| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201424330 | |
| Published online | 17 March 2015 | |
TPCI: the PLUTO-CLOUDY Interface
A versatile coupled photoionization hydrodynamics code⋆
1 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
e-mail: msalz@hs.uni-hamburg.de
2 Dipartimento di Fisica Generale, Universitá di Torino, via Pietro Giuria 1, 10125 Torino, Italy
Received: 3 June 2014
Accepted: 10 February 2015
We present an interface between the (magneto-) hydrodynamics code PLUTO and the plasma simulation and spectral synthesis code CLOUDY. By combining these codes, we constructed a new photoionization hydrodynamics solver: the PLUTO-CLOUDY Interface (TPCI), which is well suited to simulate photoevaporative flows under strong irradiation. The code includes the electromagnetic spectrum from X-rays to the radio range and solves the photoionization and chemical network of the 30 lightest elements. TPCI follows an iterative numerical scheme: first, the equilibrium state of the medium is solved for a given radiation field by CLOUDY, resulting in a net radiative heating or cooling. In the second step, the latter influences the (magneto-) hydrodynamic evolution calculated by PLUTO. Here, we validated the one-dimensional version of the code on the basis of four test problems: photoevaporation of a cool hydrogen cloud, cooling of coronal plasma, formation of a Strömgren sphere, and the evaporating atmosphere of a hot Jupiter. This combination of an equilibrium photoionization solver with a general MHD code provides an advanced simulation tool applicable to a variety of astrophysical problems.
Key words: methods: numerical / hydrodynamics / radiation: dynamics / planets and satellites: atmospheres
A copy of the code is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/576/A21
© ESO, 2015
1. Introduction
Hydrodynamic flows powered by strong irradiation (photoevaporation) can be found throughout the Universe from the evaporation of cosmological minihaloes (Shapiro et al. 2004) and the formation and evolution of H ii regions (O’Dell 2001) to the evaporation of circumstellar disks (Owen et al. 2010). The discovery of expanding hot-Jupiter atmospheres (Vidal-Madjar et al. 2003) has added another environment possibly dominated by photoevaporative mass loss (Lammer et al. 2003). Although photoevaporative phenomena occur on widely different spacial scales, the essential physical processes are similar: the absorption of ionizing radiation causes an increase in temperature and pressure, which results in a hydrodynamic wind.
Coupled photoionization and hydrodynamic simulations are essential for the progress of research in these fields. We created a new interface between an extensive equilibrium solver for the state of a gas or plasma under strong irradiation (CLOUDY) and a 3D (magneto-) hydrodynamics simulation code (PLUTO), the PLUTO-CLOUDY Interface (TPCI). The codes and the interface are publicly available123. The interface can be used to study photoevaporative processes under a wide range of conditions. However, we designed the code to study the environment of hot-Jupiter atmospheres, and a short introduction provides an idea of our requirements for the new simulation tool.
The photoevaporation of hot-Jupiter atmospheres is the result of a complex interplay of various physical processes. The absorption of extreme ultraviolet radiation (EUV, λ = 100 − 912 Å) heats the upper atmosphere of planets and in extreme cases triggers expansion and evaporation (Watson et al. 1981). Our focus lies on active host stars such as Corot-2 (Schröter et al. 2011), where the effect of X-rays (λ< 100 Å) on the mass-loss rate cannot be neglected (Cecchi-Pestellini et al. 2006). With standard abundances, metals dominate the absorption of X-rays (Morrison & McCammon 1983) and are in many cases important for the cooling of gases that are devoid of molecules and dust (e.g., in H ii regions, see Osterbrock & Ferland 2006). Thermal conduction can be a major heat source if strong temperature gradients occur in the atmospheres (Watson et al. 1981). Furthermore, hot Jupiters are most likely tidally locked, and eventually multidimensional simulations are needed to solve the disparate flows from the day and night side of the planets. Finally, planetary magnetic fields (Trammell et al. 2011) or the interaction with the stellar wind (Tremblin & Chiang 2013) also affect the evaporation process.
In this paper, we describe and validate the one-dimensional version of our numerical scheme without focusing on a particular science application. We start by describing our new coupled photoionization hydrodynamics simulation scheme (Sect. 2.1) and comparing it to available numerical codes (Sect. 2.2). The theoretical background and additional aspects of the interface are explained in Sects. 2.3 to 2.8. To verify the results of the code and demonstrate the range of applications, four problems were drawn from different fields and were solved with TPCI (Sect. 3). Our last test case is a simplified simulation of the escaping atmosphere of the hot Jupiter HD 209458b, which we compare to previous studies of the same system (Sect. 3.4). In Sect. 4 we discuss the results and indicate future applications for TPCI.
2. The PLUTO-CLOUDY Interface (TPCI)
2.1. Overview
We introduce an interface between two popular codes: the (magneto-) hydrodynamics code PLUTO (Mignone et al. 2012) and the photoionization simulation code CLOUDY (Ferland et al. 2013). The interface allows studying steady-state and slowly evolving photoevaporative flows, in which the medium is in ionization and chemical equilibrium at all times during the simulation.
The numerical scheme follows a clear division between the solution of the (magneto-) hydrodynamic equations in PLUTO and the solution of the ionization and chemical equilibrium in CLOUDY (see Fig. 1). Basically, the photoionization solver is called by the hydrodynamic code with the density and temperature distributions and solves the microphysical state of the gas under the given conditions and with the specified irradiation. It returns the radiative heating or cooling distribution, which then affects the hydrodynamic evolution. The two steps are alternated during the simulation.
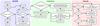 |
Fig. 1 Flowchart of the PLUTO-CLOUDY Interface. Affiliation of modules is indicated by colored boxes. PLUTO solves the hydrodynamic evolution and CLOUDY the ionization and chemical equilibrium state of the gas under strong irradiation. Communication is achieved through the interface, which also handles the interpolation between the two different grid structures. |
PLUTO is a freely distributed modular code for solving HD/MHD equations (Mignone et al. 2007, 2012). It is a Godunov-type code that computes intercellular fluxes by solving the Riemann problem at cell interfaces. Parabolic terms in the differential equations such as viscosity or conductivity can be included by operator splitting, which is also the case for source terms such as optically thin cooling or gravity. For TPCI we used the static grid version of the code.
CLOUDY is a photoionization and microphysics equilibrium solver for static structures, irradiated by an arbitrary source (Ferland et al. 1998, 2013). It accounts for the electromagnetic spectrum from hard X-rays to the radio regime. The 30 lightest elements, from hydrogen to zinc, are included, and the solver balances radiative and collisional ionization and recombination, but also more complicated physical processes such as inner shell ionization or charge exchange4. In TPCI CLOUDY is called with a fixed temperature and density structure and solves the ionization and chemical equilibrium for the given conditions, which results in an imbalance of radiative heating and cooling. The program has been thoroughly tested to approach LTE at high densities and can be used within the temperature range from 3 K to 1010 K and for number densities of up to 1015 cm-3. In cold regions CLOUDY approaches the fully molecular limit, including about 103 chemical reactions mostly from the UMIST database (Le Teuff et al. 2000). The ionization and chemical network is solved completely within CLOUDY, and only the mean molecular weight of the medium is passed to PLUTO. Since CLOUDY is a static equilibrium solver, advection of species is in general not included in TPCI. However, in 1D simulations with with a bulk flow antiparallel to the direction of irradiation, advective effects on the ionization equilibrium can be included via a CLOUDY internal iterative solver. Diffusion of elements is not included in this approach.
The coupled simulation codes use independent grid structures, and communication is achieved by linear interpolation on tabulated structures. TPCI is capable of performing true 3D MHD simulations coupled to pseudo-3D photoionization simulations along 1D parallel slices through the computational domain. One-dimensional simulations with the interface are serial, while 2D or 3D simulations are parallelized through the message passing interface (MPI). Here, we restrict the verification to 1D problems without magnetic fields. However, multidimensional simulations are not treated differently in the interface.
In the design of the interface we followed the paradigm to apply only minimal changes to both programs so as not to interfere with the well-tested numerical schemes while exploiting most of the capabilities of both codes. To this end, CLOUDY was used as an external library for solving the equilibrium state of the gas. Several input and output extensions were necessary to enable the use of CLOUDY within TPCI: we adapted the code to accept tabulated density, temperature, and velocity structures, and the methods for retrieving the results from CLOUDY were expanded to include all necessary data in the communication with PLUTO.
The setup of TPCI follows the setup of the individual codes. While the usual input script for CLOUDY simulations is specified directly in the interface, the input files for the PLUTO code have not been changed. For the output of the hydrodynamic variables the standard PLUTO output options are available. Through the CLOUDY output much additional information is available, such as the number densities of all ions and molecules, the important radiative heating and cooling agents with contribution to the total heating or cooling rate, and the irradiating, transmitted, and reflected spectra. In general, anybody who is familiar with the two simulation programs individually will be able to use the interface with only little additional introduction.
2.2. Other photoionization hydrodynamics simulation codes
For reference, we provide a short overview of some available radiation hydrodynamics codes and compare individual aspects of the numerical schemes with our new interface.
For instance, Owen et al. (2010) coupled the 3D photoionization and radiative transfer code MOCASSIN (Ercolano et al. 2003) with the hydrodynamic code ZEUS-2D (Stone & Norman 1992). MOCASSIN and CLOUDY are similarly extensive equilibrium photoionization solvers, but the temperature parameterization used by Owen et al. is only valid for X-ray heating.
Another example for coupling a microphysical equilibrium solver to a hydrodynamic simulation is the ionization module for the FLASH code (Fryxell et al. 2000) presented by Rijkhorst et al. (2006) and further improved by Peters et al. (2010). The 3D radiative transfer method is highly efficient in simulations with adaptive mesh refinement on distributed systems, but is computationally more demanding than the pseudo-3D scheme used here. A similarly advanced parallel radiative transfer method was introduced by Wise & Abel (2011) into the ENZO code (Bryan & Norman 1997; O’Shea et al. 2004); it is called MORRAY. The non-equilibrium chemistry solver is restricted to hydrogen and helium, however (Bryan et al. 2014).
Shapiro et al. (2004) and predating publications have extended the hydrodynamics code CORAL (Raga et al. 1995) to include radiative transfer and non-equilibrium photoionization of hydrogen, helium, and metals. The scheme uses a similar pseudo-multidimensional radiative transfer method, but neglects X-rays, which is one of our main interests. X-rays are also mostly neglected in the numerical schemes, which have been specifically designed to simulate escaping hot-Jupiter atmospheres, and the authors focus exclusively on 1D simulations (e.g., Yelle 2004; Tian et al. 2005; García Muñoz 2007; Penz et al. 2008; Murray-Clay et al. 2009; Koskinen et al. 2013).
In comparison, only TPCI solves our need for a photoionization hydrodynamics solver including hydrogen, helium, and metals as well as the absorption of EUV and X-ray emission.
2.3. Hydrodynamic simulation – PLUTO
In the following we present only the equations that are most relevant for the theoretical background of TPCI. The hydrodynamic simulation part is solved by the code PLUTO (Mignone et al. 2007, 2012). For a single fluid with mass density ρ, pressure p, and velocity v, the hydrodynamic equations in the quasi-conservative form are given by 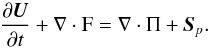 (1)Here U = (ρ,ρv,ℰ) denotes the vector of conserved variables: mass, momentum, and total energy density, which is given by ℰ = p/ (Γ − 1) + 1/2ρv2, where Γ (=5/3) is the specific heat ratio of a monatomic gas. F = (ρv,ρvv + p,(ℰ + p)v) is the hyperbolic flux tensor, and Π is the parabolic flux tensor, which in our case only contains the conductive energy flux Fc. Sp represents source terms such as gravity SG = (0,ρaG,ρv·aG) with the gravitational acceleration aG, and the radiative source term SR = (0,0,(GR − LR)), where GR and LR are the radiative heating and cooling rates.
(1)Here U = (ρ,ρv,ℰ) denotes the vector of conserved variables: mass, momentum, and total energy density, which is given by ℰ = p/ (Γ − 1) + 1/2ρv2, where Γ (=5/3) is the specific heat ratio of a monatomic gas. F = (ρv,ρvv + p,(ℰ + p)v) is the hyperbolic flux tensor, and Π is the parabolic flux tensor, which in our case only contains the conductive energy flux Fc. Sp represents source terms such as gravity SG = (0,ρaG,ρv·aG) with the gravitational acceleration aG, and the radiative source term SR = (0,0,(GR − LR)), where GR and LR are the radiative heating and cooling rates.
We follow a standard operator split scheme and include the radiative heating or cooling rate between the hydrodynamic integration steps. First, the homogeneous left-hand side of Eq. (1), namely the Euler equations, are solved. Second, PLUTO computes the included parabolic and source terms. Third, CLOUDY is called to compute the radiative source term (see Sect. 2.4), which subsequently affects the internal energy through the thermal pressure: 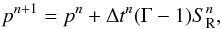 (2)where Δtn denotes the explicit time step at integration step n.
(2)where Δtn denotes the explicit time step at integration step n.
To minimize the computational effort, the radiative source term is not updated at every time step, but only if a change in either pressure or density by more than a user defined change factor triggers a call to the photoionization solver. A value of 1% for the change factor is a good compromise between accuracy and convergence speed for an initial settling phase of steady-state solutions. The accuracy can be increased by restarting the code with a smaller change factor.
2.4. Photoionization solver – CLOUDY
TPCI uses CLOUDY to solve the photoionization and the equilibrium state of the medium. We provide a compact overview of the most important processes for our applications in CLOUDY; for a more general introduction see Ferland et al. (1998, 2013). The code steps through a one-dimensional slice of the computational domain with an adaptive step width using linear interpolation on the tabulated density and temperature structures passed by PLUTO. In each cell it solves the local equilibrium state by taking into account ionization and recombination processes, chemical reactions, and atomic level transitions of all included elements.
CLOUDY separates the radiative transfer of continuum and line radiation. The continuum is diminished by absorption, 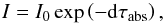 (3)where I is the intensity after the initial intensity I0 passes a slab of gas with the total optical depth dτabs. The total optical depth contains all continuous opacity sources included in CLOUDY, but in the EUV range it is dominated by ionization processes of neutral hydrogen. The continuum is furthermore diminished by scattering (Lightman & White 1988):
(3)where I is the intensity after the initial intensity I0 passes a slab of gas with the total optical depth dτabs. The total optical depth contains all continuous opacity sources included in CLOUDY, but in the EUV range it is dominated by ionization processes of neutral hydrogen. The continuum is furthermore diminished by scattering (Lightman & White 1988): 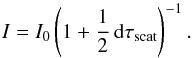 (4)The total scattering optical depth τscat also contains the opacities of several processes, of which Rayleigh scattering in the Lyman line wings dominates in the UV range.
(4)The total scattering optical depth τscat also contains the opacities of several processes, of which Rayleigh scattering in the Lyman line wings dominates in the UV range.
The escape probability mechanism (Castor 1970; Elitzur 1982) is used to approximate radiative transfer effects. The local mean intensity J, needed to solve the rate equations, is then given by 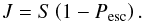 (5)Here S is the source function and Pesc the escape probability, which only depends on the optical depth. Solving the local equilibrium state is thereby decoupled from the radiative transfer equation. This approximation is exact in a single cell, where the source function is constant (Elitzur 1992). CLOUDY ensures this by choosing the adaptive grid resolution so that neither density, temperature, heating, or other properties change strongly within one cell. However, it is necessary to step through the computational domain at least twice to obtain a reasonable estimate for the optical depth in the computation of the escape probability. This iteration is needed because radiation can escape in both directions, that is, away and toward the source.
(5)Here S is the source function and Pesc the escape probability, which only depends on the optical depth. Solving the local equilibrium state is thereby decoupled from the radiative transfer equation. This approximation is exact in a single cell, where the source function is constant (Elitzur 1992). CLOUDY ensures this by choosing the adaptive grid resolution so that neither density, temperature, heating, or other properties change strongly within one cell. However, it is necessary to step through the computational domain at least twice to obtain a reasonable estimate for the optical depth in the computation of the escape probability. This iteration is needed because radiation can escape in both directions, that is, away and toward the source.
CLOUDY can include the 30 lightest elements with any abundances. These species are only present in the photoionization solver, only the mean molecular weight is passed to the hydrodynamic single fluid simulation. The ionization ladder of every element is computed by balancing the rate equations 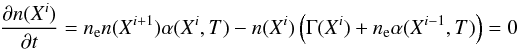 (6)for each ionization stage. Here n(Xi) is the number density of the element X in the ionization stage i, ne is the electron number density, α(Xi,T) is the temperature-dependent recombination rate from Xi + 1 to Xi summed over all levels, and Γ(Xi) is the photoionization rate given by
(6)for each ionization stage. Here n(Xi) is the number density of the element X in the ionization stage i, ne is the electron number density, α(Xi,T) is the temperature-dependent recombination rate from Xi + 1 to Xi summed over all levels, and Γ(Xi) is the photoionization rate given by 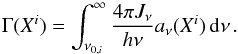 (7)Here Jν is the mean intensity at frequency ν, aν(Xi) is the photoionization cross-section, and ν0,i is the threshold frequency above which photoionization is possible. For simplicity we do not show more complex physical processes such as secondary ionizations or charge exchange in Eq. (6), which are also solved by CLOUDY, however.
(7)Here Jν is the mean intensity at frequency ν, aν(Xi) is the photoionization cross-section, and ν0,i is the threshold frequency above which photoionization is possible. For simplicity we do not show more complex physical processes such as secondary ionizations or charge exchange in Eq. (6), which are also solved by CLOUDY, however.
For the hydrodynamic part of the simulation we need the radiative heating or cooling rates. While the heating rate GR is a sum of many processes, the main heat source is usually given by photoionization: 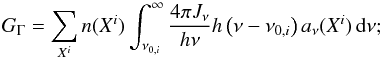 (8)the sum includes all species. Locally other heat sources such as line absorption, charge exchange, and chemical reactions can dominate the heating rate.
(8)the sum includes all species. Locally other heat sources such as line absorption, charge exchange, and chemical reactions can dominate the heating rate.
Many processes contribute to the cooling rate LR of a gas: recombination processes, free-free emission of electrons in the field of ions, line radiation, free-bound transition of H−, and chemical reactions, to name a few. Cooling due to recombinations is given by 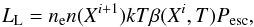 (9)where β(Xi,T) stands for the effective recombination coefficient, averaged over the kinetic energy of the electron gas. The escape probability Pesc ensures that recombinations only contribute to the cooling rate if the emitted photon escapes the medium. Another main cooling agent is line radiation of collisionaly excited elements:
(9)where β(Xi,T) stands for the effective recombination coefficient, averaged over the kinetic energy of the electron gas. The escape probability Pesc ensures that recombinations only contribute to the cooling rate if the emitted photon escapes the medium. Another main cooling agent is line radiation of collisionaly excited elements: 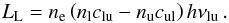 (10)Here clu denotes the collision rate between the lower and upper levels of the atom. The difference of collisional excitation and de-excitation is emitted radiatively and leads to cooling. The level populations of each ionization stage of every element are solved by balancing the equilibrium radiative and collisional transition rates in model atoms of differing complexity. Thus, CLOUDY includes a large number of lines (105 − 106, Ferland et al. 2013).
(10)Here clu denotes the collision rate between the lower and upper levels of the atom. The difference of collisional excitation and de-excitation is emitted radiatively and leads to cooling. The level populations of each ionization stage of every element are solved by balancing the equilibrium radiative and collisional transition rates in model atoms of differing complexity. Thus, CLOUDY includes a large number of lines (105 − 106, Ferland et al. 2013).
2.5. Time step control and relevant timescales
In TPCI simulations, restrictions due to hydrodynamic and microphysical timescales must be observed. PLUTO chooses the next hydrodynamic time step based on the Courant-Friedrichs-Levy (CFL) condition (Courant et al. 1928), which basically restricts disturbances in the medium to propagate by less than one cell width per time step. Radiative heating and cooling additionally limits the hydrodynamic time step in TPCI, meaning that the energy loss due to radiative cooling cannot exceed the internal energy. It is efficient to limit the next time step depending on the fraction of the energy content and the radiative source term (Frank & Mellema 1994): 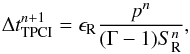 (11)and the next hydrodynamic time step is then given by
(11)and the next hydrodynamic time step is then given by ![\begin{equation} \label{eqDTmin} \Delta t^{n+1} = \mathrm{min} \left[\Delta t^{n+1}_{\mathrm{PLUTO}}, \Delta t^{n+1}_{\mathrm{TPCI}} \right] . \end{equation}](/articles/aa/full_html/2015/04/aa24330-14/aa24330-14-eq60.png) (12)Here ϵR is the user-defined maximum fractional variation parameter. The default value is ϵR = 0.1, which restricts the change in internal energy due to radiative heating or cooling to be lower than 10% in every time step.
(12)Here ϵR is the user-defined maximum fractional variation parameter. The default value is ϵR = 0.1, which restricts the change in internal energy due to radiative heating or cooling to be lower than 10% in every time step.
CLOUDY solves the equilibrium state of the medium based on a diversity of processes, each with a characteristic timescale, and the use of TPCI implies that the microphysical timescales are shorter than the hydrodynamic timescale. In gases with a temperature of about 10 000 K, hydrogen recombination usually is the microphysical process with the longest timescale (Ferland 1979): 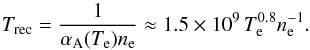 (13)TPCI locally checks whether recombination is slower than advection and issues a warning. Equation (13) holds only for ionized regions; especially molecular reactions occur on longer timescales. The CLOUDY output provides a manual method to control the longest timescales and, thus, check the validity of the approach.
(13)TPCI locally checks whether recombination is slower than advection and issues a warning. Equation (13) holds only for ionized regions; especially molecular reactions occur on longer timescales. The CLOUDY output provides a manual method to control the longest timescales and, thus, check the validity of the approach.
In 1D simulations, the advection of species can be included through a steady-state solver in CLOUDY (see Sect. 2.6). With this scheme, steady flows can be simulated in which the advective timescales are shorter than microphysical timescales. Nevertheless, the assumption of photoionization and chemical equilibrium is a strong simplification, and the validity must be considered for every application.
2.6. Advection of species
The impact of advection due to a bulk flow of the medium can be included in the simulation by using an iterative steady state solver included in CLOUDY (Henney et al. 2005). The solver is available for simulations in which the medium flows toward the source of ionizing radiation. The solution of the equilibrium state then includes source and sink terms of all species, induced by material flows: 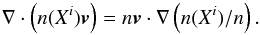 (14)In this case, PLUTO passes the velocity in addition to the density and temperature to the photoionization solver. CLOUDY computes the advective source terms using the relative density (Henney et al. 2005), which is an advective scalar.
(14)In this case, PLUTO passes the velocity in addition to the density and temperature to the photoionization solver. CLOUDY computes the advective source terms using the relative density (Henney et al. 2005), which is an advective scalar.
The steady-state solver in CLOUDY includes advection in an iterative manner, and the user must control the convergence of the solution. The module defines the advection length Δz, a measure for the resolution of advection processes. It is refined if the advective solution has converged for the current advection length. The progress is controlled by following the discretization error and the convergence error (see Henney et al. 2005, for a detailed description). The convergence error is given by 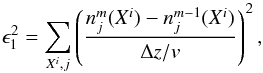 (15)where m is the iteration number and j is the zone number; the sum extends over all elements and ionization stages as well as over all zones. The error approaches zero as the changes in number densities of consecutive iterations decreases. The discretization error is defined as
(15)where m is the iteration number and j is the zone number; the sum extends over all elements and ionization stages as well as over all zones. The error approaches zero as the changes in number densities of consecutive iterations decreases. The discretization error is defined as 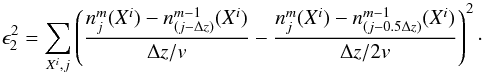 (16)(j − Δz) is a symbolic index referencing the density of the species at the distance of the advection length. The error describes the differences of the local, advective source or sink terms to the value if the advection length is refined by a factor of two. The sum again runs over all species and zones.
(16)(j − Δz) is a symbolic index referencing the density of the species at the distance of the advection length. The error describes the differences of the local, advective source or sink terms to the value if the advection length is refined by a factor of two. The sum again runs over all species and zones.
The discretization error depends on the resolution in the photoionization solver. This resolution can be up to ten times higher than in the hydrodynamic part of the simulation. For TPCI it is more important to check the advection length than the actual value of the discretization error. The advection length is refined if 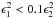 . It should generally be decreased to the hydrodynamic grid spacing, so that advective effects have the same accuracy as the rest of the simulation.
. It should generally be decreased to the hydrodynamic grid spacing, so that advective effects have the same accuracy as the rest of the simulation.
The described procedure does not follow our split scheme to solve hydrodynamic effects exclusively in PLUTO. However, at the moment we cannot solve the advection of species in PLUTO. It is possible to include advective scalars for the relative density of all species in PLUTO, but then CLOUDY would have to be called with the densities of all 30 elements and ionization stages, which is not implemented. The steady-state solver in CLOUDY is computationally demanding. One advection solution may need up to 100 iterations to converge because advective effects must be swept through the computational domain (Henney et al. 2005). Thus, including advection slows simulations down, and when searching for advective steady-state solutions, it is advisable to use the non-advective code for an initial settling of the hydrodynamic structure and then restart the simulation including advection to let the structure evolve to the final steady state. This procedure has been followed in the two test problems, which include advection of species (see Sects. 3.1 and 3.4).
2.7. Radiative acceleration
In addition to affecting the temperature of the gas, the absorption of radiation also exerts a pressure on the medium. CLOUDY records the radiative pressure produced by the absorption of radiation from the central source. The local radiative acceleration can be directly accessed after a CLOUDY call. This acceleration is handled like any external force by the PLUTO code (see Eq. (1)).
2.8. Pseudo-multidimensional simulations
Although here we focus on 1D simulations, TPCI can be used in two or three dimensions on a Cartesian grid with irradiation along the x-axis. The radiative solution is then simply split into parallel 1D simulations, which is called a pseudo-3D radiative transfer. There is no true 3D radiative transfer in CLOUDY, but the coupling of 3D radiative transfer to hydrodynamics simulations is in many cases still computationally prohibitive today (e.g., Owen et al. 2010). In problems with a strong directionality in the radiative field, the pseudo-3D approximation is valid, unless there are shadow-casting objects (Morisset et al. 2005). However, in the case of strong shadows, the induced error can also be neglected if the energy transfer into the shadow region is hydrodynamically dominated.
The 1D version of the interface is a serial code because CLOUDY requires the complete density structure to solve the plane-parallel radiative transfer through the computational domain. PLUTO is, however, capable of 3D parallel computations, which is also enabled in TPCI by not decomposing the domain along the x-axis. Each thread then deals with the full 1D structure along the x-axis for a given number of y/z-grid-points. After the complete domain has been processed, the hydrodynamic evolution continues until the next call to CLOUDY is necessary. For this approach the computational domain should be decomposed so that the available processors have the same number of y/z-points to minimize idle times.
This pseudo-3D scheme provides a convenient possibility to allow parallel simulations with low complexity. In the best case, a multidimensional simulation will have a similar execution time as a 1D simulation if every y/z-grid-point uses an individual processor. The communication overhead is small, since the main computational load usually comes from the independent CLOUDY calls.
3. Verification
In the following we present TPCI simulations of four test problems. The first two simulations verify the implementation of our numerical scheme, each with a different focus. The third test problem is included to clarify the limits of validity of TPCI. The fourth test case is a simplified simulation of a hot-Jupiter atmosphere, which already demonstrates the capabilities of TPCI in this field. The setup of each simulation is given in Table 1.
Simulations for the verification of TPCI.
3.1. Weak D-type ionization front
For the initial verification, we investigated the effects of steady-state flows in 1D simulations of ionization fronts. Such flows appear when molecular clouds are evaporated by the ionizing emission of newly formed stellar clusters. The gas is heated through ionization processes, and the cloud slowly evaporates. If the evaporation proceeds as a subsonic wind from a dense region, it is called a weak D-type ionization front, in contrast to strong ionization fronts, which involve transonic flows. (For rarefied R-type ionization fronts see Sect. 3.3.)
The results from our TPCI simulation are compared with an independent CLOUDY simulation, using the included steady-state solver, which was specifically designed to solve these photoevaporative flows (see Henney et al. 2005)5. This is a powerful test for TPCI because both simulations rely on the same photoionization solver, thus, any differences in the results can only be caused by the interaction of the hydrodynamics and the photoionization solver through the interface.
 |
Fig. 2 Pure hydrogen weak D-type ionization front. Density a), temperature b), velocity c), and degree of ionization d) are depicted. A CLOUDY simulation (red dashed lines) is compared with a TPCI simulation (blue solid lines). Initial conditions are given by the gray dotted lines. In panel c) the speed of sound is shown by the black solid line. The TPCI simulation agrees well with the independent CLOUDY simulation. Small oscillations in the high-density region that can be seen in panel c) do not affect the solution significantly. |
Figure 2 shows the simulation of a weak D-type ionization front in a pure hydrogen gas in the rest frame of the front together with the initial conditions. Cold, neutral gas (400 K) with a density of 106 cm-3 is irradiated from the right-hand side by a hot O-star with a 50 000 K blackbody spectrum. The gas shows a steady-state flow toward the source of ionizing radiation. The evaporation process is subsonic, starting with 0.1 km s-1 and reaching 7.1 km s-1 behind the ionization front. The temperature increases to 12 000 K and the density drops to 2 × 104 cm-3.
We used TPCI without the advection of species for the initial settling of the simulation and subsequently restarted the simulation including the advection as described in Sect. 2.6. The settling phase of the dynamical simulation took 3 × 104 a, after which oscillations of the ionization front were reduced to about 1% of the depth of the ionized region. These oscillations in the denser gas are caused by the reflection of waves at the left-hand boundary and at the ionization front. The depth of the ionized region in the steady-state CLOUDY simulation agrees with the dynamic TPCI simulation within the errors produced by the remaining oscillations (see Fig. 2d). The width of the ionization front is reduced by 25% in the dynamic simulation, which does not affect the overall structure, however.
The convergence of the steady-state solver in the advective TPCI and the CLOUDY simulations is shown in Fig. 3. The advection length has been iteratively refined whenever the solution converged for the current length (see Sect. 2.6). Every refinement temporarily increases the convergence error, which is then reduced over the following iterations until further refinement. The final discretization error is on the order of 10%, computed on the fine grid of the photoionization solver. This is sufficient because the advection length is similar to the coarser resolution of the hydrodynamical simulation part. Higher refinement is impossible because in this case the steady-state solver does not proceed beyond this level (see Sect. 4 for a discussion of this problem).
The comparison of the two simulations demonstrates that the interface works correctly and is capable of simulating photoevaporative flows. While the independent CLOUDY simulation with the internal steady-state solver produces smoother profiles, TPCI allows studying the dynamical evolution of the phenomenon.
 |
Fig. 3 Convergence of the models of the weak D-type ionization front. The CLOUDY simulation is shown by red, thin lines, the advective TPCI simulation by thick, blue lines. The discretization error (dotted), the convergence error (dashed), and the advection length (solid) are plotted against the iteration number of the steady-state solver in CLOUDY. The grid resolution of the TPCI simulation is indicated by the thin, black line. In both simulations the advection length is reduced to within a factor of 2 of the grid resolution in the hydrodynamic simulation part. |
3.2. Coronal flare – chromospheric evaporation wave
 |
Fig. 4 Optically thin cooling function of PLUTO (blue, dotted) and CLOUDY (red, solid). The crosses depict the actual cooling in the coronal shock simulation with TPCI. These are a factor of 1.5 lower because the simulation shows significant optical-depth effects. |
TPCI can also make use of CLOUDY to compute the cooling of collisional plasmas instead of strongly irradiated plasmas. This provides the possibility of testing the interface in the optically thin limit, where radiative losses only depend on the electron number density ne and the cooling function ΛR (e.g., Sutherland & Dopita 1993): 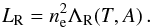 (17)The cooling function depends on temperature T and metal abundance A. A radiative transfer solver is not necessary for the simulation as long as the optical depth is negligible. Cooling in this regime is dominated by emission from ionized metals, in which case CLOUDY mostly uses transitions from the CHIANTI database (Dere et al. 1997; Landi et al. 2012). The resulting cooling function with solar abundances in CLOUDY is similar to standard optically thin cooling functions; see Fig. 4 for a comparison with the tabulated cooling function that is included in the PLUTO code.
(17)The cooling function depends on temperature T and metal abundance A. A radiative transfer solver is not necessary for the simulation as long as the optical depth is negligible. Cooling in this regime is dominated by emission from ionized metals, in which case CLOUDY mostly uses transitions from the CHIANTI database (Dere et al. 1997; Landi et al. 2012). The resulting cooling function with solar abundances in CLOUDY is similar to standard optically thin cooling functions; see Fig. 4 for a comparison with the tabulated cooling function that is included in the PLUTO code.
We can thus compare a TPCI simulation with the radiative transfer and microphysics solver with a PLUTO simulation using the included cooling function. In contrast to the ionization front simulation in the previous section, we now used the same hydrodynamics solver (i.e., PLUTO), but different solvers for the radiative cooling. Differences in the results of the test simulations can only result from the implementation of the radiative cooling from CLOUDY in PLUTO. In this simulation we included all 30 elements available in CLOUDY, which additionally tests the implementation of metals in the inteface.
We used a setup that was adapted to a strong chromospheric evaporation wave in a 1D magnetically confined coronal loop. Such evaporation fronts appear when a magnetic reconnection event releases a large amount of energy in the solar atmosphere, which leads to a solar flare (e.g., Reale & Orlando 2008). Evaporation of chromospheric plasma into the corona causes a wave that propagates at speeds of ~400 km s-1 through a coronal loop, increasing the density by up to one order of magnitude. Since optically thin cooling depends on the density squared, the cooling rate is increased and, in the long term, the evaporated plasma cools down and falls back onto the chromosphere. The magnetic loop structure usually survives the flare event.
 |
Fig. 5 Hydrodynamic evaporation wave in a flaring coronal loop. The red dashed lines show a simulation with PLUTO assuming optically thin cooling. The blue lines depict the results of TPCI, and the initial conditions are given by the gray dotted lines. The density is shown in panel a), the temperature in b), the velocity in c), and the cooling of TPCI is plotted in panel d) together with the constant heating rate. Panel d) shows the fractional abundance of the two iron ions with the strongest individual contribution to the total cooling rate. In panel b) the temperature decrement in the after-shock evolution is indicated. The sound speed is shown by the solid black line in panel c). Both simulations show the same behavior, except that in the PLUTO simulation the cooling rate is twice as strong as in the TPCI simulation, which is due to optical-depth effects and small differences of the electron density. |
For the simulation we went into the quasi-rest frame of the propagating evaporation wave (see Fig. 5 for the initial conditions). The wave front is stable at the start of the simulation, but the strength of the wave weakens as a result of cooling. This reduces the propagation speed so that during the simulation the wave front starts trailing toward the left-hand boundary. This proceeds faster in the PLUTO simulation because of the stronger cooling rate. Therefore, we do not compare contemporaneous states in both simulations but states with the same displacement from the initial shock position. There is no irradiation in this simulation.
In the test, coronal material flows in from the right-hand side of the domain with a temperature of 3 × 106 K, a hydrogen number density of 2.4 × 109 cm-3, and a velocity of −780 km s-1. The plasma is compressed to a density of 7.1 × 109 cm-3 with a temperature of 107 K and a velocity of −300 km s-1. The domain length was chosen deliberately longer than a typical magnetic loop to emphasize the cooling of the dense gas behind the shock.
To stabilize a coronal loop model, a constant mechanical coronal heating rate has to be applied (Rosner et al. 1978). This heating of unspecified source balances radiative and conductive losses throughout the loop. We applied a heating rate of 5.1/9.8 × 10-5 erg cm-3 s-1 in the TPCI/PLUTO simulations, which exactly equals the cooling rates in the pre-shock region (see Fig. 5d). Advection of species can affect the ionization stage of metals behind the shock, which in turn has a weak influence (factor <1.5) on the value of the cooling function. The increased density affects the cooling rate with a factor of ~32, however, which is why we neglected advection of species in this simulation.
Both simulations show the same behavior (see Fig. 5). The plasma is heated in the wave front and slowly cools down in the post-shock region. The cooling efficiency is a factor of two higher in the PLUTO simulation than with TPCI. This has two reasons: first, the actual cooling rate in the TPCI simulation is lower by a factor of 1.5 than in the optically thin case because CLOUDY includes optical-depth effects along the coronal loop (see Fig. 4). For example, one of the strongest emission lines of the hot plasma is a Fe xx line at 12.9 Å, which has an optical depth of 3.9 and does not escape freely. Fe+19 and Fe+18 are the most abundant iron ions in the hot gas, while Fe+16 and Fe+15 dominate in the cooler gas. Second, the PLUTO simulation computes the electron density on a simple “hydrogen-only” approximation, which in this case overestimates the electron density by a factor of 1.2. Both factors combined result in the total difference of the cooling rates (1.22 × 1.5 = 2.2).
A comparison of the two simulations shows that TPCI can also be used for collisional plasmas, especially if optical-depth effects are relevant. One drawback is the increase in computational effort by a factor of 105 compared to the much simpler, optically thin PLUTO simulation. The strong increase in computational effort results from solving the equilibrium state including all metals (see Sect. 4). For future applications the gain in accuracy by using the radiative transfer and microphysics solver must be weighed against the increased computational effort.
3.3. Formation of a Strömgren sphere
In a third setup, we used the interface to follow the heating of cool interstellar hydrogen gas after the ignition of a strong central source. This test problem demonstrates the limits of TPCI that are due to the underlying assumption of ionization and chemical equilibrium. The sudden impact of ionizing photons after ignition of the source heats the surrounding gas, and a supersonic ionization front develops (R-type). The propagation of the ionization front is only restricted by the rate of new ionizing photons emitted by the central source. The rapid expansion comes to a rest after recombinations in the ionized sphere balance the production rate of ionizing photons; the resulting sphere is called a Strömgren sphere, and the radius is given by (e.g., Osterbrock & Ferland 2006): 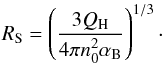 (18)Here,
(18)Here, 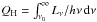 is the number of ionizing photons emitted by the central source per second, and Lν is the stellar luminosity per unit frequency interval. n0 is the initial density and αB = 2.59 × 10-13 cm3 s-1 is the hydrogen B recombination rate for a 10 000 K plasma. This rate includes recombination to all levels but the ground state because recombination to the ground state produces an ionizing photon that does not escape locally. The R-type ionization front does not raise significant bulk motion because it proceeds too fast through the interstellar medium to cause significant acceleration.
is the number of ionizing photons emitted by the central source per second, and Lν is the stellar luminosity per unit frequency interval. n0 is the initial density and αB = 2.59 × 10-13 cm3 s-1 is the hydrogen B recombination rate for a 10 000 K plasma. This rate includes recombination to all levels but the ground state because recombination to the ground state produces an ionizing photon that does not escape locally. The R-type ionization front does not raise significant bulk motion because it proceeds too fast through the interstellar medium to cause significant acceleration.
We started with an initial constant density of 104 cm-3, a temperature of 100 K, and zero velocity. The emission rate of ionizing photons is QH = 1049 s-1, which is typical for a 50 000 K hot O-star. For the CLOUDY calls we used a spherical grid with the source in the center because geometric dilution of the radiation field must be included. Since no significant bulk flows develop throughout the simulation, we simply used a Cartesian grid in PLUTO (irradiation from the center in a spherical grid has not been implemented in TPCI yet), and we also did not need to include the advection of species. We only followed the time-dependent heating of the initially cool interstellar gas.
Numerically, R-type fronts have been studied for example by Dale et al. (2007). The authors derived a simple phenomenological solution for the expansion of the ionized region after ignition of the central source, which can be used to compare the results of our code: 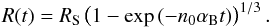 (19)This formula is derived by noting that the radius increment per time is restricted by the production rate of ionizing photons minus the recombination rate inside the already ionized region.
(19)This formula is derived by noting that the radius increment per time is restricted by the production rate of ionizing photons minus the recombination rate inside the already ionized region.
 |
Fig. 6 Expansion of an R-type ionization front. The TPCI simulation (blue solid) is compared with the theoretical evolution of Eq. (19). Three Strömgren radii for different temperatures are indicated by labeled thin black lines. The expansion of the ionized region proceeds faster in the TPCI simulation because the equilibrium solutions of the photoionization solver at each integration step are not restricted by the time since ignition of the central source. |
Figure 6 shows the propagation of the R-type ionization front in TPCI compared with the solution in Eq. (19). Especially the beginning of the simulation shows a faster expansion of the ionized region than the theoretical prediction. To understand the differences, we have to remember that CLOUDY seeks equilibrium states. Although the evolution seems to be similar to the theoretical model, the simulation is based on a different physical mechanism.
 |
Fig. 7 Temperature evolution during expansion of the R-type ionization front. The temperature versus radius is plotted at various times. The time step between consecutive lines is constant, the time is referenced by the color scheme. The temperature increases from 1000 K to 17 000 K, being nearly constant throughout the ionized region. The expansion radius of the ionized region at a given time is marked by the steep temperature decline and increases from 0.085 to 0.16 pc. The distance between consecutive lines decreases, indicating the approach to the final Strömgren radius. |
Physically, the number of ionized hydrogen atoms cannot exceed the number of emitted ionizing photons since the central source has been switched on. This is not the case in the TPCI simulation because the equilibrium photoionization solver assumes that the source already existed for an infinite amount of time. The reason that we can nevertheless follow an expansion of the ionized region is based on the fact that recombinations in the cold gas are more frequent than in an almost fully ionized 10 000 K hot region. Therefore, CLOUDY actually computes an equilibrium Strömgren sphere at every time step, but with the temperature structure that is passed from PLUTO (see Fig. 7). The Strömgren sphere increases because recombination becomes less efficient with increasing temperature. In Fig. 6 the Strömgren radii for 5000 K, 10 000 K, and 20 000 K are displayed. At the times when the TPCI simulation reaches the first two indicated Strömgren radii, the mean temperatures in the ionized region are 5600 K and 11 400 K (compare Figs. 6 and 7). The photoionization solver does not assume the simple B recombination rate as in Eq. (18), but allows photons to escape based on the optical depth. Hence, recombination in the simulation is more efficient, which causes the mean temperatures to be slightly higher at the given Strömgren radii.
This simulation clearly shows that the user must be aware of the restrictions of TPCI and what is actually simulated. The interface cannot be used to correctly simulate the expansion of an ionized region after ignition of a central source because this is an effect of a time-dependent radiation field. It could, however, be used to follow the subsequent expansion of the hot gas in the Strömgren sphere into the surrounding cool interstellar gas under unchanged irradiation by the O-star because this can be approximated by equilibrium states.
3.4. Simulation of the atmosphere of HD 209458b
The intention of the design of TPCI was simulating hot-Jupiter atmospheres, and here we present a first test case by solving a pure hydrogen atmosphere of HD 209458b as our fourth test case. The expanded atmosphere around HD 209458b was discovered by Vidal-Madjar et al. (2003), and several studies investigated the system numerically (e.g., Yelle 2004; Tian et al. 2005; García Muñoz 2007; Penz et al. 2008; Murray-Clay et al. 2009; Koskinen et al. 2013). These studies provide a solid basis for comparing the results from TPCI.
For the simulation, we made use of two more modules of PLUTO: gravitational acceleration and thermal conductivity.
3.4.1. Gravity
The simulation of the escaping hot-Jupiter atmosphere incorporates the gravitational and centrifugal acceleration in the two-body system, also referred to as tidal forces. With the planet in the center, we derive for the effective potential 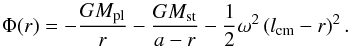 (20)Here r denotes the radial distance on the axis toward the star, Mpl and Mst are the planetary and stellar mass, a is the semi-major axis, lcm is the distance to the center of mass, and G is the gravitational constant. The angular frequency ω is given by Kepler’s third law
(20)Here r denotes the radial distance on the axis toward the star, Mpl and Mst are the planetary and stellar mass, a is the semi-major axis, lcm is the distance to the center of mass, and G is the gravitational constant. The angular frequency ω is given by Kepler’s third law 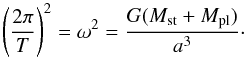 (21)In PLUTO we include the acceleration:
(21)In PLUTO we include the acceleration: 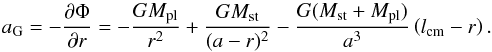 (22)By plotting the equation with the values of the system HD 209458 (Wright et al. 2011), we find that on the star-planet axis material can be bound to the planet up to 4.18 Rpl, which is the size of the planet’s Roche lobe on this axis.
(22)By plotting the equation with the values of the system HD 209458 (Wright et al. 2011), we find that on the star-planet axis material can be bound to the planet up to 4.18 Rpl, which is the size of the planet’s Roche lobe on this axis.
3.4.2. Thermal conductivity
We used a simplified approach to include thermal conductivity by adding the conductivity of an electron proton plasma and of a neutral hydrogen gas. The first dominates for temperatures in excess of 50 000 K, the latter below this.
The following coefficients are taken from Banks & Kockarts (1973). The heat flux is given by 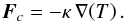 (23)For highly ionized gases, thermal conductivity is dominated by electron-ion collisions (Spitzer 1978). The conductivity coefficient is given by
(23)For highly ionized gases, thermal conductivity is dominated by electron-ion collisions (Spitzer 1978). The conductivity coefficient is given by 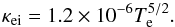 (24)The thermal conductivity coefficient of neutral hydrogen is parameterized as
(24)The thermal conductivity coefficient of neutral hydrogen is parameterized as 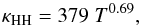 (25)and the total coefficient is given by the weighted sum
(25)and the total coefficient is given by the weighted sum 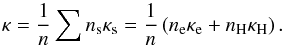 (26)In our simulations we used the direct sum of the two coefficients:
(26)In our simulations we used the direct sum of the two coefficients: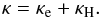 (27)In the relevant temperature range below 10 000 K the approximation is correct to within a factor of two (see Fig. 8). Since we do not expect thermal conductivity to have a significant impact on the results (García Muñoz 2007), the procedure is sufficient to verify this claim in our simulation.
(27)In the relevant temperature range below 10 000 K the approximation is correct to within a factor of two (see Fig. 8). Since we do not expect thermal conductivity to have a significant impact on the results (García Muñoz 2007), the procedure is sufficient to verify this claim in our simulation.
3.4.3. Simulation
 |
Fig. 8 Thermal conductivity coefficient. The coefficient for electron conductivity is depicted by the red dashed line, for neutral hydrogen by the green dotted line, and the blue solid line is the sum. The black dash-dotted line shows the more accurate weighted sum (Eq. (26)) derived with the actual densities of neutral hydrogen and electrons in a CLOUDY simulation without irradiation. In the temperature region below 10 000 K the simple sum is accurate to within a factor of two. |
 |
Fig. 9 Evaporating hydrogen atmosphere of HD 209458 b. Density a), temperature b), velocity c), ionization fraction d), heating and cooling rate e), and the heating fraction f) are plotted versus the planetary radius. The red dashed lines depict the initial settling phase, the blue solid lines the final TPCI simulation including advection of species. The initial conditions are given by the gray dotted lines. Panel a) also shows the density structure of an isothermal atmosphere with 500 K (black solid line). In panel c) the speed of sound is indicated (black solid line), and in panel e) the three main cooling agents in the atmosphere are shown by black thin lines. “H line emis.” is cooling due to line emission from hydrogen atoms (mainly Lyα), “ff emis.” is cooling by free-free emission of electrons, and “H recomb.” is recombination cooling of hydrogen. Additionally, thermal conductive cooling (cond.) is shown by a black dotted line. The atmosphere expands in a transonic flow. A small amount of the absorbed energy (~11%) is lost through free-free and Lyα emission. |
We used a pure hydrogen atmosphere, irradiated from the top by the host star, and simulated the escape at the substellar point. With a stretched grid the cell size is increased from 0.0005 Rpl in the lower atmosphere to 0.087 Rpl at the top. The temperature in the lower atmospheres was fixed at the planet facing boundary to 1000 K, which is approximately the average dayside brightness temperature of HD 209458b (Crossfield et al. 2012). In the simulation this was implemented by fixing the lower boundary density to 1015 cm-3 and the pressure to 140 dyn cm-2 , which is equivalent to 0.14 mbar. The gas is heated by ionizing radiation with a solar minimum EUV spectral energy distribution (Woods & Rottman 2002), which is a good approximation for an inactive G0-type dwarf (Sanz-Forcada et al. 2011; Montes et al. 2001). In the spectral range below 912 Å (XUV), the planetary atmosphere at the distance of 0.047 AU from the host star is irradiated with a flux of FXUV = 1315 erg cm-2 s-1. The derived value is similar to previous estimates, for instance, 1800 erg cm-2 s-1 in Koskinen et al. (2013). For this inactive host star (Sanz-Forcada et al. 2011), X-rays (<100 Å) contribute only 3% of the energy in the XUV spectral range. In contrast to active host stars, X-rays have no strong impact on the mass loss of HD 209458b. The initial conditions of the simulation are shown together with the results in Fig. 9. A comparable setup can be found in the simulations of Penz et al. (2008), Murray-Clay et al. (2009) or Koskinen et al. (2013).
In the expanding atmosphere neutral hydrogen is transported from the lower to the upper atmosphere, which means that advection of species is essential for the results in this simulation. To save computational time, we ran the simulation without the advection of species until a steady-state planetary wind was found and all shock waves had subsided. The resulting atmosphere was used as initial atmosphere for the final simulation including the advection of species. The convergence of the advective scheme does not proceed beyond an advection length of 0.27 Rpl. This is comparable to the grid resolution at the top of the atmosphere, but much higher than the resolution in the lower atmosphere, so that effects due to the advection of species are initially only resolved in the upper atmosphere. However, below 1.05 Rpl velocities are low and the advective timescale is longer than the hydrogen recombination timescale. Advection of species can safely be neglected below this level. Furthermore, we manually reduced the advection length to 0.01 Rpl and did not find significant changes in the solution. We therefore conclude that the advection of neutral hydrogen into the upper atmosphere is resolved throughout this simulation.
3.4.4. Results
The atmosphere expands in a steady-state transonic flow that is directed from the hot Jupiter toward the host star. We find a steep density and temperature gradient within the first 0.2 Rpl (see Fig. 9). At 1.08 Rpl the atmosphere shows a temperature minimum with only 500 K at a pressure of 0.7 μbar; the density stratification below this point differs only slightly from an isothermal atmosphere with the same temperature (see Fig. 9a). EUV radiation does not penetrate to this depth, but is mainly absorbed from 1.1 to 1.2 Rpl, where the temperature of the atmosphere strongly increases. In this pure hydrogen atmosphere free-free emission is the main radiative cooling agent below 1.08 Rpl, reemitting about 50% of the total heat input, up to 70% of which is provided by hydrogen line absorption at this depth. Hydrogen line emission, mainly Lyα radiation, dominates the radiative cooling from 1.08 to 2.0 Rpl, and recombination of hydrogen is the most efficient radiative cooling agent at higher altitudes.
Averaged over the atmosphere above the temperature minimum, 89% of the heat input is used for heating and acceleration of atmospheric gas, and eventually for lifting the material out of the gravitational potential well of the planet. The total energy gain is divided as follows: 77% of the radiative energy input is converted to gravitational potential energy, 17% to kinetic and 6% to internal energy. Note that we define the heating fraction as 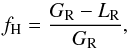 (28)here GR is the actual heating produced by the absorption of radiation, not the energy of the absorbed radiation (see Eq. (8)). In our hydrogen-only simulation, only free-free and Lyα emission decrease the radiative heating fraction significantly (see Fig. 9f). The fraction approaches 1.0 in the upper atmosphere; however, emission by helium or metals is not included in this simulation. Especially line absorption and emission by metals can significantly affect the heating and cooling rates in the lower atmosphere.
(28)here GR is the actual heating produced by the absorption of radiation, not the energy of the absorbed radiation (see Eq. (8)). In our hydrogen-only simulation, only free-free and Lyα emission decrease the radiative heating fraction significantly (see Fig. 9f). The fraction approaches 1.0 in the upper atmosphere; however, emission by helium or metals is not included in this simulation. Especially line absorption and emission by metals can significantly affect the heating and cooling rates in the lower atmosphere.
Replacing the denominator in Eq. (28) with the absorbed radiative energy gives the net heating efficiency, which is often used in hydrodynamic simulations of hot-Jupiter atmospheres to account for the fraction of energy that goes into ionizing hydrogen and also for not specifically included cooling agents. In this particular simulation, stellar emission is absorbed from 50 to 912 Å by the atmosphere (more than 50% absorption). This absorption produces 92% of the total heating rate; the remaining 8% are caused by hydrogen line absorption, mainly Lyα absorption. The heating efficiency in the XUV range is 0.71.
Thermal conduction does not play a significant role in the atmosphere since it is more than two orders of magnitude smaller than the main cooling agents at every point throughout the atmosphere (see Fig. 9e). Comparing the structure from the initial settling phase without advection of species with our final results shows that the advection of neutral hydrogen into the upper atmosphere increases the average temperature from 3000 to 5500 K. Advecting neutrals into the otherwise highly ionized region increases the heating rate because more ionization processes occur. This also boosts the heating fraction, as can be seen in Fig. 9. The final velocity exceeds the sonic speed of 10 km-1.
Our results are in excellent agreement with the C3 model of Koskinen et al. (2013) for the atmospheric evaporation at the substellar point. Assuming a spherically symmetric atmosphere, we derive a mass-loss rate of Ṁ = 4πr2ρv = 1.4 × 1011 g s-1, which is equal to 0.0023 MJup Ga-1. This value is an upper limit since we simulated the substellar point with the highest mass-loss rate. For the surface averaged mass loss, a factor of 1/4 was used by Koskinen et al., which places our result just slightly below their values, ranging from 4 − 6.5 × 1010 g s-1. Within 5% accuracy, advection of species does not change the mass-loss rate because a slightly higher velocity in the advective simulation is canceled by a lower density.
Murray-Clay et al. (2009) were the first authors to include a model for Lyα cooling in the simulation of escaping planetary atmospheres. Their spatial distribution and total cooling rate compares well with our results. Lyα cooling leads to a lower peak temperature in the atmosphere and reduces the mass-loss rate (Koskinen et al. 2013). Note, however, that deeper in the atmosphere the density is high enough that collisional de-excitation dominates and absorption of Lyα radiation is a heating agent. About one quarter of the total cooling through Lyα radiation is counterbalanced by Lyα heating in the lower atmosphere. On the other hand, Murray-Clay et al. used a gray absorption scheme, which leads to a mass-loss rate lower by a factor of four (Koskinen et al. 2013). Such differences clearly prove the advantages of the detailed photoionization solver included in TPCI. Neglecting any significant cooling or heating agent affects the mass-loss rate, which crucially depends on the available energy. This becomes even more important when metals are included in the atmosphere and an increasing number of processes must be modeled.
Although the mass-loss rate does not change when the advection of species is included in the simulation, the advection of neutral hydrogen into the upper atmosphere is important for analyzing observational results. The Lyα absorption signal of the planet during transit does change significantly because of the higher neutral hydrogen column density. The high velocities of the expanding atmosphere are crucial to transport the neutral hydrogen into the upper atmosphere.
4. Discussion and conclusion
We have presented TPCI, which is an interface between the MHD code PLUTO and CLOUDY, an equilibrium photoionization solver. TPCI enables simulations of hydrodynamic steady-state and slowly evolving flows, including multiple physical effects such as gravity and thermal conduction. It simultaneously solves the equilibrium state of a gas or plasma under strong irradiation. The code is valid from cold molecular regions to fully ionized hot plasmas and computes the radiative transfer along 1D rays.
The presented test simulations prove the validity of the combined simulations. In the introduction we have established a number of requirements for TPCI. The interface has proven its capabilities in solving the ionization and microphysical state of gases for a wide range of densities and temperatures. The second test problem (see Sect. 3.2) demonstrates the simulation of gases including metals and shows effects of X-ray radiative transfer. Multidimensional simulations or magnetic fields have not been studied in our verification of the 1D scheme. In general, we find that TPCI runs stably and reliably. The combination of the adaptable hydrodynamics code with a versatile radiative transfer and microphysics solver is generally applicable to photoevaporative flows and can for example be used to study the dynamics of H ii regions or the evaporation of protoplanetary disks. Furthermore, CLOUDY is a powerful tool for spectral analysis, and observed spectra can be directly compared with results from the simulations.
One drawback in the use of TPCI is the computational effort of the detailed photoionization solver, which usually consumes almost all of the computational time. For the simulation of the test problems we used a few days to up to two months on a single 3.1 GHz processor. One-dimensional simulations are serial, so that simulations do not perform faster on clusters. In the search for hydrodynamic steady-state situations, the best call for reducing the computational effort is to find good initial conditions to speed up the convergence and to include more complex physics step by step from pre-converged simpler solutions.
 |
Fig. 10 Execution times of CLOUDY runs on local cpu with setups based on the hot-Jupiter simulation. Simulation times vary in the shaded range based on density and temperature. Each step increases the complexity of the simulation, starting with a simulation including only hydrogen and 10 zones in CLOUDY. In this case the execution time is dominated by the initialization of CLOUDY. The next steps are with 100 and 1000 zones. We then include step by step molecules, helium, carbon, nitrogen, and oxygen, and all 30 lightest elements. Finally, we iterate twice in CLOUDY over the complete domain to correct optical-depth effects. |
Figure 10 shows execution times in single calls to the photoionization solver. The setup for the calls is based on the simulation of the hot-Jupiter atmosphere, but we used constant hydrogen number densities ranging from 105 to 1015 cm-3 and constant temperatures ranging from 1000 to 10 000 K. The actual execution times vary depending on the parameters. In a typical simulation of a hot-Jupiter atmosphere CLOUDY needs about 1000 zones for the adaptively adjusted grid, which means that execution times were about 100 s, but two iterations are needed to correctly compute the optical depth for the escape probability formalism. The settling phase of the simulation took about 10 000 calls to the photoionization solver, which explains the simulation time of about one month. For the advection of species, at least 30 iterations have to be made in the CLOUDY internal steady-state solver, but when starting from the previously converged simulation, about 200 calls to the photoionization solver suffice, which adds up to one day. In the future, the abundance of metals can be linearly increased during the simulation to prevent strong oscillation in the atmosphere and, thus, limit the CLOUDY calls to a minimum.
The convergence of the advection of species in the CLOUDY internal steady-state solver can cause problems in certain situations. The result is a solution where effects of the advection of species are only resolved on scales larger than the advection length. One possible solution is to manually reduce the advection length to the needed accuracy, which increases the computational effort, however, because more iterations in CLOUDY are needed. Furthermore, advection can only be included in 1D simulations with flows toward the irradiating source. A possible solution would be to include passive scalar fields in PLUTO for every species and solve the advection by explicitly including source and sink terms, which could be retrieved from each call to the photoionization solver. This complicates the interface, however and necessitates more essential changes of the CLOUDY source code because the number densities of each species would have to be passed to CLOUDY and source and sink terms must be retrieved. Species include all ionization stages of the 30 lightest elements plus all included molecules.
The simulation of atmospheric evaporation in the well-studied hot Jupiter HD 209458b demonstrates the capabilities of TPCI. The simulation of the hydrogen-only atmosphere shows significant differences compared to Murray-Clay et al. (2009) because the authors used a gray absorption scheme, or compared to Penz et al. (2008), who neglected Lyα cooling. Our atmosphere shows an excellent agreement with the corresponding model of Koskinen et al. (2013). We resolved a temperature minimum in the lower atmosphere because our simulation continues deeper into the atmosphere. Furthermore, we used a more comprehensive microphysics solver, which reveals significant cooling due to free-free emission in the lower atmosphere, which has previously been underestimated (Murray-Clay et al. 2009).
The increased accuracy in solving the absorption and emission processes is a clear advantage, and by using the well-tested CLOUDY code, we did not neglect any significant processes in our model. The total change in the mass-loss rate compared to the model of Koskinen et al. (2013) is lower than a factor of two in this pure hydrogen atmosphere, but larger differences can be expected when metals will be included. In the future, we will extend this initial test case to include molecules and metals and will investigate the effects of strong X-ray irradiation in the atmospheres of planets around active host stars.
Acknowledgments
We thank G. J. Ferland for a discussion of the problem. This research has made use of the Exoplanet Orbit Database and the Exoplanet Data Explorer at exoplanets.org. M.S. acknowledges support from the Deutsches Zentrum für Luft- und Raumfahrt, DLR under the project 50OR1105 and the Deutsche Forschungsgemeinschaft, DFG RTG-1351.
References
- Banks, P. M., & Kockarts, G. 1973, Aeronomy, eds. P. M. Banks, & G. Kockarts (New York: Academic Press) [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1997 [arXiv:astro-ph/9710187] [Google Scholar]
- Bryan, G. L., Norman, M. L., O’Shea, B.W., et al. 2014, ApJS, 211, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I. 1970, MNRAS, 149, 111 [NASA ADS] [Google Scholar]
- Cecchi-Pestellini, C., Ciaravella, A., & Micela, G. 2006, A&A, 458, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Courant, R., Friedrichs, K., & Lewy, H. 1928, Mathematische Annalen, 100, 32 [Google Scholar]
- Crossfield, I. J. M., Knutson, H., Fortney, J., et al. 2012, ApJ, 752, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Clarke, C. J. 2007, MNRAS, 382, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elitzur, M. 1982, Rev. Mod. Phys., 54, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 1992, Astronomical masers (Kluwer Academic Publishers), Astrophys. Space Sci. Lib., 170, 365 [Google Scholar]
- Ercolano, B., Barlow, M. J., Storey, P. J., & Liu, X.-W. 2003, MNRAS, 340, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J. 1979, MNRAS, 188, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Frank, A., & Mellema, G. 1994, A&A, 289, 937 [NASA ADS] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- García Muñoz, A. 2007, Planet. Space Sci., 55, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, S., & Shu, C.-W. 1996, NASA CR-201591 ICASE Rep. 96-50 [Google Scholar]
- Henney, W. J., Arthur, S. J., Williams, R. J. R., & Ferland, G. J. 2005, ApJ, 621, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G.-S., & Shu, C.-W. 1996, J. Comput. Phys., 126, 202 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Koskinen, T. T., Harris, M. J., Yelle, R. V., & Lavvas, P. 2013, Icarus, 226, 1678 [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Le Teuff, Y. H., Millar, T. J., & Markwick, A. J. 2000, A&AS, 146, 157 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Lightman, A. P., & White, T. R. 1988, ApJ, 335, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morisset, C., Stasińska, G., & Peña, M. 2005, MNRAS, 360, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Murray-Clay, R. A., Chiang, E. I., & Murray, N. 2009, ApJ, 693, 23 [Google Scholar]
- O’Dell, C. R. 2001, ARA&A, 39, 99 [NASA ADS] [CrossRef] [Google Scholar]
- O’Shea, B. W., Bryan, G., Bordner, J., et al. 2004 [arXiv:astro-ph/0403044] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, eds. D. E. Osterbrock, & G. J. Ferland (Sausalito, CA: University Science Books) [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Penz, T., Erkaev, N. V., Kulikov, Y. N., et al. 2008, Planet. Space Sci., 56, 1260 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., et al. 2010, ApJ, 711, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Raga, A. C., Taylor, S. D., Cabrit, S., & Biro, S. 1995, A&A, 296, 833 [NASA ADS] [Google Scholar]
- Reale, F., & Orlando, S. 2008, ApJ, 684, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Rijkhorst, E.-J., Plewa, T., Dubey, A., & Mellema, G. 2006, A&A, 452, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröter, S., Czesla, S., Wolter, U., et al. 2011, A&A, 532, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, P. R., Iliev, I. T., & Raga, A. C. 2004, MNRAS, 348, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1978, Physical processes in the interstellar medium, ed. L. Spitzer, J. Roy. Astron. Soc. Canada, 72, 349 [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, F., Toon, O. B., Pavlov, A. A., & De Sterck, H. 2005, ApJ, 621, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Toro, E. F., Spruce, M., & Speares, W. 1994, Shock Waves, 4, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trammell, G. B., Arras, P., & Li, Z.-Y. 2011, ApJ, 728, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., & Chiang, E. 2013, MNRAS, 428, 2565 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., & Abel, T. 2011, MNRAS, 414, 3458 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., & Rottman, G. J. 2002, Solar Ultraviolet Variability Over Time Periods of Aeronomic Interest, eds. M., Mendillo, A., Nagy, & J. H. Waite, 221 [Google Scholar]
- Wright, J. T., Fakhouri, O., Marcy, G. W., et al. 2011, PASP, 123, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. V. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Flowchart of the PLUTO-CLOUDY Interface. Affiliation of modules is indicated by colored boxes. PLUTO solves the hydrodynamic evolution and CLOUDY the ionization and chemical equilibrium state of the gas under strong irradiation. Communication is achieved through the interface, which also handles the interpolation between the two different grid structures. |
| In the text | |
 |
Fig. 2 Pure hydrogen weak D-type ionization front. Density a), temperature b), velocity c), and degree of ionization d) are depicted. A CLOUDY simulation (red dashed lines) is compared with a TPCI simulation (blue solid lines). Initial conditions are given by the gray dotted lines. In panel c) the speed of sound is shown by the black solid line. The TPCI simulation agrees well with the independent CLOUDY simulation. Small oscillations in the high-density region that can be seen in panel c) do not affect the solution significantly. |
| In the text | |
 |
Fig. 3 Convergence of the models of the weak D-type ionization front. The CLOUDY simulation is shown by red, thin lines, the advective TPCI simulation by thick, blue lines. The discretization error (dotted), the convergence error (dashed), and the advection length (solid) are plotted against the iteration number of the steady-state solver in CLOUDY. The grid resolution of the TPCI simulation is indicated by the thin, black line. In both simulations the advection length is reduced to within a factor of 2 of the grid resolution in the hydrodynamic simulation part. |
| In the text | |
 |
Fig. 4 Optically thin cooling function of PLUTO (blue, dotted) and CLOUDY (red, solid). The crosses depict the actual cooling in the coronal shock simulation with TPCI. These are a factor of 1.5 lower because the simulation shows significant optical-depth effects. |
| In the text | |
 |
Fig. 5 Hydrodynamic evaporation wave in a flaring coronal loop. The red dashed lines show a simulation with PLUTO assuming optically thin cooling. The blue lines depict the results of TPCI, and the initial conditions are given by the gray dotted lines. The density is shown in panel a), the temperature in b), the velocity in c), and the cooling of TPCI is plotted in panel d) together with the constant heating rate. Panel d) shows the fractional abundance of the two iron ions with the strongest individual contribution to the total cooling rate. In panel b) the temperature decrement in the after-shock evolution is indicated. The sound speed is shown by the solid black line in panel c). Both simulations show the same behavior, except that in the PLUTO simulation the cooling rate is twice as strong as in the TPCI simulation, which is due to optical-depth effects and small differences of the electron density. |
| In the text | |
 |
Fig. 6 Expansion of an R-type ionization front. The TPCI simulation (blue solid) is compared with the theoretical evolution of Eq. (19). Three Strömgren radii for different temperatures are indicated by labeled thin black lines. The expansion of the ionized region proceeds faster in the TPCI simulation because the equilibrium solutions of the photoionization solver at each integration step are not restricted by the time since ignition of the central source. |
| In the text | |
 |
Fig. 7 Temperature evolution during expansion of the R-type ionization front. The temperature versus radius is plotted at various times. The time step between consecutive lines is constant, the time is referenced by the color scheme. The temperature increases from 1000 K to 17 000 K, being nearly constant throughout the ionized region. The expansion radius of the ionized region at a given time is marked by the steep temperature decline and increases from 0.085 to 0.16 pc. The distance between consecutive lines decreases, indicating the approach to the final Strömgren radius. |
| In the text | |
 |
Fig. 8 Thermal conductivity coefficient. The coefficient for electron conductivity is depicted by the red dashed line, for neutral hydrogen by the green dotted line, and the blue solid line is the sum. The black dash-dotted line shows the more accurate weighted sum (Eq. (26)) derived with the actual densities of neutral hydrogen and electrons in a CLOUDY simulation without irradiation. In the temperature region below 10 000 K the simple sum is accurate to within a factor of two. |
| In the text | |
 |
Fig. 9 Evaporating hydrogen atmosphere of HD 209458 b. Density a), temperature b), velocity c), ionization fraction d), heating and cooling rate e), and the heating fraction f) are plotted versus the planetary radius. The red dashed lines depict the initial settling phase, the blue solid lines the final TPCI simulation including advection of species. The initial conditions are given by the gray dotted lines. Panel a) also shows the density structure of an isothermal atmosphere with 500 K (black solid line). In panel c) the speed of sound is indicated (black solid line), and in panel e) the three main cooling agents in the atmosphere are shown by black thin lines. “H line emis.” is cooling due to line emission from hydrogen atoms (mainly Lyα), “ff emis.” is cooling by free-free emission of electrons, and “H recomb.” is recombination cooling of hydrogen. Additionally, thermal conductive cooling (cond.) is shown by a black dotted line. The atmosphere expands in a transonic flow. A small amount of the absorbed energy (~11%) is lost through free-free and Lyα emission. |
| In the text | |
 |
Fig. 10 Execution times of CLOUDY runs on local cpu with setups based on the hot-Jupiter simulation. Simulation times vary in the shaded range based on density and temperature. Each step increases the complexity of the simulation, starting with a simulation including only hydrogen and 10 zones in CLOUDY. In this case the execution time is dominated by the initialization of CLOUDY. The next steps are with 100 and 1000 zones. We then include step by step molecules, helium, carbon, nitrogen, and oxygen, and all 30 lightest elements. Finally, we iterate twice in CLOUDY over the complete domain to correct optical-depth effects. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


