| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201425268 | |
| Published online | 09 February 2015 | |
Chemistry in disks
IX. Observations and modelling of HCO+ and DCO+ in DM Tauri⋆
1
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
email: teague@mpia.de
2
Univ. Bordeaux, LAB, UMR 5804, 33270
Floirac,
France
3
CNRS, LAB, UMR 5804, 33270
Floirac,
France
4
IRAM, 300 rue
de la Piscine, 38046
Saint-Martin d’Hères,
France
Received:
4
November
2014
Accepted:
29
December
2014
Aims. We study the deuteration and ionization structure of the DM Tau disk via interferometric observations and modelling of the key molecular ions, HCO+ and DCO+.
Methods. The Plateau de Bure Array is used to observe DM Tau in lines of HCO+ (1−0), (3−2) and DCO+ (3−2) with a ~ 1.5′′ angular and ~0.2 km s-1 spectral resolution. Using a power-law fitting approach the observed column densities profiles are derived and thus the isotopic ratio RD = DCO+/HCO+. Chemical modelling allowed an exploration of the sensitivity of HCO+ and DCO+ abundances to physical parameters out with temperature. A steady state approximation was employed to observationally constrain the ionization fraction x(e−).
Results. Fitting of radiative transfer models suggests that there is a chemical hole in HCO+ and DCO+, extending up to 50 AU from the star. More work is required to discern the cause of this. The observed column densities of HCO+ and DCO+ at 100 AU were (9.8+0.3-0.7) × 1012 and (1.2 ± 0.7) × 1012 cm-2 respectively. Where both HCO+ and DCO+ were present, RD was found to increase radially from 0.1 at 50 AU to 0.2 at 450 AU. This behaviour was well reproduced by the chemical model. The X-ray luminosity of the central star, the interstellar UV and CO depletion were found to be the most important physical parameters controlling the abundances of HCO+ and DCO+. Differences in the vertical extent of HCO+ and DCO+ molecular layers resulted in different responses to changing physical parameters, manifesting as radial gradients in RD. The ionization fraction was found to be x(e−) ~ 10-7 in the molecular layer, comparable to the disk averaged value. Modelling shows that while HCO+ is the most dominant charged molecular ion in our disk model, atomic ions, such as C+, S+, H+, Na+ and Mg+, dominate the charge in both the molecular layer and disk atmosphere.
Conclusions. A high value of RD is indicative of continued deuterium fractionation in a protoplanetary disk after pre/protostellar phases. Radial properties of RD can be employed to discern the importance of ionization from X-rays and UV, thus necessitating the need for more, high resolution observations of DCO+ and other deuterated species in disks. A steady-state approach commonly adopted for constraining ionization degree in prestellar cores is not applicable for disks where accurate determination of the ionization fraction in the molecular layer requires knowledge of the atomic ions present as molecular ions are relatively sparse.
Key words: protoplanetary disks / radio lines: planetary systems / circumstellar matter
© ESO, 2015
1. Introduction
In the view of recent exciting discoveries of various extrasolar planets with the Kepler satellite, including Earth-like planets in a habitable zone (Quintana et al. 2014), and recent ground-breaking Subaru, Herschel, and ALMA observations of protoplanetary disks (PPDs; e.g., Öberg et al. 2010; Sturm et al. 2013; Williams & Cieza 2011; Fedele et al. 2013; Grady et al. 2013; van der Marel et al. 2013; Rosenfeld et al. 2014), it is with great anticipation that we begin to unravel the planet formation process. Interferometric observations of PPDs provide a crucial tool in the quest to understand these enigmatic objects.
The high-resolution measurements of the dust continuum and molecular emission lines of various optical thicknesses allow for probes of physics and chemistry in distinct disk regions (for recent reviews, see Henning & Semenov 2013; Quintana et al. 2014). To make sense of these data one has to employ disk physical/thermo-chemical models that predict the thermal and density structures of disks (e.g., Woitke et al. 2009; Akimkin et al. 2013), gas-grain chemical models to calculate molecular distributions (e.g., Willacy et al. 1998; Aikawa & Herbst 1999b; Semenov et al. 2010; Walsh et al. 2010), and radiative transfer modelling to simulate molecular lines (e.g. ARTIST1, RADMC-3D2, Hogerheijde & van der Tak 2000; van Zadelhoff et al. 2002; Pinte et al. 2006; Pavlyuchenkov et al. 2007; Jørgensen et al. 2014). Another approach is to perform an iterative fitting of the observed spectra/interferometric visibilities, applying simpler power-law models of disk physical and molecular structure coupled to a fast LTE/LVG radiative transfer model (e.g., Guilloteau & Dutrey 1998; Piétu et al. 2007; Qi et al. 2008; Rosenfeld et al. 2013). A combination of these approaches have been used in series of articles by our “Chemistry In Disks” (CID) consortium (Dutrey et al. 2007, 2011; Schreyer et al. 2008; Henning et al. 2010; Semenov et al. 2010; Guilloteau et al. 2012).
In this paper we present interferometric observations of HCO+J = (3−2), J = (1−0) and DCO+J = (3−2) in DM Tau, a bona fide T-Tauri star in the Taurus-Auriga star-forming region. Owing to its large size, ~800 AU, and moderate inclination, i ≈ 35°, it has become one of the best studied PPDs. In one of the first millimeter studies of PPDs, Guilloteau & Dutrey (1994) used the 12CO and 13CO J = (2−1) lines to derive a disk mass of 1.4 × 10-3M⊙ and disk radius of ≈700 au. Later, high spectral- and spatial-resolution observations of 12CO, 13CO and C18O have allowed the detection of a vertical temperature gradient within the disk and the presence of very cold, ~ 10−15 K CO gas (Dartois et al. 2003), a better constrained disk mass of 0.05 M⊙ and an outer radius in CO of ≈800 AU.
Piétu et al. (2007) used higher resolution observations of these lines supplemented with HCO+J = (1−0) to better constrain the disk physical structure and kinematics in the radial direction. They confirmed the presence of the vertical gas temperature gradient in the DM Tau system, found that CO has an extended distribution in vertical direction, and that the slope of the CO surface distribution changes its value with radius.
In the first CID paper of Dutrey et al. (2007), a sensitive observation of N2H+ and HCO+ towards three disks (including DM Tau) was performed with PdBI, followed by advanced physico-chemical modelling. It was found that HCO+ is a major polyatomic ion in disks, and that its column density agrees with the modelled values at an evolutionary stage of a few million years. The ionization degree in the HCO+ molecular layer was also derived, ~ 2 × 10-9.
In the next CID paper by Schreyer et al. (2008) the chemical content of the DM Tau disk was compared to the disk around a hotter Herbig A0 star: AB Aur. We found that while the AB Aur disk possesses more CO, it is less abundant in other, more complex molecular species compared to the DM Tau disk. This finding gives a hint that high-energy radiation from the central star may be important not only for disk thermal structure but also for its chemical complexity (see also Fedele et al. 2011, 2013; Öberg et al. 2011a).
Another way to better characterize the thermal structure of PPDs is to observe and analyse deuterated species. Unfortunately, the key species for deuterium chemistry that can be detected at submillimeter wavelengths, namely ortho-H2D+ and para-D2H+, have been only observed in cold prestellar cores (Harju et al. 2006; Hogerheijde et al. 2006; Parise et al. 2011; Vastel et al. 2006) and have not yet been firmly detected in disks (Asensio Ramos et al. 2007; Chapillon et al. 2011). Thus, to fully characterize deuterium chemistry in disks other more readily observable tracers, such as DCO+, DCN, DNC, N2D+, along with their major isotopologues, must be used.
We must use a combination of these molecules as there are two main deuteration pathways possible, each with a different range of temperatures where they are most efficient. For example, DCO+ and N2D+ fractionation occurs mainly via H isotopologues at temperatures ≲20−30 K, whereas fractionation of DCN and DNC involves deuterated light hydrocarbon ions such as CH2D+ and C2HD+ with a pathway which remains active up to temperatures of 70−80 K (e.g., Millar et al. 1989; Aikawa & Herbst 1999a; Albertsson et al. 2013; Ceccarelli et al. 2014).
isotopologues at temperatures ≲20−30 K, whereas fractionation of DCN and DNC involves deuterated light hydrocarbon ions such as CH2D+ and C2HD+ with a pathway which remains active up to temperatures of 70−80 K (e.g., Millar et al. 1989; Aikawa & Herbst 1999a; Albertsson et al. 2013; Ceccarelli et al. 2014).
The first detection of a deuterated species in a disk was made by van Dishoeck et al. (2003), who detected DCO+ in TW Hya and discerned a disk averaged ratio of RD ≃ 0.04, a value similar to that found in pre-stellar cores (e.g., Bergin & Tafalla 2007; Caselli & Ceccarelli 2012). Guilloteau et al. (2006) have since detected DCO+ in DM Tau, with a lower ratio of RD ~ 4 × 10-3. A more recent, higher angular resolution study of Qi et al. (2008) has shown that the DCO+/HCO+ ratio in the TW Hya disk increases radially from 0.01 to 0.1 up to a radius of ≈90 au, where it drops off considerably. Later, Öberg et al. (2012) have observed isotopologues of HCN and HCO+ in TW Hya with both then SMA and ALMA, finding that the radial distribution of DCO+ and DCN is markedly different. While DCN seems to be centrally peaked, DCO+ shows an increasing column density with radius. This supports the theoretical predictions that these two deuterated ions are synthesized via distinct low- and high-temperature fractionation pathways. Recently, Mathews et al. (2013) have directly imaged the location of the CO snowline in a warmer disk around a Herbig A3 star HD 163296 with ALMA, using the optically thin DCO+ (5−4) line as a direct tracer of CO (see also Qi et al. 2013).
Additional information from the analysis of the HCO+ and DCO+ data includes the possibility to better constrain the ionization degree than with HCO+ data alone (e.g., Caselli 2002). The ionization degree is a key quantity that enables angular momentum transport in disks, thereby regulating their overall evolution and the ability to form planets via turbulence. Magnetorotational instability (MRI; Balbus & Hawley 1991) is currently the most widely accepted source of turbulence in disks (see, e.g. Flock et al. 2012), although magnetocentrifugal disk winds and other non-linear effects such as ambipolar diffusion can also be important. Öberg et al. (2011b) have used the CO, HCO+, DCO+, and N2H+ lines observed in the disk of DM Tau with SMA and estimated ionization degree through its molecular layer. In the region probed by HCO+ (T ≳ 20 K) the ionization degree was found to be 4 × 10-10, whereas in colder, deeper layers where N2H+ and DCO+ abundances are peaked, the ionization degree is lower, ~ 3 × 10-11.
The goal of this paper is to build on the previous work of Öberg et al. (2011b) to better understand the thermal and ionization structure of DM Tau. We will present higher resolution observations of HCO+J = (3−2), J = (1−0) and DCO+J = (3−2) which, combined with a chemical model of DM Tau, allow us to determine the radial dependance of HCO+ and DCO+ column densities. Furthermore, the combination of two rotational lines for HCO+ with different optical depths provide us with a tool with which to discern the HCO+ excitation structure of the disk.
The paper is structured as follows: Sect. 2 will describe the treatment of the observational data and the method in deriving a model, Sect. 3 details the computational model used and a description of the resulting “best-fit” model to our observations. In Sect. 4 we explore the deuterium fractionation and ionization fraction in the disk with a suite of chemical models to aid analysis, before finally summarising our results in Sect. 5.
 |
Fig. 1 Channel maps of: HCO+J = (1−0), top, with σ = 3.7 mJy/beam (0.32 K) and contour spacing of 2.5σ; HCO+J = (3−2), middle, with σ = 100 mJy/beam (0.64 K) and contour spacing of 2.5σ; and DCO+J = 3−2, bottom, with σ = 30 mJy/beam (0.42 K) and contour spacing of 2σ emission from DM Tau. The beam size, shown by the filled ellipse, for each line is 1.4 × 1.26″, 1.85 × 1.49″ and 1.4 × 1.33″ respectively. The velocity of each channel shown in the top left corner in km s-1 while the cross in the centre shows the position of the host star and the position angle of the major and minor axes of the disk. Dashed contours show negative values. |
2. Observational results
This section describes the process of creating a model of DM Tau by fitting HCO+ and DCO+ line emission.
Stellar and disk properties of DM Tau with values taken from Dutrey et al. (2007) and Henning et al. (2010).
2.1. PdBI data
Observations were carried out with the IRAM Plateau de Bure interferometer. Table 1 presents basic stellar properties and disk parameters of DM Tau from previous studies. We observed two transitions of HCO+, the J = (1−0) line at 89.18852 GHz and the J = (3−2) line at 267.55762 GHz and the J = (3−2) transition of DCO+ at 221.611258 GHz. The HCO+J = (1−0) data included those described in Piétu et al. (2007) and were completed by longer baselines data (baselines up to 760 m) obtained in late Feb. and early March 2008. The DCO+ data were obtained between Aug. and Dec. 2007, with baselines ranging from 15 to 175 m, yielding an angular resolution around 1.3″. The HCO+J = (3−2) data were obtained in Dec. 2008, with a similar baseline coverage than the DCO+ data.
Best-fit parameters for DM Tau with descriptions of the parameters in the text.
2.2. Data reduction
We used the IRAM package GILDAS3 for data reduction and imaging. All data were smoothed to similar spectral resolutions, 0.17 to 0.20 km s-1 for best comparison. Self-calibration was applied to all three lines and the dust thermal continuum was subtracted from the line spectra (Dutrey et al. 2007).
Channel maps of the emission lines are shown in Fig. 1, with contours in levels of 2.5σ for the HCO+ data and 2σ for DCO+. The rms noise values were calculated in a line free channel and are 3.7, 100 and 30 mJy/beam respectively. The need to plot tighter 2 σ contours for DCO+J = (3−2) highlights the lower intensity of this line relative to the HCO+ emission, which is to be expected for a deuterated isotopologue.
2.3. DiskFit fitting
Following the prescription of Piétu et al. (2007), we assume that the physical properties which affect line emission from a disk vary as a radial power law: 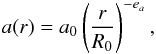 (1)where a0 is the parameter value at the reference radius R0. We adopt the standard that positive exponents, ea, imply a decrease of the physical quantity with radius. Through this prescription line emission in a disk can be described by the following parameters:
(1)where a0 is the parameter value at the reference radius R0. We adopt the standard that positive exponents, ea, imply a decrease of the physical quantity with radius. Through this prescription line emission in a disk can be described by the following parameters:
-
X0 (′′) and Y0 (′′), position of the central star;
-
VLSR (km s-1), systemic velocity;
-
PA (°) and i (°), position angle and inclination of the disk;
-
Vv (km s-1), Rv (au), v, rotation velocity at reference radius Rv, typically 100 au, with a power law exponent v. Perfect Keplerian rotation would yield v = 0.5;
-
Tm (K), RT (au), qm, gas temperature at the reference radius RT and respective power law exponent;
-
dV (km s-1), ev, turbulent component of the line widths and respective power law exponent;
-
Σm (cm-2), RΣ (au), pm, gas surface density, reference radius and power law exponent;
-
Rin and Rout (au), inner and outer radius of observed emission;
-
hm (au), Rh (au), eh, scale height of the gas, reference radius and its exponent.
It has been shown previously that power laws are reasonably accurate proxies for correct descriptions of the large-scale disk properties, such as kinematics (assuming that the self-gravity is negligible), kinetic temperature distribution, surface density (assuming the α-viscosity prescription and a constant accretion rate), and thus, also the disk scale height (e.g., Chiang & Goldreich 1997; Piétu et al. 2007).
The corresponding disk parameters were fitted to each of the observed lines with the DISKFIT software (Guilloteau & Dutrey 1998), using a combination of χ2 minimization and MCMC fitting of the observed visibilities in the uv-plane. Line emission provided information on the gas structure while continuum emission was used to fit the dust structure.
2.4. Observational results
The derived best-fit parameters for the three emission lines and the continuum are shown in Table 2. Geometrical properties of the disk (systemic velocity, inclination, position angle and Keplerian velocity at 100 AU) were found to be in good agreement with previous studies on DM Tau using the DISKFIT approach (Guilloteau & Dutrey 1998; Piétu et al. 2007; Dutrey et al. 2007).
Due to the uncertainty in optical depth of the HCO+ rotational lines, we analysed the HCO+ images in three different ways. In case A, the J = (1−0) and (3−2) images were fitted independently. The derived parameters are presented in Cols. 1, 2 of Table 2. The HCO+J = (3−2) is largely optically thick, and thus provides a good estimate of the temperature, however, the surface density cannot be well constrained from this data. A best fit outer radius of around 500 AU was found for this line. On the other hand, HCO+J = (1−0) extends further (to at least 750 AU), and is mostly optically thin. Thus, the derived temperature heavily relies on the power law extrapolation at low radii. We also note that the J = (3−2) line requires an inner radius around 50 AU. A lack of emission from the inner 50 AU may bias the temperature derived from the J = (1−0) line towards low values.
In case B, we assume the J = (1−0) and (3−2) lines to have the same excitation temperature. We fit both transitions simultaneously, and set the outer radii to 750 AU. Results are given in Col. 3. The derived temperature law is now much steeper, q = 1.00 ± 0.04, and the surface density law much flatter. The derived surface densities are also lower roughly a factor of 2 to 5 between 200 and 400 AU compared to the separate fits.
Finally, in case C, we relaxed the power law assumption, and fitted the temperature and surface densities at 5 different radii, extrapolating by power laws in between. The solution is within the errors consistent with case B, and thus we only report this latter case hereafter.
Neither approach is perfect: in case A, the extrapolation required to derive the temperature profile from the J = (1−0) line is hazardous. On the other hand, in case B we neglect the vertical temperature gradients which are expected in disks, despite the higher opacity of the J = (3−2) line naturally leading to higher excitation temperature compared to the J = (1−0) line. Alternatively, if the density is insufficient to thermalize the J = (3−2) transition, we may expect its excitation temperature to be lower than that of the J = (1−0). We shall use the results of case B hereafter. The very low temperatures derived in the outer part suggest some sub-thermal excitation, at least for the J = (3−2) transition beyond 400 AU or so. Note that apparent “ring-like” distribution of HCO+J = (3−2) is not due to simple excitation effect, as suggested by Cleeves et al. (2014). A central hole of 50 AU radius, almost fully devoid of HCO+, is required to reproduce the J = (3−2) emission.
The DCO+ line is weaker, and we can only derive the surface density by fixing all other parameters guided by those found for HCO+ as it is a reasonable assumption to assume they are cospatial in the disk. Note, however, that the derived values are quite insensitive to the assumed temperature law.
To provide a better comparison with the modelled results, we will extrapolate the power laws describing column densities and temperatures. However it must be noted that, due to the inner hole in HCO+ and smaller outer radius in DCO+ the power laws only provide a good fit to the data in the region 50 ≲ r ≲ 430 AU. In order to better comprehend these findings, we perform detailed theoretical modelling in the next Section.
3. Computational model
3.1. Disk physical structure
This section describes the methodology of creating a computational chemical disk model of DM Tau, including a description of the physical and chemical parameters used.
The DM Tau system, at a distance of 140 pc, consists of a single isolated pre-main-sequence M0.5-1.5 dwarf (Teff = 3720 K), with a mass of 0.5−0.65 M⊙, a radius of 1.2 R⊙, and an accretion rate of ~ 2−3 × 10-9M⊙ yr-1 (Mazzitelli 1989; Simon et al. 2000; McJunkin et al. 2014). It is enshrouded by an extended (~ 800 AU), cold (T ≳ 10 K) Keplerian disk (Piétu et al. 2007). According to the Spitzer IRS observations (Calvet et al. 2005), the inner DM Tau disk is cleared of small dust (≲3−4 AU) and is in a pre-transitional phase. As our interferometric observations have the highest sensitivity in disk regions ≥30 AU from the central star, we only consider the chemical evolution outside of this radius in our analysis.
 |
Fig. 2 Disk physical structure scaled vertically as z/R. Colouring shows the coupled gas and dust temperature and solid lines show the particle number densities in particles cm-3. The dashed white lines shows the 21 K isotherm, below which half of CO has frozen out. |
The DM Tau physical disk model is based on a 1+1D steady-state α-model similar to that of D’Alessio et al. (1999), where equal gas and dust temperatures are assumed. This model was extensively used in our previous studies of DM Tau-like disk chemistry (e.g., Henning et al. 2010; Semenov & Wiebe 2011; Albertsson et al. 2014b). The disk model has an outer radius of 800 AU, an accretion rate of 2 × 10-9M⊙ yr-1, a viscosity parameter α = 0.01, and a total gas mass of 0.066 M⊙ (Dutrey et al. 2007; Henning et al. 2010; Semenov & Wiebe 2011). The dissociating UV radiation of DM Tau is represented by the scaled-up interstellar UV radiation field of Draine (1978). The unattenuated stellar UV intensity at the radius of 100 AU is χ∗(100) = 410 (e.g., Bergin et al. 2003). The X-ray luminosity of DM Tau is taken to be 2 × 1029 erg s-1 (see Semenov & Wiebe 2011). The calculated disk thermal and density structure is shown in Fig. 2.
Atomic and molecular abundances used in the disk chemical model. Top: Initial abundances for modelling the pre-disk evolutionary phase Bottom: 25 initially most abundant molecules for disk chemical modelling.
3.2. Disk chemical model
The adopted chemical model is based on the advanced ALCHEMIC code (see Semenov et al. 2010) and utilizes the high-temperature, gas-grain deuterium chemistry network of Albertsson et al. (2013), with the addition of nuclear spin-state processes for H2, H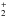 , and H
, and H isotopologues from Albertsson et al. (2014a). The chemical network without deuterated species is based on the osu.2007 ratefile4, with the recent updates to the reaction rates from Kinetic Database for Astrochemistry (KIDA; Wakelam et al. 2012). For all H-bearing reactions in this network, we derived the corresponding D-bearing reactions following the algorithm of Rodgers & Millar (1996). The cloning was not allowed for any species with the -OH endgroup.
isotopologues from Albertsson et al. (2014a). The chemical network without deuterated species is based on the osu.2007 ratefile4, with the recent updates to the reaction rates from Kinetic Database for Astrochemistry (KIDA; Wakelam et al. 2012). For all H-bearing reactions in this network, we derived the corresponding D-bearing reactions following the algorithm of Rodgers & Millar (1996). The cloning was not allowed for any species with the -OH endgroup.
Primal isotope exchange reactions for H as well as CH
as well as CH and C2H
and C2H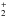 from Roberts & Millar (2000); Gerlich et al. (2002); Roberts et al. (2004); Roueff et al. (2005) were included. In cases where the position of the deuterium atom in a reactant or in a product was ambiguous, a statistical branching approach was used. This deuterium network was further extended by adding ortho- and para-forms of H2, H
from Roberts & Millar (2000); Gerlich et al. (2002); Roberts et al. (2004); Roueff et al. (2005) were included. In cases where the position of the deuterium atom in a reactant or in a product was ambiguous, a statistical branching approach was used. This deuterium network was further extended by adding ortho- and para-forms of H2, H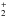 and H
and H isotopologues and the related nuclear spin-state exchange processes from several experimental and theoretical studies (Gerlich 1990; Gerlich et al. 2002; Flower et al. 2004, 2006; Walmsley et al. 2004; Pagani et al. 2009; Hugo et al. 2009; Honvault et al. 2011; Sipilä et al. 2013).
isotopologues and the related nuclear spin-state exchange processes from several experimental and theoretical studies (Gerlich 1990; Gerlich et al. 2002; Flower et al. 2004, 2006; Walmsley et al. 2004; Pagani et al. 2009; Hugo et al. 2009; Honvault et al. 2011; Sipilä et al. 2013).
To calculate UV ionization and dissociation rates, the mean FUV intensity at a given disk location is obtained by summing up the stellar χ∗(r) = 410 × (r/ 100)-2, where r is in au, and interstellar UV fluxes scaled down by the visual extinction in the radial and vertical directions, respectively. Several tens of newer photoreaction rates are adopted from van Dishoeck et al. (2006)5. The self-shielding of H2 from photodissociation is calculated by Eq. (37) from Draine & Bertoldi (1996). The shielding of CO by dust grains, H2, and the CO self-shielding is calculated using a precomputed table of Lee et al. (1996, Table 11).
The stellar X-ray radiation is modelled using observational results of Glassgold et al. (2005) and the approximate expressions (7–9) from the 2D Monte Carlo simulations of Glassgold et al. (1997a,b). Implementing Eq. (8) from Glassgold et al. (1997b), we use an exponent of n = 2.81, a cross section at 1 keV of σ-22 = 0.85 × 10-22 cm2 and total X-ray luminosity of LXR = 3 × 1029 erg s-1, yielding a typical X-ray photon energy of 3 keV. Attenuation of X-rays is calculated from Eq. (4) in Glassgold et al. (1997a). The X-ray emitting source is located at 12 stellar radii above the midplane with rates exceeding that of the CRPs in the disk regions above the midplane, particularly, at radii ~ 100−200 AU (see also Henning et al. 2010)
We assume the standard cosmic ray (CR) ionization rate ζCR = 1.3 × 10-17 s-1 and model its attenuation using Eq. (3) from Semenov et al. (2004). Note that we do not consider the scattering of low energy CR protons by the heliosphere of DM Tau, as done in Cleeves et al. (2013a). Ionization due to the decay of short-living radionuclides is taken into account, ζRN = 6.5 × 10-19 s-1 (Finocchi et al. 1997), see also Cleeves et al. (2013b).
 |
Fig. 3 Deuterium fractionation in the disk. a) Comparisons of HCO+, blue, and DCO+, red, from observations, dashed with 3σ errors, and the best fit model, solid with associated error of a factor of 3. They grey vertical bars show where the observationally derived column densities are extrapolated beyond the inner and outer edges found in parameterisation. b) and c) show the relative abundances of DCO+ and HCO+ in the best fit disk chemical model respectively. d) shows the local DCO+/HCO+ ratio in the disk model. |
The grain ensemble used to calculate disk physical structure was represented by uniform amorphous silicate particles of olivine stoichiometry with density of 3 g cm-3 and radius of 0.1 μm. Each grain provides ≈1.88 × 106 surface sites (Biham et al. 2001) for surface recombination that proceeds solely through the classical Langmuir-Hinshelwood mechanism (e.g. Hasegawa et al. 1992). The gas-grain interactions include sticking of neutral species and electrons to dust grains with 100% probability and desorption of ices by thermal, CRP-, and UV-driven processes. We do not allow H2 to stick to grains as it requires temperatures of ≲4 K. The UV photodesorption yield of 3 × 10-3 was adopted (e.g., Öberg et al. 2009a,b; Fayolle et al. 2011, 2013). Photodissociation processes of solid species are taken from Garrod & Herbst (2006), Semenov & Wiebe (2011).
In addition, dissociative recombination and radiative neutralization of molecular ions on charged grains and grain re-charging are taken into account. Upon a surface recombination, we assume there is a 1% probability for the products to leave the grain due to the partial conversion of the reaction exothermicity into breaking the surface-adsorbate bond (Garrod et al. 2007; Vasyunin & Herbst 2013). Following experimental studies on the formation of molecular hydrogen on amorphous dust grains by Katz et al. (1999), the standard rate equation approach to the surface chemistry was utilized. Overall, the disk chemical network consists of 1268 species made of 13 elements and 38 812 reactions.
The age of the DM Tau system is poorly constrained, ~3−7 Myr (Simon et al. 2000). In the chemical modelling the age of 5 Myr was considered. To set initial abundances, we calculated chemical evolution in a TMC1-like molecular cloud (nH = 2 × 104 cm-3, T = 10 K, AV = 10 mag) over 1 Myr. For that, the “low metals” elemental abundances of Graedel et al. (1982), Lee et al. (1998), Agúndez & Wakelam (2013) were used, with the equilibrium 3:1 ortho/para H2 ratio (hydrogen being fully in molecular form) and deuterium locked in HD molecule (see Table 3). The resulting abundances of modelling the pre-disk evolutionary phase were used as initial abundances for disk chemical modelling as shown in Table 3.
3.3. Modelled results
Figure 3a presents the modelled column densities for HCO+ and DCO+ in DM Tau (dashed lines) and associated 3σ errors with the observationally derived values (solid lines) overlain. Both column densities agree well within their errors. The grey boxes in Fig. 3 show where the power-law column densities are extrapolated beyond the radii where they were observed as to provide a better comparison with the chemical model which does not reproduce the inner hole.
Figures 3b and c show the relative abundance with respect to H2 of DCO+ and HCO+ throughout the disk. These clearly demonstrate the stratification of the disk with a distinct molecular layer lying ~0.5 pressure scale heights above the midplane. Both molecular layers are relatively co-spatial, in general tracing regions of high gas phase CO abundance. They are bounded by the CO snowline towards the midplane, and the photodissociation region of CO towards the disk atmosphere. DCO+ occupies a slightly tighter vertical range than HCO+ due to it also requiring efficient deuteration. The molecular layer is truncated upwards due to the higher gas temperatures, reducing the efficiency of deuterium fractionation, while the lower bound is due to reduced HD abundances with which to readily transform deuterium into DCO+.
 |
Fig. 4 Comparisons of RD(HCO+) values. The dashed black line shows the observationally derived value in DM Tau and the blue solid lines show the chemical model values at different time steps. Typical errors are a factor of 3. They grey vertical bars show where the observationally derived column densities of HCO+ and DCO+ are extrapolated beyond the inner and outer edges found in parameterisation. The orange dash-dotted line shows the value observed in TW Hya (Qi et al. 2008), the red dotted line, RD(HCO+) in HD 163296 (Mathews et al. 2013), and the yellow dashed region, values from a survey of prestellar cores (Butner et al. 1995). The top y-axis shows the temperature of the DCO+ layer derived from our parametric fitting. |
RD(HCO+) is shown in Fig. 3d with local values reaching as high as ~1. Within this region we see pronounced increases of HD and H2D+ abundances facilitating a fast transfer of deuterium from HD to DCO+. Despite these locally high values, the vertically integrated column density is more sensitive to the denser regions closer to the midplane, thereby exhibiting a lower value of RD(HCO+) ~ 0.1.
Figure 4 shows the modelled values of RD a various time steps in the model (blue lines). The observationally derived value, shown by the black dashed line, agrees qualitatively well with the t = 5 × 106 yrs value.
4. Discussion
In this section we use both the observationally-derived and best-fit modelled column densities, complemented with a further suite of chemical models, to explore both deuterium fractionation and the ionization fraction in the disk.
4.1. Deuterium fractionation of HCO+
Deuterium fractionation is typically used as a probe of the thermal history of an environment. In this section we explore physical parameters other than temperature which can alter the observed RD ≡ N(DCO+) /N(HCO+) ratios in disks through a suite of chemical models derived from our DM Tau model.
Figure 4 shows the radial profile of RD found for DM Tau observationally (dashed black line) and at various time steps in the model, t = { 103, 104, 105, 106, 5 × 106 } yrs (solid blue lines). Also marked are values for TW Hya (orange dash-dotted line; Qi et al. 2008), HD 163296 (red dotted line; Mathews et al. 2013) and an average of prestellar cores (yellow hatched region; Butner et al. 1995; Caselli et al. 2002). Enhanced values relative to the cosmic abundance of [D]/[H] ~ 10-5 are indicative of continued gaseous processing in a cold, T ≲ 20−30 K, environment; a none too surprising conclusion given the kinetic temperature probed by the line emission, T ~ 10−20 K (see Table 2). Furthermore, the radial increase is to be expected due to the radial temperature gradient in a disk. That is, the pace of deuterium fractionation and synthesis of the H isotopologues hastens in colder outer disk regions. In turn, higher abundances of the H
isotopologues hastens in colder outer disk regions. In turn, higher abundances of the H isotopologues imply more efficient formation of DCO+ in ion-molecule reactions with gaseous CO, increasing RD.
isotopologues imply more efficient formation of DCO+ in ion-molecule reactions with gaseous CO, increasing RD.
Our RD values, ranging from ≈ 0.1−0.2 between 50 AU and 430 AU, are almost two orders of magnitude higher than the disk average value of (4.0 ± 0.9) × 10-3 found by Guilloteau et al. (2006), who used HCO+J = (1−0) interferomic data and DCO+J = (3−2) single dish data. This discrepancy can be explained by the assumptions made in the calculation of HCO+ and DCO+ column densities. Firstly, it was assumed that DCO+ was radially co-spatial with the HCO+ emission which extends out to ~ 800 au, an outer radii similar to that of CO. This increased emitting region would result in a lower, disk average value for DCO+, reducing RD. Secondly, we have shown that HCO+ likely exhibits a complex molecular distribution including an inner hole in emission, see Sect. 2.4. When fitting a single transition this complexity was found to drive the parameterisation to favour steeper power laws describing column densities, consistent the HCO+J = (1−0) data from Piétu et al. (2007), yielding a much smaller RD value in the inner disk than found with our data.
In TW Hydrae, another well studied PPD, the value of RD has been measured both as a disk average (0.035 ± 0.015, van Dishoeck et al. 2003), and with spatially resolved interferomic observations yielding a value from 0.01 to 0.1 between 30 and 90 au (Qi et al. 2008). The increase found in the outer regions of the disk when moving to spatially resolved data is consistent with our findings in DM Tau. Similarly, while the TW Hya disk is smaller and less massive than DM Tau, it appears to hold comparable values for RD at similar distances to the star, namely around ~0.1 at 100 AU. More recently, Mathews et al. (2013) used ALMA science verification data of HD 163296, an A1 spectral type Herbig Ae star and comprehensive modelling to ascertain local values of RD ~ 0.3 and a disk average of 0.02. Typically disks around Herbig Ae stars are warmer and more massive than those around classical T Tauri stars, thus a reduced disk average value of RD is to be expected.
Figure 4 also clearly shows continued enhancement of RD up to ~1 Myr, indicative of continued processing of the gaseous CO during a disk lifetime. Thus, it is of no surprise that the observed value of RD in DM Tau, thought to be between 3−7 Myr, is higher than that found in low-mass prestellar cores (0.045 ± 0.015, Butner et al. 1995).
Molecular layers in a PPD are far beyond closed systems. Measurements of RD through N(DCO+)/N(HCO+) are sensitive to more than just the deuterium fractionation efficiency, but are compounded by physical parameters which can alter the abundances of HCO+ and DCO+. In the remainder of this section we explore how else the physical environment can change the observed value of RD by running a suite of chemical models and varying a single parameter. This will aid in analysis when comparing values of RD from different astrophysical environments. To motivate the choice of parameters studied, we discuss briefly the process of deuterium fractionation.
Deuterium fractionation occurs due to the energy difference between deuterium and hydrogen atoms, thereby resulting in the deuteration of H by HD to be exothermic:
by HD to be exothermic: 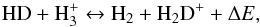 (2)where ΔE = 232 K (Roberts & Millar 2000). Hence, low energy environments are conducive to enhanced abundaces of deuterated isotopologues resulting from successive deuteration of H
(2)where ΔE = 232 K (Roberts & Millar 2000). Hence, low energy environments are conducive to enhanced abundaces of deuterated isotopologues resulting from successive deuteration of H . For H2, ΔE corresponds to Tkin ≈ 30 K resulting in inefficient fractionation above this temperature. This is clearly evident in both observational and modelled results (see Fig. 4) which show an increase in RD at larger radii where the disk is cooler. Furthermore, the larger internal energy of ortho-H2 allows for greater leverage in the back reaction of Eq. (2). It has been shown that ortho/para ratios ≳0.1 can “poison” the overall fractionation efficiency, even when the kinetic temperatures are low. Proton exchange due to collisions will reduce the initial H2 ortho/para fraction of ~ 0.75. A reduced ortho-para fraction will increase the efficiency of deuterium fractionation, see Fig. 5a. (e.g., Pagani et al. 1992, 2009, 2013; Crabtree et al. 2011; Albertsson et al. 2014a). However, the relatively high densities of the molecular layer in a disk ensure that this is a relative quick process taking ~ 105 yrs.
. For H2, ΔE corresponds to Tkin ≈ 30 K resulting in inefficient fractionation above this temperature. This is clearly evident in both observational and modelled results (see Fig. 4) which show an increase in RD at larger radii where the disk is cooler. Furthermore, the larger internal energy of ortho-H2 allows for greater leverage in the back reaction of Eq. (2). It has been shown that ortho/para ratios ≳0.1 can “poison” the overall fractionation efficiency, even when the kinetic temperatures are low. Proton exchange due to collisions will reduce the initial H2 ortho/para fraction of ~ 0.75. A reduced ortho-para fraction will increase the efficiency of deuterium fractionation, see Fig. 5a. (e.g., Pagani et al. 1992, 2009, 2013; Crabtree et al. 2011; Albertsson et al. 2014a). However, the relatively high densities of the molecular layer in a disk ensure that this is a relative quick process taking ~ 105 yrs.
 |
Fig. 5 a)N(ortho-H2)/N(para-H2) ratio from the best fit model. After ~ 105 yr the ratio reaches a steady state. b) Degree of CO freeze out in our model, N(COice)/N(COtotal) clearly demonstrating the CO ice line at r ≈ 30 AU. |
 |
Fig. 6 Computed molecular column densities for DCO+ (dashed line) and HCO+ (solid line). Black lines show the columns obtained with the best-fit model (see Sect. 3.3), red lines show the columns when the specified physical parameter is changed in the best fit model while the others are held constant. For reference, the canonical model has a single grain population of a = 0.1 μm, LX = 3 × 1029 erg s-1, χ∗(100 AU) = 410 and a CRP ionization rate of ζ = 1.3 × 10-17 s-1. |
4.1.1. Regulating CO abundance
As a parental molecule of HCO+ and DCO+, the CO abundance is intimately linked to the abundances of HCO+ and DCO+. Gaseous CO must be sufficiently abundant to efficiently convert the H and H2D+ into HCO+ and DCO+ respectively. However, CO readily freezes out at T ≈ 21 K, vastly reducing the available reaction partners, see Fig. 5b. Therefore, DCO+ is most efficiently produced where temperatures are high enough to maintain a relatively low level of CO depletion, yet cool enough to allow efficient fractionation. This is visible in Fig. 3a where N(DCO+) peaks around 50 AU.
and H2D+ into HCO+ and DCO+ respectively. However, CO readily freezes out at T ≈ 21 K, vastly reducing the available reaction partners, see Fig. 5b. Therefore, DCO+ is most efficiently produced where temperatures are high enough to maintain a relatively low level of CO depletion, yet cool enough to allow efficient fractionation. This is visible in Fig. 3a where N(DCO+) peaks around 50 AU.
For the same mass of dust, larger grains have a reduced surface area onto which CO can freeze out, reducing the depletion of CO and hence expanding its molecular layer towards the disk midplane. Figure 6a shows the change in N(HCO+) and N(DCO+) when the grain size in our best fit model is increased to 1 μm. Outside the CO snowline N(HCO+) is enhanced due to the greater availability of CO to react with H resulting in a shallower gradient. On the other hand, N(DCO+) is uniformly decreased. The decrease of DCO+ abundances is associated with less efficient fractionation of H
resulting in a shallower gradient. On the other hand, N(DCO+) is uniformly decreased. The decrease of DCO+ abundances is associated with less efficient fractionation of H in its molecular layer. Rapid ion-molecule reactions of H
in its molecular layer. Rapid ion-molecule reactions of H with volatile molecules such as CO, which are less depleted from the gas phase, compete with fractionation processes and hence lower production of deuterated H
with volatile molecules such as CO, which are less depleted from the gas phase, compete with fractionation processes and hence lower production of deuterated H isotopologues. This results in a reduced RD as a disk average and a weaker radial gradient.
isotopologues. This results in a reduced RD as a disk average and a weaker radial gradient.
4.1.2. Ionization
The other parental molecules of HCO+ and DCO+ are H and H2D+ respectively, both of which require the ionization of H2. Figs. 6b−f show how the column densities are affected when ionization sources in the best fit model are altered.
and H2D+ respectively, both of which require the ionization of H2. Figs. 6b−f show how the column densities are affected when ionization sources in the best fit model are altered.
Clearly shown in Figs. 6c and d, stellar UV and CRPs play little role in the abundance of these two species. In our disk model, UV scattering is neglected therefore the stellar UV radiation becomes quickly absorbed in radial direction by the dust, thus making little impact on the abundance of HCO+ and DCO+. Additionally, high energy CRPs can penetrate to the molecular layers, however they have such a low flux that they are of little consequence in the life-cycle of HCO+ and DCO+.
Conversely, the abundances of HCO+ and DCO+ are sensitive to the stellar X-rays, the dominant ionization source in the molecular layer. Increased values of LX lead to an enhanced abundance of HCO+ across the entire disk, as shown by Fig. 6b. DCO+ production is suppressed in the inner disk, r ≲ 100 AU, while outer regions display an enhancement. The DCO+ production is suppressed in the inner disk despite an increase in overall H isotopologue abundances within the inner molecular layer due to an increased ortho/para-H2 fraction arising from the increased X-ray luminosity injecting sufficient energy into the disk for re-equilibriation through ion-molecule and nuclear spin-state processes. The increased ortho-fraction of the H
isotopologue abundances within the inner molecular layer due to an increased ortho/para-H2 fraction arising from the increased X-ray luminosity injecting sufficient energy into the disk for re-equilibriation through ion-molecule and nuclear spin-state processes. The increased ortho-fraction of the H isotopologues slows the overall pace of the deuterium fractionation. In addition, an increase of DCO+ abundances in the outer disk is smaller than for HCO+ because the DCO+ layer is located deeper into the disk, where temperatures favor deuterium enrichment andare better shielded from impinging stellar X-ray photons than the more extended HCO+ molecular layer.
isotopologues slows the overall pace of the deuterium fractionation. In addition, an increase of DCO+ abundances in the outer disk is smaller than for HCO+ because the DCO+ layer is located deeper into the disk, where temperatures favor deuterium enrichment andare better shielded from impinging stellar X-ray photons than the more extended HCO+ molecular layer.
Reducing the stellar X-ray luminosity reduced both the HCO+ and DCO+ abundances. This is a more pronounced effect in the inner disk due to the oblique angles of incident X-rays, as found in Henning et al. (2010). The higher sensitivity of HCO+ to changing X-ray luminosities, again due to the difference in vertical extents of the molecular layers, is reflected in the gradient of RD; a lower LX leads to a less radially dependent RD. Additionally, HCO+ production is suppressed to such a low level that RD can reach ~ 1 in the outer disk.
A more puzzling result is the strong influence of interstellar UV radiation on RD. In the disk model without an IS UV field, RD becomes lower by up to an order of magnitude compared to the best-fit model. This is mainly due to a uniform decrease of the DCO+ column density throughout the disk by a factor of ~ 3, and an increase of the HCO+ column density at r ≳ 50−60 AU by a similar factor of about 3, producing a near constant RD across the radius of the disk.
The IS UV photons play two main roles for disk chemical evolution. Firstly, they partly contribute to the ionization and dissociation of disk matter in the molecular layer, particularly beyond r ≳ 100 AU. Secondly, and more importantly for RD, they bring heavy ices back to the gas phase by photodesorption and thus partly regulate surface processes. We found that in the DM Tau model without IS UV radiation, CO gets more easily converted into CO2 ice in the molecular layer at T ≲ 30−40 K through the slightly endothermic reaction of CO + OH + 80 K → CO2 + H. CO2 is unable to be photodesorbed and therefore partly dissociated in the gas. In addition, abundances of water ices increase, whereas abundances of atomic and molecular oxygen decrease. This leads to a drop in gas-phase CO abundances locally by a factor of 2−4 at all disk radii.
Furthermore, in the absence of photodesorption due to the absence of UV ionization, ions of alkali metals such as Na+ and Mg+, along with atomic ions such as S+ and C+, become less abundant and do not contribute considerably to the fractional ionization of the entire molecular layer. As a result, polyatomic ions like HCO+ and H3O+ dominate the ionization structure, resulting in a decrease by a factor of a few in ionziation fraction due to their more efficient recombination with electrons. These two factors, lower ionization degree and lower CO abundances, lead to both lower DCO+ abundances in the molecular layer and also reduced DCO+ column densities.
Contrary to DCO+, HCO+ abundances and column densities show an increase at r ≳ 50 AU in the DM Tau model without IS UV. This is related to the fact that the DCO+ molecular layer is narrower and located more deeply in the disk compared to the HCO+ molecular layer. The lack of photodesorption and photodissociation in the upper part of the HCO+ molecular layer increases abundances of CO and H isotopologues, hence boosting production of HCO+. This compensates for the decrease of gaseous CO due to its surface conversion into the CO2 ice in the lower part of the HCO+ molecular layer.
isotopologues, hence boosting production of HCO+. This compensates for the decrease of gaseous CO due to its surface conversion into the CO2 ice in the lower part of the HCO+ molecular layer.
Comparisons with previously published models highlight the importance of considering these additional processes which alter the abundance of HCO+ and DCO+. Despite the relatively well understood deuterium fractionation mechanism there are orders-of-magnitude disparity between models. Aikawa et al. (2002) modelled a smaller disk with gas extending on to 373 AU which exhibited a radial dependence of RD varying between 0.003 to 0.06, values more more in accord with the smaller TW Hya disk. Whereas a newer model of Willacy (2007) found considerably higher values ranging from RD = 0.1 at 50 AU to reaching unity outside 100 AU, suggesting high RD values are to be expected.
Hence, while N(DCO+)/ N(HCO+) provides an easily accessible measure of deuterium fractionation, a link through several environments in the cycle of molecular gas, other parameters, particularly the X-ray luminosity of the central star, the interstellar UV field and the grain evolution, are folded into this measurement. In the case of PPDs, the X-ray luminosity of the host star must be well constrained in order to fully characterise the deuterium fractionation present in the disk.
Reactions involved in the considered steady state system and the rates used in our modelling.
4.2. Ionization fraction, x(e−)
HCO+ is often touted as the most dominant ion in the warm molecular layer of a PPD. As such, it is frequently used as a proxy of the ionization in this region (Semenov et al. 2004; Dutrey et al. 2007; Qi et al. 2008; Öberg et al. 2011b). However, the large radial and vertical gradients in physical parameters characteristic of a PPD introduce several complications in deriving knowledge of the ionization fraction from a single charged species. Common practice therefore is to make a steady state approximation, a methodology that has been applied to a range of astrophysical scales: from PPDs to molecular clouds and supernova remnants (Guelin et al. 1977; Caselli 2002; Caselli et al. 2008; Vaupré et al. 2014).
Introduced by Guelin et al. (1977), this assumes a heavily reduced chemical network in a steady state of ionization. As discussed previously, the abundance of HCO+ is largely governed by two main processes: creation through ion-neutral reactions between H and CO and destruction via electronic recombination. Similar pathways hold for DCO+ but with the deuterated H2D+ in place of H
and CO and destruction via electronic recombination. Similar pathways hold for DCO+ but with the deuterated H2D+ in place of H . Caselli (2002) showed the chemical kinetics of such a network in steady state can be reduced to:
. Caselli (2002) showed the chemical kinetics of such a network in steady state can be reduced to: 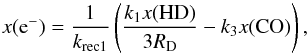 (3)where the rates and associated reactions are found in Table 4.
(3)where the rates and associated reactions are found in Table 4.
 |
Fig. 7 Constraints on the ionization fraction in DM Tau. Results from the steady state approximation are shown with: observational values, black dashed; modelled values from the entire disk, dark blue solid; modelled values from the HCO+ molecular layer, light blue solid; lower limit from Dutrey et al. (2007), light orange solid and lower limit from Öberg et al. (2011b), dark orange solid. All errors, dominated by the values from the chemical modelling, are a factor of 3. |
 |
Fig. 8 a) Ionization structure of the DM Tau disk model. The region bounded by blue lines is what we have defined as the HCO+ molecular layer. b) and c) relative contributions of charged species to the ionization level over the whole disk and the HCO+ molecular layer. As a disk average, panel b), it is clear the charge is dominated by C+ and H+, the grey region representing all other charged species. In the HCO+ molecular layer, panel c), defined as the region that contributes 90% of the total HCO+ column density, HCO+ supplies a majority of the charge with large contributions from H+, C+ and S+. |
This requires knowledge of both N(HD), of which we only have one observation of in a PPD, TW Hya (Bergin et al. 2013), and the total gas column from which to convert from column density to relative abundances, a value that cannot be well constrained observationally without several assumptions (Thi et al. 2010). Application to DM Tau is thus limited to the case where we must assume values of x(CO) and x(HD). Note that this has since been expanded to include all multiplydeuterated isotopologues of H and charged grains, however the lack of observational constraints on these would further compound the issues detailed above in the case of a PPD (Caselli et al. 2008). Note, however, that physical parameters derived from line emission will be of the molecular region and not applicable to the disk as a whole.
and charged grains, however the lack of observational constraints on these would further compound the issues detailed above in the case of a PPD (Caselli et al. 2008). Note, however, that physical parameters derived from line emission will be of the molecular region and not applicable to the disk as a whole.
Using our observationally derived RD values and values x(HD) = 2.40 × 10-5 and x(CO) = 7.24 × 10-5 taken from the best fit model, the later consistent with previous observations of DM Tau (Piétu et al. 2007), we find an ionization fraction of x(e−) ~ 10-7, as shown by the dashed black line in Fig. 7. This is consistent with the lower limits placed by Dutrey et al. (2007; light orange) and Öberg et al. (2011b; dark orange). Blue lines show x(e−) from our best fit model, the light blue considering molecular column densities integrated over the warm molecular layer probed by our HCO+ and DCO+ observations6, and those integrated over the whole disk in dark blue. Both of which qualitatively agree with the steady state values. Qi et al. (2008) found a similar ionization fraction of x(e−) ~ 10-7 in TW Hya when using the same steady state approximation.
However, disk ionization, is controlled by a myriad of atomic and molecular ions as shown by Fig. 8. Panels b) and c) show the relative contribution of the top eight most abundant ions as a function of radius for the whole disk (b) and the HCO+ molecular layer (c). It is clear that ionization as a whole is dominated by the atomic ions C+ and H+ which contribute ≳99% of the charge. Even within the molecular layer, atomic ions are the dominant charge carries with S+, H+ and C+ contributing between 50% and 90% of the total charge. While HCO+ is the dominant molecular ion, it contributes at most ~ 20% of the charge in the inner regions and is severely depleted in the outer disk, R ≳ 200 AU. Thus, while HCO+ being the most dominant molecular ion in the disk, even in the molecular layer its contribution to total charge is dwarfed by that of atomic ions such as C+, H+ and S+.
This additional source of ionization not considered in the steady state approximation can contribute to the difference in observed values of x(e−). Furthermore, it is surprising that observations sensitive to only a small region in the disk are able to recover disk average values relatively well. This is due to the density gradient towards the midplane; the disk average will draw heavily from values closer to the midplane.
5. Summary
In this paper Plateau de Bure Interferometer observations of the abundant molecules HCO+, J = (3−2), (1−0) and DCO+, J = (3−2) of DM Tau in parallel with a suit of thermo-chemical models provided the framework with which to study deuterium fractionation and the ionization fraction in DM Tau.
Using combined χ2-minimization and MCMC fitting techniques, we fitted a parametric model to the observations. HCO+ was found to exhibit a complex emission structure: (3−2) emission had a peak intensity at r ≈ 50 AU and was considerably less extended than the (1−0) emission. HCO+ (1−0) emission was found to be co-spatial with CO emission (Piétu et al. 2007). An inner hole of r ≈ 50 AU in HCO+ is needed to recreate the observations. Simultaneously fitting the (3−2) and (1−0) lines required the assumption that both lines had the same excitation temperature. DCO+ was also tentatively found to peak at r ≈ 70 AU, consistent with the CO snowline, however higher resolution observations are required to confirm this.
We find RD = N(HCO+) /N(DCO +) varies from 0.1−0.2 between 50 and 430 AU, values considerably higher than both the cosmic abundance ~10-5 and those found in prestellar cores 0.035 ± 0.015. This is indicative of continued fractionation throughout the disk lifetime. Both TW Hya and HD 163296 exhibit similar high levels of deuteration, the later peaking at RD ~ 0.3 (Qi et al. 2008; Mathews et al. 2013).
Through chemical modelling we have also explored other physical parameters which can affect RD. The most influential parameters are the level of interstellar UV and the X-ray luminosity of the central star; the dominant ionization sources in the molecular layer. X-rays interact with RD in a relatively straight forward manner: higher luminosities mean increased abundances of HCO+ and DCO+ and conversely for reduced luminosities. On the other hand, interstellar UV is more complex as it does not directly affect HCO+ and DCO+ but rather CO abundances. It enhances the DCO+ abundance across the entire disk, while suppresses the formation of HCO+ in the outer, r ≳ 50 AU, disk. These effects can be disentangled through the dependence of RD on radius with the later producing a more radially constant value of RD.
Assuming a steady state system we estimate the electron fraction of the HCO+ molecular layer to be x(e−) ~ 10-7, consistent with lower limits from Dutrey et al. (2007) and Öberg et al. (2011b). This values is high enough to induce MRI turbulence. An analysis of the dominant charge carries in the molecular layer show that HCO+ is the most dominant molecular ion, however atomic ions are considerably more dominant in all regions of the disk. Thus constraints on ionization from the abundance of HCO+ must take this into account.
Acknowledgments
R.T. is a member of the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg, IMPRS-HD, Germany. We thank the Plateau de Bure staff for performing the observations and helping with the data reduction. D. Semenov acknowledges support by the Deutsche Forschungsgemeinschaft through SPP 1385: “The first ten million years of the solar system – a planetary materials approach” (SE 1962/1-3). This research made use of NASA’s Astrophysics Data System. V.W. research is funded by the ERC starting grant 3DICE (grant agreement 336474).
References
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [CrossRef] [PubMed] [Google Scholar]
- Aikawa, Y., & Herbst, E. 1999a, ApJ, 526, 314 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Aikawa, Y., & Herbst, E. 1999b, A&A, 351, 233 [NASA ADS] [Google Scholar]
- Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akimkin, V., Zhukovska, S., Wiebe, D., et al. 2013, ApJ, 766, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Albertsson, T., Semenov, D. A., Vasyunin, A. I., Henning, T., & Herbst, E. 2013, ApJS, 207, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Albertsson, T., Indriolo, N., Kreckel, H., et al. 2014a, ApJ, 787, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Albertsson, T., Semenov, D., & Henning, T. 2014b, ApJ, 784, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Asensio Ramos, A., Ceccarelli, C., & Elitzur, M. 2007, A&A, 471, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E., Calvet, N., D’Alessio, P., & Herczeg, G. J. 2003, ApJ, 591, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Cleeves, L. I., Gorti, U., et al. 2013, Nature, 493, 644 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Biham, O., Furman, I., Pirronello, V., & Vidali, G. 2001, ApJ, 553, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Butner, H. M., Lada, E. A., & Loren, R. B. 1995, ApJ, 448, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., D’Alessio, P., Watson, D. M., et al. 2005, ApJ, 630, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P. 2002, Planet. Space Sci., 50, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., & Ceccarelli, C. 2012, A&ARv, 20, 56 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002, ApJ, 565, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Vastel, C., Ceccarelli, C., et al. 2008, A&A, 492, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Caselli, P., Bockelee-Morvan, D., et al. 2014 [arXiv:1403.7143] [Google Scholar]
- Chapillon, E., Parise, B., Guilloteau, S., & Du, F. 2011, A&A, 533, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Adams, F. C., & Bergin, E. A. 2013a, ApJ, 772, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Adams, F. C., Bergin, E. A., & Visser, R. 2013b, ApJ, 777, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Bergin, E. A., & Adams, F. C. 2014, ApJ, 794, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Crabtree, K. N., Indriolo, N., Kreckel, H., Tom, B. A., & McCall, B. J. 2011, ApJ, 729, 15 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Calvet, N., Hartmann, L., Lizano, S., & Cantó, J. 1999, ApJ, 527, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Dutrey, A., & Guilloteau, S. 2003, A&A, 399, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 1978, ApJ, 36, 595 [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., Henning, T., Guilloteau, S., et al. 2007, A&A, 464, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., Wakelam, V., Boehler, Y., et al. 2011, A&A, 535, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fayolle, E. C., Bertin, M., Romanzin, C., et al. 2011, ApJ, 739, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Fayolle, E. C., Bertin, M., Romanzin, C., et al. 2013, A&A, 556, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedele, D., Pascucci, I., Brittain, S., et al. 2011, ApJ, 732, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Fedele, D., Bruderer, S., van Dishoeck, E. F., et al. 2013, A&A, 559, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finocchi, F., Gail, H.-P., & Duschl, W. J. 1997, A&A, 325, 1264 [NASA ADS] [Google Scholar]
- Flock, M., Henning, T., & Klahr, H. 2012, ApJ, 761, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2004, A&A, 427, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerlich, D. 1990, J. Chem. Phys., 92, 2377 [NASA ADS] [CrossRef] [Google Scholar]
- Gerlich, D., Herbst, E., & Roueff, E. 2002, Planet. Space Sci., 50, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Najita, J., & Igea, J. 1997a, ApJ, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Najita, J., & Igea, J. 1997b, ApJ, 485, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Feigelson, E. D., Montmerle, T., & Wolk, S. 2005, X-Ray Flares of Sun-like Young Stellar Objects and Their Effects on Protoplanetary Disks, eds. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 165 [Google Scholar]
- Grady, C. A., Muto, T., Hashimoto, J., et al. 2013, ApJ, 762, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Graedel, T. E., Langer, W. D., & Frerking, M. A. 1982, ApJS, 48, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Guelin, M., Langer, W. D., Snell, R. L., & Wootten, H. A. 1977, ApJ, 217, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., & Dutrey, A. 1994, A&A, 291, L23 [NASA ADS] [Google Scholar]
- Guilloteau, S., & Dutrey, A. 1998, A&A, 339, 467 [NASA ADS] [Google Scholar]
- Guilloteau, S., Piétu, V., Dutrey, A., & Guélin, M. 2006, A&A, 448, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., Dutrey, A., Wakelam, V., et al. 2012, A&A, 548, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harju, J., Haikala, L. K., Lehtinen, K., et al. 2006, A&A, 454, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Semenov, D., Guilloteau, S., et al. 2010, ApJ, 714, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., & Semenov, D. 2013, Chem. Rev., 113, 9016 [Google Scholar]
- Hogerheijde, M. R., & van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
- Hogerheijde, M. R., Caselli, P., Emprechtinger, M., et al. 2006, A&A, 454, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Honvault, P., Jorfi, M., González-Lezana, T., Faure, A., & Pagani, L. 2011, Phys. Rev. Lett., 107, 023201 [NASA ADS] [CrossRef] [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jørgensen, J., Brinch, C., Girart, J. M., et al. 2014, ARTIST: Adaptable Radiative Transfer Innovations for Submillimeter Telescopes, astrophysics Source Code Library [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H.-H., Herbst, E., Pineau des Forêts, G., Roueff, E., & Le Bourlot, J. 1996, A&A, 311, 690 [NASA ADS] [Google Scholar]
- Lee, H.-H., Roueff, E., Pineau des Forets, G., et al. 1998, A&A, 334, 1047 [NASA ADS] [Google Scholar]
- Mathews, G. S., Klaassen, P. D., Juhász, A., et al. 2013, A&A, 557, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazzitelli, I. 1989, in European Southern Observatory Conference and Workshop Proceedings 33, ed. B. Reipurth, 433 [Google Scholar]
- McJunkin, M., France, K., Schneider, P. C., et al. 2014, ApJ, 780, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., Bennett, A., & Herbst, E. 1989, ApJ, 340, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009a, A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009b, A&A, 496, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2011a, ApJ, 734, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Wilner, D. J., & Andrews, S. M. 2011b, ApJ, 743, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Wilner, D. J., & Hogerheijde, M. R. 2012, ApJ, 749, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Salez, M., & Wannier, P. G. 1992, A&A, 258, 479 [NASA ADS] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Lesaffre, P., Jorfi, M., et al. 2013, A&A, 551, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Belloche, A., Du, F., Güsten, R., & Menten, K. M. 2011, A&A, 526, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlyuchenkov, Y., Semenov, D., Henning, T., et al. 2007, ApJ, 669, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Piétu, V., Dutrey, A., & Guilloteau, S. 2007, A&A, 467, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qi, C., Wilner, D. J., Aikawa, Y., Blake, G. A., & Hogerheijde, M. R. 2008, ApJ, 681, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Wilner, D. J., et al. 2013, Science, 341, 630 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Quintana, E. V., Barclay, T., Raymond, S. N., et al. 2014, Science, 344, 277 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rodgers, S. D., & Millar, T. J. 1996, MNRAS, 280, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, H., & Millar, T. J. 2000, A&A, 361, 388 [NASA ADS] [Google Scholar]
- Roberts, H., Herbst, E., & Millar, T. J. 2004, A&A, 424, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenfeld, K. A., Andrews, S. M., Hughes, A. M., Wilner, D. J., & Qi, C. 2013, ApJ, 774, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfeld, K. A., Chiang, E., & Andrews, S. M. 2014, ApJ, 782, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreyer, K., Guilloteau, S., Semenov, D., et al. 2008, A&A, 491, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., & Wiebe, D. 2011, ApJ, 196, 25 [Google Scholar]
- Semenov, D., Wiebe, D., & Henning, T. 2004, A&A, 417, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, M., Dutrey, A., & Guilloteau, S. 2000, ApJ, 545, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2013, A&A, 554, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, B., Bouwman, J., Henning, T., et al. 2013, A&A, 553, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W.-F., Mathews, G., Ménard, F., et al. 2010, A&A, 518, L125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dishoeck, E. F., Thi, W.-F., & van Zadelhoff, G.-J. 2003, A&A, 400, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday discussion, 133, Photoprocesses in protoplanetary disks (Cambridge: Royal Society of Chemistry), 231 [Google Scholar]
- van Zadelhoff, G.-J., Dullemond, C. P., van der Tak, F. F. S., et al. 2002, A&A, 395, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Caselli, P., Ceccarelli, C., et al. 2006, ApJ, 645, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Vaupré, S., Hily-Blant, P., Ceccarelli, C., et al. 2014, A&A, 568, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, C., Millar, T. J., & Nomura, H. 2010, ApJ, 722, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K. 2007, ApJ, 660, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K., Klahr, H. H., Millar, T. J., & Henning, T. 1998, A&A, 338, 995 [NASA ADS] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Stellar and disk properties of DM Tau with values taken from Dutrey et al. (2007) and Henning et al. (2010).
Atomic and molecular abundances used in the disk chemical model. Top: Initial abundances for modelling the pre-disk evolutionary phase Bottom: 25 initially most abundant molecules for disk chemical modelling.
Reactions involved in the considered steady state system and the rates used in our modelling.
All Figures
 |
Fig. 1 Channel maps of: HCO+J = (1−0), top, with σ = 3.7 mJy/beam (0.32 K) and contour spacing of 2.5σ; HCO+J = (3−2), middle, with σ = 100 mJy/beam (0.64 K) and contour spacing of 2.5σ; and DCO+J = 3−2, bottom, with σ = 30 mJy/beam (0.42 K) and contour spacing of 2σ emission from DM Tau. The beam size, shown by the filled ellipse, for each line is 1.4 × 1.26″, 1.85 × 1.49″ and 1.4 × 1.33″ respectively. The velocity of each channel shown in the top left corner in km s-1 while the cross in the centre shows the position of the host star and the position angle of the major and minor axes of the disk. Dashed contours show negative values. |
| In the text | |
 |
Fig. 2 Disk physical structure scaled vertically as z/R. Colouring shows the coupled gas and dust temperature and solid lines show the particle number densities in particles cm-3. The dashed white lines shows the 21 K isotherm, below which half of CO has frozen out. |
| In the text | |
 |
Fig. 3 Deuterium fractionation in the disk. a) Comparisons of HCO+, blue, and DCO+, red, from observations, dashed with 3σ errors, and the best fit model, solid with associated error of a factor of 3. They grey vertical bars show where the observationally derived column densities are extrapolated beyond the inner and outer edges found in parameterisation. b) and c) show the relative abundances of DCO+ and HCO+ in the best fit disk chemical model respectively. d) shows the local DCO+/HCO+ ratio in the disk model. |
| In the text | |
 |
Fig. 4 Comparisons of RD(HCO+) values. The dashed black line shows the observationally derived value in DM Tau and the blue solid lines show the chemical model values at different time steps. Typical errors are a factor of 3. They grey vertical bars show where the observationally derived column densities of HCO+ and DCO+ are extrapolated beyond the inner and outer edges found in parameterisation. The orange dash-dotted line shows the value observed in TW Hya (Qi et al. 2008), the red dotted line, RD(HCO+) in HD 163296 (Mathews et al. 2013), and the yellow dashed region, values from a survey of prestellar cores (Butner et al. 1995). The top y-axis shows the temperature of the DCO+ layer derived from our parametric fitting. |
| In the text | |
 |
Fig. 5 a)N(ortho-H2)/N(para-H2) ratio from the best fit model. After ~ 105 yr the ratio reaches a steady state. b) Degree of CO freeze out in our model, N(COice)/N(COtotal) clearly demonstrating the CO ice line at r ≈ 30 AU. |
| In the text | |
 |
Fig. 6 Computed molecular column densities for DCO+ (dashed line) and HCO+ (solid line). Black lines show the columns obtained with the best-fit model (see Sect. 3.3), red lines show the columns when the specified physical parameter is changed in the best fit model while the others are held constant. For reference, the canonical model has a single grain population of a = 0.1 μm, LX = 3 × 1029 erg s-1, χ∗(100 AU) = 410 and a CRP ionization rate of ζ = 1.3 × 10-17 s-1. |
| In the text | |
 |
Fig. 7 Constraints on the ionization fraction in DM Tau. Results from the steady state approximation are shown with: observational values, black dashed; modelled values from the entire disk, dark blue solid; modelled values from the HCO+ molecular layer, light blue solid; lower limit from Dutrey et al. (2007), light orange solid and lower limit from Öberg et al. (2011b), dark orange solid. All errors, dominated by the values from the chemical modelling, are a factor of 3. |
| In the text | |
 |
Fig. 8 a) Ionization structure of the DM Tau disk model. The region bounded by blue lines is what we have defined as the HCO+ molecular layer. b) and c) relative contributions of charged species to the ionization level over the whole disk and the HCO+ molecular layer. As a disk average, panel b), it is clear the charge is dominated by C+ and H+, the grey region representing all other charged species. In the HCO+ molecular layer, panel c), defined as the region that contributes 90% of the total HCO+ column density, HCO+ supplies a majority of the charge with large contributions from H+, C+ and S+. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


