| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 15 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322841 | |
| Published online | 27 February 2014 | |
The EUV spectrum of the Sun: SOHO CDS NIS radiances during solar cycle 23
1
INAF, Osservatorio Astronomico di Capodimonte, Salita Moiariello, 16, 80131
Naples, Italy
e-mail: andretta@oacn.inaf.it
2
DAMTP, Centre for Mathematical Sciences, University of
Cambridge, Wilberforce
Road, Cambridge
CB3 0WA,
UK
Received: 14 October 2013
Accepted: 4 December 2013
For the first time, we present and discuss EUV radiances of the solar transition region (TR) and corona obtained during a solar cycle. The measurements were obtained with the SOHO/coronal diagnostic spectrometer (CDS) during the period from 1996 to 2010. We find that limb-brightening significantly affects any characterisation of the solar radiances. We present the limb-brightening function for the main lines and find that it does not change measurably during the cycle. We confirm earlier findings that the radiance histogram of the cooler lines have a well defined, log-normal quiet-Sun component, although our results differ from previous ones. The width of the lowest-radiance log-normal distribution is constant along the cycle. Both the analysis of the centre-to-limb variation and of the radiance statistical distribution point to a constant quiet Sun emission along solar cycle 23. Lines formed above 1 MK are dramatically affected by the presence of active regions, and indeed, no “quiet Sun” region can be defined during periods of maximum activity. Much of the irradiance variability in lines formed below 1.5 MK is due to a change in the emitting area. For hotter lines, the emitting area saturates to almost 100% of full solar disk at the maximum of activity, while simultaneously the emission due to active regions increases by more than an order of magnitude. We show that structures around active regions, sometimes referred to as dark halos or dark canopies, are common and discuss their similarities and differences with coronal holes. In particular, we show how they are well visible in TR lines, contrary to coronal holes.
Key words: Sun: chromosphere / Sun: transition region / Sun: corona / Sun: UV radiation
© ESO, 2014
1. Introduction
The solar & heliospheric observatory (SOHO) coronal diagnostics spectrometer (CDS; Harrison et al. 1995) has been performing routine radiance measurements of the extreme ultraviolet (EUV) Sun since 1996; hence, it offers a unique opportunity to study the characteristics of the solar radiance along a solar cycle in many spectral lines, which are formed in different layers of the solar atmosphere. With a few minor gaps, CDS covers the important 150–800 Å EUV spectral range, of which the 308–379 and 513–633 Å are covered at first order by the two normal incidence spectrometer spectral channels (NIS 1 and 2, respectively), observed at a spectral resolution of about ~0.5 Å or better.
The main aim of this paper is to characterise the solar EUV radiances during an entire cycle (cycle 23) for the first time. Previously, the only detailed study on EUV radiances was based on data taken with full-Sun scans of the SOHO solar ultraviolet measurements of emitted radiation (SUMER, Wilhelm et al. 1995). Such a study provided, however, radiance and irradiance measurements in a few spectral lines only and for a limited time interval during the solar cycle during minimum solar conditions in 1996 (Wilhelm et al. 1998).
This paper is a part of a programme of studying the EUV spectral radiance, I, and irradiance, F, over the solar cycle. Preliminary results were presented in Del Zanna et al. (2005) and Del Zanna & Andretta (2006). A detailed in-flight CDS calibration was presented by Del Zanna et al. (2001), where responsivities for all the nine channels were provided. A detailed study of the long-term drop in sensitivity of the NIS channels during the 1998–2010 period was presented in Del Zanna et al. (2010, henceforth: Paper I), where the Del Zanna et al. (2001) responsivities were slightly revised. The new calibration allowed the first measurements of the EUV spectral irradiance along a solar cycle, as presented in Del Zanna & Andretta (2011, henceforth: Paper II). This latter paper discussed all hystorical records in detail and obtained a revised calibration for the important He ii 304 Å line, as observed in second order with the NIS 2 channel, and the most prominent line in the EUV. Large discrepancies in the He ii 304 Å radiances have been present in the literature, however recent comparisons of our measurements with those obtained with the EUNIS (EUV normal incidence spectrometer) rocket flights (see, e.g., Jordan & Brosius 2007) has uncovered errors in the EUNIS and CDS analysis software, and now excellent agreement (within a relative 10%) is found between our measurements and those obtained with EUNIS (see Wang et al. 2011a) for the He ii 304 Å line and other prominent EUV lines. Good agreement (see Paper II) was also found between our CDS measurements and those obtained with a sounding rocket flight in 2008 for a prototype of the solar dynamics observatory (SDO) extreme ultraviolet variability experiment (EVE, see Woods et al. 2012). These favourable comparisons validate our long-term calibration and therefore allow a quantitative description of the distribution of solar radiances along a solar cycle to be obtained from the CDS measurements for the first time. This has important implications in itself but also allows us to understand where the variability in the solar irradiance occurs, hence, to interpret X-UV irradiance measurements of the Sun as a star.
A new remarkable finding of Paper II was the little variability of the irradiances of lines formed at all transition-region (TR) temperatures (e.g. those from O iii, O iv, O v), as observed with SOHO/CDS. This was also shown to be evident in the data from the NASA thermosphere ionosphere mesosphere energetics dynamics (TIMED) solar EUV experiment (SEE) EUV grating spectrograph (EGS; Woods et al. 2005), which has data available since 2002. This issue is particularly important, considering that, as shown in Paper II, the mostly used models used in Earth’s upper atmosphere research (e.g. HEUVAC, Richards et al. 2006; SIP, Tobiska et al. 2008; and the older H81 of Hinteregger et al. 1981) overestimate the irradiances of TR lines by large factors, which, in turn, represent a dominant component of the solar UV irradiances.
The scheme of this work is the following: we summarise the observations used and the data reduction procedures in Sect. 2; we discuss some general properties of the statistical distributions of EUV radiances in Sect. 3.1 (including a general description of the various contributing solar features); a more detailed analysis of the properties of the quiet Sun (QS) radiances is given in Sect. 3.2 (including measurements of centre-to-limb variations and of histogram mean properties). Finally, we address the above issues concerning the variability of the EUV solar irradiance in Sect. 3.3.
2. Observations and data analysis
Since the beginning of the SOHO mission, the CDS spectrograph has been used to monitor daily the central meridian of the Sun in a few selected spectral lines. The scan of the central meridian is accomplished through a mosaic of nine spatial rasters that each cover 240 × 240″ on the Sun with a sequence of observations comprising the CDS study called SYNOP using the 2′′ slit (the majority of times). There are some variants of that study but all include the lines He i 584 Å, O v 630 Å, Mg ix 368 Å, and Mg x 625 Å. We selected a (relatively small) sample of synoptic observations spanning the 13 years of SOHO operations, which tries to uniformly cover the whole period but also avoids days when strong active regions dominated at the same time.
In addition, the study called USUN has been used since 1998 to scan the full solar disk with a mosaic of 69 rasters that each cover 240 × 240″ (see, e.g., Thompson & Brekke 2000 and Paper I for details). The movement of the slit is “sparse” in the sense that the 4′′ slit is moved in larger steps than its width. The radiance of the Sun is therefore subsampled by about a factor of 6 until to the end of 2002 (step size of 24.38′′) and by a factor of 4 afterwards (step size of 16.25′′). Exposures are also binned on board along the slit (for an equivalent pixel size of 13.44′′) to increase the count rates and reduce the telemetry load. Contrary to the SYNOP studies, the USUN studies record the full spectrum in the NIS wavelength range.
We applied standard processing for the de-biasing, flat-fielding, and 2′′ slit burn-in using the CDS routine VDS_CALIB, but we developed custom-written analysis software for all the processing (cosmic rays removal, mosaicing the rasters, long-term calibration, etc.). All the lines in the spectra were fitted with simple Gaussian profiles in the case of data prior the loss of contact of SOHO and with properly broadened profiles (with software developed by W.T. Thompson1) afterwards. The largest uncertainty in the fit is the location of the background (the scattered light), in particular for the NIS 1 channel. The fitting in the NIS channels was done on the spectra in photon events, where the scattered light “background” component is more constant. This uncertainty is more evident in SYNOP spectra due to detector windowing, which limits the possibility of estimating the background outside the line profile.
All the calibration factors have been applied after line fitting. They mostly include the wavelength-dependent long-term corrections for the drop in responsivity as detailed in Paper I (extended in Paper II), and the Del Zanna et al. (2001) responsivities, which are modified as described in Paper I (and for the He ii 304 Å as described in Paper II).
3. Discussion
The SYNOP and USUN studies are in some respects complementary: SYNOP studies are characterised by a longer time coverage (from 1996 to present) and higher spatial resolution (pixel size of 2 × 1.68″, while resolution elements in USUN scans are of 24.38 × 13.44″ or 16.25 × 13.44″) but are limited to a strip around the central meridian and to a few spectral lines. The USUN studies, on the other hand, cover the full solar disk and the full NIS spectral range, with a typically higher signal-to-noise ratio (S/N) than SYNOP observations. In our analysis, we mainly exploit the USUN studies, but we also use the SYNOP mosaics to validate and extend the USUN data.
 |
Fig. 1 Comparison of USUN and SYNOP data taken on 22 and 23 June 1998. The images show the integrated line radiances for the He i 584 Å and Mg x 625 Å lines in inverted, logarithmic scale (brighter areas correspond to fainter line radiances). The boundaries of the SYNOP FOV are also indicated. |
3.1. Statistical distribution of solar EUV radiances
3.1.1. Comparison of SYNOP and USUN statistics
A comparison of the two data sets is shown in Fig. 1 using data taken around 22 June 1998. The USUN mosaic in the He i 584 Å and Mg x 625 Å lines, started on June 22, is compared with the SYNOP scans immediately preceding and following one day. The SYNOP field of view (FOV) is indicated by a box in the USUN image. Apart from a well developed northern polar coronal hole and from a small, spotless active region crossing the meridian below the equator, the Sun is largely quiescent in the SYNOP FOV.
Figure 2 shows a comparison of the radiance histograms from the three data sets, excluding off-limb pixels; in addition, the normalised histograms obtained from USUN data both for all on-disk spectra and for spectra within the SYNOP FOV are also shown. The normalisation factor is the peak value of each histogram estimated via a Gaussian fit. Along with the histograms corresponding to the images of Fig. 1, we also show the corresponding histograms for two other strong lines, Mg ix 368 Å and O v 630 Å, in Fig. 2. In all four cases, the core of all these histograms is clearly log-normal and corresponds to the contribution from quiescent areas. We verified that the same is true for all the lines in the NIS range for which measurements with reasonable S/N could be made.
Concerning this property of the quiet-Sun statistical distribution of radiances, it is useful to recall early studies of quiet-Sun radiance distribution from the Apollo telescope mount (ATM) Skylab data (e.g. Skumanich et al. 1975; Reeves 1976), which typically analysed quiet Sun histograms as being composed by a Gaussian core and a high-radiance tail. In some cases a bi-modal distribution was fitted (e.g.: Gallagher et al. 1998, using CDS observations) and interpreted in terms of a mixture of supergranular cell-centre and network contributions. These interpretations would hint to different energy dissipation mechanisms between lower and higher radiance (or low and high magnetic field) regions within the quiescent solar atmosphere.
It was then realised by Wilhelm et al. (1998) and by Griffiths et al. (1999) using SOHO/SUMER data and by Pauluhn et al. (2000) using both SUMER and CDS data that a single, log-normal distribution fitted the data better. A single-parameter, continuous distribution would thus suggest that the same heating process is operating both at the edge the network and at the centre of superganular cells. Similar properties were inferred for the upper chromospheric lines Ly-α and Ly-β (Curdt et al. 2008). We refer to Fontenla et al. (2007) for a more detailed discussion, including a comparison with distributions of photospheric continuum and magnetic field, and of Ca ii K3 intensity.
 |
Fig. 2 Comparison of line radiance histograms of four representative lines (Mg ix 368 Å, He i 584 Å, Mg x 625 Å, and O v 630 Å) from spectra in the USUN and SYNOP mosaics, as shown in Fig. 1: USUN on-disk data (grey), USUN on-disk data within the SYNOP FOV (blue), and data from the two SYNOP mosaics (red: mosaic starting on 22 June; orange: mosaic started on 23 June). |
In addition to a log-normal quiet-Sun contribution, the radiance histograms of Fig. 2 also include contributions due to non-quiescent areas. In particular, these contributions are clearly visibile in the hotter lines and correspond respectively to the coronal hole (Mg x 625 Å radiances below ~10 photons s-1 cm-2 arcsec-2) and the small active region (Mg x 625 Å radiances above ~100 photons s-1 cm-2 arcsec-2); an additional contribution comes from near-limb pixels (limb-brightening, more apparent in the histogram from the USUN full FOV in the figure). Those contributions are less evident in the histograms of the other two lines, due to the smaller contrast and/or to the smaller areas of those features in TR lines but are nevertheless present. By analysing the histograms in the corresponding regions of interest, for instance, it can be shown that the “hump” at ~200 photons s-1 cm-2 arcsec-2 in the He i histogram does indeed correspond to the contribution of the northern hole, while the tail above ~103 photons s-1 cm-2 arcsec-2 is the contribution of the active region.
In Sect. 3.2, we exploit this feature of the EUV radiance distributions to isolate the quiet-Sun contribution to the radiance histograms by fitting the main peak of the distribution with a Gaussian. We thus are able to obtain an estimate of the median (central) radiance and width of the quiet Sun distribution for each SYNOP or USUN study.
In this regard, it is worth mentioning explicitly here that the mean value of
x is
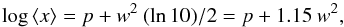 (1)given a normal distribution of a variable
y centred
at p and
with standard deviation w, and the corresponding log-normal distribution of
the variable x = 10y. The median
of x, on
the other hand, coincides with 10p. Since we analyse the
statistical properties of the logarithm of radiances in the remainder of this paper,
this difference should be kept in mind when translating the measured centres of their
normal distribution to mean radiances.
(1)given a normal distribution of a variable
y centred
at p and
with standard deviation w, and the corresponding log-normal distribution of
the variable x = 10y. The median
of x, on
the other hand, coincides with 10p. Since we analyse the
statistical properties of the logarithm of radiances in the remainder of this paper,
this difference should be kept in mind when translating the measured centres of their
normal distribution to mean radiances.
In any case, a key point is that the statistical distributions of radiances for these lines are the same in both the SYNOP and USUN data sets: neither the different spatial resolution nor other differences (detector windowing and binning, background level, S/N, etc.) produce significant differences; the only notable difference in all histograms is that USUN histograms restricted to the SYNOP FOV are generally noisier because of the lower statistics. There are some differences in some much weaker lines (such as the Fe xvi 360 Å line, also in SYNOP scans, but hardly detectable in quiet Sun areas) that can be understood in terms of the effect of the S/N and detector windowing on the determination of the background continuum.
3.1.2. Dark halos around active regions
Because of the presence of various structures on the solar disk, as noted above, only the core of the radiance histograms can be generally approximated with a log-normal distribution.
In the lower end of the tail of the histograms, one of the obvious contributions comes from coronal holes. However, a major contribution often comes from “halos” around active regions (Fig. 3) that sometimes are mistaken as disk coronal holes. That figure indeed shows that even around relatively small active regions, such halos can be seen. An example is the area south-east of NOAA AR 963 on 16 July 2007. The polar coronal holes visible on all three dates may serve as a qualitative indicator of the extent of suppression of line radiance in those halos.
These structures, which were first identified in chromospheric lines, have recently been studied by Del Zanna et al. (2011) and Wang et al. (2011b); the latter also provides a short review of historical observations. An earlier review by Feldman et al. (2000) noted that these regions are not seen in the He ii 304 Å line, contrary to genuine coronal holes. However, as shown in Fig. 3, these dark canopies, as they are sometimes called, are easily seen in that line. The real difference with coronal holes lies in the observation that these halos are easily seen in all TR lines, while coronal lines are not always suppressed, perhaps, because of emission by overarching active region (AR) loops.
Regarding the nature of these regions, Wang et al. (2011b) emphasise their association with near horizontal fibrils which contain EUV absorbing material (neutral hydrogen or helium). However, inspection of images of such regions taken with SUMER in 1996 (Feldman et al. 2003) reveals that these regions are seen as darker areas even in lines at wavelengths longer than 912 Å; a dark halo around an active region can for instance be seen in the S vi 933 Å image shown in Fig. 1 of Wilhelm et al. (1998). Therefore, the interpretation based on absorption by neutral hydrogen cannot fully explain those features. Moreover, as noted by Del Zanna et al. (2011), these regions are darker even in broadband (thin filters) Hinode XRT X-ray images, where absorption by cool material should be unimportant. We note that the observations showing that these features are seen in the X-rays, do not mean that they are hot, because the thin filters receive a significant contribution from emission lines formed at and below 1 MK.
The model proposed by Del Zanna et al. (2011), which involves interaction of active region closed loops with nearby lines opened to the solar wind, could be more promising, although it still remains to be explained why such regions are seen in TR lines, while coronal holes are not. Further discussion on this issue is in order. In the context of this paper, it only needs to be remarked that, indeed, these structures are common and seen in spectral features that form on a wide range of temperatures from the chromosphere through the transition region up to lines forming around ~106 K.
 |
Fig. 3 Radiance maps for the lines He ii 304 Å, O v 630 Å, Mg x 625 Å, and Si xii 521 Å (from top to bottom), from the CDS USUN mosaics taken on 1 November 2004, 8 November 2005, and 16 July 2007 (left to right). The active regions NOAA 693, 821, and 963, respectively, are also indicated. The logarithmic colour display table is inverted: higher-radiance areas are darker; for each line, the range of radiances is the same for all three dates. The horizontal stripes near the centre of the solar disk in the 2004 mosaics are due to a missing raster, which are filled-in here with interpolated values for display purposes. |
3.2. Some properties of quiet Sun regions
We now turn our attention to the core of radiance histograms, or the quiet Sun, thus filtering out the effects by active regions (ARs), coronal holes (CHs), and dark halos (DHs) to analyse the variability of their properties during the activity cycle. Such a study, however, may be hampered by non-negligible centre-to-limb variations. We therefore first examine the variation across the solar disk of the median radiance (Sect. 3.2.1), and then we discuss the mean properties of the radiance histograms (Sect. 3.2.2).
3.2.1. Centre-to-limb variation in the quiet Sun radiances
The centre-to-limb variation in line radiance is interesting per se, allowing for instance distinguishing between optically thin and thick lines but is also relevant for estimates of the disk-integrated line emission, which is proportional to the line irradiance in turn, aside from a constant and neglecting off-limb emission (a good approximation for all but the hottest lines, as shown in Paper II).
For an empirical estimate of the centre-to-limb variation in the quiet Sun component, we employed the same technique described in Andretta et al. (2003): for each annulus of radial distance r from disk centre and width Δr = 0.02R⊙, we computed the histogram of radiances, thus obtaining a bi-dimensional histogram as function of ρ = r/R⊙. To characterise the dependence of radiance from radial distance on the solar disk, it is usually convenient to consider the centre-to-limb variations as function of μ, the cosine of the heliocentric angle θ. We also computed, therefore, bi-dimensional histograms as a function of μ, adopting a bin size Δμ = 0.02.
 |
Fig. 4 Maps of Mg x 625 Å and O v 630 Å radiances (left-hand panels) in a logarithmic, inverted scale (brighter areas correspond to fainter line radiances) from a USUN mosaic obtained on September 2008. The corresponding bi-dimensional histograms vs. μ are shown in the upper-right and lower-right panel, respectively; the position and width of the histogram peaks are also shown (magenta dots and tee-shaped symbols). The power-law and quadratic curves fitting the peaks of the log I vs. μ histograms are shown as red and blue lines, respectively. Curves derived from plane-parallel and spherical optically thin models are shown as dashed and continuous orange lines, respectively, in both right-hand panels. Distances corresponding to μ = 0 (white light limb), 1/10, 1/3, 1/2, and 2/3 are shown as circles in the left-hand panel and as vertical lines in the right-hand panels. The rectangle corresponding to the FOV limited to | Y| < 0.85 R⊙, which is used to compute the histograms vs. μ, is also shown. |
For selected lines in the CDS/NIS range and for each USUN or SYNOP mosaic analysed, we computed a similar bi-dimensional histogram. For the calculation of the I vs. μ histogram in USUN mosaics, we excluded the polar regions to minimize the contribution of polar coronal holes during the minimum of solar activity, since we are mostly interested in the properties of the gross QS centre-to-limb variation. Adopting a rectangular coordinate system, (X,Y), with its origin at the centre of the solar disk and with the Y axis oriented along the central meridian, we then selected pixels in the region determined by | Y| < 0.85 R⊙.
Figure 4 shows two examples of these bi-dimensional histograms obtained from a USUN mosaic taken during the latest solar minimum for the coronal line Mg x 625 Å and the TR line O v 630 Å. The line-radiance maps are shown in the left-hand panels with circles indicating some representative heliocentric distances. The corresponding bi-dimensional histogram as function of μ, computed from on-disk spectra within the blue rectangle, are shown in the right-hand panels.
The measured positions of the peaks of the radiance histograms as function of μ are shown in Fig. 4 with the estimated widths (standard deviation) of the distributions. Note that the tails of the histograms are due to the small active region at ρ ~ 0.5 (μ ~ 0.85) and to the polar coronal holes (ρ > 0.75, μ < 0.67).
In a plane-parallel geometry, the total radiance of optically thin lines varies as ~μ-1. This function is shown in Fig. 4 as a dashed orange line. It is sometimes assumed (e.g.: Wilhelm et al. 1998) that solar optically thin lines should exhibit a ~μ-1 limb brightening, while significant departures from such a dependence would be characteristic of optically thick lines or of lines affected (below the Lyman edge) by absorption due to cool material. However, as shown by Andretta et al. (2003), a spherical, exponentially stratified model of line emissivity can fit observed centre-to-limb behaviour of coronal lines without invoking optical thickness effects. The centre-to-limb behaviour from such a model, which adopts a scale height corresponding to the nominal formation temperature of the Mg+9 ion (log Tmax = 6.0) (shown in Fig. 4 as a continuous orange line) fits well to the observed average centre-to-limb variation of line radiances. The match, while still better than the function μ-1, is less good in the case of the O+4 ion (log Tmax = 5.4). It, however, still serves as a warning against interpreting the empirical centre-to-limb variation in that line only in terms of optical thickness effects.
 |
Fig. 5 Average centre-to-limb variation in several strong lines from USUN mosaics (diamonds). For the He i 584 Å and O v 630 Å, where SYNOP data are available, squares indicate SYNOP data during the 2007–2009 solar minimum, while circles denote data during the 1996–1997 minimum. The quadratic (solid lines) and power-law (dashed lines) fits to the USUN data are also shown. Grey points (μ < 0.1) indicate data not used in the actual fits. |
For simplicity, we fitted the logarithm of these peak radiances as function of
μ with a
quadratic function: 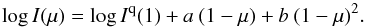 (2)To facilitate comparisons with the results
of Pietarila & Judge (2004), we also computed
power-law fits:
(2)To facilitate comparisons with the results
of Pietarila & Judge (2004), we also computed
power-law fits: 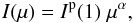 (3)note that the value α = −1 corresponds to the
plane-parallel finite-slab, optically-thin case. In the fit procedure, we only
considered histogram bins corresponding to μ > 0.1, which are further away than
~5″ from the nominal,
white-light limb. The resulting fitting curves are shown in the right-hand panels of
Fig. 4 as a blue and red curve, respectively.
(3)note that the value α = −1 corresponds to the
plane-parallel finite-slab, optically-thin case. In the fit procedure, we only
considered histogram bins corresponding to μ > 0.1, which are further away than
~5″ from the nominal,
white-light limb. The resulting fitting curves are shown in the right-hand panels of
Fig. 4 as a blue and red curve, respectively.
Once the average centre-to-limb variation in a line has been determined, it is then
possible to derive its mean disk radiance (and thus its irradiance) from a measurement
at a given μ on the solar disk, through the multiplicative
factor fcl(1), where fcl(μ) is defined by
Andretta et al. (2003) as follows: 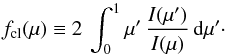 (4)The above correction factor computed at
μ = 1 is
normally the most useful value in the case of observations near disk-centre of the Sun
in a quiescent state: in the remainder, we refer to that value as simply fcl. In the
case of Eq. (2) and Eq. (3), the correction factors
(4)The above correction factor computed at
μ = 1 is
normally the most useful value in the case of observations near disk-centre of the Sun
in a quiescent state: in the remainder, we refer to that value as simply fcl. In the
case of Eq. (2) and Eq. (3), the correction factors
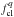 and
and
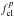 , respectively, can both be computed
analytically and will be discussed later.
, respectively, can both be computed
analytically and will be discussed later.
The centre-to-limb variation measured on each USUN or SYNOP mosaic have also been averaged to produce mean empirical centre-to-limb variations. The averages were done separately for dates corresponding to solar minimum and solar maximum. More specifically, we considered the following time intervals for the minima and maximum of solar activity:
1996–1997 minimum:: SYNOP mosaicsbetween 2 April 1996 and17 May 1997 (noUSUN studies in that time interval);
2007–2009 minimum:: USUN mosaics between 29 October 2007 and 30 November 2009; SYNOP mosaics beween 26 November 2007 and 1 December 2009;
Maximum:: USUN mosaics between 13 March 2000 and 6 August 2002; SYNOP mosaics between 5 June 2000 and 20 October 2002.
The average, empirical profiles for the solar minimum are shown in Fig. 5. At each value of μ, the standard deviation of the peak radiances for all the solar minimum dates considered provides an estimate for the errors. The average profiles at solar maximum are to be considered less reliable, given the noise introduced by solar non-quiescent structures, and are therefore not shown in that figure for clarity, but they overlap well with the more accurate solar minimum centre-to-limb profiles. |
Fig. 6 Parameters characterising the centre-to-limb variation in the O v 630 Å line during the last two solar minima. Diamonds: USUN; squares: SYNOP (2007–2009), circles: SYNOP (1996–1997). The average values are indicated by horizontal lines: dotted (USUN), solid (SYNOP, 2007–2009), and dashed (SYNOP, 1996–1997). In the upper-left panel, the centre-disk intensity, I(1), from the power-law fit are in black, while results from quadratic fits are in grey. The correction factors fcl, whose average values are listed also in Table 1, are shown in the right-hand panels; the value of centre-to-limb function at ρ = 0.85 (i.e. μ ~ 0.52), derived from the quadratic fit of Eq. (2), is shown in the lower-left panel. |
The mean empirical profiles are then again fitted with the same functions described above. The resulting fitting function are also shown in Fig. 5 in the case of solar minimum, and the fit coefficients with their standard deviations are listed in Table 1 for both activity minima and maximum.
The He i 584 Å and O v 630 Å lines have been included in the definition of SYNOP mosaics since the start of the SOHO mission; however, we do not list the results for the He i line from SYNOP mosaics here, because they are normally affected by the presence of polar coronal holes, especially during the minimum of solar activity. The effect of coronal holes is indeed clearly seen in the SYNOP average profiles of Fig. 5.
Coronal holes, on the other hand, are almost undetectable in O v 630 Å images, although a hint of a slight decrease of radiances can be seen in Fig. 5 in the SYNOP average profiles below μ ~ 0.4. We therefore use SYNOP data to measure the centre-to-limb variation in that line along the full solar cycle from the 1996–1997 to the 2007–2009 minima. Figure 6 shows the variability of the centre-to-limb fitted function for the O v 630 Å line in mosaics taken during the minimum of solar activity from both the mean profile and the individual dates. Rather than showing the fit parameters α or a and b listed in Table 1, we have chosen to show the variation in the centre-to-limb function computed at ρ = 0.85 and the factor fcl, which are quantities that are more immediately illustrative of the properties of the centre-to-limb variation. No significant variation in the centre-to-limb variation is apparent in these data. The centre-disk radiance in our data, log I(1), is constant by definition, because the long-term correction to the CDS/NIS radiometric calibration worked out in Paper I assumes a constant mean QS radiance with time. On the other hand, the variation in the radiance from centre to limb does not depend on the radiometric calibration. Therefore, its invariance between the two solar minima suggests that the structure of the transition region did not change.
Note also that parameters of the centre-to-limb functions given in Table 1 do not change between solar miminum and maximum (except for the hotter lines). The invariance of the centre-to-limb function is best seen by examining the factors fcl(1), which are consistent with constant values in all cases within the stated errors, usually within one or two standard deviations.
Fit parameters for centre-to-limb variation for various lines from USUN and (in the case of the O v 630 Å line) SYNOP mosaics.
It is useful to note also that the parameters obtained from USUN and SYNOP mosaics are consistent within the errors despite the different FOVs and spatial resolutions. However, Wilhelm et al. (1998) noticed that the limb brightening of TR lines above coronal holes is different compared to the QS (a property of TR limb brightenings already described earlier by, e.g., Doschek et al. 1976; Feldman et al. 1976). To verify whether this effect could account for the residual differences between SYNOP and USUN results shown in Fig. 6 and listed in Table 1, we computed the centre-to-limb variation in USUN mosaics as explained above but only in a strip along the central meridian similar to the SYNOP FOV (cf. Sect. 3.1.1).
For the O v 630 Å line, the factor 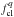 during the 2007–2009 minimum, for
instance, changes from 1.44 ± 0.02 to 1.27 ± 0.06 when restricting the analysis to the SYNOP FOV, which is
in excellent agreement with the value obtained from SYNOP data. A similar change is less
clearly seen in the fainter and cooler O iii 600 Å: the factor changes from
1.45 ± 0.02 to
1.34 ± 0.11, while the
statistics in the O iv 554 Å multiplet gives even larger uncertainties, thus
hiding this effect. While we can state that our results are consistent with the results
of Wilhelm et al. (1998) concerning the effects
of coronal holes in TR lines, the worse statistics of USUN mosaics (due to fewer spectra
in the central meridian strip) does not permit an accurate measurement of this effect.
during the 2007–2009 minimum, for
instance, changes from 1.44 ± 0.02 to 1.27 ± 0.06 when restricting the analysis to the SYNOP FOV, which is
in excellent agreement with the value obtained from SYNOP data. A similar change is less
clearly seen in the fainter and cooler O iii 600 Å: the factor changes from
1.45 ± 0.02 to
1.34 ± 0.11, while the
statistics in the O iv 554 Å multiplet gives even larger uncertainties, thus
hiding this effect. While we can state that our results are consistent with the results
of Wilhelm et al. (1998) concerning the effects
of coronal holes in TR lines, the worse statistics of USUN mosaics (due to fewer spectra
in the central meridian strip) does not permit an accurate measurement of this effect.
An inspection of the power-law exponents listed in Table 1 shows that in all cases α is negative with the exception perhaps of the He i 584 Å line, indicating a limb brightening, and its absolute value is always significantly smaller than one. We once again stress that departures from the value α = −1 do not imply significant line optical thicknesses but only an inadequacy of the plane-parallel finite-slab, optically-thin model. The majority of lines in the CDS wavelength range can still be assumed to be (effectively) optically thin, since their limb brightening can be modelled (very well in many cases) by an exponentially stratified emissivity in a spherical geometry, as shown in Fig. 4. This takes into account that the quiet-Sun component in the hotter lines, such as Si xii 521 Å line, is less clearly defined, and thus their limb brightening fits are more uncertain.
The only likely exceptions are the He i and He ii lines, which all exhibit very shallow centre-to-limb variations. While neither a plane-parallel slab nor a spherical shell geometrical model are likely to be reasonable representations of the chromosphere or of the lower TR, it is also likely that a significant optically thickness in those lines needs to be invoked, as already pointed out by Pietarila & Judge (2004). The values of α computed by the latter authors, however, are still significantly larger in absolute value than the observed values we present here. That is, they derive a limb brightnening in the helium resonance lines from their calculations which is still too strong. It is useful to note that the centre-to-limb variation in H i Ly-α, as measured with SUMER by Curdt et al. (2008) is also flat.
For what concerns a comparison to other measurements, we mention the work by Mango et al. (1978) here, who fitted measurements for the He i 584 Å, He i 537 Å, and He ii 304 Å lines with a linear function, I(μ) = I(1) [1 + C(1 − μ)], with the coefficients C = 0.10, C = 0.47, and C = 0.31, respectively. Note that the coefficient C to a second order can be related to coefficients a and b of Table 1, as a ≃ C/ln10, and b ≃ −C/(2ln10). Those fits were however made from relatively few data points and on a narrow range of μ: the data for the He i 537 Å line, in particular, were derived from the interval 0.2 < μ < 0.6. We thus do not regard a comparison with the results of our fits as very significant.
The factor fcl can be compared with the factor
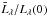 that is given in Table 4 of Wilhelm et al.
(1998), although the latter is obtained from an actual integration of data from
full-disk scans, not from an average centre-to-limb variation. The only lines in common
between Table 4 of Wilhelm et al. (1998) and
Table 1 are the He i 584 Å and O v
630 Å lines: the factor given for the former line is
that is given in Table 4 of Wilhelm et al.
(1998), although the latter is obtained from an actual integration of data from
full-disk scans, not from an average centre-to-limb variation. The only lines in common
between Table 4 of Wilhelm et al. (1998) and
Table 1 are the He i 584 Å and O v
630 Å lines: the factor given for the former line is
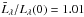 ,
which is consistent with the values of the order of unity we have found. For the latter
line, the value 1.59 is
higher than the value of ~1.3 from the QS centre-to-limb variation that is measured in
the present work. The value given by Wilhelm et al.
(1998) for the O iv 788 Å line,
,
which is consistent with the values of the order of unity we have found. For the latter
line, the value 1.59 is
higher than the value of ~1.3 from the QS centre-to-limb variation that is measured in
the present work. The value given by Wilhelm et al.
(1998) for the O iv 788 Å line,
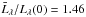 is similar to the value we find for the O iv 554 Å multiplet, fcl ~ 1.4.
is similar to the value we find for the O iv 554 Å multiplet, fcl ~ 1.4.
It should be noted that these factors allow an estimate of the disk irradiance due to QS emission only (no active regions nor coronal holes are accounted for). Furthermore, as discussed in Paper I, it is also necessary to account for off-limb emission for most lines with formation temperature of the order of ~1 MK or higher.
For the remainder of this work in any case, we adopt the quadratic fits (Eq. (2)) obtained from USUN mosaics during the 2007–2009 minimum of solar activity as a reference centre-to-limb variation.
3.2.2. Variability of quiet Sun radiances during the activity cycle
Using the characterisation of the centre-to-limb variation in line median radiances described in the previous section, we first demonstrate in Fig. 7 how the radiance histograms in some lines over the full disk are biased in both the position of the peak and the width, if the centre-to-limb variation is not taken into account. We chose to show the Mg x 625 Å, as a representative case of a coronal line with a clearly defined QS component.
Such biases in peak position and width of the QS histograms are still clearly detectable when restricting the analysis to pixels within 0.85 × RSun (corresponding to μ = 0.527 or ~70% of the disk): this is not surprising since the value at ρ = 0.85 of the centre-to-limb function is in this case ~1.6 (upper-right panel of Fig. 7). Even when restricting the analysis to just 50% of the disk, or r < 0.7 × RSun, the bias is still detectable, although to a lesser extent. In the latter case, however, the statistics are significantly worsened because both of a smaller number of pixels contributing to the histogram and a larger contribution from active region belts (outside the epochs of minimal solar activity).
 |
Fig. 7 Effect of centre-to-limb variation in the radiance histograms of the Mg x 625 Å line. The original radiance map from the USUN mosaic taken on December 15, 2008 is shown in the upper-left panel. The fit to the average centre-to-limb variation at the minimum of solar activity is shown in the upper-right panel as a solid line (i.e.: a = 0.23, b = 0.44); for comparison, the measured variation for that date (dots) is also shown, along with the value of limb brightening at ρ = 0.85 (dashed lines). The map of radiances corrected for that limb brightnening function is shown in the lower-left panel. The lower-right panel shows the radiance histograms formed from all on-disk pixels (grey-shaded histogram), as compared with the histogram from pixels with ρ < 0.85 (green-shaded histogram); the histogram from the radiances corrected for the centre-to-limb variation is shown in red. The widths of the Gaussian fit to the core of the histograms are, respectively: 0.21, 0.19, and 0.17. |
 |
Fig. 8 The contours in the upper panels show the time variability of full-disk histograms from CDS USUN mosaics after correction from centre-to-limb variation. The horizontal lines mark representative dates: 23 April 1998 (green), 30 October 2001 (orange), 1 May 2005 (red), and 15 December 2008 (grey). The gap in 1998 is due to the loss of contact of SOHO. The lower panels show the corresponding radiance histograms with the same colour coding. All the histograms are normalised to the total number of pixels; those shown in the lower panels are then also normalised to the peak of the average histogram at the solar minimum of activity. |
We chose therefore to consider all on-disk pixels but removed the average centre-to-limb variations. The resulting images were then analysed to determine the quiet-Sun component of the radiance histogram.
In the upper panels of Fig. 8, we show the evolution of radiance histograms along the cycle, once the centre-to-limb variation is removed. It is readily apparent that the quiet Sun contribution is usually still well approximated by a log-normal distribution, even around the maximum of the cycle. We therefore estimated the position of the peak and its width by fitting a Gaussian to histogram bins around the maximum of the distribution. In case of multi-component distributions, we fitted the peak corresponding to the lowest mean radiance.
In the lower panels of the same figure, we show examples of radiance histograms at different phases of the solar cycle for four representative dates from the rising phase of cycle 23 (23 April 1998: green) through its maximum (30 October 2001: orange) and from the decaying phase (1 May 2005: red), to the deep minimum before cycle 24 (15 December 2008: grey histogram). With the exception of the Si xii 521 Å and of the Si xi 303 Å histograms, the fitted component in these examples corresponds very well to the component observed during the 2008 minimum and, therefore, can be interpreted as a QS component.
 |
Fig. 9 Fit parameters of the QS or lowest-radiance component of the radiance histograms for four representative lines. Filled diamonds and circles denote USUN and SYNOP mosaics, respectively. The data points used to compute the average values of Table 2 are marked in red. |
In the Si xii 521 Å histograms, on the other hand, even the lowest-radiance components do not overlap with the quiet component measured at solar minimum. For example, the lowest component in the 2005 (red) histogram appears at around log I ~ 0.6−0.7 (radiance, I, in photons s-1 cm-2 arcsec-2) at about 0.3–0.4 dex higher than the 2008 peak. A QS component at that position is seen only as a “hump” above the Gaussian fit. A similarly small contribution is also seen in the April 2008 histogram too but is almost completely absent in the histogram corresponding to the maximum of solar activity (October 2001). Similar considerations can be made for the Si xi 303 Å histograms, although the overlap with the histogram at the minimum of activity remains significant even at the peak of the cycle.
This analysis highlights a feature of the solar EUV emission during its activity cycle: while the radiance in lines that form at temperatures lower than log T ~ 6 still shows a noticeable emission with mean radiances which are comparable to QS values during the solar minimum of activity, such a component is strongly decreased in hotter lines to the point of virtually disappearing in the hottest lines in the CDS/NIS range (log T ≳ 6.3) at epochs near the solar maximum.
A more detailed characterisation of the variability in the distribution of QS radiances along the solar cycle is given in Fig. 9, which shows how the position of the peak and width of the quiet Sun or of the lowest-radiance component of the radiance histogram vary with the cycle for four lines. The measurements shown in the figure for the He i 584 Å, O v 630 Å, and Mg x 625 Å lines are from both USUN (diamonds) and SYNOP (circles) mosaics. However, only the He i 584 Å and O v 630 Å lines (as well as the Mg ix 368 Å and Fe xvi 361 Å lines, not shown here) were included in SYNOP studies, since the beginning of the SOHO mission and thus cover both the 1996–1997 and the 2007–2009 minima; the Mg x 625 Å line was included in SYNOP mosaics only after mid-1998 during the rising phase of cycle 23.
It is readily apparent how the peak of the radiance distribution of cooler lines is nearly constant throughout the solar cycle, except for the period 1998–2002 (or 1998–2004, for the Mg x 625 Å line), where the distributions of TR lines are perturbed by the signal due to active regions. This is not easily disentangled from the QS component (see again histograms of Fig. 8).
The lowest-radiance component of the Si xii 521 Å distribution, on the other hand, is systematically higher by a factor 3 to an order of magnitude relative to the well-defined value at solar minimum. As shown in at least two of the examples of Fig. 8, a true QS component may still be seen in the radiance histograms, except at the peak of solar activity, but this component is overcome by other components associated with ARs. Hence, the variability shown in Fig. 7 of the lowest-radiance peak is to be attributed to the appearance of ARs along the cycle, not to an intrinsic variability of the QS component. In principle, with careful fitting of multiple Gaussians, or masking out the ARs on the disk, it could be possible to recover the properties of the residual QS component. Such an approach, however, is made difficult by the large area covered by AR-related emission, as discussed in Sect. 3.3. For the purpose of this paper, the current analysis is sufficient.
A remarkable feature common to all these radiance components, on the other hand, is their constant width, even in the case of the Si xii 521 Å line. This is true for the QS or lowest-radiance component but is also true for the components due to the emission by active regions (see again Fig. 8) to some extent. It is beyond the scope of this paper to analyse the properties of the histogram components due to ARs in detail, but it seems the value of these histogram widths are characteristic of each line from the data shown here.
Table 2 reports the average values at solar-minimum epochs, as defined in Sect. 3.2.1, of both the position of the peak and the width of the QS component in the radiance distribution. The data points used to compute the averages are highlighted in red in Fig. 7. We recall that the position of the peak is in practice a measure of the median radiance; the mean radiance can be computed by using Eq. (1). These average values were computed by averaging values from both USUN and, whenever available, SYNOP mosaics: from the discussion of Sect. 3.1.1, the different sampling size and resolutions of the two types of mosaics do not affect the basic properties of the radiance histograms. This is also clearly seen from the data in Fig. 9.
As already mentioned in Sect. 3, earlier analysis of radiance histograms in terms of log-normal distributions were done by Wilhelm et al. (1998) and Fontenla et al. (2007): they also report measurements for the positions and widths of the histograms.
There is no overlap in the set of lines analysed from SUMER spectra by Wilhelm et al. (1998), as noted in Sect. 3.2.1, with the exception of the 2nd order lines He i 584 Å and O v 630 Å. They found the width of the radiance histogram of the He i line to be about 0.2 dex (their Table 3), while we measure a value of 0.16 ± 0.015 dex (Table 2); in the case of the O v line, they found that its histogram has a width of about 0.26 dex, while we measure 0.19 ± 0.02 dex. They also measured the width of the distribution of the O iv 788 Å: their values range from 0.275 to 0.30 dex, while we find 0.178 ± 0.01 dex for the O iv 554 Å multiplet of the same ion.
It is not clear why the values measured by Wilhelm et al. (1998) are generally higher than those found here. We note that the procedure adopted by those authors apparently involves a Gaussian fit of the full radiance histograms, which, as we repeatedly noted in this work, may include “humps” in the wings due to features different from the QS (CHs, DHs, ARs; see also their Fig. 8). We were very careful in fitting only the core of the histograms, thus filtering out most other contributions. Moreover, the values measured by Wilhelm et al. (1998) were derived from only a very few disk scans (one to four for each line) and, indeed, usually show a considerable scatter in the widths of their histograms (see their Fig. 9), while our tabulated values refer to an average over a couple of dozens of measurements.
For completeness we report here the values obtained by Fontenla et al. (2007): they find the widths of the distributions of the 1430 Å continuum, the Ly-α line, and the Ca ii K3 filtergrams to be 0.245, 0.271, and 0.202 dex, respectively. Despite the fact that those features are formed in different regions of the atmosphere than the CDS EUV lines, the similar widths of their radiance distributions is noteworthy and, perhaps, points to a close connection between the energy dissipation mechanisms in those atmospheric regions.
From the results presented here, it is clear that this distribution for either the cooler TR lines or coronal lines that form at log T < 6.2, is not significantly altered along a solar cycle. Even for lines forming at log T > 6.2, it is more likely that a QS component similar to the one measured at epochs of minimum of solar activity is still present but is overcome by the appearance of a much stronger and diffuse emission due to ARs.
This result contradicts the findings of Kamio & Mariska (2012): from the analysis of Hinode spectra, they find the QS emission to be intrinsically variable during the time interval they considered (end of 2006 to early 2011).
Even our data, such as those shown in Fig. 7, could be still be compatible with a variability of the QS median radiance (but not of the width of the distribution) during the maximum of solar activity. However, such a variability would be rather small – of the order at most of 0.1–0.2 dex for the Mg x 625 Å line; the variation found by Kamio & Mariska (2012) is of the order of a factor between 2 and 5 for lines of similar formation temperature (like the Fe xi 180 Å line) or hotter lines. In any case, our data for Mg x clearly show that the median radiance settles to a constant value by the end of 2004, which is much earlier that the Hinode measurements.
One obvious explanation of the discrepancy is that Kamio & Mariska (2012) used a set of single-slit exposures near the disk centre. That is, their measurements are affected by a very small FOV and the occasional presence of active regions. Another problem in the Kamio & Mariska (2012) results is related to their radiometric calibration, which is now known to be at fault. Del Zanna (2013) produced a completely new Hinode EIS calibration and applied it to a careful selection of the same dataset used by Kamio & Mariska (2012) in their analysis. The Del Zanna (2013) results are that the quiet Sun radiances in lines formed at or below 1 MK do not change, which agree with the present results.
We also note that the conclusions of Kamio & Mariska (2012) rely heavily on the comparison of radiance histograms taken near the disk centre at two specific epochs: December 2006 and February 2009. In particular, they find that the peak of the radiance histogram of the Fe xii 194 Å line is at ~200 ergs cm-2 s-1 sr-1 in 2006 and ~70 ergs cm-2 s-1 sr-1 in 2009 (see their Fig. 3).
We do not have USUN scans for December 2006, but we do show in Fig. 10 (discussed in Sect. 3.3) scans for 2 October 2006, and 2 January 2007, which both show some significant activity at the equator with a broad longitudinal distribution. Indeed, inspection of EIT images around mid-December 2006 (e.g.: 12 December 2006) reveals that one active region near the equator (NOAA 10930) exhibits some long-range loops extending to a plage-like, un-numbered trailing area, at least in EIT 195 images.
We therefore speculate that the mean radiance estimated by Kamio & Mariska (2012) for December 2009 may be contaminated by solar activity. We notice that the radiance histogram for that epoch has a “hump” corresponding to the main component of the more quiescent 2009 histogram in their Fig. 3. That is perfectly analogous to what we find, for instance, in some of the histograms of our Fig. 8, as discussed earlier in this section.
3.3. On the variability of the EUV solar irradiance
A remarkable result described in Paper II is that solar EUV spectral irradiance due to TR lines varies by only modest amounts during the solar cycle (less than a factor 2 for the O v 630 Å line). This is in contrast with the strong variability of coronal lines (at least one order of magnitude for the Si xii 521 Å line). Even excluding the off-limb emission, as estimated to be non-negligible for hotter lines in Paper II, this different behaviour calls for an explanation. The analysis of the previous section of the properties of the statistical distribution of radiances may turn out useful for studying that phenomenon more in detail.
 |
Fig. 10 Maps of line radiance from USUN mosaics in four lines (top to bottom rows): Si xii 521 Å, Mg x 625 Å, O v 630 Å, and He i 584 Å. The dates of the USUN mosaics are marked by vertical, dashed lines in the lowest panel, showing the variability of the radio flux at 10.7 cm. |
Figure 8 already provides some clues to the present discussion. We already noted how the contribution of AR emission relative to the QS is significantly larger in hotter lines. At the peak of solar activity, the QS contribution virtually disappears from the distribution of hottest lines (like the Si xii 521 Å line), in contrast to the TR lines whose AR contribution always remains a mere perturbation to the main QS distribution. We also note that the AR contribution in hotter lines can easily peak at radiances at least one order of magnitude higher than the QS median value at solar minimum; conversely, the bulk of AR emission in TR lines always remains within a factor 2–3 from the QS peak of the distribution.
These observations are illustrated in Fig. 10, which shows a set of radiance maps in some CDS lines at representative times of the solar cycle. The figure is analogous to Fig. 1 of Paper II, except that the centre-to-limb variation for each line has been removed and that the colour table has been chosen to distinguish quiescent regions from emission related to solar activity. The set of images shown in this figure includes those from the same dates as shown in Fig. 8 plus six others for a more complete coverage of the cycle.
Along with the radiance maps, we also show the variability of solar flux at 2800 MHz (10.7 cm) for which we have adopted the daily measurements (scaled to 1 AU) made by the National Research Council of Canada (at the Algonquin Radio Observatory near Ottawa until 1991 and at the Dominion Radio Astrophysical Observatory near Penticton, British Columbia).
Even a casual inspection shows that regions appearing in a darker colour in Mg x 625 Å images (or in cooler lines) are bright in the hotter Si xii 521 Å line and are definitely brighter than typical QS emission in that line during solar minimum. In particular, the red-yellow areas correspond to line radiance above the peak, p, of QS radiance given in Table 2 by at least 2w, where w is the width of the log-normal QS distribution (third column of Table 2). Thus, there is a probability of 2.3% to find values belonging to the QS log-normal distribution above that threshold.
At the peak of the solar cycle (e.g. in 2001), nearly 100% of the solar disk emits in Si xii 521 Å above that threshold. Only CHs tend to remain as dark as at the minimum of activity: the QS emission nearly disappears. By contrast, spectra with O v 630 Å radiance above the threshold are less than 12% of the total over the solar disk, even at the peak of solar activity. Considering that 2.3% of the spectra belong to the tail of the QS log-normal distribution, only the remaining 10% or less is due to AR emission.
The He i and He ii lines deviate from the numbers typical of TR lines: the number of spectra with radiances above the threshold can reach about 25% of the disk. This can be explained by the effect of enhancement of those lines due coronal back-radiation from the nearby ARs or by some other enhancement mechanism differentially operating on the lines of that element (e.g. Andretta et al. 2000, 2003).
 |
Fig. 11 Estimated AR area (top panel) and contrast relative to the QS (bottom panel) during solar cycle 23 for various lines: He i 584 Å (circles), O iii 600 Å (triangles), O v 630 Å (diamonds), Mg x 625 Å (squares), Si xi 303 Å (crosses), and Si xii 521 Å (stars). |
In Fig. 11, we show how the statistical properties of the radiance histograms above the p + 2w threshold vary with the solar cycle, as compared to the bulk of the QS log-normal distribution defined by the parameters of Table 2.
The upper panel shows the fraction of disk spectra with radiance in a given line that is higher than the threshold. That number, minus the 2.3% contribution due to the tail of the QS distribution (dashed, horizontal line), can be interpreted as an estimate of the fraction of the solar disk covered by ARs at a given epoch and seen in a given line.
The lower panel shows the ratio between the mean value above the threshold p + 2w (mostly AR contribution) and the mean within the interval p ± 2w (which includes 95.5% of the QS contribution and should exclude most of CH and DH contributions). We refer to this ratio as to “AR/QS contrast”. For log-normal distributions of width 0.15 and 0.25 dex, that ratio is 2.2 and 3.5, respectively; those values, shown as horizontal, dashed lines, can be considered as lower limits for the actual measurements.
From the upper panel, the “AR area” as function of line formation temperature appears to be roughly constant for TR lines (with the exception of He i and He ii lines, see below). For coronal lines, the AR areas increase rapidly instead and yet smoothly, where it is up to almost 100% for lines forming at T > 2 MK, as noted above. This is not entirely surprising: while TR emission is expected to come from a narrow, albeit inhomogeneous layer near the solar surface, emission of hotter lines is expected to come mostly from larger AR or inter-AR loops. Thus, we speculate that this “AR” component is due either to a diffuse corona due to an enhanced activity or to a large number of overarching loops joining different active regions (the former can be due to the latter).
More intriguing is what is shown in the lower panel: the contrast betwen AR and QS remains between a factor 2 and 5 for all the lines up to the Si xi 303 Å (forming at T ~ 1.5 MK), while suddenly jumping to an order of magnitude or more (up to a factor 30) for the Si xii 521 Å line (forming at T ~ 2 MK) or for hotter lines, such as the Fe xvi 361 Å, which is not shown in the plots. The same effect can be seen in the histograms of Fig. 8: the positions of the main peaks of the Si xi 303 Å radiance distributions remain within a factor 10 or less during the cycle, while it varies by at least a factor 30 between minimum and maximum for the Si xii 521 Å line.
Such an abrupt change of AR mean emission compared to QS between the formation temperatures of Si xi and Si xii may signal the appearance at solar maximum of a hot component of the corona missing during the solar minimum. This tentative interpretation needs, however, to be addressed more carefully, including a quantitative comparison with X-ray measurements, for instance, which is a task beyond the scope of this work.
4. Conclusions
The database of CDS/NIS synoptic observations (SYNOP and USUN) taken during the lifetime of the instrument has been proven in Paper II to be very useful in the study of the solar EUV irradiance during solar cycle 23. In this work, we continued the analysis of the data by studying the properties of the solar EUV radiances of a number of strong lines. This is the first time that such an analysis is possible; hence, all the present results have particular importance.
The main points we addressed in this paper can be summarised as follows:
-
We showed that structures around active regions, sometimes referred to as dark halos or dark canopies are common, and discussed their similarities and differences with coronal holes. In particular, we show how they are well visible in TR lines, contrary to coronal holes.
-
We find that the limb-brightening for all the EUV lines in the CDS/NIS range is consistent with small or negligible optical thickness with the notable exception of the He i and He ii lines.
-
The limb-brightening significantly affects any characterisation of the solar radiances.
-
The limb-brightening function for all the lines does not change measurably during the cycle. In particular, the limb-brighenining was not different in 2008 than in 1996 in the only line, O v 630 Å, for which a comparison was possible. Our limb-brightening curves differ from those previously published.
-
We confirm earlier findings that the radiance histogram have a well defined, log-normal QS component, which is almost always identifiable in full-disk distributions, especially in coronal lines. However, our results differ from previous ones.
-
The width of the lowest-radiance, log-normal distribution (either QS or from “diffuse” corona) is constant along the cycle.
-
At solar maximum, the QS component is strongly reduced or even vanishes in lines with formation temperature T > 2 MK. More accurately, the QS component is progressively overcome by a much larger contribution from ARs.
-
We analysed the variability of solar irradiance in terms of variable area and “intrinsic” emission of active regions. We found that the emission from active regions in TR and coronal lines forming at T < 1.5 MK undergo only relatively modest changes during the cycle: thus, much of the irradiance variability is due to a change in the emitting area. For hotter lines (i.e. lines forming at T > 2 MK), the emitting area saturates to almost 100% of full solar disk at the maximum of activity, while the emission due to active regions simultaneously increases by more than an order of magnitude.
The analysis of both the centre-to-limb variation and of the radiance statistical distribution points at a constant QS emission along solar cycle 23. This result is contrary to earlier claims (e.g.: Kamio & Mariska 2012). Since both the centre-to-limb function and the widths of the radiance distributions do not depend on the radiometric calibration of the data, we are confident that our results point to truly constant properties of the quiet Sun during the activity cycle.
Finally, we remark that the availability of a good radiometric calibration, including its long-term variability, as estimated in Paper I, has been the key for the analysis of the variability of EUV emission in various lines across the solar disk and during the cycle. For instance, there were histogram components of some lines, which would have been classified as “quiescent” on the basis of a morphological analysis only (at the low resolution of this data set), even during solar maximum. On the other hand, the calibrated radiances of those components turned out to be much brighter than QS areas during solar miminum and, thus, had to be considered as major contributors to the increased irradiance in that line during solar maximum.
CDS Software Note #53: http://solar.bnsc.rl.ac.uk/swnotes/cds_swnote_53.pdf
Acknowledgments
G.D.Z. acknowledges support by STFC (UK). V.A. acknowledges partial support by the Italian Space Agency (ASI), through ASI-INAF contracts I/035/05/0 and I/05/07/0. CDS was built and operated by a consortium led by the Rutherford Appleton Laboratory (RAL), which includes UCL/Mullard Space Science Laboratory, NASA/ Goddard Space Flight Center, Max Planck Institute for Extraterrestrial Physics, Garching, and Oslo University. SOHO is a mission of international cooperation between ESA and NASA. The results obtained here could not have been achieved without the efforts of the operation and scientific staff, which successfully ran the CDS instrument, in large part at STFC/RAL (UK) and NASA/GSFC (US).
References
- Andretta, V., Jordan, S. D., Brosius, J. W., et al. 2000, ApJ, 535, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Andretta, V., Del Zanna, G., & Jordan, S. D. 2003, A&A, 400, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curdt, W., Tian, H., Teriaca, L., Schühle, U., & Lemaire, P. 2008, A&A, 492, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G. 2013, A&A, 555, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., & Andretta, V. 2006, in SOHO-17. 10 Years of SOHO and Beyond, ESA SP., 617, 124 [NASA ADS] [Google Scholar]
- Del Zanna, G., & Andretta, V. 2011, A&A, 528, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Bromage, B. J. I., Landi, E., & Landini, M. 2001, A&A, 379, 708 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Andretta, V., & Beaussier, A. 2005, Mem. Soc. Astron. Italiana, 76, 953 [NASA ADS] [Google Scholar]
- Del Zanna, G., Andretta, V., Chamberlin, P. C., Woods, T. N., & Thompson, W. T. 2010, A&A, 518, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Aulanier, G., Klein, K.-L., & Török, T. 2011, A&A, 526, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doschek, G. A., Feldman, U., VanHoosier, M. E., & Bartoe, J.-D. F. 1976, ApJS, 31, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Doschek, G. A., Vanhoosier, M. E., & Purcell, J. D. 1976, ApJS, 31, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Dammasch, I. E., & Wilhelm, K. 2000, Space Sci. Rev., 93, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Dammasch, I. E., Wilhelm, K., et al., 2003, Images of the solar upper atmosphere from SUMER on SOHO, ESA SP, 1274 [Google Scholar]
- Fontenla, J. M., Curdt, W., Avrett, E. H., & Harder, J. 2007, A&A, 468, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, P. T., Phillips, K. J. H., Harra-Murnion, L. K., & Keenan, F. P. 1998, A&A, 335, 733 [NASA ADS] [Google Scholar]
- Griffiths, N. W., Fisher, G. H., Woods, D. T., & Siegmund, O. H. W. 1999, ApJ, 512, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, R. A., Sawyer, E. C., Carter, M. K., et al. 1995, Sol. Phys., 162, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Hinteregger, H. E., Fukui, K., & Gilson, B. R. 1981, Geophys. Res. Lett., 8, 1147 [Google Scholar]
- Jordan, S. D., & Brosius, J. W. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 183 [Google Scholar]
- Kamio, S., & Mariska, J. T. 2012, Sol. Phys., 279, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Mango, S. A., Bohlin, J. D., Glackin, D. L., & Linsky, J. L. 1978, ApJ, 220, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Pauluhn, A., Solanki, S. K., Rüedi, I., Landi, E., & Schühle, U. 2000, A&A, 362, 737 [NASA ADS] [Google Scholar]
- Pietarila, A., & Judge, P. G. 2004, ApJ, 606, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, E. M. 1976, Sol. Phys., 46, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, P. G., Woods, T. N., & Peterson, W. K. 2006, Adv. Space Res., 37, 315 [Google Scholar]
- Skumanich, A., Smythe, C., & Frazier, E. N. 1975, ApJ, 200, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, W. T., & Brekke, P. 2000, Sol. Phys., 195, 45 [Google Scholar]
- Tobiska, W. K., Bouwer, S. D., & Bowman, B. R. 2008, J. Atmos. Sol.-Terr. Phys., 70, 803 [Google Scholar]
- Wang, T., Thomas, R. J., Brosius, J. W., et al. 2011a, ApJS, 197, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., Robbrecht, E., & Muglach, K. 2011b, ApJ, 733, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, K., Lemaire, P., Dammasch, I. E., et al. 1998, A&A, 334, 685 [NASA ADS] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Bailey, S. M., et al. 2005, J. Geophys. Res., 110, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Hock, R., et al. 2012, Sol. Phys., 275, 115 [Google Scholar]
All Tables
Fit parameters for centre-to-limb variation for various lines from USUN and (in the case of the O v 630 Å line) SYNOP mosaics.
All Figures
 |
Fig. 1 Comparison of USUN and SYNOP data taken on 22 and 23 June 1998. The images show the integrated line radiances for the He i 584 Å and Mg x 625 Å lines in inverted, logarithmic scale (brighter areas correspond to fainter line radiances). The boundaries of the SYNOP FOV are also indicated. |
| In the text | |
 |
Fig. 2 Comparison of line radiance histograms of four representative lines (Mg ix 368 Å, He i 584 Å, Mg x 625 Å, and O v 630 Å) from spectra in the USUN and SYNOP mosaics, as shown in Fig. 1: USUN on-disk data (grey), USUN on-disk data within the SYNOP FOV (blue), and data from the two SYNOP mosaics (red: mosaic starting on 22 June; orange: mosaic started on 23 June). |
| In the text | |
 |
Fig. 3 Radiance maps for the lines He ii 304 Å, O v 630 Å, Mg x 625 Å, and Si xii 521 Å (from top to bottom), from the CDS USUN mosaics taken on 1 November 2004, 8 November 2005, and 16 July 2007 (left to right). The active regions NOAA 693, 821, and 963, respectively, are also indicated. The logarithmic colour display table is inverted: higher-radiance areas are darker; for each line, the range of radiances is the same for all three dates. The horizontal stripes near the centre of the solar disk in the 2004 mosaics are due to a missing raster, which are filled-in here with interpolated values for display purposes. |
| In the text | |
 |
Fig. 4 Maps of Mg x 625 Å and O v 630 Å radiances (left-hand panels) in a logarithmic, inverted scale (brighter areas correspond to fainter line radiances) from a USUN mosaic obtained on September 2008. The corresponding bi-dimensional histograms vs. μ are shown in the upper-right and lower-right panel, respectively; the position and width of the histogram peaks are also shown (magenta dots and tee-shaped symbols). The power-law and quadratic curves fitting the peaks of the log I vs. μ histograms are shown as red and blue lines, respectively. Curves derived from plane-parallel and spherical optically thin models are shown as dashed and continuous orange lines, respectively, in both right-hand panels. Distances corresponding to μ = 0 (white light limb), 1/10, 1/3, 1/2, and 2/3 are shown as circles in the left-hand panel and as vertical lines in the right-hand panels. The rectangle corresponding to the FOV limited to | Y| < 0.85 R⊙, which is used to compute the histograms vs. μ, is also shown. |
| In the text | |
 |
Fig. 5 Average centre-to-limb variation in several strong lines from USUN mosaics (diamonds). For the He i 584 Å and O v 630 Å, where SYNOP data are available, squares indicate SYNOP data during the 2007–2009 solar minimum, while circles denote data during the 1996–1997 minimum. The quadratic (solid lines) and power-law (dashed lines) fits to the USUN data are also shown. Grey points (μ < 0.1) indicate data not used in the actual fits. |
| In the text | |
 |
Fig. 6 Parameters characterising the centre-to-limb variation in the O v 630 Å line during the last two solar minima. Diamonds: USUN; squares: SYNOP (2007–2009), circles: SYNOP (1996–1997). The average values are indicated by horizontal lines: dotted (USUN), solid (SYNOP, 2007–2009), and dashed (SYNOP, 1996–1997). In the upper-left panel, the centre-disk intensity, I(1), from the power-law fit are in black, while results from quadratic fits are in grey. The correction factors fcl, whose average values are listed also in Table 1, are shown in the right-hand panels; the value of centre-to-limb function at ρ = 0.85 (i.e. μ ~ 0.52), derived from the quadratic fit of Eq. (2), is shown in the lower-left panel. |
| In the text | |
 |
Fig. 7 Effect of centre-to-limb variation in the radiance histograms of the Mg x 625 Å line. The original radiance map from the USUN mosaic taken on December 15, 2008 is shown in the upper-left panel. The fit to the average centre-to-limb variation at the minimum of solar activity is shown in the upper-right panel as a solid line (i.e.: a = 0.23, b = 0.44); for comparison, the measured variation for that date (dots) is also shown, along with the value of limb brightening at ρ = 0.85 (dashed lines). The map of radiances corrected for that limb brightnening function is shown in the lower-left panel. The lower-right panel shows the radiance histograms formed from all on-disk pixels (grey-shaded histogram), as compared with the histogram from pixels with ρ < 0.85 (green-shaded histogram); the histogram from the radiances corrected for the centre-to-limb variation is shown in red. The widths of the Gaussian fit to the core of the histograms are, respectively: 0.21, 0.19, and 0.17. |
| In the text | |
 |
Fig. 8 The contours in the upper panels show the time variability of full-disk histograms from CDS USUN mosaics after correction from centre-to-limb variation. The horizontal lines mark representative dates: 23 April 1998 (green), 30 October 2001 (orange), 1 May 2005 (red), and 15 December 2008 (grey). The gap in 1998 is due to the loss of contact of SOHO. The lower panels show the corresponding radiance histograms with the same colour coding. All the histograms are normalised to the total number of pixels; those shown in the lower panels are then also normalised to the peak of the average histogram at the solar minimum of activity. |
| In the text | |
 |
Fig. 9 Fit parameters of the QS or lowest-radiance component of the radiance histograms for four representative lines. Filled diamonds and circles denote USUN and SYNOP mosaics, respectively. The data points used to compute the average values of Table 2 are marked in red. |
| In the text | |
 |
Fig. 10 Maps of line radiance from USUN mosaics in four lines (top to bottom rows): Si xii 521 Å, Mg x 625 Å, O v 630 Å, and He i 584 Å. The dates of the USUN mosaics are marked by vertical, dashed lines in the lowest panel, showing the variability of the radio flux at 10.7 cm. |
| In the text | |
 |
Fig. 11 Estimated AR area (top panel) and contrast relative to the QS (bottom panel) during solar cycle 23 for various lines: He i 584 Å (circles), O iii 600 Å (triangles), O v 630 Å (diamonds), Mg x 625 Å (squares), Si xi 303 Å (crosses), and Si xii 521 Å (stars). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


