| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322343 | |
| Published online | 06 March 2014 | |
A characteristic oxygen abundance gradient in galaxy disks unveiled with CALIFA⋆,⋆⋆
1
Instituto de Astrofísica de Andalucía (CSIC),
Glorieta de la Astronomía s/n,
Aptdo. 3004, 18080
Granada,
Spain
e-mail:
sanchez@iaa.es
2
Centro Astronómico Hispano Alemán, Calar Alto, (CSIC-MPG), C/Jesús
Durbán Remón 2-2, 04004
Almería,
Spain
3
Instituto de Astronomía,Universidad Nacional Autonóma de Mexico,
A.P. 70-264, 04510
México, D.F.,
México
4
Instituto Nacional de Astrofísica, Óptica y Electrónica,
Luis E. Erro 1,
72840
Tonantzintla,
Puebla
Mexico
5
Departamento de Investigación Básica, CIEMAT, Avda. Complutense 40, 28040
Madrid,
Spain
6
Instituto de Astrofísica de Canarias (IAC),
38205,
La Laguna, Tenerife,
Spain
7
CEI Campus Moncloa, UCM-UPM, Departamento de Astrofísica y
CC. de la Atmósfera, Facultad de CC.
Físicas, Universidad Complutense de Madrid, Avda. Complutense s/n, 28040
Madrid,
Spain
8
Departamento de Física Teórica, Universidad Autónoma de
Madrid, 28049
Madrid,
Spain
9
Departamento de Física, Universidade Federal de Santa
Catarina, PO Box 476,
88040-900
Florianópolis, SC, Brazil
10
Depto. Astrofísica, Universidad de La Laguna (ULL),
38206,
La Laguna, Tenerife,
Spain
11
School of Physics and Astronomy, University of St Andrews, North Haugh,
St Andrews, KY16 9SS, UK
12
CENTRA – Instituto Superior Tecnico, Av. Rovisco Pais 1, 1049-001
Lisbon,
Portugal
13
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte
16, 14482
Potsdam,
Germany
14
Astronomical Institute, Academy of Sciences of the Czech Republic,
Boční II 1401/1a,
141 00
Prague, Czech
Republic
15
Department of Theoretical Physics and Astrophysics, Faculty of
Science, Masaryk University, Kotlářská 2, 611
37
Brno, Czech
Republic
16
Max-Planck-Institut für Astronomie, Heidelberg, Germany
17
Sydney Institute for Astronomy, School of Physics A28,
University of Sydney, Sydney, NSW 2006, Australia
18
Australian Astronomical Observatory, PO BOX 296, Epping, NSW
1710,
Australia
19
Centro de Astrofísica and Faculdade de Ciencias, Universidade do
Porto, Rua das
Estrelas, 4150-762
Porto,
Portugal
Received:
23
July
2013
Accepted:
28
November
2013
We present the largest and most homogeneous catalog of H ii regions and associations compiled so far. The catalog comprises more than 7000 ionized regions, extracted from 306 galaxies observed by the CALIFA survey. We describe the procedures used to detect, select, and analyze the spectroscopic properties of these ionized regions. In the current study we focus on characterizing of the radial gradient of the oxygen abundance in the ionized gas, based on the study of the deprojecteddistribution of H ii regions. We found that all galaxies without clear evidence of an interaction present a common gradient in the oxygen abundance, with a characteristic slope of αO/H = −0.1 dex/re between 0.3 and 2 disk effective radii (re), and a scatter compatible with random fluctuations around this value, when the gradient is normalized to the disk effective radius. The slope is independent of morphology, the incidence of bars, absolute magnitude, or mass. Only those galaxies with evidence of interactions and/or clear merging systems present a significantly shallower gradient, consistent with previous results. The majority of the 94 galaxies with H ii regions detected beyond two disk effective radii present a flattening in the oxygen abundance. The flattening is statistically significant. We cannot provide a conclusive answer regarding the origin of this flattening. However, our results indicate that its origin is most probably related to the secular evolution of galaxies. Finally, we find a drop/truncation of the oxygen abundance in the inner regions for 26 of the galaxies. All of them are non-interacting, mostly unbarred Sb/Sbc galaxies. This feature is associated with a central star-forming ring, which suggests that both features are produced by radial gas flows induced by resonance processes. Our result suggests that galaxy disks grow inside-out, with metal enrichment driven by the local star formation history and with a small variation galaxy-by-galaxy. At a certain galactocentric distance, the oxygen abundance seems to be correlated well with the stellar mass density and total stellar mass of the galaxies, independently of other properties of the galaxies. Other processes, such as radial mixing and inflows/outflows seem to have a limited effect on shaping of the radial distribution of oxygen abundances, although they are not ruled out.
Key words: HII regions / galaxies: ISM / ISM: abundances / galaxies: abundances / galaxies: evolution / galaxies: star formation
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The nebular emission arising from extragalactic objects has played an important role in the new understanding of the Universe and its constituents brought about by the remarkable flow of data over the past few years, thanks to large surveys such as the 2dFGRS (Folkes et al. 1999), SDSS (York et al. 2000), GEMS (Rix et al. 2004), or COSMOS (Scoville et al. 2007), to name a few. Nebular emission lines have historically been the main tool at our disposal for direct measurement of the gas-phase abundance at discrete spatial positions in low-redshift galaxies. They trace the young, massive star component in galaxies, illuminating and ionizing cubic kiloparsec-sized volumes of interstellar medium (ISM). Metals are a fundamental parameter for cooling mechanisms in the intergalactic and ISM and in star formation, stellar physics, and planet formation. Measuring the chemical abundances in individual galaxies and galactic substructures over a wide range of redshifts is a crucial step toward understanding the chemical evolution and nucleosynthesis at different epochs, since the chemical abundance pattern traces the evolution of past and current stellar generations. This evolution is dictated by a complex set of parameters, including the local initial gas composition, star formation history (SFH), gas infall and outflows, radial transport and mixing of gas within disks, stellar yields, and the initial mass function (IMF). The details of these complex mechanisms are still not well established observationally, nor are they well developed theoretically, which hinders our understanding of galaxy evolution from the early Universe to the present day.
Previous spectroscopic studies have unveiled some aspects of the complex processes in play between the chemical abundances of galaxies and their physical properties. These studies have been successful in determining important relationships, scaling laws and systematic patterns: e.g., (i) luminosity-metallicity, mass-metallicity, and surface brightness vs. metallicity relations (Lequeux et al. 1979; Skillman 1989; Vila-Costas & Edmunds 1992; Zaritsky et al. 1994; Tremonti et al. 2004); (ii) effective yield vs. luminosity and circular velocity relations (Garnett 2002); (iii) abundance gradients and the effective radius of disks (Diaz 1989) systematic differences in the gas-phase abundance gradients between normal and barred spirals (Zaritsky et al. 1994; Martin & Roy 1994); and (iv) characteristic vs. integrated abundances (Moustakas & Kennicutt 2006). However, these results are limited by statistics, either in the number of observed H ii regions or in the coverage of these regions across the galaxy surface.
The advent of multi-object spectrometers and integral field spectroscopy (IFS) instruments with large fields of view now offers us the opportunity to undertake a new generation of emission-line surveys, based on samples of hundreds of H ii regions and full two-dimensional (2D) coverage of the disks of nearby spiral galaxies. In the past few years, we started a major observational program to understand the statistical properties of H ii regions and to unveil the nature of the reported physical relations, using IFS. This program was initiated with the PINGS survey (Rosales-Ortega et al. 2010), which acquired IFS mosaic data for a number of medium-sized nearby galaxies. We then continued the acquisition of IFS data for a larger sample of visually classified face-on spiral galaxies (Mármol-Queraltó et al. 2011) as part of the feasibility studies for the CALIFA survey (Sánchez et al. 2012a).
In Sánchez et al. (2012b) we presented a new method of detecting, segregating and extracting the main spectroscopic properties of H ii regions from IFS data (HIIexplorer1). Using this tool, we built the largest and homogenous catalog of H ii regions for the nearby Universe. This catalog has allowed us to establish a new scaling relation between the local stellar mass density and oxygen abundance, the so-called Σ–Z relation (Rosales-Ortega et al. 2012), and to explore the galactocentric gradient of the oxygen abundance (Sánchez et al. 2012b). We confirmed that up to ~2 disk effective radii, there is a negative gradient of the oxygen abundance in all the analyzed spiral galaxies. This result agrees with models based on the standard inside-out scenario of disk formation, which predict a relatively quick self enrichment with oxygen abundances and an almost universal negative metallicity gradient once this is normalized to the galaxy optical size (Boissier & Prantzos 1999, 2000). Indeed, the measured gradients present a very similar slope for all the galaxies (~−0.12 dex/re), when the radial distances are measured in units of the disk effective radii. We found no difference in the slope for galaxies of different morphological types: early/late spirals, barred/unbarred or grand-design/flocculent.
Beyond ~2 disk effective radii our data show evidence of a flattening in the abundance, consistent with several other spectroscopic explorations, based mostly on single objects (e.g., Bresolin et al. 2009; Yoachim et al. 2010; Rosales-Ortega et al. 2011; Marino et al. 2012; Bresolin et al. 2012). The same pattern in the abundance has been described in the case of the extended UV disks discovered by GALEX (Gil de Paz et al. 2005; Thilker et al. 2007), which show oxygen abundances that are rarely below one-tenth of the solar value. Additional results, based on the metallicity gradient of the outer disk of NGC 300 from single-star CMD analysis (Vlajić et al. 2009) support the presence of a flatter gradient toward the outer disks of spiral galaxies. In the case of the Milky Way (MW), studies using open clusters (e.g., Bragaglia et al. 2008; Magrini et al. 2009; Yong et al. 2012; Pedicelli et al. 2009), Cepheids (e.g., Andrievsky et al. 2002, 2004; Luck et al. 2003; Lemasle et al. 2008), H ii regions (e.g., Vilchez & Esteban 1996; Esteban et al. 2013), PNe (e.g., Costa et al. 2004), and a combination of different tracers (e.g., Maciel & Costa 2009) also report a flattening of the gradient in the outskirts of the Milky Way, somewhere between 10 and 14 kpc2. Despite all these results, the outermost parts of the disk have not been explored properly, either owing to the limited number of objects considered in the previous studies or to the limited spatial coverage (e.g., Sánchez et al. 2012b).
The search for an explanation of the existence of radial gradients of abundances (and the G-dwarf metallicity distribution in MW) was the reason for the early development of chemical evolution models as well as the classical closed box model (CBM). The pure CBM, which relates the metallicity or abundance of a region to its amount of gas, independently of the star formation or evolutionary history, was unable to explain the radial abundance gradient observed in our Galaxy and in other spirals. Therefore infall or outflows of gas in the MW were considered necessary to fit the data. In fact, as explained by Goetz & Koeppen (1992), there are only four possible ways to create a radial abundance gradient: 1) a radial variation of the IMF; 2) a variation of the stellar yields with galactocentric radius; 3) a star formation rate (SFR) that changes with the radius; 4) a gas infall rate that varies with radius. The first possibility is not usually considered as probable, and the second one is already included in modern models that adopt metallicity dependent stellar yields. Thus, from the seminal works of Lacey & Fall (1985), Guesten & Mezger (1982) and Clayton (1987), most of numerical chemical evolution models (e.g., Diaz & Tosi 1984; Matteucci & Francois 1989; Ferrini et al. 1992; Carigi 1994; Prantzos & Aubert 1995; Molla et al. 1996; Chiappini et al. 1997; Boissier & Prantzos 1999) explain the existence of the radial gradient of abundances by the combined effects of a SFR and an infall of gas, both varying with galactocentric radius of galaxies. In most recent times chemical evolution has been included in modern cosmological simulation codes, which already obtain spiral disks as observed, finding radial gradients of abundances that reproduce the data (Pilkington et al. 2012). It has been demonstrated (Gibson et al. 2013) that the existence and evolution of these radial gradients is, as expected, very dependent on the star formation and infall prescriptions included in the simulations.
To characterize the properties of the ISM in the Local Universe and their relations with the evolution of galaxies, we applied the previously described procedure to the IFS data provided by the CALIFA survey (Sánchez et al. 2012a)3. CALIFA is an ongoing exploration of the spatially resolved spectroscopic properties of galaxies in the Local Universe (z < 0.03) using wide-field IFS to cover the full optical extent (up to ~3–4 re) of ~600 galaxies of any morphological type, distributed across the entire color–magnitude diagram (Walcher et al., in prep.), and sampling the wavelength range 3650–7500 Å. So far, the survey has completed ~1/2 of its observations, with 306 galaxies observed (May 2013), and the first data release, comprising 100 galaxies, was delivered in November 2012 (Husemann et al. 2013).
In Sanchez et al. (2013) we presented the first results based on the catalog of H ii regions extracted from these galaxies. We studied the dependence of the ℳ–Z relation on the SFR, finding no secondary relation different from the one induced by the well known relation between the star formation and the mass. We confirmed the local Σ–Z relation unveiled by Rosales-Ortega et al. (2011), with a larger statistical sample of H ii regions.
In the current study we use the updated CALIFA catalog of H ii regions to study the radial oxygen abundance gradient up to 3–4 disk effective radii, well beyond the proposed break/flattening. The layout of this article is as follows. In Sect. 2 we summarize the main properties of the sample and data used in this study; in Sect. 3 we describe the analysis required to detect the individual clumpy ionized regions and aggregations, and to extract their spectroscopic properties, in particular the emission line ratios required to determine the abundance. The criteria to select the H ii region are explained in 3.3; the derivation of the abundance gradient for each galaxy is described in Sect. 4.1; in Sect. 4.2 we explore the dependence of the slope of these gradients with different morphological and structural properties of the galaxies; in Sect. 5.1 we describe the properties of the common gradient of the oxygen abundance for all disk galaxies up to ~2 re, and the presence of a flattening beyond this radius. The drop of the abundance for some particular galaxies is shown in Sect. 5.3. Finally, the main conclusions of this study are discussed in Sect. 6.
2. Sample of galaxies and dataset
The galaxies were selected from the CALIFA observed sample. Since CALIFA is an ongoing survey, whose observations are scheduled on a monthly basis (i.e., dark nights), the list of objects increases regularly. The current results are based on the 306 galaxies observed before May 2013, which is half of the foreseen 600 galaxies to be observed at the end of the survey. Figure 1 shows the distribution of the current sample along the color–magnitude diagram, indicating with different symbols indicating galaxies of different concentration index C (defined to be the ratio C = R90/R50, where R90 and R50 are the radii enclosing 90% and 50% of the Petrosian r-band luminosity of the galaxy; i.e., a proxy of the morphological type). The current sample covers all the color–magnitude diagram, up to Mz < −17 mag, with at least three targets per bin of about one magnitude and color (~10 galaxies on average) including galaxies of any morphological type. The CALIFA mother sample becomes incomplete below Mr > −19 mag, which corresponds to a stellar mass of ~109.5M⊙ for a Chabrier IMF. Below this mass the sample is not representative of the population of galaxies in the local universe. This corresponds to the range of masses covered by dwarf galaxies. Above this luminosity, the sample is representative of the total population at the selected redshift range (0.005 < z < 0.03) and in principle it is representative of galaxies at the Local Universe.
 |
Fig. 1 Distribution of the currently observed CALIFA galaxies in the u − z vs. Mz color–magnitude diagram. Different colors and symbols represent a classification into spheroid- and disk-dominated galaxies as well as intermediate cases, as suggested by the concentration index C (see Sect. 2 for definition). For comparison, the contours delineate the number density distribution of galaxies in the SDSS-NYU catalogue (e.g., Blanton et al. 2005). The small dots indicate the remaining objects in the CALIFA mother sample, not observed so far. |
The details of the survey, sample, observational strategy, and reduction are explained in Sánchez et al. (2012a). All galaxies were observed using PMAS (Roth et al. 2005) in the PPAK configuration (Kelz et al. 2006), covering a hexagonal field-of-view (FoV) of 74″× 64″, sufficient to map the full optical extent of the galaxies up to two to three disk effective radii. This is possible because of the diameter selection of the sample (Walcher et al., in prep.). The observing strategy guarantees a complete coverage of the FoV, with a final spatial resolution of FWHM ~ 3″, corresponding to ~1 kpc at the average redshift of the survey. The sampled wavelength range and spectroscopic resolution (3745–7500 Å, λ/Δλ ~ 850, for the low-resolution setup) are more than sufficient to explore the most prominent ionized gas emission lines, from [OII]λ3727 to [SII]λ6731, on one hand, and to deblend and subtract the underlying stellar population, on the other (e.g., Sánchez et al. 2012a; Kehrig et al. 2012; Cid Fernandes et al. 2013). The dataset was reduced using version 1.3c of the CALIFA pipeline, whose modifications with respect to the one presented in Sánchez et al. (2012a) are described in detail in Husemann et al. (2013). In summary, the data fulfill the predicted quality-control requirements with a spectrophotometric accuracy that is better than 15% everywhere within the wavelength range, both absolute and relative with a depth that allows us to detect emission lines in individual H ii regions as weak as ~10-17erg s-1 cm-2, and with a signal-to-noise ratio of S/N ~ 3–5. For the emission lines considered in the current study, the S/N is well above this limit, and the measurement errors are negligible in most of the cases. In either case, they have been propagated and included in the final error budget.
The final product of the data reduction is a regular-grid datacube, with x and y coordinates that indicate the right ascension and declination of the target and z a common step in wavelength. The CALIFA pipeline also provides the propagated error cube, a proper mask cube of bad pixels, and a prescription of how to handle the errors when performing spatial binning (due to covariance between adjacent pixels after image reconstruction). These datacubes, together with the ancillary data described in Walcher et al. (in prep.), are the basic starting points of our analysis.
The observing strategy of the CALIFA survey guarantees that the main properties of the observed sample are compatible with those of the mother sample in terms of luminosities, sizes, morphologies, and colors (Sánchez et al. 2012a; Husemann et al. 2013). Particular care was taken to not introduce any potential observational bias, since the targets are selected in a pseudo-random way based only on the visibility from the observatory on a monthly basis (i.e., dark time). In Walcher et al. (in prep.), we will describe the main properties of the CALIFA mother sample.
 |
Fig. 2 IFS-based Hα maps, in units of (log 10) 10-16 erg s-1 cm-2 arcsec-2, derived for two representative galaxies of the sample, together with the detected H ii regions shown as black segmented contours. |
In summary we can claim that with the adopted selection criteria our sample does not under-represent any kind of galaxy in the Local Universe in any observable within our 95% completeness range (−23 < Mr,SDSS < −19 mag). Obviously our results are restricted to this particular range and therefore cannot be applied to either dwarf or giant elliptical galaxies, which are under-represented or absent in our sample.
3. Analysis
The main goals of this study are to characterize the abundance gradient in galaxies and to determine whether there are any common patterns or differences depending on their individual properties. Ionized gas abundances have been well calibrated on the basis of strong-line indicators for ionized regions associated with star formation processes, i.e., the classical H ii regions. In this section we describe how we have selected those regions, extract and analyze their individual spectra, derive the corresponding oxygen abundance, and finally, analyze their radial gradient.
3.1. Detection of ionized regions
The segregation of H ii regions and the extraction of the corresponding spectra is performed using a semi-automatic procedure named HIIexplorer4. The procedure is based on some basic assumptions: (a) H ii regions are peaky and isolated structures with a strong ionized gas emission, which is significantly above the stellar continuum emission and the average ionized gas emission across the galaxy. This is particularly true for Hα because (b) H ii regions have a typical physical size of about a hundred or a few hundred parsecs (e.g., González Delgado & Perez 1997; Lopez et al. 2011; Oey et al. 2003), which corresponds to a typical projected size of a few arcsec at the distance of the galaxies.
These basic assumptions are based on the fact that most of the Hα luminosity observed in spiral and irregular galaxies is a direct tracer of the ionization of the ISM by the ultraviolet (UV) radiation produced by young high-mass OB stars. Since only high-mass, short-lived stars contribute significantly to the integrated ionizing flux, this luminosity is a direct tracer of the current SFR, independent of the previous SFH. Therefore, clumpy structures detected in the Hα intensity maps are most probably associated with classical H ii regions (i.e., those regions for which the oxygen abundances have been calibrated).
The details of HIIexplorer are given in Sánchez et al. (2012b) and Rosales-Ortega et al. (2012). We present here the basic steps in the overall process. (i) First, we create a narrow-band image of 120 Å width, centered on the wavelength of Hα shifted at the redshift of each target. The image was created by co-adding the flux within the described spectral window for each spaxel of the velocity-field corrected datacube. Then, the image is properly corrected for the underlying adjacent continuum. (ii) This image is used as an input for the automatic H ii region detection algorithm included in HIIexplorer. In this particular case, the algorithm iteratively detects the peak intensity emission above a threshold of 4 × 10-17 erg s-1 cm-2 arcsec-1, and then assigns all the adjacent pixels up to a distance of 3.5″, with a flux within a 10% of the peak intensity (Ipixel > 0.9 × Ipeak) and above a limiting flux intensity of 1 ×10-17 erg s-1 cm-2 arcsec-1 into the corresponding area. Once the first region is detected and segregated, the corresponding area is masked from the input image, and the procedure is repeated until there are no additional regions to be selected. The remaining pixels are assigned to a residual region that is assumed to be dominated by diffuse emission. The result is a segmentation map that segregates each detected cumpy ionized structure. Finally, (iii) the integrated spectra corresponding to each segmented region is extracted from the original datacube, and the corresponding position table of the detected H ii is provided. If the object was has been observed in both the low-resolution and high-resolution modes (Sánchez et al. 2012a), both corresponding spectra were extracted.
Figure 2 illustrates the process, showing the Hα intensity maps and the corresponding segmentations for two objects: (1) UGC 00312, an intermediate-to-high inclined (~70 degrees), not very massive (~0.7 × 1010M⊙) and almost bulge-less spiral galaxy, and (2) NGC 7716, a low inclination (<40 degrees), massive (~2 × 1010 M⊙) spiral, with a clear bulge. These two galaxies illustrate why we cover up to four to five disk effective radii for highly inclined galaxies (mostly along the semi-minor axis), while we cover just half of this size for mostly face-on ones, although both galaxies were diameter selected (Sánchez et al. 2012a). The galaxies analyzed in Sánchez et al. (2012b), are more like to the second type, and therefore the region beyond ~2 effective radii was mostly left unexplored.
A total of 7016 individual clumpy ionized regions are detected in a total of 227 galaxies from the sample, i.e., ~30 H ii regions per galaxy. This does not mean that on averarage there is no ionized gas in the remaining 79 galaxies. Recent results indicate that it is possible to detect low-intensity (and in most cases low-ionization) gas in all the analyzed CALIFA galaxies (Kehrig et al. 2012; Papaderos et al. 2013; Singh et al. 2013). As discussed in Papaderos et al. (2013), and in line with a substantial body of previous works (Sarzi et al. 2010; Annibali et al. 2010; Yan & Blanton 2012; Kehrig et al. 2012, among others), various lines of evidence suggest that photoionization by post-AGB stars appears to be the main driver of extended nebular emission in these systems, with non-thermal sources being potentially important only in their nuclei. The observational evidence behind this conclusion is that the nebular emission is not confined only to the nuclear regions but is extended out to r ~ 2–4 r50, i.e. it is co-spatial with the post-AGB stellar background. In most of these cases EW(Hα) typically is ~1 Å. In other cases the ionized gas does not present clear clumpy structures, required to associate them with star-forming/H ii regions. This is the case of the shock ionized regions detected in the MICE galaxies (Wild et al. 2014). Since most of this ionization is not associated with young massive stars and therefore the associated abundances are not well calibrated, it is not relevant for the present analysis.
3.2. Measurement of the emission lines
To extract the nebular physical information of each individual H ii region, the underlying stellar continuum must be decoupled from the emission lines for each of the analyzed spectra. Several different tools have been developed to model the underlying stellar population, effectively decoupling it from the emission lines (e.g., Cappellari & Emsellem 2004; Cid Fernandes et al. 2005; Ocvirk et al. 2006; Sarzi et al. 2006; Sánchez et al. 2006; Koleva et al. 2009; MacArthur et al. 2009; Walcher et al. 2011). Most of these tools are based on the same principles, i.e., they assume that the stellar emission is the result of the combination of different (or a single) simple stellar populations (SSP), or the result of a particular SFH, whose corresponding emission-line spectrum is redshifted due to a certain systemic velocity, broadened and smoothed by the effect of a certain velocity dispersion, and attenuated by a certain dust content.
We performed a simple modeling of the continuum emission using FIT3D5, a fitting package described in Sánchez et al. (2006) and Sánchez et al. (2011). A simple SSP template grid with 12 individual populations was adopted. It comprises four stellar ages (0.09, 0.45, 1.00, and 17.78 Gyr), two young and two old ones, and three metallicities (0.0004, 0.019, and 0.03), subsolar, solar, or supersolar. The models were extracted from the SSP template library provided by the MILES project (Vazdekis et al. 2010; Falcón-Barroso et al. 2011). The use of different stellar ages and metallicities or a larger set of templates does not qualitatively affect the derived quantities that describe the stellar populations. Even more, it does not quantitatively affect the estimations of the properties of the emission lines.
The analysis of the underlying stellar population is not as detailed as the one presented by Cid Fernandes et al. (2013), and it is not useful to reconstruct the SFH. However, since the spatial binning required to define these regions is based on the Hα intensity, in many cases the extracted spectra of the underlying stellar continuum do not reach the required S/N to perform a more detailed analysis. We prefer to restrict our stellar fitting to a reduced template library with few stellar populations and derive simple conclusions, such as the portion of young or old stars that contribute to the total luminosity. Therefore, we will not pay too much attention to the actual decomposition in different populations.
Throughout, we adopted the Cardelli et al. (1989) law for the stellar dust attenuation with an specific attenuation of RV = 3.1, assuming a simple screen distribution. The use of different laws like the one proposed by Calzetti (2001) does not produce significant differences in the modeling of the underlying stellar population in the wavelength range considered. A different amount of extinction, which is parametrized by the extinction in the V-band (AV), was considered for each stellar population. We consider that this is more realistic than assuming the same attenuation for all the stellar populations, since the distribution of the dust grains is not homogeneous, and it affects the old and young stellar populations in different ways.
Individual emission line fluxes were measured using FIT3D in the stellar-population subtracted spectra performing a multicomponent fitting using a single Gaussian function. When more than one emission line was fitted simultaneously (e.g., for doublets and triplets like the [N ii] lines), the systemic velocity and velocity dispersion were forced to be equal, in order to decrease the number of free parameters and increase the accuracy of the deblending process. The ratio between the two [N ii] lines included in the spectral range were fixed to the theoretical value (Osterbrock & Ferland 2006). By adopting this procedure it is possible to accurately deblend the different emission lines. A similar procedure was applied to the rest of the lines, which were fitted simultaneously (e.g., Hβ and [O iii]). The measured lines include all lines employed in determining of metallicity using strong-line methods, i.e Hα, Hβ, [O ii] λ3727, [O iii] λ4959, [O iii] λ5007, [N ii] λ6548, [N ii] λ6583, [S ii] λ6717, and [S ii] λ6731. Additionally, for those H ii regions with high S/N we were able to detect and measure intrinsically fainter lines such as [Ne III] λ3869, Hϵλ3970, Hδλ4101, Hγλ4340, He I λ5876, [O I] λ6300, and He I λ6678, although they have not been considered for the present study. FIT3D provides the intensity, equivalent width, systemic velocity and velocity dispersion for each emission line. The statistical uncertainties in the measurements were calculated by propagating the error associated with the multicomponent fitting and considering the S/N of the spectral region. By subtracting a stellar continuum model derived with a set of SSP templates, we are already correcting for the effect of underlying stellar absorption, which is particularly important in Balmer lines (such as Hβ). We performed a series of sanity tests based on the Hα/Hβ ratio to ensure that no overcorrection was done on the absorption stellar features.
We note that FIT3D fits the underlying stellar population and the emission lines together. Therefore, in addition to the parameters derived for the emission lines, the fitting algorithm provides us with a set of parameters that describe the physical components of the stellar populations. In particular, it provides the percentage of light that contributes to the continuum at 5000 Å corresponding to an old (>500 Myr, fo) or young (<500 Myr, fy) stellar population (which we consider a reliable parameter for our current stellar analysis).
 |
Fig. 3 Left panel: absolute value of the equivalent width of Hα, on a logarithmic scale, plotted against the portion of young stars in the underlying stellar population (according to the SSP modeling by FIT3D ) for the clumpy ionized regions selected with HIIexplorer. Right panel: similar distribution of the emission equivalent width of Hα, on a logarithmic scale, as a function of the luminosity portion of young stars in the underlying stellar population for the ~500 000 individual spaxels with Hα emission detected in the 306 analyzed datacubes. In both panels, the dashed horizontal line shows the demarcation limit of the EW of Hα proposed by Cid Fernandes et al. (2010) to distinguish between strong (star formation and/or AGNs) and weak (e.g., post-AGBs) ionization sources. The vertical solid line shows the currently adopted selection criteria for the H ii regions. |
 |
Fig. 4 Left panel: [O iii] λ5007/Hβ vs. [N ii] λ6583/Hα diagnostic diagram for the ~7000 ionized regions described in the text. The contours show the density distribution of these regions with the diagram plane, with the outermost contour enclosing 95% of the regions, and each consecutive one enclosing 20% less regions. The color indicates the portion of young stellar populations in the underlying continuum. Central panel: same diagnostic diagram, restricted to those ionized regions with less than a 20% of young stellar population (~1800 regions). Right panel: same diagnostic diagram, restricted to those ionized regions with more than a 20% of young stellar population (~5800 regions). In all the panels, the solid and dashed lines represent the Kauffmann et al. (2003) and Kewley et al. (2001) demarcation curves, respectively. They are usually invoked to distinguish between classical star-forming objects (below the solid line), and AGN powered sources (above the dashed line). Regions between both lines are considered intermediate ones. |
3.3. Selection of the HII regions
Classical H ii regions are gas clouds ionized by short-lived hot OB stars, associated with ongoing star formation. They are frequently selected on the basis of demarcation lines defined in the so-called diagnostic diagrams (e.g., Baldwin et al. 1981; Veilleux & Osterbrock 1987), which compare different line ratios, such as [OIII]/Hβ vs. [NII]/Hα, [OIII]/Hβ vs. [OII]/Hα, [NII]/Hα vs. [SII]/Hα or [NII]/Hα vs. [SII]/Hα. In most cases these ratios distingusih well between strong ionization sources, such as classical H ii regions and powerful AGNs (e.g., Baldwin et al. 1981). However, they are less accurate in distinguishing between low-ionization sources, such as weak AGNs, shocks or post-AGBs stars (e.g., Cid Fernandes et al. 2011; Kehrig et al. 2012). Alternative methods, based on a combination of the classical line ratios with additional information regarding the underlying stellar population have been proposed. For example, Cid Fernandes et al. (2011) propose using EW(Hα) to distinguish between retired (non star-forming) galaxies, weak AGNs, and star-forming galaxies.
The most common diagnostic diagram in the literature for the optical regime is the one that makes use of easily observed strong lines that are less affected by dust attenuation, i.e., [O iii]/Hβ vs. [N ii]/Hα (Baldwin et al. 1981). We refer hereafter to this diagnostic diagram as the BPT diagram. Different demarcation lines have been proposed for this diagram. The most popular ones are the Kauffmann et al. (2003) and Kewley et al. (2001) curves. They are usually invoked to distinguish between star-forming regions (below the Kauffmann et al. 2013 curve) and AGNs (above the Kewley et al. 2001 curve). The location between both curves is normally assigned to a mixture of different sources of ionization. Additional demarcation lines have been proposed for the region above the Kewley et al. (2001) curve to segregate between Seyfert and LINERs (e.g., Kewley et al. 2006).
Despite its benefits, this clean segregation for classification purposes may introduce biases when applied in order to select H ii regions. The Kewley et al. (2001) curve was derived on the basis of photoionization models. It corresponds to the maximum envelope in the considered plane for ionization produced by hot stars. Therefore, to the extent that these models are realistic enough, any combination of line ratios below this curve can be produced entirely by OB star photoionization. Finally, it defines all the area above it as unreachable by ionization associated with star formation. The Kauffmann et al. (2003) curve has a completely different origin. It is an empirical envelope defined to segregate star-forming galaxies and the so-called AGN branch in the BPT diagram based on the analysis of the emission lines for the SDSS galaxies. It describes the envelope of classical H ii regions found in the disks of spiral galaxies well. However, it is known that certain H ii regions can be found above this demarcation line, as shown below.
Kennicutt et al. (1989) first recognized that H ii regions in the center of galaxies distinguish themselves spectroscopically from those in the disk by their stronger low-ionization forbidden emission. The nature of this difference was not clear. It may be due to contamination by an extra source of ionization, such as diffuse emission or the presence of an AGN. However, other stellar processes, such as nitrogen enhancement due to a natural aging process of H ii regions and the surrounding ISM, can produce the same effect. These early results were confirmed by Ho et al. (1997), who demonstrated that inner star-forming regions may populate the right branch of the BPT diagram at a location above the demarcation line defined later by Kauffmann et al. (2003). However, we have found that these H ii regions are not restricted to the central regions and can be found at any galactocentric distance, even at more than 2 re (Sect. 5.1), which excludes any contamination by a central source of ionization. The nature of these H ii regions will be addressed in detail elsewhere. For the purpose of the current study it is important to define a selection criterion that does not exclude them.
Therefore, selecting H ii regions based on the Kauffmann et al. (2003) curve may bias our sample toward classical disk regions, excluding an interesting population of these objects. On the other hand it does not guarantee the exclusion of other sources of non stellar ionization that can populate this area, such as shocks (e.g., Allen et al. 2008; Levesque et al. 2010), post-AGB stars (e.g., Kehrig et al. 2012), and dusty AGNs (e.g., Groves et al. 2004). Following Cid Fernandes et al. (2010, 2011), we consider that an alternative method for distinguishing between different sources of ionization is to compare the properties of the ionized gas with those of the underlying stellar population.
We adopted a different selection criterion, using the relative contribution of young stars to the total luminosity (fy) provided by the multi-SSP analysis of the underlying stellar population, as a proxy for the star formation activity. For star-forming regions this parameter provides similar information to the EW(Hα). The lefthand panel of Fig. 3 shows the distribution of EW(Hα) against the percentage of young stars for the ~7000 clumpy ionized regions selected by HIIexplorer. For those regions with EW(Hα) > 6 Å, or with a percentage of young stars over 20%, both parameters present a strong log-linear correlation (rcorr = 0.95). The righthand panel of Fig. 3 shows the same distribution for the ~500 000 spaxels with detected Hα emission. This distribution presents the same trend as described above, but with an evident tail toward lower EW(Hα) values and a lower percentage of young stars.
The threshold imposed by HIIexplorer in the surface brightness of Hα and the requirement that the ionization is clumpy efficiently removes most of the ionization corresponding to the weak emission lines described. This is mostly diffuse emission, which peaks in the described diagram at EW(Hα) ~ 1–2 Å and fy ~ 5–10%. For early-type galaxies, this weak EW(Hα) is mostly by post-AGB stars (e.g., Kehrig et al. 2012; Papaderos et al. 2013), and therefore no correlation is expected between its intensity and the percentage of young stars (as explained in Sect. 3.1). On the other hand, high EW(Hα) could be produced by other mechanisms, such as AGNs and shocks, that are in principle not required to be correlated with the properties of the underlying stellar population. A cut in the EW(Hα) cannot remove those regions. Therefore, we consider that the percentage of young stars provides, in connection with the aforementioned spectroscopic classification criteria, a robust and physically motivated method to select genuine H ii regions.
The lefthand panel of Fig. 4 shows the distribution of the ionized regions across the BPT diagram, with contours indicating the density of regions at each location. The outermost contours encloses 95% of the detected regions, with each consecutive one encircling fewer regions. This contour is located below the Kewley et al. (2001) demarcation curve, which indicates that the ionization of our selected clumpy regions is already dominated by star formation. In fact, only ~2% of all regions are located above the Kewley et al. (2001) line, and ~80% are below the Kauffmann et al. (2003) line (i.e., where classical disk H ii regions are located). If we had adopted the latter demarcation curve as our selection criteria, we would have missed a significant number of regions.
The color code in Fig 4 indicates the average percentage of young stars at each location (i.e., the x-axis in Fig. 3), ranging from nearly 100% for the regions in the top left area of the diagram, to nearly 0% for regions at the top right location. There is a clear gradient/correlation between the percentage of young stars and the [N ii]/Hα ratio, reflecting the known downsizing-like variation in the specific SFR along the SF branch of the BPT diagram (Asari et al. 2007).
Based on these results, we classified as H ii regions those clumpy ionized regions for which young stars (<500 yr) contribute at least a 20% to the flux in the V-band. This particular percentage is the lowest for which the correlation coefficient between fy and the EW(Hα) is still higher than rcorr > 0.95 and for which the percentage of excluded regions is not higher than the one that would be excluded by adopting the more common Kauffmann et al. (2003) curve. The central panel of Fig. 4 shows the same distribution as the one shown in the lefthand panel, but restricted to the 1787 regions for which the percentage of young stars is lower than 20%. The percentage of regions above the Kewley et al. (2001) curve is significantly larger (~7%), more than a 40% above the Kauffmann et al. (2003) one. Although there are still 1043 regions below this curve, it comprises just ~15% of the original sample. This can be considered our incompleteness fraction. Although we cannot exclude that some fraction of these regions are ionized by star formation, we cannot guarantee it.
Figure 4, right panel shows the same distribution, but for the 5229 regions with a percentage of young stars over 20%, i.e., our final sample of H ii regions. Of them, only 23 are above the Kewley et al. (2001) curve (~99.5% are below it). On the other hand, there are 713 regions in the so-called intermediate region, with a significant percentage of young stars (~40% on average). These regions would have been excluded if we had adopted the Kauffmann et al. (2003) curve as our selection criteria, and we would have lost a certain number of H ii regions at any galactocentric distance. We consider that the adopted combined selection criteria are more physically driven and conservative, since they select only those regions that are associated with an underlying stellar population indicative of the presence of young stars.
 |
Fig. 5 Radial distribution of the oxygen abundance derived for the individual H ii regions with abundance errors below 0.15 dex, as a function of the deprojected galactocentric distance (i.e., corrected for inclination), normalized to the disk effective radius, for the galaxies presented in Fig. 2. The size of the symbols is proportional to the Hα intensity. The red circles represent those H ii regions below the Kauffmann et al. (2003) line, and the orange squares represent those above this curve and below the Kewley et al. (2001) demarcation lines, i.e., the regions in the so-called intermediate zone in the BPT diagram. The solid and dashed lines show the best linear regression and error-weighted linear fit derived for those values between 0.3 and 2.1 re. The results from the second fit are shown in the figure, including the zero point (a), slope (b), and correlation coefficient (r). |
4. Results
4.1. Oxygen abundance gradients
To derive the oxygen abundance for each of the selected ~5000 H ii regions, we adopted the
empirical calibrator based on the O3N2 ratio (Alloin et al.
1979; Pettini & Pagel 2004; Stasińska et al. 2006):
![\begin{eqnarray} {\rm O3N2} &=& {\rm log_{\rm 10} } \left[ \frac{I([\ion{O}{iii}]~\lambda5007)/I({\rm H}\beta)}{I([\ion{N}{ii}]~\lambda6584)/I({\rm H}\alpha)} \right] \cdot \end{eqnarray}](/articles/aa/full_html/2014/03/aa22343-13/aa22343-13-eq63.png) (1)This
ratio is basically not affected by the effects of dust attenuation, it uses emission lines
covered by our wavelength range for all the galaxies in the sample, and it shows a
monotonic single-valued behavior in its range of applicability. We adopted the functional
form and calibration by Pettini & Pagel
(2004), although its correspondence with temperature-anchored abundances at the
high-metallicity range is still under debate (Marino et
al. 2013). In that article we demonstrate that the indicator is valid for a range
of line ratios between −1.1 < O3N2 < 1.7,
which corresponds to oxygen abundances above 12 + log(O/H)> 8 dex. In our
sample of H ii regions, we do not reach the low metallicity limit for which the
calibration is still useful, most probably because we do not include low-mass/dwarf
galaxies in the considered sample of galaxies. In this regime the derived abundances have
an accuracy of ±0.08 dex,
which is an uncertainty that has been included in the error budget. The typical error
derived from the pure propagation of the errors in the measured emission lines is about
0.05 dex, although in a few cases is can be larger.
(1)This
ratio is basically not affected by the effects of dust attenuation, it uses emission lines
covered by our wavelength range for all the galaxies in the sample, and it shows a
monotonic single-valued behavior in its range of applicability. We adopted the functional
form and calibration by Pettini & Pagel
(2004), although its correspondence with temperature-anchored abundances at the
high-metallicity range is still under debate (Marino et
al. 2013). In that article we demonstrate that the indicator is valid for a range
of line ratios between −1.1 < O3N2 < 1.7,
which corresponds to oxygen abundances above 12 + log(O/H)> 8 dex. In our
sample of H ii regions, we do not reach the low metallicity limit for which the
calibration is still useful, most probably because we do not include low-mass/dwarf
galaxies in the considered sample of galaxies. In this regime the derived abundances have
an accuracy of ±0.08 dex,
which is an uncertainty that has been included in the error budget. The typical error
derived from the pure propagation of the errors in the measured emission lines is about
0.05 dex, although in a few cases is can be larger.
It is beyond the scope of the current study to make a detailed comparison of the oxygen abundances derived using the different proposed methods, such as was presented by Kewley & Ellison (2008) or López-Sánchez et al. (2012). However, we want to state clearly that all our qualitative results and most of the quantitive ones are mostly independent of the adopted oxygen abundance calibrator; i.e., despite the absolute scale among the different indicators and the differences introduced by them in the galaxy slopes, the abundance gradients statistically show the same relationships with respect to global galaxy properties, as explained below.
 |
Fig. 6 Left panel: distribution of correlation coefficients of the oxygen abundance along the radial distance, for the 193 galaxies described in the text. Central panel: distribution of zero points for the corresponding linear regression galaxy by galaxy. Right panel: distribution of slopes of the same regressions. The orange solid line represents, for each of the last two histograms, the expected histogram in case of a Gaussian distribution of the data, assuming the mean and standard-deviation of the distribution of each analyzed parameter and sampled with the same bins. |
We derive the galactocentric radial distribution of the oxygen abundance for each galaxy,
based on the abundances measured for each individual H ii region. In Appendix
A we describe the surface-brightness and
morphological analysis performed for each galaxy to derive the mean position angle,
ellipticity, and effective radius of the disk. Using this information we deprojected the
position of each H ii region for each galaxy, assuming an intrinsic ellipticity
for galaxies of q = 0.13 (Giovanelli
et al. 1995, 1997), and an inclination
given by 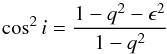 (2)where
i is the
inclination of the galaxy, and ϵ the median ellipticity provided by the
morphological analysis, defined for each galactocentric distance as
(2)where
i is the
inclination of the galaxy, and ϵ the median ellipticity provided by the
morphological analysis, defined for each galactocentric distance as
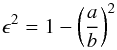 (3)where
a and
b are the
semi-major and semi-minor axes. For galaxies with an inclination below 35° we prefer not to correct for
the inclination effects of the uncertainties in the derived correction and for the very
small effect on the spatial distribution of H ii regions. We derive the
galactocentric distance for each region, which is later normalized to the disk effective
radius (re). This disk effective radius was
derived from the scalelength of the disk of each galaxy, extracted from the analysis of
the surface brightness profile in the g-band as detailed in Appendix A. For disk-dominated galaxies this effective radius is similar to the
classical effective radius, which can be derived by a pure growth curve for the full light
distribution of the galaxy. However, for galaxies with a clear bulge, it represents the
characteristic scale of only the disk part. The center of the galaxy was taken from the
WCS of the cube headers, and it was derived by a barycenter estimation described in Husemann et al. (2013).
(3)where
a and
b are the
semi-major and semi-minor axes. For galaxies with an inclination below 35° we prefer not to correct for
the inclination effects of the uncertainties in the derived correction and for the very
small effect on the spatial distribution of H ii regions. We derive the
galactocentric distance for each region, which is later normalized to the disk effective
radius (re). This disk effective radius was
derived from the scalelength of the disk of each galaxy, extracted from the analysis of
the surface brightness profile in the g-band as detailed in Appendix A. For disk-dominated galaxies this effective radius is similar to the
classical effective radius, which can be derived by a pure growth curve for the full light
distribution of the galaxy. However, for galaxies with a clear bulge, it represents the
characteristic scale of only the disk part. The center of the galaxy was taken from the
WCS of the cube headers, and it was derived by a barycenter estimation described in Husemann et al. (2013).
Finally, for each galaxy we derive the oxygen abundance gradient. Figure 5 shows two examples of these abundance gradients for the same galaxies as shown in Fig. 2 (i.e. UGC 00312, left panel, with high inclination and NGC 7716; right panel, with low inclination). As indicated above, the CALIFA FoV covers on average ~2.5 re of the observed galaxies. However, thanks to the inclination for spiral galaxies, this FoV has a wide range between ~2 re for the face-on galaxies and up to ~5 re for the edge-on ones (although the particular range also depends on the intrinsic characteristics of the galaxies).
 |
Fig. 7 Left panel: number of detected H ii regions as a function of the inclination of the galaxy. The colors of the symbols and the corresponding histogram indicate the inclination of the galaxies: (i) less than 45° (red); (ii) between 45° and 65° (green); and (iii) larger than 65° (blue). Central panel: slope of the gradients of the oxygen abundance derived for each galaxy as a function of the number of detected H ii regions. The colors of the symbols and the corresponding histogram indicate the number of detected H ii regions in each galaxy: (i) fewer than 20 H ii regions (red); (ii) between 20 and 40 H ii regions (green); and (iii) more than 40 H ii regions (blue). Right panel: slope of the gradients of the oxygen abundance derived for each galaxy based on the linear regression of the radial distribution along the slope derived by comparing the range of abundances with the corresponding range of radial distances. The colors of the symbols and the corresponding histogram indicate this parameter, showing (i) slopes lower than than −0.25 dex/re (red); (ii) between −0.25 and 0.05 dex/re (green); and (iii) larger than 0.05 dex/re (blue). The size of the symbols are inversely proportional to the derived error in the slope of the abundance gradient, in both panels. The black solid diamonds represent the mean values for the different selected subsamples, with the error bars indicating the standard deviation around this mean value. |
Following this analysis we performed a linear regression, without considering the errors of the individual abundances, and an error-weighted linear fit to the radial distribution of abundances galaxy-by-galaxy, restricted to the same spatial range. From the original 227 galaxies with detected ionized regions, we restricted the analysis to those with at least four H ii regions within the considered spatial range (0.3 < r/re < 2.1). Although Zaritsky et al. (1994) found empirically that at least five H ii regions are required to define the slope, we found that this also depends on the individual errors, the range of abundances and galactocentric distances sampled, and the actual S/N. Based on a Monte-Carlo simulation we found that the derived slope is not reliable for fewer than four H ii regions in a galaxy. This final sample comprises 193 galaxies, and a total of 4610 H ii regions. Ninety-four galaxies show at least one region beyond 2.2 disk effective radius, with a total of 484 regions (i.e, ~5 regions per galaxy in this outer region, on average).
The result of this analysis is illustrated is Fig. 6, where we show the distribution of the correlation coefficients, zero points, and slopes for each individual galaxy. For most of the galaxies there is a clear correlation between the oxygen abundance and the radial distance. The correlation coefficient (shown in the left panel of Fig. 6) is larger than rcorr > 0.4 for ~72% of the galaxies. This rcorr corresponds to a probability of good fit of ~98.5% for the typical number of H ii regions in our galaxies. Most of the galaxies for which the correlation coefficient is lower than this value are galaxies with a low number of detected H ii regions. The distribution of zero-points (mid panel) has a mean value at 12 + log(O/H)~ 8.73 dex with a standard deviation of σ ~ 0.16 dex and a range of values reflecting the mass range covered by the sample, due to the well-known ℳ–Z relation (e.g., Tremonti et al. 2004; Sanchez et al. 2013). Finally, the distribution of slopes (right panel of Fig. 6) has a clear peak, and it is remarkably symmetric. The probability of being compatible with a Gaussian distribution is 98%, based on a Lilliefors test (Lilliefors 1967) (compared with 77% derived for the distribution of zero points). Therefore, the slopes of the abundance gradients have a well-defined characteristic value of αO/H = −0.10 dex/re with a standard deviation of σ = 0.09 dex/re, so totally compatible with the value reported in Sánchez et al. (2012b) for a more reduced sample. This slope corresponds to an αO/H = −0.06 dex/rd, when normalized to the disk scalelength (rd), instead of the disk effective radius (re). If instead of this normalization scale, we adopt a more classical one, like r25 (the radius at which the surface-brightness reaches 25 mag/arcsec2 in the B-band) we obtain a similar result, although for a sharper slope of αO/H = −0.16 dex/r25, and a dispersion of σ = 0.12 dex/r25. Finally, if the physical scale (i.e., kpc) at the distance of the galaxy is used instead of any of the previous normalizations, then we find a shallower average slope of αO/H = −0.03 dex/kpc with a standard deviation of σ = 0.03 dex/kpc. Even more important, for this final case the distribution is not asymmetric, presenting a clear tail toward large slopes, up to −0.15 dex/kpc.
4.2. Abundance gradient by galaxy types
In this section we analyze the possible dependence of the slope of the gradients on the properties of the galaxies. But before addressing this issue we point out some possible limitations and biases affecting the analysis performed. The lefthand panel of Fig. 7, shows the distribution of the number of detected H ii regions as a function of the inclination of the galaxy. It is clear that although the number of H ii regions is not the only parameter that affects this error, the error is considerably larger for galaxies with fewer than ~10 regions. On the other hand the number of detected regions decreases with increasing inclination. For highly inclined galaxies (i > 70°), there are very few galaxies with more than 15 H ii regions. This is a clear selection effect, since highly inclined galaxies have less accessible portions of the disk, and therefore the number of detected regions is reduced. We have taken this bias into account in the following analysis.
The central panel of Fig. 7 shows the distribution
of the slopes as a function of the number of detected H ii regions, including
galaxies of any inclination. For galaxies with very few detected regions there is a strong
secondary peak in the distribution at αO/H ~ 0 (i.e., a
constant value). This secondary peak is more evident in the righthand panel, where we
compare the slopes derived from the linear regression (i.e., those shown in the central
panel and in Fig. 6), with a rough estimation of the
slope derived by dividing the range of abundances within the considered galactocentric
distances (0.3–2.1 re), by the differences of radial
distances, ![\begin{equation} {\rm \alpha_{\rm range} = \frac{max[12+log(O/H)]-min[12+log(O/H)]}{{\it r}_{\rm max\ O/H} - {\it r}_{\rm min\ O/H}}}\cdot \end{equation}](/articles/aa/full_html/2014/03/aa22343-13/aa22343-13-eq91.png) (4)This parameter is more
sensitive to the actual range of abundances measured for the H ii regions in each
galaxy. Most of the galaxies are concentrated in a cloud around (αO/H,αrange) = (−0.1, −0.15)
(with a wide dispersion in the second parameter). However, there is a second group of
galaxies with nearly flat or even inverse gradients, which are mostly galaxies with fewer
H ii regions or highly inclined galaxies. It is clear that for those galaxies
our derived slope is less reliable. Thus, better determinations of the slope will result
for (i) larger numbers of H ii regions; (ii) a wider range of abundances; and
(iii) a wider covered range of galactocentric distances.
(4)This parameter is more
sensitive to the actual range of abundances measured for the H ii regions in each
galaxy. Most of the galaxies are concentrated in a cloud around (αO/H,αrange) = (−0.1, −0.15)
(with a wide dispersion in the second parameter). However, there is a second group of
galaxies with nearly flat or even inverse gradients, which are mostly galaxies with fewer
H ii regions or highly inclined galaxies. It is clear that for those galaxies
our derived slope is less reliable. Thus, better determinations of the slope will result
for (i) larger numbers of H ii regions; (ii) a wider range of abundances; and
(iii) a wider covered range of galactocentric distances.
 |
Fig. 8 Top-left panel: distribution of the slopes of the abundance gradients as a function of the interaction stage of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the interaction: (i) no signatures of interaction (red); (ii) galaxies with close companions and/or in an early interaction stage (green); and (iii) galaxies under clear coalescence or evolved mergers (blue). Top-right panel: similar distribution of slopes as a function of the morphological classification of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on their morphology: (i) Early spirals, SO-Sa (red); (ii) intermediate spirals, Sab-Sb (green) and (iii) Late spirals, Sc-Sm (blue). Bottom-left panel: similar distribution of slopes as a function of the presence or absence of bars. The colors of the symbols and the corresponding histograms indicate three types of galaxies: (i) clearly unbarred (red); (ii) not clear if there is a bar or not (green) and (iii) clearly barred galaxies (blue). Bottom-right panel: similar distribution of slopes as a function of the absolute magnitude of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the luminosity: (i) luminous galaxies, Mg−SDSS < −20.25 mag (red); (ii) intermediate galaxies −19.5 < Mg−SDSS < −20.25 mag (green) and (iii) faint galaxies Mg−SDSS > −19.5 mag (blue). The size of the symbols are inversely proportional to the derived error in the slope for all the panels. The black-solid diamonds represent the mean values for the different selected subsamples, with the error bars indicating the standard deviation around this mean value. |
4.2.1. Effects of interactions in the abundance gradients
We classified our sample of galaxies based on their interaction stages to study the possible effect on the abundance gradient, with a much stronger statistical basis than any previous study. Following the classification scheme by Veilleux et al. (1995), galaxies were classified into six different groups from (i) galaxies without any evidence of interaction (class 0), like NGC 5947; (ii) galaxies with close companions at similar redshift (classes 1–2), like VV 448; and (ii) galaxies under clear interaction and/or advanced mergers (classes 3–5), including galaxies like the Mice (class 3) and ARP 220 (class 4). The details of these classification will be given elsewhere (Barrera-Ballesteros et al., in prep.).
The top panel of Fig. 8 shows the distribution of slopes of the abundance gradient for the different classes based on the interaction stage. Most of the galaxies in this study do not present any evidence of an ongoing interaction (~77%). But they do present a well centered distribution of slopes, with an average value of αO/H = −0.11 dex/re with a standard deviation of σ = 0.08 dex/re, fully compatible with the distribution for the complete sample (based on a Kolmogorov-Smirnov test, hereafter KS-test). On the other hand, the two subsamples of galaxies with evidence of early or advanced interactions present similar distributions of slopes among themselves, with shallower gradients (αO/H = −0.05 dex/re and σ = 0.07 dex/re), that are significantly different from the subsample of non-interacting galaxies: pKS = 96.19% for classes 1–2 and pKS = 99.96% for classes 3–5. It is clear that the disk effective radius is most probably ill defined for advanced mergers; however, this is irrelevant when the slope is close to zero. The righthand panel of Fig. 7 shows that most of the galaxies with a flat slope are galaxies with a narrow range of abundances across the field-of-view, and those are mostly interacting/merging galaxies. Therefore, we conclude that galaxy interactions flatten the abundance gradient.
Moreover, we restricted our analysis for the 106 galaxies with more than 10 H ii regions and with inclinations lower than 70°, taking the possible biases described in the previous section into account. We found no qualitative difference in the result. For the intermediate stage the actual number of galaxies is too low (7) to provide a significant difference (although the mean value of the slope remains the same). Finally, for the advance mergers the difference in slope remains significant (pKS = 99.81%).
4.2.2. Slopes by morphology
The top-righthand panel of Fig. 8 shows the distribution of slopes as a function of the galaxy morphological classification. This classification was performed by eye, based on independent analysis by five members of the CALIFA collaboration, and it will be described elsewhere in detail (Walcher et al., in prep.). Different tests indicate that our morphological classification is fully compatible with pre-existing ones, and their results agree with the expectations based on other photometric/morphological parameters, such as the concentration index (Fig. 1) or the Sèrsic index (Sersic 1968). We exclude from this analysis those galaxies with evidence of an ongoing interaction (i.e., classes 1–5 in the previous section), since they present a much flatter gradient. This reduces our sample to 146 galaxies.
The earlier spirals (S0/Sa) present a slightly flatter slope, αO/H,S0−Sa = −0.08 dex/re and σ = 0.08 dex/re (ngal,S0−Sa = 13), in comparison with the two groups of later type ones: αO/H,Sab−Sb = −0.12 dex/re and σ = 0.08 (ngal,Sab−Sb = 88) dex/re and αO/H,Sbc−Sm = −0.11 dex/re and σ = 0.08 dex/re (ngal,Sbc−Sm = 45). However, the corresponding t- and KS-tests indicate that the differences are not significant: pt = 98.86% and pKS = 81.31%, respectively, for the distributions with the larger differences. Therefore, statistically speaking, the slopes of spirals galaxies segregated by morphology are all equivalent.
A similar result is found if instead of normalizing the radial distances to the disk effective radius, we adopt the physical size, without any scalelength normalization. In this case we derive a much wider distribution of slopes, not compatible with a Gaussian distribution (as indicated before). The only difference is that the values for the early-type galaxies are somehow shallower and have a narrower range than do the later types, although the differences are not statistically significant.
4.2.3. Effects of bars on the abundance gradients
The bottom-lefthand panel of Fig. 8 shows the distribution of slopes for the different types of galaxies, depending on the clear presence, or not, of bars. The inspection of our sample for bars was performed by eye by five members of the CALIFA collaboration, and it will be described elsewhere in detail (Walcher et al., in prep.). Three different groups were defined, following the classical scheme: (A) galaxies with no bar, (AB) galaxies that may have a bar, but it is not clearly visible, and (B) clearly barred galaxies. The visual classification was cross-checked with an automatic search for bars, based on the change of ellipticity and PA, which has yield similar results. In a recent kinematical analysis of the Hα velocity maps using DiskFit 6, it was found that the frequency of radial motions was significantly higher in those galaxies with clear bars (Holmes et al., in prep.). As for the previous section, we only considered the 146 galaxies with no evidence of any ongoing interaction.
Again, negligible differences in statistical terms are found between the slope of the abundance gradient for barred galaxies, i.e. αO/H,B = −0.09 dex/re and σ = 0.07 dex/re (ngal,S0−Sa = 38), in comparison with the other two groups: αO/H,A = −0.12 dex/re and σ = 0.08 (ngal,A = 78) dex/re and αO/H,AB = −0.13 dex/re and σ = 0.09 dex/re (ngal,AB = 30). The corresponding t- and KS-tests indicate that the differences are not significant: pt = 93.43% and pKS = 92.44%, respectively, for the distributions with the largest differences. Therefore, if there is a change in the general slope of the gradient induced by the presence of a bar, the effect is weak and not statistically significant. The same result is found if the radial distances are normalized to the physical size, without any scalelength normalization. As in the previous case, we derive a wider distribution of slopes, but with no significant differences due to the presence or absence of bars.
4.2.4. Slopes by luminosity, stellar mass and concentration index
In the previous sections, we analyzed the possible changes of the slope of the abundance gradient on the basis of three different morphological classifications: merging/interaction stage, Hubble type, and incidence of bars. All those classifications were performed by eye, deriving a discrete segregation of the galaxies in subgroups. In this section we analyze the possible variation in the slope as a function of less-subjective parameters, which are correlated with the morphology of the galaxies: the luminosity, the stellar mass, and the concentration index C (see definition in Sect. 2).
The bottom-righthand panel of Fig. 8 illustrates this analysis by showing the distribution of slopes versus the g-band absolute magnitude of the galaxies. As in the previous sections, we excluded those galaxies with clear interactions. We split the sample into luminous (L, Mg < = −20.25 mag), intermediate (I, −20.25 < Mg < = −19.5 mag), and faint (F, Mg > −19.5 mag) galaxies. No significant difference is found between both the average slopes: αO/H,L = −0.10 dex/re and σ = 0.08 dex/re (ngal,L = 57), αO/H,I = −0.12 dex/re and σ = 0.06 dex/re (ngal,I = 42), αO/H,F = −0.12 dex/re and σ = 0.10 dex/re (ngal,F = 45). The corresponding t- and KS-tests indicate that the probability that they are different are pt = 88.11% and pKS = 87.36%, respectively, for the subsamples with the largest differences. There is not even a weak trend between both parameters, given the derived correlation coefficient r = 0.009 and a slope provided by a linear regression of a = −0.0007. Thus the abundance gradient seems to be independent of the luminosity of the galaxies.
Similar results were found for the stellar masses (derived as described in Sanchez et al. 2013), and the C-index. No clear correlation is found between the slopes of the abundance gradients and both parameters, as indicated by the derived correlation coefficients: rmass = 0.08 and rC−index = 0.24. The only difference is found for galaxies more massive than 4.5 × 1010 M⊙, with concentration indices over C > 2.4 (34 galaxies). These galaxies present an average slope of αO/H = −0.07 dex/re and σ = 0.06 dex/re, and t- and KS-tests indicate that they are significantly different from the rest of the sample: pt = 99.60% and pKS = 99.08%. However, even this difference has to be taken with care, since a visual inspection of the abundance gradients for this subsample indicates that a substantial number of them are galaxies with few detected H ii regions.
5. Discussion
The metal content of a galaxy is a fundamental parameter for understanding the evolution of the stellar populations galaxy-by-galaxy and at different locations within the same galaxy. Oxygen is the most abundant heavy element in the Universe, making it the best proxy of total metallicity. It is easily observed for a wide range of metallicities thanks to its emissivity of collisionally excited lines, which are prominent in the optical regime. An universal radial decrease in the oxygen abundance has been already suggested in many previous studies (e.g., Diaz 1989; Vila-Costas & Edmunds 1992; Bresolin et al. 2009; Yoachim et al. 2010; Rosales-Ortega et al. 2011; Marino et al. 2012; Sánchez et al. 2012b; Bresolin et al. 2012). This observational property is compatible with our current understanding of the formation and evolution of spiral galaxies (e.g., Tsujimoto et al. 2010, and references therein). Gas accretion brings gas into the inner region, where it first reaches the required density to ignite star formation. Thus the inner regions are populated by older stars, they have suffered a faster gas reprocessing, and galaxies experience an inside-out mass growth (e.g., Matteucci & Francois 1989; Boissier & Prantzos 1999). Several previous studies have analyzed the radial abundance gradients for individual galaxies or for limited samples of galaxies (e.g., Vila-Costas & Edmunds 1992; Belley & Roy 1992; Zaritsky et al. 1994; Roy & Walsh 1997; van Zee et al. 1998; Marino et al. 2012; Rosales-Ortega et al. 2011; Rich et al. 2012; Bresolin et al. 2012). These studies have found (i) a monotonic decrease in the abundance from the central regions, up to r25 and/or ~2.5–4 r0 (the scalelength of the disk), which corresponds basically to ~1.5–2.5 re; (ii) a flattening in the outer regions, for those galaxies that cover regions beyond r25; (iii) in some cases, a shallow drop in the abundance in the central regions is found (e.g., Rosales-Ortega et al. 2011, <0.3–0.5 re). In Sánchez et al. (2012b) we presented the first study of a large number (~2000) of H ii regions, extracted from 38 face-on spiral galaxies. In general, we confirmed the common pattern described above (although the sample of regions beyond ~2re was quite reduced), we found that there is not only a common pattern but a common slope of αO/H = −0.12 dex/re for all the abundance gradients between 0.3–2.1re, when normalized to the disk effective radius of the galaxies.
The results presented in the previous section point to the same conclusion as in Sánchez et al. (2012b), i.e., that independently of the wide variety of analyzed galaxies, disk galaxies in the local Universe present a common/characteristic gradient in the oxygen abundance up to about two disk effective radii. Moreover, the distribution around this mean value is compatible with a Gaussian function and therefore could be the result of random fluctuations. This result contradicts several previous studies that claim that the slope in the gas-phase abundance gradient is related to other properties of the galaxies, such as (i) the morphology, with early-type spirals showing a shallower slope and late-type ones a sharper one (e.g., McCall et al. 1985; Vila-Costas & Edmunds 1992); (ii) the mass, with more massive spirals showing a shallower slope and less massive ones a sharper one (e.g., Zaritsky et al. 1994; Martin & Roy 1994; Garnett 1998); and in particular; (iii) the presence of a bar, with barred galaxies presenting a shallower slope than unbarred ones (e.g., Zaritsky et al. 1994; Roy 1996); and (iv) the interaction stage of the galaxies, with evolved mergers presenting shallower slopes (e.g., Rich et al. 2012), which seems to be the case also for irregular galaxies and low-mass galaxies (e.g., Edmunds & Roy 1993; Walsh & Roy 1997; Kobulnicky 1998; Mollá & Roy 1999; Kehrig et al. 2008).
In the first case, the dependence of oxygen abundance on the morphology of the galaxies is a long-standing debate (e.g., McCall et al. 1985; Vila-Costas & Edmunds 1992). Early results indicated that early-type spirals (S0/Sa) present flatter gradients than late-type ones (Sc/Sm), although these results were based on a handful of observed galaxies, and it was never tested in an statistical sense, until the study presented here. Nevertheless, as described in Sect. 4.2.2, statistically speaking, the slopes of spirals galaxies segregated by morphology are all equivalent. In the case of the bars, it is well-known that at least 30% of disk galaxies have a pronounced central bar feature in the disk plane, and many more have weaker features of a similar kind (e.g., Sellwood & Wilkinson 1993). Kinematic data indicate that the bar constitutes a major non-axisymmetric component of the mass distribution, which tumbles rapidly about the axis normal to the disk plane. The theory predicts that bars are only stable inside corotation, although whether they are stable or not remains under discussion (e.g., Jogee et al. 2004; Méndez-Abreu et al. 2012). The bar and the spiral arms present two separate pattern speeds, with the bar rotating much faster, as has recently been observed (e.g., Pérez et al. 2012).
Bars have been proposed as an effective mechanism for radial migration (e.g., Di Matteo et al. 2013). Hydrodynamical simulations have shown that bars induce angular momentum transfer via gravitational torques, which result in radial flows and mixing of both stars and gas (e.g., Athanassoula 1992). This radial movement can produce a mixing and homogenization of the gas, which leads to a flattening of any abundance gradient (e.g., Friedli et al. 1994; Friedli 1998). Resonance patterns between the bar and the spiral pattern speed can shift the orbits of stars, mostly toward the outer regions (Minchev & Famaey 2010), a mechanism that also affects the gas. Another process that produces a similar effect is the coupling between the pattern speed of the spiral arms and the bar that induces angular momentum transfer at the corotation radius (e.g., Sellwood & Binney 2002). Early observational results described a flattening in the abundance gradient of barred galaxies (Zaritsky et al. 1994; Martin & Roy 1994). However, as first described in Sánchez et al. (2012b), and explained in Sect. 4.2.3 of this work, we found negligible differences in statistical terms between the slope of the abundance gradient for barred galaxies, i.e., no evidence of the claimed flattening.
A direct comparison between our derived slopes and those presented by previous results is dangerous, due to the inhomogeneity of the data. However, investigating the source of the discrepancies is needed. Zaritsky et al. (1994) presented an analysis of the abundance gradient based on a sample of 39 galaxies. Of them, 14 were new objects (comprising a total of 159 H ii regions), and the remaining ones were extracted from the literature. Finally, only seven objects of the total sample present a clear bar. Although in general their abundance estimations cover a radial range up to about two effective radii (or one isophotal radius in their nomenclature), in many cases the actual sampled spatial range is much more reduced (eg., NGC 1068 or NGC 4725, as can be seen in their Fig. 8). In other cases the slope is derived from a very low number of H ii regions (in particular some of the largest derived slopes), with values that have recently been updated to much smaller values (e.g., NGC 628, for which they derive a slope of −0.96 dex/r25, when the actual value is 5 times lower, Sánchez et al. 2011, 2012b; Rosales-Ortega et al. 2011). Therefore the individual measurements presented in this article have to be taken with care, although they were most probably the best available at the time. Finally, the claim that barred galaxies present a flatter abundance gradient than unbarred ones is based on the comparison of this parameter for seven barred with 32 unbarred galaxies (Fig. 15 of that article). The strongest difference is found in the very late-type galaxies where there are just a few objects (3 barred and 3 unbarred galaxies, with Hubble Type T > 6). Some of the reported values are hardly feasible, since slopes of −0.75 dex/r25 could imply a range of abundances that is not observed across a galaxy in more recent estimations. On the other hand, no distinction was made between interacting and non-interacting galaxies, which may introduce another source of uncertainty, since those galaxies present a flatter distribution (e.g., Rupke et al. 2010a,and this study).
Martin & Roy (1994) presented a comparison of the abundance gradient based mostly on literature data. Of the 24 analyzed galaxies, they present new data for three barred galaxies, two of them with an apparent flatter abundance gradient than unbarred galaxies of the same morphological type (NGC 925 and NGC 1073). However, the slope they presented for those galaxies, when normalized by the effective radius, cannot be considered flatter than the average (−0.185 dex/re and –0.254 dex/Re, respectively, extracted from Table 7A,B from that article). Only when they compare the gradients of the barred and unbarred galaxies normalized to the physical scale (dex/kpc) can they find a difference, although they advise that “the sample of each morphological type is small”. We have already indicated in this study the importance of defining the gradient normalized to the effective radius, since this parameter presents a clear correlation with other parameters of the galaxies, such as the absolute magnitude, the mass, and the morphological type.
Their analyzed sample comprises a heterogeneous selection of objects with the main criteria that they have at least ten H ii regions with published abundance estimates in each galaxy. Of the 24 galaxies, nine have a large inclination angle (>55°, including NGC 925), and no inclination correction has been applied in deriving of the abundance gradient. This may have an impact on the derived slopes. Finally, the three galaxies with flatter gradients (=0 dex/kpc) have been classified as merging systems, and two of them have been classified as barred galaxies. On the other hand, the galaxy with a stronger gradient is also a merging system, being classfied as unbarred. If both highly inclined objects and merging systems are excluded from the comparison, there is no clear evidence of a difference between barred and unbarred galaxies in their sample.
The same result is found for the possible variation in the slope as a function of galaxy properties that are correlated with the morphology of the galaxies such as the luminosity, the stellar mass, and the concentration index C, as described in Sect. 4.2.4. When compared with previous literature data that described correlations with these parameters, we have to consider how these results were derived (e.g., Zaritsky et al. 1994; Garnett 1998), the analyzed sample of galaxies and H ii regions, and if they refer to the slope normalized to the physical scale or to a certain galactic scalelength. For example, despite the caveats expressed before about their sample, Zaritsky et al. (1994) found a correlation between the slope and different properties of the galaxies, such as the stellar mass, the rotation velocity, and the morphological type, but only when the slope was expressed in terms of the physical size (dex/kpc). Since it is well known that the effective radius of a galaxy correlates with those parameters, both results may be compatible, as already suggested in Sánchez et al. (2012b).
 |
Fig. 9 Left panel: radial distribution for the oxygen abundance derived using the O3N2 indicator for all the galaxies in our sample. The contours show the density distribution of H ii regions in this parameter space. The outermost contour encircles 95% of the total number of H ii regions, with ~20% less in each consecutive contour. The color image shows the average stellar mass of each galaxy corresponding to each abundance and radial distance. Right panel: radial distribution for the oxygen abundance derived using the O3N2 indicator, after scaling to the average value at the disk effective radius for each galaxy. The image and contours show the density distribution of H ii regions in this parameter space. The outermost contour encircles 95% of the total number of H ii regions, with ~20% less in each consecutive contour. The solid yellow points represent the average oxygen abundances, with their corresponding standard deviations indicated as error bars for consecutive bins of 0.3 galactocentric distances per disk effective radius. The average error of the derived oxygen abundance (without considering systematic errors) is shown by a single error bar located on the top-right side of the panel. The dashed green line shows the result of the best linear regression to the data. The solid black lines in both panels represent the linear relation corresponding to the mean values of the zero points and slopes of the individual regressions derived for distribution of each individual galaxy. |
Finally, it is important to remember that in many cases, well established results are based on reduced and heterogenous samples of galaxies with an insufficient number of H ii regions explored or with comparison samples also extracted from literature data. Berg et al. (2013) explain that most old estimates of radial gradient of oxygen abundances in the literature are based on out-of-date strong-line empirical calibrations that may be uncertain. These authors measure the auroral line [O iii]λ4363 and find a gradient of –0.017 dex/kpc and –0.027 dex/kpc for NGC 638 and NGC 2403, respectively, which correspond to –0.10 and –0.15 dex/re in perfect agreement with results. These values are much fewer than the old ones, as also occurs with the estimates from Bresolin (2011) and Bresolin et al. (2012) for M 33, M 31, NGC 4258, and M 51, which are now –0.042, –0.023, –0.011, and –0.020 dex/kpc, so smaller than the old numbers reported by Zaritsky et al. (1994). In fact, the value of –0.017 dex/kpc for NGC 628 is very similar to the one found by Rosales-Ortega et al. (2011), as indicated before (compatible with the value reported by Berg et al. 2013). Therefore the procedure for measuring the gradient is important, as is the number of points or other important observational effects, such as the angular resolution, the S/N, or the annular binning that may also change the obtained radial gradient, such as it is demonstrated in Yuan et al. (2011) and Mast et al. (2014).
In the case of the effects of interactions on the abundance gradient of galaxies, theory predicts that major mergers trigger the formation of bars in the stellar and gas disks, which in turn induce vigorous gas inflows as the gas loses angular momentum to the stellar component (Barnes & Hernquist 1996). These inflows are thought to be responsible for fueling a massive central starburst and feeding AGN and/or quasar activity (Mihos & Hernquist 1996; Barnes & Hernquist 1996). For a spiral galaxy with a pre-existing metallicity gradient, gas inflow flattens the gradient by diluting the higher abundance gas in the central regions with the lower abundance gas from the outer parts (Rupke et al. 2010a,b; Kewley et al. 2010). This flattening is compounded as the spiral arms are stretched by tidal effects (Torrey et al. 2012). In addition, interactions induce central star formation processes that produce violent outflows that eject metals from the richer central regions (e.g., Wild et al. 2014). Indeed, galaxy mergers and interacting systems seem to present flatter gradients in the oxygen abundance (e.g., Kewley et al. 2010; Rich et al. 2012). The results of Sect. 4.2.1 support the same scenario, i.e., that galaxy interactions flatten the abundance gradient of spiral galaxies in a statistical sense.
5.1. The common abundance gradient
The results of the present study indicate that, when using the O3N2 strong-line abundance indicator, the oxygen abundance gradient in disk galaxies statistically present a common slope of ~–0.1 dex/re, between 0.3 and 2.1 disk effective radius, when normalized to this disk effective radius. This common slope is independent of the other properties of the galaxies, except for interaction/merging and maybe for the more massive and concentrated galaxies.
Following Sánchez et al. (2012b) it is possible to illustrate this result by presenting the radial distribution of the oxygen abundance for all the galaxies in a single figure. Since the representative abundance (i.e., the abundance at the disk effective radius) scales with the integrated mass (Sanchez et al. 2013) following the well known ℳ–Z relation (Tremonti et al. 2004), it is required to apply a global offset galaxy by galaxy and to normalize the gradient by the mean value at the disk effective radius for all the sample, i.e., 12 + log(O/H) = 8.6 dex. Figure 9 illustrates this process. In the lefthand panel, we show the contour plot of the radial distribution before rescaling to the average representative abundance. The distribution comprises ~4500 H ii regions corresponding to 193 different galaxies of any morphological type, including barred and unbarred galaxies, and covering all the CM-diagram to the completeness limit of the CALIFA survey (described in Walcher et al. in prep.). Although the radial gradient is still visible, there is a wide distribution that almost blurs the evidence of a common abundance gradient. The color-coded areas represent the integrated stellar mass of each galaxy corresponding to each represented abundance (in log units). As expected from the ℳ–Z relation, for an equal mass the abundances present a clear radial gradient, parallel to the average of the individual linear regressions derived for each galaxy, up to about two disk effective radii. This figure illustrates clearly that the common gradient is independent of the mass, as mentioned in previous sections.
The righthand panel of Fig. 9 shows the average radial distribution of the oxygen abundance after rescaling to the average representative abundance. The distribution of H ii regions is represented as a density map with both a color-coded image and a contour map (with the first contour encircling 95%) of the regions, together with the mean abundances at equal spatial bins of Δr = 0.3re with the error bars indicating the corresponding standard deviation. No significant deviation from the monotonic decrease defined by the average gradient is found up to 2.1 disk effective radii. A linear regression to the scaled distribution of H ii regions, which is restricted to the spatial range between 0.3 and 2.1 re, derives a slope of αO/H −0.107 dex/re and σ = 0.004 dex/re, which is fully compatible with the average value found for all the sample αO/H −0.09 dex/re and σ = 0.09 dex/re.
The origin of this common abundance gradient has to be directly linked to the formation and evolution of the disk in spiral galaxies. Recent results, which are based on the analysis of the SFH of CALIFA data, found undisputed evidence of the inside-out growth of the stellar mass in galaxies (Pérez et al. 2013), at least for galaxies more massive than 7 × 1010M⊙. Both the extinction-corrected color gradients in nearby galaxies (Muñoz-Mateos et al. 2007) and weak dependence of the mass-size relation with redshift (Trujillo et al. 2004, 2006; Barden et al. 2005) also support an inside-out scenario for the evolution of disks. These results are also supported by the radial distribution of the stellar ages found for the same data set (González Delgado et al. 2013).
The universal slope for the abundance gradient described in this study, independent of many of the properties of the galaxies, was proposed very recently (Sánchez et al. 2012b). This result imposes a stricter restriction to our current understanding of how disk galaxies grow. In essence, it agrees with the recently proposed Σ–Z relation (Rosales-Ortega et al. 2012) that links the gas abundance with the mass density of the underlying stellar population. It describes how the stellar mass and the gas abundance, both fundamental products of the SFH, grow side-by-side in disk galaxies, from the center to the outer parts. Together with the ℳ–Z relation, they indicate that more massive galaxies (that trace the deepest potential wells) form before and faster, thus accumulating more stellar mass and more metals. The presence of a common gradient in the abundance indicates that all disk-dominated galaxies of the same disk effective radius (Thus, the same disk mass, if they have a similar central surface brightness) synthesize metals at the same galactocentric distance with a similar efficiency.
The common slope suggests that the chemical evolution of galaxies is very similar in all disk galaxies, and it is compatible with a pseudo closed-box model. The classical closed-box model considers that each radial bin of a galaxy comprises primordial gas from which stars are born, live all their life time and die in-situ, according to given SFR and IMF prescriptions (Pagel & Patchett 1975). Therefore, if the amount of primordial gas is proportional to the depth of the potential well and the efficiency of the SFR is the same for all the galaxies, both the stellar mass and the enrichment would only be proportional to the time for a given halo mass. The efficiency of the SFR (or starformation efficiency, SFE) is defined as the SFR surface density per unit of neutral gas surface density along a line of sight. Recent results indicate that the SFE does not vary strongly where the ISM is mostly H2, in spiral galaxies (e.g., Leroy et al. 2008). Under this assumption all galaxies should have an universal gradient of their oxygen abundance with its zeropoint proportional to the total mass.
However, it is well known that the closed-box model cannot predict the correct number of metal-poor stars with respect to the observed metallicity distribution of nearby long-lived stars in the Milky Way (e.g., Gibson et al. 2003). A more realistic model overcomes this problem by allowing the disk of galaxies to form via continuous accretion of gas, driven by the gravitational force (pseudo closed-box model). This accretion can be compensated or even halted for certain galaxies and over certain periods by supernova explosions (e.g., Larson 1974). However, the outflow of gas is not expected to feature in the history of most spiral galaxies and is usually neglected in the models (Gibson et al. 2003). This modified model is consistent with the described common radial gradient if the local gas recycling is faster than other timescales involved (Silk 1993), and if the radial inflow is similar for those radial bins with the same stellar mass.
In summary, the radial gradient appears to be the consequence of different evolutionary rates along the radius. Recent chemical evolution models suggest that the inner regions evolve faster than the outer ones (Mollá & Díaz 2005), following a local downsizing evolution in agreement with the Σ–Z relation Rosales-Ortega et al. (2012); Sanchez et al. (2013). Therefore, an evolution in the slope of the radial gradient expressed in physical scales (dex/kpc) is expected, with a flattening for the more massive or more evolved galaxies (Mollá & Díaz 2005). The described characteristic slope of the radial gradient when normalized to the effective radius (dex/re) implies a tight co-evolution of the radial gradient with the scalelength of the galaxy, with more massive galaxies being larger (which is also observed).
5.2. The flattening of the abundance gradient in the outer regions
The linear regressions shown in the righthand panel of Fig. 9 have been extrapolated beyond r > 2.2 effective radii to illustrate that the abundances present a clear flattening in the outer regions, as already shown in Fig. 5 for some individual galaxies. We detected 484 H ii regions at these outer areas, corresponding to 94 individual galaxies. In most of them the derived abundance is larger than expected by the extrapolation of the monotonic decrease.
Average radial distributions of oxygen abundances, similar to the one shown in Fig. 9, were created for different subsamples of galaxies, segregated by their morphology, photometric properties and the structural parameters. The same subgroups as analyzed in the previous section were selected. No significant difference is found in either the qualitative and quantitative shape and slope of the radial gradient. It is worth noting that the flattening in the outer regions seems to be a universal property of disk galaxies, independent of the inclination, mass, luminosity, C-index, morphology, and/or presence of bars. Only in the case of the interacting galaxies, with a much lower slope in the abundance gradient in the inner disk it is unclear regardless of whether an outer flattening exists (or if all the distribution is flattened). It is also important to bear in mind that although we have adopted the O3N2-indicator, the flattening does not depend on the actual strong-line indicator selected. We tested it using the R23-based calibrator by Tremonti et al. (2004), the N2-based calibrator by Pettini & Pagel (2004), and the C-method described by Pilyugin et al. (2012), with consistent results.
As mentioned before, several previous studies found similar behavior for individual or limited samples of galaxies (e.g., Bresolin et al. 2009; Yoachim et al. 2010; Rosales-Ortega et al. 2011; Marino et al. 2012; Scarano et al. 2011; Bresolin et al. 2012). We found a first hint of this flattening in our pilot analysis of the face-on galaxies in the CALIFA feasibility sample and in PINGS data for a limited set of galaxies and H ii regions (Sánchez et al. 2012b). The same pattern in the abundance was described (i) in the extended UV disks discovered by GALEX (Gil de Paz et al. 2005; Thilker et al. 2007); (ii) in the metallicity gradient of the outer disk of NGC 300 from single-star CMD analysis (Vlajić et al. 2009); (iii) in the Milky way, based on the spectroscopic analysis of the outer H ii regions (Vilchez & Esteban 1996; Esteban et al. 2013) using open clusters (e.g., Bragaglia et al. 2008; Magrini et al. 2009; Yong et al. 2012) or Cepheids (e.g., Andrievsky et al. 2002; Luck et al. 2003; Andrievsky et al. 2004; Lemasle et al. 2008); and (iv) in the oxygen abundance gradient of different individual galaxies, such as M 83 (Bresolin et al. 2009), NGC 628 (Rosales-Ortega et al. 2011), or NGC 1512 and NGC 3621 (Bresolin et al. 2012), to cite just a few results. However, this is the first unambiguous detection of such flattening in most of the galaxies with detected H ii regions beyond ~2 effective radii.
The nature of this flattening is still under debate, in particular because it was not even clear until the current study that it is a common feature of all diskgalaxies. The observational and theoretical investigations of the metal content in the outer regions of galaxies is relatively recent. Because of their extreme conditions (e.g., very low gas densities and long dynamical timescales), the outermost regions of the galaxies are sensitive probes of the mechanisms, leading to the assembly of the disks and their evolution, so they are very important for constraining galactic chemical evolution models. The flat abundance distribution in the outer regions of galaxies usually corresponds to the lowest metallicity values in the galaxies. Nevertheless, these abundances are still relatively high. Assuming continuous star formation with the currently observed SFR, the time required to enrich the ISM up to 12 + log(O/H) ~8.2 has been estimated as ~10 Gyr. (Bresolin et al. 2012). According to cosmological hydrodynamic simulations, in the inside-out scenario for galaxy growth the outer disks of galaxies are formed in the last ~4–6 Gyr. (Scannapieco et al. 2008, 2009), making it unlikely that the in situ star formation could have enriched the ISM to the presently observed values. Therefore, in the case of isolated galaxies, alternative mechanisms of metal redistribution must play an important role.
Among the different proposed processes that could produce this abundance flattening, we wish to mention: (i) large-scale processes of angular momentum transport that produce a mix of gas abundances, including radial gas flows (e.g., Lacey & Fall 1985; Goetz & Koeppen 1992; Portinari & Chiosi 2000; Schönrich & Binney 2009; Spitoni & Matteucci 2011), resonance scattering with transient spiral density waves (Sellwood & Binney 2002), and the overlap of spiral and bar resonances (Minchev et al. 2011); (ii) minor mergers and captures of or perturbations by satellite galaxies that increase the metal content in the outer regions (Quillen et al. 2009; Bird et al. 2012); (iii) a nonlinear Schmidt-Kennicutt law that is able to trigger a highly efficient star formation process at these distances (e.g., Esteban et al. 2013); (iv) a spatial association of the flatter area with gas located in the thick disk, which is known to have different metallicity patterns (e.g., Neves et al. 2009; Ishigaki et al. 2012); (v) a plateau of the gas abundance in the intergalactic medium due to the cosmological evolution of galaxies; and the subsequent pollution of metals (Sánchez et al., in prep.); Stellar radial migration has also been proposed as a possible cause for the flattening of the metallicity gradients for stellar populations in spiral galaxies (e.g., Roškar et al. 2008b,a). However, this argument is only valid if stars and gas are not decoupled.
Detailed understanding of the nature of the flattening will require further observational and theoretical efforts. However, we can outline some of the properties of the H ii regions in this regime, which may help to constrain and distinguish between the different scenarios summarized before. Figure 10 shows the BPT diagram for the 484 H ii regions beyond 2.2 disk effective radii, together with the percentage of young stars corresponding to each region, as presented in Fig. 4. Although the number of regions here is more limited than in the whole sample, the distribution as a function of the BPT diagram is very similar. It shows a clear gradient in the stellar populations that covers a range of young stars of almost a 100% to nearly ~30%. The range of oxygen abundances measured in these regions is 8.2 < 12 + log(O/H)< 8.7. Thus, based on the analyzed parameters, these regions do not show clear differences with respect to the remaining population at small galactocentric distances.
As indicated before, even at these galactocentric distances, it is possible to find H ii regions located above the Kauffmann et al. (2003) curve (~15% beyond 2.2 effective radii). Thanks to their galactocentric distance, these regions cannot be contaminated by a non-negligible possible central ionizing source (like an AGN), and the diffuse emission is also extremely weak to affect the line ratios. A visual inspection of the Hα maps reveals that they are bona fide H ii regions, as can be appreciated in Figs. 2 and 5 for the case of UGC 312. This result reinforces our adopted selection criteria, i.e., by using the information of the underlying stellar population as proof of ongoing star formation activity, we do include H ii regions that would otherwise be discarded by using solely empirical demarcation curves based on strong emission lines like the Kauffmann et al. (2003) curve.
 |
Fig. 10 BPT diagnostic diagram similar to the one presented in Fig. 4, right panel, restricted to the H ii regions beyond 2.2 disk effective radius. The contours indicate the number density of regions, while the color-coded image represent the percentage of young stars (<500 Myr). The error bar represents the typical error in both parameters for the represented H ii regions. |
 |
Fig. 11 Radial distribution of the oxygen abundance derived for the individual H ii regions for NGC 2347, one of the galaxies showing a clear drop in this parameter in the inner regions. The symbols, lines, and labels are the same as the ones shown in Fig. 5. |
5.3. Abundance decrease in the inner regions
Some galaxies present a truncation in the monotonic increase of the oxygen abundance toward the center, or even a drop in the inner regions, at ~0.3–0.5 re (e.g., Rosales-Ortega et al. 2011; Sánchez et al. 2012b). In the Milky Way, the metallicity distributions in the Galactic bulge, in the nuclear bulge and in the Galactic bar display different trends and are difficult to assess given the obvious geometrical obstacles. However, iron abundance determinations using stellar tracers (WR, luminous blue variables, red supergiants) located along the Galactic bar and in the nuclear bulge are more metal-poor than classical Cepheids in the inner disk, suggesting that the metallicity distribution is probably approaching a plateau toward the shortest Galactocentric distances (RG < 5.5 kpc, [Fe/H] ~ 0.4 Genovali et al. 2013, and references therein). This flattening has been observed in other galaxies apart from the Milky Way (e.g., Werk et al. 2011; Bresolin et al. 2012; Sánchez et al. 2011) and has been predicted by some chemical evolution models (e.g., Mollá & Díaz 2005; Molla 2014). In some galaxies, such as NGC 628, the decrease was associated with a star-forming ring, with a clear signature in both the Hα emission and the underlying stellar population (e.g., Wakker & Adler 1995; Ganda et al. 2006; Fathi et al. 2007; Sánchez et al. 2011). This circumnuclear ring was placed at the expected location of the inner Lindblad resonance, where gas is expected to accumulate due to non-circular motions (Fathi et al. 2007). Despite this possible explanation, it is not known whether if this is a common feature of all galaxies or, on the contrary, characteristic of a physically distinct galaxy subclass.
In Sánchez et al. (2012b), we found that the drop in the inner region was present in a substantial number of the galaxies, and it was visible in the average gradient. The righthand panel of Fig. 9 shows the common abundance gradient for our current sample, which comprises many more galaxies and was properly selected to be statistically significant (Walcher et al., in prep.). There is no evidence of a central drop in the average gradient, indicating that it is not a common feature of all the galaxies.
We visually inspected of the individual gradient of each galaxy, classifying them as (i) objects without evidence of an inner drop in the abundance (146); (ii) objects with possible evidence of a drop (21); and (iii) objects with clear evidence of a drop (26). Figure 11 shows the typical abundance gradient of the last case, corresponding to NGC 2347. The galactocentric distribution shows a monotonic, linear gradient from ~0.6 to ~2.4 disk effective radius, with a hint of a flattening beyond this radius, and a clear drop in the central regions (<0.6 re). We should note here that “drop” is used as a general term, defining either a real negative gradient toward the center or just a flattenning in the inner regions. The number of detected H ii regions and the error associated with their corresponding abundances prevent us from making a firm distinction.
Half of these galaxies are morphologically classified as Sb/Sbc (13 out of 26), although a KS-test of the morphological distribution compared with the corresponding one for the full sample (or the sample without evidence of a drop), indicates that both samples are not significantly different. The same result is derived when using the galaxies with possible evidence of an inner drop. Therefore, the drop does not seem to be associated with a particular morphological type of galaxies.
As mentioned above, bars may induce radial motions of gas and stars, which may produce the described effect either by a mix of the gas content inside the bar length or by a transfer of gas toward the edge of the bar. Cavichia et al. (2014) have developed a chemical evolution model in which the bar is taken into account for driving a radial flow outward or inward the inner regions. With this model, a slight flattening of the radial gradient of abundances appears along the disk, but only in the bulge-disk interface region. Thus, at the corotation radius of the bar, there is an increase of SFR, and in consequence, the oxygen abundance increases. The net effect is that there is an apparent decrease or drop in the abundance in the central regions, when actually there is a hump around 0.5 re. If a bar were the dominant effect that produces the decrease in abundance in these galaxies, then it would be expected to detect it more frequently in barred galaxies. However, none of these effects are observed. Although the sample is still too small to provide a statistical significant statement, the percentage of barred galaxies within the galaxies with clear drop of the abundance in the inner areas (~15%, 3 out of 21, once excluded the edge on galaxies) is half of what is observed for the total sample (~28%, i.e., 53 out of 193).
As indicated in Sect. 4.2.1, interactions and mergers are events that may also produce a change in the distribution of abundances in galaxies, owing to radial motions induced by changes in the angular momentum patterns. We speculate that these kinds of disturbances may also induce the detected drop of abundances in the inner regions of galaxies (e.g., by a minor-merger or a satellite galaxy capture). However, when analyzing the interaction stage of our subsample of galaxies with an inner drop we found that none of them presents some evidence of an ongoing interaction/merging event. Therefore, it seems that this effect is due to the secular evolution of the galaxy, and not induced, in general, by the presence of an ongoing interaction (although it does not discard past interactions or a minor merger which are not evident in the morphology of the galaxies).
If the origin of the drop is the radial movements of the gas, then its presence would also have an effect on the overall distribution of abundances at larger radii. To explore whether the presence of an inner drop has any effect on determining of the slope of the abundance gradients (measured between 0.3–2.1 disk effective radii), we performed the following test. If we only consider the slopes of the abundance gradients for the galaxies with clear evidence of a drop, we obtain a mean slope αO/H,drop = −0.15 dex/re and σ = 0.06 dex/re (26 objects), which is significantly larger than the slope for the galaxies without evidence of such a drop; i.e., αO/H,drop = −0.08 dex/re and σ = 0.08 dex/re (146 objects), with a probability of being different of pKS = 99.86%. This is consistent with a radial movement toward the knee/peak point in the abundance distribution, outwards of the inner regions and inwards of the outer ones.
A detailed inspection of the Hα intensity maps of the less inclined galaxies shows that in most of them there is a star-forming ring that is spatially located inside the galactocentric distance defined by the knee in the radial distribution of the abundance. Figure 12 shows an example of this ring detected in the Hα distribution of NGC 2347. A similar result was found for NGC 628 (Sánchez et al. 2011), using data with the better physical spatial sampling provided by the PINGS survey (Rosales-Ortega et al. 2010). We speculate that the presence of the circular star formation ring and the drop in the oxygen abundance inward (together with the lack of evidence of any interaction and the low fraction of barred galaxies with these features) suggest that both features are the consequence of gas radial motions induced by resonances in the disk-speed pattern (Roškar et al. 2008b).
 |
Fig. 12 Color-coded image of the Hα intensity flux, on a logarithmic scale of 10-16 erg s-1 cm-2 arcsec-1units, corresponding to NGC 2347 (the galaxy shown in Fig. 11). The contours represent the flux intensity in the V-band, extracted from the datacube the datacube, at two intensity levels, 0.2 × 10-17 erg s-1 cm-2 arcsec-1 (corresponding to ~3σ detection limit in the continuum) and 15 × 10-17 erg s-1 cm-2 arcsec-1, included to illustrate the location of the center of the galaxy. The white ellipse indicates the location of the knee/peak in the radial abundance shown in Fig. 11. |
We will explore this hypothesis in the future with a detailed analysis of the stellar and gas kinematics, using the V1200 data available for the CALIFA objects.
6. Conclusions
In this article we described the procedures to detect, select, and analyze the spectroscopic properties of the largest homogeneous catalog of H ii regions and associations observed to date. This catalog comprises more than 5000 ionized regions associated with star formation distributed in 227 galaxies of different morphological types and evenly distributed along the color–magnitude diagram (out of 306, which comprised our original sample). We demonstrated that the combination of the properties of the ionized gas with the ongoing underlying stellar population provides a robust means for selecting bona fide H ii regions, without excluding regions that would have been ignored by other classical methods.
We used strong-line indicators to derive the oxygen abundance and the deprojected galactocentric distances to derive the radial distances of the individual H ii regions. With this information we explore the radial abundance gradients for the individual galaxies in our sample. The results of this paper show that disk galaxies in the local Universe present a common or characteristic gradient in the oxygen abundance of αO/H = −0.1 dex/re up to ~2 disk effective radii, with a small dispersion compatible with being produced by random fluctuations. No significant differences are found on the basis of the morphological type, presence or absence of bars, absolute magnitude, and/or stellar mass. A weak trend toward slightly flatter gradients is found for massive (>4.5 × 1010 M⊙) and highly concentrated galaxies (C > 2.4), although there are galaxies with few H ii regions and with the less clearly defined disk. The only clear deviation from the common slope is seen in galaxies with evidence of interaction or undergoing merging. For these galaxies the gradient is significantly flatter. Similar results are obtained with other normalization radii than re, such as the disk scalelength (rd) or the radius at which the surface brightness reaches 25 mag/arcsec2 (r25). The use of different normalization radii only changes the numerical values of the common slopes.
These results agree with the main conclusions of our previous study (Sánchez et al. 2012b), where a limited sample of 38 face-on spiral galaxies was analyzed, using similar methods to the ones described here. Both results apparently contradict previous works, in which the slope of the radial gradients show a trend toward certain morphological characteristics of the galaxies. Vila-Costas & Edmunds (1992) and Zaritsky et al. (1994) showed that barred spirals have a shallower gradient than unbarred ones. However, we must recall here that these statements are based (in general) on gradients constructed on physical/linear scales (i.e. dex kpc-1), not on normalized ones (see Appendix B for a discussion of the dependence of the results on the normalization). A slight decrease in the scatter between the different slopes was found by Vila-Costas & Edmunds (1992) and Diaz (1989), when the scalelength is normalized by the disk-scale, which agrees with our results. We conjecture that both results would begin to agree if the size-luminosity/morphological type relation was considered. In a companion article (Sánchez-Blázquez, in prep.), we analyzed the radial gradient of stellar metallicity, where we have found consistent results; i.e., when normalized to the effective radius of the disk, the slope of the stellar population gradients does not correlate with the mass or with the morphological type of the galaxies, we did not find any difference in the metallicity or age gradients in galaxies with and without bars, and the young stellar population showed a metallicity gradient that is very similar to that of the gas.
We argued that the common slope suggests that the chemical evolution of galaxies is very similar in all disk galaxies, because it is compatible with a “modified” closed-box model, in which the disk of galaxies form via continuous accretion of gas, driven by the gravitational force. In this scenario, if the amount of primordial gas is proportional to the depth of the potential well and the efficiency of the SFR is the same for all the galaxies, both the stellar mass and the chemical enrichment would just be proportional to the time, for a given halo mass. Under this assumption, all galaxies should have an universal gradient of their oxygen abundance with its zero-point proportional to the total mass. It is important to note that our results do not deny the existence of radial movements and metal mixing, although they put new constraints on their net effects on the properties of the galaxies.
Galaxies with evidence of interactions or undergoing a merger event show a clearly flatter oxygen abundance distribution, in agreement with recent results by Kewley et al. (2010) and Rich et al. (2012). This indicates that these dynamical processes can produce an effective mixing of metals. In contrast, that barred and unbarred galaxies do not present a clear difference in their abundance slope indicates that either (i) bars do not significantly enhance the efficiency of chemical mixing; (ii) they produce a proportional change in the gas abundance and stellar mass distributions, which compensate each other when normalized by the disk effective radius; or (iii) they are temporary with a life time that is shorter than chemical mixing timescale.
Another conclusion reached by this study is that the flattening of the abundance gradient at the outer regions seems to be an universal property of disk galaxies. Beyond ~2 disk effective radii, our data shows clear evidence of a flat distribution of the oxygen abundance in most of the galaxies with detected H ii regions at these radial distances. This feature has been previously reported by several authors (e.g., Bresolin et al. 2009, 2012; Marino et al. 2012; Sánchez et al. 2012b), although with less significant numbers. Although we cannot provide a conclusive answer regarding the origin of this flattening, our results suggest that its origin is most probably related to the secular evolution of galaxies, involving processes such as radial migration or the capture of evolved satellite galaxies. On the other hand, it disfavors other scenarios, such as a change in the efficiency of the star formation or the accreation of chemically polluted intergalactic media. Further analysis is required to better understand this effect.
Finally, we also presented observational evidence for a decrease in the oxygen abundance in the central region of some particular galaxies. Our analysis indicates that this drop is associated with central star-forming rings. A plausible explanation would be that both features are produced by the radial flow of gas induced by resonances in the disk pattern speed. The slight increase in the slope beyond the knee/truncation point of the oxygen abundance, the lack of this feature in interacting systems, and the fact that it is more frequent in unbarred galaxies support this scenario.
Online material
Appendix A: Effective radius of the disk
 |
Fig. A.1 Left panels: color-scale representation of 1.5′× 1.5′ postage-stamp images extracted from the SDSS g-band data (in counts), centered on two CALIFA targets (UGC 00312 and NGC 7716), together with a set of ellipses (solid-black lines) representing the recovered shape at different isophotal intensity levels by the analysis described in the text. The last dashed red-black ellipse represents the 1σ isophotal intensity level over the background, adopting the median ellipticity and position angle to plot it. Right panels: surface brightness profiles derived for the considered galaxies on the basis of the corresponding isophotal analysis (gray solid circles), together with the best fit to an exponential profile for the portion of the surface brightness dominated by the disk (gray dashed line). For NGC 7716 a previous iteration of the fitting procedure is shown, before the rejection of those values dominated by the bulge (solid-line). |
In Sánchez et al. (2012b) we showed that the abundance gradient of the analyzed galaxies presents a common gradient up to ~2 re, when normalized to the effective radius of the disk (re). To repeat the same analysis for the CALIFA dataset included in this study, in addition to the abundances of the individual H ii regions, we need to derive this structural parameter for each galaxy.
The effective radius of the disk was derived from an analysis of the azimuthal surface brightness profile (SBP). To derive the SBP, we performed an isophotal analysis of the ancillary g-band images collected for the CALIFA galaxies (extracted from the SDSS imaging survey, York et al. 2000, and Paper I).
These images were created using the SDSSmosaic tool included in IRAF7 (Zibetti et al. 2009). SDSSmosaic takes the galaxy coordinates as input argument and downloads all the individual SDSS frames and the photometric information from the SDSS DR7 web site for all five bands. These frames are then stitched together, accurate astrometry is computed, and the photometric calibration is written into the header. After that, the background is subtracted from each scan by fitting a plane surface (allowing for linear gradient along the scan direction, constant in the perpendicular direction) outside a circle centered on the source. Finally, stripes are combined in a mosaic using the program Swarp (Bertin et al. 2002). The final mosaic contains the photometric zero point (P_ZP keyword) in mag per second of exposure time (EXPTIME keyword). We extracted postage-stamp images of 3′×3′ size, centered on the CALIFA targets, for the g-band mosaic images to derive the disk effective radius.
 |
Fig. A.2 Left panel: distribution of the effective radius of the analyzed galaxies, derived from a growth curve analysis (i.e., the total light effective radius), as a function of the same effective radius derived by a similar growth curve analysis using the surface-brightness profiles derived using the ellipse task in IRAF. Right panel: distribution of the effective radius of the analyzed galaxies, derived from a growth curve analysis (i.e., the total light effective radius), as a function of the effective radius of the disk, derived from the exponential fitting to the surface brightness profile. In both panels, larger and bluer symbols correspond to earlier-type galaxies, while smaller and pinky/reddish ones correspond to later type galaxies. |
The isophotal analysis used the ellipse_isophot_seg.pl tool
included in the HIIexplorer package8).
Unlike to other tools, like ellipse included in IRAF, this tool
does not assume a priori a certain parametric shape for the isophotal distributions. The
following procedures were followed for each postage-stamp image: (i) the peak intensity
emission within a certain distance of a user defined center of the galaxy was derived.
Then, any region around a peak emission above a certain percentage of the galaxy
intensity peak is masked, which effectively masks the brightest foreground stars; (ii)
once the peak intensity is derived, the image is segmented in consecutive levels
following a logarithmic scale from this peak value, using the equation
 (A.1)where
seg(i,j) is the final segmented index at the pixel
(i,j), as an integer number; nlevels is the number of
selected levels of the isophotal analysis (100 in our case); flux(i,j)
is the intensity at the corresponding pixel (i,j) and
fluxpeak is the peak intensity at the center of the galaxy;
(iii) once the image is segmented in nlevels isophotal regions, for each of
them, a set of structural parameters was derived, including the mean flux intensity and
the corresponding standard deviation, the semi-major and semi-minor axis lengths, the
ellipticity, the position-angle, and the barycenter coordinates. These parameters are
intended to describe each isophote following an elliptical shape, but without performing
a direct fit, which is in principle more stable in lower S/N regimes. The lefthand panel
of Fig. A.1 illustrates the process, showing for
two particular objects a central section of 1.5′× 1.5′ of the postage-stamp images used
in this analysis, together with a set of ellipses plotted using the recovered shape
parameters for some particular isophotes.
(A.1)where
seg(i,j) is the final segmented index at the pixel
(i,j), as an integer number; nlevels is the number of
selected levels of the isophotal analysis (100 in our case); flux(i,j)
is the intensity at the corresponding pixel (i,j) and
fluxpeak is the peak intensity at the center of the galaxy;
(iii) once the image is segmented in nlevels isophotal regions, for each of
them, a set of structural parameters was derived, including the mean flux intensity and
the corresponding standard deviation, the semi-major and semi-minor axis lengths, the
ellipticity, the position-angle, and the barycenter coordinates. These parameters are
intended to describe each isophote following an elliptical shape, but without performing
a direct fit, which is in principle more stable in lower S/N regimes. The lefthand panel
of Fig. A.1 illustrates the process, showing for
two particular objects a central section of 1.5′× 1.5′ of the postage-stamp images used
in this analysis, together with a set of ellipses plotted using the recovered shape
parameters for some particular isophotes.
The isophotal segmentation (2nd step of the described procedure), was first introduced by Papaderos et al. (2002). Noeske et al. (2003) and Noeske et al. (2006) show that the surface-brightness profiles derived using this technique were very similar to those derived using more broadly adopted techniques, such as the 2D GALFIT code (Peng et al. 2002). We have adopted this isophotal annuli procedure in previous studies, e.g., Kehrig et al. (2012), Papaderos et al. (2013) and Mast et al. (2014). The improvement with respect to a pure isophotal segmentation was the additional derivation of the structural parameters for each isophotal region, described above (step iii).
The isophotal analysis provides an SBP, which is then analyzed to derive the required
effective radius. The righthand panel of Fig. A.1
shows two examples of the derived SBPs for those galaxies shown in the left panels. In
(Sánchez et al. 2012b), where all the galaxies
were clearly disk-dominated, the profiles were fitted using a pure exponential profile,
following the classical formula,
![\appendix \setcounter{section}{1} \begin{equation} I = I_0 \exp[ - (r/r_{\rm d})] \end{equation}](/articles/aa/full_html/2014/03/aa22343-13/aa22343-13-eq169.png) (A.2)where
I0 is the central intensity, and
rd is the disk scalelength (Freeman 1970), using a simple polynomial regression
fitting. The scalelength was then used to derive the disk effective radius, defined as
the radius at which the integrated flux is half of the total one for a disk component by
integrating the previous formula and deriving the relation:
(A.2)where
I0 is the central intensity, and
rd is the disk scalelength (Freeman 1970), using a simple polynomial regression
fitting. The scalelength was then used to derive the disk effective radius, defined as
the radius at which the integrated flux is half of the total one for a disk component by
integrating the previous formula and deriving the relation:
 (A.3)In the current
study, the sample comprises galaxies of different morphological types. In many cases the
presence of a bulge prevents us from doing a direct exponential fitting for the complete
SBP. In those cases, the effective radius of the disk diverge from the effective radius
of the complete galaxy, defined as the semi-major axis encircling half of the light of
the galaxy.
(A.3)In the current
study, the sample comprises galaxies of different morphological types. In many cases the
presence of a bulge prevents us from doing a direct exponential fitting for the complete
SBP. In those cases, the effective radius of the disk diverge from the effective radius
of the complete galaxy, defined as the semi-major axis encircling half of the light of
the galaxy.
First, to illustrate that our isophotal analysis provides consistent results with more classical analysis tools, we determined the effective radius using a classical growth-curve analysis, based both on our procedure and the surface-brightness analysis provided by the ellipse task included in IRAF. The latter analysis is part of the CALIFA sample characterization effort, which can be performed only in regular shaped targets (Walcher et al., in prep.). The lefthand panel of Fig. A.2 shows the comparison between both effective radii. Different sizes and colors are used to illustrate the morphological type of the galaxies, with smaller and pink symbols corresponding to later type galaxies, and bluer and larger symbols corresponding to earlier type ones. There is an almost one-to-one relation between both parameters, without any evident difference between different morphological types. The comparison of other shape parameters, such as the position angle or the ellipticity produce similar results.
 |
Fig. A.3 Top-left panel: distribution of the slopes of the abundance gradients as a function of the interaction stage of the galaxies, when the galactocentric distances are normalized to the effective radius derived by a growth curve analysis. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the interaction: (i) no signatures of interaction (red); (ii) galaxies with close companions and/or in an early interaction stage (green); and (iii) galaxies under clear collision or evolved mergers (blue). Top-right panel: similar distribution of slopes as a function of the morphological classification of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on their morphology: (i) early spirals, SO-Sa (red); (ii) intermediate spirals, Sab-Sb (green) and (iii) late spirals, Sc-Sm (blue). Bottom-left panel: similar distribution of slopes as a function of the presence or absence of bars. The colors of the symbols and the corresponding histograms indicate three types of galaxies: (i) clearly unbarred (red); (ii) not clear if there is a bar or not (green) and (iii) clearly barred galaxies (blue). Bottom-right panel: similar distribution of slopes as a function of the absolute magnitude of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the luminosity: (i) luminous galaxies, Mg−SDSS < −20.25 mag (red); (ii) intermediate galaxies −19.5 < Mg−SDSS < −20.25 mag (green) and (iii) faint galaxies Mg−SDSS > −19.5 mag (blue). The size of the symbols are inversely proportional to the derived error in the slope for all the panels. |
To derive the disk effective radius it is required to fit that the outer portion of the SBP clearly dominated by an exponential disk. As illustrated in the righthand panels of Fig. A.1, in some cases there is almost no deviation from an exponential disk over the full spatial range covered by the SBP (e.g., UGC 00312). However, in other cases there is a clear deviation in the inner regions due to the presence of a bulge (e.g., NGC 7716). To minimize the effect of the bulge in this derivation we perform an iterative procedure, in which the SBP, represented in surface brightness magnitudes, was fitted with a linear regression. In each stage of the iteration, the brightest value of the SBP was removed, and the regression was repeated. The iteration stops when only half of the original values remains in the SBP. From the set of regressions it was adopted that one with the highest correlation coefficient between the semi-major axis and the surface brightness magnitude.
The procedure was tested visually, as illustrated in Fig. A.1, showing that it provides a good fit for the linear regime (i.e., the disk-dominated regime), excluding in most of the cases the central regions dominated by a bulge. Obviously, the procedure works better for those galaxies that are still dominated by disk in most of the SBP, and provides the worst results for those ones dominated by a bulge. However, this would be a general limitation to any other proposed method with the same aim.
The righthand panel of Fig. A.2 shows the comparison between the effective radius derived using the growth-curve method and the disk effective radius extracted from the iterative fit of the SBP. The size and color of the symbols represent the same morphological segregation shown in the lefthand panel. As expected the late-type galaxies, which are disk-dominated, are clustered closer to the one-to-one relation, while most of the earlier-type ones with brighter bulges are shifted toward larger disk effective radii.
Appendix B: Dependence of the results on the derivation of the disk effective radius
The main result described throughout the current study is that all undisturbed galaxies with a disk present a similar radial abundance gradient with a characteristic slope, when the galactocentric distances are normalized to the disk effective radius. This characteristic slope seems to be independent of other properties of the galaxies, such as morphological types, presence of a bars and absolute magnitudes or stellar masses. However, this result relies on the definition of the disk effective radius and its derivation, based on the surface brightness profile analysis described in the previous section.
The disk effective radius is a non-standard scalelength, which we have introduced to characterize the size of the disk in galaxies with different morphologies. Therefore, it is important to illustrate how our results are affected by this adopted normalization of the radial distances. To do so we repeat the analysis using the standard effective radius derived using the growth-curve analysis (re,GC) to normalize the abundance gradients, instead of the disk effective radius. As already indicated, the growth curve effective radius has been derived independently using different procedures providing, reliable and consistent results (Fig. A.2, left panel).
Figure A.3 shows the distribution of the new slopes obtained when normalizing to these effective radius along the same structural parameters of the galaxies shown in Fig. 8. Even though individual slopes change, in particular for the galaxies of earlier type, all the results described in Sect. 4.2 remain valid:
-
Galaxies with evidence of interaction or ongoing a clear merging process present an oxygen abundance gradient flatter than those without any clear evidence of interaction. The difference is statistically significant, both using KS- or a t-test for the different distributions. The characteristic slope for non-interacting galaxies it is not affected by the selection of the normalization radius, with a mean value of αO/H = −0.11 ± 0.09 dex/re (although the dispersion suffer a slight increase).
-
The average slope for earlier type galaxies is slightly flatter when normalizing by re,GC, instead of the disk re: αO/H,Sa/S0 = −0.06 ± 0.08 dex/re,GC instead of αO/H,Sa/S0 = −0.08 ± 0.08 dex/re. However, there is no significant different in the distribution of slopes, using either a KS- or a t-test analysis.
-
Neither the average slopes nor the distribution of slopes change significantly depending on the presence or absence of a bar in the galaxies. The use of the total or disk effective radius seems to be irrelevant for comparing of abundance gradients for barred an unbarred galaxies.
-
The abundance gradient slopes normalized by re,GC do not present any dependence on the absolute magnitudes, the stellar masses, or the concentration indices of the galaxies.
In summary, although the slopes of the individual gradients for each galaxy change when normalizing by the disk re or the re,GC, in general the statistical results are basically the same. The main effect, as expected, is found in the slope of the earlier type galaxies (Sa/S0), that present slightly flatter gradients. This is expected, since for these galaxies the disk re is larger than the growth curve one, due to the presence of a bulge. For those galaxies the derivation of the disk re is also more complicated, for the same reason. However, that the slope of the abundance gradient for these galaxies becomes more similar to the one derived for the latter type ones when using the disk effective radius, indicates that (i) the use of this radius provides a better characterization for the gradient and (ii) the metal enrichment seems to be clearly dominated by the growth of the disk, rather than other non-secular processes.
Although there are recent studies that do not favor a flattening of the MW gradient in the outer disk based on Cepheids (e.g., Lemasle et al. 2013, and references therein).
Acknowledgments
S.F.S. thanks the director of CEFCA, M. Moles, for his sincere support to this project. This study makes uses of the data provided by the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://califa.caha.es/). CALIFA is the first legacy survey being performed at Calar Alto. The CALIFA collaboration would like to thank the IAA-CSIC and MPIA-MPG as major partners at the observatory, and CAHA itself, for the unique access to telescope time and support in manpower and infrastructures. The CALIFA collaboration also thanks the CAHA staff for their dedication to this project. Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck-Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC). We thank the Viabilidad, Diseño, Acceso y Mejorafunding program, ICTS-2009-10, for supporting the initial development of this project. S.F.S., F.F.R.O. and D. Mast thank the Plan Nacional de Investigación y Desarrollo funding programs, AYA2010-22111-C03-03 and AYA2010-10904E, of the Spanish Ministerio de Ciencia e Innovación, for their support for this project. S.F.S thanks the Ramón y Cajal project RyC-2011-07590 of the Spanish Ministerio de Economía y Competitividad, for their support for this project. S.F.S. and B.J. acknowledge support from the grants No. M100031241 and M100031201 of the Academy of Sciences of the Czech Republic (ASCR Internal support program of international cooperation projects – PIPPMS) and by the Czech Republic program for the long-term development of the research institution No. RVO67985815. R.G.D., E.P., and R.G.B. thank the Plan Nacional de Investigación y Desarrollo funding program AYA2010-15081. F.F.R.O. acknowledges the Mexican National Council for Science and Technology (CONACYT) for financial support under the program Estancias Posdoctorales y Sabáticas al Extranjero para la Consolidación de Grupos de Investigación, 2010-2012. I.M. and J.P. acknowledge financial support from the Spanish grant AYA2010-15169 and Junta de Andalucía TIC114 and Excellence Project P08-TIC-03531. D.M. and A.M.-I. are supported by the Spanish Research Council within the program JAE-Doc, Junta para la Ampliación de Estudios, cofunded by the FSE. R.A. Marino was also funded by the Spanish program of the International Campus of Excellence Moncloa (CEI). J.I.-P., J.M.V., A.M.-I., and C.K. have been partially funded by the projects AYA2010-21887 from the Spanish PNAYA, CSD2006 – 00070 “1st Science with GTC” from the CONSOLIDER 2010 program of the Spanish MICINN, and TIC114 Galaxias y Cosmología of the Junta de Andalucía (Spain). M.A.P.T. acknowledges support by the Spanish MICINN through grant AYA2012-38491-C02-02 and by the Autonomic Government of Andalusia through grants P08-TIC-4075 and TIC-126. CJW acknowledges support through the Marie Curie Career Integration Grant 303912. Polychronis Papaderos is supported by a Ciencia 2008 contract, funded by FCT/MCTES (Portugal) and POPH/FSE (EC). Jean Michel Gomes is supported by a grant SFRH/BPD/66958/2009 from FCT (Portugal). This paper makes use of the Sloan Digital Sky Survey data. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), theMax-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Alloin, D., Collin-Souffrin, S., Joly, M., & Vigroux, L. 1979, A&A, 78, 200 [Google Scholar]
- Andrievsky, S. M., Kovtyukh, V. V., Luck, R. E., et al. 2002, A&A, 392, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Luck, R. E., Martin, P., & Lépine, J. R. D. 2004, A&A, 413, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Annibali, F., Bressan, A., Rampazzo, R., et al. 2010, A&A, 519, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asari, N. V., Cid Fernandes, R., Stasińska, G., et al. 2007, MNRAS, 381, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Athanassoula, E. 1992, MNRAS, 259, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barden, M., Rix, H.-W., Somerville, R. S., et al. 2005, ApJ, 635, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1996, ApJ, 471, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Belley, J., & Roy, J.-R. 1992, ApJS, 78, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Skillman, E. D., Garnett, D. R., et al. 2013, ApJ, 775, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, eds. D. A. Bohlender, D. Durand, & T. H. Handley, ASP Conf. Ser., 281, 228 [Google Scholar]
- Bird, J. C., Kazantzidis, S., & Weinberg, D. H. 2012, MNRAS, 420, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Schlegel, D. J., Strauss, M. A., et al. 2005, AJ, 129, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Sestito, P., Villanova, S., et al. 2008, A&A, 480, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bresolin, F. 2011, ApJ, 730, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Ryan-Weber, E., Kennicutt, R. C., & Goddard, Q. 2009, ApJ, 695, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kennicutt, R. C., & Ryan-Weber, E. 2012, ApJ, 750, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carigi, L. 1994, ApJ, 424, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Cavichia, O., Molla, M., Costa, R. D. D., & Maciel, W. J. 2014, MNRAS, 437, 3688 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Schlickmann, M. S., et al. 2010, MNRAS, 403, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Mateus, A., & Va le Asari, N. 2011, MNRAS, 413, 1687 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Perez, E., Garcia Benito, R., et al. 2013, A&A, 557, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clayton, D. D. 1987, ApJ, 315, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, R. D. D., Uchida, M. M. M., & Maciel, W. J. 2004, A&A, 423, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diaz, A. I. 1989, in Evolutionary Phenomena in Galaxies, eds. J. E. Beckman, & B. E. J. Pagel (Cambridge University press), 377 [Google Scholar]
- Diaz, A. I., & Tosi, M. 1984, MNRAS, 208, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Haywood, M., Combes, F., Semelin, B., & Snaith, O. N. 2013, A&A, 553, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edmunds, M. G., & Roy, J.-R. 1993, MNRAS, 261, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., Carigi, L., Copetti, M. V. F., et al. 2013, MNRAS, 433, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fathi, K., Beckman, J. E., Zurita, A., et al. 2007, A&A, 466, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrini, F., Matteucci, F., Pardi, C., & Penco, U. 1992, ApJ, 387, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Folkes, S., Ronen, S., Price, I., et al. 1999, MNRAS, 308, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Friedli, D. 1998, in Abundance Profiles: Diagnostic Tools for Galaxy History, eds. D. Friedli, M. Edmunds, C. Robert, & L. Drissen, ASP Conf. Ser., 147, 287 [Google Scholar]
- Friedli, D., Benz, W., & Kennicutt, R. 1994, ApJ, 430, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Ganda, K., Falcón-Barroso, J., Peletier, R. F., et al. 2006, MNRAS, 367, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 1998, Rev. Mex. Astron. Astrofis. Conf. Ser., 7, 58 [NASA ADS] [Google Scholar]
- Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2013, A&A, 554, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibson, B. K., Fenner, Y., Renda, A., Kawata, D., & Lee, H.-C. 2003, PASA, 20, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K., Pilkington, K., Brook, C. B., Stinson, G. S., & Bailin, J. 2013, A&A, 554, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil de Paz, A., Madore, B. F., Boissier, S., et al. 2005, ApJ, 627, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Salzer, J. J., et al. 1995, AJ, 110, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Herter, T., et al. 1997, AJ, 113, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, M., & Koeppen, J. 1992, A&A, 262, 455 [NASA ADS] [Google Scholar]
- González Delgado, R. M., & Perez, E. 1997, ApJS, 108, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Guesten, R., & Mezger, P. G. 1982, Vistas Astron., 26, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997, ApJ, 487, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2013, A&A, 549, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishigaki, M. N., Chiba, M., & Aoki, W. 2012, ApJ, 753, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Jogee, S., Barazza, F. D., Rix, H.-W., et al. 2004, ApJ, 615, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kehrig, C., Vílchez, J. M., Sánchez, S. F., et al. 2008, A&A, 477, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kehrig, C., Monreal-Ibero, A., Papaderos, P., et al. 2012, A&A, 540, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Keel, W. C., & Blaha, C. A. 1989, AJ, 97, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Rupke, D., Zahid, H. J., Geller, M. J., & Barton, E. J. 2010, ApJ, 721, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A. 1998, in Abundance Profiles: Diagnostic Tools for Galaxy History, eds. D. Friedli, M. Edmunds, C. Robert, & L. Drissen, ASP Conf. Ser., 147, 108 [Google Scholar]
- Koleva, M., Prugniel, P., Bouchard, A., & Wu, Y. 2009, A&A, 501, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacey, C. G., & Fall, S. M. 1985, ApJ, 290, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Lemasle, B., François, P., Piersimoni, A., et al. 2008, A&A, 490, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemasle, B., Francois, P., Genovali, K., et al. 2013, A&A, 558, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Kewley, L. J., & Larson, K. L. 2010, AJ, 139, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Lilliefors, H. W. 1967, J. Am. Stat. Assoc., 62, 399 [CrossRef] [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., Prochaska, J. X., & Ramirez-Ruiz, E. 2011, ApJ, 731, 91 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, Á. R., Dopita, M. A., Kewley, L. J., et al. 2012, MNRAS, 426, 2630 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., Gieren, W. P., Andrievsky, S. M., et al. 2003, A&A, 401, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacArthur, L. A., González, J. J., & Courteau, S. 2009, MNRAS, 395, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Maciel, W. J., & Costa, R. D. D. 2009, in IAU Symp. 254, eds. J. Andersen, B. M., Nordströara, & J. Bland-Hawthorn, 38 [Google Scholar]
- Magrini, L., Sestito, P., Randich, S., & Galli, D. 2009, A&A, 494, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, R. A., Gil de Paz, A., Castillo-Morales, A., et al. 2012, ApJ, 754, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, R. A., Rosales-Ortega, F. F., Sánchez, S. F., et al. 2013, A&A, 559, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mármol-Queraltó, E., Sánchez, S. F., Marino, R. A., et al. 2011, A&A, 534, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, P., & Roy, J.-R. 1994, ApJ, 424, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Mast, D., Rosales-Ortega, F. F., Sanchez, S. F., et al. 2014, A&A, 561, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Sánchez-Janssen, R., Aguerri, J. A. L., Corsini, E. M., & Zarattini, S. 2012, ApJ, 761, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molla, M. 2014, Adv. Astron., accepted [arXiv:1401.0761] [Google Scholar]
- Mollá, M., & Díaz, A. I. 2005, MNRAS, 358, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Mollá, M., & Roy, J.-R. 1999, ApJ, 514, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Molla, M., Ferrini, F., & Diaz, A. I. 1996, ApJ, 466, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., & Kennicutt, Jr., R. C. 2006, ApJS, 164, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2007, ApJ, 658, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Neves, V., Santos, N. C., Sousa, S. G., Correia, A. C. M., & Israelian, G. 2009, A&A, 497, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noeske, K. G., Papaderos, P., Cairós, L. M., & Fricke, K. J. 2003, A&A, 410, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noeske, K. G., Koo, D. C., Phillips, A. C., et al. 2006, ApJ, 640, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Ocvirk, P., Pichon, C., Lançon, A., & Thiébaut, E. 2006, MNRAS, 365, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., Parker, J. S., Mikles, V. J., & Zhang, X. 2003, AJ, 126, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Herndon VA, USA: University Science Books) [Google Scholar]
- Pagel, B. E. J., & Patchett, B. E. 1975, MNRAS, 172, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Papaderos, P., Izotov, Y. I., Thuan, T. X., et al. 2002, A&A, 393, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaderos, P., Gomes, J. M., Vilchez, J. M., et al. 2013, A&A, 555, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedicelli, S., Bono, G., Lemasle, B., et al. 2009, A&A, 504, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, I., Aguerri, J. A. L., & Méndez-Abreu, J. 2012, A&A, 540, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez, E., Cid Fernandes, R., González Delgado, R. M., et al. 2013, ApJ, 764, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilkington, K., Gibson, B. K., Brook, C. B., et al. 2012, MNRAS, 425, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Mattsson, L. 2012, MNRAS, 424, 2316 [NASA ADS] [CrossRef] [Google Scholar]
- Portinari, L., & Chiosi, C. 2000, A&A, 355, 929 [NASA ADS] [Google Scholar]
- Prantzos, N., & Aubert, O. 1995, A&A, 302, 69 [NASA ADS] [Google Scholar]
- Quillen, A. C., Minchev, I., Bland-Hawthorn, J., & Haywood, M. 2009, MNRAS, 397, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, J. A., Torrey, P., Kewley, L. J., Dopita, M. A., & Rupke, D. S. N. 2012, ApJ, 753, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Barden, M., Beckwith, S. V. W., et al. 2004, ApJS, 152, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Kennicutt, R. C., Sánchez, S. F., et al. 2010, MNRAS, 405, 735 [NASA ADS] [Google Scholar]
- Rosales-Ortega, F. F., Díaz, A. I., Kennicutt, R. C., & Sánchez, S. F. 2011, MNRAS, 415, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Sánchez, S. F., Iglesias-Páramo, J., et al. 2012, ApJ, 756, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008a, ApJ, 684, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Stinson, G. S., et al. 2008b, ApJ, 675, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, J.-R. 1996, in IAU Colloq. 157: Barred Galaxies, eds. R. Buta, D. A. Crocker, & B. G. Elmegreen, ASP Conf. Ser., 91, 63 [Google Scholar]
- Roy, J.-R., & Walsh, J. R. 1997, MNRAS, 288, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Kewley, L. J., & Barnes, J. E. 2010a, ApJ, 710, L156 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Kewley, L. J., & Chien, L.-H. 2010b, ApJ, 723, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., García-Lorenzo, B., Jahnke, K., et al. 2006, New A Rev., 49, 501 [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Kennicutt, R. C., et al. 2011, MNRAS, 410, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012a, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012b, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarzi, M., Falcón-Barroso, J., Davies, R. L., et al. 2006, MNRAS, 366, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Shields, J. C., Schawinski, K., et al. 2010, MNRAS, 402, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2008, MNRAS, 389, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., White, S. D. M., Springel, V., & Tissera, P. B. 2009, MNRAS, 396, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Scarano, Jr., S., Lépine, J. R. D., & Marcon-Uchida, M. M. 2011, MNRAS, 412, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Wilkinson, A. 1993, Rep. Prog. Phys., 56, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes [Google Scholar]
- Silk, J. 1993, PNAS, 90, 4835 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, R., van de Ven, G., Jahnke, K., et al. 2013, A&A, 558, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skillman, E. D. 1989, ApJ, 347, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., & Matteucci, F. 2011, A&A, 531, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Bianchi, L., Meurer, G., et al. 2007, ApJS, 173, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Torrey, P., Cox, T. J., Kewley, L., & Hernquist, L. 2012, ApJ, 746, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Rudnick, G., Rix, H.-W., et al. 2004, ApJ, 604, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Förster Schreiber, N. M., Rudnick, G., et al. 2006, ApJ, 650, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, T., Bland-Hawthorn, J., & Freeman, K. C. 2010, PASJ, 62, 447 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L., Salzer, J. J., Haynes, M. P., O’Donoghue, A. A., & Balonek, T. J. 1998, AJ, 116, 2805 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Kim, D.-C., Sanders, D. B., Mazzarella, J. M., & Soifer, B. T. 1995, ApJS, 98, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Vilchez, J. M., & Esteban, C. 1996, MNRAS, 280, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Vlajić, M., Bland-Hawthorn, J., & Freeman, K. C. 2009, ApJ, 697, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & Adler, D. S. 1995, AJ, 109, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, Ap&SS, 331, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. R., & Roy, J.-R. 1997, MNRAS, 288, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Werk, J. K., Putman, M. E., Meurer, G. R., & Santiago-Figueroa, N. 2011, ApJ, 735, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Wild, V., Rosales-Ortega, F., Facon-Barroso, J., et al. 2014, A&A, submitted [Google Scholar]
- Yan, R., & Blanton, M. R. 2012, ApJ, 747, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., Roškar, R., & Debattista, V. P. 2010, ApJ, 716, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Carney, B. W., & Friel, E. D. 2012, AJ, 144, 95 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Yuan, T.-T., Kewley, L. J., Swinbank, A. M., Richard, J., & Livermore, R. C. 2011, ApJ, 732, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H.-W. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Distribution of the currently observed CALIFA galaxies in the u − z vs. Mz color–magnitude diagram. Different colors and symbols represent a classification into spheroid- and disk-dominated galaxies as well as intermediate cases, as suggested by the concentration index C (see Sect. 2 for definition). For comparison, the contours delineate the number density distribution of galaxies in the SDSS-NYU catalogue (e.g., Blanton et al. 2005). The small dots indicate the remaining objects in the CALIFA mother sample, not observed so far. |
| In the text | |
 |
Fig. 2 IFS-based Hα maps, in units of (log 10) 10-16 erg s-1 cm-2 arcsec-2, derived for two representative galaxies of the sample, together with the detected H ii regions shown as black segmented contours. |
| In the text | |
 |
Fig. 3 Left panel: absolute value of the equivalent width of Hα, on a logarithmic scale, plotted against the portion of young stars in the underlying stellar population (according to the SSP modeling by FIT3D ) for the clumpy ionized regions selected with HIIexplorer. Right panel: similar distribution of the emission equivalent width of Hα, on a logarithmic scale, as a function of the luminosity portion of young stars in the underlying stellar population for the ~500 000 individual spaxels with Hα emission detected in the 306 analyzed datacubes. In both panels, the dashed horizontal line shows the demarcation limit of the EW of Hα proposed by Cid Fernandes et al. (2010) to distinguish between strong (star formation and/or AGNs) and weak (e.g., post-AGBs) ionization sources. The vertical solid line shows the currently adopted selection criteria for the H ii regions. |
| In the text | |
 |
Fig. 4 Left panel: [O iii] λ5007/Hβ vs. [N ii] λ6583/Hα diagnostic diagram for the ~7000 ionized regions described in the text. The contours show the density distribution of these regions with the diagram plane, with the outermost contour enclosing 95% of the regions, and each consecutive one enclosing 20% less regions. The color indicates the portion of young stellar populations in the underlying continuum. Central panel: same diagnostic diagram, restricted to those ionized regions with less than a 20% of young stellar population (~1800 regions). Right panel: same diagnostic diagram, restricted to those ionized regions with more than a 20% of young stellar population (~5800 regions). In all the panels, the solid and dashed lines represent the Kauffmann et al. (2003) and Kewley et al. (2001) demarcation curves, respectively. They are usually invoked to distinguish between classical star-forming objects (below the solid line), and AGN powered sources (above the dashed line). Regions between both lines are considered intermediate ones. |
| In the text | |
 |
Fig. 5 Radial distribution of the oxygen abundance derived for the individual H ii regions with abundance errors below 0.15 dex, as a function of the deprojected galactocentric distance (i.e., corrected for inclination), normalized to the disk effective radius, for the galaxies presented in Fig. 2. The size of the symbols is proportional to the Hα intensity. The red circles represent those H ii regions below the Kauffmann et al. (2003) line, and the orange squares represent those above this curve and below the Kewley et al. (2001) demarcation lines, i.e., the regions in the so-called intermediate zone in the BPT diagram. The solid and dashed lines show the best linear regression and error-weighted linear fit derived for those values between 0.3 and 2.1 re. The results from the second fit are shown in the figure, including the zero point (a), slope (b), and correlation coefficient (r). |
| In the text | |
 |
Fig. 6 Left panel: distribution of correlation coefficients of the oxygen abundance along the radial distance, for the 193 galaxies described in the text. Central panel: distribution of zero points for the corresponding linear regression galaxy by galaxy. Right panel: distribution of slopes of the same regressions. The orange solid line represents, for each of the last two histograms, the expected histogram in case of a Gaussian distribution of the data, assuming the mean and standard-deviation of the distribution of each analyzed parameter and sampled with the same bins. |
| In the text | |
 |
Fig. 7 Left panel: number of detected H ii regions as a function of the inclination of the galaxy. The colors of the symbols and the corresponding histogram indicate the inclination of the galaxies: (i) less than 45° (red); (ii) between 45° and 65° (green); and (iii) larger than 65° (blue). Central panel: slope of the gradients of the oxygen abundance derived for each galaxy as a function of the number of detected H ii regions. The colors of the symbols and the corresponding histogram indicate the number of detected H ii regions in each galaxy: (i) fewer than 20 H ii regions (red); (ii) between 20 and 40 H ii regions (green); and (iii) more than 40 H ii regions (blue). Right panel: slope of the gradients of the oxygen abundance derived for each galaxy based on the linear regression of the radial distribution along the slope derived by comparing the range of abundances with the corresponding range of radial distances. The colors of the symbols and the corresponding histogram indicate this parameter, showing (i) slopes lower than than −0.25 dex/re (red); (ii) between −0.25 and 0.05 dex/re (green); and (iii) larger than 0.05 dex/re (blue). The size of the symbols are inversely proportional to the derived error in the slope of the abundance gradient, in both panels. The black solid diamonds represent the mean values for the different selected subsamples, with the error bars indicating the standard deviation around this mean value. |
| In the text | |
 |
Fig. 8 Top-left panel: distribution of the slopes of the abundance gradients as a function of the interaction stage of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the interaction: (i) no signatures of interaction (red); (ii) galaxies with close companions and/or in an early interaction stage (green); and (iii) galaxies under clear coalescence or evolved mergers (blue). Top-right panel: similar distribution of slopes as a function of the morphological classification of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on their morphology: (i) Early spirals, SO-Sa (red); (ii) intermediate spirals, Sab-Sb (green) and (iii) Late spirals, Sc-Sm (blue). Bottom-left panel: similar distribution of slopes as a function of the presence or absence of bars. The colors of the symbols and the corresponding histograms indicate three types of galaxies: (i) clearly unbarred (red); (ii) not clear if there is a bar or not (green) and (iii) clearly barred galaxies (blue). Bottom-right panel: similar distribution of slopes as a function of the absolute magnitude of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the luminosity: (i) luminous galaxies, Mg−SDSS < −20.25 mag (red); (ii) intermediate galaxies −19.5 < Mg−SDSS < −20.25 mag (green) and (iii) faint galaxies Mg−SDSS > −19.5 mag (blue). The size of the symbols are inversely proportional to the derived error in the slope for all the panels. The black-solid diamonds represent the mean values for the different selected subsamples, with the error bars indicating the standard deviation around this mean value. |
| In the text | |
 |
Fig. 9 Left panel: radial distribution for the oxygen abundance derived using the O3N2 indicator for all the galaxies in our sample. The contours show the density distribution of H ii regions in this parameter space. The outermost contour encircles 95% of the total number of H ii regions, with ~20% less in each consecutive contour. The color image shows the average stellar mass of each galaxy corresponding to each abundance and radial distance. Right panel: radial distribution for the oxygen abundance derived using the O3N2 indicator, after scaling to the average value at the disk effective radius for each galaxy. The image and contours show the density distribution of H ii regions in this parameter space. The outermost contour encircles 95% of the total number of H ii regions, with ~20% less in each consecutive contour. The solid yellow points represent the average oxygen abundances, with their corresponding standard deviations indicated as error bars for consecutive bins of 0.3 galactocentric distances per disk effective radius. The average error of the derived oxygen abundance (without considering systematic errors) is shown by a single error bar located on the top-right side of the panel. The dashed green line shows the result of the best linear regression to the data. The solid black lines in both panels represent the linear relation corresponding to the mean values of the zero points and slopes of the individual regressions derived for distribution of each individual galaxy. |
| In the text | |
 |
Fig. 10 BPT diagnostic diagram similar to the one presented in Fig. 4, right panel, restricted to the H ii regions beyond 2.2 disk effective radius. The contours indicate the number density of regions, while the color-coded image represent the percentage of young stars (<500 Myr). The error bar represents the typical error in both parameters for the represented H ii regions. |
| In the text | |
 |
Fig. 11 Radial distribution of the oxygen abundance derived for the individual H ii regions for NGC 2347, one of the galaxies showing a clear drop in this parameter in the inner regions. The symbols, lines, and labels are the same as the ones shown in Fig. 5. |
| In the text | |
 |
Fig. 12 Color-coded image of the Hα intensity flux, on a logarithmic scale of 10-16 erg s-1 cm-2 arcsec-1units, corresponding to NGC 2347 (the galaxy shown in Fig. 11). The contours represent the flux intensity in the V-band, extracted from the datacube the datacube, at two intensity levels, 0.2 × 10-17 erg s-1 cm-2 arcsec-1 (corresponding to ~3σ detection limit in the continuum) and 15 × 10-17 erg s-1 cm-2 arcsec-1, included to illustrate the location of the center of the galaxy. The white ellipse indicates the location of the knee/peak in the radial abundance shown in Fig. 11. |
| In the text | |
 |
Fig. A.1 Left panels: color-scale representation of 1.5′× 1.5′ postage-stamp images extracted from the SDSS g-band data (in counts), centered on two CALIFA targets (UGC 00312 and NGC 7716), together with a set of ellipses (solid-black lines) representing the recovered shape at different isophotal intensity levels by the analysis described in the text. The last dashed red-black ellipse represents the 1σ isophotal intensity level over the background, adopting the median ellipticity and position angle to plot it. Right panels: surface brightness profiles derived for the considered galaxies on the basis of the corresponding isophotal analysis (gray solid circles), together with the best fit to an exponential profile for the portion of the surface brightness dominated by the disk (gray dashed line). For NGC 7716 a previous iteration of the fitting procedure is shown, before the rejection of those values dominated by the bulge (solid-line). |
| In the text | |
 |
Fig. A.2 Left panel: distribution of the effective radius of the analyzed galaxies, derived from a growth curve analysis (i.e., the total light effective radius), as a function of the same effective radius derived by a similar growth curve analysis using the surface-brightness profiles derived using the ellipse task in IRAF. Right panel: distribution of the effective radius of the analyzed galaxies, derived from a growth curve analysis (i.e., the total light effective radius), as a function of the effective radius of the disk, derived from the exponential fitting to the surface brightness profile. In both panels, larger and bluer symbols correspond to earlier-type galaxies, while smaller and pinky/reddish ones correspond to later type galaxies. |
| In the text | |
 |
Fig. A.3 Top-left panel: distribution of the slopes of the abundance gradients as a function of the interaction stage of the galaxies, when the galactocentric distances are normalized to the effective radius derived by a growth curve analysis. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the interaction: (i) no signatures of interaction (red); (ii) galaxies with close companions and/or in an early interaction stage (green); and (iii) galaxies under clear collision or evolved mergers (blue). Top-right panel: similar distribution of slopes as a function of the morphological classification of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on their morphology: (i) early spirals, SO-Sa (red); (ii) intermediate spirals, Sab-Sb (green) and (iii) late spirals, Sc-Sm (blue). Bottom-left panel: similar distribution of slopes as a function of the presence or absence of bars. The colors of the symbols and the corresponding histograms indicate three types of galaxies: (i) clearly unbarred (red); (ii) not clear if there is a bar or not (green) and (iii) clearly barred galaxies (blue). Bottom-right panel: similar distribution of slopes as a function of the absolute magnitude of the galaxies. The colors of the symbols and the corresponding histograms indicate three types of galaxies based on the luminosity: (i) luminous galaxies, Mg−SDSS < −20.25 mag (red); (ii) intermediate galaxies −19.5 < Mg−SDSS < −20.25 mag (green) and (iii) faint galaxies Mg−SDSS > −19.5 mag (blue). The size of the symbols are inversely proportional to the derived error in the slope for all the panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


