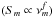| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 31 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321784 | |
| Published online | 11 September 2013 | |
Catching the radio flare in CTA 102
III. Core-shift and spectral analysis⋆
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail:
cfromm@mpifr.de
2
Observatori Astronòmic, Universitat de València,
Apartat de Correus
22085, 46071
València,
Spain
3
Departament d’Astronomia i Astrofísica, Universitat de
València, Dr. Moliner 50, 46100
Burjassot, València, Spain
4
Institut für Theoretische Physik und Astrophysik, Universität
Würzburg, Am
Hubland, 97074
Würzburg,
Germany
Received:
26
April
2013
Accepted:
24
June
2013
Context. The temporal and spatial spectral evolution of the jets of active galactic nuclei (AGN) can be studied with multi-frequency, multi-epoch very-long-baseline-interferometry (VLBI) observations. The combination of both morphological (kinematical) and spectral parameters can be used to derive source-intrinsic physical properties, such as the magnetic field and the nonthermal particle density. Such a study is of special interest during the high states of activity in AGNs, since VLBI observations can provide estimates of the location of the flaring site. Furthermore, we can trace the temporal variations in the source-intrinsic parameters during the flare, which may reflect the interaction between the underlying plasma and a traveling shock wave. The source CTA 102 exhibited such a radio flare around 2006.
Aims. In the first two papers of this series (Papers I and II), we analyzed the single-dish light curves and the VLBI kinematics of the blazar CTA 102 and suggested a shock-shock interaction between a traveling and a standing shock wave as a possible scenario to explain the observed evolution of the component associated to the 2006 flare. In this paper we investigate the core shift and spectral evolution to test our hypothesis of a shock-shock interaction.
Methods. We used eight multi-frequency Very Long Baseline Array (VLBA) observations to analyze the temporal and spatial evolution of the spectral parameters during the flare. We observed CTA 102 between May 2005 and April 2007 using the VLBA at six different frequencies spanning from 2 GHz up to 86 GHz. After the calibrated VLBA images were corrected for opacity, we performed a detailed spectral analysis. We developed methods for aligning the images and extracting the uncertainties in the spectral parameters. From the derived values we estimated the magnetic field and the density of the relativistic particles and combined those values with the kinematical changes provided from the long-term VLBA monitoring (Paper II) and single-dish measurements (Paper I).
Results. The detailed analysis of the opacity shift reveals that the position of the jet core is proportional to ν-1 with some temporal variations. The value suggests possible equipartition between magnetic field energy and particle kinetic energy densities at the most compact regions. From the variation in the physical parameters we deduced that the 2006 flare in CTA 102 is connected to the ejection of a new traveling feature (tej = 2005.9) and to the interaction between this shock wave and a stationary structure (interpreted as a recollimation shock) around 0.1 mas from the core (de-projected 18 pc at a viewing angle of ϑ = 2.6°). The source kinematics, together with the spectral and structural variations, can be described by helical motions in an overpressured jet.
Key words: galaxies: active / radiation mechanisms: non-thermal / galaxies: clusters: individual: CTA 102 / galaxies: jets / radio continuum: galaxies
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The spectral evolution of radio jets in active galactic nuclei (AGN) is probed by multi-frequency single-dish observations, and their modeling can provide estimates of the evolution of physical conditions in the source (see e.g., Marscher & Gear 1985; Türler et al. 2000). However, these observations cannot resolve the structure of the jet, and therefore only the overall spectral evolution can be obtained. One approach to extracting the spatial and temporal spectral evolution of AGN, used in the case of blazars, includes multi-epoch and multi-frequency VLBI observations. These high-resolution VLBI observations offer the unique possibility of resolving the structure of AGN jets and allow us to study the morphological and spectral evolution at parsec-scale resolutions. The analysis of these observations provides a tool for testing several jet models and extracting the source-intrinsic parameters.
Simultaneous VLBI observations at several frequencies can be used to analyze the variations in the observed base of the jet, commonly referred to as the core, with frequency (core-shift analysis; Lobanov 1998b; Hirotani 2005). These studies allow the observed core position to be related to source-intrinsic parameters, such as the magnetic field and the particle density (Lobanov 1998b; Hirotani 2005; Kovalev et al. 2008; O’Sullivan & Gabuzda 2009; Pushkarev et al. 2009). Based on the core-shift corrected maps, spectral index maps can be produced that show the spectral slope between two adjacent frequencies. The complete spectral information (i.e., turnover frequency, νm, turnover flux-density, Sm and spectral index, α0) can be extracted from multi-frequency VLBI maps by performing a spectral analysis. Such studies have been performed by, say, Lobanov (1998a), Savolainen et al. (2008), and yield the spatial distribution of the spectral values and source-intrinsic parameters, such as the particle density, N, and the magnetic field, B.
Our multi-frequency VLBI observations of CTA 102 between May 2005 and April 2007 cover the period of a large flux- density outburst in April 2006. This data set allows us to examine the changes in the physical properties of the source under these extreme circumstances. In Fromm et al. (2011, hereafter Paper I),we analyzed single-dish data of the 2006 radio flare in CTA 102 and suggested that the interaction between a propagating and a standing shock could be the driving mechanism behind the strong flare. We derived the evolution of physical parameters according to a slightly modified shock-in-jet model. The kinematic analysis of the source during the flare is presented in Fromm et al. (2013, hereafter Paper II ). This study revealed one apparently stationary component at r ~ 0.1 mas from the core and the connection of the 2006 radio flare to the ejection of a new component at epoch tej = 2005.9 ± 0.2. Based on the gradients in the evolution of the brightness temperature, we tested several jet configurations and derived estimates for the variation of the Doppler factor along the jet. From the results, we found evidence of bends in the jet, as well as of standing components that could be associated to recollimation shocks.
In this third paper of the series, we perform a full core-shift and spectral analysis to gain additional insights to clarify the jet nature. For this study we use eight multi-frequency VLBI observations with a frequency range between 2 GHz and 86 GHz during the 2006 radio flare.
The organization of the paper is the following. The data analysis tools developed for the spectral analysis of VLBI observations are described in Sect. 2. The observational results are divided into three sections: the core-shift analysis is presented in Sect. 3, the measures of the jet ridge line and width is included in Sect. 4, and the results of the spectral analysis are presented in Sect. 5. We present the derivation of the physical parameters in the jet from the observational results in Sect. 6. Finally, we discuss our results in Sect. 7 and present our conclusions in Sect. 8. A brief summary of the basic synchrotron self-absorption mechanism and the required equations for calculating the source-intrinsic parameters are given in Appendix A.
Throughout the paper we define the spectral index, α, using the relation Sν ∝ να. The optically thin spectral index, α0, can be derived from the spectral slope, s, of the relativistic electron distribution (N ∝ E−s), via the relation α0 = −(s − 1)/2. We define the optically thin spectral index as α0 < 0. We adopt the following cosmological parameters: Ωm = 0.27, ΩΛ = 0.73 and H0 = 71 km s-1 Mpc-1. This results in a linear scale of 8.11 pc mas-1 or 26.45 ly mas-1 for CTA 102 (z = 1.037). With these conventions, 1 mas yr-1 corresponds to 52.9 c. We use R for the radius of the jet and r for the distance along the jet. If not explicitly mentioned, we use cgs units throughout this paper.
2. Data analysis
For our analysis we used eight VLBI observations spanning from May 2005 until April 2007. The coverage of the 2006 radio flare in CTA 102 by our VLBI observations is presented in Fig. 1, where we show the temporal correspondence between the cm-mm light curves and the VLBA observations of CTA 102. More details about calibration, imaging, and model fitting of these VLBI images are presented in Sect. 2 of Paper II.
 |
Fig. 1 cm-mm single-dish light curves for CTA 102, covering the 2006 radio flare (see Paper I). The red dashed lines correspond to the epochs of multi-frequency VLBI observations presented in this paper. (Taken from Paper II.) |
Following the convention used in Paper II, the structure of the jet in CTA 102 can be studied by dividing it into four regions labeled as A (r > 8 mas), B (4 mas < r < 8 mas), D (2 mas < r < 4 mas), and C (r < 2 mas, the core region). Throughout our data set, we could clearly cross-identify seven features within regions A, B, and D. The analysis of the long-term monitoring of the source at 43 GHz revealed four additional features in region C (Paper II).
Figure 2 shows the VLBI observation of CTA 102 in June 2006, together with the cross-identified circular Gaussian components. A more detailed view into region C is provided in Fig. 3. All images of the source at different frequencies, together with the fitted components, are presented in the Appendix of Paper II. Table 1 presents a list of typical (average) image parameters for the CTA 102 observations at different frequencies.
 |
Fig. 2 Uniform weighted VLBA CLEAN images with fitted circular Gaussian components at different frequencies for the July 2006 observation of CTA102. The lowest contour is plotted at 10 × the off-source rms at 43 GHz and increases in steps of 2. The observing frequency and the restoring beam size are plotted above each map. For the labeling we use capital letters for the same physical region in the jet, and the numbers increase with inverse distance from the core. For a more detailed picture of the core region see Fig. 3. |
 |
Fig. 3 Zoom into the core region for the images presented in Fig. 2 corresponding to epoch 2006-06-08, showing the splitting of the C-components with increasing frequency. For map details see the caption of Fig. 2. |
2.1. Image alignment
The absolute position of the source is lost during the calibration process of VLBI observations owing to the use of closure phases. However, a proper relative alignment of the different frequency images is a basic requirement for a reliable core-shift and spectral analysis. The ideal technique for restoring the initial position of the source would be based on phase-referencing observations.
These experiments require a compact object in the neighborhood of the source. In most cases, this object would not be within the primary antenna beam of the interferometer, and this requires a nodding between the main source and the calibrator (e.g., Ros 2005). Our observations were not designed in phase-referencing mode, which makes another approach necessary.
Typical image parameters for the CTA 102 observations.
A common procedure for correcting for the frequency-dependent position of the source and especially the core is based on the assumption that the position of an optically thin region (S ∝ vα0) does not depend on the observing frequency. There are two different approaches to registering multi-frequency VLBI observations, one based on cross-identification of fitted Gaussian functions to the visibilities (denoted as components) and another based on 2D cross-correlation of the optically thin emission regions in the image plane. The advantage of the 2D approach is that the whole optically thin emission region is taken into account for the alignment, whereas the one based on fitted components takes only a single region into account. Nevertheless, if the source does not exhibit an extended jet region, the approach based on fitted features would be a better choice (see, e.g., Kadler et al. 2004; Kovalev et al. 2008; Croke & Gabuzda 2008).
In this paper we used a hybrid approach (2D cross-correlation and fitted components) depending on the amount of extended structure and on the resulting spectral index maps. We followed the work of Croke & Gabuzda (2008) and adjusted their technique to our needs. For the alignment based on cross-identified components we used the feature labeled as B2 for frequencies ν < 22 GHz and component D2 for higher frequencies. Both features could be cross-identified throughout our entire data set (see Fig. 2 and Paper II).
2.1.1. 2D cross-correlation of VLBI maps
The image parameters of a VLBI map, such as map size (ms), pixel size
(ps), and convolving beam size (bs), increase with
decreasing frequency (to optimize them with the resolution in each case). Before we
perform the cross-correlation of the VLBI images we select a set of common image
parameters. The best results for the cross correlation of two VLBI images with
frequencies, ν1 and ν2, where
ν1 > ν2,
are achieved by using the map size and beam size of the low-frequency image,
ms(ν2) and
bs(ν2), and
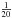 of
the high frequency beam size as pixel size ps (see also Pushkarev et al. 2012). These settings guarantee that
no structural information is lost during the alignment process. After both images are
convolved with the common beam, the optically thick core region is masked in both maps.
During the cross-correlation process, one of the images is shifted in the
Δx and the Δy directions and the cross-correlation
coefficient (see Eq. (1)) at each shift
position (Δx,Δy) is calculated. The cross-correlation
coefficient
ccΔx,Δy,
between the two maps is defined as (assuming that only the second map is shifted)
of
the high frequency beam size as pixel size ps (see also Pushkarev et al. 2012). These settings guarantee that
no structural information is lost during the alignment process. After both images are
convolved with the common beam, the optically thick core region is masked in both maps.
During the cross-correlation process, one of the images is shifted in the
Δx and the Δy directions and the cross-correlation
coefficient (see Eq. (1)) at each shift
position (Δx,Δy) is calculated. The cross-correlation
coefficient
ccΔx,Δy,
between the two maps is defined as (assuming that only the second map is shifted)
![\begin{eqnarray} cc=\frac{\sum_{i=1}^n\sum_{j=1}^m\left(S_{\nu_{1}}^{i,j}-\bar{S}_{\nu_1}\right)\left(S_{\nu_2}^{\Delta x\cdot i,\Delta y\cdot j}-\bar{S}_{\nu_2}\right)}{\left[\sum_{i=1}^n\sum_{j=1}^m\left(S_{\nu_1}^{i,j}-\bar{S}_{\nu_1}\right)^2\sum_{i=1}^n\sum_{j=1}^m\left(S_{\nu_2}^{\Delta x\cdot i,\Delta y\cdot j}-\bar{S}_{\nu_2}\right)^2\right]^{\frac{1}{2}}}, \label{cc} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq62.png) (1)where
i and j are the indices of pixels in the different
images,
(1)where
i and j are the indices of pixels in the different
images, 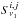 is the
flux-density of the unshifted image at the position (i,j) and
is the
flux-density of the unshifted image at the position (i,j) and
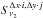 is the flux-density of the shifted map by Δx and Δy.
Finally,
is the flux-density of the shifted map by Δx and Δy.
Finally, 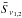 is the average flux-density in the images. The result of this approach is the
distribution of cross-correlation coefficients within the shift area. The best shift
position corresponds to the maximum cross-correlation coefficient. The finite width of
the pixel size leads to discrete values for the best shift position in steps of the used
pixel size. This dependence on the selected pixel size can be overcome by fitting a 2D
elliptical Gaussian to the cross-correlation distribution achieved. A 2D elliptical
Gaussian distribution can be written in the form
is the average flux-density in the images. The result of this approach is the
distribution of cross-correlation coefficients within the shift area. The best shift
position corresponds to the maximum cross-correlation coefficient. The finite width of
the pixel size leads to discrete values for the best shift position in steps of the used
pixel size. This dependence on the selected pixel size can be overcome by fitting a 2D
elliptical Gaussian to the cross-correlation distribution achieved. A 2D elliptical
Gaussian distribution can be written in the form 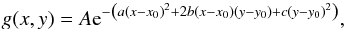 (2)where
the coefficients a, b, c are
defined by
(2)where
the coefficients a, b, c are
defined by 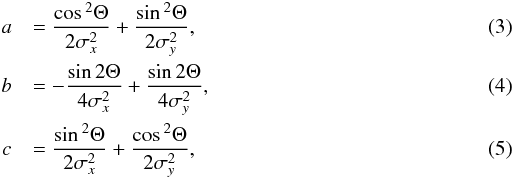 with
Θ the rotation angle, x0 and y0
the mean values, and σx and
σy the standard deviations. The fitted
parameters x0 and y0 can be
regarded as the best shift position.
with
Θ the rotation angle, x0 and y0
the mean values, and σx and
σy the standard deviations. The fitted
parameters x0 and y0 can be
regarded as the best shift position.
If the distribution of the cross-correlation coefficient is smooth and symmetric around the mean values, the distribution of the cross correlation coefficient could be described as a Gaussian distribution, and the mean values are the best choice for correcting the core shift. Otherwise, the position of the highest cross correlation coefficient is a suitable choice.
The distribution of the spectral index, α, computed from two adjacent
frequencies is highly sensitive to positional changes: 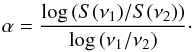 (6)In
this way, a visual check on α for both alignment methods allows us to
diagnose their performance. In principle, the distribution of the spectral index,
α, should be smooth across the jet with a decrease towards the
extended structure and a slight transversal gradient. We computed several spectral index
maps using the 2D cross-correlation approach and component approach in order to
investigate the difference between both methods. Examples are presented in Figs. 4–7 for the
alignment of two low-frequency and two high-frequency VLBI images.
(6)In
this way, a visual check on α for both alignment methods allows us to
diagnose their performance. In principle, the distribution of the spectral index,
α, should be smooth across the jet with a decrease towards the
extended structure and a slight transversal gradient. We computed several spectral index
maps using the 2D cross-correlation approach and component approach in order to
investigate the difference between both methods. Examples are presented in Figs. 4–7 for the
alignment of two low-frequency and two high-frequency VLBI images.
2.1.2. Low-frequency alignment
For the alignment of the 8 GHz and 5 GHz maps of the May 2005 observations, we used a pixel size of 0.04 mas and beam size of 3.65 × 1.52 mas and a PA of −8° for the 2D cross-correlation, and for the component based approach we used the feature labeled as B2 (see contour plots in Fig. 2). Figure 4 presents the distribution of the cross correlation coefficient between the 8 GHz and the 5 GHz images. The best shift position was found at Δx = 0.38 mas and Δy = −0.28 mas (black dashed line in Fig. 4). From the component-based approach, we obtained an image shift of Δx = 0.47 mas and Δy = −0.34 mas.
 |
Fig. 4 Distribution of the cross-correlation coefficient for the alignment of the 8 GHz and 5 GHz VLBA maps. The intersection of the white dashed lines corresponds to the maximum cross-correlation coefficient in the color-map and the intersection of the dashed black line to the peak position of the fitted 2D Gaussian. |
 |
Fig. 5 5 GHz–8 GHz spectral index maps for the May 2005 observations of CTA 102. The left panel shows the spectral index map produced by the 2D cross-correlation and the right panel the one by using the component based approach. The contours are drawn for the 8 GHz observations. The inlets show the distribution of the spectral index along the jet axis, black solid line, (inlet A) and transversal to the jet axis, dashed black line, (inlet B). |
The distribution of the spectral index shows in both cases an optically thick core
region 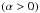 and
an optically thin jet region
and
an optically thin jet region 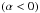 , with
the transition at a distance of r ≈ 2.7 mas away from the core. The
evolution of the spectral index along the jet axis is similar for both approaches with
minor variations (see inlet A in Fig. 5). However,
there are major differences in the transversal distribution of the spectral index (inlet
B in Fig. 5). The model fit based approach has a
strong transversal gradient in the spectral index (blue line in inlet B), which is
smoothed out by the 2D cross-correlation technique (red line in inlet B).
, with
the transition at a distance of r ≈ 2.7 mas away from the core. The
evolution of the spectral index along the jet axis is similar for both approaches with
minor variations (see inlet A in Fig. 5). However,
there are major differences in the transversal distribution of the spectral index (inlet
B in Fig. 5). The model fit based approach has a
strong transversal gradient in the spectral index (blue line in inlet B), which is
smoothed out by the 2D cross-correlation technique (red line in inlet B).
 |
Fig. 6 Distribution of the cross-correlation coefficient for the alignment of the 43 GHz and 22 GHz VLBI map. The intersection of the white dashed lines corresponds to the maximum cross-correlation coefficient in the color-map and the intersection of the dashed black line to the peak position of the fitted 2D Gaussian. |
2.1.3. High-frequency alignment
We used the 22 GHz and 43 GHz VLBA observations in the May 2005 epoch to study the alignment of high-frequency maps. The 2D cross-correlation technique resulted in a correction of Δx = 0.04 mas and Δy = 0.01 mas, using a pixel size of 0.01 mas, beam size of 0.95 × 0.33 mas, and a PA of −13° (see Fig. 6 for the distribution of the cross-correlation coefficient). Fixing component D2 (see Fig. 3), we calculated a value of Δx = 0.03 mas and Δy = 0.01 mas for the correction of the opacity shift. Since the distribution of the cross-correlation coefficient is not well described by a 2D-Gaussian, we selected the position of the highest cross-correlation coefficient as the best shift position (see white dashed line in Fig. 6).
 |
Fig. 7 22 GHz-43 GHz spectral index maps for the May 2005 observations of CTA 102. The left panel shows the spectral index map produced by the 2D cross-correlation and the right panel the one by using the component based approach. The contours are drawn for the 43 GHz observations. The inlets show the distribution of the spectral index along the jet axis, black solid line, (inlet A) and transversal to the jet axis, dashed black line, (inlet B). |
The computed spectral index maps between 22 GHz and 43 GHz are presented in Fig.
7. The distribution of the spectral indices in
the optically thick core region 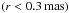 follows the same decreasing trend as in the low-frequency case (see inlet A in Fig.
7). The distributions are slightly rotated by
roughly 15°. The two different techniques, 2D cross-correlation and
component-based alignment, lead to nearly identical spectral index maps.
follows the same decreasing trend as in the low-frequency case (see inlet A in Fig.
7). The distributions are slightly rotated by
roughly 15°. The two different techniques, 2D cross-correlation and
component-based alignment, lead to nearly identical spectral index maps.
2.2. Spectral analysis
For the extraction of the spectral parameters, turnover frequency, νm, turnover flux-density, Sm, and optically thin spectral index, α0 we need at least three VLBI observations at different frequencies. In general, there are two approaches to the extraction of the spectral parameters, one based on the flux densities in each pixel (Lobanov 1998a) and the other one on the fitted components (Lobanov & Zensus 1999; Savolainen et al. 2008). The advantage of the pixel-based approach is that it provides a continuous evolution of the spectral values along the jet. If the spectrum is not homogenous because several components are located within a region of the size of the convolving beam or the turnover frequency, νm, is out of our frequency range, we can no longer obtain the turnover values. Nevertheless, the spectral index, α (Sν ∝ να) can still de derived.
As mentioned in Sect. 2.1, the convolving beam and pixel size of the maps are decreasing with increasing frequency (see Table 1). An appropriate selection of the common beam and pixel size for all the maps involved in the analysis is needed to avoid generating image artifacts (small beam size) or losing structural information (too large pixel size). There are two possible techniques that can be used to avoid these difficulties. The first one uses the beam size of the lowest frequency map and pixel size of the highest frequency map. The second one is an adaptive method, where the beam and pixel size are selected depending on the distance to the core; i.e., the closer to the core, the smaller the beam and the pixel size. Using the latter implies that the lower frequency maps have to be excluded from the spectral analysis closer to the core region to avoid image artifacts.
After one of the aforementioned methods is selected and the opacity shift is corrected in
the maps relative to a reference one (Sect. 2.1), the
pixel-to-pixel spectral analysis can be performed. The procedure is the following: i) The
aligned images are all convolved with a common beam and pixel size and are stacked on top
of each other into a datacube; ii) the dimensions of this cube are the map dimensions in
the x- and y-directions and the number of involved
frequencies in the z-direction. Thanks to the already performed image
alignment (see Sect. 2.1), each pixel at a given
frequency
[j(νu),i(νu),k(νu)]
corresponds to its counterpart at the other frequencies
![\hbox{$\left[j(\nu_p),i(\nu_p),k(\nu_p)\right]$}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq106.png) ,
where
j(νu/p),i(νu/p)
are the array indices of each VLBA map in the x- and
y-directions and
k(νu/p)
is the frequency index; iii) for each position (x,y) a frequency vector
νx,y = [ν0···νn]
and a flux-density vector
Sν,x,y = [Sν,0···Sν,n]
vector can be extracted, with n the total number of maps included in the
spectral analysis.
,
where
j(νu/p),i(νu/p)
are the array indices of each VLBA map in the x- and
y-directions and
k(νu/p)
is the frequency index; iii) for each position (x,y) a frequency vector
νx,y = [ν0···νn]
and a flux-density vector
Sν,x,y = [Sν,0···Sν,n]
vector can be extracted, with n the total number of maps included in the
spectral analysis.
By fitting the approximation of the synchrotron-self-absorbed spectrum to νx,y and Sν,x,y, the turnover frequency, νm,x,y, the turnover flux-density Sm,x,y, and the optically thin spectral index, α0,x,y, can be obtained, while fixing αt,x,y = 5/2 (assuming homogeneous synchrotron emission feature). Extending this technique to the overall source structure results in a 2D distribution of the turnover values for each multi-frequency epoch. Figure 8 illustrates our spectral analysis algorithm.
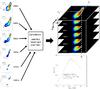 |
Fig. 8 Illustration of the basic steps within our spectral analysis algorithm: i) image alignment and convolution with common beam and pixel size; ii) stacking of the images; and iii) fitting of the synchrotron-self-absorbed spectrum. See text for more details. |
We estimated the uncertainties on the derived spectral parameters including the uncertainties of the measured parameters and the sensitivity of the computing method to the shifts between images, as described in Appendix D. In short, first we assumed that the uncertainties in the flux-density vary between 5% and 15%. We included this frequency-dependent flux-density uncertainty in our error analysis and, additionally, incorporated the flux-density errors for each pixel, based on the image signal-to-noise ratio (S/N) at each of them. To estimate the influence of the uncertainties of the opacity shifts, we assumed that the uncertainties of the obtained shift positions are within the used pixel size. Therefore, we randomly shifted each map within the allowed position, extracted the spectral parameters, and calculated the scatter of the obtained values. This was done by performing a Monte Carlo simulation for which we used up to 104 random shifts for each epoch to derive the uncertainties for the spectral parameters. We rejected turnover values that are not well constrained within our data set: i.e., spectra for which we obtained turnover frequencies, νm, lower than 75% percent of the minimum frequency in the data set. This procedure provides the most reliable turnover values and is incorporated into the presented evolution of the spectral parameters.
3. Core-shift analysis
We used the technique presented in Sect. 2.1 to align the VLBI observations of CTA 102. Owing to the difference in the image parameters, especially in the convolving beam size, we used only adjacent frequency maps in the alignment. The shift values obtained relative to the initial position are presented in Table 2.
There are two different shift directions towards the northeast (positive x- and y- directions) for frequencies higher than 22 GHz (see panel A in Fig. 9) and in the southeast direction for lower frequencies (relative to the highest frequency involved in the analysis, see panels B, C, and D in Fig. 9). An exception to this observed behavior appears in the April 2006 epoch, possibly due to the large flux-density outburst during this time.
We derived the core-shift vector from the correction of the opacity shift (see Table 2) and the position of the VLBI core (see Paper II for more details on the jet model fitting). Figure 9 shows the variation in the core-shift vector for the different frequency pairs with time.
Correction for the opacity shifts obtained by 2D cross correlation between adjacent frequencies.
 |
Fig. 9 Variation of the core-shift vector with time for different frequency pairs (panel A) (43−22) GHz, panel B) (22−15) GHz, panel C) (15−8) GHz and panel D) (8−5) GHz). The solid circles correspond to the radial distance from the reference core and the dashed lines are drawn in intervals of 30°. The color of the arrow indicates the different observational epochs. (See text for more details). |
The variation in the 43 GHz−22 GHz core-shift vector around 0.01 mas reflects the uncertainties in the alignment method used (see panel A in Fig. 9). The 22 GHz−15 GHz and 8 GHz−5 GHz shift vectors are mainly oriented in southeast direction (see panels B and D in Fig. 9), whereas the 15 GHz−8 GHz ones show some variation in the northeast to southeast direction. This variation in the direction of the core-shift vector for this frequency pair may reflect the slightly different orientation of the radio jet axis between 15 GHz and 8 GHz. For the other frequency pairs, the difference in the jet axis is not as pronounced as for the 15 GHz−8 GHz pair (see contour plots in Fig. 2).
To derive the parameter kr (see Eq. (37)), we used the highest frequency during each observation as a reference frequency and computed the relative radial core shift. Since CTA 102 has a curved structure, which is clearly visible in Fig. 2, we would have underestimated the core shift by using only the one-dimensional radial distance between two VLBA cores. Therefore, we calculated the core shift along a curved trajectory given by the x- and y-position of the image alignment. Table 3 presents the calculated core-shift values relative to the highest frequency during each observation epoch.
Since we measured the core shift relative to a reference frequency,
νref, Eq. (37)
can be rewritten in the following form (O’Sullivan &
Gabuzda 2009):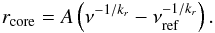 (7)We
applied Eq. (7) to the core shifts, and the
results are presented in Table 5. The weighted
average of the different kr and
A values obtained is
kr = 0.8 ± 0.1 and
A = 3.4 ± 1.6. All values are compatible with
kr ~ 1 but for the October 2006 and April
2007 observations.
(7)We
applied Eq. (7) to the core shifts, and the
results are presented in Table 5. The weighted
average of the different kr and
A values obtained is
kr = 0.8 ± 0.1 and
A = 3.4 ± 1.6. All values are compatible with
kr ~ 1 but for the October 2006 and April
2007 observations.
Core shift values relative to the reference frequency (given in the second column) for different epochs.
Physical parameters from the core-shift analysis for three different models (see text for more details).
Assuming that the jet is in equipartition and has a conical geometry, which is a valid
assumption for region C as seen from the value obtained for
kr, the magnetic field can be obtained
using Eqs. (39)–(44) (see Sect. 4 for further details on the jet width in region C) . In general, the radial
evolution of the magnetic field in the jet is given by
B ∝ r−ϵb, where
ϵ is the jet opening index
(R ∝ rϵ) and
b parametrizes the evolution of the magnetic field
(B ∝ R−b). For a jet in
equipartition the particle density has to decrease as
N ∝ R−2b or, in terms of
distance along the jet
N ∝ r−2bϵ. Assuming a
conical jet (i.e., ϵ = 1) and a toroidal magnetic field
(b = 1), an estimate can be derived for the magnetic field,
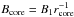 ,
and the relativistic particle density at the core,
,
and the relativistic particle density at the core, 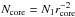 .
To calculate the magnetic field we used the shifts obtained between 22 GHz and 15 GHz
because we obtained a small variation in the core-shift orientation for this frequency pair.
We used a viewing angle of ϑ = 2.6°, a half opening angle
ϕ = 0.5°, a Doppler factor δ = 17, and an
apparent speed, βapp = 13 c, derived from the
components C1 and C2 (see Paper II). These components were ejected during our observations
and are the ones that best reflect the velocities in the core region.
.
To calculate the magnetic field we used the shifts obtained between 22 GHz and 15 GHz
because we obtained a small variation in the core-shift orientation for this frequency pair.
We used a viewing angle of ϑ = 2.6°, a half opening angle
ϕ = 0.5°, a Doppler factor δ = 17, and an
apparent speed, βapp = 13 c, derived from the
components C1 and C2 (see Paper II). These components were ejected during our observations
and are the ones that best reflect the velocities in the core region.
Table 4 presents values for the magnetic field and the particle density computed from the core-shift results using i) kr = 1, α0 = −0.5, ϑ = ϑcrit, and βapp = 13; ii) kr ≠ 1, α0 = −0.5, ϑ = 2.6°, ϕ = 0.5° , and δ = 17; and iii) kr ≠ 1 and α0 = −0.5, ϑ = 2.6°, ϕ = 0.5° and δ = 17. For calculating the particle density we assumed a fixed ratio of γmax/γmin = 105 and a lower electron Lorentz factor γmin = 1.
Parameters for the core-frequency dependency from the core-shift analysis.
 |
Fig. 10 Evolution of the core magnetic field, Bcore (top), and the relativistic particle density at the core, Ncore (bottom), as derived from the core shift analysis for three different models (For details see text). |
Figure 10 shows the evolution of Bcore,22 GHz and Ncore,22 GHz for the three models. For model i), we obtained the values around Bcore,22 GHz ~ 0.1 G and Ncore,22 GHz = 60 cm-3 (black points in Fig. 10). Using a more detailed jet parameters, while keeping kr = 1 and α0 = −0.5 leads to lower values of Bcore,22 GHz ~ 0.08 G and Ncore,22 GHz ~ 30 cm-3 as compared to model i) (red points in Fig. 10). On average, slightly lower values are computed for Bcore,22 GHz and Ncore,22 GHz if we use the obtained kr values. The average Bcore,22 GHz = 0.07 G and Ncore,22 GHz = 23 cm-3 (green points in Fig. 10).
4. Transversal jet structure and jet ridge line
A conical jet geometry was assumed in the modeling presented in the previous section. We studied the transversal jet structure of CTA 102 to test this assumption. For this, we derived the jet ridge line, that is to say, the line connecting the local flux-density maxima along the jet, and fitted a Gaussian to the flux-density profiles perpendicular to the jet ridge line (see, e.g., Pushkarev et al. 2009). Since we were interested in the average jet width and ridge line, we used stacked VLBA images, which include all the observations at a given frequency, here from 2005 until 2007. The advantage of using stacked images is that the values obtained for the width and the ridge line are less affected by individual calibration uncertainties. For the convolution of the individual images, we used the average beam size for each frequency (see Table 1).
Figure 11 shows a 15 GHz stacked VLBI image of CTA 102 overplotted with the obtained jet ridge line. We corrected the starting point of the jet ridge line at each frequency for the opacity shift using the average image shift obtained as explained in Sect. 3. The results are presented in Fig. 12.
 |
Fig. 11 Stacked 15 GHz contour map of CTA 102 obtained from observations between 2005 and 2007 convolved with a common beam size of 1.33 mas × 0.52 mas and a PA of −9° with over-plotted jet ridge line. The lowest contour level is drawn at 5× the average off-source rms (4 mJy) and the contours increase in steps of 2. |
 |
Fig. 12 Jet ridge line for CTA 102 obtained from stacked VLBA images at different frequencies after realignment. The dashed lines correspond to the radial distances and are plotted every 1 mas. |
After applying the opacity correction to the ridge lines derived at different frequencies, we obtained good spatial agreement between them (see Fig. 12). The jet ridge line at low frequencies ν < 8 GHz shows an oscillating pattern with an observed wavelength λobs,1 ~ 20 mas. Within the first 13 mas from the core, the ridge line is oriented along an observed angle of −65°. At higher frequencies, a second oscillating pattern developing on top of the first one is observed, as reported in Perucho et al. (2012) for the case of the jet in the quasar S5 0836+710. This second pattern is most visible at 15 GHz and 22 GHz and has an observed wavelength, λobs,2 ~ 5 mas. There are also indications of an additional pattern with λobs,3 < 1 mas visible at the highest frequencies, 43 GHz and 86 GHz. A full analysis of the jet ridge lines as described in Perucho et al. (2012) could lead to additional parameters of the 3D helical patterns, which are potentially connected to fluid instabilities, but this is beyond the scope of this paper.
 |
Fig. 13 Jet width of CTA 102 obtained from stacked VLBA images at different frequencies after realignment. |
Figure 13 shows the variation in the de-convolved jet
width, 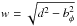 ,
with distance, where d is the FWHM of the fitted Gaussian and
bφ the size of the beam transversal to the
jet ridge line along the jet. As we did for the jet ridge line, we corrected the starting
position using the average core-shift value,
r = 3.4·ν-1.25. The constant horizontal
points for each frequency reflect the resolution limit where we cannot resolve the
transversal structure of the jet. The position of the first observed rise of the jet width
increases with decreasing frequency and is in good agreement with the position found at
neighboring frequencies, which supports the validity of the measurement. Tracing this point
back to the highest frequency available in our data set (86 GHz) leads to a distance of
0.1 mas from the jet nozzle and to a jet width of 0.05 mas, which corresponds to one
half of the convolving beam size transversal to the jet ridge line. The jet width is
varying, with several indications of collimation and recollimation along the jet. This
behavior is most visible at 15 GHz. For this frequency our analysis reveals three local
maxima of the jet width at a core distance along the ridge line of
r = 1.2 mas, r = 5.4 mas and
r = 13.3 mas. At the higher frequencies, ν = 22 GHz
and ν = 43 GHz, we also find indications of
recollimation of the jet at the same positions.
,
with distance, where d is the FWHM of the fitted Gaussian and
bφ the size of the beam transversal to the
jet ridge line along the jet. As we did for the jet ridge line, we corrected the starting
position using the average core-shift value,
r = 3.4·ν-1.25. The constant horizontal
points for each frequency reflect the resolution limit where we cannot resolve the
transversal structure of the jet. The position of the first observed rise of the jet width
increases with decreasing frequency and is in good agreement with the position found at
neighboring frequencies, which supports the validity of the measurement. Tracing this point
back to the highest frequency available in our data set (86 GHz) leads to a distance of
0.1 mas from the jet nozzle and to a jet width of 0.05 mas, which corresponds to one
half of the convolving beam size transversal to the jet ridge line. The jet width is
varying, with several indications of collimation and recollimation along the jet. This
behavior is most visible at 15 GHz. For this frequency our analysis reveals three local
maxima of the jet width at a core distance along the ridge line of
r = 1.2 mas, r = 5.4 mas and
r = 13.3 mas. At the higher frequencies, ν = 22 GHz
and ν = 43 GHz, we also find indications of
recollimation of the jet at the same positions.
We approximated the jet width with a power law in each of the four different regions C, D, B, and A, in which we divided the jet. The jet width can be parametrized as a power law, R ∝ rϵ where ϵ is the jet opening index. The jet opening index obtained for each of these regions is presented in Table 6. A single power law fit applied to the jet width gives ϵ = 0.6 ± 0.1 for the four regions.
The results of the jet width analysis show that CTA 102 embeds a pinching jet width; i.e., it consists of regions where the jet cross-section is opening or closing. At r < 1 mas the jet shows a nearly conical geometry ϵ = 0.8 ± 0.1. Farther downstream (r > 4 mas), the jet geometry differs significantly from conical.
5. Spectral analysis
Here we present the result of the spectral analysis for the different jet regions as introduced in Paper II (see the previous section). We show the spectral parameters along the jet ridge line and averaged values transversally to it, which reflect possible transversal gradients in the spectral parameters across the jet. The 2D distribution of the spectral parameters is presented in Appendix C
Since the spectral turnover is outside our frequency range for regions B and A, we fitted a power law Sν ∝ να to the measured flux densities. The uncertainties on the spectral parameters were calculated using a Monte-Carlo simulation taking into the uncertainties of the image alignment and the flux densities of the individual pixels into account. Since the uv-coverage is changing with frequency we only used those uv-radii covered throughout the selected frequency range. For more details see Appendix B and Fromm (in prep.) for the detailed treatment of the capabilities and the limitations of the pixel based spectral analysis applied to multi-frequency VLBI images.
5.1. Region C (r < 1 mas)
The core region is characterized by an inverted spectrum (increasing flux-density with increasing frequency) throughout our data set, except for the May 2005 observations. Therefore, we applied a power-law fit to obtain the 2D distribution of the spectral index α. The region could be best studied using the high-frequency VLBI maps (ν > 8 GHz), a common beam size of 0.95 × 0.33 mas with a PA of −13° (which corresponds to the average beam of the 22 GHz observations), and a pixel size of 0.03 mas. These image settings allowed us to extract the spectral index without generating image artifacts in the low-frequency maps or losing structural information in the high-frequency maps.
Estimates for the exponent ϵ, defining the jet geometry, R ∝ rϵ.
The spectral index along the jet axis is presented in Fig. 14, where we used the 43 GHz core of each observation as the origin of coordinates. The core region of the September 2005 and January 2007 observations of CTA 102 could not be explained with a single power law due to the rise of a flare, that is, the increase in the high-frequency flux densities, here the 43 GHz flux densities (see Fig. 1). Therefore, we excluded these two epochs from the analysis of the core region. Within r < 0.3 mas of the core, the spectral index is positive (α > 0), which corresponds to an inverted spectrum, and farther downstream α decreases with distance. There is a variation of α with distance and time. The latter is most visible between May 2005 and October 2006, when the slope of the spectral index along the jet changes from −1.6 (May 2005) to −1.1 (June 2006) and back to −1.3 (October 2006). This could be an indication of the injection of relativistic particles and the connected energy losses during the propagation of a relativistic shock wave.
 |
Fig. 14 Evolution of the spectral index along the jet ridge line, α (Sν ∝ να) for region C (r < 1 mas), where we used a beam size of 0.95 × 0.33 mas with a PA of −13°. For readability only one error bar per epoch is shown. |
Since our frequency coverage for the May 2005 observations ranges from 5 GHz to 86 GHz, estimates of the values at the spectral turnover could be derived. For this epoch, we only present axial turnover values, since we could hardly resolve the transversal structure of the source with the selected beam size. Figure 15 shows the spatial evolution of the turnover frequency, νm, the turnover flux-density, Sm, and the optically thin spectral index, α0 along the jet ridge line. The optically thin spectral index decreases from −0.1 at r = 0.15 mas to −0.45 at r = 0.5 mas. At the same distance, the turnover frequency changes from νm = 30 GHz to νm = 15 GHz at r = 0.5 mas. A drop in the turnover flux-density, Sm, occurs at r = 0.2 mas from Sm = 2.3 Jy to Sm = 1.2 Jy.
In the turnover frequency-turnover flux-density plane, the spatial evolution shows a constant turnover flux-density Sm = 2.3 Jy for r < 0.15 mas, while the turnover frequency decreases (see Fig. 16). For r > 0.15 mas, both the turnover frequency and the turnover flux-density decline. This decrease in the turnover position agrees with the expected behavior, when the (adiabatic) expansion losses are the dominant energy loss mechanism (Marscher & Gear 1985). The constant turnover flux-density measured across the region at r < 0.1 mas could be caused by the smearing of the flux-density during the convolution.
5.2. Region D (1 mas < r < 4 mas)
 |
Fig. 15 Spatial evolution of the turnover values along the jet ridge line for the May 2005 observation (2005.39). We used a beam size of 0.95 × 0.33 mas with a PA of −13° and pixel size of 0.03 mas. The error estimates were derived from a Monte Carlo simulation (see text for more details). Top panel: Turnover frequency, νm; middle panel: turnover flux-density, Sm; bottom panel: optically thin spectral index, α0 |
For the spectral analysis of region D, we used a beam size of 1.33 × 0.52 mas and a pixel size of 0.04 mas and included the 5 GHz and 8 GHz VLBI maps in the analysis. This extended frequency range meant we could derive the turnover values by applying Eq. (25). We rejected turnover frequencies below 5 GHz and optically thin spectral indices, α0 > −0.2.
The values obtained for the turnover frequency in this region are between 5.0 GHz and 10.0 GHz. The axial turnover frequencies exhibit a curved distribution, where the value of the peak and its position vary in time (see left panel in Fig. 17). This curvature could be an artifact of the convolution. However, the transversally averaged values show a monotonic decrease in the turnover frequency (see the right panel in Fig. 17).
The evolution of the turnover flux-density, Sm, shows a clear decreasing trend with time and a slight shift in the position of the flux-density maxima with distance from the core (see Fig. 18). The optically thin spectral index shows an increasing trend with distance from α0 ~ −1.0 to α0 ~ −0.5, but the large uncertainties in the optically thin spectral index do not allow us to detect a significant temporal variation (see Fig. 19).
 |
Fig. 16 Turnover frequency–turnover flux-density plane for region C for the May 2005
observations. The number correspond to the distance from the core in mas and the
solid red line to a power law fit |
 |
Fig. 17 Evolution of the turnover frequency, νm, for region D (1 mas < r < 4 mas) along the jet axis, where we used a beam size of 1.33 × 0.52 mas with a PA of −9°. For reasons of readability only one error bar per epoch is shown. Left: values along the jet ridge line. Right: average values transversal to the jet ridge line. |
We can see significant changes in the turnover frequency and turnover flux-density with time and position in region D. Figure 20 shows the variation of the turnover values in the turnover frequency – turnover flux-density (νm − Sm) plane for a fixed position at r = 1.5 mas. The kinematic analysis of CTA 102 revealed a traveling component, labeled as D2, within this region and a possible standing component at r = 1.5 mas (see region D in Paper II). The evolution in the νm − Sm plane shows an increase in both νm and Sm between 2005.3 and 2006.3 followed by an increase in 2006.44. For t > 2006.44, the turnover flux-density is lower than in 2005.3 and the turnover frequency varies slightly.
 |
Fig. 20 Turnover frequency-turnover flux-density plane for region D at a fixed position of r = 1.5 mas, where the numbers represent the temporal evolution. Left: axial values. Right: transversal averaged values (for more details see text). |
The kinematical results (Paper II) and the present spectral study point towards a situation in which component D2 crosses region D during the time span of our observations, possibly interacting with a standing emission region at r ≃ 1.5 mas. Following the classical shock-in-jet model, we would expect a continuous decrease in turnover flux-density and turnover frequency, since at this position, r = 1.5 mas (deprojected 86 pc), the main energy loss mechanism should be adiabatic expansion losses. However, we detect an increase in Sm at this position, which could stem from a re-acceleration of relativistic electrons or an increase in the particle density (see also Paper I). From the spectral analysis of region C, we know that the turnover flux-density and turnover frequency are monotonically decreasing (see Fig. 16). Therefore, the increase in the νm − Sm plane requires a region of locally increased density and/or magnetic field. Such a local increase in the physical parameters could be created by a recollimation shock. The results of the kinematic analysis in region D (Paper II) and the study of the transversal jet width (Sect. 4) support this assumption.
5.3. Region B (4 mas < r < 10 mas)
This region is characterized by three nearly stationary components (see Paper II) and by a constant jet width (see Sect. 4). Figure 21 shows the value of the spectral index along the jet. This region could be best studied by using a frequency range from 5 GHz to 15 GHz, a beam size of 2.32 × 0.97 mas, a PA of −7°, and a pixel size of 0.10 mas. The spectral index at r ~ 2.0 mas lies between −0.8 < α < −0.6, which is consistent with the continuation of the observed evolution in region D (see Fig. 19). For r > 2.0 mas an increase in the spectral index can be observed, followed by a plateau of nearly constant value at r = 4.0 mas (left panel in Fig. 21). For longer distances, the spectral index decreases with distance until r ~ 7.0 mas. Farther downstream there is an additional rise in the spectral index, although less pronounced than the one at r = 4 mas.
 |
Fig. 21 Evolution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 10 mas) along the jet ridge line. For reasons of readability only one error bar per epoch is shown. Left: values along the jet ridge line. Right: average values transversal to the jet ridge line. |
5.4. Region A (8 mas < r < 14 mas)
For region A we used the VLBI images at 5 GHz, 8 GHz, and 15 GHz and a beam of 3.65 × 1.52 mas, a PA of −8°, and a pixel size of 0.15 mas. In contrast to region B, the spectral index decreases from α ~ −1.0 to α ~ −1.2 without major variations, most visible in the transversally averaged values (see Fig. 22). The increase in the averaged values for the May 2005 observations (2005.39) is due to a region of high spectral indices at the edges of the jet (see Fig. C.7 in Appendix B). The sparse sampling of the uv coverage, especially on short ranges leads to strong variation in the outermost structure. Additional to the uv-sampling, antenna or weather problems (e.g., rain) mainly affect the low frequencies and especially the outer structure of the source, lead to strong flux variations and therefore variations in the spectral index. Therefore, we restricted ourself to distances r < 14 mas in the spectral analysis of the outermost structure.
 |
Fig. 22 Evolution of the spectral index, α (Sν ∝ να) for region A (8 mas < r < 14 mas) along the jet ridge line. For reasons of readability, only one error bar per epoch is shown. Left: values along the jet ridge line. Right: average values transversal to the jet ridge line. |
6. Spatial and temporal evolution of physical parameters
6.1. Position of the jet nozzle
For the core region C, we could only derive the turnover frequency, νm, and the turnover flux-density, Sm for the May 2005 observations due to an extended frequency range up to 86 GHz. The spectral turnover values allow us to compute the magnetic field and the normalization coefficient of the relativistic electron distribution using Eqs. (32) and (33), respectively. Furthermore, we could provide some estimates of the number density of the relativistic particles and of the magnetization, σ, of the plasma using the first-order model presented in Sect. 6.4 and the jet width (see Sect. 4).
In this section we use the opacity-corrected core position; i.e., the radial origin corresponds to the location where τ = 1 for ν → ∞ using the results of the core-shift analysis (see Table 5 in Sect. 3). In Table 7 we present the offset corrections for all epochs.
Results of the core-shift analysis.
6.2. Core region in May 2005
For calculating the magnetic field and the normalization coefficient of the relativistic electron distribution, we need to know the evolution of the jet width and an estimate for the Doppler factor along the jet. Since the turnover values for region C were obtained using the average beam size of the 22 GHz VLBI maps (see Sect. 5.1), we used the jet width calculated for this frequency (see Sect. 4). Based on the flux-density evolution of the component labeled as C2, we calculated a variability Doppler factor δvar = 17 ± 3. A parameter space study based on the gradients in the brightness temperature, Tb, revealed that the Doppler factor increases within region C (see Paper II). Accordingly with the numbers obtained in Paper II, we adopted an exponent of d = −0.6 (δ = R−d) and an upper value of δ = 17 for the following analysis.
The magnetic field computed from the aforementioned parameters is presented in the upper panel of Fig. 23. The magnetic field intensity decreases from 60 mG at r = 0.1 mas to 30 mG at r = 0.4 mas. The results of an approximation of the evolution with a power law (B ∝ rb′) gives an exponent b′ = −0.3 ± 0.1 for the whole range (0.02 mas < r < 0.4 mas, dashed red line in the upper panel of Fig. 23). The flat spectral index for r < 0.1 mas could be due to convolution effects. Therefore, we also fitted the evolution of the magnetic field intensity for r > 0.1 mas and obtained an exponent of b′ = 0.7 ± 0.1 (solid red line in the upper panel of Fig. 23). Similar values for the magnetic field, B, were obtained using the core-shift (see magnetic field values in Sect. 3). Since both methods are independent, the result of the magnetic field can be regarded as a meaningful estimate.
The normalization coefficient of the relativistic electron distribution spans from 5.0 erg−2α0 cm-3 to 10-3 erg−2α0 cm-3. We used a power law (K ∝ rk′) to fit the evolution of K with distance along the jet and obtained k′ = −3.6 ± 0.3 for the entire region (dashed red line in the lower panel of Fig. 23). As in the case of the magnetic field, the values for K steepen for r > 0.1 mas. A power law fit for this region results in k′ = −4.6 ± 0.2 (solid red line in the lower panel of Fig. 23). The values of the normalization coefficient cannot be directly compared owing to the varying spectral index along the jet (see bottom panel in Fig. 15 and Eq. (33)).
 |
Fig. 23 Evolution of the magnetic field B (top panel) and the normalization coefficient, K (bottom panel) for the May 2005 observation. The solid and dashed red lines correspond to power law fits (see text for details). |
The slopes obtained from the variation of the magnetic field, B, and the normalization coefficient, K, (see Fig. 23) correspond to the evolution along the jet and include the influence of the jet geometry (e.g., the magnetic field along the jet is given by B ∝ rϵb). We thus have to take the evolution of the jet radius into account to derive the geometry of the magnetic field. The evolution of the transversal jet size with distance in region C can be fitted with an exponent ϵ = 0.8 ± 0.1 (R ∝ rϵ). This results in b = −0.4 ± 0.1 for the overall region and to b = −0.9 ± 0.2 for r > 0.1 mas. For the evolution of the normalization coefficient K, we computed an exponent of k = −4.5 ± 0.7 for 0.02 mas < r < 0.45 mas and k = −5.7 ± 0.8 for r > 0.1 mas.
Assuming adiabatic expansion losses as the main energy loss mechanism, and following
Marscher & Gear (1985); Lobanov & Zensus (1999), the slope in the
νm − Sm
plane is given by 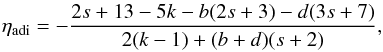 (8)with
b the exponent for the evolution of the magnetic field intensity
(B ∝ R−b),
k the exponent for the evolution of the normalization coefficient of
the relativistic electron distribution
(K ∝ R−k),
d the exponent for the evolution of the Doppler factor
(δ ∝ R−d), and
s the spectral slope
(N = Kγ−s).
A power law fit to the variation in the turnover flux-density with respect to the turnover
frequency provides an exponent η = 0.8 ± 0.1 (see Fig. 16). Together with estimates on b,
k, and d, we obtained the average spectral slope
⟨ s ⟩ = 2.3 ± 0.6, by solving Eq. (8) for s. This value for the spectral slope agrees,
within the uncertainties, with the results of the parameter space study based on the
observed brightness temperature gradients for the adopted value of
d = −0.6 (see panel 2 in Fig. 16 of Paper II).
(8)with
b the exponent for the evolution of the magnetic field intensity
(B ∝ R−b),
k the exponent for the evolution of the normalization coefficient of
the relativistic electron distribution
(K ∝ R−k),
d the exponent for the evolution of the Doppler factor
(δ ∝ R−d), and
s the spectral slope
(N = Kγ−s).
A power law fit to the variation in the turnover flux-density with respect to the turnover
frequency provides an exponent η = 0.8 ± 0.1 (see Fig. 16). Together with estimates on b,
k, and d, we obtained the average spectral slope
⟨ s ⟩ = 2.3 ± 0.6, by solving Eq. (8) for s. This value for the spectral slope agrees,
within the uncertainties, with the results of the parameter space study based on the
observed brightness temperature gradients for the adopted value of
d = −0.6 (see panel 2 in Fig. 16 of Paper II).
6.3. Region D
For calculating the magnetic field and the normalization coefficient for region D, we used the jet width obtained from the stacked 15 GHz VLBI maps (see Fig. 13 in Sect. 4). The jet expands until r ~ 1.5 mas and collimates between 1.5 mas < r < 2.4 mas. Power law fits applied to the expansion and collimation regions give ϵ = 0.8 ± 0.1 and ϵ = −0.5 ± 0.1 (where ϵ is the jet opening index, R ∝ rϵ). The kinematic analysis of region D shows a decreasing trend for the Doppler factor, which is based on only two data points, owing to the lack of traveling components within this region. Because of this, we used the average of ⟨ δ ⟩ = 7 to calculate the magnetic field and the normalization coefficient.
 |
Fig. 24 Evolution of the magnetic field B (top panel) and the normalization coefficient, K (bottom panel) for region D. The lefthand side corresponds to the axial values and the righthand side to the transversally averaged value along the jet. |
The upper panels in Fig. 24 show the spatial and temporal evolution of the axial (left panel) and transversally averaged (right panel) magnetic field intensity. The axial magnetic field varies between 6 mG and 0.5 mG, and the transversal averaged magnetic field spans from 10 mG to 0.5 mG. Like the turnover frequency for region D, the magnetic field intensity on-axis shows a parabola-shaped distribution (there is a rise and a decrease within the region), whereas the transversally averaged magnetic field decreases with distance. However, both show an increase between 2005.39 and 2006.29, which could be due to the passage of a traveling feature through this region (see component D2 in Paper II).
The evolution of the normalization coefficient, K, with distance to the core is presented in the lower panels of Fig. 24. The lefthand panel shows the on-axis values, and the righthand panel shows the transversally averaged ones. In both cases, K decreases in the region 1.0 mas < r < 1.5 mas and increases farther downstream. The variation in K is larger for the axial values (from 5 × 10-5 erg2α0 cm-3 to 10-11 erg2α0 cm-3) than for the transversally averaged values (between 10-11 erg2α0 cm-3 and 10-7 erg2α0 cm-3). The values for K depend on the optically thin spectral index and cannot therefore be directly compared. In contrast to the magnetic field intensity, the shape of the distribution is comparable for both values, and the increase in K could reflect a reacceleration of relativistic particles.
Owing to the large scatter and uncertainties in B and K, we use the time-averaged value at each position in the following. The evolution of these time-averaged values with distance could be approximated by a power law, and the results for the exponents are presented in Fig. 25 and Table 8.
 |
Fig. 25 Evolution of the time averaged magnetic field B (top panel) and the normalization coefficient, K (bottom panel) for region D. The black points and lines correspond to averaged axial values and the red points and lines to the transversally averaged values along the jet. |
For r < 1.4 mas, b′ is for both on-axis and transversally averaged values in Fig. 25, comparable with the expected value for a poloidal field (b′ ~ 2), within the uncertainties. However, there is a significant difference between the value on-axis and the averaged one, indicating that the field is poloidal on average, but could have a toroidal component closer to the axis. The strong decrease in the value of K on-axis results in an exponent k′ ~ 30 (not given in the table), which reflects the huge scatter in the temporal evolution of K (see Fig. 24). For the transversally averaged normalization coefficient, K, we obtained an exponent of k = −12 ± 4.
For r > 1.4 mas (within region D), the difference in the exponent between the on-axis values and the transversally averaged ones is greater. On-axis, the exponent indicates that the magnetic field is not organized in poloidal geometry, whereas the transversally averaged value of the field would keep the poloidal structure from the previous region. For both the on-axis and the transversally averaged normalization coefficients the exponent is k ~ 20. The unclear geometry of the magnetic field close to the jet axis in region D, together with the kinematic analysis for this region, could be interpreted in terms of an additional shock-shock interaction, as already suggested in Paper II. Such an interaction could lead to strong variations in magnetic field intensity and orientation. In particular, an increase in the transversal component (radial) is expected at the shock. Numerical simulations show that, at the position of recollimation shocks, there is an adiabatic compression that causes a (symmetric) bump in the spectral index (Mimica et al. 2009).
6.4. Derivation of the evolution of γmin and γmax
Marscher (1987) pointed out that the energy
limits,
Emin = γminmec2
and
Emax = γminmec2
in the expression describing the synchrotron spectrum are difficult to estimate. From the
results obtained in this paper, we can now put constraints on the evolution of the minimum
and maximum Lorentz factors of the non-thermal population along the jet in CTA 102.
However, here we present a first-order approximation for the evolution of the lower,
γmin, and upper, γmax electron
Lorentz factors. We consider two different jet geometries, i) a conical pressure matched
jet
(dk = p0/pa = 1)
as a reference model; and ii) an overpressured jet
(dk ≠ 1). Based on these two different
assumptions, and using some of the parameters obtained from the core-shift, ridge-line,
and spectral analysis, we computed the evolution of the electron Lorentz factor assuming;
iii) only adiabatic losses; and iv) synchrotron and adiabatic losses. For this calculation
we used an adiabatic index  ,
which corresponds to an ultra-relativistic
e−e+ plasma.
,
which corresponds to an ultra-relativistic
e−e+ plasma.
Conical jet:
the first step in the calculation of the evolution of the electron Lorentz factor is
to define the properties of the jet. In the case of a pressure-matched jet, the profile
is conical and is characterized by its radius at the jet nozzle,
R0, and its opening angle, ϕ. The opening
angle, ϕ, can be obtained either from the measured bulk Lorentz factor
ϕ ~ 1/Γ (e.g., Königl 1981) or from the transversal size of the jet (e.g., Pushkarev et al. 2009). The jet width,
R0, at the nozzle can be calculated in the following way:
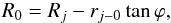 (9)with
Rj the jet width obtained at a position,
rj, where the jet can be transversally
resolved and rj − 0 the distance to the jet
nozzle including the opacity shift correction (see Sect. 8.0.1). Finally the jet width
for a conical geometry can be written as a power law:
(9)with
Rj the jet width obtained at a position,
rj, where the jet can be transversally
resolved and rj − 0 the distance to the jet
nozzle including the opacity shift correction (see Sect. 8.0.1). Finally the jet width
for a conical geometry can be written as a power law: 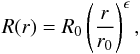 (10)where
ϵ = 1 and r0 is a normalization distance.
(10)where
ϵ = 1 and r0 is a normalization distance.
Overpressured jet:
an initial overpressure at the jet nozzle leads to the formation of recollimation
shocks farther downstream (e.g., Daly & Marscher
1988). Such stationary features can be detected and identified with VLBI
observations. To calculate the jet width at the nozzle, we used the approximation
presented by Daly & Marscher (1988):
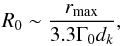 where
rmax is the deprojected distance between the jet nozzle
and the recollimation shock, Γ0 is the bulk Lorentz factor of the fluid, and
dk = p0/pext
is the initial overpressure.
where
rmax is the deprojected distance between the jet nozzle
and the recollimation shock, Γ0 is the bulk Lorentz factor of the fluid, and
dk = p0/pext
is the initial overpressure.
Assuming a locally homogeneous ambient medium, the distance between the jet nozzle and
the location of maximal jet width is roughly 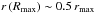 (Komissarov & Falle 1997). Using
R0, the jet opening index, ϵ, can be
derived for
(Komissarov & Falle 1997). Using
R0, the jet opening index, ϵ, can be
derived for 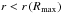 . For
. For
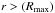 , the
jet is collimated by the ambient pressure, reaching a local minimum in the radius at the
position of the standing shock. As in the case of the jet opening region, and given the
jet width at the position of the standing shock, ϵ can be computed for
this region. If there are additional recollimation shocks with known distances from the
previous shock and jet width, one can proceed as for the first recollimation shock and
define the jet geometry.
, the
jet is collimated by the ambient pressure, reaching a local minimum in the radius at the
position of the standing shock. As in the case of the jet opening region, and given the
jet width at the position of the standing shock, ϵ can be computed for
this region. If there are additional recollimation shocks with known distances from the
previous shock and jet width, one can proceed as for the first recollimation shock and
define the jet geometry.
For each case (conical and overpressured jet), the evolution of the maximum and minimum Lorentz factors of the non-thermal population considering adiabatic and synchrotron losses, and adiabatic losses alone, can be computed as follows.
Adiabatic and synchrotron losses:
to provide an estimate for the variation in the electron Lorentz factor
γ along the jet, the energy-loss equation, which includes both
radiative and adiabatic losses (see, e.g., Georganopoulos
& Marscher 1998; Mimica et al.
2009), has to be solved as
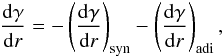 (11)where
γ corresponds to the electron Lorentz factor and r
to the distance along the jet. The synchrotron and adiabatic losses are given by
(11)where
γ corresponds to the electron Lorentz factor and r
to the distance along the jet. The synchrotron and adiabatic losses are given by
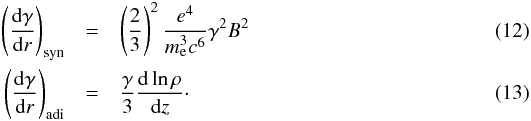 Parametrizing
the magnetic field,
B = B0(r/r0)−b,
and the jet geometry,
R = R0(r/r0)ϵ,
the energy loss equation can be simplified to
Parametrizing
the magnetic field,
B = B0(r/r0)−b,
and the jet geometry,
R = R0(r/r0)ϵ,
the energy loss equation can be simplified to
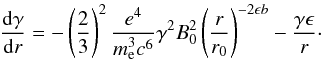 (14)This
differential equation has the following analytical solution:
(14)This
differential equation has the following analytical solution:
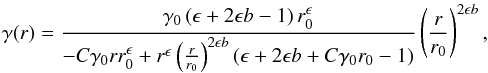 (15)where
(15)where
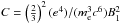 , and
, and
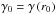 corresponds to the initial value.
corresponds to the initial value.
An estimate of the jet parameters at the jet nozzle is done by assuming that they must be similar to those at the first recollimation shock, which we locate at r ≃ 0.1 mas. This is justified because the conditions (pressure and density) at the position of the standing shock wave are roughly the same as those at the jet nozzle (in a locally homogeneous ambient medium, see e.g., Daly & Marscher 1988; Komissarov & Falle 1997). These parameters, as obtained from this work and paper II, are listed in Table 9.
 |
Fig. 26 Evolution of source-intrinsic parameters for an overpressured jet, dk ≠ 1, (left panels) and for a conical jet, dk = 1, (right panels). The upper panels show the variation in the jet width, R, in pc along the jet; the middle panels the evolution of the magnetic field, B, in G; and the bottom panels the variation ointhe upper and lower electron Lorentz factors, γmin,max. The solid and dashed red lines correspond to a model where we take both synchrotron and adiabatic losses into account. To demonstrate the influence of radiative losses, we also computed the evolution of the electron Lorentz factor only for adiabatic losses (solid and dashed lines in bottom panels). See text for more details. The bottom x-axis is drawn in pc, and to allow for the direct comparison with the observations we plotted the upper x-axis in mas. |
Figure 26 shows the results of our calculations for an overpressured (left panels) and a conical jet (right panels) using the parameters presented in Table 9. The x-axes are given in pc (bottom) and in mas (top) to facilitate the comparison with observations. The panels show (from top to bottom) the evolution of the jet width with distance along the jet (fitted from the evolution of the jet radius with distance in Fig. 13), the evolution of the magnetic field intensity (from Figs. 23 for the core and 25 for region D), and the computed evolution of the maximum and minimum electron Lorentz factor, γmin,max. The red solid and dashed lines in the bottom panels correspond to the variation in the electron Lorentz factor taking synchrotron and adiabatic losses into account and the black solid and dashed lines show the evolution of the electron Lorentz factor with only adiabatic losses.
For both jet models, the evolution of the upper electron Lorentz factor, γmax, decreases fast if the synchrotron losses are taken into account. The adiabatic losses are the dominant energy loss mechanism for r > 3 pc, which is visible in the similar slopes of the solid black and red lines. In contrast, the evolution of the lower electron Lorentz factor, γmin, is hardly affected by synchrotron losses.
The calculations show that in the case of an overpressured jet, the magnetic field increases at the position of the recollimation shocks (at r ~ 20 pc and r ~ 270 pc) and at the same position, both the minimum and the maximum electron Lorentz factor increase. This increase in the Lorentz factor corresponds to the local increase in the particle density, i.e., adiabatic compression (see, e.g., Mimica et al. 2009). Farther downstream, the jet expands and the magnetic field and the Lorentz factor decrease again. At the second recollimation shock, there is again a local increase in both magnetic field and electron Lorentz factor. This behavior is also visible in the case of adiabatic losses alone.
As opposed to the overpressured jet, the evolution of the magnetic field and the electron Lorentz factor are continuously decreasing for a conical jet (see right panels in Fig. 26).
6.5. Particle density, Ntot and relativistic energy density, Ue
Using the values computed for γmin and γmax, together with the magnetic field, B, and the normalization coefficient, K, we could compute estimates for the evolution of the total particle density, Ntot, and the relativistic energy density, Ure for regions C and D. The values of Ntot and Ure in region D were obtained from the average magnetic field and normalization coefficient (see Fig. 25). Figure 27 presents the results of our calculations taking radiative and adiabatic losses and only adiabatic losses into account. The panels show the evolution of the total particle density, Ntot (panel i), the relativistic energy density, Ure (panel ii), the magnetization σ = UB/Ure (panel iii), and the electron Lorentz factor (panel iv). The circle and diamond markers in panel iv correspond to the upper and lower electron Lorentz factors. Since our model for the evolution of the electron Lorentz factor does not take traveling shock waves into account, the average values of B and K in region D reflect a calculated steady state. However, the possible passage of a traveling component through this region was reported in Paper II, so this may be the reason for differences between the model and the observed behavior.
 |
Fig. 27 Evolution of the source-intrinsic parameters taking radiative and adiabatic losses into account (red points) and only adiabatic losses (black points). The different panels show the variation in the total particle density, Ntot (panel i), the relativistic energy density, Ure (panel ii), the magnetization σ = UB/Ure (panel iii) and the electron Lorentz factor (panel iv). The circle and diamond markers in panel iv) correspond to the upper and lower electron Lorentz factors. For more details see text. |
The total particle density for region C
(r < 1 mas) takes values between (200–15)
cm-3 if we consider only adiabatic losses and in the range of (100–10)
cm-3 if we also take radiative, here synchrotron losses, into account (panel
i in Fig. 27). Farther downstream in region D
(1 mas < r < 4 mas),
the particle density drops to roughly 1 cm-3 and increases at
r ~ 1.5 mas to 5 cm-3 (location of a possible standing
shock). The values for both models lead to similar values since
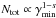 (see Eq. (34)) and the evolution of the
lower electron Lorentz factor are not affected by radiative losses (see panel iv).
(see Eq. (34)) and the evolution of the
lower electron Lorentz factor are not affected by radiative losses (see panel iv).
The influence of radiative losses is clearly visible in the evolution of the relativistic
energy density, Ure, for region C (panel ii in Fig. 27). The energy density takes values in the range of
(5 × 10-1–5 × 10-3) erg cm-3 if only adiabatic losses
are considered and from (10-2−10-3) erg cm-3 if both
synchrotron and adiabatic losses are included. Since the spectral slope for region C is
s < 2, the relativistic energy density is
mainly proportional to γmax (see Eq. (35)). As shown in Sect. 6.4, radiative losses strongly affect the variation in
γmax. The difference between the two models nearly
disappears in region D, where we obtain values between 10-4 erg cm-3
and 10-5 erg cm-3. The dependence of Ure
changes from 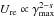 to
to 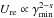 since s > 2 within region D (see Eq. (35)). As in the case of
Ntotal, the relativistic energy density increases by a
factor 6 at r ~ 1.5 mas.
since s > 2 within region D (see Eq. (35)). As in the case of
Ntotal, the relativistic energy density increases by a
factor 6 at r ~ 1.5 mas.
For both models, the jet is particle dominated (σ < 1) for r > 0.1 mas (see panel iv in Fig. 27). However, the mentioned differences in Ure lead to a difference of a factor 50 in the value of σ between the two models. The magnetization increases from a calculated value around σ ~ 0.01 in region C to σ ~ 0.1 in region D (see the third panel in Fig. 27) due to the increase in the magnetic field close to the location where we think that a standing shock is located, and drops to σ ~ 0.01 at r = 1.5 mas due to the increase in the particle density (first panel in Fig. 27) and the related rise in the relativistic energy density (second panel in Fig. 27).
7. Discussion
7.1. Region C (core)
Region C covers the first milliarcsecond of the radio jet. The component ejected after the 2006 flare (C2) evolves during the time spanned by the observations (2005–2007) within this region. This component has a velocity of 0.25 ± 0.04 mas/yr, which translates into an apparent velocity of 13 ± 2 c. In two years the component has covered an apparent distance of 0.5 mas. Unfortunately, we do not have enough resolution to identify C2 with accuracy in the spectral index maps of the region (see Figs. 14 and 2 in Appendix C).
However, following the temporal evolution of the spectral index distributions (both the axial and the transversally averaged values, see Fig. 14), we observe that the first significant increase (beyond errors) in the spectral index in the region occurs at ~2006.4 (blue dots). At this time, C2 should be crossing the region around 0.1 mas from the position of the 43 GHz core (0 mas in the plot, see Fig. A.25 in Paper II), which is the expected location of a stationary feature from our results in Papers I and II.
In Paper I, we deduced that the flare started around 2005.6 from the spectral evolution of the source as derived from the single-dish data. This evolution was interpreted in terms of the shock-in-jet model (Marscher & Gear 1985). The νm, Sm plot after this flare revealed a Compton stage, which lasted until 2005.8, followed by an adiabatic stage. However, in the period 2006.0–2006.3, there was a reversal of the expected evolution, with an increase in the peak flux (Sm), while the peak frequency (νm) basically stayed constant. Finally, after 2006.3 the component returned to the expected spectral evolution dominated by adiabatic losses. This second and unexpected peak in Sm could be understood as due to injection of relativistic particles into the system, or to the existing particles going through a compression (Mimica et al. 2009). It was discussed in terms of the interaction of the component ejected after the flare with a standing shock close to the core region. The authors initially interpreted this stage as a new Compton stage due to its similar behavior in the νm, Sm plot. However, it could well be explained as a break within the adiabatic stage. This possibility is being tested using numerical simulations (Fromm et al., in prep.).
The observed increase in the spectral index in region C (Fig. 14) from the 2005 epoch (black dots) to that in 2006.3 (blue dots) fits well into the description given in the previous paragraph. After the passage of C2 through the innermost region, it should arrive at the expansion region between ≃0.1 mas and ≃1 mas (see Fig. 13). Then, the observed decrease in the spectral index can also be understood within the evolution of C2 inside the core. The rises of the spectral index in 2006.9 (light blue dots in Fig. 14) is compatible with no changes within errors. However, the increase in 2007.4 (brown dots in Fig. 14) is clearly beyond errors and very similar to that in 2006.3. Although there is no evidence of any component crossing the core or the 0.1 mas standing feature at this epoch, component C3 is identified between 0 and 0.1 mas from the 43 GHz core position (see Fig. 16 in Paper II). Therefore this new increase could be related to the ejection of a new component.
The observed decrease in the spectral index with distance at each epoch can be easily understood in terms of synchrotron and adiabatic cooling times, which are shorter for higher frequencies (see, e.g., Blandford & Königl 1979), so a steepening of the spectral distribution with distance is expected. In summary, the spectral evolution of region C until 2007 is consistent with the propagation of a shock produced by the perturbation ejected in the 2006 radio flare.
7.2. Region D
Figures 17–19 show the peak frequency, peak flux, and the spectral index, respectively, of the spectral distribution of the jet along region D for the different epochs. The whole picture fits well with the passage of component D2 through the region, as shown by both the axial and averaged values of Sm. The peak in emission propagates from r ≃ 1 mas to r ≃ 1.5 mas in two years, which agrees with the velocity of the component D2 (0.16 ± 0.01 mas/yr, see Table 3 in Paper II).
There is a discrepancy between the axial and averaged profile shapes of α0 and νm in the 1.0–1.5 mas interval, which could be related to edge effects (i.e., at the edges of the studied region) in the axial values produced by the alignment procedure. The result is compatible with a smooth decrease in the peak frequency with distance in the region. The large errors in the derivation of the spectral index make it difficult to make any statement regarding its evolution in space and time within the region, but the result seems to indicate that it does not undergo strong changes.
Figure 13 indicates that the jet is recollimating between 1 mas and 2 mas, and this is confirmed in Fig. 8 of Paper II, which shows the continuous presence of a component at ≃1.5 mas from the core, first identified as D1 and later as D2 in this figure. This was also reported by Jorstad et al. (2005). The interaction between D2, and this standing feature could be responsible for the bump in emission at epochs 2005.39 to 2006.44 seen in the Sm plot (black, red, dark blue, and dark green points) and for the spectral index being possibly constant or slightly increasing within the region. A reconfinement region should generate a compression of the emitting particle distribution and be seen as a symmetric bump in the spectral index profile along the jet (Mimica et al. 2009).
7.3. Regions B and A
The spectral index profile within region B (see Fig. 21) shows a clear indication of one or two bumps at 4–5 mas. The fairly symmetric shape of the bumps is an indication of a compression of the particles (Mimica et al. 2009). This could be also the case between 1.5 and 2.5 mas (region B, see below and Fig. 21), but we do not have data to probe this hypotheses. In addition, the kinematics of the source between 4 mas and 5 mas indicate that the components are stationary. Finally, the jet width is constant between r ≃ 4 mas and r ≃ 8 mas. These facts favor the standing shock scenario. From the data, it is difficult to say whether the whole region includes several such shocks (as indicated by the fitted components) or whether it is a single, long reconfinement region similar to those observed in numerical simulations (Perucho & Martí 2007). In this respect, the maximum of emission in the radio maps corresponds to component B2 (see Fig. 2), which is at r ≃ 6 mas from the core, but the first bump in the spectral index is observed around r ≃ 4 mas.
Regarding region A, Fig. 22 shows the profile of the spectral index at the different epochs. A new plateau in the jet width, starting around 10 mas (see Fig. 13), could have an influence on the little change observed across this region at most epochs. However, within errors, the result is compatible with a smooth decrease in the spectral index with distance, as expected from adiabatic losses (see, e.g., Mimica et al. 2009).
7.4. The jet in CTA 102. A overall perspective
From the accumulated evidence in Papers I, II, and this work, we can discuss the general nature of the jet in CTA 102. First of all, the jet shows kinks and helical structures with different wavelengths showing up at different observing frequencies (see also Perucho et al. 2012). The regions in the stacked image (0–1 mas, 1–2 mas, 5–8 mas, and >10 mas) coincide with the transversal displacement of the ridge line in the east-west direction at 15 GHz, which is a central frequency to the whole analysis. The latter is the main reason why the jet viewing angle at this frequency plays a crucial role in selecting regions for our analysis.
Following the conclusions derived in Paper II, the jet flow should be accelerating in order to explain the observed increase in the Doppler factor at the core region (0.1 to 1 mas, see Fig. 13 in Paper II). Moreover, acceleration of the flow is also expected in a hot flow after compression in a standing shock, as has been claimed for 0.1 mas.
Farther downstream, the changes in the brightness temperature along the jet include discontinuous jumps at r ≃ 1−2 mas and r ≃ 4−5 mas (see Fig. 14 in Paper II), which cannot be accounted for in terms of a continuous change in the viewing angle. At the same positions (1–2 mas and 4 mas), the jet-width profile flattens (see Fig. 13) and the spectral index shows “bumps” in some cases (e.g., r ≃ 4−5 mas, Fig. 21). Both facts point to the presence of reconfinement shocks. Therefore, the jet morphology at, e.g., 15 GHz, indicates that helical motion is responsible for the highest relative flux in regions D, B, and A. However, the spectral properties and, to some extent also the kinematics, favor the overpressured jet scenario and the existence of recollimation regions at r ≃ 0.1 mas (deprojected 16 pc from the core), at r ≃ 1−2 mas (deprojected 160–320 pc from the core), at r ≃ 5 mas (deprojected 800 pc from the core), and possibly at r ≃ 10 mas (deprojected 1600 pc from the core). The increasing distance between the positions of the subsequent shock candidates suggest that the jet propagates in a decreasing density ambient medium. However, it is difficult to know whether, for instance, there is only one or more standing shocks in region B (components B1, B2, and B3 at 4 mas ≤ r ≤ 8 mas, see Paper II). The lack of correspondence of the plateaus in the jet radius (including stationary components and bumps in the spectral index profiles) with the boosted regions of the jet can be taken as evidence of their independent nature.
Interestingly, the width of the jet at 2 GHz increases in region D, whereas it remains unchanged at higher frequencies. Only at r ≃ 10 mas does the jet width at 2 GHz become flatter. This result should be understood in terms of transversal jet structure and of different internal and external dynamics in the jet, which can be compared to simulations or theoretical models of overpressured jets (Begelman et al. 1984; Perucho & Martí 2007; Nalewajko 2012). On the largest scales, the 2 GHz jet width is ≃6 mas (≃50 pc), whereas at 5 GHz the jet width is ≃3.5 mas (≃30 pc), which can give an idea of the width of the shear/mixing layer surrounding the jet (see, e.g., Perucho & Martí 2007; Wang et al. 2011). A deeper study of the ridge line and jet transversal structure will be presented elsewhere.
In conclusion, from the present data, we claim that a complex interaction between different structures is probably taking place in CTA 102.
8. Conclusions
In this paper we studied in detail the radio spectral variations in the jet of CTA 102 during the 2006 major flare. The core-shift analysis revealed that, on average, the observed VLBI core position behaves like r ∝ ν-1. We calculated the magnetic field at the core to be Bcore ~ 100 mG and the particle density Ncore ~ 40 cm-3.
The spectral analysis of the core region showed a significant increase in the spectral index, α, during the period of the flare with a steepening of α for r > 0.1 mas. The increase in the spectral index agrees with the possible interaction of a traveling component C2 and a standing shock at this position. The location coincides with the first detection of the jet expansion.
Within this region, adiabatic losses are dominant, and the evolution of the magnetic field intensity indicates a toroidal geometry, with values of (9–50) mG. Farther downstream, we found evidence of the possible crossing of the feature D2 through another possible standing feature at r ≃ 1.5 mas. The analysis of the transversal structure showed evidence of recollimation of the jet. The spectral evolution of this region revealed an increase in the turnover frequency and turnover flux-density during the period of the interaction between the components. The evolution of the magnetic field intensity in this region is compatible with a mixture of toroidal and poloidal structure between 10 mG and 1 mG.
Between r = 3 mas and r = 8 mas, there are additional regions of recollimation, as shown by the jet width and the spectral index, which further support our hypothesis of an overpressured jet.
Summarizing the results of this series of papers, we conclude that the jet of CTA 102 cannot be simply described by an overpressured or a helical jet, since we found evidence of both during our analysis. The morphology of VLBI images and the jet ridge line shows a clear helical pattern. The kinematic analysis reveals several standing components, and the jet width exhibits regions with jet collimation, both being indications of an overpressured jet. The symmetric variations around the locations of this stationary components is additional proof for the existence of recollimation shocks in CTA 102. All these facts lead to the conclusion that the jet of CTA 102 is best described by helical patterns or flow motion developing within an overpressured jet. Whether the observed helical structure corresponds to a pattern, as reported in Perucho et al. (2012), or the flow follows this helical path should be studied in detail in future.
The limited resolution and frequency range meant we could not derive the spectral evolution of the VLBA core and for jet features farther downstream (r > 1 mas). Moreover, the interaction between a traveling shock wave and a recollimation shock is a highly nonlinear process that requires a more detailed investigation. Such a study is only possible by performing numerical simulations and the full radiative transfer calculations including a self-consistent treatment of the relativistic electron distribution (Mimica et al. 2009). We plan to further study shock-shock interaction in parsec-scale jets using relativistic hydrodynamic simulations and extend our analysis to other sources.
Online material
Appendix A
In this section we review the basic equations of synchrotron self-absorption and present the relations needed for the performed spectral analysis (see e.g., Pacholczyk 1970; Marscher 1987; Lobanov 1998a; Türler et al. 1999).
The emission at frequency ν,
ϵν, and absorption coefficients,
κν, of a power law distribution of
relativistic electrons,
N(E) = KE−s,
where K is the normalization coefficient of the distribution and
s the spectral slope of the relativistic electron distribution, can
be written as (for details see Pacholczyk 1970)
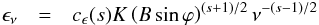 (16)
(16)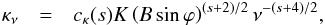 (17)where
B is the magnetic field, ϕ the pitch angle and
ν the frequency. The constants
cϵ(s) and
cκ(s) are given by
(17)where
B is the magnetic field, ϕ the pitch angle and
ν the frequency. The constants
cϵ(s) and
cκ(s) are given by
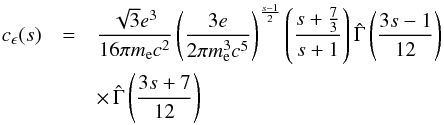 (18)
(18)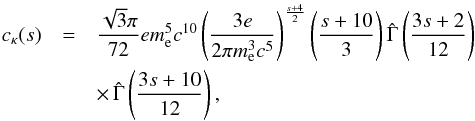 (19)with
e the electron charge, me the electron
rest-mass, c the speed of light, and
(19)with
e the electron charge, me the electron
rest-mass, c the speed of light, and
 the complete Euler-Gamma function. For a random magnetic field, the constants above have
to be averaged over the pitch angle ϕ, i.e., multiplied by
cϵ,b and
cκ,b, respectively, with
the complete Euler-Gamma function. For a random magnetic field, the constants above have
to be averaged over the pitch angle ϕ, i.e., multiplied by
cϵ,b and
cκ,b, respectively, with 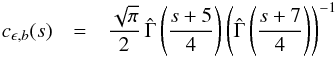 (20)
(20)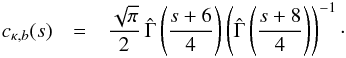 (21)The
specific intensity, Iν, can be written as
(21)The
specific intensity, Iν, can be written as
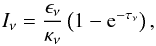 (22)where
ϵν and
κν are the emission and absorption
coefficients and
τν = κνx
is the optical depth, with x the distance along the line of sight.
Defining ν1 as the frequency where
τν = 1, Eq. (22) takes the following form (Pacholczyk 1970):
(22)where
ϵν and
κν are the emission and absorption
coefficients and
τν = κνx
is the optical depth, with x the distance along the line of sight.
Defining ν1 as the frequency where
τν = 1, Eq. (22) takes the following form (Pacholczyk 1970): ![\begin{eqnarray} I_{\nu}=I_{\nu_{1}}\left(\frac{\nu}{\nu_1}\right)^{\alpha_t}\left[1-\exp\left(\frac{\nu}{\nu_{1}}\right)^{\alpha_0-\alpha_t}\right], \label{inu} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq498.png) (23)where
αt is the optically thick spectral index
(αt = 5/2 for a
homogenous source), and α0 < 0 is
the optically thin spectral index. The optically thin spectral index is connected to the
spectral slope, s, by the following relation:
(23)where
αt is the optically thick spectral index
(αt = 5/2 for a
homogenous source), and α0 < 0 is
the optically thin spectral index. The optically thin spectral index is connected to the
spectral slope, s, by the following relation:
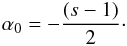 (24)Using
the transformation from intensities to flux densities Eq. (23) can be expressed in terms of the observed turnover flux-density,
Sm, and turnover frequency,
νm (Türler et al. 1999):
(24)Using
the transformation from intensities to flux densities Eq. (23) can be expressed in terms of the observed turnover flux-density,
Sm, and turnover frequency,
νm (Türler et al. 1999): 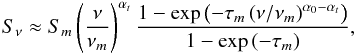 (25)where
(25)where
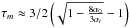 is the optical depth at the turnover. Depending on the value of
ν/νm,
Eq. (25) describes an optically thick
(ν < νm)
or optically thin
(ν > νm)
spectrum with their characteristic shapes
Sν ∝ ν5/2
and
Sν ∝ ν−(s − 1)/2,
respectively.
is the optical depth at the turnover. Depending on the value of
ν/νm,
Eq. (25) describes an optically thick
(ν < νm)
or optically thin
(ν > νm)
spectrum with their characteristic shapes
Sν ∝ ν5/2
and
Sν ∝ ν−(s − 1)/2,
respectively.
Magnetic field, B, and particle density, K
Once the turnover frequency, νm, and the
turnover flux-density, Sm are obtained
(see Sect. 2.2), estimates for the magnetic
field, B, and the normalization coefficient, K,
(see, e.g., Marscher 1987) can be derived.
Following Lind & Blandford (1985), the
emission, ϵν, and absorption coefficient,
κν, have to be corrected for
relativistic and cosmological effects. In the following, primed variables correspond
to the observer’s frame, and the equations are derived for a random magnetic field
(isotropic pitch angle, ϕ), with all parameters in cgs units.
Introducing these corrections we obtain
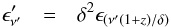 (26)
(26)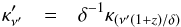 (27)with
δ = Γ-1(1 − βcosϑ)-1
the Doppler factor, with
β = v/c,
ϑ the viewing angle, and z the redshift. The
optically thin flux,
(27)with
δ = Γ-1(1 − βcosϑ)-1
the Doppler factor, with
β = v/c,
ϑ the viewing angle, and z the redshift. The
optically thin flux, 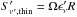 (with Ω the solid angle
and R the size of the emission region), is given by
(with Ω the solid angle
and R the size of the emission region), is given by 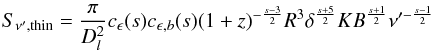 (28)and
the optical depth, τν, by:
(28)and
the optical depth, τν, by: 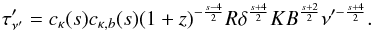 (29)Using
the obtained turnover values, the flux-density,
(29)Using
the obtained turnover values, the flux-density,
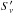 , in Eq.
(28) and the frequency,
ν′, in Eq. (29) can be replaced by the turnover flux-density,
, in Eq.
(28) and the frequency,
ν′, in Eq. (29) can be replaced by the turnover flux-density,
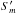 , and the
turnover frequency,
, and the
turnover frequency,  :
: 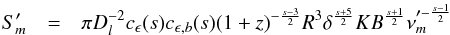 (30)
(30)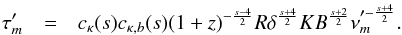 (31)The
equations above can be solved for the magnetic field, B, and the
normalization coefficient, K:
(31)The
equations above can be solved for the magnetic field, B, and the
normalization coefficient, K: ![\begin{eqnarray} B&=&\frac{\pi^{2}}{D_{l}^{4}}\left[\frac{c_{\epsilon}(s)c_{\epsilon,b}(s)}{c_{\kappa}(s)c_{\kappa,b}(s)}\right]^{2}(1+z)^{7}R^{4}\delta\nu^{\prime5}_{m}S_{m}^{\prime-2}\tau_{m}^{\prime2} \label{bfield} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq526.png) (32)
(32)![\begin{eqnarray} K&=&\frac{D_{l}^{2s+4}}{(\pi)^{s+2}}\left[c_{\epsilon}(s)c_{\epsilon,b}(s)\right]^{-(s+2)}\left[c_{\kappa}(s)c_{\kappa,b}(s)\right]^{s+1} \nonumber \\ &&\times\,(1+z)^{-(3s+5)}R^{-(2s+5)}\delta^{-(s+3)}\tau_{m}^{\prime-(s+1)}S_{m}^{\prime s+2}\nu_{m}^{\prime-(2s+3)}. \label{knorm} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq527.png) (33)
(33)
8.0.1. Number of particles, N, relativistic energy density, Ue, and magnetization σ
The number of particles, N, and the total energy distribution of
the relativistic particles, Ue, can be calculated by
integrating the distribution function
N(E) = KE−s
within the limits
E1 = γminmec2
and
E2 = γmaxmec2:
![\begin{eqnarray} N&=&\frac{K}{s-1}\left(m_{\rm e}c^{2}\right)^{1-s}\gamma_\mathrm{min}^{1-s}\left[1-\left(\frac{\gamma_\mathrm{max}}{\gamma_\mathrm{min}}\right)^{1-s}\right] \label{Ntot} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq532.png) (34)
(34)![\begin{eqnarray} U_{\rm e}&=&\left\{ \begin{array}{ll} \frac{K}{2-s}\left(m_{\rm e}c^{2}\right)^{2-s}\gamma_\mathrm{max}^{2-s}\left[1-\left(\frac{\gamma_\mathrm{min}}{\gamma_\mathrm{max}}\right)^{2-s}\right]& \textrm{if }1<s<2\\[3mm] \frac{K}{s-2}\left(m_{\rm e}c^{2}\right)^{2-s}\gamma_\mathrm{min}^{2-s}\left[1-\left(\frac{\gamma_\mathrm{max}}{\gamma_\mathrm{min}}\right)^{2-s}\right] & \textrm{if }s>2\\[3mm] K\ln\left(\frac{\gamma_\mathrm{max}}{\gamma_\mathrm{min}}\right) & \textrm{if } s=2. \end{array}\right. \label{ue} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq533.png) (35)Together
with the magnetic energy density,
Ub = B2/(8π),
we can define the ratio between the magnetic energy density and the energy density
of the relativistic particles:
(35)Together
with the magnetic energy density,
Ub = B2/(8π),
we can define the ratio between the magnetic energy density and the energy density
of the relativistic particles:
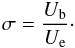 (36)
(36)
Core shift
Assuming that the position of the observed VLBI core is identical with the
(τ = 1)-surface, Lobanov
(1998a) used Eq. (29) to
derive the frequency-dependent position of the core, the so-called core shift. A
conical jet geometry was assumed in that work:
R ∝ r, a decreasing magnetic field,
B = B1r−b
and a decreasing particle density,
K = K1r−k,
where the constants B1 and K1
correspond to the magnetic field and electron normalization coefficient at 1 pc. By
inserting these assumptions into Eq. (29) and solving the equation for r, one obtains
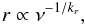 (37)where
kr = [2k + 2b(3−2α0) −2]/(5−2α0),
and α0 is the optically thin spectral index.
(37)where
kr = [2k + 2b(3−2α0) −2]/(5−2α0),
and α0 is the optically thin spectral index.
Measurements of the core shift yield estimates of several physical parameters, such
as the distance to the central engine and the magnetic field at the core (Lobanov 1998a; Hirotani 2005; O’Sullivan & Gabuzda
2009; Pushkarev et al. 2012). The
core-shift measure is defined as
![\begin{eqnarray} \Omega_{r\nu}=4.85 \times 10^{-9}\frac{\Delta r_{\nu_1,\nu_2} D_L\nu_1^{1/k_r}\nu_2^{1/k_r}}{(1+z)^2\left(\nu_2^{1/k_r}-\nu_1^{1/k_r}\right)}\,[\mathrm{pc\,GHz}], \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq544.png) (38)with
Δrν1,ν2
the core shift between the frequencies ν1 and
ν2 in mas and
Dl the luminosity distance in pc.
Following Hirotani (2005), the magnetic field at
1 pc is given by
(38)with
Δrν1,ν2
the core shift between the frequencies ν1 and
ν2 in mas and
Dl the luminosity distance in pc.
Following Hirotani (2005), the magnetic field at
1 pc is given by ![\begin{eqnarray} B_1\approx\frac{2\pi m_{\rm e}^2 c^4}{e^3}\left[\frac{e^2}{m_{\rm e} c^3}\left(\frac{\Omega_{r\nu}}{r_1\sin\vartheta}\right)^{k_r}\right]^{\frac{5-2\alpha_0}{7-2\alpha_0}}\left[ \pi C\left(\alpha_0\right)\frac{r_1 m_{\rm e} c^2}{e^2}\right. \nonumber \\ \times \left. \frac{-2\alpha_0}{\gamma_\mathrm{min}^{2\alpha_0+1}} \frac{\varphi}{\sin{\vartheta}}K\left(\gamma,\alpha_0\right) \left(\frac{\delta}{1+z}\right)^{\frac{3}{2}-\alpha_0}\right]^{\frac{-2}{7-2\alpha_0}}, \label{b1coreshiftg} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq547.png) (39)where
(39)where
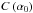 and
K(γ,α0) are defined as
and
K(γ,α0) are defined as
![\begin{eqnarray} C\left(\alpha_0\right)&=&\frac{3^{1-\alpha_0}}{8}\sqrt{\pi}\hat{\Gamma}\left(\frac{7-2\alpha_0}{4}\right)\hat{\Gamma}\left(\frac{5-6\alpha_0}{12}\right)\hat{\Gamma}\left(\frac{25-6\alpha_0}{12}\right) \nonumber \\ &&\times \left[\hat{\Gamma}\left(\frac{9-2\alpha_0}{4}\right)\right]^{-1} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq550.png) (40)
(40)![\begin{eqnarray} K\left(\gamma,\alpha_0\right)&=&\frac{2\alpha_0+1}{2\alpha_0}\frac{\left[\left(\gamma_\mathrm{max}/\gamma_\mathrm{min}\right)^{2\alpha}-1\right]}{\left[\left(\gamma_\mathrm{max}/\gamma_\mathrm{min}\right)^{2\alpha+1}-1\right]}\cdot \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq551.png) (41)The
distance to the central engine is given by
(41)The
distance to the central engine is given by 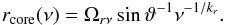 (42)Assuming
a conical jet in equipartition between the magnetic energy density and the kinetic
energy density (which implies kr = 1,
see e.g. Lobanov 1998a), and a spectral index
of α0 = −0.5, the equations above simplify to the
following relations:
(42)Assuming
a conical jet in equipartition between the magnetic energy density and the kinetic
energy density (which implies kr = 1,
see e.g. Lobanov 1998a), and a spectral index
of α0 = −0.5, the equations above simplify to the
following relations: ![\begin{eqnarray} &&B_1\approx 0.025\left[\frac{\Omega_{r\nu}^{3}(1+z)^{2}}{\varphi \delta^2\sin^2\vartheta}\right]^{1/4}, \label{b1coreshift} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq554.png) (43)
(43)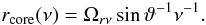 (44)The
particle density N1 can be written for both cases i)
kr = 1 and
α0 = −0.5; and ii)
kr ≠ 1 and
α0 ≠ −0.5, as
(44)The
particle density N1 can be written for both cases i)
kr = 1 and
α0 = −0.5; and ii)
kr ≠ 1 and
α0 ≠ −0.5, as
![\begin{eqnarray} N_1=\frac{K\left(\gamma,\alpha_0\right)}{8\pi m_{\rm e} c^2}\gamma_\mathrm{min}^{-1}B_1^2\, \left[\mathrm{cm^{-3}}\right]. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21784-13/aa21784-13-eq557.png) (45)Taking
kr = 1,
α0 = −0.5, and the fraction of
103 and 105 between the upper and lower electron Lorentz
factor, the equation above can be written as
(45)Taking
kr = 1,
α0 = −0.5, and the fraction of
103 and 105 between the upper and lower electron Lorentz
factor, the equation above can be written as
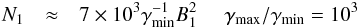 (46)
(46)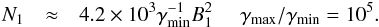 (47)
(47)
Appendix B
We performed several tests to investigate the influence of the non-identical uv-range on the spectral indices derived from images at different wavelengths and therefore with different projected baselines in wavelength units. For extracting the spectral parameters, we used both a power-law fit Sν ∝ ν+ α and the approximation of the synchrotron-self-absorbed spectrum (see Eq. (25)). Table 10 gives the average uv-ranges for the different frequencies. The image parameters, i.e., convolving beam size and pixel size, used are presented in Table 11.
Image parameters used for the spectral analysis.
 |
Fig. B.1 Influence of the uv-range on the 2D distribution of the spectral index, α (Sν ∝ να) for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increase by factors of 2. |
 |
Fig. B.2 Influence of the uv range on the 2D distribution of the turnover frequency, νm for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13°, and a pixel size of 0.03 mas. The left panel shows the turnover frequency for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 86 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
In Fig. 28 we show the 2D distribution of the
spectral index for region C using a frequency range from 15 GHz to 43 GHz. The
lefthand panel shows the distribution for a non-identical uv-range and the middle panel
the distribution for a limited uv-range, here from 27 Mλ to
450 Mλ. The difference in α between the two maps
shows that the central region is only marginally affected by the used uv-range
(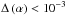 )
and the discrepancies increase with distance from the center. The largest discrepancy is
found in the edges of the distribution where
)
and the discrepancies increase with distance from the center. The largest discrepancy is
found in the edges of the distribution where 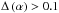 .
.
 |
B.5 Influence of the uv range on the 2D distribution of the turnover frequency, νm for region D (1 mas < r < 4 mas) using a beam size of 1.33 × 0.52 mas with a PA of −7° and a pixel size of 0.04 mas. The left panel shows the turnover frequency for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increase by factors of 2. |
 |
B.8 Influence of the uv range on the 2D distribution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 8 mas) using a beam size of 2.32 × 0.97 mas with a PA of −7° and a pixel size of 0.10 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
 |
Fig. B.9 Influence of the uv-range on the 2D distribution of the spectral index, α (Sν ∝ να) for region A and region B (4 mas < r < 21 mas) using a beam size of 3.65 × 1.52 mas with a PA of −8° and a pixel size of 0.10 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 8 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
For the May 2005 observations of CTA 102, we could derive the spectral turnover, i.e., νm and Sm, using a frequency range from 8 GHz to 86 GHz. The uv-range is set at (66−250) Mλ, and the difference in the spectral values as compared to the unlimited uv-range is shown in Figs. 29–31. The wide frequency range and the short uv-range lead to strong variation in the spectral parameters at the edges of the distribution up to 70% for α, 60% for νm, and 30% for Sm. Despite these large discrepancies at the edges, the values along the jet axis show variations up to 10%.
As mentioned in Sect. 5.2 for region D, the turnover frequency lies within our frequency range, and we can derive the turnover frequency, the turnover flux-density, and the optically thin spectral index, α0. For the analysis we used a beam size of (1.33 × 0.52) mas at a PA of −9° and a frequency range from 5 GHz to 22 GHz. We limited the uv-range to 14 Mλ to 144 Mλ and compared the results of the spectral analysis to the outcome of the unlimited uv range (see Figs. 32–34). In general, the discrepancies between the two methods are greatest at the edges of the distribution. However, in contrast to the distribution of α, there are also regions in the center of the distribution that show large differences between maps.
The difference between the turnover flux-density derived by using limited and full uv ranges is at most 10%, and a similar value is obtained for the optically thin spectral index. For the turnover frequency, the differences are much greater and can reach 50% at the edges of the distribution. The limiting of the uv range affects the distribution of the turnover flux-density less and the turnover frequency and optically thin spectral index more.
For region B (4 mas < r < 8 mas) we used a frequency range from 5 GHz to 15 GHz and the difference in the uv ranges leads only to small variations in the spectral index. As for region C, the largest differences in α can be found at the edges of the distribution. It is worth mentioning that those differences are less than 10% (see Fig. 35).
Besides the influence of the uv range, we tested the impact of the frequency range on the obtained spectral parameters. Therefore, we enlarged the frequency range from 5 GHz to 43 GHz for regions B and A. The result for the spectral index is presented in Fig. 36. The difference in α increased by a factor of 3 as compared to values calculated using a frequency range from 5 GHz to 15 GHz (see Fig. 35) and regions of increased residuals extend into the central distribution of α.
In sum, our test show that:
-
i)
if the frequency range is not more than a factor 4,the difference in the uv radii influences mainly the edges of thedistribution;
-
ii)
for the calculation of the turnover values the uv-range affects the overall distribution of the spectral parameters significantly, especially at the edges of the analyzed jet region. Therefore, the uv range should in general be matched.
Appendix C
Here we present the 2D distribution of the spectral index, α (Sν ∝ να) or the turnover values (νm, Sm and α0) for regions C, D, B, and A. In Table 11 we summarize the used image parameters for the spectral analysis.
 |
fig. C.1 2D distribution of the spectral index, α (Sν ∝ να) for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The color map in each panel shows for a given epoch (indicated in the top right corner) the distribution of α and the contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
 |
fig. C.2 2D distribution of the turnover frequency, νm, the turnover flux-density, Sm, and the optically thin spectral index, α0 for region C (r < 1 mas) for the May 2005 observations using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The contours correspond to the 86 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
 |
fig. C.3 2D distribution of the turnover frequency, νm for region D (1 mas < r < 4 mas) using a beam size of 1.33 × 0.52 mas with a PA of −7° and a pixel size of 0.04 mas. The color map in each panel shows for a given epoch (indicated in the top right corner) the distribution of νm and the contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
 |
fig. C.6 2D distribution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 8 mas) using a beam size of 2.32 × 0.07 mas with a PA of −7° and a pixel size of 0.1 mas. The color map in each panel shows for a given epoch (indicated in the top left corner) the distribution of α and the contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
 |
fig. C.7 2D distribution of the spectral index, α (Sν ∝ να) for region A (8 mas < r < 14 mas) using a beam size of 3.65 × 1.52 mas with a PA of −8° and a pixel size of 0.15 mas. The color map in each panel shows for a given epoch (indicated in the top left corner) the distribution of α and the contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
Appendix D
An accurate estimate of the uncertainties of the spectral parameters determined in Sect. 5, namely, α0, α, Sm, νm, B, and K from Eq. (32)–(33) has to take the flux-density uncertainties into account on the individual pixels and the uncertainties caused by the image alignment. We address those uncertainties by using the Monte Carlo technique.
We assume that the uncertainties on the obtained image shift are close to the used pixel size (see Sect. 2.1). Assuming additionally a normal distribution for the scatter of the image shifts, we computed 104 random image shifts and performed a spectral analysis for each shift value(see Sect. 2.2). Figure D.1 shows the distribution of the image shifts using 1000 random shifts for the May 2005 observations relative to the 86 GHz image. The different colors correspond to the absolute shifts between the reference VLBI map (here 86 GHz) and the other VLBI maps included in the spectral analysis. The initial shift positions for each frequency are indicated by the hexagon.
 |
fig. D.1 Calculated random shifts obtained from a normal distribution using the initial shift value as mean and the uncertainty as standard deviation. Different colors correspond to different frequency pairs (see plot legend) and black hexagons indicate the initial shift position. For more details see text. |
 |
fig. D.2 Result of the Monte Carlo simulation for the May 2005 observations at the position x = 0.15 mas, y = −0.13 mas (relative to the brightness peak). The left panel shows the 86 GHz contours where the lowest contour is plotted at 5× the rms value and increased by factors of 2. The solid black line corresponds to the jet axis and the red point indicates the selected position. The right panels show from top to bottom the distribution of the optically thin spectral index, α0, the turnover flux-density, Sm, and the turnover frequency, νm. The solid red lines indicate the mean of the distribution and the dashed red lines one standard deviation. The values for the spectral values are plotted in the upper left corner of the contour plot. Notice the asymmetric error bars and the tailed distribution of the spectral parameters. |
 |
fig. D.3 Monte Carlo simulation results for magnetic field, B, and the normalization coefficient, K. The other panels show the distribution of the spectral parameters, which are used to calculate B and K. The solid green lines indicate the mean of the distribution and the dashed green lines one standard deviation. The values obtained for B and K are plotted in the lower right corner. Notice the asymmetric error bars and the tailed distribution for all parameters. |
The uncertainties on the spectral parameters for each pixel were calculated from the obtained distribution. Since the equation of the synchrotron spectrum and the spectral slope are highly nonlinear (Eq. (25)), the spectral parameters are log-normally distributed. We computed the mean and the standard deviation from those distributions. The distributions calculated from the random shifts for one selected position are presented in Fig. D.2 and clearly show the log-normal distribution of the spectral parameters.
Once the variation in the spectral parameters was obtained, we used these results tocalculate the uncertainties of the magnetic field, B, and the normalization coefficient of the relativistic electron distribution, K. Again, we used a Monte Carlo approach and selected 104 random values from the log-normal distribution of the spectral parameters and computed the scatter in B and K using Eqs. (32) and (33) and the estimates of the jet width, R, and the Doppler factor, δ presented in Sect. 6. The dependence of the magnetic field and the normalization coefficient on the spectral parameters is highly nonlinear, which results in strongly skewed distributions. In Fig. D.3 we present the distributions of the spectral parameters, the magnetic field and the normalization coefficient.
The uncertainties on the spectral index, α, (Sν ∝ να) in the different regions are calculated in the same way.
Acknowledgments
C.M.F. was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. Part of this work was supported by the COST Action MP0905 Black Holes in a violent Universe through the scientific stays, STSM-MP0905-140211-004292, STSM-MP0905-300711-008633 and STSM-MP0905-110711-008634. E.R. acknowledges partial support from MINECO grant AYA2009-13036-C02-02 and the Generalitat Valenciana grant PROMETEO-2009-104. M.P. acknowledges financial support from the MINECO grants AYA2010-21322-C03-01, AYA2010-21097-C03-01, and CONSOLIDER2007-00050, and from the Generalitat Valenciana grant PROMETEO-2009-103. M.P. acknowledges partial support from MINECO through a Juan de la Cierva contract. P.M. acknowledges the support from the European Research Council (grant CAMAP-259276). This work is based on observations with VLBA. The VLBA is operated by the NRAO, a facility of the NSF under cooperative agreement by Associated Universities Inc.
References
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Croke, S. M., & Gabuzda, D. C. 2008, MNRAS, 386, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Daly, R. A., & Marscher, A. P. 1988, ApJ, 334, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Fromm, C. M., Perucho, M., Ros, E., et al. 2011, A&A, 531, A95 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromm, C. M., Ros, E., Perucho, M., et al. 2013, A&A, 551, A32 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georganopoulos, M., & Marscher, A. P. 1998, ApJ, 506, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Hirotani, K. 2005, ApJ, 619, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Kadler, M., Ros, E., Lobanov, A. P., Falcke, H., & Zensus, J. A. 2004, A&A, 426, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komissarov, S. S., & Falle, S. A. E. G. 1997, MNRAS, 288, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A. 1981, ApJ, 243, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalev, Y. Y., Lobanov, A. P., Pushkarev, A. B., & Zensus, J. A. 2008, A&A, 483, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K. R., & Blandford, R. D. 1985, ApJ, 295, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998a, A&AS, 132, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobanov, A. P. 1998b, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 1999, ApJ, 521, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 1987, in Superluminal Radio Sources, eds. J. A. Zensus, & T. J. Pearson, 280 [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mimica, P., Aloy, M.-A., Agudo, I., et al. 2009, ApJ, 696, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K. 2012, MNRAS, 420, L48 [Google Scholar]
- O’Sullivan, S. P., & Gabuzda, D. C. 2009, MNRAS, 400, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1970, Series of Books in Astronomy and Astrophysics (San Francisco, California, USA: W. H. Freemann and Company) [Google Scholar]
- Perucho, M., & Martí, J. M. 2007, MNRAS, 382, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Kovalev, Y. Y., Lobanov, A. P., Hardee, P. E., & Agudo, I. 2012, ApJ, 749, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pushkarev, A. B., Kovalev, Y. Y., Lister, M. L., & Savolainen, T. 2009, A&A, 507, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pushkarev, A. B., Hovatta, T., Kovalev, Y. Y., et al. 2012, A&A, 545, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ros, E. 2005, Future Directions in High Resolution Astronomy: The 10th Anniversary of the VLBA, PASP, 340, 482 [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., & Tornikoski, M. 2008, Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, PASP, 386, 451 [Google Scholar]
- Türler, M., Courvoisier, T. J.-L., & Paltani, S. 1999, A&A, 349, 45 [NASA ADS] [Google Scholar]
- Türler, M., Courvoisier, T. J.-L., & Paltani, S. 2000, A&A, 361, 850 [NASA ADS] [Google Scholar]
- Wang, Y., Knigge, C., Croston, J. H., & Pavlovski, G. 2011, MNRAS, 418, 1138 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Correction for the opacity shifts obtained by 2D cross correlation between adjacent frequencies.
Core shift values relative to the reference frequency (given in the second column) for different epochs.
Physical parameters from the core-shift analysis for three different models (see text for more details).
All Figures
 |
Fig. 1 cm-mm single-dish light curves for CTA 102, covering the 2006 radio flare (see Paper I). The red dashed lines correspond to the epochs of multi-frequency VLBI observations presented in this paper. (Taken from Paper II.) |
| In the text | |
 |
Fig. 2 Uniform weighted VLBA CLEAN images with fitted circular Gaussian components at different frequencies for the July 2006 observation of CTA102. The lowest contour is plotted at 10 × the off-source rms at 43 GHz and increases in steps of 2. The observing frequency and the restoring beam size are plotted above each map. For the labeling we use capital letters for the same physical region in the jet, and the numbers increase with inverse distance from the core. For a more detailed picture of the core region see Fig. 3. |
| In the text | |
 |
Fig. 3 Zoom into the core region for the images presented in Fig. 2 corresponding to epoch 2006-06-08, showing the splitting of the C-components with increasing frequency. For map details see the caption of Fig. 2. |
| In the text | |
 |
Fig. 4 Distribution of the cross-correlation coefficient for the alignment of the 8 GHz and 5 GHz VLBA maps. The intersection of the white dashed lines corresponds to the maximum cross-correlation coefficient in the color-map and the intersection of the dashed black line to the peak position of the fitted 2D Gaussian. |
| In the text | |
 |
Fig. 5 5 GHz–8 GHz spectral index maps for the May 2005 observations of CTA 102. The left panel shows the spectral index map produced by the 2D cross-correlation and the right panel the one by using the component based approach. The contours are drawn for the 8 GHz observations. The inlets show the distribution of the spectral index along the jet axis, black solid line, (inlet A) and transversal to the jet axis, dashed black line, (inlet B). |
| In the text | |
 |
Fig. 6 Distribution of the cross-correlation coefficient for the alignment of the 43 GHz and 22 GHz VLBI map. The intersection of the white dashed lines corresponds to the maximum cross-correlation coefficient in the color-map and the intersection of the dashed black line to the peak position of the fitted 2D Gaussian. |
| In the text | |
 |
Fig. 7 22 GHz-43 GHz spectral index maps for the May 2005 observations of CTA 102. The left panel shows the spectral index map produced by the 2D cross-correlation and the right panel the one by using the component based approach. The contours are drawn for the 43 GHz observations. The inlets show the distribution of the spectral index along the jet axis, black solid line, (inlet A) and transversal to the jet axis, dashed black line, (inlet B). |
| In the text | |
 |
Fig. 8 Illustration of the basic steps within our spectral analysis algorithm: i) image alignment and convolution with common beam and pixel size; ii) stacking of the images; and iii) fitting of the synchrotron-self-absorbed spectrum. See text for more details. |
| In the text | |
 |
Fig. 9 Variation of the core-shift vector with time for different frequency pairs (panel A) (43−22) GHz, panel B) (22−15) GHz, panel C) (15−8) GHz and panel D) (8−5) GHz). The solid circles correspond to the radial distance from the reference core and the dashed lines are drawn in intervals of 30°. The color of the arrow indicates the different observational epochs. (See text for more details). |
| In the text | |
 |
Fig. 10 Evolution of the core magnetic field, Bcore (top), and the relativistic particle density at the core, Ncore (bottom), as derived from the core shift analysis for three different models (For details see text). |
| In the text | |
 |
Fig. 11 Stacked 15 GHz contour map of CTA 102 obtained from observations between 2005 and 2007 convolved with a common beam size of 1.33 mas × 0.52 mas and a PA of −9° with over-plotted jet ridge line. The lowest contour level is drawn at 5× the average off-source rms (4 mJy) and the contours increase in steps of 2. |
| In the text | |
 |
Fig. 12 Jet ridge line for CTA 102 obtained from stacked VLBA images at different frequencies after realignment. The dashed lines correspond to the radial distances and are plotted every 1 mas. |
| In the text | |
 |
Fig. 13 Jet width of CTA 102 obtained from stacked VLBA images at different frequencies after realignment. |
| In the text | |
 |
Fig. 14 Evolution of the spectral index along the jet ridge line, α (Sν ∝ να) for region C (r < 1 mas), where we used a beam size of 0.95 × 0.33 mas with a PA of −13°. For readability only one error bar per epoch is shown. |
| In the text | |
 |
Fig. 15 Spatial evolution of the turnover values along the jet ridge line for the May 2005 observation (2005.39). We used a beam size of 0.95 × 0.33 mas with a PA of −13° and pixel size of 0.03 mas. The error estimates were derived from a Monte Carlo simulation (see text for more details). Top panel: Turnover frequency, νm; middle panel: turnover flux-density, Sm; bottom panel: optically thin spectral index, α0 |
| In the text | |
 |
Fig. 16 Turnover frequency–turnover flux-density plane for region C for the May 2005
observations. The number correspond to the distance from the core in mas and the
solid red line to a power law fit |
| In the text | |
 |
Fig. 17 Evolution of the turnover frequency, νm, for region D (1 mas < r < 4 mas) along the jet axis, where we used a beam size of 1.33 × 0.52 mas with a PA of −9°. For reasons of readability only one error bar per epoch is shown. Left: values along the jet ridge line. Right: average values transversal to the jet ridge line. |
| In the text | |
 |
Fig. 18 Same as Fig. 17 for the turnover flux-density, Sm. |
| In the text | |
 |
Fig. 19 Same as Fig. 17 for the optically thin spectral index, α0. |
| In the text | |
 |
Fig. 20 Turnover frequency-turnover flux-density plane for region D at a fixed position of r = 1.5 mas, where the numbers represent the temporal evolution. Left: axial values. Right: transversal averaged values (for more details see text). |
| In the text | |
 |
Fig. 21 Evolution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 10 mas) along the jet ridge line. For reasons of readability only one error bar per epoch is shown. Left: values along the jet ridge line. Right: average values transversal to the jet ridge line. |
| In the text | |
 |
Fig. 22 Evolution of the spectral index, α (Sν ∝ να) for region A (8 mas < r < 14 mas) along the jet ridge line. For reasons of readability, only one error bar per epoch is shown. Left: values along the jet ridge line. Right: average values transversal to the jet ridge line. |
| In the text | |
 |
Fig. 23 Evolution of the magnetic field B (top panel) and the normalization coefficient, K (bottom panel) for the May 2005 observation. The solid and dashed red lines correspond to power law fits (see text for details). |
| In the text | |
 |
Fig. 24 Evolution of the magnetic field B (top panel) and the normalization coefficient, K (bottom panel) for region D. The lefthand side corresponds to the axial values and the righthand side to the transversally averaged value along the jet. |
| In the text | |
 |
Fig. 25 Evolution of the time averaged magnetic field B (top panel) and the normalization coefficient, K (bottom panel) for region D. The black points and lines correspond to averaged axial values and the red points and lines to the transversally averaged values along the jet. |
| In the text | |
 |
Fig. 26 Evolution of source-intrinsic parameters for an overpressured jet, dk ≠ 1, (left panels) and for a conical jet, dk = 1, (right panels). The upper panels show the variation in the jet width, R, in pc along the jet; the middle panels the evolution of the magnetic field, B, in G; and the bottom panels the variation ointhe upper and lower electron Lorentz factors, γmin,max. The solid and dashed red lines correspond to a model where we take both synchrotron and adiabatic losses into account. To demonstrate the influence of radiative losses, we also computed the evolution of the electron Lorentz factor only for adiabatic losses (solid and dashed lines in bottom panels). See text for more details. The bottom x-axis is drawn in pc, and to allow for the direct comparison with the observations we plotted the upper x-axis in mas. |
| In the text | |
 |
Fig. 27 Evolution of the source-intrinsic parameters taking radiative and adiabatic losses into account (red points) and only adiabatic losses (black points). The different panels show the variation in the total particle density, Ntot (panel i), the relativistic energy density, Ure (panel ii), the magnetization σ = UB/Ure (panel iii) and the electron Lorentz factor (panel iv). The circle and diamond markers in panel iv) correspond to the upper and lower electron Lorentz factors. For more details see text. |
| In the text | |
 |
Fig. B.1 Influence of the uv-range on the 2D distribution of the spectral index, α (Sν ∝ να) for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increase by factors of 2. |
| In the text | |
 |
Fig. B.2 Influence of the uv range on the 2D distribution of the turnover frequency, νm for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13°, and a pixel size of 0.03 mas. The left panel shows the turnover frequency for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 86 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| In the text | |
 |
Fig. B.3 Same as Fig. 29 for the turnover flux-density, Sm. |
| In the text | |
 |
B.4 Same as Fig. 29 for the optically thin spectral index, α0. |
| In the text | |
 |
B.5 Influence of the uv range on the 2D distribution of the turnover frequency, νm for region D (1 mas < r < 4 mas) using a beam size of 1.33 × 0.52 mas with a PA of −7° and a pixel size of 0.04 mas. The left panel shows the turnover frequency for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increase by factors of 2. |
| In the text | |
 |
B.6 Same as Fig. 32 for the turnover flux-density, Sm. |
| In the text | |
 |
B.7 Same as Fig. 34 for the optically thin spectral index, α0. |
| In the text | |
 |
B.8 Influence of the uv range on the 2D distribution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 8 mas) using a beam size of 2.32 × 0.97 mas with a PA of −7° and a pixel size of 0.10 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| In the text | |
 |
Fig. B.9 Influence of the uv-range on the 2D distribution of the spectral index, α (Sν ∝ να) for region A and region B (4 mas < r < 21 mas) using a beam size of 3.65 × 1.52 mas with a PA of −8° and a pixel size of 0.10 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 8 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| In the text | |
 |
fig. C.1 2D distribution of the spectral index, α (Sν ∝ να) for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The color map in each panel shows for a given epoch (indicated in the top right corner) the distribution of α and the contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| In the text | |
 |
fig. C.2 2D distribution of the turnover frequency, νm, the turnover flux-density, Sm, and the optically thin spectral index, α0 for region C (r < 1 mas) for the May 2005 observations using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The contours correspond to the 86 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
| In the text | |
 |
fig. C.3 2D distribution of the turnover frequency, νm for region D (1 mas < r < 4 mas) using a beam size of 1.33 × 0.52 mas with a PA of −7° and a pixel size of 0.04 mas. The color map in each panel shows for a given epoch (indicated in the top right corner) the distribution of νm and the contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
| In the text | |
 |
fig. C.4 Same as Fig. C.3 for the turnover flux-density, Sm. |
| In the text | |
 |
fig. C.5 Same as Fig. C.3 for the optically thin spectral index, α0. |
| In the text | |
 |
fig. C.6 2D distribution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 8 mas) using a beam size of 2.32 × 0.07 mas with a PA of −7° and a pixel size of 0.1 mas. The color map in each panel shows for a given epoch (indicated in the top left corner) the distribution of α and the contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
| In the text | |
 |
fig. C.7 2D distribution of the spectral index, α (Sν ∝ να) for region A (8 mas < r < 14 mas) using a beam size of 3.65 × 1.52 mas with a PA of −8° and a pixel size of 0.15 mas. The color map in each panel shows for a given epoch (indicated in the top left corner) the distribution of α and the contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| In the text | |
 |
fig. D.1 Calculated random shifts obtained from a normal distribution using the initial shift value as mean and the uncertainty as standard deviation. Different colors correspond to different frequency pairs (see plot legend) and black hexagons indicate the initial shift position. For more details see text. |
| In the text | |
 |
fig. D.2 Result of the Monte Carlo simulation for the May 2005 observations at the position x = 0.15 mas, y = −0.13 mas (relative to the brightness peak). The left panel shows the 86 GHz contours where the lowest contour is plotted at 5× the rms value and increased by factors of 2. The solid black line corresponds to the jet axis and the red point indicates the selected position. The right panels show from top to bottom the distribution of the optically thin spectral index, α0, the turnover flux-density, Sm, and the turnover frequency, νm. The solid red lines indicate the mean of the distribution and the dashed red lines one standard deviation. The values for the spectral values are plotted in the upper left corner of the contour plot. Notice the asymmetric error bars and the tailed distribution of the spectral parameters. |
| In the text | |
 |
fig. D.3 Monte Carlo simulation results for magnetic field, B, and the normalization coefficient, K. The other panels show the distribution of the spectral parameters, which are used to calculate B and K. The solid green lines indicate the mean of the distribution and the dashed green lines one standard deviation. The values obtained for B and K are plotted in the lower right corner. Notice the asymmetric error bars and the tailed distribution for all parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.