| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 31 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321784 | |
| Published online | 11 September 2013 | |
Online material
Appendix A
In this section we review the basic equations of synchrotron self-absorption and present the relations needed for the performed spectral analysis (see e.g., Pacholczyk 1970; Marscher 1987; Lobanov 1998a; Türler et al. 1999).
The emission at frequency ν,
ϵν, and absorption coefficients,
κν, of a power law distribution of
relativistic electrons,
N(E) = KE−s,
where K is the normalization coefficient of the distribution and
s the spectral slope of the relativistic electron distribution, can
be written as (for details see Pacholczyk 1970)
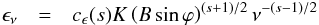 (16)
(16)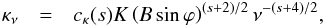 (17)where
B is the magnetic field, ϕ the pitch angle and
ν the frequency. The constants
cϵ(s) and
cκ(s) are given by
(17)where
B is the magnetic field, ϕ the pitch angle and
ν the frequency. The constants
cϵ(s) and
cκ(s) are given by
 (18)
(18)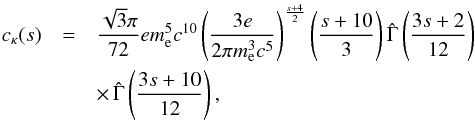 (19)with
e the electron charge, me the electron
rest-mass, c the speed of light, and
(19)with
e the electron charge, me the electron
rest-mass, c the speed of light, and
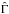 the complete Euler-Gamma function. For a random magnetic field, the constants above have
to be averaged over the pitch angle ϕ, i.e., multiplied by
cϵ,b and
cκ,b, respectively, with
the complete Euler-Gamma function. For a random magnetic field, the constants above have
to be averaged over the pitch angle ϕ, i.e., multiplied by
cϵ,b and
cκ,b, respectively, with 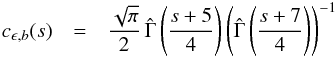 (20)
(20)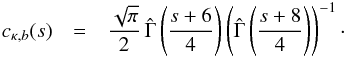 (21)The
specific intensity, Iν, can be written as
(21)The
specific intensity, Iν, can be written as
 (22)where
ϵν and
κν are the emission and absorption
coefficients and
τν = κνx
is the optical depth, with x the distance along the line of sight.
Defining ν1 as the frequency where
τν = 1, Eq. (22) takes the following form (Pacholczyk 1970):
(22)where
ϵν and
κν are the emission and absorption
coefficients and
τν = κνx
is the optical depth, with x the distance along the line of sight.
Defining ν1 as the frequency where
τν = 1, Eq. (22) takes the following form (Pacholczyk 1970): 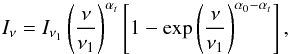 (23)where
αt is the optically thick spectral index
(αt = 5/2 for a
homogenous source), and α0 < 0 is
the optically thin spectral index. The optically thin spectral index is connected to the
spectral slope, s, by the following relation:
(23)where
αt is the optically thick spectral index
(αt = 5/2 for a
homogenous source), and α0 < 0 is
the optically thin spectral index. The optically thin spectral index is connected to the
spectral slope, s, by the following relation:
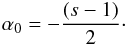 (24)Using
the transformation from intensities to flux densities Eq. (23) can be expressed in terms of the observed turnover flux-density,
Sm, and turnover frequency,
νm (Türler et al. 1999):
(24)Using
the transformation from intensities to flux densities Eq. (23) can be expressed in terms of the observed turnover flux-density,
Sm, and turnover frequency,
νm (Türler et al. 1999): 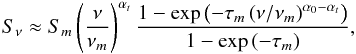 (25)where
(25)where
 is the optical depth at the turnover. Depending on the value of
ν/νm,
Eq. (25) describes an optically thick
(ν < νm)
or optically thin
(ν > νm)
spectrum with their characteristic shapes
Sν ∝ ν5/2
and
Sν ∝ ν−(s − 1)/2,
respectively.
is the optical depth at the turnover. Depending on the value of
ν/νm,
Eq. (25) describes an optically thick
(ν < νm)
or optically thin
(ν > νm)
spectrum with their characteristic shapes
Sν ∝ ν5/2
and
Sν ∝ ν−(s − 1)/2,
respectively.
Magnetic field, B, and particle density, K
Once the turnover frequency, νm, and the
turnover flux-density, Sm are obtained
(see Sect. 2.2), estimates for the magnetic
field, B, and the normalization coefficient, K,
(see, e.g., Marscher 1987) can be derived.
Following Lind & Blandford (1985), the
emission, ϵν, and absorption coefficient,
κν, have to be corrected for
relativistic and cosmological effects. In the following, primed variables correspond
to the observer’s frame, and the equations are derived for a random magnetic field
(isotropic pitch angle, ϕ), with all parameters in cgs units.
Introducing these corrections we obtain
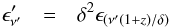 (26)
(26)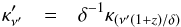 (27)with
δ = Γ-1(1 − βcosϑ)-1
the Doppler factor, with
β = v/c,
ϑ the viewing angle, and z the redshift. The
optically thin flux,
(27)with
δ = Γ-1(1 − βcosϑ)-1
the Doppler factor, with
β = v/c,
ϑ the viewing angle, and z the redshift. The
optically thin flux, 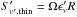 (with Ω the solid angle
and R the size of the emission region), is given by
(with Ω the solid angle
and R the size of the emission region), is given by 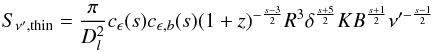 (28)and
the optical depth, τν, by:
(28)and
the optical depth, τν, by: 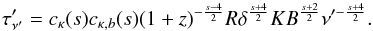 (29)Using
the obtained turnover values, the flux-density,
(29)Using
the obtained turnover values, the flux-density,
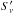 , in Eq.
(28) and the frequency,
ν′, in Eq. (29) can be replaced by the turnover flux-density,
, in Eq.
(28) and the frequency,
ν′, in Eq. (29) can be replaced by the turnover flux-density,
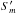 , and the
turnover frequency,
, and the
turnover frequency, 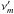 :
:  (30)
(30)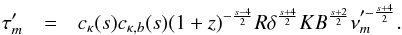 (31)The
equations above can be solved for the magnetic field, B, and the
normalization coefficient, K:
(31)The
equations above can be solved for the magnetic field, B, and the
normalization coefficient, K: 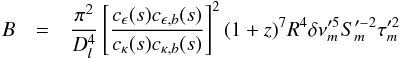 (32)
(32)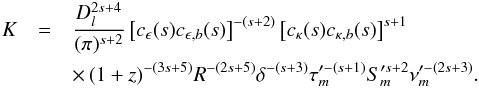 (33)
(33)
8.0.1. Number of particles, N, relativistic energy density, Ue, and magnetization σ
The number of particles, N, and the total energy distribution of
the relativistic particles, Ue, can be calculated by
integrating the distribution function
N(E) = KE−s
within the limits
E1 = γminmec2
and
E2 = γmaxmec2:
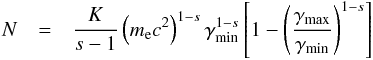 (34)
(34)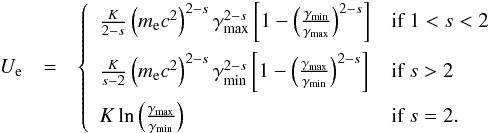 (35)Together
with the magnetic energy density,
Ub = B2/(8π),
we can define the ratio between the magnetic energy density and the energy density
of the relativistic particles:
(35)Together
with the magnetic energy density,
Ub = B2/(8π),
we can define the ratio between the magnetic energy density and the energy density
of the relativistic particles:
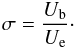 (36)
(36)
Core shift
Assuming that the position of the observed VLBI core is identical with the
(τ = 1)-surface, Lobanov
(1998a) used Eq. (29) to
derive the frequency-dependent position of the core, the so-called core shift. A
conical jet geometry was assumed in that work:
R ∝ r, a decreasing magnetic field,
B = B1r−b
and a decreasing particle density,
K = K1r−k,
where the constants B1 and K1
correspond to the magnetic field and electron normalization coefficient at 1 pc. By
inserting these assumptions into Eq. (29) and solving the equation for r, one obtains
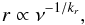 (37)where
kr = [2k + 2b(3−2α0) −2]/(5−2α0),
and α0 is the optically thin spectral index.
(37)where
kr = [2k + 2b(3−2α0) −2]/(5−2α0),
and α0 is the optically thin spectral index.
Measurements of the core shift yield estimates of several physical parameters, such
as the distance to the central engine and the magnetic field at the core (Lobanov 1998a; Hirotani 2005; O’Sullivan & Gabuzda
2009; Pushkarev et al. 2012). The
core-shift measure is defined as
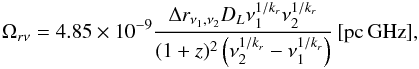 (38)with
Δrν1,ν2
the core shift between the frequencies ν1 and
ν2 in mas and
Dl the luminosity distance in pc.
Following Hirotani (2005), the magnetic field at
1 pc is given by
(38)with
Δrν1,ν2
the core shift between the frequencies ν1 and
ν2 in mas and
Dl the luminosity distance in pc.
Following Hirotani (2005), the magnetic field at
1 pc is given by 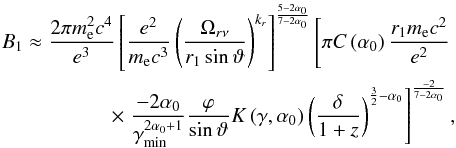 (39)where
(39)where
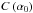 and
K(γ,α0) are defined as
and
K(γ,α0) are defined as
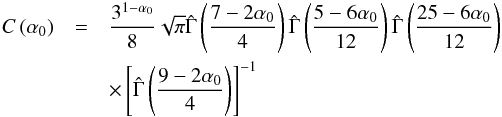 (40)
(40)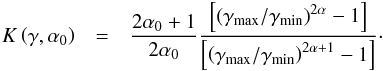 (41)The
distance to the central engine is given by
(41)The
distance to the central engine is given by 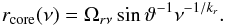 (42)Assuming
a conical jet in equipartition between the magnetic energy density and the kinetic
energy density (which implies kr = 1,
see e.g. Lobanov 1998a), and a spectral index
of α0 = −0.5, the equations above simplify to the
following relations:
(42)Assuming
a conical jet in equipartition between the magnetic energy density and the kinetic
energy density (which implies kr = 1,
see e.g. Lobanov 1998a), and a spectral index
of α0 = −0.5, the equations above simplify to the
following relations: 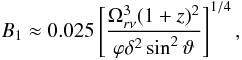 (43)
(43)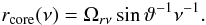 (44)The
particle density N1 can be written for both cases i)
kr = 1 and
α0 = −0.5; and ii)
kr ≠ 1 and
α0 ≠ −0.5, as
(44)The
particle density N1 can be written for both cases i)
kr = 1 and
α0 = −0.5; and ii)
kr ≠ 1 and
α0 ≠ −0.5, as
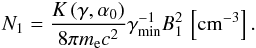 (45)Taking
kr = 1,
α0 = −0.5, and the fraction of
103 and 105 between the upper and lower electron Lorentz
factor, the equation above can be written as
(45)Taking
kr = 1,
α0 = −0.5, and the fraction of
103 and 105 between the upper and lower electron Lorentz
factor, the equation above can be written as
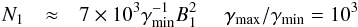 (46)
(46)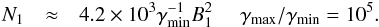 (47)
(47)
Appendix B
We performed several tests to investigate the influence of the non-identical uv-range on the spectral indices derived from images at different wavelengths and therefore with different projected baselines in wavelength units. For extracting the spectral parameters, we used both a power-law fit Sν ∝ ν+ α and the approximation of the synchrotron-self-absorbed spectrum (see Eq. (25)). Table 10 gives the average uv-ranges for the different frequencies. The image parameters, i.e., convolving beam size and pixel size, used are presented in Table 11.
Image parameters used for the spectral analysis.
 |
Fig. B.1
Influence of the uv-range on the 2D distribution of the spectral index, α (Sν ∝ να) for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increase by factors of 2. |
| Open with DEXTER | |
 |
Fig. B.2
Influence of the uv range on the 2D distribution of the turnover frequency, νm for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13°, and a pixel size of 0.03 mas. The left panel shows the turnover frequency for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 86 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| Open with DEXTER | |
 |
Fig. B.3
Same as Fig. 29 for the turnover flux-density, Sm. |
| Open with DEXTER | |
In Fig. 28 we show the 2D distribution of the
spectral index for region C using a frequency range from 15 GHz to 43 GHz. The
lefthand panel shows the distribution for a non-identical uv-range and the middle panel
the distribution for a limited uv-range, here from 27 Mλ to
450 Mλ. The difference in α between the two maps
shows that the central region is only marginally affected by the used uv-range
(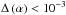 )
and the discrepancies increase with distance from the center. The largest discrepancy is
found in the edges of the distribution where
)
and the discrepancies increase with distance from the center. The largest discrepancy is
found in the edges of the distribution where 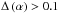 .
.
 |
B.4
Same as Fig. 29 for the optically thin spectral index, α0. |
| Open with DEXTER | |
 |
B.5
Influence of the uv range on the 2D distribution of the turnover frequency, νm for region D (1 mas < r < 4 mas) using a beam size of 1.33 × 0.52 mas with a PA of −7° and a pixel size of 0.04 mas. The left panel shows the turnover frequency for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increase by factors of 2. |
| Open with DEXTER | |
 |
B.6
Same as Fig. 32 for the turnover flux-density, Sm. |
| Open with DEXTER | |
 |
B.7
Same as Fig. 34 for the optically thin spectral index, α0. |
| Open with DEXTER | |
 |
B.8
Influence of the uv range on the 2D distribution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 8 mas) using a beam size of 2.32 × 0.97 mas with a PA of −7° and a pixel size of 0.10 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| Open with DEXTER | |
 |
Fig. B.9
Influence of the uv-range on the 2D distribution of the spectral index, α (Sν ∝ να) for region A and region B (4 mas < r < 21 mas) using a beam size of 3.65 × 1.52 mas with a PA of −8° and a pixel size of 0.10 mas. The left panel shows the spectral index for an unlimited uv range, the middle panel for limited uv range, and the right panel the residuals between them. The contours correspond to the 8 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| Open with DEXTER | |
For the May 2005 observations of CTA 102, we could derive the spectral turnover, i.e., νm and Sm, using a frequency range from 8 GHz to 86 GHz. The uv-range is set at (66−250) Mλ, and the difference in the spectral values as compared to the unlimited uv-range is shown in Figs. 29–31. The wide frequency range and the short uv-range lead to strong variation in the spectral parameters at the edges of the distribution up to 70% for α, 60% for νm, and 30% for Sm. Despite these large discrepancies at the edges, the values along the jet axis show variations up to 10%.
As mentioned in Sect. 5.2 for region D, the turnover frequency lies within our frequency range, and we can derive the turnover frequency, the turnover flux-density, and the optically thin spectral index, α0. For the analysis we used a beam size of (1.33 × 0.52) mas at a PA of −9° and a frequency range from 5 GHz to 22 GHz. We limited the uv-range to 14 Mλ to 144 Mλ and compared the results of the spectral analysis to the outcome of the unlimited uv range (see Figs. 32–34). In general, the discrepancies between the two methods are greatest at the edges of the distribution. However, in contrast to the distribution of α, there are also regions in the center of the distribution that show large differences between maps.
The difference between the turnover flux-density derived by using limited and full uv ranges is at most 10%, and a similar value is obtained for the optically thin spectral index. For the turnover frequency, the differences are much greater and can reach 50% at the edges of the distribution. The limiting of the uv range affects the distribution of the turnover flux-density less and the turnover frequency and optically thin spectral index more.
For region B (4 mas < r < 8 mas) we used a frequency range from 5 GHz to 15 GHz and the difference in the uv ranges leads only to small variations in the spectral index. As for region C, the largest differences in α can be found at the edges of the distribution. It is worth mentioning that those differences are less than 10% (see Fig. 35).
Besides the influence of the uv range, we tested the impact of the frequency range on the obtained spectral parameters. Therefore, we enlarged the frequency range from 5 GHz to 43 GHz for regions B and A. The result for the spectral index is presented in Fig. 36. The difference in α increased by a factor of 3 as compared to values calculated using a frequency range from 5 GHz to 15 GHz (see Fig. 35) and regions of increased residuals extend into the central distribution of α.
In sum, our test show that:
-
i)
if the frequency range is not more than a factor 4,the difference in the uv radii influences mainly the edges of thedistribution;
-
ii)
for the calculation of the turnover values the uv-range affects the overall distribution of the spectral parameters significantly, especially at the edges of the analyzed jet region. Therefore, the uv range should in general be matched.
Appendix C
Here we present the 2D distribution of the spectral index, α (Sν ∝ να) or the turnover values (νm, Sm and α0) for regions C, D, B, and A. In Table 11 we summarize the used image parameters for the spectral analysis.
 |
fig. C.1
2D distribution of the spectral index, α (Sν ∝ να) for region C (r < 1 mas) using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The color map in each panel shows for a given epoch (indicated in the top right corner) the distribution of α and the contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| Open with DEXTER | |
 |
fig. C.2
2D distribution of the turnover frequency, νm, the turnover flux-density, Sm, and the optically thin spectral index, α0 for region C (r < 1 mas) for the May 2005 observations using a beam size of 0.95 × 0.33 mas with a PA of −13° and a pixel size of 0.03 mas. The contours correspond to the 86 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
| Open with DEXTER | |
 |
fig. C.3
2D distribution of the turnover frequency, νm for region D (1 mas < r < 4 mas) using a beam size of 1.33 × 0.52 mas with a PA of −7° and a pixel size of 0.04 mas. The color map in each panel shows for a given epoch (indicated in the top right corner) the distribution of νm and the contours correspond to the 43 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
| Open with DEXTER | |
 |
fig. C.4
Same as Fig. C.3 for the turnover flux-density, Sm. |
| Open with DEXTER | |
 |
fig. C.5
Same as Fig. C.3 for the optically thin spectral index, α0. |
| Open with DEXTER | |
 |
fig. C.6
2D distribution of the spectral index, α (Sν ∝ να) for region B (4 mas < r < 8 mas) using a beam size of 2.32 × 0.07 mas with a PA of −7° and a pixel size of 0.1 mas. The color map in each panel shows for a given epoch (indicated in the top left corner) the distribution of α and the contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 5× the rms value and increases by factors of 2. |
| Open with DEXTER | |
 |
fig. C.7
2D distribution of the spectral index, α (Sν ∝ να) for region A (8 mas < r < 14 mas) using a beam size of 3.65 × 1.52 mas with a PA of −8° and a pixel size of 0.15 mas. The color map in each panel shows for a given epoch (indicated in the top left corner) the distribution of α and the contours correspond to the 15 GHz VLBI observations, where the lowest contour is plotted at 10× the rms value and increases by factors of 2. |
| Open with DEXTER | |
Appendix D
An accurate estimate of the uncertainties of the spectral parameters determined in Sect. 5, namely, α0, α, Sm, νm, B, and K from Eq. (32)–(33) has to take the flux-density uncertainties into account on the individual pixels and the uncertainties caused by the image alignment. We address those uncertainties by using the Monte Carlo technique.
We assume that the uncertainties on the obtained image shift are close to the used pixel size (see Sect. 2.1). Assuming additionally a normal distribution for the scatter of the image shifts, we computed 104 random image shifts and performed a spectral analysis for each shift value(see Sect. 2.2). Figure D.1 shows the distribution of the image shifts using 1000 random shifts for the May 2005 observations relative to the 86 GHz image. The different colors correspond to the absolute shifts between the reference VLBI map (here 86 GHz) and the other VLBI maps included in the spectral analysis. The initial shift positions for each frequency are indicated by the hexagon.
 |
fig. D.1
Calculated random shifts obtained from a normal distribution using the initial shift value as mean and the uncertainty as standard deviation. Different colors correspond to different frequency pairs (see plot legend) and black hexagons indicate the initial shift position. For more details see text. |
| Open with DEXTER | |
 |
fig. D.2
Result of the Monte Carlo simulation for the May 2005 observations at the position x = 0.15 mas, y = −0.13 mas (relative to the brightness peak). The left panel shows the 86 GHz contours where the lowest contour is plotted at 5× the rms value and increased by factors of 2. The solid black line corresponds to the jet axis and the red point indicates the selected position. The right panels show from top to bottom the distribution of the optically thin spectral index, α0, the turnover flux-density, Sm, and the turnover frequency, νm. The solid red lines indicate the mean of the distribution and the dashed red lines one standard deviation. The values for the spectral values are plotted in the upper left corner of the contour plot. Notice the asymmetric error bars and the tailed distribution of the spectral parameters. |
| Open with DEXTER | |
 |
fig. D.3
Monte Carlo simulation results for magnetic field, B, and the normalization coefficient, K. The other panels show the distribution of the spectral parameters, which are used to calculate B and K. The solid green lines indicate the mean of the distribution and the dashed green lines one standard deviation. The values obtained for B and K are plotted in the lower right corner. Notice the asymmetric error bars and the tailed distribution for all parameters. |
| Open with DEXTER | |
The uncertainties on the spectral parameters for each pixel were calculated from the obtained distribution. Since the equation of the synchrotron spectrum and the spectral slope are highly nonlinear (Eq. (25)), the spectral parameters are log-normally distributed. We computed the mean and the standard deviation from those distributions. The distributions calculated from the random shifts for one selected position are presented in Fig. D.2 and clearly show the log-normal distribution of the spectral parameters.
Once the variation in the spectral parameters was obtained, we used these results tocalculate the uncertainties of the magnetic field, B, and the normalization coefficient of the relativistic electron distribution, K. Again, we used a Monte Carlo approach and selected 104 random values from the log-normal distribution of the spectral parameters and computed the scatter in B and K using Eqs. (32) and (33) and the estimates of the jet width, R, and the Doppler factor, δ presented in Sect. 6. The dependence of the magnetic field and the normalization coefficient on the spectral parameters is highly nonlinear, which results in strongly skewed distributions. In Fig. D.3 we present the distributions of the spectral parameters, the magnetic field and the normalization coefficient.
The uncertainties on the spectral index, α, (Sν ∝ να) in the different regions are calculated in the same way.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


