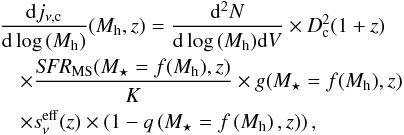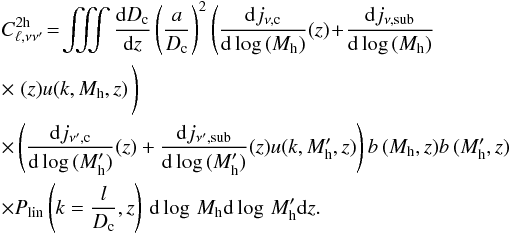| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321688 | |
| Published online | 02 September 2013 | |
The redshift evolution of the distribution of star formation among dark matter halos as seen in the infrared⋆
1
Laboratoire AIM-Paris-Saclay, CEA/DSM/Irfu – CNRS – Université Paris
Diderot, CEA-Saclay,
pt courrier 131,
91191
Gif-sur-Yvette,
France
e-mail:
matthieu.bethermin@cea.fr
2
Computational Cosmology, Department of Physics, University of
Durham, South Road,
Durham, DH1 3LE, UK
3
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove
Drive, Pasadena,
California,
USA
4
California Institute of Technology, MC249-17, Pasadena, CA
91125,
USA
5
Institut d’Astrophysique Spatiale, CNRS (UMR 8617), Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay,
France
Received:
12
April
2013
Accepted:
8
June
2013
Recent studies have revealed a strong correlation between the star formation rate (SFR) and stellar mass of the majority of star-forming galaxies, the so-called star-forming main sequence. An empirical modeling approach (the 2-SFM framework) that distinguishes between the main sequence and rarer starburst galaxies is capable of reproducing most statistical properties of infrared galaxies, such as number counts, luminosity functions, and redshift distributions. In this paper, we extend this approach by establishing a connection between stellar mass and halo mass with the technique of abundance matching. Based on a few simple assumptions and a physically motivated formalism, our model successfully predicts the (cross-)power spectra of the cosmic infrared background (CIB), the cross-correlation between CIB and cosmic microwave background (CMB) lensing, and the correlation functions of bright, resolved infrared galaxies measured by Herschel, Planck, ACT, and SPT. We use this model to infer the redshift distribution of CIB-anisotropies and of the CIB × CMB lensing signal, as well as the level of correlation between CIB-anisotropies at different wavelengths. We study the link between dark matter halos and star-forming galaxies in the framework of our model. We predict that more than 90% of cosmic star formation activity occurs in halos with masses between 1011.5 and 1013.5 M⊙. If taking subsequent mass growth of halos into account, this implies that the majority of stars were initially (at z > 3) formed in the progenitors of clusters (Mh(z = 0) > 1013.5 M⊙), then in groups (1012.5 < Mh(z = 0) < 1013.5 M⊙) at 0.5 < z < 3, and finally in Milky-Way-like halos (1011.5 < Mh(z = 0) < 1012.5 M⊙) at z < 0.5. At all redshifts, the dominant contribution to the SFR density stems from halos of mass ~1012 M⊙, in which the instantaneous star formation efficiency – defined here as the ratio between SFR and baryonic accretion rate – is maximal (~70%). The strong redshift-evolution of SFR in the galaxies that dominate the CIB is thus plausibly driven by increased accretion from the cosmic web onto halos of this characteristic mass scale. Material (effective spectral energy distributions, differential emissivities of halos, relations between Mh and SFR) associated to this model is available at http://irfu.cea.fr/Sap/Phocea/Page/index.php?id=537.
Key words: galaxies: star formation / galaxies: halos / galaxies: statistics / diffuse radiation / dark matter / submillimeter: galaxies
The effective SEDs are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/557/A66
© ESO, 2013
1. Introduction
A detailed understanding of galaxy formation in the cosmological context is one of the main problems of modern astrophysics. The star formation rate (SFR) of galaxies across cosmic time is one of the key observables to understand their evolution. However, measurements of SFR are difficult, because most of the UV light emitted by young massive stars is absorbed by interstellar dust. This light is reradiated in the infrared between 6 μm and 1 mm. The cosmic infrared background (CIB), detected for the first time in FIRAS data (Puget et al. 1996; Fixsen et al. 1998; Hauser et al. 1998), is the relic of all dust emissions since the recombination. It is the strongest background after the cosmic microwave background (CMB), and it contains half of the energy emitted after recombination (Hauser & Dwek 2001; Dole et al. 2006). Identifying the sources responsible for this background and their physical properties is thus crucial to understanding the star formation history in the Universe. Unfortunately, because of the confusion caused by the limited resolution of the current infrared/millimeter facilities (Condon 1974; Dole et al. 2004), only a small fraction of this background can be directly resolved into individual sources at wavelengths longer than 250 μm (Oliver et al. 2010; Béthermin et al. 2012c), where the CIB becomes dominated by z > 1 sources (Lagache et al. 2003, 2005; Béthermin et al. 2011, 2012c). We thus have to study the statistical properties of the unresolved background, if we want to unveil the infrared properties of galaxies that host the bulk of the obscured star formation at high redshift.
We can use statistical tools to measure the photometric properties of galaxies emitting the CIB. P(D) analysis (Condon 1974; Patanchon et al. 2009) is a method measuring the flux distribution of sources below the confusion limit by considering only the pixel histogram of an infrared/millimeter map. Glenn et al. (2010) has managed to measure the number counts (flux distribution) of SPIRE sources down to one order of magnitude below the confusion limit using P(D), and they resolve about two-thirds of the CIB into individual sources. Strong constraints on contributions to the CIB were also derived by stacking analyses (Dole et al. 2006; Marsden et al. 2009). This method allows measuring the mean flux of a population individually detected at a shorter wavelength1, but not in the far-infrared/millimeter, by stacking cutout images centered on short-wavelength detections. Number counts below the confusion limit were measured with a method based on stacking (Béthermin et al. 2010a,b). In addition to this, Béthermin et al. (2012c) also measured counts per redshift slice using an input catalog containing both 24 μm fluxes and redshifts and a complex reconstruction of the counts based on stacking. These analyses provided constraints on the CIB redshift distribution. Nevertheless, an empirical model is still needed to deduce the obscured star formation history from number counts at various wavelengths (e.g. Le Borgne et al. 2009; Valiante et al. 2009; Franceschini et al. 2010; Béthermin et al. 2011; Marsden et al. 2011; Rahmati & van der Werf 2011; Lapi et al. 2011; Gruppioni et al. 2011).
Large-scale CIB anisotropies measured by Spitzer (Lagache et al. 2007; Grossan & Smoot 2007; Pénin et al. 2012b), BLAST (Viero et al. 2009), the South Pole Telescope (SPT, Hall et al. 2010), Herschel (Amblard et al. 2011; Viero et al. 2013), and Planck (Planck Collaboration 2011) also provide degenerate constraints on the evolution of infrared-galaxy emissivities and the link between infrared galaxies and dark matter halos. This degeneracy can be broken by combining anisotropy information with infrared number counts (see above). The first generation of models used to predict/interpret CIB anisotropies was based on a combination of an evolutionary model of emissivities of infrared galaxies and a linear bias or a halo occupation distribution (HOD) model describing the spatial distribution of galaxies (Knox et al. 2001; Lagache et al. 2007; Amblard & Cooray 2007; Viero et al. 2009; Hall et al. 2010; Planck Collaboration 2011; Amblard et al. 2011; Pénin et al. 2012a; Xia et al. 2012). The emissivities are deduced from a model of galaxy evolution (e.g. Béthermin et al. 2011; Lapi et al. 2011) or represented by a simple parametric function (Hall et al. 2010; Amblard et al. 2011). However, these models assume that there is no dependency between clustering and luminosity and in general a single HOD or linear bias for all redshifts. Consequently, these models have difficulty fitting all wavelengths simultaneously. Shang et al. (2012) propose a new approach assuming an infrared-light-to-mass ratio that varies with halo mass and redshift (see also the De Bernardis & Cooray 2012 approach, which focused on 250 μm). This new model is also able to roughly reproduce the number counts (LFs respectively), though their description of infrared galaxies is simplistic (a single SED for all galaxies at all redshifts, no scatter on the mass-to-light ratio). Another approach was proposed by Addison et al. (2012), who combine a backward-evolution counts model that is very similar to the Béthermin et al. (2011) approach and a scale-dependent effective bias of infrared galaxies to predict the CIB power spectrum. This simplified approach is very efficient in fitting the data, but is purely descriptive and provides little information on the physical link between galaxies and dark matter halos.
In this paper, we propose a new approach to modeling both CIB anisotropies and galaxy number counts based on the observed relation between physical properties in galaxies and their evolution with redshift. We use the stellar mass (M⋆) as a gateway to link the halo mass (Mh) and SFR. The stochastic link between SFR and M⋆ is modeled following the Béthermin et al. (2012a) model (hereafter B12), which is based on the observed main sequence (MS) of star-forming galaxies (i.e., a strong correlation between stellar mass and SFR evolving with redshift, Noeske et al. 2007; Elbaz et al. 2007; Daddi et al. 2007; Rodighiero et al. 2011) and provides one of the best fits of mid-infrared-to-radio number counts. It contains two types of star-forming galaxies with different spectral energy distributions (SEDs): secularly star-forming MS galaxies and a population of episodic, probably merger-driven starbursts with a strong excess of SFR compared to the main sequence following the two-star-formation-mode (2SFM) formalism introduced in Sargent et al. (2012). The relation between stellar and halo mass is derived by abundance matching (Vale & Ostriker 2004; Conroy & Wechsler 2009; Behroozi et al. 2010) and assuming a monotonic relation without scatter between these quantities. Béthermin et al. (2012b) used this technique to connect SFR and Mh for MS galaxies in a qualitative way (see also Wang et al. 2013). This paper improves and extends the approach of Béthermin et al. (2012b) in order to predict the anisotropy of the CIB and the clustering of infrared galaxies. This new formalism also permits us to describe the quenching of star formation in massive galaxies and their satellites in a phenomenological way and involves a refined treatment of subhalos.
In Sect. 2, we present the philosophy of our approach. In Sect. 3, we explain the ideas on which our model is based, especially how we assign infrared properties to galaxies hosted by a dark matter halo. In Sects. 4 and 5, we describe the formalism used to compute the power spectrum of CIB anisotropies and angular correlation functions of infrared galaxies, respectively. In Sect. 6, we present the results of our modeling and an extensive comparison with observations. In Sect. 7, we discuss the successes, but also the limitations, of our model. In Sect. 8, we describe the properties of the CIB predicted a posteriori by our model, such as redshift distribution or correlation between bands. In Sect. 9, we discuss how the history of star formation history proceeds depending on the mass of dark matter halos. We conclude in Sect. 10. In Appendix A, we provide tables of conversion from multipole ℓ to angle θ and from frequencies to wavelengths, since we use both conventions interchangeably in the paper.
In this paper, we assume a WMAP-7 cosmology (Larson et al. 2011) and a Chabrier (2003) initial mass function.
2. Philosophy of our approach
The majority of previous CIB models were purely phenomenological, and they describe the emissivity and clustering of infrared galaxies using a large set of free parameters. This approach is useful for deriving quantities, such the mass where star formation is most efficient. However, it is sometimes hard to test the validity of these models since a good fit can be obtained easily considering their number of free parameters. Kim et al. (2012) proposes a physical approach based on a semi-analytical galaxy formation model, which unfortunately has substantial discrepancies with the data. We propose an alternative phenomenological approach, which represents an intermediate solution between a fully empirical and a physical model. We minimize the number of free parameters and build our analysis on the observed relation between physical quantities (e.g., the specific SFR in main-sequence galaxies calibrated from optical, near-infrared, far-infrared, and radio data). We thus do not aim to fine tune the various parameters of the model, but rather to test whether the scaling laws measured from external datasets (measurements on small samples extrapolated to all galaxies, optical/near-infrared measurements of stellar mass, or SFR) are compatible with the data under different scenarios. For this reason, we chose an approach based on abundance matching with no free parameters to describe the link between stellar mass and halo mass and use the B12 model, which follows the same philosophy to link infrared properties and stellar mass.
3. Connecting star formation and halo mass by abundance matching
In this section, we describe how we stochastically assign properties of star formation to galaxies as a function of the host halo mass by combining prescriptions from previous models. In Sects. 3.1 and 3.2, we present the halo and stellar mass functions used in this paper. We then describe how we connect stellar and halo mass by abundance matching in Sect. 3.3. Section 3.4 describes how we stochastically attribute a SFR from the stellar mass using recipes based on the B12 model. Finally, we describe how we deduce infrared properties of the galaxies from their physical properties in Sect. 3.5 using the B12 model.
3.1. Halo mass function
In our analysis, we used the halo mass function (HMF) of Tinker et al. (2008) (in our notation 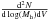 ).
We chose halo mass (Mh) to be defined by an overdensity of
Δ = 200 (often called M200). This HMF evolves with redshift
and was calibrated on N-body simulations. We also need the mass function
of subhalos, which are supposed to host satellite galaxies. The one we adopt here comes
from Tinker & Wetzel (2010), and provides
the mass distribution of subhalos in a parent halo of total mass
Mh:
).
We chose halo mass (Mh) to be defined by an overdensity of
Δ = 200 (often called M200). This HMF evolves with redshift
and was calibrated on N-body simulations. We also need the mass function
of subhalos, which are supposed to host satellite galaxies. The one we adopt here comes
from Tinker & Wetzel (2010), and provides
the mass distribution of subhalos in a parent halo of total mass
Mh:  (1)where
msub is the subhalo mass. In our analysis we neglect
sub-structures inside subhalos. The mass function of subhalos is thus
(1)where
msub is the subhalo mass. In our analysis we neglect
sub-structures inside subhalos. The mass function of subhalos is thus
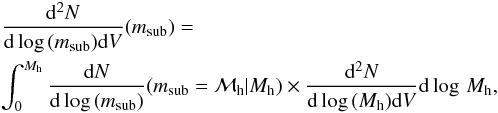 (2)we
also introduce a pseudo “total” mass function, given by the sum of the mass functions of
halos and subhalos:
(2)we
also introduce a pseudo “total” mass function, given by the sum of the mass functions of
halos and subhalos: 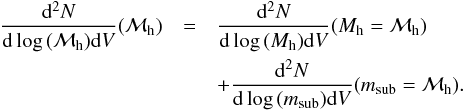 (3)Here
ℳh may stand for either the total mass of a halo
(Mh) for a main structure or the mass of the subhalo for a
substructure (msub). This function will be useful for our
abundance-matching procedure presented Sect. 3.3,
because we assume that the properties of galaxies are linked with ℳh. However,
this is not exactly a mass function, because subhalos are counted twice, namely both in
the total mass function and in the subhalo mass function. Figure 1 (lefthand column) shows the contribution of main and subhalos at
z ~ 0.5. The majority of high-mass halos are main halos, while a large
fraction of low-mass halos are substructures of more massive halos. At
ℳh = 1012 M⊙, ~1/3 of halos are
subhalos of more massive halos.
(3)Here
ℳh may stand for either the total mass of a halo
(Mh) for a main structure or the mass of the subhalo for a
substructure (msub). This function will be useful for our
abundance-matching procedure presented Sect. 3.3,
because we assume that the properties of galaxies are linked with ℳh. However,
this is not exactly a mass function, because subhalos are counted twice, namely both in
the total mass function and in the subhalo mass function. Figure 1 (lefthand column) shows the contribution of main and subhalos at
z ~ 0.5. The majority of high-mass halos are main halos, while a large
fraction of low-mass halos are substructures of more massive halos. At
ℳh = 1012 M⊙, ~1/3 of halos are
subhalos of more massive halos.
3.2. Stellar mass function
We used the same stellar mass function (SMF) of star-forming galaxies as B12, in order to
be consistent with this model, which is used to link the stellar mass to the infrared
properties (see Sect. 3.4). This mass function is
parametrized by an evolving Schechter (1976)
function: 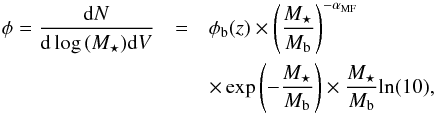 (4)with
a redshift-invariant characteristic mass Mb and faint-end
slope αMF. The characteristic density
φb is constant between z = 0 and
z = 1 but decreases at z > 1
as
(4)with
a redshift-invariant characteristic mass Mb and faint-end
slope αMF. The characteristic density
φb is constant between z = 0 and
z = 1 but decreases at z > 1
as 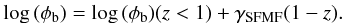 (5)The
various parameters were chosen to reproduce the observed evolution of the mass function of
star-forming galaxies. Their values are given in B12. We checked that our results are not
modified significantly if we use the double-Schechter fits of the measured SMF of Ilbert et al. (2013) instead of this simplified
parametric form.
(5)The
various parameters were chosen to reproduce the observed evolution of the mass function of
star-forming galaxies. Their values are given in B12. We checked that our results are not
modified significantly if we use the double-Schechter fits of the measured SMF of Ilbert et al. (2013) instead of this simplified
parametric form.
 |
Fig. 1 Illustration of the method used to connect various quantities by abundance matching as described in Sect. 3.3. The dashed line illustrates the connection between various quantities. We arbitrarily chose to plot results at z = 0.5. Upper left panel: integral HMF and contribution of main halos (dotted orange line) and subhalos (dot-dashed purple line). Upper right panel: integral SMF and contribution of star-forming (long-dashed blue line) and quenched (three-dot-dashed red line). Lower left panel: variation with halo mass of the fraction of halos that are subhalos. Lower right panel: fraction of quenched galaxies as a function of stellar mass. |
To correctly populate dark matter halos, we also need to account for the population of non-star-forming galaxies (called quenched galaxies hereafter), which are essentially red, passively-evolving, elliptical galaxies below the main sequence. Star formation activity in these objects is weak, and this population was thus ignored in the B12 model because of their negligible infrared emission. These galaxies do, however, contribute significantly to the mass function at high mass (e.g. Ilbert et al. 2013, see Fig. 1 upper righthand panel) and thus are generally the kind of galaxy that is encountered in massive halos. We used the mass function of quiescent galaxies from Ilbert et al. (2010) at z < 2 and Ilbert et al. (2013) at z > 2, fitted by a Schechter (1976) function. log (φb), log (Mb), and α are interpolated between the center of each redshift bins and extrapolated at z > 3. The total mass function (showed Fig. 1 upper right panel) is the sum of the contribution of both quenched and star-forming galaxies. The fraction of quenched galaxies at a given stellar mass and redshift is called q(M⋆,z). The upper righthand panel of Fig. 1 shows the mass function and its decomposition into quenched and star-forming galaxies. The lower right panel shows the fraction of quenched galaxies as a function of stellar mass. At high mass (M⋆ > 1011 M⊙) and low redshift (z < 1), the majority of galaxies are quenched, when the other regimes are dominated by star-forming galaxies.
3.3. Connecting stellar mass and halo mass through abundance matching
The abundance-matching technique is based on the hypothesis of a monotonic link between
two quantites. This is a fair assumption for the link between the stellar and halo mass of
a central galaxy at any given redshift (More et al.
2009; Moster et al. 2010; Behroozi et al. 2010). In this work, we follow Behroozi et al. (2010) and Watson & Conroy (2013) by assuming that subhalos and main
halos follow the same
M⋆-Mh relation.
Under this assumption, we associate halo mass to a stellar mass by putting the
nth most massive galaxy (in term of stellar mass) into the
nth most massive halo. In practice, we do not use catalogs, but rather
analytic mass functions. The nonparametric function linking stellar and halo mass
(M⋆ = f(ℳh)) is
thus the solution of the implicit equation
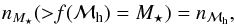 (6)where
nM⋆(> M⋆)
is the number density (in comoving units) of galaxies more massive than
M⋆ (i.e., the integral of the mass
function), and nℳh the equivalent for halo mass. We
can thus associate halo mass to stellar mass by taking the halo mass at which the number
density of galaxies and halos are the same, as illustrated by Fig. 1 (upper panels). Figure 2 shows
the resulting M⋆-ℳh relation,
which evolves little with redshift and displays a break at
ℳh ~ 1012 M⊙, as classically found in
the literature (e.g., Moster et al. 2010; Behroozi et al. 2010; Leauthaud et al. 2012).
(6)where
nM⋆(> M⋆)
is the number density (in comoving units) of galaxies more massive than
M⋆ (i.e., the integral of the mass
function), and nℳh the equivalent for halo mass. We
can thus associate halo mass to stellar mass by taking the halo mass at which the number
density of galaxies and halos are the same, as illustrated by Fig. 1 (upper panels). Figure 2 shows
the resulting M⋆-ℳh relation,
which evolves little with redshift and displays a break at
ℳh ~ 1012 M⊙, as classically found in
the literature (e.g., Moster et al. 2010; Behroozi et al. 2010; Leauthaud et al. 2012).
In this approach, we neglect the effect of the scatter on the stellar-to-halo-mass ratio, which would further complicate our analysis of CIB anisotropies. This induces a bias on the estimation of f. However, this effect is smaller than the statistical uncertainties for Mh > 1014.5 M⊙ (Behroozi et al. 2010), which host mainly passive galaxies (see Fig. 1). The scatter around f could also induce a bias on the estimate of the observables as the CIB anisotropies. However, the large-scale anisotropies are sensitive to the mean emissivity of galaxies and are not affected by the scatter. The small-scale Poisson term can be computed directly from a count model without assumptions on the dark matter (see Sect. 4). The angular correlation of bright resolved galaxies can be affected by the scatter on halo mass, but the scatter between stellar and halo mass (~0.15 dex) has the same order of magnitude as the scatter between stellar mass and SFR, which is taken into account by our model (~0.15–0.2 dex). The impact of the scatter of the stellar mass-halo mass relation on the correlation function is thus expected to be relatively small.
 |
Fig. 2 Relation between the halo mass and the stellar mass at various redshifts found by our abundance matching procedure described in Sect. 3.3. |
3.4. Connecting star formation rate to stellar mass
In the previous section, we explained how we can assign a stellar mass to a galaxy
knowing its halo mass. Unfortunately, we cannot link SFR to stellar mass by abundance
matching by assuming a monotonic relation. This hypothesis is only valid for main-sequence
galaxies, but not for quenched ones, for which
sSFR ≪ sSFRMS, and starburst galaxies, for
which sSFR ≫ sSFRMS, where sSFR is the
specific SFR; i.e.,
SFR/M⋆,
and sSFRMS is the typical value of this parameter in
main-sequence galaxies. For quenched galaxies, we neglect the star formation and thus take
SFR = 0 M⊙ yr-1 for simplicity.
For star-forming galaxies (main-sequence and starburst), we assume that SFR follows a
double log-normal distribution at fixed redshift and stellar mass (Sargent et al. 2012, B12):  (7)The
first term describes the sSFR distribution of main-sequence galaxies
(pMS), and the second one that of starbursts
(pSB). Star formation in starburst is boosted on average by
a factor BSB2, and
σMS and σSB are the dispersions
around the central values. The evolution of the main-sequence is parametrized as in B12:
(7)The
first term describes the sSFR distribution of main-sequence galaxies
(pMS), and the second one that of starbursts
(pSB). Star formation in starburst is boosted on average by
a factor BSB2, and
σMS and σSB are the dispersions
around the central values. The evolution of the main-sequence is parametrized as in B12:
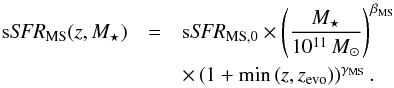 (8)The
starburst ratio rSB (i.e., the relative normalization of the
two log-normal distributions) is also provided by the B12 model:
(8)The
starburst ratio rSB (i.e., the relative normalization of the
two log-normal distributions) is also provided by the B12 model:
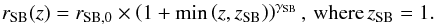 (9)
(9)
The values of the parameters in our base model (model A) are the ones provided in B123. We also used a second version of the model (model B) for which the high redshift trend was slightly modified, following the findings of a slowly increasing sSFR at high redshift (Stark et al. 2013; de Barros et al. 2012; Gonzalez et al. 2012). These higher values are the consequence of an improved modeling of the contribution of nebular line emissions to flux in near-infrared broad-band filters. For this modified version, we assume an evolution of sSFR at z > 2.5 in (1 + z). To avoid overpredicting bright millimeter counts, we compensate this increase of sSFR by a quicker decrease in the characteristic density of the stellar mass function in the same redshift range ((1 + z)-0.8 instead of (1 + z)-0.4), thus keeping the same number of bright objects. As shown in Fig. 3, both these scenarios are compatible with the data, because of the large scatter on the measurements. In Sects. 6 and 7, we discuss which scenario is actually favored by infrared observations.
 |
Fig. 3 Upper panel: evolution of sSFR in main-sequence galaxies of 5 × 109 M⊙. Lower panel: evolution of the characteristic density φb of the mass function with redshift. Both panels: model A (B12 model) is represented with a solid line and model B (modified version with higher sSFR and lower density at high redshift) with a long-dashed line. We use the compilation of data points of Sargent et al. (2012). |
3.5. Infrared outputs of galaxies
In massive galaxies, the bulk of the UV light coming from young stars is absorbed by dust
and re-emitted in the infrared. We can thus assume that the bolometric infrared (8–1000
μm) luminosity LIR is proportional to SFR
(Kennicutt 1998, the conversion factor is
K = SFR/LIR = 1 × 10-10 M⊙ yr if we assume a Chabrier 2003, IMF). In low-mass
galaxies, a significant part of the UV light escapes from the galaxy and infrared emission
is no longer proportional to SFR. Star formation rates can then be estimated from an
uncorrected UV and an infrared component
(SFR = SFRUV + SFRIR).
The infrared luminosity is then given by
if we assume a Chabrier 2003, IMF). In low-mass
galaxies, a significant part of the UV light escapes from the galaxy and infrared emission
is no longer proportional to SFR. Star formation rates can then be estimated from an
uncorrected UV and an infrared component
(SFR = SFRUV + SFRIR).
The infrared luminosity is then given by 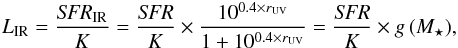 (10)where
rUV is the ratio between obscured and unobscured star
formation. We use the
rUV-M⋆
relation of Pannella et al. (2009) to compute
g(M⋆):
(10)where
rUV is the ratio between obscured and unobscured star
formation. We use the
rUV-M⋆
relation of Pannella et al. (2009) to compute
g(M⋆):
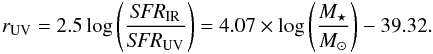 (11)g(M⋆)
tends to 0 at low mass and 1 at high mass. The UV light from young stars thus totally
escapes the low-mass galaxies, but is fully reprocessed and emitted as infrared radiation
in massive galaxies. This is due to a larger amount of dust in massive galaxies, which
causes a greater attenuation.
(11)g(M⋆)
tends to 0 at low mass and 1 at high mass. The UV light from young stars thus totally
escapes the low-mass galaxies, but is fully reprocessed and emitted as infrared radiation
in massive galaxies. This is due to a larger amount of dust in massive galaxies, which
causes a greater attenuation.
We used the same SED templates as B12, based on Magdis et al. (2012). There are different templates for main-sequence and starburst galaxies, both of which are assumed to evolve with redshift. We did not adopt a single template for a given type of galaxy at a given redshift, but assumed a scatter on the mean interstellar radiation field ⟨ U ⟩, following B12. These SEDs were calibrated using z < 2 data, which show a rise in the (rest-frame) dust temperature with redshift. At higher redshift, we assume no evolution. This assumption is discussed in Sect. 7. In this paper, we neglect the contribution of active galactic nuclei, which is only significant in the mid-infrared (B12).
4. Computing CIB power spectrum
We aim to compare the CIB anisotropies predicted by our model to observations in order to test its validity. This section presents the formalism used to derive the power spectrum (cross-spectrum) of the CIB at a given waveband (between two wavebands, respectively). One of the key benefits of the relation we established between SFR and ℳh is that we can then rely on the well-known clustering properties of dark matter halos to predict the clustering of star-forming galaxies, and thus of CIB anisotropies. We use a method similar to Shang et al. (2012). However, we modified their formalism to obtain a more natural notation and avoid renormalization of all terms by the total emissivity of infrared galaxies at a given redshift.
4.1. Mean infrared emissivities of dark matter halos
 |
Fig. 4 Effective SEDs of infrared galaxies used in our model at various redshifts. The upper panel shows the SEDs in νLν units normalized at LIR = 1 L⊙ as a function of rest-frame wavelength. The lower panel shows the ratio between the observed flux density and LIR as a function of observed wavelength. |
One of the key ingredients to compute is the mean emissivities of the halos. Classical
CIB models assume that clustering and emissivity are independent, so they compute the
total emissivity of galaxies at a given redshift. This approximation is not exact, and
both emissivity and clustering vary with halo mass (see e.g. Béthermin et al. 2012b). We thus introduce the differential emissivity
djν/dlog (Mh)
of dark matter halos as a function of halo mass. This differential emissivity is the sum
of the contribution of central galaxy and satellite galaxies:
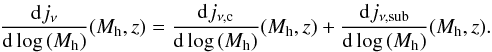 (12)The
contribution of central galaxies to the differential emissivity is computed from mean
infrared flux of galaxies hosted by a halo of mass Mh and the
HMF:
(12)The
contribution of central galaxies to the differential emissivity is computed from mean
infrared flux of galaxies hosted by a halo of mass Mh and the
HMF:
where Dc is the comoving distance and
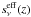 is the effective SED of
infrared galaxies at a given redshift; i.e., the mean flux density received from a
population of star-forming galaxies with a mass corresponding to a mean infrared
luminosity of 1 L⊙ (see Fig. 4), and
is the effective SED of
infrared galaxies at a given redshift; i.e., the mean flux density received from a
population of star-forming galaxies with a mass corresponding to a mean infrared
luminosity of 1 L⊙ (see Fig. 4), and 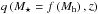 is
the fraction of quenched galaxies (i.e. non-star-forming galaxies) as defined in Sect.
3.2. Because the shape of sSFR distribution is
invariant with mass in our model, the mean flux density coming from a more massive
population can thus be obtained just by rescaling this SED and taking the attenuation
(g(M⋆) defined in Eq.
(10)) and the
SFR-M⋆ relation into account. The
effective SED is thus the mean of each type of SED weighted by their contributions to the
background (provided by Eq. (7)):
is
the fraction of quenched galaxies (i.e. non-star-forming galaxies) as defined in Sect.
3.2. Because the shape of sSFR distribution is
invariant with mass in our model, the mean flux density coming from a more massive
population can thus be obtained just by rescaling this SED and taking the attenuation
(g(M⋆) defined in Eq.
(10)) and the
SFR-M⋆ relation into account. The
effective SED is thus the mean of each type of SED weighted by their contributions to the
background (provided by Eq. (7)):
![\begin{eqnarray} s_\nu^{\rm eff}(z) = \int \left [ p_{\rm MS} \times \langle s_\nu^{\rm MS} \rangle + p_{\rm SB} \times \langle s_\nu^{\rm SB} \rangle \right] \, {\rm d}\mbox{s}\textit{SFR}, \label{eq:effsed} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21688-13/aa21688-13-eq93.png) (14)where
(14)where
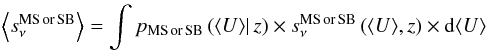 (15)where
⟨ U ⟩ is the intensity of the radiation field (strongly linked to dust
temperature), p(⟨ U ⟩ |z) its
probability distribution (this encodes the information on the scatter of dust
temperatures), and
(15)where
⟨ U ⟩ is the intensity of the radiation field (strongly linked to dust
temperature), p(⟨ U ⟩ |z) its
probability distribution (this encodes the information on the scatter of dust
temperatures), and 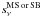 the flux density received from an
LIR = 1 L⊙ main-sequence or
starburst source with a radiation field ⟨ U ⟩ at redshift
z. The average SED of all MS or SB galaxies at any given redshift
the flux density received from an
LIR = 1 L⊙ main-sequence or
starburst source with a radiation field ⟨ U ⟩ at redshift
z. The average SED of all MS or SB galaxies at any given redshift
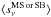 takes the scatter on
⟨ U ⟩ into account. The infrared luminosity of these effective
templates is slightly larger than 1 L⊙ because of the
asymmetry of sSFR distribution caused by starburst. The effective SEDs4 from Eq. (14) used in
this work are available at the CDS.
takes the scatter on
⟨ U ⟩ into account. The infrared luminosity of these effective
templates is slightly larger than 1 L⊙ because of the
asymmetry of sSFR distribution caused by starburst. The effective SEDs4 from Eq. (14) used in
this work are available at the CDS.
 |
Fig. 5 Differential emissivities at 100 μm (3000 GHz) and 1.38 mm (217 GHz) as a function of halo mass at various redshifts predicted by model C. The solid lines are the contributions of all the galaxies to the infrared flux of a main halo, when the dotted lines indicate only the contribution of central galaxies. |
The contribution of satellite galaxies to differential emissivity is the sum of the
contribution of all galaxies in subhalos of a main halo of mass
Mh. It depends on the mass function of main halos, the mass
function of subhalos in main halos of this mass, and the mean flux density of galaxies
hosted by subhalos: 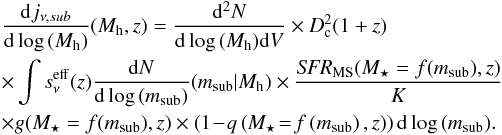 (16)
(16)
In this formula, we assume that the quenching of satellite galaxies only depends on their stellar mass (or subhalo mass). We also propose an alternative scenario where quenching depends on the mass of the main halo and not on the mass of the subhalo. In this scenario, satellite galaxies become quenched at the same time as the central galaxy in the same parent halo. In practice, we replace msub by Mh in the last factor of Eq. (16), which can then be moved outside the integral. This scenario is motivated by the tendency for the fraction of quenched satellite galaxies to be higher in dense environments (e.g. Park et al. 2007). This phenomenon is often called environmental quenching. The modified version of model B where this modification was performed is called model C.
In our computation, the flux densities are not the monochromatic flux densities at the center of the passband filters of each instrument, but are computed by taking the real filter profiles into account. Figure 5 illustrates the variation in differential emissivities with halo mass, redshift, and wavelength. The shape of the SEDs implies that long wavelengths have stronger emissivities at high redshift. The halo mass dominating the emissivities is always ~1012 M⊙, in agreement with previous works (e.g. Conroy & Wechsler 2009; Béthermin et al. 2012b; Wang et al. 2013; Behroozi et al. 2013a).
4.2. Power spectrum
The CIB power spectrum can be represented as the sum of three contributions (Amblard & Cooray 2007; Viero et al. 2009; Planck Collaboration 2011; Amblard et al. 2011; Pénin et al. 2012a; Shang et al. 2012):
-
two-halo term: correlated anisotropies between galaxies indifferent halos, which dominates on scales larger than a fewarcminutes;
-
one-halo term: correlated anisotropies of galaxies inside the same main halo, which have a significant impact on scales of a few arcminutes;
-
Poisson term: non correlated Poisson anisotropies, also called shot noise, which dominate on small scales.
The cross power spectrum of CIB
Cℓ,νν′
between two frequency bands (ν and ν′) is
thus:  (17)The
two-halo and one-halo terms, which correspond to large- and intermediate-scale
anisotropies, respectively, are computed from the mean emissivities of galaxies and are
not affected by the stochasticity of the connexions between galaxies and halos. The
computation of the anisotropies caused by the Poisson fluctuations of the number of
galaxies in a line of sight requires no assumption regarding the link between dark matter
halos and galaxies. They are deduced from the B12 model. Each term is calculated
independently, but based on the same consistent model.
(17)The
two-halo and one-halo terms, which correspond to large- and intermediate-scale
anisotropies, respectively, are computed from the mean emissivities of galaxies and are
not affected by the stochasticity of the connexions between galaxies and halos. The
computation of the anisotropies caused by the Poisson fluctuations of the number of
galaxies in a line of sight requires no assumption regarding the link between dark matter
halos and galaxies. They are deduced from the B12 model. Each term is calculated
independently, but based on the same consistent model.
4.2.1. Two-halo term
The two-halo term is computed from the following formula, summing on redshift, but also over all cross-correlation between halos of various masses:
This formula assumes the Limber (1953) flat-sky
approximation. The first factor is geometrical. The next two factors contain
differential emissivities. The factor
u(k,Mh,z)
is the Fourier transform of the halo profile assumed here to be NFW (Navarro et al. 1997). In contrast to Shang et al. (2012), this term is only placed in
front the subhalo-emissivity term, assuming that subhalos are distributed following the
NFW profile. The central galaxy is assumed to be at the center of the halo. The
clustering term  is the
cross power spectrum between halo of mass Mh and
is the
cross power spectrum between halo of mass Mh and
 , under the
assumption that
, under the
assumption that 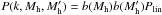 (Cooray & Sheth 2002). Here,
Plin is the linear matter power spectrum computed with the
transfer function of Eisenstein & Hu
(1999). Equation (18) can be
significantly simplified by introducing
(Cooray & Sheth 2002). Here,
Plin is the linear matter power spectrum computed with the
transfer function of Eisenstein & Hu
(1999). Equation (18) can be
significantly simplified by introducing
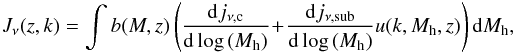 (19)which
is an emissivity weighted by the bias corresponding to each halo mass. We can then
simplify Eq. (18):
(19)which
is an emissivity weighted by the bias corresponding to each halo mass. We can then
simplify Eq. (18): 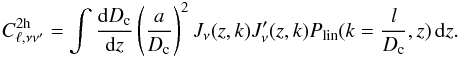 (20)This
way of computing
(20)This
way of computing 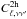 reduces the number of integrals, because Jν
can be calculated only once per frequency channel and then can be used to derive all the
cross-spectra. In addition, Jν can also be
used to compute the cross-correlation between CIB and CMB lensing (see Sect. 4.3).
reduces the number of integrals, because Jν
can be calculated only once per frequency channel and then can be used to derive all the
cross-spectra. In addition, Jν can also be
used to compute the cross-correlation between CIB and CMB lensing (see Sect. 4.3).
4.2.2. One-halo term
The one-halo term is computed with
![\begin{eqnarray} C_{\ell,\nu \nu'}^{1{\rm h}} &=& \iint \frac{{\rm d}D_{\rm c}}{{\rm d}z} \left( \frac{a}{D_{\rm c}} \right )^2 \times \Bigg[ \frac{{\rm d}j_{\nu,\textrm{c}}}{{\rm d}\log\,(M_{\rm h})} \frac{{\rm d}j_{\nu',\textrm{sub}}}{{\rm d}\log\,(M_{\rm h})} u(k, M_{\rm h},z)\nonumber\\ && +\frac{{\rm d}j_{\nu,\textrm{sub}}}{{\rm d}\log\,(M_{\rm h})} \frac{{\rm d}j_{\nu',\textrm{c}}}{{\rm d}\log\,(M_{\rm h})} u(k, M_{\rm h},z) \nonumber\\ &&+ \frac{{\rm d}j_{\nu,\textrm{sub}}}{{\rm d}\log\,(M_{\rm h})} \frac{{\rm d}j_{\nu',\textrm{sub}}}{{\rm d}\log\,(M_{\rm h})} u^2(k, M_{\rm h},z)\Bigg]\nonumber\\ && \times \left ( \frac{{\rm d}^2N}{{\rm d}\log\,(M_{\rm h}){\rm d}V}\right )^{-1} {\rm d}z \, {\rm d}\log\,M_{\rm h}. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21688-13/aa21688-13-eq116.png) (21)The
first factor describes geometry. The second one represents the various
(cross-)correlations between satellite and central galaxies. There is only a factor
u for (cross-)correlation between satellites and central, because the
central is assumed to be at the center of the halo and the satellites follow the NFW
profile, and u2 for satellite-satellite combinations.
Finally, we have to renormalize by the inverse of the mass function, because the two
dj/dlog (Mh)
factors implicitly contain two times the number of halos, when this should appear only
once (Cooray & Sheth 2002). This notation
avoid to have to renormalize by jν as in
Shang et al. (2012).
(21)The
first factor describes geometry. The second one represents the various
(cross-)correlations between satellite and central galaxies. There is only a factor
u for (cross-)correlation between satellites and central, because the
central is assumed to be at the center of the halo and the satellites follow the NFW
profile, and u2 for satellite-satellite combinations.
Finally, we have to renormalize by the inverse of the mass function, because the two
dj/dlog (Mh)
factors implicitly contain two times the number of halos, when this should appear only
once (Cooray & Sheth 2002). This notation
avoid to have to renormalize by jν as in
Shang et al. (2012).
4.2.3. Poisson term
The Poisson term is independent of large-scale halo and only depends on the flux
distribution of galaxies (number counts). These Poisson anisotropies for the auto power
spectrum can be computed from (Lagache et al.
2003): 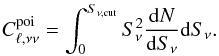 (22)Here
dN/dSν
are the differential number counts (see e.g. B12 for the computational details) and
Sν,cut is the flux cut at which sources
are removed from the maps. The Poisson term of the cross-spectrum is slightly more
complex to compute:
(22)Here
dN/dSν
are the differential number counts (see e.g. B12 for the computational details) and
Sν,cut is the flux cut at which sources
are removed from the maps. The Poisson term of the cross-spectrum is slightly more
complex to compute: 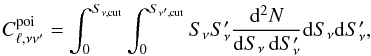 (23)where
d2N/dSνdSν′
are the multivariate counts (i.e. number of sources with a flux between
Sν and
Sν + dSν
in one band and
(23)where
d2N/dSνdSν′
are the multivariate counts (i.e. number of sources with a flux between
Sν and
Sν + dSν
in one band and 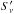 and
and
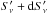 in the
other).
in the
other).
In practice, multivariate counts are hard to compute, and summing the contribution of
various redshift, types of galaxies, infrared luminosity, and radiation field is easier
(the derivation of this formula is presented in Appendix B): 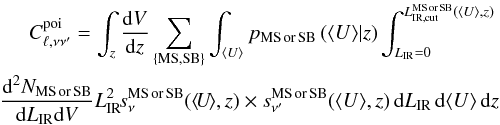 (24)where
(24)where
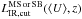 is the infrared luminosity
where the source is detected in at least one of the bands (depends on redshift, type of
galaxy and radiation field), and
d2NMS or SB/dLIR dV
is the infrared luminosity function (main-sequence or starburst contribution).
is the infrared luminosity
where the source is detected in at least one of the bands (depends on redshift, type of
galaxy and radiation field), and
d2NMS or SB/dLIR dV
is the infrared luminosity function (main-sequence or starburst contribution).
4.3. Cross-correlation between CIB and CMB lensing
In addition to cross-correlations between the CIB in various bands, we can also test the predictive power of our model for correlation between the CIB and the reconstructed gravitational potential derived from distortions of the CMB due to gravitational lensing by large scale halos at z ~ 1−3 (e.g. Hanson et al. 2009). This correlation is a direct probe of the link between the gravitational potential of dark matter halos and infrared emission from star-forming galaxies.
Because the CMB lensing signal is due to dark matter halo, this signal can be modeled
with a two-halo term replacing the term of emissivity by a term linked to the
gravitational potential (adapted from Planck Collaboration
2013): 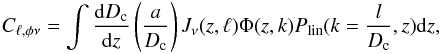 (25)Φ(z,ℓ)
is given by (Challinor & Lewis 2005)
(25)Φ(z,ℓ)
is given by (Challinor & Lewis 2005)
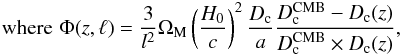 (26)where
H0 is the Hubble constant, ΩM the matter density
in units of the critical density, and
(26)where
H0 is the Hubble constant, ΩM the matter density
in units of the critical density, and 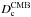 the
comoving distance between CMB and us. The impact of subhalos on CMB lensing (1-halo) is
quite small and can be neglected for this work.
the
comoving distance between CMB and us. The impact of subhalos on CMB lensing (1-halo) is
quite small and can be neglected for this work.
 |
Fig. 6 Halo occupation distribution, i.e. mean number of detected galaxies in a halo, including its substructures, as a function of its total mass Mh, of S160 > 5 mJy (left) and S850 > 3 mJy (right) sources at z = 0.1 (top) and z = 2 (bottom) for central (solid line) and satellite (dashed line) galaxies predicted by the model. The HOD of central galaxies is the same for all versions of the models and represented in black. Satellite HODs are plotted in blue (red) for model A/B (C). |
5. Computation of angular correlation function of resolved infrared galaxies
In addition to the anisotropies of the faint infrared sources responsible for the unresolved background, our model also provides predictions of the angular correlations of the individually detected bright sources. A formalism taking the selection function of the resolved sources into account has to be employed so we cannot use the same formalism as for the power spectrum. In this paper, we only consider samples selected using a flux threshold (Sν,cut) at a given wavelength for simplicity. In this section, we first explain how we compute the HOD (i.e. the mean number of central and satellite galaxies as a function of halo mass and redshift) for a given selection of resolved sources and then how we derive the correlation function from the HODs.
5.1. Halo occupation distribution
The mean number of central galaxies in a given halo of total mass
Mh is
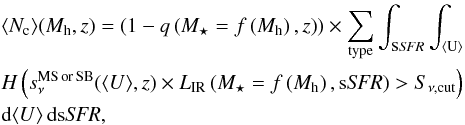 (27)where
(27)where
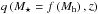 is
the fraction of quenched objects, and H is a function having a value of 1
if the condition is true and 0 otherwise. This condition is only true if the source is
sufficiently bright to be detected
(Sν > Sν,cut).
This depends on halo mass, type of galaxy (MS or SB), sSFR, and ⟨ U ⟩.
is
the fraction of quenched objects, and H is a function having a value of 1
if the condition is true and 0 otherwise. This condition is only true if the source is
sufficiently bright to be detected
(Sν > Sν,cut).
This depends on halo mass, type of galaxy (MS or SB), sSFR, and ⟨ U ⟩.
The number of satellites depends on the total mass of the parent halo
Mh and is connected to the subhalo via
 (28)This
formula works only when we assume the same infrared luminosity versus halo mass relation
for main and subhalos (models A and B), and consequently the HOD of the satellite in a
given subhalo of mass msub is the same as for the central in a
main halo of identical mass
Mh = msub. For model C
(satellites quenched at the same time as the centrals), the factor
⟨ Nc ⟩ (msub,z)
has to be multiplied by
(28)This
formula works only when we assume the same infrared luminosity versus halo mass relation
for main and subhalos (models A and B), and consequently the HOD of the satellite in a
given subhalo of mass msub is the same as for the central in a
main halo of identical mass
Mh = msub. For model C
(satellites quenched at the same time as the centrals), the factor
⟨ Nc ⟩ (msub,z)
has to be multiplied by 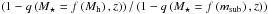 to take into account that in this version of the model the quenching is linked to the mass
of the central and not the satellite.
to take into account that in this version of the model the quenching is linked to the mass
of the central and not the satellite.
Figure 6 shows the HOD of S160 > 5 mJy (sources detected by the deepest PACS surveys) and S850 > 3 mJy (typical submillimeter galaxies) sources at low (z = 0.1) and high (z = 2) redshift. The number of central galaxies decreases very quickly at low mass. This sharp cut is due to the selection in infrared flux and the rather tight correlation between infrared luminosity and halo mass for central galaxies. At low redshift, the probability to detect an infrared galaxy in a massive halo is fairly low because the vast majority of central galaxies are quenched and thus have little infrared emission. The HOD of the satellites strongly depends on the version of the model. If the quenching of satellites is decorrelated from the quenching of the centrals (models A and B), the number of the detected satellite increases quickly with the halo mass. This is not the case for model C, for which the satellites are quenched at the same time as the centrals.
5.2. Angular auto-correlation function
The angular correlation function (ACF) can be compute from the HOD of galaxies and their
redshift distribution (see Cooray & Sheth
2002 for a review): 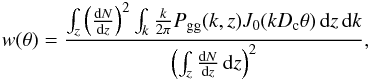 (29)where
J0 is the zeroth order Bessel function, and
dN/dz the redshift distribution of
galaxies, which can be computed from counts per redshift slice following Béthermin et al. (2011). The value
Pgg is the sum of two terms corresponding to the clustering
of galaxies in two different halos and inside the same halo:
(29)where
J0 is the zeroth order Bessel function, and
dN/dz the redshift distribution of
galaxies, which can be computed from counts per redshift slice following Béthermin et al. (2011). The value
Pgg is the sum of two terms corresponding to the clustering
of galaxies in two different halos and inside the same halo:
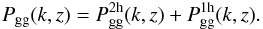 (30)Following
the standard conventions, we write the two-halo term as
(30)Following
the standard conventions, we write the two-halo term as
![\begin{eqnarray} P_{\rm gg}^{\rm 2h}(k,z) = \left [ \int_{M_{\rm h}} \frac{{\rm d}^2N}{{\rm d}\log\,(M_{\rm h}) {\rm d}V} b(M_{\rm h}) \frac{\langle N_{\rm gal} \rangle}{\bar{n}_{\rm gal}} {\rm d}M_{\rm h}\right ]^2 P_{\rm lin}(k,z), \end{eqnarray}](/articles/aa/full_html/2013/09/aa21688-13/aa21688-13-eq158.png) (31)where
⟨ Ngal ⟩ = ⟨ Nc ⟩ + ⟨ Nsub ⟩.
The one-halo term is
(31)where
⟨ Ngal ⟩ = ⟨ Nc ⟩ + ⟨ Nsub ⟩.
The one-halo term is 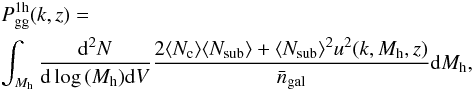 (32)where
(32)where
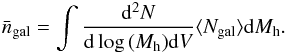 (33)
(33)
 |
Fig. 7 Left and center panels: CIB power spectrum predicted by our model and comparison with IRAS (160 μm, Pénin et al. 2012b, open circles), Spitzer (100 μm, Lagache et al. 2007, crosses, Pénin et al. 2012b, asterisks), Herschel (250, 350, and 500 μm, Viero et al. 2013, triangles), Planck (350, 550, 850, and 1380 μm, Planck Collaboration 2011, squares), and SPT (1380 μm, Hall et al. 2010, diamonds) measurements. The dotted, dot-dashed, and dotted lines represent the Poisson, 1-halo, and 2-halo terms. Right panel: number counts of infrared galaxies. Data are taken from the compilation of measurements in Béthermin et al. (2011) and B12. Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. The flux cuts used to compute the model predictions are 1 Jy at 100 μm, 100 mJy at 160 μm, 0.3 mJy at 250 μm, 350 μm, and 500 μm, 0.54 Jy at 550 μm, 0.325 Jy at 850 μm, 20 mJy at 1.38 mm. |
 |
Fig. 8 Cross-power spectrum between SPIRE bands measured by Viero et al. (2013) and comparison with our model. Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
6. Comparison with the observations
6.1. CIB power spectrum and number counts
We compared the predictions of our model with the CIB power spectrum measured with IRAS (100 μm, Pénin et al. 2012b), Spitzer (160 μm, Lagache et al. 2007; Pénin et al. 2012b), Herschel (250, 350, and 500 μm, Viero et al. 2013), Planck (350, 550, 850, and 1380 μm, Planck Collaboration 2011), and SPT (1380 μm, Hall et al. 2010) measurements in Fig. 7 (left and center). The level of the Poisson anisotropies is significantly affected by the flux cut used to mask bright sources, and their level increases with the chosen flux cut. The correlated anisotropies (1-halo and 2-halo) are less affected by the flux cut. When we compare several datasets at the same wavelength, we thus compute the model predictions for the flux cut of the experiment, which is the most sensitive on small scales. The flux cuts used to compute the model predictions are thus 1 Jy at 100 μm, 100 mJy at 160 μm, 0.3 mJy at 250 μm, 350 μm, and 500 μm, 0.54 Jy at 550 μm (545 GHz), 0.325 Jy at 850 μm (353 GHz), 20 mJy at 1.38 mm (217 GHz). The overall agreement with the data is very good for a model not fitted on the data. However, some tensions between models A and B and data at short and large wavelengths provide interesting information.
The anisotropies at 100 μm are dominated by galaxies at low redshift (see Sect. 8) and are thus not affected by the evolution of galaxies at z > 2.5. Consequently, there is no difference between models A and B. In contrast, model C (with quenching of satellite around massive quenched central) predicts a lower level of anisotropies at ℓ < 5000, which is in better agreement with the data, especially around ℓ = 2000. The “environmental quenching” in model C reduces the one-halo term compared to model B (by a factor of 4 at ℓ = 2000), but does not significantly affect the two-halo term (~15%) and does not change the Poisson level at all. However, the former difference is not very significant (~2σ), and CIB anisotropies are obviously not the best probe of such environmental effects.
The interpretation of Spitzer/MIPS 160 μm data is trickier. While our model agrees with the measurements of Lagache et al. (2007) (crosses) and Pénin et al. (2012b) (asterisks) at ℓ > 2000, they are a factor 3–10 higher than our model on larger scales. Such a large difference is hard to explain especially when considering that the model agrees well with the data at 100 and 250 μm. This could be caused by problems in cirrus subtraction. In addition, MIPS suffers from strong 1/f noise and is probably not the best instrument for measuring large-scale anisotropies.
Between 250 and 550 μm, our model agrees nicely with Planck and Herschel measurements. At longer wavelengths (850 μm and 1.4 mm), model A overpredicts anisotropies on large scales by a factor 2 at 1.4 mm, while models B and C agree with the data, except for a 2σ tension at 1.4 mm in the two lowest multipole bins. However, measuring the CIB at 217 GHz is difficult because it strongly relies on the correct subtraction of the CMB. Future analyses will either confirm or refute the presence of this discrepancy. The three models agree with the number counts at 850 μm and 1.1 mm. The difference between models A and B/C is the sSFR at z > 2.5 and the characteristic density of the mass function of star-forming galaxies. Model A assumes a flat sSFR at z > 2.5, while models B and C assume rising sSFR at z > 2.5 compensated for by a decrease in the characteristic density of the mass function to preserve the agreement with the number counts. In these two versions, the number of bright objects is thus the same, but the number of faint objects is different (see e.g. number counts around 1 mJy at 1.1 mm). Model A overpredicts the CIB anisotropies because of too high emissivity of high-redshift faint galaxies.
 |
Fig. 9 Cross-power spectrum between BLAST and ACT measured by Hajian et al. (2012) and comparison with our model. Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
 |
Fig. 10 Comparison between the cross power spectrum between CIB and CMB lensing predicted by our model and the measurements by Planck Collaboration (2013) (diamonds) and Holder et al. (2013) with SPT and Herschel (triangles). Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
 |
Fig. 11 Auto-correlation function of various flux-selected sample of infrared galaxies and comparison with our model (same color coding as in Fig. 7). The data come from Magliocchetti et al. (2011) at 100 μm and 160 μm and Cooray et al. (2010) and Maddox et al. (2010) at 250, 350, and 500 μm. We used the same flux cuts as Magliocchetti et al. (2011) and Cooray et al. (2010). Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
In the case of model C (which includes satellite-quenching), the one-halo term never dominates the anisotropies regardless of wavelength or scale. Concerning models A and B (without satellite-quenching), the one-halo term contributes to the CIB anisotropies by a similar amount as do the two-halo and Poisson terms at ℓ ~ 2000 at 100 μm, 160 μm, and 250 μm. On other scales and wavelengths, it represents a minor contribution. This result contradicts models assuming no mass-luminosity dependence (e.g. Planck Collaboration 2011; Pénin et al. 2012a), but is consistent with the approaches assuming a dependence (e.g. Shang et al. 2012). This reduction of the one-halo term is caused by the satellites being hosted by low mass subhalos and thus having low infrared luminosities.
6.2. CIB cross-power spectrum
In addition to auto power spectra, we can compare the predictions of our model with cross power spectra. They are useful for verifying that the level of correlation between bands is correct. This also is an indirect test of whether SED libraries and redshift distributions used in the model are correct. We compared our models with measurements of Viero et al. (2013) between SPIRE bands (see Fig. 8). All versions of our model agree with the data, except a systematic 2σ tension for the point at ℓ = 700 in the three bands, which could be due to cosmic variance (one 2σ outlier for 18 points is statistically expected). The trends of Hajian et al. (2012) (see Fig. 9) are also reproduced well, but our model is systematically lower than the data at ℓ = 1500. However, the stability of BLAST on large scales is not as good as for SPIRE. A future analysis of the cross-correlation between SPIRE and ACT and/or between Planck bands will thus be useful for further investigating of this discrepancy.
6.3. Cross correlation between CIB and CMB lensing
In Fig. 10, we compare the predictions of the cross-correlation between CIB and CMB lensing with the measurements from Planck Collaboration (2013) and Holder et al. (2013). In the former work, both CMB lensing and CIB fluctuations are measured from Planck data. In the latter, the CMB lensing is estimated from SPT data, and the CIB is measured using Herschel. At ℓ >1000, all versions of the model agree well with the data. At ℓ <1000, the various versions of the model tend to be be systematically higher than the data. Models B and C (with modified evolution at high redshift) are closer to the data, but slightly overpredict the cross-correlation by ~1σ at 857 GHz, 545 GHz, and 353 GHz. Future work will investigate this tension.
6.4. Clustering of resolved galaxies
The clustering of bright resolved infrared sources is also an important test of our model. Figure 11 shows the comparison between the clustering measurements of various flux-selected samples and our model predictions. At 100 and 160 μm, our model agrees well with the Herschel/PACS measurements of Magliocchetti et al. (2011). In Herschel/SPIRE bands, the comparison is trickier. There are strong disagreements between the measurements of Cooray et al. (2010) and Maddox et al. (2010). In fact, measuring the correlation function of SPIRE sources (250, 350, and 500 μm) is very difficult because these data are strongly confusion-limited (Nguyen et al. 2010). The background is thus hard to estimate, and the completeness of the catalog can vary depending on the local source density. We agree with Maddox et al. (2010) on scales larger than 0.1 deg, but not on smaller scales at 250 μm and 350 μm, where systematics could be due to background subtraction. Our model disagrees with the measurements of Cooray et al. (2010), which are systematically higher. More reliable measurements of the correlation function of SPIRE sources, controlling the systematic effects, are thus needed to check the validity of our model accurately.
7. Successes and limitations of our model
In the previous sections, we presented a natural way of extending the B12 model of infrared galaxies by linking their properties to their host halo. We tested the validity of this approach by comparing the prediction of this extended model to the measured spatial distribution of both individually detected infrared galaxies (where the measurements are reliable) and the unresolved background. This comparison shows the good predictive power of our approach, suggesting that our assumptions are fair. Using this model to interpret both the origin of CIB anisotropies (Sect. 8) and the link between star-forming galaxies and dark matter halos (Sect. 9.3) is thus legitimate. For simplicity, we perform this analyses only with model C, which provides the best agreement with the data.
Few models are able to reproduce both the number counts from mid-infrared to the millimeter wavelengths and CIB anisotropies from the far-infrared to the millimeter regimes. Addison et al. (2012) proposed a fully empirical model based on the evolution of the luminosity function and the bias of galaxies. This approach is as efficient as ours when it comes to fitting counts, but provides very little insight into the physical evolution of galaxies. Cai et al. (2013) – an updated and extended version of models presented in Lapi et al. (2011) and Xia et al. (2012) models – is also very efficient at reproducing all these observables, despite too low a level of the CIB anisotropies below 350 μm. However, their approach has many free parameters (32 for the evolution of the luminosity function of the various low-z galaxy populations, ten for the physically-modeled population of high-z proto-spheroidal galaxies, and four for the clustering of galaxies), and uses a description of the clustering based on an HOD standard that is not coupled to the physical model describing the evolution of their protospheroidal galaxies. The strength of our approach is to propose a set of 18 parameters for the evolution of galaxies, which are all constrained using external constraints (measurements of the evolution of the sSFR and the SMF, mean SEDs measured by stacking, etc.), and a formalism to compute the clustering without any free parameters, allowing a consistent description of the occupation of dark-matter halos by infrared galaxies.
However, some limitations of this model have to be kept in mind. First, the SED of infrared galaxies at high redshift (z > 2) was not measured and it is not clear if the dust temperature will increase or decrease at high redshift, because of the uncertainties on the mass-metallicity and mass-attenuation relation as discussed in Magdis et al. (2012). The good agreement between the model and the CIB anisotropies at long wavelengths suggests that our hypothesis of nonevolution is reasonable. The SED of low-mass galaxies (M⋆ < 1010 M⊙) is not well constrained, but the contribution of these low-mass galaxies to the CIB is small making this scenario hard to test. Second, the sSFR and the SMF of star-forming galaxies at very high redshift (z > 3) are also uncertain, but the effects of z > 3 galaxies on the CIB are pretty small, and these data thus cannot accurately constrain the evolution of infrared galaxies at very high redshift. Finally, we assumed an universal relation between stellar mass and UV attenuation, but this relation could also break at very high redshift, where the amount of metals is smaller and galaxies could thus contain less dust. For all these reasons, the predictions of the models at z > 2 must be interpreted with caution.
 |
Fig. 12 Predicted redshift distribution of the CIB and its anisotropies. Upper left panel: CIB SED and contribution per redshift slice (colored solid lines). Black squares: total extrapolated CIB from deep number counts (Teplitz et al. 2011; Béthermin et al. 2010a; Berta et al. 2011; Béthermin et al. 2012c; Zemcov et al. 2010). Cyan solid line: absolute CIB spectrum measured by COBE/FIRAS (Lagache et al. 2000). Green triangles: absolute CIB measurements performed by COBE/DIRBE at 100 μm, 140 μm, and 240 μm (updated in Dole et al. 2006). Yellow diamond: absolute measurements of Pénin et al. (2012a) at 160 μm with Spitzer/MIPS. Orange arrows: upper limits derived from opacity of the Universe to TeV photons (Mazin & Raue 2007). Lower left panel: normalized redshift distribution of the mean level (up), Poisson anisotropies (middle), large scale anisotropies at ℓ = 1000 (bottom). Various colors correspond to various bands. Right panel: contribution of various redshifts to the CIB (solid line) and comparison with lower limits derived by stacking from Berta et al. (2011) at 100 μm, Jauzac et al. (2011) at 160 μm and Béthermin et al. (2012c) at 250 μm, 350 μm, and 500 μm (arrows). The dashed lines are the model predictions taking the selection used to derive the lower limits into account. The flux density cuts are the same as previously (see Sect. 6 and Fig. 7). |
8. Where do the CIB and its anisotropies come from?
In this section, we discuss the predictions of the model concerning the redshift distribution of the various signals we studied (CIB auto-spectra, CIB cross-spectra, CIB × CMB lensing). We base our analysis on the model C as justified in Sect. 7.
8.1. Redshift distribution of CIB mean level and anisotropies
The CIB SED can be predicted directly from the Béthermin et al. (2012a) count model. Figure 12 (upper left panel) shows the SED of the CIB and its decomposition per redshift slice. Compared to the Béthermin et al. (2011) model, this new model has a slightly higher contribution of 1 < z < 2 sources. This new model agrees well with both absolute measurements and the total contribution of infrared galaxies extrapolated from the number counts.
 |
Fig. 13 Predicted redshift distribution of auto and cross power spectra at large (ℓ = 1000, left) and small scale (Poisson level). We focus on three frequencies: 857 GHz (350 μm), 545 GHz (550 μm), and 217 GHz (1382 μm) to illustrate the difference between cross spectrum between two distant wavelengths and the auto-spectrum at an intermediate wavelength. The flux density cuts are the same as previously (see Sect. 6 and Fig. 7). |
Predicted correlation (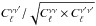 )
of CIB anisotropies between bands on small (Poisson level, upper part) and large
scales (l = 1000, lower part).
)
of CIB anisotropies between bands on small (Poisson level, upper part) and large
scales (l = 1000, lower part).
The three lower lefthand panels of Fig. 12 show the redshift distribution of the intensity of the CIB (top), but also of its anisotropies on small (middle) and large scales (bottom). To allow an easier comparison between bands, we normalized the redshift distributions in order to have ∫d(νIν)/dz dz = 1 and ∫dCℓ/dz dz = 1. Between 100 μm (3000 GHz) and 850 μm (353 GHz), the redshift distribution evolves strongly toward higher redshift. At longer wavelengths, there is almost no evolution, because all the sources below z ~ 7 are seen in the Rayleigh-Jeans regime and the color is roughly the same at all redshifts. This trend is seen for both intensity and anisotropies, regardless of scale. There are, however, small differences between these three quantities. For instance, the redshift distribution of the Poisson level5 at 100 μm is dominated by z < 0.5 sources, when a significant fraction of ℓ = 1000 anisotropies is caused by galaxies at z ~ 1. This is because the Poisson anisotropies are dominated by a small number of low-z bright galaxies just below the flux cut. Anisotropies on large scales are dominated by normal star-forming galaxies at z ~ 1 which dominate the background and the two-halo term of anisotropies.
Finally, we checked that the redshift distributions predicted by our model agree with the lower limits derived by stacking of 24 μm sources. We compare them with the lower limits from Berta et al. (2011) at 100 μm, Jauzac et al. (2011) at 160 μm and Béthermin et al. (2012c) at 250 μm, 350 μm, and 500 μm, which agree well with our model. We used our model to simulate the selection corresponding to these various works and found good overall agreement below z ~ 2.5. At higher redshift and for a 24 μm selection, these predictions are underestimated. This is expected because our SED templates only take the dust emission into account, when the λ < 8 μm rest-frame emission is significantly affected by stellar emissions. We thus underestimate the number of 24 μm detections and consequently also their contribution to the CIB.
8.2. Redshift distribution of CIB cross-correlation between bands
Cross power spectra between bands provide complementary information to the auto-spectra. Figure 13 shows the redshift distribution of a selection of cross and auto-spectra. On both large (ℓ = 1000, left) and small scales (Poisson), the redshift distribution of the cross-spectra between two distant bands (e.g., 857 and 217 GHz here) is fairly close to the redshift distribution for an intermediate band (e.g., 545 GHz here), except for a difference in Poisson level at very low z caused by different flux cuts. Considering the quite fine spectral coverage of our data, we thus cannot claim that cross-spectra probe different redshift ranges.
In contrast, the correlation (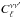 /
/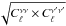 )
between bands provides a useful test of the validity of the models (especially their SEDs
and redshift distributions). This correlation varies with scale. We thus focused on
Poisson level and ℓ = 1000. The results are summarized in Table 1. The level of correlation is also important for CMB
experiments to know whether the CIB at high frequency is a good proxy for the CIB emission
at low frequency. For instance, the correlation between 857 GHz and 143 GHz is 0.904 at
ℓ = 1000, but only 0.75 for the Poisson level. This correlation is
predicted to rise to 0.996 between 353 GHz and 143 GHz (0.963 for the Poisson level).
According to our model, the CIB at 353 GHz thus provides a very good proxy for CIB in the
CMB channels.
)
between bands provides a useful test of the validity of the models (especially their SEDs
and redshift distributions). This correlation varies with scale. We thus focused on
Poisson level and ℓ = 1000. The results are summarized in Table 1. The level of correlation is also important for CMB
experiments to know whether the CIB at high frequency is a good proxy for the CIB emission
at low frequency. For instance, the correlation between 857 GHz and 143 GHz is 0.904 at
ℓ = 1000, but only 0.75 for the Poisson level. This correlation is
predicted to rise to 0.996 between 353 GHz and 143 GHz (0.963 for the Poisson level).
According to our model, the CIB at 353 GHz thus provides a very good proxy for CIB in the
CMB channels.
 |
Fig. 14 Comparison between the predicted redshift distributions of CIB × CIB and CIB × CMB lensing signal in various IRAS/Planck bands. Solid red line: redshift distribution of the cross-correlation between CIB and CMB lensing at l = 1000 in various bands. Dashed blue line: redshift distribution of CIB auto power spectrum. |
8.3. Redshift distribution of CIB × CMB lensing signal
The cross-correlation between CIB and lensing provides supplementary information probing a slightly different redshift range. Figure 14 shows a comparison between the predicted redshift distributions of the CIB auto-spectrum and the cross-spectrum between CIB and CMB lensing for various bands. While the redshift distribution of the auto-spectrum evolves strongly between 100 (3000 GHz) and 850 μm (353 GHz), this evolution is weaker for the cross-correlation with CMB lensing that mainly probes the z = 1−2 redshift range. CIB × CMB lensing is thus a good probe of the mean SED of galaxies contributing to the CIB at this epoch. However, apart from the 100 μm band, the redshift range probed by CIB × CMB lensing is relatively similar to that of the CIB power spectrum, but it is an independent and more direct probe of the link between dark matter and star-forming objects, because the lensing of the CMB by the large scale structures is a very well known and modeled physical process.
9. Star formation and dark matter halos
In this section, we discuss the prediction of our model in the context of our current understanding of galaxy formation. We use model C, as discussed in Sect. 7.
9.1. Evolution of infrared-light-to-mass ratio with redshift
The infrared-light-to-halo-mass ratio is a key ingredient of our CIB model. Figure 15 shows this relation for various hypotheses. We
consider two different definitions of the infrared luminosity inside the halos: the
infrared luminosity of a central galaxy lying exactly at the core of the main-sequence
(top panels) and the mean infrared luminosity of central galaxies (lower panels) hosted by
halos of a given mass. This second quantity takes into account that a fraction of galaxies
are passive, while the first quantity only takes the star-forming galaxies into account.
We also use both the instantaneous halo mass (left panels) and the halo mass at
z = 0. The conversion between instantaneous halo mass and halo mass at
z = 0 is performed assuming an accretion following the fits of Fakhouri & Ma (2010) to their own numerical
simulations of dark matter: 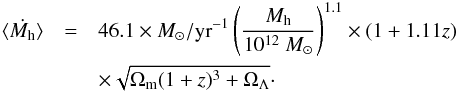 (34)The
mass at z = 0
(34)The
mass at z = 0 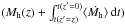 is a convenient quantity to use
when discussing the evolution of structures with time.
is a convenient quantity to use
when discussing the evolution of structures with time.
 |
Fig. 15 Relation between infrared luminosity of galaxies and their halo mass. The top panels correspond to the infrared luminosity for a central galaxy exactly on the main sequence. The bottom panels shows the mean infrared luminosity of the central galaxies. The left panels show results as the instantaneous halo mass and right panel as a function of halo mass at z = 0. The dashed lines correspond to the limit between normal galaxies (i.e. < 1011 L⊙), LIRGs (1011 < LIR < 1012 L⊙), ULIRGs (1012 < LIR < 1013 L⊙), and HyLIRGs (<1013 L⊙). |
The shape of the infrared luminosity as a function of instantaneous halo mass evolves
little with redshift. However, its normalization varies strongly. For the same halo mass,
infrared luminosity is much more intense at high redshift. This results will be
interpreted further in Sect. 9.3. At low mass, the
infrared luminosity decreases quickly. This is mainly caused by the quickly dropping
M⋆-ℳh relation at
ℳh < 1012 M⊙(see
Fig. 2), while the sSFR is roughly the same at all
stellar masses (s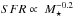 ).
This break is slightly amplified by the fact that a smaller fraction of UV light from
young stars is reprocessed into infrared emission at lower masses (Eq. (10)). At high mass, we found a sublinear
relation, even if we consider only objects on the main sequence. This behavior is also
driven by the shape of the M⋆-ℳh
relation, which is sublinear at
Mh > 1012 M⊙.
This trend is stronger if we consider the mean infrared luminosity and take the quenched
galaxies into account. At z < 1, the infrared
luminosity decreases when halo mass becomes higher than
1013 M⊙, so our model predicts a very weak star
formation in a dense environment at low redshift, in agreement with, say Feruglio et al. (2010). This trend is caused by the
large fraction of quenched galaxies at high stellar mass (see Fig. 1). The contribution of satellites is small except in massive halos
(<1013 M⊙), where the
central is inefficient in forming stars.
).
This break is slightly amplified by the fact that a smaller fraction of UV light from
young stars is reprocessed into infrared emission at lower masses (Eq. (10)). At high mass, we found a sublinear
relation, even if we consider only objects on the main sequence. This behavior is also
driven by the shape of the M⋆-ℳh
relation, which is sublinear at
Mh > 1012 M⊙.
This trend is stronger if we consider the mean infrared luminosity and take the quenched
galaxies into account. At z < 1, the infrared
luminosity decreases when halo mass becomes higher than
1013 M⊙, so our model predicts a very weak star
formation in a dense environment at low redshift, in agreement with, say Feruglio et al. (2010). This trend is caused by the
large fraction of quenched galaxies at high stellar mass (see Fig. 1). The contribution of satellites is small except in massive halos
(<1013 M⊙), where the
central is inefficient in forming stars.
The infrared luminosity as a function of halo mass at z = 0 exhibits strong downsizing. The progenitors of 1014 M⊙ initially host a very intense SFR (ULIRG regime, 1012 < LIR < 1013 L⊙) at high redshift (z = 5), which continues to grow up to z ~ 2. Then, the infrared luminosity decreases because star formation is less efficient in massive halos (see Sect. 9.3). The less massive halos need more time to ignite intense star formation. Dark matter halos similar to that of MilkyWay (~1012 M⊙ at z = 0) host significant infrared emission only below z = 1.
We can compare the predictions of our model with estimates based on clustering of various
samples of galaxies. Submillimeter galaxies (defined here to have
S850 > 3 mJy) are essentially ULIRGs
at z ~ 2.4 (e.g. Chapman et al.
2003) and the B12 model predicts that these objects generally lie on the main
sequence. Blain et al. (2004) show that the
correlation length of SMGs is compatible with typical host halos of
1013 M⊙, which is consistent with our model
prediction of an infrared luminosity of
4 × 1012 L⊙ for a main-sequence galaxy in a
1013 M⊙ halo at z = 2.4 (see
Fig. 15). We can also check the consistency of our
results with measurements based on Spitzer 24 μm
observations. Magliocchetti et al. (2008) measured
the clustering of two samples of sources with
S24 > 400 μJy with
a mean redshift of 0.79 and 2.02, respectively. This flux selection corresponds, at the
mean redshift of each sample, to an infrared luminosity of
2.6 × 1011 L⊙ and
2.6 × 1012 L⊙, respectively for a main-sequence
SED. For an object exactly on the main sequence, this corresponds to an instantaneous halo
mass of 2.7 × 1012 M⊙ and
1.2 × 1013 M⊙, in agreement with the minimal
mass found by Magliocchetti et al. (2008) of
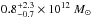 and
and
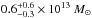 , respectively.
Farrah et al. (2006) measured the halo mass of
5.8 μm IRAC peakers with 24 μm detections and found a
1σ range for log (Mh) of 13.7–14.1. This
population of massive star-forming galaxies has a mean redshift of 2.017 and a mean
infrared luminosity of 8.9 ± 0.6 L⊙ (Fiolet et al. 2010), which is associated in our model to
log (Mh) = 14.1.
, respectively.
Farrah et al. (2006) measured the halo mass of
5.8 μm IRAC peakers with 24 μm detections and found a
1σ range for log (Mh) of 13.7–14.1. This
population of massive star-forming galaxies has a mean redshift of 2.017 and a mean
infrared luminosity of 8.9 ± 0.6 L⊙ (Fiolet et al. 2010), which is associated in our model to
log (Mh) = 14.1.
9.2. Contribution of various halo masses to star formation history
The total SFR of both central and satellite galaxies hosted by a given halo can be derived from our model. In combination with the halo mass function, we can then compute the contribution of each halo mass to the SFR. The results of this analysis are presented in Fig. 16. If we consider instantaneous halo mass (left panels), the bulk of the star formation is hosted by halos between 1011.5 M⊙ and 1013.5 M⊙ regardless of the redshift, suggesting the existence of a characteristic mass which favors star formation. The fractional contribution of each mass slice is inferred to have evolved slowly with redshift, except at z > 3. However, there are significant uncertainties in the behavior of the galaxies at high redshift, and these results should be taken with caution.
 |
Fig. 16 Contribution of various halo mass to the star formation history. Upper panels shows the contribution of each slice to star formation density and lower panels their fractional contribution. We use slice of instantaneous halo mass in the left panels and mass at z = 0 in the right panels. |
 |
Fig. 17 Instantaneous star formation efficiency (defined here as SFR/BAR, where BAR is the baryonic accretion rate) as a function of halo mass at various redshift predicted by our model. The predictions from model C are plotted with a solid line. At z = 5 model A predicts a different efficiency distribution and is represented by a dashed line. Upper panels shows this efficiency only for main-sequence galaxies and lower panels for mean efficiency. We use slice of instantaneous halo mass in the left panels and mass at z = 0 in the right panels. |
Because of the growth of dark matter halos, the same halo mass at various redshifts corresponds to progenitors of different types of halos. To take this into account, we also considered slices of z = 0 halo mass (right panels). The SFR density is predicted to have been successively dominated by progenitors of massive clusters (Mh > 1014.5 M⊙) at z > 4.7, small clusters and large group (1013.5 < Mh < 1014.5 M⊙) at 2.8 < z < 4.7, small groups (1012.5 < Mh < 1013.5 M⊙) at 0.5 < z < 2.8, and Milky Way-like halos (1011.5 < Mh < 1012.5 M⊙) at z < 0.5. Star formation thus initially occurs in the progenitor of the most massive halos before becoming less efficient and then propagating to less massive halos. This strong downsizing explains why the SFR densities at redshifts 1 and 2 are similar: z > 2 infrared luminosity density is dominated by a low density (~ 3 × 10-3 Mpc-4) of ULIRGs and z ~ 1 is dominated by higher density (~ 3 × 10-3 Mpc-3) of LIRGs (e.g. Béthermin et al. 2011).
9.3. Efficiency of star formation as a function of halo mass and redshift
To conclude, we derive an estimate of the instantaneous star formation efficiency (ISFE)
in different halos by computing the ratio between SFR and baryonic accretion rate (BAR).
Here, we assume the BAR to be the total matter accretion as given by Fakhouri & Ma (2010) multiplied by the universal baryonic
faction (BAR = 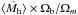 with
with
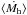 defined in Eq. (34)). This simplified definition neglects that
the gas is not transformed instantaneously into stars and that large gas reservoirs are
present in (e.g., Daddi et al. 2010; Tacconi et al. 2013) and around (Cantalupo et al. 2012) high-z galaxies. Figure 17 shows predictions for the variation in this
efficiency as a function of halo mass at various redshifts. Star-formation efficiency in
main-sequence galaxies as a function of instantaneous halo mass (upper left panel) slowly
evolves between z = 0 and z = 2 with a slight increase
in the mass of maximum efficiency with redshift (from
8 × 1011 M⊙ at z = 0 to
3 × 1012 M⊙ at z = 2). At
z = 5, this maximal efficiency is lower, and the halo mass where it
occurs is higher. The increase in the mass of maximum efficiency could be due to a delay
in the ignition of star-formation activity, because the BAR in
~1012 M⊙ halos is higher at high redshift.
However, large uncertainties exist at high redshift where we have few constraints on
star-forming galaxies. For instance, if we use model A (flat sSFR at
z > 2.5) instead of model C (rising sSFR) to
perform our calculations this effect is much smaller (dashed line in Fig. 17). In our framework, this results is a consequence of
the combined evolution of the sSFR, the
M⋆-Mh relation,
and the specific halo growth. We can also try to interpret this evolution physically.
Below the mass scale at which peak efficiency is reached, the gravitational potential of
the halo is lower and supernova feedback is probably sufficiently strong to remove gas
from the galaxy (e.g. Silk 2003; Bertone et al. 2005). At higher masses, the slow
decrease in the star formation efficiency could be caused by the transition from cold
streams below
Mh ~ 1012 M⊙ to
isotropic cooling above this mass (e.g. Dekel &
Birnboim 2006; Faucher-Giguère et al.
2011). At high mass, the cooling time of gas becomes much longer than the free fall
time because of the hot atmosphere in the massive halos (e.g. Kereš et al. 2005; Birnboim et al.
2007). Unlike the ISFE in main sequence galaxies, the mean ISFE (lower left
panel), that considers that a fraction of galaxies are quenched, exhibits a strong break
at
Mh > 1012 M⊙
at z = 0 and a moderate break at the same mass at z = 1.
This break could be caused by a suppression of isotropic gas cooling by energy injection
in the halo atmosphere by active galactic nuclei activity (e.g. Cattaneo et al. 2006; Somerville
et al. 2008; Ostriker et al. 2010).
defined in Eq. (34)). This simplified definition neglects that
the gas is not transformed instantaneously into stars and that large gas reservoirs are
present in (e.g., Daddi et al. 2010; Tacconi et al. 2013) and around (Cantalupo et al. 2012) high-z galaxies. Figure 17 shows predictions for the variation in this
efficiency as a function of halo mass at various redshifts. Star-formation efficiency in
main-sequence galaxies as a function of instantaneous halo mass (upper left panel) slowly
evolves between z = 0 and z = 2 with a slight increase
in the mass of maximum efficiency with redshift (from
8 × 1011 M⊙ at z = 0 to
3 × 1012 M⊙ at z = 2). At
z = 5, this maximal efficiency is lower, and the halo mass where it
occurs is higher. The increase in the mass of maximum efficiency could be due to a delay
in the ignition of star-formation activity, because the BAR in
~1012 M⊙ halos is higher at high redshift.
However, large uncertainties exist at high redshift where we have few constraints on
star-forming galaxies. For instance, if we use model A (flat sSFR at
z > 2.5) instead of model C (rising sSFR) to
perform our calculations this effect is much smaller (dashed line in Fig. 17). In our framework, this results is a consequence of
the combined evolution of the sSFR, the
M⋆-Mh relation,
and the specific halo growth. We can also try to interpret this evolution physically.
Below the mass scale at which peak efficiency is reached, the gravitational potential of
the halo is lower and supernova feedback is probably sufficiently strong to remove gas
from the galaxy (e.g. Silk 2003; Bertone et al. 2005). At higher masses, the slow
decrease in the star formation efficiency could be caused by the transition from cold
streams below
Mh ~ 1012 M⊙ to
isotropic cooling above this mass (e.g. Dekel &
Birnboim 2006; Faucher-Giguère et al.
2011). At high mass, the cooling time of gas becomes much longer than the free fall
time because of the hot atmosphere in the massive halos (e.g. Kereš et al. 2005; Birnboim et al.
2007). Unlike the ISFE in main sequence galaxies, the mean ISFE (lower left
panel), that considers that a fraction of galaxies are quenched, exhibits a strong break
at
Mh > 1012 M⊙
at z = 0 and a moderate break at the same mass at z = 1.
This break could be caused by a suppression of isotropic gas cooling by energy injection
in the halo atmosphere by active galactic nuclei activity (e.g. Cattaneo et al. 2006; Somerville
et al. 2008; Ostriker et al. 2010).
Regardless of the redshift and halo mass, the SFR in main-sequence galaxies is always
lower than the BAR onto the dark matter halos (see Fig. 17). For a Chabrier (2003) IMF, the
maximal efficiency is ~0.7. Appendix C discusses
the case of a Salpeter (1955) IMF. This is
consistent with the standard assumption that main-sequence galaxies host secular star
formation. This is not the case for episodic starbursts, which on average forms four times
more stars for the same halo mass than main-sequence galaxies and thus transform much more
gas into stars than they receive from cosmic accretion. They thus tend to exhaust their
gas reservoir rapidly. The main-sequence galaxies do not need to store gas to fuel their
star formation. This could seem to contradicts the fact that the specific halo growth
(sHG) is larger by a factor of two than the sSFR around z = 2, as pointed
out by Weinmann et al. (2011). However, the ratio
between sSFR and sHG is 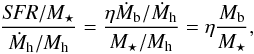 (35)where
η is the instantaneous star formation efficiency
(SFR/Ṁb), and
Ṁb the baryonic accretion into the halo. The ratio between
sSFR and sHG can thus be much higher than unity in halos of
~ 1012 M⊙, because even if η is
lower than 1, the ratio between baryonic mass and stellar mass is ~4 (e.g., Leauthaud et al. 2012), because of the low efficiency
of conversion of baryons into stars in the past (when the halos had a lower mass and thus
a lower ISFE).
(35)where
η is the instantaneous star formation efficiency
(SFR/Ṁb), and
Ṁb the baryonic accretion into the halo. The ratio between
sSFR and sHG can thus be much higher than unity in halos of
~ 1012 M⊙, because even if η is
lower than 1, the ratio between baryonic mass and stellar mass is ~4 (e.g., Leauthaud et al. 2012), because of the low efficiency
of conversion of baryons into stars in the past (when the halos had a lower mass and thus
a lower ISFE).
We can also discuss how the efficiency varies as a function of z = 0 halo mass (right panels). We predict a strong evolution of the typical halos where the ISFE is maximal. The progenitors of massive halos form stars very efficiently at high redshift, while Milky-Way-like halos are very inefficient. The opposite trend is expected at low redshift. This picture is consistent with the strong downsizing of the star-forming galaxy population discussed in the previous sections, but also with the work of Behroozi et al. (2013b). Their analysis was based only on the evolution of the SMF, and SFR were derived assuming a single galaxy population. Our approach is based on the infrared observations that directly probe the SFR in galaxies and which take the diversity of galaxies into account using three distinct populations: secularly star-forming galaxies on the main-sequence, episodic, merger-driven starbursts, and passive elliptical galaxies. Compared to Behroozi et al. (2013a), our mean ISFE is much lower in local massive halos, which almost exclusively host quenched galaxies, but we agree with their estimate if we take only a main-sequence population (more consistent with their single galaxy population).
Normal spiral galaxies at z = 0, LIRGs at z = 1, and ULIRGs at z = 2 dominate the star-formation density at these redshift and are essentially main sequence galaxies (Sargent et al. 2012). All of these are hosted by halos of similar mass, which are characterized by a very efficient conversion of accreted baryons into stars. The huge difference between their SFR can thus be explained by the accretion, which is stronger at high redshift. These objects can thus be viewed as different facets of the same universal process of secular star formation.
10. Conclusion
We have studied the connection between star formation and dark matter halos focusing on infrared observations. We developed a new modeling approach based on the 2SFM framework, which was already able to successfully reproduce the infrared luminosity function and number counts (Sargent et al. 2012, B12). This framework links stellar mass with star formation and infrared properties, when assuming two different modes of star formation in secularly star-forming galaxies and episodic starbursts. We extended this formalism to the connection between stellar mass and halo mass using the technique of abundance matching. Our formalism accounts for the facts that a significant fraction of massive galaxies are passive and do not form stars (especially at low redshift).
-
We developed a method of computing the CIB anisotropies(including power-spectra between different frequen-cies), the cross-correlation between CIB and CMB lensing,and auto-correlation functions of bright resolved galax-ies using the prescription of the 2SFM formalism. To per-form this computation, we produced effective SEDs ofall galaxies at a given redshift, and these are available on-line6.
-
We find that a slowly rising sSFR at z > 2.5 and a quenching of satellite of massive passive galaxies at low redshift (our model C) matches the infrared data reasonably well suggesting that this model is a valid description of the link between infrared galaxies and dark matter halos. The other versions of the model with flat sSFR and no quenching of satellites show some small discrepancies with the power-spectra, but cannot be conclusively ruled out.
-
Our model is able to predict the redshift distribution of CIB anisotropies. We found that the mean redshift where the CIB is emitted varies strongly between 100 μm and 850 μm but only a little at longer wavelengths. Consequently, the CIB anisotropies in the various bands above 850 μm are strongly correlated (>0.9).
-
We found a quick rise in the far-infrared-light-to-mass ratio with redshift in Mh > 1012 M⊙ halos and a strong break at lower mass at all redshifts. We found that more than 90% of the star formation is hosted by halos with masses between 1011.5 and 1013.5 M⊙ at all redshifts. The progenitors of clusters (Mh(z = 0) > 1013.5 M⊙) host the bulk of the star formation at z >3. Star formation activity then propagates to groups (1012.5 < Mh(z = 0) < 1013.5 M⊙) at 0.5 < z < 3 and Milky Way-like halos (1011.5 < Mh(z = 0) < 1012.5 M⊙) at z < 0.5. We also found that there is a characteristic halo mass (~ 1012 M⊙) where the star formation efficiency is maximal (~70% at all redshift). The large difference of SFR in galaxies dominating the background at low and high redshift would thus be driven by a difference of accretion rate in the halos close to this mass.
Our simple modeling framework is very efficient in explaining the current observations of the infrared Universe. However, future large submillimeter surveys (e.g. NIKA, CCAT) will resolve the bulk of the CIB into individual sources and will probably improve measurements of the clustering properties of infrared galaxies. We expect that deviation from our model will appear on small scales, where environmental effects could have a strong impact, thereby revealing a more complex and varied infrared Universe.
24 μm is often used because ~80% of the background is resolved into sources at this wavelength (Papovich et al. 2004; Béthermin et al. 2010a).
A detailed discussion of the SFR-enhancements of starbursts and their description in the 2-SFM framework is provided in Sargent et al. (2013).
Parameters provided in B12 are given assuming a Salpeter (1955) IMF when this paper assumes a Chabrier (2003) IMF. A correction of 0.24 dex thus has to be applied to some of the parameters to take this difference in IMF into account.
We used the same flux cuts as in Sect. 6.
Acknowledgments
We thank Steve Maddox for providing data and discussion about clustering measurements, Marco Viero and Amir Hajian for providing data, Paolo Serra for useful discussion, and the anonymous referee for very constructive comments. M.B., E.D., and M.S. acknowledge the support provided by the grants ERC-StG UPGAL 240039 and ANR-08-JCJC-0008. L.W. acknowledges support from an ERC StG grant (DEGAS-259586). This research was carried out in part at the Jet Propulsion Laboratory, run by the California Institute of Technology under a contract from NASA.
References
- Addison, G. E., Dunkley, J., & Bond, J. R. 2012, MNRAS, submitted [arXiv:1210.6697] [Google Scholar]
- Amblard, A., & Cooray, A. 2007, ApJ, 670, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Amblard, A., Cooray, A., Serra, P., et al. 2011, Nature, 470, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Conroy, C., & Wechsler, R. H. 2010, ApJ, 717, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013a, ApJ, 762, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013b, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Magnelli, B., Nordon, R., et al. 2011, A&A, 532, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertone, S., Stoehr, F., & White, S. D. M. 2005, MNRAS, 359, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Dole, H., Beelen, A., & Aussel, H. 2010a, A&A, 512, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Cousin, M., & Bavouzet, N. 2010b, A&A, 516, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Lagache, G., Le Borgne, D., & Penin, A. 2011, A&A, 529, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2012a, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Doré, O., & Lagache, G. 2012b, A&A, 537, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Le Floc’h, E., Ilbert, O., et al. 2012c, A&A, 542, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnboim, Y., Dekel, A., & Neistein, E. 2007, MNRAS, 380, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Blain, A. W., Chapman, S. C., Smail, I., & Ivison, R. 2004, ApJ, 611, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Z.-Y., Lapi, A., Xia, J.-Q., et al. 2013, ApJ, 768, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Cantalupo, S., Lilly, S. J., & Haehnelt, M. G. 2012, MNRAS, 425, 1992 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Dekel, A., Devriendt, J., Guiderdoni, B., & Blaizot, J. 2006, MNRAS, 370, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Challinor, A., & Lewis, A. 2005, Phys. Rev. D, 71, 103010 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Blain, A. W., Ivison, R. J., & Smail, I. R. 2003, Nature, 422, 695 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Condon, J. J. 1974, ApJ, 188, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & Wechsler, R. H. 2009, ApJ, 696, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., Amblard, A., Wang, L., et al. 2010, A&A, 518, L22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- de Barros, S., Schaerer, D., & Stark, D. P. 2012 [arXiv:1207.3663] [Google Scholar]
- De Bernardis, F., & Cooray, A. 2012, ApJ, 760, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dole, H., Le Floc’h, E., Pérez-González, P. G., et al. 2004, ApJS, 154, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Dole, H., Lagache, G., Puget, J., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1999, ApJ, 511, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fakhouri, O., & Ma, C.-P. 2010, MNRAS, 401, 2245 [NASA ADS] [CrossRef] [Google Scholar]
- Farrah, D., Lonsdale, C. J., Borys, C., et al. 2006, ApJ, 643, L139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faucher-Giguère, C.-A., Kereš, D., & Ma, C.-P. 2011, MNRAS, 417, 2982 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Aussel, H., Le Floc’h, E., et al. 2010, ApJ, 721, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Fiolet, N., Omont, A., Lagache, G., et al. 2010, A&A, 524, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Franceschini, A., Rodighiero, G., Vaccari, M., et al. 2010, A&A, 517, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glenn, J., Conley, A., Béthermin, M., et al. 2010, MNRAS, 409, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, V., Bouwens, R., llingworth, G., et al. 2012 [arXiv:1208.4362] [Google Scholar]
- Grossan, B., & Smoot, G. F. 2007, A&A, 474, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruppioni, C., Pozzi, F., Zamorani, G., & Vignali, C. 2011, MNRAS, 416, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hajian, A., Viero, M. P., Addison, G., et al. 2012, ApJ, 744, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, N. R., Keisler, R., Knox, L., et al. 2010, ApJ, 718, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, D., Rocha, G., & Górski, K. 2009, MNRAS, 400, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Hauser, M. G., & Dwek, E. 2001, ARA&A, 39, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Holder, G. P., Viero, M. P., Zahn, O., et al. 2013, ApJ, 771, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fevre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jauzac, M., Dole, H., Le Floc’h, E., et al. 2011, A&A, 525, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, H.-S., Lacey, C. G., Cole, S., et al. 2012, MNRAS, 425, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Knox, L., Cooray, A., Eisenstein, D., & Haiman, Z. 2001, ApJ, 550, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Haffner, L. M., Reynolds, R. J., & Tufte, S. L. 2000, A&A, 354, 247 [Google Scholar]
- Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Bavouzet, N., Fernandez-Conde, N., et al. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., González-Nuevo, J., Fan, L., et al. 2011, ApJ, 742, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Le Borgne, D., Elbaz, D., Ocvirk, P., & Pichon, C. 2009, A&A, 504, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leauthaud, A., George, M. R., Behroozi, P. S., et al. 2012, ApJ, 746, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1953, ApJ, 117, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Maddox, S. J., Dunne, L., Rigby, E., et al. 2010, A&A, 518, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Magliocchetti, M., Cirasuolo, M., McLure, R. J., et al. 2008, MNRAS, 383, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Magliocchetti, M., Santini, P., Rodighiero, G., et al. 2011, MNRAS, 416, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, G., Chapin, E. L., Halpern, M., et al. 2011, MNRAS, 417, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Mazin, D., & Raue, M. 2007, A&A, 471, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- More, S., van den Bosch, F. C., Cacciato, M., et al. 2009, MNRAS, 392, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, H. T., Schulz, B., Levenson, L., et al. 2010, A&A, 518, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Oliver, S. J., Wang, L., Smith, A. J., et al. 2010, A&A, 518, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, J. P., Choi, E., Ciotti, L., Novak, G. S., & Proga, D. 2010, ApJ, 722, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Carilli, C. L., Daddi, E., et al. 2009, ApJ, 698, L116 [Google Scholar]
- Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Park, C., Choi, Y.-Y., Vogeley, M. S., et al. 2007, ApJ, 658, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Patanchon, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1750 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pénin, A., Doré, O., Lagache, G., & Béthermin, M. 2012a, A&A, 537, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pénin, A., Lagache, G., Noriega-Crespo, A., et al. 2012b, A&A, 543, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013, A&A, submitted [arXiv:1303.5078] [Google Scholar]
- Puget, J., Abergel, A., Bernard, J., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
- Rahmati, A., & van der Werf, P. P. 2011, MNRAS, 418, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2013, ApJ, submitted [arXiv:1303.4392] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Shang, C., Haiman, Z., Knox, L., & Oh, S. P. 2012, MNRAS, 421, 2832 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2003, MNRAS, 343, 249 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Somerville, R. S., Hopkins, P. F., Cox, T. J., Robertson, B. E., & Hernquist, L. 2008, MNRAS, 391, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Schenker, M. A., Ellis, R., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- Teplitz, H. I., Chary, R., Elbaz, D., et al. 2011, AJ, 141, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., & Wetzel, A. R. 2010, ApJ, 719, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Vale, A., & Ostriker, J. P. 2004, MNRAS, 353, 189 [Google Scholar]
- Valiante, E., Lutz, D., Sturm, E., Genzel, R., & Chapin, E. L. 2009, ApJ, 701, 1814 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Wang, L., Zemcov, M., et al. 2013, ApJ, 772, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Farrah, D., Oliver, S. J., et al. 2013, MNRAS, 431, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D. F., & Conroy, C. 2013, ApJ, 772, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Weinmann, S. M., Neistein, E., & Dekel, A. 2011, MNRAS, 417, 2737 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, J.-Q., Negrello, M., Lapi, A., et al. 2012, MNRAS, 422, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Zemcov, M., Blain, A., Halpern, M., & Levenson, L. 2010, ApJ, 721, 424 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Conversions tables
Appendix A.1: Wavenumber, multipole, and angle
On small scales (Spitzer, Herschel), where curvature of the sky is negligible, people generally use wavenumber (k) in their measurements of the CIB power spectrum. This is not the case for large-scale measurements (SPT, ACT, Planck) for which people used mutlitpole (ℓ). The conversion between the two is just ℓ = 2πk. This also corresponds to a characteristic angular scale θ = π/ℓ. Table A.1 provides conversion for the range of values used in this paper.
Conversion between wavenumber, multipole, and angle.
 |
Fig. B.1 Same figure as 17 but assuming a Salpeter (1955) IMF. The black dashed line corresponds to an SFE of 1. |
Appendix A.2: From wavelengths to frequencies
Infrared astronomers use wavelengths in μm, the CMB community frequencies in GHz. For quick reference, we provide the conversion between these two conventions for the passbands discussed in this paper in Table A.2.
Conversion between wavelength and frequency for various passbands used in this paper.
Appendix B: Computation of the cross-Poisson term
The number of sources per steradian nij with
an infrared luminosity in the interval
[LIR,i,LIR,i + ΔLIR,i]
and a redshift in
[zj,zj + Δzj]
is 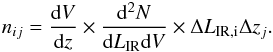 (B.1)We
also need to separate the galaxies by mode of star formation (main-sequence or starburst)
and ⟨ U ⟩ parameter. The number of main-sequence or starburst galaxies
(B.1)We
also need to separate the galaxies by mode of star formation (main-sequence or starburst)
and ⟨ U ⟩ parameter. The number of main-sequence or starburst galaxies
 in the same LIR and z bins and with
⟨ U ⟩ in
[⟨ U ⟩ k, ⟨ U ⟩ k + Δ ⟨ U ⟩ k]
is
in the same LIR and z bins and with
⟨ U ⟩ in
[⟨ U ⟩ k, ⟨ U ⟩ k + Δ ⟨ U ⟩ k]
is  (B.2)Since
we assume Poisson statistics, the variance on the number of galaxies in this bin equals
(B.2)Since
we assume Poisson statistics, the variance on the number of galaxies in this bin equals
 .
For the covariance between the fluxes at the two frequencies caused by this subpopulation
we have
.
For the covariance between the fluxes at the two frequencies caused by this subpopulation
we have 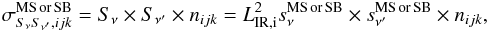 (B.3)because
the fluxes in the two bands are perfectly correlated for sources with the same SED.
Finally, we sum over the entire population (all LIR,
z, and ⟨ U ⟩) to compute the level of the Poisson
term:
(B.3)because
the fluxes in the two bands are perfectly correlated for sources with the same SED.
Finally, we sum over the entire population (all LIR,
z, and ⟨ U ⟩) to compute the level of the Poisson
term:  (B.4)which
in integral limit becomes
(B.4)which
in integral limit becomes ![\appendix \setcounter{section}{2} \begin{eqnarray} &&C_{\ell,\nu \nu'}^{\rm poi} = \int_z \frac{{\rm d}V}{{\rm d}z} \sum_{\rm \{MS, SB\}} \int_{\langle U \rangle} p_{\rm MS\, or \, SB} \left(\langle U \rangle|z \right ) \int_{L_{\rm IR}=0}^{L_{\rm IR,cut}^{\rm MS \, or \, SB}(\langle U \rangle,z)} \nonumber\\[4mm] &&\frac{{\rm d}^2N_{\rm MS\, or \, SB}}{{\rm d}L_{\rm IR} {\rm d}V} L_{\rm IR}^2 s_\nu^{\rm MS\, or \, SB}(\langle U \rangle,z) \times s_{\nu'}^{\rm MS\, or \, SB}(\langle U \rangle,z)\, {\rm d}L_{\rm IR} \, {\rm d}\langle U \rangle \, {\rm d}z.\nonumber\\ \end{eqnarray}](/articles/aa/full_html/2013/09/aa21688-13/aa21688-13-eq255.png) (B.5)
(B.5)
Appendix C: Star formation efficiency in the case of a Salpeter IMF
In Sect. 9.3, we computed the SFE assuming a Chabrier (2003) IMF. The results are slightly different if we assume a Salpeter (1955) IMF (see Fig. B.1). In this case, the galaxies close to the mass of maximum ISFE form more stars than they accrete baryons, and large gas reservoirs are required to allow the secular star formation in these objects. These reservoirs could have been replenished during the phase of low star-formation efficiency, when the halo was less massive.
All Tables
Predicted correlation (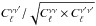 )
of CIB anisotropies between bands on small (Poisson level, upper part) and large
scales (l = 1000, lower part).
)
of CIB anisotropies between bands on small (Poisson level, upper part) and large
scales (l = 1000, lower part).
Conversion between wavelength and frequency for various passbands used in this paper.
All Figures
 |
Fig. 1 Illustration of the method used to connect various quantities by abundance matching as described in Sect. 3.3. The dashed line illustrates the connection between various quantities. We arbitrarily chose to plot results at z = 0.5. Upper left panel: integral HMF and contribution of main halos (dotted orange line) and subhalos (dot-dashed purple line). Upper right panel: integral SMF and contribution of star-forming (long-dashed blue line) and quenched (three-dot-dashed red line). Lower left panel: variation with halo mass of the fraction of halos that are subhalos. Lower right panel: fraction of quenched galaxies as a function of stellar mass. |
| In the text | |
 |
Fig. 2 Relation between the halo mass and the stellar mass at various redshifts found by our abundance matching procedure described in Sect. 3.3. |
| In the text | |
 |
Fig. 3 Upper panel: evolution of sSFR in main-sequence galaxies of 5 × 109 M⊙. Lower panel: evolution of the characteristic density φb of the mass function with redshift. Both panels: model A (B12 model) is represented with a solid line and model B (modified version with higher sSFR and lower density at high redshift) with a long-dashed line. We use the compilation of data points of Sargent et al. (2012). |
| In the text | |
 |
Fig. 4 Effective SEDs of infrared galaxies used in our model at various redshifts. The upper panel shows the SEDs in νLν units normalized at LIR = 1 L⊙ as a function of rest-frame wavelength. The lower panel shows the ratio between the observed flux density and LIR as a function of observed wavelength. |
| In the text | |
 |
Fig. 5 Differential emissivities at 100 μm (3000 GHz) and 1.38 mm (217 GHz) as a function of halo mass at various redshifts predicted by model C. The solid lines are the contributions of all the galaxies to the infrared flux of a main halo, when the dotted lines indicate only the contribution of central galaxies. |
| In the text | |
 |
Fig. 6 Halo occupation distribution, i.e. mean number of detected galaxies in a halo, including its substructures, as a function of its total mass Mh, of S160 > 5 mJy (left) and S850 > 3 mJy (right) sources at z = 0.1 (top) and z = 2 (bottom) for central (solid line) and satellite (dashed line) galaxies predicted by the model. The HOD of central galaxies is the same for all versions of the models and represented in black. Satellite HODs are plotted in blue (red) for model A/B (C). |
| In the text | |
 |
Fig. 7 Left and center panels: CIB power spectrum predicted by our model and comparison with IRAS (160 μm, Pénin et al. 2012b, open circles), Spitzer (100 μm, Lagache et al. 2007, crosses, Pénin et al. 2012b, asterisks), Herschel (250, 350, and 500 μm, Viero et al. 2013, triangles), Planck (350, 550, 850, and 1380 μm, Planck Collaboration 2011, squares), and SPT (1380 μm, Hall et al. 2010, diamonds) measurements. The dotted, dot-dashed, and dotted lines represent the Poisson, 1-halo, and 2-halo terms. Right panel: number counts of infrared galaxies. Data are taken from the compilation of measurements in Béthermin et al. (2011) and B12. Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. The flux cuts used to compute the model predictions are 1 Jy at 100 μm, 100 mJy at 160 μm, 0.3 mJy at 250 μm, 350 μm, and 500 μm, 0.54 Jy at 550 μm, 0.325 Jy at 850 μm, 20 mJy at 1.38 mm. |
| In the text | |
 |
Fig. 8 Cross-power spectrum between SPIRE bands measured by Viero et al. (2013) and comparison with our model. Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
| In the text | |
 |
Fig. 9 Cross-power spectrum between BLAST and ACT measured by Hajian et al. (2012) and comparison with our model. Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
| In the text | |
 |
Fig. 10 Comparison between the cross power spectrum between CIB and CMB lensing predicted by our model and the measurements by Planck Collaboration (2013) (diamonds) and Holder et al. (2013) with SPT and Herschel (triangles). Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
| In the text | |
 |
Fig. 11 Auto-correlation function of various flux-selected sample of infrared galaxies and comparison with our model (same color coding as in Fig. 7). The data come from Magliocchetti et al. (2011) at 100 μm and 160 μm and Cooray et al. (2010) and Maddox et al. (2010) at 250, 350, and 500 μm. We used the same flux cuts as Magliocchetti et al. (2011) and Cooray et al. (2010). Models A, B, and C are represented by a long green dash, a short blue dash, and a solid red line, respectively. |
| In the text | |
 |
Fig. 12 Predicted redshift distribution of the CIB and its anisotropies. Upper left panel: CIB SED and contribution per redshift slice (colored solid lines). Black squares: total extrapolated CIB from deep number counts (Teplitz et al. 2011; Béthermin et al. 2010a; Berta et al. 2011; Béthermin et al. 2012c; Zemcov et al. 2010). Cyan solid line: absolute CIB spectrum measured by COBE/FIRAS (Lagache et al. 2000). Green triangles: absolute CIB measurements performed by COBE/DIRBE at 100 μm, 140 μm, and 240 μm (updated in Dole et al. 2006). Yellow diamond: absolute measurements of Pénin et al. (2012a) at 160 μm with Spitzer/MIPS. Orange arrows: upper limits derived from opacity of the Universe to TeV photons (Mazin & Raue 2007). Lower left panel: normalized redshift distribution of the mean level (up), Poisson anisotropies (middle), large scale anisotropies at ℓ = 1000 (bottom). Various colors correspond to various bands. Right panel: contribution of various redshifts to the CIB (solid line) and comparison with lower limits derived by stacking from Berta et al. (2011) at 100 μm, Jauzac et al. (2011) at 160 μm and Béthermin et al. (2012c) at 250 μm, 350 μm, and 500 μm (arrows). The dashed lines are the model predictions taking the selection used to derive the lower limits into account. The flux density cuts are the same as previously (see Sect. 6 and Fig. 7). |
| In the text | |
 |
Fig. 13 Predicted redshift distribution of auto and cross power spectra at large (ℓ = 1000, left) and small scale (Poisson level). We focus on three frequencies: 857 GHz (350 μm), 545 GHz (550 μm), and 217 GHz (1382 μm) to illustrate the difference between cross spectrum between two distant wavelengths and the auto-spectrum at an intermediate wavelength. The flux density cuts are the same as previously (see Sect. 6 and Fig. 7). |
| In the text | |
 |
Fig. 14 Comparison between the predicted redshift distributions of CIB × CIB and CIB × CMB lensing signal in various IRAS/Planck bands. Solid red line: redshift distribution of the cross-correlation between CIB and CMB lensing at l = 1000 in various bands. Dashed blue line: redshift distribution of CIB auto power spectrum. |
| In the text | |
 |
Fig. 15 Relation between infrared luminosity of galaxies and their halo mass. The top panels correspond to the infrared luminosity for a central galaxy exactly on the main sequence. The bottom panels shows the mean infrared luminosity of the central galaxies. The left panels show results as the instantaneous halo mass and right panel as a function of halo mass at z = 0. The dashed lines correspond to the limit between normal galaxies (i.e. < 1011 L⊙), LIRGs (1011 < LIR < 1012 L⊙), ULIRGs (1012 < LIR < 1013 L⊙), and HyLIRGs (<1013 L⊙). |
| In the text | |
 |
Fig. 16 Contribution of various halo mass to the star formation history. Upper panels shows the contribution of each slice to star formation density and lower panels their fractional contribution. We use slice of instantaneous halo mass in the left panels and mass at z = 0 in the right panels. |
| In the text | |
 |
Fig. 17 Instantaneous star formation efficiency (defined here as SFR/BAR, where BAR is the baryonic accretion rate) as a function of halo mass at various redshift predicted by our model. The predictions from model C are plotted with a solid line. At z = 5 model A predicts a different efficiency distribution and is represented by a dashed line. Upper panels shows this efficiency only for main-sequence galaxies and lower panels for mean efficiency. We use slice of instantaneous halo mass in the left panels and mass at z = 0 in the right panels. |
| In the text | |
 |
Fig. B.1 Same figure as 17 but assuming a Salpeter (1955) IMF. The black dashed line corresponds to an SFE of 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.