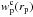| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321463 | |
| Published online | 29 August 2013 | |
The VIMOS Public Extragalactic Redshift Survey (VIPERS) ⋆
Galaxy clustering and redshift-space distortions at z ≃ 0.8 in the first data release
1
SUPA, Institute for Astronomy, University of Edinburgh, Royal
Observatory, Blackford
Hill, Edinburgh
EH9 3HJ,
UK
e-mail:
sdlt@roe.ac.uk
2
INAF – Osservatorio Astronomico di Brera, via Brera 28, 20122
Milano, via E. Bianchi 46, 23807
Merate,
Italy
3
Dipartimento di Fisica, Università di
Milano-Bicocca, P.zza della Scienza
3, 20126
Milano,
Italy
4
Dipartimento di Matematica e Fisica, Università degli Studi Roma
Tre, via della Vasca Navale
84, 00146
Roma,
Italy
5
INFN, Sezione di Roma Tre, via della Vasca Navale 84,
00146
Roma,
Italy
6
INAF – Osservatorio Astronomico di Roma,
via Frascati 33, 00040
Monte Porzio Catone ( RM), Italy
7
INAF – Osservatorio Astrofisico di Torino,
10025
Pino Torinese,
Italy
8
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
9
Canada-France-Hawaii Telescope, 65–1238 Mamalahoa Highway,
Kamuela,
HI
96743,
USA
10
Centre de Physique Théorique, UMR 6207 CNRS-Université de
Provence, Case 907,
13288
Marseille,
France
11
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
12
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Milano,
via Bassini 15, 20133
Milano,
Italy
13
Laboratoire Lagrange, UMR7293, Université de Nice
Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300
Nice,
France
14
Institute of Astronomy and Astrophysics, Academia Sinica,
PO Box 23-141,
10617
Taipei,
Taiwan
15
Dipartimento di Fisica e Astronomia - Università di Bologna,
viale Berti Pichat
6/2, 40127
Bologna,
Italy
16
INAF – Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11,
34143
Trieste,
Italy
17
Institute of Physics, Jan Kochanowski University,
ul. Swietokrzyska
15, 25-406
Kielce,
Poland
18
Department of Particle and Astrophysical Science, Nagoya
University, Furo-cho, Chikusa-ku,
464-8602
Nagoya,
Japan
19
INFN, Sezione di Bologna, viale Berti Pichat 6/2,
40127
Bologna,
Italy
20
Institute d’Astrophysique de Paris, UMR7095 CNRS, Université
Pierre et Marie Curie, 98bis
Boulevard Arago, 75014
Paris,
France
21
Institute of Cosmology and Gravitation, Dennis Sciama Building,
University of Portsmouth, Burnaby
Road, Portsmouth,
PO1 3FX,
UK
22
Astronomical Observatory of the Jagiellonian University,
Orla 171,
30-001
Cracow,
Poland
23
National Centre for Nuclear Research, ul. Hoza 69,
00-681
Warszawa,
Poland
24
Universitätssternwarte München, Ludwig-Maximillians Universität,
Scheinerstr. 1,
81679
München,
Germany
25
Max-Planck-Institut für Extraterrestrische Physik,
84571
Garching b. München,
Germany
26
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Bologna,
via Gobetti 101, 40129
Bologna,
Italy
27
INAF – Istituto di Radioastronomia, via Gobetti 101,
40129
Bologna,
Italy
28
Università degli Studi di Milano, via G. Celoria 16, 20130
Milano,
Italy
29
Dipartimento di Fisica dell’Università di Trieste,
Sezione di Astronomia, via Tiepolo
11, 34131
Trieste,
Italy
Received:
13
March
2013
Accepted:
10
July
2013
We present the general real- and redshift-space clustering properties of galaxies as measured in the first data release of the VIPERS survey. VIPERS is a large redshift survey designed to probe in detail the distant Universe and its large-scale structure at 0.5 < z < 1.2. We describe in this analysis the global properties of the sample and discuss the survey completeness and associated corrections. This sample allows us to measure the galaxy clustering with an unprecedented accuracy at these redshifts. From the redshift-space distortions observed in the galaxy clustering pattern we provide a first measurement of the growth rate of structure at z = 0.8: fσ8 = 0.47 ± 0.08. This is completely consistent with the predictions of standard cosmological models based on Einstein gravity, although this measurement alone does not discriminate between different gravity models.
Key words: cosmology: observations / large-scale structure of Universe / galaxies: high-redshift / galaxies: statistics
Based on observations collected at the European Southern Observatory, Cerro Paranal, Chile, using the Very Large Telescope under programmes 182.A-0886 and partly 070.A-9007. Also based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The VIPERS web site is http://www.vipers.inaf.it/
© ESO, 2013
1. Introduction
Over the past decades galaxy redshift surveys have provided a wealth of information on the inhomogeneous universe, mapping the late-time development of the small metric fluctuations that existed at early times, and whose early properties can be viewed in the cosmic microwave background (CMB). The growth of structure during this intervening period is sensitive both to the type and amount of dark matter, and also to the theory of gravity, so there is a strong motivation to make precise measurements of the rate of growth of cosmological structure (e.g. Jain & Khoury 2010).
Of course, galaxy surveys do not image the mass fluctuations directly, unlike gravitational lensing. But the visible light distribution does have some advantages as a cosmological tool in comparison with lensing. The number density of galaxies is sufficiently high that the density field of luminous matter can be measured with a finer spatial resolution, probing interesting non-linear features of the clustering pattern with good signal-to-noise. The price to be paid for this is that the complicated biasing relation between visible and dark matter has to be confronted; but this is a positive factor in some ways, since understanding galaxy formation is one of the main questions in cosmology. Redshift surveys provide the key information needed to meet this challenge: global properties of the galaxy population and their variation with environment and with epoch.
The final advantage of redshift surveys is that the radial information depends on
cosmological expansion and is corrupted by peculiar velocities. Although the lack of a
simple method to recover true distances can be frustrating at times, it has come to be
appreciated that this complication is in fact a good thing. The peculiar velocities induce
an anisotropy in the apparent clustering, from which the properties of the peculiar
velocities can be inferred much more precisely than in any attempt to measure them directly
using distance estimators. The reason peculiar velocities are important is that they are
related to the underlying linear fractional density perturbation δ via the
continuity equation: 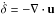 ,
where u is the peculiar velocity field. This can be expressed
more conveniently in terms of the dimensionless scale factor,
a(t), and the Hubble parameter,
H(t), as
,
where u is the peculiar velocity field. This can be expressed
more conveniently in terms of the dimensionless scale factor,
a(t), and the Hubble parameter,
H(t), as
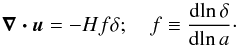 (1)The growth rate can
be approximated in most models by
f(a) ≃ Ωm(a)γ,
where γ ≃ 0.545 in standard Λ-dominated models, but where models of
non-standard gravity display a growth rate in which the effective value of
γ can differ by 30% (Linder &
Cahn 2007).
(1)The growth rate can
be approximated in most models by
f(a) ≃ Ωm(a)γ,
where γ ≃ 0.545 in standard Λ-dominated models, but where models of
non-standard gravity display a growth rate in which the effective value of
γ can differ by 30% (Linder &
Cahn 2007).
The possibility of using the redshift-space distortion signature as a probe of the growth rate of density fluctuations, together with that of using the Baryonic Acoustic Oscillations (BAO) as a standard ruler to measure the expansion history, is one of the main reasons behind the recent burst of activity in galaxy redshift surveys. The first paper to emphasise this application as a test of gravity theories was the analysis of the VVDS survey by Guzzo et al. (2008), and subsequent work especially by the SDSS LRG (Samushia et al. 2012), WiggleZ (Blake et al. 2012; Contreras et al. 2013), 6dFGS (Beutler et al. 2012) and BOSS (Reid et al. 2012) surveys has exploited this method to make measurements of the growth rate at z < 1.
Surveys such as SDSS LRG, WiggleZ, or BOSS are characterised by a large volume (0.5−2 h-3Gpc3), and a relatively sparse galaxy population with number density of about 10-4 h3 Mpc-3. Statistical errors are in this case minimised thanks to the large volume probed, at the expenses of selecting a very specific galaxy population (e.g. blue star forming or very massive galaxies), often with a complex selection function. The goal of the VIMOS Public Extragalactic Redshift Survey1 (VIPERS) has been that of constructing a survey with broader science goals and properties comparable to local general-purpose surveys such as the 2dFGRS. The adopted strategy has been to optimise the features of the ESO VLT multi-object spectrograph VIMOS in order to measure about 400 spectra at IAB < 22.5 over an area of 200 square arcmin, in a single exposure of less than 1 hour. The survey is being performed as a “Large Programme” within the ESO general user framework and aims at measuring redshifts for about 105 galaxies at 0.5 < z < 1.2.
The prime goal of VIPERS is an accurate measurement of the growth rate of large-scale structure at redshift around unity. The survey should enable us in particular to use techniques aimed at improving the precision on the growth rate (McDonald & Seljak 2009) thanks to its high galaxies sampling of about 10-2 h3 Mpc-3. In general, VIPERS is intended to provide robust and precise measurements of the properties of the galaxy population at an epoch when the Universe was about half its current age, representing one of the largest spectroscopic surveys of galaxies ever conducted at these redshifts. Examples can be found in the parallel papers that are part of the first science release (Marulli et al. 2013; Malek et al. 2013; Davidzon et al. 2013).
This paper presents the initial analysis of the real-space galaxy clustering and redshift-space distortions in VIPERS, together with the resulting implications for the growth rate. The data are described in Sect. 2; Sect. 3 describes the survey selection effects; Sect. 4 describes our methods for estimating clustering, which are tested on simulations in Sect. 5; Sect. 6 presents the real-space clustering results; Sect. 7 gives the redshift-space distortions results, and Sect. 8 summarises our results and concludes.
Throughout this analysis, if not specified otherwise, we assume a fiducial Λ-cold dark matter (ΛCDM) cosmological model with (Ωm,Ωk,w,σ8,ns) = (0.25,0, −1,0.8,0.95) and a Hubble constant of H0 = 100 h km s-1 Mpc-1.
2. Data
The VIPERS galaxy target sample is selected from the optical photometric catalogues of the
Canada-France-Hawaii Telescope Legacy Survey Wide (CFHTLS-Wide, Goranova et al. 2009). VIPERS covers 24 deg2 on the sky,
divided over two areas within the W1 and W4 CFHTLS fields. Galaxies are selected to a limit
of 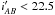 ,
applying a simple and robust gri colour pre-selection to efficiently remove
galaxies at z < 0.5. Coupled with a highly
optimised observing strategy (Scodeggio et al. 2009),
this allows us to double the galaxy sampling rate in the redshift range of interest, with
respect to a pure magnitude-limited sample. At the same time, the area and depth of the
survey result in a relatively large volume,
5 × 107 h-3 Mpc3, analogous to that
of the Two Degree Field Galaxy Redshift Survey (2dFGRS) at z ≃ 0.1 (Colless et al. 2001, 2003). Such a combination of sampling rate and depth is unique amongst current
redshift surveys at z > 0.5. VIPERS spectra are
collected with the VIMOS multi-object spectrograph (Le Fèvre
et al. 2003) at moderate resolution (R = 210) using the LR Red
grism, providing a wavelength coverage of 5500–9500 Å and a typical radial velocity error of
σv = 175(1 + z) km s-1.
The full VIPERS area of 24 deg2 will be covered through a mosaic of 288 VIMOS
pointings (192 in the W1 area, and 96 in the W4 area). A discussion of the survey data
reduction and management infrastructure is presented in Garilli et al. (2012). An early subset of the spectra used here is analysed and
classified through a Principal Component Analysis (PCA) in Marchetti et al. (2013). A complete description of the survey construction, from
the definition of the target sample to the actual spectra and redshift measurements, is
given in the parallel survey description paper (Guzzo et al.
2013).
,
applying a simple and robust gri colour pre-selection to efficiently remove
galaxies at z < 0.5. Coupled with a highly
optimised observing strategy (Scodeggio et al. 2009),
this allows us to double the galaxy sampling rate in the redshift range of interest, with
respect to a pure magnitude-limited sample. At the same time, the area and depth of the
survey result in a relatively large volume,
5 × 107 h-3 Mpc3, analogous to that
of the Two Degree Field Galaxy Redshift Survey (2dFGRS) at z ≃ 0.1 (Colless et al. 2001, 2003). Such a combination of sampling rate and depth is unique amongst current
redshift surveys at z > 0.5. VIPERS spectra are
collected with the VIMOS multi-object spectrograph (Le Fèvre
et al. 2003) at moderate resolution (R = 210) using the LR Red
grism, providing a wavelength coverage of 5500–9500 Å and a typical radial velocity error of
σv = 175(1 + z) km s-1.
The full VIPERS area of 24 deg2 will be covered through a mosaic of 288 VIMOS
pointings (192 in the W1 area, and 96 in the W4 area). A discussion of the survey data
reduction and management infrastructure is presented in Garilli et al. (2012). An early subset of the spectra used here is analysed and
classified through a Principal Component Analysis (PCA) in Marchetti et al. (2013). A complete description of the survey construction, from
the definition of the target sample to the actual spectra and redshift measurements, is
given in the parallel survey description paper (Guzzo et al.
2013).
The dataset used in this and the other papers of the early science release, will represent the VIPERS Public Data Release 1 (PDR-1) catalogue. It will be publicly available in the fall of 2013. This catalogue includes 55 358 redshifts (27 935 in W1 and 27 423 in W4) and corresponds to the reduced data frozen in the VIPERS database at the end of the 2011/2012 observing campaign; this represents 64% of the final survey in terms of covered area. A quality flag has been assigned to each object in the process of determining their redshift from the spectrum, which quantifies the reliability of the measured redshifts. In this analysis, we use only galaxies with flags 2 to 9 inclusive, corresponding to a sample with a redshift confirmation rate of 98%. The redshift confirmation rate and redshift accuracy have been estimated using repeated spectroscopic observations in the VIPERS fields (see Guzzo et al. 2013, for details). The catalogue, which we will refer to just as the VIPERS sample in the following, corresponds to a sub-sample of 45 871 galaxies with reliable redshift measurements.
The redshift distribution of the sample is presented in Fig. 1. We can see in this figure that the survey colour selection allows an efficient removal of galaxies below z = 0.5. It is important to notice that the colour selection does not introduce a sharp cut in redshift but a redshift window function which has a smooth transition from zero to one in the redshift range 0.4 < z < 0.6, with respect to the full population of i′ < 22.5 galaxies. This effect on the radial selection of the survey, which we refer to as the colour sampling rate (CSR) in the following, is only present below z = 0.6. Above this redshift, the colour selection has no impact on the redshift selection and the sample becomes purely magnitude-limited at i′ < 22.5 (Guzzo et al. 2013). If we weight the raw redshift distribution by the global survey completeness function described in the next sections, one obtains the N(z) represented by the empty histogram in Fig. 1. For convenience, we scaled down the corrected N(z) by 40%, the average effective survey sampling rate, to aid the comparison between the shapes of the two distributions. The difference in shape between these two N(z) shows the effect of incompleteness in the survey, which is only significant at about z > 0.9 (see also Davidzon et al. 2013).
 |
Fig. 1 Redshift distribution of the combined W1+W4 galaxy sample when including only reliable redshifts (filled histogram) and that corrected for the full survey completeness (empty histogram) scaled down by 40% (see text). The curve shows the best-fitting template redshift distribution given by Eq. (2) applied to the uncorrected observed distribution. |
The observed redshift distribution in the sample can be well described by a function of the
form 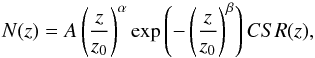 (2)in units of
deg-2·(Δz = 0.03)-1 and where
(A,z0,α,β) = (3.103,0.191,8.603,1.448).
The CSR is the incompleteness introduced by the VIPERS colour selection. It is primarily a
function of redshift and can be estimated from the ratio between the number of galaxies with
i′ < 22.5 satisfying the VIPERS colour
selection and the total number of galaxies with
i′ < 22.5 as a function of redshift.
We calibrated this function using the VLT-VIMOS Deep Survey Wide spectroscopic sample
(VVDS-Wide, Garilli et al. 2008) which has a
CFHTLS-based photometric coverage and depth that is similar to that of VIPERS, but which is
free from any colour selection (see Guzzo et al.
2013, for details). The CSR is well described by a function of the form
(2)in units of
deg-2·(Δz = 0.03)-1 and where
(A,z0,α,β) = (3.103,0.191,8.603,1.448).
The CSR is the incompleteness introduced by the VIPERS colour selection. It is primarily a
function of redshift and can be estimated from the ratio between the number of galaxies with
i′ < 22.5 satisfying the VIPERS colour
selection and the total number of galaxies with
i′ < 22.5 as a function of redshift.
We calibrated this function using the VLT-VIMOS Deep Survey Wide spectroscopic sample
(VVDS-Wide, Garilli et al. 2008) which has a
CFHTLS-based photometric coverage and depth that is similar to that of VIPERS, but which is
free from any colour selection (see Guzzo et al.
2013, for details). The CSR is well described by a function of the form ![\begin{equation} {\it CSR}(z)=\left[\frac{1}{2}-\frac{{\rm erf}\left(b(z_t-z)\right)}{2}\right], \label{eq:csr} \end{equation}](/articles/aa/full_html/2013/09/aa21463-13/aa21463-13-eq57.png) (3)with
(b,zt) = (17.465,0.424).
(3)with
(b,zt) = (17.465,0.424).
The fitting of N(z) is important in measuring galaxy clustering: the form of the mean redshift distribution must be followed accurately, but features from large-scale structure must not be allowed to bias the result. We discuss this issue in detail in Sect. 5.
3. Angular completeness
3.1. Slit assignment and footprint
To obtain a sample of several square degrees with VIMOS, one needs to perform a series of individual observations or pointings. The VIPERS strategy consists in covering the survey area with only one pass. This has been done in order to maximise the volume probed. The survey strategy and the fact that the VIMOS field-of-view is composed of four quadrants delimited by an empty cross, create a particular footprint on the sky which is reproduced in Figs. 4 and 5. In each pointing, slits are assigned to a number of potential targets which meet the survey selection criteria. This is shown in Fig. 2, which illustrates how the slits are positioned in the pointing W1P082. Given the surface density of the targeted population, the multiplex capability of VIMOS, and the survey strategy, a fraction of about 45% of the parent photometric sample can be assigned to slits. We define the fraction of target which have a measured spectrum as the target sampling rate (TSR) and the fraction of observed spectra with reliable redshift measurement as the spectroscopic sampling rate (SSR). The number of slits assigned per pointing is maximised by the SSPOC algorithm (Bottini et al. 2005), but the elongated size of the spectra means that the resulting sampling rate is not uniform inside the quadrants. The dispersion direction of the spectra in VIPERS are aligned with the Dec direction and consequently, the density of spectra along this direction is lower with respect to that along the RA direction. This particular sampling introduces an observed anisotropic distribution of pair separation, which has to be accounted for to measure galaxy clustering correctly.
 |
Fig. 2 Illustration of the slit assignment in pointing W1P082. The slits are shown in red and associated rectangles represent the typical dispersion of the spectra. All objects meeting the survey selection criteria (potential spectroscopic targets) are represented by black circles. |
The two empty stripes between the four quadrants in each pointing introduce a particular pattern in the measured correlation functions if not accounted for. We correct for that by applying detailed binary masks of the spectroscopic observations to a random sample of unclustered objects, so that both data and random catalogues contain no objects in these stripes. These masks account for the detailed VIMOS field-of-view geometry as well as for the presence of vignetted areas at the boundaries of the pointings. On top of these spectroscopic masks, we apply a set of photometric masks which discard areas where the parent photometry is affected by defects such as large stellar haloes and where the survey selection is compromised (see Guzzo et al. 2013).
3.2. Small-scale incompleteness
We can characterise the amount of missing small-scale angular pairs induced by the VIPERS
spectroscopic strategy, by measuring the angular pair completeness as a function of
angular separation. This quantity, defined as the ratio between the number of pairs in the
spectroscopic sample and that in the parent photometric sample, can be written in terms of
angular two-point correlation functions as (Hawkins et al.
2003) 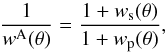 (4)where
ws(θ) and
wp(θ) are respectively the angular
correlation function of the spectroscopic and parent samples. This function is shown in
Fig. 3. No significant difference is seen between the
W1 and W4 fields, as expected. The amount of missing angular pairs is only significant
below θ = 0.03 deg, which corresponds to a transverse comoving scale of
about 1 h-1 Mpc at z = 0.8.
(4)where
ws(θ) and
wp(θ) are respectively the angular
correlation function of the spectroscopic and parent samples. This function is shown in
Fig. 3. No significant difference is seen between the
W1 and W4 fields, as expected. The amount of missing angular pairs is only significant
below θ = 0.03 deg, which corresponds to a transverse comoving scale of
about 1 h-1 Mpc at z = 0.8.
This fraction varies with redshift, although in practice we cannot measure it at different redshifts since we do not have a measured redshift for all galaxies in the parent sample. For this reason we use the global wA(θ) (averaged over all observed redshifts) to correct for the small-scale angular incompleteness effect. We will show in Sect. 5 that the level of systematic error introduced by using wA(θ) instead of wA(θ|z) is very small, of the order of a few percent. When measuring the angular correlation functions, we include the completeness weights introduced in the following section, in a similar way as for the three-dimensional correlation function estimation.
 |
Fig. 3 Completeness fraction of angular galaxy pairs due to the slit-spectroscopy strategy in the W1 and W4 fields for all galaxies at 0.5 < z < 1.0. This has been obtained from the parent and spectroscopic sample angular correlation function. |
 |
Fig. 4 Variations of the target success rate (TSR) with quadrants. The TSR quantifies our ability of obtaining spectra from the potential targets meeting the survey selection in the parent photometric sample. The quadrants filled in black correspond to failed observations where no spectroscopy has been taken. |
 |
Fig. 5 Variations of the spectroscopic success rate (SSR) with quadrants. The SSR quantifies our ability of determining galaxy redshifts from observed spectra. The quadrants filled in black correspond to failed observations where no spectroscopy has been taken. |
It is important to mention that the small-scale angular incompleteness effect is a general issue for large galaxy redshift surveys, in which one has to deal with the mechanical constraints of multi-object spectrographs and survey strategy. The incompleteness due to slit assignment in VIPERS is to some extent similar to the fibre collision problem in surveys using fibre spectroscopy such as 2dFGRS or SDSS, while the magnitude of the effect is much more severe in our case. Recently, a new method has been developed to accurately correct for fibre collision (Guo et al. 2012). Although this method is quite general, it is not applicable here. The exclusion between spectroscopically observed objects in VIPERS is essentially uni-directional, meaning that not all close pairs are excluded. Therefore calculations such as that shown in Fig. 4 are possible from the set of one-pass observations, whereas the correction scheme of Guo et al. (2012) can only be used for SDSS where overlapping observations are included. Thus we need to revise the correction methods developed for such surveys to apply them to VIPERS.
3.3. Large-scale incompleteness
In addition to the non-uniform sampling inside the pointings, the survey has variations of completeness from quadrant to quadrant. This incompleteness is the combined effect of the TSR and SSR. The latter, which characterises our ability of determining a redshift from a galaxy spectrum, is determined empirically as the ratio between the number of reliable redshifts and the total number of observed spectra. The TSR and SSR in each quadrant are shown in in Figs. 4 and 5. From these figures one can see clearly that both TSR and SSR functions vary according to the position on the sky, although the SSR tends to have stronger variations. The variations of TSR reflect the changes in angular galaxy density in the parent catalogue. Indeed, because of the finite maximum number of slits that can be assigned and the fact that each quadrant has a different number of potential targets, the less dense quadrants tend to be better sampled than the denser ones. On the other hand, variations in observational conditions from pointing to pointing induce changes in SSR. These different observational conditions translate into variations of the signal-to-noise of the measured spectra and so in our ability of extracting a redshift measurement from them. These effects are taken into account in the clustering estimation by weighting each galaxy according to the reciprocal of the TSR and SSR.
4. Clustering estimation
We characterise the galaxy clustering in the VIPERS sample by measuring the two-point
statistics of the spatial distribution of galaxies in configuration space. We estimate the
two-point correlation function ξ(r) using the Landy & Szalay (1993) estimator 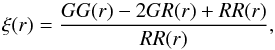 (5)where
GG(r), GR(r), and
RR(r) are respectively the normalised galaxy-galaxy,
galaxy-random, and random-random number of pairs with separation inside
[r − Δr/2,r + Δr/2].
Note that here r is a general three-dimensional galaxy separation, not
specifically the real-space separation. This estimator minimises the estimation variance and
circumvent discreteness and finite volume effects (Landy
& Szalay 1993; Hamilton 1993). A
random catalogue must be constructed in this estimator, whose aim is to accurately estimate
the number density of objects in the sample. It must be an unclustered population of objects
with the same radial and angular selection functions as the data. In this analysis, we use
random samples with 20 times more objects than in the data to minimise the shot noise
contribution in the estimated correlation functions.
(5)where
GG(r), GR(r), and
RR(r) are respectively the normalised galaxy-galaxy,
galaxy-random, and random-random number of pairs with separation inside
[r − Δr/2,r + Δr/2].
Note that here r is a general three-dimensional galaxy separation, not
specifically the real-space separation. This estimator minimises the estimation variance and
circumvent discreteness and finite volume effects (Landy
& Szalay 1993; Hamilton 1993). A
random catalogue must be constructed in this estimator, whose aim is to accurately estimate
the number density of objects in the sample. It must be an unclustered population of objects
with the same radial and angular selection functions as the data. In this analysis, we use
random samples with 20 times more objects than in the data to minimise the shot noise
contribution in the estimated correlation functions.
VIPERS has a complex angular selection function which has to be taken into account
carefully when estimating the correlation function. For this, we weight each galaxy by the
survey completeness weight, as well as each pair by the angular pair weights described in
the previous section (Eq. (4)). The survey
completeness weights correspond to the inverse of the effective sampling rate ESR in each
quadrant Q, defined as 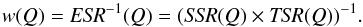 (6)By applying these
weights we effectively up-weight galaxies in the pair counts. It is important to note that
here we keep the spatial distribution of the random objects uniform across the survey
volume. We recall that survey completeness weights account for the quadrant-to-quadrant
variations of the survey completeness described in Sect. 3.3 but do not correct for the internal quadrant incompleteness. For that we use
the angular pair weights wA(θ) which are
applied to the GG pair counts. In principle the ESR is also a function of redshift and
galaxy type (see Davidzon et al. 2013). However,
given the statistics of the sample it is impossible to measure the additional dependence of
this function on redshift and galaxy properties. Therefore, we decided to only account for
its quadrant-to-quadrant variations. We discuss the accuracy of this approximation in Sect.
5.
(6)By applying these
weights we effectively up-weight galaxies in the pair counts. It is important to note that
here we keep the spatial distribution of the random objects uniform across the survey
volume. We recall that survey completeness weights account for the quadrant-to-quadrant
variations of the survey completeness described in Sect. 3.3 but do not correct for the internal quadrant incompleteness. For that we use
the angular pair weights wA(θ) which are
applied to the GG pair counts. In principle the ESR is also a function of redshift and
galaxy type (see Davidzon et al. 2013). However,
given the statistics of the sample it is impossible to measure the additional dependence of
this function on redshift and galaxy properties. Therefore, we decided to only account for
its quadrant-to-quadrant variations. We discuss the accuracy of this approximation in Sect.
5.
Additional biases can arise if the radial selection function exhibits strong variations
with redshift. The effect is particularly significant for magnitude-limited catalogues
covering a large range of redshifts and in which the radial selection function rapidly drops
at high redshift. In that case, the pair counts is dominated by nearby, more numerous
objects: distant objects, although probing larger volumes, will have less weight. To account
for this we use the minimum variance estimator of Davis
& Huchra (1982) for which the galaxy counts are essentially weighted by the
inverse of the volume probed by each galaxy. This weighting scheme, usually referred as the
J3 weighting, is defined as (Hamilton 1993)  (7)where
z is the redshift of the object, s is the redshift-space
pair separation,
(7)where
z is the redshift of the object, s is the redshift-space
pair separation, 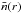 the galaxy number density at z and
J3(s) is defined as
the galaxy number density at z and
J3(s) is defined as
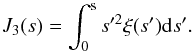 (8)Each pair is then
weighted by,
(8)Each pair is then
weighted by, 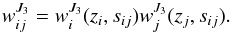 (9)However, we find that
applying J3 weighting does not significantly change the
amplitude and shape of the correlation function in our sample, and tends to produce noisy
correlation functions especially for high-redshift sub-samples. We thus decided not to apply
this correction in this analysis.
(9)However, we find that
applying J3 weighting does not significantly change the
amplitude and shape of the correlation function in our sample, and tends to produce noisy
correlation functions especially for high-redshift sub-samples. We thus decided not to apply
this correction in this analysis.
The final weight assigned to GG, GR, and
RR pairs combine the survey completeness and angular pair weights as
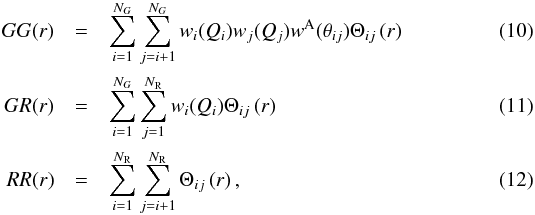 where
Θij(r) is equal to unity for
rij in
[r − Δr/2,r + Δr/2]
and null otherwise.
where
Θij(r) is equal to unity for
rij in
[r − Δr/2,r + Δr/2]
and null otherwise.
We measure correlation functions using both linear and logarithmic binning. We define the separation associated with each bin as the bin centre and as the mean pair separation inside the bin, respectively for the linear and logarithmic binning (Zehavi et al. 2011). The latter definition is more accurate than using the bin centre, in particular at large r when the bin size is large.
The galaxy real-space correlation function ξ(r) is not
directly measurable from redshift survey catalogues because of galaxy peculiar velocities
that affect redshift measurements. Galaxy peculiar velocities introduce distortions in the
galaxy clustering pattern and as a consequence we can only measure redshift-space
quantities. We measure the anisotropic redshift-space correlation function
ξ(rp,π) in which the
redshift-space galaxy separation vector has been divided in two components,
rp and π, respectively perpendicular and
parallel to the line-of-sight (Fisher et al. 1994).
This decomposition, which assumes the plane-parallel approximation, allows us to isolate the
effect of peculiar velocities as these modify only the component parallel to the
line-of-sight. Redshift-space distortions can then be mitigated by integrating
ξ(rp,π) over
π, thus defining the projected correlation function
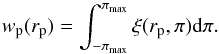 (13)We measure
wp(rp) using an optimal value of
πmax = 40 h-1 Mpc, allowing us
to reduce the underestimation of the amplitude of
wp(rp) on large scales and at the
same time to avoid including noise from uncorrelated pairs with separations of
π > 40 h-1 Mpc. The
projected correlation function allows us to measure real-space clustering (but see the later
parts of Sect. 5). To combine the correlation function
measurements from the two fields, we measure the mean of one plus the correlation functions
in W1 and W4 weighted by the square of the number density, so that the combined correlation
function ξ(rp,π) is obtained
from
(13)We measure
wp(rp) using an optimal value of
πmax = 40 h-1 Mpc, allowing us
to reduce the underestimation of the amplitude of
wp(rp) on large scales and at the
same time to avoid including noise from uncorrelated pairs with separations of
π > 40 h-1 Mpc. The
projected correlation function allows us to measure real-space clustering (but see the later
parts of Sect. 5). To combine the correlation function
measurements from the two fields, we measure the mean of one plus the correlation functions
in W1 and W4 weighted by the square of the number density, so that the combined correlation
function ξ(rp,π) is obtained
from 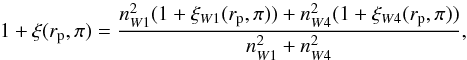 (14)where
nW1 and
nW4 are the observed galaxy number
densities in the W1 and W4 fields, respectively.
(14)where
nW1 and
nW4 are the observed galaxy number
densities in the W1 and W4 fields, respectively.
5. Tests of the clustering estimation
5.1. Simulation data
To test the robustness of our clustering estimation we make use of a large number of mock galaxy samples, which are designed to be a realistic match to the VIPERS sample. We create two sets of mock samples based on the halo occupation distribution (HOD) technique. These two sets only differ by the input halo catalogue that has been used. In the first set of mocks, we used the haloes extracted from the MultiDark dark matter N-body simulation (Prada et al. 2012). This simulation, which assumes a flat ΛCDM cosmology with (Ωm, ΩΛ, Ωb, h, n, σ8) = (0.27, 0.73, 0.0469, 0.7, 0.95, 0.82), covers a volume of 1 h-3 Gpc3 using N = 20483 particles. In the simulation, the haloes have been identified using a friends-of-friends algorithm with a relative linking length of b = 0.17 times the inter-particle separation (i.e. 0.083 h-1 Mpc) . The mass limit to which halo catalogues are complete is 1011.5 h-1 M⊙. Because this limiting mass is too large to host the faintest galaxies observed with VIPERS, we use the method of de la Torre & Peacock (2013) to reconstruct haloes below the resolution limit. This method is based on stochastically resampling the halo number density field using constraints from the conditional halo mass function. For this, one needs to assume the shapes of the halo bias factor and halo mass function at masses below the resolution limit and use the analytical formulae obtained by Tinker et al. (2008, 2010). With this method we are able to populate the simulation with low-mass haloes with a sufficient accuracy to have unbiased galaxy two-point statistics in the simulated catalogues (see de la Torre & Peacock 2013, for details). The minimum reconstructed halo mass we consider for the purpose of creating VIPERS mocks is 1010 h-1 M⊙.
We then apply to the complete halo catalogues the algorithm presented in Carlson & White (2010) to remap halo positions and velocities in the initial simulation cube onto a cuboid of the same volume but different geometry. This is done to accommodate a maximum number of disjoint VIPERS W1 and W4 fields within the 1 h-3 Gpc3 volume of the simulation. This process allows us to create 26 and 31 independent lightcones for W1 and W4 respectively over the redshift range 0.4 < z < 1.3. The lightcones are built by considering haloes from the different snapshots, disposing them according to their distance from the coordinate origin of the lightcone. The lightcones are then populated with galaxies using the HOD technique. In this process, we populate each halo with galaxies according to its mass, the mean number of galaxies in a halo of a given mass being given by the HOD. It is common usage to differentiate between central and satellite galaxies in haloes. While the former are put at rest at halo centres, the latter are randomly distributed within each halo according to a NFW radial profile. The halo occupation function and its dependence on redshift and luminosity/stellar mass must be precisely chosen in order to obtain mock catalogues with realistic galaxy clustering properties. We calibrated the halo occupation function directly on the VIPERS data. We performed an analytic HOD modelling of the projected correlation function for different samples selected in luminosity and redshift that we will present in Sect. 6. We obtain from this a series of HOD parameters at different redshifts and for different cuts in B-band absolute magnitude, which we then interpolate to obtain a general redshift- and B-band absolute magnitude-dependent halo occupation function ⟨Ngal(m|z,MB)⟩. We use the latter function to populate the haloes with galaxies. Finally, we add velocities to the galaxies and measure their redshift-space positions. While the central galaxies are assigned the velocity of their host halo, satellite galaxies have an additional random component for which each Cartesian velocity component is drawn from a Gaussian distribution with a standard deviation that depends on the mass of the host halo. Details about the galaxy mock catalogue construction are given in Appendix A.
The second set of mocks that we built is based on halo catalogues created with the Pinocchio code2 (Monaco et al. 2002). This code follows the evolution of a set of particles on a regular grid using an ellipsoidal model to compute collapse times and identify dark matter haloes, and the Zel’dovich approximation to displace the haloes from their initial position. While the recovery of haloes works well on an object-by-object basis, their positions and velocities on scales below 10 h-1 Mpc suffer by the lack of accuracy of the Zel’dovich approximation. The halo positions and velocities obtained with this method are less accurate than those from the N-body simulation, and the halo clustering is generally underestimated on scales below 3 h-1 Mpc (e.g. Monaco et al. 2002). However, this approach has the advantage of being very fast and can be used to generate a large number of independent halo catalogue realisations. We created 200 independent halo mock realisations assuming the same cosmology as the MultiDark N-body simulation. The remaining steps in generating galaxy mock samples are similar to those used for the mocks based on the MultiDark simulation. The only difference is that here we do not need to divide each simulation into sub-volumes to generate different lightcones: we can directly create volumes of the size of the lightcones.
The final step in obtaining fully realistic VIPERS mocks is to add the detailed survey selection function. The procedure that we follow is similar to that used in the VVDS and zCOSMOS surveys, which were also based on VIMOS observations (Meneux et al. 2006; Iovino et al. 2010; de la Torre et al. 2011). We start by applying the magnitude cut i′ < 22.5 and the effect of the colour selection on the radial distribution of the mocks. The latter is done by depleting the mocks at z < 0.6 so as to reproduce the CSR. The mock catalogues that we obtain are then similar to the parent photometric sample in the data. We next apply the slit-positioning algorithm with the same setting as for the data. This allows us to reproduce the VIPERS footprint on the sky, the small-scale angular incompleteness and the variation of TSR across the fields. Finally, we deplete each quadrant to reproduce the effect of the SSR. Thus we are able to produce realistic mock galaxy catalogues that contain the detailed survey completeness function and observational biases of VIPERS.
 |
Fig. 6 Comparison of different estimators of the radial distribution in the combined W1+W4 sample. The filled histogram shows the number of galaxies in fine bins of radial comoving distance. The different curves correspond to random radial distribution realisations normalised to the number of objects in the data, obtained using the Vmax (solid), Gaussian filtering (dashed and dot-dashed), or analytical (dotted) methods. The vertical line shows the minimum redshift considered in this analysis, i.e. z = 0.5. |
 |
Fig. 7 Impact of the use of different estimators of the radial distribution on the shape of the projected correlation function. The projected correlation functions obtained using the Vmax (solid), Gaussian filtering (dashed and dot-dashed), or analytical (dotted) methods are shown in the top panel, while the relative fractional differences with respect to the Vmax method are presented in the bottom panel. |
5.2. Effects of systematics on the correlation function
5.2.1. Effects related to the radial selection function
We first study the impact on our correlation function measurements of using different methods to estimate the radial selection. A key aspect in three-dimensional clustering estimation is to have a smooth and unbiased redshift distribution from which the random sample can be drawn. In particular, when the data sample used to estimate the radial distribution is not very large, one generally has to deal with strong features associated with prominent structures; these must not be allowed to induce spurious clustering in the random sample.
There are several empirical methods for avoiding this problem. One can for instance interpolate the binned observed distribution using cubic splines, filter the observed distribution with a kernel sufficiently large to erase the strong features in the distribution, or fit the observed distribution with a smooth template N(z) and then randomly sample it. In general most of the methods are parametric and have to be calibrated. An alternative non-parametric method is the Vmax method. This method consists in randomly sampling the maximum volumes Vmax probed by each galaxy in the survey (e.g. Kovač et al. 2010; Cole 2011). The Vmax value for each galaxy corresponds to the volume between the minimum and the maximum redshifts zmin and zmax at which the galaxy is observable in the survey.
Figure 6 applies three such approaches to estimate the galaxy radial distribution in the combined W1+W4 sample: the analytical N(z) of Eq. (2); the Gaussian filtering method; and the Vmax method. This figure shows the recovered N(Dc) in the random sample with each method, with Dc being the radial comoving distance; in practice we work with N(Dc) instead of N(z). We find that the methods give different estimates of the radial distribution. In the case of the Gaussian filtering, a kernel size of 150 h-1 Mpc is needed to smear out the peaks in the distribution, otherwise the recovered N(Dc) is still affected by large structures in the field – particularly by that at Dc ≃ 1600 h-1 Mpc. As expected, the filtering method tends to artificially broaden the N(Dc) distribution, whereas the analytical and Vmax methods are much smoother by construction and do not broaden the N(Dc). We find that the Vmax estimate shows a slightly flatter distribution at the level of the peak of the distribution, which seems visually to be more consistent with the data. In Fig. 7 we show the effect of using these different estimates of the radial distribution on the shape of the measured correlation function. Gaussian filtering with a kernel size of 150 h-1 Mpc and analytical N(z) estimates both yield slightly smaller amplitudes of the projected correlation function on scales of above 10 h-1 Mpc than the Vmax method. Gaussian filtering with a kernel size of 100 h-1 Mpc globally underestimates the clustering amplitude on wp(rp) as expected, by about 5%. The analytical and Vmax methods give very similar answers, except on scales above 5 h-1 Mpc where the former tends to produce a smaller clustering amplitude by 5−15% with respect to the latter. This comparison shows that the Vmax method is more robust as it uniquely allows us to restore some correlation signal at large separation. For this reason and the fact that it is non-parametric we finally decided to use the Vmax estimate to measure two-point correlation functions.
5.2.2. Effects related to the angular selection function
The most crucial aspect of the galaxy clustering estimation in VIPERS is to account for the angular selection function. We test our methodology and the different assumptions discussed in Sect. 4 using the MultiDark mock samples. We measure the accuracy with which we can estimate the two-point correlation function, by confronting the two-point correlation functions measured in the parent catalogues with those measured in the observed mocks when different completeness corrections are included. We measure the average relative difference between the corrected observed mocks and the parent measurement for different statistics. For this test, we consider two galaxy samples encompassing respectively all galaxies in the redshift intervals 0.5 < z < 0.75 and 0.75 < z < 1.0, using the same redshift distribution in the parent and observed mock samples to construct the radial selection function of the random sample.
 |
Fig. 8 Systematic error on the projected correlation function and impact of different corrections. This is calculated considering all VIPERS galaxies in the redshift intervals 0.5 < z < 0.75 (top panel) and 0.75 < z < 1 (bottom panel). |
It is common usage in clustering analysis to account for the angular survey completeness by down-weighting the random pair counts. This is usually done by keeping the galaxy counts unweighted and depleting the random sample so as to reproduce the survey angular completeness. The same effect can be achieved by using a uniform angular distribution of random objects but weighting each of them by the inverse of the weight defined in Eq. (6). If we do that and set all the angular pair weights to unity, we obtain the systematic error on wp(rp) shown with the dotted curves in Fig. 8. We concentrate first on the results in the interval 0.5 < z < 0.75. We can see in this figure that the recovered clustering with this method is underestimated by about 10% at about 1 < rp < 20 h-1 Mpc, and then drops rapidly to 35% below. The strong underestimation on small scales is due to the small-scale angular incompleteness effect inside the quadrants. The approach of modulating the random density is dubious in the context of VIPERS, since it treats the sampling variations as a pattern imposed on the large-scale structure. But because of the VIMOS slit allocation, these variations are strongly coupled with the true clustering (i.e. the observed sky distribution of VIPERS galaxies is rather uniform). It is therefore safer if we keep the random sample uniform but upweight the galaxies as described in Sect. 4. In this case, we obtain the dot-dashed lines in Fig. 8: these represent an improved estimation of wp(rp), reducing the underestimation by 5–6%. As expected, further including the angular pairs weights permits us to remedy in part the underestimation on scales below 1 h-1 Mpc, where the systematic error reaches 15% (solid lines).
So far, we have used the global survey completeness and angular weights, i.e. neglecting the redshift dependence. As an exercise we use the redshift information from the parent mocks to compute the true redshift-dependent weights and we obtain the dashed lines in the figure. Including the redshift dependence in the weights has the effect of improving the recovery of the projected correlation function by about 2% over all probed scales. However, this improvement is rather modest – indicating that the use of the redshift-independent weights is a good approximation. Our best estimate of wp(rp) therefore allows us to recover the true correlation function of the mocks at 0.5 < z < 0.75 with about 7% and 16% underestimation respectively above and below 1 h-1 Mpc. In the redshift interval 0.75 < z < 1 (shown in th bottom panel of Fig. 8), we find the same behaviour except that the correlation function is globally better recovered with an underestimation smaller than 2–3% at rp > 0.6 h-1 Mpc with the best method.
This test demonstrates that our methodology gives an accurate estimate of the galaxy clustering in VIPERS, even if there remains some residual systematic errors of up to 7% on the scales above 1 h-1 Mpc and 15% on smaller scales. We find that the effect varies with redshift, being more important at the lowest redshifts probed by VIPERS. Overall these systematics remain within the Poisson plus sample variance errors, shown with shaded regions in Fig. 8 and obtained from the standard deviation of wp(rp) among the parent mock catalogues.
5.3. Impact of possible residual zero-point uncertainties in the photometry
At the time of writing, photometry from the latest CFHTLS release (T0007) has become available (Hudelot et al. 2012). We have compared magnitudes and colours of objects in the VIPERS sample with the new CFHTLS-T0007 photometry. For VIPERS, the most important feature of T0007 compared to previous releases is that each tile in the CFHTLS has now been rescaled to an absolute calibration provided by a new photometric pre-survey taken at CFHT for this purpose. In addition, in order to ensure that seeing variations between tiles and filters are correctly accounted for, this scaling has been done using aperture fluxes that are rescaled based on the seeing on each individual tile; detailed tests at Terapix have shown that mag_auto magnitudes, which are affected by seeing variations, are not sufficiently precise for the percent-level photometric accuracy that is the objective of T0007.
An important consequence of this work for VIPERS is that the effect of seeing variation and photometric calibration errors are now cleanly separated; the stellar-locus fitting technique used to define the VIPERS selection using colours based on mag_auto magnitudes mixes both these effects. To estimate the size of colour and magnitude offsets between T0007 and the actual VIPERS selection (based on T0005) colours of stars on each VIPERS tiles measured from Terapix IQ20 magnitudes (used to calibrate T0007) and from mag_auto magnitudes in both releases have been compared. We find that these offsets shift the colour-colour locus we devised to remove lower-redshift z < 0.5 galaxies (Guzzo et al. 2013).
We test the effect of these possible variations of the colour selection across the fields in the context of galaxy clustering estimation. For this we use photometric redshifts and quantify the variations in N(z) due to tile-to-tile variations of the colour selection, assuming the T0007 photometry as the reference. When comparing the N(zphot) in the different tiles, we find that the redshift distribution varies in shape and amplitude at z < 0.6 but only in amplitude above. The typical amplitude variations are of the order of about 5% (Guzzo et al. 2013). We then measure the ratio between the N(z) per tile and that averaged over the fields and use it as a redshift-dependent correction factor. To test how these variations of the colour selection affect the measured correlation function, we vary the N(z) in the random sample for each quadrant using the correction factor previously defined on the averaged N(z). The projected correlations obtained with and without this correction are shown in Fig. 9.
 |
Fig. 9 Effect of correcting for quadrant-to-quadrant variations of the colour selection in the estimation of the projected correlation function, when using the CFHTLS-T0007 sample as the reference photometric catalogue. The top panel shows the projected correlation functions with and without the correction applied, while the bottom panel presents their relative fractional difference. |
We can see that the correction has the effect of decreasing the amplitude of the projected correlation function by about 2–4% on scales below 10 h-1 Mpc. We find a similar effect on the redshift-space angle-averaged correlation function ξ(s). The amplitude and direction of the systematic effect follows our expectations, since spurious tile-to-tile fluctuations, if not properly corrected, enhance the amplitude of clustering. This test suggests that indeed such tile-to-tile variations of colour selection are present in the data. It is interesting to note that this systematic effect goes in the opposite direction to the effects of slit-positioning and associated incompleteness. In the end, because this possible effect remains very small, we do not attempt to correct it for the clustering analysis.
6. Real-space clustering
Before studying redshift-space distortions in VIPERS, we begin by looking at the clustering in real space. The projected correlation function for all galaxies in the redshift range 0.5 < z < 1 is shown in Fig. 10. It is measured in logarithmic bins of Δlog rp = 0.2 over the scales 0.1 < rp < 30 h-1 Mpc. The error bars are estimated from the MultiDark mocks.
 |
Fig. 10 Top panel: projected correlation functions of VIPERS galaxies in the
redshift interval
0.5 < z < 1 for the
individual W1 and W4 fields as well as for the combined sample. As a comparison, the
± 1σ dispersion among the mean
wp(rp) in the mocks is
shown with the shaded region and the non-linear mass prediction in the assumed
cosmology with the dotted curve. Bottom panel: relative difference
between the measured wp(rp)
in the W1 and W4 fields and the combined projected correlation function
|
The measured wp(rp) functions in
the W1 and W4 fields are very similar, in particular on scales below
5 h-1 Mpc. The combined projected correlation function in
this redshift interval gives an accurate probe of the clustering up to scales of about
30 h-1 Mpc. We can compare the galaxy projected correlation
function to predictions for the mass non-linear correlation function and thus estimate the
global effective linear bias of these galaxies. We use the HALOFIT (Smith et al. 2003) prescription for the non-linear mass power spectrum to
compute the projected correlation function of mass at the mean redshift of the sample. By
comparing the amplitudes of the measured galaxy and predicted mass correlations on scales of
rp > 1.7 h-1 Mpc
(rp > 3.4 h-1 Mpc),
and assuming a linear biasing relation of the form 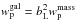 ,
we obtain a linear bias of bL = 1.35 ± 0.02
(bL = 1.33 ± 0.02).
,
we obtain a linear bias of bL = 1.35 ± 0.02
(bL = 1.33 ± 0.02).
 |
Fig. 11 Measured and best-fitting HOD model projected correlation functions wp(rp), for different luminosity-threshold subsamples of galaxies at 0.7 < z < 0.9. The wp(rp) for the MB − 5log (h) < −20.5, MB − 5log (h) < −21.0, and MB − 5log (h) < −21.5 cases have been multiplied by respectively 2, 3, and 4 to improve the clarity of the figure. |
To make a detailed interpretation of the observed clustering of galaxies and produce realistic mock samples of the survey, we model our wp(rp) measurements within the context of the HOD (Seljak 2000; Peacock & Smith 2000; Berlind & Weinberg 2002; Cooray & Sheth 2002). This method defines the mean distribution of galaxies within haloes; under the assumption of the abundance, large-scale bias, and density profile of haloes, one can then completely specify the clustering of galaxies and predict wp(rp). We define four B-band absolute magnitude-threshold samples in the redshift bin 0.7 < z < 0.9 in which we measured wp(rp). We model the projected correlation functions using HOD formalism, within a flat ΛCDM cosmology with parameters identical to those used in the MultiDark simulation (see Sect. 5.1). We restrict the fit to scales above rp = 0.2 h-1 Mpc and below rp = 30 h-1 Mpc and correct empirically the measured projected correlation function for the residual underestimation at different scales, using the ratio between the parent and recovered wp(rp) in the observed mocks for the same galaxy selection. We assume that there is negligible error in taking this small correction to be independent of cosmology. In the fitting procedure we used both the sample number density and wp(rp) constraints in order to estimate the HOD parameters and their errors by exploring the full parameter space of the model.
In our HOD model the occupation number is parameterised as 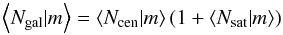 (15)where
⟨Ncen|m⟩ and
⟨Nsat|m⟩ are the average number of central
and satellite galaxies in a halo of mass m. This model explicitly assumes
that the first galaxy in haloes, when haloes have reached a sufficient mass, has to be
central. Central and satellite galaxy occupations are defined as in (Zheng et al. 2005):
(15)where
⟨Ncen|m⟩ and
⟨Nsat|m⟩ are the average number of central
and satellite galaxies in a halo of mass m. This model explicitly assumes
that the first galaxy in haloes, when haloes have reached a sufficient mass, has to be
central. Central and satellite galaxy occupations are defined as in (Zheng et al. 2005): ![\begin{eqnarray} \label{ncen} \left<N_{\rm cen}|m\right> &=& \frac{1}{2}\left[1+{\rm erf}\left(\frac{\log~m - \log M_{\rm min}}{\sigma_{\log~m}}\right)\right], \\ \label{nsat} \left<N_{\rm sat}|m\right> &=& \left(\frac{m-M_0}{M_1}\right)^{\alpha} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21463-13/aa21463-13-eq168.png) where
Mmin, σlog m,
M0, M1, and α are
the HOD parameters. The parameter M0 is generally poorly
constrained and we decided in this analysis to fix
M0 = Mmin (see also White et al. 2011; de la
Torre & Guzzo 2012).
where
Mmin, σlog m,
M0, M1, and α are
the HOD parameters. The parameter M0 is generally poorly
constrained and we decided in this analysis to fix
M0 = Mmin (see also White et al. 2011; de la
Torre & Guzzo 2012).
In the halo model formalism, the galaxy power spectrum or two-point correlation function can be written as the sum of two components: the 1-halo term that describes the correlations of galaxies inside haloes and the 2-halo term that characterises the correlations of galaxies sitting in different haloes. We follow the formalism of van den Bosch et al. (2013) to define the projected correlation in the context of this model. In particular we use their improved prescriptions for the treatment of the halo-exclusion and residual redshift-space distortions effects on wp(rp), induced by the finite πmax values used in the data (van den Bosch et al. 2013). We use the halo bias factor and mass function of Tinker et al. (2008) and Tinker et al. (2010) respectively, and assume that satellite galaxies trace the mass distribution within haloes. We make the assumption of a NFW (Navarro et al. 1996) radial density profile and use the concentration-mass relation obtained by Prada et al. (2012) from the MultiDark simulation. The details of the implementation of the HOD model are given in de la Torre et al. (in prep.).
 |
Fig. 12 Dependence of Mmin and M1 HOD parameters on redshift and absolute magnitude threshold in B-band. The absolute magnitude threshold samples are plot in terms of their implied number density ng. The VIPERS results are compared to the pervious measurements performed in the DEEP2 (Zheng et al. 2007), BOSS (White et al. 2011), and CFHTLS (Coupon et al. 2012) surveys. |
We present in Fig. 11 the measurements and best-fitting HOD models for the four different volume-limited absolute magnitude-threshold samples. We find that the model reproduces the observations well. To have a global characterisation of the clustering properties of galaxies in VIPERS, we extend this modelling to two additional redshift bins at 0.5 < z < 0.7 and 0.9 < z < 1.1. The best-fitting Mmin and M1 parameters for the different sub-samples are shown in Fig. 12 and compared to previous measurement in the same range of redshift and number density. Because in the different surveys the subsamples are not selected with the same absolute magnitude band of selection, it is convenient to compare the HOD parameters in terms of redshift and the number density probed by each sample. Note that here we compare measurements only from analyses using the same HOD parameterisation, although the exact implementation of the models can differ slightly. The VIPERS sample allows us to constraint these parameters with an unprecedented accuracy over the redshift range 0.5 < z < 1.1. Our results are consistent with previous measurements, in particular with the DEEP2 (Zheng et al. 2007) and CFHTLS (Coupon et al. 2012) analyses. Our HOD analysis is aimed at modelling the global clustering properties in VIPERS, but we refer the reader to Marulli et al. (2013) and de la Torre et al. (in prep.) for detailed analysis and interpretation of the luminosity and stellar dependence of galaxy clustering and luminosity-dependent halo occupation respectively.
We use the derived HOD parameters to define a global luminosity- and redshift-dependent occupation number which is then used to create accurate HOD mocks of the survey. To interpolate between the different redshifts, we assume a global luminosity evolution proportional to redshift, so that the magnitude threshold values scale linearly with redshift (Brown et al. 2008; Coupon et al. 2012). We find that one can approximate ⟨Ngal(m|z,MB)⟩ using Eq. (15) with
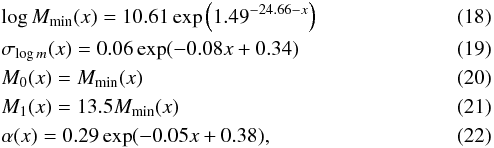 where
x = MB − 5log (h) + z.
Mmin and M1 are found to be
strongly correlated in such a way that M1 is approximately equal
to 10–20 times Mmin depending on the redshift probed and the
model implementation (e.g. Beutler et al. 2013). In
our analysis we find that M1(x) can be
approximated by 13.5 times Mmin(x). The
function
⟨Ngal(m|z,MB)⟩
is shown in Fig. 13 for the different values of
x probed with VIPERS. We checked the consistency of this parameterisation
and verify that the wp(rp)
predicted by the mocks and that measured are in good agreement for all probed redshift and
luminosity thresholds.
where
x = MB − 5log (h) + z.
Mmin and M1 are found to be
strongly correlated in such a way that M1 is approximately equal
to 10–20 times Mmin depending on the redshift probed and the
model implementation (e.g. Beutler et al. 2013). In
our analysis we find that M1(x) can be
approximated by 13.5 times Mmin(x). The
function
⟨Ngal(m|z,MB)⟩
is shown in Fig. 13 for the different values of
x probed with VIPERS. We checked the consistency of this parameterisation
and verify that the wp(rp)
predicted by the mocks and that measured are in good agreement for all probed redshift and
luminosity thresholds.
7. Redshift-space distortions
The main goal of VIPERS is to provide with the final sample accurate measurements of the growth rate of structure in two redshift bins between z = 0.5 and z = 1.2. The growth rate of structure f can be measured from the anisotropies observed in redshift space in the galaxy correlation function or power spectrum. Although this measurement is degenerate with galaxy bias, the combination fσ8 is measurable and still allows a fundamental test of modifications of gravity since it is a mixture of the differential and integral growth. In this Section, we present an initial measurement of fσ8 from the VIPERS first data release.
7.1. Method
With the first epoch VIPERS data we can reliably probe scales below about 35 h-1 Mpc. The use of the smallest non-linear scales, i.e. typically below 10 h-1 Mpc, is difficult because of the limitations of current redshift-space distortion models, which cannot describe the non-linear effects that relate the evolution of density and velocity perturbations. However, with the recent developments in perturbation theory and non-linear models for redshift-space distortions (e.g. Taruya et al. 2010; Reid & White 2011; Seljak & McDonald 2011), we can push our analysis well into mildly non-linear scales and obtain unbiased measurements of fσ8 while considering minimum scales of 5–10 h-1 Mpc (de la Torre & Guzzo 2012).
 |
Fig. 13 Evolution of the B-band absolute magnitude-dependent HOD. The curves show ⟨Ngal(m|z,MB)⟩ for values of x = MB − 5log (h) + z ranging from x = −19 to x = −22 with steps of Δx = 0.25, respectively from left to right. |
With the VIPERS first data release, we perform an initial redshift-space distortion analysis, considering a single redshift interval of 0.7 < z < 1.2 to probe the highest redshifts where the growth rate is little-konwn. We select all galaxies above the magnitude limit of the survey in that interval. The effective pair-weighted mean redshift of the subsample is z = 0.80. The measured anisotropic correlation function ξ(rp,π) is shown in the top panel of Fig. 14. We have used here a linear binning of Δrp = Δπ = 1 h-1 Mpc. One can see in this figure the two main redshift-space distortion effects: the elongation along the line-of-sight, or Finger-of-God effect, which is due to galaxy random motions within virialised objects and the squashing effect on large scales, or Kaiser effect, which represents the coherent large-scale motions of galaxies towards overdensities. The latter effect is the one we are interested in since its amplitude is directly related to the growth rate of perturbations. Compared to the first measurement at such high redshift done with the VVDS survey (Guzzo et al. 2008), this signature is detected with much larger significance, with the flattening being apparent to rp > 30 h-1 Mpc.
The anisotropic correlation has been extensively used in the literature to measure the
growth rate or the distortion parameter β (e.g. Hawkins et al. 2003; Guzzo et al.
2008; Cabré & Gaztañaga 2009;
Beutler et al. 2012; Contreras et al. 2013). However, with the increasing size and
statistical power of redshift surveys, an alternative approach has grown in importance:
the use of the multipole moments of the anisotropic correlation function. This approach
has the main advantage of reducing the number of observables, compressing the cosmological
information contained in the correlation function. In turn, this eases the estimation of
the covariance matrices associated with the data. We adopt this methodology in this
analysis and fit for the two first non-null moments
ξ0(s) and
ξ2(s), where most of the relevant
information is contained, and ignore the contributions of the more noisy subsequent
orders. The multipole moments are measured from ξ(s,μ)
which is obtained exactly as for
ξ(rp,π), except that the
redshift-space separation vector s is now decomposed into
the polar coordinates (s,μ) such that
rp = s(1 − μ2)1/2
and π = sμ. The multipole moments are related to
ξ(s,μ) as, 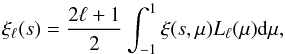 (23)where
Lℓ is the Legendre polynomial of order
ℓ. In practice the integration of Eq. (23) is approximated by a Riemann sum over the binned
ξ(s,μ). We use a logarithmic binning in
s of Δlog (s) = 0.1 and linear binning in
μ with Δμ = 0.02.
(23)where
Lℓ is the Legendre polynomial of order
ℓ. In practice the integration of Eq. (23) is approximated by a Riemann sum over the binned
ξ(s,μ). We use a logarithmic binning in
s of Δlog (s) = 0.1 and linear binning in
μ with Δμ = 0.02.
 |
Fig. 14 Anisotropic correlation functions of galaxies at 0.7 < z < 1.2. The top panel shows the results for the VIPERS first data release, deduced by the Landy-Szalay estimator counting pairs in cells of side 1 h-1 Mpc. The lower two panels show the results of two simulations, which span the 68% confidence range on the fitted value of the large-scale flattening (see Sect. 7.4). |
7.2. Covariance matrix, error estimation, and fitting procedure
The different bins in the observed correlation function and associated multipole moments
are correlated to some degree, and this must be allowed for in order to fit the
measurements with theoretical models. We estimate the covariance matrix of the monopole
and quadrupole signal using the MultiDark (MD) and Pinocchio (PN) HOD mocks. The generic
elements of the matrix can be evaluated as
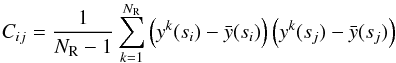 (24)where
NR is the number of mock realisations,
y(s) is the quantity of interest, and the indices
i,j run over the data points.
(24)where
NR is the number of mock realisations,
y(s) is the quantity of interest, and the indices
i,j run over the data points.
The number of degrees of freedom in the multipole moments varies between 11 and 15
depending on the scales considered. Because we have only 26 MD mock realisations, the
covariance matrix elements cannot be constrained accurately with the MD mocks only: the
covariance matrix is unbiased, but it can have substantial noise. To mitigate the noise
and obtain an accurate estimate of the covariance matrix, we apply the shrinkage method
(Pope & Szapudi 2008), using the
covariance matrix obtained with the 200 PN mocks as the target matrix. The PN mocks are
more numerous and therefore each element of the associated covariance matrix is very well
constrained, although the covariance may be biased to some extent. This bias is related to
inaccuracies in the predicted moments, which are mainly driven by the limited accuracy of
the Zel’dovich approximation used in the PN mocks to predict the peculiar velocity field.
The shrinkage technique allows the optimal combination of an empirical estimate of the
covariance with a target covariance, minimising the total mean squared error compared to
the true underlying covariance. An optimal covariance matrix C is then
obtained with 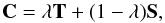 (25)where λ
is the shrinkage intensity and the target T and empirical S
covariance matrices correspond respectively to those obtained from the PN and MD mocks.
λ is calculated from (Pope &
Szapudi 2008)
(25)where λ
is the shrinkage intensity and the target T and empirical S
covariance matrices correspond respectively to those obtained from the PN and MD mocks.
λ is calculated from (Pope &
Szapudi 2008) 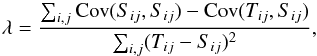 (26)where
Cov(Aij,Bij)
stands for the covariance between the elements (i,j) of the matrices
A and B. We note that, since the empirical and target matrices
are independent, the term
Cov(Tij,Sij)
vanishes in the numerator of Eq. (26). The
effect of shrinkage estimation on the MD covariance matrix is shown in Fig. 15.
(26)where
Cov(Aij,Bij)
stands for the covariance between the elements (i,j) of the matrices
A and B. We note that, since the empirical and target matrices
are independent, the term
Cov(Tij,Sij)
vanishes in the numerator of Eq. (26). The
effect of shrinkage estimation on the MD covariance matrix is shown in Fig. 15.
To measure the growth rate of structure we perform a maximum likelihood analysis of the
data given models of redshift-space distortions by adopting the likelihood function ℒ:
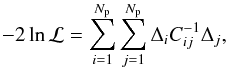 (27)where
Np is the number of points in the fit, Δ is the data-model
difference vector, and C is the covariance matrix. The likelihood is
performed on the quantity
y(s) = s2ξℓ(s),
rather than simply
y(s) = ξℓ(s)
to reduce the range of variations of multipole values at different s in
the fit. In the end, the quantity which is matched with model predictions is the
concatenation of s2ξ0 and
s2ξ2 for the set of separations
considered.
(27)where
Np is the number of points in the fit, Δ is the data-model
difference vector, and C is the covariance matrix. The likelihood is
performed on the quantity
y(s) = s2ξℓ(s),
rather than simply
y(s) = ξℓ(s)
to reduce the range of variations of multipole values at different s in
the fit. In the end, the quantity which is matched with model predictions is the
concatenation of s2ξ0 and
s2ξ2 for the set of separations
considered.
As a final remark, we note that we use the direct inverse of the covariance matrix without applying the correction discussed by Hartlap et al. (2007), as it is not clear how the size of the correction is affected by the shrinkage estimation technique. The resulting errors derived from the likelihood are well matched to the distribution of best-fit values from the mocks, which gives us confidence that only a small correction, if any, would be necessary.
7.3. Models
The formalism that describes redshift-space anisotropies in the power spectrum can be
derived from writing the mass density conservation in real and redshift space (Kaiser 1987). In particular, in the plane-parallel
approximation, which is assumed in this analysis, the anisotropic power spectrum of mass
has the general compact form (Scoccimarro et al.
1999) ![\begin{eqnarray} P^{\rm s}(k,\nu)&=&\int \frac{\d^3\boldsymbol{r}}{(2\pi)^3} {\rm e}^{-{\rm i}\boldsymbol{k} \cdot \boldsymbol{r}}\left<{\rm e}^{-{\rm i}kf\nu \Delta u_\parallel} \right. \nonumber \\ \label{eq:rspk}&& \left.\times [\delta(\boldsymbol{x})+\nu^2 f \theta(\boldsymbol{x})][\delta(\boldsymbol{x}^\prime)+\nu^2 f \theta(\boldsymbol{x}^\prime)]\right> \end{eqnarray}](/articles/aa/full_html/2013/09/aa21463-13/aa21463-13-eq238.png) (28)where
ν = k∥/k,
u∥(r) = −v∥(r)/(faH(a)),
v∥(r) is the line-of-sight
component of the peculiar velocity, δ is the density field,
θ is the divergence of the velocity field,
Δu∥ = u∥(x) − u∥(x′)
and
r = x − x′.
Although exact, Eq. (28) is impractical
for direct use on redshift survey measurements and several models have been proposed to
approximate it. In the assumption that galaxies linearly trace the underlying mass density
field with a bias b, we can build three empirical models. These take the
form,
(28)where
ν = k∥/k,
u∥(r) = −v∥(r)/(faH(a)),
v∥(r) is the line-of-sight
component of the peculiar velocity, δ is the density field,
θ is the divergence of the velocity field,
Δu∥ = u∥(x) − u∥(x′)
and
r = x − x′.
Although exact, Eq. (28) is impractical
for direct use on redshift survey measurements and several models have been proposed to
approximate it. In the assumption that galaxies linearly trace the underlying mass density
field with a bias b, we can build three empirical models. These take the
form, 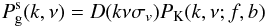 (29)where,
(29)where,
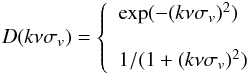 and,
and,
![\begin{eqnarray} P_{\rm K}(k,\nu;f,b) &= & \nonumber \\ &&\left\{ \nonumber \begin{array}{ll} {b^2 \Pdd(k)+2\nu^2 fb \Pdd(k) +\nu^4 f^2 \Pdd(k)} &{\rm (model~A)} \\ \\ {b^2 \Pdd(k)+2\nu^2 fb \Pdt(k) +\nu^4 f^2 \Ptt(k)} & {\rm (model~B)} \\ \\ b^2 \Pdd(k)+2\nu^2 fb \Pdt(k) +\nu^4 f^2 \Ptt(k) \\[2mm] {+ C_A(k,\nu;f,b) + C_B(k,\nu;f,b).} & {\rm (model~C)} \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21463-13/aa21463-13-eq248.png) In
these equations Pδδ,
Pδθ,
Pθθ are respectively the non-linear mass
density–density, density–velocity divergence, and velocity divergence–velocity divergence
power spectra and σv is an effective pairwise
velocity dispersion that we can fit for and then treat as a nuisance parameter. The
expressions for
CA(k,ν;f,b)
and
CB(k,ν;f,b)
are given in Appendix A of de la Torre & Guzzo
(2012). These empirical models can be seen in configuration space, as a
convolution of a damping function
D(kμσv),
which we assume to be Gaussian or Lorentzian in Fourier space, and a term involving the
density and velocity divergence correlation functions and their spherical Bessel
transforms. While the first term essentially (but not only) describes the Finger-of-God
effect, the second, PK(k,ν,b), describes the
Kaiser effect. We note that model A is the classical dispersion model (Peacock & Dodds 1994) based on the linear Kaiser (1987) model; model B is the generalisation
proposed by Scoccimarro (2004) that accounts for
the non-linear coupling between the density and velocity fields, making explicitly
appearing the velocity divergence auto-power spectrum and density–velocity divergence
cross-power spectrum; model C is an extension of model B that contains the two additional
correction terms proposed by Taruya et al. (2010)
to correctly account for the coupling between the Kaiser and damping terms. We refer the
reader to de la Torre & Guzzo (2012) for a
thorough description of these models.
In
these equations Pδδ,
Pδθ,
Pθθ are respectively the non-linear mass
density–density, density–velocity divergence, and velocity divergence–velocity divergence
power spectra and σv is an effective pairwise
velocity dispersion that we can fit for and then treat as a nuisance parameter. The
expressions for
CA(k,ν;f,b)
and
CB(k,ν;f,b)
are given in Appendix A of de la Torre & Guzzo
(2012). These empirical models can be seen in configuration space, as a
convolution of a damping function
D(kμσv),
which we assume to be Gaussian or Lorentzian in Fourier space, and a term involving the
density and velocity divergence correlation functions and their spherical Bessel
transforms. While the first term essentially (but not only) describes the Finger-of-God
effect, the second, PK(k,ν,b), describes the
Kaiser effect. We note that model A is the classical dispersion model (Peacock & Dodds 1994) based on the linear Kaiser (1987) model; model B is the generalisation
proposed by Scoccimarro (2004) that accounts for
the non-linear coupling between the density and velocity fields, making explicitly
appearing the velocity divergence auto-power spectrum and density–velocity divergence
cross-power spectrum; model C is an extension of model B that contains the two additional
correction terms proposed by Taruya et al. (2010)
to correctly account for the coupling between the Kaiser and damping terms. We refer the
reader to de la Torre & Guzzo (2012) for a
thorough description of these models.
 |
Fig. 15 Covariance matrix for the redshift-space distortions analysis. While the lower triangle represents the covariance matrix obtained directly from the MD mocks, the upper triangle corresponds to that obtained after performing shrinkage estimation. |
In the end, the model 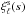 are obtained from their Fourier
counterparts,
are obtained from their Fourier
counterparts, 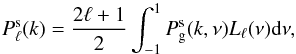 (30)as
(30)as 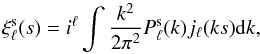 (31)where
jℓ denotes the spherical Bessel functions.
(31)where
jℓ denotes the spherical Bessel functions.
The redshift-space distortion models involve the knowledge of the underlying mass non-linear power spectra of density and velocity divergence at the effective redshift of the sample. Although the real-space non-linear correlation function of galaxies can be recovered from the deprojection of the observed projected correlation function (e.g. Bianchi et al. 2012) and thus be used to some extent as an input of the model (e.g. Hamilton 1992), it is not feasible for the more advanced models which involve the velocity divergence power spectrum. The non-linear power spectra can, however, be predicted from perturbation theory or simulations for different cosmological models. In the case of a ΛCDM cosmology, the shape of the non-linear power spectra depends on the parameters P = (Ωm,Ωb,h,ns,σ8) and can be obtained to a great accuracy from semi-analytical prescriptions such as HALOFIT. In this analysis we use the latest calibration of HALOFIT by Bird et al. (2012) to obtain Pδδ and use the fitting functions of Jennings (2012) to predict Pθθ and Pδθ from Pδδ. The latter fitting functions are accurate at the few percent level up to k ≃ 0.3 at z = 1.
In the models, the bias and growth rate parameters b and
f are degenerate with the normalisation of the power spectrum parameter
σ8. Thus, in practice only the combination of
bσ8 and
fσ8 can be constrained if no assumption is
made on the actual value of σ8. This can be done by
renormalising the power spectra in the models so that
 , thus reparameterising the
models such that the parameters (b,f) are replaced by
(bσ8,fσ8)
in Eq. (29). This parameterisation can be
used for model A and B, although not for model C in which the correction term
CA involves the additional combinations:
, thus reparameterising the
models such that the parameters (b,f) are replaced by
(bσ8,fσ8)
in Eq. (29). This parameterisation can be
used for model A and B, although not for model C in which the correction term
CA involves the additional combinations:
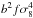 ,
,
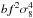 , and
, and
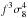 (see Taruya et al. 2010; de
la Torre & Guzzo 2012). The correction term
CA, which partially describes the effects
of the non-linear coupling between the damping and Kaiser terms, mostly affects the
monopole and quadrupole moments of the redshift-space power spectrum on scales of
k > 0.1 (Taruya
et al. 2010). Therefore, in principle
CA could help breaking the degeneracy
between f and σ8 although this has to be
verified in detail. In the end, in the case of model C we decided to treat
(f,b,σ8,σv)
as separate parameters in the fit.
(see Taruya et al. 2010; de
la Torre & Guzzo 2012). The correction term
CA, which partially describes the effects
of the non-linear coupling between the damping and Kaiser terms, mostly affects the
monopole and quadrupole moments of the redshift-space power spectrum on scales of
k > 0.1 (Taruya
et al. 2010). Therefore, in principle
CA could help breaking the degeneracy
between f and σ8 although this has to be
verified in detail. In the end, in the case of model C we decided to treat
(f,b,σ8,σv)
as separate parameters in the fit.
7.4. Detailed tests against mock data
 |
Fig. 16 Systematic and statistical errors on fσ8 obtained from the mock samples, for different models and minimum scales smin in the fit. The horizontal dashed line shows the expectation value while the shaded area marks the 15% region around the fiducial value. Note that the points have been slightly displaced horizontally around smin values of 5 h-1 Mpc, 6 h-1 Mpc, and 7 h-1 Mpc to improve the clarity of the figure. |
 |
Fig. 17 Monopole and quadrupole moments of the redshift-space correlations, as a function of scale. The shallow curves show the results for the 26 individual MultiDark simulation mocks; the points are for the measured VIPERS data at 0.7 < z < 1.2, with assigned error bars based on the scatter in the mocks. The solid and dotted lines correspond to the best fitting models to the data for model B with Gaussian or Lorentzian damping function respectively. |
We perform the redshift-space distortion analysis of the VIPERS data in the context of a flat ΛCDM cosmological model. Before considering the redshift-space distortions in the data, we first test the methodology and expected errors on fσ8 using the mock samples. We fix the shape of the mass non-linear power spectrum to that of the simulation (since the observed real-space correlations are of high accuracy) and perform a likelihood analysis of each individual MD mock. In the case of model C we also fix the normalisation of the power spectrum as discussed above. The distribution of best-fitting fσ8 values gives us a direct estimate of the probability distribution function of the parameter for a given fitting method, and serves as a check on the errors from the full likelihood function. We estimate the median and 68% confidence region of the distribution. These are shown in Fig. 16 for the different models presented in the previous section and for various minimum scales smin in the fit.
Model A is known to be the most biased model (e.g. Okumura & Jing 2011; Bianchi et al. 2012; de la Torre & Guzzo 2012) and our results confirm these findings. We thus decided not to describe in the following the detailed behaviour of this model and focus on models B and C. We find that in general model B tends to be less biased than model C, which is surprising at first sight as model C is the most advanced and supposed to be the most accurate (Kwan et al. 2012; de la Torre & Guzzo 2012). This could be due to the quite restricted scales that we consider and the limited validity of its implementation on scales below s ≃ 10 h-1 Mpc, as the maximum wavenumber to which we can predict Pδθ and Pθθ is about k = 0.3. We defer the investigation of this issue to the redshift-space distortion analysis of the final sample and concentrate here on model B. The shape of the damping function in the models also affects the recovered fσ8, as expected given the minimum scales we consider, although in the case of model B the change in fσ8 is at most 5%. Including smaller scales in the fit reduces the statistical error but at the price of slightly larger systematic error. Therefore from this test we decided to use model B and a compromise value for the minimum scale of smin = 6 h-1 Mpc.
7.5. The VIPERS result for the growth rate
These comprehensive tests of our methodology give us confidence that we can now proceed to the analysis of the real VIPERS data and expect to achieve results for the growth rate that are robust, and which can be used as a trustworthy test of the nature of gravity at high redshifts.
As explained earlier, we assume a fixed shape of the mass power spectrum consistent with the cosmological parameters obtained from WMAP9 (Hinshaw et al. 2012) and perform a maximum likelihood analysis on the data, considering variations in the parameters that are not well determined externally. The best-fitting models are shown in Fig. 17 when considering either a Gaussian or a Lorentzian damping function. Although the mock samples tend to slightly prefer models with Lorentzian damping as seen in Fig. 16, we find that the Gaussian damping provides a much better fit to the real data and we decided to quote the corresponding fσ8 as our final measurement.
We measure a value of 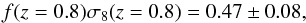 (32)which is consistent with
the General Relativity prediction in a flat ΛCDM Universe with cosmological parameters
given by WMAP9, for which the expected value is
f(0.8)σ8(0.8) = 0.45. We find that our
result is not significantly altered if we adopt a Planck cosmology (Planck Collaboration 2013) for the shape of the mass power spectrum,
changing our best-fitting fσ8 by only 0.2%.
This shows that given the volume probed by the survey, we are relatively insensitive to
the additional Alcock-Paczynski distortions (Alcock
& Paczynski 1979) on the correlation function. The marginalised
likelihood distribution of fσ8 is shown
superimposed on the mock results in Fig. 18. We see
that the preferred values of the growth rate are consistent with the mocks, in terms of
the width of the likelihood function being comparable to the scatter in mock fitted
values. To illustrate the degree of flattening of the anisotropic correlation function
induced by structure growth, we show in the middle and bottom panels of Fig. 14
ξ(rp,π) for two MD mocks
for which the measured fσ8 roughly coincide
with the 1σ limits around the best-fit
fσ8 value obtained in the data. We
therefore conclude that the initial VIPERS data prefer a growth rate that is fully
consistent with predictions based on standard gravity. Our measurement of
fσ8 is also in good agreement with previous
measurements at lower redshifts from 2dFGRS (Hawkins et
al. 2003), 2SLAQ (Ross et al. 2007), VVDS
(Guzzo et al. 2008), SDSS LRG (Cabré & Gaztañaga 2009; Samushia et al. 2012), WiggleZ (Blake et
al. 2012), BOSS (Reid et al. 2012), and
6dFGS (Beutler et al. 2012) surveys as shown in Fig.
19. In particular, it is compatible within
1σ with the results obtained in the VVDS (Guzzo et al. 2008) and WiggleZ (Blake et
al. 2012) surveys at a similar redshift, although WiggleZ measurements tend to
suggest lower fσ8 values, smaller than
expected in standard gravity (but see Contreras et al.
2013).
(32)which is consistent with
the General Relativity prediction in a flat ΛCDM Universe with cosmological parameters
given by WMAP9, for which the expected value is
f(0.8)σ8(0.8) = 0.45. We find that our
result is not significantly altered if we adopt a Planck cosmology (Planck Collaboration 2013) for the shape of the mass power spectrum,
changing our best-fitting fσ8 by only 0.2%.
This shows that given the volume probed by the survey, we are relatively insensitive to
the additional Alcock-Paczynski distortions (Alcock
& Paczynski 1979) on the correlation function. The marginalised
likelihood distribution of fσ8 is shown
superimposed on the mock results in Fig. 18. We see
that the preferred values of the growth rate are consistent with the mocks, in terms of
the width of the likelihood function being comparable to the scatter in mock fitted
values. To illustrate the degree of flattening of the anisotropic correlation function
induced by structure growth, we show in the middle and bottom panels of Fig. 14
ξ(rp,π) for two MD mocks
for which the measured fσ8 roughly coincide
with the 1σ limits around the best-fit
fσ8 value obtained in the data. We
therefore conclude that the initial VIPERS data prefer a growth rate that is fully
consistent with predictions based on standard gravity. Our measurement of
fσ8 is also in good agreement with previous
measurements at lower redshifts from 2dFGRS (Hawkins et
al. 2003), 2SLAQ (Ross et al. 2007), VVDS
(Guzzo et al. 2008), SDSS LRG (Cabré & Gaztañaga 2009; Samushia et al. 2012), WiggleZ (Blake et
al. 2012), BOSS (Reid et al. 2012), and
6dFGS (Beutler et al. 2012) surveys as shown in Fig.
19. In particular, it is compatible within
1σ with the results obtained in the VVDS (Guzzo et al. 2008) and WiggleZ (Blake et
al. 2012) surveys at a similar redshift, although WiggleZ measurements tend to
suggest lower fσ8 values, smaller than
expected in standard gravity (but see Contreras et al.
2013).
 |
Fig. 18 Marginalised likelihood distribution of fσ8 in the data (solid curve) and distribution of fitted values of fσ8 for the 26 individual MultiDark simulation mocks (histogram). These curves show a preferred value and a dispersion in the data that is consistent at the 1σ level with the distribution over the mocks. |
 |
Fig. 19 A plot of fσ8 versus redshift, showing VIPERS result contrasted with a compilation of recent measurements. The previous results from 2dFGRS (Hawkins et al. 2003), 2SLAQ (Ross et al. 2007), VVDS (Guzzo et al. 2008), SDSS LRG (Cabré & Gaztañaga 2009; Samushia et al. 2012), WiggleZ (Blake et al. 2012), BOSS (Reid et al. 2012), and 6dFGS (Beutler et al. 2012) surveys are shown with the different symbols (see inset). The thick solid (dashed) curve corresponds to the prediction for General Relativity in a ΛCDM model with WMAP9 (Planck) parameters, while the dotted, dot-dashed, and dot-dot-dashed curves are respectively Dvali-Gabadaze-Porrati (Dvali et al. 2000), coupled dark energy, and f(R) model expectations. For these models, the analytical growth rate predictions given in di Porto et al. (2012) have been used. |
Finally we compare our measurement to the predictions of three of the most plausible modified gravity models studied in di Porto et al. (2012). We consider Dvali-Gabadaze-Porrati (DGP, Dvali et al. 2000), f(R), and coupled dark energy models and show their predictions in Fig. 19 (see di Porto et al. 2012, for the detail of their analytical predictions). We find that our fσ8 measurement is currently unable to discriminate between these modified gravity models and standard gravity given the size of the uncertainty, although we expect to improve the constraints with the analysis of the VIPERS final dataset.
8. Conclusions
We have analysed in this paper the global real- and redshift-space clustering properties of galaxies in the VIPERS survey first data release. We have presented the selection function of the survey and the corrections that are needed in order to derive estimates of galaxy clustering that are free of observational biases. This has been achieved by using a large set of simulated mock realisations of the survey to quantify in detail the systematics and uncertainties on our clustering measurements.
The first data release of about 54 000 galaxies at 0.5 < z < 1.2 in the VIPERS survey allows a measurement of the real-space clustering of galaxies through the measurement of the projected two-point correlation function, to an unprecedented accuracy over 0.5 < z < 1.2. This permits detailed modelling of the halo occupation distribution at these redshifts to be carried out. From an initial HOD modelling of B-band luminosity selected samples, we have been able to accurately determine the characteristic halo masses for halo occupation in the redshift interval 0.5 < z < 1.0. These measurements are invaluable for creating realistic synthetic mock samples.
The main goal of VIPERS is to provide an accurate measurement of the growth rate of structure through the characterisation of the redshift-space distortions in the galaxy clustering pattern. With the first data release we have been able to provide an initial measurement of fσ8 at z = 0.8. We find a value of fσ8 = 0.47 ± 0.08 which is in agreement with previous measurements at lower redshifts. This allows us to put a new constraint on gravity at the epoch when the Universe was almost half its present age. Our measurement of fσ8 is statistically consistent with a Universe where the gravitational interactions between structures on 10 h-1 Mpc scales can be described by Einstein’s theory of gravity.
The present dataset represents the half-way stage of the VIPERS project, and the final survey will be large enough to subdivide our measurements and follow the evolution of fσ8 out to redshift one. This will allow us to address some issues such as the suggestion from the WiggleZ measurements that fσ8 is lower than expected at z > 0.5. Our measurement at z = 0.8 already argues against such a trend to some extent, but the larger redshift baseline and tighter errors from the final VIPERS dataset can be expected to deliver a definitive verdict on the high-redshift evolution of the strength of gravity.
We have used in this analyis a new version of this code, optimised to work on massively parallel computers, which is described in Monaco et al. (2013).
Acknowledgments
We acknowledge the crucial contribution of the ESO staff for the management of service observations. In particular, we are deeply grateful to M. Hilker for his constant help and support of this programme. Italian participation to VIPERS has been funded by INAF through PRIN 2008 and 2010 programmes. LG acknowledges support of the European Research Council through the Darklight ERC Advanced Research Grant (#291521). O.L.F. acknowledges support of the European Research Council through the EARLY ERC Advanced Research Grant (#268107). Polish participants have been supported by the Polish Ministry of Science (grant N N203 51 29 38), the Polish-Swiss Astro Project (co-financed by a grant from Switzerland, through the Swiss Contribution to the enlarged European Union), the European Associated Laboratory Astrophysics Poland-France HECOLS and a Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowship for Foreign Researchers (P11802). G.D.L. acknowledges financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 202781. W.J.P. and R.T. acknowledge financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 202686. W.J.P. is also grateful for support from the UK Science and Technology Facilities Council through the grant ST/I001204/1. E.B., F.M. and L.M. acknowledge the support from grants ASI-INAF I/023/12/0 and PRIN MIUR 2010-2011. P.M. acknowledges the support from the grant PRIN MIUR 2010-2011. This work made use of the facilities of HECToR, the UK’s national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc and NAG Ltd, and funded by the Office of Science and Technology through EPSRC’s High End Computing Programme. We are grateful to Ken Rice for assisting us with accessing HECToR facilities. The MultiDark Database used in this paper and the web application providing online access to it were constructed as part of the activities of the German Astrophysical Virtual Observatory as result of a collaboration between the Leibniz-Institute for Astrophysics Potsdam (AIP) and the Spanish MultiDark Consolider Project CSD2009-00064. The Bolshoi and MultiDark simulations were run on the NASA’s Pleiades supercomputer at the NASA Ames Research Center.
References
- Alcock, C., & Paczynski, B. 1979, Nature, 281, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., & Weinberg, D. H. 2002, ApJ, 575, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2012, MNRAS, 423, 3430 [NASA ADS] [CrossRef] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2013, MNRAS, 429, 3604 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, D., Guzzo, L., Branchini, E., et al. 2012, MNRAS, 427, 2420 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, S., Viel, M., & Haehnelt, M. G. 2012, MNRAS, 420, 2551 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Brough, S., Colless, M., et al. 2012, MNRAS, 425, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Bottini, D., Garilli, B., Maccagni, D., et al. 2005, PASP, 117, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Zheng, Z., White, M., et al. 2008, ApJ, 682, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Cabré, A., & Gaztañaga, E. 2009, MNRAS, 393, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, J., & White, M. 2010, ApJS, 190, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S. 2011, MNRAS, 416, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Peterson, B. A., Jackson, C., et al. 2003 [arXiv:astro-ph/0306581] [Google Scholar]
- Contreras, C., Blake, C., Poole, G. B., et al. 2013, MNRAS, 430, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Kilbinger, M., McCracken, H. J., et al. 2012, A&A, 542, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davidzon, I., Bolzonella, M., Coupon, J., et al. 2013, A&A, in press DOI: 10.1051/0004-6361/201321511 [Google Scholar]
- Davis, M., & Huchra, J. 1982, ApJ, 254, 437 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., & Guzzo, L. 2012, MNRAS, 427, 327 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., & Peacock, J. A. 2013, MNRAS, in press [arXiv:1212.3615] [Google Scholar]
- de la Torre, S., Meneux, B., De Lucia, G., et al. 2011, A&A, 525, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- di Porto, C., Amendola, L., & Branchini, E. 2012, MNRAS, 419, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Dvali, G., Gabadadze, G., & Porrati, M. 2000, Phys. Lett. B, 485, 208 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fisher, K. B., Davis, M., Strauss, M. A., Yahil, A., & Huchra, J. P. 1994, MNRAS, 267, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Le Fèvre, O., Guzzo, L., et al. 2008, A&A, 486, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garilli, B., Paioro, L., Scodeggio, M., et al. 2012, PASP, 124, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Tormen, G., Sheth, R. K., & van den Bosch, F. C. 2010, MNRAS, 404, 502 [NASA ADS] [Google Scholar]
- Goranova, Y., Hudelot, P., Magnard, F., et al. 2009, The CFHTLS T0006 Release, http://terapix.iap.fr/cplt/table_syn_T0006.html [Google Scholar]
- Guo, H., Zehavi, I., & Zheng, Z. 2012, ApJ, 756, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Pierleoni, M., Meneux, B., et al. 2008, Nature, 451, 541 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2013, A&A, submitted [arXiv:1303.2623] [Google Scholar]
- Hamilton, A. J. S. 1992, ApJ, 385, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, A. J. S. 1993, ApJ, 417, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hartlap, J., Simon, P., & Schneider, P. 2007, A&A, 464, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawkins, E., Maddox, S., Cole, S., et al. 2003, MNRAS, 346, 78 [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2012, ApJS, accepted [arXiv:1212.5226] [Google Scholar]
- Hudelot, P., Goranova, Y., Mellier, Y., et al. 2012, T0007: The Final CFHTLS Release, http://terapix.iap.fr/cplt/T0007/doc/T0007-doc.pdf [Google Scholar]
- Iovino, A., Cucciati, O., Scodeggio, M., et al. 2010, A&A, 509, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jain, B., & Khoury, J. 2010, Ann. Phys., 325, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Jennings, E. 2012, MNRAS, 427, L25 [NASA ADS] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Cucciati, O., et al. 2010, ApJ, 708, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Kwan, J., Lewis, G. F., & Linder, E. V. 2012, ApJ, 748, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Proc. SPIE 4841, eds. M. Iye, & A. F. M. Moorwood, 1670 [Google Scholar]
- Linder, E. V., & Cahn, R. N. 2007, Astropart. Phys., 28, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Malek, K., Solarz, A., Pollo, A., et al. 2013, A&A, 557, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchetti, A., Granett, B. R., Guzzo, L., et al. 2013, MNRAS, 428, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bolzonella, M., Branchini, E., et al. 2013, A&A, 557, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McDonald, P., & Seljak, U. 2009, J. Cosmol. Astropart. Phys., 10, 7 [Google Scholar]
- Meneux, B., Le Fèvre, O., Guzzo, L., et al. 2006, A&A, 452, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monaco, P., Sefusatti, E., Borgani, S., et al. 2013, MNRAS, 433, 2389 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, P., Theuns, T., & Taffoni, G. 2002, MNRAS, 331, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Okumura, T., & Jing, Y. P. 2011, ApJ, 726, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., & Dodds, S. J. 1994, MNRAS, 267, 1020 [NASA ADS] [Google Scholar]
- Peacock, J. A., & Smith, R. E. 2000, MNRAS, 318, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2013, A&A, submitted [arXiv:1303.5076] [Google Scholar]
- Pope, A. C., & Szapudi, I. 2008, MNRAS, 389, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., & White, M. 2011, MNRAS, 417, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., Samushia, L., White, M., et al. 2012, MNRAS, 426, 2719 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, N. P., da Ângela, J., Shanks, T., et al. 2007, MNRAS, 381, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Samushia, L., Percival, W. J., & Raccanelli, A. 2012, MNRAS, 420, 2102 [NASA ADS] [CrossRef] [Google Scholar]
- Scoccimarro, R. 2004, Phys. Rev. D, 70, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Scoccimarro, R., Couchman, H. M. P., & Frieman, J. A. 1999, ApJ, 517, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., Le Fèvre, O., & Guzzo, L. 2009, The Messenger, 135, 13 [NASA ADS] [Google Scholar]
- Seljak, U. 2000, MNRAS, 318, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., & McDonald, P. 2011, J. Cosmol. Astropart. Phys., 11, 39 [Google Scholar]
- Skibba, R., Sheth, R. K., Connolly, A. J., & Scranton, R. 2006, MNRAS, 369, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Taruya, A., Nishimichi, T., & Saito, S. 2010, Phys. Rev. D, 82, 063522 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., Norberg, P., Mo, H. J., & Yang, X. 2004, MNRAS, 352, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., More, S., Cacciato, M., Mo, H., & Yang, X. 2013, MNRAS, 430, 725 [NASA ADS] [CrossRef] [Google Scholar]
- White, M., Blanton, M., Bolton, A., et al. 2011, ApJ, 728, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Coil, A. L., & Zehavi, I. 2007, ApJ, 667, 760 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Galaxy mock catalogue construction
We provide in this appendix some details about the method that we used to create realistic galaxy catalogues based on the Halo Occupation Distribution (HOD) and Stellar-to-Halo Mass Relation (SHMR) formalisms. From the MultiDark simulation and Pinocchio halo lightcones described in Sect. 5.1, we created two types of galaxy mock catalogues: one containing B-band absolute magnitudes and associated quantities, and a second one containing stellar masses. We note that the stellar mass mock catalogues have not been explicitly used in this analysis, but in the accompanying VIPERS analyses of Marulli et al. (2013) and Davidzon et al. (2013).
For the first set of catalogues we use the HOD formalism and populated dark matter haloes
according to their mass by specifying the absolute B-band
magnitude-dependent halo occupation. We parametrised the latter using Eq. (15) and used the HOD parameters obtained from
the data and given in Sect. 6. We positioned central
galaxies at halo centres with probability given by a Bernoulli distribution function with
mean taken from Eq. (16) and assigned host
halo mean velocities to these galaxies. The number of satellite galaxies per halo is set
to follow a Poisson distribution with mean given by Eq. (17). We assumed that satellite galaxies follow the spatial and
velocity distribution of mass and randomly distributed their halo-centric radial position
so as to reproduce a Navarro et al. (1996) (NFW)
radial profile, 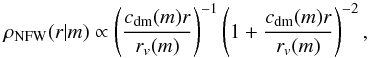 (A.1)where
cdm is the concentration parameter and
rv(m) is the virial
radius defined as
(A.1)where
cdm is the concentration parameter and
rv(m) is the virial
radius defined as 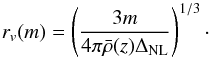 (A.2)In this equation,
(A.2)In this equation,
 is the mean matter density at redshift z and ΔNL = 200 is the
critical overdensity for virialisation in our definition. We assumed the
mass–concentration relation of Bullock et al.
(2001):
is the mean matter density at redshift z and ΔNL = 200 is the
critical overdensity for virialisation in our definition. We assumed the
mass–concentration relation of Bullock et al.
(2001): 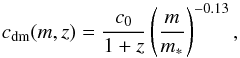 (A.3)where
c0 = 11 and m∗ is the non-linear
mass scale at z = 0 defined such as
σ(m∗,0) = δc.
Here δc and σ(m,0) are
respectively the critical overdensity (we fixed δc = 1.686)
and the standard deviation of mass fluctuations at z = 0. The latter is
defined as
(A.3)where
c0 = 11 and m∗ is the non-linear
mass scale at z = 0 defined such as
σ(m∗,0) = δc.
Here δc and σ(m,0) are
respectively the critical overdensity (we fixed δc = 1.686)
and the standard deviation of mass fluctuations at z = 0. The latter is
defined as 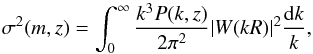 (A.4)where
(A.4)where
![\hbox{$R=\left[3m/\left(4\pi\bar{\rho}(z)\right)\right]^{1/3}$}](/articles/aa/full_html/2013/09/aa21463-13/aa21463-13-eq306.png) ,
P(k,z) is the linear mass power spectrum at redshift
z in the adopted cosmology, and W(x)
is the Fourier transform of a top-hat filter. In order to assign satellite galaxy
velocities, we assumed halo isotropy and sphericity, and drew velocities from Gaussian
distribution functions along each Cartesian dimension with velocity dispersion given by
(van den Bosch et al. 2004):
,
P(k,z) is the linear mass power spectrum at redshift
z in the adopted cosmology, and W(x)
is the Fourier transform of a top-hat filter. In order to assign satellite galaxy
velocities, we assumed halo isotropy and sphericity, and drew velocities from Gaussian
distribution functions along each Cartesian dimension with velocity dispersion given by
(van den Bosch et al. 2004):
 where
ψ(r) is the gravitational potential,
G is the gravitational constant,
f(x) = ln(1 + x) − x/(1 + x),
and
where
ψ(r) is the gravitational potential,
G is the gravitational constant,
f(x) = ln(1 + x) − x/(1 + x),
and 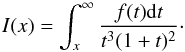 (A.7)In these mocks, the
absolute B-band magnitude for each galaxy was obtained following Skibba et al. (2006). From the mean rest-frame
B − i′ colour and K-corrections observed in
the data we then derived absolute and apparent i′-band
magnitudes for each simulated galaxy.
(A.7)In these mocks, the
absolute B-band magnitude for each galaxy was obtained following Skibba et al. (2006). From the mean rest-frame
B − i′ colour and K-corrections observed in
the data we then derived absolute and apparent i′-band
magnitudes for each simulated galaxy.
For the mock catalogues with stellar masses, we followed the SHMR approach which is based
on the assumption of a monotonic relation between halo/subhalo masses and the stellar
masses of the galaxies associated with them. We first populated the haloes in the
lightcones with subhaloes. For this we randomly distributed subhaloes around each distinct
halo following a NFW profile so that their number density satisfies the subhalo mass
function of Giocoli et al. (2010):
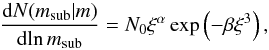 (A.8)where
msub is the subhalo mass,
ξ = msub/m,
α = −0.8, β = 12.2715, and
N0 = 0.18. We then assigned a galaxy to each halo and
subhalo, with a stellar mass given by the SHMR of Moster
et al. (2013). The galaxy velocities were assigned in a similar way as for the
HOD catalogues, with galaxies associated with distinct haloes and subhaloes being
considered as central and satellite galaxies respectively.
(A.8)where
msub is the subhalo mass,
ξ = msub/m,
α = −0.8, β = 12.2715, and
N0 = 0.18. We then assigned a galaxy to each halo and
subhalo, with a stellar mass given by the SHMR of Moster
et al. (2013). The galaxy velocities were assigned in a similar way as for the
HOD catalogues, with galaxies associated with distinct haloes and subhaloes being
considered as central and satellite galaxies respectively.
All Figures
 |
Fig. 1 Redshift distribution of the combined W1+W4 galaxy sample when including only reliable redshifts (filled histogram) and that corrected for the full survey completeness (empty histogram) scaled down by 40% (see text). The curve shows the best-fitting template redshift distribution given by Eq. (2) applied to the uncorrected observed distribution. |
| In the text | |
 |
Fig. 2 Illustration of the slit assignment in pointing W1P082. The slits are shown in red and associated rectangles represent the typical dispersion of the spectra. All objects meeting the survey selection criteria (potential spectroscopic targets) are represented by black circles. |
| In the text | |
 |
Fig. 3 Completeness fraction of angular galaxy pairs due to the slit-spectroscopy strategy in the W1 and W4 fields for all galaxies at 0.5 < z < 1.0. This has been obtained from the parent and spectroscopic sample angular correlation function. |
| In the text | |
 |
Fig. 4 Variations of the target success rate (TSR) with quadrants. The TSR quantifies our ability of obtaining spectra from the potential targets meeting the survey selection in the parent photometric sample. The quadrants filled in black correspond to failed observations where no spectroscopy has been taken. |
| In the text | |
 |
Fig. 5 Variations of the spectroscopic success rate (SSR) with quadrants. The SSR quantifies our ability of determining galaxy redshifts from observed spectra. The quadrants filled in black correspond to failed observations where no spectroscopy has been taken. |
| In the text | |
 |
Fig. 6 Comparison of different estimators of the radial distribution in the combined W1+W4 sample. The filled histogram shows the number of galaxies in fine bins of radial comoving distance. The different curves correspond to random radial distribution realisations normalised to the number of objects in the data, obtained using the Vmax (solid), Gaussian filtering (dashed and dot-dashed), or analytical (dotted) methods. The vertical line shows the minimum redshift considered in this analysis, i.e. z = 0.5. |
| In the text | |
 |
Fig. 7 Impact of the use of different estimators of the radial distribution on the shape of the projected correlation function. The projected correlation functions obtained using the Vmax (solid), Gaussian filtering (dashed and dot-dashed), or analytical (dotted) methods are shown in the top panel, while the relative fractional differences with respect to the Vmax method are presented in the bottom panel. |
| In the text | |
 |
Fig. 8 Systematic error on the projected correlation function and impact of different corrections. This is calculated considering all VIPERS galaxies in the redshift intervals 0.5 < z < 0.75 (top panel) and 0.75 < z < 1 (bottom panel). |
| In the text | |
 |
Fig. 9 Effect of correcting for quadrant-to-quadrant variations of the colour selection in the estimation of the projected correlation function, when using the CFHTLS-T0007 sample as the reference photometric catalogue. The top panel shows the projected correlation functions with and without the correction applied, while the bottom panel presents their relative fractional difference. |
| In the text | |
 |
Fig. 10 Top panel: projected correlation functions of VIPERS galaxies in the
redshift interval
0.5 < z < 1 for the
individual W1 and W4 fields as well as for the combined sample. As a comparison, the
± 1σ dispersion among the mean
wp(rp) in the mocks is
shown with the shaded region and the non-linear mass prediction in the assumed
cosmology with the dotted curve. Bottom panel: relative difference
between the measured wp(rp)
in the W1 and W4 fields and the combined projected correlation function
|
| In the text | |
 |
Fig. 11 Measured and best-fitting HOD model projected correlation functions wp(rp), for different luminosity-threshold subsamples of galaxies at 0.7 < z < 0.9. The wp(rp) for the MB − 5log (h) < −20.5, MB − 5log (h) < −21.0, and MB − 5log (h) < −21.5 cases have been multiplied by respectively 2, 3, and 4 to improve the clarity of the figure. |
| In the text | |
 |
Fig. 12 Dependence of Mmin and M1 HOD parameters on redshift and absolute magnitude threshold in B-band. The absolute magnitude threshold samples are plot in terms of their implied number density ng. The VIPERS results are compared to the pervious measurements performed in the DEEP2 (Zheng et al. 2007), BOSS (White et al. 2011), and CFHTLS (Coupon et al. 2012) surveys. |
| In the text | |
 |
Fig. 13 Evolution of the B-band absolute magnitude-dependent HOD. The curves show ⟨Ngal(m|z,MB)⟩ for values of x = MB − 5log (h) + z ranging from x = −19 to x = −22 with steps of Δx = 0.25, respectively from left to right. |
| In the text | |
 |
Fig. 14 Anisotropic correlation functions of galaxies at 0.7 < z < 1.2. The top panel shows the results for the VIPERS first data release, deduced by the Landy-Szalay estimator counting pairs in cells of side 1 h-1 Mpc. The lower two panels show the results of two simulations, which span the 68% confidence range on the fitted value of the large-scale flattening (see Sect. 7.4). |
| In the text | |
 |
Fig. 15 Covariance matrix for the redshift-space distortions analysis. While the lower triangle represents the covariance matrix obtained directly from the MD mocks, the upper triangle corresponds to that obtained after performing shrinkage estimation. |
| In the text | |
 |
Fig. 16 Systematic and statistical errors on fσ8 obtained from the mock samples, for different models and minimum scales smin in the fit. The horizontal dashed line shows the expectation value while the shaded area marks the 15% region around the fiducial value. Note that the points have been slightly displaced horizontally around smin values of 5 h-1 Mpc, 6 h-1 Mpc, and 7 h-1 Mpc to improve the clarity of the figure. |
| In the text | |
 |
Fig. 17 Monopole and quadrupole moments of the redshift-space correlations, as a function of scale. The shallow curves show the results for the 26 individual MultiDark simulation mocks; the points are for the measured VIPERS data at 0.7 < z < 1.2, with assigned error bars based on the scatter in the mocks. The solid and dotted lines correspond to the best fitting models to the data for model B with Gaussian or Lorentzian damping function respectively. |
| In the text | |
 |
Fig. 18 Marginalised likelihood distribution of fσ8 in the data (solid curve) and distribution of fitted values of fσ8 for the 26 individual MultiDark simulation mocks (histogram). These curves show a preferred value and a dispersion in the data that is consistent at the 1σ level with the distribution over the mocks. |
| In the text | |
 |
Fig. 19 A plot of fσ8 versus redshift, showing VIPERS result contrasted with a compilation of recent measurements. The previous results from 2dFGRS (Hawkins et al. 2003), 2SLAQ (Ross et al. 2007), VVDS (Guzzo et al. 2008), SDSS LRG (Cabré & Gaztañaga 2009; Samushia et al. 2012), WiggleZ (Blake et al. 2012), BOSS (Reid et al. 2012), and 6dFGS (Beutler et al. 2012) surveys are shown with the different symbols (see inset). The thick solid (dashed) curve corresponds to the prediction for General Relativity in a ΛCDM model with WMAP9 (Planck) parameters, while the dotted, dot-dashed, and dot-dot-dashed curves are respectively Dvali-Gabadaze-Porrati (Dvali et al. 2000), coupled dark energy, and f(R) model expectations. For these models, the analytical growth rate predictions given in di Porto et al. (2012) have been used. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.