EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A115 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A115
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201220475
Published online 17 May 2013

© ESO, 2013

1. Introduction

Independent of the various formation scenarios for high-mass stars that are discussed extensively in the literature (e.g., Zinnecker & Yorke 2007; Beuther et al. 2007), the initial conditions required to allow high-mass star formation at all are still poorly characterized. The initial debate even ranged around the question whether high-mass starless gas clumps should exist at all, or whether the collapse of massive gas clumps starts immediately without any clear starless phase in the high-mass regime (e.g., Motte et al. 2007). Recent studies indicate that the time where massive gas clumps exist without embedded star formation is relatively short (on the order of 50 000 yrs), but nevertheless, high-mass starless gas clumps do exist (e.g., Russeil et al. 2010; Tackenberg et al. 2012).

Current questions in that field are: Are high-mass gas clumps dominated by a single fragment or do we witness already strong fragmentation during earliest evolutionary stages (e.g., Bontemps et al. 2010)? What are the kinematic properties of the gas? Are the clumps sub- or super-virial? Do we see streaming motions indicative of turbulent flows (e.g., Bergin et al. 2004; Vázquez-Semadeni et al. 2006; Heitsch et al. 2008; Banerjee et al. 2009)?

To address these questions high spatial resolution is mandatory. Furthermore, to study the dense gas, dust continuum as well as spectral line observations are required. Therefore we tackle these questions via a dedicated study of the genuine high-mass starless gas clump IRDC 18310-4 that was first identified by Sridharan et al. (2005). Their early study based on 1.2 mm continuum emission, 8 μm extinction and NH3 emission revealed an infrared dark gas clump with a mass of ~ 840 M⊙, a temperature of ~18 K, and a NH3(1,1) line-width measured with the Effelsberg 100 m telescope with 40′′ spatial resolution of ~ 1.7 km s-1. The kinematic distance of the source is ~4.9 ± 0.26 kpc (Ragan et al. 2012a, recalculated following Reid et al. 2009) and its velocity of rest vlsr ~ 86.5 km s-1 (Sridharan et al. 2005).

The target region is at a projected separation of ~3.4′ (at the given distance corresponding to ~5.1 pc) from the luminous high-mass protostellar object (HMPO) IRAS 18310-0825 (Sridharan et al. 2002; Beuther et al. 2002) but otherwise in no outstanding part of our Galaxy. This region is part of the Herschel Earliest Phases of Star Formation (EPoS) key project that studies a large sample of high- and low-mass star-forming regions at the earliest evolutionary stages (Ragan et al. 2012a; Launhardt et al. 2013; Henning et al. 2010; Linz et al. 2010; Beuther et al. 2010, 2012b; Stutz et al. 2010).

Except for these characterizations, little additional information exist for that region. Here, we present Herschel far-infrared continuum observations as well as single-dish and interferometrically obtained N2H+(1–0) observations from the Nobeyama 45 m telescope and the Plateau de Bure Interferometer (PdBI). The latter data also allow us to image high-spatial-resolution 3 mm continuum data.

2. Observations

2.1. Herschel

The cloud complex with a size of ~6′ × 6′ was observed with PACS (Poglitsch et al. 2010) on Herschel (Pilbratt et al. 2010) on April 19th, 2011 (PACS OBS ID 134221906[0-3]). Scan maps in two orthogonal directions with scan leg lengths of ~10′ were obtained with the medium scan speed of 20′′/s. The raw data have been reduced up to level-1 with the HIPE software (Poglitsch et al. 2010; Ott 2010), version 6.0, build 1932. Besides the standard steps, we applied a 2nd level deglitching, in order to remove bad data values from a given pixel map by σ-clipping the flux values which contribute to each pixel. We used the time-ordered option and applied a 25σ threshold. The final level-2 maps were processed using Scanamorphos version 8 (Roussel 2012). Since the field of view contains bright emission on scales larger than the map, we applied the “galactic” option and included the non-zero-acceleration telescope turn-around data. The flux correction factors provided by the PACS ICC team were applied. The 70 μm extinction feature and the PdBI continuum and line data exhibited a small offset of approximately 3′′ in RA and 1′′ in Dec. Although the interferometer positional accuracy is usually superior because of the extremely well-known positions of the reference quasars, we double-checked the 70 μm PACS data via a comparison to the Spitzer MIPSGAL 24 μm survey which has also a very high spatial accuracy (Carey et al. 2009). Again, the same offset between MIPSGAL 24 μm and Herschel 70 μm was found. These Herschel data were taken at still an early Herschel time, and positional offsets on this order are known during that time. Therefore, we shifted the 70 μm map by this little offset in the high-resolution overlays from Fig. 2 onwards. The spatial resolution of the 70, 100 and 160 μm data is 5.6′′,6.8′′ and 11.4′′, respectively.

Maps at 250, 350, and 500 μm were obtained with SPIRE (Griffin et al. 2010) on March 11th, 2010 (SPIRE OBS ID 1342192067). Two times two 20′ scan legs were used to cover the source. The data were processed up to level-1 within HIPE, developer build 5.0, branch 1892, calibration tree 5.1 using the standard photometer script (POF5_pipeline.py, dated 2.3.2010) provided by the SPIRE ICC team. The resulting level-1 maps have been further reduced using Scanamorphos, version 9 (patched, dated 08.03.2011). This version included again the essential de-striping for maps with less than 3 scan legs per scan. In addition, we used the “galactic” option and included the non-zero-acceleration telescope turn-around data. Corrections for the transition from point sources to extended sources were applied according to the SPIRE Manual. The spatial resolution of the 250, 350 and 500 μm data is 18.1′′,24.9′′ and 36.6′′, respectively.

2.2. Plateau de Bure Interferometer

We observed IRDC 18310-4 with the PdBI during five nights in October and November 2009 at 93 GHz in the C and D configurations covering projected baselines between approximately 13 and 175 m. The observations were conducted in a track-sharing mode together with the IRDC 18454-1 in the neighborhood of W43 (Beuther et al. 2012b). The 3 mm receivers were tuned to 92.835 GHz in the lower sideband covering the N2H+(1–0) as well as the 3.23 mm continuum emission. At the given frequency, the primary beam of the PdBI is ~54′′. For continuum measurements we placed six 320 MHz correlator units in the band, the spectral lines were excluded in averaging the units to produce the final continuum image. Temporal fluctuations of amplitude and phase were calibrated with frequent observations of the quasars 1827+062 and 1829-106. The amplitude scale was derived from measurements of MWC 349 and 3c454.3. We estimate the final flux accuracy to be correct to within ~15%. The phase reference center is RA (J2000.0) 18:33:39.468 and Dec (J2000.0) –08:21:07.65, and the velocity of rest vlsr is 86.5 km s-1 for the two velocity components, respectively. The data were imaged with a robust weighting scheme close to uniform weighting. The synthesized beam of the line and continuum data is 4.3′′ × 3.0′′ with a PA of 14 degrees. The 3σ continuum rms is 0.24 mJy beam-1. The 3σ rms of the N2H+(1–0) data measured from an emission-free channel with a spectral resolution of 0.2 km s-1 is 21 mJy beam-1. Data calibration and imaging was performed with the GILDAS software package1.

2.3. Nobeyama 45 m telescope

The N2H+ data has been observed using the BEARS receiver at the NRO 45 m telescope in Nobeyama, Japan, in April 2010. The receiver has been tuned to 93.17346 MHz, covering the full hyperfine structure of the N2H+(1 − 0) transition with average system temperatures of Tsys ~ 200 K. At this frequency the telescope beam is 18.2′′ and the observing mode provides a spectral resolution of 0.2 km s-1 at a bandwidth of 32 MHz. The software package nostar (Sawada et al. 2008) was used for the data reduction, sampling the data to a pixel size of 7′′ with a spheroidal convolution and smoothing the spectral resolution to 0.5 km s-1. The rms of the final map is ~ 0.11 K per 0.5 km s-1 wide channel. Strong winds hampered the pointing for part of the observations, contributing to spatial uncertainties.

2.4. Merging of PdBI and Nobeyama data

To combine the N2H+(1 − 0) from the Nobeyama 45 m with the PdBI data, the Nobeyama data were converted into units of Jy, and then the combination was done within the GILDAS software package by the task uvshort. The synthesized beam of the combined dataset is 5.1′′ × 3.2′′ with a PA of 8 degrees. The 3σ rms of the merged N2H+(1–0) data measured from an emission-free channel with a spectral resolution of 0.2 km s-1 is 54 mJy beam-1.

thumbnail Fig. 1

Compilation of the continuum data from 70 μm to 500 μm wavelength in color-scale as labeled in each panel. The scale is chosen in each image individually to highlight the most important features. Contour levels of the 870 μm data start at the 3σ levels of 0.189 mJy beam-1 and continue in in 3σ steps. The white small box in the top-left panel marks the smaller region discussed in the remaining figures. A scale-bar is shown in the bottom-left panel.

thumbnail Fig. 2

Zoom into the central IRDC 18310-4. The color-scale shows the 70 μm extinction feature, and the contours present the 3.2 mm PdBI continuum emission starting at 3σ and continuing in 2σ steps (1σ = 0.08 mJy beam-1). The mm-labels, a synthesized beam and a scale-bar are shown as well. The phase reference center is close to mm1 at RA (J2000.0) 18:33:39.468 and Dec (J2000.0) − 08:21:07.65, and the primary beam of the observations with ~54′′ is larger than the shown image size.

2.5. APEX and the IRAM 30 m continuum data

The 1.2 mm continuum data were first presented in Beuther et al. (2002) and the APEX 870 μm data are part of the ATLASGAL survey of the Galactic plane (Schuller et al. 2009). Beam sizes of the two datasets are 10.5′′ and 19.2′′, respectively. The 1σ rms values are 12 and 63 mJy beam-1, respectively.

3. Results

3.1. Continuum emission

Figure 1 presents an overview of the far-infrared to submm continuum data obtained toward the whole cloud complex with Herschel and APEX. While the IRAS source and an additional far-infrared source in the north are bright at all presented wavelengths, our target region IRDC 18310-4 shows considerable structure changes between 70 μm and 870 μm. While it is a strong emission source at long wavelengths, the source is only depicted as an absorption shadow at 70 and 100 μm. While we cannot exclude that some ongoing low-mass star formation may exist below our detection threshold, non-detections at far-infrared wavelengths are among the best indicators for genuine high-mass starless gas clumps.

The longest wavelengths 1.2 mm continuum data with a spatial resolution of 10.5′′ first presented in Beuther et al. (2002) are best suited to re-estimate the gas mass and column densities of IRDC 18310-4. Peak and integrated 1.2 mm fluxes are 132 mJy beam-1 and 717 mJy for that region, respectively. Assuming optically thin thermal emission from dust, a gas-to-dust mass ratio of 186 (Jenkins 2004; Draine et al. 2007) and a temperature of 18 K derived from NH3 observations (Sridharan et al. 2005) as well as the Herschel continuum data (see below), we can estimate masses and column densities for different dust properties. Using standard ISM dust properties (Mathis et al. 1977, MRN1977, (κ1.2mm ~ 0.4 cm2 g-1)), the clump mass and peak column density are ~1600 M⊙ and 2.5 × 1023 cm-2, respectively. If we use instead the dust properties discussed in Ossenkopf & Henning (1994) for thin ice mantles at densities of 105 cm-3 (OH94, κ1.2mm ~ 0.8 cm2 g-1), the corresponding values for mass and column density are ~800 M⊙ and 1.3 × 1023 cm-2, respectively. These two estimates can be considered as brackets around the real gas masses and column densities of that region.

Table 1

Core parameters from the PdBI 3.2 mm data.

Assuming a standard initial mass function (e.g., Kroupa 2001) and a relatively high star formation efficiency of ~30% which should be appropriate for such dense gas clumps (e.g., Alves et al. 2007), one needs approximately 1000 M⊙ initial gas mass to form a cluster with at least one 20 M⊙ star in the end. Given the mass ranges estimated above, IRDC 18310-4 should be capable of high-mass star formation. Considering column density thresholds, Tackenberg et al. (2012) recently estimated that the initial gas column density for the Orion Nebula Cluster should have been approximately 1.8 × 1023 cm-2, which roughly agrees with the theoretical column density threshold from Krumholz & McKee (2008). Comparing this to the peak column density derived from the 1.2 mm data above, it also indicates that this region may form high-mass stars in the future. Commerçon et al. (2011) recently pointed out that not only high column density and heating can prevent fragmentation but that the magnetic field may be as important.

Figure 2 presents a zoom toward our central target region IRDC 18310-4. With the PdBI 3.2 mm continuum data, we can identify four sub-sources (mm1 to mm4, in the following also called cores, in contrast to the larger-scale environment labeled clump) above a 5σ threshold. While we detect a few more 3σ features, for the following analysis we only consider the 5σ detections mm1 to mm4. The cores are marginally resolved, and the source separation between mm1 to mm3 is done “by eye” at the lowest flux decrements between the cores. Outer edges are chosen at the 3σ level. Peak and integrated fluxes for these four cores are presented in Table 1. Using the dust emission again to estimate gas masses and column densities with the same assumptions outlined above (MRN1977, κ3.2  mm ~ 0.06 cm2 g-1), OH94, κ3.2  mm ~ 0.17 cm2 g-1), for these four cores we find masses between 18 and 107 M⊙ and peak column densities between 1.1 × 1023 and 6.1 × 1023 cm-2, respectively (Table 1). While we obviously filter out a significant fraction of the flux with the interferometer (~73%), this region still hosts relatively massive cores within a high-mass gas clump reservoir.

While the locations of mm1, mm3 and mm4 are largely associated with the 70 μm extinction feature (although mm1 and mm3 are both shifted a bit to the edge), it is surprising that mm2 lies at the edge of the dark extinction feature at a narrowing of the extinction. Although we cannot identify a clear and isolated 70 μm or shorter wavelength point source at this position, the slight increase of 70 μm emission toward the mm2 peak is consistent with a very young embedded object that just started to heat up the environment. In this picture, it may be that mm2 is in a little more advanced evolutionary stage compared to the other mm peak positions.

Another characteristic of the fragmentation of the gas clump is the projected nearest neighbor separation which is listed in Table 2. Since the beam is elongated in approximately north-south direction, we can resolve in east-west direction a separation between mm1 and mm2 of about ~2.9′′, which corresponds at the given distance of 4.9 kpc to a projected linear separation of of ~14 200 AU. The projected nearest neighbor separations to the other cores is even larger, between ~ 35 000 and ~47 000 AU (Table 2). In comparison to these values, the approximate Jeans-length where gas clumps should fragment into sub-structures at approximate temperatures and densities of 18 K and 105 cm-3 is ~ 17 000 AU. Hence, we see fragmentation above and below this approximate Jeans-length which is reasonable since gas clumps have a density structure and therefore not one unique fragmentation scale.

Table 2

Projected nearest neighbor separations.

thumbnail Fig. 3

The color-scale presents the dust temperature map derived from the Herschel far-infrared continuum data. Contours outline the structure of the 70 μm extinction, and the stars mark the positions of the four mm-sources from Fig. 2.

We also use the Herschel data to derive the temperature structure of the region fitting the SEDs pixel by pixel (see also Stutz et al. 2010 for details of the fitting). We excluded the 500 μm data to achieve a higher spatial resolution for the temperature map of 24.9′′, corresponding to the beam of the Herschel 350 μm data. Figure 3 presents the results and we see a clear drop of the far-infrared dust temperature from the outside to the center of our region where temperatures around 18 K are measured. This is very similar to the gas temperature derived toward that region by NH3 observations (Sridharan et al. 2005), and it is further evidence that no internal heating source exists so far.

thumbnail Fig. 4

Bottom panel: integrated N2H+(1 − 0) emission (the whole hyperfine structure between 76 and 94 km s-1) observed with the Nobeyama 45 m telescope toward the entire complex containing IRAS 18310-0825 in the south-east and IRDC 18310-4 in the north-west. The contours show the 1.2 mm continuum data presented first by Beuther et al. (2002). The contouring is from 10 to 90% of the peak emission of 400 mJy beam-1. Top panel: zoom into IRDC 18310-4 where the color scale presents a 1st moment map (intensity-weighted peak velocity) of the main hyperfine component complex between 84 and 90 km s-1. The black contours are the same 1.2 mm map as in the bottom panel, and the white contours outline the 70 μm extinction feature. The stars mark the positions of the four PdBI 3.2 mm sources.

3.2. Spectral line emission

To study the kinematics of the gas, Fig. 4 presents the N2H+(1 − 0) data (critical density at 20 K is 1.6 × 105 cm-3) of the region observed by Tackenberg et al. (2013). Although the N2H+ emission toward IRDC 18310-4 is a bit weaker than toward the HMPO IRAS 18310-0825, we nevertheless see a clear N2H+ peak toward our target region. Zooming into IRDC 18310-4, the top panel of Fig. 4 shows a 1st moment map (intensity-weighted peak velocity) extracted from these data using only the main hyperfine structure peak (see also Fig. 5). This figure shows that the overall velocity structure of the region is relatively uniform with no pronounced velocity structure and only weak gradients across the whole region (<1 km s-1 over ~1 pc extent).

Figure 5 shows a spectrum extracted toward the peak position. Observing the whole N2H+(1−0) hyperfine structure simultaneously allows us to fit the optical depth and by that derive accurate spectral line parameters. For the single-dish spectrum toward the peak position, we find a line-width of 2.7 km s-1 at a velocity of 86.1 km s-1. The fitted peak velocity is very close to that measured previously in NH3 (86.5 km s-1, Sridharan et al. 2005). Following MacLaren et al. (1988), we can estimate a virial mass assuming the FWHM/2 of the Nobeyama beam as the radius of the core. Employing possible density structures of 1/r and 1/r2 as border conditions, the virial mass of this region is between 305 and 202 M⊙, respectively. Compared to the total gas masses derived from the single-dish dust continuum data described in the previous section (Sect. 3.1), the virial mass is considerably lower (between factors 2.6 and 7.7, depending on the assumptions for the dust properties and density structure). This implies that the whole region is gravitationally unstable on these scales and likely already undergoing collapse.

thumbnail Fig. 5

Compilation of N2H+(1 − 0) Nobeyama 45 m single-dish spectrum toward IRDC 18310 (black histogram with green fit) and PdBI spectrum toward mm1 (red histogram). The PdBI data are multiplied by 5 for clarity. Fit results to the whole N2H+(1 − 0) hyperfine structure are given in the panel.

Since our PdBI observations are not only sensitive to the continuum but also to the N2H+(1 − 0) emission, we have kinematic information at high spatial resolution as well. Figure 5 also shows an N2H+(1 − 0) spectrum extracted toward the peak of mm1 just from the PdBI data (scaled up by a factor 5), and one clearly sees kinematic differences between the large and the small scale. To account for the differences and to complement the PdBI data with the missing flux information, we merged the PdBI and Nobeyama data into one single data-cube (see Sect. 2.4).

Figure 6 presents the spectra extracted from the merged data-cube toward the mm peak positions. All these spectra show that we have at least two separated velocity components in the region, one approximately peaking at ~86.5 km s-1 and the other at ~89.3 km s-1 (these values are averages from the full hyperfine structure fits to mm1 to mm3, see Fig. 6).

thumbnail Fig. 6

Spectra and N2H+(1 − 0) hyperfine spectral line fits extracted from the PdBI+Nobeyama N2H+(1 − 0) data toward the mm-peak positions marked in Fig. 2. Fit results and source labels are presented in each panel.

thumbnail Fig. 7

PdbI only (left panel) and merged PdBI+Nobeyama 45 m N2H+(1 − 0) data (right panel). The color-scale shows the 70 μm extinction feature, and the contours present the integrated N2H+(1 − 0) emission of three different velocity components as indicated in the figure. To avoid hyperfine-splitting overlap, these integrated maps were created from the isolated hyperfine component − 8.0 km s-1 apart from the central component, and then the velocity shifted to the center to be comparable with other line measurements. The contouring is done from 15 to 95% of the peak emission of each dataset, respectively. The mm-labels, a synthesized beam and a scale-bar are shown as well.

The comparison of the PdBI only spectrum and the Nobeyama only spectrum in Fig. 5 shows that the lower-velocity PdBI component corresponds relatively well to the single-dish spectrum whereas the higher-velocity PdBI component does not have a proper single-dish spectrum counterpart. This strongly indicates that the ~86.5 km s-1 component is the main component also present in the ambient gas, whereas the higher velocity component at ~89.3 km s-1 appears to be mainly associated with a dense sub-part moving with respect to the ambient gas.

To visualize spatial differences between these two spectral components, we imaged the N2H+ data for both velocity structures separately. Figure 7 shows the integrated emission derived for the velocity regimes [85.5, 88.5] and [88.5, 89.7] km s-1, respectively. The left panel shows the PdBI- only data whereas the right panel presents the combined PdBI+Nobeyama 45 m data. To avoid any artifacts of overlapping hyperfine structure lines, we produced these images from only the isolated hyperfine structure component offset by − 8.0 km s-1 (F = 0 − 1). While the lower-velocity component agrees well with the mid-infrared absorption structure encompassing mm1, mm3 and mm4, the higher-velocity component is peaking mainly in the direction of mm2. It is at first sight surprising to note that the higher-velocity component in the PdBI-only data shows an extension toward mm4 whereas this is lost in the merged dataset. Most likely this is because that extension is on small scales and comparably weak that it gets lost by the merging process. Additionally, it is possible that the single-dish data add more noise in the combined dataset, which make this weaker extension harder to detect. In addition to this, the merged dataset shows one additional velocity component at even higher velocities between 89.7 and 90.6 km s-1 that is more diffusely distributed north of the main IRDC 18310-4 structures. It is unclear whether this is just another unrelated gas component or whether that gas is structurely related to the red-shifted component between 88.5 and 89.7 km s-1. Nevertheless, both main velocity components strongly overlap and hence both contribute to the N2H+ emission from mm1 and mm2 (see spectra in Fig. 6). Furthermore, the PdBI-only data indicate that mm4 is located at an interface region between both components. In contrast to this, mm3 appears a bit different because it is located at the edge of the integrated emission of both components.

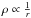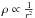Table 1 lists the line widths of the two components as well as the estimated virial masses following MacLaren et al. (1988) for different density profiles ( and ). The assumed radius of the sources is 1/2 of the FWHM which corresponds at the given distance to ~ 9000 AU. It is obvious that the narrow higher-velocity component barely contributes to the stability of the cores, and that the broader low-velocity component is far more important to stabilize the structures. Considering the spread in virial masses for different density profiles as well as for the gas masses based on the dust continuum emission and the assumed different dust properties (Table 1), the cores appear closer to virial equilibrium. This is different to the overall virial to gas mass ratio based on the single-dish data for the whole region that is significantly smaller than 1 (see above). However, one has to keep in mind that the virial masses are calculated from the merged PdBI+Nobeyama N2H+data whereas the core masses are calculated from the PdBI data only. If one compares the main component of the N2H+ spectrum toward mm1 without and with the Nobeyama short spacing information (Figs. 5 and 6), one finds that the combined data reveal a FWHM about a factor 1.7 higher than the interferometer data only. Since the line-widths is squared in the estimate of the virial mass, the derived virial masses of the combined data are usually a factor of a few larger than with interferometer data only. This implies that the comparison of masses from the combined PdBI+Nobeyama line data with the PdBI-only continuum data is not reliable. With the missing flux problem, the core masses from the PdBI-only data are underestimated, implying that the ratio of virial to gas mass on the core scales should be smaller than 1 as well. Hence, the cores are also prone to collapse.

Figure 8 presents the integrated N2H+ emission as well as the first and second moment maps (intensity-weighted peak velocities and line widths). In particular the 1st moment map shows that we have no strong velocity gradients across the filament but that the velocity peaks are dominated by the two components discussed above. The 2nd moment map appears as if it had a line width increase toward mm2, however that is only because the 2nd moment algorithm assumes a single component, and therefore the two real components appear as one broader feature in that direction.

thumbnail Fig. 8

N2H+(1 − 0) moment maps of the PdBI-only data toward IRDC 18310-4. The left, middle and right panel show in color the 0th moment (integrated intensity), 1st moment (intensity-weighted peak velocity) and 2nd moment (intensity-weighted linewidth), respectively. The moments were again extracted for the isolated hyperfine component − 8.0 km s-1 from the line center. The 1st moment was calculated from this isolated hyperfine component and then shifted toward by + 8.0 km s-1 to the vlsr of the source again. The white contours outline the 70 μm extinction feature and the stars mark the 3.2 mm peak positions from Fig. 2. The synthesized beam and a scale-bar are shown again.

thumbnail Fig. 9

Comparison between starless gas-clumps from low- via intermediate- to high-mass star formation. The 875 μm data for the prototypical low-mass core B68 are taken from Nielbock et al. (2012), and the N2H+(1–0) data for the intermediate-mass star-forming region IRDC 19175 are from Beuther & Henning (2009). Each panel presents a linear scale-bar of 50 000 AU and the synthesized beam, average densities are mentioned as well.

4. Discussion

4.1. Linear scales and densities from low- to high-mass starless gas clumps

How do linear scales and average densities compare between star-forming regions from low- to high-mass? To compare the different mass regimes with the high-mass starless region presented in this paper, we selected the low-mass starless core B68 (e.g., Alves et al. 2001; Nielbock et al. 2012) which resembles typical other low-mass globules (e.g., Launhardt et al. 2010), and the intermediate-mass starless star-forming region IRDC 19175 (Beuther & Henning 2009). Figure 9 presents data for all three regions. It is interesting to note that all three regions have approximately the same linear spatial extent on the order of 50 000 AU. However, while the linear size between the three regions does not vary considerably, the total gas reservoirs for the three complexes are very different, ranging from ~3.1 M⊙ for the low-mass core B68 (Nielbock et al. 2012), ~87 M⊙ for the intermediate-mass region IRDC 19175 (Beuther & Henning 2009) to values between ~800 and ~1600 M⊙ (depending on the dust model, see Sect. 3.1) for the high-mass region IRDC 18310-4 (see Table 3 for a list of the source parameters). Assuming that the three regions resemble typical starless gas clumps in the different mass regimes, these data imply that not the linear sizes are important but the mass reservoir squeezed within such regions, i.e., the densities.

While the peak density of the B68 core is ~ 3.4 × 105 cm-3 (Nielbock et al. 2012), the average density of the region is considerably lower. We estimate an average density for B68 from the total mass of 3.1 M⊙ (recent analysis of Herschel data, Nielbock et al. 2012) divided by a sphere with approximate radius of ~ 150′′ at a given distance of ~ 150 pc. Using these numbers the average gas density of the low-mass starless core B68 is approximately 1.2 × 104 cm-3 over a region corresponding to a sphere with ~45 000 AU diameter.

For the intermediate-mass star-forming region IRDC 19175, average core densities are estimated by Beuther & Henning (2009) to ~ 6 × 105 cm-3 over regions corresponding to spheres with ~3500 AU diameter. Estimating an average density from the total mass of 87 M⊙ over a volume corresponding to an effective radius of the 1.2 mm continuum map in Beuther & Henning (2009) results only in slightly lower values around ~2.6 × 105 cm-3 over a region corresponding to a sphere with ~48 000 AU diameter.

To compare these values with our high-mass star-forming region IRDC 18310-4, we estimate an average density for the core mm1 via averaging the peak column densities listed in Table 1 for the two different dust models, and assuming that the 3rd dimension has the same size as our synthesized beam. This results in average densities for mm1 of ~1.5 × 106 cm-3 over a region corresponding to a sphere with ~18 000 AU diameter. To get the density over a slightly larger regions, we use the average column density derived in Sect. 3.1 for the two different dust models from the single-dish 1.2 mm continuum data and again assume the 3rd dimension to have the same spatial extent as the single-dish beam of 10.5′′. This results in average densities of ~2.5 × 105 cm-3 over a region corresponding to a sphere with ~51 000 AU diameter.

Table 3

Star-forming region parameters.

These large density differences obviously also have a strong impact on the fragmentation properties of the starless gas clumps. While the low-density low-mass core B68 does not fragment at all, the higher-density intermediate- to high-mass starless clumps do fragment significantly. To better understand these properties, we estimate the Jeans length for the average B68 density of 1.2 × 104 cm-3, the approximate average large-scale densities of IRDC 19175 and IRDC 18310-4 of ~2.5 × 105 cm-3, and the higher core densities of the two regions of ~6 × 105 cm-3 and ~ 1.5 × 106 cm-3, respectively. Assuming average temperatures of 15 K for all these starless regions, the corresponding Jeans-length are ~44 000 AU (B68), ~10 000 AU (average large-scale densities of IRDC 19175 & IRDC 18310-4), ~6000 AU (average core density of IRDC 19175) and ~4000 AU (average core density of IRDC 18310-4), respectively. This relatively simple isothermal Jeans-analysis already explains the observations well: The large Jeans-length for B68 is reflected in the fact that this low-mass starless core does not fragment on the given scales (Fig. 9). Furthermore, as already discussed in Beuther & Henning (2009), the different Jeans-lengths for B68 (located close to the Pipe nebula) and IRDC 19175 correspond well to the observed core separations in the low-mass Pipe nebula and the intermediate-mass IRDC 19175 region, respectively. For the high-mass region IRDC 18310-4, we are still spatial resolution limited and only observe the fragmentation on the scales of our observed resolution elements (see also Table 2). In future higher-spatial-resolution observations, we expect to resolve this region into even more and closer spaced cores.

Calculating the Jeans-mass instead of the Jeans-length for the average densities of B68, IRDC 19175 and IRDC 18310-4, we find 1.7, 0.36 and 0.37 M⊙, respectively. The Jeans-masses for the higher core densities are correspondingly smaller (Table 3). For the low-mass region B68 that value is on the order of the whole mass (3.1 M⊙), and also for the intermediate-mass region IRDC 19175, the estimate masses of the individual cores are mostly below 1 M⊙. Hence Jeans-masses and core masses approximately agree in these two cases. In contrast to that, the Jeans-mass in IRDC 18310-4 is significantly lower than the mass estimates we derived from the dust continuum data (Table 1). Therefore, similar as discussed in the previous paragraph, for the high-mass region IRDC 18310-4, we are still spatial resolution limited, and it is highly likely that the here presented cores mm1 to mm4 will fragment even further when observed at higher spatial resolution.

Assuming that these example regions resemble starless gas clumps over the whole mass regime, one may conclude that gravitational instability in the classical Jeans-analysis explains the fragmentation properties of starless gas clumps from low- to high-mass reasonably well. The major difference between the regions appears to be their densities and mass reservoirs squeezed into the respective spatial scales. Similar Jeans fragmentation scales have also been observed toward more evolved regions, e.g., the young cluster NGC 2264 (Teixeira et al. 2006). In contrast to the larger-scale cloud fragmentation where turbulence plays a major role (e.g., Padoan & Nordlund 2002; Mac Low & Klessen 2004), these data indicate that the fragmentation on smaller clump and core scales appears to be dominated by gravity.

4.2. Kinematic signatures of a dynamic cloud collapse

Independent of the cloud formation models – do clouds evolve slower via ambipolar diffusion processes (e.g., Mouschovias et al. 2006; McKee & Ostriker 2007) or faster via more dynamic gas flows (e.g., Vázquez-Semadeni et al. 2006; Heitsch et al. 2008; Banerjee et al. 2009) – the gas has to show dynamic signatures of contraction and/or infall over large spatial scales. During molecular cloud formation the diffuse HI gas converts to the denser molecular phase. Within molecular clouds, filamentary sub-structures are likely important, and recent data indicate that hierarchical, often also filamentary structures feed the central and densest filaments or gas clumps (e.g., Myers 2009; Schneider et al. 2010; Schmalzl et al. 2010; Hennemann et al. 2012). These central cluster-forming clumps have then to collapse and form the multiple and clustered stellar associations in the end. Statistical signatures of infall from single-dish average line profiles exist. However, they are often ambiguous, and one finds signatures for infall as well outflowing motions (e.g., Fuller et al. 2005). More coherent infall motions on larger scales have only rarely been reported (e.g., Motte et al. 2005; Schneider et al. 2010). Going from the cluster-forming scales down to cores forming individual or multiple, bound objects, dynamic studies in the past have mostly concentrated on more evolved evolutionary stages like high-mass protostellar objects (HMPOs) or ultracompact Hii regions (e.g., Keto 2002; Sollins et al. 2005; Sandell et al. 2009; Qiu et al. 2011; Goddi et al. 2011; Beuther et al. 2012a).

While the above infall studies dealt with the average infall motions of the entire star-forming gas clumps, only recently spatially resolved dynamical studies of sub-structures and cores within the natal gas became possible (e.g., Beuther & Henning 2009; Zhang & Wang 2011; Wang et al. 2011; Csengeri et al. 2011a,b). In contrast to the above discussed single-dish studies where often infall signatures are derived from line profiles of optically thick lines, Ragan et al. (2012b) also find signatures of collapse and fragmentation via high-spatial-resolution NH3 observations of IRDCs. Furthermore, the studies by Csengeri et al. (2011a,b) revealed multiple velocity components in optically thin gas tracers like H13CO+ or N2H+ that were interpreted as signatures of shear motions possibly caused by converging gas flows.

The spectra we found (Figs. 5 and 6) also show multiple velocity components in the dense gas tracer N2H+. Figure 7 even identifies that the different velocity components are dominated by different mm cores within the large-scale gas clump. In addition to the work by Csengeri et al. (2011a,b), multiple velocity components in optically thin dense gas tracers were also found by Beuther & Henning (2009) as well as in recent work by Ragan et al. (in prep.) with the PdBI toward the G11.11 filament, and by Bihr et al. (submitted) with VLA NH3 observations toward IRDCs. Combining our new data with the results recently found by the other groups, based on high-spatial resolution interferometer observations there emerges a regular signature of multiple velocity components in optically thin dense gas tracers. Typical separations line widths of these multiple velocity components are around ~2 km s-1 and ~1 km s-1, respectively.

thumbnail Fig. 10

N2H+ (1−0) isolated hyperfine line profiles viewed through various lines of sight through a massive star forming region. The central image with a side-length of 0.8 pc shows the column density of the region and the surrounding line profiles are calculated for a 0.09 pc beam centered directly on the embedded core and viewed along the direction each panel touches the central image.

Confronting these observational results with theory, Rowan Smith has recently started to simulate the spectral line emission from dynamically collapsing clumps of a large-scale collapsing gas cloud modeled initially by Smith et al. (2009) and Bonnell et al. (2011). First results about cores associated with low-mass star formation were presented in Smith et al. (2012), and the simulations for high-mass collapsing gas clumps are currently conducted (Smith et al. 2013). Figure 10 shows an example of non-Gaussian optically thin line profiles produced from a simulation of a massive star-forming gas clump with 370 M⊙ (Smith et al. 2009, 2013). The N2H+ (1−0) line profiles were calculated using an assumed abundance ratio of 10-10 relative to molecular hydrogen (Aikawa et al. 2005). The radiative transfer code RADMC-3D (Dullemond 2012) was used to calculate the line emission given the temperatures and densities from the original simulation. (For a full description of our method see Smith et al. 2012). Here, only the isolated hyperfine component F = 0 − 1 (see Fig. 6) offset by ~8.0 km s-1 from the central component is shown. The line profiles are synthesized over a beam of FWHM 0.09 pc and calculated for a variety of viewing angles. No artificial noise is added to the data.

Clearly, these simulations find similar signatures of multiple N2H+ components within the dynamically collapsing gas clump. Typical peak separations and line widths are similar to what is found in the observational data. The multiple components seen in Fig. 10 arise in the simulations due to the clumpy nature of the high-mass star-forming region. Across the region there is a large scale supersonic collapse motion running from around +2 km s-1 on one side to − 2 km s-1 on the other. Dense clumps of gas at different positions along this velocity gradient all contribute to the total emission and produce peaks in the line profile at their individual velocities. A full analysis of line profiles from massive star formations will be presented in Smith et al. (submitted).

This interpretation is also consistent with our finding that the ratio of viral mass to total gas mass is significantly smaller than 1 for the entire region, implying that the large-scale gas clump is prone to collapse, similar to the findings of Ragan et al. (2012b) for their sample of IRDCs. Since the virial mass to core mass ratio is smaller than 1 on the core scales as well, the region is consistent with a globally collapsing gas clumps on almost all scales.

We can also estimate the dynamical crossing time as well as the free-fall time of the region. Using the typical velocity difference between the two gas components of ~2.8 km s-1 as the velocity dispersion of the clumps, and the approximate extent of the 70 μm absorption feature of ~30′′ (corresponding to 147 000 AU at the given distance), the dynamical crossing time for IRDC 18310-4 is ~ 2.5 × 105 yrs. In comparison to that, estimating the free-fall time for a 1000 M⊙ gas clump of with a radius of half the previously used extend, we get an approximate free-fall time-scale of ~1.2 × 105 yrs. Although there is a difference of about a factor 2 between the two estimates, these are just approximate values and they agree order-of-magnitude wise. This again implies that a dynamical collapse of the whole gas clump is a feasible model for this region.

Combining our observational results with the modeling of line profiles for dynamically collapsing gas clumps, we identify signatures that even this very young, still starless high-mass gas clump is actively collapsing and thus at the verge of star formation. The fact that similar signatures were recently found toward other regions as well, indicates that multiple velocity components of optically thin gas tracers are an excellent tool to identify and study the earliest stages of dynamical infall in high-mass star formation.

5. Conclusions

Since the evolutionary time-scale for high-mass starless gas clumps is extremely short (e.g., Motte et al. 2007; Russeil et al. 2010; Tackenberg et al. 2012), so far they had barely been studied in great depth at high spatial resolution (some notable recent papers in that field are Csengeri et al. 2011a; Ragan et al. 2012b). To better understand the fragmentation and dynamical properties of the most massive gas clumps during their earliest evolutionary stages, here we present an interferometric PdBI kinematic and continuum study of a prototypical high-mass starless gas clump that remains far-infrared dark up to 100 μm wavelengths.

The gas reservoir between ~800 and ~1600 M⊙ (depending on the assumed dust properties) splits up at a spatial resolution of 4.3′′ × 3.0′′ (linear scales 21   000 × 15   000 AU) into 4 cores. A comparison of this high-mass starless region with typical low-mass (B68) and intermediate-mass (IRDC 19175) star-forming forming regions reveals that the overall spatial size of the low-mass to high-mass star-forming regions does not vary significantly. While the linear extent of the regions is similar, the mass reservoir squeezed into this spatial size on the order of 0.25 pc, and hence the densities do vary by about 2 orders of magnitude. A classical gravitational instability Jeans analysis is capable to explain the fragmentation properties of the gas clumps over the whole mass range presented.

In addition to the fragmentation properties, we find multiple spectral velocity components toward the resolved gas cores. Recent radiative transfer hydrodynamic simulations of dynamical collapsing high-mass gas clumps are consistent with these multiple velocity components. This also agrees with a ratio between estimated viral and total mass of the whole region <1.

In summary, although this massive gas clump does not have any embedded protostellar source down to our Herschel far-infrared detection limits, the fragmentation and dynamical properties of the gas and dust are consistent with early collapse motion and clustered star formation.

Acknowledgments

We like to thank Joao Alves for interesting discussions about the comparison between high- and low-mass star-forming regions. Furthermore, thanks a lot to a careful referee who helped improving the paper.

References

  1. Aikawa, Y., Herbst, E., Roberts, H., & Caselli, P. 2005, ApJ, 620, 330 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., & Klessen, R. S. 2009, MNRAS, 398, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bergin, E. A., Hartmann, L. W., Raymond, J. C., & Ballesteros-Paredes, J. 2004, ApJ, 612, 921 [NASA ADS] [CrossRef] [Google Scholar]
  6. Beuther, H., & Henning, T. 2009, A&A, 503, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beuther, H., Churchwell, E. B., McKee, C. F., & Tan, J. C. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 165 [Google Scholar]
  9. Beuther, H., Henning, T., Linz, H., et al. 2010, A&A, 518, L78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Beuther, H., Linz, H., & Henning, T. 2012a, A&A, 543, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Beuther, H., Tackenberg, J., Linz, H., et al. 2012b, A&A, 538, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bonnell, I. A., Smith, R. J., Clark, P. C., & Bate, M. R. 2011, MNRAS, 410, 2339 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bontemps, S., Motte, F., Csengeri, T., & Schneider, N. 2010, A&A, 524, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
  15. Commerçon, B., Hennebelle, P., & Henning, T. 2011, ApJ, 742, L9 [NASA ADS] [CrossRef] [Google Scholar]
  16. Csengeri, T., Bontemps, S., Schneider, N., Motte, F., & Dib, S. 2011a, A&A, 527, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Csengeri, T., Bontemps, S., Schneider, N., et al. 2011b, ApJ, 740, L5 [NASA ADS] [CrossRef] [Google Scholar]
  18. Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dullemond, C. P. 2012, Astrophysics Source Code Library, 2015 [Google Scholar]
  20. Fuller, G. A., Williams, S. J., & Sridharan, T. K. 2005, A&A, 442, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Goddi, C., Moscadelli, L., & Sanna, A. 2011, A&A, 535, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
  23. Heitsch, F., Hartmann, L. W., Slyz, A. D., Devriendt, J. E. G., & Burkert, A. 2008, ApJ, 674, 316 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hennemann, M., Motte, F., Schneider, N., et al. 2012, A&A, 543, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Henning, T., Linz, H., Krause, O., et al. 2010, A&A, 518, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Jenkins, E. B. 2004, in Origin and Evolution of the Elements, eds. A. McWilliam, & M. Rauch, 336 [Google Scholar]
  27. Keto, E. 2002, ApJ, 568, 754 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  29. Krumholz, M. R., & McKee, C. F. 2008, Nature, 451, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Launhardt, R., Nutter, D., Ward-Thompson, D., et al. 2010, ApJS, 188, 139 [NASA ADS] [CrossRef] [Google Scholar]
  31. Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Linz, H., Krause, O., Beuther, H., et al. 2010, A&A, 518, L123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Mac Low, M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
  34. MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  36. McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
  37. Motte, F., Bontemps, S., Schilke, P., et al. 2005, in Massive Star Birth: A Crossroads of Astrophysics, eds. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 151 [Google Scholar]
  38. Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Mouschovias, T. C., Tassis, K., & Kunz, M. W. 2006, ApJ, 646, 1043 [NASA ADS] [CrossRef] [Google Scholar]
  40. Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
  43. Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
  44. Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
  45. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  46. Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Qiu, K., Zhang, Q., & Menten, K. M. 2011, ApJ, 728, 6 [NASA ADS] [CrossRef] [Google Scholar]
  48. Ragan, S., Henning, T., Krause, O., et al. 2012a, A&A, 547, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Ragan, S. E., Heitsch, F., Bergin, E. A., & Wilner, D. 2012b, ApJ, 746, 174 [NASA ADS] [CrossRef] [Google Scholar]
  50. Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
  51. Roussel, H. 2012 [arXiv:1205.2576] [Google Scholar]
  52. Russeil, D., Zavagno, A., Motte, F., et al. 2010, A&A, 515, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Sandell, G., Goss, W. M., Wright, M., & Corder, S. 2009, ApJ, 699, L31 [NASA ADS] [CrossRef] [Google Scholar]
  54. Sawada, T., Ikeda, N., Sunada, K., et al. 2008, PASJ, 60, 445 [NASA ADS] [Google Scholar]
  55. Schmalzl, M., Kainulainen, J., Quanz, S. P., et al. 2010, ApJ, 725, 1327 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Smith, R. J., Clark, P. C., & Bonnell, I. A. 2009, MNRAS, 396, 830 [NASA ADS] [CrossRef] [Google Scholar]
  59. Smith, R. J., Shetty, R., Stutz, A. M., & Klessen, R. S. 2012, ApJ, 750, 64 [NASA ADS] [CrossRef] [Google Scholar]
  60. Smith, R. J., Shetty, R., Beuther, H., Klessen, R. S., & Bonnell, I. A. 2013, ApJ, accepted [arXiv:1304.4950] [Google Scholar]
  61. Sollins, P. K., Zhang, Q., Keto, E., & Ho, P. T. P. 2005, ApJ, 624, L49 [NASA ADS] [CrossRef] [Google Scholar]
  62. Sridharan, T. K., Beuther, H., Schilke, P., Menten, K. M., & Wyrowski, F. 2002, ApJ, 566, 931 [NASA ADS] [CrossRef] [Google Scholar]
  63. Sridharan, T. K., Beuther, H., Saito, M., Wyrowski, F., & Schilke, P. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
  64. Stutz, A., Launhardt, R., Linz, H., et al. 2010, A&A, 518, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Tackenberg, J., Beuther, H., Henning, T., et al. 2012, A&A, 540, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Tackenberg, J., Beuther, H., Henning, Th., et al. 2013, A&A, submitted [Google Scholar]
  67. Teixeira, P. S., Lada, C. J., Young, E. T., et al. 2006, ApJ, 636, L45 [NASA ADS] [CrossRef] [Google Scholar]
  68. Vázquez-Semadeni, E., Ryu, D., Passot, T., González, R. F., & Gazol, A. 2006, ApJ, 643, 245 [NASA ADS] [CrossRef] [Google Scholar]
  69. Wang, K., Zhang, Q., Wu, Y., & Zhang, H. 2011, ApJ, 735, 64 [NASA ADS] [CrossRef] [Google Scholar]
  70. Zhang, Q., & Wang, K. 2011, ApJ, 733, 26 [NASA ADS] [CrossRef] [Google Scholar]
  71. Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Core parameters from the PdBI 3.2 mm data.

In the text
Table 2

Projected nearest neighbor separations.

In the text
Table 3

Star-forming region parameters.

In the text

All Figures

thumbnail Fig. 1

Compilation of the continuum data from 70 μm to 500 μm wavelength in color-scale as labeled in each panel. The scale is chosen in each image individually to highlight the most important features. Contour levels of the 870 μm data start at the 3σ levels of 0.189 mJy beam-1 and continue in in 3σ steps. The white small box in the top-left panel marks the smaller region discussed in the remaining figures. A scale-bar is shown in the bottom-left panel.
In the text
thumbnail Fig. 2

Zoom into the central IRDC 18310-4. The color-scale shows the 70 μm extinction feature, and the contours present the 3.2 mm PdBI continuum emission starting at 3σ and continuing in 2σ steps (1σ = 0.08 mJy beam-1). The mm-labels, a synthesized beam and a scale-bar are shown as well. The phase reference center is close to mm1 at RA (J2000.0) 18:33:39.468 and Dec (J2000.0) − 08:21:07.65, and the primary beam of the observations with ~54′′ is larger than the shown image size.
In the text
thumbnail Fig. 3

The color-scale presents the dust temperature map derived from the Herschel far-infrared continuum data. Contours outline the structure of the 70 μm extinction, and the stars mark the positions of the four mm-sources from Fig. 2.
In the text
thumbnail Fig. 4

Bottom panel: integrated N2H+(1 − 0) emission (the whole hyperfine structure between 76 and 94 km s-1) observed with the Nobeyama 45 m telescope toward the entire complex containing IRAS 18310-0825 in the south-east and IRDC 18310-4 in the north-west. The contours show the 1.2 mm continuum data presented first by Beuther et al. (2002). The contouring is from 10 to 90% of the peak emission of 400 mJy beam-1. Top panel: zoom into IRDC 18310-4 where the color scale presents a 1st moment map (intensity-weighted peak velocity) of the main hyperfine component complex between 84 and 90 km s-1. The black contours are the same 1.2 mm map as in the bottom panel, and the white contours outline the 70 μm extinction feature. The stars mark the positions of the four PdBI 3.2 mm sources.
In the text
thumbnail Fig. 5

Compilation of N2H+(1 − 0) Nobeyama 45 m single-dish spectrum toward IRDC 18310 (black histogram with green fit) and PdBI spectrum toward mm1 (red histogram). The PdBI data are multiplied by 5 for clarity. Fit results to the whole N2H+(1 − 0) hyperfine structure are given in the panel.
In the text
thumbnail Fig. 6

Spectra and N2H+(1 − 0) hyperfine spectral line fits extracted from the PdBI+Nobeyama N2H+(1 − 0) data toward the mm-peak positions marked in Fig. 2. Fit results and source labels are presented in each panel.
In the text
thumbnail Fig. 7

PdbI only (left panel) and merged PdBI+Nobeyama 45 m N2H+(1 − 0) data (right panel). The color-scale shows the 70 μm extinction feature, and the contours present the integrated N2H+(1 − 0) emission of three different velocity components as indicated in the figure. To avoid hyperfine-splitting overlap, these integrated maps were created from the isolated hyperfine component − 8.0 km s-1 apart from the central component, and then the velocity shifted to the center to be comparable with other line measurements. The contouring is done from 15 to 95% of the peak emission of each dataset, respectively. The mm-labels, a synthesized beam and a scale-bar are shown as well.
In the text
thumbnail Fig. 8

N2H+(1 − 0) moment maps of the PdBI-only data toward IRDC 18310-4. The left, middle and right panel show in color the 0th moment (integrated intensity), 1st moment (intensity-weighted peak velocity) and 2nd moment (intensity-weighted linewidth), respectively. The moments were again extracted for the isolated hyperfine component − 8.0 km s-1 from the line center. The 1st moment was calculated from this isolated hyperfine component and then shifted toward by + 8.0 km s-1 to the vlsr of the source again. The white contours outline the 70 μm extinction feature and the stars mark the 3.2 mm peak positions from Fig. 2. The synthesized beam and a scale-bar are shown again.
In the text
thumbnail Fig. 9

Comparison between starless gas-clumps from low- via intermediate- to high-mass star formation. The 875 μm data for the prototypical low-mass core B68 are taken from Nielbock et al. (2012), and the N2H+(1–0) data for the intermediate-mass star-forming region IRDC 19175 are from Beuther & Henning (2009). Each panel presents a linear scale-bar of 50 000 AU and the synthesized beam, average densities are mentioned as well.
In the text
thumbnail Fig. 10

N2H+ (1−0) isolated hyperfine line profiles viewed through various lines of sight through a massive star forming region. The central image with a side-length of 0.8 pc shows the column density of the region and the surrounding line profiles are calculated for a 0.09 pc beam centered directly on the embedded core and viewed along the direction each panel touches the central image.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.