| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219642 | |
| Published online | 30 April 2013 | |
Comprehensive time series analysis of the transiting extrasolar planet WASP-33b⋆,⋆⋆
1
Konkoly Observatory,
1121
Budapest,
Hungary
e-mail:
kovacs@konkoly.hu
2
Department of Physics and Astrophysics, University of North
Dakota, 58202-7129
Grand Forks, ND, USA
3
Department of Astrophysical Sciences, Princeton
University, 08544
Princeton, NJ, USA
4
Harvard–Smithsonian Center for Astrophysics, 02138
Cambridge,
MA,
USA
Received: 22 May 2012
Accepted: 5 March 2013
Context. HD 15082 (WASP-33) is the hottest and fastest rotating star known to harbor a transiting extrasolar planet (WASP-33b). The lack of high precision radial velocity (RV) data stresses the need for precise light curve analysis and gathering further RV data.
Aims. By using available photometric and RV data, we perform a blend analysis, compute more accurate system parameters, confine the planetary mass, and, attempt to cast light on the observed transit anomalies.
Methods. We combined the original HATNet observations and various followup data to jointly analyze the signal content and extract the transit component and used our RV data to aid the global parameter determination.
Results. The blend analysis of the combination of multicolor light curves yields the first independent confirmation of the planetary nature of WASP-33b. We clearly identify three frequency components in the 15–21 d-1 regime with amplitudes 7–5 mmag. These frequencies correspond to the δ Scuti-type pulsation of the host star. None of these pulsation frequencies or their low-order linear combinations are in close resonance with the orbital frequency. We show that these pulsation components explain some but not all of the observed transit anomalies. The grand-averaged transit light curve shows that there is a ~1.5 mmag brightening shortly after the planet passes the mid-transit phase. Although the duration and amplitude of this brightening varies, it is visible even through the direct inspections of the individual transit events (some 40–60% of the followup light curves show this phenomenon). We suggest that the most likely explanation of this feature is the presence of a well-populated spot belt which is highly inclined to the orbital plane. This geometry is consistent with the inference from the spectroscopic anomalies. Finally, we constrain the planetary mass to Mp = 3.27 ± 0.73 MJ by using our RV data collected by the TRES spectrograph.
Key words: planets and satellites: individual: WASP-33b / stars: variables: delta Scuti / methods: data analysis
Appendix A is available in electronic form at http://www.aanda.org
Photometric time series and lightcurves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A44
© ESO, 2013
1. Introduction
The short-period (P = 1.22 d) transiting extrasolar planet WASP-33b was discovered by Christian et al. (2006) in the course of the transit survey conducted by the WASP project (Pollacco et al. 2006). The host star, HD 15082, is a bright, V = 8.3 mag A-type star with a high projected rotational velocity of ~90 km s-1. As a result, high precision radial velocity (RV) measurements usually demanded by the planet verification and planet mass estimation processes are very difficult to take. Followup spectroscopic observations by Collier Cameron et al. (2010, hereafter CC10) could only yield an upper limit of 4.1 MJ on the planetary mass but no bisector analysis could be performed due to the several km s-1 scatter of the measured RV values. However, due to the large rotational velocity, the authors were able to utilize the surface velocity field mapping capability of the orbiting planet and showed very clearly that the orbital revolution was highly inclined (i.e., retrograde) in respect to the stellar rotational axis.
The WASP-33 system stands out from the other transiting systems not only for its highest rotation rate and highest Teff of 7400 K (CC10) but also because of the planet’s highest substellar temperature (T0 = 3800 K, see Sect. 9). Due to the high incident flux and the early spectral type of the star we expect that a large amount of UV radiation is deposited in the planet’s atmosphere. This, together with its high Roche-lobe filling factor (see Budaj 2011) make this system perhaps the best candidate for studying effective planetary envelope evaporation and mass flow onto the host star.
Due to its brightness and significant transit depth of ~14 mmag, the WASP-33 system is highly suitable for followup photometric observations. Some 801 events have been observed over the years by professional and amateur astronomers. Most of these light curves (LCs) display various anomalies, such as transit depth variation, mid-transit humps, tilted full transit phase, asymmetric ingress/egress phases and small-amplitude oscillations. Although not all of these variations are necessarily real, it is clear that the system is peculiar and very much worth for further attention.
WASP-33 was also observed by HATNet (Bakos et al. 2002, 2004) in the course of the search for transiting extrasolar planets (TEPs). After assigning the “candidate” status to the target in January 2010, a followup reconnaissance spectroscopy conducted by the TRES spectrograph (Fűrész 2008) has led to the conclusion that the rotational velocity was very high. Nevertheless, we continued the spectroscopic followup and found that the low velocity amplitude may suggest the presence of a planetary companion. After the SuperWASP announcement we stopped pursuing this target but here we utilize both the RV and the photometric (HATNet and our early followup) data.
In this paper we perform a comprehensive time series analysis by utilizing the HATNet data, the followup LCs deposited at the Exoplanet Transit Database (ETD, see Poddany et al. 2010), other published photometric data and new LCs from the Fred Lawrence Whipple and Konkoly observatories2. Our goal is to verify the planetary nature of WASP-33b purely from photometry (the “Kepler-way” of system validation – see, e.g., Muirhead et al. 2012), to derive more accurate system parameters and examine the possible causes of light curve anomalies. We also use our RV archive, based on the observations obtained by the TRES spectrograph, to improve the mass estimate of the planet.
Photometric datasets on WASP-33.
2. HATNet detection
WASP-33 is located in two HATNet fields, internally labeled as #166 and 167. The observations were made through Bessel I filter between November 06, 2003 and January 30, 2007 by the telescopes located at the Arizona (FLWO) and Hawaii (Mauna Kea) sites of HATNet. Altogether 12 149 data points have been gathered in three seasons, spanning 1181 days. The data were collected with an integration time of ~5 min. We detected a robust transit signal by using the method of box-fitting least squares (BLS, Kovács et al. 2002) after applying the trend filtering algorithm (TFA, Kovács et al. 2005) to remove systematics (note that the signal was detectable with high S/N without using TFA; however, filtering out systematics helped to increase S/N by a factor of two and substantially clean the folded light curve).
The BLS spectrum of the TFA-filtered data is shown in Fig. 1. The detection is very strong with the standard (sub)harmonics at integer frequency ratios. With the peak frequency of 0.819759 d-1 the signal was reconstructed (i.e., filtered out from systematics) by using a modified trapezoidal transit model with rounded bottom (to simulate limb darkening, with 15% maximum deviation from the trapezoidal flat bottom) and an arbitrary out of transit variation (represented by 40 bin averages of the light curve through the full orbital phase). The reconstructed light curve is plotted in Fig. 2. Except for the transit, we do not see any significant variation. We looked for an additional possible transit signal in the [0, 2] d-1 frequency band in the pre-whitened signal by the above main transit. The result of this test was negative. A Fourier frequency analysis (or discrete Fourier transform – DFT) in the same frequency band also concluded without finding a signal. The upper limit of any sinusoidal signal in the above frequency range is 0.5 mmag. Both of these tests strongly suggest that we have a genuine transit signal at hand (see also the blend analysis in Sect. 4).
The total transit duration (from the first to the last contact) is 2.7 h, the ingress/egress (each) last for 14 min. These values agree well with the ones derived in other, accurate followup works (e.g., by CC10). However, the measured transit depth (computed with the above transit model) is 13 mmag, which is in the lower tail of the distribution of the transit depths derived from the nine followup observations in the same color (see Table 1 and Appendix). The average value of the depth from these data is 14 mmag, with a standard deviation of 1.5 mmag, much higher than the formal errors. If we consider only the most accurate data gathered by larger telescopes (i.e., Konkoly, CC10), we get a range of 13–17 mmag, indicating that the transit depth might indeed vary.
We note that the lower value of the transit depth derived from the HATNet data is not too likely to come from a third-light effect due to the close, 2.9 mag fainter neighbor 2MASS 02265167+3732133. This object lies 1 pix outside of the 2.4 pix radius of the aperture used by the photometric code. With a PSF FWHM of 2.4 pix some contamination is possible but this is most likely to be small.
 |
Fig. 1 BLS spectrum of the TFA-filtered/reconstructed time series based on the observations of WASP-33 by HATNet. The label in the upper right corner shows, from left to right, the pre-whitening order, peak frequency, transit depth (assuming trapezoidal transit shape) and the S/N of the peak frequency. The BLS amplitude is normalized to unity at the highest peak and refers to the signal without correction for blending by the nearby companion (see text). |
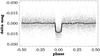 |
Fig. 2 Folded light curve of the TFA-filtered/reconstructed time series based on the observations of WASP-33 by HATNet (dots). The best-fitting simplified light curve model (with bin averaging in the out-of-transit part) is shown by the thick line. |
3. Followup datasets
We use four photometric datasets in this paper: (i) the HATNet survey LC; (ii) the amateur/professional data deposited at the ETD site; (iii) the published followup LC of Herrero et al. (2011) and Sada et al. (2012); (iv) our own followup data obtained at the Whipple and Konkoly observatories. The list of all these datasets is given in Table 1. Several of them suffered from various trends due to instrumental or reduction effects. We attempted to correct these trends by fitting the following model light curve to the observations 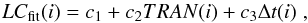 (1)where TRAN(i) is the simplified transit model3 described in Sect. 2, Δt(i) = HJD(i) − HJDmid, with HJDmid denoting the middle of the observing time for the given followup observation, c1, c2 and c3 are the regression coefficients to be determined by a standard least squares method, together with the transit parameters hidden in TRAN(i). The light curves used in the analysis presented in this paper have been derived by subtracting the best fitting linear trend, as given by the coefficients c1 and c3. The detrended light curves, the transit parameters and the trend coefficient c3 are presented in the Appendix (see Table A.1, Figs. A.3 and A.4). We also employed heliocentric corrections for most of the ETD LCs, as given at the ETD site. Since the HATNet data cover the full orbital phase, for the purpose of incorporating them in the analysis of the followup observations when constructing the average transit LC, we cut them in the phase interval [−0.1, + 0.1].
(1)where TRAN(i) is the simplified transit model3 described in Sect. 2, Δt(i) = HJD(i) − HJDmid, with HJDmid denoting the middle of the observing time for the given followup observation, c1, c2 and c3 are the regression coefficients to be determined by a standard least squares method, together with the transit parameters hidden in TRAN(i). The light curves used in the analysis presented in this paper have been derived by subtracting the best fitting linear trend, as given by the coefficients c1 and c3. The detrended light curves, the transit parameters and the trend coefficient c3 are presented in the Appendix (see Table A.1, Figs. A.3 and A.4). We also employed heliocentric corrections for most of the ETD LCs, as given at the ETD site. Since the HATNet data cover the full orbital phase, for the purpose of incorporating them in the analysis of the followup observations when constructing the average transit LC, we cut them in the phase interval [−0.1, + 0.1].
The orbital period and center of transit times were updated through a BLS analysis of all available followup (non-flagged items in Table 1) and the HATNet data. The result is shown in Table 2, where, for comparison, we also added the result derived from HATNet only. These values agree well with those of CC10, albeit our period fits better the transit center of Herrero et al. (2011).
Result of the BLS analysis.
3.1. ETD data
Due to its brightness, WASP-33 is high on the list of any followup programs, especially those conducted by amateur astronomers. As of June, 2012, there are 82 entries listed at the ETD site on this object. Most of them have been collected by skilled amateur astronomers. In the analysis presented in this paper we use a large number of these followup data and omit only those that have especially high noise or very peculiar shape. In some cases these datasets are suspect to instrumental or environmental effects. Some of those that showed reasonably low noise level were flagged and left in Table 1 for reference and further discussion in Sect. 6.
3.2. FLWO data
As part of the HATNet follow-up program we obtained a light curve of WASP-33 on the night of March 3/4, 2010 using the KeplerCam imager on the FLWO 1.2 m telescope and a Sloan z′ filter. These observations began during ingress and ended before third contact. The images were calibrated and reduced to a light curve following the procedure discussed in Bakos et al. (2010).
3.3. Konkoly data
 |
Fig. 3 Photometric observations of WASP-33 at the Konkoly and Fred Lawrence Whipple observatories. The Konkoly data have been taken through Cousins I, the FLWO data through Sloan z filters. Data points are binned in 0.001 phase (i.e., in 105 s intervals). |
The transit was detected on November 12/13, 2011 by the 60/90 cm Schmidt telescope located at Piszkestető, Hungary. We gathered 2352 exposures with 4 s integration time. The 4 K × 4 K images of the Apogee Alta CCD Camera were trimmed to 1 K × 1 K to speed up readout time. We used a filter in the Bessel I band. Since the field is reasonably sparse around WASP33, we performed simple aperture photometry after the standard calibration procedure, including astrometry (Pál 2009). Five comparison stars of similar brightness were used in a ~0.3° × 0.3°deg field of view centered on the target. After correcting for differential extinction (without the color term), we constructed the final light curve by averaging the data in 60 s bins. As shown in Fig. 3, the light curve exhibits both some oscillations (probably related to the δ Scuti-type pulsations of the host star) and a hump in the middle of the transit.
Yet another event was observed on the night of November 24/25, 2011 with the Andor iXON 888 electron multiplying CCD (EMCCD) camera attached to the 50 cm Cassegrain telescope at Piszkestető. Altogether 12 051 exposures were taken with ~1 s integration time, basically corresponding to the same sampling time due to the frame transfer mode. The field of view was 6′ × 6′ with a pixel resolution of 0.36 arcsec. As above, we used a Bessel filter in the I band. After the standard calibration (dark removal and flat field correction) a special photometric data reduction was applied on the reduced images in the following steps (Regaly et al., in prep.): (i) ~30 successive images were averaged after proper shifts due to atmospheric effects; (ii) the stellar fluxes on the co-averaged images were measured by an aperture photometric method in which the fuzzy apertures were determined by pixel-by-pixel S/N ratios; (iii) the individual stellar fluxes were corrected for airmass and by using only three reference stars – the small field of view did not allow to use more – we were able to reach an accuracy of ~3 × 10-3 mag on the above, 30 s-binned LC. The short-lasting glitches before the ingress and egress phases are attributed to amplified guiding errors due to the nearby faint companion.
 |
Fig. 4 Folded/binned HATNet light curve of WASP-33 (dots) vs the best-fitting blend model (continuous line). There are 400 bins throughout the full orbital period. The standard deviations of the bin averages are very similar, they scatter around 0.8–1.2 mmag. The large out of transit variation of the presumed blended eclipsing binary excludes the possibility of a blend scenario by very high significance. |
4. Blend analysis
CC10 previously validated the planetary nature of WASP-33b based on their Doppler tomography analysis of the system. They found that the Doppler tomography and transit light curve provide consistent values for the fractional area of WASP-33 that is eclipsed by WASP-33b, and concluded that there cannot be significant photometric dilution from a third body. To provide an independent validation of the planetary nature of WASP-33b, we conducted a blend analysis of the available light curves and absolute photometry following the procedure described in Hartman et al. (2011). (We recall that the traditional bisector span analysis does not work in the case of this star, due to its high rotational speed and the concomitant low accuracy of the radial velocity/bisector span values).
We use the TFA-reconstructed HATNet LC and the summed-up followup LCs observed in V, R, I and z colors. (We did not use the non-specified filter-less ETD-posted measurements, their B data and the J and the Hα observations of Sada et al. 2012). The HATNet data consists of 12 149 data points, whereas the followup observations in the four colors listed above, contribute by another 8361 data points (with 2891, 1759, 3260 and 451 data points and 6, 7, 8 and 1 events in V, R, I and z colors, respectively). Concerning the accuracy of these averaged single color followup LCs in a ~1 min binning, we note that the bin averages have an overall standard deviation of 1–2 mmag. (Slightly before/after the ingress/egress the scatter is higher, due to the sparser coverage of these parts by the followup observations). Since the difference is small, for the blend analysis, we used all time series without filtering out by the δ Scuti components (see Sect. 5). In finding the best fitting blend model we used the observed LCs in all colors listed above. In this process the individual colors were treated separately and the best fit was defined as the best overall fit counting all colors.
We find that a model consisting of a single star with a transiting planet is strongly preferred (with greater than 10σ confidence) over a blend between an eclipsing binary star system and another star (either foreground, or physically associated with the binary). The best-fit blend model shows both a significant out-of-transit variation (>3 mmag peak-to-peak) and a secondary eclipse (~1 mmag depth) which are both ruled out by the HATNet light curve (see Sect. 2 and Fig. 4).
This result enables us to derive more accurate system parameters by using the datasets employed in the blend analysis. We present the this global parameter determination in Sect. 8.
5. The δ Scuti pulsation components
It has been recognized quite early (see CC10) that the host star of WASP-33b is also a variable (i.e., pulsating) star. The followup work by Herrero et al. (2011) clearly showed that WASP-33 was a δ Scuti-type star. This finding was later confirmed by Smith et al. (2011), Sada et al. (2012) and quite recently by Deming et al. (2012) in various infrared bands, involving both ground and space observations. The possibility of pulsations is not too surprizing, since the physical parameters of the star fit well into the δ Scuti instability strip (although the relation between pulsation and physical parameters is not that simple in this part of the Hertzsprung-Russel diagram – see Balona & Dziembowski 2011, especially in the case of Am stars, such as the host of this system – see CC10; Balona et al. 2011).
Herrero et al. (2011) find that the frequency at ~21.3 d-1 is in close (but high-order) resonance with the orbital frequency, which brings up the interesting possibility of tidally excited stellar oscillations by the planetary motion. In spite of this and other works mentioned above, so far, a clear detection and an accurate determination of the underlying frequency components is still missing.
We Fourier (DFT) analyzed the HATNet dataset after subtracting the transit signal. The analysis was performed in the [0.0,30.0] d-1 frequency band. The resulting spectra, shown in Fig. 5, clearly display the presence of three discrete sinusoidal components. The low (sub-mmag) amplitudes of all components and the relatively close frequency spacing of two of the components explain why the earlier attempts failed to identify all these components4.
 |
Fig. 5 Successive pre-whitened DFT spectra of the HATNet data after subtracting the transit component. The labels are defined in the same way as in Fig. 1. |
In employing these oscillations to clean up the followup light curves, we have to consider that the HATNet data were accumulated between 2003 and 2007 which implies that the frequency values derived solely from the HATNet data are not accurate enough to employ them for a useful prediction in the followup era (i.e., after 2010). Therefore, we filtered out the transit component from the followup data and analyzed the so-obtained residuals with the HATNet data (also without the transit signal)5. The Fourier decomposition resulted from this analysis is given in Table 3.
We may look at various linear combinations of these frequencies to see if Herrero’s et al. (2011) resonance hypothesis still holds. We find that with these well-resolved components there is no longer such a simple relation between the pulsation and orbital periods. The δ Scuti pulsation seems to be independent of the planetary companion.
Fourier decomposition of the δ Scuti pulsation of WASP-33.
We inspected the relation between the predicted δ Scuti pulsation and the oscillations observed/suspected in the individual followup LCs. The general conclusion is that we have a reasonable overall correlation between the two variations, although the observed amplitudes are larger and there are phase shifts occasionally. In Fig. 6 we show an example on the stronger phase coherence and lack of complete ceasing of the transit anomaly after the subtraction of the δ Scuti components.
 |
Fig. 6 Example of the temporal coherence between the observed oscillations and the ones predicted by the three high-frequency δ Scuti pulsation components (see Table 3). The observations of Herrero et al. (2011) have been plotted. Note that the amplitude of the pulsation is smaller than those of the observed oscillations. |
6. The mid-transit hump
The 42 followup light curves (in addition HATNet) listed in Table 1 show a remarkable variety, with various oscillations and distortions, occasionally going to the extreme. Obviously, it is important to clarify if these changes are of astrophysical origin or just the result of unknown instrumental or environmental/weather-related effects. To get some information on the reality of certain specific features, we examine those LCs given in Table 1 that were observed by different observers on the same nights. One such a night is 2010-10-20/21. Figure 7 shows that the two ETD observers Claudio Lopresti and Ramon Naves derived the same type of LCs, with a characteristic hump in the middle of the transit.
 |
Fig. 7 Example of the consistency of followup observations made on the same date of 2010-10-20/21 by different observers. This is an example of a “regular” transit. Lighter dots are for the data of Claudio Lopresti (ETD), whereas the heavier ones for those of Ramon Naves (ETD). Continuous line shows the model fit to the grand-averaged transit light curve. The agreement between the two datasets is very good. Both indicate a small but significant brightening in the middle of the transit. |
In the above example the average shape of the LCs (except for the center hump) are in agreement with the one we expect from a standard transit. Vastly different (but consistent) LCs emerged from the observations made on 2012-01-01/02. The data come from two different sites and different telescopes from the ETD contributors Ramon Naves and Jordi Lopesino. The resulting LCs are plotted in Fig. 8. The distortion is enormous but seems to be real from these independent datasets. (Nevertheless, as the referee noted, the relative proximity of the two telescopes used in these observations raises further suspicion on a possible weather-related issue of the phenomenon).
 |
Fig. 8 Example of the consistency of followup observations made on the same date of 2012-01-01/02 by different observers. This is an example of a “strongly discrepant” transit. Lighter dots are for the data of Ramon Naves (ETD), whereas the heavier ones for those of Jordi Lopesino (ETD). Continuous line shows the model fit to the grand-averaged transit light curve. The agreement between the two datasets is very good which indicates that the large transit anomaly might be real. |
It is also worthwhile to compare observations made on the same night through different filters. Interestingly, the only available datasets of this kind gathered by the Kitt Peak survey (Sada et al. 2012) also show peculiarities which are consistent in the two filters (see Fig. 9). We see in both colors a step-wise variation and a substantially shallower transit depth in color J. The difference is too large to be accounted for by a limb darkening effect.
 |
Fig. 9 Example of the consistency of followup observations made on the same date of 2011-10-13/14 through different filters (Sada et al. 2012). This is an example of a “mildly discrepant” transit. Heavier dots are for the observations made through the Hα, whereas the lighter ones for the J filter. The larger scatter in the Hα band is likely due to the smaller aperture of the telescope used with this filter (0.5 m vs. 2.1 m for the J filter). Continuous line shows the model fit to the grand-averaged transit light curve. Both light curves clearly show the step-like variation of the flux with the break in the middle of the transit. |
There are altogether seven parallel observations in the database shown in Table 1. They are all in very good agreement with each other (including “amateur” and “professional” data, i.e., the ones gathered on 2011-11-12/13), except for the event observed on 2011-12-24/25 by Ramon Naves and Konkoly. While the Konkoly data (see Fig. 3) display a regular transit shape, the parallel dataset shows a skewed transit (see Fig. A.4). We think that this signals the need for substantial caution, especially in the case of excessive transit anomalies.
There is one characteristic feature that appears in several LCs: we see a hump/brightening of a few mmag near the center of the transit. This anomaly has been noted also by Herrero et al. (2011) and by Lubos Brat at the ETD site6. Since the hump seems to appear at the same orbital phase in each case, we decided to attempt a more definite detection of this feature by adding up all non-discrepant LCs (i.e., the not labeled ones in Table 1) to increase the S/N.
In summing up the LCs, one might be concerned about three effects influencing the final result: (i) the data were gathered in various filters that yield slightly different transit shapes due to the color dependence of the limb darkening; (ii) the LCs are of different quality; (iii) the phenomenon may not appear in all transits and then, averaging might decrease the S/N of the detection.
If we had more accurate and less uniformly sampled data, concern (i) could be an important one. Due to limb darkening, the transit depth increases by ~1.4 mmag as we switch from filter I to filter B. The difference shrinks to ~1.0 mmag if we compare filters I and V. If we have roughly uniform coverage in the bins by all colors, then large part of the transit will be shifted in magnitude roughly by the same amount. This results in a conservation of the transit distortion, depending on the limb darkening very weakly. We did not see any improvement in the overall standard deviation of the bin averages when we scaled the transits by the expected depth dependence on color. Within this framework we also included the “Clear” (C, no-filter) data, although it is not clear without detailed consideration of the optical setting in each case what filter “C” really means. In selecting the reference model, we took the one corresponding to color “B”. Various models corresponding to colors B − I gave increasing residual standard deviations toward redder colors (when fitted to the averaged LC by omitting the central hump). Redder colors tend to give more wavy residuals and worse fits to the ingress/egress parts but still a significant central hump (see Fig. A.2).
Concern (ii), the problem of different quality, was considered first within the standard framework of calculating the average of random variables of different variances. However, subsequent tests with various other ways of averaging have led to the conclusion of using the simplest way of averaging, with unit weights applied to all data points, no matter which LC are they attached to. We used the linear trend-filtered data (as derived in Sect. 3) in a binned simple summation of the non-flagged LCs in Table 1.
Concern (iii) is very important, and, it seems to be justified on the basis of the current followup database (even if we consider that most of the followup data are too noisy to make statements on each individual events). For example, the Kitt Peak data (cf. Fig. 9) clearly show that we have a stepwise anomaly rather than a slightly off-centered hump (at least on the night of the observations). The low-noise observations of Josep Gaitan (LC #34 in Table 1) show apparently a flat bottom, whereas the LCs shown in Fig. 8 may support the possibility of large, asymmetric distortions (with the caveats mentioned above). Counterexamples on these varying anomalies are LCs #11 and #25 that show slight but steady humps that survive after pre-whitening by the δ Scuti components. We think that the noise level of the currently available data does not allow a clear selection of all LCs showing the specific distortion we are searching for. Therefore, the inclusion of all, non-peculiar LCs in the averaging process seems like a reasonable approach in the present situation.
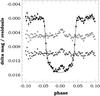 |
Fig. 10 Transit light curve obtained by summing up 32 light curves (see non-flagged items in Table 1). We combined the data in 0.002 phase units. Error bars show the ±1σ ranges of the bin averages. Continuous line shows the reference model light curve (see text). The dots in the middle of the plot show the residuals (arbitrarily shifted) for the dataset without prewhitening by the δ Scuti components (light-shaded filled circles) and for the prewhitened one (dark-shaded filled circles). |
The result of the averaging process described above is displayed in Fig. 10. We see that the ~1.5 mmag hump is significant in this grand-averaged light curve. It is also visible that it is slightly off-centered. The hump is slightly less significant, if we subtract the δ Scuti component. Since the pulsation components are not in resonance with the orbital period, this effect of decreasing the hump amplitude is attributed to our inability to separate the two phenomena. This assumption is supported by the test we made with the predicted pulsation on the timebase of the followup data. Here we folded the predicted pulsational light curves by the orbital period and checked if the so-folded LC showed any structure, indicating a piling-up close to the transit center. We did not see such an effect, instead, we saw a roughly uniform distribution. On the other hand, there are cases when the observed wiggles do coincide with the δ Scuti component (see, e.g., Fig. 6). Therefore, a few such coincidences might already be sufficient to cause some decrease of the hump.
Finally we note in passing that by adding further followup data and/or using different mixtures of them – but of course, by keeping the reliable ones – do not result in a considerable change in the significance of the central hump. Following the recommendation of the referee, in the Appendix (see Fig. A.1) we show the grand-averaged LCs obtained from three different mixtures of followup data. Although with a somewhat lower significance, the anomaly is clearly exhibited in all average LCs, even though the new set of 13 LCs are noisier by ~20% on the average than the set presented in this paper.
7. Radial velocity data – further constraining the planetary mass
As a part of our regular routine on following up planetary candidates, spectral observations were taken with the Tillinghast Reflector Echelle Spectrograph (TRES, Fűrész 2008) on the 1.5 m Tillinghast Reflector at the Fred Lawrence Whipple Observatory in Arizona. Using the medium fiber, which has a resolving power of δλ/λ ~ 44 000 and a wavelength range of 3200–8900 Å, we obtained a total of 12 observations taken between February 1, 2010 and October 25, 2010, to get complete phase coverage of our target. The spectra were extracted and analyzed using the procedures outlined in Buchhave et al. (2010). The radial velocities were measured by cross correlating a single spectral order (of the Mg b triplet in 5150–5280 Å) against a synthetic template. Significant velocity variations were seen in the single order velocities but the scatter was fairly large, presumably due to the rapid rotation of this star. In an attempt to improve the accuracy, we calculated the multi-order velocities by cross correlating the spectra against each other order-by-order and summing the correlation functions. This increases the S/N by effectively reducing the measurement errors. We used the strongest observation as a template and covered the wavelength range of ~3980–5660 Å. The 12 RV values together with their errors and spectral S/N values are listed in Table 4.
Radial velocities measured by TRES on WASP-33.
For consistency check with other spectroscopic/photometric results concerning the physical parameters of the star, we computed Teff, vrotsini and [M/H] by using the weighted average of the Mg b triplet in three adjacent orders. Because the planetary nature of the system can be regarded as proven, we tamed the well-known ill-conditioning of the physical parameter determination by fixing the gravity log g as follows from the relation g = 4a/(Δttr)2. (Here a is the semi-major axis and Δttr is the transit duration and we assumed a circular orbit with small planet-star mass ratio – see, e.g., Seager & Mallén-Ornelas 2003; Sozzetti et al. 2007; and Beatty et al. 2007). With log g = 4.2, for the strongest (highest S/N) spectra we got Teff = 7700 ± 50 K, vrotsini = 96 ± 0.5 km s-1 and [m/H] = −0.10 ± 0.08. In a comparison with CC10, we see that our temperature and rotational velocity are higher by 270 K and 10 km s-1, whereas the metallicity is lower by 0.2 dex. Taking the formal errors given both by CC10 and us, these values differ by 2.4, 19 and 1 sigma for Teff, vrotsini and [M/H], respectively. Although the differences in Teff and [M/H] are tolerable, we do not know what causes the formally highly significant discrepancy in vrotsini. For this reason and for the overall better consistency of the temperature and metallicity values derived by CC10, we use their values in the determination of the system parameters in Sect. 8.
We fitted a sinusoidal signal (assuming zero eccentricity) to the 11 RV values by omitting the point with the lowest S/N (which one is also an outlier in the fit). Since we fixed the period and the transit center according to the values obtained by the combined analysis of the HATNet and followup data, there remained two parameters to fit: (i) the RV semi-amplitude K; and (ii) the zero point shift. The resulting fit is shown in Fig. 11. Although the S/N of the fit is not particularly high, it is still possible to give a reasonable estimate on the RV amplitude and planetary mass. We get K = 0.443 ± 0.095 km s-1 and, assuming a stellar mass and a semi-major axis of 1.495 ± 0.030 Msun and 0.02556 ± 0.0002 AU respectively (see CC10), we get a planetary mass of 3.04 ± 0.66 MJ7. This is in agreement with the broad upper limit of 4.1 MJ given by CC10 and also suggests that WASP-33b falls in the more massive class of planets. In Sect. 8 we get a more complete set of system parameters (including the planetary mass) by using a global fit to all observed quantities.
 |
Fig. 11 Phased radial velocity curve with the fitted sinusoidal (assuming zero eccentricity). We fixed the period and the transit epoch as given by the joint analysis of the HATNet and followup data. Due to its large error, the gray-shaded data point at phase ~0.3 was left out of the fit. |
8. System parameters
By using the RV data and the LCs employed in the blend analysis (in all three colors), we can derive more accurate system parameters. In this process we essentially followed the method described in our discovery papers (e.g., Bakos et al. 2011). In short, we combine the parameter determination from the LC, RV and spectroscopic data through the intermediary of the stellar evolution isochrones (i.e., by using the Yale-Yonsei models of Yi et al. 2001). The errors are estimated by a Markov Chain Monte Carlo method as an integral part of the parameter determination. Because we are using composite data, we did not perform trend filtering during the fit (we made a trend filtering as part of the data preparation – see Sect. 3). One other difference from the Bakos et al. (2011) procedure is that we used a Mandel & Agol (2002) model for the HATNet data rather than a simplified flat-bottom transit model. To determine the physical parameters of the planet we used the atmospheric parameters (Teff, [Fe/H] and log g) for WASP-33 taken from Collier Cameron et al. (2010) together with the constraint on the stellar density which comes from modeling the transit light curves. The orbital period and the moment of the transit center was fixed to the values we got by the BLS analysis of the full dataset (see Sect. 3). The eccentricity was also fixed to zero, as suggested by the infrared occultation data by Smith et al. (2011) and Deming et al. (2012). Furthermore, because of the central hump, during the global analysis we omitted the data points in the phase interval [−0.007,0.014].
Table 5 lists the so-obtained parameters and their errors from the Monte Carlo method mentioned above. In comparing with the set derived by CC10, we see that the parameters are in good/fair agreement but our planet radius is ~10% larger. This difference comes mainly from the exclusion of the central hump region from our analysis (including the hump, the difference shrinks down to ~4%). Our errors, directly related to the light curve, are substantially lower. The absolute parameters (e.g., stellar mass) are of similar accuracy, or worse in our case. The reason for that is not entirely clear but might come from differences in the computational details and differences in the error limits. We agree also on the low age of the system, however our age estimate is limited to values higher than 0.1 Gyr, to avoid confusion with pre-main sequence evolution tracks. It is worthwhile to note that systems with high temperature host stars are better candidates for accurate age estimates, due to the larger age spread in the same stellar density interval (see Fig. 5 of Collier Cameron et al. 2010).
System parameters of WASP-33.
9. Discussion
To exhibit the special position of WASP-33b among the currently known TEPs, in Table 6 we summarize the relevant properties (from the point of view of this section) of the top 10 planets ordered by the value of the Roche-filling factor (Budaj 2011). We see that WASP-33b is among the possible candidates for intensive star-planet interaction, including mass transfer. In the process of planet mass loss, the dynamical/gravitational distortion is coupled with the high temperature of the host star and the higher UV (continuum) flux impinging the planet surface facing the star. Considering that HD 209458 (together with HD 189733b – see Lecavelier des Etangs et al. 2010) has already been shown loosing mass (cf. Vidal-Madjar et al. 2003), and HD 209458 has a rather low Roche-filling factor, it is expected that those with much higher filling factors are very good candidates for observing mass-loosing planets. The high planet temperature, UV radiation and the bright apparent magnitude make WASP-33 especially a good target for observing mass loss.
Although there are TEPs with strong stellar variability (e.g., CoRoT-Exo-4b, see Aigrain et al. 2008), the transit anomalies detected in WASP-33 are unmatched. (Except for the extraordinary object KIC 12557548, supposedly a Mercury size ultra short period planet, showing dramatic changes in the transit depth and shape – see Rappaport et al. 2012). The changes seen in the available followup data (even if we suspect that a considerable part of them may be of instrumental origin) are very large compared with the mild short-lasting humps attributed to stellar spot activity in some TEPs (e.g., CoRoT-2, HAT-P-11, WASP-4 and Kepler-17, see Nutzman et al. 2011; Sanchis-Ojeda & Winn 2011a; Sanchis-Ojeda et al. 2011b; and Désert et al. 2011, respectively). Some of the anomalies observed are recurrent, appearing in similar phases in the transit (e.g., two spot belts in HAT-P-11, several of them in Kepler-17). This has led to the utilization of these quasi-stationary anomalies to estimate stellar obliquity, independently of the Rossiter-McLaughlin effect. This is very promising, although for a more reliable application of the method one needs well-covered, nearly continuous set of data, characteristic only of space observations. Even if this type of data are available, sufficiently long-lived, constant latitude spots are necessary to disentangle different geometric scenarii (e.g., HAT-P-11, see Sanchis-Ojeda & Winn 2011a).
First 10 TEPs ordered by the Roche-filling factor f(Roche).
Disregarding other light curve anomalies, since the hump near the center of the transit of WASP-33b seems to be recurrent, it is important to find an explanation on the physical origin of this feature. We investigated the following possibilities (in the order of likelihood).
-
(a)
Recurring spots (a belt of spots or a single spot that rotatesresonantly with the orbital period).
-
(b)
Low spherical order distortions due to the δ Scuti pulsations.
-
(c)
Variation of the projected planet size due to tidal distortion of the planet.
-
(d)
Additional bodies (moons, planets).
-
(e)
Gravity darkening due to fast rotation.
Recurring spots.
Possibility (a) would have seemed to be a plausible explanation if we had forgotten about the spectral classification of the star. Metallic line A stars are supposed to be quiet objects with no or very weak magnetic fields, a prerequisite of spot activity. Furthermore, the element diffusion that causes the observability of the chemical peculiarities requires the absence of any mixing process, such as pulsation, if it excites random motion, i.e., turbulence. Nevertheless, as an important “by-product” of the SuperWASP survey, Smalley et al. (2011) have shown that nearly 13% of the examined 1600 stars classified as type Am are δ Scuti and γ Dor stars pulsating with low amplitudes. Although it is not mentioned in their paper, some of the γ Dor stars might be actually spotted stars with small spots. If this is true, then spots should not form a well-populated belt at a given latitude of activity, since in this case we could not observe a light variation. On the other hand, in the case of WASP-33 we did not detect a variation in the total flux above 0.5 mmag in the [0, 2] d-1 band, relevant for any rotational-related activities (see Sect. 2). Therefore, the spot belt assumption is more plausible. Then, this is consistent with the high tilt of the planetary orbit and the stellar rotational axis as suggested by the spectroscopic anomaly observed by Collier Cameron et al. (2010). Interestingly, Kepler-17 also shows a strikingly similar central hump in the grand-averaged transit light curve (Désert et al. 2011). While in the case of this system the hump can be explained by the presence of separate spots (since they cause observable effect in the average light variation), as mentioned above, no such a variation is seen in WASP-33.
Low spherical order distortions.
Explanation suggested in (b) sounds exciting, since it would explain in a natural way the steady-looking hump as a result of non-radial pulsation with l = 3, m = 0 spherical quantum numbers. The obvious condition for this model to work is the existence of a stroboscopic effect between the orbital and the pulsation frequencies. Since there is no such an effect (i.e., resonance), this model cannot produce a (quasi-)steady hump in the same orbital phase.
Variation of planet size.
Model (c) looks also a viable alternative for a moment but a glimpse on the possible distortion caused by the aspect dependence of a distorted planet in the short phase of transit (see Leconte et al. 2011), clearly excludes this model from any further considerations as an explanation of the short-lasting central hump.
Additional bodies.
Possibility (d) is listed only for completeness, as an unlikely resort to a more exotic explanation of a steady transit anomaly. We would not only need an additional planet (or moon) on a resonant orbit but the stability condition would require this object to be of extreme low density. The observed hump of ~1.5 mmag implies an object radius of ~0.6 RJ. With an “ordinary” gaseous planet density of 1 g cm-3 (i.e., the same as of WASP-33b), this results in a ~0.2 MJ object mass, which is certainly a reasonably high value to make the configuration unlikely to be stable.
Gravity darkening.
The observability of gravity darkening exerted by fast rotation (possibility (e)) has been brought up in the context of the high-precision photometric data attainable by the Kepler satellite (Barnes 2009). It has apparently been observed in KOI-13, a short-period eclipsing binary with fast rotating components (vrot ~ 70 km s-1) in the Kepler field (Szabó et al. 2011). The amplitude of the observed anomaly is only ~0.2 mmag. Barnes’ tests with a model system of an Altair (α Aquilae)-type host star (with vrot ~ 200 km s-1, e.g., van Belle et al. 2001) indicate that the central hump might be as large as 1 mmag in this case (see his Figs. 5 and 8). To extrapolate this result to the case of WASP-33, we can compare the ratios of the centrifugal and Newtonian components of the surface gravity 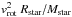 . This yields an estimate of the fractional change of
. This yields an estimate of the fractional change of 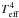 (in the classical von Zeipel approximation), the major contributor to the observed flux. We get that this ratio is about 6-times larger for Barnes’ model than for WASP-33. We conclude that model (e) is not preferred for WASP-33, since gravity darkening contributes probably at the level less than ~0.2 mmag to the distortion of the transit shape.
(in the classical von Zeipel approximation), the major contributor to the observed flux. We get that this ratio is about 6-times larger for Barnes’ model than for WASP-33. We conclude that model (e) is not preferred for WASP-33, since gravity darkening contributes probably at the level less than ~0.2 mmag to the distortion of the transit shape.
As discussed in Sect. 6, there are anomalies in WASP-33 that are of much more substantial than the central hump. Even if several of these might come from observational errors, the explanation of the remaining ones (sloping full transit phase, different steepness of the ingress/egress phases, varying transit depth, asymmetric shifts in the ingress/egress phases) should imply major changes in the stellar flux. For example, the overall increase in the temporal transit depth (see notes added to Table 1) can only be explained if we assume a temporal but substantial dimming of the stellar light (or a sudden increase of the planet radius due to a violent Roche-lobe overflow). We do not have any idea on the explanation of the asymmetric distortions of the transit shape (but the case of KIC 12557548 is tempting – see Rappaport et al. 2012).
The issue of the variability of the nearby comparison stars as an explanation of the unusual transit anomalies has come up early in this work. The HATNet data allowed us to study the variability of the some 140 objects in the trimmed field of the Konkoly Schmidt telescope (see Sect. 3). Since fainter stars contribute very little to the flux if only few comparison stars are used, we concentrated only on the 10 bright close neighbors employed by most of the followup works. Assuming that standard DFT and BLS analyses are the proper means to qualify their variability (i.e., no sudden – non-periodic – dimming or brightening occur in these stars), we found that none of them show the level of variability that could cause the observed strong anomalies. There are only two stars worth for further consideration, the rest do not show a significant variation above 0.5–1 mmag. Star 2MASS 02263566+3735479 often appears as one of the comparison stars in the various followup works. This is a variable object with f = 3.12274 d-1 and a Fourier amplitude of A = 2.6 mmag. The variability is slightly nonlinear (has a non-zero 2f component). The star is seldom used alone and even if it is done so, its variability introduces only some small, slightly nonlinear distortion (i.e., a trend) in the transit shape, that can be partially filtered out. Followup light curves using dominantly this comparison star do not show intriguing peculiarities. On the other hand, the very nearby bright (although still 2.9 mag fainter) star 2MASS 02265167+3732133 could be problematic if the aperture is not correctly set in the photometry. The HATNet data show that this object has some remaining systematics (i.e., 1 d-1 variation) at the 4–10 mmag level. By judging from the accompanying maps at the ETD site, we think that most of the followup LCs were processed by small-enough apertures and this companion did not cause any important distortion in the target light curve.
Finally, we draw attention to the extremely young age of the system (see Table 6). Although the early phase of planet formation, including the consumption of the gas component and the inward migration of the planet have probably ended, the debris disk might still be present (e.g., Krivov 2010). This might still be observable in the far infrared. Furthermore, the retrograde orbit and the young age pose the intriguing question on the nature of the body that was able to perturb WASP-33b at such an early phase of evolution, right after the planet formation in a flat disk structure. The observations of Moya et al. (2011) by adaptive optics in the near infrared is a step in the direction of finding the perturber. If the low-luminosity object (a brown dwarf or a dwarf star) found by Moya et al. (2011) is/was gravitationally bounded to WASP-33, then perhaps a close violent encounter with WASP-33b at an early phase of planet formation in this stellar binary caused the near driving out of this planet by causing a perturbation that left it now on a retrograde orbit. Although planet-planet scattering due to dynamical instability in a plane-confined resonant multiplanetary system can also lead to highly inclined orbits (i.e., Libert & Tsiganis 2012), this does not seem to be sufficient to excite retrograde orbits.
10. Conclusions
WASP-33b is a peculiar planet both in term of its host star and in respect of the size of its tidal distortion and the radiation level received from its star. These properties, combined with its brightness, have made this target a very attractive one for various followup studies, in particular for photometric ones.
Although our work primarily focused on the (time-domain) photometric properties of the system, by using our archival radial velocity (RV) data gathered by the TRES spectrograph we were able to give a better estimate the mass of WASP-33b. The derived mass of 3.27 ± 0.73 MJ is in agreement with the earlier raw upper limit of 4.1 MJ given by Collier Cameron et al. (2010). With the significant RV signal we can state that WASP-33b belongs to the more massive class of extrasolar planets.
By using the HATNet database, we searched for the signature of short-period oscillations of the host star as reported earlier by some followup works (in particular, that of Herrero et al. 2011). We confirmed the presence of δ Scuti-type pulsations, and, for the first time, we resolved the pulsation in three discrete components in the 15–21 d-1 range. All three peaks have sub-mmag amplitudes. Due to the well-known difficulties (mode identification, need for full evolutionary model structure, mode selection, etc. – see, e.g., Casas et al. 2009) in using these components in a pulsation analysis to constrain the stellar parameters, we employed these oscillations only to test their effect on the finally derived grand-averaged transit light curve (which effect has proven to be negligible for the current data). Opposite to what was suggested by some earlier works (i.e., Herrero et al. 2011), neither the frequencies nor their linear combinations are in close resonance with the orbital period.
Due to the lack of high precision RV data, we excluded possible blend scenarios primarily on the basis of the HATNet light curve. The absence of the predicted out of transit variation of the best-fitting blend model is a very strong support of the suspected genuine star-planet configuration based on the spectral tomography performed by Collier Cameron et al. (2010). As a “by-product” of the blend analysis we also derived more precise system parameters (see Table 5).
In addition to the high rotational speed and high temperature of the host star, the most remarkable peculiarity of this system is the numerous transit anomalies observed in the various followup light curves. In addition to the δ Scuti pulsations, these are extra features of the system. Interestingly, one type of anomalies, the slightly off-centered ~1–2 mmag hump within the transit, seems to persist in more than half of the followup data so that it becomes very nicely visible in the grand-averaged light curve, using 32 followup light curves and the HATNet survey data. We attempted to give a phenomenological explanation of this feature by invoking, e.g., low-spherical order stellar pulsation, a belt-like starspot structure and variation in the projected cross section of a tidally distorted planet. We think that the star spot hypothesis could be a viable one but the existence of spots is questionable on the basis of the Am classification of the star.
WASP-33 is a very interesting system for the substantial transit anomalies, for the retrograde orbit of the planet and for the young age of the parent star. The data used in the present work have been able to give a more accurate estimate of the basic system parameters and to show the quasi-permanent nature of the central small hump within the transit. However, because of the ~0.1% effect, we were unable to show if this feature (perhaps with varying amplitudes) is present during all transit events. Also, because of the observational systematics and relatively high noise level, the reality of several (but not all) other anomalies can also be questioned. Therefore, gathering high-precision (sub-mmag/min) photometric transit data would be crucial in understanding this puzzling system.
Online material
Appendix A: Individual and various grand-averagedlight curves, effect of limb darkening, transitand trend parameters
 |
Fig. A.1 Grand-averaged transit light curves obtained from various datasets. White: our basic set of 32 LCs as presented in Sect. 6; gray: 32 LCs from the basic set and 13 LCs recommended by the referee from the ETD in her/his second report. (These LCs come from the following followups (name-date-filter): CLopresti-2010-09-11-R, SGajdos-2010-10-27-V, SKorotkiy-2010-10-25-R, JGarlitz-2010-11-19-R, LBrat-2010-11-27-C, Dhusar-2010-12-03-R, SShadick-2011-02-10-I, DSergison-2011-09-29-R, CGillier-2011-09-29-R, SShadick-2011-10-01-I, SShadick-2011-10-30-I, ABourdanov-2011-12-10-C, ERomas-2011-12-10-B.) Black: as for the gray set but omitting 11 stars recommended by the referee in her/his 3rd report. (These omitted LCs come from the following followups (name-date-filter): SGajdos-2010-10-27-V, SKorotkiy-2010-10-25-R, LBrat-2010-11-27-C, and #6, #15, #18, #24, #26, #33, #34, #36 from our basic set as given in Table 1). Notation and data sampling is the same as in Fig. 10. The residuals have been shifted vertically for better visibility. |
 |
Fig. A.2 Effect of the assumed average color of the grand-averaged light curve (Fig. 10) on the transit anomaly. The continuous curves show the best fitting models from B (the deepest curve) through V, R to I (the shallowest curve). The dots represent the (shifted) residuals remaining after subtracting the model light curves corresponding to B and I (upper and lower sets of points, respectively). The “kinks” in the I residuals in the ingress/egress parts suggest that shorter wavebands give a better representation of the mixture of colors the grand-averaged light curve is assembled from. |
 |
Fig. A.3 Light curves for the first half of the dataset as listed in Table 1. Phase was computed from the ephemeris given for the full dataset in Table 2. The light curves were linearly detrended as described in Sect. 3. The filters and the internal identification numbers (see Table 1) are given in each panel in the upper left and right corners, respectively (the sign ? is overplotted on the internal ID if the light curve is not included in the analysis presented in this paper). The reference model light curve is plotted by continuous line in each panel. Since the main purpose of the plot to display primarily the ETD light curves, for simplicity we left out #01 (HATNet), #02 (FLWO) and #30 (Konkoly), shown in other figures in the paper. |
Simplified transit model fits to the individual transit events of WASP-33.
We checked also the available SuperWASP data (http://www.wasp.le.ac.uk/public/) but the noise level was too high to permit an in-depth analysis.
In principle, due to the periodic light blocking effect of the transiting planet, we should deal with both variable stellar oscillations and transit shapes. However, due to the small size of the planet and the small amplitude of the pulsations, these are rather small effects, i.e., in the order of less than 2% on the pulsation amplitudes. We also disregard the possible color dependence of the pulsation amplitudes in the different filters (see, e.g., Liakos & Niarchos 2011).
The high-precision LC presented in a poster by Hardy & Dhillon (in prep., see www.ing.iac.es/astronomy/science/staff/posters/Liam_Hardy_poster.pdf) also shows a brightening near the transit center.
Acknowledgments
The results presented in this paper have been greatly benefited from the archive of Exoplanet Transit Database (ETD) maintained by Stanislav Poddany, Lubos Brat and Ondrej Pejcha. We thank for their prompt and helpful feedback on our questions occurring during the analysis. We also thank to the numerous professional amateur observers who feed this site. Useful correspondence on the transit anomalies with ETD contributors Ramon Naves and Eugene Sokov are appreciated. Thanks are due to Pedro Valdes Sada, who sent us the data on WASP-33 gathered at Kitt Peak. We thank Attila Szing for performing the observations on November 24/25, 2011 and András Pál for making his astrometric routine available to us. Thanks are also due to Katalin Oláh for discussions on stellar activity, to Jan Budaj for helping us to revisit the Roche-filling factor and to the referee whose thorough review helped us substantially in revising the paper. G.K. and T.K. acknowledge the support of the Hungarian Scientific Research Foundation (OTKA) through grant K-81373. G.Á.B. and J.D.H. acknowledges partial support from NSF grant AST-1108686. Zs.R. has been supported by the Hungarian OTKA Grants K-83790 and MB08C-81013, and the “Lendület” Program of the Hungarian Academy of Science. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Aigrain, S., Collier Cameron, A., Ollivier, M., et al. 2008, A&A, 488, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., Ripepi, V., Catanzaro, G., et al. 2011, MNRAS, 414, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á, Lázár, J., Papp, I., Sári, P., & Green, E. M. 2002, PASP, 114, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Hartman, J., Torres, G., et al. 2011, ApJ, 742, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. W. 2009, ApJ, 705, 683 [Google Scholar]
- Beatty, T. G., Fernández, J. M., & Latham, D. W. 2007, ApJ, 663, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Bakos, G. Á, Hartman, J. D., et al. 2010, ApJ, 720, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Budaj, J. 2011, AJ, 141, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Casas, R., Moya, A., & Suárez, J. C. 2009, ApJ, 697, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Christian, D. J., Pollacco, D. L., Skillen, I., et al. 2006, MNRAS, 372, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., & Mcdonald, I. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Fraine, J. D., Sada, P. V., et al. 2012, ApJ, 754, 106 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2013, A&A, 550, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Désert, J.-M., Charbonneau, D., & Demory, B.-O. 2011, ApJS, 197, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Fűrész, G. 2008, Ph.D. Thesis, University of Szeged, Hungary [Google Scholar]
- Gillon, M., Smalley, B., Hebb, L., et al. 2009a, A&A, 496, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Demory, B.-O., Triaud, A. H. M. J., et al. 2009b, A&A, 506, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F. T., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2011, ApJ, 742, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Morales, J. C., Ribas, I., & Naves, R. 2011, A&A, 526, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovács, G., Bakos, G., & Noyes, R. W. 2005, MNRAS, 356, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V. 2010, A&A, 10, 383 [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A., Ehrenreich, D., Vidal-Madjar, A., et al. 2010, A&A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leconte, J., Lai, D., & Chabrier, G. 2011, A&A, 528, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libert, A.-S., & Tsiganis, K. 2012, MNRAS, 412, 2353 [Google Scholar]
- Liakos, A., & Niarchos, P. 2011, IBVS, 5967 [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Moya, A., Bouy, H., Marchis, F., et al. 2011, A&A, 535, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muirhead, P. S., Johnson, J. A., Apps, K., et al. 2012, ApJ, 747, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Nutzman, P. A., Fabrycky, D. C., & Fortney, J. J. 2011, ApJ, 740, 10 [Google Scholar]
- Pál, A. 2009, Ph.D. Thesis [arXiv:0906.3486] [Google Scholar]
- Poddany, S., Brat, L., & Pejcha, O. 2010, New Astron., 15, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Levine, A., Chiang, E., et al. 2012, ApJ, 752, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sada, P. V., Deming, D., Jennings, D. E., et al. 2012, PASP, 124, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., & Winn, J. N. 2011, ApJ, 743, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Holman, M. J., et al. 2011, ApJ, 733, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Smalley, B., Kurtz, D. W., Smith, A. M. S., et al. 2011, A&A, 535, A3 [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, A., Anderson, D., Skillen, I., et al. 2011, MNRAS, 416, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2009, ApJ, 691, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, Gy. M., Szabó, R., Benkő, J. M., et al. 2011, ApJ, 736, L4 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Ciardi, D. R., Thompson, R. R., et al. 2001, ApJ, 559, 1155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., & Désert, J.-M. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 BLS spectrum of the TFA-filtered/reconstructed time series based on the observations of WASP-33 by HATNet. The label in the upper right corner shows, from left to right, the pre-whitening order, peak frequency, transit depth (assuming trapezoidal transit shape) and the S/N of the peak frequency. The BLS amplitude is normalized to unity at the highest peak and refers to the signal without correction for blending by the nearby companion (see text). |
| In the text | |
 |
Fig. 2 Folded light curve of the TFA-filtered/reconstructed time series based on the observations of WASP-33 by HATNet (dots). The best-fitting simplified light curve model (with bin averaging in the out-of-transit part) is shown by the thick line. |
| In the text | |
 |
Fig. 3 Photometric observations of WASP-33 at the Konkoly and Fred Lawrence Whipple observatories. The Konkoly data have been taken through Cousins I, the FLWO data through Sloan z filters. Data points are binned in 0.001 phase (i.e., in 105 s intervals). |
| In the text | |
 |
Fig. 4 Folded/binned HATNet light curve of WASP-33 (dots) vs the best-fitting blend model (continuous line). There are 400 bins throughout the full orbital period. The standard deviations of the bin averages are very similar, they scatter around 0.8–1.2 mmag. The large out of transit variation of the presumed blended eclipsing binary excludes the possibility of a blend scenario by very high significance. |
| In the text | |
 |
Fig. 5 Successive pre-whitened DFT spectra of the HATNet data after subtracting the transit component. The labels are defined in the same way as in Fig. 1. |
| In the text | |
 |
Fig. 6 Example of the temporal coherence between the observed oscillations and the ones predicted by the three high-frequency δ Scuti pulsation components (see Table 3). The observations of Herrero et al. (2011) have been plotted. Note that the amplitude of the pulsation is smaller than those of the observed oscillations. |
| In the text | |
 |
Fig. 7 Example of the consistency of followup observations made on the same date of 2010-10-20/21 by different observers. This is an example of a “regular” transit. Lighter dots are for the data of Claudio Lopresti (ETD), whereas the heavier ones for those of Ramon Naves (ETD). Continuous line shows the model fit to the grand-averaged transit light curve. The agreement between the two datasets is very good. Both indicate a small but significant brightening in the middle of the transit. |
| In the text | |
 |
Fig. 8 Example of the consistency of followup observations made on the same date of 2012-01-01/02 by different observers. This is an example of a “strongly discrepant” transit. Lighter dots are for the data of Ramon Naves (ETD), whereas the heavier ones for those of Jordi Lopesino (ETD). Continuous line shows the model fit to the grand-averaged transit light curve. The agreement between the two datasets is very good which indicates that the large transit anomaly might be real. |
| In the text | |
 |
Fig. 9 Example of the consistency of followup observations made on the same date of 2011-10-13/14 through different filters (Sada et al. 2012). This is an example of a “mildly discrepant” transit. Heavier dots are for the observations made through the Hα, whereas the lighter ones for the J filter. The larger scatter in the Hα band is likely due to the smaller aperture of the telescope used with this filter (0.5 m vs. 2.1 m for the J filter). Continuous line shows the model fit to the grand-averaged transit light curve. Both light curves clearly show the step-like variation of the flux with the break in the middle of the transit. |
| In the text | |
 |
Fig. 10 Transit light curve obtained by summing up 32 light curves (see non-flagged items in Table 1). We combined the data in 0.002 phase units. Error bars show the ±1σ ranges of the bin averages. Continuous line shows the reference model light curve (see text). The dots in the middle of the plot show the residuals (arbitrarily shifted) for the dataset without prewhitening by the δ Scuti components (light-shaded filled circles) and for the prewhitened one (dark-shaded filled circles). |
| In the text | |
 |
Fig. 11 Phased radial velocity curve with the fitted sinusoidal (assuming zero eccentricity). We fixed the period and the transit epoch as given by the joint analysis of the HATNet and followup data. Due to its large error, the gray-shaded data point at phase ~0.3 was left out of the fit. |
| In the text | |
 |
Fig. A.1 Grand-averaged transit light curves obtained from various datasets. White: our basic set of 32 LCs as presented in Sect. 6; gray: 32 LCs from the basic set and 13 LCs recommended by the referee from the ETD in her/his second report. (These LCs come from the following followups (name-date-filter): CLopresti-2010-09-11-R, SGajdos-2010-10-27-V, SKorotkiy-2010-10-25-R, JGarlitz-2010-11-19-R, LBrat-2010-11-27-C, Dhusar-2010-12-03-R, SShadick-2011-02-10-I, DSergison-2011-09-29-R, CGillier-2011-09-29-R, SShadick-2011-10-01-I, SShadick-2011-10-30-I, ABourdanov-2011-12-10-C, ERomas-2011-12-10-B.) Black: as for the gray set but omitting 11 stars recommended by the referee in her/his 3rd report. (These omitted LCs come from the following followups (name-date-filter): SGajdos-2010-10-27-V, SKorotkiy-2010-10-25-R, LBrat-2010-11-27-C, and #6, #15, #18, #24, #26, #33, #34, #36 from our basic set as given in Table 1). Notation and data sampling is the same as in Fig. 10. The residuals have been shifted vertically for better visibility. |
| In the text | |
 |
Fig. A.2 Effect of the assumed average color of the grand-averaged light curve (Fig. 10) on the transit anomaly. The continuous curves show the best fitting models from B (the deepest curve) through V, R to I (the shallowest curve). The dots represent the (shifted) residuals remaining after subtracting the model light curves corresponding to B and I (upper and lower sets of points, respectively). The “kinks” in the I residuals in the ingress/egress parts suggest that shorter wavebands give a better representation of the mixture of colors the grand-averaged light curve is assembled from. |
| In the text | |
 |
Fig. A.3 Light curves for the first half of the dataset as listed in Table 1. Phase was computed from the ephemeris given for the full dataset in Table 2. The light curves were linearly detrended as described in Sect. 3. The filters and the internal identification numbers (see Table 1) are given in each panel in the upper left and right corners, respectively (the sign ? is overplotted on the internal ID if the light curve is not included in the analysis presented in this paper). The reference model light curve is plotted by continuous line in each panel. Since the main purpose of the plot to display primarily the ETD light curves, for simplicity we left out #01 (HATNet), #02 (FLWO) and #30 (Konkoly), shown in other figures in the paper. |
| In the text | |
 |
Fig. A.4 As in Fig. A.3 but for the second half of the dataset. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


