| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220755 | |
| Published online | 26 March 2013 | |
CoRoT 102918586: a γ Doradus pulsator in a short-period eccentric eclipsing binary⋆,⋆⋆
1
INAF – Osservatorio astronomico di Roma, via Frascati 33,
00040
Monteporzio C.,
Italy
e-mail:
maceroni@oa-roma.inaf.it
2
Institut d’Astrophysique et Géophysique, Université de
Liège, Allée du 6
Août, 4000
Liège,
Belgium
3
ESA Estec, Keplerlaan 1, 2201 AZ
Noordwijk, The
Netherlands
4
Thüringer Landessternwarte Tautenburg, Sternwarte 5,
07778
Tautenburg,
Germany
5
Department of Physics, University of Zagreb,
Bijenička cesta 32,
10000
Zagreb,
Croatia
6
INAF, Osservatorio Astronomico di Brera, via E. Bianchi
46, 23807
Merate,
Italy
Received: 16 November 2012
Accepted: 30 January 2013
Pulsating stars in eclipsing binary systems are powerful tools to test stellar models. Binarity enables us to constrain the pulsating component’s physical parameters and this knowledge drastically improves the input physics for asteroseismic studies. The study of stellar oscillations then allows us to improve our understanding of stellar interiors and stellar evolution. The space mission CoRoT discovered several promising objects suitable for these studies. They were photometrically observed with unprecedented accuracy, but needed spectroscopic follow-up. A promising target was the relatively bright eclipsing system CoRoT 102918586, which turned out to be a double-lined spectroscopic binary and also showed clear evidence of γ Dor type pulsations. With the aim of combining the information from binarity and pulsation and fully exploiting the potential of CoRoT photometry we obtained phase resolved high-resolution spectroscopy with the Sandiford spectrograph at the McDonald 2.1m telescope and the FEROS spectrograph at the ESO 2.2 m telescope. Spectroscopy yielded both the radial velocity curves and, after spectra disentangling, the component effective temperatures, metallicity, and line-of-sight projected rotational velocities. The CoRoT light curve was analyzed with an iterative procedure, devised to disentangle eclipses from pulsations. The eclipsing binary light curve analysis, combined with the spectroscopic results, provided an accurate determination of the system parameters, and the comparison with evolutionary models provided strict constraints on the system age. Finally, the residuals obtained after subtraction of the best–fitting eclipsing binary model were analyzed to determine the pulsator properties. We achieved a complete and consistent description of the system. The primary star pulsates with typical γ Dor frequencies and shows a splitting in period that is consistent with high order g-mode pulsations in a star of the corresponding physical parameters. The value of the splitting, in particular, is consistent with pulsations in ℓ = 1 modes.
Key words: binaries: eclipsing / binaries: spectroscopic / stars: oscillations / stars: individual: CoRoT 102918586 / stars: fundamental parameters
Based on photometry collected by the CoRoT space mission and spectroscopy obtained with the Sandiford spectrograph attached at the 2.1 m telescope at McDonald Observatory, USA and the FEROS spectrograph attached to the ESO 2.2 m telescope at ESO, La Silla, Chile. The CoRoT space mission was developed and is operated by the French space agency CNES, with participation of ESA’s RSSD and Science Programs, Austria, Belgium, Brazil, Germany and Spain.
McDonald spectra, light curves, and the two disentangled spectra are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/552/A60
© ESO, 2013
1. Introduction
In the last six years the CoRoT space mission has acquired more than 150 000 high-accuracy light curves with dense and almost continuous sampling over time intervals from one to five months. While the main goals of CoRoT are exoplanet hunting by the transit technique and asteroseismology of bright stars, a precious by-product is the identification of a large number of variable stars, most of them new discoveries.
Eclipsing binaries (EBs) outnumber all other variables found by CoRoT and some among them reveal additional regular variability superimposed on the binary light curve. The origin of the additional variability is very often rotation modulated surface activity, in some cases, however, there is clear evidence of pulsations, including the non-radial pulsations typical of δ Sct, γ Dor, and slowly pulsating B stars (SPB).
Precious insights in stellar structures can be obtained from asteroseismology. Pulsating EBs have a fundamental asset: studying non-radial oscillations in EB components has the advantage that the masses and radii can be independently derived, with a pure geometrical method, by combining the information from the light and the radial velocity curves, with uncertainties in the best cases below 1% (e.g., Southworth et al. 2005). Moreover, additional useful constraints derive from the requirement of the same chemical composition and age. Since the precise measurement of the mass and radius poses powerful constraints on the pulsational properties, EBs with pulsating components potentially provide direct tests of the modeling of complex dynamical processes occurring in stellar interiors (such as mixing length, convective overshooting, diffusion). Furthermore, a close eclipsing binary containing a pulsating component is the ideal laboratory to study the effect of tides on stellar pulsations.
The trade off with these advantages is the more complex structure and analysis of the data, as it is necessary to disentangle the two phenomena at the origin of the observed time series, but the results for the first CoRoT targets of this type studied so far (e.g., Maceroni et al. 2009; Damiani et al. 2010; Sokolovsky et al. 2010) are quite encouraging.
Most EBs observed by CoRoT belong to the exoplanet field, whose targets are in the V-magnitude range 11−16.5. Each CoRoT run provides the light curves of several thousand exo-targets (up to twelve thousand for the first runs and about half that number after the loss of one of the two data processing units in March ’09). The variable stars are automatically classified by the CoRoT Variability Classifier (Debosscher et al. 2009) which yields the membership probability for 29 different variability classes.
The detailed inspection of the light curves of EBs and of pulsating stars of the first CoRoT runs allowed us to select a small number of variables showing both eclipses and oscillations. All of them were new discoveries and the only available spectroscopic measurements (if any) were low-dispersion spectra from a ground–based survey of CoRoT fields (see next section). We organized a program aimed at obtaining phase resolved echelle spectroscopy of the suitable targets in the sample. In this paper we present the results relative to the brightest object of our sample: CoRoT 102918586, which was classified as EB and γ Dor candidate.
The γ Dor variables are A-F stars of luminosity class IV-V pulsating in high-order gravity-modes, with typical frequencies in the range 0.3−3 days. The driving mechanism of pulsations is the modulation of the radiative flux by convection at the base of the convective envelope (Guzik et al. 2000; Dupret et al. 2005). The g-modes probe the deep stellar interior, and for this reason are of great interest for asteroseismic studies.
Before the CoRoT and Kepler space missions sixty-six γ Dor variables were known, according to Henry et al. (2007), and about 50% of them were found in binary stars (12 visual binaries, 10 double-lined, and 6 single-lined spectroscopic binaries, no EB). The first γ Dor in an eclipsing binary (VZ CVn) was announced by Ibanoǧlu et al. (2007) but the quality and the coverage of their ground-based photometry was insufficient for a detailed asteroseismic study. Two new candidates γ Dor in EBs (CoRoT 102931335 and CoRoT 102980178) were identified by Damiani et al. (2010) and Sokolovsky et al. (2010), but their faintness prevented the collection of spectroscopic data and, therefore, the full exploitation of the EB assets. Many other similar objects were later identified in the CoRoT and Kepler archives, but again, without spectroscopic information.
CoRoT 102918586 is, therefore, the first γ Dor in an EB which can be studied in great detail, thanks to the quality of the CoRoT photometry, to its brightness (making it possible to acquire high-dispersion spectroscopy), and to the fortunate occurrence that it is a double-lined spectroscopic binary.
This paper is organized as follows: Sects. 2 and 3 describe the available data and their reduction; Sect. 4 deals with the light and radial velocity curve analysis; Sect. 5 is devoted to the analysis of the disentangled component spectra, providing the atmospheric parameters; Sect. 6 presents a comparison between the physical elements derived from the analysis and stellar evolutionary models; and, finally, Sect. 7 analyzes the pulsational properties of the components.
2. CoRoT photometry
CoRoT 102918586 is one of the ~10 000 exoplanet targets observed by CoRoT during the “Initial Run” (IRa01), the first scientific run which lasted about 60d. The limited pre-launch information on this target was collected in Exo-dat database1 (Deleuil et al. 2009). The target is relatively bright (V = 12.45 ± 0.03). Prior to CoRoT observations its binary nature was unknown. We derived a spectral classification F0 V by carefully re-analyzing (Maceroni et al. 2010) low-resolution spectra (R ≈ 1300), which were obtained with the AAOmega multi-object facilities of the Anglo-Australian Observatory, in the frame of a program aimed at acquiring a first spectroscopic snap-shot of the CoRoT fields (Guenther et al. 2012; Sebastian et al. 2012). This spectral classification is in excellent agreement with the results obtained later on from the Sandiford and FEROS observations.
The point-spread function (PSF) on the CoRoT exoplanet field detectors is actually a mini-spectrum (R ~ 3), thanks to an objective prism in the optical path of the CoRoT exoplanet channel. Three-color photometry (the so-called red, green, and blue colors) is obtained by splitting the PSF into three sub-integrating areas for target stars brighter than V ≤ 15.2. These colors do not correspond to any standard photometric system, (Auvergne et al. 2009), but they are useful for photometrically ruling out the false positives that mimick a planetary transit signal (Carone et al. 2012). Therefore, even if chromatic light curves were available for our target, our analysis is based mainly on the white light curve which was obtained by summing all the channels.
This original light curve contains ~78 000 points, with a first section (HJD < 2 454 162d) sampled in the long integration mode (512s) and the rest in the short integration mode (32s). Having checked the absence of high-frequency components, we rebinned the time series to the longer step and corrected a long-term trend, dividing the light curve by a third order Legendre polynomial. We then discarded the obvious outliers with a sigma-clip algorithm. The result of these preliminary operations is shown in Fig. 1; the total number of points is reduced to 8062. Hereafter we will refer to this curve as LC0.
The first step of our iterative procedure was the pre-whitening of LC0, with the result of the harmonic fit obtained with Period04 (Lenz & Breger 2005), i.e., a non-linear least square fit of the frequency, amplitude, and phase of the sinusoidal components, as derived from the discrete Fourier transform (DFT) of the time series. The Period04 program was applied to LC0 after eclipse masking. The harmonic fit was obtained with the twenty-four frequencies having an amplitude signal-to-noise ratio S/N > 4, according to the criterion proposed by Breger et al. (1993). The first thirteen frequencies in order of amplitude, are listed in Table 1 together with corresponding amplitudes, phases, and S/Ns.
In this type of analysis of a single light curve a problem often arises concerning the nature of the orbital period harmonics. On the one hand there could be pulsations excited at orbital overtones by tidal action. On the other, features that belong to the orbital variation (e.g., out of eclipse variations due to proximity effect or eccentricity) produce orbital overtones in the frequency spectrum. Furthermore, any deviation of the binary model from the real configuration generates orbital overtones in the residuals obtained by subtraction of the binary model. The analysis of CoRoT 102918586 is a good example in this respect: the first inspection of the light curve and the knowledge of the luminosity class of the primary star suggested a binary configuration with two components of similar surface brightness (and hence almost equally deep minima) in a circular orbit, and with an orbital period of ≈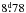 . This implied, as well, small fractional radii of the components and very little tidal deformation.
. This implied, as well, small fractional radii of the components and very little tidal deformation.
While it was possible to obtain an excellent fit of binary + pulsations with this model (Maceroni et al. 2010), explaining the presence of several orbital overtones in the harmonic fit (see Table 1) was problematic, as tidal forces should be weak in spherical components describing circular orbits.
 |
Fig. 1 CoRoT 102918586 de-trended white-light light curve after rebinning to 512s and normalization to the mean value (eclipses excluded). |
The alternative hypothesis, suggested in the above-mentioned paper, was a completely different system configuration: the minima seen in the curve are the same, single eclipse. In that case the system should be formed either by very different stars, or have an elliptic orbit with an orientation in space that would produce an eclipse only when the components are close to periastron passage (e.g., a case similar to that of HD 174884, Maceroni et al. 2009). This second hypothesis turned out to be the true one after the collection of the first series of spectra; the orbit was elliptic, with half the orbital period, and its inclination angle and longitude of periastron yielded a single, grazing, eclipse (see Sect. 3).
Results of the preliminary harmonic analysis.
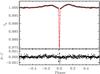 |
Fig. 2 Upper panel: phased light curve of the eclipsing binary as residuals of the harmonic fit, orbital overtones excluded. Full line: final fit with PHOEBE. Lower panel: fit residuals. The displayed curve is the final result of our procedure (after two steps of iterative pre-whitenening, see text). |
The contribution to LC0 only due to eclipses (i.e., the residuals of subtraction of the harmonic fit), was then recomputed subtracting only the 20 frequencies not corresponding to orbital overtones. This orbit-only light curve (Fig. 2, denoted as LCEB hereafter) is no longer flat out of eclipse and shows two almost equal bumps on the sides of the single minimum, which is exactly the expected shape for a longitude of periastron close to 90 degrees, i.e. a line of view coplanar with the system semi-axis.
The light curve in Fig. 2 is phased with the ephemeris 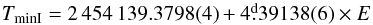 (1)that was derived by a linear fit to the minimum times, previously computed with a parabolic fit to the lower section of each minimum. The figure also shows the synthetic light curve of the best-fitting binary model computed with PHOEBE (Prša & Zwitter 2005) and described in Sect. 4.
(1)that was derived by a linear fit to the minimum times, previously computed with a parabolic fit to the lower section of each minimum. The figure also shows the synthetic light curve of the best-fitting binary model computed with PHOEBE (Prša & Zwitter 2005) and described in Sect. 4.
For the sake of brevity, we only show the final result of the iterative process used to extract LCEB from LC0. The steps of the procedure were:
-
1.
prewhitening of LC0 with 20 out of the 24 frequencies obtainedin the first harmonic fit, as already described;
-
2.
phasing with the ephemeris of Eq. (1) and further binning with a variable step, to limit computing time for PHOEBE fitting (namely computation of normal points in phase bins of 0.001 and 0.002 in and out of eclipse);
-
3.
subtraction of the PHOEBE fit model from LC0 and new harmonic fit of this full time series;
-
4.
prewhitening of LC0 with the results of the previous step, yielding a new “orbit-only” light curve.
The procedure was stopped after this last stage because there was no significant change in the parameters of the binary model and in the results of the harmonic fit.
The resulting LCEB, which is phased and binned as in step 2, is shown in Fig. 2, together with the residuals of the PHOEBE fit. Note that the larger scatter of residuals at primary minimum, and at the predicted position of the secondary minimum, is partly due to the smaller number of points in the variable width bins.
3. High resolution spectroscopy of CoRoT 102918586
CoRoT 102918586 is the brightest target of the sample of CoRoT binaries with pulsating components we selected for spectroscopic follow-up. We collected echelle spectra with two different instruments, namely the Sandiford spectrograph attached to the Cassegrain focus of the 2.1 m Otto Struve telescope at McDonald Observatory (Texas, USA), and the fiber-fed FEROS spectrograph mounted on the ESO 2.2 m telescope in La Silla, Chile.
Seven Sandiford spectra were acquired in December 2009 and three in January 2011. We used a 1″ slit, which gives a resolving power of R = 47 000. The small size of the CCD detector enables it to cover only ~1000 Å. We, therefore, set the spectrograph’s grating angle to encompass the 5050−6030 Å wavelength spectral region, which is a good compromise between S/N and number of spectral lines suitable for radial velocity (RV) measurements. Two consecutive spectra of 20−30 min were secured in each observing night and subsequently co-added to remove cosmic rays hits. The inspection of the first seven spectra, acquired at McDonald in December 2009, revealed that CoRoT 102918586 is a double-lined spectroscopic binary with an orbital period of about 4.39 days.
Seven more spectra were taken with FEROS in December 2010. The FEROS spectrograph is fed with a 2″ fibre which yields a resolution of R = 48 000 and a spectral coverage from 3800 to 8500 Å. We adopted the same observing strategy as that used in the Sandiford observations.
The reduction process involved the usual steps of de-biasing, flat-fielding, background subtraction and wavelength calibration by means of measurements of a ThAr calibration lamp. The spectral sections of interest were then normalized to the continuum and barycentric corrections were computed for the time of mid-exposure. The FEROS spectra had a typical S/N of 50−60 in the region 5500−5800 Å and of 30−40 at 4800 Å, while Sandiford spectra have a typical S/N 40−50 at 5500 Å.
The component radial velocities were derived with a standard cross-correlation algorithm, IRAF’s2 tool FXCOR. In the case of FEROS spectra, we used the wavelength interval 4500−4800 Å, rich in metallic lines. As a cross-correlation template, when using FEROS, we chose a nearby bright CoRoT primary target (HD 49933) of similar spectral type (F2) and we used the RV standard HD 22484 for reference. Instead, the cross correlation template used for the Sandiford spectra was the spectroscopic standard HD 50692 (Nidever et al. 2002). The radial velocities of the components were derived by fitting two Gaussian curves (with the FXCOR “deblend” function); the fit errors depend on the separation of the CCF peaks.
The radial velocity curves, showing excellent agreement between the two data sets, are shown in Fig. 3, the corresponding values in Table 2. Both Sandiford and FEROS uncertainties include those of the RV standard stars (0.1 km s-1; Nidever et al. 2002; Holmberg et al. 2007); the FEROS data (the last seven rows in Table 2) also include the uncertainty on the template velocity (0.1 km s-1).
Radial velocities of CoRoT 102918586.
 |
Fig. 3 Upper panel: phased radial velocity curves of CoRoT 102918586 components. Filled circles are FEROS measurements, filled squares Sandiford data; uncertainties are smaller than the symbol size; continuous line is the best-fit radial velocity curve obtained with PHOEBE for the primary component, dashed line for the secondary component. Lower panel: fit residuals, with the same symbols. |
4. Light and radial velocity curve analysis
4.1. Binary model
The light and radial velocity curve solutions were performed with the current (“devel”) version of PHOEBE, which includes flux computation with the CoRoT transmission functions, for both the seismology and the exoplanet field (for details see Maceroni et al. 2009).
We preferred to avoid the simultaneous solution of light and radial velocity curves because the RV data were acquired at different epochs with respect to photometry. Furthermore, the data sets are very different in terms of observed point number and accuracy. The two solutions were connected, however, by keeping fixed in each of them the parameters better determined by the other type of data.
In the light curve solution we adjusted the inclination i, the secondary effective temperature Teff,2, and the surface potentials Ω1,2; the primary passband luminosity L1 was separately computed rather than adjusted, as this allows for a smoother convergence to the minimum. The eccentricity e, mass ratio q, and the longitude of periastron ω were fixed to the values derived from the fit of the radial velocity curves (where we also adjusted the system semi-axis a and the barycentric velocity γ).
We adopted a square root law for limb darkening that employs two coefficients xLD and yLD per star and per passband. The coefficients are determined by PHOEBE interpolating limb darkening coefficient tables for the given atmospheric parameters. These tables were computed by synthesizing spectral energy distributions for many passbands and at different emergent angles, and fitting the linear cosine law, the non-linear log law, and the square root law by least squares (see Maceroni et al. 2009). The gravity darkening and albedo coefficients were kept fixed at their theoretical values g = 1.0 and A = 1.0 for radiative envelopes (von Zeipel 1924).
The exoplanet fields were selected with the purpose of maximizing the number of late type dwarfs which, thanks to higher contrast, are better suited for the detection of transiting planets. As a consequence the exo-fields are usually relatively crowded. Moreover, the target PSFs, as we have already mentioned, are enlarged by the miniprism. To limit contamination each target flux is recorded only in a specific (software) mask whose size and form depends on the star characteristics. Nevertheless, contamination by faint unresolved targets is rather common. Information on the degree of contamination has been independently acquired by ground-based photometry programs with a much higher space resolution (Deeg et al. 2009). For our system the contamination is non-negligible, estimated to 15% of the total flux (Deeg 2012, priv. comm.), a value similar to that appearing in the Exodat database (14.4%). We added, therefore, the former value as “third light”.
The primary effective temperature was kept fixed, as it is well known that the solution of a single light curve is sensitive only to relative values of the effective temperatures. We started with a value of 7200 K (an estimate from the spectral type) and finally used 7400 K (suggested later on by the analysis of the disentangled spectra). As expected, the change of Teff,1 reflected into a similar shift for Teff,2. The analysis of the line profiles (see Sect. 5) suggested rotational velocities very close to spin-orbit synchronization for both components; therefore, we adopted a ratio of rotational to orbital period f1,2 = 1.
The system model corresponding to the best fit is formed by two almost twin stars; the low inclination, the eccentricity, and the orientation of the orbit are at the origin of the single minimum, which is a grazing eclipse of the larger star. The system parameters from the light and radial velocity curve solution are collected in Table 3. The unicity of the solution and the derivation of parameter uncertainties are discussed in the next section.
Parameters from PHOEBE fits of light and RV curves, and derived physical parameters of CoRoT 102918586.
 |
Fig. 4 Projection of the cost function along inclination (top left), primary surface potential (top right), and secondary temperature (bottom left). The minimum value is indicated by a filled dot. Bottom right panel: the correlation of rs with inclination for the best-fitting models (cost function value ≤1% above the minimum). |
4.2. Unicity of the solution and parameter uncertainties
The light curve fit is based on the minimization procedure of a cost function measuring the deviation between model and observations in the space of adjusted parameters. In PHOEBE the minimization is performed by iterative non-linear least-squares in the Levenberg-Marquart variant, or by the Nelder and Mead’s downhill simplex. As a consequence, it suffers from the well-known problems of these methods: the minimization algorithm can be trapped in a local minimum, or degeneracy among parameters and data noise can transform the minimum into a large and flat-bottomed region, or an elongated flat valley rather than a single point. Furthermore, the correlation among the parameters implies uncertainties in the derived values which are significantly larger than the formal errors derived by the least square minimization. In the specific case of a detached binary with almost grazing eclipses, one expects a strong degeneracy among fractional radii (i.e., surface potentials) and inclination.
To handle these problems we performed a heuristic scan of the hyper-surface describing the cost function value in the space of the adjusted parameters. Minimizations were first performed starting from random assigned input points, allowing the region(s) of minima to be located. The lowest minimum region was then explored in greater detail by mapping the cost function at randomly chosen points. Figure 4 displays the lower envelope of the projections on different parameter plans of the cost-function hyper-surface.
We chose the interval corresponding to a variation of 1% of the absolute minimum value as uncertainty on the parameters. The choice of this threshold value is based on the comparison with the results of an independent estimate of uncertainties from bootstrap resampling (BR), a very useful technique to estimate parameter confidence levels of the least-squares solutions (see, for instance, Press et al. 1992). In short, BR consists in generating many different data samples by random resampling the available data with repetitions (bootstrapping), performing the minimization procedure for each sample, and deriving confidence intervals from the resulting distribution of parameters. The interval of a given parameter containing 68.3% of the solutions has the same meaning as the 1-σ interval of the Gaussian distribution. The estimate by BR was performed both for the radial and the light curve solution, according to the scheme described in detail in Maceroni & Rucinski (1997) and Maceroni et al. (2009). The main point is that the procedure is performed within the minimum already established by a single iterated solution (that is, using only one set of residuals and parameter derivatives). The 68.3% interval for the inclination from BR is ±0.07. A comparison with the first panel of Fig. 4 allows the derivation of the threshold value of 1% used in the following.
To illustrate the correlation between the sum of radii and the inclination, we use the quantity 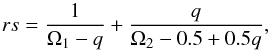 (2)where Ω1, Ω2 are the surface potentials; rs is a good approximation of the sum of the star fractional radii in the case of spherical components. In Fig. 4 we show the relation between rs and i for the sample of points with a cost function value <1% above the minimum. As expected the correlation is very strong. The projection on the y-axis of the distribution provides an estimate of the uncertainty on rs (~0.001) taking the correlation with i into account. This is larger than the formal error on the same quantity, which can be derived from the LS fit results, by a factor of ~8.
(2)where Ω1, Ω2 are the surface potentials; rs is a good approximation of the sum of the star fractional radii in the case of spherical components. In Fig. 4 we show the relation between rs and i for the sample of points with a cost function value <1% above the minimum. As expected the correlation is very strong. The projection on the y-axis of the distribution provides an estimate of the uncertainty on rs (~0.001) taking the correlation with i into account. This is larger than the formal error on the same quantity, which can be derived from the LS fit results, by a factor of ~8.
The uncertainties on the adjusted and derived parameters reported in Table 3 correspond to the 1% threshold (and to the similar BR results), all significantly larger than the formal errors of the LS fits. The formal errors from the LS fit are typically a factor of ten smaller. The error on the primary temperature, which is fixed in the solution, derives from the analysis of the disentangled spectra.
5. Spectroscopic analysis
5.1. Effective temperatures
Thanks to Doppler shifts the spectra of binary stars are complex and they vary in the course of the orbital cycle. Usually, the spectral lines of the components are overlapping, especially around eclipses, which in turn makes the radial velocities difficult to measure and inaccurate. The method of spectral disentangling, (spd), overcomes these difficulties (Simon & Sturm 1992; Hadrava 1995). In a self-consistent way it returns the optimal set of orbital elements and the individual spectra of the components. The advantages of spd are obvious: separated spectra could be analyzed as single star spectra, without the interfering signal of the companion. This allows the spectroscopic determination of the effective temperatures and of detailed elemental abundances (Hensberge et al. 2000; Pavlovski & Hensberge 2005; Frémat et al. 2005; Clausen et al. 2008; Hareter et al. 2008; Pavlovski & Southworth 2009; Tkachenko et al. 2009). The effective temperature determined from hydrogen line profiles, and/or from the strength of temperature sensitive lines, supersedes in accuracy and precision those derived from broad-band or Strömgren photometry, for example. The same is true for the metallicity derived from a detailed abundance study rather than from photometric color indices.
For the purpose of spectroscopic diagnostics of the component spectra spd was performed on the time-series of the FEROS spectra, since only these spectra cover the hydrogen Balmer lines on which the determination of the effective temperatures is based. We used FDBinary3 (Ilijic et al. 2004) which performs spectral disentangling in the Fourier space according to the prescription of Hadrava (1995). In spite of the very limited number of spectra spd performed quite well and, thanks to fair phase distribution of the observations (Hensberge et al. 2008), did not produce strong undulations in disentangled spectra.
 |
Fig. 5 Best-fitting synthetic composite spectrum of CoRoT 102918586 (red solid line). The spectral window is centered on the Hβ line. The FEROS spectrum observed on HJD 2 455 558.64812 is shown in light gray. The primary lines are blue-warded with respect to the secondary lines. |
The determination of the effective temperature from the profiles of the hydrogen Balmer lines suffers from degeneracy in Teff and log g, and that is a major limitation in setting up the appropriate model atmosphere for a detailed abundance study. However, the complementary analysis of the light and RV curves of eclipsing double-lined spectroscopic binaries also provides an independent and accurate determination of the surface gravity of the components. In well-determined solutions, the accuracy in log g is around 0.01 dex or less, and that is indeed our case, so the degeneracy in Teff and log g could be lifted.
The components’ spectra are diluted in a binary star spectrum proportional to their relative light contribution to the total light of the system. In the observed spectra of a binary system there is no information on the absolute spectral line strengths and, unless there is at least one spectrum taken in eclipse, there is an ambiguity in disentangled component spectra. Therefore, a renormalization of the disentangled spectra of the individual components to their own continuum should be performed using some additional information as discussed in detail by Pavlovski & Hensberge (2010) and Pavlovski & Southworth (2012).
In the present analysis we used a constrained optimal fitting method (Tamajo et al. 2011). In the new release of the computer code for constrained optimal fitting of disentangled component spectra the following parameters can be adjusted for both stars: effective temperature, surface gravity, light dilution factor, Doppler shift, projected rotational velocity, and the vertical shift to adjust for the continuum. In spectral disentangling the disentangled component spectra are shifted and an additive factor should be applied to return them to the continuum level (Ilijic et al. 2004; Pavlovski & Hensberge 2005; Tkachenko et al. 2009).
The disentangled spectra were then analyzed to derive the atmospheric parameters of each component. To this purpose a comprehensive grid of theoretical spectra was calculated for Teff = 5000 to 15 000 K in steps of 250 K, and log g = 2.5 to 5.0 in steps of 0.5 dex. The atlas9 model atmospheres of Castelli et al. (1997) and the uclsyn spectral synthesis package (Smalley et al. 1997) were used for the construction of the grid (which is for fixed solar metallicity but was used only in the initial determination of Teff from the Balmer lines, see below). A genetic algorithm was then used (Charbonneau 1995) for the optimization of model parameters. Further detailed description of the code is given in Pavlovski et al. (in prep.).
Only the hydrogen Balmer lines Hγ and Hβ were selected for the optimal fitting, excluding from the fit the blends due to the various metal lines. The surface gravities and the light factors of both components were fixed according to the light curve solution (Table 3). Since the Balmer lines are almost insensitive to rotational broadening, with the exception of the very core of the lines, the projected rotational velocities were also kept fixed. Their values were derived from the clean metal lines in an iterative cycle with the determination of the effective temperatures from Balmer lines yielding vrotsini = 20.5 ± 0.5 km s-1 and vrotsini = 14.5 ± 0.5 km s-1 for the primary and secondary component, respectively. With the surface gravities, the light dilution factors and projected rotational velocities for both components fixed, the only free parameters in the optimal fitting were the effective temperatures, the Doppler shifts of disentangled spectra to reference frame of the synthetic spectra, and the vertical adjustment of the continuum level for both components separately.
The mean values of the effective temperatures derived, separately for two Balmer lines in these calculations read Teff = 7400 ± 90 K for the primary, and Teff = 7100 ± 110 K for the secondary component. The latter is in excellent agreement with the value derived from the light curve solution in Table 3. The quality of the fit for the composite Hβ line in one of the observed spectra is shown in Fig. 5.
 |
Fig. 6 Short spectral stretch of two observed composite spectra at different orbital phases from the FEROS dataset. The two individual disentangled spectra are shown at the bottom along the best-fitting synthetic spectra calculated for the effective temperatures and surface gravities derived in Sects. 4 and 5 (Tables 3 and 4). |
5.2. Abundances
The important outcome of spectral disentangling is the gain in S/N. That is evident from the short section of the component disentangled spectra which are displayed in the lower part of Fig. 6, together with two composite observed spectra at different orbital phases.
We estimated an enhancement in S/N, thanks to spectral disentangling and binning of disentangled spectra, by the factor of about 2.2 and 1.6, for the primary and the secondary respectively. The difference is due to the unequal contribution of the components to the total light. The increase in S/N makes, in turn, the abundance study possible.
First, we estimated the microturbulent velocity ξt. In the spectra of F-type stars, Fe i lines serve to the purpose since they are the most numerous. The microturbulent velocities for the primary and secondary components, minimizing the scatter in the abundances from different iron lines, are ξt,p = 1.8 ± 0.1 km s-1 and ξt,s = 1.0 ± 0.1 km s-1.
Iron appears in two ionization stages, Fe i and Fe ii, which were used as additional diagnostics of the effective temperatures (Smalley 2005). The null-dependence of the iron abundance on the excitation potential slightly changed the Teff values, in a larger amount for the secondary component. However, the Fe i lines outnumber the Fe ii lines, and the solution is not well constrained. Differences of about 0.20 dex are found in the iron abundances from Fe i and Fe ii, for the primary and secondary component, which are larger than the estimated errors in abundance determination. In both cases the iron abundances are larger from the Fe ii lines. Similar differences were also found for other ions which appear in two ionization stages. However, the Fe i lines outnumber the Fe ii lines by factor of 5 and 6 for the primary and secondary components, respectively, and we eventually adopted the abundances derived from the Fe i lines. Still, this enables a slight correction of the Teff values derived in the previous subsection, and the final Teff values adopted are listed in Table 4. The final elemental abundances adopted as derived in LTE approximation, are listed in Table 5. The abundances relative to hydrogen are given in the second and fourth columns (log N(H) = 12.00), those relative to the solar values, with the solar abundances as given by Grevesse & Noels (1993), in the third and fifth columns. We conclude that within 1σ errors the abundances for both components are close to the solar value. The iron abundances [Fe/H]p = 0.11 ± 0.05 and [Fe/H]s = −0.10 ± 0.04 give an approximate metallicity for the components Zp = 0.020 ± 0.001 and Zs = 0.016 ± 0.001, with Z⊙ = 0.02 from Grevesse & Noels (1993). Because of the uncertainties in the light ratio between the components, which in turn could affect our determination of Teff values, we conclude that the metallicity of both components can be assumed to be solar.
Atmospheric parameters of CoRoT 102918586 componentsa.
Photospheric elemental abundances of CoRoT 102918586.
 |
Fig. 7 Evolution of the component radii. Upper panel: based on models without overshooting, αOV = 0; lower panel: αOV = 0.2. The light gray bands describe the time evolution of the radii for stars in the mass range M1,2 ± ΔM1,2, from Table 3. The darker areas fill the intersection with the R1,2 ± ΔR1,2 lines from the same table. The vertical lines bound the time interval respecting the constraint of coevality. |
6. Physical properties of CoRoT 102918586
A comparison with theoretical models of the given mass and chemical composition provides further information on the physical properties of the system. For instance, the inspection of the evolution of the stellar radii with time, combined to the constraint of coevality, allows an accurate determination of the system age. We prefer to use the evolution of the radius, instead, for instance, of the position in the Hertzsprung–Russell (H-R) diagram, because the radii are directly and precisely determined from the radial velocity and light curve solutions, while the computation of temperature and luminosity implies the use of color transformations and bolometric corrections.
The evolutionary tracks shown in Fig. 7 were obtained from stellar evolution modeling with the code CLES (Code Liégeois d’Évolution Stellaire, Scuflaire et al. 2008). The computations were made with the equation of state from OPAL (OPAL05, Rogers & Nayfonov 2002). The opacity tables for the Grevesse & Noels (1993, GN93) solar mixture are also from OPAL (Iglesias & Rogers 1996) and are extended to low temperatures using the Ferguson et al. (2005) opacity values. The nuclear reaction rates are those of the NACRE compilation (Angulo 1999) except for 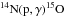 , updated by Formicola et al. (2004).
, updated by Formicola et al. (2004).
Models with and without overshooting were computed with the mixing-length theory (MLT) of convection (Böhm-Vitense 1958). The value of αMLT was kept fixed, adopting the solar value of 1.8. In the temperature range of interest here, however, its value does not affect the stellar radius. For the models with overshooting, the overshoot length was expressed in terms of the local pressure scale height Hp, as αOVHp, and the αOV value was fixed at αOV = 0.2. The chemical composition was assumed to be solar, according to the results of the previous section. The computations were done without including microscopic diffusion.
Figure 7 shows, for both components, the region of the R (log t) diagram bounded by the evolutionary tracks of mass M ± ΔM from Table 3. The intersection with the lines R ± ΔR of the same table provides the possible age range for each star; the further constraint of coevality narrows the range to the final value of 540 ± 120 Myr in the case of no-overshooting, and to 580 ± 100 Myr for αOV = 0.2. In both cases it is a young system with two Main Sequence (MS) stars which have burnt less than 20% of their initial hydrogen content.
Because of its young age, the binary has the time reach only spin-orbit synchronization while orbit circularization is still on the way. The eccentricity is quite high for the orbital period, as can be seen from the location of CoRoT 102918586 in the period-eccentricity diagram of stars of similar spectral type (see Fig. 8). For periods smaller than ~10 days the circularization process is expected to be efficient enough to change the system eccentricity in a few Gyr. So in Fig. 8 the younger stars born with high eccentricity trace the upper envelope of the distribution, and will evolve with time towards lower and lower values.
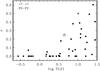 |
Fig. 8 Location of CoRoT 102918586 (starred symbol) in the period-eccentricity diagram for stars of spectral type A8-F2 (derived from the database of the 9th Catalogue of Spectroscopic Binary Orbits, Pourbaix et al. 2004). |
7. Pulsational properties
The final frequency spectrum after subtraction of the binary model is shown in Fig. 9. The plot is restricted to the frequency interval containing meaningful features as for higher frequencies we only detected signal related to the satellite orbit.
As mentioned before, to evaluate the frequency significance we used the criterion suggested by Breger et al. (1993), i.e. a value of S/N ≥ 4 for the peak. The twenty-eight frequencies satisfying this constraint are listed in Table 6. The errors in the table are derived according to Kallinger et al. (2008) and are sensibly larger that the formal errors of the LS fit, the remark column lists the closest frequency combinations, taking the uncertainties into account.
The first three dominant frequencies of the amplitude spectrum are separated by ~0.05 d-1. The fourth frequency is the beating of the third highest amplitude frequency (F3 of Table 6) and Forb = 0.22772 d-1. Other combinations of these four highest amplitude frequencies are also clearly visible. Figure 9 also shows the window DFT, whose main features are the peaks at 13.972 d-1 and its day aliases, caused by the satellite orbital frequency, and a peak at 2.005 d-1caused by the South Atlantic Anomaly crossing. The gray line is the significance threshold which is four times the local mean of the residual spectrum.
The Forb overtones present in the initial analysis of Table 1 have disappeared or are very weak, which is an indirect confirmation of the successful removal of the orbit-only binary light curve. The low frequency components (F < 0.1 d-1) are presumably leftovers of the detrending procedure with a low-order polynomial.
 |
Fig. 9 Final amplitude spectrum of CoRoT 102918586 and, in the inset, the window DFT. The vertical dotted lines correspond to the orbital period overtones, the broken lines to 2F3 and 3F3. The gray line is the threshold of significance (S/N ≥ 4) computed as explained in the text. |
Frequencies derived from the analysis of the final set of residuals, after subtraction of the EB model, with an amplitude S/N ≥ 4.
An oscillatory pattern of the kind superimposed on our EB light curve is not necessarily caused by pulsations. A study of the large sample of variables detected by the Kepler satellite and classified as γ Dor (Balona et al. 2011) has shown that the variability of “symmetric” type, i.e. symmetric with respect to its mean value, may be due to stellar spots experiencing differential rotation, and that the Kepler sample of γ Dor is contaminated by non-pulsating stars. In this case the dominant frequency is that of stellar rotation and the beating is caused by slightly different rotation rates of migrating spots.
In our case, however, even if the oscillatory pattern does show symmetry with respect to its mean value, we can exclude this hypothesis, because spectroscopy provided an accurate measurement of vrotsini (and we have the value of the inclination from the light curve analysis). Both stars have rotation frequencies close to the orbital frequency (1.1 and 0.9 Forb for the primary and secondary, respectively), and Forb ≃ Frot is much smaller than the dominant frequency of the amplitude spectrum. If the rotation axes were not aligned with the orbital axis, the stellar rotation frequencies could be higher, but the disalignement should be conspicuous: the factor ≃5 between the dominant frequencies and Forb requires an inclination of the rotation axis as low as 10°. Besides, the similarity between the rotation frequencies, as derived in the hypothesis of alignment, and the orbital frequency would remain an unexplained coincidence.
We adopt, therefore, the simplest scenario in which the periodic variations are not caused by rotation but by stellar pulsations.
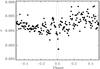 |
Fig. 10 Standard deviation, with respect to the local mean of the binned residual light curve (see text). The vertical lines bound the in-eclipse phases. The dip around phase zero suggests that the pulsations belong to the eclipsed component, i.e., to the primary star. |
The dominant frequencies seen in the spectrum (F1−F3) fall in the range of excited high order g-modes typical of γ Dor pulsators.
We have, therefore, computed with the non-adiabatic pulsation code MAD (Dupret et al. 2003) the instability domain for stellar models with the physical characteristics of the components. In particular, in the case of models without overshooting the range is between 0.50−4.16 (ℓ = 1) and 0.52−5.52 d-1 (ℓ = 2) for the primary, and between 0.55−4.7 (ℓ = 1) and 0.55−5.42 d-1(ℓ = 2) for the secondary component. The values change only slightly for the models with overshooting, becoming between 0.51−3.83 (ℓ = 1) and 0.55−5.02 d-1(ℓ = 2) for the primary, and between 0.55−4.16 (ℓ = 1) and 0.53− 5.33 d-1 (ℓ = 2) for the companion. Since the range is very similar for both stars, it is impossible to identify the pulsator in this way.
We have found, however, possible indirect evidence that the pulsating star is the primary, or at least that the higher amplitude frequencies belong to the primary. This might be the reason why the dispersion of the phased light curve decreases during eclipse. To show this effect we re-binned the residual light curve (after subtraction of the best binary model) in 200 equal phase-bins and computed the local standard deviation, which is shown in Fig. 10 as a function of the orbital phase. There is an evident dip around phase zero. However, taking into account that we have only thirteen (narrow) minima in the whole light curve, implying a poor sampling of pulsation in eclipse, and that only a small fraction of the primary surface is out of view during a grazing eclipse, we think that this conclusion should be taken with caution.
Most frequencies shown in Table 6 can be re-conducted to a combination of the first three frequencies and the orbital frequency. The main features in the spectrum are three groups centered around F3, F5 and F22 (1.1716, 2.3520 and 3.5254 d-1, respectively). Each of those frequencies is the center of a structure with side peaks spaced by about 0.05 d-1. This fact could suggest an interpretation in terms of rotational splitting of the central frequency. In particular both F5 and F22 have two peaks each side (one in the case of F22 just below the significance threshold, Fig. 9). This occurence could be interpreted – at first sight – as quintuplets due the effect of rotation of an ℓ = 2 mode, which are considered the ones preferentially excited by tidal forces (e.g., Kosovichev & Severnyj 1983).
There are, however, several arguments against this hypothesis. The first is, again, the known values of the component rotation. Since the star is rotating slowly enough (its rotation frequency is 1.5% of the critical value as defined by Townsend (2005) and smaller than the dominant pulsation frequencies), the splitting can be expressed according to the first order approximation by Ledoux (1951): 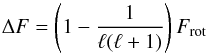 (3)where ℓ is the degree of the mode and Frot = 0.253 d-1 the rotation frequency. In our case, with ℓ = 2, ΔF ≃ 0.21 d-1, ΔF is about four times the measured value. In the case of a dipolar mode, ℓ = 1, the resulting splitting of the corresponding triplet would be smaller but still ~2.5 times larger than the derived value.
(3)where ℓ is the degree of the mode and Frot = 0.253 d-1 the rotation frequency. In our case, with ℓ = 2, ΔF ≃ 0.21 d-1, ΔF is about four times the measured value. In the case of a dipolar mode, ℓ = 1, the resulting splitting of the corresponding triplet would be smaller but still ~2.5 times larger than the derived value.
Even if we interpret the measured value as reflecting the average value of the stellar rotation (which is probably not rigid), we would end up with a star whose (observed) surface rotation rate is much faster than that of its interior. That might be the case of late-type (solar and later) components in close binaries, which might be spun up starting from a slow rotation regime as a consequence of angular momentum loss by magnetic braking and spin-orbit synchronization by tidal action. Depending on the core-surface coupling, the external layers could, in this case, rotate faster than the interior. The components of CoRoT 102918586 , however, are early F stars, so the previous scenario does not apply. Furthermore, it has to be noticed that the actual value of the spacings F3−F2 and F1−F3 are not exactly 0.05 but rather 0.0461 ± 0.0016 and 0.0531 ± 0.0020, respectively and, again on the basis of the slow rotation, one would expect symmetrical peaks. Last, but not least, there exists an alternative and more convincing interpretation of the central frequencies as combinations: F5 is closer to F1+F2 than to 2F3, and F22 is closer to F1+F2+F3 than to 3F3. The remarks in Table 6 correspond to the best matching combinations. So we can safely conclude that the patterns in Fig. 9 are not related to stellar rotation.
The comparison of the frequency spectrum with those of other γ Dor stars observed by CoRoT and Kepler suggests that the pattern we see is quite common in (presumably) single stars as well (see, e.g., Balona et al. 2011; Hareter et al. 2010). For instance, the light curve4 of CoRoT 102732872 (an F3V star, pulsating with a main frequency of 1.09 d-1) closely resembles that of CoRoT 102918586 after removal of the EB contribution. The former star is one of the few γ Dor which, according to Hareter et al. (2010), shows a pattern of regularly spaced peaks in period (as expected in the case of high-order g-modes). We computed, therefore, the mean period spacing of the three independent frequencies  (or 3110s ± 90s) and compared it with the theoretical asymptotic period spacing of the ℓ = 1 high-order g-modes, as expected for the stellar parameters from Table 3 and Sect. 6.
(or 3110s ± 90s) and compared it with the theoretical asymptotic period spacing of the ℓ = 1 high-order g-modes, as expected for the stellar parameters from Table 3 and Sect. 6.
The computed range of period spacing for the primary star, relative to the stellar models in the age interval derived in Sect. 6, is 3070−3200s for the models without overshooting, and 3300−3390s for those with αOV = 0.2. For the secondary star the values are, respectively 2800−3030s and 3160−3300s. A consistent interpretation is, therefore, that the observed pattern is caused by non-radial dipolar pulsations of the primary component.
8. Discussion and conclusions
CoRoT 102918586 is the first γ Dor in an eclipsing binary for which it was possible to collect observations of such quality to allow a very detailed study which provided both an accurate determination of the physical parameters and of the pulsational properties. Masses and radii have uncertainties ≤1%, the effective temperatures of 1.5%, and the derived age turned out to be 600 Myr, within a range of ~100 Myr.
Our results depict the system as a young eccentric binary formed by two similar MS stars (the mass ratio is 0.9); the single eclipse is due to the orientation of the binary orbit in space and the primary component is the origin of the observed γ Dor pulsations. We cannot completely exclude that the similar secondary component pulsates as well, but we suggest the dominant pulsation frequencies belong to the primary on the basis of the measured decrease of the pulsation amplitude during the eclipse.
Spectra disentangling of the FEROS spectra allowed us to derive the effective temperatures and the component chemical abundances, which turned out to be close to solar. The abundance pattern for the γ Dor pulsating stars was studied by Bruntt et al. (2008), and more recently by Tkachenko et al. (2012), particularly in regard to the links with the chemically peculiar λ Boo and Am-type stars suggested by Gray & Kaye (1999) and Sadakane (2006). Their comprehensive detailed abundance analysis did not reveal any sign of chemical peculiarities in their sample of γ Dor stars, yielding the conclusion that the metallicity is quite close to the solar value. Previously, on the basis of the Strömgren photometric m1 index, Handler (1999) also noted that all the γ Dor candidates in his sample had metallicities close to the solar value. Our finding for the γ Dor pulsating component in the binary system CoRoT 102918586 corroborates this general conclusion.
The results of our asteroseismic study are limited by the lack of calibrated multicolor photometry in CoRoT and/or of spectroscopy of sufficiently high S/N to allow the study of line profile variations caused by pulsation (unfeasible given the system magnitude). As a consequence, we could not completely identify the pulsation modes. On the other hand, from the comparison of the period splitting with the theoretically expected values, we at least have indications that the primary component is pulsating in a ℓ = 1 mode. Those are not the modes preferentially excited by tidal forces, which have been detected (or suggested) in other cases. Handler et al. (2002) propose that a number of frequencies, exact multiple of the orbital frequency, found in the γ Dor component of HD 209295 (a single-lined spectroscopic binary) could be triggered by tidal interaction. Another case is that of HD 174884 (Maceroni et al. 2009), an eccentric eclipsing binary formed by two B-type stars.
In CoRoT 102918586 , however, we find little or no influence of binarity on the pulsations. The pulsation pattern is very similar to that of single γ Dor stars and the only sign of the orbital motion is found in the beating of the orbital frequency with the dominant frequencies of pulsation. This might be due to a weak tidal interaction: our system is less eccentric than the above-mentioned cases, has a longer period, and the components have smaller fractional radii (by a factor of ~1/2 compared to HD 174884 and even smaller in the case of HD 209295, whose components’ radii, however, can only be estimated). One expects, therefore, a weaker tidal torque as this is very strongly dependent on the star fractional radius (e.g., Zahn 2005).
The final model of the system, characterized by an internal consistency among the results from different data sets and treatments, proves the success of the iterative method used to separate pulsations from the eclipsing binary light curve. That was not obvious, and we do not think that this result is generally valid, because eclipses certainly modify the observed oscillatory pattern, while we subtracted the same oscillations at all phases. A reason for the success in this case is that we dealt with a grazing eclipse, which decreases the determinacy of the light curve solution but makes this particular problem less severe.
A straightforward, first-order, correction could be to weight the pulsation amplitude with the contribution to the total light of the pulsating component during eclipses, but the definitive solution is the inclusion of non-radial pulsation in the binary model, taking into account the deformation of the surfaces by non-radial pulsations and the consequent brightness variation. That is, however, a challenging task, as we do not know a priori in which modes the star oscillates, and adding the parameters governing the oscillations to the minimization procedure greatly increases its complexity (and its unicity problems).
The light curve and its plot are available from the public section of the CoRoT-N2 archive at the CoRoT Data Center (IAS): http://idoc-corot.ias.u-psud.fr/
Acknowledgments
This work is partly based on public CoRoT data and we are very grateful to the CoRoT scientific team for making available to us the mission results in the CoRoT archives. We thank Artie Hatzes, P.I. of the echelle-spectroscopy program at McDonald Observatory, for including our binary in their list of CoRoT exoplanet targets, Jonas Debosscher for providing the results of the classification of CoRoT variables, and Hans Deeg for checking the level of contamination of our target. We would also like to express our gratitude to Andrej Prša for making publicly available and maintaining PHOEBE (and for his constant, patient, support) and to Marc-Antoine Dupret for making available to us his MAD code. Finally, we thank Markus Hareter, Conny Aerts and Maryline Briquet for suggestions and fruitful discussions, and the unknown referee for constructive criticisms. We acknowledge the generous financial support from: the Istituto Nazionale di Astrofisica (INAF) under PRIN-2010 Asteroseismology: looking inside the stars with space- and ground-based observations (C.M., M.R.) and the Agenzia Spaziale Italiana (ASI) in the frame of the ESS program (C.M.); the Belgian PRODEX Office under contract C90199 CoRoT Data Exploitation (J.M.); the German DLR under grant 50OW0204 (D.G.); the Croatian MZOS under research grant 119-0000000-3135 (K.P.). This research has made use of the Exo-Dat database, operated at LAM-OAMP, Marseille, France, on behalf of the CoRoT/Exoplanet program and of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Angulo, C. 1999, in AIP Conf. Ser., 495, 365 [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balona, L. A., Guzik, J. A., Uytterhoeven, K., et al. 2011, MNRAS, 415, 3531 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Bruntt, H., De Cat, P., & Aerts, C. 2008, A&A, 478, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carone, L., Gandolfi, D., Cabrera, J., et al. 2012, A&A, 538, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Clausen, J. V., Torres, G., Bruntt, H., et al. 2008, A&A, 487, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiani, C., Maceroni, C., Cardini, D., et al. 2010, Ap&SS, 328, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Debosscher, J., Sarro, L. M., López, M., et al. 2009, A&A, 506, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., Gillon, M., Shporer, A., et al. 2009, A&A, 506, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., De Ridder, J., De Cat, P., et al. 2003, A&A, 398, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Frémat, Y., Lampens, P., & Hensberge, H. 2005, MNRAS, 356, 545 [Google Scholar]
- Gray, R. O., & Kaye, A. B. 1999, AJ, 118, 2993 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in La Formation des Éléments Chimiques, eds. B. Hauck, S. Paltani, & D. Raboud (Lausanne: AVCP), 205 [Google Scholar]
- Guenther, E. W., Gandolfi, D., Sebastian, D., et al. 2012, A&A, 543, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJ, 542, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
- Handler, G. 1999, MNRAS, 309, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Handler, G., Balona, L. A., Shobbrook, R. R., et al. 2002, MNRAS, 333, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Hareter, M., Kochukhov, O., Lehmann, H., et al. 2008, A&A, 492, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hareter, M., Reegen, P., Miglio, A., et al. 2010 [arXiv:1007.3176] [Google Scholar]
- Henry, G. W., Fekel, F. C., & Henry, S. M. 2007, AJ, 133, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553 [NASA ADS] [Google Scholar]
- Hensberge, H., Ilijić, S., & Torres, K. B. V. 2008, A&A, 482, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ibanoǧlu, C., Taş, G., Sipahi, E., & Evren, S. 2007, MNRAS, 376, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, ASP Conf. Ser., 318, 111 [NASA ADS] [Google Scholar]
- Kallinger, T., Reegen, P., & Weiss, W. W. 2008, A&A, 481, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosovichev, A. G., & Severnyj, A. B. 1983, Pis ma Astronomich. Zh., 9, 424 [Google Scholar]
- Ledoux, P. 1951, ApJ, 114, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Comm. Asteroseismol., 146, 53 [Google Scholar]
- Maceroni, C., & Rucinski, S. M. 1997, PASP, 109, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Maceroni, C., Montalbán, J., Michel, E., et al. 2009, A&A, 508, 1375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maceroni, C., Cardini, D., Damiani, C., et al. 2010 [arXiv:1004.1525] [Google Scholar]
- Nidever, D. L., Marcy, G. W., Butler, R. P., Fischer, D. A., & Vogt, S. S. 2002, ApJS, 141, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovski, K., & Hensberge, H. 2005, A&A, 439, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlovski, K., & Southworth, J. 2009, MNRAS, 394, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovski, K., & Hensberge, H. 2010, ASP Conf. Ser., 435, 207 [Google Scholar]
- Pavlovski, K., & Southworth, J. 2012, IAU Symp., 282, 359 [Google Scholar]
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN, The Art of Scientific Computing (Cambridge University Press) [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Sadakane, K. 2006, PASJ, 58, 1023 [NASA ADS] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Sebastian, D., Guenther, E. W., Schaffenroth, V., et al. 2012, A&A, 541, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, K. P., & Sturm, E. 1992, A&A, 281, 286 [Google Scholar]
- Smalley, B. 2005, Mem. Soc. Astron. It. Suppl., 8, 130 [Google Scholar]
- Smalley, B., Smith, M. G., & Dworetsky, M. L. 1997, UCLSYN: users manual, The University College of London [Google Scholar]
- Sokolovsky, K., Maceroni, C., Hareter, M., et al. 2010, Comm. Asteroseismol., 161, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Smalley, B., Maxted, P. F. L., Claret, A., & Etzel, P. B. 2005, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Tamajo, E., Pavlovski, K., & Southworth, J. 2011, A&A, 526, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Lehmann, H., & Mkrtichian, D. E. 2009, A&A, 504, 991 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Lehmann, H., Smalley, B., Debosscher, J., & Aerts, C. 2012, MNRAS, 422, 2960 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D. 2005, MNRAS, 360, 465 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 2005, in Tidal Evolution and Oscillations in Binary Stars, eds. A. Claret, A. Giménez, & J.-P. Zahn, ASP Conf. Ser., 333, 4 [Google Scholar]
All Tables
Parameters from PHOEBE fits of light and RV curves, and derived physical parameters of CoRoT 102918586.
Frequencies derived from the analysis of the final set of residuals, after subtraction of the EB model, with an amplitude S/N ≥ 4.
All Figures
 |
Fig. 1 CoRoT 102918586 de-trended white-light light curve after rebinning to 512s and normalization to the mean value (eclipses excluded). |
| In the text | |
 |
Fig. 2 Upper panel: phased light curve of the eclipsing binary as residuals of the harmonic fit, orbital overtones excluded. Full line: final fit with PHOEBE. Lower panel: fit residuals. The displayed curve is the final result of our procedure (after two steps of iterative pre-whitenening, see text). |
| In the text | |
 |
Fig. 3 Upper panel: phased radial velocity curves of CoRoT 102918586 components. Filled circles are FEROS measurements, filled squares Sandiford data; uncertainties are smaller than the symbol size; continuous line is the best-fit radial velocity curve obtained with PHOEBE for the primary component, dashed line for the secondary component. Lower panel: fit residuals, with the same symbols. |
| In the text | |
 |
Fig. 4 Projection of the cost function along inclination (top left), primary surface potential (top right), and secondary temperature (bottom left). The minimum value is indicated by a filled dot. Bottom right panel: the correlation of rs with inclination for the best-fitting models (cost function value ≤1% above the minimum). |
| In the text | |
 |
Fig. 5 Best-fitting synthetic composite spectrum of CoRoT 102918586 (red solid line). The spectral window is centered on the Hβ line. The FEROS spectrum observed on HJD 2 455 558.64812 is shown in light gray. The primary lines are blue-warded with respect to the secondary lines. |
| In the text | |
 |
Fig. 6 Short spectral stretch of two observed composite spectra at different orbital phases from the FEROS dataset. The two individual disentangled spectra are shown at the bottom along the best-fitting synthetic spectra calculated for the effective temperatures and surface gravities derived in Sects. 4 and 5 (Tables 3 and 4). |
| In the text | |
 |
Fig. 7 Evolution of the component radii. Upper panel: based on models without overshooting, αOV = 0; lower panel: αOV = 0.2. The light gray bands describe the time evolution of the radii for stars in the mass range M1,2 ± ΔM1,2, from Table 3. The darker areas fill the intersection with the R1,2 ± ΔR1,2 lines from the same table. The vertical lines bound the time interval respecting the constraint of coevality. |
| In the text | |
 |
Fig. 8 Location of CoRoT 102918586 (starred symbol) in the period-eccentricity diagram for stars of spectral type A8-F2 (derived from the database of the 9th Catalogue of Spectroscopic Binary Orbits, Pourbaix et al. 2004). |
| In the text | |
 |
Fig. 9 Final amplitude spectrum of CoRoT 102918586 and, in the inset, the window DFT. The vertical dotted lines correspond to the orbital period overtones, the broken lines to 2F3 and 3F3. The gray line is the threshold of significance (S/N ≥ 4) computed as explained in the text. |
| In the text | |
 |
Fig. 10 Standard deviation, with respect to the local mean of the binned residual light curve (see text). The vertical lines bound the in-eclipse phases. The dip around phase zero suggests that the pulsations belong to the eclipsed component, i.e., to the primary star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


