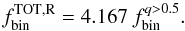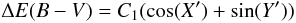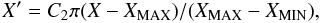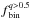| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 41 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201016384 | |
| Published online | 16 March 2012 | |
The ACS survey of Galactic globular clusters
XII. Photometric binaries along the main sequence⋆
1 Instituto de Astrofìsica de Canarias, 38200 La Laguna, Canary Islands, Spain
e-mail: milone@iac.es
2 Department of Astrophysics, University of La Laguna, 38200 La Laguna, Tenerife, Canary Islands, Spain
3 Dipartimento di Astronomia, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
4 INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
5 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
6 Department of Astronomy, University of Florida, 211 Bryant Space Science Center, Gainesville, FL 32611, USA
7 Max Plank Institute for Astrophysics, Postfach 1317, 85741 Garching, Germany
8 Lund Observatory, Box 43, 221-00 Lund, Sweden
9 Department of Physics and Astronomy, Dartmouth College, 6127 Wilder Laboratory, Hanover, NH 03755, USA
10 Department of Physics and Astronomy, University of Victoria, PO Box 3055, STN CSC, Victoria, BC, V8W 3P6 Canada
11 P. Universidad Católica de Chile, Departamento de Astronomía y Astrofísica, Casilla 306, Santiago 22, Chile
12 Centro de Estudios de Física del Cosmos de Aragón (CEFCA), 44001 Teruel, Spain
13 Dept. of Astronomy, University of Virginia, PO Box 400325, Charlottesville, VA 22904-4325, USA
14 Department of Astronomy and Astrophysics, Pennsylvania State University, 525 Davey Laboratory, State College, PA 16801, USA
Received: 21 December 2010
Accepted: 31 October 2011
Context. The fraction of binary stars is an important ingredient to interpret globular cluster dynamical evolution and their stellar population.
Aims. We investigate the properties of main-sequence binaries measured in a uniform photometric sample of 59 Galactic globular clusters that were observed by HST WFC/ACS as a part of the Globular Cluster Treasury project.
Methods. We measured the fraction of binaries and the distribution of mass-ratio as a function of radial location within the cluster, from the central core to beyond the half-mass radius. We studied the radial distribution of binary stars, and the distribution of stellar mass ratios. We investigated monovariate relations between the fraction of binaries and the main parameters of their host clusters.
Results. We found that in nearly all the clusters, the total fraction of binaries is significantly smaller than the fraction of binaries in the field, with a few exceptions only. Binary stars are significantly more centrally concentrated than single MS stars in most of the clusters studied in this paper. The distribution of the mass ratio is generally flat (for mass-ratio parameter q > 0.5). We found a significant anti-correlation between the binary fraction in a cluster and its absolute luminosity (mass). Some, less significant correlation with the collisional parameter, the central stellar density, and the central velocity dispersion are present. There is no statistically significant relation between the binary fraction and other cluster parameters. We confirm the correlation between the binary fraction and the fraction of blue stragglers in the cluster.
Key words: techniques: photometric / binaries: general / stars: Population II / globular clusters: general
Tables 1–3 and Appendices are only available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The knowledge of the binary frequency in Globular clusters (GCs) is of fundamental importance in many astrophysical studies. Binaries play an important role in the cluster dynamical evolution, as they represent an important source of heating. They are also important for the interpretation of the stellar populations in GCs. A correct determination of the stellar mass and luminosity functions in GCs requires accurate measure of the fraction of binaries. Stellar evolution in a binary system can be different from isolated stars in the field. Exotic stellar objects, like blue stragglers (BSSs), cataclysmic variables, millisecond pulsars and low mass X-ray binaries represent late evolutionary stages of close binary systems. The determination of the fraction of binaries plays a fundamental role towards the understanding of the origin and evolution of these peculiar objects.
There are three main techniques used in literature to measure the fraction of binaries in GCs (Hut et al. 1992). The first one identifies binaries by measuring their radial velocity variability (e.g. Latham 1996). This method relies on the detection of each individual binary system but, due to actual limits in sensitivity of spectroscopy, these studies are possible only for the brightest GC stars. Moreover, this technique is sensitive to binaries with short orbital periods, and the estimated fraction of binaries depends on the eccentricity distribution. The second approach is based on the search for photometric variables (e.g. Mateo 1996). As in the previous case, it is possible to infer specific properties of each binary system (like the measure of orbital period, mass ratio, orbital inclination). Unfortunately, this method is biased towards binaries with short periods and large orbital inclination. The estimated fraction of binaries depends on the assumed distribution of orbital periods, eccentricity and mass ratio. Both of these techniques have a low discovery efficiency and are very expensive in terms of telescope time because of the necessity to repeat measures in different epochs.
A third method, based on the analysis of the number of stars located on the red side of the MS fiducial line, may represent a more efficient approach to measure the fraction of binaries in a cluster for several reasons:
-
the availability of a large number (thousands) of stars makes it astatistically robust method;
-
it is efficient in terms of observational time: two filters are enough for detecting binaries, and repeated measurements are not needed;
-
it is sensitive to binaries with any orbital period and inclination.
This latter approach has been used by many authors (e.g. Aparicio et al. 1990, 1991; Romani & Weinberg 1991; Bolte 1992; Rubenstein & Baylin 1997; Bellazzini et al. 2002; Clark et al. 2004; Richer et al. 2004; Zhao & Baylin 2005; Sollima et al. 2007, 2009; Bedin et al. 2008; Milone et al. 2009, 2010a, 2012c) to study the populations of binaries in individual stellar clusters. The relatively small number of clusters that have been analyzed is a consequence of the intrinsic difficulties of the method:
-
high photometric quality is required and high resolution isnecessary to minimize the fraction of blends in the central regionsof GCs;
-
differential reddening (often present) spreads the MS and makes it more difficult to distinguish the binary sequence from the single-star MS population;
-
an accurate analysis of photometric errors as well as a correct estimate of field contamination are necessary to distinguish real binaries from bad photometry stars and field objects.
The first study of binaries in a large sample of GCs comes from Sollima et al. (2007), who investigated the global properties of binaries in 13 low-density GCs. These authors found that the total fraction of binaries ranges from 0.1 to 0.5 in the core depending on the cluster, thus confirming the deficiency of binaries in GCs compared to the field where more than half of stars are in binary systems (Mayor et al. 1992; Dunquennoy & Mayor 1991; Fischer & Marcy 1992; Halbwachs et al. 2003; Rastegaev et al. 2010; Raghavan et al. 2010). At variance with the high fraction of binaries in field sdB stars (Masted et al. 2001; Napiwotzki et al. 2004), a lack of close binaries among GC hot horizontal branch stars (the cluster counterpart of field sdBs) has been confirmed by Moni Bidin et al. (2006, 2009).
Sollima et al. (2010) extended the study of binaries to five high-latitude open clusters with ages between ~0.3−4.3 Gyr and found that the fraction of binaries are generally larger than in GCs and range between ~0.3 and 0.7 in the core. Very high binary fractions have been observed also in some young star clusters and for pre-main sequence T-Tauri stars, where the total binary fraction might be as high as 0.9 (e.g. Prosser et al. 1994; Petr et al. 1998; McCaughrean 2001; Duchêne 1999).
These findings suggest that the star formation condition, as well as the environment, could play a fundamental role on the evolution of binary systems. The binary populations in star clusters has been investigated in detail, mainly through Monte-Carlo and Fokker-Plank simulations (e.g. Giersz & Spurzem 2000; Fregeau et al. 2003; Ivanova et al. 2005), N-body (e.g. Shara & Hurley 2002; Trenti et al. 2007; Hurley et al. 2007; Fregeau et al. 2009; Marks et al. 2011) and fully analytical computations (Sollima 2008).
While the evolution of binaries stimulated by interactions with cluster stars could play the major role, there are many processes that also influence the binary population in stellar systems. For instance binary systems can form by tidal-capture (e.g. Hut et al. 1992; Kroupa 1995a). Destruction of binaries may occur via coalescence of components through encounters or tidal dissipation between the components (Hills 1984; Kroupa 1995b; Hurley & Shara 2003). Stellar evolutionary processes can significantly effect the property of binaries and binary-binary interaction can led to collisions and mergers (e.g. Fregeau et al. 2004). The comparison of simulation results with observed binary fraction is hence a powerful tool to shed light on both the cluster and the binaries evolution.
In this paper, we report the observational results of our search for photometric binaries among GCs present in the HST Globular Cluster Treasury catalog (Sarajedini et al. 2007; Anderson et al. 2008), which is based on HST ACS/WFC data We exploited both the homogeneity of this dataset, and the high photometric accuracy of the measures to derive the fraction of binaries in the densest regions of 59 GCs. We deserve to future works any attempt to interpret the empirical findings presented in this paper.
2. Observations and data reduction
Most of the data used in this paper come from the HST ACS/WFC images taken for GO 10775 (PI Sarajedini), an HST Treasury project, where a total of 66 GCs were observed through the F606W and F814W filters. For 65 of them, the database consists in four or five F606W and F814W deep exposures plus a short exposure in each band. The pipeline used for the data reduction allowed us to obtain precise photometry from nearly the tip of the red giant branch (RGB) to several magnitudes below the main sequence turn-off (MSTO), typically reaching ~0.2 m⊙.
The GO 10775 data set as well as the methods used for its photometric reduction have been presented and described in Papers II and IV of this series (Sarajedini et al. 2007 and Anderson et al. 2008)1.
The uniform and deep photometry offers a database with unprecedented quality that made possible a large number of studies (see e.g. Sarajedini et al. 2010 and references therein).
In this paper we study the main sequence binary population in a subset of 59 GCs. We excluded three clusters (Lynga 7, NGC 6304, and NGC 6717) that are strongly contaminated by field stars and for which there exist no archive HST data which could allow us to obtain reliable proper motions and separate them from cluster members. We also excluded Palomar 2 because of its high differential reddening, and NGC 5139 (ω Centauri), and NGC 6715 because of the multiple main sequences (Siegel et al. 2007; Bellini et al. 2010 and references therein). The triple MS of NGC 2808 made the binary-population extremely complicated and we presented it in a separate paper (Milone et al. 2012c).
In addition, we also used archive HST WFPC2, WFC3 and ACS/WFC images from other programs to obtain proper motions, when images overlapping the GO10775 images were available. Table 1 summarizes the archive data used in the present paper.
The recipes of Anderson et al. (2008) have been used to reduce the archive ACS/WFC data. The WFPC2 data are analyzed by using the programs and the techniques described in Anderson & King (1999, 2000, 2003). We measured star positions and fluxes on the WFC3 images with a software mostly based on img2xym_WFI (Anderson et al. 2006). Details on this program will be given in a stand-alone paper. Star positions and fluxes have been corrected for geometric distortion and pixel-area using the solutions provided by Bellini & Bedin (2009).
2.1. Selection of the star sample
Binaries that are able to survive in the dense environment of a GC are so close that even the Hubble Space Telescope (HST) is not able to resolve the single components. For this reason, light coming from each star will combine, and the binary system will appear as a single point-like source. In this paper we will take advantage from this fact to search for binaries by carefully studying the region in the CMD where their combined light puts them.
If we consider the two components of a binary system and indicate with m1, m2, F1, and F2 their magnitudes and fluxes, the binary will appear as a single object with a magnitude:
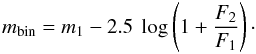 In the case of a binary formed by two MS stars (MS-MS binary) the fluxes are related to the two stellar masses (ℳ1, ℳ2), and its luminosity depends on the mass ratio q = ℳ2/ℳ1 (in the following we will assume ℳ2 < ℳ1, q < 1). The equal-mass binaries form a sequence that is almost parallel to the MS, ~ 0.75 mag brighter. When the masses of the two components are different, the binary will appear redder and brighter than the primary and populate a CMD region on the red side of the MS ridge line (MSRL) but below the equal-mass binary line.
In the case of a binary formed by two MS stars (MS-MS binary) the fluxes are related to the two stellar masses (ℳ1, ℳ2), and its luminosity depends on the mass ratio q = ℳ2/ℳ1 (in the following we will assume ℳ2 < ℳ1, q < 1). The equal-mass binaries form a sequence that is almost parallel to the MS, ~ 0.75 mag brighter. When the masses of the two components are different, the binary will appear redder and brighter than the primary and populate a CMD region on the red side of the MS ridge line (MSRL) but below the equal-mass binary line.
 |
Fig. 1 Model MS-MS binary sequences with different mass ratios for NGC 2298. The dashed-dotted line is the MSRL while, continuous black lines indicate the sequences of constant q and blue lines mark sequences of constant ℳ1. |
In Fig. 1 we used our empirical MSRL and the mass-luminosity relations of Dotter et al. (2007) to generate sequences of MS-MS binary systems with different mass ratios.
An obvious consequence of this analysis is that our capability in detecting binaries mainly depends on the photometric quality of the data. Distinguishing the binary populations in clusters requires high-resolution images and high-precision photometry. Not all stars in clusters can be measured equally well. Crowding, saturation, and image artifacts such as diffraction spikes, bleeding columns, hot pixels, and cosmic rays can prevent certain stars from being measured well. The first challenge to this project will be to identify which stars can be measured well and which are hopeless.
In addition to the basic stellar positions and photometry, the software described in Anderson et al. (2008) calculates several useful parameters that will help us reach this goal. The following parameters are provided for every star:
-
the rms of the positions measured in different exposures andtransformed into a common reference frame (rmsX and rmsY);
-
the average residuals of the PSF fit for each star (qF606W and qF814W);
-
the total amount of flux in the 0.5 arcsec aperture from neighboring stars relative to the star’s own flux (oF606W and oF814W).
True binary stars will be so close to each other as to be indistinguishable from single stars in our images, so the binarity has no impact on the above diagnostics2. Therefore, it is safe to use the above diagnostics to indicate which stars are likely measured well and which ones are likely contaminated. As an example, in the six panels of Fig. 2, we show these parameters as a function of the instrumental3mF606W and mF814W magnitudes, and illustrate the criteria that we have used to select the sample of stars with the best photometry for NGC 2298.
 |
Fig. 2 Diagnostic parameters that we have used to select the sample of NGC 2298 stars with high-quality photometry. The parameters are plotted as a function of the instrumental mF606W and mF814W magnitudes. Red circles indicate the median rmsX, Y, and qF606W,F814W per intervals of 0.4 mag. Red lines separate the well measured stars (thin points) from those that are more likely to have poorer photometry (thick points). See text for details. |
 |
Fig. 3 CMD of all the measured stars (left), of stars that passed our criteria of selection (middle), and CMD of rejected stars (right) |
We note a clear trend in the quality fit and the rms parameters as a function of the magnitude. At all magnitudes, there are outliers that are likely sources with poorer photometry and that need to be removed before any analysis. Because of this, we adopted the following procedure to select the best measured stars. We began by dividing all the stars of each cluster into bins of 0.4 mag; for each of them, we computed the median values of the parameters rmsX, Y and qF606W,F814W defined above and the 68.27th element of the percentile distribution (hereafter σ). We added to the median of each bin four times σ, and fitted these points with a spline to obtain the red lines of Fig. 2. All stars below the red line have been flagged as “well-measured” according to that diagnostic.
The parameters oF606W and oF814W do not show a clear trend with magnitude. We flagged as “well-measured” all the stars with oF606W < 1 and oF814W < 1.
In Fig. 3 we compare the color-magnitude diagram (CMD) of all the measured stars of NGC 2298 (left), the CMD of stars that pass all the selection criteria (middle), and the CMD of rejected stars (right). The sample of stars that have been used in the analysis that follows includes stars flagged as “well-measured” with respect to all the parameters we used as diagnostics of the photometric quality.
The photometric catalog by Anderson et al. (2008) also provides the rms of the mF606W and mF814W magnitude measures made in different exposures. However, a star can have a large magnitude rms either because of poor photometry or because it is a binary system with short period photometric variability. In order to avoid the exclusion of this class of binaries, we have not used the rms of magnitude measures as diagnostics of the photometric quality in the selection of our stellar sample.
2.2. Artificial-star tests
Artificial-star (AS) tests played a fundamental role in this analysis; they allowed us to determine the completeness level of our sample, and to measure the fraction of chance-superposition “binaries”. The GC Treasury reduction products (see Anderson et al. 2008) also contain a set of AS tests. The artificial stars were inserted with a flat luminosity function in F606W and with colors that lie along the MSRL for each cluster. Typically, 105 stars were added for each cluster, with a spatial density that was flat within the core, and declined as r-1 outside of the core. The stars were added one at a time, and as such they will never interfere with each other.
Each star in the input AS catalog is added to each image with the appropriate position and flux. The AS routine measures the images with the same procedure used for real stars and produces the same output parameters as in Sect. 2. We considered an artificial star as recovered when the input and the output fluxes differ by less than 0.75 mag and the positions by less than 0.5 pixel. We applied to the recovered ASs the same criteria of selection described in Sect. 2 for real stars and based on the rms in position and on the qF606W,F814W and oF606W,F814W parameters. In what follows, including the completeness measure, we used only the sample of ASs that passed all the criteria of selection.
Since completeness depends on crowding as well as on stellar luminosity, we measured it applying a procedure that accounts for both the stellar magnitude and the distance from the cluster center. We divided the ACS field into 5 concentric annuli and, within each of them, we examined AS results in 9 mag bins, in the interval −14 < mF814W < −5. For each of these 9 × 5 grid points we calculated the completeness as the ratio of recovered to added stars within that range of radius and magnitude. Finally, we interpolated the grid points and derived the completeness value associated with each star. This grid allowed us to estimate the completeness associated to any star at any position within the cluster. Results are shown in Fig. 4 for NGC 2298. The stars used to measure the binary fraction have all completeness larger than 0.50.
 |
Fig. 4 Left: completeness as a function of the mF814W magnitude in five annuli (the inner and outer radius of each annulus, in ACS pixels, are quoted in the inset) for NGC 2298. Right: completeness contours in the radial distance versus mF814W magnitude plane. The completeness levels corresponding to the red and gray continuous lines are quoted in the figure. Dotted lines indicate differences of completeness of 0.05 ranging from 0.05 to 0.95. |
3. Photometric zero point variations
In some clusters, the distribution of foreground dust can be patchy, which causes a variation of the reddening with position in the field, resulting in a non-intrinsic broadening of the stellar sequences on the CMDs. In addition to these spreads, small unmodelable PSF variations, mainly due to focus changes, can introduce slight shifts in the photometric zero point as a function of the star location in the chip (see Anderson et al. 2008 for details). The color variation due to inaccuracies in the PSF model is usually ~0.005 (Anderson et al. 2008, 2009; Milone et al. 2010). In some clusters, differential reddening effects may be much larger. An appropriate correction for these effects is a fundamental step, as it can greatly sharpen the MS, with a consequent improved analysis of the MS binary fraction.
3.1. Differential reddening
 |
Fig. 5 Panel a: observed CMD of NGC 2298; the arrow indicates the direction of reddening. The continuous lines are the axes (“abscissa” and “ordinate”) of the reference frame introduced in the procedure for the measurements of reddening variations. The position of NGC 2298 stars in this reference frame is shown in panel b where we draw the fiducial line of the MS as a dashed red line. Stars between the dotted lines (black points) have been used as reference stars. Panel C shows the rectified “ordinate” vs. Δ “abscissa” diagram. |
In order to correct for differential reddening, we started by defining a photometric reference frame where the abscissa is parallel to the reddening line, as shown in Fig. 5 for NGC 2298. To do this, we have first arbitrarily defined a point (O), near the MSTO in the CMD of Panel a. Then we have translated the CMD such that the origin of the new reference frame corresponds to O. Finally, we have rotated the CMD counterclockwise by an angle:
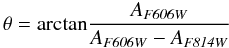 as shown in Fig. 5b. The two quantities AF606W and AF814W are the absorption coefficients in the F606W and F814W ACS bands corresponding to the average reddening for each GC. They are derived by assuming, for each GC, the average E(B − V) listed in the Harris (1996, 2003) catalog and linearly interpolating among the reddening and the absorption values given in Table 3 of Bedin et al. (2005) for a cool star. The reason for rotating the CMD is that it is much more intuitive to determine a reddening difference on the horizontal axis rather than along the oblique reddening line.
as shown in Fig. 5b. The two quantities AF606W and AF814W are the absorption coefficients in the F606W and F814W ACS bands corresponding to the average reddening for each GC. They are derived by assuming, for each GC, the average E(B − V) listed in the Harris (1996, 2003) catalog and linearly interpolating among the reddening and the absorption values given in Table 3 of Bedin et al. (2005) for a cool star. The reason for rotating the CMD is that it is much more intuitive to determine a reddening difference on the horizontal axis rather than along the oblique reddening line.
The value of θ depends weakly on the stellar spectral type, but this variation can be ignored for our present purposes. For simplicity, in this section, we will indicate as “abscissa”, the abscissa of the rotated reference frame, and as “ordinate”, its ordinate.
At this point, we adopt an iterative procedure that involves the following four steps:
-
1.
We generate the red fiducial line shown inFig. 5b. In order to determine this line, we used onlyMS stars. We divided the sample of these MS reference stars into“ordinate” bins of 0.4 mag. Foreach bin, we calculated the median “abscissa” that has beenassociated with the median “ordinate” of the stars in the bin. Thefiducial has been derived by fitting these median points with acubic spline. Here, it is important to emphasize that the use of themedian allows us to minimize the influence of the outliers ascontamination by binary stars left in the sample, field stars or starswith poor photometry.
-
2.
For each star, we calculated the distance from the fiducial line along the reddening direction (Δ “abscissa”). In the right panel of Fig. 5, we plot “ordinate” vs. Δ “abscissa” for NGC 2298.
-
3.
We selected the sample of stars located in the regions of the CMD where the reddening line define a wide angle with the fiducial line so that the shift in color and magnitude due to differential reddening can be more easily separated from the random shift due to photometric errors. These stars are used as reference stars to estimate reddening variations associated to each star in the CMD and are marked in Fig. 5 as heavy black points.
-
The basic idea of our procedure, which is applied to each star (target) individually, is to measure the differential reddening suffered by the target star by using the position in the “ordinate” vs. “abscissa” diagram of a local sample of reference stars located in a small spatial region around the target with respect to the fiducial sequence. We must adopt an appropriate size for the comparison region in order to obtain the best possible reddening correction. The optimal size is a compromise between two competing needs. On one hand, we want to use the smallest possible spatial cells, so that the systematic offset between the “abscissa” and the fiducial ridgeline will be measured as accurately as possible for each star’s particular location. On the other hand, we want to use as many stars as possible, in order to reduce the error in the determination of the correction factor. As a compromise, for each star, we typically selected the nearest 30 − 100 reference stars4 and calculate the median Δ “abscissa” that is assumed as the reddening correction for that star. In this way, our differential reddening correction will be done at higher spatial frequencies in the more populated parts of the observed field. In calculating the differential reddening suffered by a reference star, we excluded this star in the computation of the median Δ “abscissa”. As an example, in Fig. 6 we illustrate this procedure for a star in the NGC 2298 catalog. The position of all the stars within the ACS/WFC field of view is shown in the upper-left panel where reference stars are represented by black crosses, and the remaining stars are indicated with gray points. Our target is plotted as a blue asterisk. The 35 closest neighboring reference stars are marked with red circles. The lower-left panel is a zoom showing the location of the selected stars in a 700 × 700 pixel box centered on the target. The positions of the 35 closest neighboring reference stars in the “ordinate” vs. Δ “abscissa” plane are shown in the upper right panel, and their histogram distribution is plotted in the bottom-right one. Clearly, neighboring stars define a narrow sequence with Δ “abscissa” ~−0.15. Their median Δ “abscissa”, which is indicated by the continuous red line, is assumed to be the best estimate of the differential reddening suffered by the target star.
After the median Δ“abscissa” have been subtracted to the “abscissa” of each star in the rotated CMD, we obtain an improved CMD which has been used to derive a more accurate selection of the sample of MS reference stars and derive a more precise fiducial line. After step 4, we have a newly corrected CMD. We re-run the procedure to see if the fiducial sequence needs to be changed (slightly) in response to the adjustments made and iterated. Typically, the procedure converges after about four iterations. Finally, the corrected “abscissa” and “ordinate” are converted to mF606W and mF814W magnitudes.
 |
Fig. 6 Visualization of the local approach for the estimate of the differential reddening suffered by the target star indicated with the blue asterisk. Upper left: position of NGC 2298 stars in the ACS/WFC field of view (gray points). Red circles highlight the 35 reference stars in the lower left panel. Reference stars are indicated with black crosses, among them, the 35 closest neighbours (of the target star) are marked with red circles. The lower left panel is a zoom of a 700 × 700 pixel centered on the target star. Upper right: “ordinate” vs. Δ “abscissa” for all the stars in the NGC 2298 field of view. The median Δ “abscissa” of the 35 closest neighbor is indicated by the continuous red vertical line and corresponds to the differential reddening value suffered by the target star. The histogram of the Δ “abscissa” distribution of the 35 closest neighbors is shown in the bottom right panel. |
From star-to-star comparison of the original and the corrected magnitudes we can estimate star to star variations in E(B − V) and derive the reddening map in the direction of our target GCs. As an example, in Fig. 7, we divide the field of view into 8 horizontal slices and 8 vertical slices and plot Δ E(B − V) as a function of the Y (upper panels) and X coordinate (right panels). We have also divided the whole field of view into 32 × 32 boxes of 128 × 128 ACS/WFC pixels and calculated the average Δ E(B − V) within each of them. The resulting reddening map is shown in the lower-left panel where each box is represented as a gray square. The levels of gray are indicative of the amount of differential reddening as shown in the upper right plot. The analysis of the intricate reddening structures in our GC fields is beyond the purposes of the present work and will be presented in a separate paper (King et al., in prep.).
Figure 8 shows the CMDs of twelve of the GCs studied in this paper including NGC 2298. These are the clusters that revealed the largest differential reddening ΔE(mF606W − mF814W) > 0.05.
3.2. PSF variations
Some GCs have a reddening that is close to zero and therefore we expect negligible variations of reddening within their field of view. In these cases, we need to apply only a correction for the photometric zero point spatial variation due to small, unmodelable PSF variations. Usually, these PSF variations affect each filter in a different way, so their most evident manifestation is a slight shift in the color of the cluster sequence as a function of the location in the field (Anderson et al. 2008). For this reason, when the average reddening of the cluster (from Harris 1996) is lower than 0.10 mag, we did not follow the recipes for the correction of differential reddening described in the previous section, but corrected our photometry for the effects of the variations of the photometric zero point along the chip. We used a procedure that slightly differs from the one of Sect. 3.1. The only difference from what done in GCs with high reddening is that we did not rotated the CMD and so we did not apply the correction along the reddening line, but along the color direction.
 |
Fig. 7 Bottom-left: map of differential reddening in the NGC 2298 field of view. The gray levels correspond to the magnitude of the variation in local reddening as indicated in the upper-right panel. We divided the field of view into 8 horizontal slices and 8 vertical slices. Upper-left and lower-right panels plot Δ E(B − V) as a function of the Y and X coordinate. |
 |
Fig. 8 CMDs of twelve GCs before (left) and after (right) the correction for differential reddening. For each cluster we give the average reddening from the Harris (1996) catalog. |
 |
Fig. 9 CMDs of NGC 288 before (top) and after (bottom) correction for photometric zero points variations. Right panels show a zoom of CMD around the SGB and upper-MS region. |
 |
Fig. 10 Comparison of the CMD of nine GCs studied in this paper before (left) and after (right) the correction for photometric zero points variations. |
The results of this procedure are illustrated in Fig. 9 where we compare the original and the correct CMD of NGC 288. The improvement in the quality of our CMD is exemplified by the comparison in right panels figures that show a zoom of the SGB and the upper-MS.
Other examples of the improvement in the photometry coming from this procedure are shown in Fig. 10 where we plot the nine GCs studied in this paper for which we measured the largest color variations. The average color variations are typically around 0.005 mag for each cluster with E(B − V) < 0.10 studied in this paper and never exceed 0.035 mag.
 |
Fig. 11 Gray areas in the upper panels are the regions A, and B of the NGC 2298 CMD adopted to select all the (single and binary) cluster stars (left) and the candidate binaries with q > 0.5 (right), in a range of 3 mF814W magnitudes. In all panels, the MSRL is represented as a green continuous line, while the green dashed line is blue shifted from the MSRL by three times the color error. The red continuous line is the locus of MS-MS binaries with mass ratio q = 0.5, while the red dotted line is the locus of MS-MS binaries whose components have equal mass. The red dashed dotted line is displaced to the red from the dotted line by 3 times the color error. Lower panels show the observed CMD of NGC 2298 (left), the artificial stars CMD (middle), and the CMD of field stars (right). |
4. The measure of the fraction of binaries with high mass ratio
Binaries with large mass ratios have a large offset in luminosity from the MSRL and are relatively easy to detect. On the contrary, a small mass ratio doesn’t pull them very far off of the MSRL, making them hard to distinguish from single MS stars. Finally, the low signal to noise photometry of faint stars limits the range where binaries can be detected and studied.
In practice, the limited photometric precision and accuracy makes impossible the direct measure of the overall population of binaries without assuming a specific distribution of mass ratios f(q). For this reason, in this paper, we followed two different approaches to study the binary population in our target GCs.
-
1.
We isolated different samples of high mass-ratio binaries (i.e.the binary systems with q > 0.5, 0.6 and 0.7). For them, we obtained a direct measure of their fraction with respect to the total number of MS stars, and studied the properties of each group (Sect. 4).
-
2.
We determined the total fraction of binaries by assuming a given f(q) (Sect. 5.2).
In each cluster, we estimated the fractions of high q binary stars in the F814W magnitude interval ranging from 0.75 (mF814W,bright) to 3.75 (mF814W,faint) magnitudes below the MSTO5. In this work we used the MSTO magnitudes from Marín-Franch et al. (2009), who used our same photometric data base. The choice of this magnitude interval represents a compromise between the necessity of a large set of stars and the need to avoid faint stars to be able to measure the binary fraction also in clusters with poorer photometry (because of crowding).
To illustrate our setup, Fig. 11 shows the various regions we studied in the CMD of NGC 2298 in order to measure the fraction of binaries with mass ratio q > 0.5 for this cluster. The upper half of the figure displays two regions of the CMD: region A (upper left) and region B (upper right).
Region A includes all the stars that we can consider to be cluster members. It includes: all the single MS stars and the MS+MS binaries with a primary star that have mF814W,bright < mF814W < mF814W,faint. The green continuous line is the MS fiducial line, drawn as described in Sect. 3. To include stars that have migrated to the blue due to measuring error, we extend region A up to the green dashed line, which is displaced to the blue from the MSRL by 3 times the the average color error for a star at that magnitude. The red dotted line is the locus of MS-MS binaries whose components have equal mass; we set the limit of region A by drawing the red dot-dashed line, displaced to the red from the dotted line by 3 times the rms color error. The upper-right panel of Fig. 11 shows Region B, which is chosen in such a way that it contains all the binaries with q > 0.5. It starts at the locus of binaries with mass ratio, q = 0.5, marked by the continuous red line and ends at the dotted-dashed red line, which is the same line defined in the upper-left panel.
The lower half of Fig. 11 shows where observed stars and ASs fall within these two regions. The left-lower panel plots the observed stars and the middle panel shows ASs. We note that a significant number of ASs fall in region B. Only a fraction of them can be explained by photometric errors; in many cases two stars fell at positions so close together that a pair of stars has blended into a single object, which would simulate a binary. Obviously, in the real CMD, regions A and B are also populated by field stars, as shown in the right panel for NGC 2298. We will explain how the field star CMD is built in Sect. 4.1.
To determine the fraction of binaries with q > 0.5 we started by measuring the number of stars, corrected for completeness, in regions A (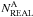 ) and B (
) and B (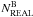 ). They are calculated as
). They are calculated as 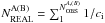 , where
, where 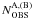 is the number of stars observed in the region A (B) and Ci is the completeness (coming from AS tests). Then, we evaluated the corresponding numbers of artificial stars (
is the number of stars observed in the region A (B) and Ci is the completeness (coming from AS tests). Then, we evaluated the corresponding numbers of artificial stars (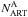 and
and 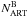 ) and field stars (
) and field stars (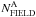 and
and 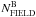 ). In the following Sects. 4.1 and 4.2 we will describe the methods that we used to estimate
). In the following Sects. 4.1 and 4.2 we will describe the methods that we used to estimate 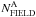 and
and 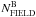 and
and 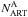 and
and 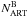 .
.
The fraction of binaries with q > 0.5 is calculated as6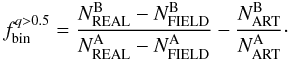 (1)Similarly, we have calculated the fraction of binaries with q > 0.6 and q > 0.7. To do this it is necessary to move redward the left-hand side (red solid line) of Region B, according to what is shown in Fig. 1.
(1)Similarly, we have calculated the fraction of binaries with q > 0.6 and q > 0.7. To do this it is necessary to move redward the left-hand side (red solid line) of Region B, according to what is shown in Fig. 1.
The error associated to each quantity of Eq. (1) is the Poisson error and the error on the obtained binary fraction is calculated by following the standard errors propagation. Therefore it represents a lower limit for the uncertainty of the binary fraction. We note that the binary fractions strongly differ from one cluster to another with 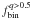 ranging from ~ 0.01 to ~ 0.40.
ranging from ~ 0.01 to ~ 0.40.
In order to analyze the radial distribution of binary stars in GCs and provide information useful for dynamical models of our target clusters, we have calculated both the total binary fraction and the fraction of binaries with q > 0.5 at different radial distances from the cluster center. More specifically, we defined three different regions:
-
a circle with a radius of one core radius(rC sample);
-
an annulus between the core and the half-mass radius (rC − HM sample);
-
a region outside the half-mass radius (roHM sample).
The values of the core radius and the half-mass radius are from the Harris (1996) catalog. It should be noted that, even if our data are homogeneous, in the sense that they came from the same instrument (ACS/WFC/HST) and have been reduced adopting the same techniques, their photometric quality vary from cluster to cluster, mainly because of the different stellar densities (which affects the crowding). For this reason, for some GCs that have poor photometry in their central regions, we have measured the fraction of binaries only outside a minimum radius (RMIN) where it is possible to distinguish binaries with q > 0.5 from single MS stars. The adopted values of RMIN are listed in Table 2. The fractions of binaries with q > 0.5, q > 0.6, q > 0.7 (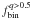 ,
, 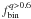 and
and 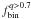 ) for the clusters in our sample are listed in Cols. 3 − 5 of Table 2, respectively. In Col. 6 there is also our best-estimate of the total binary fraction (i.e. the fraction of binaries in the whole range 0 < q < 1) that will be estimated in Sect. 5.2. We give both the fractions of binaries calculated over the ACS/WFC field and those in each of the three regions defined above.
) for the clusters in our sample are listed in Cols. 3 − 5 of Table 2, respectively. In Col. 6 there is also our best-estimate of the total binary fraction (i.e. the fraction of binaries in the whole range 0 < q < 1) that will be estimated in Sect. 5.2. We give both the fractions of binaries calculated over the ACS/WFC field and those in each of the three regions defined above.
Following these considerations, it was possible to include in the rC sample only 43 out of the original 59 GCs. In addition, the limited ACS field of view reduced the number of GCs with rC − HM and roHM samples to 51 and 45 clusters, respectively.
 |
Fig. 12 Vector-point diagram of proper motions, in equatorial coordinates, for twenty GCs. Only stars in the mF814W interval indicated in each panel are shown. |
4.1. Field contamination
The best ways to quantify foreground/background contamination of regions A and B consists in identifying field stars on the basis of their proper motion, which usually differs from the cluster motion. For several clusters of the sample considered in this paper there are previous epoch HST images with a sufficiently long temporal baseline and precision to allow the measurement of proper motions. We used archive material to determine the proper motions of 20 GCs that are critically contaminated by field stars: ARP 2, NGC 104, NGC 362, NGC 5286, NGC 5927, NGC 6121, NGC 6218, NGC 6352, NGC 6388, NGC 6441, NGC 6397, NGC 6496, NGC 6535, NGC 6626, NGC 6637, NGC 6652, NGC 6656, NGC 6681, NGC 6838, and TERZAN 7. The procedure to measure proper motions is outlined in Sect. 4.1.1
In order to determine field objects contamination in the CMDs of the remaining clusters, we run a program developed by Girardi et al. (2005), which uses a model to predict star numbers in any Galactic field. Details of this procedure are given in Sect. 4.1.2.
 |
Fig. 13 Leftmost column: mF814W vs. mF606W − mF814W CMD for all the stars of NGC 6656 with available measures of proper motions. Second Column: proper motion diagrams of the stars in the left panels in mas yr-1, in intervals of 1.4 mag. Third column: the proper motion selected CMD of cluster members. Rightmost column: the CMD of field stars. |
4.1.1. Proper motions
Proper motions are measured by comparing the positions of stars measured at two or more different epochs. For the majority of the clusters only two epochs were available and we followed a method that has been widely described in many other papers (e.g. see Bedin et al. 2008; Anderson & van der Marel 2010). In the cases of NGC 104, NGC 362, NGC 5927, NGC 6121, NGC 6397, and NGC 6656 we used a sample of images taken at three or even more different epochs and determined proper motions with the procedure given by McLaughlin et al. (McLaughlin2006). We refer the interested reader to these paper for a detailed description.
Results are shown in Fig. 12 which plots proper motions for twenty GCs. We plotted only stars in the F814W magnitude range indicated by the numbers quoted in the insets7 Since we measured proper motions relative to a sample of cluster members, the zero point of the motion is the mean motion of the cluster. Therefore, the bulk of stars clustered around the origin of the vector-point diagrams (VPD) consists mostly of cluster members, while field stars are distributed over a larger range of proper motions.
Proper motions offer a unique opportunity to estimate the number of field stars that populate the regions A and B of the CMD. In order to identify field objects, we began to isolate stars whose proper motions clearly differ from the cluster mean motion by using the procedure that is illustrated in Fig. 13 for NGC 6656 (where cluster and field stars are well separated in the VPD), and in Fig. 14 for NGC 6838 (where the separation is less evident).
In the left panel of Figs. 13 and 14 we show the CMD for all the stars for which proper motions measurements are available. The second column of the two figures shows the VPD of the stars in four different magnitude intervals. The red circle is drawn to identify the stars that have member-like motions. In the following, we will indicate as RCL and ROUT the VPD regions within and outside the red circles. We fixed the radius of the circles at 3.25σ, where σ is the average proper-motion dispersion in the two dimensions. If we assume that proper motions of cluster stars follow a bivariate Gaussian distribution, the circle should include 99.5% of the members in each magnitude interval. The third panel shows the CMD of stars with cluster-like proper motion, while selected field objects are plotted on the right panel.
We emphasize here that, as we will see in detail in the following, proper motions are used to evaluate the numbers of field stars that randomly fall within the CMD regions A and B (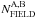 ) and not to isolate a sample of cluster stars. This approach will allow us to determine the binary fraction by means of Eq. (1) in the whole ACS/WFC field of view and not only in the spatial regions covered by multi-epochs images where proper motions are available. To determine the values of
) and not to isolate a sample of cluster stars. This approach will allow us to determine the binary fraction by means of Eq. (1) in the whole ACS/WFC field of view and not only in the spatial regions covered by multi-epochs images where proper motions are available. To determine the values of 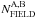 we have to account for three factors:
we have to account for three factors:
-
1.
to accurately measure
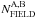 we need a correct estimate of the fraction of field stars that share cluster-like proper motions;
we need a correct estimate of the fraction of field stars that share cluster-like proper motions; -
2.
proper motions are not available for the whole ACS/WFC field of view because, usually, there is only a partial overlap between the images at different epochs. As a consequence of this we need an accurate measurement of the area of the overlapping region;
-
3.
proper motions may not be available for a fraction of stars in the ACS/WFC catalogs even if they are in the overlapping region because these stars are not measured in the second-epoch images (that in many cases come from WFPC2), because they either are too faint or in a too crowded region.
Specifically the number of field stars in the region A has been evaluated as 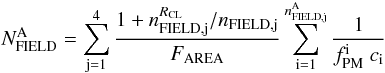 (2)where:
(2)where:
-
nFIELD,j and
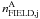 are the total number of field objects and the number of field objects within Region A for which we have measured proper motions, in the magnitude interval j (see the rightmost column of Figs. 13 and 14), respectively.
are the total number of field objects and the number of field objects within Region A for which we have measured proper motions, in the magnitude interval j (see the rightmost column of Figs. 13 and 14), respectively. -
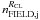 is the fraction of field objects that share proper motions similar to the cluster;
is the fraction of field objects that share proper motions similar to the cluster; -
FAREA is the fraction of the ACS/WFC field of view with multi-epoch observations;
-
ci is the completeness of the ACS/WFC catalog calculated in Sect. 2.2;
-
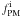 is a factor that accounts for the availability of proper motions (as in point 3 above).
is a factor that accounts for the availability of proper motions (as in point 3 above).
And the same is done to evaluate the number of field stars in the Region B. In the following, we describe the procedure used to determine nRCL, FAREA, and 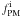 .
.
Field stars with cluster-like proper motions The VPDs of Fig. 12 show that almost all the clusters have some field stars that share the mean cluster motion. The fraction of these sources with respect to the cluster stars depends on several factors, such as the astrometric quality of the data, the temporal baseline, the line of sight, and the motion of the cluster with respect to the field. Their fraction is almost negligible in NGC 6656 and other cases, but makes a significant contribution to the binary fraction in most of the GCs of Fig. 12. We now describe a method to determine the fraction of field stars with cluster-like proper motion in order to accurately infer 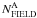 and
and 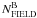 in Eq. (1).
in Eq. (1).
We note that, for the purposes of this paper, we do not need to isolate these intruders. It is sufficient to estimate their total amount, and, more specifically, the amount of field stars with cluster-like motions that populate the CMD region associated with MS-MS binaries or MS single stars.
We independently calculated, for the GCs with reliable proper motions, the number of field stars with cluster-like proper motions for each of the four magnitude intervals of Figs. 13, and 14. In the cases of GCs where cluster and field stars are clearly separated in the proper motion diagram (ARP 2, NGC 104, NGC 362, NGC 5286, NGC 6121, NGC 6218, NGC 6388, NGC 6397, NGC 6496, NGC 6535, NGC 6637, NGC 6624, NGC 6652, NGC 6656, and Terzan 7) we used the method that is illustrated in Fig. 15 for NGC 6656. All the field and cluster stars with reliable proper motions are located within the dotted circle of the left panel VPD We considered as probable cluster members all the objects that are plotted as thin gray dots in the yellow area (region RCL) of the zoomed VPD in the right panel, while remaining objects are flagged as field stars and are represented as heavier points.
The distribution of field stars in the VPD is clearly elongated and the isodensity contours can be approximately described by ellipses. In Fig. 15 we show the two isodensity contours that are tangent to the region RCL and define the red region (RT). The number of field stars within RCL is assumed to be:
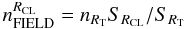 where SRCL and SRT are the areas of regions RCL and RT and nRT is the number of stars within RT.
where SRCL and SRT are the areas of regions RCL and RT and nRT is the number of stars within RT.
 |
Fig. 15 Setup to estimate the fraction of field stars with cluster-like proper motions in NGC 6656. |
In the cases of NGC 5927, NGC 6352, NGC 6441, NGC 6681, and NGC 6838, where the separation of field and cluster stars is less evident, we followed a different recipe, which is illustrated in in Fig. 16 for NGC 6838. The upper panels show the CMD (left) and the VPD (right) for stars in the third interval of magnitudes (j = 3) of Fig. 14. We selected, on the CMD, a sample of stars that, on the basis of their color and magnitude, are probable background/foreground objects. These stars are marked as heavy black points in the lower CMD of Fig. 16, while in the right-lower panel we show their position in the VPD.
If we assume that the fraction of selected objects within RCL with respect to the total number of selected field objects (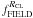 ) is representative of the overall fraction of field stars that share cluster proper motions we can impose:
) is representative of the overall fraction of field stars that share cluster proper motions we can impose: 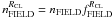 . The contribution of
. The contribution of 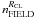 to the measure of the binary fraction is, for all the clusters smaller than 0.01.
to the measure of the binary fraction is, for all the clusters smaller than 0.01.
 |
Fig. 16 Estimate of the contamination of field stars that share cluster proper motions in NGC 6838. Upper panels show the CMD (left) and the VPD (right) for stars with 18.15 < mF814W < 19.45. Lower panels display the CMD (left) and the VPD (right) for those objects that, on the basis of their position on the CMD, are probable field stars. |
In order to investigate the reliability of this approach, we applied it also to the 15 GCs for which proper motions allow us to almost completely separate cluster stars from field ones. In all cases, we found full consistency between the two approaches, with the the fraction of binaries with q > 0.5 listed in Table 2 differing by less than 0.01.
The spatial coverage of multi-epoch images For most clusters, there is only a partial overlap among the different epoch images. In the following we will refer to the region that has been observed in at least two epochs as “RII”. Figure 17 shows the example for NGC 6656, where we indicate as light gray points all the stars for which we have only photometry, and mark with black points the stars with both photometric and proper motion measurements. As our field is just a few square arcmins, we can assume that the background/foreground population is uniformly distributed within it, and therefore we estimate the total number of field stars in our field of view as the product of the number of field stars in the region RII and the ratio between the area of the total field of view and the area of RII. In this paper, we will refer to this ratio as: FAREA.
 |
Fig. 17 Map of all the stars NGC 6656 (light gray points) with mF814W < 18.25. Black points mark all the stars with available proper motions. The contour of region “RII” is colored in red. |
Completeness correction for field stars In the procedure that we have applied to determine the cluster membership using proper motions, we have automatically excluded all the stars that might be members but have poor astrometry. An accurate estimate of the fraction of these stars is necessary to infer the correct values of 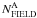 and
and 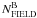 . To estimate the fraction of cluster stars lost by applying the proper motion selection criteria, we applied the procedure illustrated in Fig. 18 for NGC 6656. In panel a we show the mF814W vs. mF606W − mF814W CMD for all the stars in the region “RII”. Proper motion measurements are available only for a fraction (fPM) of these stars. Their CMD is shown in panel b, while the CMD for stars with no available proper motions is plotted in panel (c).
. To estimate the fraction of cluster stars lost by applying the proper motion selection criteria, we applied the procedure illustrated in Fig. 18 for NGC 6656. In panel a we show the mF814W vs. mF606W − mF814W CMD for all the stars in the region “RII”. Proper motion measurements are available only for a fraction (fPM) of these stars. Their CMD is shown in panel b, while the CMD for stars with no available proper motions is plotted in panel (c).
To determine fPM we started by dividing the CMD into bins of 0.5 mF814W magnitudes. In each of them, we counted the total number of observed stars (NOBS) and the number of star with a reliable estimate of proper motions (NPM). The fraction of stars with a proper motions in that bin is: fPM = NPM/NOBS.
We then calculated the median mF814W magnitude of the observed stars (mMED) in each bin. We associated to each bin the corresponding value of fPM and mMED. The (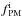 ) for each i-star is calculated by interpolation with a spline. In panel (d) of Fig. 18 we show the final fPM as a function of mF814W. For the GCs studied here always we have fPM > 0.4 at the level of 3.75 F814W magnitudes below the MSTO.
) for each i-star is calculated by interpolation with a spline. In panel (d) of Fig. 18 we show the final fPM as a function of mF814W. For the GCs studied here always we have fPM > 0.4 at the level of 3.75 F814W magnitudes below the MSTO.
 |
Fig. 18 Panel a): CMD for all the stars within the region “RII”; Panel b): CMD for stars with a reliable estimate of proper motions; Panel c): CMD for stars within “RII” for which there are not reliable measurements of proper motions; Panel d): fraction of stars with good proper motions with respect to the total number of stars within “RII” as a function of mF814W. |
4.1.2. Galactic model
In order to estimate the number of background/foreground stars in the field of view of the GCs studied in this paper, and for which we do not have reliable measurements of proper motions, we used the theoretical Galactic model described by Girardi et al. (2005). This model was used to generate a synthetic CMD (in the ACS/WFC F606W and F814W bands) containing the expected field stars in the cluster area that we are studying. The synthetic CMDs were used to count the number of field stars in the CMD regions A, and B (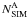 ,
, 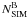 ) defined in Fig. 11. Obviously, the number of stars in simulated CMDs may differ from that of observed field stars. To minimize the effect of such uncertainties on the measure of the fraction of binaries in GCs, we defined in the CMD a region F on the red side of equal-mass binaries fiducial sequence, that is delimited on the blue side by the red dashed-dotted line of Fig. 11 and is likely not populated by cluster stars, as illustrated in Fig. 19 for NGC 2298. We determined the numbers of stars within F in the observed and in the simulated CMDs (
) defined in Fig. 11. Obviously, the number of stars in simulated CMDs may differ from that of observed field stars. To minimize the effect of such uncertainties on the measure of the fraction of binaries in GCs, we defined in the CMD a region F on the red side of equal-mass binaries fiducial sequence, that is delimited on the blue side by the red dashed-dotted line of Fig. 11 and is likely not populated by cluster stars, as illustrated in Fig. 19 for NGC 2298. We determined the numbers of stars within F in the observed and in the simulated CMDs (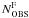 and
and 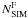 respectively).
respectively).
The number of field stars in the CMD regions A is then calculated as: 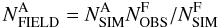 (3)and a similar equation is used to estimate the number of field stars in the region B.
(3)and a similar equation is used to estimate the number of field stars in the region B.
As anticipated in Sect. 2, we removed from our list all clusters for which we had no proper motion (two epochs data) and for which Girardi et al. (2005) model was prediction a field star contamination larger than 1%, with the only exception of E3 (a 2.4% expected contamination) and NGC 6144 (1.3%). Therefore, for clusters for which we have to rely on a Galactic model to estimate the foreground//background stars, the contamination is expected to be minimal. On the other hand, we kept into the sample all cluster for which we could use proper motion to estimate field stars, independently from the level of contamination. In order to investigate whether the estimate of field stars from Galactic models is reliable, we applied the synthetic CMDs method also in the 15 GCs for which we have reliable proper motion measurements. We found that, in the cases of GCs with a small field-star contamination, the fraction of binaries with q > 0.5 derived following the two approaches is identical within the uncertainties, with differences smaller than 0.01. For some GCs with a significant background/foreground population, namely NGC 5927, NGC 6352, NGC 6388, NGC 6441, NGC 6637, and NGC 6681, the fractions of binaries derived using a Galactic model differ from those derived using proper motions by 0.01 to 0.03 (for NGC 6441).
 |
Fig. 19 Observed CMD of NGC 2298 (left) and simulated CMD of field stars in the NGC 2298 field of view (right). |
4.2. Estimate of the fraction of apparent binaries
Chance superpositions of two physically unrelated stars that happen to lie nearly along the line of sight (apparent binaries) and superposition of a faint star and a positive background fluctuation may reproduce the color and luminosity of a genuine binary system, and populate the CMD region occupied by binaries. In a crowded stellar field, like the core of a GC, a reliable measure of the binary fraction requires good accuracy in deriving the number of chance superpositions.
We can identify and reject a significant fraction of these objects by analyzing the stellar profile, and the PSF-fit errors. For this reason, in this work, we limited our study to the objects that pass the selection criteria described in Sect. 2.1.
In order to account for the blends that have not been rejected, a statistical estimate of their number and distribution in the CMD is necessary. In this paper, we used extensive artificial-star test experiments to evaluate directly the effects of blends.
Specifically, in this subsection, we illustrate the procedure adopted to determine the relative numbers of artificial stars in the regions A and B of the CMD of Fig. 11 (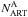 and
and 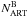 ) that are used to calculate the last term of Eq. (1).
) that are used to calculate the last term of Eq. (1).
This analysis requires that the artificial star sample that we will compare to observed data reproduce as much as possible all the details of real stars. In particular we need the best possible match between the luminosities, the radial distribution and the photometric errors of observed and simulated stars.
The data set described in Anderson et al. (2008) includes an extensive set of artificial-star tests for each cluster. The same quality parameters were determined for the artificial stars as for the real stars, so we apply the same selection criteria to them as we did to the real stars in Sect. 2.1.
To apply these generic artificial-star tests to the real cluster distribution, for each real star observed, we took a set of the artificial stars within ± 0.10 mag and with radial distances within 100 pixels of that of the star. These are the stars that were used to estimate the measurement errors (random and systematic) of the stars in the cluster.
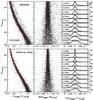 |
Fig. 20 Left: the observed (top) and simulated (bottom) CMD of NGC 2298 with the fiducial line overplotted; Middle: the CMDs rectified by subtraction of the fiducial line; Right: color distribution of the rectified CMDs. The σ in the inset are those of the best-fitting Gaussian. |
The result of this procedure is a catalog of simulated stars that reproduces both the radial and the luminosity distributions of real stars. Several effects contribute to the observed width of the main sequence. In addition to photon noise, we have the contribution of spatial variations of the PSF and residual differential reddening that are beyond the sensitivity of the method that we used to correct them, as well as scattered light, possible star-to star metallicity variations, etc. However, for the purposes of this work, it is not necessary to distinguish the contributions of the single sources of the broadening and we can include them in the photometric errors (σ).
Since MS-MS binary systems and apparent binaries both lie on the red side of the MS, we can use the MS scatter to the blue side of the MS as an estimate of the photometric error. We note that the blue portion of the MS may be contaminated by MS-white dwarf binaries but their influence on σ is expected to be negligible, and further reduced by the applied “kappa-sigma” rejection algorithm, as described below.
In order to estimate σ, we used the following iterative procedure, which has been applied to both the observed and artificial-star CMD. First of all, we subtracted the color of the MSRL from the color of each star. Then we divided this CMD into several intervals of magnitude, each one containing the same number of stars, and constructed a histogram of the color distribution for each magnitude interval. The size of each interval is a compromise between maximizing the number of stars to reduce the statistical errors and minimizing the magnitude intervals to account for the variations of the photometric error as a function of the luminosity. For these reasons, the size of the adopted interval varies from one cluster to another, depending on the number of sampled stars.
We used least-squares to fit each histogram with a Gaussian that had three fitting parameters: its center, its amplitude, and its dispersion σ. Then, we rejected all stars for which color is far more than 3σ from the fiducial line, because most of these objects must be field stars or binaries. Finally we used the remaining sample for a new Gaussian fit.
All the stars with negative color in the rectified CMD (i.e., those on the blue side of the MS) are used for a new Gaussian fit, but, this time, we fixed the center and the amplitude of the Gaussian and considered σ as the only free parameter. The best fitting σ is adopted as the average photometric error in that magnitude interval. The errors corresponding to a given magnitude in the CMD are obtained by interpolations.
As expected, the artificial star color distribution is narrower than the real star one. We need to properly estimate the difference between the artificial-star photometric error and the photometric error of real stars, since, as it will be clearer in next section, we need an artificial-star CMD with the correct photometric error in order to estimate the photometric outliers which contaminate the binary region.
The smaller color dispersion of the artificial star CMD comes from the fact that the measurement errors of artificial stars are smaller than the corresponding error of real stars. This difference is due to the fact that, in fitting artificial stars, we use exactly the same PSF that was used to originate them, while we cannot expect the same perfect match of the PSF with the real PSF of real stars. In addition, and for the same reason, artificial-star photometry is not affected by zero point photometric errors, and errors associated with the differential reddening correction.
The difference between the MS color spread of observed and simulated stars might be also due to multiple stellar populations. Indeed, nearly all the GCs studied so far host two or more generations of stars with a different light-elements. In few GCs, there are also star-to-stars iron variations (see Milone et al. 2010b for a recent review).
Among the clusters studied in this paper, multiple MSs associated to helium variation have been identified in 47 Tuc, NGC 6752, and NGC 6397 where the mF606W − mF814W color difference between the He-rich and He-poor MS is about 0.01 mag (Anderson et al. 2009; Milone et al. 2010a, 2012a,b) i.e. has the same order of magnitude as the color errors of the best measured MS stars. NGC 6656 (M22) is the only cluster of this paper where two groups of stars with a different iron content have been identified. In this case theoretical isochrones show that the measured [Fe/H] difference of ~0.15 dex do not produce any appreciable mF606W − mF814W color bimodality among MS stars (Marino et al. 2009, 2011). In general the MSs corresponding to the different stellar populations observed in the majority of GCs (and hence formed by stars that could have different overall CNO abundance, and light elements variations) are almost overimposed when observed in the mF606W − mF814W color (Sbordone et al. 2011).
As an example, the difference in color dispersion between the real and the artificial star CMDs of NGC 2298 are shown in Fig. 20. In order to compare the real and the artificial star color distribution it is necessary to appropriately re-scale the latter. For this, we considered the measured dispersions as a function of the mF814W magnitude for both observed and simulated MSs, and calculated by least squares the 4th order polynomials (PREAL and PARTS) that best fit each of them. As an example, Fig. 21 (upper panel) shows the measured dispersions and the best fitting functions for the case of NGC 2298. In this paper, we considered the spread of the MS stars as a reliable indicator of the photometric errors to be associated to color measures. We believe that it represents a much more accurate estimate for the observed MS breadth than the one given by the rms value obtained from magnitude measures of the single AS MS stars. In fact it also accounts for residuals photometric zero point errors, errors associated to the reddening correction method and possible intrinsic spread due to the presence of multiple stellar populations.
The difference between the observed and simulated MS dispersion is expressed as: 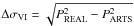 . Assuming that any spread of MS stars around the MS fiducial line comes only from photometric errors, ΔσVI indicates how the artificial-star color errors underestimate our real-star photometric error. As a final, fundamental step for the following discussion, we made the artificial-star CMD similar to the observed one by adding to each artificial star additional random noise in color, extracted from a Gaussian distribution with dispersion ΔσVI. In the bottom panels of Fig. 21 we compare the observed CMD of NGC 2298 and the CMDs of artificial stars before and after the application of the color spread. The latter CMD has been used to calculate the ratio between
. Assuming that any spread of MS stars around the MS fiducial line comes only from photometric errors, ΔσVI indicates how the artificial-star color errors underestimate our real-star photometric error. As a final, fundamental step for the following discussion, we made the artificial-star CMD similar to the observed one by adding to each artificial star additional random noise in color, extracted from a Gaussian distribution with dispersion ΔσVI. In the bottom panels of Fig. 21 we compare the observed CMD of NGC 2298 and the CMDs of artificial stars before and after the application of the color spread. The latter CMD has been used to calculate the ratio between 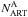 and
and 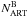 used in Eq. (1).
used in Eq. (1).
 |
Fig. 21 Upper panel: MS dispersion as a function of mF814W magnitude for NGC 2298. Circles and triangles correspond to real and artificial stars, respectively. The corresponding best fitting 4th order polynomials are represented by dotted and dashed lines. Lower panels: comparison of the observed CMD of NGC 2298 (left) and the CMDs of artificial stars before (middle) and after (right) the application of color spread. |
5. Results
In this section we illustrate and discuss the main results of this work. Specifically:
-
in Sect. 5.1 we analyze the mass-ratio distributionof binaries in each of the 59 GCs studied in thispaper in the range 0.5 < q < 1. Results from individual clusters are used toestimate the average mass-ratio distribution of binaries;
-
attempt to calculate the total fraction of MS-MS binaries is proposed in Sect. 5.2;
-
Sect. 5.3 gives a summary of the literature measurements of the binary fraction in GCs and compares them with ours.
-
in Sect. 5.4 we investigate the distribution of binaries as a function of the primary star mass (magnitude);
-
the radial distribution of binaries in each GC is studied in Sect. 5.5;
-
finally, monovariate relations between the binary fraction and the main parent cluster parameters (absolute luminosity, central velocity dispersion, metallicity, age, central density, ellipticity, core and half mass relaxation time, HB morphology, collisional parameter) are discussed in Sect. 5.6.
5.1. Mass-ratio distribution
 |
Fig. 22 As an example, we show with gray and black shaded areas the five CMD regions (B1,2,...,5) used to determine the mass-ratio distribution of binary stars in NGC 2298. |
 |
Fig. 23 Mass-ratio distribution for the binary population in the ACS field of 29 GCs. Black filled-circles show the normalized fraction of binaries in five mass-ratio intervals, while red open-circles indicate the νbin,i values obtained by using only two bins with 0.5 < q < 0.7, and 0.7 < q < 1. Horizontal segments mark the adopted mass-ratio interval, while observational errors are plotted as the vertical lines and shadowed areas. |
This section, presents the mass-ratio distribution of the binary population for our target GCs in the range of 0.5 < q < 1. To do this, we have divided Region B of the CMD into five intervals of mass ratio (B1, 2 ,..., 5) as shown in Fig. 22 for NGC 2298. We chose the size of these regions in such a way that each of them covers almost the same area in the portion of the CMD populated by binary systems with q > 0.5. The sub-region B5 includes also the gray area on the right side of equal-mass binaries fiducial that is populated by binary systems with q ~ 1 but large photometric errors.
The fraction of binaries in each sub-region Bi is calculated over the entire WFC field of view following the procedures described in Sect. 4. Each sub-region includes binary stars within a given mass-ratio interval (Δqi) as labeled in Fig. 22. To account for the different mass-ratio values of each sub-region, and analyze the mass-ratio distribution, we derived the normalized fraction of binaries:
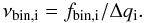 8 Results for all clusters are shown with black symbols in Figs. 23 and 24. To increase the statistics, we have also divided Region B into two large mass ratio intervals with 0.5 < q < 0.7 and 0.7 < q < 1 and calculated νbin in each of them. The results we obtained by using these q bins are marked with red open circles in Figs. 23 and 24.
8 Results for all clusters are shown with black symbols in Figs. 23 and 24. To increase the statistics, we have also divided Region B into two large mass ratio intervals with 0.5 < q < 0.7 and 0.7 < q < 1 and calculated νbin in each of them. The results we obtained by using these q bins are marked with red open circles in Figs. 23 and 24.
The mass-ratio distribution is almost flat for most of the GCs of our sample but in few cases we cannot exclude possible deviations from this general trend. To investigate this statement we compared the observations with a flat distribution, calculated for each cluster the reduced χ2 and quoted it in Figs. 23 and 24. Montecarlo simulations demonstrate that in the case of a flat distribution we expect the 50% of the total number of clusters having χ2 < 1.1 and the 99% χ2 < 3.8. We found χ2 values higher than 3.8 in four GCs namely NGC 6366 (χ2 = 4.92), NGC 6496 (χ2 = 6.38), TERZAN 7 (χ2 = 4.45) and E 3 (χ2 = 13.62).
To compare the trend of the fraction of binaries as a function of q for different GCs we divided νbin,i by two times the fraction of binaries with q > 0.59.
Results are in Fig. 25. Black points indicate the measurements for all the GCs, while red points with error bars are the averages in each mass-ratio bin. The gray line is the best fitting line. Its slope is indicated in the figure and suggests that the mass-ratio distribution is nearly flat for q > 0.5. In the Appendix we will demonstrate that this result is not affected by any significant systematic error.
Since we have determined the mass-ratio distribution over the entire ACS/WFC field of view, our conclusions should indicate the general behavior of the binaries in GCs. Unfortunately, due to the relatively small numbers of binaries, we could not extend this analysis to each sample of rC, the rC − HM, and the roHM stars. In these regions, due to mass-segregation effects, the mass-ratio distribution could differ from that shown in Fig. 25.
 |
Fig. 25 Black points show the normalized fractions of binaries, νbin measured in five mass-ratio intervals as a function of q for all the GCs studied in this paper. To compare the fraction of binaries in different clusters we divided νbin by two times the fraction of binaries with q > 0.5. For clarity, black points have been randomly scattered around the corresponding q value. Red points with error bars are the means in each mass-ratio bin, while the gray line is the best fitting line, whose slope is quoted in the inset. |
Up to now, there are few observational constraints on the overall mass-ratio distribution of the binary population in GCs. One of the few measures of f(q) for binary systems, available in the literature, comes from Fisher et al. (2005) who estimated the the mass-ratio distribution function from spectroscopic observations of field binaries within 100 parsecs from the Sun. The f(q) derived by Fisher et al. (2005) is shown in the upper panel of Fig. 26. Binaries with q < ~ 0.9 have a nearly flat distribution while there is a large concentration of binaries formed by two components of similar mass. Tout (1991) studied the binary systems located in the local field and suggests that f(q) can be derived by randomly extracting secondary stars from the observed initial mass function (IMF). The mass-ratio distribution that we obtain by randomly extracting pairs of stars from a Kroupa (2002) IMF is displayed in the upper panel of Fig. 26 for MS binaries with a primary with 0.47 < M < 0.76 M⊙ which is the typical mass interval corresponding to the magnitude interval we analyzed in the present work. In this case, the f(q) shape rapidly decreases from low to high mass-ratio values with only the 24% of binaries having q > 0.5.
 |
Fig. 26 Upper panel: mass-ratio distribution derived by Fisher et al. (2005). Lower panel: mass-ratio distribution simulated from random extraction from a Kroupa (2002) IMF in the primary star mass intervals quoted in the inset. |
In order to investigate whether the observations of Fig. 25 are consistent with any of the two mass-ratio distributions described above, we calculated the normalized fraction of binaries we expect in the CMD of a GCs where binary stars follow the distribution by Fisher et al. (2005) and the distribution obtained from random extraction of secondary stars from a Kroupa (2002) IMF (νbin,F, νbin,R). We also divided each of these quantity by two times the fraction of binaries with q > 0.5 of the corresponding CMD (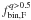 ,
, 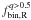 ) in close analogy to what done for real stars.
) in close analogy to what done for real stars.
Results are in Fig. 27 where the values of 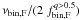 and
and 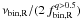 are plotted as a function of q. The best-fitting least-squares lines are colored gray and their slopes are quoted in the inset. Red points are the observed average binary frequencies of Fig. 25. The large reduced-χ square values obtained from the comparison of the theoretical and the observed points, and quoted in the figure, indicate that neither the Fisher et al. (2005) nor the Tout (1991) distribution properly matches the distribution we observe in GCs.
are plotted as a function of q. The best-fitting least-squares lines are colored gray and their slopes are quoted in the inset. Red points are the observed average binary frequencies of Fig. 25. The large reduced-χ square values obtained from the comparison of the theoretical and the observed points, and quoted in the figure, indicate that neither the Fisher et al. (2005) nor the Tout (1991) distribution properly matches the distribution we observe in GCs.
 |
Fig. 27 Frequency of binaries divided by two times the fraction of binaries with q > 0.5 expected for the cases of Fisher et al. (2005) mass-ratio distribution (upper panel) and from the distribution obtained by randomly extracting secondary stars from a Kroupa (2002) IMF (bottom panels). Red points with the error bars are the mean values of the observed binary frequency normalized by two times |
5.2. The total binary fraction
The procedure described in the previous section allowed us to directly measure the fraction of binaries with q > 0.5 without any assumptions regarding f(q). On the other hand, because of the photometric errors, binaries with small mass ratios (q < 0.5) are indistinguishable from single MS stars in this dataset, therefore, any attempt to determine the total fraction of MS-MS binaries without assumption on the mass-ratio distribution is impossible with this approach.
The approach we follow to estimate the total fraction of binaries is similar to that used by Sollima et al. (2007) and consists of assuming a form for f(q). Since none of the two mass-ratio distributions available from literature properly matches the observed distribution in order to estimate the total fraction of binaries (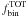 ), we extrapolated the results of Sect. 5.1 adopting a flat f(q) also for binary systems with q < 0.5; i.e., we assumed a constant mass-ratio distribution for all q values. In this case as
), we extrapolated the results of Sect. 5.1 adopting a flat f(q) also for binary systems with q < 0.5; i.e., we assumed a constant mass-ratio distribution for all q values. In this case as 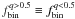 the total fraction of binaries is simply
the total fraction of binaries is simply
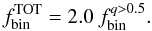 The final
The final 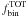 are listed in the fifth column of Table 2 for the rC, the rC − HM, the roHM sample, and the WFC field.
are listed in the fifth column of Table 2 for the rC, the rC − HM, the roHM sample, and the WFC field.
For completeness, we note that, according to Fisher et al. (2005), 66.5% of binary systems have mass ratio larger than 0.5. Hence, assuming a Fisher et al. (2005) mass ration distribution, the total fraction of binaries should be:
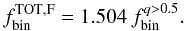 If we assume that binary stars are formed by random associations between stars of different masses, only 24% of binaries have q > 0.5, and the total fraction of binaries becomes:
If we assume that binary stars are formed by random associations between stars of different masses, only 24% of binaries have q > 0.5, and the total fraction of binaries becomes:
5.3. Comparison with previous measurements of the binary fraction in GCs
To date, the fraction of binaries has been measured for 30 GCs. In Table 3 we list the photometric binary fraction in Galactic GCs from previous measurements and available in the literature. For each GC we listed the measured fraction of binaries (fbin), specified if the latter is a lower limit, an upper limit or a measure of the total fraction of binaries. We also indicate the spatial region where this measure was done and give the reference. Although for some GCs of our sample the fraction of binaries were already estimated in previous works, caution must be used to compare the results presented in this paper with literature ones. In particular, it should be noted that the inferred values of the total fraction of binaries are tightly related to the assumed f(q). Many authors just determined lower limits to the binary fraction, as they studied binary systems with large q that are clearly separated from single MS stars. Without any indication on the mass-ratio interval analyzed, a quantitative comparison of results with these studies is not possible.
 |
Fig. 28 Comparison of the core binary fractions of 13 GCs measured in this paper (red circles) and in Sollima et al. (2007, black circles). In both cases has been assumed the mass-ratio distribution from Fisher et al. (2005). Blue triangles indicate the binary fraction estimated in this work assuming a flat q distribution. |
From the comparison between Tables 2 and 3 we note that in some cases the fraction of binaries measured in the same cluster region by different authors strongly differs from the results presented here. As an example, in the case of NGC 6752, Rubenstein & Bailyn (1997) estimated an high fraction of binaries in the core (fbin = 0.27 ± 0.12), in disagreement with the results presented in this paper (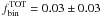 ) and in Milone et al. (2010) (
) and in Milone et al. (2010) (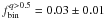 ). To investigate these different results, Milone et al. (2010) re-examined the Rubenstein & Bailyn (1997) findings first by analyzing the same data with the improved photometric techniques that are now available, and then using the better datasets that have been collected more recently. They concluded that the disagreement comes from the use of the stellar photometry tools they used, which allow a better separation of stellar blends. Similarly, the large fraction of binaries detected by Albrow et al. (2001) in NGC 104, and Fisher et al. (1995) are not confirmed by our study.
). To investigate these different results, Milone et al. (2010) re-examined the Rubenstein & Bailyn (1997) findings first by analyzing the same data with the improved photometric techniques that are now available, and then using the better datasets that have been collected more recently. They concluded that the disagreement comes from the use of the stellar photometry tools they used, which allow a better separation of stellar blends. Similarly, the large fraction of binaries detected by Albrow et al. (2001) in NGC 104, and Fisher et al. (1995) are not confirmed by our study.
Sollima et al. (2007) have recently measured the fraction of binaries in the core of 13 low-density GCs by using the same images studied in this paper. First, they analyzed the color distribution of MS stars to directly derive the minimum fraction of binary systems required to reproduce the observed CMD morphologies, then they inferred two different estimates of the total fraction of binaries by assuming the mass-ratio distribution obtained from random extractions from a de Marchi et al. (2005) IMF, and from the distribution measured by Fisher et al. (2005).
Even if we have shown that the Fisher et al. (2005) distribution is not consistent with what found in the present work and because the images are the same as in this paper, for a meaningful comparison with Sollima et al. (2007), in Fig. 28 we compare the total fraction of binaries in the core that we obtained by assuming the Fisher et al. (2005) distribution (red circles) with the values from Sollima et al. (2007). Blue triangles correspond to the binary fraction estimated in this paper assuming a flat q distribution. For eight out of thirteen GCs, results are in agreement, at the level of less than three σ. In the cases of ARP 2, NGC 6101, NGC 6723, NGC 6981, and Terzan 7 the fraction of binaries measured in this work is systematically smaller than those found by Sollima and collaborators.
5.4. The binary fraction as a function of primary-star mass
In this section we investigate the distribution of binary systems as a function of the magnitude. To do this, we calculated the fraction of binaries over the entire WFC/ACS field of view in the three magnitude intervals, containing all the single MS stars and the binary systems with a primary star: [0.75,1.75], [1.75,2.75], [2.75,3.75], F814W magnitudes below the MSTO respectively. In the cases of NGC 6388 and NGC 6441 we used smaller magnitudes intervals of [0.75,1.25], [1.25,1.75], [1.75,2.25] F814W magnitudes below the MSTO. We divided the CMD regions A and B defined in Sect. 4 and illustrated in Fig. 11 into three subregions (named Ab, Ai, Af and Bb, Bi, Bf) as shown in Fig. 29 and calculated the fraction of binaries in each magnitude interval see Eq. (1).
 |
Fig. 29 Dark and light gray areas indicate the CMD regions used to measure the fraction of binaries in three magnitude intervals. |
Results are shown in Figs. 30 and 31 where we plot the fractions of binaries with mass ratio q > 0.5 calculated in three magnitude bins as a function of the difference between the mean F814W magnitude of the bin and the F814W magnitude of the MS turn off (ΔmF814W). Red points indicate the fraction of binaries in the full interval [0.75:3.75] ([0.75:2.15] for NGC 6388 and NGC 6441), while the shadowed area indicates the error associated to this measure.
In general we find no evidence for a significant trend in the fraction of binaries with magnitude (which is a proxy for primary mass), as suggested by the reduced-χ2 values quoted in Figs. 30 and 31. Montecarlo simulations show that in the case of a flat distribution the 50% and 99% of objects have χ2 values smaller than 1.1 and 5.5 respectively. Possible exceptions to this rule of a flat trend are represented by NGC 5897 and NGC 6652 for which we have estimated χ2 values higher than 5.5. And large χ2 > 5.0 are obtained also for NGC 6144, NGC 6637, and NGC 6723.
In order to further analyze the general trend of the binary fraction with the magnitude for all the GCs studied in this paper we divided the values of 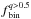 measured in each magnitude bin by the fraction of binaries with q > 0.5 in the interval between 0.75 and 3.75 mag below the MS turn off. Results are shown in Fig. 32 and confirm that the fraction of binaries is nearly flat in the analyzed magnitude range.
measured in each magnitude bin by the fraction of binaries with q > 0.5 in the interval between 0.75 and 3.75 mag below the MS turn off. Results are shown in Fig. 32 and confirm that the fraction of binaries is nearly flat in the analyzed magnitude range.
Finally, we used isochrones to estimate the average mass of the single stars and the primary component of binary systems in the regions Ab, Ai, and Af. To do this we converted the mean F814W magnitudes of the single stars contained in each of these regions into masses through the Dotter et al. (2007) mass-luminosity relations. Figure 33 shows the ratio 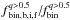 as a function of the average mass estimated above and suggests that the binary fraction is nearly flat in the analyzed mass interval.
as a function of the average mass estimated above and suggests that the binary fraction is nearly flat in the analyzed mass interval.
We recall here, that the results presented in this subsection come from the analysis of the binary fractions measured over the entire ACS/WFC field of view. Due to the relatively small numbers of binaries, we did not extended this analysis to each group of rC, the rC − HM, and the roHM stars.
 |
Fig. 30 Fraction of binaries with mass ratio q > 0.5 for 29 GCs measured in three magnitude intervals (black points) and in the interval between 0.75 and 3.75 F814W magnitudes below the MS turn off (red points) as a function of ΔmF814W. Horizontal segments indicate the magnitude coverage corresponding to each point. |
 |
Fig. 31 As in Fig. 30 for the remaining 30 GCs. In the cases of NGC 6388 and NGC 6441 the binary fraction has been measured in the interval between 0.75 and 2.25 F814W magnitudes below the MS turn off. |
 |
Fig. 32 Fraction of binaries with q > 0.5 measured in three magnitude intervals (black points) as a function of ΔmF814W for the 59 GCs studied in this work. To compare the fraction of binaries in different clusters we have divided the fraction of binaries in each bin by the value of |
 |
Fig. 33 Fraction of binaries with q > 0.5 measured in three magnitude intervals and normalized by |
5.5. The radial distribution
 |
Fig. 34 Fraction of binaries with q > 0.5 as a function of the radial distance from the cluster center for 29 GCs. The dotted and dashed vertical lines mark the core and the half mass radius respectively. Black filled-circles show binary fractions in four radial intervals while red open-symbols indicate the binary fraction for the rC, rC − HM, and roHM sample. Horizontal black segments indicate the radial coverage corresponding to each point while observational errors are plotted as vertical lines and shadowed areas. |
In order to investigate how the fraction of high-mass-ratio binaries depends on the radial distance, we divided the ACS field of view into four concentric annuli, and calculated the fraction of binaries by following the recipes described in Sects. 4 and 5.2. We chose the size of the annulus such that the number of stars that populate the CMD region A is equal in each of them.
Results are shown in Figs. 34 and 35 where we plotted 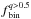 as a function of the explored radial distance for all the GCs studied in this paper. and confirm that, in most of the GCs where the fraction of binaries has been calculated both in the core and in the outer regions, binaries are significantly more centrally concentrated than single MS stars.
as a function of the explored radial distance for all the GCs studied in this paper. and confirm that, in most of the GCs where the fraction of binaries has been calculated both in the core and in the outer regions, binaries are significantly more centrally concentrated than single MS stars.
In Fig. 36, for the 43 GCs studied in this paper for which we measured the core binary fraction, we plot the fraction of binaries with q > 0.5 in units of core-binary fraction as a function of the radial distance in units of core radii While it would be naive to assume a similar radial distribution of binaries for all Galactic GCs, it seems clear that the fraction of binaries normalized to the core binary fraction is correlated with radius, and that the binary fraction typically decreases by a factor of ~2 at two core radii with respect to the core binary fraction. The latter behavior was also suggested by Sollima et al. (2007) on the basis of their analysis of the radial distribution of binaries in seven GCs. In the cluster envelope, the binary-fraction trend with radius tends to flatten.
5.6. Correlation between the binary fraction and the parent-cluster parameters
In this section we investigate whether the binary fraction is correlated with any of the physical and morphological parameters of their host GCs. In particular, our analysis makes use of the following quantities: Relative ages. We used the most recent age measures by Marín-Franch et al. (2009). Relative ages were obtained from the same photometric database used in this paper by comparing the relative position of the clusters’ MS turnoffs, using MS fitting to cross-compare clusters within the sample. Typical errors on the relative age measurements are between 2% and 7%. We also used absolute ages from Salaris & Weiss (2002) and De Angeli et al. (2005). Absolute ages are not available for 15 GCs, namely: E3, NGC 4147, NGC 4833, NGC 5024, NGC 5286, NGC 5927, NGC 5986, NGC 6144, NGC 6388, NGC 6441, NGC 6496, NGC 6541, NGC 7089, PAL 1, and TERZAN 8. Metallicity. We performed our analysis with both the metallicity scales defined by Zinn & West (1984) and Carretta & Gratton (1997), which were also used by Marín-Franch et al. (2009) to determine relative ages. BSS Frequency. We used the counts of BSS derived by Moretti et al. (2008) from the WFPC2 photometric catalogs published by Piotto et al. (2002). In particular, we used the normalized number of BSS, which is the absolute number of BSS in a given region divided by the total luminosity coming from the stars in the same region (in unit of 104 L⊙). Rate of stellar collisions per year. King et al. (2002) have shown that the rate of stellar collisions per cluster and per year is 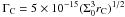 , where Σ0 is the central surface brightness in units of L ⊙ ,V pc-2 and rC is the core radius in units of parsecs. We calculated the probability (Γ∗) that a given star will have a collision in 1 yr, by dividing the collision rate by the total number of stars in the cluster. This is calculated by assuming a mass-luminosity ratio of 2 and a mean mass for colliding stars of 0.4 M⊙.
, where Σ0 is the central surface brightness in units of L ⊙ ,V pc-2 and rC is the core radius in units of parsecs. We calculated the probability (Γ∗) that a given star will have a collision in 1 yr, by dividing the collision rate by the total number of stars in the cluster. This is calculated by assuming a mass-luminosity ratio of 2 and a mean mass for colliding stars of 0.4 M⊙.
 |
Fig. 36 Binary fraction with q > 0.5 (in units of core binaries) as a function of the distance from the cluster center in units of core radii. |
We also compared the measured fraction of binaries with the encounter frequency adopted by Pooley & Hut (2006) in the approximation used for virialized systems: 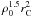 where rC is the core radius and ρ0 the central stellar density.
where rC is the core radius and ρ0 the central stellar density.
The other parameters involved in this analysis are the absolute visual magnitude MV, the ellipticity (e), the central concentration (c), the core relaxation timescale, τc, the half-mass relaxation timescale τhm, and the logarithm of the central luminosity density ρ0, and are taken from the Harris (1996) compilation. We also used three different parameters related to the cluster HB morphologies, as discussed in Sect. 5.6.3. Ellipticity (e) measurements are not available for six clusters, namely ARP2, E3, NGC 288, PALOMAR 12, Terzan 7 and Terzan 8.
Figures B.1–B.11 show the monovariate correlations. Note that, in our study of the core population of binaries, we did not include the post-core-collapse (PCC) GCs, because, for these objects, the definition of core radius is not reliable (Trager et al. 1993). Specifically, PCC clusters are marked with red crosses in these figures but are not used to study the statistical significance of the correlations. Figures B.1–B.11 show that there are no significant correlations between the binary fractions and the cluster ellipticity, core and half mass relaxation time, central concentration and metallicity as suggested by the small values of the Pearson correlation coefficient. Some marginal correlation with the central density can not be excluded.
In the following we will discuss some of the relevant relations between the cluster parameters listed above and the fraction of binaries calculated in three radial regions defined in Sect. 4. A noteworthy correlation of the binary fraction is with the central velocity dispersion (r ~ −0.6). as shown in Fig. B.1−B.3. The central velocity dispersions σV come from Meylan (1989), and are available only for a subsample of the GCs that are studied in the present work.
5.6.1. fbin versus MV, Γ∗, and BSS frequency
The most significant correlation we found is the correlation between the cluster binary fraction and its absolute magnitude. Clusters with fainter absolute luminosity (smaller mass) have higher binary fractions. This correlation is present in all binary groups, i.e. for binaries inside the cluster core, for binaries located between the core and the half-mass radius, for binaries outside the half-mass radius, and for binaries with q > 0.5 (Fig. B.4). An anticorrelation between the fraction of binaries and the mass of the host GCs is predicted by theoretical models (Sollima 2008; see also Fregeau et al. 2009). These authors suggest that this correlation could be the due to the fact that cluster mass and the efficiency of binary destruction have the same dependence on the cluster density and velocity dispersion.
This anticorrelation might extend to open cluster masses. In fact, Sollima et al. (2010) found a dependence of the fraction of binaries and the cluster mass in a sample of five open clusters. Sollima et al. (2010) suggests that the binary disruption within the cluster core is the dominant process that determine the fraction of binaries in star clusters.
Noteworthy, a similar anticorrelation between the frequency of BSSs and the absolute luminosity of the parent cluster has been found by Piotto et al. (2004), Leigh et al. (2007), and Moretti et al. (2008). Interestingly enough, Fig. B.5 shows that the fraction of binaries is indeed correlated with the fraction of BSSs. Sollima et al. (2008) observed a similar correlation between the BSS specific frequency and the fraction of binaries in the core of 13 low-density Galactic GCs. These authors suggested that the evolution of primordial binaries could be the dominant BSS formation process (see also Knigge et al. 2009; and Leigh et al. 2011). However, Davies et al. (2004) provided a simple model showing that the correlation between the BSS frequency and the cluster mass may be the result of the evolution of the binary fraction due to encounters. Here, we can only note that, Figs. B.6 and B.7 seem to suggest a mild correlation between binary fraction and the collisional parameter, while there is no significant correlation between the BSS frequency and the collisional parameter (e.g. Piotto et al. 2004; Davies et al. 2004; Leigh et al. 2007; Moretti et al. 2008). It is clear that the connection between binaries and BSSs is far from trivial. The interpretation of the correlation of binary fraction with cluster parameters, and with BSS fraction is beyond the purposes of the present paper.
5.6.2. fbin versus age
Figures B.8 and B.9 plot the fraction of binaries with q > 0.5 in the core as a function of relative ages by Marín-Franch et al. (2009) and the absolute ages from and from Salaris & Weiss (2002) and De Angeli et al. (2005) respectively. There is no evident trend between ages and the binary fraction.
Sollima et al. (2007) compared the fraction of binaries measured in the core of thirteen clusters, with the cluster ages from Salaris & Weiss (2002) and De Angeli et al. (2005) and found an anticorrelation between age and binary fraction suggesting age as the dominant parameter that determines the fraction of binaries in a GC. Our sample of 59 GCs does not confirm such correlation. Sollima et al. (2007) sample is limited to low density clusters. In order to verify whether the binary fraction dependence on age is limited to low density clusters, in Fig. B.10 we plot the binary fraction for the rC sample as a function of the age from De Angeli et al. (2005) and the relative age from Marin Franch et al. (2009) for clusters with central density log (ρ0) < 2.75 (same central density limit of Sollima et al. 2007 sample). We also note that the youngest low density clusters in our sample have a larger binary fraction, but the fact that at least one old GCs (E3) hosts a large binary fraction suggests that more data are needed to confirm any systematic trend.
5.6.3. HB morphology
Binaries have been considered as a possible second parameter of the HB morphology by several authors. In particular, the existence of a link between field B-type subdwarf (sdB) – which are the counterpart in the field of the extremely hot horizontal branch (EHB) stars in GCs – and binary systems is well-established, both on observational and theoretical grounds. A large population of binaries has been found among field sdBs (e.g. Napiwotzki et al. 2004 and references therein). However, the formation scenario of EHB stars in GCs may be different. In fact, several radial-velocity surveys for the measurement of the binary fraction among EHB stars have revealed a significant lack of binary systems (Moni Bidin et al. 2006, 2009).
In order to investigate possible relations between the fraction of binaries and the HB shape we used three different parameters:
-
1.
the median color difference between the HB and the RGB [Δ(V − I)],measured by Dotter et al. (2010)for 60 GCs using the same CMDs of this paper;
-
2.
The HB morphology index from Mackey & van den Bergh (2005);
-
3.
the effective temperature of the hottest HB stars (Teff,HB), measured by Recio-Blanco et al. (2006). Δ(V − I), HB index, and Teff,HB measures are available for 56, 55, and 28 GCs studied in this paper.
Monovariate relation between the fraction of binaries with q > 0.5 and these parameters are shown in Fig. B.11. We find no significant relations between the fraction of binaries and the HB parameters, confirming the small or null impact of the binary population on the HB morphology. Similar results are obtained for binaries with q > 0.6 and q > 0.7.
6. Summary
In this paper we have analyzed the properties of the population of MS binaries of a sample of 59 GCs. The main dataset consists in the ACS/WFC images of the Globular Clusters Treasury project (GO10775, PI Sarajedini) that allowed us to obtain uniform and deep photometry for an unprecedented number of GCs (see Sarajedini et al. 2007; and Anderson et al. 2008 for details). We have also used ACS/WFC, WFC3 and WFPC2 data from the archive to obtain proper motions when images overlapping the GO10775 data are available. The CMDs have been corrected for the effects of differential reddening and photometric zero point variations due to small inaccuracies in the PSF model.
We have measured the fraction of binaries with mass ratio q > 0.5 and estimated the total fraction of binaries for MS stars that are between 0.75 and 3.75 mag fainter than the MS turn off. We have found that:
-
in nearly all the GCs the fraction of binaries is significantlysmaller than in the field, where the binary fraction is larger than 0.5 (e.g. Duquennoyet al. 1991; Fisher & Marcy 1992)with a few relevant exceptions (E3, Palomar 1) where the totalbinary fraction is greater than ~0.4;
-
we have obtained the fraction of binaries in five intervals of q (for q > 0.5) and found that the mass-ratio distribution is generally flat;
-
there is no evidence for a significant correlation of the binary fraction with primary mass of the binary system;
-
we measured the fraction of binaries in the cluster core, in the region between the core and the half-mass radius, and outside the half-mass radius and studied their radial distribution. Binary stars are more centrally concentrated than single MS stars with the fraction of binaries generally decreasing by a factor of ~2 from the center to about two core radii;
-
we investigated monovariate relations between the fraction of binaries (in the rC, rC − HM, and roHM sample) and the main parameters of their host GCs (absolute magnitude, HB morphology, age, ellipticity, metallicity, collisional parameter, half mass and core relaxation time, central concentration, central velocity dispersion, and central luminosity density);
-
we found a significant anticorrelation between the fraction of binaries in a GC and its absolute luminosity (mass);
-
we found a marginal correlation between the cluster central density and the central velocity dispersion;
-
we did not find any significant relation between the binary fraction and the HB morphological parameters;
-
we confirm a significant correlation between the fraction of binaries and the fraction of BSSs, indicating that the main formation mechanism of BSSs must be related to binary evolution.
Online material
Description of the HST additional archive data sets used in this paper, other than those from GO-10775.
Fraction of binaries with mass ratio q > 0.5, q > 0.6 and q > 0.7, and total fraction of binaries measured in different regions.
Collection of literature binary fraction estimates.
Appendix A: Reliability of the measured binary fraction
In this appendix we investigate whether the fraction of binaries with q > 0.5 that we measured with the procedure described in Sect. 4 are reliable or are affected by any systematic uncertainty due to the method we used. The basic idea of this test consists of simulating a number of CMDs with a given fraction of binaries, measuring the fraction of binaries in each of them, and comparing the added fraction of binaries with the measured ones.
Simulation of the CMD. We started by using artificial stars to simulate a CMD made of single stars following the procedure already described in Sect. 4.2. To simulate binary stars to be added to the simulated CMD we adopted the following procedure:
-
we selected a fraction
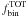 of single stars equal to the fraction of binaries that we want to add to the CMD and derived their masses by using the Dotter et al. (2007) mass-luminosity relation. In our simulations we assumed the values of
of single stars equal to the fraction of binaries that we want to add to the CMD and derived their masses by using the Dotter et al. (2007) mass-luminosity relation. In our simulations we assumed the values of 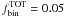 , 0.10, 0.30, and 0.50;
, 0.10, 0.30, and 0.50; -
for each of them, we calculated the mass ℳ2 = q × ℳ1 of the secondary star and obtained the corresponding mF814W magnitude. Its color was derived by the MSRL. For simplicity we assumed a flat mass-ratio distribution;
-
finally, we summed up the F606W and F814W fluxes of the two components, calculated the corresponding magnitudes, added the corresponding photometric error, and replaced the original star in the CMD with this binary system.
As an example, in the upper panels of Fig. A.1 we show the artificial star CMD made of single stars only (left panel), and the CMD where we added a fraction 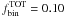 of binaries (right panel), for the case of NGC 2298.
of binaries (right panel), for the case of NGC 2298.
Simulation of the differential reddening. To probe how well the reddening correction works, we considered a simple model. The simulation of the differential reddening suffered by any single star is far from trivial as we have poor information on the structure of the interstellar medium between us and each GC. For simplicity, in this work we assumed that reddening variations are related to the positions (X, Y) of each stars by the following relations:
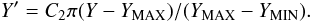 Here XMIN,MAX and YMIN,MAX are the minimum and the maximum values of the coordinates X and Y, C1 is a free parameter that determines the maximum amplitude E(B − V) variation, and C2 governs the number of differential reddening peaks within the field of view.
Here XMIN,MAX and YMIN,MAX are the minimum and the maximum values of the coordinates X and Y, C1 is a free parameter that determines the maximum amplitude E(B − V) variation, and C2 governs the number of differential reddening peaks within the field of view.
 |
Fig. A.1 Artificial stars CMD for NGC 2298 (upper-left) and simulated CMD with a fraction of |
 |
Fig. A.2 Bottom-left: Map of differential reddening added to the simulated CMD of NGC 2298. The gray levels indicate the reddening variations as indicated in the upper-right panel. Upper-left and bottom-right panels show ΔE(B − V) as a function of the Y and X coordinate respectively for stars into 8 vertical and horizontal slices. |
In this work, we used for each GC the value of C1 that ranges from 0.005 to 0.05 to account for the observed reddening variation in all the GCs, while we arbitrarily assumed three values of C2 = 3, 5, and 8 to reproduce three different fine-scales of differential reddening. As an example, in Fig. A.2 we show the map of differential reddening added to the simulated CMD of NGC 2298 that is obtained by assuming C1 = 0.025 and C2 = 5.
 |
Fig. A.3 Difference between the measured fraction of binaries and the fraction of binaries in input as a function of the parameter C1 for four difference values of the input binary fraction. Black lines indicate the average difference. Red circles, gray triangles and black crosses indicate simulations with C2 = 3, 5, and 8 respectively. |
 |
Fig. A.4 Fractions of binaries per unit q measured in five mass-ratio intervals as a function of q for all the simulated GCs. To compare the q distribution in simulated clusters with different fraction of binaries, we divided νbin by two times the fraction of binaries with q > 0.5. For clarity, black points have been randomly scattered around the corresponding q value. The means normalized binary fractions in each mass-ratio bin are represented by red points with error bars, while the gray line is the best fitting line, whose slope is quoted in the inset. |
Then, we have transformed the values of ΔE(B − V) corresponding to the position of each stars into ΔAF606W, and ΔAF814W and added these absorption variations to the F606W and the F814W magnitudes. The CMD obtained after we added differential reddening is shown in the bottom left panel of Fig. A.1 for NGC 2298. We applied to this simulated CMD the procedure to correct for differential reddening described in Sect. 3.1 and obtain the corrected CMD shown in the bottom right panel. For each of these binary-enhanced simulated CMD, we also generated a CMD made of artificial stars by following the approach described in Sect. 4.2. In our investigation we did not account for field stars. For each combination of the 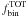 and C2 we have simulated 200 CMDs with random values of the C1.
and C2 we have simulated 200 CMDs with random values of the C1.
Measurements of the binary fraction. Finally, we used the procedure of Sect. 4 to measure the fraction of binaries with mass ratio q > 0.5 defined as:
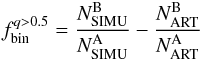 where
where 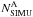 and
and 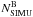 are the numbers of stars in the regions A and B in the CMD, as defined in Fig. 11 in the binary-enhanced simulated CMD and
are the numbers of stars in the regions A and B in the CMD, as defined in Fig. 11 in the binary-enhanced simulated CMD and 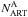 and
and 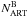 the numbers of stars in the same regions of the artificial stars CMD.
the numbers of stars in the same regions of the artificial stars CMD.
 |
Fig. A.5 Fraction of binaries with q > 0.5 in three magnitude intervals as a function of ΔmF814W for all the simulated GCs. To compare the measured fraction of binaries in different clusters we have divided the measured binary fractions in each magnitude interval by the value of |
Results are shown in Fig. A.3 where we plotted the difference between the measured and the input fraction of binaries versus the parameter C1 for four difference values of the input binary fraction. We found that, for input binary fraction of 0.05, 0.10 and 0.30, the average difference are negligible (<0.5%), as indicated by the the black lines and the numbers quoted in the inset. In the case of a large binary fraction (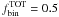 ) the measured fraction of binaries with q > 0.5 is systematically underestimated by ~0.03. Apparently our results do not depend on the value of the parameter C2. Simulations with C2 = 3, 5, and 8 (indicated in Fig. A.3 with red circles, gray triangles, and black crosses, respectively) give indeed the same average differences. Our comparison between the fraction of binaries added to the simulated CMD and the measured ones demonstrate that the fraction of binaries determined in this work and listed in Table 2 are not affected by any significant systematic errors related to the procedure we adopted.
) the measured fraction of binaries with q > 0.5 is systematically underestimated by ~0.03. Apparently our results do not depend on the value of the parameter C2. Simulations with C2 = 3, 5, and 8 (indicated in Fig. A.3 with red circles, gray triangles, and black crosses, respectively) give indeed the same average differences. Our comparison between the fraction of binaries added to the simulated CMD and the measured ones demonstrate that the fraction of binaries determined in this work and listed in Table 2 are not affected by any significant systematic errors related to the procedure we adopted.
We have also determined the fraction of binaries in five mass-ratio intervals by following the approach described in Sect. 5.1 for real stars. To this aim, we have divided the region B of the CMD defined in Sect. 11 into five subregions as illustrated in Fig. 22 for real stars. The size of each region is chosen in such a way that each of them covers a portion of the CMD with almost the same area. The resulting mass-ratio distribution is shown in Fig. A.4, where we have plotted the fraction of binaries per unit q as a function of the mass ratio. As already done in the case of real stars, to compare the mass-ratio distribution in simulated CMDs with different binary fraction, we have divided νbin by two times the measured fraction of binaries with q > 0.5. The best fitting gray line closely reproduce the flat mass-ratio distribution in input with νbin = 1.
Finally we have measured in the simulated CMDs the fraction of binaries with q > 0.5 in three intervals [0.75,1.75], [1.75,2.75], and [2.75,3.75] F814W magnitudes below the MSTO. To do this we used the procedure already described in Sect. 5.4 for real stars and we have normalized the 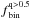 value measured in each magnitude bin by the fraction of binaries with q > 0.5 measured in the whole interval between 0.75 and 3.75 F814W magnitudes below the MSTO. Results are shown in
value measured in each magnitude bin by the fraction of binaries with q > 0.5 measured in the whole interval between 0.75 and 3.75 F814W magnitudes below the MSTO. Results are shown in
Fig. A.5 where we have plotted the normalized binary fractions as a function of ΔmF814W. The best-fitting gray line is nearly flat, and well reproduces the input magnitude distribution.
These tests demonstrate that both the mass-ratio distribution determined in Sect. 5.1 for the 59 GCs studied in this work and shown in Fig. 25 as well as the binary fractions measured in different magnitude intervals in Sect. 5.4 are not biased by significant systematic errors related to the procedure we adopted.
Appendix B
 |
Fig. B.1 Fraction of binaries with q > 0.5 in the core as a function of some parameters of their host GCs. Clockwise: ellipticity, central concentration, central velocity dispersion, logarithm of the central luminosity density, half-mass and core relaxation timescale, and metallicity. In each panel we quoted the Pearson correlation coefficient (r). PCC clusters are marked with red crosses and are not used to calculate r (see text for details). |
 |
Fig. B.4 Upper-left: fraction of binaries with q > 0.5 in the core as a function of the absolute visual magnitude of the host GC. Dashed line is the best fitting straight line whose slope (s) and intercept (i) are quoted in the figure together with the Pearson correlation coefficient (r). PCC clusters are marked with red crosses and are not used to calculate neither the best-fitting line nor r. For completeness in the upper-right panels we show the same plot for the fraction of binaries with q > 0.6, and q > 0.7. Lower panels: fraction of binaries with q > 0.5 in the rC − HM (left) and roHM (right) sample as a function of MV. |
 |
Fig. B.5 Fraction of binaries with q > 0.5 as a function of the BSS frequency in the core. PCC GCs are marked with red points. |
 |
Fig. B.6 Fraction of binaries with q > 0.5, q > 0.6, and q > 0.7 in the rC region (upper panels) and fraction of binaries with q > 0.5 in the rC − HM and roHM regions (bottom panels) as a function of the collisional parameter (Γ∗). The adopted symbols are already defined in Fig. B.4. |
 |
Fig. B.7 As in Fig. B.6. In this case we used the encounter frequency adopted by Pooley & Hut (2006) in the approximation used for virialized systems. |
 |
Fig. B.8 Fraction of binaries with q > 0.5, q > 0.6, and q > 0.7 in the rC region (upper panels) and fraction of binaries with q > 0.5 in the rC−HM and roHM regions (bottom panels) as a function of the relative age measured by Marín-Franch et al. (2009). The adopted symbols are already defined in Fig. B.4. |
 |
Fig. B.9 As in Fig. B.8 but in this case we used the age measures from Salaris & Weiss (2002) and De Angeli et al. (2005). |
 |
Fig. B.10 Fraction of binaries with q > 0.5 in the rC sample for low density clusters (log (ρ0) < 2.75) as a function of the relative age from Marín-Franch et al. (2009) (left panel) an absolute age from Salaris & Weiss (2002) and De Angeli et al. (2005) (right panel). |
 |
Fig. B.11 Fraction of binaries with q > 0.5 as a function of the temperature of the hottest HB stars (bottom), the HB morphology index (middle), and the median color difference between the HB and the RGB (top). |
Due to a partial guiding failure, we only obtained part of the NGC 5987 data. In this case the dataset consists in three long exposures in F814W and five in F606W, while only the F606W short exposure was successfully obtained. For this cluster we obtained useful magnitudes and colors for stars fainter than the sub giant branch and with masses larger then ~0.2 m⊙.
In the cases of NGC 6388 and NGC 6441 we used a smaller magnitude interval between 0.75 and 2.25 mag below the MSTO. This exception is due to the fact that, as we will see in Sect. 4.1.1, we do not have reliable proper motions to estimate the numbers of faint field stars in the CMDs of these two GCs.
The first term on the right-hand side of the equation gives the fraction of cluster stars (both binaries and blends) observed in Region B, with respect to the number of cluster stars observed in Region A. The second right-hand term is the fraction of blends and is calculated as the ratio of the number of ASs in Regions B and A.
Note that the magnitude range used to create Fig. 12 is larger than that used to estimate the field star contamination which enters into Eq. (1) for the the binary fraction calculation.
If we assume that:
-
φ(q) is the continuous function that describes the distribution of the number of binaries as a function of the mass ratio.
-
N is the total number of stars (both binaries and single stars)
-
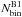 ,
, 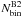 , ...,
, ..., 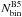 the number of binaries in each region
B1,2,...,5.
the number of binaries in each region
B1,2,...,5.
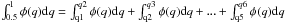 where [q1:q2], [q2:q3], ..., [q5:q6] are the mass-ratio intervals corresponding to the CMD regions of Fig. 22. We have:
where [q1:q2], [q2:q3], ..., [q5:q6] are the mass-ratio intervals corresponding to the CMD regions of Fig. 22. We have: 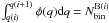 ; i = 1,2,...,5. At this point, the best we can do to gather information on φ(q) is to use the approximation:
; i = 1,2,...,5. At this point, the best we can do to gather information on φ(q) is to use the approximation: 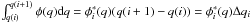 and calculate:
and calculate: 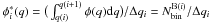 . If we normalize
. If we normalize 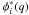 by the total number of stars we find that the normalized fraction of binaries differs from
by the total number of stars we find that the normalized fraction of binaries differs from 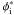 by a factor 1/N:
by a factor 1/N: 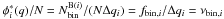 . Since the total number of stars changes from one cluster to each other, we use here νbin,i as the best approximation of the mass-ratio distribution in each q interval.
. Since the total number of stars changes from one cluster to each other, we use here νbin,i as the best approximation of the mass-ratio distribution in each q interval.
Since νbin,i depends on the fraction of binaries, which changes from one cluster to each other, to compare results from different clusters, we have to normalize it by the total fraction of binaries. Due to the lack of information on binaries with q < 0.5, we normalized νbin,i by 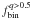 . We also multiplied the latter by a factor of two to normalize to one. (Note that, by chance,
. We also multiplied the latter by a factor of two to normalize to one. (Note that, by chance, 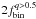 corresponds to the total fraction of binaries for the case of flat mass-ratio distribution.)
corresponds to the total fraction of binaries for the case of flat mass-ratio distribution.)
Acknowledgments
We wish to warmly tank Ivan R. King without whom most of the results presented in this review would not have been possible. We are really gratefull to the referee for the excellent and huge work she/he did. We also thank Andrea Bellini for carefully reading this manuscript, Antonio Sollima for usefull discussion, and Edoardo La Gioia for helping us in the images treatment. A.P.M., A.A., and G.P. are founded by the ministry of science and technology of the Kingdom of Spain (grant AYA 2010-16717). A.P.M. and A.A. are also founded by the Istituto de Astrofisica de Canarias (grant P3-94). G.P. and A.P.M. acknowledge partial support by MIUR under the program PRIN2007 (prot. 20075TP5K9) and by ASI under the program ASI-INAF I/016/07/0.
References
- Albrow, M. D., Gilliland, R. L., Brown, T. M., et al. 2001, ApJ, 559, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Alcaino, G., Liller, W., Alvarado, F., et al. 1998, AJ, 115, 1492 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J. 1997, Ph.D. Thesis, Univ. of California, Berkley [Google Scholar]
- Anderson, J., & King, I. R. 1999, PASP, 111, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., & King, I. R. 2000, PASP, 112, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., & King, I. R. 2003, PASP, 115, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., & King, I. R. 2006, ACS Instrument Science Report 2006-01 (Baltimore: STScI) [Google Scholar]
- Anderson, J., & van der Marel, R. P. 2010, ApJ, 710, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., Sarajedini, A., Bedin, L. R., et al. 2008, AJ, 135, 2055, Paper IV [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., Piotto, G., King, I. R., Bedin, L. R., & Guhathakurta, P. 2009, ApJ, 697, L62 [Google Scholar]
- Aparicio, A., Bertelli, G., Chiosi, C., & Garcia-Pelayo, J. M. 1990, A&A, 240, 262 [NASA ADS] [Google Scholar]
- Aparicio, A., Bertelli, G., Chiosi, C., & Garcia-Pelayo, J. M. 1991, A&AS, 88, 155 [NASA ADS] [Google Scholar]
- Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, MNRAS, 357, 1048 [Google Scholar]
- Bedin, L. R., Salaris, M., Piotto, G., et al. 2008, ApJ, 679, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Fusi Pecci, F., Messineo, M., Monaco, L., Rood, R. T., 2002, AJ, 123, 509 [Google Scholar]
- Bellini, A., & Bedin, L. R. 2009, PASP, 121, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Bedin, L. R., Piotto, G., et al. 2010, AJ, 140, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bolte, C. D. 1992, ApJS, 8, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catelan, M., Prieto, G. E., Zoccali, M., et al. 2008, Hot Subdwarf Stars and Related Objects, 392, 347 [NASA ADS] [Google Scholar]
- Clark, L. L., Sandquist, E. L., & Bolte, M. 2004, AJ, 138, 3019 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, A. M., & Bolton, A. S. 2002, in Stellar Collisions, Mergers and their Consequences, ed. M. M. Shara (San Francisco: ASP Conf. Ser.), 263, 163 [Google Scholar]
- Cote, P., & Fisher, P. 1996, AJ, 112, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Cote, P., Welch, D. L., Fischer, P., et al. 1994, ApJS, 90, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. B., Piotto, G., & de Angeli, F. 2004, MNRAS, 349, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D. S., Richer, H. B., Anderson, J., et al. 2008, AJ, 135, 2155 [NASA ADS] [CrossRef] [Google Scholar]
- De Angeli, F., Piotto, G., Cassisi, S., et al. 2005, AJ, 130, 116 [NASA ADS] [CrossRef] [Google Scholar]
- de Marchi, G., & Paresce, F. 1995, A&A, 304, 211 [NASA ADS] [Google Scholar]
- de Marchi, G., Paresce, F., & Portegies Zwart, S. 2005, The Initial Mass Function 50 Years Later, 327, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2007, AJ, 134, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Elson, R. A. W., Gilmore, G. F., Santiago, B. X., & Casertano, S. 1995, AJ, 110, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Marcy, G. W. 1992, ApJ, 396, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, J., Schroder, K. P., & Smith, R. C. 2005, MNRAS, 361, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Fregeau, J. M., Gürkan, M. A., Joshi, K. J., & Rasio, F. A. 2003, ApJ, 593, 772 [Google Scholar]
- Fregeau, J. M., Ivanova, N., & Rasio, F. A. 2009, ApJ, 707, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Pryor, C., Williams, T. B., & Hesser, J. E., 1994, AJ, 107, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- Giersz, M., & Spurzem, R. 2000, MNRAS, 317, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., & Griffin, R. F. 1979, AJ, 84, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Halbwachs, J. L., Mayor, M., Udry, S., & Arenou, F. 2003, A&A, 397, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E., 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1984, AJ, 89, 1811 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., & Shara, M. M. 2003, ApJ, 589, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Aarseth, S. J., & Shara, M. M. 2007, ApJ, 665, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P., McMillan, S., Goodman, J., et al. 1992, PASP, 104, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Belczynski, K., Fregeau, J. M., & Rasio, F. A., 2005, MNRAS, 358, 572 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- King, I. R. 2002, Introduction to Classical Stellar Dynamics (Moscow URSS) [Google Scholar]
- Knigge, C., Leigh, N., & Sills, A. 2009, Nature, 457, 288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroupa, P. 1995a, MNRAS, 277, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 1995b, MNRAS, 277, 1507 [NASA ADS] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Latham, D. W. 1996 in The Origins, Evolution and Destinies of Binary Stars in Clusters, ed. E. F. Milone, & J. C. Mermilliod (San Francisco: ASP Conf. Ser.), 90, 21 [Google Scholar]
- Leigh, N., Sills, A., & Knigge, C. 2007, ApJ, 661, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Leigh, N., Sills, A., & Knigge, C. 2011, MNRAS, 1171 [Google Scholar]
- Mackey, A. D., & van den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Duquennoy, A., Halbwachs, J.-L., & Mermilliod, J.-C. 1992, IAU Colloq. 135, Complementary Approaches to Double and Multiple Star Research, 32, 73 [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, A. F., Milone, A. P., Piotto, G., et al. 2009, A&A, 505, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Sneden, C., Kraft, R. P., et al. 2011, A&A, 532, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marks, M., Kroupa, P., & Oh, S. 2011, MNRAS, 417, 1684 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M., 1996 in The Origins, Evolution and Destinies of Binary Stars in Clusters, ed. E. F. Milone, & J. C. Mermilliod (San Francisco: ASP Conf. Ser.) [Google Scholar]
- McCaughrean, M. J. 2001, The Formation of Binary Stars, 200, 169 [NASA ADS] [Google Scholar]
- McLaughlin, D. E., Anderson, J., Meylan, G., et al. 2006, ApJS, 166, 249 er., 90, 21 [Google Scholar]
- Meylan, G. 1989, A&A, 214, 106 [NASA ADS] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., & Anderson, J. 2009, A&A, 497, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Piotto, G., King, I. R., et al. 2010a, ApJ, 709, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2010b, SF2A-2010: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, 319 [Google Scholar]
- Milone, A. P., Marino, A. F., Piotto, G., et al. 2012a, ApJ, 745, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012b, ApJ, 744, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012c, A&A, 537, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., Moehler, S., Piotto, G., et al. 2006, A&A, 451, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., Moehler, S., Piotto, G., Momany, Y., & Recio-Blanco, A. 2009, A&A, 498, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moretti, A., De Angeli, F., & Piotto, G. 2008, A&A, 483, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2004, Ap&SS, 291, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Petr, M. G., Coudé du Foresto, V., Beckwith, S. V. W., Richichi, A., & McCaughrean, M. J. 1998, ApJ, 500, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Zoccali, M., King, I. R., et al. 1999, AJ, 118, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piotto, G., De Angeli, F., & King, I. R. 2004, ApJ, 604, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., & Hut, P. 2006, ApJ, 646, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Prosser, C. F., Stauffer, J. R., Hartmann, L., et al. 1994, ApJ, 421, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Pryor, C. P., Latham, D. W., & Hazen, M. L., 1988, AJ, 96, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., Gans, P. B., Palin, J. M., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rastegaev, D. A. 2010, AJ, 140, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., Aparicio, A., Piotto, G., de Angeli, F., & Djorgovski, S. G. 2006, A&A, 452, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richer, H. B., Fahlman, G. G., Brewer, J., et al. 2004, AJ, 127, 2771 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., & Weinberg, M. D., 1991, ApJ, 372, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Rubenstein, E. P., & Bailyn, C. D., 1997, ApJ, 474, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Weiss, A. 2002, A&A, 388, 492 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658, Paper I [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Salaris, M., Weiss, A., & Cassisi, S. 2011, A&A, 534, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shara, M. M., & Hurley, J. R. 2002, ApJ, 571, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, M. H., Dotter, A., Majewski, S. R., et al. 2007, ApJ, 667, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A. 2008, MNRAS, 388, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Ferraro, F. R., Fusi Pecci, F., & Sarajedini, A. 2007, MNRAS, 380, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Carballo-Bello, J. A., Beccari, G., et al. 2010, MNRAS, 401, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A. 1991, MNRAS, 250, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Djorgovski, S., & King, I. R. 1993, Structure and Dynamics of Globular Clusters, 50, 347 [Google Scholar]
- Trenti, M., Heggie, D. C., & Hut, P. 2007, MNRAS, 374, 344 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Anderson, J., Cox, C., et al. 2007, Instrument Science Report ACS 2007-07, 7 [Google Scholar]
- Veronesi, C., Zaggia, S., Piotto, G., Ferraro, F. R., & Bellazzini, M. 1996, in Formation of the Galactic Halo Inside and Out, ed. H. Morrison, & Ata Sarajedini (San Francisco: ASP), ASP Conf. Ser., 92, 301 [Google Scholar]
- von Braun, K., & Mateo, M. 2001, AJ, 121, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., & Mateo, M. 1994, AJ, 108, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, B., & Bailyn, C. D. 2005, AJ, 129, 1934 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Description of the HST additional archive data sets used in this paper, other than those from GO-10775.
Fraction of binaries with mass ratio q > 0.5, q > 0.6 and q > 0.7, and total fraction of binaries measured in different regions.
All Figures
 |
Fig. 1 Model MS-MS binary sequences with different mass ratios for NGC 2298. The dashed-dotted line is the MSRL while, continuous black lines indicate the sequences of constant q and blue lines mark sequences of constant ℳ1. |
| In the text | |
 |
Fig. 2 Diagnostic parameters that we have used to select the sample of NGC 2298 stars with high-quality photometry. The parameters are plotted as a function of the instrumental mF606W and mF814W magnitudes. Red circles indicate the median rmsX, Y, and qF606W,F814W per intervals of 0.4 mag. Red lines separate the well measured stars (thin points) from those that are more likely to have poorer photometry (thick points). See text for details. |
| In the text | |
 |
Fig. 3 CMD of all the measured stars (left), of stars that passed our criteria of selection (middle), and CMD of rejected stars (right) |
| In the text | |
 |
Fig. 4 Left: completeness as a function of the mF814W magnitude in five annuli (the inner and outer radius of each annulus, in ACS pixels, are quoted in the inset) for NGC 2298. Right: completeness contours in the radial distance versus mF814W magnitude plane. The completeness levels corresponding to the red and gray continuous lines are quoted in the figure. Dotted lines indicate differences of completeness of 0.05 ranging from 0.05 to 0.95. |
| In the text | |
 |
Fig. 5 Panel a: observed CMD of NGC 2298; the arrow indicates the direction of reddening. The continuous lines are the axes (“abscissa” and “ordinate”) of the reference frame introduced in the procedure for the measurements of reddening variations. The position of NGC 2298 stars in this reference frame is shown in panel b where we draw the fiducial line of the MS as a dashed red line. Stars between the dotted lines (black points) have been used as reference stars. Panel C shows the rectified “ordinate” vs. Δ “abscissa” diagram. |
| In the text | |
 |
Fig. 6 Visualization of the local approach for the estimate of the differential reddening suffered by the target star indicated with the blue asterisk. Upper left: position of NGC 2298 stars in the ACS/WFC field of view (gray points). Red circles highlight the 35 reference stars in the lower left panel. Reference stars are indicated with black crosses, among them, the 35 closest neighbours (of the target star) are marked with red circles. The lower left panel is a zoom of a 700 × 700 pixel centered on the target star. Upper right: “ordinate” vs. Δ “abscissa” for all the stars in the NGC 2298 field of view. The median Δ “abscissa” of the 35 closest neighbor is indicated by the continuous red vertical line and corresponds to the differential reddening value suffered by the target star. The histogram of the Δ “abscissa” distribution of the 35 closest neighbors is shown in the bottom right panel. |
| In the text | |
 |
Fig. 7 Bottom-left: map of differential reddening in the NGC 2298 field of view. The gray levels correspond to the magnitude of the variation in local reddening as indicated in the upper-right panel. We divided the field of view into 8 horizontal slices and 8 vertical slices. Upper-left and lower-right panels plot Δ E(B − V) as a function of the Y and X coordinate. |
| In the text | |
 |
Fig. 8 CMDs of twelve GCs before (left) and after (right) the correction for differential reddening. For each cluster we give the average reddening from the Harris (1996) catalog. |
| In the text | |
 |
Fig. 9 CMDs of NGC 288 before (top) and after (bottom) correction for photometric zero points variations. Right panels show a zoom of CMD around the SGB and upper-MS region. |
| In the text | |
 |
Fig. 10 Comparison of the CMD of nine GCs studied in this paper before (left) and after (right) the correction for photometric zero points variations. |
| In the text | |
 |
Fig. 11 Gray areas in the upper panels are the regions A, and B of the NGC 2298 CMD adopted to select all the (single and binary) cluster stars (left) and the candidate binaries with q > 0.5 (right), in a range of 3 mF814W magnitudes. In all panels, the MSRL is represented as a green continuous line, while the green dashed line is blue shifted from the MSRL by three times the color error. The red continuous line is the locus of MS-MS binaries with mass ratio q = 0.5, while the red dotted line is the locus of MS-MS binaries whose components have equal mass. The red dashed dotted line is displaced to the red from the dotted line by 3 times the color error. Lower panels show the observed CMD of NGC 2298 (left), the artificial stars CMD (middle), and the CMD of field stars (right). |
| In the text | |
 |
Fig. 12 Vector-point diagram of proper motions, in equatorial coordinates, for twenty GCs. Only stars in the mF814W interval indicated in each panel are shown. |
| In the text | |
 |
Fig. 13 Leftmost column: mF814W vs. mF606W − mF814W CMD for all the stars of NGC 6656 with available measures of proper motions. Second Column: proper motion diagrams of the stars in the left panels in mas yr-1, in intervals of 1.4 mag. Third column: the proper motion selected CMD of cluster members. Rightmost column: the CMD of field stars. |
| In the text | |
 |
Fig. 14 As in Fig. 13, but for NGC 6838. |
| In the text | |
 |
Fig. 15 Setup to estimate the fraction of field stars with cluster-like proper motions in NGC 6656. |
| In the text | |
 |
Fig. 16 Estimate of the contamination of field stars that share cluster proper motions in NGC 6838. Upper panels show the CMD (left) and the VPD (right) for stars with 18.15 < mF814W < 19.45. Lower panels display the CMD (left) and the VPD (right) for those objects that, on the basis of their position on the CMD, are probable field stars. |
| In the text | |
 |
Fig. 17 Map of all the stars NGC 6656 (light gray points) with mF814W < 18.25. Black points mark all the stars with available proper motions. The contour of region “RII” is colored in red. |
| In the text | |
 |
Fig. 18 Panel a): CMD for all the stars within the region “RII”; Panel b): CMD for stars with a reliable estimate of proper motions; Panel c): CMD for stars within “RII” for which there are not reliable measurements of proper motions; Panel d): fraction of stars with good proper motions with respect to the total number of stars within “RII” as a function of mF814W. |
| In the text | |
 |
Fig. 19 Observed CMD of NGC 2298 (left) and simulated CMD of field stars in the NGC 2298 field of view (right). |
| In the text | |
 |
Fig. 20 Left: the observed (top) and simulated (bottom) CMD of NGC 2298 with the fiducial line overplotted; Middle: the CMDs rectified by subtraction of the fiducial line; Right: color distribution of the rectified CMDs. The σ in the inset are those of the best-fitting Gaussian. |
| In the text | |
 |
Fig. 21 Upper panel: MS dispersion as a function of mF814W magnitude for NGC 2298. Circles and triangles correspond to real and artificial stars, respectively. The corresponding best fitting 4th order polynomials are represented by dotted and dashed lines. Lower panels: comparison of the observed CMD of NGC 2298 (left) and the CMDs of artificial stars before (middle) and after (right) the application of color spread. |
| In the text | |
 |
Fig. 22 As an example, we show with gray and black shaded areas the five CMD regions (B1,2,...,5) used to determine the mass-ratio distribution of binary stars in NGC 2298. |
| In the text | |
 |
Fig. 23 Mass-ratio distribution for the binary population in the ACS field of 29 GCs. Black filled-circles show the normalized fraction of binaries in five mass-ratio intervals, while red open-circles indicate the νbin,i values obtained by using only two bins with 0.5 < q < 0.7, and 0.7 < q < 1. Horizontal segments mark the adopted mass-ratio interval, while observational errors are plotted as the vertical lines and shadowed areas. |
| In the text | |
 |
Fig. 24 As in Fig. 23 for the remaining 30 GCs. |
| In the text | |
 |
Fig. 25 Black points show the normalized fractions of binaries, νbin measured in five mass-ratio intervals as a function of q for all the GCs studied in this paper. To compare the fraction of binaries in different clusters we divided νbin by two times the fraction of binaries with q > 0.5. For clarity, black points have been randomly scattered around the corresponding q value. Red points with error bars are the means in each mass-ratio bin, while the gray line is the best fitting line, whose slope is quoted in the inset. |
| In the text | |
 |
Fig. 26 Upper panel: mass-ratio distribution derived by Fisher et al. (2005). Lower panel: mass-ratio distribution simulated from random extraction from a Kroupa (2002) IMF in the primary star mass intervals quoted in the inset. |
| In the text | |
 |
Fig. 27 Frequency of binaries divided by two times the fraction of binaries with q > 0.5 expected for the cases of Fisher et al. (2005) mass-ratio distribution (upper panel) and from the distribution obtained by randomly extracting secondary stars from a Kroupa (2002) IMF (bottom panels). Red points with the error bars are the mean values of the observed binary frequency normalized by two times |
| In the text | |
 |
Fig. 28 Comparison of the core binary fractions of 13 GCs measured in this paper (red circles) and in Sollima et al. (2007, black circles). In both cases has been assumed the mass-ratio distribution from Fisher et al. (2005). Blue triangles indicate the binary fraction estimated in this work assuming a flat q distribution. |
| In the text | |
 |
Fig. 29 Dark and light gray areas indicate the CMD regions used to measure the fraction of binaries in three magnitude intervals. |
| In the text | |
 |
Fig. 30 Fraction of binaries with mass ratio q > 0.5 for 29 GCs measured in three magnitude intervals (black points) and in the interval between 0.75 and 3.75 F814W magnitudes below the MS turn off (red points) as a function of ΔmF814W. Horizontal segments indicate the magnitude coverage corresponding to each point. |
| In the text | |
 |
Fig. 31 As in Fig. 30 for the remaining 30 GCs. In the cases of NGC 6388 and NGC 6441 the binary fraction has been measured in the interval between 0.75 and 2.25 F814W magnitudes below the MS turn off. |
| In the text | |
 |
Fig. 32 Fraction of binaries with q > 0.5 measured in three magnitude intervals (black points) as a function of ΔmF814W for the 59 GCs studied in this work. To compare the fraction of binaries in different clusters we have divided the fraction of binaries in each bin by the value of |
| In the text | |
 |
Fig. 33 Fraction of binaries with q > 0.5 measured in three magnitude intervals and normalized by |
| In the text | |
 |
Fig. 34 Fraction of binaries with q > 0.5 as a function of the radial distance from the cluster center for 29 GCs. The dotted and dashed vertical lines mark the core and the half mass radius respectively. Black filled-circles show binary fractions in four radial intervals while red open-symbols indicate the binary fraction for the rC, rC − HM, and roHM sample. Horizontal black segments indicate the radial coverage corresponding to each point while observational errors are plotted as vertical lines and shadowed areas. |
| In the text | |
 |
Fig. 35 As in Fig. 34 for the remaining GCs. |
| In the text | |
 |
Fig. 36 Binary fraction with q > 0.5 (in units of core binaries) as a function of the distance from the cluster center in units of core radii. |
| In the text | |
 |
Fig. A.1 Artificial stars CMD for NGC 2298 (upper-left) and simulated CMD with a fraction of |
| In the text | |
 |
Fig. A.2 Bottom-left: Map of differential reddening added to the simulated CMD of NGC 2298. The gray levels indicate the reddening variations as indicated in the upper-right panel. Upper-left and bottom-right panels show ΔE(B − V) as a function of the Y and X coordinate respectively for stars into 8 vertical and horizontal slices. |
| In the text | |
 |
Fig. A.3 Difference between the measured fraction of binaries and the fraction of binaries in input as a function of the parameter C1 for four difference values of the input binary fraction. Black lines indicate the average difference. Red circles, gray triangles and black crosses indicate simulations with C2 = 3, 5, and 8 respectively. |
| In the text | |
 |
Fig. A.4 Fractions of binaries per unit q measured in five mass-ratio intervals as a function of q for all the simulated GCs. To compare the q distribution in simulated clusters with different fraction of binaries, we divided νbin by two times the fraction of binaries with q > 0.5. For clarity, black points have been randomly scattered around the corresponding q value. The means normalized binary fractions in each mass-ratio bin are represented by red points with error bars, while the gray line is the best fitting line, whose slope is quoted in the inset. |
| In the text | |
 |
Fig. A.5 Fraction of binaries with q > 0.5 in three magnitude intervals as a function of ΔmF814W for all the simulated GCs. To compare the measured fraction of binaries in different clusters we have divided the measured binary fractions in each magnitude interval by the value of |
| In the text | |
 |
Fig. B.1 Fraction of binaries with q > 0.5 in the core as a function of some parameters of their host GCs. Clockwise: ellipticity, central concentration, central velocity dispersion, logarithm of the central luminosity density, half-mass and core relaxation timescale, and metallicity. In each panel we quoted the Pearson correlation coefficient (r). PCC clusters are marked with red crosses and are not used to calculate r (see text for details). |
| In the text | |
 |
Fig. B.2 As in Fig. B.1 for the rC − HM sample. |
| In the text | |
 |
Fig. B.3 As in Fig. B.1 for the roHM sample. |
| In the text | |
 |
Fig. B.4 Upper-left: fraction of binaries with q > 0.5 in the core as a function of the absolute visual magnitude of the host GC. Dashed line is the best fitting straight line whose slope (s) and intercept (i) are quoted in the figure together with the Pearson correlation coefficient (r). PCC clusters are marked with red crosses and are not used to calculate neither the best-fitting line nor r. For completeness in the upper-right panels we show the same plot for the fraction of binaries with q > 0.6, and q > 0.7. Lower panels: fraction of binaries with q > 0.5 in the rC − HM (left) and roHM (right) sample as a function of MV. |
| In the text | |
 |
Fig. B.5 Fraction of binaries with q > 0.5 as a function of the BSS frequency in the core. PCC GCs are marked with red points. |
| In the text | |
 |
Fig. B.6 Fraction of binaries with q > 0.5, q > 0.6, and q > 0.7 in the rC region (upper panels) and fraction of binaries with q > 0.5 in the rC − HM and roHM regions (bottom panels) as a function of the collisional parameter (Γ∗). The adopted symbols are already defined in Fig. B.4. |
| In the text | |
 |
Fig. B.7 As in Fig. B.6. In this case we used the encounter frequency adopted by Pooley & Hut (2006) in the approximation used for virialized systems. |
| In the text | |
 |
Fig. B.8 Fraction of binaries with q > 0.5, q > 0.6, and q > 0.7 in the rC region (upper panels) and fraction of binaries with q > 0.5 in the rC−HM and roHM regions (bottom panels) as a function of the relative age measured by Marín-Franch et al. (2009). The adopted symbols are already defined in Fig. B.4. |
| In the text | |
 |
Fig. B.9 As in Fig. B.8 but in this case we used the age measures from Salaris & Weiss (2002) and De Angeli et al. (2005). |
| In the text | |
 |
Fig. B.10 Fraction of binaries with q > 0.5 in the rC sample for low density clusters (log (ρ0) < 2.75) as a function of the relative age from Marín-Franch et al. (2009) (left panel) an absolute age from Salaris & Weiss (2002) and De Angeli et al. (2005) (right panel). |
| In the text | |
 |
Fig. B.11 Fraction of binaries with q > 0.5 as a function of the temperature of the hottest HB stars (bottom), the HB morphology index (middle), and the median color difference between the HB and the RGB (top). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.