| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117489 | |
| Published online | 24 January 2012 | |
Modeling the evolution of infrared galaxies: clustering of galaxies in the cosmic infrared background
1 Univ. Paris Sud, Institut d’Astrophysique Spatiale, UMR8617, 91405 Orsay, France
e-mail: aurelie.penin@ias.u-psud.fr
2 CNRS, 91405 Orsay, France
3 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
4 California Institute of Technology, Pasadena, CA 91125, USA
Received: 16 June 2011
Accepted: 25 September 2011
Context. Star-forming galaxies are highly biased tracers of the underlying dark matter density field. Their clustering can be studied through the cosmic infrared background (CIB) anisotropies. These anisotropies have been measured from 100 μm to 2 mm in the past few years.
Aims. In this paper, we present a fully parametric model allowing joint analysis of these recent observations.
Methods. To develop a coherent model at various wavelengths, we rely on two building blocks. The first one is a parametric model that describes the redshift evolution of the luminosity function of star-forming galaxies. It compares favorably to measured differential number counts and luminosity functions. The second is a halo model-based description of the clustering of galaxies. Starting from a fiducial model, we investigate parameter degeneracies using a Fisher analysis. We then discuss how halos of different masses and redshifts and how LIRGs and ULIRGs contribute to the CIB angular power spectra.
Results. From the Fisher analysis, we conclude that we cannot constrain the parameters of the model of evolution of galaxies using clustering data only. The use of combined data of Cℓ, counts, and luminosity functions improves the constraints slightly but does not remove any degeneracies. In contrast, the measurement of the anisotropies allows us to set interesting constraints on the halo model parameters, even if some strong degeneracies remain. Using our fiducial model, we establish that the 1-halo and 2-halo terms are not sensitive to the same mass regime. We also illustrate how the 1-halo term can be misinterpreted with the Poisson noise term.
Conclusions. We present a new model of the clustering of infrared galaxies. Our framework allows a coherent and joint analysis of various probes of infrared galaxies: number counts, luminosity functions, and clustering measurements; however, such a model has a few limitations, such as the parameters of the halo occupation that suffer from strong degeneracies.
Key words: infrared: galaxies / large scale structure of Universe / galaxies: high-redshift
© ESO, 2012
1. Introduction
Infrared star-forming galaxies are mainly characterized by a very high star formation rate, tens or even hundreds times higher than for the Milky Way, ~10–100 M⊙/year (Kennicutt 1998). A large number of young stars are embedded in dust that absorbs UV starlight and reemits it in the infrared (IR), from 5 μm to 1 mm. As a result, infrared star-forming galaxies emit most of their energy (~95%) in the IR. In the far IR (λ > 200 μm) and submillimeter, observations are limited by confusion, and small spatial scales are lost because of the poor angular resolution of the instruments. Thus we observe the cosmic infrared background (CIB) (Puget et al. 1996; Fixsen et al. 1998) which is the contribution of infrared star-forming galaxies integrated over the age of the Universe, and its anisotropies. In the near and mid IR a large fraction of the CIB is resolved into sources, whereas only a few percent is in the far IR. These fractions can be improved thanks to statistical methods. For instance, at long wavelength, Oliver et al. (2010) directly resolved 15%, 10% and 6% of the CIB at 250, 350, and 500 μm in Herschel/SPIRE data, whereas Papovich et al. (2004) resolved 70% of the CIB at 24 μm. Berta et al. (2010) resolved 45% and 52% of the CIB at 100 and 160 μm, respectively, by integrating number counts in Herschel/PACS data. By stacking 24 μm sources they increased these fractions to 50% and 75% respectively. As a result, sources detected at 24 μm are the main sources of the CIB around its peak at ~200 μm. The CIB is dominated by objects that get more and more massive as the redshift increases from luminous IR galaxies (LIRGs) with 1011 L⊙ < LIR < 1012 L⊙ at 0.8 < z < 1.2 with intermediate mass, to extreme LIRGs with 1012 L⊙ < LIR < 1014 L⊙ that dominate at z > 2 and with masses > 1011 M⊙ (Caputi et al. 2006).
Magliocchetti et al. (2007) and Farrah et al. (2006) derived the two-point correlation function of ultra LIRGs at z ≃ 1.6 − 2.7 and 1.5 < z < 3, respectively. They brought to light the very strong clustering of infrared star-forming galaxies and their embedding in very massive halos of ≃ 1013 M⊙. Cooray et al. (2010) computed the angular correlation function with Herschel/SPIRE data. They find that 250 μm sources are in DM halos with masses around 1012 M⊙ that lie at z ~ 2.1 whereas bright 500 μm sources are in more massive halos ≃1013 M⊙ at z ~ 2.6. More recently, Magliocchetti et al. (2011) have derived the 3D correlation function of infrared sources using Herschel/PACS data up to a redshift of 3. They find that their galaxies lie in halos with > 1012.4 M⊙, a value that agrees with previous studies. However, the two-point correlation function is not easily computed using IR data because of confusion. As said before, confusion can be circumvented through the use of statistical methods. Indeed, clustering can be measured in the correlated CIB anisotropies (CIBA). It has first been detected as an excess of signal on intermediate scales by Lagache et al. (2007) and Grossan & Smoot (2007) at 160 μm in the Spitzer Multi-band Imaging Photometer (MIPS) data. These measurements have been followed by the detection in the Balloon-borne Large Aperture Sub-millimeter Telescope (BLAST) data at 250, 350, and 500 μm (Viero et al. 2009) and by that of the South Pole Telescope team (Hall et al. 2010) at 1.3 and 2 mm. More recently Pénin et al. (2011) have measured the clustering signal by accurately removing the cirrus contamination at 100 and 160 μm. The power spectrum of the CIBA has also been computed using Herschel/SPIRE at 250, 350, and 500 μm (Amblard et al. 2011), taking advantage of its angular resolution, and using Planck/HFI at 350, 550, 850 μm and 1.3 mm (Planck Collaboration et al. 2011) taking advantage of its sky coverage. Therefore, the clustering of infrared star-forming galaxies in the CIBA has been detected over a wide range of wavelengths and angular scales. All these results have been analyzed in several ways, hardly comparable. As a first analysis, Lagache et al. (2007) derived the linear bias, the proportionality coefficient between the fluctuations of the dark matter (DM) density field and emissivities of galaxies. They found b = 2.4 ± 0.2 and Viero et al. (2009) found b = 3 ± 0.3, which implies that these galaxies are highly biased tracers of DM. The difference between these two biases may be explained by the fact that higher redshift infrared star-forming galaxies are probed at longer wavelength (Lagache et al. 2005; Fernandez-Conde et al. 2008) and thus are found to be more biased. New measurements needed more complex models. Viero et al. (2009), Amblard et al. (2011), and Planck Collaboration et al. (2011) introduced a halo occupation distribution for the study of CIBA. It describes the DM distribution and especially how galaxies are distributed in one DM halo. It appears that each wavelength must be fitted separately, which indicates an evolution of the clustering with the redshift (Planck Collaboration et al. 2011). Most of the models determined the mass of the halos where infrared star-forming galaxies lie and thus where star formation occurs.
With the long term purpose of analyzing all these new measurements in a consistent way, we present a new model of the clustering in CIBA. We use the halo model formalism (Cooray & Sheth 2002) which has often been used in the past few years to predict and to interpret galaxy clustering. We link it to a recent model of infrared star-forming galaxies evolution that reproduces number counts and luminosity functions well (Béthermin et al. 2011). This model of clustering has been successfully used to fit Planck data (Planck Collaboration et al. 2011).
The paper is organized as follows. We describe the model and its parameters in Sect. 2. We set a fiducial model inspired by Viero et al. (2009), the Planck Collaboration et al. (2011), and Amblard et al. (2011) and compute angular power spectra for several instruments with which we carry out a Fisher analysis in Sect. 4. Section 5 is dedicated to interpreting measurements, such as the redshift and halo-mass contribution to the power spectrum, the linear bias, the influence of the mean emissivities, and the contribution of LIRGs and ULIRGs to power spectra. We finally conclude in Sect. 6. Throughout this study we use the Wilkinson Microwave Anisotropy Probe 7-year Cosmology (Larson et al. 2011).
2. Why a new model?
As said previously several models of clustering in the CIB already exist so why constructing a new one? There have been several measurements of the clustering, and different models have been applied to analyzing each measurement. Moreover, their approaches are different, so comparing the results is difficult if not impossible. Thus one single model that ties together all available measurements is appealing, especially for analyzing them simultaneously and searching for any evolution of the clustering. Such a model requires three ingredients: a DM distribution, a relation between galaxies and DM halos and an evolution of infrared star-forming galaxies.
Lagache et al. (2007), Amblard & Cooray (2007), and Viero et al. (2009) used the model of galaxy evolution of Lagache et al. (2003). This model was the most up to date model at that time. It fitted differential number counts and luminosity function measurements from 24 to 850 μm (IRAS, Spitzer/SCUBA). However, it does not reproduce new measurements very well, especially the differential number counts from Herschel. This is a phenomenological model in which the evolution of the luminosity function was tuned to reproduce the constraints available at that time. It overpredicts the luminosity density at high-z. Moreover, it does not reproduce the observed redshift distribution of the CIB very well (Jauzac et al. 2011). It predicts a peak at z ~ 1 that is not observed. The angular power spectra of CIBA strongly depend on the redshift distribution of the sources through the emissivities (see Sect. 3.2). Therefore, a “valid” distribution in redshift is important and a more robust model in agreement with most recent measurements is needed.
Hall et al. (2010) use the galaxy templates from Lagache et al. (2003) to check a simple model with a “single SED”. This model only has a few parameters that can be changed easily and thus adapted to each of their wavelengths. They fixed the shape of the power spectrum and only changed its amplitude depending on the wavelength. Amblard & Cooray (2007) use the same model of infrared galaxies evolution and used the luminosity function as a function of redshift at 350 μm coming from Lagache et al. (2003) that they matched to conditional luminosity functions (CLFs). Other wavelengths are extrapolated from the 350 μm. Finally Amblard et al. (2011) avoid using any model of galaxies evolution by letting free the redshift distribution of the cumulative flux coming from the background faint galaxies in several redshift bins.
Concerning the distribution of DM, Viero et al. (2009) and Amblard et al. (2011) use the formalism of the halo model and the same halo occupation number, whereas Lagache et al. (2007) and Hall et al. (2010) consider a linear power spectrum for dark matter. Amblard & Cooray (2007) also use the halo model formalism through CLFs. By integrating CLFs on the luminosity, the halo mass function is recovered, however, this approach depends on too many parameters that cannot be constrained simultaneously.
Parameters of our model.
To construct a new model, we link an up-to-date model of galaxy evolution to a recent version of the halo model. We use the model of evolution of galaxies of Béthermin et al. (2011). It reproduces Herschel measurements well as well as older ones (from 15 μm to 1.1 mm). It also reproduces the redshift distribution of the CIB of Jauzac et al. (2011) very well. We use an updated version of the halo model of Viero et al. (2009) which is the halo occupation distribution (HOD) introduced by Tinker & Wetzel (2010). This HOD reproduces the angular correlation function of optical galaxies, red (star-forming), and blue (quiescent) galaxies at 0.4 < z < 2. Therefore we make a strong assumption here, assuming that this description would work on star-forming galaxies. Given the current lack of understanding of the details of the process of star-formation and its evolution with redshift, it is difficult to define what would be a better HOD prescription so we stay with this one. We studied power spectra coming from our model for several wavelengths/instruments: 100 μm IRAS, 160 μm Spitzer/MIPS, 250, 350, 500 μm Herschel/SPIRE, and 850 μm, 1.3, and 2 mm Planck/HFI. A list of the available data of CIBA power spectra is given in Table 2.
3. The model
3.1. The parametric model of star-forming galaxy evolution
To reproduce the angular power spectrum of the CIBA we need a model for the redshift evolution of star-forming galaxies. We use the model presented in Béthermin et al. (2011). It is a backward evolution model based on a parametrized luminosity function and on galaxies’ spectral energy distribution templates.
Béthermin et al. (2011) consider a luminosity function (LF) that behaves like a power law for L ≪ L⋆ and like a Gaussian for L ≫ L⋆ (Saunders et al. 1990): ![\begin{eqnarray} \Phi(L_{\rm IR})&=& \frac{{\rm d}N(L_{\rm IR})}{{\rm d}V{\rm d}\log_{10}(L_{\rm IR})}\\ &=&\Phi^{\star}(z)\left(\frac{L_{\rm IR}}{L^{\star}(z)}\right)^{1-\alpha}\exp{\left[-\frac{1}{2\sigma^2}\log_{10}^2\left(1+\frac{L_{\rm IR}}{L^{\star}(z)}\right)\right]} \label{eq:lum_func} \end{eqnarray}](/articles/aa/full_html/2012/01/aa17489-11/aa17489-11-eq55.png) where Φ(LIR) is the number of galaxies with the infrared bolometric luminosity LIR within the comoving volume dV and the bin dlog 10L. The normalization constant Φ⋆ fixes the density of sources. The low and high luminosity parts have different slopes, 1 − α and 1 − α − 1/σ2/ln2(10), respectively, and L⋆ represents the luminosity at the break. The parameters that describe the luminosity function are listed in Table 1.
where Φ(LIR) is the number of galaxies with the infrared bolometric luminosity LIR within the comoving volume dV and the bin dlog 10L. The normalization constant Φ⋆ fixes the density of sources. The low and high luminosity parts have different slopes, 1 − α and 1 − α − 1/σ2/ln2(10), respectively, and L⋆ represents the luminosity at the break. The parameters that describe the luminosity function are listed in Table 1.
The luminosity function evolves with the redshift through L⋆ and φ⋆:  Exponents rL and rφ are not identical for all z. Two breaks are imposed to reproduce the evolution of the LF. The first one zbreak is a free parameter and is found to be around 1. The second one is fixed at z = 2 to avoid divergence at high z. Between these two breaks, the values of rL and rφ change as shown in Table 1.
Exponents rL and rφ are not identical for all z. Two breaks are imposed to reproduce the evolution of the LF. The first one zbreak is a free parameter and is found to be around 1. The second one is fixed at z = 2 to avoid divergence at high z. Between these two breaks, the values of rL and rφ change as shown in Table 1.
Béthermin et al. (2011) use the SED library of Lagache et al. (2004). It contains two galaxy populations: star-forming and late-type galaxies. The latter emit half or less of their energy in the IR whereas the former emit more than 95% of their energy in the IR. The fraction of each population depends on luminosity. Indeed, late-type dominate at low luminosity whereas star-forming dominate at high luminosity. For a given bolometric luminosity, the fraction of star-forming is: ![\begin{eqnarray} f_{\rm SF}&=&\frac{\Phi_{\rm SF}}{\Phi}\\ &=& \frac{1+\tanh[\sigma_{\rm pop}(L)\log_{10}(L_{\rm IR}/L_{\rm pop})]}{2} \end{eqnarray}](/articles/aa/full_html/2012/01/aa17489-11/aa17489-11-eq69.png) where Lpop is the luminosity where ΦSF = Φlate − type, and σpop characterizes the width of the transition between the two populations.
where Lpop is the luminosity where ΦSF = Φlate − type, and σpop characterizes the width of the transition between the two populations.
Differential number counts are then derived for each population and then summed. At flux S, 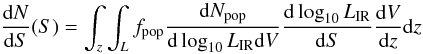 (7)where dN/dS is the number of sources per flux unit in a unit solid angle and pop = late-type or pop = star-forming.
(7)where dN/dS is the number of sources per flux unit in a unit solid angle and pop = late-type or pop = star-forming.
 |
Fig. 1 CIB per redshift bins from the model of Béthermin et al. (2011). The high redshift contribution increases with the wavelength. |
The model of Béthermin et al. (2011) is described by thirteen free parameters. Best fit parameters and confidence areas are computed using Monte-Carlo Markov chains on available and trustworthy differential number counts and luminosity functions at certain wavelengths. Béthermin et al. (2011) fitted number counts of Spitzer/MIPS at 24, 70, and 160 μm (Béthermin et al. 2010), those of Herschel/SPIRE at 250, 350, and 500 μm (Oliver et al. 2010), and those of Aztec at 1.1 mm (Austermann et al. 2010; Scott et al. 2010). A couple of luminosity functions at different redshifts are also fitted: the 8 μm one at z = 2 from Caputi et al. (2007), others derived from Rodighiero et al. (2009) (a local LF at 24 μm, a 15 μm one at z = 0.6, a 12 μm LF at z = 1) and a 60 μm one at z = 0 from Saunders et al. (1990). Moreover, absolute measurements of the CIB are also used as a model constraint (Lagache et al. 1999). We do not describe and discuss all the fits here (for a full discussion see Béthermin et al. 2011). Using the best fit, this model also provides the redshift distribution of the CIB as shown in Fig. 1. We see that higher redshifts contribution increases with wavelength: the redshift slice 0.3 < z < 1 dominates up to 400 μm, whereas z > 2 dominates in the submillimeter. This model provides very good agreement with the CIB redshift distribution (Jauzac et al. 2011).
We now study how these thirteen free parameters can be constrained with power spectra of the CIBA.
3.2. The angular power spectrum
According to Haiman & Knox (2000) and Knox et al. (2001), and using the Limber approximation, the angular power spectrum of the anisotropies of the CIB at wavelengths λ and λ′ is 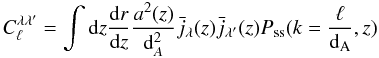 (8)where ℓ is the multipole, r the conformal distance from the observer, a(z) the scale factor, dA the comoving angular diameter distance, and
(8)where ℓ is the multipole, r the conformal distance from the observer, a(z) the scale factor, dA the comoving angular diameter distance, and 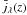 the mean emissivity per comoving unit volume at wavelength λ as a function of z. When λ = λ′ we recover the auto power spectrum. Pss(k) is the galaxy three-dimensional power spectrum.
the mean emissivity per comoving unit volume at wavelength λ as a function of z. When λ = λ′ we recover the auto power spectrum. Pss(k) is the galaxy three-dimensional power spectrum.
The emissivities are computed using the following parametric luminosity functions: 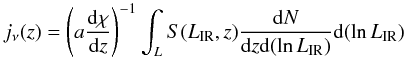 (9)where dN/dzd(lnL) is the number of galaxies per redshift bin dz and per luminosity bin d(lnL) and S the flux. Each galaxy population (late-type and star-forming) emissivity is computed and summed to get the overall emissivity. Figure 2 shows emissivities as a function of redshift. The two discontinuities at z ~ 0.9 and z = 2 are due to the breaks imposed by the parametrization of the model of galaxies. It is clear that, as the wavelength increases, the contribution from the high-redshift part increases. Emissivities are color-corrected according to their instrument and wavelengths to give Cℓ in Jy2/sr (for the photometric convention νIν = cst).
(9)where dN/dzd(lnL) is the number of galaxies per redshift bin dz and per luminosity bin d(lnL) and S the flux. Each galaxy population (late-type and star-forming) emissivity is computed and summed to get the overall emissivity. Figure 2 shows emissivities as a function of redshift. The two discontinuities at z ~ 0.9 and z = 2 are due to the breaks imposed by the parametrization of the model of galaxies. It is clear that, as the wavelength increases, the contribution from the high-redshift part increases. Emissivities are color-corrected according to their instrument and wavelengths to give Cℓ in Jy2/sr (for the photometric convention νIν = cst).
 |
Fig. 2 Emissivities versus the redshift for different wavelengths. |
In the context of the halo model, Pss(k) is the sum of the clustering in one single halo (1h) and in two different halos (2h): 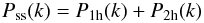 (10)where
(10)where ![\begin{eqnarray} P_{\rm 1h}(k) & = & \int_M {{\rm d}N\over {\rm d}M}{\langle N_{\rm gal}(N_{\rm gal}-1) \rangle \over \bar n_{\rm gal}^2} U(k,M)^p {\rm d}M \\ P_{\rm 2h}(k) & = & P_{\rm lin}(k)\left[\int_M {{\rm d}N\over {\rm d}M}b(M){\langle N_{\rm gal} \rangle \over \bar n_{\rm gal}} U(k,M) {\rm d}M\right]^2 . \label{eq:p12h} \end{eqnarray}](/articles/aa/full_html/2012/01/aa17489-11/aa17489-11-eq96.png) Here M is the halo mass, Plin(k) the dark matter linear power spectrum (computed with the fit of Eisenstein & Hu 1998), U(k,M) the normalized Fourier transform of the halo density profile that is assumed to be that of Navarro et al. (1996) truncated at the virial radius, b(M) is the halo bias, ⟨ Ngal ⟩ the probability of having Ngal galaxies in a halo of mass M, and we consider that p = 2 (Cooray & Sheth 2002). The mean number density of galaxies
Here M is the halo mass, Plin(k) the dark matter linear power spectrum (computed with the fit of Eisenstein & Hu 1998), U(k,M) the normalized Fourier transform of the halo density profile that is assumed to be that of Navarro et al. (1996) truncated at the virial radius, b(M) is the halo bias, ⟨ Ngal ⟩ the probability of having Ngal galaxies in a halo of mass M, and we consider that p = 2 (Cooray & Sheth 2002). The mean number density of galaxies 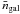 is given by
is given by 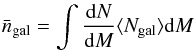 (13)where dN/dM is the halo mass function. We use the universal form given by Tinker et al. (2008), as well as its redshift evolution. We use its associated halo bias (see Eq. (A1) in Tinker et al. 2010).
(13)where dN/dM is the halo mass function. We use the universal form given by Tinker et al. (2008), as well as its redshift evolution. We use its associated halo bias (see Eq. (A1) in Tinker et al. 2010).
The halo occupation number introduces galaxies in the halos statistically. Recent data and simulations suggest a necessary distinction between the major galaxy that lies at the center of the halo and the satellite galaxies that populate the rest of the halo. Above a given mass threshold, most halos will host a central galaxy. Above a second higher mass threshold, they will also host satellite galaxies. Ngal can thus be written as 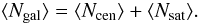 (14)According to the prescription of Tinker & Wetzel (2010), the occupation function of central galaxies is
(14)According to the prescription of Tinker & Wetzel (2010), the occupation function of central galaxies is ![\begin{equation} \langle N_{\rm cen}\rangle = \frac{1}{2}\left[1+\mbox{erf}\left(\frac{\log M-\log M_{\rm min}}{\sigma_{\log M}}\right)\right]\label{eq:hod_cent} \end{equation}](/articles/aa/full_html/2012/01/aa17489-11/aa17489-11-eq108.png) (15)where Mmin is the halo mass at which a halo has a 50% probability of hosting a central galaxy and σlog M controls the width of the transition between zero and one central galaxy. There is a smooth transition between low-mass halos that do not contain bright enough galaxies to be seen in the data (M ≪ Mmin) and more massive ones that always contain a bright central galaxy (M ≫ Mmin). The satellite occupation function is
(15)where Mmin is the halo mass at which a halo has a 50% probability of hosting a central galaxy and σlog M controls the width of the transition between zero and one central galaxy. There is a smooth transition between low-mass halos that do not contain bright enough galaxies to be seen in the data (M ≪ Mmin) and more massive ones that always contain a bright central galaxy (M ≫ Mmin). The satellite occupation function is ![\begin{equation} \langle N_{\rm sat}\rangle = \frac{1}{2}\left[1+\mbox{erf}\left(\frac{\log M-\log 2M_{\rm min}}{\sigma_{\log M}}\right)\right]\left(\frac{M}{M_{\rm sat}}\right)^{\alpha_{\rm sat}}\label{eq:hod_sat}. \end{equation}](/articles/aa/full_html/2012/01/aa17489-11/aa17489-11-eq111.png) (16)It has a cut-off of the same form as the central occupation with a transition mass that is twice higher than that of the central one to prevent halos having a low probability of hosting a central galaxy to contain satellite galaxies. The number of satellite galaxies grows with a slope of αsat. Both number of galaxies and their sum are plotted in Fig. 3.
(16)It has a cut-off of the same form as the central occupation with a transition mass that is twice higher than that of the central one to prevent halos having a low probability of hosting a central galaxy to contain satellite galaxies. The number of satellite galaxies grows with a slope of αsat. Both number of galaxies and their sum are plotted in Fig. 3.
With this model, the angular power spectrum of CIBA depends on only four halo model parameters αsat, Mmin, Msat, and σlog M. Cosmology is fixed at WMAP7 values. Our parameters are listed in Table 1 with their meaning and their fiducial values that we set in Sect. 4.
The long-term purpose of our model is to look for best fits of these parameters for Spitzer/MIPS, IRIS, Planck, Herschel, and SPT data and study their evolution with wavelength. However this is beyond the scope of this paper, so we do not compare the data to the power spectra coming from our model. Our first aim here is to study the parameter space and to particularly investigate the behavior of the halo bias, the halo mass-contribution to the power spectrum, and its redshift distribution. To do so we consider a set of fiducial halo parameters that are identical at all wavelengths.
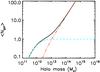 |
Fig. 3 Number of galaxies versus dark matter halo mass. The blue dashed line shows the central galaxies, the red dotted-dashed line shows satellite galaxies and the black continuous line shows the total. We use the parameters of our fiducial model (see Sect. 4), that is to say log Mmin = 11.5, Msat = 10Mmin and α = 1.4 |
4. Power spectra and parameter degeneracies
In this section, we present the CIB power spectra computed with the model explained in the previous section for several wavelengths in the far-IR and submillimeter. We then study the degeneracies of the parameters, looking first at the galaxies model parameters and second at the HOD parameters.
4.1. Power spectra
Our fiducial model is set with the HOD parameters log Mmin = 11.5, Msat = 10Mmin, and α = 1.4 at all wavelengths. These values are motivated by the parameter fit of Viero et al. (2009), Planck Collaboration et al. (2011), and Amblard et al. (2011). As the halo parameters slightly depend on the wavelength (in reality but it is not the case here), the power spectra presented in this section may not be seen as an exact prediction but as a basis for a qualitative study. For this fiducial model, we present in Fig. 4 the power spectra for different experiments and selected wavelengths, from 100 μm to 2 mm.
 |
Fig. 4 CIB anisotropies power spectra at several wavelengths. The continous black line shows the power spectra of the clustering. The dotted black line is the 1-halo term of the power spectrum, and the dashed line is the 2-halo term. The blue horizontal line represents the shot noise level and the red dot-dashed curve is the total power spectrum. Titles of the plots give the reference for the shot noise level and the bandpass filters used. |
The comparison to measurements also requires introducing of a shot noise term owing to the finite number of galaxies. We compute it using our galaxy evolution model (Béthermin et al. 2011). 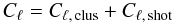 (17)where Cℓ, clus is the power spectrum of the clustering, Cℓ, shot the shot noise, and Cℓ, shot depends on the flux cut applied to the data when removing or masking the brightest sources. Typical flux cuts for different far-IR and submillimeter experiments are given in Table 2. In Fig. 4, we only show one shot noise level per wavelength corresponding to the instrument given in the plot titles, for purposes of clarity.
(17)where Cℓ, clus is the power spectrum of the clustering, Cℓ, shot the shot noise, and Cℓ, shot depends on the flux cut applied to the data when removing or masking the brightest sources. Typical flux cuts for different far-IR and submillimeter experiments are given in Table 2. In Fig. 4, we only show one shot noise level per wavelength corresponding to the instrument given in the plot titles, for purposes of clarity.
The instrument noise is not shown here but is often negligible, because the CIB is measured with a very high S/N even on spatial scales close to the angular resolution. Looking at this plot, we see clearly that the interplay between 2h, 1h, and shot noise terms will make interpretation of measurements quite difficult. The contribution of the 1-halo term decreases with the wavelength, which can prevent its measurement if the resolution of the instrument is low. For example, Planck with its 5′angular resolution at high frequency, cannot directly measure the shot noise level, and the 1-halo term can be easily misinterpreted as shot noise. Conversely, the 1-halo term dominates a wide range of scales at 100 and 160 μm and thus can be measured accurately at these wavelengths.
High wavelengths probe higher redshifts than short ones, and halos are relatively smaller at high redshifts than are those in the local Universe, since the latter had time to accrete more matter. Therefore the scale of the intersection between the 1- and 2-halo terms shifts towards higher ℓ as the wavelength increases. It goes from ℓ ~ 50 at 100 μm to ℓ ~ 1000 at 2 mm. Viero et al. (2009) also observed this trend. At 250 μm the crossing is at k ~ 0.03 arcmin-1 (ℓ ~ 648) whereas it is at k ~ 0.06 arcmin-1 (ℓ ~ 1296) at 500 μm. The exact crossing point differs from ours because of the HOD parameterization.
Shot noise levels in Jy2/sr from Béthermin et al. (2011) for available measurements of CIBA power spectra.
4.2. Variation in power spectra with the galaxy-evolution model parameters
To do an overall study of how our model parameters can be constrained, i.e. to investigate how degenerated they are, we construct the Fisher matrix associated to the power spectra. We write the Fisher matrix for angular power spectrum measurements as 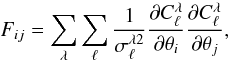 (18)where σℓ are the errors on the measurements and they include both the cosmic variance and the instrumental noise at a multipole ℓ:
(18)where σℓ are the errors on the measurements and they include both the cosmic variance and the instrumental noise at a multipole ℓ: 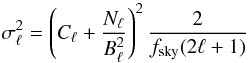 (19)where fsky is the fraction of the sky we consider, Nℓ is the level of the instrumental noise and
(19)where fsky is the fraction of the sky we consider, Nℓ is the level of the instrumental noise and 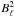 the power spectrum of the beam. To compute the Fisher matrices, we generate mock power spectra using our fiducial model and error bars derived following Eq. (19), from 100 μm to 1.3 mm. The range of multipoles is taken to be consistent with the available data. At 350 and 550 μm, we assume combined power spectra for Planck and Herschel, and we thus extend Planck power spectra to the Herschel limit in multipole. We plot Cℓ in Jy2/sr. They can be converted in μK2 using the coefficients given in Table 3.
the power spectrum of the beam. To compute the Fisher matrices, we generate mock power spectra using our fiducial model and error bars derived following Eq. (19), from 100 μm to 1.3 mm. The range of multipoles is taken to be consistent with the available data. At 350 and 550 μm, we assume combined power spectra for Planck and Herschel, and we thus extend Planck power spectra to the Herschel limit in multipole. We plot Cℓ in Jy2/sr. They can be converted in μK2 using the coefficients given in Table 3.
Conversion factors from Jy2/sr to μKCMB.
The bottom left hand panel of Fig. 5 shows confidence ellipses coming from Cℓ when trying to measure only the galaxy model parameters rL⋆, hz and rL⋆, lz. Clearly, they are very poorly constrained. For instance, rL⋆, hz = 0.145 ± 15.55, or rL⋆, lz = 2.93 ± 20.0. For reference, the constraints obtained using current number counts are rL⋆, hz = 0.145 ± 1.05 and rL⋆, lz = 2.93 ± 0.27, as shown in the top left hand panel of Fig. 5. These parameters enter into the expression of the Cℓ through the emissivities that are integrated on all redshifts, making them hard to measure from clustering measurements alone.
As a matter of fact, the lack of information in Cℓ partially comes from the large number of parameters in the model of evolution of galaxies. To quickly quantify this we vary only a few of these parameters (rL ⋆ , lz, rL⋆, hz, zbreak, rφ ⋆ , lz, and rφ ⋆ , hz) assuming that the others are perfectly known. Fixing all but these parameters corresponds to assuming that only the redshift evolution of the LF is unknown, clearly an irrealistic assumption. Not surprisingly, while some of the degeneracies remain in these reduced parameter space, on the whole, parameters are better contrained. For instance, we now obtain rL⋆, lz = 2.93 ± 0.10 and rL⋆, hz = 0.145 ± 7.05, which are about two orders of magnitude and a factor 2 improvement, respectively, as compared to the numbers above.
To illustrate this lack of information in Cℓs further, we show how they change with only one parameter, rL⋆, lz. We make it vary by ± 2σ from its best fit (σ coming from Béthermin et al. 2011). This parameter governs the evolution of the luminosity function for 0 < z < zbreak. A higher rL⋆, lz means a faster increase of the luminosity, thus a higher value of L⋆(z = zbreak). The top panel of Fig. 6 shows the influence of this parameter on the counts at 160 μm. A higher (smaller, respectively) rL⋆, lz implies higher (smaller) number counts thus more (less) galaxies on a wide range of fluxes. This leads to higher (smaller) emissivities as shows in the second and third panels of Fig. 6. This results in a modification of ~20% on the emissivities and from 15 to 35% on power spectra depending on the scale. This ratio is not constant is because the ratio of the emissivities is not constant with redshift (3rd panel of Fig. 6). We can see that all power spectra are consistent within error bars and thus we can hardly distinguish between them. Therefore, it is hard to constrain the evolution model of galaxies using only power spectra.
More relevant data are required. We compare our confidence ellipses with those obtained with luminosity functions and number count data. To do so we use the covariance matrix of Béthermin et al. (2011). The error bars are in general much smaller, and there are only a few degeneracies. For instance, as shown in the left hand panel of Fig. 5, rL⋆, hz, and rφ⋆, hz are still strongly degenerate, but they are now much better constrained.
 |
Fig. 5 1σ (dashed green), 2σ (dash-dot blue), 3σ (black) likelihood contours of the galaxy evolution model parameters rL⋆, hz, rL⋆, lz, and rφ⋆, hz. Top, middle and bottom panels show the contours computed using counts/LF data, Cℓ data only, and combined counts/LF and Cℓ data, respectively. The continous line shows the direction of degeneracy using only counts/LF, the dotted line shows that using Cℓ and the dashed line is uses all data. |
 |
Fig. 6 Counts at 160 μm, emissivities, and clustering power spectrum for three values of rL⋆, lz, the best fit, and the best fit ± 2σ. Pink crosses are data: Béthermin et al. (2010) for the counts and Lagache et al. (2007) for the power spectrum. Top panel: differential number counts at 160 μm. 2nd panel: mean emissivities at 160 μm. 3rd panel: ratio of the modified emissivities compared to the best fit one at 160 μm. 4th panel: power spectra of the clustering at 160 μm. Bottom panel: ratio of the modified power spectra compared to the best fit one at 160 μm. A small change in rL⋆, lz leads to a 20% modification of the emissivities and on 15–35% on the Cℓ. |
So far, we have investigated how galaxy evolution parameters are degenerated and constrained using LF/counts and Cℓ separately. The next step is to look at the degeneracies when combining all these data. To do so, we add the two Fisher matrices coming from the counts/LF and the Cℓ. The bottom panels of Fig. 5 show the confidence ellipses for rL⋆, hz, rL⋆, lz, and rφ⋆, hz using the combined data. The axis scales are different. The continous/dashed/dotted lines in Fig. 5 indicate the degeneracy directions. They are different, which illustrates the complementarity of the two data sets, and the constraints can be greatly improved. For example, the errors on rφ⋆, hz are decreased by a factor of 1.5, but the errors on rL⋆, hz do not change. However, this plot also clearly shows that, overall, the number counts and LF measurements are much more powerful when looking at constraining the LF. However, Cℓ can still constrain the global evolution of galaxies through their mean emissivities. A first attempt was made by Amblard et al. (2011), who did not use a model of galaxies to compute the emissivities, but instead bin them in several redshift intervals and considered the values of the emissivities in these four bins as free parameters. They also required that the integrated source density is within the 68% confidence level ranges of the CIB obtained by FIRAS.
4.3. Halo occupation distribution parameters and their degeneracies
The shape of the clustering power spectra strongly depends on the HOD parameters as shown in Fig. 7. We vary Mmin, Msat, and αsat. Each panel shows the power spectrum at 160 μm measured by Lagache et al. (2007) in addition to the ones coming from the model. In each plot we vary only one HOD parameter and hold the others fixed to the values of the fiducial model, αsat = 1.4, Mmin = 1011.5 M⊙, and Msat = 1012.5 M⊙. Both the shape and amplitude vary strongly. That some similar changes are observed using different parameters suggest strong degeneracies. We compute the Fisher matrix as in Sect. 4.2, and likelihood contours at 1- and 2-σ are shown in Fig. 8. The error bars on σlog M are very large, so we fix its value to 0.65, following Tinker & Wetzel (2010), who studied the galaxy-clustering in optical surveys. Using only Cℓ we are not able to constrain its value. Mmin and Msat happen to be highly degenerated in the direction Msat = 3.3Mmin.
In previous works using optically selected galaxies, α is usually set to 1 (Gao et al. 2004) and Mmin and Msat are the only parameters to be fitted to the data. Indeed, α is hardly constrained. For instance Tinker & Wetzel (2010) used the same halo distribution number on a sample of red and blue galaxies in the range 0.4 < z < 2. They fitted their correlation function well by fixing α = 1 and leaving Mmin and Msat free. But when they left α free in addition to the two others, they obtain unrealistic values for α (Tinker & Wetzel 2010). However, setting α = 1 might not be appropriate for CIBA. The halo model is commonly used in galaxy catalogs that are not deeper than z ~ 2 and CIBA probe higher redshifts, especially at long wavelengths. Moreover optically-selected galaxies are not only star-forming galaxies, and there is no reason why optically selected galaxies and star-forming galaxies should behave in the same way. Magliocchetti et al. (2008) used a similar form of the halo model to analyze the angular correlation function of 24 μm sources at 0.6 < z < 1.2 and 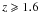 . Using two halo density profiles (NFW and a steeper one ρ ~ r-3), they derived α ~ 0.7 for the steeper profile and α ~ 0.8 for the NFW one. They get the same results for both sets of data. In contrast, Cooray et al. (2010) computed the angular correlation function of sources detected at 250, 350, and 500 μm in Herschel/SPIRE data. They use the same halo distribution as ours to get α = 1.3 ± 0.4, α < 1.8, and < 1.6 at 250, 350, and 500 μm, respectively. Finally, the Planck Collaboration et al. (2011) derive values of α that are compatible with one. The discrepancy with Magliocchetti et al. (2008) may be due to the different properties of the bright galaxies selected at 24 μm and those that contribute to the CIBA at longer wavelengths. Here by combining all CIBA measurements from 100 μm to 1.3 mm and low to high multipoles, α is well constrained, and it is not strongly degenerated with other parameters. Values of α > 1 imply that higher mass halos contribute relatively more than smaller mass ones compared to the halos with optical galaxies such as those used by Tinker & Wetzel (2010).
. Using two halo density profiles (NFW and a steeper one ρ ~ r-3), they derived α ~ 0.7 for the steeper profile and α ~ 0.8 for the NFW one. They get the same results for both sets of data. In contrast, Cooray et al. (2010) computed the angular correlation function of sources detected at 250, 350, and 500 μm in Herschel/SPIRE data. They use the same halo distribution as ours to get α = 1.3 ± 0.4, α < 1.8, and < 1.6 at 250, 350, and 500 μm, respectively. Finally, the Planck Collaboration et al. (2011) derive values of α that are compatible with one. The discrepancy with Magliocchetti et al. (2008) may be due to the different properties of the bright galaxies selected at 24 μm and those that contribute to the CIBA at longer wavelengths. Here by combining all CIBA measurements from 100 μm to 1.3 mm and low to high multipoles, α is well constrained, and it is not strongly degenerated with other parameters. Values of α > 1 imply that higher mass halos contribute relatively more than smaller mass ones compared to the halos with optical galaxies such as those used by Tinker & Wetzel (2010).
 |
Fig. 7 CIBA power spectrum at 160 μm obtained using several values of αsat,Mmin, and Msat. The level of the Poisson noise has also been added to the power spectra (black continous line). Pink dots are the data from Lagache et al. (2007) at 160 μm. When fixed, the parameters are those of the fiducial model, αsat = 1.4, Mmin = 1011.5 M⊙, and Msat = 1012.5 M⊙. Left panel: the blue line is for αsat = 1.8, the green one for αsat = 1.4 and the black one for αsat = 1. Middle panel: the blue line is the clustering power spectrum for Mmin = 1012.5 M⊙, the green one for Mmin = 1011.5 M⊙, and the black one for Mmin = 1010.5 M⊙. Right panel: the blue line is for Msat = 1013.5 M⊙, the green one for Msat = 1012.5 M⊙, and the black one for Msat = 1011.5 M⊙. |
In our analysis of the degeneracies of the halo parameters we have only considered a set of parameters identical for all wavelengths, which is not the case in reality. It could thus be that the degeneracies depend on wavelength. We therefore checked that the degeneracies did not change significantly when we compute the Fisher matrix with various set of parameters corresponding to the wavelength best-fit models.
The halo parameters cannot be constrained by counts or luminosity functions, as they only intervene in the clustering of galaxies in the equation of the Cℓ (see Eq. (8)). Therefore we cannot carry a joint analysis of the degeneracies of the halo parameters using counts/LF and Cℓ data all together. In principle, we could extrapolate the number count measurements to constrain the total number of galaxies, which also depends on the HOD parameters, but this would be a difficult measurement as it would strongly depends on the flux cut, for example.
Emissivities are given by the model of galaxy evolution, but we want to investigate the degeneracies if they are binned in redshift and if their values considered as free parameters as in Amblard et al. (2011). They did this analysis at redshift between 0 and 4. To be coherent with what has been done previously and to take advantage of our redshift range from 0 to 7, we split the whole redshift range in four bins, 0 < z < 0.9, 0.9 < z < 2, 2 < z < 3.5, 3.5 < z < 7. For each bin i we take the mean value of the emissivity that we call bj,i with i = { 1,2,3,4 } and compute the Cℓ at 350 μm (assuming a combined Planck and Herschel power spectrum) and the associated Fisher matrix. Confidence levels are given in Fig. 9. First we see that the halo occupation number degeneracies do not change much (see the previous paragraph) apart from the error bars, which are much larger. Mmin is still strongly degenerated with Msat such as Msat = 2.7Mmin. The direction of the degeneracy is roughly the same as derived using emissivities of the model, as well as those of σlog M and Msat and Mmin. Therefore, the degeneracy directions are all similar, using the emissivities or leaving them free.
 |
Fig. 8 1σ (blue) and 2σ (green) likelihood contours of the halo model parameters computed with mock data from 100 μm to 1.3 mm. |
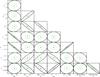 |
Fig. 9 1σ (green) and 2σ (black) likelihood contours of the halo model parameters computed with mock data at 350 μm. Instead of using emissivities coming from the model of galaxies, we split Cℓ into four redshift bins, on which we use the mean value of the emissivity on each bin bj,i that we consider as free parameters. |
 |
Fig. 10 Contribution of halo masses and redshift to the Cℓ from 100 μm to 2 mm. The first column shows the redshift and mass contribution to the 1-halo term (ℓ = 2002) and the second column represents the same contributions to the 2-halo term (ℓ = 100). The light gray corresponds to the highest contribution to the Cℓs. The step of the color range is logarithmic, and the scale is the same for both columns. |
 |
Fig. 11 Redshift distribution for several wavelengths for halo parameters different from the values of the fiducial model. The left panels are for log Mmin = 10.5 instead of log Mmin = 11.5 and the right panels for α = 1 instead of αsat = 1.4. |
The degeneracies of the bj with the halo parameters depend on the redshift. Indeed, αsat is highly degenerated with bj1 (0 < z < 0.9) and bj2 (0.9 < z < 2) and not at all with bj3 (2 < z < 3.5) and bj4 (3.5 < z < 7). Therefore αsat is constrained by z > 2 galaxies, whereas the other halo parameters behave in the opposite way: they are not degenerate with bj1 and bj2 but are with bj3 and bj4. This redshift dependency is emphasized by their own degeneracies: bj1 and bj2 are strongly correlated, and the same is true for bj3 and bj4. The degeneracies using other wavelengths are only slightly different, we do not show them here. In general, the couples (bj1,bj2) and (bj3,bj4) are always strongly degenerate and the bj,i are degenerate with the halo parameters, as shown in Fig. 9. Such a degeneracy dependence with the redshift still has to be understood.
To compare our results with those of Amblard et al. (2011), we did a similar analysis using their redshift bins, that is to say, 0 < z < 1, 1 < z < 2, 2 < z < 3 and 3 < z < 4. We observe the same behavior as described previously but different from their results. They used Monte Carlo Markov chains to compute the degeneracies, and the two-dimensional probability distributions usually have two peaks (see their Fig. S 13). Their Si are equivalent to our bj,i and S1 is degenerate with the three others Si, whereas there is no degeneracy between S3 and S4. We do not discuss the degeneracy of the halo parameters with Si as their parameterization of the halo occupation number slightly differ from ours.
Using bj,i and fitting them on the data avoids us to rely on a model of evolution of galaxies. However, they are poorly constrained with the present data. Moreover, the degeneracies between the bj,i and the halo parameters strongly depend on the halo parameterization used.
5. Interpreting measurements
Now that we have determined a model and the associated parameters degeneracies, we discuss their physical interpretation.
5.1. Redshift and halo-masses contribution to the power spectrum
The left hand panel of Fig. 15 shows the contribution to the Cℓ by several redshift bins. As stated previously, the shorter the wavelength, the more important is the relative contribution from the low redshift. For example, while z < 0.7 contributes significantly at 100 and 160 μm, it becomes much less important in the millimeter range. Reversely, the high-redshift bin (z > 3) is negligible at short wavelength but has an increasing contribution when the wavelength increases. The redshift distribution can change with the choice of the halo parameters as shown in Fig. 11. We changed the values of αsat in the left hand panels and that of Mmin in the right panels (the change is in the 1σ error bars of the best fit found by Planck Collaboration et al. 2011), the other parameters are those of the fiducial model. We recover the trend noticed above more or less emphasized.
Furthermore, not only does the redshift of the galaxies probed depend on the wavelength, but so does the mass of the halos in which they are embedded. Figure 10 shows the contribution of mass and redshift to the 1- and 2-halo terms (at ℓ = 2002 and ℓ = 100, respectively) from 100 μm to 2 mm. High-mass halos (M > 1013 M⊙) contribute more to the 1-halo term from 100 μm to 2 mm at low redshift, and this dominant mass range stays constant with wavelength. More massive halos contain more galaxies than smaller ones, therefore the galaxies contained in those halos contribute more to the angular power spectrum. This can be explained qualitatively in the following way. According to the mass function, at say z = 0.5, there are one thousand times more halos of M = 1011 M⊙/h than halos of mass M = 1014M⊙/h. According to the HOD, one out of one hundred 1011M⊙/h halo hosts a galaxy, whereas M = 1014M⊙/h mass halos hosts on average ten galaxies. Since the contribution to the one-halo terms goes like 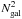 , more massive halos contribute relatively more to the one-halo term. This trend is less prononced for the two-halo term since it goes like Ngal. At all wavelengths, as the redshift increases, the dominant mass range decreases to M ~ 1011 − 13 M⊙ as halos at higher redshifts are smaller than those at z = 0.
, more massive halos contribute relatively more to the one-halo term. This trend is less prononced for the two-halo term since it goes like Ngal. At all wavelengths, as the redshift increases, the dominant mass range decreases to M ~ 1011 − 13 M⊙ as halos at higher redshifts are smaller than those at z = 0.
The 2-halo term does not exhibit the same behavior: at short wavelengths, halos in a wide range of mass 1011 − 1015 M⊙ at low z contribute to the power spectrum. In parallel, intermediate masses contribute at higher z. As the wavelength increases, the relative contribution between high mass at low z and intermediate mass at high z becomes close to unity. It ends up in an equal contribution from high mass at low z and from intermediate mass at high z at 2 mm. Intermediate mass halos are more abundant which explains their high contribution. Both the 1 and 2-halo terms are sensitive to different mass regimes which evolve with the wavelength and thus with the redshift.
Magliocchetti et al. (2008) selected 24 μm sources at 1.5 < z < 3 and deduced from their correlation function that they lie in 1013 M⊙ halos. Viero et al. (2009) found an Meff ~ 1013.2 M⊙ for unresolved galaxies at z > 1 at 250, 350, and 500 μm. Brodwin et al. (2008) derive the angular autocorrelation function of dust-obscured galaxies selected with a color criterion. They determined that they are in halos with an average mass of 1012.2 M⊙. Gilli et al. (2007) selected star-forming galaxies at 24 μm, derived the projected correlation function and found that LIRGs lie in halos M > 3 × 1013 M⊙. All these results agrees with ours. Overall, halos with masses such as 1012 − 13 M⊙ contribute the most to power spectra at all redshifts. However, we want to reemphasize here that these conclusions are model-dependent and depend on the particular emissivity model used, as discussed before. This is particularly true for the higher-z contribution, say z > 2.
 |
Fig. 12 Linear bias for several values of k (in (Mpc/h)-1) and HOD bias. Light blue squares and diamonds bias values from resolved galaxies and pink crosses represent biases from unresolved galaxies measurements (see Table 4). The big blue squares represent the HOD biases coming from resolved galaxies from Cooray et al. (2010). Light blue diamonds and squares show HOD and linear biases, respectively. |
5.2. Linear bias
Within our halo model we derive the linear bias as a function of the redshift 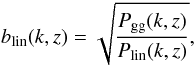 (20)where Pgg(k,z) is the galaxy-galaxy power spectrum coming from our model, Plin(k,z) is the linear DM power spectrum and blin(k,z) the linear bias.
(20)where Pgg(k,z) is the galaxy-galaxy power spectrum coming from our model, Plin(k,z) is the linear DM power spectrum and blin(k,z) the linear bias.
We will call the effective bias coming from the HOD model, bHOD. On large scale u(k → 0,M) ~ 1, so the HOD bias from Eq. (12) is 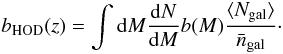 (21)In Fig. 12 we plot the linear biases and the HOD bias for our fiducial model as a function of redshift for k = 1 (Mpc/h)-1 and k = 10-2 (Mpc/h)-1, where we also add current measurements detailed in Table 4.
(21)In Fig. 12 we plot the linear biases and the HOD bias for our fiducial model as a function of redshift for k = 1 (Mpc/h)-1 and k = 10-2 (Mpc/h)-1, where we also add current measurements detailed in Table 4.
Linear and effective bias measurements.
In the linear regime, the HOD and linear biases are identical, which is the case at k = 10-2 (Mpc/h)-1 but not at k = 1 (Mpc/h)-1. On small spatial scales, the u(k → 0,M) ~ 1 is not true therefore it is strongly different from the linear bias for k = 1 as shown in Fig. 12.
For both scales, our linear biases as well as the HOD bias does not agree with measurements. Neither of them show the same trend as the data points. The measured linear biases, as well as the HOD biases, grow quicker towards higher values than the biases extracted from our model.
HOD bias measurements are from different HOD. Cooray et al. (2010) use the same halo occupation number to fit the correlation function, and they find different parameters than ours. When using their parameters set, we do recover their results. The discrepancy could be explained by the fact that these measurements result from correlation function analysis, thus from resolved sources that are not the population we are studying here.
Concerning the linear bias determined with unresolved galaxies (Lagache et al. 2007; Viero et al. 2009), our linear bias does not agree with the measurements either. Indeed when using unresolved sources, the determination of the bias requires the use of emissivities, which are strongly model dependent (see Sect. 5.3), and this can affect the bias.
5.3. Influence of the mean emissivities
Previous models such as those of Lagache et al. (2007) and Viero et al. (2009) have used emissivities coming from Lagache et al. (2004). In Fig. 13, we plot the emissivity used in this paper, as well as the Lagache et al. (2004) ones for reference. The peak at z ~ 1 in our emissivities is due to the parameterization of the LF. Despite the shapes of the emissivities of Lagache et al. (2004) and ours are different, they display similar trends. The relative contributions of high redshifts increases with wavelength, while the contribution of low redshifts decreases. According to Jauzac et al. (2011), the model of Lagache et al. (2004) predicts too much power at high z. As the latter is forced to reproduce levels of the CIB and number counts, it does not predict enough power at low z. Therefore it predicts more galaxies at high z and less at low z. To illustrate how it influences our results, we show in Fig. 14 the ratios of the power spectra computed with our emissivities and those from Lagache et al. (2004). Up to 550 μm the ratio is around 1 up to ℓ ~ 10 000, and it increases strongly at higher ℓ. At longer wavelength, the difference is much larger. It is in line with the overprediction of power at high redshift of the model of Lagache et al. (2004). The same halo parameters have been used for this plot; however, it is clear that when fitting the model to the data with both emissivities, we will not find the same halo parameters.
 |
Fig. 13 Emissivities used by Viero et al. (2009) coming from Lagache et al. (2004) (red continous line) and ours (black dotted line) coming from Béthermin et al. (2011) at several wavelengths. |
 |
Fig. 14 Power spectra ratios computed using the emissivities of Lagache et al. (2004) (Cℓ, lag) and Béthermin et al. (2011) (Cℓ,us), for several wavelengths. |
As said previously, the Lagache et al. (2004) model predicts too much power at high z, thus we need to compare the contribution in redshift to the Cℓ. They are given in Fig. 15. In both cases we observe the same trend: high redshift contributes more and more as the wavelength increases. However, this evolution goes faster with the Lagache et al. (2004) emissivities . For instance, at 250 μm, the contribution of 1.5 < z < 3 galaxies is within an order of magnitude of those of 0.7 < z < 1.5, whereas in our case the former is more than one order of magnitude less than to the latter. As we go towards longer wavelengths, the two highest redshift bins have an increasing contribution, and both dominate the power spectrum at 850 μm using Lagache et al. (2004) emissivities whereas using our emissivities 0.7 < z < 1.5 galaxies also contribute strongly. At 1.3 and 2 mm both the highest redshift bins contribute the most, but in our case, only the highest redshift bin dominate and the 1.5 < z < 3 bin has a smaller contribution. Therefore the shape of the emissivities strongly influences our results, parameters determination, and redshift distribution. The interpretation of clustering measurements is thus based using a reliable model of evolution of galaxies.
5.4. Contribution of LIRGs and ULIRGs
Star-forming galaxies are split to several categories according to their luminosities. Normal, luminous infrared, and ultra luminous infrared galaxies have luminosities of LIR < 1011 L⊙, 1011 L⊙ < LIR < 1012 L⊙, and LIR > 1012 L⊙, respectively. LIRGs dominate the infrared energy output at z ~ 1 and ULIRGs at z ~ 2 (Pérez-González et al. 2005; Le Floc’h et al. 2005; Caputi et al. 2007) therefore we look at their contribution to the Cℓ and to their evolution with the wavelength. To do so we split the emissivities in the following way: 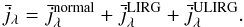 (22)This contribution is squared in the Cℓ. Therefore cross terms appear:
(22)This contribution is squared in the Cℓ. Therefore cross terms appear: 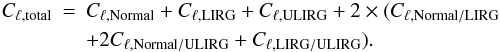 (23)We plot in Fig. 16 the contributions of normal, LIRGs, and ULIRGs. The sum of the three contributions does not make the total power spectrum because the cross terms are not shown.
(23)We plot in Fig. 16 the contributions of normal, LIRGs, and ULIRGs. The sum of the three contributions does not make the total power spectrum because the cross terms are not shown.
Normal galaxies and LIRGs both dominate the power spectrum up to 550 μm. The contribution of LIRGs increases slightly and finally dominates from 850 μm to 2 mm. ULIRGs never clearly dominate the power spectrum at long wavelengths; however, their relative contribution increases at long wavelengths, from 850 μm to 2 mm.
Therefore, we do recover what is expected from previous works. Normal galaxies dominate at low redshift, LIRGs at z ~ 1, and ULIRGs contribute in the same way as the others at high redshift, hence at long wavelengths.
 |
Fig. 15 Redshift contribution to the Cℓ at several wavelengths using our emissivities on the left and using Lagache et al. (2004) emissivity on the right. In both cases, the contribution of high redshift increases with the wavelength but the evolution goes faster with Lagache et al. (2004) emissivities. These redshift distributions are strongly varying with the halo parameters (see Fig. 10). |
 |
Fig. 16 Contribution to the Cℓ of normal galaxies, LIRGs, and ULIRGs at several wavelengths. When computing power spectra by splitting the contributions of normal galaxies, LIRGs, and ULIRGs, cross terms appear. We do not not show them on that plot, therefore the sum of the three power spectra do not make the total. |
6. Conclusion
We presented a new model of the clustering of star-forming galaxies in the CIB anisotropies. We interfaced a parametric model of star-forming galaxy evolution with a halo distribution approach. The model is fully parametric. Fixing the cosmology depends on the parameters of the model of galaxies and the HOD. We computed power spectra from 100 μm to 2 mm for IRAS, Spitzer/MIPS, Herschel/SPIRE and Planck/HFI spectral bands. We showed how power spectra can depend on the parameters, and we concluded that the parameters of the model of galaxies can hardly be constrained using only Cℓ. Number counts and luminosity functions data are required. After fixing them at the mean values found by Béthermin et al. (2011), we explored the HOD parameters constraints and degeneracies. The combination of Cℓ and counts/LF data do not break the degeneracies, but constraints are slightly improved. Some of the parameters are strongly degenerate, especially Mmin and Msat with Msat = xMmin with x ~ 3 where x is the direction of the degeneracy.
We have shown that the 1-halo term can be detected at all wavelengths and that galaxies at high redshift lie in smaller halos than those at lower redshift. The level of the shot noise might not be reached with certain instruments such as Planck because of their angular resolution. However, this does not apply to the South Pole Telescope and to Herschel because they have a better angular resolution.
Using our fiducial model, we computed the halo mass and redshift contribution to the power spectra. Higher redshift galaxies contribute more at long wavelengths. Not surprisingly, the 1- and 2- halo terms do not have the same mass dependence. We found that high-mass halos contribute the most to the 1-halo term, whereas the 2-halo term is dominated by intermediate mass halos, which are more numerous. Our model strongly depends on the emissivity given by the evolution model of galaxies, and we compare the resulting Cℓs with those obtained using the emissivities coming from Lagache et al. (2004). We have shown that the halo parameters are dependent on the emissivities when data are fitted.
To avoid using a model of galaxy evolution, we split the redshift range into four bins and computed the Cℓ using the mean emissivity on these four redshift bins as in Amblard et al. (2011). We considered these four parameters as free. They are not very well constrained, they cannot give any constraints on models of galaxies.
We investigate the contribution of LIRGs and ULIRGs to the power spectra and its evolution with the wavelength. Our results agree with previous studies of normal galaxies, LIRGs, and the ULIRG contribution to the CIB and to the luminosity functions. Normal galaxies dominate the power spectrum at low redshift. As the redshift increases, LIRGs dominate Cℓ. Meanwhile, the contribution of ULIRGs keeps increasing up to 2 mm.
The main unknown in CIB anisotropies power spectrum measurements is the redshift distributions of CIB galaxies. The coming results from Planck and Herschel will enable a big leap in how the clustering of star-forming galaxies and its redshift evolution are understood by measuring the cross power spectra between wavelengths. These new measurements will help to break some degeneracies up and will allow more precise measurements of the star formation density at high redshift and the characteristic mass of the dark matter halo at which the efficiency of the star formation is at his maximum.
Acknowledgments
Part of the research described in this paper was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. The authors would like to thank Mathieu Langer for very useful comments that improved this manuscript.
References
- Amblard, A., & Cooray, A. 2007, ApJ, 670, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Amblard, A., Cooray, A., Serra, P., et al. 2011, Nature, 470, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Austermann, J. E., Dunlop, J. S., Perera, T. A., et al. 2010, MNRAS, 401, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Magnelli, B., Lutz, D., et al. 2010, A&A, 518, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Beelen, A., & Aussel, H. 2010, A&A, 512, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Lagache, G., Le Borgne, D., & Penin, A. 2011, A&A, 529, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brodwin, M., Dey, A., Brown, M. J. I., et al. 2008, ApJ, 687, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K. I., Dole, H., Lagache, G., & Puget, J. 2006, A&A, 454, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caputi, K. I., Lagache, G., Yan, L., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., Amblard, A., Wang, L., et al. 2010, A&A, 518, L22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Farrah, D., Lonsdale, C. J., Borys, C., et al. 2006, ApJ, 641, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez-Conde, N., Lagache, G., Puget, J. L., & Dole, H. 2008, A&A, 481, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, J. W., & Atacama Cosmology Telescope Team 2010, BAAS, 41, 599 [NASA ADS] [Google Scholar]
- Gao, L., White, S. D. M., Jenkins, A., Stoehr, F., & Springel, V. 2004, MNRAS, 355, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Daddi, E., Chary, R., et al. 2007, A&A, 475, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossan, B., & Smoot, G. F. 2007, A&A, 474, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haiman, Z., & Knox, L. 2000, ApJ, 530, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, N. R., Keisler, R., Knox, L., et al. 2010, ApJ, 718, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Jauzac, M., Dole, H., Le Floc’h, E., et al. 2011, A&A, 525, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Knox, L., Cooray, A., Eisenstein, D., & Haiman, Z. 2001, ApJ, 550, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Abergel, A., Boulanger, F., Désert, F. X., & Puget, J. 1999, A&A, 344, 322 [NASA ADS] [Google Scholar]
- Lagache, G., Dole, H., & Puget, J. L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Dole, H., Puget, J. L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Bavouzet, N., Fernandez-Conde, N., et al. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Magliocchetti, M., Silva, L., Lapi, A., et al. 2007, MNRAS, 375, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Magliocchetti, M., Cirasuolo, M., McLure, R. J., et al. 2008, MNRAS, 383, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Magliocchetti, M., Santini, P., Rodighiero, G., et al. 2011, MNRAS, 1055 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Wang, L., Smith, A. J., et al. 2010, A&A, 518, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Pénin, A., Lagache, G., Noriega-Crepo, A., et al. 2011, A&A, submitted [arXiv:1105.1463] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puget, J., Abergel, A., Bernard, J., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
- Saunders, W., Rowan-Robinson, M., Lawrence, A., et al. 1990, MNRAS, 242, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Saunders, W., Rowan-Robinson, M., & Lawrence, A. 1992, MNRAS, 258, 134 [NASA ADS] [Google Scholar]
- Scott, K. S., Yun, M. S., Wilson, G. W., et al. 2010, MNRAS, 405, 2260 [NASA ADS] [Google Scholar]
- Tinker, J. L., & Wetzel, A. R. 2010, ApJ, 719, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Wechsler, R. H., & Zheng, Z. 2010, ApJ, 709, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1766 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Shot noise levels in Jy2/sr from Béthermin et al. (2011) for available measurements of CIBA power spectra.
All Figures
 |
Fig. 1 CIB per redshift bins from the model of Béthermin et al. (2011). The high redshift contribution increases with the wavelength. |
| In the text | |
 |
Fig. 2 Emissivities versus the redshift for different wavelengths. |
| In the text | |
 |
Fig. 3 Number of galaxies versus dark matter halo mass. The blue dashed line shows the central galaxies, the red dotted-dashed line shows satellite galaxies and the black continuous line shows the total. We use the parameters of our fiducial model (see Sect. 4), that is to say log Mmin = 11.5, Msat = 10Mmin and α = 1.4 |
| In the text | |
 |
Fig. 4 CIB anisotropies power spectra at several wavelengths. The continous black line shows the power spectra of the clustering. The dotted black line is the 1-halo term of the power spectrum, and the dashed line is the 2-halo term. The blue horizontal line represents the shot noise level and the red dot-dashed curve is the total power spectrum. Titles of the plots give the reference for the shot noise level and the bandpass filters used. |
| In the text | |
 |
Fig. 5 1σ (dashed green), 2σ (dash-dot blue), 3σ (black) likelihood contours of the galaxy evolution model parameters rL⋆, hz, rL⋆, lz, and rφ⋆, hz. Top, middle and bottom panels show the contours computed using counts/LF data, Cℓ data only, and combined counts/LF and Cℓ data, respectively. The continous line shows the direction of degeneracy using only counts/LF, the dotted line shows that using Cℓ and the dashed line is uses all data. |
| In the text | |
 |
Fig. 6 Counts at 160 μm, emissivities, and clustering power spectrum for three values of rL⋆, lz, the best fit, and the best fit ± 2σ. Pink crosses are data: Béthermin et al. (2010) for the counts and Lagache et al. (2007) for the power spectrum. Top panel: differential number counts at 160 μm. 2nd panel: mean emissivities at 160 μm. 3rd panel: ratio of the modified emissivities compared to the best fit one at 160 μm. 4th panel: power spectra of the clustering at 160 μm. Bottom panel: ratio of the modified power spectra compared to the best fit one at 160 μm. A small change in rL⋆, lz leads to a 20% modification of the emissivities and on 15–35% on the Cℓ. |
| In the text | |
 |
Fig. 7 CIBA power spectrum at 160 μm obtained using several values of αsat,Mmin, and Msat. The level of the Poisson noise has also been added to the power spectra (black continous line). Pink dots are the data from Lagache et al. (2007) at 160 μm. When fixed, the parameters are those of the fiducial model, αsat = 1.4, Mmin = 1011.5 M⊙, and Msat = 1012.5 M⊙. Left panel: the blue line is for αsat = 1.8, the green one for αsat = 1.4 and the black one for αsat = 1. Middle panel: the blue line is the clustering power spectrum for Mmin = 1012.5 M⊙, the green one for Mmin = 1011.5 M⊙, and the black one for Mmin = 1010.5 M⊙. Right panel: the blue line is for Msat = 1013.5 M⊙, the green one for Msat = 1012.5 M⊙, and the black one for Msat = 1011.5 M⊙. |
| In the text | |
 |
Fig. 8 1σ (blue) and 2σ (green) likelihood contours of the halo model parameters computed with mock data from 100 μm to 1.3 mm. |
| In the text | |
 |
Fig. 9 1σ (green) and 2σ (black) likelihood contours of the halo model parameters computed with mock data at 350 μm. Instead of using emissivities coming from the model of galaxies, we split Cℓ into four redshift bins, on which we use the mean value of the emissivity on each bin bj,i that we consider as free parameters. |
| In the text | |
 |
Fig. 10 Contribution of halo masses and redshift to the Cℓ from 100 μm to 2 mm. The first column shows the redshift and mass contribution to the 1-halo term (ℓ = 2002) and the second column represents the same contributions to the 2-halo term (ℓ = 100). The light gray corresponds to the highest contribution to the Cℓs. The step of the color range is logarithmic, and the scale is the same for both columns. |
| In the text | |
 |
Fig. 11 Redshift distribution for several wavelengths for halo parameters different from the values of the fiducial model. The left panels are for log Mmin = 10.5 instead of log Mmin = 11.5 and the right panels for α = 1 instead of αsat = 1.4. |
| In the text | |
 |
Fig. 12 Linear bias for several values of k (in (Mpc/h)-1) and HOD bias. Light blue squares and diamonds bias values from resolved galaxies and pink crosses represent biases from unresolved galaxies measurements (see Table 4). The big blue squares represent the HOD biases coming from resolved galaxies from Cooray et al. (2010). Light blue diamonds and squares show HOD and linear biases, respectively. |
| In the text | |
 |
Fig. 13 Emissivities used by Viero et al. (2009) coming from Lagache et al. (2004) (red continous line) and ours (black dotted line) coming from Béthermin et al. (2011) at several wavelengths. |
| In the text | |
 |
Fig. 14 Power spectra ratios computed using the emissivities of Lagache et al. (2004) (Cℓ, lag) and Béthermin et al. (2011) (Cℓ,us), for several wavelengths. |
| In the text | |
 |
Fig. 15 Redshift contribution to the Cℓ at several wavelengths using our emissivities on the left and using Lagache et al. (2004) emissivity on the right. In both cases, the contribution of high redshift increases with the wavelength but the evolution goes faster with Lagache et al. (2004) emissivities. These redshift distributions are strongly varying with the halo parameters (see Fig. 10). |
| In the text | |
 |
Fig. 16 Contribution to the Cℓ of normal galaxies, LIRGs, and ULIRGs at several wavelengths. When computing power spectra by splitting the contributions of normal galaxies, LIRGs, and ULIRGs, cross terms appear. We do not not show them on that plot, therefore the sum of the three power spectra do not make the total. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


