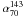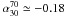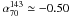| Issue |
A&A
Volume 536, December 2011
Planck early results
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116471 | |
| Published online | 01 December 2011 | |
Planck early results. XIII. Statistical properties of extragalactic radio sources in the Planck Early Release Compact Source Catalogue⋆
1
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
2
Agenzia Spaziale Italiana Science Data Center, c/o ESRIN, via Galileo Galilei, Frascati, Italy
3
Astroparticule et Cosmologie, CNRS (UMR7164), Université Denis Diderot Paris 7, Bâtiment Condorcet, 10 rue A. Domon et Léonie Duquet, Paris, France
4
Astrophysics Group, Cavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge CB3 0HE, UK
5
Atacama Large Millimeter/submillimeter Array, ALMA Santiago Central Offices, Alonso de Cordova 3107, Vitacura, Casilla 763 0355, Santiago, Chile
6
Australia Telescope National Facility, CSIRO, PO Box 76, Epping, NSW 1710, Australia
7
CITA, University of Toronto, 60 St. George St., Toronto, ON M5S 3H8, Canada
8
CNRS, IRAP, 9 Av. Colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
9
California Institute of Technology, Pasadena, California, USA
10 Centre of Mathematics for Applications, University of Oslo, Blindern, Oslo, Norway
11
DAMTP, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
12
DSM/Irfu/SPP, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
13
DTU Space, National Space Institute, Juliane Mariesvej 30, Copenhagen, Denmark
14
Departamento de Física, Universidad de Oviedo, Avda. Calvo Sotelo s/n, Oviedo, Spain
15
Departamento de Matemáticas, Universidad de Oviedo, Avda. Calvo Sotelo s/n, Oviedo, Spain
16
Department of Astronomy and Astrophysics, University of Toronto, 50 Saint George Street, Toronto, Ontario, Canada
17
Department of Physics & Astronomy, The Open University, Milton Keynes, MK7 6AA, UK
18
Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, British Columbia, Canada
19
Department of Physics and Astronomy, University of Southern California, Los Angeles, California, USA
20
Department of Physics, Gustaf Hällströmin katu 2a, University of Helsinki, Helsinki, Finland
21
Department of Physics, Purdue University, 525 Northwestern Avenue, West Lafayette, Indiana, USA
22
Department of Physics, University of California, Berkeley, California, USA
23
Department of Physics, University of California, One Shields Avenue, Davis, California, USA
24
Department of Physics, University of California, Santa Barbara, California, USA
25
Department of Physics, University of Illinois at Urbana-Champaign, 1110 West Green Street, Urbana, Illinois, USA
26
Dipartimento di Fisica G. Galilei, Universitàdegli Studi di Padova, via Marzolo 8, 35131 Padova, Italy
27
Dipartimento di Fisica, Università La Sapienza, P. le A. Moro 2, Roma, Italy
28
Dipartimento di Fisica, Università degli Studi di Milano, via Celoria, 16, Milano, Italy
29
Dipartimento di Fisica, Università degli Studi di Trieste, via A. Valerio 2, Trieste, Italy
30
Dipartimento di Fisica, Università di Ferrara, via Saragat 1, 44122 Ferrara, Italy
31
Dipartimento di Fisica, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, Roma, Italy
32
Discovery Center, Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
33
Dpto. Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
34
European Southern Observatory, ESO Vitacura, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago, Chile
35
European Space Agency, ESAC, Planck Science Office, Camino bajo del Castillo, s/n, Urbanización Villafranca del Castillo, Villanueva de la Cañada, Madrid, Spain
36
European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
37
Haverford College Astronomy Department, 370 Lancaster Avenue, Haverford, Pennsylvania, USA
38
Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University of Helsinki, Helsinki, Finland
39
IFSI/INAF, via del Fosso Cavaliere 100, 00133, Roma, Italy
40
INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78, Catania, Italy
41
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, Padova, Italy
42
INAF – Osservatorio Astronomico di Roma, via di Frascati 33, Monte Porzio Catone, Italy
43
INAF – Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, Trieste, Italy
44
INAF/IASF Bologna via Gobetti 101, Bologna, Italy
45
INAF/IASF Milano, via E. Bassini 15, Milano, Italy
46
INRIA, Laboratoire de Recherche en Informatique, Université Paris-Sud 11, Bâtiment 490, 91405 Orsay Cedex, France
47
IPAG: Institut de Planétologie et d’Astrophysique de Grenoble, Université Joseph Fourier, Grenoble 1/CNRS-INSU, UMR 5274, 38041 Grenoble, France
48
ISDC Data Centre for Astrophysics, University of Geneva, Ch. d’Écogia 16, Versoix, Switzerland
49
Imperial College London, Astrophysics group, Blackett Laboratory, Prince Consort Road, London, SW7 2AZ, UK
50
Infrared Processing and Analysis Center, California Institute of Technology, Pasadena, CA 91125, USA
51
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université Paris-Sud 11, Bâtiment 121, Orsay, France
52
Institut d’Astrophysique de Paris, CNRS UMR 7095, Université Pierre & Marie Curie, 98bis boulevard Arago, Paris, France
53
Institute of Astronomy and Astrophysics, Academia Sinica, Taipei, Taiwan
54
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
55 Institute of Theoretical Astrophysics, University of Oslo, Blindern, Oslo, Norway
56
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, Tenerife, Spain
57
Instituto de Física de Cantabria (CSIC-Universidad de Cantabria), Avda. de los Castros s/n, Santander, Spain
58
Istituto di Fisica del Plasma, CNR-ENEA-EURATOM Association, via R. Cozzi 53, Milano, Italy
59
Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California, USA
60
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
61
Kavli Institute for Cosmology Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
62
LERMA, CNRS, Observatoire de Paris, 61 avenue de l’Observatoire, Paris, France
63
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS – Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
64
Laboratoire Traitement et Communication de l’Information, CNRS (UMR 5141) and Télécom ParisTech, 46 rue Barrault, 75634 Paris Cedex 13, France
65
Laboratoire de Physique Subatomique et de Cosmologie, CNRS, Université Joseph Fourier Grenoble I, 53 rue des Martyrs, Grenoble, France
66
Laboratoire de l’Accélérateur Linéaire, Université Paris-Sud 11, CNRS/IN2P3, Orsay, France
67
Lawrence Berkeley National Laboratory, Berkeley, California, USA
68
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
69
MilliLab, VTT Technical Research Centre of Finland, Tietotie 3, Espoo, Finland
70
National University of Ireland, Department of Experimental Physics, Maynooth, Co. Kildare, Ireland
71
Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
72
Observational Cosmology, Mail Stop 367-17, California Institute of Technology, Pasadena, CA, 91125, USA
73
SISSA, Astrophysics Sector, via Bonomea 265, 34136, Trieste, Italy
74
SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
75
School of Physicsand Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff, CF24 3AA, UK
76
Space Sciences Laboratory, University of California, Berkeley, California, USA
77
Spitzer Science Center, 1200 E. California Blvd., Pasadena, California, USA
78
Stanford University, Dept of Physics, Varian Physics Bldg, 382 via Pueblo Mall, Stanford, California, USA
79
Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
80
University of Granada, Departamento de Física Teórica y del Cosmos, Facultad de Ciencias, Granada, Spain
81
University of Miami, Knight Physics Building, 1320 Campo Sano Dr., Coral Gables, Florida, USA
82
Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478 Warszawa, Poland
Received: 8 January 2011
Accepted: 21 February 2011
The data reported in Planck’s Early Release Compact Source Catalogue (ERCSC) are exploited to measure the number counts (dN/dS) of extragalactic radio sources at 30, 44, 70, 100, 143 and 217 GHz. Due to the full-sky nature of the catalogue, this measurement extends to the rarest and brightest sources in the sky. At lower frequencies (30, 44, and 70 GHz) our counts are in very good agreement with estimates based on WMAP data, being somewhat deeper at 30 and 70 GHz, and somewhat shallower at 44 GHz. Planck’s source counts at 143 and 217 GHz join smoothly with the fainter ones provided by the SPT and ACT surveys over small fractions of the sky. An analysis of source spectra, exploiting Planck’s uniquely broad spectral coverage, finds clear evidence of a steepening of the mean spectral index above about 70 GHz. This implies that, at these frequencies, the contamination of the CMB power spectrum by radio sources below the detection limit is significantly lower than previously estimated.
Key words: surveys / radio continuum: general / galaxies: active
© ESO, 2011
1. Introduction
Planck1 (Tauber et al. 2010; Planck Collaboration 2011a) is the third-generation space mission to measure the anisotropy of the cosmic microwave background (CMB). It observes the sky in nine frequency bands covering 30–857 GHz with high sensitivity and angular resolution from 31′ to 5′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1K. Polarization is measured in all but the highest two bands (Leahy et al. 2010; Rosset et al. 2010). A combination of radiative cooling and three mechanical coolers produces the temperatures needed for the detectors and optics (Planck Collaboration 2011b). Two data processing centres (DPCs) check and calibrate the data and make maps of the sky (Planck HFI Core Team 2011b; Zacchei et al. 2011). Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for galactic and extragalactic astrophysics as well as cosmology. Early astrophysics results are given in Planck Collaboration (2011h–z).
The Planck Early Release Compact Source Catalogue (ERCSC, Planck Collaboration 2011c) reports data on sources detected during the first 1.6 full-sky surveys, and thus offers, among other things, the opportunity of studying the statistical properties of extragalactic sources over a broad frequency range never fully explored by blind surveys. We will focus here on counts of extragalactic radio sources and on their spectral properties in the 30–217 GHz range2.
Although knowledge of the statistical properties at high radio frequency for this population of extragalactic sources has greatly improved in the recent past – thanks to many ground-based observational campaigns and to the Wilkinson microwave anisotropy probe (WMAP) surveys from space – above about 70 GHz these properties are still largely unknown or very uncertain. This is essentially due to the fact that very large area surveys at mm wavelengths are made difficult by the small fields of view of ground-based radio telescopes and by the long integration times required.
The most recent estimates on source number counts up to ~50−70 GHz, and the optical identifications of the corresponding bright point sources (see, e.g., Massardi et al. 2008, 2010), show that these counts are dominated by radio sources whose average spectral index is “flat”, i.e., α ≃ 0.0 (with the usual convention Sν ∝ να). This result confirms that the underlying source population is essentially made of flat spectrum radio quasars (FSRQ) and BL Lac objects, collectively called blazars3, with minor contributions coming from other source populations (Toffolatti et al. 1998; de Zotti et al. 2005). At frequencies > 100 GHz, however, there is now new information for sources with flux densities below about 1Jy coming from the South Pole Telescope (SPT) collaboration (Vieira et al. 2010), with surveys over 87 deg2 at 150 and 220 GHz, and from the Atacama Cosmology Telescope (ACT) survey over 455 deg2 at 148 GHz (Marriage et al. 2011).
The “flat” spectra of blazars are generally believed to result from the superposition of different components in the inner part of AGN relativistic jets, each with a different synchrotron self-absorption frequency (Kellermann & Pauliny-Toth 1969). At a given frequency, the observed flux density is thus dominated by the synchrotron-emitting component which becomes self-absorbed and, in the equipartition regime, the resulting spectrum is approximately flat. However, this “flat” spectrum cannot be maintained up to very high frequencies, because of electron energy losses in the dominant jet-emission component (i.e., electron ageing), or the transition to the optically-thin regime, with the onset of a “steep” spectrum with a standard spectral index α = −0.7 to −0.8. A slightly steepened spectrum may also be caused by the superposition of many jet components. The redshift moves the observed steepening to lower frequencies and, thus, a greater fraction of blazar sources are observed with a steep spectrum at sub-mm wavelengths. With current data it is not yet possible to decide among the different scenarios. However, given their sensitivity and full sky coverage, Planck surveys are uniquely able to shed light on this transition from an almost “flat” to a “steep” regime in the spectra of blazar sources.
The outline of this paper is as follows. In Sect. 2.1 we briefly sketch the main properties of the ERCSC. In Sect. 2.2 we summarize the source validation. In Sect. 2.3 we describe the complete sample selected at 30 GHz, used for the analysis of spectral properties. In Sect. 3 we present the source counts over the frequency range 30–217 GHz. In Sect. 4 we investigate the spectral index distributions in different frequency intervals. Finally, in Sect. 5 we summarize our main conclusions.
2. The Planck ERCSC
2.1. Overview
The Planck ERCSC (Planck Collaboration 2011c) lists positions and flux densities for the compact sources recovered from the Planck first 1.6 full sky survey maps in nine frequency channels between 30 and 857 GHz. Thus about 60% of the sources have been covered twice, with a time separation of about 6 months. Sources near the ecliptic poles, where the scan circles intersect, are often covered multiple times. ERCSC flux densities are therefore averages over different observing time periods. They have been calculated by aperture photometry, using the most recent definition of the beam shapes and sizes (Planck HFI Core Team 2011b; Zacchei et al. 2011). In the frequency range considered in this paper, the Planck photometric calibration is based on the CMB dipole and on the modulation induced on it by the spacecraft orbital motion. According to Zacchei et al. (2011) the absolute photometric calibration at LFI frequencies (30, 44 and 70 GHz) is at the ~1% level, while Planck HFI Core Team (2011b) reports on a relative photometric accuracy, between the frequency channels from 100 to 353 GHz, better than 2% and, more likely, at the ~1% level.
The final version of the ERCSC (see also Planck Collaboration 2011c for more details) has been created by specifically applying the so-called “PowellSnakes”detection method (Carvalho et al. 2009) to the Planck full sky (dipole subtracted) anisotropy maps in the frequency channels from 30 to 143 GHz and the SExtractor package (Bertin & Arnouts 1996) in the four channels at higher frequencies (from 217 to 857 GHz). A “compact” source is accepted in the ERCSC if it survived a set of primary and secondary selection criteria. The primary criterion utilized the feedback from the Monte Carlo Quality Assessment system and introduced a signal-to-noise ratio cut to ensure that >90% of the sources in the catalogue are reliable and have a flux density accuracy better than 30%. The secondary criterion comprised a set of cuts that removed the extended sources with an elongation >3.0 (the ratio between the major and minor axis, in pixels, of the detected source) and sources that could be potentially spurious. For instance a source is dropped whenever >5% of the pixels within 2 × FWHM of its position had invalid values (see the ERCSC Explanatory Supplement for more details). The overriding requirement in constructing the ERCSC is source reliability and not completeness.
 |
Fig.1 Comparison between the ERCSC flux densities at 30 GHz (left panel) and at 44 GHz (right panel) with the almost simultaneous ATCA measurements (PACO project) at 32.2 and 39.7 GHz, respectively. No correction for the slightly different frequencies has been applied. |
 |
Fig.2 Euclidean normalized differential number counts at the LFI frequencies. The red circles with Poisson error bars show the counts of sources with counterparts in our reference 30 GHz sample. In each panel, the solid curves show the total number counts of extragalactic radio sources predicted by the de Zotti et al. (2005) model. Also shown are: the counts estimated at 31 GHz from DASI (grey dashed box; Kovac et al. 2002) and at 33 GHz from the VSA data (grey box; Cleary et al. 2005); the counts from the PACO (grey diamonds; Bonavera et al. 2011) and the WMAP 5-yr surveys (grey squares; Massardi et al. 2009), at the closest frequencies, and the counts estimated by Waldram et al. (2007) (grey dashed line), exploiting multi-frequency follow-up observations of the 15 GHz 9C sources. The vertical dashed magenta line in the upper panel indicates the flux density completeness limit, 1.0Jy, estimated for our primary sample Sect. 2.3. |
2.2. Validation and photometry check of ERCSC sources
The validation process for the compact sources included in the Planck ERCSC was performed by two different teams, selected among members of the Planck Consortia: a validation team on radio sources (VTRS) and a validation team on far-IR sources. The two teams worked separately at first, but cross-checked their results in the second phase of the process. The processing steps and main outcomes are summarized in the Explanatory Supplement released with the ERCSC. For compact radio (i.e., synchrotron dominated) sources, the VTRS (see Planck Collaboration 2011j for a more detailed discussion) has found that >97% of the ERCSC sources at 30 GHz have reliable counterparts in published catalogues at GHz frequencies (PMN: Wright et al. 1996; GB6: Gregory et al. 1996; NVSS: Condon et al. 1998; SUMSS: Mauch et al. 2003; AT20G: Massardi et al. 2008; Murphy et al. 2010). Similar (although slightly lower) percentages were found for ERCSC sources detected at 44 and 70 GHz. At higher frequencies (≥100 GHz) Planck detects an increasing fraction of dusty galaxies, undetected by low-frequency surveys. Therefore, the source reliability was confirmed by internal matches of sources detected in two neighboring Planck frequency channels: i.e., 143 and 217 GHz, or 217 and 353 GHz, etc. However, the validation of synchrotron-dominated sources is still relatively easy to perform, since all of them must be present in low-frequency catalogues.
The WMAP 7-year catalogue (Gold et al. 2011) contains a total of 471 sources detected in at least one frequency channel. Of these, 289, 281, 166 and 59 sources are detected as ≥ 5σ peaks in the 33, 41, 61, and 94 GHz maps, respectively. The ERCSC catalogue includes 88%, 63%, 81%, and 95% of the 5σ WMAP sources at 30, 44, 70, and 100 GHz,respectively. The median of the distribution of offsets between WMAP and Planck positions are 2.5′, 2.1′, 1.7′, and 1.0′ at each of the above Planck frequency (see also Planck Collaboration 2011j for a more detailed discussion on this subject). Except for the 44 GHz channel, where Planck is known to be less sensitive, most WMAP sources that failed to be included in the Planck ERCSC (31 sources at 30 GHz) are generally at the faint end of the flux density distribution (i.e., near the detection threshold) and may have flux densities boosted by the Eddington bias or the effects of confusion, or may be spurious. The absence from the ERCSC of a few brighter WMAP sources (5 sources at 30 GHz) is probably caused by their variability.
The Planck-ATCA Co-eval Observations (PACO) project (Massardi et al. 2011) has provided measurements with the Australia Telescope Compact Array (ATCA) of sources potentially detectable by Planck almost simultaneously with Planck observations. 147 ERCSC sources have PACO observations at 32.2 and 39.7 GHz within 10 days of Planck observations. All these sources are unresolved also by ATCA. As illustrated in Fig. 1, the comparison between ATCA and ERCSC flux densities at the nearest frequencies (30 and 44 GHz, respectively), shows a reassuringly close agreement. The faintest ERCSC flux densities are obviously enhanced by the effect of the Eddington bias, the noise-increased number count of point sources to a given detection threshold, which is also enhanced in the 44 GHz Planck channel, where the noise level is higher.
2.3. The 30 GHz extragalactic radio source sample
2.3.1. Identification of compact Galactic sources
To minimize the contamination of the sample by Galactic sources we have restricted ourselves to |b| > 5° and we have also excluded sources within 5° and 2.5°, respectively, of the nominal centres of the Large and Small Magellanic Clouds. Outside these regions, a search in the SIMBAD database, with a search radius of 16′, corresponding to about half the FWHM at 30 GHz, has yielded 18 associations of ERCSC sources with known Galactic objects (5 PNe, 10 Hii regions, and 3 SNRs), all within 5′ of the ERCSC position. After having removed these sources we are left with 533 compact extragalactic radio sources detected at 30 GHz, with 97% or more of them identified in external catalogues at GHz frequencies. This constitutes our primary sample.
2.3.2. Completeness and uniformity tests
An indication of the completeness limit of our sample is obtained by looking at the differential counts (see top panel in Fig. 2): a sharp decrease of the slope at faint flux densities (Sν ≲ 1 Jy at 30 GHz) signals the onset of incompleteness. Based on the ATCA 20 GHz counts (Massardi et al. 2008; Murphy et al. 2010), we expect that the slope of the counts remains approximately constant over the limited flux density range covered by the ERCSC. Therefore, the flux density interval (or bin size) containing a fixed number of sources must decrease as a power of the central flux density. As shown in the top panel of Fig. 3, at 30 GHz this happens down to a flux density of about 0.9Jy, where the curve abruptly flattens.
We need also to test whether the spatial distribution of sources in our sample is consistent with being statistically uniform, as it must be in the case of extragalactic sources. Deviations from uniformity may be expected at lower Galactic latitudes, both because of residual contamination by unrecognized Galactic sources and through the effect of a stronger Eddington bias due to fluctuations of diffuse Galactic emission. The bottom panel of Fig. 3 shows no significant deviations from a uniform distribution on the sky for |b| > 5° if we adopt a completeness limit of ≃1.0Jy at 30 GHz. Remarkably, the average source density at |b| > 5°, D = 24.23 (in sources per sr), is very similar to the value found at |b| > 30°, D = 23.71, which guarantees that we are not losing extragalactic sources, in this frequency range, when going down to lower Galactic latitudes, and that the residual contamination due to unrecognized Galactic sources is negligible. Larger deviations from uniformity are found if we adopt fainter completeness limits. Taking into account both results, we therefore adopt Sν = 1.0 Jy as an estimate for the completeness limit at 30 GHz. Our primary sample is made of 290 sources above the adopted Sν = 1.0Jy flux density limit. As a comparison, Massardi et al. (2009) detected 281 sources at |b| > 5° and Sν > ~ 1Jy in their blind survey performed on the 5-year WMAP 33 GHz map.
In addition, we used the Planck HFI frequency channels at 143 and 217 GHz to select all the extragalactic sources in the ERCSC whose spectra are still dominated by non-thermal synchrotron emission at 217 GHz (409 sources with 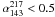 ; see Fig. 4). We limit the selection of this secondary sample to the above
; see Fig. 4). We limit the selection of this secondary sample to the above 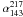 value with the purpose of excluding all possible sample contamination coming from a second population of sources dominated by thermal dust emission (
value with the purpose of excluding all possible sample contamination coming from a second population of sources dominated by thermal dust emission ( ). The choice of
). The choice of 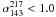 , corresponding to a minimum in the distribution, would not change our results since very few sources ( < 10) have spectral indices in the interval
, corresponding to a minimum in the distribution, would not change our results since very few sources ( < 10) have spectral indices in the interval 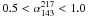 . This selection (at above 100 GHz, where there is not yet a complete match of ERCSC sources with external catalogs) is useful for comparing the outcomes from this (secondary) sample with our predictions on the statistical properties of extragalactic sources in our primary sample, selected at30 GHz.
. This selection (at above 100 GHz, where there is not yet a complete match of ERCSC sources with external catalogs) is useful for comparing the outcomes from this (secondary) sample with our predictions on the statistical properties of extragalactic sources in our primary sample, selected at30 GHz.
3. Number counts
Euclidean-normalized differential number counts per steradian estimated from the Planck ERCSC at 30–217 GHz.
Figures 2 and 5 show the number counts of extragalactic radio sources at the six Planck frequencies from 30 to 217 GHz (see also Table 1). The sharp breaks in the number counts at approximately 1.0Jy (30 GHz), 1.5Jy (44 GHz), 1.1Jy (70 GHz), 0.9Jy (100 GHz), 0.5Jy (143 GHz) and 0.4Jy (217 GHz) signal the onset of incompleteness.
The results of deeper surveys on small fractions of the sky and the WMAP differential number counts are also shown, for comparison. The agreement with WMAP data is very good. Our differential counts at 30 and 70 GHz are somewhat deeper than the WMAP ones at 33 and 61 GHz, while at 44 GHz they are somewhat shallower than the ones calculated for the 41 GHz WMAP channel. Also our counts above the completeness limits appear to join smoothly with those from deeper surveys.
At frequencies of up to 100 GHz, the predictions of the de Zotti et al. (2005) cosmological evolution model – relying on extrapolations from lower frequency data and capable of providing a very good fit to almost all data on number counts as well as on other statistics of radio sources at frequencies above 5 GHz – are in generally good agreement with our current findings. This result implies that no new radio source population shows up at bright flux densities. Very few “extreme” or “inverted-spectrum” compact radio sources are found in the Planck ERCSC. The emission and spectral properties of these sources, which are interesting in their own right, are discussed in a companion paper (Planck Collaboration 2011j).
 |
Fig.3 Completeness and uniformity tests at 30 GHz. Top panel: flux density interval, or bin size, including a fixed number of sources as a function of flux density. The change of slope at about 0.9Jy signals the onset of incompleteness. Bottom panel: uniformity test for sources with flux densities Sν ≥ 1.0Jy. The source density, D, in sources per sr, within regions at different Galactic latitudes, shows an acceptable uniformity. The horizontal grey (solid) and blue (dashed) lines show the average source density at Galactic latitudes above |b| = 5 and |b| = 30°, respectively. As it is apparent, the two values are very close to each other, within the 1σ level calculated for the overall population in the two sky areas considered here, and well inside the 1σ normalized Poisson error bars. We also checked that at flux densities below about 0.9–1.0Jy statistically more relevant deviations from a uniform distribution begin to appear. |
At higher frequencies (i.e., at 143 and 217 GHz) we also plotted the number counts obtained by using the sample of radio sources selected at 143 and 217 GHz (blue diamonds; see Sect. 2.3 and Fig. 4 for more details). These number counts (calculated from our secondary sample, 284 sources at above 0.5 Jy) turn out to be in almost perfect agreement with the ones obtained in the previous Section from our primary sample selected at 30 GHz (290 sources at Sν ≥ 1.0), thus confirming that no bright extragalactic radio sources are missed by our selection criteria and that the underlying parent population turns out to be (statistically) the same.
Figure 5 shows that the de Zotti et al. (2005) model over-predicts the bright counts by a factor of about 2 at 143 GHz and about 2.6 at 217 GHz, while it is consistent with the fainter SPT (Vieira et al. 2010) and ACT (Marriage et al. 2011) counts. As discussed in the next Section, the discrepancy between the model and our current data is due to a steepening of the spectra of ERCSC sources above about 70 GHz, not predicted by the model but, at least partially, already suggested by other data sets (González-Nuevo et al. 2008; Sadler et al. 2008).
An implication of this result is that the contamination of the CMB angular power spectrum by extragalactic radio sources below the detection limit at 143 and 217 GHz is lower than predicted by the de Zotti et al. (2005) model. Assuming a Poisson distribution (clustering effects are reduced to negligible values by the very broad luminosity function of radio sources, e.g., Toffolatti et al. 2005; de Zotti et al. 2010) and simply scaling down the model counts by the factors mentioned above, the amplitude of the angular power spectrum of unresolved sources goes down by roughly the same factor4. This is, however, an upper limit to the correction factor, especially at 217 GHz, because if we apply the factor calculated above to all flux densities we would end up with a clear underestimate of the faint counts measured by Vieira et al. (2010). Therefore, if we consider much fainter source detection limits, as foreseen for future experiments in the sub-mm, the amplitude of the angular power spectrum due to unresolved sources stays essentially at the same level as predicted by the De Zotti et al. model.
4. Spectral index distributions
 |
Fig.4 Spectral index distribution of ERCSC sources between 143 and 217 GHz. Only sources detected at 143 GHz and at 217 GHz have been considered: no upper limits on flux densities have been used in this calculation. |
 |
Fig.5 Euclidean normalized differential number counts at the HFI frequencies (100, 143, and 217 GHz). The red circles with Poisson error bars show the counts of sources with counterparts in our reference 30 GHz sample. At 143 and 217 GHz the blue diamonds (shifted to the left by half of the bin size, for clarity) show the counts obtained after removing sources with 143–217 GHz spectral index indicative of dust emission (see Sect. 2.3.2). Again, in each panel, the solid curves show the total number counts of extragalactic radio sources predicted by the de Zotti et al. (2005) evolution model. Also shown are the SPT (grey squares; Vieira et al. 2010) and ACT (grey stars; Marriage et al. 2011, counts of radio sources. At 100 GHz we also show the estimated counts by Sadler et al. (2008) from follow-up observations of a sample of sources selected from the 20 GHz ATCA survey (grey dashed line). |
Median and standard deviations of the spectral index distributions between 30 GHz and the selected frequency.
To study the spectral properties of the extragalactic radio sources in the Planck ERCSC we used our reference 30 GHz sample above the estimated completeness limit (1.0Jy; Sect. 2.3). Not all of these sources were detected at the ≥ 5σ level in each of the Planck frequency channels considered. Whenever a source was not detected in a given channel we replaced its (unknown) flux density by a 5σ upper limit, where for σ we used the average r.m.s. error estimated at each Planck frequency. The upper limits have been redistributed among the flux density bins by using a Survival Analysis technique and, more specifically, by adopting the Kaplan-Meyer estimator (as implemented in the ASURV code, Lavalley et al. 1992). Since the fraction of upper limits is always small (it reaches approximately 30% only in our less sensitive channel at 44 GHz), the spectral index distributions are reliably reconstructed at each frequency.
Table 2 gives the median spectral indices between 30 GHz and the other frequencies considered here and the dispersions of the spectral index distributions. A moderate steepening of spectral indices at higher frequencies is clearly apparent. Hints in this direction were previously found by González-Nuevo et al. (2008) from their analysis of the NEWPS sample (López-Caniego et al. 2007) and also by Sadler et al. (2008). Additional evidence of spectral steepening is presented in Planck Collaboration (2011k).
Our 30–100 GHz spectral index is close to the α ≃ −0.39 found by Sadler et al. (2008) between 20 and 95 GHz, for a sample with 20 GHz flux density S > 150mJy. Moreover, our 30–143 GHz median spectral index is in very good agreement with the one found by Marriage et al. (2011) for their bright (Sν > 50 mJy) 148 GHz-selected sample with complete cross-identifications from the Australia Telescope 20 GHz survey, i.e. 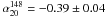 . On the other hand, (Vieira et al. 2010) find that their much fainter synchrotron emitting radio sources selected at 150 GHz are consistent with a flatter spectral behaviour (mean
. On the other hand, (Vieira et al. 2010) find that their much fainter synchrotron emitting radio sources selected at 150 GHz are consistent with a flatter spectral behaviour (mean 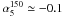 ) between 5 GHz and 150 GHz. Massardi et al. (2010) find mean spectral indices
) between 5 GHz and 150 GHz. Massardi et al. (2010) find mean spectral indices 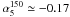 and
and 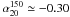 for AT20G sources with 150 GHz flux density S > 50mJy. A flattening of the mean/median high-frequency spectral indices at flux densities fainter than the ones probed by the Planck ERCSC may help to account for the unusually “flat” normalized counts at 143 and 217 GHz.
for AT20G sources with 150 GHz flux density S > 50mJy. A flattening of the mean/median high-frequency spectral indices at flux densities fainter than the ones probed by the Planck ERCSC may help to account for the unusually “flat” normalized counts at 143 and 217 GHz.
 |
Fig.6 Spectral index distributions for different frequency intervals calculated by taking into account all sources selected at 30 GHz with Sν > 1Jy. There is clear evidence for a steepening above 70 GHz. |
In Fig. 6 we compare the distributions of spectral indices over different frequency intervals. There is a clear shift toward steeper values above 70 GHz: the median values vary from 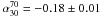 (σ = 0.18) to
(σ = 0.18) to 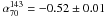 (σ = 0.22). On the other hand, the distribution of spectral indices between 143 and 217 GHz is close to the one found for
(σ = 0.22). On the other hand, the distribution of spectral indices between 143 and 217 GHz is close to the one found for 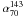 (
(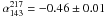 ; σ= 0.23). This latter result is again very similar to the corresponding value calculated for all the sources detected at 143 and 217 GHz with
; σ= 0.23). This latter result is again very similar to the corresponding value calculated for all the sources detected at 143 and 217 GHz with 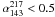 , i.e.,
, i.e., 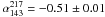 , as shown in Fig. 4. Moreover, in the paper Planck Collaboration (2011k) an average value of α = − 0.56 (σ = 0.29) at HFI frequencies is found for their sample of 84 bright blazars selected at 37 GHz, with flux densities measured in at least 3 HFI channels, in full agreement with our present findings.
, as shown in Fig. 4. Moreover, in the paper Planck Collaboration (2011k) an average value of α = − 0.56 (σ = 0.29) at HFI frequencies is found for their sample of 84 bright blazars selected at 37 GHz, with flux densities measured in at least 3 HFI channels, in full agreement with our present findings.
Figure 7 presents the contour levels of the distribution of 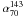 vs.
vs. 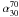 (obtained using Survival Analysis) in the form of a 2D probability field: the colour scale can be interpreted as the probability of a given pair of spectral indices.
(obtained using Survival Analysis) in the form of a 2D probability field: the colour scale can be interpreted as the probability of a given pair of spectral indices.
 |
Fig.7 Contour levels of the distribution of |
As already noted, at high Planck frequencies most of the extragalactic radiosources are blazars. From the contour plot of Fig. 7 it is possible to see that the maximum probability corresponds to 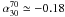 and
and  . A secondary maximum can also be seen at
. A secondary maximum can also be seen at 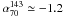 . However, a physical interpretation of these features goes beyond the purposes of this work and, moreover, more data at higher frequencies are needed. A detailed discussion on the modelling of the spectra of this source population is presented in a companion paper (Planck Collaboration 2011k).
. However, a physical interpretation of these features goes beyond the purposes of this work and, moreover, more data at higher frequencies are needed. A detailed discussion on the modelling of the spectra of this source population is presented in a companion paper (Planck Collaboration 2011k).
5. Conclusions
We have exploited the ERCSC to estimate the bright counts of extragalactic radio sources at six frequencies (30, 44, 70, 100, 143, and 217 GHz) and to investigate the spectral properties of sources in a complete sample selected at 30 GHz. The counts at 30, 44, and 70 GHz are in good agreement with those derived from WMAP data at nearby frequencies. The completeness limit of the ERCSC is somewhat deeper than that of WMAP at 30 and 70 GHz and somewhat shallower at 44 GHz. At higher frequencies the ERCSC has allowed us to obtain the first estimate of the differential number counts at bright flux density levels. At 30, 143 and 217 GHz, the present counts join smoothly to those from deeper surveys over small fractions of the sky.
The de Zotti et al. (2005) model is consistent with the present counts at frequencies up to 100 GHz, but over-predicts the counts at higher frequencies by a factor of about 2.0 at 143 GHz and about 2.6 at 217 GHz. This implies that the contamination of the CMB power spectrum by radio sources below the 1Jy detection limit is lower than previously estimated. No significant changes are found, however, if we consider fainter source detection limits, i.e., 100mJy, given the convergence between predicted and observed number counts.
The analysis of the spectral index distribution over different frequency intervals, within the uniquely broad range covered by Planck in the mm and sub-mm domain, has highlighted an average steepening of source spectra above about 70 GHz. The median values of spectral indices vary from 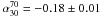 (σ = 0.18) to
(σ = 0.18) to 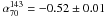 (σ = 0.22). This steepening accounts for the discrepancy between the de Zotti et al. (2005) model predictions and the observed differential number counts at HFI frequencies. The current outcome is also in agreement with the findings of Planck Collaboration (2011k) on a complete sample of blazars selected at 37 GHz. The change detected in the spectral behaviour of extragalactic radio sources in the Planck ERCSC at frequencies above 70 − 100 GHz can be tentatively explained by electron ageing or by the transition to the optically thin regime, predicted in current models for radio emission in blazar sources. However, with present data it is not yet possible to clarify the situation. In the near future, the data of the Planck Legacy Survey will surely prove very useful in settling this open issue.
(σ = 0.22). This steepening accounts for the discrepancy between the de Zotti et al. (2005) model predictions and the observed differential number counts at HFI frequencies. The current outcome is also in agreement with the findings of Planck Collaboration (2011k) on a complete sample of blazars selected at 37 GHz. The change detected in the spectral behaviour of extragalactic radio sources in the Planck ERCSC at frequencies above 70 − 100 GHz can be tentatively explained by electron ageing or by the transition to the optically thin regime, predicted in current models for radio emission in blazar sources. However, with present data it is not yet possible to clarify the situation. In the near future, the data of the Planck Legacy Survey will surely prove very useful in settling this open issue.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries: France and Italy) with contributions from NASA (USA), and telescope reflectors provided in a collaboration between ESA and a scientific consortium led and funded by Denmark.
In all our calculations we have used the effective central frequencies for the Planck channels (Mennella et al. 2011; Planck HFI Core Team 2011a), although we indicate their nominal values. The most relevant difference is at 30 GHz, with a central frequency of 28.5 GHz.
Blazars are jet-dominated extragalactic objects characterized by a strongly variable and polarized emission of the non-thermal radiation, from low radio energies up to the high energy gamma rays (Urry & Padovani 1995). Detailed analyses of spectral energy distributions (SEDs) of complete blazar samples built by using simultaneous Planck, Swift and Fermi data are given in (Planck Collaboration 2011k).
As an example, the amplitude of the power spectrum of radio sources, in terms of values, below, e.g., Jy at 217 GHz, corresponds to K, if calculated from the Planck ERCSC differential number counts of Table 1. For comparison, undetected radio sources sum up K, if we integrate the differential number counts of the de Zotti et al. (2005) cosmological evolution model up to Jy.
Acknowledgments
The Planck Collaboration thanks the referee, Ronald Ekers, for his insightful comments, which helped improve the paper. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. The Planck Collaboration acknowledges the support of: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and DEISA (EU). A description of the Planck Collaboration and a list of its members can be found at http://www.rssd.esa.int/index.php?project=PLANCK&page=Planck_Collaboration
References
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonavera, L., Massardi, M., Bonaldi, A., et al. 2011, MNRAS, 416, 559 [NASA ADS] [Google Scholar]
- Carvalho, P., Rocha, G., & Hobson, M. P. 2009, MNRAS, 393, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Cleary, K. A., Taylor, A. C., Waldram, E., et al. 2005, MNRAS, 360, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- de Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&ARv, 18, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- González-Nuevo, J., Massardi, M., Argüeso, F., et al. 2008, MNRAS, 384, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1969, ApJ, 155, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Kovac, J. M., Leitch, E. M., Pryke, C., et al. 2002, Nature, 420, 772 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lavalley, M. P., Isobe, T., & Feigelson, E. D. 1992, BAAS, 24, 839 [Google Scholar]
- Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Caniego, M., González-Nuevo, J., Herranz, D., et al. 2007, ApJS, 170, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Marriage, T. A., Juin, J. B., Lin, Y., et al. 2011, ApJ, 731, 100 [Google Scholar]
- Massardi, M., Ekers, R. D., Murphy, T., et al. 2008, MNRAS, 384, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., López-Caniego, M., González-Nuevo, J., et al. 2009, MNRAS, 392, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Bonaldi, A., Negrello, M., et al. 2010, MNRAS, 404, 532 [NASA ADS] [Google Scholar]
- Massardi, M., Bonaldi, A., Bonavera, L., et al. 2011, MNRAS, 415, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., Murphy, T., Buttery, H. J., et al. 2003, MNRAS, 342, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, A., Bersanelli, M., Butler, R. C., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, T., Sadler, E. M., Ekers, R. D., et al. 2010, MNRAS, 402, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011e, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011f, A&A, 536, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011g, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011h, A&A, 536, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011i, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011j, A&A, 536, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011k, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011l, A&A, 536, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011m, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011n, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011o, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011p, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011q, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011r, A&A, 536, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011s, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011t, A&A, 536, A24 [Google Scholar]
- Planck Collaboration 2011u, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011v, The Explanatory Supplement to the Planck Early Release Compact Source Catalogue (ESA) [Google Scholar]
- Planck Collaboration 2011w, A&A, 536, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2008, MNRAS, 385, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toffolatti, L., Argueso Gomez, F., de Zotti, G., et al. 1998, MNRAS, 297, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Toffolatti, L., Negrello, M., González-Nuevo, J., et al. 2005, A&A, 438, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vieira, J. D., Crawford, T. M., Switzer, E. R., et al. 2010, ApJ, 719, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Waldram, E. M., Bolton, R. C., Pooley, G. G., & Riley, J. M. 2007, MNRAS, 379, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. E., Griffith, M. R., Hunt, A. J., et al. 1996, ApJS, 103, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Euclidean-normalized differential number counts per steradian estimated from the Planck ERCSC at 30–217 GHz.
Median and standard deviations of the spectral index distributions between 30 GHz and the selected frequency.
All Figures
 |
Fig.1 Comparison between the ERCSC flux densities at 30 GHz (left panel) and at 44 GHz (right panel) with the almost simultaneous ATCA measurements (PACO project) at 32.2 and 39.7 GHz, respectively. No correction for the slightly different frequencies has been applied. |
| In the text | |
 |
Fig.2 Euclidean normalized differential number counts at the LFI frequencies. The red circles with Poisson error bars show the counts of sources with counterparts in our reference 30 GHz sample. In each panel, the solid curves show the total number counts of extragalactic radio sources predicted by the de Zotti et al. (2005) model. Also shown are: the counts estimated at 31 GHz from DASI (grey dashed box; Kovac et al. 2002) and at 33 GHz from the VSA data (grey box; Cleary et al. 2005); the counts from the PACO (grey diamonds; Bonavera et al. 2011) and the WMAP 5-yr surveys (grey squares; Massardi et al. 2009), at the closest frequencies, and the counts estimated by Waldram et al. (2007) (grey dashed line), exploiting multi-frequency follow-up observations of the 15 GHz 9C sources. The vertical dashed magenta line in the upper panel indicates the flux density completeness limit, 1.0Jy, estimated for our primary sample Sect. 2.3. |
| In the text | |
 |
Fig.3 Completeness and uniformity tests at 30 GHz. Top panel: flux density interval, or bin size, including a fixed number of sources as a function of flux density. The change of slope at about 0.9Jy signals the onset of incompleteness. Bottom panel: uniformity test for sources with flux densities Sν ≥ 1.0Jy. The source density, D, in sources per sr, within regions at different Galactic latitudes, shows an acceptable uniformity. The horizontal grey (solid) and blue (dashed) lines show the average source density at Galactic latitudes above |b| = 5 and |b| = 30°, respectively. As it is apparent, the two values are very close to each other, within the 1σ level calculated for the overall population in the two sky areas considered here, and well inside the 1σ normalized Poisson error bars. We also checked that at flux densities below about 0.9–1.0Jy statistically more relevant deviations from a uniform distribution begin to appear. |
| In the text | |
 |
Fig.4 Spectral index distribution of ERCSC sources between 143 and 217 GHz. Only sources detected at 143 GHz and at 217 GHz have been considered: no upper limits on flux densities have been used in this calculation. |
| In the text | |
 |
Fig.5 Euclidean normalized differential number counts at the HFI frequencies (100, 143, and 217 GHz). The red circles with Poisson error bars show the counts of sources with counterparts in our reference 30 GHz sample. At 143 and 217 GHz the blue diamonds (shifted to the left by half of the bin size, for clarity) show the counts obtained after removing sources with 143–217 GHz spectral index indicative of dust emission (see Sect. 2.3.2). Again, in each panel, the solid curves show the total number counts of extragalactic radio sources predicted by the de Zotti et al. (2005) evolution model. Also shown are the SPT (grey squares; Vieira et al. 2010) and ACT (grey stars; Marriage et al. 2011, counts of radio sources. At 100 GHz we also show the estimated counts by Sadler et al. (2008) from follow-up observations of a sample of sources selected from the 20 GHz ATCA survey (grey dashed line). |
| In the text | |
 |
Fig.6 Spectral index distributions for different frequency intervals calculated by taking into account all sources selected at 30 GHz with Sν > 1Jy. There is clear evidence for a steepening above 70 GHz. |
| In the text | |
 |
Fig.7 Contour levels of the distribution of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.