| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201016086 | |
| Published online | 28 July 2011 | |
The JCMT Spectral Legacy Survey: physical structure of the molecular envelope of the high-mass protostar AFGL2591
1
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: matthijs.vanderwiel@uleth.ca
2
SRON Netherlands Institute for Space Research, PO Box 800, 9700 AV, Groningen, The Netherlands
3
Jodrell Bank Centre for Astrophysics, Alan Turing Building, University of Manchester, Manchester, M13 9PL, UK
4
Department of Physics and Astronomy, University of Calgary, Calgary, T2N 1N4, AB, Canada
5
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University of Belfast, Belfast, BT7 1NN, UK
Received: 5 November 2010
Accepted: 27 January 2011
Context. The understanding of the formation process of massive stars ( ≳ 8 M⊙) is limited by a combination of theoretical complications and observational challenges. The high UV luminosities of massive stars give rise to chemical complexity in their natal molecular clouds and affect the dynamical properties of their circumstellar envelopes.
Aims. We investigate the physical structure of the large-scale (~104–105 AU) molecular envelope of the high-mass protostar AFGL2591.
Methods. Observational constraints are provided by spectral imaging in the 330–373 GHz regime from the JCMT Spectral Legacy Survey and its high-frequency extension. While the majority of the ~160 spectral features from the survey cube are spatially unresolved, this paper uses the 35 that are significantly extended in the spatial directions. For these features we present integrated intensity maps and velocity maps. The observed spatial distributions of a selection of six species are compared with radiative transfer models based on (i) a static spherically symmetric structure; (ii) a dynamic spherical structure; and (iii) a static flattened structure.
Results. The maps of CO and its isotopic variations exhibit elongated geometries on scales of ~100″, and smaller scale substructure is found in maps of N2H+, o-H2CO, CS, SO2, C2H, and various CH3OH lines. In addition, a line-of-sight velocity gradient is apparent in maps of all molecular lines presented here, except SO, SO2, and H2CO. We find two emission peaks in warm (Eup ~ 200 K) CH3OH separated by 12″ (12 000 AU), indicative of a secondary heating source in the envelope. The spherical models are able to explain the distribution of emission for the optically thin H13CO+ and C34S, but not for the optically thick HCN, HCO+, and CS or for the optically thin C17O. The introduction of velocity structure mitigates the optical depth effects, but does not fully explain the observations, especially in the spectral dimension. A static flattened envelope viewed at a small inclination angle does slightly better.
Conclusions. Based on radiative transfer modeling, we conclude that a geometry of the envelope other than an isotropic static sphere is needed to circumvent line optical depth effects. We propose that this could be achieved in circumstellar envelope models with an outflow cavity and/or an inhomogeneous structure on scales ≲ 104 AU. The picture of inhomogeneity is supported by substructure observed in at least six different species.
Key words: stars: formation / ISM: molecules / ISM: individual objects: AFGL2591 / techniques: imaging spectroscopy
© ESO, 2011
1. Introduction
A collapsing protostellar cloud is heated by gravitational contraction of the envelope and radiation from the central protostar. Therefore, the disposal of thermal energy through (molecular) transition lines is crucial in the process of star formation. Molecular signatures from star-forming regions are an important probe in studies of star formation. While the energy budget is reasonably well understood for protostars with masses ≲ 8 M⊙ (e.g., Evans 1999; Larson 2003), the problem is more complex for high-mass stars ( ≳ 8 M⊙). Not only do they require more material and involve (orders of magnitude) more energy, high-mass stars also form in more deeply embedded natal clouds and, generally, in more clustered environments. In addition, high-mass protostars are rarely observed because they form less often, and if they do, their formation timescales are much shorter than for their low-mass counterparts (see Zinnecker & Yorke 2007, for a review). In addition, young high-mass stars have the ability of significantly altering the chemical composition of their parental clouds by the copious amounts of UV-radiation they emit (Stäuber et al. 2004). It is exactly this impact that high-mass stars have on the surrounding interstellar medium – both when they form and when they explode as supernovae – which makes it important to study their formation process in a broader context.
Due to the above challenges in the study of high-mass star formation, it is as yet unclear whether a high-mass star forms following a process similar to low-mass star formation (core contraction → envelope collapse → disk accretion → disk evaporation), or whether other processes such as competitive accretion or stellar mergers are in play (e.g., Bonnell et al. 2001; Bonnell & Bate 2005; Hocuk & Spaans 2010). In either case, much higher accretion rates and more energetic feedback processes must be involved in high-mass star formation, providing additional challenges for theoretical modeling. Investigations into the physical and chemical structure (on various scales) of the molecular envelopes of massive young stars can shed light on the accretion process and the energy distribution and dissipation in regions of high-mass star formation (Evans 1999; Cesaroni 2005). One hypothesis to consider is whether high-mass star formation in its first stages proceeds less isotropically than low-mass star formation, undergoing nonspherical accretion even before material reaches a potential circumstellar disk.
This paper studies the molecular envelope of AFGL2591, an isolated massive star-forming region located in the Cygnus-X region at galactic coordinates 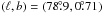 . The distance to AFGL2591 is between 0.5 and 2.0 kpc (see Van der Tak et al. 1999; Schneider et al. 2006). While the commonly assumed average distance for the Cygnus-X complex is 1.7 kpc (Motte et al. 2007), the distance to individual objects in this local spiral arm structure varies. For consistency with earlier work on this source, we adopt a distance of 1.0 kpc and we refer to discussion in Van der Tak et al. (1999) concerning the effects of a greater assumed source distance. The protostar is estimated by Van der Tak & Menten (2005) to have a mass of 16 M⊙. The object emits most of its energy in the infrared, owing to re-radiation of optical/UV radiation from the central object by the surrounding gas and dust. It has a bolometric luminosity of ~2 × 104 L⊙ (at 1 kpc) and exhibits powerful large (>1′) bipolar molecular outflows (Lada et al. 1984; Hasegawa & Mitchell 1995).
. The distance to AFGL2591 is between 0.5 and 2.0 kpc (see Van der Tak et al. 1999; Schneider et al. 2006). While the commonly assumed average distance for the Cygnus-X complex is 1.7 kpc (Motte et al. 2007), the distance to individual objects in this local spiral arm structure varies. For consistency with earlier work on this source, we adopt a distance of 1.0 kpc and we refer to discussion in Van der Tak et al. (1999) concerning the effects of a greater assumed source distance. The protostar is estimated by Van der Tak & Menten (2005) to have a mass of 16 M⊙. The object emits most of its energy in the infrared, owing to re-radiation of optical/UV radiation from the central object by the surrounding gas and dust. It has a bolometric luminosity of ~2 × 104 L⊙ (at 1 kpc) and exhibits powerful large (>1′) bipolar molecular outflows (Lada et al. 1984; Hasegawa & Mitchell 1995).
Previous modeling of the molecular envelope of AFGL2591 has assumed a spherical morphology and found that observations of molecular lines and dust can be explained using a power-law density profile (Van der Tak et al. 1999, 2000; Doty et al. 2002; Stäuber et al. 2005; Benz et al. 2007; De Wit et al. 2009). Van der Tak et al. (1999) suggested there are cavities in the envelope, carved out by the outflows, as a solution to optical depth effects that prevent molecular line radiation from escaping the cloud if the envelope is spherical and isotropic. After evidence of such cavities was observed at high spatial resolution (~2″) in the near-infrared by Preibisch et al. (2003), the idea was invoked again by Bruderer et al. (2010a,b) to allow far-UV radiation from the protostar to directly excite molecular species in the envelope. The overall structure of the envelope, however, is still assumed to be spherical.
This paper is structured as follows. In Sect. 2 we describe the unbiased submillimeter spectral imaging survey of the molecular envelope of AFGL2591 and the resulting maps of integrated intensity and velocity structure for 35 molecular transitions are presented in Sect. 3. While this paper focuses on the spatial domain in order to investigate the large-scale (>104 AU) envelope, a full exploitation of the spectral domain will be addressed in Van der Wiel et al. (2011b, in prep.). Section 4 describes various approaches to modeling a selection of six molecular emission lines using a radiative transfer code. Section 5, finally, is devoted to discussing the results of the radiative transfer modeling, a phenomenological interpretation of the lines that are not modeled, and general conclusions.
2. Observations
2.1. HARP-B and the JCMT Spectral Legacy Survey
The observations presented here were taken with the 16-element Heterodyne Array Receiver Programme B (HARP-B) and the Auto-Correlation Spectral Imaging System (ACSIS) correlator (Smith et al. 2008; Dent et al. 2000; Buckle et al. 2009) at the James Clerk Maxwell Telescope1 (JCMT) on Mauna Kea, Hawai’i. The strength of the multipixel HARP-B instrument lies in the combination of high-resolution (1 MHz, ≈ 1 km s-1) heterodyne spectroscopy with instantaneous mapping capabilities.
The JCMT Spectral Legacy Survey (SLS, Plume et al. 2007) has been allocated a total of 456 h to map four Galactic targets in the spectral region between 330 and 360 GHz. The targets are the Orion Bar, a prototypical photodissociation region (Van der Wiel et al. 2009); NGC1333 IRAS 4, a low-mass star-forming region; W49A, an active star formation complex (Roberts et al. 2011); and the isolated high-mass star-forming region AFGL2591, which is the topic of this study. The SLS is complemented at higher frequencies (360–373 GHz) by HARP maps from separate proposals between 2007 and 2010. Observations for the SLS (330–360 GHz) started immediately after the commissioning of the HARP-B instrument; AFGL2591 was observed in November 2007, March, July and September 2008, May–July 2009, and May–July 2010. The high-frequency maps were observed in August and September 2007 and July 2008. AFGL2591 is the first of the four SLS targets for which the spectral imaging was completed in the 330–360 and 360–373 GHz spectral regions.
The 16 receptors of the HARP receiver are distributed in a 4 × 4 pattern, regularly spaced at 30″ intervals. The harp4_mc jiggle position switch mode was used to create maps of a 2′ × 2′ area with pixels spaced by 7.5″, roughly half of the JCMT beam width at the relevant frequencies (15″ at 345 GHz). While the SLS observations were done in relatively wet weather at 0.12 < τ225 GHz < 0.20, the observations above 360 GHz require τ225 GHz < 0.08, since the Earth’s atmosphere becomes increasingly opaque as the frequency approaches 375 GHz. Apart from the weather constraints, the observing strategy and reduction method are identical for the high-frequency data and the SLS data.
The spectra of AFGL2591 are calibrated by measurements at an off position 340″ east of the target. After inspection of the calibrated data product, we note that there is a possibility of 12CO 3–2 contaminating emission at the off position. There is no evidence of contamination from the off position for other spectral lines. Redundancy for bad receptors is built in by consecutive observations at an offset of 15″ or by rotation of the entire array during periods where more than three of the sixteen receptors were not functioning. Redundancy for frequency spikes is provided by offsetting the central frequency of consecutive observations, each spanning 1 GHz bandwidth, by 200 or 400 MHz. Pointing was checked regularly and corrections were generally <2–3″.
2.2. HARP-B data processing
The raw time series files are processed in blocks of 1 GHz bandwidth, using standard procedures from the Starlink software package. Each scan file is inspected for bad receptors, baseline issues and frequency spikes, which are masked before scan files at the same frequency are summed and converted from time series into three-dimensional data cubes (RA × Dec × frequency). The generally noisy band edges are discarded, typically leaving 0.82 GHz of usable bandwidth per block. Baselines are fitted to line-free regions in every cube using a spline algorithm. The generally nearly linear baselines are subsequently subtracted. The baseline corrected cubes are mosaicked into a larger cube spanning (2′)2 on the sky and 330.0–373.3 GHz in frequency. The noise level is reduced by exploiting the frequency overlap between subsequent frequency settings. The spectrum with native frequency bins of 1 MHz (0.8–0.9 km s-1 between 373 and 330 GHz) is resampled to uniform 1 km s-1 velocity resolution. Intensities are corrected for the JCMT main beam efficiency of 0.61 ± 0.03 (Buckle et al. 2009) in the 345 GHz window and are therefore given in terms of main beam temperature Tmb. To convert observed TA∗ values to flux density units (Jy), multiplication by a factor 29.4 would be necessary.
 |
Fig. 1 Root-mean-square (rms) noise statistics of the data product, calculated in 1 km s-1 channels. The square symbols denote the median rms in all map pixels over a selected frequency range, with their error bars indicating the rms of the rms noise across all map pixels in the same frequency range. The triangle symbols mark the rms value in the least noisy (pointing up) and noisiest pixel (pointing down) in the map. The horizontal dashed line indicates the survey target noise for this object. |
Figure 1 shows the median of the root-mean-square (rms) noise in the resulting data cube in some selected line-free frequency ranges, as well as the spread in rms across the map pixels. The noise in Tmb units in both the 330–360 GHz and the 360–373 GHz ranges are generally close to the Tmb target noise level of 65 mK (converted from 25 mK in 2.5 km s-1 channels in TA∗ units). The lowest noise values are usually found near the spatial center of the cube.
2.3. Submillimeter continuum images
The analysis in this paper uses subsidiary submillimeter continuum images of AFGL2591. These 450 and 850 μm images have previously been presented by Van der Tak et al. (2000). The raw images, available from the JCMT archive at the Canadian Astronomy Data Centre, are processed using the standard ORAC-DR pipeline for SCUBA jiggle maps. An extinction correction is applied, based on sky-dip measurements of the sky optical depth. The resulting maps have units of mJy beam-1 and are sampled in 3″ pixels. The FWHM beam size is 8″ for the 450 μm map and 14″ for the 850 μm map. This makes the latter map especially suitable for comparison with our HARP-B spectral maps.
3. Observed spatial distribution
3.1. Selection of spatially resolved maps
While the majority of the ~160 spectral lines show a spatial distribution that is confined to the beam size of the JCMT (14–15″ FWHM at the relevant frequency), in this paper we select the lines that are spatially resolved. The selection is made by fitting a two-dimensional Gaussian profile to a spatially resampled (3 75 pixels) integrated line intensity (
75 pixels) integrated line intensity (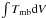 ) map for each spectral feature. Features are registered in Table 1 if aFWHM > BFWHM + 3σa, with aFWHM and σa the fitted long axis and associated error and BFWHM the JCMT beam size. Spatial extent parameters in Table 1 are given as measured in the observed maps, without beam deconvolution. We select a total of 35 spectral features with this method.
) map for each spectral feature. Features are registered in Table 1 if aFWHM > BFWHM + 3σa, with aFWHM and σa the fitted long axis and associated error and BFWHM the JCMT beam size. Spatial extent parameters in Table 1 are given as measured in the observed maps, without beam deconvolution. We select a total of 35 spectral features with this method.
The association of spectral features to molecular transitions is done using the CDMS catalog (Müller et al. 2005). When multiple molecular transitions fall within a few MHz of a measured line frequency, we choose the simplest molecule and/or the lowest upper level energy. For the 35 lines selected above, which are relatively strong (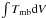 ≳ 2 K km s-1), the identifications listed in Table 1 are unambiguous. Some features are marked as a blend of several (hyperfine) transitions of the same or different molecules.
≳ 2 K km s-1), the identifications listed in Table 1 are unambiguous. Some features are marked as a blend of several (hyperfine) transitions of the same or different molecules.
Maps of integrated line intensity for each of the lines with extended emission are shown in Figs. 2–4. Intensity is integrated over the velocity interval indicated in Table 2 for each map. The intervals are determined manually, with the aim of incorporating all emission belonging to the spectral line in question without including any signal from neighboring lines. Intervals are generally symmetric around the systemic Vlsr of −5.8 km s-1 for AFGL2591, the interval width depending on the width of the line (CO 3–2 integrated over [−29,6] km s-1 is the most extreme case). In the maps of integrated line intensity (Figs. 2–4), contours are drawn based on resampled maps with pixels of 3 75. Contour levels are scaled to the maximum intensity in each map listed in Table 2. For comparison, SCUBA 850 μm continuum emission is shown on the background of each integrated line intensity map. In addition, we show an example of a map that is not extended according to our criterion: SO2 152,14–141,13 in Fig. 5. In any further discussion of SO2 morphology, we do not consider the 152,14–141,13 mentioned here, but only the three transitions 53,3–42,2, 233,21–232,22, and 232,22–231,23 that are listed in Table 1.
75. Contour levels are scaled to the maximum intensity in each map listed in Table 2. For comparison, SCUBA 850 μm continuum emission is shown on the background of each integrated line intensity map. In addition, we show an example of a map that is not extended according to our criterion: SO2 152,14–141,13 in Fig. 5. In any further discussion of SO2 morphology, we do not consider the 152,14–141,13 mentioned here, but only the three transitions 53,3–42,2, 233,21–232,22, and 232,22–231,23 that are listed in Table 1.
Molecular lines with observed spatially extended emission.
Maximum integrated intensity values and velocity parameters.
 |
Fig. 2 Maps of emission from the 3–2 transitions of CO, 13CO, C17O, transitions of N-bearing molecules, HCO+ and H13CO+ 4–3. White contours represent integrated line emission and are at 90%, 80%, ..., 10% of the maximum intensity, listed in Table 2. The contour at 50% is thicker. An extra contour is added for HNC 4–3 at 5% of the maximum intensity. The beam size at the relevant frequency is indicated in the top right corner of each panel. To avoid noise in the figures, contours below 0.7 K km s-1 are not shown. SCUBA 850 μm continuum emission is shown in color scale and thin black contours; the color scale is stretched from 10 to 5600 mJy beam-1. |
3.2. Spatial distribution of integrated line intensity
The emission of all molecular tracers from Table 1, with the exception of CO, its isotopologs, and SO2, is distributed over a central region ~20–50″ in diameter (Figs. 2–4). The flattened morphologies of roughly half of the maps are consistent with a position angle of the major axis between 65° and 95° (Table 1). The only maps in which more extended emission is visible are those of the 3–2 transition of CO, 13CO, and C17O (Fig. 2), while SO2 emission is the most concentrated. Maps of CO and 13CO trace not only the smaller scale morphology already noted above for other molecules, but also an additional larger scale envelope (up to ~100″) at lower intensity with a different orientation at a position angle of ~20°. The large scale (0.07–0.30 pc from the central position) extends to the region where previous modeling by Van der Tak et al. (2000) suggests that the molecular hydrogen density is < 105 cm-3 and dust and gas temperatures < 40 K.
A “plume” extending to the north at position angle ~10° is apparent in maps of CO, C17O, HCN, HNC, N2H+, HCO+, o-H2CO, and CH3OH 11–00 A + , 70–60 A + and 7-1–6-1 E (Figs. 2–4). Its intensity level is generally at ~10% of the maximum, but it is stronger in the CH3OH lines relative to the peak intensity. The feature appears to emerge from a position roughly 15″ east of the peak position. Alternatively, it might trace a warped structure of the collapsing molecular cloud. The plume is also apparent in the 850 μm continuum map (Fig. 2). We recognize the same feature in the 13CO 3–2 map in Fig. 3 of Van der Tak et al. (1999). The northern warped plume is not present in maps of C2H or in any of the sulfur-bearing molecules. This difference in observed morphology is not just an effect of signal-to-noise, since some of the latter transitions have peak line strengths (Table 2) comparable to the maps that do show the plume. The velocity structure of this plume is destribed in Sect. 3.3.
Maps of CO and isotopologs, CN 37/2–25/2 ΔF = 1 (Fig. 2), CS, o-H2CO (Fig. 3), C2H and CH3OH 40–3-1 (Fig. 4) show a hint of two separate southern “arms” ~30″ south of their main peak, separated by ≳ 20″ in the east-west direction. Alternatively, this feature can be described as one indentation.
The spatial distribution of N2H+ 4–3 emission (Fig. 2, top right panel) is strikingly different from those of other molecular transitions observed here. It is stretched significantly in the east-west direction, mostly owing to the spatial separation of the velocity components described in Sect. 3.3. Whereas various other species manifest two southern “arms” (see above), only N2H+ shows the same on the northern side, giving rise to a four-directional morphology.
The emission from HNC 4–3 and from the three CN transitions (Fig. 2) peaks at a position offset ~3″ to the southwest of the peaks of the dust emission and the other molecular maps. Most other molecular maps have peak positions at ΔDec between −3″ and −1″, and the 850 μm dust emission peaks at ΔDec = −1″ (Table 1). Moreover, the peaks of the SO maps, especially 78–67, appear to be shifted ~4–5″ to the southeast (Fig. 3). In contrast, the CS and C34S maps (Fig. 3) have peak positions offset 2–3″ to the north. Finally, the two C2H maps, although not obvious from their fitted peak positions, are displaced to the northwest (Fig. 4). We note that these position offsets are only marginally significant compared to the pointing accuracy (Sect. 2).
A spatially resolved two-peak structure is apparent in the map of CH3OH 121–120 (Eup = 197 K) in the top right panel of Fig. 4. The two peaks are separated by roughly 12″ (12 000 AU). The southeast warm CH3OH peak is associated to the infrared source detected by Van der Tak et al. (1999, their Fig. 1), the canonical center of the envelope of dust and gas. We discuss this two-peak structure further in Sect. 5.2. The only other molecular transitions shown in this paper with an upper level energy above 100 K are the two SO2 23–23 transitions, where a double-peak structure is not seen. The N2H+ morphology does not coincide with the spatially separated warm methanol pockets, neither in angular separation, nor in position angle.
The high-excitation J = 23–23 transitions SO2 transitions in Fig. 3 appear to be stretched in a direction perpendicular to the outflow direction. The fitted position angle for these two maps does not reflect the actual orientation of the extended emission (cf. Table 1 and Fig. 3), perhaps due to the boxy non-Gaussian shape of the emission. The real position angle for these maps would plausibly be around 140°–150°.
3.3. Velocity structure
The velocity structure of the molecular gas can be illustrated by line profiles in velocity space and by “channel maps”. First, the velocity profiles of all 35 lines at the central spatial position are fitted by a Gaussian to determine the centroid velocity and linewidth (Table 2). We find centroid velocities between − 5 and − 7 km s-1, with a median of − 5.8 km s-1. This is slightly lower than the previously determined velocity of − 5.5 km s-1 (Van der Tak et al. 1999). Gaussian linewidths range from 3 to 7 km s-1, with a median of 3.9 km s-1.
Second, to show the velocity structure of the overall molecular envelope, each integration interval from Table 2 is divided into three velocity bins: a central bin defined as the [−1.5, + 1.5] km s-1 interval, relative to the systemic Vlsr of −5.8 km s-1, and “blue” and “red” bins composed of all emission below and above the central velocity bin, respectively. The resulting channel maps are presented in Figs. 6 and 7. We only show a map of velocity structure for those transitions that show significant emission in at least two of the three velocity bins. In addition, we present a velocity map where emission is divided over seven velocity bins for the bright 13CO 3–2 transition (Fig. 8).
A general west-east gradient from blueshifted (approaching) to redshifted (receding) emission is perceived in the CO species, N2H+, CN, HCO+, HCN, and HNC (Fig. 6). The same trend is seen in the red and blue peak positions in maps of C2H and CS (Fig. 7). Although the typical angular separation between the peak of the blue and red components at ≲ 10″ is less than the FWHM of the telescope beam, the high signal-to-noise ratio in our maps allows for a relative position determination down to a fraction of the beam size. Moreover, the total extent of the blue and red lobes for the molecules mentioned above is significantly separated, with red contours reaching positions ≳ 30″ east, and blue contours ≳ 30″ west of the central position. Conversely, blue and red components are coincident for SO and SO2. H2CO maps show no clear velocity pattern. Velocity structure in maps of CH3OH is complicated by blueshifted emission from the northeastern plume (see below, and Sect. 3.2). Velocity structure in the spatially separated peaks of CH3OH 121–120 is not discernable in our observations. As a result, the line-of-sight velocity of the two pockets must be within 1 km s-1 of each other. In addition, the majority of the velocity maps exhibits emission that is stronger in the blueshifted bin than in the redshifted bin. Exceptions are HNC 4–3 and the p-H2CO transitions, where the red emission is stronger than the blue emission, and the SO transitions, where intensity levels in the red and blue bin are comparable.
Upon inspection of the Gaussian line profiles parametrized by Vcentroid and FWHM in Table 2, the full integration interval is notably wider than the Gaussian profile for the CO species, as well as for C2H, CS, HCN, and HCO+. This is due to our original choice of incorporating all emission from a particular molecular transition in the corresponding 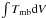 map (Sect. 3.1). The non-Gaussian part of the line intensity at the central spatial position mainly lies on the blueshifted side for these lines (see also Fig. 9 and the notes in Table 2). For most of the lines mentioned above, the line wings are relatively weak, comprising up to 20% of the total integrated line intensity, but the single Gaussian profile is an especially poor representation for the main isotopic CO 3–2 line profile, where as much as 45% of the integrated line intensity falls outside of the fitted Gaussian. We note that wings might be present even in other (weaker) lines, which would be invisible in the noise of the observations (Sect. 2).
map (Sect. 3.1). The non-Gaussian part of the line intensity at the central spatial position mainly lies on the blueshifted side for these lines (see also Fig. 9 and the notes in Table 2). For most of the lines mentioned above, the line wings are relatively weak, comprising up to 20% of the total integrated line intensity, but the single Gaussian profile is an especially poor representation for the main isotopic CO 3–2 line profile, where as much as 45% of the integrated line intensity falls outside of the fitted Gaussian. We note that wings might be present even in other (weaker) lines, which would be invisible in the noise of the observations (Sect. 2).
The velocity components of the N2H+ 4–3 line are special in the sense that they are spatially resolved: the emission peaks of the blue and red N2H+wings in Fig. 6 are separated by more than one beam size. For other species, the different components overlap in velocity space, as well as spatially. Like for several other species, emission is significantly stronger in the blueshifted approaching component than in the receding component. In the four-arm structure noted for N2H+ in Sect. 3.2, the southeast arm consists exclusively of emission from the red velocity bin.
The northern plume noted in Sect. 3.2 has more contribution from the blueshifted component of the emission than from the redshifted and central velocity bins, as shown in Figs. 6 and 7. This is particularly clear in velocity maps of CH3OH.
4. Radiative transfer modeling
Section 4.1 deals with dust continuum modeling and describes the derived density structure of the envelope. The spatial distribution of molecular emission from a radiative transfer model is addressed in Sect. 4.2. Section 4.3 explores the effects of different density structures on molecular emission. Finally, the model from Sect. 4.2 is adjusted to examine the effects of velocity structure (Sect. 4.4) and a flattened morphology (Sect. 4.5).
4.1. Dust continuum models
We use the dusty code (Ivezic et al. 1999) to create a grid of dust continuum models starting from the density profile of material in a spherical (n ∝ r − α) envelope around a luminous source. Parameters that vary across the grid include the temperature at the inner edge of the dust envelope, and the power-law index α of the density distribution. The internal luminosity is fixed at 2 × 104 L⊙ at a 1 kpc distance. A self-consistent dust temperature and radiation field is derived within the envelope, where scattering, absorption, and emission processes are considered along a radial path. The intrinsically one-dimensional models are resampled onto a radial grid of sky coordinates to obtain an intensity map, which is subsequently convolved with a synthetic telescope beam.
The resulting radial intensity profile of each model is compared with the 450 and 850 μm SCUBA continuum maps (Sect. 2). The best-fit dusty model for 450 μm has α = 1.10, whereas the one for 850 μm has α = 1.45. We take the modeled dust opacity, τν, and use the relation 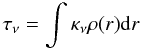 (1)to derive the scaling factor ρ0 in the mass density, ρ(r) = ρ0(r/r0) − α. Here, we assume values for the absorption coefficients κ850 = 0.03 cm2 g-1 and κ450 = 0.07 cm2 g-1. The mass density scaling factor ρ0 is divided by the mass of a hydrogen molecule in order to convert to gas number density (n0). The description of density and temperature used for the α = 1.5 models in Sects. 4.3 and 4.4 is derived from an α = 1.50 dusty model, which is very similar to the best-fit solution with α = 1.45.
(1)to derive the scaling factor ρ0 in the mass density, ρ(r) = ρ0(r/r0) − α. Here, we assume values for the absorption coefficients κ850 = 0.03 cm2 g-1 and κ450 = 0.07 cm2 g-1. The mass density scaling factor ρ0 is divided by the mass of a hydrogen molecule in order to convert to gas number density (n0). The description of density and temperature used for the α = 1.5 models in Sects. 4.3 and 4.4 is derived from an α = 1.50 dusty model, which is very similar to the best-fit solution with α = 1.45.
Van der Tak et al. (2000) constrained the slope of the power-law density profile, α, using CS line observations. With the index allowed to take on values of 0.5, 1.0, 1.5, or 2.0, they found that the best fit to several observed CS lines is given by α = 1.0. The observed 450 μm continuum map also shows good correspondence to the radial intensity profile of an α = 1.0 model, but the 850 μm continuum map is fit better with α = 1.5 (Sect. 5.3 of Van der Tak et al. 2000). We have independently confirmed the result that 850 μm dust emission favors a steeper density gradient (α = 1.45) than 450 μm (α = 1.10). In addition, De Wit et al. (2009) find that a power-law density profile with α = 1.0 fits the radial intensity profile of high-resolution (0.3″ half-power beamwidth) 24.5 μm observations, but they also report that a fit to the spectral energy distribution prefers α = 1.5. Based on the above arguments, we choose a density profile with α = 1.0 for the molecular radiative transfer in Sects. 4.2, 4.4, 4.5. An exploration of different values of α is addressed in Sect. 4.3.
 |
Fig. 5 Spatial distribution of integrated SO2 152,14–141,13 emission (white contours), which is not extended. The color scale and black contours represent 850 μm continuum, like in Fig. 2. |
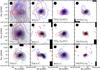 |
Fig. 6 Channel maps for the CO isotopologs, N-bearing species, HCO+ and H2CO. The velocity range is divided in three velocity bins with respect to the systemic velocity of −5.8 km s-1: [−1.5, + 1.5] km s-1 is shown in gray scale stretched between 0.7 K km s-1 (white) and the maximum intensity in the central channel (black); all emission at relative velocities below −1.5 km s-1 is shown in blue contours, and all emission at relative velocities above +1.5 km s-1 in red contours. The lowest contour level is manually fine-tuned to emphasize velocity structure in each case without showing too much noise. Consecutive contour levels are drawn in steps of 10% of the maximum intensity in the brightest channel. Lowest contours: 15.0 K km s-1 for CO, 5.0 K km s-1 for 13CO, 0.8 K km s-1 for C17O, 0.35 K km s-1 for HCN and HNC, 0.4 K km s-1 for N2H+, 0.8 K km s-1 for CN 35/2–23/2, 1.0 K km s-1 for CN 37/2–25/2, and 0.8, 0.4 and 0.3 K km s-1 for the three respective H2CO transitions. The FWHM of the telescope beam is indicated in the top left corner of each panel. |
 |
Fig. 7 Channel maps for sulfur-bearing species, CH3OH, and C2H. Colors and contours have the same meaning as in Fig. 6, except lowest contours: 0.6 K km s-1 for SO 78–67, 0.4 K km s-1 for SO 88–87 and 98–87, 0.6 K km s-1 for CS 7–6, 0.2 K km s-1 for SO2 53,3–42,2, 0.35, 0.6, 0.35 and 0.3 K km s-1 for the four consecutive CH3OH transitions, and 0.4 K km s-1 for both C2H transitions. |
4.2. Static spherical model
In the quantitative modeling of the physical structure of the envelope that gives rise to the molecular emission, we focus on C17O, HCN, CS, C34S, HCO+, and H13CO+. This set of species is chosen to cover a variety of atomic constituents and to have observed line strengths that provide the highest signal-to-noise available in our sample. While CS and HCO+ are juxtaposed with rarer isotopic variants, the isotopolog H13CN is not included because its line signal is blended with an SO2 transition (see Table 1). The maps of C17O, HCN, CS and HCO+ have observed major to minor axis ratios below 1.5 (Table 1), and they have a largely homogeneous spatial distribution. This makes them suitable tracers of the quiescent overall envelope of AFGL2591. Section 5.2 addresses the interpretation of distributions for species that are not explicitly modeled here but do appear in Table 1.
We use the radiative transfer code ratran (Hogerheijde & Van der Tak 2000) to test one-dimensional source models for AFGL2591. This relies on molecular data files from lamda (Schöier et al. 2005), with collisional rate coefficients calculated by Green & Thaddeus (1974, HCN), Turner et al. (1992, CS), Flower (1999, HCO+, and Yang et al. (2010, CO). Motivated by the dust modeling described in Sect. 4.1, we adopt a physical model from Van der Tak et al. (1999, 2000), which assumes a power-law density profile of the form: 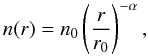 (2)with n0 = 5.3 × 104 cm-3 at r0 = 2.7 × 104 AU, and α = 1. The model cloud is truncated at a radius of 6.2 × 104 AU (62″), and has a total H2 mass of 193 M⊙. The innermost shell of our model extends from r = 0 to ~ 200 AU, and has an H2 density of 1.2 × 107 cm-3 and a temperature of 372 K. The density singularity at r = 0 is thus avoided by the discrete sampling over our finite number of model shells. A centrally peaked temperature profile ranging down to 25 K was derived from dust emission by Van der Tak et al. (2000). Molecular abundances are kept constant as a function of position in the envelope. A constant turbulence is incorporated, parametrized by the 1/e halfwidth velocity of 2 km s-1, consistent with the typical value of 3–4 km s-1 of the measured FWHM linewidths (Table 2). Initially, no infall, outflow, rotation or other velocity gradients are included. We refer to this model as the “static spherical model”.
(2)with n0 = 5.3 × 104 cm-3 at r0 = 2.7 × 104 AU, and α = 1. The model cloud is truncated at a radius of 6.2 × 104 AU (62″), and has a total H2 mass of 193 M⊙. The innermost shell of our model extends from r = 0 to ~ 200 AU, and has an H2 density of 1.2 × 107 cm-3 and a temperature of 372 K. The density singularity at r = 0 is thus avoided by the discrete sampling over our finite number of model shells. A centrally peaked temperature profile ranging down to 25 K was derived from dust emission by Van der Tak et al. (2000). Molecular abundances are kept constant as a function of position in the envelope. A constant turbulence is incorporated, parametrized by the 1/e halfwidth velocity of 2 km s-1, consistent with the typical value of 3–4 km s-1 of the measured FWHM linewidths (Table 2). Initially, no infall, outflow, rotation or other velocity gradients are included. We refer to this model as the “static spherical model”.
We use the ray tracing routine of ratran to produce spectral maps with 0.5″ pixels at the distance of 1 kpc. These maps are intentionally oversampled compared to the spatial resolution of our observations, and they are subsequently convolved with a Gaussian beam profile appropriate for the molecular transition under consideration.
The spatial distribution of observed integrated line emission is probed by a slice along the “long axis” (position angle 75°) and another slice along the “short axis” (position angle 165°) of the flattened large-scale cloud. These slices are compared with the static spherical model in Fig. 10. The two observed slices provide a measure of the nonspherical morphology of the cloud in the plane of the sky. Any modeled intensity profile which differs from the observed profiles by more than the difference between the observed “long axis” and “short axis” profiles should be regarded as incorrect.
 |
Fig. 8 Emission from the 13CO 3–2 transition divided over seven velocity bins. Line intensity is summed over the velocity range indicated in each panel (in km s-1) and represented as black contour lines. Contour levels are 90%, 80%, ..., 10% of the maximum integrated intensity in the velocity bin: 3.9, 14, 41, 124, 50, 8.1, and 0.95 K km s-1 in the respective bins. As in Fig. 2, the 50%-level contour is thicker, and any contours below 0.7 K km s-1 are not drawn. The total integrated 13CO 3–2 line intensity over the entire velocity range is shown in color scale in each panel, for reference. |
We attempt to match the modeled peak line strengths to the observed ones by adjusting individual molecular abundance values, keeping isotopic ratios fixed at CS/C34S = 20 and HCO+/H13CO+ = 60. We find abundances, relative to H2, of 2 × 10-9 for C34S and 2.5 × 10-10 for H13CO+. Consequently, the abundances of CS and HCO+ are then fixed at 4 × 10-8 and 1.5 × 10-8, respectively. Since we do not have an unblended optically thin isotopolog for HCN, we take 2 × 10-8 and for C17O we adopt 5 × 10-8 as an abundance. These abundance values are consistent with earlier estimates by Van der Tak et al. (1999).
The shapes of the modeled intensity profiles as a function of radius correspond to the observations as long as the line emission is predominantly optically thin (Fig. 10, C34S, H13CO+), but the emission of both HCN and HCO+ grows optically thick before the modeled line intensity reaches the observed value. This results in modeled emission profiles that are too weak near the center of the cloud, and fall off less steeply than the observed intensity profile. A deviation from the fixed isotopic ratio is briefly investigated. However, since the cloud is already optically thick at the center, a higher molecular abundance for the main isotopic species does not increase the emerging line intensity at the central position, while the intensity at more optically thin lines of sight away from the center does increase, thereby adding to the mismatch of the overall spatial profile. Moreover, with observed variations in the isotopic ratio restricted to a factor ≲ 3 (e.g., Chin et al. 1996), our results are not affected.
The modeled intensity of CS 7–6 is obtained by first adjusting the C34S abundance to match the observed peak intensity and simply scaling the CS abundance by the canonical factor 20 (see above). The modeled main isotopic CS 7–6 emission appears to be stronger than observed, but we note that this discrepancy is well within the intensity calibration uncertainty of 15% of the observations.
In the spectral dimension, each observed line has a roughly symmetric and single-peaked shape, as illustrated in Fig. 9 for HCO+ 4–3. Spectral line shapes are similar for other species. Considering the line profiles resulting from the radiative transfer models, individual optically thin lines (C34S 7–6, H13CO+ 4–3, C17O 3–2) have very comparable shapes, matching observed line shapes. However, for the main isotopologs HCN and HCO+, the high optical depth at line center is prominently displayed in the form of a self-absorbed line profile (Fig. 9).
A particular explanation is required for the spatial distribution of C17O, which is also discrepant with respect to the observed distribution but is optically thin in the modeled line. See Sect. 5.1 for more discussion.
To help the line emission escape the molecular cloud, the opacity at line center might be diminished for HCN and HCO+ by introducing a velocity gradient in the protostellar cloud (Sect. 4.4), or by adjusting the geometry of the envelope (Sect. 4.5). In the originally optically thick cases this might result in extra emerging line intensity. On the other hand, the integrated line intensity of the optically thin H13CO+ and C34S, for which the static spherical models already match the observations, should be conserved.
4.3. Steeper density profiles
We recall that we adopt α = 1 in Sect. 4.2 for the density profile given by Eq. (2) for the static spherical model. The dynamic spherical models (Sect. 4.4) and the flattened models (Sect. 4.5) are based on the same density power-law. The validity of this assumption is addressed in Sect. 4.1. Below we illustrate how steeper density profiles affect our results.
Because the value of α is not unambiguously equal to 1.0, we run test models with α = 2.0 and α = 1.5 for the static spherical model for HCO+. Both models have self-consistent temperature profiles derived in earlier work (Van der Tak et al. 2000) or by the dust modeling described in Sect. 4.1. The qualitative trend is that a steeper density profile results in a steeper temperature gradient.
In the static α = 2.0 model, the HCO+ 4–3 integrated line intensity emanating from the center is about 20% higher than for the α = 1.0 model at the same abundance (cf. Fig. 10). However, it still only reproduces 60% of the observed peak integrated intensity. Doubling the HCO+ abundance from 1.5 × 10-8 to 3 × 10-8 increases the central 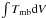 value by only a few percent, with the optical depth at the model center at line center increasing from 28 to 52. Therefore, even with further increased abundance, the α = 2.0 model will still underproduce the observed peak
value by only a few percent, with the optical depth at the model center at line center increasing from 28 to 52. Therefore, even with further increased abundance, the α = 2.0 model will still underproduce the observed peak 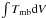 level. On the other hand, the spatial profile of
level. On the other hand, the spatial profile of 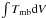 does fall off more steeply than for α = 1.0, bringing the shape closer to the observations, but we note that the H13CO+
does fall off more steeply than for α = 1.0, bringing the shape closer to the observations, but we note that the H13CO+ profile becomes too sharp to match the observations. Moreover, the fixed 1/60 ratio between the abundances of H13CO+ and HCO+ results in an overproduction of the central H13CO+
profile becomes too sharp to match the observations. Moreover, the fixed 1/60 ratio between the abundances of H13CO+ and HCO+ results in an overproduction of the central H13CO+ , simultaneously with the underproduction of HCO+ emission. Thus, we conclude that a density distribution with α = 2.0 does not improve the match to the observed intensity distribution compared to the α = 1.0 case (Sect. 4.2).
, simultaneously with the underproduction of HCO+ emission. Thus, we conclude that a density distribution with α = 2.0 does not improve the match to the observed intensity distribution compared to the α = 1.0 case (Sect. 4.2).
In the static α = 1.5 model, the HCO+ 4–3 integrated line intensity distribution is more peaked than in the α = 1.0 case from Sect. 4.2. However, the peak 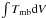 value, which was a factor ~ 2 too low for α = 1.0, is increased by only ≲ 10% for α = 1.5. At the same time, H13CO+ emission toward the central position is overproduced by a factor of 2. We conclude, as for α = 2.0 and 1.0, that a density power-law slope of 1.5 fails to explain the spatial distribution of line emission if we consider an optically thick and an optically thin tracer simultaneously.
value, which was a factor ~ 2 too low for α = 1.0, is increased by only ≲ 10% for α = 1.5. At the same time, H13CO+ emission toward the central position is overproduced by a factor of 2. We conclude, as for α = 2.0 and 1.0, that a density power-law slope of 1.5 fails to explain the spatial distribution of line emission if we consider an optically thick and an optically thin tracer simultaneously.
 |
Fig. 9 Top: velocity profiles of observed HCO+ 4–3 (histogram), compared to those from various models, all at the central spatial position. The profiles from the spherical (1D) model and the infall model follow from an HCO+ abundance of 1.5 × 10-8, and the abundance for the model used for the flattened model profile is 6 × 10-9. Bottom: velocity profiles of observed and modeled H13CO+, with abundances scaled by a factor 60 with respect to H12CO+. |
 |
Fig. 10 Position dependence of integrated line intensities for static spherical ratran models (Sect. 4.2) of C17O, HCN, CS, C34S, HCO+ and H13CO+. Black solid and dashed lines represent two perpendicular slice directions in the observed maps, red lines represent radial dependence of integrated line strength in the 1D static models. At the line center, the sky ray tracing routine calculates the following optical depths through the center of the model sphere: 0.095 for C17O, 33 for HCN, 10 for CS, 0.38 for C34S, 34 for HCO+ and 0.64 for H13CO+. Abundance values (X) are presented in the form a (b), representing a × 10b. |
4.4. Dynamic spherical models
In this section we attempt to diminish the optical depth near the emission line frequencies by introducing velocity structure in the modeled cloud. Velocity structure can be considered as either random (turbulent) motion or systematic motion. We investigate the effects of a radial turbulence gradient and of a systematic infall signature on the line opacity and on the distribution of emerging intensity.
While the originally constant turbulence of 2 km s-1 is consistent with nonthermal linewidths found in other massive star-forming regions (Caselli & Myers 1995), we introduce a gradient ranging from 10 km s-1 in the central shell of the model down to 1 km s-1 in the outer shell. Even with this deliberately extreme turbulence gradient, the resultant line optical depth is not reduced significantly, whereas the line shapes become broader in velocity space, as expected. Since this broadening is inconsistent with the observed FWHM of ~4 km s-1 for most lines, we refrain from further exploring this particular type of differential dynamics.
Apart from a turbulence gradient, a systematic radial velocity gradient could be viable. If our envelope is to be forming a centrally condensed object, an infalling rather than an expanding velocity field seems reasonable. An infall signature is classically regarded as the double-peaked spectral line profile with a stronger blue than red peak in optically thick lines (see, e.g., Fig. 5 of Evans 1999). Such a signature is either not present in our source or is unresolved by the observations (spectral resolution 1 km s-1). Any unresolved double-peak structure would have to be separated by <2 km s-1, yielding an upper limit to the infall velocity of 1 km s-1 near the dust sublimation radius, ~100 AU (e.g., De Wit et al. 2009), close to the protostar. This limit is conservative, since even observations at slightly higher spectral resolution (Mitchell et al. 1992; Van der Tak et al. 1999) show no sign of infall in line profiles of, e.g., 13CO and CS.
Choi et al. (1995) and Hogerheijde & Sandell (2000) have considered one or more off-center positions to constrain models of infalling protostellar envelopes. They find that inside-out infall models with α = 1.5 are among the possible fits for some protostellar envelopes. We emphasize that different α values are found for different protostellar envelopes, although the power-law index of the density profile α is generally between 1.0 and 2.0. Hogerheijde & Sandell (2000) highlight that the density and velocity structure are degenerate.
 |
Fig. 11 Position dependence of integrated line intensities for HCO+ and H13CO+ 4–3 resulting from an infall model with α = 1.5 (Sect. 4.3). Optical depths at line center through the center of the model cloud are 4.6 for HCO+ and 0.06 for H13CO+. |
To enable a direct comparison between results from the static and the infalling models, we retain the spherical α = 1.0 envelope from Sect. 4.2 and add a radial velocity profile applicable for the freefall region of an inside-out collapsing cloud (following Shu 1977): 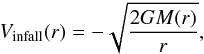 (3)where r represents radial distance from the cloud center and G is the gravitational constant. The enclosed mass M in Eq. (3) is defined as M(r) = Mcentral + Menv(<r). We set Mcentral = 16 M⊙ to account for the central protostellar object; Menv(<r) represents the gas mass in the envelope contained in a sphere of radius r. The turbulent velocity is again constant at 2 km s-1 in the infalling model. Relative molecular abundances are kept the same as in Sect. 4.2.
(3)where r represents radial distance from the cloud center and G is the gravitational constant. The enclosed mass M in Eq. (3) is defined as M(r) = Mcentral + Menv(<r). We set Mcentral = 16 M⊙ to account for the central protostellar object; Menv(<r) represents the gas mass in the envelope contained in a sphere of radius r. The turbulent velocity is again constant at 2 km s-1 in the infalling model. Relative molecular abundances are kept the same as in Sect. 4.2.
The velocity gradient has the desired effect of decreasing the optical depth at the line center and through the center of the spherical model by a factor ≳ 3. As in the spherical static case (Sect. 4.2), the modeled profiles of the rarer isotopologs C34S and H13CO+ still match the observations after the introduction of infall. The spatial profile of 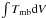 of HCN 4–3 and HCO+ 4–3 benefit from the reduced optical depth. However, it is insufficient to reproduce the observed peak
of HCN 4–3 and HCO+ 4–3 benefit from the reduced optical depth. However, it is insufficient to reproduce the observed peak 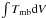 value for HCN, as well as the spatial profile of HCO+. On the other hand, the infall model for CS 7–6 overproduces line intensity at the central position by ~70%. In general, a significant discrepancy remains for the optically thick lines, in terms of both shape of the spatial profile and the peak integrated line intensity value. More importantly, the velocity gradient introduced in Eq. (3) results in a very asymmetric and double-peaked velocity profile for optically thick lines, and a wider profile (FWHM ≳ 6 km s-1, Fig. 9) for optically thin lines such as H13CO+ 4–3. Concluding, the observed spectral line profiles indicate that an infall model is inadequate for the molecular envelope studied here.
value for HCN, as well as the spatial profile of HCO+. On the other hand, the infall model for CS 7–6 overproduces line intensity at the central position by ~70%. In general, a significant discrepancy remains for the optically thick lines, in terms of both shape of the spatial profile and the peak integrated line intensity value. More importantly, the velocity gradient introduced in Eq. (3) results in a very asymmetric and double-peaked velocity profile for optically thick lines, and a wider profile (FWHM ≳ 6 km s-1, Fig. 9) for optically thin lines such as H13CO+ 4–3. Concluding, the observed spectral line profiles indicate that an infall model is inadequate for the molecular envelope studied here.
Finally, we test an α = 1.5 model for the infalling case, dynamically consistent with the physical description by Shu (1977). The spatial distribution of 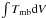 (Fig. 11) for this model comes closer than any other to a simultaneous explanation of an optically thick (HCO+) and an optically thin (H13CO+) tracer, with abundances half of those for the α = 1.0 models. However, when the spectral direction is also taken into account, the same discrepancies emerge as for the other infall models. We conclude that the adjustment of the density power-law slope from 1.0 to 1.5 does not alleviate the mismatch between infall models and the observed spectral line profiles. In fact, the static models in Sects. 4.2 and 4.5 produce better matches to the observed spectral line profiles than the infall models.
(Fig. 11) for this model comes closer than any other to a simultaneous explanation of an optically thick (HCO+) and an optically thin (H13CO+) tracer, with abundances half of those for the α = 1.0 models. However, when the spectral direction is also taken into account, the same discrepancies emerge as for the other infall models. We conclude that the adjustment of the density power-law slope from 1.0 to 1.5 does not alleviate the mismatch between infall models and the observed spectral line profiles. In fact, the static models in Sects. 4.2 and 4.5 produce better matches to the observed spectral line profiles than the infall models.
4.5. Static model with flattened geometry
After considering a static spherical model (Sect. 4.2) and dynamic spherical models (Sect. 4.4), we now explore a morphological model of the molecular envelope which is flattened in one direction. The spatial axes of the model perpendicular to the line of sight are constrained by the observed morphology of the molecular cloud, which indicates a projected cloud structure not far from circular (major to minor axis ratios < 1.5). On the other hand, the cloud can be flattened significantly in the direction along the line of sight. Moreover, if a small inclination of the short axis of the modeled system with respect to the line of sight (“viewing angle”) is introduced, we expect to be able to explain part of the noncircular geometry in the observed maps. Geometrically, the observed major/minor axis ratios on the sky of ≲ 1.5 would constrain a flattened structure to be positioned at an inclination angle ≲ 45°.
For the density structure of the flattened model, we take an ellipsoidal adaptation of the spherical description from Eq. (2), where two of the three spatial axes are identical to the spherical case and the third axis is compressed. The spherical density structure is first translated into cylindrical coordinates (R,z) and subsequently flattened by compressing the z-direction by a factor of 3. The density scaling factor n0 is scaled up by the same factor, such that the total molecular mass of the model is conserved. The temperature structure in the cloud is taken to depend on the cumulative column density toward the central position, which is extracted from the one-dimensional case (Sect. 4.2). There is no bulk velocity structure in this model. The turbulent velocity is constant at 2 km s-1, as in the spherical static and spherical infalling models from Sects. 4.2 and 4.4. For the radiative transfer, we use the axisymmetric version of the ratran code (Hogerheijde & Van der Tak 2000).
 |
Fig. 12 Position dependence of integrated line intensities for HCO+ 4–3, compared with integrated line intensity profiles from flattened ellipsoidal physical models (Sect. 4.5). Model slices are shown for an HCO+ abundance of 1.2 × 10-8 (left column) and 6 × 10-9 (right column). The viewing angle i varies from 60° (top) to 40° (middle) to 20° (bottom). Values of optical depth at line center through the center of the model, as determined by the ray tracing routine, are for X = 1.2 × 10-8: 42, 28, 23 at i = 60,40,20°, respectively; and for X = 6 × 10-9: 23, 15, 13 at i = 60,40,20°, respectively. |
Figure 12 presents the result of radiative transfer using the ellipsoidally flattened model for HCO+ 4–3. We choose two relative molecular abundances, X = 1.2 × 10-8 and 6.0 × 10-9, and three inclination angles for the ray tracing, i = 20,40, and 60°, where 0° is “face-on” (viewing along the z-axis) and 90° is “edge-on”. The best match is given by X = 6 × 10-9, i = 20° (Fig. 12, bottom right panel). The figure shows that in all cases, the modeled HCO+ 4–3 distribution is much more extended than what is observed. We note that the flattened envelope at X = 6 × 10-9 and i = 20° does explain the observed 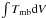 of HCO+ 4–3 at the central position, with a molecular abundance of 6 × 10-9, whereas the spherical models (Sect. 4.2, 4.4) underpredict the observed
of HCO+ 4–3 at the central position, with a molecular abundance of 6 × 10-9, whereas the spherical models (Sect. 4.2, 4.4) underpredict the observed 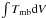 at the central position, even with more than double the abundance (X = 1.5 × 10-8). The flattened model also has a significantly lower optical depth of 13 (X = 6 × 10-9, i = 20°) at line center through the center of the model, where the spherical models have τ > 20 for HCO+ 4–3. For i = 40°, at the same low abundance, the optical depth is 15, and for i = 60° it is 23, comparable to opacities in the spherical models.
at the central position, even with more than double the abundance (X = 1.5 × 10-8). The flattened model also has a significantly lower optical depth of 13 (X = 6 × 10-9, i = 20°) at line center through the center of the model, where the spherical models have τ > 20 for HCO+ 4–3. For i = 40°, at the same low abundance, the optical depth is 15, and for i = 60° it is 23, comparable to opacities in the spherical models.
There is also a discrepancy between the modeled and observed HCO+ 4–3 line shape in velocity space. The observed line profile has a roughly Gaussian shape with one single peak centered on the known source velocity. Although an optical depth of 13 at line center is lower than in the spherical models, Fig. 9 shows that the flattened model still results in a very thick line profile, where most of the photons find a way out of the cloud at > 2 km s-1 away from the line center. As seen before, the modeled 4–3 line of the isotopic variant H13CO+ is optically thin (τ = 0.3), and therefore produces a better match to the observed line profile (Fig. 9, bottom panel).
To test how sensitive the emerging integrated intensity profiles are to the adopted flattening factor of 3, we also investigate the 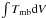 map of HCO+ 4–3 resulting from a model with a flattening factor of 6. The peak observed
map of HCO+ 4–3 resulting from a model with a flattening factor of 6. The peak observed 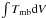 value is now best matched with an HCO+ abundance of ~2 × 10-9 (at i = 20°), with an optical depth at line center of ~ 5. As previously, the spatial profile of
value is now best matched with an HCO+ abundance of ~2 × 10-9 (at i = 20°), with an optical depth at line center of ~ 5. As previously, the spatial profile of 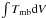 is shallower than in the observed map. As a result, model geometries with flattening factors of 3 and 6 both fail to explain the observed intensity distribution of HCO+ 4–3. While we consider flattening factors of a few to be reasonable, much flatter models would result in a geometrical description of the envelope that resembles a sheet, for which no supporting evidence exists.
is shallower than in the observed map. As a result, model geometries with flattening factors of 3 and 6 both fail to explain the observed intensity distribution of HCO+ 4–3. While we consider flattening factors of a few to be reasonable, much flatter models would result in a geometrical description of the envelope that resembles a sheet, for which no supporting evidence exists.
5. Discussion
5.1. Physical structure of the modeled envelope
In Sect. 4 we compared the observed spatial distribution of a selection of molecular tracers with spherical static and infalling models and with a static ellipsoidally flattened model. The spectral lines of the rare isotopic variants C34S and H13CO+ can be explained by the static spherical model from Sect. 4.2, both in terms of integrated intensity at emission center and the shape of the spatial profile. But for the main isotopic species HCN, HCO+, and CS, as well as for C17O, this representation of the molecular envelope fails to reproduce the observed integrated intensity levels. We conclude that for HCN, HCO+, and CS, the line optical depths of ≥ 10 (see Fig. 10) are preventing radiation from escaping the model envelope. Attempts to compensate for the missing intensity by increasing the molecular abundance logically result in even higher line opacities and do not result in more photons escaping the cloud. Moreover, as the abundance is increased, the already self-absorbed spectral line profiles become more discrepant compared to the observations.
 |
Fig. 13 Relative level populations of the J = 3 and J = 2 levels of C17O, and the J = 4 level of H13CO+, as determined by the Monte Carlo method in ratran for the static spherical model. The population of each J level is given relative to the total population for that species. The gas temperature profile (Tkin) of the model cloud is shown by the solid blue line. The energy level of the J = 3 rotational state of C17O is indicated by the dotted horizontal line. |
Unlike the other two lines that show a large discrepancy in spatial distribution of the emission (HCN 4–3 and HCO+ 4–3), the modeled C17O 3–2 emission is optically thin (τ = 0.1) at line center through the center of the model cloud. The low optical depth is confirmed by inspection of modeled line profiles in velocity space, which are represented well by a Gaussian, both on and off center. We suspect that the relative overproduction of C17O 3–2 away from the central position is caused by excitation effects. Figure 13 shows that the level populations of the J = 3 level determined by the Monte Carlo method peaks at 18 000 AU (outside the FWHM of the central beam of 15″ ≡ 15 000 AU), and declines steeply toward smaller radii. If higher J-levels are examined, it becomes apparent that the high kinetic temperatures in the center of the envelope leaves lower levels such as J = 3, with an energy of only 32 K above ground, sparsely populated.
The mismatch with the observed spatial distribution of C17O could imply that either the description of the excitation conditions (i.e., temperature) is inadequate or an additional component of cold, tenuous gas should be added to the model. The current truncation radius of 64 kAU, at which point the temperature is 22.6 K, is derived from CS line observations by Van der Tak et al. (2000). An extension of the model envelope beyond this radius to lower densities and lower temperatures, would contribute to a cold, tenuous component. The latter explanation is favored, since adjusting the temperature profile would affect many molecular species, whereas adding low-density material would mostly affect CO and its isotopes. However, two test models with extended envelopes, following the same density slope as in Sect. 4.2 and with a temperature extrapolated following r-0.4, suggest that the truncation radius alone cannot explain the discrepancy. We define one model with additional shells extending to 126 kAU and a temperature ranging down to 17.0 K, and another extending to 221 kAU and a temperature of 13.6 K. The spatial distribution of integrated C17O 3–2 intensity resulting from the first model is steeper, but still too flat to match the observed distribution. The 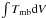 profile resulting from the second extended model is very similar to the first one, suggesting that a further extension of the envelope would not bring the modeled intensity distribution closer to the observations. Furthermore, we point out that by incorporating the observed blueshifted component of C17O 3–2 and other emission we could be contaminating our view of the quiescent molecular envelope.
profile resulting from the second extended model is very similar to the first one, suggesting that a further extension of the envelope would not bring the modeled intensity distribution closer to the observations. Furthermore, we point out that by incorporating the observed blueshifted component of C17O 3–2 and other emission we could be contaminating our view of the quiescent molecular envelope.
An attempt to reduce line opacity by introducing velocity structure (Sect. 4.4) is moderately successful in the sense that line optical depths are indeed decreased, but not sufficient to explain the spatial distribution of integrated line intensity for species such as HCO+ and HCN. Moreover, that the spectral linewidths produced by the infall model are incompatible with observations of both optically thick and optically thin lines (Fig. 9) could mean that, if any velocity gradient exists in the molecular envelope, complete freefall is not the correct approach. Part of the envelope may be radiatively, magnetically or turbulently supported against collapse, while other (outer) parts are in fact still collapsing.
Finally, the flattening of the spherical cloud in one spatial direction (Sect. 4.5) also reduces optical depths, but only when viewed under a moderate inclination angle (~20°, see Fig. 12). A high inclination angle has the additional effect of producing spatial profiles that are more asymmetric than what is observed. If the envelope of AFGL2591 is flattened in reality, we thus expect the system to be viewed almost face-on. Both trial HCO+ abundance values in Sect. 4.5 are consistent with 1 × 10-8 to within the uncertainty margin of a factor 2 quoted by Van der Tak et al. (1999).
In addition, it is apparent from Fig. 9 that neither the infall model nor the flattened model result in velocity profiles of the emission lines that are as narrow as the observed linewidths. We emphasize that the discrepancy of the velocity profile for both the optically thin and thick lines is larger for the infall model than for the static flattened model. It is an interesting result that the change from static spherical to static ellipsoidal leaves the line shape of the optically thin H13CO+ 4–3 intact, while it also manages to let more of the optically thick H12CO+ 4–3 line intensity escape the cloud.
For HCN specifically, Boonman et al. (2001) and Stäuber et al. (2005) have suggested an abundance that is enhanced by as much as a factor 100 in the central few hundred AU. We introduce an abundance jump from 1 × 10-8 at Tgas < 230 K to 1 × 10-6 above 230 K in the framework of our static spherical model (Sect. 4.2), which originally has a constant abundance. The threshold for the abundance jump is motivated by gas-phase chemistry (Boonman et al. 2001; Van der Tak et al. 1999), rather than by sublimation from grain surfaces, which puts the evaporation threshold at ~100 K for H2O ices and at ~25 K for CO ices. While this abundance jump is in principle a candidate for explaining the missing line intensity from the central region of the envelope (cf. Fig. 10), the abundance jump model underproduces the observed HCN 4–3 intensity toward the central position by ~40%, while simultaneously overproducing the off-center intensity. This is caused by the fact that only the central few hundred AU enjoys a gas temperature above 230 K, the effects of which are washed out by the ~15″ (15 000 AU) FWHM of the telescope beam; hence, the very inner part of the envelope affected by the enhanced abundance is too small to modify the 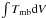 profile on the spatial scales probed by the SLS observations. Alternatively, the lack of modeled HCN 4–3 from the center of the envelope can be explained (partly) by the critical density, which is on the order of 108 cm-3 for HCN 4–3 (at 100 K) and only ~107 cm-3 for HCO+ 4–3. Compared to the maximum density of 1.2 × 107 cm-3 in the central shell of the spherical models (Sects. 4.2, 4.4), it is found that HCN is not thermalized.
profile on the spatial scales probed by the SLS observations. Alternatively, the lack of modeled HCN 4–3 from the center of the envelope can be explained (partly) by the critical density, which is on the order of 108 cm-3 for HCN 4–3 (at 100 K) and only ~107 cm-3 for HCO+ 4–3. Compared to the maximum density of 1.2 × 107 cm-3 in the central shell of the spherical models (Sects. 4.2, 4.4), it is found that HCN is not thermalized.
The dust continuum modeling in Sect. 4.1 indicates that a spherical description of the envelope with a single power-law density profile cannot simultaneously explain the 450 μm and the 850 μm continuum maps. This could indicate a deviation from spherical symmetry. Test runs of line radiative transfer models with density indices steeper than 1.0 (Sect. 4.3) demonstrate that model descriptions with α = 1.5 or 2.0 do not provide a more satisfying match to the observed emission in spatial and spectral dimensions simultaneously. Other envelopes around young high-mass stars are generally well fit by power-law density profiles with α between 1.0 and 2.0, as studied in the samples by Van der Tak et al. (2000) and Hatchell & Van der Tak (2003). Density slopes in low-mass protostellar envelopes are found to occupy the same range (Jørgensen et al. 2002). The slope of α = 1.0 for AFGL2591 is on the shallow end of this interval, but a direct correlation between α and evolutionary stage is not found in comparative studies by, e.g., Van der Tak et al. (2000).
In conclusion, the model descriptions employed in this study only match the observed molecular line intensity distributions if the line under consideration is optically thin. From a modeling point of view, signatures from these lines are not sensitive to the detailed distribution of the material in the envelope, as long as roughly the right amount of material is present at the right density and temperature. Conversely, we find a profound mismatch for optically thick lines, exactly those that are observational probes of the geometry of the envelope and the distribution of the material. Below we propose several solutions to the shortcomings of our models.
-
Instead of choosing between either velocity structure ornonspherical morphology, a combination of these twoingredients might yield a closer match for the observed molecularemission in the spatial domain. In the spectral domain, however,we do not expect a nonspherical infalling model to exhibit lineshapes that will match the observations(cf. Fig. 9).
-
A second route to lower optical depths is to adopt an outflow cavity in the envelope, in combination with a favorable viewing angle, as proposed by Van der Tak et al. (1999) and later investigated by Preibisch et al. (2003) and Bruderer et al. (2010a).
-
A third option is to introduce inhomogeneous (“clumpy”) structure to alleviate optical depth effects along selected lines of sight (Wang et al. 1993; Spaans & Van Dishoeck 1997). The spatial scales of these inhomogeneities should then be such that they are largely unresolved by the observations presented here, i.e., smaller than ~104 AU.
5.2. Further evidence of substructure
The models described in Sect. 4 are an attempt to explain the large-scale morphology of the molecular envelope of AFGL2591 by focusing on a selection of molecular species, but we have also noted additional irregular structure in other tracers in Sects. 3.2 and 3.3. Various maps of molecular species that we did not model explicitly are therefore interesting to approach from a phenomenological perspective.
The northeastern “arm”, together with the southern indentation seen in six different species, might indicate a quadrupolar outflow. This could be interpreted as a set of two bipolar outflows originating in two separate protostars, instead of the previously assumed bipolar outflow associated with a single protostar. However, apart from the velocity separation seen in N2H+, there is no overwhelming kinematic evidence of this additional outflow direction. Alternatively, the “arms” at position angles ~130° and ~310° (N2H+ velocity map in Fig. 6) may also be infalling gas streams, perhaps belonging to a larger scale filamentary structure (Klessen et al. 2005).
The northeastern plume is especially bright in several CH3OH transitions with varying Eup. This indicates that its origin does not lie in excitation effects. Combined with the observation that the plume is absent in C2H and the sulfur-bearing species, we suggest that chemical effects are at play. Grain surface chemistry is known to be an important formation route for CH3OH (Charnley et al. 1997; Herbst & Van Dishoeck 2009), which could have evaporated from grain mantles under the influence of a local shock front.
The shape and direction (position angle ~230°) of blueshifted components of 13CO, C17O, HCO+, o-H2CO, and N2H+ coincide with the direction of the known approaching molecular outflow (Hasegawa & Mitchell 1995). It is interesting to note that, contrary to most molecules in Figs. 6 and 7 where both the envelope and the outflow contribute to the observed emission, N2H+ 4–3 in particular appears to trace the outflow rather than the bulk envelope. We base this on the significantly flattened morphology of its integrated line emission map, as well as on the velocity gradient which is more pronounced for N2H+ than for the other molecules observed here. The N2H+ molecule has previously been used as a tracer of dense material (e.g., Caselli et al. 2002a,b; Crapsi et al. 2004; Di Francesco et al. 2004), but usually from observations of the J = 1–0 or 3–2 transition. We note that maps of N2H+ 4–3 are rare in the literature. Moreover, Busquet et al. (2011) have found significant depletion of N2H+ relative to NH3 in dense parts of hot cores, again derived from N2H+ 1–0 observations, so apart from the pronounced velocity structure, density-dependent depletion could contribute to the atypical distribution of N2H+ emission seen in our map (Fig. 2). Conversely, the N2H+ emission could trace the evaporation of N2 (Bergin et al. 2002) along outflow cavity walls.
Although only marginally significant compared to the pointing uncertainties, that high-density tracers such as HNC and CN have peak positions offset to the south relative to other species could be a result of density anisotropies. C2H being offset to the northwest could arise from chemical processes influenced by anisotropic UV-radiation.
The warm CH3OH 121–120 A ∓ transition, with Eup = 197 K, shows a two-peak structure (see Sect. 3), indicative of two separated heating sources. While four emission sources with separations ≲ 6″ have been seen in interferometric observations of this source (Van der Tak et al. 1999; Trinidad et al. 2003; Benz et al. 2007), the warm components separated by >10″ (>10 000 AU) described here have not been seen before. Although the 121–120 transition is not listed in studies of masing CH3OH lines (e.g., Cragg et al. 1992), we cannot exclude the possibility that it is a maser. If it is, then a linewidth narrower than the 5 km s-1 that we observe would need to be confirmed by higher angular resolution observations. An intrinsically narrow line profile is potentially smeared out by our 15″ beam, which encompasses emission from a considerable portion of the molecular cloud. Moreover, excitation analysis of an ensemble of CH3OH lines, planned in Van der Wiel et al. (2011b, in prep.) will reveal whether or not the 121–120 emission fits in the picture of thermal emission.
5.3. Conclusions and outlook
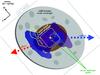 |
Fig. 14 Overview of observed substructure in the circumstellar envelope of AFGL2591. The “outer” and “inner” envelopes, as well as the four-arm structure of N2H+, the warm CH3OH spots, and the CH3OH plume are described in this work. The directions of the approaching (blue) and receding (red) outflows are indicated. The yellow star marks the position of the central heating source (infrared source from Van der Tak et al. 1999). VLA1 and VLA2 are radio continuum sources detected by Trinidad et al. (2003). The near-IR loops from Preibisch et al. (2003) are indicated in dashed yellow. For reference, the fields of view of JCMT/HARP-B and the interferometric maps from VLA and OVRO are indicated. |
To summarize, this study uses the unbiased spectral imaging from the JCMT Spectral Legacy Survey to investigate the structure of the protostellar envelope of AFGL2591. We employed 35 spatially resolved molecular line signatures to investigate the envelope in three dimensions: two spatial axes with a resolution element of ~104 AU in projected distance and the line-of-sight velocity axis with a resolution of 1 km s-1.
Figure 14 provides an overview of selected observations from the literature and from this study, which are indicative of substructure in the envelope of AFGL2591. With this overview we aim to support the suggestion that inhomogeneous substructure on scales of a few 1000 AU and smaller should be present in molecular envelopes around protostars. The two separated spots of warm CH3OH, a warped asymmetric plume feature, a flattened morphology of warm SO2, and the multiple “arm” structures seen in CO, HCN, H2CO, N2H+, and CS (Sect. 5.2) could arise from local underdense patches with associated lower cumulative column densities, higher (UV)-flux conditions, and consequently higher gas temperatures and altered chemistry. At the same time, such a picture could resolve optical depth effects for the quiescent envelope tracers discussed in Sects. 4 and 5.1. Therefore, our results warrant further theoretical modeling efforts for protostellar envelopes in the direction of clumpy models and of flattened model structures, possibly including cavities and velocity structure. We emphasize the value of the spectral imaging survey provided by the SLS, which allows for the simultaneous employment of several molecular tracers to characterize the physical properties of the large-scale envelope of AFGL2591.
An unbiased Herschel/HIFI spectral survey of AFGL2591 in the 490–1240 GHz regime is currently under analysis (Van der Wiel et al. 2011a, in prep.). This will give insight into the excitation conditions in the molecular envelope, but does not contain any spatial information. Moreover, spectral mapping of a consistent set of molecular tracers such as those presented here, but at higher angular resolution, will be needed to confirm the “clumpy” picture sketched above. The set of tracers should be chosen to be sensitive to the overall quiescent envelope, as well as to pockets of warm (>200 K) actively heated gas. Although our specific target is far into the northern sky, the obvious candidate observatory to study similar high-mass star-forming envelopes in the southern sky is the Atacama Large Millimeter and Submillimeter Array2. This facility will be able to map high-J lines of simple molecules like CO, HCN, HCO+ – and their rarer isotopic variants – at subarcsecond angular resolution.
Acknowledgments
The authors are grateful to the anonymous referee whose constructive comments helped to improve the manuscript and to the editor, Malcolm Walmsley, for additional suggestions. We acknowledge the JCMT staff for their support. This research uses the facilities of the Canadian Astronomy Data Centre operated by the National Research Council of Canada with the support of the Canadian Space Agency.
References
- Benz, A. O., Stäuber, P., Bourke, T. L., et al. 2007, A&A, 475, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Alves, J., Huard, T., & Lada, C. J. 2002, ApJ, 570, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 2005, MNRAS, 362, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., Clarke, C. J., & Pringle, J. E. 2001, MNRAS, 323, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Boonman, A. M. S., Stark, R., Van der Tak, F. F. S., et al. 2001, ApJ, 553, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S., Benz, A. O., Stäuber, P., & Doty, S. D. 2010a, ApJ, 720, 1432 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S., Benz, A. O., Van Dishoeck, E. F., et al. 2010b, A&A, 521, L44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buckle, J. V., Hills, R. E., Smith, H., et al. 2009, MNRAS, 399, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Busquet, G., Estalella, R., Zhang, Q., et al. 2011, A&A, 525, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., & Myers, P. C. 1995, ApJ, 446, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002a, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002b, ApJ, 565, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R. 2005, Ap&SS, 295, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Rodgers, S. D. 1997, ApJ, 482, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Chin, Y., Henkel, C., Millar, T. J., Whiteoak, J. B., & Mauersberger, R. 1996, A&A, 312, L33 [NASA ADS] [Google Scholar]
- Choi, M., Evans, II, N. J., Gregersen, E. M., & Wang, Y. 1995, ApJ, 448, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Cragg, D. M., Johns, K. P., Godfrey, P. D., & Brown, R. D. 1992, MNRAS, 259, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2004, A&A, 420, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Wit, W. J., Hoare, M. G., Fujiyoshi, T., et al. 2009, A&A, 494, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dent, W., Duncan, W., Ellis, M., et al. 2000, in Imaging at Radio through Submillimeter Wavelengths, ed. J. G. Mangum, & S. J. E. Radford, ASP Conf. Ser., 217, 33 [Google Scholar]
- Di Francesco, J., André, P., & Myers, P. C. 2004, ApJ, 617, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Doty, S. D., Van Dishoeck, E. F., Van der Tak, F. F. S., & Boonman, A. M. S. 2002, A&A, 389, 446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, II, N. J. 1999, ARA&A, 37, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R. 1999, MNRAS, 305, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S., & Thaddeus, P. 1974, ApJ, 191, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Mitchell, G. F. 1995, ApJ, 451, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., & Van der Tak, F. F. S. 2003, A&A, 409, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., & Van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hocuk, S., & Spaans, M. 2010, A&A, 522, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hogerheijde, M. R., & Sandell, G. 2000, ApJ, 534, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., & Van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
- Ivezic, Z., Nenkova, M., & Elitzur, M. 1999 [astro-ph/9910475] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & Van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S., Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Durán-Rojas, C. 2005, ApJ, 620, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Thronson, Jr., H. A.,Smith, H. A., Schwartz, P. R., & Glaccum, W. 1984, ApJ, 286, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 2003, Reports of Progress in Physics, 66, 1651 [Google Scholar]
- Mitchell, G. F., Hasegawa, T. I., & Schella, J. 1992, ApJ, 386, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Plume, R., Fuller, G. A., Helmich, F., et al. 2007, PASP, 119, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., Balega, Y. Y., Schertl, D., & Weigelt, G. 2003, A&A, 412, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, H., Van der Tak, F. F. S., Fuller, G. A., Plume, R., & Bayet, E. 2011, A&A, 525, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2006, A&A, 458, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., Van der Tak, F. F. S., Van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H., Buckle, J., Hills, R., et al. 2008, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, 7020, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference SeriesPresented at the [Google Scholar]
- Spaans, M., & Van Dishoeck, E. F. 1997, A&A, 323, 953 [NASA ADS] [Google Scholar]
- Stäuber, P., Doty, S. D., Van Dishoeck, E. F., Jørgensen, J. K., & Benz, A. O. 2004, A&A, 425, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stäuber, P., Doty, S. D., Van Dishoeck, E. F., & Benz, A. O. 2005, A&A, 440, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trinidad, M. A., Curiel, S., Cantó, J., et al. 2003, ApJ, 589, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E., Chan, K., Green, S., & Lubowich, D. A. 1992, ApJ, 399, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Tak, F. F. S., & Menten, K. M. 2005, A&A, 437, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van der Tak, F. F. S., Van Dishoeck, E. F., Evans, II, N. J., Bakker, E. J., & Blake, G. A. 1999, ApJ, 522, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Tak, F. F. S., Van Dishoeck, E. F., Evans, II, N. J., & Blake, G. A. 2000, ApJ, 537, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Wiel, M. H. D., Van der Tak, F. F. S., Ossenkopf, V., et al. 2009, A&A, 498, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., Jaffe, D. T., Evans, II, N. J., et al. 1993, ApJ, 419, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Root-mean-square (rms) noise statistics of the data product, calculated in 1 km s-1 channels. The square symbols denote the median rms in all map pixels over a selected frequency range, with their error bars indicating the rms of the rms noise across all map pixels in the same frequency range. The triangle symbols mark the rms value in the least noisy (pointing up) and noisiest pixel (pointing down) in the map. The horizontal dashed line indicates the survey target noise for this object. |
| In the text | |
 |
Fig. 2 Maps of emission from the 3–2 transitions of CO, 13CO, C17O, transitions of N-bearing molecules, HCO+ and H13CO+ 4–3. White contours represent integrated line emission and are at 90%, 80%, ..., 10% of the maximum intensity, listed in Table 2. The contour at 50% is thicker. An extra contour is added for HNC 4–3 at 5% of the maximum intensity. The beam size at the relevant frequency is indicated in the top right corner of each panel. To avoid noise in the figures, contours below 0.7 K km s-1 are not shown. SCUBA 850 μm continuum emission is shown in color scale and thin black contours; the color scale is stretched from 10 to 5600 mJy beam-1. |
| In the text | |
 |
Fig. 3 Like Fig. 2, but for H2CO, SO, SO2, and CS. Maximum intensities are listed in Table 2. |
| In the text | |
 |
Fig. 4 Like Fig. 2, but for CH3OH and C2H. Maximum intensities are listed in Table 2. |
| In the text | |
 |
Fig. 5 Spatial distribution of integrated SO2 152,14–141,13 emission (white contours), which is not extended. The color scale and black contours represent 850 μm continuum, like in Fig. 2. |
| In the text | |
 |
Fig. 6 Channel maps for the CO isotopologs, N-bearing species, HCO+ and H2CO. The velocity range is divided in three velocity bins with respect to the systemic velocity of −5.8 km s-1: [−1.5, + 1.5] km s-1 is shown in gray scale stretched between 0.7 K km s-1 (white) and the maximum intensity in the central channel (black); all emission at relative velocities below −1.5 km s-1 is shown in blue contours, and all emission at relative velocities above +1.5 km s-1 in red contours. The lowest contour level is manually fine-tuned to emphasize velocity structure in each case without showing too much noise. Consecutive contour levels are drawn in steps of 10% of the maximum intensity in the brightest channel. Lowest contours: 15.0 K km s-1 for CO, 5.0 K km s-1 for 13CO, 0.8 K km s-1 for C17O, 0.35 K km s-1 for HCN and HNC, 0.4 K km s-1 for N2H+, 0.8 K km s-1 for CN 35/2–23/2, 1.0 K km s-1 for CN 37/2–25/2, and 0.8, 0.4 and 0.3 K km s-1 for the three respective H2CO transitions. The FWHM of the telescope beam is indicated in the top left corner of each panel. |
| In the text | |
 |
Fig. 7 Channel maps for sulfur-bearing species, CH3OH, and C2H. Colors and contours have the same meaning as in Fig. 6, except lowest contours: 0.6 K km s-1 for SO 78–67, 0.4 K km s-1 for SO 88–87 and 98–87, 0.6 K km s-1 for CS 7–6, 0.2 K km s-1 for SO2 53,3–42,2, 0.35, 0.6, 0.35 and 0.3 K km s-1 for the four consecutive CH3OH transitions, and 0.4 K km s-1 for both C2H transitions. |
| In the text | |
 |
Fig. 8 Emission from the 13CO 3–2 transition divided over seven velocity bins. Line intensity is summed over the velocity range indicated in each panel (in km s-1) and represented as black contour lines. Contour levels are 90%, 80%, ..., 10% of the maximum integrated intensity in the velocity bin: 3.9, 14, 41, 124, 50, 8.1, and 0.95 K km s-1 in the respective bins. As in Fig. 2, the 50%-level contour is thicker, and any contours below 0.7 K km s-1 are not drawn. The total integrated 13CO 3–2 line intensity over the entire velocity range is shown in color scale in each panel, for reference. |
| In the text | |
 |
Fig. 9 Top: velocity profiles of observed HCO+ 4–3 (histogram), compared to those from various models, all at the central spatial position. The profiles from the spherical (1D) model and the infall model follow from an HCO+ abundance of 1.5 × 10-8, and the abundance for the model used for the flattened model profile is 6 × 10-9. Bottom: velocity profiles of observed and modeled H13CO+, with abundances scaled by a factor 60 with respect to H12CO+. |
| In the text | |
 |
Fig. 10 Position dependence of integrated line intensities for static spherical ratran models (Sect. 4.2) of C17O, HCN, CS, C34S, HCO+ and H13CO+. Black solid and dashed lines represent two perpendicular slice directions in the observed maps, red lines represent radial dependence of integrated line strength in the 1D static models. At the line center, the sky ray tracing routine calculates the following optical depths through the center of the model sphere: 0.095 for C17O, 33 for HCN, 10 for CS, 0.38 for C34S, 34 for HCO+ and 0.64 for H13CO+. Abundance values (X) are presented in the form a (b), representing a × 10b. |
| In the text | |
 |
Fig. 11 Position dependence of integrated line intensities for HCO+ and H13CO+ 4–3 resulting from an infall model with α = 1.5 (Sect. 4.3). Optical depths at line center through the center of the model cloud are 4.6 for HCO+ and 0.06 for H13CO+. |
| In the text | |
 |
Fig. 12 Position dependence of integrated line intensities for HCO+ 4–3, compared with integrated line intensity profiles from flattened ellipsoidal physical models (Sect. 4.5). Model slices are shown for an HCO+ abundance of 1.2 × 10-8 (left column) and 6 × 10-9 (right column). The viewing angle i varies from 60° (top) to 40° (middle) to 20° (bottom). Values of optical depth at line center through the center of the model, as determined by the ray tracing routine, are for X = 1.2 × 10-8: 42, 28, 23 at i = 60,40,20°, respectively; and for X = 6 × 10-9: 23, 15, 13 at i = 60,40,20°, respectively. |
| In the text | |
 |
Fig. 13 Relative level populations of the J = 3 and J = 2 levels of C17O, and the J = 4 level of H13CO+, as determined by the Monte Carlo method in ratran for the static spherical model. The population of each J level is given relative to the total population for that species. The gas temperature profile (Tkin) of the model cloud is shown by the solid blue line. The energy level of the J = 3 rotational state of C17O is indicated by the dotted horizontal line. |
| In the text | |
 |
Fig. 14 Overview of observed substructure in the circumstellar envelope of AFGL2591. The “outer” and “inner” envelopes, as well as the four-arm structure of N2H+, the warm CH3OH spots, and the CH3OH plume are described in this work. The directions of the approaching (blue) and receding (red) outflows are indicated. The yellow star marks the position of the central heating source (infrared source from Van der Tak et al. 1999). VLA1 and VLA2 are radio continuum sources detected by Trinidad et al. (2003). The near-IR loops from Preibisch et al. (2003) are indicated in dashed yellow. For reference, the fields of view of JCMT/HARP-B and the interferometric maps from VLA and OVRO are indicated. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


