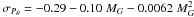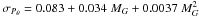| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 18 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015768 | |
| Published online | 11 March 2011 | |
Radiative hydrodynamic simulations of red supergiant stars
III. Spectro-photocentric variability, photometric variability, and consequences on Gaia measurements
1
Institut d’Astronomie et d’Astrophysique, Université Libre de
Bruxelles,
CP. 226, Boulevard du Triomphe,
1050
Bruxelles,
Belgium
e-mail: achiavas@ulb.ac.be
2
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, Postfach 1317,
85741
Garching b. München,
Germany
3
Department of Astronomy, University of Vienna,
Türkenschanzstrasse 17,
1180
Wien,
Austria
4
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot,
Place Jules Janssen,
92190
Meudon,
France
5
Université de Lyon, 69003 Lyon; École Normale Supérieure de Lyon,
46 allée d’Italie, 69007 Lyon; CNRS, UMR 5574, Centre de Recherche Astrophysique de
Lyon; Université Lyon 1, 69622
Villeurbanne,
France
6
Department of Physics and Astronomy, Division of Astronomy and
Space Physics, Uppsala University, Box 515, S-751
20
Uppsala,
Sweden
7
Istituto Nazionale di Astrofisica, Osservatorio Astronomico di
Capodimonte, via Moiariello 16, 80131
Naples,
Italy
8
Zentrum für Astronomie der Universität Heidelberg,
Landessternwarte, Königstuhl
12, 69117
Heidelberg,
Germany
9
UMR 6525 H. Fizeau, Univ. Nice Sophia Antipolis, CNRS,
Observatoire de la Côte d’Azur, Av.
Copernic, 06130
Grasse,
France
Received:
16
September
2010
Accepted:
17
December
2010
Context. It has been shown that convection in red supergiant stars (RSG) gives rise to large granules that cause surface inhomogeneities and shock waves in the photosphere. The resulting motion of the photocentre (on time scales ranging from months to years) could possibly have adverse effects on the parallax determination with Gaia.
Aims. We explore the impact of the granulation on the photocentric and photometric variability. We quantify these effects in order to better characterise the error that could possibly alter the parallax.
Methods. We use 3D radiative-hydrodynamics (RHD) simulations of convection with CO5BOLD and the post-processing radiative transfer code Optim3D to compute intensity maps and spectra in the Gaia G band [325–1030 nm].
Results. We provide astrometric and photometric predictions from 3D simulations of RSGs that are used to evaluate the possible degradation of the astrometric parameters of evolved stars derived by Gaia. We show in particular from RHD simulations that a supergiant like Betelgeuse exhibits a photocentric noise characterised by a standard deviation of the order of 0.1 AU. The number of bright giant and supergiant stars whose Gaia parallaxes will be altered by the photocentric noise ranges from a few tens to several thousands, depending on the poorly known relation between the size of the convective cells and the atmospheric pressure scale height of supergiants, and to a lower extent, on the adopted prescription for galactic extinction. In the worst situation, the degradation of the astrometric fit caused by this photocentric noise will be noticeable up to about 5 kpc for the brightest supergiants. Moreover, parallaxes of Betelgeuse-like supergiants are affected by an error of the order of a few percents. We also show that the photocentric noise, as predicted by the 3D simulation, does account for a substantial part of the supplementary “cosmic noise” that affects Hipparcos measurements of Betelgeuse and Antares.
Key words: stars: atmospheres / supergiants / astrometry / parallaxes / hydrodynamics / stars: individual: Betelgeuse
© ESO, 2011
1. Introduction
The main goal of the Gaia mission (Perryman et al. 2001; Lindegren et al. 2008) is to determine high-precision astrometric parameters (i.e., positions, parallaxes, and proper motions) for one billion objects with apparent magnitudes in the range 5.6 ≤ V ≤ 20. These data along with multi-band and multi-epoch photometric and spectrocopic data will allow us to reconstruct the formation history, structure, and evolution of the Galaxy. Among all the objects that will be observed, late-type stars present granulation-related variability that is considered, in this context, as “noise” that must be quantified in order to better characterise any resulting error on the parallax determination. A previous work by Ludwig (2006) has shown that effects caused by the granulation in red giant stars are unlikely to be important except for the extreme giants.
Red supergiant (RSG) stars are late-type stars with masses between 10 and 40 M⊙. They have effective temperature Teff ranging from 3450 (M5) to 4100 K (K1), luminosities in the range of 2000 to 300 000 L⊙, and radii up to 1500 R⊙ (Levesque et al. 2005). Their luminosities place them among the brightest stars, and they are visible up to very large distances. Based on detailed radiation-hydrodynamics (RHD) simulations of RSGs (Freytag et al. 2002 and Freytag & Höfner 2008), Chiavassa et al. (2009) (Paper I hereafter) and Chiavassa et al. (2010a) (Paper II hereafter) show that these stars are characterised by vigorous convection, which imprints a pronounced granulation pattern on the stellar surface. In particular, RSGs give rise to large granules that are comparable to the stellar radius in the H and K bands, and an irregular pattern in the optical region.
This paper is the third in the series aimed at exploring the convection in RSGs. The main purpose is to extract photocentric and photometric predictions that will be used to estimate the number of RSGs, detectable by Gaia, for which the parallax measurement will be affected by the displacements of their photometric centroid (hereafter “photocentre”).
2. Radiative hydrodynamic simulations of red supergiant stars
The numerical simulation used in this work has been computed with CO5BOLD (Freytag et al. 2002; Freytag & Höfner 2008). The model, extensively introduced in Paper I, has a mass of 12 M⊙, employs an equidistant numerical mesh with 2353 grid points with a resolution of 8.6 R⊙ (or 0.040 AU), a luminosity average over spherical shells and over time (i.e., over five years) of L = 93 000 ± 1300 L⊙, an effective temperature of Teff = 3490 ± 13 K, a radius of R = 832 ± 0.7 R⊙, and a surface gravity log g = −0.337 ± 0.001. The uncertainties are measures of the temporal fluctuations. This is our most successful RHD simulation so far because it has stellar parameters closest to Betelgeuse (Teff = 3650 K, log g = 0.0, Levesque et al.2005; or log g = −0.3, Harper et al.2008). We stress that the surface gravity of Betelgeuse is poorly known, and this is not without consequences for the analysis that will be presented in Sect. 6.1 (see especially Fig. 18).
For the computation of the intensity maps and spectra based on snapshots from the RHD simulations, we used the code Optim3D (see Paper I), which takes into account the Doppler shifts caused by the convective motions. The radiative transfer is computed in detail using pre-tabulated extinction coefficients per unit mass generated with MARCS (Gustafsson et al. 2008) as a function of temperature, density, and wavelength for the solar composition (Asplund et al. 2006). The tables include the same extensive atomic and molecular data as the MARCS models. They were constructed with no micro-turbulence broadening, and the temperature and density distributions are optimised to cover the values encountered in the outer layers of the RHD simulations.
3. Predictions
In this section we provide a list of predictions from 3D simulations that are related to the Gaia astrometric and photometric measurements.
3.1. Photocentre variability
We computed spectra and intensity maps in the Gaia G band for the whole simulation-time sequence, namely ~five years with snapshots ~23 days apart. The corresponding spectrum is presented in Fig. 1 and the images in Fig. 2.
 |
Fig. 1 Transmission curve of the Gaia G band white light passband (solid black line), the blue (dotted blue line) and red (dashed red line) photometric filters (Jordi et al. 2010; Jordi & Carrasco 2007) together with the synthetic spectrum computed from the RHD simulation described in the text. |
Paper II showed that the intensity maps in the optical region show high-contrast patterns that are characterised by dark spots and bright areas. The brightest areas exhibit an intensity 50 times brighter than the dark ones with strong changes over some weeks. Paper II reported robust interferometric comparisons of hydrodynamical simulations with existing observations in the optical and H band regions, which argued for the presence of convective cells of various sizes on the red supergiant Betelgeuse. The Gaia G band images (Fig. 2) are comparable with what has been found in Paper II. The resulting surface pattern, though related to the underlying granulation pattern, is also connected to dynamical effects. In deed, the emerging intensity depends on (i) the opacity run through the atmosphere (and in red supergiants, TiO molecules produce strong absorption at these wavelengths; see spectrum in Fig. 1) and on (ii) the shocks and waves that dominate at optical depths smaller than 1.
 |
Fig. 2 Maps of the linear intensity (the range is [0–230 000] erg/s/cm2/Å) in the Gaia G band. Each panel corresponds to a different snapshot of the model described in the text with a step of about 230 days (~five years covered by the simulation). |
The surface appearance of RSGs in the Gaia G band strongly affects the
position of the photocentre and causes temporal fluctuations. The position of the
photocentre is given as the intensity-weighted mean of the
x − y positions of all emitting points tiling the
visible stellar surface according to ![\begin{eqnarray} P_x=\frac{\sum_{i=1}^{N} \sum_{j=1}^{N} I(i,j)*x(i,j)}{\sum_{i=1}^{N} \sum_{j=1}^{N} I(i,j)} \\[1.5mm] P_y=\frac{\sum_{i=1}^{N} \sum_{j=1}^{N} I(i,j)*y(i,j)}{\sum_{i=1}^{N} \sum_{j=1}^{N} I(i,j)}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq22.png) where
I(i,j) is the emerging intensity for the grid point
(i,j) with coordinates x(i,j),
y(i,j) of the simulation, and N = 235
is the total number of grid points. Figure 3 shows
that the photocentre excursion is large, since it goes from 0.005 to 0.3 AU over five
years of simulation (the stellar radius is ~4 AU, Fig. 2). The temporal average value of the photocentre displacement is
where
I(i,j) is the emerging intensity for the grid point
(i,j) with coordinates x(i,j),
y(i,j) of the simulation, and N = 235
is the total number of grid points. Figure 3 shows
that the photocentre excursion is large, since it goes from 0.005 to 0.3 AU over five
years of simulation (the stellar radius is ~4 AU, Fig. 2). The temporal average value of the photocentre displacement is
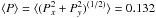 AU, and
σP = 0.065 AU.
AU, and
σP = 0.065 AU.
 |
Fig. 3 Photocentre position computed from the snapshots of Fig. 2, in the Gaia G band filter. The total simulated time is ~five years and the snapshots are 23 days apart. The snapshots are connected by the line segments. The dashed lines intersect at the position of the geometrical centre of the images. Note that the photocentric shift stays in the first quadrant for most of the 5 year simulation, and reflects the long lifetime of the large convective cell best visible in the infrared H band (Fig. 4). |
 |
Fig. 4 Map of the linear intensity in the IONIC filter (H band as described in Paper I). The range is [0–3.1 × 105] erg cm-2 s-1 Å-1. The snapshot corresponds to the top left snapshot at t = 21.976 year in Fig. 2. The large convective cell visible in this figure is swamped in smaller-scale photospheric structures in the Gaia G band images. |
At this point it is important to define the characteristic time scale of the convective-related surface structures. RHD simulations show that RSGs are characterised by two characteristic time scales:
-
(i)
the surface of the RSG is covered by a few large convective cellswith a size of about 1.8–2.3 AU (~60% of the stellar radius) that evolve on a time scale of years (see Fig. 4 and Paper I). This is visible in the infrared, and particularly in the H band where the H− continuous opacity minimum occurs and consequently the continuum-forming region is more evident;
-
(ii)
in the optical region, as in Fig. 2, short-lived (a few weeks to a few months) small-scale (about 0.2–0.5 AU, ~10% of the stellar radius) structures appear. They result from the opacity run and dynamics at optical depths smaller than 1 (i.e., further up in the atmosphere with respect to the continuum-forming region).
Both time scales have an effect on the photocentre excursion during the five years covered by the simulation. On one hand, the value of σP is mostly fixed by the short time scales corresponding to the small atmospheric structures. On the other hand, the fact that ⟨ Px ⟩ and ⟨ Py ⟩ do not average to zero (according to Fig. 3, the photocentre stays most of the time in the same quadrant, because of the large convective cell that is visible in the H band; see Fig. 4 and Paper I) indicates that the five year period covered by the simulation is not yet long enough with respect to the characteristic time scale of the large-scale (continuum) cells.
The top panel of Fig. 5 shows the temporal photocentre displacement over the ~five years of simulation, which is comparable to the total length of the Gaia mission. As seen in the figure, for t < 22 year, the random displacement is small and increases to a maximum value of 0.30 AU at t ~ 23 year.
In relation with the astrometric implications of this photocentre displacement, which will be discussed in Sect. 4, it must be stressed that neither ⟨ P ⟩ nor σP (the latter corresponding to the time sampling of the photocentric motion with a rather arbitrary time interval of 23 days) are the relevant quantities; it is instead the standard deviation of P sampled as Gaia will do (both timewise and directionwise), which turns out to be relevant. This quantity is computed below.
The bottom panel of Fig. 5 shows that there is no obvious correlation between the photocentre variability and the emerging intensity integrated in the Gaia G band. Ludwig (2006) showed analytically that this lack of correlation is to be expected.
 |
Fig. 5 Top panel: modulus of the photocentre displacement as a function
of time. Bottom panel: photocentre displacement as a function of
the integrated flux in the Gaia G band,
|
Gaia will scan the sky, observing each object on average 70−80 times. The main information that will be used to determine the astrometric characteristics of each stars will be the along-scan (AL) measurement. This is basically the projection of the star position along the scanning direction of the satellite with respect to a known reference point. By fitting those data through a least-squares minimisation, the position, parallax, and proper motion of the star can be derived. The possibility of extracting these parameters is ensured by Gaia’s complex scanning law1, which guarantees that every star is observed from many different scanning angles.
In presence of surface brightness asymmetries the photocentre position will not coincide with the barycentre of the star and its position will change as the surface pattern changes with time. The result of this phenomenon is that the AL measurements of Gaia will reflect proper motion, parallactic motion (that are modelled to obtain the astrometric parameters of the star) and photocentric motion of convective origin. The presence of the latter will be regarded as a source of additional noise.
The impact of those photocentre fluctuations on the astrometric quantities will depend on
several parameters, some of which are the stellar distance and the time sampling (fixed by
the scanning law) of the photocentric motion displayed in Fig. 3. To better assess this impact, we proceeded as follows. The Gaia
Simulator (Luri et al. 2005) was used to derive
scanning angles and time sampling for stars regularly spaced (one degree apart) along the
galactic plane where the supergiants are found. We computed the photocentre coordinates at
the Gaia transit times by linear interpolation of the photocentre positions of the model
(as provided by Fig. 3), after subtracting
⟨ Px ⟩ (=0.055 AU) and
⟨ Py ⟩ (=0.037 AU; as we will explain
below, a constant photocentric offset has no astrometric impact on the parallax). We then
computed their projection on the AL direction, which we denote
Pθ, θ being the position
angle along the scanning direction on the sky. This projection
Pθ relates to the modulus
P of the photocentre vector plotted in Fig. 5 through the relation 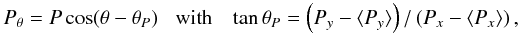 (3)and similarly, we define
(3)and similarly, we define
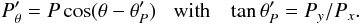 (4)The resulting run
of the standard deviation of the photocentre displacement with time for two representative
stars (one located at l = 0° with 59 transits and the other
located at l = 241° with 227 transits) is shown in Fig. 6, which reveals that the time sampling is, as expected,
strongly dependent upon the star position on the sky. The transits separated by
2−6 × 10-4 years correspond to the star being observed in succession by the
two fields of view (separated by 106.5 degrees on the sky) by the satellite spinning at a
rate of six hours per cycle, whereas the longer intervals are fixed by the satellite
precession rate.
(4)The resulting run
of the standard deviation of the photocentre displacement with time for two representative
stars (one located at l = 0° with 59 transits and the other
located at l = 241° with 227 transits) is shown in Fig. 6, which reveals that the time sampling is, as expected,
strongly dependent upon the star position on the sky. The transits separated by
2−6 × 10-4 years correspond to the star being observed in succession by the
two fields of view (separated by 106.5 degrees on the sky) by the satellite spinning at a
rate of six hours per cycle, whereas the longer intervals are fixed by the satellite
precession rate.
 |
Fig. 6 Along-scan photocentre displacement Pθ (in AU) against time for two different samplings of the photocentre displacement of Fig. 3, corresponding to the Gaia scanning law applied to stars located along the galactic plane at longitudes of 0° and 241°, as indicated on the figures. The top panel of each pair provides the distribution of time intervals between successive measurements. |
Finally, we computed the standard deviation of those projections, and obtained σPθ values ranging from 0.06 to 0.10 AU (Fig 7), with ⟨ |Pθ| ⟩ ranging from 1 × 10-4 to 8 × 10-2 AU. In the remainder of this paper, we will adopt σPθ = 0.08 AU. This quantity, which represents about 2.0% of the stellar radius (~4 AU; Sect. 2), is a measure of the mean photocentre noise induced by the convective cells in the model, and it is this value that needs to be compared with theGaia or Hipparcos measurement uncertainty to evaluate the impact of granulation noise on the astrometric parameters. This will be done in Sects. 4 and 5.
We note that
σPθ = 0.08 AU is
in fact larger than σP = 0.065 AU, and this
can be understood as follows. First, from Eq. (4) and basic statistical principles, the following relation may be easily
demonstrated: 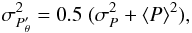 (5)under the obvious
hypothesis of statistical independence between the scanning directions θ
and the photocentric positions
Px,Py.
With ⟨ P ⟩ = 0.132 AU, and
σP = 0.065 AU obtained in Sect. 3.1, the above relation predicts
(5)under the obvious
hypothesis of statistical independence between the scanning directions θ
and the photocentric positions
Px,Py.
With ⟨ P ⟩ = 0.132 AU, and
σP = 0.065 AU obtained in Sect. 3.1, the above relation predicts
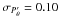 AU, in agreement with the
actual predictions based on Eq. (4). If one
considers instead Pθ from Eq. (3) (thus projecting the ’re-centred’
photocentric displacement), there is a small reduction of the standard deviation according
to
AU, in agreement with the
actual predictions based on Eq. (4). If one
considers instead Pθ from Eq. (3) (thus projecting the ’re-centred’
photocentric displacement), there is a small reduction of the standard deviation according
to 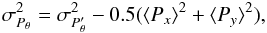 (6)yielding
σPθ = 0.088 AU,
in agreement with the detailed calculations shown in Fig. 7.
(6)yielding
σPθ = 0.088 AU,
in agreement with the detailed calculations shown in Fig. 7.
 |
Fig. 7 Run of σPθ (expressed in AU; solid blue curve and left-hand scale) with galactic longitude for stars located along the galactic plane, with a number of transit observations given by the red dots (and right-hand scale). |
3.2. Photometric variability
Another aspect of RSG variability can affectGaia spectrophotometry. The blue and red photometric bands of Fig. 1 produce two spectra of the observed source at low spectral resolution (R ~ 50). The photometric system has the advantage of continuously covering a wide range of wavelengths providing a multitude of photometric bands, but it has the great disadvantage of being extremely hard to calibrate in flux and wavelength. The photometric system ofGaia will be used to characterise the star’s effective temperature, surface gravity, and metallicity (Thévenin 2008). The vigorous convective motions and the resulting surface asymmetries of RSGs cause strong fluctuations in the spectra that will affectGaia spectrophotometric measurements (Fig. 8). In the blue photometric range (top panel), the fluctuations go up to 0.28 mag and up to 0.15 mag in the red filter (bottom panel) over the five years of simulation. These values are of the same order as the standard deviation of the visible magnitude excursion in the last 70 years for Betelgeuse, 0.28 mag (according to AAVSO2).
 |
Fig. 8 Spectral fluctuations in the blue and red Gaia photometric bands (Fig. 1) for RSGs: the black curve is the average flux over ~five years covered by the simulation, while the grey shade denotes the maximum and minimum fluctuations. The spectra were smoothed to theGaia spectral resolution (R ~ 50, Thévenin 2008). |
The light curve of the simulation in the (blue - red)Gaia colour index is displayed in Fig. 9. The temporal average value of the colour index is (blue -red) = 3.39 ± 0.06 at one sigma and there are some extreme values at, for example, t ~ 22.4 year, t ~ 23 year, and t ~ 25.2 year.
Therefore, the uncertainties on [Fe/H], Teff, and log g given by Bailer-Jones (2010) for stars with G < 15 should be revised upwards for RSGs because of temporal fluctuations from convection.
3.3. Direct imaging and interferometric observables
The simulation presented in this work was already tested against the observations at different wavelengths including the optical region (Papers I and II). However, it is now also possible to compare the predictions in theGaia G band to CHARA interferometric observations obtained with the new instrument VEGA (Mourard et al. 2009) that is integrated within the CHARA array at Mount Wilson Observatory. For this purpose, we computed intensity maps in the blue and red bands of Fig. 1 and calculated visibility curves for 36 different position angles with a step of 5° following the method explained in Paper I. Figure 10 shows the intensity maps together with the corresponding visibility curves. The angular visibility fluctuations are larger in the blue band (bottom left panel) because there is a larger contribution from molecular opacities (mainly TiO) that shade the continuum brightness of the star (top left panel): therefore the surface brightness contrast is higher. However, in both photometric bands the signal in the second lobe, at higher frequencies, is ~0.2 dex higher than the uniform disc (UD) result, which is measurable with CHARA. The approach we suggest to follow in order to check the reliability of the 3D simulation is the following: to search for angular visibility variations, as a function of wavelength, observing with the same telescope configuration covering high spatial frequencies and using the Earth’s rotation to study 6–7 different position angles in one night. The error bar should be kept smaller than the predicted fluctuations: ~40% in the blue band, and ~20% in the red band at the peak of the second visibility lobe.
 |
Fig. 9 (blue – red)Gaia colour index, computed in the blue and red photometric filters of Fig. 1, as a function of time. |
 |
Fig. 10 Top panels: maps of the linear intensity (the range is [0–230 000]
erg/s/cm2/Å) computed in the blue and red photometric filters of
Fig. 1. Bottom panels:
visibility curves from the above maps computed for 36 different position angles
5° apart (grey lines). The black curve is the average visibility, while
the dashed line is a uniform disc of about the same radius as the simulation
snapshot. The conversion factor to the more customary unit arcsec-1 on
the abscissa axis is arcsec |
To investigate the behaviour of the local flux fluctuations, closure phases will bring invaluable information on the asymmetry of the source. However, the final consistency check will be an image reconstruction to directly compare the granulation size and shape and the intensity contrast, provided by the planned second generation recombiner of the VLTI and CHARA optical interferometry arrays. The European Extremely Large Telescope (E-ELT, planned to be operating in 2018) with a mirror size five times larger than a single VLT Unit Telescope will be capable of near IR observations of surface details on RSGs (Fig. 11).
4. Impact of photocentric noise on astrometric measurements
The basic operating mode of astrometric satellites like Hipparcos orGaia is to scan the sky
and to obtain along-scan3 positions
ηAL, as was already briefly sketched in Sect. 3.1. The core astrometric data analysis then consists in
solving a least-squares problem (for the sake of simplicity, we neglect the AC term) (Lindegren 2010) ![\begin{equation} \label{Eq:xi1} \stackrel{\large\mathrm{min}}{{\vec{p},\vec{a}}} \;\; \left(\sum_{i}^{N_{\mathrm{transit}}}\frac{\left[\eta_{i} - \eta(\vec{p},\vec{a};t_{i})\right]^2}{\sigma^2_{\eta_{i}}}\right) \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq81.png) (7)for
the astrometric parameters p, and the set of satellite
attitude parameters a, given the
Ntransit along-scan positions
ηi at times
ti, the model predictions
η(p,a;ti),
and the formal error
σηi on the
along-scan position ηi (including centroiding
errors and errors caused by imperfect calibration or imperfectly known satellite attitude
for instance). If ηi is affected by some
supplementary noise coming from the photocentric motion (which is not going to be included
in σηi), then this
photocentric noise of variance
(7)for
the astrometric parameters p, and the set of satellite
attitude parameters a, given the
Ntransit along-scan positions
ηi at times
ti, the model predictions
η(p,a;ti),
and the formal error
σηi on the
along-scan position ηi (including centroiding
errors and errors caused by imperfect calibration or imperfectly known satellite attitude
for instance). If ηi is affected by some
supplementary noise coming from the photocentric motion (which is not going to be included
in σηi), then this
photocentric noise of variance 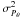 will degrade the
goodness-of-fit in a significant manner, provided that
σPθ ≳ ση.
This statement is easily demonstrated from Eq. (7), by writing
will degrade the
goodness-of-fit in a significant manner, provided that
σPθ ≳ ση.
This statement is easily demonstrated from Eq. (7), by writing 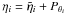 , with
the first term
, with
the first term 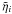 representing the astrometric motion, and the second term representing the along-scan
photocentric shift:
representing the astrometric motion, and the second term representing the along-scan
photocentric shift: ![\begin{equation} \label{Eq:xi2} \chi^2 \equiv \sum_{i=1}^{N_{\mathrm{transit}}} \frac{\left[\tilde{\eta_{i}} + P_{\theta_i} - \eta(\vec{p},\vec{a};t_{i})\right]^2}{\sigma^2_{\eta_{i}}}. \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq93.png) (8)For the sake of simplicity,
we will assume below that ση is the same for
all measurements. The above equation may be further simplified in the case where there is no
correlation between the astrometric and photocentric shifts, so that the cross-product term
(8)For the sake of simplicity,
we will assume below that ση is the same for
all measurements. The above equation may be further simplified in the case where there is no
correlation between the astrometric and photocentric shifts, so that the cross-product term
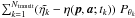 is null. This
absence of correlation only holds if the photocentric shift occurs on time scales different
from one year (no correlation with the parallax), and shorter than a few years (no
correlation with the proper motion4). Although this
assumption of absence of correlation turns out not to be satisfied in real cases (we will
return to this issue in the discussion of Fig. 21), it
nevertheless offers insights into the situation, and we therefore pursue the analytical
developments by writing
is null. This
absence of correlation only holds if the photocentric shift occurs on time scales different
from one year (no correlation with the parallax), and shorter than a few years (no
correlation with the proper motion4). Although this
assumption of absence of correlation turns out not to be satisfied in real cases (we will
return to this issue in the discussion of Fig. 21), it
nevertheless offers insights into the situation, and we therefore pursue the analytical
developments by writing ![\begin{eqnarray} \label{Eq:xi3} \chi^ 2 & = & \frac{1}{\sigma^2_{\eta}} \left[\sum_{i=1}^{N_{\mathrm{transit}}} \left[\tilde{\eta}_{i} - \eta(\vec{p},\vec{a};t_{i})\right]^2 + \sum_{i=1}^{N_{\mathrm{transit}}} P_{\theta_i}^2\right] \nonumber\\ & = & \chi^ 2_0 + N_{\mathrm{transit}} \; \frac{\sigma^2_{P_{\theta}}}{\sigma^2_{\eta}}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq96.png) (9)where
(9)where
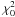 is the chi-square
obtained in the absence of photocentric motion, and we assumed
is the chi-square
obtained in the absence of photocentric motion, and we assumed
 since asymptotically
⟨ Pθ ⟩ = 0. It is important to stress here
that it is indeed the standard deviation of the photocentre displacement (sampled
the same way as the astrometric data have been) – rather than its average value –
that matters. In the extreme case of a constant (non-zero) photocentre shift, there will
obviously be no impact on the astrometric parameters.
since asymptotically
⟨ Pθ ⟩ = 0. It is important to stress here
that it is indeed the standard deviation of the photocentre displacement (sampled
the same way as the astrometric data have been) – rather than its average value –
that matters. In the extreme case of a constant (non-zero) photocentre shift, there will
obviously be no impact on the astrometric parameters.
 |
Fig. 11 Snapshot of 3D simulation (upper left of Fig. 2) convolved to the PSF of a 42 m telescope (for a star at a distance of 152.4 pc, see solution #2 in Table 2) like the European Extremely Large Telescope. |
The degradation of the fit caused by the photocentric noise may be quantified through the
goodness-of-fit parameter F2, defined as ![\begin{equation} \label{Eq:F2} F2 = \left(\frac{9\nu}{2}\right)^{1/2} \left[\left(\frac{\chi^2}{\nu}\right)^{1/3}+\frac{2}{9\nu}-1\right], \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq101.png) (10)where
ν is the number of degrees of freedom of the
χ2 variable. The above definition corresponds to the
“cube-root transformation” of the χ2 variable (Stuart & Ord 1994). The transformation of
(χ2,ν) to F2 eliminates the
inconvenience of having the distribution depending on the additional variable
ν, which is not the same for the different stars. F2
follows a normal distribution with zero mean and unit standard deviation. The
goodness-of-fit F2 thus appears to be an efficient way to detect any
photocentric noise. It may be compared to its value F20 in the
absence of photocentric noise by assuming
(10)where
ν is the number of degrees of freedom of the
χ2 variable. The above definition corresponds to the
“cube-root transformation” of the χ2 variable (Stuart & Ord 1994). The transformation of
(χ2,ν) to F2 eliminates the
inconvenience of having the distribution depending on the additional variable
ν, which is not the same for the different stars. F2
follows a normal distribution with zero mean and unit standard deviation. The
goodness-of-fit F2 thus appears to be an efficient way to detect any
photocentric noise. It may be compared to its value F20 in the
absence of photocentric noise by assuming 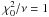 and
Ntransit/ν ~ 1; then
Eq. (9) writes
and
Ntransit/ν ~ 1; then
Eq. (9) writes
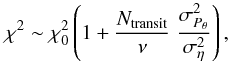 (11)thus leading to
(11)thus leading to
![\begin{equation} \label{Eq:DeltaF2} F2 = F2_0 + \left(\frac{9\nu}{2}\right)^{1/2}\; \left[ \left(1+ \frac{\sigma^2_{P_{\theta}}}{\sigma^2_{\eta}}\right)^{1/3} -1 \right]. \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq109.png) (12)For Gaia, the second
term of the above equation may be evaluated as a function of
σPθ/ση
by adopting ν = 70, as represented in Fig. 12. Because F2 follows a normal distribution with zero mean and
unit standard deviation, the fit degradation will become noticeable if F2
increases by 2 or so, implying
σPθ/ση ≳ 0.6.
This translates into a condition on the distance:
(12)For Gaia, the second
term of the above equation may be evaluated as a function of
σPθ/ση
by adopting ν = 70, as represented in Fig. 12. Because F2 follows a normal distribution with zero mean and
unit standard deviation, the fit degradation will become noticeable if F2
increases by 2 or so, implying
σPθ/ση ≳ 0.6.
This translates into a condition on the distance: ![\begin{equation} \label{Eq:d} d\; [\mbox{kpc}] \la \frac{\sigma_{P_{\theta}} \; [\mbox{AU}]} {0.6\; \sigma_{\eta}\; [\mbox{mas}]}\cdot \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq113.png) (13)The error on the
along-scan position η should not be confused with the end-of-mission error
on the parallax (σϖ), which ultimately results
from the combination of Ntransit transits, with
Ntransit ranging from 59 to 120 for Gaia, with an average of
(13)The error on the
along-scan position η should not be confused with the end-of-mission error
on the parallax (σϖ), which ultimately results
from the combination of Ntransit transits, with
Ntransit ranging from 59 to 120 for Gaia, with an average of
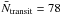 (Lindegren 2010), and from 10 to 75 for Hipparcos
(Fig. 3.2.4 of Vol. 1 of the Hipparcos and Tycho Catalogues). The number of transits depends
(mostly) on the ecliptic latitude.
(Lindegren 2010), and from 10 to 75 for Hipparcos
(Fig. 3.2.4 of Vol. 1 of the Hipparcos and Tycho Catalogues). The number of transits depends
(mostly) on the ecliptic latitude.
For Hipparcos, the individual ση values for
each transit may be found in the Astrometric Data files (van
Leeuwen & Evans 1998; van Leeuwen
2007a), and are of the order of 1.7 mas for the brightest stars (see Sect. 5 and Fig. 15). For
Gaia, the quantity ση may be obtained from the
relation 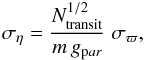 (14)where
m = 1.2 denotes an overall end-of-mission contingency margin, and
gpar = 1.91 is a dimensionless geometrical factor depending on
the scanning law, and accounting for the variation of Ntransit
across the sky, since σϖ is an effective
sky-average value (see de Bruijne 2005). A current
estimate of σϖ is 7.8 μas for
the brightest stars (Lindegren 2010), yielding
ση of the order of 30 μas.
To avoid saturation on objects brighter than G = 12.6, a special CCD gating
strategy will be implemented so that the error budget may be assumed to be a constant for
G ≤ 12.6 (de Bruijne 2005; Lindegren 2010). As we show in Sect. 6, only the bright-star regime matters for our purpose. Inserting these
values in Eq. (13), we thus find
(14)where
m = 1.2 denotes an overall end-of-mission contingency margin, and
gpar = 1.91 is a dimensionless geometrical factor depending on
the scanning law, and accounting for the variation of Ntransit
across the sky, since σϖ is an effective
sky-average value (see de Bruijne 2005). A current
estimate of σϖ is 7.8 μas for
the brightest stars (Lindegren 2010), yielding
ση of the order of 30 μas.
To avoid saturation on objects brighter than G = 12.6, a special CCD gating
strategy will be implemented so that the error budget may be assumed to be a constant for
G ≤ 12.6 (de Bruijne 2005; Lindegren 2010). As we show in Sect. 6, only the bright-star regime matters for our purpose. Inserting these
values in Eq. (13), we thus find
![\begin{equation} \label{Eq:M-d2-Hip} d\; [\mbox{kpc}] \le 0.98 \; \sigma_{P_\theta} \; [\mbox{AU}] \quad\qquad\mathrm{for\; Hipparcos,}\;\;\; \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq125.png) (15)and
(15)and
![\begin{equation} \label{Eq:M-d2-Gaia} d \; [\mbox{kpc}] \le 55.5 \; \sigma_{P_\theta} \; [\mbox{AU}]\quad\qquad\mathrm {for\; Gaia.}\;\;\; \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq126.png) (16)Adopting
σPθ = 0.08 AU for
Betelgeuse-like supergiants (Sect. 3.1) yields
d < 0.08 kpc for Hipparcos and
d < 4.4 kpc for Gaia. This limit has to be
interpreted as marking the maximum distance up to which a photocentric motion with
σPθ = 0.08 AU
will increase the astrometry goodness-of-fit by 2. The validity of these conditions will be
further evaluated in Sects. 5 and 6.
(16)Adopting
σPθ = 0.08 AU for
Betelgeuse-like supergiants (Sect. 3.1) yields
d < 0.08 kpc for Hipparcos and
d < 4.4 kpc for Gaia. This limit has to be
interpreted as marking the maximum distance up to which a photocentric motion with
σPθ = 0.08 AU
will increase the astrometry goodness-of-fit by 2. The validity of these conditions will be
further evaluated in Sects. 5 and 6.
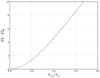 |
Fig. 12 Degradation of the goodness-of-fit F2 in the presence of a photocentric motion described in terms of the ratio σPθ/ση, where ση is the instrumental error. Remember that F2 follows a normal distribution with zero mean and unit standard deviation. |
Properties of the spots observed at the surface of Betelgeuse during the Hipparcos mission.
With this photocentric noise, the astrometric data reduction process may adopt one of the following three approaches:
-
(i)
Neither the model definition, nor the measurement-errordefinition are modified (meaning that the quantitiesσi entering Eq. (9) are the same as before, and that no attempt is whatsoever made to model the granulation). With respect to a star with similar properties (same apparent magnitude and location on the sky), a star with global-scale convection cells will then be recognised by a goodness-of-fit F2 value higher than expected depending upon the ratio σPθ/ση (see Fig. 12). Under those conditions, the resulting formal uncertainty on the parallax would not be especially large, though; actually, it would be exactly identical to the parallax uncertainty in the absence of photocentric motion. This is because the formal errors on the parameters p (among which the parallax) only depend on the measurement errors ση (which were kept the same with or without photocentric noise), and not on the actual measured values (which will be different in the two situations). This is demonstrated in Appendix A. But of course, the error on the parallax derived in this way is underestimated, because it does not include the extra source of noise introduced by the photocentric motion. The next possibility alleviates this difficulty.
-
(ii)
An estimate of the photocentric noise may be quadratically added to
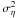 appearing in
Eq. (8). The error on the parallax
will then be correctly estimated (and will be larger than the one applying to similar
non-convective stars); the goodness-of-fit will no longer be unusually large. This is
the method adopted for the so-called “stochastic solutions” in the Hipparcos
reduction, an example of which will be presented in Sect. 5. These solutions, called “DMSA/X”, added some extra-noise (in the
present case: the photocentric noise) to the measurements to get an acceptable fit.
appearing in
Eq. (8). The error on the parallax
will then be correctly estimated (and will be larger than the one applying to similar
non-convective stars); the goodness-of-fit will no longer be unusually large. This is
the method adopted for the so-called “stochastic solutions” in the Hipparcos
reduction, an example of which will be presented in Sect. 5. These solutions, called “DMSA/X”, added some extra-noise (in the
present case: the photocentric noise) to the measurements to get an acceptable fit.
-
(iii)
The model is modified to include the photocentric motion. This would be the best solution in principle, because it would allow us to alleviate any possible error on the parallax, as they may occur with the two solutions above. However, the 3D simulations reveal that it is very difficult to model the complex convective features seen in visible photometric bands by a small number of spots with a smooth time behaviour. This solution was therefore not been attempted.
The astrometric parameters themselves may change of course, for either of the above solutions, especially when the photocentric motion adds to the parallactic motion a signal with a characteristic time scale close to one year. If on the contrary, the photocentric motion has a characteristic time scale very different from one year, the photocentric motion averages out and leaves no imprint on the parallax. A similar situation is encountered if there is an unrecognized orbital motion on top of the parallactic motion: only if the unaccounted orbital signal has a period close to one year will the parallax be strongly affected (see Pourbaix & Jorissen 2000, for a discussion of specific cases). As explained in Sect. 3.1, RSGs large convective cells evolve over time scales of years. In addition, they slightly change their position on the stellar surface within the five years of simulated time (Chiavassa PhD Thesis5), but, unfortunately, it is difficult to measure the granule size exactly (Berger et al. 2010) and consequently to give a consistent estimate of this displacement.
 |
Fig. 13 Top panel: interferometric observations of the surface of Betelgeuse obtained with the William Herschel Telescope at a wavelength of 710 nm, in January 1991 (Wilson et al. 1992) and January 1992 (Tuthill et al. 1997). North is at the top and East is to the left. The two images have been taken from Freytag et al. (2002). The spot properties are summarised in Table 1. Bottom panel: Hipparcos epoch photometry of Betelgeuse with the vertical lines indicating the epoch of the two interferometric observations. |
5. A look at Betelgeuse’s Hipparcos parallax
Hipparcos data (ESA 1997) may hold signatures of global-scale granulation in supergiants. The three nearby supergiants α Sco (Antares; HIP 80763), α Ori (Betelgeuse; HIP 27989) and α Her (Rasalgethi; HIP 84345) are ideal targets for this purpose, since Tuthill et al. (1997) indeed found surface features on all three stars, implying photocentric displacements of the order of 1 mas (estimated from the product of the fraction of flux belonging to a bright spot with its radial distance from the geometric centre; see Table 1).
Parallaxes for Betelgeuse computed from various data sets.
By chance, observations of the disc of Betelgeuse at the time of the Hipparcos mission were done by Wilson et al. (1992) and Tuthill et al. (1997) and are shown in Fig. 13. Tuthill et al. reveal that the two bright spots present in January 1991 merged one a year later (January 1992), with a much fainter spot appearing at the edge of the extended disc. Because the simulation used in this work shows excellent fits to the visibility curves, closure phases, and reconstructed images based on William Herschel Telescope data in the same filters as those used in Fig. 13, and because RSGs are slow rotators, it is most likely that the spots in Fig. 13 are caused by convection. Their properties have been summarised in Table 1, along with the corresponding photocentric displacement. The observed photocentric displacements agree with the model predictions, as can be evaluated from σPθ [mas] = σPθ [AU] × ϖ [mas] = 0.5 mas, since σPθ = 0.08 AU for a supergiant (Sect. 4) and ϖ = 6.56 ± 0.83 mas for Betelgeuse (see Table 2; in the remainder of this section, all quantities from Hipparcos refer to van Leeuwen’s new reduction, 2007b).
Considering that the instrumental uncertainty on an individual measurement is 1.9 mas for a star like Vega (V = 0.03), which is as bright as Betelgeuse (V = 0.42) (according to Vega’s intermediate astrometric data file in van Leeuwen 2007a), Betelgeuse’s convective noise with σPθ = 0.5 mas should be just noticeable on top of the instrumental noise, and possibly have some detectable impact on the astrometric data of Betelgeuse. For Vega, van Leeuwen (2007a) found a very good astrometric solution, whose residuals Δη have a standard deviation σΔη of 1.78 mas, fully consistent with the formal errors on η (top panel of Fig. 15). The extreme brightness of Vega thus did not prevent us from finding a good astrometric solution. On the other hand, neither the original Hipparcos processing nor van Leeuwen’s revised processing could find an acceptable fit to the Betelgeuse and Antares astrometric data, and a so-called “stochastic solution” (DMSA/X) had to be adopted (the kind of solution labelled (ii) in the discussion of Sect. 4), meaning that some supplementary noise (called “cosmic noise”) had to be added to yield acceptable goodness-of-fit values F2.
 |
Fig. 14 Parallax standard errors for supergiants in the Hipparcos Catalogue, after van Leeuwen’s reprocessing. The dashed line represents 1.5 times the standard parallax error for stars with precise parallaxes (<10%; solid line) in van Leeuwen’s reprocessing (see Fig. 2.19 of van Leeuwen 2007a), whereas the solid line represents the fiducial relation between the Hipparcos magnitude and the standard parallax error. Large red circles correspond to stars redder than V − I = 2. |
 |
Fig. 15 Abscissa residuals Δη (in mas on the sky; red dots) along with the corresponding error bar from van Leeuwen (2007a) for Betelgeuse and Vega, as a function of time, expressed in years from 1991.25. Filled star symbols correspond to the along-scan projections Pθ of the synthetic photocentre displacements of Fig. 3. The red dashed lines and black solid lines depict the ± 1σ interval around the mean for the Hipparcos data points and model predictions, respectively. Note that these displacements were computed in the Gaia G filter instead of the Hipparcos Hp filter. A test on a given snapshot has shown that the difference is negligible: Px = 0.11 AU with the Hp filter, as compared to 0.13 AU with the G filter. |
The cosmic noise amounts to 2.4 and 3.6 mas for Betelgeuse and Antares, respectively, in van Leeuwen’s reprocessing. These values correspond to the size of the error bars displayed in Figs. 15 and 16. Rasalgethi was not flagged as DMSA/X, but rather as DMSA/C (indicating the presence of a close companion), but its high goodness-of-fit value F2 = 46.63 is indicative also of increased noise. Consequently, all three supergiants have a parallax standard error larger than expected6 given its Hipparcos magnitude Hp, as revealed by Fig. 14, which displays σϖ against the median magnitude for all supergiants (luminosity classes I and II, of all spectral types) in the Hipparcos catalogue. The chromaticity correction has been a serious concern for the reduction of the Hipparcos data of very red stars (see Platais et al. 2003, for a detailed discussion of this problem), and one may wonder whether the increased noise of the three supergiants under consideration could perhaps be related to this effect. Because the very red supergiants (with V − I > 2.0) show no appreciable offset from the rest of the sample in Fig. 14 (at least for the brightest supergiants, down to Hp = 8), this possibility may be discarded, and the different behaviour of Rasalgethi, Antares, and Betelgeuse in Fig. 14 seems instead related to their large apparent brightness, which is caused by their proximity to the Sun.
Could the poor accuracy of Betelgeuse’s parallax and its cosmic noise be related to its surface features, as already suggested in general terms by Barthès & Luri (1999), Gray (2000), Platais et al. (2003), Svensson & Ludwig (2005), Bastian & Hefele (2005), Ludwig (2006), Eriksson & Lindegren (2007)?
The bottom panel of Fig. 15 shows the along-scan residuals Δη for Betelgeuse against time (and Fig. 16 does the same for Antares and Rasalgethi), compared with the photocentre displacements Px and Py determined from the 3D simulation of Sect. 3.1.
From this comparison, we conclude that the photocentric noise, as predicted by The 3D simulations, does account for a substantial part of the “cosmic noise”, but not for all of it. A possibility to reconcile predictions and observations could come from an increase of Betelgeuse’s parallax (because the observed photocentric motion would then be larger for the σPθ value fixed by the models), but this suggestion is not borne out by the recent attempt to improve upon Betelgeuse’s parallax in the recent literature (Harper et al. 2008) (solution #2 in Table 2), by combining the Hipparcos astrometric data with VLA positions, as this new value is lower than both the original Hipparcos and van Leeuwen’s values. The remaining possibility is that the 3D model discussed in Sect. 3.1 underestimates the photocentric motion. Indeed, Paper II showed that the RHD simulation fails to reproduce the TiO molecular band strengths in the optical region (see spectrum in Fig. 1). This is because the RHD simulations are constrained by execution time and therefore use a grey approximation for the radiative transfer. This is well justified in the stellar interior, but is a crude approximation in the optically thin layers. As a consequence, the thermal gradient is too shallow and weakens the contrast between strong and weak lines (Chiavassa et al. 2006). The resulting intensity maps look sharper than observations (see Paper II) and thus also the photocentre displacement should be affected. As described in Paper II, a new generation of non-grey opacities (five wavelength bins employed to describe the wavelength dependence of radiation fields) simulation is under development. This will change the mean temperature structure and the temperature fluctuations, especially in the outer layers where TiO absorption occurs.
Photocentre motion from 3D simulations.
6. Application to Gaia
6.1. Number of supergiant stars with detectable photocentric motion
In this section, we will use Eq. (16) to estimate the number of supergiants that will have a poor goodness-of-fit as a consequence of their photocentric motion. This equation requires knowledge of σPθ, which will be kept as a free parameter in this section. In Sect. 3.1, σPθ = 0.08 AU was considered as typical for Betelgeuse-like supergiants, but Sect. 5 has provided hints that 3D models with grey opacities could somewhat underestimate this quantity. Moreover, according to Freytag (2001) and Ludwig (2006), σPθ is expected to vary with the star’s atmospheric pressure scale height, which in turn depends upon the star’s absolute magnitude MG. To explore the parameter space, we therefore need to know how σPθ varies with MG. This is especially important since on top of the condition in Eq. (16) relating d to σPθ(MG), there is another constraint coming from the requirement not to saturate the CCD, namely the Gaia magnitude G should be fainter than 5.6. All these constraints may be conveniently encapsulated in boundaries in the d − MG plane, as displayed in Fig. 19.
But first, we have to clarify the relation between σPθ and MG, which appears to be a critical ingredient in the present discussion. Unfortunately, 3D hydrodynamical models in the literature are scarce. Their main properties are collected in Table 3. These simulations are of two kinds: (i) box-in-a-star models cover only a small section of the surface layers of the deep convection zone, and the numerical box includes some fixed number of convective cells, which are large enough to not constrain the cells by the horizontal (cyclic) boundaries; (ii) star-in-a-box models, like the one described in this paper (Sect. 2), cover the whole convective envelope of the star and have been used to model RSG and AGB stars so far (see Freytag & Höfner 2008, for an AGB model), whereas the former simulations cover a large number of stellar parameters from white dwarf to red giant stars. The transition where the box-in-a-star models become inadequate occurs around log g ~ 1, when the influence of sphericity becomes important; the star-in-a-box global models are then needed, but those are highly computer-time demanding and difficult to run, which is the reason why there are only very few models available so far.
 |
Fig. 17 Fits to the standard deviation σPθ of the photocentric motion predicted from 3D simulations, as listed in Table 3, against the pressure scale height Hp. The equation of the (red) solid line is log σPθ = −6.110 + 1.110log (Hp) with χ2 = 0.17: the fit considers only the box-in-a-star models (filled circles) of Svensson & Ludwig (2005). The (green) dashed line (with equation log σPθ = −6.275 + 1.174log Hp + 0.039(log Hp)2) is a fit to all the models of Table 3 (i.e., box-in-a-star models and star-in-a-box, the latter being represented by a filled square). The (blue) dotted line is an arbitrary exponential law that connects the last two points with the following equation log σPθ = −1.09−3.434exp(− 0.00149Hp). |
 |
Fig. 18 Photocentre motions determined from interferometric observations for some evolved stars (see Table 4) overplotted on the different fits of the standard deviation σPθ of the photocentric motion as a function of the pressure scale height Hp. The large open inverted triangles correspond to the standard deviations of the photocentre deviations for a given observed star. Star-in-a-box and box-in-a-star models correspond to the large filled square and circle respectively. |
Ludwig (2006) found that there is a tight
correlation between the amplitude of the photocentric motion and the size of the granular
cells. This size is related to the pressure scale height at optical-depth unity (Freytag 2001). The pressure scale height is defined as
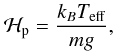 (17)where
g is the surface gravity,
kB is the Boltzmann constant and
m is the mean molecular mass
(m = 1.31 × mH = 1.31 × 1.67 × 10-24 g,
for temperatures lower than 10000 K). In the above expression, ℋp has the
dimension of length. But in the remainder of this paper, we adopt instead the simplified
definition
(17)where
g is the surface gravity,
kB is the Boltzmann constant and
m is the mean molecular mass
(m = 1.31 × mH = 1.31 × 1.67 × 10-24 g,
for temperatures lower than 10000 K). In the above expression, ℋp has the
dimension of length. But in the remainder of this paper, we adopt instead the simplified
definition 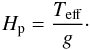 (18)The law relating the
standard deviation of the photocentre displacement to Hp may
be inferred from Fig. 17, which displays the values
from Table 3. The transition from the most evolved
box-in-a-star model (with log Hp ~ 2.57) to our star-in-a-box
model (log Hp ~ 3.85) is still unexplored; consequently, there
is no guarantee that the trend obtained at
log Hp < 2.57 may be extrapolated to
higher Hp values. Different trends are therefore considered in
Fig. 17 with a zoom in Fig. 18. The linear fit of
log σPθ as
a function of log Hp considers only the box-in-a-star models
of Svensson & Ludwig (2005); the parabolic
function is the best fit to all the models (including the star-in-a-box supergiant model).
However, there is strong evidence in the simulations that the convective pattern changes
significantly from the giant (big black circle symbol in Fig. 18) to the RSG simulations (big black squared symbol). The convective
related surface structures grow enormously in the RSGs and together with the low effective
temperature (i.e., the molecular absorption, strongly related to the temperature
inhomogenities, is more important) increase the displacement of the photocentre position
(i.e., σPθ is
larger). Thus, the parabolic fit, which considers all the simulations’ configurations
together, is not a completely correct approach because of the physical changes reported
above. Since the transition region between the box-in-a-star (giant stars) and
star-in-a-box models (RSG stars) is still unexplored, we consider an extreme transition by
adopting an arbitrary exponential law to relate the last two model simulation points
(i.e., the transition region between the box-in-a-star and star-in-a-box models). Paper I
pointed out that the reasons for the peculiar convective pattern in RSGs could be (i) in
RSGs, most of the downdrafts will not grow fast enough to reach any significant depth
before they are swept into the existing deep and strong downdrafts enhancing the strength
of neighbouring downdrafts; (ii) radiative effects and smoothing of small fluctuations
could matter; (iii) sphericity effects and/or numerical resolution (or lack of it).
(18)The law relating the
standard deviation of the photocentre displacement to Hp may
be inferred from Fig. 17, which displays the values
from Table 3. The transition from the most evolved
box-in-a-star model (with log Hp ~ 2.57) to our star-in-a-box
model (log Hp ~ 3.85) is still unexplored; consequently, there
is no guarantee that the trend obtained at
log Hp < 2.57 may be extrapolated to
higher Hp values. Different trends are therefore considered in
Fig. 17 with a zoom in Fig. 18. The linear fit of
log σPθ as
a function of log Hp considers only the box-in-a-star models
of Svensson & Ludwig (2005); the parabolic
function is the best fit to all the models (including the star-in-a-box supergiant model).
However, there is strong evidence in the simulations that the convective pattern changes
significantly from the giant (big black circle symbol in Fig. 18) to the RSG simulations (big black squared symbol). The convective
related surface structures grow enormously in the RSGs and together with the low effective
temperature (i.e., the molecular absorption, strongly related to the temperature
inhomogenities, is more important) increase the displacement of the photocentre position
(i.e., σPθ is
larger). Thus, the parabolic fit, which considers all the simulations’ configurations
together, is not a completely correct approach because of the physical changes reported
above. Since the transition region between the box-in-a-star (giant stars) and
star-in-a-box models (RSG stars) is still unexplored, we consider an extreme transition by
adopting an arbitrary exponential law to relate the last two model simulation points
(i.e., the transition region between the box-in-a-star and star-in-a-box models). Paper I
pointed out that the reasons for the peculiar convective pattern in RSGs could be (i) in
RSGs, most of the downdrafts will not grow fast enough to reach any significant depth
before they are swept into the existing deep and strong downdrafts enhancing the strength
of neighbouring downdrafts; (ii) radiative effects and smoothing of small fluctuations
could matter; (iii) sphericity effects and/or numerical resolution (or lack of it).
References used to compute the photocentric shifts from interferometric data.
To see which among these three possible trends has to be preferred, we made a compilation of photocentric displacements P from interferometric observations of various supergiants available in the literature (see Fig. 18). Supergiants and Miras have been observed several times in the last decade with interferometers, often revealing the presence of surface brightness asymmetries. In several cases (α Ori, α Her, and o Cet; see Table 4 for the data list and references; more stars will be presented in Sacuto et al., in preparation), the observations could be represented by parametric models consisting of a uniform disc plus one (or more) bright or dark spots. Using the parameters of the spots fitting the interferometric data, we computed the positions of the photocentre for all observations of a given star and from there the standard deviation of these photocentric positions, which was then plotted against Hp in Fig. 18. These observational data suggest that the exponential and quadratic fits of the simulation data are to be preferred over the linear extrapolation of the box-in-a-star values (Fig. 18). We stress, however, that the surface gravity for supergiants like α Her and α Ori are quite uncertain (see Table 4) and also the highly uncertain metallicity differences might play a role here.
 |
Fig. 19 Location in the (MG,d) plane for supergiants with a photocentre noise (of standard deviation σPθ) significantly altering the goodness-of-fit of the astrometric solution (see text), for the case of an exponential link between box-in-a-star and star-in-a-box models (see Fig. 18 and text). |
The number of stars with photocentric motions detectable by Gaia as having bad fits (i.e., high goodness-of-fit F2 values) may now be estimated as follows. The Besançon Galaxy model (Robin et al. 2004) was used to generate a sample of bright giants and supergiants (MV < 0) in the region 0 ≤ l ≤ 180 and −20 ≤ b ≤ 20 of our Galaxy (where l and b are the galactic coordinates). The reddening was added separately using the extinction model from Drimmel et al. (2003). For each one of the the 361069 stars in that sample, we assign the corresponding expected standard deviation of the photocentre displacement σPθ taken from the exponential or parabolic laws of Fig. 17 (each of these two possibilities was tested separately), with HP estimated from Eq. (18)7.
We then computed the number of stars that fulfill the condition expressed by Eq. (16), and have at the same time
G > 5.6 in order not to saturate the Gaia CCD
detectors. The conversion between V and G magnitudes has
been done from the colour equation (adopted from the Gaia Science Performance
document8,9):
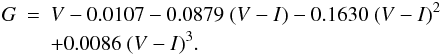 (19)With
the exponential law, we found 215 supergiants (among the 361069 of the full sample,
representing half the galactic plane) fulfilling these two conditions. They are displayed
in Fig. 19 in the
d − MG plane, and are
basically confined to a crescent delineated by the conditions
G > 5.6 (corresponding to the two lines with an
upwards concavity, labelled G > 5.6; the two
lines correspond to two values of the extinction in the G band:
AG = 0 and 1) and
d ≤ 55.5σPθ(MG)
(Eq. (16), corresponding to the green
dashed line with a downwards concavity). The latter line is based on a fiducial
relationship between
σPθ and
MG, as shown in Fig. 20. Some supergiants nevertheless fall outside the crescent defined
above, simply because of the scatter affecting the
σPθ − MG
relationship (Fig. 20). Obviously, all supergiants
of interest are bright in the G band, in the range 5.6 to about 8 and
will thus be easily identifiable during Gaia data processing.
(19)With
the exponential law, we found 215 supergiants (among the 361069 of the full sample,
representing half the galactic plane) fulfilling these two conditions. They are displayed
in Fig. 19 in the
d − MG plane, and are
basically confined to a crescent delineated by the conditions
G > 5.6 (corresponding to the two lines with an
upwards concavity, labelled G > 5.6; the two
lines correspond to two values of the extinction in the G band:
AG = 0 and 1) and
d ≤ 55.5σPθ(MG)
(Eq. (16), corresponding to the green
dashed line with a downwards concavity). The latter line is based on a fiducial
relationship between
σPθ and
MG, as shown in Fig. 20. Some supergiants nevertheless fall outside the crescent defined
above, simply because of the scatter affecting the
σPθ − MG
relationship (Fig. 20). Obviously, all supergiants
of interest are bright in the G band, in the range 5.6 to about 8 and
will thus be easily identifiable during Gaia data processing.
With the parabolic law, only one supergiant matches the conditions: it is the brightest supergiant located in the upper left corner of Fig. 20 (green point in the lower panel; note that in Fig. 19 this star is not located below the parabolic threshold line as expected, because that line is based on a mean σP − MG relation – see Fig. 20 –, and that supergiant happens to have a σP value much above average, as seen in Fig. 20). Thus, Fig. 19 suggests that the “parabolic” link between box-in-a-star and star-in-a-box models of Fig. 17 and 18 is a limiting case: for photocentric motions to be detected by Gaia, the σPθ vs MG relation has to lie above this limiting case (depicted as the green solid line in Fig. 18).
In Fig. 19 there is a cluster of stars at MG = −4.5 (corresponding to log Teff ~ 3.5 and log g ~ 0.4), which corresponds to bright giants or asymptotic giant branch (AGB) stars. They are also clearly seen in Fig. 20 as the cluster at σPθ = 0.035 AU (with the exponential law) or 0.01 AU (with the parabolic law). Because these stars belong to a population different from supergiants (with masses of the order 1 M⊙), they are not necessarily confined to the galactic plane as supergiants are. Hence another sample, now covering a quarter of the sky (0° ≤ l ≤ 180°, b ≥ 0°), was generated from the Besançon model and contains 702 211 giants and bright giants. In this sample, 938 stars satisfy the condition of detection of the photocentric motion with the exponential law, and none with the parabolic law. The relation MG − σPθ thus appears as an essential ingredient, but unfortunately quite uncertain still, especially for those among the bright giants that are pulsating as long-period variables. The pulsation makes the modelling especially difficult (see for instance Freytag & Höfner 2008; Chiavassa et al. 2010b, for an application of 3D AGB models to the star VX Sgr). Nevertheless, numerous observations have revealed their surface brightness asymmetries (e.g., Ragland et al. 2006, and references therein).
 |
Fig. 20 Upper panel: the relation between
σPθ and
MG for supergiants and bright giants,
assuming either an exponential (red plusses) or a parabola (blue crosses) to connect
the box-in-a-star with the star-in-a-box models (Fig. 18). The equation of the dashed green line (through the red plusses) is
|
6.2. Impact on the parallaxes
To evaluate the impact of the photocentric shift on the parallax, we proceeded as follows. The sampling times, scanning angles, along-scan measurements and their errors were obtained from the Gaia Object Generator v7.0 (GOG10, Isasi et al. 2010) for the supergiant stars from the sample generated using the Besançon model described in the previous section. A photocentric motion deduced from the photocentre position computed from the snapshots of the red supergiant model (see Fig. 3) was added on the along-scan measurements (the photocentric shift was converted from linear to angular shifts, according to the known stellar distance). The red supergiant model gives a single photocentre position sequence. Yet the sequence for every star should be different. Therefore the sequence was rotated for every star by a random angle before being added to the along scan measurements. The astrometric parameters were then retrieved by solving the least-squares equation (Eq. (7)), separately with and without surface brightness asymmetries. The resulting parallaxes are compared in Fig. 21.
 |
Fig. 21 Comparison of parallaxes for supergiant stars with and without surface brightness asymmetries (spots), normalised to σϖ. The stars falling on the horizontal line with ordinate 0 are very reddened stars, are consequently quite faint, and therefore have large errors on their astrometric measurements and thus on their parallax. |
Figure 23 presents the histogram of the quantity (ϖ − ϖspot)/σϖ for three different ranges of distances. Obviously the distribution, which is quite peaked at zero for distant stars, becomes wider for nearer stars, meaning that the ratio of the error on the parallax to its formal error increases with decreasing distance. Similarly, the fits of the astrometric data are worse for stars closer by, and this effect is clearly seen in Fig. 24, displaying the relation between the goodness-of-fit parameter F2 and the distance. The run of F2 with distance is consistent with that predicted by Eq. (12), for ν = 70, σPθ = 0.1 AU and ση = 0.03 mas.
Coming back to Fig. 22, it is remarkable that the relative error on the parallax, namely (ϖ − ϖspot)/ϖ is almost independent of the distance and amounts to a few percents. This is in deed easy to understand if one assumes that the difference ϖ − ϖspot must somehow be proportional to the amplitude of the excursion of the photocentre on the sky, which must in turn be related to θ, the angular radius of the star on the sky; therefore, (ϖ − ϖspot)/ϖ = αθ/ϖ = αR, where α is the proportionality constant and R is the linear radius of the star (expressed in AU). Thus we conclude that the relative error on the parallax is independent of the distance, and is simply related to the excursion of the photocentre expressed in AU.
These simulations for a sample of Betelgeuse-like supergiants therefore allow us to confirm the results obtained in Sect. 6.1 (and Fig. 19), in particular that the impact on the goodness-of-fit remains noticeable up to about 5 or 6 kpc (Fig. 24).
 |
Fig. 22 Same as Fig. 21, but normalised by the parallax. Note how the relative parallax error is almost independent of the distance. |
 |
Fig. 23 Histograms of the relative error on the parallax of supergiant stars, for different ranges of distances. |
7. Conclusion
We provided astrometric and photometric predictions from 3D simulations of RSGs to evaluate the impact of the surface brightness variations on the astrometric parameters of these stars to be derived by Gaia.
We found that the global-scale convective pattern of RSGs cause strong variability in the position of the photocentre, P. From a 3D simulation of a Betelgeuse-like supergiant, ⟨ P ⟩ = 0.132 ± 0.065 AU (i.e., more than 3% of the stellar radius) showing excursions from 0.005 to 0.3 AU over the five years of simulation. In addition, the spectra show large fluctuations in the red and blue Gaia bands of up to 0.28 mag in the blue and 0.15 mag in the red. The Gaia colour index (blue – red) also fluctuates strongly with respect to time. Therefore, the uncertainties on [Fe/H], Teff and log g should be revised upwards for RSGs because of their convective motions. We furthermore provided predictions for interferometric observables in the Gaia filters that can be tested against observations with interferometers such as VEGA at CHARA.
Then we studied the impact of the photocentric noise on the astrometric parameters. For this purpose, we considered the standard deviation of the photocentre displacement predicted by the RHD simulation, sampled as Gaia will do (both timewise and directionwise). We called this quantity σPθ, where θ is the position angle of the scanning direction on the sky, and we found σPθ = 0.08 AU for Betelgeuse-like supergiants. This photocentric noise can be combined with ση = 30 μas (the error on the along-scan position η) for Gaia to determine the maximum distance (d < 4.4 kpc) up to which a photocentric motion with σPθ = 0.08 AU will generate an astrometric noise of the order of the astrometric error on one measurement (more precisely 0.6 times that error, yielding an increase of the F2 goodness-of-fit parameter by two units). The value σPθ = 0.08 AU could even be somewhat underestimated, as we guessed from the comparison of the along-scan Hipparcos residuals for Betelgeuse with the RHD predictions. We concluded that the predicted photocentric noise does account for a substantial part of the Hipparcos “cosmic noise” for Betelgeuse and Antares, but not for all of it. This may be because the temperature stratification in the RHD models is not completely correct owing to the grey approximation used for the radiative transfer. The resulting intensity maps have higher contrast than the observations, as shown in Paper II, and the photocentre position can therefore be affected as well. New simulations with wavelength resolution (i.e., non-grey opacities) are in progress and they will be tested against these observations.
 |
Fig. 24 Same as Fig. 21 for the goodness-of-fit F2. The solid line corresponds to the prediction from Eq. (12), with ν = 70, σPθ = 0.1 AU and ση = 0.03 mas. Part of the large scatter at intermediate distances (2 to 4 kpc) is caused by a different CCD gating sequence (see de Bruijne 2005; Lindegren 2010). |
We estimated how many RSGs might have an abnormally large goodness-of-fit parameter F2. We found that the photocentric noise should be detected by Gaia for a number of bright giants and supergiants varying between 2 and about 4190 (215 supergiants in each half of the celestial sphere and 940 bright giants in each quarter of the sphere; see Sect. 6.1), depending upon the run of σPθ with the atmospheric pressure scale height HP, and to a lesser extent, depending on galactic extinction. The theoretical predictions of 3D simulations presented in this work will be tested against the multi-epoch interferometric observations of a sample of giants and supergiants (Sacuto et al., in prep.), with the hope to better constrain this σPθ − HP relation. In a forthcoming paper (Pasquato et al., in prep.), we will evaluate how the Gaia reduction pipeline behaves when facing the bright-giants and supergiants granulation. More specifically, we will show that the distance to the star is the main driver fixing which one among all the possible solution types (single-star, acceleration, orbital, stochastic) is actually delivered by the pipeline (the acceleration and orbital solutions being obviously spurious).
Finally, a very important conclusion is that the parallax for Betelgeuse-like supergiants may be affected by an error of a few percents. For the closest supergiants (d < 2.5 kpc), this error may be up to 15 times the formal error σϖ (see Fig. 21) resulting from the measurement errors and estimated from the covariance matrix. In a forthcoming paper (Pasquato et al., in prep.), we will moreover show that this error is sensitive to the time scale of the photocentric motion (which is in turn fixed by the granulation and the stellar rotation).
There is little hope to be able to correct the Gaia parallaxes of RSGs from this parallax error, without knowing the run of the photocentric shift for each considered star. Nevertheless, it might be of interest to monitor the photocentric deviations for a few well selected RSGs during the Gaia mission. Ideally, this would require imaging the stellar surface, although monitoring of the phase closure on three different base lines may already provide valuable information on the size of the inhomogeneities present on the stellar surface (see Sacuto et al., in prep.). The best-suited targets for that purpose would be supergiants with G magnitudes just above the Gaia saturation limit of 5.6, where the astrometric impact is going to be maximum, and at the same time, still within reach of the interferometers. The corresponding diameter will be of the order of 4 mas (derived from the radius 830 R⊙ for a Betelgeuse-like supergiant seen at a distance of 2 kpc if G = 5.6, AG = 1, and MG = −6.6). A search for G, K, or M supergiants (of luminosity classes I, Ia, Iab, or Ib) with 5.6 ≤ V ≤ 8 in the SIMBAD database yielded only three stars (XX Per, HD 17306, and WY Gem) matching these criteria, the latter being a spectroscopic binary, which will disturb the radius measurement and is thus unsuited for this purpose. It may therefore be necessary to select these targets from the Gaia data themselves, after the first year of the mission.
American Association of Variable Star Observers, www.aavso.org
This larger parallax standard error does not contradict Appendix A stating that, in the presence of a photocentric noise, the standard error on the parallax should stay the same. This is because this parallax standard error is obtained in the framework of a DMSA/X (“stochastic”) solution, where the measurement errors were artificially increased by a “cosmic noise” to get an acceptable goodness-of-fit value. Hence, the “design matrix” defined in Appendix A, which is directly related to the variance-covariance matrix of the astrometric parameters, has been changed to produce the stochastic solution, thus resulting in a larger parallax error. This corresponds to a solution of kind (ii) in Sect. 4.
We note in passing that in the Besançon sample there is no star matching Betelgeuse parameters if one adopts log g = −0.3 for its surface gravity, yielding log Hp = 3.85. If on the other hand, one adopts log g = 0.0, we get log Hp = 3.55 and Betelgeuse is then matched by stars from the Besançon sample. This can be seen from the lower panel of Fig. 20, since Betelgeuse has MG = −6.4, when adopting Mbol = −7.5 from the apparent bolometric flux 111.67 × 10-13 W cm-2 (Perrin et al. 2004) and the parallax 6.56 mas (van Leeuwen 2007a), V − G = 0.98 from V − I = 2.32 (ESA 1997) and Eq. (19), BCV = −2.05 from the apparent bolometric flux and V = 0.42 (Johnson et al. 1966).
Acknowledgments
E.P. is supported by the ELSA (European Leadership in Space Astrometry) Research Training Network of the FP6 Programme. S.S. acknowledges funding by the Austrian Science Fund FWF under the project P19503-N13. We thank the CINES for providing some of the computational resources necessary for this work. We thank DPAC-CU2, and especially X. Luri and Y. Isasi, for help with the use of GOG. A.C. thanks G. Jasniewicz for enlightening discussions. B.F. acknowledges financial support from the Agence Nationale de la Recherche (ANR), the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, and the “École Normale Supérieure” (ENS) of Lyon, France, and from the Istituto Nazionale di Astrofisica/Osservatorio Astronomico di Capodimonte (INAF/OAC) in Naples, Italy.
References
- Asplund, M., Grevesse, N., & Sauval, A. J. 2006, Communi. Asteroseismol., 147, 76 [Google Scholar]
- Bailer-Jones, C. A. L. 2010, MNRAS, 403, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Barthès, D., & Luri, X. 1999, Baltic Astron., 8, 285 [NASA ADS] [Google Scholar]
- Bastian, U., & Hefele, H. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 215 [Google Scholar]
- Berger et al.(2010), A&ARv, submitted [Google Scholar]
- Buscher, D. F., Baldwin, J. E., Warner, P. J., & Haniff, C. A. 1990, MNRAS, 245, 7P [NASA ADS] [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2006, in SF2A-2006: Semaine de l’Astrophysique Francaise, ed. D. Barret, F. Casoli, G. Lagache, A. Lecavelier, & L. Pagani , 455 [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiavassa, A., Haubois, X., Young, J. S., et al. 2010a, A&A, 515, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiavassa, A., Lacour, S., Millour, F., et al. 2010b, A&A, 511, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Bruijne, J. H. J. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 35 [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El Eid, M. F. 1994, A&A, 285, 915 [NASA ADS] [Google Scholar]
- Eriksson, U., & Lindegren, L. 2007, A&A, 476, 1389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ESA. 1997, The Hipparcos and Tycho Catalogues (ESA SP-1200) [Google Scholar]
- Fernie, J. D. 1995, AJ, 110, 2361 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B. 2001, in 11th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. R. J. Garcia Lopez, R. Rebolo, & M. R. Zapaterio Osorio, ASP Conf. Ser., 223, 785 [Google Scholar]
- Freytag, B., & Höfner, S. 2008, A&A, 483, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., Steffen, M., & Dorch, B. 2002, Astron Nachr., 323, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2000, ApJ, 532, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harper, G. M., Brown, A., & Guinan, E. F. 2008, AJ, 135, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Haubois, X., Perrin, G., Lacour, S., et al. 2009, A&A, 508, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isasi, Y., Figueras, F., Luri, X., & Robin, A. C. 2010, in Highlights of Spanish Astrophysics V, ed. J. M. Diego, L. J. Goicoechea, J. I. González-Serrano, & J. Gorgas (Berlin: Springer Verlag), 415 [Google Scholar]
- Johnson, H. L., Iriarte, B., Mitchell, R. I., & Wisniewski, W. Z. 1966, Communications of the Lunar and Planetary Laboratory, 4, 99 [Google Scholar]
- Jordi, C., & Carrasco, J. M. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 215 [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L. 2010, in Relativity in Fundamental Astronomy: Dynamics, Reference Frames, and Data Analysis, IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel (Cambridge: Cambridge University Press), 261, 296 [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, in A Giant Step: from Milli- to Micro-arcsecond Astrometry, ed. W. J. Jin, I. Platais, & M. A. C. Perryman (Cambridge: Cambridge University Press), IAU Symp. 248, 217 [Google Scholar]
- Ludwig, H.-G. 2006, A&A, 445, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luri, X., Babusiaux, C., & Masana, E. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 357 [Google Scholar]
- Mourard, D., Clausse, J. M., Marcotto, A., et al. 2009, A&A, 508, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, G., Ridgway, S. T., Coudé du Foresto, V., et al. 2004, A&A, 418, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Platais, I., Pourbaix, D., Jorissen, A., et al. 2003, A&A, 397, 997 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourbaix, D., & Jorissen, A. 2000, A&AS, 145, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W., Teutolsky, S., Vetterling, W., & Flannery, B. 1992 [Google Scholar]
- Ragland, S., Traub, W. A., Berger, J., et al. 2006, ApJ, 652, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2004, A&A, 416, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuart, A., & Ord, J. K. 1994, Kendall’s advanced theory of statistics. Vol. 1: Distribution theory, ed. A. Stuart, & J. K. Ord [Google Scholar]
- Svensson, F., & Ludwig, H. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 979 [Google Scholar]
- Tatebe, K., Chandler, A. A., Wishnow, E. H., Hale, D. D. S., & Townes, C. H. 2007, ApJ, 670, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Thévenin, F. 2008, Phys. Scripta T, 133, 014010 [NASA ADS] [CrossRef] [Google Scholar]
- Tuthill, P. G., Haniff, C. A., & Baldwin, J. E. 1997, MNRAS, 285, 529 [NASA ADS] [Google Scholar]
- Tuthill, P. G., Haniff, C. A., & Baldwin, J. E. 1999, MNRAS, 306, 353 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007a, Hipparcos, the New Reduction of the Raw Data (Springer Verlag) [Google Scholar]
- van Leeuwen, F. 2007b, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F., & Evans, D. W. 1998, A&AS, 130, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, R. W., Baldwin, J. E., Buscher, D. F., & Warner, P. J. 1992, MNRAS, 257, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. W., Dhillon, V. S., & Haniff, C. A. 1997, MNRAS, 291, 819 [NASA ADS] [Google Scholar]
- Young, J. S., Baldwin, J. E., Boysen, R. C., et al. 2000, MNRAS, 315, 635 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Formal errors on the parameters of a least-squares minimisation
We provide here a short demonstration of a well-known statistical result (see e.g., Press et al. 1992), which may appear counter-intuitive in the present context, namely that the presence of an extra-source of unmodelled noise will not change the formal errors on the parameters derived from a least-squares minimisation.
Consider the case where the data points
(xi,yi)(i = 1,..., N)
must be fitted by a general linear model
 (A.1)where
Xk(x)(k = 1,..., M)
are M arbitrary (but known) functions of x, which may be
wildly non-linear. The merit function is defined as
(A.1)where
Xk(x)(k = 1,..., M)
are M arbitrary (but known) functions of x, which may be
wildly non-linear. The merit function is defined as
![\appendix \setcounter{section}{1} \begin{equation} \chi^2 = \sum_{i=1}^{N} \left[\frac{y_i - \Sigma_{k=1}^M a_k\;X_k(x_i)}{\sigma_i} \right]^2 , \end{equation}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq244.png) (A.2)where
σi is the measurement error on
yi presumed to be known. To simplify the
notation, we define the design matrix A (of size
N × M) by
(A.2)where
σi is the measurement error on
yi presumed to be known. To simplify the
notation, we define the design matrix A (of size
N × M) by
 (A.3)the vector
b of (normalised) measured values, of length
N:
(A.3)the vector
b of (normalised) measured values, of length
N: 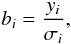 (A.4)and finally the
vector a of length M whose components are
the parameters
ak(k = 1,..., M)
to be fitted. The least-squares problem may thus be rephrased as
(A.4)and finally the
vector a of length M whose components are
the parameters
ak(k = 1,..., M)
to be fitted. The least-squares problem may thus be rephrased as
find a that minimises χ2 = |Aa − b|2,
whose solution may be written 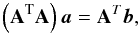 (A.5)with
(A.5)with
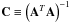 being the variance-covariance matrix describing the uncertainties11 of the estimated parameters a. The
crucial point to note here is that matrix C involves the
measurement uncertainties σi but not the
measurements yi themselves. Therefore,
changing yi, in the presence of an unmodelled
process (like photocentric motion) without changing the measurement uncertainties
σi, will not change the formal errors on
the resulting parameters a. But of course,
χ2 along with the goodness-of-fit parameter
F2 (see Eq. (10)) will
be larger if there is of a photocentric noise, as the scatter around the best astrometric
solution will be larger than expected solely from the measurement errors. Therefore, it is
F2 and its associated χ2, but not the
formal parallax error, which bear the signature of the presence of photometric noise.
being the variance-covariance matrix describing the uncertainties11 of the estimated parameters a. The
crucial point to note here is that matrix C involves the
measurement uncertainties σi but not the
measurements yi themselves. Therefore,
changing yi, in the presence of an unmodelled
process (like photocentric motion) without changing the measurement uncertainties
σi, will not change the formal errors on
the resulting parameters a. But of course,
χ2 along with the goodness-of-fit parameter
F2 (see Eq. (10)) will
be larger if there is of a photocentric noise, as the scatter around the best astrometric
solution will be larger than expected solely from the measurement errors. Therefore, it is
F2 and its associated χ2, but not the
formal parallax error, which bear the signature of the presence of photometric noise.
All Tables
Properties of the spots observed at the surface of Betelgeuse during the Hipparcos mission.
All Figures
 |
Fig. 1 Transmission curve of the Gaia G band white light passband (solid black line), the blue (dotted blue line) and red (dashed red line) photometric filters (Jordi et al. 2010; Jordi & Carrasco 2007) together with the synthetic spectrum computed from the RHD simulation described in the text. |
| In the text | |
 |
Fig. 2 Maps of the linear intensity (the range is [0–230 000] erg/s/cm2/Å) in the Gaia G band. Each panel corresponds to a different snapshot of the model described in the text with a step of about 230 days (~five years covered by the simulation). |
| In the text | |
 |
Fig. 3 Photocentre position computed from the snapshots of Fig. 2, in the Gaia G band filter. The total simulated time is ~five years and the snapshots are 23 days apart. The snapshots are connected by the line segments. The dashed lines intersect at the position of the geometrical centre of the images. Note that the photocentric shift stays in the first quadrant for most of the 5 year simulation, and reflects the long lifetime of the large convective cell best visible in the infrared H band (Fig. 4). |
| In the text | |
 |
Fig. 4 Map of the linear intensity in the IONIC filter (H band as described in Paper I). The range is [0–3.1 × 105] erg cm-2 s-1 Å-1. The snapshot corresponds to the top left snapshot at t = 21.976 year in Fig. 2. The large convective cell visible in this figure is swamped in smaller-scale photospheric structures in the Gaia G band images. |
| In the text | |
 |
Fig. 5 Top panel: modulus of the photocentre displacement as a function
of time. Bottom panel: photocentre displacement as a function of
the integrated flux in the Gaia G band,
|
| In the text | |
 |
Fig. 6 Along-scan photocentre displacement Pθ (in AU) against time for two different samplings of the photocentre displacement of Fig. 3, corresponding to the Gaia scanning law applied to stars located along the galactic plane at longitudes of 0° and 241°, as indicated on the figures. The top panel of each pair provides the distribution of time intervals between successive measurements. |
| In the text | |
 |
Fig. 7 Run of σPθ (expressed in AU; solid blue curve and left-hand scale) with galactic longitude for stars located along the galactic plane, with a number of transit observations given by the red dots (and right-hand scale). |
| In the text | |
 |
Fig. 8 Spectral fluctuations in the blue and red Gaia photometric bands (Fig. 1) for RSGs: the black curve is the average flux over ~five years covered by the simulation, while the grey shade denotes the maximum and minimum fluctuations. The spectra were smoothed to theGaia spectral resolution (R ~ 50, Thévenin 2008). |
| In the text | |
 |
Fig. 9 (blue – red)Gaia colour index, computed in the blue and red photometric filters of Fig. 1, as a function of time. |
| In the text | |
 |
Fig. 10 Top panels: maps of the linear intensity (the range is [0–230 000]
erg/s/cm2/Å) computed in the blue and red photometric filters of
Fig. 1. Bottom panels:
visibility curves from the above maps computed for 36 different position angles
5° apart (grey lines). The black curve is the average visibility, while
the dashed line is a uniform disc of about the same radius as the simulation
snapshot. The conversion factor to the more customary unit arcsec-1 on
the abscissa axis is arcsec |
| In the text | |
 |
Fig. 11 Snapshot of 3D simulation (upper left of Fig. 2) convolved to the PSF of a 42 m telescope (for a star at a distance of 152.4 pc, see solution #2 in Table 2) like the European Extremely Large Telescope. |
| In the text | |
 |
Fig. 12 Degradation of the goodness-of-fit F2 in the presence of a photocentric motion described in terms of the ratio σPθ/ση, where ση is the instrumental error. Remember that F2 follows a normal distribution with zero mean and unit standard deviation. |
| In the text | |
 |
Fig. 13 Top panel: interferometric observations of the surface of Betelgeuse obtained with the William Herschel Telescope at a wavelength of 710 nm, in January 1991 (Wilson et al. 1992) and January 1992 (Tuthill et al. 1997). North is at the top and East is to the left. The two images have been taken from Freytag et al. (2002). The spot properties are summarised in Table 1. Bottom panel: Hipparcos epoch photometry of Betelgeuse with the vertical lines indicating the epoch of the two interferometric observations. |
| In the text | |
 |
Fig. 14 Parallax standard errors for supergiants in the Hipparcos Catalogue, after van Leeuwen’s reprocessing. The dashed line represents 1.5 times the standard parallax error for stars with precise parallaxes (<10%; solid line) in van Leeuwen’s reprocessing (see Fig. 2.19 of van Leeuwen 2007a), whereas the solid line represents the fiducial relation between the Hipparcos magnitude and the standard parallax error. Large red circles correspond to stars redder than V − I = 2. |
| In the text | |
 |
Fig. 15 Abscissa residuals Δη (in mas on the sky; red dots) along with the corresponding error bar from van Leeuwen (2007a) for Betelgeuse and Vega, as a function of time, expressed in years from 1991.25. Filled star symbols correspond to the along-scan projections Pθ of the synthetic photocentre displacements of Fig. 3. The red dashed lines and black solid lines depict the ± 1σ interval around the mean for the Hipparcos data points and model predictions, respectively. Note that these displacements were computed in the Gaia G filter instead of the Hipparcos Hp filter. A test on a given snapshot has shown that the difference is negligible: Px = 0.11 AU with the Hp filter, as compared to 0.13 AU with the G filter. |
| In the text | |
 |
Fig. 16 Same as Fig. 15 for Antares and α Her. |
| In the text | |
 |
Fig. 17 Fits to the standard deviation σPθ of the photocentric motion predicted from 3D simulations, as listed in Table 3, against the pressure scale height Hp. The equation of the (red) solid line is log σPθ = −6.110 + 1.110log (Hp) with χ2 = 0.17: the fit considers only the box-in-a-star models (filled circles) of Svensson & Ludwig (2005). The (green) dashed line (with equation log σPθ = −6.275 + 1.174log Hp + 0.039(log Hp)2) is a fit to all the models of Table 3 (i.e., box-in-a-star models and star-in-a-box, the latter being represented by a filled square). The (blue) dotted line is an arbitrary exponential law that connects the last two points with the following equation log σPθ = −1.09−3.434exp(− 0.00149Hp). |
| In the text | |
 |
Fig. 18 Photocentre motions determined from interferometric observations for some evolved stars (see Table 4) overplotted on the different fits of the standard deviation σPθ of the photocentric motion as a function of the pressure scale height Hp. The large open inverted triangles correspond to the standard deviations of the photocentre deviations for a given observed star. Star-in-a-box and box-in-a-star models correspond to the large filled square and circle respectively. |
| In the text | |
 |
Fig. 19 Location in the (MG,d) plane for supergiants with a photocentre noise (of standard deviation σPθ) significantly altering the goodness-of-fit of the astrometric solution (see text), for the case of an exponential link between box-in-a-star and star-in-a-box models (see Fig. 18 and text). |
| In the text | |
 |
Fig. 20 Upper panel: the relation between
σPθ and
MG for supergiants and bright giants,
assuming either an exponential (red plusses) or a parabola (blue crosses) to connect
the box-in-a-star with the star-in-a-box models (Fig. 18). The equation of the dashed green line (through the red plusses) is
|
| In the text | |
 |
Fig. 21 Comparison of parallaxes for supergiant stars with and without surface brightness asymmetries (spots), normalised to σϖ. The stars falling on the horizontal line with ordinate 0 are very reddened stars, are consequently quite faint, and therefore have large errors on their astrometric measurements and thus on their parallax. |
| In the text | |
 |
Fig. 22 Same as Fig. 21, but normalised by the parallax. Note how the relative parallax error is almost independent of the distance. |
| In the text | |
 |
Fig. 23 Histograms of the relative error on the parallax of supergiant stars, for different ranges of distances. |
| In the text | |
 |
Fig. 24 Same as Fig. 21 for the goodness-of-fit F2. The solid line corresponds to the prediction from Eq. (12), with ν = 70, σPθ = 0.1 AU and ση = 0.03 mas. Part of the large scatter at intermediate distances (2 to 4 kpc) is caused by a different CCD gating sequence (see de Bruijne 2005; Lindegren 2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



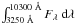
![\hbox{$^{-1}={R}_\odot^{-1} d~[{\rm pc}]\, 214.9$}](/articles/aa/full_html/2011/04/aa15768-10/aa15768-10-eq79.png)