| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912723 | |
| Published online | 26 November 2010 | |
High-resolution mapping of the physical conditions in two nearby active galaxies based on 12CO(1–0), (2–1), and (3–2) lines ⋆,⋆⋆,⋆⋆⋆
1
Observatoire de Paris, LERMA,
61 avenue de l’Observatoire
75014
Paris,
France
e-mail: frederic.boone@obspm.fr
2
Laboratoire d’Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 avenue Édouard
Belin, 31400
Toulouse,
France
3
Observatorio Astronómico Nacional (OAN) – Observatorio de Madrid,
C/ Alfonso XII 3,
28014
Madrid,
Spain
4
Institute of Astronomy and Astrophysics, Academia Sinica,
PO Box 23-141,
Taipei
106,
Taiwan
5
Department of Physics and Astronomy, Rutgers, the State University
of New Jersey, 136 Frelinghuysen
Road, Piscataway,
NJ
08854,
USA
6
Joint ALMA Office,
Av. El Golf 40, Piso 18, Las Condes,
Santiago,
Chile
7
Institut de Radio Astronomie Millimétrique,
300 rue de la Piscine,
38406
Saint-Martin-d’Hères, France
8
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
Received: 19 June 2009
Accepted: 4 October 2010
We present a detailed analysis of high resolution observations of the three lowest CO transitions in two nearby active galaxies, NGC 4569 and NGC 4826. The CO(1–0) and (2–1) lines were observed with the Plateau de Bure Interferometer and the CO(3–2) line with the Submillimeter Array. Combining these data allows us to compare the emission in the three lines and to map the line ratios, R21 = ICO(2 − 1)/ICO(1 − 0) and R32 = ICO(3 − 2)/ICO(1 − 0) at a resolution of ~2″, i.e., a linear resolution of 160 pc for NGC 4569 and 40 pc for NGC 4826. In both galaxies the emission in the three lines is similarly distributed spatially and in velocity, and CO is less excited (R32 < 0.6) than in the Galactic Center or the centers of other active galaxies studied so far. According to a pseudo-LTE model the molecular gas in NGC 4569 is cold and mainly optically thick in the CO(1–0) and (2–1) lines; less than 50% of the gas is optically thin in the CO(3–2) line. LVG modeling suggests the presence of an elongated ring of cold and dense gas coinciding with the inner Lindblad resonance (ILR) of the stellar bar in agreement with a previous analysis of the kinematics.
More excited gas is resolved in the circumnuclear disk of NGC 4826. According to our pseudo-LTE model this corresponds to warmer gas with a ~20% of the CO(3–2) emission being optically thin. LVG modeling indicates the presence of a semicircular arc of dense and cold gas centered on the dynamical center and ~70 pc in radius. The gas temperature increases and its density decreases toward the center. A near side/far side asymmetry noticeable in the CO, R32 and Paα maps suggests that opacity effects play a role. Examining published CO maps of nearby active galaxies we find similar asymmetries suggesting that this could be a common phenomenon in active galaxies. These mainly qualitative results open new perspectives for the study of active galaxies with the future Atacama Large Millimeter/submillimeter Array.
Key words: galaxies: active / galaxies: ISM / galaxies: individual: NGC 4569 / galaxies: individual: NGC 4826
Based on observations carried out with the Submillimeter Array (SMA), a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics that is funded by the Smithsonian Institution and the Academia Sinica.
Based on observations carried out with the IRAM Plateau de Bure Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
Appendix and Figs. 1, 5, 16–20, 23, 24 are only available in electronic form at http://www.aanda.org
© ESO, 2010
1. Introduction
Multitransition CO observations are essential for studying the processes at work in the centers of active galaxies. The molecular gas fuels the nuclear activity powered by accretion onto a supermassive black hole and/or intense star formation. Conversely, the molecular gas properties are affected by the influence of the active nucleus through jets, winds, and radiation. The molecular gas must also constitute the bulk of the nuclear torus responsible for the highly anisotropic extinction invoked by the unified model for active galactic nuclei (AGN; Antonucci 1993). As the most abundant molecule after H2 and with its four lowest rotational transitions coinciding with the atmospheric windows in the millimeter and submillimeter range, CO has long been recognized and used as the best molecular gas tracer. Observing a single transition allows us to map the molecular gas column density and kinematics and, thus, to identify dynamical instabilities, and measure gravitational torques and possible gas inflows. Such detailed studies are for example conducted for nearby galaxies in the context of the NUclei of GAlaxies survey (García-Burillo et al. 2003, hereafter NUGA-I) based on high resolution observations of the CO(1–0) and (2–1) lines (see also Helfer et al. 2003; Sakamoto et al. 1999, for other high resolution CO surveys). It is however necessary to observe more transitions to characterize the physical conditions of the molecular gas and identify interstellar medium (ISM) structures involved in star formation, shocks (e.g., due to the disk kinematics, AGN feedback, stellar winds, or supernova remnants), or quiescent gas reservoirs ready to ignite star formation or feed the central black hole. Other molecular or atomic lines(including those of CO isotopologues) can be observed to characterize the physical conditions, but this implies adding new unknowns, namely the relative abundances of the observed molecules or atoms (which are otherwise interesting to measure to study the ISM chemistry).
Models of the ISM in galactic centers suggest that high resolution multitransition CO observations should allow for the identification of the torus around the supermassive black hole (Wada & Tomisaka 2005) as well as the influence of the AGN on the ISM chemistry (in X-ray dominated regions, Meijerink et al. 2007; Meijerink & Spaans 2005).
While the first two CO transitions at 115 and 230 GHz have been regularly observed for some time at high spatial resolution with millimeter interferometers, the third transition at 345 GHz could only be observed with single dish telescopes until recently. CO(3–2) single dish observations complemented lower transitions’ observations and yielded a wealth of information on the excitation of the molecular gas in galaxy centers (see e.g. Papadopoulos & Seaquist 1999; Papadopoulos & Allen 2000; Dumke et al. 2001; Curran et al. 2001; Hafok & Stutzki 2003; Yao et al. 2003; Weiß et al. 2005; Bayet et al. 2006; Muraoka et al. 2007; Kohno et al. 2008; Papadopoulos et al. 2008; Wilson et al. 2009; Israel 2009) including that of our own Galaxy (Oka et al. 2007). These observations showed that the CO(3–2)/(1–0) line ratio generally increases toward the center, where it can reach values greater than unity (in temperature units) in starburst and AGN hosts as well as in the Milky Way (vs. a typical value of 0.4 in galaxy disks). It is only since the Submillimeter Array became operational (Ho et al. 2004) that it has been possible to map the CO(3–2) (and higher J-transitions see, e.g., Matsushita et al. 2009) in the central regions of galaxies with the same spatial resolution as the CO(1–0) and CO(2–1) lines observed with millimeter interferometers. Among other results, these observations have revealed gas interacting with a jet in the center of M 51 (Matsushita et al. 2004) and gas interacting with a starburst superwind or AGN outflow in NGC 6240 (Iono et al. 2007).
In this paper, we present a detailed analysis of high resolution observations of the three lowest CO transitions in two nearby active galaxies. Long-term drivers for this work are (1) to estimate the feasibility of mapping the physical conditions in the centers of galaxies based on CO line observations, and (2) to discuss the implications for the study of active galaxies with current and future instruments. We selected the two galaxies in the NUGA sample with the strongest low-J CO lines, NGC 4569 and NGC 4826, and observed the CO(3–2) line with theSubmillimeter Array (SMA). The CO(1–0) and CO(2–1) observations obtained with the IRAM Plateau de Bure Interferometer (PdBI) were presented and analyzed in NUGA-I, García-Burillo et al. (2005, hereafter NUGA-IV) and Boone et al. (2007,hereafter NUGA-VII).
NGC 4569 is a bright early type spiral galaxy in the Virgo cluster at a distance of 17 Mpc (1″ is ~80 pc). It harbours a transition-type nucleus (Ho et al. 1997) which exhibits the most pronounced nuclear starburst activity among thelow-ionization nuclear emission-line region (LINER) and transition nuclei with available UV data (Maoz et al. 1998). Hensler et al. (2003) report a bipolar outflow in X-ray and a giant Hα outflow with a scale height of 10 kpc to the west. Chyży et al. (2006) observe symmetric radio lobes extending up to 24 kpc from the galactic disk. High resolution PdBI observations allowed us to model the kinematics of the central kpc (NUGA-VII) and showed that the molecular gas concentration at a radius of 600 pc corresponds to the inner Lindblad resonance (ILR) of the large scale bar, which extends to a radius of 5 kpc (Laurikainen & Salo 2002). The inclination of the galaxy is 70 deg (Tully 1988) and its position angle 30 deg (Guhathakurta et al. 1988).
NGC 4826, also known as the “Evil Eye”, is the closest target (4.1 Mpc, i.e., 1″ is ~20 pc) of the NUGA core sample for which we have acquired ~0.5″ resolution PdBI CO observations (NUGA-IV). These observations show a large concentration of molecular gas within a radius of 80 pc forming a circumnuclear molecular disk (CND). A detailed analysis of the kinematics, however, does not reveal any evidence of fuelling of the nucleus (NUGA-I). The nucleus of NGC 4826 is also classified as a transition type (Ho et al. 1997). The inclination of the galaxy is 60 deg (Rubin 1994), and its position angle 112 deg (NUGA-I).
The paper is organized as follows. The SMA CO(3–2) observations are presented in Sect. 2. The distributions of the emission in the three lines and of the two line ratios(R21 ≡ ICO(2 − 1)/ICO(1 − 0) and R32 ≡ ICO(3 − 2)/ICO(1 − 0), where ICO is a line intensity in temperature units) are compared in Sects. 3 and 4, respectively. Mapping of the physical conditions based on radiative transfer modeling of the line ratios is performed in Sect. 5. The results obtained are discussed in Sect. 6 and conclusions are drawn in Sect. 7.
2. Observations and data processing
 |
Fig. 2 SMA CO(3–2) integrated map of NGC 4569 (grey scale given in the color bar in Jy km s-1 beam-1) overlaid with the PdBI CO(1–0) integrated map (left) with contours at 2, 6, 12, 20, and 30 Jy km s-1 beam-1 and the PdBI CO(2–1) integrated map (right) with contours at at 7, 21, 42, 70 and 87 Jy km s-1 beam-1. No primary beam correction has been applied. All maps have the same resolution (PdBI data have been tapered) and the beam (2.3″ × 2.1″) is shown at the bottom left. The black cross labelled E shows the position of the AGN (αJ2000 = 12h36m49 .s80, δJ2000 = 13°09′46 .′′3). It is also the dynamical center and the phase center for the observations. The other crosses indicate the positions of the spectra plotted in Fig. 4. |
Each galaxy was observed with the SMA in an ~8 h track at night in March 2005. The observing frequency was set to the CO(3–2) line frequency (345.796 GHz) redshifted according to the systemic velocity of the galaxy. At these frequencies the half power beam width (HPBW) of the primary beam is ~36″. The SMA was in its compact configuration with seven working antennas. Saturn was observed for bandpass calibration, bright nearby quasars (3C 273 and 3C 279 for NGC 4569, 3C 279 and 1159 + 292 for NGC 4826) were observed every ~15 min for gain calibration, and Titan and Callisto were used for flux calibration. The data were reduced using the SMA MIR package (Qi 2005). For image reconstruction the MIRIAD software1 (Sault et al. 1995) was used with natural weighting applied to the uv data.
We estimated the flux missed by the SMA due to the short spacings inherently missing in interferometric observations by comparing to the single dish data published by Wilson et al. (2009) for NGC 4569 and by Israel (2009) for NGC 4826. We compared the total flux within an aperture of ~36″ in diameter after correcting the SMA data for the primary beam attenuation and degrading to the resolution of the single dish data (14.5″). We found that 21% and 38% of the flux is missed by the SMA in NGC 4569 and NGC 4826, respectively.
We then used the single dish data to compute and add the missing short spacings to the SMA data. The corresponding large scale distribution was included in the image plane using the IMMERGE task of the MIRIAD software. One of the input parameters to this task is a factor to scale the flux of the single dish data. We controlled the value of this parameter by comparing the flux of the merged data with that of the single dish data following the same procedure as the one described above to estimate the missing flux. The factor was fixed such that the fluxes of the merged data and single dish data agreed to within 10%.
For NGC 4569 the synthesized beam HPBW is 2.6″ × 2.1″ with a position angle of − 36 deg and the rms is 115 mJy beam-1 in 10 km s-1 channels. For NGC 4826 the HPBW is 2.6″ × 1.9″ with a position angle of − 37 deg and the rms is 75 mJy beam-1 in 10 km s-1 channels.
To make the comparison between the three CO lines easier the PdBI observations (which also include the short spacings) have been degraded to the resolution of the SMA observations. This was done by apodizing the visibilities, cleaning the datacubes and restoring them with the same clean beam as the one used for the corresponding SMA map.
3. Comparison of the three CO line intensity distributions
3.1. NGC 4569
The channel maps of the CO(3–2) line emitted by NGC 4569 and observed with the SMA are presented in Fig. 1. The elongated distribution identified in most of the individual CO(1–0) and CO(2–1) channel maps (see NUGA-VII) can also be recognized in the CO(3–2) channel maps. The CO(3–2) emission appears more clumpy and irregular, however, and while emission was detected up to ±200 km s-1 relative to systemic in CO(1–0) and CO(2–1), there is no CO(3–2) emission at a level higher than 3σ for velocities greater than 130 km s-1 in absolute value. These differences between the PdBI and SMA data may be due to the lower S/N ratio of the CO(3–2) SMA data. Indeed, the integrated map (see RGB image in Fig. 3 and detailed grey scale maps in Fig. 2) shows that the CO(3–2) is well detected at the peaks of CO(1–0) and CO(2–1) line emission, i.e., the northern (B) and the southern (G) peaks that were interpreted as emission from an elongated ring at the Inner Lindblad Resonance (see NUGA-VII), and at the central ridge (D). As in the two other line maps, there is a depression in the CO(3–2) map at the location of the nucleus (E) which is also the dynamical center, and the southern peak is more prominent than the northern one.
There are, however, differences in the integrated maps as well. The depression at the center and the difference between the northern and southern peaks seem to be more pronounced in the CO(3–2) map. The CO(3–2) map also shows more emission west of the center (F) than the other line maps.
The spectra at the 8 positions marked by crosses in the integrated maps (Fig. 2) and labelled from A to H are presented in Fig. 4. The SMA spectra show negative values outside the CO(3–2) line. These are due to deconvolution errors (a single SMA track was obtained, whereas the PdBI observations include four tracks in four configurations, leading to better uv-coverage and therefore lower sidelobes). These effects are difficult to correct for without additional observations, but it can be seen that the negative offsets do not exceed 100 mJy, i.e., the deconvolution errors do not exceed the rms.
Although the CO(3–2) line has a lower S/N, the three CO lines look fairly similar in their profiles at a given position as well as in their spatial distribution, i.e., their intensity ratios are constant as a function of velocity to within ~30% over the profiles. This is particularly true at the three peaks (positions B, D and G). This implies that overall, the kinematics are the same for the three emission lines, i.e., even if different clumps or gas components are probed by the different lines they all seem to follow the same kinematics. The CO(1–0) emission seems to be relatively stronger away from the peaks (positions A, C and H); this is particularly striking to the north (at position A), but a similar trend is seen toward the south in position H.
3.2. NGC 4826
The channel maps of the CO(3–2) emission from NGC 4826 as observed with the SMA are presented in Fig. 5. The phase center is offset by ~10″ to the south of the dynamical center, which is marked by a small cross on the channel maps. The typical disk rotation pattern (a.k.a. spider diagram) clearly seen in the individual CO(1–0) and CO(2–1) channel maps (NUGA-I) can just be recognized in the CO(3–2) channel maps. The integrated map (see RGB-image in Fig. 7 and detailed greyscale maps in Fig. 6), however, shows that the CO(3–2) distribution is similar to that of the CO(1–0) and CO(2–1) lines at the same resolution. It is dominated by a nearly circular region elongated along the galactic major axis with a radius of ~2″ (40 pc) and identified as a circumnuclear disk (CND) in NUGA-I. The emission detected outside the disk seems to coincide with the spiral arms described in that same paper. This general agreement between the three CO lines suggests that the discrepancies in the channel maps are mainly due to the lower S/N of the SMA data in individual channels. This interpretation is further supported by the similarities between the individual spectra shown in Fig. 8. At the eight positions (marked on the integrated map in Fig. 6) the spectra exhibit similar profiles to within 30%.
The relative strengths of the lines appear to follow two trends. (i) The closer to the center, the stronger the CO(2–1) and CO(3–2) lines relative to CO(1–0); (ii) The CO(3–2) line is stronger relative to CO(2–1) in the central disk (positions B, C and D) and along the major axis (compare positions A and E vs. F and G), where the spiral arms connect to the disk.
4. Line ratios
 |
Fig. 3 Composite color image of NGC 4569 made from the intensity maps of the CO(1–0), CO(2–1) and CO(3–2) line emission. The line intensities are represented by the red, green and blue color intensities respectively. The intensity maps were obtained by summing all channels where the line has S/N > 3, and are corrected for primary beam attenuation. |
 |
Fig. 4 Individual spectra of CO(1–0) (black), (2–1) (blue) and (3–2) (red) lines at six different positions (see Fig. 2) in the central region of NGC 4569 extracted at the same spatial resolution of 2.6″ × 2.1″. The fluxes have been corrected for primary beam attenuation and the CO(1–0) flux is scaled up by a factor 3.5 for better readability. |
 |
Fig. 6 SMA CO(3–2) integrated map of NGC 4826 (grey scale given in the color bar in Jy km s-1 beam-1) overlaid with the PdBI CO(1–0) integrated map (left) with contours at 2, 4, 8, 12, 16, 20, and 24 Jy km s-1 beam-1 and the PdBI CO(2–1) integrated map (right) with contours at 4.1, 14.3, 24.5, 34.7, 44.9, 55.1, 65.3 and 75.5 Jy km s-1 beam-1. No primary beam correction has been applied. All maps have the same resolution (PdBI data have been tapered) and the beam (2.6 × 1.9″) is shown at the bottom left. The white cross labelled C shows the position of the dynamical center (αJ2000 = 12h56m43 .s64, δJ2000 = 21°40′59 .′′3). The other crosses indicate the positions of the spectra plotted in Fig. 8. |
 |
Fig. 7 Composite color image of NGC 4826 made from the intensity maps of the CO(1–0), CO(2–1) and CO(3–2) line emission. The line intensities are represented by the red, green and blue color intensities, respectively. The intensity maps were obtained by summing all channels where the line has S/N > 3 and are corrected for primary beam attenuation. |
 |
Fig. 8 Individual spectra of the CO(1–0) line (black), the CO(2–1) line (blue) and the CO(3–2) line (red) at 8 different positions (see Fig. 6) in the central region of NGC 4826 extracted at the same spatial resolution of 2.6″ × 1.9″. The fluxes have been corrected for primary beam attenuation and the CO(1–0) flux is scaled up by a factor 3.5 for better readability. |
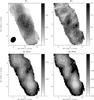 |
Fig. 9 Line ratio maps of NGC 4569 and associated uncertainties. Upper left: R21 with black contours ranging from 0.3 to 0.7 in steps of 0.1 and white contours at 0.8 and 0.9. The beam (2.3″ × 2.1″) is represented as a filled ellipse at the bottom left corner. Upper right: R32 with black contours ranging from 0.1 to 0.25 in steps of 0.05, and white contours at 0.3, 0.35 and 0.4. Lower left: R21 error map with black contours at 0.02, 0.03, and white contours at 0.04, 0.05. Lower right: R32 error map with black contours 0.05, 0.07, and white contours at 0.09, 0.11, 0.13. |
 |
Fig. 10 Line ratio maps with the same contours as in Fig. 9 (only above 0.2 for R32) overlaid on the Paα map obtained from NICMOS data (Programme ID: 9360, PI: Kennicutt). The grey scale is logarithmic; dark color corresponds to high flux. |
 |
Fig. 11 (Left) R32-vs.-R21 diagram for the galaxy NGC 4569. The x-axis represents R21 and the y-axis R32. The intensity scale gives the sky area in the map per unit area in the ratio space, it is expressed in beams per 0.01 × 0.01 ratio area. This diagram has been produced by convolving the actual distribution of pixels in the ratio-ratio plane by a Gaussian kernel with a FWHM of 0.02. Note that the pixels in the ratio maps used to compute the distribution are much smaller than the beam (see Sect. 4). The contour levels are 0.3, 0.6, 0.9, 1.2 and 1.5 beams/0.012. (Middle) R32-vs.-R21 diagram for the galaxy NGC 4826; the contour levels are 0.3, 0.5, 0.7, 0.9, 1.1 beams/0.012. (Right)LTE and pseudo-LTE models represented as black curves in the R32-vs.-R21 diagram. Curves 1 and 2 correspond to pure LTE models with NCO/dV = 1015 cm-2 pc (km s-1)-1 and NCO/dV = 12 × 1015 cm-2 pc (km s-1)-1, respectively. The temperature increases from 4 K at the bottom left to 8 K at the top right. Curves 3 and 4 correspond to pseudo-LTE models with f32 = 0.5 and f32 = 0.2 respectively (see Sect. 5.1 for the definition of f32). The column density to line width ratio is NCO/dV = 1015 cm-2 pc (km s-1)-1 and the temperature increases from 4 to 20 K along the curves from bottom left to top right. The cyan and magenta curves show the lowest contours for NGC 4569 and NGC 4826, respectively. |
 |
Fig. 12 Line ratio maps of NGC 4826 and associated uncertainties. The crosses are the same as in Fig. 6. Upper left: R21 with black contours at 0.4, 0.5, 0.6, 0.7, 0.8 and white contours at 0.77 and 0.9. The beam (2.6″ × 1.9″) is represented as a filled ellipse at the bottom left corner. Upper right: R32 with black contours at 0.1, 0.2, 0.3 and white contours at 0.4 and 0.5. Lower left: R21 error map with black contours at 0.02, 0.03 and white contours at 0.04 and 0.05. Lower right: R32 error map with black contours at 0.05, 0.07 and white contours at 0.09 and 0.11. |
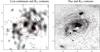 |
Fig. 13 Maps of NGC 4826. Left: R21 with the same contours as in Fig. 12 overlaid on the 2 cm radio continuum map from Turner & Ho (1994). Right: R32 with the same contours as in Fig. 12 overlaid on the Paα map from NUGA-I. Dark color corresponds to high flux. |
With the definition adopted in the introduction any line ratio would tend to 1 with increasing excitation temperature for thermalized gas in local thermal equilibrium. Line ratio maps were computed restricting the spectral window of each pixel to the channels where the CO(1–0) flux is >4–σ and the CO(3–2) flux is positive. When the spectral window was narrower than 50 km s-1, i.e., less than 5 channels, the pixel was discarded.
4.1. NGC 4569
The ratio maps with the corresponding error (standard deviation) maps are shown in Fig. 9. R21 is distributed in the range 0.2 to 0.9 with a weighted mean of 0.63. The uncertainties on R21 are in the range 0.01 to 0.05. R32 is distributed in the range 0.05 to 0.45 with a weighted mean of 0.23. The uncertainties on R32 are in the range 0.03 to 0.11. The errors on the weighted means based on the data noise only are less than 0.02. While calibration uncertainties introduce an overall error of the order of 0.05, they should have the same effect on all locations and thereby spatial trends should be unaffected. The mean values are in good agreement with the values found by Hafok & Stutzki (2003) based on single dish observations with a beam of 80″ HPBW, i.e., R21 = 0.64 ± 0.08 and R32 = 0.23 ± 0.04; and with the R32 value found by Wilson et al. (2009) within the inner 22″, i.e., 0.34 ± 0.11 (note however that the latter is not a fully independent check as we used the same CO(3–2) single dish data to complement our SMA data).
The R21 and R32 maps are different. While R21 is smooth, more or less symmetric with respect to the center, and continuously increasing toward the center with a maximum at ~1″ to the west of the galactic center, R32 is more clumpy, exhibiting several peaks, and is more asymmetric.The large-scale gradient in R32 reported by Wilson et al. (2009) does not appear in the inner 10″.
R32 is expected to probe more extreme conditions such as those occuring in star forming or shock regions. This is confirmed by the comparison to the Paα emission (Fig. 10). Although the detailed structure of R32 is not reflected in Paα, most of the pixels where R32 > 0.2 coincide with Paα emission detected in the NICMOS image. R21, instead, reaches high values outside (to the north) as well as inside the Paα emission region, although it peaks at the galactic center as the Paα. The fact that R32 tracks massive star formation in NGC 4569 better than R21 is consistent with the conclusion of Wilson et al. (2009), based on maps over larger areas, that CO(3–2) is a robust tracer of star formation.
The fact that R32 correlates with the individual CO line intensities (the three peaks in CO are also peaks in R32) also suggests that it is more sensitive to density. In contrast, the fact that R21 does not show the same structures as the individual line maps and that it increases steadily towards the center suggests that it is more sensitive to temperature. This is expected for thermalized gas with moderate opacity in the CO(3–2) line.
The left panel of Fig. 11 shows the distribution of the ratios in the R32 vs. R21 space; in the following this will be referred to as the R32-vs.-R21 diagram.This diagram was obtained by mapping each pixel (0.2″ × 0.2″ in size) of the ratio maps to the grid and convolving with a Gaussian kernel of 0.02 FWHM, corresponding to a typical uncertainty in the line ratio. Based on the line ratio error maps shown in Fig. 9 it should be kept in mind that any feature in this diagram with a size lower than ~0.05 cannot be considered as real.In addition, although the ratio maps are considered as continuous distributions (we used small pixels with respect to the beam), it should be kept in mind that the resolution is finite in the ratio maps. This diagram is used to show in a synoptic way which regions of the ratio-ratio space are populated.As expected from the differences between the R32 and R21 maps noted above, the distribution is dispersed in the diagram. The ratios populate a region going from (0.4, 0.15) to (0.8, 0.25) with an average thickness of ~0.15 in an orthogonal direction.
4.2. NGC 4826
The ratio maps with the corresponding error (standard deviation) maps are shown in Fig. 12.R21 is distributed in the range 0.2 to 0.95 with a weighted mean of 0.67. R32 is distributed in the range 0.05 to 0.60 with a weighted mean of 0.38. The errors on the ratios and the weighted means are similar to those in the case of NGC 4569. The mean values are lower than the ratios found by Israel (2009) based on single dish observations in the inner 21″, i.e., R21 = 0.98 ± 0.17 and R32 = 0.59 ± 0.09 and the inner 12″, i.e., R21 = 1.06 ± 0.22 and R32 = 0.79 ± 0.18. They are, however, within (or close to) the 2σ interval of the single dish measurements.R32 does not appear to be more clumpy than R21, in contrast to NGC 4569, and both maps look relatively symmetric with respect to the dynamical center, with both ratios increasing steadily toward the center. There are however differences. While the R21 spatial distribution appears to be close to circularly symmetric, the R32 distribution is more elongated along the galactic major axis. Furthermore, R21 seems to be more prominent to the north of the dynamical center (although its peak coincides with the dynamical center), whereas R32 forms a ridge along the major axis south of the dynamical center with its peak ~1″ to the southwest.
As in NGC 4569, high R32 values (>0.3) occur within the Paα emission region as detected by NICMOS, while this is not necessarily true for R21 (see Fig. 13 right panel). Indeed, although R21 increases toward the center as R32, it reaches high values (>0.7) north and south of the Paα emission region, which is elongated along the galactic major axis. R21 shows some correlations with the 2 cm radio continuum (see Fig. 13 left panel). In particular, the 2 cm peaks 1″ and 4″ north of the dynamical center coincide with high R21 values. At the VLA’s resolution, the 2 cm continuum is dominated by emission from HII regions and SNRs around which the molecular phase is expected to be strongly heated. If R21 is more sensitive to temperature relative to R32, this may explain the better correlation of R21 with the 2 cm continuum than R32. We emphasize, however, that this trend is weak relative to the radial increase toward the center of R21, R32 and Paα emission(as for R21/R32, previously noted by Israel 2009). In fact both line ratios are sensitive to temperature and density and their interpretation in terms of physical conditions requires radiative transfer modeling; this is the topic of the next section.
The middle panel of Fig. 11 shows the R32-vs.-R21 diagram for NGC 4826. The emission is much more widely spread in the R32-vs.-R21 diagram than for NGC 4569. The top part of the diagram with R32 > 0.3 being more populated, in particular the top right part with R21 > 0.6 and R32 > 0.3.
5. Modeling the physical conditions of the molecular gas
 |
Fig. 14 Variations of the CO line opacities with respect to temperature and density based on LVG modeling. From left to right panel: CO(1–0), (2–1) and (3–2) opacities. Used for the qualitative interpretation of the pseudo-LTE model. |
5.1. Pseudo-LTE model
The line intensity of a single component medium in local thermal equilibrium (LTE) is entirely determined by the temperature of the medium, T, and by the ratio of the column density to the local line width, NCO/dV when the line is not optically thick. In reality, the ISM is multi-component and the intensity of each line results from the sum over the beam of all the individual components’ line intensities. LTE may still be a reasonable approximation for the local emission of individual components or clumps, but the average opacity in a line toward the observer also depends on more global properties of the ISM (e.g. turbulence and complex structures). A way to improve the model is to decouple the average opacity from the average local physical conditions and consider a mixture of components. For the sake of simplicity we assume that CO(1–0) and CO(2–1) emissions are optically thick, and we consider optically thick (τ ≫ 1) and optically thin (τ ≪ 1) components for the CO(3–2) emission. This choice is justified by the variations of the line opacities with the physical conditions as shown in Fig. 14 and based on large velocity gradient model (LVG model described in Sect. 5.2). For gas with a temperature close to or below ~20 K and a density above ~103 cm-3, the CO(1–0) and (2–1) emission is mainly optically thick whereas the CO(3–2) emission optical depth can vary from thick to thin. We denote f32 the fraction of optically thin emission for CO(3–2). Treating f32 as an independent parameter allows us to avoid complex modeling of the ISM, but it should be kept in mind that this parameter is also related to the physics of the ISM. In other words, the interpretation of such a model requires further physical modeling (at least qualitative) of the opacities. We assume the line intensities are given by the LTE equations(the optically thick component is independent of NCO/dV). We refer to this modified LTE model as a pseudo-LTE model.Although this model relies on simple assumptions, we think it can be used to interpret the overall distribution of the gas in the R32-vs.-R21 diagram in terms of variations of its physical properties. In practice, we reproduce the overall distribution in the R32-vs.-R21 plot with families of pseudo-LTE models corresponding to different combinations of physical parameters. In other words, this model is not used to fit each (R21, R32) pair independently (this would not be possible given the number of unknowns); it is used to relate the different parts of the R32-vs.-R21 diagram to the physical conditions and reproduce the overall ratio distribution.
5.1.1. NGC 4569
As shown in the right panel of Fig. 11, a single-component LTE model (curves 1 and 2) cannot reproduce the line ratios observed in NGC 4569 (cyan contour). Even with high column densities per unit velocity (curve 1 corresponds to NCO/dV = 1015 cm-2 (km s-1)-1 and curve 2 to NCO/dV = 12 × 1015 cm-2 (km s-1)-1) at the low-temperature (lower left) end R32 is always lower than observed.
 |
Fig. 15 Grids of LVG models for a range of molecular hydrogen densities and kinetic temperatures. Each grid corresponds to a different value of XCO/(dV/dR), from left to right: 10-6, 10-7 and 10-8 pc (km s-1)-1. The CO(1–0) radiative temperature is represented in color scale and is overlaid with R21 black contours (0.3 to 1.3 in steps of 0.2) and R32 blue contours (0.1 to 0.6 in steps of 0.1). The line ratios increase from bottom left to top right. |
5.1.2. NGC 4826
As shown in the right panel of Fig. 11, The highest ratios observed in NGC 4826 (magenta contour) follow more or less the pseudo-LTE model represented by the curve 4 in the R32-vs.-R21 diagram. As noted in Sect. 4.2 the line ratios increase toward the galactic center (Fig. 12), although their maxima do not exactly coincide with it. Hence according to this simple model the temperature should increase toward the center and a significant fraction (~20%) of the CO(3–2) emission should be optically thin.
5.2. LVG model
5.2.1. The procedure
To interpret the observations of the three CO lines in terms of molecular gas physical conditions we have modeled the line ratios based on the large velocity gradient (LVG) assumption (Scoville & Solomon 1973; Goldreich & Kwan 1974) using the LVG code in the MIRIAD package. As opposed to the LTE assumption, the LVG assumption allows us to deal with transitions that are not necessarily thermalized. On the other hand, with the observations available we can only consider a single component. Although the single component assumption is at odds with the known complexity of the real ISM (even at the 40 pc linear resolution reached in NGC 4826), it was successfully used in many extragalactic studies to assess the physical properties of the molecular gas. For a single component the free parameters are the molecular hydrogen number density, n(H2), the kinetic temperature, Tk, and the ratio of the CO molecule fractional abundance with the velocity gradient, XCO/(dV/dR). With only two observables (the line ratios) one of the three parameters needs to be fixed.
We have implemented a maximum likelihood fitting procedure to fit two parameters assuming normal probability distributions for the line ratios. The normalized likelihood of the best fit is used as a goodness-of-fit metric, denoted ℳ. It is equal to 1 when the observed line ratios are exactly reproduced by the best fit model and it tends to 0 with increasing discrepancy.
The value of XCO/(dV/dR) was constrained as follows. We have generated three grids of models for XCO/(dV/dR) = 10-6, 10-7 and 10-8 pc (km s-1)-1. Each grid is 50 × 50 in size corresponding to 50 values of Tk in the range 5 to 200 K and 50 values of n(H2) in the range 102 to 105 cm-3. The intervals in Tk and n(H2) are logarithmic. The grids are displayed in Fig. 15. To estimate the most appropriate value of XCO/(dV/dR) we computed ℳ for each point of a R32-vs.-R21 grid assuming an uncertainty of 0.02 for R21 and 0.04 for R32. The distribution of ℳ over the R32-vs.-R21 grid thus obtained was then compared to the R32-vs.-R21 diagram of the galaxies. The three ℳ grids are plotted in Fig. 16. For both galaxies the XCO/(dV/dR) value maximizing the goodness-of-fit over the map is 10-7 pc (km s-1)-1 similar to that found by Iono et al. (2007) for NGC 6240 following a similar method; we therefore adopted this value for all the models.
As can be seen in Fig. 15, the two line ratios follow a similar distribution over the density-temperature grid, i.e., the isocontours of both line ratios are close to parallel over most of the grid. Hence, in many cases, when the uncertainties are taken into account the solution is degenerate. The confidence intervals typically have arc-shapes similar to the isocontours (see Figs. 17 and 19). However, a confidence interval does not cover the complete range of densities and temperatures, and the average values over this interval can be used to characterize qualitatively the trend of the model, i.e., whether it tends to favour high or low densities and temperatures. Thus, instead of considering the best fit solutions, we consider the average values of the temperature and density over all possible solutions, i.e., the average values over the 90% confidence interval. As the 90% confidence interval can be unbounded toward high temperatures and/or high densities we fix the maximum possible temperature to 70 K and the maximum possible density to 105 cm-3. Fixing these upper limits affects the averages but not their qualitative variations with the ratio values.
5.2.2. NGC 4569
The LVG fits to the eight individual positions marked on the map of Fig. 2 are displayed in Fig. 17. This figure shows that good LVG solutions exist for all positions but that the uncertainties are large (see the confidence intervals in the insets). This figure also shows how using the average values instead of the best fit gives more stable results. For example, the ratio values at the northern and southern peaks (B and G) are similar and should therefore give similar results. The best fit solutions are very different, the average values are more stable and therefore better adapted to a qualitative description.
Density and temperature maps obtained by applying the fitting procedure to all pixels are presented in Fig. 18. The pressure, obtained by averaging the product, T × n over the confidence interval, is displayed at the bottom left and the goodness-of-fit map is shown at the bottom right. Gas with density above 5.5 × 103 cm-3 (the lowest white contour) and temperature below 15 K is distributed around the center in an elongated ring extending from the CO(1–0) northern peak (position B) to the CO(1–0) southern peak (position G). This is consistent with the kinematic model presented in NUGA-VII where the molecular gas was distributed in an elongated ring extending from the northern peak to the southern peak and identified as the ILR. Within this ring there are two clumps of high density cold gas, one at the southern CO(1–0) peak (position G) and the other 3″ to the west of the nucleus (position F).
In the central region delineated by the ring there is also a density peak ~1.5″ north of the center (near position D) where the temperature is higher than in the ring. On average, in the central region the density is higher than outside the ring. The temperature is higher in the central region than in the ring itself but is not higher than in the region outside the ring. This reversal is not expected, as the central starburst should heat the gas, and this may reflect the limit of the method used here, i.e., averaging the physical parameters over the confidence interval can only give a trend not the absolute values. The warmest regions are to the east of the northern peak and to the south-west of the southern peak. They may correspond to diffuse hot gas near the points where the orbit crowding causes shocks (see orbits in NUGA-VII). We note however that south of the southern peak the goodness-of-fit is lower (ℳ < 0.4). There are three pressure peaks coinciding with the three density peaks.
5.2.3. NGC 4826
The LVG fits to the eight positions marked in the map of Fig. 6 are displayed in Fig. 19. This figure shows that good LVG solutions exist for all positions except the easternmost and westernmost ones (positions A and E) where R32 is too high with respect to R21.
Density and temperature maps obtained by applying the fitting procedure to all pixels are presented in Fig. 20. The pressure is displayed at the bottom left, and the goodness-of-fit map is shown at the bottom right. The densest (with density >104 cm-3) and coldest (T ~ 5 K) gas is distributed in a semicircle ~60–80 pc in radius whose center coincides with the dynamical center. Inside the region delineated by the arc the temperature increases from the arc to the north of the dynamical center.
However, as can be seen from the goodness-of-fit map in the lower right panel of Fig. 20 and as was already noted from the fit to the individual positions A and E (Fig. 19), the LVG solutions outside the arc along the major axis, i.e., the solutions giving the most diffuse and warm conditions, do not fit the observed ratios well.
6. Discussion
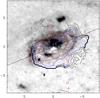 |
Fig. 21 Pressure contours of NGC 4826 (same contours as in Fig. 20lower left panel) overlaid on the Paα map. The ellipse corresponds to a ring of 90 pc radius inclined by 60 deg. The straight line indicates the major axis of the galaxy. |
6.1. Comparison of the two galaxies
NGC 4569 and NGC 4826 both harbor transition type nuclei. It is therefore interesting to compare the ISM close to the nucleus and look for similarities. At first sight, the molecular gas distributions and properties appear to be very different in the two galaxies. In NGC 4569, the gas is concentrated in an ILR ring and a clump close to the center, and the CO is not very excited. In NGC 4826, the gas is concentrated in a CND and the gas is more excited. In addition, the strong correlation between the two line ratios near the center in NGC 4826 is not seen in NGC 4569.
However, the low excitation gas in NGC 4826 (with R32 < 0.3) follows a ratio distribution similar to that of NGC 4569 (see the R32-vs.-R21 diagrams Fig. 11), and the difference in linear resolution must be taken into account. It is 4 times higher for NGC 4826 (40 pc) than for NGC 4569 (160 pc). If NGC 4826 were observed with the same linear resolution as NGC 4569 the CND would not be resolved and the ratio distribution in the upper right of the R32-vs.-R21 diagram would be averaged into a small clump in the diagram. Conversely, observing NGC 4569 with the same linear resolution as NGC 4826 could well reveal more excited gas.
Taking into account this observational bias, the most robust similarity between the two galaxies is the relatively low excitation of the CO compared to other galaxy centers. At the hundred parsec scale, R21 and R32 can be >0.8 (Eckart et al. 1990, 1991; Braine & Combes 1992; Wild et al. 1992) and >1 (Dumke et al. 2001), respectively, in galaxy centers with enhanced star formation, and the ratios lie typically in the range 0.7–1.1 and 0.5–1 around luminous AGNs (Papadopoulos & Seaquist 1999; Papadopoulos et al. 2008; Israel 2009). At the same scale R21 even reaches a value of ~2 in the prototypical Seyfert galaxy NGC 1068 (Schinnerer et al. 2000b) as well as in the Seyfert 1 galaxy NGC 1097 (Hsieh et al. 2008). R32 also reaches a value of 2 at the hundred parsec scale in the nucleus of M 51 (Matsushita et al. 2004). Finally, R32 is also lower than in the inner 200 pc of the Milky Way (a.k.a. the circumnuclear zone, CNZ), where R32 has an average value of ~0.8 (see Fig. 3 of Oka et al. 2007). Thus, at the scale of previous single dish studies and at the scale of the CNZ, the molecular gas in the centers of NGC 4569 and NGC 4826 appears to be in a rather low excitation state. R21 and R32 are also lower than the model predictions of Wada & Tomisaka (2005) for AGN tori.
6.2. Can opacity effects explain the asymmetries in NGC 4826?
The LVG modeling indicates the presence of a semicircular arc of dense gas close to the nucleus of NGC 4826. Its center of curvature agrees with the dynamical center and it lies at the south-west of the nucleus. In fact, this dense arc seems to reflect asymmetries in the CO and R32 maps (Figs. 6 and 12). Indeed, close to the nucleus the emission of the three CO lines is slightly more prominent south of the nucleus and, as was noted in Sect. 4.2, the R32 distribution is clearly more prominent to the south.
Interestingly, as can be seen in Fig. 21, the dense arc seems to coincide with regions of the CND where the Paα emission is weaker. Another interesting point is that the galaxy major axis seems to be a privileged axis for this anticorrelation, i.e., the Paα emission is more prominent on the near side (to the north east) of the galactic disk, whereas the semicircular dense arc is on the far side; the minor axis seems to be a symmetry axis for both the Paα emission and the dense gas distribution. As noted in NUGA-I, the dust lane extinction is usually stronger on the near side (an effect that turns out to be spectacular in this galaxy outside the CND), and the Paα near side/far side asymmetry is opposite to the one expected for star formation in a density wave. A possible explanation for this Paα asymmetry is that extinction is not confined to dust lanes in a density wave but rather comes from extraplanar dust around the nucleus (see e.g. Mason et al. 2006; Rhee & Larkin 2006; Quillen et al. 2008). In addition, part of the Paα emission close to the nucleus may come from material above or at the surface of molecular clouds that has been ionized by the nuclear activity rather than by young stars distributed in a spiral.
The near side/far side asymmetries and the Paα/dense gas anticorrelation suggest that the CO emission as well could be affected by opacity (for a similar conclusion based on intensity ratios averaged over a larger beam, see also Israel 2009). Opacity effects are generally not considered for extragalactic CO observations. Although the low-J CO lines are mainly optically thick, the clumpiness of the ISM and the very low probability to have two clumps on the same line of sight with the same line of sight velocity imply that molecular clouds do not shadow each other, and therefore that CO lines are good column density probes (see e.g. Dickman et al. 1986). CO morphologies observed in galaxies are thus assumed to reflect the actual gas distribution. We see however two possible reasons for opacity to play a role in the CO morphologies observed close to galactic centers. First, the column density is larger and the probability of having several clumps on the same line of sight with the same line of sight velocity may not be negligible anymore. Second, the activity of the nucleus is expected to affect the surrounding ISM and as a result the individual clumps may have strongly inhomogeneous properties fully determined by their distance and orientation relative to the nucleus; the clumps on the far side of the galaxy could thus show very different properties from those of the near side. Both effects, which we refer to as the large scale opacity effect and the clump scale opacity effect, respectively, are sketched in Fig. 22. We investigate them in more detail in the following.
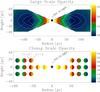 |
Fig. 22 Sketches illustrating the two opacity effects considered in Sect. 6.2. In both panels the color scale is related to the temperature in K as shown in the colorbars and the star symbol represents the AGN. The observer is assumed to be looking from the top right, so that the right-hand side of the panels corresponds to the near side and the left-hand side to the far side of the galaxy. The top panel illustrates how the densest and coldest gas distributed in a ring at 70 pc from the center could partly obscure emission from the dense torus on the near side and from the galactic disk on the far side. The white contours correspond to density levels. The dashed white lines delineate the regions that would be obscured by the densest gas. The lower panel illustrates how clumps heated by the nucleus could have inhomogeneous properties with the side exposed to the nucleus being warmer, less dense and less opaque to CO emission than the other side. |
6.2.1. Large scale opacity effect
The molecular gas disks in active nuclei are thought to flare out to radii of order 10 pc, forming the putative obscuring torus required by the unified AGN model (see e.g. Elitzur 2008, and references therein). How this structure connects to the outer disk and whether it is embedded in a larger toroidal structure is still uncertain. The hydrodynamical simulations by Wada & Tomisaka (2005) suggest that such a large molecular structure could extend out to several tens of parsecs and this seems to be confirmed by observations of the near-IR molecular hydrogen lines in nearby AGNs by Hicks et al. (2009).
If the densest and coldest gas is distributed in a ring inside such a large toroidal structure and is able to partly absorb CO emission along the line of sight, then the disk beyond the ring would be partly absorbed on the far side and the warmer inner regions of the torus would be partly absorbed on the near side (see sketch in the top panel of Fig. 22). In other words, the line of sight toward the torus on the near side would be more contaminated by emission from the disk and would not be seeing all the emission from the inner regions of the torus. The torus would be more clearly visible on the far side.
In order to check whether this effect could be compatible with the observations we consider a toy model of a flared disk (see details in Appendix A.1). The resulting integrated CO maps and line ratio maps are presented in Fig. 23. Although this simple model cannot reproduce exactly the integrated maps shown in Fig. 6, it can partly reproduce the morphology inside the CND. In particular, the emission does not peak at the nucleus but to the east and west of the nucleus, and there is more emission to the south (the far side) than to the north of the nucleus. Also, the general morphology does not change significantly in the three CO lines. The main differences between the R21 and R32 maps noted in Sect. 4.2 are also reproduced by the model. The R32 distribution is more extended along the major axis and is more prominent to the south of the nucleus (on the far side) than the R21 distribution.
6.2.2. Clump scale opacity effect
Alternatively, the asymmetry could result from the inhomogeneity of the clumps forming the toroidal structure. The side of the clumps exposed to the nucleus would be warmer and more diffuse than the other side. The dense side would be more opaque and it would hide the warmer side to the observer depending on the angle between the line of sight and the line subtended by the clump and the nucleus (see sketch in the lower panel of Fig. 22). A similar “external heating” scenario was already discussed by Baker & Scoville (1998) and Baker (2000) and by Meier & Turner (2001) to interpret asymmetries of molecular line emission in NGC 1068 and IC 342, respectively. A similar argument was also invoked and formalized by Nenkova et al. (2008b,a) to interpret the infrared observations of AGNs. To test whether such an effect could be consistent with the observations we have distributed clumps in the same toroidal structure as the one used in the model of the previous subsection. The resulting CO maps as well as the ratio maps are presented in Fig. 24. They show that this simple model can also reproduce the slight CO emission excess on the far side and the differences between the two ratio maps noted in Sect. 4.2.
6.2.3. A common property of active galaxies?
We note that in NGC 4569 as well, the CO emission and the R32 distributions close to the nucleus are more prominent on the far side (east side). In fact, although this remained unnoticed for most of them, several nearby active galaxies show a slight near side/far side asymmetry close to their nuclei with CO emission excess on the far side as well; this is for example the case for Centaurus A (Espada et al. 2009), NGC 4945 (Chou et al. 2007), NGC 3227 (Schinnerer et al. 2000a), and NGC 1068 (Schinnerer et al. 2000b). A detailed statistical study of CO asymmetries in nearby AGNs is beyond the scope of this paper, but these few cases suggest that near side/far side asymmetries could be common in AGNs.
While both torus models described above can reproduce the asymmetry observed, the first model requires a high inclination, a very specific geometry, and a high volume filling factor of the dense gas. The second model is more robust to various inclinations (although it also decreases with decreasing inclination) and configurations; it would therefore provide the best explanation for a putative generalized near side/far side asymmetry in AGNs. An alternative opacity effect was proposed by Galliano et al. (2003) to explain the asymmetry in NGC 1068. They invoked CO line absorption by a thick disk, and in their model the asymmetry resulted from a tilt between the molecular disk and the Compton thick absorber. This model however does not explain why the asymmetry should coincide with a far side/near side asymmetry.
7. Conclusion
We have observed the emission from the first three 12CO J-lines in the nuclei of two nearby galaxies, NGC 4569 and NGC 4826, with the Plateau de Bure interferometer and the SubMillimeter Array. Combining these data allows us to compare the emission in the three lines and to map the line ratios R21 and R32 at a resolution of ~2″, i.e., a linear resolution of 160 pc for NGC 4569 and 40 pc for NGC 4826. We interpret the line ratios through radiative transfer modeling and map the physical conditions of the molecular gas. The main results of this study can be summarized as follows:
-
In both galaxies the three lines are similarly distributed over thedata cubes, i.e., both spatially and in velocity.
-
In both galaxies the line ratios seem to be lower than in other galaxy centers.
-
In both galaxies the gas with R32 greater than 0.2 is confined to Paα emitting regions detected by NICMOS. R21 instead reaches high values away from the Paα emitting regions detected by NICMOS.
-
According to a pseudo-LTE model, the molecular gas in NGC 4569 is cold, mainly optically thick in the CO(1–0) and (2–1) lines and with a fraction less than 50% optically thin in the CO(3–2) line. LVG modeling suggests the presence of an elongated ring of cold and dense gas coinciding with the ILR. There are two denser and colder clumps along this ring and one denser and warmer clump close (~160 pc) to the nucleus.
-
More excited gas is resolved in the circumnuclear disk (CND) of NGC 4826. According to the pseudo-LTE model this corresponds to warmer gas with a ~20% of the CO(3–2) emission being optically thin. The LVG modeling indicates the presence of a semicircular arc of dense and cold gas centered on the dynamical center and ~70 pc in radius. The gas temperature increases and the density decreases toward the center.
-
NGC 4826 shows a near side/far side asymmetry in the CO, Paα and R32 distributions. This asymmetry suggests that the gas opacity could play a role in the CO morphology. It can be reproduced if the cold dense gas is distributed in a ring of 70 pc radius embedded in a flared toroidal structure and can partly absorb the CO emission, or if the clumps forming the toroidal structure are inhomogeneously heated by the nuclear activity and are partly optically thick.
-
Several published CO maps of nearby active galaxies seem to show a slight CO emission excess on the far side of the nuclear region similar to the one observed in NGC 4826 suggesting that this could be a common property of active galaxies. If confirmed, this would favor the interpretation based on the model with inhomogeneous clumps heated by the nuclear activity.
This study demonstrates the feasibility of mapping the molecular gas physical properties in the centers of nearby galaxies based on multitransition CO observations with current interferometers. It also shows how important these observations are for correctly interpreting the CO emission and thus understanding the processes at work in nuclear regions. While the results derived in this study are still mainly qualitative and limited by uncertainties and resolution, they suggest new areas of investigation. Analyzing multitransition interferometric CO observations for more nearby galaxies with various inclinations should provide a statistical basis for investigating the unified AGN paradigm. More importantly, with ALMA, such observations will be greatly improved in terms of sensitivity (about one order of magnitude), resolution (one order of magnitude) and imaging quality (more complete uv coverage). Furthermore, it will be possible to observe more CO transitions with a single array and thus, to better constrain the models and to derive more quantitative results on the ISM properties close to galaxy centers. For example it will be possible to keep the CO abundance as a free parameter and thus resolve the possible AGN influence on this parameter. It will also be possible to resolve the clumpy structure of the CNDs and investigate in more detail the role of pressure in these structures.
Online material
 |
Fig. 1 CO(3–2) channel maps of the galaxy NGC 4569. The velocity relative to the systemic velocity of the galaxy (vhel = −235 km s-1) is given at the top left of each map. The phase center indicated by the large cross is at the AGN position αJ2000 = 12h36m49.8s, δJ2000 = 13°09′46.3″. The beam (represented at the bottom left of each map) is 2.6″ × 2.1″ and the rms is 115 mJy beam-1. The only contour line overlaid corresponds to the 4σ level. The maps are not corrected for the primary beam attenuation. |
 |
Fig. 5 CO(3–2) channel maps of the galaxy NGC 4826. The velocity relative to the systemic velocity of the galaxy (vhel = 402 km s-1) is given at the top left of each map. The phase center indicated by the large cross is at αJ2000 = 12h56m43.76s, δJ2000 = 21°40′51.9″. The galactic nucleus is marked by the small cross. The beam (represented at the bottom left of each map) is 2.6″ × 1.9″ and the rms is 75 mJy beam-1. The only contour line overlaid corresponds to the 4σ level. |
 |
Fig. 16 Likelihood of all possible (R21, R32) pairs on a R32-vs.-R21 grid for different values of XCO/(dV/dR). The contours of the R32-vs.-R21 diagrams of NGC 4569 (blue) and NGC 4826 (magenta) are overlaid. The contours are smoothed and their levels correspond to 3 and 9 pixels per grid bin. (see Fig. 11). |
 |
Fig. 17 LVG best fits to the line ratios measured in the central region of NGC 4569 at the eight positions marked in Fig. 2. The measured line ratios are represented with the 1-σ error bars and the best fit model ratios are linked with a straight line. The inset in each plot shows the 90% confidence interval (light grey shaded area) and the 50% confidence interval (dark grey) in the density-temperature plane assuming a normal probability distribution for each ratio; the best fit solution is marked with a cross. The best fit temperature and density as well as the averages over the 90% confidence interval are given at the top right of each plot. The normalized likelihood of the best fit, P/Pmax is also given (1 means the measured values are exactly reproduced by the model). |
 |
Fig. 18 LVG result maps for NGC 4569. Upper left: H2 number density averaged over the 90% confidence interval of each LVG model. The black contours are at 5 × 102, 103, 3 × 103 cm-3 and the white contours at 5.5 × 103, 104, and 5 × 104 cm-3. Upper right: kinetic temperature averaged over the 90% confidence interval of each model. The black contours are at 5, 10, 15, 20, 25 K and the white contours at 30, 35, 40 K. Lower left: pressure averaged over the 90% confidence interval of each model. The black contours are at 104.1, 104.4, and 104.7 K cm-3 and the white contours at 105, 105.3 and 105.6 K cm-3. Lower right: the normalized likelihood (or merit), P/Pmax, of the best fit with black contours at 0.35 and 0.55 and white contours at 0.75 and 0.95. |
 |
Fig. 19 LVG best fits to the line ratios measured in the central region of NGC 4826 at the eight positions marked in Fig. 6. See caption of Fig. 17 for more details. |
 |
Fig. 20 LVG result maps for NGC 4826. Upper left: H2 number density averaged over the 90% confidence interval of each LVG model. The black contours are at 103 and 5 × 103 cm-3 and the white contours at 104 and 5 × 104 cm-3. Upper right: kinetic temperature averaged over the 90% confidence interval of each model. The black contours are at 5, 10, 20 K and the white contours at 40 and 60 K. Lower left: pressure averaged over the 90% confidence interval of each model. The black contours are at 104.7, 104.9, 105.1 and 105.3 K cm-3 and the white contours at 105.5 and 105.7 K cm-3. Lower right: goodness-of-fit with the same contours as in Fig. 18. |
 |
Fig. 23 The upper panels show the CO integrated maps produced by the flared disk toy model described in Appendix A.1. The CO(3–2) emission is shown in greyscale, and the CO(1–0) (left panel) and CO(2–1) emission (right panel) are contours. The lower left and right panels show the resulting R21 and R32 maps, respectively. |
 |
Fig. 24 The upper panels show the CO integrated maps produced by the clumpy flared disk toy model described in Appendix A.2. The CO(3–2) emission is shown in greyscale, and the CO(1–0) (left panel) and CO(2–1) emission (right panel) are contours. The lower left and right panels show the resulting R21 and R32 maps, respectively. |
Appendix A: Large torus models
 |
Fig. A.1 Radial profiles of the molecular gas density (blue) and temperature (red) used in the models. |
A.1. Model with large scale opacity
In this model the clumps are assumed to be homegeneous and the only parameter related to the clumpiness of the medium is the volume filling factor. The sizes and shapes of the individual clumps are not taken into account. The density and temperature radial profiles used are represented in Fig. A.1. The density increases exponentially with radius from nmin = 102.5 cm-3 at 10 pc to nmax = 104.9 cm-3 at 70 pc and it decreases exponentially with height above the galactic plane. Inside 70 pc the temperature is related to the density by T ∝ nα with Tmax = 50 K
at 10 pc and Tmin = 10 K at 70 pc, i.e., α = −0.3. Outside 70 pc the density decreases exponentially with radius down to nout = 102 cm-3 and the temperature is kept constant at 12 K. Overall the density and temperature profiles define a cold dense ring at 70 pc. The gas volume filling factor is proportional to the gas density (where the gas is denser, it fills more of a given volume). We assume that gas with a density higher than 0.6 × nmax has a volume filling factor of 20% and can absorb the CO line emission from gas further away on the line of sight having the same line of sight velocity. We assume circular rotation and a Gaussian line profile with a velocity dispersion of 15 km s-1 outside 70 pc and 30 km s-1 inside. The CO line intensities are computed with the LVG model. The resulting integrated CO maps and line ratio maps are presented in Fig. 23.
A.2. Model with clump scale opacity
In this model the individual clumps are assumed to be spherical and inhomogeneous and they cannot obscure each other. In each clump the hemisphere exposed to the nucleus is assumed to be warmer and less dense than the other hemisphere. In addition, the warm hemisphere is assumed to be optically thin in the CO(3–2) line, while the other hemisphere is assumed to be optically thick. CO(1–0) and (2–1) lines are assumed to be optically thick everywhere. The density and temperature profiles of the warm hemisphere of the clumps as a function of the distance to the nucleus and the height above the plane are the same as in the previous model. The temperature profile of the cold hemisphere follows the same exponential profile with the same lower value but the maximum value is fixed to 30 K instead of 50 K. Thus, the difference in temperature between the warm and cold hemispheres increases with the temperature and reaches 20 K at the maximum. The density of the gas in the clumps is related to the temperature as in the previous model and the number density of clumps is assumed proportional to this gas density. The line intensities are computed assuming LTE. The resulting CO maps as well as the ratio maps are presented in Fig. 24.
Acknowledgments
We are much indebted to Christine Wilson and Frank Israel for very kindly providing us with their single dish CO(3–2) data. F.B. thanks the Max-Planck-Institut für Radioastronomie in Bonn, where he was a postdoc at the time of the observations, for supporting the travel to the SMA. We thank the scientific and technical staffs at the SMA for their help at the observatory. The collaboration between LERMA and ASIAA was supported by the ORCHID French-Taiwanese Hubert Curien Program.
References
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Baker, A. J., & Scoville, N. Z. 1998, in The Central Regions of the Galaxy and Galaxies, ed. Y. Sofue, IAU Symp., 184, 221 [NASA ADS] [Google Scholar]
- Baker, A. J. 2000, Ph.D. Thesis [Google Scholar]
- Bayet, E., Gerin, M., Phillips, T. G., & Contursi, A. 2006, A&A, 460, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boone, F., Baker, A. J., Schinnerer, E., et al. 2007, A&A, 471, 113 (NUGA-VII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braine, J., & Combes, F. 1992, A&A, 264, 433 [NASA ADS] [Google Scholar]
- Chou, R. C. Y., Peck, A. B., Lim, J., et al. 2007, ApJ, 670, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T., Soida, M., Bomans, D. J., et al. 2006, A&A, 447, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curran, S. J., Johansson, L. E. B., Bergman, P., Heikkilä, A., & Aalto, S. 2001, A&A, 367, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickman, R. L., Snell, R. L., & Schloerb, F. P. 1986, ApJ, 309, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Dumke, M., Nieten, C., Thuma, G., Wielebinski, R., & Walsh, W. 2001, A&A, 373, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckart, A., Downes, D., Genzel, R., et al. 1990, ApJ, 348, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Eckart, A., Cameron, M., Jackson, J. M., et al. 1991, ApJ, 372, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2008, New Astron. Rev., 52, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Espada, D., Matsushita, S., Peck, A., et al. 2009, ApJ, 695, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, E., Alloin, D., Granato, G. L., & Villar-Martín, M. 2003, A&A, 412, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Hunt, L. K., et al. 2003, A&A, 407, 485 (NUGA-I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 (NUGA-IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Guhathakurta, P., van Gorkom, J. H., Kotanyi, C. G., & Balkowski, C. 1988, AJ, 96, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Hafok, H., & Stutzki, J. 2003, A&A, 398, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helfer, T. T., Thornley, M. D., Regan, M. W., et al. 2003, ApJS, 145, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Hensler, G., Bomans, D., & Boselli, A. 2003, The Cosmic Cauldron, 25th meeting of the IAU, Joint Discussion 10, 18 July 2003, Sydney, Australia, 10 [Google Scholar]
- Hicks, E. K. S., Davies, R. I., Malkan, M. A., et al. 2009, ApJ, 696, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997, ApJS, 112, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., Moran, J. M., & Lo, K. Y. 2004, ApJ, 616, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, P.-Y., Matsushita, S., Lim, J., Kohno, K., & Sawada-Satoh, S. 2008, ApJ, 683, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Iono, D., Wilson, C. D., Takakuwa, S., et al. 2007, ApJ, 659, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, F. P. 2009, A&A, 493, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kohno, K., Tosaki, T., Miura, R., et al. 2008, PASJ, 60, 457 [NASA ADS] [Google Scholar]
- Laurikainen, E., & Salo, H. 2002, MNRAS, 337, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Koratkar, A., Shields, J. C., et al. 1998, AJ, 116, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, R. E., Geballe, T. R., Packham, C., et al. 2006, ApJ, 640, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Matsushita, S., Sakamoto, K., Kuo, C.-Y., et al. 2004, ApJ, 616, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Matsushita, S., Iono, D., Petitpas, G. R., et al. 2009, ApJ, 693, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, D. S., & Turner, J. L. 2001, ApJ, 551, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meijerink, R., Spaans, M., & Israel, F. P. 2007, A&A, 461, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muraoka, K., Kohno, K., Tosaki, T., et al. 2007, PASJ, 59, 43 [NASA ADS] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Ivezić, Ž., & Elitzur, M. 2008a, ApJ, 685, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., Ivezić, Ž., & Elitzur, M. 2008b, ApJ, 685, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Nagai, M., Kamegai, K., Tanaka, K., & Kuboi, N. 2007, PASJ, 59, 15 [NASA ADS] [Google Scholar]
- Papadopoulos, P. P., & Seaquist, E. R. 1999, ApJ, 516, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., & Allen, M. L. 2000, ApJ, 537, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Kovacs, A., Evans, A. S., & Barthel, P. 2008, A&A, 491, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qi, C. 2005, MIR Cookbook, http://www.cfa.harvard.edu/~cqi/mircook.html [Google Scholar]
- Quillen, A. C., Bland-Hawthorn, J., Green, J. D., et al. 2008, MNRAS, 384, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Rhee, J. H., & Larkin, J. E. 2006, ApJ, 640, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V. C. 1994, AJ, 107, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Okumura, S. K., Ishizuki, S., & Scoville, N. Z. 1999, ApJS, 124, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Schinnerer, E., Eckart, A., & Tacconi, L. J. 2000a, ApJ, 533, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Eckart, A., Tacconi, L. J., Genzel, R., & Downes, D. 2000b, ApJ, 533, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., & Solomon, P. M. 1973, ApJ, 180, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B. 1988, Nearby galaxies catalog (Cambridge and New York: Cambridge University Press), 221 [Google Scholar]
- Turner, J. L., & Ho, P. T. P. 1994, ApJ, 421, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., & Tomisaka, K. 2005, ApJ, 619, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Weiß, A., Walter, F., & Scoville, N. Z. 2005, A&A, 438, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wild, W., Harris, A. I., Eckart, A., et al. 1992, A&A, 265, 447 [NASA ADS] [Google Scholar]
- Wilson, C. D., Warren, B. E., Israel, F. P., et al. 2009, ApJ, 693, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, L., Seaquist, E. R., Kuno, N., & Dunne, L. 2003, ApJ, 588, 771 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 2 SMA CO(3–2) integrated map of NGC 4569 (grey scale given in the color bar in Jy km s-1 beam-1) overlaid with the PdBI CO(1–0) integrated map (left) with contours at 2, 6, 12, 20, and 30 Jy km s-1 beam-1 and the PdBI CO(2–1) integrated map (right) with contours at at 7, 21, 42, 70 and 87 Jy km s-1 beam-1. No primary beam correction has been applied. All maps have the same resolution (PdBI data have been tapered) and the beam (2.3″ × 2.1″) is shown at the bottom left. The black cross labelled E shows the position of the AGN (αJ2000 = 12h36m49 .s80, δJ2000 = 13°09′46 .′′3). It is also the dynamical center and the phase center for the observations. The other crosses indicate the positions of the spectra plotted in Fig. 4. |
| In the text | |
 |
Fig. 3 Composite color image of NGC 4569 made from the intensity maps of the CO(1–0), CO(2–1) and CO(3–2) line emission. The line intensities are represented by the red, green and blue color intensities respectively. The intensity maps were obtained by summing all channels where the line has S/N > 3, and are corrected for primary beam attenuation. |
| In the text | |
 |
Fig. 4 Individual spectra of CO(1–0) (black), (2–1) (blue) and (3–2) (red) lines at six different positions (see Fig. 2) in the central region of NGC 4569 extracted at the same spatial resolution of 2.6″ × 2.1″. The fluxes have been corrected for primary beam attenuation and the CO(1–0) flux is scaled up by a factor 3.5 for better readability. |
| In the text | |
 |
Fig. 6 SMA CO(3–2) integrated map of NGC 4826 (grey scale given in the color bar in Jy km s-1 beam-1) overlaid with the PdBI CO(1–0) integrated map (left) with contours at 2, 4, 8, 12, 16, 20, and 24 Jy km s-1 beam-1 and the PdBI CO(2–1) integrated map (right) with contours at 4.1, 14.3, 24.5, 34.7, 44.9, 55.1, 65.3 and 75.5 Jy km s-1 beam-1. No primary beam correction has been applied. All maps have the same resolution (PdBI data have been tapered) and the beam (2.6 × 1.9″) is shown at the bottom left. The white cross labelled C shows the position of the dynamical center (αJ2000 = 12h56m43 .s64, δJ2000 = 21°40′59 .′′3). The other crosses indicate the positions of the spectra plotted in Fig. 8. |
| In the text | |
 |
Fig. 7 Composite color image of NGC 4826 made from the intensity maps of the CO(1–0), CO(2–1) and CO(3–2) line emission. The line intensities are represented by the red, green and blue color intensities, respectively. The intensity maps were obtained by summing all channels where the line has S/N > 3 and are corrected for primary beam attenuation. |
| In the text | |
 |
Fig. 8 Individual spectra of the CO(1–0) line (black), the CO(2–1) line (blue) and the CO(3–2) line (red) at 8 different positions (see Fig. 6) in the central region of NGC 4826 extracted at the same spatial resolution of 2.6″ × 1.9″. The fluxes have been corrected for primary beam attenuation and the CO(1–0) flux is scaled up by a factor 3.5 for better readability. |
| In the text | |
 |
Fig. 9 Line ratio maps of NGC 4569 and associated uncertainties. Upper left: R21 with black contours ranging from 0.3 to 0.7 in steps of 0.1 and white contours at 0.8 and 0.9. The beam (2.3″ × 2.1″) is represented as a filled ellipse at the bottom left corner. Upper right: R32 with black contours ranging from 0.1 to 0.25 in steps of 0.05, and white contours at 0.3, 0.35 and 0.4. Lower left: R21 error map with black contours at 0.02, 0.03, and white contours at 0.04, 0.05. Lower right: R32 error map with black contours 0.05, 0.07, and white contours at 0.09, 0.11, 0.13. |
| In the text | |
 |
Fig. 10 Line ratio maps with the same contours as in Fig. 9 (only above 0.2 for R32) overlaid on the Paα map obtained from NICMOS data (Programme ID: 9360, PI: Kennicutt). The grey scale is logarithmic; dark color corresponds to high flux. |
| In the text | |
 |
Fig. 11 (Left) R32-vs.-R21 diagram for the galaxy NGC 4569. The x-axis represents R21 and the y-axis R32. The intensity scale gives the sky area in the map per unit area in the ratio space, it is expressed in beams per 0.01 × 0.01 ratio area. This diagram has been produced by convolving the actual distribution of pixels in the ratio-ratio plane by a Gaussian kernel with a FWHM of 0.02. Note that the pixels in the ratio maps used to compute the distribution are much smaller than the beam (see Sect. 4). The contour levels are 0.3, 0.6, 0.9, 1.2 and 1.5 beams/0.012. (Middle) R32-vs.-R21 diagram for the galaxy NGC 4826; the contour levels are 0.3, 0.5, 0.7, 0.9, 1.1 beams/0.012. (Right)LTE and pseudo-LTE models represented as black curves in the R32-vs.-R21 diagram. Curves 1 and 2 correspond to pure LTE models with NCO/dV = 1015 cm-2 pc (km s-1)-1 and NCO/dV = 12 × 1015 cm-2 pc (km s-1)-1, respectively. The temperature increases from 4 K at the bottom left to 8 K at the top right. Curves 3 and 4 correspond to pseudo-LTE models with f32 = 0.5 and f32 = 0.2 respectively (see Sect. 5.1 for the definition of f32). The column density to line width ratio is NCO/dV = 1015 cm-2 pc (km s-1)-1 and the temperature increases from 4 to 20 K along the curves from bottom left to top right. The cyan and magenta curves show the lowest contours for NGC 4569 and NGC 4826, respectively. |
| In the text | |
 |
Fig. 12 Line ratio maps of NGC 4826 and associated uncertainties. The crosses are the same as in Fig. 6. Upper left: R21 with black contours at 0.4, 0.5, 0.6, 0.7, 0.8 and white contours at 0.77 and 0.9. The beam (2.6″ × 1.9″) is represented as a filled ellipse at the bottom left corner. Upper right: R32 with black contours at 0.1, 0.2, 0.3 and white contours at 0.4 and 0.5. Lower left: R21 error map with black contours at 0.02, 0.03 and white contours at 0.04 and 0.05. Lower right: R32 error map with black contours at 0.05, 0.07 and white contours at 0.09 and 0.11. |
| In the text | |
 |
Fig. 13 Maps of NGC 4826. Left: R21 with the same contours as in Fig. 12 overlaid on the 2 cm radio continuum map from Turner & Ho (1994). Right: R32 with the same contours as in Fig. 12 overlaid on the Paα map from NUGA-I. Dark color corresponds to high flux. |
| In the text | |
 |
Fig. 14 Variations of the CO line opacities with respect to temperature and density based on LVG modeling. From left to right panel: CO(1–0), (2–1) and (3–2) opacities. Used for the qualitative interpretation of the pseudo-LTE model. |
| In the text | |
 |
Fig. 15 Grids of LVG models for a range of molecular hydrogen densities and kinetic temperatures. Each grid corresponds to a different value of XCO/(dV/dR), from left to right: 10-6, 10-7 and 10-8 pc (km s-1)-1. The CO(1–0) radiative temperature is represented in color scale and is overlaid with R21 black contours (0.3 to 1.3 in steps of 0.2) and R32 blue contours (0.1 to 0.6 in steps of 0.1). The line ratios increase from bottom left to top right. |
| In the text | |
 |
Fig. 21 Pressure contours of NGC 4826 (same contours as in Fig. 20lower left panel) overlaid on the Paα map. The ellipse corresponds to a ring of 90 pc radius inclined by 60 deg. The straight line indicates the major axis of the galaxy. |
| In the text | |
 |
Fig. 22 Sketches illustrating the two opacity effects considered in Sect. 6.2. In both panels the color scale is related to the temperature in K as shown in the colorbars and the star symbol represents the AGN. The observer is assumed to be looking from the top right, so that the right-hand side of the panels corresponds to the near side and the left-hand side to the far side of the galaxy. The top panel illustrates how the densest and coldest gas distributed in a ring at 70 pc from the center could partly obscure emission from the dense torus on the near side and from the galactic disk on the far side. The white contours correspond to density levels. The dashed white lines delineate the regions that would be obscured by the densest gas. The lower panel illustrates how clumps heated by the nucleus could have inhomogeneous properties with the side exposed to the nucleus being warmer, less dense and less opaque to CO emission than the other side. |
| In the text | |
 |
Fig. 1 CO(3–2) channel maps of the galaxy NGC 4569. The velocity relative to the systemic velocity of the galaxy (vhel = −235 km s-1) is given at the top left of each map. The phase center indicated by the large cross is at the AGN position αJ2000 = 12h36m49.8s, δJ2000 = 13°09′46.3″. The beam (represented at the bottom left of each map) is 2.6″ × 2.1″ and the rms is 115 mJy beam-1. The only contour line overlaid corresponds to the 4σ level. The maps are not corrected for the primary beam attenuation. |
| In the text | |
 |
Fig. 5 CO(3–2) channel maps of the galaxy NGC 4826. The velocity relative to the systemic velocity of the galaxy (vhel = 402 km s-1) is given at the top left of each map. The phase center indicated by the large cross is at αJ2000 = 12h56m43.76s, δJ2000 = 21°40′51.9″. The galactic nucleus is marked by the small cross. The beam (represented at the bottom left of each map) is 2.6″ × 1.9″ and the rms is 75 mJy beam-1. The only contour line overlaid corresponds to the 4σ level. |
| In the text | |
 |
Fig. 16 Likelihood of all possible (R21, R32) pairs on a R32-vs.-R21 grid for different values of XCO/(dV/dR). The contours of the R32-vs.-R21 diagrams of NGC 4569 (blue) and NGC 4826 (magenta) are overlaid. The contours are smoothed and their levels correspond to 3 and 9 pixels per grid bin. (see Fig. 11). |
| In the text | |
 |
Fig. 17 LVG best fits to the line ratios measured in the central region of NGC 4569 at the eight positions marked in Fig. 2. The measured line ratios are represented with the 1-σ error bars and the best fit model ratios are linked with a straight line. The inset in each plot shows the 90% confidence interval (light grey shaded area) and the 50% confidence interval (dark grey) in the density-temperature plane assuming a normal probability distribution for each ratio; the best fit solution is marked with a cross. The best fit temperature and density as well as the averages over the 90% confidence interval are given at the top right of each plot. The normalized likelihood of the best fit, P/Pmax is also given (1 means the measured values are exactly reproduced by the model). |
| In the text | |
 |
Fig. 18 LVG result maps for NGC 4569. Upper left: H2 number density averaged over the 90% confidence interval of each LVG model. The black contours are at 5 × 102, 103, 3 × 103 cm-3 and the white contours at 5.5 × 103, 104, and 5 × 104 cm-3. Upper right: kinetic temperature averaged over the 90% confidence interval of each model. The black contours are at 5, 10, 15, 20, 25 K and the white contours at 30, 35, 40 K. Lower left: pressure averaged over the 90% confidence interval of each model. The black contours are at 104.1, 104.4, and 104.7 K cm-3 and the white contours at 105, 105.3 and 105.6 K cm-3. Lower right: the normalized likelihood (or merit), P/Pmax, of the best fit with black contours at 0.35 and 0.55 and white contours at 0.75 and 0.95. |
| In the text | |
 |
Fig. 19 LVG best fits to the line ratios measured in the central region of NGC 4826 at the eight positions marked in Fig. 6. See caption of Fig. 17 for more details. |
| In the text | |
 |
Fig. 20 LVG result maps for NGC 4826. Upper left: H2 number density averaged over the 90% confidence interval of each LVG model. The black contours are at 103 and 5 × 103 cm-3 and the white contours at 104 and 5 × 104 cm-3. Upper right: kinetic temperature averaged over the 90% confidence interval of each model. The black contours are at 5, 10, 20 K and the white contours at 40 and 60 K. Lower left: pressure averaged over the 90% confidence interval of each model. The black contours are at 104.7, 104.9, 105.1 and 105.3 K cm-3 and the white contours at 105.5 and 105.7 K cm-3. Lower right: goodness-of-fit with the same contours as in Fig. 18. |
| In the text | |
 |
Fig. 23 The upper panels show the CO integrated maps produced by the flared disk toy model described in Appendix A.1. The CO(3–2) emission is shown in greyscale, and the CO(1–0) (left panel) and CO(2–1) emission (right panel) are contours. The lower left and right panels show the resulting R21 and R32 maps, respectively. |
| In the text | |
 |
Fig. 24 The upper panels show the CO integrated maps produced by the clumpy flared disk toy model described in Appendix A.2. The CO(3–2) emission is shown in greyscale, and the CO(1–0) (left panel) and CO(2–1) emission (right panel) are contours. The lower left and right panels show the resulting R21 and R32 maps, respectively. |
| In the text | |
 |
Fig. A.1 Radial profiles of the molecular gas density (blue) and temperature (red) used in the models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


