| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A175 | |
| Number of page(s) | 26 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202346345 | |
| Published online | 20 June 2023 | |
Spectral classification of young stars using conditional invertible neural networks
I. Introducing and validating the method
1
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik,
Albert-Ueberle-Straße 2,
69120
Heidelberg, Germany
e-mail: kang@uni-heidelberg.de
2
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen,
Im Neuenheimer Feld 205,
69120
Heidelberg, Germany
3
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching bei München, Germany
4
Universitäts-Sternwarte, Ludwig-Maximilians-Universität,
Scheinerstrasse 1,
81679
München, Germany
5
Alma Mater Studiorum Università di Bologna, Dipartimento di Fisica e Astronomia (DIFA),
Via Gobetti 93/2,
40129
Bologna, Italy
6
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze, Italy
7
Université Paris Cité, Université Paris-Saclay, CEA, CNRS, AIM,
91191
Gif-sur-Yvette, France
8
INAF – Istituto di Astrofisica e Planetologia Spaziali,
Via Fosso del Cavaliere 100,
00133
Roma, Italy
Received:
7
March
2023
Accepted:
10
April
2023
Aims. We introduce a new deep-learning tool that estimates stellar parameters (e.g. effective temperature, surface gravity, and extinction) of young low-mass stars by coupling the Phoenix stellar atmosphere model with a conditional invertible neural network (cINN). Our networks allow us to infer the posterior distribution of each stellar parameter from the optical spectrum.
Methods. We discuss cINNs trained on three different Phoenix grids: Settl, NextGen, and Dusty. We evaluate the performance of these cINNs on unlearned Phoenix synthetic spectra and on the spectra of 36 class III template stars with well-characterised stellar parameters.
Results. We confirm that the cINNs estimate the considered stellar parameters almost perfectly when tested on unlearned Phoenix synthetic spectra. Applying our networks to class III stars, we find good agreement with deviations of 5–10% at most. The cINNs perform slightly better for earlier-type stars than for later-type stars such as late M-type stars, but we conclude that estimates of effective temperature and surface gravity are reliable for all spectral types within the training range of the network.
Conclusions. Our networks are time-efficient tools that are applicable to large numbers of observations. Among the three networks, we recommend using the cINN trained on the Settl library (Settl-Net) because it provides the best performance across the widest range of temperature and gravity.
Key words: methods: statistical / stars: late-type / stars: pre-main sequence
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In star-forming regions, massive stars influence the surrounding environment energetically and dynamically during their short lifetime, but the majority of stars that form in star-forming regions are low-mass stars whose masses are similar to or lower than the solar mass. These low-mass stars are not only the most numerous objects in the star-forming region (Bochanski et al. 2010), but also account for about half of the total stellar mass (Kroupa 2002; Chabrier 2003). Living longer than massive stars, these low-mass stars still remain in the pre-main-sequence phase even when the massive stars are dead. These young low-mass stars provide important information for studying stellar evolution and planet formation.
Stellar parameters (e.g. effective temperature, surface gravity, and luminosity) are estimated from photometric or spec-troscopic data by various methods. These methods are usually based on characteristic spectral features that vary depending on the type of stars. Therefore, it is important to adopt a method appropriate for the star under consideration and for the observed wavelength range.
The volume of accumulated observations has continually expanded in recent years, and therefore it has become important to develop time-efficient tools that analyse large amounts of data in a faster and more consistent way. To do this, artificial neural networks (NNs; Goodfellow et al. 2016) are currently used in many astronomical fields. For instance, NNs have been used to predict physical parameters (e.g. Fabbro et al. 2018; Ksoll et al. 2020; Olney et al. 2020; Kang et al. 2022) or to efficiently analyse images, such as identifying structures (e.g. Abraham et al. 2018) and exoplanets (e.g. de Beurs et al. 2022), or classifying observations (e.g. Wu et al. 2019; Walmsley et al. 2021; Whitmore et al. 2021). In this study, we develop NNs that can efficiently analyse numerous spectra in the optical wavelength range of young low-mass stars. We prepare our networks to analyse data observed by the Multi Unit Spectroscopic Explorer (MUSE) of the Very Large Telescope (VLT) adopting the wavelength coverage and spectral resolution of MUSE. In the follow-up paper, we will apply our tool to the spectra of young stars in the Carina nebula that were observed with VLT/MUSE.
We adopt the conditional invertible neural network (cINN) architecture developed by Ardizzone et al. (2021). Estimating physical parameters from observed measurements is a non-trivial task. Because the information we obtain from observations is limited due to information loss during the forward process (i.e. translation from physical systems into observations), different physical systems can be observed similarly or almost identically, which we call a degenerate system. The cINN architecture is specialised to solve the inverse problem of the degenerate system (i.e. from observations to physical systems). In particular, cINN has its own advantage in that cINN always provides a full posterior distribution of the physical system without any additional computations. In astronomy, the cINN approach has so far been used to characterise the internal properties of planets (Haldemann et al. 2023), analyse photometric data of young stars (Ksoll et al. 2020), study emission lines in H II regions (Kang et al. 2022), or infer the merger history of galaxies (Eisert et al. 2023).
The cINN architecture adopts a supervised learning approach that learns the hidden rules from a number of well-labelled data sets of physical parameters and observations. Because it is difficult to collect a sufficient number of well-interpreted real observations, synthetic observations have commonly been used instead to generate enough training data. In this study, we use Phoenix stellar atmosphere libraries (e.g. Allard et al. 2012; Husser et al. 2013; Baraffe et al. 2015) to train cINNs. Selecting the Settl, NextGen, and Dusty Phoenix libraries, we introduce three cINNs (Settl-Net, NextGen-Net, and Dusty-Net) that were trained on each of these libraries.
A few studies have developed NNs to analyse low-mass stars from photometric or spectroscopic data (e.g. Ksoll et al. 2020; Olney et al. 2020; Sharma et al. 2020). For example, Ksoll et al. (2020) developed a network using a cINN architecture to estimate the physical parameters of individual stars from HST photometric data, and Olney et al. (2020) used a convo-lutional neural network (CNN) to estimate physical parameters (e.g. effective temperature, surface gravity, and metallicity) from near-infrared spectra observed with the Apache Point Observatory Galactic Evolution Experiment (APOGEE) spectrograph. Sharma et al. (2020) also used a CNN to diagnose the optical spectra of stars in a wide range of spectral types, but their network only estimates the spectral type of the stars, not the other physical parameters. On the other hand, in this paper, our networks directly estimate the stellar parameters from the optical spectrum of low-mass stars, including the stars in the main sequence and pre-main-sequence phases. Moreover, our network provides a posterior distribution by adopting a cINN architecture, which is useful for studying the degeneracy between parameters.
In this paper, we focus on validating the performance of the three cINNs. We evaluate our networks not only on Phoenix synthetic observations, but also on real spectra of 36 young low-mass stars to investigate how well our cINNs work on real observations. These stars are template stars in the class III phase that have been well interpreted in the literature (e.g. Manara et al. 2013, 2017; Stelzer et al. 2013).
The paper is structured as follows. In Sect. 2 we describe the structure and principles of cINN and explain implementation details on the machine-learning side. In Sect. 3 we introduce our three networks and three training databases. In the following section (Sect. 4), we describe the class III template stars we used. Our main results are reported in Sect. 5. We validate our networks using synthetic Phoenix spectra and 36 template stars. We not only evaluate the parameter prediction power of the cINN, but also determine whether the predicted parameters explain the input observations. Section 6 presents the parts of the spectrum on which cINN relies most. In Sect. 7 we investigate the gap between Phoenix synthetic spectra and real observations. We summarise the results in Sect. 8.
2 Neural network
2.1 Conditional invertible neural network
The cINN (Ardizzone et al. 2019a,b) is a deep-learning architecture that is well suited for solving inverse problems. These are tasks in which the underlying physical properties x of a system are to be recovered from a set of observable quantities y. In nature, recovering the inverse mapping x ← y is often challenging and subject to degeneracy due to an inherent loss of information in the forward mapping x → y, such that multiple sets of physical properties may appear similar or even entirely the same in observations.
To solve these difficulties, the cINN approach introduces a set of unobservable, latent variables z with a known, prescribed prior distribution P(z) to the problem in order to encode the information that is otherwise lost in the forward mapping. The cINN achieves this by learning a mapping f from the physical parameters x to the latent variables z conditioned on the observations y, that is,
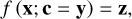 (1)
(1)
capturing all the variance of x that is not explained by y in z, while enforcing that z follows the prescribed prior P(z). Given a new observation y′ at prediction time, the cINN can then query the encoded variance by sampling the latent space according to the known prior distribution and by making use of its invert-ible architecture run in reverse to estimate the full posterior distribution p (x|y′) as
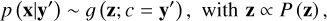 (2)
(2)
where f−1 (·, c) = ɡ(·, c) represents the inverse of the learned forward-mapping for a fixed condition c. In practice, P(z) is usually prescribed to be a multivariate normal distribution with zero mean and unit covariance, and the dimension of the latent space is chosen to be equal to that of the target parameter space, that is, dim(z) = dim(x).
The invertibility of the cINN architecture is achieved by chaining so-called (conditional) affine coupling blocks (Dinh et al. 2016). Each of these blocks performs two complementary affine transformations on the halves uı and u2 of the block input vector u, following
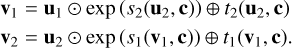 (3)
(3)
As the equation shows, these two transformations are easily inverted given the halves v1, v2 of the output vector v according to
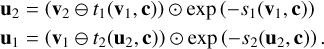 (4)
(4)
In both sets of Eqs. (3) and (4), si and ti (i є {1,2}) denote arbitrarily complex transformations, which need not themselves be invertible (as they are only ever evaluated in the forward direction) and can also be learned by the cINN itself when realised as small sub-networks (Ardizzone et al. 2019a,b).
Another advantage of the cINN architecture is that as the observations are treated as a condition and simply concatenated to the input of the subnetworks si and ti in each affine coupling layer, it allows for (a) an arbitrarily large dimension of the input y, and (b) the introduction of a conditioning network h (trained together with the cINN itself), which transforms the input observation into a more helpful, learned representation 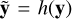 for the cINN (Ardizzone et al. 2019b).
for the cINN (Ardizzone et al. 2019b).
2.2 Implementation details
We employed a cINN consisting of 11–16 conditional affine coupling layers in the generative flow (GLOW; Kingma & Dhariwal 2018) configuration, where the transformation outputs si(·) and ti(·) are estimated by a single subnetwork ri(·) = (si(·), ti(·)). The latter choice reduces the number of sub-networks per affine layer from four to two, reducing network complexity and computation time. As sub-networks ri we employed simple fully connected architectures consisting of five to seven layers of size 256 using the rectified linear unit (ReLU, ReLU(x) = max(0, x)) as activation function.
The affine coupling layers were furthermore alternated with random permutation layers, which randomly (but in a fixed and thus invertible way) permute the output vector in between coupling layers to improve the mixing of information between the two streams u1 and u2 (Ardizzone et al. 2019a,b). For the conditioning network h, we also employed a three-layer fully connected architecture with layer size 512 and ReLU activation, extracting 256 features in the final layer.
Prior to training, we performed a linear scaling transformation on the target parameters x = {x1,…, xN} and on the input observations y = {y1…, yM}, where each target property xi and input feature yi was modified according to
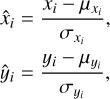 (5)
(5)
where 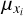 ,
, 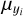 and
and 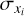 ,
, 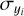 , denote the means and standard deviations of the respective parameter or feature across the training data set. These transformations ensure that the distributions of individual target parameters/input features have zero mean and unit standard deviation and are trivially inverted at prediction time. The transformation coefficients
, denote the means and standard deviations of the respective parameter or feature across the training data set. These transformations ensure that the distributions of individual target parameters/input features have zero mean and unit standard deviation and are trivially inverted at prediction time. The transformation coefficients 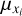 ,
, 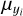 and
and 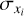 ,
, 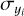 are determined from the training set and applied in the same way to new query data.
are determined from the training set and applied in the same way to new query data.
We trained the cINN approach for this problem by minimising the maximum likelihood loss as described in Ardizzone et al. (2019b) using the Adam (Kingma & Ba 2014) optimiser for the stochastic gradient descent with a step-wise learning-rate adjustment.
3 Training data
3.1 Stellar photosphere models
The approach we used to train the cINN is to use libraries of theoretical models for stellar photospheres. Our goal is to use the cINN to classify and derive photospheric parameters from medium- to low-resolution optical spectroscopy. For this purpose, we selected the most extensive set of available models that offer a spectral resolution better than R ~ 10 000. The most extensive, homogeneous, tested, and readily available1 library of theoretical photospheric spectra, including different treatments of dust and molecules formation and opacities, that is applicable in the range of effective temperatures covering the range from ~2000 to ~7000 K and gravities appropriate for pre-main-sequence stars and brown dwarfs are the Phoenix spectral libraries (e.g. Allard et al. 2012; Husser et al. 2013; Baraffe et al. 2015). We used the NextGen, Dusty, and Settl models. The latter is expected to provide the best description of the atmospheric characteristics in most cases of interest (Allard et al. 2012). We included the older NextGen models as a comparison set and the Dusty models because they appear to describe photospheres in the range of 2000 K ≤ Teff ≤ 3000 K more accurately (e.g. Testi 2009). For a more detailed description and comparison of the physical assumption in the models, we refer to the discussion and references in Allard et al. (2012).
The grid of synthetic spectra is available for regularly spaced values of Teff and log ɡ, with steps of 100 K in Teff and 0.5 in log ɡ. To compute a synthetic spectrum for a given set of (arbitrary but within the grid ranges) values of (Teff, log ɡ, and AV), we set up the following procedure: First, we identified the values of Teff and log ɡ in the grid that bracket the requested values, then we interpolated linearly in log ɡ at the values of the two bracketing Teff values, then we interpolated linearly the two resulting spectra at the requested Teff value, finally, we computed and applied the extinction following the Cardelli et al. (1989) prescription, with Rv as a user-selectable parameter (we used RV = 4.4; see Sect. 3.2). The resulting spectrum was then convolved at the MUSE resolution, using a Gaussian kernel, and was resampled on the MUSE wavelength grid.
3.2 Databases and networks
We analysed the cINN performance based on each of the three spectral libraries described in the previous section. Accordingly, we constructed a training data set for each spectral library using the interpolation scheme we outlined. For the target parameter space, we adopted the limits described below.
For NextGen and Settl, we limited Teff to the range of 2600 to 7000 K and log(g/cm s−2) from 2.5 to 5. The Dusty library has an overall smaller scope, and therefore we can only probe from 2600 to 4000 K in Teff and from 3 to 5 in log(g/cm s−2) here. For AV, we selected the same range of 0 to 10 mag for all three libraries, where we used the Cardelli et al. (1989) extinction law with RV = 4.4 to artificially redden the model spectra. We chose RV = 4.4 considering the application of our networks to the Carina nebula (Hur et al. 2012) in the follow-up study. As some of the template stars used in this paper (Sect. 4) are dereddend assuming RV = 3.1, we also experimented with training data sets using RV = 3.1. We found no significant difference in our main results and therefore continue to use RV = 4.4 in this study.
In terms of wavelength coverage, we matched the range of the template spectra described in Sect. 4 (i.e. ~5687 to ~9350 Å) and adopted the MUSE spectral resolution by subdividing the wavelength interval into a total of 2930 bins with a width of 1.25 Å. Additionally, we normalised the spectra to the sum of the total flux across all bins.
To generate the training data, we opted for a uniform random sampling approach, where we sampled both Teff and ɡ in log space and only AV in linear space within the limits specified above for the three libraries. We generated a total of 65 536 synthetic spectra models for each library. We also experimented with larger training sets, but found no significant increase in the predictive performance of our method, such that we deemed this training set size sufficient.
Finally, we randomly split each of these three initial databases 80:20 into the respective training and test sets for the cINN. The former subsets mark the data that the cINN was trained on, whereas the latter were withheld during training and served to quantify the performance of the trained cINN on previously unseen data with a known ground truth of the target parameters.
We first trained 50 networks for each library with randomised hyper-parameters of cINN, and we selected the best network based on the performance on the test set and template stars. We trained the network until the training loss and test loss converged or either of them diverged, where the latter cases were discarded. It took about 50 min to train one network (6 h for 50 networks using seven processes in parallel) with an NVIDIA GeForce RTX 2080 Ti graphic card. After they were trained, our networks can sample posterior estimates very efficiently. Using the same graphic card and sampling 4096 posterior estimates per observation, we needed about 1.1 s to sample posterior distributions for 100 observations (91 observations per second). When tested with M1 pro CPU with 8 cores, it takes about 13 s for 100 observations (7.6 observation/s).
4 Class III templates
The set of observations on which we validated our networks contained 36 spectra of well-known class III stars observed with VLT/X-Shooter (Manara et al. 2013, 2017). We refer to the original papers for details of the observations and data reduction. The templates come from different star-forming regions (Taurus, Lupus, Upper Scorpius, σ Orionis, TW Hydrae Association, and Chameleon I) and span a broad range of effective temperatures (2300–5800 K), as well as spectral types (M9.5–G5.0). We used their properties as provided by Manara et al. (2013, 2017) and Stelzer et al. (2013).
Spectral types for stars later than K5 were obtained based on the depth of the molecular absorption bands (TiO, VO, and CaH) and a few photospheric lines (e.g. Na I, Ca I, and Mg I) that are present in the optical part of the spectra (Manara et al. 2013). Earlier K-type stars were identified using the spectral indices introduced by Herczeg & Hillenbrand (2014), while G-type stars were identified based on the difference at 5150 Å of continuum estimated between 4600 and 5400 Å, and 4900 and 5150 Å (Herczeg & Hillenbrand 2014). Effective temperatures (Teff) were derived from spectral types using the relations from Luhman et al. (2003) for M-type objects and those from Kenyon & Hartmann (1995) for K- and G-type stars. Most of the templates have none or negligible extinction (AV < 0.5 mag, Manara et al. 2017); those with AV > 0.3 were dereddened before analysis assuming the extinction law from Cardelli et al. (1989) and RV = 3.1.
The surface gravity (log ɡ) of class III sources was estimated using the ROTFIT tool (Frasca et al. 2003). It compares the observed spectrum with the grid of referenced spectra and finds a best-fit by minimising the χ2 of difference between the spectra in specific wavelength ranges. Stelzer et al. (2013) and Manara et al. (2017) used BT-Settl spectra in a log g range of 0.5–5.5 dex as reference. The tool also provides Teff and radial and rotational velocities, but we used Teff derived from spectral types in the subsequent analysis. Table 1 provides a summary of the class III stars and their stellar parameters. We excluded the sources from the original paper that might be unresolved binaries or whose youth is doubtful due to the lack of the lithium absorption line at 6708 Å (Manara et al. 2013).
X-Shooter has higher spectral resolution than MUSE. The template spectra were therefore degraded to the MUSE resolution (R ~ 4000) using a Gaussian kernel and were resampled on MUSE spectra within the range of 5687.66–9348.91 Å (the common spectral range of MUSE and the optical arm of X-Shooter). Subsequently, spectra were normalised to the sum of the total flux of the stellar spectrum within the analysed spectral range.
5 Validation
5.1 Validations with synthetic spectra
In this section, we validate whether the trained networks learned the physical rules hidden in the synthetic Phoenix models well. We use the test set of each database, that is, the synthetic models that are not used for the training, but share the same physics as the training data. As mentioned in Sect. 3.2, we only used 80% of the database for training and retained the rest for validation. Each test set consists of 13 107 test models.
5.1.1 Prediction performance
We introduce an accuracy index to evaluate the parameter prediction performance of the network. The accuracy of the prediction is defined as the deviation between the posterior estimate of the parameter and the ground-truth value (x*) of the test model. In this section, we calculate the accuracy on the same physical scales as we used to build the databases in Sect. 3.2, meaning that we use the logarithmic scales for the effective temperature and surface gravity and the linear scale for the extinction magnitude. We either used all posterior estimates sampled for one test model or the maximum a posteriori (MAP) point estimate as a representative. To determine the MAP estimate from the posterior distribution, we performed a Gaussian kernel density estimation on a 1D posterior distribution and determined the point at which the probability density maximises, similar to the method used in Ksoll et al. (2020) and Kang et al. (2022). In most parts of this paper, we use the MAP estimate to quantify the accuracy of the prediction.
We evaluated the three networks (Settl-Net, NextGen-Net, and Dusty-Net) by using all 13 107 test models in the corresponding test set. For each test model, we sampled 4096 posterior estimates and measured the MAP estimates for three parameters from the 1D posterior distributions. In Fig. A.1 we present 2D histograms to compare the MAP values estimated by Settl-Net with the true values of the entire test models. Settl-Net predicts all three parameters extremely well, so that the data points all lie on the one-to-one correspondence line. The NextGen-Net and Dusty-Net also show extremely good results on the test set. The results of the other two networks are very similar to the result of Settl-Net (Fig. A.1), and therefore we do not include figures of them in this paper.
To quantify the average accuracy of the network for multiple test models, we measured the root mean square error (RMSE) following
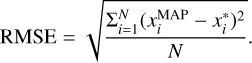 (6)
(6)
In the case of the Dusty-Net, the training ranges of the effective temperature and surface gravity are narrower than the range of the other two networks. As the total number of models is the same for all three databases (i.e. 65 536 models), the number density of the model for the effective temperature and surface gravity in the Dusty database is higher than the other two. We therefore defined the normalised RMSE (NRMSE),
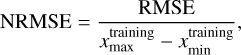 (7)
(7)
by dividing the RMSE by the training range.
In Table 2 we list the RMSE and NRMSE of each parameter for three networks. As already shown in the comparisons between the MAP values and true values (Fig. A.1), the RMSE and NRMSE for all three networks are very low around 10−4 ~ 10−2. Dusty-Net has the smallest RMSE and NRMSE for all three parameters in the three networks. In the case of the effective temperature and extinction, the differences in NRMSE between the networks are very small, whereas the difference in the NRMSE in the case of surface gravity is relatively noticeable in the three parameters. Although Dusty-Net has the best results, the low values in Table 2 demonstrate that all three networks perfectly learned the synthetic spectra.
Stellar parameters of class III template stars.
5.1.2 Resimulation
To further validate the prediction results of the cINN on the synthetic test data, we verified whether the spectra that correspond to the MAP estimates match the respective input spectrum of each test example. We did this by feeding the MAP predictions for the stellar parameters of the 13 107 test examples as an input to our spectra interpolation routine, which we introduced for the training set generation in Sect. 3.1, in order to resimulate the corresponding spectra. Afterwards, we computed the residuals, RMSEs, and R2 scores of the resimulated spectra in comparison to the corresponding input spectra. The latter serves as a goodness-of-fit measure and is defined as
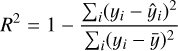 (8)
(8)
for a set of N observations yi with corresponding predictions 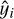 , where
, where 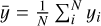 denotes the mean of the observations. It takes on values between 0 and 1, with the latter indicating a perfect match (James et al. 2017).
denotes the mean of the observations. It takes on values between 0 and 1, with the latter indicating a perfect match (James et al. 2017).
Figure 1 summarises the results for Settl-Net, showing the median relative residual against the wavelength in the left panel and the distribution of RMSEs in the right one. The corresponding plots for NextGen-Net and Dusty-Net are shown in Figs. A.2 and A.3. Out of the 13,107 test cases, we were unable to resimulate spectra for only 52, 32, and 9 MAP predictions for Settl-Net, NextGen-Net, and Dusty-Net, respectively. In these few instances alone fall either the predicted temperature or gravity (or both) outside the interpolation limits of the respective spectra library, so that the spectrum cannot be res-imulated. Notably, all of these cases are extreme edge cases that lie immediately at the training boundaries of either Teff or log(ɡ) so that the cINN MAP estimates fall ever so slightly outside the limits while still being an excellent match to the ground truth.
Figure 1 confirms the excellent precision of the MAP predictions that was demonstrated in the ground-truth comparison in Fig. A.1. With a median RMSE of the resimulated spectra of 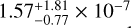 (and median R2 score of 1), the resimulated spectra correspond exactly to the corresponding input. The left panel of Fig. 1 also shows that while the overall median residual is very low, there is a systematic trend towards a larger discrepancy between resimulation and input within a shorter wavelength regime (<7250 Å). This is likely an effect of the overall low flux in the short-wavelength regime for the colder stars (<4000 K), so that even a small deviation in flux results in a comparably higher value of the relative residual. We note again, however, that with most relative deviations falling below 0.2%, the discrepancy is marginal overall even in the short-wavelength regime.
(and median R2 score of 1), the resimulated spectra correspond exactly to the corresponding input. The left panel of Fig. 1 also shows that while the overall median residual is very low, there is a systematic trend towards a larger discrepancy between resimulation and input within a shorter wavelength regime (<7250 Å). This is likely an effect of the overall low flux in the short-wavelength regime for the colder stars (<4000 K), so that even a small deviation in flux results in a comparably higher value of the relative residual. We note again, however, that with most relative deviations falling below 0.2%, the discrepancy is marginal overall even in the short-wavelength regime.
Figures A.2 and A.3 show that NextGen-Net and Dusty-Net exhibit a similar behaviour in the resimulation test, although we find slightly lower mean RMSEs with 2.28 ± 2.48 × 10−7 and 9.01 ± 7.34 × 10−8, respectively. Because the mean RMSEs in the three different spectral libraries agree within one σ, however, it is safe to say that all three networks achieve equally excellent performance in the resimulation test.
Average prediction performance of three networks (Settl-Net, NextGen-Net, and Dusty-Net) on 13 107 Phoenix synthetic models in the test set.
 |
Fig. 1 Resimulation results of Settl-Net for the entire synthetic spectra in the test set. The left panel presents the median relative error across the wavelength range of the resimulated spectra based on the MAP predictions of the cINN trained on the Settl models averaged over the 13 107 synthetic spectra in the test set. The grey envelope indicates the interquantile range between the 25 and 75% quantiles. In the right panel, we present the histogram of the RMSEs of the 13 107 resimulated spectra. The mean resimulation RMSE across the test set is 3.01 ± 4.35 × 10−7. |
5.2 Validations with class III template stars
In this section, we investigate how well our cINNs predict each parameter when they are applied to real observations by analysing the class III template stars introduced in Sect. 4. The stellar parameter values (i.e. effective temperature, surface gravity, and extinction) provided by previous papers (Manara et al. 2013, 2017; Stelzer et al. 2013) are listed in Table 1. The 36 template stars include cases for which the literature value of the effective temperature exceeds the training range of the cINNs, or for which the literature gravity value is lacking. Two out of 36 stars have temperatures below 2600 K, which is beyond the temperature range of all three databases. Moreover, 14 stars with temperatures between 4000 and 7000 K exceed the training range of the Dusty-Net. These stars were excluded from some analyses in the following sections.
Using each network, we sampled 4096 posterior estimates per star and measured MAP estimation for three parameters. We list the MAP values predicted by the three networks in Table 3.
Summary of cINN MAP predictions for the class III template spectra for the cINN models based on the three different spectral libraries.
5.2.1 Parameter comparison between the literature and cINN
In Fig. 2 we compare the stellar parameter values from the literature (xlit) with MAP predictions (xMAP). Each row shows the result of different cINNs. The first two columns are the results of effective temperature and surface gravity. Because the extinction value of the template stars is negligible, we compared the literature temperature value with the MAP extinction estimate. We calculated the uncertainty of the MAP estimate based on the width of the posterior distribution, but because the uncertainties are all very small, we do not present the uncertainty of the MAP estimate in the figure. For the uncertainty of the literature values, we adopt a one-subclass temperature interval as the uncertainty of the temperature and use the surface gravity uncertainty provided by the literature (Stelzer et al. 2013; Manara et al. 2017). According to the literature, the 1 σ uncertainty of the extinction is ~0.1–0.2 mag. We therefore indicate the range from −0.2 to 0.2 mag in grey to show the uncertainty range.
In this section, we do not use some stars in our analyses whose stellar parameter value from the literature exceeds the training range or for which any stellar parameter value is lacking, although they are presented in Fig. 2 by triangles. We used 34, 34, and 20 stars for Settl-Net, NextGen-Net, and Dusty-Net, respectively, when analysing temperatures or extinction, and we used 32, 32, and 18 stars when analysing gravity.
Comparing the temperature MAP estimates with the literature values, we confirm that the majority of stars lie close to the one-to-one correspondence line. We calculated the RMSE for each network by only using stars whose temperature literature values were within the training range (i.e. circles in Fig. 2). The average of the one-subclass temperature interval of these stars is about 140 K, therefore the RMSE values of 175.3, 192.3, and 94.02 K for Settl-Net, NextGen-Net, and Dusty-Net, respectively, are well within the interval of one to two subclasses. As shown in the figure and RMSE values, Dusty-Net agrees best with the literature value when the temperature is within its training range of 2600–4000 K. However, Dusty-Net agrees little with the literature values when the temperature is outside the training range. This implies that using cINN to analyse stars far from the training range should be done with caution. When we compare Settl-Net and NextGen-Net, which have the same training range, the MAP estimates of Settl-Net are closer to the literature values.
To compare the performance of the three networks on the temperature in more detail, we present the relative temperature deviations between the MAP predictions and the literature values sorted by their spectral type. Figure 3 also shows that MAP estimates from Dusty-Net agree well with the literature value within 5%. In the case of Dusty-Net, the deviation is within the one-subclass interval, except for one star. In the case of Settl-Net and NextGen-Net, 23 and 16 stars out of 34, respectively, deviate by less than one-subclass interval. The MAP estimates of Settl-Net and NextGen-Net agree relatively little with the literature values for hot stars of 4500 Κ (e.g. K4.0 type) or higher. However, the discrepancies are still within 10%. The average absolute relative deviations when only the templates within the training range of each network are used are 3.28, 4.49, and 2.58% for Settl-Net, NextGen-Net, and Dusty-Net, respectively (Table 4). These average errors are equivalent to 1.08, 1.12, and 0.601 subclasses.
In the case of surface gravity, the RMSEs of Settl-Net, NextGen-Net, and Dusty-Net are 0.30, 0.51, and 0.42 dex, respectively. However, because the surface gravity value from previous studies (Stelzer et al. 2013; Manara et al. 2017) was obtained by fitting the spectrum on the Settl models, the MAP estimate of Settl-Net is essentially closest to the literature value. Although Settl-Net has the lowest RMSE value, the other two networks also agree well with the literature value when the uncertainty of the literature values is considered.
To combine the results of temperature and surface gravity, we defined the combined error of two parameters as
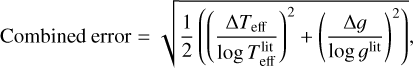 (9)
(9)
and present the combined error of each template star. We used the effective temperature in the logarithmic scale to match the scale with the surface gravity. The overall result using the combined error presented in Fig. 4 is not significantly different from Fig. 3, but when the gravity error is added, Settl-Net performs better than Dusty-Net even for low-temperature stars. In the case of NextGen-Net, the combined error is larger than in the other two networks because there are cases where temperature and gravity errors are both large. The average combined errors across the stars of Settl-Net NextGen-Net, and Dusty-Net are 3.93, 7.20, and 6.47%, respectively.
In the case of Settl-Net, all but seven stars agree well with the literature values within the 1σ uncertainty. Except for one star with a large error, most of the stars have errors smaller than 5 and 10% at most. Dusty-Net also has small errors (< 15%), but Dusty-Net has the disadvantage that it is inherently less versatile than the other two networks because of its training range. NextGen-Net also shows an error smaller than 10% for stars with spectral type earlier than M5.0.
Lastly, in the case of extinction, the deviation between MAP estimates and literature values varies depending on the temperature. For stars hotter than about 3400 Κ (i.e. M3.0 type), all three networks predict near-zero extinction, with little deviation from the literature values. In the case of NextGen-Net, some stars are slightly outside the error range, but their MAP estimates are sufficiently small. On the other hand, for cool stars below 3400 K, the discrepancy between the MAP value and the literature value grows gradually. In the case of Settl-Net and Dusty-Net, the MAP estimate does not exceed the maximum of 3, but in the case of NextGen-Net, the MAP estimates are slightly larger than for the other two networks.
In this section, we showed that the discrepancy between the network MAP prediction and literature value varies with the characteristics of the stars. Based on the overall results, a star of M6.5–K1.0 (2935–5000 K) for Settl-Net, M4.5–K1.0 (3200–5000 K) for NextGen-Net, M5.5–M0.0 (3060–4000 K) for Dusty-Net agrees especially well with the literature values. Settl-Net agreed best with the literature values overall. Dusty-Net also agrees well for stars whose temperature is within the Dusty database of 2600–4000 K. NextGen-Net has relatively large errors compared to the other two, but it still shows reliable performance for early-type stars. Because Settl-Net and NextGen-Net cover a wider range of temperatures (i.e. 2600–7000 K) and gravity (2.5–5 log(cm s−2)) than Dusty-Net, Settl-Net is the best choice among the three networks. However, all three networks agree well with the literature values considering their uncertainty.
This result shows how well our cINN predictions agree with the values obtained with the classical methods in previous studies. The differences between literature values and network predictions do not demonstrate that the network prediction is incorrect. For example, in the case of surface gravity, there is inevitably a larger discrepancy between the literature values and the MAP predictions of NextGen-Net and Dusty-Net because the literature value was also obtained by fitting spectra based on the Settl model. This means that we need to consider the methods that were used in the literature, and additional analysis is required to judge whether the cINN prediction is incorrect. The resimulation following in the next section provides a better clue to determine the correctness of our cINN predictions.
 |
Fig. 2 Comparison of MAP predictions with literature values in Table 1. Stars are basically denoted by circles, but triangles denote stars that were excluded in analyses such as RMSE calculation either because their literature temperature values exceed the cINN training range or because their literature surface gravity values are lacking. The colour indicates the temperature deviation between the MAP estimate and the literature value. We indicate the training range of each parameter with dotted green lines. In the third column, the horizontal grey area presents the 1σ uncertainty (i.e. 0.2 mag) of extinction provided by the literature. |
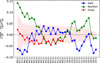 |
Fig. 3 Relative temperature deviations of the template stars between the MAP estimates and the literature values sorted by their spectral type. Different colours and symbols indicate the results of the three different cINNs. The pink area indicates the uncertainty of the literature temperature value. We only present template stars whose literature temperature value is within the network training range. |
Average absolute relative error between cINN predictions and literature values for the template stars.
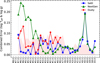 |
Fig. 4 Average relative error of the template stars between the MAP estimates and the literature values sorted by their spectral type. The average error is calculated as the rms of the relative errors of temperature and gravity, both in log scale (Eq. (9)). The pink area indicates the ltr uncertainty of the literature value. We only present template stars whose literature temperature value is within the network training range and whose literature gravity value is presented. The colour codes are the same as in Fig. 3. |
 |
Fig. 5 Resimulation results for the class III star SO797. The columns show the results for the three different spectral libraries Settl, NextGen, and Dusty. Top: comparison of the resimulated spectrum. The blue spectrum indicates the resimulation derived from the literature stellar parameters from Table 1. The red spectrum shows the corresponding resimulation based on the cINN MAP prediction. The respective input parameters for the resimulation are summarised in the table in the bottom right corner. The relative residuals (Iresim – Iin)/Iin of the resimulated spectra compared to the input spectrum are shown in the bottom panels. |
5.2.2 Resimulation
As for the synthetic test data in Sect. 5.1.2, we also evaluated the accuracy of the cINN predictions on the class III template by resimulation to quantify the agreement between the spectra corresponding to the MAP estimates with the input spectra. In this case, we also ran a resimulation for the nominal literature stellar parameters of the class III sources listed in Table 1 for comparison. Some of the class III template sources in our sample lack an estimate for log(g) in the literature. For these sources, we assumed a fixed value of log(ɡ/cms−2) = 4.0 in our resimulation, which is a reasonable guess for the spectral types in our sample. The sources in question are marked as “fixed” in the last column of Table 1. In a few templates (seven for Settl, one for NextGen, and eight for Dusty; see Table 3) the cINN extinction MAP estimate has an unphysical negative value. Since most of these are only barely below zero, we decided to allow these negative values to be accounted for during the resimulation.
Figure 5 shows an example result of the resimulation for the M4-type template star SO797 for all three spectral libraries. The top panels compare the resimulated spectra to the input spectrum, and the bottom panels show the corresponding residuals. The red curve indicates the resimulation result derived from the cINN MAP estimates, and the blue curve marks the literature-based outcome. In this particular example, the cINN recovers both Teff and log(g) quite accurately for all three spectral libraries but overestimates AV for this supposedly zero-extinction template class III source by 1.07, 1.48, and 0.73 mag based on Settl, NextGen, and Dusty, respectively. Interestingly, however, we find that the resimulated spectrum based on the cINN MAP prediction with the supposedly incorrect AV matches the input spectrum better than the spectrum derived from the literature value in all three examples, as attested by the smaller RMSE and better R2 score of 2.7 × 10−5 and 0.98 compared to 3.77 × 10−5 and 0.97 in the Settl case, for example. Figure A.4 shows another such example, which immediately shows that the cINN-based resimulated spectrum matches the input observation much better than the literature-based solution, which evidently does not capture the slope of the observed spectrum correctly.
Figures 6 and 7 and Table A.1 summarise the resimulation results for the entire class III template sample, showing the median relative residuals against the wavelength, the distributions of RMSEs and R2 scores, and a table of all RMSEs and R2 scores, respectively. The resimulation statistics vary between the libraries. Because the effective temperature limits of the libraries are lower (i.e. 2600 K), 2 of the 36 templates, namely TWA26 and DENIS1245, can a priori not be resimulated with Settl and NextGen. For Dusty, the literature sample is even smaller, with only 20 out of 36 templates due to the low upper temperature limit of 4000 K. For the resimulation of the MAP estimates, we used 31 templates with Settl-Net, 29 with NextGen-Net, and only 17 with Dusty-Net. For more details, we refer to Table A.1. For the Dusty resimulation, there are 7 templates for which the log(g) prediction is above the training set limit of 5. However, since the Dusty spectral library extends to log(ɡ/cms−2) = 5.5, we decided to run the resimulation for these 7 templates, in particular because for most of them, the log(ɡ) prediction is only barely above 5 (see Table 3).
Figure 6 shows that our observation from Fig. 5, in which the resimulated spectrum based on the cINN prediction fits the input spectrum better than the literature-based resimulation, holds for the entire template sample on average for the three networks. The distributions of the RMSEs and R2 scores of the resimulated spectra in Fig. 7 further confirm this, as the cINN-based resim-ulated spectra tend towards smaller RMSEs and slightly better R2 scores than the literature-based spectra for all three spectral libraries.
The resimulations of the seven templates for which the Dusty-based cINN prediction of log(ɡ) exceeds the learned upper limit of 5 (i.e. the cINN extrapolated) show that even when the cINN extrapolates, the set of predicted parameters corresponds to a spectrum that matches the input observation quite well, and in particular, it matches the input equally if not better than the respective spectrum resimulated from the literature values, as indicated by the R2 scores (see Table A.1 and Fig. A.5 for an example). This result shows that the cINN prediction is fairly robust even in the event of slight extrapolation.
Comparing our chosen resimulation accuracy measures to the spectral types of the class III templates in Fig. 8, we find that the RMSEs exhibit an increasing trend towards M types for all three spectral libraries. For the R2 scores, we find a notable dip in the goodness of fit for the intermediate spectral types, that is, between M2 and K3, in the resimulation of the literature and in the cINN-based values for Settl and NextGen. The beginning of this dip can also be seen in the Dusty-based results up to the temperature limit of this library at the K7 type. Interestingly, when compared to Fig. 4, the discrepancy between the cINN prediction and literature stellar properties is relatively low in this spectral type, where the cINN and literature values both correspond to an equally suboptimal fit to the observed spectra.
The resimulation test shows overall that the cINN approach predicts parameters for the real class III template spectra that correspond to spectra that not only fit the input observations very well (as shown by the good R2 scores in Fig. 7 and Table A.1), but also match better than the spectra resimulated from the literature values in most instances. This validates that cINNs find the best theoretical model that satisfies the input observation well as it is designed to.
 |
Fig. 6 Comparison of the median relative error of the resimulated spectra for the class III template stars between the resimulations based on the literature stellar parameters (blue, see Table 1) and the cINN MAP predictions (red). From top to bottom, the panels show the corresponding results for the three tested spectral libraries Settl, NextGen, and Dusty. |
6 Feature importance
6.1 Importance calculation
In this section, we evaluate the parts of the spectra on which the cINN prediction relies most. To do this, we measure the so-called permutation feature importance, an approach first described by Breiman (2001) for random forest models and later generalised by Fisher et al. (2019). We implemented the algorithm of Fisher et al. (2019) as described in Molnar (2022). It operates as described below.
First, we computed the error on the original held-out test set,
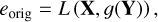 (10)
(10)
where g represents the inverse translation (x ← y) of the trained cINN, X denotes the matrix of the target parameters of the test set (ntest × nparameters), Y is the ntest × nfeatures feature matrix of the test set, and L represents a loss measure. In our case, L is the RMSE of the MAP estimates.
Next, for each feature j ∊ {1,…,nfeatures}, we generated a feature matrix Yperm j· via random permutation of the jth column in order to break the association between feature j and the target parameters x, estimate the prediction error eperm,j = L (X,ɡ (Ypermj))based on the permuted data set, and compute the feature importance of feature j as the quotient
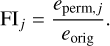 (11)
(11)
The larger FIj, the worse the model prediction becomes if feature j is scrambled via permutation, that is, the more important feature j is to the decision making of the model. The closer FIj to 1, on the other hand, the less feature j affects the predictive performance and, thus, the less relevant it is to the reasoning of the model.
In our particular case, the feature space is very high dimensional with 2930 spectral bins per spectrum. Consequently, computing the individual per spectral bin feature importance is rather computationally expensive as it requires generating the posteriors and determining the MAP estimates for each of the 2930 bins. Although the computational cost alone is not prohibitive in this case given the cINNs great efficiency, we still opted for a slightly different approach because the spectral bins themselves are also not necessarily independent of each other. Instead of using the individual bins, we grouped them together into combined features, for which we then estimated the importance. In practice, this meant that we permuted multiple columns at once (each column with its own permutation seed), corresponding to the spectral bins in a given group. For the setup in this study, we decided in particular to evaluate the feature importance across the wavelength range using groups of 10 bins, which corresponds to a spectral width of 12.5 Å. We set all groups to overlap by 5 bins (i.e. 6.25 Å) with the preceding and following groups. We averaged the feature importance for overlapping bins.
 |
Fig. 7 Average error for the resimulation spectra for the class III template stars. Top: histograms of the RMSEs for the resimulation on the class III template spectra for the three different spectral libraries. Bottom: histograms of the corresponding R2 scores for the resimulated spectra. |
6.2 Important features for M-, K-, and G-type stars
We drew three groups from the test set according to the temperature of the test model: M-type (2600–3850 K) group, K-type (3900–5110 K) group, and G-type (5150–6000 K) group, and evaluated the feature importance across the wavelength for each group per network. In the case of Dusty-Net, we only evaluated this for the M-type group because the highest temperature of the Dusty database is 4000 K.
Figure 9 presents the feature importance of Settl-Net for M-type stars. To compare the important features with the locations of stellar parameter tracers existing in the real spectrum, we plot the median flux of M-type template stars in the first row and indicate the locations of several tracers of stellar parameters (Table 5): Na I doublet 5890, 5896 Å (Teff and log ɡ, Allen & Strom 1995), Ca I 6122, 6162, 6439 Å (log ɡ, Allen & Strom 1995), Ba II, Fe I, and Ca I blend 6497 Å (Teff and log ɡ, Allen & Strom 1995; Herczeg & Hillenbrand 2014), Hα 6563 Å (Teff, Luhman et al. 2003), K I doublet 7665, 7699 Å (Teff and log ɡ, Manara et al. 2013, 2017), Na I doublet 8183, 8195 Å (Teff and log g, Kirkpatrick et al. 1991; Allen & Strom 1995; Riddick et al. 2007), Ca II IR triplet 8498, 8542, 8662 Å (Teff, Kirkpatrick et al. 1991; Allen & Strom 1995; Luhman et al. 2003), Mg I 8807 Å (Teff, Manara et al. 2013; Herczeg & Hillenbrand 2014), hydrogen Paschen series (AV, Edwards et al. 2013), CaH 6750–7050 Å (Teff and log ɡ, Kirkpatrick et al. 1993; Allen & Strom 1995), TiO 6080–6390, 7053–7270 Å (Teff, Kirkpatrick et al. 1991; Henry et al. 1994; Jeffries et al. 2007), ViO 7550–7570, 7920–8000 Å (Teff, Allen & Strom 1995; Riddick et al. 2007; Manara et al. 2013), and R1 8015–8130 Å (Teff, Riddick et al. 2007).
To evaluate whether these observational tracers act as important features in our networks, we verified whether the feature importance value corresponding to each tracer wavelength exceeded a fiducial value. We used the value of median plus one standard deviation over the entire wavelength range as a fiducial value to determine an important tracer. For tracers with multiple lines or molecular bands, we averaged the feature importance for each line or over the wavelength range. In Table 5 we mark tracers whose average importance exceeds the fiducial value. We also indicate for which parameters these lines and bands trace in real observations.
Figure 9 shows that the Na I doublet 8183, 8195 Å lines are the most important feature for Settl-Net to predict stellar parameters of M-type stars. In the case of extinction, there are two wide peaks near 7500 Å, where the redder peak overlaps with the VO molecular band. However, Na I has a similarly high importance value. In the case of temperature and gravity, K I doublet 7665, 7699 Å lines play a second important role, and in extinction, Ha does. VO and R1 molecular absorption bands as well act as important features to determine the temperature and extinction.
We present the feature importance evaluated for NextGen-Net and Dusty-Net in Fig. A.7. Na I, K I, and Ha are important features for M-type stars in all three networks. However, for NextGen-Net, there is a large bump at 7500 Å in the case oftem-perature. The results of NextGen-Net are spikier than in the other two networks overall. In the case of Dusty-Net, the importance value of the Na I doublet 5890, 5896 Å (Na ID) is relatively high compared to the other networks, and there is a very wide bump around Na I doublet 8183, 8195 Å.
Because extinction affects the overall shape of the spectrum, it is interesting that Settl-Net relies strongly on a few certain lines. Broad bumps exist in the red part of the spectrum, but there are particularly important lines and areas such as the Na I, Ha, and near VO bands. The result of NextGen-Net is similar to that of Settl-Net, but shows a slightly more spiky trend with wider peaks. Dusty-Net shows a more wavy shape across the entire wavelength range than the others.
Next, in the case of K-type stars, the results of Settl-Net and NextGen-Net are similar to each other, unlike the case of M-type stars. We therefore only present the result of Settl-Net in this paper (left panels in Fig. 10). Compared to the results of M-type stars, it is noticeable that important features are different for each parameter. In the case of temperature and extinction, the overall shapes are similar: The Ha line is the most important feature. The Na I doublet 8183, 8195 Å are no longer so important to determine temperature and extinction for K-type stars. In addition, Na I D lines and hydrogen Paschen series have relatively high importance values. On the other hand, in the case of surface gravity, the Na I doublet 8183, 8195 Å lines still play the most important role. The importance of Na I D in gravity becomes noticeable in K-type stars compared to M-type stars. Additionally, there are several peaks at K I, Mg I 8807 Å that are used as important features to determine gravity.
The result of G-type stars (i.e. right panels in Fig. 10) is similar to the K-type stars. The Hα is still the most important feature for temperature and extinction, and the Paschen series also include several peaks. For gravity, Na I D becomes more important in G-type stars and has an importance value comparable to that of Na I doublet 8183, 8195 Å. These sodium lines are the most important features to determine gravity. On the other hand, the importance of K I lines decreases in G-type stars compared to K-type stars.
These results show that the features on which our networks rely to determine parameters vary depending on the input object. In particular, when changing from M- to K-type, important features change noticeably. For example, the Na I doublet 8183, 8195 Å lines are essential features for networks to understand M-type stars, sensitive to all three stellar parameters, but for earlier-type stars (K- and G-types), it is only important to determine gravity. Similarly, the K I doublet lines are gravity-sensitive features for late-type stars, but they are less essential for earlier types. In the case of the Na I doublet 5890, 5896 Å lines, on the other hand, they are more important for hot stars than for cold stars to determine gravity.
The feature-importance tests presented in this section indicate the features that affect the judgement of the network, which is based on the Phoenix models. Some of the important features (that are essential for the network) behave very similarly to our knowledge, but others do not. Above all, the behaviour of the Na I doublet 8183, 8195 Å lines in the feature importance test agrees well with our knowledge. The Na I line, tracing the gravity (Riddick et al. 2007; Herczeg & Hillenbrand 2014; Manara et al. 2017) and the temperature of late-type stars (Kirkpatrick et al. 1991; Allen & Strom 1995; Riddick et al. 2007), is also essential for networks to determine stellar parameters of late-type stars and gravity. Based on Table 5, we find that the R1 8015–8130 Å, K I doublet 7665, 7699 Å, and Ba II, Fe I, and Ca I blend 6497 Å also behave similarly to our knowledge. On the other hand, unlike our knowledge that the Ca II IR triplet 8498, 8542, 8662 Å and Mg I 8807 Å trace the temperature (Kirkpatrick et al. 1991; Allen & Strom 1995; Luhman et al. 2003; Manara et al. 2013; Herczeg & Hillenbrand 2014), the networks do not rely much on these lines to estimate the temperature.
In the feature-importance results of extinction, we showed the interesting results that there are particularly influential features, although the extinction affects the overall shape of the spectrum, not the particular lines. One of the possible causes is the degeneracy between temperature and extinction. In our results, the features influential in determining the temperature tend to have high importance in extinction as well (e.g. the Na I doublet 8183, 8195 Å, the VO band, and Ha). Due to the degeneracy between the two parameters, the over- or under-estimation of the temperature can be compensated for by an over- or underestimate of extinction. This means that if the features important for temperature are scrambled, the determination of the extinction can also be affected. Another possible cause is that the network determines extinction based on correlations between multiple features. For example, if the network relies on the ratios of several features to Ha, Ha may have relatively higher importance than others because scrambling Hα affects all these ratios.
The feature importance only shows how much the error increases by scrambling a certain feature. Therefore, it is difficult to clearly understand the reasons for the error increment. Compared to the spectra of template stars, however, it is obvious that cINN captures important information from the point at which absorption or emission exists. Many features have been used to predict parameters in addition to the main features indicated in the figures or in the table, but the important point is that the most influential features are the same as the tracers we already know. This confirms that even though we do not exactly know how cINNs learn the hidden rules from the training data, what cINNs learned is very close to the physical knowledge we have.
 |
Fig. 8 Comparison of the resimulation accuracy measures (RMSE in the top row, R2 score in the bottom) for the three spectral libraries to the spectral type of the class III templates. In all panels, the dotted red line indicates the results for the resimulation based on the literature stellar properties, and the black line shows the cINN-based outcomes. |
 |
Fig. 9 Feature importance evaluation for M-type synthetic models in the test set using Settl-Net. We present the median flux of M-type class III template stars in the first row. The grey area indicates the interquantile range between the 25 and 75% quantiles. The other three rows show the feature importance across the wavelength for each stellar parameter. Vertical lines and shades indicate the location of typical tracers of stellar parameters listed in Table 5. |
 |
Fig. 10 Feature importance evaluation for K-type synthetic models (left) and for G-type synthetic models (right) in the test set using Settl-Net. The panels in the first row show the median flux of K-type and G-type class III template stars, respectively. Lines and shades are the same as Fig. 9. |
Tracers whose feature importance values are higher than the fiducial value of median plus one standard deviation are indicated, meaning that marked tracers are significantly important features for determining each stellar parameter.
7 Simulation gap and the best network
In Sects. 5.1.1 and 5.2.1 we showed that for the synthetic models, our cINNs predict stellar parameters perfectly and for the template stars, network predictions agree well with the literature values within an error of 5–10%. The difference between literature values and network predictions slightly varies depending on the characteristics of the template stars. In Sects 5.1.2 and 5.2.2 we confirmed that resimulation of the spectrum based on the network prediction restored the original input spectrum well. This means that the network successfully finds the most suitable model that satisfies the given observational data, as the network is designed to do. In other words, the very good resimulation results indicate that cINNs provided us with the best results within the physics it has learned.
Interestingly, the resimulated spectrum based on the network prediction is closer to the original input spectrum than the resim-ulated spectrum based on the literature values for template stars (see Fig. 5 and Table A.1), despite the discrepancy between the network prediction and literature value. This can be considered to be one of the following two cases. One is because there is a simulation gap, that is, a gap between the physics within training data (i.e. the Phoenix atmosphere models), and the physics of the real world. The other is because of misclassification, meaning that the literature value used as a reference in this paper is inaccurate. In the former case, no matter how perfectly trained the network is in terms of machine learning, it encounters inherent limitations. The simulation gap can be improved with better training data.
The three Phoenix libraries used in this paper reflect many important physics and characteristics of stellar atmosphere, but they do not reflect reality perfectly. Therefore, we suspect that the parameter predictions differ from the literature values because of the simulation gap, even though the resimulation results are almost perfect. In this section, we introduce a method for quantifying the simulation gap using the trained cINN and for determining how large the gap is between the Phoenix models and reality. Finally, we draw comprehensive conclusions about the performance and usage of our cINNs.
7.1 Quantifying the simulation gap
As explained in Sect. 2.1, cINN consists of the main network that connects parameters (x) and latent variables (z) and the conditioning network (h) that transforms the input observation (y) into the useful representative (i.e. condition, c). Both are trained together, and the conditioning network in this paper compresses 2930 features (y1…,y2930) included in one spectrum into 256 conditions (c1,…, c256). If the condition of the real observational data that are passed through the conditioning network (cobs) follows the same probability distribution as the condition of the training data (ctrain), this means that there is no simulation gap because the conditioning network extracts only important features from the spectrum.
However, unlike the latent variables that were set up to follow a prescribed distribution (i.e. a standard normal distribution), the distribution of conditions does not follow a certain known distribution. Therefore, we built a network (k) that transformed the distribution of conditions (p(c)) into a prescribed probability distribution. The k network based on the cINN architecture is described as k(c) = s, and the output s was trained to follow a standard normal distribution. By definition of the cINN architecture, the dimensions of c and s are the same.
Using the conditioning network h and transformation network k, we checked the simulation gap between the Phoenix models and template stars by comparing the distribution of the transformed condition of template stars k(h(ytpl)) = stpl with the distribution of transformed condition of the training data strain, which follows a known distribution. We evaluated the simulation gap based on the R2 score between two probability distributions, p(strain) and p(stpl). The larger the R2 value, the smaller the simulation gap.
7.2 Simulation gap
We trained transformation networks (k) for each cINNs (Settl-Net, NextGen-Net, and Dusty-Net) and compared the probability distribution of the transformed conditions of the training data and template stars. Figure 11 shows that the distribution of the training data (blue line) follows the prescribed standard normal distribution well (pink line), but the distribution of the template stars (black) differs from that of the training data. Each star has 256 condition components, but we present all these components in one distribution. The R2 scores for all template stars are 0.805, 0.709, and 0.425 for Settl, NextGen, and Dusty, respectively. The Dusty model seems to have the widest simulation gap, but we need to consider that Dusty-Net has a narrower training range than the parameter space of the template stars.
As the performance of the cINN varies depending on the temperature of the template star, we divided the stars into three groups based on the prediction performance of the networks shown in Sect. 5.2.1 (see Figs. 3 and 4). For example, Settl-Net and NextGen-Net predicted parameters that agreed well with the literature values, especially for stars with temperatures between ~3000 and ~5000 K. We therefore divided the stars into three groups based on 3000 and 5000 K for Settl-Net and NextGen-Net. In the case of Dusty-Net, we divided groups based on 3000 and 4000 K due to the temperature upper limit of 4000 K for the Dusty training set.
In the case of the Settl and NextGen libraries (Fig. 12), the earlier the spectral type, the smaller the gap, and Settl has a smaller gap than NextGen in the overall temperature range. While the simulation gap is small for hot stars above 3000 K, the gap is large for later-type stars below 3000 K. In the case of NextGen, in particular, the simulation gap is very large for stars below 3000 K. In the case of Dusty, the simulation gap for the coldest group (T < 3000 K) is also very large and comparable to that for hot stars (T > 4000 K), which is beyond the temperature range of the Dusty library.
The large gap for the lowest temperature group (T < 3000 K) is an obvious result because perfectly implementing the atmosphere of late-type stars through the simulation is a much more difficult task than for the earlier-type stars. For late-type stars, condensation of vapour is essential, but the relevant physical processes are complex, making it very difficult to produce a good atmosphere model. Thus, these results demonstrate the inherent limitations of modelling low-temperature stars. These results show that the degree of the simulation gap varies with the characteristics of the star, just as the difference between the prediction of cINN and the literature value varies, as shown in Sect. 5.2.1.
Interestingly, Settl and NextGen both have the smallest simulation gaps for early-type stars with temperatures above 5000 K. However, in Figs. 3 and 4, the difference between the MAP prediction and the literature value of this group is slightly larger than that of the intermediate-temperature group (3000–5000 K). The smallest simulation gap (Fig. 12) and good resimulation results better than the resimulation of literature values (Fig. A.4 and Table A.1) imply that MAP estimates of our networks for early-type stars above 5000 K are sufficiently reliable. Therefore, we suggest that the parameter estimations by our networks may be more accurate than the literature values for early-type stars above 5000 K.
 |
Fig. 11 Probability distributions of transformed conditions of the training data (blue) and template stars (black) for three networks. The gap between the blue and black lines indicates the gap between the Phoenix model and the template spectrum. The R2 value between the blue and black line and the number of template stars used is presented in the upper left corner of each panel. |
7.3 Best network
The simulation gap is clearly large for late-type stars. Interestingly, however, our cINNs nevertheless predict the temperature and surface gravity well. First of all, all three networks had poor predictions of extinction for late-type stars below 3000 K. It is therefore very difficult for the network to estimate extinction accurately for stars in this temperature range, and the estimated extinction is not very reliable compared to the other two stellar parameters. However, Settl-Net, NextGen-Net, and Dusty-Net estimated the temperature accurately with maximum errors of less than 10, 5, and 15%, respectively, despite the large simulation gap. This is a sufficiently accurate prediction considering the temperature interval between one subclass of stellar spectral type (see Fig. 3). Using the combined error in Fig. 4, we demonstrate that Dusty-Net and Settl-Net predict the surface gravity and temperature accurately within 5% for late-type stars as well as early-type stars, despite the simulation gap of late-type stars. This shows that our networks are still applicable to low-temperature stars despite the limitations of the training data. The performance of NextGen-Net was relatively poor for low-temperature stars compared to the other two networks, which is explained by the large simulation gap shown in Fig. 12.
On the other hand, for earlier-type stars with relatively small simulation gaps, the network performs more reliably. Except for one or two outliers, Settl-Net and NextGen-Net both accurately predict temperature and gravity within an error of 5–10% at most. NextGen-Net tends to estimate extinction and temperature slightly higher than Settl-Net. NextGen-Net apparently adopts a degenerate solution that satisfies the same input spectrum by increasing both extinction and temperature slightly. Overall, Settl-Net, with the smallest simulation gap, shows the best performance of the three networks.
We conclude that Settl-Net is the best network considering the parameter prediction performance and the simulation gap. For low-temperature stars (e.g. M-type stars), Dusty-Net also shows comparable performance to Settl-Net. However, because the stellar parameter coverage (i.e. temperature and gravity) of Settl-Net is wider than that of Dusty-Net, Settl-Net is more versatile and usable. Based on our overall results, we therefore recommend using Settl-Net when applying the network to real observations. The only limitation to be cautious of is the estimation of extinction. Regardless of the spectral type of the stars, a cINN estimates temperature and gravity accurately, but we caution about estimating extinction when the estimated temperature is below 3000 K.
 |
Fig. 12 Probability distributions of transformed conditions of the training data and template stars. Each column represents three networks (Settl-Net, NextGen-Net, and Dusty-Net), and each row represents the group of template stars depending on their temperature |
8 Summary
We introduced a novel tool for estimating stellarparameters from the optical spectrum of an individual young low-mass star. cINN is one of the deep-learning architectures that specialise in solving a degenerate inverse problem. The degenerate problem here means that due to the inevitable information loss during the forward process from the physical system to observation, different physical systems are mapped onto similar or almost identical observations. Many of the main tasks in astrophysics involve solving degenerate inverse problems, such as estimating physical properties from observations. We developed a cINN for young low-mass stars to efficiently diagnose their optical spectra and estimate stellar parameters such as effective temperature, surface gravity, and extinction.
The cINN adopts a supervised learning approach, meaning that the network is trained on the database consisting of numerous well-labelled data sets of physical parameters and observations. However, it is difficult to collect a sufficient number of well-interpreted observations in reality. Therefore, we instead used synthetic observations to generate enough training data. In this work, we used three Phoenix stellar atmosphere libraries (i.e. Settl, NextGen, and Dusty) to produce the database for the training and evaluation of the network. By interpolating the spectrum in the temperature - gravity space and adding the extinction effect on the synthetic spectra, we produced a database for each Phoenix library consisting of 65 536 synthetic models. To produce the databases, we randomly sampled three parameters from the given parameter ranges. The Settl and NextGen databases cover the temperature range of 2600–7000 K and the log(ɡ/cm s−2) range of 2.5−5. The Dusty database covers the temperature of 2600–4000 K and log(g/cm s−2) of 3–5. All three databases have extinction values within 0–10 mag. Then, we built and trained cINNs using each database, but only used 80% of the synthetic models in the database to train the network and retained the rest for evaluation. We presented three cINNs that learned different Phoenix atmosphere models: Settl-Net, NextGen-Net, and Dusty-Net.
We validated the performance of our cINNs in various methods. Our main results are listed below.
All three networks provided perfect predictions on the test set with an RMSE lower than 0.01 dex for all three parameters, demonstrating that the cINNs are well trained. Additionally, we resimulated the spectrum using the parameters estimated by the network using our interpolation method and compared it with the original input spectrum. The resim-ulated spectra perfectly match the input spectra of the test models with RMSE of about 10−7. These results prove that our three cINNs perfectly learned the hidden rules in each training data set.
To test the performance on the real observational data, we analysed 36 class III template stars that were interpreted by Manara et al. (2013, 2017) and Stelzer et al. (2013) with our cINNs. We demonstrated that the stellar parameters estimated by our cINNs agree well with the literature values.
Each network has a slightly different error depending on the temperature of the given star. Settl-Net works especially well for M6.5–K1.0 (2935–5000 K) stars, and NextGen-Net works well for M4.5–K1.0 (3200–5000 K) stars. Dusty-Net works well for M5.5–M0.0 (3060–4000 K) stars. The temperature upper limit of the Dusty training data is 4000 K, and Dusty-Net works well for stars within its training range. For stars in other temperature ranges, the three networks perform well, with an error smaller than 10%.
The most difficult parameter for cINNs to predict is the extinction of cold stars with temperatures lower than 3200 K. All three networks tend to estimate a higher extinction than the literature value for cold stars. However, cINNs estimate extinction well for hot stars with temperatures above 3200 K.
We resimulated spectra based on cINN estimations and literature values and compared them with the original input spectrum. Interestingly, most of the resimulated spectra based on cINN estimations are closer to the input spectra than the resimulated spectra derived from the literature values. This implies that our cINNs understand the physics in each Phoenix library well and are able to find the best-fitting Phoenix model (i.e. parameters) for the given observation.
The resimulations are perfect even though the prediction of the network is slightly different from the literature. This can be explained by the gap between the Phoenix model and reality, the so-called the simulation gap. We quantified the simulation gap between each library and template stars using the conditioning networks included in our cINNs. We confirm that the simulation gaps are relatively large for cold stars below 3000 K, where the cINNs have difficulty in estimating extinction. We confirm that the simulation gap is small for hot stars, where the cINNs predict the parameters well.
The overall results imply that although there is an obvious gap between the Phoenix model and reality, especially for cold stars below 3000 K, our networks can nonetheless provide reliable predictions for all stars within an error of 5–10%, especially for temperature and gravity. Extinction estimated by cINN is also reliable unless the estimated temperature is lower than 3200 K.
We investigated on which parts of the spectrum the cINN relies most to predict stellar parameters and compared the important features with typically used stellar parameter tracers. We find that cINN relies on different features depending on the physical parameters and on the input observations (e.g. spectral types). We confirm that the main features are equivalent to the typically used tracers, such as Hα 6563 Å and the Na I doublet 8183, 8195 Å.
Our overall results show that our cINNs perform reliably enough to be applicable to real observational data. Of the three networks introduced in this paper, we recommend Settl-Net trained on the Settl library as the best network because of its remarkable performance and versatility in the parameter space.
Acknowledgements
This work was partly supported by European Union’s Horizon 2020 research and innovation program and the European Research Council via the ERC Synergy Grant “ECOGAL” (project ID 855130), and the Marie Sklodowska-Curie grant DUSTBUSTERS (project No 823823), by the Deutsche Forschungsgemeinschaft (DFG) via the Collaborative Research Center “The Milky Way System” (SFB 881 − funding ID 138713538 − subprojects A1, B1, B2 and B8), by the Heidelberg Cluster of Excellence (EXC 2181 −390900948) “STRUCTURES”, funded by the German Excellence Strategy, and by the German Ministry for Economic Affairs and Climate Action in project “MAINN” (funding ID 50OO2206). We also thank for computing resources provided by the Ministry of Science, Research and the Arts (MWK) of the State of Baden-Württemberg through bwHPC and DFG through grant INST 35/1134−1 FUGG and for data storage at SDS@hd through grant INST 35/1314−1 FUGG.
Appendix A Supplemental materials
In this appendix, we present supplementary figures and the table mentioned in our main results (sections 5–6).
Appendix A.1 Prediction performance
We evaluated the performance of three networks (Settl-Net, NextGen-Net, and Dusty-Net) on 13,107 synthetic test models drawn from the corresponding database by comparing the MAP predictions from the network and the true values of the models. We present the result of Settl-Net in Fig. A.1 as representative because the other two networks (NextGen-Net and Dusty-Net) also show very similar results. The figure shows that the network estimates all three parameters perfectly with very small RMSEs.
 |
Fig. A.1 2D histograms comparing the MAP values estimated by Settl-Net and the true values for the entire test models of the Settl database. The colours indicate the number of models at each point in the 2D histograms. In the lower right corner, we present the RMSE and the number of test models (Ntest). |
Appendix A.2 Resimulation
We validated the cINN predictions on the synthetic test data (Sect. 5.1.2) and on real template spectra (Sect. 5.2.2) by res-imulating the spectra corresponding to the MAP estimates with our spectral library interpolator (Sect. 3.1) and comparing the result to the respective input spectra.
Analogously to Fig. 1, Figs. A.2 and A.3 show the median relative error of the resimulated spectra (left panel) and the distributions of the RMSEs (right panel) for the 13,107 synthetic test spectra when evaluated with the cINN models trained on NextGen and Dusty, respectively.
Table A.1 provides a summary of the resimulation results for the cINN predictions on the class III template spectra (see Sect. 5.2.2 and also Tables 1 and 3). We list the RMSEs and R2 scores of the resimulated spectra with respect to the corresponding input spectra for the resimulation based on the literature and cINN-predicted parameters for all three spectral libraries.
Figures A.4 and A.5 provide additional examples of the resimulation results by comparing the resimulated spectra to the input spectra and the outcomes between the three libraries, analogously to Fig. 5. In particular, these two figures show examples in which the resimulated spectra based on the cINN MAP estimates appear to match the input spectra notably better than the respective resimulation outcome based on the literature properties of the given class III templates.
Lastly, Fig. A.6 provides an overview of the resimulation results for all class III template spectra for the cINN trained on the Settl library, corresponding to the top left panels in Figs. 5, A.4, and A.5.
 |
Fig. A.2 Resimulation results of NextGen-Net for the entire synthetic spectra in the test set. Left: Median relative error across the wavelength range of the resimulated spectra based on the MAP predictions of the cINN trained on the NextGen models averaged over the 13,107 synthetic spectra in the test set. The grey envelope indicates the interquantile range between the 25% and 75% quantiles. Right: Histogram of the RMSEs of the 13,107 resimulated spectra. The mean resimulation RMSE across the test set is 2.28 ± 2.48 × 10−7. |
 |
Fig. A.3 Resimulation results of Dusty-Net for the entire synthetic spectra in the test set. Left: Median relative error across the wavelength range of the resimulated spectra based on the MAP predictions of the cINN trained on the Dusty models averaged over the 13,107 synthetic spectra in the test set. Here the grey envelope indicates the interquantile range between the 25% and 75% quantiles. Right: Histogram of the RMSEs of the 13,107 resimulated spectra. The mean resimulation RMSE across the test set is 9.01 ± 7.34 × 10−8. |
Summary of the resimulation test for the literature values and cINN MAP predictions for the three different spectral libraries, listing the RMSEs and R2 scores of the resimulated spectra.
 |
Fig. A.6 Resimulation results for all class III templates for the cINN trained on the Settl library. In each panel, the black curve indicates the observed spectrum, and the red and blue curves correspond to the spectra that were resimulated based on the cINN MAP estimates and literature properties, respectively. The latter values are summarised in the table in each panel. If either the red or blue or both curves are lacking, the corresponding set of parameters could not be resimulated. For the RMSEs and R2 scores of the resimulated spectra, see Table A.1. |
Appendix A.3 Feature importance
We investigated the important feature on which NextGen-Net and Dusty-Net rely most. We divided the synthetic observations into three groups depending on their spectral types (e.g. M-, K-, and G-types). We present the results of NextGen-Net and Dusty-Net for M-type stars in Fig. A.7. We do not present the results of NextGen-Net for K- and G-type stars because the overall results are similar to that of Settl-Net presented in Fig. 10.
 |
Fig. A.7 Feature importance evaluation for M-type synthetic models in the test set using NextGen-Net (left) and Dusty-Net (right). The first row shows the median flux of M-type class III template stars. The lines and shades are the same as in Fig. 9. |
References
- Abraham, S., Aniyan, A. K., Kembhavi, A. K., Philip, N. S., & Vaghmare, K. 2018, MNRAS, 477, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, Philos. Trans. R. Soc. London Ser. A, 370, 2765 [Google Scholar]
- Allen, L. E., & Strom, K. M. 1995, AJ, 109, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Ardizzone, L., Kruse, J., Rother, C., & Köthe, U. 2019a, in Analyzing inverse problems with invertible neural networks, in 7th International Conference on Learning Representations [Google Scholar]
- Ardizzone, L., Lüth, C., Kruse, J., Rother, C., & Köthe, U. 2019b, ArXiv e-prints [arXiv:1907.02392] [Google Scholar]
- Ardizzone, L., Kruse, J., Lüth, C., et al. 2021, Lect. Notes Comput. Sci., 12544, 373 [CrossRef] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bochanski, J. J., Hawley, S. L., Covey, K. R., et al. 2010, AJ, 139, 2679 [NASA ADS] [CrossRef] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45, 5 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- de Beurs, Z. L., Vanderburg, A., Shallue, C. J., et al. 2022, AJ, 164, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Dinh, L., Sohl-Dickstein, J., & Bengio, S. 2016, ArXiv e-prints [arXiv:1605.08803] [Google Scholar]
- Edwards, S., Kwan, J., Fischer, W., et al. 2013, ApJ, 778, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Eisert, L., Pillepich, A., Nelson, D., et al. 2023, MNRAS, 519, 2199 [Google Scholar]
- Fabbro, S., Venn, K. A., O’Briain, T., et al. 2018, MNRAS, 475, 2978 [Google Scholar]
- Fisher, A., Rudin, C., & Dominici, F. 2019, J. Mach. Learn. Res., 20, 1 [Google Scholar]
- Frasca, A., Alcalá, J. M., Covino, E., et al. 2003, A&A, 405, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (Cambridge, MA: MIT Press) [Google Scholar]
- Haldemann, J., Ksoll, V., Walter, D., et al. 2023, A&A, 672, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, T. J., Kirkpatrick, J. D., & Simons, D. A. 1994, AJ, 108, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [Google Scholar]
- Hur, H., Sung, H., & Bessell, M. S. 2012, AJ, 143, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, G., Witten, D., Hastie, T., & Tibshirani, R. 2017, An Introduction to Statistical Learning with Applications in R, Corrected at 8th Printing edn., Springer Texts in Statistics (New York, NY: Springer) [Google Scholar]
- Jeffries, R. D., Oliveira, J. M., Naylor, T., Mayne, N. J., & Littlefair, S. P. 2007, MNRAS, 376, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, D. E., Pellegrini, E. W., Ardizzone, L., et al. 2022, MNRAS, 512, 617 [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [Google Scholar]
- Kingma, D. P., & Ba, J. 2014, ArXiv e-prints [arXiv:1412.6980] [Google Scholar]
- Kingma, D. P., & Dhariwal, P. 2018, ArXiv e-prints [arXiv:1807.03039] [Google Scholar]
- Kirkpatrick, J. D., Henry, T. J., & McCarthy, D. W. Jr. 1991, ApJS, 77, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Kelly, D. M., Rieke, G. H., et al. 1993, ApJ, 402, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
- Ksoll, V. F., Ardizzone, L., Klessen, R., et al. 2020, MNRAS, 499, 5447 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Briceño, C., Stauffer, J. R., et al. 2003, ApJ, 590, 348 [Google Scholar]
- Manara, C. F., Testi, L., Rigliaco, E., et al. 2013, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Frasca, A., Alcalá, J. M., et al. 2017, A&A, 605, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molnar, C. 2022, Interpretable Machine Learning, 2nd edn. (India: Lulu.com) [Google Scholar]
- Olney, R., Kounkel, M., Schillinger, C., et al. 2020, AJ, 159, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Riddick, F. C., Roche, P. F., & Lucas, P. W. 2007, MNRAS, 381, 1067 [Google Scholar]
- Sharma, K., Kembhavi, A., Kembhavi, A., et al. 2020, MNRAS, 491, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Frasca, A., Alcalá, J. M., et al. 2013, A&A, 558, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testi, L. 2009, A&A, 503, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walmsley, M., Lintott, C., Géron, T., et al. 2021, MNRAS, 509, 3966 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmore, B. C., Lee, J. C., Chandar, R., et al. 2021, MNRAS, 506, 5294 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C., Wong, O. I., Rudnick, L., et al. 2019, MNRAS, 482, 1211 [NASA ADS] [CrossRef] [Google Scholar]
We downloaded the theoretical spectra from the websites https://osubdd.ens-lyon.fr/phoenix/ and http://svo2.cab.inta-csic.es/theory/newov2/
All Tables
Average prediction performance of three networks (Settl-Net, NextGen-Net, and Dusty-Net) on 13 107 Phoenix synthetic models in the test set.
Summary of cINN MAP predictions for the class III template spectra for the cINN models based on the three different spectral libraries.
Average absolute relative error between cINN predictions and literature values for the template stars.
Tracers whose feature importance values are higher than the fiducial value of median plus one standard deviation are indicated, meaning that marked tracers are significantly important features for determining each stellar parameter.
Summary of the resimulation test for the literature values and cINN MAP predictions for the three different spectral libraries, listing the RMSEs and R2 scores of the resimulated spectra.
All Figures
 |
Fig. 1 Resimulation results of Settl-Net for the entire synthetic spectra in the test set. The left panel presents the median relative error across the wavelength range of the resimulated spectra based on the MAP predictions of the cINN trained on the Settl models averaged over the 13 107 synthetic spectra in the test set. The grey envelope indicates the interquantile range between the 25 and 75% quantiles. In the right panel, we present the histogram of the RMSEs of the 13 107 resimulated spectra. The mean resimulation RMSE across the test set is 3.01 ± 4.35 × 10−7. |
| In the text | |
 |
Fig. 2 Comparison of MAP predictions with literature values in Table 1. Stars are basically denoted by circles, but triangles denote stars that were excluded in analyses such as RMSE calculation either because their literature temperature values exceed the cINN training range or because their literature surface gravity values are lacking. The colour indicates the temperature deviation between the MAP estimate and the literature value. We indicate the training range of each parameter with dotted green lines. In the third column, the horizontal grey area presents the 1σ uncertainty (i.e. 0.2 mag) of extinction provided by the literature. |
| In the text | |
 |
Fig. 3 Relative temperature deviations of the template stars between the MAP estimates and the literature values sorted by their spectral type. Different colours and symbols indicate the results of the three different cINNs. The pink area indicates the uncertainty of the literature temperature value. We only present template stars whose literature temperature value is within the network training range. |
| In the text | |
 |
Fig. 4 Average relative error of the template stars between the MAP estimates and the literature values sorted by their spectral type. The average error is calculated as the rms of the relative errors of temperature and gravity, both in log scale (Eq. (9)). The pink area indicates the ltr uncertainty of the literature value. We only present template stars whose literature temperature value is within the network training range and whose literature gravity value is presented. The colour codes are the same as in Fig. 3. |
| In the text | |
 |
Fig. 5 Resimulation results for the class III star SO797. The columns show the results for the three different spectral libraries Settl, NextGen, and Dusty. Top: comparison of the resimulated spectrum. The blue spectrum indicates the resimulation derived from the literature stellar parameters from Table 1. The red spectrum shows the corresponding resimulation based on the cINN MAP prediction. The respective input parameters for the resimulation are summarised in the table in the bottom right corner. The relative residuals (Iresim – Iin)/Iin of the resimulated spectra compared to the input spectrum are shown in the bottom panels. |
| In the text | |
 |
Fig. 6 Comparison of the median relative error of the resimulated spectra for the class III template stars between the resimulations based on the literature stellar parameters (blue, see Table 1) and the cINN MAP predictions (red). From top to bottom, the panels show the corresponding results for the three tested spectral libraries Settl, NextGen, and Dusty. |
| In the text | |
 |
Fig. 7 Average error for the resimulation spectra for the class III template stars. Top: histograms of the RMSEs for the resimulation on the class III template spectra for the three different spectral libraries. Bottom: histograms of the corresponding R2 scores for the resimulated spectra. |
| In the text | |
 |
Fig. 8 Comparison of the resimulation accuracy measures (RMSE in the top row, R2 score in the bottom) for the three spectral libraries to the spectral type of the class III templates. In all panels, the dotted red line indicates the results for the resimulation based on the literature stellar properties, and the black line shows the cINN-based outcomes. |
| In the text | |
 |
Fig. 9 Feature importance evaluation for M-type synthetic models in the test set using Settl-Net. We present the median flux of M-type class III template stars in the first row. The grey area indicates the interquantile range between the 25 and 75% quantiles. The other three rows show the feature importance across the wavelength for each stellar parameter. Vertical lines and shades indicate the location of typical tracers of stellar parameters listed in Table 5. |
| In the text | |
 |
Fig. 10 Feature importance evaluation for K-type synthetic models (left) and for G-type synthetic models (right) in the test set using Settl-Net. The panels in the first row show the median flux of K-type and G-type class III template stars, respectively. Lines and shades are the same as Fig. 9. |
| In the text | |
 |
Fig. 11 Probability distributions of transformed conditions of the training data (blue) and template stars (black) for three networks. The gap between the blue and black lines indicates the gap between the Phoenix model and the template spectrum. The R2 value between the blue and black line and the number of template stars used is presented in the upper left corner of each panel. |
| In the text | |
 |
Fig. 12 Probability distributions of transformed conditions of the training data and template stars. Each column represents three networks (Settl-Net, NextGen-Net, and Dusty-Net), and each row represents the group of template stars depending on their temperature |
| In the text | |
 |
Fig. A.1 2D histograms comparing the MAP values estimated by Settl-Net and the true values for the entire test models of the Settl database. The colours indicate the number of models at each point in the 2D histograms. In the lower right corner, we present the RMSE and the number of test models (Ntest). |
| In the text | |
 |
Fig. A.2 Resimulation results of NextGen-Net for the entire synthetic spectra in the test set. Left: Median relative error across the wavelength range of the resimulated spectra based on the MAP predictions of the cINN trained on the NextGen models averaged over the 13,107 synthetic spectra in the test set. The grey envelope indicates the interquantile range between the 25% and 75% quantiles. Right: Histogram of the RMSEs of the 13,107 resimulated spectra. The mean resimulation RMSE across the test set is 2.28 ± 2.48 × 10−7. |
| In the text | |
 |
Fig. A.3 Resimulation results of Dusty-Net for the entire synthetic spectra in the test set. Left: Median relative error across the wavelength range of the resimulated spectra based on the MAP predictions of the cINN trained on the Dusty models averaged over the 13,107 synthetic spectra in the test set. Here the grey envelope indicates the interquantile range between the 25% and 75% quantiles. Right: Histogram of the RMSEs of the 13,107 resimulated spectra. The mean resimulation RMSE across the test set is 9.01 ± 7.34 × 10−8. |
| In the text | |
 |
Fig. A.4 Resimulation results for the class III star RXJ0445.8+1556. Same as Fig. 5. |
| In the text | |
 |
Fig. A.5 Resimulation results for the class III star CD_29_8887A. Same as Fig. 5. |
| In the text | |
 |
Fig. A.6 Resimulation results for all class III templates for the cINN trained on the Settl library. In each panel, the black curve indicates the observed spectrum, and the red and blue curves correspond to the spectra that were resimulated based on the cINN MAP estimates and literature properties, respectively. The latter values are summarised in the table in each panel. If either the red or blue or both curves are lacking, the corresponding set of parameters could not be resimulated. For the RMSEs and R2 scores of the resimulated spectra, see Table A.1. |
| In the text | |
 |
Fig. A.7 Feature importance evaluation for M-type synthetic models in the test set using NextGen-Net (left) and Dusty-Net (right). The first row shows the median flux of M-type class III template stars. The lines and shades are the same as in Fig. 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.