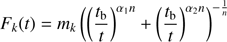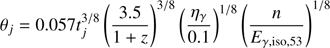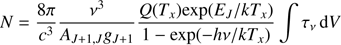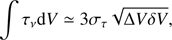| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833094 | |
| Published online | 07 December 2018 | |
X-shooter and ALMA spectroscopy of GRB 161023A
A study of metals and molecules in the line of sight towards a luminous GRB⋆
1
Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomí, s/n, 18008 Granada, Spain
e-mail: deugarte@iaa.es
2 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, 2100 Copenhagen Ø, Denmark
3 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
4 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
5 Department of Particle Physics and Astrophysics, Weizmann Institute of Science, 234 Herzl Street, Rehovot 761000, Israel
6 Joint ALMA Observatory, Alonso de Córdova 3107, Vitacura 763 0355, Santiago, Chile
7 INAF – Osservatorio Astronomico di Roma, Via Frascati 33, 00040 Monteporzio Catone, Italy
8 ASI-Space Science Data Centre, Via del Politecnico snc, 00133 Rome, Italy
9 Space Science Group, School of Physics, University College Dublin, Belfield, Dublin 4, Ireland
10 Astrophysics Research Institute, Liverpool John Moores University, IC2, Liverpool Science Park, 146 Brownlow Hill, Liverpool L3 5RF, UK
11 Instituto de Astrofísica y Centro de Astroingeniería, Facultad de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
12 INAF, Istituto Astrofisica e Planetologia Spaziali, Via Fosso del Cavaliere 100, 00133 Roma, Italy
13 Department of Physics and Earth Science, University of Ferrara, Via Saragat 1, 44122 Ferrara, Italy
14 IRAP, Université de Toulouse, CNRS, UPS, CNES, Toulouse, France
15 Department of Physics, University of Warwick, Coventry CV4 7AL, UK
16 Department of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK
17 Millennium Institute of Astrophysics (MAS), Nuncio Monseñor Sótero Sanz 100, Providencia, Santiago, Chile
18 Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301, USA
19 INAF – Osservatorio Astronomico di Brera, Via Bianchi 46, 23807 Merate (LC), Italy
20 School of Physics, University of Western Australia, M013, Crawley, WA 6009, Australia
21 European Southern Observatory, Karl-Schwarzschild Str. 2, 85748 Garching bei München, Germany
22 Department of Astronomy and Space Sciences, Istanbul University, 34119 Beyazıt, Istanbul, Turkey
23 Cosmic Dawn Center, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
24 Centre for Astrophysics and Cosmology, University of Nova Gorica, Vipavska 11c, Ajdovščina 5270, Slovenia
25 Department of Physics and Astronomy, Clemson University, Clemson, SC 29634, USA
26 Centre for Astrophysics and Cosmology, Science Institute, University of Iceland, Dunhagi 5, 107 Reykjavík, Iceland
27 Department of Physics, University of the Free State, 9300 Bloemfontein, South Africa
28 Astronomical Observatory Institute, Faculty of Physics, Adam Mickiewicz University, ul. Słoneczna 36, 60-286 Poznań, Poland
29 Department of Physics, University of Bath, Claverton Down, Bath BA2 7AY, UK
30 CAS Key Laboratory of Space Astronomy and Technology, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China
31 Australian Astronomical Observatory, PO Box 915 North Ryde, NSW 1670, Australia
Received:
25
March
2018
Accepted:
21
July
2018
Context. Long gamma-ray bursts (GRBs) are produced during the dramatic deaths of massive stars with very short lifetimes, meaning that they explode close to the birth place of their progenitors. Over a short period they become the most luminous objects observable in the Universe, being perfect beacons to study high-redshift star-forming regions.
Aims. We aim to use the afterglow of GRB 161023A at a redshift z = 2.710 as a background source to study the environment of the explosion and the intervening systems along its line of sight.
Methods. For the first time, we complement ultraviolet (UV), optical and near-infrared (NIR) spectroscopy with millimetre spectroscopy using the Atacama Large Millimeter Array (ALMA), which allows us to probe the molecular content of the host galaxy. The X-shooter spectrum shows a plethora of absorption features including fine-structure and metastable transitions of Fe, Ni, Si, C, and O. We present photometry ranging from 43 s to over 500 days after the burst.
Results. We infer a host-galaxy metallicity of [Zn/H] = −1.11 ± 0.07, which, corrected for dust depletion, results in [X/H] = −0.94 ± 0.08. We do not detect molecular features in the ALMA data, but we derive limits on the molecular content of log(NCO/cm−2) < 15.7 and log(NHCO+/cm−-12, which are consistent with those that we obtain from the optical spectra, log(NH2/cm−2)< 15.2 and log(NCO/cm−2) < 14.5. Within the host galaxy, we detect three velocity systems through UV, optical and NIR absorption spectroscopy, all with levels that were excited by the GRB afterglow. We determine the distance from these systems to the GRB to be in the range between 0.7 and 1.0 kpc. The sight line to GRB 161023A shows nine independent intervening systems, most of them with multiple components.
Conclusions. Although no molecular absorption was detected for GRB 161023A, we show that GRB millimetre spectroscopy is now feasible and is opening a new window on the study of molecular gas within star-forming galaxies at all redshifts. The most favoured lines of sight for this purpose will be those with high metallicity and dust.
Key words: gamma-ray burst: individual: GRB 161023A / techniques: spectroscopic / ISM: abundances / ISM: molecules / galaxies: ISM / submillimeter: ISM
Full Tables A.1 and A.2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/620/A119
© ESO 2018
1. Introduction
Long-duration gamma-ray bursts (GRBs) are produced by the deaths of very massive stars. As such, the lives of their progenitors are short and these are expected to explode within or near the star-forming regions in which they were formed. Their early emission outshines the rest of the Universe in gamma-rays for a few seconds. In optical they can also reach extreme luminosities during the first seconds, having reached a record absolute magnitude of −38.7 mag (in the rest-frame U-band; Bloom et al. 2009). Their afterglows are produced as material that has been ejected through jets at ultra-relativistic velocities collides with the interstellar medium, decelerating and emitting synchrotron radiation. This long-lasting emission can be usually detected at optical wavelengths for several days after the burst onset, and for weeks or even months at radio frequencies.
Gamma-ray bursts are consequently not only interesting sources for the study of some of the most extreme physics in the Universe, but can also be used as extremely luminous beacons that shine from the heart of star-forming regions. These beacons of light allow us to probe the region in which the GRB formed, its host galaxy, the intergalactic medium, and any intervening systems along the line of sight (e.g. Pollack et al. 2009). In fact, they are one of the only means of studying star-forming galaxies at very high redshift from the inside, independently of their size and luminosity (Fynbo et al. 2008). However, when studying the closest environment of the GRB, we have to consider that the intense radiation released during the GRB explosion has a detectable effect on the surroundings of the GRB. Afterglow emission has been shown to excite spectral lines up to distances of the order of 1 kpc within the host galaxy (e.g. Vreeswijk et al. 2007; D’Elia et al. 2009a).
The most significant drawback when studying GRBs and using them as light beacons is that they also fade very rapidly. This implies that, even using the largest telescopes, we need to have a very fast reaction time and use instrumentation that allows us to observe a broad spectral range simultaneously. This is the reason why instruments like the Gamma-ray Burst Optical/Near-infrared Detector (GROND; Greiner et al. 2008), with its seven-band simultaneous imaging capability, or X-shooter, capable of obtaining spectroscopy from 3000 to 24 800 Å in a single shot, were built. To observe the very early light curve and probe the phase when the gamma-ray emission is still ongoing, even faster approaches, such as robotic observatories (i.e. French et al. 2004; Boër et al. 1999), are needed.
The advances in millimetre and submillimetre instrumentation are giving us a new way of observing astronomical sources. For GRB studies, these wavelengths have the advantage that the peak emission is normally reached within hours to days after the burst, unlike the gamma-ray emission that peaks within seconds or the optical emission that reaches maximum within tens of seconds. In particular the Atacama Large Millimeter Array (ALMA) is now capable of responding to target-of-opportunity alerts with reaction times of the order of a day and with unprecedented sensitivities. These wavelengths are interesting because they normally cover the location of the peak synchrotron frequency during the first day and also cover some of the most prominent molecular transitions.
In this paper we present imaging and spectroscopy of the afterglow of GRB 161023A, including for the first time millimetre spectroscopy in search of several molecular features. This burst, at a redshift of z = 2.710, is amongst the group of most luminous afterglows detected to date, in both the optical and millimetre wavelengths.
Section 2 presents the observations and some details on the data reduction of the different data sets. Section 3 presents the results derived from these observations. In Sect. 4 we discuss these results, place them into the context of previous observations, and provide our conclusions. Throughout the paper we use the convention where Fν ∝ tανβ, and a cosmology with H0 = 71 km s−1 Mpc−1, ΩM = 0.3, and ΩV = 0.7 (Spergel et al. 2003).
2. Observations and data reduction
2.1. High-energy observations
GRB 161023A was first identified by INTEGRAL (INTErnational Gamma-Ray Astrophysics Laboratory) as a long gamma-ray burst that triggered the IBIS (Imager on-Board the INTEGRAL Satellite) detector at 22:38:40 UT on 23 October 2016 (Mereghetti et al. 2016), which we use as the trigger reference time T0 throughout this paper. The GRB had a T90 duration of ∼80 s in the IBIS observations. Only lower limits on the fluence of the burst were given using the IBIS data, as the brightness of the event resulted in saturation of the detectors. The burst was also observed by Konus-Wind at 22:39:12.321 UT (the later detection with respect to INTEGRAL is due to the lower sensitivity of Konus with respect to IBIS) which measured a duration of ∼50 s. The burst had a fluence of (4.2 ± 0.6) × 10−5 erg cm−2 in the 20 keV–10 MeV observer-frame energy range and a peak energy of 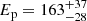 keV (Frederiks et al. 2016). Finally, the burst was also detected by AstroSat CZTI (Cadmium Zinc Telluride) in the 40–200 keV range with a T90 duration of 44 s (Sharma et al. 2016). The light curve showed a single peak at 22:39:10.00 UT.
keV (Frederiks et al. 2016). Finally, the burst was also detected by AstroSat CZTI (Cadmium Zinc Telluride) in the 40–200 keV range with a T90 duration of 44 s (Sharma et al. 2016). The light curve showed a single peak at 22:39:10.00 UT.
Using the Konus-Wind fluence and spectral fit, together with the redshift of z = 2.710 (Tanvir et al. 2016, refined in this paper), we determine the isotropic-equivalent released energy in the 1 keV–10 MeV rest-frame band to be Eiso, γ = (6.3 ± 0.9)×1053 erg, which is toward the upper end of the typical energy release of GRBs (Butler et al. 2007; Amati et al. 2002; Ackermann et al. 2013). We also use the redshift to transform the peak energy to rest frame, 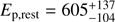 keV. These values lie well within the expected values for the Ep − Eiso correlation for long GRBs (Amati et al. 2009).
keV. These values lie well within the expected values for the Ep − Eiso correlation for long GRBs (Amati et al. 2009).
Follow-up observations of the burst were performed by the Neil GehrelsSwift Observatory (Gehrels et al. 2004), which detected an X-ray counterpart starting 34.8 ks after the trigger (D’Aì et al. 2016). The analysis of the X-ray afterglow data (Evans et al. 2009) showed a spectral slope of 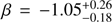 , and a decay with a slope of
, and a decay with a slope of 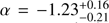 (considering a single power-law decay). The intrinsic equivalent hydrogen column density derived from the X-ray attenuation is consistent with the Galactic value of NH = 3.18 × 1020 cm−2, allowing us to only derive a 3-σ upper limit at the redshift of the host galaxy of NH < 3.0 × 1022 cm−2.
(considering a single power-law decay). The intrinsic equivalent hydrogen column density derived from the X-ray attenuation is consistent with the Galactic value of NH = 3.18 × 1020 cm−2, allowing us to only derive a 3-σ upper limit at the redshift of the host galaxy of NH < 3.0 × 1022 cm−2.
2.2. Optical and infrared photometry
A bright optical counterpart to GRB 161023A was quickly identified by the MASTER II (Mobile Astronomical System of TElescope Robots) robotic telescope (Gorbovskoy et al. 2016), starting at 22:39:24 UT (T0 + 44 s). The afterglow brightness reached a maximum ∼3 min after the burst, with a magnitude of ∼12.5. Early follow-up was also obtained by the Watcher robotic telescope which started observing 43 s after the trigger (Martin-Carrillo et al. 2016), using 5 s images for the first ten minutes and then switching to 60 s exposures. The evolution as seen by Watcher also had an early rise in brightness, reaching a maximum 200 s after the burst at r′ = 12.8 mag, after which it decayed to r′ = 14.4 mag 893 s after the burst. Later observations were reported by TAROT (Télescopes à Action Rapide pour les Objets Transitoires), ranging from 64 to 143 min after the burst (Klotz et al. 2016b), the Faulkes Telescope South 10.6 h after the burst (Guidorzi et al. 2016), the Zadko telescope 0.55 days after the GRB (Klotz et al. 2016a), and the GROND detector (Greiner et al. 2008) mounted on the 2.2 m MPG (Max-Planck-Gesellschaft) telescope, at ESO’s (European Southern Observatory) La Silla observatory, Chile, for which the first epoch, starting 25.2 h after the burst, was reported by Krühler & Greiner (2016).
In this paper we present the observations performed with the 0.4 m Watcher telescope (French et al. 2004), the 0.25 m TAROT La Silla telescope, the 2.0 m Faulkes South telescope, the 1.0 m Zadko Gingin telescope, and the 2.2 m MPG telescope with GROND. Our photometric data set also includes an r′ -band observation obtained during the acquisition of the X-shooter spectrum at ESO’s Very Large Telescope (VLT). We have added observations obtained using the FORS2 (FOcal Reducer/low dispersion Spectrograph 2) instrument at the VLT as part of a different programme (Wiersema et al., in prep.). Finally, we include a deep observation obtained with FORS2 in March 2018 in search of the host galaxy, which remains undetected down to a strong 3-σ limit of 26.5 mag. The photometry of all these data was obtained based on Sloan magnitudes of secondary standard stars based on GROND observations of SDSS (Sloan Digital Sky Survey) fields. In the case of FORS2 the observations performed with the Rspecial filter were calibrated directly with the Sloan r′. The photometric data are presented in Table A.1 and shown in Fig. 1.
 |
Fig. 1. Light curve of GRB 161023A in optical and near-infrared bands. Downward pointing triangles are 3-σ upper limits. The grey vertical lines mark the times of the X-shooter and ALMA observations. The solid and dashed lines show the fits of the photometric data to broken power laws, as explained in Sect. 3.1. Plotted in brown is the tail of the gamma-ray emission detected by Konus-Wind. |
The field of GRB 161023A was also observed at late times with the Infrared Array Camera (IRAC; Fazio et al. 2004) on the Spitzer Space Telescope (Werner et al. 2004), as part of the extended Swift GRB HOst gAlaxy Legacy Survey (SHOALS; Perley et al. 2016a). We acquired 108 dithered images of 100 s each for a total exposure time of 3.0 h, all using the 3.6 μm filter (channel 1). The post-basic calibrated data image was downloaded from the Spitzer legacy archive; no source is detected at the position of the GRB to a limit of > 25.3 mag.
2.3. X-shooter spectroscopy
The X-shooter spectrograph (Vernet et al. 2011), installed on ESO’s Very Large Telescope (Chile) observed the optical counterpart of GRB 161023A at a mean epoch 2.795 h after the burst. The observation consisted of 2 × 600 s exposures covering the spectral range between 3000 and 24 800 Å.
The spectral resolution is slightly different in the three arms. Furthermore, when the seeing is smaller than the slit width, the actual resolution is better than the nominal resolution for the given arm and slit. We determine the real spectral resolution following the procedure outlined in Selsing et al. (2018) and find resolutions of 38.5 km s−1, 31.4 km s−1, and 35.5 km s−1 for the UVB (UV-Blue), VIS (Visible), and NIR (near-IR) arms, respectively.
In the X-shooter spectrum we identify numerous absorption features (see Table A.2 and Fig. 2) including the hydrogen Lyman series down to the Lyman limit, S II, Si II, Si IV, C IV, Al II, Fe II, Ni II, Zn II, Mg II, Mg I, Mn II and O I, many of which have been reported by Tanvir et al. (2016). Several elements also show fine-structure lines and metastable transitions, at a redshift of z = 2.710, which are expected to be excited by the radiation of the GRB, confirming that this is indeed the redshift of the GRB. The absorption features also show several velocity components, as will be discussed in the following section. In addition, the spectrum shows multiple intervening systems along the line of sight ranging from ∼1200 km s−1 bluewards of the GRB redshift, down to z = 1.14 (see Sect. 3.4). This data set is available through the GRBSpec database1 (de Ugarte Postigo et al. 2014).
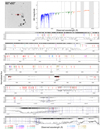 |
Fig. 2. X-shooter spectrum of GRB 161023A. Top left panel: acquisition image indicating the position of the slit. Top right panel: flux-calibrated spectrum. each colour represents one of the X-shooter arms. Horizontal gray bars mask the regions affected by strong telluric absorption bands. Below panels: normalised spectrum together with the 2D spectrum. Each of the different absorption systems are marked in a different colour, as indicated at the bottom. At the top of the 1D spectra we mark the telluric features with black lines, their widths being proportional to their intensity, as done in de Ugarte Postigo et al. (2010). |
2.4. ALMA observations
Millimetre observations were carried out in ALMA Bands 3 and 7 two days after the burst, from 25 October 2016 23:03:11.0 to 26 October 2016 00:22:33.3 UT, and from 26 October 2016 00:44:44.1 to 26 October 2016 01:42:38.4 UT, respectively. The configuration used 38 array elements with baselines ranging from 18 m to 1.2 km, equivalent to 5-374 kλ (Band 3) and 21-1300 kλ (Band 7). Integration time on source was 51 min (with PWV 1.0 mm) and 38 min (with PWV 0.74 mm), respectively. In Band 3, the correlator was set up in two low-resolution (15.6 MHz bins) 1.875 GHz wide spectral windows centred at ∼106 GHz and ∼108 GHz, and three high-resolution (one 0.122 MHz and two 0.244 MHz bins) 468.75 MHz wide spectral windows centred at 93.5, 96.4 and 96.8 GHz, respectively. In Band 7, the correlator was set up in four low-resolution (15.6 MHz) 1.875 GHz windows centred at 337.5, 339.4, 347.5, and 349.5 GHz.
The data were calibrated with CASA (Common Astronomy Software Applications, version 4.7, McMullin et al. 2007) using the calibration script provided in the ALMA archive, and subsequently images were produced by using the combined emission in each spectral window. The resolution achieved using natural weighting was 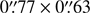 (PA 50°) and
(PA 50°) and 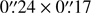 (PA 70°) for Bands 3 and 7, respectively. Moreover, data cubes were produced for the individual spectral windows that were imaged at the original resolution for the low-resolution windows and binned to 12 MHz for the high-resolution windows. The flux calibration was based on observations of the quasars J1924–2914 and J2056–4714 for Bands 3 and 7, respectively. In Table 1 we show the flux measurements obtained for the afterglow of GRB 161023A in each of the different spectral windows.
(PA 70°) for Bands 3 and 7, respectively. Moreover, data cubes were produced for the individual spectral windows that were imaged at the original resolution for the low-resolution windows and binned to 12 MHz for the high-resolution windows. The flux calibration was based on observations of the quasars J1924–2914 and J2056–4714 for Bands 3 and 7, respectively. In Table 1 we show the flux measurements obtained for the afterglow of GRB 161023A in each of the different spectral windows.
Flux measurements for the afterglow of GRB 161023A.
From the ALMA observations we derive the most precise coordinates (J2000) for the afterglow of GRB 161023A:
RA: 20:44:05.1718 (±0. s0003)
Dec: −47:39:47.921 (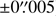 )
)
In the 350 GHz (Band 7) image obtained by ALMA, we identify four additional tentative sources detected at ≳3σ, as shown in Fig. 3. The coordinates and flux densities of these sources are given in Table 2. In the deep Spitzer image, shown in the middle panel, sources S2 and S3 are not detected. However, S4 is part of a bright extended galaxy and S1 is also detected at 24.9 ± 0.3 mag. The host galaxy of GRB 161023A is not detected down to a 3-σ limit of > 25.3 mag at 3.6 μm. Within the deep FORS2 image (bottom panel), we do not detect any optical counterparts to sources S2 or S3. As in the Spitzer image, S4 is detected in the outskirts of a bright spiral galaxy. S1 is faintly detected at a magnitude of r′ = 26.27 ± 0.24. The 3-σ limit for the host galaxy is r′ > 26.5 mag.
 |
Fig. 3. Top panel: continuum image obtained with ALMA at 350 GHz. The GRB afterglow is clearly seen in the centre of the image. Several other faint objects can be seen within the field-of-view, which measures 15″ × 15″. North is up and East is to the left. Centre panel: Spitzer image of the field in the 3.6 μm band, showing a slightly larger region. The box indicates the area of the upper figure. Sources S1 and S4 are detected. Bottom panel: late deep image obtained with FORS2 at VLT in the Rspecial band. Whereas ALMA sources S2, and S3 have no corresponding optical counterparts, S4 could be part of a nearby spiral galaxy to the South West and S1 is marginally detected. |
Sources tentatively detected in the neighbourhood of GRB 161023A in the 350 GHz band, with typical positional errors of 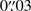 .
.
3. Results
3.1. Spectral energy distribution and light curves in the context of the fireball model
The standard fireball model (Sari et al. 1998, 1999) describes the temporal evolution of the afterglow light curve as a series of power laws. Similarly, the spectra of the afterglow are expected to be synchrotron radiation, which is described by several spectral power laws that meet at characteristic break frequencies: νm is the typical frequency of the electrons, νa the self-absorption frequency, and νc is the cooling frequency. Depending on several parameters that characterise the properties of the ejecta and the media with which the shock interacts, we obtain different spectral and temporal slopes for the different observed bands. The most relevant parameters that define these slopes are the electron index p, which describes the distribution of shock-accelerated electrons in the circumburst medium, and the density profile of the external medium with which the ejecta interacts. The density profile is often found to be uniform ∝r0 (as for an interstellar medium), but in some cases the data have been seen to be fit better with a wind medium, ∝r−2. This standard fireball is often complemented with the presence of a reverse-shock component at early times, with a sharper temporal rise and decay than expected for the forward shock of the fireball (Sari & Piran 1999; Kobayashi 2000; Kobayashi & Sari 2000).
To make a rough analysis in the context of this model we perform temporal and spectral fits of our data. In this analysis we ignore the first four Watcher r′-band datapoints, which are likely linked to the tail of the prompt gamma-ray emission, and behave in a similar way to that of the afterglow of GRB 080603A (Guidorzi et al. 2011). We then fit the early rise and subsequent decay with a smoothly broken power law:
Where mk is the normalisation for each band (left as a free and non-shared parameter), α1, 2 are the temporal slopes, tb is the break time, and n is the smoothness of the break (see e.g. Zeh et al. 2006 for more details). While for the early fit (between 0.001 and 0.1 d) we only use the r′ band, as we have no other colour information, the “normal” decay (after 0.1 d) and the late steep decay are fit in all bands with another smoothly broken power law, where we share all parameters in the different bands, except for the different normalisations. Such a fit takes the maximum amount of available data into account, leading to a more tightly constrained Spectral Energy Distribution (SED). We note that the “normal” decay slope result is identical in both fits. From these fits, we derive the following parameters for the optical light curve (see Fig. 1): the initial rise to peak αrise = 5.44 ± 0.13, the break from rise to decay tb, 1 = 0.00181 ± 0.00002 days (156 ± 2 s), the “normal” decay slope α1 = −1.063 ± 0.002, the break from normal to steep decay tb, 2 = 2.81 ± 0.30 days, and the post-break decay slope α2 = −2.25 ± 0.15. The break smoothness for the peak was left as a parameter free to vary and we find n1 = 0.605 ± 0.025, a very smooth rollover. The second break is also not sharp, we find n2 = 2.41 ± 0.60. As we find no evidence for a host-galaxy contribution to the light curve (especially considering the late deep limit from VLT/FORS2), we do not include a host value in the fit.
We have created an SED at the time of the ALMA observation (t − t0 = 50 h) spanning from the millimetre data all the way to the X-ray domain, observed with Swift/XRT, which is shown in Fig. 4. For this fit we interpolate the X-ray band to 50 h using the fits of the previous section. The optical and the X-ray data seem to be on the same synchrotron spectral segment: The optical to X-ray spectral slope, βOX = −1.021 ± 0.015, is consistent with the X-ray index, 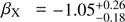 (a value obtained from the Swift/XRT pages2 that was calculated by fitting all the X-ray data), and is also very similar to the one obtained from the GROND photometry when performing a direct fit without assuming any host galaxy extinction (βO = −1.03 ± 0.05). The ALMA data are below the extrapolation, meaning that a spectral break must lie in-between the NIR and submillimetre wavelengths. This scenario is consistent with a standard fireball expanding in a medium with an electron index of p = 2.03, which implies β = −1.015 at frequencies higher than νc and β = −0.515 between νm and νc. However, the spectral slope between the two ALMA observations (βALMA = −0.29 ± 0.03) is shallower than β = −0.515, but is not compatible with β = +0.3, which would be expected below the νm frequency. This indicates that the peak spectral frequency is between the two bands. This is confirmed when we look at the spectral slope defined within the side bands of Band 3 which, thanks to their high signal-to-noise ratio (S/N) and in spite of the short wavelength range allow us to determine a slope of βBand 3 = +0.39 ± 0.13 consistent with the expected β = +1/3. The larger errors in Band 7 prevent us from determining the spectral slope, although a flux density decreasing toward shorter wavelengths is favoured.
(a value obtained from the Swift/XRT pages2 that was calculated by fitting all the X-ray data), and is also very similar to the one obtained from the GROND photometry when performing a direct fit without assuming any host galaxy extinction (βO = −1.03 ± 0.05). The ALMA data are below the extrapolation, meaning that a spectral break must lie in-between the NIR and submillimetre wavelengths. This scenario is consistent with a standard fireball expanding in a medium with an electron index of p = 2.03, which implies β = −1.015 at frequencies higher than νc and β = −0.515 between νm and νc. However, the spectral slope between the two ALMA observations (βALMA = −0.29 ± 0.03) is shallower than β = −0.515, but is not compatible with β = +0.3, which would be expected below the νm frequency. This indicates that the peak spectral frequency is between the two bands. This is confirmed when we look at the spectral slope defined within the side bands of Band 3 which, thanks to their high signal-to-noise ratio (S/N) and in spite of the short wavelength range allow us to determine a slope of βBand 3 = +0.39 ± 0.13 consistent with the expected β = +1/3. The larger errors in Band 7 prevent us from determining the spectral slope, although a flux density decreasing toward shorter wavelengths is favoured.
 |
Fig. 4. Spectral energy distribution of GRB 161023A at the time of the ALMA observations, 50 h after the GRB. |
By using the light-curve slopes together with the spectral slopes determined in the previous paragraphs, we can constrain the model even more. We use the closure relations (Gao et al. 2013) to determine that the fireball was expanding in an environment with an electron index of p = 2.06 ± 0.04. According to these assumptions, the spectral slopes are expected to be βmodel = −0.53 ± 0.02 for the case νm < ν < νc and βmodel = −1.03 ± 0.2 for νc < ν (consistent with the observed βOX = −1.021 ± 0.015). The temporal slopes for ν > νc, where we expect to have both optical and X-ray data, would be αmodel = −1.04 ± 0.03 before the jet break (consistent with the observed α1 = −1.063 ± 0.002), and αmodel = −2.06 ± 0.04 after the jet break (consistent with the observed α2 = −2.25 ± 0.15).
The joint fit of all data after 0.1 days, as described above, allows us to derive a very precise g′r′i′z′JHKS SED that takes all multi-colour data into account. We find no evidence for colour evolution; this would manifest itself in a high χ2 value as well as significant residuals from the fit, which we do not see. Fitting the SED with dust models from Pei (1992), considering the filter response curves, we find that the best fit is given by SMC (Small Magellanic Cloud) -like dust (in accordance with the majority of GRB sightlines, Kann et al. 2010; Greiner et al. 2011; Bolmer et al. 2018), although an LMC (Large Magellanic Cloud) -like extinction profile can not be ruled out. For SMC dust, we find small but significant line-of-sight extinction AV = 0.09 ± 0.03 mag and an intrinsic spectral slope β = −0.66 ± 0.08 (see Fig. 5).
 |
Fig. 5. Fits to the g′r′i′z′JHKS SED of the GRB 161023A afterglow. We use the analytical expressions for the dust attenuation curves for MW (dotted blue line), LMC (dashed green line), and SMC (solid black line) dust from Pei (1992). A fit with no dust is also shown (red solid line). SMC and LMC dust both give good fits with a small amount of extinction, whereas MW dust or the complete absence of line-of-sight extinction is ruled out. The flux density is determined at the time of the light-curve break assuming n = ∞, but since this is a multi-band joint fit, scaling is essentially arbitrary (the evolution is achromatic). |
Finally, using the light-curve break time we can estimate the half-opening angle of the jet. The observed break time of tb, obs = 2.81 ± 0.30 days implies a rest-frame break time of tb, rest = 0.758 ± 0.082 day. Using the method described by Racusin et al. (2009) based on that of Frail et al. (2001), the jet half-opening angle (in radians) is defined as
where tj is the break time in days, z is the redshift, and Eγ, iso, 53 is the rest-frame isotropic equivalent energy radiated in gamma-rays between 1 keV and 10 MeV in units of 1053 erg. We assume a uniform interstellar medium (ISM) density of n = 1 cm−3 and a radiative efficiency of nγ = 0.1, and we note that the dependence on these values is only 1/8, therefore having a small effect on θj. Using this equation and these assumptions, we estimate a jet half-opening angle of θj = 3.74 ± 0.09 deg (the errors are only derived from the measurements of tb and Eγ, iso, so there could be an additional systematic error due to our parameter assumptions but, due to the power of 1/8 dependencies, they are expected to be small). This can be compared to the sample of Racusin et al. (2009), who found a mean aperture of ⟨θj⟩ = 6.5 deg. A narrow opening angle allows GRB 161023A to have the large luminosity that we see while constraining the overall energetics of the event.
We note that the spectral slope derived from the optical and NIR data fit is in conflict with the picture derived before from the light curves and broadband SED. A possibility would be that, due to the proximity of the cooling break (see Fig. 4), the curvature is due to the intrinsic shape of the spectrum and not only due to extinction (see Filgas et al. 2011 for a good example). This would imply that the extinction would strictly be an upper limit. Furthermore, the proximity of the cooling frequency νc at the time of the broadband SED implies that we would have expected it to cross the optical bands shortly before the time of the SED. This would result in a shallower decay slope at earlier times, which the light curve does not seem to show. We would also expect a colour change to be present in such a case, although the lack of early multi-band photometry prevents us from doing a thorough analysis of this. We also notice that the light-curve slope towards the early optical peak is too steep and thus inconsistent with the expected values for a forward shock. Therefore, it is possible that the early peak that we are seeing is, in fact, dominated by a reverse shock. The effect of this reverse shock, combined with other possible contributions such as flares, or energy injections, often seen in GRB light curves, may be contributing to mask the pure fireball evolution expected at early times. A more detailed analysis of the broadband model describing the GRB emission is beyond the scope of this paper.
3.2. Luminosity of the afterglow of GRB 161023A
Peaking at r′ = 12.6 mag (AB system, corrected for Galactic foreground extinction), the afterglow of GRB 161023A is one of the brightest that has been detected so far. Combining the information we derived for the spectral slopes and the temporal evolution in the previous section, together with the redshift, we can use the method of Kann et al. (2006) to place the afterglow of GRB 161023A into the luminosity context of a large afterglow sample (Kann et al. 2006, 2010, 2011; 2018). We derive a magnitude shift from the original z = 2.71 frame (i.e as observed) to z = 1 of 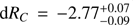 mag. We show the light curves in Fig. 6, highlighting that of GRB 161023A. This plot represents how GRB afterglows would be observed if they were completely unaffected by extinction and were all at z = 1. Following the very early rapid variability, the afterglow rises rapidly to a slow rollover peak. For αrise ≠ −αdecay, the peak time of the light curve is not identical to the light-curve break time as determined in Sect. 3.1. Following Molinari et al. (2007), we derive a peak time tpeak = 0.00274 days (64 s post-GRB in the rest frame), and a peak mRC = 9.75 ± 0.13 mag at z = 1, equivalent to an absolute magnitude of MU = −34.43 ± 0.13 mag. The very early afterglow of GRB 161023A (t < 0.01 days) is not among the most luminous early peaks (Fig. 6), but it still shows one of the most luminous peaks that roll over slowly and are likely not completely dominated by a reverse shock, since the post-peak decay is slower than one would expect for such a case (Kobayashi 2000); most other early optical peaks are clearly linked to reverse-shock flashes or central-engine activity (e.g. Akerlof et al. 1999; Boër et al. 2006; Kann et al. 2007; Racusin et al. 2008; Bloom et al. 2009; Martin-Carrillo et al. 2014) – we note that the luminosity is similar to that of the prompt flash of GRB 130427A (Vestrand et al. 2014). The only other afterglows that show peaks that evolve similarly to that of GRB 161023A but that are more luminous belong to GRB 061007 (Rykoff et al. 2009), GRB 080810 (Page et al. 2009), and finally the possible case of the ultra-luminous GRB 080607 (Perley et al. 2011), which peaked so early that the rise (and possibly peak) was not detected in spite of extremely rapid follow-up. Then, between 0.5 and a few days in the z = 1 frame, the afterglow of GRB 161023A is seen to become one of the most luminous afterglows detected so far.
mag. We show the light curves in Fig. 6, highlighting that of GRB 161023A. This plot represents how GRB afterglows would be observed if they were completely unaffected by extinction and were all at z = 1. Following the very early rapid variability, the afterglow rises rapidly to a slow rollover peak. For αrise ≠ −αdecay, the peak time of the light curve is not identical to the light-curve break time as determined in Sect. 3.1. Following Molinari et al. (2007), we derive a peak time tpeak = 0.00274 days (64 s post-GRB in the rest frame), and a peak mRC = 9.75 ± 0.13 mag at z = 1, equivalent to an absolute magnitude of MU = −34.43 ± 0.13 mag. The very early afterglow of GRB 161023A (t < 0.01 days) is not among the most luminous early peaks (Fig. 6), but it still shows one of the most luminous peaks that roll over slowly and are likely not completely dominated by a reverse shock, since the post-peak decay is slower than one would expect for such a case (Kobayashi 2000); most other early optical peaks are clearly linked to reverse-shock flashes or central-engine activity (e.g. Akerlof et al. 1999; Boër et al. 2006; Kann et al. 2007; Racusin et al. 2008; Bloom et al. 2009; Martin-Carrillo et al. 2014) – we note that the luminosity is similar to that of the prompt flash of GRB 130427A (Vestrand et al. 2014). The only other afterglows that show peaks that evolve similarly to that of GRB 161023A but that are more luminous belong to GRB 061007 (Rykoff et al. 2009), GRB 080810 (Page et al. 2009), and finally the possible case of the ultra-luminous GRB 080607 (Perley et al. 2011), which peaked so early that the rise (and possibly peak) was not detected in spite of extremely rapid follow-up. Then, between 0.5 and a few days in the z = 1 frame, the afterglow of GRB 161023A is seen to become one of the most luminous afterglows detected so far.
 |
Fig. 6. Top panel: comparison of the light curves of a large sample of GRB afterglows shifted to a common redshift of z = 1 (adapted from Kann et al. 2018). The afterglow of GRB 161023A is amongst the most luminous afterglows observed so far. More details can be found in the text. Bottom panel: comparison of the observed peak fluxes in the mm/submm bands (adapted from de Ugarte Postigo et al. 2012a). |
At millimetre wavelengths it is also one of the most luminous events ever recorded (see Fig. 6). In the observer frame, it is not among the brightest, where GRB 030329 is still the record holder (Sheth et al. 2003; Resmi et al. 2005), followed by the recent GRB 171205A (de Ugarte Postigo et al. 2017), GRB 100621A (Greiner et al. 2013), GRB 111005A (Michałowski et al. 2018), GRB 100418A (de Ugarte Postigo et al. 2012a, and in prep.) and GRB 110715A (Sánchez-Ramírez et al. 2017), all of which happened at redshifts z < 1. However, it is close to the group of most luminous millimetre GRB afterglows, which lie close to a peak luminosity of 1033 erg s−1 Hz−1. Within the most luminous events we find GRB 980329 (Smith et al. 1999), GRB 080129 (Greiner et al. 2009), GRB 090313 (Melandri et al. 2010) and GRB 050904 (de Ugarte Postigo et al. 2012a), with GRB 161023A being the fifth most luminous event for which we have millimetre data.
3.3. Host galaxy
Although we do not have direct observations of the host-galaxy emission lines, we are able to study the galaxy from within its interior using the afterglow light as a beacon that shines from the explosion site of the GRB. In this section we present different types of absorption line analysis that give us insight into the dynamics, abundances, dust depletion, molecular content, and structure of the host galaxy.
3.3.1. Constraints from photometric upper limits
The Spitzer non-detection at the GRB location can be used to constrain the properties of the host galaxy. The measured limit of > 25.3 mag corresponds to an absolute magnitude limit of > − 20.0 mag at a rest wavelength of 1 μm. For a continuous star formation history, this non-detection places a limit on the mass of the host to be < 4 × 109 M⊙ (alternatively, the empirical method of Perley et al. 2016b provides a consistent upper limit). This limit is about the mass of the Large Magellanic Cloud, or about 0.05 L* at the redshift of the burst. Assuming minimal dust (< 0.5 mag) and a > 10 Myr stellar population, the FORS2 r′-band non-detection limits the star formation rate to < 2 M⊙ yr−1, although it could be substantially higher in the presence of dust extinction.
3.3.2. Line strength analysis
We perform an analysis of the strong features detected at the redshift of the GRB in the X-shooter spectrum following the prescription of de Ugarte Postigo et al. (2012b), obtaining a value for the Line Strength Parameter of LSP = −0.51 ± 0.72. This number is indicative of the strength of absorption features and implies that the lines in the spectrum of GRB 161023A are slightly weaker than the average of the sample presented in that paper (an average value would have returned an LSP equal to zero). We create a line-strength diagram, shown in Fig. 7, which reveals a very low equivalent width (EW) in the Zn II/Cr II features, slightly low Fe II and slightly low ionisation (C IV/C II, Si IV/Si II). Overall the line-strength parameter is below average, although the very weak Zn II/Cr II feature is responsible for lowering it and for increasing the uncertainty in the value of the LSP.
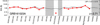 |
Fig. 7. Equivalent width diagram obtained for the spectral features of the GRB 161023A afterglow with X-shooter. It shows the strength of the lines measured for our GRB (in red) as compared to the average and standard deviation of strengths of a sample of GRB afterglows (in black), as described by de Ugarte Postigo et al. (2012b). The gray areas mask features that were not measured because they fell on telluric bands. |
3.3.3. Column densities and abundances in the host galaxy
We fit the absorption lines of the host complex with Voigt profiles using the FITLYMAN environment in Midas (Fontana & Ballester 1995). We use as zero velocity the highest redshift component, which we find to be at z = 2.71064 ± 0.00003. All transitions commonly observed in GRB afterglow spectra from Lyα to Mg I are detected in our X-shooter data. The Ca II doublet lies on the red end of the atmospheric band between J and H band and cannot be fitted. Mn II transitions of λ2594 and 2606 Å are detected but lie in a region contaminated by skylines beyond 9600 Å and were not fitted. O I is clearly saturated and has only one transition available for fitting, hence only an upper limit can be given, assuming a b-parameter of 15 km s−1. Corresponding fine-structure transitions of Fe, Ni, Si, and C are measured, as well as metastable transitions of Ni and Fe up to Fe II 5s, although Fe II 2s could not be fitted due to issues with skylines and blending with Fe II 3s. We further detect the strong high-ionisation lines of C IV, Si IV, and N V as well as several transitions of O VI, S IV, S VI and possibly P V in the Lyα forest. The detection of P V is not secure as it seems somewhat redshifted compared to the other high-ionisation lines, however, both transitions of P V do show absorption at the same (redshifted) velocity. We hence urge caution concerning the detection of this line.
Whenever possible we fitted at least two transitions of the same elementary species and ionisation state to make sure that one of them is not contaminated by a transition from an intervening system, an atmospheric line, or the Lyα forest in case of the high-ionisation transitions. The majority of neutral and single ionised lines show three velocity components. Al II and Si II*λ1309 have an additional component between component I and III, also for O I** we need an additional component to properly fit the absorption complex. Si IIλ1526 looks like an extended absorption system; however, the additional components red and blue of the four main components are C IV doublets from an extended intervening system at z = 2.65, as is some absorption within the complex that would correspond to a component II, but which in reality is C IVλ 1548 from the intervening system (see Sect. 3.4). To determine the b-parameter, we fitted the unblended and unsaturated transitions of Fe II 1608 and Si II* 1309 and used the fitted b-parameters for all single ionised and fine-structure/metastable transitions respectively, with exceptions for lines with additional components. Somewhat different b-parameters were derived for the neutral and high-ionisation species using the strongest, non-saturated absorption line for each ionisation or fine-structure state. The fitted column densities for the individual components of all resonant and fine-structure/metastable transitions and the common b-parameters are listed in Table 3. In Figs. 8–10 we plot some of the transitions and the corresponding fits.
Components and column densities (N) with their corresponding b-parameters in the GRB system.
 |
Fig. 8. Voigt profile fits of low-ionisation features (red) at the redshift of the host galaxy overplotted on the normalised spectra. The error spectrum is shown with a dotted blue line. The different velocity components are marked with roman numbers at the top and vertical dotted lines. |
 |
Fig. 9. Voigt profile fits of high-ionisation features at the redshift of the host galaxy, using the same plotting scheme as in Fig. 8. |
 |
Fig. 10. Voigt profile fits of fine-structure and metastable features at the redshift of the host galaxy, using the same plotting scheme as in Fig. 8. |
The abundances derived for the high-ionisation lines as well as HI and the value for the metallicity are in good agreement with Heintz et al. (2018) who used the same data set but a different Voigt-profile fitting code. Using the total column density of S II we derive a metallicity of3 [S/H] = −1.15 ± 0.04 for the host galaxy. A similar metallicity is derived from Zn, [Zn/H] = −1.11 ± 0.07. This is a rather average metallicity for a GRB host at this redshift (Thöne et al. 2013; Sparre et al. 2014; Cucchiara et al. 2015). We tried to disentangle different components in the Ly absorption series which we detect down to Ly 9 in order to derive separate metallicities for the three different components. However, all Lyman transitions are either contaminated by other Lyman forest lines or transitions from intervening systems in the red and blue wing or completely saturated, making a separation of three possible sub-components impossible. Hence we can only derive a metallicity for the entire host system including all absorption components.
3.3.4. Dust depletion in the host
Above we determined the metallicity of the host from two of the elements least depleted by dust, although there might be some issues with sulphur that can show depletion up to 1 dex in very dusty systems (Jenkins 2009) but can under most circumstances be treated as a mildly depleted element together with zinc. Indeed, if we determine the metallicity from other elements we obtain lower values (see Table 4). For oxygen we obtain a limit of [O/H] < −0.46. Oxygen is also considered to be undepleted, however, the transition is usually saturated, and there is no other transition available at the observable wavelengths, hence a determination of metallicity is often difficult, which is also the case for GRB 161023A. Carbon is an equally difficult case with only one, often saturated transition at λ1335, which is furthermore blended with two of its fine-structure transitions.
Abundances, dust depletion and corrected metallicities using different elements (according to De Cia et al. 2016).
Parameters for the molecular transitions studied in the spectrum of GRB 161023A.
If the different metallicities are due to dust depletion only, we should be able to verify this by comparing them to common dust-depletion patterns. De Cia et al. (2016, 2018) recently extended the analysis of Jenkins (2009) for relative abundances along Galactic sight lines to the (higher) abundances measured in damped Lyman-α system (DLA) sight lines and determined the depletion δX and the nucleosynthetic over-/under-abundances αX of different elements relative to [Zn/Fe]. The authors furthermore provide new depletion patterns, substituting the commonly used patterns for the warm/cool disk and halo by Savage & Sembach (1996). Since we detect Zn and Fe in all components, we can derive depletion values for both the combined host absorption and the three main components. In Fig. 11 we plot δX of different elements in order of increasing depletion and for the different absorption-line components. We determined δX from fits relative to [Zn/Fe] where δX = A2 + B2 × [Zn/Fe] (see De Cia et al. 2016, Eq. (5)) and the coefficients for each element, A2 and B2 are given in De Cia et al. (2016, Table 3) The values obtained for δX in our spectra of GRB 161023A are given in Table 4 for the different components. Component IV (the bluest component) has the highest depletion with values close to Milky Way gas which is quite rare for quasi-stellar object (QSO) -DLAs (see De Cia et al. 2016). However, this is the component where zinc is only marginally detected, hence we caution against any strong conclusions being derived from it.
 |
Fig. 11. Dust-depletion sequence of the host of GRB 161023A and the three main components resolved. The relative abundances are [Zn/Fe] = 0.7 for the total host system and 0.52, 0.6 and 1.34 for components I, II and IV respectively. As comparison, we show dust-depletion patterns from fitting DLA absorption systems (see De Cia et al. 2016). In the bottom panel we plot the dust-corrected metallicities (see also Table 4). |
With the depletion values derived from [Zn/Fe], we can now determine the total abundances corrected for dust depletion and hence establish a corrected metallicity of the host [X/H]tot = [X/H] − δX (see De Cia et al. 2018, Eqs. (1) and (2)), which we also list in Table 4 and plot in the bottom panel of Fig. 11. If nucleosynthesis effects played a major role, we would expect deviations of some corrected metallicities, however, for GRB 161023A all are consistent within errors. GRB 161023A shows that possible nucleosynthetic over- or under-abundances are difficult to measure, even in GRB absorption systems at high S/N and with many different elements detected. To derive a final metallicity for the host of GRB 161023A, we take the average of all depletion-corrected metallicities from lines with well-constrained column densities and available depletion patterns: Zn, S, Si, Mg, and Fe. Taking into account the errors for the individual corrected metallicities, we infer an average, dust-corrected metallicity of −0.95 ± 0.05, which we adopt as the metallicity for the host of GRB 161023A.
The depletion values furthermore allow us to calculate the dust-to-metals (dtm) ratio normalised to the Galactic value (𝒟𝒯ℳ) where 𝒟𝒯ℳ = (1 − 10δX)/dtm(Gal) and the Galactic ratio dtm(Gal) is 0.98 (De Cia et al. 2013). The 𝒟𝒯ℳ values for different elements are listed in Table 4. The 𝒟𝒯ℳ values for Fe, Si, and Mg, elements that can be depleted onto dust grains, are in good agreement and well within the spread of values for other DLAs at a metallicity of ∼ − 1.0 (see Fig. 16 in De Cia et al. 2016). The exception here is component IV, which has a high depletion factor as mentioned above and has a 𝒟𝒯ℳ at the upper end of the distribution for DLAs at that metallicity. We note, however, that we are not able to resolve the metallicity for different components. Finally, from the 𝒟𝒯ℳ we can also derive an overall extinction of the sight lines in the host (see De Cia et al. 2016, Eq. (8)) and obtain an estimate of AV = 0.04 mag, not far from the value obtained from the SED fit (Sect. 3.2).
3.3.5. Limits on the detection of molecules from ALMA spectroscopy
The ALMA observing windows of Band 3 were tuned to cover the range in which we would expect to observe several molecular transitions at the redshift of the GRB. In particular, we covered the CO(2-3) and the HCO+(3-4) transitions. Although there is no detection of any absorption features, these observations can be used to determine a limit on the column density of each of the molecules along the line of sight toward the GRB within its host galaxy. The column density of a specific molecule with a transition from level J to J+1 (absorption) is given by the relation (assuming local thermodynamic equilibrium conditions, based on the formulation of Wiklind & Combes 1995, 1997)
where ν is the observed frequency, AJ + 1, J is the Einstein coefficient of the transition, gJ + 1 is 2(J+1)+1, Q(Tx) is the partition function, and Tx is the rotational temperature, which, as a lower limit, we can assume to be that of the cosmic microwave background (CMB) at the redshift of the burst (Tx = 2.725(1 + z) = 10.1 K). The energy of the lower level is EJ, ∫τν dV is the observed optical depth integrated over the line for a given transition, where V is the velocity relative to the line rest frame, h is the Planck constant, and k is the Boltzmann constant. In our case we can get a limit on the value of the integral by using Eq. (5) from Wiklind & Combes (1997),
ΔV being the velocity width of the line, δV the spectral resolution and στ the rms of the opacity, which is equivalent to
where σnorm is the rms of the continuum-normalised spectrum. Assuming a δv = 13 km s−1, similar to the b-parameters measured for the absorption lines in the X-shooter spectrum (see Sect. 3.3.3), we get a limit value of 3.9 km s−1 for the integral for any of the three transitions that we are considering.
In this case, our attempt to detect absorption features in the line of sight of the GRB yielded only non-detections, from which we derive the abundance of molecules in the GRB host galaxy. Here, the host-galaxy environment is nearly dust-free, and has a lower-than-average metal content, in spite of the large amount of metal features that have been detected. In the future, millimetre and submillimetre absorption spectroscopy will have better chances of success if the search is focused towards bright bursts (to increase the S/N) and/or highly-extinguished lines of sight, with plenty of dust and a high column density of metals, generally known as optically dark bursts.
3.3.6. Limits on the detection of molecules from X-shooter spectroscopy
We use the method developed in Bolmer et al. (in prep.) to search for absorption of molecular hydrogen and carbon monoxide at the redshift of the individual absorption components given in Table 3. We use the PyMC Markov chain Monte Carlo (MCMC) python package4 to fit parts of the normalised X-shooter spectrum with the Lyman-Werner absorption bands of molecular hydrogen or the CO bandheads, including any number of blending ion lines for each of the individual absorption components, with the column density and b as a free parameter (the Voigt profiles are convolved with the instrumental resolution). In the case of molecular hydrogen, we here use the rotational levels from J = 0 to J = 5 with a common b parameter but individual column densities. Although the Lyman and Werner bands fall between 910 Å and 1152 Å (rest frame), we limit the fitted part of the spectrum to the range between 1040.7 Å and 1078.4 Å, corresponding to 3862.0 Å to 4001.6 Å in the observer frame, due to the sparseness of intervening systems and absorption lines in that region (see Fig. 2). Additionally we exclude several parts of the spectrum as indicated by the grey shaded areas in Fig. 13. The spectrum shows evidence for absorption from Ar I, which was thus included in the fit. We find no evidence for absorption from molecular hydrogen with an upper limit of NJ0 − 5(H2)< 1015.2 cm−2 (3σ), when assuming b = 2.0 km s−1 (smaller b values lead to higher upper limits for the column density and therefore give the most conservative result).
 |
Fig. 12. Regions of the ALMA spectra covering the CO(3-2) (top panel) and HCO+(4-3) (bottom panel) features. We do not see any significant absorption in any of the cases, allowing us only to place limits on the molecular content of the line of sight. The grey spectrum has a resolution of 2 km s−1 whereas the black line is for a binned resolution of 10 km s−1. The red vertical lines mark the expected location of features at the redshift of the three velocity components seen in the optical spectra. |
 |
Fig. 13. X-shooter spectrum from 3862.0 Å to 4001.6 Å. In green and red we indicate ion lines as well as the Lyman-Werner absorption bands of molecular hydrogen for each of the three absorption components given in Table 3. The blue line shows the model with NJ0 − 5(H2)< 1015.2 cm−2, including absorption from Ar I in the GRB host galaxy. The grey shaded areas were excluded from the fit. |
We also find no evidence for absorption by carbon monoxide with an upper limit of NJ0 − 6(CO)< 1014.5 cm−2 (3σ) when simultaneously fitting the rotational levels from J = 0 to J = 6 of CO AX(0-0), AX(1-0), and AX(2-0) when assuming b = 2.0 km s−1. The result is shown in Fig. 14.
 |
Fig. 14. Three parts of the X-shooter spectrum covering CO AX(0-0), AX(1-0), and AX(2-0) lines, showing no indication for absorption from carbon monoxide down to NJ0 − 6(CO)< 1014.5 cm−2. |
3.3.7. Distance scales from the fine-structure lines
Excited states in the surrounding medium of the GRB are routinely detected in afterglow spectra (see, e.g., Hartoog et al. 2013 and references therein). There is a general consensus that these features are produced by indirect UV pumping by the afterglow, that is, through the population of higher levels followed by the depopulation into the states responsible for the absorption features. This was demonstrated both by the detection of variability of fine-structure lines in multi-epoch spectroscopy (Vreeswijk et al. 2007; D’Elia et al. 2009a), and through the column-density ratios of different excited levels when multiple spectra were not available (Ledoux et al. 2009; D’Elia et al. 2009b).
The latter scenario holds for GRB 161023A, where no multi-epoch observations are available. In fact, the high column density of the first metastable level of Fe II (a4F9/2, or 5s in Table 3) with respect to the fine-structure levels of the ground state (1s–4s) can hardly be explained with a level population distribution given by a Boltzmann function (Vreeswijk et al. 2007), meaning that collisional excitations can be rejected at very high significance. The lack of multi-epoch spectroscopy does not completely rule out the possibility that the exciting UV flux comes from regions with high star formation rates and not from the GRB alone. In fact, fine-structure emission lines are present in high-redshift Lyman-break galaxies, but usually with lower column densities than observed in GRBs (see Shapley et al. 2003). Assuming that the UV flux comes from the GRB, we can estimate the GRB-absorber distance, comparing the observed column densities to those predicted by a time-dependent photo-excitation code for the time when the spectroscopic observations were acquired. The photo-excitation code is that used by Vreeswijk et al. (2007) and D’Elia et al. (2009a), to which we refer the reader for more details. Our equations take into account the (4π)−1/2 correction factor to the flux experienced by the absorbing gas described by Vreeswijk et al. (2011). We assume that the species for which we are running the code are in the ground state before the UV flash from the GRB reaches the gas. The behaviour of the GRB emission before the X-shooter observation was estimated using the light curve and spectral indices derived in Sect. 3.1, with no spectral variation assumed during the time interval between the burst and our observation.
We here concentrate on the Fe II levels because the multiple excited lines allow for a more precise fitting of the data. The initial column densities of the ground states were computed from the observed column densities of all the levels of each ion, that is, we are assuming that the species are not excited at t = 0. The initial values for the three components in which excited levels are 20 km s−1, which is the average value for the transitions of Fe II in the three components. Allowing for a variation in the range 10 − 30 km s−1 does not change our results significantly. We find the following values for the GRB-absorber distance: dI = 990 ± 60 pc, dII = 820 ± 90 pc, and dIV = 700 ± 140 pc for the three components. While for components II and IV the reduced χ2 values (in the range 1 − 2) give a good agreement between data and model, for component I this is not the case. We allow for a variation of the total column density of Fe II to explore the possibility that the limited resolution of X-shooter may not allow us to distinguish between two sub-components at the velocity of component I, one close to the GRB and responsible for the excited level and one further away, not related to these transitions. However, the best fit to our data is still obtained with the original column density. We then try to compare data and model allowing for larger error bars in the excited levels and we obtain a satisfactory fit. The best value of the GRB absorber does not vary, but the computed error is somewhat larger (∼140 pc instead of 60 pc). This is a possible indication that the errors on the excited levels in the strongest component I are somewhat underestimated by the Voigt fitting procedure, since we cannot fully exclude saturation in this component.
3.3.8. Dynamical analysis of the different components
All resonant and fine-structure/metastable transitions show the same velocity structure of three (for some stronger lines four) absorption components at 0, –76 (–142) and –188 km s−1 with a slightly different velocity for the second component of Mg I and Mg II. Both resonant and fine-structure transitions have the red-most component as the strongest absorption component which we therefore define as v = 0 km s−1. The only exception is Mg I which has as strongest component the blue-most component, which is also obvious in the blend of Zn II 2026 and Mg I 2026, where the strongest component in the complex is the bluest line of Mg I. O I, on the other hand, shows a normal pattern like the other single ionised and fine-structure transitions. Such an “outlier” behaviour for Mg I, but not for example for O I, was also found in the host of GRB 100219A (Thöne et al. 2013). This might be an indication for Mg, or at least neutral Mg, being associated with gas different from the bulk of the ISM, for example in the halo of the galaxy.
The relative strength of the fine-structure versus resonant components seems to be similar in all three components, implying that the impact of the GRB radiation reaches across all of the absorbing gas, which is not usually the case (see e.g. Thöne et al. 2008, 2013; D’Elia et al. 2014). This is in line with the distance of the absorption components derived from the modelling of the fine-structure line strength (see Sect. 3.3.7). Despite large uncertainties, our analysis shows that the least-redshifted component is actually the one closest to the GRB. If the GRB were located somewhere inside the central parts of the host, we would expect a more ordered spatial distribution of absorbing clouds along the sight line in the host, as this has usually been observed in GRB hosts (see e.g. D’Elia et al. 2010, 2011; Thöne et al. 2013). However, here we see clouds at very different velocities within only a few 100 pc. In addition, there is a large total velocity distribution of more than 250 km s−1, too high for the velocity field expected for a galaxy with a mass as low as for GRB 161023A, besides that, those galaxies often do not even show ordered velocity fields. This points to a more turbulent gas distribution than has been usually observed for GRB hosts.
All high-ionisation lines again show the same velocity structure (except for P V as noted above), however, with relative strengths different for the resonant and fine-structure lines. The structure consists of a deep central absorption at –114 km s−1 with additional components in the wings. We also note a small additional component redwards of the main absorption line at +6 km s−1 for Si IV, C IV and possibly O VI, although the latter could be contaminated by Ly forest absorption. The velocities of the main component and the additional component at +6 km s−1 are almost consistent with component I and III of the resonant lines. We can only speculate whether this is a coincidence or whether it implies that the material is actually at the same position in the galaxy but with very different relative strengths. High- and low-ionisation transitions frequently do not trace each other (see e.g. Thöne et al. 2008, 2013; Hartoog et al. 2015). Heintz et al. (2018) made a complete study of high-ionisation lines from the X-shooter GRB sample, including data from this burst. They found two classes of high-ionisation systems: those at the bulk velocity of the host absorption and those blueshifted by a few 100 km s−1, the latter being associated with systems with log(NH/cm−2) < 21.5. This is interpreted as the high-ionisation absorption being associated with the HII region of the GRB and photoionised by the event, but at low NH the absorption only occurs at the edge of the HII region. An earlier study claimed that high-ionisation absorptions at several 1000 km s−1 from the GRB redshift (Fox et al. 2008) were likely all associated with galaxies near the GRB host, along the sight line; in fact, the closest intervening system of GRB 161023A is only 1200 km s−1 from the GRB redshift (see Sect. 3.4). Also, only C IV and S IV have been detected in these systems, but none of the absorption species with high ionisation energies such as N V.
The total absorption complex spans a velocity of nearly 200 km s−1, which is consistent with the value of the velocity field of a relatively large galaxy. Arabsalmani et al. (2018) established correlations between metallicity and velocity for GRB hosts based on earlier works on DLAs, for example by Ledoux et al. (2006). If the absorption can be associated entirely with rotation in the host, we can obtain a mass estimate of the host according to the Tully-Fischer relation at z ∼ 2.6 in Übler et al. (2017) and get log(M * /M⊙) ∼ 10.5, within the range of GRB hosts at that redshift (see e.g. Perley et al. 2016b). As described above, the presence of fine-structure absorption at almost equal relative strength compared to the resonant absorption implies that the absorbing gas might be concentrated in only a part of the galaxy or that the GRB is located in the “foreground” part of its host, hence the velocity width would only imply a lower limit on the total mass of the host.
3.4. Intervening systems
Additionally, beyond the GRB host-galaxy absorption, we observe nine different intervening absorption systems, many of them with several velocity components. Only one other GRB so far has a similarly high number of identified intervening systems, GRB 130606A (Hartoog et al. 2015), which, however, was at a much higher redshift of z = 5.91. In Table 6 we present the systems that we have identified and their detected absorption features as well as the different redshifts of the individual components, the table with the column densities of all intervening systems and their absorption lines can be found in the Appendix, Table B.1. In Figs. B.1–B.9 in the Appendix we plot the strongest lines for each intervening system to show the absorption profiles.
Intervening systems along the line of sight to GRB 161023A.
The intervening system with the highest redshift is only ∼1200 km s−1 from the central redshift of the host galaxy. While this is probably too far for it to be associated with the host itself, it is likely a smaller satellite galaxy of the host or another companion in a galaxy group to which the host belongs, and not related to the outflow from the GRB as, for example suggested in Fox et al. (2008). This is also supported by the fact that we detect Fe II absorption in this system and not only high-ionisation lines. The next-highest intervening system at z = 2.6 seems to have an extended halo of hydrogen and we can fit a velocity complex of nearly 500 km s−1 in both Lyα/Lyβ (Lyγ is contaminated by another Ly forest system) and C IVλλ1548, 1550. The 1548 Åline of the latter is contaminating the Si IIλ1526 absorption complex of the host galaxy but the 1550 Å line is separated and can be fit with the corresponding components. The system could be even larger with a width of ∼1000 km s−1 evident in Lyα, but since Lyβ seems to be contaminated we cannot verify its existence. Another large halo might be present in the system at z = 2.5, with a velocity width of ∼450 km s−1 and four to five different components in Lyα and Lyβ. A very interesting system is the one at z = 1.24, with six components in both Mg II lines (and 4 in Mg I and Fe II) spanning a width of almost 500 km s−1. Velocity widths above ∼400 km s−1 are very unusual for intervening absorbers both in the sight lines towards GRBs and QSO-DLAs (see e.g. Arabsalmani et al. 2018; Berg et al. 2016).
Only two intervening systems are sub-DLAs or Lyman limit systems (LLS), the one at z = 2.69 (sub-DLA, with log log(NH/cm−2) = 19.2) and the one at z = 2.40 (LLS, log(NH/cm−2) = 18.6), the other intervening systems have log log(NH/cm−2)< 17. Most of our intervening systems show absorption of high-ionisation lines of C IV and Si IV, usually associated with the haloes of galaxies. We detect Mg II, Mg I absorption only at the redshift of the GRB and for the two lowest redshift systems, at z = 1.14 and 1.24. In spite of the large number of intervening systems detected in the line of sight toward GRB 161023A, only the one at z = 1.24 can be considered a strong Mg absorber with a rest frame EW of 1.73 ± 0.02 Å for the Mg IIλ2796 line. Strong intervening Mg absorbers are commonly found along GRB and QSO sight lines (see e.g. Vergani et al. 2009; Cucchiara et al. 2013; Christensen et al. 2017).
4. Discussion and conclusions
GRB 161023A was an exceptionally luminous GRB. Although being at a redshift of z = 2.710, its afterglow reached a peak magnitude of r′ = 12.6 mag (equivalent to an absolute magnitude of MU = −34.43 ± 0.13 mag). It was also energetic in the high-energy regime, although not extraordinary, emitting Eiso, γ = (6.3 ± 0.9)×1053 erg. The burst is consistent with the Ep − Eiso, γ correlation (Amati et al. 2009). Its afterglow was amongst the few most luminous ever detected, both in optical and millimetre wavelengths. As such, this burst is a perfect example of how GRB afterglows can be exceptional beacons to study lines of sight across a big fraction of the Universe’s history, at the same time as they allow us to study their own host galaxy from the inside.
Our earliest observations, using the Watcher telescope, started just 40 s after the GRB onset. The very early optical light curve is characterised by optical flickering simultaneous to the gamma-ray emission. After 80 s, the emission rapidly rises, peaking at about 240 s and henceforth decaying steadily. This peak may represent a reverse-shock flash transitioning into a classical forward-shock afterglow, but a more detailed analysis is beyond the scope of this paper. This afterglow emission shows a constant decay until 2.81 days after the burst, when it steepens due to what we interpret as a jet break. From this break time we estimate a relatively narrow jet half opening angle of θj = 3.74 ± 0.09 deg, well below the average value of 6.5 deg. This narrow jet contributed to the unusual observed luminosity of the event.
We construct an SED at the time of the ALMA observations, 2.1 days after the burst, combining millimetre data from ALMA, NIR and optical data from GROND, and X-ray data from Swift/XRT. We find that the Band 3 data are below the characteristic frequency νm whereas the Band 7 data are already above νm but still below νc. The optical data seem to be in the same regime as the X-ray data, both beyond νc, although the cooling break is probably not far from the NIR data at the time of the ALMA observation.
Taking advantage of the brightness of GRB 161023A we performed early spectroscopy at UV, optical and NIR wavelengths with X-shooter at ESO VLT and, for the first time, also in millimetre wavelengths with ALMA, in search of possible absorption from the CO and HCO+ molecules.
The X-shooter spectrum shows a plethora of absorption features. We fit the absorption features using Voigt profiles to determine the column densities of all species at the redshift of the GRB, which shows three different velocity components within a range of 200 km s−1. This was done independently for low- and high-ionisation lines, which showed a slightly different velocity structure, as has been seen before (Heintz et al. 2018), and also for fine-structure and metastable levels, which are expected to be indirectly excited by the UV emission of the GRB.
Using these column densities we derive a metallicity of [S/H] = − 1.15 ± 0.04 and [Zn/H] = − 1.11 ± 0.07 for the host galaxy, which is an average metallicity for a GRB host at this redshift. Thanks to the good S/N of the spectrum and the abundance of resolved features of different species we can study the dust-depletion patterns of the three velocity components observed within the host galaxy of the GRB using recently established correlations based on [Zn/Fe] for QSO-DLAs by De Cia et al. (2016, 2018). We measure only a mild depletion for components I and III and the average of the host with [Zn/Fe] = 0.5 − 0.7. Component IV, which is the one closest to the GRB, might have a higher depletion, similar to MW-disc-like extinction, but we caution against over-interpreting our findings as Zn absorption is very weak in this component. The dust-corrected average metallicity of the host of GRB 161023A is −0.94 ± 0.08. The dust-to-metals ratio derived from the depletion analysis is average for a DLA at that redshift and metallicity (De Cia et al. 2016). The estimate of the total extinction of AV = 0.04 mag is not far from the value derived from SED fitting.
We assume that the fine-structure and metastable levels detected for Fe II are excited by indirect UV pumping, as has been shown for other GRBs in the past. Combining the column densities of these species and the information on spectral and decay slopes of the afterglow to predict how the afterglow would have excited them, we estimate the physical distance to the three systems detected in the host galaxy: dI = 990 ± 60 pc, dII = 820 ± 90 pc, and dIV = 700 ± 140 pc. Hence, the closest system to the GRB afterglow is in this case the one that is blueshifted the furthest in the spectrum.
The ALMA observations did not yield a detection of molecules but allow us to impose limits on the column density of CO and HCO+ along the GRB line of sight, and can be used as a guide for future observations. We determine a limit for the CO molecule from the CO(2-3) transition of log(NCO/cm−2) < 15.7 and for HCO+ of log(NHCO+/cm−2) < 13.2. On the other hand, the redshift of the GRB is ideal for the search for molecular features in the ultraviolet range. Based on a search for the rotational Lyman-Werner bands of hydrogen molecules in the Lyman-α forest we impose a detection limit of log(NH2/cm−2) < 15.2. We also look for carbon monoxide in the X-shooter spectrum, determining a limit of log(NCO/cm−2) < 14.5. These values can be compared to the ones shown in Table 7 for a sample of GRB afterglow spectra in which a search for molecules was performed. The limit obtained for NH2 in GRB 161023A would have been good enough to allow the detection of molecular hydrogen features for similar column densities as those previously measured in some GRBs. Furthermore, for a case like GRB 080607, the most extreme line of sight regarding molecular content, ALMA would have easily detected CO features. The host galaxy of GRB 161023A has a molecular fraction smaller than 10−5. This is much lower than cases like GRBs 080607, 120815A or 121024A, which are all in the range between 0.03 and 0.1, but consistent with the measurement of GRB 120327A at 10−5.2, and comparable with the sample of Ledoux et al. (2009), which showed no detections down to limits that reached 10−8. In Fig. 15 we compare the molecular fraction and the metallicity of GRBs and quasar DLAs. We notice that although there does not seem to be a direct correlation between the molecular fraction and the metallicity, detections of H2 in both GRB and quasar DLA spectra have only been achieved for higher metallicities: in the case of GRBs, only for [X/H] > −1.2. Furthermore, there seems to be a clustering of molecular fractions between −3 < log(f)< − 0.5 with a gap of more than an order of magnitude until the following detection. There does not seem to be a correlation either for the molecular fraction with extinction. It is known, however, that high-extinction lines of sight normally imply high column densities of hydrogen and consequently will make the detection of H2 easier. Furthermore, the presence of molecules such as CO are known to be correlated with dust clouds, implying that their detection will be more likely in highly extinguished lines of sight. As a unique significant example, the extreme sight line toward GRB 080607 had both, close-to-solar metallicity and high extinction.
Measurements of different parameters of GRBs for which molecular searches have been performed.
 |
Fig. 15. Molecular fraction of GRB (in green, Table 7) and quasar DLAs (in yellow, from Noterdaeme et al. 2008) compared to their metallicity. In both cases the molecular fraction is higher at higher metallicity. |
We note that both ultraviolet and millimetre methods complement each other well at this redshift. However, at lower redshifts (z ≲ 2.2) the UV method stops being useful as the features are no longer visible from ground-based observatories and at higher redshifts (z ≳ 4.0) the Lyman forest becomes more populated and less transparent and the analysis becomes unpractical. On the other hand, millimetre observations do not have this redshift constraint. Moreover, most of these molecules are correlated with the presence of dust, implying that the best chance of measuring them is along dusty sight lines. However, this same dust strongly attenuates ultraviolet radiation, making optical studies much more complicated than millimetre ones, as these are not affected by extinction. Hence, we expect that in the future, searches for molecules at millimetre wavelengths will be more successful for very bright afterglows and for those with very high optical extinction due to dust (dark bursts).
The sight line of GRB 161023A is amongst the ones with the largest number of intervening systems detected up to now (Fynbo et al. 2009; Hartoog et al. 2015; Selsing et al. 2018). We find nine independent absorption systems ranging from z = 1.138 to z = 2.695, most of them with multiple velocity components, for a total of 34 different components. Only one system has a detection of strong Mg II. We performed Voigt profile fits to the components for which a fit was feasible. The ALMA observations allowed us to serendipitously tentatively identify four emitters at 350 GHz within 7″ of the GRB. Future studies may tell if any of these systems are related to the intervening systems detected in the spectrum.
Acknowledgments
AdUP and CT acknowledge support from Ramón y Cajal fellowships RyC-2012-09975 and RyC-2012-09984 and the Spanish Ministry of Economy and Competitiveness through projects AYA2014-58381-P and AYA2017-89384-P, AdUP furthermore from the BBVA foundation. DAK acknowledges support from the Spanish research project AYA 2014-58381-P, and from Juan de la Cierva Incorporación fellowship IJCI-2015-26153. FEB acknowledges support from CONICYT-Chile (Basal-CATA PFB-06/2007) and the Ministry of Economy, Development, and Tourism’s Millennium Science Initiative through grant IC120009, awarded to The Millennium Institute of Astrophysics, MAS. Part of the funding for GROND (both hardware as well as personnel) was generously granted from the Leibniz-Prize to Prof. G. Hasinger (DFG grant HA 1850/28-1).JB acknowledges support through the Sofja Kovalevskaja Award to P. Schady from the Alexander von Humboldt Foundation of Germany. MJM acknowledges the support of the National Science Centre, Poland through the POLONEZ grant 2015/19/P/ST9/04010; this project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 665778. AG acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0031 and project grant No. J1-8136) and networking support by the COST Action GWverse CA16104. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programmes 098.A-0055, 098.D-0710 and 0100.D-0649. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2016.1.00862.T. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan) and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech.
References
- Ackermann, M., Ajello, M., Asano, K., et al. 2013, ApJS, 209, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Akerlof, C., Balsano, R., Barthelmy, S., et al. 1999, Nature, 398, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amati, L., Frontera, F., & Guidorzi, C. 2009, A&A, 508, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arabsalmani, M., Møller, P., Perley, D. A., et al. 2018, MNRAS, 473, 3312 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, T. A. M., Ellison, S. L., Sánchez-Ramírez, R., et al. 2016, MNRAS, 463, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Perley, D. A., Li, W., et al. 2009, ApJ, 691, 723 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boër, M., Bringer, M., Klotz, A., et al. 1999, A&AS, 138, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boër, M., Atteia, J. L., Damerdji, Y., et al. 2006, ApJ, 638, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmer, J., Greiner, J., Krühler, T., et al. 2018, A&A, 609, A62 [Google Scholar]
- Butler, N. R., Kocevski, D., Bloom, J. S., & Curtis, J. L. 2007, ApJ, 671, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., Vergani, S. D., Schulze, S., et al. 2017, A&A, 608, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucchiara, A., Prochaska, J. X., Zhu, G., et al. 2013, ApJ, 773, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Cucchiara, A., Fumagalli, M., Rafelski, M., et al. 2015, ApJ, 804, 51 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., Sbarufatti, B., Burrows, D. N., et al. 2016, GRB Coordinates Network, 20112 [Google Scholar]
- De Cia, A., Ledoux, C., Savaglio, S., Schady, P., & Vreeswijk, P. M. 2013, A&A, 560, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cia, A., Ledoux, C., Mattsson, L., et al. 2016, A&A, 596, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cia, A., Ledoux, C., Petitjean, P., & Savaglio, S. 2018, A&A, 611, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Goldoni, P., Thöne, C. C., et al. 2010, A&A, 513, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Lundgren, A., Martín, S., et al. 2012a, A&A, 538, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Fynbo, J. P. U., Thöne, C. C., et al. 2012b, A&A, 548, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Blazek, M., Janout, P., et al. 2014, in Software and Cyberinfrastructure for Astronomy III, Proc. SPIE, 9152, 91520B [Google Scholar]
- de Ugarte Postigo, A., Schulze, S., Bremer, M., et al. 2017, GRB Coordinates Network, Circular Service, 22187 [Google Scholar]
- D’Elia, V., Fiore, F., Perna, R., et al. 2009a, ApJ, 694, 332 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, V., Fiore, F., Perna, R., et al. 2009b, A&A, 503, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Elia, V., Fynbo, J. P. U., Covino, S., et al. 2010, A&A, 523, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Elia, V., Campana, S., Covino, S., et al. 2011, MNRAS, 418, 680 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, V., Fynbo, J. P. U., Goldoni, P., et al. 2014, A&A, 564, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Filgas, R., Greiner, J., Schady, P., et al. 2011, A&A, 535, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontana, A., & Ballester, P. 1995, The Messenger, 80, 37 [NASA ADS] [Google Scholar]
- Fox, A. J., Ledoux, C., Vreeswijk, P. M., Smette, A., & Jaunsen, A. O. 2008, A&A, 491, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Frederiks, D., Golenetskii, S., Aptekar, R., et al. 2016, GRB Coordinates Network, 20111 [Google Scholar]
- French, J., Hanlon, L., McBreen, B., et al. 2004, in Gamma-Ray Bursts: 30 Years of Discovery, eds. E. Fenimore, & M. Galassi, AIP Conf. Ser., 727, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Friis, M., De Cia, A., Krühler, T., et al. 2015, MNRAS, 451, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Møller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Jakobsson, P., Prochaska, J. X., et al. 2009, ApJS, 185, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, H., Lei, W.-H., Zou, Y.-C., Wu, X.-F., & Zhang, B. 2013, New Astron., 57, 141 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gorbovskoy, E., Lipunov, V., Tyurina, N., et al. 2016, GRB Coordinates Network, 20102 [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., McBreen, S., et al. 2009, ApJ, 693, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., Klose, S., et al. 2011, A&A, 526, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greiner, J., Krühler, T., Nardini, M., et al. 2013, A&A, 560, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guidorzi, C., Kobayashi, S., Perley, D. A., et al. 2011, MNRAS, 417, 2124 [NASA ADS] [CrossRef] [Google Scholar]
- Guidorzi, C., Kobayashi, S., Steele, I. A., Mundell, C. G., & Gomboc, A. 2016, GRB Coordinates Network, 20107 [Google Scholar]
- Hartoog, O. E., Wiersema, K., Vreeswijk, P. M., et al. 2013, MNRAS, 430, 2739 [NASA ADS] [CrossRef] [Google Scholar]
- Hartoog, O. E., Malesani, D., Fynbo, J. P. U., et al. 2015, A&A, 580, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heintz, K. E., Watson, D., Jakobsson, P., et al. 2018, MNRAS, 479, 3456 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., & Zeh, A. 2006, ApJ, 641, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Masetti, N., & Klose, S. 2007, AJ, 133, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2010, ApJ, 720, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2011, ApJ, 734, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Schady, P., Olivares, E. F., et al. 2018, A&A, 617, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klotz, A., Turpin, D., Atteia, J. L., et al. 2016a, GRB Coordinates Network, 20109 [Google Scholar]
- Klotz, A., Turpin, D., Atteia, J. L., et al. 2016b, GRB Coordinates Network, 20110 [Google Scholar]
- Kobayashi, S. 2000, ApJ, 545, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S., & Sari, R. 2000, ApJ, 542, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Ledoux, C., Fynbo, J. P. U., et al. 2013, A&A, 557, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krühler, T., & Greiner, J. 2016, GRB Coordinates Network, Circular Service, 20113 [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ledoux, C., Vreeswijk, P. M., Smette, A., et al. 2009, A&A, 506, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin-Carrillo, A., Hanlon, L., Topinka, M., et al. 2014, A&A, 567, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin-Carrillo, A., Murphy, D., Hanlon, L., et al. 2016, GRB Coordinates Network, 20108 [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Melandri, A., Kobayashi, S., Mundell, C. G., et al. 2010, ApJ, 723, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Gotz, D., Ferrigno, C., Fotopoulou, S., & Borkowski, J. 2016, GRB Coordinates Network, 20103 [Google Scholar]
- Michałowski, M. J., Xu, D., Stevens, J., et al. 2018, A&A, 616, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, E., Vergani, S. D., Malesani, D., et al. 2007, A&A, 469, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., & Srianand, R. 2008, A&A, 481, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, K. L., Willingale, R., Bissaldi, E., et al. 2009, MNRAS, 400, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Morgan, A. N., Updike, A., et al. 2011, AJ, 141, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Krühler, T., Schulze, S., et al. 2016a, ApJ, 817, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Tanvir, N. R., Hjorth, J., et al. 2016b, ApJ, 817, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, L. K., Chen, H.-W., Prochaska, J. X., & Bloom, J. S. 2009, ApJ, 701, 1605 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Sheffer, Y., Perley, D. A., et al. 2009, ApJ, 691, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Racusin, J. L., Karpov, S. V., Sokolowski, M., et al. 2008, Nature, 455, 183 [Google Scholar]
- Racusin, J. L., Liang, E. W., Burrows, D. N., et al. 2009, ApJ, 698, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Resmi, L., Ishwara-Chandra, C. H., Castro-Tirado, A. J., et al. 2005, A&A, 440, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rykoff, E. S., Aharonian, F., Akerlof, C. W., et al. 2009, ApJ, 702, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Ramírez, R., Hancock, P. J., Jóhannesson, G., et al. 2017, MNRAS, 464, 4624 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Piran, T. 1999, ApJ, 520, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Selsing, J., Malesani, D., Goldoni, P., et al. 2018, A&A, submitted [arXiv:1802.07727] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, V., Kumar, V., Bhattacharya, D., et al. 2016, GRB Coordinates Network, Circular Service, 20114 [Google Scholar]
- Sheth, K., Frail, D. A., White, S., et al. 2003, ApJ, 595, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, I. A., Tilanus, R. P. J., van Paradijs, J., et al. 1999, A&A, 347, 92 [NASA ADS] [Google Scholar]
- Sparre, M., Hartoog, O. E., Krühler, T., et al. 2014, ApJ, 785, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Kruehler, T., De Cia, A., et al. 2016, GRB Coordinates Network, 20104 [Google Scholar]
- Thöne, C. C., Wiersema, K., Ledoux, C., et al. 2008, A&A, 489, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thöne, C. C., Fynbo, J. P. U., Goldoni, P., et al. 2013, MNRAS, 428, 3590 [NASA ADS] [CrossRef] [Google Scholar]
- Übler, H., Förster Schreiber, N. M., Genzel, R., et al. 2017, ApJ, 842, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, S. D., Petitjean, P., Ledoux, C., et al. 2009, A&A, 503, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vestrand, W. T., Wren, J. A., Panaitescu, A., et al. 2014, Science, 343, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Vreeswijk, P. M., Ledoux, C., Smette, A., et al. 2007, A&A, 468, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vreeswijk, P. M., Ledoux, C., Smette, A., et al. 2011, A&A, 532, C3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wiklind, T., & Combes, F. 1995, A&A, 299, 382 [NASA ADS] [Google Scholar]
- Wiklind, T., & Combes, F. 1997, A&A, 324, 51 [NASA ADS] [Google Scholar]
- Zeh, A., Klose, S., & Kann, D. A. 2006, ApJ, 637, 889 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Photometry and spectroscopy tables
Optical/NIR observations.
Equivalent widths of the spectral features measured in the X-shooter spectrum.
Appendix B: Voigt profile fit of intervening systems
In this appendix we present the results of the Voigt profile fits to the intervening systems.
 |
Fig. B.1. Intervening system at z = 1.138. This and the following plots use the same scheme as in Fig. 8, with the only difference that the fits of the intervening systems are shown in blue. |
 |
Fig. B.2. Intervening system at z = 1.243. |
 |
Fig. B.3. Intervening system at z = 1.9267. |
 |
Fig. B.4. Intervening system at z = 2.231. |
 |
Fig. B.5. Intervening system at z = 2.311. |
 |
Fig. B.6. Intervening system at z = 2.404. |
 |
Fig. B.7. Intervening system at z = 2.525. |
 |
Fig. B.8. Intervening system at z = 2.659. The additional absorption in C IVλ 1548 belongs to Si IIλ1526 in the GRB host. |
 |
Fig. B.9. Intervening system at z = 2.695. |
Column densities (N) and b-parameters from Voigt profile fits to the intervening systems along the line of sight to GRB 161023A ordered by redshift.
All Tables
Sources tentatively detected in the neighbourhood of GRB 161023A in the 350 GHz band, with typical positional errors of  .
.
Components and column densities (N) with their corresponding b-parameters in the GRB system.
Abundances, dust depletion and corrected metallicities using different elements (according to De Cia et al. 2016).
Parameters for the molecular transitions studied in the spectrum of GRB 161023A.
Measurements of different parameters of GRBs for which molecular searches have been performed.
Equivalent widths of the spectral features measured in the X-shooter spectrum.
Column densities (N) and b-parameters from Voigt profile fits to the intervening systems along the line of sight to GRB 161023A ordered by redshift.
All Figures
 |
Fig. 1. Light curve of GRB 161023A in optical and near-infrared bands. Downward pointing triangles are 3-σ upper limits. The grey vertical lines mark the times of the X-shooter and ALMA observations. The solid and dashed lines show the fits of the photometric data to broken power laws, as explained in Sect. 3.1. Plotted in brown is the tail of the gamma-ray emission detected by Konus-Wind. |
| In the text | |
 |
Fig. 2. X-shooter spectrum of GRB 161023A. Top left panel: acquisition image indicating the position of the slit. Top right panel: flux-calibrated spectrum. each colour represents one of the X-shooter arms. Horizontal gray bars mask the regions affected by strong telluric absorption bands. Below panels: normalised spectrum together with the 2D spectrum. Each of the different absorption systems are marked in a different colour, as indicated at the bottom. At the top of the 1D spectra we mark the telluric features with black lines, their widths being proportional to their intensity, as done in de Ugarte Postigo et al. (2010). |
| In the text | |
 |
Fig. 3. Top panel: continuum image obtained with ALMA at 350 GHz. The GRB afterglow is clearly seen in the centre of the image. Several other faint objects can be seen within the field-of-view, which measures 15″ × 15″. North is up and East is to the left. Centre panel: Spitzer image of the field in the 3.6 μm band, showing a slightly larger region. The box indicates the area of the upper figure. Sources S1 and S4 are detected. Bottom panel: late deep image obtained with FORS2 at VLT in the Rspecial band. Whereas ALMA sources S2, and S3 have no corresponding optical counterparts, S4 could be part of a nearby spiral galaxy to the South West and S1 is marginally detected. |
| In the text | |
 |
Fig. 4. Spectral energy distribution of GRB 161023A at the time of the ALMA observations, 50 h after the GRB. |
| In the text | |
 |
Fig. 5. Fits to the g′r′i′z′JHKS SED of the GRB 161023A afterglow. We use the analytical expressions for the dust attenuation curves for MW (dotted blue line), LMC (dashed green line), and SMC (solid black line) dust from Pei (1992). A fit with no dust is also shown (red solid line). SMC and LMC dust both give good fits with a small amount of extinction, whereas MW dust or the complete absence of line-of-sight extinction is ruled out. The flux density is determined at the time of the light-curve break assuming n = ∞, but since this is a multi-band joint fit, scaling is essentially arbitrary (the evolution is achromatic). |
| In the text | |
 |
Fig. 6. Top panel: comparison of the light curves of a large sample of GRB afterglows shifted to a common redshift of z = 1 (adapted from Kann et al. 2018). The afterglow of GRB 161023A is amongst the most luminous afterglows observed so far. More details can be found in the text. Bottom panel: comparison of the observed peak fluxes in the mm/submm bands (adapted from de Ugarte Postigo et al. 2012a). |
| In the text | |
 |
Fig. 7. Equivalent width diagram obtained for the spectral features of the GRB 161023A afterglow with X-shooter. It shows the strength of the lines measured for our GRB (in red) as compared to the average and standard deviation of strengths of a sample of GRB afterglows (in black), as described by de Ugarte Postigo et al. (2012b). The gray areas mask features that were not measured because they fell on telluric bands. |
| In the text | |
 |
Fig. 8. Voigt profile fits of low-ionisation features (red) at the redshift of the host galaxy overplotted on the normalised spectra. The error spectrum is shown with a dotted blue line. The different velocity components are marked with roman numbers at the top and vertical dotted lines. |
| In the text | |
 |
Fig. 9. Voigt profile fits of high-ionisation features at the redshift of the host galaxy, using the same plotting scheme as in Fig. 8. |
| In the text | |
 |
Fig. 10. Voigt profile fits of fine-structure and metastable features at the redshift of the host galaxy, using the same plotting scheme as in Fig. 8. |
| In the text | |
 |
Fig. 11. Dust-depletion sequence of the host of GRB 161023A and the three main components resolved. The relative abundances are [Zn/Fe] = 0.7 for the total host system and 0.52, 0.6 and 1.34 for components I, II and IV respectively. As comparison, we show dust-depletion patterns from fitting DLA absorption systems (see De Cia et al. 2016). In the bottom panel we plot the dust-corrected metallicities (see also Table 4). |
| In the text | |
 |
Fig. 12. Regions of the ALMA spectra covering the CO(3-2) (top panel) and HCO+(4-3) (bottom panel) features. We do not see any significant absorption in any of the cases, allowing us only to place limits on the molecular content of the line of sight. The grey spectrum has a resolution of 2 km s−1 whereas the black line is for a binned resolution of 10 km s−1. The red vertical lines mark the expected location of features at the redshift of the three velocity components seen in the optical spectra. |
| In the text | |
 |
Fig. 13. X-shooter spectrum from 3862.0 Å to 4001.6 Å. In green and red we indicate ion lines as well as the Lyman-Werner absorption bands of molecular hydrogen for each of the three absorption components given in Table 3. The blue line shows the model with NJ0 − 5(H2)< 1015.2 cm−2, including absorption from Ar I in the GRB host galaxy. The grey shaded areas were excluded from the fit. |
| In the text | |
 |
Fig. 14. Three parts of the X-shooter spectrum covering CO AX(0-0), AX(1-0), and AX(2-0) lines, showing no indication for absorption from carbon monoxide down to NJ0 − 6(CO)< 1014.5 cm−2. |
| In the text | |
 |
Fig. 15. Molecular fraction of GRB (in green, Table 7) and quasar DLAs (in yellow, from Noterdaeme et al. 2008) compared to their metallicity. In both cases the molecular fraction is higher at higher metallicity. |
| In the text | |
 |
Fig. B.1. Intervening system at z = 1.138. This and the following plots use the same scheme as in Fig. 8, with the only difference that the fits of the intervening systems are shown in blue. |
| In the text | |
 |
Fig. B.2. Intervening system at z = 1.243. |
| In the text | |
 |
Fig. B.3. Intervening system at z = 1.9267. |
| In the text | |
 |
Fig. B.4. Intervening system at z = 2.231. |
| In the text | |
 |
Fig. B.5. Intervening system at z = 2.311. |
| In the text | |
 |
Fig. B.6. Intervening system at z = 2.404. |
| In the text | |
 |
Fig. B.7. Intervening system at z = 2.525. |
| In the text | |
 |
Fig. B.8. Intervening system at z = 2.659. The additional absorption in C IVλ 1548 belongs to Si IIλ1526 in the GRB host. |
| In the text | |
 |
Fig. B.9. Intervening system at z = 2.695. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.