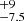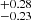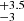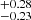| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A320 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202449916 | |
| Published online | 17 October 2024 | |
Spin-orbit alignment in very low mass tight binaries: results for the 2MASS J0746425+200032AB and 2MASS J1314203+132001AB systems using spectroscopic and optically derived rotational estimates
1
Department of Physics, College of Science, Al-Nahrain University, Baghdad, Iraq
2
Vatican Observatory Research Group, Steward Observatory, University of Arizona, Tucson, AZ 85721, USA
3
Department of Computer and Software Engineering, Technological University of the Shannon, Athlone, Co. Westmeath, Ireland
4
Physics, School of Natural Sciences, College of Science & Engineering, University of Galway, Galway, Ireland
5
Centre for Astronomy, College of Science & Engineering, University of Galway, Galway, Ireland
Received:
9
March
2024
Accepted:
9
August
2024
Context. Constraining the coplanarity status of very low mass (VLM) tight binary systems provides valuable information towards understanding the dominant mechanisms in star and planetary formation at the lower end of the initial mass function.
Aims. We sought to constrain the v sin i degeneracies of two nearby tight VLM binary systems, 2MASS J0746+20AB and 2MASS J1314+13AB, by independently determining each companion’s rotational period and so characterize each system’s spin-orbit alignment.
Methods. Long observational baseline high cadence I band photometry data were obtained for both systems using the Galway Ultra Fast Imager (GUFI) on the Mount Graham International Observatory’s Vatican Advanced Technology Telescope. Previously known rotational periods determined in other passbands were used as a basis for recovering additional periodic modulations in the time-series data.
Results. Using the known rotational period of 3.32 hours for 2MASS J0746425+200032A, we recovered an underlying periodic modulation of 2.14 ± 0.11 hours, which we associate with 2MASS J0746425+200032B. Breaking each components’ v sin i corresponds to equatorial inclination angles of 32 ± 4 degrees and 37 ± 4 degrees for components A & B respectively. We recover a weaker 2.06 ± 0.05 hours modulation separate from the known 3.79 hour signature for J1314203+132001B, which we associate with J1314203+132001A. We place a lower limit on J1314203+132001A’s equatorial inclination angle to be in the range of 24.5−3+3.5 degrees, which deviates from the system’s orbital plane previously determined to be 49.34−0.23+0.28 degrees.
Conclusions. We confirm long term, consistent periodic modulations from both binary systems and report the first definitive rotational period for J1314203+132001A of 2.06 ± 0.05 hours, in addition to coplanarity to within 10 degrees in the spin-orbit alignment of the 2MASS J0746425+200032AB system. The lack of separate v sin i values for the 2MASS J1314203+132001AB system limits a definitive assessment but best estimates suggest coplanarity to be unlikely.
Key words: techniques: photometric / binaries close / stars: low-mass / stars: rotation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Over the past decade, several surveys have revealed that many very low mass (VLM) stars are optically variable sources, with some displaying sustained periodic variability consistent with that expected from prior v sin i rotational estimates (Clarke et al. 2002b; Koen 2006; Rockenfeller et al. 2006; Lane et al. 2007; Littlefair et al. 2008; Harding et al. 2013a), and for others, non-periodic variability or evidence of periodic variability at time scales not correlating with spectroscopically derived rotation estimates (Gelino et al. 2002; Lane et al. 2007; Maiti 2007). There are three plausible sources for producing such optical variability as the dwarf rotates: magnetically-induced spots, suspended localized atmospheric dust clouds, and auroral hot spots, or alternatively a mixture of some or all three (Martín et al. 2001; Gelino et al. 2002; Rockenfeller et al. 2006; McLean et al. 2011; Harding et al. 2013a; Hallinan et al. 2015; Croll et al. 2016; Pineda et al. 2017). What distinguishes each emission mechanism are their distinctive rotational signatures in differing passbands, and in particular whether their inferred rotational periods are consistent with the range derived from any spectroscopically derived v sin i estimates. If the latter is indeed the case, then it becomes possible to break the degeneracy in i, and in so doing constrain the dwarf’s viewing geometry. This is particularly relevant for those systems for which regular periodic coherent radio emission has been detected and suspected to originate in a functioning auroral zone, as the beamed radio emission would be expected to be projected perpendicular to the rotating magnetosphere axis and so be associated with high i values. In these cases, the optical rotational signature has been hypothesized to be dominated by the effect of auroral currents impacting the dwarf photosphere (Hallinan et al. 2015), in effect sustaining the regular feature associated with the corresponding optical modulation. Whilst evidence of a stable rotational period does not restrict an interpretation involving starspots (Rockenfeller et al. 2006; Lane et al. 2007; Croll et al. 2016), or the presence of weather systems (Bailer-Jones & Mundt 2001; Gelino et al. 2002; Enoch et al. 2003; Maiti 2007; Littlefair et al. 2008; Goldman et al. 2008; Clarke et al. 2008; Artigau et al. 2009; Radigan et al. 2012, 2014; Gillon et al. 2013; Buenzli et al. 2014; Crossfield et al. 2014), the difficulty remains of explaining the basis for the inherent stability of both these phenomena and their ability to sustain long lasting coherent structures sufficient to yield such regular periodic modulations over time.
We have conducted long term observational campaigns for several nearby VLM targets, both binary and non-binary, whose proximity, estimated high v sin i rotational periods and location at the substellar boundary have motivated us to determine if it is possible to detect unambiguous periodic optical modulations consistent with the long term sustenance of such surface, atmospheric and/or magnetospheric structures. Using the high speed Galway Ultra-Fast Imager (GUFI) on the 1.8m Vatican Advanced Technology Telescope (VATT) to date we have been able to fully characterize such signatures successfully from five field dwarfs and two binary systems (Harding et al. 2013b; Dulaimi et al. 2023).
Observations of tight VLM binaries are of particular relevance to the study of how such systems are formed and evolve, part of a wider debate on the formation of exoplanetary systems more generally. Differing formation models are expected to yield distinct rotational signatures in such systems, with a disk fragmentation origin favoring coplanar orientations within the system’s orbital plane (Adams et al. 1989; Bonnell & Bate 1994) in contrast to the alternative turbulent fragmentation and/or dynamical interaction models that would be expected to yield more complex spin-orbit orientations (Goodwin et al. 2004; Fisher 2004).
An influential study by Hale (1994) on the spin-orbit alignment of solar-type binary and multiple systems (86 stars in 73 stellar systems in total) indicated the presence of a bimodal relationship in coplanarity based on separation distance, with systems a ≤ 30 au preferentially aligned, suggesting a bias towards a disk fragmentation origin below this distance scale. However a reappraisal of the same sample incorporating more accurate astrometric and spectroscopic data analyzed using a more rigorous Bayesian formalism suggested that no such preferential alignment exists (Justesen & Albrecht 2020). Importantly, these latter authors highlighted the impact that uncertainties regarding stellar properties play in such assessments, ranging from the difficulty in accurately ascertaining stellar rotational periods from chromospheric activity indices, to the use of inferred stellar radii, to uncertainties in v sin i estimates. Whilst an examination of the projected spin-orbit alignment Δi of solar-type binaries in Justesen & Albrecht (2020) from separations ranging from 3-120 au does appear to be consistent with their conclusions, the limited sample of sources less than 10 au is notable for both its sparsity and apparent trend towards Δi → 0.
An open question remains as regards the coplanarity properties of low mass binary systems, particularly those tight systems with separations < 10 au. The question arises as to whether a similar lack of preferential alignment dominates here too, as proposed by Justesen & Albrecht (2020)’s study of solar-type binary systems. This may well be the case if both classes of binary systems share the same origins – however whilst uncertainty remains as regards the overall binary fraction of VLM stars and brown dwarfs, ranging from 2% to 50%, it is generally accepted that this is far less than the binary fraction of G dwarf systems (Bardalez Gagliuffi et al. 2014). Of relevance too is the potential role that the presence of magnetic fields might have in the formation of such systems, potentially resulting in a loss of system angular momentum to perturbations on spin inclinations (Li et al. 2004).
In Harding et al. (2013b) we were able to directly identify a separate rotational signature from the tight (2.7 au) VLM binary (L0+L1.5) 2MASSW J0746425+200032AB from the one already known from previous radio observations, and combining this with each component’s previously very well constrained v sin i and radii, we confirmed the system’s coplanarity to within 10 degrees. In this communication, we present our most recent results for our high precision optical observations of the binary systems 2MASS J0746425+200032AB and 2MASS J1314203+132001AB. Both targets have previously exhibited periodic optical variability (McLean et al. 2011; Harding et al. 2013a; Williams et al. 2015), high spectroscopically-derived rotation rates, and they are also known radio sources (Berger et al. 2009; McLean et al. 2011; Forbrich et al. 2016; Zic et al. 2019; Zhang et al. 2020). Our motivation was twofold. Firstly, to assess long term stability in any inferred optical periods, and in particular, to identify the presence of periodic optical modulation from 2MASS J0746425+200032B and 2MASS J1314203+132001A, as none has been determined to date from both dwarfs. Secondly, to use such rotational signatures to constrain each system’s coplanarity and in so doing, provide further insight into the formation of tight binary VLM systems.
2. Target selection
2.1. 2MASS J0746425+200032AB
2MASS J0746425+200032AB (hereafter known as 2M J0746+20AB) is a system of two L-dwarfs. It was discovered by Kirkpatrick et al. (2000) and was later unequivocally determined to be a binary system by Reid et al. (2001) with a separation of 2.7 au. Bouy et al. (2004) subsequently determined the spectral types of both components (L0 ± 0.5 for A and L1.5 ± 0.5 for B). The 2M J0746+20AB system is located at a distance of only 12.2 pc (Dahn et al. 2002). The A and B components have estimated effective temperatures of 1900 K and 2225 K, and bolometric magnitudes of log Lbol/L⊙ ≈ −3.64 and –3.77 (Vrba et al. 2004; Konopacky et al. 2010). The initial total mass measurement by Bouy et al. (2004) yielded 0.146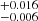 M⊙, which placed the system in the very low mass binary regime, with the most recent VLBI based observations of Zhang et al. (2020) yielding the most accurate mass estimates to date of A (0.07954 ± 0.00034 M⊙) and B (0.0756 ± 0.00025 M⊙). Blake et al. (2010) and Konopacky et al. (2012) separately measured resolved v sin i for 2M J0746+20AB, and obtained almost identical values for each component: 33 ± 3 km s−1. Table 1 summarizes the system’s properties.
M⊙, which placed the system in the very low mass binary regime, with the most recent VLBI based observations of Zhang et al. (2020) yielding the most accurate mass estimates to date of A (0.07954 ± 0.00034 M⊙) and B (0.0756 ± 0.00025 M⊙). Blake et al. (2010) and Konopacky et al. (2012) separately measured resolved v sin i for 2M J0746+20AB, and obtained almost identical values for each component: 33 ± 3 km s−1. Table 1 summarizes the system’s properties.
Properties of the 2M J0746+20AB binary system.
Initial observations of this system by Bouy et al. (2004) also revealed evidence for Hα variability, indicative of chromospheric and/or enhanced magnetic activity. The subsequent detection of a single, highly polarized burst of coherent radio emission at 4.86 GHz (Antonova et al. 2008) implied a magnetic field strength of ∼1.7 kG from one of the components. Following this observation, Berger et al. (2009) conducted joint simultaneous Karl G. Jansky Very Large Array (VLA)/Hα/X-ray observations to confirm the presence of correlated, coronal incoherent gyrosynchrotron processes from both dwarfs. These authors detected variable, coherent radio emission at 4.86 GHz with a period of 2.07 ± 0.002 hours, in addition to quasi-sinusoidal Hα emission with the same period. They suggested that the source of both periodic emissions originated from the same binary component, 2M J0746+20A, as the magnetic field strength was consistent with that of Antonova et al. (2008). Lynch et al. (2015) used the VLA at 5 and 7 GHz to obtain multi-epoch radio observations of 2M J0746+20AB, and reported a period of 2.071481 ± 0.000002 hours, which lies within the uncertainty range of the 2.072 ± 0.001 hours period measured by Berger et al. (2009). Using the Giant Metrewave Radio Telescope array at 600 MHz and 1.3 GHz, Zic et al. (2019) demonstrated the presence of stable radio emission in both bands, with suggestions of a dominant circularly polarized coherent component at 1.3 GHz. Recently, Zhang et al. (2020) reported found that both binary components are radio emitters in Very Large Baseline Array (VLBA) observations – observed over seven epochs between 2010 and 2017 at 5 GHz, consistent emission was detected from 2M J0746+20B, and a majority of observations demonstrated emission from 2M J0746+20A, in all cases circularly polarized, consistent with an electron cyclotron maser instability (ECMI) mechanism, and likely auroral emission process, for both dwarfs. These authors confirmed a 2.1 ± 0.2 hours periodicity to the bursts originating from 2M J0746+20B, and a weaker ∼3.2 ± 0.2 hours periodic modulation from 2M J0746+20A.
In terms of optical variability other than Hα, weak evidence of periodicity (of a few hours) was reported by Clarke et al. (2002a) and Bailer-Jones (2004). A high precision I-band photometric study of the unresolved system by Harding et al. (2013b) recovered a significant periodic signal of 3.32 ± 0.15 hours, which these authors proposed originated from 2M J0746+20A in contrast to the 2.07 ± 0.002 hours radio source previously detected in the radio by Berger et al. (2009), and estimated maximum possible rotation periods for 2M 0746+20A and 2M J0746+20B of ∼4.22 hours and ∼2.38 hours, respectively. Thus far no definitive periodic optical variability had been detected for 2M 0746+20B. We chose to monitor this binary system to confirm an unambiguous optical rotational period consistent with those determined from previous radio observations for 2M 0746+20B, as well as to confirm the presence of stable rotational signatures from both dwarfs that, taken together with the long term radio periodicities identified by Zhang et al. (2020) for both components, would strengthen the case for the presence of sustained auroral activity for the 2M J0746+20AB system.
2.2. 2MASS J1314203+132001AB
2MASS J1314203+132001AB (hereafter known as 2M J1314+13AB) was discovered as a radio-emitting source in 2007 during a VLA survey of nearby mid-and late-M dwarfs (McLean et al. 2011). Lucky imaging at z′ and i′ bands resolved it into a binary with a separation of ∼1.6 au, where the secondary component is fainter than the primary by ∼1 mag in the i′ band (Law et al. 2006). Lepine et al. (2009) measured its parallactic distance of 16.39 ± 0.75 pc, in addition to determining both components’ M7.0 ± 0.5 spectral type. More recently, the joint analysis of Keck adaptive optics and VLBA radio interferometry observations determined that the system is located at a revised distance of 17.249 ± 0.013 pc (Forbrich et al. 2016). A combination of spectral analysis and resolved JHKL′-band photometry has estimated effective temperatures of 3200 ± 500 K and 3100 ± 500 K for the A and B components, respectively (Schlieder et al. 2014). Dupuy et al. (2016) and Forbrich et al. (2016) determined that A and B have nearly identical (to within ±2%) masses of 92.8 ± 0.6 MJ (0.0885 ± 0.0006 M⊙) and 91.7 ± 1.0 MJ (0.0875 ± 0.0010 M⊙). These mass estimates are in good agreement with Schlieder et al. (2014), who also used the evolutionary models of Baraffe et al. (2003) and derived masses of ∼0.0925 M⊙ and ∼0.0868 M⊙ for the A and B components, respectively. McLean et al. (2011) inferred the radii of both components to be ∼0.13 R⊙ (∼1.29 RJ), which is 30% larger than the ∼0.1 R⊙ (∼0.99 RJ) model predictions by Demory et al. (2009) for a field-age M7 dwarf. The high levels of magnetic activity present in both 2M J1314+13AB components may alter their radii, making them over sized by ∼20% (Williams et al. 2015). More recent studies (Dupuy et al. 2016; Forbrich et al. 2016), which present the most precise data so far, found model radii of ∼1.831 RJ and ∼1.808 RJ, respectively. Table 2 summarizes the system’s properties.
Properties of the 2M J1314+13AB binary system.
The 2M J1314+13AB system has strong chromospheric Hα emission, confirming the presence of significant magnetic activity (Lepine et al. 2009). Activity in radio emission has also been reported in several studies, with the detection of highly circularly polarized periodic radio pulses most likely due to ECMI processes. McLean et al. (2011) detected persistent radio emission from 2M J1314+13AB, with a flat spectrum over a range of frequencies (1.43, 4.86, 8.46 and 22.5 GHz), varying sinusoidally with a period of 3.89 ± 0.05 hours at two of these frequencies (4.86 and 8.46 GHz). These multi-epoch VLA observations coincided with simultaneous optical observations that yielded periodic, correlated, optical modulation in g′ and i′ band filters with a period of ∼3.79 hours, and a measured v sin i of 45 ± 5 km s−1. These authors suggested the optical-radio period difference could be due to differential rotation, with ΔΩ ≈ 1 rad day −1 between the equatorial and polar regions of this target. Using the MEarth array of optical telescopes Williams et al. (2015) subsequently detected two optical periodicities, 3.7859 ± 0.0001 hours and 3.7130 ± 0.0002 hours, and ruled out that the two similar rotation periods could be a result of differential rotation, as it is not expected to occur in the mass range of VLM stars. Instead, they attributed the previously identified differential rotation as being due to the unusually magnetically active state of the binary system, which is known to output the highest X-ray and radio luminosities detected from an ultracool dwarf to date (Williams et al. 2015). VLBA observations revealed that the origin of the radio emission is only from the secondary component (Forbrich et al. 2016). Based on all of this reported radio and optical activity, we chose to monitor the binary system to investigate the existence of such variations at optical wavelengths in both components, and in particular 2M J1314+13A, for which no optical variability has yet been seen.
3. Optical observations
Observations of 2M J0746+20AB and 2M J1314+13AB were carried out on the 1.83 m Vatican Advance Technology Telescope (VATT), using the L3-CCD based Galway Ultra Fast Imager (GUFI) photometer and VATT I-Arizona (∼7200–9100 Å) broadband filter for both targets. Using its near-IR optimised focal reducer, GUFI’s 512 × 512 pixel format recorded a FOV of ∼3′ × 3′ at a plate scale of 0.35″ pixel−1 (Harding et al. 2013b). Data for both targets were typically taken with exposure times of 5 seconds, with a smaller amount at 3 or 10 second cadence. A total of 72.3 hours of optical observations were made of 2M J0746+20AB over the course of three separate epochs (March, November and December 2017), as listed in Table A.1. We monitored 2M J1314+13AB for a total of 47.2 hours, encompassing three separate epochs (February 2017, March 2017 and May 2018).
4. Pipeline data reduction and variability analysis
All data obtained was processed using the custom L3-GUFI pipeline. This initially implements de-biasing (using zero-integration frames) and flat-fielding (using twilight flat-fields). Using a fringing template created from the median of a subset of dithered, reduced, I-band science frames, all frames are de-fringed, followed by a registration step to correct for any potential guiding drift. Co-addition of frames in one-minute batches is applied to increase the signal to noise ratio while maintaining time resolution appropriate to the target. The pipeline then performs differential photometry on the calibrated time-series frames, measuring both the target (2M J0746+20AB or 2M J1314+13AB) and selected comparison stars in the same frame to ensure that any variability was intrinsic to the target. The GUFI field-of-view offered between 4–6 comparison stars while monitoring both targets. The differential light curves (one per night per target) were assessed in order to check for any remaining systematic trends due, for example, to the effects of increasing or decreasing air mass – none were evident during these observations.
Using the IRAF task phot, we calculated the error in each differential magnitude of the target star. The error in magnitude was then converted to an error in flux to match the photometric light curve units. In this paper, a photometric error model described by Bailer-Jones & Mundt (2001) was used to quantify formal (e.g. Poisson noise) and informal photometric errors (e.g. fringing residuals). After extracting the differential photometric time-series for each epoch, we used both Lomb-Scargle (LS) periodogram analysis (Lomb 1976; Scargle 1982, 1989) and Phase Dispersion Minimization (PDM) (Stellingwerf 1978) to search for periodic signals. We selected a number of LS power peaks above the noise-floor (> 5σ significance), and for the PDM analyses, we ran 105 Monte-Carlo simulations per assay to determine the statistical significance of the potential outcomes. The data were then phase-folded on the most significant periodicities.
We used a bootstrapping distribution of the periods with the highest LS powers to determine the period uncertainty, in addition to applying a χ2 goodness-of-fit to compute the uncertainty of the period on each night. We used a sinusoidal fitting model to assess the amplitude of each target light curve, adopting the identified rotation period and varying the amplitude and phase of the sinusoidal function, using a χ2 goodness-of-fit test to determine the best fit for both parameters, along with their associated uncertainties. Sufficient period precision was not attained to allow us to phase-connect light curves together between the separate observational epochs for each target system.
Due to the close separation of both binary systems – ∼2.7 au for 2M J1314+13AB and ∼1.6 au for 2M J0746+20AB – GUFI could not resolve each binary as a pair of point sources. Consequently the photometric apertures used enclosed the combined flux of both the A and B components in each binary system. Due to the likely periodic variation of both components, these differential fluxes were expected to consist of superimposed variability at different periods. We developed a Python based script Light Curve Fitter (LCF) which uses a χ2 /lsf fitting model, where lsf corresponds to the least-squared fit of the LCF algorithm, to subtract out specified periodic signals within a given photometric time series. For both systems previous observations in the optical and radio have already identified a dominant periodic signature associated with one companion. Our strategy for both binary systems was to use our LCF script to subtract and subsequently remove each system’s previously identified periodicity, and test the residual time series for additional periodic signals. Reversing these steps with any such identified secondary periodicities was then implemented to recover the original modulation, and taken together, to determine estimates on the precision.
5. Results
5.1. 2MASS J0746425+200032AB
Fixed aperture photometry using 5–6 reference stars was implemented for the 2M J0746+20AB observational data. The resulting photometric time series (see Figure 1) were processed using our LCF script with a period of 3.32 hours (the known rotational period for 2M 0746+20A) on each of the nightly light curves independently. We analysed the resulting time-series and identified a secondary periodic signature, with mean peak-to-peak amplitude variability of 0.0011–0.0053 mag in I-band (Table 3, Figures 2, 3 and 4). We attribute this 2.14 ± 0.11 hours periodicity to the secondary 2M J0746+20B, with the phase folded residual time series data showing weak sinusoidal modulation (Figure 5). This rotational signal agrees with the estimates of Berger et al. (2009) and Lynch et al. (2015) who both reported radio pulses with a period of ∼2.07 hours, and the more accurate radio periodicity of 2.1 ± 0.1 hours revealed by long term VLBA observations (Zhang et al. 2020). As such our analysis confirms the detection of 2M J0746+20B’s rotational period in the optical passband for the first time.
 |
Fig. 1. Representative I-band photometric timeseries from four out of sixteen nights when 2M J0746+20AB was observed. Target flux relative to 5–6 reference stars is plotted against Modified Heliocentric Julian Date (MHJD). The HJD time above each figure denotes the start-point of each observation night. Both components of the binary contribute to the variability seen here. Possibly aperiodic variations are observed in some light curves (e.g. 29th December 2017). The arrow marked on the 24th November 2017 light curve indicates a period of full cloud coverage, and this data has been removed. The December 24th 2017 data were taken during bad weather conditions (thin cloud). The impact is shown clearly by an increase in the photometric error bars and an increase in the scatter of the light curve itself. |
Amplitude variability and photometric error analysis of 2M J0746+20A and 2M J0746+20B.
 |
Fig. 2. 2M J0746+20B: The same light curves as Figure 1, after running LCF to subtract out the 3.32 hours rotational period of the primary component 2M J0746+20A. Each figure shows relative flux vs. Modified Heliocentric Julian Date (MHJD) time. Photometric error bars for 2M J0746+20AB are applied here as listed in Table 3. |
 |
Fig. 3. A. Lomb Scargle (LS) periodograms of all epochs of 2M J0746+20B, after subtraction of the primary’s 3.32 hours period: power spectra vs. frequency days−1. Dashed, horizontal red lines denote the 5σ false alarm probability of the peaks. The period obtained for the combined dataset is 2.14 ± 0.11 hours, a newly discovered optical period. This periodicity lies within the period uncertainty range of Berger et al. (2009), Lynch et al. (2015) and Zhang et al. (2020) who measured the radio period at 2.072 ± 0.001 hours, 2.071481 ± 0.000002 hours and 2.1 ± 0.1 hours, respectively, as well as being consistent with the 2.07 hours period of quasi-sinusoidal Hα emission (Berger et al. 2009). B. The same LS periodogram, zoomed into the area around the highest peak. The dashed red line corresponds to our detected optical secondary period of 2.14 ± 0.11 hours. |
 |
Fig. 4. A. Phase Dispersion Minimization (PDM) plot for all epochs of 2M J0746+20B, after subtraction of the primary’s 3.32 hours period. The theta statistic was determined from 105 Monte-Carlo simulations. The minima theta indicates the most likely rotational period of ∼2.14 hours, in agreement with the rotation period resulting from the LS periodogram seem in Figure 3. B. The same PDM theta plot, zoomed into the area around the minimum theta statistic. |
 |
Fig. 5. A. Phase-folded light curve of 2M J0746+20B from all epochs combined, after subtracting out the ∼3.32 hours periodicity attributed to the rotational period of the primary component. These unbinned data are folded to our newly discovered rotation period in the optical of ∼2.14 hours. B. The same data in plot A except binned in phase by a factor of 10 for clarity. |
This process was repeated again on the original I-band time series of 2M J0746+20AB by re-running LCF and subtracting the 2.14 hours period (Figure 6). We then re-ran our statistical analysis tools on the residual data points (Figures 7 and 8), and phase folded on the detected primary period to confirm whether 2M J0746+20A is a periodic source (Figure 9). We confirm periodic optical variability of 3.32 ± 0.08 hours with mean peak-to-peak amplitude variability of 0.0014–0.0154 mag (Table 3), largely consistent with a previous study by Harding et al. (2013b), who reported a period of ∼3.32 hours for the slower component. Our period is consistent with the VLBA derived 3.2 ± 0.2 hours periodicity measured by Zhang et al. (2020). This demonstrates that the variability parameters of the primary 2M J0746+20A are stable on timescales of many years.
 |
Fig. 6. 2M J0746+20A: The same light curves as in Figure 1, after running LCF to subtract out the secondary component’s signature. Each figure shows relative flux vs. Modified Heliocentric Julian Date (MHJD) time. Note the difference in scale on the y-axis for the 24th November 2017 plot, due to the light curve exhibiting a larger amplitude variation of 1.54%. Photometric error bars for 2M J0746+20AB are applied here as listed in Table 3. |
 |
Fig. 7. A. Lomb-Scargle (LS) periodograms of all three epochs of the I-band GUFI photometric data of 2M J0746+20A, after subtraction of the putative ∼2.14 hours rotational period of the secondary component. The x-axis is plotted in days−1, since each epoch was time-stamped in units of Modified Heliocentric Julian Date (MHJD). The red dashed and dotted horizontal lines represent a 5σ false-alarm probability of the peaks, as defined by the LS periodogram algorithm. The mean peak-to-peak amplitude variability of 2M J0746+20A varied between 0.0014 to 0.0154 mag on different nights. B. The same LS periodogram, zoomed into the area around the highest peak. The vertical red dashed line corresponds to 3.32 ± 0.08 hours. |
 |
Fig. 8. A. Phase Dispersion Minimization (PDM) plots for all epochs of 2M J0746+20A, after subtraction of the putative ∼2.14 hours rotational period of the secondary component, showing theta statistic against frequency days−1. The deepest minimum of the quantity theta marks the most likely rotational period of ∼3.32 hours. B. The same PDM theta plot, zoomed into the area around the deepest minimum theta statistic that corresponds to the primary’s period of rotation established in this work, consistent with the rotation period resulting from LS periodogram analysis. |
 |
Fig. 9. A. Phase-folded light curve of 2M J0746+20A from all three epochs, after subtracting out the secondary period of 2.14 hours. These unbinned data points are folded to a period of ∼3.32 hours. The observed sinusoidal variability to the same reported period from Harding et al. (2013b), shows that this dwarf is stable on timescales of years. B. The same data in plot A except binned in phase by a factor of 20 for clarity. |
Our observations thus demonstrate the presence of periodic optical emission from both components in the 2M J0746+20AB system, at periods that match those previously determined from several radio observations, most notably the VLBA study of Zhang et al. (2020). We remark however that on some nights we only observed periodic I-band modulation of 2M J0746+20A, and some nights only 2M J0746+20B showed modulation, and on some nights both were variable (Figures 1, 2 and 6). Whilst it is possible such variability is a consequence of local meteorology on both dwarfs, the striking consistency in periods between the underlying optical periods and that of the unambiguous coherent, presumed auroral emission, present over many years as determined by Zhang et al. (2020) does suggest that the optical signature has a likely magnetic basis, either via magnetic spots and/or auroral processes.
5.2. 2MASS J1314203+132001AB
The 2M J1314+13AB data were processed with fixed aperture photometry using 4 reference stars, yielding nightly photometric time series (Figure 10). As was the case previously, we used the previously determined periodic signal of 3.79 hours (McLean et al. 2011; Williams et al. 2015) together with our LCF script to subtract this dominant signal. Our resulting analysis of the residual time-series determined the presence of a 2.06 ± 0.05 hours modulation (Figures 11, 12 and 13), with a peak-to-peak sinusoidal amplitude that varied between 0.0011–0.0086 mag (Table 4). We reversed the LCF procedure using this newly determined periodicity, and recovered a 3.79 ± 0.05 hours signal (Figures 14, 12 and 13) with peak-to-peak sinusoidal variability on different nights varying between 0.0022–0.0154 mag (Table 4). The latter is consistent with the periodicity determined by Williams et al. (2015), and the ∼3.89 ± 0.05 hours periodic radio pulses reported by McLean et al. (2011). VLBA observations Forbrich et al. (2016) determined the source of the ∼3.8 hours modulation as originating from the secondary component 2M J1314+13B, and so we attribute the 2.06 ± 0.05 hours modulation to more than likely originate from 2M J1314+13A, the first such estimate of its rotational period. This result is in contradiction with prior expectations given the both components’ physical similarities (Table 1) and common origin (Dupuy et al. 2016; Forbrich et al. 2016), similar rotation properties were presumed for both components (McLean et al. 2011; Forbrich et al. 2016; Pineda et al. 2017).
 |
Fig. 10. I-band light curves of 2M J1314+13AB from three of the observation epochs. Each figure shows relative flux vs. HJD time. The HJD time above each figure denotes the start-point of each observation night. Photometric error bars were applied to each data point as listed in Table 4. Both A and B components contribute to the variability seen here. The arrows marked on the 24th Feb 2017 light curve indicates an interval of complete cloud cover; therefore these data were removed. |
Amplitude variability and photometric error analysis of 2M J1314+13A and 2M J1314+13B.
 |
Fig. 11. The same light curves as Figure 10, after subtracting out the signal of 2M J1314+13B. These lightcurves plot relative flux vs. Modified Heliocentric Julian Date (MHJD). Photometric error bars of each 2M J1314+13AB measurement are applied here as listed in Table 3. |
 |
Fig. 12. Lomb-Scargle (LS) periodograms for each permutation of binary component and photometric technique, after isolating signal for each binary component by running LCF. Panel A: Periodogram of all epochs of the I-band GUFI photometric data of 2M J1314+13A, after subtraction of the putative rotational period of the secondary component. We discovered optical variability of 2.06 ± 0.05 hours detected as the highest peak in the periodogram. Panel B: Periodogram of all epochs of the I-band GUFI photometric data of 2M J1314+13B, after subtracting out the primary period. We indicated a periodicity of 3.79 ± 0.05 hours detected as the highest peak in the periodogram. The vertical red dashed line (shown in close-up in the inset plot) corresponds to the detected optical periods using each technique for each component. The dashed-dotted line on each plot corresponds to the 5σ false-alarm probability in each case. |
 |
Fig. 13. Phase Dispersion Minimization (PDM) plots of the entire ∼1.3 year baseline for each permutation of binary component and photometric technique after running LCF. The arrow marked on each figure indicates the most significant periods after trying 105 Monte-Carlo simulations. Panel A: PDM of all epochs of the I-band data sets of 2M J1314+13A. We discovered sinusoidal photometric variability with a period of ∼2.06 hours. Panel B: PDM of all epochs of the GUFI I-band data of 2M J1314+13B. We detected a period of ∼3.78 hours. Panels C and D: close-ups of the region where theta reaches its minimum, yielding our reported periods. |
Again our observations indicate periodic optical emission from both components of the 2MASS J1314203+132001AB system, with recovery of the well known ∼3.8 hours rotational period from 2M J1314+13B – stable over a timescale of up to 8 years – and the first such detection from 2M J1314+13A with a period of 2.06 ± 0.05 hours. 2M J1314+13AB is an M7 binary dwarf and so the formation and long-term suspension of dust clouds are unlikely. Such longevity is more consistent with magnetically-induced spots being the cause of the rotational modulation for both binary components (McLean et al. 2011). Alternatively, correlations observed in simultaneous optical - in particular Hα – and radio observations are explicable in the context of an active auroral electrodynamic engine on 2M J1314+13B (McLean et al. 2011). Forbrich et al. (2016) further used their astrometric observations to explain how such auroral currents can be generated. Given the lack of any discernible radio emission from 2M J1314+13A, it is more likely this dwarf lacks the conditions to support and sustain stable aurora, and so its modulation is a consequence of magnetic spots, possibly with a variable cycle. Further, more detailed observations of this system are required to resolve this conundrum in the observational data acquired to date.
6. Constraining the spin-orbit alignment of both binary systems
6.1. 2M J0746+20AB
To derive the spin-orbit alignment of the 2M J0746+20AB system we use the radii estimate of 0.99 ± 0.03 RJ and 0.96 ± 0.02 RJ (Harding et al. 2013b), and the v sin i measurements of 19 ± 2 km s−1 and 33 ± 3 km s−1 from spectroscopic observations (Konopacky et al. 2012) for A and B respectively. These data, when combined with our derived periods for both components allow us to conclude that the axes are oriented with respect to the observer at 32 ± 4 degrees and 37 ± 4 degrees, respectively (Figures 15 and 16). The uncertainty on these equatorial inclination estimates were determined using a Monte Carlo formalism. These findings are entirely consistent with an equatorial inclination angle of 32 ± 4 degrees for component A (Harding et al. 2013b), and 36 ± 4 degrees for component B (Harding et al. 2013b; Lynch et al. 2015), and confirm that the rotational and orbital planes of 2M J0746+20AB are consistent with a coplanar alignment to within 10 degrees, suggesting a likely disk fragmentation origin for this binary system.
 |
Fig. 15. Equatorial rotational velocity vs. inclination angle of the orbital plane for 2M J0746+20A. The solid red curve plots the v sin i of 2M J0746+20A (Konopacky et al. 2012). The black vertical solid line and top x-axis scale refer to the alignment of the spin and orbit axes. The right-hand y− axis corresponds to the radius of the dwarf, ∼0.99 RJ (∼0.0995 R⊙) where RJ ∼ 69 911 km, as calculated by Harding et al. (2013b). This radius corresponds to an equatorial velocity of ∼36 km s−1 from this work, highlighted as the solid blue line. The 41.8 degree orbital inclination angle is adopted from Konopacky et al. (2012). The dashed lines in all cases represent the associated errors. We measured equatorial inclination of 32 ± 4 degrees marked with the solid green line, which is exactly consistent with what has been found in the previous study of Harding et al. (2013b) and also confirm that the 2M J0746+20A equatorial inclination is within 10 degrees of the orbital inclination angle. |
 |
Fig. 16. Same axis layout and illustration as Figure 15, except for the case of 2M J0746+20B. Its v sin i of 33 ± 3 km s−1 (Konopacky et al. 2012) is shown by the red solid line, where the dashed lines represent the errors in this measurement. We highlight the adopted radius of ∼0.96 RJ (∼0.0964 R⊙) (Harding et al. 2013b) with the dotted green vertical track, which appears to have an equatorial inclination angle of 37 ± 4 degrees, aligned with the orbital plane of the system to within ∼5 degrees. We calculated an equatorial velocity of ∼55 km s−1 which is marked by the solid blue line, in exact agreement with Harding et al. (2013b) who used the ∼2.07 hours radio period for the secondary member in their work. |
6.2. 2M J1314+13AB
In the case of the M7 dwarf 2M J1314+13AB, we used the latest radii estimates (Dupuy et al. 2016) of 1.831 ± 0.018 RJ and 1.808 ± 0.018 RJ for 2M J1314+13A and 2M J1314+13B. We assigned the periods of rotation of 2.06 ± 0.05 hours and 3.79 ± 0.05 hours discovered here for components A and B, respectively. Unlike 2M J0746+20AB, we do not currently possess v sin i measurements for each of the components in 2M J1314+13AB, thus limiting our ability to unambiguously constrain the system’s spin-orbit geometry. If we assign the system’s combined v sin i value of 45 ± 5 km s−1 (McLean et al. 2011) to 2M J1314+13B, and use the same Monte Carlo approach as applied to the case of 2M J0746+20AB, we can explore its spin-orbital orientation, and find evidence for such an alignment with an estimated spin axis orientation of 50.6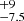 degrees. This result is consistent with Dupuy et al. (2016), who previously determined system’s orbital plane (orbital inclination i = 49.34
degrees. This result is consistent with Dupuy et al. (2016), who previously determined system’s orbital plane (orbital inclination i = 49.34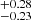 degrees) as shown in Figure 17.
degrees) as shown in Figure 17.
 |
Fig. 17. Equatorial rotational velocity vs. inclination angle of the orbital plane for 2M J1314+13B. The green solid curve plots the v sin i of 2M J1314+13B (45 ± 5 km s−1) (McLean et al. 2011). The black horizontal lines show the inferred equatorial velocity of 58.2 ± 0.2 km s−1 for 2M J1314+13B. The dashed green and black lines correspond to the error in this measurement. We find that our photometric period of rotation, combined with the latest estimated radius of 1.808 ± 0.018 RJ (Dupuy et al. 2016), results in an equatorial inclination angle of 50.6 |
Under the unrealistic assumption that the v sin i of 45 ± 5 km s−1, McLean et al. (2011) originates solely from 2M J1314+13B, we can use the current estimate of the radius of 2M J1314+13A (1.831 ± 0.018 RJ) (Dupuy et al. 2016) and our measured rotation period (2.06 ± 0.05 hours) to derive a v sin i for the primary component of 83.8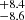 km s−1. A more realistic interpretation of the measured v sin i is that it is a combination of the contributions from both components, and that the the fainter source would have a weaker signal (about 1 mag fainter in the Sloan z′ filter; therefore its flux is ∼40% of the flux of the dominant component and < 30% of the combined flux Law et al. 2006) contributing to the observed v sin i, which likely places it within the 45 ± 5 km s−1 range. This being so, we estimate the lower limit of the primary’s equatorial inclination angle to be in the range of 24.5
km s−1. A more realistic interpretation of the measured v sin i is that it is a combination of the contributions from both components, and that the the fainter source would have a weaker signal (about 1 mag fainter in the Sloan z′ filter; therefore its flux is ∼40% of the flux of the dominant component and < 30% of the combined flux Law et al. 2006) contributing to the observed v sin i, which likely places it within the 45 ± 5 km s−1 range. This being so, we estimate the lower limit of the primary’s equatorial inclination angle to be in the range of 24.5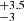 degrees, and so not coplanar with the system’s orbital plane (the vertical magenta line in Figure 18). However, for spin axes be aligned with the orbital plane, we inferred that an inclination of ∼64.8 degrees is expected for 2M J1314+13A (the vertical black dashed line in Figure 18). Definitive resolution of this system’s orientation, and in particular our ability to determine if 2M J1314+13AB has an evolutionary history similar to that of 2M J0746+20AB, speaking to a common disk fragmentation model origin, will require resolved v sin i estimates for both components.
degrees, and so not coplanar with the system’s orbital plane (the vertical magenta line in Figure 18). However, for spin axes be aligned with the orbital plane, we inferred that an inclination of ∼64.8 degrees is expected for 2M J1314+13A (the vertical black dashed line in Figure 18). Definitive resolution of this system’s orientation, and in particular our ability to determine if 2M J1314+13AB has an evolutionary history similar to that of 2M J0746+20AB, speaking to a common disk fragmentation model origin, will require resolved v sin i estimates for both components.
 |
Fig. 18. Same axis layout and illustration as Figure 17, but here we plot the results obtained from the scenario that the v sin i of 45 ± 5 km s−1 (red solid curve) is a combination from both components. The dashed red line corresponds to the measured error in the v sin i. The horizontal green dashed line in the plot represents the 1.831 ± 0.018 RJ radius estimate for the secondary component (Dupuy et al. 2016). The magenta vertical solid line shows the corresponding tentative equatorial inclination angle of 24.5 |
7. Conclusions
We identify a newly discovered optical variability in the secondary component of the ultracool dwarf binary 2M J0746+20AB with a period of 2.14 ± 0.11 hours. This value lies within the period uncertainty range of Berger et al. (2009), Lynch et al. (2015) and Zhang et al. (2020) who reported radio periodicity of 2.072 ± 0.001 hours, 2.071481 ± 0.000002 hours and 2.1 ± 0.1 hours, respectively. Berger et al. (2009) also detected quasi-sinusoidal Hα emission modulated with the same period, although not in phase, and confirmed the presence of a ∼1.7 kG magnetic field, which is consistent with that originally estimated by Antonova et al. (2008). The recent observation of this system by a collaboration using the Giant Metrewave Radio Telescope array at 600 MHz and 1.3 GHz (Zic et al. 2019) demonstrated the presence of stable radio emission at both bands, with suggestions of a dominant coherent component at 1.3 GHz, although sensitivity and instrumentation constraints limited their ability to definitively assert this as being the case, nor indeed to discern any pulsed or periodic modulations in the radio data. Whilst low frequency (i.e. 600 MHz) emission is expected to be dominated by incoherent gyrosynchrotron processes, the tentative detection of highly polarized emission at 1.3 GHz is consistent with auroral emission, albeit from a higher magnetic field environment. All these findings support the idea of a correlation between radio, spectroscopic and photometric wavelengths in both components, and therefore the observed optical variability in 2M J0746+20A and 2M J0746+20B may be attributed to stellar rotation coupled with active and sustained localized auroral regions on both components, with the work of Zhang et al. (2020) suggesting some variability in that associated with 2M J0746+20A. We confirm the proposition of Harding et al. (2013b) regarding the spin-orbit alignment of 2M J0746+20AB, with the system being in coplanar alignment to within 10 degrees.
Up to now only one component of the 2M J1314+13AB binary system has been associated with a periodic modulation, presumed to be the rotational signature of 2M J1314+13B, evident in prior optical and radio observations with a period of ∼3.8 hours. We were able to identify an additional periodic signal of 2.06 ± 0.05 hours in our I-band photometry, presumed to originate from 2M J1314+13A, in addition to recovering a 3.79 ± 0.05 hours modulation in our observations of 2M J1314+13AB using the GUFI photometer at VATT. This is the first detection of any modulated emission from the primary component of this system. Our observations also confirm that the emission mechanisms associated with the secondary are associated with stable and sustained processes; as such periodic emission has been detected at this modulation over an 8 year baseline. Unlike 2M J0746+20AB, VLBA observations as reported by Forbrich et al. (2016) only detected emission from 2M J1314+13B, and so whilst an argument can be made for the presence of a dominant auroral engine on this component, the paucity of modulated emission at any passband for 2M J1314+13A, despite its faster rotational period, is indicative of either a mis-aligned spin axis compared to its companion, or a weaker magnetic environment yielding sporadic activity, or both. 2M J1314+13AB lacks individual v sin i estimates for both components, limiting our ability to fully constrain the system’s spin-orbit alignment. Assuming that the combined value of 45 ± 5 km s−1 originates solely from 2M J1314+13B allows us to determine excellent agreement between the orbital plane estimate of Dupuy et al. (2016) and the component’s inferred spin axis. A much more reasonable interpretation posits that the combined v sin i is being dominated by the brighter (∼1 mag) 2M J1314+13B, and that the primary’s v sin i is within this observed range. That being so, it would suggest that the primary is in fact not in coplanar alignment with its companion or the system more generally, and so perhaps explain the paucity of modulated emission to date, in addition to challenging a common disk fragmentation origin hypothesis for such dwarf binaries. The acquisition of individual v sin i for the 2M J1314+13AB binary system would be invaluable in resolving this matter.
We note a geometric effect associated with the inference of coplanarity using existing RV/rotation observations, namely our inability to definitively rule out the likelihood that both components have rotational axes orthogonal with respect to each other despite presenting the same apparently coplanar inclination angle (Harding et al. 2013b). To date, the only means whereby such definitive estimates of absolute spin orientation in multi-component systems have been made is by using the Rossiter-McLaughlin effect, but this only possible to implement for the case of eclipsing binaries (Albrecht 2012). State-of-the-art spectro-interferometry could directly measure spin-spin alignment in visual binary systems (Le Bouquin et al. 2009) although these have yet to be performed, likely a consequence of the challenging nature of such observations. Previous efforts simulating the formation of low mass binary systems argued for the dominance of turbulent fragmentation (Offner et al. 2010) although model constraints limited the systems studied to > 200 au separation, and did not provide any information on resulting component spin orientations. Developing modeling formalisms capable of simulating the formation of more closely separated systems in addition to estimates of the latter could offer a more comprehensive means of understanding the lower end of the initial stellar multiplicity distribution under differing formation contexts (Lee et al. 2020), and in so doing, provide a probabilistic framework to assess the likelihood of coplanar orthogonal spin orientations in tight binary systems as determined from RV or rotational observations.
Confirmation of of spin-orbit coplanarity for the 2M J0746+20AB system underlines its great potential as a case study for modeling VLM tight binary formation, particularly given the system’s longevity and both components common stellar classification and associated strong magnetic fields. However one must exercise caution in drawing inferences more generally, especially given our conclusion that the second system studied, 2M J1314+13AB, as likely being non-coplanar and requiring additional observations to confirm that this is indeed the case. This is further complicated by the coplanarity status of a third tight binary, LP349-25AB, for which we previously have presented evidence indicative of coplanarity (Harding et al. 2013a). Additional observations of these and other systems, and their formation contexts, are needed to reasonably characterize spin-orbit alignment in the very low mass binary regime, and so determine more far reaching implications, if any, for understanding of star and planet formation more generally. Critical to this will be the development of magneto-hydrodynamic codes capable of accurately modeling such formation scenarios at ∼au scales, so as to accurately capture the physical interactions that are likely to dominate and so shape the resulting spin-orbit scenarios we observe.
Acknowledgments
S.D gratefully acknowledges financial support from the Ministry of higher education in Iraq and Nahrain University who funded this work, and the Dean of Graduate Studies at the University of Galway. Funding to support the development of the GUFI instrument is gratefully acknowledged from Science Foundation Ireland (Grant Number 07/RFP/PHYF553). Based on observations with the VATT: the Alice P. Lennon Telescope and the Thomas J. Bannan Astrophysics Facility.
References
- Adams, F. C., Ruden, S. P., & Shu, F. H. 1989, ApJ, 347, 959 [Google Scholar]
- Albrecht, S. 2012, IAU Symp., 282, 379 [NASA ADS] [Google Scholar]
- Antonova, A., Doyle, J., Hallinan, G., Bourke, S., & Golden, A. 2008, A&A, 487, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artigau, É., Bouchard, S., Doyon, R., & Lafrenière, D. 2009, ApJ, 701, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. 2004, A&A, 419, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C., & Mundt, R. 2001, A&A, 367, 218 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. 2003, A&A, 402, 701 [CrossRef] [EDP Sciences] [Google Scholar]
- Bardalez Gagliuffi, D. C., Burgasser, A. J., Gelino, C. R., et al. 2014, ApJ, 794, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Rutledge, R., Phan-Bao, N., et al. 2009, ApJ, 695, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C. H., Charbonneau, D., & White, R. J. 2010, ApJ, 723, 684 [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 1994, MNRAS, 269, L45 [CrossRef] [Google Scholar]
- Bouy, H., Duchêne, G., Köhler, R., et al. 2004, A&A, 423, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buenzli, E., Apai, D., Radigan, J., Reid, I. N., & Flateau, D. 2014, ApJ, 782, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, F., Oppenheimer, B., & Tinney, C. 2002a, MNRAS, 335, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, F., Tinney, C., & Covey, K. 2002b, MNRAS, 332, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, F., Hodgkin, S., Oppenheimer, B., Robertson, J., & Haubois, X. 2008, MNRAS, 386, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Muirhead, P. S., Han, E., et al. 2016, MNRAS, submitted [arXiv:1609.03586] [Google Scholar]
- Crossfield, I., Biller, B., Schlieder, J., et al. 2014, Nature, 505, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Dahn, C. C., Harris, H. C., Vrba, F. J., et al. 2002, AJ, 124, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Ségransan, D., Forveille, T., et al. 2009, A&A, 505, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dulaimi, S., Golden, A., Boyle, R. P., & Butler, R. F. 2023, MNRAS, 521, 4695 [CrossRef] [Google Scholar]
- Dupuy, T. J., Forbrich, J., Rizzuto, A., et al. 2016, ApJ, 827, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Brown, M. E., & Burgasser, A. J. 2003, AJ, 126, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, R. T. 2004, ApJ, 600, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Forbrich, J., Dupuy, T. J., Reid, M. J., et al. 2016, ApJ, 827, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Gelino, C. R., Marley, M. S., Holtzman, J. A., Ackerman, A. S., & Lodders, K. 2002, ApJ, 577, 433 [CrossRef] [Google Scholar]
- Gillon, M., Triaud, A., Jehin, E., et al. 2013, A&A, 555, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldman, B., Cushing, M., Marley, M., et al. 2008, A&A, 487, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodwin, S. P., Whitworth, A. P., & Ward-Thompson, D. 2004, A&A, 414, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hale, A. 1994, AJ, 107, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Littlefair, S., Cotter, G., et al. 2015, Nature, 523, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, L. K., Hallinan, G., Boyle, R. P., et al. 2013a, ApJ, 779, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, L. K., Hallinan, G., Konopacky, Q. M., et al. 2013b, A&A, 554, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Justesen, I., & Albrecht, S. 2020, A&A, 642, A212 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirkpatrick, J. D., Reid, I. N., Liebert, J., et al. 2000, AJ, 120, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C. 2006, MNRAS, 367, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Konopacky, Q., Ghez, A., Barman, T. S., et al. 2010, ApJ, 711, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Konopacky, Q., Ghez, A., Fabrycky, D., et al. 2012, ApJ, 750, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, C., Hallinan, G., Zavala, R., et al. 2007, ApJ, 668, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Law, N., Hodgkin, S., & Mackay, C. 2006, MNRAS, 368, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bouquin, J. B., Absil, O., Benisty, M., et al. 2009, A&A, 498, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., Offner, S. S. R., Hennebelle, P., et al. 2020, Space Sci. Rev., 216, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lepine, S., Thorstensen, J. R., Shara, M. M., & Rich, R. M. 2009, AJ, 137, 4109 [NASA ADS] [CrossRef] [Google Scholar]
- Li, P. S., Norman, M. L., Mac Low, M.-M., & Heitsch, F. 2004, ApJ, 605, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S., Dhillon, V., Marsh, T., et al. 2008, MNRAS, 391, L88 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Lynch, C., Mutel, R., & Güdel, M. 2015, ApJ, 802, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Maiti, M. 2007, AJ, 133, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, E. L., Osorio, M. R. Z., & Lehto, H. J. 2001, ApJ, 557, 822 [CrossRef] [Google Scholar]
- McLean, M., Berger, E., Irwin, J., Forbrich, J., & Reiners, A. 2011, ApJ, 741, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Kratter, K. M., Matzner, C. D., Krumholz, M. R., & Klein, R. I. 2010, ApJ, 725, 1485 [Google Scholar]
- Pineda, J. S., Hallinan, G., & Kao, M. M. 2017, ApJ, 846, 75 [Google Scholar]
- Radigan, J., Jayawardhana, R., Lafreniere, D., et al. 2012, ApJ, 750, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Radigan, J., Lafrenière, D., Jayawardhana, R., & Artigau, E. 2014, ApJ, 793, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N., Burgasser, A., Cruz, K., Kirkpatrick, J. D., & Gizis, J. 2001, AJ, 121, 1710 [NASA ADS] [CrossRef] [Google Scholar]
- Rockenfeller, B., Bailer-Jones, C. A., Mundt, R., & Ibrahimov, M. A. 2006, MNRAS, 367, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Scargle, J. D. 1989, ApJ, 343, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Schlieder, J. E., Bonnefoy, M., Herbst, T., et al. 2014, ApJ, 783, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [Google Scholar]
- Vrba, F. J., Henden, A., Luginbuhl, C., et al. 2004, AJ, 127, 2948 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. K. G., Berger, E., Irwin, J., Berta-Thompson, Z., & Charbonneau, D. 2015, ApJ, 799, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Hallinan, G., Brisken, W., Bourke, S., & Golden, A. 2020, ApJ, 897, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Zic, A., Lynch, C., Murphy, T., Kaplan, D. L., & Chandra, P. 2019, MNRAS, 483, 614 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Observation Details
2M J0746+20AB & 2M J1314+13AB observations.
All Tables
Amplitude variability and photometric error analysis of 2M J0746+20A and 2M J0746+20B.
Amplitude variability and photometric error analysis of 2M J1314+13A and 2M J1314+13B.
All Figures
 |
Fig. 1. Representative I-band photometric timeseries from four out of sixteen nights when 2M J0746+20AB was observed. Target flux relative to 5–6 reference stars is plotted against Modified Heliocentric Julian Date (MHJD). The HJD time above each figure denotes the start-point of each observation night. Both components of the binary contribute to the variability seen here. Possibly aperiodic variations are observed in some light curves (e.g. 29th December 2017). The arrow marked on the 24th November 2017 light curve indicates a period of full cloud coverage, and this data has been removed. The December 24th 2017 data were taken during bad weather conditions (thin cloud). The impact is shown clearly by an increase in the photometric error bars and an increase in the scatter of the light curve itself. |
| In the text | |
 |
Fig. 2. 2M J0746+20B: The same light curves as Figure 1, after running LCF to subtract out the 3.32 hours rotational period of the primary component 2M J0746+20A. Each figure shows relative flux vs. Modified Heliocentric Julian Date (MHJD) time. Photometric error bars for 2M J0746+20AB are applied here as listed in Table 3. |
| In the text | |
 |
Fig. 3. A. Lomb Scargle (LS) periodograms of all epochs of 2M J0746+20B, after subtraction of the primary’s 3.32 hours period: power spectra vs. frequency days−1. Dashed, horizontal red lines denote the 5σ false alarm probability of the peaks. The period obtained for the combined dataset is 2.14 ± 0.11 hours, a newly discovered optical period. This periodicity lies within the period uncertainty range of Berger et al. (2009), Lynch et al. (2015) and Zhang et al. (2020) who measured the radio period at 2.072 ± 0.001 hours, 2.071481 ± 0.000002 hours and 2.1 ± 0.1 hours, respectively, as well as being consistent with the 2.07 hours period of quasi-sinusoidal Hα emission (Berger et al. 2009). B. The same LS periodogram, zoomed into the area around the highest peak. The dashed red line corresponds to our detected optical secondary period of 2.14 ± 0.11 hours. |
| In the text | |
 |
Fig. 4. A. Phase Dispersion Minimization (PDM) plot for all epochs of 2M J0746+20B, after subtraction of the primary’s 3.32 hours period. The theta statistic was determined from 105 Monte-Carlo simulations. The minima theta indicates the most likely rotational period of ∼2.14 hours, in agreement with the rotation period resulting from the LS periodogram seem in Figure 3. B. The same PDM theta plot, zoomed into the area around the minimum theta statistic. |
| In the text | |
 |
Fig. 5. A. Phase-folded light curve of 2M J0746+20B from all epochs combined, after subtracting out the ∼3.32 hours periodicity attributed to the rotational period of the primary component. These unbinned data are folded to our newly discovered rotation period in the optical of ∼2.14 hours. B. The same data in plot A except binned in phase by a factor of 10 for clarity. |
| In the text | |
 |
Fig. 6. 2M J0746+20A: The same light curves as in Figure 1, after running LCF to subtract out the secondary component’s signature. Each figure shows relative flux vs. Modified Heliocentric Julian Date (MHJD) time. Note the difference in scale on the y-axis for the 24th November 2017 plot, due to the light curve exhibiting a larger amplitude variation of 1.54%. Photometric error bars for 2M J0746+20AB are applied here as listed in Table 3. |
| In the text | |
 |
Fig. 7. A. Lomb-Scargle (LS) periodograms of all three epochs of the I-band GUFI photometric data of 2M J0746+20A, after subtraction of the putative ∼2.14 hours rotational period of the secondary component. The x-axis is plotted in days−1, since each epoch was time-stamped in units of Modified Heliocentric Julian Date (MHJD). The red dashed and dotted horizontal lines represent a 5σ false-alarm probability of the peaks, as defined by the LS periodogram algorithm. The mean peak-to-peak amplitude variability of 2M J0746+20A varied between 0.0014 to 0.0154 mag on different nights. B. The same LS periodogram, zoomed into the area around the highest peak. The vertical red dashed line corresponds to 3.32 ± 0.08 hours. |
| In the text | |
 |
Fig. 8. A. Phase Dispersion Minimization (PDM) plots for all epochs of 2M J0746+20A, after subtraction of the putative ∼2.14 hours rotational period of the secondary component, showing theta statistic against frequency days−1. The deepest minimum of the quantity theta marks the most likely rotational period of ∼3.32 hours. B. The same PDM theta plot, zoomed into the area around the deepest minimum theta statistic that corresponds to the primary’s period of rotation established in this work, consistent with the rotation period resulting from LS periodogram analysis. |
| In the text | |
 |
Fig. 9. A. Phase-folded light curve of 2M J0746+20A from all three epochs, after subtracting out the secondary period of 2.14 hours. These unbinned data points are folded to a period of ∼3.32 hours. The observed sinusoidal variability to the same reported period from Harding et al. (2013b), shows that this dwarf is stable on timescales of years. B. The same data in plot A except binned in phase by a factor of 20 for clarity. |
| In the text | |
 |
Fig. 10. I-band light curves of 2M J1314+13AB from three of the observation epochs. Each figure shows relative flux vs. HJD time. The HJD time above each figure denotes the start-point of each observation night. Photometric error bars were applied to each data point as listed in Table 4. Both A and B components contribute to the variability seen here. The arrows marked on the 24th Feb 2017 light curve indicates an interval of complete cloud cover; therefore these data were removed. |
| In the text | |
 |
Fig. 11. The same light curves as Figure 10, after subtracting out the signal of 2M J1314+13B. These lightcurves plot relative flux vs. Modified Heliocentric Julian Date (MHJD). Photometric error bars of each 2M J1314+13AB measurement are applied here as listed in Table 3. |
| In the text | |
 |
Fig. 12. Lomb-Scargle (LS) periodograms for each permutation of binary component and photometric technique, after isolating signal for each binary component by running LCF. Panel A: Periodogram of all epochs of the I-band GUFI photometric data of 2M J1314+13A, after subtraction of the putative rotational period of the secondary component. We discovered optical variability of 2.06 ± 0.05 hours detected as the highest peak in the periodogram. Panel B: Periodogram of all epochs of the I-band GUFI photometric data of 2M J1314+13B, after subtracting out the primary period. We indicated a periodicity of 3.79 ± 0.05 hours detected as the highest peak in the periodogram. The vertical red dashed line (shown in close-up in the inset plot) corresponds to the detected optical periods using each technique for each component. The dashed-dotted line on each plot corresponds to the 5σ false-alarm probability in each case. |
| In the text | |
 |
Fig. 13. Phase Dispersion Minimization (PDM) plots of the entire ∼1.3 year baseline for each permutation of binary component and photometric technique after running LCF. The arrow marked on each figure indicates the most significant periods after trying 105 Monte-Carlo simulations. Panel A: PDM of all epochs of the I-band data sets of 2M J1314+13A. We discovered sinusoidal photometric variability with a period of ∼2.06 hours. Panel B: PDM of all epochs of the GUFI I-band data of 2M J1314+13B. We detected a period of ∼3.78 hours. Panels C and D: close-ups of the region where theta reaches its minimum, yielding our reported periods. |
| In the text | |
 |
Fig. 14. The same light curves as Figure 12, after subtracting out the primary component. |
| In the text | |
 |
Fig. 15. Equatorial rotational velocity vs. inclination angle of the orbital plane for 2M J0746+20A. The solid red curve plots the v sin i of 2M J0746+20A (Konopacky et al. 2012). The black vertical solid line and top x-axis scale refer to the alignment of the spin and orbit axes. The right-hand y− axis corresponds to the radius of the dwarf, ∼0.99 RJ (∼0.0995 R⊙) where RJ ∼ 69 911 km, as calculated by Harding et al. (2013b). This radius corresponds to an equatorial velocity of ∼36 km s−1 from this work, highlighted as the solid blue line. The 41.8 degree orbital inclination angle is adopted from Konopacky et al. (2012). The dashed lines in all cases represent the associated errors. We measured equatorial inclination of 32 ± 4 degrees marked with the solid green line, which is exactly consistent with what has been found in the previous study of Harding et al. (2013b) and also confirm that the 2M J0746+20A equatorial inclination is within 10 degrees of the orbital inclination angle. |
| In the text | |
 |
Fig. 16. Same axis layout and illustration as Figure 15, except for the case of 2M J0746+20B. Its v sin i of 33 ± 3 km s−1 (Konopacky et al. 2012) is shown by the red solid line, where the dashed lines represent the errors in this measurement. We highlight the adopted radius of ∼0.96 RJ (∼0.0964 R⊙) (Harding et al. 2013b) with the dotted green vertical track, which appears to have an equatorial inclination angle of 37 ± 4 degrees, aligned with the orbital plane of the system to within ∼5 degrees. We calculated an equatorial velocity of ∼55 km s−1 which is marked by the solid blue line, in exact agreement with Harding et al. (2013b) who used the ∼2.07 hours radio period for the secondary member in their work. |
| In the text | |
 |
Fig. 17. Equatorial rotational velocity vs. inclination angle of the orbital plane for 2M J1314+13B. The green solid curve plots the v sin i of 2M J1314+13B (45 ± 5 km s−1) (McLean et al. 2011). The black horizontal lines show the inferred equatorial velocity of 58.2 ± 0.2 km s−1 for 2M J1314+13B. The dashed green and black lines correspond to the error in this measurement. We find that our photometric period of rotation, combined with the latest estimated radius of 1.808 ± 0.018 RJ (Dupuy et al. 2016), results in an equatorial inclination angle of 50.6 |
| In the text | |
 |
Fig. 18. Same axis layout and illustration as Figure 17, but here we plot the results obtained from the scenario that the v sin i of 45 ± 5 km s−1 (red solid curve) is a combination from both components. The dashed red line corresponds to the measured error in the v sin i. The horizontal green dashed line in the plot represents the 1.831 ± 0.018 RJ radius estimate for the secondary component (Dupuy et al. 2016). The magenta vertical solid line shows the corresponding tentative equatorial inclination angle of 24.5 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.