| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A290 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202449768 | |
| Published online | 17 October 2024 | |
Evolution of the star formation rate and ΣSFR of galaxies at cosmic morning (4 < z < 10)
1
INAF – Osservatorio Astronomico di Roma, Via Frascati 33 00078 Monte Porzio Catone, Italy
2
Scuola Normale Superiore, Piazza dei Cavalieri 7, 50126 Pisa, Italy
3
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
4
INAF – Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
5
Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, Via Marzolo 8, I-35131 Padova, Italy
6
Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
7
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Texas A& M University, College Station, TX 77843-4242, USA
8
Racah Institute of Physics, The Hebrew University of Jerusalem, Jerusalem 91904, Israel
9
NSF’s National Optical-Infrared Astronomy Research Laboratory, 950 N. Cherry Ave., Tucson, AZ 85719, USA
10
The University of Texas at Austin, 2515 Speedway Blvd Stop, C1400 Austin, TX 78712, USA
11
University of Massachusetts Amherst, 710 North Pleasant Street, Amherst, MA 01003-9305, USA
12
Institute of Physics, Laboratory of Galaxy Evolution, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
13
Department of Physics and Astronomy, University of Louisville, Natural Science Building 102, 40292 KY, Louisville USA
14
, Center for Astrophysics | Harvard & Smithsonian, 60 Garden St., Cambridge, MA 02138, USA
15
Black Hole Initiative at Harvard University, 20 Garden St., Cambridge, MA 02138, USA
16
ESA/AURA, Space Telescope Science Institute, 3800 San Martin Drive, Baltimore, MD 21218, USA
17
Department of Physics and Astronomy, University of California, Los Angeles, 430 Portola Plaza, Los Angeles, 90095 CA, USA
18
Aix Marseille Université, CNRS, CNES, LAM, 38, rue Frédéric Joliot-Curie, 13388 Marseille, CEDEX 13, France
19
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
20
Cavendish Laboratory, University of Cambridge, 19 JJ Thomson Avenue, Cambridge CB3 0HE, UK
21
Astronomy Centre, University of Sussex, Falmer, Brighton BN1 9QH, UK
22
Institute of Space Sciences and Astronomy, University of Malta, Msida, MSD 2080, Malta
23
Departamento de Astronomía, Universidad de La Serena, Av. Juan Cisternas 1200 Norte, La Serena, Chile
24
ARAID Foundation. Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Unidad Asociada al CSIC, Plaza San Juan 1, E-44001 Teruel, Spain
25
Laboratory for Multiwavelength Astrophysics, School of Physics and Astronomy, Rochester Institute of Technology, 84 Lomb Memorial Drive, Rochester, NY 14623, USA
Received:
27
February
2024
Accepted:
19
June
2024
The galaxy-integrated star formation rate (SFR) surface density measurement (ΣSFR) has been proposed as a valuable diagnostic of the mass accumulation in galaxies given it is more tightly related to the physics of star formation and stellar feedback than other indicators. In this work, we assembled a statistical sample of 230 galaxies observed with JWST in the GLASS and CEERS spectroscopic surveys to estimate Balmer line-based dust attenuations and SFRs (i.e., from Hα, Hβ, and Hγ), along with the UV rest-frame effective radii. We studied the evolution of galaxy SFR and ΣSFR in the first 1.5 billion years of our Universe, from a redshift of z ∼ 4 to z ∼ 10. We found that ΣSFR is mildly increasing with redshift with a linear slope of 0.16 ± 0.06. We explored the dependence of SFR and ΣSFR on stellar mass, showing that a star-forming main sequence and a ΣSFR main sequence are present out to z = 10. This dependence exhibits a similar slope compared to the same relations at lower redshifts, but with a higher normalization. We find that the specific SFR (sSFR) and ΣSFR are correlated with the [O III] λ5007 Å/[O II] λ3727 Å ratio and with indirect estimates of the escape fraction of Lyman continuum photons; hence, they are likely to play an important role in the evolution of ionization conditions at higher redshifts and in the escape of ionizing radiation. We also searched for spectral outflow signatures in the Hα and [O III] emission lines in a subset of galaxies observed at high resolution (R = 2700) by the GLASS survey, finding an outflow incidence of 2/11 (=20%32%9%) at z < 6, but no evidence at z > 6 (0/6, < 26%). Finally, we find a positive correlation between AV and ΣSFR, and a flat trend as a function of sSFR, indicating that there is no evidence of a drop in AV in extremely star-forming galaxies between z ∼ 4 and ∼10. This result might be at odds with a dust-clearing outflow scenario, which may instead take place at redshifts of z ≥ 10, as suggested by some theoretical models.
Key words: galaxies: evolution / galaxies: high-redshift / galaxies: ISM / galaxies: star formation / galaxies: statistics
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The cosmic evolution of galaxy star formation rates (SFRs) is one of the fundamental predictions of astrophysical models and cosmological simulations. It also stands as one of the most widely studied processes observationally. Indeed, it provides essential insights into cosmic structure formation across all scales, the accretion of gas into these structures, the efficiency of conversion into stars, and, ultimately, the diffusion of baryonic material in the intergalactic medium (IGM) through stellar feedback (White & Rees 1978; White & Frenk 1991; Springel & Hernquist 2003; Shapley 2011; Hopkins et al. 2012; Behroozi et al. 2013; Madau & Dickinson 2014).
The SFR is intimately linked to other galaxy properties, most importantly the stellar mass (M⋆). A correlation between SFR and M⋆, known as the main sequence of star formation (Noeske et al. 2007), has been determined across over five orders of magnitude in M⋆ at all redshifts. While the slope, m, of this relation remains rather constant with redshift, with m ranging between 0.5 and 1.2, depending on both selection effects and the method to measure the SFRs (see Speagle et al. 2014 for a review), its normalization increases at earlier cosmic epochs. Indeed, focusing on the specific SFR (sSFR=SFR/M⋆), that is, the SFR normalized by the total stellar mass content, it follows a rather smooth, monotonic increase by at least one order of magnitude from a redshift of 0 up to the Epoch of Reionization (EoR, Speagle et al. 2014; Pannella et al. 2015; Schreiber et al. 2015; Santini et al. 2017; Davidzon et al. 2018; Leslie et al. 2020; Popesso et al. 2023), which is supported by theoretical models and simulations (Furlong et al. 2015; Henriques et al. 2015; Behroozi et al. 2019; Donnari et al. 2019; Di Cesare et al. 2023).
In addition to the SFR and the sSFR, a quantity that is gaining increasing attention (now that JWST has been equipped to resolve galaxy sizes out to the EoR) is the surface density of star formation (ΣSFR). This quantity represents the SFR normalized by the surface area where it occurs and encapsulates information about the spatial distribution of star formation. It is usually defined by the expression ΣSFR = SFR/(2π × re2), where re is the half-light radius. As galaxies become increasingly more compact at higher redshifts, since the dependence on the size is quadratic, ΣSFR increases more rapidly with redshift compared to the sSFR. In particular, it can rise by more than three orders of magnitudes in typical star-forming galaxies from z ∼ 0 to z ∼ 6 (Wuyts et al. 2011; Holwerda et al. 2015), reaching extreme conditions at the epoch of reionization (ΣSFR ≳ 10 M⊙/yr/kpc2). Therefore, it is even more essential to characterize the peculiar conditions of SF in the first phases of galaxy assembly.
Being more intimately related to the physics of star formation, such as the gas mass surface density through the Kennicutt-Schmidt relation (Kennicutt 1989; Kennicutt et al. 2007) and the effectiveness of stellar feedback, ΣSFR is thought to regulate the redshift evolution of the sSFR and M⋆ (Lehnert et al. 2015). Moreover, for the same reason, Salim et al. (2023) introduced the term “ΣSFR main sequence” to indicate the ΣSFR versus M⋆ relation, and they claim that this is even more fundamental than the sSFR – M⋆ relation. Along this new “main sequence”, star-forming galaxies have remarkably similar values of ΣSFR at z ∼ 0 (as also found independently by Schiminovich et al. 2007 and Förster Schreiber et al. 2019), with only a weak dependence (i.e., a positive correlation) on stellar mass across over three orders of magnitudes from 108 to 1011 M⊙. This is indicative of a more universal and self-regulated nature of ΣSFR. This relation exists up to at least z ∼ 2 (Salim et al. 2023), even though it becomes slightly steeper compared to z ∼ 0, which they interpret as evidence of bulge formation in the central regions of more massive systems.
The level of ΣSFR influences that of other galaxy properties. First, the increase in ΣSFR is tightly coupled to the increase of the interstellar medium (ISM) gas pressure and of the electron density, ne, with redshift (Jiang et al. 2019; Reddy et al. 2023). The increase of ne (and consequently ΣSFR) at fixed stellar mass may be entirely responsible for the higher ionization parameter of high redshift galaxies (Reddy et al. 2023). Thus, ΣSFR assumes the primary role that was previously attributed to metallicity. Secondly, ΣSFR is tightly related to the feedback of star formation, regulating the power of the outflows and how efficiently the gas is removed from the galaxies, thus affecting the future evolution of the entire system. For instance, previous works have shown that ΣSFR correlates with the mass loading factor of the outflow (Llerena et al. 2023) and with the maximum outflow velocity (Kornei et al. 2012; Bordoloi et al. 2014; Heckman & Borthakur 2016; Sugahara et al. 2019; Prusinski et al. 2021; Calabrò et al. 2022a). Similarly, an enhanced ΣSFR and stellar feedback reduce the gas and dust covering fraction in galaxies by creating channels that allow Lyα and Lyman-continuum (LyC) photons to escape into the IGM (Reddy et al. 2022). This picture is supported by observations suggesting a relation between ΣSFR and the escape fraction fesc of ionizing photons (Heckman 2001; Naidu et al. 2020; Flury et al. 2022), according to which galaxies with higher ΣSFR at both low and intermediate redshift have larger fractions of LyC leakers; also, LyC leakers have higher ΣSFR than the average galaxy population.
The key role of ΣSFR in driving outflows and easing the escape of ionizing radiation is also supported by models and simulations. For example, Sharma et al. (2016) and Sharma et al. (2017) implement galactic winds in the EAGLE cosmological simulations in such a way that they are capable of increasing fesc to more than 20% when ΣSFR reaches a value of 0.1 M⊙/yr/kpc2. With this recipe, they are able to explain the redshift evolution of the average fesc of galaxies and the volume filling factor of ionized gas up to z ∼ 8. Naidu et al. (2020) presented an empirical model e the evolution of fesc in galaxies is only dependent on ΣSFR, which thus assumes a key role in reionization. With this tight connection between fesc and ΣSFR, they claim that the bulk of reionization (∼80%) must be driven by a small number of galaxies (< 5%), the so-called “oligarchs”, with extremely high ΣSFR (∼10–20 M⊙/yr/kpc2), compact size, and relatively high UV luminosity (MUV < −18) and stellar mass (M⋆ > 108 M⊙).
The SFR in the first phases of galaxy assembly can also reach the super-Eddington regime, a condition in which the radiation pressure from young stars overcomes the gravitational force, leading to a galaxy-wide outflow that can clear the galaxy of its dust and gas content, pushing them away to large radii in a short timescale of the order of a few Myr (Ferrara et al. 2023; Ferrara 2024). These extreme conditions of star formation are invoked to explain the stunning abundance of UV luminous, very blue, and massive galaxies at z > 10 found since the first extragalactic observations with JWST (e.g., Naidu et al. 2022; Castellano et al. 2022).
The goal of this paper is to investigate how the SFR and the SFR surface density evolve in the first 1.5 billion years of our Universe. The investigation of galaxy assembly during the reionization epoch is perfectly-timed. On the one hand, the advent of JWST has allowed us to measure more compact galaxy sizes compared to previous telescopes and to resolve internal structures at much finer levels. On the other hand, the unique sensitivity of JWST in the rest-frame optical and UV of galaxies has allowed us to perform large photometric and spectroscopic surveys, such as GLASS (Treu et al. 2022) and CEERS (Finkelstein et al., in prep.), targeting statistically representative samples of galaxies during reionization down to M⋆ of 107 M⊙, and constraining the low SFR levels expected for these low-mass systems. This is essential to trace the scaling relations followed by the global galaxy population since the earliest epochs of their formation. In addition to the evolution of star formation, we are interested in exploring how ΣSFR is related to other galaxy properties and compare the observed values to those required by models and simulations to trigger galaxy wide outflows and to carve channels for the escape of Lyman continuum radiation.
The paper is organized as follows. In Section 2, we describe the spectroscopic observations, sample selection, and the derivation of all the physical properties investigated in this paper. In Section 3, we show our results, including the redshift evolution of the ΣSFR from z = 4 to z = 10, the SFR and the “ΣSFR main sequence”. Finally, in Section 4, we compare our findings with theoretical model predictions, and explore the relation between ΣSFR and other galaxy properties to understand its role in the reionization process. Then we analyze the presence of outflows in NIRSpec galaxies and connect them to the star formation rate and dust attenuation. For our analysis, we adopt a Chabrier 2003 initial mass function (IMF), and we assume a standard cosmology with H0 = 70 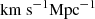 , Ωm = 0.3, and ΩΛ = 0.7.
, Ωm = 0.3, and ΩΛ = 0.7.
2. Methodology
The aim of this work is to analyze fundamental scaling relations describing the evolution of star formation in galaxies; hence, it is important to assemble a statistical sample as large as possible. Here, we use the data obtained by two JWST-based Early Release Science (ERS) programs, namely GLASS and CEERS, which represent the largest publicly available JWST survey thus far, with hundreds of high-redshift galaxies observed in the optical and near-infrared rest-frame. In the following part we analyze each survey in more detail, and explain how we derive the physical properties of galaxies from the available spectroscopic, imaging, and photometric datasets.
2.1. Spectroscopic observations and sample selection
We first considered spectra acquired through NIRSpec MSA observations by the GLASS-JWST ERS Program (PID 1324, PI: Treu; Treu et al. 2022) and by a JWST DDT program (PID 2756, PI: W. Chen; Roberts-Borsani et al. 2022). Both of them targeted galaxies residing over the central regions of the Frontier Field galaxy cluster Abell 2744. However, they were obtained using two different setups and different exposure times. The former were taken in high-resolution grating mode with three spectral configurations (G140H/F100LP, G235H/F170LP, and G395H/F290LP), covering a wavelength range from 1.5 to 5.14 μm at R ∼2000–3000, and with a total integration time (per grating) of 4.9 hours. The latter instead were taken in low-resolution mode with the CLEAR filter + prism configuration, which provides a continuous wavelength coverage from 0.6 to 5.3 μm at R ∼30–300. The prism resolution in the red part of the spectrum is enough to resolve and detect redshifted rest-frame optical emission lines, such as Hβ and [O III] λ5007 Å. The exposure time in this case is of 1.23 hours. The details of the spectral reduction, wavelength and flux calibration are described in detail in Mascia et al. (in prep.). Since GLASS-JWST observations target sources behind a lensing cluster, we adopt the magnification factors (μ) listed by Mascia et al. (2023), based on the latest lensing model of Bergamini et al. (2023), to correct line fluxes, SFRs, and galaxy sizes.
We also consider the spectra obtained by the CEERS survey through the NIRSpec MSA mode. The CEERS spectroscopic data were acquired over 3 different observing epochs and in 8 different pointings. The NIRSpec pointings named p4, p5, p7, p8, p9, and p10 were observed with the three NIRSpec medium resolution (G140M, G235M, and G395M) gratings, covering the observed-frame wavelength range 0.97–5.10 μm with a resolving power R ∼1000. In addition, p4, p5, p8, p9, p11, and p12 were also observed with the low resolution prism. In all cases, the exposure time is of 3107s per spectrum. Three-shutter slitlets with a three-point nodding pattern were also used to enable accurate background subtraction. After the observing run, some galaxies have spectra obtained with both the prism and M-grating configuration, in which case we prioritize the latter, as the higher resolution of the M-grating improves the detection of faint emission lines with low signal-to-noise ratio (S/N). The main steps of the reduction, the optimal extraction of the final 1D spectra, including also the wavelength and flux calibration, follow those described in other works of our collaboration, namely Fujimoto et al. (2023), Kocevski et al. (2023), and Arrabal Haro et al. (2023). A more detailed description of the NIRSpec data processing and a final spectroscopic catalog of the entire survey will also be presented in Arrabal Haro et al. (in prep.).
To build a sample of high redshift galaxies for our analysis, we visually checked all the 1D spectra provided by the above surveys in order to assign a first value to the spectroscopic redshift zspec based on the visual identification of relatively bright, optical emission lines, including [O II] λ3727 Å, Hβ, [O III] λ5007 Å, and Hα. This process was guided by the previous knowledge of the photometric redshifts of all the sources, obtained with the EAZY code (Brammer et al. 2008). In the next section, we describe a more precise measurement of zspec. We also remark that the spectroscopic redshifts were checked and confirmed independently by other team members in both the GLASS and CEERS collaborations. Part of our spectroscopic sample is already published by other works (e.g., Arrabal Haro et al. 2023; Mascia et al. 2023, 2024), in which case we just checked the consistency of our zspec measurements.
Among the sample observed with NIRSpec by either the GLASS or CEERS survey, we selected galaxies with a spectroscopic redshift zspec ≥ 4. The reason for this lower limit is twofold. First, we aim to study the properties of the galaxy population as we approach the epoch of reionization, where most of the scaling relations addressed in this work are still largely unexplored compared to cosmic noon (1 < z < 3). Secondly, targets with z ≥ 4 were the main priority of the GLASS and CEERS spectroscopic surveys, thus, we have better statistics at our disposal in this range. This condition yields a final sample of 230 galaxies that we consider in our analysis. Among this sample, 19 have H-grating spectroscopic data (R∼2700) in GLASS, 93 have M-grating spectroscopy from CEERS (R∼1000), while 15 and 114 are observed in prism configuration (R∼100) in the Abell 2744 and EGS fields, respectively. The global population spans a redshift range between z = 4 and 10.4, with a median value zmed = 5.4 (see Fig. 1-top). The number of sources decreases toward higher redshifts, with 11 selected galaxies residing at redshift ≥8.
 |
Fig. 1. Redshift distribution of stellar masses (top panel) and SFRs (bottom panel) for the galaxies selected in this paper. We highlight the redshift histogram of the entire sample on top of the first diagram, while the M⋆ and SFRs histograms are added on the right part of each panel. Galaxies coming from the CEERS and GLASS surveys are differentiated with a yellow and blue color, respectively. We note that GLASS probes galaxies with slightly lower masses and SFRs on average, thanks to the gravitational lensing magnification effect. The gray vertical bars in the top right corners represent the typical uncertainties (∼0.2 dex) for the stellar masses and SFRs. The 90% mass completeness limits at z ∼ 5 and z ∼ 9 are highlighted, respectively, with black and lime horizontal segments. |
We can notice in Fig. 1 that the GLASS sample includes 5 galaxy members of a spectroscopically confirmed protocluster at redshift ∼8 (Morishita et al. 2023). Furthermore, four galaxies in the same field have spectroscopic redshifts ranging between 4.01–4.05. All of them are more than 1′ away from each other, but the whole group lies within a projected radius of 80″ (i.e., ∼0.6 pMpc at redshift 4). This is much larger than the protocluster at z ∼ 8, but more similar to the size of some galaxy overdensities identified at redshifts ∼3 (e.g., Calabrò et al. 2022b).
Given the variety of observational programs considered, it is useful to better investigate the properties of our selected sample to assess potential biases on our analysis. The GLASS observations with NIRSpec cover approximately 50 arcmin2 in the sky. Given the relatively long exposure times, they are among the deepest available so far, as we can detect emission lines with fluxes down to a few 10−18 erg/s/cm2. In addition, the lensing magnification is ideal for improving the detection of the intrisically faint, low-mass galaxy population at the epoch of reionization. The primary science targets of the NIRSpec observations were placed into open Microshutters (MSA), and were chosen based on previous spectrophotometric catalogs available from the GLASS team and from the literature. Many of them already had a confirmed spectroscopic redshift, while the remaining systems were photometrically selected at z > 4 using previous HST observations in the region of Abell 2744 (see Treu et al. 2022 for more details). The CEERS spectroscopic observations cover instead a larger area in the sky of about 90 arcmin2, but they are shallower compared to GLASS. Some of the spectroscopic targets are HST-selected in the UV rest-frame (among which we find those galaxies falling outside of the NIRCam coverage), while additional targets benefitted from NIRCam observations undertaken in the first observing run (prior to NIRSpec observations), and therefore are optically selected, even though they might still be biased to UV-bright LBG-type objects as they are chosen based on their photometric redshift. While a more detailed description will be included in Finkelstein et al. (in prep.), we note that it is difficult to precisely assess the selection function even within the same survey. It is thus a better approach to carry out an a posteriori analyis of the galaxy properties as a whole.
Even though GLASS probes slightly lower masses and SFRs on average compared to CEERS, due to the gravitational lensing effect, the two subsets are similarly distributed in redshift, as shown in the top histogram of Fig. 1 (top). Also, they are located along the same M⋆ versus SFR relation. Moreover, in the redshift evolution of ΣSFR, and in all the other diagrams analyzed in this paper, removing the small GLASS subset does not significantly change the results and the best-fit relations, meaning that they satisfy the same physical trends. We also note from Fig. 1 that both subsets may suffer from slight incompleteness at redshift ≥8, where we may lose a fraction of galaxies at the lowest masses and SFRs (respectively log M⋆/M⊙ < 8 and log SFR/(M⊙/yr) < 0. However, as explained in Section 3.3, our galaxies can be fairly considered as representative of the star-forming main sequence for most part of our redshift range.
Finally, even though the standard STScI reduction pipeline adopted for our spectra already includes a slit loss correction, we further checked the absolute flux calibration of the output 1D spectra by comparing them to the available broadband photometry (see Section 2.3 for the specific filters used). For all galaxies, we considered total fluxes estimated in the CEERS and GLASS collaborations. In the first survey, these fluxes are obtained by first performing the photometry in elliptical Kron apertures and then applying aperture corrections estimated from simulations by matching the image PSFs between different filters, as detailed in Finkelstein et al. (2024). A similar procedure for obtaining total fluxes was followed for the GLASS survey by Paris et al. (2023), using the code A-PHOT (Merlin et al. 2019). Despite the fact that the calibration corrections for individual photometric bands do not show a significant wavelength dependence, as also found by other works in the collaboration (e.g., Napolitano et al. 2024), we limited the comparison to the redder spectral range at 2 μm < λ < 5 μm; this is because the S/N of the continuum rapidly drops at lower wavelengths, making this check and comparison more difficult. A second reason for this choice is that we are interested only in optical rest-frame lines, which mostly lie in the red part of the spectrum. For the correction, we applied a constant multiplicative factor to the spectrum; this factor was obtained as the median value of the corrections derived independently for all the photometric bands whose central wavelengths reside in the above spectral range.
2.2. Line measurements and derivation of star formation rates
We measured the emission line properties with a similar methodology to that adopted in Calabrò et al. (2019) and Calabrò et al. (2023). In brief, we used a python version of the χ2 minimization routine MPFIT (Markwardt 2009) to fit the following emission lines: [O II] λ3727 Å, Hγ, [O III] λ5007 Å, Hβ, and Hα, together with their underlying continuum in a spectral window of ±5000 km/s around the line. We assumed a Gaussian function for the emission lines, while the continuum was modeled with a first-order polynomial. We assume for the lines a common redshift and line velocity width σ, with a tolerance of 100 (1000) km/s on the line centroid and σ for the H- or M-grating and prism spectra, respectively. The fit yields the exact redshift of the sources, the line widths, the line fluxes, and their corresponding uncertainties. The quality of the fit is controlled through the reduced χ2 and visual inspection for each galaxy. We consider the lines as detected when they are above a S/N of 3, while for non-detected lines, we adopted 3σ upper limits, which were then propagated across all the physical quantities derived. As discussed in Calabrò et al. (2023), the underlying stellar absorption for Balmer lines can be neglected as it does not produce significant variations of the emission line fluxes for galaxies in our stellar mass range. Moreover, our galaxies typically have younger ages, lower metallicities, and lower dust content compared to the lower redshift CEERS sample analyzed in Calabrò et al. (2023); therefore, the underlying absorption is expected to be even smaller (Groves et al. 2012). For this reason, we did not correct the emission line fluxes for stellar absorption. We also noticed that in low resolution spectra acquired with the prism configuration, Hα is blended with the [NII] doublet. However, our galaxies are all very low-mass and with sub-solar metallicities, for which the expected contamination is less than 10%, according to lower redshift studies (Faisst et al. 2018). A negligible contribution of [N II] to Hα for galaxies at z > 4 was also found by the photoionization models described in Simmonds et al. (2023) and supported by the results from our high resolution dataset. As a consequence, we do not attempt to make any correction on the Hα flux in prism spectra. Finally, two sources at redshifts 5 < z < 6 with clear broad Hα components and narrow [O III] λ5007 Å, indicative of broad-line AGN emission, are removed from the sample. We refer to Calabrò et al. (2023) for a more detailed discussion of the emission line measurement.
As the first step of our analysis, we computed the gas-phase attenuation, AV, from the available Balmer lines (among Hγ, Hβ, and Hα) assuming a dust-screen, Milky Way like extinction law (Cardelli et al. 1989). If only one Balmer line is detected, we adopted an AV as inferred from the SED fitting procedure described later in Section 2.3. As shown in the Appendix of Calabrò et al. (2023), hydrogen recombination lines across a large range of wavelengths (∼0.4 to ∼2 μm) are overall in agreement with the predictions of typical dust attenuation models, even when the lines reside in different gratings, indicating that their relative calibration and the inferred values of AV are generally reliable. From the fluxes of the [O II] λ3727 Å and [O III] λ5007 Å lines, we also derived the O32 index, defined as the logarithm of the reddening corrected [O III] λ5007 Å/[O II] λ3727 Å ratio.
We then derived the star formation rates as follows. We first computed the observed, dust-corrected Hα luminosity LHα. If Hα was not detected, we considered the fluxes of Hβ (or Hγ as last possibility), corrected for dust attenuation and rescaled to Hα assuming the intrinsic ratios of 2.86 and 6.10 (respectively, for Hβ and Hγ), valid for a case B recombination, a temperature T = 10 000K, and an electron density ne = 102 cm−3 (Osterbrock 1989). We then converted LHα to SFR assuming the calibration of Reddy et al. (2022) as SFR = LHα × 10−41.67. This is the most suitable calibration according to the typical subsolar metallicities expected for our galaxies at z > 4; it also reflects the greater efficiency of ionizing photon production in metal poor stellar populations. In our sample, we obtained the SFR from Hα in 153 galaxies, from Hβ in 67 systems, while for ten galaxies, it is inferred from Hγ. The resulting SFR distribution is shown in Fig. 1 (bottom), where our galaxies span values between ∼0.1 and 300 M⊙/yr, with a median SFR of ∼5 M⊙/yr.
We note some possible caveats of our analysis, affecting the relation between the SFR and Hα luminosity. For example, the diffuse warm ionized gas (DIG) or collisional excitation in the ISM might contribute to the observed Hα emission, leading us to slightly overestimate the SFRs. On the other hand, part of the ionizing radiation may be absorbed by dust and helium, or might escape from the galaxy, reducing the amount of Lyman continuum (LyC) photons available for hydrogen line emission. This might lead us to slightly underestimate the total SFR of the galaxy. Modeling and testing these effects is difficult, especially at high redshifts. However, despite these uncertainties, the simple analysis performed in this paper and the dust correction through the Balmer decrement should work well as a first approximation, as shown by Tacchella et al. (2022).
We also note that the dust correction is another potential source of uncertainty. This is due both to a poor theoretical understanding of dust production mechanisms and dust growth in the ISM at high redshift (see discussion in Markov et al. 2023) and to the lack of observational constraints. For this reason, different dust attenuation and extinction laws measured in the local Universe are usually adopted in the literature also at early epochs. We remark that our choice for dust correction is the same adopted by similar works on NIRSpec galaxies at the epoch of reionization (e.g., Llerena et al. 2024). Adopting a Calzetti et al. (2000) attenuation law, as done, for example, in Mascia et al. (2024), does not significantly alter the results.
2.3. Photometric data and estimation of stellar masses through SED fitting
We derived stellar masses for our galaxies through an SED fitting procedure using the code CIGALE (Boquien et al. 2019), version 2022.1. We fit Bruzual & Charlot (2003) stellar population models with Chabrier IMF to the available observed photometry ranging from 0.5 to 8 μm. There is a homogeneous photometric coverage for all the galaxies in our sample. In particular, all the galaxies observed by the GLASS survey are covered by JWST/NIRCam imaging from the UNCOVER program (JWST-GO-2561; Bezanson et al. 2022). For this subset, fluxes and uncertainties are obtained in the F115W, F150W, F200W, F277W, F356W, F410M, and F444W filters, using the catalog of Paris et al. (2023). The majority of our NIRSpec sources in the EGS field are also covered by JWST/NIRCam observations from the CEERS survey in the same filters listed above (Bagley et al. 2023). For this subset, we took the fluxes and uncertainties from Finkelstein et al. (2024). For all the NIRCam sources, we used the total flux estimates mentioned in Section 2.1. However, a subset of CEERS sources (79) do not have JWST imaging. To ensure that in this case, we also have access to complete coverage of the UV and optical rest-frame emission for the SED fitting, we considered the following broadband filters: HST/ACS F606W and F814W, HST/WFC3 F125W, F140W, and F160W, CFHT/WIRCAM J, H, and Ks, Spitzer IRAC 3.6 and 4.5 μm. In particular, we used the total photometric fluxes and associated uncertainties from the multi-wavelength catalog assembled by Stefanon et al. (2017).
The SED fitting with CIGALE was performed as follows. The redshift of the galaxy was fixed to the spectroscopic value estimated in Section 2.2. We considered a main stellar population with metallicities Z* = 0.0004, 0.004, 0.008, or 0.02, and a delayed SFH parameterized by an e-folding time that can assume the following values: 10, 100, 500, and 1000 Myr, and with a grid of 18 possible stellar ages ranging from 50 Myr to 1.3 Gyr. We also included the possibility of a recent exponential burst with SFH ∝exp−t/τburst, where τ can assume the values 1, 20, and 50 Myr, while the ages were allowed to range from 5 to 50 Myr. We also allowed the mass fraction of the late burst population to vary from 0 to 80% of the total mass formed in the entire galaxy history. We included contribution from nebular emission, where the nebular component is parametrized with an electron density ne of 100 cm−3, subsolar gas-phase metallicity equal to the stellar metallicity, and ionization parameter between −3 and −2. Finally, the dust attenuation of the stellar and nebular components were modeled with a Milky Way extinction curve (Cardelli et al. 1989) and parametrized with a color excess E(B-V)stellar ranging from 0 to 3 in steps of 0.05, a total to selective extinction RV = 3.1, and a stellar continuum to nebular attenuation ratio of 0.44 (Calzetti 2001). Therefore, for each galaxy, AV was computed as RV × E(B-V). The intergalactic medium (IGM) transmission is also taken into account following the model of Meiksin (2006). After the SED-fitting, we correct the stellar masses of the GLASS sources for the effects of lensing, using the magnification factors mentioned above. As demonstrated by Furtak et al. (2021), this approach yields consistent results compared to correcting the photometry before the SED-fitting.
We find stellar masses M⋆ ranging from 107 to 1010.5 M⊙ (see Fig. 1-top), with a nearly symmetric distribution around a median log10M⋆/M⊙ = 8.7 (1σ = 0.7). Combining these results with the SFR measurements described in the previous section, we find that the bulk of our galaxy population has sSFRs between 1 and 100 Gyr−1, with median value of 10 Gyr−1. For galaxies fitted with E(B–V) = 0, we also set an upper limit on their dust attenuation as E(B–V) = 0.05, corresponding to our grid step and to the average uncertainties obtained with this methodology. Comparing the values of AV, nebular obtained from the SED fitting to those estimated from Balmer lines, we find that they are overall consistent with the 1 : 1 relation, even though with a large scatter.
For galaxies with multiple coverage, we also checked that removing NIRCam photometry and using only the remaining bands (HST + Spitzer + ground) in the SED fitting yields M⋆ values that are in agreement with estimates based on JWST photometry in the entire range spanned by our sample. Therefore, we did not introduce systematic biases (related to the measurement method) on the derived parameters for the subset that is not covered by JWST imaging. Our stellar masses are consistent with those obtained using the code ZPHOT (Fontana et al. 2000) with a similar setup and SFH to our CIGALE run, indicating that this quantity is rather robust and not significantly affected by the exact fitting procedure. Finally, we also tested a nebular attenuation equal to the stellar attenuation, but this choice did not produce significant variations in the final results of this paper.
2.4. Galaxy sizes and SFR surface density estimation
We measured the major-axis half-light radius re of our galaxies by fitting their rest-frame UV images with the python software GALIGHT (Ding et al. 2021). A subset of 151 galaxies is covered by JWST imaging, in which case we adopted the background-subtracted mosaics described in Bagley et al. (2023) and Paris et al. (2023), for the CEERS and GLASS subset, respectively. For the remaining subset of 79 galaxies (all in the CEERS field), we use instead HST imaging (Koekemoer et al. 2011). To homogeneously probe the same rest-frame UV window, we performed the measurements in the F115W band for galaxies at z < 5.5, in the F150W filter for those at slightly higher redshifts (5.5 < z < 7.5), and in F200W for systems at z > 7.5. In cases where only HST imaging is available, we adopted the F125W and F160W band for galaxies at redshifts lower and higher than 5.5, respectively.
To measure the galaxy sizes, we first produced 3″ × 3″ cutouts, which are given as input to the GALIGHT code. All sources in the cutout, including the central galaxy of interest, were fitted simultaneously assuming that they are well represented by a Sersic profile. We constrained the following parameters to keep the fit within physically meaningful values: the Sersic index n is free to vary from 0.2 to 8.0, and the axis ratio q is set in the range 0.1 < q < 1. After running GALIGHT, sources are flagged according to the quality of the fit, with a flag = 0 assigned to reliable fits, and flag = 1 for sources that are not fitted well by the above procedure (indicative of a more complex shape), as checked visually in the observed versus best-fit luminosity profile that is output by the code. As a result, 213 galaxies with a good size quality flag were considered when analyzing the ΣSFR, as described in the following sections.
The size uncertainties are assessed in accordance with Yang et al. (2022) and rescaled based on the S/N derived from the photometry. Previous studies (e.g., Kawinwanichakij et al. 2021) have shown that the outcomes from GALIGHT are robust, and consistent with estimations made through conventional softwares like Galfit (Peng et al. 2002). A subset of our galaxies are indistinguishable from point sources. In particular, we performed a subset of simulations, finding that 0.025″ and 0.1″ are the smallest measurable sizes in JWST and HST images, respectively. Therefore, we set these values as upper limits. In our sample, 64 galaxies of 213 (∼30%) are unresolved and have upper limits on re. We also notice that for the galaxies lying in the GLASS field (which are all covered by JWST imaging), the sizes are corrected for the effect of lensing. In particular, we divided the original sizes by 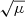 assuming an isotropic magnification, which represents a reasonable approximation considering the low magnification factors (median μ ≃ 2) found in our sample.
assuming an isotropic magnification, which represents a reasonable approximation considering the low magnification factors (median μ ≃ 2) found in our sample.
With the estimated sizes, we compute the galaxy-integrated SFR surface densities for all the objects. A subset of 25 extremely compact galaxies have an upper limit on the size but also an upper limit on the SFR. We exclude these galaxies from the analysis as their ΣSFR would be totally unconstrained. As a result, the investigation of the redshift evolution of ΣSFR and its dependence on other galaxy properties ought to be made on a sample of 188 galaxies. The distribution of ΣSFR for this galaxy subset has a median value of log10ΣSFR = 0.6 (in units of M⋆/yr/kpc2, 1σ = 0.8), with individual systems spanning the logarithmic range between −1.5 and 2.5.
The UV rest-frame based re values adopted in this paper probe the size of star formation in the last ∼100 Myr (i.e., the continuum emission from young and massive stars), a slightly longer timescale than the Hα (or Hβ) based SFRs, which are sensitive to the last 10–30 Myr of star formation. Ideally, more suitable emission line-based sizes could be derived through IFU spectral observations or from imaging observations in photometric bands dominated by emission lines. To check whether the latter case occurs within our sample, we have estimated for all the galaxies the emission line contribution to the observed photometry. In particular, we compared for all the available photometric bands the in-band fluxes obtained by integrating the observed spectrum across each filter transmission curve and by summing the emission lines only. With this procedure, we find that the maximum emission line contribution to the photometry is of ∼20% on average, exceeding 60% in 9 galaxies (∼3.5% of the sample). However, for this small subset, the optical rest-frame sizes (in bands where the emission lines dominate) are in agreement with those estimated in the rest-frame UV, suggesting that using the latter does not significanly alter the final ΣSFR on average. Moreover, recent independent studies at similar redshifts based on JWST-NIRCam observations (e.g., Ono et al. 2024; Morishita et al. 2024) have shown that rest-frame UV sizes are in agreement with rest-frame optical sizes (where we might have contribution from strong optical emission lines).
2.5. Estimating sample completeness and potential selection effects
In this section, we explain how we derived an approximate estimation of the mass completeness limits for our sample. The majority of our NIRSpec selected galaxies at redshifts 4 ≤ z ≤ 10 is made of JWST-NIRCam selected sources within a magnitude limit in F277W of ∼28.5 mag. Using the recent results of Cole et al. (2023) and rescaling them to account for the different limiting magnitudes in F277W, we estimated a 90% mass completeness limit of 107.8 M⊙ at z ∼ 5 and of 108.4 M⊙ at z ∼ 9 (i.e., ∼0.2 dex lower than the limits of Cole et al. 2023). This redshift-dependent completeness has effects on the stellar mass and SFR distributions shown in Fig. 1 and is likely responsible for the strong rise observed at z > 7.5 of the minimum stellar mass and SFR probed within our sample.
We also note that no additional selection effects have been added to the spectroscopic sample by our analysis, as we have a SFR measurement (or at least an upper limit) and a size measurement from UV rest-frame imaging for all the galaxies selected in Section 2.1. The galaxies without a measurement of ΣSFR (because of an upper limit on both the SFR and the size) or without a size (because of a complex shape) are randomly distributed in redshift and in the M⋆ – SFR plane, so they do not produce systematic biases in the results.
We also investigate the effect of surface brightness dimming on source identification and sample selection. To this aim, we performed a set of Monte Carlo simulations, creating mock observations of galaxies in the F277W band following a similar approach to that adopted Treu et al. (2023) (see their Section 3.2). We placed the sources at different redshifts from z = 4 to z = 10 (in steps of 0.5), assuming for simplicity a single Sersic light profile for the galaxies, with n = 1 (consistent with observations of EoR galaxies, Yang et al. 2022), q = 1, and re ranging from 0.1 to 1.5 kpc (in steps of 0.05 kpc). The background level was set to match the exposure time (5207 s) in CEERS and then 50 simulations were run for each configuration, applying each time a detection algorithm (using the photutils package in python) with an S/N detection threshold of 3. From these simulations, we study how the detection rate varies as a function of redshift and re for different total magnitudes of the source, from 28.5 (the magnitude limit of our sample) to 27, in steps of 0.3 mag.
We find that at z ≃ 9, the maximum size for which a galaxy can be detected in F277W (at fixed total observed magnitude) is smaller than at z ≃ 4 by ∼0.2–0.25 dex. However, galaxies become intrinsically smaller at higher redshifts. For example, Ward et al. (2024) have shown that the typical re of galaxies decreases by a factor of ∼2 (0.3 dex) from z = 4 to 9 (at fixed stellar mass); also, the mass-size relation leads to the result of smaller sizes at high-z. This suggests that, within our “magnitude-limited” sample, size incompleteness does not play a significant role in the observed evolution of ΣSFR at higher redshifts. For example, assuming for galaxies at redshifts 8 < z < 10 an average F277W magnitude of ∼28, and a minimum detected SFR of 5 M⊙/yr (Fig. 1-bottom), we are able to probe ΣSFR values down to log10ΣSFR/(M⊙/yr/kpc2) ∼0.4, which is more than 2σ below the z − ΣSFR relation extrapolated without the highest redshift bin.
3. Results
Here, we explore the redshift evolution of ΣSFR for our selected sample and then focus on fundamental scaling relations involving M⋆, SFR, and ΣSFR in the entire redshift range between ∼4 and ∼10. To characterize all the 2D distributions presented in this paper and quantify the level of correlation between two quantities, we adopted two different approaches throughout this work. Both take into account (in a different way) the presence of upper and lower limits in the data. We explain them in detail in the next subsection for the redshift versus ΣSFR diagram, but the same steps of the analysis are followed for the other diagrams.
3.1. Fitting methods
As a first approach to characterize the redshift evolution of ΣSFR, we computed the median redshift and the median ΣSFR of galaxies falling in different, well defined bins of increasing spectroscopic redshift (4–5, 5–6, 6–7, 7–8, > 8), which are shown as black empty diamonds in Fig. 2. In each bin, we also calculated the median absolute deviation (MAD) of ΣSFR, indicated with black error bars. In this calculation, we assign half of the ΣSFR value to galaxies with 3σ upper limits, or twice the value in case of 3σ lower limit on ΣSFR. In data science, imputation of upper (lower) limits with half (double) the detection limit is a common approach, and simulation studies have found that this is a better choice compared to assuming the detection limit itself or a zero value (for upper limits), as it introduces the least bias into the estimates (Beal 2001). Then we are able to derive a global, best-fit linear relation and 1σ limits through Monte Carlo simulations. In particular, we performed 1000 realizations of our data varying the data points according to their x and y axis 1σ uncertainties. For each realization, we repeated the same process of median ΣSFR estimation in each of the previously defined redshift bins and fit these median values with a first order polynomial. Finally, we derived the best-fit relation as the median slope and normalization of all the different realizations, including the uncertainties as their standard deviation.
 |
Fig. 2. Redshift evolution of ΣSFR from z = 4 to 10. The median values and MAD of ΣSFR in bins of increasing redshift are shown with black empty diamonds and black vertical error bars, while the best-fit to the bins is represented with a black dashed line with a gray region indicating its 1σ uncertainty. The best-fit obtained with the Bayesian linear regression is shown with a blue continuous line, with the blue dotted lines and the blue shaded regions representing the 1σ uncertainty and the ‘posterior plot’, respectively. Theoretical model predictions and comparison observations are included as specified in the legend. |
In the second analysis method, we used the Python package PyMC1. This is an advanced tool for statistical modeling featuring next-generation Markov chain Monte Carlo (MCMC) sampling algorithms such as the No-U-Turn Sampler (NUTS; Hoffman & Gelman 2024), a self-tuning variant of Hamiltonian Monte Carlo (HMC; Duane et al. 1987). HMC and NUTS can manage complex posterior distributions and fitting models, taking advantage of gradient information from the likelihood to achieve much faster convergence than traditional sampling methods. A first advantage of this approach is that it can be applied to the entire dataset without dividing the sample in multiple bins as in the previous case. A second advantage is that it implements the methods of the Bayesian survival analysis in the linear regression to deal with upper and lower limits on the y axis. Most importantly, this method does not impute the limits (i.e., does not strictly substitute them with a different value), but instead integrates them out through the likelihood. In pratice, the entire dataset is fitted with a linear relation, obtaining a first guess of the line parameters. Then, pyMC is run by assuming Gaussian priors for the slope and intercept, with σ = 1 and the first guesses as centers. At this step, normal measurements, upper and lower limits are considered simultaneously in the fit. Finally, the full posterior distributions of the slope and intercept are used to calculate the mean linear relation, the 1σ uncertainty, and for showing the ‘posterior plot, that is, a stack of random draws from the posterior distribution of the slope and intercept. We report in Table 1 the best-fit parameters obtained for the main relations studied in this paper and using both the linear regression methods described above.
Best-fit linear relations of the diagrams analyzed in this work.
3.2. The redshift evolution of the SFR surface density
Our results for the evolution of ΣSFR are shown globally in Fig. 2, where the median ΣSFR and MAD in five increasing bins of redshift (defined as 4–5, 5–6, 6–7, 7–8, and > 8) are represented with empty diamonds and vertical error bars, while the best-fit to the bins is highlighted with a black dashed line and a gray shaded area indicating its 1σ uncertainty. In addition, we also consider the Bayesian fitting method, plotting the mean linear relation as a blue continuous line, the 1σ uncertainty as blue dotted lines, and the ‘posterior plot’ as a blue shaded region around the mean relation.
Regardless of the analysis approach, we find a mild evolution of ΣSFR from z ≃ 4 to z ∼ 8, with a slight but statistically significant increase by a factor of two (0.3 dex), going from 2.5 M⊙/yr/kpc2 to ∼5 M⊙/yr/kpc2. We note that in the short cosmic epoch that we are exploring (around one billion years of cosmic history), the linear relation yields a good description of the increase in ΣSFR. In all cases we obtain a positive correlation with best-fit slopes of 0.16 ± 0.06 and 0.21 ± 0.03, respectively from the Bayesian regression and the fit to the bins. Therefore, in all cases we can exclude a flat trend at least at 2σ level.
Fitting the median ΣSFR in the five redshift bins, the slope is slightly higher compared to the other method, as due to a sudden rise of ΣSFR in the last bin at 8 < z < 10, where we reach a median ΣSFR of ∼20 M⊙/yr/kpc2. However, we notice that the median ΣSFR derived in the last bin is consistent with the Bayesian fit within 1σ. We have also removed the galaxies in the last redshift bin and fitted again the sample with the two methods, but we do not obtain significantly different results. Therefore the upturn of ΣSFR at z > 8 is not significant from our data. This trend might be due to the different sample completeness limits between lower and higher redshifts, as discussed in Section 2.5, and might reflect the rise observed at z ≳ 7.5 of the minimum stellar mass and SFR probed by our NIRSpec sample (Fig. 1). We also remark that in that redshift regime we are limited by the poor statistics, and a larger sample is required to better constrain the ΣSFR evolution at z > 8.
Both the normalization and the slope of our ΣSFR – redshift relation are consistent with most of the previous observations. In particular, our Bayesian best-fit line falls exactly between the observed median relations estimated by Shibuya et al. (2015) up to redshift 8 in two different bins of SFR (1< SFR/M⊙/yr < 10 and 10< SFR/M⊙/yr < 100). Compared to these results, our findings indicate that the increase of ΣSFR can be extended up to at least redshift 10. The median ΣSFR between redshift 4 and 9 are overall consistent with those calculated by Morishita et al. (2024) with a sample similar to our study in terms of stellar masses and SFRs probed (fuchsia empty stars in Fig. 2). Moreover, NIRSpec galaxies ranging 8 < z < 10 have ΣSFR comparable to those recently derived in photometrically selected systems observed by JADES at much higher redshifts (10–13) by Robertson et al. (2023). Finally, our results are slightly higher, but still marginally consistent, than the range of ΣSFR (1–20 M⊙/yr/kpc2) measured by Holwerda et al. (2015) for 6 galaxies at redshifts 9 < z < 10 identified with HST in the CANDELS survey, even though these are intrinsically brighter systems compared to those analyzed in this work.
3.3. Main sequence of star formation at z > 4
We go on to focus on the fundamental scaling relations describing the evolution of the galaxy population. The most important is that involving the star formation rate and the stellar mass, which show a tight correlation at all redshifts, known as the star-forming main sequence (SFMS, Noeske et al. 2007, Daddi et al. 2007, Santini et al. 2017). This relation is fundamental to understand the process of gas conversion into stars and subsequent build-up of stellar mass across cosmic time. While the slope is relatively constant with redshift, ranging from ∼0.6 to ∼1, depending on the sample selection and specific tracer used for the SFR, all studies agree that the normalization increases monotonically from lower to higher redshift up to at least z ∼ 7.
In Fig. 3, we show the M⋆ versus SFR diagram for our selected spectroscopic sample. In order to check and better appreciate variations with redshift, we divide the sample in two redshift bins, that is, 4 < z < 6 and 6 < z < 10 (top and bottom panels, respectively). In both cases, we further divide the sample in different bins of stellar masses from 107.5 to 1010.5 M⊙ in steps of 0.5 dex (slightly larger in the first bin) when performing the first approach of the analysis explained in Section 3.1. We perform the fit considering only the galaxies above the mass completeness limits estimated in Section 2.5, that is, log10 (M⋆/M⊙) above 7.8 in the low redshift bin, and > 8.4 in the high redshift bin. With all the fitting methods, we find in both redshift ranges a tight and significant correlation between M⋆ and the SFR, indicating that the SFMS is in place up to the highest redshifts (z ∼ 10) explored by this work. Adopting the Bayesian regression as the reference method, the SFMS in the two redshift bins have similar slopes (0.63 ± 0.07 at z < 6 and 0.63 ± 0.10 at z > 6), and the normalization of the relation is not significantly different between the two redshift bins in the M⋆ range from ∼108 to ∼1010.5 M⊙.
 |
Fig. 3. Star-forming main sequence of galaxies selected in this work in the redshift range 4 < z < 6. The best-fit relations are derived in the mass range where we have 90% mass completeness. For comparison, the high redshift and low-mass extrapolation of the MS relations by Schreiber et al. (2015) and Speagle et al. (2014) (obtained at lower redshifts and higher M⋆) are shown with dashed orange and dotted fuchsia lines, respectively. Bottom panel shows the same as the top, but for the redshift range 6 < z < 10. The Bayesian best-fit relation obtained in the lower redshift bin in included as a pink continuous line for comparison. |
Recently, Cole et al. (2023) studied the SFMS using photometrically selected galaxies from the CEERS survey at redshifts 4.5–12, with stellar masses and SFRs estimated through SED fitting. If we focus on the stellar mass ranges where we are both mass complete at 90% (i.e., log10 (M⋆/M⊙) > 8 at lower redshifts, and > 8.6 at higher redshifts), we find consistent relations with similar slopes and normalizations. This also confirms that the spectroscopic selection is not significantly biased compared to a pure photometrical selection. We have also performed a fit by including all the galaxies down to the lowest measured stellar masses, but we obtain best-fit relations that are not significantly different from those estimated above. This suggests that, even though we are incomplete at lower stellar masses, this effect might not be large.
Cole et al. (2023) also found that 10Myr-averaged SFRs are significantly more scattered around the median relation compared to 100 Myr-averaged values by ∼0.3 dex (see their Fig. 7), which these authors interpret as evidence of the stochasticity of star formation. We have here the possibility to analyze the scatter of the main sequence relation using the Balmer lines as tracers of very recent star formation. To this aim, we computed the intrinsic scatter of the M⋆ – SFR relations by subtracting in quadrature, for all the redshift and M⋆ bins, the scatter due to the measurement uncertainty from the total observed scatter, as done in Huang et al. (2023). We find that the intrinsic scatter log(σintrinsic, Hα/(M⊙/yr)) ranges between 0.3 and 0.6 in both the low and high redshift bins, with a median of 0.5 across the entire stellar mass range. This result is consistent with the range of σ10 Myr reported by Cole et al. (2023), and ∼0.4 dex higher than σ100 Myr found by the same study, thus providing a spectroscopic confirmation of the relatively larger scatter of the main sequence when SFRs are averaged over short timescales of ≪100 Myr.
Both the slope and normalization of our relations are generally in agreement with the extrapolations at redshift 5 and 7.5 (and down to a stellar mass of 107 M⊙) of the SFMS relations derived for more massive and lower redshift star-forming galaxies by Speagle et al. (2014) and Schreiber et al. (2015), with a slightly better consistency with the shallower slope found by Speagle et al. (2014). We note that the evolution of SFR at fixed stellar mass expected in this redshift range (∼0.15 dex) is smaller than the intrinsic scatter of the relation and too small to be appreciated with our dataset, given the uncertainties obtained in the fit.
3.4. The main sequence of SFR surface density
The galaxy integrated ΣSFR has been proposed as an alternative and more physical measurement of the current SF activity of galaxies, the reason being a closer connection to the gas density and the efficiency of stellar feedback compared to the specific SFR. For example, the incidence of outflows has been shown to correlate better with the ΣSFR rather than with the offset from the standard SFMS (Förster Schreiber et al. 2019). Moreover, ΣSFR also incorporates, by construction, information about the galaxy structure and morphology. For this reason, an alternative main sequence relation has been defined as the main locus occupied by star-forming galaxies in the ΣSFR – M⋆ plane. Compared to the sSFR, the ΣSFR properties of galaxies are more uniform at varying stellar masses, such that ΣSFR is approximately constant across the main sequence, as found by Schiminovich et al. (2007) and Salim et al. (2023) for relatively low redshift galaxies (z ≲ 1). However, there could also be deviations from this flat relation, indicating additional (or lower) star formation activity associated with different galaxy structures. For example, moderately positive correlations between ΣSFR and M⋆ are observed at M⋆ > 109 M⊙ by Salim et al. (2023) for star-forming galaxies from z = 0 to z = 2, which are interpreted as the build-up of a central bulge component in those galaxies.
We now explore the ΣSFR versus M⋆ diagram for the NIRSpec galaxies, divided in two redshift bins (4 < z < 6 and 6 < z < 10), as done for the classical SFMS. In the fit we consider only the galaxies above the mass completeness limits defined before for each redshift. Our results are shown in Fig. 4. We find that in both redshift bins there is a very mild correlation, with ΣSFR slightly increasing in more massive galaxies: the best-fit slopes obtained with the Bayesian regression method are of 0.19 ± 0.09 and 0.30 ± 0.15, respectively, in the low and high redshift bins. This tells us that the data points are still consistent (within 3σ) with a constant ΣSFR as a function of M⋆ in the entire redshift of our work. Considering the large range spanned by ΣSFR (by more than three orders of magnitude), it is indeed remarkable to observe a median variation of only less than 0.5 dex across more than ∼3 orders of magnitude of stellar mass, from log M⋆ = 7.5 to ∼10.5. For the higher redshift sample we also find a slightly higher normalization of the ΣSFR-main sequence by ∼0.5 dex (at M⋆ = 109 M⊙) compared to the subset at z < 6.
 |
Fig. 4. ΣSFR main sequence for our selected galaxies in the lower redshift bin (4 < z < 6, top) and higher redshift bin (6 < z < 10, bottom). The lines, shaded areas, and markers are the same as in Fig. 2. The average location of massive (M⋆ > 109 M⊙) star-forming galaxies at redshift ∼0 presented by Salim et al. (2023) is highlighted with a cyan dashed line. |
The very mild increase of ΣSFR with M⋆ is in agreement with previous observations of star-forming galaxies at comparable masses but at lower redshifts (Förster Schreiber et al. 2019; Schiminovich et al. 2007; Salim et al. 2023). In such comparisons, we do not find clear evidence of a sudden or significant upturn of the relation in the entire mass range that we explore. However, the normalization of the ΣSFR-main sequence is significantly higher compared to lower redshift studies. The median ΣSFR of our galaxies at z ∼ 5 is of ∼2.5 M⊙/yr/kpc2 (log ΣSFR = 0.4). At fixed stellar mass, and focusing on the overlapping stellar mass region (8 < log M⋆/M⊙ < 10), our ΣSFR values are higher compared to the local Universe by approximately 2 dex at z ∼ 5 and 2.5 dex at z ∼ 10, indicating a strong evolution of ΣSFR with cosmic time. This is consistent with the average ΣSFR evolution found over this cosmic epoch by other observations (e.g., Shibuya et al. 2015) and simulations (e.g., Sharma et al. 2017). It can be explained as the combined effect of the higher average SFRs (by ∼1 dex, Speagle et al. 2014) and more compact sizes (re ∼0.5 dex lower, Ward et al. 2024) of galaxies at z ∼ 5 compared to the local Universe, at a fixed stellar mass of ∼109.5 M⊙.
4. Discussion
In this section, we further analyze our results to better understand how the fundamental quantity ΣSFR is related to other phsyical properties of the galaxies during and immediately after the epoch of reionization.
4.1. Comparison to predictions of theoretical models
We compare our observations to some theoretical models that have been introduced to explain galaxy evolution across cosmic epochs. Focusing on the redshift evolution of ΣSFR, we first consider the empirical model of Naidu et al. (2020). As mentioned in Section 1, the main assumption of this model is that fesc is solely dependent on ΣSFR as fesc = a × ΣSFRb, with a = 1.6 ± 0.3 and b = 0.4 ± 0.1. As shown in Fig. 2, this model yields an evolution of ΣSFR up to redshift ∼8 (lime curve) that is fully in agreement with our best-fit relation.
As an additional test, we compare our observations to the physical model presented by Ferrara et al. (2023) and Ferrara (2024). In detail, we take the redshift evolution of the SFR predicted by their model, and derive the ΣSFR by combining it with the empirical size evolution found by Morishita et al. (2024). At the median stellar mass of the sample plotted in Fig. 2 (log M⋆/M⊙ = 8.6), we obtain a slightly increasing trend of ΣSFR, highlighted with a dash-dotted orange line, whose slope is remarkably consistent with our data and with the model of Naidu et al. (2020). Even though is has a slightly higher normalization of ∼ + 0.2 dex, this is well below the uncertainties of our best-fit relation. We note that the prediction is very sensitive not only to the stellar mass considered (lower M⋆ have systematically lower ΣSFR), but especially to the effective radius. Indeed, considering the uncertainties on the best-fit redshift-size relation of Morishita et al. (2024), we would obtain an uncertainty on the normalization of the predicted ΣSFR evolution of ∼0.8 dex, higher than the median absolute deviation (MAD) of our sample.
Finally, we also took the CEERS mock galaxy catalog (Yung et al. 2022) for comparison. This catalog covers an area overlapping with the observed EGS field, and contains galaxies over 0 < z ≲ 10. The galaxies in the mock lightcone were simulated with the Santa Cruz SAM for galaxy formation (Somerville & Davé 2015; Somerville et al. 2021). The free parameters in the model were calibrated to reproduce a set of galaxy properties observed at z ∼ 0 and have been shown to well-reproduce the observed evolution in high-redshift (z ≳ 4) one-point distribution functions of MUV, M*, and SFR (Yung et al. 2019a,b). The effective radii of these simulated galaxies are determined as described in Brennan et al. (2015) and are shown to be in good agreement with CEERS observations at 3 < z < 6 (Kartaltepe et al. 2023).
From the mock lightcone, we extracted a random sample of galaxies with a redshift and a stellar mass distribution similar to our observed sample, and then apply a magnitude cut as F277W < 29.15 to match the depth of the CEERS survey (Finkelstein et al. 2024), where most of our galaxies come from. With this selection method, fitting the median ΣSFR in five bins of redshift as done for the real data, we obtained an increasing trend of ΣSFR with redshift that is very similar to the observational result. In addition, the SAM best-fit relation has a slightly lower normalization than the observed one by ∼0.2 dex. As in the previous case, this is due to predictions on galaxy sizes, which are slightly larger on average compared to our values and to the size evolution obtained by Morishita et al. (2024). Despite this, the difference in ΣSFR normalization is rather small and below the 1σ uncertainties. Therefore, the SCSAM yields a good representation of the observed properties of galaxies in the entire redshift range from 4 to ∼10. A similar good consistency between SCSAM model predictions and observations is obtained also for all the other diagrams studied in Section 3 and in Section 4. The models analyzed in this section also agree on the strong evolution of ΣSFR from z = 0 to the reionization epoch mentioned in Section 3.4. To conclude, our results are consistent not only with previous observations, but also with a variety of theoretical models that are commonly adopted in the literature.
4.2. SFR surface density and ionization properties
The SFR surface densities of galaxies have been shown recently to be tightly related and to have a key influence on their ionizing properties (Reddy et al. 2022). We know from simulations, galaxy models, and observations, that high redshift galaxies have higher ionization parameters (at fixed stellar mass) compared to local analogs (e.g., Brinchmann et al. 2008; Nakajima et al. 2013; Steidel et al. 2014; Kewley et al. 2015; Shapley et al. 2015; Hirschmann et al. 2017, 2023; Euclid Collaboration 2024). This redshift evolution of ionization conditions is usually explained as a combined effect of lower metallicity, harder stellar ionizing spectra, and higher gas densities at z ≫ 0. The latter increasing trend, also found with the electron density ne (Isobe et al. 2023), which is more easily measurable from optical emission lines, reflects the denser, more compact molecular clouds, and ultimately also higher values of ΣSFR. Significant correlations were indeed found observationally between ne and ΣSFR (Shimakawa et al. 2015; Jiang et al. 2019; Reddy et al. 2023), confirming the close relation between the two quantities, and the important role of ΣSFR in the evolution of the ISM properties across cosmic time (see also Papovich et al. 2022).
We test here the connection between ΣSFR and the ionization conditions, comparing the measured values of ΣSFR to the O32 index defined in Section 2.2, which is usually adopted as an observational proxy for the ionization parameter. The result is shown in Fig. 5. The O32 values, represented on the y-axis, range between −0.3 and 1.3, with a median of ∼0.6. We observe an increase of O32 with ΣSFR, with a slope of 1.5 ± 0.2, indicating that the correlation is statistically significant at more than 3σ level. We notice also that the galaxies in the top right part of the diagram, with ΣSFR ≥ 1 and O32 ≥0.7, have similarly high ΣSFR and O32 to photometrically selected extreme emission line galaxies (EELGs) identified in the CEERS field by Llerena et al. (2024). We refer to that paper for a more detailed discussion of those galaxies. Overall, these findings corroborate previous results, supporting the close relation between ΣSFR and the ionization properties of galaxies. We also note that excluding the small subset of galaxies at z > 8 with very high ΣSFR does not significantly change this global picture.
 |
Fig. 5. ΣSFR as a function of the O32 index for our selected sample in the entire range 4 < z < 10. The lines, shaded areas, and markers are the same as in Fig. 2. The diamonds colored in orange highlight our strong LyC leaking candidates, according to the criteria defined by Flury et al. (2022). |
Finally, seven galaxies observed at high resolution in GLASS have a S/N of [O II] λ3727 Å> 3 and a physically meaningful flux ratio [O II]3729/[O II]3726 in the range 0.3–1.5 (Osterbrock 1989). From this flux ratio, we derived for those galaxies the electron density ne, using the python package PYNEB (Luridiana et al. 2015) and assuming an electron temperature T = 10 000 K, as above. We find that most of the galaxies cluster within a range of densities going from 200 to 400 cm−2 (median ne = 280 cm−2). The poor statistics does not allow us to test possible correlations between ne and ΣSFR, even though we notice that the galaxy ID 100003 with the highest density in the sample (> 104cm−2, the only one outside the range 200–400 cm−2), also has the highest ΣSFR (∼102 M⊙/yr/kpc2). We defer a more detailed analysis to a future work with a larger sample.
4.3. SFR surface density and escape of Lyman continuum photons
Enhanced values of the O32 index and ΣSFR are usually associated with increased fractions of ionizing photons that escape from the galaxies. The connection between ΣSFR (or O32) and fesc is found from multiple observations and with different approaches. Lyman continuum leaking sources (LyC), identified through direct or indirect methods, are found to have ΣSFR significantly higher than the average value of the star-forming population at a given redshift (e.g., Cen 2020). In the other direction, galaxies with enhanced ΣSFR show larger fractions of LyC leakers. For example, Heckman (2001) and Heckman (2002) claimed that galaxies with ΣSFR above 0.1 M⊙/yr/kpc2 are capable to launch strong star-forming driven winds, which might be responsible for creating channels though which Lyc photons can leak. Steidel et al. (2018), based on a sample of LBGs at z ∼ 3, suggested that ΣSFR and fesc are highly correlated quantities. Similarly, the O32 index is considered as a valid indicator of LyC leaking, according to Izotov et al. (2020). Also, Flury et al. (2022) found that 40% of local galaxies with ΣSFR > 10 M⊙/yr/kpc2 and O32 higher than 0.7 are LyC leakers; hence, they adopted these two conditions at higher redshifts to define a source as a strong LyC leaker candidate.
Following these observational findings, hydrodynamical simulations and models have started to implement the effects of spatially concentrated star formation in the form of turbulence and stellar-driven winds (Ma et al. 2016; Sharma et al. 2016), showing that an increased ΣSFR is responsible for launching galaxy-wide outflows and for carving ionizing channels in the ISM where the Lyman continuum radiation of young massive stars and supernovae is free to propagate outside. According to the model of Naidu et al. (2020), fesc reaches unity when ΣSFR is one-third of the maximum ΣSFR ( = 1000 M⊙/yr/kpc2) that can be sustained without radiation pressure instabilities (Hopkins et al. 2010).
Triggered by this extensive observational and theoretical background, we used our dataset to explore the relation between ΣSFR and fesc at redshifts 4 < z < 10. We find that at z ≥ 4, it is almost impossible to directly detect the Lyman continuum emission due to the very low IGM transmission (Vanzella et al. 2015), and at z > 5 it becomes virtually impossible. For this reason, we determined fesc in an indirect way using the empirical relation presented in Mascia et al. (2023), which provides an estimation of the escape fraction using three galaxy parameters: the UV beta slope, the physical size re, and the O32 index; we note that these are among the properties that are better correlated with fesc. This relation is calibrated on the low-redshift (0.2 < z < 0.4) Lyman Continuum survey (LzLCS), for which Flury et al. (2022) performed direct measurements of the Lyman continuum flux and fesc from imaging observations.
In Fig. 6 (top), we show ΣSFR as a function of fesc. Using our two analysis approaches, we find in all cases a significant correlation between these two parameters, according to which galaxies with higher ΣSFR have systematically higher fesc than galaxies with lower ΣSFR. In detail, fesc increases from log ΣSFR = − 1 to 3, with a best-fit slope of 0.37 ± 0.05 by fitting the median values in seven bins of ΣSFR defined with the following grid [−1, −0.5, 0, 0.5, 1, 1.5, 2, 3]. These results do not significantly change if we exclude from the analysis the galaxies at z > 8 that are responsible for the ΣSFR enhancement in the last redshift bin observed in Fig. 2. This indicates that galaxies with more concentrated SFR have the conditions that should facilitate the escape of LyC photons. A subset of ∼20% of our galaxy sample have ΣSFR and O32 satisfying the conditions established by Flury et al. (2022) for being strong LyC leaker candidates, showing similar properties to the LyC leakers studied at redshift ∼0.3. These systems, indicated with orange diamonds in Fig. 6 and in Fig. 5, tend to have higher fesc estimates compared to the average galaxy population at these redshifts.
 |
Fig. 6. Diagram comparing ΣSFR and fesc for galaxies at 4 < z < 10 with an estimate of fesc(top). The lines, shaded areas, and markers are the same as in Fig. 2. sSFR versus fesc for this NIRSpec sample is shown in the bottom panel. The orange diamonds represent strong LyC leaking candidates according to Flury et al. (2022), as highlighted in Fig. 5. The two galaxies for which we detect outflow signatures in their H-grating spectra from GLASS are shown as big darkred stars. The sample representative error of 0.3 dex on fesc is added below the legend. We include with blue empty squares the LzLCS sample of 66 galaxies at 0.2 < z < 0.4, with measurements (including direct estimates of fesc) performed by Flury et al. (2022). |
We compare our observations to the direct measurements of fesc and physical properties estimated by Flury et al. (2022) for the LzLCS galaxy sample (shown as blue empty squares) in Fig. 6. We find a similar slope of the best-fit relation, even though we derive a higher normalization by ∼0.5 dex. The large difference in normalization of the ΣSFR – fesc relation mostly depends on the fact that, at fixed ΣSFR, high-redshift galaxies have a lower UV slope on average compared to the low redshift systems analyzed in Flury et al. (2022); hence, they have a lower dust attenuation and a lower metallicity (see Calabrò et al. 2021 for the relation between attenuation and metallicity). This translates into an increased capability to form channels through the ISM for the escape of ionizing radiation. Indeed, the normalization offset almost disappears when considering a subset from the LzLCS with a median UV slope similar to the NIRSpec galaxies (βmedian ≃ −2.1). A minor part of the offset is also due to our sample probing slightly lower stellar masses (by ∼0.3 dex) than the sample of Flury et al. (2022).
We also find that the slope of our correlation is consistent with the 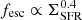 relation predicted by the Naidu et al. (2020) model. We find a lower normalization of our relation by ∼0.3 dex compared to their fiducial model with a = 1.6, possibly suggesting a lower value of this parameter. For completeness, we also report in Fig. 6 (top) the model with a = 0.8, which is not ruled out in their work (as shown in their Fig. 6) and whose prediction is much closer to our best-fit relation. However, their fesc versus ΣSFR relation relies on measurements by Steidel et al. (2018), which are based on a sample of star-forming galaxies at redshift z ∼ 3. The difference may thus originate from the different redshifts probed by our works, hence from the effects discussed above.
relation predicted by the Naidu et al. (2020) model. We find a lower normalization of our relation by ∼0.3 dex compared to their fiducial model with a = 1.6, possibly suggesting a lower value of this parameter. For completeness, we also report in Fig. 6 (top) the model with a = 0.8, which is not ruled out in their work (as shown in their Fig. 6) and whose prediction is much closer to our best-fit relation. However, their fesc versus ΣSFR relation relies on measurements by Steidel et al. (2018), which are based on a sample of star-forming galaxies at redshift z ∼ 3. The difference may thus originate from the different redshifts probed by our works, hence from the effects discussed above.
A big caveat to the above analysis is that the two quantities on the x and y axis are not completely independent: ΣSFR correlates with the size, while fesc is strongly dependent on the size by construction. While this is unavoidable, we also remark that, the fesc estimation is based also on other galaxy properties and not just on the re. However, in order to provide a more independent measurement, we also compare the estimated values of fesc to the sSFRs, which do not directly depend on the physical extension of the galaxies (Fig. 6, bottom panel). We find that the sSFR is still correlated to fesc, although with a shallower slope and lower significance compared to the same relation with ΣSFR. Also, in this case the slope of our best-fit relation is similar to what is found for the LzLCS galaxy sample at z ∼ 0.3, suggesting that the level of star formation activity in a galaxy (regardless of the normalization method) has an impact on the escape of ionizing radiation. Overall, we are aware that all these quantities (i.e., fesc, ΣSFR, sSFR, size, UV slope, and O32) are all interrelated somehow and not fully independent, as many of them depend on the same physical processes. This tells us that the best candidates as LyC leaking galaxies have rather peculiar and similar properties, being characterized by blue UV slopes, compact sizes, high O32, and also enhanced star formation activity in the form of ΣSFR and sSFR.
4.4. Connecting star formation and outflows
We have seen in the previous section that ΣSFR is tightly related to the ionizing properties of galaxies and their ability to spread ionizing photons in their surrounding medium. The underlying physical mechanism through which ΣSFR impacts on fesc is that galaxies with more compact and enhanced star formation activity facilitate the launch of galaxy scale outflows through stellar feedback, which includes radiation from young stars, stellar winds, and supernova explosions. Indeed, several studies have found higher gas outflow velocities and mass loading factors in galaxies with higher ΣSFR (Calabrò et al. 2022a; Llerena et al. 2023), corroborating the close relation between ΣSFR and outflows. From the theoretical point of view, Sharma et al. (2016) and Sharma et al. (2017) predict that outflows are ubiquitous in galaxies with ΣSFR ≥10 M⊙/yr/kpc2. The final connection between outflows and fesc is then supported by a variety of works from the literature, both observational and theoretical (Heckman et al. 2011; Amorín et al. 2012; Borthakur et al. 2014; Sharma et al. 2017; Hogarth et al. 2020), according to which outflows can clear pathways in the surrounding neutral gas, favoring the escape of ionizing photons. Recently, Amorín et al. (2024) found a clear correlation between the velocity width of the [O III] λ5007 Å and Hα broad-line wings and fesc for a sample of 20 Lyman continuum emitters at z ∼ 0.3, with the stronger emitters also having the highest values of ΣSFR. In this subsection, we investigate spectral outflow signatures in our sample and study how they relate to the host galaxy properties. We also test the impact of outflows in an indirect way through the effect that they may have on the dust attenuation.
4.4.1. Exploring spectral outflow signatures in our sample
To study the presence of outflows of ionized gas, we use the GLASS high resolution grating spectra and perform a single Gaussian and a double-component (narrow+broad) Gaussian fit to the Hα and [O III] λ5007 Å lines (when available), which are the lines with the highest S/N in this redshift range, thus the most suited for exploring low S/N outflow features. In detail, Hα was fitted alone, as the contribution from [N II] λ6583 Å can be neglected at first order, while [O III] λ5007 Å was fitted together with Hβ and [O II] λ4959 Å as explained in Section 2.2. In the double Gaussian fit, we add a second broad component, allowing the intrinsic velocity width σ of the narrow component to vary between 10 and 250 km/s, and σ of the broad component from 100 to 800 km/s, which is the limit expected for star-forming driven outflows (Calabrò et al. 2022a). We constrain the velocity shift between the two Gaussian centroids to < 300 km/s, of the same order of the spectral resolution. We do not set any constraints on the flux ratio of the two components. In case of the Hβ + [O III] triplet, a broad component is added to all the three lines. Finally, we use the Akaike Information Criterion (AIC) criterion (Akaike 1974) to decide if the double Gaussian provides a significantly better fit to the line profile compared to a single Gaussian fit. In particular, we consider the double component as the final solution if the difference (AICsingle − AICdouble) = ΔAIC is > 10 (Burnham & Anderson 2004; Bosch et al. 2019), and if both the narrow and broad best-fit Gaussians are detected with a flux S/N > 3. The above threshold ensures that the double component model is 100 times more probable than the single component model to minimize the information loss.
With the above criteria, we find that a broad component is required to fit [O III] and Hα of two galaxies: ID 160133 and ID 110000 (Fig. 7). Both galaxies have ΔAIC > 15 in [O III] (the highest S/N line), indicating a very strong case for the double component model. For the galaxy ID 110000, Hα has a ΔAIC slightly lower than 10 (∼8), but the double Gaussian is still highly favored (50 times more probable than a single component). We primarily interpret these components as an outflow, with σbroad = 250 ± 4 km/s and 200 ± 10 km/s, respectively. We measure a broad to narrow line flux ratio of 0.16 (0.3) and a broad to narrow σ ratio of 3.4 (2.8). These galaxies lie at redshifts 4.02 and 5.76, respectively, and both have a modest log ΣSFR /(M⊙ yr−1 kpc−2) of 0.6 ± 0.2 (0.4 ± 0.2), comparable to the average galaxy population at their redshifts, and log sSFR /(yr−1) of −7.6 ± 0.2 (−8.5 ± 0.3). These systems are highlighted as big darkred stars in Fig. 6. The indirect estimation of fesc for these two galaxies yields a value of ≃0.11 (≃0.04), which is slightly above (slightly below) the median fesc of galaxies at similar ΣSFR. We also note that these outflow velocities would correspond to strong leakers (fesc ≥4-10%) if we assume the σbroad–fesc correlation of Amorín et al. (2024). Intriguingly, both galaxies with outflow signatures show low surface brigthness clumpy structures around the main cores from high-resolution JWST images. This makes the scenario of gas accretion an interesting, alternative possibility that cannot be excluded with our spectroscopic data.
 |
Fig. 7. Single Gaussian (1G) and double Gaussian (2G, narrow + broad) best fits to the [O III] λ5007 Å+Hβ and Hα lines, as indicated in each panel label, for the two galaxies (ID GLASS 160133 and 110000) in which we detect a significant outflow signature in both emission lines (upper and lower four panels, respectively). In each panel, the upper part shows the observed spectrum with the best fit line in red (red (green) line for the narrow (broad) component in the double Gaussian fit), the middle part represents the error spectrum, while the bottom part is the residual after subtracting the best fit result. The spectra are in the observed frame wavelength. |
To better understand these results, we compare them to those obtained with a comparable dataset by Carniani et al. (2024), which includes 52 galaxies with R = 2700 spectra from the JWST-JADES program at redshifts, stellar masses, and SFRs similar to our work. They detect broad additional components in Hα or [O III] in a fraction of galaxies going from 15% to 40%, which they interpret as evidence of outflows. They find that the outflow incidence increases with SFR but is rather stable (at the level of 20–30%) as a function of M⋆ and sSFR. Limiting the comparison to the redshift range between 4 and ∼6 (where most of their galaxies lie), and assuming the simple interpretation (also favored by their work) of an outflow scenario, we derive in GLASS an outflow incidence of 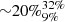 (2 out of 11 galaxies with detected [O III]), with uncertainties derived following Gehrels (1986). This result is comparable to Carniani et al. (2024). We also notice that our flux and σ ratios between the narrow and broad Gaussian components fall within their observed range. All this suggests that we are probably probing the same physical phenomenon. Interestingly, we do not observe instead any outflow signatures in the 6 GLASS sources at z > 6 (upper limit of 26%). In this case, we cannot make comparisons as this redshift range is poorly sample by the other work. Within our sample, the number of high redshift sources with high resolution spectra is so low that the outflow incidence at z > 6 is still compatible with that derived at lower redshift. However, we can exclude from this analysis that outflows become more important at higher redshifts.
(2 out of 11 galaxies with detected [O III]), with uncertainties derived following Gehrels (1986). This result is comparable to Carniani et al. (2024). We also notice that our flux and σ ratios between the narrow and broad Gaussian components fall within their observed range. All this suggests that we are probably probing the same physical phenomenon. Interestingly, we do not observe instead any outflow signatures in the 6 GLASS sources at z > 6 (upper limit of 26%). In this case, we cannot make comparisons as this redshift range is poorly sample by the other work. Within our sample, the number of high redshift sources with high resolution spectra is so low that the outflow incidence at z > 6 is still compatible with that derived at lower redshift. However, we can exclude from this analysis that outflows become more important at higher redshifts.
Furthermore, we do not find significant evidence of outflows in individual galaxies among the CEERS sample observed at medium resolution (R≃1000). To understand whether this is expected, and to test the effect of resolution on the outflow detectability, we perform a set of Monte Carlo simulations. In detail, we simulate spectra at different redshifts injecting an emission line at a specific wavelength (0.53 μm rest frame) assuming different line fluxes to produce a variety of S/N of the emission feature (from 3 to ∼60). We also set a broad to narrow intrinsic flux ratio in the range between 0.1 and 0.7, and different σ ratios ranging 2 to 12, with σnarrow, intrinsic fixed to 50 km/s. We vary the intrinsic broad line centroid within a resolution element. We then perform a single Gaussian and double Gaussian (narrow + broad) fit as done for the observed data, imposing the same requirements for taking the double component as the final best fit. Running these simulations (100 for each configuration) we find that the recovery rate is of the order of 2% or less for the typical range of outflow parameters expected from our works and from previous findings. This rate is not strongly dependent on the specific assumptions, except for the most extreme cases such as width and flux ratios > = 5 and > = 0.5, respectively. Therefore, the lack of significant outflow signatures in the CEERS sample is likely due to their lower spectral resolution.
Increasing the S/N of the emission lines, for example through spectral stacking, can slightly increase the outflow recovery rate at median resolution and the possibility of detecting faint broad components in case of high outflow velocities. We thus stack the entire dataset selected in this work with H- or M-grating observations. We first downgrade by convolution the GLASS high resolution spectra to R = 1000, convert the spectra to rest-frame using the spectroscopic redshifts determined in Section 2.2, resample them to a common wavelength grid, and normalize them to the median flux estimated around the specific lines analyzed. Then, we apply for each pixel a median stacking with 5σ clipping, and finally perform the line measurements as done for individual galaxies. As shown by our simulations, this stacking approach tends to broaden a line systematically (regardless of the S/N or intrinsic line width) by ∼50 km/s, as due to the impact of the spectral resolution on the redshift estimation uncertainty when converting to rest-frame.
Stacking the spectra around the [O III] λ5007 Å line, which is the highest S/N line available for the largest number of galaxies in our sample, and fitting the Hβ+[O III] triplet with a single and double Gaussian as described before, we find that the double component model is not strongly favored according to the previous condition (ΔAIC = 3), thus there is no significant evidence of outflow. Given the lower S/N, we are not able to appreciate significant differences in the fit or to detect any outflow signatures if we divide the sample in two or more bins of redshift, sSFR, or ΣSFR.
To conclude, we find outflow incidence rates in individual galaxies observed by GLASS that are consistent to those obtained by similar works in the same redshift range. As highlighted by Carniani et al. (2024), the relatively low incidence rate is not necessarily evidence of a minor role of outflows, as this could be related to the outflow geometry. For example, an incidence rate of ∼20% can be obtained if outflows have a biconical morphology with an opening angle of ∼37deg. This also suggests that to robustly constrain the role of outflows in the ΣSFR − fesc correlation (hence, to confirm in a direct way the outflow-driven LyC photon escape scenario at the EoR), we need to study how the outflow fraction varies as a function of ΣSFR and fesc, which requires better statistics than what is available in the present analysis. This scientific question will be addressed in the future with a larger sample of galaxies with deep, high-resolution NIRSpec data.
4.4.2. Investigating the attenuation and the outflow incidence of extremely star-forming galaxies
Approaching the epoch of cosmic dawn, galaxies tend to have denser ISM and more concentrated star formation activity, as shown in the previous sections. For electron densities exceeding ∼200 cm−3, the radiation pressure from young stars starts to dominate over the thermal pressure sustained by supernovae explosions (Ferrara 2024). Assuming the (1 + z)p redshift evolution of ne, we expect this transition to occur for the average galaxy population in a redshift range between 3 and 7, depending on the value of the exponent p between 1 and 2 (see Isobe et al. 2023). In these conditions of gas density and pressure, supernova explosions rapidly lose energy due to radiative losses, and the energy is converted into sound waves through shocks on a short timescale (see, e.g., Martizzi et al. 2015, Gatto et al. 2015, Kim & Ostriker 2015, Walch & Naab 2015, Fielding et al. 2017), making supernova-driven outflows highly inefficient in early galaxies. Some theoretical models predict that in compact galaxies with extreme star formation activity, a super-Eddington regime could be established, according to which radiation driven outflows can dramatically decrease the dust optical depth by pushing it to larger radii in a few Myr (Ferrara 2024). This drastic event is expected when the sSFR exceeds ∼10−7.6 yr−1. The consequence of this process is the formation of a system that has negligible dust attenuation, hence a very blue SED. This model was introduced to explain the excess of UV-bright and blue galaxies (compared to theoretical expectations) discovered during the first JWST observing campaigns (e.g., Naidu et al. 2022; Castellano et al. 2022). However, it is still unclear whether it is the right physical explanation to the observational findings and when exactly this proposed mechanism might start to dominate.
To test this scenario, we analyzed the outflow incidence rate in galaxies with extremely high sSFR. First, we found that the fraction of galaxies in super Eddington regime (i.e., sSFR > 10−7.6 yr−1) in all the redshift range explored in this work (4 < z < 10) is consistent with the model predictions by Ferrara (2024), increasing from ∼15% at redshift 4 to ∼40% at redshift 10. Among these galaxies, if we consider only those five observed by GLASS at high resolution, we find an outflow incidence rate of 1/5 (∼20%); otherwise, we have 1/3 if we limit the analysis to systems with a compact morphology, that is, with an effective radius of 150 pc or less. In both cases, these fractions are compatible with the incidence rate obtained from the full sample.
An alternative method to testing the effect of star formation on the dust content of galaxies, including the dust clearing scenario, is to analyze how the galaxy attenuation, AV, is related to the star-forming properties. To this aim, in Fig. 8, we color code the points in the z − ΣSFR diagram as a function of AV. We can see that galaxies at z > 7 have a large variety of AV: while some galaxies have upper limits on AV consistent with 0, some others have higher values that can reach AV = 2 in magnitude. Therefore, we do not see evidence for a sudden drop in AV with redshift down to the very low values (AV ≃10−2–10−3) expected by the dust-clearing scenario, nor that the global galaxy population at z > 7 is dominated by systems with AV ≃ 0, even if the majority of this high-z subset also has sSFRs largely exceeding the super-Eddington conditions defined above.
 |
Fig. 8. Redshift evolution of ΣSFR (analogous to Fig. 2), color-coded by the attenuation, AV, estimated as described in the text. Galaxies with AV values derived from the emission lines are encapsulated within bigger blue squares. |
We can better understand this result by plotting AV as a function of sSFR for the entire redshift range (top panel of Fig. 9). We can see that galaxies with higher sSFR show a large variety of AV. Globally, the median AV slightly increases with sSFR but it is consistent also with a flat relation (m = 0.07 ± 0.09). In the bottom panel of Fig. 9 we analyze instead the relation between AV and ΣSFR. Here we find a positive correlation between the two quantities, with a best-fit slope of 0.28 ± 0.07 with the Bayesian method, indicating that galaxies with more concentrated star formation (i.e., higher ΣSFR) have higher dust attenuations on average. This positive correlation is similar to what is found in lower redshift studies (e.g., Reddy et al. 2015; Tomičić et al. 2017), and it reflects the fact that galaxies accumulate more dust in their ISM as a consequence of their increased (and more compact) star formation activity. Dividing our sample in two redshift bins (lower and higher than 6), we find no significant differences in the global trends seen in both panels of Fig. 9.
 |
Fig. 9. Diagrams comparing AV to sSFR and ΣSFR (top and bottom panels, respectively) for our selected galaxies in the redshift range of 4 < z < 10. The lines, shaded areas, and markers are the same as in Fig. 2. |
In conclusion, we can hypothesize several different explanations to our results. First, dust clearing radiatively driven outflows (in super Eddington conditions) have been proposed to explain the excess of bright and very blue galaxies at z ≥ 10. We should note that the two NIRSpec galaxies at z ≃ 10 in our sample are both dust poor, consistent with this scenario. We are focusing instead on a cosmic epoch where the feedback from supernovae is likely contributing to the acceleration of winds, as incorporated in several models and simulations (e.g., Sharma et al. 2017). Therefore, supernovae feedback remains the most plausible explanation for the outflows observed in NIRSpec galaxies at z < 6. However, we should also be aware of the possible lesser role played by supernovae as we approach the reionization epoch, following the argument explained above. Galaxies at cosmic dawn are also expected to be younger than analogs at lower redshifts, with consequently shorter times available to supernovae to impact the surrounding ISM in a stable way.
Secondly, the fraction of halo gas entrained by the outflowing shell might be conspicuous at the level of 10% or more. Consequently, the gas outflow velocities can be relatively low (see equation 15 in Ferrara 2024), to the level of 50–100 km/s that are not easily detectable even in high resolution spectral mode. Another alternative explanation is that we are observing the galaxies in an intermediate phase of dust accumulation, possibly coincident with a period of gas accretion and dust creation by the first star formation episodes, which has not yet reached the conditions of dust opacity for developing a sudden blow-out event. In this particular phase, whose duration is not well known, the galaxies might still retain most of their gas and dust content, showing attenuations significantly higher than 0, while maintaining a low-level outflowing activity.
5. Summary
We summarize the main findings of this paper as follows. We analyze a spectroscopic sample of galaxies in the redshift range from 4 to 10 observed with JWST-NIRSpec by the CEERS and GLASS surveys. Using the Balmer lines and UV-based effective radii, we study the evolution of the SFR and ΣSFR over this cosmic epoch.
-
We find that ΣSFR increases mildly in this redshift range (best-fit slope = 0.16 ± 0.06), rising by a factor of 2 from z = 4 to 10. This trend is consistent with the predictions from several semi-analytic models of galaxy evolution, such as the Santa Cruz models (Somerville & Davé 2015) and those from Ferrara (2024) and Naidu et al. (2020).
-
A star-forming main sequence relation holds out to a redshift of ∼10, with a best-fit slope of ∼0.7, consistent with the relations obtained for star-forming galaxies at lower redshifts.
-
We derive, for the first time at z > 4, the ΣSFR main sequence, finding a very mild increase (consistent with a flat relation) of ΣSFR with stellar mass. The slope of the best-fit relation is in agreement with observations at 0 < z < 2, while the normalization is about ∼2.5 dex higher (at z ∼ 10) compared to the Local Universe, resulting from the strong evolution of the average ΣSFR in star-forming galaxies during the last 13 billion years.
-
We show that ΣSFR is tightly related to the ionizing source properties, as probed by the O32 index. This corroborates recent studies proposing ΣSFR as a key quantity responsible for the higher ionization parameter observed in high redshift galaxies (Reddy et al. 2023).
-
We find correlations among ΣSFR and sSFR with the escape fraction, estimated in an indirect way using the prescription of Mascia et al. (2023), calibrated on direct measurements of fesc from the low-redshift Lyman continuum survey (Flury et al. 2022). The slopes of both correlations are in agreement with observations of low-redshift LyC leakers and with those predicted by the models of Naidu et al. (2020). This suggests that ΣSFR and sSFR play an important role in the escape of ionizing radiation.
-
We detect outflow signatures in Hα and [O III] λ5007 Å lines for ∼20% of the galaxies at z < 6 observed in H-grating NIRSpec mode, in agreement with the outflow incidence found in galaxies at similar redshifts by Carniani et al. (2024). This relatively low incidence might be related to the outflow geometry. In particular, a biconical outflow morphology with an opening angle of ∼37deg is able to explain the observed fraction. A larger sample is instead necessary to study the outflow incidence at varying ΣSFR and fesc so that we may have a more direct confirmation of the SFR-outflow connection. In addition, this would give us a better picture of the outflow-driven LyC photon escape scenario at the EoR.
-
We find a positive correlation between AV and ΣSFR, along with a flat trend as a function of sSFR, indicating that there is no evidence of a drop in AV in extremely star-forming galaxies between z = 4 and 10. This might be at odds with a dust-clearing outflow scenario being in place at z ≥ 10.
Observing a larger number of galaxies at high resolution and testing the correlation between ΣSFR and outflow velocity predicted by supernovae feedback models can help us further constrain the properties and physical origin of the outflows detected both in our and in similar works at z ∼ 4 to 10. It will also enable us to further clarify the relation between star formation and outflows in the epoch of reionization. Enlarging the sample of spectroscopically confirmed galaxies at z > 10 is essential for testing possible transformations of the ISM properties occurring at this cosmic epoch in the future.
Acknowledgments
We thank the referee for the detailed and constructive comments. AC acknowledges support from the INAF Large Grant for Extragalactic Surveys with JWST. We acknowledge support from the PRIN 2022 MUR project 2022CB3PJ3 – First Light And Galaxy aSsembly (FLAGS) funded by the European Union – Next Generation EU. We thank Stefano Carniani for useful discussion on the main topic of the paper.
References
- Akaike, H. 1974, IEEE Trans. Autom. Contr., 19, 716 [Google Scholar]
- Amorín, R., Vílchez, J. M., Hägele, G. F., et al. 2012, ApJ, 754, L22 [CrossRef] [Google Scholar]
- Amorín, R. O., Rodríguez-Henríquez, M., Fernández, V., et al. 2024, A&A, 682, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023, ApJ, 951, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Bagley, M. B., Finkelstein, S. L., Koekemoer, A. M., et al. 2023, ApJ, 946, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Beal, S. L. 2001, J Pharmacokinet Pharmacodyn, 28, 481 [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P., Wechsler, R. H., Hearin, A. P., et al. 2019, MNRAS, 488, 3143 [NASA ADS] [CrossRef] [Google Scholar]
- Bergamini, P., Acebron, A., Grillo, C., et al. 2023, ApJ, 952, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Bezanson, R., Labbe, I., Whitaker, K. E., et al. 2022, ApJ, submitted [arXiv:2212.04026] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bordoloi, R., Lilly, S. J., Hardmeier, E., et al. 2014, ApJ, 794, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Borthakur, S., Heckman, T. M., Leitherer, C., et al. 2014, Science, 346, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch, G., Hägele, G. F., Amorín, R., et al. 2019, MNRAS, 489, 1787 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [Google Scholar]
- Brennan, R., Pandya, V., Somerville, R. S., et al. 2015, MNRAS, 451, 2933 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Pettini, M., & Charlot, S. 2008, MNRAS, 385, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Burnham, K. P., & Anderson, D. R. 2004, Sociol. Methods Res., 33, 261 [Google Scholar]
- Calabrò, A., Daddi, E., Puglisi, A., et al. 2019, A&A, 623, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calabrò, A., Castellano, M., Pentericci, L., et al. 2021, A&A, 646, A39 [EDP Sciences] [Google Scholar]
- Calabrò, A., Pentericci, L., Talia, M., et al. 2022a, A&A, 667, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calabrò, A., Guaita, L., Pentericci, L., et al. 2022b, A&A, 664, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calabrò, A., Pentericci, L., Feltre, A., et al. 2023, A&A, 679, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carniani, S., Venturi, G., Parlanti, E., et al. 2024, A&A, 685, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellano, M., Fontana, A., Treu, T., et al. 2022, ApJ, 938, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R. 2020, ApJ, 889, L22 [Google Scholar]
- Cole, J. W., Papovich, C., Finkelstein, S. L., et al. 2023, ArXiv e-prints [arXiv:2312.10152] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Oppenheimer, B. D., & Finlator, K. 2011, MNRAS, 415, 11 [Google Scholar]
- Davidzon, I., Ilbert, O., Faisst, A. L., et al. 2018, ApJ, 852, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cesare, C., Graziani, L., Schneider, R., et al. 2023, MNRAS, 519, 4632 [Google Scholar]
- Ding, X., Birrer, S., Treu, T., et al. 2021, ArXiv e-prints [arXiv:2111.08721] [Google Scholar]
- Donnari, M., Pillepich, A., Nelson, D., et al. 2019, MNRAS, 485, 4817 [Google Scholar]
- Duane, S., Kennedy, A. D., Pendleton, B. J., et al. 1987, Phys. Lett. B, 195, 216 [CrossRef] [Google Scholar]
- Euclid Collaboration (Scharré, L., et al.) 2024, A&A, 689, A276 [CrossRef] [EDP Sciences] [Google Scholar]
- Faisst, A. L., Masters, D., Wang, Y., et al. 2018, ApJ, 855, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A. 2024, A&A, 684, A207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrara, A., Pallottini, A., & Dayal, P. 2023, MNRAS, 522, 3986 [NASA ADS] [CrossRef] [Google Scholar]
- Fielding, D., Quataert, E., Martizzi, D., et al. 2017, MNRAS, 470, L39 [CrossRef] [Google Scholar]
- Finkelstein, S. L., Leung, G. C. K., Bagley, M. B., et al. 2024, ApJ, 969, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Flury, S. R., Jaskot, A. E., Ferguson, H. C., et al. 2022, ApJS, 260, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fontana, A., D’Odorico, S., Poli, F., et al. 2000, AJ, 120, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Übler, H., Davies, R. L., et al. 2019, ApJ, 875, 21 [Google Scholar]
- Fujimoto, S., Arrabal Haro, P., Dickinson, M., et al. 2023, ApJ, 949, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Furlong, M., Bower, R. G., Theuns, T., et al. 2015, MNRAS, 450, 4486 [Google Scholar]
- Furtak, L. J., Atek, H., Lehnert, M. D., et al. 2021, MNRAS, 501, 1568 [Google Scholar]
- Gatto, A., Walch, S., Low, M.-M. M., et al. 2015, MNRAS, 449, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [Google Scholar]
- Groves, B., Brinchmann, J., & Walcher, C. J. 2012, MNRAS, 419, 1402 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M. 2001, Gas and Galaxy Evolution, 240, 345 [NASA ADS] [Google Scholar]
- Heckman, T. M. 2002, Extragalactic Gas at Low Redshift, 254, 292 [NASA ADS] [Google Scholar]
- Heckman, T. M., & Borthakur, S. 2016, ApJ, 822, 9 [CrossRef] [Google Scholar]
- Heckman, T. M., Borthakur, S., Overzier, R., et al. 2011, ApJ, 730, 5 [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2015, MNRAS, 451, 2663 [Google Scholar]
- Hirschmann, M., Charlot, S., Feltre, A., et al. 2017, MNRAS, 472, 2468 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Charlot, S., Feltre, A., et al. 2023, MNRAS, 526, 3610 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, M. D., & Gelman, A. 2024, J. Mach. Learn. Res., 15, 1593 [Google Scholar]
- Hogarth, L., Amorín, R., Vílchez, J. M., et al. 2020, MNRAS, 494, 3541 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Bouwens, R., Oesch, P., et al. 2015, ApJ, 808, 6 [CrossRef] [Google Scholar]
- Hopkins, P. F., Murray, N., Quataert, E., et al. 2010, MNRAS, 401, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2012, MNRAS, 421, 3522 [Google Scholar]
- Huang, R., Battisti, A. J., Grasha, K., et al. 2023, MNRAS, 520, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, Y., Ouchi, M., Nakajima, K., et al. 2023, ApJ, 956, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Worseck, G., et al. 2020, MNRAS, 491, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, T., Malhotra, S., Yang, H., et al. 2019, ApJ, 872, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Kartaltepe, J. S., Rose, C., Vanderhoof, B. N., et al. 2023, ApJ, 946, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Kawinwanichakij, L., Silverman, J. D., Ding, X., et al. 2021, ApJ, 921, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1989, ApJ, 344, 685 [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Zahid, H. J., Geller, M. J., et al. 2015, ApJ, 812, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., & Ostriker, E. C. 2015, ApJ, 802, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Kocevski, D. D., Barro, G., McGrath, E. J., et al. 2023, ApJ, 946, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kornei, K. A., Shapley, A. E., Martin, C. L., et al. 2012, ApJ, 758, 135 [Google Scholar]
- Lehnert, M. D., van Driel, W., Le Tiran, L., et al. 2015, A&A, 577, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leslie, S. K., Schinnerer, E., Liu, D., et al. 2020, ApJ, 899, 58 [Google Scholar]
- Llerena, M., Amorín, R., Pentericci, L., et al. 2023, A&A, 676, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Llerena, M., Amorín, R., Pentericci, L., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202449904 [Google Scholar]
- Luridiana, V., Morisset, C., & Shaw, R. A. 2015, A&A, 573, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, X., Hopkins, P. F., Faucher-Giguère, C.-A., et al. 2016, MNRAS, 456, 2140 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Markov, V., Gallerani, S., Pallottini, A., et al. 2023, A&A, 679, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
- Martizzi, D., Faucher-Giguère, C.-A., & Quataert, E. 2015, MNRAS, 450, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Mascia, S., Pentericci, L., Calabrò, A., et al. 2023, A&A, 672, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mascia, S., Pentericci, L., Calabrò, A., et al. 2024, A&A, 685, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meiksin, A. 2006, MNRAS, 365, 807 [Google Scholar]
- Menci, N., Gatti, M., Fiore, F., et al. 2014, A&A, 569, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merlin, E., Pilo, S., Fontana, A., et al. 2019, A&A, 622, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morishita, T., Roberts-Borsani, G., Treu, T., et al. 2023, ApJ, 947, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Morishita, T., Stiavelli, M., Chary, R.-R., et al. 2024, ApJ, 963, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Tacchella, S., Mason, C. A., et al. 2020, ApJ, 892, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Oesch, P. A., van Dokkum, P., et al. 2022, ApJ, 940, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2013, ApJ, 769, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, L., Pentericci, L., Santini, P., et al. 2024, A&A, 688, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Ono, Y., Harikane, Y., Ouchi, M., et al. 2024, PASJ, 76, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei, 1989, 408 [NASA ADS] [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [Google Scholar]
- Papovich, C., Simons, R. C., Estrada-Carpenter, V., et al. 2022, ApJ, 937, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Paris, D., Merlin, E., Fontana, A., et al. 2023, ApJ, 952, 20 [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., et al. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Concas, A., Cresci, G., et al. 2023, MNRAS, 519, 1526 [Google Scholar]
- Prusinski, N. Z., Erb, D. K., & Martin, C. L. 2021, AJ, 161, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Kriek, M., Shapley, A. E., et al. 2015, ApJ, 806, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Topping, M. W., Shapley, A. E., et al. 2022, ApJ, 926, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Topping, M. W., Sanders, R. L., et al. 2023, ApJ, 952, 167 [CrossRef] [Google Scholar]
- Roberts-Borsani, G., Morishita, T., Treu, T., et al. 2022, ApJ, 938, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, Nat. Astron., 7, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Tacchella, S., Osborne, C., et al. 2023, ApJ, 958, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Fontana, A., Castellano, M., et al. 2017, ApJ, 847, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Schiminovich, D., Wyder, T. K., Martin, D. C., et al. 2007, ApJS, 173, 315 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapley, A. E. 2011, ARA&A, 49, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Reddy, N. A., Kriek, M., et al. 2015, ApJ, 801, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, M., Theuns, T., Frenk, C., et al. 2016, MNRAS, 458, L94 [CrossRef] [Google Scholar]
- Sharma, M., Theuns, T., Frenk, C., et al. 2017, MNRAS, 468, 2176 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [Google Scholar]
- Shimakawa, R., Kodama, T., Steidel, C. C., et al. 2015, MNRAS, 451, 1284 [Google Scholar]
- Simmonds, C., Tacchella, S., Maseda, M., et al. 2023, MNRAS, 523, 5468 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., & Davé, R. 2015, ARA&A, 53, 51 [Google Scholar]
- Somerville, R. S., Olsen, C., Yung, L. Y. A., et al. 2021, MNRAS, 502, 4858 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., et al. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
- Stefanon, M., Yan, H., Mobasher, B., et al. 2017, ApJS, 229, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Rudie, G. C., Strom, A. L., et al. 2014, ApJ, 795, 165 [Google Scholar]
- Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2018, ApJ, 869, 123 [Google Scholar]
- Sugahara, Y., Ouchi, M., Harikane, Y., et al. 2019, ApJ, 886, 29 [Google Scholar]
- Tacchella, S., Smith, A., Kannan, R., et al. 2022, MNRAS, 513, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Tomičić, N., Kreckel, K., Groves, B., et al. 2017, ApJ, 844, 155 [CrossRef] [Google Scholar]
- Treu, T., Roberts-Borsani, G., Bradac, M., et al. 2022, ApJ, 935, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Calabrò, A., Castellano, M., et al. 2023, ApJ, 942, L28 [CrossRef] [Google Scholar]
- Vanzella, E., de Barros, S., Castellano, M., et al. 2015, A&A, 576, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walch, S., & Naab, T. 2015, MNRAS, 451, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, E., de la Vega, A., Mobasher, B., et al. 2024, ApJ, 962, 176 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, L., Morishita, T., Leethochawalit, N., et al. 2022, ApJ, 938, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Yung, L. Y. A., Somerville, R. S., Finkelstein, S. L., et al. 2019a, MNRAS, 483, 2983 [NASA ADS] [CrossRef] [Google Scholar]
- Yung, L. Y. A., Somerville, R. S., Popping, G., et al. 2019b, MNRAS, 490, 2855 [NASA ADS] [CrossRef] [Google Scholar]
- Yung, L. Y. A., Somerville, R. S., Ferguson, H. C., et al. 2022, MNRAS, 515, 5416 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Redshift distribution of stellar masses (top panel) and SFRs (bottom panel) for the galaxies selected in this paper. We highlight the redshift histogram of the entire sample on top of the first diagram, while the M⋆ and SFRs histograms are added on the right part of each panel. Galaxies coming from the CEERS and GLASS surveys are differentiated with a yellow and blue color, respectively. We note that GLASS probes galaxies with slightly lower masses and SFRs on average, thanks to the gravitational lensing magnification effect. The gray vertical bars in the top right corners represent the typical uncertainties (∼0.2 dex) for the stellar masses and SFRs. The 90% mass completeness limits at z ∼ 5 and z ∼ 9 are highlighted, respectively, with black and lime horizontal segments. |
| In the text | |
 |
Fig. 2. Redshift evolution of ΣSFR from z = 4 to 10. The median values and MAD of ΣSFR in bins of increasing redshift are shown with black empty diamonds and black vertical error bars, while the best-fit to the bins is represented with a black dashed line with a gray region indicating its 1σ uncertainty. The best-fit obtained with the Bayesian linear regression is shown with a blue continuous line, with the blue dotted lines and the blue shaded regions representing the 1σ uncertainty and the ‘posterior plot’, respectively. Theoretical model predictions and comparison observations are included as specified in the legend. |
| In the text | |
 |
Fig. 3. Star-forming main sequence of galaxies selected in this work in the redshift range 4 < z < 6. The best-fit relations are derived in the mass range where we have 90% mass completeness. For comparison, the high redshift and low-mass extrapolation of the MS relations by Schreiber et al. (2015) and Speagle et al. (2014) (obtained at lower redshifts and higher M⋆) are shown with dashed orange and dotted fuchsia lines, respectively. Bottom panel shows the same as the top, but for the redshift range 6 < z < 10. The Bayesian best-fit relation obtained in the lower redshift bin in included as a pink continuous line for comparison. |
| In the text | |
 |
Fig. 4. ΣSFR main sequence for our selected galaxies in the lower redshift bin (4 < z < 6, top) and higher redshift bin (6 < z < 10, bottom). The lines, shaded areas, and markers are the same as in Fig. 2. The average location of massive (M⋆ > 109 M⊙) star-forming galaxies at redshift ∼0 presented by Salim et al. (2023) is highlighted with a cyan dashed line. |
| In the text | |
 |
Fig. 5. ΣSFR as a function of the O32 index for our selected sample in the entire range 4 < z < 10. The lines, shaded areas, and markers are the same as in Fig. 2. The diamonds colored in orange highlight our strong LyC leaking candidates, according to the criteria defined by Flury et al. (2022). |
| In the text | |
 |
Fig. 6. Diagram comparing ΣSFR and fesc for galaxies at 4 < z < 10 with an estimate of fesc(top). The lines, shaded areas, and markers are the same as in Fig. 2. sSFR versus fesc for this NIRSpec sample is shown in the bottom panel. The orange diamonds represent strong LyC leaking candidates according to Flury et al. (2022), as highlighted in Fig. 5. The two galaxies for which we detect outflow signatures in their H-grating spectra from GLASS are shown as big darkred stars. The sample representative error of 0.3 dex on fesc is added below the legend. We include with blue empty squares the LzLCS sample of 66 galaxies at 0.2 < z < 0.4, with measurements (including direct estimates of fesc) performed by Flury et al. (2022). |
| In the text | |
 |
Fig. 7. Single Gaussian (1G) and double Gaussian (2G, narrow + broad) best fits to the [O III] λ5007 Å+Hβ and Hα lines, as indicated in each panel label, for the two galaxies (ID GLASS 160133 and 110000) in which we detect a significant outflow signature in both emission lines (upper and lower four panels, respectively). In each panel, the upper part shows the observed spectrum with the best fit line in red (red (green) line for the narrow (broad) component in the double Gaussian fit), the middle part represents the error spectrum, while the bottom part is the residual after subtracting the best fit result. The spectra are in the observed frame wavelength. |
| In the text | |
 |
Fig. 8. Redshift evolution of ΣSFR (analogous to Fig. 2), color-coded by the attenuation, AV, estimated as described in the text. Galaxies with AV values derived from the emission lines are encapsulated within bigger blue squares. |
| In the text | |
 |
Fig. 9. Diagrams comparing AV to sSFR and ΣSFR (top and bottom panels, respectively) for our selected galaxies in the redshift range of 4 < z < 10. The lines, shaded areas, and markers are the same as in Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


