| Issue |
A&A
Volume 688, August 2024
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202347803 | |
| Published online | 12 August 2024 | |
Individual particle approach to diffusive shock acceleration
Effect of the non-uniform flow velocity downstream of the shock⋆
1
INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
2
Institute for Applied Problems in Mechanics and Mathematics, National Academy of Sciences of Ukraine, Naukova St. 3-b, 79060 Lviv, Ukraine
e-mail: oleh.petruk@gmail.com
Received:
25
August
2023
Accepted:
25
April
2024
Aims. The momentum distribution of particles accelerated at strong non-relativistic shocks may be influenced by the spatial distribution of the flow speed around the shock. This phenomenon becomes evident in the cosmic-ray-modified shock, where the particle spectrum itself determines the profile of the flow velocity upstream. However, the effects of a non-uniform flow speed downstream are unclear. Hydrodynamics indicates that the spatial variation of flow speed over the length scales involved in the acceleration of particles in supernova remnants (SNRs) could be noticeable.
Methods. In the present paper, we address this question. We initially followed Bell’s approach to particle acceleration and then also solved the kinetic equation. We obtained an analytical solution for the momentum distribution of particles accelerated at the cosmic-ray-modified shock with spatially variable flow speed downstream.
Results. We parameterised the downstream speed profile to illustrate its effect on two model cases: the test particle and non-linear acceleration. The resulting particle spectrum is generally softer in Sedov SNRs because the distribution of the flow speed reduces the overall shock compression accessible to particles with higher momenta. On the other hand, the flow structure in young SNRs could lead to harder spectra. The diffusive properties of particles play a crucial role as they determine the distance the particles can return from to the shock, and, as a consequence, the flow speed that they encounter downstream. We discuss a possibility that the plasma velocity gradient could be (at least partially) responsible for the evolution of the radio index and for the high-energy break visible in gamma rays from some SNRs. We expect the effects of the gradient of the flow velocity downstream to be prominent in regions of SNRs with higher diffusion coefficients and lower magnetic field, that is, where acceleration of particles is not very efficient.
Key words: acceleration of particles / shock waves / ISM: supernova remnants
Movie is available at https://www.aanda.org.
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The theory of diffusive shock acceleration (DSA) was introduced in four independent papers and was initially formulated in two alternative approaches. The first approach was through the kinetic equation (Krymskii 1977; Axford et al. 1977; Blandford & Ostriker 1978), while the second was based on the microscopic description (Bell 1978a). Although Bell’s approach is quite intuitive, most of the results related to DSA have been derived by considering the diffusion–convection equation.
The approach of Bell (1978a) deserves more attention as it may be used to derive the known solutions of the kinetic equation and help with new problems. To illustrate the possibilities of the Bell approach, we obtained the solution of Blasi (2002) for the non-linear acceleration (NLA) problem, which we present in Sect. 2.
It has been known for a long time that the spectrum of accelerated particles is affected by the non-uniformity of the plasma flow (e.g. Bogdan & Volk 1983. The NLA solution indeed reflects the non-uniform velocity distribution upstream of the shock, where the particles of higher energies diffuse farther upstream and are scattered back to the shock by scattering centres whose speed differs from the speed of the centres affecting particles of the smaller momenta, which are able to penetrate to shorter distances in the preshock region. This leads to the formation of a concave particle spectrum (e.g. Malkov & Drury 2001; Blasi 2002) instead of a simple power-law derived from the linear approach, where the plasma speed u is considered uniform both upstream and downstream of the shock (e.g. Drury 1983).
The common boundary condition for DSA problems is a zero gradient of the flow velocity behind the shock. However, if du/dx ≠ 0 in the upstream medium affects the particle spectrum shape, this leads us to wonder what the effects might be of also considering a non-zero gradient downstream.
The diffusion length of particles accelerated at the shock can reach ∼0.1 of the shock radius. At this distance downstream in real objects – for example, in supernova remnants (SNRs) –, the flow velocity differs from the immediate post-shock value. Hence, we may expect a ‘downstream’ effect similar to the ‘upstream’ one from the non-linear approach. Moreover, it is known from self-similar solutions (e.g. Chevalier 1982; Sedov 1959) and hydrodynamic simulations (e.g. recent Patnaude et al. (2015), Orlando et al. (2015), Gabler et al. (2021) for the case of the core-collapse supernovae (SNe) and Ferrand et al. (2019, 2021) for the type Ia SNe), that the structure of the flow undergoes essential changes during the early evolution of SNRs. Therefore, we may expect the shape of the spectrum of accelerated particles to vary with time due to the variable non-uniformity of the downstream flow.
In the present paper, we address this effect in the framework of the Bell approach to particle acceleration at shocks. Section 3 presents details of our motivation to answer this question, where we consider the spatial profiles of the plasma velocity behind the SNR shocks from numerical simulations. Appendix A includes an animation of the evolution of the flow speed. In Sect. 4, we use the generalised description of the Bell approach from Sect. 2 to DSA with the non-uniform downstream flow. We consider two practical cases: test-particle and non-linear (NLA) acceleration of particles. Appendix B provides relevant details of the presented derivations. In Sect. 5, we discuss possible scenarios where the effect could be visible. Our conclusions are presented in Sect. 6. Appendix C presents the derivation of the same solution as in Sect. 4 but this time by solving the kinetic equation.
2. NLA in the framework of the Bell approach
Let us consider the shock reference frame with the shock at the coordinate x = 0. In this frame, the flow velocity of the shock u is in the positive x direction. Particles are accelerated by repeating the acceleration cycle multiple times, that is, crossing the shock from downstream (x > 0, index ‘2’) to upstream (x < 0, index ‘1’) and then again to downstream. The approach of Bell (1978a) consists in finding the increase in the particle momentum per cycle and the probability of participating in the next acceleration cycle, then considering many repetitions. We refer the reader to Sect. 3.3 of Jones & Ellison (1991) for the extended formulation of the approach. In the present section, we generalise this approach to the modified shock.
The main idea behind DSA is that the spatial structure of the flow determines the change in the particle momentum ṗ ≡ dp/dt:
The average momentum gain is derived by integration of this expression,
where vx = dx/dt is the projection of the particle velocity v on the x-axis, and by averaging over the flux. The classic formula
comes from (2) for any xa < 0 and xb > 0 if we assume that the upstream u1(x) and the downstream u2(x) velocities of the flow are uniform in their domains.
Under NLA conditions, the pressure of accelerated particles modifies the structure of the flow upstream of the shock, creating some profile u1(x). The pressure of these particles downstream is negligible compared to the thermal pressure, and so the uniformity of u2(x) = const remains unaffected.
Let us first consider the problem in a simplified and more intuitive way. We assume that particles with the momentum p can move away from the shock to a maximum distance |xp| upstream, where the flow speed is up1 = u1(xp) (Blasi 2002). Changing xa to xp in Eq. (2), we arrive at the formula (for more accurate derivation, refer to Sect. 4.1)
In order to participate in the next acceleration cycle, the particle should return to the shock from downstream against the flow direction; that is, its velocity component vx should be −vx > u2. Therefore, the ratio of particle fluxes in the positive and negative x directions gives the probability of continuing acceleration for particles with an isotropic distribution of v (Jones & Ellison 1991)
The probability to participate in at least N number of cycles is
Decomposition of the logarithm of P to the first order on u2/vi results in
The original approach generalised the equation for the momentum increase (4) to N cycles, and its logarithm is decomposed to first order in u2/vi. We instead express 4/vi from Eq. (4) and use this to substitute (7). Then, considering that the ratio Δpi/pi ∼ u2/c ≪ 1 is small for relativistic particles and the number N is high, we make a transition from the summation to the integration: ∑Δpi/pi → ∫dp′/p′. After that, we obtain the probability for a particle to be accelerated to momentum p (or higher) from the injection momentum po on the steady background of the non-uniform profile of the flow velocity upstream:
This probability and the definition of the isotropic distribution function fo(p) (Jones & Ellison 1991),
where index ‘o’ refers to the shock location (x = 0) and n is the number density of particles participating in the acceleration process by returning from downstream, results in the same steady-state distribution function of accelerated particles at the modified shock as derived by Blasi (2002) from the alternative approach of solving the kinetic equation,
where η is the injection efficiency, and n1 and u1 should be taken at the same point – for example, in the immediate preshock location (at x = −0). It is clear that the shape of the particle spectrum depends on the effective compression factor σeff(p) = up1/u2, which is ‘seen’ by particles with momentum p. The function (10) transforms to the power-law test-particle version if we assume that the flow velocity upstream is uniform, meaning the same convergence of the flow for particles of any momentum: σeff(p) = u1/u2. The non-linearity of this solution lies in the fact that σeff(p) itself depends on f(p), which requires another equation for these two functions. Blasi (2002) developed a way to relate σeff(p) to f(p) by considering the hydrodynamics of the flow. In their notation, σeff(p) = RtotU(p), where Rtot = u0/u2 represents the total compression factor of the shock and u0 is the flow speed far upstream.
3. Profiles of the flow velocity
Studies of cosmic-ray-modified shocks demonstrate that the spatial non-uniformity of the plasma velocity upstream of the shock affects the shape of the momentum distribution of accelerated particles. It is natural to ask how the downstream flow structure modifies the particle spectrum. Numerical simulations of CR acceleration, which accounts for the complex hydrodynamic structure of the flow inside SNRs, demonstrate that the volume-averaged CR spectra can have a variety of possible shapes (e.g. Telezhinsky et al. 2012, 2013; Brose et al. 2020). In the present paper, we would like to consider the effect of the non-uniform flow in the vicinity of a single shock where the CR acceleration takes place.
The length scales involved in the particle acceleration at the forward shock are of the order of the diffusion length, which may eventually be up to a few times 0.1R, where R is the SNR radius. Most of the mass swept up by the forward shock is located immediately behind the adiabatic shock within about 10% of the radius. The ratio of densities is ρ(0.9R)/ρ(R) = 0.49 for the Sedov shock in the uniform medium. The variation of the flow velocity in the laboratory reference frame is not as strong, that is, v(0.9R)/v(R) = 0.82, but it is not negligible.
The leading motivation for the present study is the fact that the velocity of the flow u(x) is non-uniform downstream of the shock on the length scale involved in the particle acceleration; indeed it varies spatially from the value u2 at x = +0 in accordance with the profile determined by the hydrodynamics. However, the length scale is small enough to avoid considering the effect of the shock curvature on particle acceleration. In fact, the distance 0.1R on the SNR surface corresponds to the sector with a central angle in arctan(0.1) = 5.7 degrees. Therefore, we can consider the one-dimensional acceleration problem within such a small sector with a plane shock.
For a presentation of the profiles u(x) we can expect downstream, we refer to our previous paper (Petruk et al. 2021). There, we investigate the MHD evolution of the remnants of three SN models, namely thermonuclear SNIa, and two core-collapse SNe: SNIc and SNIIP. We adopted a uniform ISM to model the type SNIa explosion, whereas the core-collapse SNe evolved in a circumstellar bubble with a density shaped by ρCS = Dr−2, where the value of D depends on the explosion model. Core-collapse SNe produce a range of explosion conditions, unlike the thermonuclear explosion of a WD star (SNIa event). To account for this, we selected the two most representative cases, that is, a blue supergiant (SNIc) and a red supergiant (SNIIP) undergoing the core collapse. The SNIc and SNIIP models differ in the effective explosion mass and number density of a wind-blown bubble. We performed all numerical simulations with the PLUTO MHD code (Mignone et al. 2007, 2012). The spherically symmetric uniform grid has 20 000 zones, providing a very detailed spatial resolution during the entire simulation period. Petruk et al. (2021) provide more details on the technical model setup and on initial conditions for the explosion models.
Figure 1 shows the spatial distributions of the flow speed for the three models at the age of 500 yr and for three different SNR ages in the case of the SNIa model. The plots in the left column correspond to the laboratory frame, and those in the right column correspond to the shock frame. The velocity profile u2(x) may rise or decline with distance from the shock. The distribution evolves with time, for example, changing from a decreasing to an increasing function of x in the SNIa model (Fig. 1 bottom right plot). The animation in Appendix A shows the detailed evolution of the velocity distributions up to 10 000 yr in these three models.
 |
Fig. 1. Profiles of the flow velocity v(r) in the observer reference frame (left) and u(x) in the shock reference frame (right) for the three models of SNRs. Upper row: Three SNe models at 500 yr. Lower row: SNIa model at the ages 20, 200, and 1000 yr. On the plots to the left, the explosion centre is at r = 0 with the zero velocity v there. On the plots to the right, the horizontal axes display x = 1 − r/R. Therefore, negative values correspond to the upstream region, whereas positive values correspond to the downstream region. The centre of the explosion on the right-hand side plots is at x = 1, and the velocity u at this point is equal to the upstream velocity u1. We conducted the numerical simulations for the unmodified shocks, and therefore u is spatially constant upstream. The dashed line represents the velocity profile from the Sedov (1959) solution. |
4. Particle acceleration on the background of the non-uniform flow velocities upstream and downstream
4.1. Distribution function
Let us consider the particle acceleration on the flow where the velocity profiles are non-uniform both upstream and downstream of the shock. We start again from Eq. (1). To calculate the increase of momentum per acceleration cycle, we need to spatially separate the integration:
where the function 𝒳i(x) is the probability of finding a cosmic ray with a given momentum at a given coordinate x. The momentum of a particle is modified not only at the shock transition (where the flow speed changes from u1(0) to u2(0)) but also in the convergent (or divergent) flows upstream and downstream.
The formula (11) considers one-dimensional flow. We use it along with the velocity profiles calculated in Sect. 3 using the spherical geometry. There are two important factors we must keep in mind. First, the centre of the SNR is at the point x = R in the shock reference frame. Therefore, the upper limit in the last integral should be R. However, for the sake of generalisation, we use the notation +∞, because the acceleration region is much smaller than the radius R of the SNR. Second, there is a geometrical effect. In the laboratory frame, the integration over the SNR volume is given by rNdr, where N = 0, 1, 2 for the plane, cylindrical, and spherical shocks, respectively. By integrating over x in the shock reference frame, we assume that this effect is accounted for by the probabilities 𝒳i(x).
The spatial distribution of particles is given by the functions f(x, p). Therefore, the probability for the accelerated particle to be at a coordinate x is
where fo(p)≡f(0, p) is the distribution function at the shock. Clearly, 𝒳0(x) = 1.
Equation (1) reads ṗ = p(u1(0) − u2(0))δ(x)/3 for the second integral in (11). Then, the expression (11) may be written as
with the notations
The transition to the classical test-particle case is provided by du/dx = 0.
The probabilities 𝒳i(x) are related to particles that participate in the acceleration around the shock. They do not account for particles escaping upstream or advected downstream. In particular, by equating the diffusive and convective flows in the problem of the test-particle acceleration, we have (Drury 1983)
where D1 is the diffusion coefficient. For the NLA problem (Amato & Blasi 2005; Caprioli et al. 2010), the expression for this probability is more complex. However, the same references suggest its accurate approximation:
where σs = u1(0)/u2(0) is the subshock compression ratio. The probability 𝒳1(x) ≃ exp(u1x/D1) ≃ exp(−x/xp), where xp ≃ −D1/u1 is the coordinate that corresponds to the diffusion length for particles with momentum p. This can be roughly approximated by the Heaviside step function 𝒳1(x) ≈ ℋ(x − xp), which is why we used up ≈ u1(xp) in Sect. 2.
In the test-particle problem, a formula similar to Eq. (16) can be derived in the same way for the region behind the shock. In the future, a derivation of f2(x, p) and 𝒳2(x) in a more general case – considering NLA effects and du2/dx ≠ 0– should be taken into account. In the present paper, we assume that the probability downstream is similar to that upstream, which means that 𝒳2(x) ≃ exp(−x/xp) ≈ ℋ(xp − x), and thus up2 ≈ u2(xp). In fact, at a given point x downstream, only a fraction ξ of particles with momentum p can return to the shock and continue acceleration. A fraction 1 − ξ is advected downstream from this point and never returns to the shock. The fraction ξ decreases with distance from the shock because the particles can return from about one diffusion length. This distance is xp ≃ D2(p)/u2 ∝ pα/u2 with positive α; that is, there are progressively fewer particles with momentum p able to return, being farther from the shock.
Equation (13) gives the average Δp/p for the first half-cycle (upstream–downstream) of acceleration. When we also consider the second half-cycle (downstream–upstream) and take the average over the flux, we obtain the expression for the average momentum increase:
The presented equation accounts for the fact that the plasma velocity profiles are not constant upstream and downstream, contrary to what is assumed in the classical picture of the test-particle acceleration at the shock.
This equation shows that the momentum change depends on the difference between the two utmost values of the flow speed that are ‘reachable’ for accelerating particles with a given momentum.
In Sect. 2, the probability for a particle to cross the shock from downstream to upstream and to consequently participate in the next acceleration cycle is given by the ratio of the particle fluxes in the positive and negative x directions for the isotropic distribution of v and a uniform profile of the plasma velocity downstream u2(x) = const (Jones & Ellison 1991). In our case, u2 varies with the distance from the shock.
Let us consider a simple and intuitive assumption that particles with a given momentum p can reach the maximum coordinate xp2 downstream of the shock and that this distance is greater for particles with greater momenta. Particles must return to the shock from this point to continue acceleration. Therefore, a component of a particle velocity vx must be larger than the flow speed up2 ≈ u2(xp) there. With these assumptions, we can write the expression for the probability from (5) as
The probability for n cycles is
Decomposition of the logarithm to first order on up2, i/vi then gives
Appendix B presents a more general derivation of this expression.
Let us now use 4/vi from (18) to substitute this equation and convert the sum ∑Δpi/pi to the integral ∫dp′/p′. As a result, we derive the probability of a particle being accelerated to momentum p (or higher) on a steady background of the non-uniform profiles of the flow velocity upstream and downstream:
The isotropic distribution function fo(p) is defined by Eq. (9) with n the number density of all accelerated particles, making it a fraction n = ηn0 of all the incoming particles. The flux is conserved: n(x)u(x) = const. Therefore, we can take n at any point; we use n = ηn1u1/up2. Thus, the definition (9) finally yields the distribution function
Known solutions may be easily derived from equation (23). Namely, u2(x) = const results in the non-linear solution of Blasi (2002). If u1(x) = const as well, then we have the common test-particle power-law spectrum for the momentum distribution of accelerated particles.
For the cosmic-ray-modified shock, a way to calculate up1 with an integro-differential equation – that accounts for the changes in the flow hydrodynamics introduced by fo(p) – was developed by Blasi (2002) and Blasi et al. (2005). In these latter studies, the flow is assumed to follow the adiabatic law in the preshock region. Amato & Blasi (2006) and Caprioli et al. (2009) examined the impact of other effects related to the precursor – such as turbulent heating and magnetic field amplification – on the plasma velocity profile upstream.
Equation (23) describes the momentum distribution of accelerated particles at the shock and is derived in the frame of the approach of Bell (1978a) to the particle acceleration. The solution of the same problem derived in the frame of an alternative approach, namely by solving the kinetic equation for DSA, is presented in Appendix C.
4.2. Spectral index
The ‘local’ spectral index s(p), that is, the local slope of the particle distribution fo(p) at a given momentum p, is defined as
Applying it to the function (23), we have
This expression represents the spectral index for particles accelerated around the shock with a non-uniform spatial distribution of the flow speed u(x) upstream and downstream.
Let us introduce the effective compression factor that is ‘seen’ by particles with the momentum p (as shown in Fig. 2):
 |
Fig. 2. Schematic representation of the structure of the flow velocity u(x) (solid line). The shock is located at the coordinate x = 0. The upstream profile of u(x) is shown for the case of the cosmic-ray-modified shock. |
The spectral index for the cosmic-ray-modified shock (it is given by Eq. (8) in Blasi 2002) comes from (25) by assuming u2 = const and therefore σeff = up1/u2:
Equation (25) gives the classic test-particle index,
for u1 = const and u2 = const, namely by using the substitution σeff = σs = u1/u2. In the general case, where u1(x)≠const and u2(x)≠const, the contribution to s(p) from the first term in Eq. (25) is the same as for the unmodified shock (28) but with the effective compression factor σeff instead of σs. This contribution is modified somewhat by the second term in Eq. (25), which represents the ‘local’ (in the momentum space) slope of the difference up1 − up2. Below, we consider the effects of the spatially non-uniform u2(x) on a few practical cases.
4.3. Benchmark problems
4.3.1. Test particles at the Sedov shock
We start from the acceleration of the test particles, that is, u1 = const, at the adiabatic shock with the Sedov profile for u2(x). For simplicity and clarity, we use the approximation by Taylor (1950) for the distribution of the flow velocity downstream of the shock, namely
In the laboratory frame, the immediate post-shock value is v2(R) = 3V/4, V is the shock speed, r is the distance from the explosion centre, and R is the shock radius. The accuracy of the approximation is better than 4% for > 0.7R (Fig. 1 in Petruk 2000). In the shock reference frame, the profile is
where u2(0) = u1/σs. We calculate up2 with the expression up2 ≈ u2(xp), which follows from the definition (15) and 𝒳2(x) ≈ ℋ(xp − x). In order to parametrise the dependence of the diffusion length xp on p, we take
where D is the spatially constant diffusion coefficient of the form D2 ∝ pα with α ≥ 0. Therefore,
where 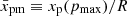 is the diffusion length for particles with the maximum momentum pmax normalised to R. In such a model, we can evaluate the spectral index analytically:
is the diffusion length for particles with the maximum momentum pmax normalised to R. In such a model, we can evaluate the spectral index analytically:
In order to decipher the sensitivity of the problem to 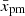 , we consider a few values of this parameter. We take these values for granted in the present section and explore their role further in Sect. 5.3.
, we consider a few values of this parameter. We take these values for granted in the present section and explore their role further in Sect. 5.3.
In Fig. 3, we can see the local spectral index and the distribution function for the model we are considering. It is evident that the effect of the function u2(x), which increases with x, leads to a higher s for higher p. (We note that in the observer frame, the flow speed v decreases downstream with distance from the shock.) This is because the effective compression factor σeff decreases with growing p (Fig. 2). Therefore, the momentum distribution function fo(p) descends more rapidly than a common power law (Fig. 3).
 |
Fig. 3. Local slopes s(p) and the distribution functions fo(p)/no for the unmodified Sedov shock. The parameters are |
It is worth noting that the shapes of the particle distributions shown in Fig. 3 are only due to the plasma velocity gradient downstream of the shock. We applied only the sharp high-energy cutoff to the spectrum of particles ℋ(pmax − p), where ℋ(x) is the Heaviside step function. For comparison, the spectrum is just the power law up to the maximum momentum N(p) = Kp − sℋ(pmax − p) in the case of constant flow speed u2(x) = const.
The classical test-particle index for the case of u2 = const is s = 4. From Fig. 3, we observe that the local index s(p) for the Sedov velocity profile is close to this value for particles with low momenta p, that is, for the particles that are accelerated from small distances 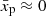 , where deviations of the flow velocity from u2(0) are minor. The index s(p) increases with p for Sedov shock, and its maximum value happens for particles around pmax which are able to return to the shock from deeper downstream locations, that is, from around
, where deviations of the flow velocity from u2(0) are minor. The index s(p) increases with p for Sedov shock, and its maximum value happens for particles around pmax which are able to return to the shock from deeper downstream locations, that is, from around 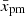 .
.
The effect described in the present paper is sensitive to α. For a fixed 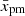 , the effect is more prominent for smaller α (Fig. 3) because particles with low momenta may return to the shock from deeper
, the effect is more prominent for smaller α (Fig. 3) because particles with low momenta may return to the shock from deeper 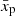 downstream regions.
downstream regions.
Electrons in the magnetic field B = 10 μG emitting most of their energy through the synchrotron radiation at the radio frequency 5 GHz have an energy of 10 GeV. It is apparent from Fig. 3 that, at this energy, the spectral index differs by a few percent from the usual value. For example, the radio index is 0.52 for α = 1/3 and 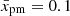 instead of having the common value of 0.5. The differences are larger for smaller α. In the limit of a momentum-independent D (i.e. α = 0), the spectral index is also momentum independent. In such a toy model, its value depends on the distance xp, which is the same for any p, as follows from the Eq. (32). Numerically, for the Sedov profile of u2(x), the values are s = 4.4 for
instead of having the common value of 0.5. The differences are larger for smaller α. In the limit of a momentum-independent D (i.e. α = 0), the spectral index is also momentum independent. In such a toy model, its value depends on the distance xp, which is the same for any p, as follows from the Eq. (32). Numerically, for the Sedov profile of u2(x), the values are s = 4.4 for 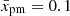 and s = 4.2 for
and s = 4.2 for 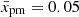 . The radio index at 5 GHz is 0.7 and 0.6, respectively.
. The radio index at 5 GHz is 0.7 and 0.6, respectively.
4.3.2. Cosmic-ray-modified Sedov shock
Let us consider the acceleration of particles on the cosmic-ray-modified shock with the upstream profile u1(x)≠const and the downstream distribution for u2(x) given by Eq. (30), as in a Sedov SNR. The goal is to compare the spectra of particles with the case u2(x) = const.
An intrinsic property of the non-linearity of the cosmic-ray modification of the shock is in the dependence of the plasma speed profile upstream of the shock u1(x) on the particle distribution function fo(p). If we have u2(x) = const downstream of the shock, then the NLA solution of Blasi (2002) holds. In our problem, we should account for the spatial variation u2(x) as well. We show above that the non-uniform profile u2(x) affects the shape of the distribution function fo(p). Therefore, the profile u1(x) upstream will be differently modified by cosmic rays compared to the uniform u2(x) distribution. In turn, this modified upstream profile affects fo(p) as well.
We calculated the NLA solution for such a problem numerically in a self-consistent way by following the approach described by Blasi (2002), Blasi et al. (2005). Namely, we found the function up1(p) by iteratively solving the integro-differential equation, which depends on fo(p), and accounts for the adiabatic evolution of the flow in the shock precursor, for the relation between the injection efficiency and the compression factor at the subshock, and – our addition – for the flow velocity structure downstream. The distribution function fo(p) may then be found from Eq. (23). The iterations are repeated until the boundary condition up1(pmax) = u0 is satisfied. We considered the following set of parameters: the Mach number ℳo = 100, the flow speed far upstream u0 = 6.5 × 108 cm s−1, the maximum momentum pmax = 104mpc, and the injection efficiency η = 1.30 × 10−4. The red line on Fig. 4 shows the solution for u2(x) = const, while the blue lines correspond to models with the velocity gradient downstream of the shock.
 |
Fig. 4. Plots of s(p) and fo(p)/no for the cosmic-ray-modified shock with u2(x) = const (red line) and with up2(p) given by the Eq. (32) with α = 1 (solid blue line), α = 1/3 (dashed blue line), |
Qualitatively, we can understand the behaviour of the momentum distribution of accelerated particles from Fig. 2. In this scheme, we show a model of the cosmic-ray-modified shock (represented by the velocity profile in the x < 0 domain) with increasing function u2(x) downstream (in the x > 0 domain). If we first consider the uniform u2(x) (dashed grey horizontal line in Fig. 2), we can observe that particles with the lowest momenta ‘see’ the compression σs. Particles with larger momenta are affected by continuously higher compression σeff(p), which raises due to the velocity profile upstream. This is the main characteristic of the NLA solution shown by the red line in Fig. 4: the higher the effective compression, the lower the spectral index s and the harder the distribution fo(p). However, the increasing function u2(x) (solid line downstream in Fig. 2) progressively weakens this trend for higher momenta. As a result, the shape of the spectrum may be less concave compared to the pure NLA case or have a complex shape with an inflection point (blue lines in Fig. 4). In contrast, the decreasing u2(x) causes stronger effective compression compared to the uniform u2 downstream and strengthens the NLA concavity.
The effective compression factors are typically high in the NLA problem. They often lead to emission spectra with steep shapes, which are not observed in SNRs. To make σeff lower compared to the pure NLA case, Caprioli et al. (2009) considered the relative Alfenic speed vA of the scattering centres (i.e. u + vA instead of u in the diffusion–convection equation). Our model with a rising flow speed in the shock reference frame could be a natural way to lower σeff and make the spectrum flatter in circumstances where the cosmic-ray shock modification is an essential component.
It is worth noting that the injection efficiency we consider for Fig. 4 is not high, and the shock modification is not very strong. Indeed, the compression factor σtot ≡ u0/u2(0) is 5.434 for the red line, 5.359 for the blue solid line, and 4.897 for the blue dashed line. If the back-reaction of accelerated particles is higher –for example if σtot has a value of about 10 or more– then the upstream profile u1(x) plays the dominating role in shaping fo(p) compared to the effect from the downstream distribution u2(x).
5. Discussion
We show in the previous section that the spatial variation of the flow speed downstream of the shock results in deviation of the momentum distribution of accelerated particles from the classic power law. The spectrum of emission produced by these particles should also be affected. This leads us to wonder whether this effect can be seen in any observables and what its strength might be. Let us look for an answer in the frame of the test-particle acceleration, that is, when assuming that u1 = const.
5.1. Evolution of the radio index of young SNRs
Previously, we explored magneto-hydrodynamic properties of young SNRs in examples of remnants from the three types of SNe (Petruk et al. 2021). Section 3 shows (see also the animation in Appendix A) that the temporal changes in the plasma velocity structure downstream of the shock u2(x, t) are essential during the development of an SNR from the early stage (Chevalier 1982; Dwarkadas & Chevalier 1998) to the Sedov (1959) epoch. These changes may cause time variations in the momentum distribution of particles and consequently in the evolution of the radio index of SNRs.
Figure 5 shows the evolution of the effective compression factor for particles with the maximum momentum 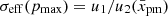 with
with 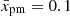 for three models of an SNR. The flow dynamics are different between the models. Specifically, the flow speed within
for three models of an SNR. The flow dynamics are different between the models. Specifically, the flow speed within 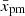 from the shock is almost the same in the SNIIP model, which is one of the representative cases for the DSA theory that assumes u2(x) = const. On the other hand, the SNIa model demonstrates prominent changes in conditions for the shock particle acceleration during its evolution.
from the shock is almost the same in the SNIIP model, which is one of the representative cases for the DSA theory that assumes u2(x) = const. On the other hand, the SNIa model demonstrates prominent changes in conditions for the shock particle acceleration during its evolution.
 |
Fig. 5. Effective compression factor |
These differences may be present in the evolution of the radio index. To expose the effect, we approximate the profile of u2(x, t) for the downstream region close to the shock using the linear function with a variable coefficient k:
This approximation is justifiable by the shape of the u2(x) profiles within the interval of x from zero to ∼0.1R (Fig. 1 and animation in Appendix A). The function up2(p) is then
instead of Eq. (32) and the local slope of the particle distribution is, instead of Eq. (33),
The evolution of the radio index (s − 3)/2 calculated with this expression for s(p, t) is shown in Fig. 6. In the model SNIa, which displays the most prominent changes in the structure of the plasma speed (Fig. 5), the radio index varies from 0.46 to 0.54 over about 1000 yr (red solid line, s changes from 1.9 to 2.1 respectively). The range for the radio index variation could be even wider if particles probe deeper interiors of SNR during acceleration (i.e. when (xpm > 0.1R or α smaller in the assumed dependence xp(p), Eq. (32)), as shown by the dashed line in Fig. 6. It is also consistent with Fig. 3.
 |
Fig. 6. Evolution of the radio index at 5 GHz for the three models of SNRs and electrons with energy of 10 GeV (so, the magnetic field strength is 10 μG), pmax = 104mpc, |
We can conclude that the spectral index in the SNIa model is smaller than the value 0.5 up to SNR ages of ≈100 yr and higher at later times, as shown in Fig. 6. The reason is given by Eq. (36), which shows that the classic value s = 4 (and the radio index 0.5) corresponds to k = 0. Furthermore, this formula reveals that s could have a value of less than 4 when k < 0 (which happens when the flow velocity u2 decreases with x, and thus the effective compression factor 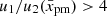 , as seen in Fig. 5) or above 4 when k > 01.
, as seen in Fig. 5) or above 4 when k > 01.
It is worth noting that the left vertical line in Fig. 3 corresponds to electrons that mostly determine the radio index shown in Fig. 6. We see that the deviation of their spectrum from the power law is minor. However, the deviation is more significant for particles with higher momenta, which emit X-rays and gamma-rays.
5.2. High-energy spectral break
A spectral feature is observed in the gamma-ray spectra of several SNRs that is attributed to a change in the slope of the proton spectrum, which is typically referred to as the broken power law. The change in the slope Δs ≈ 0.4 − 1 and should be added to proton spectrum models around the break momentum pbr, which has values from pbr = 10 GeV/c to pbr = 240 GeV/c to fit the observed spectra of some SNRs (e.g. Ackermann et al. 2013; H.E.S.S. Collaboration 2015, 2018).
Such a feature is also visible in radio (Loru et al. 2019) and microwave (Planck Collaboration XXXI 2016) spectra of SNRs, although it has roots in the momentum distribution of electrons.
Our results suggest that the particles accelerated at the shock with spatially variable flow velocity downstream have a momentum distribution with a smooth change of slope over a wide range of momenta. The radio-to-X-ray synchrotron spectrum is convex for evolved SNRs (when u2(x) is an increasing function; Sect. 3), which could mimic the ‘break’ if not very sharp. Our calculations in Sect. 4.2 show that the slope changes between the particle energies 1 Gev and 300 Gev as Δs = 0.11 (from s = 4.02) or Δs = 0.30 (from s = 4.3) for Sedov shock and parameters 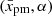 from (0.1, 0.3) to (0.2, 0.1). Comparing these values of Δs with those required by observations, we see that the model could (at least partially) be responsible for the broken power law.
from (0.1, 0.3) to (0.2, 0.1). Comparing these values of Δs with those required by observations, we see that the model could (at least partially) be responsible for the broken power law.
The difference in s(p) from the standard value s = 4 increases towards the maximum energy faster for larger 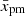 (i.e. the maximum distance from the shock the particles can be and still return to it), for higher values of k (i.e. how fast the flow speed u2 grows with x), and for lower values of α (which is a measure of the extent to which the diffusion coefficient depends on the particle momentum).
(i.e. the maximum distance from the shock the particles can be and still return to it), for higher values of k (i.e. how fast the flow speed u2 grows with x), and for lower values of α (which is a measure of the extent to which the diffusion coefficient depends on the particle momentum).
This last point leads us to an important conclusion: the shape of the accelerated particle distribution in the momentum space is sensitive to the dependence of D on p if the flow speed is not spatially uniform. It is clear from Eq. (36) that the larger the absolute value of k, the higher the sensitivity.
In our model, the diffusion coefficient is a power-law function of the particle momentum D ∝ pα across the whole range of p. As a result, the momentum spectrum of particles changes smoothly over the wide range of p. The observed spectral feature may reflect the change in the dependence of the diffusion coefficient on p around the break momentum pbr.
Figure 7 illustrates this concept, showing the same models as Fig. 3 but with a different diffusion coefficient for particles with the highest momenta. Namely, this coefficient is
 |
Fig. 7. Distribution functions for the same cases as in Fig. 3. The only difference is the diffusion coefficient. It is the same as in Fig. 3 up to the momentum 0.1pmax and independent of p for higher momenta. Above 0.1pmax, the slopes s for the solid blue and red lines are 2.33 and 2.16, respectively. We note that all the lines will be straight horizontal up to pmax in the case of a uniform flow speed u2(x) = const. |
with pbr = 0.1pmax. We see a sharp break around p ∼ 103/mc in the solid lines representing the Bohm diffusion up to the break. The slope change is Δs = 0.33 for xpm = 0.1 and Δs = 0.16 for xpm = 0.05, meaning that it depends on the depth of the ‘zone’ downstream sampled by the accelerating particles. It is interesting to note that the slope s = 2.33 above pbr around the lower boundary of the values of s ≈ 2.3 − 2.6 is required to fit the observed gamma-ray spectra of some SNRs at photon energies of ≳1 TeV. The index s may even be higher in our model for appropriate xpm and k.
We would like to emphasize that D(p) only influences s(p) if the flow speed is non-uniform, that is, in either the downstream or the upstream direction. If u2(x) = const and u1(x) = const, then particles of all momenta sample the same difference between u1 and u2 and therefore s is independent of p.
5.3. Evolution of the diffusion length
The effect we are considering depends on the spatial extent of the downstream region probed by particles accelerating at the shock. We expect the effect from the non-uniform flow velocity downstream of the shock to be noticeable in real SNRs if the diffusion length xpm is higher than about 5% of the radius R.
The Larmor radius of a proton or electron with energy E = ETeV × 1012 eV in the magnetic field B = Bμ × 10−6 G is rL = 10−3ETeV/Bμ pc. The length-scale downstream, which is involved in the formation of fo(p), is of the order of the diffusion length xp ≃ D2/u2. If diffusion is Bohm-like, then DB = ηrLc/3 and
The diffusion length could be up to xp ∼ 105rL (for η = 100 and a slow shock V = 300 km s−1). Under such extreme circumstances, even the radio-emitting electrons may effectively ‘feel’ the non-uniformity of the distribution of the flow speed, because the diffusion length may be up to xp ∼ 0.1 pc for 10 GeV electrons in 10 μG magnetic field. Particles with energy Emax = 10 TeV may have xp ∼ 0.1 pc in more common situations, such as in a magnetic field with a strength of 50 μG behind the shock with a speed of 6000 km s−1 and η = 10.
In order to examine the sensitivity of the problem to the parameter 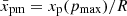 , we adopt fixed values for it and repeat the calculations in the previous sections. Let us examine how
, we adopt fixed values for it and repeat the calculations in the previous sections. Let us examine how 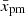 evolves in the two alternative scenarios: the efficient acceleration with the Bohm diffusion and the test-particle case with the Kolmogorov diffusion coefficient.
evolves in the two alternative scenarios: the efficient acceleration with the Bohm diffusion and the test-particle case with the Kolmogorov diffusion coefficient.
The turbulent component of the magnetic field δB causes the scattering of particles. Equation (38) yields
where V3000 is the shock speed in units of 3000 km s−1 and we used δB2 = σBδB1. It follows that the normalized diffusion length varies over time due to the expansion of the SNR, the evolution of pmax, and the magnetic field: 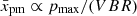 . We know the dependencies R(t) and V(t) for our SNR models from simulations.
. We know the dependencies R(t) and V(t) for our SNR models from simulations.
Under the efficient acceleration regime, we consider both the ordered B1 and the random δB1 components. At the young shocks, the Bell non-resonant instability operates with δB1 > B1. The saturated level of magnetic energy is approximately equal to the V/c fraction of energy Ecr stored in CRs (Bell 2004):
where ξcr is the fraction of the kinetic energy transferred to CRs. When this δB1 is less than the strength of the ordered field B1, the resonant waves are responsible for the particle scatterings with (Amato & Blasi 2006)
where 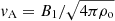 , Pcr = (γcr − 1)Ecr the CR pressure, γcr = 4/3 and δB1/B1 ≤ 1. The highest value of δB1 for the resonant waves could be B1. We assume δB1 = B1 in situations where these formulae give δB1 < B1 for the non-resonant and δB1 > B1 for the resonant, at the same time. Numerically, for the plasma with a mean particle mass in units of the proton mass μ = 0.609,
, Pcr = (γcr − 1)Ecr the CR pressure, γcr = 4/3 and δB1/B1 ≤ 1. The highest value of δB1 for the resonant waves could be B1. We assume δB1 = B1 in situations where these formulae give δB1 < B1 for the non-resonant and δB1 > B1 for the resonant, at the same time. Numerically, for the plasma with a mean particle mass in units of the proton mass μ = 0.609,
Figure 8 shows the variation of δB1 with the SNR age in our models.
 |
Fig. 8. Evolution of δB1 in three models of SNRs. |
The mean acceleration time tacc(pmax) could be estimated from a classic integral (Eq. (3.31) in Drury 1983) assuming D ∝ pα, u1 = V, u2 = V/σtot:
where βa accounts for the fraction of time a particle spends upstream and downstream.
As expected, the acceleration time for diffusion with α < 1 is longer in 1/α times than in the case of the Bohm diffusion (α = 1), for example, for the Kolmogorov diffusion with α = 1/3, it is greater in 3 times.
One of three processes determines the maximum momentum of accelerated particles pmax. The condition tacc(pmax) = t gives the maximum momentum limited by the SNR age. For the Bohm-like diffusion, we have
The synchrotron loss time, which is only applicable to electrons, is
with 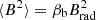 , where Brad = max(δB1, B1) and βb accounts for the time particles spend in the upstream and downstream (Reynolds 1998):
, where Brad = max(δB1, B1) and βb accounts for the time particles spend in the upstream and downstream (Reynolds 1998):
The equation tacc(pmax) = trad(pmax) provides
The third important time to account for is the time required for the growth of the Bell instability, which produces the magnetic field (Bell et al. 2013; Cardillo et al. 2015). In this case, the maximum momentum is estimated using equation (5) of Cristofari et al. (2020):
where e is the electron charge, ω = −dlnno(R)/dlnR is the ambient density steepness (denoted m in Cardillo et al. 2015), and Λ ≈ 12 for pmax ∼ 100 TeV. This expression is valid for any type of diffusion and when the non-resonant δB1 > B1.
In an alternative scenario, we assume the test-particle acceleration and the Kolmogorov diffusion. We set the diffusion coefficient the same as the Bohm-like one at the particle energy Eo, that is, 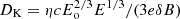 . Then
. Then
The ‘test-particle’ relativistic protons do not amplify the magnetic field. Therefore, we do not account for pmax, gr in this scenario. The magnetic field strength for the diffusion coefficient and the radiative losses is the ordered one at the parallel shock, δB1 = Brad = B1 = B2.
The two scenarios for the evolution of the diffusion length 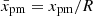 are summarised in Table 1. Figures 9 and 10 show the results of the calculations.
are summarised in Table 1. Figures 9 and 10 show the results of the calculations.
 |
Fig. 9. Evolution of the maximum momentum pmax (a) and the normalized diffusion length |
 |
Fig. 10. Same as in Fig. 9 but for the scenario of efficient acceleration. Dot-dashed lines represent pmax due to the Bell instability, which operates up to the time when the non-resonant δB1 > B1. |
Parameters for two considered scenarios.
In the test-particle case, the maximum momentum in our models is limited predominantly by the age of the system (Fig. 9a). Interestingly, the three lines for 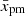 (Fig. 9b) are similar in shape to the evolution of the deceleration parameter m = Vt/R (Fig. 2 of Petruk et al. 2021). Indeed, if we express D from the relations tacc = t or tacc = trad and plug this into
(Fig. 9b) are similar in shape to the evolution of the deceleration parameter m = Vt/R (Fig. 2 of Petruk et al. 2021). Indeed, if we express D from the relations tacc = t or tacc = trad and plug this into 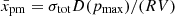 , we get
, we get
which is valid for diffusion of any type. If the age of the systems limits pmax, then the correlation 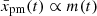 is clear. When the radiative losses limit the maximum energy of particles, then
is clear. When the radiative losses limit the maximum energy of particles, then 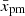 also scales with parameters determining trad (Fig. 9b: blue line after t = 1.3 kyr and green line after t = 2.3 kyr). This could be essential in real SNRs when radiative losses limit pmax; for example when MF is amplified to high values. In this case, in a Sedov SNR for example,
also scales with parameters determining trad (Fig. 9b: blue line after t = 1.3 kyr and green line after t = 2.3 kyr). This could be essential in real SNRs when radiative losses limit pmax; for example when MF is amplified to high values. In this case, in a Sedov SNR for example, 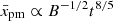 , which might provide a way to determine the properties of a magnetic field from the non-thermal spectra of SNRs. When pmax is age limited, the normalised diffusion length for particles with maximum momentum is determined solely by the shock compression and diffusion type (represented by α). In particular, for the Bohm-like (Kolmogorov) diffusion and unmodified shock,
, which might provide a way to determine the properties of a magnetic field from the non-thermal spectra of SNRs. When pmax is age limited, the normalised diffusion length for particles with maximum momentum is determined solely by the shock compression and diffusion type (represented by α). In particular, for the Bohm-like (Kolmogorov) diffusion and unmodified shock, 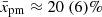 of the SNR radius in young SNRs (when m ≈ 1) or
of the SNR radius in young SNRs (when m ≈ 1) or 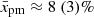 in SNRs at the Sedov stage (when m = 0.4).
in SNRs at the Sedov stage (when m = 0.4).
In the scenario of efficient acceleration, pmax is limited by the growth rate of the Bell instability up to t ≈ 3 kyr (Fig. 10a, cf. Fig. 8). Eqs. (39), (40), and (48) then yield
The dependence on the shock speed is not strong, and the evolution of 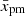 is slow. Indeed, we see in Fig. 10b that the region downstream involved into the acceleration process is about 1 ÷ 3% of the radius when the Bell instability is effective. However, if the diffusion is Bohm-like with η = 2 ÷ 3, then
is slow. Indeed, we see in Fig. 10b that the region downstream involved into the acceleration process is about 1 ÷ 3% of the radius when the Bell instability is effective. However, if the diffusion is Bohm-like with η = 2 ÷ 3, then 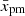 could reach 5% of the SNR radius. At times after ∼3 kyr, when the non-resonant instability is not effective in scattering the particles, then the SNR age limits the maximum momentum. At this stage, the diffusion length does not depend on η (Eqs. (41) and (44)) and may be up to ∼0.1R.
could reach 5% of the SNR radius. At times after ∼3 kyr, when the non-resonant instability is not effective in scattering the particles, then the SNR age limits the maximum momentum. At this stage, the diffusion length does not depend on η (Eqs. (41) and (44)) and may be up to ∼0.1R.
Thus, the downstream structure of the flow might have some influence on the shape of the non-thermal spectra of SNRs in both of the scenarios considered here. The effect is not sufficiently strong to modify the spectral indices in every SNR, but may do so in some cases under certain circumstances.
5.4. Limitations
The non-uniformity of the plasma speed behind the shock affects the cosmic-ray spectrum to a larger extent if particles can penetrate deeply downstream while accelerating at the shock. If so, they can probe a larger (for decreasing u2(x)) difference between the upstream up1 and downstream up2 flow speeds and experience a higher burst in momentum: Δp ∝ up1 − up2. The distance from the shock depends on the properties of diffusion, xp2 ≃ D/u2. Therefore, in order for the effect from the downstream gradient of u2 to be visible in the spectrum, the diffusion coefficient needs to be large. In our estimates, we considered xp1 to be 5 ÷ 10% of the SNR radius R for the particles with the maximum momentum pmax = 104mpc ≈ 10 TeV/c. This corresponds to a diffusion coefficient for particles with such a momentum of D ∼ 0.1Ru2 ∼ 3 × 1025 cm2 s−1 (we used R ∼ 1 pc and u2 ∼ 103 km s−1 for this estimate), which is well within typical values used in the literature. On the contrary, to be capable of providing the proton acceleration to energies beyond 100 TeV, the diffusion coefficient should be the smallest one, namely the Bohm coefficient D = rLc/3 in a magnetic field of a few hundred μG, which requires substantial magnetic field amplification. Under such conditions, the diffusion length for particles with energy Emax = 10 TeV is D2/u2 ≃ rLc/u2 ∼ 0.01 pc, which is just ∼1% of R for particles with the maximum momentum. Of course, the variation of the plasma speed provided by the SNR hydrodynamics on such length scales downstream does not affect the shape of the CR spectrum. On the other hand, the length scale 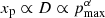 also increases with the rise in maximum momentum.
also increases with the rise in maximum momentum.
In general, we expect the effect of the downstream velocity gradient to be prominent in SNRs – or in some local regions in SNRs – where the particle acceleration is not very efficient, that is, with a lower magnetic field and higher diffusion coefficient. In the present paper, the conditions studied therefore do not provide the highest Emax ∼ PeV energies. Instead, the maximum energy Emax ≈ 10 TeV we used in our examples is a value that can be reached in SNRs with a common interstellar magnetic field and without the fastest diffusion regime. It seems that the conditions for very efficient acceleration (amplified B of ∼ a few mG, the smallest Bohm diffusion coefficient), while crucial for the investigation of PeVatrons, are not widespread in SNRs. Such conditions could be expected locally, that is, present only in some small regions of the SNR shock surface. For an illustration of this point, we refer the reader to Fig. 4 of Long et al. (2003). The thinnest radial profile of the X-ray surface brightness in region A of SN1006 is due to the very fast radiative cooling of electrons in the high magnetic field. This profile provides evidence of effective acceleration with magnetic field amplification there. However, two other profiles B and C, which are close, are thicker (i.e. magnetic field is weaker in these regions). Therefore, the high magnetic strength inferred from the thinnest profile may not be generally attributed to the whole SNR. The less efficient particle acceleration could be in operation throughout other regions of the SNR shock surface.
Another important point is related to the dependence of the diffusion coefficient on the particle momentum; that is, the value of the index α. The effect of the gradient of u2 could be more prominent with smaller particle momenta if the index α is less than unity (as in the Kolmogorov or Kraichnan diffusion coefficients), because xp(p)∝xp(pmax)pα (see Figs. 3, 4, 7).
Interestingly, numerical studies of non-linear particle acceleration (where the kinetic particle equation is solved along with a system of hydrodynamic equations for the flow) by different groups (Kang & Jones 1995, 2007; Gieseler et al. 2000; Kang et al. 2002; Berezhko & Völk 1997, 2000; Zirakashvili & Aharonian 2010; Zirakashvili & Ptuskin 2012) used either the Bohm or the Bohm-like diffusion coefficient and did not find an appreciable impact of the downstream velocity gradient on the particle spectrum.
We find one report where the effect appears visible (though it is difficult to separate from the possible influence of other factors). Brose et al. (2020) numerically solved a system of equations for cosmic rays, magnetic turbulence, and plasma hydrodynamics in SNR. Their Fig. 2 compares the particle spectra for the Bohm diffusion (red lines) and the diffusion coefficient calculated self-consistently from the magnetic turbulence (green lines). In the latter case, the coefficient becomes Kolmogorov-like for most energies (Brose 2023, priv. commun.). The differences between the spectra shapes for α = 1 and α = 1/3 at the ages of 10 and 60 kyr are similar to ours in Fig. 3.
In summary, the effect of the non-uniform u2(x) on the particle spectrum could be prominent in SNRs where adoption of Kolmogorov (α = 1/3) or Kraichnan diffusion (α = 1/2) in magnetic fields with standard strength B of a few tens of μG is acceptable, or in the case of a more efficient acceleration with the Bohm-like diffusion coefficient with η > 1.
In contrast, such values of α, B, and η are not compatible with the highest maximum energies of cosmic rays observed in several SNRs and are not consistent with a modern view of anisotropic cascade of MHD turbulence in the sources of highly efficient particle acceleration based on the Bohm diffusion and high values of amplified B.
6. Conclusions
The aim of the present study is to investigate the possible effect of a spatially variable distribution of the flow speed downstream of the shock on the momentum distribution of particles accelerated at the shock. To this end, we generalised the approach of Bell (1978b), which is an alternative way to describe the particle acceleration at the shock. This generalisation is itself of general academic interest.
We applied this generalised individual particle approach to the NLA solution of Blasi (2002), which assumes u2(x) = const, and then to a more general problem with u2(x)≠const. In order to cross-check our results, we derived in Appendix C the same general solution for fo(p) by solving the kinetic equation.
The formula for the general solution (23) is similar to the known NLA solution. The difference consists in the substitution of the constant u2 with up2(p).
In Sect. 3, we present profiles of the flow speed derived in numerical MHD simulations of remnants evolving after supernova explosions of different types. We demonstrate that the flow speed may vary prominently on the spatial scales involved in the acceleration of particles around the SNR shocks.
Then, we calculated the momentum spectra of particles for several practical cases to demonstrate the effect and its limitations. In these applications, we treat the problem by taking the formula (35) for the function up2(p).
Such a simplified description of up2(p) allows us to study the effect of a non-uniformity of the flow speed on the particle spectrum accelerated in the test-particle limits or the NLA regime (Sect. 4.3).
In Sect. 5, we suggest two cases where the phenomenon might affect – at least partially – some observed properties of SNRs. The overall effect may be visible from equation (36) written for the test-particle limit. If the flow speed in the frame of the shock rises with distance from the shock (i.e. k > 0, as in evolved SNRs) and particles with higher p reach larger x, then s grows with p. This results in a convex spectrum of particles. If the flow speed declines (k < 0), then s decreases and the spectrum is concave. The typical assumption of uniform flow downstream (k = 0) results in the classic formulae.
An important conclusion apparent from Eq. (36) is that the diffusion coefficient (represented by α in this formula) only directly affects the shape of fo(p) if the flow speed is not uniform upstream and/or downstream. Diffusion properties of accelerating particles are important in shaping the fo(p) because the diffusion coefficient determines the diffusive lengths for particles with different momenta. The momentum increase of a particle is sensitive to the differences in the flow velocities it probes u1(xp1)−u2(xp2). Therefore, the same speed profile u2(x) affects the spectrum fp(p) in a different way in models with distinct diffusion coefficients.
The effect of interest is rather sensitive to the diffusion properties of cosmic rays. Particles should diffuse far downstream to probe a hydrodynamic variation of u2(x). Therefore, their diffusion length and diffusion coefficient should be high. As the acceleration of cosmic rays in SNRs to energies beyond 100 TeV is only likely to be achievable through the Bohm diffusion mechanism in an amplified magnetic field (where the diffusion length is therefore small), the significance of the downstream gradient of plasma velocity in SNRs capable of generating PeV cosmic rays can generally be disregarded.
Movie
Movie 1 (SNe_vx_animation) Access here
Acknowledgments
We acknowledge Elena Amato for useful discussions. OP acknowledges the OAPa grant number D.D.75/2022 funded by Direzione Scientifica of Istituto Nazionale di Astrofisica, Italy. The study was partially supported by the INAF mini-grant 1.05.23.04.04. This project has received funding through the MSCA4Ukraine project, which is funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the MSCA4Ukraine Consortium as a whole nor any individual member institutions of the MSCA4Ukraine Consortium can be held responsible for them. We thank the Armed Forces of Ukraine for providing security to perform this work. This research used an HPC cluster at DESY, Germany, and the HPC system MEUSA at INAF-Osservatorio Astronomico di Palermo, Italy.
References
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Amato, E., & Blasi, P. 2005, MNRAS, 364, L76 [NASA ADS] [Google Scholar]
- Amato, E., & Blasi, P. 2006, MNRAS, 371, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Axford, W. I., Leer, E., & Skadron, G. 1977, Int. Cosmic Ray Conf., 11, 132 [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Bell, A. R., Schure, K. M., Reville, B., & Giacinti, G. 2013, MNRAS, 431, 415 [Google Scholar]
- Berezhko, E. G., & Völk, H. J. 1997, Astropart. Phys., 7, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., & Völk, H. J. 2000, A&A, 357, 283 [NASA ADS] [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Blasi, P. 2002, Astropart. Phys., 16, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Gabici, S., & Vannoni, G. 2005, MNRAS, 361, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdan, T. J., & Volk, H. J. 1983, A&A, 122, 129 [NASA ADS] [Google Scholar]
- Brose, R., Pohl, M., Sushch, I., Petruk, O., & Kuzyo, T. 2020, A&A, 634, A59 [EDP Sciences] [Google Scholar]
- Caprioli, D., Blasi, P., Amato, E., & Vietri, M. 2009, MNRAS, 395, 895 [Google Scholar]
- Caprioli, D., Amato, E., & Blasi, P. 2010, Astropart. Phys., 33, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Cardillo, M., Amato, E., & Blasi, P. 2015, Astropart. Phys., 69, 1 [Google Scholar]
- Chevalier, R. A. 1982, ApJ, 258, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Cristofari, P., Blasi, P., & Amato, E. 2020, Astropart. Phys., 123, 102492 [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [Google Scholar]
- Dwarkadas, V. V., & Chevalier, R. A. 1998, ApJ, 497, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrand, G., Warren, D. C., Ono, M., et al. 2019, ApJ, 877, 136 [Google Scholar]
- Ferrand, G., Warren, D. C., Ono, M., et al. 2021, ApJ, 906, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Wongwathanarat, A., & Janka, H.-T. 2021, MNRAS, 502, 3264 [CrossRef] [Google Scholar]
- Gieseler, U. D. J., Jones, T. W., & Kang, H. 2000, A&A, 364, 911 [NASA ADS] [Google Scholar]
- H.E.S.S. Collaboration (Abramowski, A., et al.) 2015, A&A, 574, A100 [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, F. C., & Ellison, D. C. 1991, Space Sci. Rev., 58, 259 [Google Scholar]
- Kang, H., & Jones, T. W. 1995, ApJ, 447, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., & Jones, T. W. 2007, Astropart. Phys., 28, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., Jones, T. W., & Gieseler, U. D. J. 2002, ApJ, 579, 337 [CrossRef] [Google Scholar]
- Krymskii, G. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Long, K. S., Reynolds, S. P., Raymond, J. C., et al. 2003, ApJ, 586, 1162 [Google Scholar]
- Loru, S., Pellizzoni, A., Egron, E., et al. 2019, MNRAS, 482, 3857 [CrossRef] [Google Scholar]
- Malkov, M. A., & Drury, L. O. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Orlando, S., Miceli, M., Pumo, M. L., & Bocchino, F. 2015, ApJ, 810, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Patnaude, D. J., Lee, S.-H., Slane, P. O., et al. 2015, ApJ, 803, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Petruk, O. 2000, A&A, 357, 686 [NASA ADS] [Google Scholar]
- Petruk, O., Kuzyo, T., Orlando, S., Pohl, M., & Brose, R. 2021, MNRAS, 505, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XXXI. 2016, A&A, 586, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, S. P. 1998, ApJ, 493, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press Inc.) [Google Scholar]
- Taylor, G. 1950, Proc. Royal Soc. London Ser. A, 201, 159 [NASA ADS] [Google Scholar]
- Telezhinsky, I., Dwarkadas, V. V., & Pohl, M. 2012, Astropart. Phys., 35, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Telezhinsky, I., Dwarkadas, V. V., & Pohl, M. 2013, A&A, 552, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2012, Astropart. Phys., 39, 12 [Google Scholar]
Appendix A: Evolution of the flow velocity downstream of the forward shock. Animation
The online animation shows the time development of the profiles of the flow speed v(r) in the observer reference frame (left) and u(x) in the shock reference frame (right) for the same models of SNRs as described in Sect. 3 and shown in Fig. 1, up to 10 000 yr. The horizontal axes represent r on the right plot and x = 1 − r/R on the left plot. Vertical axes are normalised to v2(0) (left) and u1(0) (right). The dashed line on each plot corresponds to the flow speed in the Sedov (1959) solution.
Appendix B: Probability of return
The probability of return P in one acceleration cycle is given by the ratio P = F−x/F+x where F−x and F+x are the fluxes of particles with momentum p in the negative and positive x-directions (Jones & Ellison 1991). In our case, the flow speed varies with x and we need to integrate over all places where the probability 𝒳2(p,x) of finding particles with this momentum is above zero, i.e.
Transition to the rightmost equalities assumes that 𝒳2 = 1 at x = +0 and 𝒳2 = 0 for x = +∞. The simplified treatment of the probability in Sect. 4.1 may be recovered by taking approximately
and considering that dℋ(xp − x)/dx = −δ(x − xp). Then
where up2 = u2(xp), as follows from approximation (B.2), and the definition
In a more general treatment, we neglect the terms of the order (u2/v)2 in (B.1). Then, (1 ± u2/v)2 ≈ 1 ± 2u2/v and, with the use of definition (B.4), the probability of return in one cycle becomes
In many cycles, we have the product of the probabilities for individual cycles. Decomposition of the logarithm of the product into the series to first order in up2/v yields equation (21).
Appendix C: Solution of the kinetic equation
This Appendix presents an alternative approach to deriving the expression (23) from the kinetic equation.
We consider the standard steady-state equation for the particle distribution function f(x, p):
together with the typical conditions: the flow speed is along the x axis, in the positive x direction; the shock is located at the coordinate x = 0; the velocity jump du/dx = (u2 − u1)δ(x) through the point x = 0; f(−0, p) = f(+0, p); f(x, p) = 0 at x = ±∞ and df/dx = 0 at x = −∞; the momentum part of the injection term
where po is the injection momentum, η is the injection efficiency (the fraction of particles that start acceleration), po is the injection momentum, δ(x) is the delta-function, and the indices ‘1’ and ‘2’ mark upstream and downstream locations.
We consider the general situation where the flow speed profiles are not spatially constant: u1(x)≠const, u2(x)≠const. The approach to solving equation (C.1) is similar to solving the non-linear problem (Blasi 2002; Blasi et al. 2005); that is, we have to account for the spatial variations of the flow velocity.
The integration of the main equation (C.1) from −∞ to x = −0 results in
where fo(p) is the distribution function at the shock. The integration of the equation (C.1) from x = −0 to x = +0 and from x = +0 to +∞ yields
Integration of the last integral in (C.5) by parts transforms it to
We introduce the notations
where u3 and f3(p) are at the downstream infinity and ux is an unknown function, as well as (cf. with equations (14)-(15))
With all these, equation (C.4) may be rewritten as the equation for the distribution function at the shock fo(p):
The solution of this equation is
The unknown function ux should be ux = up2 in order (i) to match the expression (23) derived in the frame of the approach of Bell, (ii) to give the Blasi (2002) solution with u2 = const (cf. eq.(8) in Blasi et al. 2005), and (iii) to yield the classic test-particle solution fo ∝ p−3u1/(u1 − u2) with u1 = const and u2 = const (then up1 = u1 and up2 = u2).
Strictly speaking, ux in the solution (C.12) is ux = u3f3(p)/fo(p) (see eq. C.7). The equality ux = up2 is valid in the case (i) above at least to the level of approximation for the spatial ‘part’ of the distribution function f2(x, p) adopted in the present paper, i.e. f2(x,p) ≈ fo(p)ℋ(xp − x). Indeed, let us consider some point xp′ downstream. The advected flux of particles with momentum p′ from this point toward x > xp′ is proportional to u2(xp′)fo(p′). The flux conservation gives u3f3(p′) = u2(xp′)fo(p′). Similarly, u3f3(p″) = u2(xp″)fo(p″) for particles with another momentum p″, and so on. Therefore, u3f3(p) = u2(xp)fo(p) holds for any momentum p of relativistic particles. From the definition (15) and 𝒳2(x) = ℋ(xp − x), we have that u2(xp) = up2. Thus, u3f3(p)/fo(p) = up2 and, from (C.7), ux = up2.
It would be desirable in the future to determine the distribution f3(p) from more general considerations. This task is related to the problem of distinguishing between the distribution functions of two populations of particles, namely those that continue to participate in acceleration and those advected downstream. Nevertheless, the exact evolution of particles advected toward the downstream infinity seems unimportant in the determination of the distribution function at the shock because they are ‘removed’ from the accelerator. Therefore, one may set up the boundary condition (C.7) as u3f3(p) = up2fo a priori.
All Tables
All Figures
 |
Fig. 1. Profiles of the flow velocity v(r) in the observer reference frame (left) and u(x) in the shock reference frame (right) for the three models of SNRs. Upper row: Three SNe models at 500 yr. Lower row: SNIa model at the ages 20, 200, and 1000 yr. On the plots to the left, the explosion centre is at r = 0 with the zero velocity v there. On the plots to the right, the horizontal axes display x = 1 − r/R. Therefore, negative values correspond to the upstream region, whereas positive values correspond to the downstream region. The centre of the explosion on the right-hand side plots is at x = 1, and the velocity u at this point is equal to the upstream velocity u1. We conducted the numerical simulations for the unmodified shocks, and therefore u is spatially constant upstream. The dashed line represents the velocity profile from the Sedov (1959) solution. |
| In the text | |
 |
Fig. 2. Schematic representation of the structure of the flow velocity u(x) (solid line). The shock is located at the coordinate x = 0. The upstream profile of u(x) is shown for the case of the cosmic-ray-modified shock. |
| In the text | |
 |
Fig. 3. Local slopes s(p) and the distribution functions fo(p)/no for the unmodified Sedov shock. The parameters are |
| In the text | |
 |
Fig. 4. Plots of s(p) and fo(p)/no for the cosmic-ray-modified shock with u2(x) = const (red line) and with up2(p) given by the Eq. (32) with α = 1 (solid blue line), α = 1/3 (dashed blue line), |
| In the text | |
 |
Fig. 5. Effective compression factor |
| In the text | |
 |
Fig. 6. Evolution of the radio index at 5 GHz for the three models of SNRs and electrons with energy of 10 GeV (so, the magnetic field strength is 10 μG), pmax = 104mpc, |
| In the text | |
 |
Fig. 7. Distribution functions for the same cases as in Fig. 3. The only difference is the diffusion coefficient. It is the same as in Fig. 3 up to the momentum 0.1pmax and independent of p for higher momenta. Above 0.1pmax, the slopes s for the solid blue and red lines are 2.33 and 2.16, respectively. We note that all the lines will be straight horizontal up to pmax in the case of a uniform flow speed u2(x) = const. |
| In the text | |
 |
Fig. 8. Evolution of δB1 in three models of SNRs. |
| In the text | |
 |
Fig. 9. Evolution of the maximum momentum pmax (a) and the normalized diffusion length |
| In the text | |
 |
Fig. 10. Same as in Fig. 9 but for the scenario of efficient acceleration. Dot-dashed lines represent pmax due to the Bell instability, which operates up to the time when the non-resonant δB1 > B1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



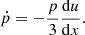
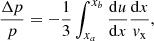
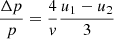
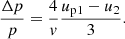
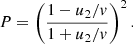
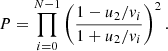
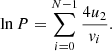
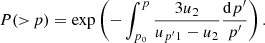
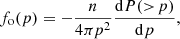
![$$ \begin{aligned} f_{\rm o}(p)=\displaystyle \frac{\eta n_{1}}{4\pi p_{\rm o}^3}\frac{3u_{1}}{u_{\rm p1}-u_2} \exp \left[-\int _{p_{\rm 0}}^{p}\frac{3u_{p^\prime 1}}{u_{p^\prime 1}-u_2}\frac{\mathrm{d}p^\prime }{p^\prime }\right],\end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq10.gif)
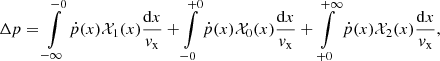
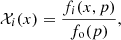
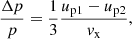
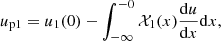
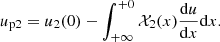
![$$ \begin{aligned} \mathcal{X}_1(x)=\exp \left[\int _{0}^{x}\frac{u_1(x^\prime )\mathrm{d}x^\prime }{D_1(x^\prime ,p)}\right], \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq16.gif)
![$$ \begin{aligned} \mathcal{X}_1(x)=\exp \left[\frac{s(p)}{3}\frac{\sigma _{\rm s}-1}{\sigma _{\rm s}}\int _{0}^{x}\frac{u_1(x^\prime )\mathrm{d}x^\prime }{D_1(x^\prime ,p)}\right] ,\end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq17.gif)
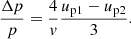
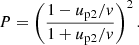
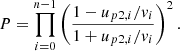
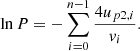
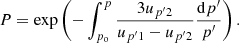
![$$ \begin{aligned} f_{\rm o}(p)=\frac{\eta n_1}{4\pi p_{\rm o}^3}\frac{3u_1}{u_{p1}-u_{p2}} \exp \left[-\int _{p_{\rm o}}^{p}\frac{3u_{{p^\prime }1}}{u_{p^\prime 1}-u_{{p^\prime }2}}\frac{\mathrm{d}{p^\prime }}{{p^\prime }}\right]. \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq23.gif)
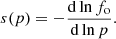
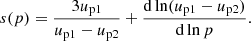
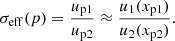
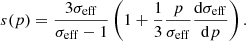
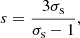
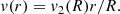
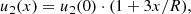
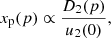
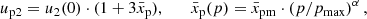
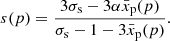
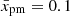
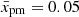
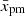
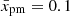
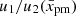
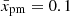
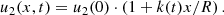
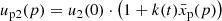
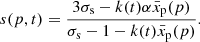
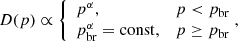
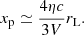
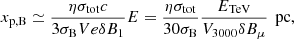
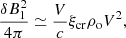
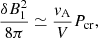
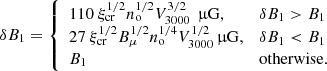
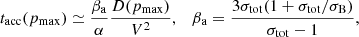
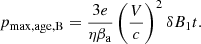
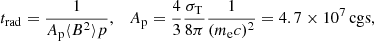
![$$ \begin{aligned} p_{\rm max,rad,B}=\left[\frac{3e}{\eta \beta _{\rm a}\beta _{\rm b}A_{\rm p}}\left(\frac{V}{c}\right)^2\frac{\delta B_1}{B_{\rm rad}^2}\right]^{1/2}. \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq74.gif)
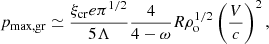
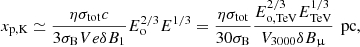
![$$ \begin{aligned} p_{\rm max,age,K}=\left[\frac{ec^{2/3}}{\eta \beta _{\rm a} E_{\rm o}^{2/3}}\left(\frac{V}{c}\right)^2B_1t\right]^{3}, \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq78.gif)
![$$ \begin{aligned} p_{\rm max,rad,K}=\left[\frac{ec^{2/3}}{\eta \beta _{\rm a}\beta _{\rm b}A_{\rm p} E_{\rm o}^{2/3}}\left(\frac{V}{c}\right)^2 \frac{\delta B_1}{B_{\rm rad}^2}\right]^{3/4}. \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq79.gif)
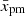
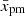
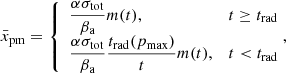
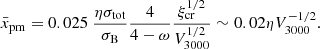
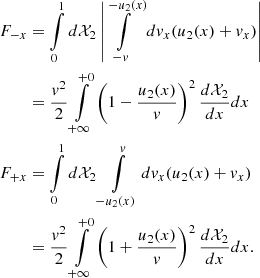
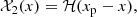
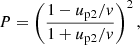
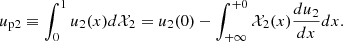
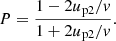
![$$ \begin{aligned} u\frac{\partial {f}}{\partial {x}}=\frac{\partial }{\partial {x}}\left[D\frac{\partial {f}}{\partial {x}}\right]+\frac{1}{3}\frac{du}{dx}p\frac{\partial {f}}{\partial {p}}+Q_{\rm o}(p)\delta (x) ,\end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq102.gif)
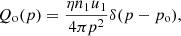
![$$ \begin{aligned} \left[D\frac{\partial {f}}{\partial {x}}\right]_1=u_{\rm p1}f_{\rm o}-\frac{p}{3}\frac{\partial }{\partial {p}}\int _{-\infty }^{-0}f\frac{du}{dx}dx, \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq104.gif)
![$$ \begin{aligned} \left[D\frac{\partial {f}}{\partial {x}}\right]_2-\left[D\frac{\partial {f}}{\partial {x}}\right]_1 +\frac{p}{3}\frac{\partial {f_{\rm o}}}{\partial {p}}(u_2-u_1) +Q_{\rm o}(p)=0 \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq105.gif)
![$$ \begin{aligned} \left[D\frac{\partial {f}}{\partial {x}}\right]_2= \frac{p}{3}\frac{\partial }{\partial {p}}\int _{+0}^{+\infty }f\frac{du}{dx}dx -\int _{+0}^{+\infty }u\frac{\partial {f}}{\partial {x}}dx-u_{\rm x}f_{\rm o} . \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq106.gif)
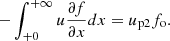
![$$ \begin{aligned} \left[D\frac{\partial {f}}{\partial {x}}\right]_{+\infty }=-u_3f_3\equiv -u_{\rm x}f_{\rm o} ,\end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq108.gif)
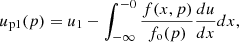
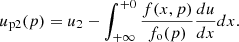
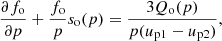
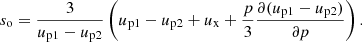
![$$ \begin{aligned} f_{\rm o}(p)=\frac{\eta n_1}{4\pi p_{\rm o}^3}\frac{3u_1}{u_{\rm p1}-u_{\rm p2}} \exp \left[-\int _{p_{\rm o}}^{p}\frac{3(u_{\rm p1}-u_{\rm p2}+u_{\rm x})}{u_{\rm p1}-u_{\rm p2}}\frac{dp^{\prime }}{p^{\prime }}\right]. \end{aligned} $$](/articles/aa/full_html/2024/08/aa47803-23/aa47803-23-eq113.gif)