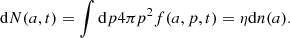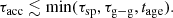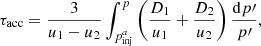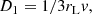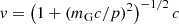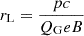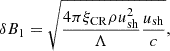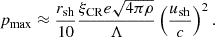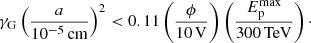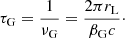| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202452436 | |
| Published online | 13 January 2025 | |
Diffusive shock acceleration of dust grains at supernova remnants
1
Laboratoire Univers et Théories, Observatoire de Paris, Université PSL, Université Paris Cité, CNRS, F-92190 Meudon, France
2
Université Paris-Saclay, CNRS/IN2P3, IJCLab, 91405 Orsay, France
⋆ Corresponding author; pierre.cristofari@obspm.fr
Received:
30
September
2024
Accepted:
26
October
2024
Context. Diffusive shock acceleration (DSA) is a prominent mechanism for energizing charged particles up to very large rigidities at astrophysical collisionless shocks. In addition to ions and electrons, it has been proposed that interstellar dust grains could also be accelerated through diffusive shock acceleration; for instance, at supernova remnants (SNRs).
Aims. Considering interstellar dust grains of various sizes and compositions, we investigate the possibility of grain acceleration at young SNR shocks (throughout the free expansion and Sedov-Taylor phases) and the maximum energies reached by the accelerated grains. We investigate the potential implications for the abundance of refractory species relative to volatile elements in the cosmic-ray composition.
Methods. We rely on semi-analytical descriptions of particle acceleration at strong shocks, and on self-similar solutions for the dynamics of SNR shock waves. For simplicity, type Ia thermonuclear SNRs expanding in a uniform interstellar medium are considered.
Results. We find that the acceleration of dust grains at relativistic speed is possible, up to a Lorentz factor of ∼102 and a kinetic energy of Ek/nuc ∼ 102 GeV/nuc for the smaller grains of size a ∼ 5 × 10−7 cm. We find that the subsequent sputtering of grains can produce nuclei with a sufficient rigidity to be injected in the process of diffusive shock acceleration. Such a scenario can help naturally account for the overabundance of refractory elements in the Galactic cosmic-ray composition, provided that a fraction, η ∼ 10−3 − 10−2, of dust grains swept up by an SNR are energized through DSA.
Key words: acceleration of particles / astroparticle physics / shock waves / cosmic rays / dust / extinction / ISM: supernova remnants
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Dust grains have been shown to be potentially accelerated in interstellar shock waves through diffusive shock acceleration (DSA). Several works have discussed this possibility (Epstein 1980; Ellison et al. 1997), and how the rapid grain destruction following the acceleration could play a role in the production of cosmic rays (CRs; Cesarsky & Bibring 1981; Bibring & Cesarsky 1981).
In the former work of Epstein (1980), dust grains are seen as significant ions of a huge mass-to-charge ratio; that is, large rigidity. The possible acceleration is then counterbalanced by the multiple losses suffered by the dust grains (Ellison et al. 1997; Hoang et al. 2015): interactions with ambient radiation fields, gas and dust, which can lead to thermal sublimation, Coulomb explosions, grain-grain collisions, or sputtering.
As is discussed in Hoang et al. (2015), the acceleration of dust grains to relativistic speeds is challenging (as for instance in the case of acceleration through radiation pressure), and the numerous interactions with the interstellar medium (ISM) and radiations fields are also expected to limit their survival to distances typically of ≲pc or ≲kpc depending on the size and composition of grains, and thus limit the possibility of detecting relativistic dust grains in our atmosphere.
On the other hand, the acceleration of dust grains to relativistic or sub-relativistic speeds is of special interest in the context of the composition of Galactic CRs. Indeed, several measurements have indicated that the refractory elements (i.e., the ones likely to be found in dust phases, such as Mg, Al, Si, Ca, Fe, Co, or Ni) are overabundant compared to volatile elements (i.e., the ones likely to be found in gas phases). The acceleration of dust grains has been shown to potentially play a role in explaining this measurement (Meyer et al. 1997; Ellison et al. 1997). It was more specifically suggested that refractories could be injected in the ISM as Galactic CRs from a population of energized dust grains formed in core collapse supernovae sputtered in the reverse and forward shocks (Lingenfelter et al. 1998; Lingenfelter 2019). However, the abundance of the refractories in the Galactic CRs is somewhat similar to the one of the standard cosmic composition, which argues against the sole implication of core collapse supernovae. In particular, since a substantial fraction ∼70% of Fe originates from thermonuclear supernovae, these objects should also play a role (Tatischeff et al. 2021).
In this paper, we follow the approach of Ellison et al. (1997) to discuss the maximum momentum, velocity, and kinetic energy reached by dust grains accelerated through DSA throughout the lifetime of a typical benchmark supernova remnant (SNR). We consider realistic composition and size distributions (Mathis et al. 1977) for dust grains in the ISM and reassess the various interaction processes of the grains in SNR shocks. We then study the acceleration of refractories from sputtered energized dust grains to discuss the observed overabundance of refractory elements in the Galactic CR composition.
2. Dust grains at supernova remnant shocks
2.1. Physical properties
As in Ellison et al. (1997), we have considered dust grains of a characteristic size, a, and electric potential, ϕ, so that the charge on a spherical grain is of order q ∼ 4πϵ0aϕ (ϵ0 is the vacuum permittivity). This corresponds to a grain charge of
The number of atoms in the (spherical) grain is
with nd = ρd/(μ amu) the atomic number density of the dust grain, μ the average atomic weight of the grain atoms, and amu the atomic mass unit (amu = 1.66 × 10−24 g). In the case of a nonspherical (Min et al. 2007) or asperous grain, NG is expected to be smaller. The mass of a spherical grain is
The atomic weight is AG = μNG with μ the average atomic weight of the grain atoms. The corresponding mass-to-charge ratio is
which can reach values ≳105 − 6 for some dust grains, several orders of magnitude above ions.
The considered dust grains move through the plasma at a velocity, βG, and Lorentz factor, γG, and thus have a rigidity, R:
where p is the grain momentum, c the speed of light, and mp the proton mass.
We considered a size distribution for dust grains following Mathis et al. (1977). The number of dust grains whose size is between a and a + da reads
normalized so that ∼1% of the ISM mass is found in dust of sizes between amin = 5 × 10−7 cm and amax = 5 × 10−5 cm.
It is customary to distinguish between at least two types of dust grains in the ISM: carbonaceous and silicate grains (Draine 2003), with typical properties that are reported in Table 1. Polycyclic aromatic hydrocarbons are not considered in the present study.
Physical properties of graphite and silicate dust grains. nd is the atomic number density, ρd the mass density, and μ the average atomic weight.
2.2. Interactions of dust grains at supernova remnant shocks
Accelerated dust grains can interact with the various constituents of the ISM: photons, ambient gas, and dust grains. We are especially interested in the mechanisms that can lead to the destruction of accelerated dust grains. A few relevant mechanisms affecting the survival of dust grains include: thermal sublimation, Coulomb explosions, and sputtering or grain-grain collisions. For the acceleration at SNR shock waves, sputtering and grain-grain collisions are most relevant.
Indeed, in the case of thermal sublimation, the dust grains heated by interactions with particles and various photon fields in the ISM can lead to the complete destruction of the grains, but the typical timescale associated with thermal sublimation makes the process important for grain destruction if a powerful bolometric source such as a massive star is located within a few AU (Guhathakurta & Draine 1989; Waxman & Draine 2000; Hoang et al. 2015). We thus neglect this effect in this paper.
Coulomb explosions and field emission can occur as the result of an increased charge of the dust grains (Draine & Salpeter 1979). The increase in the potential of the dust grains, ϕ, and tensile strength, S = (ϕ/a)2/4π, is only bearable up to a maximum value where the grain explodes. When a dust grain is sufficiently charged, the emission of individual ions (ion field emission) can also gradually destroy the grain without an explosion. At least two mechanisms can account for the increase in the dust grain charge: collisional charging and photoelectric emission. Collisional charging happens in the high-energy regime when incident electrons and ions cannot be stopped or recombine in the grain but rather lead to the production of secondary electrons, which can potentially escape from the grain, and thus increase the grain charge. The photoelectric emission occurs when the absorption of high energy photons leads to the emission of primary photoelectric electrons, Auger electrons, or secondary electrons (excited by primary photoelectric electrons or Auger electrons). Photoelectric emission is generally relevant for dust grains close to stars (typically a few astronomical units; Hoang et al. 2015), but it can be neglected for the accelerations of grains at SNRs.
2.2.1. Sputtering
Sputtering can lead to the destruction of dust grains. Sputtering corresponds to the ejection of matter (atoms from the dust grains) in the energetic collision of a dust grain and a particle of the ISM. The direct knock-on sputtering of accelerated dust grains is efficient in the low-energy regime (E < 0.1 MeV/u). In the high-energy regime, electronic sputtering, whereby electronic excitations lead to the ejection of atoms, becomes dominant (Dasgupta 1979; Bringa & Johnson 2004).
Ellison et al. (1997), following the approach of Dwek (1987), evaluated the loss time, accounting for frictional interactions of dust grain with the background plasma (neglecting grain-grain collision), as
where nH is the H number density in the ambient medium. The timescale for sputtering can be estimated by considering that about ∼0.5 − 1% of collisions with ambient gas atoms lead to the sputtering of an atom from the grain surface, and that, on average, a collision reduces AG by μ:
In addition to the knock-on sputtering, thermal sputtering can also be considered through a typical timescale (Draine 2011):
where T is the temperature of the considered plasma. This effect is significantly more important downstream in the shock-heated plasma.
2.2.2. Grain-grain collisions
The timescale associated with grain-grain collisions is estimated as
where aT is the typical radius of the target dust grain, and where the interactions with the grains of various sizes, a, are accounted for with the integral over a. Assuming a distribution as in Mathis et al. (1977) (Eq. (6)), dn/da = ngasAMRNa−3.5, with typically AMRN ≈ 3 × 10−25 cm2.5 valid between amin = 5 × 10−7 cm and amax = 5 × 10−5 cm, so that 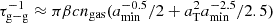 ; that is, τg − g is governed by the maximum of
; that is, τg − g is governed by the maximum of 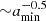 and
and 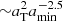 , while amax is of little importance. Moreover, other distributions of dust grains at SNR shocks (e.g., log-parabola function Bocchio et al. 2016, or more elaborate Zubko et al. 2004; Weingartner & Draine 2001) have been shown to provide good descriptions of the dust around SNRs. In the context of this paper, such distributions can potentially affect the timescales discussed above – for instance in the grain-grain collision, in which the prescriptions used in Bocchio tend to increase the characteristic timescale of grain-grain interactions – however they do not significantly impact our results.
, while amax is of little importance. Moreover, other distributions of dust grains at SNR shocks (e.g., log-parabola function Bocchio et al. 2016, or more elaborate Zubko et al. 2004; Weingartner & Draine 2001) have been shown to provide good descriptions of the dust around SNRs. In the context of this paper, such distributions can potentially affect the timescales discussed above – for instance in the grain-grain collision, in which the prescriptions used in Bocchio tend to increase the characteristic timescale of grain-grain interactions – however they do not significantly impact our results.
3. Diffusive shock acceleration
The general theory of DSA predicts that the acceleration of charged particles (and thus of dust grains in our approach) follows a power law in momentum. The distribution function of dust grains of size a will read
where the slope in the test-particle limit is s = 3r/(r − 1) = 4 for a strong shock of compression factor r = 4. Here, p0 = mpc, and the normalization of the spectrum of accelerated dust grains can be estimated assuming that a fraction, ξ, of the number of dust grains of size a enter DSA. In principle, this fraction can change for grains of different sizes. The question of how ions are injected in the DSA process is complex and still open. For protons, whose distribution in momentum is expected to follow a Maxwellian distribution, it is usual to assume that only protons with sufficient momentum are injected in DSA, with a condition that typically reads pinj ≈ χpth, with χ ∼ 3 − 5 (Blasi et al. 2005), and 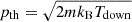 being the momentum at the thermal peak of the Maxwellian downstream. As DSA is a rigidity-dependent mechanism, we can assume that the same condition on the minimum rigidity is required for other ions (and dust grains) to get injected in the acceleration process.
being the momentum at the thermal peak of the Maxwellian downstream. As DSA is a rigidity-dependent mechanism, we can assume that the same condition on the minimum rigidity is required for other ions (and dust grains) to get injected in the acceleration process.
Still, we remark that all dust grains in the rest frame of the plasma downstream arrive from upstream with a velocity of v = (1 − 1/r)ush, where ush is the velocity of the SNR shock wave in the observer rest frame. Their corresponding momentum (and rigidity) with respect to the plasma downstream is m(a)v, largely satisfying the usual conditions on the minimum rigidity required to enter DSA cycles. We can then assume that η, the fraction of dust grains from upstream energized through DSA, is the same for all dust grains. Moreover, their temperature is expected to remain very low compared to the plasma temperature, and thus, unlike protons, the “thermal distribution” is irrelevant for dust grains. The number of accelerated dust grains, dN(a, t), of a size between a and a + da at a time, t, reads
The maximum momentum of dust grains accelerated through DSA can be limited by losses suffered by the dust grains, and by their escape upstream from the acceleration region. Following Ellison et al. (1997), the maximum momentum reached due to losses can be estimated by equating the acceleration time, τacc, with the minimum of the typical loss timescales and the age of the accelerator:
The typical loss times, τsp, τg − g, are discussed in Sect. 2.2.1. The typical acceleration time is
where D1, u1 (D2, u2) are the diffusion coefficient and velocity upstream (downstream).
In order to investigate the maximum energy of accelerated particles, we assume a Bohm-like diffusion coefficient,
where
is the velocity and
the Larmor radius of dust grains of mass, mG, momentum, p, and charge, QG, in a magnetic field, B.
At young SNR shocks, magnetic field values on the order of a few ∼100 μG have been inferred from observations (Vink 2012). Although the exact processes at play are not known, a consensual picture is that the streaming of accelerated particles upstream the shock excite instabilities in the plasma, leading to magnetic field amplification. The dominant mechanism at fast expanding shocks (young SNRs) corresponds to the growth of “non-resonant” instabilities (Bell modes; Bell 2004; Bell et al. 2013; Schure & Bell 2014), and the corresponding magnetic field, attained when the growth in instabilities saturates, typically reads
where ρ is the hydrogen density in the ISM and Λ = ln(pmax/mc). The associated maximum momentum for protons is (Bell et al. 2013)
The maximum energy reached by dust grains can also be limited by their escape upstream from the acceleration region. In the DSA process, accelerated particles are reflected back toward the shock by scattering on turbulence generated by nonthermal particles in the precursor, mostly protons. The maximum energy of the confined grains is then determined by the lowest frequency of the excited turbulence, which corresponds to the gyrofrequency of protons at their maximum (relativistic) energy: 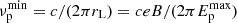 . The grain confinement condition can be expressed in terms of the grain gyrofrequency as
. The grain confinement condition can be expressed in terms of the grain gyrofrequency as 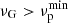 , which can be written in terms of Lorentz factors as
, which can be written in terms of Lorentz factors as 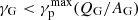 or also
or also 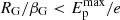 . We then obtain rom Eq. (5); for example for silicate grains, the condition
. We then obtain rom Eq. (5); for example for silicate grains, the condition
This equation shows that relatively large silicate grains with a ≳ 30 − 50 nm are never confined in the shock precursor, and thus cannot be accelerated by the DSA mechanism.
In addition, the acceleration can only take place provided that the gyration time of the accelerated dust grains is shorter than the acceleration time: τG ≪ tacc, with
The timescales relevant for Emax are illustrated in Fig. 1, and the obtained maximum velocities, kinetic energy per nucleon, and Lorentz factor are shown in Fig. 2 in the case of silicate grains. The maximum Lorentz factors set by the escape or by the losses considered are also plotted in Fig. 2 (bottom panel), illustrating that the escape is typically the most stringent condition in the first few 10−2 kyr.
 |
Fig. 1. Timescales relevant to the acceleration of a silicate dust grain of size a = 10−6 cm and shock velocity ush = 109 cm/s vs. the grain velocity, β, in units of c. The relevant typical times shown are: the acceleration time, τacc (solid black), the grain-grain interaction time, τg − g (solid thin green), the gyration time (dashed blue), the grain loss time from frictional interactions with the background plasma (dashed red), the associated sputtering time (dash-dotted thin orange), and the thermal sputtering time (dotted thin orange). |
Considering silicates or graphite grains does not substantially affect the quantities shown in Fig. 2. However, considering a different average magnetic field value impacts the maximum energy, as for instance an average magnetic field of ∼3 μG leads to a maximum Lorentz factor of ∼3, and a kinetic energy of ∼5 GeV/nuc for the smaller grains of a = 5 × 10−7 cm.
 |
Fig. 2. Maximum velocity (top), kinetic energy (middle), and Lorentz factor (bottom) of accelerated silicate grains, with the grain size increasing from thin to thick. The dashed red curve in the top panel shows the evolution of the shock velocity. In the bottom panel, the dashed blue and dotted green lines correspond to the maximum Lorentz factor obtained with the escape condition (Eq. (20)) and with the loss condition (Eq. (13)), respectively. |
The influence of the average magnetic field, as well as the grain average atomic weight, μ, and the potential, ϕ, on the maximum Lorentz factor of the accelerated dust grains is additionally illustrated in Fig. 3.
 |
Fig. 3. Maximum Lorentz factor of dust grains with a = 5 × 10−7 cm for various grain average atomic weight and potential. The thickness of the lines accounts for the change in potential (from 1 V to 100 V). The black, red, and blue lines correspond, respectively, to a magnetic field amplified due to the growth of non-resonant streaming instabilities (Bell), to a fixed value of 100 μG, and to a fixed value of 3 μG. The solid lines assume a mean mass μ = 5, and the dashed lines μ = 56. |
As was mentioned previously, in the rest frame of the downstream plasma, the grains, if assumed to be advected in the plasma, arrive with a velocity of (1 − 1/r)ush, and thus with large momenta (rigidities) compared to ions in the plasma. The rigidity of the dust grain arriving from the upstream plasma, and the maximum rigidity of the dust grain that underwent DSA, are shown in Fig. 4 in the case of silicate grains.
 |
Fig. 4. Rigidity of silicate dust grains arriving downstream (top panel) and at maximum energized through DSA (bottom panel). |
4. The abundance of refractory elements
A substantial fraction of dust grains in an SNR environment is expected to be destroyed (Slavin et al. 2015). This is also expected for accelerated dust grains, for which sputtering is expected to play an important role. Interestingly, the atoms sputtered from the accelerated dust grains have a higher rigidity than the atoms sputtered from the thermal grains, or the grains simply advected in the plasma. We have examined the case of silicate dust grains, under the hypothesis that all Si atoms in the ISM are locked in such grains. The Si abundance in CRs compared to that in the Solar System (SS) composition has been found to be typically ∼20 times greater than the CR-to-SS abundance ratio for protons (Tatischeff et al. 2021). The acceleration and sputtering of dust grains in SNR shocks has been proposed as a possible way to explain the observed overabundance of refractory elements in the CR composition.
Focusing on the case of silicates, we computed throughout the lifetime of an SNR (up until the end of the Sedov-Taylor phase) the amount of accelerated protons throught DSA, under the usual assumption that at each time a fraction of the ram pressure is converted into CR protons, PCR, p = ξpρush2(t), with ξCR ∼ 0.1, which corresponds to a cumulative ratio of accelerated-to-swept-up protons of ηp ∼ 10−5 at the end of the Sedov-Taylor phase.
Additionally, we computed the number of dust grains accelerated, and the number of sputtered silicon with a rigidity larger than the minimum injection ridigity of the protons required to enter DSA: these silicon nuclei are thus considered to have a sufficient rigidity to be accelerated through DSA and contribute to the CR composition. The typical rigidity of the sputtered silicon is illustrated in Fig. 5, showing that throughout the entire SNR lifetime, all dust grains typically smaller than ∼4 × 10−6 can be sputtered to produce silicon that can get into DSA. At a given time, t, the amount of sputtered silicon was estimated by comparing the sputtering timescale given in Eq. (8) to the dynamical timescale at a given time, tdyn = min(t, tadv), where tadv ∼ D1/ush2, with D1 the diffusion coefficient of dust grains upstream. In such an approach, we implicitly consider that all the silicon sputtered upstream will be advected to the shock, and enter DSA, provided that the rigidity satisfies the criterion on injection. The sputtering needs to occur upstream of the shock so that the sputtered ions can be swept into the shock for subsequent acceleration by DSA. The silicon sputtered downstream is quickly advected downstream and lost inside the SNR. Ionization losses for silicon are also taken into account through their typical timescales as in Ellison et al. (1997) but do not significantly affect our calculation.
 |
Fig. 5. Rigidity of silicon sputtered from accelerated silicate dust grains. The hatched black area corresponds to the region where the rigidity of the sputtered silicon is lower than the rigidity required for the injection into DSA. |
We next estimated the cumulative ratio of accelerated-to-swept-up silicon and protons denoted Rsi and Rp. The main free parameter in our calculation is the fraction of dust grains energized through DSA, η. The scaling of Rsi is proportional to η, and Rp ∝ ηCR, so that in order to obtain a ratio, Rsi/Rp ∼ 20, assuming a typical value of ηCR ∼ 10−5, the efficiency of acceleration of dust grains needs to be on the order of η ∼ 5 × 10−3. In other words: Rsi/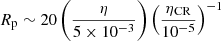 (as is shown in Fig. 6).
(as is shown in Fig. 6).
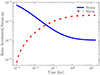 |
Fig. 6. Ratio of the cumulative accelerated ions to cumulative swept-up ions. The solid blue line corresponds to protons, and the dotted red line to silicon considering sputtering as the main destruction mechanism for the dust grains. The calculation was carried out with the number of CRs or dust grains (ηCR = 10−5, and ηa ∼ 5 × 10−3 in order to get a silicon-proton ratio of ∼20) at the end of the Sedov-Taylor phase. |
Under the assumption that the increase fraction of silicon in CRs comes from accelerated and sputtered dust grains, an efficiency of acceleration of dust grains, η ∼ 10−3 − 10−2, is required; that is, 2−3 orders of magnitude more than for protons for which η ∼ 10−5. The need for an increased efficiency for dust grains is easily understood since, as was discussed in the previous section, only smaller dust grains can be accelerated through DSA (βmax larger than the shock velocity), and thus a large number of accelerated small dust grains are needed, so that these dust grains can subsequently be sputtered.
Such increased efficiency is easily accounted for given that the dust grains arriving from upstream have rigidities vastly larger than the minimum rigidity required for protons to enter DSA. In this calculation, the typical total ratio of the accelerated dust silicates to the silicates swept up by the SNR shock is found to be on the order of ∼2 × 10−4, which corresponds to an efficiency of ηa ∼ 5 × 10−3, where the grains smaller than ≲5 × 10−6 cm are efficiently energized through DSA. This amounts to an acceleration of ∼5 × 10−3 of the total mass of dust grains swept up by the SNR throughout its active life.
The results of our calculation are illustrated in Fig. 6. In our simplified approach, all CR Si ions originate from the sputtering of accelerated silicate grains, which are assumed to be all destroyed at the end of the adiabatic phase (∼20 kyr). All the non-accelerated silicates are also substantially destroyed from various processes, as often at least ∼50% are estimated to be destroyed at SNR shocks from various processes (Zhu et al. 2019), but the rigidity of silicon arriving downstream. Non-accelerated silicates are also substantially destroyed at SNR shocks from various processes (Zhu et al. 2019), but the rigidity of Si ions sputtered from non-accelerated silicates in the downstream medium is smaller than the rigidity required to enter into the DSA process.
For this calculation, we have normalized the number of accelerated grains through η (Eq. (12)), but it is also possible to normalize f(a, p, t) in pressure, assuming that a fraction, ξa, of the partial pressure for grains, n(a)m(a)daush2, is accelerated through DSA. The normalization in pressure allows one to easily obtain Rsi/Rp ∼ 20, provided that 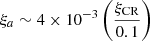 .
.
However, several aspects could strongly affect the efficiency of acceleration of dust grains. The charging of dust grains – for instance, through collisional charging (McKee et al. 1987; Weingartner et al. 2006) – can also have a significant impact on the efficiency of acceleration, and an increase of a factor of ∼100 in the charge leads a grain of size a = 5 × 10−7 cm to a rigidity smaller than the one required for injection into DSA. Second, as is discussed in Sect. 2.2.1, the sputtering rates are not well constrained, and any increase in the sputtering timescale would allow for larger values of η.
5. Conclusions
The DSA at SNR shocks is found to be able to energize dust grains up to relativistic energies; for example, γ ∼ 102, Ek ∼ 102 GeV/nuc for grains of size a ∼ 5 × 10−7 cm. The maximum energy of small grains with a ≲ 5 × 10−6 cm is limited by the losses or destruction at play. For grains larger than a ≳ 5 × 10−6, the escape of the grains from the shock precursor prevents their acceleration.
Additionally, the sputtering of ions from accelerated dust grains can help account for the overabundance of refractories in CRs, as the enhanced rigidity of sputtered ions allow them to be in turn injected in DSA more efficiently. A silicon-to-proton abundance ratio of ∼20, as was found in the measurement of CRs (Tatischeff et al. 2021), can be accounted for, provided that the efficiency of acceleration of dust grains is typically on the order of ηa ∼ 10−3 − 10−2; in other words, 2−3 orders of magnitude larger than the one for protons, ηCR ∼ 10−5.
Several effects require further investigation in order for us to clearly understand the details of the acceleration of dust grains, such as: (1) the importance of dust grain destruction in the SNR environment, and especially close to the shock discontinuity (i.e., sputtering, destruction by charging, ...); (2) the injection of dust grains in the DSA process; (3) the charging of the dust grains, which can affect both the injection and the maximum rigidity; (4) nonlinear effects of DSA on the acceleration of grains, and the potential consequences of grain acceleration on the acceleration of other ions present in the plasma; (5) the importance of the grain distribution in size, for example the presence of large dust grains (∼10−4 cm) was shown to potentially be reflected and accelerated in the pre-shock gas before being destroyed, and thus possibly affected the shock environment in which CR or dust grain acceleration is taking place (Slavin et al. 2004); and (6) the case of remnants from core-collapse supernovae, expanding in very diverse environments, needs also to be taken into account.
Acknowledgments
PC acknowledges support from the GALAPAGOS PSL Starting Grant. The authors warmly thank J. Raymond and J. Slavin for fruitful discussions and constructive comments on the manuscript.
References
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Bell, A. R., Schure, K. M., Reville, B., & Giacinti, G. 2013, MNRAS, 431, 415 [Google Scholar]
- Bibring, J. P., & Cesarsky, C. J. 1981, Int. Cosm. Ray Conf., 2, 289 [NASA ADS] [Google Scholar]
- Blasi, P., Gabici, S., & Vannoni, G. 2005, MNRAS, 361, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchio, M., Marassi, S., Schneider, R., et al. 2016, A&A, 587, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bringa, E. M., & Johnson, R. E. 2004, ApJ, 603, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Cesarsky, C. J., & Bibring, J. P. 1981, in Origin of Cosmic Rays, eds. G. Setti, G. Spada, & A. W. Wolfendale, 94, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Dasgupta, A. K. 1979, Ap&SS, 63, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 438 [Google Scholar]
- Dwek, E. 1987, ApJ, 322, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Drury, L. O., & Meyer, J.-P. 1997, ApJ, 487, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, R. I. 1980, MNRAS, 193, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Guhathakurta, P., & Draine, B. T. 1989, ApJ, 345, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Lazarian, A., & Schlickeiser, R. 2015, ApJ, 806, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Lingenfelter, R. E. 2019, ApJS, 245, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Lingenfelter, R. E., Ramaty, R., & Kozlovsky, B. 1998, ApJ, 500, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- McKee, C. F., Hollenbach, D. J., Seab, G. C., & Tielens, A. G. G. M. 1987, ApJ, 318, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, J.-P., Drury, L. O., & Ellison, D. C. 1997, ApJ, 487, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Waters, L. B. F. M., de Koter, A., et al. 2007, A&A, 462, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schure, K. M., & Bell, A. R. 2014, MNRAS, 437, 2802 [CrossRef] [Google Scholar]
- Slavin, J. D., Jones, A. P., & Tielens, A. G. G. M. 2004, ApJ, 614, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. D., Dwek, E., & Jones, A. P. 2015, ApJ, 803, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Tatischeff, V., Raymond, J. C., Duprat, J., Gabici, S., & Recchia, S. 2021, MNRAS, 508, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
- Waxman, E., & Draine, B. T. 2000, ApJ, 537, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Weingartner, J. C., Draine, B. T., & Barr, D. K. 2006, ApJ, 645, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, H., Slane, P., Raymond, J., & Tian, W. W. 2019, ApJ, 882, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Physical properties of graphite and silicate dust grains. nd is the atomic number density, ρd the mass density, and μ the average atomic weight.
All Figures
 |
Fig. 1. Timescales relevant to the acceleration of a silicate dust grain of size a = 10−6 cm and shock velocity ush = 109 cm/s vs. the grain velocity, β, in units of c. The relevant typical times shown are: the acceleration time, τacc (solid black), the grain-grain interaction time, τg − g (solid thin green), the gyration time (dashed blue), the grain loss time from frictional interactions with the background plasma (dashed red), the associated sputtering time (dash-dotted thin orange), and the thermal sputtering time (dotted thin orange). |
| In the text | |
 |
Fig. 2. Maximum velocity (top), kinetic energy (middle), and Lorentz factor (bottom) of accelerated silicate grains, with the grain size increasing from thin to thick. The dashed red curve in the top panel shows the evolution of the shock velocity. In the bottom panel, the dashed blue and dotted green lines correspond to the maximum Lorentz factor obtained with the escape condition (Eq. (20)) and with the loss condition (Eq. (13)), respectively. |
| In the text | |
 |
Fig. 3. Maximum Lorentz factor of dust grains with a = 5 × 10−7 cm for various grain average atomic weight and potential. The thickness of the lines accounts for the change in potential (from 1 V to 100 V). The black, red, and blue lines correspond, respectively, to a magnetic field amplified due to the growth of non-resonant streaming instabilities (Bell), to a fixed value of 100 μG, and to a fixed value of 3 μG. The solid lines assume a mean mass μ = 5, and the dashed lines μ = 56. |
| In the text | |
 |
Fig. 4. Rigidity of silicate dust grains arriving downstream (top panel) and at maximum energized through DSA (bottom panel). |
| In the text | |
 |
Fig. 5. Rigidity of silicon sputtered from accelerated silicate dust grains. The hatched black area corresponds to the region where the rigidity of the sputtered silicon is lower than the rigidity required for the injection into DSA. |
| In the text | |
 |
Fig. 6. Ratio of the cumulative accelerated ions to cumulative swept-up ions. The solid blue line corresponds to protons, and the dotted red line to silicon considering sputtering as the main destruction mechanism for the dust grains. The calculation was carried out with the number of CRs or dust grains (ηCR = 10−5, and ηa ∼ 5 × 10−3 in order to get a silicon-proton ratio of ∼20) at the end of the Sedov-Taylor phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



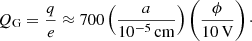
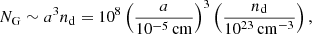
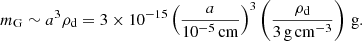
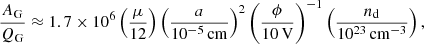
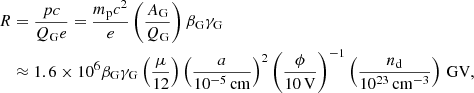
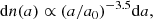
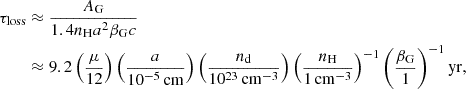
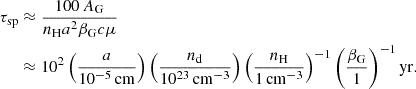
![$$ \begin{aligned} \tau _{\rm sp, thermal}\approx 10^{5} \left[1 + \left(\frac{T}{10^6\,\mathrm{K}}\right)^{-3}\right] \left(\frac{a}{10^{-5}\,\mathrm{cm}}\right) \left(\frac{n_{\rm H}}{1\,\mathrm{cm}^{-3}}\right)^{-1} \mathrm{yr}, \end{aligned} $$](/articles/aa/full_html/2025/01/aa52436-24/aa52436-24-eq9.gif)
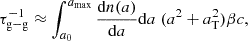
![$$ \begin{aligned} f (a,p,t) = A (a,t) \left(\frac{p}{p_0}\right)^{-s} \exp \left[-\frac{p}{{p_{\rm max}(a,t)}}\right], \end{aligned} $$](/articles/aa/full_html/2025/01/aa52436-24/aa52436-24-eq14.gif)