| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A293 | |
| Number of page(s) | 10 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202449887 | |
| Published online | 20 June 2024 | |
A model of umbral oscillations inherited from subphotospheric fast-body modes
1
Astronomy Program, Department of Physics and Astronomy, Seoul National University, Seoul 08826, Republic of Korea
e-mail: jcchae@snu.ac.kr
2
Bay Area Environmental Research Institute, NASA Research Park, Moffett Field, CA 94035, USA
3
Lockheed Martin Solar and Astrophysics Laboratory, 3251 Hanover St, Palo Alto, CA 94306, USA
4
Solar and Space Weather Group, Korea Astronomy and Space Science Institute, Daejeon 34055, Republic of Korea
Received:
7
March
2024
Accepted:
17
April
2024
Recently, complex horizontal patterns of umbral oscillations have been reported, but their physical nature and origin are still not fully understood. Here we show that the two-dimensional patterns of umbral oscillations of slow waves are inherited from the subphotospheric fast-body modes. Using a simple analytic model, we successfully reproduced the temporal evolution of oscillation patterns with a finite number of fast-body modes. In this model, the radial apparent propagation of the pattern is associated with the appropriate combination of the amplitudes in radial modes. We also find that the oscillation patterns are dependent on the oscillation period. This result indicates that there is a cutoff radial mode, which is a unique characteristic of the model of fast-body modes. In principle, both internal and external sources can excite these fast-body modes and produce horizontal patterns of umbral oscillations.
Key words: magnetohydrodynamics (MHD) / waves / Sun: chromosphere / Sun: oscillations / sunspots
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Umbral oscillations are a magnetohydrodynamic (MHD) process conspicuous in every sunspot umbra. Following their initial detection (Beckers & Tallant 1969), subsequent works revealed that the umbral oscillations are the slow MHD waves propagating upwards from the photosphere to the corona with a group speed of around the speed of sound (Lites 1984; Centeno et al. 2006; Felipe et al. 2010; Krishna Prasad et al. 2017). Because the temperature minimum region between the photosphere and the chromosphere acts as a high-pass filter, the wave power peaks around the cutoff frequency (ωc) of around 6 mHz in the chromosphere (Roberts 1983; Centeno et al. 2006). Theoretical studies have revealed that even a portion of low-frequency waves (ω < ωc) can propagate upwards due to the effects of the temperature gradient (Schmitz & Fleck 1998; Chae & Litvinenko 2018) and the radiative relaxation of nonadiabatic heating and cooling (Roberts 1983; Centeno et al. 2006; Chae et al. 2023). The most plausible sources of the umbral oscillations have been considered to be either the magnetoconvection inside a sunspot, such as an umbral dot (Lee 1993; Jacoutot et al. 2008; Jess et al. 2012), or the absorption of the incident f and p mode waves (Braun & Duvall 1987; Spruit & Bogdan 1992; Cally & Bogdan 1997).
Interestingly, observational studies recently reported waves that appear to move across the magnetic field, forming ring-like patterns (Zhao et al. 2015; Cho & Chae 2020; Cho et al. 2021) or spiral-shaped wave patterns (SWPs) (Sych & Nakariakov 2014; Su et al. 2016; Felipe et al. 2019; Kang et al. 2019). There are two models that can reproduce these patterns: a model of propagating waves excited in the subphotosphere (e.g., Zhao et al. 2015; Cho & Chae 2020), and a model of slow-body resonant modes (e.g., Edwin & Roberts 1982; Stangalini et al. 2022). The wave-propagation model assumes that there is a localized disturbance in the high-β region of the subphotosphere. This disturbance excites fast MHD waves, and these waves propagate quasi-isotropically. The wavefront reaching the equipartition layer (β ∼ 1) has a time delay as a function of horizontal distance, and this time delay causes ring-like patterns to propagate across the magnetic field (Zhao et al. 2015). After reaching β ∼ 1, the fast waves are partially converted to the slow waves by the mode-conversion process (Zhugzhda & Dzhalilov 1984; Cally 2001; Schunker & Cally 2006). This model successfully reproduces the ring-like wavefronts (Cho & Chae 2020; Cho et al. 2021) and the SWPs (Kang et al. 2019) observed in the chromosphere. To explain the SWPs, Kang et al. (2019) additionally assumed that the point-like source generates nonaxisymmetric modes. However, it is not yet clear as to whether or not the exciting source assumed in this model really exists, and if it does, how such a source can generate nonaxisymmetric modes also remains unclear.
The other model to explain the complex wave patterns is the model of slow-body resonant modes. Eigenmode waves are known to appear when the flux tube resonates with external driving (Edwin & Roberts 1982, 1983; Roberts 2019). Considering the cylindrical geometry, Jess et al. (2017) successfully identified the first-order azimuthal mode from chromospheric umbral oscillations. Recently, Albidah et al. (2022) found higher-mode oscillation patterns in circular and elliptical sunspots. In addition, in a large-scale sunspot with complex geometry, Stangalini et al. (2022) successfully reproduced the oscillation patterns by the superposition of more than 30 slow-body resonant modes in Cartesian geometry. However, it is difficult to understand how a systematic horizontal pattern can be established from the resonance of slow-body waves that are very inefficient in transferring energy in the horizontal direction across magnetic fields.
In the present work, we propose another model: a model of umbral oscillations inherited from subphotospheric fast-body modes. In this model of fast-body modes, we suppose that the driving and resonance of the flux tube occur in the subphotosphere, resulting in the subphotospheric fast-body modes. These fast modes are partially converted to slow waves in the equipartition layer. These slow waves come to have two-dimensional patterns with resonant modes because they inherit the fast modes from the subphotosphere.
In Sect. 2, we propose the simple analytic model of the subphotospheric fast-body modes. In Sect. 3, we show observations of two-dimensional patterns in the pore and present a method to analyze them. In Sect. 4, we compare the observation and the model. Finally, in Sect. 5, we summarize and discuss our model.
2. The model
We regard the patterns of umbral oscillations as the inherited patterns of fast-body modes in the subphotosphere (see Fig. 1). We conjecture that the inheritance is realized by the process of fast-to-slow-mode conversion in the equipartition layer (e.g., Zhugzhda & Dzhalilov 1984; Cally 2001) after the fast-body modes have formed in the subsurface. These converted slow waves (blue solid line) propagate upwards to the detection layer along the magnetic field. As a consequence, the observed horizontal patterns of umbral oscillations can be identified with the patterns of fast-body modes (red solid line) in the subphotosphere.
 |
Fig. 1. Illustration of our model of umbral oscillations inherited from subphotospheric fast-body modes. The yellow area represents the high-β region (cs > vA) below the sunspot surface, and the white area represents the low-β region (cs < vA). The black solid line between the two regions represents the equipartition layer (cs = vA) where the mode conversion can occur. The gray vertical lines illustrate the magnetic field lines of the flux tube, and the vertical dashed line indicates the boundary of the flux tube. The red line demonstrates the vertical velocity vz of fast body waves, and the blue line represents vz of converted slow waves. The dash-dotted horizontal line represents the detection layer of the chromosphere. The two panels in the bottom right corner show the vertical velocity fluctuation of two azimuthal modes of m = 0 and 2. The top right panel shows a horizontal cross-section view of the modeled oscillation patterns. |
For simplicity, we adopt a vertical magnetic flux tube with a radius R where density ρ, Alfvén speed vA, sound speed cs, and tube speed 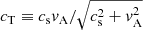 are uniform inside the flux tube. The magnetoacoustic body mode of vertical velocity with angular frequency ω, azimuthal mode m, radial wavenumber kr, and vertical wavenumber kz is given by the solution in cylindrical coordinates (Edwin & Roberts 1983; Roberts 2019),
are uniform inside the flux tube. The magnetoacoustic body mode of vertical velocity with angular frequency ω, azimuthal mode m, radial wavenumber kr, and vertical wavenumber kz is given by the solution in cylindrical coordinates (Edwin & Roberts 1983; Roberts 2019),
where Akr, m, ω is a complex constant and Jm is the first kind of the Bessel function of an azimuthal mode m. Here, the radial wavenumber kr depends on ω and kz as in the expression
and is to be determined from the boundary condition at r = R:
which is obtained from the continuity of total pressure and radial velocity vr (Edwin & Roberts 1983). Here, Km is the second kind of the modified Bessel function, the prime operator (′) denotes the derivative of the Bessel function, and the subscript e stands for quantities in the external region r > R.
For the body wave solution, kr should be real and hence 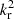 has to be positive (Edwin & Roberts 1983). This requirement is satisfied for fast-body waves when the vertical phase speed vp ≡ ω/kz lies between the internal sound speed and the external sound speed:
has to be positive (Edwin & Roberts 1983). This requirement is satisfied for fast-body waves when the vertical phase speed vp ≡ ω/kz lies between the internal sound speed and the external sound speed:
Similarly, we obtain the condition for the slow-body wave solution:
indicating that vp should be in between the internal Alfvén speed and the tube speed.
We note that Eq. (3) has a simple solution,
in the limit of zero-external density (ρe = 0). This condition might be satisfied when the external medium is much hotter than the interior. As Jm is an oscillatory function, there are several values of kr(n) with different values of radial mode n. In other words, kr(n)R is the nth root of Eq. (6). Generally speaking, kr is specified by m, n, and R.
The zero-density limit is useful for understanding the characteristics of the body waves when only considering the internal atmospheric conditions such as cs, and vA. Eqs. (2) and (6) are solved for the expression
with the parameters
We note that the larger value, kz, +, corresponds to slow waves and the smaller one, kz, −, to fast waves.
The relationship in Eq. (7) can be used to calculate kz as a function of ω or equivalently the oscillation period P = 2π/ω when m and n are specified in the cases of slow-body waves and fast-body waves. As an illustration, we consider a flux tube of R = 3.5 Mm, cs = 6.3 km s−1, and vA = 0.56cs at a depth of β = 3.8 below the surface (Fig. 2). Here, the choice of cs has been made by extrapolating the Maltby M sunspot model (Maltby et al. 1986) to the depth of 100 km. As the condition cs, e > cs > vA is satisfied in this flux tube, both fast-body waves and slow-body waves can occur if vp is within a specified range.
 |
Fig. 2. Period P as a function of vertical wavenumber kz for (a) the slow-body waves and (b) the fast-body waves for n = 1, 2, 3, 4, 5, and 10 with m = 2 in the subphotospheric condition (cs, e > cs > vA). The white area in panel a marks the range of vA > vp > cT within which the slow-body wave solution can exist, and that in panel b represents the range within which the fast-body wave can exist (cs, e > vp > cs). The inset figure in panel a shows the magnified figure in the ranges of 0.011 < kz < 0.012 km s−1 and 155 < P < 165 s. The dashed line represents the period of 160 s. The color-shaded regions in panel b represent the regions with the same cutoff radial mode nM; yellow is nM = 2, green is nM = 3, blue is nM = 4 and purple is nM ≥ 5. We have taken the internal sound speed of cs = 6.3 km s−1, internal Alfvén speed of vA = 0.56cs, and external sound speed of cs, e = 1.7cs. |
We first consider slow-body modes (see Fig. 2a). These waves can exist within the vp range marked as a white area and satisfying vA > vp > cT. We find that the curve representing the solution for kz(P) with m = 2 of any value of n fits into this range. An important property of slow waves is that for a specified period, there exists an infinite number of solutions with n = 1, …, ∞ with any value of m.
We now consider fast-body modes. Figure 2b presents the solution for kz(P) for each value of n with m = 2. Even though this solution is independent of the physical condition outside the flux tube, it can have a physical meaning as fast waves only when the condition cs, e > vp > cs is satisfied. With the choice of cs, e = 1.7cs, the physically meaningful range of vp is marked as a white area. A distinct property of fast waves is that for a specified period, there exists a finite number of solutions with n ≤ nM for each m, where nM is the highest radial mode that can be trapped in the flux tube satisfying the condition of Eq. (4). In other words, for a given period, there exists a cutoff (nM) in the radial mode in fast-body waves. For example, for the waves with a period of 160 s, which corresponds to the dashed line, the cutoff radial mode is nM = 4. We note that nM depends on P as well as m in fast waves, whereas nM = ∞ always in slow waves.
As we regard the observed pattern of velocity fluctuation as the inheritance of the fast-body waves in the subphotosphere, it can be modeled by a superposition of all modes, as in
where An, m, ω represents the real amplitude and the phase is described by θm, ω and tm, n, ω. We note that kz is determined from Eq. (7) for given ω, m, and n. The inheritance is simply achieved by choosing z to represent the detection layer, assuming a constant phase lag between the chromosphere and the subphotosphere in all the waves. For reasons of practicality, we set z = 0 to represent the detection layer, θ0, ω = 0, and t0, 1, ω = 0 for a reference without loss of generality.
3. Data and method
We now describe how to obtain vz(t, r, θ; ω) in the detection layer from the observation, and how to determine the parameters n, An, m, ω, θm, and tm, n from vz(t, r, θ; ω) for each m with significant power. We applied our model to a small sunspot, a pore observed in NOAA 12078 at (-301″, 162″) on June 3, 2014, from 16:49 UT to 17:56 UT (Fig. 3a). The data –taken with the Fast Imaging Solar Spectrograph (FISS, Chae et al. 2013) at the Goode Solar Telescope (GST)– have been used in several studies (Chae et al. 2015, 2022; Kang et al. 2019). The time cadence of the data is 20 s, the spatial sampling is 0.16″, the spectral sampling is 19 mÅ, and the spectral range is −5 Å to 5 Å of Hα. We calibrated the raw data following the reduction pipeline described in detail by Chae et al. (2013). We calculated the line-of-sight (LOS) Doppler velocity vLOS(t, x, y) at every pixel (x, y) at different times using the lambdameter (bisector) method (e.g., Chae et al. 2014) with a chord of 0.1 Å.
 |
Fig. 3. Detection of a pattern of umbral oscillations. (a) Continuum intensity map of the GST/FISS constructed at the −43.5 Å of the Hα line center and chromospheric intensity map constructed at the line center at 17:44:07 UT on June 3, 2014. (b) Two-dimensional wave patterns of the chromospheric Doppler velocity map temporally filtered in 5.5 − 9 mHz. The black contour displays the boundary of the pore, and the red cross symbol marks the center position of the SWP. (c) Azimuthally decomposed wave patterns for m = 0 and ±2 modes. (d) Modeled LOS velocity fluctuation map constructed by the superposition of 12 modes (m × n, where m = 0, 2, −2 and n = 1, 2, 3, 4). The dashed circle shows the boundary of the modeled flux tube. (e) All modes of trapped fast-body waves for the modeled LOS velocity map. Here m represents the azimuthal mode and n refers to the radial mode. The color limit of panels b–e is −3.5 to 3.5 km s−1, where the positive sign signifies the redshift. The temporal evolutions of panels b–d are shown in Fig. 5. |
In the present study, we focus on the two-armed SWPs that occurred around 17:44:07 UT (t = 40 s). The wavelet power spectrum of velocity fluctuations vLOS(t, xc, yc) at the center of these SWPs indicates that most power is concentrated in the 2 − 3 min band with a peak of around P = 160 s (Fig. 4). We confined our analysis to this band, with the peak frequency ω = 2π/P = 0.04 rad s−1. We extracted the velocity at this band vLOS(t, x, y; ω) by applying the 5.5 − 9 mHz passband filtering to the time series of LOS velocity vLOS at every pixel (x, y) on the image plane. As an illustration, Fig. 3b shows vLOS(t, x, y; ω) at t = 40 s.
 |
Fig. 4. Wavelet power spectrum of the Doppler velocity averaged over 3 × 3 pixels at the center of the oscillation patterns. The black dashed line represents the time t = 0 at 17:43:27 UT, which is the middle time of the wave packet of spiral-shaped wave patterns. The red contour indicates the 95% confidence level, and the hashed region shows the cone of influence. Among the total observing duration (of −3200 s to 780 s), the diagram shows only the time range of −780 s to 780 s. |
Now we describe how we extracted the azimuthal component of mode m from vLOS(t, x, y; ω). We first set the polar coordinates with the origin at the center of the oscillation patterns, and obtained vLOS(t, r, θ) in these coordinates using interpolation. Second, we performed the Fourier transform of vLOS(t, r, θ) over θ for every t and r, which we then multiplied by the filter function that is set to one for the specific value of m and zero for the other values. By applying the inverse Fourier transform over θ for every t and r, and mapping the data back to the image coordinates, we obtained the azimuthal component of velocity vLOS(t, x, y; ω, m). We found that the velocity data are satisfactorily reproduced by the summation of m = 0 mode and m = 2 mode only, as illustrated in Fig. 3c. The m = 1 mode has not been included here because it has insignificant power (see Fig. 1d in Kang et al. 2019).
To reproduce this vLOS(t, x, y; ω, m), we obtained the parameters tn, n, ω, An, m, ω, and θm, ω from Eq. (11) using the following method. First, we remapped vz(t, r, θ; ω) to the image coordinates, vz(t, x, y; ω). Second, we obtained the values of tn, m, ω, An, m, ω, and θm, ω for each m by comparison with vLOS(t, x, y; ω, m), maximizing the Pearson correlation value between the model and the observation at a reference time of t = 40 s. The temporal evolution of the pattern is reproduced by changing time t in Eq. (11). In this process, we empirically find that tn, m, ω mostly affects the overall shape of the pattern and An, m, ω reflects the width of the arms and their radial speed. In particular, the inner shape of the patterns is highly affected by high-order n, and the outer part is associated with low-order n. Finally, we reconstructed the patterns summing up azimuthal modes of m = 0, m = 2, and m = −2 (Fig. 3d). All of the modeling parameters are shown in Table 1 and illustrated in Fig. 3e.
4. Results
Figure 5 indicates that our model of subphotospheric fast-body modes can successfully reproduce the observed horizontal patterns of umbral oscillations. Here the observed patterns have been temporally filtered in the frequency range of 5.5 − 9 mHz. The observation displays the two rotating spiral arms that appear to propagate outwards, which is successfully reproduced by the model constructed by the superposition of a total of 12 modes; m = 0, ±2, and n = 1, 2, 3, 4. As can be seen from the figure, this model is very similar in appearance to the observation, with the Pearson correlation coefficient being as large as cc = 1.00. The standard deviation of the residual is as small as 0.13 km s−1 and is roughly twice the standard error of the LOS velocity of 0.07 km s−1. We note that our model has the advantage that the temporal evolution is fully described with the set of model parameters computed at the reference time using Eq. (11), without having to repeat the fit at individual time steps (cf. Stangalini et al. 2022).
 |
Fig. 5. Temporal evolution of the spiral-shaped wave patterns. (a) Observed LOS velocity map temporally filtered in the frequency range of 5.5 − 9 mHz. (b) LOS velocity map additionally filtered in the azimuthal mode of m = 0, and 2. (c) Modeled velocity map constructed by the superposition of a total of 12 modes; m = 0, ±2, and n = 1, 2, 3, 4. (d) Residual between the filtered map (b) and the model (c). The model parameters are shown in Table 1. Columns show the temporal evolution of each map from t = 0 to t = 80 s. Here, the time t = 0 s is equal to 17:43:27 UT, which is the middle time of the wave packet shown in Fig. 4. The black solid contour indicates the boundary of the pore, and the black dashed circle represents the boundary of the flux tube of the model. The correlation values between (b) and (c) are shown in the top corner of each panel of (c). |
Table 1 lists the values of the model parameters. We first consider the case of m = 2. In this case, the amplitude is larger than 2 km s−1 for n = 1, 2, 3 but is smaller than 1 km s−1 for n = 4, being as small as one-quarter of the value for n = 3. This means that the patterns are fairly well described by the low radial modes up to n = 3, and including n = 4 is more than sufficient. In order to clarify this point, we attempted to include n = 5. The amplitude of the n = 5 mode is found to be less than that of n = 4 by a factor of 2. Furthermore, its inclusion only slightly reduces the residual error. Therefore, we conclude that the inclusion of higher modes is physically meaningless and the observation can be successfully reproduced by a small number of modes. The rapid decrease in the amplitude over n around n = 4 indicates that the cutoff radial mode nM may be equal to 4. In the case of m = 0, we may obtain a similar conclusion as in the case of m = 2 described above. In the case of m = −2, the amplitude for n = 1, 2, 3 is small, not being much larger than that for n = 4. Nevertheless, as the amplitude of n = 4 mode is, in this case, comparable to the corresponding values in the cases of m = 0 and m = 2, and the amplitude of n = 5 is found to be smaller than that of n = 4, it is likely that nM = 4 for m = −2 as well.
We investigated how the cutoff radial mode depends on the frequency. To this end, we processed the observed patterns in two other bands: a lower frequency band of 2 − 4 mHz (4.2 − 8.3 min) and a higher frequency band of 12 − 20 mHz (0.8 − 1.4 min) as shown in Fig. 6. We find that in the lower frequency band (panel a), spiral arms are absent. In the higher frequency band (panel b), the spiral arms not only exist but also appear to be more tightly wrapped than the 5.5 − 9 mHz band pattern as shown in Fig. 5. The observed patterns in these two bands can also be well reproduced by the fast-body wave models as shown in the bottom panels. In each band, we tried different values of the maximum n values for each m. As a result, we found that the pattern of the 2 − 4 mHz band can be reproduced satisfactorily by setting nM = 2, and the pattern in the 12 − 20 mHz band by setting nM = 6. With these values, the lower frequency pattern is well modeled with 6 modes, and the higher frequency pattern with 18 modes. The Pearson correlation between each observed pattern and the corresponding model is found to be stronger than 0.97.
 |
Fig. 6. Oscillation patterns in low and high-frequency bands. Top panels show the observed oscillation patterns at 17:44:07 UT, which are spatially filtered in m = 0 and 2 modes and temporally filtered in (a) 2.5 − 4 mHz and (b) in 12 − 20 mHz. Bottom panels show the model for each frequency band. The contour represents the boundary of the pore, and the dashed circle illustrates the boundary of the flux tube. All panels only show a 3 Mm radius from the center because the outer region is affected by the running penumbral waves and error. |
Combined with nM = 4 obtained above for the 5.5 − 9 mHz band pattern, it is noteworthy that nM increases with frequency. This result was empirically obtained from comparison of the models with observations and is exactly what the dispersion relation for subphotospheric fast-body modes predicts (Fig. 2b), supporting our model of umbral oscillations inherited from subphotospheric fast-body modes.
5. Discussion
In this study, we successfully reproduced the two-armed spiral-shaped wave patterns in the pore from the superposition of 12 subphotospheric fast-body modes. We find that the patterns of umbral oscillations depend on the oscillation frequency, comparing the patterns in three different bands. In addition, these oscillation patterns consist of the finite number of the radial mode: nM = 4 for the 3 min period band, nM = 2 for the 5 min band, and nM = 6 for the 1 min band. These results are in agreement with the concept of the cutoff radial mode in the model of the subphotospheric fast-body modes.
Our model is based on several assumptions for the sake of simplicity. We believe these assumptions are not detrimental. It is assumed that the flux tube is uniform, has a circular shape, and is surrounded by an external medium of zero density. In Appendix A, we discuss these assumptions in detail and find that they are tolerable enough to allow a reasonable interpretation of the observed patterns. In addition, the magnetic field is assumed to be purely vertical. Because of this assumption, we confined the modeling region to the inside of a circular pore where magnetic field inclination is almost vertical (Chae et al. 2015).
We now consider how fast waves become trapped. In a flux tube, the fast waves can be either refracted or reflected when they reach the boundary, because the external sound speed and the internal sound speed differ from each other (cs, e > cs). In particular, the waves can be fully reflected if the incident angle of the waves is larger than the critical angle (θc = arcsin(cs/cs, e)) of the total internal reflection, similar to the light in an optical fiber. Therefore, only the waves with an incident angle of larger than the critical angle can be fully reflected and finally form resonance modes.
In this regard, the cutoff in the radial mode occurs for the fast-body modes. In slow-body waves, the incident angles of all radial modes are large because these waves tend to be directed along magnetic fields (kz ≫ kr). As a consequence, all the slow waves are trapped inside the flux tube. In contrast, in fast-body waves, with small kz, the radial directionality (kr/kz) becomes stronger for a higher n, because the higher n has a larger value of kr by definition and has a smaller value of kz for a given period (see Fig. 2b); this means that the incident angle becomes smaller. As a result, the fast-body waves have a cutoff in radial modes. We note that higher radial modes with incident angles smaller than θc can propagate across the boundary as leaky waves. In our case, for example, the n = 4 mode with a period of 160 s has an incident angle of about 43°, which is larger than θc ≈ 42°, but the incident angle of the n = 5 mode is about 26°. Thus, only the radial mode with n ≤ 4 can be trapped in the flux tube.
Our model is similar to the other two models of umbral oscillation patterns in several respects. It is like the wave propagation model in that the observed slow waves are regarded as the inheritance of the subphotospheric fast waves. It is also similar to the slow resonance model in that the oscillation patterns are described as the superposition of several modes.
Our model has a distinct advantage in describing the observed frequency-dependent patterns. As shown in Fig. 6, we find that the oscillation pattern at each frequency band is a superposition of radial modes, the number of which depends on frequency. This frequency dependence is not at all expected in the wave propagation model if one single source drives the waves. In the wave propagation model, the horizontal pattern depends only on the depth of the source and the wave propagation speed (Zhao et al. 2015; Cho & Chae 2020), and so the pattern should be the same regardless of the oscillation frequency, unless the wave propagation speed depends on frequency. Of course, the waves can form frequency-dependent patterns if the vertically elongated source, or more than two localized sources at different depths, generate waves of different frequencies, but this frequency dependence has not yet been reported in previous simulation works. The observed frequency dependence cannot be explained by the slow resonance model either. In this latter model, an infinite number of radial modes can exist regardless of frequency (Edwin & Roberts 1983), which is not compatible with the finding that the pattern can be described by only a few radial modes. In our model, in contrast, this finding is easily described by the existence of the cutoff radial mode increasing with frequency.
One might attribute the appearance of the cutoff radial mode to the dependence of the efficiency of the fast-to-slow conversion on the radial mode. Nevertheless, this is not the case. It is likely that the efficiency decreases with the radial mode because the conversion efficiency is known to become high when the wave vector is aligned with the magnetic field in order to ensure kz/kr ≫ 1 (Schunker & Cally 2006). However, this expected decrease is gradual, unlike the observed sharp drop in amplitude (see Table 1), which is naturally interpreted as the occurrence of the cutoff.
Our model requires the trapping of fast waves in the subphotosphere. We note that the fast-body modes can exist at regions satisfying the condition of Eq. (4). This condition is not satisfied in the photosphere, or above it, where vA > cs, e > cs. Nor is it satisfied in the deep region where cs ∼ cs, e. Therefore, it is likely that the trapping of fast waves is occurring in the shallow region in the subphotopshere. Indeed, we estimated the trapping region by calculating the sound speed and the Alfvén speed in the subphotosphere using the Maltby model (Maltby et al. 1986), and found that the fast-body modes of the observed two-armed SWPs may be formed in a shallow region from −300 km to −50 km below the equipartition layer. In this region, plasma β is found to range from 3 to 10. We think that this region is for horizontal trapping only, and is not for vertical trapping. In the vertical direction, fast waves might come from below or from above.
Our model of fast-body modes has a couple of noticeable characteristics. First, the apparent radial propagation of the pattern is reproduced by an appropriate combination of amplitudes in the radial modes. For example, Time–distance (TD) maps in Fig. 7 clearly show that the speed of radial propagation increases with the ratios of the n = 1 mode amplitude to that of the other modes. In this regard, our model is in contrast with the wave propagation model, where the speed of the radial motion depends on the depth of the localized source (Zhao et al. 2015; Felipe & Khomenko 2017; Kitiashvili et al. 2019; Cho & Chae 2020). Second, fast-body modes, in principle, can be excited by arbitrary sources, either internally or externally. Among these two possible sources, we conjecture that the predominant source may be the external f and p modes in the subphotosphere, because f and p modes ubiquitously occur in the quiet Sun region regardless of the existence of a sunspot, and the p-mode absorption is an effective mechanism to absorb incoming p-mode waves (e.g., Braun & Duvall 1987; Cally & Bogdan 1997). In addition, irrespective of the excitation source, the fast-body modes, once established, display the pattern of umbral oscillations apparently propagating out of the center of the cross-section of the flux tube. In the wave propagation model, in contrast, the source is assumed to be a localized disturbance in the subphotosphere, which is related to the center of the oscillation patterns observed in the chromosphere (Cho & Chae 2020; Kang et al. 2024).
 |
Fig. 7. Time–distance map of modeled m = 0 mode waves for three different cases. (a) TD map with the amplitudes of A0, 1 = 2.25, A0, 2 = 2.0, and A0, 3 = 0.5 in units of km s−1. (b) TD map with the amplitudes of A0, 1 = 1.5, A0, 2 = 2.25 and A0, 3 = 1.5 in units of km s−1. (c) TD map with the amplitudes of A0, 1 = 0.5, A0, 2 = 2.0 and A0, 3 = 2.25 in units of km s−1. All of them have the phase differences of t0, 1 = 0, t0, 2 = −20 and t0, 3 = −40 in seconds. The solid lines represent the gradients of the ridges, and their values are shown in each panel. |
Our model has difficulty in explaining the observed change of the center of the pattern. From the observation of a sunspot with the light bridge, Cho et al. (2021) reported that the center of the wave pattern was located at different positions inside the same umbra at different times. It is difficult to explain this observation with our model as far as we currently understand, unless the shape of the sunspot significantly changed during the observation. This is a challenging problem for our model. To obtain a solution, further numerical and observational studies are necessary.
Acknowledgments
We appreciate the referee’s positive evaluation and the constructive comments. This research was supported by the National Research Foundation of Korea (RS-2023-00273679). J. Chae was supported by the National Research Foundation of Korea (RS-2023-00208117). E.-K. Lim was supported by the Korea Astronomy and Space Science Institute under R&D program of the Korean government (MSIT; No. 2024-1-850-02, 2024-1-810-03). We gratefully acknowledge the use of data from the Goode Solar Telescope (GST) of the Big Bear Solar Observatory (BBSO). BBSO operation is supported by US NSF AGS-2309939 and AGS-1821294 grants and New Jersey Institute of Technology. GST operation is partly supported by the Korea Astronomy and Space Science Institute and the Seoul National University.
References
- Albidah, A. B., Fedun, V., Aldhafeeri, A. A., et al. 2022, ApJ, 927, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M., & Tallant, P. E. 1969, Sol. Phys., 7, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, D. C., Duvall, T. L. J., & Labonte, B. J., 1987, ApJ, 319, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Cally, P. S. 2001, ApJ, 548, 473 [Google Scholar]
- Cally, P. S., & Bogdan, T. J. 1997, ApJ, 486, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [Google Scholar]
- Chae, J., & Litvinenko, Y. E. 2018, ApJ, 869, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Park, H.-M., Ahn, K., et al. 2013, Sol. Phys., 288, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Yang, H., Park, H., et al. 2014, ApJ, 789, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Song, D., Seo, M., et al. 2015, ApJ, 805, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Cho, K., Lim, E.-K., & Kang, J. 2022, ApJ, 933, 108 [CrossRef] [Google Scholar]
- Chae, J., Lim, E.-K., Lee, K., et al. 2023, ApJ, 944, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, K., & Chae, J. 2020, ApJ, 892, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, K., Chae, J., & Madjarska, M. S. 2021, A&A, 656, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1982, Sol. Phys., 76, 239 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [Google Scholar]
- Felipe, T., & Khomenko, E. 2017, A&A, 599, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felipe, T., Khomenko, E., Collados, M., & Beck, C. 2010, ApJ, 722, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Kuckein, C., Khomenko, E., & Thaler, I. 2019, A&A, 621, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jacoutot, L., Kosovichev, A. G., Wray, A., & Mansour, N. N. 2008, ApJ, 684, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Jess, D. B., De Moortel, I., Mathioudakis, M., et al. 2012, ApJ, 757, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Jess, D. B., Van Doorsselaere, T., Verth, G., et al. 2017, ApJ, 842, 59 [Google Scholar]
- Kang, J., Chae, J., Nakariakov, V. M., et al. 2019, ApJ, 877, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, J., Chae, J., & Geem, J. 2024, ApJ, 960, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kitiashvili, I. N., Kosovichev, A. G., Mansour, N. N., Wray, A. A., & Sandstrom, T. A. 2019, ApJ, 872, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Krishna Prasad, S., Jess, D. B., Klimchuk, J. A., & Banerjee, D. 2017, ApJ, 834, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. W. 1993, ApJ, 404, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 1984, ApJ, 277, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
- Roberts, B. 1983, Sol. Phys., 87, 77 [Google Scholar]
- Roberts, B. 2019, MHD Waves in the Solar Atmosphere (Cambridge: Cambridge University Press) [Google Scholar]
- Schmitz, F., & Fleck, B. 1998, A&A, 337, 487 [Google Scholar]
- Schunker, H., & Cally, P. S. 2006, MNRAS, 372, 551 [Google Scholar]
- Spruit, H. C., & Bogdan, T. J. 1992, ApJ, 391, L109 [Google Scholar]
- Stangalini, M., Verth, G., Fedun, V., et al. 2022, Nat. Commun., 13, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Su, J. T., Ji, K. F., Cao, W., et al. 2016, ApJ, 817, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Sych, R., & Nakariakov, V. M. 2014, A&A, 569, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J., Chen, R., Hartlep, T., & Kosovichev, A. G. 2015, ApJ, 809, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, I. D., & Dzhalilov, N. S. 1984, A&A, 132, 45 [NASA ADS] [Google Scholar]
Appendix A: Dependence of the model on the assumptions
Our model, for simplicity, assumes the zero-density limit, circular shape, and uniformity inside the flux tube. Here we discuss how each of these assumptions affects the model.
A.1. Zero-density limit
As a boundary condition, our model assumes that mass density is zero outside the flux tube. In this zero-density limit, the node is always located at the boundary of the flux tube, which leads to the very simple boundary condition of Eq. (6). However, in the general case, the external density is not zero and, hence, the node does not occur exactly at the boundary. To examine the difference, we solve the full boundary condition in Eq. (3) and present the solution in Fig. A.1. As a result, we find that the node is located slightly inside the boundary. The mode has slightly larger values of kr, kz for a given period than in the case of zero-density limit (see Fig. A.1). An important point here is that the differences are sufficiently small, as can be seen from the similarity of the curves shown in Fig. A.1 to those in Fig. 2b. This result suggests that the assumption of a zero-density limit is sufficiently justified to allow interpretation of the oscillation patterns, unless precise modeling is required.
 |
Fig. A.1. Numerical solution of Eq. (3) with the same parameters as Figure 2b but without the assumption of zero-density limit. As the fast-wave solution is confined within the range of cs, e > vp > cs, curves are confined to the white area. |
A.2. Circular shape
The geometry of the flux tube can change the shape of the pattern (Albidah et al. 2022). If the cross-section of the flux tube is not circular, the center of the oscillation pattern is not located at the center of the flux tube. In our study, the effect of noncircular shape does not seem to be strong because the pore has a relatively circular shape. In our model, we identified the center of the two-armed SWPs at the center of the flux tube, which is found to be 1″ from the center of the pore determined by the ellipse fitting of the morphology. We think the deviation of this amount is tolerable, and so the assumption of the circular shape is sufficiently justified for our purposes. We also note that the geometry of the flux tube does not affect the presence of the cutoff radial mode, which is the most important characteristic of our model here.
A.3. Uniformity
For simplicity, our model assumes that all the physical parameters are uniform both horizontally and vertically in the subphotosphere. The assumption of uniformity holds better in the horizontal direction than in the vertical direction. The vertical uniformity is hindered by the gravitational stratification of pressure and density. Nevertheless, it may not be detrimental in our model because the vertical extent of the subphotosphere (∼250 km) is not much larger than the local pressure scale height (∼200 km).
A.4. Trapping
The existence of the modes implicitly assumes that the waves are trapped somehow inside the flux tube. The trapping requires not only horizontal confinement but also vertical confinement. It is obvious that horizontal confinement occurs at the lateral boundaries. This leads us to question where the vertical confinement might occur. Our model of fast-body modes implicitly assumes that the vertical confinement occurs outside the subphotosphere: both above and below it. In the region above the photosphere, density rapidly decreases with height and the Alfvén speed rapidly increases with height, which causes the fast waves to be reflected downward. In the deep interior below the subphotosphere of our interest, the temperature rapidly increases with depth, and the propagation speed of the fast waves rapidly increases with depth, which causes the waves to be reflected upward.
All Tables
All Figures
 |
Fig. 1. Illustration of our model of umbral oscillations inherited from subphotospheric fast-body modes. The yellow area represents the high-β region (cs > vA) below the sunspot surface, and the white area represents the low-β region (cs < vA). The black solid line between the two regions represents the equipartition layer (cs = vA) where the mode conversion can occur. The gray vertical lines illustrate the magnetic field lines of the flux tube, and the vertical dashed line indicates the boundary of the flux tube. The red line demonstrates the vertical velocity vz of fast body waves, and the blue line represents vz of converted slow waves. The dash-dotted horizontal line represents the detection layer of the chromosphere. The two panels in the bottom right corner show the vertical velocity fluctuation of two azimuthal modes of m = 0 and 2. The top right panel shows a horizontal cross-section view of the modeled oscillation patterns. |
| In the text | |
 |
Fig. 2. Period P as a function of vertical wavenumber kz for (a) the slow-body waves and (b) the fast-body waves for n = 1, 2, 3, 4, 5, and 10 with m = 2 in the subphotospheric condition (cs, e > cs > vA). The white area in panel a marks the range of vA > vp > cT within which the slow-body wave solution can exist, and that in panel b represents the range within which the fast-body wave can exist (cs, e > vp > cs). The inset figure in panel a shows the magnified figure in the ranges of 0.011 < kz < 0.012 km s−1 and 155 < P < 165 s. The dashed line represents the period of 160 s. The color-shaded regions in panel b represent the regions with the same cutoff radial mode nM; yellow is nM = 2, green is nM = 3, blue is nM = 4 and purple is nM ≥ 5. We have taken the internal sound speed of cs = 6.3 km s−1, internal Alfvén speed of vA = 0.56cs, and external sound speed of cs, e = 1.7cs. |
| In the text | |
 |
Fig. 3. Detection of a pattern of umbral oscillations. (a) Continuum intensity map of the GST/FISS constructed at the −43.5 Å of the Hα line center and chromospheric intensity map constructed at the line center at 17:44:07 UT on June 3, 2014. (b) Two-dimensional wave patterns of the chromospheric Doppler velocity map temporally filtered in 5.5 − 9 mHz. The black contour displays the boundary of the pore, and the red cross symbol marks the center position of the SWP. (c) Azimuthally decomposed wave patterns for m = 0 and ±2 modes. (d) Modeled LOS velocity fluctuation map constructed by the superposition of 12 modes (m × n, where m = 0, 2, −2 and n = 1, 2, 3, 4). The dashed circle shows the boundary of the modeled flux tube. (e) All modes of trapped fast-body waves for the modeled LOS velocity map. Here m represents the azimuthal mode and n refers to the radial mode. The color limit of panels b–e is −3.5 to 3.5 km s−1, where the positive sign signifies the redshift. The temporal evolutions of panels b–d are shown in Fig. 5. |
| In the text | |
 |
Fig. 4. Wavelet power spectrum of the Doppler velocity averaged over 3 × 3 pixels at the center of the oscillation patterns. The black dashed line represents the time t = 0 at 17:43:27 UT, which is the middle time of the wave packet of spiral-shaped wave patterns. The red contour indicates the 95% confidence level, and the hashed region shows the cone of influence. Among the total observing duration (of −3200 s to 780 s), the diagram shows only the time range of −780 s to 780 s. |
| In the text | |
 |
Fig. 5. Temporal evolution of the spiral-shaped wave patterns. (a) Observed LOS velocity map temporally filtered in the frequency range of 5.5 − 9 mHz. (b) LOS velocity map additionally filtered in the azimuthal mode of m = 0, and 2. (c) Modeled velocity map constructed by the superposition of a total of 12 modes; m = 0, ±2, and n = 1, 2, 3, 4. (d) Residual between the filtered map (b) and the model (c). The model parameters are shown in Table 1. Columns show the temporal evolution of each map from t = 0 to t = 80 s. Here, the time t = 0 s is equal to 17:43:27 UT, which is the middle time of the wave packet shown in Fig. 4. The black solid contour indicates the boundary of the pore, and the black dashed circle represents the boundary of the flux tube of the model. The correlation values between (b) and (c) are shown in the top corner of each panel of (c). |
| In the text | |
 |
Fig. 6. Oscillation patterns in low and high-frequency bands. Top panels show the observed oscillation patterns at 17:44:07 UT, which are spatially filtered in m = 0 and 2 modes and temporally filtered in (a) 2.5 − 4 mHz and (b) in 12 − 20 mHz. Bottom panels show the model for each frequency band. The contour represents the boundary of the pore, and the dashed circle illustrates the boundary of the flux tube. All panels only show a 3 Mm radius from the center because the outer region is affected by the running penumbral waves and error. |
| In the text | |
 |
Fig. 7. Time–distance map of modeled m = 0 mode waves for three different cases. (a) TD map with the amplitudes of A0, 1 = 2.25, A0, 2 = 2.0, and A0, 3 = 0.5 in units of km s−1. (b) TD map with the amplitudes of A0, 1 = 1.5, A0, 2 = 2.25 and A0, 3 = 1.5 in units of km s−1. (c) TD map with the amplitudes of A0, 1 = 0.5, A0, 2 = 2.0 and A0, 3 = 2.25 in units of km s−1. All of them have the phase differences of t0, 1 = 0, t0, 2 = −20 and t0, 3 = −40 in seconds. The solid lines represent the gradients of the ridges, and their values are shown in each panel. |
| In the text | |
 |
Fig. A.1. Numerical solution of Eq. (3) with the same parameters as Figure 2b but without the assumption of zero-density limit. As the fast-wave solution is confined within the range of cs, e > vp > cs, curves are confined to the white area. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



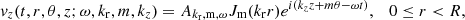
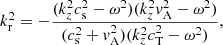
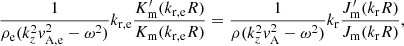
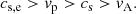
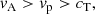
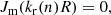
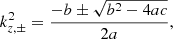
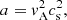
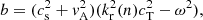
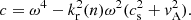
![$$ \begin{aligned}&{v_z (t, r, \theta , z; \omega )} = \sum _{n,m}^{n_{\rm M}} v_z (t, r, \theta , z; \omega , k_{\rm r}, m) \nonumber \\&\qquad \qquad = \sum _{n, m}^{n_{\rm M}} A_{n, m, \omega } J_m(k_{r;n, m} r) e^{i[k_z z + m (\theta -\theta _{m,\omega })-\omega (t-t_{n,m,\omega })]}, \end{aligned} $$](/articles/aa/full_html/2024/06/aa49887-24/aa49887-24-eq13.gif)