| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202450051 | |
| Published online | 17 May 2024 | |
Letter to the Editor
Abell 0399–Abell 0401 radio bridge spectral index: First multi-frequency detection
1
Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna, Via P. Gobetti 93/2, 40129 Bologna, Italy
2
INAF – Istituto di Radioastronomia, Via P. Gobetti 101, 40129 Bologna, Italy
e-mail: giada.pignataro2@unibo.it
3
Department of Physics and Electronics, Rhodes University, PO Box 94 Makhanda, 6140, South Africa
4
South African Radio Astronomy Observatory (SARAO), Black River Park, 2 Fir Street, Observatory, Cape Town, 7925, South Africa
5
Hamburger Sternwarte, Universitat Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
6
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
7
Thüringer Landessternwarte, Sternwarte 5, 07778 Tautenburg, Germany
8
ASTRON, the Netherlands Institute for Radio Astronomy, Postbus 2, 7990 AA Dwingeloo, The Netherlands
Received:
20
March
2024
Accepted:
30
April
2024
Aims. Recent low-frequency radio observations at 140 MHz discovered a bridge of diffuse emission with a length of 3 Mpc that connects the galaxy clusters Abell 0399 and Abell 0401. We present follow-up observations at 60 MHz to constrain the spectral index of the bridge, which has only been detected at 140 and 144 MHz so far.
Methods. We analysed deep (∼18 h) LOw Frequency ARray (LOFAR) Low Band Antenna (LBA) data at 60 MHz to detect the bridge at very low frequencies. We then conducted a multi-frequency study with LOFAR HBA data at 144 MHz and uGMRT data at 400 MHz. Assuming second-order Fermi mechanisms for the re-acceleration of relativistic electrons driven by turbulence in the radio bridge regions, we compared the observed radio spectrum with theoretical synchrotron models.
Results. The bridge is detected in the 75″ resolution LOFAR image at 60 MHz, and its emission fully connects the region between the two galaxy clusters. Between 60 MHz and 144 MHz, we found an integrated spectral index value of α60144 = −1.44 ± 0.16 for the bridge emission. For the first time, we produced spectral index and related uncertainties maps for a radio bridge. We produce a radio spectrum that shows a significant steepening between 144 and 400 MHz.
Conclusions. This detection at low frequencies provides important information for models of particle acceleration and magnetic field structure on very extended scales. The spectral index gives important clues about the origin of inter-cluster diffuse emission. The steepening of the spectrum above 144 MHz can be explained in a turbulent re-acceleration framework, assuming that the acceleration timescales are longer than ∼200 Myr.
Key words: galaxies: clusters: general / large-scale structure of Universe
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Matter is primarily accreted onto galaxy clusters along the filaments of the so-called cosmic-web, and the subsequent merger of these systems releases an extreme amount of energy into the intra-cluster medium (ICM; Markevitch & Vikhlinin 2007). Radio observations have provided strong evidence for the processes that channel this energy into particle acceleration and magnetic field amplification in the form of diffuse emission with steep synchrotron spectra (α < −1, with a flux density Sν ∝ να). Galaxy clusters contain different types of diffuse radio sources: radio relics, mini haloes, and radio haloes (for an extensive review, see van Weeren et al. 2019). Recent studies unveiled diffuse radio emission on an even larger scale (Govoni et al. 2019; Botteon et al. 2020; Hoeft et al. 2021). This emission extends beyond the cluster centres and traces the densest region of cosmic-web filaments, where the gas is compressed during the first phase of the merger between clusters. Multi-frequency studies of synchrotron emission from radio bridges between clusters can shed light on the mechanisms of particle acceleration and on the properties of the magnetic fields at poorly probed scales (Vazza et al. 2019).
The galaxy clusters Abell 0399 and Abell 0401 (hereafter, A399 and A401) are a local (z ∼ 0.07, Oegerle & Hill 2001) pair found in a pre-merger state (Bonjean et al. 2018) where X-ray observations (Fujita et al. 1996, 2008; Akamatsu et al. 2017) revealed 6 − 7 keV ionised plasma in the region between the clusters. The gas in this region is also detected via the Sunyaev–Zeldovich (SZ) effect by Planck (Planck Collaboration Int. VIII 2013; Planck Collaboration XXII 2016; Bonjean et al. 2018) and the Atacama Cosmology Telescope (ATC; Hincks et al. 2022; Radiconi et al. 2022). The first radio bridge connecting two galaxy clusters was discovered in this system (Govoni et al. 2019). The bridge was detected at 140 MHz with the LOw Frequency ARray (LOFAR) and extends for approximately 3 Mpc, which is the projected separation of the two clusters that also host radio haloes. Following the discovery of the bridge, the A399–A401 system was extensively studied at radio frequencies. de Jong et al. (2022) presented a 40-h, deep LOFAR observation at 144 MHz and investigated the properties of the diffuse emission in the bridge further. They were able to detect the bridge at high significance and measured a flux density of S144 = 550 ± 60 mJy over 2.7 Mpc2. To cause diffuse emission on scales like this, electrons would need to be generated or re-accelerated in situ because their synchrotron lifetimes are short. Govoni et al. (2019) proposed the model of Fermi-I re-acceleration of fossil electrons by weak shocks crossing the region, which would result in spectral indices similar to those of radio relics (α ∼ −1.3). Alternatively, Brunetti & Vazza (2020) showed that this emission could also be explained by a Fermi-II re-acceleration process. In this scenario, the fossil relativistic particles are re-accelerated by turbulence in amplified magnetic fields over megaparsec scales. This would result in steep observed synchrotron spectra between 150 MHz and 1.5 GHz (α < −1.5). Recently, Nunhokee et al. (2023) presented Westerbork Synthesis Radio Telescope (WSRT) observations at 346 MHz that were not sufficiently deep to observe the bridge, and therefore, they placed a limit on the bridge spectral index (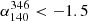 ). A similar procedure to place limits on the emission of radio bridges was defined in Pignataro et al. (2024). The non-detection of bridge emission in high-sensitivity upgraded Giant Metrewave Radio Telescope (uGMRT) data at 400 MHz results in a more stringent constraint on the steep bridge spectral index (
). A similar procedure to place limits on the emission of radio bridges was defined in Pignataro et al. (2024). The non-detection of bridge emission in high-sensitivity upgraded Giant Metrewave Radio Telescope (uGMRT) data at 400 MHz results in a more stringent constraint on the steep bridge spectral index (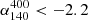 ), disfavouring the Fermi-I acceleration scenario.
), disfavouring the Fermi-I acceleration scenario.
Other than the detection in A399–A401, only a few other radio bridges associated with merging clusters are known. Botteon et al. (2018,2020) reported the bridge in Abell 1758N-S, for which they also measured a spectral index for a patch of emission. Moreover, a candidate bridge was reported in Abell 1430 (Hoeft et al. 2021), and a bridge between a relic and a halo in A1550 (Pasini et al. 2022). Recently, a few more bridges between clusters and groups have been discovered (see Bonafede et al. 2021; Venturi et al. 2022). However, for none of these objects has the spectral index of the extended diffuse emission been determined so far.
In this Letter, we present a multi-frequency study conducted with new LOFAR Low Band Antenna (LBA) data at 60 MHz. For the first time, these data allow us to determine the spectral index of the radio bridge in the A399–A401 bridge between 60 and 144 MHz. We assumed a ΛCDM cosmology, with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7. With these assumptions, at the average distance of the A399–A401 system (z ∼ 0.07), 1′=83 kpc and the luminosity distance is DL = 329 Mpc.
2. Observations and data reduction
The observations of A399–A401 lasted for 18 h and were carried out using the LOFAR LBA system in the frequency range of 30 − 77 MHz (proposal code: LC13_022, P.I.: Bonafede). The correlated data were initially pre-processed for radio frequency interference (RFI) and demix procedure (Van der Tol 2009; de Gasperin et al. 2020a). In this case, both Cygnus A and Cassiopia A were demixed. The data were also averaged from 1 to 4 s integration time and from 64 to 8 channels per subband to reduce memory and computational load. The data were then calibrated with the pipeline of the Library for Low Frequencies (LiLF). We briefly summarise its main steps here, and a full description can be found in de Gasperin et al. (2019, 2020b). The pipeline obtains solutions from the calibrator (3C196) and applies them to correct the target data. In this part, the pipeline isolates the systematic effects of the polarisation alignment, the bandpass, and Faraday rotation well. The clock drift is left mixed with the total electron content (TEC), and both are transferred to the target. Additional calibration is then needed to correct for the differential ionospheric effects that strongly affect the lower frequencies (de Gasperin et al. 2018), especially for observations at low elevation, as is the case of this target (Dec +13°). This is done for the target field with direction-independent (DI) self-calibration and then with a direction-dependent (DD) calibration. After a round of calibration, we inspected the data and found very strong artefacts produced by a radio galaxy (3C79) outside the first primary beam null. To mitigate this effect, we reduced the observation bandwidth to eliminate the frequencies at which the source is brightest and the primary beam is largest. This reduced the frequency range to 44 − 77 MHz, with the central frequency at 60 MHz. Then, we proceeded with a new round of DI phase and amplitude self-calibration, which performs two cycles and corrects for the systematic errors in the target field. From the sky model produced in the last round of DI calibration, the bright sources were selected as calibrators for the DD calibration, which removed the differential ionospheric errors in the direction of each calibrator within the field of view. Both steps are described in detail in de Gasperin et al. (2019). Finally, the pipeline performs the target extraction (van Weeren et al. 2021; Biava et al. 2021; Pasini et al. 2022), where the DD solutions found are used to subtract all sources outside a radius of approximately 0.5° around the target system. To refine the calibration towards the target, a few cycles of phase self-calibration at an increasing time resolution are performed on the extracted field. At this point, we can use the final calibrated extracted visibilities of the target to image at different resolutions with WSClean v3.1 (Offringa & McKinley 2014).
We produced a final primary-beam-corrected image at the central frequency of 60 MHz at a resolution of 75″ with an rms noise of σrms = 3 mJy beam−1. This is shown in Fig. 1 (left panel). We then produced a high-resolution image excluding baselines shorter than 900λ (i.e. emission on scales more extended than ∼4′) to recover only the compact sources, and we then subtracted their components from the visibilities. The 75″ resolution source-subtracted image of the target field is shown in Fig. 1 (right panel). The radio bridge is detected at 2σrms and continuously connects the two radio haloes. Its morphology is patchier at the 3σrms level.
 |
Fig. 1. Radio images at 60 MHz of the A399–A401 clusters pair. Left panel: low-resolution (75″, the beam size is indicated in the bottom left corner) image with compact sources and the σrms = 3 mJy beam−1 produced with the parameters listed in Table 1. Right panel: same as the left panel, but after subtraction of the compact source. The contour levels (in white) start at 2σrms, 3σrms, and 5σrms and then increase to 20σrms with factors of 2. A negative contour at −3σrms is shown in red. |
3. Results and discussion
3.1. Spectral analysis
In order to understand the origin and properties of the large-scale emission, we investigate the integrated spectral index and spectral index distribution of the bridge emission. To perform the spectral index analysis, the LBA data were imaged with the same parameters as the HBA data at 144 MHz presented in de Jong et al. (2022). The imaging parameters are listed in Table 1. In particular, we matched the uv-min and weighting scheme to recover the same angular scales and reach a similar resolution between LBA and HBA observations. To ensure that we corrected for possible shifts introduced by the phase self-calibration, we checked that the locations of the peaks of some point-sources in the field matched in both images. We then convolved the images to the same restoring beam (80″ resolution). Additionally, we performed a flux density alignment on the uv-subtracted image HBA maps presented in de Jong et al. (2022), as is usually done for LoTSS pointings (Shimwell et al. 2019, 2022), and applied a scale factor of 0.9 to the data. Finally, we only considered the emission above the 2σrms contour in both images and computed the spectral index map with the associated error map, assuming a flux calibration error of 10% (as done for LoLSS, de Gasperin et al. 2021).
WSClean imaging parameters used to produce the low-resolution source-subtracted images for spectral index analysis.
We show the resulting spectral index and spectral index error maps between 60 and 144 MHz with a resolution of 80″ in Fig. 2. We only considered the emission outside the grey mask as part of the radio bridge, while we masked the radio haloes and other features of diffuse emission that are unrelated to the bridge emission. Figure 2 (top panel) shows the distribution of the spectral index along the bridge, and the occurrence of each value is represented in the histogram. The distribution appears uniform overall. Most values lie between −1.5 ≤ α ≤ −1.2. The error map (Fig. 2, bottom panel) shows the associated errors, which are mostly around Δα ∼ 0.2.
 |
Fig. 2. Spectral index maps. Top panel: spectral index map of the emission in the radio bridge in A399–A401 between 60 and 144 MHz, with a resolution of 80″. The distribution of the spectral index values (histogram at the top) only refers to the bridge emission inside the 2σrms level, which is not covered by the grey mask over the radio haloes. Bottom panel: associated spectral index error map. The LOFAR LBA contours at 2σrms and 3σrms are overlaid in black. |
Within the 2σrms level contours of the LBA image, we measure a flux density of S60 MHz = 1.77 ± 0.18 Jy and S144 MHz = 0.50 ± 0.05 Jy1, leading to an integrated spectral index value for the radio bridge of 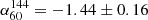 . This is the first estimate of a radio bridge spectral index, and it provides important information on the models of magnetic field amplification and particle re-acceleration processes on megaparsec-scales.
. This is the first estimate of a radio bridge spectral index, and it provides important information on the models of magnetic field amplification and particle re-acceleration processes on megaparsec-scales.
3.2. Theoretical models
The origin of the radio emission from radio bridges is still being investigated. The megaparsec-scale size of the bridge requires an in situ mechanism that accelerates the relativistic particles so that they travel over these scales (Brunetti & Jones 2014). Govoni et al. (2019) suggested a shock-driven emission model, where multiple weak shocks re-accelerate a pre-existing population of electrons. However, they showed that it is difficult to account for the extension and strength of the bridge emission only via a shock prior to the collision between A399 and A401. Moreover, the high-sensitivity study of de Jong et al. (2022) reported no filamentary structures or shock surfaces in the bridge region, which disfavours the shock origin. We wished to investigate the spectrum of the bridge emission with the measured flux densities at LOFAR frequencies. Additionally, we wished to incorporate data from the uGMRT observations at a central frequency of 400 MHz presented in Pignataro et al. (2024), where the bridge emission was undetected. This also allows for a comprehensive comparison of the radio spectrum with the synchrotron spectrum predicted by theoretical models. In Pignataro et al. (2024), we found a limit on the bridge emission by following the injection procedure. In order to incorporate the limit in the radio spectrum produced in this work, we again performed the procedure by injecting the 60 MHz emission model, where the emission appears to be less extended in than the 144 MHz detection.
Following an extended approach to the injection procedure with the 60 MHz observation as a starting model, we find a limit for the spectral index between 60 MHz and 400 MHz of 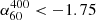 at a 95% confidence level. The injection method is discussed in Appendix A.
at a 95% confidence level. The injection method is discussed in Appendix A.
The radio spectrum of the bridge is shown in Fig. 3 (top panel), and the plotted values are listed in Table 2. The observations at 60 and 140 MHz and the upper limit derived at 400 MHz show a steepening towards increasing frequency. This feature, as well as the steep spectrum found between 144 and 400 MHz, is hard to reconcile with a shock-origin scenario. However, spectral steeping is a key prediction of the turbulent re-acceleration model presented in Brunetti & Vazza (2020). These authors investigated several re-acceleration scenarios coupled with the result of a cosmological simulation and showed that the steepening changes as a function of the magnetic field amplification efficiency (ηB) and particle acceleration times (τacc). In particular, they identified for their analysis a simulated system that resembles the A399–A401 bridge (Govoni et al. 2019; Domínguez-Fernández et al. 2019). The initial spectrum of relativistic electrons was evolved by solving the Fokker-Planck equations assuming a single-zone model, that is, assuming average quantities, such as thermal densities and magnetic fields, which are measured in each cell in the simulated bridge region at a fixed time. This was done for different values of particle acceleration times (τacc), from ∼10 Myr up to ∼10 Gyr (see Brunetti & Vazza 2020, Fig. 2). The spectrum shown in Fig. 3 (bottom panel) was obtained from the spectrum presented in Brunetti & Vazza (2020, see Fig. 3, for ηB ∼ 0.05). To reproduce our observed data, we re-scaled the spectrum from a surface of ∼3.9 Mpc2 to ∼2.2 Mpc2, which is the area covered by the LBA detection, excluding the radio haloes. Additionally, it was necessary to exclude all cells with a generated τacc < 200 Myr, which make up ∼3% of the volume of the simulated bridge. Therefore, the observed LOFAR luminosities and the uGMRT limit set a constraint on the particles acceleration times to values longer than 200 Myr, which are generated in the majority of the cells in the simulation.
 |
Fig. 3. Radio spectra. Top panel: bridge emission radio spectra in integrated flux density. The grey arrow represents the uGMRT limit. Bottom panel: radio luminosity of the bridge emission compared to a synchrotron theoretical model (red curve) produced by the relativistic particle populations with acceleration times τacc > 200 Myr. |
Radio quantities for the bridge emission at the three frequencies.
Finally, we investigated how the spectral index value could vary in different areas of the bridge. The distribution of the spectral index is likely related to the contribution of turbulence and re-acceleration processes across the extended emission. We created a grid covering the emission inside the 2σrms contours in the 60 MHz image (Fig. 4, left panel). Each grid cell was one beam size (80″ × 80″). We extracted a value of the spectral index between 60 and 144 MHz in each coloured cell. We computed the spectral index over the 2σrms LBA detection and therefore considered the emission component with steepest spectra and/or weakest surface brightness. To check this bias, we extracted the 1σrms emission in the red cell and evaluated a limit on the spectral index with the 2σrms emission in the 144 MHz image. The distribution of the spectral index in the bridge is shown in the top right panel of Fig. 4, and in the bottom right panel we show the distribution of the residuals, Δα, between each value of the spectral index we extracted and the mean α value. The values of each cell are consistent around the mean value inside the standard deviation for most points. Even though a larger scatter is observed for some cells (0.5 < Δα < 0.9), they do not appear to be spatially correlated. The red arrows represent the limits extracted from the red cells, which are generally flatter than the mean value. However, we also note the limits at the level of the measured spectral index, or steeper. The spectral index is consistent with being constant throughout the region, and there is no evidence for any systematic trend in the bridge region.
 |
Fig. 4. Spectral index distribution. Left panel: LBA radio image at 60 MHz and resolution of 80″. The 2σrms contours and the grid to extract the spectral index between 60 and 144 MHz are overlaid. Different areas of the bridge are covered by differently coloured cells. The coloured cells cover the LBA emission above 2σrms, and the red cells cover the 1σrms LBA emission and 2σrms HBA emission. Top right: spectral index distribution across the bridge. The black points show values extracted from each cell, separated by colour, and the red arrows indicate 1σrms limits extracted from the red cells. The dashed horizontal green line shows the mean spectral index, and the filled horizontal green region represents the standard deviation. Bottom right: distribution of residuals (Δα) of α with respect to the mean spectral index. |
4. Conclusions
For the first time, we have determined the spectral index for the emission of a radio bridge that connects the two pre-merging galaxy clusters A399 and A401. The radio bridge was only detected at 144 MHz before, and therefore, we analysed new LOFAR LBA data at 60 MHz to constrain the spectral index of the emission.
We measured an integrated spectral index for the bridge between 60 and 144 MHz of 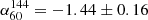 . We also investigated the spectral index distribution, which gives insights into the contribution of turbulence and re-acceleration processes causing the extended emission. In the spectral index and associated errors maps, the distribution shows no systematic gradients in the bridge regions.
. We also investigated the spectral index distribution, which gives insights into the contribution of turbulence and re-acceleration processes causing the extended emission. In the spectral index and associated errors maps, the distribution shows no systematic gradients in the bridge regions.
Combining the two LOFAR detections and the uGMRT limit found at 400 MHz, we produced a comprehensive comparison of the obtained radio spectrum of the bridge with the synchrotron spectrum predicted by theoretical models. The steepening of the spectrum between 144 and 400 MHz is hardly reconcilable with a scenario of a shock acceleration origin (as proposed in Govoni et al. 2019), but it can be explained by the turbulent acceleration models investigated by Brunetti & Vazza (2020). Our observations allowed us to constrain the particle acceleration time and in turn the volume-filling factor of the particle distribution in the turbulent re-acceleration model. Short acceleration times (corresponding to re-acceleration in regions that occupy a small fraction of the bridge volume) generate shallower spectra, which are disfavoured by our observations. Conversely, a long acceleration time (τacc > 200 Myr) for particles that occupy most of the bridge volume is consistent with our data. The fact that the emission in the 60 MHz image appears to be less volume-filling than at 144 MHz is likely related to the sensitivity limitations of the LBA observations. The Fermi-II origin scenario suggested by these observations requires significant turbulent motions in most of the bridge volume. Moreover, the aforementioned scenario assumes a volume-filling reservoir of low-energy electrons (γ ≤ 103), whose existence requires further observational evidence and is not yet quantitatively predicted by simulations either. Finally, the B ≥ 0.3 μG magnetic field required by this model is large for a peripheral region like this, and it might be detected by the next generation of polarisation surveys (Heald et al. 2020).
This is in agreement with the flux density measured in de Jong et al. (2022), the difference is due only to different areas.
Acknowledgments
A.B. acknowledges financial support from the ERC Starting Grant “DRANOEL”, number 714245. Fd.G. acknowledges support from the ERC Consolidator Grant ULU 101086378. F.V. acknowledges the financial support from the Cariplo “BREAKTHRU” funds Rif: 2022-2088 CUP J33C22004310003. A.B. acknowledges financial support from the European Union – Next Generation EU. M.B. acknowledges funding by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306. R.Jv.W. acknowledges support from the ERC Starting Grant ClusterWeb 804208. J.M.G.H.Jd.J. acknowledges this publication is part of the project CORTEX (NWA.1160.18.316) of the research programme NWA-ORC which is (partly) financed by the Dutch Research Council (NWO). This work made use of the Dutch national e-infrastructure with the support of the SURF Cooperative using grant no. EINF-1287.
References
- Akamatsu, H., Fujita, Y., Akahori, T., et al. 2017, A&A, 606, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardi, G., Venturi, T., Cassano, R., et al. 2016, MNRAS, 456, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Biava, N., de Gasperin, F., Bonafede, A., et al. 2021, MNRAS, 508, 3995 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Cassano, R., Brüggen, M., et al. 2017, MNRAS, 470, 3465 [Google Scholar]
- Bonafede, A., Brunetti, G., Vazza, F., et al. 2021, ApJ, 907, 32 [Google Scholar]
- Bonjean, V., Aghanim, N., Salomé, P., Douspis, M., & Beelen, A. 2018, A&A, 609, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botteon, A., Shimwell, T. W., Bonafede, A., et al. 2018, MNRAS, 478, 885 [Google Scholar]
- Botteon, A., van Weeren, R. J., Brunetti, G., et al. 2020, MNRAS, 499, L11 [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 1430007 [Google Scholar]
- Brunetti, G., & Vazza, F. 2020, Phys. Rev. Lett., 124, 051101 [Google Scholar]
- de Gasperin, F., Mevius, M., Rafferty, D. A., Intema, H. T., & Fallows, R. A. 2018, A&A, 615, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gasperin, F., Dijkema, T. J., Drabent, A., et al. 2019, A&A, 622, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gasperin, F., Vink, J., McKean, J. P., et al. 2020a, A&A, 635, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gasperin, F., Brunetti, G., Brüggen, M., et al. 2020b, A&A, 642, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gasperin, F., Williams, W. L., Best, P., et al. 2021, A&A, 648, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, J. M. G. H. J., van Weeren, R. J., Botteon, A., et al. 2022, A&A, 668, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domínguez-Fernández, P., Vazza, F., Brüggen, M., & Brunetti, G. 2019, MNRAS, 486, 623 [Google Scholar]
- Duchesne, S. W., Johnston-Hollitt, M., Riseley, C. J., Bartalucci, I., & Keel, S. R. 2022, MNRAS, 511, 3525 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Koyama, K., Tsuru, T., & Matsumoto, H. 1996, PASJ, 48, 191 [NASA ADS] [Google Scholar]
- Fujita, Y., Tawa, N., Hayashida, K., et al. 2008, PASJ, 60, S343 [Google Scholar]
- Govoni, F., Orrù, E., Bonafede, A., et al. 2019, Science, 364, 981 [Google Scholar]
- Heald, G., Mao, S. A., Vacca, V., et al. 2020, Galaxies, 8, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hincks, A. D., Radiconi, F., Romero, C., et al. 2022, MNRAS, 510, 3335 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, M., Dumba, C., Drabent, A., et al. 2021, A&A, 654, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [Google Scholar]
- Nunhokee, C. D., Bernardi, G., Manti, S., et al. 2023, MNRAS, 522, 4421 [CrossRef] [Google Scholar]
- Oegerle, W. R., & Hill, J. M. 2001, AJ, 122, 2858 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Pasini, T., Edler, H. W., Brüggen, M., et al. 2022, A&A, 663, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pignataro, G. V., Bonafede, A., Bernardi, G., et al. 2024, A&A, 682, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. VIII. 2013, A&A, 550, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radiconi, F., Vacca, V., Battistelli, E., et al. 2022, MNRAS, 517, 5232 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Hardcastle, M. J., Tasse, C., et al. 2022, A&A, 659, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van der Tol, S. 2009, PhD Thesis, Technical University of Delft, The Netherlands [Google Scholar]
- van Weeren, R. J., de Gasperin, F., Akamatsu, H., et al. 2019, Space Sci. Rev., 215, 16 [Google Scholar]
- van Weeren, R. J., Shimwell, T. W., Botteon, A., et al. 2021, A&A, 651, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Ettori, S., Roncarelli, M., et al. 2019, A&A, 627, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Merluzzi, P., et al. 2022, A&A, 660, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Injection procedure
As explained in 3.2, to incorporate the upper limit on the bridge emission at 400 MHz with uGMRT observations in the radio spectrum, it is necessary to perform the injection procedure (see e.g. Venturi et al. 2008; Bernardi et al. 2016; Bonafede et al. 2017; Duchesne et al. 2022; Nunhokee et al. 2023) starting from the emission detected at 60 MHz. We extended the procedure presented in Pignataro et al. (2024) and took the spatial variations in the noise pattern in the uGMRT image into account. This follows from a generalisation of the injection approach, where we do not only inject at the centre of the image (i.e. the location at which the bridge is detected at lower frequencies), but also in different locations in the field. Analysing the noise pattern in the final uGMRT image over which the injection is performed, we find a non-uniform distribution. Therefore, to place a more conservative limit on the flux density of the bridge, we injected the visibilities three times: once at the known location of the bridge in the centre of the image, once north-east of the centre, and once south-west of the centre. The final limit is the result of an average of the three injections.
The injection procedure can be summarised as follows (see Pignataro et al. 2024 for an extensive description):
-
From the model image of the LOFAR detection at 60 MHz, we created a mask that only included the emission from the bridge.
-
The bridge model image was extrapolated to the central frequency of the uGMRT observation with a varying spectral index between −4 ≤ α ≤ 0 with steps of Δα = 0.25. The model images were additionally multiplied with the uGMRT primary beam model to take the attenuation of the primary beam in the uGMRT observation into account.
-
The final bridge model images were then Fourier transformed into visibilities (WSClean -predict, Offringa & McKinley 2014) that were injected into the uGMRT source-subtracted calibrated visibilities. The prediction of the model visibilities in the original dataset takes into account the missing short baselines or flagged data of the uGMRT observation. We then deconvolved and imaged with the same parameters, uv sampling, and image and visibility weighting as for the non-injected data images. In this way, we produced a mosaic with a resolution of 80″ as the injected image at the central frequency of 400 MHz for each spectral index, α.
-
We defined the ratio
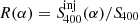 , which measures how bright, given a certain spectral index value, α, the injected bridge emission is (i.e. the flux density
, which measures how bright, given a certain spectral index value, α, the injected bridge emission is (i.e. the flux density 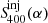 ) with respect to the image background (S400). We computed the ratio R(α) each time we performed the injection in a different location. We then computed the average of the three ratios, ⟨R(α)⟩.
) with respect to the image background (S400). We computed the ratio R(α) each time we performed the injection in a different location. We then computed the average of the three ratios, ⟨R(α)⟩. -
We finally evaluated the cumulative probability distribution function of ⟨R(α)⟩. We find that the spectral index of the bridge has a limit of αl < −1.75 with a 95% confidence level. This is different from the confidence level presented in Pignataro et al. (2024) because we started from a different injected model and followed a more robust procedure.
The limit on the spectral index translates into an upper limit on the bridge-integrated flux density that is S400 < 60 mJy.
All Tables
WSClean imaging parameters used to produce the low-resolution source-subtracted images for spectral index analysis.
All Figures
 |
Fig. 1. Radio images at 60 MHz of the A399–A401 clusters pair. Left panel: low-resolution (75″, the beam size is indicated in the bottom left corner) image with compact sources and the σrms = 3 mJy beam−1 produced with the parameters listed in Table 1. Right panel: same as the left panel, but after subtraction of the compact source. The contour levels (in white) start at 2σrms, 3σrms, and 5σrms and then increase to 20σrms with factors of 2. A negative contour at −3σrms is shown in red. |
| In the text | |
 |
Fig. 2. Spectral index maps. Top panel: spectral index map of the emission in the radio bridge in A399–A401 between 60 and 144 MHz, with a resolution of 80″. The distribution of the spectral index values (histogram at the top) only refers to the bridge emission inside the 2σrms level, which is not covered by the grey mask over the radio haloes. Bottom panel: associated spectral index error map. The LOFAR LBA contours at 2σrms and 3σrms are overlaid in black. |
| In the text | |
 |
Fig. 3. Radio spectra. Top panel: bridge emission radio spectra in integrated flux density. The grey arrow represents the uGMRT limit. Bottom panel: radio luminosity of the bridge emission compared to a synchrotron theoretical model (red curve) produced by the relativistic particle populations with acceleration times τacc > 200 Myr. |
| In the text | |
 |
Fig. 4. Spectral index distribution. Left panel: LBA radio image at 60 MHz and resolution of 80″. The 2σrms contours and the grid to extract the spectral index between 60 and 144 MHz are overlaid. Different areas of the bridge are covered by differently coloured cells. The coloured cells cover the LBA emission above 2σrms, and the red cells cover the 1σrms LBA emission and 2σrms HBA emission. Top right: spectral index distribution across the bridge. The black points show values extracted from each cell, separated by colour, and the red arrows indicate 1σrms limits extracted from the red cells. The dashed horizontal green line shows the mean spectral index, and the filled horizontal green region represents the standard deviation. Bottom right: distribution of residuals (Δα) of α with respect to the mean spectral index. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


