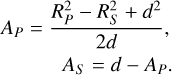| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348880 | |
| Published online | 17 May 2024 | |
Signature of the atmospheric asymmetries of hot and ultra-hot Jupiters in light curves
1
Laboratoire de Météorologie Dynamique, IPSL, CNRS, Sorbonne Université, Ecole Normale Supérieure, Université PSL, Ecole Polytechnique, Institut Polytechnique de Paris,
75005
Paris,
France
e-mail: aurelien.falco@lmd.ipsl.fr
2
IPGP, Université Paris Cité, Université Paris-Saclay, CEA, CNRS, AIM,
91191
Gif-sur-Yvette,
France
3
Laboratoire AIM, CEA, CNRS, Univ. Paris-Sud, UVSQ, Université Paris-Saclay,
91191
Gif-sur-Yvette,
France
4
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS,
B18N, allée Geoffroy Saint-Hilaire,
33615
Pessac,
France
5
Observatoire Astronomique de l’Université de Genève, département d’astronomie
Chemin Pegasi 51,
1290
Versoix,
Switzerland
Received:
7
December
2023
Accepted:
16
February
2024
With the new generation of space telescopes such as the James Webb Space Telescope (JWST), it is possible to better characterize the atmospheres of exoplanets. The atmospheres of Hot and ultra-hot Jupiters are highly heterogeneous and asymmetrical. The difference between the temperatures on the day and night sides is especially extreme in the case of ultra-hot Jupiters. We introduce a new tool to compute synthetic light curves from 3D general circulation model (GCM) simulations, developed in the Pytmosph3R framework. We show how rotation induces a variation in the flux during the transit that is a source of information on the chemical and thermal distribution of the atmosphere. We find that the day–night gradient linked to ultra-hot Jupiters has an effect close to stellar limb darkening, but opposite to tidal deformation. We confirm the impact of the atmospheric and chemical distribution on variations in the central transit time, though the variations found are smaller than those in available observational data, which could indicate that the east–west asymmetries are underestimated, due to the chemistry or clouds.
Key words: techniques: spectroscopic / planets and satellites: atmospheres / planets and satellites: gaseous planets
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
One-dimensional plane-parallel geometry is sufficient to explain low-resolution data in the case of cold planets, since the atmosphere is more or less homogeneous (MacDonald et al. 2020). However, in the case of hot Jupiters, this assertion does not hold anymore. Such planets, tidally locked and very close to their host star, present a strong dichotomy between their inflated hot day side and their cold and shrunken night side (Showman & Guillot 2002; Showman et al. 2008; Menou & Rauscher 2009; Wordsworth et al. 2011; Heng et al. 2011; Charnay et al. 2015; Kataria et al. 2016; Drummond et al. 2016; Tan & Komacek 2019; Pluriel et al. 2020, 2022). It is necessary, then, to use models with more than one dimension to explain spectral features.
In the case of transmission spectroscopy, the sampled atmospheric space is limited to a narrow region around the terminator (Brown 2001; Kreidberg 2018), and we may extract information about the day and night sides from the signal Fortney et al. (2010), Caldas et al. (2019), Wardenier et al. (2022). Morning-evening asymmetries may also have an impact on the spectrum (Line & Parmentier 2016; Parmentier et al. 2016; MacDonald et al. 2020; Espinoza & Jones 2021). Even so, retrieval techniques – that is, the inference of input parameters for the atmospheric simulation based on the fitting of a spectral observation – mostly relied on 1D models until quite recently. Studies have now started to include more dimensions (MacDonald & Lewis 2022; Nixon & Madhusudhan 2022; Zingales et al. 2022) for the fitting of observations.
Observations not only have spectral information, but also temporal information about how the observed flux varies over time, and especially during the transit of one or more exoplanets. Konings et al. (2022) have also shown that stellar flares are also expected to have a time-dependent impact on transmission spectra (this effect will not be considered in this study).
The question is what information light curves (variations in the flux during the transit of an exoplanet) provide. Through time-resolved high-resolution spectroscopy, it is possible to detect species by cross-correlation of the features of each species (Prinoth et al. 2023). Prinoth et al. (2023) emphasize that the observational data is expected to fluctuate during the transit and is influenced by the characteristics of the atmosphere, such as the thermal dissociation occurring at very high temperatures on the day side of ultra-hot Jupiters. Using low-resolution spectral information, light curves can provide evidence of morning and evening asymmetries (Line & Parmentier 2016; von Paris et al. 2016). They also allow us to probe other regions of the atmospheres, due to the rotation of the planet. Light curve models have historically relied on 1D spherical models (Kreidberg 2015; Tsiaras et al. 2016), though recent tools extend the concept to different shapes and dimensions (Maxted 2016; Akinsanmi et al. 2019; Jones & Espinoza 2020; Barros et al. 2022; Grant & Wakeford 2022).
There is a similar trend in emission spectroscopy. For example, Chubb & Min (2022) rely on a 3D model to study phase curves, enabling them to extract information such as a shift of the hot spot in the simulation.
In this work, we consider 3D general circulation model (GCM) simulations (Wordsworth et al. 2011; Leconte et al. 2013), from which we can extract information such as a temperature map and the chemical composition of the atmosphere. Caldas (2018), Caldas et al. (2019) introduced a tool, namely Pytmosph3R, which produces transmission spectra from the simulation data. A new, more user-friendly and open-source implementation of Pytmosph3R has since been introduced, namely Pytmosph3R 2.0 (Falco et al. 2022). The present paper is linked to a new release (2.2), which introduces light curves, among other functionalities. Section 2 describes the transit model parameters and details. Section 3 shows the biases of a homogeneous spherical 1D light curve model (a solid sphere, or a completely opaque ball), as generally used by the literature, to a full 1D atmospheric model. It is followed by a discussion (Sect. 5) on the impact of a 2D day–night temperature gradient approximation, as well as a full 3D GCM simulation on the shape of the resulting light curve, when taking into account rotation or when it is ignored. This has been studied for a hot Jupiter (WASP-39b) and an ultra-hot Jupiter (WASP-121b), both cases being presented in Sect. 4. We compare the effect of the rotation of a tidally locked planet to stellar limb darkening in Sect. 6, and to the ellipsoid approximation (Maxted 2016; Barros et al. 2022) in Sect. 7.
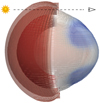 |
Fig. 1 Ray of light crossing the atmosphere of WASP-121b. The color map indicates the local temperature, ranging from around 400 K (in blue) to 3300 K (in red). The inflation of the day side is directly due to the increase in the scale height (due to the hydrostatic equilibrium). This simulation includes a super-rotating equatorial jet (visible in gray). |
2 Transit model
We briefly reintroduce here the method that we use to compute the transit depth of an exoplanet. Let us consider a situation like the one represented in Fig. 1.
Γ𝒯 is defined as the polar coordinate system of the transmittance grid, 𝒯, located in the plane of the sky, orthogonal to the planet-observer axis. The points in this coordinate system are noted (r, θ). In this coordinate system, the point (RP, 0) is the projection of the northernmost point on the planet of radius RP on the transmittance grid. The transmittance grid, 𝒯, is composed of Nr radial points and Nθ angular points.
The rays of light crossing the atmosphere are partially absorbed by the interaction of the rays with the molecules present in the atmosphere. The opacity of each ray can be calculated through the optical depth, which has already been detailed in Caldas et al. (2019), Falco et al. (2022).
2.1 Transmittance map and spectrum
A transmittance map can be computed from the optical depth, τ, via
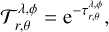 (1)
(1)
for each ray (r, θ) in the transmittance grid, wavelength, λ, and phase, ϕ. In the case of a homogeneous stellar disk, the relative dimming of the stellar flux of the planet and its atmosphere during transit is given by
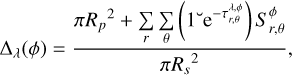 (2)
(2)
with 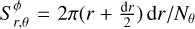 , for phases, ϕ, when the planet is completely in front of the star. Rp is the radius of the planet, Rs the radius of the star, and dr the distance between two consecutive r.
, for phases, ϕ, when the planet is completely in front of the star. Rp is the radius of the planet, Rs the radius of the star, and dr the distance between two consecutive r.
However, during the ingress and egress, the surface area of 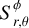 will change according to its intersection with the stellar disk. The details of this calculation are laid out in Appendix A.
will change according to its intersection with the stellar disk. The details of this calculation are laid out in Appendix A.
In this study, light curves were generated for 30 000 wavelength points between 0.5 and 10 μm.
2.2 Transit parameters
The transit is parameterized by the inclination of the orbit of the planet, its distance to the star, a (i.e., the semi-major axis, or the orbit radius, since we consider the orbit to be spherical in the current study), and the number of phases at which we calculate the forward model.
The calculation of the transmittance map, 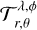 , is quite costly, so we calculate N𝒯 transmittance maps, a number that can be different from the number of phases, Nϕ, for which we calculate Eq. (2). In practice, we therefore calculate
, is quite costly, so we calculate N𝒯 transmittance maps, a number that can be different from the number of phases, Nϕ, for which we calculate Eq. (2). In practice, we therefore calculate 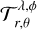 for phases
for phases
![${\phi _{\cal T}} = \left\{ {{\phi _j},\forall j \in \left[ {1,{N_{\cal T}}} \right]} \right\},$](/articles/aa/full_html/2024/05/aa48880-23/aa48880-23-eq7.png) (3)
(3)
preferably with a low N𝒯, and using these reference points, ϕ𝒯, we interpolate 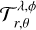 for the phases, ϕλ:
for the phases, ϕλ:
![${\phi _\lambda } = \left\{ {{\phi _i},\forall i \in \left[ {1,{N_\phi }} \right]} \right\},$](/articles/aa/full_html/2024/05/aa48880-23/aa48880-23-eq9.png) (4)
(4)
which enables us to calculate Eq. (2) for all phases, ϕλ. The advantage of doing so is that Nϕ can be much larger than N𝒯 and we can therefore compute numerous time steps without enduring the full cost of the computation of a transmittance map for each and every one of them.
An alternative method to improve speed without significantly compromising accuracy is to distribute the points, ϕλ, in a way that allocates more points for segments of the transit where the light curve is expected to exhibit a more intricate fluctuation. Considering homogeneous stellar disks in this study, this will take place during the ingress and egress. We considered the orbit to be spherical at this time. The phase at which the atmosphere will emerge from the transit (when it is not superimposed with the stellar disk anymore) – that is, the start of the egress – is equal to
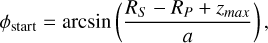 (5)
(5)
where zmax is the maximum altitude of the simulation, and a is the planet’s orbit radius. Similarly, the egress stage will stop at phase
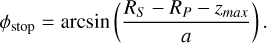 (6)
(6)
These functions are valid only for circular orbits. They also depend on the scale of the simulation and the lower pressures for which the atmosphere has been computed.
We consider the egress to take place between ϕstart and ϕend, and the ingress between −ϕend and −ϕstart. The egress space defined by these points is discretized into Negress phases, the ingress into Ningress phases, and the rest of the phases (Nϕ, − Negress − Ningress) discretize the plateau in between, when the entire atmosphere of the planet is completely superimposed with the stellar disk.
In practice, we set Ningress = Negress, and the implementation sets as Negress = Nϕ/3 by default. Setting a higher phase resolution for the egress or ingress allows us to better replicate the fineness of the egress or ingress, during which the intersection between the atmosphere's projection and the stellar disk is going to change drastically at each phase. During the rest of the transit, the main change in the transmittance is induced by the rotation of the planet. This can be approximated with a lower phase resolution, Nϕ, interpolated between the N𝒯 phases (for which a transmittance map is computed). The matter of choosing N𝒯 is discussed in Appendix B, considering a balance between accuracy and computational time.
Parameters of the 1D and 2D atmospheres.
3 Homogeneously opaque solid sphere one-dimensional fitting of the transmittance of a one-dimensional atmosphere
We study here the biases of 1D and homogeneously spherical light curve models, meaning those in which the entire solid sphere (or ball) is considered to be completely opaque. We show here that these models are able to retrieve the signal of a 1D atmosphere almost consistently all along the transit, except during the ingress or egress. To that end, we thus compared two models:
the 1D atmosphere, for which the light curve was generated via Pytmosph3R 2.2 (see details in Table 1); and
the homogeneously spherical model, which was generated via batman.
batman is a python package introduced by Kreidberg (2015) for modeling 1D transit and eclipse light curves, which were used as a reference point. A simple representation of the two models is shown in Fig. 2.
The diffuse opacity of the atmosphere (which generally decreases with the altitude) calculated by Pytmosph3R cannot be reproduced via a homogeneously opaque solid sphere. This effect is only visible when the atmosphere partially absorbs the star light; in other words, during the ingress or egress. This is shown in Fig. 3.
Though the integration of the opacity of the atmosphere over its apparent disk in Pytmosph3R is equal to the circular surface calculated by batman, the atmosphere calculated by Pytmosph3R extends over a larger space than that of batman, and is more transparent at high altitude, as is shown by the schematics in Fig. 2. Therefore, during the egress, the upper part of the atmosphere in Pytmosph3R disappears from the transit before the equivalent disk in batman does, and the opacity of batman will thus be overestimated at the early stage of the egress. Reversely, it is underestimated in the late stage of the egress. The same holds true during the ingress.
The strength of this effect is relatively small (almost one order of magnitude) compared to the biases introduced by the spherical approximation in the presence of east–west or day–night asymmetries, which will be discussed in the following sections.
 |
Fig. 2 Projected opacity of a planet on the observer's field of view when considering (or not) an atmosphere. Left: diffuse opacity due to atmospheric content (Pytmosph3R). Right: homogeneously opaque solid sphere approximation (batman). |
 |
Fig. 3 Relative flux (Eq. (2)) at a wavelength, λ = 7μm, of the spherical approximation (batman) compared to the diffuse opacity of a 1D (Table 1) atmospheric simulation (Pytmosph3R) (see Fig. 2 for the schematics). The effect is similar in the case of a 2D day–night (Table 1) simulation (Pytmosph3R) without rotation (i.e., N𝒯 = 1). The same effect holds true in 3D cases, since the opacity of each case will decrease with the altitude, although it will be dominated by other effects. |
4 From hot to ultra-hot Jupiters
In the later sections, we will study the effects of asymmetries in hot and ultra-hot Jupiters on the associated light curves. For that purpose, we have selected three cases that we detail below.
4.1 Ultra-hot Jupiters WASP-121b
In this study, we took a SPARC/MITgcm simulation (Showman et al. 2009) of WASP-121b (Parmentier et al. 2018) as a reference for ultra-hot Jupiters. Its temperature map is shown in Fig. 4. This simulation has a strong day–night temperature gradient and also a shift of the hot spot toward the east. The chemistry includes He, H, H2, H2O, CO, TiO, and VO, for which some of the relevant distribution maps are displayed in Fig. 5.
The star temperature was set to 6460 K, its radius was set to 1.458 R⊙ (solar radii), and the orbital radius of WASP-121b was set to 0.025 au.
 |
Fig. 4 Temperature maps of WASP-121b. Top: high-altitudinal cut. Bottom: equatorial cut, for which the atmosphere scale has been multiplied by ten for visual reasons. In this simulation, the hot spot is slightly shifted to the east. |
4.2 Two-dimensional day–night gradient
To be able to distinguish the signal due to day–night variations from the signal due to east–west variations in ultra-hot Jupiters, we took as an example a 2D description of the atmosphere, for which the temperature was defined using Eq. (7) following a day–night gradient, as was proposed by Caldas et al. (2019).
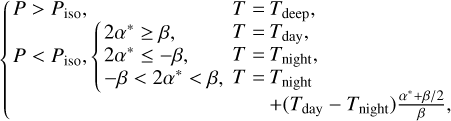 (7)
(7)
The atmosphere is thus symmetrical around the star–observer axis; that is, there are no morning-evening or east–west asymmetries. The parameters used in this study for this 2D case are listed in Table 1.
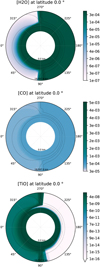 |
Fig. 5 Abundance maps of WASP-121b. Top: H2O. Middle: CO. Bottom: TiO. All are equatorial cuts, for which the atmosphere scale has been multiplied by ten for visual reasons. |
4.3 Hot Jupiter WASP-39b
hot Jupiters and ultra-hot Jupiters have a notable difference concerning the strength of the equatorial jet and the resulting east–west asymmetries. We will take here the example of the hot Jupiter WASP-39b, which is based on the Met Office Unified Model (Drummond et al. 2018). For our simulation of WASP-39b, we used a constant chemistry and chose two species that display a readily identifiable spectral signature; that is, H2O and CO2, with a VMR of 3.57×10−3 for H2O and 1.25×10−4 for CO2. We used a He/H2 ratio of 0.2577. These abundances were not extracted from James Webb Space Telescope (JWST) observational data of WASP-39b. Our C/O ratio (0.03) is quite low compared to the ratios (>0.3) retrieved by Rustamkulov et al. (2023) for WASP-39b and should thus be taken with caution. It should be noted that there is no CO in our simulation, while it should be a substantial part of the carbon-bearing species, and thus the C/O ratio. This study is focused on the observational implications of thermal asymmetries of hot Jupiters rather than simulating the exact case of WASP-39b. Temperature maps of our simulation for WASP-39b are displayed in Fig. 6. This figure shows the temperature structure of the atmosphere of a simulation corresponding to WASP-39b, sliced at an altitude of 7800 km and at the equatorial plane. The simulation presents a strong jet going eastward, with the hot spot shifted by more than 60°. The temperature of the equatorial jet is also still very hot on the night side (>1300 K) at an altitude of 7800 km, and the temperatures in the overall equatorial inner annulus (up to around 104 km) are all higher than 1400 K. Above this altitude, the cold spot (900 K) is located between the west limb and the anti-stellar point (longitudes ~200°−280°). The west limb is more or less uniform, with a temperature around 1200 K.
This is quite different from the case of WASP-121b, in which the eastward shift of the hot spot is much less pronounced and does not reach the night side. The day–night gradient is therefore much stronger. The cold spot also covers more angle on the night side.
The star temperature was set to 5326.6 K, its radius was set to 1 R⊙, and the orbital radius of WASP-39b was set to 0.0486 au.
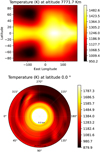 |
Fig. 6 Temperature maps for hot Jupiter WASP-39b. Top: latitude–longitude map, at an altitude of 7772 km. Bottom: equatorial slice. The simulation goes up to an altitude of 29 950 km. |
5 Biases of one-dimensional light curve retrievals of rotating hot to ultra-hot Jupiters due to atmospheric asymmetries
Using Pytmosph3R 2.2, we tried to unravel the biases inherent in 1D light curve models by generating light curves of 2D or 3D atmospheric models. For this purpose, we again used the 1D solid-sphere model batman (Kreidberg 2015), but also Juliet (Espinoza et al. 2019), a wrapper of multiple tools (including batman) that offers the possibility of fitting data through Bayesian inference (naturally here we focused on fitting light curves).
The parameters used for the Juliet retrievals are listed in Table 2. They include the time of inferior conjunction (mid-transit), or the central transit time, normalized by the orbital period of the planet, and the planet radius and the orbit radius (considering a circular orbit) normalized by the host star’s radius.
Appendix C discusses the impact of the time or phase resolution on the input light curve calculated by Pytmosph3R during a retrieval. The parameters used by Pytmosph3R in the calculation of the light curves are listed in Table B.1 (i.e., the ingress and egress are discretized with a higher resolution). As is explained in Appendix C, all the light curves were re-interpolated over Nϕ = 300 phases before feeding them to the retrieval in order to be statistically more adequate.
5.1 Biases during the ingress and egress for a translating ultra-hot Jupiter with a three-dimensional atmosphere (no rotation)
Let us start with a simple case, and assume that we can neglect rotation during the transit due to its brevity (we set the number of computed transmittances, N𝒯, to 1). We use the term "translation" to refer to a transit for which rotation was not considered. We took the case of the ultra-hot Jupiter WASP-121b as an example and generated its light curve using Pytmosph3R 2.2. We also generated the corresponding 1D solid sphere, homogeneously opaque, setting the input planet radius of batman to the apparent radius at mid-transit of the light curve of WASP-121b.
The difference between the 1D (batman) and 3D (Pytmosph3R) light curves is shown in Fig. 7. We can see on this figure the east–west asymmetry of the simulation. The spherical model (batman) finds an apparent disk larger than Pytmosph3R during the ingress and overestimates it during the egress. This effect is similar to Fig. 12 from von Paris et al. (2016), for example. This is due to the lower temperature in the west limb of the simulation, and higher temperature in the east limb as the hot spot on the day side is slightly shifted toward eastern longitudes, as is shown in Fig. 4. We will see that this effect can be partially reduced by changing the central time, T0 (Sect. 5.3).
 |
Fig. 7 Difference between the flux (Eq. (2)) of a 1D solid sphere (batman) and the flux of a 3D simulation of an ultra-hot Jupiter (Pytmosph3R) without rotation (i.e., N𝒯 = 1). The ultra-hot Jupiter is WASP-121b (Fig. 4). The x axis shows the wavelength; the y axis shows the transit phase. |
5.2 The translation approximation
Rotation is usually excluded from the current models, the planets being thought to be too cold and the transits too short for the rotation to usually have an effect on the light curve. We will try to characterize here the effects of the tidally locked rotation that can be expected, from a pure geometrical perspective (i.e., ignoring Doppler effects). In the "translation" case, the planet slides along the plane of the sky, ignoring the tidally locked rotation. Figure 8 shows the difference between light curves generated for WASP39b, the 2D day–night gradient, and WASP-121b, each with and without rotation (N𝒯 = 8 and N𝒯 = 1, respectively).
In the case of WASP-39b (top plot), we can see that the signal is stronger in the early stage than the late stage. This is due to the fact that the cold spot is located near the western longitudes (~200°−280°, see Fig. 6). This cold spot moves toward the edge of the west limb during the late stage, accentuating the decrease in the apparent radius in the west. Indeed, the scale height of the atmosphere is linearly dependent on the temperature (H = RT/mg, with R standing for the ideal gas constant, m the mean molar mass, g the surface gravity, and T the atmosphere temperature). The cold spot moves toward the anti-stellar point during the early stage, and is therefore less probed by stellar rays crossing the atmosphere on the star-observer axis. At the same time, the higher temperatures of the day side move to the west limb, increasing its scale height. The effect is stronger for wavelengths with a high apparent radius (see Figs. 11 or 13, for example). The signals during the ingress and egress are also boosted, reaching a peak of almost 200 ppm. This peak during the ingress and egress is due to the overall day–night temperature difference.
To understand this effect, let us focus on the 2D day–night gradient simulation (middle plot of Fig. 8), for which the gradient between the day temperatures and the night temperatures is much stronger. The light curves in this case are symmetric with respect to the mid-transit, meaning that ∆λ(ϕ) = ∆λ(−ϕ). The variations between different wavelengths are solely linked to the height of the absorption lines. In this case, the greatest differences between the rotation case and the translation case occur (by far) during the ingress and egress, due to the (hotter) day side partially obscuring the star when the (colder) night side is out of the transit zone. For a visualization, one can see how the east limb is much larger (due to the day side being more visible) in the last transmittance map (late transit) in Fig. 9. This figure shows the example of WASP-121b, although the same effect is happening for the 2D day–night gradient. The west limb (which corresponds to a larger fraction of the night side) is much smaller and is going to disappear first from the signal during the egress. If we go back to Fig. 8, we can also see in the 2D case that, in the early and late stages, the differences between rotation and translation can go as low as −450 ppm due to the projection average area of the atmosphere being smaller (see again the same transmittance maps in Fig. 9). This difference follows a U-shaped curve during the transit, excluding the ingress and egress (the difference is close to zero at mid-transit but increasingly negative for phases far from mid-transit).
Our simulation of WASP-121b presents a very strong day–night asymmetry, but also a smaller east–west asymmetry. The U-shaped signal of the day–night gradient (as is discussed above for the 2D case) is again visible in the background in the 3D case (bottom plot of Fig. 8), but the east–west asymmetry breaks the symmetry of the pattern. The differences during the late-transit are positive. They are due to the shift of the hot spot on the day side to the east, as it moves toward the east limb during the late stage and is therefore more visible. The differences amount to more than 100 ppm during the ingress and egress (reaching a peak of 600 ppm in wavelengths with larger apparent radii). During the early and late stages, they can go as low as −450 ppm due to the day–night gradient and reach +100 ppm due to the shift of the hot spot.
Appendix B also shows the errors and the times expected for different numbers of transmittances maps N𝒯 calculated during the transit (for faster calculation, interpolating between each phase, see Sect. 2.2), in the case of an ultra-hot Jupiter.
 |
Fig. 8 Residuals between translation (N𝒯 = 1) and rotation (N𝒯 = 8) fluxes. Top: WASP-39b (Fig. 6). Middle: two-dimensional day–night gradient (Table 1). The east–west symmetry leads to the signal being identical at phases ϕ and −ϕ. Bottom: WASP-121b (Fig. 4). The x axis shows the wavelength; the y axis shows the transit phase. |
 |
Fig. 9 Transmittance maps for phases −13, 0, and 13°, i.e., early-, mid-, and late-transit, respectively, at λ = 0.6 μm of WASP-121b. The atmosphere scale has been multiplied by ten for visual reasons. The inner black circle represents the planet core. The total apparent surface is greater at mid-transit due to the hot day side being apparent all around the limb. The night side is more apparent during the early and late stages (lower scale height). |
5.3 Central time variations and east–west effects
We are interested here in studying the relationship between the atmosphere characteristics and the variations in the central time, T0, retrieved by the 1D spherical model of Juliet.
Rustamkulov et al. (2023) have published the variations in the central transit time, or time of inferior conjunction, T0 (see their extended data Fig. 3), for WASP-39b. They show variations in T0 between −50 and +60 s, depending on the wavelength (going from 0.5 to 6 μm). We have generated a synthetic light curve with Pytmosph3R for which we retrieve T0, for wavelengths going from 1 to 5 μm. We have done so for the hot Jupiter WASP-39b, considering a tidally locked rotation, and for the ultra-hot Jupiter WASP-121b. The results are shown in Fig. 10.
In the case of the 2D day–night model, as is shown in the middle plot of Fig. 8, the shape of the transit is symmetrical before and after the mid-transit; that is, ∆λ(ϕ) = ∆λ(−ϕ), due to the symmetry of the simulation along the star-observer axis. Therefore, retrievals by Juliet find no variation in the time of inferior conjunction, T0.
Figure 10 shows that the variations in the central time, T0, are stronger in the case of the hot Jupiter WASP-39b than in the case of the ultra-hot Jupiter WASP-121b. This is due to the fact that east–west asymmetries are stronger in the case of the hot Jupiter than that of the ultra-hot Jupiter. The amplitude of the variations is around 5 s for all wavelengths (from 3 to 8 s) in the case of the ultra-hot Jupiter WASP-121b, meaning that the retrieval method finds a solid-sphere equivalent planet that transits 5 s late compared to the actual planet. It is 10 s at minimum (around 1 μm) and goes up to 22 s (around 4.5 μm) for the hot Jupiter WASP-39b. For WASP-39b, the spectral features are clearly visible. As for errors on the flux discussed above, wavelengths with larger apparent radii are also linked to a larger bias in the transit timing.
In the case of WASP-39b, Rustamkulov et al. (2023) show an amplitude of more than 50 s on the same spectral range. Thus, we manifestly do not account for the whole amplitude of the variations in T0. This could be due to cloud coverage or the chemical structure of the simulation. As was mentioned before, we considered a quite simple constant chemistry for this simulation. The observational (Rustamkulov et al. 2023) and simulated data (this study) central time variations both follow the spectral features and especially the H2O and CO2 bands. Both data can also be fitted by a non-zero slope linear regression. Let us assume a linear fit under the form ax + b, where x is within 1−5 μm. In the case of the observational data (Rustamkulov et al. 2023), we obtain a = 2.07 and b = −4.77, while we obtain a = 1.40 and b = 12.68 for our simulation of WASP-39b. The differences between the slope values (a) may be due to the stellar spectrum (if the real stellar temperature is different from ours, which is 5326.6 K) but also to our choice of chemistry, which does not correspond to the actual observations of WASP-39b. Indeed, a potential discrepancy in our simulation is the absence of CO, as there is a CO band around 5 μm. The differences might also arise from an overestimated amount of H2O, as the water bands dominate the wavelengths shortward of 3 μm.
In our translation simulation of WASP-121b (displayed in orange in the bottom plot of Fig. 10) the shift in the transit timing (on the order of 5 s for all wavelengths) is in line with previous results. Indeed, Line & Parmentier (2016) found that light curve residuals could be reduced by a factor of ten when shifting the transit timing of ~10−5 and ~10−4 days, following the scale height difference between the morning and evening limbs of the planet.
The value found for T0 in this translating case is also impacted by the chemistry. For example, the value found for λ = 0.6 μm in the translation case is higher than in the other one, due to the distribution of TiO in the simulation. TiO is less symmetrically distributed than its counterparts H2O and CO, and therefore its east–west asymmetry leads to an overestimation of T0. Other spectral features have less impact over the variations in T0 and one might have difficulties in distinguishing the water or CO bands from the error bars.
When we account for the tidally locked rotation of WASP-121b (blue curve in Fig. 10), the central time is shifted by the same order of magnitude, around 5 s. However, there are some differences, including in the spectral region dominated by the opacity of TiO (<1 μm), where the shift is slightly smaller. This could be linked to the distribution of TiO in the atmosphere, which is indeed present at higher altitude on the east limb, but also in both terminators. The fact that the planet rotates seems to reduce the difference between the east and west limbs, due to the fact that the oversized east limb (see Fig. 5) is reduced by being partly masked from the observer during the early and late stages, and the east–west differences are therefore less visible than in the translation case. In the translation case, the east–west asymmetries present in both limbs stay constant throughout the whole transit. Concerning the impact of the chemistry, we can hardly see the spectral signatures in either the rotating case or the translating case. Spectral signatures are much more significant in the variations of T0 in the hot Jupiter WASP-39b than in the ultra-hot Jupiter WASP-121b.
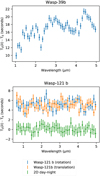 |
Fig. 10 Time of inferior conjunction, T0, retrieved by Juliet for the tidally locked hot Jupiter WASP-39b (top) and the ultra-hot Jupiter WASP-121b (bottom, including legend) for wavelengths from 1 to 5 μm, at a resolution similar to NIRSpec. In the case of WASP-121b, three cases are displayed (indicated by the colors): 1) the light curve of the 3D simulation of WASP-121b without rotation (i.e., translation) in orange, 2) the same including rotation in blue, and 3) a 2D day–night temperature gradient (symmetric transit) in green. |
 |
Fig. 11 Values retrieved by Juliet for (RP/RS)2 of WASP-39b in the translation case (in orange; the planet does not rotate during the transit), the rotation case (in blue), and the input value of (RP/RS)2 at mid-transit (in black). Error bars are included (less than 1 ppm). |
5.4 Reduced radius retrieved due to the rotation of the planet
Due to the shape of the signal during the transit (a U shape due to the day–night gradient or a slope due to east–west asymmetries), which cannot be simulated by a 1D spherical model, 1D retrievals will tend to average the observed radius over the whole duration of the transit.
In the case of WASP-39b, the radius retrieved for the rotation and the translation case is displayed in Fig. 11. In the 2D day–night case, the radius retrieved for the rotation and the translation case is displayed in Fig. 12. In the case of WASP-121b, the radius retrieved for the rotation and the translation case is displayed in Fig. 13.
One may notice that the retrieved values for the planet radius are almost always inferior to the input value. This is due to the fact that the input value shown in the plot is taken at mid-transit. For light curves that have a U shape, the average value of the signal will always be lower than the mid-transit value, since it is the maximum value of the whole transit. This is more readily visible in Fig. 14. The input radius given to batman is the maximum apparent radius, RP, of the light curve generated via Pytmosph3R, and hence the residual of batman is always equal to zero when the light curve of Pytmosph3R reaches its minimum. In this case, there is no meaningful value of RP for either batman or Juliet since the 1D model used cannot reproduce the nonlinear curve shape during transit due to the asymmetries in the input model.
The differences between the Juliet retrieved light curves and the 2D day–night simulation are almost constantly at their maximum in mid-transit (Fig. 14), and thus the retrieved apparent radii in Fig. 12 also have the largest errors among the three examples. Indeed, in the cases of WASP-39b and WASP-121b, the light curves in some wavelengths follow a slope instead of a U-shaped curve, and the maximum difference between the retrieved value of RP and its initial value is therefore not at mid-transit but during the early and late stages (the retrieved value being an average of the overall slope, it is closer to the intermediate value of RP in mid-transit).
If we take a closer look at Fig. 14, we can see that Juliet always overestimates the apparent radius during the early and late stages of the transit (which is equivalent to saying that it underestimates the relative flux). This is due to the fact that the projection of our 3D simulation of WASP-121b over the observer's field of view is larger in mid-transit, as was explained in previous sections (the hot temperatures from the day side contribute to the absorption all around the terminator), and smaller during early and late stages, due to the hot day-side temperatures being replaced by the night side's on the east and the west limbs, respectively (see Fig. 9 for a visualization).
During the ingress and egress, Juliet underestimates the apparent radius compared to the input simulation due to the day side being the major part of the atmosphere obscuring the star (the night side exits the transit before the day side and enters after the day side).
In conclusion, a 1D model would be biased up to a few hundred ppm depending on the current phase of the transit due to the rotation of the tidally locked planet. One might need to take this effect into account in the calculation of the limb darkening associated with the star.
 |
Fig. 12 Values retrieved by luliet for (Rp/Rs)2 of the 2D day–night gradient in the rotation case (see Sect. 5.4), the same when also retrieving limb-darkening (LD) coefficients (see Sect. 6), and the input value of (RP/RS)2 at mid-transit (in black). |
 |
Fig. 13 Same as Fig. 12 for WASP-121b, but with the retrievals of the rotation and translation cases (discussed in Sect. 5.4) and the retrieval using limb darkening (discussed in Sect. 6). |
 |
Fig. 14 Light curves for the two-dimensional rotation case. Left: light curves generated by Pytmosph3R (dashed line) compared to the fit provided by Juliet (solid line, with retrieved values for T0 and RP). Right: residuals of Juliet (orange) to Pytmosph3R, with batman (assuming T0 = 0 and RP taken at mid-transit from Pytmosph3R) given as a reference. It should be noted that Juliet itself uses batman as a forward model; the difference only comes from the retrieved values of T0 and RP. |
 |
Fig. 15 Light curves retrieved with limb-darkening (Juliet) and without (batman) and residuals. For each case (2D day–night and WASP-121b): Left: light curves generated by Pytmosph3R (dashed line) compared to Juliet (solid line, with retrieved limb darkening, T0 and RP). Right: residuals of Juliet (orange) to Pytmosph3R, with batman (no limb darkening, T0 = 0 and RP taken at mid-transit from Pytmosph3R) given as a reference. |
6 Rotation of the atmospheric signal versus limb darkening
Since the 2D day–night gradient introduces a reduction of the signal during the early and late stages, the effect could be mistaken for the limb darkening of the star. When considering limb darkening, the flux emitted by the star when the planet is obscuring the edge of the star is lower than when it obscurs the center. Limb darkening therefore also induces a U-shaped signal in the transit light curve, which is coincidentally similar to the effect of the day–night gradient of the planet, although the U-shaped signal does not have the same properties. We will consider here a quadratic law for the limb darkening.
In this section, we retrieve the light curves generated via Pytmosph3R for the 2D day–night gradient case and WASP-121b. The limb-darkening-specinc parameters retrieved by Juliet are listed in Table 2.
Figure 15 shows the differences between the 1D retrieved model, including limb darkening, and the input light curve calculated via Pytmosph3R for WASP-121b. Let us keep in mind here that the ingress-egress reductions are mainly due to the T0 shift, as is discussed in Sect. 5.3. We are therefore more interested in the full transit. We can see that the U shape of the limb-darkening light curve (here using a quadratic law) is a better match for most wavelengths, as it can better fit the U shape or slope of the Pytmosph3R light curve.
However, this better fit does not represent the original data, in which no limb darkening was used. The limb-darkening coefficients retrieved are shown in Fig. 16. The values of these retrieved coefficients vary from one wavelength to another. Around 1 μm, the shape of the light curve is almost flat for the 2D day–night gradient, and thus the limb-darkening coefficient is very low. The shape of the spectral features can be easily distinguished in the values of q1.
The retrieved apparent radius, shown in Fig. 13, is therefore even more biased when it comes to the day–night thermal difference (top plot). East-west effects of the simulation of WASP-121b (bottom plot) seem to reduce this bias. Indeed, the retrieved values of the limb-darkening coefficients in the case of WASP-121b are much smaller than for the 2D day–night gradient, as is shown by Fig. 16, and the resulting retrieved light curve is consequently closer to a retrieval without limb darkening.
There are two caveats to this study. The first one is that we generated the forward light curves without limb darkening. This is an implementation issue, as the computation of the intersection area of the transmittance grid with the stellar disk (see Appendix A) relies on the assumption that the stellar flux is uniform over the disk. To take into account the limb darkening of the stellar flux, one should use a different method; that is, integrate the flux over each cell by discretizing the cell following the radial dimension, allowing us to plug in the limb darkening law, based on the radial coordinate. One downside of this integration is its additional cost, which would slow down the overall computation. This has not been implemented in our model yet.
The second caveat is that these limb-darkening fits were done using the quadratic law. It could be interesting to see how other laws behave, although studying other limb-darkening laws in addition to the generation of limb-darkening forward 3D light curves deserves the focus of an entire study and is thus not addressed further here. We emphasize that the retrieved limb-darkening coefficients depend on the wavelength and we therefore conclude that light curves retrievals of ultra-hot Jupiters should be realized over multiple wavelengths to avoid being biased by the day–night gradient of the planet's atmosphere.
 |
Fig. 16 Values retrieved by Juliet for the limb-darkening coefficients, q1 and q2, in the 2D day–night gradient case and WASP-121b. The scale for q2 (indicated on the right) is different in the two plots. |
7 Atmosphere versus ellipsoid rotation in the case of ultra-hot Jupiters
Barros et al. (2022) propose using an ellipsoid model to fit the light curve of Wasp-103b, using elle, a tool developed by Maxted (2016) that provides an ellipsoid light curve model that also has the ability to conduct a Bayesian analysis. They suggest that this model fits the data better than a spherical model. However, as we can see in Fig. 17, the light curve generated by Pytmosph3R (with a spherical core, it should be noted) is better fitted by the spherical model. We used a Love number equal to 1.39 in this study, corresponding to WASP-121b (Hellard et al. 2020).
The deformation of the ellipsoid has the reverse shape to that of the atmospheric signal of the day–night temperature gradient (see the light curve at 0.6 μm, for example). This is due to the apparent surface projected onto the plane of the sky. As is shown in Fig. 18, the ellipsoid covers more surface during the early and late stages compared to the mid-transit stage. The atmospheric signal due to the day–night dichotomy of ultra-hot Jupiters has a reverse effect, as was mentioned before: the atmosphere covers more surface during the mid-transit stage due to the hot day side being visible all around the limb, while the night side is more visible during the early and late stages, decreasing the scale height of the atmosphere and the apparent surface (see Fig. 9).
For hot Jupiters, when the atmospheric signal is more influenced by east–west effects than by day–night thermal differences, this is less visible.
We can therefore only conclude that if the ellipsoid model is indeed fitting better the original data of Wasp-103b, the actual Love number found may be underestimated due to the signal linked to the atmosphere, and more especially if there is a strong day–night dichotomy. A coupling between a tidally deformed core and an atmospheric model would be needed to study both effects simultaneously.
 |
Fig. 17 Ellipsoid light curves compared to light curves generated via Pytmosph3R (i.e., spherical core, but atmospheric envelope). Rotation is taken into account for both methods. Left: light curves generated by Pytmosph3R (dashed line) compared to the spherical model (dotted line) and the ellipsoid model (solid line). Right: residuals of the spherical model (Sphere) versus Pytmosph3R (P3) and the ellipsoid model (Love). |
8 Conclusion
In this paper, we have introduced a novel framework to compute light curves from a 3D GCM simulation. The parameters of the model include the planet's orbit radius, period (optional, but necessary for the conversion between phase and time), and inclination, as well as the number of phases and transmittances for computing the light curve. The documentation for this tool, Pytmosph3R 2.2, is available here.
We used Pytmosph3R to generate light curves in either 2D (with a day–night temperature gradient) representative of an ultra-hot Jupiter, or in 3D (with simulations of WASP-121b and WASP-39b) and studied how 1D models behave in retrieving such data. The 1D light curve retrieval model used is Juliet (Espinoza et al. 2019), which is based on the 1D light curve model batman (Kreidberg 2015).
Our conclusions are that the 2D day–night dichotomy of an ultra-hot Jupiter has two impacts on the light curve: 1) the planet's apparent radius decreases in the early and late stages of the transit, compared to the mid-transit, leading to a U-shaped light curve, and 2) the planet's apparent radius increases during the ingress and egress due to the day side obscuring the star longer than the night side.
The light curve's U shape due to the day–night thermal dichotomy may be confused with limb darkening. However, the limb-darkening coefficients depend on the wavelength, and could therefore be distinguished from the atmospheric signal in this way. East-west asymmetries might also enable this degeneracy to be broken.
Furthermore, we find that the atmospheric signal of a day–night strong temperature gradient has a signature opposite to the tidal deformation of the planet's core (not taking into account east–west asymmetries), and therefore the Love number retrieved by an ellipsoid model may be underestimated if the atmospheric signature in the light curve is not taken into account.
The east–west asymmetries of the ultra-hot Jupiter simulation (WASP-121b) are also visible in the light curve data, and will mostly translate as a shift in the time of the mid-transit (or central transit time) T0 for the light curve retrieval code. As the hot spot is shifted to the east in our simulation, the planet's apparent radius appears larger during the late (egress) stage compared to the early (ingress) stage. We included TiO/VO in our simulations. However, recent studies show that WASP-121b might be depleted in TiO/VO Hoeijmakers et al. (2024). This does not change the general conclusions of the study.
The east–west asymmetries are stronger in the case of the hot Jupiter WASP-39b, leading to a larger shift in the central transit time, T0, retrieved by the 1D retrieval model. This simulation of WASP-39b is linked to a shift that can be as large as 20 s and that varies from one wavelength to another. Between 1 and 5 μm, the amplitude of these variations is around 17 s. This is less than the real observations by JWST (Rustamkulov et al. 2023), which could be due to the chemistry or cloud structure in the atmosphere.
A very promising tool that could better describe the spatial deformations of the atmosphere comes under the form of transmission strings, namely harmonica (Grant & Wakeford 2022). In this tool, the planet's radius is described as a function of the angle around the limb, parameterized in terms of Fourier series. Further studies could investigate how well this model may retrieve a full 3D GCM light curve generated via Pytmosph3R.
 |
Fig. 18 Projection of an ellipsoid for early-, mid-, and late-transit phases (not to scale). This can be compared to Fig. 9. |
Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement n°679030/WHIPLASH). AF would also like to acknowledge financial support by LabEx UnivEarthS (ANR-10-LABX-0023 and ANR-18-IDEX-0001) and by the CNES (Centre National d'Études Spatiales).
Appendix A Area of intersection between transmittance cells and the stellar disk
The transmittance map is defined using the polar coordinate system, Γ𝒯, and a grid of Nr radial points and Nθ angular points. To properly evaluate the opacity of each cell in this grid, defined by its boundaries, (r1, r2, θ1, θ2), we need to calculate the surface of intersections between the star apparent disk and this cell 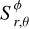 (see Eq. (2)). This is illustrated by Fig. A.1.
(see Eq. (2)). This is illustrated by Fig. A.1.
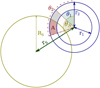 |
Fig. A.1 Area of intersection, A (in red), of one cell (r1, r2, θ1, θ2) in the transmittance grid with a stellar disk of radius Rs. The star center is located at (rs,θs). The coordinates follow the transmittance coordinate system Γ𝒯. |
The star's projected center is defined as the point at coordinates (rs, θs) in Γ𝒯. Its Cartesian coordinates are xs = D sin (θS) and ys = D cos(θS). The boundary of the stellar disk is defined as a circle of radius RS around that point. The points (0, 0), (rS, As) and (r, θ) form a triangle whose sides are equal to rS, r, and Rs. The law of cosines states:
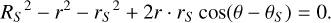 (A.1)
(A.1)
For a fixed angle, θ, we can rewrite Eq. (A.1) as
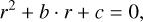 (A.2)
(A.2)
with b = −2r · rS cos (θ − θS) and с = rS2 − RS2, which is a polynomial equation of degree 2 that can easily be solved to get r. The angle, θ, can be computed from a fixed r by rewriting Eq. (A.1) as
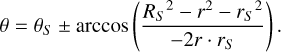 (A.3)
(A.3)
It should be noted that for both Eqs. (A.2) and (A.3), there are zero, one, or two solutions. We can apply Eqs. (A.2) and (A.3) to find all intersections of the star boundary (circle of radius RS) with the radial and angular points of the transmittance grid. A cell of the transmittance grid is defined using its boundaries, (r1, r2, θ1, θ2). The area of the cell (r1, r2, θ1, θ2) can be expressed as
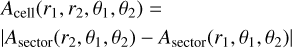 (A.4)
(A.4)
(see Fig. A.1 for an illustration of the intersection area). Therefore, following Eq. (A.4), we now reduced the problem to finding the area of a sector of the transmittance grid, Asector(r, θ1, θ2), as is illustrated in Fig. A.2. As is shown in this figure, this intersection can be expressed as the sum of simpler geometric objects, composed of circular segments and triangles. We express below the intersection for the maximum number of intersections. If an intersection is outside the sector, we can simply select the nearest corner instead. If there are no intersections (no solution to either Eq. (A.2) or Eq. (A.3)), two circular segments will join. Examples of such cases are shown in Fig. A.3.
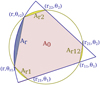 |
Fig. A.2 Intersection of one sector (r, θ1, θ2) of the transmittance grid (boundaries in blue) with the star (boundaries in yellow). The intersection area can be subdivided into the sum of circular segments (yellow when the circle is the star; blue when the circle is the planet) and triangles (subparts of A0, in red). Here, the maximum number of intersections has been displayed. Fig. A.3 shows examples of cases with fewer intersections. |
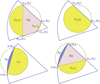 |
Fig. A.3 Examples of cases with fewer intersections between the sector (r, θ1, θ2) and the star. Some areas have merged together. |
The area of a triangle can be computed from its sides, a, b, and c, using Heron's formula:
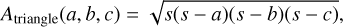 (A.5)
(A.5)
where s = (a + b + c)/2.
The area of a circular segment of angular width, α, for a circle of radius, R, is given by
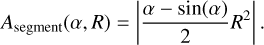 (A.6)
(A.6)
Finally, we consider the core of the planet to be completely opaque, and therefore the surface area of intersection of a core of radius RP with the stellar disk of radius RS, of which the centers are at a distance, rS, is equal to the area of intersection of two disks. If d ≥ RS + RP, then the surface area of intersection is zero. Otherwise, if d ≥ |RS − RP|, the surface is equal to the area of the smallest circle. Alternatively, we can use
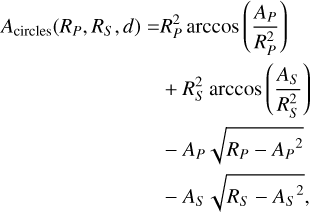 (A.7)
(A.7)
These equations are equivalent to Eq. (3) from Kreidberg (2015).
Appendix B Convergence and computational cost
We have previously validated the computation of transmission spectra in Pytmosph3R in Falco et al. (2022) by studying the stability of the model when changing the position of the observer in the frame of reference of the planet.
We have also validated our light curve implementation using batman in the case in which no atmosphere is present, but this comes down to validating the equations calculating the intersection area of two circles; that is, Eq. (A.7), or its equivalent, Eq. (3) in Kreidberg (2015).
We have in addition studied the convergence of the light curve module in Pytmosph3R. Studying a case that is symmetric along the star-observer axis (translation 2D day–night temperature map defined in Eq. (7), or 1D), the number of angular points in the transmittance map (Nθ) should have no effect on the resulting integral. We have observed an accuracy of less than 1 ppm for all Nθ in the 2D case of Table 1. The parameters used for generating light curves with Pytmosph3R are listed in Table B.1.
Pytmosph3R parameters used for generating light curves.
We have also introduced a number of transmittance maps, N𝒯, to calculate all along the transit in Sect. 2.2. For the rest of the Nϕ phases, the transmittance map is interpolated from the N𝒯 maps. We assume that the N𝒯 maps are regularly distributed in the phase space. This induces an error in the resulting light curve. Fig. B.1 shows the errors that one can expect when using a number of transmittance maps, N𝒯, that is too low for a hot Jupiter (2D study case of Table 1). With N𝒯 = 1, we can actually see the effect of not including rotation in the model, which is not negligible. This is discussed more at length in Sect. 4.2.
 |
Fig. B.1 Increasing the number of steps in which we compute the transmittance increases the accuracy of the computed light curve. The legend indicates the number of transmittance maps, N𝒯, used, as well as their difference to N𝒯 = 20 and the corresponding standard deviation. The standard deviation for N𝒯 = 8 is less than 1 ppm and is therefore an acceptable number compared to current instrumental errors (Rustamkulov et al. 2023). The 2D study case was used for this experiment (Table1). |
Computing one transmittance map scales with the number of molecules, the spectral resolution, and the atmospheric resolution used. We can see in Fig. B.2 how interpolating between the N𝒯 transmittances can prove to be very effective.
Overall, N𝒯 = 8 seems to be an acceptable trade-off between computational time and accuracy. It even seems acceptable to use N𝒯 = 5, though this might prove to be inadequate in some cases.
 |
Fig. B.2 Cost of increasing the number of transmittances N𝒯 computed for 30000 wavelengths. The 2D study-case has been used for this experiment (Table 1). |
Appendix C Time or phase resolution in light curve retrieval
When generating a light curve with Pytmosph3R, the default option will discretize the ingress or egress with a higher resolution (in the time, or phase, dimension), compared to the rest of the transit, as a trade-off between accuracy and computational time. We therefore discuss here the difference between light curves:
generated using Pytmosph3R with no resampling, here with parameters from Table B.1; that is, Negress = 30 and Nϕ = 100, and
interpolated from the above over Nϕ = 300 equally distributed phases.
The values retrieved by Juliet are shown in Fig. C.1 for both cases, and the corresponding light curves are shown in Fig. C.2.
The egress or ingress (which lasts a shorter amount of time than the rest of the transit) is overrepresented from a statistical point of view in case one. This leads to a bias in the retrieval, in which the algorithm will try to minimize the egress or ingress more that the rest of the transit. To avoid this statistical bias, we can interpolate the signal over a finer phase grid, or we can change the weight of each point using the error bars used in the retrieval. We have used the first method here, though they are equivalent from a statistical point of view.
We can see that in case one in Fig. C, the apparent radius during the main transit (when the planet, including its atmosphere, is fully in front of the star, excluding the ingress or egress) is underestimated by Juliet by more than 50 ppm at 0.6 μm. This is more than the maximum residual during the ingress or egress, though this varies from wavelength to wavelength.
 |
Fig. C.1 Values retrieved by Juliet for the light curve generated by Pytmosph3R in the 3D case (Fig. 4), without rotation, at wavelengths 0.6, 1, 3, 3.9, and 7 μm. The parameters for the retrieval are described in Table 2. The parameters for the input light curve (Pytmosph3R) are given in Table B.1. Top: Negress = 30 and Nϕ = 100. Bottom: Interpolation over Nϕ = 300 phases. |
In case two (Fig. C), the maximum residual always occurs during ingress or egress, and more precisely when only a small portion is either in front or out of the star (due to the atmosphere opacity, in a similar way as is explained in Fig. 3 and Fig. 2).
 |
Fig. C.2 Comparison between Pytmosph3R, batman (T0 = 0), and Juliet (values retrieved in Fig.C.1). For each subfigure: Left: Light curves generated by Pytmosph3R (dashed line) compared to Juliet (solid line). Right: Residuals of batman (blue) and Juliet (orange) compared to Pytmosph3R. The residual of Juliet is lower on average than that of batman, mainly because of the shift in T0. Using Negress = 30 and Nϕ = 100 leads to a statistical overrepresentation of the egress or ingress in the retrieval, which can be corrected using an interpolation over Nϕ = 300 phases (see Fig. C.2). |
In conclusion, we highly recommend that a user of Pytmosph3R be aware of this statistical bias. When computing a light curve with a higher resolution over the ingress or egress (for computational reasons), one should always either interpolate it over an equally distributed sample, or change the error bars accordingly, before using it in retrieval methods.
This study does not take into account other biases that unfold when changing the temporal binning of light curves and we refer interested readers to Kipping (2010) for more information.
References
- Akinsanmi, B., Barros, S. C. C., Santos, N. C., et al. 2019, A&A, 621, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Akinsanmi, B., Boué, G., et al. 2022, A&A, 658, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Caldas, A. 2018, PhD thesis, Université de Bordeaux, France [Google Scholar]
- Caldas, A., Leconte, J., Selsis, F., et al. 2019, A&A, 623, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnay, B., Meadows, V., Misra, A., Leconte, J., & Arney, G. 2015, ApJ, 813, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Chubb, K. L., & Min, M. 2022, A&A, 665, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drummond, B., Tremblin, P., Baraffe, I., et al. 2016, A&A, 594, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drummond, B., Mayne, N. J., Manners, J., et al. 2018, ApJ, 869, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., & Jones, K. 2021, AJ, 162, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., Kossakowski, D., & Brahm, R. 2019, MNRAS, 490, 2262 [Google Scholar]
- Falco, A., Zingales, T., Pluriel, W., & Leconte, J. 2022, A&A, 658, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortney, J. J., Shabram, M., Showman, A. P., et al. 2010, ApJ, 709, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, D., & Wakeford, H. R. 2022, MNRAS, 519, 5114 [Google Scholar]
- Hellard, H., Csizmadia, S., Padovan, S., Sohl, F., & Rauer, H. 2020, ApJ, 889, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., Frierson, D. M. W., & Phillipps, P. J. 2011, MNRAS, 418, 2669 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Kitzmann, D., Morris, B. M., et al. 2024, A&A, in press https://doi.org/10.1051/0004-6361/202244968 [Google Scholar]
- Jones, K., & Espinoza, N. 2020, J. Open Source Softw., 5, 2382 [NASA ADS] [CrossRef] [Google Scholar]
- Kataria, T., Sing, D. K., Lewis, N. K., et al. 2016, ApJ, 821, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [Google Scholar]
- Konings, T., Baeyens, R., & Decin, L. 2022, A&A, 667, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
- Kreidberg, L. 2018, in Handbook of Exoplanets, eds. H. J. Deeg, & J. A. Belmonte, 100 [Google Scholar]
- Leconte, J., Forget, F., Charnay, B., et al. 2013, A&A, 554, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Line, M. R., & Parmentier, V. 2016, ApJ, 820, 78 [Google Scholar]
- MacDonald, R. J., & Lewis, N. K. 2022, ApJ, 929, 20 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, R. J., Goyal, J. M., & Lewis, N. K. 2020, ApJ, 893, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L. 2016, A&A, 591, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menou, K., & Rauscher, E. 2009, ApJ, 700, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, M. C., & Madhusudhan, N. 2022, ApJ, 935, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, V., Fortney, J. J., Showman, A. P., Morley, C., & Marley, M. S. 2016, ApJ, 828, 22 [Google Scholar]
- Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pluriel, W., Zingales, T., Leconte, J., & Parmentier, V. 2020, A&A, 636, A66 [EDP Sciences] [Google Scholar]
- Pluriel, W., Leconte, J., Parmentier, V., et al. 2022, A&A, 658, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinoth, B., Hoeijmakers, H. J., Pelletier, S., et al. 2023, A&A, 678, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rustamkulov, Z., Sing, D. K., Mukherjee, S., et al. 2023, Nature, 614, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., Cooper, C. S., Fortney, J. J., & Marley, M. S. 2008, ApJ, 682, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Fortney, J. J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, X., & Komacek, T. D. 2019, ApJ, 886, 26 [Google Scholar]
- Tsiaras, A., Waldmann, I. P., Rocchetto, M., et al. 2016, ApJ, 832, 202 [NASA ADS] [CrossRef] [Google Scholar]
- von Paris, P., Gratier, P., Bordé, P., Leconte, J., & Selsis, F. 2016, A&A, 589, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardenier, J. P., Parmentier, V., & Lee, E. K. H. 2022, MNRAS, 510, 620 [Google Scholar]
- Wordsworth, R. D., Forget, F., Selsis, F., et al. 2011, ApJ, 733, L48 [Google Scholar]
- Zingales, T., Falco, A., Pluriel, W., & Leconte, J. 2022, A&A, 667, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Ray of light crossing the atmosphere of WASP-121b. The color map indicates the local temperature, ranging from around 400 K (in blue) to 3300 K (in red). The inflation of the day side is directly due to the increase in the scale height (due to the hydrostatic equilibrium). This simulation includes a super-rotating equatorial jet (visible in gray). |
| In the text | |
 |
Fig. 2 Projected opacity of a planet on the observer's field of view when considering (or not) an atmosphere. Left: diffuse opacity due to atmospheric content (Pytmosph3R). Right: homogeneously opaque solid sphere approximation (batman). |
| In the text | |
 |
Fig. 3 Relative flux (Eq. (2)) at a wavelength, λ = 7μm, of the spherical approximation (batman) compared to the diffuse opacity of a 1D (Table 1) atmospheric simulation (Pytmosph3R) (see Fig. 2 for the schematics). The effect is similar in the case of a 2D day–night (Table 1) simulation (Pytmosph3R) without rotation (i.e., N𝒯 = 1). The same effect holds true in 3D cases, since the opacity of each case will decrease with the altitude, although it will be dominated by other effects. |
| In the text | |
 |
Fig. 4 Temperature maps of WASP-121b. Top: high-altitudinal cut. Bottom: equatorial cut, for which the atmosphere scale has been multiplied by ten for visual reasons. In this simulation, the hot spot is slightly shifted to the east. |
| In the text | |
 |
Fig. 5 Abundance maps of WASP-121b. Top: H2O. Middle: CO. Bottom: TiO. All are equatorial cuts, for which the atmosphere scale has been multiplied by ten for visual reasons. |
| In the text | |
 |
Fig. 6 Temperature maps for hot Jupiter WASP-39b. Top: latitude–longitude map, at an altitude of 7772 km. Bottom: equatorial slice. The simulation goes up to an altitude of 29 950 km. |
| In the text | |
 |
Fig. 7 Difference between the flux (Eq. (2)) of a 1D solid sphere (batman) and the flux of a 3D simulation of an ultra-hot Jupiter (Pytmosph3R) without rotation (i.e., N𝒯 = 1). The ultra-hot Jupiter is WASP-121b (Fig. 4). The x axis shows the wavelength; the y axis shows the transit phase. |
| In the text | |
 |
Fig. 8 Residuals between translation (N𝒯 = 1) and rotation (N𝒯 = 8) fluxes. Top: WASP-39b (Fig. 6). Middle: two-dimensional day–night gradient (Table 1). The east–west symmetry leads to the signal being identical at phases ϕ and −ϕ. Bottom: WASP-121b (Fig. 4). The x axis shows the wavelength; the y axis shows the transit phase. |
| In the text | |
 |
Fig. 9 Transmittance maps for phases −13, 0, and 13°, i.e., early-, mid-, and late-transit, respectively, at λ = 0.6 μm of WASP-121b. The atmosphere scale has been multiplied by ten for visual reasons. The inner black circle represents the planet core. The total apparent surface is greater at mid-transit due to the hot day side being apparent all around the limb. The night side is more apparent during the early and late stages (lower scale height). |
| In the text | |
 |
Fig. 10 Time of inferior conjunction, T0, retrieved by Juliet for the tidally locked hot Jupiter WASP-39b (top) and the ultra-hot Jupiter WASP-121b (bottom, including legend) for wavelengths from 1 to 5 μm, at a resolution similar to NIRSpec. In the case of WASP-121b, three cases are displayed (indicated by the colors): 1) the light curve of the 3D simulation of WASP-121b without rotation (i.e., translation) in orange, 2) the same including rotation in blue, and 3) a 2D day–night temperature gradient (symmetric transit) in green. |
| In the text | |
 |
Fig. 11 Values retrieved by Juliet for (RP/RS)2 of WASP-39b in the translation case (in orange; the planet does not rotate during the transit), the rotation case (in blue), and the input value of (RP/RS)2 at mid-transit (in black). Error bars are included (less than 1 ppm). |
| In the text | |
 |
Fig. 12 Values retrieved by luliet for (Rp/Rs)2 of the 2D day–night gradient in the rotation case (see Sect. 5.4), the same when also retrieving limb-darkening (LD) coefficients (see Sect. 6), and the input value of (RP/RS)2 at mid-transit (in black). |
| In the text | |
 |
Fig. 13 Same as Fig. 12 for WASP-121b, but with the retrievals of the rotation and translation cases (discussed in Sect. 5.4) and the retrieval using limb darkening (discussed in Sect. 6). |
| In the text | |
 |
Fig. 14 Light curves for the two-dimensional rotation case. Left: light curves generated by Pytmosph3R (dashed line) compared to the fit provided by Juliet (solid line, with retrieved values for T0 and RP). Right: residuals of Juliet (orange) to Pytmosph3R, with batman (assuming T0 = 0 and RP taken at mid-transit from Pytmosph3R) given as a reference. It should be noted that Juliet itself uses batman as a forward model; the difference only comes from the retrieved values of T0 and RP. |
| In the text | |
 |
Fig. 15 Light curves retrieved with limb-darkening (Juliet) and without (batman) and residuals. For each case (2D day–night and WASP-121b): Left: light curves generated by Pytmosph3R (dashed line) compared to Juliet (solid line, with retrieved limb darkening, T0 and RP). Right: residuals of Juliet (orange) to Pytmosph3R, with batman (no limb darkening, T0 = 0 and RP taken at mid-transit from Pytmosph3R) given as a reference. |
| In the text | |
 |
Fig. 16 Values retrieved by Juliet for the limb-darkening coefficients, q1 and q2, in the 2D day–night gradient case and WASP-121b. The scale for q2 (indicated on the right) is different in the two plots. |
| In the text | |
 |
Fig. 17 Ellipsoid light curves compared to light curves generated via Pytmosph3R (i.e., spherical core, but atmospheric envelope). Rotation is taken into account for both methods. Left: light curves generated by Pytmosph3R (dashed line) compared to the spherical model (dotted line) and the ellipsoid model (solid line). Right: residuals of the spherical model (Sphere) versus Pytmosph3R (P3) and the ellipsoid model (Love). |
| In the text | |
 |
Fig. 18 Projection of an ellipsoid for early-, mid-, and late-transit phases (not to scale). This can be compared to Fig. 9. |
| In the text | |
 |
Fig. A.1 Area of intersection, A (in red), of one cell (r1, r2, θ1, θ2) in the transmittance grid with a stellar disk of radius Rs. The star center is located at (rs,θs). The coordinates follow the transmittance coordinate system Γ𝒯. |
| In the text | |
 |
Fig. A.2 Intersection of one sector (r, θ1, θ2) of the transmittance grid (boundaries in blue) with the star (boundaries in yellow). The intersection area can be subdivided into the sum of circular segments (yellow when the circle is the star; blue when the circle is the planet) and triangles (subparts of A0, in red). Here, the maximum number of intersections has been displayed. Fig. A.3 shows examples of cases with fewer intersections. |
| In the text | |
 |
Fig. A.3 Examples of cases with fewer intersections between the sector (r, θ1, θ2) and the star. Some areas have merged together. |
| In the text | |
 |
Fig. B.1 Increasing the number of steps in which we compute the transmittance increases the accuracy of the computed light curve. The legend indicates the number of transmittance maps, N𝒯, used, as well as their difference to N𝒯 = 20 and the corresponding standard deviation. The standard deviation for N𝒯 = 8 is less than 1 ppm and is therefore an acceptable number compared to current instrumental errors (Rustamkulov et al. 2023). The 2D study case was used for this experiment (Table1). |
| In the text | |
 |
Fig. B.2 Cost of increasing the number of transmittances N𝒯 computed for 30000 wavelengths. The 2D study-case has been used for this experiment (Table 1). |
| In the text | |
 |
Fig. C.1 Values retrieved by Juliet for the light curve generated by Pytmosph3R in the 3D case (Fig. 4), without rotation, at wavelengths 0.6, 1, 3, 3.9, and 7 μm. The parameters for the retrieval are described in Table 2. The parameters for the input light curve (Pytmosph3R) are given in Table B.1. Top: Negress = 30 and Nϕ = 100. Bottom: Interpolation over Nϕ = 300 phases. |
| In the text | |
 |
Fig. C.2 Comparison between Pytmosph3R, batman (T0 = 0), and Juliet (values retrieved in Fig.C.1). For each subfigure: Left: Light curves generated by Pytmosph3R (dashed line) compared to Juliet (solid line). Right: Residuals of batman (blue) and Juliet (orange) compared to Pytmosph3R. The residual of Juliet is lower on average than that of batman, mainly because of the shift in T0. Using Negress = 30 and Nϕ = 100 leads to a statistical overrepresentation of the egress or ingress in the retrieval, which can be corrected using an interpolation over Nϕ = 300 phases (see Fig. C.2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.