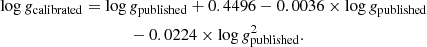EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 684 (April 2024) A&A, 684 (2024) A70 Full HTML
Open Access
Issue
A&A
Volume 684, April 2024
Article Number A70
Number of page(s) 18
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202348336
Published online 05 April 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Mechanisms of formation and evolution of our Galaxy are strongly encoded into the kinematics, chemistry, and ages of its stars. The chemical elements synthesised in stellar interiors and ejected through stellar winds and late-stage ejection mechanisms like explosions add new ingredients to the interstellar medium (ISM) for the next stellar generations, driving the chemical evolution of the Milky Way. The stellar yields vary as a function of the nucleosynthesis paths stars of different initial masses and metallicities go through, of the mass loss efficiency along their lifetimes, and of how much the ejected layers are contaminated by the nucleosynthesis products, which strongly depends on the way chemicals are transported (mixed) in stellar interiors. Stars rarely exhibit their initial chemical compositions because of different types of in situ (magneto-)hydrodynamical mixing processes that can modify their internal and surface chemical properties along their nucleosynthetic life as well as the main stellar parameters and lifetimes (e.g. Vauclair et al. 1978; Charbonnel 1995; Palacios et al. 2003; Talon et al. 2006; Lagarde et al. 2012a; Maeder et al. 2014; Pignatari et al. 2016; Limongi & Chieffi 2018; Deal et al. 2020; Bouret et al. 2021; Dumont et al. 2021; Guerço et al. 2022). Understanding these mixing processes is crucial for stellar physics and Galactic archeology, with unique and complementary constraints coming from the large Galactic astrometric, spectroscopic, and asteroseismic surveys that are presently revolutionizing our knowledge of the links between Galactic and stellar evolution (e.g. Miglio et al. 2021; Lagarde et al. 2021).

High-precision astrometric data, including trigonometric parallaxes as well as abundances of certain chemical elements for nearly 5.6 million stars provided by Gaia (Gaia Collaboration 2021; Recio-Blanco et al. 2023), offer exclusive information on the position of stars in the Hertzsprung–Russel diagram (HRD) and on their membership in different Galactic populations. Spectroscopic surveys provide chemical abundances and radial velocities for stars in different populations in our Galaxy (e.g. Gaia-ESO survey Gilmore et al. 2022; Randich et al. 2022; APOGEE Majewski et al. 2017; GALAH Buder et al. 2021). Finally, asteroseismology provides key information on the internal structure of the stars, and hence on the age, evolutionary stage, and mass, through the detection of rich oscillation spectra (including non-radial oscillation modes; e.g. Baglin et al. 2006; Borucki et al. 2010; Chaplin & Miglio 2013). For the first time we have the ability to obtain (1) very precise stellar gravity values (typically one order of magnitude more precise than currently achievable by high-resolution spectroscopy of bright stars); (2) precise estimates of the stellar masses and radii of giant stars, which can be used to infer precise distances for field stars; (3) more accurate (model-dependent) age estimates of giant stars even several kiloparsecs from the sun. The major spectroscopic surveys have taken care to observe the stars in the asteroseismic surveys, for example with the APOKASC consortium pointing to the Kepler stars observed by APOGEE (Pinsonneault et al. 2018), CoRoGEE (CoRoT+APOGEE, Anders et al. 2017a,b), RAVE+K2 (Valentini et al. 2019), CoRoGES (CoRoT+Gaia-ESO, Valentini et al. 2016), or APO-K2 (Schonhut-Stasik et al. 2024). For both (and related) stellar and galactic objectives, we can thus start to use golden stellar samples for which astrometric, spectroscopic, and seismic data can be combined for stars of different masses, metallicities, and evolutionary stages (e.g. Lagarde et al. 2015, 2021; Montalbán et al. 2021).

For this study we built for the first time a golden sample to probe the mixing processes that have been revealed to occur in low- and intermediate-mass red-giant-branch (RGB) stars by previous spectroscopic observations of light elements such as lithium, carbon, and nitrogen in samples without asteroseismic coverage (e.g. Charbonnel & Balachandran 2000; Smiljanic et al. 2009, 2010; Charbonnel et al. 2020; Mikolaitis et al. 2010; Tautvaišienė et al. 2013; Lagarde et al. 2015; Takeda et al. 2019; Magrini et al. 2021). We focus on the best chemical indicator to constrain the mixing efficiency in giant stars, namely the carbon isotopic ratio (e.g. Dearborn et al. 1976; Brown & Wallerstein 1989; Smith & Suntzeff 1989; Bell et al. 1990; Gilroy & Brown 1991; Gratton et al. 2000; Charbonnel et al. 1998; Tautvaišienė et al. 2010, 2013; Morel et al. 2014; Takeda et al. 2019; McCormick et al. 2023; Aguilera-Gómez et al. 2023). To the best of our knowledge, only four giant field stars with asteroseismic diagnostics coming from the CoRoT satellite and measured carbon isotopic ratios are available in the literature (Morel et al. 2014). Previous spectroscopic studies have shown that the atmospheric value of this quantity first changes during the first dredge-up (1DUP) on the subgiant branch, when the deepening convective envelope engulfs the 13C peak that was built inside the stars through the CNO cycle during the main sequence (e.g. Iben 1967; Charbonnel 1994). The amplitude of the decrease in the 12C/13C ratio then depends on the stellar mass and metallicity, and on rotation-induced mixing while the star was on the main sequence (e.g. Charbonnel & Lagarde 2010). The surface 12C/13C ratio drops again later, together with the Li abundance and the C/N ratio when the stars move across the so-called RGB bump (e.g. Fusi Pecci et al. 1990; Charbonnel 1994). To date, the only explanation for this second pattern that is not predicted in classical stellar evolution models is the thermohaline instability or double-diffusive mixing process (Charbonnel & Zahn 2007a). Simplified prescriptions for this mechanism (Kippenhahn et al. 1980) in 1D stellar evolution models explain the observed behaviour of the carbon isotopic ratio together with that of Li, C, and N in field and open cluster RGB stars with various masses and metallicities (Charbonnel & Lagarde 2010; Lagarde et al. 2012a). Some other 1D models challenge its ability to explain simultaneously the behaviour of these three indicators, in particular in low-metallicity globular cluster red giants (e.g. Angelou et al. 2011; Henkel et al. 2017; Tayar & Joyce 2022; but see also Fraser et al. 2022). Additionally, multi-D hydrodynamical models points towards lower efficiency of this mechanism in stellar interiors than expected to explain the observations (e.g. Denissenkov 2010; Denissenkov & Merryfield 2011; Traxler et al. 2011; Brown et al. 2013), while in specific conditions other effects induced by rotation and magnetic field might significantly enhance the fingering transport rate (Sengupta & Garaud 2018; Harrington & Garaud 2019; Fraser et al. 2023). Since the thermohaline instability is also expected to significantly lower the amount of 3He released by low- and intermediate-mass stars as required by Galactic evolution models (Charbonnel & Zahn 2007a,b; Lagarde et al. 2011, 2012b; see also Eggleton et al. 2006), it is fundamental to better understand if, how, and by how much this mechanism actually modifies the surface composition of red giants and their chemical yields.

Our study deals with both observational and theoretical aspects. First, we present the carbon isotopic ratios and CNO abundances we determined from our spectroscopic observations of 71 giant stars previously observed by the Kepler satellite during its four-year run. The asteroseismic properties of these objects (such as Δν, νmax, and ΔΠℓ = 1) are also available, allowing a precise determination of their mass, radius, age, and evolutionary stage. This sample is therefore the largest sample of stars for which surface properties from spectroscopy including the carbon isotopic ratio and internal properties from asteroseismology are available. Thanks to the Gaia satellite, the kinematics of these stars is also accessible, making it the best characterised RGB sample so far. Then, we compare our observations and additional data from the literature to the predictions of stellar evolution models computed with the code STAREVOL (e.g. Lagarde et al. 2012a; Amard et al. 2019), taking into account the thermohaline instability. For this comparison we use the Besançon Galaxy model (hereafter BGM), a state-of-the-art Galactic stellar population synthesis model (Lagarde et al. 2017), to compute mock catalogues that we statistically compare to our data.

The paper is structured as follows. In Sect. 2 we present the spectroscopic and atmospheric characterisation for our sample stars. In Sect. 3 we present complementary properties of our sample coming from the Kepler and Gaia satellites, and we present the literature data gathered to probe the behaviour of the carbon isotopic ratio over the largest possible range of [Fe/H] and mass. In Sect. 5 we discuss the efficiency of extra-mixing on the RGB comparing our observations with the theoretical trends provided by the BGM simulations described in Sect. 4. Our conclusions are presented in Sect. 6.

2. Observations and spectral analysis

To construct our golden sample, we chose to observe field stars at two different evolutionary phases: during the central helium-burning phase and on the RGB at a lower luminosity than the RGB bump (see Sect. 3.1).

2.1. Observations

We performed two observing runs using the high-resolution FIbre-fed Echelle Spectrograph (FIES; Telting et al. 2014) on the Nordic Optical Telescope (NOT). We used the medium-resolution configuration (R = 46 000), which provided a large continuous wavelength range from about 4100 to 8500 Å. It contains the forbidden [O I] line, C2 bands, strong 12C14N features, and the 13C14N line at 8004 Å suitable to determine the C/N and 12C/13C ratios (see Sect. 2.2). The first run, from June 27 to July 2, 2018, under the programme P57-105, was dedicated to the observation of 41 stars with masses < 1.5 M⊙. On the second run, from July 25 to 28, 2019, under the programme P59-103, we completed our observations targeting more massive (1.5–2.2 M⊙) and low-metallicity stars ([Fe/H] < −0.2). The observed targets are listed in Table B.1. The exposure times were chosen to obtain a signal-to-noise ratio of 80 or higher. We performed the data reduction with the dedicated software (FIEStool) available at the telescope. FIEStool provides a fully reduced spectrum using the nightly calibration frames.

2.2. Spectral analysis

In this work, we used an equivalent widths method for the determination of the main stellar atmospheric parameters and a spectral synthesis approach for the determination of the abundances of chemical elements. Both analysis techniques make use of the one-dimensional, plane-parallel, local thermodynamical equilibrium (LTE) model stellar atmospheres MARCS (Gustafsson et al. 2008), the Gaia-ESO linelist (Heiter et al. 2015), and solar abundances by Grevesse et al. (2007).

2.2.1. Atmospheric parameters

For the determination of the main atmospheric parameters, we adopted a two-step approach. At first we used the classical equivalent widths method, which is based on the analysis of Fe I and Fe II atomic lines. The equivalent widths were measured with a DAOSPEC code (Stetson & Pancino 2008), and then the abundances were calculated using a MOOG code (Sneden 1973). The initial iron line list included 112 Fe I and 15 Fe II lines. The line list was carefully compiled to avoid blended and strong lines; we discarded lines that were larger than 150 mÅ in observed stars. On average 103 Fe I and 13 Fe II lines remained and were used for the analysis. The available Fe II lines are usually scarce and weak in comparison to the Fe I, and their measurements greatly influence the determination of log g. Surface gravities are considered to be more accurate when determined from asteroseismic properties (Morel & Miglio 2012; Creevey et al. 2013). Thus, in the second step, we determined stellar surface gravities using the Kepler asteroseismic data from Mosser et al. (2012) and the spectroscopic effective temperatures calculated in our work during the first step. Then we fixed the asteroseismic log g value and re-determined the other parameters to get the required balance of abundances from the Fe I lines in relation to their excitation potential and equivalent widths. This way, we eliminated the weakest point of spectroscopic analysis, which is the accurate log g determination. The difference between purely spectroscopic parameters and those that had fixed asteroseismic log g values are plotted in Fig. 1. No clear trends can be observed in the comparisons of surface gravity or effective temperature. The average differences are −33 ± 36 (K) for effective temperatures and −0.10 ± 0.09 (dex) for the surface gravity.

2.2.2. Abundance determination

For the spectral analysis we used a differential model atmosphere technique. The spectral synthesis was performed to determine the carbon, nitrogen, oxygen, and magnesium abundances, and in determining the carbon isotopic ratios. The calculations were performed using a TURBOSPECTRUM code (Alvarez & Plez 1998). For the carbon abundance determination we used two regions: the C2 Swan (0,1) band head at 5135.5 Å and the C2 Swan (0,1) band head at 5635.2 Å. The 12C/13C ratio was obtained from the 13C/12N feature at 8004.7 Å. An interval of 6470–6490 Å and of 7980–8005 Å, with up to seven strong 12C/14N features was used to determine nitrogen abundances. The forbidden [O I] line at 6300.31 Å was used for the oxygen abundance derivation. This oxygen line is blended by 58Ni and 60Ni. The oscillator strength values for these two nickel lines were taken from Johansson et al. (2003). In several cases the oxygen line at 6300.31 Å was contaminated by the telluric absorption line and could not be used for the investigation of oxygen abundance. As C and O abundances are bound together, when the oxygen abundance was unavailable the magnesium abundance was used as a proxy to determine carbon and nitrogen abundances. The spectral synthesis of three spectral lines at 5711.1, 6318.7, and 6319.2 Å was used for the Mg abundance determination.

Synthetic spectra were calibrated to the solar spectrum by Kurucz (2005) with log A⊙(C) = 8.39, log A⊙(N) = 7.78, log A⊙(O) = 8.66, log A⊙(Mg) = 7.53, and log A⊙(Fe) = 7.45 taken from Grevesse et al. (2007). Solar atmospheric parameters were taken from Pavlenko et al. (2012): Teff = 5777 K, log g = 4.44, [Fe/H] = 0.00, vt = 0.75 km s−1, v sin i = 1.6 km s−1. The calibration required slight changes to the log gf values of the original line list. Several examples of the synthetic spectra fits are presented in Figs. 2–4.

thumbnail Fig. 1.

Comparison of effective temperatures, surface gravities and metallicities determined during the first (spectroscopic) and the second (asteroseismic) steps of the parameter determination process.

thumbnail Fig. 2.

Examples of fits to the carbon and oxygen lines in a spectrum of KIC4457200. The middle line represents the best fit for [C/H] = 0.01 and [O/H] = 0.12, whereas the other two lines indicate ±0.10 dex for the corresponding abundances.

thumbnail Fig. 3.

Examples of fits to the 12C14N and 13C14N molecular lines in a spectrum of KIC4457200. The middle line represents the best fit for 12C/13C = 12, whereas the other two lines indicate ±2 in the 12C/13C ratio.

thumbnail Fig. 4.

Example of fits to the magnesium lines for KIC4457200. The middle line represents the best fit for [Mg/H] = 0.22, whereas the other two lines indicate ±0.10 dex for the magnesium abundance.

Figure 5 shows the differences for A(C), A(N), and A(O) abundances determined from spectroscopic and seismic atmospheric parameters. The differences do not exceed the uncertainties of the method of abundance determinations (lower than 0.5%), and there is no visible impact on the 12C/13C value.

thumbnail Fig. 5.

Differences in abundances of C, N, and O derived using the spectroscopic and asteroseismic atmospheric parameters.

2.2.3. Evaluation of uncertainties

The calculated medians of asteroseismic atmospheric parameter determination errors in our stellar sample are σTeff = 51 K, σlog g = 0.22 dex, σ[Fe/H] = 0.11 dex, and σvt = 0.22 km s−1. In Table 1 we present changes in abundances caused by the median values of atmospheric parameter determination errors of each individual atmospheric parameter, calculated keeping other parameters fixed. For this investigation we took KIC7366121, which has Teff = 4806 K, log g = 2.56 dex, [Fe/H] = −0.10 dex, and vt = 1.4 km s−1.

Table 1.

Effects on the derived chemical abundances and abundance ratios resulting from uncertainties in atmospheric parameters and abundances.

Carbon, nitrogen, and oxygen are bound by the molecular equilibrium in the stellar atmospheres, and therefore these chemical elements require a more detailed analysis. We started from derivations of carbon and oxygen abundances and iterated this operation until the determinations of carbon and oxygen abundances converged. Finally the abundance of nitrogen was derived using both carbon and oxygen values. An error in one of the elements bounded by the molecular equilibrium (carbon, nitrogen, or oxygen) typically influences the abundance determination of another, as well as measurement of C/N and 12C/13C ratios. These effects are also presented in Table 1. As expected, only the oxygen abundance exhibits a larger sensitivity to surface gravity variations, and the C/N ratio is sensitive to variations of C and N abundances. Other values are not very sensitive to uncertainties.

2.3. Comparisons with other studies

In this section we present a comparison between our derivations and the abundances published in the literature.

APOGEE DR17 catalogue. For comparison with the APOGEE data, we used the clean and calibrated abundances which verify the following: Fifty-three stars in our sample are in common with the APOGEE data release 17 catalogue (Abdurro’uf et al. 2022). Solar abundances from Grevesse et al. (2007) are used to derived surface abundances such as [C/Fe], [N/Fe], [O/Fe], and [M/Fe].

FE_H_FLAG=0 AND
C_FE_FLAG=0 AND
N_FE_FLAG=0 AND
O_FE_FLAG=0 AND
MG_FE_FLAG=0.

Gaia catalogue. Our sample has 70 stars in common with the Gaia DR3 catalogue (Gaia Collaboration 2023a). Using the quality flags on the global parameters and on the abundances given in Gaia Collaboration (2023b) and Recio-Blanco et al. (2023), we only selected stars with the best determinations of [N/Fe], [Mg/Fe], and [Fe/H]1. We used the following criteria (Astronomical Data Query Language (ADQL) queries used in this study are presented in Appendix A):

3500<Teff<7000 & 0<log g<5 AND
vbroadT=0 & vbroadG=0 & vbroadM=0 AND
vradT=0 & vradG=0 & vradM=0 AND
fluxNoise=0 & extrapol<3 & KMtypestars<2 AND
NegFlux=0 & nanFlux=0 & emission=0 &
nullFluxErr=0

For [N/Fe]:
NUpLim<2 & NUncer=0 AND
nfe_gspspec_nlines>=2 AND
nfe_gspspec_linescatter<0.1 AND
[N/Fe]_unc<0.15

For [Mg/Fe]:
MgUpLim<2 & MgUncer=0 AND
[Mg/Fe]_unc<0.2

For [Fe/H]:
FeUpLim<2 & FeUncer=0 AND
[M/H]_unc<0.2.

Sixty-two stars verify the selection criteria for the iron abundance, 19 stars for the magnesium abundance, and 15 for the nitrogen abundance. The abundances were derived using Grevesse et al. (2007) solar abundances. As proposed by Recio-Blanco et al. (2023) we applied a correction to the Gaia published abundances of [N/Fe], [Mg/Fe], and [Fe/H], and of log g (see Appendix A).

PASTEL sample. Twenty stars in our sample are in common with the last release of PASTEL catalogue (Soubiran et al. 2022).

LAMOST DR7 catalogue. Eight stars in our sample are in common with the LAMOST data release 7 catalogue (Luo et al. 2022).

Figure 6 shows the differences between the abundance determinations published in the literature using spectra coming from different large surveys and those derived in this study. This comparison is done for [Fe/H], [C/H], [N/H], [O/H], and [Mg/H] abundance ratios and for log g and Teff. We note a good agreement between our log g and Teff determination with those of previous studies excepted for the Gaia DR3 catalogue. This implies a close agreement (within ±0.2 dex) for the abundances. However, we note that our [O/H] and [Mg/H] abundances are systematically higher than those of the other surveys. Considering the [Fe/H] ratio, the median differences are around 0.01–0.02 dex according to the APOGEE DR17, LAMOST DR7, and PASTEL surveys, while the difference is larger considering the Gaia DR3 catalogue (0.095 dex). A slight overabundance of carbon is visible in the LAMOST survey. The biggest difference is visible between the value of [N/H] determined by Gaia DR3 and our study with a median difference around −0.20 dex. Nevertheless, our study seems to be in agreement with the APOGEE and LAMOST spectroscopic surveys for this element. Thus, the Gaia [N/Fe] values should therefore be treated with caution, and an additional calibration would probably be necessary (cf. de Laverny, P., et al., priv. comm.). In the Gaia survey, the nitrogen calibration is based on a small number of reference stars.

thumbnail Fig. 6.

Differences between [X/H], log g, and Teff coming from the literature and derived in this study. The comparisons are done using the Gaia DR3 (blue stars), APOGEE DR17 (green circles), LAMOST DR7 (orange squares), and PASTEL (purple diamonds) catalogues. The shaded regions indicate ±0.2 dex and ±100 K.

3. Overview of the stellar sample

3.1. Asteroseismic properties

The first asteroseismic quantities available for our sample is the average large separation, Δν, which is expected to be proportional to the square root of the mean stellar density (e.g. Ulrich 1986). The frequency νmax at which the oscillation modes reach their strongest amplitudes is approximately proportional to the acoustic cut-off frequency (e.g. Brown et al. 1991; Belkacem et al. 2011) is also available. We use the large frequency separation Δν, and the frequency corresponding to the maximum observed oscillation power νmax to determine the stellar radius and mass of our solar-like oscillating giants. We used the code PARAM (Rodrigues et al. 2017) to infer the radius, mass, and age of the red giant component by using a combination of seismic and non-seismic constraints. On the one hand, the average large frequency separation is computed using the radial mode frequencies of the models in the grid, not added as an a posteriori correction to the scaling relation between Δν and the square root of the stellar mean density. On the other hand, νmax in the model grid is computed using a simple scaling relation (Kjeldsen & Bedding 1995) by considering νmax, ⊙ = 3090 μHz. The grid of stellar evolution models used in PARAM is the same as the reference grid adopted in Khan et al. (2019) and Miglio et al. (2021) (grid G2). We obtained seismic masses for 69 sample stars.

Finally, the asymptotic period spacing of gravity modes for ΔΠℓ = 1 provides information on stellar structure. This quantity allows us to distinguish two giants having the same luminosity, one at the RGB bump and the other at the clump undergoing central He burning (Bedding et al. 2011; Mosser et al. 2011). As the stellar structure, and more particularly the presence of the convective core affects the domain where the g-modes are trapped, ΔΠℓ = 1 is larger in clump stars than in RGB stars. Figure 7 presents the period spacing of g-modes for our sample derived by Mosser et al. (2012) compared to that derived by Mosser et al. (2014) and Vrard et al. (2016). The figure shows good agreement between the different ΔΠℓ = 1 determinations. We adopt the values derived by Mosser et al. (2012) to classify the stars in our sample. Using this value, we find that our sample contains 9 and 62 RGB and core He-burning stars, respectively. This classification remains correct no matter which of the three different values is considered here.

thumbnail Fig. 7.

Asymptotic period spacing of g-modes, ΔΠℓ = 1, computed by Mosser et al. (2014; orange circles) and by Vrard et al. (2016; blue triangles) as a function of ΔΠℓ = 1 derived by Mosser et al. (2012). We considered all stars with ΔΠℓ = 1≤140 s as first-ascent RGB stars and all stars with ΔΠℓ = 1 > 140 s as core He-burning stars. The error bars on the ΔΠℓ = 1 determination are smaller than the size of the symbols.

3.2. Masses derived using SPInS

In order to better appreciate the possible uncertainties in the determination of the mass and age of our sample stars, we independently determined these quantities with the Stellar Parameters INferred Systematically (SPInS) tool (Lebreton & Reese 2020). We used the stellar evolution models computed with the STAREVOL code by Lagarde et al. (2017, 2019). The same grid is used in the Besançon Galaxy model in Sect. 4 for consistency.

The SPInS tool characterises stars through a Markov chain Monte Carlo (MCMC) approach, with different possible sets of input observable quantities. We chose two different combinations: (1) spectroscopic observables, where we considered the spectroscopic observables derived from our spectra (Teff, the surface gravity log g, and the iron abundances [Fe/H]) and (2) spectroscopic + asteroseismic observables, where we also included the asteroseismic quantities Δν, νmax, and ΔΠℓ = 1. In this case, the Δν in the stellar evolution models is computed from scaling relations. In both cases we assumed a Kroupa initial mass function (IMF; Kroupa 2001; Kroupa et al. 2013) as a prior as well as a truncated uniform stellar formation rate between 0 and 13.8 Gyr, which is roughly the age of the Universe.

Figure 8 shows the relative difference between the stellar mass we determined with SPInS and the seismic mass we computed with PARAM. While differences up to ∼50% can be obtained when we use only the spectroscopic input in SPInS, the masses derived with PARAM and SPInS agree within ∼20%, when we include the asteroseismic input. This is mainly thanks to ΔΠℓ = 1, which lifts the degeneracy between red giant stars and core He-burning stars in the HRD. We note that this is a very good agreement, considering the uncertainties of the input physics that can affect the modelling of red giant stars. In Sect. 5.2 we discuss in particular the impact of the assumptions on the mass loss rate.

thumbnail Fig. 8.

Relative difference of the stellar masses derived from SPInS and the seismic masses derived with PARAM (ΔM/M = (MSPINS − Mseismic)/Mseismic) using or not asteroseismic diagnostics (red and blue stars, respectively). The dashed lines represent a relative difference of ±20%.

For the rest of the study, we use the seismic masses derived by PARAM. In addition, for the purpose of consistency and further discussion, we determine the stellar properties (M, age) of all the literature samples discussed in Sect. 3.4, using the same SPInS configuration and using only spectroscopic observables.

3.3. Kinematics from Gaia data

In order to determine whether the stars in our sample belong to a specific Galactic stellar population, we used the kinematics derived by Kordopatis et al. (2023; for more details, see their Sect. 2.4). They computed the stellar positions (galactocentric Cartesian X, Y, and Z positions, and cylindrical radius R) as well as the galactocentric cylindrical velocities (Vr, Vφ, and VZ) using the astrometric parameter from Gaia EDR3 (Gaia Collaboration 2021) as well as distances computed by Bailer-Jones et al. (2021). Figure 9 displays the velocity components in a Toomre diagram. This diagram is used extensively to identify the main components of our Galaxy, such as the thin and thick discs and the halo, using only kinematics. We assume that the stars outside the blue circle belong to the thick disc, while the others belong to the thin disc (e.g. Yoshii 1982; Gilmore & Reid 1983; Recio-Blanco et al. 2014). Using these criteria for guidance, our sample is therefore composed of 7 stars from the thick disc and 63 stars from the thin disc.

thumbnail Fig. 9.

Toomre diagram for the stars in our sample. The dashed curves indicate constant space motion. The stars are colour-coded according to their metallicity.

3.4. Compilation of 12C/13C form others studies

Because of the limitations of the Kepler field and of our selection criteria, our golden sample contains only relatively metal-rich stars (i.e. with [Fe/H] higher than ∼ − 0.6 dex), with luminosities around that of the RGB bump and of the clump (see Fig. 10). We thus miss carbon isotopic ratios for brighter RGB stars and for metal-poor field giants to test possible correlations between the metallicity, the position on the RGB, and the mixing efficiency. We thus collect this information from the literature studies that are listed in Table 2 (Gratton et al. 2000; Tautvaišienė et al. 2010, 2013; Morel et al. 2014; Takeda et al. 2019; Aguilera-Gómez et al. 2023). For this EXTENDED SAMPLE, however, asteroseismic constraints are missing, making the determination of the stellar masses and evolution phases more uncertain than in our golden sample, as described below. Figure 10 presents the Kiel diagram for our golden and the extended samples. We derived the stellar mass of all of the stars in the literature sample using SPInS tool and the list of input parameters of set (1) described in Sect. 3.2; we used the values of Teff, log g, and [Fe/H] published in the original papers. We were aware of the systematics that can be induced by the sample inhomogeneity. However, this allowed us to explore a mass range between 0.6 and 4.2 M⊙ and a [Fe/H] range between −2.1 and 0.4 dex, thus scanning different Galactic stellar populations, and to probe the dependency of the mixing with the stellar mass and metallicity.

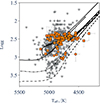thumbnail Fig. 10.

Kiel diagram for the stars in our sample (orange symbols). RGB and core He-burning stars are represented by circles and squares, respectively. Stars compiled from the literature for which the carbon isotopic ratio (and log g) is determined are represented by grey star symbols (see Sect. 3.4). Stellar evolutionary tracks computed with STAREVOL for the 1.4 M⊙ model (dashed line) and 2.0 M⊙ model (dash-dotted line) at solar metallicity and 2.5 M⊙ at [Fe/H] = −0.23 (solid line) are also plotted.

Table 2.

Properties of the star samples used in this study.

Figure 11 shows the carbon isotopic ratio as a function of [Fe/H], stellar mass, and age for both our golden and extended samples. In the first row from the left we show the data for all the stars. In the middle and the third rows, we eliminated the literature stars for which no evolution stage indication was provided in the original papers. We split the remaining stars with respect to their evolution phase, and we show the error bars on the masses, which are much higher for the extended sample than for the golden sample stars for which asteroseismic data provide more reliable estimates. Our golden sample contains mostly clump stars, and only four RGB stars with luminosity values close to that of the clump for which 12C/13C is derived. The literature sample contains more putative RGB stars, for which definitive information about their actual evolution phase would require asteroseismic information. In any case, the observed trends are very similar between the golden and the extended samples. As can be seen in Fig. 11, the golden sample undoubtedly confirms that the carbon isotopic ratio is lower at the surface of core He-burning stars compared to RGB stars with slightly lower luminosity than the RGB bump. The dispersion of 12C/13C observed at the surface of RGB stars in the extended sample is greater than for clump stars (see middle panel of Fig. 11). This depicts the combined effects of 1DUP (all the RGB stars have a luminosity that is high enough to have already undergone the 1DUP), and of additional mixing in decreasing the carbon isotopic ratio while the stars are climbing along the red giant branch until it reaches a “plateau” value where the stars lie during the helium-burning phase. However, future asteroseismic studies are required to definitively pinpoint the actual phase where the extra-mixing occurs along or at the tip of the RGB. Finally, 12C/13C decreases clearly when the stellar metallicity and mass decrease, while it seems to decrease slowly with the stellar age (see Fig. 11). These behaviours are consistent with other previously published studies, but they will have to be confirmed in the future when asteroseismology studies become feasible for low-metallicity red giants.

thumbnail Fig. 11.

12C/13C vs. [Fe/H] (top panel), mass (middle panel), and age (bottom panel) for stars in our sample (orange symbols). The abundances are from Gratton et al. (2000), Tautvaišienė et al. (2010, 2013), Morel et al. (2014), Takeda et al. (2019), Charbonnel & Balachandran (2000) and Aguilera-Gómez et al. (2023) are also plotted. When the information is available in the original papers, first-ascent giant and core He-burning stars are plotted in the middle and right column, respectively. For our golden sample stars, the asteroseismic masses and ages we obtained with PARAM are shown. For the literature sample, the masses and ages obtained with SPInS with only spectroscopic but no asteroseismic constraints are shown.

4. Forward modelling using the Besançon Galaxy model

The stars we consider in both the golden and the extended sample belong to different stellar populations of the Milky Way, each with a different formation and history. Additionally, they cover a large range in terms of mass and [Fe/H], and they lie either on the RGB or the clump. In order to exploit the full potential of these observations by taking into account both the evolution of the Milky Way and the evolution of stars, which can affect the stellar properties to different degrees, we run simulations with a Galactic stellar population synthesis model. We use the Besançon Galaxy model (BGM; e.g. Lagarde et al. 2017) that provides forward modelling and realistic data simulations (mock catalogues) where selection biases on observables from specific surveys can be accurately reproduced.

The BGM is built on a Galactic formation and evolution scenario that reflects our present understanding of the Milky Way. We consider four stellar populations, a thin disc, a thick disc, a bar, and a halo; each stellar population has a specific density distribution. The stellar content of each population is modelled through an initial mass function (IMF) and a star formation history (SFH; Czekaj et al. 2014), and follows stellar evolutionary tracks (implemented in Lagarde et al. 2017, 2019) taking into account different transport processes (see Sect. 5.1). The resulting stellar properties are used to compute the observational properties using atmosphere models and assuming a 3D extinction map. A Galactic dynamical model is used to compute radial velocities and proper motions (Robin et al. 2017). Our sample stars belong mostly to the thin and thick discs. The main ingredients to describe these two populations are the following:

  • The initial mass functions for the two stellar populations are from the analysis of the Tycho-2 data (Mor et al. 2018).

  • The SFH of the thin disc is from Mor et al. (2018). The SFH of the thick disc is modelled assuming a two-episode formation (Robin et al. 2014) with Gaussian age distributions from 8 to 12 Gyr and from 10 to 13 Gyr for the young and the old thick discs, respectively.

  • Considering the thin disc, the iron abundance [Fe/H] and its dispersion are estimated assuming the age-metallicity relation deduced from Haywood (2006; for more details, see Czekaj et al. 2014),

    (1)

    with the stellar age given in gigayears, and a radial metallicity gradient of −0.07 dex kpc−1 limited to galactocentric radii between 5 and 12 kpc. Considering the thick disc, a mean metallicity is assumed for the young thick disc and the old thick disc (−0.5 and −0.8 dex, respectively) with a dispersion of 0.3 dex.

  • The adopted [α/Fe] versus [Fe/H] relations follow the trend observed in the DR17 of APOGEE for both stellar populations. For [Fe/H] ≤ 0.1,

    (2)

    For [Fe/H] > 0.1, [α/Fe] is assumed to be solar. An intrinsic Gaussian dispersion of 0.02 dex is added to these relations.

  • The adopted velocity dispersions as a function of age were constrained from the RAVE survey (DR4, Kordopatis et al. 2013) and proper motions from the TGAS part of the Gaia DR1 (Gaia Collaboration 2016) by Robin et al. (2017, see their Table 4).

  • The rotation curve is given by Sofue (2015). The asymmetric drift is also taken into account following Robin et al. (2017). The dynamical statistical equilibrium is ensured by assuming the Stäckel approximation of the potential from Bienaymé et al. (2015, 2018).

  • The 3D extinction map adopted is a combination of the 3D maps published by Marshall et al. (2006) and by Lallement et al. (2018). Simulations were conducted using this extinction, but to account for small-scale variations in the distribution of interstellar matter, a dispersion around the average value was introduced on a star-by-star basis. This dispersion was equivalent to 10% of the mean extinction.

Stellar properties of the mock sample are directly deduced from stellar evolution models. Lagarde et al. (2017) improved the BGM including stellar evolutionary models computed with the STAREVOL code (e.g. Lagarde et al. 2012a; Amard et al. 2019) for stars between 0.2 and 6.0 M⊙ at six metallicities ([Fe/H] = –2.14, –1.8, –0.54, –0.23, 0 and 0.51) with different α-enhancement (0, 0.15, and 0.3) to simulate properties of stars in different stellar populations (Lagarde et al. 2019). Thanks to this improvement, the BGM provides the global properties (e.g. surface gravity, effective temperature), chemical abundances (for 54 stable and unstable species), and asteroseismic properties (e.g. δν, νmax, ΔΠℓ = 1). Importantly for our study, we compare the observed abundances of our golden and extended samples to the predictions of the BGM for two sets of stellar models (Sect. 5). The first set corresponds to “classical” models that include no transport process for chemicals except convection, and hence only the effect of the 1DUP is accounted for. The second set takes into account the additional effects of thermohaline instability during the red giant branch (see Sect. 5.1). We use a diffusion coefficient for thermohaline mixing that is based on the Ulrich (1972) prescription corrected for non-perfect gas and with an aspect ratio of 6 for the instability “fingers” as in Charbonnel & Zahn (2007a; see also Lagarde et al. 2012a, 2017).

For this study, we computed simulations for the Kepler fields according to the following criteria: Apparent magnitude range of 4.5 < H < 10.5; Stars with an effective temperature lower than 5300 K to select only giant stars; Stars within the observed domains of the large separation (Δν) and the frequency of maximum power (νmax; 3 < Δν < 12 μHz; 25 < νmax < 150 μHz); We select core He-burning stars in the simulation according to the period spacing of g-modes ΔΠℓ = 1 > 140 s. Finally, we apply an error to the surface abundances predicted by the BGM. We assume the observational errors for C, N, O, [Fe/H], 12C/13C, and 12C/14N; the theoretical error bars are generated with a uniform noise.

5. Comparison between BGM predictions and observations

We first recall the theoretical impact of thermohaline mixing on the surface abundances along stellar evolution tracks. We then use simulations of the Kepler field computed with the BGM which include stellar models taking into account or not thermohaline mixing, and study its effects on the surface abundances of stars in the Kepler field and its dependency on stellar metallicity, mass, and age.

5.1. Surface abundance variations predicted by the stellar evolution models

Properties of stars simulated by the BGM are deduced from STAREVOL evolutionary tracks, which may or may not account for the impact of thermohaline mixing on surface properties. Figure 12 presents some of these tracks and the impacts of thermohaline instability on the surface values of 12C/13C, [C/O], and [N/O] as a function of effective temperature. After the main sequence, once a star has burnt its hydrogen in the centre, it evolves into the red giant branch. The core of the star contracts and the convective envelope expands and dives towards deeper regions where H-burning occurred while the star was on the main sequence. This episode, called the first dredge-up (1DUP), changes the surface abundances of chemical elements such as carbon and nitrogen. The 1DUP induces a decrease in 12C/13C and in [C/O], while [N/O] increases (see Fig. 12). The post-1DUP values of 12C/13C and [C/O] are lower when mass increases and metallicity decreases, while [N/O] has the opposite behaviour.

thumbnail Fig. 12.

Hertzsprung–Russell diagram of a 1.0 M⊙ model at solar metallicity (top left panel). Also shown are the evolution of 12C/13C (top right panel), [C/O] (bottom left panel), and [N/O] (bottom right panel) for the 1.0 M⊙ and 1.5 M⊙ model at solar metallicity (blue and purple lines, respectively) and for 1.0 M⊙ at [Fe/H] = –0.54 (orange line) from the subgiant branch to the RGB tip and later from the core He-burning to AGB phase. The tracks show the predicted behaviour from stellar evolution models taking into account or not the effects of thermohaline mixing (solid and dashed lines, respectively). The position of the beginning of the first dredge-up, the RGB bump, and the core He-burning phase are indicated in each panel (triangle, star, and square, respectively).

When the effects of thermohaline mixing are not taken into account, the surface abundances do not change along the red giant branch and during the central helium-burning phase until the 2DUP (see dashed lines on Fig. 12). In particular, the post-1DUP carbon isotopic ratio ranges between ∼25 and 30, which is higher than its observational value in clump stars and in RGB stars that have passed the RGB bump (see Fig. 11). After the end of core He-burning the surface abundance ratios change again slightly when the convective envelope deepens again as the star reaches the early AGB phase.

On the other hand, we see in Fig. 12 that the double diffusive thermohaline instability has a significant impact on the surface abundances of the light elements, such as the carbon isotopes and nitrogen (also on lithium, not shown here, but see e.g. Charbonnel & Zahn 2007a; Charbonnel & Lagarde 2010; Charbonnel et al. 2020; Magrini et al. 2021 who use models with the same prescription and assumptions for the thermohaline diffusion coefficient). From the RGB bump luminosity to the RGB tip, the surface abundance of 12C decreases, while that of 13C and N increase, and O stays constant, resulting in a decrease in the 12C/13C and C/O ratios and an increase in the N/O ratio (see the solid lines on Fig. 12). The surface abundances do not change during the core He-burning phase until the second dredge-up occurs, similarly to the classical case. With the prescription we use in the models, the efficiency of this instability varies with the stellar mass and metallicity (for more details see Lagarde et al. 2012a). The less massive the star and the lower its metallicity, the more efficient the mixing. We discuss below how these differences affect the predictions of the BGM model.

5.2. 12C/13C predicted and observed in the Kepler field

Figures 13–15 show the carbon isotopic ratio as a function of [Fe/H], stellar mass, and age predicted by the BGM based on STAREVOL evolution tracks and compared with the observed abundances of our Kepler golden sample with asteroseismic masses and ages from PARAM. The simulations performed with the BGM show only the core He-burning stars, unlike the observations where, in addition to the core He-burning stars (squares), we also show the four stars with a luminosity lower than the RGB bump and for which we could determine the carbon isotopic ratio (circles). Since the thermohaline mixing is efficient only above the RGB bump, the 12C/13C ratio observed at the surface of these four first-ascent RGB stars are well reproduced by simulations that do or do not include thermohaline mixing, within the error bars (which are larger for the less evolved stars that may not have finished the 1DUP, and hence are less enriched in 13C). These stars act as indicators of the mixing efficiency between two different evolutionary stages (i.e. before the stars reach the RGB bump and the core He-burning phase). As already anticipated, all the core He-burning stars show carbon isotopic ratios lower than predicted by classical models, but they are well reproduced when thermohaline mixing is accounted for.

thumbnail Fig. 13.

12C/13C vs. [Fe/H] for core He-burning and RGB stars in our sample (squares and circles, respectively) compared with the BGM simulations for core He-burning stars only (dots) of the Kepler field and taking into account or not the effects of thermohaline mixing (right and left panels, respectively). The stellar mass is colour-coded for both observations (using seismic determinations from PARAM) and simulations (predicted by BGM using STAREVOL stellar evolution models from Lagarde et al. 2017, 2019). In the right panel the mass loss rate is decreased on the RGB by a factor of two compared to the left and middle panels (see text for details).

thumbnail Fig. 14.

Same as Fig. 13 for 12C/13C as a function of stellar mass. In the right panel, the mass loss rate is decreased on the RGB by a factor of two compared to the left and right panels (see text for details). The stellar age is colour-coded for both observations and BGM simulations. The green lines in the middle panel show the 12C/13C at the core He-burning phase predicted by stellar evolution models computed by Lagarde et al. (2012a) and including both thermohaline and rotation-induced mixing (at V/Vcrit ∼ 0.3) at [Fe/H] = 0 and [Fe/H] = −0.86 (dotted and dashed line, respectively).

thumbnail Fig. 15.

Same as Fig. 13 for 12C/13C as a function of stellar age, with the stellar metallicity colour-coded for both observations and simulations. The green lines in the right pannel have the same meaning as in Fig. 14.

The simulations indicate that under the presence of thermohaline mixing, 12C/13C decreases as [Fe/H] decreases, reaching a plateau value of around 6–7 at the lowest metallicities (see Fig. 13). The core He-burning stars of our golden sample confirms this “banana-shaped” behaviour (already seen in Fig. 11), which combines the various observations published in the literature. The model perfectly reproduces this observational behaviour, confirming the importance of a mixing process such as the thermohaline mixing for understanding the carbon abundance of giant-field stars. However, since we compare BGM model predictions for ages and masses based on stellar evolution models to data with seismic ages and masses from PARAM, we do not expect a perfect match when it comes to these two quantities. In particular, the predicted masses of the simulated stellar population depend on the mass loss rate prescription used in the stellar evolution models. Lagarde et al. (2017, 2019) used the Reimers (1975) mass loss prescription with the η parameter equal to 0.5. We compare in Fig. 14 the BGM masses for this value and for η = 0.25 (see also Fig. 13). For this, we simply consider that the difference between the initial and the clump masses of each star of the simulated population is decreased by a factor of two. This leads to an even better agreement with the asteroseismic masses, and hence between the observed and predicted carbon isotopic ratio as a function of mass.

Generally, and as previously noted by Charbonnel & Lagarde (2010) and Lagarde et al. (2012a), three different mass domains can be considered to measure the efficiency of thermohaline instability: (1) For low-mass (M < 1.25 M⊙) and low-metallicity stars, thermohaline mixing is the most efficient transport process, decreasing the surface abundance of 12C and increasing the surface abundances of 13C and nitrogen. This is why the simulations presented here reproduce very well the 12C/13C observed in this mass and metallicity domain (see Figs. 14 and 13). Interestingly, the simulations favour a lower mass loss rate on the RGB than was used in the stellar evolution models. As these stars are also the oldest stars in our Galaxy, the simulations also explain very well the 12C/13C observed at the surface of the oldest stars (see Fig. 15). (2) For intermediate-mass stars (1.25 ≤ M ≤ 2.2 M⊙) our simulations including the effects of thermohaline mixing have slightly higher 12C/13C values than the observations, but they are in very good agreement when we consider mass loss rates lower than in the original stellar evolution models (see Fig. 14). In addition to thermohaline mixing on the RGB, rotation-induced mixing on the main sequence (not included in the stellar tracks used in the BGM simulations, but see the green lines in the figures) has also been shown to lower the surface carbon isotopic of RGB stars in this particular mass range (see e.g. Fig. 17 in Charbonnel & Lagarde 2010 to see the impact of different initial velocities). (3) More massive stars do not experience thermohaline mixing as they do not go through the RGB bump during their short first ascent of the red giant branch, making thermohaline instability irrelevant for them. The selection of stars for this study was specifically aimed at testing the efficiency of thermohaline mixing, which is why there are no stars in this mass range.

Finally, we show in Fig. 15 the predicted behaviour of the carbon isotopic ratio as a function of the ages of the stars of the simulated population, and compare with the observed behaviour for the golden sample. We see that the uncertainties on the ages obtained with PARAM are larger than the uncertainties of the masses (see e.g. Chaplin & Miglio 2013, for a discussion).

thumbnail Fig. 16.

12C/13C as a function of log(C/O) for core He-burning and RGB stars in our sample (orange squares and circles, respectively) compared to the BGM simulations for core He-burning stars only. The simulations (grey dots) take into account the thermohaline mixing (middle and right panels) or not (left panel). The C/O ratio derived by Blanton et al. (2017) for stars in common is also shown, using our carbon isotopic ratios (blue stars in middle panel). The abundances derived by Gałan et al. (2017, 2023), and Gratton et al. (2000) are also compared with the simulation in the right panel. The 12C/13C at the core He-burning phase predicted by stellar evolution models computed by Lagarde et al. (2012a) and including both thermohaline and rotation-induced mixing (at V/Vcrit ∼ 0.3) are shown at [Fe/H] = 0 and [Fe/H] = −0.86 (green dotted and solid lines, respectively).

thumbnail Fig. 17.

Same as Fig. 16. 12C/13C, but as a function of log(N/O).

5.3. CNO abundance ratios

As shown in Sect. 5.1, the thermohaline mixing has a significant effect on the C and N surface abundances, but leaves the O values unchanged. Figures 16 and 17 present the 12C/13C as a function of C/O and N/O observed for giants in our sample (left and middle panels). First-ascent RGB stars have a carbon isotopic ratio as well as C/O and N/O in agreement with the post 1DUP value. Observations of core He-burning stars show that a low 12C/13C is associated with low C/O and N/O ratios. The predicted behaviour of 12C/13C with C/O and N/O for core He-burning stars is correct, although our simulations predict a higher N/O ratio than our observations. In order to understand this discrepancy in the nitrogen abundances derived from our observations and simulations, we also show the APOGEE DR17 data for C/O and N/O for the stars we have in common (blue star symbols in the middle panels of Figs. 16 and 17, using our carbon isotopic values). As already shown in Sect. 2.3, the abundances of [C/Fe] and [N/Fe] are higher in the APOGEE DR17 catalogue than in our study, while [O/Fe] is lower. This is why C/O and N/O are higher in the APOGEE DR17 catalogue than in our study. An explanation for these differences might be found in slightly different atmospheric parameters (ours are asteroseismic) and spectral lines used (in the APOGEE survey the infrared OH, CO, and CN lines were investigated, while we investigated optical [O I], C2, and CN lines). In any case, the observational trends for 12C/13C versus C/O and N/O are similar in both samples, and it can be explained only when thermohaline mixing is accounted for in the simulations.

In addition to the APOGEE data, we also show in Figs. 16 and 17 the values of 12C/13C as well as the CNO abundances determined by Gałan et al. (2017) for a sample of atypical stars (yellow circles in the right panels of Figs. 16 and 17). These are known as symbiotic stars, which are binaries composed of a star in the later stages of evolution and a stellar remnant. The authors derived the photospheric composition of the giant stars in the binary system, and found enhanced 14N, depleted 12C, and decreased 12C/13C. These observations show a C/O ratio in agreement with our observations and APOGEE DR17, but a much higher N/O ratio. These higher N/O ratio values are well reproduced by BGM simulations and by models including the effects of both thermohaline and rotation-induced mixing.

In our sample of stars we also have 12 atypical eruptive stars. Eruptive variables are stars that vary in brightness because of violent processes and flares occurring in their chromospheres and coronae. The light changes are usually accompanied by shell events or mass outflow in the form of stellar winds or variable intensity and/or by interactions with the surrounding interstellar medium (Good 2003). Even though occasional flashes, according to theoretical predictions, may be very energetic and may alter the stellar chemical composition (e.g. Sackmann et al. 1974), in our sample of eruptive stars the CNO and 12C/13C abundances do not differ from the core He-burning stars.

Finally, using the kinematics from the Gaia satellite, we separate our sample of stars into two populations: those belonging to the Galactic thin disc and those to the thick disc (see Sect. 3.3). Figure 18 shows the carbon isotopic ratio as a function of the N/O ratio for core He-burning stars only for these two populations using our data and that of APOGEE. Although the 12C/13C vs. N/O trends are the same in the simulations and in the observations for both N/O determinations, there is a shift between the observations and the simulations. Part of the shift comes from the differences between our values for N/O and those from APOGEE, as discussed above. Furthermore, the thick disc stars have a very low N/O ratio, but are also the stars for which the difference in N/O ratio between APOGEE and our determination is the largest. Since our study contains only three core He-burning thick disc stars with a 12C/13C ratio and a N/O ratio, a more detailed study of the nitrogen and oxygen observed at the surface of a large number of thick disc stars is needed to understand this difference.

thumbnail Fig. 18.

12C/13C vs. log(N/O) for core He-burning stars in our sample (left panel) and vs. log(N/O) derived by APOGEE DR17 (right panel) compared to the BGM simulations including the effects of thermohaline mixing. Thin and thick disc stars according to their Gaia kinematics are represented by the orange and blue symbols. The same colour-coding is used in the BGM simulation.

6. Conclusions

Thanks to the rich observational context, the surface properties of stars are derived from spectroscopic observations, such as their photospheric composition, while asteroseismology allows us to determine their masses and ages more accurately. One of the key elements in effectively constraining the mixing occurring in giant stars is the carbon isotopic ratio. Only seven studies have derived and published the 12C/13C in field giant stars; only one used asteroseismic constraints for a few objects. The compilation of these studies presented in Sect. 3.4 shows that 12C/13C increases with [Fe/H] and the mass, and seems to decrease with age. In this study we therefore compiled a catalogue of 71 stars in the Kepler field with the best properties to constrain the efficiency of the mixing taking place between the end of the 1DUP and the central He-burning phase. We carried out a spectroscopic follow-up using the FIbre-fed Echelle Spectrograph on the Nordic Optical Telescope for a sample of giant Kepler stars. We determined the atmospheric properties (Teff, log g) as well as the chemical abundances in C, N, O, Mg, Fe, O, and the 12C/13C isotopic ratio for 71 giant stars (see Sect. 2.2.2). We validated some of our determinations by comparing them with those already published in the literature by various surveys (Gaia Recio-Blanco et al. 2023; PASTEL Soubiran et al. 2022; LAMOST DR7 Luo et al. 2022; and APOGEE DR17 Blanton et al. 2017).

Because our sample stars were observed by the Kepler satellite, we were able to determine their masses and ages from seismic observables (Δν, νmax), and we could unambiguously determine whether they are first-ascent RGB stars or are in the core He-burning phase using ΔΠℓ = 1 (see Sect. 3.1). We show that our sample is composed of 9 red giant stars and 62 core He-burning stars. In order to estimate possible uncertainties, we determined the masses and ages of stars in our sample using the Stellar Parameters INferred Systematically tool (Lebreton & Reese 2020) and our stellar evolution models (Lagarde et al. 2017), and found good consistency between the two determinations.

To harness the complete potential of our extensive catalogue, considering both the Milky Way evolution and the impact of stellar evolution (which can influence stellar properties to varying degrees) we employed simulations generated through the Besançon stellar population synthesis model of our Galaxy (BGM). We built mock catalogues using the BGM in which stellar evolution models take into account (and not) the effects of thermohaline instability (Lagarde et al. 2017, 2019). To date, thermohaline mixing is the sole physical mechanism suggested in the literature to account for the photospheric composition of evolved red giant stars, even with simplistic analytical prescriptions similar to those used in our stellar evolution models and that are not yet able to capture the full picture of this complex double diffusive instability (Sengupta & Garaud 2018; Harrington & Garaud 2019; Fraser et al. 2022). In this study we focused on discussing this non-canonical extra mixing in red giant stars. This was achieved by investigating the changes in the 12C/13C ratio throughout the red giant branch and the helium-burning phases. Additionally, we analysed how this ratio varies with respect to stellar age, mass, and metallicity. Finally, we investigated CNO abundances as a function of carbon isotopic ratio. Our main results can be summarised as follows:

  • Thanks to asteroseismology, we confirm that the carbon isotopic ratio at the surface of core He-burning stars is lower than that of first-ascent RGB stars. Thermohaline instability develops from the luminosity of the RGB bump, decreasing surface abundances of 12C and increasing 13C. Simulations including this mixing therefore show a lower 12C/13C ratio during the core He-burning phase compared with the red giant phase just before the RGB bump (e.g. 12C/13C ∼ 8 and 30, respectively for a 1.0 M⊙ at [Fe/H] = −0.54).

  • Considering only core He-burning stars, we confirm that the carbon isotopic ratio measured at the surface of these objects increases with [Fe/H] and stellar mass, while it decreases with stellar age. Simulations done with the BGM and including the effects of thermohaline mixing explain these trends in an exceptional way (see Sect. 5.1). Standard models that do not include the effects of thermohaline mixing show inverse trends that can explain the surface abundances of giant stars just after the 1DUP, but not the abundances of more evolved stars such as core He-burning stars.

  • Our spectroscopic analysis shows that low 12C/13C values are correlated with low C/O and N/O ratios. These behaviours are predicted well by simulations that include the effects of thermohaline mixing. As already shown by Charbonnel & Lagarde (2010) and Lagarde et al. (2019), thermohaline mixing decreases the carbon abundance, while the nitrogen abundance increases and the oxygen abundance remains constant. Although the observed behaviours are reproduced well, with some notable shifts in N/O between our values and values from the literature, it should be noted that there are the stars belonging to the thick disc that show a mismatch between the nitrogen abundances derived from the spectra and from the simulations.

The relatively large sample we gathered in our pioneer study is still limited due to the limitations of the asteroseismic missions in terms of either their coverage across the Galactic volume or the duration of observations. These limitations subsequently constrain the level of precision attainable for deducing key stellar properties, including the age of stars. However, the Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015) and the forthcoming PLATO (Rauer et al. 2014) space missions are set to offer stellar age estimates as well as evolutionary states across various directions within the Milky Way, encompassing a substantial number of stars. Furthermore, future spectroscopic surveys will provide a complementary chemical vision of our Galaxy, allowing investigation of the CNO – mass, age or metallicity relation and probing all stellar populations in the Milky Way.

1

We deduced [Fe/H] by adding [M/H] and [Fe/M].

Acknowledgments

Based on observations made with the Nordic Optical Telescope, owned in collaboration by the University of Turku and Aarhus University, and operated jointly by Aarhus University, the University of Turku and the University of Oslo, representing Denmark, Finland and Norway, the University of Iceland and Stockholm University at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. The observational project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 730890 (OPTICON). N.L., C.C., C.R. acknowledge financial support from “Programme National de Physique Stellaire” (PNPS) and from the “Programme National Cosmology et Galaxies (PNCG)” of CNRS/INSU, France. C.C. thanks the Swiss National Science Foundation (SNF; Project 200020-192039). R.M., A.D., G.T., B.B. acknowledge funding from the Lithuanian Science Council (LMTLT, grant No. P-MIP-23-24). The “Stellar Parameters INferred Systematically” (SPInS) code is a spin-off of the “Asteroseismic Inference on a Massive Scale” (AIMS) project, one of the deliverables of the SpaceINN network, funded by the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 312844. SPInS was initially created for the 5th International Young Astronomer School “Scientific Exploitation of Gaia Data” held in Paris, (26 February–2 March 2018), as a simple tool to estimate stellar ages, as well as other stellar properties.

References

  1. Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [CrossRef] [Google Scholar]
  2. Aguilera-Gómez, C., Jones, M. I., & Chanamé, J. 2023, A&A, 670, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
  4. Amard, L., Palacios, A., Charbonnel, C., et al. 2019, A&A, 631, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Anders, F., Chiappini, C., Rodrigues, T. S., et al. 2017a, A&A, 597, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Anders, F., Chiappini, C., Minchev, I., et al. 2017b, A&A, 600, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Angelou, G. C., Church, R. P., Stancliffe, R. J., Lattanzio, J. C., & Smith, G. H. 2011, ApJ, 728, 79 [NASA ADS] [CrossRef] [Google Scholar]
  8. Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, 36th COSPAR Scientific Assembly, 36, 3749 [Google Scholar]
  9. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  10. Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [Google Scholar]
  11. Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bell, R. A., Briley, M. M., & Smith, G. H. 1990, AJ, 100, 187 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bienaymé, O., Robin, A. C., & Famaey, B. 2015, A&A, 581, A123 [Google Scholar]
  14. Bienaymé, O., Leca, J., & Robin, A. C. 2018, A&A, 620, A103 [EDP Sciences] [Google Scholar]
  15. Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [Google Scholar]
  16. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  17. Bouret, J. C., Martins, F., Hillier, D. J., et al. 2021, A&A, 647, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Brown, J. A., & Wallerstein, G. 1989, AJ, 98, 1643 [Google Scholar]
  19. Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [Google Scholar]
  20. Brown, J. M., Garaud, P., & Stellmach, S. 2013, ApJ, 768, 34 [NASA ADS] [CrossRef] [Google Scholar]
  21. Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
  23. Charbonnel, C. 1994, A&A, 282, 811 [NASA ADS] [Google Scholar]
  24. Charbonnel, C. 1995, ApJ, 453, L41 [NASA ADS] [CrossRef] [Google Scholar]
  25. Charbonnel, C., & Balachandran, S. C. 2000, A&A, 359, 563 [Google Scholar]
  26. Charbonnel, C., & Lagarde, N. 2010, A&A, 522, A10 [CrossRef] [EDP Sciences] [Google Scholar]
  27. Charbonnel, C., & Zahn, J.-P. 2007a, A&A, 467, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Charbonnel, C., & Zahn, J. 2007b, A&A, 476, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Charbonnel, C., Brown, J. A., & Wallerstein, G. 1998, A&A, 332, 204 [NASA ADS] [Google Scholar]
  30. Charbonnel, C., Lagarde, N., Jasniewicz, G., et al. 2020, A&A, 633, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Creevey, O. L., Thévenin, F., Basu, S., et al. 2013, MNRAS, 431, 2419 [NASA ADS] [CrossRef] [Google Scholar]
  32. Czekaj, M. A., Robin, A. C., Figueras, F., Luri, X., & Haywood, M. 2014, A&A, 564, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Deal, M., Goupil, M. J., Marques, J. P., Reese, D. R., & Lebreton, Y. 2020, A&A, 633, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Dearborn, D. S. P., Eggleton, P. P., & Schramm, D. N. 1976, ApJ, 203, 455 [CrossRef] [Google Scholar]
  35. Denissenkov, P. A. 2010, ApJ, 723, 563 [NASA ADS] [CrossRef] [Google Scholar]
  36. Denissenkov, P. A., & Merryfield, W. J. 2011, ApJ, 727, L8 [NASA ADS] [CrossRef] [Google Scholar]
  37. Dumont, T., Charbonnel, C., Palacios, A., & Borisov, S. 2021, A&A, 654, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Eggleton, P. P., Dearborn, D. S. P., & Lattanzio, J. C. 2006, Science, 314, 1580 [Google Scholar]
  39. Fraser, A. E., Joyce, M., Anders, E. H., Tayar, J., & Cantiello, M. 2022, ApJ, 941, 164 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fraser, A. E., Reifenstein, S. A., & Garaud, P. 2023, ApJ, submitted [arXiv:2302.11610] [Google Scholar]
  41. Fusi Pecci, F., Ferraro, F. R., Crocker, D. A., Rood, R. T., & Buonanno, R. 1990, A&A, 238, 95 [NASA ADS] [Google Scholar]
  42. Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 650, C3 [EDP Sciences] [Google Scholar]
  44. Gaia Collaboration (Vallenari, A., et al.) 2023a, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Gaia Collaboration (Recio-Blanco, A., et al.) 2023b, A&A, 674, A38 [CrossRef] [EDP Sciences] [Google Scholar]
  46. Gałan, C., Mikołajewska, J., Hinkle, K. H., & Joyce, R. R. 2017, MNRAS, 466, 2194 [CrossRef] [Google Scholar]
  47. Gałan, C., Mikołajewska, J., Hinkle, K. H., & Joyce, R. R. 2023, MNRAS, 526, 918 [CrossRef] [Google Scholar]
  48. Gilmore, G., & Reid, N. 1983, MNRAS, 202, 1025 [Google Scholar]
  49. Gilmore, G., Randich, S., Worley, C. C., et al. 2022, A&A, 666, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Gilroy, K. K., & Brown, J. A. 1991, ApJ, 371, 578 [NASA ADS] [CrossRef] [Google Scholar]
  51. Good, G. A. 2003, Observing Variable Stars (London, Berlin: Springer) [CrossRef] [Google Scholar]
  52. Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
  53. Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
  54. Guerço, R., Smith, V. V., Cunha, K., et al. 2022, MNRAS, 516, 2801 [CrossRef] [Google Scholar]
  55. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Harrington, P. Z., & Garaud, P. 2019, ApJ, 870, L5 [CrossRef] [Google Scholar]
  57. Haywood, M. 2006, MNRAS, 371, 1760 [NASA ADS] [CrossRef] [Google Scholar]
  58. Heiter, U., Lind, K., Asplund, M., et al. 2015, Phys. Scr., 90, 054010 [Google Scholar]
  59. Henkel, K., Karakas, A. I., & Lattanzio, J. C. 2017, MNRAS, 469, 4600 [Google Scholar]
  60. Iben, I., Jr. 1967, ApJ, 147, 624 [NASA ADS] [CrossRef] [Google Scholar]
  61. Johansson, S., Litzén, U., Lundberg, H., & Zhang, Z. 2003, ApJ, 584, L107 [NASA ADS] [CrossRef] [Google Scholar]
  62. Khan, S., Miglio, A., Mosser, B., et al. 2019, A&A, 628, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Kippenhahn, R., Ruschenplatt, G., & Thomas, H.-C. 1980, A&A, 91, 175 [NASA ADS] [Google Scholar]
  64. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
  65. Kordopatis, G., Gilmore, G., Steinmetz, M., et al. 2013, AJ, 146, 134 [Google Scholar]
  66. Kordopatis, G., Schultheis, M., McMillan, P. J., et al. 2023, A&A, 669, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  68. Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in Planets, Stars and Stellar Systems, eds. T. D. Oswalt, & G. Gilmore, et al., Galactic Structure and Stellar Populations, 5, 115 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 189 [Google Scholar]
  70. Lagarde, N., Charbonnel, C., Decressin, T., & Hagelberg, J. 2011, A&A, 536, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012a, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Lagarde, N., Romano, D., Charbonnel, C., et al. 2012b, A&A, 542, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Lagarde, N., Miglio, A., Eggenberger, P., et al. 2015, A&A, 580, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Lagarde, N., Robin, A. C., Reylé, C., & Nasello, G. 2017, A&A, 601, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Lagarde, N., Reylé, C., Robin, A. C., et al. 2019, A&A, 621, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Lagarde, N., Reylé, C., Chiappini, C., et al. 2021, A&A, 654, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Lebreton, Y., & Reese, D. R. 2020, A&A, 642, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  80. Luo, A. L., Zhao, Y. H., Zhao, G., et al. 2022, VizieR Online Data Catalog: V/156 [Google Scholar]
  81. Maeder, A., Przybilla, N., Nieva, M.-F., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Magrini, L., Lagarde, N., Charbonnel, C., et al. 2021, A&A, 651, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [Google Scholar]
  84. Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. McCormick, C., Majewski, S. R., Smith, V. V., et al. 2023, MNRAS, 524, 4418 [CrossRef] [Google Scholar]
  86. Miglio, A., Chiappini, C., Mackereth, J. T., et al. 2021, A&A, 645, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Mikolaitis, Š., Tautvaišienė, G., Gratton, R., Bragaglia, A., & Carretta, E. 2010, MNRAS, 407, 1866 [NASA ADS] [CrossRef] [Google Scholar]
  88. Montalbán, J., Mackereth, J. T., Miglio, A., et al. 2021, Nat. Astron., 5, 640 [Google Scholar]
  89. Mor, R., Robin, A. C., Figueras, F., & Antoja, T. 2018, A&A, 620, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Morel, T., & Miglio, A. 2012, MNRAS, 419, L34 [NASA ADS] [CrossRef] [Google Scholar]
  91. Morel, T., Miglio, A., Lagarde, N., et al. 2014, A&A, 564, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Mosser, B., Benomar, O., Belkacem, K., et al. 2014, A&A, 572, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Palacios, A., Talon, S., Charbonnel, C., & Forestini, M. 2003, A&A, 399, 603 [CrossRef] [EDP Sciences] [Google Scholar]
  96. Pavlenko, Y. V., Jenkins, J. S., Jones, H. R. A., Ivanyuk, O., & Pinfield, D. J. 2012, MNRAS, 422, 542 [NASA ADS] [CrossRef] [Google Scholar]
  97. Pignatari, M., Herwig, F., Hirschi, R., et al. 2016, ApJS, 225, 24 [NASA ADS] [CrossRef] [Google Scholar]
  98. Pinsonneault, M. H., Elsworth, Y. P., Tayar, J., et al. 2018, ApJS, 239, 32 [Google Scholar]
  99. Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
  101. Recio-Blanco, A., de Laverny, P., Kordopatis, G., et al. 2014, A&A, 567, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Recio-Blanco, A., de Laverny, P., Palicio, P. A., et al. 2023, A&A, 674, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Reimers, D. 1975, MSRSL, 8, 369 [NASA ADS] [Google Scholar]
  104. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  105. Robin, A. C., Reylé, C., Fliri, J., et al. 2014, A&A, 569, A13 [CrossRef] [EDP Sciences] [Google Scholar]
  106. Robin, A. C., Bienaymé, O., Fernández-Trincado, J. G., & Reylé, C. 2017, A&A, 605, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
  108. Sackmann, I. J., Smith, R. L., & Despain, K. H. 1974, ApJ, 187, 555 [NASA ADS] [CrossRef] [Google Scholar]
  109. Schonhut-Stasik, J., Zinn, J. C., Stassun, K. G., et al. 2024, AJ, 167, 50 [NASA ADS] [CrossRef] [Google Scholar]
  110. Sengupta, S., & Garaud, P. 2018, ApJ, 862, 136 [CrossRef] [Google Scholar]
  111. Smiljanic, R., Gauderon, R., North, P., et al. 2009, A&A, 502, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Smiljanic, R., Pasquini, L., Charbonnel, C., & Lagarde, N. 2010, A&A, 510, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Smith, V. V., & Suntzeff, N. B. 1989, AJ, 97, 1699 [NASA ADS] [CrossRef] [Google Scholar]
  114. Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas at Austin, USA [Google Scholar]
  115. Sofue, Y. 2015, PASJ, 67, 75 [Google Scholar]
  116. Soubiran, C., Brouillet, N., & Casamiquela, L. 2022, A&A, 663, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
  118. Takeda, Y., Omiya, M., Harakawa, H., & Sato, B. 2019, PASJ, 71, 119 [NASA ADS] [CrossRef] [Google Scholar]
  119. Talon, S., Richard, O., & Michaud, G. 2006, ApJ, 645, 634 [Google Scholar]
  120. Tautvaišienė, G., Barisevičius, G., Berdyugina, S., Chorniy, Y., & Ilyin, I. 2010, Balt. Astron., 19, 95 [Google Scholar]
  121. Tautvaišienė, G., Barisevičius, G., Chorniy, Y., Ilyin, I., & Puzeras, E. 2013, MNRAS, 430, 621 [CrossRef] [Google Scholar]
  122. Tayar, J., & Joyce, M. 2022, ApJ, 935, L30 [NASA ADS] [CrossRef] [Google Scholar]
  123. Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nachr., 335, 41 [Google Scholar]
  124. Traxler, A., Garaud, P., & Stellmach, S. 2011, ApJ, 728, L29 [Google Scholar]
  125. Ulrich, R. K. 1972, ApJ, 172, 165 [NASA ADS] [CrossRef] [Google Scholar]
  126. Ulrich, R. K. 1986, ApJ, 306, L37 [Google Scholar]
  127. Valentini, M., Chiappini, C., Miglio, A., et al. 2016, Astron. Nachr., 337, 970 [Google Scholar]
  128. Valentini, M., Chiappini, C., Bossini, D., et al. 2019, A&A, 627, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  129. Vauclair, S., Vauclair, G., Schatzman, E., & Michaud, G. 1978, ApJ, 223, 567 [Google Scholar]
  130. Vrard, M., Mosser, B., & Samadi, R. 2016, A&A, 588, A87 [CrossRef] [EDP Sciences] [Google Scholar]
  131. Yoshii, Y. 1982, PASJ, 34, 365 [NASA ADS] [Google Scholar]

Appendix A: Queries of Gaia data samples

The following ADQL queries to the Gaia DR3 catalogue through the Gaia archive can be used to retrived the data sample used in this study. We follow the recommendations given in Recio-Blanco et al. (2023) and use the definition given in Gaia Collaboration (2023b).

FROM gaiadr3.astrophysical_parameters
WHERE (teff_gspspec>3500 AND
teff_gspspec<7000) AND
(logg_gspspec>0 AND logg_gspspec<5) AND
(flags_gspspec LIKE '0%') AND (flags_gspspec
LIKE '_0%') AND (flags_gspspec LIKE '__0%') AND
(flags_gspspec LIKE '___0%') AND (flags_gspspec
LIKE '____0%') AND (flags_gspspec LIKE
'_____0%') AND (flags_gspspec LIKE '______0%')
AND ((flags_gspspec LIKE '_______0%') OR
(flags_gspspec LIKE '_______1%') OR
(flags_gspspec LIKE '_______2%') ) AND
((flags_gspspec LIKE '____________0%') OR
(flags_gspspec LIKE '____________1%') ) AND
(flags_gspspec LIKE '________0%') AND
(flags_gspspec LIKE '_________0%') AND
(flags_gspspec LIKE '__________0%') AND
(flags_gspspec LIKE '___________0%')

Listing 1. ADQL query with simple cuts in the limiting parameters for the general sample

GENERAL SAMPLE AND
((nfe_gspspec_upper-nfe_gspspec_lower)<0.30) AND
((flags_gspspec LIKE '_____________0%') OR
(flags_gspspec LIKE '_____________1%')) AND
(flags_gspspec LIKE '______________0%') AND
(nfe_gspspec_nlines>=2) AND
(nfe_gspspec_linescatter<0.1)

Listing 2. ADQL query for the nitrogen abundance sample

GENERAL SAMPLE AND
((Mgfe_gspspec_upper-Mgfe_gspspec_lower)<0.40)
AND
((flags_gspspec LIKE '_______________0%') OR
(flags_gspspec LIKE '_______________1%')) AND
(flags_gspspec LIKE '________________0%')

Listing 3. ADQL query for the magnesium abundance sample

GENERAL SAMPLE AND
((mh_gspspec_upper-mh_gspspec_lower)<.4) AND
((flags_gspspec LIKE '___________________________0%')
    OR
(flags_gspspec LIKE '___________________________1%'))
    AND
(flags_gspspec LIKE '____________________________0%')

Listing 4. ADQL query for the iron abundance sample

We also calibrated the Gaia abundances of iron, nitrogen, and magnesium as well as log g using the following formulae:

(A.1)

(A.2)

(A.3)

(A.4)

Appendix B: Stellar properties about the giants in our sample

Table B.1.

Information about the giants stars in our sample.

All Tables

Table 1.

Effects on the derived chemical abundances and abundance ratios resulting from uncertainties in atmospheric parameters and abundances.

In the text
Table 2.

Properties of the star samples used in this study.

In the text
Table B.1.

Information about the giants stars in our sample.

In the text

All Figures

thumbnail Fig. 1.

Comparison of effective temperatures, surface gravities and metallicities determined during the first (spectroscopic) and the second (asteroseismic) steps of the parameter determination process.
In the text
thumbnail Fig. 2.

Examples of fits to the carbon and oxygen lines in a spectrum of KIC4457200. The middle line represents the best fit for [C/H] = 0.01 and [O/H] = 0.12, whereas the other two lines indicate ±0.10 dex for the corresponding abundances.
In the text
thumbnail Fig. 3.

Examples of fits to the 12C14N and 13C14N molecular lines in a spectrum of KIC4457200. The middle line represents the best fit for 12C/13C = 12, whereas the other two lines indicate ±2 in the 12C/13C ratio.
In the text
thumbnail Fig. 4.

Example of fits to the magnesium lines for KIC4457200. The middle line represents the best fit for [Mg/H] = 0.22, whereas the other two lines indicate ±0.10 dex for the magnesium abundance.
In the text
thumbnail Fig. 5.

Differences in abundances of C, N, and O derived using the spectroscopic and asteroseismic atmospheric parameters.
In the text
thumbnail Fig. 6.

Differences between [X/H], log g, and Teff coming from the literature and derived in this study. The comparisons are done using the Gaia DR3 (blue stars), APOGEE DR17 (green circles), LAMOST DR7 (orange squares), and PASTEL (purple diamonds) catalogues. The shaded regions indicate ±0.2 dex and ±100 K.
In the text
thumbnail Fig. 7.

Asymptotic period spacing of g-modes, ΔΠℓ = 1, computed by Mosser et al. (2014; orange circles) and by Vrard et al. (2016; blue triangles) as a function of ΔΠℓ = 1 derived by Mosser et al. (2012). We considered all stars with ΔΠℓ = 1≤140 s as first-ascent RGB stars and all stars with ΔΠℓ = 1 > 140 s as core He-burning stars. The error bars on the ΔΠℓ = 1 determination are smaller than the size of the symbols.
In the text
thumbnail Fig. 8.

Relative difference of the stellar masses derived from SPInS and the seismic masses derived with PARAM (ΔM/M = (MSPINS − Mseismic)/Mseismic) using or not asteroseismic diagnostics (red and blue stars, respectively). The dashed lines represent a relative difference of ±20%.
In the text
thumbnail Fig. 9.

Toomre diagram for the stars in our sample. The dashed curves indicate constant space motion. The stars are colour-coded according to their metallicity.
In the text
thumbnail Fig. 10.

Kiel diagram for the stars in our sample (orange symbols). RGB and core He-burning stars are represented by circles and squares, respectively. Stars compiled from the literature for which the carbon isotopic ratio (and log g) is determined are represented by grey star symbols (see Sect. 3.4). Stellar evolutionary tracks computed with STAREVOL for the 1.4 M⊙ model (dashed line) and 2.0 M⊙ model (dash-dotted line) at solar metallicity and 2.5 M⊙ at [Fe/H] = −0.23 (solid line) are also plotted.
In the text
thumbnail Fig. 11.

12C/13C vs. [Fe/H] (top panel), mass (middle panel), and age (bottom panel) for stars in our sample (orange symbols). The abundances are from Gratton et al. (2000), Tautvaišienė et al. (2010, 2013), Morel et al. (2014), Takeda et al. (2019), Charbonnel & Balachandran (2000) and Aguilera-Gómez et al. (2023) are also plotted. When the information is available in the original papers, first-ascent giant and core He-burning stars are plotted in the middle and right column, respectively. For our golden sample stars, the asteroseismic masses and ages we obtained with PARAM are shown. For the literature sample, the masses and ages obtained with SPInS with only spectroscopic but no asteroseismic constraints are shown.
In the text
thumbnail Fig. 12.

Hertzsprung–Russell diagram of a 1.0 M⊙ model at solar metallicity (top left panel). Also shown are the evolution of 12C/13C (top right panel), [C/O] (bottom left panel), and [N/O] (bottom right panel) for the 1.0 M⊙ and 1.5 M⊙ model at solar metallicity (blue and purple lines, respectively) and for 1.0 M⊙ at [Fe/H] = –0.54 (orange line) from the subgiant branch to the RGB tip and later from the core He-burning to AGB phase. The tracks show the predicted behaviour from stellar evolution models taking into account or not the effects of thermohaline mixing (solid and dashed lines, respectively). The position of the beginning of the first dredge-up, the RGB bump, and the core He-burning phase are indicated in each panel (triangle, star, and square, respectively).
In the text
thumbnail Fig. 13.

12C/13C vs. [Fe/H] for core He-burning and RGB stars in our sample (squares and circles, respectively) compared with the BGM simulations for core He-burning stars only (dots) of the Kepler field and taking into account or not the effects of thermohaline mixing (right and left panels, respectively). The stellar mass is colour-coded for both observations (using seismic determinations from PARAM) and simulations (predicted by BGM using STAREVOL stellar evolution models from Lagarde et al. 2017, 2019). In the right panel the mass loss rate is decreased on the RGB by a factor of two compared to the left and middle panels (see text for details).
In the text
thumbnail Fig. 14.

Same as Fig. 13 for 12C/13C as a function of stellar mass. In the right panel, the mass loss rate is decreased on the RGB by a factor of two compared to the left and right panels (see text for details). The stellar age is colour-coded for both observations and BGM simulations. The green lines in the middle panel show the 12C/13C at the core He-burning phase predicted by stellar evolution models computed by Lagarde et al. (2012a) and including both thermohaline and rotation-induced mixing (at V/Vcrit ∼ 0.3) at [Fe/H] = 0 and [Fe/H] = −0.86 (dotted and dashed line, respectively).
In the text
thumbnail Fig. 15.

Same as Fig. 13 for 12C/13C as a function of stellar age, with the stellar metallicity colour-coded for both observations and simulations. The green lines in the right pannel have the same meaning as in Fig. 14.
In the text
thumbnail Fig. 16.

12C/13C as a function of log(C/O) for core He-burning and RGB stars in our sample (orange squares and circles, respectively) compared to the BGM simulations for core He-burning stars only. The simulations (grey dots) take into account the thermohaline mixing (middle and right panels) or not (left panel). The C/O ratio derived by Blanton et al. (2017) for stars in common is also shown, using our carbon isotopic ratios (blue stars in middle panel). The abundances derived by Gałan et al. (2017, 2023), and Gratton et al. (2000) are also compared with the simulation in the right panel. The 12C/13C at the core He-burning phase predicted by stellar evolution models computed by Lagarde et al. (2012a) and including both thermohaline and rotation-induced mixing (at V/Vcrit ∼ 0.3) are shown at [Fe/H] = 0 and [Fe/H] = −0.86 (green dotted and solid lines, respectively).
In the text
thumbnail Fig. 17.

Same as Fig. 16. 12C/13C, but as a function of log(N/O).
In the text
thumbnail Fig. 18.

12C/13C vs. log(N/O) for core He-burning stars in our sample (left panel) and vs. log(N/O) derived by APOGEE DR17 (right panel) compared to the BGM simulations including the effects of thermohaline mixing. Thin and thick disc stars according to their Gaia kinematics are represented by the orange and blue symbols. The same colour-coding is used in the BGM simulation.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.