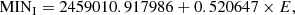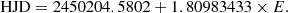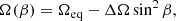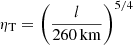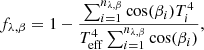| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 26 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348324 | |
| Published online | 09 April 2024 | |
A star under multiple influences
Magnetic activity in V815 Her, a compact 2+2 hierarchical system⋆
1
Konkoly Observatory, HUN-REN Research Centre for Astronomy and Earth Sciences, Konkoly Thege Miklós út 15-17, 1121 Budapest, Hungary
e-mail: kovari@konkoly.hu
2
HUN-REN CSFK, MTA Centre of Excellence, Konkoly Thege Miklós út 15-17, 1121 Budapest, Hungary
3
Leibniz-Institute for Astrophysics Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
4
Institute for Physics and Astronomy, University of Potsdam, Karl-Liebknecht-Strasse 24/25, 14476 Potsdam, Germany
5
Baja Astronomical Observatory of University of Szeged, Szegedi út, Kt. 766, 6500 Baja, Hungary
6
HUN-REN-SZTE Stellar Astrophysics Research Group, Szegedi út, Kt. 766, 6500 Baja, Hungary
7
ELTE Gothard Astrophysical Observatory, Szent Imre h. u. 112, 9700 Szombathely, Hungary
8
Moholy-Nagy University of Art and Design, Centre for Data Science and Digital Development, Zugligeti út 9, 1121 Budapest, Hungary
Received:
19
October
2023
Accepted:
10
January
2024
Context. Close binaries with magnetically active components are astrophysical laboratories for studying the effects of binarity on activity. Of particular interest are binary and multiple star systems that contain a solar-type active component with an internal structure similar to the Sun, allowing us to study how the dynamo of a solar-type star would work under different conditions.
Aims. We have conducted a comprehensive investigation of V815 Her using photometric and spectroscopic data to understand the origin of the activity and what influences it in the short and long term.
Methods. Using space photometry we performed light curve modeling in order to derive astrophysical and orbital parameters for the eclipsing binary subsystem V815 Her B. Using archival photometric data covering a century we carried out a time frequency analysis. Spectral synthesis was applied to determine the basic astrophysical parameters of the rapidly rotating primary using high-resolution STELLA spectra recorded in 2018.
Results. Photometric analysis of archived data revealed multiple cycles on timescales between ∼6.5 and ∼26 yr, some of which may be harmonic. From TESS photometry we obtained an orbital solution for the V815 Her B subsystem. By placing the primary component on the Hertzsprung–Russell-diagram, we could deduce an age of ≈30 Myr, in line with the high Li-6707 abundance. The STELLA spectra covering the 200 day-long observing season enabled us to create 19 time-series Doppler images, which revealed a constantly changing spotted surface on a timescale of a few weeks. From the consecutive image pairs we built up the average cross-correlation function map to measure the surface differential rotation of the spotted star, from which we derive a weak solar-type surface shear.
Conclusions. We found evidence that the V815 Her B component previously apostrophized as a “third body” is actually an eclipsing close binary subsystem of two M dwarfs with a period of 0.5 d, that is, V815 Her is a 2+2 hierarchical quadruple system. The system is apparently young, only a few times ten million years old, consistent with the spotted primary V815 Her Aa being a zero-age main-sequence star. Spot activity on the primary was found to be vivid. Fast starspot decay suggests that convective-turbulent erosion plays a more significant role in such a rapidly rotating star. The weak surface shear of V815 Her Aa due to differential rotation is presumably confined by tidal forces of the close companion V815 Her Ab. The slowly increasing photometric cycle of about 6.5 yr on average is interpreted as a spot cycle of V815 Her Aa, which is probably modulated by the eccentric wide orbit.
Key words: stars: activity / stars: imaging / stars: individual: V815 Her / stars: late-type / starspots
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Close binaries that contain magnetically active components may be regarded as astrophysical laboratories for studying the effect of binarity on activity. Tidal forces in such systems are supposed to modify the operation of the magnetic dynamo, by altering the flux emergence patterns at the surface (Holzwarth & Schüssler 2003a,b). Amplified dynamo operation is expected, for instance, when fast rotation is sustained by weakening magnetic braking through angular momentum transport in a close binary system (Song et al. 2018). Although, other binarity-related effects like early evolution accretion processes can also result in faster rotation (Meibom et al. 2007). In all probability, the gravitational influence of a close companion can suppress the differential rotation of the convection zone (Scharlemann 1982; Collier Cameron 2007) or even force the formation of active longitudes at certain phases fixed to the orbit (Oláh 2006; Kővári et al. 2021). Especially interesting are those binaries and multiple star systems that contain active G-type main-sequence (MS) stars with an inner structure (convective zone) similar to that of the Sun, making it possible to investigate how the solar-type dynamo would work under different circumstances.
In accordance with the above, this time we chose the active G dwarf component of the single-lined though a quaternary star system V815 Her (= HD 166181) for our study. In the beginning, it was believed that the G star with its enhanced magnetic activity inferred from strong Ca II H&K emission is the primary member of a single-lined binary (SB1) system with an orbital period of ≈1.81 days (Nadal et al. 1974). Later using new spectroscopic data taken in 1992 at Kitt Peak National Observatory Dempsey et al. (1996) found a significant radial velocity difference of 11 km s−1 compared to the data of Nadal et al. (1974), which was attributed to a possible third body with an orbital period of many years. This idea was revisited by Fekel (2004) who, using new observations from 2002, calculated long-period orbital elements for the outer companion in the system for the first time with a preliminary period of 6.3 yr. With additional radial velocity measurements from 2003, this value was soon refined to 2092.2 ± 5.8 d (Fekel et al. 2005). From their mass estimates for the system components of the long-period orbit, Fekel et al. (2005) also suggested that the unseen component might also be a close binary. An important step forward in the story was that the outer component has been resolved by direct imaging within the frame of the Gemini Deep Planet Survey (GDPS) by Lafrenière et al. (2007) who confirmed the astrometric solution of Fekel et al. (2005) for the third body. Going even further, in our paper we present space photometry from NASA’s Transiting Exoplanet Survey Satellite (TESS) to demonstrate that the suspected third body itself is indeed an eclipsing close binary system of two unseen but very likely M dwarfs, that is, V815 Her is in fact a four-star system consisting of two close binaries orbiting each other.
According to photometric observations, it has long been known that the G (most probably G5–G6) active component features cool spots on its surface (Mekkadan et al. 1980). Strassmeier et al. (1989) reported automatic photoelectric telescope (APT) data from 1984–1986 in U, B, and V colors and found that the photometric period associated with the rotation of the G star was 1.8195 d and 1.8356 d for 1985 and 1986, respectively, that is, ≈1% longer than the orbital period from Nadal et al. (1974). From an extended study using long-term APT data taken in B and V between 1984 and 1998, Jetsu et al. (2000) found seasonal photometric period changes attributable to surface differential rotation of the spotted star. In addition, their time-series analysis revealed that one dominant active longitude was present for the full 14 yr-long observing period, while another weaker one emerged during some of the seasons. These APT data were reanalyzed in Savanov (2009) to reconstruct temperature inhomogeneities of the stellar surface. Again, two active longitudes were found, separated by about a 0.5 rotation phase (cf. Jetsu et al. 2000), showing the so-called flip-flop phenomenon, that is, when dominance switches quasi-periodically from one active longitude to the other.
Like the photosphere, the chromosphere and corona of the G component show the signatures of strong magnetic activity over a wide range of the electromagnetic spectrum. In addition to the strong and narrow Ca II H&K emission (Nadal et al. 1974; Bopp 1984) UV observations from the International Ultraviolet Explorer (IUE) satellite (Fekel et al. 1986) also indicate an active chromosphere. The absolute luminosity in the Mg II k line supports this enhanced activity (Cardini et al. 2003), however, the lack of hot component in the UV spectra suggests that the companions without contribution should be M-dwarfs or fainter. Moreover, the G star performs extreme-ultraviolet radiation measured during the ROSAT Wide Field Camera All-Sky Survey (Pounds et al. 1993) and by the Extreme Ultraviolet Explorer (EUVE) satellite (Malina et al. 1994). Due to the ROSAT mission, V815 Her is known for its bright X-ray corona (Dempsey et al. 1993a,b). Indeed, its coronal luminosity of LX = 3.183 × 1030 erg (Makarov 2003) classifies V815 Her as one of the 100 brightest stellar X-ray sources within 50 pc. Accordingly, with such an active corona, the star is known as a radio source as well (Drake et al. 1992).
V815 Her is not associated with any particular moving group (but see Wichmann et al. 2003, who cited the star as Pleiades-like). The strong Li line in the optical spectrum (Fekel et al. 2005) indicates that the G component is indeed young, near the zero-age main sequence (ZAMS). This observation is consistent with the star being listed in the Two Micron All Sky Survey Point Source Catalog (2MASS/PSC, Haakonsen & Rutledge 2009) due to its infrared excess, most probably related to primordial protoplanetary material.
In our paper, we perform a Doppler imaging study for the G star for the first time with reconstructing 19 time-series Doppler images using high-resolution optical spectra taken during a 9-month long observing run in 2018. The paper is organized as follows. In Sect. 2 we present the analysis of photometric data. Using TESS observations we analyze the newly discovered eclipses and give an orbital solution for the unseen, but most likely M+M dwarf binary companion V815 Her B in the quadruple system. In Sect. 3 we derive precise astrophysical parameters of the active G component for the Doppler imaging study presented in Sect. 4. Results are discussed in Sect. 5, and summarized in Sect. 6.
2. Photometric data and analysis
2.1. New light curve and orbital solution for V815 Her B using TESS data
The Transiting Exoplanet Survey Satellite has observed V815 Her during sectors 26, 40, and 531. The sector 26 observations were carried out in 2-min cadence mode, so the light curves produced by the Science Processing Operations Center (SPOC) became directly available, while the sector 40 and 53 observations were carried out only in the 600-min cadenced full frame image (FFI) mode. Hence, we downloaded the 2-min cadence Pre-search Data Conditioned Simple Aperture Photometry (PDCSAP) data from the Mikulski Archive for Space Telescopes, while we processed the sector 40 and 53 FFI data with the software package FITSH (Pál 2012). V815 Her (= TIC 320959269) is listed as a TESS planet host candidate with a supposed planetary orbit of 0.26 d. However, from a closer inspection, after removing the spot variability of the G star using the 1.8 d rotational period, it became clear to us that the depths of successive minima are slightly different, that is, primary and secondary minima alternate. Evidently, instead of a planet orbiting with a period of 0.26 d we found a close eclipsing binary with a double-length period of 0.52 d bound to V815 Her A in the wide orbit.
To prepare data for the computation of the orbital solution of this new close binary we fit the spotted light curve of the G star with a time-series three-spot model (see Fig. 1), which could properly follow the ever-changing light variation instead of a constant rotational period and its harmonics. For the fit we used an upgraded version of the SpotModeL code originally presented in Ribárik et al. (2003). For the light curve modeling the fixed parameters used were only crudely approximated (temperature, limb darkening, etc.) since the main goal was only to fit the light curve as smoothly as possible. The data were also cleaned from obvious outliers and a possible flare. The resulting model was subtracted from the original data and binned to 0.005 days (7.2 min) which were then used for binary modeling.
 |
Fig. 1. Fitted TESS light curve of V815 Her from sector 40. The blue dots indicate the observations, while the red line indicates the time-series three-spot model fit. |
For the eclipsing binary (EB) light curve modeling the residual curves of the three TESS sectors were converted into the flux domain, and normalized to unity. Then they were phase-folded with the previously determined eclipsing period of  -day and binned into 500 evenly spaced phase cells. The fluxes in each cell were simply averaged, and these 500 mean flux values were rendered to the mid-phase moments of each cell. In such a manner we obtained evenly spaced, folded, binned, mean light curves separately for sectors 26, 40, and 53, which are plotted in Fig. 2.
-day and binned into 500 evenly spaced phase cells. The fluxes in each cell were simply averaged, and these 500 mean flux values were rendered to the mid-phase moments of each cell. In such a manner we obtained evenly spaced, folded, binned, mean light curves separately for sectors 26, 40, and 53, which are plotted in Fig. 2.
 |
Fig. 2. Folded and fitted TESS sector 26, 40, and 53 light curves of the wide binary companion V815 Her B. Cleaned observations are marked with blue dots, the original orbital solutions without assuming surface inhomogeneities are drawn with gray lines, while the models drawn with red lines fit also the light curve variations arising from stellar spots. The residuals of both fits are plotted on the bottom parts of all panels. We note that the eclipses in sectors 40 and 53 (middle and bottom panels) are shifted from phases 0.0 and 0.5, indicating timing variations, which are discussed in detail in the text. |
The EB light curve analyses of these prepared datasets were carried out with software package LIGHTCURVEFACTORY (see Borkovits et al. 2019, 2020, and further references therein). We analyzed the data of the three sectors separately. During our Markov chain Monte Carlo (MCMC) based parameter search process, the following seven light curve parameters were adjusted: the total duration of an eclipse (which is a direct observable, and closely related to the sum of the fractional radii of the two stars); the RBb/RBa ratio of the stellar radii; the TBa effective temperature of the primary; the logarithm of the ratio of the effective temperatures log(TBb/TBa); the “third” light ℓ, which allows us to take into account the light contamination caused by the much brighter binary V815 Her A; the EB’s inclination iB; and finally the T0 time of the reference epoch2. Regarding the other orbital elements, the folded mean light curve in Fig. 2 reveals that the secondary eclipses occur just at (or, at least, very close to) phase 0.5, that is, in the mid-times between the consecutive primary eclipses. In addition, the durations of primary and secondary eclipses appear to be similar. Thus, we assume a circular EB orbit and, accordingly, we fix the eccentricity at eB = 0.
The adjustment of the effective temperature of the primary TBa needs some further explanation. In general, in the case of a single photometric band EB light curve, the temperature ratio of the two stars is well determined, while the individual effective temperatures themselves play only a minor role in forming the light curve, so they are ill-determined. In such a case, the usual solution is to take one of the temperatures (for instance TBa) from some external source (e.g., spectroscopy or spectral energy distribution analysis) and keep it fixed. However, in the present case, TBa was treated as a free parameter in order to check the physical reliability and consistency of our solution. This was done as follows. We know that the brighter binary should be a very young object. We reasonably assume that the two binaries are coeval, and thus, the two stars of binary B locate also on (or, very near to) the ZAMS. Hence, we expect that the empirical mass–luminosity and mass–radius relations of Tout et al. (1996) are applicable for these stars. Therefore, with the combined and inverted use of these relations, we can calculate the masses and radii of the components from the effective temperatures. Then we can compare the total mass of binary B, obtained from our analysis to the minimum mass inferred from the orbital solution of Fekel et al. (2005). Moreover, we can compare the stellar radii, calculated directly through the mass–radius relations of Tout et al. (1996) to that calculated from the combination of the fractional radii (which are direct outputs of the light curve analysis) and the masses, inferred again from the Tout et al. (1996) relations.
Finally, we also note, that a first inspection of the folded mean light curve of binary B reveals that, despite the averaging over ∼25 orbital cycles, the out-of-eclipse light variations did not average out perfectly. One possible origin of these out-of-eclipse light variations might be the surface brightness inhomogeneities (e.g., starspots), which, for the (almost) synchronized stellar rotations may have “survived” the averaging for the orbital period. We model these variations together with the EB light curve modeling simultaneously in a purely mathematical way, that is, independent of their real origin, as follows. In each trial step, after the removal of the model EB light curve from the input light curve data, the residual is modeled with harmonic functions of two fixed frequencies (namely, the twice of the orbital frequency and, the orbital frequency itself), of which the four (plus one) coefficients are obtained via matrix inversion. Then, this mathematical model of the residual light curve is added to the EB model light curve and the actual χ2 value is calculated for this mixed model curve.
In Table 1 we tabulate the median values and the 1σ statistical uncertainties of the parameters (including several derived, physical ones) that were obtained from our analysis for the sector 26 data. We also display the synthetic model fits (both with and without the mathematically modeled out-of-eclipse light variations) derived from the best-fit solution in Fig. 2. We note that in the case of the analysis of sector 40 and 53 light curves we obtained mostly similar parameters within the tabulated 1-σ uncertainties and, hence, we do not tabulate these results separately. The two exceptions are the ℓ extra flux and the T0 epoch of the primary minimum. Regarding the former one, in sectors 40 and 53 we obtained smaller ℓ parameters with ∼5 − 10%, which we explain with a smaller level of contaminated fluxes in the TESS pixels. What physically more interesting is, the shift of the phase of the primary eclipses, which can also be seen in the consecutive panels of Fig. 2. In order to understand the nature and origin of this effect, we carried out a detailed analysis of the times of eclipsing minima.
Adjusted and derived astrophysical and orbital parameters for V815 Her B.
2.2. Eclipse timing variation analysis of V815 Her B
We determined mid-eclipse times for all the observed primary and secondary eclipses of V815 Her B for the available TESS cleaned time series (see Sect. 2.1). The individual times of minima are tabulated in Table A.1. We derived an eclipse timing variation (ETV) curve using the linear ephemeris
where the zero epoch is given in Barycentric Julian Date (BJD). We plot the obtained ETV curve in Fig. 3. As one can see, the ETV curve displays clearly a nonlinear behavior, which reveals that the observed eclipsing period is varying.
 |
Fig. 3. Eclipse timing variations of V815 Her B calculated from the mid-minima times of primary and secondary eclipses based on TESS observations. The red dots and blue squares represent the primary and secondary eclipses, respectively. The black line represents the theoretical LTTE curve derived from the former third-body RV solution of Fekel et al. (2005). See text for details. |
As a next step, we demonstrate that this variation can be explained by the light-travel time effect (LTTE) caused by the revolution of the eclipsing binary V815 Her B around its brighter counterpart V815 Her A, and the parameters of this LTTE orbit is in accordance with the former RV solution of Fekel et al. (2005). This indicates, that this currently discovered EB is identical with the third component suspected formerly through RV measurements. In order to demonstrate this fact, we derive LTTE solution from the outer RV orbit of Fekel et al. (2005, their Table 2). While doing so, one should be cautious about a few things. First, the argument of pericenter of the outer orbit (ωA) given in the RV solution refers to the orbit of component A, while in the LTTE solution of component B, the argument of pericenter of component B (ωB = ωA + 180°) is present. Moreover, the projected semi-major axis aA sin iout of the orbit of component A around the center of mass of the whole quadruple system, which was deduced from the amplitude of the RV curve, should also be transformed to the projected semi-major axis of component B (aB sin iout = mA/mB × aA sin iout). For this step, we must know the mass ratio of the two binaries. For the formerly known, brighter component we accept mA = mAa + mAb = 1.27 M⊙ (Fekel et al. 2005), while our solution gives the mass of component B to be mB = mBa + mBb = 0.63 M⊙, which results in an outer mass ratio of mA/mB = 2.02. Taking into account these constraints, and plotting the theoretical ETV curve against the measured ones, one can see a nice agreement (see Fig. 3), which, in our readings demonstrate nicely that the spectroscopic multiplicity of V815 Her is confirmed independently through TESS photometry, and the third spectroscopic component itself is a close, eclipsing binary, forming such a way a close quadruple system with a 2+2 hierarchy. For comparison, the periods and geometrical parameters of the wide (V815 Her AB) and the two close orbits (V815 Her A and B) in the 2+2 hierarchical system are given in Table 2.
Comparison of the periods and geometry in V815 Her.
2.3. Long-term photometric behavior using archival data
V815 Her has data from scanned photographic plates in the Digital Access to a Sky Century @ Harvard (DASCH, Grindlay et al. 2009) database for about hundred years between 1890–1990 supplemented with photoelectric data collected in Jetsu et al. (2000) with an overlap of 5 yr. We stitched the two datasets together by shifting the photoelectric B band light curve to match the median of the DASCH light curve in the 5 yr overlap. These data cannot depict the rotational modulation of the G star, but can be used to search for long-term variability and trends. We combine the photographic and photoelectric datasets in Fig. 4.
 |
Fig. 4. Long-term photometry and time-frequency analysis of V815 Her. Top: DASCH light curve of ≈100 yr for V815 Her from scanned photographic plates (black dots) supplemented with photoelectric data (blue dots) spanning more than a century between 1890–1998 with 5 yr’ overlap. The spline smoothed data are indicated by a red line. Bottom: time-frequency analysis for the available photographic+photoelectric data of V815 Her using the TiFrAn code (Kolláth & Oláh 2009). The plot indicates dominant cycles of different lengths and amplitudes on timescales corresponding to ∼6.5, ∼9.1, ∼11.5, ∼13 and ∼26 yr, the latter two are probably multiples of the 6.5-yr period. Dashed lines indicate the 2092 d period of the wide orbit and its double at 4184 d (≈11.5 yr). See the text for more. |
Looking for possible activity cycles we used our Time Frequency Analyzer package TiFrAn (Kolláth & Oláh 2009) with Choi-Williams distribution kernel which gives good resolution in the frequency domain and somewhat less in the time-domain. The data were averaged in bins of 365 days. Although there is a huge difference between the observational noise of the photographic and photoelectric data, the magnitude of the noise does not alter the frequency pattern. The different kernels of TiFrAn and their features are discussed in detail in Kolláth & Oláh (2009).
The data and results are plotted in Fig. 4. We reveal a cycle with a slowly increasing period, which has a steady amplitude at ∼6.5 yr. Two other cycles of ∼9.1 and ∼13 yr with similarly strong amplitudes are present throughout the observations. Between them, we also find an ∼11.5-yr cycle which is still clearly visible despite its weaker amplitude. This fits quite well to twice the period of the outer orbit, that is, 11.45 yr (= 4184 d); see the lower dashed line in Fig. 4. The longest persistent feature (ignoring the one corresponding to the total data length) points toward a timescale around ∼24–26 yr with weakening amplitude. The cycle lengths of ∼13 and ∼26 yr are perhaps harmonics of ∼6.5 yr, although in contrast to the slow growth of the 6.5-yr cycle over time, the 13-yr cycle seems to decrease toward the end of the time series. At this point, it is difficult to interpret the possible physical background of each cycle that appears in the brightness change. In any case, we attempt to list some ideas in Sect. 5.
3. Spectroscopic data and astrophysical properties of V815 Her Aa
3.1. STELLA-SES spectra
The spectroscopic observations were carried out with the 1.2-m STELLA-II telescope of the STELLA robotic observatory (Strassmeier et al. 2010) located at Izaña Observatory in Tenerife, Spain. STELLA-II is equipped with the fiber-fed, fixed-format STELLA Echelle Spectrograph (SES) providing an average spectral resolution of R = 55 000 along the covered 3900–8800 Å wavelength range. Further details on the performance of the system and the data-reduction procedure can be found in Weber et al. (2008, 2012).
Altogether 621 high-resolution spectra were recorded between 07 March and 11 November, 2018. With a default exposure time of 3000 s an average signal-to-noise ratio (S/N) of ≈200:1 could be reached and only 18 spectra had to be discarded due to their poor quality. This dataset were used for both the spectral synthesis detailed in the next section and the Doppler-inversions (see Sect. 4). The observing log is summarized in Table B.1. Assuming synchronized rotation for the G star in the close binary subsystem V815 Her A, the rotational phases are calculated using the orbital period from Fekel et al. (2005) according to the following equation:
The zero phase is the time of maximum radial velocity, that is, the primary component is closest to us in ϕ = 0.75 phase, accordingly, the λ = 270° longitude of the primary is facing the secondary.
3.2. Spectral synthesis
For the determination of some of the basic astrophysical parameters, we used the spectral synthesis code SME (Piskunov & Valenti 2017). Ten good quality (S/N ∼ 200) STELLA-SES echelle spectra were randomly selected to carry out spectral synthesis independently on each. During the computations, local thermodynamical equilibrium (LTE) was assumed and MARCS atmospheric models (Gustafsson et al. 2008) were used. Atomic line data were taken from the VALD line database (Kupka et al. 1999). A global macroturbulence relationship was adopted from Valenti & Fischer (2005, see their Eq. (1)). The parameters, Teff effective temperature, log g surface gravity, [Fe/H] metallicity, and vmic microturbulence were determined iteratively; for details on the fitting method see Kriskovics et al. (2019). For the fits the equatorial rotational velocity v sin i was kept at 30 km s−1 since the Doppler-inversion (see Sect. 4 in this paper) proved to be artifact-free at this value, while using, for example, 27 km s−1 and 33 km s−1 caused severely artifact-ridden results having unrealistic equatorial brightening with polar darkening or polar brightening with equatorial darkening, respectively. We note that if v sin i was treated as a free parameter as well, the process yielded only slightly different results compared to the value of 30 km s−1.
Lithium 6707 Å abundance was determined also by SME using LTE synthesis together with 3D-NLTE departure coefficients taken from Harutyunyan et al. (2018). We selected the same ten spectra of high S/N as above, for which we determined the lithium abundance separately. Averaging these yielded logarithmic abundances of A(Li)LTE = 1.66 ± 0.04 and A(Li)NLTE = 1.75 ± 0.04. Here, logarithmic abundance is defined as A(Li) = log(NLi/NH)+12 where NLi and NH are the number densities of lithium and hydrogen, respectively. Figure 5 shows an example fit to the observed Li I 6707 Å spectral region. In a solar-like star like the G component in the V815 Her system, Li-6707 is gradually depleting during the pre-MS evolution over a few tens of Myr (e.g., Hillenbrand 2009). According to Somers & Pinsonneault (2015), in the Pleiades, A(Li) typically decreases from the initial 3.3 to below ∼1.0 by the age of ∼100 Myr, however, highly dependent on the evolutionary models applied. Nevertheless, the correspondingly estimated age of a few tens of Myr is also consistent with the result of our spectral energy distribution analysis; see Sect. 3.3.
 |
Fig. 5. Example plot of the observed Li I 6707Å spectral region (black) fitted with a synthetic spectrum (blue). |
3.3. Analysis with VOSA
We performed a spectral energy distribution (SED) synthesis using the virtual observatory (VO) SED analyzer tool VOSA (Bayo et al. 2008) to build the SED of V815 Her from the available VO catalogs and surveys (GALEX, Tycho, SDSS, Pan-STARRS, Gaia, 2MASS, AKARI/IRC, WISE, and IRAS). For fitting the resulting SED in Fig. 6 ATLAS9 Kurucz ODFNEW/NOVER models (Castelli & Kurucz 2003) were used with the nearest grid values of Teff = 5500 K effective temperature, log g = 4.5 surface gravity, and [Fe/H] = 0.2 metallicity.
 |
Fig. 6. SED for V815 Her generated by the VOSA SED analyzer tool (Bayo et al. 2008). The synthetic spectrum (blue line) is fitted to the archival photometry (red dots) from the available VO catalogs and surveys using ATLAS9 Kurucz ODFNEW/NOVER models with Teff = 5500 K effective temperature, log g = 4.5 surface gravity, and [Fe/H] = 0.2 metallicity. |
It is noteworthy that the SED (see Fig. 6) shows an excess toward infrared (IR) wavelengths. This could be the characteristics of a very young age since pre-MS stars of ≲10 Myr (Williams & Cieza 2011) usually possess primordial protoplanetary disk, which causes excess in near-IR (cf. Sect. 3.2).
In Fig. 7 we plotted the star on the Hertzsprung–Russell-diagram (HRD) along with theoretical isochrones and evolutionary tracks for the most suitable Geneva model (Haemmerlé et al. 2019). According to the plot, the age of the G star with M/M⊙ ≲ 1.0 mass ratio is ≈30 million years. We note, however, that errors of age determination increase toward the ZAMS as the isochrones line up more and more densely. Nevertheless, this age determination is in agreement with the measured Li-6707 abundance in Fig. 5.
 |
Fig. 7. Position of V815 Her Aa (black dot) on the HRD plotted by using the VOSA SED analyzer tool (Bayo et al. 2008). Evolutionary tracks for the Geneva model (Haemmerlé et al. 2019) indicate an age of 30 Myr for a M ≲ 1 M⊙ ZAMS star. |
3.4. Luminosity and size
The Gaia EDR3 parallax of π = 31.1649 ± 0.1225 mas (Gaia Collaboration 2016, 2021) yields a distance of d = 32.087 ± 0.127 pc for V815 Her. Assuming 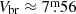 for the brightest V magnitude with B − V of 0
for the brightest V magnitude with B − V of 0 71 (cf. Fekel et al. 2005), and neglecting interstellar extinction yields an absolute visual magnitude of
71 (cf. Fekel et al. 2005), and neglecting interstellar extinction yields an absolute visual magnitude of 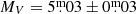 . Taking the BC = −0.132 bolometric correction from Flower (1996) gives a bolometric magnitude of
. Taking the BC = −0.132 bolometric correction from Flower (1996) gives a bolometric magnitude of 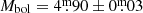 . This gives L/L⊙ = 0.87 ± 0.03 when using a value of
. This gives L/L⊙ = 0.87 ± 0.03 when using a value of 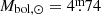 for the Sun.
for the Sun.
Assuming an inclination of i = 75 ± 5° (cf. Fekel et al. 2005), the projected equatorial rotational velocity v sin i of 30 km s−1 with ±1.5 km s−1 error (see Sect. 3.2) would yield a stellar radius of R/R⊙ = 1.1 ± 0.1. We note, that at a distance of ≈32 pc the estimated limb-darkened angular diameter of the G star of 0.346(±0.009) mas (Mid-infrared stellar Diameters and Fluxes compilation Catalog V10, Cruzalebes et al. 2019) would yield a similar radius of ≈1.2 R⊙. Although the ≳1.1 R⊙ size is a bit larger than predicted for a nonmagnetic G5 ZAMS star, still, such inflation is indeed to be expected for a ZAMS star with enhanced surface magnetic activity (cf. Jackson et al. 2016, and their references). When combining this radius with the effective temperature, the Stefan–Boltzmann law would give L/L⊙ ratio of 1.05 ± 0.15, still in line with the value derived from the bolometric magnitude, if the estimated errors are taken into account. Moreover, the 1.1 R⊙ radius, when combined with the most likely mass ratio of M/M⊙ ≲ 1.0 (cf. Fig. 7 and Fekel et al. 2005) would yield log g ≈ 4.31 for the G component in a pretty good agreement with the one obtained from SME. In Table 3 we summarize the astrophysical parameters of the G star determined in our study, along with the others adopted from the literature.
Derived and adopted astrophysical parameters for V815 Her Aa.
4. Surface temperature maps of the G star
4.1. Imaging code iMAP
To reconstruct the surface temperature maps we use the state-of-the-art Doppler imaging code iMAP (Carroll et al. 2012). This code carries out multiline inversion on a list of photospheric lines. We selected 38 nonblended absorption lines from the 5049–6750 Å region with suitable line-depth, temperature sensitivity and well-defined continuum. The stellar surface is modeled on a 5° ×5° spherical grid. Each local line profile is computed with a full radiative solver (Carroll et al. 2008). The local line profiles are disk integrated, and the individually modeled disk-integrated lines are averaged. Atomic line data are taken from the Vienna Atomic Line Database (VALD, Kupka et al. 1999). Model atmospheres from Castelli & Kurucz (2003) are interpolated for the necessary temperature, gravity, or metallicity values. When solving the radiative transfer, local thermodynamical equilibrium (LTE) is assumed. Additional input parameters are micro- and macroturbulence, and the projected equatorial velocity (see Sect. 3). For the surface temperature reconstructions iMAP uses an iterative regularization based on a Landweber algorithm (Carroll et al. 2012). The iterative regularization has been proven to always converge on the same image solution, therefore, no additional constraints are imposed (see Appendix A in Carroll et al. 2012).
4.2. Time-series Doppler images
From the STELLA-SES spectra described in Sect. 3.1 we formed consecutive and independent data subsets in such a way that each of them covers the entire rotation phase in sufficient density. As a result, we created enough subsets for 19 time-series Doppler images. For the temporal distribution of the Doppler images see Table 4. The 19 time-series Doppler images of V815 Her Aa are plotted in Fig. 8, while the corresponding line-profile fits are given in Figs. C.1–C.3. In order to follow the change in the spot distribution even more spectacularly, in Appendix D, we also present our Doppler images in the Mercator projection. The surface temperature maps indicate a constantly changing surface structure on a time scale of a few weeks. Even the coverage of the visible pole with a spot is not continuous: in images S05–S06 and S08–S10 and in S18 we see strong polar spots, which, for example, are almost absent in images S03, in S07 and S19. Spot temperature ranges are not constant either, the highest contrast (see, e.g., S08) reaches 1800 K, while the smallest temperature contrast (S07) is only a few hundred degrees. The lifespan of the longest-lived spots can typically be estimated at 2–3 weeks. However, with few exceptions, it is difficult to clearly point out the corresponding spots in successive images. The obvious main reason for this is rapid spot evolution, in which surface differential rotation is most likely involved. What is certain is that during the observed period we do not see a permanent polar spot, nor is there any sign of the formation of an active longitude. For further discussion of surface evolution see Sect. 5.4.
 |
Fig. 8. Nineteen time-series Doppler images of V815 Her for the 2018 observing season. From top to bottom, in chronological order, Doppler images S01–S10 are on the left, and Doppler images S11–S19 are on the right. |
Temporal distribution of the subsequent datasets for each individual Doppler image.
4.3. Surface differential rotation
The latitude dependent surface rotation can usually be inferred from the cross-correlation of two successive Doppler images (Donati & Collier Cameron 1997). However, random changes in spot distribution can easily mask the expected cross-correlation pattern of differential rotation. Therefore, for the detection of the surface shear operating in the background, we use ACCORD (e.g., Kővári et al. 2012, 2015), a technique which enables the averaging of latitudinal cross-correlations in the case of a sufficient number of pairs of Doppler images not too distant in time, this way suppressing the effect of randomness and amplifying the correlation pattern attributed to surface differential rotation.
The overall correlation pattern in the resulting average cross-correlation map (Fig. 9) is fitted by a rotational law in the form
 |
Fig. 9. Average cross-correlation function map derived from 18 individual cross correlations. The stronger the correlation, the darker the shade. The map indicates how much longitude shift occurs at a given latitude due to surface shear during ∼6 Prot (which is the average time difference between the mean-HJDs of the consecutive maps; see Table 4). |
where Ω(β) is the latitude (β) dependent angular velocity, while Ωeq is the angular velocity at the equator, and ΔΩ = Ωeq − Ωpole gives the difference between the equatorial and polar angular velocities. The dimensionless surface shear parameter α is defined as αDR = ΔΩ/Ωeq. The resulting fit indicates a weak solar-type differential rotation, with Ωeq = 199.06 ± 0.40° day−1 and ΔΩ = 1.99 ± 0.60° day−1, yielding αDR = 0.010 ± 0.003 shear parameter. In comparison, the solar pole-to-equator angular velocity difference is ΔΩ⊙ = 4.1° day−1, that is, twice that of V815 Her. In the average correlation map, the stronger correlations are observed at latitudes higher than ≈30°, this is probably due to the fact that at lower latitudes the spots have less contrast, and perhaps in connection with this, their lifetime is also shorter. According to the rotational law that best fits the average cross-correlation pattern, it is most likely that the equatorial regions of the G star are (most) synchronized to the orbit. We note that the errors of the fitted rotation law plotted in Fig. 9 were estimated based on the error bars of the locations with the best correlations at the different latitude bands. However, this is the error of the fitting process, which does not necessarily reflect the true errors resulting from the method.
5. Discussions
5.1. Multiplicity and dynamical evolution
The multiple nature of the V815 Her system makes it very special, as the size of the wide (i.e., AB, in other words “outer” or “long”) orbit of the 2+2 hierarchical quadruple is relatively small, only aAB ≈ 1.6 AU (cf. Table 2). The investigation of similar systems is also exciting because their secular gravitational evolution can have a significant impact on the future fate of the components. Long-term gravitational effects in such quadruple systems can have a serious impact on the evolution of the orbital eccentricities, since both binaries can act as a distant perturber on the other pair. Unfortunately, the evolution of such a 2+2 hierarchy is still an under-researched topic (but see Vokrouhlický 2016). It is certain, however, that this interaction is not only dynamic (e.g., Kozai oscillations, also known as von Zeipel–Lidov–Kozai mechanism or Lidov–Kozai cycles; for a recent review see Ito & Ohtsuka 2019), but due to the small size and large eccentricity of the wide orbit, as well as the compactness of the subsystems, tidal effects must also be taken into account (cf. Fabrycky & Tremaine 2007).
Due to the Kozai mechanism, in hierarchical triple systems a distant third body (as well as a distant close binary in a 2+2 system) may even decircularize the inner orbit (e.g., Hamers 2021, see also their references). The time scale of these Kozai cycles is in the order of 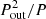 , that is, few times 103 yr. As a matter of fact, this can be seen in action on HD 74438 (Merle et al. 2022), a 2+2 hierarchical system in a highly eccentric wide orbit, where the eccentricity of one of the inner orbits was probably pumped by gravitational effects. According to this, the circularized close binaries of V815 Her will not necessarily remain so either. However, Kozai oscillations can be suppressed drastically when tidal friction enters the picture, shrinking and circularizing the inner orbit(s) on the tidal dissipation timescale (Fabrycky & Tremaine 2007). For both inner binaries, this timescale should be on the order of 105 yr (Van Eylen et al. 2016), that is, much shorter than ∼107-yr age of the Aa component and so the assumed age of the four-star system (in case the components are coeval). For this reason, we do not expect a large-amplitude Kozai oscillation in the case of V815 Her.
, that is, few times 103 yr. As a matter of fact, this can be seen in action on HD 74438 (Merle et al. 2022), a 2+2 hierarchical system in a highly eccentric wide orbit, where the eccentricity of one of the inner orbits was probably pumped by gravitational effects. According to this, the circularized close binaries of V815 Her will not necessarily remain so either. However, Kozai oscillations can be suppressed drastically when tidal friction enters the picture, shrinking and circularizing the inner orbit(s) on the tidal dissipation timescale (Fabrycky & Tremaine 2007). For both inner binaries, this timescale should be on the order of 105 yr (Van Eylen et al. 2016), that is, much shorter than ∼107-yr age of the Aa component and so the assumed age of the four-star system (in case the components are coeval). For this reason, we do not expect a large-amplitude Kozai oscillation in the case of V815 Her.
We note that in Merle et al. (2022) HD 74438 is reported to be one of the shortest period 2+2 quadruple systems with P ≈ 5.7 yr for the wide orbit, coincidentally almost exactly the same as the AB orbital period of V815 Her. Indeed, along with a few compact and coplanar (or even doubly eclipsing) 2+2 four-star system (Tokovinin 2018; Borkovits et al. 2021; Kostov et al. 2023; Zasche et al. 2023), V815 Her is among the shortest period 2+2 hierarhical systems. However, considering the size of the wide orbit, the V815 Her system is much more compact compared to HD 74438, which can be a significant difference in terms of the strength of secondary (i.e., tidal) effects; see also Sect. 5.3 below in this paper.
5.2. The V815 Her B close binary subsystem
The components of the low-mass eclipsing binary V815 Her B of the quadruple system are plotted on the mass-radius diagram on Fig. 10 together with other eclipsing binary components from the literature. Note that the oversize of the primary of V405 And were determined by two different methods using independent data (cf. caption of Fig. 10). In the figure the noneclipsing component V815 Her Aa is also given for reference to the age determination. Together with V815 Her Ba+Bb three other systems are plotted in color (see the legends in Fig. 10). While the masses of both the primaries and secondaries of these four systems are very similar to each other, laying on the two sides of the full-convection limit of ≈0.35 M⊙ (Chabrier & Baraffe 1997), the primaries show about twofold difference in radius. The fully convective secondaries are quite similar to each other in size, except for Thor-42 (Murphy et al. 2020). This detailed study of Thor-42 was not able to simultaneously model the mass, radius, temperature and luminosity of the components.
 |
Fig. 10. Mass-radius relation of low-mass eclipsing binary stars with well-determined parameters. The gray dots represent the targets taken from Schweitzer et al. (2019, their Table B.2). Other colored symbols in the legend show the positions of TIC 18480699 (Hebb et al. 2006), V405 And ((1) Vida et al. 2009, (2) Ribeiro et al. 2011), Thor 42 (Murphy et al. 2020), and V815 Her Aa, Ba, and Bb (present paper). Nonmagnetic, solar metallicity isochrones are taken from Baraffe et al. (2015). |
The relative oversize of low-mass magnetically active stars compared to inactive stars is a known phenomenon (cf. Mullan & MacDonald 2001). Kraus et al. (2011) suggested rotation as a third parameter of the mass-radius relation. Fast rotation, maintained by the binarity influence the magnetic field and through this, the strength of the magnetic activity of the late-type dwarfs. MacDonald & Mullan (2021) modeled Thor-42 using both magnetoconvection and starspots and through this they were able to reconcile all stellar parameters of the system, but at a different age that Murphy et al. (2020) found. This result underlines the importance of magnetic field in estimating fundamental parameters of active stars. We may say that the apparent discrepancy between the ages of the components of the V815 Her quadruple system shown in Fig. 10 could be largely due to the magnetic activity of the components which, in the same time, could also be different star-by-star.
5.3. Brightness change along the wide orbit
In the top panel of Fig. 11 we plot the V observations of V815 Her between 1984–98 from Jetsu et al. (2000). In these data we found a long-term brightness modulation, which showed an exciting coincidence with the approximate period of 5.73 yr of the outer (AB) orbit. Therefore, in the bottom panel of Fig. 11 we replot the V data along with the folded light curve phased with the period of the wide orbit taken from Fekel et al. (2005). It is interesting that near zero phase (which is the periastron of the wide orbit), the brightness decreases, while away from it the brightness gradually increases. The question arises as to whether this is just a coincidence or really a change related to the wide orbit, and if it is the latter, then what is causing it.
 |
Fig. 11. V light curve of V815 Her from Jetsu et al. (2000) between 1984–98. Below the panel of the time series, in the lower panel we present the light curve folded with the period of the wide orbit of 5.73 yr (= 2092.2 d). As zero phase the time of the periastron passage was set. The continuous color gradient helps to distinguish successive phases. |
On the other hand, the time-frequency analysis of the photometric data on a much longer term plotted in Fig. 4 does not show a strong cycle corresponding exactly to the period of the outer orbit, instead we see a strong signal of a 6.5-yr cycle with gradually increasing period, and strangely, a signal that appears almost exactly at twice the orbital period. Nevertheless, it cannot be ruled out that the slowly changing, roughly 6.5-y photometric period is the changing activity cycle of the Aa component, which is perhaps triggered along the wide orbit. According to Fekel et al. (2005) the eccentricity of the wide orbit is quite large (≈0.77), therefore gravitational effects exerted on the G star by V815 Her B change significantly along the outer orbit. Tidal interactions have indeed a potential impact on the internal structure and the turbulent/mixing processes (e.g., Toledano et al. 2007; Koenigsberger et al. 2021), ultimately, therefore, for the operation of the magnetic dynamo. This may also result in a change of the strength of spot activity of the G star, which ultimately causes the long-term change in brightness. We note here that such a possible binary-induced, that is, tidally triggered activity was reported in Strassmeier et al. (2011).
An alternative explanation could be that the brightness change along the wide orbit is somehow related to the dust-gas material component of any kind (circumstellar or circumbinary) present in the quadruple star system. Assuming that there is a circumbinary disk around the Ba+Bb binary (consistently with the infrared surplus indicated by Fig. 6), such a disk if tilted to the plane of the wide orbit, can reflect the radiation of the G star differently, depending on their mutual position, that is, the orbital phase. In our case, the reflected light can only be estimated cautiously in the case of a disk of unknown composition, size and geometry. However, if we estimate the contribution of the reflection from the disk to ≲1% (which is a rough upper estimate, cf. Bromley et al. 2021), then we can only explain a few percent of the long-term change in the mean brightness with reflection (say, ≲0.02 mag). Therefore, we conclude that changing spot activity results in the modulated brightness along the outer orbit, even though light reflected from any disk contributes little, if at all.
5.4. Surface evolution of V815 Her Aa
5.4.1. Spot decay and turbulent-driven magnetic diffusion
According to observations, the lifetime of sunspots depends on their area, based on which linear and nonlinear spot decay theories were born (e.g., Bumba 1963; Krause & Ruediger 1975; Petrovay & van Driel-Gesztelyi 1997; Hathaway & Choudhary 2008; Litvinenko & Wheatland 2015; Muraközy 2021; Forgács-Dajka et al. 2021), etc.). The underlying theories assume different mechanisms that also depend on the morphology of the sunspots/sunspot groups. When starspot lifetimes and starspot decay are discussed based on the solar analogy, the question arises as to whether it is a matter of scaling or other considerations are necessary (see, e.g., Namekata et al. 2019, and their references). The average spot area on V815 Her is about a factor of ∼100 larger compared to long-lived big sunspots (see Fig. 8). We note however, that the spatial resolution of our Doppler images does not reach the size range of sunspots, but in principle they are able to resolve surface structures corresponding to the largest sunspot groups. In this context, it is perhaps more reasonable to compare the starspots of our Doppler images with groups of sunspots instead of large individual sunspots.
As for the spot lifetime, based on our time-series Doppler images, the spotted surface of V815 Her is completely rearranged in a few steps, typically within ∼25–50 days (cf. Fig. 8 and Table 4). This is therefore the approximate upper limit of spot lifetime. At the same time, the lifespan of individual spots can vary widely. The shortest-lived spots can only be observed in one or at most two consecutive images, so their lifetime is ∼10–15 days.
We emphasize here, that it is difficult to discuss on the starspot decay in the context of sunspot theory without knowledge of the true morphology of starspots, that is, we do not know whether we are reconstructing monolithic spots on the Doppler images or clusters of smaller spots. It is even possible that one does not exclude the other, nevertheless, usually the limited spatial resolution of observations does not allow us to make a clear distinction (but see Järvinen et al. 2018). Moreover, spot decay may strongly be influenced by surface and subsurface flows.
Işik et al. (2007) modeled the temporal decay of the surface magnetic flux when assuming different spot configurations while large-scale flows (differential rotation, meridional circulation) are switched on and off. Their results indicate that spot conglomerates decay faster compared to large monolithic spots, and flows also play an important role in speeding up the decay. We note that the ΔΩ ≈ 2° d−1 surface shear on V815 Her is much weaker than on the Sun (see Sect. 4.3). If we take into account the tl lap time, that is, the time taken for the equator to lap the poles, then in the case of V815 Her we get 360° /ΔΩ = 180 d (i.e., about twice the solar lap time of ∼88 d). This is much longer than the observed spot lifetimes on V815 Her, therefore, differential rotation is likely to play a minor role (if at all) in spot decay. However, even with flows, the simulations in Işik et al. (2007) generally predict longer spot lifetimes than what we see on V815 Her.
Bradshaw & Hartigan (2014) argued that, assuming the same physical background and starting from the Gnevyshev–Waldmeier (hereafter GW) rule, the decay of sunspots and starspots can be scaled by the value of magnetic diffusivity through the turbulent scale length (which is connected to the supergranulation on the Sun). They suggested an anomalous turbulent-driven magnetic diffusion, which can account for the decay of either sunspots or starspots by scaling the characteristic supergranule/diffusion lengths.
By following the empirical GW rule, that is, assuming a linear relationship between the maximum As spot area and its ts lifetime, based on our time-series Doppler images, taking ts ∼ 20 d and Rs ∼ 10°, equivalent of 1.3 × 105 km, as average spot lifetime and corresponding characteristic maximum size, respectively, we can estimate a characteristic value of the spot decay rate ΔAs/Δts of about −4.0 × 104 km2 s−1. In Appendix F, we also present a more detailed study to measure the spot decay rate. Although the method is not mature enough yet, it is certainly more quantitative than the above estimate. We note that this detailed study yields even faster decay of about −7.0 × 104 km2 s−1.
Now, using ts = 20 d and Rs = 1.3 × 105 km (see above), we get from 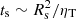 (Bradshaw & Hartigan 2014, their Eq. (3)) a value of ηT ≈ 104 km2 s−1 for the turbulent diffusivity. According to Chae et al. (2008, their Eq. (19)), from
(Bradshaw & Hartigan 2014, their Eq. (3)) a value of ηT ≈ 104 km2 s−1 for the turbulent diffusivity. According to Chae et al. (2008, their Eq. (19)), from
this value would yield a turbulent scale length of l = 4.2 × 105 km or ≈0.55 R*, that is, in the order of the stellar radius. Indeed, if we assumed an even faster spot decay from Appendix F, we would get about twice this amount. This large turbulent scale length is probably an overestimate, which may result from an overestimation of the maximum spot size. However, if, for example, several smaller spots were assumed instead of a monolithic spot, the turbulent scale length could also be reduced to a more plausible value (cf. Bradshaw & Hartigan 2014). Finally, we should also note that our measurement of the spot decay rate can be significantly distorted if, in addition to the spot shrinking, a rapid flux emergence occurs simultaneously in the same region. This would limit the validity of the interpretation that the observed spot decay rate and turbulent diffusion are directly related.
5.4.2. Latitudinal and longitudinal distribution of spots
In order to make it easier to assess the distribution of spots on the time-series Doppler maps, for each temperature reconstruction we calculated the sums of the f filling factor values along the λ longitude and β latitude (we have 72 longitude and 36 latitude pixels on a 5° ×5° spherical grid). When calculating fλ and fβ, we took into account the geometric distortion on the spherical surface according to the following formula:
where Ti and βi are the temperature and the latitude of the ith pixel, while the limit of the summation is the image pixel number over either the longitude (nλ = 72), or the latitude (nβ = 33, since we do not see the star below β = −75°). The resulting spot filling factors for the nineteen Doppler images are shown in Appendix E. Based on the latitudinal distribution of the spots, we see that especially in the case of low spot coverage, the spots tend to appear at mid-latitudes. In these cases (e.g., S01–S02–S03–S04, S07, S12–S13, S18) a somewhat equatorially symmetric distribution is seen. On the other hand, at other times spots tend to appear at high latitudes, closer to the visible pole. We note however, that, since we cannot see the other pole and its immediate surroundings, we cannot say whether the appearance of the polar spots shows any symmetry to the equator.
Granzer et al. (2000) studied the dynamics of magnetic flux tubes in young stars by numerical simulations and found that at a rotation rate of V815 Her Aa the spot emergence latitude is most likely between 25° −50° (see their ZAMS star model of 1 solar mass with ∼10 Ω/Ω⊙ rotation). However, similarly to V815 Her Aa, the coexistence of low-to-mid latitude spots and high latitude (or polar) spots on G-K type MS stars has already been supported by numerous Doppler imaging studies (e.g., Strassmeier 2009, and references therein). Moreover, EK Dra, the rapidly rotating young Sun, showed a very similar starspot distribution in the recent Doppler imaging study by Şenavcı et al. (2021), in which the polar and mid-latitude (>20°) spots are also consistent with flux emergence and transport simulations. According to Granzer et al. (2000), after flux emergence at mid latitudes a poleward flux transport by meridional circulation and/or magnetic stresses could explain the formation of polar spots (for the formation of polar spots on rapid rotators see also Schrijver & Title 2001; Işık et al. 2018). Maybe a weak sign of this can be seen in some of our subsequent Doppler image pairs (S04–S05, S13–S14, S16–S17), where the formation of the polar spot is preceded by a nearby lower latitude spot, although the available time resolution is not enough for a strict conclusion. Here, we note that the internal structure of V815 Her Aa is indeed affected by its close companion Ab, and this may be important also from the point of view of magnetic flux tube dynamics (e.g., Schuessler et al. 1996; Holzwarth & Schüssler 2003a,b).
The longitudinal spot distribution, in contrast, is more random, we see no definite indication of the existence of active longitudes. Although the changes can still mostly be followed in successive images, however, no systematic pattern can be seen in the evolution of the spotted surface over the entire period.
5.4.3. Surface differential rotation
From our cross-correlation study, we infer that the active G star has a weak solar-type differential rotation. Actually, this finding is in a fair agreement with the recent results obtained for two similar close binary systems V471 Tau (Kővári et al. 2021) and EI Eri (Kriskovics et al. 2023) in which the active component preserves its rapid rotation as a result of synchronization, but at the same time the degrees of surface shear due to differential rotation is presumably confined by tidal interaction. These observations support the idea that differential rotation is suppressed in low-mass stars tidally locked in close binary systems (see also Collier Cameron 2007, and their references). From a theoretical point of view, this kind of behavior is not unexpected, since a marked initial differential rotation structure would converge to rigid body-like rotation due to tidal shear energy dissipation (Koenigsberger et al. 2021). Our Fig. 9 also suggests that the equatorial region of V815 Her Aa is synchronized the most with the orbital period of V815 Her A. We note that this is consistent with tidal perturbations being expected to be strongest around equatorial latitudes.
6. Summary
The V815 Her system undoubtedly evolves dynamically and most likely magnetically, while the two subsystems, V815 Her A and B, interact gravitationally. Our main conclusions are summarized as follows:
-
The wide component in V815 Her previously apostrophized as a “third body” is actually an eclipsing close binary subsystem of two M dwarfs, that is, V815 Her is a 2+2 hierarchical quadruple system.
-
V815 Her is presumably a young system, supported by the infrared surplus indicated by the spectral energy distribution in Fig. 6. The young age is also supported by the lithium abundance that has not yet been depleted. In accordance with this, the evolutionary state of V815 Her Aa is a ZAMS star, with an age of ∼30M yr.
-
A rapid spot evolution can be observed on the surface of the active G component V815 Her Aa, the spot distribution can change completely on a time range of few times ten days.
-
We measured a weak solar-type surface differential rotation on the G star, which is probably suppressed by the tidal force of the close companion.
-
Based on the long-term photometric data, we found a slowly increasing cycle length of about 6.5 yr on average, which we interpret as a spot cycle. The length of the spot cycle is not necessarily closely related to the 5.73-yr period of the wide orbit, but we would not rule out the possibility of this at this point. We suspect that the reason for the slow change may be the modulation due to the eccentricity of the wide orbit.
The case of V815 Her is a good example of the particular importance of tidal effects for the dynamo mechanism. For this reason, our quartet is certainly interesting for further study of how gravitational evolution of the system affects activity.
Acknowledgments
We thank our referee, Dr. Emre Işık, for his very useful and constructive feedback, in which he made several important comments that contributed to the further development of the paper. Authors gratefully thank Dr. Attila Moór from Konkoly Observatory for the discussion about protoplanetary and debris disks and the light reflected from them. This work was supported by the Hungarian National Research, Development and Innovation Office grants OTKA K131508, KKP-143986 and by the Lendület Program of the Hungarian Academy of Sciences, project No. LP2018-7/2019. Authors acknowledge the financial support of the Austrian-Hungarian Action Foundation (98öu5, 101öu13, 112öu1). L.K. acknowldeges the support of the Hungarian National Research, Development and Innovation Office grant PD-134784. L.K. and K.V. are Bolyai János research Fellows. K.V. is supported by the Bolyai+ grant ÚNKP-22-5-ELTE-1093, B.S. is supported by the ÚNKP-22-3 New National Excellence Program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund. STELLA was made possible by funding through the State of Brandenburg (MWFK) and the German Federal Ministry of Education and Research (BMBF). The facility is a collaboration of the AIP in Brandenburg with the IAC in Tenerife. This publication makes use of VOSA, developed under the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/ through grant PID2020-112949GB-I00. VOSA has been partially updated by using funding from the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement no 776403 (EXOPLANETS-A). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This publication makes use of the Digital Access to a Sky Century at Harvard (DASCH), a project to digitize the photographic plate collection held at Harvard College Observatory. DASCH has been supported by NSF grants AST-0407380, AST-0909073, and AST-1313370, for which we are grateful.
References
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bopp, B. W. 1984, ApJS, 54, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Rappaport, S., Kaye, T., et al. 2019, MNRAS, 483, 1934 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Rappaport, S. A., Hajdu, T., et al. 2020, MNRAS, 493, 5005 [Google Scholar]
- Borkovits, T., Rappaport, S. A., Maxted, P. F. L., et al. 2021, MNRAS, 503, 3759 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, L., Sipőcz, B., Robitaille, T., et al. 2021, https://doi.org/10.5281/zenodo.5796924 [Google Scholar]
- Bradshaw, S. J., & Hartigan, P. 2014, ApJ, 795, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Bromley, B. C., Leonard, A., Quintanilla, A., et al. 2021, AJ, 162, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bumba, V. 1963, Bull. Astron. Inst. Czechosl., 14, 91 [NASA ADS] [Google Scholar]
- Cardini, D., Cassatella, A., Badiali, M., Altamore, A., & Fernández-Figueroa, M. J. 2003, A&A, 408, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, T. A., Strassmeier, K. G., Rice, J. B., & Künstler, A. 2012, A&A, 548, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, A20 [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Chae, J., Litvinenko, Y. E., & Sakurai, T. 2008, ApJ, 683, 1153 [Google Scholar]
- Collier Cameron, A. 2007, Astron. Nachr., 328, 1030 [CrossRef] [Google Scholar]
- Cruzalebes, P., Petrov, R. G. P., Robbe-Dubois, S., et al. 2019, VizieR Online Data Catalog: II/361 [Google Scholar]
- Dempsey, R. C., Linsky, J. L., Fleming, T. A., & Schmitt, J. H. M. M. 1993a, ApJS, 86, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Dempsey, R. C., Linsky, J. L., Schmitt, J. H. M. M., & Fleming, T. A. 1993b, ApJ, 413, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Dempsey, R. C., Neff, J. E., O’Neal, D., & Olah, K. 1996, AJ, 111, 1356 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, S. A., Simon, T., & Linsky, J. L. 1992, ApJS, 82, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C. 2004, Rev. Mex. Astron. Astrofis. Conf. Ser., 21, 45 [Google Scholar]
- Fekel, F. C., Moffett, T. J., & Henry, G. W. 1986, ApJS, 60, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., Barlow, D. J., Scarfe, C. D., Jancart, S., & Pourbaix, D. 2005, AJ, 129, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Forgács-Dajka, E., Dobos, L., & Ballai, I. 2021, A&A, 653, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granzer, T., Schüssler, M., Caligari, P., & Strassmeier, K. G. 2000, A&A, 355, 1087 [NASA ADS] [Google Scholar]
- Grindlay, J., Tang, S., Simcoe, R., et al. 2009, in Preserving Astronomy’s Photographic Legacy: Current State and the Future of North American Astronomical Plates, eds. W. Osborn& L. Robbins, ASP Conf. Ser., 410, 101 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haakonsen, C. B., & Rutledge, R. E. 2009, ApJS, 184, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Haemmerlé, L., Eggenberger, P., Ekström, S., et al. 2019, A&A, 624, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamers, A. S. 2021, MNRAS, 500, 3481 [Google Scholar]
- Harutyunyan, G., Steffen, M., Mott, A., et al. 2018, A&A, 618, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hathaway, D. H., & Choudhary, D. P. 2008, Sol. Phys., 250, 269 [Google Scholar]
- Hebb, L., Wyse, R. F. G., Gilmore, G., & Holtzman, J. 2006, AJ, 131, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A. 2009, in The Ages of Stars, eds. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, IAU Symp., 258, 81 [NASA ADS] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003a, A&A, 405, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003b, A&A, 405, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Işik, E., Schüssler, M., & Solanki, S. K. 2007, A&A, 464, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Işık, E., Solanki, S. K., Krivova, N. A., & Shapiro, A. I. 2018, A&A, 620, A177 [Google Scholar]
- Ito, T., & Ohtsuka, K. 2019, Monogr. Environ. Earth Planets, 7, 1 [Google Scholar]
- Jackson, R. J., Jeffries, R. D., Randich, S., et al. 2016, A&A, 586, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Järvinen, S. P., Strassmeier, K. G., Carroll, T. A., Ilyin, I., & Weber, M. 2018, A&A, 620, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jetsu, L., Hackman, T., Hall, D. S., et al. 2000, A&A, 362, 223 [NASA ADS] [Google Scholar]
- Koenigsberger, G., Moreno, E., & Langer, N. 2021, A&A, 653, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolláth, Z., & Oláh, K. 2009, A&A, 501, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostov, V. B., Borkovits, T., Rappaport, S. A., et al. 2023, MNRAS, 522, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kővári, Zs., Korhonen, H., Kriskovics, L., et al. 2012, A&A, 539, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Kriskovics, L., Künstler, A., et al. 2015, A&A, 573, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Kriskovics, L., Oláh, K., et al. 2021, A&A, 650, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., Tucker, R. A., Thompson, M. I., Craine, E. R., & Hillenbrand, L. A. 2011, ApJ, 728, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, F., & Ruediger, G. 1975, Sol. Phys., 42, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kriskovics, L., Kővári, Zs., Vida, K., et al. 2019, A&A, 627, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kriskovics, L., Kővári, Zs., Seli, B., et al. 2023, A&A, 674, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007, ApJ, 670, 1367 [Google Scholar]
- Litvinenko, Y. E., & Wheatland, M. S. 2015, ApJ, 800, 130 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, J., & Mullan, D. J. 2021, ApJ, 907, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V. 2003, AJ, 126, 1996 [NASA ADS] [CrossRef] [Google Scholar]
- Malina, R. F., Marshall, H. L., Antia, B., et al. 1994, AJ, 107, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Mathieu, R. D., & Stassun, K. G. 2007, ApJ, 665, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Mekkadan, M. V., Raveendran, A. V., & Mohin, S. 1980, Inf. Bull. Var. Stars, 1791, 1 [NASA ADS] [Google Scholar]
- Merle, T., Hamers, A. S., Van Eck, S., et al. 2022, Nat. Astron., 6, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Mullan, D. J., & MacDonald, J. 2001, ApJ, 559, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Muraközy, J. 2021, ApJ, 908, 133 [Google Scholar]
- Murphy, S. J., Lawson, W. A., Onken, C. A., et al. 2020, MNRAS, 491, 4902 [Google Scholar]
- Nadal, R., Pedoussaut, A., Ginestet, N., & Carquillat, J. M. 1974, A&A, 37, 191 [NASA ADS] [Google Scholar]
- Namekata, K., Maehara, H., Notsu, Y., et al. 2019, ApJ, 871, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K. 2006, Ap&SS, 304, 145 [Google Scholar]
- Pál, A. 2012, MNRAS, 421, 1825 [Google Scholar]
- Petrovay, K., & van Driel-Gesztelyi, L. 1997, Sol. Phys., 176, 249 [Google Scholar]
- Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pounds, K. A., Allan, D. J., Barber, C., et al. 1993, MNRAS, 260, 77 [NASA ADS] [Google Scholar]
- Ribárik, G., Oláh, K., & Strassmeier, K. G. 2003, Astron. Nachr., 324, 202 [CrossRef] [Google Scholar]
- Ribeiro, T., Baptista, R., & Kafka, S. 2011, AJ, 142, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Savanov, I. S. 2009, Astron. Rep., 53, 941 [CrossRef] [Google Scholar]
- Scharlemann, E. T. 1982, ApJ, 253, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2001, ApJ, 551, 1099 [Google Scholar]
- Schuessler, M., Caligari, P., Ferriz-Mas, A., Solanki, S. K., & Stix, M. 1996, A&A, 314, 503 [Google Scholar]
- Schweitzer, A., Passegger, V. M., Cifuentes, C., et al. 2019, A&A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Şenavcı, H. V., Kılıçoğlu, T., Işık, E., et al. 2021, MNRAS, 502, 3343 [NASA ADS] [CrossRef] [Google Scholar]
- Somers, G., & Pinsonneault, M. H. 2015, MNRAS, 449, 4131 [NASA ADS] [CrossRef] [Google Scholar]
- Song, H. F., Meynet, G., Maeder, A., et al. 2018, A&A, 609, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [Google Scholar]
- Strassmeier, K. G., Hall, D. S., Boyd, L. J., & Genet, R. M. 1989, ApJS, 69, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 970306 [CrossRef] [Google Scholar]
- Strassmeier, K. G., Carroll, T. A., Weber, M., et al. 2011, A&A, 535, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A. 2018, ApJS, 235, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Toledano, O., Moreno, E., Koenigsberger, G., Detmers, R., & Langer, N. 2007, A&A, 461, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tout, C. A., Pols, O. R., Eggleton, P. P., & Han, Z. 1996, MNRAS, 281, 257 [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [Google Scholar]
- Van Eylen, V., Winn, J. N., & Albrecht, S. 2016, ApJ, 824, 15 [Google Scholar]
- Vida, K., Oláh, K., Kővári, Zs., et al. 2009, A&A, 504, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D. 2016, MNRAS, 461, 3964 [CrossRef] [Google Scholar]
- Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, in Advanced Software and Control for Astronomy II, eds. A. Bridger& N. M. Radziwill, SPIE Conf. Ser., 7019, 70190L [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., Granzer, T., & Strassmeier, K. G. 2012, in Software and Cyberinfrastructure for Astronomy II, eds. N. M. Radziwill& G. Chiozzi, SPIE Conf. Ser., 8451, 84510K [NASA ADS] [CrossRef] [Google Scholar]
- Wichmann, R., Schmitt, J. H. M. M., & Hubrig, S. 2003, A&A, 399, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [Google Scholar]
- Zasche, P., Henzl, Z., Mašek, M., et al. 2023, A&A, 675, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Times of eclipsing minima from TESS light curves
Times of minima of V815 Her B from TESS light curves.
Appendix B: Log of spectroscopic data
Observing log of STELLA-SES spectra of V815 Her.
Appendix C: Fitted line profiles
 |
Fig. C.1. Fitted line profile subsets corresponding to the Doppler images S01-S08 presented in Fig. 8. The phase values of each profile are shown on the right side of the panels. |
 |
Fig. C.2. Fitted line profile subsets corresponding to the Doppler images S09-S16 presented in Fig. 8. The phase values of each profile are shown on the right side of the panels. |
 |
Fig. C.3. Fitted line profile subsets corresponding to the Doppler images S17-S19 presented in Fig. 8. The phase values of each profile are shown on the right side of the panels. |
Appendix D: Doppler images in Mercator projection
 |
Fig. D.1. Doppler images S01-S10 (left, top to bottom) and S11-S19 (right, top to bottom) plotted in Mercator projection. The maps and the temperature scale correspond to those shown in Fig. 8. The ticks on the bottom edge indicate the phases of the observations used for that map. |
Appendix E: Spot filling factors
 |
Fig. E.1. The spot filling factors for the nineteen Doppler images in the arrangement corresponding to Fig. D.1. For each temperature map, the histogram of the spot filling factor is shown in two panels: on the left side (in red), summed along the latitude, and on the right side (in blue), summed up along the longitude. |
Appendix F: Measuring spot decay rate
Relying strictly on our time-series Doppler images, below we attempt to quantitatively measure the spot decay rate ΔAs/Δts for V815 Her. For this we set up a simple statistic, in which we tracked the evolution of well-separated and easy-to-follow spots on our series of surface snapshots.
First, we identified spots on all 19 Doppler maps with the Photutils (Bradley et al. 2021) image segmentation function called detect_sources on the 72×36 pixel images to detect spots below a specific threshold value. We required each spot to have at least ten pixels at least 50 K below the quiescent photosperic temperature. As a next step, we used the deblend_sources function to deblend the overlapping spots, with the minimum size of ten pixels. We ended up with 99 individual spots on all of the images. For each spot, we calculated the centroid position by weighting with temperature, and the area, taking into account the distortion of pixels with the cosine of the latitude. Then, we manually identified matching spots on consecutive image pairs. However, tracking decaying spots is made more difficult by interactions between neighboring spots (e.g., merging) or the emergence of new fluxes. Therefore, we only matched unambigous spot pairs, where it was reasonable to assume that we see the evolution of the same feature. The maximum allowed angular separation between the centroids of the subsequent images of the evolving spot was set to be 40°.
As an example, in Fig. F.1 we show the identification of the individual spots for S01 and S02 Doppler images (top and middle panels, respectively) and the spot pairing (see the bottom panel). For each spot pair, we calculated the decay rate as ΔA/Δt, where ΔA is the change in spot area, and Δt is the time difference between the two images. The average decay rate for the 18 spot pairs showing negative ΔA (i.e., shrinking) is ΔA/Δt = −7.0±1.3 104 km2 s−1. For identification, we provide a list of these spots in Table F.1, while the list of spot pairs found on consecutive Doppler images that we considered to represent successive evolutionary phases (i.e., spot decay) of the same spot is as follows: #2−#11; #3−#12; #4−#10; #5−#13; #9−#16; #12−#18; #20−#23; #21−#25; #29−#34; #34−#37; #36−#40; #42−#45; #43−#48; #47−#52; #48−#53; #60−#63; #69−#75; #78−#83.
 |
Fig. F.1. Demonstrating how spot segmentation and identification works. As an example, the upper panel shows the identified spots with their ID numbers (see also Table F.1) of the S01 Doppler image, and the middle one shows the identified spots of the S02 Doppler image. In the bottom panel, the spots of S01 are represented by red contours, the spots of S02 by green contour lines, and the paired spots are connected by gray lines. |
Identified starspots with their derived parameters.
Finally, we note that the method presented here is not mature yet. For example, it is not possible to separate the effects of flux emergence and flux decay if they occur simultaneously in the same unresolved spotted region. For this reason and the other sources of error mentioned above (e.g., interacting spots, arbitrarily taken threshold values, etc.), we consider our method only suitable for order of magnitude estimation for the time being.
All Tables
Temporal distribution of the subsequent datasets for each individual Doppler image.
All Figures
 |
Fig. 1. Fitted TESS light curve of V815 Her from sector 40. The blue dots indicate the observations, while the red line indicates the time-series three-spot model fit. |
| In the text | |
 |
Fig. 2. Folded and fitted TESS sector 26, 40, and 53 light curves of the wide binary companion V815 Her B. Cleaned observations are marked with blue dots, the original orbital solutions without assuming surface inhomogeneities are drawn with gray lines, while the models drawn with red lines fit also the light curve variations arising from stellar spots. The residuals of both fits are plotted on the bottom parts of all panels. We note that the eclipses in sectors 40 and 53 (middle and bottom panels) are shifted from phases 0.0 and 0.5, indicating timing variations, which are discussed in detail in the text. |
| In the text | |
 |
Fig. 3. Eclipse timing variations of V815 Her B calculated from the mid-minima times of primary and secondary eclipses based on TESS observations. The red dots and blue squares represent the primary and secondary eclipses, respectively. The black line represents the theoretical LTTE curve derived from the former third-body RV solution of Fekel et al. (2005). See text for details. |
| In the text | |
 |
Fig. 4. Long-term photometry and time-frequency analysis of V815 Her. Top: DASCH light curve of ≈100 yr for V815 Her from scanned photographic plates (black dots) supplemented with photoelectric data (blue dots) spanning more than a century between 1890–1998 with 5 yr’ overlap. The spline smoothed data are indicated by a red line. Bottom: time-frequency analysis for the available photographic+photoelectric data of V815 Her using the TiFrAn code (Kolláth & Oláh 2009). The plot indicates dominant cycles of different lengths and amplitudes on timescales corresponding to ∼6.5, ∼9.1, ∼11.5, ∼13 and ∼26 yr, the latter two are probably multiples of the 6.5-yr period. Dashed lines indicate the 2092 d period of the wide orbit and its double at 4184 d (≈11.5 yr). See the text for more. |
| In the text | |
 |
Fig. 5. Example plot of the observed Li I 6707Å spectral region (black) fitted with a synthetic spectrum (blue). |
| In the text | |
 |
Fig. 6. SED for V815 Her generated by the VOSA SED analyzer tool (Bayo et al. 2008). The synthetic spectrum (blue line) is fitted to the archival photometry (red dots) from the available VO catalogs and surveys using ATLAS9 Kurucz ODFNEW/NOVER models with Teff = 5500 K effective temperature, log g = 4.5 surface gravity, and [Fe/H] = 0.2 metallicity. |
| In the text | |
 |
Fig. 7. Position of V815 Her Aa (black dot) on the HRD plotted by using the VOSA SED analyzer tool (Bayo et al. 2008). Evolutionary tracks for the Geneva model (Haemmerlé et al. 2019) indicate an age of 30 Myr for a M ≲ 1 M⊙ ZAMS star. |
| In the text | |
 |
Fig. 8. Nineteen time-series Doppler images of V815 Her for the 2018 observing season. From top to bottom, in chronological order, Doppler images S01–S10 are on the left, and Doppler images S11–S19 are on the right. |
| In the text | |
 |
Fig. 9. Average cross-correlation function map derived from 18 individual cross correlations. The stronger the correlation, the darker the shade. The map indicates how much longitude shift occurs at a given latitude due to surface shear during ∼6 Prot (which is the average time difference between the mean-HJDs of the consecutive maps; see Table 4). |
| In the text | |
 |
Fig. 10. Mass-radius relation of low-mass eclipsing binary stars with well-determined parameters. The gray dots represent the targets taken from Schweitzer et al. (2019, their Table B.2). Other colored symbols in the legend show the positions of TIC 18480699 (Hebb et al. 2006), V405 And ((1) Vida et al. 2009, (2) Ribeiro et al. 2011), Thor 42 (Murphy et al. 2020), and V815 Her Aa, Ba, and Bb (present paper). Nonmagnetic, solar metallicity isochrones are taken from Baraffe et al. (2015). |
| In the text | |
 |
Fig. 11. V light curve of V815 Her from Jetsu et al. (2000) between 1984–98. Below the panel of the time series, in the lower panel we present the light curve folded with the period of the wide orbit of 5.73 yr (= 2092.2 d). As zero phase the time of the periastron passage was set. The continuous color gradient helps to distinguish successive phases. |
| In the text | |
 |
Fig. C.1. Fitted line profile subsets corresponding to the Doppler images S01-S08 presented in Fig. 8. The phase values of each profile are shown on the right side of the panels. |
| In the text | |
 |
Fig. C.2. Fitted line profile subsets corresponding to the Doppler images S09-S16 presented in Fig. 8. The phase values of each profile are shown on the right side of the panels. |
| In the text | |
 |
Fig. C.3. Fitted line profile subsets corresponding to the Doppler images S17-S19 presented in Fig. 8. The phase values of each profile are shown on the right side of the panels. |
| In the text | |
 |
Fig. D.1. Doppler images S01-S10 (left, top to bottom) and S11-S19 (right, top to bottom) plotted in Mercator projection. The maps and the temperature scale correspond to those shown in Fig. 8. The ticks on the bottom edge indicate the phases of the observations used for that map. |
| In the text | |
 |
Fig. E.1. The spot filling factors for the nineteen Doppler images in the arrangement corresponding to Fig. D.1. For each temperature map, the histogram of the spot filling factor is shown in two panels: on the left side (in red), summed along the latitude, and on the right side (in blue), summed up along the longitude. |
| In the text | |
 |
Fig. F.1. Demonstrating how spot segmentation and identification works. As an example, the upper panel shows the identified spots with their ID numbers (see also Table F.1) of the S01 Doppler image, and the middle one shows the identified spots of the S02 Doppler image. In the bottom panel, the spots of S01 are represented by red contours, the spots of S02 by green contour lines, and the paired spots are connected by gray lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.