| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202245767 | |
| Published online | 14 June 2023 | |
EI Eridani: A star under the influence
The effect of magnetic activity in the short and long term★
1
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
Konkoly Thege út 15–17,
1121
Budapest, Hungary
2
CSFK, MTA Centre of Excellence, Budapest,
Konkoly Thege Miklós út 15–17,
1121
Hungary
e-mail: kriskovics.levente@csfk.org
3
Eötvös Loránd University,
Budapest, Hungary
4
Center of Excellence in Information Systems, Tennessee State University,
Nashville, TN
37209, USA
5
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam, Germany
Received:
22
December
2022
Accepted:
18
April
2023
Context. Homogeneous photometric time series spanning decades provide a unique opportunity to study the long-term cyclic behavior of active spotted stars such as our target EI Eridani. In addition, with ultraprecise space photometry data, it is possible to investigate the accompanying flare activity in detail. However, the rotation period of ≈2 days for EI Eri makes it impossible to achieve time-resolved surface images from a single ground-based observing site. Therefore, for this purpose, spectroscopic data from a multi-site observing campaign are needed.
Aims. We use our photometric time series of more than 40 yr to analyze the long-term behavior of EI Eri. We investigate flare activity using photometric data obtained with the Transiting Exoplanet Survey Satellite (TESS). The MUlti-SIte Continuous Spectroscopy (MUSICOS) campaign in 1998 was designed to achieve high-resolution, multi-wavelength spectroscopic observations from many sites around the globe, which meant that uninterrupted phase coverage of EI Eri became available. We use these data to reconstruct successive surface-temperature maps of the star in order to study the changes of starspots on a very short timescale.
Methods. We used long-term seasonal period analysis of our photometric time series to study changes in the rotational period. We also applied short-term Fourier-transform to look for activity cycle-like changes. We also studied the phase and frequency distribution of hand-selected flares. We applied our multi-line Doppler imaging code to reconstruct four consecutive Doppler images. These images were also used to measure surface differential rotation with our cross-correlation technique. In addition, we carried out tests to demonstrate how Doppler imaging is affected by the fact that the data came from several different instruments with different spectral resolutions.
Results. Seasonal period analysis of the light curve reveals a smooth, significant change in period, possibly indicating the evolution of active latitudes. Temperature curves from B − V and V − I show slight differences, indicating the activity of EI Eri is spot dominated. Short-term Fourier transform reveals smoothly changing cycles of between 4.5 and 5.5 yr and of between 8.9 and 11.6 yr. The time-resolved spotted surface of EI Eri from Doppler imaging enabled us to follow the evolution of the different surface features. Cross-correlating the consecutive Doppler maps reveals surface shear of α = 0.036 ± 0.007. Our tests validate our approach and show that the surface-temperature distribution is adequately reconstructed by our method. The tests also indicate how accurately the cross-correlation method can reproduce the surface shear as a function of the spectral resolution.
Key words: stars: activity / stars: imaging / starspots / stars: individual: EI Eridani
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
EI Eridani = HD 26337 (G5IV, Prot = 1.945 days, V = 7.m1) is a well-known, rapidly rotating (υ sin i = 51 km s−1), active RS CVn-type, non-eclipsing, single-lined spectroscopic binary. It was identified as an active star by Bidelman & MacConnell (1973) based on its Ca II H&K emission, which was later confirmed by Fekel (1980). Later on, Fekel et al. (1982) identified it as an RS CVn type variable. These authors also detected photometric variability with an amplitude of V ≈ 0.m2 and a period of roughly two days. Fekel et al. (1986) derived an orbital period of 1.9472 days, while Hall et al. (1987) detected a photometric period of 1.945 ± 0.005 days from UBV photometry.
Its long-term photometric variability and behavior have been extensively studied over the last four decades. Hall et al. (1987) reported seasonal changes in the photometric period on the order of one percent. Strassmeier et al. (1989) found a seasonal change of 0.043 days in the rotational period throughout three seasons. Oláh et al. (2012) also reported a ±2% deviation from the orbital period on a three-decade-long dataset.
It was Rodono & Cutispoto (1992) who first suggested a long-term cycle of roughly 10 yr. Strassmeier et al. (1997) also found an 11 ± 1 yr cycle in the sinusoidal change of a 16 yr photometric time series, without any apparent relation between the cycle and the change of the seasonal periods. Oláh & Strassmeier (2002) also found photometric cycles of roughly 2.4 and 12.2 yr, which were later confirmed and refined by Oláh et al. (2009), who provided values of ≈2.9–3.1 and ≈14yr. Moreover, these authors reported a cycle with a length of roughly 4.1–4.9 yr. EI Eri is also known to exhibit flares. Pandey & Singh (2012) estimates the peak energy during flares in the 0.3–10 keV energy band to be ≈1031–1032 erg using observations obtained by the XMM-Newton X-ray observatory.
EI Eri has been among the prime targets for Doppler imaging over recent decades since the first application of the technique. Strassmeier (1990), Strassmeier et al. (1991), and Hatzes & Vogt (1992) reported a permanent polar spot with a radically changing appendage. The presence of the polar feature was confirmed by Washuettl et al. (2001), and later by Washuettl et al. (2009) and Kővári et al. (2009). These authors also reported constantly changing low-latitude features over 6-10 rotations (approximately two-three weeks). However, as the rotational period of EI Eri is very close to two days, covering a rotation with optimal phase coverage from a singular observing site takes around a month, but reaching adequate coverage also requires at least two weeks of time series. On images reconstructed using these datasets, shorter-lived features are suppressed and smeared out, which means the resulting Doppler images cannot be used to show rapid changes. It also makes differential rotation measurements less reliable. As conventional, ground-based optical observing runs are regularly interrupted by daybreak, the only solution to this issue is a multisite campaign. Consequently, EI Eri was chosen as one of the main targets for the MUSICOS campaign in 1998 organized at ESTEC/ESA by Bernard Foing and Joana Oliveira (for general details of the campaign, see Catala & Foing 1988). MUSICOS stands for MUlti-SIte COntinuous Spectroscopy and was designed to achieve high-resolution, multiwavelength spectroscopic observations from many sites around the globe so that uninterrupted phase coverage of selected objects can be obtained.
The MUSICOS dataset presented in this paper was used to create preliminary Doppler images in order to measure surface differential rotation by Kővári et al. (2009). These authors also confirm the presence of a stable polar spot with a slightly changing shape, and short-lived spots at lower latitudes, even though the rapid changes are somewhat masked by the artifacts that could be the result of the single-line inversion approach that was used. Kővári et al. (2009) also derived a surface differential rotation parameter of α = ∆Ω/Ωeq = 0.0037. This is congruent with the estimation of Oláh et al. (2012) based on long-term photometry.
This paper is structured as follows. After presenting the observations in Sect. 2, we present our study of the long-term spot activity – including photometric cycles – and the seasonal change of rotational periods of EI Eri using a photometric time series covering four decades, an unprecedented length (see Sect. 3.1). In Sect. 3.2, we describe how we used photometric data from the Transiting Exoplanet Survey Satellite (TESS) to investigate the flaring activity. In Sect. 4, we present our investigation of the rapid changes of the spot configuration using spectral time series from the MUSICOS 98 campaign. We show how we applied a multi-line Doppler imaging code on the MUSICOS dataset to reconstruct four Doppler images of EI Eri in order to investigate the short-term changes of the spotted surface. In Appendix A, we present the tests we performed in order to verify that the spectra with different spectral resolutions used for Doppler imaging do not introduce artifacts and bias the results.
Sites and telescopes involved in this work.
2 Observations
2.1 Photometric observations
Photometric observations in Johnson V and IC colors were carried out with the Wolfgang-Amadeus twin Automatic Photoelectric Telescope (APT), two robotic 75 cm telescopes for photoelectric photometry at Fairborn Observatory in the Sonoran desert near Tucson, Arizona (Strassmeier et al. 1997). The observations were made differentially with HD 25852 as the comparison star (V = 7.m83, V − IC = 1.m03) and HD 26409 as the check star.
Johnson B and V data were gathered with the Tennessee State University’s T3 0.4 m Automatic Photoelectric Telescope (APT) located also at Fairborn Observatory. For this dataset, HD 26409 was used as a comparison star. Part of the V dataset was published in Jetsu et al. (2017). All photometry was transformed to the Johnson-Cousins BV(RI)C system. In addition, older photometric observations starting from 1980 were used from the literature (see Oláh et al. 2009; Strassmeier et al. 1997, Table 5). The light curves of the ground-based photometry are shown in Fig. 1. TESS 120 s cadence data from sectors 5 and 32 are also available for EI Eri and were included in the photometric analysis, see Sect. 3.2.
2.2 Spectroscopic observations
The MUSICOS 1998 campaign involved eight northern and southern sites and ten telescopes to fulfill the needs of six scientific programs and took place from November 20 to December 14, 1998. For this work, we used data from seven instruments at six observing sites. These instruments are summarized in Table 1. Figure 2 shows the distribution of these observatories: Observatoire Haute-Provence (OHP), Xinglong Observatory (BXO), Kitt Peak National Observatory (KPNO), ESO La Silla (ESO), La Palma (INT), and Mt. Stromlo Observatory (MSO).
For this specific program, a total of 90 high-resolution spectra of EI Eri were obtained within a time period of 21 days (November 23-December 13). The observing log is summarized in Table B.1. The various observing sites made use of different spectrographs (long slit, echelle), which leads to data sets of different quality, different wavelength range, and different spectral resolution. Fortunately, the region around 6400–6450 Å – which contains frequently used Doppler imaging lines (Fe I 6400, Fe I 6408, Fe I 6421, Fe I 6430 and Ca I 6439) – is present in all of them. Several spectra were discarded due to low signal-to-noise ratio or contaminated line profiles, resulting in 59 selected spectra. The data were reduced using standard reduction techniques for echelle spectra in the NOAO packages of IRAF: bias subtraction, flat-field correction to remove pixel-to-pixel variations, and the curvature of the blaze function. For OHP, HEROS, and Xinglong observations, the MIDAS package was used. Background subtraction and flat-field correction using exposures of a tungsten lamp were applied. Wavelength calibration was performed by taking the spectra of a Thorium-Argon lamp. The spectra were normalized by a low-order polynomial fit or a cubic spline fit to the observed continuum.
As the dataset is comprised of spectra from seven different instruments with different spectral resolutions, which can cause problems during the Doppler inversions, we decided to decrease the resolution of all spectra to the lowest available resolution of 20 000. In Appendix A, we present a series of tests to validate this approach.
The observations are phased with the following ephemeris (Kővári et al. 2009):
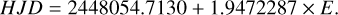 (1)
(1)
Table B.1 shows the observing log, while Fig. 2 shows the phase distribution of the different measurements.
 |
Fig. 1 Available ground-based photometry, calculated temperature curves and yearly rotational periods for EI Eri. Top panel: ground-based Johnson V light curve of EI Eri from the Potsdam Wolfgang APT at Fairborn Observatory and from the literature (grey dots) and from Jetsu et al. (2017) and present paper (black dots). Middle panel: temperatures from B − V (blue) and V – I (red). The dashed line and the grey area denote the effective temperature from spectral synthesis with 1σ error (Teff = 5580 ± 70 K, see Sect. 4.1). Black dot shows the averaged surface temperature value from the four Doppler maps (〈T〉 = 5467 ± 25 K, see Sect. 4.3). Bottom panel: yearly rotational periods from the V light curves with grey and black points, as on the upper panel and the two available TESS sectors (grey triangles). The dashed lines show the maximal (pole) and minimal (equator) rotational periods calculated using the differential rotation from the Doppler maps (see Sect. 4.4), while the dotted line denotes the orbital period. |
 |
Fig. 2 Observing sites and phase distribution of the data. Left panel: MUSICOS sites involved in this work, namely Observatoire Haute-Provence (OHP), Xinglong Observatory (BXO), Kitt Peak National Observatory (KPNO), ESO La Silla (ESO), La Palma (INT), and Mt. Stromlo Observatory (MSO). Right panel: phases of the observations plotted against the reduced Julian Date. Different colors denote different instruments (see legend). Observations plotted with filled circles were used for Doppler imaging, while the empty circles denote omitted observations. The vertical dashed lines separate the four subsets used for Doppler imaging. |
 |
Fig. 3 Short-term Fourier transform of all available V observations of EI Eri. A smoothly changing cycle is seen between 4.5 and 5.5 yr (and between the half of these values), and a longer one which moves between 8.9 and 11.6 yr. |
3 Photometric analysis
3.1 Analysis of the long-term photometry
Due to differential rotation, the period measured from photometry can change slightly depending on the latitude where the dominant spots reside. Figure 1 shows the measured rotational period of EI Eri in seasonal blocks using the peak of the Lomb-Scargle periodogram (Lomb 1976; Scargle 1982) with uncertainties calculated from the width of the peaks at 90% power. The periods from the literature and Potsdam APT data (gray dots) are consistent with the data from Jetsu et al. (2017) and the present paper (black dots), and with the two points from the TESS light curves (gray triangles) within one season. There is a smooth and significant change in the period, indicating the evolution of active latitudes.
The middle panel of Fig. 1 shows the temperatures calculated from B − V and V − I color indices by linearly interpolating the grid of Worthey & Lee (2011) at the given log g and metallicity. The dashed line and the gray area denote Teff = 5580 ± 70 K from spectral synthesis with 1σ error (for details, see Sect. 4.1). The average temperature calculated from the Doppler maps is plotted with a black dot, and the 1σ error is computed from the four different values for the four different maps (for details on the inversion, see Sect. 4.3).
To look for activity cycles, we used short-term Fourier transform (Kolláth & Oláh 2009) for the present dataset, which is 41 yr in length, 13 yr longer than the one used in Oláh et al. (2009). As the algorithm requires uniform sampling in time, a cubic spline interpolation was used. We find that the previously identified structures on the STFT diagram are still present, indicating roughly the same cyclic behavior. The signal of the longest, high-amplitude feature in Fig. 3 is suppressed, but above about 13.6 yr, which is one-third of the length of the data, all signals have the same amplification. Smoothly changing cycles are seen between 4.5 and 5.5, and between 8.9 and 11.6 yr, which are not harmonics, as the speed and the direction of their changes are different. A weak cycle-like feature of about 2.5 yr is also seen at the beginning of the time span.
3.2 Flares
We manually identified 41 flares in the two available TESS sectors (see Fig. 4). To calculate their energies in the TESS band, we followed similar procedures as in Oláh et al. (2022), using a BT-NextGen model spectrum (Hauschildt et al. 1999) convolved with the TESS transmission curve to get the quiescent stellar luminosity of LTESS = 4.69 × 1033 erg s−1, and integrating over the flare light curves to get the equivalent durations. The flare frequency distribution (FFD) in Fig. 5 shows a broken power-law shape. Two-component fits of the FFD yield power-law indices of 1.41 ± 0.02 and 2.26 ± 0.08 (one minus the slope of the fitted line) for the first and second parts, respectively, while a fit for all datapoints gives 1.66 ± 0.04 (for further discussion, see Sect. 5).
Figure 6 shows the phase distribution of flares in the reference frame of the orbit using the ephemeris from Eq. (1). While the spot configuration of EI Eri changes quickly, the orbiting secondary component provides a solid reference frame. To test whether there is a significant increase in the occurrence of flares at given phases, we ran a two-sided Kuiper’s test (Kuiper 1960). This test compares the measured data to a given distribution; it is similar to the Kolmogorov-Smirnov test, but is invariant under a cyclic transformation, which makes it applicable for comparing cyclic phase distributions (the Kolmogorov-Smirnov test would give different results for different starting epochs). The test rejects the null hypothesis of a uniform flare-phase distribution with a p-value of 0.006. The increase in flare rate appears on the side facing the secondary component.
 |
Fig. 4 TESS observations from Sector 5 (left) and Sector 32 (right). The identified flares are marked in black. |
 |
Fig. 5 Flare-frequency distribution from the TESS data. The dashed line denotes a fit for all of the points with a power-law index of 1.66 ± 0.04, while the two solid lines show a two-component fit (1.41 ± 0.02 and 2.26 ± 0.08); see Sect. 3.2. |
 |
Fig. 6 Phase distribution of the TESS flares on the primary component in the reference frame of the binary orbit. The relative radii and separation of the circles are for scale. The colors are realistic digital colors for the given spectral types from Harre & Heller (2021). The gray area shows a Gaussian kernel density estimation with the bandwidth of 2°. Black ticks denote the orbital phase values of the flare observations. |
4 Doppler imaging
4.1 Astrophysical parameters for the inversion
Precise astrophysical parameters are fundamental for Doppler inversion. Therefore, we carried out a detailed spectroscopic analysis based on spectral synthesis using the code SME (Piskunov & Valenti 2017) and MARCS atmospheric models (Gustafsson et al. 2008). Atomic line parameters were taken from the VALD database (Kupka et al. 1999). Macroturbulence was estimated using the following equation (Valenti & Fischer 2005):
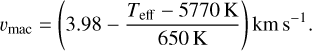 (2)
(2)
Astrophysical parameters were fitted one-by-one iteratively as described in Kriskovics et al. (2019). The results are summarized in Table 2.
Astrophysical parameters from spectral synthesis.
4.2 The Doppler imaging code iMap
The Doppler imaging code iMap (Carroll et al. 2012) used in this work carries out multi-line Doppler inversion on a list of photospheric lines. As the wavelength coverage of our dataset is limited, we used five (Fe I 6400, Fe I 6408, Fe I 6421, Fe I 6430 and Ca I 6439) virtually unblended lines with well-defined continuum, suitable line depth, and temperature sensitivity. The stellar surface was divided into 6° × 6° segments. For each local line profile, the code utilizes a full radiative solver (Carroll et al. 2008).
The local line profiles are then disk integrated, and the individually modeled, disk-integrated lines are averaged. Atomic line data are taken from VALD (Kupka et al. 1999). Model atmospheres are taken from Castelli & Kurucz (2003) and are interpolated for the necessary temperature, gravity, and metallicity values. Due to the high computational capacity requirements, local thermodynamic equilibrium (LTE) radiative transfer is used instead of spherical model atmospheres, but imperfections in the fitted line shapes are well compensated by the multi-line approach. Additional input parameters are micro- and macro-turbulence, and υsini. Table 2 summarizes the astrophysical parameters used during the inversion. Inclination was set to i = 56° (adopted from Washuettl et al. 2009).
For the surface reconstruction, an iterative regularization method based on a Landweber algorithm is used (Carroll et al. 2012), meaning no additional constraints are imposed in the image domain.
4.3 Time-resolved surface evolution
The 59 selected spectra were divided into four subsets (hereafter DI1, DI2, DI3, and DI4) corresponding to the following Julian Date intervals: 2451141.3758–2451144.9045, 2451145.6007–2451148.7618, 2451148.9391–2451150.7474 and 2451150.9827–2451156.5520, with lengths of roughly 1.8, 1.6, 1.0, and 2.9 rotations, respectively. Imaging lines were selected from the spectral region that was covered by all of the spectra in order to make the resulting maps comparable. This gives us a unique opportunity to study the short-term spot evolution of EI Eri. The selected spectral lines are Fe I 6400, Fe I 6408, Fe I 6421, Fe I 6430, and Ca I 6439.
The resulting four Doppler images (DI1-DI4) are shown in Fig. 7. The corresponding line profile fits are shown in Fig. C.1, with corresponding root mean square deviations of 0.0030, 0.0030, 0.0036, and 0.0040, respectively. The four maps show a persistent polar feature (with a spot temperature of ∆T ≈ 1100 K below the temperature of the unspotted surface. (Here we refer to our tests presented in Appendix A, where we also discuss the accuracy of the spot temperature determination.) Associated with the dominant polar spot, a less prominent appendage appears in DI2 around the phase value of ϕ ≈ 0.35, which is further strengthened in DI3. In DI4, the appendage starts to fade, but is still present. The overall contrast of the polar feature seems to increase from DI1 towards DI4. In addition, several low-latitude features show rapid evolution as well. In DI1, the barely visible spot at ϕ ≈ 0.45 in the lower hemisphere becomes stronger in DI2, and after a slight retrograde shift seen in DI3, it disappears completely in DI4, being present for ~4.5 rotations. Around the phase value of 0.2, a low-latitude feature emerges in DI2 and becomes increasingly prominent over time. In DI2 at ϕ ≈ 0.7, a low-latitude spot forms and strengthens along DI3 and DI4, while gradually shifting toward the visible pole.
It is worth emphasizing that the evolution of the different surface features can be followed quite nicely through the four independently reconstructed maps. Therefore, we believe that most of the recovered surface features are real and not imaging artifacts.
 |
Fig. 7 Four consecutive Doppler images of EI Eri obtained for the MUSICOS 1998 data. The corresponding time intervals for the four images from top to bottom are 2451141.3758–2451144.9045, 2451145.6007–2451148.7618, 2451148.9391–2451150.7474, and 2451150.9827–2451156.5520. |
 |
Fig. 8 Measured surface differential rotation of EI Eri and its comparison to other stars. Left panel: average cross-correlation map for EI Eri. The correlation peaks (white circles) are fitted with a quadratic differential rotation law. The resulting fit (continuous line) indicates a solar-type differential rotation with a shear parameter α = 0.036 ± 0.007. Right panel: extended version of the surface shear coefficient versus rotational period plot from Kővári et al. (2017). Squares denote results from the cross-correlation technique, while circles show differential rotational coefficients from the sheared image method. White and gray symbols correspond to single and binary stars, respectively. Symbol size increases from dwarfs to subgiants to giants. EI Eri is represented by the blue square at Prot ≈ 2 days. The Sun is plotted with a dotted circle. The dotted and dash-dotted lines denote the linear fits to the points corresponding to singles and binaries, respectively, with slopes of |α| ∝ (0.0049 ± 0.00001)Prot and |α| ∝ (0.0014 ± 0.00003)Prot. |
4.4 Differential rotation
A method often used to measure surface differential rotation is cross-correlation of consecutive Doppler images (Donati & Collier Cameron 1997). However, rapid spot evolution can easily hinder the correlation pattern; for example, through the formation or dimming of spots or interaction between nearby spots, all of which can be seen in the Doppler images of EI Eri. To overcome this, and strengthen the signal of differential rotation, we used our code ACCORD (e.g Kővári et al. 2012), which uses the average of the cross-correlations of consecutive Doppler images. The latitudinal correlation peaks in the resulting average correlation map are fitted with a quadratic rotational law in the form
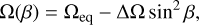 (3)
(3)
where Ω(β) is the angular velocity at β latitude, Ωeq is the angular velocity of the equator, and ∆Ω = Ωeq − Ωpole gives the difference between the equatorial and polar angular velocities. With these, the dimensionless surface shear parameter α is defined as α = ∆Ω/Ωeq.
For the average cross-correlation, we formed three pairs of consecutive Doppler images, that is DI1–DI2, DI2–DI3, and DI3–DI4. After the cross-correlation of the image pairs, we normalized each resulting correlation map to the same time difference so that they can be averaged. For a more detailed description of the ACCORD method, see Kővári et al. (2015) and their references. In the left panel of Fig. 8, the average correlation pattern is fitted with a quadratic differential rotation law, which yields α = 0.036 ± 0.007 (Ωeq = 186.922 ± 0.384 degrees day−1, ∆Ω = 6.768 ± 1.349 degrees day−1). The errors are estimated from the amplitudes and the full width at half maximum values (FWHMs) of the Gaussian functions fitted to each longitudinal strip.
In the right panel of Fig. 8 (an updated plot of Kővári et al. 2017), we compare the surface shear of EI Eri to the surface shear of other well-known active stars as a function of the corresponding rotational periods. Our resulting shear value of 3.6% for EI Eri is in good agreement with the value expected according to the plot. However, we note that the differential rotation pattern can be somewhat diminished by the relatively low spectral resolution; see the tests we performed to investigate this question in Appendix A.
5 Discussion
5.1 Long-term photometric behavior
Kolláth & Oláh (2009) found shorter cycles of 2.9–3.1 and 4.1–4.9 yr and a longer cycle of roughly 14 yr on EI Eri. Our cycle lengths derived from a dataset of 13 yr longer, that is, of roughly 2.5, 4.5–5.5, and 8.9–11.6 yr, are in good agreement with these previous findings (in Fig. 3, the longest 13.6 yr cycle is suppressed because the dataset is only three times longer than this value). The cycle lengths are smoothly changing, which is a well-documented behavior of activity cycles; see examples in Oláh et al. (2009), or the solar case in Kolláth & Oláh (2009). Visual inspection of the curve of seasonal rotational period changes (bottom panel of Fig. 1) hints at a cycle-like behavior of around 3500–4000 days (roughly 9.5–11 yr). The similarity between the lengths of the cycle-like features of the long-term photometry and the change of the seasonal rotational periods at around 9–11 yr is indeed remarkable. However, there are problems in interpreting the photometric results due to the huge spots and the inclination of the stellar disk to the line of sight, which makes the tracing of the positions and sizes of the spots complicated. Therefore, we are not able to match brightness changes to changes in rotational periods (as in a butterfly diagram).
The temperatures calculated from B − V and V − I color indices show slightly different amplitudes. The higher temperature of the facular-plage regions contributes to the signal in the B bandpass, although the spots from the photosphere also have a lower contribution in B, whereas the signal in the I filter has no or negligible contribution from the areas of higher temperature. The spot/plage ratio can be different from star to star, and also within spot cycles of the same star. The difference between the B − V and V − I color indices could indicate that the activity of EI Eri is dominated by spots rather than plages. This is also supported by the large spotted areas present on the Doppler maps and the fact that the temperature from B − V correlates with the effective temperature from the spectral synthesis, while the average temperature from the Doppler images is within the interval of the temperatures calculated from V − I. However, we note that the photometric accuracy of the color indices may hinder this result. Uncertainties of on the order of 0.01 magnitudes translate to an error of about 30 K in temperature. Nevertheless, the average temperature calculated by summing up the temperature elements of the surface of the Doppler images agrees very well with the temperature values of the same season resulting from V − I, which suggests the results from the color indices are reasonably accurate.
5.2 Flare activity
The possible origin of breakpoints in FFDs was discussed by Mullan & Paudel (2018) for flare stars showing a critical energy value on the FFD when the flaring loop size exceeds the local scale height (which depends on local field strengths and densities). On the high energy side of this breakpoint, the power-law index is steeper, and the opposite is true for the other part of the curve.
Extrapolating their results, Oláh et al. (2021) gave examples of broken power-law FFDs for two giant stars with FFDs with different breakpoints but similar energy ranges suggesting different atmospheric properties and strengths of magnetic fields. In the case of the subgiant EI Eri, this rationale may hold as well. The median flare duration of about 1.5 h and the energy range shown in Fig. 5 are fully consistent with the general trends seen in the flare energy-flare duration diagram given by Maehara et al. (2021, see their Fig. 14), placing EI Eri somewhere between G dwarfs and giants on the flare energy-flare duration diagram.
When an active star is in a close binary system, tidal effects may play a role in determining the position of the emerging magnetic flux tubes that are supposed to be the origin of activity on stars. Such effects, supposing different physical circumstances (such as the strength of the magnetic field, the depth of the convection zone where the flux tubes originate, local density, etc.), were investigated in two papers by Holzwarth & Schüssler (2003a,b), who showed that clustering of flux-tube emergence positions in the orbital reference frame of close binaries may appear. Our results, plotted in Fig. 6, where the observed flare phases are shown in the reference frame of the orbit, show a clustering on the hemisphere facing the secondary that may originate from the tidal effects described above.
5.3 Rapid spot evolution and differential rotation
Rapid spot evolution is not unheard of on subgiants. Strassmeier & Bartus (2000) found fast-evolving, low-latitude features on V711 Tau, a similar binary subgiant (although we note that V711 Tau is somewhat cooler and its secondary is more massive). These authors found that in several cases, low-latitude features changed shape and became cooler on a scale of a few days, which is similar to what we found on EI Eri. Gradual strengthening of the polar feature is also observed on V711 Tau and EI Eri; this might indicate spot migration towards the poles. Moreover, Harutyunyan et al. (2016) reported rapid spot evolution on another subgiant, HU Vir, with a prominent, high-latitude, but not polar feature, which drastically changes shape from one rotation to the next. However, we note that due to the nature of Doppler imaging, we have no information about the spot evolution on timescales shorter than the ≈10d rotational period of HU Vir.
Polar features have been observed to persist for years on subgiants (see e.g., Hussain 2002, and references therein), and are also a fairly common and well-explained phenomenon (even from a theoretical viewpoint) on fast-rotating active stars (e.g., Işik et al. 2007). However, rapid spot changes on the scale of a few days are much more difficult to explain with models. Işik et al. (2007) even point out that the lifetime of their simulated bipolar magnetic regions (BMRs) are longer on a star similar to V711 Tau than on a solar analog. According to the simulation presented by these latter authors, a large BMR above β = 70° in latitude can be present for more than 2 yr. This may even be consistent with the permanent polar features of EI Eri.
However, BMRs and spots can behave differently: BMRs consist of spots, plages, and short-lived structures. Whether large spots on Doppler images are single magnetic structures or clusters of smaller spots is also a matter of debate. Accordingly, it is possible that the evolution timescales applicable to homogeneous, large spots are different from those applicable to several smaller spots. Işik et al. (2007) showed that a cluster of spots (that still cannot be resolved by Doppler imaging) dissipates the fastest in their simulation, especially when large-scale flows (e.g., meridional circulation) are introduced, with a decay time of at least a few tens of days.
Strassmeier & Bartus (2000) theorized that magnetic reconnection could play an important role in this phenomenon: it may induce magnetic field diffusion from the stronger flux tubes (i.e., the cooler spots) toward the weaker (warmer) ones, resulting in increased magnetic pressure and therefore more suppressed convection and rapid cooling in the warmer spots. These authors also estimated that on V711 Tau, the Alfvén-velocity for the photosphere region corresponding to τ = 1 optical depth results in a magnetic interaction timescale between spots, which is on the order of 1 day. Therefore, energy transport by Alfvén-waves may contribute to the rapid spot changes.
Rempel & Cheung (2014) carried out three-dimensional numerical simulations to study spot emergence and decay. These authors found that in the first phase of spot decay, the process is dominated by downward convective motion, while in the second phase, plasma intrusions fragment larger spots. The latter could be consistent with the assumptions of Strassmeier & Bartus (2000). Also, Rempel & Cheung (2014) pointed out that strong, subsurface large-scale convective motions can play a significant role in spot decay (however, their simulation box was limited to the upper part of the convective zone).
Namekata et al. (2019, in their Fig. 6,) compare observed stellar spot lifetimes on different solar-type stars. The results of these authors suggest that if spot evolution is driven by the same mechanism in all evolutionary stages, the typical spot lifetime on EI Eri should be in the range of 10–30 days. Our findings (and previous ones in the literature; see above) are in agreement with these results, as most of the active nests are present on all of the Doppler images, which altogether cover 15 days, although with changing shape and contrast (in agreement with Strassmeier & Bartus 2000). The TESS light curves (Fig. 1) also supports this; for example, a new nest seems to form around JD=2457143, which is persistent for at least ≈10 days, although with different amplitude. However, we note that datasets spanning a much longer time period are required to confirm or disprove this.
The surface differential rotation parameter of α = 0.036 ± 0.007 fits well to the observation that rapidly rotating subgiants exhibit relatively low surface shear. Harutyunyan et al. (2016) measured α = −0.029 ± 0.005 on HU Vir, another K subgiant in a binary. On the K subgiant IL Hya, Kővári & Weber (2004) reported α ≈0.03. Our results are also in good agreement with the empirical relation of |α| ≈ 0.013Prot for binaries originally suggested by Kővári et al. (2017) (see also the right panel of our Fig. 8).
6 Summary
Our study of the main component of the single-lined RS CVn binary EI Eri based on a photometric time series spanning four decades and a multisite high-resolution spectroscopic campaign yielded the following results:
Based on a 41 yr photometric dataset, we derive a roughly 2.5, a 4.5–5.5, and a 8.9–11.6 yr photometric cycle for EI Eri. The apparent periodicity in the seasonal changes of the rotational period coincides with the longest cycle. The long-term B − V and V − I multicolor photometry indicates spotdominated activity, rather than plage dominated;
The FFD of 41 flares shows a broken power-law shape with power-law indices of 1.41 ± 0.02 and 2.26 ± 0.08. According to Mullan & Paudel (2018), this might indicate that there is a critical energy break point on the FFD, where the flaring loop size exceeds the local scale height, resulting in higher energy flares and steeper power-law indices. The phase distribution of the flares indicates that magnetic-flux emergence is affected by tidal effects (Holzwarth & Schüssler 2003a,b), and flares are concentrated on the hemisphere facing the secondary;
Using our MUSICOS spectral time series, we derived four consecutive, independent Doppler-images of EI Eri, covering 1.8, 1.6, 1.0, and 2.9 rotations, enabling us to study very short-term spot evolution on the rapidly evolving surface. The resolution of the spectra was blurred down to the lowest available resolution in order to avoid artifacts caused by different resolution. This approach was validated by a series of tests. The Doppler images reveal a strong, evolving, but always present polar cap and several emerging and disappearing low-latitude features of constantly evolving shape and contrast. The approximate lifetime of these structures coincides with the lower limit proposed by Namekata et al. (2019), although datasets covering longer time periods are needed in order to obtain conclusive verification of this;
Cross correlating the consecutive Doppler images reveals a weak, solar-like surface differential rotational pattern of α = 0.036 ± 0.007, which is in good agreement with the empirical law for binaries proposed by Kővári et al. (2017).
Our paper also includes tests to show that our multi-instrument time series can be used for Doppler imaging without introducing artifacts, if treated properly. The method presented here could help in achieving proper phase coverage of stars for which this can only be achieved in time intervals comparable to or longer than the typical spot evolution timescale.
Acknowledgements
The authors would like to thank Albert Washuettl and the original MUSICOS team for organizing and gathering the data used in this work. The authors acknowledge the Hungarian National Research, Development and Innovation Office grants OTKA K-131508, KKP-143986 (Élvonal), and 2019-2.1.11-TéT-2019-00056. L.K. acknowledges the Hungarian National Research, Development and Innovation Office grant OTKA PD-134784. L.K. and K.V. are Bolyai János research Fellows. K.V. is supported by the Bolyai+ grant ÚNKP-22-5-ELTE-1093, BS is supported by the ÚNKP-22-3 New National Excellence Program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund. G.W.K. acknowledges long-term support from NASA, NSF, and the State of Tennessee through its Centers of Excellence Program.
Appendix A Resolution tests
MUSICOS 1998 data of EI Eri were obtained from seven different instruments with different spectral resolutions (and therefore there are spectra with different resolutions in each subset), which can induce artifacts on the Doppler maps due to the different levels of detail of the spectral features and the different instrumental profiles. To counteract this, we used a Gaussian kernel to decrease the resolution of the spectra to our lowest available resolution. As this has not been done before, we carried out tests in order to explore the effects of this treatment on the high-resolution dataset of Vl358 Ori (Kriskovics et al. 2019). We created datasets of decreased resolution, corresponding to R=20 000, 30 000, 40 000, 50 000, 60 000, and 70 000, and compared them to the original maps. For details on the original dataset, astrophysical parameters, and inversion, we refer to Kriskovics et al. (2019).
Doppler images for the datasets of decreased resolution were derived with the same inversion settings and astrophysical parameters. Hotter features were purposely not suppressed in order to see whether or not artifacts are introduced on lower resolutions. Figure A.1 shows examples for both rotations corresponding to R=60 000, 40 000, and 20 000, along with the originals. Visual comparison of the test maps and the original ones reveal that the overall structure did not change on the maps corresponding to lower spectral resolutions, except for a few smaller features that gradually faded as the resolution decreased. However, spot temperatures can significantly change in the case of the strongest active regions, especially on the maps corresponding to R=20 000. This is expected, as the blurring makes the bumps caused by the spots on the line profiles shallower. Figure A.2 shows the difference maps of the original and the R = 20 000 map. It is apparent that in the case of the strong polar feature, there is about 600 K difference in the recovered spot temperature, while smaller features did not change significantly. Finally, it is important to note that artifacts are not introduced by the lower resolution.
Based on these tests, we conclude that degrading the MUSICOS spectra to a reduced spectral resolution of R=20 000 is still sufficient to investigate the rapid spot evolution and differential rotation of EI Eri, despite the fact that there is some fading of the spectral features due to a decrease in contrast, which affects the measurement of the differential rotation at some level.
The reliability of measuring differential rotation by cross-correlation of consecutive Doppler maps is based on the reliability of the spot reconstruction (for details of the cross-correlation technique, see Sect. 4.4). Therefore, we tested how the reduced spectral resolution affects the surface shear parameter derived from cross-correlation. To this end, the two consecutive rotations of V1358 Ori (see Fig. A.1) were cross-correlated with different levels of spectral resolution. Two example cross-correlation maps are shown in Fig. A.3, which correspond to R=20 000 (α = 0.01 ± 0.0025) and R=70 000 (α = 0.015 ± 0.003). We note that the original cross-correlation map presented in Kriskovics et al. (2019) with a spectral resolution of R=80 000 resulted in α=0.016. The derived α surface shear values are plotted against the spectral resolution in Fig. A.4. It is apparent that the resolution affects the derived shear coefficient in a unique way; that is, at low resolution the dependence has some linear trend, while at mid to high resolution (R>40 000) there is no real trend, and the derived α values agree with each other within the estimated error bars. Nevertheless, on our lowest resolution (R=20 000), the measured surface differential rotation underestimates the actual value by ≈60%.
 |
Fig. A.1 Doppler imaging test for two consecutive rotations of V1358 Ori. Images on the left correspond to the first rotation, while images on the right correspond to the second one. The four rows from top to bottom correspond to data of different spectral resolution: R = 80 000 (original data taken from Kriskovics et al. 2019), and reduced levels of R = 60 000, R = 40 000, and R = 20 000, respectively. |
 |
Fig. A.2 Difference images of the original V1358 Ori Doppler images (Kriskovics et al. 2019) and those that correspond to a spectral resolution reduced to R=20 000. The left panel corresponds to the first rotation and the right panel to the second; cf. Fig. A.1. |
 |
Fig. A.3 Example cross-correlation test maps of V1358 Ori with their fitted surface differential rotation functions obtained for different spectral resolutions of R=20 000 (left) and R=70 000 (right). The derived surface shear coefficients are α = 0.010 ± 0.0025 and α = 0.015 ± 0.003, respectively. For the original cross-correlation map see Kriskovics et al. (2019). |
 |
Fig. A.4 The α surface differential rotation parameter values obtained for spectroscopic test datasets with different levels of R spectral resolution. |
Appendix B Observing log
Observing log of the MUSICOS 1998 data.
Columns from left to right: the Heliocentric Julian Dates (HJD), the observing facilities, the rotational phases (according to Eq. 1), and whether the measurement was used or not.
Appendix C Line profile fits
 |
Fig. C.1 Fitted line profile subsets (S1-S4) corresponding to the four Doppler images (DI1-DI4) presented in Fig. 7. The phase distributions of each subset are shown in the right panel of Fig. 2. |
References
- Bidelman, W. P., & MacConnell, D. J. 1973, AJ, 78, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, T. A., Strassmeier, K. G., Rice, J. B., & Künstler, A. 2012, A&A, 548, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, 210, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, A20 [NASA ADS] [Google Scholar]
- Catala, C., & Foing, B. H. 1988, in Comptes-rendus du premier atelier MUSICOS: Multi-Site Continous Spectroscopy; Spectroscopie Multi-Sites en Continu [Google Scholar]
- Donati, J. F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C. J. 1980, SAO Special Rep., 389, 133 [NASA ADS] [Google Scholar]
- Fekel, F. C., Hall, D. S., Henry, G. W., Landis, H. J., & Renner, T. R. 1982, Inform. Bull. Variable Stars, 2110, 1 [Google Scholar]
- Fekel, F. C., Moffett, T. J., & Henry, G. W. 1986, ApJS, 60, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, D. S., Osborn, S. A. G., Seufert, E. R., et al. 1987, AJ, 94, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Harre, J.-V., & Heller, R. 2021, Astron. Nachr., 342, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Harutyunyan, G., Strassmeier, K. G., Künstler, A., Carroll, T. A., & Weber, M. 2016, A&A, 592, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P., & Vogt, S. S. 1992, MNRAS, 258, 387 [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003a, A&A, 405, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003b, A&A, 405, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hussain, G. A. J. 2002, Astron. Nachr., 323, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Işik, E., Schüssler, M., & Solanki, S. K. 2007, A&A, 464, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jetsu, L., Henry, G. W., & Lehtinen, J. 2017, ApJ, 838, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Kolláth, Z., & Oláh, K. 2009, A&A, 501, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., & Weber, M. 2004, Publ. Astron. Dept. Eötvös Loránd Univ., 14, 221 [Google Scholar]
- Kővári, Zs., Washuettl, A., Foing, B. H., et al. 2009, in AIP Conf. Ser., 1094, 15th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, ed. E. Stempels, 676 [Google Scholar]
- Kővári, Zs., Korhonen, H., Kriskovics, L., et al. 2012, A&A, 539, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Z., Kriskovics, L., Künstler, A., et al. 2015, A&A, 573, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Oláh, K., Kriskovics, L., et al. 2017, Astron. Nachr., 338, 903 [Google Scholar]
- Kriskovics, L., Kővári, Zs., Vida, K., et al. 2019, A&A, 627, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, N. H. 1960, Nederl. Akad. Wetensch. Proc. Ser. A, 63, 38 [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&As, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Maehara, H., Notsu, Y., Namekata, K., et al. 2021, PASJ, 73, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Mullan, D. J., & Paudel, R. R. 2018, ApJ, 854, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Namekata, K., Maehara, H., Notsu, Y., et al. 2019, ApJ, 871, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., & Strassmeier, K. G. 2002, Astron. Nachr., 323, 361 [CrossRef] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kővári, Zs., Vida, K., & Strassmeier, K. G. 2012, in From Interacting Binaries to Exoplanets: Essential Modeling Tools, 282, eds. M. T. Richards, & I. Hubeny, 478 [Google Scholar]
- Oláh, K., Kővári, Z., Günther, M. N., et al. 2021, A&A, 647, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Seli, B., Kővári, Z., Kriskovics, L., & Vida, K. 2022, A&A, 668, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, J. C., & Singh, K. P. 2012, MNRAS, 419, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rempel, M., & Cheung, M. C. M. 2014, ApJ, 785, 90 [Google Scholar]
- Rodono, M., & Cutispoto, G. 1992, A&As, 95, 55 [NASA ADS] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Strassmeier, K. G. 1990, ApJ, 348, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., & Bartus, J. 2000, A&A, 354, 537 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Hall, D. S., Boyd, L. J., & Genet, R. M. 1989, ApJS, 69, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Rice, J. B., Wehlau, W. H., et al. 1991, A&A, 247, 130 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodonó, M. 1997, A&As, 125, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [Google Scholar]
- Washuettl, A., Strassmeier, K. G., & Collier-Cameron, A. 2001, in ASP Conf. Ser., 223, 11th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. R. J. Garcia Lopez, R. Rebolo, & M. R. Zapaterio Osorio, 1308 [Google Scholar]
- Washuettl, A., Strassmeier, K. G., & Weber, M. 2009, Astron. Nachr., 330, 366 [CrossRef] [Google Scholar]
- Worthey, G., & Lee, H.-C. 2011, ApJS, 193, 1 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Available ground-based photometry, calculated temperature curves and yearly rotational periods for EI Eri. Top panel: ground-based Johnson V light curve of EI Eri from the Potsdam Wolfgang APT at Fairborn Observatory and from the literature (grey dots) and from Jetsu et al. (2017) and present paper (black dots). Middle panel: temperatures from B − V (blue) and V – I (red). The dashed line and the grey area denote the effective temperature from spectral synthesis with 1σ error (Teff = 5580 ± 70 K, see Sect. 4.1). Black dot shows the averaged surface temperature value from the four Doppler maps (〈T〉 = 5467 ± 25 K, see Sect. 4.3). Bottom panel: yearly rotational periods from the V light curves with grey and black points, as on the upper panel and the two available TESS sectors (grey triangles). The dashed lines show the maximal (pole) and minimal (equator) rotational periods calculated using the differential rotation from the Doppler maps (see Sect. 4.4), while the dotted line denotes the orbital period. |
| In the text | |
 |
Fig. 2 Observing sites and phase distribution of the data. Left panel: MUSICOS sites involved in this work, namely Observatoire Haute-Provence (OHP), Xinglong Observatory (BXO), Kitt Peak National Observatory (KPNO), ESO La Silla (ESO), La Palma (INT), and Mt. Stromlo Observatory (MSO). Right panel: phases of the observations plotted against the reduced Julian Date. Different colors denote different instruments (see legend). Observations plotted with filled circles were used for Doppler imaging, while the empty circles denote omitted observations. The vertical dashed lines separate the four subsets used for Doppler imaging. |
| In the text | |
 |
Fig. 3 Short-term Fourier transform of all available V observations of EI Eri. A smoothly changing cycle is seen between 4.5 and 5.5 yr (and between the half of these values), and a longer one which moves between 8.9 and 11.6 yr. |
| In the text | |
 |
Fig. 4 TESS observations from Sector 5 (left) and Sector 32 (right). The identified flares are marked in black. |
| In the text | |
 |
Fig. 5 Flare-frequency distribution from the TESS data. The dashed line denotes a fit for all of the points with a power-law index of 1.66 ± 0.04, while the two solid lines show a two-component fit (1.41 ± 0.02 and 2.26 ± 0.08); see Sect. 3.2. |
| In the text | |
 |
Fig. 6 Phase distribution of the TESS flares on the primary component in the reference frame of the binary orbit. The relative radii and separation of the circles are for scale. The colors are realistic digital colors for the given spectral types from Harre & Heller (2021). The gray area shows a Gaussian kernel density estimation with the bandwidth of 2°. Black ticks denote the orbital phase values of the flare observations. |
| In the text | |
 |
Fig. 7 Four consecutive Doppler images of EI Eri obtained for the MUSICOS 1998 data. The corresponding time intervals for the four images from top to bottom are 2451141.3758–2451144.9045, 2451145.6007–2451148.7618, 2451148.9391–2451150.7474, and 2451150.9827–2451156.5520. |
| In the text | |
 |
Fig. 8 Measured surface differential rotation of EI Eri and its comparison to other stars. Left panel: average cross-correlation map for EI Eri. The correlation peaks (white circles) are fitted with a quadratic differential rotation law. The resulting fit (continuous line) indicates a solar-type differential rotation with a shear parameter α = 0.036 ± 0.007. Right panel: extended version of the surface shear coefficient versus rotational period plot from Kővári et al. (2017). Squares denote results from the cross-correlation technique, while circles show differential rotational coefficients from the sheared image method. White and gray symbols correspond to single and binary stars, respectively. Symbol size increases from dwarfs to subgiants to giants. EI Eri is represented by the blue square at Prot ≈ 2 days. The Sun is plotted with a dotted circle. The dotted and dash-dotted lines denote the linear fits to the points corresponding to singles and binaries, respectively, with slopes of |α| ∝ (0.0049 ± 0.00001)Prot and |α| ∝ (0.0014 ± 0.00003)Prot. |
| In the text | |
 |
Fig. A.1 Doppler imaging test for two consecutive rotations of V1358 Ori. Images on the left correspond to the first rotation, while images on the right correspond to the second one. The four rows from top to bottom correspond to data of different spectral resolution: R = 80 000 (original data taken from Kriskovics et al. 2019), and reduced levels of R = 60 000, R = 40 000, and R = 20 000, respectively. |
| In the text | |
 |
Fig. A.2 Difference images of the original V1358 Ori Doppler images (Kriskovics et al. 2019) and those that correspond to a spectral resolution reduced to R=20 000. The left panel corresponds to the first rotation and the right panel to the second; cf. Fig. A.1. |
| In the text | |
 |
Fig. A.3 Example cross-correlation test maps of V1358 Ori with their fitted surface differential rotation functions obtained for different spectral resolutions of R=20 000 (left) and R=70 000 (right). The derived surface shear coefficients are α = 0.010 ± 0.0025 and α = 0.015 ± 0.003, respectively. For the original cross-correlation map see Kriskovics et al. (2019). |
| In the text | |
 |
Fig. A.4 The α surface differential rotation parameter values obtained for spectroscopic test datasets with different levels of R spectral resolution. |
| In the text | |
 |
Fig. C.1 Fitted line profile subsets (S1-S4) corresponding to the four Doppler images (DI1-DI4) presented in Fig. 7. The phase distributions of each subset are shown in the right panel of Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


