| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 14 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202347900 | |
| Published online | 04 March 2024 | |
Observation of solar radio burst events from Mars orbit with the Shallow Radar instrument
1
University of Texas at Austin Institute for Geophysics, J.J. Pickle Research Campus, 10100 Burnet Road, 78758 Austin, TX, USA
e-mail: christopher.gerekos@austin.utexas.edu
2
Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91011, USA
3
Department of Physics and Astronomy, University of Turku, Turku, Finland
4
Naval Postgraduate School, Monterey, CA, USA
5
Fondazione Bruno Kessler, Via Sommarive 18, 38123 Povo, Trento, Italy
6
School of Physics and Astronomy, University of Leicester, University Rd, Leicester LE1 7RH, UK
7
Center for mathematical Plasma Astrophysics, Department of Mathematics, Katholieke Universiteit Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
8
Solar-Terrestrial Centre of Excellence, Royal Observatory of Belgium, Avenue Circulaire 3, 1180 Uccle, Belgium
9
Department of Aerospace Engineering Sciences, College of Engineering and Applied Sciences, University of Colorado Boulder, Boulder, CO, USA
Received:
7
September
2023
Accepted:
19
December
2023
Context. Multispacecraft and multiwavelength observations of solar eruptions, such as flares and coronal mass ejections, are essential to understanding the complex processes behind these events. The study of solar burst events in the radio frequency spectrum has relied almost exclusively on data from ground-based observations and a few dedicated heliophysics missions such as STEREO or Wind.
Aims. By reanalysing existing data from the Mars Reconnaissance Orbiter (MRO) Shallow Radar (SHARAD) instrument, a Martian planetary radar sounder, we discovered the instrument was also capable of detecting solar radio bursts and that it was able to do so with unprecedented resolution for a space-based solar instrument. In this study, we aim to demonstrate the reliability and value of SHARAD as a new solar radio observatory.
Methods. We characterised the sensitivity of the instrument to type III solar radio bursts through a statistical analysis of correlated observations using STEREO and Wind as references. Using 38 correlated detections, we established the conditions under which SHARAD can observe solar bursts in terms of acquisition geometry. As an example of scientific application, we also present the first analysis of type III characteristic times at high resolution beyond 1 AU.
Results. A simple logistic model based purely on geometrical acquisition parameters can predict burst show versus no-show in SHARAD data with an accuracy of 79.2%, demonstrating the reliability of the instrument in detecting solar bursts and laying the foundation for using SHARAD as a solar radio observatory. The extremely high resolution of the instrument, both in temporal and frequency directions; its bandwidth; and its position in the Solar System enable SHARAD to make significant contributions to heliophysics. Notably, it could provide data on plasma processes on the site of the burst generation and along the propagation path of associated fast electron beams.
Key words: space vehicles / space vehicles: instruments / techniques: radar astronomy / Sun: corona / Sun: coronal mass ejections (CMEs) / Sun: radio radiation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Sun is routinely capable of accelerating electrons to suprathermal energies through eruptive phenomena such as flares, coronal mass ejections, and the subsequent shock waves that they drive. Through various mechanisms, these suprathermal electrons emit radiation in the entire electromagnetic spectrum and particularly in the longer radio wavelengths. Based on the source (streaming electrons, shock waves, etc.), the emission can manifest itself with different morphological properties on the dynamic radio spectrogram. Early observations have distinguished five main spectral types (I–V; Kundu 1965), and further sub-classifications have been made since.
In the past two decades, radio frequency observatories onboard heliophysics missions such as the Solar TErrestrial RElations Observatory Ahead & Behind (STEREO A & B/WAVES; Bougeret et al. 2008) and Wind/WAVES (Bougeret et al. 1995) have been used to understand various aspects of interplanetary radio emissions. Recently, these missions have been combined with the Radio Frequency Spectrometer (RFS, part of the FIELDS suite; Bale et al. 2016; Pulupa et al. 2017) onboard the Parker Solar Probe (PSP; Fox et al. 2016) and the radio and plasma waves (RPW; Maksimovic et al. 2020) instrument onboard Solar Orbiter (SolO; Müller & Marsden 2013) for multi-vantage point studies of hecto-kilometric (H-K) radio emissions (e.g. Jebaraj et al. 2023a; Dresing et al. 2023). While they do not provide the same time-frequency resolution as ground-based instrumentation, observing radio emissions simultaneously from multiple vantage points opens the possibility of investigating the generation and propagation of radio waves (Musset et al. 2021). Previous multi-vantage point observations of solar burst events made beyond 1 AU include Lecacheux et al. (1989) and Bonnin et al. (2008).
Planetary radar sounders are a class of spacecraft-mounted remote sensing instruments that operate by recording reflections of electromagnetic waves off a solid planetary body. Such reflections arise when an incoming electromagnetic field encounters a change in the dielectric constant of the medium, such as the space-surface interface, subsurface layering, or subsurface inclusions. The source of this incoming field can be the instrument itself, in which case the radar will transmit a coded waveform (usually a linear chirp) with the power of a few Watts. This mode of operation is known as ‘active sounding’ (Skolnik 1980). Conversely, the incoming field can be a signal of opportunity of astrophysical origin, according to a recently proposed mode of operation known as ‘passive sounding’ (Romero-Wolf et al. 2015). Radar sounders typically operate in the deca-hectometre (D-H) wavelength bands.
One particularly productive planetary radar sounder has been the Shallow Radar (SHARAD) instrument (Seu et al. 2004) onboard the National Aeronautics and Space Administration (NASA) Mars Reconnaissance Orbiter (MRO) mission, which was launched towards Mars in 2005 and began observations a year later. SHARAD is sensitive in the 13.3–26.7 MHz band, has a time resolution of 1.43 ms before pre-summing, and a frequency resolution of 7.41 kHz (Seu et al. 2004; Croci et al. 2011). The radiating element of SHARAD is a 10-m long thin-wire dipole antenna (Croci et al. 2011). When operating SHARAD, the spacecraft is nominally oriented so that its −Z direction points towards the Martian surface, although some variations in the roll angle have been considered to accommodate the unforeseen lobe distribution of the SHARAD antenna pattern (Croci et al. 2011; Campbell et al. 2021). Amongst other discoveries enabled by SHARAD, Grima et al. (2009) characterised the ice purity in the layers of the Martian polar caps, Holt et al. (2008) found evidence of buried glaciers at mid-latitudes, and Campbell et al. (2013a) constrained the roughness and near-surface density of the Martian surface.
In this work, we show how SHARAD can be used to observe solar radio burst (SRB) events at unprecedented resolution in the D-H band from space, also marking the first attempt to use a planetary radar sounder as a solar radio observatory. We note that Gurnett et al. (2010) mentioned having seen SRBs in data from the Mars Advanced Radar for Subsurface and Ionosphere Sounding (MARSIS), another Martian radar sounder (Picardi et al. 2004) operating at markedly lower frequencies than SHARAD (1.3–5.5 MHz in sounding mode), but these were treated as parasitic signals, and no attempt has yet been made to study SRBs with this instrument. In order to demonstrate the potential of SHARAD for heliophysics, we devised a purpose-built algorithm for detection of SHARAD-detectable type III bursts in the STEREO/WAVES and Wind/WAVES datasets. We propagated these events in time from the orbits of these spacecraft to the orbit of Mars and searched for any instance when the SHARAD receiver was on and when the Sun was not occulted by Mars, as seen from MRO. This search for SHARAD type III burst-containing candidates yielded 179 distinct SHARAD radargrams, of which 38 contain solar burst. Through a multivariate statistical analysis of the candidates, we quantified the importance of the acquisition geometry for burst detection. As, by construction, all of our SHARAD-detected bursts have at least one correlated observation, we also present comparisons of a few selected bursts observed by SHARAD and the source solar spacecraft, and we provide succinct commentary on their features. As an example of scientific application of this dataset, we analyse the characteristic times of our dataset of type III bursts following a methodology close to that of Reid & Kontar (2018) and compare the frequency-dependence scaling laws we obtained with those obtained on Earth.
This manuscript is structured as follows. Section 2 presents our methodology for finding correlated observation opportunities and building the proposed list of SHARAD candidates. Section 3 contains a summary of our observations. Section 4 presents the statistical analysis of the sensitivity of SHARAD to type III SRBs. Section 5 contains in-depth analyses of representative SHARAD spectrograms, including the type III characteristic time analysis at 1.5 AU. Section 6 concludes this paper with a discussion of the proposed dataset and its perspectives. Appendix A presents a SHARAD duty cycle analysis, and Appendix B contains a quicklook mosaic of all the SHARAD-captured bursts we have found.
2. Methods and datasets
In this section we present the methodology we used to detect SRBs in STEREO and Wind data and to search for corresponding SHARAD candidates, focusing on type III bursts. The critical parts of the code have been made available along with an accompanying flowchart as Supplementary Material 1 (Gerekos 2023a).
2.1. Solar radio burst detections from STEREO and Wind
Data from the STEREO and Wind iterations of the WAVES instrument was used for the compilation of SHARAD-detectable type III bursts for a number of reasons, including the availability of round-the-clock observations, the existence of some degree of homogeneity of the data properties across STEREO and Wind, and the partial bandwidth overlap with SHARAD. These properties ensure that a relatively unified algorithm can be built to search for bursts in three different spacecraft and to collect a large number of co-observation opportunities.
We used the 60-second averaged WAVES products from both STEREO and Wind covering a period starting on 6 December 2006 (first SHARAD acquisition) and ending on 31 December 2021. An initial screening for bursts was made by integrating the spectrograms over their entire range of frequencies, yielding a one-dimensional time-series of power flux, and by detecting prominences that are one standard deviation higher than the background through the MATLAB proprietary function findpeaks. This was done for each 24h-spanning data product. A three-step fuzzy logic algorithm was then applied on these peaks in order to reject prominences due to interferences or instrument malfunction and to reject genuine type III bursts that do not have significant energy above 13 MHz, about the lowest frequency available to SHARAD. Therefore, the algorithm tests peak flatness, peak asymmetry, and high-frequency content. (For more details, please see Gerekos 2023a.)
Given the large number of type III bursts that these missions recorded and the nature of our study, the algorithm is rather restrictive, as false positives are more dangerous than false negatives. With this method, we detected 5676 bursts with STEREO A, 4340 bursts with STEREO B, and 3538 events with Wind.
2.2. SHARAD candidate selection
Each of the events we detected has an associated timestamp t that corresponds to the time of detection of peak power. We propagated this time of detection at the observer (STEREO A, B, or Wind) to Martian orbit by considering the radial distance separating the solar spacecraft and Mars at that time. This step rests on the hypothesis that the isocontours of burst detection time form circles around the Sun. This radial distance difference was converted into a delay τ by assuming propagation at the speed of light in vacuum. In other words, if t′ is the supposed time of detection at Mars, we can write
where vw, vO, and vM represent the position of the observer (STEREO A, B, or Wind), the position of the Sun, and the position of Mars, respectively, and where r represents a radial distance from the Sun. These positions can be extracted from the appropriate SPICE kernels. The corresponding Mars detection time t′ was computed for all the events detected in the previous step. Then, a SHARAD data product was considered a candidate if it satisfied the two following conditions: (i) SHARAD is operating at t′, and (ii) the Sun is not occulted by Mars at t′ as seen from MRO. The first criterion was verified by testing that the start and stop time, t1 and t2, of a given SHARAD data product is such that t1 ≤ t′≤t2, where t1 and t2 are found in the SHARAD product metadata. The second criterion could be easily tested using a SPICE query.
After application of these criteria, we were left with 226 SHARAD detections comprising 179 distinct SHARAD data products (a given event recorded by different solar observatories may correspond to the same SHARAD product). This very strong reduction in the numbers of events, compared with that of Sect. 2.1, is explained by the very low duty cycle of SHARAD activity (see Appendix A) and by the fact that a majority of radar sounding observations were done on the Martian nightside (Campbell et al. 2013b). A complete list of these SHARAD candidates is given as Supplementary Material 2 (Gerekos 2023b).
2.3. Spectrogram and time profile generation
The SHARAD Experimental Data Records (EDR; Slavney & Orosei 2007a) are real-valued baseband waveforms containing 3600 samples per rangeline. A rangeline is a one-dimensional fast-time collection of samples that forms the basic acquisition unit of a radargram, and a radargram is a collection of consecutive rangelines. With SHARAD, rangelines are acquired at a frequency of 700 Hz, and each have a duration of 135 μs. The SHARAD dynamic spectra shown in this manuscript are the absolute value of the fast Fourier transform of the EDR product in decibel scale, and only the positive-frequency components are displayed (1800 samples). In addition to possible SRBs, these opportunistically acquired SHARAD SRB spectrograms contain a number of signals of non-solar origin: electromagnetic interference (EMI) and reflections of the active chirp. These are highlighted in Fig. 1 for product 2533401, which contains a type III burst. For canonical exploitation of radar data, that is, the geologic analysis of backscattered echoes, the EDR data must at least undergo an operation known as ‘range-compression’ to be interpretable (Cumming & Wong 2005; Gerekos 2020), and they usually undergo additional azimuth processing as well. On SHARAD, range-compressed and azimuth-processed EDRs are known as Reduced Data Records (RDR; Slavney & Orosei 2007b) and constitute the ‘usual’ form of SHARAD data. The corresponding RDR product for 2533401 is also shown in Fig. 1 for context. The processed radargram depicts a slightly rough surface located in the northern Martian lowlands with a small crater near the end of the acquisition. The solar burst is clearly visible as the noisy part in the centre.
 |
Fig. 1. Comparison of the Reduced Data Record (top) and spectrogram of the Experimental Data Record (bottom) for SHARAD product 2533401. Also depicted are annotations for the main signals present in the spectrogram. This product contains a type III burst (outlined by the dashed black curve); it is affected by various EMI sources, which are the narrow band signals that are persistent in time and manifest themselves as horizontal traces and the strongest of which are highlighted with horizontal arrows; and it contains traces of the reflection of the active chirp, which are wideband signals with short durations in time and manifest themselves as vertical traces, the strongest of which (or groups of which) are highlighted by vertical arrows. The band of flat spectral gain is delimited by the dashed orange lines at 15 and 25 MHz. |
It must be noted that SHARAD has not been calibrated on the ground, meaning there is no formally generated data products in physical units of spectral flux (Slavney & Orosei 2007b). The gain per frequency band across the whole bandwidth (13.3–26.7 MHz) has also not been completely characterised, although it was optimised to be spectrally flat in the 15–25 MHz range (Bernardini et al. 2004). Calibrating SHARAD a posteriori is an ongoing effort (Campbell et al. 2021; Castaldo et al. 2013).
No gain de-trending or active chirp removal algorithms have been applied to the spectrograms shown in this work, as our exploitation of the data in this work remains exploratory. Instead, a basic filtering using a Gaussian kernel of 3 pixels was applied globally for image rendition concerns. The time profiles represent a 100-pixel moving average of the raw spectra.
3. Observations
The 179 SHARAD candidates obtained from our search algorithm were visually examined for the presence of solar bursts. Of these candidates, 38 products contained a clear, scientifically exploitable burst. The list of all candidates, including those without a burst, has been made available as Supplementary Material 2 (Gerekos 2023b) to allow for possible future reanalyses that would look for subtler signatures, and the subset of SHARAD candidates that contain an unambiguous solar burst is summarised in Table 1. A quicklook mosaic of these products is further provided in Appendix B.
All the SHARAD candidates where a burst (type III unless otherwise indicated) was identified within the product.
Several of these bursts display extensive fine structures, and some bursts have a peculiar dynamic spectra unlike the typical type III profile. Interestingly, a type II event (SHARAD product 3544101) was also picked up by our algorithm.
The temporal and spatial distributions of the 226 SHARAD candidate events, with and without a burst, is shown in Fig. 2. The number of SHARAD candidates throughout the surveyed years closely follows the solar cycle, and the fraction of these candidates that were confirmed to contain a burst stays at around 25% for every year. The additional variability in the number of candidates can be explained by the variation in the yearly SHARAD duty cycle (see Appendix A). This consistency suggests that the geometric selection criteria described in Sect. 2.2 do not introduce any particular bias. When considering the spatial spread of the observations, it can be observed that the sources of the observations (STEREO A, B, and Wind) are rather evenly distributed, whereas the corresponding SHARAD candidates are more concentrated on the negative X-side of the Solar System in the J2000 system of coordinates. However, when considering the SHARAD candidates containing a burst, the distribution of the sources shows a similar unbalance. The first feature is simply explained by the fact that a great proportion of bursts were recorded in 2014 and that Mars was in that particular sector during that year, whereas the second observation hints at the angular difference dependence for detectability (see Sect. 4). The dedicated solar missions may have been at any place in the Solar System during the peak years, but it was being angularly closest to Mars that lead to better chances of a SHARAD observation.
 |
Fig. 2. Visual summary of the generated dataset. (a) Temporal distribution of the SHARAD burst candidates. In grey is the count of all SHARAD candidates per year, with the burst-containing subsets colour-coded according to the source of the observation. The histogram follows the solar cycle, and the proportion of burst-containing products is stable. (b) Spatial distributions of SHARAD burst candidates. Indicated are the positions of MRO, STEREO A, STEREO B, and Wind for all SHARAD candidates. The lines are drawn between the source of the observation and the corresponding SHARAD candidate for every candidate with a burst. |
4. SHARAD sensitivity to type III bursts
Of the 179 SHARAD candidates picked up by the algorithm described in Sect. 2, 38 contain a prominent burst, representing 21.23% of the candidates, and 141 were identified as not containing a burst. In this section, we discuss these figures and quantify the effects of several geometrical factors on this cross-detection rate.
A parameter that likely influences the detection of SRBs with SHARAD is the absolute power of the burst as detected by the source of observations (STEREO A, B, or Wind), as some bursts seen by the observer may not have been seen by SHARAD because of its own sensitivity threshold. However, it is not a parameter we can uniformly analyse: Wind/WAVES data have not yet been formally calibrated at the time of the analysis, and issues of cross-calibration of STEREO/WAVES and Wind/WAVES are still unsettled (Krupar, pers. comm., 2022). Parameters of geometrical nature, however, can be analysed uniformly. The non-isotropic nature of type III bursts (Musset et al. 2021) is expected to lead to a preferential detection if the angle between the source spacecraft and MRO with respect to the Sun (marked as ϕ in Fig. 3) is small. It is also expected that the orientation of MRO plays a major role in the detectability of bursts due to the antenna pattern of SHARAD (Croci et al. 2007). In processed radar sounding data, variations of gain of up to 4 dB have been observed by Campbell et al. (2021). The position of the high-gain antenna and the orientation of the solar panels of MRO are also known to considerably affect the antenna pattern of SHARAD (Campbell et al. 2021). Due to the complexity and interdependence of these effects, however, we chose to focus on the orientation of the antenna only.
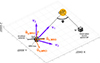 |
Fig. 3. Illustration of several key quantities in the definition of relevant angles. In this illustration, yaw is about 60°, pitch is about 20°, and roll is close to 90°. |
Since the orientation towards the Sun is the most relevant parameter, we defined the pitch, yaw, and roll angles with respect to that direction as follows. We first defined a set of three reference unit vectors:
where vO = (0, 0, 0) is the position of the Sun in the J2000 system of coordinates and vMRO is that of MRO. By construction, 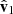 always points from MRO towards the Sun. The normal to the ecliptic plane is indicated by
always points from MRO towards the Sun. The normal to the ecliptic plane is indicated by 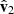 , and
, and 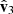 completes the orthonormal basis. With these vectors, we defined the following projections of the
completes the orthonormal basis. With these vectors, we defined the following projections of the 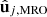 , (j = x, y, z) vectors, which form the basis of MRO-fixed orthonormal unit vectors (Croci et al. 2007):
, (j = x, y, z) vectors, which form the basis of MRO-fixed orthonormal unit vectors (Croci et al. 2007):
In Fig. 3, the vectors 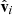 , (i = 1, 2, 3) and
, (i = 1, 2, 3) and 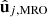 , (j = x, y, z) are represented in purple and orange, respectively. The projection of
, (j = x, y, z) are represented in purple and orange, respectively. The projection of 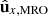 onto the
onto the 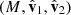 plane is represented by wx; wx′ is the projection of
plane is represented by wx; wx′ is the projection of 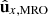 onto the
onto the 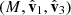 plane; and wz is the projection of
plane; and wz is the projection of 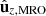 onto the
onto the 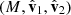 plane.
plane.
These constructions allowed us to define the desired Sun-based pitch, yaw, and roll angles as follows:
where sgn(⋅) is the sign function. A 0° value for both yaw and pitch indicates a situation where 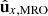 is aligned with
is aligned with 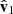 and thus has the antenna axis pointed towards the Sun. An ideal dipole in this configuration would see zero gain in the direction of the Sun. A 90° yaw angle places the antenna axis perpendicular to the Sun in the horizontal plane (the projection
and thus has the antenna axis pointed towards the Sun. An ideal dipole in this configuration would see zero gain in the direction of the Sun. A 90° yaw angle places the antenna axis perpendicular to the Sun in the horizontal plane (the projection 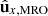 onto the
onto the 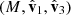 plane is perpendicular to
plane is perpendicular to 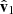 ), whereas a 90° pitch angle places the antenna perpendicular to the Sun in the vertical plane (the projection
), whereas a 90° pitch angle places the antenna perpendicular to the Sun in the vertical plane (the projection 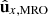 onto the
onto the 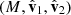 plane is perpendicular to
plane is perpendicular to 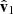 ). Both situations would place the main lobe of an ideal dipole to point towards the Sun. Lastly, the roll angle controls the rotation around the antenna axis. It thus affects the relative positions of SHARAD and the MRO bus (and other elements such as the high-gain antenna and the solar panels) with respect to the Sun. The gain of an ideal dipole is agnostic to roll, but here these large structures on the spacecraft are expected to play a role.
). Both situations would place the main lobe of an ideal dipole to point towards the Sun. Lastly, the roll angle controls the rotation around the antenna axis. It thus affects the relative positions of SHARAD and the MRO bus (and other elements such as the high-gain antenna and the solar panels) with respect to the Sun. The gain of an ideal dipole is agnostic to roll, but here these large structures on the spacecraft are expected to play a role.
We made two types of statistical analysis based on the observer separation angle, MRO pitch, MRO yaw, and MRO roll: (i) a principal component analysis (PCA) and (ii) histograms and probability of detection for each angle taken independently. The results can be seen in Figs. 4 and 5a-d, respectively.
 |
Fig. 4. Multivariate logistic regression using the feature vectors generated by the principal component analysis. |
 |
Fig. 5. Sensitivity of SHARAD to geometrical acquisition parameters. Histograms of the number of burst detections (‘Yes’) and burst no-detections (‘No’) along with the probability p of detection (ratio of ‘Yes’ to ‘Yes’ + ‘No’) for J2000 separation, yaw, pitch, and roll angles, respectively. The bars of the histograms are stacked, meaning the total number of events n in a given angular bin is immediately accessible on the graph. The error bars associated with the probability curve correspond to the standard error of a binary outcome, that is, σ = [p(1 − p)/n]1/2. |
Regarding the components of the PCA, which are orthogonalised linear combinations of the four angles, the first three components contained 96.45% of all variability in the original data, the first two 73.41%, and the first component only 47.13% of all variability. The correlation between any pair of angles was weak (< 0.2), except for yaw and roll, which are strongly anti-correlated (−0.8), a result of the attitude control on MRO, itself on a polar orbit (Zurek & Smrekar 2007). We also performed a multivariate logistic regression using these PCA feature vectors to classify the bursts as ‘Yes’ or ‘No’, based on a selectable threshold to convert the continuous output of the predictive model in the [0, 1] range to a ‘Yes-No’ binary. This predictive model has a classification accuracy that peaks at 0.792 for a threshold of 0.49 when using all four feature vectors. A threshold near 0.5 is the most natural for an application such as this one. Thus, the fact that the logistic regression accuracy peaks at this value conforms to the idea of a sensible model. Using only the first two components of the PCA, the predictive model retains similar accuracy, highlighting a degree of correlation between the four considered angles, as discussed.
From the J2000 separation angle histogram, it is clear that detection is preferentially successful at low angles, with a probability of cross-detection reaching 0.7 when the angle between MRO and the source of observation is around 20°. Regarding orientation, the probability of detection peaks when the pitch and yaw are both close to 90°. These angles put the radar axis perpendicular to the Sun (the former, vertically and the latter, horizontally), which is the configuration for which maximal gain is expected. The absence of observations for some ranges of angles can be traced to MRO orbit specifics coupled with the no-occultation condition we imposed on the candidates. The probability of detection also peaks when the roll angle approaches ±180°, that is, when 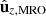 is aligned but opposite to
is aligned but opposite to 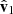 (see Fig. 3). For a favourable yaw and pitch, such roll angles place SHARAD ‘in front’ of the Sun, with the bus and the other large structures ‘behind’ it. Intuitively, this is also a configuration that is expected to maximise the SHARAD gain, as it approaches that of traditional radar sounding (Campbell et al. 2021).
(see Fig. 3). For a favourable yaw and pitch, such roll angles place SHARAD ‘in front’ of the Sun, with the bus and the other large structures ‘behind’ it. Intuitively, this is also a configuration that is expected to maximise the SHARAD gain, as it approaches that of traditional radar sounding (Campbell et al. 2021).
5. Analysis and discussion
It is well understood that the morphology of the intensity-time profiles of a type III radio burst correspond to the growth of the instability (Voshchepynets et al. 2015; Voshchepynets & Krasnoselskikh 2015; Krasnoselskikh et al. 2019; Tkachenko et al. 2021; Jebaraj et al. 2023c) and the propagation of radio waves (Fokker 1965; Arzner & Magun 1999). The emission, which is a combination of all these processes, is systematically asymmetric in intensity-time profiles (Suzuki & Dulk 1985). Rapid variations in the peak intensity across the observing frequencies is not uncommon in decametre type III bursts (Kontar et al. 2017) and are to be expected when the electron beam evolves in an inhomogeneous medium. These variations may then be used to probe the plasma through which the beam propagates, assuming that the emission is close to the electron plasma frequency.
Figure 6a illustrates a typical type III burst observed on 22 December 2011. STEREO A/WAVES also detected this burst, albeit at a lower resolution. Figure 6b displays a group of type III bursts observed on 1 January 2012. Due to limited resolution in the H-K wavelengths, different type III bursts within one are difficult to deconvolve. SHARAD, with its superior capabilities at lower frequencies, revealed nine bursts where STEREO A/WAVES only detected two. Figure 6c presents a type III burst with fine structures called ‘striae’ elements. These bursts can emerge due to electron beam evolution in inhomogeneous plasma, where stronger emissions occur in regions with smaller density inhomogeneities (Jebaraj et al. 2023c). Pulse broadening is mainly due to velocity dispersion of the electron beam exciter (Reid & Ratcliffe 2014), but the Langmuir wave growth can also be hindered in inhomogeneous plasma, resulting in less intense, longer-duration bursts (Voshchepynets et al. 2015; Voshchepynets & Krasnoselskikh 2015). In this example, SHARAD detects three distinct type III bursts, while STEREO A/WAVES observes a single burst without discernible fine structures, underscoring the significance of high time and frequency resolution.
 |
Fig. 6. In-depth analysis of three representative elements of the SHARAD burst dataset: (a) SHARAD product 2533401, which is also displayed in Fig. 1; (b) SHARAD product 2546401; (c) SHARAD product 6763001. For each case, the plots in the first row represent a map of the Solar System. The second row shows the STEREO-captured original burst, in calibrated units. The third row shows the SHARAD spectrogram. The plots in the fourth row contain time profiles for selected frequencies extracted from the SHARAD spectrogram, along with the 15.0125 MHz line from STEREO for comparison. In the case of 2533401, the dashed black lines on the SHARAD spectrogram show the bounds of the corresponding time profiles. The calibrated STEREO data was sourced from Krupar et al. (2022). |
While it is possible to distinguish fine structures and intensity variations using STEREO and Wind observations, their frequency resolution of more than 4% would mean that only large scale inhomogeneities can be probed (Jebaraj et al. 2023c). On the other hand, SHARAD provides the resolution capable of resolving the fine-scale intensity variations, which may then be used in tandem with modern missions, such as the Parker Solar Probe during its close encounters. However, a complete characterisation of the spectral gain of SHARAD as well as its sources of EMI is likely to be needed for full exploitation of its spectral resolution.
In this sense, the limitations of SHARAD for heliophysics are twofold. The first limitation is due to the instrument-specific limitations that we have previously mentioned. Empirically, uneven spectral gain can be addressed by a de-trending of the time-averaged spectral power for each burst. Regarding EMI, notch filtering has been applied successfully to SHARAD products to enhance the quality of range-compressed observations (Campbell et al. 2021). While these methods are promising for heliophysics-oriented analysis of SHARAD data, one must ensure they do not compromise the natural signals of interest. For this reason, we devolve the study of fine structures within the very high-resolution SHARAD dynamic spectra of type III bursts to a future study. The second limitation arises from using SHARAD opportunistically. The limited number of bursts that we observed in our dataset can be traced to the low duty cycle of SHARAD, the preference for nighttime observations for radar sounding of Mars, and the nadir-pointing geometry favoured for radar sounding of Mars.
5.1. Time-profile characteristics at 1.5 AU
A consequence of the very high temporal resolution of SHARAD is that the fast Gaussian-like rise and the slower exponential decay are effortless to identify, as evidenced by the examples shown in Fig. 6. For this reason, we propose to study the statistics of the frequency dependence of the rise time tr and decay time td, computed by fitting an exponentially modified Gaussian function (Dulk et al. 1984; Reid & Kontar 2018; Jebaraj et al. 2023b) and by computing the half widths at half maximum (HWHM) on either side of the peak intensity. Reid & Kontar (2018) conducted a comparable study with 31 type III bursts recorded by LOFAR (Van Haarlem et al. 2013) in the 30–80 MHz range. The characteristic times of type III bursts in the frequency range of 15–25 MHz, which provides a natural continuation to Reid & Kontar (2018), has not been explored beyond 1 AU at the resolutions we have access to in this work and constitute a novel result.
The time-profile analysis was run on all the ‘canonical’ type III bursts detected by SHARAD, that is, all those listed in Table 1 with an asterisk in the ‘Notes’ column. This excludes those with peculiar morphologies (e.g. 2712401), those with an extensive fine structure (e.g. 3617602), and those that are not a type III (e.g. 3544101). A similar sieving was done in Reid & Kontar (2018). When a given SHARAD data product contained several bursts, all those that were exploitable within the product were included. This left 26 individual bursts to analyse. Of these bursts, all frequency lines containing EMI were ignored. For a given product, the EMI lines were identified through a global time-average of the dynamic spectrum, the application of a median filter with kernel size 101, and the detection of all frequency lines that were above this trend line. We also excluded the frequency lines at the edges of the instrument’s capabilities and ran our analysis in the 15–25 MHz range, the bandwidth the instrument was optimised for. After exclusion of EMI and edge frequencies, about 800 frequency lines per burst (out of 1800) were still available for time-profile analysis. In total, we analysed about 25 000 profiles.
The function resulting from the convolution of an exciter function and an exponential decay is able to accurately represent the intensity-time profiles of type III bursts (Aubier & Boischot 1972; Barrow & Achong 1975). With the choice of a Gaussian function as the exciter (De Groot 1966), this function is referred to as an exponentially modified Gaussian function. It is more general than both the Gaussian used in Reid & Kontar (2018) and the exponential decay functions historically used to study type III bursts (Evans et al. 1973; Dulk 2000), and it yields particularly accurate fits in our study of lower-frequency bursts due to its asymmetry. The characteristic times extracted from this function are therefore the most faithful. The five-parameter function we used to fit the time profiles of this paper is given by
where a controls the overall scaling of the burst, and b controls its floor; μ is the mean of the Gaussian sector of the function, and σ2 is its variance. Lastly, λ controls the decay rate of the exponential sector. The error function is defined as erf(z)≡2(π)−1/2∫0ze−t2dt. The rise time tr and decay time td are then computed as the two HWHMs of the fitted curve. In Fig. 7, we show an example of a SHARAD profile along with its fitted function and a graphical representation of tr and td.
 |
Fig. 7. Example of a time-profile extraction and fit on SHARAD product 2545801 using the EMI-free frequency band of 15.5056 MHz. The dashed vertical black lines on the dynamic spectrum represent the portion of the product that was fed into the fitting subroutine. The coefficients displayed next to the fitted curve correspond directly to those of Eq. (11). The rise and decay time tr and td were derived as the first and second HWHM. The maximum was computed as the difference between the maximum of the curve and the floor parameter b. |
Along with the quantities of interest, we also recorded the r2 coefficient for each fit in order to exclude fits of bad quality. Bad fits can occur when the signal-to-noise ratio of the burst is very low, when several closely spaced bursts force the cropping to be constrained around each of them, or when the profile is contaminated by reflections of the active SHARAD chirp. Due to the abundance of data points, we were able to apply very strict fit quality criteria, considering only the profiles for which r2 > 0.95, and still be left with about 7000 data points in the final analysis.
The results for tr(f), td(f), and the derived quantities FWHM(f) = (td + tr)(f) and td(tr) can be seen in Fig. 8, and the best-fit power laws for each plot are given in Eqs. (13) through (16), respectively. These laws were obtained by directly fitting a power function using MATLAB’s unweighted non-linear fit method, instead of linearly fitting the data in logarithm space. This was done so as to (i) minimise the non-linear transformation applied on to the data and (ii) conform with the procedure of Reid & Kontar (2018):
 |
Fig. 8. Analysis of rise time and decay time of the suitable type III bursts recorded by SHARAD after fitting an exponentially modified Gaussian function onto every frequency line that is unhampered by EMI. The colour-coding of the dots represents profiles from an individual burst, with some colours being reused. The black line is the best power-law fit, the equations for which are given in formulae (13) through (16). |
5.1.1. Rise and decay time
Both the SHARAD rise time exponent −0.85 ± 0.14 (Eq. (13)) and the SHARAD decay time exponent −0.83 ± 0.14 (Eq. (14)) are consistent with Reid & Kontar (2018), who found −0.77 ± 0.14 and −0.89 ± 0.15, respectively, using LOFAR. Interestingly, (Reid & Kontar 2018) found the decay time to decrease more sharply with frequency, whereas we found that the rise time and the decay time share a similar behaviour. The rise time is closely linked to the exciter function, that is, the growth of Langmuir waves, and inherits its characteristics (Krasnoselskikh et al. 2019), and it is thus expected to behave similarly at different points of the Solar System for a given frequency. The decay time, on the other hand, is not completely immune to propagation effects, and can be thought of as a convolution between the characteristics of the source and the electromagnetic wave propagation effects (Reid & Kontar 2018). We therefore did not exclude that the subtle discrepancy we observed for the decay time at 1.5 AU is partly due to such effects, although it seems unlikely given the frequency range of SHARAD. However, it is widely understood that these effects are minimal for higher harmonics (Melrose 1980). Recent studies by Jebaraj et al. (2023b) have found that type III bursts predominantly occur as fundamental/harmonic pairs. We did not differentiate between fundamental and harmonic components in this study, so we cannot exclude some kind of selection bias towards the former either. At any rate, these broadly-consistent results can be interpreted as validation of the appropriateness of SHARAD, but a thorough investigation of the fundamental versus harmonic content of our SHARAD-detected burst dataset should yield interesting insights. We defer this research to a future study.
5.1.2. Burst duration
The burst duration is commonly computed as the full width at half maximum (FWHW) of the time profile in the literature (Barrow & Achong 1975; Reid & Kontar 2018; Kontar et al. 2019). In our case, this quantity is readily available as the sum of the fall and decay times, FWHM = tr + td. Our duration values are somewhat higher than those suggested by Kontar et al. (2019), whose study examines a much wider range of frequencies (100 kHz – 100 MHz), but they are comparable to those of Melnik et al. (2011), who studied particularly powerful bursts in a similar frequency range as that of SHARAD. The durations of the SHARAD bursts are, however, slightly shorter than those detected by Barrow & Achong (1975) with the University of West Indies Radio Observatory. Our analysis yielded a frequency dependence with an exponent of −0.84 ± 0.14 (Eq. (15)), which is compatible with that of both Kontar et al. (2019) and Reid & Kontar (2018), who respectively found −0.98 ± 0.05 and −0.86 ± 0.11. A graphical summary of these comparisons can be found in Fig. 9.
 |
Fig. 9. Comparison of the type III burst durations (FWHM) derived from SHARAD data (Eq. (15) and Fig. 8) with that of Kontar et al. (2019), Reid & Kontar (2018), Melnik et al. (2011), Barrow & Achong (1975). The shaded area around the law obtained in this study corresponds to the 95% confidence interval for the parameters of the fitted function (functional prediction interval). |
5.2. Burst asymmetry
When computing the decay time as a function of the rise time (Eq. (16)), we found that the former is almost always greater than the latter, as expected, outliers notwithstanding. The exponent of the decay time’s frequency dependence close to one also matches with the literature (Reid & Kontar 2018).
6. Conclusions and outlook
In this manuscript, we demonstrated that planetary radar sounders such as SHARAD can be used as high-resolution solar radio observatories. We presented a quantitative analysis of the sensitivity of SHARAD to solar burst events based on the statistics of correlated observations from a geometric standpoint, and we extracted the characteristic times of type III bursts from this dataset.
Our findings show that SHARAD observations can bring large advancements in the understanding of the generation and propagation of the radio bursts at distances even as far as the Mars orbit. In addition to studying characteristic times at 1.5 AU, the capabilities of SHARAD could be leveraged to study fine structures and provide additional points of observation in burst triangulation. Moreover, its bandwidth completes the spectrum between typical dedicated solar missions and Earth radio telescopes. From the perspective of radar science, correlated observations with STEREO can also help in the absolute calibration of SHARAD since STEREO/WAVES data are absolutely calibrated. Since bursts can be compared one-to-one between the observer(s) and SHARAD, the power that SHARAD should have detected for a given burst can be predicted, taking into account an estimation of the directional gain of SHARAD (for instance, through EM simulations) and the effects of longitudinal variations (for instance, by selecting situations where the observer and MRO are aligned or by a method such as that of Musset et al. 2021). Conversely, it is also possible to start from current indirect calibrations of SHARAD to estimate the absolute power of detected bursts.
It must be noted that the catalogue of type III bursts we present is limited to correlated observations only. There are likely more bursts within the SHARAD archive that could be found through direct inspection. For example, a survey of the MARSIS dataset is planned amongst future work in order to produce a complete catalogue of MARSIS SRB observations (Sánchez-Cano et al., in prep.), which will be compared with SHARAD to get a fuller frequency spectrum of the co-observed bursts. The main limitation of using radar sounder data of the Sun is the fact that sounders typically operate for no more than a few minutes or tens of minutes a day, and they cannot function as a round-the-clock survey instrument.
The results presented here can also be used for future planetary missions. In this decade, two missions carrying radar sounder instruments are being launched towards the Jupiter system: the Radar for Icy Moons Exploration (RIME) onboard the ESA Jupiter Icy Moons Explorer (JUICE) probe and the Radar for Europa Assessment and Sounding Ocean to Near-Surface (REASON) onboard the NASA Europa Clipper mission (Blankenship et al. 2023; Bruzzone et al. 2011). Additionally, one mission is being sent towards Venus: the Subsurface Radar Sounder (SRS) onboard the ESA Envision mission (Bruzzone et al. 2020). Maturing the scientific exploitation of solar bursts with SHARAD opens a path to also utilising these new instruments as solar observatories.
Acknowledgments
Christopher Gerekos dedicates this manuscript to the memory of his beloved mother Patricia Brabants (1965–2023). This work was supported by the G. Unger Vetlesen Foundation and by JPL’s Innovative Spontaneous Concepts in Research and Technology Development program. Part of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. I.C.J. is grateful for support by the Academy of Finland (SHOCKSEE, grant No. 346902). B.S.-C. acknowledges support through STFC Ernest Rutherford Fellowship ST/V004115/1. M.L. acknowledges support through STFC grant ST/W00089X/1. J.M. acknowledges funding by the BRAIN-be project SWiM (Solar Wind Modeling with EUHFORIA for the new heliospheric missions). The authors wish to express their gratitude to Bruce Campbell, Dirk Plettemeier, Marco Mastrogiuseppe, Vratislav Krupar, Marc Pulupa, Vladimir Krasnoselskikh, and Milan Maksimovic for the excellent discussions.
References
- Arzner, K., & Magun, A. 1999, A&A, 351, 1165 [NASA ADS] [Google Scholar]
- Aubier, M., & Boischot, A. 1972, A&A, 19, 343 [NASA ADS] [Google Scholar]
- Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
- Barrow, C., & Achong, A. 1975, Sol. Phys., 45, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardini, F., Croci, R., Fois, F., et al. 2004, Alenia Spazio S.p.A., Doc. No. MAN-SHR-0007-ALS, 16 [Google Scholar]
- Blankenship, D. D., Moussessian, A., Chapin, E., et al. 2023, AGU Fall Meeting Abstracts, P41G-3264 [Google Scholar]
- Bonnin, X., Hoang, S., & Maksimovic, M. 2008, A&A, 489, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bougeret, J.-L., Kaiser, M. L., Kellogg, P. J., et al. 1995, Space Sci. Rev., 71, 231 [CrossRef] [Google Scholar]
- Bougeret, J. L., Goetz, K., Kaiser, M. L., et al. 2008, Space Sci. Rev., 136, 487 [CrossRef] [Google Scholar]
- Bruzzone, L., Alberti, G., Catallo, C., et al. 2011, Proc. IEEE, 99, 837 [CrossRef] [Google Scholar]
- Bruzzone, L., Bovolo, F., Thakur, S., et al. 2020, in IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium (IEEE), 5960 [CrossRef] [Google Scholar]
- Campbell, B. A., Putzig, N. E., Carter, L. M., et al. 2013a, J. Geophys. Res.: Planets, 118, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, B. A., Putzig, N. E., Foss, F. J., & Phillips, R. J. 2013b, IEEE Geosci. Remote Sens. Lett., 11, 632 [Google Scholar]
- Campbell, B. A., Morgan, G. A., Bernardini, F., et al. 2021, Icarus, 360, 114358 [NASA ADS] [CrossRef] [Google Scholar]
- Castaldo, L., Alberti, G., Cirillo, G., & Orosei, R. 2013, in 2013 Signal Processing Symposium (SPS) (IEEE), 1 [Google Scholar]
- Croci, R., Fois, F., Flamini, E., Mecozzi, R., & Seu, R. 2007, in 2007 4th International Workshop on, Advanced Ground Penetrating Radar, (IEEE), 241 [CrossRef] [Google Scholar]
- Croci, R., Seu, R., Flamini, E., & Russo, E. 2011, Proc. IEEE, 99, 794 [CrossRef] [Google Scholar]
- Cumming, I. G., & Wong, F. H. 2005, Digital Processing of Synthetic Aperture Radar Data (Boston, London: Artech House) [Google Scholar]
- De Groot, T. 1966, Rech. Astron. Obs. Utrecht, 18, 1 [Google Scholar]
- Dresing, N., Rodríguez-García, L., Jebaraj, I. C., et al. 2023, A&A, 674, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dulk, G. A. 2000, Geophys. Monogr. Ser., 119, 115 [NASA ADS] [Google Scholar]
- Dulk, G. A., Steinberg, J. L., & Hoang, S. 1984, A&A, 141, 30 [NASA ADS] [Google Scholar]
- Evans, L. G., Fainberg, J., & Stone, R. 1973, Sol. Phys., 31, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Fokker, A. D. 1965, Bull. Astron. Inst. Netherlands, 18, 111 [NASA ADS] [Google Scholar]
- Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
- Gerekos, C. 2020, PhD Thesis, Università degli Studi di Trento, Italy [Google Scholar]
- Gerekos, C. 2023a, Zenodo, http://dx.doi.org/10.5281/zenodo.10386038 [Google Scholar]
- Gerekos, C. 2023b, Zenodo, http://dx.doi.org/10.5281/zenodo.8039090 [Google Scholar]
- Grima, C., Kofman, W., Mouginot, J., et al. 2009, Geophys. Res. Lett., 36 [Google Scholar]
- Gurnett, D., Morgan, D., Granroth, L., et al. 2010, Geophys. Res. Lett., 37 [Google Scholar]
- Holt, J. W., Safaeinili, A., Plaut, J. J., et al. 2008, Science, 322, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Jebaraj, I. C., Kouloumvakos, A., Dresing, N., et al. 2023a, A&A, 675, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jebaraj, I. C., Krasnoselskikh, V., Pulupa, M., Magdalenic, J., & Bale, S. D. 2023b, ApJ, 955, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Jebaraj, I. C., Magdalenic, J., Krasnoselskikh, V., Krupar, V., & Poedts, S. 2023c, A&A, 670, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P., Yu, S., Kuznetsov, A. A., et al. 2017, Nat. Commun., 8, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Chen, X., Chrysaphi, N., et al. 2019, ApJ, 884, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnoselskikh, V., Voshchepynets, A., & Maksimovic, M. 2019, ApJ, 879, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Krupar, V., Nguyen, Q. N., Bonnin, X., Cecconi, B., & Maksimovic, M. 2022, STEREO/Waves/LFR-HFR L3 DF Data Collection (Version 1.0) (PADC/MASER) [Google Scholar]
- Kundu, M. R. 1965, Solar Radio Astronomy (New York: Interscience Publication) [Google Scholar]
- Lecacheux, A., Steinberg, J.-L., Hoang, S., & Dulk, G. 1989, A&A, 217, 237 [Google Scholar]
- Maksimovic, M., Bale, S. D., Chust, T., et al. 2020, A&A, 642, A12 [EDP Sciences] [Google Scholar]
- Melnik, V. N., Konovalenko, A. A., Rucker, H. O., et al. 2011, Sol. Phys., 269, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1980, Space Sci. Rev., 26, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D., Marsden, R. G., & St Cyr, O. C., & Gilbert, H. R., 2013, Sol. Phys., 285, 25 [Google Scholar]
- Musset, S., Maksimovic, M., Kontar, E., et al. 2021, A&A, 656, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Picardi, G., Biccari, D., Seu, R., et al. 2004, Planet. Space Sci., 52, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Pulupa, M., Bale, S. D., Bonnell, J. W., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 2836 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A., & Kontar, E. P. 2018, A&A, 614, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, H. A. S., & Ratcliffe, H. 2014, Res. Astron. Astrophys., 14, 773 [Google Scholar]
- Romero-Wolf, A., Vance, S., Maiwald, F., et al. 2015, Icarus, 248, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Seu, R., Biccari, D., Orosei, R., et al. 2004, Planet. Space Sci., 52, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Skolnik, M. I. 1980, Introduction to Radar Systems (New York: McGraw Hill Book Co.), 590 [Google Scholar]
- Slavney, S., & Orosei, R. 2007a, Shallow radar experimental data record software interface specification, Planetary Data System (PDS) [Google Scholar]
- Slavney, S., & Orosei, R. 2007b, Shallow radar reduced data record software interface specification, Planetary Data System (PDS) [Google Scholar]
- Suzuki, S., & Dulk, G. A. 1985, in Solar Radiophysics: Studies of Emission from the Sun at Metre Wavelengths, eds. D. J. McLean, & N. R. Labrum (Cambridge University Press), 289 [Google Scholar]
- Tkachenko, A., Krasnoselskikh, V., & Voshchepynets, A. 2021, ApJ, 908, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchepynets, A., & Krasnoselskikh, V. 2015, J. Geophys. Res. (Space Phys.), 120, 139 [NASA ADS] [Google Scholar]
- Voshchepynets, A., Krasnoselskikh, V., Artemyev, A., & Volokitin, A. 2015, ApJ, 807, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Zurek, R. W., & Smrekar, S. E. 2007, J. Geophys. Res.: Planets, 112 [CrossRef] [Google Scholar]
Appendix A: SHARAD duty cycle analysis
To provide additional context on the discussion of the general properties of the dataset and to highlight the targeted nature of the instrument (as opposed to a survey instrument such as WAVES), we present a brief analysis of the activity duty cycle of SHARAD over the past years. Starting from the SHARAD EDR label files, we extracted the radargram start time and stop time for each radargram in the entire SHARAD dataset for the period of study (6 December 2006 to 31 December 2021) in order to compute the duration of that radargram. Taking the cumulative sum of all these durations for each year, we obtained the durations shown in Table A.1. In an average year, SHARAD is on for about a million seconds, corresponding to a duty cycle of about 3%. Aside from the solar cycle, part of the variability of the number of candidates counted in Figure 2a can be traced to the fraction of the time SHARAD was operating (for instance, the dip in candidates in 2013).
SHARAD operating time throughout the surveyed years.
Appendix B: Quicklook of SHARAD burst products
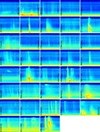 |
Fig. B.1. Dynamic spectra of all SHARAD-detected solar radio burst products. The y-axis goes from 13.3 to 26.7 MHz for all images. The x-axis bounds are specified in Table 1. The dynamic range of the image can vary from acquisition to acquisition. |
All Tables
All the SHARAD candidates where a burst (type III unless otherwise indicated) was identified within the product.
All Figures
 |
Fig. 1. Comparison of the Reduced Data Record (top) and spectrogram of the Experimental Data Record (bottom) for SHARAD product 2533401. Also depicted are annotations for the main signals present in the spectrogram. This product contains a type III burst (outlined by the dashed black curve); it is affected by various EMI sources, which are the narrow band signals that are persistent in time and manifest themselves as horizontal traces and the strongest of which are highlighted with horizontal arrows; and it contains traces of the reflection of the active chirp, which are wideband signals with short durations in time and manifest themselves as vertical traces, the strongest of which (or groups of which) are highlighted by vertical arrows. The band of flat spectral gain is delimited by the dashed orange lines at 15 and 25 MHz. |
| In the text | |
 |
Fig. 2. Visual summary of the generated dataset. (a) Temporal distribution of the SHARAD burst candidates. In grey is the count of all SHARAD candidates per year, with the burst-containing subsets colour-coded according to the source of the observation. The histogram follows the solar cycle, and the proportion of burst-containing products is stable. (b) Spatial distributions of SHARAD burst candidates. Indicated are the positions of MRO, STEREO A, STEREO B, and Wind for all SHARAD candidates. The lines are drawn between the source of the observation and the corresponding SHARAD candidate for every candidate with a burst. |
| In the text | |
 |
Fig. 3. Illustration of several key quantities in the definition of relevant angles. In this illustration, yaw is about 60°, pitch is about 20°, and roll is close to 90°. |
| In the text | |
 |
Fig. 4. Multivariate logistic regression using the feature vectors generated by the principal component analysis. |
| In the text | |
 |
Fig. 5. Sensitivity of SHARAD to geometrical acquisition parameters. Histograms of the number of burst detections (‘Yes’) and burst no-detections (‘No’) along with the probability p of detection (ratio of ‘Yes’ to ‘Yes’ + ‘No’) for J2000 separation, yaw, pitch, and roll angles, respectively. The bars of the histograms are stacked, meaning the total number of events n in a given angular bin is immediately accessible on the graph. The error bars associated with the probability curve correspond to the standard error of a binary outcome, that is, σ = [p(1 − p)/n]1/2. |
| In the text | |
 |
Fig. 6. In-depth analysis of three representative elements of the SHARAD burst dataset: (a) SHARAD product 2533401, which is also displayed in Fig. 1; (b) SHARAD product 2546401; (c) SHARAD product 6763001. For each case, the plots in the first row represent a map of the Solar System. The second row shows the STEREO-captured original burst, in calibrated units. The third row shows the SHARAD spectrogram. The plots in the fourth row contain time profiles for selected frequencies extracted from the SHARAD spectrogram, along with the 15.0125 MHz line from STEREO for comparison. In the case of 2533401, the dashed black lines on the SHARAD spectrogram show the bounds of the corresponding time profiles. The calibrated STEREO data was sourced from Krupar et al. (2022). |
| In the text | |
 |
Fig. 7. Example of a time-profile extraction and fit on SHARAD product 2545801 using the EMI-free frequency band of 15.5056 MHz. The dashed vertical black lines on the dynamic spectrum represent the portion of the product that was fed into the fitting subroutine. The coefficients displayed next to the fitted curve correspond directly to those of Eq. (11). The rise and decay time tr and td were derived as the first and second HWHM. The maximum was computed as the difference between the maximum of the curve and the floor parameter b. |
| In the text | |
 |
Fig. 8. Analysis of rise time and decay time of the suitable type III bursts recorded by SHARAD after fitting an exponentially modified Gaussian function onto every frequency line that is unhampered by EMI. The colour-coding of the dots represents profiles from an individual burst, with some colours being reused. The black line is the best power-law fit, the equations for which are given in formulae (13) through (16). |
| In the text | |
 |
Fig. 9. Comparison of the type III burst durations (FWHM) derived from SHARAD data (Eq. (15) and Fig. 8) with that of Kontar et al. (2019), Reid & Kontar (2018), Melnik et al. (2011), Barrow & Achong (1975). The shaded area around the law obtained in this study corresponds to the 95% confidence interval for the parameters of the fitted function (functional prediction interval). |
| In the text | |
 |
Fig. B.1. Dynamic spectra of all SHARAD-detected solar radio burst products. The y-axis goes from 13.3 to 26.7 MHz for all images. The x-axis bounds are specified in Table 1. The dynamic range of the image can vary from acquisition to acquisition. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



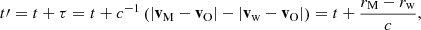
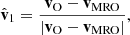
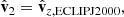
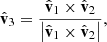
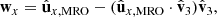
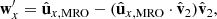
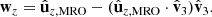
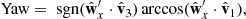
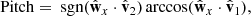
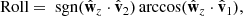
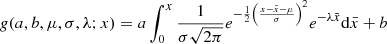
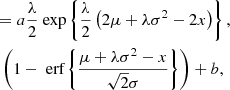
![$$ \begin{aligned}&t_r = \left(38\pm 16\right) \left( \frac{f \text{[MHz]}}{1 \text{[MHz]}} \right)^{-0.85 \pm 0.14}, \end{aligned} $$](/articles/aa/full_html/2024/03/aa47900-23/aa47900-23-eq35.gif)
![$$ \begin{aligned}&t_d = \left(58\pm 24\right) \left( \frac{f \text{[MHz]}}{1 \text{[MHz]}} \right)^{-0.83 \pm 0.14}, \end{aligned} $$](/articles/aa/full_html/2024/03/aa47900-23/aa47900-23-eq36.gif)
![$$ \begin{aligned}&FWHM = \left(97\pm 40\right) \left( \frac{f \text{[MHz]}}{1 \text{[MHz]}} \right)^{-0.84 \pm 0.14},\end{aligned} $$](/articles/aa/full_html/2024/03/aa47900-23/aa47900-23-eq37.gif)
![$$ \begin{aligned}&t_d = \left(1.654\pm 0.025\right) \left( \frac{t_r \text{[s]}}{1 \text{[s]}} \right)^{0.985 \pm 0.007}. \end{aligned} $$](/articles/aa/full_html/2024/03/aa47900-23/aa47900-23-eq38.gif)