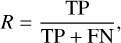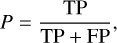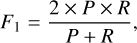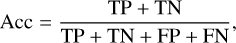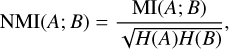EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A104 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A104
Number of page(s) 16
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/202347341
Published online 13 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

It is accepted that stars are formed in dense molecular cores and clumps (e.g. Krumholz & McKee 2005; Zinnecker & Yorke 2007; Krumholz et al. 2009; Hacar et al. 2013; Könyves et al. 2015). The condensation of these structures from the ambient cloud represents a critical step in the star formation process. Understanding the properties of dense cores and clumps is of utmost importance in astrophysics, particularly concerning the mechanism for determining the initial stellar mass function (IMF; e.g. Motte et al. 1998; Alves et al. 2007; Könyves et al. 2010; Bresnahan et al. 2018; Arzoumanian et al. 2019). Although great progress has been made in determining the form of the IMF (e.g. Chabrier 2003; Nutter & Ward-Thompson 2007; Olmi et al. 2009; Könyves et al. 2015; Benedettini et al. 2018), a detailed explanation of its form and possible environment depends on an understanding of the nature and evolution of the molecular clumps (Marsh et al. 2016). Meanwhile, the mass distribution within clumps provides important information not only on the mechanisms that influence clump formation, evolution, and destruction (e.g. Rosolowsky 2005; Colombo et al. 2014; Faesi et al. 2016), but also on the factors regulating star formation (Liu et al. 2022). Thus, the clumps of molecular interstellar medium (ISM) surveys play an important role in our understanding of the location and mode of star formation in the Milky Way. Therefore, numerous CO line emission surveys have been launched, such as the Galactic Ring Survey (GRS, Jackson et al. 2006), the Mopra Southern Galactic Plane CO survey (Burton et al. 2013), the Milky Way Image Scroll Painting (MWISP, Jiang & Li 2013), the CO Heterodyne Inner Milky Way Plane Survey (CHIMPS, Rigby et al. 2016), and the Structure, Excitation, and the FOREST Unbiased Galactic plane Imaging survey with the Nobeyama 45m telescope (FUGIN, Umemoto et al. 2017). With the increasing size of the survey data, some algorithms for the automatic detection of molecular clumps have emerged.

Some of these detection algorithms are based on unsupervised machine learning (e.g. Williams et al. 1994; Rosolowsky et al. 2008; Berry 2015; Luo et al. 2022; Jiang et al. 2022, 2023). The ClumpFind algorithm described in Williams et al. (1994) has been widely used for the identification of cores and clumps (e.g. Kirk et al. 2006; Rathborne et al. 2009; Ikeda & Kitamura 2011; Tanaka et al. 2013; Gómez et al. 2014; Shimajiri et al. 2015). The algorithm works well with reasonable parameters to identify cores or clumps. Pineda et al. (2009) and Ikeda & Kitamura (2009) both investigated the effect of threshold levels on the core mass function (CMF). Ikeda & Kitamura (2009) showed that in Orion A, core properties and CMF exhibited a weak dependence on thresholds within the 2-5σ range, which is consistent with the findings of Pineda et al. (2009). The Dendrogram algorithm described by Rosolowsky et al. (2008) is well-suited to representing the hierarchical structure of isosurfaces in molecular line data cubes, illustrating variations in topology as contour levels change (Rani et al. 2023). This latter has been widely used in conjunction with continuum, atomic hydrogen (HI), and molecular line data (Takekoshi et al. 2019; Nakanishi et al. 2020; Zhang et al. 2021). Cheng et al. (2018) used the Dendrogram algorithm to identify dense cores and clumps and found that the spectral index of the core mass function is consistent with the index of the Salpeter IMF (α ≃ 1.35, Salpeter 1955). FellWalker uses ascending pathways to delineate clumps, a method that has been employed in various SCUBA-2 surveys (e.g. Rumble et al. 2015; Eden et al. 2017, 2019; Johnstone et al. 2017; Juvela et al. 2018; Mannfors et al. 2021). FellWalker has also been applied by Zhang et al. (2018) to Herschel column density maps. Li et al. (2020) found that FellWalker performed well in extracting the total flux of the clumps in a large sample of simulated clump experiments.

Luo et al. (2022) adopted the local density clustering method to identify clumps; they consider that the clumps are local dense regions embedded within molecular gas of lower average bulk density (Blitz & Stark 1986; Lada 1992; Bergin & Tafalla 2007). The central idea of this approach comes from Alex Rodriguez (2014), who recognise the cluster centres as local density maxima that are far away from any points of higher density. This idea forms the basis of a clustering procedure in which the number of clusters arises intuitively through a ‘decision graph’. Additionally, a multi-Gaussian model is used to simultaneously fit overlapping molecular clumps, allowing the extraction of clump parameters. This algorithm has been validated through simulations and synthetic data, demonstrating its ability to accurately describe the morphology and flux of molecular clumps (Luo et al. 2022). Jiang et al. (2022) introduced a molecular-clump-detection method based on morphology, gradient, and a merging rule, demonstrating good performance for crowded simulated clumps at different signal-to-noise ratios. Furthermore, Jiang et al. (2023) introduced a Gaussian facet model for fitting local surfaces, and employed the extremum determination theorem of multivariate functions to determine clump centres.

All these algorithms allow iterative adjustment of parameters to achieve the desired detection requirements. However, adequate prior knowledge is a prerequisite to choosing suitable algorithm parameters, and this knowledge of the clumps is finite in unknown regions. An alternative approach to determining the final parameters of the algorithm is to analyse the clumps detected by the algorithm with initial parameters. Researchers can gain insights into algorithm performance by examining and comparing the results with ground truth, which can be simulated or previously validated data. In practice, optimising algorithm parameters to enhance detection reliability often results in weak structures going undetected. Conversely, striving for comprehensive detection may introduce false positives, for which further manual verification is necessary. Therefore, to achieve reliable and comprehensive detection, the detection algorithm should aim to detect as many instances as possible, followed by manual verification to refine the results. Automated verification as a substitute for manual verification becomes increasingly necessary in the era of large data sets.

Supervised deep learning, such as galaxy-morphology-classification tasks (Zhu et al. 2019; Lukic et al. 2020; Cheng et al. 2020; He et al. 2021; Gupta et al. 2022), has become increasingly popular in astronomy because of its high efficiency and accuracy. Its success has been demonstrated repeatedly in industry, especially for pattern recognition, image description, and anomaly detection. However, this method requires training with a large number of labelled samples, requiring significant effort in data cleansing and manual labelling. The best-trained model reflects the properties of the feature space covered by the training data set. This may lead to supervised deep learning consequently giving limited results if the training data set from the real Universe is considerably biased. This problem impacts the universality of supervised deep learning. By contrast, unsuper-vised learning (Han et al. 2022) can avoid these disadvantages as it can use enough unlabelled data to train itself; however the accuracy of unsupervised learning is ~10% less than that of supervised learning (Cheng et al. 2020, 2021).

In many practical applications, users usually have labelled samples of small sizes and train them with semi-supervised deep learning to improve accuracy. Joint clustering and deep extracted feature learning methods as types of semi-supervised deep learning (Zhan et al. 2020) have shown remarkable performance. Here, the algorithm learns transferable image or video representations without large amounts of manual annotation and requires little domain knowledge while achieving encouraging performances. In this study, we propose a semi-supervised deep learning method for molecular-clump verification named SS-3D-Clump, which utilises deep features extracted from data, and incorporates Constrained-KMeans (Basu et al. 2002) - one of the classical semi-supervised clustering algorithms - to verify the candidate clumps.

Our method first employs ClumpFind (Williams et al. 1994) and Dendrogram (Rosolowsky et al. 2008) to obtain clump candidates, but other clump-extraction algorithms could be used. Then, the deep features of the clump candidate are extracted by the feature-extraction part of SS-3D-Clump. Using the deep features as a foundation, the Constrained-KMeans algorithm efficiently generates pseudo-labels for candidates using small, manually verified, labelled samples as seeds. The SS-3D-Clump classifier also assigns predict-labels to the candidates based on their deep features. The difference between these two labels can then be used to optimise the parameters of the SS-3D-Clump model. The SS-3D-Clump iteratively groups the deep features with a standard clustering algorithm, namely Constrained-KMeans, and uses the subsequent assignments as supervision to update the network weights. Finally, we integrated the SS-3D-Clump model with existing molecular-clump-detection algorithms to form a framework for the automated detection and verification of molecular clumps. The code in this study is publicly available online1.

Section 2 introduces the molecular clump data, which are used to validate the generalisation of the SS-3D-Clump model, as well as the detection algorithm for extracting molecular clump candidates and the basic information of the clump dataset. Section 3 describes the main components and implementation details of SS-3D-Clump. Section 4 presents our experiments and results. Sections 5 and 6 contain a discussion and our conclusions, respectively.

thumbnail Fig. 1

Face-on view of an imaginary Milky Way (credit: R. Hurt, NASA/JPL-Caltech/SSC). The Galactic centre (red asterisk) is at (0, 0) and the Sun (green filled circle) is at (0, 8.5).

2 Experiment data

2.1 CO data

The Milky Way Imaging Scroll Painting (MWISP2) project (Su et al. 2019) is a completed northern Galactic plane CO survey using the 13.7 millimetre-wavelength telescope at Delingha, China (hereafter the DLH telescope). The MWISP project is led by the Purple Mountain Observatory with full support from the staff members at Delingha. The survey simultaneously observed the 12CO, 13CO, and C18O (J = 1−0) lines for regions of l = 10° to l = 230° and −5.25° ≤ b ≤ 5.25° over 10 yr. We select three sectors in the first, second, and third Galactic quadrants from the MWISP survey area, as shown in Fig. 1. The three sectors, highlighted in red, orange, and green, represent regions of different molecular gas distributions in the first, second, and third quadrants of the Galactic plane, respectively.

The sector in the first quadrant (hereafter Q1S) spans Galactic longitudes of 10°–20° and Galactic latitudes of −5°.25°−5°.25, covering an area of 100 deg2. The CO data in Q1S are the collection of molecular clouds along sight lines passing through several spiral arms, from near to far. Q1S is chosen as the high-density region (HDR). The sector in the second quadrant (hereafter Q2S) spans Galactic longitudes of 100°–110° and Galactic latitudes of −5°.25–5°.25, covering an area of 100 deg2. Q2S passes through fewer spiral arms than Q1S, and is chosen as the moderate-density region (MDR). The sector in the third quadrant (hereafter Q3S) spans Galactic longitudes of 180°−195° and Galactic latitudes of −5°.25–5°.25, covering an area of 150 deg2. Q3S is chosen as the low-density region (LDR).

Table 1

Parameters of the ClumpFind algorithm.

2.2 Clump extraction

Star-forming regions are messy and chaotic environments, with structures on many scales (Wurster & Rowan 2023). The entire region is typically referred to as a cloud; dense regions embedded within the cloud are clumps; and the very dense regions in the clumps are cores (Alves et al. 2007). There is general agreement in the literature over these three terms, although there is ambiguity amongst the specific definitions and divisions between the levels. For example, Rathborne et al. (2009) identified molecular clouds and clumps using the ClumpFind algorithm, using 13CO (J = 1−0) emission line data observed by the Galactic Ring Survey (GRS, Jackson et al. 2006). Takekoshi et al. (2019) analysed the statistical properties of C18O (J = 1−0) clumps in the Cygnus X cluster-forming region using data from the Nobeyama 45 m radio telescope, with the clumps identified using the Dendrogram algorithm (Rosolowsky et al. 2008). Liu et al. (2022) refer to centrally concentrated structures as clumps and treat Dendrogram-defined leaves accordingly. In this study, we apply ClumpFind and Dendrogram algorithms to the MWISP13 CO (J = 1−0) data to identify molecular clumps in the three sectors Q1S, Q2S, and Q3S.

The ClumpFind algorithm was developed by Williams et al. (1994) to detect emission regions in astronomical data; it can be implemented within the CUPID package (Berry et al. 2007)3, which is part of the Starlink project (Currie et al. 2014; Berry et al. 2022). ClumpFind works by contouring the data and following them down to lower intensities. It is capable of detecting not only 2D molecular line data but also 3D data in the positionposition-velocity (PPV) space. The ClumpFind algorithm has been widely used in various applications (Kainulainen et al. 2009), and is efficient at identifying peaks, especially in crowded areas. However, it tends to overestimate sizes and there can be a significant fraction of spurious detections caused by noise spikes (Congiu et al. 2023). This prompts the need to post-process the results of ClumpFind using a dedicated automated verification algorithm (Sect. 3). Table 1 presents the main parameters of ClumpFind used for clump detection, while the remaining parameters were set to their default values4.

The Dendrogram (Rosolowsky et al. 2008) implemented in astrodendro5 is an abstraction of the changing topology of the isosurfaces as a function of contour level. It uses a tree diagram to describe hierarchical structures over a range of scales in a 2D or 3D datacube (Zhang et al. 2021). There are two types of structures returned in the results: leaves, which have no substructure, and branches, which can split into multiple branches or leaves. There are two main parameters in the algorithm: Tmin and ΔT. Here, Tmin is the minimum value to be considered in the data set. In the fiducial case, we adopt Tmin = 3σ. ΔT describes how significant a leaf has to be in order to be considered an independent entity. We adopt a fiducial value of ΔT = 2σ, which means a clump must have a peak flux reaching 5σ above the noise.

thumbnail Fig. 2

ClumpFind and Dendrogram applied to the same data. The green circles represent the centroids of clumps detected by ClumpFind, while the blue plus symbols represent the results of Dendrogram.

2.3 Manual verification and data set

To mitigate the effects of false positives, Rigby et al. (2019) visually inspected each CHIMPS clump by three independent reviewers and assigned a reliability flag. Rojas et al. (2022) visually inspected and classified the lens candidates into two catalogues using high-resolution imaging and spectroscopy. The dense molecular cores and clumps are defined as compact (~0.1 and 1 pc, respectively) and dense (≳104–105 H2 cm−3) structures (e.g. Williams et al. 2000; Zhang et al. 2009; Ohashi et al. 2016; Motte et al. 2018).

First, by cross-matching the identification results of the two algorithms described in Sect. 2.2, any ‘extremely’ high-confidence clumps can be obtained. As shown in Fig. 2, drawn using the Cube Analysis and Rendering Tool for Astronomy (CARTA; Comrie et al. 2021), the green circles and blue plus symbols represent the centroids of clumps detected by ClumpFind and Dendrogram, respectively. Meanwhile, for 13CO clumps, if a corresponding entity is found in C18O, this indicates a high-confidence 13CO clump, as shown in Fig. 3. The upper and lower subplots on the left of Fig. 3 represent the velocity channel map of 13CO clumps at −5.6 km s−1 and the integrated map within the velocity range of −7.3 to −4.5 km s−1, respectively. The two subplots on the right of Fig. 3 show the corresponding results for C18O.

Then, those clump candidates that were not identified by both algorithms simultaneously and for which no corresponding entity is found in C18O are referred to here as low-confidence clumps, and manual verification is conducted for labelling. In order to achieve a more consistent verification among users, we all agreed to follow the guidelines for molecular clumps solely from an observational perspective, such as the intensity and spectral line information of clumps. First, the density in clump regions is significantly higher than the average density within the molecular cloud. Second, clumps are typically localised regions within the molecular cloud rather than the entire cloud, and exhibit sufficient contrast with the surrounding gas to be recognised as clumps. Third, the spectral profiles of clumps appear Gaussian-like along the velocity direction.

To enhance the efficiency of verifying clump candidates, we created a verification assistant tool6 that can display integrated maps and spectral information of the clump candidates, helping users record their verification results. The various steps carried out to perform the visual manual verification can be summarised as follows: (a) Three individuals verify the low-confidence clump candidates and decide whether they are molecular clumps or not. The label (Yes or No) of the molecular clump candidates is finalised when the verification results of the three individuals are consistent. (b) Clump candidates with inconsistencies among the three users are referred to as ambiguity clumps. Hogg & Lang (2008) argue that catalogue entities should not be fixed values but likelihoods, which were used by Scaringi et al. (2009) to address issues related to subjectivity and transparency, especially when dealing with ‘ill-defined’ astronomical objects such as broad-absorption-line quasars. Therefore, these candidates were verified by a group of five members and assigned a confidence value indicating their membership in molecular clumps.

Following steps (a) and (b) above, we can obtain labelled and ambiguity clumps, forming the test dataset and ambiguity dataset. In addition, all positive samples in the seed are the high-confidence clumps mentioned earlier. The remaining unverified samples are included in the training dataset. Figure 4 shows examples of datasets verified manually. For each13 CO clump, ClumpFind returns a mask in PPV space. Each 13CO clump sample is identified by a unique index (e.g. 1, 2). We use the mask to extract its data portion and place it inside a cube with the size set to 30 px × 30 px × 30 px, which matches the input size of the model described in Sect. 3.2. In the data cube, the intensity values of the regions not marked by the mask for the molecular clumps are set to 0. Those clumps that exceed the data cube size retain only their main parts, making up 4.79% of the dataset. Finally, we extracted the background of the molecular clump data and filled it into the region with a mask value of 0, resulting in the final clump sample data. Detailed information about the datasets of three sectors are listed in Table 2.

thumbnail Fig. 3

Examples of 13CO clumps having corresponding entities in C18O. The upper and lower subplots on the left illustrate the velocity channel map of 13CO clumps at −5.6 km s−1 and the integrated map spanning the velocity range of −7.3 to −4.5 km s−1, respectively. The two subplots on the right depict the corresponding results for C18O.
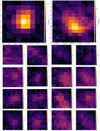thumbnail Fig. 4

Integrated intensity maps of clumps from the dataset. The top row shows two samples of positive clumps, while the subsequent four rows showcase 16 samples of ambiguous datasets.

3 Method introduction

Clustering-based unsupervised representation learning has recently received significant attention, with various methods now proposed for jointly optimising feature learning and image clustering. Notably, these methods have demonstrated outstanding potential in learning unsupervised features on small datasets. To scale up to large datasets like ImageNet, Caron et al. (2018) proposed DeepCluster, which iteratively clusters features extracted from data to gain the cluster assignments and updates the con-volutional neural network (CNN) with subsequently assigned pseudo-labels for each epoch. Although deep clustering methods can learn effective representations from large-scale unlabelled data, the alternating updates of feature clustering and CNN parameters can cause instability during training (Zhan et al. 2020). Inspired by the seed-constrained KMeans algorithm, we introduce it into our unsupervised representation learning step to address the instability issue in model training.

In this paper, we propose a semi-supervised deep learning method named SS-3D-Clump, which is based on the Constrained-KMeans algorithm for molecular clump verification, and the overall framework of SS-3D-Clump is shown in Fig. 5. The SS-3D-Clump algorithm employs an iterative process of grouping the deep features using the Constrained-KMeans algorithm. The assignments generated during this process are then used as supervision to update the network weights.

Table 2

Number of molecular clumps in three regions and the counts in the training and test datasets.

3.1 Constrained-KMeans

Given a dataset, X, KMeans clustering of the dataset generates a K-partitioning 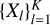{ Xl }l=1K$\left\{ {{X_l}} \right\}_{l = 1}^K$ of X so that the KMeans objective is locally minimised. Let S ⊆ X, which is referred to as the seed set here, be the subset of data points on which supervision is provided as follows: for each xi ∈ S, the user provides the cluster Xl of the partition to which it belongs. We assume that corresponding to each partition Xl of X, there is typically at least one seed point xi ∈ S. We get a disjoint K-partitioning 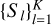{ Sl }l=1K$\left\{ {{S_l}} \right\}_{l = 1}^K$ of the seed set S, so that all xi ∈ Sl belong to Xl according to the supervision. This partitioning of the seed set S forms the seed clustering and is used to guide the KMeans algorithm.

In Constrained-KMeans (Basu et al. 2002), seed clustering is used to initialise the KMeans algorithm. Instead of initialising KMeans from K random means, the mean of the l-th cluster is initialised with the mean of the lth partition S of the seed set. This approach allows a more targeted initialisation of the KMeans algorithm and can lead to improved clustering results; it has been applied in various domains (Hasanaj et al. 2021, 2022). In the subsequent steps, the cluster memberships of the data points in the seed set are not recomputed in the assign_cluster steps of the algorithm, the cluster labels of the seed data are kept unchanged, and only the labels of the non-seed data are re-estimated. The details of the algorithm are provided in Fig. 6. We use the publicly available code euxhenh7.

To demonstrate the working principle of the Constrained-KMeans algorithm, we simulated five clusters with a two-dimensional Gaussian distribution as labelled seed data (Fig. 7) and then randomly generated points within the coverage of these five clusters. The random points were then clustered using the Constrained-KMeans algorithm. The left panel of Fig. 7 shows five clusters coloured cyan, blue, green, red, and orange, respectively. Yellow marks the unclustering points. Using the points from the five clusters as the initial seed, the unlabelled points are suitable for assigning proper labels in the right panel of Fig. 7.

thumbnail Fig. 5

Structure of the SS-3D-Clump. The proposed method involves iteratively clustering deep features and using cluster assignments as pseudo-labels to learn the parameters of the 3D CNN and classifier networks.
thumbnail Fig. 6

Constrained-KMeans algorithm.
thumbnail Fig. 7

Illustration of the clustering principle of the Constrained-KMeans algorithm using two-dimensional scatter plot clustering.

3.2 Structure of 3D CNN and classifer networks

We conducted experiments on the 13CO J = 1−0 data of the giant molecular complex M16 (Zhan et al. 2016), covering a 5 deg2 area within the HDR. We manually check the 13CO clumps detected by ClumpFind, and assigned labels to a portion of the clumps in M16. The 13CO clumps in M16 were selected to determine the feature dimensions for Constrained-Kmeans. The results are shown in Table 3, where Acc_KMeans represents the accuracy of Constrained-KMeans clustering based on the features extracted by the 3D CNN after the model’s stable training compared with the labels in the dataset. We reiterate that ‘precision’, F1, and ‘accuracy’ are defined as in Sect. 4.1.

Table 3 shows that most indicators are high when the feature dimension is set to 256. The experimental results show that the feature dimension significantly affects the clustering performance, with the best results achieved when the feature dimension is set to 256. The structure of the 3D CNN and classifier is shown in Fig. 8; it consists of five 3D convolutional layers with 16, 32, 32, 32, and 32 filters, and four fully connected networks (FCNs). The ReLU activation function is applied between each layer, and dropout is used during the training process.

3.3 Implementation details in SS-3D-Clump

In summary, SS-3D-Clump first uses 3D CNN to extract deep features. The extracted features are then clustered using the constrained-KMeans algorithm to obtain pseudo-labels, and the weights of the 3D CNN and classifier networks are optimised based on the loss generated between the pseudo-labels and the labels predicted by the classifier. As mentioned by Zhan et al. (2020), the alternating updates of feature clustering and CNN parameters can cause instability during training.

In the initial stages of the model, the extracted features may exhibit unclear clustering patterns. As a result, the pseudo-labels generated from the clustering algorithm may contain numerous errors, leading to a lack of convergence during the early stages of training. In unsupervised algorithms, dealing with imbalanced class samples is an inevitable challenge. When encountering extreme class imbalance, the model faces difficulties in effectively correcting errors in the prediction of the minority class. This is due to the limited contribution of loss from the small number of samples belonging to that class.

To address the first issue, namely the lack of convergence in SS-3D-Clump in the early stages of training, we introduced the Constrained-KMeans algorithm discussed in Sect. 3.1. This algorithm provides constraints on and guidance in clustering deep features by using a small set of labelled seed samples. These seed samples remain unchanged throughout the model training iterations. Additionally, from the clustering results of the Constrained-KMeans algorithm, we select a subset of samples based on the distance between the sample and the cluster centre within each class. For example, we may choose the top 40% of samples sorted by distance in ascending order. These selected samples are then used to construct the pseudo-labels and update the model’s weight coefficients based on the discrepancy between the pseudo-labels and the predicted labels.

To address the second issue of extreme class imbalance occurring in SS-3D-Clump, we apply class-wise weighting during backpropagation. This weighting is based on the number of samples from each class participating in the model training. By doing so, we ensure an equal contribution of the loss generated by samples from each class to the updates of the model. In this study, positive and negative samples contribute equally, with each class contributing 50% to the overall loss.

Table 3

Performance in terms of recall, precision, and F1 score for different parameters of the 3D CNN model.

thumbnail Fig. 8

Network structure and detailed parameters of SS-3D-Clump. The SS-3D-Clump receives a 30 px × 30 px × 30 px cube as input and has two neurons in the output layer, representing the two-class verification of molecular clumps. It comprises a 3D CNN and an FCN. The input data in SS-3D-Clump undergo processing steps including ‘Stem’, ‘ResB 1’, and Conv3D. The resulting data are then flattened and passed into the FCN to generate the final output. ‘Stem’ comprises 16 3D Convolution kernels of size 3 and stride 2, and is followed by the ReLU activation function, and 32 MaxPooling layers with a kernel size of 2 and stride of 2. ‘ResB 1’ consists of alternating 3D CNN and Batch Normalization layers, with the ReLU activation function applied in each layer; it incorporates residual connections inspired by the ResNet architecture. The FCN consists of five layers with the following numbers of neurons: 4096, 512, 256, 16, and 2.

4 Experiment

4.1 Evaluation indicators

After completing the training of the SS-3D-Clump, we used the test datasets mentioned in Sect. 2.3 to measure the performance of the model. To quantify the performance of the model, we calculated the precision (P), recall (R), F1 score (F1), and accuracy (Acc) of the SS-3D-Clump model in the test datasets. The calculation formulas of R, P, F1, and Acc are as follows:

R=TPTP+FN,$R = {{{\rm{TP}}} \over {{\rm{TP}} + {\rm{FN}}}},$(1) P=TPTP+FP,$P = {{{\rm{TP}}} \over {{\rm{TP}} + {\rm{FP}}}},$(2) F1=2×P×RP+R,${F_1} = {{2 \times P \times R} \over {P + R}},$(3) Acc=TP+TNTP+TN+FP+FN,${\rm{Acc}} = {{{\rm{TP}} + {\rm{TN}}} \over {{\rm{TP}} + {\rm{TN}} + {\rm{FP}} + {\rm{FN}}}},$(4)

where TP (true positive) is the number of true sources that were indeed predicted to be true, FP (false positive) is the number of sources predicted to be true but in reality are false, TN (true negative) is the number of false sources that were indeed predicted to be false, and FN (false-negative) is the number of true sources that were predicted to be false.

We measure the information shared between two different assignments A and B of the same data as the normalised mutual information (NMI), which is defined as

NMI(A;B)=MI(A;B)H(A)H(B),${\rm{NMI}}\left( {A;B} \right) = {{{\rm{MI}}\left( {A;B} \right)} \over {\sqrt {H\left( A \right)H\left( B \right)} }},$(5)

where MI denotes the mutual information and H the entropy. This measure can be applied to any assignment coming from the clusters or the true labels. If the two assignments A and B are independent, the NMI is equal to 0. If one of them is deterministically predictable from the other, the NMI is equal to 1.

To evaluate the performance of SS-3D-Clump, especially the true-positive and false-positive rates, we employed the receiver operating characteristic (ROC) curve. This curve provides a more comprehensive assessment of the performance of SS-3D-Clump under different threshold settings during the classification process (James et al. 2013; Rojas et al. 2022; Demianenko et al. 2023). Another valuable tool for classifier evaluation is the area under the curve (AUC) of the ROC curve. The larger the AUC, the better the classifier works. An excellent model has an AUC that is close to 1, indicating that it has a high level of separability. An AUC equal to 0.5 means the model cannot classify the data.

thumbnail Fig. 9

Performance of the SS-3D-Clump model during the training process in HDR. Left panel: evolution of clustering capability in SS-3D-Clump across training epochs. Middle panel: evolution of cluster reassignments in each clustering iteration of SS-3D-Clump. Right panel: overall performance of SS-3D-Clump in the test dataset.
thumbnail Fig. 10

Performance of the SS-3D-Clump model during the training process in MDR, with the same content as described in Fig. 9.
thumbnail Fig. 11

Performance of the SS-3D-Clump model during the training process in LDR, with the same content as described in Fig. 9.

4.2 Results

We applied the SS-3D-Clump model to the HDR, MDR, and LDR. Appendix B presents the results of the verification of several molecular clump candidates by the SS-3D-Clump model. These results are consistent with the manual verifications. Figures 9, 10, and 11 illustrate the performance of the algorithm during the training process in the three respective regions.

Table 4 summarises the evaluation metrics for molecular-clump verification in the corresponding test datasets of the trained models in the three regions.

The left panel of Fig. 9 illustrates the evolution of the NMI between the assignments generated by the Constrained-Kmeans algorithm and the labels of the test dataset during training. This measure assesses the model’s ability to predict class-level information. We only use this metric for this analysis and not in any model-selection process. As time progresses, the dependency between the clusters and the labels increases, indicating that our features progressively capture information related to object classes.

Measuring the NMI between the clusters at epoch t−1 and t provides insights into the actual stability of our model. The middle panel of Fig. 9 displays the evolution of this measure during training, showing that the NMI increases over time, meaning that there are fewer reassignments and that the clusters are stabilising. The right panel of Fig. 9 shows the overall performance on the test dataset during model training. After 12 epochs, the F1 has reached a high level (93.7%) and has stabilised.

Figure 10 illustrates the performance of the SS-3D-Clump model during the training process on the MDR. The middle panel indicates that, in this dataset, the rate of label swapping between the model’s previous and current iterations is already low after 25 epochs of training. After 25 epochs, the model’s modifications start to become more gradual but consistently move in a more precise direction. After 25 epochs, modifications of the model begin to stabilise while consistently improving its accuracy. This observation indirectly suggests that the labels generated by the Constrained-KMeans clustering based on the features extracted by the SS-3D-Clump model closely correspond to the actual labels of the molecular clumps; it demonstrates the model’s robust capability to effectively classify categories within the extracted feature space.

Figure 11 depicts the performance of the SS-3D-Clump model on the LDR. From the left to right panels, the model has achieved stable convergence after 20 epochs of training. The middle panel reveals that in the initial epochs of training, following the model’s random initialisation, there were frequent label modifications in the clustering process within the extracted feature space. However, as training progressed, this phenomenon gradually diminished. This indicates that the SS-3D-Clump introduces seed samples to constrain the KMeans algorithm, preventing arbitrary label modifications between adjacent iterations and ensuring the stability of the model during the clustering process.

The results shown in Table 4 and Figs. 9, 10, and 11 indicate that SS-3D-Clump achieved high performance on the test datasets by leveraging the features extracted by 3D CNN and generating pseudo-labels through Constrained-KMeans. This approach effectively transformed unsupervised learning into supervised learning and benefited from the constraints provided by several seed samples.

Table 4

Performance metrics of the SS-3D-Clump model applied to the labelled test datasets in three regions, using molecular clump candidates detected by ClumpFind for semi-supervised deep learning.

thumbnail Fig. 12

Evaluation metrics for SS-3D-Clump performance. The red dot is in the ‘elbow’ of the ROC curve and shows the best balance between completeness and purity.

5 Discussion

5.1 SS-3D-Clump model generalisation

By applying the trained and converged SS-3D-Clump models obtained from the three regions, we can observe the recognition results on the corresponding clump test datasets in Table 5. The table shows that the accuracy of recognition decreases when a model trained on one region is applied to the molecular clump data from the other regions, which is likely because the distribution of clumps may not be entirely consistent across different regions. As a result, we retrained the model on the corresponding region and applied it to the test dataset of that region for evaluation. The results are shown in the ‘Retraining’ column of Table 5. For example, when the SS-3D-Clump model trained in HDR was applied to the test dataset in MDR, the accuracy decreased from 0.929 to 0.718. However, after fine-tuning the model on the MDR dataset, the accuracy improved to 0.984.

Furthermore, we combined the datasets from the selected high-, medium-, and low-density regions to create a comprehensive dataset of molecular clumps. Using this dataset, we trained the existing HDR-trained model to obtain the final SS-3D-Clump model. The performance of this model on the complete test dataset, which includes data from all three density regions, resulted in a recall rate of 0.960, a precision rate of 0.951, an F1 score of 0.955, and an accuracy of 0.940. We provide the ROC curve of SS-3D-Clump in Fig. 12. We achieve an AUC of 0.977, indicating that the model accurately distinguishes between clump and non-clump samples in the test sample. The value (P = 0.88) corresponds to the ‘elbow’ of the ROC curve (Fig. 12), which is, in principle, the ideal compromise between completeness and purity. When applying the model to verify molecular clump candidates in a completely unknown region, we can use the obtained candidates to further train the model based on the final SS-3D-Clump model. Once the model training is completed, verifying those candidates in that region can be accomplished using the trained model.

Appendix C presents the intermediate feature extraction results by the SS-3D-Clump model on the molecular clump. Some of the feature maps indicate that the model can extract crucial features of the molecular clumps, such as their intensity, rotational angles on the l − b plane, and background noise. These extracted features provide valuable information for verifying and characterising molecular clumps. Appendix D displays the feature maps of the model at different training epochs, along with the verification of molecular clumps in the test dataset. These results show that the SS-3D-Clump model enhances its feature-extraction capabilities as the number of training epochs increases. This improvement enables the feature-based classification network to verify molecular clumps.

Finally, we applied the final SS-3D-Clump model to the molecular clump candidates in the respective regions for their verification. The top of Fig. 13 shows the peak distribution of the molecular clumps in the three regions. The peak positions of the clump distributions in LDR and MDR are both at 1.89K, while the peak of the distribution is at 1.68 K in HDR. The bottom of Fig. 13 shows the peak distribution of the clumps excluded by the final SS-3D-Clump. It can be observed that in LQR, the peak value distribution of the false clumps identified by SS-3D-Clump is concentrated around 1 K, while the distribution of peak values for false clumps in the MQR and HQR are clustered in the range of 1.2–1.4 K. The peak values of false clumps in LQR are noticeably lower than those in the other two regions, which may be attributed to the overall weaker peak intensity of clumps in the LQR. The statistical results show that out of 25 673 molecular clump candidates in HDR, the SS-3D-Clump model excluded 6685 false molecular clumps. Out of 13 455 candidates in MDR, 3775 false clumps were eliminated by the model. The model removed a LDR consisting of 7515 candidates and 4244 false clumps. Ultimately, 18 952, 9670, and 3271 clumps were retained in the HDR, MDR, and LDR, respectively.

Figure 14 presents a scatter plot of the confidence scores for ambiguous clumps verified separately through manual and SS-3D-Clump. Manual verification represents the average score from assessments by five users. The horizontal axis of Fig. 14 represents the confidence score of SS-3D-Clump in identifying ambiguous clumps, while the vertical axis represents the scores from manual verification. Figure 14 shows that there is a certain level of correlation between the results of manual and SS-3D-Clump recognition of ambiguous clumps, with a correlation value of 0.59. From the statistical histograms of their recognition results for ambiguous samples, manual recognition shows a concentration of confidence scores around 0.6, while SS-3D-Clump’s recognition results are distributed more evenly from 0.1 to 0.9. Manual recognition tends to be more conservative and cautious when verifying ambiguous samples (confidence scores concentrated around 0.6), while the recognition results of SS-3D-Clump demonstrate its relatively increased capability in verifying ambiguous samples.

Table 5

Performance of the SS-3D-Clump model trained on datasets from three regions when applied to the other regions.

thumbnail Fig. 13

Peak distribution of clumps excluded and retained by SS-3D-Clump. Top: peak distribution of clumps in the three regions. The peak positions of the distributions in LDR and MDR are consistent at 1.89 K, while in HDR, the peak position is at 1.68 K. Bottom: peak distribution of clumps excluded by the final SS-3D-Clump.

5.2 Comparison with FellWalker

The FellWalker algorithm developed by Berry (2015) is a watershed algorithm designed to segment a data array into clusters of emission by tracing the steepest ascent path to identify significant peaks. It starts from pixels above a specified threshold and follows the steepest gradient to reach a peak. The algorithm searches for higher-intensity pixels in the neighbourhood and continues uphill. When a peak surpasses the intensity of all neighbouring pixels, the visited pixels are labelled as belonging to a cluster.

We conducted a comparison between FellWalker and a combination of FellWalker and SS-3D-Clump (Fell+SS-3D-Clump). Firstly, we selected a local region in the first quadrant of the Milky Way: 13° ≤ b ≤ 16°, −1.5° ≤ b ≤ 0.5°, and 0 km s−1 ≤ v ≤ 70 km s−1, as shown in Fig. 15. We applied FellWalker to detect clump candidates in this region. For the identified candidates from FellWalker, we used the final SS-3D-Clump model mentioned in Sect. 5.1 for training. After completing the training, we verified the candidates to obtain the results of Fell+SS-3D-Clump.

The detection accuracy and false detection rate of FellWalker and Fell+SS-3D-Clump are compared based on manual verification of their detection results. The detection performance of FellWalker and Fell+SS-3D-Clump in the selected region is shown in Table 6. FellWalker detected 3444 candidate molecular clumps. Upon manual verification, 2876 were confirmed as true positives, 568 as false positives, and 49 as ambiguous (as shown in Fig. 16) according to the verification criteria provided in Sect. 2.3. Among the 2876 confirmed true candidates, 2000 were obtained through cross-matching (matching the detections from both FellWalker and Dendrogram algorithms), and 263 had corresponding entities in the C18O data. Specifically, 138 clumps met both criteria of cross-matching and having corresponding entities in the C18O data.

Therefore, the accuracy of FellWalker is 83.4% with a false detection rate of 16.6%. Fell+SS-3D-Clump identified 2655 molecular clump candidates, with 2679 being true positives and 10 being false positives when compared to the results of manual verification. Thus, Fell+SS-3D-Clump has an accuracy of 99.7% with a false detection rate of 0.3%. The combination of FellWalker with the SS-3D-Clump model significantly improves the accuracy from 83.4% to 99.7% and reduces the false detection rate to 0.3%. Notably, the true number of molecular clumps in the real data is unknown, and so the recall rate of both algorithms cannot be calculated. Assuming the total number of molecular clumps in the selected region is 2832 (i.e. the results of manual verification on FellWalker’s detected candidates), and that 2648 are identified after verification with the SS-3D-Clump model, the recall rate of Fell+SS-3D-Clump is 93.5%. This further demonstrates that the SS-3D-Clump model can improve accuracy and reduce false detection rates while sacrificing a certain level of recall rate.

thumbnail Fig. 14

Scatter plot of confidence scores for ambiguous clumps identified manually and with SS-3D-Clump. Horizontal axis: SS-3D-Clump recognition confidence. Vertical axis: manual identification scores.
thumbnail Fig. 15

Integrated intensity maps of 13CO emission for the selected region.
Table 6

Number of molecular clumps detected by the FellWalker and Fell+SS-3D-Clump algorithms, as well as a comparison with manual verification results.

thumbnail Fig. 16

Integrated intensity maps of eight ambiguous clumps detected by FellWalker.

6 Conclusion

This paper introduces SS-3D-Clump, a semi-supervised deep clustering method for automated verification of molecular clumps. By using a 3D CNN to extract features of molecular clumps and by training the model with unlabelled samples using semi-supervised learning, SS-3D-Clump achieves high accuracy in verifying these objects. Our main conclusions can be summarised as follows:

  • 1.

    The SS-3D-Clump model, trained on a dataset constructed from three different density regions, achieves an accuracy of 0.940, a recall rate of 0.960, a precision rate of 0.951, and an F1 score of 0.955 on the corresponding test dataset.

  • 2.

    The SS-3D-Clump model effectively captures the key features of molecular clumps, such as intensity, rotation angle, and background noise, using a 3D convolutional neural network.

  • 3.

    The SS-3D-Clump model exhibits strong generalisation ability, allowing it to adapt to new and unlabelled samples while consistently achieving high accuracy rates across different regions of molecular clump data.

  • 4.

    The SS-3D-Clump model can be integrated with existing molecular clump detection algorithms to form a framework for the automated detection and verification of molecular clumps.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (U2031202, 11903083, 11873093 and 12203029). This research made use of the data from the Milky Way Imaging Scroll Painting (MWISP) project, which is a multi-line survey in 12CO/13CO/C18O along the northern galactic plane with PMO-13.7 m telescope. We are grateful to all the members of the MWISP working group, particularly the staff members at PMO-13.7m telescope, for their long-term support. MWISP was sponsored by National Key R&D Program of China with grant 2017YFA0402701 and CAS Key Research Program of Frontier Sciences with grant QYZDJ-SSW-SLH047. Software: CUPID (Berry et al. 2007), CARTA (Comrie et al. 2021), Astropy (Astropy Collaboration 2018), TensorFlow (TensorFlow Developers 2021), Scikit-Learn (Pedregosa et al. 2011).

Appendix A Manual verification of molecular clumps

For the molecular-clump candidates detected by the ClumpFind, we integrated them in three directions to generate the l − b, l − v, and b – v maps for each candidate. We also plotted the peak spectrum and average spectrum of each molecular clump candidate. Figure A.1 shows the corresponding images of six molecular-clump candidates. The first two rows of the four subplots in the figure display four candidates recognised as true molecular clumps, while the two subplots of the last row show two candidates recognised as false molecular clumps.

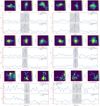thumbnail Fig. A.1

Information on the molecular clump. The top three subplots offer the l − b, l – v, and b – v map integrations in three directions for a clump, while the middle and bottom panels of the figure show the peak spectrum and average spectrum of the clump, respectively.

As shown in the top-left subplot of Fig. A.1, the top row consists of three subplots illustrating the integration of the molecular clump candidate in three directions, resulting in the l − b, l – v, and b – v maps, respectively. In the middle row, the subplots display the peak spectrum of the candidate, where the blue dashed line represents the velocity position corresponding to the peak intensity. The bottom row exhibits the average spectrum of the candidate, with the blue dashed line indicating the velocity position of the centroid of the molecular clump candidate. The shaded regions in both spectrum subplots represent the velocity range associated with the molecular clump. Using information from the integrated maps and spectra of the molecular clump candidates shown in the subplots of Fig. A.1, we conducted manual verification of a test dataset consisting of selected regions in the three quadrants, as described in Section 2.3. Our primary focus during the verification process was to assess whether or not the integrated maps of the candidate exhibits local density enhancements surrounded by weaker density components and whether or not the candidate’s spectrum exhibits a Gaussian profile. Three individuals independently performed the verification to minimise subjective bias in the manual verification, and the designation of a molecular clump was only confirmed when all three verifications matched.

Appendix B Verification results by the SS-3D-Clump model

Figure B.1 shows the recognition results of the SS-3D-Clump on some molecular clump candidates. The first two rows display the results for four molecular clumps, while the last row shows the results for two non-molecular clumps. The first row of each subplot presents the maximum value, total flux, and number of pixels for the respective molecular clump. The second row labels the molecular clump with its centroid position (e.g. the centroid position of the molecular clump shown in the top right corner is: l = 11.186°, b = −1.171°, v = 38.893 km/s). The second number in the third row represents the probability the model assigns to the sample belonging to a clump (e.g. the sample in the top right corner has a 100% probability of belonging to a molecular clump).

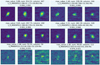thumbnail Fig. B.1

Molecular-clump candidates verified by the SS-3D-Clump.

Appendix C Visualisation of intermediate results of the SS-3D-Clump model

To qualitatively evaluate the filters of the SS-3D-Clump model, we plotted the intermediate results of the SS-3D-Clump model using manually verified positive and negative molecular clump samples as input. Figure C.1 shows the intermediate results of the SS-3D-Clump model when the positive molecular clump sample is used as input. The left panel displays the integrated map of the molecular clump in the l − b plane (integrated along the first axis of data). The middle panel consists of four subplots (arranged in a 2×2 grid), representing four out of the sixteen results obtained after the ‘Stem’ operation in the SS-3D-Clump model. These subplots display the integrated maps along the first axis (the remaining subplots show integrated maps along the first axis). The right panel displays 32 results obtained after the ‘ResB 1’ operation.

Figure C.1 shows that in the feature extraction process of the SS-3D-Clump model, some of the convolutional filters capture the main components of the molecular clump, resulting in higher intensity in the central region compared to the surrounding areas. By contrast, other filters extract background information related to the molecular clump. Figure C.2 presents similar results, except that the input to the SS-3D-Clump model is the manually verified negative samples of the molecular clump, resulting in relatively uniform intensity across the images. Figure C.2 shows that when inputting negative samples of the molecular clump, the features extracted by the SS-3D-Clump model do not exhibit the same pattern as the results after the Stem operation in Fig. C.1. These features do not show a significant enhancement in intensity in the central regions of the images; instead, they appear relatively flat. Although some features in certain feature maps show more vigorous intensity in the central region of the feature image, the surrounding features also exhibit some intensity.

By comparing the differences between Figs C.1 and C.2, we can roughly infer that the SS-3D-Clump model has the ability to effectively separate the main components of the molecular clump from the background noise during the feature extraction process. The SS-3D-Clump model generates feature maps where the intensity in the central region is significantly higher than in the surrounding regions. These features help the classifier network of the model to verify the molecular clump further.

thumbnail Fig. C.1

Features extracted from the SS-3D-Clump model for positive samples of molecular clump are shown. The left subplot represents the integrated map of the molecular clump in l − b. The middle four subplots arranged in a 2 × 2 grid depict the feature maps obtained after the ‘Stem’ feature extraction in the SS-3D-Clump model (16 feature maps, with four shown here). These feature maps capture the main components of the molecular clump and background noise. The right side exhibits 32 subplots showing the features extracted through the ‘ResB 1’ operation in the SS-3D-Clump model.
thumbnail Fig. C.2

Feature-extraction results of the SS-3D-Clump model for negative samples of the molecular clump.

Appendix D Training process of the SS-3D-Clump model

thumbnail Fig. D.1

Recognition results of the SS-3D-Clump model and the probability distribution of the output molecular clumps for each round during the training process.

Figure D.1 illustrates the recognition results of the SS-3D-Clump model on the molecular clump candidates in the HDR test dataset. The subplots from the top-left to the bottom-right represent the histogram of probabilities assigned by the SS-3D-Clump model, trained from the first to the sixteenth epoch. In each subplot, the x-axis represents the probability given by the SS-3D-Clump model for recognising a candidate as a molecular clump. The blue histogram represents the probability distribution for all molecular clump candidates in the test dataset. The green histogram represents the probability distribution of the candidates correctly recognised as negative samples by the SS-3D-Clump model. By contrast, the orange represents the probability distribution of the candidates correctly recognised as positive samples.

In the initial epochs, the predicted probability values of the SS-3D-clump model are concentrated around 50%, and there are no two distinct clusters (i.e. no two peaks in the distribution of probability values). As the model continues to train, two peaks appear in the distribution at the eighth epoch, and there is a clear boundary between the two peaks. The peaks also move towards the two ends, indicating that the model has started to possess the ability to classify. Moreover, the model’s predictions are in close agreement with the true data labels. Each subplot in Fig. D.2 represents the feature maps extracted by the SS-3D-Clump model from the molecular-clump positive samples after each training epoch. The figure displays the variations of four feature maps during the 16 epochs of model training. The bottom-right subplot exhibits feature maps that mainly contain background noise information of the molecular clump. The feature maps in the top-right subplot likely capture the intensity information regarding the molecular clump, as indicated by the colour bar, with an integrated intensity reaching around 40 after 16 training epochs, while the other three feature maps reach a value of about 10. The feature maps in the bottom-left subplot may contain directional information regarding the molecular clump in the / - b direction. By contrast, the feature map in the top-left subplot appears to include the molecular clump’s main components and background noise information.

The commonalities among the four subplots in Fig. D.2 indicate that as the training epochs of the SS-3D-Clump model increase, the SS-3D-Clump model can extract more prominent features. Additionally, by examining the probability distribution histograms in Fig. D.1, we can make a preliminary inference that as the SS-3D-Clump model improves its feature extraction, the classifier network within the model becomes more accurate in verifying and classifying molecular clump samples.

thumbnail Fig. D.2

Feature maps extracted by the SS-3D-Clump model from molecular clump-positive samples at each training epoch are shown. The figure displays the variations of four feature maps over 16 epochs. The bottom-left subplot represents background noise information. The top-right subplot captures the intensity of the molecular clump, reaching an integrated intensity of approximately 40 after 16 epochs, while the other three feature maps have intensities of around 10. The bottom-right subplot may contain directional information in the l − b direction. The top-left subplot includes the main components of the molecular clump and background noise.

References

  1. Alex Rodriguez, A. L. 2014, Science, 344, 1492 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Arzoumanian, D., André, P., Könyves, V., et al. 2019, A&A, 621, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  5. Basu, S., Banerjee, A., & Mooney, R. J. 2002, in Machine Learning, Proceedingsof the Nineteenth International Conference (ICML 2002), University of New South Wales, Sydney, Australia, July 8–12, 2002 [Google Scholar]
  6. Benedettini, M., Pezzuto, S., Schisano, E., et al. 2018, A&A, 619, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [Google Scholar]
  8. Berry, D. S. 2015, Astron. Comput., 10, 22 [Google Scholar]
  9. Berry, D. S., Reinhold, K., Jenness, T., & Economou, F. 2007, in ASP Conf. Ser., 376, Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, 425 [Google Scholar]
  10. Berry, D., Graves, S., Bell, G. S., et al. 2022, inASP Conf. Ser., 532, Astronomical Society of the Pacific Conference Series, eds. J. E. Ruiz, F. Pierfedereci, & P. Teuben, 559 [Google Scholar]
  11. Blitz, L., & Stark, A. A. 1986, ApJ, 300, L89 [CrossRef] [Google Scholar]
  12. Bresnahan, D., Ward-Thompson, D., Kirk, J. M., et al. 2018, A&A, 615, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Burton, M. G., Braiding, C., Glueck, C., et al. 2013, PASA, 30, e044 [NASA ADS] [CrossRef] [Google Scholar]
  14. Caron, M., Bojanowski, P., Joulin, A., & Douze, M. 2018, arXiv e-prints [arXiv:1807.05520] [Google Scholar]
  15. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  16. Cheng, Y., Tan, J. C., Liu, M., et al. 2018, ApJ, 853, 160 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cheng, T.-Y., Conselice, C. J., Aragón-Salamanca, A., et al. 2020, MNRAS, 493, 4209 [Google Scholar]
  18. Cheng, T.-Y., Huertas-Company, M., Conselice, C. J., et al. 2021, MNRAS, 503, 4446 [NASA ADS] [CrossRef] [Google Scholar]
  19. Colombo, D., Hughes, A., Schinnerer, E., et al. 2014, ApJ, 784, 3 [NASA ADS] [CrossRef] [Google Scholar]
  20. Comrie, A., Wang, K.-S., Hsu, S.-C., et al. 2021, https://doi.org/10.5281/zenodo.4905459 [Google Scholar]
  21. Congiu, E., Blanc, G. A., Belfiore, F., et al. 2023, A&A, 672, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Currie, M. J., Berry, D. S., Jenness, T., et al. 2014, in ASP Conf. Ser., 485, Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, 391 [Google Scholar]
  23. Demianenko, M., Malanchev, K., Samorodova, E., et al. 2023, A&A, 677, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Eden, D. J., Moore, T. J. T., Plume, R., et al. 2017, MNRAS, 469, 2163 [Google Scholar]
  25. Eden, D. J., Liu, T., Kim, K.-T., et al. 2019, MNRAS, 485, 2895 [NASA ADS] [CrossRef] [Google Scholar]
  26. Faesi, C. M., Lada, C. J., & Forbrich, J. 2016, ApJ, 821, 125 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gómez, L., Wyrowski, F., Schuller, F., Menten, K. M., & Ballesteros-Paredes, J. 2014, A&A, 561, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Gupta, R., Srijith, P., & Desai, S. 2022, Astron. Comput., 38, 100543 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Han, Y., Zou, Z., Li, N., & Chen, Y. 2022, Res. Astron. Astrophys., 22, 085006 [CrossRef] [Google Scholar]
  31. Hasanaj, E., Wang, J., Sarathi, A., Ding, J., & Bar-Joseph, Z. 2021, https://doi.org/10.1101/2021.03.19.436162 [Google Scholar]
  32. Hasanaj, E., Wang, J., Sarathi, A., Ding, J., & Bar-Joseph, Z. 2022, Nat.Commun., 13, 1 [NASA ADS] [CrossRef] [Google Scholar]
  33. He, Z., Qiu, B., Luo, A.-L., et al. 2021, MNRAS, 508, 2039 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hogg, D. W., & Lang, D. 2008, in AIP Conf. Ser., 1082, Classification and Discovery in Large Astronomical Surveys, ed. C. A. L. Bailer-Jones, 331 [Google Scholar]
  35. Ikeda, N., & Kitamura, Y. 2009, ApJ, 705, L95 [Google Scholar]
  36. Ikeda, N., & Kitamura, Y. 2011, ApJ, 732, 101 [NASA ADS] [CrossRef] [Google Scholar]
  37. Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
  38. James, G., Witten, D., Hastie, T., Tibshirani, R., et al. 2013, An Introduction toStatistical Learning, 112 (Springer) [Google Scholar]
  39. Jiang, Z., & Li, J. 2013, in Protostars and Planets VI, Posters 1B003 [Google Scholar]
  40. Jiang, Y., Zheng, S., Jiang, Z., et al. 2022, Astron. Comput., 40, 100613 [NASA ADS] [CrossRef] [Google Scholar]
  41. Jiang, Y., Chen, Z., Zheng, S., et al. 2023, ApJS, 267, 32 [NASA ADS] [CrossRef] [Google Scholar]
  42. Johnstone, D., Ciccone, S., Kirk, H., et al. 2017, ApJ, 836, 132 [NASA ADS] [CrossRef] [Google Scholar]
  43. Juvela, M., He, J., Pattle, K., et al. 2018, A&A, 612, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Kainulainen, J., Lada, C. J., Rathborne, J. M., & Alves, J. F. 2009, A&A, 497, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kirk, H., Johnstone, D., & Francesco, J. D. 2006, ApJ, 646, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  46. Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [Google Scholar]
  48. Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
  49. Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 699, 850 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lada, E. A. 1992, ApJ, 393, L25 [NASA ADS] [CrossRef] [Google Scholar]
  51. Li, C., Wang, H.-C., Wu, Y.-W., Ma, Y.-H., & Lin, L.-H. 2020, Res. Astron. Astrophys., 20, 031 [CrossRef] [Google Scholar]
  52. Liu, L., Bureau, M., Li, G.-X., et al. 2022, MNRAS, 517, 632 [NASA ADS] [CrossRef] [Google Scholar]
  53. Lukic, V., de Gasperin, F., & Brüggen, M. 2020, Galaxies, 2020, 8 [NASA ADS] [Google Scholar]
  54. Luo, X., Zheng, S., Huang, Y., et al. 2022, Res. Astron. Astrophys., 22, 015003 [CrossRef] [Google Scholar]
  55. Mannfors, E., Juvela, M., Bronfman, L., et al. 2021, A&A, 654, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Marsh, K. A., Kirk, J. M., André, P., et al. 2016, MNRAS, 459, 342 [Google Scholar]
  57. Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
  58. Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [Google Scholar]
  59. Nakanishi, H., Fujita, S., Tachihara, K., et al. 2020, PASJ, 72, 43 [CrossRef] [Google Scholar]
  60. Nutter, D., & Ward-Thompson, D. 2007, MNRAS, 374, 1413 [Google Scholar]
  61. Ohashi, S., Sanhueza, P., Chen, H.-R. V., et al. 2016, ApJ, 833, 209 [NASA ADS] [CrossRef] [Google Scholar]
  62. Olmi, L., Ade, P. A. R., Anglés-Alcázar, D., et al. 2009, ApJ, 707, 1836 [NASA ADS] [CrossRef] [Google Scholar]
  63. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  64. Pineda, J. E., Rosolowsky, E. W., & Goodman, A. A. 2009, ApJ, 699, L134 [NASA ADS] [CrossRef] [Google Scholar]
  65. Rani, R., Moore, T. J. T., Eden, D. J., et al. 2023, MNRAS, 523, 1832 [NASA ADS] [CrossRef] [Google Scholar]
  66. Rathborne, J. M., Lada, C. J., Muench, A. A., et al. 2009, ApJ, 699, 742 [Google Scholar]
  67. Rigby, A. J., Moore, T. J. T., Plume, R., et al. 2016, MNRAS, 456, 2885 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rigby, A. J., Moore, T. J. T., Eden, D. J., et al. 2019, A&A, 632, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Rojas, K., Savary, E., Clément, B., et al. 2022, A&A, 668, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Rosolowsky, E. 2005, PASP, 117, 1403 [NASA ADS] [CrossRef] [Google Scholar]
  71. Rosolowsky, E. W., Pineda, J. E., Kauffmann, J., & Goodman, A. A. 2008, ApJ, 679, 1338 [Google Scholar]
  72. Rumble, D., Hatchell, J., Gutermuth, R. A., et al. 2015, MNRAS, 448, 1551 [NASA ADS] [CrossRef] [Google Scholar]
  73. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  74. Scaringi, S., Cottis, C. E., Knigge, C., & Goad, M. R. 2009, MNRAS, 399, 2231 [NASA ADS] [CrossRef] [Google Scholar]
  75. Shimajiri, Y., Kitamura, Y., Nakamura, F., et al. 2015, ApJS, 217, 7 [NASA ADS] [CrossRef] [Google Scholar]
  76. Su, Y., Yang, J., Zhang, S., et al. 2019, ApJS, 240, 9 [Google Scholar]
  77. Takekoshi, T., Fujita, S., Nishimura, A., et al. 2019, ApJ, 883, 156 [NASA ADS] [CrossRef] [Google Scholar]
  78. Tanaka, T., Nakamura, F., Awazu, Y., et al. 2013, ApJ, 778, 34 [NASA ADS] [CrossRef] [Google Scholar]
  79. TensorFlow Developers, T. 2021, https://doi.org/10.5281/zenodo.4724126 [Google Scholar]
  80. Umemoto, T., Minamidani, T., Kuno, N., et al. 2017, PASJ, 69, 78 [Google Scholar]
  81. Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [Google Scholar]
  82. Williams, J. P., Blitz, L., & McKee, C. F. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell, 97 [Google Scholar]
  83. Wurster, J., & Rowan, C. 2023, MNRAS, 523, 3025 [NASA ADS] [CrossRef] [Google Scholar]
  84. Zhan, X.-L., Jiang, Z.-B., Chen, Z.-W., Zhang, M.-M., & Song, C. 2016, Res. Astron. Astrophys., 16, 56 [Google Scholar]
  85. Zhan, X., Xie, J., Liu, Z., Ong, Y. S., & Loy, C. C. 2020, in 2020 IEEE/CVFConference on Computer Vision and Pattern Recognition (CVPR) [Google Scholar]
  86. Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268 [Google Scholar]
  87. Zhang, G.-Y., Xu, J.-L., Vasyunin, A. I., et al. 2018, A&A, 620, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Zhang, S., Zavagno, A., López-Sepulcre, A., et al. 2021, A&A, 646, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Zhu, X.-P., Dai, J.-M., Bian, C.-J., et al. 2019, Ap&SS, 364, 55 [NASA ADS] [CrossRef] [Google Scholar]
  90. Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [Google Scholar]
4

See the details of ClumpFind in starlink.eao.hawaii.edu

All Tables

Table 1

Parameters of the ClumpFind algorithm.

In the text
Table 2

Number of molecular clumps in three regions and the counts in the training and test datasets.

In the text
Table 3

Performance in terms of recall, precision, and F1 score for different parameters of the 3D CNN model.

In the text
Table 4

Performance metrics of the SS-3D-Clump model applied to the labelled test datasets in three regions, using molecular clump candidates detected by ClumpFind for semi-supervised deep learning.

In the text
Table 5

Performance of the SS-3D-Clump model trained on datasets from three regions when applied to the other regions.

In the text
Table 6

Number of molecular clumps detected by the FellWalker and Fell+SS-3D-Clump algorithms, as well as a comparison with manual verification results.

In the text

All Figures

thumbnail Fig. 1

Face-on view of an imaginary Milky Way (credit: R. Hurt, NASA/JPL-Caltech/SSC). The Galactic centre (red asterisk) is at (0, 0) and the Sun (green filled circle) is at (0, 8.5).
In the text
thumbnail Fig. 2

ClumpFind and Dendrogram applied to the same data. The green circles represent the centroids of clumps detected by ClumpFind, while the blue plus symbols represent the results of Dendrogram.
In the text
thumbnail Fig. 3

Examples of 13CO clumps having corresponding entities in C18O. The upper and lower subplots on the left illustrate the velocity channel map of 13CO clumps at −5.6 km s−1 and the integrated map spanning the velocity range of −7.3 to −4.5 km s−1, respectively. The two subplots on the right depict the corresponding results for C18O.
In the text
thumbnail Fig. 4

Integrated intensity maps of clumps from the dataset. The top row shows two samples of positive clumps, while the subsequent four rows showcase 16 samples of ambiguous datasets.
In the text
thumbnail Fig. 5

Structure of the SS-3D-Clump. The proposed method involves iteratively clustering deep features and using cluster assignments as pseudo-labels to learn the parameters of the 3D CNN and classifier networks.
In the text
thumbnail Fig. 6

Constrained-KMeans algorithm.
In the text
thumbnail Fig. 7

Illustration of the clustering principle of the Constrained-KMeans algorithm using two-dimensional scatter plot clustering.
In the text
thumbnail Fig. 8

Network structure and detailed parameters of SS-3D-Clump. The SS-3D-Clump receives a 30 px × 30 px × 30 px cube as input and has two neurons in the output layer, representing the two-class verification of molecular clumps. It comprises a 3D CNN and an FCN. The input data in SS-3D-Clump undergo processing steps including ‘Stem’, ‘ResB 1’, and Conv3D. The resulting data are then flattened and passed into the FCN to generate the final output. ‘Stem’ comprises 16 3D Convolution kernels of size 3 and stride 2, and is followed by the ReLU activation function, and 32 MaxPooling layers with a kernel size of 2 and stride of 2. ‘ResB 1’ consists of alternating 3D CNN and Batch Normalization layers, with the ReLU activation function applied in each layer; it incorporates residual connections inspired by the ResNet architecture. The FCN consists of five layers with the following numbers of neurons: 4096, 512, 256, 16, and 2.
In the text
thumbnail Fig. 9

Performance of the SS-3D-Clump model during the training process in HDR. Left panel: evolution of clustering capability in SS-3D-Clump across training epochs. Middle panel: evolution of cluster reassignments in each clustering iteration of SS-3D-Clump. Right panel: overall performance of SS-3D-Clump in the test dataset.
In the text
thumbnail Fig. 10

Performance of the SS-3D-Clump model during the training process in MDR, with the same content as described in Fig. 9.
In the text
thumbnail Fig. 11

Performance of the SS-3D-Clump model during the training process in LDR, with the same content as described in Fig. 9.
In the text
thumbnail Fig. 12

Evaluation metrics for SS-3D-Clump performance. The red dot is in the ‘elbow’ of the ROC curve and shows the best balance between completeness and purity.
In the text
thumbnail Fig. 13

Peak distribution of clumps excluded and retained by SS-3D-Clump. Top: peak distribution of clumps in the three regions. The peak positions of the distributions in LDR and MDR are consistent at 1.89 K, while in HDR, the peak position is at 1.68 K. Bottom: peak distribution of clumps excluded by the final SS-3D-Clump.
In the text
thumbnail Fig. 14

Scatter plot of confidence scores for ambiguous clumps identified manually and with SS-3D-Clump. Horizontal axis: SS-3D-Clump recognition confidence. Vertical axis: manual identification scores.
In the text
thumbnail Fig. 15

Integrated intensity maps of 13CO emission for the selected region.
In the text
thumbnail Fig. 16

Integrated intensity maps of eight ambiguous clumps detected by FellWalker.
In the text
thumbnail Fig. A.1

Information on the molecular clump. The top three subplots offer the l − b, l – v, and b – v map integrations in three directions for a clump, while the middle and bottom panels of the figure show the peak spectrum and average spectrum of the clump, respectively.
In the text
thumbnail Fig. B.1

Molecular-clump candidates verified by the SS-3D-Clump.
In the text
thumbnail Fig. C.1

Features extracted from the SS-3D-Clump model for positive samples of molecular clump are shown. The left subplot represents the integrated map of the molecular clump in l − b. The middle four subplots arranged in a 2 × 2 grid depict the feature maps obtained after the ‘Stem’ feature extraction in the SS-3D-Clump model (16 feature maps, with four shown here). These feature maps capture the main components of the molecular clump and background noise. The right side exhibits 32 subplots showing the features extracted through the ‘ResB 1’ operation in the SS-3D-Clump model.
In the text
thumbnail Fig. C.2

Feature-extraction results of the SS-3D-Clump model for negative samples of the molecular clump.
In the text
thumbnail Fig. D.1

Recognition results of the SS-3D-Clump model and the probability distribution of the output molecular clumps for each round during the training process.
In the text
thumbnail Fig. D.2

Feature maps extracted by the SS-3D-Clump model from molecular clump-positive samples at each training epoch are shown. The figure displays the variations of four feature maps over 16 epochs. The bottom-left subplot represents background noise information. The top-right subplot captures the intensity of the molecular clump, reaching an integrated intensity of approximately 40 after 16 epochs, while the other three feature maps have intensities of around 10. The bottom-right subplot may contain directional information in the l − b direction. The top-left subplot includes the main components of the molecular clump and background noise.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.