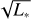| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 25 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202348224 | |
| Published online | 07 February 2024 | |
Mid-infrared spectra of T Tauri disks: Modeling the effects of a small inner cavity on CO2 and H2O emission
1
Leiden Observatory, Leiden University,
2300 RA
Leiden,
The Netherlands
e-mail: vlasblom@strw.leidenuniv.nl
2
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching,
Germany
3
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale,
91405
Orsay,
France
Received:
10
October
2023
Accepted:
17
November
2023
Context. The inner few AU of disks around young stars, where terrestrial planets are thought to form, are best probed in the infrared. The James Webb Space Telescope is now starting to characterize the chemistry of these regions in unprecedented detail, building on earlier results of the Spitzer Space Telescope that the planet-forming zone of disks contain a rich chemistry. One peculiar subset of sources characterized by Spitzer are the so-called CO2-only sources, in which only a strong 15 μm CO2 feature was detected in the spectrum.
Aims. One scenario that could explain the weak or even non-detections of molecular emission from H2O is the presence of a small, inner cavity in the disk. If this cavity were to extend past the H2O snowline, but not past the CO2 snowline, this could strongly suppress the H2O line flux with respect to that of CO2. For this work, we aimed to test the validity of this statement.
Methods. Using the thermo-chemical code Dust And LInes (DALI), we created a grid of T Tauri disk models with an inner cavity, meaning we fully depleted the inner region of the disk in gas and dust starting from the dust sublimation radius and ranging until a certain cavity radius. Cavity radii varying in size from 0.1 to 10 AU were explored for this work. We extended this analysis to test the influence of cooling through H2O ro-vibrational lines and the luminosity of the central star on the CO2 /H2O flux ratio.
Results. We present the evolution of the CO2 and H2O spectra of a disk with inner cavity size. The line fluxes show an initial increase as a result of an increasing emitting area, followed by a sharp decrease. As such, when a large-enough cavity is introduced, a spectrum that was initially dominated by H2O lines can become CO2-dominated instead. However, the cavity size needed for this is around 4–5 AU, exceeding the nominal position of the CO2 snowline in a full disk, which is located at 2 AU in our fiducial, L* = 1.4 L⊙ model. The cause of this is most likely the alteration of the thermal structure by the cavity, which pushes the snowlines outward. In contrast, our models show that global temperature fluctuations, for example due to changes in stellar luminosity, impact the fluxes of H2O and CO2 roughly equally, thus not impacting their ratio much. Alternative explanations for bright CO2 emission are also briefly discussed.
Conclusions. Our modeling work shows that it is possible for the presence of a small inner cavity to explain strong CO2 emission in a spectrum. However, the cavity needed to do so is larger than what was initially expected. As such, this scenario will be easier to test with sufficiently high angular resolution (millimeter) observations.
Key words: astrochemistry / line: formation / molecular processes / radiative transfer / protoplanetary disks
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The formation of terrestrial planets is thought to occur mostly within the inner few AU of protoplanetary disks around young stars (Morbidelli et al. 2012). To understand the composition of these planets and their atmospheres, investigating the chemistry of their birth environment is crucial. This environment is certainly not static, as the inner disk hosts strong variations in temperature, density, and UV irradiation with position. Additionally, the presence of substructures and drift of icy grains can further alter the composition of the inner disk. Tracing the inner disk structure can be done though infrared (IR) spectroscopy. Previous surveys conducted with, for example, the Spitzer Space Telescope have found most disks to contain a rich chemistry, with the molecules H2O, CO2,CO, HCN, and C2H2 commonly detected in the 10–20 µm range (Carr & Najita 2008; Pontoppidan et al. 2010; Salyk et al. 2011; Pontoppidan et al. 2014). Now, the James Webb Space Telescope (JWST; Gardner et al. 2023; Rigby et al. 2023) provides even better insights into the complexities of these warm, inner regions. The higher sensitivity and higher spectral resolution of JWST compared with Spitzer boosts the line-to-continuum ratio, allowing it to detect much weaker emission from less abundant, minor species and for an even better quantitative interpretation of molecular emission, due to these bands being much less blended than they were when observed with Spitzer.
In the mid-IR wavelength range probed by the Mid-InfraRed Instrument (MIRI; Wright et al. 2015, 2023; Rieke et al. 2015), emission lines from H2O and CO2 are often prominently detected (Kamp et al. 2023; van Dishoeck et al. 2023), as was also already the case with Spitzer. To interpret these findings, many sophisticated models of the inner disks of T Tauri stars have been developed over the years (e.g., Agúndez et al. 2008; Woitke et al. 2009; Walsh et al. 2010; Najita et al. 2011; Bruderer et al. 2012), with several of them being specifically focused on the formation and evolution of H2O (Glassgold et al. 2009; Bethell & Bergin 2009; Meijerink et al. 2009; Ádámkovics et al. 2014; Du & Bergin 2014). Recent modeling results have shown that the H2O and CO2 abundances and their emission are sensitive to the gas temperature (see, e.g., Walsh et al. 2015; Woitke et al. 2018; Anderson et al. 2021), making their emission and their relative flux levels interesting tracers of the inner disk’s physical and chemical conditions. Namely, H2O and CO2 share a common pathway in their gas-phase formation. Both molecules are formed from OH, but which of the two is formed most is determined by the gas temperature (Charnley 1997; van Dishoeck et al. 2013; Walsh et al. 2015). At temperatures between 100 and 250 K, OH reacts with CO to form CO2 via the reaction OH + CO → CO2 + H. Above a temperature of roughly 300 K, the energy barrier of the reaction OH + H2 → H2O + H at 1740 K (Baulch et al. 1992) can be overcome, and due to H2 being more abundant than CO, the vast majority of the OH is turned into H2O instead of CO2.
However, in some sources observed with Spitzer, only the 15 µm band from CO2 was detected, whereas H2O emission seemed absent in these observations (Pontoppidan et al. 2010). These sources became known as the “CO2-only sources”. One of these sources, GW Lup, has now been observed with JWST-MIRI as a part of the MIRI mid-INfrared Disk Survey (MINDS) (Grant et al. 2023; Kamp et al. 2023). While more molecules than just CO2 were detected, thanks to the higher sensitivity and resolving power of JWST compared to Spit𝓏er, the spectrum of GW Lup still stands out from typical IR T Tauri disk spectra in that its CO2 line flux is especially strong. Its CO2 flux is much stronger than the surrounding H2O lines at 15 µm, which is not something that is commonly seen in these sources. As such, even emission from 13CO2 was detected in this disk, which had not been achieved before. Also the disk’s CO2 /H2O column density ratio, estimated with 0D local thermodynamic equilibrium (LTE) slab models, is found to be particularly high compared with other sources, at a value of approximately 0.7 (Grant et al. 2023).
A possible scenario to explain the presence of such a large CO2/H2O flux ratio was put forth: the presence of a small (few AU) cavity in the inner disk. Such a cavity in the millimeter dust continuum could, for example, be carved by a companion and would unlikely be resolved with the Atacama Large Millimeter/sub-millimeter Array (ALMA). If that cavity would extend beyond the H2O snowline, it could suppress the H2O emission. Additionally, it would also prevent any remaining H2O within the cavity to be efficiently replenished by radial drift. If the cavity does not extend further than the CO2 snowline, however, this would not happen to the CO2 emission. If the H2O emission can be suppressed with respect to the CO2 emission in this manner, it could lead to the source’s spectrum exhibiting a large CO2/H2O flux ratio, as is seen in the CO2-only sources. This scenario is illustrated in Fig. 1. In this work, we set out to test this by modeling the effects of a small cavity on the H2O and CO2 spectra of a T Tauri disk. However, there are also other scenarios that should be considered, which we mention here and discuss in more detail in Sect. 4.
First, the presence of a dust trap with only a small perturbation on the gas surface density, rather than a small, deep cavity, between the H2O and CO2 snowlines could have a similar effect on the H2O and CO2 line fluxes. A dust trap at this location could halt the drift of icy pebbles, preventing the sublimation of H2O ice but not that of CO2 ice, allowing the CO2 gas to be continuously replenished while the H2O gas is depleted. This could also lead to the spectrum exhibiting a large CO2/H2O flux ratio.
Second, since the gas temperature in a disk is largely set by the stellar luminosity, it would not be surprising for lower-luminosity stars to be more CO2-rich, as the CO2 and H2O abundances are sensitive to the gas temperature. In fact, low-mass stars have been shown, both by observations and models, to be richer in carbon-bearing species than their higher-mass counterparts (e.g., Pascucci et al. 2013; Walsh et al. 2015). However, very-low-mass stars often show strong emission from hydrocarbons such as C2H2 (see, e.g., Tabone et al. 2023a; Arabhavi et al. 2023 for recent examples with JWST), and this is not seen in these CO2-only sources. Still, the CO2-only class of sources could represent an in-between case, between the cold, very-low-mass stars rich in carbon-bearing species and the hotter, higher-mass stars rich in oxygen-bearing species.
Finally, the amount of small grains in the disk atmosphere can also impact molecular line fluxes. Since the gas-to-dust ratio has a strong impact on the line strengths (see, e.g., Meijerink et al. 2009; Woitke et al. 2018; Greenwood et al. 2019), the typically weak H2O fluxes in the CO2-only sources could point to these sources having a larger amount of dust in the upper layers, and thus a smaller gas-to-dust ratio. This may also impact the relative CO2 /H2O flux ratios. After all, the smaller gas-to-dust ratio leads to the disk atmosphere being cooler, which promotes the gas-phase formation of CO2 over H2O. This effect can be tentatively seen in Bosman et al. (2022b).
For this work, we make use of the thermo-chemical code Dust And LInes (DALI; Bruderer et al. 2012; Bruderer 2013), which has previously been used to model CO2 mid-IR emission by Bosman et al. (2017). We include the most recent updates to the code as described in Bosman et al. (2022a, b). The work by these authors introduces H2O UV-shielding (Bethell & Bergin 2009) and so-called (photo-)chemical heating to the code. The latter refers to the process in which excess energy released by the photodissociation of molecules and the subsequent chemical reactions involving the dissociation products is used to heat the gas (Glassgold & Najita 2015). The work by Bosman et al. (2022a,b) finds both of these processes to be especially important in matching modeled spectra to typical Spit𝓏er observations, where there had previously been some difficulty to do so (see Woitke et al. 2018; Anderson et al. 2021). In particular, models previously had a tendency to greatly overproduce the CO2 flux with respect to the H2O flux, leading to much higher CO2 /H2O flux ratios than most sources show. The inclusion of H2O UV-shielding and extra chemical heating were shown by Bosman et al. (2022b) to help mitigate this problem. The reasoning behind this relies again on the common gas-phase formation pathway of CO2 and H2O. Namely, the extra chemical heating increases the temperature in the upper layers of the disk, and thus stimulates the H2O production in this region. As the H2O becomes more abundant in the disk, eventually it will reach the column densities required for it to start UV-shielding (Bethell & Bergin 2009). This will further drive the balance from CO2 toward H2O, even at a slightly lower temperature. The H2O is then photodissociated at a much lower rate and this also reduces the production rate of OH, which quenches the formation of CO2. Moreover, CO2 does not benefit from self-shielding at these column densities, so its photodissociation rate will be higher. So, the inclusion of both of these effects boosts the H2O production in the disk and allows the models to closer match the fact that H2O emission is typically stronger than CO2 emission in observed mid-IR spectra. Of course, this goes in the opposite direction to what we are interested in (sources with H2O emission fainter than CO2), but these effects are still important to include to better match what is generally observed in mid-IR spectra, rather than only our specific subset of CO2-only sources.
The structure of this work is as follows: we describe our modeling setup in Sect. 2 and the results in Sect. 3. The implications of our modeling work are discussed in Sect. 4 and our main conclusions are summarized in Sect. 5.
 |
Fig. 1 Cartoon illustrating the scenario that is tested in this work. On the top, a full disk is shown, leading to an observed spectrum with bright H2O lines (illustrated in blue) and a relatively weaker 15 µm CO2 feature (illustrated in green). On the bottom, a disk with a small inner cavity is illustrated. This could, for example, be carved by a companion. The cavity extends beyond the H2O snowline but not beyond the CO2 snowline, leading to an observed spectrum that shows a bright CO2 feature and relatively weak H2O lines. The values given for the locations of the H2O and CO2 snowlines are the midplane snowline locations of our fiducial, L* = 1.4 L⊙ full disk model based on AS 209. |
Summary of all model parameters.
2 Methods
In this work, we present 5 grids of thermo-chemical models made with DALI which have small inner cavities. The fiducial grid, which is presented in the main body of this work, consists of models that are based on those presented in Bosman et al. (2022a,b), which in turn are based on the model of the disk around the pre-main-sequence K5 star AS 209 presented in Zhang et al. (2021). All grids contain models with inner cavities ranging in size from 0.1 to 10 AU, as well as a full disk model without a cavity. The importance of H2O ro-vibrational cooling as well as input stellar luminosity are tested with additional grids which are presented in Appendices A and B. We summarize the model parameters of all grids in Table 1 and provide the main details of our setup below.
The code DALI generates the physical-chemical models in three main steps (see Bruderer et al. 2012; Bruderer 2013). In the first step, the local radiation field and dust temperature are determined at all locations in the disk by solving a dust radiative transfer calculation with a 2D Monte Carlo method. In the next step, the chemical abundances are calculated, assuming steady state chemistry and using an initial guess for the gas temperature. These abundances are then used as input for the non-LTE excitation calculation for several specified atoms and molecules that make up the main coolants of the model. The code then solves for the thermal balance to obtain an improved estimate for the gas temperature. Since the previously calculated quantities – the chemical abundances and the atomic and molecular excitation – are both dependent on the gas temperature, this process is repeated in an iterative sequence until a convergent solution is reached. Once convergence is achieved, a raytracing tool can be used in a third step to obtain line fluxes, spectra and spectral image cubes.
The radial structure of the gas and dust of a full, smooth disk (with no cavity or gap present) is parameterized as follows
![${\Sigma _{{\rm{gas }}}}(R) = {\Sigma _{\rm{c}}}{\left( {{R \over {{R_{\rm{c}}}}}} \right)^{ - \gamma }}\exp \left[ { - {{\left( {{R \over {{R_{\rm{c}}}}}} \right)}^{2 - \gamma }}} \right]{\rm{, }}$](/articles/aa/full_html/2024/02/aa48224-23/aa48224-23-eq1.png) (1)
(1)
based on a self-similar solution to a viscously evolving disk (Lynden-Bell & Pringle 1974; Hartmann et al. 1998). Here, Σgas is the gas surface density, Σc is the gas surface density at the characteristic radius Rc, and γ is the power-law index. The vertical scale height of the gas is given by
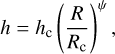 (2)
(2)
where hc is the characteristic scale height at the characteristic radius and ψ is the flaring index of the disk. The dust is separated into two populations by their grain size: small grains have sizes between 5 nm and 1 µm and large grains have sizes between 5 nm and 1 mm, with both populations following an MRN distribution (Mathis et al. 1977). The small grains are well coupled to the gas, and they follow the same radial and vertical distribution (Miotello et al. 2016). Poly-cyclic aromatic hydrocarbons (PAHs) are not considered in this work. The large grains have a mass fraction determined by fℓ and have a similar vertical distribution with a reduced scale height of χhc. From the four models presented in Bosman et al. (2022a,b), we base all of our grids on the thin (hc = 0.08) model with the largest value for the large dust fraction (fℓ = 0.999), meaning that almost all of the dust is large and has thus settled to the midplane, which gives these models a gas-to-dust ratio of 105 in the upper layers of the disk.
The chemical network used for this work is the same as the one used in Bosman et al. (2022a, b). This network builds on the standard DALI chemical network, based on UMIST06 (Woodall et al. 2007), by including H2O UV-shielding and more efficient H2 formation at high temperatures. Specifically, several H2 formation routes via three-body reactions have been included (see Appendix A in Bosman et al. 2022a) and the chemisorp-tion binding energy of H has been increased from 10 000 to 30 000 K, which allows H2 to form on grains at dust temperatures between 300 and 900 K (Cazaux & Tielens 2002, 2004; Wakelam et al. 2017; Thi et al. 2020). The binding energies for H2O and CO2 are 4820 and 2690 K respectively, following Sandford & Allamandola (1993), Aikawa et al. (1997). Isotope chemistry, as implemented in Miotello et al. (2014) and Visser et al. (2018), is not included in this network. The H2O, 12CO2, and 13CO2 spectra are calculated using DALI’s “fast line ray-tracer” (Bosman et al. 2017, Appendix B). For this procedure, we assume that the disk is located at a distance of 121 pc (the distance to AS 209; Gaia Collaboration 2018) and has a face-on orientation. Since 13C is not included in the chemical network, the 13CO2 spectrum is derived by scaling its abundance with 12CO2 according to the ISM 12C /13C ratio of 77 (Wilson & Rood 1994). All spectra are then convolved to a resolving power of R = 3000, comparable to that of MIRI in this wavelength range. We focus our analysis of the spectra mainly on the 13–17 µm wavelength range, since the lines in this region trace similar regions within the disk. The molecular data file for H2O is taken from the Leiden Atomic and Molecular Database, in which levels with energies up to 7200 K are included (Tennyson et al. 2001), line transitions come from the BT2 list (Barber et al. 2006) and colli-sional rate coefficients are from Faure & Josselin (2008). The molecular data for CO2 come from Bosman et al. (2017), for which the energy levels, line positions and line strengths are taken from the HITRAN database (Rothman et al. 2013), with collisional rate coefficients based on Allen et al. (1980), Nevdakh et al. (2003), Jacobs et al. (1975).
As stated previously, our fiducial grid consists of models that are based on the AS 209 model presented in Zhang et al. (2021). Hence, we use the stellar input spectrum from this paper and thus these models have a central source with spectral type K5, an effective temperature of 4300 K and a stellar luminosity of 1.4 L⊙. The grids of models presented in this work contain a small, inner cavity. In this context, we use the word “cavity” to mean a gap in the disk that starts at the sublimation radius and extends until a certain specified radius, referred to as the “cavity size”. Thus, in our use of the word, a disk with a cavity has no inner disk present. Our grids of models contain cavity sizes Rcav between 0.1 and 10 AU. The cavity itself is devoid of gas and dust. Each grid also contains a full disk model, for which the “cavity size” is equal to the sublimation radius, which has a value of 0.08 AU for our fiducial grid. The outer radius, Rout, of all models is set to 100 AU.
Since the mid-IR emission of H2O and CO2 that we model in this work traces the innermost regions of the disk, it is very important for our models to have sufficient resolution at the cavity wall. This is especially true for our models with larger cavity sizes, to prevent that all emission traces only a single or a few cells. As such, we have slightly modified how the grid is set up from Rcav to Rout. In the normal DALI setup (see Bruderer 2013, for details), this region contains a single, logarithmic grid. We cover this area with two grids instead, a logarithmic grid that covers the cavity wall, and a linear grid that covers the rest of the disk. This allows us to get the very high resolution needed at the edge of the cavity. The transition point between the two grids is chosen to ensure a smooth transition in grid cell size, and lies well beyond the relevant emitting regions.
Aside from our fiducial grid of models, we created four additional grids to test the influence of cooling through H2O ro-vibrational lines and the luminosity of the central star on the CO2 /H2O flux ratio of our model spectra. As such, one additional grid including H2O ro-vibrational cooling (which is not included in our fiducial grid, to be consistent with the work by Bosman et al. 2022a,b), is presented in Appendix A. A further three grids are presented in Appendix B which contain central sources with luminosities of L* = 0.2, 0.4, and 0.8 L⊙ respectively. We touch on the main results from these tests in Sects. 3.4 and 3.5, and further details on the specific model setup for these grids can be found in the appendices.
3 Results
3.1 Temperature and abundance structure
In Fig. 2, the abundance maps of H2O and CO2 are presented (left and middle columns) for the models with no cavity, a 1 AU cavity, and a 5 AU cavity (top, middle, and bottom rows respectively). The right hand column presents the corresponding gas temperature. The H2O gas abundance maps clearly show how H2O is present in three main reservoirs (see also Woitke et al. 2009). The inner disk midplane contains the most abundant reservoir of H2O. Here, inside the H2O snowline, the gas temperature is high enough so that the molecule is effectively formed through gas-phase reactions between OH and H2, and the column density is high enough for the molecule to be fully self-shielded from UV radiation. In the warm, upper layers of the disk between Z/R ~ 0.2 – 0.3, the gas temperature is still high enough for gas-phase formation of H2O to occur, but due to the lower density, this is now balanced by photodissociation, leading to a slightly lower H2O abundance. Finally, a cold photodesorption layer is present in the outer disk around Z/R ~ 0.1 where the temperature is too low to effectively form H2O via gas-phase reactions or for H2O to be thermally sublimated. As such, this reservoir is solely supplied by photodesorped H2O, making it the least abundant reservoir. The first two reservoirs are also clearly present for CO2, though the midplane reservoir is located further into the disk since CO2 forms more effectively at lower temperatures and its sublimation temperature is lower. The gap seen between the midplane reservoir and the warm, upper layer of CO2 is caused by H2O UV-shielding, since CO2 in this region is preferentially destroyed by photodissociation due to its inability to self-shield, and the relatively high gas temperature allows for H2O to be preferentially formed (see also Bosman et al. 2022b).
The H2O and CO2 snowlines are indicated in the figure with solid light blue and pink lines, respectively, and it shows that their nominal midplane positions are at approximately 0.5 and 2 AU respectively for the full disk model. The figure also shows that, as a cavity is introduced into the model, the snowlines will move outward slightly from their nominal positions. As such, the warm H2O and CO2 midplane reservoirs do not vanish immediately once the cavity size has surpassed their respective nominal snowline positions. Due to this fact, the concept of the “nominal snowline position” is perhaps not the most useful reference to compare the cavity sizes to, since the actual snowline positions in the cavity models will differ. Still, since it is a constant reference point compared to the moving ‘real’ snowlines, we use it for our comparisons in the rest of this work.
The origin of 90% of the H2O 113,9 − 100,10 line (Eup = 2438 K) emission at 17.22 µm and the CO2 V2 = 1−0 Q(20) line (Eup = 1196 K) emission at 14.97 µm are indicated in yellow and red contours respectively. This shows how most of the emission from these molecules is not tracing a deep column of gas, but rather the thin, warm surface layer. Below this warm surface layer, the line emission becomes optically thick, so the IR emission does not probe the deeper reservoirs. The dust τ = 1 surface at 15 µm is indicated with a dashed, dark blue line, showing that the dust becomes optically thick around Z/R = 0.1. This is rather low down in the disk, which can be attributed to the fact that the mass fraction of large dust grains is rather large (fℓ = 0.999). These are well settled to the midplane, and thus there is little small dust in the disk upper layers.
 |
Fig. 2 Abundance maps of H2O (left column) and CO2 (middle column) for the models with no cavity (top row), a 1 AU cavity (middle row) and a 5 AU cavity (bottom row). The H2O and CO2 snowlines (defined as ngas/nice = 1) are indicated with solid light blue and pink lines, respectively. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The right column shows the gas temperature, with dashed black lines indicating 100 and 300 K. The yellow contours indicate the region in which 90% of the H2O 113,9 − 100,1o line emission at 17.22 µm (Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 v2 = 1 − 0 Q(20) line emission (Eup = 1196 K). |
 |
Fig. 3 Generated H2O, 12CO2 and 13CO2 spectra for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row). The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple respectively). |
3.2 H2O and 12CO2 spectra
The generated H2O, 12CO2, and 13CO2 continuum-subtracted spectra are presented in Fig. 3 for the models with no cavity, a 1 AU cavity, and a 5 AU cavity, which are shown in the top, middle, and bottom panels respectively. This figure shows that the spectrum for the full disk is dominated by H2O emission, and becomes CO2-dominated only once a large-enough cavity is introduced. This thus confirms the plausibility of our initial hypothesis, stating that the observation of bright CO2 emission in the mid-IR spectrum of a disk could be caused by that disk containing a small, inner cavity.
To summarize the evolution of the spectra across all cavity sizes concisely, the integrated fluxes of several H2O line complexes as well as the 12CO2 and 13CO2 Q-branches are plotted as a function of cavity size in Fig. 4. Properties of the line complexes whose fluxes are shown in these figures, such as the wavelength range over which the flux is calculated and the upper-level energy Eup of the most prominent transitions within that wavelength range, can be found in Table 2. For 12CO2 and 13CO2 we chose to calculate the fluxes of their respective v2 = 1−0 Q-branches, since they are these molecules’ most prominent features in the mid-IR wavelength range. For 12CO2, the integration range used is the same as in Salyk et al. (2011) and Anderson et al. (2021). We also calculate the fluxes of the 12CO2 v = 100−010 13.9 µm hot band and the v2 = 1−0 P(25) line, since these lines are more comparable in flux to the 13CO2 Q-branch. For H2O, we calculate the fluxes of the 15.17 and 17.22 µm line complexes as was also done for Spit𝓏er data in Pontoppidan et al. (2010). We also include a blend of two lines with higher Eup values at 12.4 µm that are also analyzed in Banzatti et al. (2017). Additionally, we include the line complexes at 23.94 and 26.70 µm as they are also discussed in the analysis of JWST-MIRI data of H2O-rich source Sz 98 by Gasman et al. (2023), and they have slightly higher Aul values. Finally, we also include a line complex at 23.65 µm that is likely to be detected in H2O-rich sources with JWST-MIRI (see Sect. 4.2) and two individual, unblended lines at ~15.6 µm. All of the lines considered here are (marginally) optically thick in all models and thus their fluxes scale with the temperature and emitting area, rather than scaling linearly with the total number of molecules 𝒩tot = NπR2. Analyzing the evolution of these fluxes as a function of cavity size gives some insight into the evolution of the spectrum as a whole as a cavity is introduced in a disk.
All depicted lines can be seen to increase in flux as a small cavity (≲3–4·AU) is introduced (Fig. 4). This seems slightly counter-intuitive, since there is now less molecular gas present in the inner region of the disk, but this same effect has also been seen in other works (see, e.g., analysis by Antonellini et al. 2016; Woitke et al. 2016, 2018). The explanation for this most likely lies with the fact that the cavity wall is now directly irradiated by the star, and thus also directly heated. As discussed above, the snowlines are pushed outward as a result of this.
Additionally, since the cavity wall is now directly exposed, more of the IR emission will be tracing the cavity wall directly, instead of the disk surface. Since the cavity wall area grows as 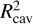 , the emission is now tracing a larger surface area of warm gas, causing the line flux to increase.
, the emission is now tracing a larger surface area of warm gas, causing the line flux to increase.
However, for larger cavity sizes (≳5 AU), the line flux drops off steeply. At these cavity sizes, the direct irradiation of the cavity wall can no longer heat the gas enough to produce a large column of gas. Only a very small region right at the cavity wall remains hot enough for gas-phase formation of CO2 and H2O and as such, the line flux drops off. This can also be quite clearly seen when considering the emitting regions shown in Fig. 2. For smaller cavity sizes, the molecular emission traces a warm, thin surface layer of gas, but for a cavity size of 5 AU and larger this layer is absent. This observed trend in flux (the initial increase followed by a sharp drop-off) is consistent with previous work by Antonellini et al. (2016) and Woitke et al. (2018). Interestingly, the work by Anderson et al. (2021) shows a different behavior. In their work, they vary the inner radius of their model between 0.2 and 1 AU and observe a substantial decrease in molecular line flux, instead of the initial increase in flux that would be expected for such small cavity sizes.
Comparing the evolution of the CO2 and H2O line fluxes in Fig. 4, we can see that the H2O line fluxes drop off at smaller cavity sizes than the CO2 fluxes (~4 AU vs. ~5–6 AU). This is to be expected, since H2O has a higher binding energy, and is formed more efficiently at higher temperatures than CO2, thus it is located further into the disk. As such, we can see from Fig. 3 that this can lead to a spectrum that was H2O-dominated when it had no cavity to a spectrum becoming CO2-dominated once a large-enough cavity is introduced. This is in line with what was expected from the scenario that was proposed. However, we expected this switch from H2O-dominated to CO2-dominated to occur when the disk had a cavity that extended beyond the nominal H2O snowline position, but not beyond the nominal CO2 snowline position. From our modeling work, this clearly does not hold up. This is best seen in Fig. 5, where the flux of the 12CO2 Q-branch is now divided by the H2O line fluxes from the left panel of Fig. 4. This figure clearly shows that it takes a cavity of 5 AU or larger for the relative CO2 /H2O flux to reach its maximum, that is for the spectrum to become CO2-dominated. Still, for cavity sizes of 5 AU and smaller, the relative CO2 /H2O fluxes do show an overall upward trend, which shows that this scenario produces the expected outcome, namely that it becomes more likely to clearly distinguish the CO2 Q-branch from the H2O lines in this wavelength range as a small cavity is introduced into the disk. It should be noted that Fig. 5 shows a noticeable downturn in the relative CO2 /H2O flux for cavity sizes larger than 5 AU. This is caused by both the H2O and CO2 line fluxes rapidly dropping off for these models, and thus the relative fluxes begin to equalize.
 |
Fig. 4 Integrated fluxes of several H2O (left panel), 12CO2, and 13CO2 (middle and right panels) line complexes plotted as a function of cavity size. Properties of these line complexes can be found in Table 2. Nominal H2O and CO2 midplane snowlines in the full disk model are indicated with colored bars. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
Line properties.
 |
Fig. 5 Ratio of the 12CO2 Q-branch flux and the fluxes of several H2O line complexes, plotted as a function of cavity size. Properties of these line complexes can be found in Table 2. |
3.3 13CO2 spectrum
Aside from 12CO2, the spectrum of 13CO2 and the integrated flux of its Q-branch are also presented in Fig. 3 and in the middle and right panels of Fig. 4, respectively. From these two figures, it is clear that the 13CO2 Q-branch has a similar intensity to the surrounding 12CO2 P-branch lines for cavity sizes up to ~2 AU (see also Bosman et al. 2017, 2022b). For cavity sizes of 4–5 AU, the flux of the 13CO2 Q-branch reaches its peak and becomes roughly 2 times brighter than the 12CO2 P-branch lines. For even larger cavity sizes, the flux drops off steeply again. The peak in flux of the 13CO2 Q-branch at cavity sizes of 4–5 AU could indicate that the emission in starting to trace deeper into the disk.
When looking at the CO2 emitting region in the bottom panels of Fig. 2, this indeed seems to be the case. This is further supported by the flux of the 12CO2 v = 100−010 hot band that is shown in the right panel of Fig. 4. Bosman et al. (2022b) show that, if the v = 100−010 hot band is brighter than the v2 = 1−0 P(19)-P(27) lines, this is indicative of the emission tracing deep, warm CO2. In our models, we see that this is most prominently the case around cavity sizes of 4–5 AU. This analysis also shows that the 13CO2 emission will be best observable right after the point of transition from a H2O-dominated to a CO2-dominated spectrum, and that it has the potential to become quite prominent compared to the 12CO2 P-branch lines. 13CO2 has been detected in the gas-phase for the first time in the GW Lup disk by Grant et al. (2023). In the context of the hypothesis that this disk has a small cavity, this detection is in line with our expectations. The authors compare the peak intensity of the 13CO2 Q-branch to that of the 12CO2 P(27) line, finding a ratio of 1.4. In our work, we find the ratio of peak intensities for models with cavity sizes of 4–5 AU to be similar to the finding by Grant et al. (2023).
3.4 Inclusion of H2O ro-vibrational cooling
When computing the spectra, we realized that cooling by mid-IR and near-IR molecular lines can significantly impact the H2O fluxes. Specifically, cooling by the ro-vibrational transitions of H2O has not been included in the results shown so far. This was done to be consistent with work by Bosman et al. (2022a,b), who do not include H2O ro-vibrational cooling since this yielded low fluxes compared with observations (A. Bosman, priv. comm.). Indeed, we find that the inclusion of this cooling lowers the H2O fluxes by a factor of 2–3, since the disk gas temperature is lowered precisely in the layer from which H2O predominantly emits in the mid-IR. Since this effect is highly localized to a specific layer in the inner disk, H2O fluxes at longer wavelengths, such as those in the far-IR or ALMA wavelength range, will likely be much less affected, if at all. The effect on the temperature structure can be seen in Fig. 6, where the gas and dust temperatures (solid and dashed lines respectively) are shown for a vertical cut of the disk taken at 0.3 AU. The model without H2O ro-vibrational cooling (indicated in black) is hotter by, at most, a factor of 2 compared to the model in which this cooling is included (indicated in red). This increase in temperature is limited to a narrow range of disk heights that coincides with the H2O emitting layer (indicated in gray). The inclusion of H2O ro-vibrational transitions in the heating and cooling balance allows the gas more ways to cool in this layer, hence the lower temperature.
The fact that this particular layer is sensitive to such effects is not surprising. Looking at the gas temperature maps for our models in the right column in Fig. 2, we can see that the H2O emitting region lies just below the hot, T > 1000 K disk atmosphere where most gas is atomic. In the layer below this hot atmosphere, which our molecular emission is tracing, the gas is molecular, but the gas and dust are still thermally decoupled, as can also be seen in Fig. 6. As such, the gas temperature in this layer is particularly sensitive to changes in the thermochemistry. This is also seen in Bosman et al. (2022a), where the authors show how the inclusion of H2O UV-shielding and chemical heating leads to changes in gas temperature in this layer.
To investigate the effects of H2O ro-vibrational cooling, we created an additional grid in which we did include H2O ro-vibrational cooling. The analysis shown in the previous three subsections was repeated for this grid and is presented in Appendix A. Comparisons between the H2O and CO2 abundance maps, the gas temperature map, and the generated spectra from the two grids are shown in Figs. A.1–A.3. The integrated fluxes of several H2O, 12CO2, and 13CO2 lines (analogous to Fig. 4) are presented in Fig. A.4, and the relative CO2/H2O fluxes of these lines (analogous to Fig. 5) are presented in Fig. A.5.
The resulting decrease in H2O flux from the inclusion of H2O ro-vibrational cooling is on the order of a factor 2–3. This may not be a very significant change by itself, but when the H2O flux is compared to the CO2 flux, the spectra change from being dominated by the H2O lines to being dominated by the CO2 Q-branch feature. Thus, whereas our fiducial models (the models without H2O ro-vibrational cooling) were H2O-dominated until a large-enough cavity was introduced, the models with H2O ro-vibrational cooling are always CO2-dominated. Regardless, when a cavity is introduced, both grids show a similar trend. As can be seen in Figs. A.3 and A.4, the fluxes first slightly increase when a small cavity is introduced, which is then followed by a decrease in flux once that cavity becomes large enough. This shows that the trends in flux found in this work are robust, but the model assumptions for the full disk spectrum, determining whether the model is H2O- or CO2-dominated, are important.
 |
Fig. 6 Gas and dust temperatures (solid and dashed lines, respectively) as a function of height in the disk Z/R for the models with and without H2O ro-vibrational cooling, indicated in black and red, respectively. Both are full disk models without a cavity. The height in the disk at which H2O emits is indicated in gray. The vertical cut through the disk is taken at a distance of 0.3 AU. |
3.5 Lower-luminosity central sources
To better compare our models to the CO2-only source GW Lup, we also present the results obtained from models that have a lower-luminosity input spectrum than our fiducial AS 209 spectrum in Appendix B. H2O ro-vibrational cooling was not included, just like our fiducial grid. The input spectra used for these grids have L* = 0.2, 0.4, and 0.8 L⊙ compared to the L* = 1.4 L⊙ of the fiducial grid, to ensure that we cover a decent luminosity range. For reference, GW Lup has a luminosity of roughly 0.3 L⊙ (Alcalá et al. 2017; Andrews et al. 2018). We started our analysis with our fiducial, AS 209 model rather than a lower-luminosity model more comparable to GW Lup in order for our fiducial models to be directly comparable to the work by Bosman et al. (2022a,b). A comparison of the H2O and CO2 abundance maps as well as the gas temperature map between all four luminosity grids is presented in Figs. B.1–B.3. The generated H2O, 12CO2, and 13CO2 spectra are presented in Fig. B.4, the integrated fluxes of several H2O, 12Co2, and 13CO2 lines (analogous to Fig. 4) are presented in Fig. B.5, and the relative CO2/H2O fluxes of these lines (analogous to Fig. 5) are presented in Fig. B.6.
The spectra of these models are all, just like the fiducial model, H2O-dominated when no cavity is present, and they all become CO2-dominated once a large enough cavity is introduced. So, the lower-luminosity input spectrum and resulting decrease in global disk gas temperature by itself is not enough to make these models CO2-dominated. The overall trend they follow is also the same as what was described above: the H2O and CO2 line emission initially becomes brighter as a small cavity is introduced, and once that cavity becomes significantly larger than the molecule’s nominal snowline position, the emission drops off sharply. This is shown using the 17.22 µm H2O flux, the CO2 Q-branch flux and the ratio of these two for the grids of all four luminosities in Fig. 7. This figure clearly shows that the drop in line flux from H2O and CO2 occurs at smaller cavity sizes for models with a lower-luminosity input spectrum. The CO2 /H2O flux ratio shows a similar trend between all four models: there is an upward trend for smaller cavity sizes and a downturn for larger cavity sizes. However, as one would expect, the lower-luminosity models reach their peak CO2 /H2O flux ratio (and thus become CO2-dominated) at smaller cavity sizes (e.g., ~23 AU for a L* = 0.2 L⊙ source vs. ~4–5 AU for a L* = 1.4 L⊙ source). Still, these values lie well beyond each model’s nominal midplane CO2 snowline position. We discuss the consequences and possible causes of this in Sect. 4.1. Additionally, from Fig. 7 we can see that the CO2 and H2O line fluxes approximately scale with the stellar luminosity as 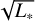 , as is also found by Tabone et al. (2023b). This is shown more clearly in Fig. B.7, which shows the same data as Fig. 7, but with the x-axis rescaled by a factor
, as is also found by Tabone et al. (2023b). This is shown more clearly in Fig. B.7, which shows the same data as Fig. 7, but with the x-axis rescaled by a factor 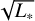 . In this figure, the peaks of the line fluxes now all roughly coincide, whereas they are shifted with respect to each other in Fig. 7. From all of this, we can conclude that our main findings from the fiducial grid also hold for lower-luminosity sources.
. In this figure, the peaks of the line fluxes now all roughly coincide, whereas they are shifted with respect to each other in Fig. 7. From all of this, we can conclude that our main findings from the fiducial grid also hold for lower-luminosity sources.
4 Discussion
4.1 A cavity as an explanation for strong CO2 emission
In this work, we test the scenario proposed by Grant et al. (2023) to explain the strong CO2 emission that some IR spectra of T Tauri disks show: the presence of a small, inner cavity, located between the H2O and CO2 snowlines, could suppress the H2O emission, thus leading the source’s spectrum to show a large CO2/H2O flux ratio. With this modeling work, we show that this is indeed a possibility: a spectrum that was H2O-dominated when it had no cavity can become CO2-dominated instead once a large-enough cavity is introduced. We expected the cavity size needed for a spectrum to switch to be larger than the nominal position of the H2O snowline, but not larger than that of the CO2 snowline. From our modeling, however, we consistently find that this switch occurs for a cavity size that is well beyond the nominal position of the CO2 snowline in a full disk. Some discussion on possible causes and consequences is thus warranted.
Some possible causes can be understood by looking back at Fig. 2. As was already pointed out in Sect. 3.1, the reservoir of warm molecular gas does not disappear immediately once a cavity exceeding the position of its snowline is introduced. For example, the midplane H2O snowline is clearly within 1 AU in the model without a cavity (top left panel of Fig. 2), but when a 1 AU cavity is introduced, the warm H2O reservoir near the cavity wall is still quite prominent. Clearly, the snowlines move outward when a cavity is present. As such, it makes sense that the emission also remains prominent. Additionally, we see from Fig. 2 that the H2O and CO2 emission originates from a thin, warm surface layer at Z/R ~ 0.2 in the disk. Looking at the right column of this figure, we can see that this warm layer remains present in the disk until a cavity size of roughly 5 AU, when we also see that the molecular emission is starting to trace regions slightly deeper down in the disk. The continued presence of this warm layer, combined with the continued presence of molecular gas near the cavity wall, likely explains why the molecular emission remains bright, even though a cavity far larger than the nominal CO2 snowline position has been introduced.
To turn an otherwise H2O-dominated spectrum into a CO2-dominated one, the cavity that needs to be introduced must be larger than was initially expected. This makes it less likely for this phenomenon to be the sole explanation for the existence of the CO2-only sources found by Spit𝓏er. Specifically for sources with higher luminosity, for which cavity sizes of 4–5 AU are needed, the presence of such a cavity could more easily be ruled out observationally (see Sect. 4.2). Additionally, our modeling work shows that small, local temperature changes can have a big impact on a disk’s CO2/H2O flux ratio. The difference in temperature caused by the inclusion of H2O ro-vibrational cooling is, at most, only a factor of two, and it is localized to a very specific layer in the disk, yet that is enough to switch from a H2O-dominated spectrum to a CO2-dominated one. Global temperature changes on the other hand, for example those caused by changes in stellar luminosity, do not seem to have much of an impact on the CO2/H2O flux ratio, instead impacting both molecules’ fluxes equally.
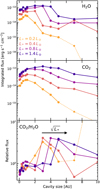 |
Fig. 7 Flux of the 17.22 µm H2O line complex (top), the CO2 Q-branch (middle), and their ratio (bottom) for the grids with L* = 0.2, 0.4, 0.8, and 1.4 L⊙. |
4.2 Observing a small inner cavity
To confirm this scenario producing a large CO2 /H2O flux ratio, one would want to observe a small cavity in sources that are known to have a CO2-dominated mid-IR spectrum. Here, we discuss some methods that could be used to do so. First, our modeling work has shown that the cavity needed to make a source’s spectrum CO2-dominated can be quite large, ~5 AU. With sufficiently high angular resolution mm observations, for example comparable to that of the DSHARP program (Andrews et al. 2018; 0″.035, ~5 AU diameter for a source at 150 pc), such a cavity’s presence could be confirmed or ruled out. A source’s SED can also provide a measure of any inner cavity present in the disk, though this is in part degenerate with the exact dust properties (see, e.g., Woitke et al. 2016). In this work, we assume an inner cavity to be completely devoid of dust, but this does not need to be the case. If there was a sufficient amount of small grains left in the cavity, this could mask its presence in the SED.
Velocity-resolved line profiles, for example those of the fundamental CO ro-vibrational transitions at 4.7 µm, could provide a better measure of the inner gas radius (e.g., Brown et al. 2013; Banzatti et al. 2022). This could be obtained with the VLT CRIRES+ or the Keck NIRSPEC spectrographs. Such data exist for many disks, but not yet for most CO2-rich sources. Finally, one could attempt to resolve the inner dust disk directly through IR interferometric observations with, for example, VLTI GRAVITY at 2 µm or MATISSE in the L, M and N bands (see, e.g., Varga et al. 2021; Bohn et al. 2022; GRAVITY Collaboration 2021). In this case, however, the distinction between an inner cavity (no inner disk present) and an inner gap (with inner disk present) may not be clear. Additionally, this technique may be limited to the brightest sources due to the limited sensitivity of these instruments.
4.3 Comparison to observations
Having determined the relative CO2/H2O fluxes in our models, we can compare them to some disks recently observed with JWST-MIRI as part of the MINDS program. For four sources, the integrated fluxes of the H2O 12.40, 15.17, and 17.22 µm line complexes, as well as the 12CO2 Q-branch, are calculated and their ratios are presented as vertical colored lines in Fig. 8. Two of these sources are clearly H2O-rich: DR Tau (Temmink et al., in prep.; see also Salyk et al. 2008) and Sz 98 (Gasman et al. 2023; see also van Dishoeck et al. 2023; Kamp et al. 2023). The other two are clearly CO2-rich: GW Lup (Grant et al. 2023) and CX Tau (Vlasblom et al., in prep.). Plotted as black lines are these same flux ratios calculated from our fiducial grid of models, as presented in Fig. 5. The CO2 /H2O flux ratios of DR Tau and Sz 98 are roughly in line with our H2O-dominated models, those that have no or only a small cavity. The flux ratios of GW Lup and CX Tau are even larger than those of our CO2-dominated models, indicating that these sources have even fainter H2O emission than what our models predict. This could be an indication that an additional explanation beyond just the presence of a cavity may be needed for these high flux ratios (see Sect. 4.4). Still, it is clear that GW Lup and CX Tau are the best candidates for having a small, inner cavity.
GW Lup is an M1.5 star at a distance of 155 pc with a luminosity of L* = 0.33 L⊙ that has been observed as part of the DSHARP program (see Alcalá et al. 2017; Andrews et al. 2018). Its dust disk is rather extended with an outer radius of ~ 120 AU in mm continuum and its radial intensity profile does not show a decrease toward the center, which would hint at the possible presence of a dust cavity (Huang et al. 2018). Of all of the sources presented in the DSHARP survey, there are a few sources that do show a decrease in intensity toward the center of their disks, however from their radial intensity profiles we can estimate these possible cavities or gaps to be roughly 10 AU in radius. Since GW Lup has a stellar luminosity roughly consistent with the two lowest-luminosity grids presented in this work, we can estimate that it would need a cavity of approximately 3 AU in size to explain its bright CO2 emission. Such a cavity would likely not be visible at the distance GW Lup is located, even at DSHARP resolution. Instead, velocity-resolved CO data or VLTI observations could provide further insights.
CX Tau is an M2.5 star at a distance of 128 pc with a luminosity of L* = 0.22 L⊙ (Herczeg & Hillenbrand 2014). Its dust disk is very compact, having a 68% dust radius of only ~15 AU. Its gas disk, on the other hand, is much more extended (~75 AU), strongly pointing to radial drift being an important mechanism in this disk (Facchini et al. 2019). CX Tau was observed with Spit𝓏er (see Najita et al. 2007; Furlan et al. 2011) and though its molecular features were never analyzed in detail, it can certainly be classified as a CO2-only source. Following our modeling, a cavity of roughly 2 AU in radius could explain its high CO2 flux. Interestingly, this source has been classified as a transition disk in the past based on its lack of near-IR excess, though this classification does not hold when considering color criteria (compare Najita et al. 2007 and Furlan et al. 2011). However, high-resolution ALMA data (taken at the same resolution as the DSHARP program) do not show any signs of an inner cavity. Analysis by Facchini et al. (2019) shows that, when adding a parameter Rtrunc to their fit of the disk’s intensity profile within which the dust continuum intensity is set to zero, an upper limit of Rtrunc = 0.54 AU encloses 95% of their MC realizations. As such, it is unlikely that the disk has an inner cavity much larger than this. From our models, we can conclude that such a cavity would not be enough to explain the high CO2 flux and relatively low H2O flux.
 |
Fig. 8 Ratio of the 12CO2 Q-branch flux and the fluxes of the 12.40, 15.17, and 17.22 µm H2O line complexes from our fiducial grid of models, plotted as a function of cavity size, shown with dashed, dotted and solid black lines, respectively. Vertical colored lines, with bars indicating the uncertainty, indicate the same CO2 /H2O flux ratios calculated for JWST-MIRI observations of GW Lup (Grant et al. 2023), Sz 98 (Gasman et al. 2023), DR Tau (Temmink et al., in prep.), and CX Tau (Vlasblom et al., in prep.), all taken as a part of the MINDS program. |
4.4 Alternative scenarios
So far, we have tested the effects of a deep cavity in the gas and dust on the H2O and CO2 spectra of a T Tauri disk, and we have also tested the influence of the stellar luminosity on this scenario. Naturally, there are many other parameters or variations to be made that could be interesting for further study. Here we discuss three of them, and we present a few additional models to provide a quick insight into these scenarios, though we leave a thorough investigation for future work.
4.4.1 Gas and dust inside the cavity
All of the models presented here so far consider a cavity that is fully depleted in both gas and dust. However, this is not necessarily representative for all disks, since their stars are often still accreting at a decent rate. It is possible for some amount of gas and dust to still be flowing through the cavity, or there may still be a small inner disk present. Observations of many transitional disks show that gas is present inside large dust cavities (see, e.g., van der Marel et al. 2015, 2016), at various levels of depletion, and small inner disks have been found inside the large cavities as well (Francis & van der Marel 2020).
Naturally, if the cavity is not fully depleted in gas, this may contribute to the spectrum. To understand how this could impact our results, we examine each of these two scenarios with six additional models. All of these models contain a 5 AU cavity, since this model shows a spectrum that is dominated by a bright CO2 Q-branch in our fiducial grid. As such, this helps us quantify how much gas and dust inside the cavity is needed to impact our results. We create three models in which some gas and dust are present over the full extent of the cavity, depleted by factors of 103,104, and 105 with respect to the outer disk. We also create three models in which a small inner disk is present out to 0.5 AU, and the rest of the cavity is empty. This inner disk is then also depleted in gas and dust by the same factors with respect to the outer disk.
In Fig. 9, we show the H2 column density as a function of disk radius for these six additional models. The models with an 0.5 AU inner disk are indicated using solid lines and the models with gas inside the entire extent of the cavity are indicated using dashed lines. To understand what level of gas depletion in the inner disk could be considered realistic, we can compare our models to the work of Leemker et al. (2022). They find an upper limit on the total hydrogen column density NH ~ 1022 cm−2 inside the cavity of LkCa15, consistent with the finding of ~1021 cm−2 from Salyk et al. (2009). Looking at studies from, for example, Salyk et al. (2009) and Brown et al. (2013), who derive the CO column density in the inner disk, it is seen that total hydrogen columns of 1021–23 cm−2 are common. This corresponds best to our models with depletion factors of 104 and 105.
The spectra generated for these six models, compared with the fiducial model with a 5 AU cavity, are presented in Fig. 10. The three models with gas and dust inside the entire cavity are (including the fiducial model) are shown in the left column, and the three models with an 0.5 AU inner disk (plus fiducial model) are shown in the right column. This figure shows that, if enough gas and dust is present inside the cavity, this can indeed start to impact our results. For depletion factors of 103 and less, the gas inside the cavity contributes significantly to the spectrum. This enhances the H2O emission with respect to the CO2, since this gas is hot enough to contain abundant H2O. Depletion factors larger than 104 are needed for the contribution from the gas inside the cavity to be negligible and for most of the emission to originate from outside of the cavity. So, we can see from these tests that the cavity needs to be sufficiently depleted of gas and dust for our previous results to hold. The necessary depletion factors are consistent with a typical amount of gas in the inner disk, following, for example, Salyk et al. (2009), Brown et al. (2013), and Leemker et al. (2022).
The gas and dust are depleted by equal factors in the models previously shown, but one could also envision a scenario in which the cavity contains significantly more gas than dust (for example due to the dust being locked up in larger bodies). In this case, the gas temperature inside the cavity will rise significantly (see, e.g., Leemker et al. 2022), making the molecular emission brighter. We do not expect this to significantly affect the CO2 /H2O ratio, however, since the emission from both molecules will likely be boosted by roughly equal amounts.
 |
Fig. 9 H2 column density, integrated until τdust = 1 at 15 µm, as a function of disk radius for the models with an 0.5 AU inner disk (solid lines) and gas inside a 5 AU cavity (dashed lines). The models with depletion factors of 103, 104, and 105 are indicated with green, blue, and black lines, respectively. |
4.4.2 Effect of the gas-to-dust ratio
It is well known that the amount of small grains in the upper layers of the disk can also have a significant effect on the observed mid-IR fluxes. It was shown by Meijerink et al. (2009) that mid-IR H2O lines observed with Spit𝓏er likely originate from a region where the gas-to-dust ratio is locally increased by 1–2 orders of magnitude compared to the canonical interstellar medium (ISM) value of 100. This is necessary to match the observed line strengths and line-to-continuum ratios of typical sources. We incorporate this into our models by assuming an overall gas-to-dust mass ratio of 100, but we assume that a significant fraction (99.9%) of the dust is large and is settled to the midplane. This leaves the disk atmosphere relatively depleted in dust, and this area will have a gas-to-dust ratio of 105 instead. This yields large line fluxes and high line-to-continuum ratios, which strongly decrease as the amount of dust in the upper layers of the disk increases (see, e.g., Woitke et al. 2018; Greenwood et al. 2019). The CO2-only sources often have weak H2O fluxes, possibly pointing to smaller gas-to-dust ratios in these sources. The CO2/h2O flux ratio may also be impacted by the gas-to-dust ratio, as a larger amount of dust in the disk atmosphere will cool this region more, possibly stimulating the gas-phase formation of CO2 over the formation of H2O.
To provide a preliminary test to this scenario, we present two additional models (based on our fiducial grid) in which we vary the fraction of large grains, fℓ, and thus the gas-to-dust ratio in the upper layers of the disk (see also Sect. 2). The two additional models are full disk models, so they do not have a cavity, and they have fℓ = 0.9 and 0.99 (corresponding to gas-to-dust ratios of 103 and 104 in the upper layers, respectively). The spectra for these models are presented in Fig. 11. This shows that a lower gas-to-dust ratio in the upper layers (fℓ = 0.9) can indeed produce a CO2-dominated spectrum, completely without the need to introduce a cavity into the model. However, one can also see that the absolute flux levels drop significantly (see also Bosman et al. 2017; Woitke et al. 2018). This could provide a diagnostic to test whether a source is more likely to be CO2-dominated due to a small cavity or due to a small gas-to-dust ratio, since the drop in CO2 flux could become too large to be consistent with the latter.
It is likely that the relative evolution of CO2 and H2O line emission with gas-to-dust ratio is an effect of both temperature and chemistry. The effect of the gas-to-dust ratio on the gas temperature is presented in Fig. 12, where the gas temperature is plotted as a function of the CO2 and H2O column densities (solid and dashed lines, respectively) for all three models. This figure clearly shows a decrease in gas temperature in the upper layers of the disk as fℓ, and thus the gas-to-dust ratio, decreases. Since CO2 is preferentially formed over H2O at lower temperatures, this could explain the shift in flux ratio. The lower temperature could also be a cause of the lower absolute flux of both molecules.
Large gas-to-dust ratios in the upper layers of the disk are needed to reproduce mid-IR fluxes (Meijerink et al. 2009; Bosman et al. 2022a), so that may point to a cavity being a better explanation. Still, this scenario is very interesting to consider, especially in relation to disks such as GW Lup and CX Tau, which (as we discuss in Sect. 4.3) show even higher CO2 /H2O flux ratios than this work predicts, yet all of the observational evidence collected so far does not necessarily point to a large-enough cavity being present in these disks. Another interesting example to consider here is IM Lup, a known CO2-only disk as observed by Spit𝓏er (Pontoppidan et al. 2010; Bosman et al. 2017). Bosman et al. (2023) speculate that this disk could have a high abundance of small grains in its upper layers due to strong radial drift and vertical mixing. The authors speculate that this could hide the disks H2O emission behind optically thick dust, yet pumping by IR continuum photons could boost other emission features such as the CO2 Q-branch, providing an alternative explanation as to why this disk is CO2-bright. More in-depth testing is needed to confirm this theory, though it further highlights that a more thorough exploration of the gas-to-dust ratio and how it impacts mid-IR molecular emission is warranted. This will be done in future work.
 |
Fig. 10 Generated H2O, 12CO2, and 13CO2 spectra for the models with gas inside a 5 AU cavity, but no inner disk (left column) or an 0.5 AU inner disk inside a 5 AU, completely empty cavity (right column). The gas and dust inside the cavity or the inner disk are depleted by factors of 103, 104, and 105 (first, second, and third rows respectively). The fourth row shows, in both panels, the fiducial model with a 5 AU cavity, where the cavity is completely empty. The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple, respectively). |
 |
Fig. 11 Generated H2O, 12CO2, and 13CO2 spectra for the models with fℓ = 0.9, 0.99, and 0.999 (the fiducial model). All are full disk models with no cavity present. The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple, respectively). |
 |
Fig. 12 Gas temperature in a vertical cut at 0.3 AU, plotted as a function of CO2 (solid lines) and H2O (dashed lines) column density. This is shown for the full disk models with fℓ = 0.9 (blue), 0.99 (green), and 0.999 (black; the fiducial model). |
4.4.3 A dust trap instead of a cavity
One final alternative scenario that is qualitatively considered here is that of a dust trap with only a small perturbation in the gas surface density. If a dust trap were located between the H2O and CO2 snowlines, this could prevent the flow of H2O-ice-rich pebbles from reaching the disk region inside the H2O snowline, preventing the enhancement of the H2O gas that is formed in situ by sublimation of ices (e.g., Banzatti et al. 2017, 2020). This could lead to the inner regions of the disk becoming relatively depleted in H2O gas, especially if the gas in the inner disk (in which H2O can still form in the gas-phase) is accreted onto the star at a rapid rate. This would not be true for the CO2 gas, since this could be replenished by sublimation of ices. This higher abundance of CO2 compared to H2O in the inner disk could then possibly explain the relatively stronger CO2 emission.
Dust traps and the radial drift of ices can also have some interesting effects on the C/O ratio in the inner regions. Modeling work from Mah et al. (2023) shows that, even without a dust trap present, the C/O ratio in the inner regions of the disk will increase over time due to the inward advection of C-rich gas from beyond the H2O snowline. They also show that this process is significantly faster for low-mass stars, potentially explaining their high observed C/O ratios. Similarly, a dust trap could trap O-rich ices outside the H2O snowline, raising the C/O ratio in the inner regions. If this O-depletion is significant enough, the emission from the inner disk may get a significant contribution from hydrocarbons. The emission from both H2O and CO2 would likely be strongly reduced in such a case. Since CO2 contains two O atoms, and would thus be doubly affected by the O-depletion caused by the dust trap, the dust trap would likely need to be located sufficiently close to the H2O snowline for the emission of CO2 to be stronger than that of H2O. DALI does not take pebble transport into account, but such a scenario could still be modeled with the code by varying the initial abundances of C and O, and thus the C/O ratio, with disk radius. Such an exploration is also left for future work.
5 Conclusions
Some sources observed with Spit𝓏er and JWST show a very high CO2 /H2O flux ratio. In this work, we present DALI thermochemical models to investigate one scenario which may cause this: the presence of a small, inner cavity in the disk that extends beyond the H2O snowline, but not beyond the CO2 snowline. We also test for the effects of stellar luminosity as well as H2O ro-vibrational cooling. Our main results are summarized below.
A spectrum that is H2O-dominated when no cavity is present in the disk can become CO2-dominated by introducing a large-enough cavity into the disk.
The cavity size needed to achieve this is roughly 4–5 AU for our fiducial, L* = 1.4 L⊙ model (vs. 2–3 AU for the L* = 0.2 L⊙ model) and is found to be consistently larger than the nominal midplane CO2 snowline location in a full disk, contrary to our initial hypothesis. As such, the presence of this small, inner cavity could more easily be tested observationally.
The inclusion of H2O ro-vibrational transitions in DALI’s heating and cooling balance creates a small decrease in gas temperature of at most a factor of two in the layer from which H2O emits, which in turn lowers the H2O line fluxes by roughly the same amount. In our models, this local gas temperature change results in the spectrum becoming CO2-dominated whereas it would be H2O-dominated were these transitions not included.
Global temperature changes, such as those caused by a difference in stellar luminosity, do not seem to affect the relative CO2 /H2O flux ratio much, instead impacting both molecules’ fluxes equally.
Comparison with JWST-MIRI data of four T Tauri disks from the MINDS GTO program finds two disks which are clearly H2O-dominated (DR Tau and Sz 98) and two which are clearly CO2-dominated (GW Lup and CX Tau), the latter of which may have a small, inner cavity. The observational evidence for this is so far inconclusive.
If enough gas and dust is still present inside the cavity, this could boost the H2O lines with respect to the CO2. However, for typical inner disk hydrogen column densities, this effect is negligible.
A lower gas-to-dust ratio can also lead to a spectrum becoming CO2-dominated, without the presence of a cavity, though this also causes the absolute line fluxes to drop steeply. A more thorough exploration of this and other possible scenarios will be conducted in future work.
Acknowledgements
We thank the anonymous referee for the constructive comments on the manuscript. We also thank Arthur Bosman for the insightful discussions, Ardjan Sturm for comments on the manuscript, and the MINDS GTO team for providing the MIRI data shown in this work. Astrochemistry in Leiden is supported by funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 101019751 MOLDISK). B.T. is a Laureate of the Paris Region fellowship program, which is supported by the Ile-de-France Region and has received funding under the Horizon 2020 innovation framework program and Marie Sklodowska-Curie grant agreement No. 945298.
Appendix A Including H2O rovibrational cooling
We created an additional grid of models to test the effects of H2O ro-vibrational cooling. As described in Sect. 2, in the second step of DALI’s model creation, the excitation balance of several specified atoms and molecules is calculated. For this purpose, a file specifying all of the molecule’s transitions is supplied. On the Leiden Atomic and Molecular Database, two versions of such a file are available for H2O, one including the molecule’s rovibrational and pure rotational transitions, and one containing only its pure rotational transitions. For the calculation of the fiducial grid (as well as the lower-luminosity grids), only the pure rotational transitions of H2O are considered in DALI’s heating and cooling balance, as is also done in the work by Bosman et al. (2022a,b), on which the fiducial grid is based. For the additional grid presented in this section, the ro-vibrational transitions of H2O are also included. The inclusion of H2O ro-vibrational cooling is the only change made to the models for this additional grid, all other parameters are kept the same. As is shown in Sect. 3.4, this inclusion causes a small, localized decrease in the gas temperature, which in turn translates into a decrease in the H2O line fluxes. All models presented in this work also contain cooling through CO ro-vibrational transitions (vibrational levels v ≤ 2 included, collisional rate coefficients from Yang et al. 2010) and OH pure rotational transitions (collisional rate coefficients from Offer et al. 1994). Cooling through CO2 emission lines is not considered in any of the models.
 |
Fig. A.1 Abundance maps of H2O (first and second columns) and CO2 (third and fourth columns) for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the fiducial grid without H2O ro-vibrational cooling (first and third columns) and the grid with H2O ro-vibrational cooling (second and fourth columns). The H2O and CO2 snowlines (defined as ngas/nice = 1) are indicated with solid light blue and pink lines, respectively. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The yellow contours indicate the region in which 90% of the H2O 113,9 − 100,10 line emission at 17.22 µm (Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
 |
Fig. A.2 Gas temperature map for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the fiducial grid without H2O ro-vibrational cooling (left column) and the grid with H2O ro-vibrational cooling (right column). Temperature contours of 100 and 300 K are indicated with dashed, black lines. The yellow contours indicate the region in which 90% of the H2O 1139 − 10010 line emission at 17.22 µm(Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
 |
Fig. A.3 Generated H2O, 12CO2, and 13CO2 spectra for the fiducial grid without H2O ro-vibrational cooling (left column) and the grid with H2O ro-vibrational cooling (right column). The spectra are shown for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row). The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple respectively). |
 |
Fig. A.4 Integrated fluxes of several H2O (left panel), 12CO2, and 13CO2 (middle and right panels) line complexes plotted as a function of cavity size for grid with H2O ro-vibrational cooling. Properties of these line complexes can be found in Table 2. Nominal H2O and CO2 midplane snowlines in the full disk model are indicated with colored bars. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
 |
Fig. A.5 Ratio of the 12CO2 Q-branch flux and the fluxes of several H2O line complexes, plotted as a function of cavity size for the grid with H2O ro-vibrational cooling. Properties of these line complexes can be found in Table 2. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
Appendix B Lower-luminosity grids
As described in Sect. 1, the stellar luminosity may affect the H2O and CO2 spectra of a disk as well, with disks around lower-luminosity stars being colder and thus potentially having a more CO2-dominated spectrum. Hence, we performed our analysis not just for our fiducial grid of models based on AS 209, but also for three grids with central stars with luminosities of 0.2, 0.4, and 0.8 L⊙. For comparison, the “CO2-only” source GW Lup observed with JWST by Grant et al. (2023) has L* = 0.3 L⊙. For these grids, the input spectra consist of a blackbody at temperatures of 3500, 3750 and 4000 K respectively, all with an additional 10000 K component modeling the UV luminosity generated by accretion (Kama et al. 2016; Visser et al. 2018). The lower luminosity input spectra are generated to have far-ultraviolet (FUV; 911–2067 Å) luminosities of log LFUV/L⊙ = −3.45, −2.92, and −2.62 for the L = 0.2, 0.4, and 0.8 L⊙ grids respectively. This corresponds to a mass accretion rate of log 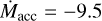 for the lowest luminosity spectrum, whereas for the two higher-luminosity spectra this corresponds to a mass accretion rate of log
for the lowest luminosity spectrum, whereas for the two higher-luminosity spectra this corresponds to a mass accretion rate of log 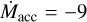 . The dust sublimation radius is located at 0.03, 0.04, and 0.06 AU for the L* = 0.2, 0.4, and 0.8 L⊙ grids respectively.
. The dust sublimation radius is located at 0.03, 0.04, and 0.06 AU for the L* = 0.2, 0.4, and 0.8 L⊙ grids respectively.
 |
Fig. B.1 Abundance maps of H2O for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the grids with an input stellar spectrum with L* = 0.2 L⊙ (first column), L* = 0.4 L⊙ (second column), L, = 0.8 L⊙ (third column), and L* = 1.4 L⊙ (the fiducial grid, fourth column). The H2O snowline (defined as ngas/nice = 1) is indicated with a solid light blue line. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The yellow contours indicate the region in which 90% of the H2O 113,9 − 100,10 line emission at 17.22 µm (Eup = 2438 K) originates. |
 |
Fig. B.2 Abundance maps of CO2 for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the grids with an input stellar spectrum with L* = 0.2 L⊙ (first column), L* = 0.4 L⊙ (second column), L* = 0.8 L⊙ (third column), and L* = 1.4 L⊙ (the fiducial grid, fourth column). The CO2 snowline (defined as ngas/nice = 1) is indicated with a solid light pink line. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
 |
Fig. B.3 Gas temperature maps for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the grids with an input stellar spectrum with L* = 0.2 L⊙ (first column), L* = 0.4 L⊙ (second column), L* = 0.8 L⊙ (third column), and L* = 1.4 L⊙ (the fiducial grid, fourth column). Temperature contours of 100 and 300 K are indicated with dashed black lines. The yellow contours indicate the region in which 90% of the H2O 1139 − 10010 line emission at 17.22 µm (Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
 |
Fig. B.4 Generated H2O, 12CO2, and 13CO2 spectra for the grids with L* = 0.2, 0.4, and 0.8 L⊙. The spectra are shown for the models with no cavity (top row), a 1 AU cavity (middle row), and a 2 AU, 3 AU, or 4 AU cavity (cavity size at which the spectrum becomes CO2-dominated, bottom row, left, middle, and right panels respectively). The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple respectively). Note that the scaling on the y-axis is different for each column. |
 |
Fig. B.5 Integrated fluxes of several H2O (left panel), 12CO2, and 13CO2 (middle and right panels) line complexes plotted as a function of cavity size for the grids with input spectra with L* = 0.2, 0.4,0.8 L⊙. Properties of these line complexes can be found in Table 2. Nominal H2O and CO2 midplane snowlines in the full disk model are indicated with colored bars. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
 |
Fig. B.6 Ratio of the 12CO2 Q-branch flux and the fluxes of several H2O line complexes, plotted as a function of cavity size for the models with input spectra with L* = 0.2, 0.4, 0.8 L⊙. Note the different vertical scales of these panels. Properties of these lines can be found in Table 2. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
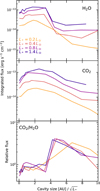 |
Fig. B.7 Flux of the 17.22 µm H2O line complex (top), the CO2 Q-branch (middle), and their ratio (bottom) for the grids with L* = 0.2, 0.4, 0.8, and 1.4 L⊙, plotted as a function of cavity size scaled with |
References
- Ádámkovics, M., Glassgold, A. E., & Najita, J. R. 2014, ApJ, 786, 135 [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Goicoechea, J. R. 2008, A&A, 483, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aikawa, Y., Umebayashi, T., Nakano, T., & Miyama, S. M. 1997, ApJ, 486, L51 [Google Scholar]
- Alcalá, J. M., Manara, C. F., Natta, A., et al. 2017, A&A, 600, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D., Scragg, T., & Simpson, C. 1980, Chem. Phys., 51, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. E., Blake, G. A., Cleeves, L. I., et al. 2021, ApJ, 909, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Antonellini, S., Kamp, I., Lahuis, F., et al. 2016, A&A, 585, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arabhavi, A. M., Kamp, I., & Henning, T. 2023, Science, submitted [Google Scholar]
- Banzatti, A., Pontoppidan, K. M., Salyk, C., et al. 2017, ApJ, 834, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Pascucci, I., Bosman, A. D., et al. 2020, ApJ, 903, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Abernathy, K. M., Brittain, S., et al. 2022, AJ, 163, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Barber, R. J., Tennyson, J., Harris, G. J., & Tolchenov, R. N. 2006, MNRAS, 368, 1087 [Google Scholar]
- Baulch, D., Cobos, C., Cox, R., et al. 1992, J. Phys. Chem. Ref. Data, 21, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Bethell, T., & Bergin, E. 2009, Science, 326, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Bohn, A. J., Benisty, M., Perraut, K., et al. 2022, A&A, 658, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosman, A. D., Bruderer, S., & van Dishoeck, E. F. 2017, A&A, 601, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosman, A. D., Bergin, E. A., Calahan, J., & Duval, S. E. 2022a, ApJ, 930, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Bosman, A. D., Bergin, E. A., Calahan, J. K., & Duval, S. E. 2022b, ApJ, 933, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Bosman, A. D., Appelgren, J., Bergin, E. A., Lambrechts, M., & Johansen, A. 2023, ApJ, 944, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Pontoppidan, K. M., van Dishoeck, E. F., et al. 2013, ApJ, 770, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S. 2013, A&A, 559, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A&A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carr, J. S., & Najita, J. R. 2008, Science, 319, 1504 [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2002, ApJ, 575, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B. 1997, ApJ, 481, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Du, F., & Bergin, E. A. 2014, ApJ, 792, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Facchini, S., van Dishoeck, E. F., Manara, C. F., et al. 2019, A&A, 626, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., & Josselin, E. 2008, A&A, 492, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Francis, L., & van der Marel, N. 2020, ApJ, 892, 111 [Google Scholar]
- Furlan, E., Luhman, K. L., Espaillat, C., et al. 2011, ApJS, 195, 3 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gardner, J. P., Mather, J. C., Abbott, R., et al. 2023, PASP, 135, 068001 [NASA ADS] [CrossRef] [Google Scholar]
- Gasman, D., van Dishoeck, E. F., Grant, S. L., et al. 2023, A&A, 679, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassgold, A. E., & Najita, J. R. 2015, ApJ, 810, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Meijerink, R., & Najita, J. R. 2009, ApJ, 701, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, S. L., van Dishoeck, E. F., Tabone, B., et al. 2023, ApJ, 947, L6 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Sanchez-Bermudez, J., et al.) 2021, A&A, 654, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenwood, A. J., Kamp, I., Waters, L. B. F. M., Woitke, P., & Thi, W. F. 2019, A&A, 631, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [Google Scholar]
- Huang, J., Andrews, S. M., Dullemond, C. P., et al. 2018, ApJ, 869, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, R., Pettipiece, K., & Thomas, S. 1975, Phys. Rev. A, 11, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Kama, M., Bruderer, S., van Dishoeck, E. F., et al. 2016, A&A, 592, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., Henning, T., Arabhavi, A., et al. 2023, Faraday Discuss., 245, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Leemker, M., Booth, A. S., van Dishoeck, E. F., et al. 2022, A&A, 663, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Mah, J., Bitsch, B., Pascucci, I., & Henning, T. 2023, A&A, 677, L7 [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Meijerink, R., Pontoppidan, K. M., Blake, G. A., Poelman, D. R., & Dullemond, C. P. 2009, ApJ, 704, 1471 [Google Scholar]
- Miotello, A., Bruderer, S., & van Dishoeck, E. F. 2014, A&A, 572, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miotello, A., van Dishoeck, E. F., Kama, M., & Bruderer, S. 2016, A&A, 594, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Lunine, J. I., O’Brien, D. P., Raymond, S. N., & Walsh, K. J. 2012, Ann. Rev. Earth Planet. Sci., 40, 251 [Google Scholar]
- Najita, J. R., Strom, S. E., & Muzerolle, J. 2007, MNRAS, 378, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Ádámkovics, M., & Glassgold, A. E. 2011, ApJ, 743, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Nevdakh, V. V., Orlov, L. N., & Leshenyuk, N. S. 2003, J. Appl. Spectrosc., 70, 276 [CrossRef] [Google Scholar]
- Offer, A. R., van Hemert, M. C., & van Dishoeck, E. F. 1994, J. Chem. Phys., 100, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Herczeg, G., Carr, J. S., & Bruderer, S. 2013, ApJ, 779, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Blake, G. A., et al. 2010, ApJ, 720, 887 [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Bergin, E. A., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 363 [Google Scholar]
- Rieke, G. H., Ressler, M. E., Morrison, J. E., et al. 2015, PASP, 127, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J., Perrin, M., McElwain, M., et al. 2023, PASP, 135, 048001 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L., Gordon, I., Babikov, Y., et al. 2013, J. Quant. Spectrosc. Radiat. Transf., 130, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., et al. 2008, ApJ, 676, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2009, ApJ, 699, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., Najita, J. R., & Carr, J. S. 2011, ApJ, 731, 130 [Google Scholar]
- Sandford, S. A., & Allamandola, L. J. 1993, ApJ, 417, 815 [CrossRef] [Google Scholar]
- Tabone, B., Bettoni, G., van Dishoeck, E. F., et al. 2023a, Nat. Astron., 7, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Tabone, B., van Dishoeck, E. F., & Black, J. H. 2023b, A&A, submitted [Google Scholar]
- Tennyson, J., Zobov, N. F., Williamson, R., Polyansky, O. L., & Bernath, P. F. 2001, J. Phys. Chem. Ref. Data, 30, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Thi, W. F., Hocuk, S., Kamp, I., et al. 2020, A&A, 634, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., Pérez, L., & Isella, A. 2015, A&A, 579, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2016, A&A, 585, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [Google Scholar]
- van Dishoeck, E. F., Grant, S., Tabone, B., et al. 2023, Faraday Discuss., 245, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Varga, J., Hogerheijde, M., van Boekel, R., et al. 2021, A&A, 647, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., Bruderer, S., Cazzoletti, P., et al. 2018, A&A, 615, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Bron, E., Cazaux, S., et al. 2017, Mol. Astrophys., 9, 1 [Google Scholar]
- Walsh, C., Millar, T. J., & Nomura, H. 2010, ApJ, 722, 1607 [Google Scholar]
- Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. F. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A&A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Thi, W. F., et al. 2018, A&A, 618, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, G. S., Wright, D., Goodson, G. B., et al. 2015, PASP, 127, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, G. S., Rieke, G. H., Glasse, A., et al. 2023, PASP, 135, 048003 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [Google Scholar]
- Zhang, K., Booth, A. S., Law, C. J., et al. 2021, ApJS, 257, 5 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Cartoon illustrating the scenario that is tested in this work. On the top, a full disk is shown, leading to an observed spectrum with bright H2O lines (illustrated in blue) and a relatively weaker 15 µm CO2 feature (illustrated in green). On the bottom, a disk with a small inner cavity is illustrated. This could, for example, be carved by a companion. The cavity extends beyond the H2O snowline but not beyond the CO2 snowline, leading to an observed spectrum that shows a bright CO2 feature and relatively weak H2O lines. The values given for the locations of the H2O and CO2 snowlines are the midplane snowline locations of our fiducial, L* = 1.4 L⊙ full disk model based on AS 209. |
| In the text | |
 |
Fig. 2 Abundance maps of H2O (left column) and CO2 (middle column) for the models with no cavity (top row), a 1 AU cavity (middle row) and a 5 AU cavity (bottom row). The H2O and CO2 snowlines (defined as ngas/nice = 1) are indicated with solid light blue and pink lines, respectively. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The right column shows the gas temperature, with dashed black lines indicating 100 and 300 K. The yellow contours indicate the region in which 90% of the H2O 113,9 − 100,1o line emission at 17.22 µm (Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 v2 = 1 − 0 Q(20) line emission (Eup = 1196 K). |
| In the text | |
 |
Fig. 3 Generated H2O, 12CO2 and 13CO2 spectra for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row). The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple respectively). |
| In the text | |
 |
Fig. 4 Integrated fluxes of several H2O (left panel), 12CO2, and 13CO2 (middle and right panels) line complexes plotted as a function of cavity size. Properties of these line complexes can be found in Table 2. Nominal H2O and CO2 midplane snowlines in the full disk model are indicated with colored bars. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
| In the text | |
 |
Fig. 5 Ratio of the 12CO2 Q-branch flux and the fluxes of several H2O line complexes, plotted as a function of cavity size. Properties of these line complexes can be found in Table 2. |
| In the text | |
 |
Fig. 6 Gas and dust temperatures (solid and dashed lines, respectively) as a function of height in the disk Z/R for the models with and without H2O ro-vibrational cooling, indicated in black and red, respectively. Both are full disk models without a cavity. The height in the disk at which H2O emits is indicated in gray. The vertical cut through the disk is taken at a distance of 0.3 AU. |
| In the text | |
 |
Fig. 7 Flux of the 17.22 µm H2O line complex (top), the CO2 Q-branch (middle), and their ratio (bottom) for the grids with L* = 0.2, 0.4, 0.8, and 1.4 L⊙. |
| In the text | |
 |
Fig. 8 Ratio of the 12CO2 Q-branch flux and the fluxes of the 12.40, 15.17, and 17.22 µm H2O line complexes from our fiducial grid of models, plotted as a function of cavity size, shown with dashed, dotted and solid black lines, respectively. Vertical colored lines, with bars indicating the uncertainty, indicate the same CO2 /H2O flux ratios calculated for JWST-MIRI observations of GW Lup (Grant et al. 2023), Sz 98 (Gasman et al. 2023), DR Tau (Temmink et al., in prep.), and CX Tau (Vlasblom et al., in prep.), all taken as a part of the MINDS program. |
| In the text | |
 |
Fig. 9 H2 column density, integrated until τdust = 1 at 15 µm, as a function of disk radius for the models with an 0.5 AU inner disk (solid lines) and gas inside a 5 AU cavity (dashed lines). The models with depletion factors of 103, 104, and 105 are indicated with green, blue, and black lines, respectively. |
| In the text | |
 |
Fig. 10 Generated H2O, 12CO2, and 13CO2 spectra for the models with gas inside a 5 AU cavity, but no inner disk (left column) or an 0.5 AU inner disk inside a 5 AU, completely empty cavity (right column). The gas and dust inside the cavity or the inner disk are depleted by factors of 103, 104, and 105 (first, second, and third rows respectively). The fourth row shows, in both panels, the fiducial model with a 5 AU cavity, where the cavity is completely empty. The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple, respectively). |
| In the text | |
 |
Fig. 11 Generated H2O, 12CO2, and 13CO2 spectra for the models with fℓ = 0.9, 0.99, and 0.999 (the fiducial model). All are full disk models with no cavity present. The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple, respectively). |
| In the text | |
 |
Fig. 12 Gas temperature in a vertical cut at 0.3 AU, plotted as a function of CO2 (solid lines) and H2O (dashed lines) column density. This is shown for the full disk models with fℓ = 0.9 (blue), 0.99 (green), and 0.999 (black; the fiducial model). |
| In the text | |
 |
Fig. A.1 Abundance maps of H2O (first and second columns) and CO2 (third and fourth columns) for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the fiducial grid without H2O ro-vibrational cooling (first and third columns) and the grid with H2O ro-vibrational cooling (second and fourth columns). The H2O and CO2 snowlines (defined as ngas/nice = 1) are indicated with solid light blue and pink lines, respectively. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The yellow contours indicate the region in which 90% of the H2O 113,9 − 100,10 line emission at 17.22 µm (Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
| In the text | |
 |
Fig. A.2 Gas temperature map for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the fiducial grid without H2O ro-vibrational cooling (left column) and the grid with H2O ro-vibrational cooling (right column). Temperature contours of 100 and 300 K are indicated with dashed, black lines. The yellow contours indicate the region in which 90% of the H2O 1139 − 10010 line emission at 17.22 µm(Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
| In the text | |
 |
Fig. A.3 Generated H2O, 12CO2, and 13CO2 spectra for the fiducial grid without H2O ro-vibrational cooling (left column) and the grid with H2O ro-vibrational cooling (right column). The spectra are shown for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row). The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple respectively). |
| In the text | |
 |
Fig. A.4 Integrated fluxes of several H2O (left panel), 12CO2, and 13CO2 (middle and right panels) line complexes plotted as a function of cavity size for grid with H2O ro-vibrational cooling. Properties of these line complexes can be found in Table 2. Nominal H2O and CO2 midplane snowlines in the full disk model are indicated with colored bars. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
| In the text | |
 |
Fig. A.5 Ratio of the 12CO2 Q-branch flux and the fluxes of several H2O line complexes, plotted as a function of cavity size for the grid with H2O ro-vibrational cooling. Properties of these line complexes can be found in Table 2. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
| In the text | |
 |
Fig. B.1 Abundance maps of H2O for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the grids with an input stellar spectrum with L* = 0.2 L⊙ (first column), L* = 0.4 L⊙ (second column), L, = 0.8 L⊙ (third column), and L* = 1.4 L⊙ (the fiducial grid, fourth column). The H2O snowline (defined as ngas/nice = 1) is indicated with a solid light blue line. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The yellow contours indicate the region in which 90% of the H2O 113,9 − 100,10 line emission at 17.22 µm (Eup = 2438 K) originates. |
| In the text | |
 |
Fig. B.2 Abundance maps of CO2 for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the grids with an input stellar spectrum with L* = 0.2 L⊙ (first column), L* = 0.4 L⊙ (second column), L* = 0.8 L⊙ (third column), and L* = 1.4 L⊙ (the fiducial grid, fourth column). The CO2 snowline (defined as ngas/nice = 1) is indicated with a solid light pink line. The dashed, dark blue line shows the dust τ = 1 surface at 15 µm. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
| In the text | |
 |
Fig. B.3 Gas temperature maps for the models with no cavity (top row), a 1 AU cavity (middle row), and a 5 AU cavity (bottom row) for the grids with an input stellar spectrum with L* = 0.2 L⊙ (first column), L* = 0.4 L⊙ (second column), L* = 0.8 L⊙ (third column), and L* = 1.4 L⊙ (the fiducial grid, fourth column). Temperature contours of 100 and 300 K are indicated with dashed black lines. The yellow contours indicate the region in which 90% of the H2O 1139 − 10010 line emission at 17.22 µm (Eup = 2438 K) originates. The red contours indicate the origin of 90% of the CO2 0110 − 0000 Q(20) line emission (Eup = 1196 K). |
| In the text | |
 |
Fig. B.4 Generated H2O, 12CO2, and 13CO2 spectra for the grids with L* = 0.2, 0.4, and 0.8 L⊙. The spectra are shown for the models with no cavity (top row), a 1 AU cavity (middle row), and a 2 AU, 3 AU, or 4 AU cavity (cavity size at which the spectrum becomes CO2-dominated, bottom row, left, middle, and right panels respectively). The vertical colored bars indicate the integration ranges for the H2O 15.17 and 17.22 µm flux (blue), as well as the 12CO2 and 13CO2 Q-branches (green and purple respectively). Note that the scaling on the y-axis is different for each column. |
| In the text | |
 |
Fig. B.5 Integrated fluxes of several H2O (left panel), 12CO2, and 13CO2 (middle and right panels) line complexes plotted as a function of cavity size for the grids with input spectra with L* = 0.2, 0.4,0.8 L⊙. Properties of these line complexes can be found in Table 2. Nominal H2O and CO2 midplane snowlines in the full disk model are indicated with colored bars. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
| In the text | |
 |
Fig. B.6 Ratio of the 12CO2 Q-branch flux and the fluxes of several H2O line complexes, plotted as a function of cavity size for the models with input spectra with L* = 0.2, 0.4, 0.8 L⊙. Note the different vertical scales of these panels. Properties of these lines can be found in Table 2. Data points are connected by dashed lines if the line flux drops below 10−15 erg s−1 cm−2, indicating that the lines will become more difficult to observe. |
| In the text | |
 |
Fig. B.7 Flux of the 17.22 µm H2O line complex (top), the CO2 Q-branch (middle), and their ratio (bottom) for the grids with L* = 0.2, 0.4, 0.8, and 1.4 L⊙, plotted as a function of cavity size scaled with |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.