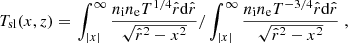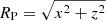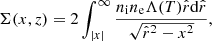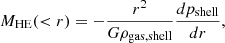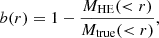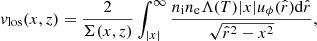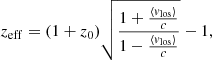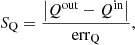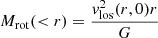| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202347656 | |
| Published online | 31 January 2024 | |
Gas rotation and dark matter halo shape in cool-core clusters of galaxies
1
Dipartimento di Fisica e Astronomia “Augusto Righi” – Alma Mater Studiorum – Università di Bologna, Via Piero Gobetti 93/2, 40129 Bologna, Italy
e-mail: tommaso.bartalesi3@unibo.it
2
INAF, Osservatorio di Astrofisica e Scienza dello Spazio, Via Piero Gobetti 93/3, 40129 Bologna, Italy
e-mail: stefano.ettori@inaf.it
3
INFN, Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
Received:
4
August
2023
Accepted:
24
October
2023
Aims. We study the possibility that the gas in cool-core clusters of galaxies has non-negligible rotation support, the impact of gas rotation on mass estimates from current X-ray observations, and the ability of forthcoming X-ray observatories to detect such rotation.
Methods. We present three representative models of massive cool-core clusters with a rotating intracluster medium (ICM) in equilibrium in cosmologically motivated spherical, oblate, or prolate dark matter halos, represented by physical density–potential pairs. In the models, the gas follows a composite-polytropic distribution, and has rotation velocity profiles consistent with current observational constraints and similar to those found in clusters formed in cosmological simulations. We show that the models are consistent with available measurements of the ICM properties of the massive cluster population: the thermodynamic profiles, the shape of the surface brightness distribution, the hydrostatic mass bias, and the broadening of X-ray emitting lines. Using the configuration for the microcalorimeter onboard the XRISM satellite, we generated a set of mock X-ray spectra for our cluster models, which we then analyzed to make predictions about the rotation speed that will be obtained with such an instrument. We then assessed what fraction of the hydrostatic mass bias of our models could be accounted for by detecting the rotation speed with XRISM spectroscopy over the range (0.1 − 1)r500, sampled with three nonoverlapping pointings.
Results. Current data leave room for rotating ICM in cool-core clusters, with peaks in the rotation speed as high as 600 km s−1. We show that such rotation, if present, will be detected with upcoming X-ray facilities such as XRISM and that 60 − 70% of the hydrostatic mass bias due to rotation can be accounted for using the line-of-sight velocity measured from X-ray spectroscopy with XRISM, with a residual bias smaller than 3% at an overdensity of 500. In this way, XRISM will allow us to pin down any mass bias of a different origin from the rotation.
Key words: galaxies: clusters: general / galaxies: clusters: intracluster medium / dark matter / X-rays: galaxies / X-rays: galaxies: clusters
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Accurately estimating the mass of galaxy clusters is crucial to understanding the formation and evolution of cosmic structures and to constraining the parameters that define the cosmological background (see Pratt et al. 2019 for a review). Clusters of galaxies are permeated by a hot (∼107 − 108 K), rarefied (∼10−2 − 10−4 particles per cm3), optically thin, gaseous component known as the intracluster medium (ICM), which emits X-rays via thermal Bremsstrahlung and emission lines from collisional excitation of the inner shell electrons of heavy metals. Assuming that the ICM is in hydrostatic equilibrium, X-ray observations can thus be used to infer the mass of galaxy clusters (see Ettori et al. 2013 for a review). Mass estimates obtained in this way can be very precise but inaccurate (e.g., Ettori et al. 2019), given that the hydrostatic equilibrium does not account for the residual non-thermalized (kinetic) energy in the ICM (see e.g., Rasia et al. 2006; Piffaretti & Valdarnini 2008; Lau et al. 2009, 2013; Suto et al. 2013; Biffi et al. 2016; Angelinelli et al. 2020; Gianfagna et al. 2021). This effect that brings hydrostatic masses to underestimate the “true” mass is often referred to as hydrostatic mass bias. Measurements of this bias can be obtained by comparison with more direct mass estimators (e.g., Zhang et al. 2010; Mahdavi et al. 2013; Lovisari et al. 2020). In particular, being the most massive gravitationally bound structures in the Universe, galaxy clusters are effective gravitational lenses that provide a complementary and typically more accurate method of inferring the total (i.e., baryon plus dark matter (DM)) mass (see e.g., Meneghetti et al. 2010; Rasia et al. 2012). Alternatively, the dynamical mass of a cluster can be estimated by exploiting measurements of the orbital velocities of its member galaxies (see e.g., Ferragamo et al. 2021).
Even though in the X-ray observations the gas clumpiness, the temperature distribution, and the use of the spectroscopic measurements in reconstructing the thermal properties of the ICM can contribute non-negligibly to the hydrostatic mass bias (see e.g., Rasia et al. 2006; Roncarelli et al. 2013; Pearce et al. 2020; Towler et al. 2023), most of this bias is expected to be due to the motions in the ICM: in particular, turbulence bulk motion, and rotation (see e.g., Nagai et al. 2007b; Nelson et al. 2014; Biffi et al. 2016; Angelinelli et al. 2020). Most of these previous works have focused on the relative importance of bulk and random motions for the total budget of the hydrostatic mass bias, with only a few studies dedicated to the contribution from the ICM rotational support (e.g., Fang et al. 2009). There are essentially only two direct ways of measuring gas rotation in galaxy clusters: the rotational kinetic Sunyaev–Zeldovich effect (Cooray & Chen 2002, Chluba & Mannheim 2002 and also Sunyaev & Zeldovich 1980; see Baldi et al. 2018 and Altamura et al. 2023b for future perspectives) and the Doppler shift of the centroids of the X-ray emitting lines or their Doppler broadening. The latter measurements require X-ray spectrometers at high-energy resolutions (ΔE ≲ 10 eV at E ≈ 6 − 7 keV is required to detect a line-of-sight (LOS) speed of ≈500 km s−1; e.g., Sunyaev et al. 2003; Bianconi et al. 2013), which are thus far reached only by a calorimeter on board the International X-ray Astronomy Mission ASTRO-H/Hitomi1 satellite (see Hitomi Collaboration 2016 for its results). The loss of Hitomi has prevented us from depicting a comprehensive overview of the kinematics of the ICM; however, the forthcoming microcalorimeter Resolve on board the X-Ray Imaging and Spectroscopy Mission2 (XRISM) satellite (with ΔE ≃ 7 eV FWHM at E = 6 − 7 keV), launched in September 2023, is expected to provide some key elements that will improve our understanding of the ICM kinematics. Nowadays, only upper limits on the velocity broadening of X-ray emitting lines are available: using X-ray Multi-Mirror Mission3 (XMM-Newton) reflection grating spectrometer (RGS) data, Pinto et al. (2015) find, in most cool cores of clusters, groups, and massive elliptical galaxies in their observed sample, broadening velocities of ≈500 km s−1 (see also Sanders et al. 2011 and Bambic et al. 2018). Even though some objects have higher upper limits (of ≈1000 km s−1), we interpret 500 km s−1 as the current upper limit on the rotation speed of the ICM in typical clusters, which leaves open the possibility that the ICM has non-negligible rotation support in relaxed clusters4.
In the cosmological context, the rotation of both DM and gas is expected to be induced primarily by the large-scale processes involving the entire cluster (such as tidal torques from neighbouring overdensities; Peebles 1969). In massive clusters (virial masses ≳5 × 1014 M⊙) formed in cosmological N-body hydrodynamical non-radiative simulations, Baldi et al. (2017) have found that the rotation support of the ICM tends to be higher than that of the DM, with values of the gas spin parameter on average 13% higher than those of the halo spin parameter. In principle, the rotation support of the ICM can be further enhanced by unimpeded radiative cooling, because of conservation of angular momentum (see e.g., Kley & Mathews 1995), but in real clusters heating mechanisms are also at work. In fact, including radiative cooling, active galactic nucleus (AGN) and stellar feedback models in cosmological simulations, Baldi et al. (2017) have found that the rotation support of the ICM is similar to that found in non-radiative simulations.
Based on the properties of the ICM in the central regions, clusters of galaxies are classified as cool-core and non-cool-core clusters (e.g., Sect. 6.4.3 of Cimatti et al. 2019). Given that we are interested in rotation support of the ICM, in this work we focus on cool-core clusters, which tend to be relaxed (e.g., Pratt et al. 2010; Mahdavi et al. 2013) and thus good targets for symmetric equilibrium models of the ICM. By definition, cool-core clusters are characterized by lower central ICM entropy, which is broadly interpreted as a signature of cooling. In fact, the measured values of the central entropy are much higher than predicted in a standard cooling-flow model (e.g., McDonald et al. 2013). This suggests that, in a time-averaged sense, over ∼10 Gyr, radiative cooling is balanced by some form of heating, a picture also supported by the fact that radiative cosmological simulations without heating suffer from the “overcooling” problem, which produces photometric features inconsistent with observations (e.g., Fang et al. 2009; Lau et al. 2011, 2012; Nagai et al. 2013). There is a growing consensus that AGN feedback provides the dominant heating contribution in the inner cluster regions (see McNamara & Nulsen 2012; Hlavacek-Larrondo et al. 2022 for reviews and Nobels et al. 2022; Huško et al. 2022 for recent results). However, it must be stressed that modeling the complex interplay of heating and cooling is also challenging for state-of-the-art simulations. For instance, clusters formed in currently available cosmological simulations including an AGN feedback model can suffer from the “entropy-core” problem, in the sense that their inner entropy profiles do not match those observed in real clusters (Altamura et al. 2023a).
The rotation of the ICM could also be relevant to the energy balance of cool cores, given that the ICM is known to be weakly magnetized. If the magnetized, rotating ICM is unstable to the magnetorotational instability (Balbus & Hawley 1991), the nonlinear evolution of the instability will lead to turbulent heating, which could contribute to offsetting the radiative cooling of the ICM and to halting the cooling flows, lending a hand to the AGN feedback (see Nipoti & Posti 2014; Nipoti et al. 2015).
In this work, we propose three models representative of typical, nearby, massive cool-core clusters, with cosmologically motivated dark halos of different shapes (Sect. 2) and a rotating ICM with a rotation speed consistent with observed upper limits (Sect. 3). In Sect. 4, we compare the intrinsic and observable properties of the ICM in our cluster models to the observational data of real galaxy clusters. In Sect. 5, we assess the detectability of the rotation support of our models, building mock X-ray spectra of the rotating ICM in our cluster models, and using the configurations for Resolve. Section 6 concludes.
Throughout this article, when using the Hubble parameter H(z) = H0E1/2(z), where 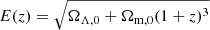 , we assume Ωm, 0 = 0.3, ΩΛ, 0 = 0.7, and Hubble constant H0 = 70 km s−1 Mpc−1.
, we assume Ωm, 0 = 0.3, ΩΛ, 0 = 0.7, and Hubble constant H0 = 70 km s−1 Mpc−1.
2. Dark matter halo models
We introduce here the gravitational potentials that we used to build our cluster models. Given that the mass content of clusters is dominated by the DM, these gravitational potentials must be essentially representative of those produced by the cluster DM halos.
Cosmological N-body DM-only simulations predict for most halos an aspherical shape, set at the time of the last major merger (Allgood et al. 2006). In general, the angle-averaged density profile of these simulated halos is well fitted by the Navarro–Frenk–White (NFW; Navarro et al. 1996) profile
where r is the distance from the halo center, ρn is a characteristic density, and rs is the scale radius. The density distribution of DM in real clusters is also well represented by this profile: for instance, from X-ray and Sunyaev-Zeldovich effect observations, Ettori et al. (2019) infer that the NFW profile successfully models the angle-averaged density profiles of the halos of the observed clusters. It is thus natural to take the NFW density profile (Eq. (1)) as a reference for building realistic flattened halo models. In the following sections we describe how we build axisymmetric halo models by suitably modifying the spherical NFW model.
2.1. Flattened NFW density–potential pairs
Ciotti & Bertin (2005) presented a technique for constructing analytic axisymmetric and triaxial density–potential pairs by modifying a parent spherical density distribution with the given density profile 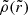 , where
, where 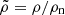 and
and 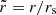 , with ρn a characteristic density and rs a scale radius. The generic density–potential pair of this family can be written in Cartesian coordinates (x, y, z) as
, with ρn a characteristic density and rs a scale radius. The generic density–potential pair of this family can be written in Cartesian coordinates (x, y, z) as
where 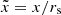 ,
, 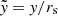 ,
, 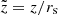 ,
, 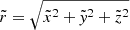 , and
, and 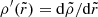 , and
, and
where 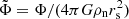 , Φ is the gravitational potential, and
, Φ is the gravitational potential, and 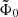 ,
, 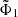 , and
, and 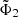 are functions depending on
are functions depending on 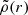 , whose definitions can be found in Ciotti & Bertin (2005). Here ϵ > 0 and η > 0 are dimensionless parameters that must be such that
, whose definitions can be found in Ciotti & Bertin (2005). Here ϵ > 0 and η > 0 are dimensionless parameters that must be such that 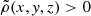 everywhere. We note that, though constructed exploiting the technique of the homeoidal expansion, the density–potential pairs given by the above formulae do not require ϵ and η to be much smaller than unity (see Sect. 2 of Ciotti & Bertin 2005).
everywhere. We note that, though constructed exploiting the technique of the homeoidal expansion, the density–potential pairs given by the above formulae do not require ϵ and η to be much smaller than unity (see Sect. 2 of Ciotti & Bertin 2005).
Here, we assumed as a parent spherical density profile the NFW model (Eq. (1)), which in dimensionless form reads
Using Eq. (4) as 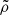 , Eq. (2) becomes
, Eq. (2) becomes
The dimensionless gravitational potential generated by the density profile Eq. (5) is given by Eq. (3), where
and
The second term in the r.h.s. of Eq. (5) breaks the spherical symmetry of the distribution, subtracting density along the 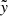 and
and 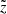 directions. It is evident that the dimensionless density distribution Eq. (5) would assume negative values if the directional subtraction of parent density were sufficiently large. When we consider the NFW as the parent density profile, the condition that at any point of space
directions. It is evident that the dimensionless density distribution Eq. (5) would assume negative values if the directional subtraction of parent density were sufficiently large. When we consider the NFW as the parent density profile, the condition that at any point of space 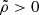 , with
, with 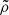 given by Eq. (5), imposes ϵ, η ≤ 1/3 (see Ciotti & Bertin 2005 for the method to limit ϵ and η).
given by Eq. (5), imposes ϵ, η ≤ 1/3 (see Ciotti & Bertin 2005 for the method to limit ϵ and η).
In particular, in this work we consider prolate (η = ϵ) and oblate (ϵ = 0) axisymmetric density–potential pairs, having as a parent density distribution Eq. (4), which we refer to as prolate NFW and oblate NFW models, respectively. The prolate NFW model (η = ϵ), renaming x as z, and vice versa, has density distribution
(shown for η = 1/3 in the left panel of Fig. 1) and gravitational potential
 |
Fig. 1. Isodensity (dashed) and isopotential (solid) contours in the meridional plane of the prolate (left panel) and oblate (right panel) NFW models with η = 1/3. The size of the box is ≈r200/rs (see Sect. 2.2). |
(shown for η = 1/3 in the left panel of Fig. 1), where 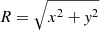 is the radius in the equatorial plane and
is the radius in the equatorial plane and 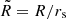 . The oblate NFW model (ϵ = 0), maintaining now the names of the variables x, y, and z as in Eqs. (2) and (3), has density distribution
. The oblate NFW model (ϵ = 0), maintaining now the names of the variables x, y, and z as in Eqs. (2) and (3), has density distribution
(shown for η = 1/3 in the right panel of Fig. 1) and gravitational potential
(shown for η = 1/3 in the right panel of Fig. 1).
In both cases, z is the symmetry axis. Given that the first-order terms of Eqs. (9) and (11) are 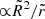 or
or 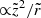 , respectively, the subtraction of the parent density is more significant in the outer regions. For η → 1/3, it induces a peanut-shaped distribution sufficiently far from the center (see Fig. 1).
, respectively, the subtraction of the parent density is more significant in the outer regions. For η → 1/3, it induces a peanut-shaped distribution sufficiently far from the center (see Fig. 1).
2.2. Realistic halo models for massive clusters
A variety of halo shapes are expected from cosmological simulations (e.g., Bett 2012; Henson et al. 2017; see also Sect. 7.5.3 of Cimatti et al. 2019), depending mainly on the halo merging history. When approximating the halos as ellipsoids, even if the majority of them is triaxial, the fact that the ratio of two of the three principal semiaxes is close to unity justifies the use of the spheroidal approximation for the description of these halos. However, for one of our models we adopted the spherical approximation, which is appropriate when the smallest-to-largest axial ratio is close to unity.
Using the density–potential pairs presented in Sect. 2.1, we built our halo models as follows. The prolate and oblate NFW models (represented by Eqs. (9)–(10) and (11)–(12), respectively, which both give for η = 0 the spherical NFW model) were parameterized by ρn, rs, and η. To be as far as possible consistent with the predictions of cosmological simulations on the smallest-to-largest axial ratio (see Allgood et al. 2006), in our spheroidal halo models we assumed the largest possible flattening (η = 1/3) compatible with a ubiquitously positive DM density distribution (see Sect. 2.1).
When a spherical NFW model is considered in the cosmological context, the parameters ρn and rs can be expressed as functions of two other parameters, the virial mass, MΔ, and the concentration, cΔ, which are routinely measured in cosmological simulations (e.g., Dutton & Macciò 2014) and estimated for the halos of observed clusters of galaxies (e.g., Ettori et al. 2010). MΔ is the mass measured within a sphere of the radius, rΔ, within which the average halo density is Δρcrit(z), where the dimensionless quantity Δ is the overdensity and ρcrit(z) = 3H2(z)/(8πG) is the critical density of the Universe at redshift z. The halo concentration is cΔ = rΔ/r−2, where r−2 is the radius at which the logarithmic slope of the angle-averaged density profile is −2. For the spherical NFW model rs = r−2 = rΔ/cΔ, where
and we infer ρn from cΔ as
We now focus on the case of the standard overdensity value Δ = 200, and thus consider r200, M200, and c200 = r200/r−2. To construct our specific spherical NFW, hereafter referred to as the “spherical dark matter” (SDM) model, we set M200 = 1015 M⊙ and c200 = 3.98, in agreement with the mass–concentration relation of Dutton & Macciò (2014) at redshift z ≈ 0.
For the spheroidal halo models, we first computed the mass within the sphere of radius r,
where ρ(R, z) is given by Eqs. (9) or (11) for the prolate and oblate NFW models, respectively. We then estimated r200 and r−2 in the following way. The average density within the sphere of radius r is ⟨ρ⟩(r) = 3M(r)/(4πr3), while the angle-averaged density profile, ρshell(r), was estimated by measuring the average density within concentric spherical shells,
where δr = 0.8 kpc is the thickness of the shell centered on the radius r. rΔ was thus defined to be such that ⟨ρ⟩(rΔ)≃Δρcrit(z), and r−2 to be such that
The above equations could thus be used to estimate M200 = M(r200) and c200 for our flattened halo models. In practice, to build the oblate and prolate NFW halo models, hereafter referred to as “oblate dark matter” (ODM) and “prolate dark matter” (PDM) models, respectively, we selected pairs of values of ρn and rs such that M200 ≈ 1015 M⊙ and c200 is consistent with the z ≈ 0 mass–concentration relation of Dutton & Macciò (2014). The parameters of the SDM, PDM, and ODM halo models are reported in Table 1. The corresponding density and gravitational potential profiles along the symmetry axis and in the equatorial plane are shown in Fig. 2. The upper panel of Fig. 2 shows that, comparing models with approximately the same mass, because of the outward-increasing directional subtraction of parent density discussed in Sect. 2.1 (see Fig. 1), the prolate model has a steeper ρ(R, 0) and a shallower ρ(0, z) than the density profile of the spherical model, and vice versa for the oblate model. Analogous (but weaker) trends are found in the gravitational potential profiles (lower panel of Fig. 2).
 |
Fig. 2. Profiles of density (upper panel) and gravitational potential (lower panel) of SDM (red lines), ODM (blue lines), and PDM (green lines) halo models (see Table 1). In particular, for our axisymmetric models we plot the density and gravitational potential profiles along the symmetry axis (dashed lines) and in the equatorial plane (dotted lines). The top axis in both panels indicates the distance from the center, normalized to r500 of the SDM halo model (r500 = 1345 kpc; we note that the values of r500 in our three halo models differ by less than 2%). |
Parameters of the adopted NFW halo models.
3. Building cool-core clusters models with a rotating ICM
In this section, we present axisymmetric rotating models of the ICM that, in the absence of net cooling or heating, is in equilibrium in a given axisymmetric gravitational potential, representative of an isolated cluster. The ICM is sufficiently dense to cool on timescales much shorter than the Hubble time in the cluster core, and thus to flow into the center of the gravitational potential well. However, as already mentioned in the introduction, the effect of cooling is expected to be efficiently counteracted by heating mechanisms, such as AGN and stellar feedback. Thus, the adoption of stationary models of the ICM is justified as long as there is balance between cooling and heating in a time-averaged sense (e.g., McCourt et al. 2012), provided the cluster does not undergo major interactions.
3.1. The equilibrium of a rotating ICM in a cool-core cluster
Assuming that the total gravitational potential of the cluster, Φ, is time-independent and axisymmetric, we can build simple models of a stationary rotating ICM by considering that the angular velocity of the gas is stratified over cylinders (and thus that the gas distribution is barotropic, i.e., with pressure stratified over density5). Under these hypotheses, neglecting magnetic fields (which are dynamically unimportant for the ICM; see, e.g., Bruggen 2013), the gas mass density, ρgas(R, z), and pressure, p(R, z), are related by ∇p = −ρgas∇Φeff, where
is the effective potential, uϕ(R) is the gas rotation velocity, and (R⋆, z⋆) is a reference point (e.g., Tassoul 1978).
From observations and hydrodynamical simulations, there is evidence that the ICM is well described by polytropic distributions, essentially independent of the halo mass (e.g., Ghirardini et al. 2019b), in which the pressure is stratified over the density as a power law, 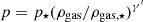 , where γ′ is the polytropic index, p⋆ = p(R⋆, z⋆), and ρgas, ⋆ = ρgas(R⋆, z⋆).
, where γ′ is the polytropic index, p⋆ = p(R⋆, z⋆), and ρgas, ⋆ = ρgas(R⋆, z⋆).
In this work, we model the ICM in a cool-core cluster through a two-component composite polytropic distribution (e.g., Bianconi et al. 2013), by assuming polytropic index 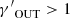 in the outer region and
in the outer region and 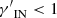 in the cool core. It is convenient to adopt (R⋆, z⋆) = (Rbreak, 0), where Rbreak is a model parameter that defines the size of the cool core. For any outward-increasing axisymmetric potential, defining ΔΦeff(R, z) = Φeff(R, z)−Φeff(Rbreak, 0), we have ΔΦeff(R, z) > 0 in the outer region and ΔΦeff(R, z)≤0 in the cool core. Assuming the ideal gas equation of state, the polytropic distributions of temperature and density of the ICM, in our models of cool-core clusters, are given by
in the cool core. It is convenient to adopt (R⋆, z⋆) = (Rbreak, 0), where Rbreak is a model parameter that defines the size of the cool core. For any outward-increasing axisymmetric potential, defining ΔΦeff(R, z) = Φeff(R, z)−Φeff(Rbreak, 0), we have ΔΦeff(R, z) > 0 in the outer region and ΔΦeff(R, z)≤0 in the cool core. Assuming the ideal gas equation of state, the polytropic distributions of temperature and density of the ICM, in our models of cool-core clusters, are given by
and
where ΔΦeff(R, z) > 0, and by
and
where ΔΦeff(R, z)≤0. Here, n = ρgas/(μmp) is the gas number density, n⋆ = ρgas, ⋆/(μmp), and T⋆ = p⋆/(kBn⋆); μ, mp, and kB are the mean molecular weight (taken equal to 0.6), the proton mass and the Boltzmann constant, respectively.
3.2. Rotation law and effective potential
Though the ICM rotation velocity curve is poorly constrained observationally (see Liu & Tozzi 2019, for an attempt), it is reasonable to expect that it could have a relatively steep rise of azimuthal velocity in the cluster center, a peak at intermediate radii, and a gradual fall in the outskirts (see Baldi et al. 2017; Altamura et al. 2023b). In particular, following Bianconi et al. (2013), we adopted the rotation law
where S ≡ R/R0, R0 is a reference radius and u0 a reference speed.
Substituting the rotation law (23) in Eq. (18), and integrating the rotational component of the effective potential, we get the analytic effective potential associated with this rotation law,
where
3.3. Three representative models of massive cool-core clusters with a rotating ICM
Without focusing on a particular cluster, we propose three models with a rotating ICM representative of the observed population of massive (M200 ≈ 1015 M⊙) cool-core clusters, dubbed “spherical rotating model” (SRM), “oblate rotating model” (ORM), and “prolate rotating model” (PRM). In all these models, we assumed that the gas follows a two-component composite polytropic distribution described by Eqs. (19)–(22), and that the rotation law has the functional form (23). The effective potential is thus in the form of Eqs. (24)–(25). In all cases, to compute the intrinsic and emission properties of the ICM, we assumed a metallicity, Z = 0.3 Z⊙ (where Z⊙ is the solar metallicity reported in Anders & Grevesse 1989), implying n/ne = 1.94, where n = ni + ne is the gas number density, ne is the electron number density, and ni is the ion number density (assuming full ionization).
In the SRM model the total gravitational potential, Φ, is given by the spherical gravitational potential of the SDM halo model described in Sect. 2.2. In the ORM and PRM models, the total gravitational potential is axisymmetric, being, respectively, the potential of the ODM oblate halo model and of the PDM prolate halo model, described in Sect. 2.2. The values of the plasma parameters, Rbreak, n⋆, T⋆, 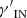 , and
, and 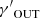 , and of the parameters of the rotation pattern, R0 and u0, are reported for all the models in Table 2. The ICM rotation speed profiles of the three models, with peak rotation speeds in the range of 400–600 km s−1, are shown in Fig. 3. In the same figure we plot, for comparison, the average rotation speed profiles of clusters formed in the MUSIC6 (Baldi et al. 2017) and MACSIS7 (Altamura et al. 2023b) cosmological simulations. Our rotation speed profiles are in between the average profiles found by Baldi et al. (2017) and Altamura et al. (2023b), and can thus be considered, in this sense, to be cosmologically motivated. Moreover, in Sect. 4 we show that our three rotating models are realistic, in the sense that they have properties consistent with the currently available observational data of real massive clusters.
, and of the parameters of the rotation pattern, R0 and u0, are reported for all the models in Table 2. The ICM rotation speed profiles of the three models, with peak rotation speeds in the range of 400–600 km s−1, are shown in Fig. 3. In the same figure we plot, for comparison, the average rotation speed profiles of clusters formed in the MUSIC6 (Baldi et al. 2017) and MACSIS7 (Altamura et al. 2023b) cosmological simulations. Our rotation speed profiles are in between the average profiles found by Baldi et al. (2017) and Altamura et al. (2023b), and can thus be considered, in this sense, to be cosmologically motivated. Moreover, in Sect. 4 we show that our three rotating models are realistic, in the sense that they have properties consistent with the currently available observational data of real massive clusters.
 |
Fig. 3. Profiles of ICM rotation speed of our cluster models with spherical (SRM; dashed blue curve), oblate (ORM; dash-dotted red curve), and prolate (PRM; dotted green curve) halos. For comparison, we also show as solid curves the average rotation speed profiles of the ICM found in clusters formed in cosmological simulations: in particular, the cyan and orange curves are obtained from the functional forms given by, respectively, Baldi et al. (2017) and Altamura et al. (2023b), assuming rΔ and MΔ as in the SDM model. In the top axis, the radial coordinate in the meridional plane is normalized to r500 of the SRM model. The vertical line indicates R = Rbreak for the spherical model, approximately enclosing the cool-core region (red arrow), which has roughly the same extent in all models (see Table 2). |
Parameters of the cluster models with a rotating ICM.
4. Comparison with observations
Here we compare with the observational data some properties of the cool-core cluster models with a rotating ICM presented in Sect. 3.3.
4.1. Thermodynamic profiles of the ICM
Two directly observable quantities of the ICM are the emission measure, which is a proxy for the gas density, and the spectroscopic temperature (Tsp), which is the temperature associated with the emission in the X-ray spectrum. Despite the difficulty of finding an analytic expression of the spectroscopic temperature, Mazzotta et al. (2004) found a good approximation of it, called the spectroscopic-like temperature, which, for an axisymmetric cluster with a symmetry axis, z, orthogonal to the LOS, is given by
where T is the gas temperature (in this work, given by Eqs. (20), (22)) and 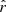 is the radius in the plane at height z, parallel to the equatorial plane. Here, x and z are the coordinates in the plane of the sky, with the origin in the cluster center.
is the radius in the plane at height z, parallel to the equatorial plane. Here, x and z are the coordinates in the plane of the sky, with the origin in the cluster center.
According to the cosmological framework of the formation and evolution of cosmic structures, the population of galaxy clusters is expected to be homogeneous, with “universal” profiles of the thermodynamic quantities (density, temperature, pressure, and entropy) of the ICM that depend only on the mass and redshift of the halo (see e.g., Vikhlinin et al. 2006; Pratt et al. 2010; Arnaud et al. 2010; Eckert et al. 2012; Ghirardini et al. 2019a; Ettori et al. 2023). This is particularly true in the regions dominated by the action of gravity.
Recently, the combination of high-quality data of the thermal Sunyaev–Zeldovich effect (Sunyaev & Zeldovich 1972) and of X-ray observations has allowed Ghirardini et al. (2019a) to reconstruct the universal thermodynamic profiles of the XMM Cluster Outskirts Project (X-COP) sample (Eckert et al. 2017) out to r200 with an unprecedented accuracy8 (see also Vikhlinin et al. 2006 and Nagai et al. 2007a for a discussion on the reliability of the reconstruction method).
We thus compare our models of the rotating ICM in equilibrium in cool-core clusters of M200 ≈ 1015 M⊙ with these thermodynamic profiles in Figs. 4–6, where the observed temperature is Tsp. We note that in the inner regions of the cool core (i.e., r < 60 kpc) the spectroscopic-like temperature of the models departs significantly from the observed profile of the spectroscopic temperature, but this discrepancy is not very meaningful, given the observational limitations on the recovery of the thermodynamic properties in such central regions. The thermodynamic properties of the SRM, ORM, and PRM models, with different halo shapes and rotation patterns, are thus reasonably representative of the average properties of the ICM in massive cool-core clusters.
 |
Fig. 4. Thermodynamic profiles of the ICM in the SRM model. Upper panels: radial (dotted) and vertical (dashed) profiles of electron number density (left panel) and spectroscopic-like temperature (right panel) for the SRM model (blue lines) compared with the corresponding average observed profiles (solid red lines) and their scatter (shaded red band), taken from Ghirardini et al. (2019a, G19 in the legends). Here, ne, shell (solid green line; left panel) is the angle-averaged (see Sect. 2.2) density profile of the SRM model, and Tsl, mean(RP) = [Tsl(RP,0)+Tsl(0,RP)]/2 (solid green line; right panel) is its average spectroscopic-like temperature profile. Lower panels: departure of average profile (solid green lines; see above) of density (left panel) and spectroscopic-like temperature (right panel) of the SRM model from the average observed profiles (solid red lines) with their scatter (shaded red band). The spherical radius, r, and the radius in the plane of the sky, |
 |
Fig. 5. Density (left panel) and spectroscopic-like temperature (right panel) profiles of the ORM model. The figure display is the same as Fig. 4, but for the ORM model r500 ≃ 1346 kpc and T200 ≃ 6.45 keV. |
 |
Fig. 6. Density (left panel) and spectroscopic-like temperature (right panel) profiles of the PRM model. The figure display is the same as Fig. 4, but for the PRM model r500 ≃ 1366 kpc and T200 ≃ 6.53 keV. |
Once they have shown that the ICM pressure is stratified over the ICM density following a piecewise power law function, in the X-COP sample Ghirardini et al. (2019b) find polytropic indices that, depending on the cluster radius, span from 0.75 (in the inner region) to 1.25 (in the outer region), independent of the cluster mass. The polytropic indices of our rotating ICM models (SRM, ORM, and PRM), 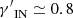 and
and 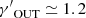 (see Table 2), are fully consistent with those of the observed clusters.
(see Table 2), are fully consistent with those of the observed clusters.
We note that reproducing the observed thermodynamic profiles under the assumption of a rotating ICM is not guaranteed: this is discussed in Appendix A, where we present an illustrative example of a model with a strongly rotating ICM, which fails to reproduce some characteristic features of the observed population of massive clusters.
4.2. Flattening of the X-ray surface brightness distributions
The gas rotation and halo flattening leave a trace in the shape of the X-ray surface brightness distribution. Here, we compare the shape of the X-ray surface brightness distribution in our models and in real massive clusters. One way to account for the departure of the iso-surface brightness contours from the circular shape is through an average axial ratio, based on the inertia tensor of the surface brightness distribution (see Buote & Canizares 1992, 1994).
Assuming that our models are being observed edge-on (i.e., with a symmetry axis orthogonal to the LOS), the surface brightness is
where Λ(T) is the cooling function (in particular we take Λ from Tozzi & Norman 2001, for Z = 0.3 Z⊙).
Using Eq. (27), we computed the surface brightness distribution of our models, which is shown for the ORM and PRM models in Fig. 7.
 |
Fig. 7. Surface brightness maps of the ORM (left panel) and PRM (right panel) models. The boxes (with an origin in the cluster center) extend out to ≈r500 (see white arrows). |
Given that the inertia tensor of the surface brightness distribution is in a diagonal form for a cluster observed edge-on, its diagonal terms are 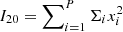 , and
, and 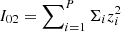 , where Σi is the surface brightness (given by Eq. (27)) at the grid point of plane-of-the-sky coordinates (xi, zi), called hereafter pixel, and P is the total number of pixels. From the definition of diagonal terms, it follows that the average axial ratio is ζ = Imin/Imax, where Imax = max{I20, I02} and Imin = min{I20, I02}.
, where Σi is the surface brightness (given by Eq. (27)) at the grid point of plane-of-the-sky coordinates (xi, zi), called hereafter pixel, and P is the total number of pixels. From the definition of diagonal terms, it follows that the average axial ratio is ζ = Imin/Imax, where Imax = max{I20, I02} and Imin = min{I20, I02}.
In this work, we compare our models to the results obtained for the XMM Cluster Heritage Project (CHEX-MATE) sample9 (Arnaud 2021), which contains both cool-core and non-cool-core clusters observed within their r500. To match the clusters of this sample, we computed the average axial ratio of our cluster models only in the plane-of-the-sky region defined by Rbreak ≤ |x|≤r500 and Rbreak ≤ |z|≤r500. In Fig. 8 we present the cumulative distribution of the average axial ratios of CHEX-MATE clusters, where the 25th, 50th, and 75th percentiles are ζ = 0.77, ζ = 0.85, and ζ = 0.89, respectively (see also Fig. B.1 of Campitiello et al. 2022).
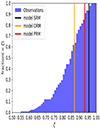 |
Fig. 8. Comparison of the average axial ratio of surface brightness distribution of the SRM, ORM, and PRM models (black, yellow, and red vertical lines, respectively), with the cumulative distribution of the average axial ratios measured for the CHEX-MATE clusters (blue) by Campitiello et al. (2022). |
The SRM, ORM, and PRM models have, respectively, ζ = 0.96, ζ = 0.87, and ζ = 0.93, corresponding to the 93rd, 62nd, and 85th percentiles of the distribution of the CHEX-MATE sample, and thus are consistent with the less flattened population of massive clusters. The halos formed in cosmological simulations (having an average ellipticity ≈0.5; e.g., Allgood et al. 2006) tend to be more flattened than our aspherical halo models (having an ellipticity ∼0.3). The relatively high values of ζ of our cluster models are a consequence of the method adopted to build the density–potential pairs of our oblate and prolate halo models: given the requirement of a everywhere positive halo density, the Ciotti & Bertin (2005) method prevented us from building highly flattened halos (see Sect. 2). However, the flattening of our ICM models is due only to rotation and halo shape, while mergers, substructures, and anisotropic turbulence, all neglected in our models, are likely present in real clusters, where they can contribute to lower ζ.
4.3. Hydrostatic mass bias
The mass recovered under the assumption of hydrostatic equilibrium and spherically symmetric gravitational potential is (e.g., Lau et al. 2013)
where pshell and ρgas, shell are, respectively, the angle-averaged (see Sect. 2.2) pressure and density profiles. The hydrostatic mass bias profile is
where Mtrue is the angle-averaged mass (Eq. (15)) of the halo model that generates the gravitational potential, in which the ICM is in equilibrium. Using Eqs. (28) and (29), we computed b(r) for our cluster models, which we plot in Fig. 9, finding in all cases that the hydrostatic mass bias, except for the central region, tends to decrease with radius.
 |
Fig. 9. Profiles of the hydrostatic mass bias of the SRM (blue dashed line), ORM (red dash-dotted line) and PRM (green dotted line) models, compared to the observational measurements (points): in particular, to average hydrostatic mass biases, taken from Fig. 5 of Ettori et al. (2019, black points), from Tables 2 and 4 of Lovisari et al. (2020, orange points), and from Table 4 of Mahdavi et al. (2013, brown points). The vertical error bars of observational data indicate 1σ uncertainty for b. In the bottom axis, the radius is normalized to r500 of the corresponding model, with the SRM model radii, r2500, r1000, r500, and r200, reported on the plot top. The top axis reports the corresponding overdensity, Δ, of the SRM model (for the ORM and PRM models the overdensity values are very similar to those of the SRM model). The radius corresponding to a given overdensity was computed from the true mass profile, which, in the case of observational data, was assumed to be obtained from the weak gravitational lensing analysis. The red arrow indicates the extent of the cool core. |
The mass estimates from weak gravitational lensing are believed to be significantly less biased than those from X-ray observations (e.g., Meneghetti et al. 2010; Lee et al. 2018), at least for nonmerging clusters (Lee et al. 2023). Thus, when we consider the hydrostatic mass bias of real clusters, we take the cluster mass from weak lensing as an estimate of Mtrue. In particular, in Fig. 9 we compare the hydrostatic mass bias of our cluster models to the following measurements:
-
The error-weighted average of the hydrostatic mass biases of the massive clusters in the X-COP sample, which are classified as relaxed, at true (i.e., obtained from weak lensing measurements) r500 and r200. The hydrostatic and weak lensing masses were determined by Ettori et al. (2019) and Herbonnet et al. (2020), respectively.
-
The average hydrostatic mass bias of a large subsample of the Planck Sunyaev–Zeldovich effect galaxy clusters (62 clusters of true masses in the range 3 × 1014 − 2 × 1015 M⊙, at z < 0.5) at 1 Mpc and true r500. The hydrostatic masses were determined by Lovisari et al. (2020), while the weak lensing masses were taken from Sereno (2015).
-
The average hydrostatic mass bias of the relaxed cluster subsample (most of which are found to have prominent cool cores) of the Canadian Cluster Comparison Project (50 clusters at 0.15 < z < 0.55, selected with the X-ray spectroscopic temperature > 3 keV), at true r2500, r1000, and r500. The hydrostatic and weak lensing masses were determined by Mahdavi et al. (2013) and Hoekstra et al. (2012), respectively.
As shown by Fig. 9, the rotation support assumed in our cluster models is realistic, in the sense that it induces a hydrostatic mass bias comparable to or lower than those detected in real clusters (with the exception of the estimate of Mahdavi et al. 2013 at r2500; see Sect. 5.4 for a discussion). On the basis of the comparison of the thermodynamic profiles of the ICM, the shape of the surface brightness distribution, and the hydrostatic mass bias of our cluster models with observations, we conclude that our models are consistent with the main cluster observables that are currently able to constrain the rotation speed of the ICM in cool-core clusters.
5. Measuring rotation with X-ray spectroscopy
In the near future, the advent of the microcalorimeters, soft X-ray spectrometers such as Resolve on board XRISM, a JAXA/NASA collaborative mission with ESA participation, will provide us with X-ray spectra at high spectral resolutions (Tashiro et al. 2018), allowing us to measure the LOS component of the ICM velocity (e.g., Ota et al. 2018), and thus estimate its rotation support. In this section, using the configurations for Resolve, we present a set of mock X-ray spectra of the rotating ICM in our cluster models and we assess the detectability of rotation with X-ray spectroscopy.
5.1. Building mock spectra of the rotating ICM
Here, we present our mock spectra, focusing primarily on the kinematic signatures. Given that, for a temperature of the ICM higher than 3 keV, a mock multi-temperature source spectrum (i.e., constructed from a multi-temperature model) and the best fit to this spectrum with a single-temperature model are indistinguishable in the X-rays (Mazzotta et al. 2004), we directly simulated the X-ray thermal emission of the ICM of our models through a single-temperature model. In particular, we used the velocity broadened astrophysical plasma emission code10 (BAPEC), in which a parameter accounts for a general broadening of the X-ray emission lines, including the thermal broadening of the ionized metals, and any other contribution in the form of “Doppler broadening” due to the cumulative effect of the different Doppler shifts caused by a distribution of the velocities of the ions. With this model, the Doppler shift of the lines is parametrized by an effective redshift (zeff), which can be different from the cluster’s redshift, z0, due to the action of a coherent, bulk motion, and their equivalent width is regulated by the metallicity, which we fixed to 0.3 Z⊙. We observed our models of cool-core clusters edge-on, to maximize the contribution of rotation to the LOS velocity, which is thus
where Σ is given by Eq. (27) and uϕ by Eq. (23), with parameters u0 and R0 reported in Table 2. To decouple the rotation from the contributions to the broadening of X-ray emitting lines, we observed sufficiently large regions, to be spatially resolved by the spectrometer Resolve, where the ICM was either approaching or receding: in particular, we simulated the observation of regions R1, R2, and R3, reported in Table 3. The LOS speed of the ICM in our cluster models is consistent with the observed upper limit on the rotation speed of 500 km s−1 in the cool cores of real galaxy clusters (e.g., Sanders et al. 2011; Pinto et al. 2015; Bambic et al. 2018): for all models, |vlos| ≲ 450 km s−1 in region R1, which belongs to the inner region. The energy shift of a 6 keV line due to the rotation speed of 400 km s−1 is 8 eV. Resolve, thanks to its energy resolution of ∼7 eV at E = 6 keV11, has the potential to detect such an energy shift, unlike the currently available X-ray CCD detectors with an energy resolution on the order of ≈100 eV. Assuming positive vlos for an approaching ICM, we computed zeff as
Characteristics of the mock pointings.
where we always take z0 = 0.05. In this section, ⟨…⟩ refers to the average over the integration region in the plane of the sky: following Roncarelli et al. (2018), we used nineΛ(T) as a weight for the average along the LOS, except for the spectroscopic-like temperature, which was defined by Eq. (26).
At E > 2 keV, the strongest and better-modeled lines of the X-ray spectra are due to the transitions of inner shell electrons of the iron in the ICM (see e.g., Zhuravleva et al. 2012; Ota et al. 2018, and Fig. 10, where we show a typical spectrum of the ICM, discussed in detail below). The iron thus represents the reference element for the calculations on the line broadening. Previous works have shown that, though being formally independent of the line broadening, the best-fitting Doppler shift of X-ray emitting lines is decisively affected by their broadening. In particular, on the basis of the results of the fits to mock observations of the rotating ICM, Bianconi et al. (2013) point out that, at a fixed signal-to-noise ratio, the best-fitting Doppler shift of the centroids of the X-ray emission lines suffers from a higher error when increasing their overall broadening above ≈300 km s−1. Such a consideration leads us to take into account the following contributions to the broadening of the strong iron-emitting lines:
-
The random motion of iron ions produces thermal broadening (σTH), which is accounted for by the spectroscopic-like temperature (Eq. (26)) in the BAPEC model. In our mock spectra, 90 km s−1 < σTH < 110 km s−1. We notice that the adopted value of the spectroscopic-like temperature represents a weighted average of the observed distribution in the integrated spectra, with typical dispersions around this central value in the range (0.37 − 0.53) keV for all the models.
-
The turbulence, which is believed to be ubiquitous in galaxy clusters on the basis of hydrodynamical simulations (e.g., Vazza et al. 2017) and observations (e.g., Schuecker et al. 2004), is expected to induce a non-negligible contribution (on the order of a few hundred km/s) to the broadening of the iron-emitting lines, known as turbulent broadening, σturb (e.g., Zhuravleva et al. 2012). In the following analysis, we consider a σturb of either 0 or 500 km/s, the latter one considered as an upper limit on the turbulent velocity dispersion in typical galaxy clusters (see e.g., Pinto et al. 2015).
 |
Fig. 10. Representative spectrum of the ICM in equilibrium in our cluster models. Left panel: fit (upper panel; red line) and residuals (lower panel) to the mock spectrum of the receding ICM (black crosses), in equilibrium in the SRM model, for the plane-of-the-sky region R1, taking σturb = 500 km s−1. FeXXV and FeXXVI (with rest-frame energies close to 6.7 and 6.9 keV, respectively), referred to as Fe–K, are the prominent emission lines in the upper panel. In the lower panel, the green line traces the null residuals. We rebinned the data for display purposes (we recall that, using the C-Statistics, the data without backgrounds are not binned). Right panel: zoom on the range 6 − 7 keV of the yellow band in the left panel, where the emission lines FeXXV and FeXXVI are emphasized. Here, we rebinned the data in a different way from the left panel for display purposes. |
In order to mimic an observation as realistically as possible, we introduced a typical absorption due to the Milky Way (NH = 5 × 1020 cm−2; e.g., HI4PI Collaboration 2016), using the PHotoelectric ABSorption model12 (PHABS). Assuming also the parameters of Table 4, an exposure time of 100 ks, and convolving in the range 0.5 − 8 keV with instrumental response functions of Resolve13 in Xspec14 (Arnaud 1996), we built mock spectra of the rotating ICM of our cluster models (see an example in Fig. 10). We did not consider any background in our mock spectra, working in the ideal condition of the analysis of very bright regions. To account for the different behavior of response matrices at different energies, for any region under consideration, we present two mock spectra: one for an “approaching”, blue-shifted ICM and another for a “receding”, red-shifted ICM, with typical differences in energy of the line centroids of a few tens of eV (see Fig. 10). Moreover, to assess the impact of the turbulence on the fit to the shape of the emitting lines, for any region under consideration we present a couple of mock spectra: one with σturb = 500 km s−1 and another without turbulence. The emission at 6–7 keV (yellow vertical band in the left-hand panel of Fig. 10) provides the most valuable information for measuring the LOS speed (see also Ota et al. 2018) because of the relatively high emissivity of the iron-emitting lines FeXXV and FeXXVI (see also the right-hand panel of Fig. 10).
Input parameters of our mock spectra.
Using the C-statistics (Cash 1979), as suggested by Ota et al. (2018; see also Humphrey et al. 2009; Kaastra 2017), and thawing all the parameters except NH, we then fit the absorbed BAPEC model to the mock spectrum in Fig. 10. With the purpose of studying Resolve’s ability to detect the ICM rotation (see Sect. 5.2), in Table 5 we report the expectation values and the statistical errors of the parameters of the fit to the X-ray emission lines: the effective redshift, zeff (that regulates the energy shift of their centroids), the turbulent velocity, σturb (that contributes to their broadening), the metallicity Z (that regulates their intensity), and the spectroscopic temperature, T (that is related to a contribution to their broadening).
Results of the spectral analysis of the mock spectra of the ICM.
5.2. Significativity of the recovered observable quantities
In this section, we discuss how the BAPEC parameters zeff, σturb, Z, and T were recovered from the fit of our mock spectra, once convolved with the Resolve response matrices in the X-rays.
We thus introduce the significativity of the “best-fit” quantity, Qout (reported in Table 5):
where Qin and errQ are the input parameter (reported in Table 4) and the error of Qout to ≃68% of confidence (reported in Table 5), respectively. SQ measures at which level of confidence the “best-fit” parameters match the input values: SQ ≤ 1 means that the spectral analysis recovers the input parameter Qin within ≃68% of confidence. A lower SQ thus corresponds to a better recovery of the observable property, Qin, via the spectral best-fitting. Using Q = {T, zeff, Z} in Eq. (32), we estimated their significance, reported in Table 5, where we refer to the significance of zeff as Seff. The input parameters of the spectroscopic temperature, metallicity, and effective redshift in most spectral analyses were recovered within a 1σ confidence level. To illustrate the results of these mock observations, we focus on the best and worst recoveries of the rotation speed of the ICM. First, we compare the effective redshift measured in region R1 of the SRM cluster model with a receding, nonturbulent ICM (see the third column and the first row of Table 5) to the corresponding input zeff (see the fourth column and the first row of Table 4): the output zeff perfectly matches the input zeff (i.e., Seff = 0, using Eq. (32)). Second, we compare the effective redshift measured in region R3 of the SRM cluster model with a receding, turbulent ICM (see the third column and the sixth row of Table 5) to the corresponding input, zeff (see the fourth column and the third row of Table 4): the output zeff matches the input zeff at 1.6σ. Though each measurement depends on the signal-to-noise ratio, this exercise shows the ability of Resolve to measure the rotation speed of the ICM at a high significance, assuming that the cluster cosmological redshift and Milky Way absorption are known. We note that the statistical errors associated with the “best-fit” spectroscopic temperature, effective redshift, and metallicity (Table 5) depend on the signal-to-noise ratio: these errors decrease by raising the signal-to-noise ratio; in other words, by increasing the exposure time (here assumed to be 100 ks) and enlarging the plane-of-the-sky integration region (see Table 3). For instance, comparing the SRM-R3-R spectral analyses with σturb = 0 and σturb = 500 km s−1 (see Table 5), we note that, keeping the signal-to-noise ratio fixed, the increase in σturb induces a greater error in the “best-fit” effective redshift and turbulent velocity. Most importantly, in this case the input zeff is recovered within 1σ if the input σturb = 0 and out of 1σ if the input σturb = 500 km s−1. From the entire set of our results, the significativity of the effective redshift appears to be sensitive to the input turbulent velocity dispersion: the spectral best-fitting recovers, on average, the input zeff with a higher Seff (i.e., within a higher confidence level) when we increase the input σturb. This outcome is in line with the picture that emerged from the X-ray mock observations of galaxy clusters from hydrodynamical simulations, where the increase in the complexity of the velocity field (here, obtained with an increasing turbulent velocity dispersion, at a fixed rotation speed) reduces our ability to recover the kinematic properties of the ICM (e.g., Roncarelli et al. 2018).
We also studied the covariance among the BAPEC best-fit parameters. We find that the off-diagonal correlation coefficients are significantly lower than 0.2, implying no relevant cross-correlation between zeff, σturb, Z, and T. A partial exception is the ≈0.2 correlation coefficient between Z and σturb for all the models: this weak correlation is due to the way Z is measured (Z is estimated by measuring the equivalent width of emitting lines). In conclusion, we find that the cross-correlations have a negligible impact on our measurements of the ICM rotation speed.
Using the configurations for Resolve, we conclude that, even in the presence of the turbulence of 500 km s−1, the LOS component of the rotation velocity is recovered through the fitting procedure within a 1σ confidence level in most analyses of the mock spectroscopic data. The analysis of our cool-core cluster models shows that current observational constraints, such as the rotation speed of the ICM based on the upper limits on the broadening of the X-ray emitting lines, the measurements of the thermodynamic profiles, and the flattening of the surface brightness distribution and of the hydrostatic mass bias, leave room for rotation of the ICM up to 600 km s−1 in typical clusters. Further tests of our cluster models with rotating ICM will be provided by future measurements of the LOS velocity with XRISM/Resolve that will put stringent and direct constraints on the intrinsic kinematics of the ICM in galaxy clusters.
5.3. Assessing the hydrostatic mass bias with X-ray spectroscopy
In our cluster models, the ICM is in equilibrium and departs from the hydrostatic condition owing only to rotation. Here, we point out the perspectives and limitations on the use of X-ray spectroscopy for the mapping of non-negligible rotation support of the ICM.
As discussed above, the LOS velocity, vlos(x, z) (see Eq. (30)), can be recovered from the measurements of the properties of the X-ray emitting lines (see e.g., Biffi et al. 2013; Roncarelli et al. 2018). Thus, a proxy for the rotational contribution to the hydrostatic mass bias, defined in Eq. (29), is Mrot/Mtrue, where
is the mass associated with the gas rotation support, and Mtrue the same halo mass as in Eq. (29).
Using in Eq. (33) the true LOS rotation speed, vlos, given by Eq. (30), we computed the Mrot profiles of our cluster models (see curves in Fig. 11). Then, to find the LOS velocity ⟨vlos⟩ as measured from the best fits to our mock spectra, we used Eq. (31), where zeff is now the best-fit value to the mock spectrum of the receding ICM without turbulence (reported in Table 5). Substituting vlos(r, 0) with ⟨vlos⟩ in Eq. (33), where we considered the radius, r, equal to the value of the plane-of-the-sky x coordinate (reported in Table 3 for the region under consideration), we estimated the mass associated with gas rotation support at the centers of the regions chosen for our mock observations. Following this method, from the normal distribution with a mean and standard deviation equal to the best-fit effective redshift and its error (both reported in Table 5), respectively, we inferred the errors (as 16th and 84th percentiles) on Mrot as estimated from X-ray spectroscopy for our cluster models.
 |
Fig. 11. Fraction of the hydrostatic mass bias due to rotation (b) of the SRM (blue), ORM (red), and PRM (green) models, which we recovered from the true (dashed lines) and best-fit (points) LOS velocities using Eq. (33). The horizontal error bars indicate the extent of the region of the mock observations, while the vertical error bars indicate the 1σ errors on Mrot estimated from X-ray spectroscopy. The radius was normalized to r500 as in Fig. 9, with the SRM radii, r2500, r1000, and r500, indicated in the top axis. |
Figure 11 shows that Mrot estimated from the best-fit zeff recovers within 1σ statistical errors (vertical error bars) the mass associated with the rotation support estimated from the true LOS velocity (Eq. (30)). This is consistent with the fact that the best-fit effective redshift from the spectral analysis recovers within a 1σ confidence level the input effective redshift (Sect. 5.2). However, as shown by the curves in Fig. 11, Mrot/Mtrue based on Eq. (33), where we take the true LOS speed, is lower than the hydrostatic mass bias, b, measured from the theoretical angle-averaged pressure profile of the ICM (see Sect. 4.3). The reason for this discrepancy (pointed out also by Ota et al. 2018) is that the mean LOS velocity at a projected distance d from the symmetry axis is lower than the rotation speed of the ICM at an intrinsic distance d from the symmetry axis.
Focusing on the hydrostatic mass biases of our cluster models as measured from X-ray spectroscopy (points with error bars in Fig. 11), we conclude that the estimates of the rotation support over the range (0.1 − 1)r500 obtained through the “best-fit” LOS rotation speed resolved by Resolve are able to account for 55 − 70% of the hydrostatic mass bias of our models. It follows that a Resolve-like correction for the rotation support of the ICM is expected to leave a residual hydrostatic mass bias due to rotation smaller than 3% at r500 for systems similar to our model clusters. The error bars in Fig. 11 are larger in the outermost bin for all the models: this is a consequence of the increase in the statistical uncertainties of the spectral parameters due to the lower signal present in those regions of our cluster models.
Moreover, the poor angular resolution of Resolve (with a point spread function with a half power diameter of ≈1.7 arcmin) prevented us from sampling the hydrostatic mass bias profile in a larger independent number of radial bins. This will be possible in the future with the Advanced Telescope for High Energy Astrophysics15 (ATHENA; Nandra et al. 2013), thanks to its expected arcsec resolution combined with the performance of the onboard X-ray microcalorimeter X-IFU (see e.g., Roncarelli et al. 2018).
5.4. Discussion on the hydrostatic bias
In Sect. 4.3, we discussed how the measurements of the hydrostatic mass bias can be used to limit the rotation speed of the ICM. In Table 6, we quote the hydrostatic mass bias due to rotation in our cluster models at some characteristic overdensities available to observations. A general trend is that the observed hydrostatic mass bias decreases with increasing overdensity (see e.g., Zhang et al. 2010; Mahdavi et al. 2013; Sereno & Ettori 2015; Lovisari et al. 2020). A similar trend is also recovered in hydrodynamical simulations (see e.g., Nagai et al. 2007b; Lau et al. 2009; Meneghetti et al. 2010; Rasia et al. 2012; Gianfagna et al. 2021). This behavior results in tension with the hydrostatic mass bias profiles recovered from our models, which increase with increasing Δ (see Fig. 9). Cosmological hydrodynamical simulations show that the support from turbulence in galaxy clusters increases with radius (see e.g., Fang et al. 2009; Lau et al. 2009; Towler et al. 2023), overcoming the rotational contribution well within r500. Thus, the observed trend of the hydrostatic mass bias is expected to follow the increase in the turbulent support of the ICM moving outward, with a non-negligible contribution from the rotation only in the inner regions. Indeed, the few data available at r2500 (see Fig. 9), where hydrodynamical simulations suggest comparable support from rotation and turbulence, suggest a hydrostatic bias marginally consistent (within 2σ) with the predictions of our models.
Characteristic values of the hydrostatic mass bias of our cluster models.
In the near future, new instruments and space telescopes will permit more accurate determinations of the hydrostatic mass bias at different overdensities in a larger sample of galaxy clusters. In particular, the aforementioned XRISM and eRosita16 (onboard the Spectrum-Roentgen-Gamma mission and, only in the future, the observatory Athena), together with currently available X-ray observatories (XMM-Newton and Chandra17), will continue to provide the measurements of the hydrostatic mass through X-ray observations. The ESA optical/infrared space telescope Euclid18 and other ground-based campaigns will complement with weak lensing mass estimates the information on the mass budget in larger samples of galaxy clusters, allowing us to refine our comprehension of the statistical properties of the hydrostatic mass bias.
6. Conclusions
In this work, we have presented three representative, realistic models of massive (M200 ≈ 1015 M⊙) cool-core galaxy clusters with rotating ICM in equilibrium in DM halos consistent with observational findings and theoretical predictions on the halo shape and mass-concentration relation (Sect. 2). While one of the models has a spherical NFW halo, the other two have, respectively, physically consistent oblate and prolate NFW halos, built analytically using the method of Ciotti & Bertin (2005). Our cool-core cluster models, which have a barotropic ICM rotation with velocity peaks as high as 600 km s−1 (see Fig. 3), have an ICM temperature and density profiles consistent with the corresponding universal profiles of real clusters. Cosmological hydrodynamical simulations can also be used to calibrate these analytic models (for instance, on the location of Rbreak, the parameter that defines the size of the cool core) once any overcooling problem (see e.g., Kravtsov & Borgani 2012) is properly solved, and realistic cooling cores are produced in systems that did not experience a major merger in the central region (e.g., Rasia et al. 2015). The shape of surface brightness contours, the discrepancy between hydrostatic and true masses, and the broadening of X-ray emission lines of the models are also consistent with currently available observations.
We obtained a set of mock X-ray spectra of the rotating ICM from the aforementioned three cluster models, using the configuration for the microcalorimeter Resolve onboard XRISM, for different turbulence conditions. In this way, we estimated how well the rotation speed and the hydrostatic mass bias due to rotation are recovered based on the results of Resolve-like spectral analysis (Sect. 5).
The main conclusions of this work are the following:
-
The existence of realistic cluster models with peaks in the rotation speed of the ICM in the range of 400–600 km s−1 leaves open the possibility that the rotation support of the ICM is non-negligible in real cool-core galaxy clusters.
-
Even with turbulent velocity dispersion as high as 500 km s−1, a Resolve-like X-ray spectral analysis recovers the input LOS rotation speed at a high significance.
-
Measuring the LOS velocity from X-ray spectroscopy with XRISM accounts for 55 − 70% of the hydrostatic mass bias due to rotation. In this way, XRISM will allow us to pin down any mass bias of a different origin from the rotation (for instance, due to turbulence; see e.g., Ettori & Eckert 2022).
On the one hand, improving spatial and spectral resolution in X-rays will open a new window in which the combination of the intrinsic thermodynamic profiles with the rotation and turbulent velocity dispersion profiles can be used to validate models of the ICM, providing robust estimates of the cluster mass. On the other hand, Sect. 5.3 shows the need for a functional form that properly maps the intrinsic rotation speed through the LOS rotation speed as resolved in massive clusters. Most of the limitations of this mapping come from the possible degeneracy present in the interpretation of the observational data. Possible contaminants that can limit our interpretation of the physical state of the ICM are, for example, unresolved gas clumps, multiphase gas, metallicity inhomogeneities, and complex velocity fields not properly mapped, both in the plane of the sky and along the LOS (see also Sect. 5.2). We postpone further study on this topic to future work.
X-ray observations will enable us to guess both the rotation axis and the maximal rotation speed (see e.g., Ota et al. 2018; Liu & Tozzi 2019) in some favorable conditions (broadly speaking, bright enough sources and X-ray detectors with sufficient spatial and spectral resolution). Once these X-ray observations are available, the kinetic Sunyaev–Zeldovich (see e.g., some observational constraints in Sayers et al. 2013, 2019; Mroczkowski et al. 2019, for a review) can be resolved (thanks also to the forthcoming ground-based Simons Observatory; Ade et al. 2019) and compared to the X-ray constraints to provide a consistent picture of the ICM peculiar velocity along the LOS.
The presented results strongly encourage future spectroscopic observations of relaxed galaxy clusters with XRISM/Resolve (in the forthcoming decade) and/or ATHENA/X-IFU (in the far future; see also Roncarelli et al. 2018) to quantify the level of the ICM rotation speed, and to improve X-ray based mass estimates of real clusters, with important implications for the use of galaxy clusters as accurate cosmological probes (see e.g., Pratt et al. 2019).
As pointed out by Nipoti & Posti (2014) and Nipoti et al. (2015), if the ICM is weakly magnetized (as found by the observational works reviewed by Bruggen 2013) and significantly rotating, the magnetorotational instability could also have relevant effects. Thus, the possibility that the ICM has non-negligible rotation support with a speed as high as 600 km s−1 in real clusters acquires a great interest for its implications not only for the mass estimates, but also for our understanding of the energy balance and evolution of the cool cores, because the magnetorotational instability could play a role in regulating their energetic budget.
Indications of rotation support of the galactic component have been found in some clusters from spectroscopic observations of member galaxies (see e.g., Oegerle & Hill 1992; Hwang & Lee 2007; Ferrami et al. 2023). The differences in the rotation speed profiles of the ICM and member galaxies are an interesting issue to be explored with future facilities.
The synthetic clusters of Baldi et al. (2017) were selected from the MUSIC-2 sample (Sembolini et al. 2013) having M200 > 5 × 1014 h−1 M⊙, where h = H0/(100 km s−1 Mpc−1). The corresponding curve in Fig. 3 was built using data taken from Table 4 of Baldi et al. (2017), for the gas-VP2b rotation curve in the so-called AGN simulation.
The MACSIS cluster sample (Barnes et al. 2017) has friends-of-friends masses ≳1015 M⊙ at redshift z = 0. The corresponding curve in Fig. 3 was built using data taken from Table B.2 of Altamura et al. (2023b) for the M500 < 9.7 × 1014 M⊙ subsample in the so-called gas-aligned case.
The X-COP sample consists of 13 nearby, massive galaxy clusters selected on the basis of signal-to-noise ratio of the Sunyaev–Zeldovich effect as resolved in the Planck maps (Planck Collaboration XXIX 2014). Five of these objects are classified as relaxed, cool-core systems accordingly to their central entropy.
The CHEX-MATE sample is a signal-to-noise limited sample of 118 galaxy clusters detected by Planck via their Sunyaev–Zel’dovich effect; it is composed by two subsamples: the Tier-1, including the population of clusters at the most recent time (z < 0.2) and the Tier-2, with the most massive objects to have formed thus far in the history of the Universe; see http://xmm-heritage.oas.inaf.it/ for further details.
The ESA satellite ATHENA, is scheduled to be launched not before 2036 (see https://www.the-athena-x-ray-observatory.eu/en).
Acknowledgments
We thank the referee Edoardo Altamura for useful suggestions. S.E. acknowledges the financial contribution from the contracts ASI-INAF Athena 2019-27-HH.0, “Attività di Studio per la comunità scientifica di Astrofisica delle Alte Energie e Fisica Astroparticellare” (Accordo Attuativo ASI-INAF n. 2017-14-H.0), and from the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant agreement n. 871158).
References
- Ade, P., Aguirre, J., Ahmed, Z., et al. 2019, J. Cosmol. Astropart. Phys., 2019, 056 [Google Scholar]
- Allgood, B., Flores, R. A., Primack, J. R., et al. 2006, MNRAS, 367, 1781 [NASA ADS] [CrossRef] [Google Scholar]
- Altamura, E., Kay, S. T., Bower, R. G., et al. 2023a, MNRAS, 520, 3164 [CrossRef] [Google Scholar]
- Altamura, E., Kay, S. T., Chluba, J., & Towler, I. 2023b, MNRAS, 524, 2262 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta., 53, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Angelinelli, M., Vazza, F., Giocoli, C., et al. 2020, MNRAS, 495, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Arnaud, M. 2021, A&A, 650, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Baldi, A. S., De Petris, M., Sembolini, F., et al. 2017, MNRAS, 465, 2584 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, A. S., De Petris, M., Sembolini, F., et al. 2018, MNRAS, 479, 4028 [NASA ADS] [CrossRef] [Google Scholar]
- Bambic, C. J., Pinto, C., Fabian, A. C., Sanders, J., & Reynolds, C. S. 2018, MNRAS, 478, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, D. J., Kay, S. T., Henson, M. A., et al. 2017, MNRAS, 465, 213 [Google Scholar]
- Bett, P. 2012, MNRAS, 420, 3303 [Google Scholar]
- Bianconi, M., Ettori, S., & Nipoti, C. 2013, MNRAS, 434, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Biffi, V., Dolag, K., & Böhringer, H. 2013, MNRAS, 428, 1395 [Google Scholar]
- Biffi, V., Borgani, S., Murante, G., et al. 2016, ApJ, 827, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bruggen, M. 2013, Astron. Nachr., 334, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., & Canizares, C. R. 1992, ApJ, 400, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., & Canizares, C. R. 1994, ApJ, 427, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Campitiello, M. G., Ettori, S., Lovisari, L., & CHEX-MATE Collaboration 2022, Eur. Phys. J. Web. Conf., 257, 00007 [CrossRef] [EDP Sciences] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Chluba, J., & Mannheim, K. 2002, A&A, 396, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cimatti, A., Fraternali, F., & Nipoti, C. 2019, Introduction to Galaxy Formation and Evolution: From Primordial Gas to Present-Day Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
- Ciotti, L., & Bertin, G. 2005, ApJ, 437, 419 [NASA ADS] [Google Scholar]
- Cooray, A., & Chen, X. 2002, ApJ, 573, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Eckert, D., Vazza, F., Ettori, S., et al. 2012, A&A, 541, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., et al. 2017, Astron. Nachr., 338, 293 [Google Scholar]
- Ettori, S., & Eckert, D. 2022, A&A, 657, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2010, A&A, 524, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Donnarumma, A., Pointecouteau, E., et al. 2013, Space Sci. Rev., 177, 119 [Google Scholar]
- Ettori, S., Ghirardini, V., Eckert, D., et al. 2019, A&A, 621, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Lovisari, L., & Eckert, D. 2023, A&A, 669, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fang, T., Humphrey, P., & Buote, D. 2009, ApJ, 691, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Ferragamo, A., Barrena, R., Rubiño-Martín, J. A., et al. 2021, A&A, 655, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrami, G., Bertin, G., Grillo, C., Mercurio, A., & Rosati, P. 2023, A&A, 676, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019a, ApJ, 621, A41 [Google Scholar]
- Ghirardini, V., Ettori, S., Eckert, D., & Molendi, S. 2019b, A&A, 627, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gianfagna, G., De Petris, M., Yepes, G., et al. 2021, MNRAS, 502, 5115 [NASA ADS] [CrossRef] [Google Scholar]
- Henson, M. A., Barnes, D. J., Kay, S. T., McCarthy, I. G., & Schaye, J. 2017, MNRAS, 465, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Herbonnet, R., Sifón, C., Hoekstra, H., et al. 2020, MNRAS, 497, 4684 [NASA ADS] [CrossRef] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hitomi Collaboration (Aharonian, F., et al.) 2016, Nat, 535, 117 [CrossRef] [Google Scholar]
- Hlavacek-Larrondo, J., Li, Y., & Churazov, E. 2022, Handbook of X-ray and Gamma-ray Astrophysics, 5 [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Humphrey, P. J., Liu, W., & Buote, D. A. 2009, ApJ, 693, 822 [Google Scholar]
- Huško, F., Lacey, C. G., Schaye, J., Schaller, M., & Nobels, F. S. J. 2022, MNRAS, 516, 3750 [CrossRef] [Google Scholar]
- Hwang, H. S., & Lee, M. G. 2007, ApJ, 662, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S. 2017, A&A, 605, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Mathews, W. G. 1995, ApJ, 438, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Nagai, D., Kravtsov, A. V., & Zentner, A. R. 2011, ApJ, 734, 93 [CrossRef] [Google Scholar]
- Lau, E. T., Nagai, D., Kravtsov, A. V., Vikhlinin, A., & Zentner, A. R. 2012, ApJ, 755, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Nagai, D., & Nelson, K. 2013, ApJ, 777, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, B. E., Le Brun, A. M. C., Haq, M. E., et al. 2018, MNRAS, 479, 890 [Google Scholar]
- Lee, W., Cha, S., Jee, M. J., et al. 2023, ApJ, 945, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, A., & Tozzi, P. 2019, MNRAS, 485, 3909 [NASA ADS] [CrossRef] [Google Scholar]
- Lovisari, L., Ettori, S., Sereno, M., et al. 2020, A&A, 644, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., et al. 2013, ApJ, 767, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Rasia, E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] [Google Scholar]
- McCourt, M., Sharma, P., Quataert, E., & Parrish, I. J. 2012, MNRAS, 419, 3319 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2013, ApJ, 774, 23 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mroczkowski, T., Nagai, D., Basu, K., et al. 2019, Space Sci. Rev., 215, 17 [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007a, ApJ, 668, 1 [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007b, ApJ, 655, 98 [Google Scholar]
- Nagai, D., Lau, E. T., Avestruz, C., Nelson, K., & Rudd, D. H. 2013, ApJ, 777, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Nelson, K., Lau, E. T., Nagai, D., Rudd, D. H., & Yu, L. 2014, ApJ, 782, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., & Posti, L. 2014, ApJ, 792, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Posti, L., Ettori, S., & Bianconi, M. 2015, J. Plasma Phys., 81, 495810508 [NASA ADS] [CrossRef] [Google Scholar]
- Nobels, F. S. J., Schaye, J., Schaller, M., Bahé, Y. M., & Chaikin, E. 2022, MNRAS, 515, 4838 [CrossRef] [Google Scholar]
- Oegerle, W. R., & Hill, J. M. 1992, AJ, 104, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, N., Nagai, D., & Lau, E. T. 2018, PASJ, 70, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Pearce, F. A., Kay, S. T., Barnes, D. J., Bower, R. G., & Schaller, M. 2020, MNRAS, 491, 1622 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1969, ApJ, 155, 393 [Google Scholar]
- Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, C., Sanders, J. S., Werner, N., et al. 2015, AAP, 575, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, ApJ, 571, A29 [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Biviano, A., et al. 2019, Space Sci. Rev., 215, 25 [Google Scholar]
- Rasia, E., Ettori, S., Moscardini, L., et al. 2006, MNRAS, 369, 2013 [CrossRef] [Google Scholar]
- Rasia, E., Meneghetti, M., Martino, R., et al. 2012, New J. Phys., 14, 055018 [Google Scholar]
- Rasia, E., Borgani, S., Murante, G., et al. 2015, ApJ, 813, L17 [Google Scholar]
- Roncarelli, M., Ettori, S., Borgani, S., et al. 2013, MNRAS, 432, 3030 [NASA ADS] [CrossRef] [Google Scholar]
- Roncarelli, M., Gaspari, M., Ettori, S., et al. 2018, ApJ, 618, A39 [Google Scholar]
- Sanders, J. S., Fabian, A. C., & Smith, R. K. 2011, MNRAS, 410, 1797 [NASA ADS] [Google Scholar]
- Sayers, J., Mroczkowski, T., Zemcov, M., et al. 2013, ApJ, 778, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Montaña, A., Mroczkowski, T., et al. 2019, ApJ, 880, 45 [Google Scholar]
- Schuecker, P., Finoguenov, A., Miniati, F., Böhringer, H., & Briel, U. G. 2004, A&A, 426, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sembolini, F., Yepes, G., De Petris, M., et al. 2013, MNRAS, 429, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M. 2015, MNRAS, 450, 3665 [Google Scholar]
- Sereno, M., & Ettori, S. 2015, MNRAS, 450, 3633 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1980, MNRAS, 190, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., Norman, M. L., & Bryan, G. L. 2003, Astron. Lett., 29, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Suto, D., Kawahara, H., Kitayama, T., et al. 2013, ApJ, 767, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Tashiro, M., Maejima, H., Toda, K., et al. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 10699, 1069922 [NASA ADS] [Google Scholar]
- Tassoul, J.-L. 1978, Sov. Astron., 24, 255 [NASA ADS] [Google Scholar]
- Towler, I., Kay, S. T., & Altamura, E. 2023, MNRAS, 520, 5845 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., & Norman, C. 2001, ApJ, 546, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Jones, T. W., Brüggen, M., et al. 2017, MNRAS, 464, 210 [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [Google Scholar]
- Zhang, Y.-Y., Okabe, N., Finoguenov, A., et al. 2010, ApJ, 711, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Zhuravleva, I., Churazov, E., Kravtsov, A., & Sunyaev, R. 2012, MNRAS, 422, 2712 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: An extreme cluster model with a rotating ICM
In this appendix, with the purpose of illustrating the effect of strong ICM rotation on the observable properties of galaxy clusters, we present a cluster model (of M200 ≈ 1015 M⊙) with a rotating ICM, which, unlike the three models presented in Sect. 3.3, is not realistic because, though it has a realistic gas density distribution, it has a temperature distribution substantially different from that of real clusters. This extreme cluster model, which we refer to as the “extreme rotating model” (ERM), has gravitational potential generated by the ODM halo model (see Sect. 2.2) and the gas rotation law given by Eq. (23), with values of the parameters u0 and R0 (see Tab. A.1) such that the rotation speed peak is 750 km s−1 at a radius of 150 kpc (see bottom panel of Fig. A.1). The values of the other gas parameters (Rbreak, 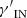 ,
, 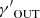 , n⋆ and T⋆; see Tab. A.1) were chosen so that the angle-averaged gas density profile of the ERM model is consistent with the universal gas density profile of observed cool-core clusters (top panel of Fig. A.1). However, this choice of parameter values implies that, due to the strong rotation support, the temperature profile of the ERM model is grossly inconsistent with the universal temperature profile derived for observed cool-core clusters (middle panel of Fig. A.1).
, n⋆ and T⋆; see Tab. A.1) were chosen so that the angle-averaged gas density profile of the ERM model is consistent with the universal gas density profile of observed cool-core clusters (top panel of Fig. A.1). However, this choice of parameter values implies that, due to the strong rotation support, the temperature profile of the ERM model is grossly inconsistent with the universal temperature profile derived for observed cool-core clusters (middle panel of Fig. A.1).
 |
Fig. A.1. Thermodynamic (top and middle panels) and rotation speed profiles (bottom panel) of the ICM in the ERM model. Top and middle panels: same as the left and right panels of Fig. 4, respectively, but for the ERM model. Bottom panel: rotation speed profile of the ICM in the ERM model. The red arrow indicates the approximate extent of the cool core, defined as in Fig. 3. |
Parameters of the ERM model.
Given the rotation speed curve and the gravitational potential assumed for the ERM model, we were not able to find a combination of values of the plasma parameters such that both the density and the spectroscopic-like temperature profiles are consistent with those observed for massive cool-core clusters. Though this does not allow us to place an upper limit on the peak of the rotation speed of the ICM, it is a strong indication that rotation speeds higher than ≈600 km s−1 are problematic not only for the spectroscopic constraints on the broadening of the X-ray emission line, but also for constraints imposed by the shape of the universal thermodynamic profiles. Comparing further the polytropic indices, 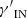 and
and 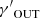 , of our ICM distributions to those observed, we also note that the ERM model, which has lower
, of our ICM distributions to those observed, we also note that the ERM model, which has lower 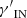 and higher
and higher  than our realistic models (see Tab.s 2 and A.1), is in tension with the results of Ghirardini et al. (2019b) on the polytropic indices of observed clusters (see Sect. 4.1).
than our realistic models (see Tab.s 2 and A.1), is in tension with the results of Ghirardini et al. (2019b) on the polytropic indices of observed clusters (see Sect. 4.1).
All Tables
All Figures
 |
Fig. 1. Isodensity (dashed) and isopotential (solid) contours in the meridional plane of the prolate (left panel) and oblate (right panel) NFW models with η = 1/3. The size of the box is ≈r200/rs (see Sect. 2.2). |
| In the text | |
 |
Fig. 2. Profiles of density (upper panel) and gravitational potential (lower panel) of SDM (red lines), ODM (blue lines), and PDM (green lines) halo models (see Table 1). In particular, for our axisymmetric models we plot the density and gravitational potential profiles along the symmetry axis (dashed lines) and in the equatorial plane (dotted lines). The top axis in both panels indicates the distance from the center, normalized to r500 of the SDM halo model (r500 = 1345 kpc; we note that the values of r500 in our three halo models differ by less than 2%). |
| In the text | |
 |
Fig. 3. Profiles of ICM rotation speed of our cluster models with spherical (SRM; dashed blue curve), oblate (ORM; dash-dotted red curve), and prolate (PRM; dotted green curve) halos. For comparison, we also show as solid curves the average rotation speed profiles of the ICM found in clusters formed in cosmological simulations: in particular, the cyan and orange curves are obtained from the functional forms given by, respectively, Baldi et al. (2017) and Altamura et al. (2023b), assuming rΔ and MΔ as in the SDM model. In the top axis, the radial coordinate in the meridional plane is normalized to r500 of the SRM model. The vertical line indicates R = Rbreak for the spherical model, approximately enclosing the cool-core region (red arrow), which has roughly the same extent in all models (see Table 2). |
| In the text | |
 |
Fig. 4. Thermodynamic profiles of the ICM in the SRM model. Upper panels: radial (dotted) and vertical (dashed) profiles of electron number density (left panel) and spectroscopic-like temperature (right panel) for the SRM model (blue lines) compared with the corresponding average observed profiles (solid red lines) and their scatter (shaded red band), taken from Ghirardini et al. (2019a, G19 in the legends). Here, ne, shell (solid green line; left panel) is the angle-averaged (see Sect. 2.2) density profile of the SRM model, and Tsl, mean(RP) = [Tsl(RP,0)+Tsl(0,RP)]/2 (solid green line; right panel) is its average spectroscopic-like temperature profile. Lower panels: departure of average profile (solid green lines; see above) of density (left panel) and spectroscopic-like temperature (right panel) of the SRM model from the average observed profiles (solid red lines) with their scatter (shaded red band). The spherical radius, r, and the radius in the plane of the sky, |
| In the text | |
 |
Fig. 5. Density (left panel) and spectroscopic-like temperature (right panel) profiles of the ORM model. The figure display is the same as Fig. 4, but for the ORM model r500 ≃ 1346 kpc and T200 ≃ 6.45 keV. |
| In the text | |
 |
Fig. 6. Density (left panel) and spectroscopic-like temperature (right panel) profiles of the PRM model. The figure display is the same as Fig. 4, but for the PRM model r500 ≃ 1366 kpc and T200 ≃ 6.53 keV. |
| In the text | |
 |
Fig. 7. Surface brightness maps of the ORM (left panel) and PRM (right panel) models. The boxes (with an origin in the cluster center) extend out to ≈r500 (see white arrows). |
| In the text | |
 |
Fig. 8. Comparison of the average axial ratio of surface brightness distribution of the SRM, ORM, and PRM models (black, yellow, and red vertical lines, respectively), with the cumulative distribution of the average axial ratios measured for the CHEX-MATE clusters (blue) by Campitiello et al. (2022). |
| In the text | |
 |
Fig. 9. Profiles of the hydrostatic mass bias of the SRM (blue dashed line), ORM (red dash-dotted line) and PRM (green dotted line) models, compared to the observational measurements (points): in particular, to average hydrostatic mass biases, taken from Fig. 5 of Ettori et al. (2019, black points), from Tables 2 and 4 of Lovisari et al. (2020, orange points), and from Table 4 of Mahdavi et al. (2013, brown points). The vertical error bars of observational data indicate 1σ uncertainty for b. In the bottom axis, the radius is normalized to r500 of the corresponding model, with the SRM model radii, r2500, r1000, r500, and r200, reported on the plot top. The top axis reports the corresponding overdensity, Δ, of the SRM model (for the ORM and PRM models the overdensity values are very similar to those of the SRM model). The radius corresponding to a given overdensity was computed from the true mass profile, which, in the case of observational data, was assumed to be obtained from the weak gravitational lensing analysis. The red arrow indicates the extent of the cool core. |
| In the text | |
 |
Fig. 10. Representative spectrum of the ICM in equilibrium in our cluster models. Left panel: fit (upper panel; red line) and residuals (lower panel) to the mock spectrum of the receding ICM (black crosses), in equilibrium in the SRM model, for the plane-of-the-sky region R1, taking σturb = 500 km s−1. FeXXV and FeXXVI (with rest-frame energies close to 6.7 and 6.9 keV, respectively), referred to as Fe–K, are the prominent emission lines in the upper panel. In the lower panel, the green line traces the null residuals. We rebinned the data for display purposes (we recall that, using the C-Statistics, the data without backgrounds are not binned). Right panel: zoom on the range 6 − 7 keV of the yellow band in the left panel, where the emission lines FeXXV and FeXXVI are emphasized. Here, we rebinned the data in a different way from the left panel for display purposes. |
| In the text | |
 |
Fig. 11. Fraction of the hydrostatic mass bias due to rotation (b) of the SRM (blue), ORM (red), and PRM (green) models, which we recovered from the true (dashed lines) and best-fit (points) LOS velocities using Eq. (33). The horizontal error bars indicate the extent of the region of the mock observations, while the vertical error bars indicate the 1σ errors on Mrot estimated from X-ray spectroscopy. The radius was normalized to r500 as in Fig. 9, with the SRM radii, r2500, r1000, and r500, indicated in the top axis. |
| In the text | |
 |
Fig. A.1. Thermodynamic (top and middle panels) and rotation speed profiles (bottom panel) of the ICM in the ERM model. Top and middle panels: same as the left and right panels of Fig. 4, respectively, but for the ERM model. Bottom panel: rotation speed profile of the ICM in the ERM model. The red arrow indicates the approximate extent of the cool core, defined as in Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



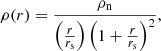
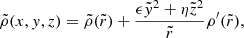
![$$ \begin{aligned} \tilde{\Phi }(x,{ y},z) = \tilde{\Phi }_0 (\tilde{r}) + (\epsilon + \eta ) [\tilde{\Phi }_1 (\tilde{r}) - \tilde{\Phi }_0 (\tilde{r})] + (\epsilon \tilde{{ y}}^2 + \eta \tilde{z}^2) \tilde{\Phi }_2 (\tilde{r}), \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq12.gif)
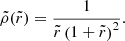
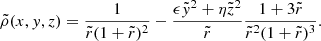
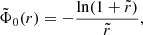
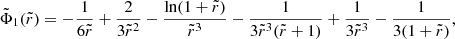
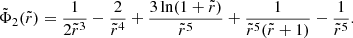
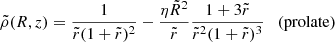
![$$ \begin{aligned} \tilde{\Phi }(R,z)&~{=} -\frac{\ln (1+\tilde{r})}{\tilde{r}} +2\eta \left[-\frac{1}{6 \tilde{r}} + \frac{2}{3 \tilde{r}^2} - \frac{\ln (1+\tilde{r})}{\tilde{r}^3}\right.\nonumber \\&\quad ~{-}\left.\frac{1}{3 \tilde{r}^3 (\tilde{r} +1)} + \frac{1}{3 \tilde{r}^3} - \frac{1}{3 (1+\tilde{r})} + \frac{\ln (1+\tilde{r})}{\tilde{r}}\right]\\&\quad ~{+}~\eta \tilde{R}^2 \left[ \frac{1}{2 \tilde{r}^3}- \frac{2}{ \tilde{r}^4} + \frac{3 \ln (1+\tilde{r})}{\tilde{r}^5}+\right.\nonumber \\&\quad ~{+} \left.\frac{1}{ \tilde{r}^5 (\tilde{r} +1)} - \frac{1}{\tilde{r}^5}\right]\quad \mathrm{(prolate)}\nonumber \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq30.gif)
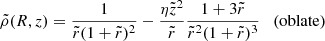
![$$ \begin{aligned} \tilde{\Phi }(R,z)&= - \frac{\ln (1+\tilde{r})}{\tilde{r}} +\eta \left[-\frac{1}{6 \tilde{r}} + \frac{2}{3 \tilde{r}} - \frac{\ln (1+\tilde{r})}{\tilde{r}^3}+\right.\nonumber \\&\quad - \frac{1}{3 \tilde{r}^3 (1+\tilde{r})}+ \left.\frac{1}{3 \tilde{r}^3} - \frac{1}{3 (1+\tilde{r})} + \frac{\ln (1+\tilde{r})}{\tilde{r}}\right]\\&\quad +\eta \tilde{z}^2 \left[ \frac{1}{2 \tilde{r}^3} - \frac{2}{ \tilde{r}^4}+ \frac{3 \ln (1+\tilde{r})}{\tilde{r}^5}+ \frac{1}{ \tilde{r}^5 (1+\tilde{r})}+\right.\nonumber \\&\quad \left.- \frac{1}{\tilde{r}^5}\right]\quad \mathrm{(oblate)}\nonumber \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq34.gif)
![$$ \begin{aligned} r_{\Delta }=\left[\frac{M_{\Delta }}{(4/3)\pi \Delta \rho _{\mathrm{crit}}(z)} \right]^{1/3}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq37.gif)
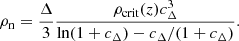
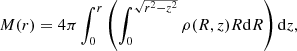
![$$ \begin{aligned} \rho _{\mathrm{shell}}(r)=\frac{3[M(r+\delta r/2)-M(r-\delta r/2)]}{4 \pi [(r+\delta r/2)^3-(r-\delta r/2)^3]}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq40.gif)
![$$ \begin{aligned} \left[\frac{\mathrm{d}\ln \rho _{\mathrm{shell}}}{\mathrm{d}\ln r}\right]_{r=r_{-2}}\simeq -2. \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq41.gif)
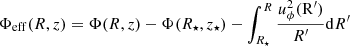
![$$ \begin{aligned} n(R,z)=n_\star \left[1- \frac{{\gamma ^{\prime }}_{\mathrm{OUT}}-1}{{\gamma ^{\prime }}_{\mathrm{OUT}}} \frac{\upmu m_{\rm p}}{k_{\rm B} T_{\star }} \Delta \Phi _{\mathrm{eff}}(R,z)\right]^{\frac{1}{{\gamma ^{\prime }}_{\mathrm{OUT}}-1}} \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq46.gif)
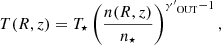
![$$ \begin{aligned} n(R,z)=n_\star \left[1- \frac{{\gamma ^{\prime }}_{\mathrm{IN}}-1}{{\gamma ^{\prime }}_{\mathrm{IN}}} \frac{\upmu m_{\rm p}}{k_{\rm B} T_{\star }} \Delta \Phi _{\mathrm{eff}}(R,z)\right]^{\frac{1}{{\gamma ^{\prime }}_{\mathrm{IN}}-1}} \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq48.gif)
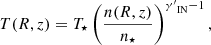
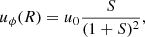
![$$ \begin{aligned} \Phi _{\mathrm{eff}}(R,z)= \Phi (R,z)-\Phi (R_\star ,z_\star ) -\left[I(R)-I(R_\star )\right], \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq51.gif)
![$$ \begin{aligned} I(R^\prime )=u_{\mathrm{0}}^2\left[\frac{1}{3}\left(1+\frac{R^\prime }{R_{\mathrm{0}}}\right)^{-3}-\frac{1}{2}\left(1+\frac{R^\prime }{R_{\mathrm{0}}}\right)^{-2}\right]. \end{aligned} $$](/articles/aa/full_html/2024/02/aa47656-23/aa47656-23-eq52.gif)