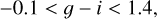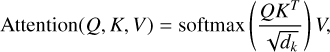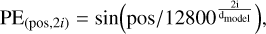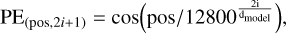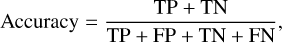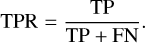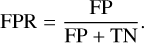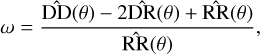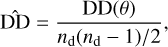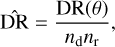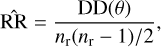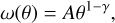| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 23 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202347649 | |
| Published online | 26 January 2024 | |
Shedding light on low-surface-brightness galaxies in dark energy surveys with transformer models★
1
National Centre for Nuclear Research,
Warsaw,
Poland
e-mail: hareesh.thuruthipilly@ncbj.gov.pl; junais@ncbj.gov.pl; agnieszka.pollo@ncbj.gov.pl
2
Jagiellonian University,
Kraków,
Poland
3
Wits Centre for Astrophysics, School of Physics, University of the Witwatersrand,
Johannesburg,
South Africa
Received:
3
August
2023
Accepted:
17
October
2023
Context. Low-surface-brightness galaxies (LSBGs), which are defined as galaxies that are fainter than the night sky, play a crucial role in our understanding of galaxy evolution and in cosmological models. Upcoming large-scale surveys, such as Rubin Observatory Legacy Survey of Space and Time and Euclid, are expected to observe billions of astronomical objects. In this context, using semiautomatic methods to identify LSBGs would be a highly challenging and time-consuming process, and automated or machine learning-based methods are needed to overcome this challenge.
Aims. We study the use of transformer models in separating LSBGs from artefacts in the data from the Dark Energy Survey (DES) Data Release 1. Using the transformer models, we then search for new LSBGs from the DES that the previous searches may have missed. Properties of the newly found LSBGs are investigated, along with an analysis of the properties of the total LSBG sample in DES.
Methods. We created eight different transformer models and used an ensemble of these eight models to identify LSBGs. This was followed by a single-component Sérsic model fit and a final visual inspection to filter out false positives.
Results. Transformer models achieved an accuracy of ~94% in separating the LSBGs from artefacts. In addition, we identified 4083 new LSBGs in DES, adding an additional ~17% to the LSBGs already known in DES. This also increased the number density of LSBGs in DES to 5.5 deg−2. The new LSBG sample consists of mainly blue and compact galaxies. We performed a clustering analysis of the LSBGs in DES using an angular two-point auto-correlation function and found that LSBGs cluster more strongly than their high-surface-brightness counterparts. This effect is driven by the red LSBG. We associated 1310 LSBGs with galaxy clusters and identified 317 ultradiffuse galaxies among them. We found that these cluster LSBGs are getting bluer and larger in size towards the edge of the clusters when compared with those in the centre.
Conclusions. Transformer models have the potential to be equivalent to convolutional neural networks as state-of-the-art algorithms in analysing astronomical data. The significant number of LSBGs identified from the same dataset using a different algorithm highlights the substantial impact of our methodology on our capacity to discover LSBGs. The reported number density of LSBGs is only a lower estimate and can be expected to increase with the advent of surveys with better image quality and more advanced methodologies.
Key words: methods: data analysis / techniques: image processing / Galaxy formation / galaxies: clusters: general / galaxies: evolution
LSBG catalog is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/682/A4
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Low-surface-brightness galaxies (LSBGs) are most often defined as galaxies with a fainter central surface brightness than the night sky or galaxies with a B-band central surface brightness µ0(B) of below a certain threshold. In the literature, this threshold value varies from µ0(B) ≥ 23.0 mag arcsec−2 (Bothun et al. 1997) to µ0(B) ≥ 22.0 mag arcsec−2 (Burkholder et al. 2001).
It is estimated that the LSBGs only contribute a few percent (< 10%) of the local luminosity and of the stellar mass density of the observable Universe (Bernstein et al. 1995; Driver 1999; Hayward et al. 2005; Martin et al. 2019). However, LSBGs are considered to account for a significant fraction (30% ~ 60%) of the total number density of galaxies (McGaugh 1996; Bothun et al. 1997; O’Neil & Bothun 2000; Haberzettl et al. 2007; Martin et al. 2019), and as much as 15% of the dynamical mass content of the Universe (Driver 1999; Minchin et al. 2004). These numbers imply that LSBGs can contribute significantly to our understanding of the physics of galaxy evolution and cosmological models. However, as their name indicates, LSBGs are very faint systems, and due to the observational challenges in detecting them, LSBGs remain a mostly unexplored realm.
In recent years, despite observational challenges, advances in digital imaging have improved our ability to detect LSBGs. The first and largest LSBG to be identified and verified is Malin 1, serendipitously discovered by Bothun et al. (1987) during a survey of galaxies of low surface brightness in the Virgo cluster. Notably, Malin 1 is the largest spiral galaxy known today (e.g., Impey et al. 1988; Junais et al. 2020; Galaz et al. 2022). Current searches for LSBGs have shown that they exhibit a wide range of physical sizes (Greene et al. 2022) and can be found in various types of environments: for example, from satellites of local nearby galaxies (Danieli et al. 2017; Cohen et al. 2018), ultrafaint satellites of the Milky Way (McConnachie 2012; Simon 2019), galaxies found in the field (Leisman et al. 2017; Prole et al. 2021), to members of massive galaxy clusters like Virgo (Mihos et al. 2015, 2017; Junais et al. 2022) and Coma (van Dokkum et al. 2015; Koda et al. 2015).
LSBGs have also been separated into several subclasses based on their physical size, surface brightness, and gas content. Ultradiffuse galaxies (UDGs) represent a subclass of LSBGs characterised by their considerable size, which is comparable to that of Milky Way-like galaxies, yet they exhibit very faint luminosities akin to dwarf galaxies. Although the term ‘UDG’ was coined by van Dokkum et al. (2015), such galaxies were identified in several earlier studies in the literature (Sandage & Binggeli 1984; McGaugh & Bothun 1994; Dalcanton et al. 1997; Conselice et al. 2003a). Similarly, giant LSBGs (GLS-BGs) form another subclass of LSBGs that are extremely gas-rich (MHI > 1010 M⊙), faint, and extended (Sprayberry et al. 1995; Saburova et al. 2023). The formation and evolution of extreme classes such as UDGs and GLSBGs are still debated (Amorisco & Loeb 2016; Di Cintio et al. 2017; Saburova et al. 2021; Benavides et al. 2023; Laudato & Salzano 2023).
In order to understand the formation mechanism(s) giving rise to the various types LSBGs in different environments, in it crucial to study them extensively across different environments (galaxy clusters vs field) over a large area of the sky. Recently, Greco et al. (2018) detected 781 LSBGs in the Hyper Suprime-Cam Subaru Strategic Program (HSC SSP) in a blind search covering around 200 deg2 of the sky from the Wide layer of the HSC SSP. Similarly, in a recent study, Tanoglidis et al. (2021b) used a support vector machine (SVM) and visual inspection to analyse the first three years of data from the Dark Energy Survey (DES). These authors identified more than 20000 LSBGs, thus building the largest LSBG catalogue available.
A common feature observed in both of these untargeted searches for LSBGs was the significant presence of low-surface-brightness artefacts. As pointed out in Tanoglidis et al. (2021b), these artefacts predominantly consist of diffuse light from nearby bright objects, galactic cirrus, star-forming tails of spiral arms, and tidal streams. These artefacts typically pass the simple selection cuts based on photometric measurements and often make up the majority of the LSBG candidate sample. These contaminants need to be removed, which is often accomplished using semi-automated methods, which has a low success rate, and visual inspection, which is more precise but time-consuming.
For example, in HSC SSP, Greco et al. (2018) applied selection cuts on the photometric measurements from SourceExtractor (Bertin & Arnouts 1996), which led to the selection of 20838 LSBG candidates. Using a galaxy modelling pipeline based on imfit (Erwin 2015), the sample size was subsequently reduced to 1521. However, after visual inspection, only 781 candidates were considered confident LSBGs, which is around 4% of the preliminary candidate sample and 50% of the sample selected by the pipeline. Similarly, in DES, Tanoglidis et al. (2021b) shortlisted 419 895 LSBG candidates using the selection cuts on SourceExtractor photometric measurements. After applying a feature-based machine learning (ML) classification (SVM) on the photometric measurements, the candidate sample was further reduced to 44979 objects. However, a significant number of false positives still remained, and only 23 790 were later classified as confident LSBGs. Therefore, these numbers indicate that the occurrence of LSBGs in these methods is roughly 5% for the initial selection and 50% for the subsequent selection.
Upcoming large-scale surveys, such as Legacy Survey of Space and Time (LSST; Ivezić et al. 2019) and Euclid (Euclid Collaboration 2022), are expected to observe billions of astronomical objects. In this scenario, it would be impractical to rely solely on photometric selection cuts or semi-automated methods – such as galaxy model fitting – to identify LSBGs confidently. Furthermore, the accuracy of the classification methodology in distinguishing between LSBGs and artefacts must be improved in order to achieve meaningful results. This situation therefore demands more effective and efficient automation methodologies in searches for LSBGs.
Recently, advancements in deep learning have been widely applied in astronomy, opening up a plethora of opportunities. Particularly for analysing astronomical images, convolutional neural networks (CNNs) have emerged as a state-of-the-art technique. For example, CNNs have been used for galaxy classification (Pérez-Carrasco et al. 2019), galaxy merger identification (Pearson et al. 2022), supernova classification (Cabrera-Vives et al. 2017), and finding strong gravitational lenses (Schaefer et al. 2018; Davies et al. 2019; Rojas et al. 2022). One of the fascinating features of CNNs is their ability to directly process the image as input and learn the image features, making them one of the most popular and robust architectures in use today. Generally, the learning capacity of a neural network increases with the number of layers in the network. The first layers of the network learn the low-level features, and the last layers learn more complex features (Russakovsky et al. 2015; Simonyan & Zisserman 2015).
One of the main requirements for creating a trained CNN is a sufficiently large training dataset that can generalise the features of the data being analysed. Recently, Tanoglidis et al. (2021a) used a catalogue of over 20000 LSBGs from DES to distinguish LSBGs from artefacts using a CNN for the first time and achieved an accuracy of 92% and a true positive rate of 94%.
While CNNs have been the dominant choice for analysing image data in astronomy, the current state-of-the-art models for computer vision are transformers. Transformers were initially introduced in natural language processing (NLP) as an attention-based model (Vaswani et al. 2017). The fundamental concept behind the transformer architecture is the attention mechanism, which has also found a broad range of applications in machine learning (Zhang et al. 2018; Fu et al. 2019; Parmar et al. 2019; Zhao et al. 2020; Tan et al. 2021). In the case of NLP, attention calculates the correlation of different positions of a single sequence to calculate a representation of the sequence. Later the idea was adapted to computer vision and has been used to produce state-of-the-art models for various image processing tasks, such as image classification (Wortsman et al. 2022) and image segmentation (Chen et al. 2023).
Generally, two categories of transformers are present in the literature. The first type integrates both CNNs and attention to perform the analysis. An example of this type is the detection transformer (DETR) originally proposed for end-to-end object detection by Carion et al. (2020). The key idea behind using CNNs and transformers together is to leverage the strengths of both architectures. CNNs excel at local feature extraction, capturing low-level details and spatial hierarchies, while attention layers excel at modelling global context and long-range dependencies. The second class of transformers contains the models that do not use a CNN and operate entirely based on self-attention mechanisms. An example of this type is the Vision Transformer (ViT) proposed for object classification by Dosovitskiy et al. (2021). ViTs have demonstrated remarkable performance in image classification tasks and have surpassed the accuracy of CNN-based models on various benchmark datasets (Dosovitskiy et al. 2021; Yu et al. 2022; Wortsman et al. 2022).
Although transformers were introduced very recently in astronomy, they have already found a wide variety of applications. For example, the transformer models have been used to detect and analyse strong gravitational lensing systems (Thuruthipilly et al. 2022b,a; Huang et al. 2023; Jia et al. 2023), to represent light curves that can be used for classification or regression (Allam & McEwen 2021), and to classify multi-band light curves of different supernovae (SN) types (Pimentel et al. 2023).
In this paper, we explore the capability of transformers to classify LSBGs from artefacts in DES and compare the performance of transformers with the CNNs presented in Tanoglidis et al. (2021a). We also use the transformer models to look for new LSBGs that previous searches may have missed. For comparison purposes, throughout this work, we follow the LSBG definition from Tanoglidis et al. (2021b), which is based on the g-band mean surface brightness ( ) and the half-light radii (r1/2). We consider LSBGs as galaxies with
) and the half-light radii (r1/2). We consider LSBGs as galaxies with 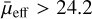 mag arcsec−2 and r1/2 > 2.5″.
mag arcsec−2 and r1/2 > 2.5″.
The paper is organised as follows. Section 2 discusses the data we used to train our models and to look for new LSBGs. Section 3 provides a brief overview of the methodology used in our study, including the model architecture, information on how the models were trained, and details of the visual inspection. The results of our analysis are presented in Sect. 4. A detailed discussion of our results and the properties of the newly identified LSBGs are presented in Sects. 5 and 6, respectively. A further analysis of the clustering of LSBGs is presented in Sect. 7 and a detailed discussion on the UDGs identified as a subsample of LSBGs is presented in Sect. 8. Section 9 concludes our analysis by highlighting the significance of LSBGs, the impact of our methodology on our capacity to discover LSBGs, and future prospects with regard to the upcoming survey LSST.
2 Data
2.1 Dark Energy Survey
The Dark Energy Survey (DES; Abbott et al. 2018, 2021) is a six-year observing program (2013–2019) covering ~5000 deg2 of the southern Galactic cap in the optical and near-infrared regime using the Dark Energy Camera (DECam) on the 4 m Blanco Telescope at the Cerro Tololo Inter-American Observatory (CTIO). The DECam focal plane comprises 62 2k × 4k charge-coupled devices (CCDs) dedicated to science imaging and 12 2k × 2k CCDs for guiding, focus, and alignment. The DECam field of view covers 3 deg2 with a central pixel scale of 0.263 arcsec pixel−1 (Flaugher et al. 2015). To address the gaps between CCDs, DES uses a dithered exposure pattern (Neilsen et al. 2019) and combines the resulting individual exposures to form co-added images, which have dimensions of 0.73 × 0.73 degrees (Morganson et al. 2018). The DES has observed the sky in grizY photometric bands with approximately ten overlapping dithered exposures in each filter (90 s in griz-bands and 45 s in Y-band).
2.2 DES DR1 and the gold catalogue
In this work, we use the image data from the Dark Energy Survey Data Release 1 (DES DR1; Abbott et al. 2018) and the DES Y3 Gold catalogue (DES Y3_gold_2_2.1) obtained from the first three years of the DES observations (Sevilla-Noarbe et al. 2021). The DES DR1 comprises optical and near-infrared imaging captured over 345 different nights between August 2013 and February 2016. The median 3σ surface brightness limits of the g, r, and i-bands of DES DR1 are 28.26, 27.86, and 27.37 mag arcsec−2, respectively (Tanoglidis et al. 2021b). It is worth mentioning that the DES source detection pipeline has not been optimised for detecting large, low-surface-brightness objects (Morganson et al. 2018). Therefore, the above-mentioned surface brightness values can be considered as the limits for detecting faint objects in each band. The gold catalogue shares the same single-image processing, image co-addition, and object detection as the DES DR1. The objects in the gold catalogue were detected using SourceExtractor (Bertin & Arnouts 1996) and have undergone selection cuts on minimal image depth and quality, additional calibration, and deblending. The median coadd magnitude limit of the DES Y3 Gold catalogue at a signal-to-noise ratio (S/N) = 10 is g = 24.3 mag, r = 24.0 mag, and i = 23.3 mag (Sevilla-Noarbe et al. 2021). The DES Y3 Gold catalogue contains around 319 million astronomical objects, which we used for searching LSBGs in DES. For a detailed review and discussion of the data from the DES, please refer to Abbott et al. (2018) and Sevilla-Noarbe et al. (2021).
We reduced the number of objects processed in our study using preselections, in a similar way to Greco et al. (2018) and Tanoglidis et al. (2021b). We first removed objects classified as point-like objects in the DES Y3 Gold catalogue based on the i-band SourceExtractor SPREAD_MODEL parameter and EXTENDED_CLASS_COADD, as described in Tanoglidis et al. (2021b). In addition, we constrained the g-band half-light radius (FLUX_RADIUS_G) and surface brightness (MUE_MEAN_MODEL_G) within the range of 2.5″ < r1/2 < 20″ and 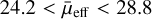 mag arcsec−2, respectively. Furthermore, we also limited our sample to objects with colours (using the MAG_AUTO magnitudes) in the range:
mag arcsec−2, respectively. Furthermore, we also limited our sample to objects with colours (using the MAG_AUTO magnitudes) in the range:
These colour cuts are based on Greco et al. (2018) and Tanoglidis et al. (2021b). As mentioned by Greco et al. (2018), these colour requirements will remove the spurious detections due to optical artefacts detected in all bands and blends of high-redshift galaxies. Finally, we also restricted the axis ratio (B_IMAGE/A_IMAGE) of each object to be greater than 0.3 in order to remove artefacts such as the highly elliptical diffraction spikes. Our complete selection criteria were based on the selection criteria presented in Appendix B of Tanoglidis et al. (2021b). After the preliminary selections using the SourceExtractor parameters from the DES Y3 Gold catalogue, our sample contains 419 784 objects.
2.3 Training data
All of the trained, validated, and tested models in this study used the labelled dataset of LSBGs and artefacts identified from DES by Tanoglidis et al. (2021b). Below, we briefly summarise the primary steps taken by Tanoglidis et al. (2021b) in constructing the LSBG catalogue. (i) The SourceExtractor parameters from the DES Y3 Gold catalogue presented by Sevilla-Noarbe et al. (2021) were used to create the initial selection cuts, as discussed in Sect. 2.2. (ii) The candidate sample was further reduced using an SVM to classify artefacts and LSBGs. The SVM was trained with a manually labelled set of approximately 8000 objects (640 LSBGs) and using the SourceExtractor parameters as features for learning. (iii) From the candidate sample generated through SVM, over 20 000 artefacts were excluded upon visual inspection. Most of the rejected objects that had passed the SVM feature-based selection were found to be astronomical artefacts (such as galactic cirrus, star-forming extensions of spiral arms, and tidal streams) rather than instrumental artefacts (such as scattered light emitted by nearby bright objects) during visual inspection, (iv) Objects that passed the visual inspection were subjected to Sérsic model fitting and Galactic extinction correction. Following this, new selection cuts were applied to the updated parameters, and the final LSBG catalogue containing 23 790 LSBGs was created.
For training our classification models, we selected LSBGs from the LSBG catalogue as the positive class (label – 1) and the objects rejected in the third step (visual inspection) by Tanoglidis et al. (2021b) as the negative class (label – 0). The catalogues for the positive and negative classes are publicly available, and we used these catalogues to create our training dataset1. The selection of the artefacts and LSBGs for training was random, and after selection, we had 18 474 artefacts and 23 103 LSBGs. However, when we further inspected these LSBGs and artefacts, we found that there were 797 objects belonging to both classes. After conducting a thorough visual examination, we identified that these are, in fact, LSBGs that had been mistakenly categorized as artefacts in the publicly accessible artefact catalogue. However, we avoided these 797 objects from our training set in order to avoid contamination and ambiguity among classes during training. We generated multi-band cutouts for each object in the flexible image transport system (FITS) format using the cutout service provided in the DES public data archive. Each cutout corresponds to a 67.32″ × 67.32″ (256 × 256 pixels) region of the sky and is centred at the coordinates of the object (LSBG or artefact). We resized the cutouts from their initial size to 64 × 64 pixels to reduce computational costs. The cutouts of g, r, and z-bands were stacked together to create the dataset for training the models. Examples of LSBGs and artefacts used for training the model are shown in Fig. 1. Our training catalogue contains 39 983 objects, of which 22 306 are LSBGs and 17 677 are artefacts. Before training, we randomly split the full sample into a training set, a validation set, and a test set, consisting of 35 000, 2500, and 2483 objects, respectively.
 |
Fig. 1 Four examples of LSBGs (a) and artefacts (b) used in the training data. Each image of the LSBG and artefact corresponds to a 67.32″ × 67.32″ region of the sky. Images were generated by combining the g, r, and z bands using APLpy package (Robitaille & Bressert 2012). |
3 Methodology
3.1 Transformers and attention
As mentioned in Sect. 1, the central idea behind every transformer architecture is attention. Before applying attention, the input sequence is transformed into three vectors in multi-head attention: query (Q), key (K), and value (V). The dot product between the query and key vectors is used to obtain attention scores. The attention scores are then used to weight the value vector, producing a context vector that is a weighted sum of the value vectors. For our work, the vectors (Q, V, and K) are identical, and this method is termed self-attention. This approach enables the transformer to model long-range dependencies and capture complex patterns in the input sequence. Mathematically, the attention function is defined as
where Q, K, and V are the query, key, and value vectors and dk is the dimension of the vector K. The softmax function, by definition, is the normalised exponential function that takes an input vector of K real numbers and normalises it into a probability distribution consisting of K probabilities proportional to the exponential of the input numbers. The building blocks of our transformer models are layers applying self-attention and are termed transformer encoders. Please refer to Vaswani et al. (2017) for a detailed discussion on transformer encoders.
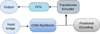 |
Fig. 2 Scheme of the general architecture of the detection transformer (LSBG DETR) taken from Thuruthipilly et al. (2022b). The extracted features of the input image by the CNN backbone are combined with positional encoding and are passed on to the encoder layer to assign attention scores to each feature. The weighted features are then passed to the feed-forward neural network (FFN) to predict the probability. |
3.2 LSBG detection transformer (LSBG DETR)
We implemented four transformer models that use a CNN backbone and self-attention layers to classify the labels, which we call LSBG detection transformer (LSBG DETR) models in general. The LSBG DETR architecture is inspired by transformer models from Thuruthipilly et al. (2022b), which were used to explore diverse structures and hyperparameters in order to optimise classification performance. Each individual model is followed by a number indicating its chronological order of creation. The LSBG DETR models have an eight-layer CNN backbone to extract feature maps from the input image. The feature maps produced by the CNN backbone are then passed on to the transformer encoder layer to create an attention map that helps the transformer component focus on the most relevant features for classification. The transformer encoder layer has subcomponents known as heads, which, in parallel, apply the self-attention to the input vector split into smaller parts. Output generated by the transformer encoder is then passed on to a feed-forward neural network (FFN) layer to predict the probability that the input is an LSBG. Another point to be noted is that the transformers are permutation invariant; we therefore add positional encoding to address this issue and retain the positional information of features. For the LSBG DETR, we used fixed positional encoding defined by the function
where pos is the position, i is the dimension of the positional encoding vector, and dmodel is the dimension of the input feature vector. We follow the positional encoding defined in Vaswani et al. (2017), and for a detailed discussion on positional encoding and its importance, we refer to Liutkus et al. (2021); Su et al. (2021); Chen et al. (2021). The general structure of the LSBG DETR is shown in Fig. 2. For a detailed discussion on the transformer models similar to LSBG DETR, we refer to Carion et al. (2020) and Thuruthipilly et al. (2022b).
3.3 LSBG Vision
We created four transformer models similar to the ViT introduced by Google Brain (Dosovitskiy et al. 2021), which we call LSBG vision transformers (LSBG ViT) in general. Similar to LSBG DETR models, each individual model is followed by a number indicating its chronological order of creation. One of the main features of LSBG ViT models is that they do not use any convolutional layers to process the image, unlike LSBG DETR. In the ViT architecture, the input image is divided into fixed-size patches, which are flattened into a sequence of ID vectors. As the transformers are permutation invariant, the positional embedding is added to the patch embedding before they are fed into the transformer layers. The positional embedding is typically a fixed-length vector that is added to the patch embedding, and is learned during training along with the other model parameters. The combined ID sequence is then passed through a stack of transformer layers. An additional learnable (class) embedding is affixed to the input sequence, which encodes the class of the input image. This class embedding for each input is calculated by applying self-attention to positionally embedded image patches. Output from the class embedding is passed on to a multi-layer perceptron (MLP) head to predict the output class. A schematic diagram of the vision transformer is shown in Fig. 3. For a detailed discussion on ViT models, please refer to Dosovitskiy etal. (2021).
3.4 Training
All of the LSBG DETR and LSBG ViT models were trained with an initial learning rate of α = 10−4. We used the exponential linear unit (ELU) function as the activation function for all the layers in these models (Clevert et al. 2016). We initialise the weights of our model with the Xavier uniform initialiser (Glorot & Bengio 2010), and all layers are trained from scratch by the ADAM optimiser with the default exponential decay rates (Kingma & Ba 2015). We used the early stopping callback from Keras2 to monitor the validation loss of the model and stop training once the loss was converged. The models LSBG DETR 1 and 4 were each given 8 heads and were trained for 150 and 93 epochs, respectively. Similarly, the LSBG DETR 2 and 3 were given 12 heads and were trained for 134 and 105 epochs, respectively. Regarding the LSBGS ViT models, the hyperparameters we varied were the size of the image patches, the number of heads, and the number of transformer encoder layers. The hyperparameters for the all the LSBG DETR models were customised based on the results from Thuruthipilly et al. (2022b), who extensively investigated the hyperparameter configurations of DETR models. When it comes to the LSBG ViT models, we maintained the hyperparameters from the LSBG DETR models, such as learning rate, batch size – except for adjustments in image patch size –, the count of attention heads, and the number of transformers encoder layers. We varied these parameters and the four best models are presented in Table 1. In the spirit of reproducible research, our code for LSBG DETR and LSBG ViT is publicly available3.
3.5 Ensemble models
We took two classes of transformers (LSBG DETR and LSBG ViT) with four models in each class, and used an ensemble model of these four models for each class to look for new LSBGs from DES DR1. Ensemble models in deep learning refer to combining multiple models to create a single model that performs better than the individual models. The idea behind ensemble models is to reduce the generalisation error and increase the stability of the system by taking into account multiple sources of information. Various kinds of ensemble learning exist in the literature, and they have been found helpful in a broad range of machine learning problems (Wang et al. 2022). For a detailed review of ensemble methods, please refer to Domingos & Hulten (1999) and Dietterich (2000). One of the easiest and most common ensemble methods is model averaging. In model averaging, multiple models are trained independently on the same training data, and the outputs of the models are averaged to make the final prediction. One of the main advantages of model averaging is that it is computationally efficient and does not require any additional training time; it also allows the use of different types of model architecture and can take advantage of their strengths and weaknesses and improve overall performance. Here we use averaging to create the ensemble models for LSBG DETR and LSBG ViT.
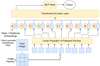 |
Fig. 3 Scheme of the general architecture of the LSBG ViT. The input image is split into small patches and flattened into a sequence of 1D vectors and combined with positional encoding. The numbered circular patches represent the position encoding, and the counterpart represents the flattened 1D sequence of the image patches. The combined 1D sequence is passed to the transformer layers. The extra learnable class embedding encodes the class of the input image after being updated by self-attention and passes it on to an MLP head to predict the output. |
Name of the model, size of the image patches (s), number of heads (h), number of transformer encoder layers (T), and the number of epochs taken to train the four vision models (e) in chronological order of creation.
3.6 Sérsic fitting
The candidates identified independently by both LSBG DETR and LSBT ViT ensemble models were subjected to a single-component Sérsic fitting using Galfit (Peng et al. 2002). This was done to re-estimate the 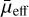 and r1/2 values of the LSBG candidates initially used for our sample selection. We employed a single-component Sérsic-fitting method to align with the LSBG search methodology of Tanoglidis et al. (2021b), who also used a similar approach. However, we also note that Sérsic fitting does not always capture the full light from a galaxy.
and r1/2 values of the LSBG candidates initially used for our sample selection. We employed a single-component Sérsic-fitting method to align with the LSBG search methodology of Tanoglidis et al. (2021b), who also used a similar approach. However, we also note that Sérsic fitting does not always capture the full light from a galaxy.
We used the magnitude (MAG_AUTO) and radius (FLUX_ RADIUS) values from the gold catalogue as an initial guess for the Galfit procedure. Moreover, the Sérsic index (n) and axis ratio (q) were initialised to be at a fixed value of 1 and were allowed to vary only within the range of 0.2 < n < 4.0 and 0.3 < q < 1.0, respectively. A similar fitting procedure was used for both the g-band and i-band images of our sample. After the fitting, we excluded all the sources with poor or failed fits with either a reduced χ2 > 3 or if their Galfit magnitude estimates diverge from their initial MAG_AUTO values by more than 1 mag. We also excluded the cases where the estimated n and q values do not converge and are on the edge of the range specified above. For the remaining galaxies, we re-applied our g-band sample selection criteria of 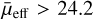 mag arcsec−2 and r1/2 > 2.5″, following Tanoglidis et al. (2021b). The
mag arcsec−2 and r1/2 > 2.5″, following Tanoglidis et al. (2021b). The 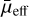 values were calculated using the relation given by Eq. (7):
values were calculated using the relation given by Eq. (7):
where 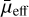 is the mean surface brightness within the effective radius, m is the total magnitude, and r1/2 is the half-light radius in a specific band estimated from Galfit. For all our measurements, we also applied a foreground Galactic extinction correction using the Schlegel et al. (1998) maps normalised by Schlafly & Finkbeiner (2011) and a Fitzpatrick (1999) dust extinction law.
is the mean surface brightness within the effective radius, m is the total magnitude, and r1/2 is the half-light radius in a specific band estimated from Galfit. For all our measurements, we also applied a foreground Galactic extinction correction using the Schlegel et al. (1998) maps normalised by Schlafly & Finkbeiner (2011) and a Fitzpatrick (1999) dust extinction law.
3.7 Visual inspection
We considered for visual inspection only those candidates (i) identified independently by LSBG DETR and LSBT ViT ensemble models and (ii) that passed the selection criteria for being an LSBG with the updated parameters from the Galfit. This refined sample was subjected to visual inspection by two authors independently. Candidates identified as LSBGs by both authors were treated as confident LSBGs, and candidates identified as LSBGs by only one author were reinspected together to make a decision. As visual inspection is time-consuming, we only resorted to this at the last step and tried to reduce the number of candidates shortlisted for visual inspection.
To aid in visual inspection, we used two images for every candidate. We generated images enhancing the low-surface-brightness features using the APLpy package (Robitaille & Bressert 2012) and images downloaded from the DESI Legacy Imaging Surveys Sky Viewer (Dey et al. 2019). Furthermore, the g-band Sérsic models from Galfit were also used to visually inspect the quality of the model fitting. Each candidate was then categorised into three classes based on the Galfit model fit and the images: LSBG, non-LSBG (Artifacts), or misfitted LSBGs. If the model of the galaxy was fitted correctly and the candidate showed LSBG features, it was classified as an LSBG. If the candidate showed LSBG features but the model did not fit correctly, we classified it as a misfitted LSBG. Finally, if the candidate did not show LSBG features, we classified it as an artefact or non-LSBG.
3.8 Metrics for comparing models
Here, we use accuracy, true positive rate (TPR), false positive rate (FPR), and area under the receiver operating characteristic (AUROC) curve as the metrics with which to compare the performance of the created transformer models. The classification accuracy of a model is defined as:
where TP is the number of true positives, TN is the number of true negatives, FP is the number of false positives, and FN is the number of false negatives. As identifying LSBGs with less contamination is our primary focus, rather than the overall accuracy of the classifier, TPR and FPR are more informative metrics for evaluating the performance of the classifier. The TPR is the ratio of LSBGs identified by the model to the total number of LSBGs, which can be expressed as
In the literature, sensitivity is another term used to represent the true positive rate (TPR), and it measures how well a classifier detects positive instances (in this case, LSBGs) from the total number of actual positive instances in a dataset. Similarly, FPR can be considered a contamination rate because it measures how often the classifier incorrectly classifies negative instances as positive. The FPR is defined as
All the quantities defined above are threshold dependent and vary as a function of the chosen probability threshold. By constructing the receiver operating characteristic curve (ROC) and finding the AUROC, one could define a threshold-independent metric for comparing the models. The ROC curve is constructed by plotting the true positive rate (TPR) and FPR as functions of the threshold. The area under the ROC curve (AUROC) measures how well a classifier distinguishes between classes and is a constant for the model, unlike the accuracy, which varies with a threshold. If the AUROC is 1.0, the classifier is perfect with TPR = 1.0 and FPR = 0.0 at all thresholds. A random classifier has an AUROC ~ 0.5, with TPR almost equal to FPR for all thresholds.
4 Results
4.1 Model performance on the testing set
We created four models of each transformer, namely LSBG DETR and LSBG ViT, with different hyperparameters to generalise our results for both transformers. Each model was implemented as a regression model to predict the probability of an input being an LSBG, and we set 0.5 as the threshold probability for classifying an input as an LSBG. Further, we use an ensemble of the four models as the final model for LSBG DETR and LSBG ViT. Table 2 describes the architecture, accuracy and AUROC of all the models, including the ensemble models on the test dataset, as mentioned in Sect. 2.3.
As mentioned earlier, the more insightful metrics are the TPR and the FPR rather than overall accuracy. These metrics can be visualised using a confusion matrix, which is shown in Fig. 4 for the ensemble models using a threshold of 0.5. The LSBG DETR ensemble had a TPR of 0.96 and an FPR of 0.07, indicating that the LSBG DETR ensemble model can accurately identify 96% of all LSBGs in the DES data, with an estimated 7% contamination rate in the predicted sample. Similarly, the LSBG ViT Ensemble model can identify 97% of all the LSBGs in DES but with 11% contamination.
The receiver operator characteristic (ROC) curve of the LSBG DETR and LSBG ViT ensemble models are shown in Fig. 5. In terms of accuracy and AUROC, the LSBG DETR models performed slightly better than the LSBG ViT models. It is clear from Fig. 5 that both the ensemble models have a TPR ~0.75 even for a high threshold such as 0.9. Indicating that both the ensemble models can confidently identify around ~75% of all the LSBGs in DES and assign these candidates with a probability of greater than 0.9.
4.2 Search for LSBGs in the full coverage of DES
As the LSBG DETR model and the LSBG ViT model have different architectures and feature extraction principles, we regard the ensemble models of these two as separate independent transformer classifiers. In order to search for new LSBGs from DES, we employed the transformer ensemble model on the 419 782 objects that satisfied the selection criteria defined in Sect. 2.2. The candidates scoring above the threshold probability of 0.5 were catalogued as potential LSBG candidates. The LSBG DETR ensemble classified 27 977 objects as LSBGs, among which 21005 were already identified by Tanoglidis et al. (2021b). Similarly, the LSBG ViT ensemble classified 30 508 objects as LSBGs, among which 21 396 LSBGs were also identified by Tanoglidis et al. (2021b). Therefore, finally, 6972 and 9112 new candidates were classified as potential LSBGs by the LSBG DETR and LSBG ViT ensembles, respectively. However, only the 6560 candidates identified by both the ensemble models independently were considered for further analysis in order to reduce the number of false positives. As there is a possibility that there might be duplicates of the same candidates existing in the selected sample, we ran an automated spatial cross-match to remove duplicate objects separated by <5″. The origin of these duplicates can be traced back to the fragmentation of larger galaxies into smaller parts by SourceExtractor. After removing the duplicates, the number of potential LSBG candidates reduced from 6560 to 6445. As discussed in Sect. 3.6, these candidates were subjected to single-component Sérsic model fitting using Galfit.
During the Galfit modelling, 999 candidates had failed fits and were consequently removed from the sample, because our objective is to produce a high-purity sample with accurate Sérsic parameters. We visually inspected these unsuccessful fits and found that in most cases the presence of a very bright object near the candidate was the cause of the poor Sérsic fit. Of the remaining 5446 candidates, 4879 passed the 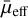 and r1/2 selection criteria outlined in Sect. 2.2 with the updated parameters. These 4879 candidates were inspected visually to identify the genuine LSBGs. After independent visual inspections by the authors, 4190 candidates were classified as LSBGs and 242 candidates were found to be non-LSBGs. During visual inspection, 447 candidates were found to be possible LSBGs with unreliable measurements from Galfit. These candidates are excluded from our final sample, and here we only report the candidates most confidently identified as LSBGs during visual inspection. After correcting for the Galactic extinction correction, our final sample reduced to 4083 new LSBGs from DES DR1. The schematic diagram showing the sequential selection steps used to find the new LSBG sample is shown in Fig. 6. A sample catalogue listing the properties of the newly identified LSBGs is shown in Table 3, and some examples of the new LSBGs that we have found are plotted in Fig. 7.
and r1/2 selection criteria outlined in Sect. 2.2 with the updated parameters. These 4879 candidates were inspected visually to identify the genuine LSBGs. After independent visual inspections by the authors, 4190 candidates were classified as LSBGs and 242 candidates were found to be non-LSBGs. During visual inspection, 447 candidates were found to be possible LSBGs with unreliable measurements from Galfit. These candidates are excluded from our final sample, and here we only report the candidates most confidently identified as LSBGs during visual inspection. After correcting for the Galactic extinction correction, our final sample reduced to 4083 new LSBGs from DES DR1. The schematic diagram showing the sequential selection steps used to find the new LSBG sample is shown in Fig. 6. A sample catalogue listing the properties of the newly identified LSBGs is shown in Table 3, and some examples of the new LSBGs that we have found are plotted in Fig. 7.
The distributions of the r1/2, 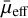 , Sérsic index (n), and axis ratio (q) of the new sample of LSBGs are plotted in Fig. 8. The majority of the LSBGs in this new sample have r1/2 < 7″ and
, Sérsic index (n), and axis ratio (q) of the new sample of LSBGs are plotted in Fig. 8. The majority of the LSBGs in this new sample have r1/2 < 7″ and  mag arcsec−2. The Sérsic index of the new LSBG sample predominantly lies between 0.5 and 1.5 and has a median value of 0.85. This pattern is similar to the trend identified by Poulain et al. (2021) in the case of dwarf ellipticals, suggesting that a significant portion of the LSBG sample could be comprised of such sources. In the case of the axis ratio, the new LSBG sample has a median axis ratio of 0.72 and has a distribution lying in the range of 0.3–1. The median value of 0.72 suggests that most galaxies in this sample have a slightly flattened or elongated shape. A detailed discussion of the properties of the new LSBGs identified in this work and their comparison with LSBGs identified by Tanoglidis et al. (2021b) is presented in Sect. 5.
mag arcsec−2. The Sérsic index of the new LSBG sample predominantly lies between 0.5 and 1.5 and has a median value of 0.85. This pattern is similar to the trend identified by Poulain et al. (2021) in the case of dwarf ellipticals, suggesting that a significant portion of the LSBG sample could be comprised of such sources. In the case of the axis ratio, the new LSBG sample has a median axis ratio of 0.72 and has a distribution lying in the range of 0.3–1. The median value of 0.72 suggests that most galaxies in this sample have a slightly flattened or elongated shape. A detailed discussion of the properties of the new LSBGs identified in this work and their comparison with LSBGs identified by Tanoglidis et al. (2021b) is presented in Sect. 5.
 |
Fig. 4 Confusion matrix of LSBG DETR and LSBG ViT models plotted for a threshold = 0.5. Class 0 represents the artefacts, and Class 1 represents the LSBGs. |
 |
Fig. 5 Receiver operating characteristic curve of the ensemble models. The red and blue lines represent the variation of FPR and TPR as a function of the threshold for LSBG DETR and LSBG Vision ensembles, respectively. The red and blue points mark the TPR and FPR for a threshold = 0.9. |
Architecture, accuracy, TPR, FPR, and AUROC of all the models in chronological order of creation.
5 Discussion
5.1 Transformers as LSBG detectors
In this study, we introduce the use of transformers as classifier models for finding the undiscovered LSBGs in DES. Currently, in the literature, one of the reported deep-learning-based models for classifying LSBGs and artefacts is a CNN model named DeepShadows created by Tanoglidis et al. (2021a). These authors used the catalogue of LSBGs and artefacts identified from DES reported in Tanoglidis et al. (2021b) to generate the training data. The DeepShadows model achieved an accuracy of 92% in classifying LSBGs from artefacts and had a TPR of 94% with a threshold of 0.5. Moreover, the DeepShadows model also achieved an AUROC score of 0.974 on this training dataset. However, the DeepShadows was not applied to the complete DES data and its performance was not evaluated. Nevertheless, DeepShadows was the first deep-learning model used to classify LSBGs and artefacts. In addition, Tanoglidis et al. (2021a) showed that the DeepShaodws was a better classifier than the support vector machine or random forest models. However, in our work, all of our transformer models were able to surpass the DeepShadows model in every metric individually, which can be seen from Table 2. Namely, in their respective classes, LSBG DETR 1 and LSBG ViT 2 had the highest accuracies (94.36 and 93.79%), respectively.
Earlier searches for LSBGs used semi-automated methods such as pipelines based on imfit by Greco et al. (2018) or simple machine-learning models such as SVMs by Tanoglidis et al. (2021b). However, the success rate of these methods was very low, and 50% of the final candidate sample produced by these methods was made up of false positives, which had to be removed by visual inspection. Here we explore the possibilities of transformer architectures in separating LSBGs from artefacts. We used two independent ensemble models of LSBG DETR and LSBG ViT models and single-component Sérsic model fitting to filter the LSBG candidates. Only 5% of our final sample was made up of non-LSBGs, which is a significant improvement on the results of previous methods in the literature. Following the definition of an LSBG as described in Tanoglidis et al. (2021b), we identified 4083 new LSBGs from DES DR1, increasing the number of identified LSBGs in DES by 17%. Our results highlight the significant advantage of using deep-learning techniques to search for LSBGs in the upcoming large-scale surveys.
To gain further insight into the fraction of false positives from our method, we evaluated the performance of these models during training. We encountered around 7 and 11% artefacts from the LSBG DETR ensemble and LSBG ViT sample, respectively, during training on the test dataset. However, using a combination of these models, we reduced the artefact fraction to less than 5% during visual inspection. Most of the non-LSBGs we encountered during visual inspection were faint compact objects that blended in the diffuse light from nearby bright objects. We use the term ‘non-LSBG’ instead of artefacts here because, during visual inspection, we classified some potential LSBGs as non-LSBGs; these are objects for which the g-band images contained instrumental artefacts or lacked sufficient signal in the g-band. As the machine learning model takes three bands as input (g, r and z), this suggests that the model was able to study and generalise the nature of LSBGs in each band and was able to predict whether or not it was an LSBG based on the signal from the other bands. However, as we define LSBGs based on their g-band surface brightness and radius in this work, we classified the galaxies without reliable g-band data as non-LSBGs. Some non-LSBGs we encountered during visual inspection are shown in Figs. 9 and 10. With the upcoming surveys of deeper imaging, these galaxies might be classified as LSBGs, which might further reduce the non-LSBGs in our candidate sample.
When discussing the non-LSBGs from the candidate sample, we must also mention that some of the candidates identified as LSBGs by the ensemble models (567 out of 5446) did not meet the selection criteria for being an LSBG after being fitted with Galfit. These galaxies had r1/2 ranging from 2″ to 20″, with a median of 3.85″, which is similar to the new LSBG sample we found. However, the majority of these galaxies have a mean surface brightness of between 24.0 and 24.2 mag arcsec−2, with a median of 24.16 mag arcsec−2. This suggests that the machine learning model understood the criteria for angular size for LSBGs during its training, but it did not learn the strict condition regarding surface brightness. This situation is similar to a human expert analysing a galaxy image to determine whether or not it is an LSBG. Features such as the size of the galaxy are easily identifiable to the human eye. However, determining the surface brightness accurately with only the human eye would be challenging, and there may be possible errors near the threshold region, similar to our machine learning model. One could therefore say that the machine learning model is behaving in approximately the same way as a human visual expert.
Judging from the performance of our model on the training data, we cannot assert that we have discovered all the possible existing LSBGs from the DES DR1. As we can see from Fig. 4, the TPRs for the individual ensemble models were 0.96 and 0.97, respectively. This means that the model has not found all the possible LSBGs and a minor fraction of LSBGs is yet to be found in DES DR1. Moreover, to reduce the FPR and the burden during visual inspection, we only visually inspected the candidates identified commonly by both the ensemble models and that passed the criteria for correctly fitting by Gal fit.
We also note that, in this work, we are using two different ensemble models, each being an ensemble of four models. As mentioned earlier, each ML model can be considered equivalent to a human inspector, and the ensemble models help balance out the disadvantages of the other models in the ensemble. A closer look at the individual probability distribution of these models shows that there are 310 candidates among the 4 083 confirmed LSBG candidates, which had a probability of less than 0.5 for at least one model among the individual models. However, as we used an average ensemble model, we were able to identify these LSBGs by balancing out the probability, which demonstrates the advantage of using an ensemble model over a single model.
Here, we use visual inspection as the final step to confirm the authenticity of an LSBG detected by the models. However, it is essential to acknowledge the potential for human bias during the visual inspection, which can impact the accuracy and reliability of the results. For example, during the visual inspection, there was disagreement over the labelling of approximately 10% of the candidate sample. Most of these galaxies had a mean surface brightness of greater than 25.0 mag arcsec−2, which suggests that even for human experts, it is challenging to characterise extremely faint LSBGs. With better imaging, this might change, but we must acknowledge that there will always be some human bias and error associated with human inspection. Also, we must consider that in the upcoming surveys, such as LSST and Euclid, there will be too much data to make visual inspection a viable possibility. In this scenario, relying solely on improved automated methods to purify the sample and accepting a small fraction of false positives could be a feasible solution.
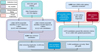 |
Fig. 6 Schematic diagram showing the sequential selection steps used to find the new LSBG sample. |
Sample of new LSBGs identified in this work.
 |
Fig. 7 Cutouts of nine confirmed new LSBGs after visual inspection. The unique identification number (co object id) for each galaxy in DES DR1 is given below each image. The images were generated by combining the g, r, and z bands using the APLpy package (Robitaille & Bressert 2012), and each image corresponds to a 67.32″ × 67.32″ region of the sky with the LSBG at its centre. |
 |
Fig. 8 Normalised distribution of half-light radius (top left panel), mean surface brightness (top right panel), Sérsic index (bottom left panel), and axis ratio (bottom right panel) of the new sample of LSBGs. The dashed line shows the median of the distribution. |
 |
Fig. 9 Examples of candidates (Coadd object id - 149796289 and 374192591) classified as non-LSBGs during visual inspection because of glitches in the g-band near the galaxy. The panels a and c show the RGB image created using the g, r, and z bands with APLpy package (Robitaille & Bressert 2012). Panels b and d show the image in the g band. Each image corresponds to a 67.32″ × 67.32″ region of the sky with the candidate at its centre. |
 |
Fig. 10 Examples of candidates classified as non-LSBG during visual inspection because of lack of sufficient signal in the g-band (a) are shown in the top panel. Candidates classified as non-LSBG during visual inspection because of being artefacts are shown in the lower panel (b). The RGB images are created using the g, r, and z bands with the APLpy package (Robitaille & Bressert 2012). Each image corresponds to a 67.32″ × 67.32″ region of the sky with the candidate at its centre. |
 |
Fig. 11 Normalised distribution of colour of the LSBGs from the new sample identified in this work and the LSBGs identified by Tanoglidis et al. (2021b) plotted in the left panel. The right panel shows the colour as a function of mean surface brightness in the g-band for the new sample identified in this work and the LSBGs identified by Tanoglidis et al. (2021b). The dashed line shows the separation between red and blue LSBGS. |
6 The new sample of DES DR1 LSBGs
6.1 The newly identified LSBG sample
The optical colour of a galaxy can provide insights into its stellar population. Conventionally, based on their colour, the galaxies are divided into red and blue galaxies, and it has been shown that colour is strongly correlated to the morphology of a galaxy (Strateva et al. 2001). Blue galaxies are usually found to be highly actively star-forming spiral or irregular systems. In contrast, red galaxies are mostly found to be spheroidal or elliptical. In addition, the red galaxies have also been found to tend to cluster together compared to the blue galaxies (Bamford et al. 2009).
The LSBGs found by Tanoglidis et al. (2021b) have found a clear bimodality in the g – i colour distribution, which is similar to the LSBGs found by Greco et al. (2018). In the left panel of Fig. 11, we present the g – i colour distribution of the 4083 new LSBGs and the 23 790 LSBGs found by Tanoglidis et al. (2021b). We follow the criteria defined by Tanoglidis et al. (2021b) to define red galaxies as galaxies with g – i > 0.6 and blue galaxies as galaxies with g – i < 0.6, where g and i represent the magnitude in each band. In the right panel of Fig. 11, we present the colour as a function of mean surface brightness in g-band for the new sample identified in this work and the LSBGs identified by Tanoglidis et al. (2021b). There are 1112 red LSBGs and 2944 blue LSBGs in the new LSBG sample4. From Fig. 11, we can see that we have identified a relatively large fraction of blue LSBGs compared to Tanoglidis et al. (2021b) and a considerable fraction of new red LSBGs with g – i ≥ 0.80 and a mean surface brightness of less than 25.0 mag arcsec−2. The bias against blue LSBGs and highly red LSBGs in the sample created by Tanoglidis et al. (2021b) may have been caused by the bias in the training set used to create the SVM, which preselected the LSBG candidates. This bias could have occurred because a large fraction of their training set consisted of LSBGs near the Fornax cluster, which are mainly red LSBGs.
Looking at the distribution of 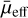 values of the new sample, both the red and blue LSBGs have a similar mean surface brightness range, with median
values of the new sample, both the red and blue LSBGs have a similar mean surface brightness range, with median 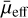 of 24.75 and 24.68 mag arcsec−2, respectively. Both red LSBG and blue LSBG populations from the new sample have sizes ranging from 2.5″ to 20″. However, as mentioned above, most of these LSBGs have radii of less than 7″, with a median of 4.01″ for blue LSBGs and 3.59″ for red LSBGs. In comparison, blue LSBGs tend to have larger angular radii compared to red LSBGs. The Sérsic index distribution is similar in both the red and blue LSBGs in the new sample and they have an almost equal median value (0.847 and 0.845 for red and blue LSBGs, respectively). A median Sérsic index of around 0.84 indicates that the majority of the galaxies are closer to a disc-shaped geometry, irrespective of their colour. The distribution of the axis ratio of the red LSBGs from the new sample is clearly different from that of the blue LSBGs, as shown in Fig. 12. The median of the axis ratio distribution of the blue and red LSBGs is 0.7 and 0.8, respectively. This indicates that, in general, the red LSBGs are rounder than the blue LSBGs.
of 24.75 and 24.68 mag arcsec−2, respectively. Both red LSBG and blue LSBG populations from the new sample have sizes ranging from 2.5″ to 20″. However, as mentioned above, most of these LSBGs have radii of less than 7″, with a median of 4.01″ for blue LSBGs and 3.59″ for red LSBGs. In comparison, blue LSBGs tend to have larger angular radii compared to red LSBGs. The Sérsic index distribution is similar in both the red and blue LSBGs in the new sample and they have an almost equal median value (0.847 and 0.845 for red and blue LSBGs, respectively). A median Sérsic index of around 0.84 indicates that the majority of the galaxies are closer to a disc-shaped geometry, irrespective of their colour. The distribution of the axis ratio of the red LSBGs from the new sample is clearly different from that of the blue LSBGs, as shown in Fig. 12. The median of the axis ratio distribution of the blue and red LSBGs is 0.7 and 0.8, respectively. This indicates that, in general, the red LSBGs are rounder than the blue LSBGs.
 |
Fig. 12 Normalised distribution of axis ratio (left panel) of red and blue LSBGs from the new sample. The vertical lines show the median for each class. |
6.2 Why are there additional LSBGs?
Another aspect worthy of investigation at this moment is the extent to which the new LSBG sample is different from the LSBGs identified by Tanoglidis et al. (2021b). More specifically, one might wonder why this many LSBGs were previously missed, and whether or not this is somehow related to the nature of the galaxies themselves. Apart from the Sérsic index, all other Sérsic parameters of the new and old samples have a similar distribution. The distribution of the Sérsic index for the new sample identified in this work and that of the LSBG sample identified by Tanoglidis et al. (2021b) are shown in Fig. 13. The new LSBG sample has a Sérsic index predominantly in the range n < 1, which is lower than the Sérsic index distribution of LSBGs identified by Tanoglidis et al. (2021b). However, this does not point to any reason why these LSBGs were missed in the previous search, and moreover, Tanoglidis et al. (2021b) also mentioned an under-representation of red LSBGs with small Sérsic index in their sample.
To answer the aforementioned question, a close inspection of the methodology of Tanoglidis et al. (2021b) shows that most of the new LSBGs (82%) we identified here were missed by the SVM in their first preselection step. This demonstrates the importance of methodology in preselecting the samples. As the methodologies used by Tanoglidis et al. (2021b) and Greco et al. (2018) show considerable similarity (e.g. usage of SVM), this indicates that Greco et al. (2018) might have also missed some LSBGs from the HSC-SSP survey and that the fraction should be greater in comparison to Tanoglidis et al. (2021b). It should be noted that there is a slight overlap in the regions of observation by Greco et al. (2018) and DES, as shown in Fig. 14. There are 198 LSBGs identified by Greco et al. (2018) from HSC-SSP in the field of view of DES and detected in the DES Y3 Gold catalogue. Among these 198 LSBGs, Tanoglidis et al. (2021b) recovered 183 LSBGs, and we recovered 10 additional LSBGs from this field, taking the total number of recovered LSBGs to 193. We would also like to point out that there are additional LSBGs (~200) in our total sample in the same region that were missed by Greco et al. (2018), despite the fact that the HSC-SSP data used by Greco et al. (2018) are about two orders of magnitude deeper than the DES DR1. However, we also missed some LSBGs (~150) that were identified by Greco et al. (2018). These LSBGs were not detected in the DES Y3 Gold catalogue and were subsequently missed by the searches by Tanoglidis et al. (2021b) and ours. Given that the DES data release 2 (DES DR 2) are of greater depth (~0.5 mag; Abbott et al. 2021), we should expect an increase in the number of LSBGs from DES. Therefore, there is a potential for using transfer learning with transformers in the future search for LSBGs from DES DR 2 (Abbott et al. 2021) and HSC-SSP Data Release 3 (Aihara et al. 2022).
With the addition of the new 4083 LSBGs, the number of LSBGs in the DES increased to 27 873, effectively increasing the average number density of LSBGs in DES to ~5.5 deg−2. In addition, it should be noted that there are still around 3000 candidates identified by the ensemble models, which were not analysed further for verification of their possible LSBG nature, potentially indicating that the number of LSBGs in DES might increase further in future. The average number density of 5.5 deg−2 reported here can therefore only be taken as a lower limit. Earlier, Greco et al. (2018) estimated that the average number density of LSBGs in HSC-SSP is ~3.9 deg−2. However, this estimate was based on LSBG samples with  mag arcsec−2, unlike the
mag arcsec−2, unlike the 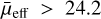 mag arcsec−2 selection we adopted in this work. For a similar selection on mue > 24.2mag arcsec−2 in the combined sample presented here (LSBGs identified in this work plus LSBGs identified by Tanoglidis et al. 2021b), we obtain a higher number density of 4.9 deg−2, compared to the previous estimates (3.9 deg−2 from Greco et al. 2018 and 4.5 deg−2 from Tanoglidis et al. 2021b).
mag arcsec−2 selection we adopted in this work. For a similar selection on mue > 24.2mag arcsec−2 in the combined sample presented here (LSBGs identified in this work plus LSBGs identified by Tanoglidis et al. 2021b), we obtain a higher number density of 4.9 deg−2, compared to the previous estimates (3.9 deg−2 from Greco et al. 2018 and 4.5 deg−2 from Tanoglidis et al. 2021b).
As discussed above, the number density of LSBGs will be influenced by the methodology used to search for them. Similarly, one other intrinsic factor that can influence the number density is the completeness of the survey. Improved imaging techniques can reveal fainter objects, leading to an increase in the number density. The completeness of a survey can be determined by plotting the galaxy number count, and one could also obtain a rough idea of the redshift distribution of the objects of interest by comparing this count with the Euclidean number count. Figure 15 shows the number count of LSBGs identified in DES (this work and Tanoglidis et al. 2021b) and HSC (Greco et al. 2018). As expected, HSC has higher completeness than DES. However, HSC still has a lower number density than DES, which is evident from comparing the peaks of both number counts. The slope of the number counts near 0.6 (representing Euclidean geometry) for both HSC and DES suggests that most identified LSBGs are local (Yasuda et al. 2001). Furthermore, Greene et al. (2022) analysed the LSBG sample from HSC and estimated that the 781 LSBGs identified by Greco et al. (2018) have a redshift of less than 0.15.
With the increasing number of LSBGs identified from different surveys, a further open question at this moment refers to the precise definition of an LSBG. A different definition for an LSBG could be used, consequently leading to finding a completely different sample of LSBGs from the same dataset, which in turn could affect the conclusions of the study. The current discrepancies in defining LSBGs largely stem from the predominant reliance on surface brightness-based definitions, which are inherently dependent on the observational band in use. Different observation bands may involve distinct threshold values. Depending on the band we use, the LSBG definition will likely vary. In this scenario, one potential solution is to define an LSBG based on the stellar mass density of the galaxy. Current definitions based on the stellar mass density define an LSBG as a galaxy with a stellar mass density of Σstar ≲ 107 M⊙ kpc−2 (e.g. Carleton et al. 2023). Following Eq. (1) of Chamba et al. (2022), we estimated the stellar mass surface density using our observed i-band surface brightness 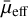 and the stellar mass-to-light ratio obtained from the g – i colour (Du et al. 2020). The stellar mass surface density distributions of the LSBGs from DES and HSC-SSP are shown in Fig. 16. Here, we can see that most of the LSBGs satisfy this condition, and only a small percentage stay above the threshold of 107 M⊙ kpc−2. On average, the LSBGs from DES have a higher stellar mass surface density than those from HSC-SSP, which could be attributed to the higher depth in the data used by Greco et al. (2018). However, as argued by Chamba et al. (2022), accurate estimation of the stellar mass density requires deep photometry in multiple bands. In our case, we employed a single colour, and as a result, the constraints we derived on the stellar mass density may be limited in accuracy.
and the stellar mass-to-light ratio obtained from the g – i colour (Du et al. 2020). The stellar mass surface density distributions of the LSBGs from DES and HSC-SSP are shown in Fig. 16. Here, we can see that most of the LSBGs satisfy this condition, and only a small percentage stay above the threshold of 107 M⊙ kpc−2. On average, the LSBGs from DES have a higher stellar mass surface density than those from HSC-SSP, which could be attributed to the higher depth in the data used by Greco et al. (2018). However, as argued by Chamba et al. (2022), accurate estimation of the stellar mass density requires deep photometry in multiple bands. In our case, we employed a single colour, and as a result, the constraints we derived on the stellar mass density may be limited in accuracy.
 |
Fig. 13 Normalised distribution of the Sérsic index of the LSBGs identified in this work and by Tanoglidis et al. (2021b). The vertical lines show the median for each class. |
 |
Fig. 14 Sky distribution of the LSBGs identified from DES (black dots) by Tanoglidis et al. (2021b) and in this work and the LSBGs identified from HSC-SSP (blue dots) by Greco et al. (2018). |
 |
Fig. 15 Number count of galaxies as a function of i-band magnitude, with the y-axis displaying the logarithm of the number density as a function of apparent magnitude. The red line with the blue error bars represents the data from HSC, and the black dashed line with green error bars represents the data from DES. |
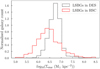 |
Fig. 16 Normalised distribution of stellar mass surface density of LSBGs identified in HSC (red line) and DES (black line). |
7 Clustering of LSBGs in DES
The on-sky distributions of the red and blue LSBGs identified in this work, along with those identified by Tanoglidis et al. (2021b), are shown in Figs. 17 and 18. In the local Universe, ‘normal’ high-surface-brightness red galaxies tend to cluster together, while blue galaxies are much more dispersed in the field (Zehavi et al. 2005). Such a trend is also clearly visible for the LSBG sample. As seen in Fig. 17, red LSBGs tend to form concentrated nodes. In contrast, the blue LSBGs are distributed much more homogeneously in the sky, as seen in Fig. 18.
A two-point auto-correlation function is a statistical tool commonly used to quantify the galaxy clustering (Peebles 1980). Here we use the angular two-point auto-correlation function, ω(θ), computed using the Landy & Szalay (1993) estimator, which is defined as
where
where DD(θ) is the number of pairs in the real sample with angular separation θ, RR(θ) is the number of pairs within a random sample, DR(θ) is the number of cross pairs between the real and random samples, nd is the total number of real data points, and nr is the total number of random points.
We use a random sample of 4491746 points generated from the DES footprint mask. To compute ω(θ) we employ treecorr (Jarvis 2015). Errors are estimated using jackknife resampling where the sky is divided into 100 equal-sized batches for resampling (Efron & Gong 1983). For samples of high-surface-brightness galaxies (HSBGs), the angular correlation function can very often be well fitted by a single power law (Peebles & Hauser 1974; Peebles 1980; Hewett 1982; Koo & Szalay 1984; Neuschaefer et al. 1991):
where A is the amplitude that represents the strength of the clustering, and γ represents the rate at which the strength of the clustering reduces as we go to large angular scales. This power-law behaviour is usually observed on a wide range of angular scales; however, it is not universal, especially on the smallest scales. Full modelling of the shape of the correlation function requires accounting for the different processes governing galaxy clustering on small scales (corresponding to galaxies located in the same dark matter halo) and at larger scales (corresponding to clustering of different haloes). This modelling is usually done using the halo occupation distribution models (HODs; Ma & Fry 2000; Peacock & Smith 2000; Zheng et al. 2005; Kobayashi et al. 2022). However, in this work, we perform only a preliminary analysis and base interpretation of our data on the power-law fitting alone.
To compare the clustering of the LSBGs with the clustering of the HSBGs, we constructed a control sample of HSBGs from the DES data. To this purpose, we selected galaxies in the surface brightness range 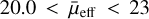 mag arcsec−2 and in the magnitude range 17 < g < 23 mag (which is the same magnitude range as our LSBG sample). Additionally, we applied a photometric redshift z < 0.1 cut in order to keep the HSBGs sample consistent with the LSBGs, which are also expected to be mostly local (Greene et al. 2022). For this end, we used the photometric redshifts from the DES Y3 Gold catalogue calculated using the Directional Neighbourhood Fitting (DNF) algorithm (Sevilla-Noarbe et al. 2021; De Vicente et al. 2016). In addition, we also applied the selection cuts on the parameters from SourceExtractor such as SPREAD_MODEL,EXTENDED_CLASS_COADD and on colours (using the MAG_AUTO magnitudes) as described in Sect. 2.2.
mag arcsec−2 and in the magnitude range 17 < g < 23 mag (which is the same magnitude range as our LSBG sample). Additionally, we applied a photometric redshift z < 0.1 cut in order to keep the HSBGs sample consistent with the LSBGs, which are also expected to be mostly local (Greene et al. 2022). For this end, we used the photometric redshifts from the DES Y3 Gold catalogue calculated using the Directional Neighbourhood Fitting (DNF) algorithm (Sevilla-Noarbe et al. 2021; De Vicente et al. 2016). In addition, we also applied the selection cuts on the parameters from SourceExtractor such as SPREAD_MODEL,EXTENDED_CLASS_COADD and on colours (using the MAG_AUTO magnitudes) as described in Sect. 2.2.
Initially, we computed the angular two-point auto-correlation function for the samples of LSBGs and HSBGs. We then split the samples into red and blue galaxies to measure their clustering properties separately. For LSBGs, we followed the criterion defined in Sect. 6, that is, a colour cut of g – i = 0.6 mag to separate blue and red sources. As seen from the colour histogram presented in Fig. 19, the HSBGs show a bimodality around g – i = 1.0 mag, which can be most likely attributed to their different stellar masses. Consequently, we use the boundary g – i = 1.0 mag to divide our HSBG sample into red and blue subsamples. The properties of all the samples used for the measurement of the galaxy clustering, together with the best-fit power-law parameters, are listed in Table 4. The two-point autocorrelation functions for all the samples described above are shown in Fig. 20.
As is clear from Fig. 20, the angular two-point autocorrelation function of the red LSBGs does not follow a power law at small angular scales. Therefore, the power-law fits were only performed in the range of 0.15 deg to 7 deg to prevent them being affected by the one-halo effects. In part well fitted by the power law, for the red LSBGs, ω(θ) is significantly steeper than for the blue LSBGs; however, it flattens at smaller scales, that is, between 0.01 deg and 0.2 deg. This behaviour is also transmitted to the full sample of LSBGs. In contrast, the blue LSBGs follow a power-law behaviour, with a lower clustering amplitude and a much shallower slope, at almost all angular scales. This behaviour of the angular correlation function might be explained by the observations by van der Burg et al. (2016) and Wittmann et al. (2017) that the number of LSBGs close to the cores of galaxy clusters decreases. Such suppression may reduce the clustering power on small scales, leading to a flattening of the autocorrelation function, which is seen for the red LSBGs, which are mostly associated with clusters.
Notable differences are also seen in the clustering of the LSBGs and the HSBGs. Not surprisingly, red samples – both of HSBGs and LSBGs – are more clustered than their blue counterparts. At the same time, the red LSBG sample has a significantly higher clustering amplitude than the reference red HSBG sample. Red LSBGs also display a steeper slope of ω(θ) at angular scales larger than 0.15 deg, but at smaller scales, their ω(θ) flattens, unlike in the case of red HSBGs for which we can even observe hints of an upturn, which can be associated with a one-halo term. This picture is consistent with a scenario in which red LSBGs are mostly associated with dense structures like clusters; however, these LSBGs do not populate the centres of these structures but rather their outskirts. In contrast, red HSBGs display the usual behaviour of red passive galaxies, appearing in a variety of environments, with a tendency to cluster and gather most strongly in the cluster centres.
Blue LSBGs have a significantly lower clustering amplitude than their HSBG counterparts. At the same time, the slope of their ω(θ) at scales larger than 0.15 deg remains very similar. The blue HSBGs and LSBGs follow the usual distribution of blue star-forming galaxies, dispersed in the field and avoiding clusters. These results are consistent with the results obtained by Tanoglidis et al. (2021b) for their sample of DES LSBGs. These latter authors compared the clustering of LSBGs with very bright galaxies in the magnitude range of 14 < g < 18.5 mag from the 2MPZ catalogue (Bilicki et al. 2014), finding that LSBGs had higher clustering amplitude in the range of 0.1–2 degrees, which is similar to our observations.
However, our results contradict the early estimates from Bothun et al. (1993) and Mo et al. (1994), who infer that the LSBGs tend to show weak spatial clustering. However, their analyses were limited by a small data sample (~400 LSBGs), a small area of the sky, and most likely selection biases. Given the low accuracy of photometric redshifts for LSBGs in our sample, we do not attempt to reconstruct their spatial clustering in this work. Further analysis is planned as a follow-up to this study.
 |
Fig. 17 Sky distribution of the red LSBGs identified in this work (red dots) and of the LSBGs identified (black dots) by Tanoglidis et al. (2021b). |
 |
Fig. 18 Sky distribution of the blue LSBGs identified from the new sample (blue dots) and of the LSBGs identified (black dots) by Tanoglidis et al. (2021b). |
 |
Fig. 19 Colour distribution of the HSBGs from the DES DR1. The vertical line at g – i = 1.0 shows the colour separation of the HSBGs into red and blue galaxies. |
 |
Fig. 20 Angular autocorrelation function for the full sample of LSBGs (grey line with open circles) and the sample of HSBGs (black line with crosses) is shown in the left panel. The angular autocorrelation function of the red LSBGs (red line), blue LSBGs (blue line), red HSBGs (orange line), and blue HSBGs (purple line) is shown in the right panel. The vertical green shaded region represents the region fitted for a power law (ω = Aθ1–γ), and the corresponding γ values are shown in the legend. |
Best-fitting power-law parameters for the angular two-point autocorrelation function for HSBGs and LSBGs along with information on the number of galaxies, median g-band magnitude, and the mean surface brightness for each sample.
8 Identification of ultradiffuse galaxies
As discussed in Sect. 1, UDGs are a subclass of LSBGs that have extended half-light radii of r1/2 ≥ 1.5 kpc and a central surface brightness of µ0 > 24 mag arcsec−2 in g-band (van Dokkum et al. 2015). A significant population of UDGs has been discovered in the Coma cluster by van Dokkum et al. (2015) and other investigations have revealed a large number of UDGs in other galaxy clusters (Koda et al. 2015; Mihos et al. 2015; Lim et al. 2020; La Marca et al. 2022). Later studies showed that thousands of UDGs can be found in single individual clusters and that the abundance of UDGs scales almost linearly with host halo mass (van der Burg et al. 2016; Mancera Piña et al. 2018).
In order to search our sample of LSBGs – identified in DES – for cluster UDGs, we cross-matched our total LSBG sample (23 790 LSBGs from Tanoglidis et al. 2021b and the 4083 new LSBGs we identified) with the X-ray-selected galaxy cluster catalogue from the ROSAT All-Sky Survey (RXGCC; Xu et al. 2022). All the LSBGs at an angular distance from the centre of the cluster of less than R2005 (i.e. the virial radius of the cluster) were associated with that cluster. Here, R200 is the radius at which the average density of a galaxy cluster is 200 times the critical density of the Universe at that redshift. We find 1310 LSBGs from the combined catalogue and 123 LSBGs from our new sample to be associated with 130 and 53 clusters, respectively. Using the redshift of the cluster provided in Xu et al. (2022), and assuming that any associated LSBG is at the same redshift as the cluster, we estimated the half-light radius of those LSBGs and their projected comoving distance from the cluster centre. It should be noted that, as we perform our cross-matching with only projected distances, some of the LSBGs associated with clusters could be non-cluster members that are projected along the field. However, this is unlikely to be the case for all of them, and given that we do not have any other distance estimate for the LSBGs, we chose to adopt this method. However, it should also be noted that UDGs are not exclusively located in clusters; they can also be observed in groups (Cohen et al. 2018; Marleau et al. 2021) and even in field environments (Prole et al. 2019). In this section, we focus on the LSBGs and UDGs associated with the clusters.
Among the 1310 cluster LSBGs, we further classify 317 cluster UDG candidates based on their half-light radius (r1/2 ≥ 1.5 kpc) and their central surface brightness (µ0 > 24.0 mag arcsec−2) in g-band. As we have not confirmed the physical distances to these galaxies, and therefore cannot be certain of their physical sizes, they can only be regarded as UDG candidates. From here onward, when referring to UDGs in this paper, it is important to note that we are discussing UDG candidates and not confirmed UDGs. These 317 UDGs are distributed within 80 clusters, making it the largest sample of clusters in which UDGs have been studied. It should also be noted that Tanoglidis et al. (2021b) also identified 41 UDGs from their LSBG sample in DES by associating the nine most overdense regions of LSBGs with known clusters. However, these authors did not study the properties of those 41 UDGs in detail, and the 276 UDGs among the 317 UDGs reported here are completely new. The UDGs presented here have a median rı/2 of 2.75 kpc and µ0 of 24.51 mag arcsec−2. Six of the newly identified UDGs are shown in Fig. 21.
As seen from Fig. 22, the majority of the cluster UDGs (253 out of 317) are red in colour (ɡ–i > 0.6 mag), which is similar to the trend of cluster LSBGs (909 out of 1310). This is consistent with theoretical predictions for cluster UDGs (Benavides et al. 2023). Mancera Piña et al. (2019) found a similar distribution for the ɡ – r colour of 442 UDGs observed in eight galaxy clusters. The joint distribution of the red and blues UDGs in the space of r1/2 and µ0 is shown in Fig. 23. The red UDGs presented here have a median r1/2 of 2.75 kpc and µ0 of 24.52 mag arcsec−2. Similarly, the blue UDGs have a median r1/2 of 2.78 kpc and µ0 of 24.41 mag arcsec−2. Most of the red and blue UDGs have a half-light radius in the range 1.5 < r1/2 < 6 kpc. However, there is a small fraction of UDGs (6 out of 317) with r1/2 > 10 kpc; these are all red and have µ0 < 25.0 mag arcsec−2, and could be regarded as good potential candidates for follow-up studies.
For all the cluster LSBGs, we can see a gradient in colour as shown in Fig. 24, where LSBGs towards the outskirts of clusters tend to be bluer than those in the centre. This is similar to the behaviour found in Virgo cluster LSBGs from Junais et al. (2022). However, for the cluster UDGs presented in this study, the colour gradient appears much weaker, showing an almost flat distribution in comparison to the LSBGs. A similar weak trend, where more blue UDGs are found towards the cluster centre, was also noted by Mancera Piña et al. (2019). On the other hand, Román & Trujillo (2017) and Alabi et al. (2020) reported a more pronounced colour trend as a function of cluster-centric distance, while La Marca et al. (2022) did not find any significant trend. However, when directly comparing the trends in the colour of UDGs in the cluster, one should keep in mind that these trends will be affected by several factors, such as the bands used to determine colour, sample size, and the studied cluster, as we can see from the results in the literature. For example, our sample size (>300) is similar to the sample size of Mancera Piña et al. (2019), and we obtain similar results, whereas our findings are different from those of Román & Trujillo (2017); Alabi et al. (2020) and La Marca et al. (2022), who use smaller sample sizes (<40).
The trend observed in the half-light radius (Fig. 24) for both the cluster LSBGs and UDGs is quite evident. As we move towards the outer regions of the cluster centre, both LSBGs and UDGs show an increase in size. This behaviour is in agreement with the findings of Román & Trujillo (2017). The gradients we observe in colour and size with respect to the cluster-centric distance are consistent with the proposed UDG formation scenarios, such the galaxy harassment (Conselice 2018), tidal interactions Mancera Piña et al. (2019), and ram-pressure stripping (Conselice et al. 2003b; Buyle et al. 2005). Such trends are also similar to what is observed for dwarf galaxies in the literature (Venhola et al. 2019), providing further support for the argument that UDGs can be considered a subset of dwarf galaxies (Conselice 2018; Benavides et al. 2023).
The sample of UDG candidates presented here will be the subject of a follow-up analysis. Additionally, it should be noted that all the UDGs reported here are cluster UDGs. The actual number of UDGs in the LSBG catalogue (including low-density environments) might be more than this, and therefore the reported number is only a lower limit on the total number of UDGs.
 |
Fig. 21 Cut-outs of six confirmed new UDGs. The unique identification number (Coadd Object Id) for each galaxy in DES DR1 is given below each image. The images were generated by combining the g, r, and z bands using the APLpy package (Robitaille & Bressert 2012), and each image corresponds to a 33.66″ × 33.66″ region of the sky with the UDG at its centre. |
 |
Fig. 22 Colour distribution of the 1310 cluster LSBGs and 317 cluster UDGs from the DES DR1. |
 |
Fig. 23 Joint distribution of the red (red dots) and blue (blue cross) UDGs in the space of r1/2 and µ0 in the ɡ-band. The vertical lines in the histogram on the x-axis and y-axis show the median for each class. |
9 Conclusions
In this paper, we explore the possibility of using transformers to distinguish LSBGs from artefacts in optical imaging data. We implemented four transformer models that combined the use of CNN backbone and self-attention layers to classify the labels; we call them LSBG DETR (LSBG detection transformers) models. Similarly, we created four transformer models that directly apply attention to the patches of the images without any convolutions; we call these models LSBG vision transformers. We compared the performances of these two different architectures to that of the LSBG identification CNN model called DeepShadows presented in Tanoglidis et al. (2021a). We find that the transformer models perform better than DeepShadows. We then used the ensemble of our transformer models to look for new LSBGs in the DES DR1 data that the previous searches may have missed. We follow the definition of an LSBG used by Tanoglidis et al. (2021b); that is, we define LSBGs as galaxies with a ɡ-band mean surface brightness of 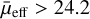 mag arcsec−2 and a half-light radius of r1/2 > 2.5″. Following this definition, we identified 4083 new LSBGs from the DES DR1, increasing the number of identified LSBGs in DES by 17%.
mag arcsec−2 and a half-light radius of r1/2 > 2.5″. Following this definition, we identified 4083 new LSBGs from the DES DR1, increasing the number of identified LSBGs in DES by 17%.
Our sample selection and LSBG identification pipeline consist of the following steps:
- 1.
We preselect the objects from the DES Y3 Gold catalog based on the selection criteria described in Tanoglidis et al. (2021b) using the SourceExtractor parameters.
- 2.
We applied the ensemble of transformer models to this sample of preselected objects. We chose the objects identified independently by both the LSBG DETR ensemble and the LSBG ViT ensemble for further follow-up inspection to clarify any LSBG identifications.
- 3.
We performed a Sérsic fitting using Galfit and reapplied the selection cuts to further reduce the number of false positives. After this step, 4879 LSBG candidates were retained for subsequent visual inspection.
- 4.
Following visual inspection, we report the presence of 4083 new LSBGs identified by the transformer ensemble models.
Following Tanoglidis et al. (2021b), we divided the total LSBG sample into two subsamples according to their ɡ – i colour. Among the 4083 new LSBGs presented here, 72% were identified as blue LSBGs, which is higher than the 67% observed in the sample presented by Tanoglidis et al. (2021b). Additionally, we also find that we have a higher fraction of red LSBGs with colour ɡ – i > 0.8 compared to the sample of LSBGs presented by Tanoglidis et al. (2021b). We speculate that the bias might originate from the training set used by Tanoglidis et al. (2021b) to train the SVM model to preselect the LSBG candidate sample.
By combining the previously identified 23 790 LSBGs from Tanoglidis et al. (2021b) with the LSBGs newly identified in our work, the total number of known LSBGs in the DES is increased to 27 873. This increases the number density of LSBGs in the DES from 4.13 to 4.91 deg−2 for LSBGs with 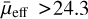 mag arcsec−2 and from 4.75 to 5.57 deg−2 for LSBGs with
mag arcsec−2 and from 4.75 to 5.57 deg−2 for LSBGs with 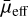 mag arcsec−2. It should be stressed that this is a lower limit to the number density, and will likely increase in the future with the improved imaging quality and methodology of surveys such as LSST and Euclid.
mag arcsec−2. It should be stressed that this is a lower limit to the number density, and will likely increase in the future with the improved imaging quality and methodology of surveys such as LSST and Euclid.
We also carried out an analysis of the clustering of LSBGs in DES. We find that the LSBGs tend to cluster more strongly than the HSBGs from DES, which is similar to the findings of Tanoglidis et al. (2021b). Upon further examination, we observe that the strong clustering tendency observed among LSBGs primarily stems from the red LSBGs, while the behaviour of blue LSBGs resembles that of blue HSBGs, which have weaker clustering tendencies. Additionally, we note a decrease in the number of red LSBGs near the centre of the galaxy cluster, resulting in a flattening of the auto-correlation function on smaller scales, which is similar to the conclusions of Wittmann et al. (2017).
Additionally, we cross-matched the LSBGs with the X-ray-selected galaxy cluster catalogue from the ROSAT All-Sky Survey (RXGCC; Xu et al. 2022) to find LSBGs associated with the clusters. Using the redshift information of the clusters, we identify 317 UDGs, among which 276 are reported for the first time. We also observe a colour gradient among the cluster LSBGs, where LSBGs located towards the outskirts of clusters exhibit a bluer colour compared to those at the centre, which is similar to findings of Junais et al. (2022) for the Virgo cluster LSBGs. However, this trend is relatively weak for the cluster UDGs in our study, unlike the LSBGs. A clear trend can also be seen in the half-light radius of the cluster LSBGs and UDGs as a function of cluster-centric distance. The LSBGs and UDGs grow in size from the cluster centre to the outskirts. These coherent trends in colour and size are in agreement with proposed UDG formation mechanisms, such as galaxy harassment (Conselice 2018), tidal interactions Mancera Piña et al. (2019), and ram-pressure stripping (Conselice et al. 2003b; Buyle et al. 2005), giving more support to the argument that UDGs are a subset of dwarf galaxies (Conselice 2018; Benavides et al. 2023).
The upcoming large-scale surveys, LSST and Euclid, are expected to cover around 18 000 and 14 5000 deg2 of the sky, respectively (Ivezić et al. 2019; Euclid Collaboration 2022). Extrapolating our results on the number density of LSBGs, we expect more than 100000 and 80000 LSBGs to be found from LSST and Euclid, respectively. In this scenario, an improved and efficient methodology for distinguishing LSBGs from artefacts will be highly significant, and we propose that transformer models could significantly speed up this process. With the aid of transfer learning, we are planning to extend our study to HSC SSP DR3 and thus pave the way towards straightforward LSBG detection in LSST and Euclid.
 |
Fig. 24 g – i colour of the cluster LSBGs (black points) and r1/2 as a function of the projected distance from their cluster centre (in units of the cluster radius R200); left and right panels, respectively. The UDGs are marked as red hollow circles. The green line and the grey-shaded region are the linear best fit and the 1σ scatter for the cluster LSBGs, respectively. The blue dashed line is the linear best fit for the cluster UDGs. |
We used the R500 values and the redshiſts provided by Xu et al. (2022) to obtain the R200 cross-matching radius. Following Ettori & Balestra (2009), we assume R200 ≈ R500/0.65, where R500 is the radius at which the average density of a galaxy cluster is 500 times the critical density of the universe at that redshift.
Acknowledgements
S.J. and K.M. are grateful for support from the Polish National Science Centre via grant UMO-2018/30/E/ST9/00082. U.S. acknowledges support from the National Research Foundation of South Africa (grant no. 137975). This research was partially supported by the Polish National Science Centre grant UMO-2018/30/M/ST9/00757 and the Polish Ministry of Science and Higher Education grant DIR/WK/2018/12.
References
- Abbott, T. M. C., Abdalla, F. B., Allam, S., et al. 2018, ApJS, 239, 18 [Google Scholar]
- Abbott, T. M. C., Adamów, M., Aguena, M., et al. 2021, ApJS, 255, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., AlSayyad, Y., Ando, M., et al. 2022, PASJ, 74, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Alabi, A. B., Romanowsky, A. J., Forbes, D. A., Brodie, J. P., & Okabe, N. 2020, MNRAS, 496, 3182 [NASA ADS] [CrossRef] [Google Scholar]
- Allam, Tarek, J., & McEwen, J. D. 2021, arXiv e-prints [arXiv:2105.06178] [Google Scholar]
- Amorisco, N. C., & Loeb, A. 2016, MNRAS, 459, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Benavides, J. A., Sales, L. V., Abadi, M. G., et al. 2023, MNRAS, 522, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G. M., Nichol, R. C., Tyson, J. A., Ulmer, M. P., & Wittman, D. 1995, AJ, 110, 1507 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bilicki, M., Jarrett, T. H., Peacock, J. A., Cluver, M. E., & Steward, L. 2014, ApJS, 210, 9 [Google Scholar]
- Bothun, G. D., Impey, C. D., Malin, D. F., & Mould, J. R. 1987, AJ, 94, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Bothun, G. D., Schombert, J. M., Impey, C. D., Sprayberry, D., & McGaugh, S. S. 1993, AJ, 106, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Bothun, G., Impey, C., & McGaugh, S. 1997, PASP, 109, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Burkholder, V., Impey, C., & Sprayberry, D. 2001, AJ, 122, 2318 [NASA ADS] [CrossRef] [Google Scholar]
- Buyle, P., De Rijcke, S., Michielsen, D., Baes, M., & Dejonghe, H. 2005, MNRAS, 360, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Vives, G., Reyes, I., Förster, F., Estévez, P. A., & Maureira, J.-C. 2017, ApJ, 836, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Carion, N., Massa, F., Synnaeve, G., et al. 2020, in Computer Vision – ECCV 2020, eds. A. Vedaldi, H. Bischof, T. Brox, & J.-M. Frahm (Cham: Springer International Publishing), 213 [Google Scholar]
- Carleton, T., Cohen, S. H., Frye, B. L., et al. 2023, ApJ, 953, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Chamba, N., Trujillo, I., & Knapen, J. H. 2022, A&A, 667, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, P.-C., Tsai, H., Bhojanapalli, S., et al. 2021, in Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (Online and Punta Cana, Dominican Republic: Association for Computational Linguistics), 2974 [CrossRef] [Google Scholar]
- Chen, Z., Duan, Y., Wang, W., et al. 2023, in The Eleventh International Conference on Learning Representations [Google Scholar]
- Clevert, D., Unterthiner, T., & Hochreiter, S. 2016, in 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, May 2-4, 2016, Conference Track Proceedings, eds. Y. Bengio, & Y. LeCun [Google Scholar]
- Cohen, Y., van Dokkum, P., Danieli, S., et al. 2018, ApJ, 868, 96 [Google Scholar]
- Conselice, C. J. 2018, Res. Notes Am. Astron. Soc., 2, 43 [Google Scholar]
- Conselice, C. J., Gallagher, John S. I., & Wyse, R. F. G. 2003a, AJ, 125, 66 [CrossRef] [Google Scholar]
- Conselice, C. J., O’Neil, K., Gallagher, J. S., & Wyse, R. F. G. 2003b, ApJ, 591, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Spergel, D. N., Gunn, J. E., Schmidt, M., & Schneider, D. P. 1997, AJ, 114, 635 [Google Scholar]
- Danieli, S., van Dokkum, P., Merritt, A., et al. 2017, ApJ, 837, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, A., Serjeant, S., & Bromley, J. M. 2019, MNRAS, 487, 5263 [NASA ADS] [CrossRef] [Google Scholar]
- De Vicente, J., Sánchez, E., & Sevilla-Noarbe, I. 2016, MNRAS, 459, 3078 [NASA ADS] [CrossRef] [Google Scholar]
- Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
- Di Cintio, A., Brook, C. B., Dutton, A. A., et al. 2017, MNRAS, 466, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Dietterich, T. G. 2000, Multiple Classifier Systems (Berlin: Springer) 1 [Google Scholar]
- Domingos, P., & Hulten, G. 1999, in Proceedings of the fifth ACM SIGKDD international conference on knowledge discovery and data mining, ACM, 155 [CrossRef] [Google Scholar]
- Dosovitskiy, A., Beyer, L., Kolesnikov, A., et al. 2021, in 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021 (OpenReview.net) [Google Scholar]
- Driver, S. P. 1999, ApJ, 526, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Du, W., Cheng, C., Zheng, Z., & Wu, H. 2020, AJ, 159, 138 [CrossRef] [Google Scholar]
- Efron, B., & Gong, G. 1983, Am. Stat., 37, 36 [Google Scholar]
- Erwin, P. 2015, ApJ, 799, 226 [Google Scholar]
- Ettori, S., & Balestra, I. 2009, A&A, 496, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [Google Scholar]
- Fu, J., Liu, J., Tian, H., et al. 2019, in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Los Alamitos, CA, USA: IEEE Computer Society), 3141 [CrossRef] [Google Scholar]
- Galaz, G., Frayer, D. T., Blaña, M., et al. 2022, ApJ, 940, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Glorot, X., & Bengio, Y. 2010, in JMLR Proceedings, 9, Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, AISTATS 2010, Chia Laguna Resort, Sardinia, Italy, May 13–15, 2010, eds. Y. W. Teh & D. M. Titterington (JMLR.org), 249 [Google Scholar]
- Greco, J. P., Greene, J. E., Strauss, M. A., et al. 2018, ApJ, 857, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J.E., Greco, J. P., Goulding, A. D., et al. 2022, ApJ, 933, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Haberzettl, L., Bomans, D. J., & Dettmar, R. J. 2007, A&A, 471, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayward, C. C., Irwin, J. A., & Bregman, J. N. 2005, ApJ, 635, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P. C. 1982, MNRAS, 201, 867 [Google Scholar]
- Huang, K.-W., Chen, G. C.-F., Chang, P.-W., et al. 2023, in Computer Vision – ECCV 2022 Workshops, ed. L. Karlinsky, T. Michaeli, & K. Nishino (Cham: Springer Nature Switzerland), 143 [Google Scholar]
- Impey, C., Bothun, G., & Malin, D. 1988, ApJ, 330, 634 [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
- Jarvis, M. 2015, Astrophysics Source Code Library [record ascl:1508.007] [Google Scholar]
- Jia, P., Sun, R., Li, N., et al. 2023, AJ, 165, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Junais, Boissier, S., Epinat, B., et al. 2020, A&A, 637, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Junais, Boissier, S., Boselli, A., et al. 2022, A&A, 667, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kingma, D. P., & Ba, J. 2015, in 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7–9, 2015, Conference Track Proceedings, eds. Y. Bengio, & Y. LeCun [Google Scholar]
- Kobayashi, Y., Nishimichi, T., Takada, M., & Miyatake, H. 2022, Phys. Rev. D, 105, 083517 [CrossRef] [Google Scholar]
- Koda, J., Yagi, M., Yamanoi, H., & Komiyama, Y. 2015, ApJ, 807, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, D. C., & Szalay, A. S. 1984, ApJ, 282, 390 [NASA ADS] [CrossRef] [Google Scholar]
- La Marca, A., Iodice, E., Cantiello, M., et al. 2022, A&A, 665, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [Google Scholar]
- Laudato, E., & Salzano, V. 2023, Euro. Phys. J. C, 83, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Leisman, L., Haynes, M. P., Janowiecki, S., et al. 2017, ApJ, 842, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, S., Côté, P., Peng, E. W., et al. 2020, ApJ, 899, 69 [CrossRef] [Google Scholar]
- Liutkus, A., Cífka, O., Wu, S., et al. 2021, Proc. Mach. Learn. Res., 139, 7067 [Google Scholar]
- Ma, C.-P., & Fry, J. N. 2000, ApJ, 543, 503 [Google Scholar]
- Mancera Piña, P. E., Peletier, R. F., Aguerri, J. A. L., et al. 2018, MNRAS, 481, 4381 [Google Scholar]
- Mancera Piña, P. E., Aguerri, J. A. L., Peletier, R. F., et al. 2019, MNRAS, 485, 1036 [CrossRef] [Google Scholar]
- Marleau, F. R., Habas, R., Poulain, M., et al. 2021, A&A, 654, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, G., Kaviraj, S., Laigle, C., et al. 2019, MNRAS, 485, 796 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W. 2012, AJ, 144, 4 [Google Scholar]
- McGaugh, S. S. 1996, MNRAS, 280, 337 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Bothun, G. D. 1994, AJ, 107, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Durrell, P. R., Ferrarese, L., et al. 2015, ApJ, 809, L21 [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J. J., et al. 2017, ApJ, 834, 16 [Google Scholar]
- Minchin, R. F., Disney, M. J., Parker, Q. A., et al. 2004, MNRAS, 355, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., McGaugh, S. S., & Bothun, G. D. 1994, MNRAS, 267, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Morganson, E., Gruendl, R. A., Menanteau, F., et al. 2018, PASP, 130, 074501 [NASA ADS] [CrossRef] [Google Scholar]
- Neilsen, E. J.Jr., Annis, J. T., Diehl, H. T., et al. 2019, arXiv e-prints [arXiv:1912.06254] [Google Scholar]
- Neuschaefer, L. W., Windhorst, R. A., & Dressler, A. 1991, ApJ, 382, 32 [NASA ADS] [CrossRef] [Google Scholar]
- O’Neil, K., & Bothun, G. 2000, ApJ, 529, 811 [CrossRef] [Google Scholar]
- Parmar, N., Ramachandran, P., Vaswani, A., et al. 2019, in Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, 68 [Google Scholar]
- Peacock, J. A., & Smith, R. E. 2000, MNRAS, 318, 1144 [Google Scholar]
- Pearson, W. J., Suelves, L. E., Ho, S. C. C., et al. 2022, A&A, 661, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peebles, P. J. E. 1980, The Large-scale Structure of the Universe (Princeton: Princeton university Press) [Google Scholar]
- Peebles, P. J. E., & Hauser, M. G. 1974, ApJS, 28, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
- Pérez-Carrasco, M., Cabrera-Vives, G., Martinez-Marin, M., et al. 2019, PASP, 131, 108002 [CrossRef] [Google Scholar]
- Pimentel, Ó., Estévez, P. A., & Förster, F. 2023, AJ, 165, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Poulain, M., Marleau, F. R., Habas, R., et al. 2021, MNRAS, 506, 5494 [NASA ADS] [CrossRef] [Google Scholar]
- Prole, D. J., van der Burg, R. F. J., Hilker, M., & Davies, J. I. 2019, MNRAS, 488, 2143 [NASA ADS] [Google Scholar]
- Prole, D. J., van der Burg, R. F. J., Hilker, M., & Spitler, L. R. 2021, MNRAS, 500, 2049 [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
- Rojas, K., Savary, E., Clément, B., et al. 2022, A&A, 668, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Román, J., & Trujillo, I. 2017, MNRAS, 468, 4039 [Google Scholar]
- Russakovsky, O., Deng, J., Su, H., et al. 2015, Int. J. Comput. Vis., 115, 211 [Google Scholar]
- Saburova, A. S., Chilingarian, I. V., Kasparova, A. V., et al. 2021, MNRAS, 503, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Saburova, A. S., Chilingarian, I. V., Kulier, A., et al. 2023, MNRAS, 520, L85 [Google Scholar]
- Sandage, A., & Binggeli, B. 1984, AJ, 89, 919 [Google Scholar]
- Schaefer, C., Geiger, M., Kuntzer, T., & Kneib, J.-P. 2018, A&A, 611, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Sevilla-Noarbe, I., Bechtol, K., Carrasco Kind, M., et al. 2021, ApJS, 254, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D. 2019, ARA&A, 57, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Simonyan, K., & Zisserman, A. 2015, in 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7–9, 2015, Conference Track Proceedings, eds. Y. Bengio, & Y. LeCun [Google Scholar]
- Sprayberry, D., Impey, C. D., Bothun, G. D., & Irwin, M. J. 1995, AJ, 109, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I., Ivezić, Ž., Knapp, G. R., et al. 2001, AJ, 122, 1861 [CrossRef] [Google Scholar]
- Su, J., Lu, Y., Pan, S., Wen, B., & Liu, Y. 2021, arXiv e-prints [arXiv:2104.09864] [Google Scholar]
- Tan, A., Nguyen, D. T., Dax, M., Nießner, M., & Brox, T. 2021, Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, The Eleventh Symposium on Educational Advances in Artificial Intelligence, EAAI 2021, Virtual Event, February 2-9, 2021, 9799 [Google Scholar]
- Tanoglidis, D., Ćiprijanović, A., & Drlica-Wagner, A. 2021a, Astron. Comput., 35, 100469 [NASA ADS] [CrossRef] [Google Scholar]
- Tanoglidis, D., Drlica-Wagner, A., Wei, K., et al. 2021b, ApJS, 252, 18 [Google Scholar]
- Thuruthipilly, H., Grespan, M., & Zadrozny, A. 2022a, arXiv e-prints [arXiv:2212.12915] [Google Scholar]
- Thuruthipilly, H., Zadrozny, A., Pollo, A., & Biesiada, M. 2022b, A&A, 664, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Burg, R. F. J., Muzzin, A., & Hoekstra, H. 2016, A&A, 590, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dokkum, P. G., Abraham, R., Merritt, A., et al. 2015, ApJ, 798, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Vaswani, A., Shazeer, N., Parmar, N., et al. 2017, in Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4–9, 2017, Long Beach, CA, USA, 5998 [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2019, A&A, 625, A143 [EDP Sciences] [Google Scholar]
- Wang, X., Kondratyuk, D., Christiansen, E., et al. 2022, in International Conference on Learning Representations [Google Scholar]
- Wittmann, C., Lisker, T., Ambachew Tilahun, L., et al. 2017, MNRAS, 470, 1512 [Google Scholar]
- Wortsman, M., Ilharco, G., Gadre, S. Y., et al. 2022, in ICML, 23965–23998 [Google Scholar]
- Xu, W., Ramos-Ceja, M. E., Pacaud, F., Reiprich, T. H., & Erben, T. 2022, A&A, 658, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yasuda, N., Fukugita, M., Narayanan, V. K., et al. 2001, AJ, 122, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, J., Wang, Z., Vasudevan, V., et al. 2022, arXiv e-print [arXiv:2205.01917] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2005, ApJ, 630, 1 [Google Scholar]
- Zhang, H., Goodfellow, I. J., Metaxas, D. N., & Odena, A. 2018, arXiv e-prints [arXiv:1805.08318] [Google Scholar]
- Zhao, H., Jia, J., & Koltun, V. 2020, arXiv e-prints [arXiv:2004.13621] [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Name of the model, size of the image patches (s), number of heads (h), number of transformer encoder layers (T), and the number of epochs taken to train the four vision models (e) in chronological order of creation.
Architecture, accuracy, TPR, FPR, and AUROC of all the models in chronological order of creation.
Best-fitting power-law parameters for the angular two-point autocorrelation function for HSBGs and LSBGs along with information on the number of galaxies, median g-band magnitude, and the mean surface brightness for each sample.
All Figures
 |
Fig. 1 Four examples of LSBGs (a) and artefacts (b) used in the training data. Each image of the LSBG and artefact corresponds to a 67.32″ × 67.32″ region of the sky. Images were generated by combining the g, r, and z bands using APLpy package (Robitaille & Bressert 2012). |
| In the text | |
 |
Fig. 2 Scheme of the general architecture of the detection transformer (LSBG DETR) taken from Thuruthipilly et al. (2022b). The extracted features of the input image by the CNN backbone are combined with positional encoding and are passed on to the encoder layer to assign attention scores to each feature. The weighted features are then passed to the feed-forward neural network (FFN) to predict the probability. |
| In the text | |
 |
Fig. 3 Scheme of the general architecture of the LSBG ViT. The input image is split into small patches and flattened into a sequence of 1D vectors and combined with positional encoding. The numbered circular patches represent the position encoding, and the counterpart represents the flattened 1D sequence of the image patches. The combined 1D sequence is passed to the transformer layers. The extra learnable class embedding encodes the class of the input image after being updated by self-attention and passes it on to an MLP head to predict the output. |
| In the text | |
 |
Fig. 4 Confusion matrix of LSBG DETR and LSBG ViT models plotted for a threshold = 0.5. Class 0 represents the artefacts, and Class 1 represents the LSBGs. |
| In the text | |
 |
Fig. 5 Receiver operating characteristic curve of the ensemble models. The red and blue lines represent the variation of FPR and TPR as a function of the threshold for LSBG DETR and LSBG Vision ensembles, respectively. The red and blue points mark the TPR and FPR for a threshold = 0.9. |
| In the text | |
 |
Fig. 6 Schematic diagram showing the sequential selection steps used to find the new LSBG sample. |
| In the text | |
 |
Fig. 7 Cutouts of nine confirmed new LSBGs after visual inspection. The unique identification number (co object id) for each galaxy in DES DR1 is given below each image. The images were generated by combining the g, r, and z bands using the APLpy package (Robitaille & Bressert 2012), and each image corresponds to a 67.32″ × 67.32″ region of the sky with the LSBG at its centre. |
| In the text | |
 |
Fig. 8 Normalised distribution of half-light radius (top left panel), mean surface brightness (top right panel), Sérsic index (bottom left panel), and axis ratio (bottom right panel) of the new sample of LSBGs. The dashed line shows the median of the distribution. |
| In the text | |
 |
Fig. 9 Examples of candidates (Coadd object id - 149796289 and 374192591) classified as non-LSBGs during visual inspection because of glitches in the g-band near the galaxy. The panels a and c show the RGB image created using the g, r, and z bands with APLpy package (Robitaille & Bressert 2012). Panels b and d show the image in the g band. Each image corresponds to a 67.32″ × 67.32″ region of the sky with the candidate at its centre. |
| In the text | |
 |
Fig. 10 Examples of candidates classified as non-LSBG during visual inspection because of lack of sufficient signal in the g-band (a) are shown in the top panel. Candidates classified as non-LSBG during visual inspection because of being artefacts are shown in the lower panel (b). The RGB images are created using the g, r, and z bands with the APLpy package (Robitaille & Bressert 2012). Each image corresponds to a 67.32″ × 67.32″ region of the sky with the candidate at its centre. |
| In the text | |
 |
Fig. 11 Normalised distribution of colour of the LSBGs from the new sample identified in this work and the LSBGs identified by Tanoglidis et al. (2021b) plotted in the left panel. The right panel shows the colour as a function of mean surface brightness in the g-band for the new sample identified in this work and the LSBGs identified by Tanoglidis et al. (2021b). The dashed line shows the separation between red and blue LSBGS. |
| In the text | |
 |
Fig. 12 Normalised distribution of axis ratio (left panel) of red and blue LSBGs from the new sample. The vertical lines show the median for each class. |
| In the text | |
 |
Fig. 13 Normalised distribution of the Sérsic index of the LSBGs identified in this work and by Tanoglidis et al. (2021b). The vertical lines show the median for each class. |
| In the text | |
 |
Fig. 14 Sky distribution of the LSBGs identified from DES (black dots) by Tanoglidis et al. (2021b) and in this work and the LSBGs identified from HSC-SSP (blue dots) by Greco et al. (2018). |
| In the text | |
 |
Fig. 15 Number count of galaxies as a function of i-band magnitude, with the y-axis displaying the logarithm of the number density as a function of apparent magnitude. The red line with the blue error bars represents the data from HSC, and the black dashed line with green error bars represents the data from DES. |
| In the text | |
 |
Fig. 16 Normalised distribution of stellar mass surface density of LSBGs identified in HSC (red line) and DES (black line). |
| In the text | |
 |
Fig. 17 Sky distribution of the red LSBGs identified in this work (red dots) and of the LSBGs identified (black dots) by Tanoglidis et al. (2021b). |
| In the text | |
 |
Fig. 18 Sky distribution of the blue LSBGs identified from the new sample (blue dots) and of the LSBGs identified (black dots) by Tanoglidis et al. (2021b). |
| In the text | |
 |
Fig. 19 Colour distribution of the HSBGs from the DES DR1. The vertical line at g – i = 1.0 shows the colour separation of the HSBGs into red and blue galaxies. |
| In the text | |
 |
Fig. 20 Angular autocorrelation function for the full sample of LSBGs (grey line with open circles) and the sample of HSBGs (black line with crosses) is shown in the left panel. The angular autocorrelation function of the red LSBGs (red line), blue LSBGs (blue line), red HSBGs (orange line), and blue HSBGs (purple line) is shown in the right panel. The vertical green shaded region represents the region fitted for a power law (ω = Aθ1–γ), and the corresponding γ values are shown in the legend. |
| In the text | |
 |
Fig. 21 Cut-outs of six confirmed new UDGs. The unique identification number (Coadd Object Id) for each galaxy in DES DR1 is given below each image. The images were generated by combining the g, r, and z bands using the APLpy package (Robitaille & Bressert 2012), and each image corresponds to a 33.66″ × 33.66″ region of the sky with the UDG at its centre. |
| In the text | |
 |
Fig. 22 Colour distribution of the 1310 cluster LSBGs and 317 cluster UDGs from the DES DR1. |
| In the text | |
 |
Fig. 23 Joint distribution of the red (red dots) and blue (blue cross) UDGs in the space of r1/2 and µ0 in the ɡ-band. The vertical lines in the histogram on the x-axis and y-axis show the median for each class. |
| In the text | |
 |
Fig. 24 g – i colour of the cluster LSBGs (black points) and r1/2 as a function of the projected distance from their cluster centre (in units of the cluster radius R200); left and right panels, respectively. The UDGs are marked as red hollow circles. The green line and the grey-shaded region are the linear best fit and the 1σ scatter for the cluster LSBGs, respectively. The blue dashed line is the linear best fit for the cluster UDGs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.