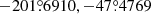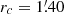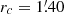EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 681 (January 2024) A&A, 681 (2024) A54 Full HTML
Open Access
Issue
A&A
Volume 681, January 2024
Article Number A54
Number of page(s) 14
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202347834
Published online 10 January 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The vast spectroscopic and photometric evidence obtained over the past three decades has conclusively shown that globular clusters (GCs) host multiple populations of stars with prominent variations in the abundance of light elements (C, N, O, Na, Mg, and Al; Carretta et al. 2009; Mészáros et al. 2015; Pancino et al. 2017; Masseron et al. 2019). Previously, the observed large intrinsic spreads in light elements were mainly thought to be associated with significant variations in iron abundance only in a small subset of the entire GC population (i.e., ω Centauri, M54, Terzan5, and Liller1; Norris & Da Costa 1995; Sarajedini & Layden 1995; Ferraro et al. 2009; Crociati et al. 2023). However, recent photometric and spectroscopic studies have found evidence suggesting that small-to-moderate iron spreads (from less than 0.05 up to 0.3 dex) may be relatively common in massive clusters (Legnardi et al. 2022; Lardo et al. 2022, 2023; Lee 2022, 2023; Monty et al. 2023).

All of the observed chemical differences are structured in well-defined patterns, such as the C-N, Na-O, and Mg–Al anticorrelations (see, e.g., Gratton et al. 2004, 2012, 2019; Carretta et al. 2009; Pancino et al. 2017; Mészáros et al. 2020). The overall observational evidence is interpreted as the characteristic signature of self-enrichment within clusters, where low-velocity material processed through the hot CNO cycle and its secondary NeNa and MgAl chains (e.g., Langer et al. 1993; Prantzos et al. 2007) is incorporated in a subsequent generation of stars. The majority of theoretical models for the formation of multiple populations do indeed involve the occurrence of two or more episodes (in some clusters only two main populations are detected) of star formation where CNO-enriched stars – the second population (2P) – were formed out of matter polluted by massive stars with a field-like composition – the first population (1P) – within the first 100–200 Myr of the cluster life.

A number of polluters were proposed in the literature, including intermediate-mass stars in their asymptotic giant branch (AGB) phase (D’Ercole et al. 2010), fast rotating massive stars (FRMS; Krause et al. 2013), novae (Maccarone & Zurek 2012; Denissenkov et al. 2014), interacting binary stars (de Mink et al. 2009), and supermassive stars (Denissenkov & Hartwick 2014). Nonetheless, all self-enrichment models put forward so far have failed to reproduce the observed chemical anticorrelations and the number ratio between 1P and 2P stars (see e.g., Bastian & Lardo 2018, and references therein for a discussion).

The Mg–Al anticorrelation is of special relevance in this context because, in contrast to other anticorrelations (such the C-N and Na-O ones), its extension significantly differs from one cluster to another and is absent in some GCs (Mészáros et al. 2015). These two elements are involved in the hot MgAl cycle, which works at temperatures higher than those of the CNO and NeNa cycles (≳108 K; Ventura et al. 2016). As a result, the analysis of these two elements can place substantial constraints on the nature of polluters responsible for the chemistry seen in GCs. Additionally, compared to the other elements involved in chemical anomalies (C, N, O, and Na; Denisenkov & Denisenkova 1990), Mg and Al are not affected by deep mixing processes occurring during the red giant branch phase; therefore, their chemical abundances reflect the initial chemical composition of the gas from which stars formed.

ω Centauri (NGC 5139) is a highly complex stellar cluster, usually classified as a GC according to its morphology and mass. It is the most massive among the GCs with a mass of (3.94 ± 0.02)×106 M⊙ (Baumgardt & Hilker 2018); it spans a wide metallicity range (−2.2 ≲ [Fe/H] ≲ −0.5 dex) with at least four main populations with a different iron content (Norris & Da Costa 1995; Pancino et al. 2002; Johnson & Pilachowski 2010; Marino et al. 2011). The multimodal iron distribution seen in ω Centauri suggests that this system underwent multiple star formation events lasting a few billion years (Smith et al. 2000; Sollima et al. 2005a; Romano et al. 2010; Villanova et al. 2014), at variance with the genuine GCs. The prevalent interpretation is that ω Centauri is the remnant of an old nucleated dwarf galaxy that the Milky Way accreted in the past (Bekki & Freeman 2003). ω Centauri also exhibits large star-to-star variations in light elements, which manifest as correlations and anticorrelations (Norris & Da Costa 1995; Smith et al. 2000; Johnson & Pilachowski 2010; Marino et al. 2011; Mészáros et al. 2021).

ω Centauri is the only GC-like system showing all the anticorrelations usually observed in (some or all) genuine GCs, that is, Na–O (Johnson & Pilachowski 2010; Marino et al. 2011), Na–Li (Mucciarelli et al. 2018a), Mg–Al (Norris & Da Costa 1995; Smith et al. 2000; Mészáros et al. 2021), and Mg–Si and Mg–K (Mészáros et al. 2020; Alvarez Garay et al. 2022). All of these chemical anomalies point to the extreme NeNa and MgAl chains playing a crucial role in the formation of multiple populations in ω Centauri. In particular, proton capture reactions operating at temperatures higher than 108 K could explain the anticorrelations between Mg and Si and Mg and K. In the case of the Mg–Si anticorrelation, the previously synthesized Al is used to produce Si, whereas proton capture on Ar nuclei leads to the synthesis of K in the Mg–K anticorrelation.

Using the same sample analyzed in Alvarez Garay et al. (2022, hereafter AG22), in this study we provide the chemical abundances of those elements (Mg, Al, and Si) participating in the MgAl cycle in ω Centauri for a total of 439 member stars along the Red Giant Branch (RGB). The structure of this paper is as follows: the data are presented in Sect. 2; the chemical analysis is detailed in Sect. 3; the metallicity distribution and Mg–Al–Si abundance variations are illustrated and discussed in Sect. 4; in Sect. 5 a comparison is provided with the analysis done by Mészáros et al. (2021); and findings and conclusions are summarized in Sect. 6.

2. Observations and atmospheric parameters

This study is a continuation of our recent work (AG22) in which we analyzed the extension of the Mg–K anticorrelation among the RGB stars of ω Centauri (Fig. 1 in AG22 shows the position in the color-magnitude diagram of the considered stars). The dataset is the same as the one used in AG22, and consists of high-resolution spectra collected with the multiobject spectrograph FLAMES (Pasquini et al. 2002), mounted on UT2 (Kueyen) at the ESO-VLT Observatory in Cerro Paranal, within the ESO program 095.D-0539 (P.I. Mucciarelli). The observations were performed in the GIRAFFE mode that allows one to allocate up to 132 fibers simultaneously. The adopted setups are HR11 (with a wavelength range from 5597 to 5840 Å and a spectral resolution of 29 500) and HR18 (with a wavelength range from 7648 to 7889 Å and a spectral resolution of 20 150). The first setup allowed us to measure up to five lines of Si, while the second setup allowed us to measure the Al doublet at 7835 and 7836 Å.

All of the observed targets are on the RGB of ω Centauri, and their membership was confirmed by multiple literature sources (Norris & Da Costa 1995; Johnson & Pilachowski 2010; Marino et al. 2011). A total of 439 stars were analyzed: 345 of them are in common with Johnson & Pilachowski (2010), 82 with Marino et al. (2011), and 12 with Norris & Da Costa (1995). Further, we considered only stars that are not contaminated by neighbor stars within the GIRAFFE fibers’ size.

Four configurations of targets were defined and each of them was observed with both HR11 and HR18 setups. Due to the brightness of the targets (10.7 < G < 14.5), for each configuration two exposures of 1300 s and two of 300 s each were sufficient to reach a signal-to-noise ratio (S/N)∼70 and S/N ∼ 100 for HR11 and HR18, respectively. The observation of each configuration was split into two exposures in order to get rid of the effects of cosmic rays and other transient effects. Finally, during each exposure, about 15 fibers were dedicated to observe empty sky regions in order to sample the sky background.

The spectra were reduced using the dedicated GIRAFFE ESO pipeline1 that performs bias subtraction, flat-fielding, wavelength calibration, and spectral extraction. For each exposure, the spectra of sky regions were median-combined together, and the derived master-sky spectrum was subtracted from each stellar spectrum.

Atmospheric parameters (effective temperature, surface gravity, and microturbolent velocity) for all sample stars were adopted from AG22; however, for the convenience of the reader, we summarize the procedure we adopted here. We used photometric information from Gaia early Data Release 3 (Gaia Collaboration 2016, 2021). The spatial distribution of the sample relative to the cluster center is illustrated in Fig. 1.

thumbnail Fig. 1.

Coordinate positions of FLAMES targets are displayed by the red circles. The black cross denotes the cluster center ( − 201 . ° 6910 , − 47 . ° 4769 $ -201{{\overset{\circ}{.}}}6910, -47{{\overset{\circ}{.}}}4769 $) according to van Leeuwen et al. (2000). The dashed black circles show 2.5 and 5 times the core radius ( r c = 1 . ′ 40 $ r_c = 1{{\overset{\prime}{.}}}40 $; Harris 1996). We note that 424 out of the 439 stars that were analyzed in this study are contained within the green circle, which is 10 times the core radius.

Effective temperatures (Teff) were computed using the empirical (BP − RP)0 − Teff relation by Mucciarelli et al. (2021), based on the infrared flux method, and assuming a color excess of E(B − V) = 0.12 ± 0.02 (Harris 2010). In the calculation of the dereddened color (BP − RP)0, we followed the scheme proposed by Gaia Collaboration (2018). Internal errors in Teff due to the uncertainties in photometric data, reddening, and the (BP − RP)0 − Teff relation are in the range 85–115 K.

Surface gravities (log g) were estimated from the Stefan–Boltzmann relation, adopting a typical mass of 0.80 M⊙, assuming the photometric Teff, the bolometric corrections for the dereddened G-band magnitude from Andrae et al. (2018), and a true distance modulus DM0 = 13.70 ± 0.06 (Del Principe et al. 2006). We computed the uncertainties in gravities by propagating the uncertainties in Teff, the distance modulus, and photometry. These uncertainties are on the order of 0.1 dex. We would like to point out that an incorrect attribution of the targets to an evolutionary stage (AGB stars attributed to the RGB sequence) has a negligible impact on the derived abundances: a difference of 0.2 M⊙ in the attribution mass does indeed lead to a modification in log g of ∼0.1, corresponding to a variation in the measured Mg, Al, Si, and Fe abundances of about 0.005 dex or less. To assess the impact of the 0.1 dex change in log g on elemental abundances, we performed calculations while keeping the other atmospheric parameters fixed to their best values and only varying log g by the specified value. Our results indicate that such a difference leads to an extremely small change in the measured abundance ratios, amounting to less than 0.005 dex. This negligible variation arises from the fact that all the measured elements (Fe, Mg, Al, and Si) are in their neutral stage, rendering them almost insensitive to variations in log g.

Microturbolent velocities (vt) were obtained adopting the log g–vt calibration by Kirby et al. (2009). This relation provides values of vt of about 1.6–2.0 km s−1. We assumed a conservative error of 0.2 km s−1 in the determination of vt uncertainties. All of the relevant information about the observed targets (Id, Gaia G magnitude, radial velocity, and the derived atmospheric parameters) are reported in Table 1 in AG22.

3. Abundance analysis

In this work we adopted Fe and Mg abundances from AG22, while we derived abundances for Al and Si. In Table 1 all of the obtained elemental abundances are reported.

Table 1.

Abundance ratios for the GIRAFFE targets of ω Centauri.

Chemical analysis was performed using one-dimensional, local thermodynamic equilibrium (LTE), plane-parallel geometry model atmospheres computed with the code ATLAS9 (Castelli & Kurucz 2003) that treats the line opacity through the opacity distribution functions (ODF) method. All of the models were calculated using the ODFs computed by Castelli & Kurucz (2003) with α-enhanced chemical composition and without the inclusion of the approximate overshooting in the calculation of the convective flux.

Si abundances were derived through the comparison between measured and theoretical equivalent widths (EWs) using the code GALA (Mucciarelli et al. 2013). We measured the EWs of selected lines with the code DAOSPEC (Stetson & Pancino 2008) through the wrapper 4DAO (Mucciarelli 2013). Our lines were selected in order to be unblended and not saturated at the resolution of the GIRAFFE setups. The atomic data for our transitions are from the Kurucz-Castelli linelist2.

Al abundances were derived using our own code SALVADOR, which performs a χ2 minimization between the observed line and a grid of suitable synthetic spectra calculated on the fly using the code SYNTHE (Kurucz 2005) in which only the Al abundance is varying. Al abundances were derived through spectral synthesis and not via an EW, as we did for Si, because the Al doublet at 7835–7836 Å is contaminated by CN lines. At low metallicities, the impact of CN contamination is negligible; however, as metallicity increases, its impact becomes more pronounced3. Since most of the stars in our sample do not have published C and N abundances, we fixed [N/Fe] = +1.5 dex as a reasonable N value (according to Marino et al. 2012) and treated C as a free parameter to fit the CN affecting the Al doublet. Taking these assumptions into account, [C/Fe] abundance ratios between −0.5 and +0.3 dex provide the best fits to the CN lines. Finally, all of the derived abundance ratios were referred to the solar abundances of Grevesse & Sauval (1998).

We again followed the same approach used in AG22 to estimate star-to-star uncertainties associated with the chemical abundances. Internal errors, associated with the measurement process, were estimated as the line-to-line scatter divided by the root mean square of the number of lines. For Si, when only one line was available, we calculated the internal error by varying the EW of our lines of 1σEW (i.e., the EW error provided by DAOSPEC). For Al, we adopted 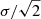σ / 2 $ \sigma/\sqrt{2} $ for all of the stars in which we used both lines, while for the stars in which only one line was available, we estimated the internal error by resorting to a Monte Carlo simulation.

Errors associated with the adopted atmospheric parameters were computed by recalculating chemical abundances, varying only one parameter at a time by its uncertainty and keeping the other parameters fixed to their best value. The uncertainties of the abundance ratios [Al/Fe] and [Si/Fe] were obtained following Eq. (2) in AG22.

4. Results

Depending on the metallicity range, ω Centauri exhibits (anti)correlations with different amplitudes. Given the wide range of metallicities present in the system, it is crucial to analyze the chemical anomalies not only as a whole, but also in distinct metallicity regimes. This approach provides a more comprehensive understanding of the mechanisms underlying the complex chemical patterns observed in ω Centauri.

4.1. Fe, Mg, Al, and Si abundances

According to the literature, ω Centauri hosts stars covering a broad range of metallicities. The metallicity distribution function (MDF hereafter) that we found in our investigation is shown in Fig. 2. In particular, to identify distinct populations in the data, we employed the scikit-learn4 implementation of Gaussian mixture models (GMMs), which allowed us to identify four distinct groups corresponding to the following peaks in [Fe/H]: −1.85, −1.55, −1.15, and −0.80 dex. For comparison, we considered the analyses performed by Johnson & Pilachowski (2010) and Mészáros et al. (2021) in which they studied a total sample of 855 and 1141 stars, respectively, covering the cluster’s entire metallicity range. In particular, Johnson & Pilachowski (2010) found the presence of five distinct metallicity peaks that are located at [Fe/H] = −1.75, −1.50, −1.15, −1.05, and −0.75 dex (in their distribution the peaks at −1.15 and −1.05 dex were combined due to the difficulty in separating the two populations), while Mészáros et al. (2021) found four peaks at [Fe/H] = −1.65, −1.35, −1.05, and −0.7 dex. The three MDFs exhibit a good agreement with each other, in terms of [Fe/H] extension and the relative position and intensity of the peaks.

thumbnail Fig. 2.

Histogram displaying the MDF of ω Centauri. Also shown as a dashed black line is the Gaussian kernel fit of the distribution. Four Gaussian components can be identified. They represent the MP, M-int1, M-int2, and MR subpopulations, and are plotted in the figure as dotted, dashed, solid, and dash-dotted lines, respectively.

With the exception of the peak at −1.15 dex, our measurements of the metallicity peaks are slightly lower (by about 0.05–0.1 dex) compared to those reported by Johnson & Pilachowski (2010). On the other hand, the metallicity peaks in our study are systematically lower by about 0.1–0.2 dex than the ones from Mészáros et al. (2021). These discrepancies are likely to be attributed to the very different method and set of lines used to calculate the metallicities from the H band (Mészáros et al. 2021) and optical spectra.

Finally, following the results obtained from our distribution and a nomenclature similar to the one adopted by Sollima et al. (2005b), we divided our population into the following four subpopulations: metal-poor (MP, [Fe/H] ≤ −1.69 dex), metal-int1 (M-int1, −1.68 ≤ [Fe/H] ≤ −1.34 dex), metal-int2 (M-int2, −1.33 ≤ [Fe/H] ≤ −0.94 dex), and metal-rich (MR, [Fe/H] ≥ −0.93 dex). The main information for the four subpopulations is reported in Table 2.

Table 2.

Mean metallicity ⟨[Fe/H]⟩, its associated dispersion (σ), the sample size (N), and number fraction of the four metallicity subpopulations identified in ω Centauri (see text for details).

In Fig. 3 we can observe the behavior of [Mg/Fe], [Al/Fe], and [Si/Fe] as a function of [Fe/H] for the stars that we analyzed in this work. In the left panel, we can see that the [Mg/Fe] distribution is split into two different branches, with the upper branch that covers a [Fe/H] range from ∼ − 2.1 dex up to ∼ − 1.3 dex and is characterized by enriched values of [Mg/Fe]. On the other hand, the lower branch covers a range of [Fe/H] from ∼ − 1.9 dex up to ∼ − 0.5 dex, with Mg abundances ranging from subsolar values up to the highest values [Mg/Fe] ∼ +0.6 dex at the highest metallicities. For the [Al/Fe] distribution, the behavior is completely different. In the MP subpopulation, there is indeed a large spread in [Al/Fe] with abundances from [Al/Fe] ∼ −0.15 dex up to [Al/Fe] ∼ +1.3 dex. At higher metallicities ([Fe/H] > −1.7 dex), there is the presence of a branch that reaches its maximum extension in the Al abundance at [Fe/H] ∼ −1.3 dex and then there is a clear decrease in the Al abundances down to [Al/Fe] ∼ +0.6 in the MR subpopulation. Finally, a minor group of stars with [Al/Fe] < 0.9 dex is in the M-int1, M-int2, and MR subpopulations. The number of stars in this latter group significantly diminishes at the highest metallicities, with only three stars present in the MR subpopulation. Finally, the behavior of [Si/Fe] as a function of [Fe/H] is bimodal at [Fe/H] < −1.3 dex, even though the separation between the two branches is not so evident (they are separated by ∼0.2 dex). At higher metallicities, all of the stars are characterized by enhanced [Si/Fe] with a spread fully compatible with the typical uncertainties.

thumbnail Fig. 3.

Distribution of [Mg/Fe] (left panel), [Al/Fe] (middle panel), and [Si/Fe] (right panel) as a function of [Fe/H] for the stars belonging to our sample. The error bar in the top-right corner represents the typical error associated with the measurements.

4.2. Mg–Al anticorrelation

We observe a large spread in both [Mg/Fe] and [Al/Fe] abundances ratios, with [Mg/Fe] ranging from 0.70 dex down to subsolar values (the minimum abundance value is −0.44 dex) with a mean value [Mg/Fe] = +0.26 dex (σ = 0.23 dex), while [Al/Fe] ranges from +1.70 dex down to −0.15 dex with a mean value [Al/Fe] = +0.93 dex (σ = 0.44 dex). For the 323 stars for which both Mg and Al abundances are available, a discrete Mg–Al anticorrelation can be detected, as can be seen in Fig. 4. In particular, groups of stars with a different metallicity exhibit different Mg–Al distributions. Especially, the MP and M-int1 subpopulations show a clear Mg–Al anticorrelation (see top panels of Fig. 4), whereas the other two subpopulations show a chemical anomaly that is either less clear or not present at all (see bottom panels of Fig. 4).

thumbnail Fig. 4.

Trend of [Mg/Fe] as a function of [Al/Fe] for the MP, M-int1, M-int2, and MR subpopulations (from top to bottom, left to right). The size of each point indicates its probability of belonging to that particular metallicity subpopulation – the larger the symbol, the higher the probability – while gray dots represent the entire sample. The error bar in the top-right corner represents the typical measurement error associated with the data.

In the 144 stars that make up the MP subpopulation, we recognize the presence of a distinct Mg–Al anticorrelation, with all of the Mg-poor ([Mg/Fe] < 0.0 dex) stars having [Al/Fe] ∼ +1.15 dex. On the other hand, the Mg-rich stars ([Mg/Fe] > 0.0 dex) are distributed from [Mg/Fe] ∼ 0.15 up to [Mg/Fe] ∼ +0.5 dex and they cover a wide range of [Al/Fe] (from ∼ − 0.15 up to ∼ + 1 dex). Finally, we observe that the two groups of stars are clearly separated by a sort of gap in [Mg/Fe] between −0.1 and +0.1 dex. For the Mg-rich group (112 out of 144 stars), we ran a Spearman correlation test and calculated the correlation coefficient (Cs) and the corresponding two-tailed probability that an absolute value Cs larger than the observed one can be obtained starting from uncorrelated variables, in order to better quantify the amplitude of this anticorrelation. In this instance, we found Cs = −0.70, which resulted in zero chance that the observed anticorrelation could have come from uncorrelated data.

We can also clearly discern a Mg–Al anticorrelation in the M-int1 subpopulation (135 stars). We can easily distinguish two principal groups of stars in this metallicity class, which have similarities with the previous group. The first subgroup has high [Mg/Fe] values (ranging from ∼ + 0.4 to ∼ + 0.6 dex) and a wide range of [Al/Fe] values (from ∼ + 0.3 to ∼ + 1.0 dex). The second group, however, has a smaller range of [Al/Fe] (from ∼ + 1.3 up to ∼ + 1.7 dex) but a wider range of [Mg/Fe] (from ∼ + 0.35 down to ∼ − 0.2 dex). There are a considerable number of Mg-poor stars in this latter group. The Spearman test was also run in this instance, and the results show that Cs = −0.60 and a p value that is consistent with zero.

From the top panels of Fig. 4, we can clearly note that all of the stars in the Mg-poor group of the MP subpopulation have lower Al abundances ([Al/Fe] ∼ 0.2 dex lower) than the stars in the same Mg-poor group belonging to the M-int1 subpopulation. We investigated whether this effect is artificial or not, but neither the stellar parameters nor the evolutionary state were found to be related. Additionally, we can see the spectra of some stars from the MP and M-int1 subpopulations in Fig. 5 around the Al doublet. Even though they are members of different subpopulations, all stars share similar atmospheric parameters and metallicity. In particular, stars were selected to have metallicities between −1.78 ≤ [Fe/H] ≤ −1.69 dex and −1.68 ≤ [Fe/H] ≤ −1.63 dex for the MP and the M-int1 subpopulations, respectively. The figure undoubtedly demonstrates that Al lines are weaker in the Mg-poor stars corresponding to the MP subpopulation.

thumbnail Fig. 5.

Spectral region around the Al doublet at 7835–7836 Å for sample stars with similar atmospheric parameters. The solid blue lines denote stars belonging to the Mg-poor group in the MP subpopulation, whereas the dashed green lines represent again Mg-poor stars but in the M-int1 subpopulation. A clear difference in the strength of the Al lines can be appreciated between the two metallicity subgroups.

The existence of the Mg–Al anticorrelation in the 26 stars that make up the M-int2 subpopulation is less certain. The abundances of the stars range from ∼ + 0.1 to ∼ + 0.6 dex for [Mg/Fe] and from ∼ + 1 to ∼ + 1.7 dex for [Al/Fe], with Mg abundances that are between those of the Mg-rich stars in the previous two subpopulations. Only one star stands out among these values, having much lower Al and greater Mg abundances than the other stars in the same group. We are not able to tell whether discrete star groups are present in this subpopulation.

Finally, for the MR subpopulation (18 stars), there is no evidence of an anticorrelation, with the stars that have [Mg/Fe] ≳ +0.35 dex and [Al/Fe] ≲ +1.1 dex. This result is not surprising since the presence of the Mg–Al anticorrelation is detected in almost all GCs that are more metal poor than [Fe/H] ≲ −1 (Shetrone 1996; Mészáros et al. 2015; Pancino et al. 2017). In summary, an anticorrelation between the abundance of Mg and Al has been observed in ω Centauri, with the strength of the correlation being dependent on the metallicity of the individual stars being considered. A clear anticorrelation can be detected, in particular, for all stars with [Fe/H] ≲ −1.3 dex. However, for stars in the range between −1.3 < [Fe/H] < −0.9 dex, the anticorrelation is less obvious and, ultimately, for stars more metal-rich than [Fe/H] ≳ −0.9 dex, there is no sign of the Mg–Al anticorrelation.

Different studies carried out by Norris & Da Costa (1995), Smith et al. (2000), and Mészáros et al. (2021) found evidence of a significant spread in the Mg and Al abundances in ω Centauri. In particular, Mészáros et al. (2021) found evidence of an extended Mg–Al anticorrelation among the stars with [Fe/H] < −1.2 dex. However, our study represents the first clear detection of a discrete Mg–Al anticorrelation, specifically within the MP and M-int1 subpopulations, with different Mg and Al distributions at different metallicities. Furthermore, 73% of our stars have [Al/Fe] > 0.5 dex. The existence of a such fraction of stars with high values of Al indicates that the majority of stars in our sample belong to the so-called 2P, which was born from material processed in the polluter stars by the MgAl chain at high temperatures (Ventura et al. 2016; Dell’Agli et al. 2018).

4.3. Mg–Si anticorrelation and Al–Si correlation

For a total of 370 stars, the abundances of Mg and Si were simultaneously measured. With a mean value of +0.45 dex (σ = 0.10 dex), [Si/Fe] varies from +0.68 dex down to +0.08 dex. A Mg–Si anticorrelation is present in this sample, which is mostly contributed by the population’s MP subgroup (see Fig. 6). In fact, the Mg-poor and the Mg-rich stars may be clearly distinguished from one another in this subpopulation. The first group is distinguished by a mean value of [Si/Fe] = +0.55 dex, whereas the second group has a mean value of [Si/Fe] +0.35 dex, even if there are certain stars (the minority) with [Si/Fe] > +0.5 dex. In comparison to the Mg-rich group, the Mg-poor group is therefore increased by roughly +0.2 dex, which is significantly larger than the typical error associated with the [Si/Fe] measurements (0.1 dex). It is worth noting that the Si enhancement (Al depletion) in ω Centauri is primarily observed in stars with low Mg abundances, particularly in the most metal-poor population.

thumbnail Fig. 6.

As for Fig. 4, but for [Si/Fe] and [Al/Fe].

We have used the Spearman correlation test to examine the Mg–Si anticorrelation in the MP subpopulation, much like we did for the Mg–Al anticorrelation. Our results show that Cs = 0.45 and the p value is consistent with zero. This suggests that the presence of a Mg–Si anticorrelation in the MP subpopulation of ω Centauri is real. Besides the MP subpopulation, only the M-int1 subpopulation displays a clear anticorrelation between Mg and Si abundances, despite the challenge of distinguishing between the various subgroups within this population.

An Al–Si correlation can be observed in ω Centauri, as we can appreciate in Fig. 7. In this case, Si and Al are available at the same time for a total of 381 stars. Numerous previous studies have theorized that the Al–Si correlation in GCs is the result of a leakage from the MgAl chain into 28Si via proton capture reaction at extremely high temperatures (e.g., Yong et al. 2005; Mészáros et al. 2015; Masseron et al. 2019).

thumbnail Fig. 7.

As for Fig. 4, but for [Mg/Fe] and [Si/Fe].

All of the (anti)correlations associated with the MgAl chain are seen in the MP and M-int1 subpopulations of ω Centauri when Mg, Al, and Si are analyzed together while taking the various metallicity groups into account. In particular, the Mg-depleted and Al (mildly) enhanced stars, which are assumed to be the product of the extreme MgAl processing in the polluter stars, correspond to the majority of Si-enhanced stars. The proton capture processes in these stars took place at temperatures greater than 108 K. Contrarily, only a (weak) Mg–Al anticorrelation is found in the M-int2 subpopulation, whereas the other two anticorrelations are either nonexistent or just weakly confirmed. Finally, there is no indication of any chemical anomaly linked to the MgAl chain in the MR subpopulation. This result is expected given that the polluter stars are unable to attain the temperatures required to begin the Mg destruction through proton capture at those metallicities ([Fe/H] ≳ −0.9 dex).

5. Comparison with Mészáros et al. (2021)

Age spectroscopic analysis measuring Mg, Al, and Si abundance variations in ω Centauri was performed by Mészáros et al. (2021). In particular, they studied a total sample of 982 stars with a high signal-to-noise ratio (S/N > 70), observed by the SDSS-IV/APOGEE-2 survey (Majewski et al. 2017). Mészáros et al. (2021) found behaviors of the three abundance ratios qualitatively similar to ours. They found a Mg–Al anticorrelation, the shape of which clearly depends on the metallicity of the considered stars (see their Fig. 4). In particular, at high metallicities ([Fe/H] > −1.2 dex), the presence of a Mg–Al anticorrelation is less evident, but with a bimodal distribution in the Al abundances; on the other hand, at the highest values of [Fe/H], the Mg–Al anticorrelation disappears and the Al abundances are nearly constant. These findings are well in agreement with our results and indicate a weakening of the Mg–Al anticorrelation extension toward higher metallicities. Despite the similarities in the morphology, some relevant differences between our results and those by Mészáros et al. (2021) are present (see top panel of Fig. 8).

thumbnail Fig. 8.

Trend of [Mg/Fe] as a function of [Al/Fe] for the stars analyzed in this study (top-left panel), and for the stars analyzed by Mészáros et al. (2021; top-right panel). In the bottom panels, we display only the stars belonging to the MP subpopulation for each sample, respectively.

Differences in the Mg–Al anticorrelation in the MP subpopulation: if we consider the MP subpopulation in both samples5 (see bottom panel of Fig. 8), we can observe some interesting differences. In both samples we can detect a clear gap between the Mg-poor and Mg-rich stars. However, at variance with us, in the subgroup of stars with [Mg/Fe] > 0.0 dex, Mészáros et al. (2021) did not detect a clear Mg–Al anticorrelation. They did indeed observe almost a constant [Mg/Fe], with a large spread in [Al/Fe] (from [Al/Fe] ∼ −0.25 dex up to [Al/Fe] ∼ +1.25 dex).

Discreteness of the Al-rich group: if we consider the MP and M-int1 subpopulations, we can observe that Al-rich stars are well separated by a gap. To test whether this observed discreteness is real or not, in our sample we considered the most Al-rich stars ([Al/Fe] > +1. dex) in both MP and M-int1 subpopulations, and we measured if they are compatible in having the same Al. We found a mean value [Al/Fe] = +1.16 ± 0.01 dex (σ = 0.08 dex) for the MP subsample, and [Al/Fe] = +1.33 ± 0.01 dex (σ = 0.11 dex) for the M-int1 subsample (see Fig. 9). These values indicate that these two subsamples are compatible at a level of 8.54 σ, thus strongly suggesting that they do not display the same Al abundances. On the other hand, this discreteness is not observed in the dataset of Mészáros et al. (2021). This difference could be due to our higher precision in the abundance measure that allows us to distinguish different abundance substructures.

thumbnail Fig. 9.

Trend of [Mg/Fe] as a function of [Al/Fe] for the stars analyzed in this study. The blue dots and the green crosses represent the MP and M-int1 stars with [Al/Fe] > 1 dex, respectively. The gray dots represent the entire sample. The error bar in the top-right corner represents the typical measurement error associated with the data. The dashed line indicates the value [Al/Fe] = 1 dex. The distributions of the two subsamples are shown in the right panel with the corresponding colors.

Differences in the 2P/1P ratio: the most striking difference is in the fraction of 2P stars sampled by the two studies, with us having two-thirds of stars belonging to 2P, while Mészáros et al. (2021) have only half. We obtained these fractions of 2P by performing a population analysis, on both Mg–Al anticorrelations, using the GMM algorithm. We considered the overall distributions on the Mg–Al plane for both anticorrelations, without making any division among the metallicity subpopulations. The aim of this type of analysis was not to uncover the presence of distinct subpopulations within the two distributions, but rather to separate the populations between so-called enriched (with high Al abundances) and primordial (with low Al abundances) stars. In the case of our Mg–Al anticorrelation, the GMM algorithm revealed that the enriched stars constitute 73% (σ = 6%) of the entire population, while for the Mészáros et al. (2021) Mg–Al anticorrelation, the enriched population forms 52% (σ = 3%) of the total sample. To further investigate this result, we repeated the GMM analysis at various distances from the cluster center, taking into account the fact that our sample is more radially concentrated relative to the stars analyzed in Mészáros et al. (2021). Specifically, our targets are located at a distance of about 15 core radii, while the stars studied in Mészáros et al. (2021) extend up to 30 core radii (as shown in the right panel of Fig. 10).

thumbnail Fig. 10.

Left panel: fraction of the enriched stars as a function of the distance from the cluster center, as defined by van Leeuwen et al. (2000). The blue circles represent the stars analyzed in this study, whereas the orange squares display the stars studied by Mészáros et al. (2021). In the Y axis, the error bars represent the error associated with the fraction of enriched stars, while in the X axis, they represent the extension of the stars contained in each radial ring. The dashed gray line and the gray area show the mean and the standard deviation for the genuine GCs observed so far, respectively (Bastian & Lardo 2015). Right panel: coordinate positions of stars analyzed by Mészáros et al. (2021). The black cross represents the same cluster center used in Fig. 1. The dashed black circles show 5, 20, and 30 times the core radius ( r c = 1 . ′ 40 $ r_c = 1{{\overset{\prime}{.}}}40 $; Harris 1996). The green circle represents 10 times the core radius and it encloses 554 out of 982 stars.

To investigate the radial distribution of the percentage of enriched stars, we divided our sample into three radial annuli: stars located within 3 core radii (105 stars), stars between 3 and 5 core radii (110 stars), and stars beyond 5 core radii (108 stars). In the case of Mészáros et al. (2021), we examined stars located within 5 core radii (80 stars), between 5 and 7.3 core radii (169 stars), between 7.3 and 9.6 core radii (171 stars), between 9.6 and 13.0 core radii (174 stars), and beyond 13.0 core radii (169 stars). In the left panel of Fig. 10, we can observe the fraction of enriched stars in both samples. In particular, in the innermost region our value is slightly higher (but within the errors) compared to the mean value observed in other GCs (see Bastian & Lardo 2015 for a detailed discussion). On the other hand, except for the value within 5 core radii, the fraction of enriched stars found by Mészáros et al. (2021) is constantly below the mean value observed in other GCs, even though in the overlapping regions the two distributions are consistent within the uncertainties. This may be due to the different radial distribution of the two samples, as it is well known that 2P stars are more centrally concentrated than 1P stars in ω Centauri (as well as in many other clusters; e.g., Bellini et al. 2009; Bastian & Lardo 2015).

We speculate that the difference in the fraction of enriched stars between Mészáros et al. (2021) and our study may partially explain why the Mg–Al anticorrelation exhibits distinct shapes. Mészáros et al. (2021) did indeed analyze more external regions of ω Centauri, and the higher fraction of 1P stars in their sample could potentially contribute to explain the observed differences in the Mg–Al anticorrelation shape.

Differences in the behavior with [Fe/H]: in Fig. 11 we can observe a comparison between the stars analyzed here and the ones studied by Mészáros et al. (2021) for the distributions of [Mg/Fe], [Al/Fe], and [Si/Fe] as a function of [Fe/H]. If, on the one hand, we have similar behaviors in all three elements, there are also some interesting differences. In the [Mg/Fe] versus [Fe/H] plane, the presence of the two branches in our sample is clear, while in the case of Mészáros et al. (2021), their presence is barely visible. This effect may be attributed to the predominance of Mg-rich stars in their sample, as well as potential limitations in the measurement accuracy that could prevent a clear separation of the two branches in their analysis. Regarding [Al/Fe], our distribution and the one found by Mészáros et al. (2021) cover a similar range of abundances. However, in the case of Mészáros et al. (2021), the absence of Al-rich stars at [Fe/H] > −1 dex did not allow them to observe if either is present or not a trend in the [Al/Fe] distribution against the metallicity. Moreover, their sample presents a population with [Al/Fe] ≲ +0.5 dex that constitutes half of the entire sample (these stars represent the 1P stars) and it is distributed at almost every metallicity, with a decrease toward the highest metallicities. Finally, the [Si/Fe] distribution in the case of Mészáros et al. (2021) is characterized by a constant and enhanced [Si/Fe] abundance ratio over the entire range in metallicity, at variance with the bimodality we observe in our sample at [Fe/H] < −1.3 dex. We would like to note that for the stars analyzed by Mészáros et al. (2021), we applied their criteria, limiting our selection only to stars with S/N > 70, Teff < 5500 K, and with errors in the single abundances < 0.2 dex. Furthermore, it is worth mentioning that few stars were observed with [Fe/H] > −1 dex in the [X/Fe] (where X represents Mg, Al, and Si) versus [Fe/H] diagrams.

thumbnail Fig. 11.

Distribution of [Mg/Fe] (left panel), [Al/Fe] (middle panel), and [Si/Fe] (right panel) as a function of [Fe/H]. In the top are displayed the stars here analyzed (blue dots), while in the bottom the stars analyzed by Mészáros et al. (2021; orange dots). The error bar in the top-right corner in the top figures represents the typical error associated with the measurements.

6. Discussion and conclusions

In this work, we have investigated the multiple populations of ω Centauri by evaluating the effects of the MgAl cycle in the stars of this system. We derived the Fe, Mg, Al, and Si abundances for a total of 439 giant stars from the analysis of high-resolution spectra obtained with the multi-object spectrograph VLT/FLAMES. Here we summarize our most important findings:

  1. We found a multimodal MDF that is nicely reproduced by the combination of four Gaussian distributions, in good agreement with Johnson & Pilachowski (2010). Our sample is dominated by a MP subpopulation that contributes 44% to the total population. The secondary peaks at higher metallicities contribute 35%, 14%, and 7%, respectively.

  2. Based on our metallicity distribution, we divided the entire sample into four subpopulations (MP, M-int1, M-int2, and MR), which we used to investigate the strength of the (anti)correlations associated with the MgAl chain. Our analysis revealed a clear Mg–Al anticorrelation, with the shape and extension of the correlation varying significantly with the metallicity of the stars being considered. A clear-cut and discrete Mg–Al anticorrelation is present in all stars with a metallicity lower than ∼ − 1.3 dex, while for higher values of [Fe/H], the anticorrelation is less evident or possibly not present at all.

  3. We also detected Mg–Si and Al–Si (anti)correlations, whose extensions vary as a function of the metallicity, and as for the Mg–Al anticorrelation, their presence is evident for the stars with [Fe/H] ≲ −1.3 dex. All of the observed (anti)correlations found here confirm the results found in previous works by Norris & Da Costa (1995), Smith et al. (2000), and Mészáros et al. (2021). These results constitute a fingerprint of Mg burning at very high temperatures (≳108 K) through the MgAl chain, at least in the MP and M-int1 subpopulations (Ventura et al. 2016).

  4. Our Mg–Al anticorrelation presents a discrete shape in the MP and M-int1 subpopulations. In particular, in the MP subpopulation, we can observe (1) a Mg–Al anticorrelation analogous to the one observed in genuine single-metallicity GCs (Mészáros et al. 2015; Pancino et al. 2017), with small variations in Mg abundances (∼0.3 dex), and almost 1 dex of variation in the Al abundances; (2) a distinct component of Mg-poor stars that are all enriched in Al at [Al/Fe] ∼ +1.15 dex. This kind of subpopulation has been observed only among the most metal-poor GCs such as M15, M92, and NGC 5824 (Masseron et al. 2019; Mucciarelli et al. 2018b), or massive GCs such as NGC 2808 (e.g., Carretta et al. 2018). The Mg–Al anticorrelation in the M-int1 subpopulation is dominated by the most Al-rich stars, with a second group of stars at lower Al values and enhanced in Mg. The Al-rich stars in MP and M-int1 subpopulations are clearly separated by ∼0.2 dex, with a gap not detected by Mészáros et al. (2021).

  5. In the [Al/Fe] versus [Fe/H] plane, we can clearly recognize a trend as a function of the metallicity for the stars with [Al/Fe] ≳ +0.5 dex. We can observe that the [Al/Fe] distribution reaches its maximum at [Fe/H] ∼ −1.3 dex and then there is a decrease in the Al abundances toward the highest metallicities.

  6. By comparing our results with those of Mészáros et al. (2021), we observe that the fraction of 2P stars decreases from the cluster center toward the outer regions. This finding confirms that the formation of 2P stars is more prevalent in the central regions of the cluster (see Marino et al. 2012, and references therein). The prevalence of 2P in our sample can be the key factor at the origin of all the observed differences between our sample and that of Mészáros et al. (2021).

6.1. ω Centauri as a GC

ω Centauri exhibits the most extensive chemical anomalies associated with the MgAl chain, making it a unique opportunity to impose additional constraints on the potential nature of the polluters responsible for the multiple populations. The MgAl chain is indeed far more sensitive to temperature than the CNO and NeNa cycles (Ventura et al. 2016). Additionally, the presence of stars enhanced in Al (and Si) and depleted in Mg in the MP and M-int1 components of ω Centauri necessitates the occurrence of proton capture processes at temperatures that cannot be reached in all the polluter stars suggested in the literature.

If the polluters responsible for the observed anticorrelations are AGB and super-AGB stars, then the chemical anomalies observed here and the trend of Al abundances with respect to metallicity for stars with [Al/Fe] > +0.5 dex can be readily explained. In the metal-poor domain, represented by the MP and M-int1 populations here, the clear Mg–Al trend is due to the strong hot bottom burning (HBB) experienced by low-mass, massive AGB stars, where the ignition of proton-capture nucleosynthesis at temperatures above 108 K favors the depletion of the overall Mg in favor of Al (Ventura et al. 2016). In this context, the lower peak value of Al exhibited by MP stars with respect to the M-int1 counterparts is due to the activation of the full MgAlSi nucleosynthesis in the most metal-poor AGBs, with the efficient activation of the 27Al proton capture reaction, which destroys part of the Al synthesized by Mg burning (Dell’Agli et al. 2018). This understanding is confirmed by the Mg–Si and Al–Si trends detected in MP stars. In the M-int2 subpopulation, the Mg spread is shorter than in the MP and M-int1 subpopulations, since the HBB temperatures experienced by AGB stars of metallicity [Fe/H] ∼ −1 are not sufficiently hot to favor an extended destruction of the Mg. The lack of a Mg–Si anticorrelation in this subpopulation is a signature of the inefficiency of the advanced MgAl chain reaction 26Al(p, γ)27Si(e−, ν)27Al(p, γ)28Si at high metallicities. High metallicities do indeed prohibit an efficient Si production. Finally, the short extension of the Mg–Al trend shown by the most metal-rich stars witnesses the action of proton-capture reactions by the two least abundant 25Mg and 26Mg isotopes, whereas the HBB temperatures at these metallicities are not sufficiently hot to activate the proton capture process efficiently by the most abundant 24Mg isotope: the overall Mg spread is narrow in this case. Therefore, our study shows for the first time the presence in ω Centauri of the two channels of Al production and destruction (Ventura et al. 2013; Dell’Agli et al. 2018). In conclusion, at [Fe/H] ≲ −1.3 dex, the Al production channel is always activated, with the destruction channel that becomes significant at the lowest metallicities. On the other hand, at [Fe/H] ≳ −1.3 dex, the Al production channel weakens as the metallicity increases, while the destruction channel is not present at all since we do not have any Si production through Al burning.

While the AGB model appears to qualitatively account for observed chemical anomalies, it is important to note that different levels of dilution of the AGB ejecta with pristine gas are required to reproduce the observed (anti)correlations (Dell’Agli et al. 2018). Based on their Mg and Al abundance values, 2P stars with less extreme compositions may have formed from AGB ejecta mixed with up to 70% pristine gas, whereas the most extreme populations (characterized by heavy Mg depletion and Al enhancement) may have formed from AGB gas with either very limited or no dilution with pristine material. However, the precise physics and timing of the dilution process during the early evolution of the cluster remain unknown and can possibly require some degree of fine tuning.

FRMS (Krause et al. 2013) or interacting binaries (de Mink et al. 2009) are among the polluter candidates since they are able to activate the CNO cycle and the secondary chains, but they require very high masses (on the order of ∼100 M⊙ or above) and some adjustement of the reaction rates in order to reproduce the observed Mg–Al anticorrelations in GCs (Prantzos et al. 2017). Supermassive stars (∼1000 M⊙; Denissenkov & Hartwick 2014) have central temperatures high enough at the beginning of the main sequence to allow the simultaneous burning of He, Na, and Mg. Moreover, the models show that in these stars Si can be produced, but at temperatures where Mg is heavily destroyed. This is in contrast with what we find in ω Centauri. Also novae were suggested as polluters (Maccarone & Zurek 2012; Denissenkov et al. 2014). The fundamental issue with stars of this type is that all the light elements that are enhanced in 2P stars (Na, Al, and Si) are regularly overproduced in quantities that are significantly greater than the reported levels. However, as nova outbursts are multiparameter phenomena, more research on the parameter space is required to determine the precise amount of light elements ejected by these stars into the intracluster medium.

Even though many different scenarios have been proposed up to this point, none of them are fully free from serious flaws (e.g., Renzini et al. 2015, 2022; Bastian & Lardo 2018; Milone & Marino 2022). In particular, all of the self-enrichment models cannot explain that 2P stars generally outnumber their 1P counterparts (see Bastian & Lardo 2015 for a discussion).

The available chemical evidence suggests that the ω Centauri chemical enrichment history was very complex and influenced by a simultaneous contribution of core-collapse supernovae (CC-SNe), as demonstrated by the observed spread in Fe, enhanced [α/Fe] ratios, and high [Na/Fe] and [Al/Fe] abundances (see Johnson & Pilachowski 2010, and references therein), and likely AGB stars, which are responsible for the observed light-element variations. In contrast to regular (non nucleated) galaxies or genuine GCs, the ω Centauri chemical history has been controlled by its ability to retain both high- and low-velocity ejecta.

6.2. ω Centauri as a nuclear remnant

In the above discussion, we have considered our results in the perspective of the origin of the multiple populations in GCs (Gratton et al. 2012; Bastian & Lardo 2018; Gratton et al. 2019), exploiting the constraints provided by the extreme chemical manifestations of this syndrome that are observed to occur in ω Centauri. We have also made some attempt to interpret general trends within the entire sample assuming that they are produced by a single chemical evolution path, driven by self-enrichment. However, the latter is just a hypothesis, since, depending on the actual nature of the system, other kinds of processes may have been involved in the origin of the present-day status of ω Centauri. In this section, we want to reconsider the observational scenario from a different perspective.

The idea that ω Centauri can be the nuclear remnant of a dwarf galaxy whose main body was completely disrupted by the interaction with the Milky Way dates back decades and was the subject of extensive literature (see, e.g., Gnedin et al. 2002; Bekki & Freeman 2003; Bekki & Tsujimoto 2019, and references therein). The strict analogy with the stellar nucleus of the currently disrupting Sgr dSph galaxy was firstly noted and discussed by Bellazzini et al. (2008) and Carretta et al. (2010a). In recent times the possible association of ω Centauri with a specific dwarf accretion event, Gaia-Sausage-Enceladus (GSE; Helmi et al. 2018; Belokurov et al. 2018), lent further support to this hypothesis (Myeong et al. 2018; Massari et al. 2019; Limberg et al. 2022).

There is general consensus that the (widely diffused, see, e.g., Böker et al. 2004) stellar nuclei are formed by the spiral-in to the center of the host galaxy of massive star clusters, by dynamical friction, and/or by central in situ star formation, with the first channel possibly being the preferred one in M ≲ 109 M⊙ galaxies (Neumayer et al. 2020, and references therein). Such a multiple-channel formation path can greatly help in accounting for the extremely complex abundance patterns observed in ω Centauri.

In this context, we want to highlight two facts that emerge particularly clearly from our analysis and that suggest that the system may indeed be a nuclear remnant that was built up by the merging of GCs plus in situ star formation at the center of the (now disrupted) progenitor dwarf galaxy (see also Ibata et al. 2019, 2021):

  • The MDF is clearly multimodal, with the strongest peak being the most MP one. This is at odds with what is observed in local dwarfs (Kirby et al. 2011; Hasselquist et al. 2021). In these sites, where the buildup of the MDF should be dominated by the chemical evolution of a self-enriching stellar system embedded in a dark matter halo, MDFs typically have a very clean single mode toward the metal-rich side of the distribution plus an extended metal-poor tail. It is interesting to note that this is also true for the Sgr dSph when the MDF is sampled outside the nucleus (Mucciarelli et al. 2017; Minelli et al. 2021), while strong bi-modality emerges in the nuclear region (Bellazzini et al. 2008; Mucciarelli et al. 2017; Alfaro-Cuello et al. 2019, 2020).

  • If we consider the different subgroups as classified by the GMM described in Sect. 4.1, we can infer the intrinsic metallicity dispersion with the maximum likelihood analysis described in Mucciarelli et al. (2012), following Pryor & Meylan (1993) and Walker et al. (2006). Doing this, we obtain mean metallicities of the various components in excellent agreement with the results of the GMM, and the intrinsic metallicity dispersions (σint) and the associated uncertainties reported in Table 3. It is very interesting to note that both the MP and the M-int1 components are fully consistent with null dispersion, that is, the most likely outcome of the analysis, with tiny uncertainty. Null or very small metallicity dispersion is a defining characteristic of GCs (Willman & Strader 2012; Gratton et al. 2019). On the other hand, the M-int2 metallicity distribution is strongly incompatible with zero dispersion and nothing relevant can be said on the MR population as the uncertainty on σint is huge.

Table 3.

Intrinsic metallicity dispersion of the four subpopulations.

Taken at face value, these results suggest that ω Centauri may indeed be the nuclear remnant of a dwarf galaxy that was originally built up by the merging of two massive metal-poor GCs (both more massive than 106 M⊙, according to Table 2 and the total mass by Baumgardt & Hilker 2018, M = 3.94 ± 0.02 × 106 M⊙), with each one displaying its own extended light elements’ anticorrelations typical of GCs in this mass regime, plus some more metal-rich components, with significant metallicity dispersion, possibly formed in situ, similar to the case of the nucleus of Sgr dSph (Carretta et al. 2010a,b; Alfaro-Cuello et al. 2019, 2020).

It is important to keep in mind that the reliability of the results reported in Table 3 depends on the accuracy of the errors on the individual [Fe/H] estimates, which is notoriously difficult to assess properly. However, there is little doubt that the intrinsic metallicity dispersion observed in our MP and Mint1 samples, if not null, is very small and compatible with that observed in other massive GCs (Carretta et al. 2010b,c; Lardo et al. 2023), and hence the hypothesis that they trace the population of ancient GCs that merged at the center of the progenitor dwarf galaxy to build the backbone of its stellar nucleus appears sustainable in any case.

It may be legitimate to ask oneself the reason why the possibility that the M-int1 and, in particular, the MP components can be single-metallicity populations has not emerged so clearly in previous studies. The comparisons between the distribution in various chemical planes suggest that our set of measures has a higher precision than comparable samples by other authors, allowing us to gain deeper insight into the trends and distributions in these planes (see, e.g., Fig. 11). As a quantitative test in this sense, we considered the subsamples of MP stars in common with Johnson & Pilachowski (2010; 170 stars) and with Mészáros et al. (2021; 70 stars). Since we were dealing with exactly the same set of stars, the intrinsic metallicity dispersion σint was fixed. We can compute the observed metallicity dispersion σoss, in the very reasonable hypothesis of Gaussian distribution, as 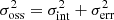σ oss 2 = σ int 2 + σ err 2 $ \sigma_{\rm oss}^2 = \sigma_{\rm int}^2 + \sigma_{\rm err}^2 $, where σerr is the contribution of the measuring error that is different from the set of measures (ours) to set of measures (Johnson & Pilachowski 2010; Mészáros et al. 2021). The one having the largest σoss necessarily also has the largest σerr, and hence lower precision. For the MP stars in common with Johnson & Pilachowski (2010), we obtain σoss = 0.077 dex from our measures and σoss = 0.137 dex from their measures. For the MP stars in common with Mészáros et al. (2021), we obtain σoss = 0.085 dex from our measures and σoss = 0.103 dex from their measures. Therefore, at least for the considered samples, in both cases our [Fe/H] measures are significantly more precise than theirs. This is clearly a factor enhancing our capability to disentangle the various components of the overall MDF and to properly estimate their metallicity dispersion. The differences in the spatial distribution of the various samples may also play a role since the different components may have different radial distributions (Bellini et al. 2009; Johnson & Pilachowski 2010) and as our sample is more centrally concentrated than those by Johnson & Pilachowski (2010) and, especially, by Mészáros et al. (2021).

In summary, the scenario outlined above seems to deserve a more thorough and deeper dedicated analysis, taking into account also different aspects of the problem not considered here, such as the age distribution and the kinematics of the various components. This is clearly beyond the scope of the present paper and we postpone it to a future contribution.

3

We would like to remark that the CN contamination does not affect the Fe, Mg, or Si at any metallicity.

5

We note that Mészáros et al. (2021) define their MP subpopulation at [Fe/H] ≤ −1.5 dex.

Acknowledgments

This research is funded by the project LEGO – Reconstructing the building blocks of the Galaxy by chemical tagging (P.I. A. Mucciarelli). granted by the Italian MUR through contract PRIN 2022LLP8TK_001. C.L. acknowledges funding from Ministero dell’Università e della Ricerca (MIUR) through the Programme Rita Levi Montalcini (grant PGR18YRML1). We would like to thank Donatella Romano for the useful discussions.

References

  1. Alfaro-Cuello, M., Kacharov, N., Neumayer, N., et al. 2019, ApJ, 886, 57 [Google Scholar]
  2. Alfaro-Cuello, M., Kacharov, N., Neumayer, N., et al. 2020, ApJ, 892, 20 [CrossRef] [Google Scholar]
  3. Alvarez Garay, D. A., Mucciarelli, A., Lardo, C., Bellazzini, M., & Merle, T. 2022, ApJ, 928, L11 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bastian, N., & Lardo, C. 2015, MNRAS, 453, 357 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [Google Scholar]
  7. Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [Google Scholar]
  8. Bekki, K., & Freeman, K. C. 2003, MNRAS, 346, L11 [Google Scholar]
  9. Bekki, K., & Tsujimoto, T. 2019, ApJ, 886, 121 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1147 [Google Scholar]
  11. Bellini, A., Piotto, G., Bedin, L. R., et al. 2009, A&A, 507, 1393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
  13. Böker, T., Sarzi, M., McLaughlin, D. E., et al. 2004, AJ, 127, 105 [CrossRef] [Google Scholar]
  14. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010a, ApJ, 714, L7 [Google Scholar]
  16. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010b, A&A, 520, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Carretta, E., Gratton, R. G., Lucatello, S., et al. 2010c, ApJ, 722, L1 [NASA ADS] [CrossRef] [Google Scholar]
  18. Carretta, E., Bragaglia, A., Lucatello, S., et al. 2018, A&A, 615, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, A20 [Google Scholar]
  20. Crociati, C., Valenti, E., Ferraro, F. R., et al. 2023, ApJ, 951, 17 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dell’Agli, F., García-Hernández, D. A., Ventura, P., et al. 2018, MNRAS, 475, 3098 [CrossRef] [Google Scholar]
  22. Del Principe, M., Piersimoni, A. M., Storm, J., et al. 2006, ApJ, 652, 362 [NASA ADS] [CrossRef] [Google Scholar]
  23. de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Denisenkov, P. A., & Denisenkova, S. N. 1990, Sov. Astron. Lett., 16, 275 [NASA ADS] [Google Scholar]
  25. Denissenkov, P. A., & Hartwick, F. D. A. 2014, MNRAS, 437, L21 [Google Scholar]
  26. Denissenkov, P. A., Truran, J. W., Pignatari, M., et al. 2014, MNRAS, 442, 2058 [NASA ADS] [CrossRef] [Google Scholar]
  27. D’Ercole, A., D’Antona, F., Ventura, P., Vesperini, E., & McMillan, S. L. W. 2010, MNRAS, 407, 854 [Google Scholar]
  28. Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [Google Scholar]
  29. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gnedin, O. Y., Zhao, H., Pringle, J. E., et al. 2002, ApJ, 568, L23 [Google Scholar]
  33. Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [Google Scholar]
  34. Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
  35. Gratton, R., Bragaglia, A., Carretta, E., et al. 2019, A&ARv, 27, 8 [Google Scholar]
  36. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
  37. Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
  38. Harris, W. E. 2010, arXiv e-prints [arXiv:1012.3224] [Google Scholar]
  39. Hasselquist, S., Hayes, C. R., Lian, J., et al. 2021, ApJ, 923, 172 [NASA ADS] [CrossRef] [Google Scholar]
  40. Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
  41. Ibata, R. A., Bellazzini, M., Malhan, K., Martin, N., & Bianchini, P. 2019, Nat. Astron., 3, 667 [Google Scholar]
  42. Ibata, R., Malhan, K., Martin, N., et al. 2021, ApJ, 914, 123 [NASA ADS] [CrossRef] [Google Scholar]
  43. Johnson, C. I., & Pilachowski, C. A. 2010, ApJ, 722, 1373 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kirby, E. N., Guhathakurta, P., Bolte, M., Sneden, C., & Geha, M. C. 2009, ApJ, 705, 328 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kirby, E. N., Lanfranchi, G. A., Simon, J. D., Cohen, J. G., & Guhathakurta, P. 2011, ApJ, 727, 78 [Google Scholar]
  46. Krause, M., Charbonnel, C., Decressin, T., Meynet, G., & Prantzos, N. 2013, A&A, 552, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 14 [Google Scholar]
  48. Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lardo, C., Salaris, M., Cassisi, S., & Bastian, N. 2022, A&A, 662, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Lardo, C., Salaris, M., Cassisi, S., et al. 2023, A&A, 669, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Lee, J.-W. 2022, ApJS, 263, 20 [NASA ADS] [CrossRef] [Google Scholar]
  52. Lee, J.-W. 2023, ApJ, 948, L16 [NASA ADS] [CrossRef] [Google Scholar]
  53. Legnardi, M. V., Milone, A. P., Armillotta, L., et al. 2022, MNRAS, 513, 735 [NASA ADS] [CrossRef] [Google Scholar]
  54. Limberg, G., Souza, S. O., Pérez-Villegas, A., et al. 2022, ApJ, 935, 109 [NASA ADS] [CrossRef] [Google Scholar]
  55. Maccarone, T. J., & Zurek, D. R. 2012, MNRAS, 423, 2 [NASA ADS] [CrossRef] [Google Scholar]
  56. Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [Google Scholar]
  57. Marino, A. F., Milone, A. P., Piotto, G., et al. 2011, ApJ, 731, 64 [Google Scholar]
  58. Marino, A. F., Milone, A. P., Piotto, G., et al. 2012, ApJ, 746, 14 [CrossRef] [Google Scholar]
  59. Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Masseron, T., García-Hernández, D. A., Mészáros, S., et al. 2019, A&A, 622, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Mészáros, S., Martell, S. L., Shetrone, M., et al. 2015, AJ, 149, 153 [Google Scholar]
  62. Mészáros, S., Masseron, T., García-Hernández, D. A., et al. 2020, MNRAS, 492, 1641 [Google Scholar]
  63. Mészáros, S., Masseron, T., Fernández-Trincado, J. G., et al. 2021, MNRAS, 505, 1645 [Google Scholar]
  64. Milone, A. P., & Marino, A. F. 2022, Universe, 8, 359 [NASA ADS] [CrossRef] [Google Scholar]
  65. Minelli, A., Mucciarelli, A., Romano, D., et al. 2021, ApJ, 910, 114 [CrossRef] [Google Scholar]
  66. Monty, S., Yong, D., Marino, A. F., et al. 2023, MNRAS, 518, 965 [Google Scholar]
  67. Mucciarelli, A. 2013, arXiv e-prints [arXiv:1311.1403] [Google Scholar]
  68. Mucciarelli, A., Bellazzini, M., Ibata, R., et al. 2012, MNRAS, 426, 2889 [Google Scholar]
  69. Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
  70. Mucciarelli, A., Bellazzini, M., Ibata, R., et al. 2017, A&A, 605, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Mucciarelli, A., Salaris, M., Monaco, L., et al. 2018a, A&A, 618, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Mucciarelli, A., Lapenna, E., Ferraro, F. R., & Lanzoni, B. 2018b, ApJ, 859, 75 [NASA ADS] [CrossRef] [Google Scholar]
  73. Mucciarelli, A., Bellazzini, M., & Massari, D. 2021, A&A, 653, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Myeong, G. C., Evans, N. W., Belokurov, V., Sanders, J. L., & Koposov, S. E. 2018, ApJ, 863, L28 [NASA ADS] [CrossRef] [Google Scholar]
  75. Neumayer, N., Seth, A., & Böker, T. 2020, A&ARv, 28, 4 [Google Scholar]
  76. Norris, J. E., & Da Costa, G. S. 1995, ApJ, 447, 680 [Google Scholar]
  77. Pancino, E., Pasquini, L., Hill, V., Ferraro, F. R., & Bellazzini, M. 2002, ApJ, 568, L101 [NASA ADS] [CrossRef] [Google Scholar]
  78. Pancino, E., Romano, D., Tang, B., et al. 2017, A&A, 601, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Pasquini, L., Avila, G., Blecha, A., et al. 2002, Messenger, 110, 1 [NASA ADS] [Google Scholar]
  80. Prantzos, N., Charbonnel, C., & Iliadis, C. 2007, A&A, 470, 179 [CrossRef] [EDP Sciences] [Google Scholar]
  81. Prantzos, N., Charbonnel, C., & Iliadis, C. 2017, A&A, 608, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 357 [Google Scholar]
  83. Renzini, A., D’Antona, F., Cassisi, S., et al. 2015, MNRAS, 454, 4197 [Google Scholar]
  84. Renzini, A., Marino, A. F., & Milone, A. P. 2022, MNRAS, 513, 2111 [NASA ADS] [CrossRef] [Google Scholar]
  85. Romano, D., Tosi, M., Cignoni, M., et al. 2010, MNRAS, 401, 2490 [NASA ADS] [CrossRef] [Google Scholar]
  86. Sarajedini, A., & Layden, A. C. 1995, AJ, 109, 1086 [Google Scholar]
  87. Shetrone, M. D. 1996, AJ, 112, 1517 [NASA ADS] [CrossRef] [Google Scholar]
  88. Smith, V. V., Suntzeff, N. B., Cunha, K., et al. 2000, AJ, 119, 1239 [Google Scholar]
  89. Sollima, A., Pancino, E., Ferraro, F. R., et al. 2005a, ApJ, 634, 332 [NASA ADS] [CrossRef] [Google Scholar]
  90. Sollima, A., Ferraro, F. R., Pancino, E., & Bellazzini, M. 2005b, MNRAS, 357, 265 [NASA ADS] [CrossRef] [Google Scholar]
  91. Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
  92. van Leeuwen, F., Le Poole, R. S., Reijns, R. A., Freeman, K. C., & de Zeeuw, P. T. 2000, A&A, 360, 472 [NASA ADS] [Google Scholar]
  93. Ventura, P., Di Criscienzo, M., Carini, R., & D’Antona, F. 2013, MNRAS, 431, 3642 [Google Scholar]
  94. Ventura, P., García-Hernández, D. A., Dell’Agli, F., et al. 2016, ApJ, 831, L17 [Google Scholar]
  95. Villanova, S., Geisler, D., Gratton, R. G., & Cassisi, S. 2014, ApJ, 791, 107 [Google Scholar]
  96. Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2006, AJ, 131, 2114 [Google Scholar]
  97. Willman, B., & Strader, J. 2012, AJ, 144, 76 [Google Scholar]
  98. Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Abundance ratios for the GIRAFFE targets of ω Centauri.

In the text
Table 2.

Mean metallicity ⟨[Fe/H]⟩, its associated dispersion (σ), the sample size (N), and number fraction of the four metallicity subpopulations identified in ω Centauri (see text for details).

In the text
Table 3.

Intrinsic metallicity dispersion of the four subpopulations.

In the text

All Figures

thumbnail Fig. 1.

Coordinate positions of FLAMES targets are displayed by the red circles. The black cross denotes the cluster center ( − 201 . ° 6910 , − 47 . ° 4769 $ -201{{\overset{\circ}{.}}}6910, -47{{\overset{\circ}{.}}}4769 $) according to van Leeuwen et al. (2000). The dashed black circles show 2.5 and 5 times the core radius ( r c = 1 . ′ 40 $ r_c = 1{{\overset{\prime}{.}}}40 $; Harris 1996). We note that 424 out of the 439 stars that were analyzed in this study are contained within the green circle, which is 10 times the core radius.
In the text
thumbnail Fig. 2.

Histogram displaying the MDF of ω Centauri. Also shown as a dashed black line is the Gaussian kernel fit of the distribution. Four Gaussian components can be identified. They represent the MP, M-int1, M-int2, and MR subpopulations, and are plotted in the figure as dotted, dashed, solid, and dash-dotted lines, respectively.
In the text
thumbnail Fig. 3.

Distribution of [Mg/Fe] (left panel), [Al/Fe] (middle panel), and [Si/Fe] (right panel) as a function of [Fe/H] for the stars belonging to our sample. The error bar in the top-right corner represents the typical error associated with the measurements.
In the text
thumbnail Fig. 4.

Trend of [Mg/Fe] as a function of [Al/Fe] for the MP, M-int1, M-int2, and MR subpopulations (from top to bottom, left to right). The size of each point indicates its probability of belonging to that particular metallicity subpopulation – the larger the symbol, the higher the probability – while gray dots represent the entire sample. The error bar in the top-right corner represents the typical measurement error associated with the data.
In the text
thumbnail Fig. 5.

Spectral region around the Al doublet at 7835–7836 Å for sample stars with similar atmospheric parameters. The solid blue lines denote stars belonging to the Mg-poor group in the MP subpopulation, whereas the dashed green lines represent again Mg-poor stars but in the M-int1 subpopulation. A clear difference in the strength of the Al lines can be appreciated between the two metallicity subgroups.
In the text
thumbnail Fig. 6.

As for Fig. 4, but for [Si/Fe] and [Al/Fe].
In the text
thumbnail Fig. 7.

As for Fig. 4, but for [Mg/Fe] and [Si/Fe].
In the text
thumbnail Fig. 8.

Trend of [Mg/Fe] as a function of [Al/Fe] for the stars analyzed in this study (top-left panel), and for the stars analyzed by Mészáros et al. (2021; top-right panel). In the bottom panels, we display only the stars belonging to the MP subpopulation for each sample, respectively.
In the text
thumbnail Fig. 9.

Trend of [Mg/Fe] as a function of [Al/Fe] for the stars analyzed in this study. The blue dots and the green crosses represent the MP and M-int1 stars with [Al/Fe] > 1 dex, respectively. The gray dots represent the entire sample. The error bar in the top-right corner represents the typical measurement error associated with the data. The dashed line indicates the value [Al/Fe] = 1 dex. The distributions of the two subsamples are shown in the right panel with the corresponding colors.
In the text
thumbnail Fig. 10.

Left panel: fraction of the enriched stars as a function of the distance from the cluster center, as defined by van Leeuwen et al. (2000). The blue circles represent the stars analyzed in this study, whereas the orange squares display the stars studied by Mészáros et al. (2021). In the Y axis, the error bars represent the error associated with the fraction of enriched stars, while in the X axis, they represent the extension of the stars contained in each radial ring. The dashed gray line and the gray area show the mean and the standard deviation for the genuine GCs observed so far, respectively (Bastian & Lardo 2015). Right panel: coordinate positions of stars analyzed by Mészáros et al. (2021). The black cross represents the same cluster center used in Fig. 1. The dashed black circles show 5, 20, and 30 times the core radius ( r c = 1 . ′ 40 $ r_c = 1{{\overset{\prime}{.}}}40 $; Harris 1996). The green circle represents 10 times the core radius and it encloses 554 out of 982 stars.
In the text
thumbnail Fig. 11.

Distribution of [Mg/Fe] (left panel), [Al/Fe] (middle panel), and [Si/Fe] (right panel) as a function of [Fe/H]. In the top are displayed the stars here analyzed (blue dots), while in the bottom the stars analyzed by Mészáros et al. (2021; orange dots). The error bar in the top-right corner in the top figures represents the typical error associated with the measurements.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.