EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 681 (January 2024) A&A, 681 (2024) A98 Full HTML
Open Access
Issue
A&A
Volume 681, January 2024
Article Number A98
Number of page(s) 6
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202347789
Published online 23 January 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

In certain aspects, Mercury’s magnetosphere is a scaled-down version of the Earth’s magnetosphere. However, the typical solar wind dynamic pressure at Mercury is about five times higher than at the Earth, and the average IMF magnitude is about four times stronger (Winslow et al. 2013). Together with the weak intrinsic magnetic field of Mercury, a small and dynamic magnetosphere, compared to the Earth, is formed that interacts with the solar wind and its embedded interplanetary magnetic field (IMF; Slavin & Holzer 1979; Anderson et al. 2008; Slavin et al. 2018). In addition to a stronger dependency on the solar wind relative to the Earth, Mercury’s magnetosphere also reacts faster to solar wind changes. The Dungey cycle, which describes the plasma circulation and magnetic flux transfer in the magnetosphere, takes only about 2min, as MESSENGER observations show (Slavin et al. 2009, 2021). The timescale is significantly shorter than the Dungey cycle at the Earth (about 1 h, Baker et al. 1996), suggesting that the Hermean system is more dynamic and can only be considered quasi-stationary for a few minutes. Compared to the other terrestrial planets, Mercury is unique in (1) the lack of a significant ionosphere and (2) the existence of a large, electrically conducting core (Smith et al. 2012). These features significantly impact the magnetospheric current system and induction effects (Jia et al. 2015; Exner et al. 2018, 2020; Ganushkina et al. 2015).

The pioneering work by Ness et al. (1975) used the first in situ measurements of Mercury’s magnetosphere (Mariner 10, Dunne & Burgess 1978) to provide initial insights. Siscoe & Christopher (1975) and Slavin & Holzer (1979) used this data together with observational data from the Earth to evaluate the solar wind stand-off distance at Mercury to about (1.3−2.1)RM (RM = 2440 km being the radius of Mercury), depending on the upstream solar wind condition. More than three decades later, MESSENGER (Solomon et al. 2007) observations revealed a more detailed insight and narrowed the estimate for the solar wind stand-off distance to (1.35−1.55) RM (Winslow et al. 2013). The average subsolar distance of the bow shock is (1.89− 2.29) RM (Slavin et al. 2009; Winslow et al. 2013). Previous studies support these results and further examine the interaction between Mercury and the solar wind, using both measurements and (numerical) models, under average solar wind conditions and varying IMF conditions (e.g., Trávníček et al. 2009; Baker et al. 2013; Jia et al. 2015; Fatemi et al. 2018, 2020) or during extreme events, such as CMEs (e.g., Exner et al. 2018; Jia et al. 2019).

The BepiColombo space mission (Benkhoff et al. 2010) will perform a total of six swingbys near Mercury before its final arrival at the planet in 2025. While the nominal mission does not begin before the arrival in the final science orbits, traversing Mercury’s magnetosphere at various angles during the swingbys and reaching approaches as close as about 200 km gives unique science opportunities to investigate the planet’s global magnetosphere.

While there is no significant ionosphere, Mercury possesses a tenuous exosphere consisting mainly of sodium (Cheng et al. 1987; Milillo et al. 2005). This gas envelope is predominantly generated by multiple surface processes of the solar wind and solar radiation interaction with the planetary surface (Wurz et al. 2010,2022; Cassidy et al. 2015; Gamborino & Wurz 2018; Exner et al. 2020). Hence, there are two main sources for plasma in the magnetosphere: exospheric particles and solar wind particles.

Due to limited observational coverage of previous missions, the plasma motion of planetary and solar wind ions through Mercury’s equatorial low-altitude nightside magnetosphere is largely derived from scaled-down models based on the magnetosphere of Earth. However, global numerical modeling efforts have revealed particular plasma signatures, including partial plasma rings (Delcourt et al. 2003; Trávníček et al. 2007; Exner et al. 2018; Yagi et al. 2010, 2017), and increased exospheric densities (Exner et al. 2020) at these low altitudes. The second swingby trajectory of BepiColombo (henceforth called MSB2) is strongly equatorial, as the spacecraft passed through the southern magnetosphere and had its closest approach (CA) on the dawnward nightside at 199 km on June 23, 2022, obtaining measurements in the previously non-covered low altitudes (see Fig. 1).

In this study, we investigate the observed particle densities and energies due to solar wind particle entry. A proton energy spectrum is computed that gives insights into regions along the trajectory where, for instance, particles are accelerated or heated. Magnetic field data from the MGF instrument (Baumjohann et al. 2020) on board the Mio spacecraft of Bepi-Colombo are used to determine the outbound IMF parameters. The determined IMF direction and strength agrees well with commonly observed IMF conditions at Mercury resulting from the Parker spiral (James et al. 2017). We address two scientific questions in this study:

How deep do solar wind particles penetrate Mercury’s magnetosphere? What do the energy spectra of the penetrating ions look like? To tackle these questions, we employed a numerical hybrid plasma approach utilizing the AIKEF model.

2 Hybrid plasma approach

Using a hybrid plasma model to study the interaction between the solar wind and the planet Mercury offers several advantages. The most important one in the context of this study is the advantage of a kinetic description of the ions as it enables the resolution of non-Maxwellian distributions. In addition, such models are computationally inexpensive compared to fully kinetic (particle in cell, or PIC) simulations, as the electrons are described as a fluid and the electron kinetics that happen on much smaller length and time scales than those of ions are omitted (Winske & Omidi 1996). Therefore, physical processes down to ion kinetic time and length scales can be reasonably described using hybrid models. Hybrid modeling has been applied to investigate Mercury’s plasma environment by, for example, Trávníček et al. (2007, 2009); Paral et al. (2010); Paral & Rankin (2013); Müller et al. (2011,2012); Herčík et al. (2013); Fatemi et al. (2017, 2018); Exner et al. (2018, 2020); Jarvinen et al. (2020); Aizawa et al. (2021); Lu et al. (2022).

In this work, we used the Adaptive Ion-Kinetic Electron-Fluid code, or AIKEF (Müller et al. 2011). It is a global 3D hybrid plasma simulation code where ions are treated kinetically and electrons are a massless charge-neutralizing fluid. A Cartesian mesh grid is used where the electromagnetic fields are computed on the nodes of the numerical mesh. While the number of particles per unit volume gives the resolution in velocity space, the resolution of the numerical mesh gives the spatial resolution. Mercury’s surface is treated as a perfect plasma absorber, which means that particles impacting the surface are removed from the simulation box. Magnetic reconnection is handled self-consistently through anomalous resistivity (Raeder et al. 1998; Jia et al. 2009). (For a detailed explanation on how the electromagnetic fields are propagated and how the AIKEF model is implemented, see Müller et al. 2011.)

thumbnail Fig. 1

Overview of the AIKEF simulation box. In the top-right corner, there is an exemplary unrefined block that is further divided into cells that define the grid resolution (size ratios: block to simulation box = cell to block). The black arrows denote the difference between the MASO and MSM coordinate system, which is shifted 0.2RM in the +Z direction. The subsolar point is defined to be on the MSM X-axis; see modelled bow shock (green, solid line) and magnetopause (blue, dotted). The MSB2 trajectory with its closest approach is shown in red; the orange outline encloses the refined area (grid resolution doubled).

Simulation setup

The size of the simulation box is 12 RM x 12 RM × 12 RM (see Fig. 1). We set the separation between the physical nodes to 114 km, which corresponds to 2.8 di,sw, with di,sw = 40 km being the ion inertial length in the solar wind (see Table 1). However, the spatial resolution near the planet (−2.1 RM < X < 3.9 RM; −4.1 RM < Y < 4.1 RM; −1.9 RM < Z < 1.9 RM) is twice as high when using mesh refinement, resulting in a node distance of 57 km (or 1.4 di,sw). The model utilizes the right-handed Mercury Anti Solar Orbital (MASO) coordinate system where the X-axis is directed as the solar wind velocity (i.e., anti-sunward), the Z-axis is the positive normal to the orbital plane (anti-parallel to Mercury’s dipole moment), and the Y-axis is the orthogonal complement roughly pointing toward Mercury’s orbital movement direction (i.e., dawnside). To reach a quasi-steady state, the total run time of the simulation is about 760 seconds in the simulation domain, which corresponds to about 6 Dungey cycles (Slavin et al. 2009). Apart from the IMF direction derived from the BepiColombo Mio MGF measurements during the outbound trajectory phase (Baumjohann et al. 2020), all other physical input parameters are adapted from the average values obtained from 4yr of MESSENGER observations (Winslow et al. 2013; Anderson et al. 2012), see Table 1.

In this study, our simulations account only for protons (H+ ions) of solar wind origin as the dominant ion species. The effects of heavier solar wind ions or ions of planetary origin, such as Na+ (Potter & Morgan 1985), are neglected.

Table 1

Input parameters used for the AIKEF model.

3 Results and discussion

3.1 Magnetospheric regions and penetration depth

In Figs. 2a and c, the quasi-steady state magnetosphere of Mercury is depicted through the ion number density ni as meridional and equatorial “slices” through the simulation. Additionally, panels b and d illustrate the electric current density |J| = 1/μ0|∇ × B|, where B represents the magnetic field and μ0 the vacuum permeability, once again in meridional and equatorial planes. The projection of the mostly equatorial MSB2 trajectory is displayed in all subplots of Fig. 2. Crossings of BepiColombo through different magnetospheric regions are highlighted in panel a: (1) inbound magnetopause crossing, between (2) and (3) grazing of the magnetotail, (4) the outbound magnetopause crossing after the closest approach, and (5) the outbound bow shock crossing at about 2 RM.

We find it important to note here that Fig. 2 displays only one slice through the simulation, and hence the MSB2 trajectory intersects each of these planes only at one point (marked with crosses). This also accounts for the tail current sheet that is tilted (Romanelli et al. 2022) and intersects the equatorial plane, for instance at YMASO = 0.5 RM (see Figs. 2a and b). Magnetospheric regions and boundaries become more evident when considering the particle distributions in Fig. 3.

In general, considering Figs. 2a and c, solar wind protons are spread throughout the magnetosphere. The lowest number densities of >0.01 cm−3 are found at the dayside magnetopause, and a density of about (0.1−1) cm−3 can be observed in the tail lobes (comparable to MESSENGER results, Zhao et al. 2020). The density in the dayside magnetosheath is about 130 cm−3, and the highest density of 250 cm−3 can be seen at the cusp regions, where the particles can precipitate onto the surface, which is a driving mechanism for planetary ions that make up Mercury’s exosphere (Raines et al. 2022; Exner et al. 2020).

Our results indicate a dawn-dusk asymmetry of the magnetosheath thickness in the equatorial plane (see Figs. 2a and Figs. b). As the model itself is symmetric about the X-axis, the difference might be caused by the IMF direction and also influenced by the upstream solar wind condition resulting in a foreshock on the dawnside. There are several widely used models that assess the locations of the bow shock and magnetopause, including the classic Shue model (Shue et al. 1997), a paraboloid model proposed by Alexeev et al. (2008), and the KT14 and KT16 models (Korth et al. 2015, 2017), among others. These models often assume (anti-)parallel IMF conditions, leading to a rotational symmetry around the X-axis. However, studies on the Earth’s magnetosphere have shown clear signatures of asymmetries at the quasi-perpendicular (dusk) side of the bow shock, meaning that the angle between the bow shock normal and the IMF direction, θbn, is greater than 45°, and the magnetosheath is thicker than on the quasi-parallel (dawn) side due to the greater extent of the shock (Sundberg et al. 2013; Dimmock et al. 2016). Models that include this dawn-dusk asymmetry have been developed (e.g., by Tsyganenko 2002). This effect is also observable in our simulation, as can be seen in Figs. 2a and b. Compared to the modeled bow shock (Slavin et al. 2009) using empirical parameters from Winslow et al. (2013), a difference in the general shape as well as a slight shift to the dusk side is evident in the simulation. Moreover, while in Figs. 2a and b, the quasi-perpendicular bow shock is a clear shock front, the quasi-parallel shock shows the development of a foreshock region. We find it important to note here that in Fig. 2 the ion density is shown in the geographical equatorial plane, deviating slightly from the shifted Mercury Solar Magnetospheric (MSM) XY-plane (see Fig. 1), in which the modeled bow shock and magnetopause are shown. The magnetopause seems to be symmetric around ZMASO = 0.2 RM, comparing well to the magnetopause model from Korth et al. (2015).

Evaluating the areas of the highest electric current densities in Fig. 2d, the subsolar magnetopause and bow shock stand-off distances (at ZMASO = 0.2 RM) are respectively RMP =1.45 RM and RBS =1.85 RM, generally reproducing the empirical models by Slavin et al. (2009) and Winslow et al. (2013). The bow shock stand-off distance is about 2% smaller than the minimal expected value of 1.89 RM (Winslow et al. 2013). This might be caused by numerical inaccuracies due to the limited grid resolution in the simulation.

At the subsolar magnetopause (most) solar wind protons can penetrate down to 1100 km toward the planetary surface and are deflected around the planet and its intrinsic magnetic field. This is illustrated by the density drop toward the planet and by the thin black lines depicting the ion bulk flow velocity in Figs. 2a and c. The penetration depth decreases slightly toward the dawnside direction, as can be seen in Fig. 2a. In addition, one can see trapped particles in terms of closed streamlines at X = 0 RM, Y = 1.5 RM in Fig. 2a. As the MSB2 trajectory passes right through this area, these particles are also seen in the energy spectrum in Fig. 3 and are discussed in the following section.

3.2 Penetrating ion energy profile

To predict the ion energy profile along the spacecraft trajectory through the magnetosphere, we used a method that extracts the particle data from the completed simulation snapshot. This approach offers the flexibility to adjust the trajectory with minimal computational effort, regardless of the complexity of the underlying simulation.

To determine the plasma energy distribution along MSB2, we extracted all particles within a constant distance of 5 ion inertial lengths (in the solar wind) and gathered their velocity distribution. Subsequently, an omnidirectional velocity distribution and thus energy spectrum of the ions was obtained without the direct limitation of a limited mesh grid resolution. Ideally, if one aims to reconstruct measurements by a particle detector, the radius of the “particle cloud” at each trajectory point should be determined by the thermal velocity of the particles and the measurement or exposure time of the instrument. Notably, the larger the radius, the higher the number of particles within the cloud, resulting in improved statistical accuracy. We chose a radius of 5 ion inertial lengths in the solar wind (roughly 200 km) in order to obtain sufficient data points (N > 1000 per trajectory point) to compute a spectrum.

The resulting ion kinetic energy spectrum along the trajectory is presented in Fig. 3. It shows the particle distribution functions as histograms at each trajectory point alongside one another. The displayed energy ranges from 1 eV to 20keV, with 60 logarithmic energy bins per histogram. We note that while Fig. 3 uses time as the X-axis, the analysis is based on adjusting the spatial position within a quasi-stationary state at the end of the simulation. To guide the eye, we indicate the solar wind initialization temperature of 1 keV with a horizontal dashed line in Fig. 3.

During MSB2, the BepiColombo spacecraft entered the magnetosphere at the post-terminator duskside flank of the mag-netosheath. Due to the size of the simulation box used, the spectrum in Fig. 3a starts at 08:45 UTC, and the spacecraft is already located in the magnetosheath. The particle energy peaks are just under 1 keV, which equates to the solar wind input energy. Due to the distance of X > +4 RM at Y ~ −3 RM, the solar wind that was decelerated and heated at the bow shock accelerates again to solar wind speed (Gershman et al. 2013).

Nevertheless, considering the width of the energy distribution at about 09:10 UTC in Fig. 3a, a few particles have energies that exceed 1 keV due to acceleration mechanisms at the dusk-side flank of the inbound magnetopause. After (1) in Fig. 3, the energy decreases gradually to about 50 eV at 09:33 UTC. This lowering of the energy by one order of magnitude is seen as being a result of a passage from the magnetopause through the tail plasma lobes. Between 09:35 UTC and 09:40 UTC, marked with (2), a particle population with an energy range of about 20− 200 eV is observed. Taking into account Figs. 2c and d, this is interpreted as a grazing of the tail current sheet from its southern boundary. In the area between (3) and (4), the density increases, and there is a particle population with energies of a few electron volts up to a maximum of 1 keV.

Starting from (3) in Fig. 3, the energy first decreases until about 09:47 UTC and then increases again until (4). This population can be identified with the trapped particles seen in Fig. 2a. These particles have a predominantly negative x-velocity component (see Fig. 3b), meaning they move in a sunward direction, and compared to Fig. 2a, a convection pattern can be identified. These accelerated particles are due to magnetotail reconnection and drift planetward and toward the magnetopause. Between the closest approach and (4) there is another particle population accelerated to higher energies centered at about 6 keV and reaching up to 10 keV. These particles are accelerated near the (dawnside) flanks of the tilted tail current sheet. Due to the proximity to the downtail reconnection site, the energies are higher compared to the generally lower energy population between (3) and (4). Point (4) roughly marks the outbound magnetopause crossing. In the dayside magnetosheath, ranging from (4) to (5), the energy ranges from a 10 eV up to about 4 keV. At around 09:54 UTC, point (5), the spacecraft traversed through the bow shock into the solar wind. Between (5) and about 10:05 UTC, there are also ions with a sunward velocity component, despite the solar wind bulk flow (see Fig. 3b), that potentially describe a field-aligned ion beam in the foreshock region that was identified in Figs. 2a and c.

While precise times are indicated, we note that an averaging effect exists in the energy spectrum as a result of employing a radius of about 200 km for the computation of the particle spectrum. Consequently, boundary regions become “blurred” and timings may not be exact. Moreover, the indicated particle energies may deviate from the real-world scenario, especially the low-energy population in the magnetopshere. In that regard, our simulation results are more appropriately viewed as a qualitative representation of the real flyby.

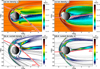thumbnail Fig. 2

AIKEF MSB2 simulation overview. Panels a and b show modeled plasma density ni and electric current density |J| in the XY (equatorial) plane (MASO). Panels c and d illustrate the same parameters but in the XZ (meridonial) plane. The black thin lines in panels a and c represent the bulk flow velocity, whereas the black thin lines in b and d indicate magnetic field lines. The red thick lines with a white outline correspond to the projected MSB2 trajectory, with crosses indicating the points where the simulation “slice” is intersected. The models for magnetopause and bow shock are illustrated by the black dashed (Winslow et al. 2013) and black solid (Slavin et al. 2009; Winslow et al. 2013) lines.
thumbnail Fig. 3

Model results for the proton energy spectrum along BepiColombo Mercury swingby 2 trajectory. Panel a shows all particles, and panel b only shows particles moving in a sunward (υx < 0) direction. The white horizontal dashed line represents the solar wind energy input parameter, and CA denotes the closest approach. The numbers 1−5 indicate magnetopsheric region or boundary crossings: (1) inbound magnetopause crossing, (2 to 3) grazing of the magnetotail, (4) the outbound magnetopause crossing, and (5) the outbound bow shock crossing. The white bar between 09:19 UTC and 10:02 indicates the area where a higher resolution (refinement) was used.

4 Summary and conclusion

We used a global 3D hybrid plasma simulation to investigate the entry of solar wind protons into Mercury’s magnetosphere. Particle densities as well as the electric current were used to evaluate magnetopsheric regions and boundaries. We utilized solar wind upstream IMF conditions derived from averaged measurements obtained by the BepiColombo MGF instrument during the MSB2 phase that are also commonly observed near Mercury (James et al. 2017). The MSB2 trajectory was used as an example to evaluate proton energy distributions throughout the southern magnetosphere and to quantitatively estimate boundary crossings.

The magnetopause and bow shock stand-off distances at the subsolar point are RMP = 1.45 RM and RBS = 1.85 RM. The magnetopause distance falls within the range of anticipated values (Winslow et al. 2013), and likewise, the bow shock distance corresponds well with values documented by Slavin et al. (2009); Winslow et al. (2013). Looking at the general shape of the magnetosphere, a clear difference between empirical models and our simulation can be seen (Fig. 2). The asymmetry in the equatorial plane has been found to be a result of the oblique IMF direction during MSB2. Solar wind particles enter the magnetopshere as they pass through the bow shock and are deflected around the magnetopause. They follow magnetic field lines at the cusps toward the surface and can also enter the magnetopshere through magnetic reconnection at the magnetotail. During these reconnection processes, the particles are accelerated and convect around the planet toward the dayside magnetopause.

We initialized the simulation with solar wind protons that exhibit an average kinetic energy of 1 keV. The resulting energies of these protons influenced by Mercury’s magnetosphere vary by three orders of magnitude, ranging from a few electron volts near the dawnside terminator lower than a few 100 km surface altitude (around the closest approach of MSB2) up to about 4 keV in the magnetosheath region on the pre-terminator dawnside, which is consistent with earlier observations by MESSENGER (Zhao et al. 2020). Moreover we observed a grazing of the magnetotail plasma sheet. After the bow shock crossing, there are indications for an ion beam in the foreshock region of Mercury.

For this study, we utilized a steady state snapshot of Mercury’s magnetosphere. While the positions of boundaries and energy distributions were investigated and estimated, the dynamics of the system are not covered. Mercury’s magnetospheric system, however, is constantly changing due to IMF variability (Fatemi et al. 2018; Exner et al. 2018) and the fast Dungey cycle of about 2 min Slavin et al. (2009). Therefore, our results should be regarded as a quantitative representation, especially if compared to particle measurements during MSB2. The flyby interval of about one to 2 h might allow reconfigurations that potentially affect boundary positions and orientations.

Future work will entail comparing modeled data with ion measurements. This could include investigating dynamic effects, methods to obtain directional particle spectra, and incorporating ion species of planetary origin to investigate exospheric processes. Moreover, simulations with varying IMF and solar wind conditions can be used to provide forecast scenarios for all upcoming Mercury swingbys, contributing to mission/operation planning of BepiColombo.

Acknowledgements

This work was financially supported by the Austrian Research Promotion Agency (FFG) ASAP PICAM-4 under contract 885349. D.T. acknowledges the Mio MGF team (W. Baumjohann as PI, A. Matsuoka as Co-PI) for providing the mean values of interplanetary magnetic field for the BepiColombo flyby-2 outbound trajectory. Furthermore, D.T. acknowledges constructive discussions with colleagues from the Space Research Insitute (IWF) Graz. W.E. has been supported by an ESA research fellowship. W.E. and U.M. acknowledge the North-German Supercomputing Alliance (HLRN) for providing HPC resources that have contributed to the research results reported in this paper. VisIt 3.2.2 has been used to generate the 2D-plots (Childs et al. 2012).

References

  1. Aizawa, S., Griton, L. S., Fatemi, S., et al. 2021, Planet. Space Sci., 198, 105176 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alexeev, I. I., Belenkaya, E. S., Yu. Bobrovnikov, S., Slavin, J. A., & Sarantos, M. 2008, J. Geophys. Res.: Space Phys., 113, A12210 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anderson, B. J., Acuña, M. H., Korth, H., et al. 2008, Science, 321, 82 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anderson, B. J., Johnson, C. L., Korth, H., et al. 2012, J. Geophys. Res.: Planets, 117, E00L12 [Google Scholar]
  5. Baker, D. N., Pulkkinen, T. I., Angelopoulos, V., Baumjohann, W., & McPherron, R. L. 1996, J. Geophys. Res., 101, 12975 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baker, D. N., Poh, G., Odstrcil, D., et al. 2013, J. Geophys. Res.: Space Phys., 118, 45 [NASA ADS] [CrossRef] [Google Scholar]
  7. Baumjohann, W., Matsuoka, A., Narita, Y., et al. 2020, Space Sci. Rev., 216, 125 [NASA ADS] [CrossRef] [Google Scholar]
  8. Benkhoff, J., van Casteren, J., Hayakawa, H., et al. 2010, Planet. Space Sci. , 58, 2 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cassidy, T. A., Merkel, A. W., Burger, M. H., et al. 2015, Icarus, 248, 547 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cheng, A., Johnson, R., Krimigis, S., & Lanzerotti, L. 1987, Icarus, 71, 430 [NASA ADS] [CrossRef] [Google Scholar]
  11. Childs, H., Brugger, E., Whitlock, B., et al. 2012, in High Performance Visualization–Enabling Extreme-Scale Scientific Insight, 357 [Google Scholar]
  12. Delcourt, D. C., Grimald, S., Leblanc, F., et al. 2003, Ann. Geophys., 21, 1723 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dimmock, A. P., Nykyri, K., Osmane, A., & Pulkkinen, T. I. 2016, Adv. Space Res., 58, 196 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dunne, J. A., & Burgess, E. 1978, Natl. Aeronautics Space Admin., SP, 424 [Google Scholar]
  15. Exner, W., Heyner, D., Liuzzo, L., et al. 2018, Planet. Space Sci., 153, 89 [NASA ADS] [CrossRef] [Google Scholar]
  16. Exner, W., Simon, S., Heyner, D., & Motschmann, U. 2020, J. Geophys. Res. (Space Phys.), 125, e27691 [NASA ADS] [Google Scholar]
  17. Fatemi, S., Poppe, A., Delory, G., & Farrell, W. 2017, J. Phys.: Conf. Ser., 837, 012017 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fatemi, S., Poirier, N., Holmström, M., et al. 2018, A&A, 614, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Fatemi, S., Poppe, A. R., & Barabash, S. 2020, J. Geophys. Res.: Space Phys., 125, e27706 [CrossRef] [Google Scholar]
  20. Gamborino, D., & Wurz, P. 2018, Planet. Space Sci., 159, 97 [CrossRef] [Google Scholar]
  21. Ganushkina, N. Y., Liemohn, M. W., Dubyagin, S., et al. 2015, Ann. Geophys., 33, 1369 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gershman, D. J., Slavin, J. A., Raines, J. M., et al. 2013, J. Geophys. Res.: Space Phys., 118, 7181 [NASA ADS] [CrossRef] [Google Scholar]
  23. Herčík, D., Trávnícek, P. M., Johnson, J. R., Kim, E.-H., & Hellinger, P. 2013, J. Geophys. Res.: Space Phys., 118, 405 [CrossRef] [Google Scholar]
  24. James, M. K., Imber, S. M., Bunce, E. J., et al. 2017, J. Geophys. Res.: Space Phys., 122, 7907 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jarvinen, R., Alho, M., Kallio, E., & Pulkkinen, T. I. 2020, MNRAS, 491, 4147 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jia, X., Walker, R. J., Kivelson, M. G., Khurana, K. K., & Linker, J. A. 2009, J. Geophys. Res. (Space Phys.), 114, A09209 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jia, X., Slavin, J. A., Gombosi, T. I., et al. 2015, J. Geophys. Res.: Space Phys., 120, 4763 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jia, X., Slavin, J. A., Poh, G., et al. 2019, J. Geophys. Res.: Space Phys., 124, 229 [NASA ADS] [CrossRef] [Google Scholar]
  29. Korth, H., Tsyganenko, N. A., Johnson, C. L., et al. 2015, J. Geophys. Res.: Space Phys., 120, 4503 [NASA ADS] [CrossRef] [Google Scholar]
  30. Korth, H., Johnson, C. L., Philpott, L., Tsyganenko, N. A., & Anderson, B. J. 2017, Geophys. Res. Lett., 44, 10 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lu, Q., Guo, J., Lu, S., et al. 2022, ApJ, 937, 1 [NASA ADS] [CrossRef] [Google Scholar]
  32. Milillo, A., Wurz, P., Orsini, S., et al. 2005, Space Sci. Rev., 117, 397 [CrossRef] [Google Scholar]
  33. Müller, J., Simon, S., Motschmann, U., et al. 2011, Comput. Phys. Commun., 182, 946 [CrossRef] [Google Scholar]
  34. Müller, J., Simon, S., Wang, Y.-C., et al. 2012, Icarus, 218, 666 [CrossRef] [Google Scholar]
  35. Ness, N., Behannon, K., Lepping, R., & Whang, Y. 1975, J. Geophys. Res., 80, 2708 [NASA ADS] [CrossRef] [Google Scholar]
  36. Paral, J., & Rankin, R. 2013, Nat. Commun., 4, 1645 [NASA ADS] [CrossRef] [Google Scholar]
  37. Paral, J., Trávnícek, P. M., Rankin, R., & Schriver, D. 2010, Geophys. Res. Lett., 37, L19102 [NASA ADS] [CrossRef] [Google Scholar]
  38. Potter, A., & Morgan, T. 1985, Science, 229, 651 [NASA ADS] [CrossRef] [Google Scholar]
  39. Raeder, J., Berchem, J., & Ashour-Abdalla, M. 1998, J. Geophys. Res.: Space Phys., 103, 14787 [NASA ADS] [CrossRef] [Google Scholar]
  40. Raines, J. M., Dewey, R. M., Staudacher, N. M., et al. 2022, J. Geophys. Res.: Space Phys., 127, e2022JA030397 [CrossRef] [Google Scholar]
  41. Romanelli, N., DiBraccio, G. A., Slavin, J., Bowers, C., & Weber, T. 2022, Geophys. Res. Lett., 49, e2022GL101643 [Google Scholar]
  42. Shue, J.-H., Chao, J., Fu, H., et al. 1997, J. Geophys. Res., 102, 9497 [NASA ADS] [CrossRef] [Google Scholar]
  43. Siscoe, G., & Christopher, L. 1975, Geophys. Res. Lett., 2, 158 [NASA ADS] [CrossRef] [Google Scholar]
  44. Slavin, J. A., & Holzer, R. E. 1979, J. Geophys. Res.: Space Phys., 84, 2076 [NASA ADS] [CrossRef] [Google Scholar]
  45. Slavin, J. A., Acuña, M. H., Anderson, B. J., et al. 2009, Science, 324, 606 [NASA ADS] [CrossRef] [Google Scholar]
  46. Slavin, J. A., Baker, D. N., Gershman, D. J., et al. 2018, in Mercury. The View after MESSENGER, eds. S. C. Solomon, L. R. Nittler, & B. J. Anderson, 461 [CrossRef] [Google Scholar]
  47. Slavin, J. A., Imber, S. M., & Raines, J. M. 2021, Magnetospheres in the Solar System, 34, 535 [CrossRef] [Google Scholar]
  48. Smith, D. E., Zuber, M. T., Phillips, R. J., et al. 2012, Science, 336, 214 [NASA ADS] [CrossRef] [Google Scholar]
  49. Solomon, S. C., McNutt, R. L., Gold, R. E., & Domingue, D. L. 2007, Space Sci. Rev., 131, 3 [NASA ADS] [CrossRef] [Google Scholar]
  50. Sundberg, T., Boardsen, S. A., Slavin, J. A., et al. 2013, J. Geophys. Res.: Space Phys., 118, 6457 [NASA ADS] [CrossRef] [Google Scholar]
  51. Trávníček, P., Hellinger, P., & Schriver, D. 2007, Geophys. Res. Lett., 34, L05104 [Google Scholar]
  52. Trávníček, P. M., Hellinger, P., Schriver, D., et al. 2009, Geophys. Res. Lett., 36, L07104 [Google Scholar]
  53. Tsyganenko, N. 2002, J. Geophys. Res.: Space Phys., 107, 1179 [NASA ADS] [Google Scholar]
  54. Winske, D., & Omidi, N. 1996, J. Geophys. Res.: Space Phys., 101, 17287 [NASA ADS] [CrossRef] [Google Scholar]
  55. Winslow, R. M., Anderson, B. J., Johnson, C. L., et al. 2013, J. Geophys. Res. (Space Phys.), 118, 2213 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wurz, P., Whitby, J. A., Rohner, U., et al. 2010, Planet. Space Sci., 58, 1599 [CrossRef] [Google Scholar]
  57. Wurz, P., Fatemi, S., Galli, A., et al. 2022, Space Sci. Rev., 218, 10 [NASA ADS] [CrossRef] [Google Scholar]
  58. Yagi, M., Seki, K., Matsumoto, Y., Delcourt, D. C., & Leblanc, F. 2010, J. Geophys. Res.: Space Phys., 115, A10253 [NASA ADS] [CrossRef] [Google Scholar]
  59. Yagi, M., Seki, K., Matsumoto, Y., Delcourt, D. C., & Leblanc, F. 2017, J. Geophys. Res.: Space Phys., 122, 10,990 [CrossRef] [Google Scholar]
  60. Zhao, J.-T., Zong, Q.-G., Slavin, J. A., et al. 2020, Geophys. Res. Lett., 47, e88075 [Google Scholar]

All Tables

Table 1

Input parameters used for the AIKEF model.

In the text

All Figures

thumbnail Fig. 1

Overview of the AIKEF simulation box. In the top-right corner, there is an exemplary unrefined block that is further divided into cells that define the grid resolution (size ratios: block to simulation box = cell to block). The black arrows denote the difference between the MASO and MSM coordinate system, which is shifted 0.2RM in the +Z direction. The subsolar point is defined to be on the MSM X-axis; see modelled bow shock (green, solid line) and magnetopause (blue, dotted). The MSB2 trajectory with its closest approach is shown in red; the orange outline encloses the refined area (grid resolution doubled).
In the text
thumbnail Fig. 2

AIKEF MSB2 simulation overview. Panels a and b show modeled plasma density ni and electric current density |J| in the XY (equatorial) plane (MASO). Panels c and d illustrate the same parameters but in the XZ (meridonial) plane. The black thin lines in panels a and c represent the bulk flow velocity, whereas the black thin lines in b and d indicate magnetic field lines. The red thick lines with a white outline correspond to the projected MSB2 trajectory, with crosses indicating the points where the simulation “slice” is intersected. The models for magnetopause and bow shock are illustrated by the black dashed (Winslow et al. 2013) and black solid (Slavin et al. 2009; Winslow et al. 2013) lines.
In the text
thumbnail Fig. 3

Model results for the proton energy spectrum along BepiColombo Mercury swingby 2 trajectory. Panel a shows all particles, and panel b only shows particles moving in a sunward (υx < 0) direction. The white horizontal dashed line represents the solar wind energy input parameter, and CA denotes the closest approach. The numbers 1−5 indicate magnetopsheric region or boundary crossings: (1) inbound magnetopause crossing, (2 to 3) grazing of the magnetotail, (4) the outbound magnetopause crossing, and (5) the outbound bow shock crossing. The white bar between 09:19 UTC and 10:02 indicates the area where a higher resolution (refinement) was used.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.