EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 670 (February 2023) A&A, 670 (2023) A174 Full HTML
Open Access
Issue
A&A
Volume 670, February 2023
Article Number A174
Number of page(s) 8
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202245162
Published online 22 February 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The plasma environment of Mercury still remains one of the least explored among the terrestrial planets in the Solar System. The global intrinsic magnetic field of Mercury, first discovered in 1974, sustains a small magnetosphere in a harsh and highly variable solar wind (Slavin et al. 2009). Positions of magnetospheric boundaries (bow shock, magnetopause) and main regions (magnetosheath, magnetosphere) are usually given while considering a stationary solar wind. This assumption of a stationary solar wind is valid for the Earth and the giant planets, whose magnetic fields are so strong that they result in a magnetic cavity that the solar wind takes hours (at Earth) or days (at Jupiter and Saturn) to cross (Badman & Cowley 2007). On the other hand, Mercury’s closed magnetic field lines do not extend more than ten planetary radii downstream of the planet, a distance that the solar wind covers in about one minute (Slavin et al. 2021). Variations of the solar wind on a timescale of the order of a single minute may thus be crucial in shaping the magnetic environment of Mercury. From this point of view, Mercury is an exception within the Solar System, but probably representative of many exoplanets with a small intrinsic magnetic field.

At Mercury, the position of the magnetospheric boundaries (see e.g., Winslow et al. 2013) are thus expected to change in response to variations of the solar wind parameters on timescales down to only ten seconds. Recent data from Parker Solar Probe and Helios, collected by Dakeyo et al. (2022), show that the fluctuations cover a of plasma densities, velocities, and temperatures, while the direction and intensity of the IMF have been observed to change significantly on timescales as short as ten minutes (James et al. 2017). Also, due to the smallness of the planetary intrinsic magnetic field, fluctuations in the solar wind dynamic pressure can be strong enough to push the day-side magnetopause down to the planet’s surface. For these reasons, the Hermean magnetosphere is said to be highly dynamic, an aspect which has only recently started attracting attention among the community (Sun et al. 2022).

BepiColombo (joined mission from ESA and JAXA) is the third mission dedicated to the exploration of Mercury. Launched in 2018, it will deploy two coordinated orbiting spacecraft in December 2025. BepiColombo’s scientific objectives cover a wide range of subjects, from planetary interior to a test of Einstein’s relativity theory (Benkhoff et al. 2010). Exploration of the Hermean plasma environment and its interaction with the solar wind is one of the key science questions of the mission (Milillo et al. 2020). On board the Mio spacecraft (the magnetospheric orbiter, under the auspices of JAXA), the Plasma Wave Investigation, PWI (Kasaba et al. 2020) carries the Spectroscopie des Ondes Radio et Bruit Electrostatique Thermique (SORBET) instrument (Moncuquet et al. 2006; Kasaba et al. 2020), a radio high-frequency spectrometer. SORBET is primarily designed to measure in situ the electron macroscopic density and temperature through the quasi-thermal noise (QTN) technique (Meyer-Vernet & Perche 1989; Issautier et al. 2001; Meyer-Vernet et al. 2017). The QTN method is based on the analysis of the spectrum of the electrostatic fluctuations (or electrostatic noise) induced on an electric antenna by the motion of the surrounding thermal particles. The point is that the noise can be formally calculated as a function of both the particle velocity distribution (PVD) and the antenna geometry. It can therefore be used to deduce the density, the temperature, and other moments of the PVD. In particular, if the antenna is longer than the local Debye length, the spectrum of the electrostatic noise shows a strong peak at the plasma frequency, from where the electron plasma density is immediately obtained, even for a non-calibrated spectrum (for a recent example, see Moncuquet et al. 2020). We note that, unfortunately, the PWI electric antennas will not be deployed during the cruise phase until orbital insertion in December 2025. As a consequence, PWI/SORBET is only very partially operational during the cruise phase.

On 1 October 2021 and 23 June 2022, BepiColombo accomplished its first two Mercury flybys Mangano et al. (2021; or ‘swing-bys’) denoted as MSB1 and MSB2, respectively, (out of six in total). The trajectory of BepiColombo is shown on Fig. 1 along with models of the bow shock and magnetopause location, from Slavin et al. (2009). During both MSB1 and MSB2, Mio is under the sun shield (MOSIF; Murakami et al. 2020) and has no easy access to the whole surrounding plasma. During these flybys, SORBET was switched on and connected to the stowed WPT antenna.

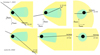thumbnail Fig. 1.

The first two Mercury flyby trajectories of BepiColombo seen from three different angles, in the MeSO frame (Mercury Sun Orbit), are shown along a model of the magnetopause (cyan) and bow shock (yellow), (model from Slavin et al. 2009). The spacecraft position is at 22:40 UTC on 1 October 2021 for MSB1 (top panels) and at 07:30 UTC on 23 June 2022 for MSB2 (bottom panels).

Despite the impossibility to accurately measure the quasi-thermal noise with stowed antennas, a meticulous analysis of the spectra recorded by SORBET has revealed drops and rises of the QTN minimal plateau of the collected spectral density, which may be interpreted as large variations of the local plasma density, as explained in Sect. 2. Comparisons with global magnetohydrodynamic simulations, described in Sect. 3, show that these drops and rises of the plasma density occur when the spacecraft crosses relevant physical boundaries such as the bow shock and the magnetopause (see Sect. 4). The signature of the boundaries on the electron density profiles could not be seen by MESSENGER with no embarked instrument dedicated to the measurements of thermal electrons (only supra-thermal electrons were partially measured inside the magnetosphere Ho et al. 2016). We have taken the opportunity provided by the BepiColombo flybys of Mercury to point to the crucial interest of having access to density measurements for the identification and the understanding of the plasma boundaries around Mercury. On BepiColombo, both SORBET and the Mercury Electron Analysers (MEA), from the MPPE instrumental suite (Saito et al. 2010), can provide such measurements. Fortunately, as shown in this paper, even with non-deployed antennas, SORBET has been found to be able to detect the variations of the electron density. We must emphasise that after orbit insertion around Mercury in December 2025, the antennas will be deployed, opening the door to high-quality density and temperature measurements via the QTN technique.

2. Meticulous analysis of SORBET spectra via a stowed electric antenna

The data discussed in this work were obtained serendipitously during the MSB1 and MSB2 by PWI, but only from the non-deployed electric dipole antenna known as Wire Probe anTenna (WPT, spherical probes of 60 mm diameter just at the outside of the spacecraft side panel but behind MOSIF) and connected to the SORBET radio receiver in the band [2.5 − 640] kHz, called TNR band, hereafter. The question arises as to why this measurement is serendipitous. During both MSB1 and MSB2, PWI/SORBET was switched ‘on’ to check the HF measurements of the high-frequency part of a search coil. However, because SORBET delivers two inseparable synchronised channels in the TNR band, we also got the signal from the stowed WPT antenna in the same telemetry packets; while the WPT preamp was switched on too (we note it was not the case during the near Earth flyby in March 2020 but during all other flybys). The signal from WPT only rarely exceeded the instrumental sensitivity during the cruise phase since otherwise it is grounded to the spacecraft side panel with about several kilo-ohm as the stowed scheme. However, it did so during MSB1 and, to a much lesser extent, during MSB2.

First, it is important to mention that the data process sketched here is only a byproduct of the QTN spectroscopy, far below the expected and nominal performances of SORBET after antennas deployment (Moncuquet et al. 2006; Kasaba et al. 2020). Second, let us then remark that the QTN is ubiquitous in the spectral domain but may be dominant only at frequencies near the electron plasma frequency.

With the stowed antenna immersed in a low-density plasma, the QTN is tiny and often falls below the receiver sensitivity. However, under favourable conditions, the QTN may exceed the SORBET sensitivity threshold. This will generally happen near and below the plasma frequency, fp. The QTN rapidly vanishes for increasing frequencies above fp.

With no clear QTN peak at fp (a sharp peak requires a long dipole, i.e., a deployed antenna) a substitute method rests on the detection of the thermal plateau of the QTN. The thermal plateau is a flat minimum of the intensity of the QTN located just below fp. This yields the rationale of the method used here, mainly intended to frame the local plasma frequency within upper and lower limits and, thus, the electron density surrounding the spacecraft body itself.

At this point, we go on to describe the data processing in more details. In each spectrum, we first searched for the frequency of the minimum noise over all the TNR band. Since the QTN is strongest at fp and quickly vanishes above fp, this frequency defines a rough but absolute upper limit for fp. We call this frequency fp, sup. The upper white curve on Fig. 2 is a profile of fp, sup. We then mimicked the plasma peak detection algorithm (which will be used onboard after the deployment of the antennas as described in detail in Kasaba et al. 2020) to detect the steepest positive slope in the TNR band in the range from 10 to 160 kHz (corresponding to an electron density in the approximate range from 1 to 300 electron/cc). This provides a candidate fp, labelled fp, proxy and corresponding to the red curve on Fig. 2, which we adopted as the upper limit for a possible QTN plateau. We then searched the frequency of the minimum noise below fp, proxy, which thus defines a lower limit for fp, named fp, inf, corresponding to the lower white curve on Fig. 2. We validated fp, inf in the case when an almost constant noise minimum is observed over at least four of the TNR frequencies below fp, proxy.

thumbnail Fig. 2.

Radio spectrograms (frequency versus time) between 10 and 160 kHz of SORBET spectrometer obtained during Mercury’s flyby on 1October 2021 (MSB1 on top), and 23 June 2022 (MSB2 on bottom), respectively (the cadence was one spectrum every 4 s), with a color bar chart on the right indicating the level (in dB). Superimposed upper and lower white curves (dots) show the plasma frequency limits, fp, sup and fp, inf, respectively, as determined by the QTN plateau detection. The red dots shows the fp, proxy as explained in the text, and, on top panel only, the smoothed black curve indicates the frequency of the spectral absolute minimum strictly below fp, sup.

If, for a given spectrum, the QTN plateau could not be obtained with the above procedure, it was eliminated from the process. Roughly 25% spectra had to be eliminated for MSB1 and 75% for MSB2. With SORBET connected to the WPT antenna, a spectrum of 128 log-spaced frequencies is obtained every 4 s. We note that the low-frequency part of the dynamic spectrum (≲15 kHz) does sometimes reveal an intense level of fluctuations. These fluctuations are not QTN, but are due to the so-called ‘shot noise’, which is known to scale as f−2, but it is indeed very much amplified or dampened by the spacecraft floating potential, making it almost impossible to exploit it properly. Obviously, if the shot noise level is dominant over the QTN at frequencies close to the plasma frequency, our procedure for finding fp, proxy must fail. Indeed, the determination of fp, inf rests on the identification of a constant level of fluctuations for f < fp, proxy, so that spectra with a significant contribution from the shot noise at frequencies just below fp, proxy are automatically culled out. 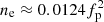From the plasma frequency, fp, or any estimates of it, we deduced the electron density, ne, through the standard relation n e = ϵ 0 m e (2π/e) 2 f p 2 $ n_{\rm e} = \epsilon_0 m_{\rm e} (2\pi/e)^2 f_{\rm p}^2 $ or n e ≈0.0124 f p 2 $ n_{\rm e} \approx 0.0124 f_{\rm p}^2 $ SI units.

Figure 3 shows the estimated electron density for the first two Mercury’s flybys. The top and bottom blue curves are indeed the upper and lower limits (if any), respectively, and the medium blue line shows the simple average of both. We note that from this method, we deduced the total electron density without any discrimination between core and suprathermal particles.

thumbnail Fig. 3.

Estimate of the electron density from QTN thermal plateau detection (see method in the text), during the first Mercury’s flyby from 22:00 to 0:30 UTC (MSB1 on top) and the second one from 9:00 to 10:30 UTC (MSB2 on bottom), respectively, using the stowed WPT antenna. In each panel, we plotted in blue the upper and lower (if any) limits of the density and the average of both. The different dashed lines correspond to some identified density drops, as explained in the text. The red dashed line indicates the closest approach (CA).

The range between the lower and the upper limits for the electron densities is admittedly rather large. However, the temporal profiles allow the identification of boundaries separating regions of significant differences of densities. After crossing of some of these boundaries, the density remains too low for the QTN plateau tracking method to succeed during a long period of time.

This occurs when the collected noise is systematically too low, that is, very close to the SORBET sensitivity threshold (which roughly corresponds to the crossing between the fp, inf curve and the illustrative black curve on top panel of Fig. 2). Those identified boundaries are marked by dashed black lines on the Fig. 3. Note that the method used in this paper does not allow us to deduce the electron temperature, since we cannot deduce any calibrated level of the thermal plateau.

We now briefly compare the results and their reliability for the two flybys: for MSB1, we validated a QTN plateau for about 75% of the recorded spectra. The electron density was found on average (provided a lower limit could be obtained) between about 13 and 70 electron/cc. These values are compatible with densities commonly measured at 0.4 AU, most recently by Parker Solar Probe (Moncuquet et al. 2020).

For MSB2, the ambient plasma (in the solar wind or in Mercury’s magnetosphere) was more tenuous than for MSB1 with a density roughly 40% lower. The magnetosphere was traversed by BepiColombo in a shorter time and the QTN plateau could be identified on only about 25% of the recorded spectra. Thus, MBS2 presents much more density variations features than MSB1 and with fewer high-drop variations. Therefore, the small number of boundaries determined in the same way as at MSB1 (dashed lines on the bottom panel of Fig. 3) are less reliable and merely illustrate the limitations of the method used here. In the following sections, we comment the discontinuities observed during MSB1 in the frame of 3D simulations of the magnetosphere.

3. Magnetohydrodynamic 3D simulations for the global picture

We used the PLANET-MAG-AMRVAC code (Pantellini et al. 2015) to run 3D magneto-hydrodynamic simulations of Mercury’s magnetosphere. The code is based on the generic MHD solver of MPI-AMRVAC1. Numerical settings and equations solved are described in Aizawa et al. (2021). The simulation domain is delimited by two spherical shells at distances 0.8 RM and 16 RM from the planet’s center (RM = 2440 km is the radius of Mercury). The equations are solved on a spherical grid (r, θ, ϕ), with a resolution of (96,48,48). At the inner boundary, a typical cell spans 70 km in the radial direction, 100 km in longitude, and 50 km in latitude. For r in the range from 0.8 to 1.0 RM, namely, in Mercury’s mantle, the plasma density is arbitrarily set to ten times the solar wind density. The planetary magnetic field at the inner boundary is from the multi-polar model of Anderson et al. (2012) up to the octopole term. Inside the mantle, plasma velocity is null. Three simulations are run for 5.5 min of real time, which is long enough to reach a steady-state. The solar wind and IMF conditions are summarised in Table 1.

Table 1.

Solar wind parameters for three different simulations.

Selected values are inspired by recent measurements by Dakeyo et al. (2022) at 0.38 AU, the actual distance of Mercury from the Sun at the time of MSB1 and MSB2. IMF orientation is BX, MeSO = +0.813BSW, BY, MeSO = +0.465BSW, and BZ, MeSO = +0.348BSW in the Mercury-Sun-Orbit (MeSO) reference frame; this is based on a comparison of global simulations with on-board measurements along the MSB1 trajectory before the closest approach (CA) by W. Exner, L. Griton and D. Heyner (priv. comm.). The IMF intensity BSW was set to either 30 or 20 nT, which are typical values for Mercury. Those values result in typical low Alfvenic Mach numbers (i.e., MA ≃ 3 − 5 as defined by Gershman et al. 2013) for simulations 1 and 2, as well as a slightly higher Alfvenic Mach number in simulation 3 (MA ≃ 7).

4. Boundaries of the Hermean magnetosphere from changes of electrons

As explained in Sect. 2, during MSB1 and MSB2, SORBET provided only estimates of the electron density. However, during MSB1 in particular, the obtained density profiles turned out to be sufficiently stable in time to allow the identification of boundaries separating unequally dense regions. During MSB1, a first sharp increase of plasma density is met around 22:26 UTC. This increase corresponds to the bow shock crossing in Simulation 1, for which the solar wind is dense (ne = 80 cm−3) and slow (vSW = 300 km s−1), as shown by the first red star in Fig. 4. Afterwards, a significant fall of plasma density takes place at 23:01:40 UTC. This fall, encountered in all three simulations, best coincides with the second simulation, with ne = 60 cm−3 and vSW = 400 km s−1. Then, the density increases again at 23:19:00 UTC. This increase happens earlier in simulation 1 and 2 and better fits the timing of simulation 3, which corresponds to a faster solar wind with a lower density (ne = 40 cm−3 and vSW = 500 km s−1). After the closest approach at 23:34:00, all three simulations present the same fall as the SORBET data for approximately three minutes. After that, only simulation 1 shows a significant rise, with the outbound crossing taking place ten minutes earlier than the time suggested by the data at 23:55 UTC.

thumbnail Fig. 4.

Results of the three simulations (silver, grey, and black points) along the trajectory of BepiColombo during MSB1, on 1–2 October 2021, against the density measurements by SORBET, as described in Sect. 2. Vertical red dashed line stands for the time of closest approach and the four vertical dashed lines highlight (from left to right) the inbound crossing of the bow shock, inbound crossing of the magnetopause, outbound crossing of magnetopause, and outbound bow shock crossing (as deduced from SORBET data), respectively. The three red stars show the time when each of the three simulations best fits the density variations observed by SORBET.

However, the orientation of the IMF in all three simulations was chosen following the inbound magnetic field measurements (from private communication by D. Heyner and W. Exner). After the closest approach, the orientation of the IMF may have changed significantly. We shall not comment MSB2 further as no clear correspondence could be established between the plasma boundaries observed during MSB2 (as shown on Fig. 3) and the boundaries in the simulations.

This data against simulation comparison demonstrates that the electron density will be a key element of the analysis of the Hermean boundaries when BepiColombo arrives at Mercury in 2025 and the antennas of Mio were deployed.

In fact, studying the boundaries only with magnetic field data – which are the only data continuously provided by the MESSENGER spacecraft – may be tricky on the night side of Mercury. On the night side, there is no strong current at the magnetopause. Magnetic field lines in the magnetosheath are nearly aligned to planetary open magnetic field lines and the magnetopause boundary is difficult to identify on the magnetic field data only. However, as observed by SORBET during MSB1 and in the corresponding MHD simulations (see Fig. 5), this magnetopause is very well defined when looking at the electron density. Indeed, right after the magnetosheath, the boundary with the magnetic cavity is essentially maintained by an equilibrium of the thermal pressure. However, there is also a boundary with a strong electric current in the night side of the Hermean magnetosphere. This strong current exists at the boundary between the last closed magnetic field lines (the magnetic flux tubes which are connected to the planet on both sides), and the open field lines in region 2 in Fig. 5. This boundary delimits an inner region (which is sometimes called a ‘plasmasphere’) bounded by the closed magnetic field lines.

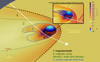thumbnail Fig. 5.

Visualisation of simulation 1 (paraview) with additional annotations. The yellow-to-purple background is the plane containing the trajectory of BepiColombo during MSB1 (white line) on 1–2 October 2021, coloured according to plasma electron density ne in cm−3. At the center, the sphere is coloured according to the radial magnetic field (negative in blue, positive in red), in normalised units. This is to show where the magnetic equator of Mercury is with respect to the plane containing the trajectory of the spacecraft. In the black frame, the magnetic field lines crossing the trajectory of BepiColombo are displayed in blue when they are connected on both sides to the planet, and in red when they are open planetary or solar wind magnetic field lines. The thick black dashed line stands for the bow shock, thin green dashed line stands for the magnetopause, and blue thick line stands for the boundary between closed and open field lines. Those boundaries delimit three regions: (1) the magnetosheath, (2) the magnetic cavity, and (3) the closed field lines region with a much higher electron density than in the magnetosheath (plasmasphere).

The plasmasphere inside Mercury’s magnetosphere was extensively discussed by Herčík & Trávníček (2016), from hybrid simulations and proton energy measurements from the FIPS instrument on board MESSENGER. Herčík & Trávníček (2016) concluded that the plasmasphere is always present around Mercury, its shape highly depends on the orientation of the IMF around Mercury’s magnetosphere, and that it contains quasi-trapped populations of protons from different sources (both from the planetary surface and the solar wind). In the context of our MHD simulations, it should be noted that the plasma density in this region may be higher than in reality, for it is dependent on the inner boundary condition and the value of the plasma density set to ten times the solar wind density in the planetary mantle. On the contrary, the density estimated from SORBET measurements might be underestimated around the time of closest approach, as higher density cannot be correctly measured while the antenna are not fully deployed and the accurate QTN method cannot be used.

To summarise, even with undeployed antennas, SORBET measurements allowed the identification of the main boundary crossings along MSB1 inbound trajectory: bow shock, magnetopause, and plasmasphere. After the closest approach, boundary crossings are less clear. The MSB2 measurements displayed on Fig. 3 present too many drops and increases to be easily identified as boundaries or clearly defined regions. A comparison with measurements from the Mercury Electron Analysers (MPPE/MEA onboard Mio, Sauvaud et al. 2010, Saito et al. 2010) could help their interpretation and is under process with the MEA team.

5. In anticipation of BepiColombo’s deployment at Mercury

Following four additional flybys of Mercury, its arrival on Mercury is scheduled on December 2025. At that time, the final Mercury orbit insertion will occur and Mio and MPO satellites will separate from each other. This crucial phase of operations will also imply the deployment of both antenna sensors, WPT and MEFISTO, respectively, connected to the SORBET receiver. Three months of commissioning will enable to deduce the base capacitance and to calibrate in space the voltage power spectrum (in V2/Hz). Then, the quasi-thermal noise method will be exploited continuously along Mio orbit and thus used in routine to explore the Hermean magnetosphere and exosphere, as well as the solar wind. From this technique, we will provide, on the pioneering BepiColombo mission, the mapping of the electron density and temperature, which is one of the key scientific objectives of the PWI instrument, as explained by Moncuquet et al. (2006) and Kasaba et al. (2020).

Meanwhile the numerical simulation effort will continue, along with an extensive analysis of the MESSENGER data, to better understand the physics that happen at the boundaries of such a dynamic plasma environment as Mercury. In particular, systematic detection of the plasmasphere, magnetic cavity, and magnetosheath should be improved through different kinds of algorithm (including machine-learning techniques). This would facilitate optimised studies of those regions as different kinds of plasma laboratories in which interesting plasma physics phenomena (such as particle-wave interactions, plasma instabilities) can occur in different conditions than they would in the context of more well known planetary magnetospheres.

6. Summary and conclusion

While awaiting BepiColombo’s orbit insertion around Mercury in December 2025, this short paper aims at presenting the measurements acquired by Mio PWI/SORBET during BepiColombo’s first (MSB1) and second (MSB2) swing-bys of Mercury, respectively, on 1–2 October 2021 and 23 June 2022:

  1. At MSB1, with the SORBET receiver connected to the stowed antenna WPT, we were able to use simplified QTN spectroscopy to frame the electron density between the upper and lower limits. We note that the latter ones would be reliable only when the density does not decrease below 10 cm−3 along the BepiColombo trajectory.

  2. We provide an estimation of the density (framed by reliable error bars). We note the signal we can exploit is tiny, at the limit of SORBET and WPT preamp sensitivity, and the method only accounts for large variations of the density. That is mainly interesting to determine sharp boundaries (drops and rises) in the plasma encountered along the BepiColombo trajectory.

  3. Electron density falls and increases obtained during MSB1 are compared to three MHD numerical simulations, with three different kinds of solar wind (vSW = 300 km s−1, vSW = 400 km s−1, and vSW = 500 km s−1 respectively). This need for three different simulations reveals how fast changes in the solar wind can affect Mercury’s magnetosphere within only one hour.

  4. This data compared against the simulations reveals that serendipitous measurements by SORBET were just good enough to detect the main boundaries of Mercury’s plasma environment along the inbound trajectory of MSB1: bow shock, magnetosheath, magnetopause, magnetic cavity, and plasmasphere inside the closed magnetic field lines.

  5. This provides us with the opportunity to recall the major role electron densities (and temperatures) will play in the detection and characterisation of Mercury’s magnetospheric boundaries once the antennae are deployed in December 2025.

Acknowledgments

The authors thank the BepiColombo teams at JAXA, ESA and CNES, especially J. Benkhoff, G. Murakami, K. Amsif and A. Jean-Antoine Piccolo. In particular, the authors thank the PWI team, the MPPE/MEA team including N. André and S. Aizawa and the MAG team, especially D. Heyner and W. Exner, for fruitful discussions.

References

  1. Aizawa, S., Griton, L. S., Fatemi, S., et al. 2021, Planet. Space Sci., 198, 105176 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anderson, B. J., Johnson, C. L., Korth, H., et al. 2012, J. Geophys. Res. Planets, 117 [Google Scholar]
  3. Badman, S. V., & Cowley, S. W. H. 2007, Ann. Geophys., 25, 941 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benkhoff, J., van Casteren, J., Hayakawa, H., et al. 2010, Planet. Space Sci., 58, 2 [NASA ADS] [CrossRef] [Google Scholar]
  5. Dakeyo, M., Démoulin, H., & Stevens, 2022, ArXiv e-prints [arXiv:2207.03898] [Google Scholar]
  6. Gershman, D. J., Slavin, J. A., Raines, J. M., et al. 2013, J. Geophys. Res. Space Phys., 118, 7181 [NASA ADS] [CrossRef] [Google Scholar]
  7. Herčík, D., Trávníček, P. M., & Štverák, t., & Hellinger, P., 2016, J. Geophys. Res. Space Phys., 121, 413 [CrossRef] [Google Scholar]
  8. Ho, G. C., Starr, R. D., Krimigis, S. M., et al. 2016, Geophys. Res. Lett., 43, 550 [NASA ADS] [CrossRef] [Google Scholar]
  9. Issautier, K., Moncuquet, M., Meyer-Vernet, N., Hoang, S., & Manning, R. 2001, Physics of Space: Growth Points and Problems, 309 [CrossRef] [Google Scholar]
  10. James, M. K., Imber, S. M., Bunce, E. J., et al. 2017, J. Geophys. Res. Space Phys., 122, 7907 [NASA ADS] [CrossRef] [Google Scholar]
  11. Kasaba, Y., Kojima, H., Moncuquet, M., et al. 2020, Space Sci. Rev., 216, 65 [NASA ADS] [CrossRef] [Google Scholar]
  12. Mangano, V., Dóa, M., Fränz, M., et al. 2021, Space Sci. Rev., 217, 23 [NASA ADS] [CrossRef] [Google Scholar]
  13. Meyer-Vernet, N., & Perche, C. 1989, J. Geophys. Res. Space Phys., 94, 2405 [NASA ADS] [CrossRef] [Google Scholar]
  14. Meyer-Vernet, N., Issautier, K., & Moncuquet, M. 2017, J. Geophys. Res. Space Phys., 122, 7925 [NASA ADS] [CrossRef] [Google Scholar]
  15. Milillo, A., Fujimoto, M., Murakami, G., et al. 2020, Space Sci. Rev., 216, 93 [NASA ADS] [CrossRef] [Google Scholar]
  16. Moncuquet, M., Matsumoto, H., Bougeret, J.-L., et al. 2006, AdvSpR, 38, 680 [NASA ADS] [Google Scholar]
  17. Moncuquet, M., Meyer-Vernet, N., Issautier, K., et al. 2020, ApJS, 246, 44 [Google Scholar]
  18. Murakami, G., Hayakawa, H., Ogawa, H., et al. 2020, Space Sci. Rev., 216, 113 [CrossRef] [Google Scholar]
  19. Pantellini, F., Griton, L., & Varela, J. 2015, Planet. Space Sci., 112, 1 [NASA ADS] [CrossRef] [Google Scholar]
  20. Saito, Y., Sauvaud, J. A., Hirahara, M., et al. 2010, Planet. Space Sci., 58, 182 [Google Scholar]
  21. Sauvaud, J. A., Fedorov, A., Aoustin, C., et al. 2010, AdSpR, 46, 1139 [NASA ADS] [Google Scholar]
  22. Slavin, J. A., Anderson, B. J., Zurbuchen, T. H., et al. 2009, Geophys. Res. Lett., 36 [Google Scholar]
  23. Slavin, J. A., Imber, S. M., & Raines, J. M. 2021, in Magnetospheres in the Solar System (American Geophysical Union (AGU)), 535 [CrossRef] [Google Scholar]
  24. Sun, W., Dewey, R. M., Aizawa, S., et al. 2022, Sci. China Earth Sci., 65, 25 [NASA ADS] [CrossRef] [Google Scholar]
  25. Winslow, R. M., Anderson, B. J., Johnson, C. L., et al. 2013, J. Geophys. Res. Space Phys., 118, 2213 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Solar wind parameters for three different simulations.

In the text

All Figures

thumbnail Fig. 1.

The first two Mercury flyby trajectories of BepiColombo seen from three different angles, in the MeSO frame (Mercury Sun Orbit), are shown along a model of the magnetopause (cyan) and bow shock (yellow), (model from Slavin et al. 2009). The spacecraft position is at 22:40 UTC on 1 October 2021 for MSB1 (top panels) and at 07:30 UTC on 23 June 2022 for MSB2 (bottom panels).
In the text
thumbnail Fig. 2.

Radio spectrograms (frequency versus time) between 10 and 160 kHz of SORBET spectrometer obtained during Mercury’s flyby on 1October 2021 (MSB1 on top), and 23 June 2022 (MSB2 on bottom), respectively (the cadence was one spectrum every 4 s), with a color bar chart on the right indicating the level (in dB). Superimposed upper and lower white curves (dots) show the plasma frequency limits, fp, sup and fp, inf, respectively, as determined by the QTN plateau detection. The red dots shows the fp, proxy as explained in the text, and, on top panel only, the smoothed black curve indicates the frequency of the spectral absolute minimum strictly below fp, sup.
In the text
thumbnail Fig. 3.

Estimate of the electron density from QTN thermal plateau detection (see method in the text), during the first Mercury’s flyby from 22:00 to 0:30 UTC (MSB1 on top) and the second one from 9:00 to 10:30 UTC (MSB2 on bottom), respectively, using the stowed WPT antenna. In each panel, we plotted in blue the upper and lower (if any) limits of the density and the average of both. The different dashed lines correspond to some identified density drops, as explained in the text. The red dashed line indicates the closest approach (CA).
In the text
thumbnail Fig. 4.

Results of the three simulations (silver, grey, and black points) along the trajectory of BepiColombo during MSB1, on 1–2 October 2021, against the density measurements by SORBET, as described in Sect. 2. Vertical red dashed line stands for the time of closest approach and the four vertical dashed lines highlight (from left to right) the inbound crossing of the bow shock, inbound crossing of the magnetopause, outbound crossing of magnetopause, and outbound bow shock crossing (as deduced from SORBET data), respectively. The three red stars show the time when each of the three simulations best fits the density variations observed by SORBET.
In the text
thumbnail Fig. 5.

Visualisation of simulation 1 (paraview) with additional annotations. The yellow-to-purple background is the plane containing the trajectory of BepiColombo during MSB1 (white line) on 1–2 October 2021, coloured according to plasma electron density ne in cm−3. At the center, the sphere is coloured according to the radial magnetic field (negative in blue, positive in red), in normalised units. This is to show where the magnetic equator of Mercury is with respect to the plane containing the trajectory of the spacecraft. In the black frame, the magnetic field lines crossing the trajectory of BepiColombo are displayed in blue when they are connected on both sides to the planet, and in red when they are open planetary or solar wind magnetic field lines. The thick black dashed line stands for the bow shock, thin green dashed line stands for the magnetopause, and blue thick line stands for the boundary between closed and open field lines. Those boundaries delimit three regions: (1) the magnetosheath, (2) the magnetic cavity, and (3) the closed field lines region with a much higher electron density than in the magnetosheath (plasmasphere).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.