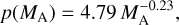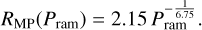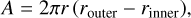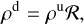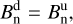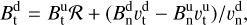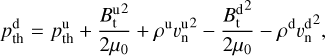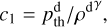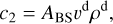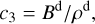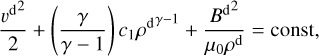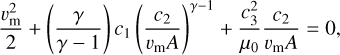| Issue |
A&A
Volume 668, December 2022
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245008 | |
| Published online | 13 December 2022 | |
Solar-wind-dependent streamline model for Mercury’s magnetosheath
A hydrodynamic magnetosheath model for Mercury
1
Space Research Institute (IWF), Austrian Academy of Sciences (OeAW),
Schmiedlstrasse 6,
8042
Graz, Austria
e-mail: daniel.schmid@oeaw.ac.at
2
IGEP, TU Braunschweig,
Mendelssohnstrasse 3,
38106
Braunschweig, Germany
3
University of Pisa,
Lungarno Antonio Pacinotti 43,
56126
Pisa, Italy
Received:
19
September
2022
Accepted:
27
October
2022
Context. Mercury’s magnetosphere and magnetosheath are unique in the Solar System plasmas as they are highly time dependent, since the planet has only a small-scale magnetosphere originating from the weak intrinsic planetary magnetic field. Yet, it is believed that the plasma therein reaches a quasi-stationary state, that is, the ground state of magnetospheric dynamics, when the solar wind smoothly passes by the magnetosphere without energy or momentum exchange in quiet conditions.
Aims. Here, we aim to construct a semi-analytical streamline model for Mercury’s magnetosheath to extend the modeling effort from the magnetospheric plasma to the magnetosheath plasma. The magnetosheath model should have the capability of determining the plasma density and the bulk velocity as a function of the radial distance from the planet, the zenith angle to the Sun, and the solar wind condition.
Methods. Our magnetosheath model was constructed with (1) the steady-state continuity equation around a magnetospheric obstacle where the bow shock and magnetopause location may depend on the solar wind condition, (2) the jump conditions at the bow shock, and (3) the adiabatic behavior in the magneotsheath.
Results. Our magnetosheath model reasonably explains and reproduces the in-situ measurements around Mercury by the MErcury Surface, Space Environment, GEochemistry and Ranging (MESSENGER) spacecraft as well as numerical simulations.
Conclusions. The presented streamline model of Mercury’s magnetosheath serves as a useful tool for the on-going two spacecraft BepiColombo mission when analyzing the plasma data by tracing the plasma parcel along the streamline both forward from one spacecraft to another and backward, locating the shock crossing coordinate, or when estimating the elapsed time of plasma parcel after the shock crossing.
Key words: planets and satellites: terrestrial planets / magnetohydrodynamics (MHD) / planet-star interactions
© D. Schmid et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Planetary magnetospheres constitute an obstacle to the solar wind, because the interplanetary magnetic field (IMF) embedded in the solar wind cannot simply penetrate the magnetosphere. Therefore, a bow shock emerges upstream of the planet, where the super-magnetosonic solar wind plasma is slowed and heated. The region between the bow shock and the magnetopause (outer boundary of the planetary magnetosphere) with the subsonic, heated solar wind plasma is the so-called magnetosheath. Planetary magnetosheaths play an important role as they convey energy between the solar wind and the magnetosphere.
Mercury, the innermost planet in the Solar System, is unique and challenging in space plasma physics, as the planet sustains a small magnetosphere (with a subsolar distance of only about 0.5 RM (Mercury radii, 1 RM ~ 2440 km) from the surface to the magnetopause), corresponding to a time scale of the magnetospheric response to a change in the solar wind from seconds to minutes (e.g., Fujimoto et al. 2007; Slavin et al. 2009; Anderson et al. 2013; Korth et al. 2015). This makes a marked contrast to the Earth’s magnetospheric case with a timescale extending from hours to days (e.g., Dungey 1961; Sergeev et al. 1996; Baumjohann et al. 2006). The magnetosphere can potentially exhibit a series of instabilities, oscillations, and reconfigurations (see e.g., Romanelli et al. 2020; Boardsen et al. 2009; Le et al. 2013; Sundberg et al. 2013, 2015; Schmid et al. 2021b). Moreover, here, understanding the ground-level state or quasistationary picture of the magnetosphere plays an important role.
The magnetosphere is also unique in the absence of a conducting dense ionosphere, yet the existence of spatially extended dilute sodium exosphere (e.g., Ip 1986; Exner et al. 2020). Moreover, the magnetosphere is exposed to a stronger and more radially directed magnetic field (due to the Parker spiral nature and the planet’s proximity to the Sun) and a denser plasma than that around the Earth’s orbit (e.g., James et al. 2017).
Efforts are being made to reveal Mercury’s magnetosphere and its dynamics in various ways (see, e.g., Sun et al. 2021, for a review). In the observational sense, MESSENGER (Solomon et al. 2007) performed in situ plasma and magnetic field measurements over 4yr (2011–2015), and BepiColombo (Benkhoff et al. 2010, 2021) is providing the flyby data from 2021 to 2025 and will provide the in-orbit data upon its arrival in 2025. In the computational sense, multi-fluid, magnetohydrodynamic, and hybrid simulations play a leading role in the simulations of Mercury’s magnetic field interacting with the solar wind and help to interpret the observational results (e.g., Baumjohann et al. 2010).
Over the years, (multi-fluid) magnetohydrodynamic (Jia et al. 2015; Kabin et al. 2000; Benna et al. 2010; Dong et al. 2019), hybrid (Kallio & Janhunen 2004; Trávnícek et al. 2010; Wang et al. 2010; Richer et al. 2012; Hercík et al. 2013; Fatemi et al. 2017; Exner et al. 2018, 2020) simulations, and most recently a global, fully kinetic simulation (Lavorenti et al. 2022) of the solar wind interaction with Mercury’s magnetosphere have been developed to reconstruct the Hermean space environment (see also Aizawa et al. 2021). Under the assumption of field-aligned conditions (i.e., plasma flow along the magnetic field), the computational complexity of the magnetohydrodynamic (MHD) theory is significantly reduced (see e.g., Cowley 1960; 1960). For example, Spreiter & Rizzi (1974) developed a series of magnetosheath plasma flow models, the so-called Spreiter-Stahara models (see Spreiter & Stahara 1994, for a review), to describe the solar wind flow around the Earth’s magnetopause. The practice of field-aligned MHD has also been applied to exploit the solar wind flow around Venus (1996). It should be mentioned, however, that all of these models are purely numerical. Although single fluid MHD simulations can be easily accomplished on a modest desktop PC, Schmid et al. (2021a) proposed an analytical magnetosheath flow model for Mercury (hereafter referred to as the S21 model) that has the capacity to give a first order approximation of the plasma flow without the need for exact solar wind conditions. The S21 model is based on the terrestrial magnetic field model developed by Kobel & Flückiger (1994), which has been rescaled to the space environment around Mercury following the procedure proposed by Soucek & Escoubet (2012). The basic idea is that under a radial IMF configuration the magnetic field lines represent the plasma streamlines around the planet. In this sense, the plasma flow velocity direction in the magnetosheath can be expressed analytically by the magnetic field direction of the rescaled Kobel & Flückiger (1994) magnetic field model. The essential advantage of the S21 model is that it is easy to implement and only depends on the upstream solar wind parameters. However, the S21 model uses several pre-fixed parameters: First, the bow shock and the magnetopause positions are chosen to be statistically representative using the MESSENGER data (Winslow et al. 2013), but depending on the upstream plasma parameters, these positions may vary in the individual realizations. Second, the original model assumes a constant plasma density and thus a constant velocity along the streamline, that means the downstream solar wind velocity immediately behind the shock is assumed to be constant along the entire streamline. Naturally, this assumption underestimates the velocity within the magnetosheath (especially far downstream in the magnetosheath).
In this work, we modified and extended the S21 model, where we adapt the bow shock and magnetopause location/shape to the upstream solar wind and IMF conditions and estimated the change in plasma density and velocity along the streamlines based on simple hydrodynamic considerations. In view of the upcoming two-spacecraft BepiColombo mission on Mercury, this model can serve as a crucial and useful analysis tool to trace the magnetosheath plasma along the streamlines, offering the opportunity to study the growth or damping rate of a particular wave mode or evolution of turbulence energy spectra along the streamline.
2 Model description
In the following, we use the aberrated Mercury-Solar-Magnetospheric (MSM) coordinate system, where the X-axis is anti-parallel with the solar wind velocity, aberrated by the orbital motion of Mercury around the sun (38.9–59.0 km s−1); the Y - axis points in the opposite direction to Mercury’s orbital motion; and the Z-axis completes the right-hand coordinate system and is shifted northward by 479 km from the Mercury-Sun line to account for Mercury’s apparent dipole offset (Anderson et al. 2012).
In this coordinate system, the bow shock and magnetopause are considered to be rotationally symmetric around the XMSM- axis and thus easiest expressed in polar coordinates, with 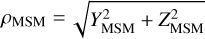 being the distance to the XMSM-axis and θ = tan−1(ρ/x) the angle between XMSM-axis and any point {x,ρ}MSM in the Xρ-MSM plane. That means the modeled magnetosheath is constructed as axi-symmetric around the direction from the apparent offset dipole position to the Sun.
being the distance to the XMSM-axis and θ = tan−1(ρ/x) the angle between XMSM-axis and any point {x,ρ}MSM in the Xρ-MSM plane. That means the modeled magnetosheath is constructed as axi-symmetric around the direction from the apparent offset dipole position to the Sun.
Our magnetosheath model is based on the terrestrial magnetic field model developed from Kobel & Flückiger (1994) (hereafter KF94 model). In the KF94 model, the bow shock (BS) and magnetopause (MP) are modeled by parabolic surfaces with a common focus by
where bBS = 1/(4RBS − 2RMP) and bMP = 1/(2RMP) are defined by the subsolar stand-off distances of the bow shock and magnetopause, R{BS,MP}, respectively. The basic idea of KF94 is to uniquely determine the scalar potential between the magnetopause and bow shock (Eq. (1)), which in turn determines the spatial magnetic field configuration between these two boundaries. In the following all quantities related to the KF94 model are denoted by a tilde~symbol. Assuming a steady state, the continuity equation is reduced to a divergence-free condition of mass flux. By imposing the existence of a scalar potential and rewriting the mass flux by the gradient of this scalar potential, the continuity equation is reduced to the Laplace equation for this scalar potential (see Génot et al. 2011). In the special case where the magnetic field is radially oriented (away from the sun), the magnetic field lines determined by the KF94-model represent the plasma streamlines around the planet, and the KF94 solution is significantly simplified to (Génot et al. 2011; Soucek & Escoubet 2012)
where 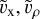 is the flow velocity at any given point r = {x,ρ}MSM within the magnetosheath, and
is the flow velocity at any given point r = {x,ρ}MSM within the magnetosheath, and 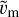 corresponds to the so far unknown flow velocity magnitude, which will be determined later and in the meantime is set to
corresponds to the so far unknown flow velocity magnitude, which will be determined later and in the meantime is set to 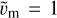 . The constant C = RMP(2RBS − RMP)/(2RBS − 2RMP) is defined by the bow shock and magnetopause stand-off distances, and d = |r − r0| is the difference between the given point r and the parabolic surface focus at {RMP/2, 0}.
. The constant C = RMP(2RBS − RMP)/(2RBS − 2RMP) is defined by the bow shock and magnetopause stand-off distances, and d = |r − r0| is the difference between the given point r and the parabolic surface focus at {RMP/2, 0}.
Equations (2) and (3) (with 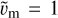 ) yield the direction of the plasma flow at r anywhere within the magnetosheath of the KF94-model, which is confined by Eq. (1). Based on the method introduced by Soucek & Escoubet (2012), Schmid et al. (2021a) rescaled the plasma flow direction to the best-fit parameters of the Hermean bow shock and magnetopause determined by Winslow et al. (2013). Thereto, the relative distance,
) yield the direction of the plasma flow at r anywhere within the magnetosheath of the KF94-model, which is confined by Eq. (1). Based on the method introduced by Soucek & Escoubet (2012), Schmid et al. (2021a) rescaled the plasma flow direction to the best-fit parameters of the Hermean bow shock and magnetopause determined by Winslow et al. (2013). Thereto, the relative distance,  , between the bow shock and magnetopause in the KF94 model,
, between the bow shock and magnetopause in the KF94 model,
is calculated to transform the flow velocity 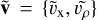 into Mercury’s space environment accordingly. The bow shock is modeled by a conic section of the following form (Slavin et al. 2009):
into Mercury’s space environment accordingly. The bow shock is modeled by a conic section of the following form (Slavin et al. 2009):
with x0 = 0.5 RM being the best-fit value of the distance of the focus of the conic section from the dipole center along XMSM, p = 2.75 RM the best-fit value of the focal parameter, and e = 1.04 the best-fit value of the eccentricity. With these best-fit parameters, the extrapolated subsolar bow shock stand-off distance is RBS = 1.9 RM; the magnetopause is given by (Korth et al. 2015)
with α = 0.5 being the best-fit flaring parameter and RMP = 1.42 RM the subsolar magnetopause stand-off distance. We note that in the S21 model the position and location of the bow shock and magnetopause are fixed according to these best-fit parameters. After the transformation of the velocity vector from the KF94 model into MSM coordinates, the streamline can be back-traced from point r to the bow shock by iteratively calculating the position of an adjacent point r′ = r + v∆t with an arbitrarily small time increment ∆t.
The S21 model assumes a constant velocity along the back-traced streamline. Thus, the velocity magnitude immediately downstream of the shock directly corresponds to the velocity magnitude at a given point r. Using the Rankine–Hugoniot (RH) equations, which relate the upstream (u) with the downstream (d) plasma conditions before and after the bow shock, the downstream velocity vector component parallel 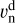 and perpendicular
and perpendicular 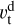 to the shock normal
to the shock normal 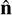 and tangent
and tangent 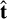 is given by
is given by
where R = ρd/ρu is the compression ratio between the upstream and downstream mass density, 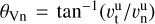 is the angle between the upstream velocity vector and the shock normal,
is the angle between the upstream velocity vector and the shock normal, 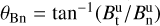 is the angle between upstream magnetic field vector and shock normal, and
is the angle between upstream magnetic field vector and shock normal, and 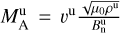 is the upstream Alfvén Mach number. All parameters pertain to the upstream side, except for the compression ratio R. However, R can also be expressed by exclusively upstream parameters with the following (see, e.g., Anderson 1963):
is the upstream Alfvén Mach number. All parameters pertain to the upstream side, except for the compression ratio R. However, R can also be expressed by exclusively upstream parameters with the following (see, e.g., Anderson 1963):
with γ being the polytropic index that is assumed to be γ = 5/3. By solving Eq. (9) for R the downstream velocity magnitude, 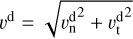 can be obtained. Thus, the magnetosheath velocity magnitude, vm = vd, at point r is entirely determined by only the upstream solar wind parameters.
can be obtained. Thus, the magnetosheath velocity magnitude, vm = vd, at point r is entirely determined by only the upstream solar wind parameters.
As mentioned above, however, the obtained velocity and density (ρd = ρuR) are assumed to be constant along the entire streamline. In the following, we extend and further develop the orginal S21 model to an enhanced model that encompasses (1) the varying bow shock and magnetopause location/shape and (2) the change of the plasma density and velocity along the streamlines, determined only by the upstream solar wind parameters.
In the S21 model, the bow shock and magnetopause location and shape are pre-fixed to be statistically representative by incorporating the fitting parameters against the MESSENGER observations (Winslow et al. 2013, see above). These boundary positions, of course, vary with respect to the solar wind conditions such as the ram pressure and the IMF magnitude. We therefore improved the model by setting the bow shock and magnetopause locations depending on the solar wind conditions. By doing so, the magnetosheath plasma and magnetic field can be compared more flexibly for each observational realization.
Winslow et al. (2013) showed that the solar wind Mach number and ram pressure are the most dominant factors influencing the Hermean bow shock and magnetopause location, respectively. They found that the focal parameter, P in Eq. (5), of the bow shock is systematically affected by the upstream Alfvén Mach number, MA in a power-law fashion, as
and that the magnetopause stand-off distance is effectively determined by the ram pressure Pram = ρu · vu2, also in a power-law fashion as
They found that there was no statistically significant variation of the flaring parameters of the bow shock (reflected in the eccentricity parameter e in Eq. (5)) and/or magnetopause (reflected in the flaring parameter α in Eq. (6)) with the upstream solar wind conditions.
Using the upstream parameters (IMF magnetic field vector, B, solar wind proton number density, np, and velocity, VSW) from, for example, the solar wind propagation model of Tao et al. (2005), it is thus possible to adjust the bow shock and magnetopause in Eqs. (5) and (6) accordingly. Figure 1 shows a comparison of the modeled bow shock and magnetopause for different solar wind parameters. The red lines indicate the bow shock and magnetopause under a high Alfvénic Mach number (MA = 20) and solar wind ram pressure (Pram = 30 nPa) observed around August 7, 2013, 102000 UT, and the blue lines under a low Alfvénic Mach number (MA = 2) and solar wind ram pressure (Pram = 5 nPa) around March 8, 2012, 201000 UT. The solid black line shows the bow shock and magnetopause used in the S21 model, which are based on the best-fit parameters from Winslow et al. (2013).
With the adjusted bow shock and magnetopause we now evaluate the change of the flow speed vm along the streamline by applying the following steps:
First, we apply the method proposed in the S21-model (see Sect. 4.1 in Schmid et al. 2021a) and back-trace the streamline from the given point r within the magnetosheath by iteratively solving Eqs. (2)–(3) and Eq. (4), until the bow shock is reached  . Second, the back-tracing procedure is repeated for two neighboring points (here we chose r ± 0.001 RM, which is numerically sufficient) to calculate the neighboring streamlines directly above (denoted by router) and below (denoted by rinner) the back-traced streamline in order to obtain a flux tube around the streamline of interest (that in step 1). In the third step, we calculate the change in the cross-section of the flux tube along the streamline of interest. For a locally cylindrical or conic flux tube (i.e., the cross-section is bounded by a circle), the cross-sectional area A can be determined along the streamline as
. Second, the back-tracing procedure is repeated for two neighboring points (here we chose r ± 0.001 RM, which is numerically sufficient) to calculate the neighboring streamlines directly above (denoted by router) and below (denoted by rinner) the back-traced streamline in order to obtain a flux tube around the streamline of interest (that in step 1). In the third step, we calculate the change in the cross-section of the flux tube along the streamline of interest. For a locally cylindrical or conic flux tube (i.e., the cross-section is bounded by a circle), the cross-sectional area A can be determined along the streamline as
where router and rinner are the corresponding points of the outer and inner streamlines’ normal to point r of the streamline of interest. In the fourth step, we follow the procedure of Schmid et al. (2021a) and determine the bow shock normal, 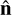 , and tangent,
, and tangent, 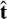 , where the flux tube intersects the bow shock (see their Eq. (12)). In the last step, we use the upstream solar wind parameters from, the Tao et al. (2005) model and apply the Rankine-Hugoniot conditions to determine the downstream velocity vector from Eqs. (7) and (8) by solving Eq. (9) for the compression ratio R, and then calculate the downstream plasma mass density, ρd, magnetic field magnitude,
, where the flux tube intersects the bow shock (see their Eq. (12)). In the last step, we use the upstream solar wind parameters from, the Tao et al. (2005) model and apply the Rankine-Hugoniot conditions to determine the downstream velocity vector from Eqs. (7) and (8) by solving Eq. (9) for the compression ratio R, and then calculate the downstream plasma mass density, ρd, magnetic field magnitude, 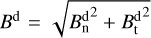 , and thermal pressure,
, and thermal pressure, 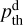 , with
, with
where Eq. (13) is the definition of the density jump, Eq. (14) the normal component of the divergence-free magnetic field condition, Eq. (15) the induction equation for the frozen-in magnetic field, and Eq. (16) the pressure conservation across the shock.
With Eq. (12) and Eqs. (13)–(16), the flux-tube area ABS and all plasma parameters immediately behind the bow shock can be individually determined. On the assumption of an adiabatic expansion (compression) of the flux tube from the bow shock along the streamline (constant entropy within the fluxtube),
the conservation of mass within the flux tube,
frozen-in flux within the flux tube,
and constant total energy described by Bernoulli’s equation (see, e.g., Kuznetsova & Pudovkin 1978),
the plasma velocity at any point r along the streamline, ~m, can be evaluated by rearranging Eqs. (17)–(20) into a conservation law,
using the corresponding flux-tube cross-section area A at point r. Eq. (21) has two real solutions in vm that are both physically relevant; while the smaller value of vm (low-speed solution) is valid for all points along the streamline that are located between the bow shock and the point of maximal fluxtube compression (i.e. where A is minimal), the larger value of vm (high-speed solution) is valid for all points behind the maximal fluxtube compression and the given point r or when the fluxtube is expanding (e.g. far away from the magnetopause and/or subsolar region). Subsequently, using Eq. (18) with vm and the flux-tube crosssection area, A, we can also determine the plasma density at a given point, r.
 |
Fig. 1 Comparison of modeled bow shock (dashed) and magnetopause (dot-dashed) for different solar wind parameters. The red lines indicate the bow shock and magnetopause under high Alfvénic Mach number (MA = 20) and solar wind ram pressure (Pram = 30 nPa) around August 7, 2013, 102000 UT, and the blue lines indicate it under low Alfvénic Mach number (MA = 2) and solar wind ram pressure (Pram = 5 nPa) around March 8, 2012, 201 000 UT. The solid black line shows the bow shock and magnetopause used in the S21 model based on the best-fit parameter from Winslow et al. (2013). |
3 Results
The functionality of the developed magnetosheath model is tested against the MESSENGER data and numerical simulation results.
3.1 Model in average solar wind conditions
After modifying the solar wind velocity vector of the Tao et al. (2005) model by the orbital motion of Mercury obtained from the Navigation and Ancillary Information Facility (NAIF; Acton 1996) database (see Eq. (16) in Schmid et al. 2021a), the average input solar wind plasma parameters during the entire MESSENGER operation service between 2011 and 2015 are as follows: plasma density nu ≈ 40 cm−3, temperature Tu ≈ 18 eV ≡ 208 880 K, plasma velocity vu ≈ -400 km s−1, and magnetic field magnitude Bu ≈ 20 nT. These values yield an Alfvén Mach number of MA ≈ 5.8, ram pressure of Pram ≈ 10.7 nPa, and plasma beta β = 2 µ0nukBTu/Bu2 ≈ 0.72, where µ0 is the permeability of free space and fes the Boltzmann constant.
Figure 2 shows the ratio between the flux-tube cross-section area at the bow shock, ABS, and the flux-tube cross-section along the streamlines. The black lines illustrate streamline examples. Dark blue areas indicate a compression of the flux tube (A/ABS < 1), and light blue to red areas denote an expansion (A/ABS > 1)∙ The results show that close to the subsolar point, the flux tubes significantly expand before being strongly compressed at the magnetopause close to the terminator due to the draping of the streamlines around the magnetopause, whereas streamlines away from the magnetopause gradually expand downstream from the bow shock because of the missing barrier provided by the magnetopause.
Figure 3 depicts the flow velocity on the streamlines in the magnetosheath. Close to the sub-solar region the magnetosheath plasma flow decelerates from ~150 km s−1 to ~70 km s−1 toward the magnetopause, although the flux tube is expanding. This is expected due to the strong compression of the flux tube further downstream close to the terminator, where the downstreaming plasma is throttled. After the point of maximal compression, the plasma flow gradually accelerates along the streamline until the initial solar wind velocity is reached.
Figure 4 shows the magnetosheath plasma density distribution. As expected, the plasma density behind the bow shock decreases with increasing solar zenith angle 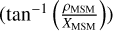 due to the decreasing compression ratio. Directly behind the bow shock the plasma density remains below ~ 160 cm−3, corresponding to the upper limit of the compression ratio (R = 4, determined by the limit of high Alfvén Mach number (MA —> ∞) under a polytropic index of γ = 5/3). However, for flux tubes that are compressed close to the magnetopause, the plasma density can increase beyond ~ 160 cm−3, again as a result of the backlog of the incoming plasma from the bow shock.
due to the decreasing compression ratio. Directly behind the bow shock the plasma density remains below ~ 160 cm−3, corresponding to the upper limit of the compression ratio (R = 4, determined by the limit of high Alfvén Mach number (MA —> ∞) under a polytropic index of γ = 5/3). However, for flux tubes that are compressed close to the magnetopause, the plasma density can increase beyond ~ 160 cm−3, again as a result of the backlog of the incoming plasma from the bow shock.
It should be mentioned, however, that Eq. (21) yields solutions only, when the polynomial function of vm has a root. A descriptive illustration of what happens when Eq. (21) does not yield a solution, is given in Fig. 5. Panel a illustrates three examples of streamlines with the corresponding shock frame of references (normal and tangent vectors 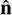 and
and 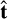 , respectively). Panel b shows the flux-tube cross-section area change along the three streamlines. Panels c and d show the 1-D curves of the density and velocity profiles along the three streamlines from the bow shock. The red streamline is located far away from the magnetopause where the density/velocity monotonically decreases/increases because of the solely expanding flux tube (A/ABS > 1)∙ Here, the polynomial function becomes negative everywhere along the streamline and thus possesses two solutions. The physically meaningful solutions in this case are the larger velocity solutions. The green streamline, located slightly closer to the magnetopause, shows a local maximum (minimum) in the ID density (velocity) profile. This behavior is expected, since the flux tube is slightly compressed when deflected around the magnetopause (A/ABS < 1)∙ Again, Eq. (21) yields two solutions, with the smaller velocity solution before the compression and the larger after the point of strongest compression. The blue streamline is located in close proximity to the magnetopause. In this extreme case, the flux tube rapidly expands downstream of the bow shock ahead of the magnetopause (see also Fig. 2). As the streamline is deflected around the magnetopause it is strongly compressed, before again expanding downstream of the terminator. This behavior is also reflected in the density and velocity profiles. The density increases from the bow shock to the point of maximum fluxtube expansion and then decreases while the fluxtube is compressed. Around the maximal flux-tube compression (A/ABS ≤ 0.75, gray shaded area in Fig. 5) the cross-section becomes so small that the polynomial function of vm in Eq. (21) stays positive and thus does not yield a solution. Behind this region, however, Eq. (21) yields a solution and the velocity (density) increases (decreases) with the gradual flux-tube expansion again.
, respectively). Panel b shows the flux-tube cross-section area change along the three streamlines. Panels c and d show the 1-D curves of the density and velocity profiles along the three streamlines from the bow shock. The red streamline is located far away from the magnetopause where the density/velocity monotonically decreases/increases because of the solely expanding flux tube (A/ABS > 1)∙ Here, the polynomial function becomes negative everywhere along the streamline and thus possesses two solutions. The physically meaningful solutions in this case are the larger velocity solutions. The green streamline, located slightly closer to the magnetopause, shows a local maximum (minimum) in the ID density (velocity) profile. This behavior is expected, since the flux tube is slightly compressed when deflected around the magnetopause (A/ABS < 1)∙ Again, Eq. (21) yields two solutions, with the smaller velocity solution before the compression and the larger after the point of strongest compression. The blue streamline is located in close proximity to the magnetopause. In this extreme case, the flux tube rapidly expands downstream of the bow shock ahead of the magnetopause (see also Fig. 2). As the streamline is deflected around the magnetopause it is strongly compressed, before again expanding downstream of the terminator. This behavior is also reflected in the density and velocity profiles. The density increases from the bow shock to the point of maximum fluxtube expansion and then decreases while the fluxtube is compressed. Around the maximal flux-tube compression (A/ABS ≤ 0.75, gray shaded area in Fig. 5) the cross-section becomes so small that the polynomial function of vm in Eq. (21) stays positive and thus does not yield a solution. Behind this region, however, Eq. (21) yields a solution and the velocity (density) increases (decreases) with the gradual flux-tube expansion again.
 |
Fig. 2 Ratio between flux-tube cross-section area at the bow shock, ABS, and the flux-tube cross-section area anywhere along the streamline, A, for the case of an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. The black lines illustrate streamline examples. |
 |
Fig. 3 Plasma flow velocity distribution within the Hermean magnetosheath, for the case of an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. Again, the black lines illustrate streamline examples. |
 |
Fig. 4 Plasma density distribution within magnetosheath for the case of an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. |
 |
Fig. 5 Flux-tube cross-section area change, density and velocity profile for three examples of streamlines. Panel a shows the course of the streamlines (red, green, and blue) with the corresponding shock frame of references (normal and tangent vectors ft and î, respectively) used for the Rankine–Hugoniot relations. Panel b shows the flux-tube cross-section area change along the streamlines. Panels c and d show the 1-D curves of the density and velocity profiles along the three streamlines (red, green, and blue) from the bow shock to XMSM = −4RM, respectively. Again, the average solar wind parameters during the entire MESSENGER service between 2011 and 2015 are used with an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. The gray shaded area indicates the region where the flux tube becomes extremely compressed around the magnetopause (A/ABS ≤ 0.75), and Eq. (21) does not yield a solution. |
3.2 Comparison of the model with previous numerical model results
To evaluate the results of the developed magnetosheath model, we compare the results of our model with the results of a global MHD simulation (Yagi) that was recently presented in Aizawa et al. (2021), where they cross-compared various 3D simulation codes with MESSENGER observations during orbit 1415 (November 8, 2012). Thereto, we apply the same solar wind parameters that were used as input parameters for their model: nu = 40 cm−3, temperature of Tu = 12 eV, plasma velocity of vu = −459 km s−1, and a normal and tangential magnetic field component of 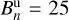 nT and
nT and 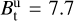 nT. These values yield an Alfvén Mach number of MA ≈ 5.1, ram pressure of pdyn ≈ 14.1 nPa, and plasma beta of β ≈ 0.27.
nT. These values yield an Alfvén Mach number of MA ≈ 5.1, ram pressure of pdyn ≈ 14.1 nPa, and plasma beta of β ≈ 0.27.
Figure 6a shows the magnetic field observations of MESSENGER (Anderson et al. 2007) during orbit 1415. The spacecraft entered the magnetosphere on the nightside and returned to the solar wind on the dayside, thus crossing the bow shock (BS) and magnetopause (MP) twice. The vertical red lines indicate the crossing times for both inbound (in) and outbound (out) crossings visually determined from the MESSENGER data.
The plasma density and velocity distribution derived from our model are displayed in Figs. 6b and c, respectively. In addition, MESSENGER’s trajectory is plotted as a black line. In the first step, we compare the modeled bow shock and magnetopause position to the in situ measurements of MESSENGER during the orbit. The vertical gray lines in panel a mark the boundary crossings estimated by our model. The modeled bow shock and magnetopause, derived by Eqs. (5) and (6) and modified according to Eqs. (10) and (11) are in good agreement with the in situ magnetic field observations of MESSENGER, indicating that the position of the magnetopause and bow shock are accurately determined by our model.
In the second step, we compare the plasma density and velocity predicted by our model and the Yagi model. Figures 6d, e and f, g shows the modeled density and velocity profile along the spacecraft trajectory within the nightside and dayside magnetosheath, respectively. For the nightside encounter (panels d and e), the bow shock and magnetopause crossing locations, BSin and MPin, are very similar, and the determined density and velocity values at the bow shock agree well. However, in our model the density (velocity) decreases toward the magnetopause and is slightly smaller (larger) than that modeled by the Yagi model. We note that in our model the magnetopause is considered as an impermeable boundary, while in the Yagi model the complete magnetospheric environment is modeled with a low permeable magnetopause, which might explain the different values.
The bow shock and magnetopause crossing on the dayside magnetosheath (panels f and g), on the other hand, takes place about 5 min later than predicted by the Yagi model, but is in good agreement with the visually determined boundaries from the magnetic field measurements. Again, the density and velocity profiles of both models show a similar trend: After the magnetopause crossing (MPout), the density decreases and the velocity increases toward the bow shock (BSout)∙ This can also be observed in the Yagi model, but on much smaller timescales. We note that the dayside magnetosheath in the Yagi model is generally thinner. That means the gradient of the density and velocity profile of the Yagi model is expected to be larger. Thus, for the dayside encounter the model results also seem to be in good agreement.
 |
Fig. 6 Comparison of the model results with the observations of MESSENGER and the results of a global MHD simulation. Panel a shows the magnetic field observations of MESSENGER on November 8, 2012 during orbit 1415. The vertical red lines indicate the bow shock (BS) and magnetopause (MP) crossing determined by visual inspection. The gray dashed lines indicate the boundary crossings determined by our model. Panels b and c show the modeled plasma density and velocity distribution within the magnetosheath for the same solar wind parameters used in Aizawa et al. (2021). The black line indicate the trajectory of MESSENGER for the time interval in panel a. The modeled plasma density/velocity along MESSENGER’s trajectory within the nightside magnetosheath and dayside magnetosheath are shown in panels d and e, and f and g, respectively. |
4 Summary and outlook
In this work, we continue and further develop the Hermean magnetosheath plasma flow model introduced by Schmid et al. (2021a) with a hydrodynamic approach, which allows us to determine the plasma velocity and density along the streamline under varying solar wind conditions and can therefore be adapted to each observational case. On the assumption of adiabatic expansion (compression), conservation of mass and frozen-in flux along the streamline (with an arbitrarily small cross-section) it is possible to determine both the plasma velocity and density, according to Eq. (21). However, close to the magnetopause the flux tube is extremely compressed and the polynomial function is nonzero and does not yield a solution. One physical explanation of why the model becomes imprecise near the magnetopause (i.e., where strong flux-tube compression takes place) might be that the assumption of an adiabatic compression becomes violated. It is possible that plasma cooling effects through, for example, charge exchange may become significant close to the magnetopause, which causes the breakdown of the adiabatic behavior (Galeev et al. 1985). In a future work, such cooling effects may be included and evaluated against in situ plasma measurements of, for example, the upcoming BepiColombo mission.
In general, however, the model produces similar plasma densities and velocities as those derived by previous MHD simulations and commensurates the plasma boundary locations identified by the magnetic field measurements of MESSENGER. It easy to implement and computationally less expensive than more complex numerical models. Thus, it provides a good reference point for comparison with observations, also in respect of the upcoming two-spacecraft BepiColombo mission. The presented model has the potential to estimate the solar wind parameters using the magnetosheath plasma observation of Mio during periods in Mercury’s orbit when even Mio (Mercury Magnetospheric Orbiter, MMO) stays mainly in the magnetosphere and magnetosheath (apo-herm on the night side) and hardly encounters the solar wind (Milillo et al. 2020).
Moreover, the model can help us to better understand the highly dynamic processes in the Hermean space environment. The model basically considers a ground state (steady state) of the solar-wind-magnetosphere system. This is essential because the magnetospheric dynamics are regarded as excited states, and the ground state must therefore be properly described or modeled to achieve one of the goals of BepiColombo to better understand, for example, the current systems, instabilities, substorms, and plasma waves in the space environment around Mercury. In this context, it would be useful to extend this semi-analytical magnetosheath model also to the magnetosphere. In a future work, the model presented in this work could therefore be encompassed with the MHD magnetosphere model developed by Alexeev et al. (2008).
Acknowledgements
The plasma data of the heliospheric Tao model are open access and can be retrieved on the AMDA website (http://amda.cdpp.eu/, Centre de Données de la Physique des Plasmas (CDPP), 2018) via the WorkSpace Explorer: DataBase/Solar Wind Propagation Models/Tao Model/SW Input OMNI (Tao et al. 2005). The orbital motion data of Mercury are provided by the Navigation and Ancillary Information Facility (NAIF) and can be retrieved on the NAIF website under https://wgc.jpl.nasa.gov:8443/webgeocalc (Acton 1996). The data of the Yagi model can be found under https://doi.org/10.1016/j.pss.2021.105176. An IDL program to evaluate the streamlines within Mercury’s magnetosheath, which is based on solar wind parameters of the Tao solar wind propagation model, can be retrieved from OSF: https://osf.io/9jgqn/7view_only=2624aca3774c4ba8885dcb21a13e1b08 (last access: 25 August 2022) (Schmid et al. 2021a). The work of Y.N. is financially supported by the Austrian Research Promotion Agency (FFG) ASAP PICAM-4 under contract 885349. DH was supported by the German Ministerium fur Wirtschaft und Energie and the German Zentrum fur Luft- und Raumfahrt under contract 50 QW 1501. K.P. was supported by DFG (German Research Foundation) under contract HE 8016/3-1. The collaboration of some of the authors (D.S. and M.V.; D.S., D.H. and S.A.) was facilitated by support from the International Space Science Institute (ISSI) in ISSI Team 517 (Towards a Unifying Model for Magnetic Depressions in Space Plasmas) and 525 (Modelling Mercury’s Dynamic Magnetosphere in Anticipation of BepiColombo).
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [Google Scholar]
- Aizawa, S., Griton, L. S., Fatemi, S., et al. 2021, Planet. Space Sci., 198, 105176 [NASA ADS] [CrossRef] [Google Scholar]
- Alexeev, I.I., Belenkaya, E. S. Bobrovnikov, S. Yu., Slavin, J. A., & Sarantos, M. 2008, J. Geophys. Res.: Space Physics, 113, A12 [Google Scholar]
- Anderson, J. E. 1963, Magnetohydrodynamic Shock Waves (Cambridge: MIT Press) [CrossRef] [Google Scholar]
- Anderson, B. J., Acuña, M. H., Lohr, D., et al. 2007, Space Sci. Rev., 131, 417 [CrossRef] [Google Scholar]
- Anderson, B. J., Johnson, C. L., Korth, H., et al. 2012, J. Geophys. Res.: Planets, 117, 1 [Google Scholar]
- Anderson, B. J., Johnson, C. L., & Korth, H. 2013, Geophys. Geosyst., 14, 3875 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhoff, J., Casteren, J., Hayakawa, H., et al. 2010, Planet. Space Sci., 58, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhoff, J., Murakami, G., Baumjohann, E., et al. 2021, Space Sci. Rev., 217, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Baumjohann, W., Matsuoka, A., Glassmeier, K.-H., et al. 2006, Adv. Space Res., 38, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Baumjohann, W., Matsuoka, A., Magnes, W., et al. 2010, Planet. Space Sci., 58, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Benna, M., Anderson, B. J. Baker, D. N., et al. 2010, Icarus, 209, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Boardsen, S. A., Slavin, J. A., Anderson, B. J., Korth, H., & Solomon, S. C. 2009, Geophys. Res. Lett., 36, L18106 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, M. D. 1960, Jet Propulsion, 30, 271 [Google Scholar]
- De Zeeuw, D. L., Nagy, A. F., Gombosi, T. I., Powell, K. G., & Luhmann, J. G. 1996, J. Geophys. Res: Planets, 101, 4547 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, C., Wang, L., Hakim, A., et al. 2015, Geophys. Res. Lett., 46, 11584 [Google Scholar]
- Dungey, J. W. 1961, Phys. Rev. Lett., 6, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Exner, W., Heyner, D., Liuzzo, L., et al. 2018, Planet. Space. Sci., 153, 89 [Google Scholar]
- Exner, W., Simon, S., Heyner, D., & Motschmann, U. 2020, J. Geophys. Res.: Space Phys., 125, e2019JA027691 [CrossRef] [Google Scholar]
- Fatemi, S., Poirier, N., Homström, M., et al. 2017, A&A, 614, A132 [Google Scholar]
- Fujimoto, M., Baumjohann, W., Kabin, K., et al. 2007, Space Sci. Rev., 132, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Galeev, A. A., Cravens, T. E., & Gombosi, T. I. 1985, Astrophys. J., 289, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Génot, V., Broussillou, L., Budnik, E., et al. 2011, Ann. Geophys., 29, 1849 [CrossRef] [Google Scholar]
- Hercík, D., Trávnícek, P. M., Johnson, J. R., Kim, E.-H., & Hellinger, P. 2013, J. Geophys. Res: Space Phys., 118, 405 [CrossRef] [Google Scholar]
- Imai, I. 1960, Rev. Mod. Phys., 32, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Ip, W. H. 1986, Geophys. Res. Lett, 13, 423 [NASA ADS] [CrossRef] [Google Scholar]
- James, M. K., Imber, S. M., Bunce, E. J., et al. 2017, J. Geophys. Res: Space Phys., 122, 7907 [NASA ADS] [CrossRef] [Google Scholar]
- Jia, X., Slavin, J. A., Gombosi, T. I., et al. 2015, J. Geophys. Res.: Space Phys., 120, 4763 [NASA ADS] [CrossRef] [Google Scholar]
- Kabin, K., Gombosi, T. I., DeZeeuw, D., & Powell, K. 2000, Icarus, 143, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Kallio, K., & Janhunen, P. 2004, Adv. Space Res., 33, 2176 [NASA ADS] [CrossRef] [Google Scholar]
- Kobel, E., & Flückiger, E. O. 1994, J. Geophys. Res: Space Phys., 99, 617 [Google Scholar]
- Korth, H., Tsyganenko, N. A., Johnson, C. L., et al. 2015, J. Geophys. Res: Space Phys., 120, 4503 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsova, T. V., & Pudovkin, M. I. 1978, Planet. Space. Sci., 26, 229 [Google Scholar]
- Lavorenti, F., Henri, P., Califano, F., et al. 2022, A&A, 664, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le, G., Chi, P. J., Blanco-Cano, X., et al. 2013, J. Geophys. Res: Space Phys., 118, 2809 [NASA ADS] [CrossRef] [Google Scholar]
- Milillo, A., Fujimoto, M., Murakami, G., et al. 2020, Space Sci. Rev., 216, 1572 [Google Scholar]
- Ness, N. F., Behannon, K. W., Lepping, R. P., & Whang, Y. C. 1975, J. Geophys. Res., 80, 2708 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, E., Modolo, R., Chanteur, G. M., Hess, S., & Leblanc, F. 2012, J. Geophys. Res: Space Phys., 117, A10228 [Google Scholar]
- Romanelli, N., DiBraccio, G., Gershman, D., et al. 2012, Geophys. Res. Lett., 47, 0094 [Google Scholar]
- Schmid, D., Narita, Y., Plaschke, F., et al. 2021a, Ann. Geophys., 39, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, D., Narita, Y., Plaschke, F., et al. 2021b, Geophys. Res. Lett., 48, e2021GL092606 [Google Scholar]
- Sergeev, V. A., Pellinen, R. J., & Pulkkinen, T. I. 1996, Space Sci. Rev., 75, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. A., Anderson, B. J., Zurbuchen, T. H., et al. 2009, Geophys. Res. Lett., 36 [Google Scholar]
- Solomon, S. C., McNutt, R. L., Gold, R. E., & Domingue, D. L. 2007, Space Sci. Rev., 131, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Soucek, J., & Escoubet, C. P. 2012, Ann. Geophys., 30, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Spreiter, J. R., & Rizzi, A. W. 1974, Acta Astrol., 1, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Spreiter, J. R., & Stahara, S. S. 1994, Adv. Space Res., 14, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, W., Dewey, R. M., Aizawa, S., et al. 2021, China Earth Sci., 64 [Google Scholar]
- Sundberg, T., Boardsen, S. A. Slavin, J. A., et al. 2013, J. Geophys. Res: Space Phys., 118, 6457 [NASA ADS] [CrossRef] [Google Scholar]
- Sundberg, T., Boardsen, S. A., Burgess, D., & Slavin, J. A. 2015, J. Geophys. Res: Space Phys., 120, 7342 [NASA ADS] [CrossRef] [Google Scholar]
- Tao, C., Kataoka, R., Fukunishi, H., Takahashi, Y., & Yokoyama, T. 2005, J. Geophys. Res: Space Phys., 110 [Google Scholar]
- Trávnícek, P. M., Schriver, D., Hellinger, P., et al. 2010, Icarus, 209, 11 [CrossRef] [Google Scholar]
- Wang, Y.-C., Mueller, J., & Motschmann, U. 2010, Icarus, 209, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Winslow, R. M., Anderson, B., Johnson, C., et al. 2013, J. Geophys. Res: Space Phys., 118, 2213 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Comparison of modeled bow shock (dashed) and magnetopause (dot-dashed) for different solar wind parameters. The red lines indicate the bow shock and magnetopause under high Alfvénic Mach number (MA = 20) and solar wind ram pressure (Pram = 30 nPa) around August 7, 2013, 102000 UT, and the blue lines indicate it under low Alfvénic Mach number (MA = 2) and solar wind ram pressure (Pram = 5 nPa) around March 8, 2012, 201 000 UT. The solid black line shows the bow shock and magnetopause used in the S21 model based on the best-fit parameter from Winslow et al. (2013). |
| In the text | |
 |
Fig. 2 Ratio between flux-tube cross-section area at the bow shock, ABS, and the flux-tube cross-section area anywhere along the streamline, A, for the case of an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. The black lines illustrate streamline examples. |
| In the text | |
 |
Fig. 3 Plasma flow velocity distribution within the Hermean magnetosheath, for the case of an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. Again, the black lines illustrate streamline examples. |
| In the text | |
 |
Fig. 4 Plasma density distribution within magnetosheath for the case of an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. |
| In the text | |
 |
Fig. 5 Flux-tube cross-section area change, density and velocity profile for three examples of streamlines. Panel a shows the course of the streamlines (red, green, and blue) with the corresponding shock frame of references (normal and tangent vectors ft and î, respectively) used for the Rankine–Hugoniot relations. Panel b shows the flux-tube cross-section area change along the streamlines. Panels c and d show the 1-D curves of the density and velocity profiles along the three streamlines (red, green, and blue) from the bow shock to XMSM = −4RM, respectively. Again, the average solar wind parameters during the entire MESSENGER service between 2011 and 2015 are used with an Alvén Mach number of MA = 5.8, ram pressure of Pram = 10.7 nPa, and plasma beta of β = 0.72. The gray shaded area indicates the region where the flux tube becomes extremely compressed around the magnetopause (A/ABS ≤ 0.75), and Eq. (21) does not yield a solution. |
| In the text | |
 |
Fig. 6 Comparison of the model results with the observations of MESSENGER and the results of a global MHD simulation. Panel a shows the magnetic field observations of MESSENGER on November 8, 2012 during orbit 1415. The vertical red lines indicate the bow shock (BS) and magnetopause (MP) crossing determined by visual inspection. The gray dashed lines indicate the boundary crossings determined by our model. Panels b and c show the modeled plasma density and velocity distribution within the magnetosheath for the same solar wind parameters used in Aizawa et al. (2021). The black line indicate the trajectory of MESSENGER for the time interval in panel a. The modeled plasma density/velocity along MESSENGER’s trajectory within the nightside magnetosheath and dayside magnetosheath are shown in panels d and e, and f and g, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![${\tilde r_{\left[ {{\rm{BS,MP}}} \right]}} = {{ - \cos \theta + \sqrt {{{\cos }^2}\theta + 4{R_{\left[ {{\rm{BS,MP}}} \right]}}{b_{\left[ {{\rm{BS,MP}}} \right]}}{{\sin }^2}\theta } } \over {2{b_{\left[ {{\rm{BS,MP}}} \right]}}{{\sin }^2}\theta }},$](/articles/aa/full_html/2022/12/aa45008-22/aa45008-22-eq2.png)
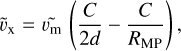
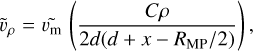
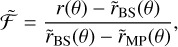
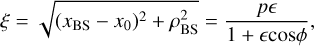
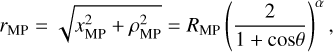
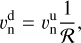
![$v_{\rm{t}}^{\rm{d}} = v_{\rm{n}}^{\rm{u}}\left( {\tan \theta {{\rm{v}}_{\rm{n}}}{{1 - 1/R} \over {\left[ {M_{\rm{A}}^{{\rm{u}}\,\,{\rm{2}}}/\left( {R{{\cos }^2}{\theta _{{\rm{Bn}}}}} \right)} \right] - 1}}\tan {\theta _{{\rm{Bn}}}}} \right),$](/articles/aa/full_html/2022/12/aa45008-22/aa45008-22-eq19.png)
![$\matrix{{{{\left( {M_{\rm{A}}^{{\rm{u}}\,{\rm{2}}} - R} \right)}^2}\left( {\gamma {\beta ^{\rm{u}}}R + M_{\rm{A}}^{{\rm{u}}\,\,{\rm{2}}}{{\cos }^2}{\theta _{{\rm{Bn}}}}\left[ {\left( {\gamma - 1} \right)R - \left( {\gamma + 1} \right)} \right]} \right)} \hfill \cr { + RM_{\rm{A}}^{{\rm{u}}\,\,{\rm{2}}}{{\sin }^2}{\theta _{{\rm{Bn}}}}\left( {\left[ {\gamma + \left( {2 - \gamma } \right)R} \right]M_{\rm{A}}^{{\rm{u}}\,\,{\rm{2}}} + R\left[ {\left( {\gamma - 1} \right)R - \left( {\gamma + 1} \right)} \right]} \right) = 0,} \hfill \cr} $](/articles/aa/full_html/2022/12/aa45008-22/aa45008-22-eq23.png)