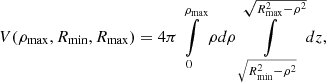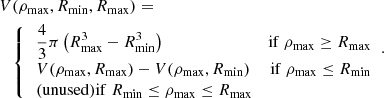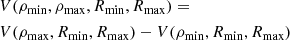| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202347125 | |
| Published online | 15 December 2023 | |
Soft X-ray emission from warm gas in IllustrisTNG circum-cluster environments
I. Sample properties, methods, and initial results
1
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, 91405 Orsay, France
e-mail: celine.gouin@ias.u-psud.fr
2
University of Alabama in Huntsville, Department of Physics and Astronomy, Huntsville, AL 35899, USA
3
Max-Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
Received:
8
June
2023
Accepted:
8
September
2023
Context. Whereas X-ray clusters are extensively used for cosmology, their idealised modelling, through the hypotheses of spherical symmetry and hydrostatic equilibrium, is being questioned more and more. The soft X-ray emission detected in tens of clusters with ROSAT was found to be higher than what was expected from the idealised hot gas modelling, pointing to our incomplete understanding of these objects.
Aims. Given that cluster environments are at the interface between the hot intra-cluster medium (ICM), warm circum-galactic medium (WCGM), and warm-hot intergalactic medium (WHIM), we aim to explore the relative soft X-ray emission of different gas phases in circum-cluster environments.
Method. By using the most massive halos in IllustrisTNG at z = 0, we have predicted the hydrodynamical properties of the gas from cluster centres to their outskirts (5 R200), and modelled their X-ray radiation for various plasma phases.
Results. First, we found that the radial profile of temperature, density, metallicity and clumpiness of the ICM are in good agreement with recent X-ray observations of clusters. Secondly, we have developed a method to predict the radial profile of soft X-ray emission in different bands, the column density of ions, and the X-ray absorption lines (O VIII, O VII, Ne IX, and Ne IX) of warm-hot gas inside and around clusters.
Conclusion. The warm gas (in the form of both WCGM and WHIM gas) is a strong emitter in soft X-ray bands and is qualitatively consistent with the observational measurements. Our results suggest that the cluster soft excess is induced by the thermal emission of warm gas in the circum-cluster environments.
Key words: methods: statistical / methods: numerical / X-rays: galaxies: clusters / galaxies: clusters: general / large-scale structure of Universe
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
X-ray emission from galaxy clusters is used extensively to probe a variety of astrophysical phenomena and to study cosmology. From the early surveys of the X-ray sky (Giacconi et al. 1972), it became apparent that clusters are powerful sources of X-ray emission, originating primarily from a hot phase (≥107 K) of the intergalactic medium that is kept bound by a massive dark matter halo that significantly outweighs visible galaxies (e.g. Bahcall & Sarazin 1977). The X-ray emission is primarily thermal in origin, with free–free bremsstrahlung providing the bulk of the emissivity, with the presence of emission lines from elements such as iron, which are not fully ionised (e.g. Mitchell et al. 1976; Serlemitsos et al. 1977).
Among some of the key uses of X-ray emission from galaxy clusters are the determination of cosmological parameters that describe dark matter and dark energy (e.g. Allen et al. 2004; Vikhlinin et al. 2009; Mantz et al. 2014, 2022) and the Hubble constant (e.g. Bonamente et al. 2006; Wan et al. 2021), the understanding of the growth of cosmic structure on the largest scales (see Walker et al. 2019, for recent review), and the study of the complex feedback mechanism between the cluster’s galaxies and their active galactic nuclei (e.g. Yang & Reynolds 2016). At the heart of all these studies is the interpretation of the detected emission as radiation from a hot intra-cluster medium (ICM) that is in approximate hydrostatic equilibrium with its underlying matter potential.
At soft X-ray wavelengths, broadly defined as photon energies substantially below the peak of the X-ray emission from the hot ICM (≤1 keV) and above the effective cut-off imposed by Galactic absorption (∼0.1 keV), X-ray emission from and near clusters is less well studied. This is due to a combination of the lower effective energy and poorer calibration of most X-ray missions (e.g. Nevalainen et al. 2010) towards lower photon energies, the effects of Galactic foregrounds (e.g. Snowden et al. 1995) that are both time and space variables, and the contamination from sub-virial phases.
Numerical simulations provide the means to study the thermodynamics of the gas in and near cluster environments. With the advanced of baryonic physic models through sub-grid and particle techniques, the current generation of large hydrodynamical simulations, such as IllustrisTNG (Nelson et al. 2019), HorizonAGN (Dubois et al. 2016), Magneticum (Hirschmann et al. 2014; Dolag et al. 2016; Ragagnin et al. 2017), and TheThreeHundred project (Cui et al. 2018), provides a statistical sample of highly resolved simulated clusters to deeply investigate their gas properties, and in particular their thermal footprint for X-ray interpretation. Probing the gas physics through state-of-the-art simulations has already revealed a departure to hydrostatic equilibrium inside clusters (e.g. Gianfagna et al. 2023), resulting from turbulence and bulk motion (e.g. Angelinelli et al. 2020) and proposed correction for this bias in X-rays (Ansarifard et al. 2020). More generally, numerous investigations have recently been carried out to probe the ICM physics by using numerical simulations, such as their chemical enrichment (Biffi et al. 2018) and their thermal and pressure profiles, to accurately predict scaling relations (e.g. Barnes et al. 2017; Pop et al. 2022) and better interpret the X-ray emission of clusters.
For our cluster gas investigation, we used the TNG300-1 simulation, the larger box of IllustrisTNG simulations (∼300 Mpc3) with the highest spatial resolution, to take advantage of both a statistical sample of clusters and an accurate modelling of the baryonic physics (Pillepich et al. 2018). Using TNG300-1 simulation, Martizzi et al. (2019) and Galárraga-Espinosa et al. (2021) have highlighted that hot gas is dominant inside clusters, as the knots of the large-scale cosmic web, whereas warm diffuse gas can be used to trace filamentary structures at z = 0. Such an improvement in our understanding of cluster and cosmic gas has recently allowed us to estimate warm and hot gas observations through OVII and OVIII emission lines for the next generation of spectrometers (Parimbelli et al. 2023; Butler Contreras et al. 2023; Tuominen et al. 2023). Focusing exclusively on cluster environments, Gouin et al. (2022) explored the gas thermodynamics in TNG300-1, showing that clusters are the interface between two dominated gas phases: the warm and the hot gas. The warm gas in filaments infalls to the connected clusters, undergoes motions of accretion and ejection at cluster borders, and then transitions into the hot gas phase, inside clusters.
This project aims to fill the gap in our theoretical and observational understanding of soft X-ray emission in and near galaxy clusters, using the Gouin et al. (2022) IllustrisTNG sample of massive clusters studied out to 5 × r200. We refer to these astrophysical volumes as the circum-cluster environment (as introduced by Yoon & Putman 2013), that is the region in and surrounding galaxy clusters, including the transition between the inner virialised ICM and the outer accreting sub-virial plasmas that is expected to contain the highest density warm-hot intergalactic medium (WHIM). The main motivation for this study of the soft X-ray emission near clusters is the expectation that a significant fraction of the Universe’s baryons at the present epoch is in a warm-hot intergalactic medium (WHIM) at log T(K)≤7 (e.g. Cen & Ostriker 1999; Davé et al. 2001). These baryons are widely expected to bridge the missing baryons gap, and thus, resolve the observational discrepancy between the lower amount of low-z baryons compared to high-z baryons (e.g. Danforth et al. 2016). Although evidence is mounting that WHIM filaments are responsible for both the emission (e.g. Tanimura et al. 2020, 2022; Mirakhor et al. 2022) and absorption of X-rays (e.g. Kovács et al. 2019; Spence et al. 2023) in amounts that are consistent with the missing fraction of baryons, the regions near clusters where filaments are expected to be densest remain relatively unexplored, in part because of the difficulties in disentangling the contributions from the virial and sub-virial phases. One exception is the detection of the cluster soft excess emission in a number of clusters with ROSAT (e.g. Bonamente et al. 2003, 2022) and other soft X-ray instruments, which is consistent with the detection of WHIM filaments projecting onto massive clusters. One of the main motivations of this project is therefore to address the contribution to the projected X-ray emission at soft X-ray energies from hot and sub-virial phases in and around massive clusters, and other aspects of cluster physics that are related to this X-ray emission.
This paper, which is intended to be the first in a series, describes the methods of analysis of the IllustrisTNG data to obtain averaged radial profiles of thermodynamic quantities of interest for the prediction of the X-ray emission, via density, temperature, chemical abundances, volume covering fraction and clumpiness of the gas phases, and initial results on the projection of the emissivity from the different gas phases in and around clusters. This paper is structured as follows: Sect. 2 presents the IllustrisTNG simulations and their analysis to obtain radial profiles; Sect. 3.1 describes our analytical method to project radial profiles on a detector plane, Sect. 4 describes the methods to obtain projected profiles of radiated power and X-ray surface brightness that can be compared with observations and preliminary results from that analysis; and Sect. 5 presents a brief discussion and our conclusions. Subsequent papers will make use of these methods for a more in-depth analysis of the emission from sub-virial gas in and around clusters, its astrophysical and cosmological implications, and related aspects of cluster physics.
2. Thermodynamical profiles from IllustrisTNG circum-cluster environments: methods and comparison with observations
2.1. Gas cells from IllustrisTNG simulation
Our study is based on the analysis of the gas cells in the TNG300-1 simulation, the high-resolution box of IllustrisTNG300 with a physical box size of 302.6 Mpc (Nelson et al. 2019). This run including the full TNG physics model, such as gas thermodynamics, has been computed over a moving-mesh code (Springel 2010), with a minimum physical gas cell radius of ∼47 pc and a the median gas cell radius of ∼31 kpc at z = 0. The equations of ideal magnetohydrodynamics are solved along this robust adaptive grid, and the full TNG physics model has been implemented with key physical processes such as microphysical gas radiative mechanisms; chemical enrichment of the gas following supernovae Ia, II, and AGB stars; and multi-mode black hole feedback (with both a thermal “quasar” mode and a kinetic “wind” mode, as described in Weinberger et al. 2018). We note that the gas metal abundances were carefully analysed in IllustrisTNG (see e.g. Torrey et al. 2017; Vogelsberger et al. 2018; Nelson et al. 2018, and references therein). The TNG300-1 simulation provides the characteristics of the gas cells on which we derive the temperature and pressure for each cell assuming a perfect monoatomic gas.
2.2. Cluster selection from IllustrisTNG simulation
Starting from the halo catalogue of the TNG300-1 simulation at z = 0, we selected all friends-of-friends halos (FoF) with masses of M200 > 1014 M⊙ h−1. In this catalogue, the radial scale of FoF halos R200 is defined as the radius of a sphere which encloses a mass M200 with an average density equal to 200 times the critical density of the Universe. From our mass selection of 153 clusters, we only considered the 138 clusters whose centres are more distant than 5 × R200 from the simulation box edges; this was done in order to fully explore cluster environments. The main properties of the IllustrisTNG cluster sample are reported in Table 1. In this table, we define also the four mass bins considered in the following analysis: the low-mass clusters M1 (with M200 ∈ 10[14.0 − 14.1] M⊙ h−1), the middle cluster mass range M2 (with M200 ∈ 10[14.1 − 14.5] M⊙ h−1), and two samples of the most massive clusters, respectively M3 with M200 > 1014.5 M⊙ h−1, and M4 with the five most massive clusters with M200 > 1014.75 M⊙ h−1.
Main properties of the all cluster sample and its four mass bins M1, M2, M3, and M4 (notice that M4 is included in M3).
2.3. Gas phases
The gas cells are separated depending on their temperature and density in order to distinguish different gas phases. We followed the temperature and density cuts of Martizzi et al. (2019), commonly used in hydrodynamical simulation analyses to explore gas phase transitions (see e.g. Galárraga-Espinosa et al. 2021). As demonstrated by Gouin et al. (2022), cluster environments are dominated by two main phases, mostly the hot ICM (T[K]> 107) inside the clusters, and the warm diffuse gas phase (WHIM: 105 < T[K]< 107 and nH[cm−3]< 10−4) outside clusters (see Figs. 1 and 2 of Gouin et al. 2022). In this study, we also defined the WARM gas as all gas cells with a warm temperature 105 < T[K]< 107, thus accounting for both the WHIM and WCGM gas phase (105 < T[K]< 107 and nH[cm−3]> 10−4). We illustrated this different gas phase definitions in the phase-space diagram Fig. 1. Although the distinction between WHIM and WCGM is used as a simple means to identify the lower and higher density portions of the WARM sub-virial phase. This density limit separating WHIM from WCGM gas should simply be considered as a guiding reference. The WHIM gas phase, dominant inside cosmic filaments (Galárraga-Espinosa et al. 2021), can be accreted onto the surroundings of halos and become denser in the form of WCGM, and inversely, WCGM gas around halos might be ejected and become more diffuse due to AGN feedback effects.
 |
Fig. 1. Phase-space of gas cells around a given cluster in the TNG300-1 simulation, shown by the normalised 2D histogram. The hot gas is defined with a temperature of T[K]> 107, and the WARM gas with temperature between 105 < T[K]< 107. The WHIM gas is a sub-sample of the WARM gas, with the condition of being diffuse, i.e., its density is nH[cm−3]< 10−4. |
In Fig. 2, we show the spatial distribution of these different gas phases for a given cluster environment (up to 5 R200). As expected from Gouin et al. (2022), the hot gas phase traces the gas distribution inside clusters, whereas WHIM gas represents the filamentary patterns around a cluster (see also Planelles et al. 2018). Interestingly, our extended definition of WARM gas shows the WHIM gas with the addition of warm clumps of gas. Indeed, by plotting only WCGM gas in Fig. 2, one can see that small dense clumps of gas are resulting from the WCGM phase. As expected by Martizzi et al. (2019), this definition of WCGM and WHIM gases therefore represents physically different gas phases.
 |
Fig. 2. Distribution of gas within 5 R200 around a given massive cluster. The first panel shows the distribution of all the gas cells, the second one only the hot gas, the third one only the WHIM gas, and the left panel the WARM gas. |
In Table 2 we summarise the different gas phases considered in this study. The hot gas phase is also referred to as a hot ICM, given that it is the hotter gas (T > 107 K) in circum-cluster environments located inside clusters. Moreover, we denote “all gas” as all the gas cells in cluster environments, independently of any temperature or density selection, as a reference to compare one particular gas phase to the full gas distribution. Figure B.1 shows the average number of cells for each gas phase as a function of cluster-centric distance, to ensure that our results are not affected by averaging gas properties over a small number of cells. Moreover, the density limit between the WHIM and WCGM gas phase (nH[cm−3] = 10−4) is also demonstrated in Fig. B.4 to show the evolution of WHIM and WCGM gas abundance as a function of this limit. Here, we focus on the full WARM gas phase given that both of its components (WHIM and WCGM gas) should have an impact on soft X-ray properties.
2.4. Numerical computation of radial thermodynamic profiles
For each thermodynamic quantity of the gas, we averaged the value by considering the gas cells (labelled by the index i and with a volume Vi) inside radial shells (labelled by the index k, with rk normalised by R200) around the cluster centre. The average of a quantity Q is given by the following:
with the k = 1, …, 50 index labelling the 50 logarithmically spaced radial distances around the centre, ranging from 0 to 5 R200, and the radial range being Rk = [rk − 1, rk]. The averages according to Eq. (1) therefore represent the volume-weighted average value of the quantity for a given gas phase (either all gas cells, hot, WHIM, or WARM gas). These averages are shown as solid lines in Figs. 3, 6, and 8 for, respectively, the electron ne and hydrogen density nH, the temperature T, and the metal abundance Z.
 |
Fig. 3. Electron density ne calculated according to the averaging of Eq. (1) is shown with a solid line, and the mass density calculated according to the averaging of Eq. (3) is shown with a dashed line. The median profiles for the entire cluster sample are given. |
The average profiles according to Eq. (1), however, do not take into account the volume covering fraction of a given phase (hot ICM, WHIM and WARM), defined as
where Vshell, k is the usual volume of a spherical shell between radii rk − 1 and rk. The volume covering fractions are shown in Fig. 4, where the covering fraction is approximately 100% for the hot phase near the cluster centre, while it is significantly less than unity for the other phases, and it changes with radius for each phase. Indeed, the volume covering fraction of a given gas phase is intrinsically related to its abundance. Therefore, it follows the same radial trend as the relative abundance of different gas phases discussed in Gouin et al. (2022), with two dominant phases in circum-cluster environments: the hot gas phase (up to ∼1 R200) and the WARM gas phase at larger radial distances.
In order to predict the X-ray emission of different gas phases, it is also useful to determine the radial profiles of the mass density, accounting for the volume covered by a given phase. This is obtained via
where mi is the mass of contained in the i-th gas cell that is included in the radial bin Rk. In Eq. (3), the density is in units of (M⊙ h−1)⋅(Mpc h−1)−3 and includes all the gas (such as electrons, hydrogen, and all other ions). These mass density profiles are shown as dashed lines in Fig. 3, after a normalisation that results in the conversion to units of equivalent H atoms cm−3 to match the units of the electron and hydrogen density in the same figure. One can first notice that when taking into account the volume fraction of a given gas phase, the radial profile of the phase drastically changes. For example, we see that the WARM gas is denser than the hot ICM inside clusters (the solid red line is higher than the black one), which can be explained by the fact that colder gas can more easily collapse and become denser. However, given that WARM gas is extremely rare compared to the ICM gas phase inside clusters (see Fig. 4 and as illustrated in Fig. 2), its mass density (weighted by volume fraction, dashed lines) is much lower than the ICM. For a given phase, the difference between solid and dashed density curves in Fig. 3 is therefore simply explained by the different radial dependencies of the volume covering fractions.
All of these thermodynamic profiles have been computed for each simulated cluster and then averaged for all the clusters and for the three different cluster mass bins. The detail on the averaging procedure over the cluster population is detailed in Appendix B, where we also discuss the difference between mean and median averages. Indeed, individual clumps in some circum-cluster environments can artificially boost the mean thermodynamic profiles. We also report, in Tables C.1 and C.2, the values of density, volume fraction, temperature, metal abundance of the different gas phases in and around the clusters averaged overall, and M1, M2, and M3 clusters.
2.5. Radial thermodynamic profiles – comparisons to observations
The hot ICM mass density is compared with selected recent observations in Fig. 5, namely the Ghirardini et al. (2019) analysis of the X-COP sample of 12 massive clusters, the Eckert et al. (2012) results of a sample of 31 nearby clusters, and the detailed analysis of the Coma cluster by Mirakhor & Walker (2020), all covering a radial range approximately equal to at least r200. The IllustrisTNG profile of the average hot ICM nH density (dashed line in Fig. 5) is in excellent agreement with the observational results, especially for the most massive cluster sample M3 whose masses are most directly comparable to those of the Ghirardini et al. (2019), Eckert et al. (2012) and Mirakhor & Walker (2020) observations.
 |
Fig. 5. Zoomed-in view of Fig. 3, the median radial profiles of the mass density for the ICM gas phase for all the clusters (left panel), and the most massive ones (M3 mass bin, right panel). We highlight the comparison with X-COP observations (Ghirardini et al. 2019), those of a sample of 31 nearly clusters by Eckert et al. (2012), and the Coma cluster (Mirakhor & Walker 2020). |
The radial profiles of the mean temperature of the different phases are shown in Fig. 6. A comparison of the hot ICM temperature profiles with the observational results from Ghirardini et al. (2019) and Mirakhor & Walker (2020) is shown in Fig. 7, where we also show projected profiles according to the Mazzotta et al. (2004) density-square weights. The Ghirardini et al. (2019) temperature profiles are scaled according to the temperature at r500 (T500), and therefore Fig. 6 shows two observational constraints corresponding to two values of T500 that correspond approximately to the most massive sample and to the least massive sample. The radial profile of the hot ICM temperature for the M3 sample is in perfect agreement with the Ghirardini et al. (2019) constraints for T500 = 5 keV. The Coma radial profile has a slightly higher temperature, given that its mass of M200 = 8.550 ± 0.55 M⊙ corresponds to one of the largest in our IllustrisTNG sample.
 |
Fig. 7. Zoomed-in view of Fig. 6 for hot ICM temperature profiles and comparison with selected observations. TSL is the projected spectroscopic temperature according to the density-square weights of Mazzotta et al. (2004; uncertainty bands are similar to those of the 3D temperatures, and they are not shown). Left: All clusters. Right: Mass sample M3. |
The average metal abundance profiles are shown in Fig. 8. The metal abundance of the hot ICM is in excellent agreement with the Ghizzardi et al. (2021) constraints at all radii. Mernier et al. (2017), on the other hand, found a significantly higher metal abundance at lower radii, progressively reaching the A ≃ 0.2 solar value towards the virial radius, in agreement with the IllustrisTNG profiles. This higher metallicity inside clusters might be induced by the WARM gas phase, as is suggested by our predictions according to Fig. 8.
2.6. Clumpiness of the gas
Inhomogeneities in the gas have a direct impact on several physical quantities derived from observations of galaxy clusters and the warm-hot phases. As is explained in detail in Sect. 4 below, the measured X-ray surface brightness is proportional to the square of the density. Therefore, it is the average 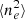 , and not ⟨ne⟩, that is the primary observable in X-rays. In turn, this means that inferences on such fundamental quantities as the gas mass and the total mass as inferred by hydrostatic equilibrium, both functions of ne, rely on an estimate of the linear density and therefore on an assessment of inhomogeneities in the plasma (for a review, see e.g. Walker et al. 2019).
, and not ⟨ne⟩, that is the primary observable in X-rays. In turn, this means that inferences on such fundamental quantities as the gas mass and the total mass as inferred by hydrostatic equilibrium, both functions of ne, rely on an estimate of the linear density and therefore on an assessment of inhomogeneities in the plasma (for a review, see e.g. Walker et al. 2019).
Following Nagai & Lau (2011), we used the following averages of the electron density,
to define the clumping factor as
A value of the clumping factor greater than one indicates gas that is not uniformly distributed over the respective spherical shell of provenance, but rather with regions of significantly higher or lower (including null) density, contributing to a variance in the distribution of the densities that results in 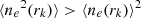 . Table C.3 also reports the values of
. Table C.3 also reports the values of 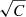 for selected radii, for the three gas phases, and for the three mass bins.
for selected radii, for the three gas phases, and for the three mass bins.
Figure 9 shows the median radial profile of the clumping factor average over all the clusters and for different gas phases. Considering the full gas distribution (purple line), the clumpiness of the gas is very low inside clusters and becomes significantly clumpy beyond the virial radius, while the density of the hot ICM is quite uniform within r200. However, the WARM gas clumpiness (red line) is higher inside clusters, as suggested previously in the illustration in Fig. B.2. Therefore, we conclude that the WARM gas phase is colder, with larger metallicity and more clumpiness than the hot ICM in circum-cluster environments. In contrast, WHIM gas alone is by definition more diffuse, and thus with a lower clumping factor than WARM gas. Interestingly, we also found that all gas phases follow the same radial trend with low clumpiness inside clusters and rapidly increase beyond the virial radius.
 |
Fig. 9. Median radial profiles of clumping factor average over all the clusters. In addition to the usual ICM, WHIM, and WARM phases, we also report the clumpiness obtained by using all the gas cells (no phase selection). |
The measurements of the clumping factor of Nagai & Lau (2011), using the simulations of Kravtsov (1999) and Kravtsov et al. (2002), shows an increasing radial trend that reaches a value of C ≃ 10 at 2 × R200, somewhat higher than our results yet qualitatively consistent with an increasing importance of clumpiness at larger distances from the cluster’s centre. This radial evolution of clumpiness is also consistent with previous numerical investigations (see e.g. Vazza et al. 2013; Roncarelli et al. 2013; Ansarifard et al. 2020). More recently, Angelinelli et al. (2021) performed a similar analysis with the Itasca simulations (see Fig. 5 in their paper), resulting in quantitatively similar results that indicate an increasing radial trend of the clumpiness with the radius reaching an approximate value of 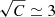 at 5 × r500 ≃ 3 × r200 (their definition of the clumpiness factor includes the square-root operation). An interesting point is to consider either mean or median averaging of clumping factor, a point discussed in Appendix B, showing that median is less sensitive to individual gas inhomogeneities in the full cluster sample (see also Towler et al. 2023, reaching a similar conclusion). Finally, Planelles et al. (2017) revealed that the inclusion of AGN feedback in simulations is helping the hot ICM to be more homogeneous, reducing the clumping factor values, and they also found a similar clumpiness radial trend with a slightly higher value of
at 5 × r500 ≃ 3 × r200 (their definition of the clumpiness factor includes the square-root operation). An interesting point is to consider either mean or median averaging of clumping factor, a point discussed in Appendix B, showing that median is less sensitive to individual gas inhomogeneities in the full cluster sample (see also Towler et al. 2023, reaching a similar conclusion). Finally, Planelles et al. (2017) revealed that the inclusion of AGN feedback in simulations is helping the hot ICM to be more homogeneous, reducing the clumping factor values, and they also found a similar clumpiness radial trend with a slightly higher value of 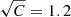 at r200.
at r200.
Observationally, it is challenging to measure the gas clumping directly, primarily due to the limited spatial resolution of the X-ray instruments and the small angular size of most distant clusters. Morandi et al. (2017) were able to estimate a clumping factor of C ∼ 2 − 3 at r200 for the lower mass galaxy group NGC 2563, again in agreement with the IllustrisTNG predictions, although for a system of lower mass than the clusters in our sample. For the nearby Virgo cluster, Mirakhor & Walker (2021) measured a small value of the clumping factor (C ≃ 1.1) at small radii from the centre (r ≪ r200) from X-ray observations, again in quantitative agreement with our measurements. Moreover, Eckert et al. (2015a) used a sample of 31 clusters (z = 0.04 − 0.2) observed by ROSAT to measure the clumping factor at the level of 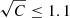 within r500, and to set constraints of the order of
within r500, and to set constraints of the order of 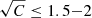 beyond that radius.
beyond that radius.
In Fig. 10, we compare our ICM clumpiness radial profile of most massive clusters with previous AGN simulation from Planelles et al. (2017) and the observational measurements from Eckert et al. (2015a) and Mirakhor & Walker (2021). Inside clusters (< 1 R200), a good agreement is found with both previous numerical predictions and recent observations. Interestingly, at larger radii (> 1 R200), Planelles et al. (2017) showed a somewhat lower clumping factor than our prediction, although with the same increasing radial trend as our profile. This difference can be due to different AGN modelling that accurately reproduces observed statistical trends at z = 0 in IllustrisTNG (Pillepich et al. 2018; Nelson et al. 2019). The accurate AGN feedback modelling in IllustrisTNG might be the reason for the agreement of our prediction of the hot ICM clumpiness with recent observations beyond the virial radius.
 |
Fig. 10. Comparison of hot ICM clumpiness factor for the most massive cluster (M3 mass bin) with the simulations of Planelles et al. (2017) in a sample of clusters in a comparable mass range; clumpiness in Coma from Mirakhor & Walker (2020); and Eckert et al. (2015b) measurements. |
2.7. The gas mass fraction
Finally, we report a first analysis of the gas mass fraction of our cluster sample to explore its validity in terms of the baryon mass budget and compare it to current observational measurements. The baryonic budget of IllustrisTNG simulations (Nelson et al. 2019) follows the cosmological parameters from the Planck 2015 results (Planck Collaboration XIII 2016).
In our case, we use the average profiles of the hot ICM density and temperature to estimate the gas mass fraction, under the assumption of hydrostatic equilibrium. Gas mass fractions can be used to probe the hydrostatic mass bias in observations (Wicker et al. 2023). Therefore, we only focused on the gas cells here and estimated the total mass according to the hydrostatic equilibrium (e.g. Sarazin 1988) within a radius r as
where μ is the mean molecular weight of the plasma (see Sect. 4.1 for details), and ne and T are the electron density and temperature at a given radius r from the centre of the clusters. Figure 11 shows the radial profile of the gas mass and of the total mass, for the entire cluster sample. Within the virial radius, the gas mass fraction is in excellent agreement with the ratio of the cosmological parameters Ωb/ΩM as measured by the Planck mission (Planck Collaboration VI 2020) and from various X-ray measurements of the gas mass fraction (e.g. Mantz et al. 2022, 2014; Ettori et al. 2009; Vikhlinin et al. 2006; Lyskova et al. 2023). This agreement is further evidence that the definition of the hot ICM phase in the IllustrisTNG simulation used in this work does indeed reproduce key features of observed clusters.
 |
Fig. 11. Cumulative radial profiles of gas mass and hydrostatic mass for entire cluster sample. The X-ray measurements of Ettori et al. (2009) and Vikhlinin et al. (2006) are for r ≤ r500, and the Mantz et al. (2022) gas mass fraction was calculated in a radial shell of 0.8 − 1.2 × r2500, where r2500 ≃ 0.45 × r500. |
For completeness, Fig. 11 includes the radial range beyond r200 where it is known that hydrostatic equilibrium is challenged by the presence of non-thermal pressure support (e.g. Fusco-Femiano & Lapi 2018). The application of hydrostatic equilibrium to regions where gas is supported by additional forms of pressure results in a higher-than-true total mass, and in fact our radial profile of the gas mass fraction has a sharp drop. In principle, our analysis can be complemented by a study of the radial distribution of dark matter in IllustrisTNG, which, however, goes beyond the scope of this paper (see Barnes et al. 2021 for details on hydrostatic mass bias for mock X-rays in IllustrisTNG simulations).
3. Methods of analysis: from thermodynamic profiles to X-ray emission
In this section, we present the methods used to predict the X-ray emissivity from the thermodynamic profiles of simulated clusters (described in Sect. 2.4). The average X-ray emissivity of clusters is computed by first projecting the average radial profiles with the method described in Sect. 3.1, and then by calculating the X-ray cooling and associated quantities as described in Sect. 3.2. A brief description of the atomic code and associated quantities is provided in Sect. 3.3. The scientific results of this analysis are then presented in Sect. 4.
3.1. Projection of the radial profile
The radial profiles of thermodynamic properties in Fig. 3 up to Fig. 9 are a function of the 3D radius, as measured by the IllustrisTNG simulation. Observations of the thermodynamic quantities, such as density and temperature, and of the associated X-ray surface brightness (see Sect. 4), require either a de-projection of the observations (as, e.g. is done in the case of observations such as those of Ghirardini et al. 2019), or a projection onto a (focal) plane of the 3D profiles obtained from the simulations. This section describes the method of projection that we used for this project, so that we can compare our results with X-ray observations directly, without the need to de-project the observations.
In hydrodynamical N-body simulations, it is customary to project such quantities as the temperature of each plasma cell in order to obtain a temperature that is comparable to observations. For example, projection of the temperature of a gas cell with a weight equal to 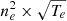 leads to the popular ‘spectroscopic’ temperature that is commonly used to compare temperatures in simulations with X-ray observations (see Mazzotta et al. 2004). Alternatively, observations of such projected quantities as the temperature or the surface brightness can be de-projected using geometric methods that typically assume spherical symmetry. Such methods have been progressively honed since the initial efforts of, for example, Fabian et al. (1981) and Kriss et al. (1983), and are common practice especially in X-ray astronomy (e.g. Buote 2000; Ettori 2002) and beyond (McLaughlin 1999).
leads to the popular ‘spectroscopic’ temperature that is commonly used to compare temperatures in simulations with X-ray observations (see Mazzotta et al. 2004). Alternatively, observations of such projected quantities as the temperature or the surface brightness can be de-projected using geometric methods that typically assume spherical symmetry. Such methods have been progressively honed since the initial efforts of, for example, Fabian et al. (1981) and Kriss et al. (1983), and are common practice especially in X-ray astronomy (e.g. Buote 2000; Ettori 2002) and beyond (McLaughlin 1999).
The problem presented by our analysis of the IllustrisTNG simulations is that of the projection of functions of radial profiles of thermodynamic quantities (e.g. to obtain the surface brightness) that were obtained according to Eq. (1). These radial profiles therefore represent the average properties of a certain volume, under the assumption of radial symmetry. This problem therefore differs from the usual problem of projecting quantities associated with individual simulation cells or particles of a given mass and volume, as considered, for example, in the projection of Mazzotta et al. (2004). For this project, what is required is the identification of the volumes that pertain to those quantities, that is, the volume of intersection between a shell of a sphere (representing the circum-cluster region) and a concentric cylinder (representing the sightline). A simple avenue would be that of identifying these volumes numerically. Instead, we chose to identify these volumes analytically. Since to the best of our knowledge these integrals were not previously reported in the astrophysical literature, we chose to evaluate them and report the results in Appendix A.
The projection of the radial profiles follows the geometry of Fig. A.1, where the spherically symmetric distribution of matter is represented by onion-like shells of increasing radial distance r from the centre. To each of those shells correspond the average thermodynamic quantities (e.g. density, temperature, and abundance) that are calculated according to Eq. (1). The usual spherical coordinates (r, θ, ϕ) are related to the cylindrical coordinates (ρ, θ, z) by the usual transformations ρ = r sin ϕ, z = r cos ϕ, where the z direction in cylindrical coordinates represents the sightline1. Given the spherical symmetry of the radial profiles, the z coordinate of the cylindrical system is chosen to represent the distance along the sightline, and the (ρ, θ) plane represents the focal plane. The volume of intersection of a spherical shell between radii Rmin = rk − 1 and Rmax = rk and a concentric cylindrical shell between radii ρmin and ρmax can be calculated using the steps that are described in detail in Appendix A. This volume of intersection is used in conjunction with the average thermodynamic quantities that belong to that radius, as further described below in this section.
3.2. X-ray cooling function, surface brightness, and luminosity
In X-ray astronomy, it is customary to refer to the power P emitted by an astrophysical plasma, in units of erg s−1, as the luminosity of the source. This luminosity is related to the plasma emissivity Λ(T, A) or cooling function, which is defined as the power emitted per unit nenH by the plasma, following the convention of Raymond & Smith (1977) and Smith et al. (2001), and therefore in units of erg cm3 s−1. The plasma emissivity is therefore the power emitted by a unit volume of the plasma, rescaled by the nenH, and it is a function of the temperature T and metal composition of the plasma, the latter usually being described as a fraction A of solar abundances of heavy elements. Both the IllustrisTNG simulations and the APEC code of Smith et al. (2001) use the Anders & Grevesse (1989) abundances, and therefore those metal abundances are used in this paper2.
The plasma cooling function is related to the X-ray surface brightness via
where the integral is along the sightline l, and the (1 + z)4 factor provides the cosmological dimming in an expanding universe, with z the redshift of the source (see e.g. Eq. (2) in Bonamente et al. 2006). It is intended to represent the amount of energy collected, per unit time, per unit solid angle, and per unit area of an ideal detector in the focal plane of a focusing telescope. In our sample, we consider clusters at z = 0, and the cosmological dimming factor therefore has no role. The surface brightness is the quantity that is usually collected in X-ray observations of diffuse sources such as galaxy clusters (e.g. Ghirardini et al. 2019).
Another observational quantity commonly used is the emission integral sometimes referred to as emission measure defined by
and representing an integral over a volume V of an extended source. The emission integral is proportional to the normalisation constant of an optically thin plasma, such as APEC, used to fit a spectrum from a spatially resolved area in the detector (e.g. a radial annulus around the centre of the cluster), with V representing the 3D volume responsible for the emission. For example, the APEC code (and other commonly used codes such as mekal, Mewe et al. 1985, 1986; Kaastra 1992) as implemented in the X-ray fitting software XSPEC, which returns the normalisation constant
where DA is the angular diameter distance to the source, z its redshift, and the constant 10−14 is used for convenience so that the normalisation constant has values in the neighborhood of unity for a variety of astronomical sources of interest, including galaxy clusters.
For the purpose of comparing the amount of energy radiated by different phases, and at different projected radial distance from the centre of the cluster, it is necessary to use quantities that are closely related to observations. We assumed radial symmetry throughout this work, and therefore considered the 3D radius r as the only geometric parameter, with Rk a radial range between 3D radii rk − 1 and rk, as used in Sect. 2.4. The total power radiated within a projected radial range Ck (i.e. projected radii ρk − 1 and ρk), is thus an integral along the sightline representing a cylindrical shell within those projected radii,
where the volume V is the intersection between the sphere and the concentric cylindrical annulus. In practice, given that 3D radial profiles are evaluated in discrete concentric shells, the power can be evaluated as a sum over all volumes resulting from the intersection of the cylindrical shell (representing the sightline) with the spherical shells (representing the cluster), such as,
where Vik is the volume of intersection of cylindrical shell with radii in the fixed Ck range with a spherical shell with radii in the variable Ri range, as described in Sect. 3.1 and Eq. (A.9). This projected power is proportional to the count rate of photons that are detected by a given instrument, and in a given band, and therefore it is a useful proxy to establish the relative level of emission of the phases as a function of projected radius.
In Eq. (11), Vik is the volume of the intersection between the i-th spherical shell of density ne, i, and a cylindrical shell with inner and outer radii representing the k-th annulus on the focal plane, the latter were chosen, for convenience, as the same as those of the k-th spherical shell. Details of these volumes of intersection were given in Sect. 3.1, with Vik obtained from Eq. (A.9) with the two cylindrical radii correspond to the index k, and the two spherical radii to the index i. Given that the radial profiles are given as a function of r/r200, the volume in Eq. (11) must be multiplied by the value of 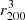 in cm3 to obtain the luminosity in cgs units.
in cm3 to obtain the luminosity in cgs units.
3.3. The PyAtomDB code and atomic data
This project makes use of the AtomDB data and models of X-ray and extreme ultraviolet emitting astrophysical spectra for hot and optically thin plasma. These data were originally developed by Smith et al. (2001) as the Astrophysical Plasma Emission Database (APED) and the Astrophysical Plasma Emission Code (APEC). These codes result from a development started with Raymond & Smith (1977) that was followed by the codes of Mewe et al. (1985, 1986) and Kaastra (1992). Over the years, as new and improved calculations in atomic data became available, AtomDB was improved by Foster et al. (2012) and eventually led to the PyAtomDB project that is easily accessible through python (Foster & Heuer 2020). The latter is the version that we use in this project.
In particular, this project uses the PyAtomDB function calc_power to calculate the X-ray emissivity of a plasma in collisional ionisation equilibrium (CIE; e.g. Mazzotta et al. 1998). The code uses the Anders & Grevesse (1989) solar abundances that can be re-scaled, either individually or as a whole, by an overall metal abundance A as a fraction of solar. Moreover, the emissivity can be conveniently decomposed into the contribution from each element (i.e. using return_line_emissivity), and, for each element, it is possible to calculate the contribution from each transition; e.g., it is possible to calculate the power of the O VII resonance line at 21.602 Å, or that of any other X-ray line of interest.
Given that the emissivity calculated via atomDB is rescaled by the product (ne ⋅ nH) of the plasma, which is a function of the metal abundances, it is also necessary to specify the mean weights of the various plasma species. In general, the number density of species j is related to the total mass density of the medium ρ via
where Xj is the fraction by mass of the j-th species (say, H, He, electrons, heavy ions, etc.),
and mj is the atomic mass of the species (∼mp for hydrogen, ∼4mp for helium, etc.). The mass density ρ (in a given shell) includes all species that are present in the plasma,
where z labels all metals, defined as elements with atomic number Z > 2. It is customary to define the hydrogen mass fraction as X, that of helium as Y, and that of all other metals combined as Z (not to be confused with the same letter that is also used for the overall metal abundance). It is then true that the sum of the mass fractions is
According to typical solar abundance ratios, the number density of He is approximately 10% of that of H. Specifically, nHe ≃ 0.1 ⋅ nH according to Anders & Grevesse (1989), while Lodders (2003) found a number ratio of nHe = 0.084 ⋅ nH. Assuming that Z = 0 (negligible contribution from metals to mass), and an 8.4% ratio by number of helium-to-hydrogen, the mass fractions are approximately X = 0.749 and Y = 0.251.
It is now convenient to define themean molecular weights of a given species via
In particular, the mean molecular or atomic weight μ is the average weight (in units of the proton mass mp) of a given particle using the density of all particles, n = ne + nH + nHe + nx. It therefore follows that
where the other terms can be ignored inasmuch as there is a small fraction of metals. Clearly, Eqs. (14) and (15) are equivalent.
Characteristic values for the mean atomic weights in the ICM, assuming fully ionised plasma with primordial abundances (metal mass fraction Z = 0), are μH = 1.335, μe = 1.143, μHe = 15.94, and μ = 0.593. This means that one electron traces an equivalent mass of 1.143 protons, and one hydrogen atom traces approximately the mass of 1.335 protons. When metals are taken into account, their values are slightly larger, while the ratio μH/μe = ne/nH ≃ 1.168 remains approximately the same. From the IllustrisTNG simulations we measure a ratio of approximately ne/nH = 1.16 for all species, at all radii, which is consistent with these calculations.
Collisional ionisation equilibrium (CIE) is believed to apply in the hot ICM, and with good approximation to the lower density warm-hot phase at log T(K) = 5 − 7. Utilising the CIE approximation, it is therefore also possible to predict column densities of any ion of interest along a sightline at any projected radius from the centre of the cluster, and for any phase. This gives us the ability to study the detectability of absorption lines from a give atomic species. In this initial study, we focus on four ions that are prominent in CIE at the temperatures of the warm-hot phase, namely O VII, O VIII, Ne IX, and Ne X (e.g. Mazzotta et al. 1998), and probe both their soft X-ray emission and their column densities. A more detailed analysis on their detectability (through current and upcoming X-ray instruments) will be presented in a follow-up paper. Table 3 provides the atomic data for the lines of interest.
Atomic data for selected X-ray lines of interest, for ions that are expected to be abundant in the warm-hot phase.
4. Results: X-ray emission from IllustrisTNG circum-cluster environments
This section presents the results of the X-ray emissivity from the IllustrisTNG circum-cluster environments. These predictions have been estimated from the methods described in Sect. 3, which use the average thermodynamic radial profiles of clusters described in Sect. 2.4.
4.1. The soft X-ray emission near clusters: initial results
We used Eq. (11) to measure the average luminosity (proportional to the count rate) of the three phases as a function of radial distance from the centre of a cluster, with the density and other thermodynamic quantities at each radius averaged for a given mass bin as described in Sect. 2.4. Given that the radial profiles are normalised to the r200 of each cluster in the IllustrisTNG simulations, the volumes Vi, k obtained from Eq. (A.9) are multiplied by 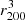 in units of cm3.
in units of cm3.
Figure 12 features the luminosity per unit area, or surface brightness according to Eq. (7) in a soft X-ray band of choice, as a function of the projected radius, for all the clusters. As illustrated in Fig. 12, it is clear that just outside of the virial radius, the luminosity of the warm gas becomes dominant, relative to that of the hot ICM. Inside clusters (< 1 R200), the ICM gas dominates the soft X-ray surface brightness. Moreover, the WHIM gas has a very low luminosity inside clusters, while the entire WARM phase has a ≥1% surface brightness compared to the hot ICM. As discussed previously in Sect. 2, we expect that the soft X-luminosity of warm gas inside clusters is mostly the result of WCGM gas clumps, whereas outside clusters it is mostly induced by WHIM gas. Indeed, beyond 1 R200, the soft X-ray luminosity of WHIM gas becomes higher than ICM luminosity.
 |
Fig. 12. X-ray surface brightness SX (proportional to luminosity per unit area) in a soft X-ray band of choice (0.2–1 keV) for the various phases of the gas for all clusters. |
In Fig. 12, we also highlight the contribution of the total emission by selected ions (O VII, O VIII, Ne IX and Ne X), inclusive of their continuum and line emission. Focusing on the metal-line emission, we found that surface brightness of metals generally decreases beyond the virial radius, with O VIII being the brightest line followed by Ne X, in agreement with previous predictions with OWLS simulations (see Fig. 1 of van de Voort & Schaye 2013). Moreover, our emission of O VII is also consistent with Tuominen et al. (2023), which found that O VII drops dramatically beyond the virial radii of halos in the EAGLE simulations. In detail, beyond the virial radius of massive clusters, the distribution and oxygen ions (primarily O VI and O VII) are expected to follow cosmic filaments (as described in Artale et al. 2022; Tuominen et al. 2023), and thus, oxygen ions might be good tracers of WHIM gas in filaments connected to clusters (Gouin et al. 2022). In fact, Nelson et al. (2018) used the IllustrisTNG simulation to show that O VI, O VII, and O VIII are mostly induced by the WHIM gas phase. Further details on ions abundances and their emissions as a function of their location (e.g. inside or outside filaments) and gas phases will be discussed in detail in another publication.
In order to address the agreement with measurements of the X-ray luminosity from the hot ICM, Fig. 13 shows a bolometric luminosity in a broad X-ray band (0.1–100 keV; black lines) and the bolometric contribution from free–free bremsstrahlung emission from hydrogen alone, for the three cluster mass bins, according to
 |
Fig. 13. X-ray luminosity in a broad X-ray band (0.1–100 keV) for the hot ICM phase, for the three cluster mass bins: M1 (dotted lines), M2 (dashed lines), and M3 (solid lines). This broad-band luminosity is compared with bolometric luminosities of massive clusters from Pratt et al. (2009). |
where 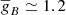 is the velocity and frequency-averaged Gaunt factor (e.g. Rybicki & Lightman 1979). This bremsstrahlung component is part of the AtomDB code, and it is shown in Fig. 13 as an illustration of the relative importance of the continuum H emission and other components of the X-ray radiation. Moreover, in Fig. 13, the bolometric X-ray luminosities from the REXCESS sample of massive clusters out to r500 ≃ 0.65 r200 are shown as green crosses (Pratt et al. 2009). This figure shows that their measurements are consistent with the IllustrisTNG simulated clusters, which spread over a range of cluster masses from 1014 to 1015 M⊙ h−1.
is the velocity and frequency-averaged Gaunt factor (e.g. Rybicki & Lightman 1979). This bremsstrahlung component is part of the AtomDB code, and it is shown in Fig. 13 as an illustration of the relative importance of the continuum H emission and other components of the X-ray radiation. Moreover, in Fig. 13, the bolometric X-ray luminosities from the REXCESS sample of massive clusters out to r500 ≃ 0.65 r200 are shown as green crosses (Pratt et al. 2009). This figure shows that their measurements are consistent with the IllustrisTNG simulated clusters, which spread over a range of cluster masses from 1014 to 1015 M⊙ h−1.
4.2. The soft X-ray emission near clusters due to WARM gas
Figure 14 shows the ratio of WHIM-to-ICM and WARM-to-ICM phases, for the same soft X-ray band as in Fig. 12. This result allows us to highlight the relative importance of the WARM and WHIM gas in the X-ray emission of circum-cluster gas, relative to the usual hot ICM gas. These ratios are consistent with an increasing radial trend in the relative count rate from warm sub-virial gas, relative to the virialised ICM, which reaches a ratio of 100% just outside the virial radius. Moreover, the high-density WARM gas is also capable of producing around 10% of soft X-ray excess emission, compared with that from the hot ICM, towards the interior of the cluster. For most massive clusters (M3 mass bin), in the left panel Fig. 14, the ratio WARM-to-ICM is constant at a value of 10% from radius 0.2 r200 up to 0.7 × r200. These results are quantitatively consistent with the presence of soft X-ray excess emission that was detected by ROSAT and other instruments towards Coma out to the virial radius (e.g. Bonamente et al. 2003; Bonamente 2023) and in the inner regions of several other clusters (e.g. Bonamente et al. 2002). Figure 15 shows the mass budgets associated with the soft excess emission. In the inner regions of the clusters, the soft, excess-emitting warm gas is at the level of a few percent of the hot ICM gas, and radially increasing in importance also as a function of cluster mass (see differences between left and right panels, corresponding, respectively, to all clusters and the most massive ones). An in-depth analysis of the soft excess emission from clusters, which was originally discovered in extreme-ultraviolet observations of Coma and the Virgo clusters (Lieu et al. 1996a,b), will be presented in a follow-up paper.
 |
Fig. 14. Ratios of differential X-ray surface brightness or count rates of warm phases, relative to the hot ICM; left panel for all clusters and right for mass sample M3. The figure also shows the contribution of individual ions, primarily through their line emission, to the total emission from warm sub-virial phases. |
 |
Fig. 15. Ratio of warm gas and WHIM masses relative to hot ICM mass, corresponding to the soft excess fluxes of Fig. 14. Left panel is for all clusters, and right is for mass sample M3. The solid curves represent the total integrated mass out to that radius. |
A comparison of the Bonamente et al. (2022) soft excess emission in Coma with the IllustrisTNG prediction is illustrated in the top panel of Fig. 16, where only the most massive clusters (M200 > 1014.75 M⊙ h−1) are used for the prediction, to match Coma’s virial mass as measured by Mirakhor & Walker (2020) as M(r200) = (8.50 ± 0.55) × 1014 M⊙. One can see that our numerical prediction of soft X-ray excess via WARM gas emission (red line), is in very good agreement with Coma soft excess (green data points). This emission from warm-hot gas near the virial radius matches the level of soft excess emission detected with ROSAT, indicating a thermal origin for the emission, above the contribution from the hot ICM. We note that the large scatter of ratio profile, especially from 0.5 to 0.9 r200, is due to the presence or absence of WARM gas clumps (from one cluster to another), which drastically increase the soft excess and thus induce this large scatter traced by the error bars. The bottom panel of Fig. 16 shows the predictions for the entire mass sample M3 to illustrate the mass dependence of the soft excess emission. A more detailed study of the soft excess as a function of cluster properties will be presented in a separate paper.
 |
Fig. 16. Ratio of differential count rates from warm-hot phases, relative to the hot ICM. Same as in Fig. 14, but for the most massive clusters at M200 > 1014.75 M⊙ h−1 from sample M4 (top panel) to match the mass of the Coma cluster; and for the mass sample M3 (bottom panel). The data points are the soft excess emission measured by Bonamente et al. (2022) in the 0.2–1.0 keV band, based on the ROSAT analysis of Bonamente et al. (2003). |
Similar studies were recently performed with the Magneticum simulation (Churazov et al. 2023), finding that the emission from the diffuse WHIM phase alone was not sufficient to explain the observational result of Bonamente et al. (2022). This is also clearly shown by our results when only the WHIM gas is considered (blue curve in Fig. 16). A qualitatively similar result was also obtained by the Cheng et al. (2005) simulations, which identified low-entropy and high-density warm gas as the likely phase responsible for the soft excess within the virial radius.
4.3. Soft X-ray absorption lines: column density of ions
Our analysis of the IllustrisTNG simulations also measures the column density of any ion of interest, which can be used to address the feasibility of detecting the warm sub-virial gas in absorption. For example, in Fig. 17 we illustrate the average projected column density of four ions of interest for X-ray absorption studies, namely O VII, O VIII, Ne IX, and Ne X. There have been several reports of possible absorption lines associated from intervening warm-hot gas (recently, e.g. Bonamente et al. 2016; Kovács et al. 2019; Ahoranta et al. 2020, 2021; Spence et al. 2023), although usually with limited significance. In particular, given the lower chance alignment of a bright background extragalactic source (e.g. a quasar) with a galaxy cluster along our sightline, there have been, to date, no attempts to detect the warm-hot gas in absorption near clusters. Our preliminary results of Fig. 17 indicate that there is especially a substantial amount of O VIII that is in fact within the reach of upcoming X-ray missions such as the proposed Light Element Mapper (LEM) mission (Kraft et al. 2022).
 |
Fig. 17. Projected column densities of selected X-ray ions for all the clusters. Solid curves are for the hot gas phase, dashed curves for the WARM phase, and dotted curves for the WHIM phase. |
These predictions of X-ray absorption lines in circum-cluster environments are done with the IllustrisTNG simulation and already show a good agreement with observations of O VI column density at low redshift (Nelson et al. 2018). Moreover, as recently highlighted by Butler Contreras et al. (2023) using CAMELS simulations, O VII absorption predictions are quite sensitive to change with supernova feedback models. Qualitatively, our prediction of O VII column density is in agreement with Butler Contreras et al. (2023), which found that the OVII absorbers with column densities log NOVII < 14 cm−2 fall within 1 Mpc from the centre of halos. They thus predicted that the simulated O VII column density are higher in halos and their outskirts than in the large-scale cosmic web. Based on CAMELS simulations, we also referred to Parimbelli et al. (2023), which provides forecasts on WHIM observations with a typical next-generation spectrometer such as X-IFU on board Athena (Barret et al. 2023; Nandra et al. 2013). Along this line, the EAGLE simulations analysed by Wijers & Schaye (2022) estimated the detectability of X-ray metal-line emission from intra-cluster gas and found that O VII and O VII emission lines will be detectable out to the virial radius by the proposed Athena X-IFU instrument. These initial results of X-ray absorption lines from the different gas phase in circum-cluster environments illustrate an example of numerical predictions done through our methodology (Sect. 4) and will be explored in more detail a subsequent publication, including the effects of gas clumping and the volume covering fraction.
5. Discussion and conclusions
This paper outlines the methods of analysing the thermodynamic quantities of simulated galaxy clusters from IllustrisTNG simulations (with M200 > 1014 M⊙ h−1 at z = 0) for the purpose of studying the X-ray emission in the circum-cluster environment. Given the wealth of information provided by these simulations, this paper is intended to be the first in a series of publications in which we analyse the properties of sub-virial gas in and around galaxy clusters, with emphasis on its soft X-ray emission and the effect of the emission on related cluster observables.
Starting from this simulated cluster sample, we extracted azimuthally averaged radial profiles of the density, temperature, and metallicity for different gas phases (e.g. Martizzi et al. 2019; Galárraga-Espinosa et al. 2021): the hot ICM phase at log T(K) > 7 and the WARM phase at 5 ≤ log T(K)≤7. The latter was further divided into WHIM (log nH(cm−3)≤ − 4) and WCGM gas, as it had higher densities. The goal was to provide a simple yet accurate set of averaged quantities that are representative of the hot virialised gas and of the cooler sub-virial gas that is preferentially found in either filamentary structures (WHIM), or in higher density regions such as the surroundings of haloes (WCGM). Indeed, based on this same simulated cluster sample, Gouin et al. (2022) found that gas in the circum-cluster environment is at the interface between the warm gas infalling in filaments connected to clusters, and the hot virialised gas inside clusters (see also Vurm et al. 2023; Lokken et al. 2023).
A first step in our analysis was to validate the IllustrisTNG data with results from observations of galaxy clusters. Temperature profiles of the hot ICM are well studied in X-rays, and the IllustrisTNG profiles (see Sect. 2.4 and Fig. 6) are in excellent agreement with the X-ray measurements of a large sample of X-ray clusters of Ghirardini et al. (2019) and with the Mirakhor & Walker (2020) radial profile of the Coma cluster, one of the nearest and most massive clusters. A similar agreement applies to the measurement of the chemical abundance of the ICM (see Fig. 8), especially towards the virial radius where the abundance of the gas reaches approximately a value of 20% solar. Another key factor for the prediction of X-ray emission is the amount of inhomogeneities in the plasma, since the emissivity is proportional to the square of the plasma density. Accordingly, we measured the clumpiness parameter (see Sect. 2.6), and, as expected, we found that the inhomogeneities is increasing with the radial distance from clusters (Nagai & Lau 2011; Roncarelli et al. 2013; Angelinelli et al. 2021). Our clumpiness radial profile is, moreover, in good agreement with the Eckert et al. (2015b) results, suggesting a good modelling of AGN feedback, a key ingredient for the study of gas inhomogeneities (Planelles et al. 2017). Interestingly, separating gas in various phases, we show that both the hot ICM, WARM, and WHIM gas phases have significant different levels of inhomogeneities, within and beyond the virial radius (see Fig. 9).
To study the X-ray radiation from the various plasma phases, we devised a simple analytical method to project the radial profiles of the thermodynamical quantities of interest. This projection, in conjunction with the X-ray emissivity codes and databases provided by the pyatomdb project (e.g. Foster & Heuer 2020), makes it possible to predict the X-ray luminosity and surface brightness profiles projected on a detector plane. A key test for the reliability of our IllustrisTNG data is the ability to reproduce the X-ray luminosity of the ICM of observed clusters (see Fig. 13), with bolometric luminosities in the range of log LX(erg s−1) = 44 − 45, similar to that of observed clusters (e.g. Pratt et al. 2009).
This paper also presents initial results for the analysis of the X-ray emission from the warm sub-virial gas. To date, there are no significant observational constraints on soft X-ray emission from circum-cluster sub-virial plasma, due to the challenges associated with the detection of X-rays in emission at those temperatures. The preliminary analysis in Sect. 4 shows a fundamental new result that is the key takeaway of this initial paper: the warm sub-virial gas, either in the form of low-density WHIM gas or as higher density WCGM, features a surface brightness that is at the same level as that from the ICM near the virial radius, and it becomes the dominant source of soft X-ray radiation at larger distances from the centre. This is a key new result that had not previously been noted, and it will be the basis for a more detailed investigation in an separate publication. For example, Fig. 14 shows that the average soft X-ray emission from the WARM gas in the entire cluster sample reaches 100% of the hot ICM emission at r/r200 ≃ 0.8 − 1 (left panel), with a similar result for the most massive clusters alone (right panel). It is therefore clear that ignoring this emission component would lead to biases in the inference of such quantities as cluster masses measured from X-rays. In the inner cluster regions, the relative importance of the soft X-ray emission from warm gas is usually at a lower level of ∼1–10%. In particular, focusing on the Coma cluster and its soft X-ray emission (Bonamente 2023), we found that the most massive IllustrisTNG clusters reproduce well Coma’s soft X-ray excess (see Fig. 16), supporting our finding that WARM gas is a crucial ingredient to understanding soft X-ray emission in circumcluster environments. Our method of analysis is also able to identify which ions are present as a function of radial distance, thanks to the capabilities of the pyAtomDB codes. This feature can be used to guide observational searches for the WARM gas, and it will be explored in future publications.
In summary, the preliminary results presented in this paper are consistent with a thermal origin for the cluster soft excess emission detected in a number of clusters, such as in Coma (Bonamente et al. 2003, 2022) and in other clusters (Bonamente et al. 2002). The emission, which is at the ∼10% level in the inner regions and rising in importance towards the virial radius, is naturally explained by the warm-hot sub-virial phases seen in these IllustrisTNG simulations. A more detailed analysis of the soft X-ray emission is deferred to a follow-up publication, where we also plan to present results as a function of cluster masses and other structural properties, such as the degree of connectivity that is used as a proxy for the possible presence of WHIM filaments (Gouin et al. 2022), whether such emission is due to the denser WCGM or to lower-density WHIM filaments, and its dependence on cluster properties.
Although the symbol ρ is also used to denote volume density, e.g., in Eq. (3), we opted to use this symbol for the radial coordinate in cylindrical coordinates, and the corresponding 2D radial coordinates in the focal plane (see Appendix A). The reader should be able to distinguish them according to the context.
Acknowledgments
This research has been supported by the funding for the ByoPiC project from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement ERC-2015-AdG 695561 (ByoPiC, https://byopic.eu). C.G. thanks the very useful comments and discussions with all the members of the ByoPiC team, and in particular N. Aghanim. We thank the IllustrisTNG Collaboration for providing free access to the data used in this work. C.G. is supported by a KIAS Individual Grant (PG085001) at Korea Institute for Advanced Study.
References
- Ahoranta, J., Nevalainen, J., Wijers, N., et al. 2020, A&A, 634, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahoranta, J., Finoguenov, A., Bonamente, M., et al. 2021, A&A, 656, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, S. W., Schmidt, R. W., Ebeling, H., Fabian, A. C., & van Speybroeck, L. 2004, MNRAS, 353, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Angelinelli, M., Vazza, F., Giocoli, C., et al. 2020, MNRAS, 495, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Angelinelli, M., Ettori, S., Vazza, F., & Jones, T. W. 2021, A&A, 653, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansarifard, S., Rasia, E., Biffi, V., et al. 2020, A&A, 634, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artale, M. C., Haider, M., Montero-Dorta, A. D., et al. 2022, MNRAS, 510, 399 [Google Scholar]
- Bahcall, J. N., & Sarazin, C. L. 1977, ApJ, 213, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, D. J., Kay, S. T., Bahé, Y. M., et al. 2017, MNRAS, 471, 1088 [Google Scholar]
- Barnes, D. J., Vogelsberger, M., Pearce, F. A., et al. 2021, MNRAS, 506, 2533 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Albouys, V., Herder, J.-W. D., et al. 2023, Exp. Astron., 55, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Biffi, V., Mernier, F., & Medvedev, P. 2018, Space Sci. Rev., 214, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M. 2022, Statistics and Analysis of Scientific Data (Springer) [CrossRef] [Google Scholar]
- Bonamente, M. 2023, MNRAS, 522, 1987 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Lieu, R., Joy, M. K., & Nevalainen, J. H. 2002, ApJ, 576, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Joy, M. K., & Lieu, R. 2003, ApJ, 585, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Joy, M. K., LaRoque, S. J., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Nevalainen, J., Tilton, E., et al. 2016, MNRAS, 457, 4236 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Mirakhor, M., Lieu, R., & Walker, S. 2022, MNRAS, 514, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A. 2000, ApJ, 539, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Butler Contreras, A., Lau, E. T., Oppenheimer, B. D., et al. 2023, MNRAS, 519, 2251 [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, L.-M., Borgani, S., Tozzi, P., et al. 2005, A&A, 431, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churazov, E., Khabibullin, I. I., Dolag, K., Lyskova, N., & Sunyaev, R. A. 2023, MNRAS, 523, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W., Knebe, A., Yepes, G., et al. 2018, MNRAS, 480, 2898 [Google Scholar]
- Danforth, C. W., Keeney, B. A., Tilton, E. M., et al. 2016, ApJ, 817, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Cen, R., Ostriker, J. P., et al. 2001, ApJ, 552, 473 [Google Scholar]
- Dolag, K., Komatsu, E., & Sunyaev, R. 2016, MNRAS, 463, 1797 [Google Scholar]
- Dubois, Y., Peirani, S., Pichon, C., et al. 2016, MNRAS, 463, 3948 [Google Scholar]
- Eckert, D., Vazza, F., Ettori, S., et al. 2012, A&A, 541, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Roncarelli, M., Ettori, S., et al. 2015a, MNRAS, 447, 2198 [Google Scholar]
- Eckert, D., Jauzac, M., Shan, H., et al. 2015b, Nature, 528, 105 [Google Scholar]
- Ettori, S. 2002, MNRAS, 330, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Hu, E. M., Cowie, L. L., & Grindlay, J. 1981, ApJ, 248, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, A. R., & Heuer, K. 2020, Atoms, 8, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [Google Scholar]
- Fusco-Femiano, R., & Lapi, A. 2018, MNRAS, 475, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Galárraga-Espinosa, D., Aghanim, N., Langer, M., & Tanimura, H. 2021, A&A, 649, A117 [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019, A&A, 621, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghizzardi, S., Molendi, S., van der Burg, R., et al. 2021, A&A, 646, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacconi, R., Murray, S., Gursky, H., et al. 1972, ApJ, 178, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Gianfagna, G., Rasia, E., Cui, W., et al. 2023, MNRAS, 518, 4238 [Google Scholar]
- Gouin, C., Gallo, S., & Aghanim, N. 2022, A&A, 664, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirschmann, M., Dolag, K., Saro, A., et al. 2014, MNRAS, 442, 2304 [Google Scholar]
- Kaastra, J. 1992, Internal SRON-Leiden Rep., Ver. 2 [Google Scholar]
- Kovács, O. E., Bogdán, Á., Smith, R. K., Kraft, R. P., & Forman, W. R. 2019, ApJ, 872, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R., Markevitch, M., Kilbourne, C., et al. 2022, ArXiv e-prints [arXiv:2211.09827] [Google Scholar]
- Kravtsov, A. V. 1999, Ph.D. Thesis, New Mexico State University, USA [Google Scholar]
- Kravtsov, A. V., Klypin, A., & Hoffman, Y. 2002, ApJ, 571, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Kriss, G. A., Cioffi, D. F., & Canizares, C. R. 1983, ApJ, 272, 439 [Google Scholar]
- Lieu, R., Mittaz, J. P. D., Bowyer, S., et al. 1996a, ApJ, 458, L5 [CrossRef] [Google Scholar]
- Lieu, R., Mittaz, J. P. D., Bowyer, S., et al. 1996b, Science, 274, 1335 [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
- Lokken, M., Cui, W., Bond, J. R., et al. 2023, MNRAS, 523, 1346 [NASA ADS] [CrossRef] [Google Scholar]
- Lyskova, N., Churazov, E., Khabibullin, I. I., et al. 2023, MNRAS, 525, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Allen, S. W., Morris, R. G., et al. 2014, MNRAS, 440, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Morris, R. G., Allen, S. W., et al. 2022, MNRAS, 510, 131 [Google Scholar]
- Martizzi, D., Vogelsberger, M., Artale, M. C., et al. 2019, MNRAS, 486, 3766 [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazzotta, P., Rasia, E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E. 1999, AJ, 117, 2398 [Google Scholar]
- Mernier, F., de Plaa, J., Kaastra, J. S., et al. 2017, A&A, 603, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511 [NASA ADS] [Google Scholar]
- Mirakhor, M. S., & Walker, S. A. 2020, MNRAS, 497, 3204 [Google Scholar]
- Mirakhor, M. S., & Walker, S. A. 2021, MNRAS, 506, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Mirakhor, M. S., Walker, S. A., & Runge, J. 2022, MNRAS, 509, 1109 [Google Scholar]
- Mitchell, R. J., Culhane, J. L., Davison, P. J. N., & Ives, J. C. 1976, MNRAS, 175, 29P [CrossRef] [Google Scholar]
- Morandi, A., Sun, M., Mulchaey, J., Nagai, D., & Bonamente, M. 2017, MNRAS, 469, 2423 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., & Lau, E. T. 2011, ApJ, 731, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Nelson, D., Kauffmann, G., Pillepich, A., et al. 2018, MNRAS, 477, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, D., Springel, V., Pillepich, A., et al. 2019, Comput. Astrophys. Cosmol., 6, 2 [Google Scholar]
- Nevalainen, J., David, L., & Guainazzi, M. 2010, A&A, 523, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parimbelli, G., Branchini, E., Viel, M., Villaescusa-Navarro, F., & ZuHone, J. 2023, MNRAS, 523, 2263 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planelles, S., Fabjan, D., Borgani, S., et al. 2017, MNRAS, 467, 3827 [Google Scholar]
- Planelles, S., Mimica, P., Quilis, V., & Cuesta-Martínez, C. 2018, MNRAS, 476, 4629 [NASA ADS] [CrossRef] [Google Scholar]
- Pop, A.-R., Hernquist, L., Nagai, D., et al. 2022, MNRAS, submitted [arXiv:2205.11528] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragagnin, A., Dolag, K., Biffi, V., et al. 2017, Astron. Comput., 20, 52 [Google Scholar]
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Roncarelli, M., Ettori, S., Borgani, S., et al. 2013, MNRAS, 432, 3030 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley-Interscience) [Google Scholar]
- Sarazin, C. L. 1988, in Cambridge Astrophysics Series (Cambridge: Cambridge University Press) [Google Scholar]
- Serlemitsos, P. J., Smith, B. W., Boldt, E. A., Holt, S. S., & Swank, J. H. 1977, ApJ, 211, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [Google Scholar]
- Snowden, S. L., Freyberg, M. J., Plucinsky, P. P., et al. 1995, ApJ, 454, 643 [Google Scholar]
- Spence, D., Bonamente, M., Nevalainen, J., et al. 2023, MNRAS, 523, 2329 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, MNRAS, 401, 791 [Google Scholar]
- Tanimura, H., Aghanim, N., Kolodzig, A., Douspis, M., & Malavasi, N. 2020, A&A, 643, L2 [EDP Sciences] [Google Scholar]
- Tanimura, H., Aghanim, N., Douspis, M., & Malavasi, N. 2022, A&A, 667, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torrey, P., Hopkins, P. F., Faucher-Giguère, C.-A., et al. 2017, MNRAS, 467, 2301 [NASA ADS] [CrossRef] [Google Scholar]
- Towler, I., Kay, S. T., & Altamura, E. 2023, MNRAS, 520, 5845 [NASA ADS] [CrossRef] [Google Scholar]
- Tuominen, T., Nevalainen, J., Heinämäki, P., et al. 2023, A&A, 671, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van de Voort, F., & Schaye, J. 2013, MNRAS, 430, 2688 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Eckert, D., Simionescu, A., Brüggen, M., & Ettori, S. 2013, MNRAS, 429, 799 [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [Google Scholar]
- Vogelsberger, M., Marinacci, F., Torrey, P., et al. 2018, MNRAS, 474, 2073 [NASA ADS] [CrossRef] [Google Scholar]
- Vurm, I., Nevalainen, J., Hong, S. E., et al. 2023, A&A, 673, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, S., Simionescu, A., Nagai, D., et al. 2019, Space Sci. Rev., 215, 7 [Google Scholar]
- Wan, J. T., Mantz, A. B., Sayers, J., et al. 2021, MNRAS, 504, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberger, R., Springel, V., Pakmor, R., et al. 2018, MNRAS, 479, 4056 [Google Scholar]
- Wicker, R., Douspis, M., Salvati, L., & Aghanim, N. 2023, A&A, 674, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijers, N. A., & Schaye, J. 2022, MNRAS, 514, 5214 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H. Y. K., & Reynolds, C. S. 2016, ApJ, 818, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, J. H., & Putman, M. E. 2013, ApJ, 772, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Zhuravleva, I., Churazov, E., Kravtsov, A., et al. 2013, MNRAS, 428, 3274 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Methods for the projection of radial profiles
This appendix describes the analytical method to obtain the volume of intersection of a spherical shell of radii Rmin and Rmax, representing the volume of a thermodynamic quantity such as density or temperature, with a concentric cylindrical shell of (projected) radii ρmin and ρmax, representing the volume of integration along the sightline. The result is an analytical formula for the volume V(ρmin, ρmax, Rmin, Rmax), which is used in (11) and elsewhere in this work for the projection of radial profiles.
A.1. The volume of intersection of a sphere with a concentric cylinder
This initial problem consists of finding the volume of intersection of a whole sphere of radius R with a concentric cylinder of radius ρmax. If ρmax ≥ R, the intersection is the entire sphere, so the interesting case is when ρmax ≤ R.
The volume element in cylindrical coordinates is dV = r dr dθdz, and the limits of integration to obtain the volume of intersection are
where z(ρ, R) represents the maximum value of the Cartesian z coordinate for a fixed value of the ρ cylindrical radius, and it is given by
Equation A.2 means that as the cylindrical coordinate spans its range between 0 and ρmax, the maximum value of z for integration decreases from the sphere’s radius R at the centre (ρ = 0) to a smaller value, 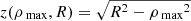 , of course in the interesting case of ρmax ≤ R. This leads to a volume of intersection of
, of course in the interesting case of ρmax ≤ R. This leads to a volume of intersection of
which can be immediately solved with a change of variable u = R2 − ρ2, du = −2ρdρ, again assuming ρmax ≤ R, whereby
This integral leads to the results that the volume of intersection of a sphere of radius R with a concentric cylinder of radius ρmax is given by
This volume is shown as the grey area in Figure A.1.
 |
Fig. A.1. Volumes of intersection for the projection of a 3D radial distribution onto a 2D plane. In grey is the volume of intersection of concentric sphere and cylinder. In blue is the volume of intersection of a spherical shell with radii Rmin, Rmax with a cylinder of radius ρmax(in red). The volume of interaction represents the volume contribution from the spherical shell (assumed to have uniform thermodynamical properties) to a circular region of radius ρ (dashed red line). For a cylindrical shell of radii ρmin and ρmax (in orange), the area of intersection represents the contribution to the annulus by the shell. Given the azimuthal symmetry of both sphere and cylinder, the polar angle θ is not displayed. |
A.2. Volume of intersection of a spherical shell with a concentric cylinder
The next problem is intersecting a spherical shell with radii Rmin, Rmax, with the same concentric cylinder of radius ρmax. The volume of interaction represents the volume contribution from the spherical shell to a circular region of radius ρmax in the plan of the detector.
For this volume, the cylindrical coordinates have the following ranges:
where the new limits for the z coordinate enforce the two radii of the spherical shell. This geometry is represented in Figure A.1.
With the limits of integration according to Eq. A.6, the volume of intersection is given by
provided that ρmax ≤ Rmin, so that the lower limit of integration remains described by Eq. A.2. The case of Rmin ≤ ρmax ≤ Rmax (i.e. in Figure A.1 the red dashed line would be between the values r = 7 and 8) is not used in practice, and it will be discussed separately. This integral is given by
In Eq. A.8, the top case corresponds to a spherical shell that is completely enclosed by the cylinder. The middle case corresponds to the situation illustrated in Figure A.1, where Eq. A.7 applies, and therefore the integral is the difference of the two contributions given by Eq. A.5 (which has the limitation ρmax ≤ Rmin). The last case is not used, since we chose the boundaries of the annuli to be the same as those of the spherical shells.
A.3. Volume of intersection of a spherical shell with a concentric cylindrical shell
Finally, the volume of interest is the intersection of a spherical shell with a concentric cylindrical shell of radii ρmin, ρmax, and it is represented by the orange shaded area in Figure A.1. To simplify calculations, we chose the same radial bins for the 3D radius r and for the projected cylindrical radius ρ, in such a way that the radii ρmin, ρmax always fall at the boundaries of the Rmin, Rmax spherical radii (i.e. as for the orange dashed lines in Figure A.1, but not the red line, which was used only for illustration purposes). With this choice, it is also not necessary to evaluate the case at the bottom of Eq. A.8.
Given the linearity of the integral, the volume of intersection is given with
as the difference of the two contributions according to Eq. A.8. This volume is used to integrate the total power or luminosity emitted by a given radial region along the sightline, given that the radiation is expected to be optically thin, and, therefore, the surface brightness is added linearly along the sightline.
Appendix B: Statistical analysis of the radial profiles
The radial profiles of the thermodynamic quantities (Figures 3 through 9) are obtained by averaging the quantity of interest for each of the 138 clusters at each of the 50 radii. The mean number of cells per gas phase as a function of the radial distance is shown in Fig. B.1. We then obtain a distribution of the averaged quantity, for all clusters that have data at that radius. At a given radius, not all of the clusters have data, and therefore certain data points — such as those at the lowest radii for the electron density of the WARM phase in Fig. 3, bottom right panel — result from the use of only a small fraction of all the clusters in the sample. When fewer than three clusters have data, we chose not to report that quantity.
 |
Fig. B.1. Mean number of gas cells, as depending of the cluster centric distance, for two mass bins M1 and M3, and considering the two dominant gas phases (WARM and Hot gas). |
With the distribution of the value of the quantity for the ≤ 138 that have data at that radius, we can then calculate key statistics such as the mean, median, and standard deviation. In Fig. B.2, we show selected distributions to illustrate the method of analysis. For example, typical distributions of the ICM density use all of the 138 clusters as in the top panel of Fig. B.2, while often a smaller number of clusters have WHIM or WARM particles at small distances from the cluster centre. The bottom panel of Fig. B.2 illustrates a typical situation with the distribution of the clumpiness factor C for the WARM and WHIM phases, whereas the distribution is significantly skewed, resulting in a large difference between the mean and the median. Radial profiles of the ratio of the mean to the median of the distributions, for the hot ICM and WARM nH density and for the clumpiness factor, are shown in Fig. B.3, to illustrate the difference between the two statistics. We chose to report the median as the most representative value of the distribution and its standard deviation as obtained from a Monte Carlo bootstrap resampling method, as a measure of the variability in the distribution.
 |
Fig. B.2. Distribution of values of selected quantities from the analysis of the 138 IllustrisTNG clusters, for the radial bin 11. Top: hot ICM density; Bottom: clumpiness factor for WARM phase. |
The choice to use the median as a representative value for a parameter is well documented in the statistical literature because of its greater insensitivity to outliers compared to the sample mean (for a review, see e.g. Bonamente 2022). In fact, most studies of the clumpiness of the gas use the median as a representative value (e.g. Planelles et al. 2017; Nagai & Lau 2011), and, similarly, for other thermodynamic quantities (e.g. Zhuravleva et al. 2013; Eckert et al. 2015b). Towler et al. (2023) also investigates the difference between the mean and median of certain thermodynamical quantities in simulations (see their Fig. 6) and concludes that mean of the density–related quantities are indeed more susceptible to bias due to the effect of substructures compared to the median. In our simulations, we also found this to be true; in fact, in the top panel of Fig. B.3 the datapoint corresponding to r/r200 = 2.75 is not plotted, as it falls significantly above the scale (for a mean/median ratio above 10,000) due to the effect of a small clump of hot gas near that radius that is likely unrelated to the hot ICM of one cluster in the sample (cluster number 130).
 |
Fig. B.3. Radial distribution of the ratio of the mean to the median for selected quantities. Top: nH density for the hot ICM and the WARM gas; Bottom: clumpiness factor. |
Finally, we discuss the density limit between the WHIM and WCGM gas (which was set at nH[cm−3] = 10−4). In Fig. B.4, we illustrate the evolution of WHIM and WCGM gas abundance as a function of this limit (similar to Gouin et al. 2022). Physically, the main reason for this threshold at nH[cm−3] = 10−4 is the separation between diffuse gas and the gas associated to haloes (living in denser regions), and the value is the one allowing to perform this separation in the TNG model (Martizzi et al. 2019). As we can see in Fig. B.4, the lower the density limit for WHIM gas definition, the smaller the fraction outside clusters. As a consequence, the WCGM gas phase becomes more abundant. In our case, we defined diffuse warm gas (WHIM) with a density threshold of nH[cm−3]< 10−4, and we focus on the WARM gas phase (WCGM+WHIM). This is physically motivated because our interest is on the impact of the full warm gas on the soft X-ray emission, in contrast to the hot ICM.
 |
Fig. B.4. Averaged mass fraction of gas phases as depending of the cluster distance, for different density thresholds of WHIM gas (respectively nH < 1e − 4, 5e − 5, 1e − 5 cm−3). |
Appendix C: Tables of radial evolution of cluster properties
This appendix reports the average radial profiles of the thermodynamic properties of gas, and namely the density and volume covering fraction in Table C.1, temperature and metal abundance in Table C.2, and clumping factor in Table C.3. Each average quantity is reported as a function of phase (ICM, WHIM, and WARM) and for selected radial distances from the cluster’s centre. In each table, the first block is for the median quantity of all the clusters and the other blocks, respectively, for the three mass bins in order of increasing average mass (M1, M2, and M3).
Density and volume covering fractions of the hot ICM, WHIM, and WARM gas phases in the IllustrisTNG clusters for representative radii (see Fig. 3 and 4). The four blocks correspond, respectively, to all clusters followed by the mass samples M1, M2, and M3.
Temperature and chemical abundance of the hot ICM, WHIM, and WARM gas phases in the IllustrisTNG clusters, for representative radii (see Fig. 6 and 8). The four blocks correspond, respectively, to all clusters followed by the mass samples M1, M2, and M3.
Clumping factor of the hot ICM, WHIM, and WARM gas phases in the IllustrisTNG clusters for representative radii (see Fig. 9) and considering all the gas. The four blocks correspond, respectively, to all clusters, followed by the mass samples M1, M2, and M3.
All Tables
Main properties of the all cluster sample and its four mass bins M1, M2, M3, and M4 (notice that M4 is included in M3).
Atomic data for selected X-ray lines of interest, for ions that are expected to be abundant in the warm-hot phase.
Density and volume covering fractions of the hot ICM, WHIM, and WARM gas phases in the IllustrisTNG clusters for representative radii (see Fig. 3 and 4). The four blocks correspond, respectively, to all clusters followed by the mass samples M1, M2, and M3.
Temperature and chemical abundance of the hot ICM, WHIM, and WARM gas phases in the IllustrisTNG clusters, for representative radii (see Fig. 6 and 8). The four blocks correspond, respectively, to all clusters followed by the mass samples M1, M2, and M3.
Clumping factor of the hot ICM, WHIM, and WARM gas phases in the IllustrisTNG clusters for representative radii (see Fig. 9) and considering all the gas. The four blocks correspond, respectively, to all clusters, followed by the mass samples M1, M2, and M3.
All Figures
 |
Fig. 1. Phase-space of gas cells around a given cluster in the TNG300-1 simulation, shown by the normalised 2D histogram. The hot gas is defined with a temperature of T[K]> 107, and the WARM gas with temperature between 105 < T[K]< 107. The WHIM gas is a sub-sample of the WARM gas, with the condition of being diffuse, i.e., its density is nH[cm−3]< 10−4. |
| In the text | |
 |
Fig. 2. Distribution of gas within 5 R200 around a given massive cluster. The first panel shows the distribution of all the gas cells, the second one only the hot gas, the third one only the WHIM gas, and the left panel the WARM gas. |
| In the text | |
 |
Fig. 3. Electron density ne calculated according to the averaging of Eq. (1) is shown with a solid line, and the mass density calculated according to the averaging of Eq. (3) is shown with a dashed line. The median profiles for the entire cluster sample are given. |
| In the text | |
 |
Fig. 4. Volume covering fractions; same sample as in Fig. 3. |
| In the text | |
 |
Fig. 5. Zoomed-in view of Fig. 3, the median radial profiles of the mass density for the ICM gas phase for all the clusters (left panel), and the most massive ones (M3 mass bin, right panel). We highlight the comparison with X-COP observations (Ghirardini et al. 2019), those of a sample of 31 nearly clusters by Eckert et al. (2012), and the Coma cluster (Mirakhor & Walker 2020). |
| In the text | |
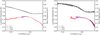 |
Fig. 6. Radial profiles of temperatures; same samples as in Fig. 5. |
| In the text | |
 |
Fig. 7. Zoomed-in view of Fig. 6 for hot ICM temperature profiles and comparison with selected observations. TSL is the projected spectroscopic temperature according to the density-square weights of Mazzotta et al. (2004; uncertainty bands are similar to those of the 3D temperatures, and they are not shown). Left: All clusters. Right: Mass sample M3. |
| In the text | |
 |
Fig. 8. Radial profiles of abundances, same samples as in Fig. 5. |
| In the text | |
 |
Fig. 9. Median radial profiles of clumping factor average over all the clusters. In addition to the usual ICM, WHIM, and WARM phases, we also report the clumpiness obtained by using all the gas cells (no phase selection). |
| In the text | |
 |
Fig. 10. Comparison of hot ICM clumpiness factor for the most massive cluster (M3 mass bin) with the simulations of Planelles et al. (2017) in a sample of clusters in a comparable mass range; clumpiness in Coma from Mirakhor & Walker (2020); and Eckert et al. (2015b) measurements. |
| In the text | |
 |
Fig. 11. Cumulative radial profiles of gas mass and hydrostatic mass for entire cluster sample. The X-ray measurements of Ettori et al. (2009) and Vikhlinin et al. (2006) are for r ≤ r500, and the Mantz et al. (2022) gas mass fraction was calculated in a radial shell of 0.8 − 1.2 × r2500, where r2500 ≃ 0.45 × r500. |
| In the text | |
 |
Fig. 12. X-ray surface brightness SX (proportional to luminosity per unit area) in a soft X-ray band of choice (0.2–1 keV) for the various phases of the gas for all clusters. |
| In the text | |
 |
Fig. 13. X-ray luminosity in a broad X-ray band (0.1–100 keV) for the hot ICM phase, for the three cluster mass bins: M1 (dotted lines), M2 (dashed lines), and M3 (solid lines). This broad-band luminosity is compared with bolometric luminosities of massive clusters from Pratt et al. (2009). |
| In the text | |
 |
Fig. 14. Ratios of differential X-ray surface brightness or count rates of warm phases, relative to the hot ICM; left panel for all clusters and right for mass sample M3. The figure also shows the contribution of individual ions, primarily through their line emission, to the total emission from warm sub-virial phases. |
| In the text | |
 |
Fig. 15. Ratio of warm gas and WHIM masses relative to hot ICM mass, corresponding to the soft excess fluxes of Fig. 14. Left panel is for all clusters, and right is for mass sample M3. The solid curves represent the total integrated mass out to that radius. |
| In the text | |
 |
Fig. 16. Ratio of differential count rates from warm-hot phases, relative to the hot ICM. Same as in Fig. 14, but for the most massive clusters at M200 > 1014.75 M⊙ h−1 from sample M4 (top panel) to match the mass of the Coma cluster; and for the mass sample M3 (bottom panel). The data points are the soft excess emission measured by Bonamente et al. (2022) in the 0.2–1.0 keV band, based on the ROSAT analysis of Bonamente et al. (2003). |
| In the text | |
 |
Fig. 17. Projected column densities of selected X-ray ions for all the clusters. Solid curves are for the hot gas phase, dashed curves for the WARM phase, and dotted curves for the WHIM phase. |
| In the text | |
 |
Fig. A.1. Volumes of intersection for the projection of a 3D radial distribution onto a 2D plane. In grey is the volume of intersection of concentric sphere and cylinder. In blue is the volume of intersection of a spherical shell with radii Rmin, Rmax with a cylinder of radius ρmax(in red). The volume of interaction represents the volume contribution from the spherical shell (assumed to have uniform thermodynamical properties) to a circular region of radius ρ (dashed red line). For a cylindrical shell of radii ρmin and ρmax (in orange), the area of intersection represents the contribution to the annulus by the shell. Given the azimuthal symmetry of both sphere and cylinder, the polar angle θ is not displayed. |
| In the text | |
 |
Fig. B.1. Mean number of gas cells, as depending of the cluster centric distance, for two mass bins M1 and M3, and considering the two dominant gas phases (WARM and Hot gas). |
| In the text | |
 |
Fig. B.2. Distribution of values of selected quantities from the analysis of the 138 IllustrisTNG clusters, for the radial bin 11. Top: hot ICM density; Bottom: clumpiness factor for WARM phase. |
| In the text | |
 |
Fig. B.3. Radial distribution of the ratio of the mean to the median for selected quantities. Top: nH density for the hot ICM and the WARM gas; Bottom: clumpiness factor. |
| In the text | |
 |
Fig. B.4. Averaged mass fraction of gas phases as depending of the cluster distance, for different density thresholds of WHIM gas (respectively nH < 1e − 4, 5e − 5, 1e − 5 cm−3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



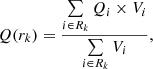
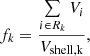
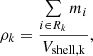
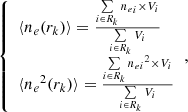
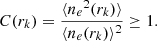
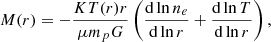
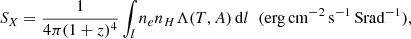
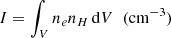
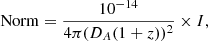
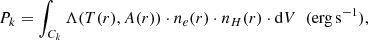
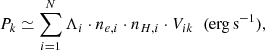
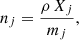
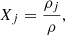
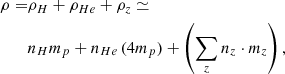
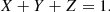
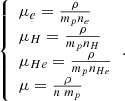
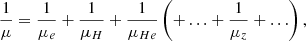
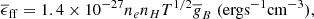
![$$ \begin{aligned} {\left\{ \begin{array}{ll} \rho \in [0, \rho _{\mathrm{max}}]\\ \theta \in [0, 2 \pi ]\\ z \in [0, z(\rho ,R)]\\ \end{array}\right.} ,\end{aligned} $$](/articles/aa/full_html/2023/12/aa47125-23/aa47125-23-eq30.gif)
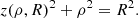
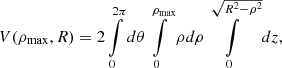
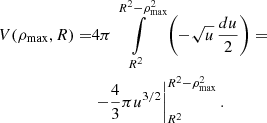
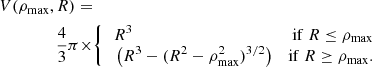
![$$ \begin{aligned} {\left\{ \begin{array}{ll} \rho \in [0, \rho _{\mathrm{max}}]\ (\mathrm{same as in previous case})\\ \theta \in [0, 2 \pi ]\ (\mathrm{same as in previous case})\\ z \in [z(\rho ,R_{\mathrm{min}}), z(\rho ,R_{\mathrm{max}})] \end{array}\right.}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47125-23/aa47125-23-eq36.gif)