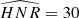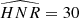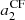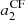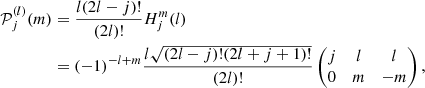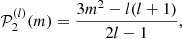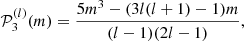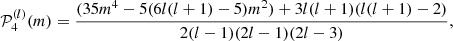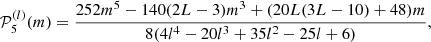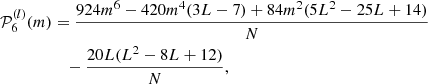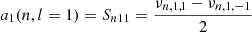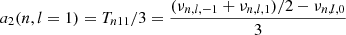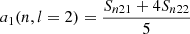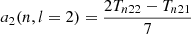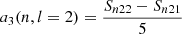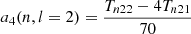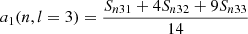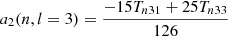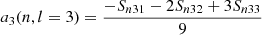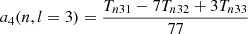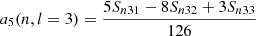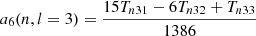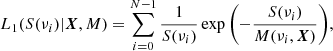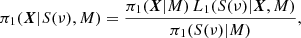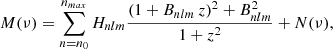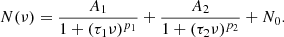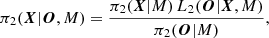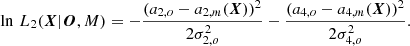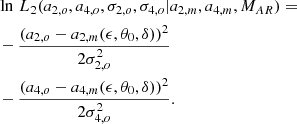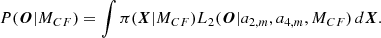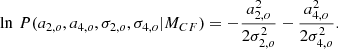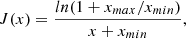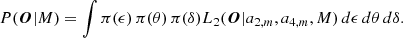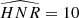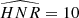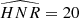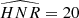| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 26 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202347095 | |
| Published online | 11 December 2023 | |
Detecting active latitudes of Sun-like stars using asteroseismic a-coefficients⋆
1
Department of Astronomical Science, School of Physical Sciences, SOKENDAI, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
2
Solar Science Observatory, National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
e-mail: othman.benomar@nao.ac.jp
3
New York University Abu Dhabi, Center for Space Science, PO Box 129188 Abu Dhabi, UAE
e-mail: ob19@nyu.edu
4
Department of Astronomy, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
5
Heidelberger Institut für Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
6
Max-Planck-Institut für Sonnensystemforschung, 37077 Göttingen, Germany
7
Institut für Astrophysik, Georg-August-Universität Göttingen, 37077 Göttingen, Germany
8
Department of Physics, The University of Tokyo, Tokyo 113-0033, Japan
Received:
5
June
2023
Accepted:
25
July
2023
Aims. We introduce a framework to measure the asphericity of Sun-like stars using a1, a2, and a4 coefficients and constrain their latitudes of magnetic activity.
Methods. We evaluated systematic errors on the inferred coefficients in function of key physical and seismic parameters (inclination of rotation axis, average rotation, height-to-noise ratio of peaks in power spectrum). The measured a-coefficients account for rotational oblateness and the effect of surface magnetic activity. We used a simple model that assumes a single latitudinal band of activity.
Results. Using solar SOHO, VIRGO, and SPM data, we demonstrate the capability of the method to detect the mean active latitude and its intensity changes between 1999 and 2002 (maximum of activity) and 2006 and 2009 (minimum of activity). We further applied the method to study the solar-analogue stars 16 Cyg A and B using Kepler observations. In 16 Cyg A, we detected an equatorial band of activity exhibiting an intensity that could be comparable to that of the Sun. However, 16 Cyg B exhibits a bimodality in a4 that is challenging to explain. We suggest that this could be a manifestation of the transition between a quiet and an active phase of activity. Validating or invalidating this hypothesis may require new observations.
Key words: asteroseismology / stars: activity / stars: rotation / stars: solar-type
All data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST) at the Space Telescope Science Institute. The specific observations analysed can be accessed via https://doi.org/10.17909/T9059R/.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The observations from the space-borne instruments MOST (Walker et al. 2003), CoRoT (Baglin et al. 2006), Kepler (Borucki et al. 2010), and TESS (Ricker et al. 2014) have been important to advancing our knowledge of stellar interiors. This is particularly true for Kepler, which could continuously observe tens of thousands of stars for nearly four uninterrupted years, enabling asteroseismic measurements that almost rival disc-integrated helioseismic measurements from a decade ago. Those precise measurements have, for example, enabled us to better understand stellar rotation and its impact on stellar evolution. The asteroseismology of Sun-like stars is based on the study of the pressure modes that are excited by turbulent convection in the outer layers of these stars. The acoustic modes may reach deep into the core or may be localised close to the stellar surface, giving access to the internal structure and dynamics of the stars. Rotation has a critical impact on the stellar structure and evolution, as it induces a material mixing process (Maeder & Meynet 2008). Rotation is also an essential ingredient of the dynamo effect (Thompson et al. 2003) and can lead to a distortion of the star’s shape due to the centrifugal force (Chandrasekhar 1969). For fast rotators, the rotational flattening must be taken into account. These stars show a variety of pulsation modes that are not present in slower rotators (e.g. Lignières et al. 2006).
Despite the Sun slow rotation rate, the solar asphericity can be measured by helioseismology. While the Sun is seen as oblate by acoustic modes during the quiet phases of its activity cycle, the modes sense a more complicated shape during activity maxima. During solar maxima, the frequencies of acoustic modes increase slightly due to the presence of active regions. The perturbation occurs near the surface and is stronger for modes that sense the active latitudes (below ≃30° for the Sun). Physically, the magnetic perturbations consist of several components that are not easy to disentangle, including stratification and wave speed perturbations (Libbrecht & Woodard 1990; Antia et al. 2000; Dziembowski et al. 2000). The magnetic perturbations affect the acoustic modes near the surface over only a few hundred kilometres, that is, on the order of 10−5 R⊙, but it is significant enough to be measured.
The origin of stellar activity is not well understood, as it depends on the complex interplay between rotation, convection, and the magnetic field (Brun & Browning 2017). Stellar magnetic cycles have been observed in most cool stars (Simon et al. 2002) over a large range of the electromagnetic spectrum, and evidence of activity cycles has been observed in X-ray (e.g. Catura et al. 1975), radio waves (White 1999; White et al. 2017), and chromospheric emission lines (Vaughan 1983; Oláh et al. 2009, 2016) as well as through luminosity variation due to surface magnetic activity in the visible light (Hartmann & Rosner 1979; Silva-Valio et al. 2010; Ceillier et al. 2017). On Sun-like stars, the level of activity is often observed to be cyclic, with activity periods ranging from a few years to decades. Although there are relationships between the stellar age, the rotation period, and the level of activity (van Saders et al. 2016), the underlying mechanisms at play are not understood.
Since the advent of space-borne photometry and the observation of Sun-like pulsators by CoRoT, it became evident that helioseismic methods used for the Sun may be applied to asteroseismic observations. This has resulted in robust estimates of the average rotational splittings, which, in combination with the surface rotation rates inferred from photometric variability, indicate that main sequence stars have nearly uniform internal rotation rates (Gizon et al. 2013; Benomar et al. 2015; Nielsen et al. 2017). All the recent seismic studies of radial differential rotation agree that angular momentum transport in the radiative zone is much more efficient than considered in theory, even in the case of stars more massive than Sun-like stars, such as γ-Doradus stars (e.g. Mosser et al. 2012; Gehan et al. 2018; Ouazzani et al. 2019). For the best Kepler observations, asteroseismology has shown evidence of latitudinal differential rotation for main sequence stars (Benomar et al. 2018a) as well as of the radial differential rotation in red-giant-branch (RGB; e.g. Deheuvels et al. 2012, 2014).
This paper aims to provide a framework to study stellar activity and its latitude by analysing its effect on pulsation frequencies. The proposed method involves the use of the a-coefficient decomposition (Schou et al. 1994; Pijpers 1997, 1998) on the stellar power spectrum to conveniently separate the perturbations caused by rotation and asphericity. The method is tested on Sun-as-a-star data and on the solar analogues 16 Cyg A and B, which are the two brightest stars in the initial Kepler observation field.
Only a few successful measurements of the asphericity of stars other than the Sun have been made so far. Using ultra-precise measurements of the frequency splittings of time-harmonic (i.e. non-stochastic) low-degree p modes, Gizon et al. (2016) inferred the oblateness of the γ Doradus–δ Scuti star KIC 11145123 to be ΔR = (1.8 ± 0.6)×10−6R ≃ 3 ± 1 km, which is smaller than expected from rotational oblateness alone, suggesting the presence of magnetic activity at low latitudes. Bazot et al. (2019) measured the asphericity of the solar-like pulsators 16 Cyg A and B and found that 16 Cyg A is likely prolate, implying that this star may have low-latitude magnetic activity on its surface.
In the spirit of the study by Gizon (2002), we perform Monte Carlo simulations to demonstrate the possibility of inferring the even a-coefficients from simulated oscillation power spectra in order to constrain the latitude of activity. Unlike Gizon (2002), who included only the a2 coefficient in the parametric model, we infer both the a2 and a4 coefficients.
In Sect. 2, we start by introducing the effects of rotation on pulsation frequencies and discuss the effect of the centrifugal force and of the activity on the mode cavities. In Sect. 3, we present the assumptions required for the asteroseismic measurement of stellar activity. We discuss the achievable accuracy of the seismic observables in Sect. 4, while in Sects. 5 and 6 we present the results on solar data and for 16 Cyg A and B. This is followed by a discussion and conclusion in Sect. 7.
2. The effects of rotation and magnetic activity
This section presents the effects of rotation and magnetic activity on pulsation modes. It also introduces the frequency model used for asteroseismic data analysis.
2.1. Frequency splittings
Slowly rotating stars without significant magnetic activity are approximately spherical, and it is common to describe the family of modes travelling inside them using spherical harmonics (see e.g. Unno et al. 1989). If the departure from spherical shape remains small enough, it is convenient to keep the spherical representation for the equilibrium model and account for distortions through a perturbation analysis. All pulsations can then be described using a set of integers (n, l, m), namely, the radial order, the mode degree, and the azimuthal order. Acoustic pressure modes observed in Sun-like stars can be identified using their frequencies νnlm.
In a non-rotating, non-active star, m-components are degenerate and cannot be resolved. When rotation or magnetic activity sets in, this degeneracy is lifted. The resulting frequency is treated as a perturbation to the degenerate frequency without rotation and activity,
with νnl as the equilibrium eigenfrequency without rotation and activity, and δνnlm as the frequency splitting. The splitting may depend on multiple physical effects perceived by the modes (Libbrecht & Woodard 1990) within their cavity of propagation. It can be a term of the order 𝒪(Ω), with Ω the rotation rate estimated at the equator, Ω = Ω(r, θ = π/2). The splitting depends directly on the stellar rotation profile Ω(r, θ). Higher-order perturbations pertaining to the shape of the mode cavity can also exist. We note that νnl differs from νnl, m = 0, as the m = 0 components may have their frequency shifted by perturbations, such as the magnetic activity (see e.g. Fig. 1).
 |
Fig. 1. Example of Lorentzian mode profiles showing the a-coefficients and their relationship with frequency spacings for l = 1 (a) and l = 2 modes (b). The orange spacing is Tn22 − Tn21, νnl is the m-averaged frequency of each multiplet, and the stellar inclination is 40°. |
Splitting can be described using the Clebsch-Gordan a-coefficient decomposition (Ritzwoller & Lavely 1991), which corresponds to a representation of the splittings on a basis of polynomials 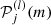 of degree j in m,
of degree j in m,
with the polynomials such that
Here, aj(n, l) is the a-coefficient of order j, and jmax = 2l is the maximum order to which the decomposition must be carried for a given degree. The standard set of polynomials used in this expansion are those normalised as per described by Schou et al. (1994).
This decomposition is extensively used in helioseismology and was used on Sun-like stars by Benomar et al. (2018a). Asteroseismology has been so far unable to observe modes of degree higher than l = 3 so that in the following, the discussion is restricted to l ≤ 3 and jmax = 2l = 6 due to the selection rule of the 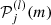 . This limitation is the consequence of full-disc integrated photometric observations. An example of splitting including odd and even aj coefficients is given in Fig. 1 for l = 1, 2.
. This limitation is the consequence of full-disc integrated photometric observations. An example of splitting including odd and even aj coefficients is given in Fig. 1 for l = 1, 2.
This theoretical model leads to a natural interpretation of the observed splittings. One may decompose the splittings into their symmetrical, Snlm, and antisymmetrical, Tnlm, parts. These components can then be respectively described as sums over the odd and even a-coefficients,
This arises from the parity relation 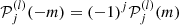 . These equations can be used to express the a-coefficients with Snlm and Tnlm. They also provide relations between the νnlm and the aj(n, l) (see Appendix A.2).
. These equations can be used to express the a-coefficients with Snlm and Tnlm. They also provide relations between the νnlm and the aj(n, l) (see Appendix A.2).
It can be seen from Appendix A.1 that the sums in Eqs. (4) and (5) respectively involve odd and even functions of m. Physically, this means that the symmetrical components of the splittings (Gough & Thompson 1990) result from large-scale perturbations sensitive to the prograde or retrograde nature or the waves, such as advection or the Coriolis force. However, the antisymmetric splittings are caused by processes that are not affected by the propagation direction of waves. This may include the centrifugal force that scales as 𝒪(Ω2) and whose effect on the oscillation frequencies varies as m2. Magnetic fields or non-spherical deformations of the equilibrium structure also contribute to the antisymmetric splittings.
We further decompose the antisymmetric splittings into a term depending on centrifugal force-induced distortions and another term accounting for activity-related distortions,
The symmetric part of the splitting corresponds to a term 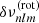 that stems from perturbations of the order 𝒪(Ω), and the total observed splitting is,
that stems from perturbations of the order 𝒪(Ω), and the total observed splitting is,
Using the Sun as an archetype of a Sun-like star, it is possible to measure these contributions to δνnlm, as shown in Sects. 2.2 and 2.3.
2.2. Expressions for 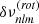 ,
, 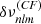 , and
, and 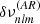
To the first order, the perturbation on the frequency due to rotation is
where R is the radius of the star and the kernel Knlm(r, θ) expresses the sensitivity of a mode to the rotation at the radial point r and co-latitude θ (Hansen et al. 1977). The rotation profile of the star is represented as Ω(r, θ). It can be shown that 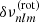 actually only depends on symmetrical splittings (Ritzwoller & Lavely 1991), which in turn depend only on odd coefficients. For example, for l = 3, it is expressed as,
actually only depends on symmetrical splittings (Ritzwoller & Lavely 1991), which in turn depend only on odd coefficients. For example, for l = 3, it is expressed as,
Centrifugal forces typically distort a spherical rotating sphere of gas into an oblate ellipsoid elongated at the equator. Functional analysis shows that the contribution of centrifugal forces to the mode splitting is proportional to Ω2R3/𝒢M. Properly integrating higher-order terms of the perturbation expansion over the aspherical volume of the star and using asymptotic expressions for the equilibrium mode eigenfunctions (assuming n is large enough), leads to the following expression for the centrifugal-force component of the frequency splitting (Gough & Taylor 1984; Gough & Thompson 1990),
with the 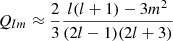 factor depending on the density.
factor depending on the density.
Equation (10) means that
with
since 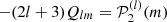 . We note that the contribution of the centrifugal force-induced deformation to the frequency splittings can be described by a linear combination of the 𝒫2j polynomials (Gough & Taylor 1984; Gough & Thompson 1990). Since the stars are assumed to be slowly rotating, one may only retain terms of the order 𝒪(Ω2), which correspond to the contribution of the a2 coefficient alone.
. We note that the contribution of the centrifugal force-induced deformation to the frequency splittings can be described by a linear combination of the 𝒫2j polynomials (Gough & Taylor 1984; Gough & Thompson 1990). Since the stars are assumed to be slowly rotating, one may only retain terms of the order 𝒪(Ω2), which correspond to the contribution of the a2 coefficient alone.
One can further approximate Eq. (12) in order to express 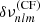 as a function of quantities that can be obtained directly from the modelling of the acoustic power spectra of Sun-like stars (Benomar et al. 2018a). We consider first that the stellar mean density of a Sun-like star scales to a good approximation with its large separation. The large separation is the average distance in the frequency space between two modes of identical degree and consecutive orders (Ulrich 1986). In solar units, this reads as ρ = (ρ⊙/Δν⊙)Δν, with the solar density ρ⊙ = (1.4060 ± 0.0005)×103 kg m−3 and Δν⊙ = 135.20 ± 0.25 μHz (García et al. 2011a). With an accuracy estimated to a few percentage points for Sun-like stars (White et al. 2011), the use of this scaling relation is thought to be a decent approximation.
as a function of quantities that can be obtained directly from the modelling of the acoustic power spectra of Sun-like stars (Benomar et al. 2018a). We consider first that the stellar mean density of a Sun-like star scales to a good approximation with its large separation. The large separation is the average distance in the frequency space between two modes of identical degree and consecutive orders (Ulrich 1986). In solar units, this reads as ρ = (ρ⊙/Δν⊙)Δν, with the solar density ρ⊙ = (1.4060 ± 0.0005)×103 kg m−3 and Δν⊙ = 135.20 ± 0.25 μHz (García et al. 2011a). With an accuracy estimated to a few percentage points for Sun-like stars (White et al. 2011), the use of this scaling relation is thought to be a decent approximation.
The second simplification uses the fact that the Clebsch-Gordan coefficient decomposition of the frequency splitting imposes a one-to-one relationship between the a-coefficients and the coefficients associated to the decomposition of the velocity field into poloidal and toroidal components (Ritzwoller & Lavely 1991). Helioseismology suggests that the Sun rotates with a near constant angular velocity down to at least r/R⊙ = 0.2 (e.g. Thompson et al. 2003), which is the maximum depth at which measurements from low-degree p modes are available. Furthermore, its outer convective zone shows a differential rotation of ≃30% from the equator to the pole, which leads to an a3, ⊙(n, l)≃4 nHz and even smaller values for higher odd a-coefficients. This is significantly smaller than a1, ⊙(n, l)≃420 nHz. Therefore, the aforementioned one-to-one relation ensures that we can retain only the leading order in the expansion of the rotation rate and treat it as an average value, given in terms of seismic observables by Ω ≃ 2πa1. This leads to
Regarding 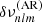 , there is no unambiguous theory to describe the effect of the near-surface magnetic activity on the shape of the cavity. Due to this and following Gizon (2002), a geometrical description is preferred to a physical model. This description assumes that the corresponding wave speed perturbation separates in the latitudinal and radial coordinates. The proposed form of the perturbation in frequency is
, there is no unambiguous theory to describe the effect of the near-surface magnetic activity on the shape of the cavity. Due to this and following Gizon (2002), a geometrical description is preferred to a physical model. This description assumes that the corresponding wave speed perturbation separates in the latitudinal and radial coordinates. The proposed form of the perturbation in frequency is
The term 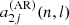 in Eq. (14) refers to the combined contribution of a magnetic field and other perturbations in the stellar structure (e.g. stratification, temperature). The geometrical weight function Alm(x) describes the effect of an active zone at the co-latitude θ on a mode of degree l and azimuthal order m. It is also the product of two contributions. The first is from the normalised spherical harmonics
in Eq. (14) refers to the combined contribution of a magnetic field and other perturbations in the stellar structure (e.g. stratification, temperature). The geometrical weight function Alm(x) describes the effect of an active zone at the co-latitude θ on a mode of degree l and azimuthal order m. It is also the product of two contributions. The first is from the normalised spherical harmonics 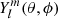 that decompose the magnetic activity effect over each mode. These are spherical-polar coordinates defined in the inertial frame with a polar axis pointing in the direction of the rotation axis. The second is from the weight distribution (or the shape of the active region) defined by F(θ|x). Here, x refers to the parameters that are necessary to describe the function F(θ|x).
that decompose the magnetic activity effect over each mode. These are spherical-polar coordinates defined in the inertial frame with a polar axis pointing in the direction of the rotation axis. The second is from the weight distribution (or the shape of the active region) defined by F(θ|x). Here, x refers to the parameters that are necessary to describe the function F(θ|x).
On the Sun, large active regions persist on the surface for one to two rotation periods and are randomly distributed in longitude over well-defined latitudes. We assume that the corresponding perturbation can be approximated by a function of latitude only. The general problem of distinct active regions on the differentially rotating surface goes beyond the scope of our study (see Papini & Gizon 2019, for the case of a single long-lived active region). In this paper, we only consider perturbations that are approximately steady in the inertial frame (i.e. latitudinal bands of activity).
In theory, a third integral over the radius is necessary to describe the dependence of the magnetic activity to the stellar depth. However, p modes are weakly sensitive to the deep structure inside stars. Therefore, the radial integral is replaced by ϵnl, the overall activity intensity. The frequency νnl allows for a dimensionless ϵnl that can be compared between stars. Section 3.2 further develops the required assumptions in order to obtain reliable information content on the active region in asteroseismology.
2.3. Modelling the frequencies
Combining Eqs. (1), (7), (8), (13), and (14) leads to
Using Eqs. (1) and (2), νnlm can also be expressed using the a-coefficients without loss of generality,
It is possible to use Eq. (15) to measure the activity parameters x by directly fitting the power spectrum. However, there are multiple benefits to using a two-step approach consisting of first using Eq. (16) for the fitting of the power spectrum to evaluate the a-coefficients (method detailed in Appendix B) and then fitting the coefficients obtained during the first step using solely Eqs. (13) and (14) (detailed in Appendix C). Firstly, and in the general case, the evaluation of Alm(x) requires the precise computation of a double integral. This is a slow process that increases the time necessary to fit the power spectrum1. Postponing to an ulterior step, the computation of Alm(x) drastically reduces the parameter space from a few tens of parameters to just a few2, effectively making the convergence rate of the fitting algorithm faster and making it easier to explore the assumptions that have to be made in Eq. (15) to have a functional approach in real cases (see the discussions in Sect. 3). Secondly, it allows us to decouple the observables from the physics, enabling the testing of various physical assumptions without having to reperform the lengthy power spectrum analysis. Finally, it eases the evaluation of the reliability of the activity determination by enabling us to pinpoint the cause of biases (if any) on either the observables (e.g. a2, a4; see Sect. 4) or on the interpretation of these observables in terms of physical parameters (see Sect. 3.3). The disadvantage of the two-step approach is that it requires more statistical assumptions, such as neglecting correlations and assuming Gaussian parameters. Although one can argue that it is possible to perform a hierarchical Bayesian analysis (e.g. Hogg et al. 2010; Campante et al. 2016) to partly alleviate this issue, such an approach is generally slow and may cancel the benefits of the two-step approach.
3. Information content in low-order a-coefficients
The general theoretical formulations of Sect. 2 demonstrate how pulsation frequencies are expressed as a function of the rotation, the centrifugal distortion, and the activity of stars. However, observational limitations need to be accounted for in order to enable a viable, robust model that extracts as much of the information content within currently existing data as possible. This necessarily requires additional assumptions, for which the rational is detailed hereafter.
3.1. Factors contributing to the splitting accuracy and precision
As explained in Kamiaka et al. (2018), the pulsation height (H) and the noise background (N) are important factors that reduce the capabilities of asteroseismic analyses. These factors are a complex function of the global stellar characteristics (mass, radius, age) of the convective motion at the surface of Sun-like stars and also depend on the instrumental limitations. The mode height and the noise background are in fact difficult to evaluate a priori. However, the height-to-noise (HNR), defined as the ratio H/N, can be used to assess the quality of the spectrum of a pulsation mode. In fact, Kamiaka et al. (2018) have shown that the HNR at maximum of mode height, 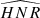 , can be used to study biases on the stellar inclination. This is because all main sequence Sun-like stars show a similar dependency on the height and on the width as a function of the frequency (see e.g. Appourchaux et al. 2014). In Sect. 4, we propose the same approach but on a-coefficients.
, can be used to study biases on the stellar inclination. This is because all main sequence Sun-like stars show a similar dependency on the height and on the width as a function of the frequency (see e.g. Appourchaux et al. 2014). In Sect. 4, we propose the same approach but on a-coefficients.
The 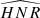 not only defines how many modes can be observed but also the maximum degree of the modes that is observed. Considering specifically the Kepler observations, stars exhibit an
not only defines how many modes can be observed but also the maximum degree of the modes that is observed. Considering specifically the Kepler observations, stars exhibit an 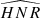 for l = 0 modes of up to 30, the highest HNR being observed for 16 Cyg A and 16 Cyg B. Kamiaka et al. (2018) showed that the capability of distinguishing rotationally split components is of great importance if one wants to obtain a reliable asteroseismic inference of the rotation characteristics and of the stellar inclination. In particular, the ratio a1/Γνmax between the a1 coefficient and the mode width determined at the maximum of mode amplitude Γνmax (see Fig. 2) determines the expected bias on the stellar inclination. As shown in Sect. 4, a1/Γνmax also controls the importance of the bias for the other low-order a-coefficients. Finally, another important factor is the spectrum resolution. The higher the resolution, the more resolved are the modes. Thus, observations Tobs of several years are the most suitable in order to resolve and measure rotationally split components. Broadly speaking, observations exceeding a year and a1/Γ > 0.4 are preferable to ensure a reliable measurement of a1. All the limitations discussed above incite us to introduce assumptions in order to ensure robust measurements of a-coefficients (i.e. mitigate biases).
for l = 0 modes of up to 30, the highest HNR being observed for 16 Cyg A and 16 Cyg B. Kamiaka et al. (2018) showed that the capability of distinguishing rotationally split components is of great importance if one wants to obtain a reliable asteroseismic inference of the rotation characteristics and of the stellar inclination. In particular, the ratio a1/Γνmax between the a1 coefficient and the mode width determined at the maximum of mode amplitude Γνmax (see Fig. 2) determines the expected bias on the stellar inclination. As shown in Sect. 4, a1/Γνmax also controls the importance of the bias for the other low-order a-coefficients. Finally, another important factor is the spectrum resolution. The higher the resolution, the more resolved are the modes. Thus, observations Tobs of several years are the most suitable in order to resolve and measure rotationally split components. Broadly speaking, observations exceeding a year and a1/Γ > 0.4 are preferable to ensure a reliable measurement of a1. All the limitations discussed above incite us to introduce assumptions in order to ensure robust measurements of a-coefficients (i.e. mitigate biases).
 |
Fig. 2. Height-to-noise ratio (black) and a1/Γ ratio (red) for 16 Cyg A. We used 16 Cyg A to make our simulations. |
3.2. Latitudinal profile of the activity
Noting that it is challenging to measure low-degree a-coefficients for the Sun (e.g. Toutain & Kosovichev 2001), we present a minimal set of assumptions on even a-coefficients that allow us to constrain the asphericity of stellar cavities. One of the first aspects that has to be considered is the form of F(θ|x), the function characterising the activity latitude θ (see Eq. (14)).
The butterfly diagram of the Sun (Fig. 3) is used as a reference for this latitudinal dependence. The data are from the Greenwich USAF/NOAA observatory3 and provide the daily area of the spots, counted manually over the period 1874-2016. Panel a of Fig. 3 shows the butterfly diagram with colours representing the area covered by the spots in units of percent of visible hemisphere. It focuses on the observations after 1985 and covers two full solar cycles. Vertical colour bands highlight three time intervals : 1985–1989 (purple), 1999–2002 (blue), and 2006–2009 (yellow). The first two are during a maximum of solar activity, while the last one is during a minimum of activity. Due to the gradual migration of the spots over time, the longer observation period (1985–1989; i.e. 4 yr) leads to a broader activity zone than the period 1999–2002. This indicates that the extension of the active region may not be trivial to measure in other stars because it will depend on the fraction of time the star is observed relative to the duration of its activity cycle. The activity cycles of Sun-like stars (if any) are a priori unknown, but Ca II H+K line emission and photometric studies (Oláh et al. 2009, 2016) suggest that it is of durations of roughly a few years to decades, which is the same as for the Sun. It indicates that over the course of several years, an active band as large as ≃40° may be expected.
 |
Fig. 3. Solar activity over time. (a) Butterfly diagram for the Sun. Vertical colour bands highlight periods of maximum (1988–1992, 1999–2002) and minimum activity (2006–2009). (b) Averaged spot area for the highlighted periods. Blue and purple marks in (b) are the weighted mean for the activity latitude. (c) Filters F(θ|X) used for this study superimposed onto solar data (1986–2016). The parameters θ0 and δ are the latitude and the extension of the active region, respectively. |
Panel b of Fig. 3 shows the cumulative area of spots as a function of the latitude as well as for the three considered periods. As noted earlier, the extension of the activity band is larger for the longest time frame. The area of the spots during the active solar phase are symmetrical towards the equator. This suggests that when the activity is strong, F(θ|x) is almost north-south symmetric. This may be inaccurate for the low activity phase, as shown for the period 2006–2009, but because 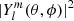 is also symmetrical towards the equator, this has no incidence on the
is also symmetrical towards the equator, this has no incidence on the 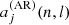 coefficients.
coefficients.
During the minimum, the total average area of the spots is a few times lower than during the maximum. It is also narrower, as the integral in Eq. (14) is small, reducing 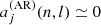 . During the phase of the minimum of activity, the activity can effectively be considered as non-existent (see Sect. 5 for the analysis on solar data) so that a2(n, l) is dominated by the centrifugal term
. During the phase of the minimum of activity, the activity can effectively be considered as non-existent (see Sect. 5 for the analysis on solar data) so that a2(n, l) is dominated by the centrifugal term 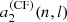 and the other even a-coefficients are null.
and the other even a-coefficients are null.
The overall latitudinal profile seemingly follows a bell shape, with sharp slopes during periods of activity. Figure 3c shows a comparison of data between 1986 and 2016 with three models for the active latitudes: a model using the gate function F(θ|x) = Π(θ0, δ), a triangular function Λ(θ0, δ), and a Gaussian function 𝒩(θ0, δ). The parameters of these were adjusted manually to approximately match the solar spot active latitudes profile. The triangular and the Gaussian functions equivalently describe the data, while the gate function initially proposed by Gizon (2002) roughly fits the data. Because spots strictly appear at latitudes below 45°, the Λ function may be the most suitable for the Sun. Nevertheless, we retained these three functions and compare them further in this work.
3.3. Assumptions on the a-coefficients
The most direct method for measuring asphericity is to evaluate it directly for each mode (n,l), that is, measuring the terms aj(n, l). As this is already difficult for low-order a-coefficients of the Sun (Chaplin et al. 2003), it seems unreasonable to expect an accurate measurement of all individual aj(n, l) using asteroseismic data. These stars have a lower signal-to-noise ratio than the Sun and severely reduced visibility at l ≥ 3 due to the integrated photometry. After a trial and error process, jointly with power spectra simulations, we could identify a set of assumptions ensuring reliable and precise measurement of a-coefficients.
We considered a fictitious star rotating as a solid-body with a solar activity level (ϵnl ≃ 5 × 10−4; Gizon 2002) with a1 = 1000 nHz. The observed oscillation frequencies of 16 Cyg A are used (Davies et al. 2015; Kamiaka et al. 2018). We derived split frequencies using Eqs. (1), (7), (13), and (14) and converted them into a-coefficients using Eqs. (A.8)–(A.19). The a-coefficients are linear functions of the frequency, which is expected, as F(θ|θ0, δ) describes a single active region. Thus, a reasonable assumption is to consider those a-coefficients as pure first order polynomial functions of frequencies. However, tests on artificial spectra showed that it is often difficult to evaluate the slope of the a-coefficients. This is because the uncertainty on any aj is at least of the same order as its variations within the range of observed frequencies. This suggests that current asteroseismic data lack the resolution and the signal-to-noise to reliably measure the frequency dependence on the a-coefficients.
Figure 4 shows 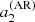 ,
, 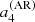 ,
, 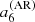 for activity described by F = Π (black) or Λ (red) or 𝒩 (blue). These are the mean coefficients for the fictitious active star, as a function of θ0 and δ. The figure indicates that there is a simple relationship between the a-coefficients, the co-latitude θ0, and the extension of the activity zone δ, independently of the shape of activity. In the case of F = Π, the lines are cut near the pole and the equator due to the condition θ0 ≥ δ/2 and θ0 ≤ π − δ/2. In the other profiles, edge effects (truncation) have a noticeable impact near the equator. The definition of δ differs between the three profiles, which explains why a factor of a few in
for activity described by F = Π (black) or Λ (red) or 𝒩 (blue). These are the mean coefficients for the fictitious active star, as a function of θ0 and δ. The figure indicates that there is a simple relationship between the a-coefficients, the co-latitude θ0, and the extension of the activity zone δ, independently of the shape of activity. In the case of F = Π, the lines are cut near the pole and the equator due to the condition θ0 ≥ δ/2 and θ0 ≤ π − δ/2. In the other profiles, edge effects (truncation) have a noticeable impact near the equator. The definition of δ differs between the three profiles, which explains why a factor of a few in 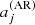 is noticeable between F = Π, Λ, and 𝒩 for a given δ. We note that adding the centrifugal effect reduces
is noticeable between F = Π, Λ, and 𝒩 for a given δ. We note that adding the centrifugal effect reduces 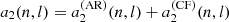 because the coefficient
because the coefficient 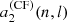 is always negative.
is always negative.
 |
Fig. 4. Average |
If an observation can constrain only a single a-coefficient (e.g. a2), there often exists a degeneracy in θ0, as multiple values of aj can be obtained for a given θ0. As the figure shows, measuring two a-coefficients alleviates this degeneracy, provided that uncertainties are small enough. In other words, the accuracy on the inference of the active region using a-coefficients is ensured only if we can simultaneously constrain two a-coefficients (e.g. a2 and a4). This is essential to distinguishing an activity near the pole (θ0 ⪅ 30°) from one near mid-latitude (30 ° ⪅θ0 ⪅ 60°) or near the equator (θ0 ⪆ 60°).
Figure 4 indicates that the loss of information resulting from the averaging does not affect the accuracy4. Figure 4 also indicates that for a star with an activity intensity and an activity zone of extension commensurate with that of the Sun (ϵnl ≃ 5 × 10−4, δ ≃ 10° when F = Π), the uncertainty for 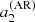 must be approximately ⪅25 nHz, for
must be approximately ⪅25 nHz, for 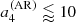 nHz, and for
nHz, and for 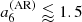 nHz to be able to detect significant departures of the coefficients. This is to be compared with the spectral resolution of 7–14 nHz for 2–4 yr of observation, which is typical of the longest Kepler observations. In Fig. 4,
nHz to be able to detect significant departures of the coefficients. This is to be compared with the spectral resolution of 7–14 nHz for 2–4 yr of observation, which is typical of the longest Kepler observations. In Fig. 4, 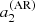 is obtained by averaging l = 1, 2, and
is obtained by averaging l = 1, 2, and 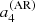 is obtained by averaging l = 2, while
is obtained by averaging l = 2, while 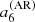 is only constrained by l = 3 modes. Averaging
is only constrained by l = 3 modes. Averaging 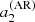 and
and 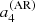 over l = 1, 2, 3 increases the maximum range of the a-coefficients by a factor of approximately 1.5 for
over l = 1, 2, 3 increases the maximum range of the a-coefficients by a factor of approximately 1.5 for 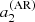 and approximately a factor of two for
and approximately a factor of two for 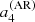 without changing the overall shape of the function. In Sun-like stars, the l = 3 modes have an HNR at least ten times lower than l = 0 modes because the height ratio between l = 3 and l = 0 modes is around 0.08 for the Sun (Toutain & Gouttebroze 1993; Toutain et al. 1998). These modes are therefore difficult to observe. Due to all the above, it is extremely challenging to measure a6 with existing data. In the following, we thus focus on assessing the reliability domains of a2 and a4 only in the following sections.
without changing the overall shape of the function. In Sun-like stars, the l = 3 modes have an HNR at least ten times lower than l = 0 modes because the height ratio between l = 3 and l = 0 modes is around 0.08 for the Sun (Toutain & Gouttebroze 1993; Toutain et al. 1998). These modes are therefore difficult to observe. Due to all the above, it is extremely challenging to measure a6 with existing data. In the following, we thus focus on assessing the reliability domains of a2 and a4 only in the following sections.
4. Bias analysis on a1, a2, and a4
In order to understand the reliability of the inference on low-degree a-coefficients, it is necessary to perform a bias analysis. This requires fitting an ensemble of emulated spectra that are representative of Sun-like stars and comparing the results with the true inputs.
4.1. Test setup
The synthetic spectra used to analyse the biases use the frequencies, heights, widths, and the noise background profile of 16 Cyg A as a template for the simulations. We wanted to specifically study the impact of the mode blending (effect of a1/Γνmax), stellar inclination (i), observation duration (Tobs), and maximum height-to-noise (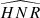 ) background on the accuracy of a1, a2, and a4. We built grids of spectra in the case of an equatorial band of activity and of a large polar activity. The grid parameters and their ranges are provided in Table 1 and discussed further in this section. The spectra were made using a spectrum simulator code5 that takes the reference star (or template) and modifies its properties to match those required by the user. The template was altered in terms of HNR following a similar approach in Kamiaka et al. (2018). The main difference is that we considered a frequency-dependent noise background. We rescaled heights according to
) background on the accuracy of a1, a2, and a4. We built grids of spectra in the case of an equatorial band of activity and of a large polar activity. The grid parameters and their ranges are provided in Table 1 and discussed further in this section. The spectra were made using a spectrum simulator code5 that takes the reference star (or template) and modifies its properties to match those required by the user. The template was altered in terms of HNR following a similar approach in Kamiaka et al. (2018). The main difference is that we considered a frequency-dependent noise background. We rescaled heights according to
Parameters set to construct artificial power spectra.
where 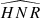 is the maximum HNR of the synthetic star,
is the maximum HNR of the synthetic star, 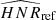 is the maximum HNR of the reference star, and Href(n, l = 0) is the l = 0 heights of the reference star.
is the maximum HNR of the reference star, and Href(n, l = 0) is the l = 0 heights of the reference star.
As for the mode blending factor f = a1/Γνmax, we calculated it fixing a1 and altering Γνmax such that
We used a fiducial value of a1 = 1000 nHz (≃2.4 the solar rotation) in the simulation. We note that this differs from Kamiaka et al. (2018), where the splitting was modified in order to obtain the desired mode blending factor.
As shown in Table 1, three HNR cases were investigated, ranging from 10 to 30. Two observation durations were considered: 2 yr and 4 yr. This is representative of the best Kepler observations (Davies et al. 2015) and of future observations from PLATO (Rauer et al. 2014). Similar to the test cases of Gizon (2002), a2 and a4 were determined for an equatorial activity of extension of the same order as in the Solar case (δ ≃ 10°) and in the case of a large polar cap (δ = 45 ° ). Both situations assume an activity of the same order as the Sun. The priors were set in a manner similar to how they would be if the power spectrum was from a real star. The evaluation of the mode parameters was performed using an MCMC method, just as for actual stars (see Appendix B for further details), but on the limit spectrum (no noise). Fitting the limit spectrum allowed us to assess the systematic errors by calculating the expectation value of the probability density function. The expected uncertainty can also be known by computing the standard deviation.
4.2. Results
To appreciate the level of inaccuracy achieved when measuring aj, j ∈ [1, 2, 4] coefficients, we calculated the bias for aj, f = a1/Γνmax, and i:
Here, the letter E refers to the expectation value (median) from the probability density function.
Figure 5 shows the resulting bias maps for a-coefficients as a function of the blending factor F and of the stellar inclination for a-coefficients corresponding to an equatorial activity band. Figure 6 is the same but for a large polar activity cap. The bias is represented as a projected three dimensional vector using the three quantities defined by Eq. (19) and for j ∈ [1, 2, 4]. To evaluate the importance of the bias on aj, the plot shows b(aj)/⟨σaj(i, F)⟩i, with ⟨σaj(i, F)⟩i as the average standard deviation of the probability density functions (PDFs) obtained by the MCMC sampling over i ∈ [30 ° ,90 ° ]. The value of ⟨σaj(i, F)⟩i (noted as σ for convenience hereafter) and its variance along the inclination axis is also shown on the plots. A value of b(aj)/σ greater than one indicates that the inaccuracy exceeds the typical expected uncertainty at 1σ and may lead to significantly biased results during the subsequent analyses of the a-coefficients. A negative bias (underestimation) for aj is indicated by a cross within the circle, while a positive bias (overestimation) is indicated by a dot. The darker the colour, the smaller the norm of the normalised bias. The size of the circle symbols is also proportional to the bias but capped to three in order to avoid excessively large symbols when i < 30° (see next paragraph for explanations). The cases with an observation duration of 2 yr are in the top panels (Figs. 5a–c) of the figure, while cases with a duration of 4 yr are shown in the bottom panels (Figs. 5d–f).
 |
Fig. 5. Bias analysis for |
 |
Fig. 6. Bias analysis for |
We note first that the biases on inclination and on F are consistent with results from Kamiaka et al. (2018). We found regions of stellar inclination below 30° provide very unreliable results, and the median of the inclination is biased toward ≃80° when the true input is i = 90°. Meanwhile, we found biases in a1 often exceed 50% in the grey area6, indicating that for an inclination below ≃30°, the median estimator of the probability density function might not be reliable. This also justifies the range for the calculation of σ. In the following paragraphs, we therefore focus the discussion of the figures for the region above 30°.
In the case of an equatorial zone of activity, we note that measurements of a1 may have negligible inaccuracies when the blending factor F is above 0.4, but it starts to be significantly deteriorated at (and probably below) f = 0.4 because |b(a1)|/σ exceeds 1.5 when i < 50°. Split components then overlap significantly, leading to important degeneracies between a-coefficients, mode widths, and the stellar inclination. Meanwhile, we note that the biases on a2 and a4 remain mild compared to the uncertainty (|b(a2)|/σ < 1 and |b(a4)|/σ < 1), even for f = 0.4.
In the case of a polar active region, |a2| represents ≃20% of the a1 coefficient. In these conditions, we note that b(a1)/σ does not exceed the unity (see Figs. 5a,d), indicating a good accuracy. The terms |b(a2)|/σ and |b(a4)|/σ are also lower than 0.5, provided that the stellar inclination is between 30° and 70°. This indicates that a large a2 coefficient is generally associated with a higher accuracy for all a-coefficients. The plot also demonstrates that a large zone in the parameter space has a moderate to small bias.
Interestingly, figures for 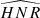 of 10 and 20 (Figs. D.1–D.4) lead to similar conclusions. Therefore, even in less favourable
of 10 and 20 (Figs. D.1–D.4) lead to similar conclusions. Therefore, even in less favourable 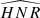 conditions, the expected uncertainty on the measurement generally encompass the bias, provided that the stellar inclination exceeds ≃30° (ensuring that m ≠ 0 have significant amplitudes) and that the mode blending factor is above 0.4. This indicates that for a majority of stars observed by Kepler, the accuracy may not be a major issue when measuring a1, a2, and a4 if a careful assessment of F and i is performed. We note, however, that the average uncertainty σ does usually increase when the
conditions, the expected uncertainty on the measurement generally encompass the bias, provided that the stellar inclination exceeds ≃30° (ensuring that m ≠ 0 have significant amplitudes) and that the mode blending factor is above 0.4. This indicates that for a majority of stars observed by Kepler, the accuracy may not be a major issue when measuring a1, a2, and a4 if a careful assessment of F and i is performed. We note, however, that the average uncertainty σ does usually increase when the 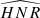 and/or the observation duration decrease, which has an impact on the precision of the determination of the active region.
and/or the observation duration decrease, which has an impact on the precision of the determination of the active region.
5. Analysis of solar data
The Sun has a well-known 11-year activity cycle that makes it an ideal subject to further test the accuracy of the method described in Sect. 4. The Sun’s activity cycle is analysed at two instants, highlighted in Fig. 3 and for which high-quality helioseismic data are available: (a) the maximum of activity between January 1999 and January 2002 and (b) the minimum of activity between January 2006 and January 2009. Data are from the Variability of Solar Irradiance and Gravity Oscillations instrument on board the SOHO spacecraft (Frohlich et al. 1997) and present very few gaps.
5.1. a-coefficients of the Sun
As for the simulated data, the analysis consists of fitting the power spectrum for cases (a) and (b) in order to measure the a1, a2, and a4 coefficients using the Bayesian modelling and the MCMC method described in Appendix B. Figures of the best fits and their discussions are provided in Appendix E. As the goal is to evaluate the accuracy of the inference of the activity zone based on the a-coefficients, the presented results are for a stellar inclination fixed to 90°, instead of having it as a free parameter. This value corresponds approximately to the stellar inclination seen by the SOHO satellite. This alleviates biases on aj coefficients that may arise due to the systematic underestimation of i when it is close to 90 degrees. However, tests we carried out with a free inclination during the maximum of activity7 led to a difference of −12 nHz in a2 and to −1.3 nHz in a4. This outcome is consistent with the expected difference from the bias map of Fig. 5. In agreement with the discussion of Sect. 4, the difference does not have a significant impact on the activity inference because the uncertainties for those parameters are larger than the observed measurement shift.
Figure 7 shows the measured probability distribution function of the relevant parameters along with their correlations during the maximum (left) and the minimum (right) of solar activity. The 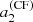 distribution in red represents the expected centrifugal effect on a2 as derived from frequency shifts
distribution in red represents the expected centrifugal effect on a2 as derived from frequency shifts 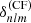 of Eq. (13). The distributions are Gaussians and show a weak correlation, reflecting the quality of the data. Between the maximum and the minimum of activity, the a2 coefficient drifted significantly, from a2 = 80 ± 19 nHz to a2 = 11 ± 21, falling within the 1σ confidence interval of the centrifugal term. Although a4 may have changed, the effect is below uncertainty levels and remains close to zero. As shown in Fig. 8, other time intervals may lead to a4 departing from zero. The figures demonstrate that a comparison of a2 and
of Eq. (13). The distributions are Gaussians and show a weak correlation, reflecting the quality of the data. Between the maximum and the minimum of activity, the a2 coefficient drifted significantly, from a2 = 80 ± 19 nHz to a2 = 11 ± 21, falling within the 1σ confidence interval of the centrifugal term. Although a4 may have changed, the effect is below uncertainty levels and remains close to zero. As shown in Fig. 8, other time intervals may lead to a4 departing from zero. The figures demonstrate that a comparison of a2 and 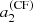 may reveal the activity of a Sun-like star. At the maximum of activity,
may reveal the activity of a Sun-like star. At the maximum of activity, 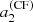 is inconsistent with a2 at 4.5σ, but it is in agreement at 1σ during the minimum of activity. Interestingly, Chaplin et al. (2003) also studied the frequency asymmetry of l = 2 modes in detail using BiSON and GOLF data with a different methodology and over a period that encompasses the maximum of 1999–2002. Their measurement considers only Tn22, so a direct comparison is not straightforward. However, we note that with an 844 day-long time series starting in February 19998, they detected a frequency shift Tn22 ≃ 190 nHz at a similar significance (≃4σ) as our measurement when averaging over all modes between ≃2000 − 3300 μHz (to be compared to our range of ≃2300 − 3600 μHz). Their Fig. 8 also shows that the global effect of the activity cycle between 1994 and 2000 is evident in the averaged Tn22, while the frequency dependence of Tn22 may have uncertainties too large to ascertain a frequency trend. This is in line with our own findings (see our Sect. 3.3).
is inconsistent with a2 at 4.5σ, but it is in agreement at 1σ during the minimum of activity. Interestingly, Chaplin et al. (2003) also studied the frequency asymmetry of l = 2 modes in detail using BiSON and GOLF data with a different methodology and over a period that encompasses the maximum of 1999–2002. Their measurement considers only Tn22, so a direct comparison is not straightforward. However, we note that with an 844 day-long time series starting in February 19998, they detected a frequency shift Tn22 ≃ 190 nHz at a similar significance (≃4σ) as our measurement when averaging over all modes between ≃2000 − 3300 μHz (to be compared to our range of ≃2300 − 3600 μHz). Their Fig. 8 also shows that the global effect of the activity cycle between 1994 and 2000 is evident in the averaged Tn22, while the frequency dependence of Tn22 may have uncertainties too large to ascertain a frequency trend. This is in line with our own findings (see our Sect. 3.3).
 |
Fig. 7. Probability density functions and their correlations obtained by MCMC for coefficients a1, a2, a3, and a4 for the Sun at maximum activity (1999–2002, left) and at minimum activity (2006–2009, right). The red curve is the expected |
 |
Fig. 8. Probability density functions and their correlations obtained by MCMC for coefficients a1, a2, a3, and a4 for the Sun between two activity cycles (2006–2011). The red curve is the expected |
A rigorous statistical evaluation of our significance requires the joint use of a2 and a4. This is discussed in Sect. 5.2, along with other activity results. Finally, we note that for an inclination of ≃90 deg, it is not possible to determine a3 because the amplitudes of the azimuthal components for l = 1, 2 are not favourable (Gizon & Solanki 2004).
5.2. Activity of the Sun
We derived the activity intensity of the Sun and its latitudinal coverage from a fit of the 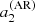 and
and 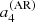 coefficients. Technical details are in Appendix C. A statistical summary of the results is presented in Table 2. The statistical significance of the activity exceeds 99.99% (highly significant) at the maximum of activity but is around 50.6% (not significant) during the minimum of activity, demonstrating the possibility of detecting activity in Sun-like stars. The choice of the function F describing the active region changes the detection significance by only a few percentage points. The three models we explored fit the data equivalently, implying that the shape of the active region cannot be determined with currently available a2 and a4 constraints.
coefficients. Technical details are in Appendix C. A statistical summary of the results is presented in Table 2. The statistical significance of the activity exceeds 99.99% (highly significant) at the maximum of activity but is around 50.6% (not significant) during the minimum of activity, demonstrating the possibility of detecting activity in Sun-like stars. The choice of the function F describing the active region changes the detection significance by only a few percentage points. The three models we explored fit the data equivalently, implying that the shape of the active region cannot be determined with currently available a2 and a4 constraints.
Statistical summary for the activity parameters and their model log-marginal likelihood ln(P(O|MAR) when F(θ|x) = Π(θ0, δ), Λ(θ0, δ), or 𝒩(θ0, δ).
Figures 9 and 10 show ϵnl = ϵ, θ0, and δ for the Sun at its maximum (1999–2002) and its minimum (2006–2009) of activity, respectively. There are no major differences between the three activity profiles, although we do note that the uncertainties are larger in the case of a triangular and a Gaussian activity zone. During the maximum of activity, ϵ ≃ 0 is clearly excluded (see inset in Fig. 9). With F = Π, we observed a log-normal distribution, with median 7.6 × 10−4, consistent with the value reported by Gizon (2002). However, the uncertainty is large, suggesting that only the order of magnitude can be constrained in Sun-like stars. At the minimum of activity, the log-normal distribution morphs into a 1/x law, similar to the Jeffreys prior. This is a sign of weaker statistical significance for the activity.
 |
Fig. 9. Inferred PDFs for (a) ϵ, (b) θ0, and (c) δ during the maximum activity of the Sun (1999–2002). The inset of (a) is a zoom into the near zero ϵ values with smaller binning. |
 |
Fig. 10. Inferred PDFs for (a) ϵ, (b) θ0, and (c) δ during the minimum activity of the Sun (2006–2009). The inset of (a) is a zoom into the near zero ϵ values with smaller binning. |
The co-latitude θ0 ≃ 75 < SPSDOUBLEDOLLAR > ° is consistent with the butterfly diagram, which suggests θ0 ≃ 80°. At the minimum of activity, and despite a non-significant detection, the probability distribution of θ0 shows a weak indication of activity at mid and high co-latitudes. Despite the high significance of the detection during the maximum of activity, δ is poorly constrained, showing that this parameter is challenging to measure on the Sun and on other Sun-like stars.
6. Analysis of 16 Cyg A and B
Due to their brightness (magnitudes V = 5.95 and 6.20), 16 Cyg A and B have modes with the highest HNR among all of Sun-like stars observed asteroseismically so far. They constitute ideal candidates to evaluate the activity. The two stars are wide binaries; there is a confirmed planet around 16 Cyg B (Cochran et al. 1997); and they were extensively studied (e.g. Neckel 1986; King et al. 1997; Deliyannis et al. 2000; Schuler et al. 2011; Takeda 2005; Metcalfe et al. 2012, 2016; Lund et al. 2014; Verma et al. 2014; Buldgen et al. 2015, 2022; Deal et al. 2015; Roxburgh 2017; Bellinger et al. 2017; Maia et al. 2019; Bazot et al. 2019; Bazot 2020; Farnir et al. 2020; Morel et al. 2021; Nsamba et al. 2022). In this section, we use the 2.5 year observation (13 September 2010 to 8 March 2013) by the Kepler space-borne instrument to measure pulsation parameters. The data are the same as those used in Bazot et al. (2019), for which instrumental issues (outliers, jumps, trends) and the quarter stitching is performed using the procedure described in García et al. (2011b). The binary system has precisely measured angular diameters, making 16 Cyg A and B two of the few Sun-like stars with known interferometric radii. The measured radii are 1.22 ± 0.02 R⊙ and 1.12 ± 0.02 R⊙ for 16 Cyg A and B, respectively (White et al. 2013). The spectroscopic parameters of these stars are very close to those of the Sun. The effective temperatures for 16 Cyg A and B are, respectively, Teff = 5825 ± 50 K and Teff = 5750 ± 50 K, and their metallicities are [M/H] = 0.10 ± 0.09 and [M/H] = 0.05 ± 0.06 (Ramírez et al. 2009), respectively. Each with an estimated age of around 7 Gyr (e.g. Metcalfe et al. 2016; Bazot 2020), the two stars are significantly older than the Sun.
6.1. Seismic constraints for 16 Cyg A
Earlier studies of 16 Cyg A have revealed around 60 modes of pulsations, with a significance in the power spectrum9. The asteroseismic analysis of Davies et al. (2015) found a stellar inclination of 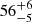 and a rotation of
and a rotation of 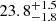 (
(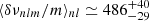 nHz). Using a refined power spectrum modelling that accounts for a1 and a3 and that parameterises the cavity asphericity (Req − Rpol)/Req, Bazot et al. (2019) reported values (i = 58.5 ± 6.8, a1 = 464 ± 43 nHz) consistent with Davies et al. (2015).
nHz). Using a refined power spectrum modelling that accounts for a1 and a3 and that parameterises the cavity asphericity (Req − Rpol)/Req, Bazot et al. (2019) reported values (i = 58.5 ± 6.8, a1 = 464 ± 43 nHz) consistent with Davies et al. (2015).
Figure 11 shows the PDFs for a1, a2, a3, and a4 for 16 Cyg A, along with their correlation and with 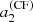 superimposed in the a2 quadrant. Table 3 synthesises the inferred values of the coefficients. The PDFs are near Gaussian, and thus the quadratic mean of the asymmetrical uncertainties is reported in the table. The a1 coefficient is significantly lower than past estimates but remains consistent at a 2σ confidence level. The difference may be due to the lower stellar inclination, i = 45 ± 4, which is also only consistent with an earlier determination at 2σ. The a3 coefficient is marginally greater but with a smaller uncertainty than Bazot et al. (2019) (they reported a3 = 11.15 ± 10.95 nHz).
superimposed in the a2 quadrant. Table 3 synthesises the inferred values of the coefficients. The PDFs are near Gaussian, and thus the quadratic mean of the asymmetrical uncertainties is reported in the table. The a1 coefficient is significantly lower than past estimates but remains consistent at a 2σ confidence level. The difference may be due to the lower stellar inclination, i = 45 ± 4, which is also only consistent with an earlier determination at 2σ. The a3 coefficient is marginally greater but with a smaller uncertainty than Bazot et al. (2019) (they reported a3 = 11.15 ± 10.95 nHz).
 |
Fig. 11. Probability density functions and their correlations obtained by MCMC of the power spectrum of 16 Cyg A and for coefficients a1, a2, a3, and a4 for 16 Cyg A. The red curve shows the expected |
Summary of the main parameters for the Sun and 16 Cyg A and B used to infer the activity.
More importantly, a2 is positive at 1σ, which is consistent with the assertion of star prolateness from Bazot et al. (2019) and is inconsistent with the centrifugal distortion term, 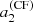 . Finally, a4 includes zero within 1σ.
. Finally, a4 includes zero within 1σ.
With respect to Figs. 5 and 6, a1/Γνmax = 0.45 ± 0.04 and i = 45 ± 4° place 16 Cyg A in a parameter space where the expected magnitude of the bias for a1, a2, and a4 is of the order of 0.5σ, 0.5σ, and 0.8σ, respectively. This remains accurate even when accounting for the slightly higher estimates of inclination from previous publications. Translated into absolute units, this corresponds to approximately b(a1)≃ + 10 nHz (overestimation), b(a2)≃ − 10 nHz (underestimation), and b(a4)≃ − 10 nHz (underestimation). These fiducial values are used in Sect. 6.3 to evaluate the effect of the potential bias on the estimates of the activity zone.
6.2. Seismic constraints for 16 Cyg B
Similar to 16 Cyg A, 16 Cyg B has around 60 observed modes. However, the reported precision for the past determination of the seismic parameters is less accurate than for 16 Cyg A, despite a similar HNR. Davies et al. (2015) and Bazot et al. (2019) both note a large degeneracy between the stellar inclination and the average rotation rate, even with a clear bimodality in the distributions obtained by Bazot et al. (2019). Their global solution of 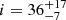 is associated with two separate solutions for a1, centred around ≃300 nHz and ≃550 nHz, that they use to infer the latitudinal differential rotation profile. Meanwhile, as for 16 Cyg A, the star is found to be prolate, indicating a surface activity.
is associated with two separate solutions for a1, centred around ≃300 nHz and ≃550 nHz, that they use to infer the latitudinal differential rotation profile. Meanwhile, as for 16 Cyg A, the star is found to be prolate, indicating a surface activity.
Figure 12 shows the measured a-coefficients. It appears that including the a4 coefficient removed the degeneracy issue observed by previous publications. The stellar inclination, a1, and a2 are precisely determined and have approximately Gaussian probability distributions, and these are reported as such in Table 3. The found rotation rate a1 corresponds to the higher solution of rotational splitting of Davies et al. (2015) and Bazot et al. (2019; see their figures of PDFs). Meanwhile, the degeneracy observed in a1 in earlier studies is moved to a4, and it exhibits two solutions. As our method of activity inference assumes Gaussian distributions, the bimodality of a4 requires separating the two apparent solutions. The mean and standard deviation of both solutions were measured using Gaussian mixture modelling (Bishop 1995; Bazot et al. 2019), enabling their separate analysis. The lowest estimate’s (a4 = −27.9 ± 6.5 nHz) weight is 30%, and the highest estimate (a4 = −1.0 ± 6.7 nHz) is more significant, as its weight is 70%. The inference of the activity from the two solutions is discussed in Sect. 6.4. We note that 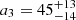 nHz is significantly higher than the reported values from Bazot et al. (2019) (a3 = 13.89 ± 13.95 nHz) and may have an impact on the rotational profile.
nHz is significantly higher than the reported values from Bazot et al. (2019) (a3 = 13.89 ± 13.95 nHz) and may have an impact on the rotational profile.
 |
Fig. 12. Probability density functions and their correlations obtained by MCMC of the power spectrum of 16 Cyg B and for coefficients a1, a2, a3, and a4 for 16 Cyg B. The red curve shows the expected |
6.3. Activity inference for 16 Cyg A
Figure 13 shows the results from the inference of the activity parameters and a statistical summary is given Table 2. Triangular and Gaussian descriptions of active latitudes give larger uncertainties than the simple gate model. However, they all suggest near-equatorial activity, with a similar detection significance level of ≃79% (without bias correction), or ≃96% with fiducial correction. As for the Sun and because the shape of the active region is a priori unknown, the average distribution of the parameters is discussed. The activity intensity has a large uncertainty, but according to the median of ϵ, it may be between the maximum and the minimum of solar activity.
 |
Fig. 13. Inferred PDFs for 16 Cyg A for raw measures (a–c) and with bias correction (d–f). The green curve is for the average PDF with F = Π, Λ, and 𝒩. The shaded area is its 1σ confidence interval. The insets in (a) and (d) are zooms into the near zero ϵ values with smaller binning. |
The posterior probability distribution of δ does not allow us to precisely constrain the extension of the activity region. As already noted in the case of the Sun, this parameter requires stringent constraints on both the a2 and a4 coefficients in order gain information about the size of the active region.
6.4. Activity inference for 16 Cyg B
Figures 14 and 15 show the results for the activity for 16 Cyg B in the two possible scenarios of a4 discussed in Sect. 6.2 (see Table 2 for the statistical summary). In the case of a4 = −27.9 ± 6.5 nHz (Fig. 14), the activity is highly significant (greater than 99.3%, with or without bias correction, whatever the activity zone model) and has a stronger intensity than in the case of the Sun. The active region is then located at θ0 ≃ 58° (θ0 ≃ 60°, after bias correction), that is, at comparable latitudes seen during a maximum of activity of the Sun. The bias correction has a negligible effect on the inferred activity latitude. Due to a4 significantly departing from zero, the extension of the active region is better constrained than in 16 Cyg A or the Sun, but it remains weakly informative.
 |
Fig. 14. Inferred PDFs of ϵ, θ0, and δ for raw results of 16 Cyg B with the lower solution a4 = −29.2 ± 5.6 nHz without bias correction (a–c) and with it (d–f). The green curve is the average PDF with F = Π, Λ, and 𝒩. The shaded area is its 1σ confidence interval. The insets of in (a) and (d) are zooms into the near zero ϵ values with smaller binning. |
The second more likely solution (probability of 70%) corresponds to a4 = −1.0 ± 6.7 nHz (Fig. 15). It is associated with an activity at co-latitudes above ≃40° and with lower activity. Its statistical significance is low, and the activity intensity may be of the same order or lower than 16 Cyg A. In fact, it looks similar to the solar case when approaching its minimum of activity. Accounting for the fiducial bias, the solution is more concentrated in the equatorial region and differs significantly from the lower probability a4 solution. Here, the uncertainty on a2 and a4 is again too large to provide a stringent constraint on the extension of the activity zone δ.
7. Discussion and conclusion
Stellar activity is a complex phenomenon emerging from the interplay between stellar plasma, rotation, and magnetism. The activity distorts the shape of the mode cavity, perturbing the pulsation frequencies. In this work, we evaluated this perturbation observationally using an a-coefficient decomposition, as it allowed us to separate observables (the a-coefficients) from their physical interpretation (the activity modelling). The separation also enabled us to demonstrate that the measurements of the average low a-coefficient, a2, and a4, under some observational conditions, are sufficient to reveal the presence of a statistically significant activity of similar intensity to the Sun and to determine its latitude. The required observational conditions were analysed using a methodology similar to Kamiaka et al. (2018), that is, by constructing a grid of artificial power spectra that allows the bias for a1, a2, and a4 to be determined. We found that if the HNR exceeds ten, then the mode blending factor f = a1/Γνmax is greater than 0.4, the inclination is above 30°, and the observation is longer than 2 years. The inaccuracy remains mild and generally smaller than the 1σ uncertainty. The uncertainty and/or the inaccuracy may, however, become too large to reliably detect any activity beyond the above-specified conditions. In particular, and in agreement with Kamiaka et al. (2018), the stellar inclination is a decisive variable for ensuring the accuracy of the measurement. Below 30°, a1 is often wrong by a factor two. This is likely due to the fit mistakenly identifying l = 2, m = ±1 as l = 2, m = ±2 and vice-versa. Other a-coefficients are then severely inaccurate. Therefore, such a bias analysis suggests that rotation studies of stellar ensembles require a careful star selection.
We proposed a method that uses the average a2 and a4 coefficients to perform a subsequent analysis of the activity, considering a geometrical model of the activity effect on the pulsation frequencies and accounting for the stellar asphericity due to the centrifugal effects. We tested this two-step approach on the Sun and showed that it is effectively able to detect the change of activity between the solar maximum of activity around 1999–2002 and the minimum of activity around 2006–2009. Although the use of averaged a-coefficients makes it difficult to evaluate the extension of the activity zone, the model successfully retrieves the mean latitude of activity during the maximum of the solar cycle.
We then applied the method to the brightest stars observed during the initial observational phase of the Kepler space instrument: 16 Cyg A and B. These stars were selected as a test bed due to the fact that they are well studied and present the highest mode signal-to-noise ratio of all the currently known main sequence stars. Davies et al. (2015) suggested that these stars have mild to no activity. However, Bazot et al. (2019), using a parametric model for describing the asphericity (Req − Rpol)/Req, found an asphericity significant at 1σ. Our current analysis, performed using the same data set, confirms this asphericity, and we found a mild (relative to the Sun) to moderate activity for both stars. It is found that 16 Cyg A has a near-equatorial band of activity during the period of observation (13 September 2010 to 8 March 2013), with a significance of the detection greater than 79.8%.
The case of 16 Cyg B is more ambiguous. A bimodality on the average splitting ⟨δνnlm/m⟩≃a1 and on the stellar inclination has already been reported in Davies et al. (2015) and Bazot et al. (2019). Our refined model suggests that this bimodality is in fact related to the l = 2 modes. Indeed, as we accounted for a1, a2, a3, and a4, we noted that the bimodality previously seen on a1 in earlier studies becomes displaced to a4. The solutions of a4 were separated using a Gaussian process algorithm, and we found that the weight (or importance) of the highest solution, close to 0 nHz, is of 70%. The lower solution, close to −28 nHz, has a weight of 30%. The associated probability distribution for stellar inclination i = 35 ± 3 is unique (instead of being bimodal in past studies). We analysed the two solutions of a4 independently. The lower solution (with lower weight) is associated with an overall activity that is stronger than the Sun, localised at latitudes of approximately 32° (with an uncertainty of ≃3°). The higher solution is linked to a lower activity and is weakly significant (probability greater than 67.1%). Although the uncertainty is large, our study suggests an activity closer to the equatorial region. In the Sun, and as evident in its butterfly diagram, the quiet phase is associated with a magnetic activity closer to the equator, while the transition to the active Sun is abrupt and characterised by the appearance of magnetic spots at latitudes of 30–40°. In that context, and although it is not possible to rule out the possibility of a statistical fluke, an interpretation of the bimodality is that the star was transitioning from a period of low activity to a more active period during the observation time of the Kepler instrument. To evaluate that hypothesis, we selected solar data between January 2006 and January 2011, which includes the end of a cycle and the start of a new one. The measured a-coefficients for that analysis are shown in Fig. 8. There is no visible bimodality on either a2 or a4. Because 16 Cyg B is evidently different than the Sun, this does not refute the hypothesis but weaken it. A firmer verification would require a follow-up observation of the star, with PLATO (Rauer et al. 2014) for example, or extensive simulations in order to attempt to reproduce the bimodality.
This work demonstrates that it is possible to determine the latitude and intensity of the activity of Sun-like stars when this activity is similar to or exceeds that of the Sun. The limited observed bias suggests that this analysis of the stellar activity could also be extended to a larger set of stars. Notably, the Kepler LEGACY stars (Lund et al. 2017) are ideal candidates, as these stars generally satisfy the criteria of reliability discussed in this conclusion and detailed in Sect. 4.
Although the a-coefficient analysis has the benefit of allowing for simplification of the bias studies and making the analysis faster, a further axis of improvement would consist of using a single analysis step, for example, by fitting the power spectrum with the model of activity directly. Contrary to the two-step analysis, such an approach does not require assumptions on the properties of probability distribution of the a-coefficients, as is currently the case. It would also make use of the full set of a-coefficients (not only their average), which may lead to smaller uncertainties. However, the two approaches would certainly need to be used in tandem, as the stability of the solution (and its accuracy) is harder to ascertain when performing a single-step fitting approach.
We fitted three parameters with our choice of Alm(x) (see Sect. 3.2).
The tool suite used here along with the data inputs and outputs are available at https://github.com/OthmanB/Benomar2022/tree/version_2
Acknowledgments
O.B. and L.G. acknowledge partial support from NYUAD Institute Grant G1502 “Center for Space Science”. L.G. is supported in part by the European Research Council (ERC) Synergy Grant WHOLE SUN 810218 and the Max Planck Society grant “Preparations for PLATO Science”. We thank Saskia Hekker for comments and advice.
References
- Anderson, E. R., Duvall, T. L., Jr, & Jefferies, S. M. 1990, ApJ, 364, 699 [Google Scholar]
- Antia, H. M., Chitre, S. M., & Thompson, M. J. 2000, A&A, 360, 335 [NASA ADS] [Google Scholar]
- Appourchaux, T. 2003, A&A, 412, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Gizon, L., & Rabello-Soares, M.-C. 1998, A&AS, 132, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Antia, H. M., Benomar, O., et al. 2014, A&A, 566, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atchadé, Y. F. 2006, Methodol. Comput. Appl. Probab., 8, 235 [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, ESA SP, 1306, 33 [NASA ADS] [Google Scholar]
- Ballot, J., Barban, C., & van’t Veer-Menneret, C., 2011, A&A, 531, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bazot, M. 2020, A&A, 635, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bazot, M., Benomar, O., Christensen-Dalsgaard, J., et al. 2019, A&A, 623, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellinger, E. P., Basu, S., Hekker, S., & Ball, W. H. 2017, ApJ, 851, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Benomar, O. 2008, Commun. Asteroseismol., 157, 98 [NASA ADS] [Google Scholar]
- Benomar, O., Appourchaux, T., & Baudin, F. 2009, A&A, 506, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benomar, O., Bedding, T. R., Stello, D., et al. 2012, ApJ, 745, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Benomar, O., Takata, M., Shibahashi, H., Ceillier, T., & García, R. A. 2015, MNRAS, 452, 2654 [Google Scholar]
- Benomar, O., Bazot, M., Nielsen, M. B., et al. 2018a, Science, 361, 1231 [Google Scholar]
- Benomar, O., Goupil, M., Belkacem, K., et al. 2018b, ApJ, 857, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Bishop, C. M. 1995, Neural Networks for Pattern Recognition (Oxford University Press, Inc.) [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
- Buldgen, G., Reese, D. R., & Dupret, M. A. 2015, A&A, 583, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Farnir, M., Eggenberger, P., et al. 2022, A&A, 661, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campante, T. L., Handberg, R., Mathur, S., et al. 2011, A&A, 534, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campante, T. L., Lund, M. N., Kuszlewicz, J. S., et al. 2016, ApJ, 819, 85 [Google Scholar]
- Catura, R. C., Acton, L. W., & Johnson, H. M. 1975, ApJ, 196, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Ceillier, T., Tayar, J., Mathur, S., et al. 2017, A&A, 605, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1969, Ellipsoidal Figures of Equilibrium (New Haven: Yale University Press) [Google Scholar]
- Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 2003, MNRAS, 343, 343 [CrossRef] [Google Scholar]
- Cochran, W. D., Hatzes, A. P., Butler, R. P., & Marcy, G. W. 1997, ApJ, 483, 457 [Google Scholar]
- Davies, G. R., Chaplin, W. J., Farr, W. M., et al. 2015, MNRAS, 446, 2959 [CrossRef] [Google Scholar]
- Deal, M., Richard, O., & Vauclair, S. 2015, A&A, 584, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deliyannis, C. P., Cunha, K., King, J. R., & Boesgaard, A. M. 2000, AJ, 119, 2437 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, T. L., Jr, Jefferies, S. M., Harvey, J. W., Osaki, Y., & Pomerantz, M. A. 1993, ApJ, 410, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., Goode, P. R., Kosovichev, A. G., & Schou, J. 2000, ApJ, 537, 1026 [CrossRef] [Google Scholar]
- Farnir, M., Dupret, M. A., Buldgen, G., et al. 2020, A&A, 644, A37 [EDP Sciences] [Google Scholar]
- Frohlich, C., Andersen, B. N., Appourchaux, T., et al. 1997, Sol. Phys., 170, 1 [CrossRef] [Google Scholar]
- García, R. A., Hekker, S., Stello, D., et al. 2011a, MNRAS, 414, L6 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Salabert, D., Ballot, J., et al. 2011b, J. Phys. Conf. Ser., 271, 012049 [CrossRef] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgobiani, D., Kosovichev, A. G., Nigam, R., Nordlund, Å., & Stein, R. F. 2000, ApJ, 530, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L. 2002, Astron. Nachr., 323, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L. 2006, Cent. Eur. Astrophys. Bull., 30, 1 [NASA ADS] [Google Scholar]
- Gizon, L., & Solanki, S. K. 2003, ApJ, 589, 1009 [Google Scholar]
- Gizon, L., & Solanki, S. K. 2004, Sol. Phys., 220, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., Ballot, J., Michel, E., et al. 2013, Proc. Nat. Acad. Sci., 110, 13267 [CrossRef] [PubMed] [Google Scholar]
- Gizon, L., Sekii, T., Takata, M., et al. 2016, Sci. Adv., 2, e1601777 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., & Taylor, P. P. 1984, Mem. Soc. Astron. Ital., 55, 215 [Google Scholar]
- Gough, D. O., & Thompson, M. J. 1990, MNRAS, 242, 25 [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with ‘Mathematica’ Support (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Handberg, R., & Campante, T. L. 2011, A&A, 527, A56 [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Cox, J. P., & van Horn, H. M. 1977, ApJ, 217, 151 [Google Scholar]
- Hartmann, L., & Rosner, R. 1979, ApJ, 230, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. 1985, ESA SP, 235, 199 [Google Scholar]
- Hogg, D. W., Myers, A. D., & Bovy, J. 2010, ApJ, 725, 2166 [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability, 3rd edn. (Oxford, UK: Oxford University Press) [Google Scholar]
- Kamiaka, S., Benomar, O., & Suto, Y. 2018, MNRAS, 479, 391 [NASA ADS] [Google Scholar]
- King, J. R., Deliyannis, C. P., Hiltgen, D. D., et al. 1997, AJ, 113, 1871 [Google Scholar]
- Libbrecht, K. G., & Woodard, M. F. 1990, Nature, 345, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Lignières, F., Rieutord, M., & Reese, D. 2006, A&A, 455, 607 [Google Scholar]
- Lund, M. N., Lundkvist, M., Silva Aguirre, V., et al. 2014, A&A, 570, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017, ApJ, 835, 172 [Google Scholar]
- Maeder, A., & Meynet, G. 2008, in Mass Loss from Stars and the Evolution of Stellar Clusters, eds. A. de Koter, L. J. Smith, & L. B. F. M. Waters, ASP Conf. Ser., 388, 3 [NASA ADS] [Google Scholar]
- Maia, M. T., Meléndez, J., Lorenzo-Oliveira, D., Spina, L., & Jofré, P. 2019, A&A, 628, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., García, R. A., Régulo, C., et al. 2010, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metcalfe, T. S., Chaplin, W. J., Appourchaux, T., et al. 2012, ApJ, 748, L10 [Google Scholar]
- Metcalfe, T. S., Egeland, R., & van Saders, J. 2016, ApJ, 826, L2 [Google Scholar]
- Morel, T., Creevey, O. L., Montalbán, J., Miglio, A., & Willett, E. 2021, A&A, 646, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, H. 1986, A&A, 159, 175 [NASA ADS] [Google Scholar]
- Nielsen, M. B., Schunker, H., Gizon, L., Schou, J., & Ball, W. H. 2017, A&A, 603, A6 [Google Scholar]
- Nigam, R., & Kosovichev, A. G. 1998, ApJ, 505, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Nsamba, B., Cunha, M. S., Rocha, C. I. S. A., et al. 2022, MNRAS, 514, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kővári, Z., Petrovay, K., et al. 2016, A&A, 590, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papini, E., & Gizon, L. 2019, Front. Astron. Space Sci., 6, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Pijpers, F. P. 1997, A&A, 326, 1235 [NASA ADS] [Google Scholar]
- Pijpers, F. P. 1998, Ap&SS, 261, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, Proc. SPIE, SPIE Conf. Ser., 9143, 914320 [NASA ADS] [Google Scholar]
- Ritzwoller, M. H., & Lavely, E. M. 1991, ApJ, 369, 557 [CrossRef] [Google Scholar]
- Roxburgh, I. W. 2017, A&A, 604, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, ApJ, 433, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Schuler, S. C., Cunha, K., Smith, V. V., et al. 2011, ApJ, 737, L32 [Google Scholar]
- Silva-Valio, A., Lanza, A. F., Alonso, R., & Barge, P. 2010, A&A, 510, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, T., Ayres, T. R., Redfield, S., & Linsky, J. L. 2002, ApJ, 579, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Stahn, T. 2010, PhD Thesis, Georg August University of Gottingen, Germany [Google Scholar]
- Takeda, Y. 2005, PASJ, 57, 83 [NASA ADS] [Google Scholar]
- Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J. 2003, ARA&A, 41, 599 [Google Scholar]
- Toutain, T., & Gouttebroze, P. 1993, A&A, 268, 309 [NASA ADS] [Google Scholar]
- Toutain, T., & Kosovichev, A. G. 2001, in SOHO 10/GONG 2000 Workshop: Helio- and Asteroseismology at the Dawn of the Millennium, eds. A. Wilson, & P. L. Pallé, ESA SP, 464, 123 [Google Scholar]
- Toutain, T., Appourchaux, T., Frohlich, C., et al. 1998, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, ed. S. Korzennik, ESA SP, 418, 973 [NASA ADS] [Google Scholar]
- Ulrich, R. K. 1986, ApJ, 306, L37 [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (University Tokyo Press) [Google Scholar]
- van Saders, J. L., Ceillier, T., Metcalfe, T. S., et al. 2016, Nature, 529, 181 [Google Scholar]
- Vaughan, A. H. 1983, IAU Symp., 102, 113 [Google Scholar]
- Verma, K., Faria, J. P., Antia, H. M., et al. 2014, ApJ, 790, 138 [Google Scholar]
- Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [Google Scholar]
- White, S. M. 1999, Sol. Phys., 190, 309 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 161 [Google Scholar]
- White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
- White, S. M., Iwai, K., Phillips, N. M., et al. 2017, Sol. Phys., 292, 88 [Google Scholar]
Appendix A: Polynomials, a-coefficients and splittings
A.1. The first six used polynomials
The 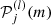 coefficients, which were introduced by Schou et al. (1994), can be obtained by normalising the
coefficients, which were introduced by Schou et al. (1994), can be obtained by normalising the 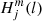 coefficients by Ritzwoller & Lavely (1991) so that
coefficients by Ritzwoller & Lavely (1991) so that 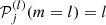 .
.
where the last factor means the Wigner 3j symbol. The coefficients can also be obtained by recurrence, using Equations (2) and (3) together with the normalisation condition 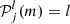 and starting with
and starting with 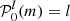 . The first six polynomials are as follows:
. The first six polynomials are as follows:
where L = l(l + 1) and N = 64l5 − 480l4 + 1360l3 − 1800l2 + 1096l − 240.
A.2. Relationship between a-coefficients and splittings
The relationships between a-coefficients and symmetric or antisymmetric splittings can be derived using Equations (4) and (5). The equations are used to convert model frequencies νnlm into a-coefficients.
A.2.1. Explicit form for low a-coefficients and l=1
The relation between a-coefficients a1(n, l = 1), a2(n, l = 1) and the modes frequencies is,
A.2.2. Explicit form for low a-coefficients and l=2
The relation between a-coefficients a1(n, l = 2), a2(n, l = 2), a3(n, l = 2), a4(n, l = 2) and the symmetric or antisymmetric splittings is,
A.2.3. Explicit form for low a-coefficients and l=3
The relation between a-coefficients a1(n, l = 3), a2(n, l = 3), a3(n, l = 3), a4(n, l = 3), a5(n, l = 3), a6(n, l = 3) and the symmetric or antisymmetric splittings is,
Appendix B: Spectrum analysis
B.1. Acoustic spectrum modelling
The analysis of the asteroseismic data is very often performed by fitting the power spectrum (e.g. Appourchaux et al. 1998, 2008). This requires devising a likelihood function and a model for the observed spectrum. As our fitting involves a Bayesian approach, the priors are also required.
B.1.1. Likelihood
The likelihood function is determined by the noise statistics of the power spectrum, which is an χ-squared with two degrees of freedom. It is also based on the assumption that the frequency bins are independent and uncorrelated. This implies that the observation duration is assumed to be much greater than the typical lifetime of the pulsation modes and that the duty cycle is sufficient to allow us to neglect any leakage induced by the window function. The observation time frame for the LEGACY sample is of the order of years, which is significantly longer than the mode lifetime. Furthermore, the duty cycle is above 95%, which was shown to be sufficient to neglect leakage (Stahn 2010). Under these conditions, the likelihood function is (Anderson et al. 1990)
where S(νi) is the power at the central frequency νi of the ith bin. Here, N is the total number of bins, and M(νi, X) is the model of the power spectrum with the set of variable X for the model M.
From Bayes theorem, the posterior probability density function is defined as
where π1(X|M) is the prior knowledge on the parameters X. We note that π1(S(ν)|M) is a normalisation constant and is essential only when comparing the significance of models (e.g. Gregory 2005; Benomar et al. 2009). We assumed the variables to be independent from each other. We evaluated the posterior using the Tempered Adaptive MCMC code10 described in Atchadé (2006) and implemented by Benomar (2008).
B.1.2. Acoustic spectrum model
The model used for the power spectrum fitting involves a sum of asymmetrical Lorentzian superimposed to a monotonically decreasing function of frequency (pink noise). The asymmetric Lorentzian is commonly used in helioseismology (Duvall et al. 1993; Nigam & Kosovichev 1998; Georgobiani et al. 2000; Toutain et al. 1998) and in asteroseismology for Sun-like stars (Benomar et al. 2018b). The sum of Lorentzian profiles is defined as,
with z = 2(ν − νnlm)/Γnlm. Each asymmetrical Lorentzian is defined by a height Hnlm, width Γnlm, central frequency νnlm, and asymmetry Bnlm. As explained by Gizon (2006); Benomar et al. (2018b), the asymmetry coefficient depends on the mode width and frequency. The normalised asymmetry coefficient 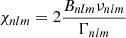 is fitted, as it is nearly constant over the range of fitted modes.
is fitted, as it is nearly constant over the range of fitted modes.
Several prescriptions exist for describing the noise background N(ν). In this work, we assumed it to be a sum of two generalised Lorentzian, sometimes referred as Harvey-like profiles (Harvey 1985), and of a white noise:
Here, N0 is the white noise, and Ak is the maximum heights of the kth generalised Lorentzian. The τk parameter is the timescale that is the inverse of the full width at half maximum of the Lorentzians, and pk is a power exponent.
The fit is performed globally over all the statistically significant peaks visible in the power spectrum of a star. This can lead to a very large number of fitted parameters (up to a few thousands), which is practically unsuitable. A model simplification is therefore preferred (similar to e.g. Appourchaux et al. (2008), Benomar et al. (2009), Campante et al. (2011), Handberg & Campante (2011)); the main simplifications recalled hereafter:
-
The m dependence on heights is controlled by its relationship with the stellar inclination (Gizon & Solanki 2003). This saves several hundreds of parameters.
-
The relative height of the different degree l is constant across the fitted range and for a given l, hence
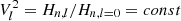 . Only the l = 0 heights Hn, l = 0 are variables. The mode visibility
. Only the l = 0 heights Hn, l = 0 are variables. The mode visibility 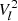 replaces the Hn, l > 0 as a variable.
replaces the Hn, l > 0 as a variable. -
Given a degree l, Γn, l, m = Γn, l is imposed. This is justified by the fact that the width depends weakly on the frequency, as all split components are assumed to have the same width.
-
Because Γn, l is nearly independent of the degree, it is possible to fit Γ(ν) = Γn, l = 0 and to interpolate it to the frequencies of the modes with degree l > 0.
These assumptions reduce the number of variables to a few tens in the case of CoRoT, Kepler, or TESS observations. The frequencies of the modes follow Equation (14) in Section 2.3.
B.2. Priors
Priors are fundamental to the Bayesian method. This section discusses π1(X|M, I), the prior used during the power spectrum fitting. We assumed the parameters of the vector X to be independent of each other such that the product rule is used to the define π1(X|M, I).
Heights, widths, frequencies, asymmetry, and inclination use non-informative priors. These are either Jeffreys priors for scale parameters, noted as 𝒥(xmin, xmax), or uniform priors, noted as 𝒰(xmin, xmax). The priors on frequencies are uniform and require a visual inspection of the power spectrum in order to assign the lower and upper bound of the prior for each mode that follows the expected pattern for main sequence Sun-like stars (equally spaced p modes) and that shows an excess of power relative to the background that exceeds 80%. The excess of power is determined using a smooth spectrum for which the noise statistics is derived by Appourchaux (2003). Mode visibilities are defined by Gaussian priors (noted as 𝒢(x0, σ)), with the mean x0 set as the solar value (see Ballot & Barban 2011), and the standard deviation σ is 10% of the mean. Table B.1 lists the type and the prior characteristic values that are used for the parameters of the modes.
Mode priors used for the fit of the power spectrum. Prior parameters on frequencies were visually determined (see Section B.2).
The prior on a1 is uniform between 0 and 1500 nHz. For 16 Cyg A and B, a uniform fixed prior is set on |a3| over the range [0, 100] nHz. However at each iteration of the optimisation process, |a3| is not allowed to exceed 20% of a1. Preventing an extremely large relative value of a3/a1 improves the fit stability and ensures a faster convergence of the algorithm. For the Sun analysis and because it is not possible to measure a3 for i ≃ 90° (due to the lack of amplitude of l = 2, m = ±1 at that inclination), a3 is fixed to zero.
The priors on a2 and a4 are also uniform. The range is defined by using the maximum range of Figure 4 (showing 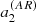 and
and 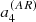 , increasing it by 50%, and adding the expected centrifugal term
, increasing it by 50%, and adding the expected centrifugal term 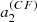 , assuming a1 = 400nHz for the Sun and a1 = 600nHz for 16 Cyg A or 16 Cyg B. The Δν reported in Table 3 is also used. For the same reason as with a3, a2/a1 cannot exceed 50%, and a4/a1 cannot exceed 20% at each iteration step of the optimisation process.
, assuming a1 = 400nHz for the Sun and a1 = 600nHz for 16 Cyg A or 16 Cyg B. The Δν reported in Table 3 is also used. For the same reason as with a3, a2/a1 cannot exceed 50%, and a4/a1 cannot exceed 20% at each iteration step of the optimisation process.
The noise priors are obtained from a global MAP approach similar to Benomar et al. (2012). This provides the best fit values and 1σ uncertainties that are to be used as priors. The noise background of the individual model analysis is described by Equation (B.4). During the global MAP fit, the model is made of that same background model plus a Gaussian envelope to account for the power excess due to the modes (e.g. Mathur et al. 2010; Huber et al. 2011).
Appendix C: Inference of the active latitudes
The determination of the activity is performed as a second step using the marginalised posterior distribution of the average a-coefficients as observables. This section describes the method and assumptions for determining the posterior distribution and computing the significance of the detection.
C.1. Posterior distribution and likelihood
Similar to the power spectrum fitting described in Appendix B, the determination of the most likely latitudes for the activity and its significance necessitate the computation of a posterior distribution,
with π2(X|O, M), π2(X|M), and L2(O|X, M) as the posterior distribution, the prior, and the likelihood, respectively. The denominator, π2(O|M), is the normalisation constant used for model comparison (marginal likelihood). The posterior distributions of the a-coefficients a2, o and a4, o obtained by power spectrum fitting are the observables contained in O. The class of the model is identified by the variable M.
For simplicity, the observables are assumed to be distributed according to uncorrelated Gaussian functions such that O = {a2, o, a4, o, σ2, o, σ4, o}, where a2, o and a4, o are the mean for the distributions of a2 and a4, while σ2, o and σ4, o are the standard deviations. This leads to a log-likelihood in the form of an χ-squared,
In Dziembowski et al. (2000), a-coefficients are weighted using the inverse of the mode inertia (see their Equation 4). This is due to the fact that the inertia account for most of the frequency variations of the coefficients. Accounting for the mode inertia is essentially relevant if the uncertainties are small enough to observe a trend when modes are fitted individually. However, in the case of the Sun and with either GOLF or BiSON data, it is difficult to perceive a frequency trend (Chaplin et al. 2003). Our own trials on VIRGO/SPM using a linear fit to describe the frequency dependence of an a-coefficient did not detect a slope that is significant at more than 1σ. A similar analysis on 16 Cyg A and B and on simulations showed evidence of large uncertainties when attempting to determine frequency variations for stars with HNR typical of Kepler observations. In fact, only the average of the a-coefficient over l and n is shown to be robustly determined (see also our discussion Section 3.3) so that inertia effects are neglected.
The activity model MAR depends on the variables X = {ϵ, θ0, δ} and a2, m(X), whereas a4, m(X) denotes the modelled a-coefficients. The log-likelihood is then
In our case, the observables are the average of the fitted modes’ coefficients, 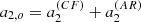 and
and 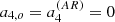 . However, to conveniently propagate all errors on the parameters of
. However, to conveniently propagate all errors on the parameters of 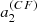 (a1, Δν, Δν⊙, ρ⊙, νnl), it is preferable to use
(a1, Δν, Δν⊙, ρ⊙, νnl), it is preferable to use 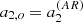 , which is obtained by subtracting the
, which is obtained by subtracting the 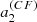 from the a2 measured by the power spectrum fitting. The distribution of Δν is computed by a linear fitting of the groupwise ensemble of samples (n, l = 0) for each measured frequency νn0. Finally, the term
from the a2 measured by the power spectrum fitting. The distribution of Δν is computed by a linear fitting of the groupwise ensemble of samples (n, l = 0) for each measured frequency νn0. Finally, the term 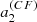 is obtained through a weighted average of all independent
is obtained through a weighted average of all independent 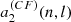 computed at the star’s posterior frequencies νnl. The subtraction of
computed at the star’s posterior frequencies νnl. The subtraction of 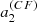 is then again performed using the samples of its posterior, enabling the posterior probability distribution function of
is then again performed using the samples of its posterior, enabling the posterior probability distribution function of 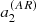 to be constructed, from which we deduced its mean a2, o and its standard deviation σ2, o. To evaluate the relevance of the activity, two models are considered. First, a model (M = MCF) without activity that accounts only for the centrifugal effects and, second, a model (M = MAR) with activity. Their details and the choice of the priors are described in the following sections individually.
to be constructed, from which we deduced its mean a2, o and its standard deviation σ2, o. To evaluate the relevance of the activity, two models are considered. First, a model (M = MCF) without activity that accounts only for the centrifugal effects and, second, a model (M = MAR) with activity. Their details and the choice of the priors are described in the following sections individually.
C.2. Model without activity MCF
The model MCF has no unknown variable requiring minimisation (see Equation (13)). For the sake of comparing this model with the model MAR, it is however important to determine the marginal likelihood of MCF, and it is then necessary to calculate the denominator of Equation (C.1), P(O|MCF), which is defined as an integral,
An absence of activity corresponds to the limit case where the a-coefficients of the activity are exactly zero. This corresponds to setting Dirac priors on a2, m = δ0 and a4, m = δ0 and implies that the marginal likelihood is the local value of the likelihood at X = {0, 0}. The model comparison is commonly performed in log-space such that
C.3. Model with activity MAR
Regarding the model with activity of Equation (C.3), priors must be set on the variables subject to optimisation. The ϵ and δ parameters are indispensable intensive parameters, and the adequate non-informative prior is then the (truncated) Jeffreys prior (Jeffreys 1961), uniform in the log-space,
where xmin and xmax are the upper and lower bounds such that if x > xmax or x < xmin, then J(x) = 0. This guarantees that the probability density is proper (the integral over x is finite). In case of weak information content in the observables, this prior is more weighted towards a null value. We set ϵmin = 5.10−4 and ϵmax = 10−2. This embraces the solar value ϵ ≃ 5.10−4 (Gizon 2002). Because δ ≃ 10° at the maximum of solar activity, we set δmin = 10°. We also note that consistent with the discussion of Figure 3 in Section 3, δmax = 45° is required. Finally, the location parameter θ0 has a uniform prior in the range [0, 90]( ° ).
The marginal likelihood of the model MAR requires evaluation of the triple integral,
The MCMC process used here involves the use of parallel Metropolis-Hasting tempered chains. The chains mix with each other in order to enhance the sampling. As explained in Benomar et al. 2009 (see their Section A.3), these parallel chains can be used to approximate the Equation (C.7). This technique is used with ten parallel chains following a geometrical temperature law Tk = 1.7k − 1, with k as the chain index such that k = 1 is the target distribution, given by equation (C.1).
Appendix D: Bias map for 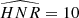 and
and 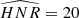
This section shows the bias on the a1, a2, and a4 coefficients in the case of 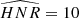 and
and 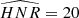 . Figures D.1 and D.3 are for the case of an equatorial band of activity, and Figures D.2 and D.4 are for a polar cap. The inaccuracy of the fit remains noticeably smaller than the standard deviation in the majority of the parameter space and for i > 30°, a1/Γνmax > 0.4. Interestingly, the relative-to-error bias on a1 is more pronounced in the case of an equatorial band of activity when {a1/Γνmax ≤ 0.4, i = [30, 60]} (Figure D.1d and D.3d). Then this bias can exceed three times the uncertainty. The accuracy of the inference of activity based on the a-coefficients is expected to weakly depend on the
. Figures D.1 and D.3 are for the case of an equatorial band of activity, and Figures D.2 and D.4 are for a polar cap. The inaccuracy of the fit remains noticeably smaller than the standard deviation in the majority of the parameter space and for i > 30°, a1/Γνmax > 0.4. Interestingly, the relative-to-error bias on a1 is more pronounced in the case of an equatorial band of activity when {a1/Γνmax ≤ 0.4, i = [30, 60]} (Figure D.1d and D.3d). Then this bias can exceed three times the uncertainty. The accuracy of the inference of activity based on the a-coefficients is expected to weakly depend on the 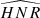 (although potentially with a large uncertainty) for most stars, except within this regime (in addition to the grey area) where the centrifugal effect will be overestimated.
(although potentially with a large uncertainty) for most stars, except within this regime (in addition to the grey area) where the centrifugal effect will be overestimated.
 |
Fig. D.1. Bias analysis for |
 |
Fig. D.2. Bias analysis for |
 |
Fig. D.3. Bias analysis for |
 |
Fig. D.4. Bias analysis for |
Appendix E: Figures of the best fits
This section presents visuals of the best MCMC fits for the power spectrum of the active Sun (Figure E.1), quiet Sun (Figure E.2), 16 Cyg A (Figure E.3), and for the two a4 solutions of 16 Cyg B (Figures E.4 and E.5). For 16 Cyg B, the solutions were separated by selecting the median for the samples only below or above a4 = 21nHz. In the case of the Sun, the impact of the activity on the profile of l = 2 is very clear, as the shifts of the m-components introduce an asymmetry in power for the overall l = 2 mode profile during the active phase. During the quiet phase, such an asymmetry is not visible.
 |
Fig. E.1. Solar power spectrum for observation between 1999 and 2002 after Gaussian smoothing over a kernel width s = 50nHz. Superimposed is the best MCMC fit. Top panel: Highlight of a l = 2, 0, 3, 1 mode group (left to right) and their fit (red). The power asymmetry due to non-symmetric m-components is visible in the data. Top panel, inset: Overall view of the modes. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. |
 |
Fig. E.2. Same as Figure E.1 but between 2006 and 2009. Top panel: Highlight of a l = 2, 0, 3, 1 mode group (left to right) and their fit (red). The power asymmetry seen for 1999-2002 is not apparent in the data. Top panel, inset: Overall view of the power spectrum. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. The residual on l = 1 is a bit high due to the visibility being fixed for all modes. |
 |
Fig. E.3. Same as Figure E.1 but for 16 Cyg A. Top panel: Highlight of a l = 2, 0, 1 mode group (left to right) and their fit (red). A very mild power asymmetry is seen in the l = 2 data. Top panel, inset: Overall view of the power spectrum. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. The residual shows an excess of power due to the low HNR≃1.7 l = 3 (not fitted here). |
 |
Fig. E.4. Same as Figure E.1 but for 16 Cyg B, a4 < −21 nHz. Top panel: Highlight of a l = 2, 0, 1 mode group (left to right) and their fit (red). A mild power asymmetry is seen in the l = 2 data. Top panel, inset: Overall view of the power spectrum. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. The residual shows an excess of power due to the low HNR≃1.6 l = 3 (not fitted here). |
 |
Fig. E.5. Same as Figure E.1 but for 16 Cyg B, a4 > −21 nHz. Top panel: Highlight of a l = 2, 0, 1 mode group (left to right) and their fit (red). Top panel, inset: Overall view of the power spectrum. Bottom. Residual of the fit with two level s of Gaussian smoothing. The residual show an excess of power due to the low HNR≃1.6 l = 3 (not fitted here). |
Similarly, although it is less pronounced than in the Sun, in the cases of 16 Cyg A and B, a weak asymmetry is visible in l = 2 modes. For 16 Cyg B, the two solutions of a4 provide sensibly similar mode profiles, as the difference is weakly apparent to the eye only for l = 2. The residuals do not show striking differences. This visually supports the fact that the goodness of fit is similar and explains that the two solutions coexist in statistical terms.
All Tables
Statistical summary for the activity parameters and their model log-marginal likelihood ln(P(O|MAR) when F(θ|x) = Π(θ0, δ), Λ(θ0, δ), or 𝒩(θ0, δ).
Summary of the main parameters for the Sun and 16 Cyg A and B used to infer the activity.
Mode priors used for the fit of the power spectrum. Prior parameters on frequencies were visually determined (see Section B.2).
All Figures
 |
Fig. 1. Example of Lorentzian mode profiles showing the a-coefficients and their relationship with frequency spacings for l = 1 (a) and l = 2 modes (b). The orange spacing is Tn22 − Tn21, νnl is the m-averaged frequency of each multiplet, and the stellar inclination is 40°. |
| In the text | |
 |
Fig. 2. Height-to-noise ratio (black) and a1/Γ ratio (red) for 16 Cyg A. We used 16 Cyg A to make our simulations. |
| In the text | |
 |
Fig. 3. Solar activity over time. (a) Butterfly diagram for the Sun. Vertical colour bands highlight periods of maximum (1988–1992, 1999–2002) and minimum activity (2006–2009). (b) Averaged spot area for the highlighted periods. Blue and purple marks in (b) are the weighted mean for the activity latitude. (c) Filters F(θ|X) used for this study superimposed onto solar data (1986–2016). The parameters θ0 and δ are the latitude and the extension of the active region, respectively. |
| In the text | |
 |
Fig. 4. Average |
| In the text | |
 |
Fig. 5. Bias analysis for |
| In the text | |
 |
Fig. 6. Bias analysis for |
| In the text | |
 |
Fig. 7. Probability density functions and their correlations obtained by MCMC for coefficients a1, a2, a3, and a4 for the Sun at maximum activity (1999–2002, left) and at minimum activity (2006–2009, right). The red curve is the expected |
| In the text | |
 |
Fig. 8. Probability density functions and their correlations obtained by MCMC for coefficients a1, a2, a3, and a4 for the Sun between two activity cycles (2006–2011). The red curve is the expected |
| In the text | |
 |
Fig. 9. Inferred PDFs for (a) ϵ, (b) θ0, and (c) δ during the maximum activity of the Sun (1999–2002). The inset of (a) is a zoom into the near zero ϵ values with smaller binning. |
| In the text | |
 |
Fig. 10. Inferred PDFs for (a) ϵ, (b) θ0, and (c) δ during the minimum activity of the Sun (2006–2009). The inset of (a) is a zoom into the near zero ϵ values with smaller binning. |
| In the text | |
 |
Fig. 11. Probability density functions and their correlations obtained by MCMC of the power spectrum of 16 Cyg A and for coefficients a1, a2, a3, and a4 for 16 Cyg A. The red curve shows the expected |
| In the text | |
 |
Fig. 12. Probability density functions and their correlations obtained by MCMC of the power spectrum of 16 Cyg B and for coefficients a1, a2, a3, and a4 for 16 Cyg B. The red curve shows the expected |
| In the text | |
 |
Fig. 13. Inferred PDFs for 16 Cyg A for raw measures (a–c) and with bias correction (d–f). The green curve is for the average PDF with F = Π, Λ, and 𝒩. The shaded area is its 1σ confidence interval. The insets in (a) and (d) are zooms into the near zero ϵ values with smaller binning. |
| In the text | |
 |
Fig. 14. Inferred PDFs of ϵ, θ0, and δ for raw results of 16 Cyg B with the lower solution a4 = −29.2 ± 5.6 nHz without bias correction (a–c) and with it (d–f). The green curve is the average PDF with F = Π, Λ, and 𝒩. The shaded area is its 1σ confidence interval. The insets of in (a) and (d) are zooms into the near zero ϵ values with smaller binning. |
| In the text | |
 |
Fig. 15. Same as Fig. 14 but for the higher solution a4 = −0.9 ± 6.8 nHz. |
| In the text | |
 |
Fig. D.1. Bias analysis for |
| In the text | |
 |
Fig. D.2. Bias analysis for |
| In the text | |
 |
Fig. D.3. Bias analysis for |
| In the text | |
 |
Fig. D.4. Bias analysis for |
| In the text | |
 |
Fig. E.1. Solar power spectrum for observation between 1999 and 2002 after Gaussian smoothing over a kernel width s = 50nHz. Superimposed is the best MCMC fit. Top panel: Highlight of a l = 2, 0, 3, 1 mode group (left to right) and their fit (red). The power asymmetry due to non-symmetric m-components is visible in the data. Top panel, inset: Overall view of the modes. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. |
| In the text | |
 |
Fig. E.2. Same as Figure E.1 but between 2006 and 2009. Top panel: Highlight of a l = 2, 0, 3, 1 mode group (left to right) and their fit (red). The power asymmetry seen for 1999-2002 is not apparent in the data. Top panel, inset: Overall view of the power spectrum. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. The residual on l = 1 is a bit high due to the visibility being fixed for all modes. |
| In the text | |
 |
Fig. E.3. Same as Figure E.1 but for 16 Cyg A. Top panel: Highlight of a l = 2, 0, 1 mode group (left to right) and their fit (red). A very mild power asymmetry is seen in the l = 2 data. Top panel, inset: Overall view of the power spectrum. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. The residual shows an excess of power due to the low HNR≃1.7 l = 3 (not fitted here). |
| In the text | |
 |
Fig. E.4. Same as Figure E.1 but for 16 Cyg B, a4 < −21 nHz. Top panel: Highlight of a l = 2, 0, 1 mode group (left to right) and their fit (red). A mild power asymmetry is seen in the l = 2 data. Top panel, inset: Overall view of the power spectrum. Bottom panel: Residual of the fit with two levels of Gaussian smoothing. The residual shows an excess of power due to the low HNR≃1.6 l = 3 (not fitted here). |
| In the text | |
 |
Fig. E.5. Same as Figure E.1 but for 16 Cyg B, a4 > −21 nHz. Top panel: Highlight of a l = 2, 0, 1 mode group (left to right) and their fit (red). Top panel, inset: Overall view of the power spectrum. Bottom. Residual of the fit with two level s of Gaussian smoothing. The residual show an excess of power due to the low HNR≃1.6 l = 3 (not fitted here). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



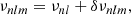
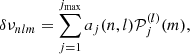
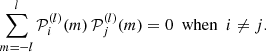
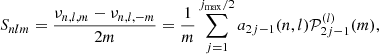
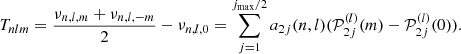
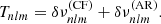
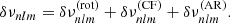
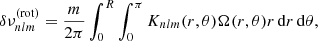
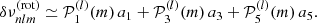
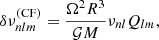
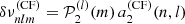
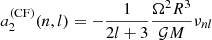
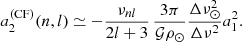
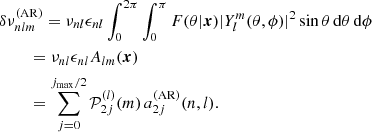
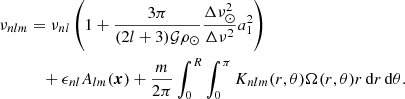
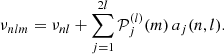
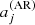
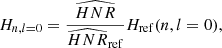
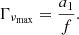
![$$ \begin{aligned} b(a_j)&= \mathrm{E} [a^{\mathrm{meas} }_j] - a^{\mathrm{true} }_j, \nonumber \\ b(F)&= \mathrm{E} [F^{\mathrm{meas} }] - F^{\mathrm{true} }, \nonumber \\ b(i)&= \mathrm{E} [i^{\mathrm{meas} }] - i^{\mathrm{true} }. \nonumber \end{aligned} $$](/articles/aa/full_html/2023/12/aa47095-23/aa47095-23-eq60.gif)