| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346767 | |
| Published online | 08 December 2023 | |
Shaping the CO snowline in protoplanetary disks
1
Niels Bohr Institute, University of Copenhagen,
Øster Voldgade 5-7,
1350
Copenhagen K, Denmark
e-mail: sacha.gavino@nbi.ku.dk
2
University of Kiel, Institute of Theoretical Physics and Astrophysics,
Leibnizstrasse 15,
24118
Kiel, Germany
3
Laboratoire d’Astrophysique de Bordeaux, Université de Bordeaux, CNRS, B18N,
Allée Geoffroy Saint-Hilaire,
33615
Pessac, France
Received:
28
April
2023
Accepted:
9
October
2023
Context. Characterizing the dust thermal structure in protoplanetary disks is a fundamental task because the dust surface temperature can affect both the planetary formation and the chemical evolution. Because the temperature depends on many parameters, including the grain size, it can be challenging to properly model the grain temperature structure. Many chemistry disk models usually employ a sophisticated single dust structure designed to reproduce the effect of a realistic population presumably composed of a large diversity of sizes. This generally represents a good approximation in most cases. Nonetheless, it dilutes the effects of the complex radiative interactions between the different grain populations on the resulting dust temperature, and thus, the chemistry.
Aims. We seek to show that the radiative interactions between dust grains of different sizes can induce a nontrivial dust temperature structure that cannot be reproduced by a single dust population and that can significantly affect the chemical outcome.
Methods. The disk thermal structures were computed using the Monte Carlo radiative transfer code RADMC-3D. The thermal structures were postprocessed using the gas-grain code NAUTILUS to calculate the evolution of the chemical abundance.
Results. We find that simultaneously using at least two independent dust grain populations in disk models produces a complex temperature structure due to the starlight that is intercepted by the upper layers of the disk. In particular, we find that micron-sized dust grains are warmer than larger grains and can even show a radial temperature bump in some conditions. This dust temperature spread between the grain populations results in the segregation of the CO snowline and in an unexpected CO gas hole in the midplane. We compare the results with observed close to edge-on class I/II disks.
Conclusions. Our study shows that the size dependence of the dust temperature significantly impacts the chemistry, and that two dust populations at least are required to account for this property of the thermal structure in protoplanetary disk models over a wide range of disk masses and dust properties.
Key words: circumstellar matter / protoplanetary disks / astrochemistry / radiative transfer / scattering / radio lines: stars
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Numerous studies have now confirmed the existence of grain growth in circumstellar disks. Grains up to millimeter sizes were detected (e.g., Testi et al. 2014; Ohashi et al. 2023). Some authors reported grain growth at a very early stage. For instance, Harsono et al. (2018) confirmed millimeter-sized grains in the very young disk (~100 000 yr) around the protostar TMC1A. These observations are especially important because they suggest that planet formation can be initiated at a very early stage of the protostellar evolution.
More specifically, it is known that the grain size distribution in protoplanetary disks is different from the distribution in the interstellar medium (ISM). Many authors have shown that the distribution can deviate from the typical Mathis, Rumpl and Nordsieck model (hereafter MRN; Mathis et al. 1977) found in the ISM (Ricci et al. 2010). In particular, the grain size range in disks is broader than in the ISM and is likely continuously distributed due to dust coagulation, fragmentation, and radial drift (e.g., Dullemond & Dominik 2005; Brauer et al. 2008; Birnstiel et al. 2010, 2018), resulting in a typical range from nanometer to centimeter sizes. The spatial distribution is also more complex. Grains with a small Stokes number are coupled to the disk gas (small Stokes numbers typically apply to small grains, and vice versa) and can be observed in the near-infrared to a very large vertical extent, whereas grains with a larger Stokes number are more efficiently settled toward the disk midplane and extend less in the vertical direction (Fromang & Nelson 2009). Moreover, inward radial drift can occur for coagulated grains (e.g., Birnstiel et al. 2010; Lambrechts & Johansen 2014), which strongly reshuffles the local dust density and size distributions.
Consequently, the extinction opacity in disks is also far harder to characterize than in the ISM. Most authors assumed size-averaged opacities from a given local distribution (e.g., Pinte et al. 2016; Birnstiel et al. 2018). The opacities are commonly averaged over a typical dust size distribution from the MRN model, and the maximum grain size is chosen to align with multiwavelength observations. More precisely, most recent studies considered a dust model composed of two grain populations: a small dust population, and a large dust population (e.g., Du & Bergin 2014; Ballering et al. 2021; Schwarz et al. 2021; Zhang et al. 2021; Murillo et al. 2022). They were meant to fit observationally constrained evidence of grain growth and size dependence to vertical and radial segregation (Gräfe et al. 2013; Pérez et al. 2015; Tazzari et al. 2016; Villenave et al. 2020). Typically, the opacity of each population was averaged over a given size range, each with a different maximum grain size amax, which parameter strongly affects the wavelength-dependent optical properties (Birnstiel et al. 2018). A single resulting temperature is then extracted (density and temperature), either by averaging out the two dust structures or by forcing dust thermal coupling during the radiative transfer simulations. The structure is later used for chemistry postprocesses. However, because surface chemistry is highly sensitive to dust surface temperatures, this treatment may overlook possible chemical effects by not considering the two dust structures independently.
Real disks are most likely composed of grains with multiple sizes with independent optical properties, resulting in polydis-persed dust grains (Birnstiel et al. 2018). We use the term ‘polydispersion’ (as opposed to monodispersion) in this study in the strict sense as defined in Deirmendjian (1969) and Bohren & Huffman (1998), that is, we speak of polydispersion when a population of scattering particles in a medium is uniform in shape and bulk material, but not uniform in size. Grains are heated both by the external field and by the resulting scattering and reemitted light from all the other grains. The absorption efficiency of grains depends on grain size and wavelengths, which results in a) a complex interaction with the local radiation field and b) a size-dependent dust temperature structure (Heese et al. 2017; Gavino et al. 2021). It is therefore expected that utmost attention should be given to the selection of the dust population, dust absorption, and scattering profiles in disk models.
We reproduce dust models here that are similar to those in recent studies (e.g., Zhang et al. 2021). However, we keep the dust structures independent so that we can analyze (i) the precise dust temperature structures resulting from polydispersed dust grains computed with dust continuum radiative transfer simulations, and (ii) the resulting chemical structure by treating the various dust populations simultaneously and independently in chemistry post-processes. We compare the results with test models composed of a single dust population meant to depict the classical treatment mentioned above. In particular, we investigate the effect of polydispersion in the regions around the disk midplane and observe the impact on the CO snowline.
The paper is structured as follows: Sect. 2 describes the disk models we used. Section 3 presents the resulting thermal structures and chemical post-process, and finally, Sect. 4 presents the origin of the temperature substructures and its potential implications for the CO gas distribution in observed disks in more detail. A summary is then provided in Sect. 5.
2 Model
We assumed that the models are static protoplanetary disks, consisting of a typical 2D parametric smooth, axisymmetric, and geometrically flared structure. Additionally, only passive heating was assumed. The disk was assumed to be in Keplerian rotation. We provide a concise description of the parametrization below, but the model is similar to that of Gavino et al. (2021).
2.1 Fiducial disk structure
2.1.1 Spatial distribution of gas
The radial gas surface density follows a simple truncated power law,
where p = 3/2 (Shakura & Sunyaev 1973; Hersant et al. 2009; Guilloteau et al. 2011; Le Gal et al. 2019), and R0 is the reference radius, which was chosen to be 100 au in the study.
The surface density at the given reference radius R0 was derived using
where Mdisk is the total disk mass, and its inner radius and outer radius are Rin and Rout, respectively.
Following Dartois et al. (2003), the gas temperature was imposed by analytical laws. The gas kinetic temperature in the midplane Tmid is given by a power law,
where Tmid,0 is the gas temperature in the midplane at R0, and we allowed for a warmer disk atmosphere using the formulation of Williams & Best (2014),
where σ = 2 is the stiffness parameter of the vertical profile. Above zatm, the temperature is vertically constant. Tatm(r) follows a power law similar to Tmid(r) and zatm is taken as being four times the midplane gas-scale height, Hg, which at the reference radius R0 is given by
where µ is the mean molecular weight equal to 2.4, mH is the proton mass, kB is the Boltzmann constant, and G is the gravitational constant. The midplane gas-scale height then follows a radial power law that varies as r3/2−q/2, a typical flared geometry.
Our assumed gas temperature and density profiles were selected for comparison with previous works and differ from those of a steady-state viscous disk with a radially constant viscosity, which would depend on r−1.1. We note, however, that a self-consistent model would have a more complex radial density profile even under the simplified viscosity assumption because of the regions of increased temperatures that result from the treatment of different dust populations.
We solved the gas density by considering the (nonisothermal) vertical hydrostatic pressure equilibrium, which we solved iteratively following Hersant et al. (2009),
where  is the gas-mass density at altitude zi, and Ω is the Keplerian rotation at the given radius. The vertical gas density structure thus slightly deviates from a Gaussian profile at altitudes z > 2 – 3Hg.
is the gas-mass density at altitude zi, and Ω is the Keplerian rotation at the given radius. The vertical gas density structure thus slightly deviates from a Gaussian profile at altitudes z > 2 – 3Hg.
Although this imposed density and gas temperature structure are not exactly self-consistent, we verified that the gas temperature Tg(r, z) is not too different from the area-weighted dust temperature (calculated from Monte Carlo simulations as described in Sect. 2.2),
as would be expected when the gas is mostly heated by thermal contact with the dust grains and not by the radiation field. Here, aj represents the grain size of bin j, and nd is the dust number density (details are given in the next section). The chemical models can be computed using the gas temperature as given by Eq. (4) or derived from the area-weighted dust temperature (Eq. (7)). We systematically verified that both cases lead to very similar abundances for the most common molecules, as expected, because the rates of the main gas-phase chemical reactions are not strong functions of the temperature1. We thus only present chemistry results from the model using the gas temperature as given by Eq. (4), the other choice results in practically identical figures.
2.1.2 Spatial distribution of dust
The vertical density distribution of any dust component is defined by the following equation:
where σd(r,a) and Hd(r,a) are the surface density and scale height, respectively, of the grain population of size a at radius r. The dust scale height is defined following (see Dubrulle et al. 1995; Youdin & Lithwick 2007; Fromang & Nelson 2009; Dong et al. 2015)
so that the dust scale height represents a fraction of the gas scale height, depending on the dimensionless stopping time, or Stokes number, St. Sc is the Schmidt number, and α is the turbulent viscosity coefficient, set to 1 and 0.01, respectively, in the whole study. The coefficient α sets the degree of turbulent viscosity and therefore the degree of settling (Shakura & Sunyaev 1973). The settling factor depends on the dust grain size a via the Stokes number, which can be defined near the midplane as
where ρm is the dust material density, and under the assumption of an Epstein regime and spherical particles (see Cuzzi et al. 2001; Birnstiel et al. 2012). The dust-to-gas mass ratio varies from one altitude to the next due to the settling, but the dust-to-gas surface density ratio is ζ at all radii. The model does not include radial drift.
We point out here that dust settling is not expected to result in a simple Gaussian distribution. For instance, the simulations and analytical approach of Fromang & Nelson (2009, their Eq. (19)) show that in a vertically isothermal disk, the dust settling results in a dust-mass distribution that is approximately Gaussian near the midplane (z < 2H), but falls more steeply than a Gaussian at high heights. Nevertheless, Eq. (19) of Fromang & Nelson (2009) is only valid for a vertical Gaussian gas density distribution. In our case, the increased temperature at high heights above z/H > 2, where the dust profile starts to be steeper, leads to a profile with broader wings than a Gaussian (our Eq. (6)).
The two effects partially cancel each other, and the settled dust distribution is thus quite likely better approximated by a simple Gaussian than in the vertically isothermal case. In order to ensure that the additional term in Eq. (19) of Fromang & Nelson (2009) does not cause major differences, we performed additional simulations using their approach. These tests showed very minor changes. We therefore only present the results using our Eq. (8).
2.1.3 Dust mass and size distribution
The size distributions follow the MRN distribution throughout, with a power law dn(a) ∝ a−d and with d = 3.5. It is possible to divide the distribution into Nd intervals (logarithmically distributed in the entire study). From this, a mass and a size can be defined for each grain bin j. Following Gavino et al. (2021), the effective discretized size value of the jth interval is given by the mass-weighted average,
where a+,j and a−,j are the maximum and minimum cutoff values of the jth interval, respectively.
The total dust mass in the disk of the population j of size aj is a fraction x(aj) of the total disk dust mass Mdust,
with ζ the dust-to-gas mass ratio, and Mdisk the total disk mass (gas + dust). The term x(aj) derives from the MRN distribution and is a fraction of the full size distribution,
where amin and amax are the minimum and maximum cutoff values, respectively, of the full size distribution, and they are such that
The fiducial physical parameters we used in all disk models are summarized in Table 1. We note that these parameters were chosen to provide an interpretative framework for the resulting thermal structure and are not intended for a direct comparison with observations. However, the models were chosen to be similar to a typical low-mass T Tauri disk.
2.2 Radiation source and radiative transfer modeling
For the stellar radiation, we considered a pre-main-sequence star emitting as a blackbody with an effective temperature of Tstar = 4100 K, a stellar luminosity of Lstar = 1 L⊙, and a stellar mass of Mstar = 1 M⊙. For the interstellar radiation field (ISRF), we considered a typical distribution from Draine (1978) with an extension of van Dishoeck & Black (1982) for wavelengths >200 nm. We used these parameters for all models described in this study. The stellar irradiation is the dominant source of thermal heating for the dust and gas. On the other hand, the photochemistry of the disk surface is mainly controlled by the far-UV (FUV) spectra of both the ISRF and stellar radiation field.
To compute the dust temperature, we performed radiative transfer calculations using the RADMC-3D code (Dullemond et al. 2012). Each dust population had its own density distribution and was allowed to be thermally decoupled from the next population. The radiative transfer calculations included the absorption opacity, scattering opacity, and the Henyey–Greenstein g parameter for the treatment of anisotropic scattering.
The structure was a spherical grid centered at the location of the star, with 300 logarithmically distributed radii, and 180 angles from 0 to π. We used 100 logarithmically distributed wavelengths from 0.1 µm to 2 mm for the radiative transfer calculation. We used 107 photon packages in each simulation.
Fiducial disk parameters
2.3 Chemical network and gas-grain simulation
We used the three-phase Nautilus Multi-Grain Code (NMGC; Ruaud et al. 2016; Iqbal & Wakelam 2018; Gavino et al. 2021), derived from the NAUTILUS gas-grain code (Hersant et al. 2009). NMGC is specifically designed for chemistry simulations of models embedding multiple independent grain populations. All dust populations are chemically active, and all chemical compounds can interact with each population independently. The chemistry model is a 1D+1 structure spanning from 4 au to 360 au from the star. All 1D structures are composed of 64 vertical spatial points from the disk midplane up to 4 Hg, defined as the surface of the disk.
NMGC uses the rate-equation approach (Hasegawa et al. 1992; Hasegawa & Herbst 1993) in which the gas phase, the grain surfaces, and the mantles are chemically active (Ruaud et al. 2016). The gas phase can exchange species with the surfaces, but not directly with the mantle. For surface chemistry, adsorption, thermal desorption, cosmic-ray-induced desorption, photodesorption, and chemical desorption, swapping from the mantle to the surface and vice versa are included. Physisorbed species can diffuse on the grain surface via tunneling or thermal hopping. For the gas phase, chemistry is driven by bimolecular, ion-neutral, and neutral-neutral reactions as well as by ionization and dissociation triggered by cosmic-ray-induced processes, and both interstellar and stellar radiation fields. Following the prescription of Gavino et al. (2021), the H2 formation rates were calculated by consistently interpolating rate curves, which were initially solved by using a stochastic treatment that considers fluctuations of hydrogen atoms on the grain surfaces by Bron et al. (2014).
We used the kinetic database for astrochemistry network (kida.uva.2014)2 (Wakelam et al. 2015), in which we included the additional reaction rates for the H2 formation on grain surfaces. The chemical evolution was simulated over a period of tchem = 2 Myr, which is well longer than the CO freeze-out timescale in the whole disk. Considering the relatively long simulation run-time, we used atomic initial conditions (except for H2) as presented in Table 2. We refer to Wakelam et al. (2019) for more information about the impact of the initial conditions on the chemical evolution.
For species other than H2 and CO, the photoprocess rates were calculated using the following equation:
Here, G0 is the unattenuated local UV flux at each radius relative to the standard ISM (Draine) value. The γ value was taken as the default value appropriate for the ISM and that for many species γ = 1 in the Kida network.
The Aυ was computed using the local UV flux calculated from the Monte Carlo radiative transfer simulation.
For a given wavelength λ and given coordinates (r, z), the local flux is the unattenuated flux F0 reduced by the dust extinction,
where the opacity is related to the extinction by the usual relation
Adopted elemental initial abundances relative to H.
2.4 Dust models and optical properties
To illustrate the importance of polydispersion, we considered four dust models. Model S (for single) was composed of a simple single dust distribution. Models C and D used two dust distributions. In model D (for Dual), each dust population had its own temperature, while for model C (for common), an averaged temperature was derived from the two temperatures of model D following Eq. (7). The difference between models C and D therefore lies entirely in the chemical computation, as we show below. Last, model M16 (for multi) was composed of 16 dust grain size bins. The four models are described below, while the thermal and chemical results are shown in Sects. 3.2 and 3.3, respectively. A summary of the four models is given in Table 3. More specifically, the number of grain size bins we used during radiative transfer and chemistry simulations as well as the effective grain size values are indicated in Cols. 2–4, respectively.
Summary of the dust disk models.
 |
Fig. 1 Dust optical properties of model D (dashed and solid lines) and S (dashed lines only). Left: absorption opacity. Middle: scattering opacity. Right: Henyey–Greenstein g parameter of the anisotropy (g = <cos(θ)>). |
2.4.1 Models S, D, and C
We adopted the opacities from the DSHARP collaboration by using the standard size-averaged smoothed optical properties of the dsharp_opac package3 as described in Birnstiel et al. (2018), with the mixed Mie coefficients used for the DSHARP project.
For model D, we reproduced the same distribution as in Zhang et al. (2021, who used the DSHARP opacities). For each of the two populations, we used a size-averaged opacity derived from a dust grain size distribution following the MRN distribution with a power-law index q = 3.5. The dust grains were composed of a mixture of water ice (Warren & Brandt 2008), astronomical silicates (Draine 2003), troilite, and refractory organics (Henning & Stognienko 1996). We considered two populations: a small population Dsmall with an upper grain radius amax,s = 1 µm, and a large population Dlarge with an upper grain radius amax,ı = 1 mm. Both populations had a lower grain radius of amin = 0.005 µm (e.g., Schwarz et al. 2018; Ballering et al. 2021; Zhang et al. 2021). The wavelength range was a logarithmic distribution of 210 values between λmin = 0.1 µm and λmax = 104 µm. Because the small population is globally less protected from photodesorption, we set its ice-mass fraction to zero (following the prescription in Zhang et al. 2021).
The resulting mass-weighted dust absorption opacities κabs, dust scattering κsca, and the g parameter of anisotropy are shown in Fig. 1. These profiles are meant to reproduce those in Zhang et al. (2021) as closely as possible. The thermal calculations as well as the chemistry post-process were performed using the two populations simultaneously.
For model S, we only used the small population opacity Dsmall (dashed lines in Fig. 1) to compute the dust temperature. A single dust structure was thus considered at all steps, including the chemistry post-process.
Model C is the same as model D because it uses the two dust size distributions and optical properties simultaneously to compute the dust temperature, but it differs during the chemistry post-process step. The two resulting dust temperatures were averaged over the dust surface area using Eq. (7) so that a single dust structure was used as input to solve the chemical evolution. Model C is therefore close to the prescription that has commonly been used in most disk models so far.
2.4.2 Model M16
Based on models of dust coagulation and fragmentation, it is expected that a dust population is not composed of only two distinct populations, but rather of a continuous size distribution (Birnstiel et al. 2010, 2018). To address this, we considered model M16, which mimics a continuous grain size distribution by splitting the MRN distribution into 16 logarithmically distributed grain size intervals, each with its own size (Eq. (11)) and associated single-grain-size opacities. Model M16 is therefore meant to be more realistic than the other models.
Similarly to the other models, we adopted a classical power-law grain size distribution ranging from amin = 5 nm to amax = 1 mm, with a size distribution index q = 3.5. However, instead of averaging the total absorption opacity over the total size distribution (as was done in the other models), the resulting opacities were discretized into the 16 bins (see Table 4).
To do this, we performed calculations for each grain bins using the Fortran subroutine included in the dsharp_opac package (Birnstiel et al. 2018), which is itself derived from the original Mie code from Bohren & Huffman (1998). To avoid unrealistic interference effects due to the spherical treatment of the Mie theory, we calculated the opacity for 30 linearly distributed grain sizes around each of the 16 bin sizes.
To simplify the discussion in the following, we differentiate three subpopulations from the 16 sizes, each of which is characterized by similar optical properties. We call small grains all grains of size <0.1 µm (four bins), intermediate grains all grains of sizes between 0.1 and 10 µm (six bins), and large grains all grains of size > 10 µm (six bins).
The resulting mass-weighted absorption opacities κabs(a) = 2πa2Qabs(a)/m(a) (g cm−2) and scattering albedos ω are shown in Fig. 2. The absorption opacities (Fig. 2a) of the large grains (solid lines) are roughly flat in short wavelengths (<100 µm), but they all asymptotically follow the same decreasing slope beyond. The large grains also prefer to emit at wavelengths comparable to their size. Intermediate- (dashed lines) and small-grain (dotted lines) opacities are strongly wavelength dependent and show structured patterns due to their material composition. These various profiles result in various equilibrium grain temperatures and thermal emissions.
The small grains and intermediate grains show little albedo or are completely opaque (Fig. 2b) at wavelengths λ > 10 µm. The albedo ω is at its maximum when 2πa ~ λ (Birnstiel et al. 2018) and can be as high as 0.9 between ~0.1 and 10 µm in the case of the intermediate grains. The albedo of the largest grains (bin 12 to bin 16) remains globally flat for λ < 100 µm at a fairly large albedo (0.5 < ω < 0.6). However, because their relative surface area is very small (<1% in the midplane), their contribution to scattering events leading to significant effects on the thermal structure is assumed to be negligible.
 |
Fig. 2 Absorption opacity and scattering albedo profiles for the 16 bin sizes in model M16. The dotted, dashed, and solid lines represent the small, intermediate, and large grains, respectively. The dashed vertical black line indicates the wavelength λmax at which the star radiates according to Wien’s law. The grain sizes are indicated in µm. We refer to Table 4 for a description of the bin sizes. |
Dust distribution in model M16.
2.4.3 Comparing models
The total disk mass was kept constant in all models. Thus, when we compare the models, their respective optical depths can differ because the dust mass is not distributed among the same dust populations. Typically, models D and C are expected to exhibit a slightly lower vertical optical depth than model S because of the large dust population in the former. However, these opacity differences are rather small, and the differences between models can mainly be attributed to their different dust temperature structures. We tested various dust models and physical disk parameters (disk mass, size distribution, opacities, and viscosity), and we show the results in Appendix A.
3 Results
In this section, we evaluate the effects of different assumptions on the dust models on the thermal and chemical outcomes. First, we describe the 2D dust structures.
 |
Fig. 3 Panels a and b: 2D dust area density (cm−1) of model D. Panel c: ratio of the large-grain area density to the small-grain area density (note the different z scale). Panel d: mass ratio of the large and small grains. The green lines mark 1 × Hg and 2 × Hg. |
3.1 Dust structures
Figure 3 shows the 2D dust area densities of model D. We show the area density because the dust surface area is one of the main parameters that drives the gas-grain interactions during chemistry. As detailed in Sect. 2, the dust populations were computed independently of one another so that the two dust populations are shown separately.
Using Eqs. (11) and (12), we can define two discretized subranges representing two populations with their own size and mass fraction values. The small dust population (Fig. 3a) is composed of grains with a size asmall = 0.02 µm, and although they represent less than 5% of the total dust mass, it contributes more to the extinction because the grains represent most of the dust surface area. The large dust population is composed of grains with a size alarge = 10.4 µm, and it represents 95.5% of the total dust mass (Fig. 3b).
The settling factor was defined using Eq. (9). The large population is more confined toward the midplane than the small population because its settling factor is significantly larger. The Stokes number ratio of the two populations is St,large/St,small = alarge/asmall = 5.2 × 102. While the settling factor of the small population is close to unity at all radii (the small dust scale height follows that of the gas), the ratio of the large dust and small dust scale height equals 0.92 at 10 au, 0.35 at 100 au and 0.20 at 500 au.
3.2 Thermal structures
3.2.1 2D temperature structures of model D
Figure 4 shows the dust temperature structures of model D computed with the thermal Monte Carlo simulation in RADMC3D. The two populations exhibit notable differences. In particular, the 25 K isothermal is located at ~30 au from the star (in the midplane) for the large grains (Fig. 4, right), which is a typically expected distance at which the CO snowline is located in a T-Tauri disk. On the other hand, the small-grain temperature drops below 25 K near 180 au only (Fig. 4, left). There is therefore a significant temperature spread with a radial distance of 150 au between the two 25 K isothermal.
 |
Fig. 4 2D dust temperature structures of model D. Left: temperature of the small grains. Right: temperature of the large grains. |
3.2.2 Comparison between models D, S, and C
To better understand the temperature structures, we further investigated the disk midplane by comparing the radial dust temperatures of model D with that of models S and C. Figure 5 shows the radial profiles in the midplane of the three models. In model D, the two populations are thermally decoupled from r ~ 30 au and the small grains are warmer than the large grains, approximately 13 K, at all radii. Moreover, the small dust population temperature shows a surprising bump between ~30 au and ~80 au. This structure therefore deviates from the expected monotonously decreasing temperature along the radial distance.
In model S, the dust optical properties are the same as for the small population of model D. We can therefore expect that their respective dust temperatures exhibit similar profiles, but Fig. 5 shows that this is not the case. The temperature profiles of the two models overlap in the optically thick (τ ≫ 1) inner region (r < 30 au) due to the very effective temperature coupling. Farther away, the two populations in model D become spread out as they become thermally decoupled. This temperature spread does not exist in model S because the dust structure is unique. This also implies that there can be no bump in model S.
The optical depth at both visible and infrared domains between the star and any radial distance in the midplane is too large (τ > 104 at 1 µm), thus the reheating of the small dust population cannot be generated by direct starlight emission. Because this bump does not exist in model S, we can assume that it originates from the interaction of the r-emission and scattered light between the two dust populations. This assumption is also supported by the vertical optical depth. The vertical solid, dashed, and dotted green lines represent the radial distances at which the vertical optical depth at 1 µm becomes smaller than 10, 5, and 1, respectively (in model D). The dust temperature starts to increase as the vertical optical depth decreases to values close to 10, where dust radiative interactions between upper layers and lower layers become possible. In model C, the temperature profile closely follows the profile of the small dust population of model D because most of the dust surface area stems from the small-grain populations (>95%).
 |
Fig. 5 Disk midplane radial profiles of the dust temperatures. The black curves show the temperature profiles of model D. The solid red curve shows the temperature profile of model S, and the yellow curve shows that of model C. The vertical solid, dashed, and dotted green lines represent the radial distances in model D at which the vertical optical depth (at 1 µm) becomes smaller than 10, 5, and 1, respectively. |
3.2.3 Model M16
We proceeded and tested the effect of polydispersion in a more realistic structure by considering model M16. Figure 6a shows the resulting radial temperature profiles of the 16 grain species in the midplane. The temperature spread is just like in model D: The intermediate grains are warmer than the small and large grains, and the difference is about 17 K between the warmest and coldest grain. The model also shows a temperature bump inside 100 au. It is clear that the grain populations can be divided into two groups, one group with a bump effect (small and intermediate grains), and another without (large grains). The division into two groups is in fact analogous to the division in model D. This suggests that a two-population model such as model D could be sufficient to properly approximate the effect of poly-dispersion that takes place in a realistic dust grain population. In order to help us understand which of the absorption, emission, or scattering processes as well as which of the grain populations contribute to the bump effect, we successively set the scattering opacity to zero inside wavelength intervals for each grain population and ran radiative transfer simulations. We find that the radiation of wavelengths between 0.7 and 2 µm scattered by the intermediate grains (5 ≤ bin ≤ 10, i.e., grain sizes between 0.1 and 10 µm) seems to be the main reason for the temperature bump. Figure 6b shows the result of the dust temperature structure computed with an albedo between 0.7 µm and 2 µm of the intermediate grains artificially set to zero. All grain temperature profiles now monotonously decrease with the distance. The temperature spread is smaller, and all small and intermediate grains roughly exhibit the same temperature.
We can conclude that when scattering is included (Fig. 6a), the temperature degeneracy of small and intermediate grains is raised, the spread is larger, and a bump is generated. A similar test with model D shows that setting the albedo to zero also suppresses the temperature bump. This effect is discussed in more detail in Sect. 4.1.2.
Another look at the temperatures shows that this temperature spread is located right in the vicinity of the CO freeze-out temperature (typically around 20–30 K in the disk midplane). We test the effect of the temperature spread on the chemical evolution in the following sections.
 |
Fig. 6 Midplane radial dust temperature profiles of model M16. The dotted curves represent the dust temperatures of the small dust grains, the dashed curves represent the temperature of the intermediate grains, and the solid curves show the dust temperatures of the large dust grains. The grain sizes are given in µm. Left: temperatures with scattering. Right: temperatures with scattering opacity of the intermediate grains set to zero. |
3.3 Chemistry post-process: The case of CO
3.3.1 Limitations
It is easy to anticipate the effects of the temperature bump on the chemical abundance of light species, particularly that of CO. However, computing the chemical evolution with as many grain sizes as in model M16 costs much cpu time (a single ID structure needs ~60 h in cpu-time to be solved on a typical laptop compared to around ~1 h for a model using a single grain) and can generate convergence issues due to the sizes and very small abundances of the largest grains. To work around this obstacle, we chose to use model D instead of M16 to compute the chemistry, based on the assumption made previously about the equivalent thermal structure in models D and M16. In other words, we assumed that the thermal spread from these models has similar chemical outcomes. In addition, to fully appreciate the effect of the temperature spread, we also computed the chemistry in models S and C.
3.3.2 CO in the gas phase
Figure 7 shows the integrated surface density of CO in all three models. While models S and C result in similar profiles, model D shows a clear depression in CO near 150 au as a result of the combined effects of the small and large grains.
In order to understand where the differences in column densities come from, we show in Fig. 8 the resulting 2D CO gas number density [cm−3] structures in (r,z) coordinates from r = 2 au to 360 au using model S (Fig. 8a), model C (Fig. 8b), and model D (Fig. 8c). The solid white lines mark the transition at which the ratio ng(CO)/(ng(CO)+ns(CO)) becomes smaller than 0.5, or in other words, the CO snowline.
The interpretation of the CO gas structure in model S is straightforward. The disk surface is vulnerable to the external UV radiation, and the photodissociation rate of CO is high enough to prevent efficient formation. In the molecular layers, the H2 shielding and CO self-shielding become sufficiently protective, and CO gas becomes the most abundant molecule (after H2) with an abundance close to the interstellar value 10−4. The grain surfaces are still too warm for effective CO condensation. Closer to the midplane, the grain surface temperatures drop, and CO becomes massively depleted onto the grain surfaces. The CO snowline delimits the molecular layer and the cold midplane. Model C shows a similar pattern with larger molecular layers. This is expected because the dust temperature is globally higher than in model S. This V-shape structure is typically observed in protoplanetary disks (see van’t Hoff et al. 2020, for a detailed description of the CO gas phase distribution in disks).
The CO gas map in model D shows a more intriguing structure. Although the structure in the upper layers is similar to models S and C, we note a CO hole from ~50 au to ~200 au that extends to ~10 au vertically. We then observe a CO gas rise between 200 au and 300 au, before CO diminishes beyond 300 au. The CO snowline exhibits an entirely different shape as well: The gas-ice transition is displaced toward the midplane between 150 au and 250 au.
Figure 5 apparently shows that the CO gas rise is located well outside the temperature bump (around ~70 au) and the CO depression is located right where the dust temperature is maximum. This striking discrepancy between CO depression and dust temperature arises because the dust distribution produces multiple condensation fronts, as shown in the following section.
 |
Fig. 7 Surface densities of CO in the gas phase for models S (dotted line), C (dashed line), and D (solid line) as a function of the radius. |
3.3.3 CO ice and snowline
Figure 9 shows the 2D number density maps of the total CO ice in models S, C, and D. All models present the typical dual structure split by the snowline, below which CO is massively depleted onto the grains. With a globally higher dust temperature, the snowline of model C is shifted toward lower layers of the disks than in model S.
In model D, the total CO ice content is the sum of CO ice adsorbed onto the small and large-grain populations. It is clear that CO ice lies below the snowline profile, and although the snowline is clearly different than in the other models, the CO ice distribution seems to follow a similar trend as the other models. Additionally, we also present the snowlines of each population taken separately (dashed red lines). The snowlines appear to be divided into two individual surfaces that overlap near 250 au. To better understand this, we provide a formal definition of the snowline in the case of multiple discretized dust grain sizes. The freeze-out temperature is tantamount to solving the balance between the desorption and adsorption rate, and it depends on multiple parameters, including the dust temperature and dust and gas densities (see for instance van't Hoff et al. 2017). Each grain population has its own density and temperature, and we can therefore define a snowline for each of them. More precisely, if nsmall (CO) and nlarge (CO) represent the CO ice number density on the small and large population, respectively, and ng(CO) is the number density of CO gas. The two dashed white lines thus correspond to the location at which the ratios ng(CO)/(ng(CO) + nsmall (CO)) and ng(CO)/(ng(CO) + nlarge(CO)) equal 0.5. On the other hand, the total snowline (white line) is the location at which
where
In the case of model D, the number of grain bins N = 2 and Eq. (19) writes  .
.
While model S and model C exhibit an expected structure of the snowline, the shape of the snowline in model D is more complex. This is discussed in more details in Sect. 4.2.
4 Discussion
4.1 Thermal decoupling and the bump effect
4.1.1 Thermal decoupling in the disk midplane
Figure 10 shows the 2D map (grays cale) of the optical depth at 1 µm in model D computed from the star to all points in the disk τ★(r, z). The optical depth values that are located below one scale height z < Hg (dashed white curve) are very high (τ★ ≫ 102), such that the disk midplane is always optically thick with regard to the star. The two dust populations are therefore expected to be strongly thermally coupled: the warmer population is cooled by the cooler population, and vice versa. However, outside 30 au, the grains become thermally decoupled (the small grains become warmer), even though the optical depth remains very high.
In more detail, the blue line marks the altitude at which the vertical optical depth calculated from the midplane equals 1. In this way, we can investigate the altitude from which radiation contributes to the heating of the midplane. At small radii (r < 30 au), the radiation that reaches the midplane is exclusively due to thermal emission from nearby dust with a very similar temperature, hence the temperature coupling. At larger radii (r > 30 au), the altitude of the blue line suddenly increases to reach the uppermost layers of the disk at about r = 100 au. On the other hand, the red lines correspond to the surface, where the optical depth from the star τ★ equals 1. The layers above that surface are therefore directly heated by the star. At the coordinates (r = 70 au, z = 11 au), the blue line crosses the red line, meaning that the optical depth from the star to this point and from there to the midplane equals 2, which is far lower than the optical depth calculated from the star through the midplane. The midplane can thus be effectively heated by stellar light coming from the disk surface.
However, because each grain has a different absorption/emission opacity, they are not heated with the same efficiency. Figure 11 shows the ratios of the absorption cross section for wavelengths at which the star typically radiates to the absorption cross section for wavelengths at which the dust typically emits (~20 µm) as a function of the grain size. In model D, the small population has a ratio close to 4, whereas the large population has a ratio close to 1.2. The starlight at 1 µm is thus more effective in heating the small grains than the large grains. Likewise, in model M16, the intermediate grains have the highest ratio values, which means that the heating is strongest for these grains.
 |
Fig. 8 2D maps of CO gas number density [cm−3]. Left: CO in model S. Middle: CO in model C. Right: CO in model D. The solid white line corresponds to the CO snowline where ng(CO)/(ngas(CO)+nice(CO)) = 0.5. The black line shows the maximum scale height below which chemistry is computed. |
 |
Fig. 9 2D maps of the number density of CO ice. Left: CO adsorbed onto dust grains in model S. Middle: same in model C. Right: CO adsorbed both onto the small and large dust populations in model D. The solid white line corresponds to the CO snowline. The dashed red lines correspond to the snowline of each population taken independently. The black line shows the maximum scale height below which chemistry is computed. |
 |
Fig. 10 2D map of the disk. The gray scale represents the values of the optical depth computed from the star to all points in the disk τ★(r,z). The red lines represent the surface where τ★(r,z) = 1. The green lines mark the location at which the total vertical optical depth at the mid-plane becomes lower than 10, 5, and 1. The solid blue line marks the altitude at which the optical depth in the z-direction toward the upper layers becomes 1. The line diverges to infinity beyond the line τυ = 1. All opacities are given at 1 µm. |
4.1.2 The bump effect
In addition, we described a surprising effect where the temperature increases again, reaches a maximum, and then monotonously decreases again. We called this the bump effect.
In Sect. 3.2 we demonstrated that scattering is at the origin of the bump effect in the dust temperatures.
To illustrate the importance of the contribution of scattered stellar radiation, we indicated the wavelength λmax for the temperature at which the star emits according to Wien’s law in Fig. 2a.
In model M16, the bump effect was caused by the scattering of stellar radiation by the intermediate grains, where a fraction of the starlight intercepted in the upper layers is scattered vertically toward the midplane. In the case of model D, this fraction is the small grains that scatter the starlight vertically (we note that the large grains are strongly settled so they cannot effectively intercept the starlight in the upper layers. They can interact with the starlight already scattered by the small dust population in the intermediate layers, however). More generally, the crucial combination for a bump to occur is the simultaneous presence of at least one scattering dust grain population with a large scattering albedo accompanied by at least one other grain population with a high opacity ratio of absorption to emission.
In model S, no bump effect is visible even in the optically thin regions. This is a result of the mechanisms needed to generate a bump: at least two dust species with different opacities are needed, so that the various dust populations can have different temperatures in regions in which temperature coupling is not relevant. Therefore, a bump effect cannot occur in a dust model that uses a single-opacity profile, regardless of how sophisticated the model is.
 |
Fig. 11 Ratios of the absorption cross section for wavelengths at which the star radiates (~1 µm) and the absorption cross section for wavelengths at which the dust emits (~20 µm) for the grains in model D (red points) and M16 (black points). |
4.1.3 Sensitivity to other parameters
Thermal decoupling and the bump effect originate from different mechanisms. While thermal decoupling always occurs in optically thin environments and does not require radiative interaction between different grains, a bump effect is generated on certain grains by the scattered light coming from other grains in their vicinity. It is therefore sensitive to the chosen optical properties, and in particular, to parameters that affect the albedo: the material composition, the size range, and so on. To illustrate this, we again performed dust continuum radiative transfer simulations for model D, but this time, using the DIANA standard opacities in Appendix A.1 and using another size distribution in Appendix A.2. We also tested the sensitivity to different disk masses (Appendix A3) and different turbulence parameters (Appendix A.4). As expected, while the magnitude of the bump is sensitive to the opacity properties, a temperature dichotomy exists in all cases, but at different radii. Finally, we refer to Appendix B, where we address the question of the possible numerical origin of the bump effect arising in optically thick regions.
4.2 Snowline shape in model D
To understand the snowline shape, we first considered the separate contributions of the two grain populations. Figure 12 shows the CO ice on each population in model D. Figure 12a represents the distribution of CO adsorbed onto the small grains only, and Fig. 12b represents CO ice adsorbed onto the large grains only. The gray line is the total snowline (Eq. (18)), and the dashed red lines are the snowlines of the individual populations.
In the midplane, the CO snowline for the small dust population is located close to 250 au, where the dust temperature has sufficiently decreased. Inside 250 au, CO ice on the small grains is virtually nonexistent because the temperature is above the freeze-out threshold for this population. For the large grains, the CO snowline in the midplane is located at a farther inward radius (~25 au), where the dust temperature drops below the freeze-out temperature for this population. We can then straightforwardly conclude that only the large dust population is at the origin of the CO gas hole that is visible in Fig. 8c.
On the other hand, the large-grain population also exhibits another midplane snowline (near ~250 au; the midplane snowline of the small grains is located here as well), so that the overall snowline of the large grains forms a closed bubble. Beyond that bubble, CO is virtually nonexistent on the large grains (Fig. 12b), even though their surface temperature is low enough for CO to adsorb. This behavior can be explained by multiple factors, but the most crucial one is the competition of interactions with CO molecules between the large and small grains. The dust surface-areas (and therefore the number of accessible sites) is never the same between the two populations. For instance, at 250 au, the ratio of the small-grain surface-area to the large-grain surface-area is  , meaning that a CO molecule has a higher probability (about 6.5 times higher) to interact with a small grain than with a large grain. Consequently, when the small grains are below the freeze-out temperature, they retain most of CO at the expense of the large grains. Hence, the sharp delimitation between the two snowlines.
, meaning that a CO molecule has a higher probability (about 6.5 times higher) to interact with a small grain than with a large grain. Consequently, when the small grains are below the freeze-out temperature, they retain most of CO at the expense of the large grains. Hence, the sharp delimitation between the two snowlines.
The rise in CO gas observed at the delimitation (Fig. 8c) is also a consequence of this competition. Between r = 150 au to r = 250 au, the desorption to adsorption rate ratio progressively increases and reaches the value 0.5 close to 250 au (for the small grains). At this location, CO interacts more with the small grains, but because these are still slightly too warm, is ultimately returned to the gas phase. In other words, the freeze-out timescale around 250 au is longer than elsewhere, and the snowline assumes this peculiar S-shape with a minimum height at 250 au.
A small isolated island of CO ice appears on small grains (Fig. 12a) at ~30 au around the midplane, which corresponds to the location of the temperature dip, at which the large grains have cooled the smaller grains sufficiently. This happens because of the specific dust mass and structure of the disk. If the disk were slightly less massive, this small island would likely not exist.
Last, with two grain populations and therefore two temperatures, model D is an efficient simplification of the dust distribution that allows us to understand the impact of a proper dust temperature onto the chemistry, and in particular, the behavior of snowlines. Nevertheless, a more realistic distribution with more grain populations and more related temperatures would necessarily produce more individual snowlines (one per grain population and temperature), which would cause a higher complexity in the resulting CO snowline. Although the resulting CO ice segregation is probably hard to probe in observed protoplanetary disks, it requires an interpretation on its own that may have significant implications for the chemical evolution and planet formation.
 |
Fig. 12 2D maps of CO ice number density (cm−3) in model D. Left: CO ice adsorbed onto the small dust population only. Right: CO ice adsorbed onto the large dust population only. The solid gray line corresponds to the total CO snowline. The dashed red lines correspond to the snowline of each population independently. The black line is the maximum scale height below which chemistry is computed. |
4.3 Radial drift and planet formation
Our model does not include any radial drift. The CO snowline shape is therefore solely due to the different dust temperatures, although its shape and precise location are also affected by dust settling.
Cleeves (2016) showed using a simple parametric model that radial drift can reshape the CO distribution and create multiple snowlines. In particular, the removal of a large fraction of dust grains from the outer disk can allow the region to become warmer by reprocessed stellar radiation from the upper layers. We showed that this reprocessing can occur even without a significant change in the dust-to-gas mass ratio and only requires different dust populations. We can therefore expect that the combination of the two mechanisms (i.e., temperature spread and radial drift) builds up the radial segregation of the snowlines.
Radial drift occurs when gas drag acts on the dust grains (the gas disk ’feels’ its own pressure and is therefore sub-Keplerian). As a consequence, the dust grains drift inward. The drift efficiency increases with the Stokes number St < 1 under the Epstein drag law (Birnstiel et al. 2012). For instance, when we consider the grain distribution in model M16, the large grains will drift more efficiently than the intermediate grains, whereas the small grains remain mostly coupled to the gas and will drift barely. Although the drift time is expected to be relatively long for the whole grain size range considered (St < 10−2 for all grains of size <1 mm at 10 au in our model), radial size-dependent segregation can occur with enough orbital periods. We can make an estimate of the radial segregation between all grain populations by considering the following drift-timescale equation (Birnstiel et al. 2012),
where Vk is the Keplerian velocity at radius r, cs is the isothermal sound speed, and  is the absolute value of the power-law index of the gas pressure. The drift timescales at 100 au of all 16 grains are given in the fourth column of Table 4. These timescales can be compared with our chemical evolution time tchem = 2 Myr. All grains larger than about 10 µm have a drift timescale < tchem, whereas the small-grain populations virtually do not drift (τdrift (100 AU) ≫ tchem). We can therefore expect a strong radial size-dependent segregation within the chemical evolution time. The colder and larger grains should be found within a smaller radial extent than the smaller grains, such that the surface-area ratios become even more in favor of the smaller grains at large radii.
is the absolute value of the power-law index of the gas pressure. The drift timescales at 100 au of all 16 grains are given in the fourth column of Table 4. These timescales can be compared with our chemical evolution time tchem = 2 Myr. All grains larger than about 10 µm have a drift timescale < tchem, whereas the small-grain populations virtually do not drift (τdrift (100 AU) ≫ tchem). We can therefore expect a strong radial size-dependent segregation within the chemical evolution time. The colder and larger grains should be found within a smaller radial extent than the smaller grains, such that the surface-area ratios become even more in favor of the smaller grains at large radii.
Accordingly, we expect that the effect found in model D, which depends on a competition between small and large dust grain populations, is moved inward by the radial drift of large grains, and one might expect an even more complex shape for the 2D snowline curve than in our model D. Likewise, this effect should be enhanced by inward drift in a more realistic distribution, like in model M16. This could have observational implications (see Sect. 4.4).
Our study ignores grain-grain collisions, which may lead to more homogeneous ice compositions for grains of different sizes. However, grain-grain collisions are a complex process. While it is conceivable that slow-velocity collisions between a small and a large grain effectively cause the ice coverage of the small grain to be incorporated in the ice coverage of the larger one, faster collisions, those that replenish the small size distribution from the large size one, are unlikely to have such a simple outcome. Grain growth has been shown by Van Clepper et al. (2022) to affect the chemistry, with an impact on the C/O gas-phase ratio as a function of disk age, but their model did not consider disruptive collisions. Our chemical model also ignores diffusion, in particular, vertical mixing, which can homogeneíze the gas-phase abundances (Hersant et al. 2009). In all cases, however, accounting for the size dependence of dust temperatures leads to higher temperatures than using a common temperature, so that this process should be considered when evaluating the chemical evolution.
On the hand, our mechanism also has implications for the chemical evolution during planet formation. Model D shows that the small grains are virtually free from CO ice inside the large-grain snowline, whereas the large grains are free from CO inside the small-grain snowline. This suggests that the process of CO ice toward complex organic molecules (COMs) takes place only on the large grains in the inner regions in which planet formation takes place, whereas it occurs only on the small grains in the outermost regions, which later act as a reservoir of solid particles after they slowly grew toward drifting larger grains (Youdin & Shu 2002; Lambrechts & Johansen 2014). Additional chemistry models that take size-dependent radial drift into account will be investigated in future work.
4.4 CO holes in observed disks
We found that model D shows a CO depression of up to three orders of magnitude in density and of a factor of 10 in surface density, forming a hole between 50 au and 200 au that is followed by a rise beyond. This behavior is reported in the case of the observations of edge-on disks.
Dutrey et al. (2017) analyzed the temperature structure of the edge-on Class II disk 2MASS J16281370-2431391 (the so-called Flying Saucer). They found a CO and CS temperature drop inside 200 au, followed by a rise between 200 and 300 au. They argued that an effective rise in the UV penetration can explain the heat up of the disk in the outer region (200 au is the outer radius of the millimeter dust disk). Similarly, Flores et al. (2021), and Villenave et al. (2022) reported a rise in the CO temperature in the outermost region in the edge-on Class II disk around SSTC2D J163131.2-242627 (Oph 16313). They also argued that an external UV field can heat the outer disk, where UV photons can penetrate more effectively.
More recently, Lin et al. (2023) detected a similar behavior in both the 12CO and 13CO emissions in the close-to edge-on Class I disk IRAS 04302+2247 (the ‘Butterfly’; Wolf et al. 2003), which closes off the freeze-out region and forms a hole. However, in contrast to the two other disks, the rise does not coincide with the outer radius of millimeter-continuum emission. Furthermore, Gräfe et al. (2013) showed that in this disk, the population of large grains has drifted inward, whereas the modeled scattered light indicates that the small-grain distribution has a larger radial extent that is invisible to the millimeter wavelength.
Hence, in these objects, the rise of CO appears beyond a more or less important drop of the dust-to-gas ratio (although it is less obvious in the case of the younger Butterfly star, where the dust is less evolved). This behavior can be qualitatively explained by Cleeves (2016), where a CO rise naturally occurs because the dust-to-gas ratio quickly drops beyond the millimeter-dust disk edge, which allows a raise in temperature.
The Cleeves (2016) model requires an effective change in the (small-grain) dust-to-gas ratio caused by radial drift. In contrast, our model shows that even for a radially relatively constant value of this ratio, the temperature difference between small and large grains can result in a similar feature. This will be investigated in a future work.
Finally, Fig. 7 shows that the CO surface density, although at a similar amplitude, clearly differs for model D compared to the other models. Model D, with two-grain temperatures, shows a dip between 70 and 230 au that reflects the CO depression observed in Fig. 12. When a disk with a moderate inclination is observed, this feature can apparently mimic an unresolved gap, which may then erroneously be attributed to planet formation.
In any case, we note that the observation of the CO snowline shape is only feasible for disks seen at high inclination, ideally, close to edge-on. In less inclined disks, the substantial CO opacity from the top layer will hide the empty region behind the upper layers. The surface density effect shown in Fig. 7 should be visible using isotopologues, however, principally 13CO.
Other manifestations of the temperature gradient may be found with other molecular probes. The differences in temperature and timescales will also affect the surface chemistry because of the temperature dependence of the atoms and molecule mobility on the dust surfaces, and thus, in return, the chemical composition of the gas phase. Grids of models may be required to quantitatively evaluate the impact and possibly determine more sensitive indicators of this behavior than the rotational lines of CO.
5 Summary
We tested the impact of polydispersion in a medium composed of multiple independent grain populations on the resulting dust temperatures and chemical evolution in protoplanetary disk models. More specifically, we compared disk models using populations with one grain, two grains, and a more realistic population with 16 individual grains with size-dependent vertical settling, densities, and optical properties and showed the effect on the CO distribution in the disks. The main results can be summarized as follows.
Multiple dust populations with different optical properties generate a systematic dust temperature spread in which the smaller grains are always warmer than the larger grains in regions of the disk in which dust can be thermally decoupled. This is true even in the midplane of massive disks. Interestingly, the temperature of micron-sized grains can show a radial bump: it slightly reincreases with radial distance as a result of stellar scattered light from the upper layers when the vertical optical depth decreases.
Our work shows that opacities derived from a size distribution are not well-suited to reproducing the temperature spread that exists in a dust population composed of multiple sizes because these opacities dilute the effects of polydispersion, regardless of how sophisticated the opacity models are. In particular, they underestimate the temperature of the small grains. This prevents the choice of a fit-all dust-opacity model to compute a realistic dust temperature. However, given the computational limitations of a dust opacity model using single-grain size opacities, such as model M16, we argue that a satisfactory compromise is to use two (maybe three) independent size-averaged dust opacities to approximate the thermal dust spread of a realistic dust grain population, providing a good choice of the composition and size range.
The grains of different sizes have different temperatures and different coupling timescales to the gas phase. They therefore do not interact in the same way with the gas-phase species, in particular, when the CO condensation/evaporation balance is considered.
The multiple temperatures significantly affect the CO gas-phase distribution. Our model with two dust populations shows a CO depletion from 50 au up to 250 au, followed by a CO gas rise at larger radii. This rise does not require additional external UV irradiation or a change in the dust-to-gas mass ratio. The effect cannot be reproduced in chemical models that use a single-dust temperature structure.
The CO ice distribution is also affected, and the snowline is reshaped. The dust temperature spread creates multiple CO condensation fronts, inducing a split in the radial snowline. This does not require radial drift, although inward drift will affect the snowline even more. A more physical model would need a larger number of grain sizes and related temperature, implying a more complex 2D CO snowline.
These results have potential implications for observations and planet formation. On one hand, CO holes followed by a rise in observed Class I/II disks have been reported recently. We speculate that the origin of these CO holes could be linked to the combination of dust temperature spreads and size-dependent dust radial segregation. On the other hand, the split in the CO snowline affects the chemical evolution during planet formation. The formation of COMs via CO surface processes in turn is also dust-size segregated, such that it affects the way in which COMs are brought toward planetary cores.
Overall, this work illustrates the necessity for modelers to consider simultaneously multiple dust grain populations with independent optical properties, both for the thermal and chemical simulations.
Acknowledgements
We thank the referee for their valuable feedback. S.G., J.K.J., and R.S. acknowledge support from the Independent Research Fund Denmark (grant No. 0135-00123B). This work was supported by A. Dutrey and S. Guilloteau thank the French CNRS programs PNP, PNPS and PCMI. J. Kobus and S. Wolf acknowledge support from the DFG grant WO 857/19-1.
Appendix A Sensitivity to different physical parameters
Appendix A.1 Grain properties and dust opacities
Here, we use another dust opacity model in order to determine the impact of grain properties onto the thermal disk structure of model D. We chose the standard DIANA opacities (Woitke et al. 2016) in the optool code (Dominik et al. 2021) and used the same dust size and wavelength distribution as described in Sect. 2.4.1. The opacity profiles are shown in Fig. A.1. The composition was a mixture of amorphous laboratory silicate (Dorschner et al. 1995) with amorphous carbon (Zubko et al. 1996) and 25 % porosity. The difference with the DSHARP opacities seems minor, but they are not exactly similar. Figure A.2 shows the effect on the dust temperatures in the midplane. The bump effect disappears, but the small-grain temperature profile always remains warmer than that of large grains, and it reaches 20K at about 250 au. Therefore, the CO chemistry is expected to behave similarly as with the DSHARP opacities. This result holds for model M16 as well.
Appendix A.2 Size range
In all the models shown above, the two grain populations have the same minimum size value amin = 0.005 µm, as in many other studies (e.g., Cleeves 2016; Schwarz et al. 2018; Ballering et al. 2021; Zhang et al. 2021; Calahan et al. 2023). This choice is partly justified by the fact that in a distribution following a power law, the opacities are mostly sensitive to amax because most of the mass is in the larger grains (Draine 2006; Birnstiel et al. 2018).
However, a few other studies adopted a prescription in which amin,l equals amax,s for the calculation of the opacities (e.g., Du & Bergin 2014), which is expected to slightly decrease the opacities at submillimeter wavelengths. Here, we test the effect of this prescription both with DSHARP and DIANA opacities on the thermal structure, that is, by using the range [0.005 µm , 1 µm] for the small grains and [1 µm, 1 mm] for the large grains. The resulting absorption opacities are shown by the red lines in Fig. A.3. A higher amin,l value decreases the absorption opacities at visible and UV wavelengths by up to an order of magnitude. The resulting dust temperature profiles are shown by the red lines in Fig. A.4. Interestingly, changing the large-grain opacities mostly affects the small dust temperature rather than that of the large one, because the scattering albedo of the large grains is increased with the new size range (the scattering opacities are also slightly decreased in the same wavelength range but less so than the absorption opacities).
It is generally assumed that a higher albedo decreases the absorbed energy in the disk and therefore decreases the overall dust temperature. This result shows that this is not exactly correct when a dust size distribution is considered: The decrease in energy input for a grain species can imply an increase in energy input for another grain species.
We also note that while the DIANA standard opacities do not raise a bump when amin,l = amin,s, they do raise a bump and increase the overall small-grain temperatures when amin,l = amax,s is chosen. This highlights the importance of a careful selection of the optical properties. In particular, this questions the widely chosen prescription of amin,l = amin,s because this result shows that the value of amin,l can have a significant impact on the dust temperature when polydispersion is considered, even for a dust distribution following a power law.
Appendix A.3 Disk mass
Using the same stellar luminosity (L★ = 1 L⊙), we compared disks of different masses to investigate the impact of the optical depth on the thermal dust decoupling. We used model D with the DSHARP opacities and changed only its mass for two extreme cases: one model is 10 × less massive than model D (Mdisk = 7.5 × 10−4M⊙), and the other is 10 × more massive (Mdisk = 7.5 × 10−2M⊙). The resulting dust temperatures in the midplane are shown in Fig. A.5.
In the less massive disk, a similar CO-ice distribution as in model D is expected. The large-grain temperature drops below 25 K inside 50 au and below 20 K at radius ~ 100 au. The small-grain temperature decreases to below 25 K at about 250 au and reaches 20 K about 350 au. In the more massive and thus more optically thick disk model, the thermal decoupling occurs, as expected, at a larger distance than for the fiducial model D (outside 50 au). A bump is present for the small grains farther away than in model D, but the temperature never exceeds 20 K. In this model, we can expect that CO molecules preferably stick on the small grains almost everywhere in the disk. However, this conclusion is only valid because we fixed the stellar luminosity to the same value (L★ = 1 L⊙), as appropriate for T Tauri stars. In practice, the more massive disks are found around Herbig Ae stars, and they will have higher temperatures because the stellar luminosity is higher, possibly sufficient to return the bump temperature to more than 20 K.
Appendix A.4 Impact of the turbulence
We also tested different values of the a parameter (which affects our model only through dust settling) in order to determine the effect of a varying ratio in the vertical concentration of solid particles to that of the gas on the bump shape and thermal dust profile. The fiducial model had an α value of 10−2. In Fig. A.6, we show the resulting dust temperatures in the midplane of model D (using the DSHARP opacities) with two other α values that are compatible with observations (Cuzzi et al. 1993; Brauer et al. 2008), model D was computed with α values of 10−3 and 10-4. In the first case (α = 10−3), the thermal structure in the midplane is roughly unchanged. For the lower value of α (10−4), the bump appears to be flatter, while the temperature spread is smaller, in particular, at large radii. Overall, the CO spatial distribution is not expected to vary much from the fiducial model D because in all cases, the small-grain temperature remains higher than that of the large ones.
 |
Fig. A.1 Dust optical properties from DIANA opacities for model D. Left: Absorption coefficients. Middle: Scattering coefficients. Right: Henyey-Greenstein g parameter of the anisotropy (g = <cos(θ)>). |
 |
Fig. A.2 Midplane radial dust temperature profiles of model D with the DIANA standard opacities. |
 |
Fig. A.3 Absorption opacity profiles from DSHARP (left) and DIANA standard opacities (right) for model D. The red line represents the opacities of the large grains when amin,l is set to 1 µm. The black lines show the standard choice of amin,l = 0.005 µm. |
 |
Fig. A.4 Disk midplane radial profiles of the dust temperatures. The parameters are that of model D. The red lines show the temperatures when using amin,l = 1 µm. For comparison, the black lines show the original temperatures using the standard sets (amin,l = 0.005 µm). Left: DSHARP opacities. Right: DIANA standard opacities. |
 |
Fig. A.5 Disk midplane radial profiles of the dust temperatures. The black curves show the temperature profiles of the small (dotted) and large (solid) grains. The parameters are that of model D, but with a different mass. |
 |
Fig. A.6 Disk midplane radial profiles of the dust temperatures. The black curves show the temperature profiles of the small (dotted) and large (solid) grains. The parameters are that of model D, but with different α values. |
Appendix B The bump effect: Simulation artifacts or physical effects
It can rightfully be argued that a dip in temperature in optically thick regions is very often the result of numerical effects. The bump effect would therefore not be a physical effect and would rather be caused by too few photon packages and/or by a too strong limitation on the maximum number of interactions a photon package is allowed to have before it is removed during a simulation. In order to ensure that the temperature bump is an actual physical effect, we performed additional test simulations in which we compared various numbers of photon packages and various maximum numbers of interactions. The results are shown in Fig. B.1. The left panels shows the temperature profile of size bin 5 from model M16 for various maximum numbers of interactions from 101 to 108 interactions. The right panel shows the same grain population for various numbers of photon packages from 106 to 109. Both tests strongly suggest that the visible bump is a real physical effect and is not due to thermal simulation effects. We also note that these simulation results were cross checked and confirmed using the 3D Monte Carlo radiative transfer code POLARIS (Reissl et al. 2016).
 |
Fig. B.1 2D dust density maps in cm −3 of the dust distribution. |
References
- Ballering, N. P., Cleeves, L. I., & Anderson, D. E. 2021, ApJ, 920, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A & A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A & A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., Zhu, Z., et al. 2018, ApJ, 869, L45 [CrossRef] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1998, Absorption and Scattering of Light by Small Particles (New York: Wiley-VCH) [CrossRef] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A & A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bron, E., Le Bourlot, J., & Le Petit, F. 2014, A & A, 569, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calahan, J. K., Bergin, E. A., Bosman, A. D., et al. 2023, Nat. Astron., 7, 49 [Google Scholar]
- Cleeves, L. I. 2016, ApJ, 816, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Dobrovolskis, A. R., & Champney, J. M. 1993, Icarus, 106, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Hogan, R. C., Paque, J. M., & Dobrovolskis, A. R. 2001, ApJ, 546, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Dutrey, A., & Guilloteau, S. 2003, A & A, 399, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deirmendjian, D. 1969, Electromagnetic scattering on spherical polydispersions (New York, NY (USA): Elsevier Scientific Publishing) [Google Scholar]
- Dominik, C., Min, M., & Tazaki, R. 2021, Astrophysics Source Code Library [record ascl:2104.010] [Google Scholar]
- Dong, R., Zhu, Z., & Whitney, B. 2015, ApJ, 809, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A & A, 300, 503 [NASA ADS] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [Google Scholar]
- Du, F., & Bergin, E. A. 2014, ApJ, 792, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A & A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
- Dutrey, A., Guilloteau, S., Piétu, V., et al. 2017, A & A, 607, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flores, C., Duchêne, G., Wolff, S., et al. 2021, AJ, 161, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., & Nelson, R. P. 2009, A & A, 496, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavino, S., Dutrey, A., Wakelam, V., et al. 2021, A & A, 654, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfe, C., Wolf, S., Guilloteau, S., et al. 2013, A & A, 553, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A & A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harsono, D., Bjerkeli, P., van der Wiel, M. H. D., et al. 2018, Nat. Astron., 2, 646 [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [Google Scholar]
- Heese, S., Wolf, S., Dutrey, A., & Guilloteau, S. 2017, A & A, 604, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henning, T., & Stognienko, R. 1996, A & A, 311, 291 [NASA ADS] [Google Scholar]
- Hersant, F., Wakelam, V., Dutrey, A., Guilloteau, S., & Herbst, E. 2009, A & A, 493, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iqbal, W., & Wakelam, V. 2018, A & A, 615, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, At & A, 572, A107 [Google Scholar]
- Le Gal, R., Brady, M. T., Öberg, K. I., Roueff, E., & Le Petit, F. 2019, ApJ, 886, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Z.-Y. D., Li, Z.-Y., Tobin, J. J., et al. 2023, ApJ, 951, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Murillo, N. M., Hsieh, T. H., & Walsh, C. 2022, A & A, 665, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohashi, S., Momose, M., Kataoka, A., et al. 2023, ApJ, 954, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Chandler, C. J., Isella, A., et al. 2015, ApJ, 813, 41 [CrossRef] [Google Scholar]
- Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [Google Scholar]
- Reissl, S., Wolf, S., & Brauer, R. 2016, A & A, 593, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A & A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [Google Scholar]
- Schwarz, K. R., Bergin, E. A., Cleeves, L. I., et al. 2018, ApJ, 856, 85 [Google Scholar]
- Schwarz, K. R., Calahan, J. K., Zhang, K., et al. 2021, ApJS, 257, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A & A, 24, 337 [NASA ADS] [Google Scholar]
- Tazzari, M., Testi, L., Ercolano, B., et al. 2016, A & A, 588, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 339 [Google Scholar]
- Van Clepper, E., Bergner, J. B., Bosman, A. D., Bergin, E., & Ciesla, F. J. 2022, ApJ, 927, 206 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1982, ApJ, 258, 533 [NASA ADS] [CrossRef] [Google Scholar]
- van't Hoff, M. L. R., Walsh, C., Kama, M., Facchini, S., & van Dishoeck, E. F. 2017, A & A, 599, A101 [CrossRef] [EDP Sciences] [Google Scholar]
- van’t Hoff, M. L. R., Harsono, D., Tobin, J. J., et al. 2020, ApJ, 901, 166 [Google Scholar]
- Villenave, M., Ménard, F., Dent, W. R. F., et al. 2020, A & A, 642, A164 [CrossRef] [EDP Sciences] [Google Scholar]
- Villenave, M., Stapelfeldt, K. R., Duchêne, G., et al. 2022, ApJ, 930, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J. C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Chapillon, E., Dutrey, A., et al. 2019, MNRAS, 484, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res.Atmos., 113, D14220 [NASA ADS] [Google Scholar]
- Williams, J. P., & Best, W. M. J. 2014, ApJ, 788, 59 [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A & A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, S., Padgett, D. L., & Stapelfeldt, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Shu, F. H. 2002, ApJ, 580, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Booth, A. S., Law, C. J., et al. 2021, ApJS, 257, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Dust optical properties of model D (dashed and solid lines) and S (dashed lines only). Left: absorption opacity. Middle: scattering opacity. Right: Henyey–Greenstein g parameter of the anisotropy (g = <cos(θ)>). |
| In the text | |
 |
Fig. 2 Absorption opacity and scattering albedo profiles for the 16 bin sizes in model M16. The dotted, dashed, and solid lines represent the small, intermediate, and large grains, respectively. The dashed vertical black line indicates the wavelength λmax at which the star radiates according to Wien’s law. The grain sizes are indicated in µm. We refer to Table 4 for a description of the bin sizes. |
| In the text | |
 |
Fig. 3 Panels a and b: 2D dust area density (cm−1) of model D. Panel c: ratio of the large-grain area density to the small-grain area density (note the different z scale). Panel d: mass ratio of the large and small grains. The green lines mark 1 × Hg and 2 × Hg. |
| In the text | |
 |
Fig. 4 2D dust temperature structures of model D. Left: temperature of the small grains. Right: temperature of the large grains. |
| In the text | |
 |
Fig. 5 Disk midplane radial profiles of the dust temperatures. The black curves show the temperature profiles of model D. The solid red curve shows the temperature profile of model S, and the yellow curve shows that of model C. The vertical solid, dashed, and dotted green lines represent the radial distances in model D at which the vertical optical depth (at 1 µm) becomes smaller than 10, 5, and 1, respectively. |
| In the text | |
 |
Fig. 6 Midplane radial dust temperature profiles of model M16. The dotted curves represent the dust temperatures of the small dust grains, the dashed curves represent the temperature of the intermediate grains, and the solid curves show the dust temperatures of the large dust grains. The grain sizes are given in µm. Left: temperatures with scattering. Right: temperatures with scattering opacity of the intermediate grains set to zero. |
| In the text | |
 |
Fig. 7 Surface densities of CO in the gas phase for models S (dotted line), C (dashed line), and D (solid line) as a function of the radius. |
| In the text | |
 |
Fig. 8 2D maps of CO gas number density [cm−3]. Left: CO in model S. Middle: CO in model C. Right: CO in model D. The solid white line corresponds to the CO snowline where ng(CO)/(ngas(CO)+nice(CO)) = 0.5. The black line shows the maximum scale height below which chemistry is computed. |
| In the text | |
 |
Fig. 9 2D maps of the number density of CO ice. Left: CO adsorbed onto dust grains in model S. Middle: same in model C. Right: CO adsorbed both onto the small and large dust populations in model D. The solid white line corresponds to the CO snowline. The dashed red lines correspond to the snowline of each population taken independently. The black line shows the maximum scale height below which chemistry is computed. |
| In the text | |
 |
Fig. 10 2D map of the disk. The gray scale represents the values of the optical depth computed from the star to all points in the disk τ★(r,z). The red lines represent the surface where τ★(r,z) = 1. The green lines mark the location at which the total vertical optical depth at the mid-plane becomes lower than 10, 5, and 1. The solid blue line marks the altitude at which the optical depth in the z-direction toward the upper layers becomes 1. The line diverges to infinity beyond the line τυ = 1. All opacities are given at 1 µm. |
| In the text | |
 |
Fig. 11 Ratios of the absorption cross section for wavelengths at which the star radiates (~1 µm) and the absorption cross section for wavelengths at which the dust emits (~20 µm) for the grains in model D (red points) and M16 (black points). |
| In the text | |
 |
Fig. 12 2D maps of CO ice number density (cm−3) in model D. Left: CO ice adsorbed onto the small dust population only. Right: CO ice adsorbed onto the large dust population only. The solid gray line corresponds to the total CO snowline. The dashed red lines correspond to the snowline of each population independently. The black line is the maximum scale height below which chemistry is computed. |
| In the text | |
 |
Fig. A.1 Dust optical properties from DIANA opacities for model D. Left: Absorption coefficients. Middle: Scattering coefficients. Right: Henyey-Greenstein g parameter of the anisotropy (g = <cos(θ)>). |
| In the text | |
 |
Fig. A.2 Midplane radial dust temperature profiles of model D with the DIANA standard opacities. |
| In the text | |
 |
Fig. A.3 Absorption opacity profiles from DSHARP (left) and DIANA standard opacities (right) for model D. The red line represents the opacities of the large grains when amin,l is set to 1 µm. The black lines show the standard choice of amin,l = 0.005 µm. |
| In the text | |
 |
Fig. A.4 Disk midplane radial profiles of the dust temperatures. The parameters are that of model D. The red lines show the temperatures when using amin,l = 1 µm. For comparison, the black lines show the original temperatures using the standard sets (amin,l = 0.005 µm). Left: DSHARP opacities. Right: DIANA standard opacities. |
| In the text | |
 |
Fig. A.5 Disk midplane radial profiles of the dust temperatures. The black curves show the temperature profiles of the small (dotted) and large (solid) grains. The parameters are that of model D, but with a different mass. |
| In the text | |
 |
Fig. A.6 Disk midplane radial profiles of the dust temperatures. The black curves show the temperature profiles of the small (dotted) and large (solid) grains. The parameters are that of model D, but with different α values. |
| In the text | |
 |
Fig. B.1 2D dust density maps in cm −3 of the dust distribution. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.












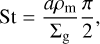





![${F_{{\rm{local}}}}\left( {\lambda ,r,z} \right) = {F_0}\left( {\lambda ,r,4{\rm{H}}} \right)exp\left[ { - \tau _\lambda ^{ext}} \right],$](/articles/aa/full_html/2023/12/aa46767-23/aa46767-23-eq17.png)



