EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A62 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A62
Number of page(s) 12
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202245195
Published online 06 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

When dark clouds collapse under their own gravity (Shu et al. 1987), the conservation of angular momentum leads to the formation of a protoplanetary disk in orbit around a forming protostar. Material with little angular momentum migrates inward and onto the protostar, while material with excess angular momentum contributes to the building up of the disk. Via the launching of magnetically-powered winds, further angular momentum can be removed from the disk (Blandford & Payne 1982; Pudritz & Norman 1983; Shu et al. 1994) and allow for the disk material to migrate inwards towards the protostar (GRAVITY Collaboration 2020).

The infall of material from envelope to disk scales is a prerequisite to star formation and is the primary signature used to determine whether a core is collapsing to form a protostar. Nevertheless, detecting such motions turns out to be surprisingly difficult. Indeed, outflows were first discovered during a search for infall signatures (Snell et al. 1979, 1980). With improvements in telescopes, infall is now frequently detected towards the youngest sources (e.g. Kristensen et al. 2012).

Infall motion is typically studied through spectrally resolved gas observations and the detection of a special type of self-absorbed, optically thick spectral line profile. In a collapsing core, the temperature of the gas increases towards the centre of the core and the blue-shifted part of the spectrum will be enhanced with respect to the red-shifted part (Leung & Brown 1977). However, such infall profiles have also been observed in regions where infall is known not to be present, for example, towards molecular outflows and shocks (Bjerkeli et al. 2012, 2011) where red-shifted and blue-shifted emission can mimic the characteristic shape of infall profiles. Furthermore, the absence of infall profiles does not rule out infall. In fact, previous surveys have revealed that most young stellar objects do not show evidence of infalling material, despite the high accretion rates inferred from outflows and/or infrared emission (e.g. Carney et al. 2016; Heiderman & Evans 2015). Therefore, we should be careful when interpreting infall profiles and, furthermore, high angular resolution observations are generally needed to distinguish between different kinematical components. Such high angular and spectral resolution is available with the Atacama Large Millimeter/submillimeter Array (ALMA).

In the general picture of star formation, we expect infall to be most prominent during the earliest stages of star formation, in other words, during the prestellar core and Class 0 (André et al. 1990) phases, when there is still ample material available in the envelope. A representative example is the infall profile in the water line observed with Herschel towards the prestellar core L1544 (Caselli et al. 2012). The ground-state ortho-water line (at 557 GHz) has turned out to be an excellent tracer of infall, and such profiles are more common towards Class 0 sources than Class I sources (Kristensen et al. 2012; Mottram et al. 2013). However, observing conditions when studying infall water line profiles are not ideal due to the limited spatial resolution available with satellites, the opaqueness of the Earth’s atmosphere when observing from the ground, and the known high abundance of water in outflows. Therefore, to characterise the inward motions on the smallest scales and to be able to separate emission from different components (e.g. disk, envelope, and outflow), high angular resolution observations are needed.

Such observations were recently presented towards one of the youngest known protostellar regions, B335, which is an isolated, dense, and almost spherical Bok globule. In a study by Evans et al. (2015), it was shown from the line profiles of HCO+ and HCN that matter is falling inwards and line profiles were consistent with previously published models (Evans et al. 2005) where the radius of the infall region is 4000 au. In a follow-up study, a combination of data from Spitzer, Herschel, ALMA, and the literature showed that B335 underwent an increase in luminosity over the last few years (Evans et al. 2023). This suggests that accretion is time-variable in B335, which could be a result of an episodic supply of infalling material. This is in line with another study of dense gas tracers (e.g. C17O) on 100–860 au scales, which revealed a complex velocity pattern indicative of asymmetric infall of material towards the central region (Cabedo et al. 2021). Furthermore, based on continuum measurements, Evans et al. (2015) showed that any disk in the centre is of very low mass, 10−3 M⊙. This is consistent with the results of Yen et al. (2015), specifically assuming that if a rotationally-supported disk is present in B335, it must be very small. It should be noted, however, that such a low value should be viewed with some skepticism. The latest modelling by Evans et al. (2023) has emphasised that part of the disk mass could be hidden behind optically thick dust. When it comes to the size of the disk in B335, a study carried out by Bjerkeli et al. (2019) at 0.035″ resolution revealed a dust continuum peak no larger than 12 au (0.07″) in diameter, where rotation is hinted at but not confirmed. On much larger scales, extended continuum emission is detected over an extent of ~1500 au. The spectral line profiles of 13CO revealed clear red-shifted absorption features in the vicinity of the continuum peak.

Detailed studies of infall in B335 are also important because it has been proposed that B335 may be an example of magnetic braking during disk formation in action (e.g. Yen et al. 2018; Maury et al. 2018; Cabedo et al. 2023). In this scenario, when a sufficiently strong magnetic field is present and aligned with the rotational axis of the core, disk formation can be suppressed through efficient removal of the angular momentum of the gas (e.g. Galli & Shu 1993a,b; Allen et al. 2003; Li et al. 2014; Wurster & Li 2018). If the magnetic field becomes strong enough, it can remove nearly all of the angular momentum in the infall region (Galli et al. 2006). Whether such magnetic braking occurs in B335 is not yet clear, but the relatively small disk (Yen et al. 2015; Bjerkeli et al. 2019), together with a known magnetically-powered outflow and apparent magnetically regulated collapse (Maury et al. 2018), may suggest that this is the case.

In this paper, we combine the 13CO (2−1) long-baseline ALMA observations presented in Bjerkeli et al. (2019), with previous observations taken with ALMA in a more compact configuration in order to examine the velocity profile on small scales in B335 and where infall velocities are highest. We also revisit the imaging of the combined continuum data presented in Bjerkeli et al. (2019) to further illuminate the small-scale structure of the region. Even though infall has previously been detected in B335, it has not previously been resolved on very small spatial scales. A kinematically resolved infall velocity map can shed light on how matter is falling towards the protostar on au scales and timescales of only a few years. Indeed, accretion streamers towards disks have recently been suggested for multiple targets (e.g. Alves et al. 2020; Segura-Cox et al. 2020; Pineda et al. 2020; Valdivia-Mena et al. 2022), where, in some cases, inflowing material has been shown to impact the disk (e.g. Garufi et al. 2022). Meanwhile, recent observations of B335 have shown that outflow emission show variability on very short timescales (e.g. Bjerkeli et al. 2019). Variable ejection is typically tied to variability close to the protostar (Audard et al. 2014), but it is important to investigate whether such variability is also manifested in the infall region on slightly larger scales.

It is worth noting that there has been some uncertainty about the distance to B335 over the years. Recently, Watson (2020) demonstrated that B335 was connected to a reflection nebula associated with the star HD 184982 at a distance of 164.5± 1.2 pc, based on Gaia measurements. In this paper, we adopt this (new) distance to B335.

The structure of the paper is as follows. The observations are described in Sect. 2. In Sect. 3, we discuss the geometry and the kinematics of the infalling material first from a purely observational point of view and then through comparisons with 3D radiative transfer models. Our summary and conclusions are presented in Sect. 4.

2 Observations and results

Our long-baseline observations were carried out between October 21–29 2017 as part of the ALMA Cycle 5 programme 2017.1.00288.S. The observational details of that observing programme, as well as details regarding calibration and imaging (carried out in CASA; McMullin et al. 2007), are described thoroughly in Bjerkeli et al. (2019). We summarise them here for completeness. The angular resolution of the observations was 0.032 by 0.023″ and the largest recoverable scale is of the order 0.3″ (~50 au), much smaller than the ~4000 au extent of the infall region as inferred in Evans et al. (2015). Our goal is therefore to combine our long-baseline observations with shorter baseline observations from 2013 (Project ID: 2013.1.00879.S), with observational details given in Yen et al. (2015). We chose to include these data to also recover emission on scales that are a factor of ten larger. Unlike the case of 12CO, there is, however, no 13CO 2−1 data available on intermediate scales. Hence, it is worth noting that sensitivity to emission on ~0.3″ scales will be slightly suppressed in the present work. In addition, we revisited the imaging of the long-baseline continuum data that was presented in Bjerkeli et al. (2019). Specifically, we lowered the robust parameter during cleaning to 0.0 and reduced the cell size from 0.01″ to 0.001″ to recover small scale emission and improve image quality in an attempt to recover any disk-like structure. All molecular line spectral cubes were imaged after continuum subtraction in the (u, υ) domain. The analysis of all the cleaned data products presented in this study was carried out in Matlab and images were convolved to a common angular resolution of 0.035 arcseconds to allow for direct comparisons. This resolution matches the resolution of the cubes presented in Bjerkeli et al. (2019).

Inspection of our improved map of the long-baseline dust continuum emission in B335 reveals a single-peaked structure elongated in the north-south direction and peaking towards the position of B335. Moreover, we observe complicated extended structures that are better revealed in our improved map. Specifically, we detect extended emission down to the 5σ level in a region extending out to a distance of ~0.1″ (17 au) from the protostar (Fig. 1).

The combined 13CO emission (Fig. 1) exhibits infall-type profiles (Fig. 2) characterised by an absorption feature at the systemic velocity of 8.3 km s−1 (Evans et al. 2005). These infall profiles persist throughout the entire region surrounding the protostar (see also Fig. 8 in Bjerkeli et al. 2019). Notably, the infall profiles are also present in the northern and southern regions, where no 12CO outflow emission is present. In addition, no significant13 CO contribution from the outflow can be detected on the investigated scales. Neither does the 13CO data show any signs of rotation on any scales. As such, we conclude that most (if not all) of the material traced by13 CO is falling towards the central region. We consequently conclude the infall shape of the line profiles is an optical depth effect. Furthermore, careful inspection of line profiles throughout the region (Fig. 2) and comparisons between integrated long-baseline and combined data emission show that line profiles differ most at larger distances from the protostar (while the ratio approaches one towards the protostellar position). This suggests that a fraction of the emission originates from scales that have not been picked up in our long baseline observations. The effect seems to be more prominent for the low-velocity gas, at greater distances from the protostar, but may still indicate that infall takes place on larger scales than what is probed here. This finding is in line with earlier, lower resolution studies of infall towards B335 (e.g. Evans et al. 2015) where the infall region was estimated to be 4000 au in size.

thumbnail Fig. 1

Continuum and 13CO emission around B335. Left: re-imaged continuum with line contours from 5x in steps of 30x. Purple ellipse shows a 2D Gaussian fit to the upper 40% of the continuum emission. All data were convolved to a common resolution of 0.035″ with the beam size shown on lower-left side of each panel. Right: moment 0 map of the 13CO emission, integrated from −5 to +5 km s−1 with respect to the systemic velocity of 8.3 km s−1, and overlaid with the continuum in black contours. Only regions with 13CO emission above 3σ are included.

3 Discussion

3.1 1.3 mm continuum and 13CO emission

In Fig. 1, the continuum emission is presented together with a 2D Gaussian fit to the centrally peaked part of the continuum (where the emission is above 1.4 mJy beam−1). The best fit to the continuum yields a FWHM of 0.059″ by 0.041″ (9.7 by 6.7 au), and a position angle of 5 degrees east of north (purple ellipse in Fig. 1). This size and position angle are both consistent with what we would expect for a disk-like structure in B335 (Yen et al. 2015; Bjerkeli et al. 2019), if present. The elongation of the centrally peaked continuum emission is perpendicular to the direction of the outflow to within the uncertainty of the outflow position angle as inferred from Herbig-Haro knots (~80°± 10°E of N, see e.g. Gålfalk & Olofsson 2007). Although it has been shown previously that the inner structure on scales of 10–15 au is consistent with rotation (Yen et al. 2015; Bjerkeli et al. 2019), an optically thin tracer of the kinematics on even smaller scales would be required to confirm the presence of a rotationally supported disk around B335. Our observations do include the C18O 2−1 line, but the signal-to-noise ratio (S/N) of the data is not sufficient to reveal the kinematics of such a disk-like structure.

Also presented in Fig. 1, we have the integrated13 CO emission map (from −5–5 km s−1) above 3σ (colours) for the region surrounding the continuum peak. This region is extended compared to the continuum emitting region, but it nevertheless shows self-absorbed line profiles, suggesting that the surrounding cloud material in the region contributes to the line profiles in the form of absorption.

3.2 Geometry and kinematics of infalling material

In a scenario where infall is spherically symmetric and increasing towards the centre, the emission will be detected across a range of velocities and a traditional intensity-weighted velocity map (e.g. Fig. A.1), a channel map (e.g. Fig. A.2), or a position-velocity diagram (see Fig. 8 in Bjerkeli et al. 2019) may not provide a clear picture of the velocity field within each beam. However, the width of a line profile at each position of the infalling gas will provide a lower limit to the true infall velocity in that position. In the case where this position is directly towards the protostar (the dominant source of gravity on the small scales examined here), we would expect the width of the line profile to almost correspond to the maximum infall velocity (at least if the S/N is sufficiently high). Meanwhile, in the case where the position is offset from the protostar, we would expect the extent of the line profile to be narrower than the maximum infall velocity. The reason for this is that since material can move at an angle with respect to the line of sight, the line profile will not capture the true maximum infall velocities (since they are at an angle with respect to the line-of-sight direction). In the spherically symmetrical case, this can be accounted for, but if infall is asymmetric, it becomes more difficult.

To further investigate the geometry and kinematics of the infalling material in B335, we fit a Gaussian profile to the blue-shifted part of the line profile in each position of the 13CO map. Since (in an infall scenario) the blue-shifted emission would suffer less from absorption than the red-shifted emission, this provides a better method to constrain the velocity field in the region. After careful comparison between observed spectra and Gaussian fits, we decided to take the velocity where the Gaussian fit meets the observed noise level at each position (Fig. A.3) as a measure of the maximum observed motion in each position of the map – in other words, we estimated a lower limit on the true infall velocity. From visual inspection of selected Gaussian fits, we conclude that a coefficient of determination (R squared”) higher than 0.25 is desirable in order to be able to accurately determine (i.e. to within approximately 1 km s−1) the extent of the line profile. Thus, in the following, we only include the positions where this requirement is fulfilled. This method of producing a velocity map is useful to assess the morphology of the infalling region, as described below. While it does not account for the skewness of the line profiles, we note that the results remain consistent with our method even if we fit the blue-shifted line profiles at each position using a log-normal distribution (Fig. A.3), which gives slightly higher velocity estimates.

In the case of spherical infall (and as mentioned previously), the velocity measurements from the Gaussian fitting to the emission line profiles would for most of the positions be lower than the true infall velocity in each given position due to projection effects. In the region around B335, we can furthermore assume that thermal broadening does not contribute significantly (less than 1 km s−1) to the width of line profiles due to the relatively low temperatures (200 K, see: Bjerkeli et al. 2019). Similarly, there is no reason to believe that there should be a significant contribution from turbulence, since there is no source that can contribute in the region outside the outflow. As such, and since we do not know the morphology of the infalling region, the velocities estimated from Gaussian fits (Fig. 3) to the blue-shifted line profiles in the spatially resolved map should be considered as lower limits on the true velocity at each given position. In fact, higher velocities would be reasonable given the asymmetric nature of the emission.

From Fig. 3, it can be seen that13CO 2−1 does not trace the outflow emanating from B335. In fact, high velocities in 13CO are found predominantly to the north and south of B335, perpendicular to the direction of the outflow. This is expected in the case of infall, since this region is not actively participating in the outflow. We stress that the B335 region is spatially resolved in these ALMA observations and, in the following, we focus our analysis on the regions to the north and the south of the protostar, where the outflow is not present. In particular (see Sect. 3.4), we focus on a position located 20 au to the north of the protostar and more than 10 au away from the outflow cavity wall.

thumbnail Fig. 2

Comparisons of long-baseline and combined data line profiles Left: long-baseline (blue) and combined data (red) line profiles for three different positions (averaged over dashed purple circles in right panels). υLSR = 8.3 km s−1, is indicated with black dashed lines in the left panels. Right: the ratio of the13 CO line flux between combined and long baseline data as a function of position, where both combined and long baseline emission exceeds 3σ. The line ratio maps suggest that information on larger scales is filtered out by the interferometer. Note: the regions used for averaging in the lower two panels are slightly bigger to improve the S/N. Black contours show the continuum starting at 5σ in steps of 10σ.

3.3 Possibility of high-velocity components and episodic flows on small scales

The lower limits on the infall velocities presented in Fig. 3 can be compared to the expected infall velocities at corresponding radii. It is reasonable to assume that most of the mass in the B335 system is in the protostar and not the (disk-)like structure surrounding it. The protostellar mass was estimated by Yen et al. (2015) and Evans et al. (2015) to be 0.05 and 0.15 M⊙, respectively. Taking the new distance estimate of 164.5 pc into account (versus the prior distance, 100 pc), this translates to a central mass in the 0.1–0.4 M⊙ range. In the case of free-fall, this implies maximum infall velocities of: 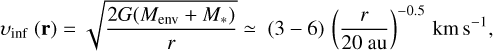(1)

where r is the distance from the protostellar position, G is the gravitational constant, Mstar is the mass of the central protostar, and Menv is the mass of the envelope inside r, which is negligible on the small scales discussed here (less than 0.1% of the total envelope mass assuming the density profile of Kristensen et al. 2012, Appendix C). At 20 au separation from the protostar, this yields velocities below the ~6 km s−1 level. Based on the observations, the lower limits that we estimated for the infall velocities (Fig. 3) are up to 50% higher than 6 km s−1, particularly towards positions located to the north and the south of the protostar. These measurements are not easily reconcilable with a magnetic braking scenario, where (in contrast) the velocities are expected to be lower than the free-fall velocities (see e.g. Lam et al. 2019, Figs. 4, 7, and 12).

We note that our infall map in Fig. 3 suggests velocity variations on the level of a few km s−1. However, given the uncertainties described above, it cannot be confirmed from the velocity map alone that fluctuations are due to episodic infall rather than noise or random motions. We also note that estimates of the infall velocity in the overlap region between the outflow and the envelope are particularly uncertain. What is clear from the map, however, is that velocities to the north and to the south are systematically higher than what is expected in the free-fall scenario, assuming the mass estimate is correct. Furthermore, velocities are not decreasing as r−0.5 as expected in a free-fall scenario. For the case in which the protostellar mass is higher than expected (e.g. 0.8 M⊙), we derived velocities that are too low at small radii close to the protostar (see Fig. 3).

We conclude that it is unlikely that the observed high infall velocities can be explained by spherical infall. Additionally, we note that anisotropic accretion along the cavity walls is observed on slightly larger scales Cabedo et al. (2021) and that B335 recently underwent a burst in luminosity (Evans et al. 2023) accompanied by an ejection event (Bjerkeli et al. 2019). Thus, it would not be entirely surprising if asymmetric and time-variable accretion also propagated to smaller scales.

thumbnail Fig. 3

Infall velocity field. Left: lower limit on the infall velocity (colour) as estimated from the FWHM of Gaussian fits to the blue-shifted components of line profiles at each position. Translucent white regions denote where 12CO emission is detected (Bjerkeli et al. 2019) and, therefore, where contamination from the outflow could be contributing. Black contours show continuum starting at 5σ in steps of 30σ, and the red ellipse show a 2D Gaussian fit to the upper 40% of the continuum emission. For the velocity map, only positions where the coefficient of determination is higher than 0.25 are included. Right: lower limit on the infall velocity as a function of distance from the continuum peak (grey dots). Maximum measured velocities at each radii are shown with black triangles. Note: this plot takes into account every pixel in the map, and therefore some of the gray dots correspond to regions coincident with the outflow. The observed lower limit on the infall velocities are compared with the spherically-symmetric free-fall scenario for three different protostellar masses (green, blue, and red solid lines).

3.4 Radiative transfer modelling

To constrain the nature of the observed 13CO infall velocities, we used the 3D line radiative transfer code LIME (Brinch & Hogerheijde 2010, v1.4.3). LIME does not put any constraints on the geometry and complexity of the models and different components can be formulated analytically. The density, temperature, abundance, and velocity structures are specified and LIME generates an unstructured Delaunay grid from the input model. Here, 50 000 grid points were used and the sampling probability was weighted by the density structure, so that the grid is finer towards the centre of the model. The13 CO collisional rate coefficients data file from the LAMBDA1 database, which is derived from Yang et al. (2010), was used. After convergence was reached, the model was ray-traced with velocity resolution similar to the observations. In all models, the micro-turbulent velocity was set to 200 m s−1 and the spatial resolution of the output was set to 0.01″.

We considered three different types of models (see Fig. 4) to investigate various scenarios that could explain the observed velocities. These are: (i) spherical free-fall towards a central protostar; (ii) episodic infall in the regions where outflow motions are not present; and (iii) free-fall towards a central protostar, but where the velocity is higher along the cavity walls, meant to mimic the possible occurrence of streamers in B335. Two cases for each model are considered, one where the mass of the central protostar is 0.1 M⊙ and one where the mass is 0.4 M⊙, making a total of six cases. A protostellar mass of 0.4 M⊙ is considerably higher than what was previously estimated in Yen et al. (2015), but this allows us to investigate to what degree the protostellar mass affects the infall velocity morphology on slightly larger scales. We note that no disk is included in any of the models. Leaving out this component will affect the computed line profiles close to the protostar, particularly since its rotation is not taken into account. It will also affect the line profile shapes particularly towards red-shifted velocities since the presence of a disk increases the optical depth towards certain positions. This choice will not, however, affect the infall velocities and line profiles on larger scales (> 10 au) where we focus our investigation, since any disk, if present, is less <10 au.

When defining the physical conditions in the models, we chose for all the parameters to be as close as possible to what has previously been published. For the first model, the density follows a power-law profile (Kristensen et al. 2012) out to 6600 au distance from the protostar: 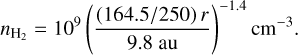(2)

We set the abundance of 13CO to a constant value of 1.7 × 10−6 with respect to H2 (Frerking et al. 1987). A surrounding envelope with a density of 109 cm−3 is included and extends from 6600 to 10 000 au. This density is unrealistically high, but chosen so that the envelope produces absorption in the line profiles near the systemic velocity that corresponds reasonably well with the observations. The velocity in the envelope (r > 6600 au) is set to zero. Within the infall region, the gas is assumed to be in free-fall (see Eq. (1)) and the temperature follows a power law of: 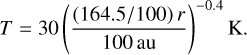(3)

This profile is taken from Yen et al. (2015), and not in perfect agreement with the observed temperatures in the inner region as derived from the CH3OH emission (Bjerkeli et al. 2019). This is, however, of less importance here since our focus is on the line profiles on larger scales.

To account for the response of the interferometer, we employed simalma in CASA to post-process our model emission maps using the ALMA Cycle 9 configuration and array set up corresponding to the observations in this study. After applying the same process as we did for the actual observations to extract the lower limit on the infall velocity (see Fig. A.3), we obtained the infall velocity maps presented in Fig. 5.

In the second (‘episodic’) model, the infall velocity is allowed to vary in the radial direction. In addition, we assume no infall takes place in the region where the outflow is present (in the east-west directions) and the temperature and density in this region is set to be constant (T = 100 K, n(H2) = 104 cm−3, respectively). As a result, the infall region is now effectively two cones with 45° opening angles to the north and south (middle column of Fig. 5). The velocity is varied relative to the free-fall velocity using a cosine function in radius, where the amplitude is allowed to change by 50% and where the period is 20 au. The mean velocity in the region is, in addition, increased by 40% relative to the free-fall velocity to account for the fact that infall only occurs in a fraction of the total region (i.e. to make up for the region where the outflow is present). The standard spherical envelope model from Kristensen et al. (2012) does not account for this modified geometry and the possible effects of our modifications on the large-scale envelope are unknown. We do find, however, that we need to vary the density in the envelope by a factor of up to five in order to match the observed line profiles. The temperature follows the same power-law profile as in the first model, but we acknowledge that it may also vary. It is worth noting that the variability in this particular model corresponds to a time-scale of approximately 20 yr. This timescale is chosen to match the observed infall velocities, but is also in line with the studies of Bjerkeli et al. (2019) and Evans et al. (2023), where the episodic ejection event that took place in 2015 can be connected to a luminosity burst that peaked in 2019. The resulting infall velocities are presented in the middle row of Fig. 5.

In the third model, we included the outflow cavity as above, but instead vary the velocities and densities in the azimuthal direction (i.e. angle with respect to the north-south axis). The absolute value of the velocity is varied with a cosine, where it is increased by a factor of two along the cavity walls and goes to zero along north and south directions. The densities and velocities are also adjusted to keep the mass and mean velocities constant, while the temperature continues to follow the power-law profile from Eq. (3). The resulting infall velocites are presented in the bottom row of Fig. 5.

It should be noted that we have found it difficult to fully account for the fluxes observed close to υLSR, while simultaneously fitting the line flux in the wings (see Fig. A.4). For the cases presented here, this amounts to model fluxes near υLSR that are up to 50% lower than the observations. The flux near υLSR is particularly low in the episodic infall scenario, while fluxes roughly correspond to observations in the streamline scenario. The reason for this is not entirely understood (but also keeping in mind that some of the observed emission could be filtered out by the interferometer), but could be due to low-velocity emission that is not captured in our simplistic description of the envelope and/or due to optical depth effects. That said, we want to emphasise that reproducing the exact line profiles is not the main purpose of this study. Instead, we are aiming to understand which scenarios can match the observed line profile widths. In fact, while the line profile width is determined by the maximum infall velocity at each position, a complex interplay between several different parameters (e.g. density, temperature, molecular abundance) determines the line profile shapes.

To test how well the derived lower limits on the infall velocity (Fig. 5) correspond with real line widths, we also extract limits from the models before employing simalma, by taking the maximum extent of the line profiles at each position. This recovers the results of the simulated models, demonstrating that our measurement technique is robust on the scales studied here. How well the derived velocities correspond with the actual infall velocities can also be determined since we know the true infall velocities in the models. In Fig. 6, we present how the derived infall velocities from the different models compare with observations and theoretical free-fall scenarios. Although we estimated that infall velocities exceed the theoretical values in approximately 10% of positions in the 0.1 M⊙ free-fall scenario and 1% of positions in the 0.4 M⊙ free-fall scenario, we attribute these discrepancies to a few instances of bad fitting. It is important to note that these discrepancies do not significantly affect the overall conclusions and for most of the positions in the map, the estimated infall velocities are below the theoretical value. This is consistent with the assumption that the width of the line provide a lower limit to the true infall velocity in each position.

While our models are simplistic, they allow us to test whether a higher protostellar mass can account for the infall velocities observed at larger distances from the protostar in the free-fall scenario. However, both low and high protostellar mass scenarios in the spherical free-fall models produce velocities that are not consistent with observations. In particular, a low protostellar mass produces overly low velocities at all radii while a high protostellar mass produce too high velocities in the central region. We also tested whether episodic infall and/or enhanced infall along the cavity walls can account for the observed high velocities. Infall velocity maps for the six different cases (and three different models) are presented in Fig. 5. Here, the images have been convolved to a common resolution of 0.035″.

From the different cases, a few important conclusions can be drawn. It is not possible to reproduce the high infall velocities observed on large scales with a pure free-fall scenario. Even in the case where the protostellar mass is high (0.4 M⊙), the velocities do not match the observed (lower limit) 8 km s−1 infall velocities on 20 au scales. To obtain such high velocities, a central protostellar mass of M = 0.8 M⊙ would be required in the free-fall scenario. That would, however, significantly increase the infall velocity close to the protostar to ~20 km s−1, which is inconsistent with the observations. In fact, no matter how the protostellar mass is varied in the free-fall scenario, the velocity profile with distance from the protostar cannot be reproduced. Hence, we conclude that a pure free-fall scenario does not provide a good match to the data at hand.

The streamline scenario provides a better fit to the observations, but only in the case where the protostellar mass is 0.4 M⊙ (Figs. 5 and 6). The scenario where velocities and densities are allowed to vary episodically in the radial direction also provides a better fit to the observations, but in the case where the protostellar mass is 0.1 M⊙ (Figs. 5 and 6). For both the aforementioned models, high-velocity gas is present on scales that are larger than what is seen in the observations and varying parameters suggests that the temperature profile is a defining parameter in this instance. A steeper slope for the temperature would provide a better match to the observed velocity field, but this would (on the other hand) reduce the intensity of the 13CO line and not match the temperature in the central region derived from the methanol emission. We note that matching the high velocities observed at ~20 au distance is particularly challenging for any of our models. The fit may be improved with a much more complex, fine-tuned velocity drop-off with distance, but such a model goes beyond the purposes of this study.

While no exact match to the observed line profiles was obtained in either of these two scenarios (Fig. A.4), it is clear that models where the infall velocities is allowed to deviate from free-fall velocities are able to both better reproduce the relatively high infall velocities on larger scales and simultaneously keep velocities sufficiently low close to the protostar (Fig. 5). At the same time, they show a spread in velocity at each radii, that is in better agreement with observations (Fig. 6). Our modelling therefore suggests that a characteristic variation in the infall velocity on small scales is present in B335. We cannot, however, from these observations alone put constraints on the cause of such variations. High temperatures and Kelvin-Helmholtz instabilities in the vicinity of the cavity wall could perhaps explain high infall velocities at an angle towards the disk. Similarly, if matter is falling in towards the disk in ‘clumps’ from the north and south, it is plausible that density or pressure fluctuations will alter the infall velocity. To better understand infall in B335, and in particular to confirm that the infall fluctuates in time, deep follow-up observations with ALMA in its longest baselines configurations and at different epochs will be required. Finally, if the current data indeed indicate that infall is occurring episodically and with a variation similar to the one we included in our modelling, it would be intriguing to monitor B335 over time for additional outbursts.

thumbnail Fig. 4

Illustration depicting the three distinct models under consideration. The yellow dot marks the protostar, the arrows denote the direction and variation in velocity, while the shading denotes deviations from spherical free-fall.
thumbnail Fig. 5

Infall velocity field LIME models for B335 for two different protostellar masses (0.1 M⊙ in the left column and 0.4 M⊙ in the right column). The models were post-processed with simalma and all plots have been convolved to a common resolution of 0.035″. Only positions where the coefficient of determination is higher than 0.25 are included and due to our relatively simple description for the envelope, our method to extract the infall velocity field does not perform sufficiently well in the regions where infall is not present (hence, the white regions).
thumbnail Fig. 6

Lower limit on the infall velocity as a function of distance. Gray regions show the measured velocities from observations (same as dots in Fig. 3) while green (0.1 M⊙) and blue (0.4 M⊙) regions show the measured velocities from the models. The theoretical spherically-symmetric free-fall curves (Fig. 3) are included for comparison. Note: the spread on measured velocities increases with distance due to lower signal-to-noise ratio. In addition, a Gaussian fitting is not possible for the few spectra very close to the protostar (hence no velocity estimates in that region). Furthermore, the number of points used to create the colored colored regions vary with distance from the centre (cf., Fig. 3). For example, the ‘bumps’ at large distances in the models are caused by a relatively small number of line-width measurements.

4 Summary and conclusions

In this paper, we present observations of 13CO (2−1) and dust continuum emission in B335. The emission line profiles were analysed and compared with 3D radiative transfer models. Our main findings are as follows:

  • The peak of the 1.3 mm continuum emission towards B335 shows an elongated structure, 10 by 7 au in size, with a position angle 5° east of north. This is consistent with a scenario where a disk has started to form.

  • 13CO emission towards B335 shows line profiles where the blue-shifted emission component is enhanced with respect to the red-shifted component. We interpret the observations of 13CO as material falling inwards towards the protostar from the north and south. The velocities do not follow a r0.5 profile, as would be expected in the case of spherically symmetric infall.

  • The relatively high velocities are not easily reconcilable with a scenario where disk growth is actively prohibited via magnetic braking.

  • Since there is no reason to believe that the infall velocity should exceed the free-fall velocity at any given location, this suggests asymmetric, perhaps time-variable infall. A scenario where the central mass is higher than 0.4 M⊙ could (in principle) account for slightly higher velocity emission on 20 au scales, but at the same time, it would not account for the velocity decrease with distance and the relatively low velocities at small distances from the protostar.

From radiative transfer modelling using toy models that include free-fall, episodic infall and infall along a streamline, we favour a scenario where the infall velocity is varying either in the radial direction or with the angle from the north-south axis.

Acknowledgements

The authors would like to thank the anonymous referee for a thorough review that helped improve the quality of the paper. In addition, the authors would like to thank Neal Evans, Yao-Lun Yang, John Tobin, Johanna Matero and Hannah Shoemaker for interesting discussions. This paper makes use of the following ALMA projects data: 2013.1.00879.S and 2017.1.00288.S. ALMA is a partnership of ESO (representing its member states, NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We acknowledge support from the Nordic ALMA Regional Centre (ARC) node based at Onsala Space Observatory. The Nordic ARC node is funded through Swedish Research Council grant No 2017-00648. P.B. acknowledges the support of the Swedish Research Council (VR) through contract 2017-04924. JPR and ZYL are supported in part by NSF grant AST-1910106 and NASA grant 80NSSC20K0533. J.P.R. would like to further acknowledge the support of the Virginia Initiative on Cosmic Origins (VICO). H.C.’s research group is supported by an OPUS research grant (2021/41/B/ST9/03958) from the Narodowe Centrum Nauki. The research of J.K.J. is supported the Independent Research Fund Denmark (grant No. DFF0135-00123B).The research of L.E.K. is supported by a research grant (19127) from VILLUM FONDEN. D.H. is supported by Center for Informatics and Computation in Astronomy (CICA) grant and grant number 110J0353I9 from the Ministry of Education of Taiwan. D.H. also acknowledges support from the National Science and Technology Council of Taiwan through grant number 111B3005191. The astrophysics HPC facility at the University of Copenhagen, supported by a research grant (VKR023406) from VILLUM FONDEN, was used for carrying out the radiative transfer modelling.

Appendix A Supplementary material

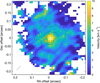thumbnail Fig. A.1

Observed 13CO intensity weighted velocity map (moment 1). Note: the velocities have been corrected w.r.t υLSR and the sign changed to allow comparison with Fig. 3. The first moment is calculated in a velocity range from −15 to +15 km s−1 with respect to υLSR, and pixels where emission is below 3σ (σ = 0.012 Jy beam−1 km s−1) are masked out.
thumbnail Fig. A.2

Channel maps of the observed 13CO emission in four different velocity bins. Only regions with emission above 3σ are included, and hence it should be noted that the range of the color bars slightly varies between panels, with the lower end indicating the 3σ level. Furthermore, velocities have been corrected w.r.t υLSR and the sign changed to allow for comparisons with Fig. 3.
thumbnail Fig. A.3

Gaussian (red) and log-normal (blue) fits to the emission (black) in four different example positions at native spatial resolution. Note: the sign of the velocity scale has been changed and corrected w.r.t. υLSR in order to capture a lower limit on the infall velocity for each position. The log-normal fits generally provide slightly higher velocity estimates (vertical blue lines) than the Gaussian fits (vertical red lines). The σ level for each spectrum is indicated with a light grey dashed line and is calculated in the line emission free regions. Estimated velocities from the Gaussian fits for each of the spectra are indicated with red text. Note: the fit towards the central position is considered to be too poor for further analysis.
thumbnail Fig. A.4

Comparison between modelled (solid line) and observed (dashed; same in all panels) line profiles towards a position 20 au north of the protostar. a) Model free-fall line profile towards a 0.1 M⊙ protostar; b) Free-fall line profile towards a 0.4 M⊙ protostar; c) Episodic infall towards a 0.1 M⊙ protostar; d) Episodic infall towards a 0.4 M⊙ protostar; e) Streamline infall along cavity walls towards a 0.1 M⊙ protostar; and f) Streamline infall along cavity walls towards a 0.4 M⊙ protostar.
thumbnail Fig. A.5

Same as Fig. 5, but before processing the models with simalma.

References

  1. Allen, A., Li, Z.-Y., & Shu, F. H. 2003, ApJ, 599, 363 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alves, F. O., Cleeves, L. I., Girart, J. M., et al. 2020, ApJ, 904, L6 [NASA ADS] [CrossRef] [Google Scholar]
  3. André, P., Martin-Pintado, J., Despois, D., & Montmerle, T. 1990, A&A, 236, 180 [NASA ADS] [Google Scholar]
  4. Audard, M., Ábrahám, P., Dunham, M. M., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 387 [Google Scholar]
  5. Bjerkeli, P., Liseau, R., Nisini, B., et al. 2011, A&A, 533, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bjerkeli, P., Liseau, R., Larsson, B., et al. 2012, A&A, 546, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bjerkeli, P., Ramsey, J. P., Harsono, D., et al. 2019, A&A, 631, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
  9. Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cabedo, V., Maury, A., Girart, J. M., & Padovani, M. 2021, A&A, 653, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cabedo, V., Maury, A., Girart, J. M., et al. 2023, A&A, 669, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Carney, M. T., Yildiz, U. A., Mottram, J. C., et al. 2016, A&A, 586, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
  14. Evans, N. J., II, Lee, J.-E., Rawlings, J. M. C., & Choi, M. 2005, ApJ, 626, 919 [NASA ADS] [CrossRef] [Google Scholar]
  15. Evans, N. J., II, Di Francesco, J., Lee, J.-E., et al. 2015, ApJ, 814, 22 [CrossRef] [Google Scholar]
  16. Evans, I., Neal, J., Yang, Y.-L., Green, J. D., et al. 2023, ApJ, 943, 90 [NASA ADS] [CrossRef] [Google Scholar]
  17. Frerking, M. A., Langer, W. D., & Wilson, R. W. 1987, ApJ, 313, 320 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gålfalk, M., & Olofsson, G. 2007, A&A, 475, 281 [CrossRef] [EDP Sciences] [Google Scholar]
  19. Galli, D., & Shu, F. H. 1993a, ApJ, 417, 220 [NASA ADS] [CrossRef] [Google Scholar]
  20. Galli, D., & Shu, F. H. 1993b, ApJ, 417, 243 [NASA ADS] [CrossRef] [Google Scholar]
  21. Galli, D., Lizano, S., Shu, F. H., & Allen, A. 2006, ApJ, 647, 374 [NASA ADS] [CrossRef] [Google Scholar]
  22. Garufi, A., Podio, L., Codella, C., et al. 2022, A&A, 658, A104 [CrossRef] [EDP Sciences] [Google Scholar]
  23. GRAVITY Collaboration (Garcia Lopez, R., et al.) 2020, Nature, 584, 547 [Google Scholar]
  24. Heiderman, A., & Evans, I., Neal, J. 2015, ApJ, 806, 231 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kristensen, L. E., van Dishoeck, E. F., Bergin, E. A., et al. 2012, A&A, 542, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Lam, K. H., Li, Z.-Y., Chen, C.-Y., Tomida, K., & Zhao, B. 2019, MNRAS, 489, 5326 [Google Scholar]
  27. Leung, C. M., & Brown, R. L. 1977, ApJ, 214, L73 [NASA ADS] [CrossRef] [Google Scholar]
  28. Li, Z.-Y., Banerjee, R., Pudritz, R. E., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 173 [Google Scholar]
  29. Maury, A. J., Girart, J. M., Zhang, Q., et al. 2018, MNRAS, 477, 2760 [Google Scholar]
  30. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASPConf. Ser., 376, 127 [NASA ADS] [Google Scholar]
  31. Mottram, J. C., van Dishoeck, E. F., Schmalzl, M., et al. 2013, A&A, 558, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Pineda, J. E., Segura-Cox, D., Caselli, P., et al. 2020, Nat. Astron., 4, 1158 [NASA ADS] [CrossRef] [Google Scholar]
  33. Pudritz, R. E., & Norman, C. A. 1983, ApJ, 274, 677 [NASA ADS] [CrossRef] [Google Scholar]
  34. Segura-Cox, D. M., Schmiedeke, A., Pineda, J. E., et al. 2020, Nature, 586, 228 [NASA ADS] [CrossRef] [Google Scholar]
  35. Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [Google Scholar]
  36. Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
  37. Snell, R. L., Loren, R. B., & Plambeck, R. L. 1979, BAAS, 11, 713 [NASA ADS] [Google Scholar]
  38. Snell, R. L., Loren, R. B., & Plambeck, R. L. 1980, ApJ, 239, L17 [NASA ADS] [CrossRef] [Google Scholar]
  39. Valdivia-Mena, M. T., Pineda, J. E., Segura-Cox, D. M., et al. 2022, A&A, 667, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Watson, D. M. 2020, Res. Notes Am. Astron. Soc., 4, 88 [Google Scholar]
  41. Wurster, J., & Li, Z.-Y. 2018, Front. Astron. Space Sci., 5, 39 [Google Scholar]
  42. Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [Google Scholar]
  43. Yen, H.-W., Takakuwa, S., Koch, P. M., et al. 2015, ApJ, 812, 129 [NASA ADS] [CrossRef] [Google Scholar]
  44. Yen, H.-W., Zhao, B., Koch, P. M., et al. 2018, A&A, 615, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1

Continuum and 13CO emission around B335. Left: re-imaged continuum with line contours from 5x in steps of 30x. Purple ellipse shows a 2D Gaussian fit to the upper 40% of the continuum emission. All data were convolved to a common resolution of 0.035″ with the beam size shown on lower-left side of each panel. Right: moment 0 map of the 13CO emission, integrated from −5 to +5 km s−1 with respect to the systemic velocity of 8.3 km s−1, and overlaid with the continuum in black contours. Only regions with 13CO emission above 3σ are included.
In the text
thumbnail Fig. 2

Comparisons of long-baseline and combined data line profiles Left: long-baseline (blue) and combined data (red) line profiles for three different positions (averaged over dashed purple circles in right panels). υLSR = 8.3 km s−1, is indicated with black dashed lines in the left panels. Right: the ratio of the13 CO line flux between combined and long baseline data as a function of position, where both combined and long baseline emission exceeds 3σ. The line ratio maps suggest that information on larger scales is filtered out by the interferometer. Note: the regions used for averaging in the lower two panels are slightly bigger to improve the S/N. Black contours show the continuum starting at 5σ in steps of 10σ.
In the text
thumbnail Fig. 3

Infall velocity field. Left: lower limit on the infall velocity (colour) as estimated from the FWHM of Gaussian fits to the blue-shifted components of line profiles at each position. Translucent white regions denote where 12CO emission is detected (Bjerkeli et al. 2019) and, therefore, where contamination from the outflow could be contributing. Black contours show continuum starting at 5σ in steps of 30σ, and the red ellipse show a 2D Gaussian fit to the upper 40% of the continuum emission. For the velocity map, only positions where the coefficient of determination is higher than 0.25 are included. Right: lower limit on the infall velocity as a function of distance from the continuum peak (grey dots). Maximum measured velocities at each radii are shown with black triangles. Note: this plot takes into account every pixel in the map, and therefore some of the gray dots correspond to regions coincident with the outflow. The observed lower limit on the infall velocities are compared with the spherically-symmetric free-fall scenario for three different protostellar masses (green, blue, and red solid lines).
In the text
thumbnail Fig. 4

Illustration depicting the three distinct models under consideration. The yellow dot marks the protostar, the arrows denote the direction and variation in velocity, while the shading denotes deviations from spherical free-fall.
In the text
thumbnail Fig. 5

Infall velocity field LIME models for B335 for two different protostellar masses (0.1 M⊙ in the left column and 0.4 M⊙ in the right column). The models were post-processed with simalma and all plots have been convolved to a common resolution of 0.035″. Only positions where the coefficient of determination is higher than 0.25 are included and due to our relatively simple description for the envelope, our method to extract the infall velocity field does not perform sufficiently well in the regions where infall is not present (hence, the white regions).
In the text
thumbnail Fig. 6

Lower limit on the infall velocity as a function of distance. Gray regions show the measured velocities from observations (same as dots in Fig. 3) while green (0.1 M⊙) and blue (0.4 M⊙) regions show the measured velocities from the models. The theoretical spherically-symmetric free-fall curves (Fig. 3) are included for comparison. Note: the spread on measured velocities increases with distance due to lower signal-to-noise ratio. In addition, a Gaussian fitting is not possible for the few spectra very close to the protostar (hence no velocity estimates in that region). Furthermore, the number of points used to create the colored colored regions vary with distance from the centre (cf., Fig. 3). For example, the ‘bumps’ at large distances in the models are caused by a relatively small number of line-width measurements.
In the text
thumbnail Fig. A.1

Observed 13CO intensity weighted velocity map (moment 1). Note: the velocities have been corrected w.r.t υLSR and the sign changed to allow comparison with Fig. 3. The first moment is calculated in a velocity range from −15 to +15 km s−1 with respect to υLSR, and pixels where emission is below 3σ (σ = 0.012 Jy beam−1 km s−1) are masked out.
In the text
thumbnail Fig. A.2

Channel maps of the observed 13CO emission in four different velocity bins. Only regions with emission above 3σ are included, and hence it should be noted that the range of the color bars slightly varies between panels, with the lower end indicating the 3σ level. Furthermore, velocities have been corrected w.r.t υLSR and the sign changed to allow for comparisons with Fig. 3.
In the text
thumbnail Fig. A.3

Gaussian (red) and log-normal (blue) fits to the emission (black) in four different example positions at native spatial resolution. Note: the sign of the velocity scale has been changed and corrected w.r.t. υLSR in order to capture a lower limit on the infall velocity for each position. The log-normal fits generally provide slightly higher velocity estimates (vertical blue lines) than the Gaussian fits (vertical red lines). The σ level for each spectrum is indicated with a light grey dashed line and is calculated in the line emission free regions. Estimated velocities from the Gaussian fits for each of the spectra are indicated with red text. Note: the fit towards the central position is considered to be too poor for further analysis.
In the text
thumbnail Fig. A.4

Comparison between modelled (solid line) and observed (dashed; same in all panels) line profiles towards a position 20 au north of the protostar. a) Model free-fall line profile towards a 0.1 M⊙ protostar; b) Free-fall line profile towards a 0.4 M⊙ protostar; c) Episodic infall towards a 0.1 M⊙ protostar; d) Episodic infall towards a 0.4 M⊙ protostar; e) Streamline infall along cavity walls towards a 0.1 M⊙ protostar; and f) Streamline infall along cavity walls towards a 0.4 M⊙ protostar.
In the text
thumbnail Fig. A.5

Same as Fig. 5, but before processing the models with simalma.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.