| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 40 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202245131 | |
| Published online | 26 April 2023 | |
Optical and near-infrared stellar activity characterization of the early M dwarf Gl 205 with SOPHIE and SPIRou
1
Aix Marseille Univ, CNRS, CNES, LAM,
Marseille,
France
e-mail: pia.cortes@lam.fr
2
LSSTC DSFP Fellow
3
Sub-department of Astrophysics, Department of Physics, University of Oxford,
Oxford
OX1 3RH,
UK
4
Laboratório Nacional de Astrofísica,
Rua Estados Unidos 154,
37504-364
Itajubá, MG,
Brazil
5
Univ. de Toulouse, CNRS, IRAP,
14 av. Belin,
31400
Toulouse,
France
6
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto,
Portugal
7
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto,
Portugal
8
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
9
Université de Montréal, Département de Physique, IREX,
Montréal, QC
H3C 3J7,
Canada
10
International Center for Advanced Studies (ICAS) and ICIFI (CONICET), ECyT-UNSAM, Campus Miguelete,
25 de Mayo y Francia,
(1650),
Buenos Aires,
Argentina
11
Science Division, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC),
Keplerlaan 1,
2201
AZ Noordwijk,
The Netherlands
12
Institut d’Astrophysique de Paris, CNRS, UMR 7095, Sorbonne Université,
98 bis bd Arago,
75014
Paris,
France
13
Observatoire du Mont-Mégantic, Université de Montréal,
Montréal, QC
H3C 3J7,
Canada
14
Observatoire de Haute-Provence, CNRS, Université d’Aix-Marseille,
04870
Saint-Michel-l’Observatoire,
France
15
Department of Physics, Shahid Beheshti University,
Tehran,
Iran
16
Laboratoire J.-L. Lagrange, Observatoire de la Côte d’Azur (OCA), Universite de Nice-Sophia Antipolis (UNS), CNRS,
Campus Val-rose,
06108
Nice Cedex 2,
France
17
Department of Physics & Astronomy, McMaster University,
1280 Main Street West,
Hamilton,
ON L8S 4K1,
Canada
18
LUPM, Université de Montpellier, CNRS,
Place Eugène Bataillon,
34095
Montpellier,
France
19
Canada-France-Hawaii Telescope, CNRS,
Kamuela,
HI 96743,
USA
20
Observatoire Astronomique de l’Université de Genève,
Chemin Pegasi 51b,
1290
Versoix,
Switzerland
21
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris Cité,
5 place Jules Janssen,
92195
Meudon,
France
22
Departamento de Matemática y Física Aplicadas, Universidad Católica de la Santísima Concepción,
Alonso de Rivera
2850,
Conceptión,
Chile
23
Astrophysics Group, University of Exeter,
Exeter
EX4 2QL,
UK
Received:
4
October
2022
Accepted:
19
January
2023
Context. The stellar activity of M dwarfs is the main limiting factor in the discovery and characterization of the exoplanets orbiting them, because it induces quasi-periodic radial velocity (RV) variations.
Aims. We aim to characterize the magnetic field and stellar activity of the early, moderately active M dwarf Gl 205 in the optical and near-infrared (NIR) domains.
Methods. We obtained high-precision quasi-simultaneous spectra in the optical and NIR with the SOPHIE spectrograph and SPIRou spectropolarimeter between 2019 and 2022. We computed the RVs from both instruments and the SPIRou Stokes V profiles. We used Zeeman–Doppler imaging (ZDI) to map the large-scale magnetic field over the time span of the observations. We studied the temporal behavior of optical and NIR RVs and activity indicators with the Lomb-Scargle periodogram and a quasi-periodic Gaussian process regression (GPR). In the NIR, we studied the equivalent width of Al I, Ti I, K I, Fe I, and He I. We modeled the activity-induced RV jitter using a multi-dimensional GPR with activity indicators as ancillary time series.
Results. The optical and NIR RVs show similar scatter but NIR shows a more complex temporal evolution. We observe an evolution of the magnetic field topology from a poloidal dipolar field in 2019 to a dominantly toroidal field in 2022. We measured a stellar rotation period of Prot = 34.4 ± 0.5 days in the longitudinal magnetic field. Using ZDI, we measure the amount of latitudinal differential rotation (DR) shearing the stellar surface, yielding rotation periods of Peq = 32.0 ± 1.8 days at the stellar equator and Ppol = 45.5 ± 0.3 days at the poles. We observed inconsistencies in the periodicities of the activity indicators that could be explained by these DR values. The multi-dimensional GP modeling yields an RMS of the RV residuals down to the noise level of 3 m s−1 for both instruments while using Hα and the BIS in the optical and the full width at half maximum (FWHM) in the NIR as ancillary time series.
Conclusions. The RV variations observed in Gl 205 are due to stellar activity, with a complex evolution and different expressions in the optical and NIR revealed thanks to an extensive follow-up. Spectropolarimetry remains the best technique to constrain the stellar rotation period over standard activity indicators, particularly for moderately active M dwarfs.
Key words: techniques: radial velocities / techniques: polarimetric / stars: activity / stars: low-mass / planets and satellites: detection
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
M dwarfs are the most abundant stars in the Milky Way (Henry et al. 2006; Reylé et al. 2021) and have become key targets for exoplanetary surveys (e.g., Morley et al. 2017). Their low mass favors the detection of the planets orbiting them as the Doppler variations are larger than those seen for Sun-like stars for a given planetary mass and equilibrium temperature. Dedicated surveys to discover and characterize exoplanets around M dwarfs are currently being carried out using transit photometry (e.g., MEarth: Nutzman & Charbonneau 2008; TRAPPIST: Gillon et al. 2011; SPECULOOS: Delrez et al. 2018; Tierras: Garcia-Mejia et al. 2020) and Doppler spectroscopy (e.g., HPF: Mahadevan et al. 2012; HARPS: Bonfils et al. 2013; HARPS-N: Covino et al. 2013; IRD: Kotani et al. 2014; CARMENES: Quirrenbach et al. 2018; MAROON-X: Seifahrt et al. 2018; SOPHIE: Hobson et al. 2018; SPIRou: Donati et al. 2020).
Transit and radial velocity (RV) surveys have shown that M dwarfs can host Earth-like planets (Bonfils et al. 2013; Kopparapu 2013; Dressing & Charbonneau 2013, 2015; Sabotta et al. 2021; Pinamonti et al. 2022). However, despite efforts to detect and characterize Earth-like planets around M dwarfs, the presence of stellar activity remains a significant limiting factor in such endeavors. Cool stars, such as M dwarfs, are known to host magnetic fields that cause the phenomena known as stellar activity (Reiners 2012).
Stellar magnetic activity produces quasi-periodic RV signals with amplitudes of a few meters per second that can easily lead to a false-positive exoplanet detection (e.g., Queloz et al. 2001; Desidera et al. 2004; Huélamo et al. 2008; Carolo et al. 2014; Bortle et al. 2021). Features over the stellar surface, particularly dark spots and bright plages, can survive and evolve on timescales of a few stellar rotation cycles and can therefore modulate the RVs at the period of the stellar rotation (Boisse et al. 2011; Scandariato et al. 2017).
Several techniques have been developed during the last decade to mitigate the effects of stellar activity in order to improve the detection of exoplanets around active stars. When the stellar rotation period is known, one can model the RV variations induced by spots by fitting sinusoidal signals and their harmonics (Boisse et al. 2011) or by simulations of the active regions (Dumusque et al. 2014a). Another approach is to use activity indicators built from spectral information. These can be proxies of the shape of the cross-correlation function (CCF), for example the full width at half maximum (FWHM) and the bisector inverse slope (BIS; Queloz et al. 2001; Boisse et al. 2011), or of the chromospheric emission in spectral lines sensitive to activity, such as the Ca II H&K and Hα (Boisse et al. 2009). A third approach, among others, is to model the stellar surface structures generating RV variations (e.g., Hébrard et al. 2016; Klein et al. 2021, 2022).
The activity-induced behavior of the spectral lines in M dwarf spectra has been studied only for a handful of lines, such as Hα, Ca II H&K, Ca II IRT, Na I D, and He I, with the Hα and CaII H&K lines the most extensively explored (e.g., Gomes da Silva et al. 2011; Newton et al. 2017; Fuhrmeister et al. 2019; Lafarga et al. 2021). The majority of the well-known activity tracers are located at optical wavelengths. Recently, some near-infrared (NIR) lines were studied, for example the He I triplet (Schöfer et al. 2019; Fuhrmeister et al. 2019, 2020) and the K I line (Fuhrmeister et al. 2022; Terrien et al. 2022). The He I triplet in absorption is not detected over the range of the whole M dwarf spectral type and disappears for stars later than M5. When in emission, it could be related to flaring events (Fuhrmeister et al. 2019). Moreover, Fuhrmeister et al. (2020) found that the variability in the He I triplet may be correlated with the Hα variability only for active M dwarfs. In the particular case of the active M dwarf AU Mic, the He I flux correlated well with the RVs (Klein et al. 2021). Regarding the K I line emission, it has been found that it is rarely correlated or anti-correlated with Hα (Fuhrmeister et al. 2022). Moreover, Terrien et al. (2022) found clear signals of Zeeman broadening in this line that are modulated by the stellar rotation in G1 699 and Teegarden’s star data.
More recently, the use of data-driven techniques, namely Gaussian processes regression (GPR; e.g., Haywood et al. 2014; Rajpaul et al. 2015; Jones et al. 2017; Gilbertson et al. 2020; Klein et al. 2021; Barragán et al. 2022a; Delisle et al. 2022) or principal component analysis (PCA; e.g., Davis et al. 2017; Cretignier et al. 2022), has shown good results in modeling the contribution of stellar activity in RVs. Nowadays, the use of GPs has become the standard procedure for modeling and filtering stellar activity in RV and transits exoplanet searches, because the GPR can easily fit the quasi-periodic activity signal. This technique is particularly successful when the information from activity indicators is used when fitting the GPs on the RV time series along with the Keplerian signal (Rajpaul et al. 2015; Barragán et al. 2019a; Suárez Mascareño et al. 2020; Faria et al. 2022; Zicher et al. 2022).
Spectropolarimetry data have been widely used to measure and constrain the properties of the large-scale magnetic field of M dwarfs (Donati et al. 2008; Morin et al. 2008, 2010). In particular, it has been shown that the longitudinal magnetic field Bℓ is a reliable magnetic activity tracer for M dwarfs and therefore can be used to determine the stellar rotation period (e.g., Morin et al. 2008, 2010; Folsom et al. 2016; Hébrard et al. 2016; Martioli et al. 2022).
Another way to mitigate stellar activity is to observe in NIR wavelengths, because for M dwarfs, the spot-induced RV jitter decreases as a function of wavelength (Martín et al. 2006; Desort et al. 2007; Reiners et al. 2010; Mahmud et al. 2011). The flux contrast between the dark spots and the stellar surface is smaller at NIR wavelengths than in the optical, generating less activity-induced RV jitter. However, this effect strongly depends on the spectral type and the spot configuration on the stellar surface (Reiners et al. 2010; Andersen & Korhonen 2015). On the contrary, the RV jitter due to the Zeeman effect increases at longer wavelengths as the induced variation is proportional to the wavelength and the magnetic field strength (Hébrard et al. 2014). In cases of low-temperature contrast, the expected gain of the NIR is hampered by the increasing Zeeman effect (Reiners et al. 2013; Klein & Donati 2020). Simultaneous observations at the optical and NIR can help to disentangle the activity contribution from the two wavelength domains (Reiners et al. 2013; Robertson et al. 2020). Moreover, multiwavelength observations have been crucial to reject the planetary nature of RV signals (e.g., TW Hydrae: Huélamo et al. 2008; AD Leo: Carleo et al. 2020; Carmona et al. 2023)
Gl 205 is an early (M1.5), relatively nearby (5.7 pc), slow-rotating M1.5 dwarf with moderate levels of activity. It has a mass of 0.55 ± 0.03 M⊙ and a radius of 0.56 ± 0.03 R⊙ (Schweitzer et al. 2019). More stellar parameters are listed in Table 1. Previously, Gl 205 was monitored with HARPS (Bonfils et al. 2013), and with HARPS-Pol and NARVAL (Hébrard et al. 2016). Using the Hα and Ca II H&K indices, Bonfils et al. (2013) found the stellar rotational period to be close to 33 days, and using spectropolarimetric data, Hébrard et al. (2016) determined a rotation period of Prot = 33.63 ± 0.37 days. Photometry data in the V band showed a periodic signal of 33 d and a possible long-trend magnetic cycle of ~1500 days (Kiraga & Stepien 2007). The discrepancies between the periodicities of several activity indicators could be explained by differential rotation shearing the stellar surface and this may induce a difference of ~ 10 days in the rotation period between the equator and the pole (Hébrard et al. 2016).
In this work, we analyze the magnetic field and stellar activity of the early-M dwarf Gl 205, which was intensively monitored over a two-year period with the SOPHIE optical spectrograph and with the SPIRou NIR spectropolarimeter. This paper is structured as follows. In Sect. 2, we describe the observations and the reduction of the SOPHIE and SPIRou data. Section 3 is dedicated to the stellar characterization of Gl 205 and Sect. 4 to the analysis of TESS photometry. We describe the magnetic field properties using the SPIRou spectropolarimetric data in Sect. 5. In Sect. 6 we compare the optical and NIR RVs and in Sect. 7 we describe and analyze the activity indicators. We filter the RV variations due to activity using a multi-dimensional GP framework in Sect. 8. In Sect. 9 we discuss our RV detection limit of Keplerian signals. In Sect. 10 we discuss our results and present the principal conclusions of this work.
2 Observations and data reduction
2.1 SOPHIE
SOPHIE is a high-resolution fiber-fed, cross-dispersed échelle spectrograph mounted on the 1.93m telescope at the Observatoire de Haute-Provence (OHP; Perruchot et al. 2008; Bouchy et al. 2013). It covers a wavelength domain from 3870 to 6940 Å across 39 spectral orders.
Observations of Gl 205 were carried out between November 2019 and January 2022 as a part of the Subprogram 3 (SP3) of the SOPHIE exoplanet consortium, which is dedicated to hunting for exoplanets around M dwarfs. So far, the main results of this program include the detection of the exoplanets Gl 96b (Hobson et al. 2018), Gl 378b (Hobson et al. 2019), and Gl 411b (Díaz et al. 2019), and the independent confirmation of Gl 617Ab (Hobson et al. 2018).
The observations were gathered using the high-resolution (HR) mode, in which the spectrograph reaches a resolving power of λ/Δλ ~ 75 000. In order to measure the instrumental drift, simultaneous calibrations with a Fabry-Pérot (FP) étalon were performed. In total, we gathered 74 spectra of the star, with a median exposure time of 930 s and a median signal-to-noise ratio (S/N) per pixel at 550 nm of 95. After removing the observations with airmass >1.6, S/N < 80, or those affected by moonlight pollution, a total of 62 observations remained.
We used the SOPHIE Data Reduction Software (DRS, Bouchy et al. 2009a) to reduce and extract the spectra. The SOPHIE observations are corrected for the charge transfer inefficiency (CTI) effect of the CCD following Bouchy et al. (2009a) and Hobson et al. (2018). The DRS automatically computes the RVs using the CCF technique, which is obtained by cross-correlation of the spectra with an empirical M2V mask. The DRS also uses the CCF to deliver stellar activity indicators, such as the depth of the CCF defined as CCF contrast, CCF FWHM, and BIS.
However, in the case of M dwarf spectra, the CCF method is not an optimal approach because of the large number of absorption lines. To use most of the Doppler information available, we used a template-matching algorithm to obtain high-precision RVs (NAIRA, Astudillo-Defru et al. 2015, 2017). First, all the available spectra are normalized by the blaze functions and scaled to unity by their median. Second, the spectra are shifted using the RVs computed by the DRS. Third, these spectra are co-added to build a high-S/N stellar template. Finally, the maximum-likelihood RV is the minimum of the Chi-square profile obtained by shifting the stellar template over an array of RVs.
A list of standard stars was used to correct the long-term variations of the RV zero-point in SOPHIE, an effect described by Courcol et al. (2015). To do so, we systematically monitored a group of G-type stars: HD 185144, HD 9407, HD 89269A, and a group of M dwarfs: Gl 514, Gl 15A, and Gl 686 (Hobson et al. 2018) on each night when this was possible.
The final RVs from NAIRA used in this work with their error bars are listed in the Table A.1, along with the activity indicators: CCF FWHM, CCF contrast, BIS, the S index, and Hα line (see Sect. 7). Figure 1 shows the SOPHIE RV time series whose average error bars are 1.9 m s−1 and the scatter is 4.8 m s−1.
 |
Fig. 1 SOPHIE and SPIRou data of Gl 205. Left: RV time series of Gl 205 from SOPHIE in blue and SPIRou in red with an offset equal to the mean RV of each instrument, RVSOPHIE = 8727.8 m s−1 and RVSPIRou = 9345.5 m s−1. The scatter in the time series is 4.7 m s−1 in the SPIRou data set and 4.8 m s−1 in SOPHIE. The labels above the time series depict the four subsets of observations described in Sect. 6. Right: GLS periodogram of the full RV time series, combining SOPHIE and SPIRou observations. The highest peak is marked with an arrow at 34.3 days. |
Stellar parameters of Gl 205.
2.2 SPIRou
The Spectro-Polarimetre InfraRouge (SPIRou, Donati et al. 2020) is a high-resolution NIR spectropolarimeter and velocimeter mounted at the Canada-France-Hawaii Telescope (CFHT) in Hawaii. With a nominal spectral range from 9800 to 23 500 Å, it covers the Y, J, H, and K bands of the infrared spectrum at a spectral resolving power of λ/Δλ ~ 70 000. The observations of Gl 205 are part of the Planet Search program (WP1) of the SPIRou Legacy Survey (SLS, Donati et al. 2020), whose main goal is to perform a systematic RV monitoring of nearby M dwarfs.
SPIRou operates as a spectropolarimeter as well as a spectrograph. A spectropolarimetric sequence consists of four subexpo-sures, each one with a different rotation angle of the half-wave Fresnel rhombs in the polarimeter. We used the spectropolari-metric mode in order to obtain a set of Stokes I (unpolarized) and Stokes V (circularly polarized) profiles spectra per spectropolari-metric sequence of four subexposures (see Sect. 5).
The star was observed from September 2019 to January 2022, collecting a total of 156 sequences of four subexposures. The median exposure time of the observations is 61 s per rhomb position (244 s for a complete sequence) and the median S/N per pixel at 1670 nm is 290. We removed 11 sequences from the analysis, each with S/N < 150 or airmass >1.7.
The data were reduced using the SPIRou data-reduction software APERO1 v0.7.194 (Cook et al. 2022). APERO performs an automatic reduction of the 4096×4096 pixels raw images, including correction for detector effects, and identification and removal of bad pixels and cosmic rays. The data are calibrated by performing flat and blaze corrections, and are then optimally extracted (Horne 1986) from both science channels (fibers A and B that carry orthogonal polarimetric states of the incoming light) and from the calibration channel (fiber C).
The pixel-to-wavelength calibration is done using an UNe hollow cathode lamp and a Fabry-Pérot etalon, following Hobson et al. (2021), in order to obtain the wavelength at the observatory rest frame. APERO then utilizes the barycorrpy2 (Kanodia & Wright 2018) Python code to compute the Barycentric Earth RV (BERV) and barycentric Julian date (BJD) of each exposure. APERO performs a telluric and night emission correction in two steps. The first step is to obtain an atmospheric absorption model built with TAPAS (Transmissions of the AtmosPhere for AStronomical data; Bertaux et al. 2014), which is applied to pre-clean the science frames. This model only leaves percentage-level residuals in deep (>50%) lines of H2O and dry absorption molecules (e.g., CH4, O2, CO2, N2O, and O3). This procedure of building a TAPAS model is also done for a set of rapid rotating hot stars observed under different atmospheric conditions in order to build a library of telluric residual models. This grid of telluric residual models has three degrees of freedom (optical depths of H2O and dry components, and a constant). The second step is to subtract this telluric residual model from the pre-cleaned data to obtain telluric-corrected spectra.
In a standard procedure, APERO automatically computes the RVs by cross-correlation of the telluric-corrected spectra with a given binary mask of stellar absorption lines. However, in this work, we made use of the RVs computed by the line-by-line (LBL) method based on the Bouchy et al. (2001) framework and optimized for SPIRou data. The LBL method is fully described by Artigau et al. (2022). This algorithm exploits the RV content per line on the spectra to obtain one single RV measurement. Usually, an M dwarf observed by SPIRou will have about 16 000 individual spectral lines. A finite-mixture model approach deals with the high-sigma outliers in the RVs of the lines that come from cosmic rays or errors in the correction for tellurics. After outlier removal, the final RV is the mean of a Gaussian distribution containing the individual RVs of all the lines, and its uncertainty is derived following Bouchy et al. (2001). This method is also applied to the simultaneous calibration fiber to correct for the instrumental drift. The LBL RVs are corrected for the instrumental drift and for the long-term zero point using a GPR with data of the most observed stars in the SPIRou Legacy Survey. The details of this procedure will be described in Vandal et al. (in prep). The log of the observations and the RV measurements from the LBL method are listed in Table A.2. Figure1 shows the SPIRou RV time series whose average error bar is 1.9 m s−1 and scatter is 4.4 m s−1.
 |
Fig. 2 TESS light curves of Gl 205. Top: sector 6 data. Middle: zoom onto the region of the two flares identified in Sector 6 using the stella package. The red line depicts the best-fit flare model. Bottom: sector 32 data. |
2.3 Transiting Exoplanet Survey Satellite
Currently, the Transiting Exoplanet Survey Satellite (TESS; Ricker 2014) is in its extended mission, after successfully completing an all-sky survey of bright stars during its primary mission. TESS observed Gl 205 with two-minute cadence during Sector 6, between December 12, 2018, and January 6, 2019, and again in Sector 32, from November 19 to December 16, 2020. We obtained the Presearch Data Conditioning (PDC) flux time series processed by the TESS Science Processing Operations Center (SPOC) from the Mikulski Archive for Space Telescopes (MAST)3. The light curves are shown in Fig. 2. We used the quality flags given by the pipeline to remove bad regions of the light curves, and therefore only kept data points with a quality flag equal to zero.
3 Stellar characterization
We use the high-resolution spectra from SOPHIE and SPIRou independently to derive the atmospheric stellar parameters of Gl 205. For the SOPHIE optical part, we made use of the ODUSSEAS (Antoniadis-Karnavas et al. 2020) code to compute the effective temperature, Teff, and the metallicity, [Fe/H]. For the SPIRou NIR spectra, we follow Cristofari et al. (2022b) to derive Teff, surface gravity (log g), overall metallicity ([M/H]), and alpha-enhancement ([α/H]). The Teff measured from the optical and NIR spectra are in good agreement. The values of stellar parameters derived for Gl 205 are listed in Table 1. In this section, we describe both techniques in detail.
3.1 SOPHIE spectra
A detailed description of the machine-learning tool ODUSSEAS can be found in Antoniadis-Karnavas et al. (2020). The method is based on measuring the pseudo equivalent widths (pEWs) of absorption lines and blended lines in the range between 5300 Å and 6900 Å. The line list consists of 4104 absorption features, the same as that used by Neves et al. (2014).
ODUSSEAS receives 1D spectra and their resolutions as input. The tool contains a supervised machine-learning algorithm based on the scikit-learn Python package (Pedregosa et al. 2011) in order to determine the Teff and [Fe/H] of M dwarf stars.
Applied to new spectra, ODUSSEAS measures the pEWs of their lines and compares them to the models generated from the reference HARPS spectra sample, which are convolved to the respective resolution of the new spectra to be analyzed. The reference data set is built with spectra taken from the HARPS M dwarf sample. In the case of the SOPHIE spectrum of the star Gl 205, the HARPS reference spectra are convolved from their original resolution of 115 000 to the SOPHIE resolution of 75 000.
For the analysis of Gl 205, the new reference data set of the upgraded ODUSSEAS version has been applied and includes spectra from 47 M dwarfs. The references for training and testing the models are the pEWs of the 47 HARPS spectra, used together with interferometry-based Teff (Rabus et al. 2019; Khata et al. 2021) and [Fe/H] derived by applying the method by Neves et al. (2012) using updated values of parallaxes from Gaia DR3.
The resulting stellar parameters of the star are calculated from the mean values of 100 determinations obtained by randomly shuffling and splitting the training (80% of the reference sample, i.e., 37 stars) and testing groups (remaining 20%, i.e., 10 stars) each time. We report parameter uncertainties derived by quadratically adding the dispersion of the resulting stellar parameters and the mean absolute errors of the machine-learning models at this resolution. We obtained an Teff = 3878 ± 81 K and [Fe/H] = 0.21 ± 0.06 dex.
3.2 SPIRou spectra
We estimate the Teff, log g, [M/H], and [α/H] from a highresolution template spectrum built from the over 500 spectra from subexposures acquired with SPIRou. The process relies on the direct comparison of the template spectrum with a grid of synthetic spectra computed from MARCS model atmospheres (Cristofari et al. 2022b,a). The comparison is performed on carefully selected spectral windows containing about 20 atomic lines and 40 molecular lines.
Prior to the comparison, synthetic spectra are broadened to account for instrumental effects, and the local continuum of the models is adjusted on windows built around the selected lines. Comparing the template spectrum to a grid of synthetic spectra with various Teff, log g, [M/H], and [α/H] results in the computation of a 3D χ2 grid on which we fit a 3D second-degree polynomial to retrieve a minimum. With this model, we derive Teff = 3770 ± 30 K, log g = 4.70 ± 0.1 dex, [M/H] = 0.43 ± 0.1 dex, and [α/Fe] = −0.08 ± 0.04.
3.3 Age and galactic population
We computed the age of Gl 205 with the stardate4 (Angus et al. 2019) Python package, which combines isochrones fitting with gyrochronology. The inputs of this code are the stellar parameters derived in Sects. 3.2 and 3.1: Teff, log g, [Fe/H], and the parallax from Table 1. As we obtained two estimations of Teff, we tested both values to see if we obtain similar results. Using the Teff from SOPHIE spectra we measure a stellar age of 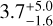 Gyr. On the other hand, using the SPIRou Teff we estimate the age at
Gyr. On the other hand, using the SPIRou Teff we estimate the age at 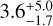 Gyr. Both estimations are in complete agreement.
Gyr. Both estimations are in complete agreement.
The rotation period of Gl 205 is higher than that of stars of similar mass in the 4 Gyr-old open cluster M67 sequence (Dungee et al. 2022). Calibrating the gyrochronology relationship with this sequence results in an age determination of 5.2 ± 0.7 (Fouqué et al. 2023), which is within the error bars of our independent estimate.
In order to identify the galactic population (thin disk, thick disk, or halo) to which Gl 205 belongs, we followed Reddy et al. (2006) to obtain the probabilities of belonging to the three populations based on the galactic velocities of the star. For Gl 205, the galactic velocities are (U, V, W) = (49, 13, 31) km s−1, computed using the position, proper motion, and parallax from Gaia DR3 (Gaia Collaboration 2020). We find a 99% probability that Gl 205 belongs to the thin disk of the Milky Way.
The ages of the stars in the thin disk span a wide range. However, it has been stated that most of them have ages of less than 5 Gyr, reaching up to 14 Gyr (Reddy et al. 2006; Haywood 2008; Holmberg et al. 2009). Our estimation of the age of Gl 205 is in agreement with these results. Regarding the metallicity, Allende Prieto et al. (2004) found that the mean metallicity of the stars in the thin disk is 〈[Fe/H]〉 = −0.09 ± 0.19. We estimated a high metallicity for Gl 205 of 0.21 ± 0.06, which is located within 2σ of the mean value.
3.4 Comparison with the literature
We compared our results with previous studies of Gl 205. Schweitzer et al. (2019) derived the photospheric parameters Teff, log g, and [Fe/H] from CARMENES VIS spectra and the stellar radius using the Stefan-Boltzmann’s law. Using the log g and the stellar radius, the authors derived the stellar mass; their results of stellar mass and radius are listed in Table 1. These authors found Teff = 3891 ± 51 K, log g = 4.64 ± 0.07 dex, and [Fe/H] = 0.23 ± 0.16 dex. Our results of [Fe/H] and Teff computed from SOPHIE spectra and the log g from SPIRou spectra are in particularly good agreement within 1σ with the values of CARMENES. The Teff derived using SPIRou spectra is within 3σ of the CARMENES result.
Neves et al. (2014) obtained [Fe/H] and Teff for Gl 205 from HARPS spectra with values of [Fe/H] = 0.19 ± 0.09 and Teff = 3670 ± 110 K. Our estimation of the metallicity from SOPHIE spectra is in good agreement with the one from HARPS and our Teff value lies within 3σ. However, the HARPS metallicity is in better agreement with our SPIRou Teff.
Using spectra of Gl 205 from the APOGEE survey, Souto et al. (2022) determined Teff = 3820 ± 110 K, log g = 4.67 ± 0.2 dex, and [Fe/H] = 0.29 ± 0.10 dex. Their result for Teff is in particularly good agreement with our value derived from SPIRou spectra. Maldonado et al. (2015) used HARPS and HARPS-N spectra to derive stellar parameters of early-M dwarfs, finding a metallicity of Gl 205 of [Fe/H] = −0.03 ± 0.19 dex. Our estimation of [Fe/H] is within 2σ of their value.
4 Light-curve analysis
In this section, we describe the analysis of the TESS light curves of Gl 205 to identify stellar flares and search for exoplanet transits. As each TESS sector has a duration of ~27 days, the rotation period of Gl 205 (see Table 1) is not covered in one single sector and therefore determination of the rotation period from the TESS data is not possible. Moreover, there is a time gap of 684 d between the sector 6 and sector 32.
4.1 Flares identification
For the identification of stellar flares, we used the Python package stella5 (Feinstein et al. 2020a). This open-source code uses convolutional neural networks (CNN) to identify flare events in the two-minute cadence TESS light curves and delivers the probability of such an event for a given time. The reported flare probability is the average prediction of the ten models available in stella. After identification, stella uses an empirical flare model (Walkowicz et al. 2011; Davenport et al. 2014) to obtain the best-fit parameters through a χ2 fit. The flare model includes a sharp Gaussian rise and an exponential decay (Feinstein et al. 2020b). Candidate events with probability higher than 50% of being a flare were considered for modeling. In the modeling process, the part of the light curves that includes the flare is detrended to account for stellar variability.
We applied the algorithm in the available TESS sectors of Gl 205 using the available trained CNNs from Feinstein et al. (2020b). We identified two flare events during sector 6 and none during sector 32 (see Fig. 2). Table 2 reports the time of the flare’s peak, its amplitude, the equivalent duration (ED) – which is measured as the area of the flare event –, the rise and fall parameters from the flare model, and the probability.
The second flare identified seems more prominent than the first, reaching a higher flux amplitude. However, both events have the same equivalent duration of about 10 hours, meaning that the energies of these events are similar but cover different timescales; while the first flare lasted 2.5 h, the second flare lasted 0.5 h.
Günther et al. (2020) performed a study of stellar flares in the first data release of TESS, finding that mid to late M dwarfs show the highest fraction of flaring stars. However, the authors warned that this may be influenced by the TESS target selection. Only 10% of the early M dwarfs in their sample are flaring stars. Moreover, fast rotators (P < 5 days) may have higher flare rates than slow rotators. Our findings in Gl 205 agree with the results of Günther et al. (2020), as we observed a low rate of flaring for this star, which is expected for early and slow-rotating M dwarfs.
Parameters of the flare events identified in the TESS light curves of Gl 205.
 |
Fig. 3 Detrended TESS light curves of Gl 205. The red line depicts the applied detrending model to remove the stellar variability using the wōtan package. Below each panel are the residuals of the model with a standard deviation of 210 ppm. |
4.2 Planet transit search
The TESS data-validation report of Gl 205 identifies a planet candidate with an orbital period of 22.2 days. However, the transit-event candidate proposed by the automatic pipeline is clearly affected by the flare of 2458471.056 BJD. We conduct our own analysis in order to identify possible transits in the light curves.
First, we removed outliers using a 3σ clipping procedure and excluded the data affected by the flares. As the light curves are affected by stellar variability, we used the Python package wōtan6 (Hippke et al. 2019) to remove the trends. This code includes several methods to perform light-curve detrending. We applied a method based on a time-windowed sliding filter with an iterative robust location estimator following the results of Hippke et al. (2019). For the detrending model, we excluded the edges of the light curves, because these zones are usually affected by strong systematic errors. Figure 3 shows the detrending model of the light curves and the residuals, which have a standard deviation of 210 ppm.
After detrending the light curves, we used the transit least squares7 algorithm (Hippke & Heller 2019) to search for periodic transit events. The algorithm searches for transit features in an automatically built grid of orbital periods and transit durations. The grid of periods depends on the time span of the data and the transit durations come from an empirical relation detailed in Hippke & Heller (2019).
We first applied the algorithm in the whole data set, including sector 6 and sector 32. The grid of periods was automatically set between 0.6 and 365 days. The maximum signal-detection efficiency (SDE) is found at an orbital period of 11.86 d but it has low significance (SDE = 8) and the periodogram is highly degenerate. The S/N of this stacked transit signal is 2.5 with only three events in the data set: one in sector 6 and two in sector 32. To confirm or rule-out this period we applied the algorithm in sector 32 independently, because two transits were identified in this sector. We find no transits in this sector and therefore discarded transit events in the two available TESS sectors of Gl 205.
 |
Fig. 4 Time series of the SPIRou longitudinal magnetic field Bℓ. The GP model using a quasi-periodic kernel is shown in red. The residuals of this model have a scatter of 0.97 G and are shown in the bottom panel. At the top of the figure, we mark the four subsets of data used in Sect. 5.2. |
5 Magnetic field analysis
The SPIRou spectropolarimetric products, in particular the Stokes I and V profiles, were obtained using the Libre-ESpRIT pipeline described in Donati et al. (1997). We applied least-squares deconvolution (LSD; Donati et al. 1997) to compute the average Stokes I (unpolarized) and Stokes V (circularly polarized) line profiles for all our SPIRou observations. We used a mask of atomic lines spanning the SPIRou spectral domain and computed from a ATLAS9 local thermodynamical equilibrium (LTE) atmosphere model (Kurucz 1993), assuming an effective temperature of 3750 K and a surface gravity of log g = 5.0. We only selected lines with a relative absorption of greater than 3% (from the unpolarized continuum) to avoid an over-representation of weak lines in our final line list. Lines affected by strong tellurics, that is, of relative absorption deeper than 20% within ± 30 km s−1 from the line center, are masked out in the LSD process. The extracted Stokes I and V profiles feature a mean central wavelength of 1700 nm, an effective Landé factor of 1.25, and a relative depth of 12% with respect to the continuum.
5.1 Stellar rotation period
The disk-integrated longitudinal magnetic field Bℓ was computed using the Stokes V and Stokes I profiles following the method of Donati et al. (1997):
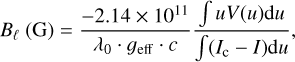 (1)
(1)
where I and V are the unpolarized and circularly polarized LSD profiles, Ic is the continuum level, u is the velocity in km s−1, λ0 is the mean wavelength, geff is the effective Landé factor, and c the speed of light in km s−1.
The Bℓ time series of Gl 205 is listed in Table A.2. The mean value of the Bℓ time series is 1.6 G, the standard deviation is 2.9 G, and the mean of the error bars is 1.0 G. We expect that the longitudinal magnetic field is modulated by the rotational period of the star, because the large-scale magnetic topology at the surface of the star is expected to evolve on a longer timescale. To measure the stellar rotation period, we first computed the generalized Lomb-Scargle (GLS) periodogram (Lomb 1976; Scargle 1982; Zechmeister & Kürster 2009) implemented in the astropy (Astropy Collaboration 2013, 2018) Python package. The GLS periodogram of the Bℓ time series shows a strong peak of periodicity at 32.7 days with a false-alarm probability (FAP) of below 1% (see Fig. 10).
However, it has been demonstrated that stellar activity shows a quasi-periodic behavior (e.g., Haywood et al. 2014; Angus et al. 2018) rather than a single sinusoidal signal, as is the case of the periodicity seen in a GLS periodogram. Moreover, the magnetic field of Gl 205 is known to evolve on a timescale of a few rotation cycles (Hébrard et al. 2016). We therefore take advantage of the flexibility of the GPs to constrain the rotational period of the star using the Bℓ time series. For this purpose, it is important to highlight that the three well-defined observational seasons of the Bℓ (see Fig. 4) are long enough to cover a few stellar rotation cycles.
The kernel of the GPR is set to be the quasi-periodic as defined in Roberts et al. (2012):
![${k_{i,j}} = {A^2}\exp \left[ { - {{{{\left( {{x_i} - {x_j}} \right)}^2}} \over {2{l^2}}} - {1 \over {{\beta ^2}}}{{\sin }^2}\left( {{{\pi \left( {{x_i} - {x_j}} \right)} \over {{P_{{\rm{rot}}}}}}} \right)} \right] + {\sigma ^2}{\delta _{i,j}},$](/articles/aa/full_html/2023/05/aa45131-22/aa45131-22-eq5.png) (2)
(2)
where xi and xj are two observation dates, A is the amplitude of the covariance, l is the decay time, β is the smoothing factor, Prot is the stellar rotation period, and σ is the uncorrelated white noise also known as the jitter term.
The posterior distributions of the hyperparameters were sampled from a Markov-chain Monte Carlo (MCMC) routine using the package emcee (Foreman-Mackey et al. 2013). We set up 50 walkers and 5000 steps after a burn-in phase of 500 steps. The priors used and the final posterior distributions are listed in Table 3 and Fig. B.1 shows the corner plot of the posterior distributions. The best-fitting model of the GPR is illustrated in Fig. 4 and has a reduced χ2 of 0.92. As a sanity check, we plot the GLS periodogram of the GP model residuals in Fig. 5, where we see that there is no periodic signal left over.
We measured a stellar rotation period of Prot = 34.4 ± 0.5 days and a decay time of  days, which implies that the active features could evolve relatively quickly, that is, on a timescale of about two rotation cycles, as the GP decay time has been shown to be a good indicator of the average timescale of evolution of the active features (Nicholson & Aigrain 2022). With this new estimation of the rotation period, we can derive the rotational velocity υ sin i. Assuming a stellar radius of 0.556 ± 0.033 M⊙ and inclination of 60° ± 10° (see Table 1), we obtained a υ sin i of 0.7 ± 0.1 km s−1. (Hébrard et al. 2016) obtained a υ sin i of 1.0 ± 0.5 km s−1 from their ZDI analysis, which is in agreement with our results.
days, which implies that the active features could evolve relatively quickly, that is, on a timescale of about two rotation cycles, as the GP decay time has been shown to be a good indicator of the average timescale of evolution of the active features (Nicholson & Aigrain 2022). With this new estimation of the rotation period, we can derive the rotational velocity υ sin i. Assuming a stellar radius of 0.556 ± 0.033 M⊙ and inclination of 60° ± 10° (see Table 1), we obtained a υ sin i of 0.7 ± 0.1 km s−1. (Hébrard et al. 2016) obtained a υ sin i of 1.0 ± 0.5 km s−1 from their ZDI analysis, which is in agreement with our results.
Priors and best-fit hyperparameters of the GP model using a quasi-periodic kernel in the SPIRou longitudinal magnetic field data Bℓ.
 |
Fig. 5 GLS periodogram of the residuals of the GPR applied in the longitudinal magnetic field Bℓ. |
5.2 Zeeman-Doppler imaging
We use Zeeman–Doppler imaging (Semel 1989; Brown et al. 1991; Donati & Brown 1997) to invert the observed Stokes V LSD profiles into distributions of the large-scale magnetic field at the surface of Gl 205. As described in Donati et al. (2006), ZDI decomposes the large-scale field vector into its poloidal and toroidal components, both expressed as weighted sums of spherical harmonics. For a given field distribution, local Stokes V profiles are computed for each resolution element of the visible hemisphere of the star using analytical expressions from the Unno-Rachkovski’s solution to the radiative transfer equation in a plane-parallel Milne-Eddington atmosphere (Unno 1956). These profiles are then (i) shifted to the local projected rotational velocity, (ii) weighted according to stellar inclination and the limb-darkening law (assumed linear with a coefficient of 0.3, Claret & Bloemen 2011), and then (iii) combined into global profiles at the times of the observations. ZDI uses a conjugate gradient algorithm to iteratively compare the synthetic profiles to the observed Stokes V LSD profiles down to a given reduced χ2. The degeneracy between multiple magnetic maps is lifted by imposing a maximum-entropy regularization condition to the fit, assuming that the map with the minimum amount of information is the most reliable (Skilling & Bryan 1984)
The intrinsic evolution of the magnetic field is not yet included in our ZDI code despite notable progress over the last few years (Yu et al. 2019; Finociety & Donati 2022). To prevent the code from focusing on the intrinsic evolution of the field rather than on its rotational modulation, we divide our observations into four subsets of data, namely S1, S2, S3, and S4, containing respectively 36, 31, 19, and 31 observations. The time windows spanned by these four data sets are indicated in Table 4 and depicted in Fig. 4. We then apply ZDI independently to each of these data sets. We note that these four seasons were defined so that the longitudinal field remains roughly periodic on timescales longer than a rotation period, ensuring that the magnetic topology does not dramatically evolve during each season and that the variation of the Stokes V profiles primarily reflects the stellar modulation rather than the intrinsic evolution of the field.
Our ZDI reconstruction includes the modeling of latitudinal differential rotation (DR) shearing the large-scale field at the surface of Gl 205 (Donati et al. 2000; Petit et al. 2002). The stellar rotation rate Ω is assumed to vary as a function of the colatitude θ such that
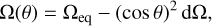 (3)
(3)
where Ωeq and dΩ stand for the rotation rate at the stellar equator and the difference in rotation rate between the equator and the pole, respectively. The best DR parameters explaining the observations are estimated using the method described in Donati et al. (2000). For a wide range of DR parameters, we apply ZDI to a fixed level of entropy. The best parameters with error bars are estimated by fitting a 2D paraboloid to the resulting χ2 distribution in the (Ωeq, dΩ) space.
The best-fitting maps of the large-scale field vector for the four subsets of data are shown in Fig. 6, and the associated magnetic properties are listed in Table 4. The best fits to the observed Stokes V LSD profiles are shown in Appendix C for the four seasons. Data sets S1 to S4 have been fitted to reduced χ2 of 1.0, 1.08, 1.1, and 1.05, starting from reduced χ2 of 2.4, 1.5, 4.1, and 1.4. As expected from the time series of longitudinal magnetic field shown in Fig. 4, we observe a significant fluctuation in the field topology throughout our observations. In Seasons S1 and S3, the field is found to be a dipole of 13–15 G (consistent with the topology found in Hébrard et al. 2016), and to be tilted at 36° and 56° to the rotation axis towards phases 0.78 and 0.84, respectively. A weaker and more complex field is found in Season S2. Though dominantly poloidal, the magnetic energy budget is much more spread into the dipolar (45%), quadripolar (20%), and octupolar (31%) than in Seasons S1 and S3 (both dipolar at more than 90%). Between Seasons S3 and S4, the field quickly evolves, that is, on a two-month timescale, from a poloidal dipole to a dominantly toroidal topology8.
The best-fitting DR parameters and associated equatorial and polar stellar rotation periods are listed in Table 4, whereas the 2D χ2 maps associated to the fit in the (Ωeq, dΩ) space are shown in Fig. 7. Consistent latitudinal DRs of 0.05–0.08 rad d−1 are detected in Seasons S1, S3, and S4, whereas solid-body rotation cannot be firmly excluded in Season S2. These values of latitudinal DRs are of the same order of magnitude as those of other early-M dwarfs with slightly faster rotation (Donati et al. 2008).
We note that more complex magnetic topologies, such as those seen in Seasons S2 and S4, are associated with larger equatorial rotation periods than simpler dipolar fields. This could reflect the fact that the field is dominated by smaller-scale structures mostly located at mid-to-high latitudes and, thus, only partially covering the stellar equator. However, the accuracy of our DR parameters is strongly limited by the relatively low latitudinal precision of our reconstruction, which is due to the very low υ sin i of the star. As a consequence, no conclusions can be drawn as to the potential evolution of the DR throughout the observations. We report an inverse-variance-weighted average of the DR values from Season S1 to S4 of Peq = 32.0 ± 1.2 d for the rotation period at the stellar equator, and Ppol = 45.5 ± 0.3 d for the rotation period at the poles.
Main results of the spectropolarimetric analysis of each of subset of data of the Gl 205 SPIRou observations with ZDI.
 |
Fig. 6 Radial, azimuthal and meridional components of the large-scale magnetic field at the surface of Gl 205 for the four subsets of data defined in Sect. 5.2. From top to bottom, the rows show the results for Seasons S1 (September-December 2019), S2 (August-October 2020), S3 (August–September 2021), and S4 (November 2021–January 2022). Each panel is a flattened polar view of the stellar surface. The circles indicate the equator (black solid line) and the –30, 30 and 60° parallels (dashed lines) and the ticks around the star mark the spectropolarimetric observations in unit of stellar rotation phase. The color bar depicts the magnetic flux in Gauss. |
 |
Fig. 7 Distribution of reduced χ2 as a function of Ωeq and dΩ extracted from the Stokes V LSD profiles in Season S1 to S4 defined in Table 4. In each map, the 1 and 3σ contours are indicated by the black solid lines. |
6 Optical and NIR RVs
6.1 Periodogram analysis
The almost simultaneous acquisition of SOPHIE and SPIRou RVs allows us to quantify the stellar activity jitter in the optical and NIR domains. We computed the GLS periodogram to look for periodicities in the RVs. The RV time series including the SOPHIE and SPIRou data is shown in Fig. 1 along with its GLS periodogram. We identified a highly significant (FAP ≪0.1%) period at 34.3 days and a second peak, also with low FAP, at 37.9 days. There is also a third peak with low FAP at ~0.5 day, which is an alias of the periodicity at 1 day due to the daily sampling.
The SOPHIE and SPIRou data sets do not show the same periodicities. In the SOPHIE RVs, there is no significant periodicity found by the GLS periodogram, however the strongest peak occurs close to the Prot/2 harmonic at ~ 17 days (see the top-right panel of Fig. 9). The SPIRou RVs, on the contrary, show a clear peak of periodicity at 34.4 days (see the top-left panel of Fig. 10) which is the expected stellar rotation period. In terms of the scatter of the RVs, the data sets have a root mean square (RMS) of 4.7 m s−1 for SPIRou and 4.8 m s−1 for SOPHIE.
6.2 Global modeling
In order to obtain a first approximation of the magnitude of the RV jitter, we applied a GP with a quasi-periodic kernel in the SOPHIE and SPIRou RV time series, following Sect. 5.1. The MCMC procedure to obtain the posterior distribution is set up with 50 walkers and 5000 steps after a burn-in phase of 500 steps. The priors applied in the hyperparameters are listed in Table 5. As we measured the stellar rotation period from the spectropolarimetric data, we applied a more constraining prior to the GP period of the RVs.
The best-fit models of the GP regressions are shown in Fig. 8 and the final posterior distributions of the GP hyperparameters are listed in Table 5. The periods found in the SOPHIE and SPIRou RVs of 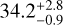 days and 39.2 ± 2.4 days, respectively, are consistent at a 3σ level with the period of the longitudinal magnetic field of 34.4 ± 0.5 d (see Sect. 5.1). The decay time found for the SOPHIE RVs is larger than for SPIRou and is consistent with more than two stellar rotations (
days and 39.2 ± 2.4 days, respectively, are consistent at a 3σ level with the period of the longitudinal magnetic field of 34.4 ± 0.5 d (see Sect. 5.1). The decay time found for the SOPHIE RVs is larger than for SPIRou and is consistent with more than two stellar rotations (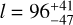 days). However, in the case of SPIRou, the decay time of
days). However, in the case of SPIRou, the decay time of 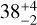 days is comparable with the rotation period of 39.2 ± 2.4 days. This effect is problematic for the quasi-periodicity of the signal. When there is a short evolution timescale, l ⩽ Prot, the periodicity of the signal is meaningless (see e.g., Rajpaul et al. 2015; Barragán et al. 2022a).
days is comparable with the rotation period of 39.2 ± 2.4 days. This effect is problematic for the quasi-periodicity of the signal. When there is a short evolution timescale, l ⩽ Prot, the periodicity of the signal is meaningless (see e.g., Rajpaul et al. 2015; Barragán et al. 2022a).
We examined the effect of applying a different prior in the decay time for the SPIRou RVs, keeping it uniform but limiting it to between 70 and 150 days to ensure at least two rotation cycles. As a result, we obtained consistent posterior distributions – within the error bars – with the values from Table 5, except for the decay time. With a different prior, we obtained a decay time of 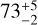 days. However, the log-likelihood of the first model (log-L = −374) is slightly higher than the model with a new prior in the decay time (log-L = −384), meaning that the first model shows a better fit to the data.
days. However, the log-likelihood of the first model (log-L = −374) is slightly higher than the model with a new prior in the decay time (log-L = −384), meaning that the first model shows a better fit to the data.
 |
Fig. 8 Time series of the SOPHIE and SPIRou RVs. Top: the best-fitting GP models using a quasi-periodic kernel in the SOPHIE and SPIRou data are shown in blue and red, respectively. The light-blue and light-red colors depict the 3σ level of the uncertainties. The residuals of this model have a scatter of 2.6 m s−1 for SOPHIE, and 2.4m s−1 for SPIRou and are shown below the time series. Middle and bottom: zoom onto the SOPHIE and SPIRou RVs divided into the seasons defined in Table 6 with their best-fitting GP models. |
6.3 Seasonal analysis
The RVs observation time span is clearly divided in three seasons (see Fig. 1), with the first epoch from 58738 BJD to 58922 BJD (September 2019 to March 2020), the second epoch from 59088 BJD to 59297 BJD (August 2020 to March 2021), and the third epoch from 59440 BJD to 59607 BJD (August 2021 to January 2022). These subsets are longer than the subsets defined in Sect. 5.2 because in order to look for periodic variability, a longer time-span is required than for the ZDI analysis. The details of the RV subsets, such as the start and ending dates as well as the number of data points included, are listed in Table 6. These RV subsets, which are depicted in Fig. 1, are defined as 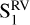 ,
,  , and
, and  in order to differentiate them from the seasons defined in Sect. 5.2.
in order to differentiate them from the seasons defined in Sect. 5.2.
Even though the seasons  and
and  overlap to some extent with S1 and S2, we cannot directly compare S3 with the RV data because only three SOPHIE observations are within this season. Therefore, we defined a fourth season of RV observations,
overlap to some extent with S1 and S2, we cannot directly compare S3 with the RV data because only three SOPHIE observations are within this season. Therefore, we defined a fourth season of RV observations, 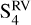 , from 59500 BJD to 59607 BJD (October 2021 to January 2022) that overlaps with S4 and allows us to measure the differences between seasons S3 and S4 of the Bℓ in the RVs data sets.
, from 59500 BJD to 59607 BJD (October 2021 to January 2022) that overlaps with S4 and allows us to measure the differences between seasons S3 and S4 of the Bℓ in the RVs data sets.
To gain insight into the variability of the RV signal, we define the amplitude A as the peak-to-valley difference and we list it alongside the RMS of the model residuals and the reduced χ2 in Table 6 for all the data sets and each RV season.
It is clearly seen in Fig. 8 that the best-fitting GP model for the SOPHIE RVs is more stable in time than that for the SPIRou RVs, and is similar to a double sinusoidal model at Prot and its first harmonic. As seen in the middle and bottom panels of Fig. 8, the signal in the SOPHIE RVs remains approximately consistent between 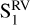 and
and  , with similar shapes and amplitudes of 10.8 ± 2.9 and 9.8 ± 3.0 m s−1, respectively. The goodness of the model is similar for the seasons
, with similar shapes and amplitudes of 10.8 ± 2.9 and 9.8 ± 3.0 m s−1, respectively. The goodness of the model is similar for the seasons  through
through  , with an RMS of between 2.3 and 2.8 m s−1. However, during
, with an RMS of between 2.3 and 2.8 m s−1. However, during 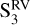 and
and 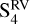 , the reduced χ2 becomes slightly poorer than for the other seasons. This may be due to the presence of outliers in the subdata set.
, the reduced χ2 becomes slightly poorer than for the other seasons. This may be due to the presence of outliers in the subdata set.
On the contrary, the SPIRou RV signal is not consistent from one season to the next (see bottom panels of Fig. 8), and exhibits a high level of variability. The amplitude of the RV signal rises slightly between 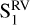 and
and  , from 13.7 ± 2.3 to 15.2 ± 2.2 m s−1, but this rise is not significant and the difference is within the error bars. As in the SOPHIE RVs, there are no important differences between the RMSs or reduced χ2 of each season, but the goodness of the model fit deteriorates for
, from 13.7 ± 2.3 to 15.2 ± 2.2 m s−1, but this rise is not significant and the difference is within the error bars. As in the SOPHIE RVs, there are no important differences between the RMSs or reduced χ2 of each season, but the goodness of the model fit deteriorates for  . As in the case of the SOPHIE RVs, this may be due to the presence of outliers; if these outliers are removed, the RMS improves to 2.4 m s−1 .
. As in the case of the SOPHIE RVs, this may be due to the presence of outliers; if these outliers are removed, the RMS improves to 2.4 m s−1 .
At this point, we cannot tell whether or not there are significant differences between 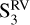 and
and  of the SOPHIE and SPIRou RVs, and we require this information in order to measure the possible impact of changes in the magnetic field topology on the RVs (see Sect. 5.2). As listed in Table 5, there is little discrepancy between these two seasons in the amplitudes, RMSs, and reduced χ2. Despite the fact that the Bℓ shows a high level of variability at these epochs, the scatter of the RVs does not increase. This may mean that the variability in the longitudinal magnetic field is not directly expressed as high RV dispersion.
of the SOPHIE and SPIRou RVs, and we require this information in order to measure the possible impact of changes in the magnetic field topology on the RVs (see Sect. 5.2). As listed in Table 5, there is little discrepancy between these two seasons in the amplitudes, RMSs, and reduced χ2. Despite the fact that the Bℓ shows a high level of variability at these epochs, the scatter of the RVs does not increase. This may mean that the variability in the longitudinal magnetic field is not directly expressed as high RV dispersion.
Priors and best-fit hyperparameters of the GP model using a quasi-periodic kernel in the SOPHIE and SPIRou RVs.
 |
Fig. 9 SOPHIE RVs and optical activity indicator. Left: time series; middle left: data folded at the Prot of 34.4 days; middle right: correlation with the RVs where the red line depicts the linear correlation between both quantities; right: GLS periodogram where the horizontal dashed black line indicates the FAP level at 1% and the vertical color lines mark the Prot at 34.4days in yellow, the first harmonic at Prot/2 in light blue, and the time range of differential rotation in light green. |
7 Activity indicators
7.1 Optical activity indicators
Using the SOPHIE data, we computed standard activity indicators that quantify distortions in the CCF profile, such as the BIS, the FWHM, and the contrast. The BIS is defined as the velocity span between the top (55% < CCF depth < 80%) and the bottom (20% < CCF depth < 40%) of the CCF. The FWHM and the contrast are direct measurements of the width and the depth of the CCF, respectively.
The time series of the BIS, FWHM, and contrast of the CCF from the SOPHIE data are shown in Fig. 9, with their corresponding GLS periodograms. No significant periodicity close to the expected stellar rotation period of Prot = 34.4 ± 0.5 days is found in their periodograms.
Within the SOPHIE spectral domain, there is the well-known Hα line (Kürster et al. 2003; Bonfils et al. 2007; Boisse et al. 2009) and the CaII H&K lines, which are measured to compute the Mount Wilson S index (Wilson 1968; Baliunas et al. 1995). The so-called S index is a measure of the emission at the core of the CaII H&K lines, located at 3922 Å and 3968 Å, and for the Hα is the flux at the core of the line at 6562 Å. To compute this index, we follow Boisse et al. (2009), who define it as the ratio between the flux in a defined range of continuum and the core of the absorption lines.
Figure 9 shows the time series of the Hα and S indices of our SOPHIE data along with their GLS periodograms. The time series of Hα shows a peak of periodicity at 33.7 d and in the case of the S index, long-term trends dominate the periodogram.
The correlation or anti-correlation between the RVs and the activity indicators usually provides information about the stellar origin of the signal (e.g., Queloz et al. 2001; Boisse et al. 2011). However, the lack of correlation can be due to phase shifts between the RVs and the activity indicators (e.g., Bonfils et al. 2007; Dumusque et al. 2014b). For example, Collier Cameron et al. (2019) measured a temporal lag of 1 and 3 days between the maxima in the RVs and the maxima of the FWHM and BIS, respectively. In the present work, we do not explore the possibility of the phase lags in our data set but we rather warn the reader about it.
The SOPHIE BIS, FWHM, and contrast are not correlated or anti-correlated with the RVS, and the S index and Hα are correlated with the RVs with Pearson’s coefficients of 0.4. We computed the p-value associated with this correlation in order to prove the significance. The p-value is defined as the probability that the observed correlation is a false positive under a true null hypothesis. In this case, the null hypothesis is that there is no correlation between the variables. The correlations between the RVs and the Hα and S indices have p-values of 8 × 10−4 and 9 × 10−4, respectively. This means that the correlations we find are statistically significant.
We applied a GPR following the same procedure as in Sect. 5.1 to study the periodicity of the signal, as we have seen how the longitudinal magnetic field and the RVs follow a quasi-periodic trend. This behavior could have an effect in the classical GLS periodogram and hide the real period of the signal. The computation of the FWHM and the contrast by the SOPHIE DRS do not provide their error bars. Therefore, we assumed equal error bars for all the data points of 0.1 % for the contrast, and 0.01 km s−1 for the FWHM.
We used the same priors as in Sect. 6, which are listed in Table 5. To obtain the posterior distribution from the MCMC we used 50 walkers and 5000 steps after a burn-in phase of 500 steps. The best-fitted GP models for the SOPHIE activity indicators are shown in Fig. E.1. The means of the posterior distributions of the GP hyperparameters are listed in Table E.1 and the corner plots of the posterior distributions are shown in Fig. E.1.
In the case of the SOPHIE activity indicators, the quasi-periodic GP fits a model with a periodicity in agreement with the expected rotation period of Prot = 34.4 ± 0.5 days. This is particularly interesting for the BIS, FWHM, and CCF contrast, because their GLS periodograms do not exhibit significant peaks of periodicity at the rotation period. The decay time of the GP model of the FWHM, BIS, and Hα are consistent with an average timescale decay of at least two rotation cycles, as also seen in the longitudinal magnetic field Bℓ.
Results of the RV analysis in the observational seasons of the SOPHIE and SPIRou.
7.2 NIR activity indicators
Within the SPIRou LBL framework, we can obtain the differential line width (dLW, Zechmeister et al. 2018) and the chromatic velocity slope. The differential line width corresponds to the second derivative of the spectral profile and can be expressed in units of FWHM. We follow the definition by Artigau et al. (2022) using this quantity as FWHMLBL. The chromatic velocity slope is defined as the RV gradient as a function of wavelength (Zechmeister et al. 2018).
The time series and the GLS periodograms of the FWHMLBL and the chromatic velocity slope are shown in Fig. 10 along with their phase-folded and correlation with RVs plots. When phase-folding FWHMLBL by the stellar rotation period of 34.4 days, it seems to be modulated in time. Moreover, FWHMLBL is slightly correlated with the RVs with a Pearson’s coefficient of 0.3 and a p-value of 4 × 10−5, which means that the found correlation is significant. The highest peak of the FWHMLBL GLS periodogram is at 34.4 days but with FAP slightly above 1%, which corresponds to the stellar rotation period. The chromatic velocity slope indicator is not correlated or anti-correlated with the RVs, but the most significant peak of periodicity in its periodogram is located at 31.3 days, which is close to the rotation period.
As for the SOPHIE activity indicators, we also computed a GP model in the SPIRou activity indicators including the FWHM, chromatic velocity slope, and pEW of the NIR spectral lines. The best-fit GP models for the FWHM and the chromatic velocity slope are shown in Fig. E.2 and the means of the posterior distribution of the hyperparameters are listed in Table E.1. The corner plots of the posterior distributions are shown in Figs. E.4 and E.5. The period measured in the FWHM and the chromatic velocity slope are in agreement – within the error bars – with the expected rotation period of 34.4 ± 0.5. Similar to the activity indicators in the optical, the measured decay time of the signal is consistent with two stellar rotation cycles. The results of the NIR spectral lines are discussed in the following subsection.
7.3 Diagnostics on NIR spectral lines
Observations in the infrared domain introduce two challenges. On the one hand, we lack well-identified and characterized spectral lines in this domain that can be used as stellar activity tracers. On the other hand, M dwarf spectra do not always show a clear flux continuum within the whole NIR wavelength range, because their spectra have a large number of absorption lines and hamper the proper measurement of equivalent widths.
We selected NIR absorption lines of chemical species that are proven activity indicators in optical or NIR wavelengths for Sun-like stars or M dwarfs in order to test their potential as activity indicators for SPIRou. These absorption lines are the titanium (Ti I) line at 10499 Å (Spina et al. 2020), the helium triplet (He I) at 10 833 Å (Schöfer et al. 2019; Fuhrmeister et al. 2019, 2020), the iron (Fe I) line at 11692 Å (Yana Galarza et al. 2019; Cretignier et al. 2020), the potassium line (K I) at 12435 Å (Barrado y Navascués et al. 2001; Robertson et al. 2016; Terrien et al. 2022), and the aluminum (Al I) line at 13154 Å (Spina et al. 2020). The specific central wavelength of these lines is listed in Table 7.
The equivalent width (EW) of spectral lines can be used as a proxy for the strength of the chromospheric activity and is defined as follows Gray (2008):
 (4)
(4)
where Fλ is the flux of the spectral line and F0 is the continuum flux surrounding the spectral line.
As the continuum in the M dwarfs spectra is unknown, we used a pseudo-continuum as in Schöfer et al. (2019), and therefore we measured the pEW. To do so, we first stacked the four consecutive exposures of each SPIRou observation to obtain one single high-S/N spectrum per epoch. We then used a Python reimplementation of the continuum-fitting routine from IRAF9 to obtain the pseudo-continuum. This pseudo-continuum is defined as the local continuum of a spectral zone of 2–5 Å, where the spectral line is at the center. The details of the wavelength range that we used to compute the pseudo-continuum are listed in Table 7.
To each spectrum per epoch, we fitted a Voigt profile in the absorption lines within an MCMC framework using the emcee (Foreman-Mackey et al. 2013) Python package. The parameters of the Voigt profile are the Gaussian width, the Cauchy-Lorentz scale, the amplitude, and the center of the line. The fitted model of the Voigt profile corresponds to Fλ in Eq. (4). We used the posterior distributions of the fitted parameters to compute the uncertainties on the pEWs using the bootstrap method. To look for periodicities in the time series of the tested spectral lines, we computed the GLS periodogram. We then considered any peak with a FAP of below 1% as significant. Table 7 shows the highest peaks of the periodicities in the GLS periodograms for each line within a range of 1 day to 100 days; this excludes periodicities coming from the 1-day alias and long-term variability.
Figure 10 displays the pEW time series of the Al I, Ti I, K I, Fe I, and He I lines along with their GLS periodograms, the phase-folded plot, and the correlation plot with RVs. The highest peak of the periodicity of each line is listed in Table 7 for all the data and for each of the RV seasons. Only Al I exhibits peaks of periodicities with a FAP of below 1% at 35 days, which is close to the expected stellar rotation of 34.4 days. Moreover, Al I shows several peaks at between 30 and 40 days, which may be related to the differential rotation. The lines best correlated with the RVs are Al I and Fe I with Pearson’s coefficients of 0.3 and 0.2, respectively. However, the correlation between the RVs and Al I is more significant, with a p-value of 4 × 10−4 versus the p-value of 0.01 for the correlation with Fe I.
Excluding Al I, the remaining spectral lines tested, namely Fe I, Ti I, K I, and He I, do not seem to be modulated by the stellar rotation and show small or no correlation with the RVs, at least from the analysis of their periodograms. The Fe I line in particular shows a peak of periodicity at 44.7 days, which is similar to the expected stellar rotation at the poles (Ppol = 45.5 days). This line could be tracing active surface features at latitudes close to the stellar pole.
The best-fitting GP models of the tested spectral lines are shown in Fig. E.2 and the final posterior distributions of the hyperparameters are listed in Table E.1. Most of the spectral lines have periodicities of longer than the measured rotation period of 34.4 ± 0.5, except for He I. However, suggested by the previous results within this work, it seems that the He I line is not sensitive to stellar activity. Moreover, it is clear that the GPs do not fully model the variability in the tested spectral lines, and we observe high values of reduced χ2. Underestimation of the uncertainties on the pEW computation could play a role in this; we will investigate this further in future works.
Thanks to the analysis of the GLS periodograms and the GPR, we can see that the periodicity of the Al I and Fe I lines as computed using these two techniques is consistent; however, the decay time is shorter than expected and does not cover two complete cycles.
Properties and periodicities of the NIR spectral lines within the SPIRou domain.
7.4 Seasonal analysis
As stellar activity shows a quasi-periodic behavior, the activity signals should be consistent over short timescales, which means we should be able to measure their periodicities with the periodograms in a seasonal analysis. We observe that the strongest peaks of the GLS periodograms of the optical activity indicators are not consistent over the three seasons of data previously defined as 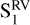 ,
, 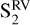 , and
, and  . The GLS periodograms for each of the three subsets are displayed in Fig. D.1. For the CCF contrast and the BIS, the periodicity close to the rotation period gains significance towards the second subset, but still has a high FAP. On the other hand, the peak at the stellar rotation period decreases in significance towards the 2021/2022 observations. During
. The GLS periodograms for each of the three subsets are displayed in Fig. D.1. For the CCF contrast and the BIS, the periodicity close to the rotation period gains significance towards the second subset, but still has a high FAP. On the other hand, the peak at the stellar rotation period decreases in significance towards the 2021/2022 observations. During  , the Hα time series shows an important power excess at a period slightly longer than the expected rotation period. During
, the Hα time series shows an important power excess at a period slightly longer than the expected rotation period. During 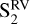 and
and  , Hα keeps some power excess around the rotation period but this is not significant.
, Hα keeps some power excess around the rotation period but this is not significant.
The SPIRou activity indicators, the FWHMLBL and the chromatic velocity slope, do not show the same seasonal behavior. As shown in Fig. D.2, the FWHMLBL has a peak of periodicity that is unrelated to the stellar rotation in  ; during
; during  and
and 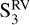 we can see some power excess close to the rotation period but with a FAP of above 10%. On the other hand, the chromatic velocity slope has a highly significant peak of periodicity that is slightly shorter than the rotation period in
we can see some power excess close to the rotation period but with a FAP of above 10%. On the other hand, the chromatic velocity slope has a highly significant peak of periodicity that is slightly shorter than the rotation period in 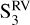 , but no peaks in
, but no peaks in 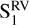 or
or  . The periodicity seen in
. The periodicity seen in 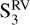 may be affected by the window function of that particular season (see Fig. D.2).
may be affected by the window function of that particular season (see Fig. D.2).
The tested NIR spectral lines also do not keep consistent periodicities across the three subsets of RVs observations  ,
,  , and
, and 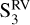 . The strongest peaks of the GLS periodograms of Al I, Ti I, K I, and Fe I change from season to season and are close to the rotation period during at least one season (see Table 7). However, this latter periodicity is ~39 d instead of the expected Prot. This may be related to active features in the stellar surface at mid latitudes where the rotation should be greater than at the equator. Regarding the Fe I line in particular, although when considering the whole data set its periodicity is larger than Prot, the periodicity of each RV season is between 30 and 40 days, which could originate from the stellar rotation modulation. This variability in the periodicity observed for the spectral lines may suggest high temporal variability in the stellar activity manifesting as highly variable active features.
. The strongest peaks of the GLS periodograms of Al I, Ti I, K I, and Fe I change from season to season and are close to the rotation period during at least one season (see Table 7). However, this latter periodicity is ~39 d instead of the expected Prot. This may be related to active features in the stellar surface at mid latitudes where the rotation should be greater than at the equator. Regarding the Fe I line in particular, although when considering the whole data set its periodicity is larger than Prot, the periodicity of each RV season is between 30 and 40 days, which could originate from the stellar rotation modulation. This variability in the periodicity observed for the spectral lines may suggest high temporal variability in the stellar activity manifesting as highly variable active features.
Although we see hints of seasonal behavior in the optical and NIR activity indicators in this work, most of their periodicities are not significant and therefore we cannot describe trends of the stellar activity during each season. For example, Hα is clearly modulated by the stellar rotation during 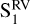 which could be due to high chromospheric activity levels. However, we do not see this behavior in other activity indicators.
which could be due to high chromospheric activity levels. However, we do not see this behavior in other activity indicators.
8 Stellar activity modeling
Rajpaul et al. (2015) describes a multi-dimensional GP framework within which the stellar activity in the RV time series can be modeled simultaneously with the Keplerian signal using the information from activity indicators. In summary, this framework assumes that the stellar activity signals and the RVs can be modeled by the same latent function, namely G(t), and its time derivative, G(t). Here, G(t) is related to the area of the visible stellar disk covered by active regions and G(t) describes the evolution of these active regions over time. Therefore, the RV variations induced by activity can be expressed as a linear combination of G(t) and G(t). Physically, this linear combination will account for the convective blueshift suppression and the evolution of spots on the stellar surface.
In principle, the ancillary time series, such as the activity indicators, should also be defined as linear combinations of G(t) and G(t) if they are affected by both processes: the area covered by active regions and its time evolution on the stellar surface (e.g., BIS). However, some activity indicators, such as  and SHK, can be described only by G(t) as they do not account for the time evolution of spots (see Rajpaul et al. 2015 and Barragán et al. 2022a for more details).
and SHK, can be described only by G(t) as they do not account for the time evolution of spots (see Rajpaul et al. 2015 and Barragán et al. 2022a for more details).
We used the Python code pyaneti10 (Barragán et al. 2019b, 2022a) to apply the multi-dimensional GP framework in our SOPHIE and SPIRou data. As the code was built for planet RV and transit modeling and there is no planet signal detected in this system, we set up a planet signal with an amplitude of K = 0 m s−1. Then only the stellar activity signal is considered in the modeling. The kernel of the GPR is set to be the same as in Eq. (2) of Sect. 5. However, the amplitude A in Eq. (2) in the multidimensional framework is replaced by the amplitude Ci, as follows:
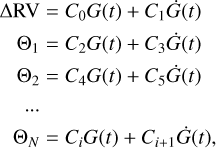 (5)
(5)
where Θ1,…,N are the activity indicators. In this way, it is guaranteed that the hyperparameters of the kernel will be shared, except for the amplitudes Ci. We follow the procedure as in Sect. 5 to obtain the posterior distributions.
We modeled the stellar activity of the SOPHIE RVs using the Hα index and the BIS as ancillary time series, as follows:
 (6)
(6)
We chose the Hα instead of the S index because the former shows a peak in periodicity at the stellar rotation period and is clearly correlated with the RVs (see Fig. 9). Details of the computation of the activity indicators are provided in Sect. 7.
The model obtained from the multidimensional GPR is shown in Fig. 11 for the RVs, the and the BIS time series. The priors and posteriors are listed in Table 8 and Fig. F.1 shows the corner plot of the posterior distributions. The RV jitter is 2.7 ± 0.6 m s−1 and the rotation period is determined at 35.4 ± 1.0 days. The residuals of the RVs have a scatter of 2.9 m s−1 and do not show any significant periodicity in the GLS periodogram.
In the case of the SPIRou data set, we used the FWHMLBL as ancillary time series as it is the activity indicator that is best correlated to the RVs and shows a significant peak at the stellar rotation period (see Fig. 10). The model is as follows:
 (7)
(7)
We only used FWHMLBL because there is no analog to the BIS or any other activity indicator that could trace the temporal evolution of the active regions in the SPIRou data set. The model obtained for the RVs and the FWHMLBL is shown in Fig. 12 and the priors and posteriors are listed in Table 8. Figure F.2 shows a corner plot of the posterior distributions. The rotation period is found at  days, the RV jitter is 2.7 ± 0.3 m s−1, and the RMS of the RV residuals is 3.1 m s−1. Also, the GLS periodogram of the RV residuals does not show any periodicity.
days, the RV jitter is 2.7 ± 0.3 m s−1, and the RMS of the RV residuals is 3.1 m s−1. Also, the GLS periodogram of the RV residuals does not show any periodicity.
We tested the Bℓ as an ancillary time series together with the FWHMLBL. The is a proven stellar activity tracer and we could therefore use its information to improve the modeling of the stellar activity signal. The stellar rotation period obtained from this test is in better agreement with the value obtained in Sect. 5 than the period obtained when only using the FWHMLBL as an ancillary time series, with a value of Prot = 34.6 ± 0.8 days. However, the scatter of the residuals is higher with a value of 3.7 m s−1.
In Fig. 11, we see the complexity in the structures describing the SOPHIE RVs, which is due to the high harmonic complexity of the signal. We can probe this with the smoothing factor β value from the GP model. The smoothing factor β is higher for the SOPHIE RVs 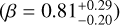 than for SPIRou
than for SPIRou  .
.
The high harmonic complexity seen in the optical can be empirically proven with the amplitudes of G(t) and G(t) (Barragán et al. 2022b). The function G(t) describes the area covered by active regions on the stellar surface as a function of time (Aigrain et al. 2012; Rajpaul et al. 2015). We see that the amplitude of G(t),  is smaller than the amplitude of Ġ(t),
is smaller than the amplitude of Ġ(t), 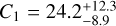 , which explains the observed complexity.
, which explains the observed complexity.
However, we see a different result in the NIR. The amplitudes of G(t) and G(t) are similar with values of  and
and  . This could be an indication that the function G(t) is not fully describing the origin of the RV variations and might be evidence of a different process dominating the stellar activity in the NIR, such as the Zeeman effect.
. This could be an indication that the function G(t) is not fully describing the origin of the RV variations and might be evidence of a different process dominating the stellar activity in the NIR, such as the Zeeman effect.
 |
Fig. 11 Multi-dimensional GP regression of the SOPHIE RVs using the Hα index and the BIS as ancillary time series. The black line indicates the GP model and the gray areas are the 1σ and 2σ levels. The residuals of the GP model are shown below each time series. The mean value has been removed from all the time series. |
9 Detection of planet RV signals
To date, no planet has been found to orbit Gl 205. From our RV analysis of Sect. 6, we do not observe periodicities that could be attributable to Keplerian signals. Considering the total time span of our SOPHIE and SPIRou observations of almost 900 days, we can discard long-period planets with orbital periods longer than 450 days. In particular, the detection of long-period planets would be highly affected by the two gaps of observations of ~100 days each (see Fig. 1). Further observation campaigns of Gl 205 may yet lead to the discovery of long-period planets around this star.
The well-defined seasons of RV observations in Fig. 1 last 184, 209, and 167 days, respectively, and therefore our highest detection sensitivity is given for planets with periods of less than 100 days and with amplitudes greater than 4.8 m s−1, which corresponds to the scatter in the RVs. Moreover, we do not observe periodicity peaks in the GLS periodograms of the SOPHIE and SPIRou RVs that are not related to the stellar rotation period.
The observed peaks of periodicity in the RVs GLS periodogram are not consistent during the three seasons of observations and are always correlated with one or more of the activity indicators studied here. Furthermore, the procedure to filter the stellar activity described in Sect. 8 allows us to discard remnant Keplerian periodic signals in the RVs. In both cases, for the SOPHIE and SPIRou data sets, the multidimensional GP absorbs most of the activity-induced RV signal, leaving an RMS of the residuals of ~3 m s−1. The GLS periodogram of these RV residuals does not exhibit any residual periodicity with a low FAP that could be attributed to a Keplerian signal.
Furthermore, we tested the coherence and consistency of the periodicities using the Stacked Bayesian generalized Lomb-Scargle (Stacked-BGLS) periodogram from Mortier & Collier Cameron (2017). This algorithm is designed to help disentangle short-lived incoherent signals produced by stellar activity from long-lived consistent Keplerian signals.
The Stacked-BGLS periodogram for the RVs from SOPHIE and SPIRou are shown together and independently in Fig. 13. We observed that there are no strong signals in the periodograms at periods of between 0 and 100 days. However, the activity close to 34 days is accompanied by other signals at close periods and shows some level of variable probability, as expected for stellar activity signals.
 |
Fig. 12 Multidimensional GP regression of the SPIRou RVs using the FWHMLBL as an ancillary time series. The black line indicates the GP model and the gray areas are the 1σ and 2σ levels. The residuals of the GP model are shown below each time series. The mean value has been removed from all the time series. |
Priors and best-fit hyperparameters of the multi-dimensional GP model using a quasi-periodic kernel in the SOPHIE and SPIRou data.
10 Discussion and conclusions
In this work, we present the long-term stellar activity and magnetic field characterization of the early, moderately active M dwarf Gl 205 using quasi-simultaneous optical and NIR high-resolution spectra from the SOPHIE/OHP and SPIRou/CFHT spectrographs. We used the SPIRou circularly polarized spectra to measure the Zeeman signature produced by the presence of the magnetic field. The longitudinal magnetic field Bℓ is modulated by the stellar rotation with a period of Prot = 34.4 ± 0.5 days, which is in agreement with previous works (Kiraga & Stepien 2007; Bonfils et al. 2013; Hébrard et al. 2016). The comparison of the periodicities found in Bℓ with those suggested by various activity indicators reinforces the accuracy of Bℓ in constraining Prot compared to the standard activity indicators for early M dwarfs.
We applied the Zeeman Doppler imaging technique to reconstruct the large-scale magnetic field map of the star Gl 205 over three seasons of observations. We observe a temporal evolution of the magnetic field topology, while the strength of the large-scale field remains mostly constant. Moreover, we confirmed the differential rotation over the stellar surface of our target, which could explain the disagreement between its rotation period measured by previous studies and that suggested by different activity proxies.
We derived RVs using the CCF technique with the SOPHIE data and the line-by-line method with the SPIRou data. Both RV data sets are comparable in amplitude and scatter with variations due to stellar activity. We applied a quasi-periodic GPR in the SOPHIE and SPIRou RVs. The periodicities found in the RV data sets are in agreement with that of the longitudinal magnetic field Bℓ.
We filtered the activity-induced RV variations using a multidimensional GPR framework. For the optical RVs, we used the Hα index and the BIS as ancillary time series and, for the NIR, we used the FWHMLBL. The obtained models fit the RVs down to the noise level, with a scatter of 2.7 m s−1 in the residuals for both instruments. As we did not detect residual periodic signals, we can rule out a priori the presence of Keplerian signatures in the given data set. Moreover, we used TESS photometry to discard the presence of transit events in the two available sectors. Nevertheless, we cannot completely rule out the presence of planets around Gl 205 because of the flexibility of the GPs. At certain periods, in particular close to the stellar rotation period, the GP could still absorb the Keplerian signature in the RVs (Rajpaul et al. 2015).
 |
Fig. 13 Stacked Bayesian generalized Lomb-Scargle periodogram of the SOPHIE, SPIRou, and SOPHIE+SPIRou RVs. The periodogram of each observation is stacked along the y-axis. The color scale indicates the logarithm of the probability, where dark red indicates higher probability. |
10.1 Magnetic field temporal evolution
The long-term follow-up of more than two years of data presented in this work allows us to characterize the evolution of the large-scale magnetic field of Gl 205. The topology evolves significantly from a poloidal dipolar field with a strength of 〈B〉 = 12 G in 2019 to a dominantly toroidal field in 2022 with a similar field strength of 〈B〉 = 12.3 G. This change in the topology occurred quickly, that is, within two months, during our last set of SPIRou observations.
Previous studies of moderately active early M dwarf samples revealed significant diversity in magnetic field topologies (Donati et al. 2008; Hébrard et al. 2016; Martioli et al. 2022), suggesting that there is no unique topology pattern for these stars. This diversity is especially visible in partly convective, slowly rotating M dwarfs. Long-term follow-up campaigns of early M dwarfs, such as Gl 410 and Gl 846 (Donati et al. 2008; Hébrard et al. 2016), revealed a temporal evolution of the topology of the magnetic field. The variability of the magnetic field seen in early M dwarfs is at least partly attributable to their differential rotation over the stellar surface (Donati et al. 2008; Morin et al. 2008; Hébrard et al. 2016).
Although most of the seasons observed in this study and that of Hébrard et al. (2016) exhibit poloidal fields for the case of Gl 205, the fact that the field is dominantly toroidal during at least one of our seasons is unexpected, given that previous studies of partly convective stars (Petit et al. 2008; See et al. 2016) suggested that only fast rotators could generate toroidal dominated fields.
Our results of the large-scale magnetic field during the four seasons of Bℓ (see Table 4) are mostly consistent with the previous magnetic field study by Hébrard et al. (2016); however, in the present work we have been able to characterize the long-term evolution of the large-scale field. The long-term SPIRou monitoring was key to revealing the true nature of the magnetic field evolution and its intrinsic variability.
10.2 Diagnostics on optical and NIR activity indicators
Previous works using photometric, spectroscopic, and spectropolarimetric data for Gl 205 measured similar rotation period values (Prot ~ 33 d). Nevertheless, the variability due to the stellar rotation are not always clear in all the activity indicator time series. Bonfils et al. (2013) showed that the strongest peaks at Prot of the Hα and S index periodograms are seasonal, meaning that they become significant when the data set is restricted to one observation season of ~300 days. Hébrard et al. (2016) measured the periodicity of Bℓ, RV, FWHM, and finding values of between 33.46 and 41.9 days, where the best result was given by the Bℓ with a rotation period of 33.63 ± 0.37 days. This discrepancy between activity indicators was explained by the presence of differential rotation over the stellar surface, but the HARPS-Pol and NARVAL data were not sufficient to confirm this rotation.
We studied stellar activity indicators of Gl 205 in the optical and NIR domains. In the optical domain, the Hα index from SOPHIE exhibits a good correlation with the RVs and is modulated by the stellar rotation period as seen by Bonfils et al. (2013) in HARPS data. This is expected, because the Hα index is a well-studied activity indicator for M dwarfs and its correlation with stellar rotation is clear in large samples (e.g., Delfosse et al. 1998; Newton et al. 2017; Jeffers et al. 2018). In particular, the Carmencita sample of Jeffers et al. (2018) shows that Hα in inactive (pEW(Hα) > −0.5 Å) early M dwarfs, including Gl 205, tend to exhibit modulations at larger periods from 10 to 100 days.
The other optical indicators included in this work do not show clear signs of tracing activity. Even though most of them tend to have incipient peaks of periodicities close to the stellar rotation in their GLS periodograms, these peaks are not significant or do not persist for longer than one season. For example, the BIS becomes significantly modulated by the stellar rotation during the season  . However, the periodicity is slightly longer than the rotation period, suggesting that the traced active features were closer to the poles. It is not surprising that the BIS is not anti-correlated with the RVs (Desort et al. 2007) in the case of Gl 205, because the SOPHIE resolution is larger than the υsini of 0.7 km s−1.
. However, the periodicity is slightly longer than the rotation period, suggesting that the traced active features were closer to the poles. It is not surprising that the BIS is not anti-correlated with the RVs (Desort et al. 2007) in the case of Gl 205, because the SOPHIE resolution is larger than the υsini of 0.7 km s−1.
In the NIR domain, we find that the FWHMLBL is the best tracer of activity in our data set as it is correlated with the RV with a Pearson’s coefficient of 0.4, and its periodogram has the strongest peak at the stellar rotation period. Previous studies found the same trend for other M dwarfs (e.g., Klein et al. 2021; Zicher et al. 2022). Moreover, we tested the performance of NIR spectral lines as possible activity tracers. The He I triplet at 10833 Å has been extensively studied in the CARMENES sample of M dwarfs (Fuhrmeister et al. 2019, 2020) showing that its variability is correlated with Ha only for active cases. In our work, we obtained large error bars from the fitting of the He I line, which is due to the large number of absorption lines around it, making it difficult to obtain a good Voigt profile. The index we derived does not appear to be modulated by the stellar rotation period.
The K line at 12435 Å is studied in detail by Fuhrmeister et al. (2022). The authors find that the K I is rarely correlated or anti-correlated with Ha because this line is less sensitive to chromospheric variability than Hα. Our results agree with the findings of Fuhrmeister et al. (2022) given that the K I line is not correlated with the RV variations and is not modulated by Prot.
Only the Al I line at 13 154 Å shows several peaks of periodicity within the range of the expected differential rotation, suggesting that this line could be tracing several active features across the stellar latitudes. Even though the Ti I at 10499 Å and Fe I at 11693 Å lines are not modulated by the stellar rotation, they appear to be affected by the magnetic field, because they follow approximately the same changes in phase. Al I and Ti I have not previously been studied as activity tracers for Sun-like or M dwarf stars, and further analysis in a larger sample would be of great benefit to prove their capacity as activity tracers as they are located in relatively clear parts of the spectrum with few telluric lines.
Interestingly, the analysis of several activity indicators over time reveals changes in the periodicities over different seasons of observations, which may indicate an evolution in the distribution of active features over the stellar surface of Gl 205. All the activity indicators studied in this work reveal different information, suggesting they may be tracing various activity processes in the stellar surface, and demonstrate the complexity of the stellar activity of Gl 205.
As explained above, the lack of correlation or anti-correlation between the RVs and the activity indicators could be the result of time lags between the time series. For that reason, we cannot completely discard the activity indicators that are not correlated with the RVs as activity tracers. Nevertheless, the existence of the correlation is evidence of stellar nature of the signal.
On the other hand, the GLS periodogram is the standard tool for detecting periodicities in time series; however, its efficiency depends on the number of data points, time span, and sampling, among other characteristics. The absence of a significant peak in periodicity by the periodogram does not directly imply that the indicator is not rotationally modulated. In this work, we compared the periodicities found in the GLS periodograms with the period of the quasi-periodic GP applied in all the activity indicators. In some cases where the GLS periodogram does not find periodicities in the dataset, the GP succeeded in constraining a periodicity close to the expected rotation period. However, in these particular cases, we know the expected stellar rotation and can therefore properly constrain the period of the GP. In blind searches of the stellar rotation period, the results may differ.
The periods found in the GP models are all within the ranges of the differential rotation of the star, namely 32–45.5 days, except for He I. In particular, these periods tend to be longer than the period measured in the longitudinal magnetic field. This may be a geometrical effect due to the inclination of Gl 205, which is 60 deg. From the point of view of the observer, there is one pole hidden, which means that we are more likely to observe active regions with longer rotation periods at greater latitudes.
Finding NIR spectral lines that could function as stellar activity tracers remains an open challenge for stellar characterization and exoplanet searches in this domain. This is particularly important for less active M dwarfs, because chromospheric lines may be better tracers of stellar activity than CCF-based activity indicators (Lafarga et al. 2021). A complementary route to face this challenge consists in identifying subsets of lines that are more or less sensitive to the activity jitter (Bellotti et al. 2022).
10.3 Optical and NIR activity-induced RV jitter
In this study, we confirm that the observed RV variations of Gl 205 in the optical and NIR are due to stellar activity, as previously stated. The RV periodicities over the three RV subdatasets and over the whole time series are always linked to one or more of the activity indicators in both domains.
Hébrard et al. (2016) defined the total RV jitter as the sum of the jitter due to the rotational modulation and the jitter originated from random components (e.g., short-lived spots). Although we are close to reaching the noise level of the data set with the multidimensional GP modeling, the remaining jitter of 2.7 ± 0.3 m s−1 for SPIRou and 2.7 ± 0.6 m s−1 for SOPHIE is equal to the random component contribution proposed for Gl 205, which is of the order of Jr = 2.7 m s−1. This jitter contribution is greater than the average error bar of 1.9 m s−1.
In the GP models applied to the RVs, we observe that the model of the optical RVs is consistent over time and resembles a sinusoid with its first harmonic. The NIR RVs, on the other hand, show a more complex behavior, with a rapidly evolving signal. The amplitudes measured from the GP model show a slightly larger value for the NIR RVs. Suárez Mascareno et al. (2018) measured the optical RV variation due to the rotational modulation and obtained a mean value of 4.4 m s−1 for early M dwarfs and 5.6 m s−1 if only targets from HADES are considered. Our results are in agreement with theirs; the SOPHIE RV semi-amplitudes through all the seasons are between 4.3 and 5.4 m s−111.
We find that the optical and NIR RVs of Gl 205 are similar in amplitude and jitter level for the whole time series, meaning that there is at least a small advantage to observing at NIR wavelengths, which is expected for early, moderately active or inactive M dwarfs. Reiners et al. (2010) showed that the gain in precision toward the NIR is seen especially for M4 and later spectral types. In the case of early M dwarfs, the best precision is obtained in the V band, although the highest S/N is reached in the J band. Moreover, this effect may not be exclusively dependent on the spectral type only, but on levels of activity as well.
Robertson et al. (2020) analyzed a small sample of fast-rotating M dwarfs to compare their optical and NIR RVs. The late M dwarf Gl 3959 exhibits comparable optical and NIR RVs from the HIRES and HPF spectrographs, while some other targets showed comparable RVs only during one season of observations. Active M dwarfs, such as Gl 388 and AU Mic, show stronger RV jitter in the optical than in the NIR, while less active stars, such as Gl 205, do not. The strength of the magnetic field may play a key role in this phenomenon, because it likely impacts the brightness contrast between magnetic and nonmagnetic features. We show here that Gl 205 has a much weaker field than those of active M dwarfs. We plan to extend the work of quasi-simultaneous observations with SOPHIE and SPIRou to more M dwarfs in order to help understand the multiwavelength stellar activity contribution in RVs studies.
We note that removing a small fraction of randomly selected Stokes V profiles in each season leads to fully consistent magnetic properties, which confirms that the field topology remains globally consistent throughout each season. In contrast, seasons S2, S3, and S4 cannot be extended without dramatically affecting the resulting magnetic topologies, which confirms that the season lengths are relatively well suited to the ZDI analysis.
We approximate the semi-amplitude as half of the amplitudes measured in Table 6.
Acknowledgements
P.C.Z. thanks Oscar Barragán for the helpful discussions about pyaneti and the multi-dimensional GPs. This work is based on observations collected with the SOPHIE spectrograph on the 1.93 m telescope at the Observatoire de Haute-Provence (CNRS), France. We thank the staff of the Observatoire de Haute-Provence for their support at the 1.93 m telescope and on SOPHIE. This work is based on observations obtained at the Canada-France-Hawaii Telescope (CFHT) which is operated from the summit of Maunakea by the National Research Council of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique of France, and the University of Hawaii. The observations at the Canada-France-Hawaii Telescope were performed with care and respect from the summit of Maunakea which is a significant cultural and historic site. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of MaunaKea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. Based on observations obtained with SPIRou, an international project led by Institut de Recherche en Astrophysique et Planétologie, Toulouse, France. This paper includes data collected by the TESS mission that are publicly available from the Mikulski Archive for Space Telescopes (MAST). We acknowledge funding from the French National Research Agency (ANR) under contract number ANR-18-CE31-0019 (SPlaSH). P.C.Z. thanks the LSSTC Data Science Fellowship Program, which is funded by LSSTC, NSF Cybertraining Grant #1829740, the Brinson Foundation, and the Moore Foundation; her participation in the program has benefited this work. B.K. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 865624, GPRV). A.A.K. acknowledges that this work was supported by FCT – Fundaçâo para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalizaçâo by these grants: UIDB/04434/2020 & UIDP/04434/2020; PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113; PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953; IF/00849/2015/CP1273/CT0003. J.F.D., C.M. and P.I.C. acknowledge funding from the European Research Council under the H2020 and innovation program (grant #740651 NewWorlds). X.D., X.B., T.F., and A.C. acknoweldge a funding from the French National Research Agency in the framework of the Investissements d Avenir program (ANR-15-IDEX-02), through the funding of the “Origin of Life” project of the Grenoble-Alpes University. S.H. acknowledges CNES funding through the grant 837319.
Appendix A RVs and activity indicators
The log of the SOPHIE and SPIRou observations with their activity indicators are listed in Tables A.1 and A.2, respectively.
SOPHIE RVs and activity indicators. The values of the RVs are given as the variation from the mean RV = 8727.9 m s−1.
SPIRou RVs and activity indicators. The values of the RVs are given as the variation from the mean RV = 9229.7 m s−1.
Appendix B Longitudinal magnetic field Bℓ, GP posterior distributions
The posterior distributions of the GP model applied in the longitudinal magnetic field are shown in Fig. B.1.
 |
Fig. B.1 Corner plot of the GP hyperparameters on the Bℓ time series sampled from our MCMC framework generated with the corner Python package (Foreman-Mackey 2016). The blue line over the posterior distributions indicates the mean and the dashed lines show the 0.16 and 0.84 quantile uncertainties. |
Appendix C ZDI inversion of the Stokes V LSD profiles
The best ZDI fit to the time series of Stokes V LSD profiles observed in September – December 2019, August – October 2020, August – September 2021, and November 2021 – January 2022 are shown in Figure C.1 and Figure C.2.
 |
Fig. C.1 Stokes V LSD profiles (thin black lines) and best-fitting ZDI profiles (thick red lines). Profiles observed between September and December 2019 (Season S1 in Table 4) are shown in the left-hand panel whereas the profiles observed between August and October 2020 (Season S2 in Table 4) are shown in the right-hand panel. The stellar rotation cycle computed using the first observation (BJD = 2 458 738.128) as a reference time and assuming a rotation period of 34.4d (see Table 3) is given on the right-hand side of each observation. The ±1σ error bars are indicated on the left-hand side of each profile. |
 |
Fig. C.2 Same as Figure C.1, but for the observations collected in Season 3 (August to September 2021, left-hand panel), and Season 4 (November 2021 and January 2022, right-hand panel). We note that we use the same rotation period and reference time as in Figure C.1 to compute the stellar rotation phases. |
Appendix D Periodogram of the activity indicators
The GLS periodograms of all the SOPHIE and SPIRou activity indicators, for each of the three subsets of observations  ,
,  , and
, and  , are shown in Figures D.1 and D.2.
, are shown in Figures D.1 and D.2.
 |
Fig. D.1 Generalized Lomb-Scargle periodograms of the SOPHIE RVs, activity indicators, and window function of the three seasons of RV observations: |
 |
Fig. D.2 Same as Figure D.1 for SPIRou data. |
Appendix E GP model of the activity indicators time series
The best-fit hyperparameters of the GP model applied in the SOPHIE and SPIRou activity indicators are listed in Table E.1. Figures E.1 and E.2 show the best GP model for each activity indicator, and Figures E.3, E.4, and E.5 show the corner plots of the posterior distributions.
 |
Fig. E.1 Time series of the SOPHIE RVs, FWHM, CCF contrast, BIS, S index, and Ha. The GP model of each time series is shown in blue with the 3σ uncertainties in light blue. |
Best-fit hyperparameters of the GP model using a quasi-periodic kernel in the SOPHIE and SPIRou activity indicators.
 |
Fig. E.2 Time series of the SPIRou longitudinal magnetic field Bℓ, RVs, FWHMLBL, chromatic velocity slope, and the pEW of K I, Ti I, Al I, Fe I, and He I. The GP model of each time series is shown in red with the 3σ uncertainties in light red. |
 |
Fig. E.3 Corner plot of the posterior distributions of the GP regression applied in the SOPHIE RVs, Hα, BIS, S index, CCF contrast, and FWHM, independently. |
 |
Fig. E.4 Corner plot of the posterior distributions of the GP regression applied in the SPIRou RVs, FWHM, chromatic velocity slope, Al I, Ti I, independently. |
 |
Fig. E.5 Same as Figure E.4, but for Fe I and He I. |
Appendix F Multi-dimensional GP corner plots
The posterior distributions of the multidimensional GP model applied in the SOPHIE and SPIRou data are shown in Figures F.1 and F.2.
 |
Fig. F.1 Corner plot with the posterior distributions of the multidimensional GP applied in the SOPHIE RVs, Hα, and BIS time series. |
 |
Fig. F.2 Corner plot with the posterior distributions of the multidimensional GP applied in the SPIRou RVs and FWHMLBL time series. |
References
- Aigrain, S., Pont, F., & Zucker, S. 2012, MNRAS, 419, 3147 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andersen, J. M., & Korhonen, H. 2015, MNRAS, 448, 3053 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, R., Morton, T., Aigrain, S., Foreman-Mackey, D., & Rajpaul, V. 2018, MNRAS, 474, 2094 [Google Scholar]
- Angus, R., Morton, T. D., Foreman-Mackey, D., et al. 2019, AJ, 158, 173 [Google Scholar]
- Antoniadis-Karnavas, A., Sousa, S. G., Delgado-Mena, E., et al. 2020, A&A, 636, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artigau, É., Cadieux, C., Cook, N. J., et al. 2022, AJ, 164, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astudillo-Defru, N., Bonfils, X., Delfosse, X., et al. 2015, A&A, 575, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astudillo-Defru, N., Forveille, T., Bonfils, X., et al. 2017, A&A, 602, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrado y Navascués, D., Garda Lopez, R. J., Severino, G., & Gomez, M. T. 2001, A&A, 371, 652 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barragán, O., Aigrain, S., Kubyshkina, D., et al. 2019a, MNRAS, 490, 698 [Google Scholar]
- Barragán, O., Gandolfi, D., & Antoniciello, G. 2019b, MNRAS, 482, 1017 [Google Scholar]
- Barragán, O., Aigrain, S., Rajpaul, V. M., & Zicher, N. 2022a, MNRAS, 509, 866 [Google Scholar]
- Barragán, O., Armstrong, D. J., Gandolfi, D., et al. 2022b, MNRAS, 514, 1606 [CrossRef] [Google Scholar]
- Bellotti, S., Petit, P., Morin, J., et al. 2022, A&A, 657, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Moutou, C., Vidal-Madjar, A., et al. 2009, A&A, 495, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bortle, A., Fausey, H., Ji, J., et al. 2021, AJ, 161, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009a, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Isambert, J., Lovis, C., et al. 2009b, in EAS Publications Series, 37, ed. P. Kern, 247 [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Díaz, R. F., Hébrard, G., et al. 2013, A&A, 549, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, S. F., Donati, J. F., Rees, D. E., & Semel, M. 1991, A&A, 250, 463 [NASA ADS] [Google Scholar]
- Carleo, I., Malavolta, L., Lanza, A. F., et al. 2020, A&A, 638, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carmona, A., Delfosse, X., Bellotti, S., et al. 2023, A&A, submitted [arXiv:2303.16712] [Google Scholar]
- Carolo, E., Desidera, S., Gratton, R., et al. 2014, A&A, 567, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Mortier, A., Phillips, D., et al. 2019, MNRAS, 487, 1082 [Google Scholar]
- Cook, N. J., Artigau, É., Doyon, R., et al. 2022, PASP, 134, 114509 [NASA ADS] [CrossRef] [Google Scholar]
- Courcol, B., Bouchy, F., Pepe, F., et al. 2015, A&A, 581, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cretignier, M., Dumusque, X., Allart, R., Pepe, F., & Lovis, C. 2020, A&A, 633, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cretignier, M., Dumusque, X., & Pepe, F. 2022, A&A, 659, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cristofari, P. I., Donati, J. F., Masseron, T., et al. 2022a, MNRAS, 516, 3802 [NASA ADS] [CrossRef] [Google Scholar]
- Cristofari, P. I., Donati, J. F., Masseron, T., et al. 2022b, MNRAS, 511, 1893 [NASA ADS] [CrossRef] [Google Scholar]
- Davenport, J. R. A., Hawley, S. L., Hebb, L., et al. 2014, ApJ, 797, 122 [Google Scholar]
- Davis, A. B., Cisewski, J., Dumusque, X., Fischer, D. A., & Ford, E. B. 2017, ApJ, 846, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Perrier, C., & Mayor, M. 1998, A&A, 331, 581 [NASA ADS] [Google Scholar]
- Delisle, J. B., Unger, N., Hara, N. C., & Ségransan, D. 2022, A&A, 659, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Gillon, M., Queloz, D., et al. 2018, SPIE Conf. Ser., 10700, 107001I [Google Scholar]
- Desidera, S., Gratton, R. G., Endl, M., et al. 2004, A&A, 420, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desort, M., Lagrange, A. M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Delfosse, X., Hobson, M. J., et al. 2019, A&A, 625, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J. F., & Brown, S. F. 1997, A&A, 326, 1135 [Google Scholar]
- Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [Google Scholar]
- Donati, J. F., Mengel, M., Carter, B. D., et al. 2000, MNRAS, 316, 699 [Google Scholar]
- Donati, J. F., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Morin, J., Petit, P., et al. 2008, MNRAS, 390, 545 [Google Scholar]
- Donati, J. F., Kouach, D., Moutou, C., et al. 2020, MNRAS, 498, 5684 [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2013, ApJ, 767, 95 [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2015, ApJ, 807, 45 [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog [Google Scholar]
- Dumusque, X., Boisse, I., & Santos, N. C. 2014a, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Bonomo, A. S., Haywood, R. D., et al. 2014b, ApJ, 789, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Dungee, R., van Saders, J., Gaidos, E., et al. 2022, ApJ, 938, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Faria, J. P., Suárez Mascareño, A., Figueira, P., et al. 2022, A&A, 658, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feinstein, A., Montet, B., & Ansdell, M. 2020a, J. Open Source Softw., 5, 2347 [Google Scholar]
- Feinstein, A. D., Montet, B. T., Ansdell, M., et al. 2020b, AJ, 160, 219 [Google Scholar]
- Finociety, B., & Donati, J. F. 2022, MNRAS, 516, 5887 [NASA ADS] [CrossRef] [Google Scholar]
- Folsom, C. P., Petit, P., Bouvier, J., et al. 2016, MNRAS, 457, 580 [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fouqué, P., Martioli, E., Donati, J. F., et al. 2023, ApJL, 927, L11 [Google Scholar]
- Fuhrmeister, B., Czesla, S., Hildebrandt, L., et al. 2019, A&A, 632, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Hildebrandt, L., et al. 2020, A&A, 640, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Nagel, E., et al. 2022, A&A, 657, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration. 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
- Garcia-Mejia, J., Charbonneau, D., Fabricant, D., et al. 2020, SPIE Conf. Ser., 11445, 114457R [NASA ADS] [Google Scholar]
- Gilbertson, C., Ford, E. B., Jones, D. E., & Stenning, D. C. 2020, ApJ, 905, 155 [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011, in European Physical Journal Web of Conferences, 11, 06002 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
- Hébrard, É. M., Donati, J. F., Delfosse, X., et al. 2014, MNRAS, 443, 2599 [CrossRef] [Google Scholar]
- Hébrard, É. M., Donati, J. F., Delfosse, X., et al. 2016, MNRAS, 461, 1465 [CrossRef] [Google Scholar]
- Henry, T. J., Jao, W.-C., Subasavage, J. P., et al. 2006, AJ, 132, 2360 [Google Scholar]
- Hippke, M., & Heller, R. 2019, A&A, 623, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hippke, M., David, T. J., Mulders, G. D., & Heller, R. 2019, AJ, 158, 143 [Google Scholar]
- Hobson, M. J., Díaz, R. F., Delfosse, X., et al. 2018, A&A, 618, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobson, M. J., Delfosse, X., Astudillo-Defru, N., et al. 2019, A&A, 625, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobson, M. J., Bouchy, F., Cook, N. J., et al. 2021, A&A, 648, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [Google Scholar]
- Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffers, S. V., Schöfer, P., Lamert, A., et al. 2018, A&A, 614, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, D. E., Stenning, D. C., Ford, E. B., et al. 2017, ArXiv e-prints [arXiv:1711.01318] [Google Scholar]
- Kanodia, S., & Wright, J. 2018, RNAAS, 2, 4 [NASA ADS] [Google Scholar]
- Khata, D., Mondal, S., Das, R., & Baug, T. 2021, MNRAS, 507, 1869 [NASA ADS] [CrossRef] [Google Scholar]
- Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
- Klein, B., & Donati, J. F. 2020, MNRAS, 493, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, B., Donati, J.-F., Moutou, C., et al. 2021, MNRAS, 502, 188 [Google Scholar]
- Klein, B., Zicher, N., Kavanagh, R. D., et al. 2022, MNRAS, 512, 5067 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Kopparapu, R. K. 2013, ApJ, 767, L8 [Google Scholar]
- Kotani, T., Tamura, M., Suto, H., et al. 2014, SPIE Conf. Ser., 9147, 914714 [NASA ADS] [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lafarga, M., Ribas, I., Reiners, A., et al. 2021, A&A, 652, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Mahadevan, S., Ramsey, L., Bender, C., et al. 2012, SPIE Conf. Ser., 8446, 84461S [NASA ADS] [Google Scholar]
- Mahmud, N. I., Crockett, C. J., Johns-Krull, C. M., et al. 2011, ApJ, 736, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Maldonado, J., Affer, L., Micela, G., et al. 2015, A&A, 577, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín, E. L., Guenther, E., Zapatero Osorio, M. R., Bouy, H., & Wainscoat, R. 2006, ApJ, 644, L75 [CrossRef] [Google Scholar]
- Martioli, E., Hébrard, G., Fouqué, P., et al. 2022, A&A 660, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morin, J., Donati, J. F., Petit, P., et al. 2008, MNRAS, 390, 567 [Google Scholar]
- Morin, J., Donati, J. F., Petit, P., et al. 2010, MNRAS, 407, 2269 [Google Scholar]
- Morley, C. V., Kreidberg, L., Rustamkulov, Z., Robinson, T., & Fortney, J. J. 2017, ApJ, 850, 121 [Google Scholar]
- Mortier, A., & Collier Cameron, A. 2017, A&A, 601, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2012, A&A, 538, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2014, A&A, 568, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newton, E. R., Irwin, J., Charbonneau, D., et al. 2017, ApJ, 834, 85 [Google Scholar]
- Nicholson, B. A., & Aigrain, S. 2022, MNRAS, 515, 5251 [NASA ADS] [CrossRef] [Google Scholar]
- Nutzman, P., & Charbonneau, D. 2008, PASP, 120, 317 [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Perruchot, S., Kohler, D., Bouchy, F., et al. 2008, SPIE Conf. Ser., 7014, 70140J [Google Scholar]
- Petit, P., Donati, J. F., & Collier Cameron, A. 2002, MNRAS, 334, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Pinamonti, M., Sozzetti, A., Maldonado, J., et al. 2022, A&A, 664, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Ribas, I., et al. 2018, SPIE Conf. Ser., 10702, 107020W [Google Scholar]
- Rabus, M., Lachaume, R., Jordán, A., et al. 2019, MNRAS, 484, 2674 [Google Scholar]
- Rajpaul, V., Aigrain, S., Osborne, M. A., Reece, S., & Roberts, S. 2015, MNRAS, 452, 2269 [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [Google Scholar]
- Reiners, A. 2012, Living Rev. Solar Phys., 9, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [Google Scholar]
- Reiners, A., Shulyak, D., Anglada-Escudé, G., et al. 2013, A&A, 552, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reylé, C., Jardine, K., Fouqué, P., et al. 2021, A&A, 650, A201 [Google Scholar]
- Ricker, G. R. 2014, J. Am. Assoc. Variable Star Observers (JAAVSO), 42, 234 [NASA ADS] [Google Scholar]
- Roberts, S., Osborne, M., Ebden, M., et al. 2012, Philos. Trans. Roy. Soc. Lond. A, 371, 20110550 [NASA ADS] [Google Scholar]
- Robertson, P., Bender, C., Mahadevan, S., Roy, A., & Ramsey, L. W. 2016, ApJ, 832, 112 [CrossRef] [Google Scholar]
- Robertson, P., Stefansson, G., Mahadevan, S., et al. 2020, ApJ, 897, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Sabotta, S., Schlecker, M., Chaturvedi, P., et al. 2021, A&A, 653, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scandariato, G., Maldonado, J., Affer, L., et al. 2017, A&A, 598, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Schöfer, P., Jeffers, S. V., Reiners, A., et al. 2019, A&A, 623, A44 [Google Scholar]
- Schweitzer, A., Passegger, V. M., Cifuentes, C., et al. 2019, A&A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- See, V., Jardine, M., Vidotto, A. A., et al. 2016, MNRAS, 462, 4442 [CrossRef] [Google Scholar]
- Seifahrt, A., Stürmer, J., Bean, J. L., & Schwab, C. 2018, SPIE Conf. Ser., 10702, 107026D [NASA ADS] [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Skilling, J., & Bryan, R. K. 1984, MNRAS, 211, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Souto, D., Cunha, K., Smith, V. V., et al. 2022, ApJ, 927, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Spina, L., Nordlander, T., Casey, A. R., et al. 2020, ApJ, 895, 52 [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., et al. 2018, A&A, 612, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Faria, J. P., Figueira, P., et al. 2020, A&A, 639, A77 [Google Scholar]
- Terrien, R. C., Keen, A., Oda, K., et al. 2022, ApJ, 927, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W. 1956, PASJ, 8, 108 [NASA ADS] [Google Scholar]
- Walkowicz, L. M., Basri, G., Batalha, N., et al. 2011, AJ, 141, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1968, ApJ, 153, 221 [Google Scholar]
- Yana Galarza, J., Meléndez, J., Lorenzo-Oliveira, D., et al. 2019, MNRAS, 490, L86 [Google Scholar]
- Yu, L., Donati, J. F., Grankin, K., et al. 2019, MNRAS, 489, 5556 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zicher, N., Barragán, O., Klein, B., et al. 2022, MNRAS, 512, 3060 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Priors and best-fit hyperparameters of the GP model using a quasi-periodic kernel in the SPIRou longitudinal magnetic field data Bℓ.
Main results of the spectropolarimetric analysis of each of subset of data of the Gl 205 SPIRou observations with ZDI.
Priors and best-fit hyperparameters of the GP model using a quasi-periodic kernel in the SOPHIE and SPIRou RVs.
Results of the RV analysis in the observational seasons of the SOPHIE and SPIRou.
Priors and best-fit hyperparameters of the multi-dimensional GP model using a quasi-periodic kernel in the SOPHIE and SPIRou data.
SOPHIE RVs and activity indicators. The values of the RVs are given as the variation from the mean RV = 8727.9 m s−1.
SPIRou RVs and activity indicators. The values of the RVs are given as the variation from the mean RV = 9229.7 m s−1.
Best-fit hyperparameters of the GP model using a quasi-periodic kernel in the SOPHIE and SPIRou activity indicators.
All Figures
 |
Fig. 1 SOPHIE and SPIRou data of Gl 205. Left: RV time series of Gl 205 from SOPHIE in blue and SPIRou in red with an offset equal to the mean RV of each instrument, RVSOPHIE = 8727.8 m s−1 and RVSPIRou = 9345.5 m s−1. The scatter in the time series is 4.7 m s−1 in the SPIRou data set and 4.8 m s−1 in SOPHIE. The labels above the time series depict the four subsets of observations described in Sect. 6. Right: GLS periodogram of the full RV time series, combining SOPHIE and SPIRou observations. The highest peak is marked with an arrow at 34.3 days. |
| In the text | |
 |
Fig. 2 TESS light curves of Gl 205. Top: sector 6 data. Middle: zoom onto the region of the two flares identified in Sector 6 using the stella package. The red line depicts the best-fit flare model. Bottom: sector 32 data. |
| In the text | |
 |
Fig. 3 Detrended TESS light curves of Gl 205. The red line depicts the applied detrending model to remove the stellar variability using the wōtan package. Below each panel are the residuals of the model with a standard deviation of 210 ppm. |
| In the text | |
 |
Fig. 4 Time series of the SPIRou longitudinal magnetic field Bℓ. The GP model using a quasi-periodic kernel is shown in red. The residuals of this model have a scatter of 0.97 G and are shown in the bottom panel. At the top of the figure, we mark the four subsets of data used in Sect. 5.2. |
| In the text | |
 |
Fig. 5 GLS periodogram of the residuals of the GPR applied in the longitudinal magnetic field Bℓ. |
| In the text | |
 |
Fig. 6 Radial, azimuthal and meridional components of the large-scale magnetic field at the surface of Gl 205 for the four subsets of data defined in Sect. 5.2. From top to bottom, the rows show the results for Seasons S1 (September-December 2019), S2 (August-October 2020), S3 (August–September 2021), and S4 (November 2021–January 2022). Each panel is a flattened polar view of the stellar surface. The circles indicate the equator (black solid line) and the –30, 30 and 60° parallels (dashed lines) and the ticks around the star mark the spectropolarimetric observations in unit of stellar rotation phase. The color bar depicts the magnetic flux in Gauss. |
| In the text | |
 |
Fig. 7 Distribution of reduced χ2 as a function of Ωeq and dΩ extracted from the Stokes V LSD profiles in Season S1 to S4 defined in Table 4. In each map, the 1 and 3σ contours are indicated by the black solid lines. |
| In the text | |
 |
Fig. 8 Time series of the SOPHIE and SPIRou RVs. Top: the best-fitting GP models using a quasi-periodic kernel in the SOPHIE and SPIRou data are shown in blue and red, respectively. The light-blue and light-red colors depict the 3σ level of the uncertainties. The residuals of this model have a scatter of 2.6 m s−1 for SOPHIE, and 2.4m s−1 for SPIRou and are shown below the time series. Middle and bottom: zoom onto the SOPHIE and SPIRou RVs divided into the seasons defined in Table 6 with their best-fitting GP models. |
| In the text | |
 |
Fig. 9 SOPHIE RVs and optical activity indicator. Left: time series; middle left: data folded at the Prot of 34.4 days; middle right: correlation with the RVs where the red line depicts the linear correlation between both quantities; right: GLS periodogram where the horizontal dashed black line indicates the FAP level at 1% and the vertical color lines mark the Prot at 34.4days in yellow, the first harmonic at Prot/2 in light blue, and the time range of differential rotation in light green. |
| In the text | |
 |
Fig. 10 Same as Fig. 9 but for SPIRou data. |
| In the text | |
 |
Fig. 11 Multi-dimensional GP regression of the SOPHIE RVs using the Hα index and the BIS as ancillary time series. The black line indicates the GP model and the gray areas are the 1σ and 2σ levels. The residuals of the GP model are shown below each time series. The mean value has been removed from all the time series. |
| In the text | |
 |
Fig. 12 Multidimensional GP regression of the SPIRou RVs using the FWHMLBL as an ancillary time series. The black line indicates the GP model and the gray areas are the 1σ and 2σ levels. The residuals of the GP model are shown below each time series. The mean value has been removed from all the time series. |
| In the text | |
 |
Fig. 13 Stacked Bayesian generalized Lomb-Scargle periodogram of the SOPHIE, SPIRou, and SOPHIE+SPIRou RVs. The periodogram of each observation is stacked along the y-axis. The color scale indicates the logarithm of the probability, where dark red indicates higher probability. |
| In the text | |
 |
Fig. B.1 Corner plot of the GP hyperparameters on the Bℓ time series sampled from our MCMC framework generated with the corner Python package (Foreman-Mackey 2016). The blue line over the posterior distributions indicates the mean and the dashed lines show the 0.16 and 0.84 quantile uncertainties. |
| In the text | |
 |
Fig. C.1 Stokes V LSD profiles (thin black lines) and best-fitting ZDI profiles (thick red lines). Profiles observed between September and December 2019 (Season S1 in Table 4) are shown in the left-hand panel whereas the profiles observed between August and October 2020 (Season S2 in Table 4) are shown in the right-hand panel. The stellar rotation cycle computed using the first observation (BJD = 2 458 738.128) as a reference time and assuming a rotation period of 34.4d (see Table 3) is given on the right-hand side of each observation. The ±1σ error bars are indicated on the left-hand side of each profile. |
| In the text | |
 |
Fig. C.2 Same as Figure C.1, but for the observations collected in Season 3 (August to September 2021, left-hand panel), and Season 4 (November 2021 and January 2022, right-hand panel). We note that we use the same rotation period and reference time as in Figure C.1 to compute the stellar rotation phases. |
| In the text | |
 |
Fig. D.1 Generalized Lomb-Scargle periodograms of the SOPHIE RVs, activity indicators, and window function of the three seasons of RV observations: |
| In the text | |
 |
Fig. D.2 Same as Figure D.1 for SPIRou data. |
| In the text | |
 |
Fig. E.1 Time series of the SOPHIE RVs, FWHM, CCF contrast, BIS, S index, and Ha. The GP model of each time series is shown in blue with the 3σ uncertainties in light blue. |
| In the text | |
 |
Fig. E.2 Time series of the SPIRou longitudinal magnetic field Bℓ, RVs, FWHMLBL, chromatic velocity slope, and the pEW of K I, Ti I, Al I, Fe I, and He I. The GP model of each time series is shown in red with the 3σ uncertainties in light red. |
| In the text | |
 |
Fig. E.3 Corner plot of the posterior distributions of the GP regression applied in the SOPHIE RVs, Hα, BIS, S index, CCF contrast, and FWHM, independently. |
| In the text | |
 |
Fig. E.4 Corner plot of the posterior distributions of the GP regression applied in the SPIRou RVs, FWHM, chromatic velocity slope, Al I, Ti I, independently. |
| In the text | |
 |
Fig. E.5 Same as Figure E.4, but for Fe I and He I. |
| In the text | |
 |
Fig. F.1 Corner plot with the posterior distributions of the multidimensional GP applied in the SOPHIE RVs, Hα, and BIS time series. |
| In the text | |
 |
Fig. F.2 Corner plot with the posterior distributions of the multidimensional GP applied in the SPIRou RVs and FWHMLBL time series. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.