| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202243904 | |
| Published online | 05 May 2023 | |
Cosmic gas highways in C-EAGLE simulations⋆
1
Tartu Observatory, University of Tartu, 61602 Tõravere, Tartumaa, Estonia
e-mail: indrek.vurm@ut.ee
2
Korea Astronomy and Space Science Institute, 776 Daedeok-daero, Yuseong-gu, 34055 Daejeon, Republic of Korea
3
Astronomy Campus, University of Science & Technology, 776 Daedeok-daero, Yuseong-gu, 34055 Daejeon, Republic of Korea
4
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
5
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
6
Departamento de Astrofísica, Universidad de La Laguna, Av. Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
7
Tuorla Observatory, Department of Physics and Astronomy, Vesilinnantie 5, University of Turku, 20014 Turku, Finland
Received:
29
April
2022
Accepted:
8
February
2023
Context. A substantial fraction of cosmic baryons is expected to hide in the form of diffuse warm-hot intergalactic medium (WHIM) at X-ray temperatures (T = 105 − 107 K). Due to the expected low density of WHIM, it has been very difficult to detect so far. A statistically significant sample of credible detections of the WHIM phase might help solve the problem of the missing cosmic baryons. While the majority of cosmic gas is approximately at rest inside the filaments of the Cosmic Web, the fraction of gas located close to galaxy clusters is falling towards them with substantial velocities. The infalling gas is influenced by the increasing density in the cluster vicinity and eventually undergoes a termination shock, which may boost its X-ray signal. Thus, the cluster outskirts are potential locations for improved detectability of the missing baryons.
Aims. The primary goal of this work is to identify optimal locations of the enhanced X-ray emission and absorption, arising from the interaction of infalling filamentary gas with cluster material. Our further goal is to improve our understanding of the various physical processes affecting WHIM as it falls towards clusters of galaxies along the cosmic filaments. We aim to utilise this information for planning future X-ray observations of WHIM in cluster outskirts.
Methods. We applied the DisPerSE filament finder to the galaxy distribution in the surroundings of a single Coma-like (M200 ∼ 1015.4 M⊙) simulated C-EAGLE cluster of galaxies. We characterised the distribution of the thermodynamic properties of the gas in such filaments and provided a physical interpretation for the results. This analysis serves as a proof of method to be applied to the full C-EAGLE sample in a future work.
Results. We captured a large fraction (∼50%) of the hot (T > 105.5 K) gas falling towards the cluster in the detected filaments in the cluster outskirts. The gas in the filaments is in approximate free fall all the way down to the radial distance of ∼2 r200 from the cluster. At smaller radii, the filament gas begins to slow down due to the increasing pressure of the ambient gas; approximately half of the filament gas nevertheless penetrates into the cluster before being decelerated. The deceleration is accompanied by the conversion of gas bulk kinetic energy into heat. As a result, the density and temperature of the gas in the filaments increase from the general Cosmic Web level of ρ ∼ 10ρav (where ρav is the cosmic mean baryon density) and T = 105 − 106 K at r ∼ 4 r200 towards ρ ∼ 100ρav and T = 107 − 108 K at the virial boundary of the very massive cluster studied in this paper.
Conclusions. The detection of the cosmic filaments of galaxies around clusters may provide a practical observational avenue for locating the densest and hottest phase of the missing baryons.
Key words: large-scale structure of Universe / intergalactic medium
Movie associated to Fig. 4 is available at https://www.aanda.org.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In cold dark matter (DM) theory, cosmological structures form by gravitational collapse of primordial density fluctuations and grow hierarchically from smaller to larger structures by mergers. Large galaxy clusters have undergone several such merger events, hence the plasma that makes up the diffuse intracluster medium in a large cluster has likely undergone several strong shocks and been heated to temperatures T = 107 − 108 K within the virial radius. The intracluster gas is virialised and in approximate hydrostatic equilibrium. The high temperature and density of the hot plasma in the inner regions of massive clusters render it relatively easily detectable with modern X-ray instruments.
However, in the cluster outskirts, the intracluster plasma becomes too tenuous to be routinely detectable with current facilities. The desired boost for the X-ray signal may be provided locally by the physical processes and conditions arising from cluster-filament interactions near the cluster boundary, whereby the filaments which connect the clusters to the Cosmic Web feed the latter with gas and galaxies (‘gas highways’, e.g. Cautun et al. 2014; Kraljic et al. 2018; Rost et al. 2021; Power et al. 2020). In this work, we mainly focus on the gas falling along the filaments towards clusters in order to devise observational strategies for detecting the gas in X-rays.
In the outer filaments (r ≳ 4r200), the main driver of gas dynamics is the gravity of the dark matter concentration near the filament spines. It accumulates gas from the surroundings and compresses the filament gas to overdensities of ∼10. The strong external shocks due to the mass flowing towards the filaments (the sonic Mach number ℳs ∼ 100; Ryu et al. 2003) heat the gas inside filaments into the warm-hot intergalactic medium (WHIM) domain of T = 105 − 107 K. Additional heating is provided by weaker internal shocks within gas that has previously been shocked during the hierarchical structure formation process and is associated with accretion onto filaments from non-linear structures as well as halo mergers and chaotic flow motions within filaments (e.g. Ryu et al. 2003; Kang et al. 2007).
Closer to the cluster (r ∼ 1 − 3r200), its dark matter and gas become important drivers of filament gas thermodynamics. In these regions, the infalling gas has substantial ram pressure which is competing against the pressure of the cluster gas. Depending on the properties of the gases, the infalling gas may slow down or even stop close to the hot and dense cluster, producing features in the velocity structure (e.g. Rost et al. 2021). When the gas falling along the filaments encounters denser environments close to the cluster, a fraction of the energy associated with ordered gas motion along the filament is converted to thermal energy via shocks. This heats the infalling material at the cluster outskirts. Also, the slowing down of the continuously accreting mass over cosmic timescales results in the increase of the gas density at the cluster outskirts. It is thus expected that between the outer filaments and the virial region of the cluster, there is a transition region with distinct thermodynamic properties. We propose a concept of the cluster-filament interface to describe this transition region.
Rost et al. (2021) used the ThreeHundred simulation to show that the gas particles falling towards galaxy clusters experience different dynamics depending on whether they are within or outside the cosmic filaments. While the filaments act as gas highways, penetrating deeper into the cluster, the particles outside filaments slow down and some even turn back. Our aim in this work is to understand, in more detail, the physics of the falling gas, inside and outside the filaments, and its interaction with the central cluster by analysing C-EAGLE simulations.
Cornuault et al. (2018, see also Mandelker et al. 2020a,b) considered the interaction of an incoming collimated gas stream with haloes of masses ranging from galaxies to clusters. They suggest that the persistence of the accretion shock, its lifetime, and the possible disruption of the filament critically depend on the relative timescales of various processes in the problem. They delineate different regimes, primarily depending on the cooling ability of the post-shock filament gas. The massive cluster CE-29 considered in the present paper falls firmly into the regime in which the post-shock gas is unable to cool over the dynamical time (‘hot mode accretion’), whereby the filament material remains hot and likely mixes with the ambient halo material. In the picture of Cornuault et al. (2018), maintaining a hot post-shock gas phase suggests that the accretion shock is persistent, meaning that it has a lifetime exceeding the dynamical (free-fall) time associated with the halo. This regime also avoids some of the complexities related to rapid cooling, such as excessive temporal and spatial gradients, highly multi-phase media, as well as some of the associated hydrodynamical instabilities and turbulence that current cosmological simulations such as C-EAGLE fail to fully capture. This lends some confidence that the shocks identified in the present numerical context have some bearing on the physical reality of filament-cluster interactions.
Several works have focussed on the infalling substructures in the outskirts of the simulated galaxy clusters. Mostoghiu et al. (2021) studied the stripping of the gas from the infalling haloes. Angelinelli et al. (2021) studied simulated galaxy clusters with the aim of deriving information for aiding in X-ray detection of the gas in filaments in the cluster outskirts. They focussed on the self-gravitating gas clumps, falling along the filaments, and suggest that assuming 0.3 Solar metal abundance, the clumps are at the verge of being detectable with current X-ray instruments via free-free and line emission in the 0.3–2.0 keV band and they will surely be detected by future missions such as ATHENA. However, the clumps contain a minority of the total baryon mass in filaments and cover a small fraction of their volumes. In order to study the physics of the gas falling towards the clusters observationally, as well as its contribution to the cosmic baryon budget, one needs a robust sampling of the gas outside the clumps. Our aim is to investigate the prospects of detecting the bulk of the gas in filaments in X-rays. The obvious problem is that the median gas overdensity in filaments is at a level of ∼10 (e.g. Tuominen et al. 2021), while the clumps have densities higher by a factor of 10–100 (Angelinelli et al. 2021). However, the larger extent of the filaments may provide an order of magnitude longer paths through the gas, compared to the clumps. In order to improve the detection chances, we focus on emission and absorption line detection with high-resolution X-ray spectroscopy, which may provide an advantage over the wide-band emission observed with low-resolution instruments, considering the cosmic background in the soft X-rays that probably dominates.
There have been some recent reports on possible X-ray detection of the dense and hot phase of intergalactic gas (WHIM) at the outskirts of galaxy clusters (e.g. Bulbul et al. 2016; Eckert et al. 2015; Reiprich et al. 2021; Werner et al. 2008; Tanimura et al. 2022). While some of the observational works focus on the bridges between cluster pairs, our aim in this paper is different: the intergalactic gas falling along the filaments from the Cosmic Web towards a cluster.
The primary goal of this work is to identify the optimal locations of the enhanced X-ray emission and absorption due to the interaction between the matter falling along filaments and the galaxy clusters. Our secondary goal is to provide some theoretical insights into the underlying physical processes governing gas dynamics in the cluster vicinity, which ultimately affect the X-ray observables. To this end, we characterise and contrast the basic thermodynamical properties of the gas within and outside filaments in the interface region, and provide a physically motivated picture of filaments acting as gas highways. Our motivation is to help harvest the currently existing X-ray data archives (e.g. XMM-Newton and Chandra) and soon arriving data (eROSITA), as well as to develop observational strategies for future X-ray missions (e.g. ATHENA).
Due to the challenges of X-ray observations of diffuse gas such as that in cosmological filaments, it is likely that in the foreseeable future detection is only feasible by stacking a large number of filaments. In fact, recent soft X-ray emission detections from cosmic filaments at the ∼4σ level using ROSAT (SRG/eROSITA) required a stacking of ∼15 000 (500) filaments from the Sloan Digital Sky Survey (Tanimura et al. 2020, 2022). As the primary goal of this paper is observational, we, therefore, limit our analysis to a level of detail sufficient for informing detection strategies, while retaining the salient features for physical interpretation. This amounts to approximations such as fixing the filament width, analysing spherically averaged quantities, as well as averaging across all filaments. We discuss the variation of individual filament properties at the level we deem sufficient from an X-ray observer’s point of view, as well as consider two specific filaments in more detail whose properties bracket the above variation.
The structure of this paper is as follows. In Sect. 2, we describe the C-EAGLE data and the overall properties of the massive mock galaxy cluster which we use in this work. We also discuss our methods of defining the filaments around the cluster and sampling the gas. After a brief discussion on the gas properties in the filaments at the outer regions of the simulation volume in Sect. 3, we characterise, in more detail, the properties of the hot gas in the cluster-filament interface in Sect. 4. A physical interpretation of the thermodynamic structure of the gas is given in Sect. 5, while in Sect. 6 we discuss implications of the infalling gas on the cosmic highway for X-ray detection. We summarise our results in Sect. 7.
2. Data
2.1. C-EAGLE
Our study is based on data from the Cluster-EAGLE (C-EAGLE) simulation project (Bahé et al. 2017; Barnes et al. 2017a). The sample of initial 30 DM halos has been selected from a large (3.2 Gpc)3 simulation (Barnes et al. 2017b), evenly sampled per logarithmic mass interval over the range of M200 = 1014−1015.4 M⊙ to cover the typical mass range of galaxy clusters. The baryonic content of the clusters has then been produced by hydrodynamical zoom simulations using the EAGLE code (Schaye et al. 2015; Crain et al. 2015) extending to the radial distance of 10r200 from the cluster centre. The initial mass of the smoothed-particle hydrodynamics (SPH) gas particles is mgas = 1.8 × 106 M⊙, and the mass of the DM particle is mDM = 9.7 × 106 M⊙.
2.2. The cluster CE-29
In the current work we focus on CE-29, the most massive (M200 = 1015.4 M⊙) halo in the C-EAGLE sample. We are analysing the data within a box of size (∼40 Mpc)3 centred on CE-29. Such a highly massive cluster is not representative of the true cluster population, where lower-mass clusters are more numerous. However, our aim in this paper is to get first insights into the physics of the cluster-filament interface and the thermodynamic conditions for the production of X-ray emitting ions. We chose the most massive cluster in order to maximise the amount of X-ray material and to establish methods for studying the hot WHIM. In future work, we will apply these methods to the lower-mass clusters in order to obtain a more realistic view of the expected observational situation.
Given the high mass of the cluster CE-29, M200 = 2.4 × 1015 M⊙ (similar to that of Coma, e.g. Kubo et al. 2007), the virial radius in spherical approximation is quite large, r200 = 2.8 Mpc. However, visual inspection indicates that the cluster is elongated. The density and velocity structures indicate that two subclusters (sc1 and sc2 in Fig. 1) are merging along the direction of the elongation. Therefore we defined the cluster boundary as an isodensity surface within which 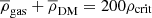 , referred to as the boundary of the virial region below. To suppress local small-scale inhomogeneities, the boundary was calculated on a smoothed density field convolved with a 3D Gaussian kernel with a 0.2 Mpc radius. The result shows that the boundary of the virial region indeed has an elongated shape: the semi-major axis length is ∼1.5r200, the semi-minor axis is ∼0.7r200, yielding an axial ratio ∼2 (the white region in Fig. 1).
, referred to as the boundary of the virial region below. To suppress local small-scale inhomogeneities, the boundary was calculated on a smoothed density field convolved with a 3D Gaussian kernel with a 0.2 Mpc radius. The result shows that the boundary of the virial region indeed has an elongated shape: the semi-major axis length is ∼1.5r200, the semi-minor axis is ∼0.7r200, yielding an axial ratio ∼2 (the white region in Fig. 1).
 |
Fig. 1. Filamentary network around cluster CE-29, as detected by DisPerSE applied to C-EAGLE galaxies. Filament spines (red lines) are shown together with the virial boundary of the cluster (white region) for approximately the full (40 Mpc)3 box (left) and zoomed to the central region (right). The locations where the filamentary network crosses the virial boundary are labelled with yellow symbols. The centres of the two merging subclusters (sc1 and sc2) are marked with black arrows. |
When characterising the radial behaviour of the thermodynamic properties of the whole system below, we use distributions averaged over spherical shells around the cluster centre. This somewhat complicates the interpretation of the results close to the cluster due to its non-spherical shape. On the other hand, the analysis of individual filaments below takes the shape of the cluster into account and considers the distance from the local cluster boundary (i.e. where the filament crosses) separately for each filament.
The spherically averaged density and temperature profiles (see Sect. 2.4 for the profile method) of the gas inside the virial boundary decrease with radial distance r from the cluster centre approximately as ρ ∝ r−2 and T ∝ r−0.45, respectively, reaching an overdensity of ∼100 and a temperature of a few times 107 K at the virial boundary (see Fig. 2).
 |
Fig. 2. Gas density (left) and temperature (right) profile within the cluster CE-29. The dashed line in the left panel shows the theoretical density profile for isothermal gas, assuming spherical symmetry and that ρgas/ρDM is constant (ρ ∝ r−2). The dashed line in the right panel shows T ∝ r−0.45 approximation. |
2.3. Filaments
We applied the Discrete Persistent Structures Extractor (DisPerSE) filament finder (Sousbie 2011) to C-EAGLE galaxies, instead of gas or dark matter density, because they constitute currently the only robust observable related to these systems. DisPerSE has been shown to trace well the different cosmological environments, including filaments (Sousbie et al. 2011). It has been widely used for detecting the cosmic web filaments using observational data (e.g. Kraljic et al. 2018; Malavasi et al. 2020; Laigle et al. 2018). The observational angle is fundamental for our purposes since our aim is to locate the enhanced X-ray emission and absorption using galaxies in, for example, SDSS and 4MOST surveys.
Applying DisPerSE with a default setting (a persistence threshold of 5σ and a smoothing level 10, see Sousbie 2013 for details) yields the filamentary network around cluster CE-29 (Figs. 1 and 3). The network has two centres within the central cluster, approximately located at the centres of the merging subclusters, which in turn are connected with a filament. Thus, we are probably witnessing the merger of two filament networks. The central filament between the two subclusters is approximately aligned with the major axis of the virial boundary of the cluster (see Sect. 2.2). This is consistent with Kuchner et al. (2020) who studied a sample of simulated clusters and found a correlation between the alignments of the major axes of the central haloes and the filaments.
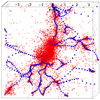 |
Fig. 3. Galaxies (red) and DisPerSE spine points (blue) from a ∼(8r200)3 region centred on the cluster CE-29. The orientation of the 3D region approximately corresponds to that shown in Figs. 1 and 4. |
The filamentary network is quite complex; there are many locations where one identifiable filament splits into two or more branches. Thus, the filament identity is valid only locally. There are nine locations where the filamentary structure is crossing the virial boundary of the cluster (see Fig. 1). We identify these locations as inner endpoints of filaments F1–3 (F4–9) associated with subcluster sc1 (sc2), respectively. When investigating the individual filaments below (Sect. 5.4), we follow the above filaments only up to the first splitting point. This limits the study of the individual filaments to distances less than ∼r200 away from the virial boundary.
2.4. Gas sampling
We first divided the computational volume of C-EAGLE into a rectangular grid of (0.2 Mpc)3 cells and computed all physical quantities relevant for our analysis within each cell based on SPH particle data. This allowed a straightforward determination of the median values as well as the distributions of physical quantities within all regions of interest, for instance within or outside filaments, at a given radial distance from the cluster etc., with minimal computational effort. We verified that the number of SPH particles per cell in filament regions is sufficiently large (∼300 on average for typical filament overdensity of 10) for robust statistics. We concentrate on the intergalactic baryons and we thus exclude particles defined as halo particles by the EAGLE team.
In each cell, we co-added the SPH particle masses and divided them with the cell volume to obtain the density. For the non-additive properties like temperature and velocity, we computed a mass-weighted SPH particle average (see Fig. 4 for the maps of the density and the temperature).
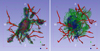 |
Fig. 4. Density (left) and temperature (right) structure approximately within the cluster-filament interface, i.e. within a ∼(8r200)3 region centred on the cluster CE-29. The filaments spines are indicated in red. In the left panel only regions of gas overdensity above 10 are indicated in order to highlight the connection of the densest infalling gas and the filaments (see the online video showing a 360° view). In the right panel, the green, blue and red surfaces approximately correspond to temperatures 2 × 107 K, 6 × 107 K, and 2 × 108 K, respectively. |
The DisPerSE procedure does not produce well-defined boundaries for the filaments, which are needed to capture the diffuse baryons within the filament volume. We rely on the results of Tuominen et al. (2021) on main EAGLE filaments, whereby most of the WHIM is located within 1 Mpc distance from the filament spines, while at 2 Mpc, the median gas density profile has already dropped to the cosmic average level. Thus, we defined as filament gas the contents of such (0.2 Mpc)3 boxes which are located within 1 Mpc of any filament spine. While the filaments cover only ∼6% of the full volume outside the virial boundary of the cluster (out to 6r200), the fraction of the diffuse hot (T ≥ 105.5 K) baryon mass located within this volume is ∼50% of the total in the same temperature range.
Our aim is to investigate quantitatively the physics of the infalling filamentary gas and its interaction with the central cluster. We thus constructed profiles of the thermodynamic properties as a function of the distance from the cluster centre. We divided the volume into concentric spherical shells of 0.5 Mpc width centred at the cluster centre and extracted the distribution of the properties of such (0.2 Mpc)3 boxes which are located within such a shell and within a filament. The median of this distribution was then assigned as a representative of the baryon properties in that shell. From this data, we constructed the median radial profiles of the baryon properties in the filaments as a function of the nominal r200 (see Sect. 4 for the results).
3. Outer filaments
In this work, we are focussing on the potentially enhanced temperatures and densities in the cluster-filament interface due to interaction with the central cluster. As a baseline for comparison, we first considered the gas properties at the largest distances from the cluster where the cluster effects should be minimised. While the temperature and density profiles of the filament gas quite monotonically decrease with the distance from the cluster centre, they start to level off at ∼4r200 (see Fig. 5, top panels). The median density of the filament gas beyond 4r200 is ∼10 times the cosmic mean baryon density. This is consistent with the general large scale structure formation scenario whereby the baryon overdensity in the Cosmic Web filaments is 10 − 100 (e.g. Cen & Ostriker 1999; Davé et al. 2001). The median temperature at these radii is ∼106 K, again consistent with the general predictions of WHIM temperatures of T = 105 − 107 K. Thus, the data implies that beyond 4r200 the filaments are approaching the general Cosmic Web network.
 |
Fig. 5. Dependences of various physical quantities on distance from the cluster center. Top left panel: Median overdensity of the gas outside the virial boundary of the cluster inside (red symbols) and outside (green symbols) the filaments. The dashed blue (orange) line shows ρ ∝ r−1.6 (ρ ∝ r−4) approximation for the density profile inside (outside) filaments. The horizontal dash-dotted line shows the median overdensity within the filaments at radii 4r200 < r < 7r200. The mean cosmic density is denoted with a horizontal dotted line. The approximate radial range of the elongated virial boundary is indicated with the vertical dashed lines. Top right panel: Same as left panel, but for the median temperature. The dashed lines indicate the piece-wise power-law approximation to the temperature profile in different zones (IF1-3 and OF1-2, see Sect. 4.2). Bottom left panel: Same as top panels, but for the median radial velocity towards the cluster. The blue curve indicates the free-fall velocity given by the mass of the cluster. Bottom right panel: Median gas and ram pressure outside the virial region of the cluster as a function of the distance from the cluster centre for the gas within (square symbols) and outside (diamond symbols) filaments. |
4. Characterising the cluster-filament interface
We now shift our focus to the main topic of interest in this paper, namely the outskirts of cluster CE-29, and will begin by characterising the gas properties within this region, both within filaments as well as outside. Due to the high elongation of the cluster (Sect. 2.2), we will not apply the formal r200 to separate the cluster and the filaments. Instead, we study the gas in the cluster-filament interface which we define as the volume within the filaments, radially limited by being outside the 3D boundary of the virial region (determined in Sect. 2.2) but within 4 times the nominal r200 from the cluster centre.
The 3D thermodynamic structure of the cluster-filament interface region (see Fig. 4) indicates that the gas is indeed concentrated along the galactic filaments all the way to the cluster boundary. This lends confidence to our aim of observationally locating the infalling gas using the DisPerSE filament detection method acting on spectroscopic galaxy surveys.
The temperature structure is more complex (see Fig. 4). The inverse correlation between infalling gas density and its susceptibility to shocks, as well as turbulent motions and outflows of hot gas driven by the cluster results in a hotter and somewhat chaotic environment in the cluster vicinity compared with larger distances, more readily affecting the more tenuous gas outside filaments; we discuss this issue further in Sects. 5.2 and 5.3. Thus, the fraction of hot gas captured within filaments is lower (∼50%, see Sect. 2.4) than that in the main Cosmic Web far from clusters (∼80%, Tuominen et al. 2021). However, focussing on filaments with X-ray observations is preferable since, while being hot, they stand out from their surroundings with their higher gas density.
Using the procedure described in Sect. 2.4, we constructed profiles of the thermodynamic properties as a function of distance from the cluster centre, in the radial range extending from the virial boundary up to 4r200. We first produced a single median profile considering the gas from all filaments, that is, all such (0.2 Mpc)3 boxes located within 1 Mpc distance from the filament spine points detected with DisPerSE. We will additionally perform a more detailed analysis of the individual profiles in Sect. 5.4. For comparison, we also specified an “outside filaments” gas region which is located safely outside the filaments, that is, the boxes further than 2 Mpc from any filament spine. In the following, we will describe the main thermodynamic and kinematic properties of gas in the interface region, as derived from the above methods.
4.1. Density
The density of the gas inside filaments decreases from the cluster level of overdensity ∼100 at the inner edge of the cluster-filament interface (r ∼ 0.7 − 1.5r200) to the typical Cosmic Web filament level of overdensity ∼10 at r = 4r200, following approximately ρ ∝ r−1.6, providing a high-density path from the cluster to the Cosmic Web (see Fig. 5, top left panel).
On the other hand, the density of the gas outside filaments drops much faster with distance, following approximately ρ ∝ r−4. At r ≳ 2.5r200, the density outside filaments decreases to the cosmic mean baryon density level. At r ≳ 4r200, the gas outside filaments is underdense by a factor of ∼10, entering the void domain (Fig. 5, top left panel).
Figure 6 shows the overdensity distributions in selected radial ranges, separately for gas within and outside filaments. At all radii, the distribution of the gas overdensity within filaments peaks at systematically higher values than outside filaments. Thus, when searching for the densest gas in the cluster outskirts in observations, it is beneficial to focus on the locations of the filaments which can be detected relatively easily using spectroscopic galaxy surveys such as Sloan Digital Sky Survey (SDSS; e.g. Tempel et al. 2014).
 |
Fig. 6. Overdensity distributions within (blue line) and outside (orange line) filaments, at different radial distances from the cluster centre. The distance is decreasing from left to right and top to bottom as indicated in the panels. We note that all distributions have been normalised independently for visual clarity. |
4.2. Temperature
Within the cluster-filament interface, the median temperature profile of the gas inside filaments suggests three different zones (see Fig. 5, top right panel). When the gas flows from the Cosmic Web domain at r > 4r200 towards r ∼ 2.5r200 (Zone IF1), the temperature increases from the WHIM temperatures of T ∼ 105 − 106 K, following T ∝ ∼r−2.6 down to r ∼ 2.5r200, reaching a level of a few times 106 K. Continuing inwards, in a relatively narrow radial range of r ∼ 1.7 − 2.5r200 (Zone IF2) the gas temperature rapidly increases by almost an order of magnitude, exceeding 107 K, following approximately T ∝ ∼r−5.1. Between ∼1.7r200 and the virial boundary (Zone IF3) the temperature profile is flatter (T ∝ ∼ r−0.9), reaching ∼5 × 107 K where the filaments enter the cluster.
Compared with the filaments, the gas outside filaments is significantly cooler near the outer edge of the interface region (r ≈ 4r200), at the expected void level of T = 103 − 104 K (Cautun et al. 2014; Tuominen et al. 2021). However, it heats up rapidly between ∼4 − 2.7r200 (Zone OF1), reaching 107 K. Inwards from this distance, the temperature profile is flatter, following approximately T ∝ r−1.0 all the way towards the virial boundary (Zone OF2). As a result, between 2 − 3r200, the gas outside the filaments is, on average, hotter than that within filaments.
At the radial range of 0.7 − 1.5r200, the temperature profiles of the gas inside and outside filaments (IF3 and the inner part of OF2 in the top right panel of Fig. 5) are very similar to those inside the cluster (see Fig. 2, right panel); the temperature varies between ∼3 − 6 × 107 K. The similarity implies a causal connection between the gas in the different domains mentioned above. We discuss this issue further in Sect. 5.3.3.
4.3. Radial velocity
The 3D distribution and the median profile of the radial velocity (see Fig. 7, top panels) indicate that at 3 − 4r200 the gases inside and outside filaments fall with the same velocity (∼1000 km s−1). From r ∼ 3r200 inwards the behaviour of the gas in the two environments starts to differ. The gas inside the filaments has a higher velocity and keeps accelerating when falling closer to the cluster, as on a cosmic gas highway. In contrast, the gas outside filaments already starts to slow down at these radii. The deceleration of the filament gas begins closer to the cluster centre, at ∼2r200.
 |
Fig. 7. Radial velocity and Mach number structure in the cluster-filament interface. Top left panel: Radial velocity structure around filament F1 (white dots). Negative (positive) values correspond to gas inflow (outflow). The values are averages in each sight line and thus the image is illustrative rather than quantitatively accurate. The black symbols indicate the boundary of the virial region. The grey surface marks the radius r = 1.5r200 from the cluster centre. Top right panel: Radial velocity repeated from Fig. 5. Bottom left panel: Radial Mach number structure around filament F1 (black dots). The subsonic regions (values below 1) are shown in blue and supersonic regions in white, i.e. in the 2D projection white regions indicate the lack of subsonic gas along the line of sight. Bottom right panel: Median ratio of bulk to sound velocity (a proxy for Mach number) of the gas outside the virial boundary as a function of distance from the cluster centre. |
The gas outside the filaments stops around the virial boundary (r ∼ 0.7 − 1.5r200), while the gas inside filaments still has a median velocity of ∼500 − 1000 km s−1 at these radii. The latter is related to the fact that individual filaments can penetrate inside the virialised region (see Fig. 1).
5. Physical interpretation
Having characterised the general radial behaviour of the infalling gas in the outskirts of CE-29 cluster, we now turn to more detailed analysis and physical interpretation of the kinematic and thermodynamical behaviour of gas in the interface region within and outside filaments. The following interpretations are specific to the CE-29 cluster. A rigorous statistical analysis of a full sample of C-EAGLE clusters is required for generalising the features reported here. While we stress the approximate nature of our spherically averaged analysis, it will be seen below that the simplifications made nevertheless retain sufficient information about the gas thermodynamics for a coherent physical interpretation. To complement the spherically averaged analysis and to inform on the inherent scatter in filament properties, we will also discuss the latter on an individual filament basis (Sect. 5.4). Furthermore, two specific filaments with markedly distinct properties will be selected for a more detailed analysis. The 3D structure of gas in the cluster vicinity will also be discussed. This will yield a better understanding of the main features of the thermodynamic properties indicated by the overall profiles, such as the different temperature zones (see Fig. 5, top right panel) and the slowing down of the infalling gas (see Fig. 5, bottom left panel).
5.1. Slowing down of the infalling gas
We first investigate how the infalling gas is slowed down depending on whether it approaches the cluster via filaments or from the outside. In Fig. 8, we show the distributions of gas radial velocities within and outside filaments in selected radial ranges. Also shown are double Gaussian fits for each distribution (see Appendix A for more details), with the rationale that the infalling gas both within and outside filaments can be broadly classified into two phases, the free-falling component and the decelerated (shocked) one. By tentatively identifying the above components with the two Gaussians, the relative magnitudes of the latter inform about the fraction of decelerated vs. free-falling gas in the two environments.
 |
Fig. 8. Radial velocity distributions within (blue line) and outside (orange line) filaments at different radial distances from the cluster centre. The distance is decreasing from left to right and top to bottom as indicated in the panels. The dashed red and green curves show double Gaussian fits to the radial velocity distributions within and outside filaments, respectively. The individual Gaussian components of the fits are shown by dotted lines. The vertical dashed black line on the bottom right panel shows vff/2 at 1.25r200; within filaments, approximately half of the gas (by mass) retains radial velocities vrad < vff/2 at r200 < r < 1.5r200. |
The ability of the accreting material to penetrate into the cluster is determined mainly by its ram pressure, defined for an approximately radial infall as 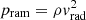 . As long as pram significantly exceeds the thermal pressure pgas = 2ρkBT/mp ahead of it, the gas remains in free-fall. At the largest radii (r > 3r200), the ambient gas pressure around the cluster CE-29 is very low compared to the ram pressure of the infalling gas (see Fig. 5, bottom right panel). Thus, the gas both inside and outside filaments is presumably dynamically affected mainly by the gravitational pull of the cluster. The velocity distributions inside and outside the filaments are consequently relatively narrow and almost identical (see Fig. 8) and comparable to the free-fall velocity derived from the cluster mass (see Fig. 5, bottom left panel).
. As long as pram significantly exceeds the thermal pressure pgas = 2ρkBT/mp ahead of it, the gas remains in free-fall. At the largest radii (r > 3r200), the ambient gas pressure around the cluster CE-29 is very low compared to the ram pressure of the infalling gas (see Fig. 5, bottom right panel). Thus, the gas both inside and outside filaments is presumably dynamically affected mainly by the gravitational pull of the cluster. The velocity distributions inside and outside the filaments are consequently relatively narrow and almost identical (see Fig. 8) and comparable to the free-fall velocity derived from the cluster mass (see Fig. 5, bottom left panel).
5.1.1. Inside filaments
The ambient gas pressure becomes comparable to the ram pressure of the gas within filaments only once the latter has reached the vicinity of the virialised region of the cluster (see Fig. 5, bottom right panel). At this stage, the filament gas begins to slow down while dissipating its kinetic energy, most likely via shocks starting at ∼2.0r200. Yet, by mass, approximately half of the gas inside filaments remains within ∼50% of the free-fall velocity (vrad < vff/2) down to the virial region (bottom right panel in Fig. 8) and therefore penetrates into the cluster (for comparison, the free-falling Gaussian component accounts for 28% of the filament by volume). The persistence of a significant free-falling component is in agreement with the results of Zinger et al. (2016, 2018), who found that gas streams associated with filaments can penetrate deep into the cluster in approximately half of the simulated clusters that they studied, and that the penetration was more efficient in dynamically unrelaxed clusters.
The dissipation associated with slowing gas down heats it up (see Fig. 5, top right panel) and its thermal pressure increases above the ram pressure, indicating that a substantial fraction of the infalling material has become subsonic and dominated by thermal (rather than kinetic) energy (see Sect. 5.4.3 for further discussion about shocks). On average, the supersonic (vrad/cs > 1) to subsonic (vrad/cs < 1) transition takes place at r ∼ 1.2r200, that is, within the radial limits of the elongated cluster virial boundary (see Fig. 7, bottom right panel).
5.1.2. Outside filaments
In contrast, outside of the virial region the density of the gas outside filaments is more than an order of magnitude below that of the filament gas. Consequently, its ram pressure is lower and its infall starts to be affected by the gas pressure ahead already at r ∼ 3r200. This is manifested via the appearance and subsequent growth of a separate low-velocity component (in terms of the absolute value) in the distribution, indicating that an increasing fraction of gas is being slowed down (Fig. 8, top right and bottom left panels). By r ≈ 2 − 2.5r200, the low-velocity component has increased sufficiently so that the overall distribution is clearly bimodal, supporting our two-phase interpretation. By that stage, much of the gas outside filaments has been slowed down; this corresponds to the radius where gas and ram (median) pressures have become comparable (Fig. 5).
As within filaments, the deceleration is accompanied by heating of the gas and transition into the subsonic domain (Fig. 7, bottom right panel). However, unlike filaments, the gas outside filaments does not retain a free-falling component near the virial radius; its radial velocity distribution can be well fitted by a single Gaussian with mean velocity 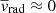 (bottom right panel on Fig. 8), suggesting that essentially all of the gas accreting in this mode has been processed through shocks by this stage.
(bottom right panel on Fig. 8), suggesting that essentially all of the gas accreting in this mode has been processed through shocks by this stage.
5.2. Gas heating outside filaments
The next goal of our analysis is to gain a better understanding of the mechanisms responsible for gas heating within the interface region, and the related temperature behaviour in different zones delineated in Fig. 5 (top right panel). We will first consider regions unassociated with filaments.
5.2.1. Zone OF1
Far from the cluster (beyond 4r200), most of the volume outside filaments is filled by cold gas with temperatures at the expected void level of T = 103 − 104 K (see Fig. 5, top right panel and Fig. 9, top left panel). The free-falling gas has a low sound speed and is consequently highly supersonic (see Fig. 7, bottom panels). The accretion of such gas is known to create “external shocks” surrounding clusters, filaments, and sheets, with very high Mach numbers (≳10, e.g. Miniati et al. 2000; Ryu et al. 2003). We assume that due to this mechanism the temperature distribution outside filaments in our data begins to acquire a new high-temperature component with T ∼ 107 K (Fig. 9, upper middle panel) near the outer boundary of Zone OF1 (r ∼ 4r200).
 |
Fig. 9. Temperature distributions within (blue line) and outside (orange line) filaments at different radial distances from the cluster centre. The distance is decreasing from left to right and top to bottom as indicated in the panels. The secondary peak discussed in the text is indicated with a black arrow in the bottom middle panel. |
In order to learn more about the structure of this region, we employed SlicerAstro software (Punzo et al. 2017) to produce thin “slices” of the full simulation box. The 3D structure reveals that within Zone OF1 (r = 4.0 − 2.7r200), where the overall temperature profile undergoes a steep rise from 104 K to 107 K outside the filaments (Fig. 5, top right panel), the infalling gas undergoes abrupt heating episodes (see Figs. 10 and 11 for an example of a thin slice through the simulation box). The locations of the corresponding temperature jumps within OF1 (e.g. at Sh1 in Figs. 10 and 11) match with the local minima on the velocity divergence ∇ ⋅ v map (bottom left panel of Fig. 11), both of which are indicative of a shock (Ryu et al. 2003; Schaye et al. 2015).
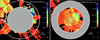 |
Fig. 10. Temperature of the gas in the OF1 (left; black region corresponds to T < 104 K) and OF2 (right; black region corresponds to T < 106 K) zones in a planar cross-section of size (24 Mpc)2 ≈ (8.5r200)2, crossing through the cluster centre. We note that the temperature scale is different for the two panels, in order to maintain the details in the two regions with very different properties. The white diamonds labelled Sh1–Sh3 mark the locations of heating events (possibly shocks) in gas outside filaments, for referencing in the text. The shaded area in the middle of the right panel shows the virial boundary of the cluster. |
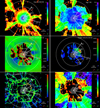 |
Fig. 11. Different gas properties in the same region as in Fig. 10. The panels show gas density (top left), temperature (top right), radial velocity separately for inflows (middle left; black region corresponds to outflow) and outflows (middle right; black region corresponds to inflow), negative gas velocity divergence (bottom left; high values correspond to strong compression), and the ratio of bulk speed to sound speed (bottom right). The shaded area in the centre indicates the virial region of the cluster. The white circles delineate the radial regions marked OF1 and OF2 in Fig. 5. White diamonds labelled Sh1 – Sh2 mark the locations of heating events (possibly shocks) in gas outside filaments, for referencing in the text; white lines indicate the cluster-centric distances of the heating events. |
Due to the very inhomogeneous spatial distribution of the heating episodes, the spherically averaged temperature profile does not exhibit a clear-cut temperature break but instead a rather smooth variation. The steepness of the temperature profile of the gas outside filaments at these radii reflects the extreme temperature gradient across the shock front, where the ∼103 K gas entering from the voids is heated by several orders of magnitude to T ∼ 107 K.
5.2.2. Zone OF2
The 3D velocity structure indicates that during the initial shock heating episode in Zone OF1, most of the accreting gas loses only a fraction of its bulk kinetic energy, continuing its infall towards the cluster (e.g. Sh1, top right and middle left panels of Fig. 11) into Zone OF2. The gas becomes subsonic in this episode (Fig. 11, bottom right panel), which places it in causal contact with the cluster, in a sense that its subsequent evolution depends on the physical conditions in the circumcluster region, which in turn are influenced by the cluster properties and evolutionary history. For example, in the case of CE-29 the infalling gas encounters an outflow of cluster gas in Zone OF2 at velocities ∼2000 − 3000 km s−1 (peaking at location Sh2 in Fig. 11, right middle panel) ejected at an earlier epoch. The outflow may be due to AGN feedback or pressure effects related to the abovementioned pre-merger state of CE-29 (Sect. 2.2, see also Biffi et al. 2022). At this location, the infalling and already heated gas undergoes another shock against the outflowing material, yielding very high temperatures (∼108 K). This heating episode and the corresponding temperature discontinuity are spatially coincident with the global minimum of the velocity divergence (Fig. 11, bottom left panel), reinforcing the shock interpretation.
The outflow-induced reheated gas structure around Sh2 is very hot (∼108 K), that is, hotter than that inside the virial boundary of the cluster, and its spatial extent appears comparable to the virial region of the cluster (see Fig. 11). Such a hot spot might be too hot to be detected via X-ray line emission since oxygen, the most common metal, is fully ionised at these temperatures. However, the detection might be feasible via the Sunyaev-Zeldovich (SZ) effect which scales linearly with the temperature. Depending on the properties (phase, mass of the sub-clusters etc.), there may be such cluster mergers where the merger outflow-induced hot spots have less extreme temperatures and thus would be useful targets for X-ray spectroscopy.
5.3. Gas heating inside filaments
Next, we analyse the temperature behaviour and gas heating inside filaments, with a goal to obtain a physical explanation for the different temperature zones (see Fig. 5, top right panel), as well as to contrast the behaviour and properties of gas within and outside filaments in the interface region.
5.3.1. Zone IF1
The temperature distribution of the gas inside filaments behaves very differently from the gas outside filaments (see Fig. 9): it has a well-defined single peak that gradually shifts from T ∼ 106 K at the largest radii to T ≈ 3 − 4 × 106 K at the inner boundary of Zone IF1 (∼2.5r200). This corresponds to the rising temperature profile in Zone IF1 (see Fig. 5, top right panel). Due to its higher density, the gas inside filaments is less sensitive to shocks (as pointed out by Rost et al. 2021) than that outside and retains the bulk of its kinetic energy until it approaches the cluster virial boundary. Consequently, the temperature of the gas inside filaments towards the inner boundary of IF1 is smaller than that outside filaments.
The gradual increase of filament gas temperature towards smaller radii within Zone IF1 can arise from a few different effects related to the increasing influence of the cluster. First, it is well established that the filament gas within the Cosmic Web is heated in the first place by the ram, turbulent and thermal pressure of the ambient gas accreting onto the filament from the sides due to the gravitational pull of the latter. As the filament approaches the cluster, the ambient conditions begin to change which also alters the physical properties of the accreting gas (in other words, the outer boundary conditions of the accretion problem change). The ambient gas also begins to slow down at larger radii from the cluster compared to the filaments (Fig. 5, bottom left panel), creating shearing motions near the filament-environment interface. The latter can give rise to instabilities and oblique shocks that heat the filament by dissipating a fraction of its kinetic energy without disrupting the filament altogether. Finally, visual inspection reveals locations where the gas structure deviates from our definition of a filament volume, that is, a cylinder with a fixed radius of 1 Mpc around the spines detected with DisPerSE. This leads to some degree of artificial mixing of gas identified as residing inside or outside filaments; since the gas temperature outside filaments rises rapidly with decreasing radius, such mixing may also contribute to the temperature rise in filaments within IF1.
5.3.2. Zone IF2
At r < 2.5r200, a possibly separate higher-temperature component starts to appear at T ∼ 107 K (see Fig. 9, bottom middle panel), which could indicate that filaments are starting to undergo termination shocks against the cluster material (see Sect. 5.4.3 for a case study). The typical temperatures and sound speeds of the filaments are already sufficiently high that the termination shocks have relatively modest Mach numbers, with a median ℳ ∼ 3−4 (see Fig. 7, bottom panels). The latter corresponds to a temperature jump of ≲10 at the shock according to the Rankine-Hugoniot conditions (see Eq. (3) below), hence the putative higher-temperature (shocked) component is not as clearly separable from the overall distribution as in the outside filament gas (see Sect. 5.2.1).
The onset of the cluster-induced shock heating is reflected in the steepening of the temperature profile in Zone IF2 (Fig. 5, top right panel), while the shock interpretation is reinforced by the filament gas starting to slow down at these radii (see discussion in Sect. 5.1 and Fig. 5). Thus the infalling filament gas undergoes qualitatively similar evolution as the gas outside filaments, while the main difference is in the distance from the central cluster where the bulk of the shock heating takes place (Zones IF2 and OF1, respectively), as well as in the strength of the respective shocks.
5.3.3. Zone IF3
The hot component in the temperature distribution becomes dominant and shifts to T ∼ 3 × 107 K by r < 2r200. At the same radii (IF3) the filament gas slows down quite rapidly and dissipates most of its kinetic energy (see Fig. 5), again consistent with the shock scenario.
We note, however, that this hot component cannot be unambiguously associated with that of the shocked filament gas – inwards from the shock, the filament gas flow may be disrupted and can mix with (1) the infalling gas outside filaments and (2) the gas associated with the cluster which has been heated by the shocks due to the gravitational collapse during the cluster formation (as in the case of filament F1 below). This is indicated by the similarity of the temperature profiles of the gas inside the cluster, inside filaments and outside filaments at similar distances from the cluster centre at r < 2r200 (see Figs. 2 and 5). Due to this complexity, delineating and interpreting the thermal state separately for the gas inside the cluster and of that infalling through filaments or outside is not straightforward at these radii.
5.4. Individual filaments
Given the above understanding of the physical processes taking place at the cluster-filament interface, we proceed on a more detailed level and investigate the filaments individually in order to avoid various averaging effects in our analysis. It is likely that in order to detect the hot infalling gas in observations, one needs to stack many filaments (see Sect. 1). Thus, the details of individual filaments may not be very important in this context, and the overall profile derived above could be sufficient for estimating the detection feasibility. However, in this work, our goal is to gain a better understanding of the underlying physical mechanisms, which manifest most clearly when considering filaments on an individual basis. Thus, we first derived the radial profiles of density and temperature for individual filaments, in order to evaluate the scatter of the thermodynamic properties between the filaments and to derive some insight into the cause of the scatter.
As discussed in Sect. 2.3, the individual filaments F1–9 are defined between the virial boundary and the first splitting point (up to ∼r200 distance from the virial boundary). Since the detectable X-rays probably originate from the close proximity of the cluster virial boundary, this radial limitation is acceptable. In order to extract the profiles of the relevant quantities, we applied a modified version of the procedure we used for the median profile described in Sect. 2.4. Namely, we are interested here in the local individual phenomena and conditions, primarily driven by the matter density of the cluster. Thus, we construct the individual profiles of the thermodynamical properties of the gas as a function of the radial distance from where the individual filament spine crosses the cluster virial boundary (rather than from the cluster centre), defined in Sect. 2.2.
At a distance further than ∼0.5 − 1.0r200 from the cluster boundary, the gas in most filaments is approaching the cluster relatively undisturbed and nearly in free fall along the cosmic gas highway, while the temperature and density vary by almost an order of magnitude between filaments (Fig. 12). Closer to the cluster, the temperature of the gas in most filaments exhibits behaviour similar to the overall median profile for all filaments taken together (Fig. 5, top right panel), that is, it increases rapidly. The location of the highest temperature gradient approximately marks the location of the termination shock for each filament – its location varies between filaments as it depends on the individual filament properties (e.g. ram pressure), as well as the local ambient conditions. The corresponding temperature jumps in each filament are smeared out over a distance comparable to the filament radius (1 Mpc), which is to be expected given that neither the filament nor the shock normal is perfectly radial (see Fig. 12, right panel). After the termination shock, the scatter in temperature and density becomes markedly smaller between filaments (roughly a factor 3) and probably reflects more the properties of the cluster that the shocked filaments have joined and mixed with, rather than the individual filament properties ahead of the shock.
 |
Fig. 12. Median gas overdensity (left) and temperature (right) within individual filaments, as a function of radial distance from the local cluster boundary (normalised to the nominal r200). |
The large scatter in temperature and density before the termination shock is likely caused by the complexity of the environmental and evolutionary factors, which are difficult to disentangle. For example, for a subset of filaments the higher ambient density and proximity of prominent clumps seem to correlate with higher filament temperatures; however, this is not the case for all filaments. A significantly larger sample of filaments is required to put such a tentative correlation on a firmer footing and to investigate how the ambient gas influences the filament not just through its density, but also through pressure, turbulent motions, etc. Finally, the snapshot data analysed in this paper cannot account for evolutionary effects, and including an explicit temporal dimension in the analysis is beyond the scope of this work.
Given the above issues we limit our study of the individual filaments to examining filaments F1 and F9 (see Figs. 13 and 14), which bracket the variation of the gas temperature and density close to the virial boundary of the cluster (see Fig. 12).
 |
Fig. 13. Overdensity (top left), temperature (top right), radial velocity (bottom left), and the ratio of bulk speed to sound speed (bottom right) of the gas around filaments F1 in a planar cross-section of size (24 Mpc)2 ≈ (8.5r200)2, crossing through the cluster centre. The grey area on the right-hand side of the figures marks regions within the cluster boundary. The white line marks the direction approximately parallel to the shock normal. |
5.4.1. Filament F1
Filament F1 appears “disturbed”: it approaches the cluster through a denser environment than other filaments (see Fig. 13, top left panel), contains a prominent halo at 3r200, and connects to another halo just at the cluster boundary (Fig. 13). Accordingly, it is significantly thicker and denser (r⊥ ∼ 2 Mpc, ρgas ∼ 100ρav) than most other filaments.
The denser filament has comparatively higher penetrating power compared with the rest and is, therefore, still in free fall (i.e. on a gas highway) when it crosses the cluster boundary. This is supported by Fig. 13 (bottom left), which shows that the filament has not decelerated (i.e. undergone a termination shock) until well inside the cluster boundary. This also accounts for its lower temperature (∼107 K) near the boundary compared with other filaments (∼3 × 107 K; Fig. 12), because the others have already been heated up by their respective termination shocks by that stage. In contrast, if one compares the filaments on their respective “gas highways” (rather than at a fixed distance from the local cluster boundary), that is, ahead of their termination shocks, then the “disturbed” filament F1 is comparatively hotter (T ∼ 107 K) than the rest (∼106 − 107 K), which is not unexpected given its more turbulent environment and higher density.
5.4.2. Filament F9
In contrast, filament F9 is one of the more isolated ones, approaching the cluster through a relatively low-density region (see Figs. 12 and 14). Hence, it is comparatively undisturbed and cool – that is, it approximately retains the properties characteristic of filaments within the Cosmic Web domain (overdensity ∼10, T ∼ 105 − 106 K) all the way to the clearly identifiable termination shock, where it exhibits an abrupt temperature jump by almost two orders of magnitude. Hence filament F9 serves as the “cleanest” representative of general scenario presented in this paper, showing a clear cosmic highway region, penetration into the interface region, and the final termination shock against the cluster material. For these reasons, we chose the shock in filament F9 for a more detailed analysis below.
5.4.3. Shock heating in filament F9
The average thermodynamic behaviour of the full filament population in the cluster vicinity (discussed in Sect. 4) is well understood in terms of the ram pressure and shock heating arguments. While a systematic study of shocks taking place within individual filaments is beyond the scope of this paper, we present here, as proof of concept, a specific example (filament F9) exhibiting a particularly prominent accretion shock. We identified a location of discontinuity of thermodynamic properties of the gas in this filament at a distance of ≈1.7r200 from the cluster centre (see Figs. 14 and 15). The Rankine-Hugoniot jump conditions for density, velocity (in the shock frame), pressure and temperature in a perpendicular plane-parallel shock are
 |
Fig. 15. Profiles of gas properties in the shock vicinity in filament F9, along the shock normal (indicated by a white line in Fig. 14). Radii above 1.7r200 (below 1.6r200) correspond to the upstream (downstream) region. |
where ℳ1 is the Mach number upstream of the shock, γ is the ratio of specific heats (γ = 5/3 for mono-atomic ideal gas), and subscripts 1 and 2 refer to quantities in the immediate upstream and downstream of the shock front, respectively.
The measured velocity jump in the cluster frame is v1/v2 ≈ 5.5 (upstream velocity v1 ≈ −2000 km s−1 in the cluster frame). This is inconsistent with a stationary shock front (since in the shock frame v1, sh/v2, sh ≤ 4, where the limiting value corresponds to ℳ → ∞) and suggests that the shock front is propagating in the direction opposite to the flow velocity. The observed ratio of the upstream bulk to sound velocities is |v1|/cs, 1 ≈ 8; with the oppositely propagating shock, it follows that |v1, sh|> |v1| and that the upstream Mach number ℳ1 = |v1,sh|/cs,1 > 8. From Eq. (1) one then obtains 3.8 ≲ v1, sh/v2, sh ≤ 4, which limits the shock velocity to a relatively narrow range around vsh ∼ 200 km s−1 in the cluster frame. This yields ℳ1 = |v1−vsh|/cs ≈ 9, where v1, sh = v1 − vsh is the upstream velocity in the shock frame.
Using the above value for the Mach number for a planar shock, the Rankine-Hugoniot conditions (Eqs. (1)–(3)) yield ρ2/ρ1 = v1, sh/v2, sh ≈ 3.9, P2/P1 ≈ 100, and T2/T1 ≈ 26. The measured discontinuities across the shock along its normal (white line in Fig. 14) are ρ2/ρ1 ≈ 2.8, P2/P1 ≈ 80 and T2/T1 ≈ 30. The theoretical and measured values are consistent within ∼20 − 40%. The differences can be ascribed to the non-planarity of the shock front, as well as the multi-dimensional nature of the gas flow in the shock vicinity (i.e. that we use values in a thin slice to represent the full system). Thus, accounting for the above uncertainties, the measured discontinuities are consistent with an accretion shock taking place in filament F9.
6. Implications for X-ray detection of the infalling gas
We continue by discussing some of the general implications of the above analysis of a simulated Coma-like C-EAGLE cluster CE-29 for the X-ray emission and absorption line detection of the infalling hot intergalactic gas in the cluster-filament interface with future instruments on board ATHENA and XRISM missions.
The gas density at the virial boundary (r ∼ 0.7 − 1.5r200) of the cluster CE-29 is ∼100 times the mean baryon density. To look for the observational signals from the infalling gas beyond the virial radius it is beneficial to follow the filaments, the Cosmic Gas Highways, which accumulate the gas over the cosmic history into the cluster-filament interface. The radial decrease of the gas density along filaments is less rapid (approximately ρ ∝ r−1.6) than outside (approximately ρ ∝ r−4) and maintains an overdensity above 10 all the way to the Cosmic Web.
By applying the DisPerSE filament detection algorithm on the galaxy distribution in the cluster outskirts we captured ∼50% of the mass of the intergalactic X-ray (T > 105.5 K) gas between the cluster boundary and a radial distance of 6r200 from the cluster centre within the filaments. Thus, a practical way of locating the infalling X-ray gas in observations is to apply filament detection methods to the spectroscopic galaxy surveys. In future work, we will investigate the effects of applying magnitude cuts mimicking the sensitivity limits of specific surveys like SDSS and 4MOST in order to obtain a more realistic efficiency of capturing the hot WHIM.
The structure of the high-temperature gas close to the virial boundary of the cluster is not well spatially correlated with the filaments, due to the chaotic nature of the cluster-related shock heating episodes induced by the infalling and outflowing gases (see Fig. 4). This is probably the reason why our capture fraction of the hot WHIM is smaller than that in the main EAGLE Cosmic Web filaments far from clusters (∼80%, Tuominen et al. 2021). However, while the filaments close to the cluster boundary have temperatures comparable to the hot ambient gas, they are preferable for the X-ray follow-up since they stand out from their surroundings with their higher gas densities.
Most of the filament gas mass (73%) up to 2r200 distance from the cluster CE-29 is hotter than 107 K. At such high temperatures most of the common X-ray elements, in particular oxygen, are fully ionised. This implies (based on the temperature only) that at these distances in the case of very massive clusters, the infalling gas may be better detectable via FeXXV-XXVI rather than oxygen lines. This capability is provided by XRISM. Further than 2r200 from CE-29 the median temperature in filaments decreases to levels suitable for OVII-VIII production and the corresponding X-ray line wavelengths will be covered by ATHENA/X-IFU. A quantitative study of the X-ray detectability of a single massive cluster such as the one studied in this paper will be the subject of follow-up work, where we will consider in detail the distribution of metal ions in the abovementioned regions and their relevant emission and absorption properties. Future work will also extend the above study to lower mass clusters, which will dominate the observational samples. Their lower gravitational potentials and virial temperatures are expected to increase the importance of the ions of the most common metal, oxygen, in the cluster-filament interfaces.
7. Summary and conclusions
In this work we analysed the thermodynamic properties of the intergalactic gas inside and outside the Cosmic Web filaments in the outskirts of the most massive (M200 = 2.4 × 1015 M⊙) cluster (CE-29) in C-EAGLE simulations. Our main conclusions can be summarized as follows:
-
Using the DisPerSE filament finder, we detected the complex filamentary network of galaxies around the two merging sub-clusters. There are nine locations where the network crosses the virial boundary of the cluster.
-
The volumes within a 1 Mpc distance from the filament spines (excluding those within r200 of the halos) capture a large fraction (∼50%) of the hot (T > 105.5 K) intergalactic gas falling towards the cluster in the cluster-filament interface. This, along with the systematically higher gas densities within filaments, holds promise for locating the hot WHIM observationally.
-
The gas inside filaments is in free fall all the way down to the radial distance of ∼2r200 from the cluster, beyond which it starts to slow down. The ordered (bulk) motion of ∼50% of the filament gas persists into the virial region. On the other hand, the gas outside filaments starts decelerating at larger radii and stops near the virial boundary.
-
The slowing down of the infalling gas starts when its ram pressure becomes comparable to the thermal and/or turbulent pressure of the ambient gas in the cluster vicinity. Owing to its higher density, the ram pressure of the free-falling filament gas is higher than that outside filaments. Hence the filaments are able to penetrate deeper, almost all the way to the cluster virial boundary, before being decelerated by the increasing cluster gas pressure. They therefore serve as cosmic gas highways transporting matter from the Cosmic Web domain into the cluster.
-
When the gas slows down, a fraction of the energy associated with ordered gas motion along the filament is converted to thermal energy via shocks. Consequently, the gas is rapidly heated close to the virial boundary of the cluster.
-
The median temperature of the filament gas increases from the typical Cosmic Web WHIM level of T = 105 − 106 K at r = 4r200 to higher than T = 107 K at the virial boundary of the studied massive cluster.
-
The rising filament temperature closer to the cluster is accompanied by a gradual increase of the filament gas density from the overdensity of ∼10 at r = 4r200 to ∼100 in the cluster boundary, following ρ ∝ r−1.6.
Our analysis indicates that the detection of the cosmic filaments of galaxies around clusters may provide a practical observational avenue for locating the densest and hottest phase of the WHIM. This holds promise for future progress in the X-ray detections of the missing baryons. However, further work is required to advance on the theoretical front. Namely, the analysis should be extended to lower mass clusters which are more prevalent in the observational domain. Also, the characterisation of the metal ion distributions within the filaments is needed for a detailed prediction of the X-ray signal.
Movie
Movie 1 associated with Fig. 4 (3D_density_4r200_DT10) Access here
Acknowledgments
The authors thank Toni Tuominen for useful discussions on EAGLE data analysis and Andrea Negri for providing the galaxy data for C-EAGLE simulations. We thank Rain Kipper for help with the analysis of our results. We acknowledge the support by the Estonian Research Council grants IUT40-2, PRG1006, and by the European Regional Development Fund (TK133). S.E.H. was supported by the project 우주거대구조를 이용한 암흑우주 연구 (“Understanding Dark Universe Using Large Scale Structure of the Universe”), funded by the Ministry of Science. C.D.V. acknowledges support by the Spanish Ministry of Science and Innovation (MICIU/FEDER) through research grant PID2021-122603NB-C22.
References
- Angelinelli, M., Ettori, S., Vazza, F., & Jones, T. W. 2021, A&A, 653, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bahé, Y. M., Barnes, D. J., Dalla Vecchia, C., et al. 2017, MNRAS, 470, 4186 [Google Scholar]
- Barnes, D. J., Kay, S. T., Bahé, Y. M., et al. 2017a, MNRAS, 471, 1088 [Google Scholar]
- Barnes, D. J., Kay, S. T., Henson, M. A., et al. 2017b, MNRAS, 465, 213 [Google Scholar]
- Biffi, V., ZuHone, J. A., Mroczkowski, T., Bulbul, E., & Forman, W. 2022, A&A, 663, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bulbul, E., Randall, S. W., Bayliss, M., et al. 2016, ApJ, 818, 131 [Google Scholar]
- Cautun, M., van de Weygaert, R., Jones, B. J. T., & Frenk, C. S. 2014, MNRAS, 441, 2923 [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cornuault, N., Lehnert, M. D., Boulanger, F., & Guillard, P. 2018, A&A, 610, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Cen, R., Ostriker, J. P., et al. 2001, ApJ, 552, 473 [Google Scholar]
- Eckert, D., Jauzac, M., Shan, H., et al. 2015, Nature, 528, 105 [Google Scholar]
- Kang, H., Ryu, D., Cen, R., & Ostriker, J. P. 2007, ApJ, 669, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Kraljic, K., Arnouts, S., Pichon, C., et al. 2018, MNRAS, 474, 547 [Google Scholar]
- Kubo, J. M., Stebbins, A., Annis, J., et al. 2007, ApJ, 671, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, U., Aragón-Salamanca, A., Pearce, F. R., et al. 2020, MNRAS, 494, 5473 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., Pichon, C., Arnouts, S., et al. 2018, MNRAS, 474, 5437 [Google Scholar]
- Malavasi, N., Aghanim, N., Douspis, M., Tanimura, H., & Bonjean, V. 2020, A&A, 642, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelker, N., Nagai, D., Aung, H., et al. 2020a, MNRAS, 494, 2641 [Google Scholar]
- Mandelker, N., van den Bosch, F.C., Nagai, D., et al. 2020b, MNRAS, 498, 2415 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F., Ryu, D., Kang, H., et al. 2000, ApJ, 542, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Mostoghiu, R., Arthur, J., Pearce, F. R., et al. 2021, MNRAS, 501, 5029 [Google Scholar]
- Power, C., Elahi, P. J., Welker, C., et al. 2020, MNRAS, 491, 3923 [Google Scholar]
- Punzo, D., van der Hulst, J. M., Roerdink, J. B. T. M., Fillion-Robin, J. C., & Yu, L. 2017, Astron. Comput., 19, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., Veronica, A., Pacaud, F., et al. 2021, A&A, 647, A2 [EDP Sciences] [Google Scholar]
- Rost, A., Kuchner, U., Welker, C., et al. 2021, MNRAS, 502, 714 [Google Scholar]
- Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T. 2013, ArXiv e-prints [arXiv:1302.6221] [Google Scholar]
- Sousbie, T., Pichon, C., & Kawahara, H. 2011, MNRAS, 414, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Tanimura, H., Aghanim, N., Kolodzig, A., Douspis, M., & Malavasi, N. 2020, A&A, 643, L2 [EDP Sciences] [Google Scholar]
- Tanimura, H., Aghanim, N., Douspis, M., & Malavasi, N. 2022, A&A, 667, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Stoica, R. S., Martínez, V. J., et al. 2014, MNRAS, 438, 3465 [CrossRef] [Google Scholar]
- Tuominen, T., Nevalainen, J., Tempel, E., et al. 2021, A&A, 646, A156 [EDP Sciences] [Google Scholar]
- Werner, N., Finoguenov, A., Kaastra, J. S., et al. 2008, A&A, 482, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinger, E., Dekel, A., Birnboim, Y., Kravtsov, A., & Nagai, D. 2016, MNRAS, 461, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Zinger, E., Dekel, A., Birnboim, Y., et al. 2018, MNRAS, 476, 56 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Statistical significance of the identification of free-falling and decelerated gas phases within and outside filaments
Figure A.1 shows the mean values of the double gaussian components fitted to the radial velocity distributions in Figure 8, along with the widths of the gaussians and the standard errors of the fitted means. At large radii, the velocity distributions both within and outside filaments are well fitted by a single gaussian, with mean values consistent with each other within errors. At r ≲ 4r200, a decelerated (shocked) component appears in the outside filament gas, which is separated by more than 1σ in velocity space from the free-falling phase. At the same radii, the filament gas distribution is still consistent with a single (free-falling) component. Importantly, the standard errors of the fitted gaussian mean values (shown by thicker bars overlaid on top of the longer bars that characterise the gaussian widths) show that the mean velocities of the free-falling and decelerated components are separated by ≫3σ whenever both components are present (we note that in some cases the above error bars are smaller than the symbol of the relevant data point and not visible in the figure), clearly indicating that the two components (as well as their underlying distributions) are statistically distinct.
Outside filaments, the decelerated component has become the dominant one by r ∼ 2.5r200, while the bulk of the filament gas still resides in the free-falling phase; the radial velocities of these components are separated by > 1σ in terms of the gaussian widths and by > 10σ in terms of the standard errors of the fitted gaussian means. The latter in particular shows that the radial velocities within and outside filaments are drawn from distinct underlying distributions, supporting the case for an environment-dependent accretion history.
 |
Fig. A.1. Results of double gaussian fitting of the radial velocity distributions, corresponding to the radial regions shown on the different panels in Figure 8. The red and green bars show the 1σ range of the fitted gaussian components within and outside filaments, respectively. The overlaid blue and purple bars show the standard errors of the fitted gaussian mean values. The relative line widths of the bars within a given radial range are proportional to the areas under the two fitted gaussian components (if the ratio is < 0.1 in a given range, only the dominant component is shown). The black horizontal bars mark the radial ranges where the fits are performed. |
All Figures
 |
Fig. 1. Filamentary network around cluster CE-29, as detected by DisPerSE applied to C-EAGLE galaxies. Filament spines (red lines) are shown together with the virial boundary of the cluster (white region) for approximately the full (40 Mpc)3 box (left) and zoomed to the central region (right). The locations where the filamentary network crosses the virial boundary are labelled with yellow symbols. The centres of the two merging subclusters (sc1 and sc2) are marked with black arrows. |
| In the text | |
 |
Fig. 2. Gas density (left) and temperature (right) profile within the cluster CE-29. The dashed line in the left panel shows the theoretical density profile for isothermal gas, assuming spherical symmetry and that ρgas/ρDM is constant (ρ ∝ r−2). The dashed line in the right panel shows T ∝ r−0.45 approximation. |
| In the text | |
 |
Fig. 3. Galaxies (red) and DisPerSE spine points (blue) from a ∼(8r200)3 region centred on the cluster CE-29. The orientation of the 3D region approximately corresponds to that shown in Figs. 1 and 4. |
| In the text | |
 |
Fig. 4. Density (left) and temperature (right) structure approximately within the cluster-filament interface, i.e. within a ∼(8r200)3 region centred on the cluster CE-29. The filaments spines are indicated in red. In the left panel only regions of gas overdensity above 10 are indicated in order to highlight the connection of the densest infalling gas and the filaments (see the online video showing a 360° view). In the right panel, the green, blue and red surfaces approximately correspond to temperatures 2 × 107 K, 6 × 107 K, and 2 × 108 K, respectively. |
| In the text | |
 |
Fig. 5. Dependences of various physical quantities on distance from the cluster center. Top left panel: Median overdensity of the gas outside the virial boundary of the cluster inside (red symbols) and outside (green symbols) the filaments. The dashed blue (orange) line shows ρ ∝ r−1.6 (ρ ∝ r−4) approximation for the density profile inside (outside) filaments. The horizontal dash-dotted line shows the median overdensity within the filaments at radii 4r200 < r < 7r200. The mean cosmic density is denoted with a horizontal dotted line. The approximate radial range of the elongated virial boundary is indicated with the vertical dashed lines. Top right panel: Same as left panel, but for the median temperature. The dashed lines indicate the piece-wise power-law approximation to the temperature profile in different zones (IF1-3 and OF1-2, see Sect. 4.2). Bottom left panel: Same as top panels, but for the median radial velocity towards the cluster. The blue curve indicates the free-fall velocity given by the mass of the cluster. Bottom right panel: Median gas and ram pressure outside the virial region of the cluster as a function of the distance from the cluster centre for the gas within (square symbols) and outside (diamond symbols) filaments. |
| In the text | |
 |
Fig. 6. Overdensity distributions within (blue line) and outside (orange line) filaments, at different radial distances from the cluster centre. The distance is decreasing from left to right and top to bottom as indicated in the panels. We note that all distributions have been normalised independently for visual clarity. |
| In the text | |
 |
Fig. 7. Radial velocity and Mach number structure in the cluster-filament interface. Top left panel: Radial velocity structure around filament F1 (white dots). Negative (positive) values correspond to gas inflow (outflow). The values are averages in each sight line and thus the image is illustrative rather than quantitatively accurate. The black symbols indicate the boundary of the virial region. The grey surface marks the radius r = 1.5r200 from the cluster centre. Top right panel: Radial velocity repeated from Fig. 5. Bottom left panel: Radial Mach number structure around filament F1 (black dots). The subsonic regions (values below 1) are shown in blue and supersonic regions in white, i.e. in the 2D projection white regions indicate the lack of subsonic gas along the line of sight. Bottom right panel: Median ratio of bulk to sound velocity (a proxy for Mach number) of the gas outside the virial boundary as a function of distance from the cluster centre. |
| In the text | |
 |
Fig. 8. Radial velocity distributions within (blue line) and outside (orange line) filaments at different radial distances from the cluster centre. The distance is decreasing from left to right and top to bottom as indicated in the panels. The dashed red and green curves show double Gaussian fits to the radial velocity distributions within and outside filaments, respectively. The individual Gaussian components of the fits are shown by dotted lines. The vertical dashed black line on the bottom right panel shows vff/2 at 1.25r200; within filaments, approximately half of the gas (by mass) retains radial velocities vrad < vff/2 at r200 < r < 1.5r200. |
| In the text | |
 |
Fig. 9. Temperature distributions within (blue line) and outside (orange line) filaments at different radial distances from the cluster centre. The distance is decreasing from left to right and top to bottom as indicated in the panels. The secondary peak discussed in the text is indicated with a black arrow in the bottom middle panel. |
| In the text | |
 |
Fig. 10. Temperature of the gas in the OF1 (left; black region corresponds to T < 104 K) and OF2 (right; black region corresponds to T < 106 K) zones in a planar cross-section of size (24 Mpc)2 ≈ (8.5r200)2, crossing through the cluster centre. We note that the temperature scale is different for the two panels, in order to maintain the details in the two regions with very different properties. The white diamonds labelled Sh1–Sh3 mark the locations of heating events (possibly shocks) in gas outside filaments, for referencing in the text. The shaded area in the middle of the right panel shows the virial boundary of the cluster. |
| In the text | |
 |
Fig. 11. Different gas properties in the same region as in Fig. 10. The panels show gas density (top left), temperature (top right), radial velocity separately for inflows (middle left; black region corresponds to outflow) and outflows (middle right; black region corresponds to inflow), negative gas velocity divergence (bottom left; high values correspond to strong compression), and the ratio of bulk speed to sound speed (bottom right). The shaded area in the centre indicates the virial region of the cluster. The white circles delineate the radial regions marked OF1 and OF2 in Fig. 5. White diamonds labelled Sh1 – Sh2 mark the locations of heating events (possibly shocks) in gas outside filaments, for referencing in the text; white lines indicate the cluster-centric distances of the heating events. |
| In the text | |
 |
Fig. 12. Median gas overdensity (left) and temperature (right) within individual filaments, as a function of radial distance from the local cluster boundary (normalised to the nominal r200). |
| In the text | |
 |
Fig. 13. Overdensity (top left), temperature (top right), radial velocity (bottom left), and the ratio of bulk speed to sound speed (bottom right) of the gas around filaments F1 in a planar cross-section of size (24 Mpc)2 ≈ (8.5r200)2, crossing through the cluster centre. The grey area on the right-hand side of the figures marks regions within the cluster boundary. The white line marks the direction approximately parallel to the shock normal. |
| In the text | |
 |
Fig. 14. As Fig. 13 but for filament F9. The yellow cross indicates the accretion shock location. |
| In the text | |
 |
Fig. 15. Profiles of gas properties in the shock vicinity in filament F9, along the shock normal (indicated by a white line in Fig. 14). Radii above 1.7r200 (below 1.6r200) correspond to the upstream (downstream) region. |
| In the text | |
 |
Fig. A.1. Results of double gaussian fitting of the radial velocity distributions, corresponding to the radial regions shown on the different panels in Figure 8. The red and green bars show the 1σ range of the fitted gaussian components within and outside filaments, respectively. The overlaid blue and purple bars show the standard errors of the fitted gaussian mean values. The relative line widths of the bars within a given radial range are proportional to the areas under the two fitted gaussian components (if the ratio is < 0.1 in a given range, only the dominant component is shown). The black horizontal bars mark the radial ranges where the fits are performed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



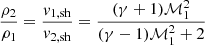
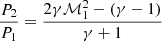
![$$ \begin{aligned} \frac{T_2}{T_1}&= \frac{[(\gamma - 1)\mathcal{M}_1^2 + 2][2\gamma \mathcal{M}_1^2 - (\gamma -1)]}{(\gamma + 1)^2 \mathcal{M}_1^2}, \end{aligned} $$](/articles/aa/full_html/2023/05/aa43904-22/aa43904-22-eq6.gif)