| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245092 | |
| Published online | 10 April 2023 | |
A machine learning approach for correcting radial velocities using physical observables
1 Institut de Ciències de l’Espai (ICE, CSIC), Campus UAB, Carrer de Can Magrans s/n, 08193 Bellaterra, Spain
e-mail: perger@ice.cat
2 Institut d’Estudis Espacials de Catalunya (IEEC), c/ Gran Capità 2-4, 08034 Barcelona, Spain
3 Department of Physics, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK
4 Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
5 School of Physical Sciences, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK
6 Centro de Astrobiología (CAB), CSIC-INTA, ESAC, Camino bajo del castillo s/n, 28692 Villanueva de la Canada, Madrid, Spain
7 Max Planck Institut für Sonnensystemforschung (MPS), Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
8 Landessternwarte, Zentrum für Astronomie der Universität Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
9 Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received:
29
September
2022
Accepted:
5
February
2023
Context. Precision radial velocity (RV) measurements continue to be a key tool for detecting and characterising extrasolar planets. While instrumental precision keeps improving, stellar activity remains a barrier to obtaining reliable measurements below 1–2 m s−1 accuracy.
Aims. Using simulations and real data, we investigate the capabilities of a deep neural network approach to producing activity-free Doppler measurements of stars.
Methods. As case studies we used observations of two known stars, ϵ Eridani and AU Microscopii, both of which have clear signals of activity-induced Doppler variability. Synthetic observations using the starsim code were generated for the observables (inputs) and the resulting Doppler signal (labels), and then they were used to train a deep neural network algorithm to predict Doppler corrections. We identified a relatively simple architecture, consisting of convolutional layers followed by fully connected layers, that is adequate for the task. The indices investigated are mean line-profile parameters (width, bisector, and contrast) and multi-band photometry.
Results. We demonstrate that the RV-independent approach can drastically reduce spurious Doppler variability from known physical effects, such as spots, rotation, and convective blueshift. We identify the combinations of activity indices with the most predictive power. When applied to real observations, we observe a good match of the correction with the observed variability, but we also find that the noise reduction is not as good as in the simulations, probably due to a lack of detail in the simulated physics.
Conclusions. We demonstrate that a model-driven machine learning approach is sufficient to clean Doppler signals from activity-induced variability for well-known physical effects. There are dozens of known activity-related observables whose inversion power remains unexplored, indicating that the use of additional indicators, more complete models, and more observations with optimised sampling strategies can lead to significant improvements in our detrending capabilities for new and existing datasets.
Key words: planetary systems / techniques: radial velocities / methods: data analysis / stars: activity / stars: chromospheres
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The majority of exoplanet discoveries in the last two decades have been thanks to two methods. One is the transit method, monitoring tens of thousands of stars simultaneously; it is most effectively done from space with instruments such as Kepler (Borucki et al. 2010) and the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015). The other is the Doppler technique, which is conducted using high-resolution spectrographs such as the HIgh Resolution Échelle Spectrograph (HIRES; Vogt et al. 1994), the High Accuracy Radial velocity Planet Searcher (HARPS; Mayor et al. 2003), HARPS-N (Cosentino et al. 2012), the Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical Échelle Spectro-graph (CARMENES; Quirrenbach et al. 2020), and the Échelle SPectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO; Pepe et al. 2021). While the field of exoplanet science is now progressing from the mere discovery of planetary companions to the analysis of atmospheres of already known transiting planets, these surveys are still collecting new data and providing complementary insight into planet formation and evolution. Significant challenges remain in the detection of small terrestrial planets around Sun-like stars, mainly due to spurious effects caused by stellar variability.
There are large datasets, collected from both photometric and spectroscopic observations, that may have the precision to detect objects of high interest but remain unexploited. In particular, radial velocities (RVs) are extracted from high-resolution spectra by measuring the wavelength shift of the different lines present in the spectra compared to a laboratory reference standard or to a template created from the stellar spectra themselves. Shifts can be caused by the motion of the stellar centre of mass caused by a planet, or they can be induced by the stellar activity. Various effects influence these measurements. Dumusque et al. (2012) give a comprehensive overview of the topic. The effects introduced by stellar surface phenomena, such as dark spots or bright faculae, induce apparent RV wobbles with typical timescales of rotation periods of stars, active region lifetimes, and stellar activity cycles, making it extremely difficult to disentangle such effects from true Doppler signals from planets, which tend to have comparable orbital periods. Most effective inversion strategies involve the joint fit of the so-called activity indices with the RVs using a handful of shared parameters in Gaussian processes (GPs), as discussed in Suárez Mascareño et al. (2015), which still has the drawback of reducing the information content of the time series, and potentially filtering out potential signals of interest.
Currently RV precisions of 1 m s−1 are regularly achieved. But this precision rarely translates into accurate measurements of true stellar motion due to the effects of stellar activity. This spurious variability is estimated to be about 2–4 m s−1 (Perger et al. 2017) for quiet old stars and as high as hundreds of m s−1 for young and active stars. To account for these effects, many empirical techniques have been proposed and applied, but with limited success. This includes: a simple fit of one or two sinusoids that account for the stellar activity (often called pre-whitening; Suárez Mascareño et al. 2015); in-depth analysis of additional activity indices, photometry, and their correlations with observed RV signals; and the application of more sophisticated noise models in Bayesian frameworks, such as GPs (Perger et al. 2019, 2021). Currently, as for many fields in astrophysics and science in general, machine learning techniques are being considered to solve similar problems. Shallue & Vanderburg (2018) and Dattilo et al. (2019) developed and applied a method for classifying potential planet signals using machine learning algorithms in the Kepler/K2 data. de Beurs et al. (2022), on the other hand, used cross-correlation functions (CCFs) created by the binary-mask technique used to extract the RVs from HARPS-N spectra of the Sun (Collier Cameron et al. 2019) and from ‘Spot Oscillation And Planet’ (SOAP) 2.0 (Dumusque et al. 2014) synthetic data and then trained a neural network (NN) algorithm to distinguish Doppler shifts due to companions from activity-induced shifts based on the information in the cross-correlation profile.
In this article, we investigate whether a machine learning framework trained using synthetic (but realistic and complex) observables is able to produce usable RV corrections without using the information about the Doppler shifts themselves. We present the setup and assumptions of our study in Sect. 2, including the different activity indices studied, two stars used as study cases, the models and software used to generate synthetic time series (starsim), and the methodologies and machine learning framework that we have developed to address the problem. The results and discussions are given in Sect. 3, and we provide the conclusions from our study in Sect. 4.
2 Setup
2.1 Tracers for stellar activity
In the Doppler technique, the stellar spectrum is measured with high spectral resolution (ℛ > 50 000). The Doppler shift of the spectrum is then obtained by cross-correlating the observed spectrum with a mask (cross-correlation technique as in Cosentino et al. 2012; Lafarga et al. 2020) or a template built from the same observations (Anglada-Escudé & Butler 2012; Zechmeister et al. 2018). The high resolution of the spectra also allows for simultaneous measurement of spectral characteristics other than the RV. In addition to this, contemporaneous photometric observations can be used to infer the coverage of spots on the star, putting constraints on the expected RV variability. When possible, this photometric monitoring is done in various filter bands (or colours) in order to determine not only the spot coverage but also properties of the spots such as their effective temperatures (Rosich et al. 2020).
The process of measuring precision Doppler shifts with the cross-correlation method consists of consolidating the information of hundreds (thousands) of spectral lines in a cross-correlation profile obtained by performing the correlation of the observed spectra with a predefined weighted mask (list of wavelengths where spectral lines should appear at zero Doppler shift). The resulting CCF profile is equivalent to the mean shape of the spectral lines for each observation. The computation of this CCF profile is typically produced by instrument pipelines such as the data reduction systems (DRS) of the instruments HARPS, HARPS-N, and ESPRESSO, and the raccoon code (Radial velocities and Activity indicators from Cross-COrrelatiON with masks; Lafarga et al. 2020) developed in the context of the CARMENES project. In this study we use raccoon to obtain Doppler shifts and precision measurements of the shape parameters of the CCF.
The RV is measured by fitting a Gaussian function and measuring its mean. Other useful measurements can be obtained from the fitted Gaussian profile, such as the full width at half maximum (FWHM; in m s−1) and the relative depth – or contrast – relative to the continuum (CON; in %). As an indicator of possible changes in the symmetry of the CCF profile, the bisector inverse slope (BIS; in m s−1) is usually measured. As abundantly discussed in the literature, all these indices (FWHM, CON, and BIS, among others) are known to be affected by the presence of spots and other physical effects that are also responsible for the observed spurious Doppler shifts. Therefore, the information needed to produce a clean RV measurement could be, in principle, available in the same observation through the indices. This production of clean RVs from other spectroscopic indices (‘inversion’ hereafter) has been the topic of many research efforts during the last decade, which have achieved only partial success.
2.2 Observational data
In order to base our experiments with synthetic data on realistic observations, we use measurements of two well-studied and representative stars: the very nearby K2-dwarf ε Eridani (Gliese 144; ε Eri hereafter), and the very young M1-dwarf AU Microscopii (Gliese 803; AU Mic hereafter). They are both quite active and show strong stellar contributions to the RVs as well as to all CCF indices. In Table 1, we provide the parameters of these test stars as found in the literature. Both datasets were chosen for having high signal to noise spectra (so observations would not be limited by photon noise), and their observing cadence was quite regular over a relatively short time interval (2–3 months).
The star ε Eri is young, nearby, and has a rotation period of about 11.2 days (Fröhlich 2007). It has a debris disk inclined by 30º (Quillen & Thorndike 2002) with respect to the sky plane, and at least one planetary companion of at least 0.7 MJup in a 7-yr period orbit (Campbell et al. 1988) causing a Doppler signal with a RV semi-amplitude of about 11 m s−1. For this study, we use 204 publicly available spectra obtained with HARPS (3750 Å < λ < 6900 Å, ℛ = 115 000) obtained on 66 quasi-consecutive nights between 5 October 2019 (BJD = 2458762 days) and 1 January 2020 (BJD = 2458850 days) with a total baseline of 88 days1. All observations within a night were consolidated in night average values to produce the 66 epochs that we use throughout the paper.
AU Mic, on the other hand, is a young star located at a distance of 9.71 pc (Plavchan et al. 2020). It rotates with a period of 4.9 days (Krist et al. 2005) and shows strong evidence of differential rotation (dΩ = 9.57 ± 0.52° day−1; Klein et al. 2021). Its debris disk is seen edge-on (Kalas et al. 2005). Since planets are supposed to form in such disks, it could host transiting planets as well. Indeed, Plavchan et al. (2020) and follow-up publications reported the detection of (at least) two transiting planetary companions with orbital periods of 8.5 days, and 18.9 days, and minimum masses of about 20 and 11 M⊕, respectively, inducing possible RV semi-amplitudes of 6 and 8 m s−1. In this study we use 75 CARMENES VIS spectra (5200 Å < λ < 9 600 Å, ℛ = 94600) obtained for this star (available from CARMENES DR1, Ribas et al. 2023), which were observed quite regularly on 37 nights from 14 July 2019 (BJD = 2458679 d) to 9 October 2019 (BJD = 2458766 d) with a total baseline of 87 days. After consolidating the data in night averages, we reach an average time spacing of 2.5 days between consecutive observations.
Our early experiments were run using DRS instrument pipeline data-products for the real data, and raccoon generated measurements on synthetic data. The mismatches were very obvious in all cases and no correction close to what was observed could be obtained from them. This indicated that a high level of consistency was needed in all the algorithms producing observables in the simulations and the real data-products. In order to be fully consistent, we use the raccoon code to retrieve RV, FWHM, BIS, and CON from the CCF using the binary masks as indicated in Table 1, and then adapted the codes in starsim to be fully consistent with them.
For the analyses that follow, it is important to separate what we consider random errors (photon noise, instrumental and other effects generating uncorrelated errors) from activity-induced variability (which has timescales of days, due to the rotation period and its harmonics), especially for the real datasets. To obtain an estimate of the random errors for all the real time series (RVs, but also the activity indices), we performed a pre-whitening procedure using sequential fitting of sinusoids using generalised Lomb–Scargle periodograms (Zechmeister & Kürster 2009). When there is no signal left below a 1% false alarm probability (FAP), we assumed that the remaining variability are these random errors, although they might contain some correlated stellar jitter below the noise level. The standard deviation of these random errors in all the series will later be used to simulate synthetic datasets with realistic observational noise. Table 2 shows the residual RMS from this procedure, and the ratio between the original RMS and the residual RMS after the pre-whitening process, expressed as a percentage. This ratio between the residual RMS compared to the original RMS expressed as a percentile is what we call the relative residual error (RRE), and it will be used in many instances throughout the paper for different time series. We used this value instead because we compared our results to the relative RV change and not to its absolute true value (which would be the accuracy). A depiction of the time series (RV and spectroscopic indices) as obtained from the observations is shown in Figs. 1 (ε Eri) and 2 (AUMic). The data in the figures can be found in Tables B.1 and B.2.
The signal of the stellar rotation period is present in all time series of ε Eri. Probably due to the differential rotation of the star, the rotation period as given in the literature manifests itself more strongly in its second harmonic at 5.6days. By using the pre-whitening procedure described earlier, we achieve RREs between 17% and 25% in all indices.
For AU Mic we find the rotation period in all the datasets except the CON series. As also discussed later, the measurement of the CON series might not be useful for this kind of target and study. For the other indices the achieved RRE is about 30% to 60%.
Next we perform a quick analysis applying a GP using the george package (Ambikasaran et al. 2015) and the quasi-periodic and cosine kernel (Perger et al. 2021), and exploring the parameter space with a Monte Carlo Markov chain (MCMC) using emcee (Foreman-Mackey et al. 2013). We show in Fig. 3 the posterior distributions for the period hyperparameters 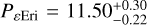 days and PAU Mic = 4.87 ± 0.01 days, and
days and PAU Mic = 4.87 ± 0.01 days, and 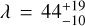 days and
days and 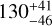 days, where λ is the characteristic decay time of the correlations (related to the average time it takes for a spot to change substantially in size or location, or even disappear) for the RVs of ε Eriand AUMic, respectively.
days, where λ is the characteristic decay time of the correlations (related to the average time it takes for a spot to change substantially in size or location, or even disappear) for the RVs of ε Eriand AUMic, respectively.
Literature and starsim parameters for ε Eridani, and AU Microscopii, and their planetary companions.
Time-series data characteristics of 66 nightly binned data points of ε Eri using HARPS (top) and of 37 nightly binned data points from AUMic using CARMENES VIS (bottom), both extracted by raccoon.
 |
Fig. 1 Nightly binned time series (left panels) and their periodograms (right panels) of ε Eri extracted with raccoon. From top to bottom they are RV, BIS, FWHM, and CON. Dashed blue horizontal lines indicate FAP levels of 0.1, 1, and 10%, and the vertical orange lines indicate the frequency of the rotation period of 11.2 days and its second harmonic. |
 |
Fig. 2 Nightly binned time series (left panels) and their periodograms (right panels) of AU Mic extracted with raccoon. From top to bottom they are RV, BIS, FWHM, and CON. For the CON, one obvious outlier is not in this diagram. Dashed blue horizontal lines indicate FAP levels of 0.1, 1, and 10%, and the vertical orange lines indicate the frequency of the rotation period of 4.9 days and its second harmonic. The vertical green lines mark the periods of the two planetary companions. |
 |
Fig. 3 Histogram of the MCMC posterior distributions for hyperparameters P (left panels) and λ (right panels) of GPs applied to ε Eri (top panels) and AU Mic (bottom panels) RV data using the quasi-periodic and cosine kernel. |
2.3 Synthetic data
We used the starsim code (Herrero et al. 2016) to model time-series data for a spotted rotating star with the characteristics of our two tests stars, ε Eri and AUMic. The current version of starsim2 (Baroch et al., in prep.) is able to produce synthetic photometry for a predefined filter from low-resolution model spectra for our study, we produce light curves in the Johnson V, R, and I filters. CCFs at each observation epoch are also generated from high-resolution Phoenix spectra (Husser et al. 2013) of a predefined wavelength range, from which RVs, and the CCF activity indices are then measured. The calculations make use of important stellar parameters, geometric effects, and of the distribution of magnetically active regions (spots hereafter) on the surface of the star. One simulation consists of a list of epochs and their corresponding RV, FWHM, BIS, CON, and V, B, and I photometric bands, all assumed to be simultaneous and without errors.
Preliminary experiments (not described here for brevity) showed that constraining the simulations to the known physical parameters of the star is rather important to improve the inversion capabilities of the algorithms used. This makes sense as NNs are known to be good tools for interpolation as long as the training set densely populates the region of the parameter space of interest. The priors of the most important stellar variables as adopted for the creation of the synthetic datasets of the two test stars are shown in Table1. For the mass, radius, effective temperature, inclination of the rotation axes, and rotation period, we used the published values in their error limits. In the case of ε Eri, we adapted a range for the rotation period in order to include the larger periodicities found by our pre-whitening, as shown in Table 2. We chose further fixed values for metallicity and surface gravity. In the algorithm, the convective blueshift is given in units of the solar shift of −325 m s−1 (e.g. Löhner-Böttcher et al. 2018; Stief et al. 2019), and the differential rotation in units of the solar value dΩ⊙ = 3.15° day−1 (following Beck 2000). Furthermore, the binary masks of the corresponding stellar type and wavelength range were used to calculate the CCFs. In each simulation, the physical properties of the star are randomly initialised within these priors, thus implicitly accounting for the uncertainty in the basic properties of the star at simulation level (training and test sets).
With starsim, it is also required to specify the distribution of the spots on the stellar surface (assumed circular) in what we call a spot map. The contribution of a spot in a simulation is taken into account when producing a CCF integrated over the stellar disk (spots have a different CCF than the photosphere because of lower temperature and different spectral features). For the spots we also use Phoenix spectra of lower temperature as given by the ΔT parameter in Table 1, and a modified bisector following what is observed on the Sun (Herrero et al. 2016). The priors of these parameter are specified by following empirical studies on a variety of stellar types in Herbst et al. (2021). In the input spot map each spot is described by five parameters: time of appearance, lifetime, longitude, co-latitude, and radius. Taking into account that the contribution from stellar activity is clearly visible in all sets at all times (no flat regions in the observational data), and to match both absolute value and variation of each time series, we use randomly 25 to 40 dark spots to ensure that at least one to two spots are visible at any observing time. All spot map parameters are also generated randomly following a uniform distribution: radii (2.5–4º), lifetime τ (5–100 days), time of appearance (t0 − τ to t0 + 100 days), co-latitude (0–180º), and longitude (0–360º). The values adopted try to encompass the intervals of the most likely values from these parameters following the GP analysis from the previous section.
To investigate the importance of sampling in the ability to correct for stellar activity, we generated simulations following five different time samplings with starsim: (i) uniform, consisting of 100 data points uniformly distributed over 100 days; (ii) random1, consisting of 100 data points randomly distributed over the same time baseline; (iii) gap1, consisting of 60 randomly distributed data points from time 0 day to 50 days and 40 data points from time 70 days to 100 days, thereby creating an artificial visibility gap as we often encounter it in actual astronomical campaigns; (iv) random2, which uses 100 randomly chosen out of the 300 data points in uniform, random1, and gap1; and (v) gap2, which has 40 data points in the first 30 days, and 60 in the last 45 days of the 300 data points, leaving open another gap. The random2 and gap2 time samplings were generated from subsets of the previous samplings to save simulation time (most computationally intensive step as discussed later). The 100 days time interval was chosen to cover the rotation period of both test stars a sufficient number of times. We then generate 600 000 and 1 000 000 simulations for ε Eri and AU Mic, respectively, for each of these time samplings.
We checked for possible linear relations between the synthetic RVs and the activity indices. Applying those relations, we reach RREs for V, I, BIS, FWHM, and CON indices of 99%, 99%, 79%, 98%, and 98% for ε Eri, and 99%, 99%, 73%, 86%, and 95% for AU Mic, respectively. If we apply a linear fit to all six datasets, we achieve RREs of 77% for ε Eri and 72% for AU Mic, respectively, showing the importance of a more sophisticated and RV-independent approach for our synthetic data.
2.4 Neural network architectures
Finding the right format for the inputs and defining an adequate NN architecture are some of the major challenges when applying NN approaches to new types of data. Neural networks with several fully connected layers have a huge number of parameters, thus enabling a fit to almost anything. However, being so general, they are slow to train (and may not even converge at all) and often lead to over-fitting (i.e. the NN is able to reproduce the training set, but performs poorly on a test sample). For an NN to be able to make non-linear predictions, more than two layers are needed. Since the data we are analysing contain strong correlations between neighbouring points, and these correlations encode the physics, we propose an NN composed of a small number of convolutional layers first, followed by three dense fully connected layers. This architecture is similar to those used in pattern recognition in images, which also looks for patterns in the spatial domain to identify features in an image. We use the open-source python package PyTorch3. We also run experiments with Keras/Tensorflow4, which is the other most popular platform for NN development. Neither the results nor the performance depended much on the choice of the framework, so all results presented here were produced using PyTorch. In all cases, we installed the ‘graphics processing unit’ (GPU-)enabled versions of the libraries to take full advantage of our hardware capabilities. The codes were developed in python. Both the starsim simulations and the training of the NN were executed on two identical dedicated machines (Intel Core i7-10700, which contains eight ‘central processing unit’ (CPU) cores, and equipped with a GPU-NVIDIA GeForce RTX 2060 SUPER each).
An input sample consists of Ni time series of indices (or channels) corresponding to the activity indices used for each test. The target (also called label) of each input sample is the corresponding RV time series of the corresponding simulation. For example, for a synthetic set with 100 epochs, a NN network trained to produce RVs from FWHM and BIS data, would have two channels (FWHM and BIS) of 100 data points each as input, and one output list with 100 RV data points. All time series are mean subtracted and normalised by the full ensemble standard deviation for that index (or label). Thereby we conserve the information of the relative strengths of the variations of the indices.
The input layer is then an array of 1 × 100 × Ni neurons. The first two layers are convolutional layers with small kernel sizes (typically three elements only), and a rather large number of channels (typically 32). This means that in the first convolu-tional layer, the information of each point and neighbours will be taken into account at the layer output. The second convolutional layer repeats the same operation, meaning that, effectively, the NN will take into account the value of each point and the ±2 closest neighbours. Tests using kernels with larger sizes or the inclusion of more convolutional layers did not improve the performance of the NN significantly. The outputs of all neurons of the second convolutional layer are then arranged in a single list (so-called flatten operation), and this is then fed to three fully connected layers with 300 neurons each (also called dense layers). The output layer is a fully connected layer with 100 neurons. Except for the output layer (which has a linear function as its response), the response functions used in all other layers were the so-called rectified linear unit (ReLU; f(x) = max(0, x)) plus a constant offset (also called bias). We tested alternative functions (such as sigmoids), finding similar performances but at the cost of more training iterations and longer training time per iteration. As a cost function, we use the standard deviation of the difference between the simulated RVs (label) and the RV predictions by the NN (output). Training a NN consists of finding a combination of neuron parameters (weights and biases) that minimises this cost function. The optimisation procedures and algorithms are already included in the aforementioned libraries (PyTorch and/or Tensorflow).
For training, we use 90% of the synthetic sets, and 10% of the sets are reserved for testing and validation. On average, we found that these architectures would reach reasonable convergence (as measured by non-significant improvement of the cost function after 5 iterations) with about 50 training epochs. As an important check, we verified that the cost function applied to the test sets would always be equal (or slightly worse) than on the training sample, thus ensuring that we were not incurring in over-fitting. We show a visual representation of the NN architecture as described here in Fig. 4, as well as some computing-time benchmark experiments in Table 3.
 |
Fig. 4 Neural network architecture used throughout this study. The input layer consists of 100 measurements of Ni activity indicators, and the output layer (or label) is the corresponding 100 RVs. The first two hidden layers are convolutional layers, each with 32 kernels applied onto the three neighbouring neurons. After the second convolutional layer, all the outputs for all the neurons are organised in a linear vector of neurons, and three subsequent, fully connected layers are used to transform this vector into the final RV prediction. The response functions of all the neurons are the so-called ReLus, which clearly outperforms other non-linear functions in terms of convergence speed and lower computational time. As discussed in the text, small modifications to this architecture do not significantly change the obtained results. |
3 Results
In this section, we perform a series of experiments to benchmark the inversion performance of different activity indicators. Each experiment consists of taking a time sampling (uniform, random, gap) and using a combination of activity indicators as the input for the NN. Then, the RRE of the RVs is computed for the full ensemble of outputs and used as a figure of merit of the procedure. We first do it with simulated datasets without uncertainties in the input nor the output RVs (Sect. 3.1), and then we replicate all the experiments for the uniform time sampling adding realistic noise (using the error value from Table 2) to the inputs to quantify the impact of uncertainties in the training set and the overall performances (Sect. 3.2).
From the first experiments, it became clear that the most computationally intensive part of this study was the simulation of the synthetic datasets and not the training of the NN. With our setup, simulating one dataset consisting of RV, FWHM, BIS, CON, V, B, and I takes about one second per CPU. Assuming 8 cores, it takes about 1.5 days to complete 106 simulations.
These simulations can be easily parallelised, the total computing time being proportional to the inverse of the number of CPUs employed. For illustrative purposes, Table 3 shows the computer time needed to perform one training iteration, showing that these are relatively small (the 50 epoch values that we use to train each NN can be reached within a few minutes). The table illustrates the advantage of using GPU-enabled computers and choosing a suitable size of a parameter called a batch size, which is the number of samples used in a single optimisation step within one training epoch. This is a key parameter to take full advantage of the parallel computing power of GPUs as abundantly discussed in NN literature. A large batch size uses many samples to adjusts all the parameters of an NN (sends a large number of samples to the GPU to perform the back propagation adjustment of the NN), but may smooth out subtle effects contained in the simulations thus making it more difficult to converge to an optimal solution. We found that an optimal batch size of 512 samples per training step was sufficient to reproduce the convergence performance of smaller batch sizes while keeping a the computing time quite low.
Numerical performance tests as a function of batch size.
Relative residual error of the RVs in percent after 50 training runs for the NNs using 540 000 starsim models for different time samplings and for different kinds and numbers of activity indices as input for ε Eri.
Relative residual error of the RVs in % after 50 training runs for the NNs using 900 000 starsim models for different time samplings and for different kinds and numbers of activity indices as input for AU Mic.
3.1 Neural network training without observational errors
Tables 4 and 5 show the RRE for each exercise, that is to say, the relative residual RV error. The combinations of activity indices used in each exercise are shown in the left column. We show further the values averaged over all time samplings (average), and the results obtained for the uniform time sampling when we inject realistic noise (see Table 2) to the input indices (see Sect. 3.2). Figure 5 visually shows the same results. Additionally, the RRE of the test sets as a function of the number of epochs is shown in Figs. 6 and 7 for both stars. There, we used the NNs trained with the uniform time sampling and without additional errors, and applied it to the test sets without (left panels) and with (right panels) the additional errors for the test input sets, respectively.
As a further illustration, we show one random synthetic RV test set from the uniform time sampling and the output of the NNs with all the combinations of input data (i.e. index time series) in the left panels of Fig. 8. From the top, we see in the first panel the usage of only one index, then two indices, then the three indices from photometry and from the CCF, and then all six index time-series data. The model itself is shown by the black dots and line. In the right panels, the difference between the RV model and its corresponding prediction by the NN is shown.
In general, we find that even using a single index, there is always a reduction in RRE. But even for data without uncertainties, not all the activity-induced RV variability can be removed from the observations. We note that this inversion error marks the floor of what is possible given the information in the corresponding index (these are intrinsic model degeneracies) and our NN implementation. Additional indices at the same epochs (additional spectroscopic observables) and/or additional non-simultaneous measurements (e.g. contemporaneous photometric observations) could improve these floor values, but one should expect worse performances when applied to real, noisy observations.
The most important take-home messages from these experiments can be summarised as follows. First, the proposed NN architecture is sufficient to produce high quality corrections to RV data. The NNs converge after only a few training epochs irrespective of the fine details of the NN algorithm (response function, training strategy or other technical details). The convergence and non-overfitting can be easily verified by checking that the RRE of the test sample (which is the merit function also used during training) is similar or slightly larger than the RRE of the training sample, which is always the case in all the experiments.
Second, line-profile indices contain enough information to successfully train the algorithms, and produce a significant correction of the activity signals in the RV time series. Despite the existence of correlations between RV and indices has been demonstrated in the past, this is the first time (to our knowledge) where it is shown that there is enough information in them to reproduce the RV activity signal.
Third, the best performing single index was found to be CON, rather than BIS, which would have been expected according to Lafarga et al. (2020). This indicates that data, model-driven approaches rather than guesswork or theoretical expectations are preferable in future activity and RV noise investigations. It is possible that other indices provide even better performances than those discussed here.
Fourth, combining multiple indices is the most effective way to achieve a higher RV reduction, given that these measurements can be obtained from the same spectra used to obtain the RV measurement. The actual reduction, and the most relevant index is star dependent (as has been suspected for some time now) and, in general, one should aim at using a combination of all possible indices that show variability consistent with stellar activity. In particular, using all the available CCF indices, the simulations indicate that we can reach a RRE of 5.1, and 2.4% for ε Eri and AU Mic, respectively. This is better than half the value as for any single index for ε Eri, but is remarkably lower (eight times) for AU Mic.
Fifth, simultaneous photometric time series seem to contain the least information of the tested indices, worsening for the redder filters. Even when combined, they only match the performance of a single CCF index as input. Especially for AU Mic, the obtained RREs are only at the 55% level, which is a rather poor performance. Using all the available filters, we can reach RREs of 9 and 49% for ε Eri and AU Mic, respectively. This is likely caused by intrinsic degeneracies when mapping photometric signals into putative spots (and corresponding RV signal), as often happens in light curve-only inversion cases. For example, a small equatorial spot can produce the same photometric signal than a small polar one, but its RV counterpart can be rather different. In any case, adding photometry always helps, and the putative use of photometric time samplings denser than the RV sampling (as often happens when using space-based photometry) remains to be investigated.
Sixth, a larger number of data points seems to improve overall performance. Probably due to the smaller number of data points (37 versus 66) and the later spectral type, the RRE of the RVs across all input data combinations is more than double in the AU Mic data compared to the ε Eri sets, and this is despite the larger training data sample (540 000 versus 900 000).
Seventh, injecting noise in the test sets does not improve performance when applied to noiseless sets. That is, when trained with synthetic data without errors, the performance on test data with errors we observed that the RV RRE is not as good, and comparable to training without errors (as discussed in the next section). This is illustrated in Figs. 6 and 7.
Eighth, the precise time sampling does not have a strong influence on the outcome, even with seasonal gaps. We remark, however, that all the test samplings used here cover the rotation period of both stars quite well (several cycles, more than one point per cycle). More tests would be needed to re-analyse old survey data, which typically spans several years and with observations clustered in seasons of a few months each year.
Finally, the time-tags of the observations were NOT used in the experiments presented here (Tables 4 and 5). Experiments ran with time-tags and all combinations of indices converged much more slowly than those without them. This is something we did not expect that requires further investigation. The outcome of a test including the time tags as inputs together with the BIS index for ε Eri is shown in Table 4.
 |
Fig. 5 RRE after the application of the trained NNs on the 540 000 and 900 000 starsim models in percentage for ε Eri (top) and AU Mic (bottom), respectively. We mark the different activity-index combinations used for the NN training. The average RV reduction for the different time samplings average is given for ε Eri in red and for AU Mic in blue. The yellow and green bars indicate the value, if the relative additional error from Table 2 was added to the input data. |
 |
Fig. 6 Evolution of the RRE of the 60 000 synthetic ε Eri test set RVs for the 50 epochs for the NNs using all different combinations of input data, i.e. activity index time series as indicated, the uniform time sampling, and no additional error on the training input sets. The curves are shown for the test sets without additional uncertainties as calculated by starsim (left panel, dashed lines) and for the case where we included the error value from Table 2 for each activity index into the test sets (right panel, full drawn lines). |
 |
Fig. 7 Evolution of the RRE of the 100 000 synthetic AU Mic test set RVs for the 50 epochs for the NNs using all different combinations of input data. See Fig. 6 for more details. |
 |
Fig. 8 Illustration of the quality of the RV correction as a function of the input indices used (random synthetic set chosen) for the ε Eri data and the uniform time sampling (black lines). The output predictions of the NNs with all the combinations of input data, i.e. index time series, are illustrated with different colours. The outcome of using only one index is shown in the top panel, further down two indices, then combinations of three indices (photometry and CCF), and then time-series data from all six indices. Radial velocities are shown as modelled by starsim. The legends contain the RV RRE of this particular set for each combination of index inputs. The residuals (differences between RV predictions and the simulated RV) are shown in the right panels. |
3.2 Neural network training with realistic observational errors
Since noise is an intrinsic characteristic of real data that shall also be learned, we considered whether we should train our NN with noisy synthetic observations. In the following, we summarise the three conclusions drawn by running tests with noisy training sets, data from which are presented in Tables 4 and 5 and Fig. 5.
First, the performance of CCF indices becomes quite affected when using noisy input indices (and their combinations) when their RRE exceeds 50% (FWHM and CON for AU Mic). Uncertainties in activity indices are not as well understood as for RV measurements, so this calls for a quick examination of possible periodic signals in all the indices to be used before deciding whether an index shall be used in the training and later de-trending of real time series. A real case example is discussed later in the section devoted to AU Mic real observations (Sect. 3.3.2), where we found that using the CON index (which does not show the same periodicities as the other indices) makes things worse.
Second, and along the same line, uncertainties in the photometry at the few percent level (which are quite easy to obtain, even from the ground) do not affect the inversion power of the photometry as an input. To illustrate this in the tests presented here, the precision of the photometric time series was arbitrarily chosen to be at 10% level, which is rather high (see Table 2). Despite this high value, this does not influence the outcome very much confirming that the lesser inversion power of the photometry comes from intrinsic physical degeneracies.
Finally, the RRE of an activity index should be 30–40% smaller than the contribution to the RV RRE caused by stellar activity variability. If larger (FWHM and CON for AU Mic), the introduction of those errors degrades performances very much (RV RREs form 16–44%, and 16–45% in these example cases).
3.3 Application to observational data
3.3.1 Results on ε Eridani
Before jumping into generating a final set of synthetic training sets, we performed an exact inversion using the starsim code to verify that the priors set in our simulations matched what would be obtained if attempting a more classic full stellar fitting approach. This process is explained in detail in Appendix A. Most importantly, the starsim inversion resulted in differences in the stellar parameters compared to the literature ones, especially the stellar radius. With this new parameters, we then produce 100 000 starsim simulations of RV, BIS, FWHM, and CON time series, each using the same original time sampling consisting in 66 observations. For the spot map, we use the random procedure as used in previous sections to avoid producing simulations too specific to the data. To train the NN, we add uncertainties and errors to the inputs and outputs as described in previous sections since in the case for the real observational data the NN performance is significantly enhanced. We then trained our NNs again on 50 training epochs. We achieved an RV RRE down to 10% on our 100 000 training sets, which is slightly larger than, but comparable to, the experiments (7.5%) in the previous section.
When applied to the real dataset, we obtain the correction shown in Fig. 9. The black curve shows the observed RVs and the red curve shows the outputs of a trained NN with inputs of BIS, FWHM, and CON from the observations. The periodograms of the real and predicted RVs are also shown in the panel below. The corresponding RV RRE is 45% (from 4.4 m s−1 to 2.0 m s−1), which is quite far from the nominal 10% inferred from the training and test samples. We argue that at the level below a few m s−1, the physics of the activity-induced effects are not yet properly included in the simulations and, possibly, some instrumental systematic errors are also affecting the result (e.g. uncertainty in the wavelength solution of each night of observation). More work on the models is needed to identify all possible sources of such mismatches. In any case, the reduction of the RMS to below 2 m s−1 already places ε Eri as a high quality target (similar ‘jitter’ as the Sun) for exoplanet searches (enough sensitivity to detect close-in super-Earths).
3.3.2 Results on AU Microscopii
We applied the same procedure to the case of AU Mic, but without performing the initial inversion with starsim. Instead, we used the stellar parameters as introduced in Table 1, the original time sampling containing 37 data points, and randomised spot maps as introduced in Sect. 2.3.
For this experiment, we created 400 000 new starsim simulations calculating RV, BIS, and FWHM, and we include again the observational errors (see Table 2) into the time series since it has been shown that it results in lower RV RREs. We then train our NN for 50 training epochs as before and reach an RV RRE of 10% for the test set. This is essentially the same value as in the previous test. We show the RV observations and the NN output in the top panel of Fig. 10. In the bottom panel, we show the periodograms of those two time series and add in green the periodogram of the difference.
As opposed to the expectations from all previous experiments, the inclusion of the CON index produced very poor performances when applied to the real data. After a close examination of the CON measurements and corresponding periodograms (see Fig. 2) it is clear that they do not contain the same characteristic periodicities as the other indices, or the RV. We attribute this to the fact that CON measurements from CARMENES are affected by additional noise sources not included in the simulations, including instrumental and astrophysical effects. For example, CON measurements are very sensitive to the continuum determination (and corresponding line-depths of the lines). Therefore, the source of this systematic error might be instrumental (e.g. change in the instrumental setup such as using simultaneous calibration lamps, sky background contribution, change in gain in the detector), but it could also be associated with astrophysical phenomena causing changes in the spectral continuum. For these reasons, we only use the BIS and FWHM indices for the performance analysis on real observations of AU Mic.
The correction obtained on the RVs is rather good, reaching to a RV RRE down to 10%, the same as for the starsim training sets. The cleaned RVs (subtraction of the computed correction to the observed ones), do not contain any trace of the rotation period. Moreover, the resulting scatter is consistent with the presence of the Doppler signals of the planets (although there are not enough observations to confirm them with only these 37 epochs). As opposed to ε Eri, most of the activity-induced variability is clearly related to the dark spot effect on a fast rotating star (peak to peak variability over 100 m s−1), which is one of the better understood RV noise phenomena. Although the relative improvement is rather good, we also note that the residual RV variability is around 13 m s−1, which is substantially poorer than the one from ε Eri. This is is again consistent with the models lacking relevant physical realism at the few m s−1 level. Using other de-trending techniques and evidence of periodic transits from photometric observations (Cale et al. 2021), the possible amplitude of two low mass companions have been inferred at the level of ~10 m s−1, which could explain part of this variability as well (Keplerian orbits have not been included in the training samples in any case). We show the residual RVs in Fig. 11, and illustrate the possible contribution of the signals of the two published planetary companions to the residual RV noise (red and green dashed curves for the individual planets, and the blue curve for their combination).
 |
Fig. 9 RVs (top panel) and periodogram (bottom panel) of observational ε Eri data in black. In red, we show the prediction produced by our NN using BIS, FWHM, and CON indices as input. In green we show the periodogram of the cleaned data, that is, the difference between the observed and modelled RVs. The rotation period and its second harmonic are indicated as vertical dashed grey lines. The level of RMS reduction is about 45%. |
 |
Fig. 10 Results for the AU Mic observations. Top panel: RVs from AU Mic as observed (black) and as modelled by the trained NN using BIS, and FWHM indices with their respective RREs. Bottom panel: periodogram of the observed RVs (black), the NN output (red), and the difference (green). Dashed black lines indicate the rotation period and its second harmonic, and dashed blue lines indicate the orbits of the two planetary companions of AU Mic. We reach RREs as low as 10%. |
 |
Fig. 11 Residual RVs of the 37 AU Mic observations after applying the NN using BIS and FWHM indices (black dots). We further show the curves introduced to the RVs by the two detected planets of AU Mic (dashed red and green lines) and their combination (blue curve). |
4 Conclusions
We have developed a model-driven machine learning approach using convolutional deep NNs to produce corrections to RV time series contaminated by stellar activity. It is model driven in the sense that synthetic datasets were used to train the algorithms. Stellar activity manifests itself in observables other than RVs, and this additional information has already been used to mitigate the influence of activity on the RVs. However, it was not entirely clear whether the information contained in the individual and combined observables was sufficient to invert the problem and produce a correction in a more general and independent way, not using the information contained in the RVs. This work applied to the test datasets demonstrates that the inversion is possible and that it is solvable, without requiring explicit expressions for all the relations of the indices with the RV variability.
We identified NN architectures that are well suited to the task (a few convolutional layers followed by a few dense layers) and determined that they can be trained with quite modest computational resources. In fact, producing realistic simulations is the most computer-intensive part of the processing.
We assessed the inversion power of the classic activity indices used in exoplanet detection papers and find that combinations of them are sufficient to provide corrections below the photon noise of state-of-the-art spectrometers when we consider the effects of spots combined with rotation and convective blueshift only (~10 cm s−1, the goal of ESPRESSO). Photometric information obtained simultaneously with the observations did not have that much inversion power, but on its own can still produce a significant reduction in RV noise. Non-simultaneous (space-based) multi-band photometry is likely to perform better, but it will require additional work and, possibly, slightly different NN architectural choices.
We applied our technique to two real datasets, achieving a significant reduction in the activity-induced RV variability, but the results are not yet at the level of the photon noise of the observations. This is likely caused by astrophysical phenomena yet to be included in the simulations, and due to systematic (instrumental and algorithmic) errors in the measurements of both the activity indicators and the RVs.
As a future step, we plan to test the machine learning framework with more models that include additional activity phenomena. In particular, models will have to include more complex phenomena, such as non-uniform convective flows (granulation, supergranulation, and meridional flows), magnetic distortion of spectral lines (Zeeman splitting), different sensitivities of some spectral lines to stellar activity, and the effect of bright and chro-mospherically active regions to apparent Doppler shifts (plages, faculae, or others).
Acknowledgements
CARMENES is an instrument at the Centro Astronómico Hispano en Andalucía (CAHA) at Calar Alto (Almería, Spain), operated jointly by the Junta de Andalucía and the Institute de Astrofísica de Andalucía (CSIC). CARMENES was funded by the Max-Planck-Gesellschaft (MPG), the Consejo Superior de Investigaciones Científicas (CSIC), the Ministerio de Economía y Competitividad (MINECO) and the European Regional Development Fund (ERDF) through projects FICTS-2011-02, ICTS-2017-07-CAHA-4, and CAHA16-CE-3978, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Institut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Cen-tro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the MINECO, the Deutsche Forschungsgemeinschaft through the Major Research Instrumentation Programme and Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. We acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 and the ERDF “A way of making Europe” through projects PID2020-120375GB-I00, PID2019-109522GB-C5[1:4], PGC2018-098153-B-C33, and the Centre of Excellence “Severo Ochoa” and “Maria de Maeztu” awards to the Institut de Ciències de l’Espai (CEX2020-001058-M) Instituto de Astrofísica de Canarias (CEX2019-000920-S), Instituto de Astrofísica de Andalucía (SEV-2017-0709), and Centro de Astrobiolog a (MDM-2017-0737); the Generalitat de Catalunya/CERCA programme; and the DFG through priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (JE 701/5-1). Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 0104.C-0863(A); also called Red Dots. We also thank the Red Dots members Carole Haswell, Mario Damasso, Fabio del Sordo and Stefan Dreizler for their participation in the preparation of the Red Dots ESO observations with HARPS, their comments and insightful discussions.
Appendix A starsim data inversion for ε Eridani
With the current version of the starsim code, we calculated the inversion of the algorithm, that is, using the observational time-series data of ε Eri to fit for stellar parameters and an average distribution of stellar spots. Differently from our initial approach, we use a fixed number of 10 different dark spots up to 15° in radius, appearing at any point of the calculated time interval randomly and stellar parameters floating around the measurements as given in Table 1. As a result, we achieve a best fit on observational RV, BIS, and FWHM time series, as shown in Fig. A.1. This is achieved for the absolute offsets for the three datasets as given in the top right of each panel. In Table A.1, we show the differences for the stellar parameters from the literature and from our best data inversion. Especially R* does differ significantly. We note that ΔCB, i, and dΩ were fixed for the inversion test. A histogram of the posterior distributions for all the inversion iterations of the five parameters of the 10 spots are shown in Fig. A.2. We can see a clear clustering around longitudes 50 to 150 and 275 to 325º, as well as co-latitudes ranging between 20 and 40º. Spots show mostly 2 to 4º radius resulting in absolute spot filling factors of 2.5 to 3.5%. Spot lifetimes seem to be mostly in between 40 to 60 d, coinciding thereby with the results from the GP, as shown in Fig. 3.
 |
Fig. A.1 Results of the starsim inversions for ε Eri using RV (top panel), FWHM (middle panel), and BIS (bottom panel). Blue dots indicate the measurements as extracted from raccoon from the observed spectra. The black curve shows the average fit and the grey area the uncertainty of the different solutions. The dashed red curve shows the solution with the largest likelihood. On the top right, the offset for each time series is indicated as well as its additional jitter, both of which show the shortcomings of the modelling of time-series data with starsim. |
Differences of important stellar parameters from the literature and from our data inversion with starsim
 |
Fig. A.2 Histogram of the posterior distribution of the five parameters of the spot maps containing ten spots of the starsim inversion applied to observational ε Eri data RV, BIS, and FWHM. |
Appendix B Tables of observational data
66 nightly binned time-series data points extracted with raccoon from 204 HARPS spectra of ε Eri.
37 nightly binned time-series data points extracted with raccoon from 75 CARMENES VIS spectra for AU Microscopii.
References
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D.W., & O’Neil, M. 2015, IEEE Trans. Pattern Anal. Mach. Intell., 38, 252 [Google Scholar]
- Anglada-Escudé, G., & Butler, R.P. 2012, ApJS, 200, 15 [CrossRef] [Google Scholar]
- Baines, E.K., & Armstrong, J.T. 2012, ApJ, 744, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, J.G. 2000, Sol. Phys., 191, 47 [CrossRef] [Google Scholar]
- Borucki, W.J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Cale, B.L., Reefe, M., Plavchan, P., et al. 2021, AJ, 162, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, B., Walker, G.A.H., & Yang, S. 1988, ApJ, 331, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Mortier, A., Phillips, D., et al. 2019, MNRAS, 487, 1082 [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 84461V [Google Scholar]
- Dattilo, A., Vanderburg, A., Shallue, C.J., et al. 2019, AJ, 157, 169 [NASA ADS] [CrossRef] [Google Scholar]
- de Beurs, Z.L., Vanderburg, A., Shallue, C.J., et al. 2022, AJ, 164, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [Google Scholar]
- Dumusque, X., Boisse, I., & Santos, N.C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D.W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, H.E. 2007, Astron. Nachr., 328, 1037 [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
- Gaidos, E., Mann, A.W., Lépine, S., et al. 2014, MNRAS, 443, 2561 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes da Silva, J., Santos, N.C., Adibekyan, V., et al. 2021, A&A, 646, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, G., Carlson, M.K., & Tobin, R.W. 2010, MNRAS, 403, 1368 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, K., Papaioannou, A., Airapetian, V.S., & Atri, D. 2021, ApJ, 907, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Ribas, I., Jordi, C., et al. 2016, A&A, 586, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husser, T.O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janson, M., Quanz, S.P., Carson, J.C., et al. 2015, A&A, 574, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalas, P., Graham, J.R., & Clampin, M. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, P.C., & McNeil, R.C. 1989, ApJS, 71, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, B., Donati, J.-F., Moutou, C., et al. 2021, MNRAS, 502, 188 [Google Scholar]
- Krist, J.E., Ardila, D.R., Golimowski, D.A., et al. 2005, AJ, 129, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Lafarga, M., Ribas, I., Lovis, C., et al. 2020, A&A, 636, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liebing, F., Jeffers, S.V., Reiners, A., & Zechmeister, M. 2021, A&A, 654, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Llop-Sayson, J., Wang, J.J., Ruffio, J.-B., et al. 2021, AJ, 162, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Löhner-Böttcher, J., Schmidt, W., Stief, F., Steinmetz, T., & Holzwarth, R. 2018, A&A, 611, A4 [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meunier, N., Lagrange, A.-M., Mbemba Kabuiku, L., et al. 2016, in 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), 104 [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perger, M., García-Piquer, A., Ribas, I., et al. 2017, A&A, 598, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perger, M., Scandariato, G., Ribas, I., et al. 2019, A&A, 624, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perger, M., Anglada-Escudé, G., Ribas, I., et al. 2021, A&A, 645, A58 [EDP Sciences] [Google Scholar]
- Plavchan, P., Barclay, T., Gagné, J., et al. 2020, Nature, 582, 497 [Google Scholar]
- Quillen, A.C., & Thorndike, S. 2002, ApJ, 578, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., CARMENES Consortium, Amado, P.J., et al. 2020, SPIE Conf. Ser., 11447, 114473C [Google Scholar]
- Ribas, I., Reiners, A., Zechmeister, M., et al. 2023, A&A, 670, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G.R., Winn, J.N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
- Rosich, A., Herrero, E., Mallonn, M., et al. 2020, A&A, 641, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N.C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shallue, C.J., & Vanderburg, A. 2018, AJ, 155, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Stief, F., Löhner-Böttcher, J., Schmidt, W., Steinmetz, T., & Holzwarth, R. 2019, A&A, 622, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J.I., & Esposito, M. 2015, MNRAS, 452, 2745 [CrossRef] [Google Scholar]
- Torres, C.A.O., Quast, G.R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, S.S., Allen, S.L., Bigelow, B.C., et al. 1994, SPIE Conf. Ser., 2198, 362 [NASA ADS] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P.J., et al. 2018, A&A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zicher, N., Barragán, O., Klein, B., et al. 2022, MNRAS, 512, 3060 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Literature and starsim parameters for ε Eridani, and AU Microscopii, and their planetary companions.
Time-series data characteristics of 66 nightly binned data points of ε Eri using HARPS (top) and of 37 nightly binned data points from AUMic using CARMENES VIS (bottom), both extracted by raccoon.
Relative residual error of the RVs in percent after 50 training runs for the NNs using 540 000 starsim models for different time samplings and for different kinds and numbers of activity indices as input for ε Eri.
Relative residual error of the RVs in % after 50 training runs for the NNs using 900 000 starsim models for different time samplings and for different kinds and numbers of activity indices as input for AU Mic.
Differences of important stellar parameters from the literature and from our data inversion with starsim
66 nightly binned time-series data points extracted with raccoon from 204 HARPS spectra of ε Eri.
37 nightly binned time-series data points extracted with raccoon from 75 CARMENES VIS spectra for AU Microscopii.
All Figures
 |
Fig. 1 Nightly binned time series (left panels) and their periodograms (right panels) of ε Eri extracted with raccoon. From top to bottom they are RV, BIS, FWHM, and CON. Dashed blue horizontal lines indicate FAP levels of 0.1, 1, and 10%, and the vertical orange lines indicate the frequency of the rotation period of 11.2 days and its second harmonic. |
| In the text | |
 |
Fig. 2 Nightly binned time series (left panels) and their periodograms (right panels) of AU Mic extracted with raccoon. From top to bottom they are RV, BIS, FWHM, and CON. For the CON, one obvious outlier is not in this diagram. Dashed blue horizontal lines indicate FAP levels of 0.1, 1, and 10%, and the vertical orange lines indicate the frequency of the rotation period of 4.9 days and its second harmonic. The vertical green lines mark the periods of the two planetary companions. |
| In the text | |
 |
Fig. 3 Histogram of the MCMC posterior distributions for hyperparameters P (left panels) and λ (right panels) of GPs applied to ε Eri (top panels) and AU Mic (bottom panels) RV data using the quasi-periodic and cosine kernel. |
| In the text | |
 |
Fig. 4 Neural network architecture used throughout this study. The input layer consists of 100 measurements of Ni activity indicators, and the output layer (or label) is the corresponding 100 RVs. The first two hidden layers are convolutional layers, each with 32 kernels applied onto the three neighbouring neurons. After the second convolutional layer, all the outputs for all the neurons are organised in a linear vector of neurons, and three subsequent, fully connected layers are used to transform this vector into the final RV prediction. The response functions of all the neurons are the so-called ReLus, which clearly outperforms other non-linear functions in terms of convergence speed and lower computational time. As discussed in the text, small modifications to this architecture do not significantly change the obtained results. |
| In the text | |
 |
Fig. 5 RRE after the application of the trained NNs on the 540 000 and 900 000 starsim models in percentage for ε Eri (top) and AU Mic (bottom), respectively. We mark the different activity-index combinations used for the NN training. The average RV reduction for the different time samplings average is given for ε Eri in red and for AU Mic in blue. The yellow and green bars indicate the value, if the relative additional error from Table 2 was added to the input data. |
| In the text | |
 |
Fig. 6 Evolution of the RRE of the 60 000 synthetic ε Eri test set RVs for the 50 epochs for the NNs using all different combinations of input data, i.e. activity index time series as indicated, the uniform time sampling, and no additional error on the training input sets. The curves are shown for the test sets without additional uncertainties as calculated by starsim (left panel, dashed lines) and for the case where we included the error value from Table 2 for each activity index into the test sets (right panel, full drawn lines). |
| In the text | |
 |
Fig. 7 Evolution of the RRE of the 100 000 synthetic AU Mic test set RVs for the 50 epochs for the NNs using all different combinations of input data. See Fig. 6 for more details. |
| In the text | |
 |
Fig. 8 Illustration of the quality of the RV correction as a function of the input indices used (random synthetic set chosen) for the ε Eri data and the uniform time sampling (black lines). The output predictions of the NNs with all the combinations of input data, i.e. index time series, are illustrated with different colours. The outcome of using only one index is shown in the top panel, further down two indices, then combinations of three indices (photometry and CCF), and then time-series data from all six indices. Radial velocities are shown as modelled by starsim. The legends contain the RV RRE of this particular set for each combination of index inputs. The residuals (differences between RV predictions and the simulated RV) are shown in the right panels. |
| In the text | |
 |
Fig. 9 RVs (top panel) and periodogram (bottom panel) of observational ε Eri data in black. In red, we show the prediction produced by our NN using BIS, FWHM, and CON indices as input. In green we show the periodogram of the cleaned data, that is, the difference between the observed and modelled RVs. The rotation period and its second harmonic are indicated as vertical dashed grey lines. The level of RMS reduction is about 45%. |
| In the text | |
 |
Fig. 10 Results for the AU Mic observations. Top panel: RVs from AU Mic as observed (black) and as modelled by the trained NN using BIS, and FWHM indices with their respective RREs. Bottom panel: periodogram of the observed RVs (black), the NN output (red), and the difference (green). Dashed black lines indicate the rotation period and its second harmonic, and dashed blue lines indicate the orbits of the two planetary companions of AU Mic. We reach RREs as low as 10%. |
| In the text | |
 |
Fig. 11 Residual RVs of the 37 AU Mic observations after applying the NN using BIS and FWHM indices (black dots). We further show the curves introduced to the RVs by the two detected planets of AU Mic (dashed red and green lines) and their combination (blue curve). |
| In the text | |
 |
Fig. A.1 Results of the starsim inversions for ε Eri using RV (top panel), FWHM (middle panel), and BIS (bottom panel). Blue dots indicate the measurements as extracted from raccoon from the observed spectra. The black curve shows the average fit and the grey area the uncertainty of the different solutions. The dashed red curve shows the solution with the largest likelihood. On the top right, the offset for each time series is indicated as well as its additional jitter, both of which show the shortcomings of the modelling of time-series data with starsim. |
| In the text | |
 |
Fig. A.2 Histogram of the posterior distribution of the five parameters of the spot maps containing ten spots of the starsim inversion applied to observational ε Eri data RV, BIS, and FWHM. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


