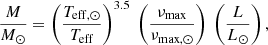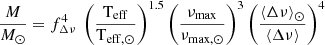EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 671 (March 2023) A&A, 671 (2023) A53 Full HTML
Open Access
Issue
A&A
Volume 671, March 2023
Article Number A53
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202245746
Published online 03 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

It is widely accepted that the large range in colour shown by low-mass stars in the central He-burning phase, called the horizontal branch (HB), is mainly due to variations in the efficiency of the H-burning shell and, hence, due to the mass of the H envelope remaining around a He core of ≃0.5 M⊙ (e.g., Salaris & Cassisi 2006). In a colour-magnitude diagram, low-mass core-He-burning (CHeB) stars appear distributed in both bluer and redder colours than the RR Lyrae instability strip (RRL-IS). Those located between the RR Lyrae and the red clump (RC; e.g., Girardi 2016) are called red horizontal branch (rHB) stars, and they have a H-rich envelope of ≈0.1 − 0.2 M⊙ (e.g., Rood & Crocker 1989; Valcarce & Catelan 2008; Girardi 2016; Tailo et al. 2020). This HB component has been clearly observed in globular clusters of different metallicities and ages (e.g., Armandroff 1988; Stetson et al. 1989; Catelan 2009; Tailo et al. 2020); however, rHB objects also exist in the field. While their identification is challenging, their census has been considered extremely important for tracing old stellar populations in the Milky Way (e.g., Kaempf et al. 2005; Chen et al. 2010, 2011). Although mainly associated with stars of low to intermediate metallicity, corresponding to the thick disc and halo population, spectroscopic studies (e.g., Afşar et al. 2012, 2018) have shown that rHB stars are also present in the metal-rich component of the Milky Way. This suggests that the progenitors of these objects have followed a non-standard evolution with significant mass loss or envelope stripping due to binary interactions. Signs of significant mass loss have been revealed in red giants observed by the Kepler space telescope (Borucki et al. 2010) in the field and in the open cluster NGC 6819 (e.g., Handberg et al. 2017; Brogaard et al. 2021; Li et al. 2022).

Stellar evolution models predict different structures for rHB and RC stars, with the latter having a similar He core as the former but a larger H envelope. We thus expect their seismic properties to be different. The exquisite precision achieved after 4 years of Kepler observations has revealed oscillation spectra of red giants with an increasing level of complexity (see Chaplin & Miglio 2013, for a review): frequency patterns in red-giant branch (RGB) stars similar to those found in main-sequence stars (universal pattern; Mosser et al. 2011); spectra of RC stars with ‘forests’ of dipole modes around the nominal acoustic mode, but still with an evident regularity (i.e., Beck et al. 2011); and ‘outlier’ spectra with a larger number of visible modes over the whole frequency domain, which are hypothesised in this paper to belong to rHB stars (see Fig. 1).

thumbnail Fig. 1.

PSD for five low-mass red giants (grey lines in the five panels) observed by Kepler. Panels a, b, and c: three low-mass CHeB stars KIC 5271626, KIC 6032981, and KIC 8694070 (first three rows in Table 1 and coloured stars in Fig. 2). Panels d and e: RC star KIC 1161618 and the RGB star KIC 2436824, for comparison. All five panels contain a smoothed PSD (red lines) computed with a box kernel of width 0.5 μHz in panels a, b, c, and d, and of width 0.1 μHz in panel e.

In this work we identify a small sample of 11 rHB candidates among the red giants in the Kepler field. Their global seismic properties and atmospheric parameters suggest that they are low-mass CHeB stars with low, intermediate, or solar metallicity. Combining numerical simulations of stellar structure and evolution and stellar oscillations, we study the consistency between the location of our rHB candidates in the Hertzsprung–Russell diagram (HRD), their theoretically predicted internal structure, and their oscillation spectra. Our rHB sample is presented in Sect. 2 and the theoretical models in Sect. 3. Section 4 discusses the properties of theoretical oscillation spectra of typical rHB and RC stars, as well as the comparison with observations. In Sect. 5 we summarise our findings.

2. Observational data

In addition to KIC 4937011, a 0.71 M⊙ CHeB star belonging to the open cluster NGC 6819 (see Handberg et al. 2017) that has a turn-off mass of ∼1.6 M⊙, we found 11 red giants in the Kepler database1 with peculiar power spectral densities (PSDs). While their global seismic parameters (mean large frequency separation, ⟨Δν⟩, frequency of maximum power, νmax, and asymptotic period spacing of the dipole modes, ΔΠ1) are compatible with low-mass CHeB stars, they have complex oscillation spectra. They have, for instance, an unusually high number of observable dipole mixed modes without the amplitude modulation around the p-like modes that is typically found in low-RGB and RC stars. This fact suggests that all dipole modes also have a significant amplitude in the outer region of the star and, hence, that g and p resonant cavities in these objects are strongly coupled.

The ability to transfer the energy of the mode from one cavity to the other, instead of it remaining trapped mainly in one of them, is quantified by the coupling factor, q (e.g., Shibahashi 1979; Takata 2016). The analysis of Kepler light curves provides the seismic parameters mentioned above, as well as the value of q (e.g., Vrard et al. 2016; Mosser et al. 2017, 2018). Theoretically, the parameter q ranges from 0 (uncoupled) to 1 (completely coupled). All the stars in our sample have q ≳ 0.4, while the median for RC stars is ≃0.25 − 0.3 (Vrard et al. 2016; Mosser et al. 2017).

On the other hand, the values of radial mode-linewidths (Γ0 > 0.2 μHz) are larger than the third quantile of the full sample of CHeB Kepler stars (median value Γ0 = 0.15 μHz; Vrard et al. 2018). Both a high q and a high Γ0 contribute to increasing the complexity of the spectra. Moreover, given the dependence of Γ0 on the effective temperature, Teff (e.g., Chaplin et al. 2009), the quadrupole modes are more difficult to detect in the hotter metal-poor subsample than in the cooler metal-rich objects.

The seismic properties (νmax, ⟨Δν⟩, ΔΠ1, and q) for our sample are reported in Tables 1 and A.1, together with the atmospheric parameters (Teff and chemical composition) from APOGEE Data Release (DR) 16 and DR17 (Ahumada et al. 2020; Abdurro’uf 2022). Twenty-five percent (3 out of 12) of the sample are metal-rich (0 ≤ [Fe/H] < 0.3) cool (4600 ≤ Teff/K ≤ 4800) stars, and the rest are low- or intermediate-metallicity (−1.4 < [Fe/H] < −0.5) stars with 5200 ≤ Teff/K ≤ 5600, that is, they belong to the ‘classical’ rHB.

Table 1.

Summary of the seismic and atmospheric properties for three rHB candidates of our sample (Sect. 2).

Tables 1 and A.1 also contain the stellar luminosity derived using Gaia-DR3 astrometry data (see Appendix A for details) and an estimate of their mass. The latter can be derived from scaling relations involving atmospheric and global seismic parameters (see e.g., Miglio et al. 2012). Here we used the one combining L, Teff, and νmax:

M M ⊙ = ( T eff , ⊙ T eff ) 3.5 ( ν max ν max , ⊙ ) ( L L ⊙ ) , $$ \begin{aligned} \frac{M}{M_\odot } = \left(\frac{T_{\rm eff,\odot }}{T_{\rm eff}}\right)^{3.5}\ \left(\frac{\nu _{\rm max}}{\nu _{\rm max,\odot }}\right) \ \left(\frac{L}{L_\odot }\right), \end{aligned} $$(1)

where the solar reference values are Teff, ⊙ = 5777 K and νmax, ⊙ = 3090 μHz (Huber et al. 2011). The mass uncertainties were calculated in quadrature by considering an uncertainty of at least 50 K in Teff as estimated from an independent analysis of APOGEE spectra (see Appendix A). In Appendix A.1 we also discuss the stellar mass values from a model-based corrected scaling relation involving Teff, ⟨Δν⟩, and νmax (Eq. (A.1)).

We notice that the mass of KIC 4937011 in Table A.1 is that of Handberg et al. (2017), and its value is nevertheless compatible with our results obtained with Eqs. (1) or (A.1). All the objects in our sample are then very low-mass stars (M ≲ 0.8 M⊙) with a high coupling2 between p-mode and g-mode cavities.

We selected three stars (those in Table 1) as representative of low-mass CHeB stars in different metallicity domains. Figure 2 shows these stars in an HRD, together with the Kepler-APOGEE red giant sample (Miglio et al. 2021, grey dots) and the red edge of the RRL-IS (Marconi et al. 2015, dashed red line). The two metal-poor stars (blue star symbols) are located between the RRL-IS and the RC, as expected for rHB stars, while the metal-rich CHeB star (orange star symbol) appears in the region of the ‘ensemble’ Kepler-RC. Its location is nevertheless redder than the RC at solar metallicity, and hence it is indeed a rHB metal-rich star, as also suggested by its mass (see also Handberg et al. 2017) and oscillation spectra. As mentioned above, rHB stars, especially metal-rich ones, must have followed a non-standard evolution to reach their current state within the age of the Universe. They are probably the progeny of strongly interacting binary systems. It has not been possible to confirm that hypothesis using the currently available Gaia-DR3 astrometry data (see Halbwachs et al. 2023, for the non-single star processing3), but we cannot exclude that they were part of binary systems in the past.

thumbnail Fig. 2.

HRD of a sample of red giants in the Kepler field. The coloured star symbols highlight the location of the first three rHB candidates in Table 1, and the grey dots in the background correspond to the Kepler-APOGEE sample in Miglio et al. (2021). The blue and red lines represent the theoretical red giant evolutionary tracks (from the RGB phase until the first thermal pulse) of low-mass stars with two different chemical compositions: M = 0.65 M⊙, [α/Fe] = 0.2, [Fe/H] = −1.00 (blue) and M = 0.75 M⊙, [α/Fe] = 0, [Fe/H] = 0 (red). The green line is the evolutionary track for a 1.5 M⊙ with solar composition, and the dashed red one is the red edge of the RRL-IS for the composition of the blue track (see Marconi et al. 2015). Solid orange and blue circles correspond to our rHB and RC reference models, with a central He mass fraction Yc ≃ 0.27.

3. Simulated data

The aim of this work is not to fit the available observational data, but to analyse the relation between the structures of rHB stars, according to stellar evolution theory, and their oscillation spectra, and to compare the latter with those observed in our sample.

From a grid of models (see Appendix B) we selected two sets of parameters that are good representatives of the mass and chemical composition of classical rHB stars (M = 0.65 M⊙, [α/Fe] = 0.2 and [Fe/H] = −1.00) and metal-rich low-mass CHeB stars (M = 0.75 M⊙, [α/Fe] = 0 and [Fe/H] = 0). For comparison, we also considered a typical RC star (M = 1.5 M⊙ with solar composition). As shown in Fig. 2, the parameters selected for our reference models do provide a good representation of the low- to intermediate-metallicity and metal-rich rHB stars in our sample. We also note that without complementary information, such as that provided by asteroseismology, a metal-rich rHB star would be mistaken for a more massive star in the RGB (see also Handberg et al. 2017).

It is generally accepted that, except for the age, the properties of a low-mass star with a He core of ≃0.5 M⊙ and a H-rich envelope of ∼0.1 − 0.2 M⊙ are largely independent of whether the star was born with a small mass or whether it originated from a more massive star (M ≲ 1.8 M⊙) that underwent significant mass loss. Therefore, it is justified to use structure models calculated without mass loss such as those in our grid.

In the following we concentrate on a metal-poor model since, as described in Sect. 2, we expect metal-poor rHB stars to present more marked differences with respect to the spectra of typical RC stars. We selected structure models with a central He mass fraction Yc ∼ 0.27 as representative of the CHeB phase. The structures and oscillation spectra of these reference models will be discussed in Sect. 4.

To simulate 4-year-long Kepler observations of such objects, we used the code AADG3 (AsteroFLAG Artificial Dataset Generator, version 3.0.2; Ball et al. 2018, and references therein). Frequencies and normalised inertiae, Enorm (see the definition in e.g., Aerts et al. 2010) of radial (ℓ = 0) and non-radial (ℓ = 1 − 3) adiabatic oscillation modes were computed using the code GYRE (version 6.0.1, Townsend & Teitler 2013; Townsend et al. 2018; Goldstein & Townsend 2020). AADG3 also requires information on mode lifetimes, a quantity that is directly related to non-adiabatic processes and therefore does not result from the GYRE computation. AADG3 uses a relation between Γ0, ν, νmax, and Teff calibrated on a small sample of main-sequence and RGB spectra. Since the temperatures of our metal-poor rHB stars are outside the domain covered by the calibration sample, and since Γ0 also depends on the evolutionary state (Vrard et al. 2018), we adopted as values of Γ0 the ones obtained from peak-bagging radial modes in the spectra of our CHeB sample (using the method described in Davies & Miglio 2016).

4. Discussion

In this section we analyse the structures and oscillation spectra of our reference models (rHB and RC), and we compare the simulated PSD with the observed ones (Sect. 4.3).

4.1. Propagation diagram

The propagation diagrams of dipole modes for our rHB and RC reference models are shown in the upper panels of Fig. 3. In each panel, we show the modified Brunt–Väisälä ( N ∼ $ \tilde{N} $) and Lamb ( S ∼ $ \tilde{S} $) frequencies (Takata 2006) as a function of the normalised radius (x = r/Rphot, with Rphot the photospheric radius), as well as the expected frequency domain of the solar-like oscillations.

thumbnail Fig. 3.

Comparison between structure and seismic properties of rHB (left panels) and RC (right panels) reference models (see Sect. 3). Upper panels: propagation diagrams of the dipole modes, with blue and orange lines corresponding to the modified Brunt–Väisälä and Lamb frequencies (Takata 2006), respectively. The grey bands represent the frequency domain of expected solar-like oscillations, and at their centre the dashed cyan lines indicate the νmax values. The insets are zoomed-in views of the evanescent zones, delimited at νmax by the red and black points. Their different extension translates to a different coupling between g and p cavities (see main text). Lower panels: normalised inertia, Enorm, and period spacing of the dipole modes, ΔP, as functions of the eigenfrequencies, with the red curve representing, for comparison, the Enorm of radial modes. The dashed green line indicates the value of the period spacing from the asymptotic theory of high-order g modes (ΔPa; Tassoul 1980), and the grey band and the dashed cyan line have the same meaning as in the upper panels.

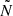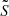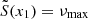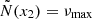The N ∼ $ \tilde{N} $ and S ∼ $ \tilde{S} $ profiles define the inner limits of the g and p cavities. For modes with a frequency close to νmax, these limits are defined by the condition S ∼ ( x 1 ) = ν max $ \tilde{S}(x_1) = \nu_{\mathrm{max}} $ and N ∼ ( x 2 ) = ν max $ \tilde{N}(x_2) = \nu_{\mathrm{max}} $, and in the region between x1 and x2 the modes are evanescent.

The extent of the evanescent zone is one of the ingredients that determine the coupling between resonant cavities (Takata 2016; Pinçon et al. 2020). From the zoomed-in boxes in Fig. 3 it appears that this region is smaller in the rHB model than in the RC one, and, therefore, we expect the coupling factor, q, to be larger in the former than in the latter. Indeed, using the structure of our reference models and the strong-coupling approximation4 for the dipole modes (Takata 2016; Pinçon et al. 2020), we obtain qrHB = 0.65 and qRC = 0.25 at ν = νmax. We note that these values are consistent, given the typical uncertainties (σq ∼ 0.2), with those measured from the observed PSDs (see Tables 1 and A.1, Vrard et al. 2016; Mosser et al. 2017, 2018).

We notice that the value of the coupling factor is also a function of the mode frequency (e.g., Pinçon et al. 2020; Jiang et al. 2020; van Rossem in prep.). As shown in Fig. 3, the size of the evanescent zone decreases (and thus q increases) with increasing frequency. The value of q varies from 0.56 to 0.74 in the solar-like frequency domain for the rHB model, and from 0.22 to 0.24 for the RC one. In Sect. 4.2 we discuss the effect of this variation on the behaviour of the period spacing.

4.2. Dipole mode properties

In this section we analyse the properties of the dipole mode spectra computed for our reference models. The bottom panels of Fig. 3 show Enorm and the period spacing, ΔP (i.e., the period difference between two consecutive modes of the same angular degree) as a function of the eigenfrequencies.

We recall that Enorm is an average of the mode energy, and its value indicates the main region probed by the mode. Modes that examine central, high-density regions have higher Enorm than modes that are preferentially trapped in the outer regions. The inertia of dipole modes of the RC model shows a significant variation between local minima and maxima (ratio up to ≈27 in the observable region), corresponding to the p-like and g-like modes, respectively. On the contrary, the inertia in the rHB is almost uniform, with a small contrast between maxima and minima (ratio up to ≈3 in the observable region). This indicates that the dipole modes in the rHB are not clearly trapped in any of the resonant cavities, that is, they have an important mixed p–g character. This behaviour is consistent with the coupling factor values derived in the previous section.

Since the amplitude of the modes is inversely proportional to the square root of the inertia (see e.g., Dupret et al. 2009), we expect a modulation of the dipole mode amplitudes around the p-like mode in the case of the RC, as observed in some Kepler red giants, while many dipole modes with similar amplitudes may be observed in the spectrum of the rHB. This implies an increasing complexity of the oscillation spectra, as shown by the stars in our sample (see Fig. 1).

The high value of q also affects the behaviour of the period spacing (see also Mosser et al. 2017). In the bottom part of the lower panels of Fig. 3, we plot ΔP as a function of the eigenfrequencies as well as the constant value (dashed green line) predicted by the asymptotic g-mode approximation (ΔPa; Tassoul 1980). In the observable frequency domain, we notice for the rHB model a significant deviation of ΔP from the asymptotic value even for modes with high inertia, as well as a decreasing trend of ΔP with increasing frequency. To show that both effects are a consequence of the high value of q and its frequency dependence, we used the Ong & Basu (2020) formalism to separate pure isolated p modes (π modes) from pure isolated g modes (γ modes), that is, pure g modes not affected by the coupling with the acoustic cavity. In Fig. 4 we plot the period spacing of dipole γ modes, and, as expected, their average value is consistent with that from the asymptotic approximation of pure high-order g modes. Therefore, the differences in the period spacing of the RC and rHB models are explained by the high coupling for the latter, which causes all dipole modes to have an important acoustic component, thus decreasing the value of ΔP.

thumbnail Fig. 4.

Period spacing as a function of the eigenfrequencies of the isolated dipole γ modes (Ong & Basu 2020). Other symbols and colours are the same as in Fig. 3. The high modulation in the period spacing above the observable frequencies is connected to structural glitches (see e.g., Bossini et al. 2015).

4.3. Power spectral density

Figure 5 shows the simulated PSDs of our reference models together with the inertia of the ℓ = 0, 1, 2, 3 modes. The contribution of each degree to the PSD is shown in Appendix C.

thumbnail Fig. 5.

Simulated PSD (grey line) as a function of the eigenfrequencies using theoretical ℓ = 0, 1, 2, 3 modes for rHB (left) and RC (right) models. The red line is a smoothed version of the PSD. The vertical dashed cyan lines correspond to νmax values, and coloured dots and lines represent the values of Enorm for the ℓ = 0, 1, 2, 3 modes.

A comparison between Figs. 1 and 5 shows many similarities between the rHB-mock spectrum and the observed ones. These spectra appear noisier than RC ones, with a large number of peaks corresponding to non-radial modes. In particular, there are observable dipole modes in the entire frequency range between two consecutive radial modes, unlike the behaviour in RC and low-RGB stars, where only a few modes around the corresponding p-like mode have observable amplitudes.

We see that the strong coupling also affects the quadrupole modes. Several of them, with frequencies close to those of the p-like modes, are expected to have similar contributions to the PSD. Moreover, because of a higher inertia at the local minima with respect to the RC model, quadrupole modes in rHB stars would have lower amplitudes. All that makes it more challenging to detect and characterise ℓ = 2 modes in CHeB metal-poor stars. Finally, ℓ = 3 modes have eigenfrequencies close to those of radial modes, and their heights are similar to the background noise. They tend to form a continuum that should be considered during the background analysis (see Appendix C).

5. Conclusions

High-quality spectra obtained from the 4-year-long Kepler observations of a large number of red giants allowed us to identify a small number of red giants (12) whose oscillation spectra appear to be very noisy or complex with respect to the typical behaviour of oscillation spectra in Kepler red giants. Their global seismic parameters are compatible with low-mass stars (M ≲ 0.8 M⊙) in the central He-burning phase, and the fit of the asymptotic relation for the dipole modes (e.g., Vrard et al. 2016) results in coupling factor values q ≳ 0.4, much higher than the typical value for stars classified as RC (q ∼ 0.25 − 0.30; e.g., Vrard et al. 2016; Mosser et al. 2017, 2018). In our sample we find stars with a low to intermediate metallicity (75%) and stars with solar metallicity. Their position in the HRD is compatible with the so-called rHB stars, that is, low-mass objects between the RRL-IS and the RC at the corresponding metallicity. Stellar evolution theory predicts for these stars a structure consisting of a He core of ∼0.5 M⊙ and an envelope of ≈0.1 − 0.2 M⊙ (e.g., Rood & Crocker 1989; Valcarce & Catelan 2008; Gratton et al. 2010; Girardi 2016; Tailo et al. 2020).

In this work we have shown that the oscillation spectra we expect for this type of star are entirely consistent with those observed in our sample. These spectra are clearly different from those of the stars that, with a similar He core but a much larger envelope, populate the RC. The main factor determining these differences is the coupling between the inner and outer regions, which reflects very different density profiles inside these stars. A second factor that increases the complexity of these spectra is the higher temperature of the less metallic stars, which decrease the lifetime of the modes. In fact, solar-like oscillations in rHB stars have also been detected in the K2 (Howell et al. 2014) light curves of the globular cluster M 4 (e.g., Wallace et al. 2019), where the complexity of the spectra and the reduced observation time (80 days) have made it difficult to extract robust ⟨Δν⟩ values (e.g., Tailo et al. 2022; Howell et al. 2022).

Stars in the rHB stage are well known and easily identified in globular clusters. Here we have also shown the ability of asteroseismology to identify these low-mass CHeB stars in the field and in solar-metallicity environments where, even with high-precision photometry, they would be hardly distinguishable from other stars in RC or RGB phases.

It is clear that 0.7 M⊙ stars, especially those of solar metallicity, must have followed a non-standard evolution during which they lost a large amount of mass (see also Li et al. 2022; Bobrick et al. 2022). This work provides us with a solid framework for the future study of these stars and of the processes that led them to their current mass. Knowledge of this is fundamental for deriving their ages with accuracy, and potentially providing another piece of the puzzle in the sequence between RC and subdwarf B stars or other stripped stars.

2

We notice that stars in the CHeB stage could have multiple cavities in the inner part due to semi-convection. This could lead to a bias when estimating q from the fit of observations with the asymptotic relation for dipole modes (e.g., Pinçon & Takata 2022). This must be considered in future work.

3

We also checked the non-single star hypothesis using the fidelity_v2 table.

4

The weak-coupling approximation (see e.g., Shibahashi 1979; Unno et al. 1989) does not hold for low-mass CHeB stars (see e.g., Vrard et al. 2016; Mosser et al. 2017; van Rossem, in prep.).

5

https://www.as.utexas.edu/ chris/moog.html

6

http://vald.astro.uu.se

Acknowledgments

We are grateful to (in alphabetical order) Emma Willett, Joel Ong, Joris De Ridder, Masao Takata and Saniya Khan for useful discussions. We are also grateful to the anonymous referee for the constructive comments. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia) and from the Two Micron All Sky Survey (https://irsa.ipac.caltech.edu/Missions/2mass.html). This research made use of Lightkurve, a Python package for Kepler and TESS data analysis (Lightkurve Collaboration 2018), and of dustmaps, a package for interstellar dust reddening and extinction (Green 2018). AM, AS, GC, JM, MM, MT acknowledge support from the ERC Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, https://www.asterochronometry.eu, G.A. n. 772293). MV acknowledge support from NASA grant 80NSSC18K1582. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement No. DNRF106).

References

  1. Abdurro’uf, Accetta K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (New York: Springer Science Business Media) [Google Scholar]
  3. Afşar, M., Sneden, C., & For, B. Q. 2012, AJ, 144, 20 [CrossRef] [Google Scholar]
  4. Afşar, M., Bozkurt, Z., Böcek Topcu, G., et al. 2018, AJ, 155, 240 [CrossRef] [Google Scholar]
  5. Ahumada, R., Prieto, C. A., Almeida, A., et al. 2020, ApJS, 249, 3 [Google Scholar]
  6. Armandroff, T. E. 1988, AJ, 96, 588 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  8. Babusiaux, C., Fabricius, C., Khanna, S., et al. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202243790 [Google Scholar]
  9. Ball, W. H., Chaplin, W. J., Schofield, M., et al. 2018, ApJS, 239, 34 [Google Scholar]
  10. Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [Google Scholar]
  11. Bobrick, A., Iorio, G., Belokurov, V., et al. 2022, MNRAS, submitted [arXiv:2208.04332] [Google Scholar]
  12. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  13. Bossini, D., Miglio, A., Salaris, M., et al. 2015, MNRAS, 453, 2290 [Google Scholar]
  14. Bossini, D., Miglio, A., Salaris, M., et al. 2017, MNRAS, 469, 4718 [Google Scholar]
  15. Brogaard, K., Arentoft, T., Jessen-Hansen, J., & Miglio, A. 2021, MNRAS, 507, 496 [NASA ADS] [CrossRef] [Google Scholar]
  16. Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [Google Scholar]
  17. Casagrande, L., & VandenBerg, D. A. 2018, MNRAS, 479, L102 [NASA ADS] [CrossRef] [Google Scholar]
  18. Catelan, M. 2009, Ap&SS, 320, 261 [Google Scholar]
  19. Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
  20. Chaplin, W. J., Houdek, G., Karoff, C., Elsworth, Y., & New, R. 2009, A&A, 500, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Chen, Y. Q., Zhao, G., Carrell, K., & Zhao, J. K. 2011, AJ, 142, 184 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chen, Y. Q., Zhao, G., Zhao, J. K., Xue, X. X., & Schuster, W. J. 2010, AJ, 140, 500 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
  24. Davies, G. R., & Miglio, A. 2016, Astron. Nachr., 337, 774 [Google Scholar]
  25. Dupret, M. A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Gai, N., Basu, S., Chaplin, W. J., & Elsworth, Y. 2011, ApJ, 730, 63 [Google Scholar]
  27. Girardi, L. 2016, ARA&A, 54, 95 [Google Scholar]
  28. Goldstein, J., & Townsend, R. H. D. 2020, ApJ, 899, 116 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D’Orazi, V. 2010, A&A, 517, A81 [CrossRef] [EDP Sciences] [Google Scholar]
  30. Green, G. 2018, J. Open Source Softw., 3, 695 [NASA ADS] [CrossRef] [Google Scholar]
  31. Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Halbwachs, J. L., Pourbaix, D., Arenou, F., et al. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202243969 [Google Scholar]
  34. Handberg, R., Brogaard, K., Miglio, A., et al. 2017, MNRAS, 472, 979 [CrossRef] [Google Scholar]
  35. Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
  36. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
  37. Howell, M., Campbell, S. W., Stello, D., & De Silva, G. M. 2022, MNRAS, 515, 3184 [NASA ADS] [CrossRef] [Google Scholar]
  38. Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [Google Scholar]
  39. Jiang, C., Cunha, M., Christensen-Dalsgaard, J., & Zhang, Q. 2020, MNRAS, 495, 621 [Google Scholar]
  40. Kaempf, T. A., de Boer, K. S., & Altmann, M. 2005, A&A, 432, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Khan, S., Hall, O. J., Miglio, A., et al. 2018, ApJ, 859, 156 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
  43. Li, Y., Bedding, T. R., Murphy, S. J., et al. 2022, Nat. Astron., 6, 673 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lightkurve Collaboration (Cardoso, J. V. D. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
  45. Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  46. Marconi, M., Coppola, G., Bono, G., et al. 2015, ApJ, 808, 50 [Google Scholar]
  47. Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [Google Scholar]
  48. Miglio, A., Chiappini, C., Mackereth, J. T., et al. 2021, A&A, 645, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Mosser, B., Belkacem, K., Goupil, M. J., et al. 2011, A&A, 525, L9 [CrossRef] [EDP Sciences] [Google Scholar]
  50. Mosser, B., Pinçon, C., Belkacem, K., Takata, M., & Vrard, M. 2017, A&A, 600, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Mosser, B., Gehan, C., Belkacem, K., et al. 2018, A&A, 618, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Ong, J. M. J., & Basu, S. 2020, ApJ, 898, 127 [NASA ADS] [CrossRef] [Google Scholar]
  53. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  54. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  55. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  56. Paxton, B., Marchant, P., Schwab, J., et al. 2016, ApJS, 223, 18 [NASA ADS] [CrossRef] [Google Scholar]
  57. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  58. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  59. Pinçon, C., & Takata, M. 2022, A&A, 661, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Pinçon, C., Goupil, M. J., & Belkacem, K. 2020, A&A, 634, A68 [Google Scholar]
  61. Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
  62. Rood, R. T., & Crocker, D. A. 1989, in IAU Colloq. 111: The Use of Pulsating Stars in Fundamental Problems of Astronomy, ed. E. G. Schmidt, 103 [Google Scholar]
  63. Salaris, M., & Cassisi, S. 2006, Evolution of Stars and Stellar Populations (New York: Wiley-VCH) [Google Scholar]
  64. Shetrone, M., Bizyaev, D., Lawler, J. E., et al. 2015, ApJS, 221, 24 [Google Scholar]
  65. Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
  66. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  67. Smith, V. V., Bizyaev, D., Cunha, K., et al. 2021, AJ, 161, 254 [NASA ADS] [CrossRef] [Google Scholar]
  68. Stetson, P. B., Vandenberg, D. A., Bolte, M., Hesser, J. E., & Smith, G. H. 1989, AJ, 97, 1360 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tailo, M., Milone, A. P., Lagioia, E. P., et al. 2020, MNRAS, 498, 5745 [CrossRef] [Google Scholar]
  70. Tailo, M., Corsaro, E., Miglio, A., et al. 2022, A&A, 662, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Takata, M. 2006, PASJ, 58, 893 [Google Scholar]
  72. Takata, M. 2016, PASJ, 68, 109 [NASA ADS] [CrossRef] [Google Scholar]
  73. Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
  74. Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [Google Scholar]
  75. Townsend, R. H. D., Goldstein, J., & Zweibel, E. G. 2018, MNRAS, 475, 879 [Google Scholar]
  76. Ulrich, R. K. 1986, ApJ, 306, L37 [Google Scholar]
  77. Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
  78. Valcarce, A. A. R., & Catelan, M. 2008, A&A, 487, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Valentini, M., Chiappini, C., Bossini, D., et al. 2019, A&A, 627, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Vrard, M., Mosser, B., & Samadi, R. 2016, A&A, 588, A87 [CrossRef] [EDP Sciences] [Google Scholar]
  81. Vrard, M., Kallinger, T., Mosser, B., et al. 2018, A&A, 616, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Wallace, J. J., Hartman, J. D., Bakos, G. Á., & Bhatti, W. 2019, ApJS, 244, 12 [NASA ADS] [CrossRef] [Google Scholar]
  83. White, T. R., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 161 [Google Scholar]
  84. Yu, J., Huber, D., Bedding, T. R., et al. 2018, ApJS, 236, 42 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Physical properties of the full sample

In this appendix we give some details concerning the origin of the physical quantities in Tables 1 and A.1. The latter complements the former, providing the properties of the rest of our sample of rHB candidates (see also the HRD of the whole sample in Fig. A.1).

thumbnail Fig. A.1.

Same as Fig. 2, but including all the CHeB stars in our sample. These stars are colour-coded according to increasing [Fe/H].

Table A.1.

Physical properties for the rest of our sample of rHB candidates.

The global seismic parameters, νmax and ⟨Δν⟩, of targets tagged with an asterisk in Tables 1 and A.1 are taken from Yu et al. (2018), while those for the NGC 6819 cluster member (KIC 4937011, tagged with R) are from Handberg et al. (2017). For the rest of the sample, we employed the approach of Davies & Miglio (2016), and the value of ⟨Δν⟩ was computed using individual frequencies and the weighted fit of the asymptotic relation for radial modes. As discussed in Handberg et al. (2017), this method gives results in good agreement with the values of ⟨Δν⟩ derived by Yu et al. (2018) and allows a forward comparison with model-based values. The asymptotic period spacing of the dipole modes, ΔΠ1, and the coupling factor, q, were derived using the stretched-period method (see e.g. Vrard et al. 2016).

The atmospheric parameters, Teff, and chemical composition come from APOGEE-DR17, except for four targets with a STAR_BAD flag in that release. For them (marked with a plus symbol in Tables 1 and A.1) we adopted the available values in APOGEE-DR16. To check the reliability of these atmospheric parameters and of the quoted uncertainties, we performed an independent analysis for the three stars (see Table 1). We used MOOG-synth5 with the assumption of local thermodynamic equilibrium and the APOGEE-DR17 linelist (Shetrone et al. 2015; Smith et al. 2021) implemented with lines from the VALD database6 and MARCS model atmospheres (Gustafsson et al. 2008). We get results in good agreement with those in APOGEE DR16 and DR17, except for the Teff uncertainties. Even for the best situation in which log g is fixed to the seismic values (e.g. Valentini et al. 2019), the uncertainty on Teff is σTeff ∼ 50 K. Therefore, although in Tables 1 and A.1 we keep the values from APOGEE, we assumed a minimum value of σTeff = 50 K when deriving the stellar mass and its uncertainty.

Bolometric luminosities, L, were estimated by combining astrometry data from Gaia DR3 (Babusiaux et al. 2023) with 2MASS photometry (Skrutskie et al. 2006) in the Ks band and bolometric correction from Casagrande & VandenBerg (2014, 2018). We applied the Gaia-DR3 parallax zero-point correction of Lindegren et al. (2021) and estimated reddening and extinction from the three-dimensional maps of Green et al. (2019). The errors in L are calculated with a Markov chain Monte Carlo method and considering the extinction and the value of Mbol,⊙ to be fixed (Mbol,⊙ = 4.75; Casagrande & VandenBerg 2014).

Stellar masses, as described in Sect. 2, were estimated using the scaling relation Eq. 1 and the values of L, Teff, and νmax just described. In the following we present the results obtained with an alternative scaling relation.

A.1. Stellar mass from the scaling relation involving ⟨Δν⟩ and νmax

In order to test the mass estimations made with Eq. 1 of Sect. 2, we employed the model-based corrected scaling relation (see e.g. Kjeldsen & Bedding 1995; Gai et al. 2011)

M M ⊙ = f Δ ν 4 ( T eff T eff , ⊙ ) 1.5 ( ν max ν max , ⊙ ) 3 ( 〈 Δ ν 〉 ⊙ 〈 Δ ν 〉 ) 4 $$ \begin{aligned} \frac{M}{M_\odot } = f_{\Delta \nu }^4 \ \left(\frac{\mathrm{T_{eff}}}{\mathrm{T_{eff,\odot }}}\right)^{1.5}\left(\frac{\nu _{\rm max}}{\nu _{\rm max,\odot }}\right)^3 \left(\frac{\left\langle \Delta \nu \right\rangle _\odot }{\left\langle \Delta \nu \right\rangle }\right)^4 \end{aligned} $$(A.1)

for two metal-rich stars (KIC5271626 and KIC4937011) and for two metal-poor stars (KIC6032981 and KIC11072164) of our sample. Here we used the solar reference values of Sect. 2 and ⟨Δν⟩⊙ = 135.1 μHz (Huber et al. 2011). The correction factor, fΔν, on the ⟨Δν⟩ scaling law (Ulrich 1986) was derived with the procedure described in Rodrigues et al. (2017), that is, by using the theoretical radial mode frequencies of stellar models to compute ⟨Δν⟩ from the weighted linear fit of the asymptotic relation (see also Miglio et al. 2021; Tailo et al. 2022). We based the iterative search for the correct fΔν on evolutionary tracks with the same metallicity (within the errors) as the four stars: solar composition for the metal-rich ones; and [Fe/H] = −1.00 with [α/Fe] = 0.2 and [α/Fe] = 0.4 for the two metal-poor ones (see Appendix B for details on the models). To correct the model-predicted ⟨Δν⟩ for the surface effects, we included the ⟨Δν⟩⊙ = 135.3 μHz of our solar-calibrated model to the correction factor fΔν (e.g. White et al. 2011). Finally, we computed the theoretical radial oscillations with the tool GYRE. The fΔν we find are nearly equal to 1.03 and 1.01 for the metal-poor and for the metal-rich stars, respectively. In deriving the masses with Eq. (A.1), we considered a minimum error of 50 K in Teff (as noted in Appendix A) and an error of 0.01 on fΔν due to the impossibility of knowing the exact position, at fixed νmax, of our observed stars along the evolutionary tracks. Therefore, these masses are compatible within the errors with those derived from Eq. 1. We also note that it is difficult to have a very precise ⟨Δν⟩ estimate for these stars because the radial modes are located in crowded regions (see Appendix C). This leads to systematic errors in the measurement of individual radial modes that can be of the order of 4% by mass.

Appendix B: Grids of stellar models

As mentioned in Sect. 3, we chose three sets of stellar parameters to represent a rHB star, a metal-rich low-mass CHeB star, and a RC star. The stellar models at the base of this work belong to a grid of stellar evolutionary models computed with the code MESA-r11532 (Modules for Experiments in Stellar Astrophysics; Paxton et al. 2011, 2013, 2015, 2016, 2018, 2019). In the computation we followed the evolution from the pre-main-sequence phase until the first thermal pulse in the asymptotic giant branch for stellar masses from 0.6 M⊙ to 2.00 M⊙, with a step of 0.05 M⊙. We considered 36 different chemical compositions, with 12 values of [Fe/H] (from −2.5 to 0.25) and three values of alpha-element enhancement: [α/Fe] = 0.0, 0.2, and 0.4. We adopted as a reference solar mixture that from Asplund et al. (2009), and high- and low-temperature radiative opacity tables were computed for these specific metal mixtures, the solar and alpha-enhanced ones. Envelope convection is described by the mixing length theory (Cox & Giuli 1968); the corresponding αMLT parameter, the same for all the grid, was derived from the solar calibration with the same physics. Below the convective envelope, we added a diffusive undershooting (Herwig 2000) with a size parameter f = 0.02 (see Khan et al. 2018). Extra mixing over the convective core limit during the central-He-burning phase was treated following the formalism by Bossini et al. (2017).

Appendix C: Contribution of individual eigenmodes to the PSDs of CHeB stars

In this section we break down the PSDs of our reference models (Fig. 5) into the contributions from the modes of different angular degrees. The smoothed PSDs for ℓ = 0, 1, 2, 3 are shown in Fig. C.1. The smoothing was chosen just for illustration purposes, that is, to resemble a Lorentzian fit of each eigenmode. The modulation around the p-like mode in the dipole modes of the RC star and the higher number of observed mixed modes in the rHB model are evident. Furthermore, the quadrupole modes of the rHB model are less visible than those of the RC model, and its octupole modes resemble a continuous background with small peaks almost coinciding with the radial modes. Finally, we note that the presence, in rHB stars, of ℓ = 1, 2, 3 modes very close to the radial ones (in some cases almost coinciding; e.g. Fig. C.1) could introduce a non-negligible influence on the analysis of the heights and the linewidths of the ℓ = 0 modes.

thumbnail Fig. C.1.

Smoothed version of the PSDs presented in Sect. 4.3. Here we show the individual degrees for the simulated rHB (top) and RC (bottom) stars. The dashed cyan line is the corresponding νmax.

All Tables

Table 1.

Summary of the seismic and atmospheric properties for three rHB candidates of our sample (Sect. 2).

In the text
Table A.1.

Physical properties for the rest of our sample of rHB candidates.

In the text

All Figures

thumbnail Fig. 1.

PSD for five low-mass red giants (grey lines in the five panels) observed by Kepler. Panels a, b, and c: three low-mass CHeB stars KIC 5271626, KIC 6032981, and KIC 8694070 (first three rows in Table 1 and coloured stars in Fig. 2). Panels d and e: RC star KIC 1161618 and the RGB star KIC 2436824, for comparison. All five panels contain a smoothed PSD (red lines) computed with a box kernel of width 0.5 μHz in panels a, b, c, and d, and of width 0.1 μHz in panel e.
In the text
thumbnail Fig. 2.

HRD of a sample of red giants in the Kepler field. The coloured star symbols highlight the location of the first three rHB candidates in Table 1, and the grey dots in the background correspond to the Kepler-APOGEE sample in Miglio et al. (2021). The blue and red lines represent the theoretical red giant evolutionary tracks (from the RGB phase until the first thermal pulse) of low-mass stars with two different chemical compositions: M = 0.65 M⊙, [α/Fe] = 0.2, [Fe/H] = −1.00 (blue) and M = 0.75 M⊙, [α/Fe] = 0, [Fe/H] = 0 (red). The green line is the evolutionary track for a 1.5 M⊙ with solar composition, and the dashed red one is the red edge of the RRL-IS for the composition of the blue track (see Marconi et al. 2015). Solid orange and blue circles correspond to our rHB and RC reference models, with a central He mass fraction Yc ≃ 0.27.
In the text
thumbnail Fig. 3.

Comparison between structure and seismic properties of rHB (left panels) and RC (right panels) reference models (see Sect. 3). Upper panels: propagation diagrams of the dipole modes, with blue and orange lines corresponding to the modified Brunt–Väisälä and Lamb frequencies (Takata 2006), respectively. The grey bands represent the frequency domain of expected solar-like oscillations, and at their centre the dashed cyan lines indicate the νmax values. The insets are zoomed-in views of the evanescent zones, delimited at νmax by the red and black points. Their different extension translates to a different coupling between g and p cavities (see main text). Lower panels: normalised inertia, Enorm, and period spacing of the dipole modes, ΔP, as functions of the eigenfrequencies, with the red curve representing, for comparison, the Enorm of radial modes. The dashed green line indicates the value of the period spacing from the asymptotic theory of high-order g modes (ΔPa; Tassoul 1980), and the grey band and the dashed cyan line have the same meaning as in the upper panels.
In the text
thumbnail Fig. 4.

Period spacing as a function of the eigenfrequencies of the isolated dipole γ modes (Ong & Basu 2020). Other symbols and colours are the same as in Fig. 3. The high modulation in the period spacing above the observable frequencies is connected to structural glitches (see e.g., Bossini et al. 2015).
In the text
thumbnail Fig. 5.

Simulated PSD (grey line) as a function of the eigenfrequencies using theoretical ℓ = 0, 1, 2, 3 modes for rHB (left) and RC (right) models. The red line is a smoothed version of the PSD. The vertical dashed cyan lines correspond to νmax values, and coloured dots and lines represent the values of Enorm for the ℓ = 0, 1, 2, 3 modes.
In the text
thumbnail Fig. A.1.

Same as Fig. 2, but including all the CHeB stars in our sample. These stars are colour-coded according to increasing [Fe/H].
In the text
thumbnail Fig. C.1.

Smoothed version of the PSDs presented in Sect. 4.3. Here we show the individual degrees for the simulated rHB (top) and RC (bottom) stars. The dashed cyan line is the corresponding νmax.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.