| Issue |
A&A
Volume 671, March 2023
|
|
|---|---|---|
| Article Number | A170 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245064 | |
| Published online | 24 March 2023 | |
The Hubble/STIS near-ultraviolet transmission spectrum of HD 189733 b
1
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042,
Graz, Austria
e-mail: patricio.cubillos@oeaw.ac.at
2
INAF – Osservatorio Astrofisico di Torino,
Via Osservatorio 20,
10025
Pino Torinese, Italy
3
Lunar and Planetary Laboratory, University of Arizona,
1629 E. University Blvd.,
Tucson, AZ
85721, USA
4
Laboratory for Atmospheric and Space Physics, University of Colorado,
600 UCB,
Boulder, CO
80309, USA
5
School of Physical Sciences, The Open University,
Walton Hall,
Milton Keynes
MK7 6AA, UK
Received:
26
September
2022
Accepted:
30
January
2023
The benchmark hot Jupiter HD 189733 b has been a key target, used to lay out the foundations of comparative planetology for giant exo-planets. As such, HD 189733 b has been extensively studied across the electromagnetic spectrum. Here we report the observation and analysis of three transit light curves of HD 189733 b obtained with Hubble/STIS in the near-ultraviolet (NUV), the last remaining unexplored spectral window to be probed with present-day instrumentation for this planet. The NUV is a unique window for atmospheric mass-loss studies owing to the strong resonance lines and large photospheric flux. Overall, from a low-resolution analysis (R = 50) we found that the planet’s NUV spectrum is well characterized by a relatively flat baseline, consistent with the optical-infrared transmission, plus two regions at ~2350 and ~2600 Å that exhibit a broad and significant excess absorption above the continuum. From an analysis at a higher resolution (R = 4700), we found that the transit depths at the core of the magnesium resonance lines are consistent with the surrounding continuum. We discarded the presence of Mg II absorption in the upper atmosphere at a ~2–4σ confidence level, whereas we could place no significant constraint for Mg I absorption. These broad absorption features coincide with the expected location of Fe II bands; however, solar-abundance hydrodynamic models of the upper atmosphere are not able to reproduce the amplitude of these features with iron absorption. This scenario would require a combination of little to no iron condensation in the lower atmosphere super-solar metallicities and a mechanism to enhance the absorption features (such as zonal wind broadening). The true nature of this feature remains to be confirmed.
Key words: planets and satellites: atmospheres / planets and satellites: gaseous planets / techniques: spectroscopic
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The hot Jupiter HD 189733 b is one of the earliest transiting exoplanets to be detected (Bouchy et al. 2005), being one of the closest transiting planets to Earth. The high mass of HD 189733b of 1.13 MJup, large radius of 1.13 RJup, and short-period 2.2-day orbit (Stassun et al. 2017) provide some of the most favorable conditions for atmospheric characterization. Consequently, HD 189733 b has become one of the most extensively observed exoplanets, and now constitutes a benchmark target for atmospheric characterization via follow-up observations and theoretical modeling.
From space, the Hubble Space Telescope (HST) has been instrumental in probing the optical to infrared transmission spectra of this planet. Collective observations with the Advanced Camera for Surveys (ACS), the Space Telescope Imaging Spec-trograph (STIS), and the Wide Field Camera 3 (WFC3) obtained nearly continuous spectra over the 0.3–1.7 µm range (Pont et al. 2008; Sing et al. 2011; Huitson et al. 2012; McCullough et al. 2014). Complementary infrared (IR) transmission photometry from the Spitzer Space Telescope between 3.6 and 8.0 µm (Désert et al. 2009; Agol et al. 2010; Knutson et al. 2012), and posterior re-analyses of the cumulative data (Pont et al. 2013; Sing et al. 2016) revealed a steep Rayleigh scattering slope dominating the optical and near-infrared spectrum. These results are consistent with the presence of high-altitude atmospheric hazes, ruling out a clear atmosphere.
Ground-based facilities further allowed the detection of several spectral features; in particular, high-resolution observations lead to the detection of narrow absorption features above the haze layer from the H Balmer lines (Jensen et al. 2012; Cauley et al. 2015) and the Na D lines (Redfield et al. 2008; Wyttenbach et al. 2015). These observations constrained the temperature of the thermosphere, revealed strong wind velocities consistent with an eastward equatorial jet (Louden & Wheatley 2015), and detected a transit early ingress, possibly caused by a hydrogen bow shock ahead of the planet (Cauley et al. 2015). We note however that these detections were contested in subsequent studies (see Barnes et al. 2016; Guilluy et al. 2020), where it was argued that the observed signal could be stellar in nature, rather than planetary. Similarly, stellar effects are also suspected to affect the steep UV slope observed by HST for this planet, although the magnitude of this contribution is not fully understood (see, e.g., McCullough et al. 2014; Rackham et al. 2019).
High-resolution spectroscopy studies of HD 189733 b at near-infrared wavelengths via the cross-correlation method yielded the detection of H2O absorption features (Birkby et al. 2013; Brogi et al. 2018) and CO (Rodler et al. 2013; Brogi et al. 2016). These observations further constrain atmospheric composition and suggest small wind speeds of ~2 km s−1 (at pressures around the 10−2−10−3 bar levels).
Infrared observations of the day-side emission during secondary eclipse revealed a lack of thermal inversion and a nearly solar H2O abundance in the lower planetary atmosphere (Crouzet et al. 2014; Todorov et al. 2014). Furthermore, infrared photometry along the entire orbital phase measured the brightness temperature variation, constraining the energy budget and the global circulation regime (Knutson et al. 2007, 2009, 2012). These observations revealed an efficient energy redistribution of the incident stellar irradiation and an eastward offset of the peak emission, relative to the substellar point. As with the conclusions from optical observations, these measurements are consistent with circulation models exhibiting an eastward advection by an equatorial super-rotating jet with wind speeds on the order of 1 km s−1 at pressures around the 1 mbar level (e.g., Showman et al. 2009, 2013).
Given the close planet to star distance, it is expected that HD 189733 b exhibits atmospheric escape. The host star, HD 189733, is an active K-dwarf star (radius 0.75 R⊙, mass 0.79 M⊙, effective temperature 5052 K; Stassun et al. 2017) that shows clear evidence of activity and spots during transit events (e.g., Sing et al. 2011; Pont et al. 2013), which makes it a particularly interesting study case for star-planet interactions (e.g., Poppenhaeger et al. 2013; Pillitteri et al. 2015; Cauley et al. 2018).
Lyman-α transit observations in the far-ultraviolet with HST/STIS detected an extended hydrogen envelope that expands hydrodynamically and escapes to space, powered by absorption of the high-energy stellar flux (X-ray and extreme ultraviolet, EUV; Lecavelier des Etangs et al. 2012; Bourrier et al. 2013). Strong temporal variations and the high velocity of the escaping gas suggest the presence of significant star–planet interactions (consistent with the active nature of the host star), which requires an acceleration mechanism in addition to stellar radiation pressure, such as the stellar wind. Although later, Guo & Ben-Jaffel (2016) found that the Lyα variability can be simply explained by invoking a thermal population of H I in the planet’s upper atmosphere without a need for complex dynamics involving stellar winds or radiation pressure. In this case changes to the star’s EUV output would explain the different absorption signals. Far-ultraviolet observations with the HST Cosmic Origins Spectrograph have also led to the detection of O I and C II in the planetary upper atmosphere (Ben-Jaffel & Ballester 2013), indicating that heavy atoms are possibly entrained and dragged upward in the hydrogen hydrodynamic outflow of the atmosphere.
The Hα absorption feature detection by Jensen et al. (2012) indicates that the upper atmosphere of HD 189733 b is neither in radiative equilibrium nor thermodynamic equilibrium, due to the large ultraviolet flux received by its active host star. In addition, Salz et al. (2018), Zhang et al. (2022), and Guilluy et al. (2020) detected a strong absorption signal from the He I triplet at 10 830 Å by means of ground-based high-resolution transmission spectroscopy with CARMENES and GIARPS, respectively. The observed He absorption favors a compact helium atmosphere with a substantial column density and no evidence of He escape. This interpretation of the He observations would seem to be consistent with the above explanation of the Lyman-alpha transit observations by Guo & Ben-Jaffel (2016).
The many observations of HD 189733 b across the electromagnetic spectrum have enabled an in-depth characterization of the composition and physical state of both the lower and upper atmosphere of the planet. However, until recently, the near-ultraviolet (NUV) window, probing both the exosphere and thermosphere, escaped the spectral coverage probed by these observations. King et al. (2021) analyzed 20 NUV photometric transits of HD 189733 b obtained from the XMM-Newton optical monitor. They detected a transit-depth signal consistent with that in the optical, ruling out extended broadband absorption toward or beyond the Roche lobe. However, to detect the NUV absorption signature from individual metallic lines, higher spectral resolution observations are required, like those from HST/STIS, with a resolving power of R ≈ 30 000 (see Sing et al. 2019; Cubillos et al. 2020).
For the slighly more strongly irradiated planet HD 209458 b, Cubillos et al. (2020) detected Fe II absorption in a 100 Å wide range around 2370 Å lying beyond the planetary Roche lobe, but did not find evidence for absorption by Mg II, neutral magnesium (Mg I), or neutral iron (Fe I). These results suggest that hydrodynamic escape is strong enough to carry heavy atoms beyond the planetary Roche lobe; however, condensate formation sequesters primarily Mg (rather than Fe) in the lower atmosphere of the planet, consistent with microphysical cloud-formation models (Gao et al. 2020). For the ultra-hot Jupiter WASP-121b, Sing et al. (2019) reported the detection of strong narrow NUV absorption features, consistent with the singly ionized magnesium (Mg II) doublet and several lines of ionized iron (Fe II), emanating from altitudes that exceed the Roche-lobe radius of the planet. These results indicate that Mg II and Fe II species are not trapped in condensates at depth, and can hydrodynamically escape the atmosphere.
To complete the spectral survey of this benchmark planet and aid the quantitative assessment of the metallicity, ionization state, and outflow rate of the upper atmosphere of HD 189733 b, here we analyzed 15 HST orbits obtained from three STIS NUV transit light curves. In Sect. 2, we describe the observations in more detail. In Sect. 3, we describe our data analysis procedure. In Sect. 4, we present the main results from the NUV data analysis. In Sect. 5, we place the observations in context by contrasting them with theoretical models of the planet. In Sect. 6, we speculate on the origin of the features seen in the NUV observations. Finally, in Sect. 7 we summarize our conclusions.
2 Observations
We observed three transits of the planet HD 189733 b obtained with HST, using the Space Telescope Imaging Spectrograph (STIS, program GO #15338, PI L. Fossati). The observations were carried out on 2018 March 10, 2018 September 19, and 2019 August 27 (visits 1, 2, and 3, respectively). Each observation used the NUV Multi-Anode Microchannel Array (NUV-MAMA) detector in ACCUM mode, E230M grating, and with an aperture of 0/2 × 0″.2.
Each transit observation (one HST visit) consists of five HST orbits. For each visit, the fourth orbit occurs during transit, whereas the first three and last HST orbits occur out of transit. The orbits are broken into exposures (frames) of ~332 s each. The first two visits contain nine frames per orbit (except for the first orbit, which contains one fewer frame to facilitate acquisition observations). The third visit contains one fewer frame per orbit, possibly due to a longer pointing adjustment time after HST returned to operations from a gyroscope failure.
Each frame consists of an echelle spectrum comprising 23 partially overlapping orders, covering the 2300–3100 Å spectral range. Each order contains 1024 wavelength samples, with a resolving power of R = λ/Δλ = 30 000, where the resolution element spans approximately two pixels (or equivalently ~0.09 Å, or ~10 km s−1). Figure 1 shows a sample spectrum from visit 1. As expected, the flux decreases toward shorter wavelengths, with a clear drop in signal-to-noise ratio (S/N) at wavelengths shorter than ~2550 Å. The stellar spectrum shows many emission features, most of which correspond to Fe II lines rising from low energy levels, but also the Mg I and Mg II resonance lines (the strongest line emission feature in the data, as shown in the insets of Fig. 1). In contrast, stellar Fe I features appear in absorption.
The input for our analysis consisted of the x1d CALSTIS-reduced fits files1 (version 3.4.2). The reduction comprises dark and flat-field correction, 1D spectral extraction of each echelle order, background subtraction, and wavelength and flux calibration. The results are the 1D spectra (erg s−1 cm−2 Å−1 ) and their uncertainties.
Following Sing et al. (2019), we also considered the Engineering Data Processing System “jitter” files, which contain 28 different engineering measurements of the HST Pointing Control System for each exposure during an observation.
 |
Fig. 1 HD 189733 system flux as observed by HST/STIS. This spectrum was constructed from the mean time series spectra obtained during the first visit, after discarding bad pixels. The spectrum is color-coded by echelle order (see color bar on the right). The insets show zoomed-in images around the location of the Mg II and Mg I resonance lines. |
3 Data analysis
The core of our analysis is based on the methodology of Cubillos et al. (2020). We separated our light curve analysis into two main steps. First we constructed white light curves by integrating the flux per transit visit and per echelle order to boost the astrophysical and instrumental signals, from which we characterized the instrumental systematics. Then we divided out the systematics model from the raw data, and combined the systematics-corrected data from all visits into spectral light curves binned at different resolving powers, from which we extracted the transmission spectra of the astrophysical signal.
3.1 Analysis of individual visits
We characterized the instrumental systematics to detrend them from the astrophysical signal and remove them from further analyses. To increase the S/N of the data, we integrated the flux over each echelle spectral order. The implicit assumption is that the instrumental systematics behave similarly over the integrated range (Kreidberg et al. 2014), in this case over each echelle order.
The analysis begins by masking bad and overly noisy data values. Following the standard practice for exoplanet HST/STIS time series analyses, we discarded the first orbit from each visit and the first frame from each orbit since they show significantly stronger instrumental systematics (see, e.g., Sing et al. 2011). Then we used the overlap between echelle orders to discard data points where the fluxes differ from each other by more than 3σ. Finally, we manually inspected the edges of the echelle spectra to exclude data points with abnormally low fluxes (typically, a handful of data points at the ends of the echelle orders). We then produced raw white light curves by summing the flux over each spectral order and propagating the uncertainties accordingly.
We fit the raw light curves with parametric transit and systematics models at each echelle order (denoted by their wavelength λ) as a function of time (t), HST orbital phase (ϕ), and jitter vector (ji):
Here Tλ(t) is a Mandel & Agol (2002) transit model and Sλ(t, ϕ, ji) is a model of the instrumental systematics. To obtain statistically robust parameter estimations, we computed the best-fitting parameters and uncertainties from a LevenbergMarquardt optimization and a Markov chain Monte Carlo (MCMC) sampling, respectively. For this matter, we employed the open-source MC3 statistical package2 (Cubillos et al. 2017), which implements the Snooker Differential-evolution MCMC algorithm of ter Braak & Vrugt (2008).
The transit model parameterizes the astrophysical signal via the orbital parameters, the planet-to-star radius ratios Rp/Rs(λ), the out-of-transit stellar fluxes Fs(λ), and limb-darkening coefficients Ci(λ). For the orbital parameters, we adopted previously measured values for the orbital period P = 2.21857567 ± 1.5 × 10−8 days, inclination i = 85°.71, and the ratio of semimajor axis to stellar radius a/Rs = 8.84 ± 0.27 (Stassun et al. 2017), which we kept fixed during the fitting and MCMC process. We fit the transit mid-time epoch, applying a Gaussian prior according to the measured optical value (T0 = 53955.025551 ± 9 × 10−6 MJD, Bonomo et al. 2017), propagating uncertainties according to the epoch of the HST observations.
For the limb-darkening parameters, we computed theoretical coefficients based on the stellar properties, since the low S/N ratios and gaps in the HST observations do not provide a good estimation. For this calculation we used the open-source routines of Espinoza & Jordán (2015) to compute limb-darkening coefficients over each wavelength range based on the PHOENIX stellar model (Husser et al. 2013) that best matches the properties of HD 189733: effective temperature Teff = 5052 K, surface gravity log ɡ = 4.49, and metallicity [M/H] = −0.02 (Stassun et al. 2017). We note that, in the absence of any better known guess, the adopted limb-darkening coefficents correspond to the photosphere of the star. If a significant fraction of the stellar flux comes from its chromosphere and transition region, as suggested by the stellar line emission, then the limb-darkening coefficients used may not be as representative as expected.
The HST/STIS time series observations exhibit a number of well-documented instrumental systematics: periodic variations in phase with the HST orbital period, which are suspected to originate from the telescope's thermal cycle (Brown et al. 2001), and visit-long variations that might be attributed to stellar activity (e.g., Wakeford et al. 2016; Sing et al. 2019). Following the example of previous studies, we model these systematics considering a family of polynomials in time (t) and HST orbital phase. Furthermore, Sing et al. (2019) showed that additional data from the HST Pointing Control System (called jitter data) can help decorrelate instrumental systematics from the astrophysi-cal signal. For each science exposure, the jitter data describe the HST fine guidance sensor (FGS) coordinates, FGS jitter, right ascension, declination, position angle, latitude, longitude, angle between HST zenith and target, Earth-limb angle, terminator angle, and magnetic field. HST stores the jitter measurements in time-tag ancillary engineering files, recorded at a high temporal resolution. For each science exposure we computed a value for each of the jitter parameters by calculating the median of the jitter values during the exposure. Therefore, our systematics model consists of a polynomial expression up to a quadratic degree in time, up to a quartic degree in HST phase, and a up to a linear degree in one of the jitter vectors
where ak, bk, and ck are the polynomial coefficients to be fit. We note that we considered an individual set of fitting parameters for each echelle order (we dropped the λ-dependence of these coefficients for clarity). For the jitter vectors ji, we considered each of the 21 vectors listed in Table 1 of Sing et al. (2019); t0 and ϕ0 are reference values for the time and phase, which are fixed at the transit mid-time t0 = T0 and at the HST mid-phase ϕ0 = 0.2, respectively; 〈 ji⟩ denotes the mean value of the jitter vector ji along the visit.
3.1.1 Systematics model selection
Given our limited understanding of the systematics affecting HST observations, we determined the optimal functional form for the systematics model S λ by comparing fits considering all possible combinations of polynomial orders in t and ϕ up to the degrees shown in Eq. (2), and each of the 21 jitter vectors, and fits with no jitter vectors. To this end, we employed a Bayesian model selection approach (see, e.g., Trotta 2007), where the posterior probability of two competing models are compared, given the data, by computing the ratio of their Bayesian evidence (also known as the Bayes factor). The main problem with this approach is that the evidence of a model is not readily calculable. Numerically, calculating the evidence entails evaluating the model likelihood throughout its parameter space (e.g., via a nested-sampling algorithm). To avoid the computational cost of this task, we adopt a simpler model selection approach where we approximate the evidence ratio via the Bayesian information criterion (BIC, Liddle 2007)
where 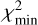 is the goodness-of-fit parameter corresponding to the maximum likelihood for the given model, k is the number of free parameters, and N is the number of data points. The Bayes ratio is then simply calculated from the difference in BIC values between the competing models B = exp{−(BIC1 − BIC2)/2} (Raftery 1995), which only requires finding the maximum likelihood for the given models. A Bayes factor B > 1 favors model 1 over model 2, or alternatively, the favored model minimizes BIC.
is the goodness-of-fit parameter corresponding to the maximum likelihood for the given model, k is the number of free parameters, and N is the number of data points. The Bayes ratio is then simply calculated from the difference in BIC values between the competing models B = exp{−(BIC1 − BIC2)/2} (Raftery 1995), which only requires finding the maximum likelihood for the given models. A Bayes factor B > 1 favors model 1 over model 2, or alternatively, the favored model minimizes BIC.
These approximations are based on various assumptions, which may not be fulfilled to different extents, such as independent and identically distributed data or (nearly) Gaussian posterior distributions, or that the forward model is correct. Therefore, we also considered a second model selection criterion based on information theory, the Akaike information criterion corrected for small sample sizes (AICc, Liddle 2007):
Just as above, the favored model minimizes AICc.
3.1.2 Model selection applied to the HST observations
For the HD 189733 b data we treated each HST visit independently, and for each visit we fit simultaneously the astrophysical and systematics parameters. For each visit we also fit all 23 echelle orders simultaneously, jointly fitting the transit mid-time epoch and adopting the same configuration of the systematics model for all orders. Table 1 lists the BIC and AICc of the global fit to all orders for the favored systematics model (with and without jitter decorrelation). Figure 2 shows an example of the light curve fits for a selected echelle order.
As seen from the raw light curves (top row of Fig. 2), the systematics are characterized by visit-long and HST-orbit-long variations. Overall, the second visit shows stronger systematics than the first visit, and the third visit shows stronger systematics than the second, which is reflected in the best-fitting BIC, AICc, and reduced χ2 values 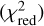 . In particular, the second and third visit systematics vary on the order of 10% of the raw flux. If we only included the more traditional polynomials in t and ϕ in the fit, we found clear systematic residual trends that vary in strength for each echelle order. The relatively new practice of jitter decorrelation introduced by Sing et al. (2019) significantly improves the fit for the second and third visits, minimizing both information criteria statistics and residual systematics (bottom row of Fig. 2). In these fits, the AICc imparts a weaker penalty per fitting parameter than the BIC, thus favoring more complex models, which notably improves the
. In particular, the second and third visit systematics vary on the order of 10% of the raw flux. If we only included the more traditional polynomials in t and ϕ in the fit, we found clear systematic residual trends that vary in strength for each echelle order. The relatively new practice of jitter decorrelation introduced by Sing et al. (2019) significantly improves the fit for the second and third visits, minimizing both information criteria statistics and residual systematics (bottom row of Fig. 2). In these fits, the AICc imparts a weaker penalty per fitting parameter than the BIC, thus favoring more complex models, which notably improves the 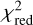 values. However, although the BIC and AICc statistics favor different models, the two criteria usually produced consistent transit depths. All the following analyses presented here focus on the best AICc analysis including jitter decorrelation.
values. However, although the BIC and AICc statistics favor different models, the two criteria usually produced consistent transit depths. All the following analyses presented here focus on the best AICc analysis including jitter decorrelation.
Figure 3 shows the resulting transmission spectra according to the best AICc models for each visit and at each echelle order. One clear feature seen in the transmission spectra is an offset between the third visit and the first two. This offset is consistent with the signature of unocculted stellar spots (see, e.g., Rackham et al. 2018; Zellem et al. 2017), which is a likely cause given the well-known active nature of HD 189733. For each visit we found that the transit radius ratios vary closely proportional to the square root of the bolometric fluxes of the observations 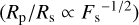 , which is a direct consequence of observations arising from a heterogeneous stellar photosphere including spots (Rackham et al. 2018). The weighted mean of the Rp/Rs values for each individual visit are 0.1585, 0.1595, and 0.1701, whereas the relative bolometric fluxes between visits are
, which is a direct consequence of observations arising from a heterogeneous stellar photosphere including spots (Rackham et al. 2018). The weighted mean of the Rp/Rs values for each individual visit are 0.1585, 0.1595, and 0.1701, whereas the relative bolometric fluxes between visits are 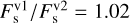 and
and 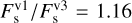 . The combined analysis in Sect. 4.1 shows an independent confirmation that we are observing stellar spot contamination in the data.
. The combined analysis in Sect. 4.1 shows an independent confirmation that we are observing stellar spot contamination in the data.
Once corrected for stellar activity, the analysis of each of the three visits produces a consistent transmission spectrum across the NUV. We obtained a mostly flat transmission spectrum between 2300 Å and 3100 Å, with a planet-to-star radius ratio of ~0.16, which becomes significantly noisier at wavelengths shorter than 2550Å, due to the much lower stellar flux. These results are also consistent with the previous NUV observation by King et al. (2021), which measured the transit depth of HD 189733 b in the UVM2 photometric band of the XMM-Newton Space Observatory (effective wavelength 2310 Å, width 480Å).
As a reference, the estimated altitude of the Roche-lobe radius as probed during transit is RL1′ = 0.44 Rs (i.e., perpendicular to the star-planet axis). This value is approximated by 2/3 the distance to the L1 Lagrange point (see, e.g., Vidal-Madjar et al. 2008). All transit depths at each echelle order are well under the Roche-lobe radius.
 |
Fig. 2 Sample transmission light curve fitting of the HST/STIS observations of HD 189733 b (fourth echelle order, |
 |
Fig. 3 HST/STIS NUV transmission spectrum of HD 189733 b (individual visits). The circles with error bars denote the transmission planet-to-star radius ratios from each echelle order and visit (see legend), corresponding to the best AICc fits. The colored dashed lines denote the mean value for each visit. The squares denote the XMM-Newton/UVM2 photometric measurement by King et al. (2021). |
BIC and AICc model comparison.
3.2 Analysis of combined visits
To search for the narrow metal line absorption features in the transmission spectrum, we need to analyze the observations at a high resolving power in order to find a compromise between sufficient S/N per wavelength channel and diluting the narrow absorption features. Therefore, we treated the data at multiple spectral resolving powers ranging from R = 10–70 (coarse sampling analysis), and then at a R = 4700 (fine sampling analysis). We proceeded in the same fashion as in Cubillos et al. (2020), that is we calibrated the wavelength solution to ensure that the spectra are well aligned, used the modeling results from the previous analysis to divide out the instrumental systematics, combined the data from all three visits into a single spectrum, and fit the transit depths at each bin. All future analyses use the best AICc dataset since it attained 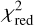 values closer to one.
values closer to one.
3.2.1 Wavelength calibration
We used a cross-correlation procedure to calibrate the wavelength solution of each echelle order in each frame and visit. First, we created a master stellar template (enhancing the S/N) by co-adding the spectra from all frames within an echelle order and visit. We then Doppler-shifted the individual frame spectra and cross-correlated them with their templates, searching for the relative velocity with respect to the template given by the shift that maximized the correlation function. Once we obtained the wavelength correction of the individual frames within an echelle order, we repeated the procedure between the template spectra of each visit to find the relative wavelength correction between all spectra. Finally, we compared our wavelength solution with a theoretical model spectrum of HD 189733 (Shulyak et al. 2004) to obtain an absolute wavelength solution at a rest reference frame. Once calibrated, we Doppler-shifted all frames within a given echelle order to a common wavelength solution using a cubic spline interpolation. To minimize the impact of the interpolation, we selected a reference point that minimized the shifts of the set of frames. For a given visit, we found offsets of less than half a pixel between the frames, and in general the wavelength solution for each echelle order follows a similar trend along the visit, with no outliers.
3.2.2 Divide-white spectral extraction
To extract a high-resolution transmission spectrum of HD 189733 b, we followed the “divide-white” spectral analysis by Kreidberg et al. (2014), as described in Cubillos et al. (2020). In this approach we first constructed a non-parametric model of the instrumental systematics by dividing the white light curves (for each echelle order and visit) by their best-fit astrophysical transit model (see Sect. 3.1). Assuming that the instrumental systematics vary weakly with wavelength, each raw spectral data point is divided by the systematics model corresponding to their orbital phase, echelle order, and visit. Data uncertainties are properly accounted for by using the white light model’s posterior distribution to estimate the uncertainties systematics model and propagating the errors. In the second step, we split the data into constant resolving-power wavelength bins, where for each spectral channel we co-added all flux contributions from all echelle orders, and propagated the errors accordingly.
To analyze the spectral light curves we fit a Mandel & Agol (2002) transit model to the systematics-corrected spectral light curves in a MCMC run. As previously, we fixed the orbital a/Rs, cos(i), and P parameters, and applied a Gaussian prior for the mid-transit epoch based on the white light fitting results. We also computed theoretical limb-darkening curves at each spectral channel, which we kept fixed during the fit. At each wavelength bin we fit a unique transit depth common to all three visits, but we fit a separate out-of-transit flux value for each visit. Additionally, we incorporated a stellar spot correction model, which we detail in the following section.
3.2.3 Stellar spot correction
To account for the spectral transit-depth variations due to unoc-culted stellar spots, we modeled the stellar flux as a linear combination of a nominal photospheric region and a spotted region. We assumed that a fraction fspot of the observed photosphere is covered by spots with a characteristic temperature Tspot, whereas the rest of the photosphere has the nominal effective temperature of the star Teff = 5052 K (with Teff ≥ Tspot). We used the PHOENIX library of high-resolution synthetic stellar spectra (Husser et al. 2013) to compute the flux of the nominal stellar photosphere Fs(Teff) and the spotted region Fspot(Tspot). This leads to the following correction term for the observed transit depth dobs(λ):
Here d(λ) is the true transit depth and ϵ(λ) is the contamination spectrum due to stellar hetereogeneities (as defined in Rackham et al. 2018). To evaluate the correction factor at any given Tspot, we interpolated in temperature between all available PHOENIX models (ranging from 2300 K to 5100 K) at a fixed metallicity ([M/H] = 0.0) and surface gravity (log(ɡ) = 4.5).
The stellar spot correction model thus contains two free parameters for each visit (fspot and Tspot), which we fit simultaneously along with the other astrophysical parameters during the MCMC. We considered a uniform prior for the fspot values between 0.0 and 0.5; it would be unlikely to find unocculted spot covering fractions greater than 50%. For the spot temperature we considered a logarithmic-uniform prior in ΔTspot = Teff −Tspot because the spectral variation of the spot correction is more pronounced at small ΔTspot values (McCullough et al. 2014). When ΔTspot ≳ 1500 K the correction becomes nearly achromatic. Regardless of the parameterization, the main conclusions of our analysis do not change when we consider a uniform prior in Tspot.
 |
Fig. 4 Near-UV transmission spectrum of HD 189733 b from the combined HST/STIS observations. The red symbols with error bars denote the systematics- and stellar spot-corrected transmission spectrum, their 1σ uncertainties, and the span of the spectral bins (the data is binned in wavelength over a resolving power of R = 50). The green symbols show our results when neglecting the stellar spot contamination in the analysis (symbols are slightly shifted in wavelength for visibility). The blue spectrum shows a theoretical model of the planet’s upper atmosphere (see Sect. 5.1) and the blue dots show the model integrated over the spectral bins. The orange curve shows an extrapolation from a fit to the optical–IR transmission spectrum of the planet (see Sect. 5.2). |
4 Planetary atmospheric signatures
4.1 Coarse-binning spectra
To boost the characterization of the astrophysical signal, we started with the analysis of the combined data binning over a relatively coarse wavelength sampling. Figure 4 shows the NUV transmission spectrum of HD 189733 b sampled at a resolving power of R = 50. This resolving power resulted in the best compromise between having a good S/N per bin and having sufficient spectral resolution to identify variability with wavelength. Appendix A shows the corresponding systematics- and stellar spot-corrected light curves for this analysis. At this resolving power we obtained a relatively flat transmission spectrum with the exception of two regions where the transit depth increases (by more than ~1σ relative to the surrounding wavelengths) located at λ ~ 2350 Å and λ ~ 2600 Å.
For completeness, we also analyzed the data at other similar resolving powers of R = ~10, 30, 70 and found consistent results. Analyses with the bins shifted by half a bin width returned consistent results as well.
The stellar spot contamination was well characterized, as shown in Fig. 5. The first two visits show a negligible spot contamination (ϵ < 1.05), with the models finding either a small spot covering fraction or a spot temperature close to the nominal stellar effective temperature (ΔTspot ≲ 10). In contrast, the third visit clearly shows a significant spot contamination ranging from ϵ(λ) ≈ 1.20 to 1.15 from short to long wavelengths. The contamination shows a weak variation with wavelength, which is not larger than the 1σ credible intervals of the constraints. Accordingly, we constrained the spot covering fraction to ƒspot > 0.11 and the spot temperature to 100 K ≲ ΔTspot < 500 K, values that are strongly correlated (see posterior pair-wise distribution in Fig. 5). Analyzing the combined data without a stellar spot model produced slightly larger transit depths (Fig. 4); however, the shape of the spectrum remains consistent with that of the spot-corrected analysis, which is consistent with the nearly wavelength-independent stellar spot correction.
In summary, the ratio of the contamination spectra of the visits (e.g., ϵv3/ϵv1 = 0.15–0.2) matches precisely the ratio of the bolometric fluxes (e.g., 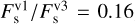 ), which reinforces the hypothesis that the variability between visits is caused by a varying stellar spot coverage at different epochs.
), which reinforces the hypothesis that the variability between visits is caused by a varying stellar spot coverage at different epochs.
 |
Fig. 5 Stellar spot contamination. The top panels show the posterior distribution of the spot parameters derived from the combined data analysis. The blue shaded areas denote the 1σ highest posterior density credible region. Visits 1 and 2 show a negligible spot contamination with either a small spot covering fraction or a negligible difference between the spot and photospheric temperatures. Visit 3 in contrast shows a non-negligible contamination of ϵ(λ) ~ 1.15–1.2, with a strong correlation between the spot covering fraction and spot temperature. The bottom panel shows the respective contamination spectra. The colored symbols and vertical spans show the median and 1σ uncertainty of the contamination, respectively. |
 |
Fig. 6 Infrared to ultraviolet transmission spectrum of HD 189733 b. The top and bottom panels show the same data, focused on different spectral regions for better visibility. The colored symbols with error bars show the transit observations, 1σ uncertainties, and wavelength span of the observations (see legend). Our data points were computed from the data binned at a resolving power of R = 33 (see Appendix A). The red curve and orange shaded areas show the spectrum posterior distribution of the optical–IR fit (median, 68%, and 95% quantiles of the distribution; see Appendix B). The blue curve shows the upper atmosphere model (shaded in a slightly paler color when below the optical-IR continuum). |
4.2 Fine-binning spectra: Magnesium resonance lines
We attempted to analyze the data binning at much higher resolving power in order to capture absorption of individual metallic lines; however, the high-resolution light curves were largely dominated by noise, and not much could be concluded from the resulting spectra. The only region where we were able to place significant constraints at high resolution is at the core of the magnesium resonance lines, which have fluxes nearly ten times larger than at other wavelengths, and thus a much better S/N. For this we selected a bin resolving power of R = 4700 (65 km s−1 wide bins), which encapsulates the core of the Mg I and Mg II resonance lines.
Figure 6 shows the high-resolution light curves centered at the Mg I and Mg II resonance (top), and the stellar spectra (middle) and transit radius-ratio spectra (bottom) around the magnesium lines. For the Mg II bins, the light curves show a clear transit signature (albeit with some residual noise for the Mg II h line), and have S/N values of the same order of magnitude as those of the low-resolution analysis. The light curve at the Mg I line, having much lower flux, is significantly noisier than the Mg II lines. For all three magnesium lines the transit depths do not show any significant excess above the low-resolution continuum values (R = 50 analysis), and are consistent with the optical-IR transmission spectrum of HD 189733 b.
For context, in the bottom panels of Fig. 6 we also show the theoretical upper atmosphere model for this planet (see Sect. 5.1 for details). While the HD 189733 b escape rate is not high enough to generate magnesium absorption signatures close to the Roche-lobe altitude (RL1′ /Rs = 0.44), the model predicts a noticeable excess absorption above the continuum. Thus, we used the binned model estimate to place non-detection limits for the Mg II measurements. We found that the observations lie 2–4σ below the prediction for a solar-abundance atmospheric model containing Mg in the upper atmosphere (Table 2). Due to the higher noise at the Mg I line, we cannot reject nor confirm the presence of Mg I absorption from our observations.
HD 189733 b transit measurements at magnesium lines.
5 The transmission spectrum of HD 189733 b from near-UV to infrared
For context, the HeI infrared metastable triplet and HI Lyman-α transit observations of HD 189733 b can be interpreted in terms of the planet hosting a compact upper atmosphere: extended, but not as much as that of other exoplanets observed in the NUV (e.g., HD 209458 b). Metals like magnesium or iron may condense in the lower atmosphere and, even if they make it to the upper atmosphere, a lower escape rate would not allow their density profiles to stretch out to high altitudes. At longer wavelengths the optical–IR observations show a strong slope toward the blue, which can be interpreted as absorption from high-altitude hazes.
To test these hypotheses and to get a better understanding of the interaction between the upper and lower atmosphere of HD 189733 b, we compare the observations to theoretical models. Since it is not possible to model all the required upper and lower atmosphere properties at once, we modeled the upper and lower regions individually, and then studied how they relate to each other.
5.1 Upper atmosphere modeling
To interpret the NUV transmission spectrum of HD 189733 b, we employed the physical model of the upper atmospheres of close-in planets (Koskinen et al. 2013a,b, 2022). Since the parts of the NUV transmission spectrum that probe the upper atmosphere are dominated by signatures of ionized metals Fe II and Mg II (Sing et al. 2019; Cubillos et al. 2020), we added the heavy elements C, O, N, Mg, Si, Fe, S, Ca, Na, and K with solar abundances to the model, in addition to H and He, with the related chemistry and physics adapted from Huang et al. (2017). We included Mg, Si, Fe, Ca with first and second ionization states, due to the relatively low ionization potential of the first ionization state, and the rest of the heavy elements with their first ionization state. The electron density is equal to the sum of the ion densities under the assumption of quasi-neutrality. The lower boundary of the escape model is at 0.1 µbar where the temperature is sufficient to dissociate molecules that are not included in the model.
We used the results from the photochemical model of Lavvas & Koskinen (2017) to obtain the mean molecular weight profile in the lower and middle atmosphere to set the lower boundary altitude and temperature of the escape model. The temperature profile in the lower and middle atmosphere was not calculated self-consistently by the photochemical model, and was instead adapted from Moses et al. (2011). Here, we used the MK profile from Lavvas & Koskinen (2017). The application of the photochemical model to HD189733b did not include Mg and Fe, which are detectable in the NUV. In order to crudely model the full profiles of the absorption lines, we added Mg and Fe to the lower and middle atmosphere, assuming solar abundances and thermal ionization according to the Saha equation (Menou 2012). This approximation does not affect our conclusions because our focus in this section is on the possible upper atmosphere signatures.
Given the temperature profile assumed for HD 189733 b here and assuming equilibrium condensation, Mg, Fe, Si, and Ca are expected to condense to form mineral clouds and rain out from the atmosphere (e.g., Wakeford & Sing 2015). We included Mg and Fe in the escape model simply to explore if the modeled absorption lines of Mg II and Fe II would be detectable in the NUV data. The rest of the heavy elements were retained for consistency with the no-condensation scenario. Although efficient mixing in the lower atmosphere could interfere with mineral cloud formation and allow for higher abundances of the relevant heavy elements in the upper atmosphere (Spiegel et al. 2009; Koskinen et al. 2013b), we do not hold a view at this point on whether this is possible on HD 189733 b.
Figures 4 and 7 show the transmission spectrum from the upper atmosphere model in blue. Here, we calibrated the model spectrum so that the measured base Rp/Rs (in the near-IR) corresponds to 2.3 mbar in the atmosphere (Lavvas & Koskinen 2017). So as not to bias the fit to any particular interpretation at this point, we did not include extinction by the high-altitude haze modeled by Lavvas & Koskinen (2017) in this forward model. Instead, the transit continuum is due to Rayleigh scattering by H2, H, and He. It is immediately clear that the model continuum falls below the extrapolation based on the optical–IR transmission spectrum of the planet, due to the lack of the high-altitude haze in the forward model. Since transit depth is not a cumulative quantity, however, the model still correctly represents absorption by Fe II and Mg II in the upper atmosphere in the absence of condensation, even if high-altitude hazes are present.
We ran the upper atmosphere model assuming globally averaged radiative forcing with the extreme UV (EUV) spectrum constructed from ϵ Eridani as an input, due to the well-known similarity to HD 189733 (Lavvas & Koskinen 2017). The reference simulation, on which the spectrum in Fig. 4 is based, assumes an isolated planet. We also ran a second simulation that includes Roche-lobe overflow (see Koskinen et al. 2022), but this had a negligible effect on the modeled spectrum, in line with the expectation that Roche-lobe overflow does not significantly enhance the escape rate or upper atmosphere densities on HD 189733 b.
It should be noted that NUV observations have the potential to offer valuable new insights to the properties of possible high-altitude hazes and/or clouds. Unfortunately, S/N is an issue for HD 189733 b that precludes clear conclusions on the origin of the continuum in the transit observations. The visible spectrum shows a strong slope indicative of small-particle hazes (Sing et al. 2016; Lavvas & Koskinen 2017) that appears to be supported to some degree by observations by the Stratospheric Observatory for Infrared Astronomy (SOFIA; Angerhausen et al. 2015); however, SOFIA found a slope offset to lower depths by ΔRp/Rs = ~0.001 (see Appendix A). The slope can, however, be enhanced by stellar activity (star spots; McCullough et al. 2014). In addition, a general circulation model (GCM) that simulates the production and transport of hazes predicts a shallower slope unless mixing by subgrid scale eddies exceeds mixing by global circulation (Steinrueck et al. 2021). The NUV observations are statistically consistent with the model that includes no haze, and generally the observed transmission falls below the extrapolation based on the visible slope (Fig. 7), with the exception of the 2350 Å region. Due to low S/N in the NUV, however, the observations are also consistent with this extrapolation. Thus, these NUV observations neither confirm nor exclude the presence of high-altitude hazes, especially if the visible slope is enhanced by star spots.
 |
Fig. 7 Infrared to ultraviolet transmission spectrum of HD 189733 b. The top and bottom panels show the same data, focused on different spectral regions for better visibility. The colored symbols with error bars show the transit observations, 1σ uncertainties, and wavelength span of the observations (see legend). Our data points were computed from the data binned at a resolving power of R = 33 (see Appendix A). The red curve and orange shaded areas show the spectrum posterior distribution of the optical–IR fit (median, 68%, and 95% quantiles of the distribution; see Appendix B). The blue curve shows the upper atmosphere model (shaded in a slightly paler color when below the optical-IR continuum). |
5.2 Lower atmosphere modeling
To constrain the lower atmosphere properties of HD 189733 b we used the open-source >Pyrat Bay framework3 (Cubillos & Blecic 2021). We modeled the atmosphere from 100 to 10−9 bar, adopting a parametric temperature profile from Madhusudhan & Seager (2009), hydrostatic equilibrium, and a composition dominated by H2 and He considering constant-with-altitude volume mixing ratios.
The Pyrat Bay radiative transfer computed the transmission spectrum between 0.2 and 33.0 µm, at a constant resolving power of R = λ/Δλ = 15 000. The opacities included line-by-line data from HITEMP for CO2, CO, and CH4 (Rothman et al. 2010; Li et al. 2015; Hargreaves et al. 2020), and from ExoMol for HCN, H2O, NH3, and SiO (Harris et al. 2006, 2008; Polyansky et al. 2018; Coles et al. 2019; Yurchenko 2015; Yurchenko et al. 2022). We extracted the dominant transitions from these line lists using the REPACK algorithm (Cubillos 2017), and then computed tabulated opacities by sampling over temperature and wavelength grid. Additionally, the model included collision-induced opacities for H2−H2 pairs (Borysow et al. 2001; Borysow 2002) and H2−He pairs (Borysow et al. 1988, 1989; Borysow & Frommhold 1989); Rayleigh-scattering opacity for H, H2, and He (Kurucz 1970); and a gray cloud deck model. Finally, the model considered a parametric haze absorber model (Lecavelier Des Etangs et al. 2008) with arbitrary slope and strength (αhaze and 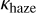 ), which are fit in the retrieval.
), which are fit in the retrieval.
The atmospheric retrieval employed the differentialevolution MCMC sampler (ter Braak & Vrugt 2008), implemented via the open-source code MC3 (Cubillos et al. 2017), guided by the transit observations from the HST STIS G430 and G750 and WFC3 G102 and G141 spectrographs, and from the Spitzer IRAC 3.6, 4.5, 5.8, 8.0 µm and MIPS 24 µm photometric bands (Pont et al. 2013; Sing et al. 2016).
Figure 7 shows the fit to the optical–IR transit observations. Appendix B presents the retrieval posterior-distribution results for all model parameters. The optical–IR observations point to a prominent haze slope, steeper than a Rayleigh slope (αhaze ~ −9.3 ± 2.3). This is a similar conclusion to that found by previous retrieval studies on this planet (e.g., Pinhas et al. 2019; Barstow 2020). From a physical perspective, the steep haze slope can be created by a combination of particle growth and efficient eddy (turbulent) mixing (Ohno & Kawashima 2020) or by stellar inhomogeneities (Rackham et al. 2018), effects that were captured by the parametric haze model (rather than being explicitly accounted for). The optical absorption is also stronger than that produced by hydrogen (as in the upper atmosphere model), leading to a higher continuum level at optical wavelengths, and when extrapolated to NUV wavelengths. The NUV observations are consistent with the optical–IR continuum model, with the exception of the few data points that extend above the continuum (mainly the 2350 Å region). Lastly, we can see that the constraint on the temperature profile becomes less precise above the 1 µbar level since optical–IR data mostly probes the lower layers of the atmosphere. At the same time, at these high altitudes the retrieved temperature profile starts to differ from the higher temperatures predicted by self-consistent models that account for high-energy flux that heats the thermosphere of the planet (Lavvas & Koskinen 2017; i.e., the models used as the base of our upper atmosphere model).
6 The nature of the NUV absorption
6.1 Fe II absorption
It is interesting that the excess NUV absorption matches precisely the locations of the two strongest Fe II bands in the region, while there does not seem to be any absorption corresponding to the Fe I band slightly blueward of the magnesium doublet. Unfortunately, the low S/N achieved when binning the data at higher resolution does not allow us to identify absorption from individual lines.
A detection of Fe II would actually be very controversial in this planet for multiple reasons. In the first place, iron is not expected to survive the cold trap at the lower layers. Even if we neglected the iron condensation, as is the case for our upper atmosphere model, we cannot match the large amplitude of the observed features when we bin the model at the resolution of the observation. Another argument against Fe II is that given the relatively cool expected temperature of the planet and the late spectral type of the star, we would also expect to observe Fe I if Fe II were detected.
If the NUV absorption indeed corresponded to Fe II, it would imply that our hydrodynamic model severely underestimates the absorption signature, and we would be in need of a mechanism to enhance the lines such that they become detectable in broader bins. This would require a significant broadening of the iron lines and super-solar abundances, even when assuming no condensation in the lower atmosphere. However, GCMs predict winds on the order of ±8 km s−1 at the terminator (Steinrueck et al. 2021). These models include regions of significant size with flows both away from and toward the Earth, due to the complexity of the circulation and rotation effects. These kinds of flows could effectively broaden metal lines in spatially unresolved transit observations.
6.2 Absorption from an unknown absorber or other source
The broadband absorption suggests the presence of an extra absorber, but the fact that the absorption matched the location of Fe II bands might be deceptive. It is certainly possible that the absorption comes from another unidentified species, possibly from either a haze or from the electronic band system of a molecular species, given the width of the absorption and the transition energies involved.
Following Lothringer et al. (2022), we explored whether SiO, for example if vaporized from strongly mixed cloud particles, could appear in the upper atmosphere. However, the atmospheric retrievals do not favor significant SiO absorption when it was included in the model. From a further heuristic exploration, we could not find any configuration of temperatures and abundances producing SiO bands at the observed strength or location. We finally tested for other candidates available in the ExoMol database and that extended into the NUV, which led us to discard both HS and OH.
One might consider that the absorption originates from an external source such as accreted material from trojan or circumplanetary satellites (Kislyakova et al. 2016; Oza et al. 2019). However, this is a highly speculative scenario; to date there is no model that demonstrates that material from an external source can produce such large absorption features, nor that it could generate exclusively an Fe II signature but not a signature from other particles like magnesium.
It also seems unlikely that the absorption features come from an as-yet-undetermined aerosol. To our knowledge there is no self-consistent GCM that couples haze production and circulation to a degree where we could state with confidence that particles could form and exist at the required high altitudes (~0.1 nbar). It is hard then to explain how aerosols would form and remain aloft at such altitudes. We also tested whether the stellar spot correction could generate the observed features (Rackham et al. 2018, 2019), but on close inspection of the spectral dependency of the spot contamination at different temperatures, we found no indication that it could mimic extra absorption at the location of the Fe II bands.
Finally, we considered the impact of stellar center-to-limb flux variation. As the stellar Fe II lines show in emission (Fig. 1), the observations should be probing the (hotter) stellar chromosphere and transition region rather than the (cooler) photosphere. Therefore, the lines may be showing limb brightening instead of limb darkening, leading to a quite different transit signature (see, e.g., Schlawin et al. 2010). Unfortunately, the limb-darkening and/or limb-brightening law for these lines is unknown, and it cannot be reasonably estimated with current instrumentation. In any case, while the unknown limb-darkening law of the emission lines introduces a degree of uncertainty in the NUV transit depths, unaccounted limb brightening would lead to underestimates in the transit depths, and thus does not explain the excess absorption seen at 2350 Å and 2600 Å.
6.3 Exoplanet NUV observations in context
To date three exoplanets have been spectroscopically observed during transit in the NUV with HST/STIS: WASP-121b (Sing et al. 2019), HD 209458 b (Cubillos et al. 2020), and HD 189733 b (this work). These three planets span a wide range of irradiation regimes, receiving a stellar flux of 364× (HD 189733 b), 769× (HD 209458 b), and 5624× (WASP-121b) that of the flux received by the Earth. The analysis of this aggregated data provides a first glance at the physical processes that shape the properties of the planets' upper atmospheres.
The upper panel of Fig. 8 shows the transmission spectra of these three planets at a resolution of R = 1300 in units of r/Rp, with Rp being the optical radius. We can see that WASP-121b exhibits enhanced transit depths coinciding with Fe II and Mg II lines, whereas the other two planets show subtler features. When comparing the transmission spectra at a resolving power of R = 130 in units of r/RRL, with RRL being the Roche-lobe terminator radius (lower panel of Fig. 8), we see that the pseudo-continuum extends to the Roche-lobe boundary, which indicates that the middle atmosphere and/or lower thermosphere of WASP-121b undergoes Roche-lobe overflow. In clear contrast, this is not the case for HD 189733 b or HD 209458 b. WASP-121b is therefore unique among these planets, and must have a much higher mass loss rate than the others, as expected. This broad behavior is qualitatively consistent with expectations based on model predictions.
The lower panel of Fig. 8 illustrates the dramatic difference between WASP-121b and the two other planets. The NUV spectra of HD 209458 b and HD 189733 b look nearly featureless when compared to that of WASP-121b. Certainly, WASP-121b is not an ordinary planet; it must have substantially higher mass-loss rates than the other two planets. Neither HD 209458 b nor HD 189733 b shows the Mg II absorption feature that survives in the spectrum of WASP-121b. As we already know, the spectrum of HD 189733 b shows a strong feature close to the blue Fe II absorption band. This feature does not extend to the Roche lobe, but the peak is ~150 surface scale heights above the optical radius. Given that heating in the thermosphere increases the scale height by a factor of ~20 above the ~1 µbar level, the peak probably probes the 1 nbar level.
Finally, we note, however, that the feature in the spectrum of HD 189733 b is not identical to the Fe II feature in the spectrum of WASP-121b. In particular, the point at ~2400 Å coincides with a strong Fe II band and should show maximum absorption toward the longer-wavelength edge. This is true for WASP-121b, but in the spectrum of HD 189733 b absorption drops instead. This poses a conundrum, however. Given the uncertainties in the data analysis, noise could be responsible for this apparent inconsistency.
 |
Fig. 8 Comparison HST/STIS NUV transmission spectra of HD 189733 b, HD 209458 b, and WASP-121b scaled by the optical transit radius Rp (top panel) and by the Roche-lobe terminator radius RRL of each planet (bottom panel). The shaded regions denote the wavelength span of the dominant Fe II and Mg II NUV bands and lines. |
7 Conclusions
HD 189733 b is the coolest hot Jupiter that has been spectrosopi-cally observed in the NUV to date. Transmission observations indicate that this is a very hazy planet, but the composition of the hazes are not really known; some of them may present additional absorption in the NUV.
By analyzing the combined NUV HST/STIS transmission spectra (three transits) at a relatively coarse resolution (R = 50), we obtained better S/Ns and spectral resolution than previous NUV observations of HD 189733 b in the NUV by King et al. (2021). The transit signature in the light curves is clear and with no significant residual systematics. We were able to constrain a continuum level that sits in between the extrapolation of the optical haze slope and the continuum of a pure-H2−He upper atmosphere model. Thus, given the uncertainties of our continuum data points, the NUV data is statistically consistent with either a hazy or clear atmosphere scenario. In addition, the NUV transmission spectrum presents strong and broad absorption features that coincide with the location of two strong Fe II bands, while there is no apparent excess absorption correlated with Fe I bands. When analyzing the data at higher resolution (R = 4700), we found that most of the light curves are dominated by noise, which does not allow us to confirm or discard iron as the source of the absorption. However, thanks to the much higher stellar flux at the location of the magnesium resonance lines, we were able to rule out the presence of Mg II excess absorption above the continuum. When compared to a solar metallicity model with magnesium in the upper atmosphere, the measured transmission Rp/Rs values at the core of the Mg II lines are 2–4σ below the model predictions. The S/N values of the data at the Mg I line are not high enough to reject or confirm excess absorption due to magnesium.
HD 189733 b has a surface gravitational acceleration twice that of HD 209458 b, and unlike WASP-121b, Roche-lobe overflow effects are not expected to be that significant. Its atmosphere is also cooler, suggesting that the formation of clouds is expected. This is closely in agreement with optical observations, where the data are consistent with a high-altitude haze, which could have a soot-like precursor. HD 189733 b upper atmosphere models assuming that magnesium did not condense in the lower atmosphere show considerable excess absorption at the core of the Mg II resonance lines. Thus, the absence of excess absorption suggests that magnesium is not escaping on HD 189733 b and that Mg−Si clouds likely form in the lower atmosphere.
At this point, the nature of the broad NUV absorption features is not known. An iron origin raises significant challenges for existing upper atmosphere models. In first place, given the relatively low temperatures of HD 189733 b, condensation is expected to sequester heavy metals into the lower layers of the atmosphere, though it is possible that condensates form primarily from other metals instead, such as magnesium (Gao et al. 2020; Woitke et al. 2020). However, even if iron is not strongly depleted, we would still need a mechanism to enhance its absorption beyond that predicted by our upper atmosphere models. The two most immediate possibilities would be to consider higher metallicities and zonal-wind velocity broadening of the absorption lines. GCM estimations of HD 189733 b predict wind velocities at ~8 km s−1 at the terminator; the question for future studies is whether these mechanisms are enough to boost the signal. Heavy metals play a key role in the modeling and interpretation of NUV transit observations and hence in our understanding of exoplanetary atmospheres as a whole. The detection of metals at Roche-lobe distances would be surprising instead of expected for HD 189733 b. Here we presented the detection of a broad absorption feature in the NUV that matches the location of Fe II bands, but cannot fully confirm the nature of the absorber. Future observational and theoretical work are both needed to understand more precisely the origin of this absorption.
Acknowledgements
We thank the anonymous referee for his/her time and valuable comments. We thank contributors to the Python Programming Language and the free and open-source community, including: PYRAT BAY (Cubillos & Blecic 2021), MC3 (Cubillos et al. 2017), REPACK (Cubillos 2017), NUMPY (Harris et al. 2020), SCIPY (Virtanen et al. 2020), MATPLOTLIB (Hunter 2007), IPYTHON (Pérez & Granger 2007), and BIBMANAGER (Cubillos 2020). This research has made use of NASA’s Astrophysics Data System Bibliographic Services. This project was funded in part by the Austrian Science Fund (FWF) Erwin Schroedinger Fellowship, programs J4595-N and J4596-N. A.G.S. and L.F. acknowledge financial support from the FFG project 865968. Based on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with program #15338.
Appendix A HD 189733 b NUV transmission spectra
Figure A.1 shows the NUV transmission spectrum binned at a coarse resolving power of R = 10, and shows a SOFIA-like offset of the transit depth for comparison.
Figure A.2 shows the systematics- and stellar spot-corrected light curves of the combined HST/STIS HD 189733 b observations, when binned over a coarse wavelength sampling with a resolving power of R = 50. We used the posterior-distribution median and the central 68% percentiles statistics to estimate the parameter values and their credible intervals.
Tables A.1, A.2, and A.3 present the estimated values of the NUV transmission planet-to-star radius ratio when analyzed at resolving powers of 50, 33, and 10, respectively.
 |
Fig. A.1 Near-UV transmission spectrum of HD 189733 b from the combined HST/STIS observations. The red symbols with error bars denote the systematics- and stellar spot-corrected transmission spectrum, their 1σ uncertainties, and the span of the spectral bins for a resolving power of R =10. The blue spectrum shows a theoretical model of the planet’s upper atmosphere. The orange curve shows the fit to the optical–IR transmission spectrum extrapolated into the NUV; the shaded areas denote the 1σ and 2σ uncertainties. The black dashed curve shows the optical–IR fit shifted downward according to a SOFIA-like offset of ΔRp/Rs = 0.001. |
 |
Fig. A.2 Transit light curves of the combined HST/STIS observations of HD 189733 b binned at a resolving power of R = 50. The colored symbols with error bars denote the systematics- and stellar spot-corrected measurements, color-coded for each visit (see legend). The solid red curve and orange area denote the best-fitting transit depths and span of their 1σ uncertainties. The light curve of each bin has been shifted in the vertical axis for visualization. The labels next to each light curve denotes the mean wavelength of the spectral bin. The scale of the vertical axis changes from left to right as the S/N of the data improves with increasing wavelength. |
HD 189733 b NUV transmission spectrum at R=50
HD 189733 b NUV transmission spectrum at R=33
HD 189733 b NUV transmission spectrum at R=10
Appendix B Lower atmosphere transmission retrieval
Table B.1 shows the parameterization, priors, and retrieved posterior values for the analysis of the HD 189733 b optical-IR transmission spectrum. Figure B.1 shows the posterior distributions of the model parameters and temperature profile.
 |
Fig. B.1 Pairwise distribution (lower left corner panels) and marginal histograms (diagonal) of the retrieved posterior parameters of the HD 189733 b optical–IR retrieval. The dashed lines indicate the marginal maximum likelihood of the parameters (i.e., the mode of the histograms or median when the parameter not well constrained). The shaded areas denote the 68% highest posterior density. The top right panel shows the posterior distribution of the temperature-profile models; the median and the span of the 68% and 95% central credible intervals. |
HD 189733b: Summary of optical–IR retrieval parameters
References
- Agol, E., Cowan, N.B., Knutson, H.A., et al. 2010, ApJ, 721, 1861, [NASA ADS] [CrossRef] [Google Scholar]
- Andrae, R. 2010, ArXiv e-prints [arXiv:1009.2755] [Google Scholar]
- Angerhausen, D., Mandushev, G., Mandell, A., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 034002 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J.R., Haswell, C.A., Staab, D., & Anglada-Escudé, G. 2016, MNRAS, 462, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Barstow, J.K. 2020, MNRAS, 497, 4183 [NASA ADS] [CrossRef] [Google Scholar]
- Ben-Jaffel, L., & Ballester, G.E. 2013, A&A, 553, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birkby, J.L., de Kok, R.J., Brogi, M., et al. 2013, MNRAS, 436, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Bonomo, A.S., Desidera, S., Benatti, S., et al. 2017, A&A, 602, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., & Frommhold, L. 1989, ApJ, 341, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, J., Frommhold, L., & Birnbaum, G. 1988, ApJ, 326, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Frommhold, L., & Moraldi, M. 1989, ApJ, 336, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Jorgensen, U.G., & Fu, Y. 2001, J. Quant. Spec. Radiat. Transf., 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Udry, S., Mayor, M., et al. 2005, A&A, 444, L15 [EDP Sciences] [Google Scholar]
- Bourrier, V., Lecavelier des Etangs, A., Dupuy, H., et al. 2013, A&A, 551, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brogi, M., de Kok, R.J., Albrecht, S., et al. 2016, ApJ, 817, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., Giacobbe, P., Guilluy, G., et al. 2018, A&A, 615, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T.M., Charbonneau, D., Gilliland, R.L., Noyes, R.W., & Burrows, A. 2001, ApJ, 552, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Cauley, P.W., Redfield, S., Jensen, A.G., et al. 2015, ApJ, 810, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Cauley, P.W., Shkolnik, E.L., Llama, J., Bourrier, V., & Moutou, C. 2018, AJ, 156, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, P.A., Yurchenko, S.N., & Tennyson, J. 2019, MNRAS, 490, 4638 [CrossRef] [Google Scholar]
- Crouzet, N., McCullough, P.R., Deming, D., & Madhusudhan, N. 2014, ApJ, 795, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Cubillos, P.E. 2017, ApJ, 850, 32 [CrossRef] [Google Scholar]
- Cubillos, P.E. 2020, https://zenodo.org/record/3634059 [Google Scholar]
- Cubillos, P.E., & Blecic, J. 2021, MNRAS, 505, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Cubillos, P., Harrington, J., Loredo, T.J., et al. 2017, AJ, 153, 3 [Google Scholar]
- Cubillos, P.E., Fossati, L., Koskinen, T., et al. 2020, AJ, 159, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Lecavelier des Etangs, A., Hébrard, G., et al. 2009, ApJ, 699, 478 [Google Scholar]
- Espinoza, N., & Jordán, A. 2015, MNRAS, 450, 1879 [Google Scholar]
- Gao, P., Thorngren, D.P., Lee, E.K.H., et al. 2020, Nat. Astron., 4, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Guilluy, G., Andretta, V., Borsa, F., et al. 2020, A&A, 639, A49 [EDP Sciences] [Google Scholar]
- Guo, J.H., & Ben-Jaffel, L. 2016, ApJ, 818, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Hargreaves, R.J., Gordon, I.E., Rey, M., et al. 2020, ApJS, 247, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G.J., Tennyson, J., Kaminsky, B.M., Pavlenko, Y.V., & Jones, H.R.A. 2006, MNRAS, 367, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C.R., Millman, K.J., van der Walt, S.J., et al. 2008, MNRAS, 390, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G.J., Larner, F.C., Tennyson, J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C., Arras, P., Christie, D., & Li, Z.-Y. 2017, ApJ, 851, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Huitson, C.M., Sing, D.K., Vidal-Madjar, A., et al. 2012, MNRAS, 422, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J.D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Husser, T.O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jensen, A.G., Redfield, S., Endl, M., et al. 2012, ApJ, 751, 86 [NASA ADS] [CrossRef] [Google Scholar]
- King, G.W., Corrales, L., Wheatley, P.J., et al. 2021, MNRAS, 506, 2453 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K.G., Pilat-Lohinger, E., Funk, B., et al. 2016, MNRAS, 461, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H.A., Charbonneau, D., Allen, L.E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H.A., Charbonneau, D., Cowan, N.B., et al. 2009, ApJ, 690, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H.A., Lewis, N., Fortney, J.J., et al. 2012, ApJ, 754, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Koskinen, T.T., Harris, M.J., Yelle, R.V., & Lavvas, P. 2013a, Icarus, 226, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Koskinen, T.T., Yelle, R.V., Harris, M.J., & Lavvas, P. 2013b, Icarus, 226, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Koskinen, T.T., Lavvas, P., Huang, C., et al. 2022, ApJ, 929, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L., Bean, J.L., Désert, J.-M., et al. 2014, Nature, 505, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R.L. 1970, SAO Special Report, 309 [Google Scholar]
- Lavvas, P., & Koskinen, T. 2017, ApJ, 847, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Bourrier, V., Wheatley, P.J., et al. 2012, A&A, 543, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, G., Gordon, I.E., Rothman, L.S., et al. 2015, ApJS, 216, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Liddle, A.R. 2007, MNRAS, 377, L74, [NASA ADS] [CrossRef] [Google Scholar]
- Lothringer, J.D., Sing, D.K., Rustamkulov, Z., et al. 2022, Nature, 604, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Louden, T., & Wheatley, P.J. 2015, ApJ, 814, L24 [CrossRef] [Google Scholar]
- Madhusudhan, N., & Seager, S. 2009, ApJ, 707, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
- McCullough, P.R., Crouzet, N., Deming, D., & Madhusudhan, N. 2014, ApJ, 791, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K. 2012, ApJ, 745, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J.I., Visscher, C., Fortney, J.J., et al. 2011, ApJ, 737, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Ohno, K., & Kawashima, Y. 2020, ApJ, 895, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Oza, A.V., Johnson, R.E., Lellouch, E., et al. 2019, ApJ, 885, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B.E. 2007, Comput. Sci. Eng., 9, 21 [CrossRef] [Google Scholar]
- Pillitteri, I., Maggio, A., Micela, G., et al. 2015, ApJ, 805, 52 [Google Scholar]
- Pinhas, A., Madhusudhan, N., Gandhi, S., & MacDonald, R. 2019, MNRAS, 482, 1485 [Google Scholar]
- Polyansky, O.L., Kyuberis, A.A., Zobov, N.F., et al. 2018, MNRAS, 480, 2597 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Knutson, H., Gilliland, R.L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [CrossRef] [Google Scholar]
- Pont, F., Sing, D.K., Gibson, N.P., et al. 2013, MNRAS, 432, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Poppenhaeger, K., Schmitt, J.H.M.M., & Wolk, S.J. 2013, ApJ, 77362, [Google Scholar]
- Rackham, B.V., Apai, D., & Giampapa, M.S. 2018, ApJ, 853, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Rackham, B.V., Apai, D., & Giampapa, M.S. 2019, AJ, 157, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Raftery, A.E. 1995, Sociol. Methodol., 25, 111 [CrossRef] [Google Scholar]
- Redfield, S., Endl, M., Cochran, W.D., & Koesterke, L. 2008, ApJ, 673, L87 [CrossRef] [Google Scholar]
- Rodler, F., Kürster, M., & Barnes, J.R. 2013, MNRAS, 432, 1980 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L.S., Gordon, I.E., Barber, R.J., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P.C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlawin, E., Agol, E., Walkowicz, L.M., Covey, K., & Lloyd, J.P. 2010, ApJ, 722, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A.P., Fortney, J.J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A.P., Fortney, J.J., Lewis, N.K., & Shabram, M. 2013, ApJ, 762, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W.W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D.K., Fortney, J.J., Nikolov, N., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D.K., Lavvas, P., Ballester, G.E., et al. 2016, Nature, 529, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D.K., Pont, F., Aigrain, S., et al. 2019, AJ, 158, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D.S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K.G., Collins, K.A., & Gaudi, B.S. 2017, AJ, 153, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Steinrueck, M.E., Showman, A.P., Lavvas, P., et al. 2021, MNRAS, 504, 2783 [NASA ADS] [CrossRef] [Google Scholar]
- ter Braak, C.J.F., & Vrugt, J.A. 2008, Stat. Comput., 18, 435 [CrossRef] [Google Scholar]
- Todorov, K.O., Deming, D., Burrows, A., & Grillmair, C.J. 2014, ApJ, 796, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2007, MNRAS, 378, 72 [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.M., et al. 2008, ApJ, 676, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T.E., et al. 2020, Nat. Methods, 17, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Wakeford, H.R., & Sing, D.K. 2015, A&A, 573, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakeford, H.R., Sing, D.K., Evans, T., Deming, D., & Mandell, A. 2016, ApJ, 819, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Helling, C., & Gunn, O. 2020, A&A, 634, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yurchenko, S.N. 2015, J. Quant. Spec. Radiat. Transf., 152, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S.N., Tennyson, J., Syme, A.-M., et al. 2022, MNRAS, 510, 903 [Google Scholar]
- Zellem, R.T., Swain, M.R., Roudier, G., et al. 2017, ApJ, 844, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, M., Cauley, P.W., Knutson, H.A., et al. 2022, AJ, 164, 237 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 HD 189733 system flux as observed by HST/STIS. This spectrum was constructed from the mean time series spectra obtained during the first visit, after discarding bad pixels. The spectrum is color-coded by echelle order (see color bar on the right). The insets show zoomed-in images around the location of the Mg II and Mg I resonance lines. |
| In the text | |
 |
Fig. 2 Sample transmission light curve fitting of the HST/STIS observations of HD 189733 b (fourth echelle order, |
| In the text | |
 |
Fig. 3 HST/STIS NUV transmission spectrum of HD 189733 b (individual visits). The circles with error bars denote the transmission planet-to-star radius ratios from each echelle order and visit (see legend), corresponding to the best AICc fits. The colored dashed lines denote the mean value for each visit. The squares denote the XMM-Newton/UVM2 photometric measurement by King et al. (2021). |
| In the text | |
 |
Fig. 4 Near-UV transmission spectrum of HD 189733 b from the combined HST/STIS observations. The red symbols with error bars denote the systematics- and stellar spot-corrected transmission spectrum, their 1σ uncertainties, and the span of the spectral bins (the data is binned in wavelength over a resolving power of R = 50). The green symbols show our results when neglecting the stellar spot contamination in the analysis (symbols are slightly shifted in wavelength for visibility). The blue spectrum shows a theoretical model of the planet’s upper atmosphere (see Sect. 5.1) and the blue dots show the model integrated over the spectral bins. The orange curve shows an extrapolation from a fit to the optical–IR transmission spectrum of the planet (see Sect. 5.2). |
| In the text | |
 |
Fig. 5 Stellar spot contamination. The top panels show the posterior distribution of the spot parameters derived from the combined data analysis. The blue shaded areas denote the 1σ highest posterior density credible region. Visits 1 and 2 show a negligible spot contamination with either a small spot covering fraction or a negligible difference between the spot and photospheric temperatures. Visit 3 in contrast shows a non-negligible contamination of ϵ(λ) ~ 1.15–1.2, with a strong correlation between the spot covering fraction and spot temperature. The bottom panel shows the respective contamination spectra. The colored symbols and vertical spans show the median and 1σ uncertainty of the contamination, respectively. |
| In the text | |
 |
Fig. 6 Infrared to ultraviolet transmission spectrum of HD 189733 b. The top and bottom panels show the same data, focused on different spectral regions for better visibility. The colored symbols with error bars show the transit observations, 1σ uncertainties, and wavelength span of the observations (see legend). Our data points were computed from the data binned at a resolving power of R = 33 (see Appendix A). The red curve and orange shaded areas show the spectrum posterior distribution of the optical–IR fit (median, 68%, and 95% quantiles of the distribution; see Appendix B). The blue curve shows the upper atmosphere model (shaded in a slightly paler color when below the optical-IR continuum). |
| In the text | |
 |
Fig. 7 Infrared to ultraviolet transmission spectrum of HD 189733 b. The top and bottom panels show the same data, focused on different spectral regions for better visibility. The colored symbols with error bars show the transit observations, 1σ uncertainties, and wavelength span of the observations (see legend). Our data points were computed from the data binned at a resolving power of R = 33 (see Appendix A). The red curve and orange shaded areas show the spectrum posterior distribution of the optical–IR fit (median, 68%, and 95% quantiles of the distribution; see Appendix B). The blue curve shows the upper atmosphere model (shaded in a slightly paler color when below the optical-IR continuum). |
| In the text | |
 |
Fig. 8 Comparison HST/STIS NUV transmission spectra of HD 189733 b, HD 209458 b, and WASP-121b scaled by the optical transit radius Rp (top panel) and by the Roche-lobe terminator radius RRL of each planet (bottom panel). The shaded regions denote the wavelength span of the dominant Fe II and Mg II NUV bands and lines. |
| In the text | |
 |
Fig. A.1 Near-UV transmission spectrum of HD 189733 b from the combined HST/STIS observations. The red symbols with error bars denote the systematics- and stellar spot-corrected transmission spectrum, their 1σ uncertainties, and the span of the spectral bins for a resolving power of R =10. The blue spectrum shows a theoretical model of the planet’s upper atmosphere. The orange curve shows the fit to the optical–IR transmission spectrum extrapolated into the NUV; the shaded areas denote the 1σ and 2σ uncertainties. The black dashed curve shows the optical–IR fit shifted downward according to a SOFIA-like offset of ΔRp/Rs = 0.001. |
| In the text | |
 |
Fig. A.2 Transit light curves of the combined HST/STIS observations of HD 189733 b binned at a resolving power of R = 50. The colored symbols with error bars denote the systematics- and stellar spot-corrected measurements, color-coded for each visit (see legend). The solid red curve and orange area denote the best-fitting transit depths and span of their 1σ uncertainties. The light curve of each bin has been shifted in the vertical axis for visualization. The labels next to each light curve denotes the mean wavelength of the spectral bin. The scale of the vertical axis changes from left to right as the S/N of the data improves with increasing wavelength. |
| In the text | |
 |
Fig. B.1 Pairwise distribution (lower left corner panels) and marginal histograms (diagonal) of the retrieved posterior parameters of the HD 189733 b optical–IR retrieval. The dashed lines indicate the marginal maximum likelihood of the parameters (i.e., the mode of the histograms or median when the parameter not well constrained). The shaded areas denote the 68% highest posterior density. The top right panel shows the posterior distribution of the temperature-profile models; the median and the span of the 68% and 95% central credible intervals. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



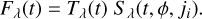
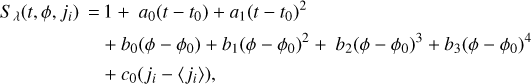
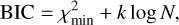
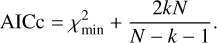
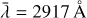
![${d_{{\rm{obs}}}}\left( \lambda \right) = {{d\left( \lambda \right)} \over {1 - {f_{{\rm{spot}}}}\left[ {1 - {{{F_{{\rm{spot}}}}\left( \lambda \right)} \mathord{\left/ {\vphantom {{{F_{{\rm{spot}}}}\left( \lambda \right)} {{F_{\rm{s}}}\left( \lambda \right)}}} \right. \kern-\nulldelimiterspace} {{F_{\rm{s}}}\left( \lambda \right)}}} \right]}} \equiv d\left( \lambda \right)\left( \lambda \right).$](/articles/aa/full_html/2023/03/aa45064-22/aa45064-22-eq14.png)