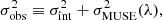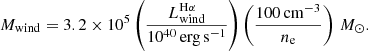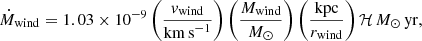| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244895 | |
| Published online | 09 February 2023 | |
Shaken, but not expelled: Gentle baryonic feedback from nearby starburst dwarf galaxies
1
INAF – Arcetri Astrophysical Observatory, Largo E. Fermi 5, 50127 Firenze, Italy
e-mail: antonino.marasco@inaf.it
2
INAF – Padova Astronomical Observatory, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
3
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Avda. Vicũna Mackenna 4860, 8970117 Macul, Santiago, Chile
4
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei Muenchen, Germany
5
Dipartimento di Fisica e Astronomia, Universitá di Firenze, Via G. Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy
6
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
7
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
8
Institute for Computational Cosmology, Department of Physics, University of Durham, South Road, Durham DH1 3LE, UK
9
AURA for the European Space Agency (ESA), Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
10
Scuola Normale Superiore, Piazza dei Cavalieri 7, Pisa 56126, Italy
11
Department of Electrical Engineering and Center of Astro-Engineering UC, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile
Received:
6
September
2022
Accepted:
16
November
2022
Baryonic feedback is expected to play a key role in regulating the star formation of low-mass galaxies by producing galaxy-scale winds associated with mass-loading factors of β ∼ 1 − 50. We test this prediction using a sample of 19 nearby systems with stellar masses of 107 < M⋆/M⊙ < 1010, mostly lying above the main sequence of star-forming galaxies. We used MUSE at VLT optical integral field spectroscopy to study the warm ionised gas kinematics of these galaxies via a detailed modelling of their Hα emission line. The ionised gas is characterised by irregular velocity fields, indicating the presence of non-circular motions of a few tens of km s−1 within galaxy discs, but with intrinsic velocity dispersion of 40 − 60 km s−1 that are only marginally larger than those measured in main-sequence galaxies. Galactic winds, defined as gas at velocities larger than the galaxy escape speed, encompass only a few percent of the observed fluxes. Mass outflow rates and loading factors are strongly dependent on M⋆, the star formation rate (SFR), SFR surface density, and specific SFR (sSFR). For M⋆ of 108 M⊙ we find β ≃ 0.02, which is more than two orders of magnitude smaller than the values predicted by theoretical models of galaxy evolution. In our galaxy sample, baryonic feedback stimulates a gentle gas cycle rather than causing a large-scale blow-out.
Key words: galaxies: dwarf / galaxies: irregular / galaxies: starburst / ISM: jets and outflows / ISM: kinematics and dynamics
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Feedback from star formation and active galactic nuclei (AGNs) is expected to profoundly affect the evolution of low-mass galaxies by launching large-scale winds that can easily escape the shallow gravitation potential of these systems. While this idea goes back to almost half a century ago (Larson 1974; Saito 1979), in the last decade, feedback has been systematically invoked as the main physical mechanism capable of resolving a number of tensions between theoretical models of galaxy evolution in the Λ cold dark matter (ΛCDM) framework and the observed properties of low-mass galaxies (for a review see Bullock & Boylan-Kolchin 2017, and references therein). On global scales, feedback offers a natural explanation to the relatively small number density of dwarf galaxies compared to that of low-mass dark matter halos (the so-called ‘missing-satellite problem’ Klypin et al. 1999; Moore et al. 1999) via the suppression of star formation in the low-mass regime (e.g., Sawala et al. 2016), in turn, shaping the mass-metallicity relation (e.g., Maiolino & Mannucci 2019; Tortora et al. 2022) by efficiently ejecting metal-enriched gas out of low-mass galaxy discs (e.g., Brooks et al. 2007). On local scales, violent and recurring feedback episodes are expected to produce a flattening of the dark matter profile in the central regions of galaxies (e.g., Governato et al. 2012), leading to slowly rising rotation curves that are similar to those seen in observations (de Blok 2010). In addition, centrally concentrated feedback episodes can selectively remove low-angular momentum material from the galaxy innermost region, leading to the formation of bulge-less, low-mass discs (e.g., Governato et al. 2010; Brook et al. 2012). While these effects had traditionally been attributed to feedback from star formation, recent theoretical studies (Silk 2017; Koudmani et al. 2021), supported by observations in the X-ray, optical, and near-infrared bands (e.g., Baldassare et al. 2017, 2018; Kaviraj et al. 2019; Birchall et al. 2020), have highlighted the importance of feedback from AGN in the evolution of dwarf galaxies, especially in the early Universe. Hereafter, we generally refer to stellar and AGN feedback as ‘baryonic’ feedback.
In spite of its importance in shaping galaxy evolution, a comprehensive and quantitative understanding of baryonic feedback physics is still missing from both the observational and the theoretical sides. Theoretical models of stellar feedback-driven winds must deal with the impracticability of modelling all the affected physical scales at the same time, ranging from a few pc and necessary for following the evolution of single supernova blast waves, up to the several tens of kpc required to track the wind propagation throughout the galaxy halos. Large-scale cosmological hydrodynamical suites such as EAGLE (Schaye et al. 2015) or Illustris TNG (Pillepich et al. 2018) do not resolve single supernovae and make use of sub-grid recipes to describe star formation and stellar feedback processes. In these models, feedback energy from single ‘star’ elements is deposited onto the surrounding gas in thermal or kinetic forms, driving galactic winds. These models are optimal to follow the long-term gas cycle in galaxies produced by feedback, but the detailed physical properties of the outflowing gas (e.g., its temperature and density distribution) depend on the feedback implementation, which varies from one simulation to another. On the other hand, detailed hydrodynamical models of stellar feedback such as that of Kim & Ostriker (2018) can accurately track the interaction between single supernova explosions and the multi-phase, magnetised interstellar medium (ISM), leading to realistic predictions for the wind launching conditions, but with the drawback that the long-term evolution of the gas in the outflow remains unknown. Similar considerations, but with even larger uncertainties, are applicable to feedback from supermassive black holes, for which the impossibility to model sub-pc scale accretion discs in large-scale simulations is combined with severe theoretical uncertainties on the AGN-driven wind propagation mechanism (e.g., King 2010; King & Pounds 2015; Richings & Faucher-Giguère 2018; Costa et al. 2020).
While observations are potentially key to constrain feedback and wind propagation models (e.g., Collins & Read 2022), they are limited by two factors. The first is that measurements of wind properties rely on assumptions on the ionisation state, 3D geometry, chemical composition, and kinematics of the gas. It is no surprise that reported mass-loading factors (defined as the ratio between the mass outflow rate and the star formation rate) range widely from 0.01 to 10 (Veilleux et al. 2005), and can vary up to a factor of 10 in the same galaxy depending on the assumed conditions (Chisholm et al. 2016, 2017). The second is that feedback-driven outflows have low surface brightness and are multi-phase, thus the study of each phase requires deep observations with a dedicated instrument. The hot (T ∼ 106 K) wind phase, caused by gas shock-heated by supernova blast waves, has been observed in the X-ray only in a small number of low-mass systems in the nearby Universe (e.g., Heckman et al. 1995; Summers et al. 2003; Ott et al. 2005). Atomic and molecular outflows, originating either from cold ISM entrained in the wind or from the cooling of the hot outflowing gas, can be traced by the H I (atomic) or CO (molecular) emission lines (e.g., Walter et al. 2002; Kobulnicky & Skillman 2008; Bolatto et al. 2013; Lelli et al. 2014a; Di Teodoro et al. 2019; Fluetsch et al. 2019, 2021), as well as the Na I absorption doublet (Schwartz & Martin 2004; Concas et al. 2019). Warm ionised winds can be traced by optical emission lines and are thought to have an origin similar to the colder phase. However, until recently (McQuinn et al. 2019, see below), only a few observational constraints on ionised winds in dwarf galaxies existed, mostly coming from the characterisation of expanding superbubbles (e.g., Marlowe et al. 1995; Martin 1996, 1998; van Eymeren et al. 2009b; Heckman et al. 2015).
Crucially, there is no consensus on which phase should dominate the outflow mass and energy budget. Models such as those of Kim & Ostriker (2018) have predicted that gas at temperatures of 0.5–2 × 104 K – thus visible in H I or Hα, depending on the ionisation conditions – dominates the wind mass-loading, whereas most of the wind energy is in the hot phase. Instead, the observations tend to find winds that are dominated in mass and kinetic power by the molecular phase (Fluetsch et al. 2019, 2021). This is the case for both for galaxies with and without an AGN; however, warm ionised gas may dominate the outflow mass budget in the most luminous quasars (Fiore et al. 2017).
Starburst dwarf galaxies, generally intended as low-mass (M⋆ < 1010 M⊙) systems which lie above the main-sequence of star formation (Noeske et al. 2007; Popesso et al. 2019), represent an ideal laboratory to study baryonic feedback in the dwarf regime, as they combine large SFRs with shallow gravitational potential wells. The conditions that trigger the starburst in these systems have continued to be highly debated, with both external and internal mechanisms proposed, such as direct accretion from extra-galactic cold flows (Dekel & Birnboim 2006), tidal perturbations from nearby companions (Noguchi 1988; Lelli et al. 2014b), wet mergers (Bekki 2008; Lelli et al. 2012), torques due to star-forming clumps (Elmegreen et al. 2012), or radial flows produced by triaxial dark matter halos (Bekki & Freeman 2002; Marasco et al. 2018). Interestingly, H I observations of starburst dwarfs have revealed a balanced mixture of regularly rotating and kinematically disturbed discs, sometimes featuring strong radial motions, although unsettled H I distributions are rare. These systems have both baryonic and gas fractions similar to those of typical dwarf irregulars, indicating that they did not eject a large amount of gas out of their potential wells (Lelli et al. 2014b). A similar conclusion was recently reached by McQuinn et al. (2019), who studied the properties of ionised winds in a sample of 12 nearby starburst dwarfs using deep Hα imaging. Their results show a very modest spatial extent of all detected ionised material, suggesting that the majority of gas expelled from dwarfs does not escape into the intergalactic medium, but remains in the galaxy halo instead. However, we note that the study of McQuinn et al. (2019) relies on narrow and broad-band imaging alone, thus, it lacks detailed information on ionised gas kinematics that only optical spectroscopy can provide.
In this study, we make use of the excellent combination of spatial and spectral resolution offered by MUSE to study the kinematics of the ionised gas in a sample of 19 nearby starburst dwarfs. These galaxies are part of a larger sample of 40 starburst systems with publicly available archival MUSE observations, which make up the ‘DWarf galaxies Archival Local survey for Interstellar medium investigatioN’ (DWALIN, Cresci et al., in prep.) sample. Our goals are to infer ionised mass outflow rates and loading factors and to study how these are related to a number of galaxy properties such as stellar masses (M⋆), star formation rates (SFRs), and mean SFR densities.
This paper is structured as follows. In Sect. 2, we provide a brief description of the DWALIN sample and present our measurements for M⋆ and the SFRs. The MUSE data analysis, which consists of the extraction and modelling of Hα velocity profiles aimed at inferring the main properties of the ionised winds, is presented in Sects. 3 and 4. Our results are discussed in light of other observational and theoretical studies in Sect. 5. Our conclusions are drawn in Sect. 6.
2. The DWALIN sample
DWALIN is a sample of 40 nearby galaxies that is specifically designed to study the gas properties in low-mass, highly star-forming systems. All galaxies in DWALIN have archival MUSE data and have been selected either: (1) from the Herschel Dwarf Galaxy Survey (DGS; Madden et al. 2013; Cormier et al. 2015), a survey of nearby (D < 200 Mpc) low-metallicity galaxies using far-infrared (FIR) and sub-millimetre data from the Herschel Space Observatory; or (2) from the Karachentsev et al. (2013) catalogue of galaxies in the local Volume (distance < 11 Mpc) and log(M/M⋆) < 9.0. A detailed description of the DWALIN sample will be provided from Cresci et al. (in prep.).
The main properties of our sample are listed in Table 1, along with our new measurements of M⋆ and SFRs determined as described in Sect. 2. Most DWALIN galaxies have M⋆ < 2 × 109 M⊙, but the sample spans more than five dex in M⋆ and SFR. Distances in DWALIN are taken from the Extragalactic Distance Database1 (EDD; Tully et al. 2009), which collects and homogenises distance measurements from a variety of sources. Specifically, for 16 galaxies, we used the Cosmicflows-3 distance catalogue (CF3, Tully et al. 2016), which provides weighted distances for about 18 000 nearby galaxies using multiple velocity-independent methods, such as Cepheids, tip of red giant branch (TRGB), type Ia supernovae, Tully–Fisher relation (TFR, Tully & Fisher 1977), and others. Some DWALIN galaxies have velocity-independent distances but do not appear in the CF3: for these objects, we used stellar distances from Jacobs et al. (2009) and Anand et al. (2021), or TFR distances from Kourkchi et al. (2022). For Leo P, we adopted the estimate of McQuinn et al. (2015) based on the luminosity of horizontal branch stars and ten RR Lyrae candidates. Finally, for the 20 galaxies that have no velocity-independent distances, we adopted estimates based on local 3D flow models (Kourkchi et al. 2020). Distance uncertainties are taken from the EDD, with the exception of those determined from the flow models, for which we have assumed an error of 20% (about twice the typical uncertainty of the CF3 measurements).
Main properties of the DWALIN galaxy sample.
An atlas of the DWALIN sample from the Sloan Digital Sky Survey (SDSS; York et al. 2000) and the Digital Sky Survey (DSS) is shown in Fig. 1, with the field of view of the archival MUSE pointings overlaid. As a preliminary step, we planned to re-reduce the archival MUSE data for all 40 DWALIN galaxies, with the goal of providing a uniform analysis of the ionised gas kinematics and wind properties across the sample. This step requires considerable computational and human resources and, at the time of this writing, it is still in progress. So far we have re-reduced the MUSE data for 19 galaxies (green frames in Fig. 1), randomly selected from DWALIN: these systems comprise the DWALIN-19 sub-sample. As the midway point of the analysis of the complete sample, in this study we focus on the ionised gas properties of this sub-sample. The analysis of the 21 remaining DWALIN galaxies will be presented in a later paper.
 |
Fig. 1. Optical DSS or SDSS images (2′ on a side) of the DWALIN sample of starburst galaxies, with the MUSE field of view overlaid (squared overlays). Green overlays show the MUSE data that have been re-reduced and analysed and are discussed in the current study. Red overlays are used for the MUSE data that will be analysed in a future study. Galaxies are ordered by their M⋆, with lowest-mass galaxies at the top left. |
The MUSE data reduction was carried out with the MUSE pipeline (Weilbacher et al. 2020) v2.8.1, using the ESO Recipe flexible execution workbench (Reflex, Freudling et al. 2013), which offers a graphical and automated way to execute with EsoRex the Common Pipeline Library (CPL) reduction recipes, within the Kepler workflow engine (Altintas et al. 2006). Details on the MUSE data reduction of individual galaxies will be provided by Cresci et al. (in prep.), while the data analysis is presented in Sect. 3.
2.1. Stellar masses and star formation rates
In order to determine homogeneous and reliable estimates of M⋆ and SFRs for all galaxies in the DWALIN sample, we employed the approach outlined by Leroy et al. (2019, see their appendix) based on the combined use of infrared and ultraviolet data. We made use of archival, publicly available near- and mid- infrared (NIR and MIR) images from the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) in bands W1 (3.4 μm) and W4 (22 μm), from the IRAC 3.6 μm and MIPS 24 μm camera on board of the Spitzer Space Telescope (Werner et al. 2004), and of near- and far- ultraviolet (NUV and FUV) images from the Galaxy Evolution Explorer (GALEX; Gil de Paz et al. 2007). The photometric analysis of these images was performed using our own routines, described in detail in Appendix A.
Leroy et al. (2019) outlined a series of methods to determine the integrated M⋆ and SFR in nearby galaxies using only WISE and/or GALEX data. All these methods are calibrated on measurements from the GALEX-SDSS-WISE Legacy Catalogue (GSWLC; Salim et al. 2016, 2018), which combine GALEX and WISE photometry with SDSS observations to infer M⋆ and SFR for about 600 000 galaxies via population synthesis modelling with the CIGALE code (Boquien et al. 2019). The impressive size of this sample and the refined spectral modelling, which accounts for energy balance and contamination by emission lines to the broad-band photometry, make GSWLC an excellent benchmark for assessing how global galaxy parameters are recovered when only a subset of the full photometric data is available.
Following Leroy et al. (2019), we used five methods to compute M⋆ and SFR depending on the data available. These are described in Table 2. We stress that each of these methods have been calibrated separately by Leroy et al. (2019), thus the coefficients adopted in the calculation of M⋆ and SFR vary between one method and another. In addition to this procedure, we used IRAC 3.6 μm (MIPS 24 μm) luminosities as a replacement for W1 (W4) luminosities when the latter were not available, after having assessed the excellent agreement between our Spitzer and WISE photometry in similar bands. In fact, we have verified that Spitzer and WISE data are practically interchangeable, both providing M⋆ and SFR measurements that are compatible within their uncertainties (computed as described in Appendix A). However, Spitzer data are less-than-optimal to use for our M⋆ and SFR estimates, given that the procedures of Leroy et al. (2019) are specifically calibrated on WISE data. Our NUV and FUV measurements are corrected for Galactic extinction using the reddening map of Schlegel et al. (1998). We make a single exception to our procedure: we take the M⋆ of Leo P from McQuinn et al. (2015), given that this very faint system is only barely detectable in our NIR images.
Methods used to determine M⋆ and SFR in this work, in descending order of preference.
The resulting M⋆ and SFRs for the DWALIN sample are listed in Table 1. In Fig. 2, we compare our measurements with those of Leroy et al. (2019) for a sample of ≈15 750 nearby galaxies, and with the main-sequence trends at z ∼ 0 from the Sloan Digital Sky Survey (SDSS; Chang et al. 2015), from the Low-Mass Local Volume Legacy (LMLVL) sample (Berg et al. 2012), and from McGaugh et al. (2017) for a sample of late-type, low-surface-brightness galaxies. The majority of the DWALIN galaxies are located above the main sequence of star formation. One possible exception is given by the faintest systems (M⋆ < 108 M⊙), for which, however, information on the obscured component of the SF is missing because W4 or MIPS data are unavailable (purple circles in Fig. 2). We stress that most of these faint galaxies may still lie in the starburst region given their low M⋆, assuming a steepening in the main-sequence relation at M⋆ ≲ 109 M⊙ as suggested by McGaugh et al. (2017). We also notice that the DWALIN-19 sub-sample (numbered systems in Fig. 2) spans the same dynamical range of its parent sample.
 |
Fig. 2. SFR vs. M⋆ plot for the DWALIN galaxy sample. Green squares, brown triangles, and blue circles indicate galaxies whose SFR measurements come from the combination of UV and MIR data, MIR data alone, or UV data alone, respectively (see text for details). ID numbers are shown for the DWALIN-19 sample studied with MUSE in this work. Gray dots show the sample of ≈15 750 nearby galaxies studied by Leroy et al. (2019). We also show the SFR–M⋆ trends at z ≃ 0 from the SDSS (Chang et al. 2015, dashed line), from the LMLVL sample (Berg et al. 2012, dotted line), and the relation derived by McGaugh et al. (2017) for a sample of low-surface brightness galaxies (dot-dashed line). |
Various studies have suggested that free-free radiation and hot dust emission can contribute to the 3–5 μm luminosity in dwarf galaxies (e.g., Smith & Hancock 2009). In this study we have assumed that such a contribution is negligible. Correcting for these effects would lead to slightly lower estimates for M⋆, shifting the DWALIN sample even further away from the main sequence of star formation.
We adopted the method of Leroy et al. (2019), so that the DWALIN sample and GSWLC sample could be compared directly. We point out, however, that M⋆ calibrations from different population synthesis models (Meidt et al. 2014; McGaugh & Schombert 2014; Herrmann et al. 2016; Norris et al. 2016; Hunt et al. 2019; Schombert et al. 2019), color-magnitude diagrams of resolved stellar populations (Eskew et al. 2012; Zhang et al. 2017), and dynamical arguments (McGaugh & Schombert 2015; Lelli et al. 2016a,b) give systematically higher values of M⋆ by a factor of ∼1.5 − 2.0.
3. Ionised gas kinematics in DWALIN
Here, we describe in detail the steps taken to infer the global kinematic properties of the ionised gas in the DWALIN-19 sample. We illustrate our procedure on the MUSE data of He 2-10 (previously studied by Cresci et al. 2017), but we proceed in the same way for all the DWALIN-19 galaxies.
3.1. Continuum subtraction and velocity cube creation
The first step of our procedure consists in the subtraction of the continuum from the MUSE spectra. This operation must be highly accurate, since even an error of few percentage points can artificially enhance or suppress the faint wings in the line profiles that may be associated with the outflow component.
Stellar absorption features are quite weak in the DWALIN-19 sample, but they are nonetheless visible, especially around the Hβ line in the most massive systems. The stellar continuum is subtracted following a procedure similar to that outlined by Cresci et al. (2017), which consists of first enhancing the stellar signal via a Voronoi tessellation (Cappellari & Copin 2003) of the MUSE data (we imposed S/N > 20 on the continuum at 5100 < λ/@@@ < 5500, on average, per 1.25 Å spectral channel) and then fitting the resulting binned cube via a multi-component model using the pPXF software (Cappellari 2017). The model adopted is built of a combination of E-MILES stellar population model templates (Sánchez-Blázquez et al. 2006; Röck et al. 2016), which cover the entire MUSE wavelength range, Gaussian features to model the main optical emission lines, and an additive third-order polynomial to account for any additional ‘smooth’ stellar feature extended over the whole λ range. A multi-Gaussian fitting could be employed in order to achieve a finer modelling of the emission lines but, at this stage, we are primarily interested in removing the stellar continuum, thus we used a single Gaussian component per line. The outcome of this process is a model cube for the stellar continuum matched to the binned data. This cube is then subtracted from the original (unbinned) data by re-scaling the model spectrum of each Voronoi cell to match the intensity level of the individual spaxels within that cell.
This procedure is generally robust, however, it is still subject to small flaws since the additional polynomial term included in our model may not be adequate to describe the residual continuum flux with sufficient accuracy. This may produce spurious, extended wings in the line profile, mimicking the presence of broad components that could be interpreted as outflows. We deal with this problem by means of a ‘local’ refinement of our continuum subtraction, using an approach that is tailored around the emission lines of interest. Specifically, we fit third-order polynomials to the continuum-subtracted spectra only around small (120 Å-wide) spectral windows, centred around each emission line of interest, after a careful masking of all the principal lines. A visual inspection of the spectra confirms that this local approach considerably improved the continuum subtraction where we needed it the most; thus, we employed it on the four emission lines that are used in the rest of the analysis: Hα, Hβ, [S II]λ6716, and [S II]λ6731.
After this additional correction, velocity cubes for the individual lines were extracted and studied separately using the multi-Gaussian decomposition method discussed below. The Hα and Hβ cubes span a velocity range of ±600 km s−1, while we build a unique cube for the [S II] doublet, centred around the doublet centre and encompassing ±900 km s−1. These velocity ranges are adequate to capture virtually all the emission coming from these bright lines, while minimising the contamination from the nearby fainter lines.
3.2. Emission-line modelling
We modeled the velocity profiles in our cubes using a combination of Gaussian components, which we then analysed a posteriori to assess the presence of outflows in our data. This approach is preferred for the DWALIN-19 galaxies which (as we show below) do not possess the highly-regular velocity fields that are typical of more massive spirals and would permit a geometric modelling of the data, for instance, via tilted ring methods (e.g., Rogstad et al. 1974; Di Teodoro & Fraternali 2015; Bouché et al. 2015; Concas et al. 2022). We proceed by distinguishing between a reference line (Hα), which is modelled first using a complete multi-Gaussian decomposition, followed by the ‘secondary’ lines (all the others) for which only the amplitudes of the Gaussian components are fitted, while the mean velocities and widths of the various components are fixed to the values determined for the reference line. Adopting this separation has two advantages. The first is that it improves the modelling of fainter lines like the [S II] doublet, for which an unconstrained fit may give unpredictable results, especially in the lowest S/N regions. The second (and more relevant advantage) is that it allows us to use the same components for very different lines, which is useful in the calculation of line ratios.
In each spaxel, the Hα line is modelled with a variable number of Gaussian components ranging from one to four. For each component we fit the amplitude, the mean velocity, and the ‘intrinsic’ velocity dispersion σint, defined as:
where σobs is the observed velocity dispersion of the Hα line in our velocity cube and σMUSE is the λ-dependent instrumental broadening, which is equal to ∼50 km s−1 (FWHM of 116 km s−1) around the Hα line (see Eq. (8) of Bacon et al. 2017). Following Marasco et al. (2020), the optimal number of components is decided spaxel-by-spaxel on the basis of a Kolgomorov–Smirnov (KS) test on the residuals of the fits determined for n and n + 1 (with 1 < n < 3) components: if the two residual distributions are statistically different2, then the n + 1 component model is preferred. Thus this method is sensitive to the relative improvements in the data fitting due to the use of increasingly complex models, but it is independent of the ‘goodness’ of the fit in absolute terms.
As the emission from the [N II] doublet can potentially contaminate the Hα line (arrows in Fig. 3), we did not model the [N II] a posteriori – as we did for all the other secondary lines. Instead, we included a single extra parameter in the Hα fit to each spaxel in order to account for the amplitude of the [N II]λ6583 line, under the assumption that it can be modelled as a re-scaled version of the Hα. Assuming a [N II]λ6583/[N II]λ6548 ratio of 3 also works to fully constrain the fainter line of the doublet.
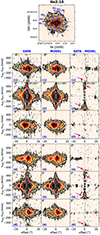 |
Fig. 3. Multi-Gaussian modelling of the Hα line in He 2-10. Top panel shows the total Hα intensity map and the six representative slices (blue-dashed segments) used to extract the position-velocity plots. These are shown in the panels below (left column: data, middle column: model, right column: residual), using a width of three spaxels. Iso-intensity contours are at 2, 5, 10, 20, 102, 103, 104 times the rms noise σ. An additional contour at −2σ is shown in grey. Arrows mark the regions where emission from the [N II] doublet leaks into the Hα cube. |
To illustrate the outcome of this procedure, Fig. 3 shows a series of position-velocity plots taken along different slices for the Hα data (left column), model (middle column), and residual (data-model, right column) velocity cubes of He 2-10. The model provides an excellent description of the data over the whole Hα intensity range which, in this particular case, spans about four orders of magnitude.
The treatment of the instrumental broadening σMUSE in Eq. (1) requires a separate discussion. A caveat associated with the implementation of σMUSE is that the MUSE line spread function (LSF) is not actually Gaussian, but instead more squared in shape. However, as we need to model a few millions velocity profiles with multiple components, fitting complex numerical LSF profiles is highly unpractical and the use of simpler Gaussian shapes becomes mandatory. Although Bacon et al. (2017) stated that a Gaussian approximation of the MUSE LSF is perfectly valid for most applications, in practice we found that some of the emission lines at the longest wavelength in our spectra were narrower than what the instrumental broadening alone would allow (that is, σobs < σMUSE in Eq. (1)). We bypassed this issue by multiplying the σMUSE predicted by Bacon et al. (2017) by a factor 𝒦 = 0.8, which we found to be the approximate value for which spectral lines at different λ have similar σint when modelled separately with a single Gaussian component defined with Eq. (1). Different values of 𝒦 would imply that σint smoothly varies across the wavelength range, which is hardly justifiable, given that the various lines probe the same phase of the ISM (warm ionised gas) with similar temperature and excitation conditions.
3.3. Ionised gas kinematics
The multi-Gaussian decomposition allows us to describe the position-velocity distribution of the ionised gas with a virtually infinite velocity resolution. We use these convenient analytical proxies for the actual velocity profiles to build Hα intensity maps, velocity fields (moment-1 maps, Fig. 4), and velocity dispersion fields (moment-2 maps, Fig. 5) for all DWALIN-19 galaxies.
 |
Fig. 4. Hα velocity fields of the DWALIN-19 galaxies, as derived from our multi-Gaussian modelling of the MUSE data. |
 |
Fig. 5. Hα velocity dispersion fields of the DWALIN-19 galaxies, as derived from our multi-Gaussian modelling of the MUSE data. Only the intrinsic line broadening is shown (see Sect. 3.2). |
As shown in Fig. 4, in the DWALIN-19 sample, the ionised gas is characterised by complex velocity fields that cannot be ascribed to pure regularly rotating discs (Fig. 4). Velocity gradients are visible in many galaxies but are often very irregular, indicating the presence of strong, localised non-circular motions that are likely induced by baryonic feedback and/or past interaction events. This kinematic complexity makes a modelling approach based on simple geometry and large-scale motions (such as in a tilted-ring model) unsuitable, which is why we opted for a different methodology. However, in spite of this complexity, the typical line-of-sight velocities of the ionised gas are on the order of some tens of km s−1 in the DWALIN-19 sample, suggesting the absence of large-scale bulk flows that are sufficiently powerful to expel a vast amount of material out of these galaxies, at least on the spatial scales probed by MUSE. Figure 5 shows that the typical velocity dispersion for the ionised gas is in the range 40–60 km s−1, with the exceptions of He 2-10 and Haro 11, both reaching values slightly above ∼100 km s−1. Thus, the ionised gas in these systems is slightly more turbulent than that of typical star-forming galaxies where σ ≈ 30 ± 10 km s−1 (e.g., Epinat et al. 2010; Green et al. 2014); this is not surprising given their higher-than-average SFR (e.g., Bacchini et al. 2020). Clearly, gas turbulence can also be increased by recent mergers and interactions events, which may trigger the starburst episode in the first place. In fact, Haro 11 is thought to be a merger system (Östlin et al. 2015), and He 2-10 shows signatures of a recent accretion event (Vanzi et al. 2009). However, the DWALIN-19 sample also features systems that are highly isolated and whose Hα velocity dispersion is above average, such as KKH046 and NGC 2915.
The kinematic complexity shown by the DWALIN-19 galaxies is likely to stem from a combination of internal and environmental mechanisms. However, even assuming a scenario where baryonic feedback is the only driver of the observed kinematics, we would conclude that its impact on the ISM is limited to promoting non-circular motions of a few tens of km s−1 over scales of some hundred parsecs as well as to producing only a marginal enhancement of the gas velocity dispersion. The impression is that most of the gas is ‘shaken’ within the ISM, rather than being violently expelled from the galaxy as a result of feedback processes. Similar results are found for the H I kinematics on larger spatial scales, which show complex velocity fields in ∼50% of starburst dwarfs but with typical line-of-sight velocities of just tens of km s−1 (Lelli et al. 2014a). Quantifying the amount of gas that is actually outflowing requires a more careful investigation of the line profiles, which we present below.
4. Ionised winds in DWALIN
The above results indicate that the DWALIN-19 galaxies are not simple rotating discs; they also lack unambiguous, spatially resolved evidence for a large-scale bulk motion in their ionised gas. In these conditions, the signature of a galactic wind can be identified through the presence of wings and/or secondary (broad) components in the line profiles.
However, even after the identification of such features, two key decisions must be made: what the wind speed and what the fraction of flux associated with the wind should be. These choices largely affect the wind properties, but they are often determined arbitrarily. With the purpose of providing a more physically motivated definition of a galaxy wind, we adopted basic prescriptions to define the flux and velocity associated with the wind component based on simple dynamical and geometrical considerations.
4.1. Towards a more physically motivated selection of the wind
We define ‘wind’ as the material whose velocity, measured with respect to the systemic velocity of the galaxy, exceeds the local escape velocity, vesc, defined as the minimum speed required to bring a test particle from its original location out to the halo’s virial radius3. This choice is motivated by the idea that material ejected with a speed higher than vesc leaves the galaxy’s virialised region and is not longer bound to that system. Clearly, this is a strong simplification of the process of gas cycling induced by feedback, as it ignores hydrodynamical effects that can alter the purely ‘ballistic’ dynamics of the cycle. On the one hand, since drag from the pre-existing CGM slows down the cloud speed, an initial velocity higher than vesc is needed to expel clouds from the virialised region. On the other hand, even for low outflow speeds, the development of hydrodynamical instabilities due to the cloud-CGM interaction can fragment the outflowing cloud into small cloudlets that, via thermal conduction, can evaporate into the CGM (e.g., Armillotta et al. 2017). As the outcome of these processes depends on the physical condition of the outflowing gas and on the detailed properties of the CGM, we prefer to neglect them in favour of a simpler and easy-to-model ballistic interpretation of the gas flow.
The vesc radial profile of each galaxy is determined using a mass model consisting of a dark matter (DM) halo, a stellar disc and a gaseous disc. For the DM halo, we assume a Navarro–Frenk–White (NFW, Navarro et al. 1997) profile, with a virial mass of M200 determined from M⋆ via the stellar-to-halo mass relation (SHMR) of Moster et al. (2013), and a concentration, c, set by the M200 − c relation of Dutton & Macciò (2014), which is therefore consistent with a ΛCDM Universe. The stellar disc is modelled with a double-exponential profile, with scale-length Rd determined either from the IRAC 3.6 μm data or (when these are unavailable) from the W1 data4 and scale-height given by Rd/5 (e.g., van der Kruit & Freeman 2011). Given the lack of a complete database of atomic and molecular gas observations for DWALIN, we used a M⋆-based proxy for the cold gas mass (Eq. (7) in Chae et al. 2021) and assumed a size of the gaseous disc equal to twice that of the stars. This formulation is overall consistent (to within 0.2–0.5 dex), with the gas content in low-mass galaxies that would be inferred from the M⋆+SFR empirical approach by Hunt et al. (2020). Both of these approaches are only rough approximations, and in the calculation of vesc, the baryon distribution plays a very marginal role as the escape speed is primarily affected by the overall depth of the gravitational potential rather than by the potential gradient (unlike the case of the circular velocity, for instance). In practice, the key ingredient is the assumed SHMR, which we have used the model of Moster et al. (2013) to calculate; this value is compatible with dynamical estimates for M⋆ and M200 in the mass range spanned by our sample (e.g., Katz et al. 2017; Posti et al. 2019). While gas-rich dwarfs may feature cores in their central mass distribution (e.g., de Blok 2010), we verified that the use of a cored DM profile such as that of Burkert (1995) makes little difference in the resulting vesc profile.
The vesc curve can be compared with the position-velocity distribution of the ionised gas using a phase-space plot. Panel a in Fig. 6 shows an example of such a plot for the Hα line of He 2-10, where we have populated the position-velocity space using the various components of our multi-Gaussian modelling considering only the intrinsic broadening in the line profiles. From this diagram, it is clear that some fraction of the ionised gas is located in regions beyond the escape speed curves, identified by white-dashed lines in the panel. However, as we discuss below, the selection of a wind component from this diagram depends on the 3D geometry and kinematics of the wind itself, which must be assumed.
 |
Fig. 6. Scheme illustrating the extraction of the wind component from the Hα velocity cube of He 2-10. (a): phase-space distribution for the whole Hα emission. Instrumental broadening is removed via the multi-Gaussian decomposition. Cyan contours encompass 50%, 70%, and 90% of the total Hα flux. White-dashed lines show the escape speed radial profile (see Sect. 4.1). (b): the two feedback scenarios of Sect. 4.2. In (b1) feedback injects turbulence in the ISM, but produces no bulk flow. In (b2) feedback produces the spherical expansion of a turbulent shell of gas (TES). (c): illustration of the effects of feedback on a single velocity profile. For both scenarios we assume vesc of 100 km s−1, a systemic velocity of 0 km s−1, and velocity dispersion of 30 km s−1 for the unperturbed gas (blue-dashed curve). The component perturbed by feedback (red-dashed curve) is derived by assuming a shell expansion speed, v, and a velocity dispersion, σ, indicated in the top-right corner. Both scenarios feature very similar broad components. In the turbulent case (c1), only the flux at |v|> vesc (highlighted in yellow) is eligible as ‘wind’. In the TES case, given that v > vesc, the whole component will be associated with a wind. (d): phase-space plots for the wind component alone, extracted by processing each Hα velocity profile as discussed in Sect. 4.2. Contours are defined as in panel a. (e): integrated Hα intensity maps of the wind component. Iso-intensity contours for the total Hα emission are shown in grey, as a reference. |
4.2. Feedback-driven turbulence and expansion
We propose two different approaches to select the wind component from the analysis of the phase-space plots. The first is more conservative in terms of wind mass, while the second is more generous, corresponding to diverse modes by which the energy and momentum injected by feedback is imparted to the ISM. The use of both approaches allows us to better assess the uncertainties in the outflow rate estimates. These two idealised feedback scenarios, along with their implications in terms of wind component selection, are illustrated in panels b and c of Fig. 6.
The first approach is based on a scenario where baryonic feedback augments the turbulence of the surrounding gas without affecting its bulk motion. In this ‘turbulence’ scenario, sketched in panel b1 of Fig. 6, the wind will be made solely by those cloudlets that are randomly scattered at sufficiently large (> |vesc|) velocities (panel c1 in Fig. 6). This scenario can be applied to our data by selecting only the portion of the emission at |v|> |vesc| in the phase space (panel d1 in Fig. 6). The resulting wind flux is multiplied by a factor 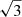 to take into account that we only see projected velocities.
to take into account that we only see projected velocities.
A completely converse model is the one where feedback does not affect the gas turbulence – but solely its bulk motion. We start by considering a spherical expanding shell of gas with a constant velocity, vwind, slightly larger than vesc. We can demonstrate that in the absence of extinction, the line-of-sight (LOS) velocity profile produced by a (spatially unresolved) expanding, homogeneous shell of non-turbulent gas is a perfectly flat distribution confined within ±vwind. This occurs because we observe the intrinsic ±vwind only along two opposite shell elements aligned with the line of sight, whereas we see a fraction of ±vwind for all the other shell elements due to projection effects. Trivially, the fact that flat velocity profiles are never observed suggests that this model is not realistic and that some amount of turbulence is always injected within the expanding gas, producing a smoother profile. In this ‘turbulent expanding shell’ (hereafter, TES) scenario, selecting only the flux at |v|> |vesc| would largely underestimate the wind mass, since we know that – by construction – the whole shell moves faster than vesc (panels b2 and c2 in Fig. 6). We apply these considerations to our data by inspecting (one by one) the components of the multi-Gaussian fit and assign them to the wind component if they have at least a fraction fesc of their flux beyond the vesc. We use fesc = 0.05 as our fiducial value, but in Sect. 4.3, we explore values uniformly distributed between 0.01 and 0.1 to assess the uncertainty of this method.
Figure 6 illustrates the application of these two feedback scenarios to the Hα data of He 2-10, showing the phase-space plots (panels d1 and d2) and the integrated Hα intensity maps (panels e1 and e2) associated with the wind component alone. As expected, the two scenarios predict a different flux for the wind, equal to 2% of the total for the turbulence case and 8% of the total for the TES case. With respect to the turbulence case, the TES scenario outputs a more defined wind structure, which features a spiral-like wind morphology. Even though the Hα flux of the wind component is small, its half-light radius is about twice that determined for the total Hα distribution. Typically, we find that Hα winds in the DWALIN-19 sample have half-light radii that are 50–80% larger than those of the total Hα distribution. This suggests a radial expansion of the material ejected from the galaxy by baryonic feedback, in agreement with expectations from ballistic models of the galactic fountain (e.g., Fraternali 2017). Plots similar to those presented in Fig. 6 are shown for all DWALIN-19 galaxies in Appendix B.
Our wind selection was performed on the reference line (Hα), but we applied it to the secondary lines too, using the following criteria: for the turbulent scenario we simply selected the emission at v > vesc, as we had already done for the Hα line, while for the TES case, we relied on our multi-Gaussian modelling (Sect. 3.2) and selected all Gaussian components in the secondary lines that are associated with the wind in the reference line. This approach allows us to have a self-consistent wind definition across different lines, which is important for the computation of the wind properties, as we discuss below.
4.3. Outflow rates and mass-loading factors
Our calculations for the (ionised) gas outflow rates follow those outlined in a number of previous studies (e.g., Liu et al. 2013; Cresci et al. 2015, 2017; Marasco et al. 2020; Tozzi et al. 2021). The main difference is that in this work, we present separate computations for the two feedback scenarios described above, which lead to different estimates of the wind rates: a more conservative one for the turbulence scenario and a less conservative one for the TES case. In the calculations that follow, all wind properties (flow rate, electron density, and extinction) are determined using integrated fluxes of the wind component.
Assuming that the ionised wind can be described as a collection of ionised gas clouds all having the same electron density, ne, and that the ionisation conditions do not vary across the FOV, its mass can be computed from the luminosity of the wind component of the Hα line, 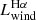 , as:
, as:
To determine 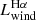 , the Hα flux of the wind component must be corrected for internal dust extinction, A(Hα). We determine A(Hα) from the Balmer decrement, assuming an intrinsic Hα/Hβ of 2.86 for a temperature T = 104 K (Osterbrock & Ferland 2006)5, a Calzetti et al. (2000) extinction law and (importantly) computing the observed Hα/Hβ total flux ratio for the wind component alone. This is relevant because (as we discuss below) the properties of wind material can differ from the average properties of the galactic ISM. Similarly, we determined ne in Eq. (2) from the [S II]λ6716/[S II]λ6731 flux ratio computed for the wind component, using the prescription from Sanders et al. (2016).
, the Hα flux of the wind component must be corrected for internal dust extinction, A(Hα). We determine A(Hα) from the Balmer decrement, assuming an intrinsic Hα/Hβ of 2.86 for a temperature T = 104 K (Osterbrock & Ferland 2006)5, a Calzetti et al. (2000) extinction law and (importantly) computing the observed Hα/Hβ total flux ratio for the wind component alone. This is relevant because (as we discuss below) the properties of wind material can differ from the average properties of the galactic ISM. Similarly, we determined ne in Eq. (2) from the [S II]λ6716/[S II]λ6731 flux ratio computed for the wind component, using the prescription from Sanders et al. (2016).
The distributions of the resulting A(Hα) and ne are shown in Fig. 7, where we compare the values determined for the wind in each galaxy (red and green histograms) with those inferred for the entire galaxy (grey-shaded histograms). Clearly, the ionised wind has on average a higher electron density and extinction compared to the rest of the galaxy. A higher ne for the (stellar- or AGN-driven) ionised winds has been found in several other studies (Arribas et al. 2014; Perna et al. 2017; Rose et al. 2018; Mingozzi et al. 2019; Davies et al. 2020; Fluetsch et al. 2021); it may be driven by the compression of the gas caused by the expanding superbubbles in the star-forming disc (e.g., Keller et al. 2014). In particular, our findings agree well with prior measurements of local ultra-luminous infrared galaxies from Fluetsch et al. (2021), where the typical ne is ∼150 cm−3 in the disc and ∼500 cm−3 in the outflow.
 |
Fig. 7. Extinction A(Hα) (top panel) and electron density ne (bottom panel) distribution in our sample. The grey-shaded histograms show mean values representative for the whole galaxy. The solid green and red lines refer to the wind component computed in the turbulence and TES scenarios, respectively. Winds are characterised by higher A(Hα) and ne than in the rest of the galaxy. |
Measurements for dust extinction in the wind are more widely debated in the literature, with different groups finding both higher (Holt et al. 2011; Villar Martín et al. 2014) and lower (Rose et al. 2018; Mingozzi et al. 2019; Fluetsch et al. 2021) values in the outflow than in the rest of the ISM. A visual inspection of the spaxel-by-spaxel distribution of A(Hα) for the wind in single DWALIN-19 galaxies often shows a peak at values closer to (or below) that of the ISM (0.5–1 mag), followed by a tail that extends towards very large values and increases the mean A(Hα) for this component. Our findings of a higher mean extinction agree qualitatively with predictions from radiation pressure-driven models of stellar feedback (e.g., Ishibashi & Fabian 2016). High density and extinction are also requirements for the formation of molecules in the wind (Richings & Faucher-Giguère 2018). We show below that ionised winds in DWALIN-19 have much lower mass-loading factors than what cosmological models would predict, thus the presence of a significant molecular component in the outflow can potentially mitigate this tension. Our measurements for the wind extinction and electron density in each galaxy are listed in Table 3.
The mass outflow rate, Ṁwind, at a given radius rwind is derived using the simplified assumptions of spherical (or multi-conical) geometry and a constant outflow speed vwind. Following Lutz et al. (2020), we have
where ℋ is a multiplicative factor that depends on the adopted outflow history. We take ℋ = 1, adequate for a temporally constant Ṁwind during the flow time rwind/vwind, which is typically ∼6 Myr in our sample. For simplicity, we consider rwind to be equal to the half-light radius of the wind component, which can be easily determined from our phase-space diagrams, and vwind to be equal to the escape speed computed at r = rwind. Thus in our approach the wind speed is not directly measured from the data but is assumed from our mass model, for consistency with the wind selection method (Sect. 4.1). Wind speeds, radii, and outflow rates are listed in Table 3 for each galaxy in the DWALIN-19 sample.
The uncertainties quoted in Table 3 come from multiple sources. For the turbulence scenario, uncertainties on A(Hα) and ne originate from statistical errors on the multi-Gaussian models of the Balmer and [S II] lines used to infer such quantities. These are propagated to Ṁwind and β estimates, although the errors on the latter are dominated by uncertainties in the SFRs. For the TES scenario, rather, we also account for fesc, which we take free to vary between 0.01 and 0.1. fesc is the dominant source of uncertainty for all quantities in the TES case.
Figure 8 summarises the properties of the ionised winds in the DWALIN-19 sample, showing mass outflow rates, Ṁwind, (left-hand column) and mass-loading factors, β ≡ Ṁwind/SFR, (right-hand column), derived as mean values of the two methods discussed above, as a function of galaxy M⋆ (top row), SFR (second row), mean SFR density (ΣSFR6, third row), and SFR-to-M⋆ ratio (or specifc SFR, sSFR, bottom row). Error-bars on the Ṁwind measurements come from the quadratic sum of two uncertainties: the first is given by half the difference between the values determined in the turbulence and TES scenarios and the second is the largest error-bar of the two scenarios, provided by Table 3. The former uncertainty is typically dominant since, as expected, the TES scenario outputs outflow rates that are larger on average by a factor of 2 (and up to a factor of 6) than the turbulence case (see Table 3).
 |
Fig. 8. Summary of the wind properties in the DWALIN-19 sample. Ionised gas outflow rate, Ṁwind, (left-hand panels) and mass-loading factors β (right-hand panels) as a function of galaxy M⋆ (first row), SFR (second row), mean SFR surface density (third row), and sSFR (fourth row). Each galaxy is labelled with an ID number (see legend on top). Data points are based on the average of values from the turbulence and TES scenarios; error-bars account both for the difference between the two scenarios and for the uncertainties associated with each of them (see text). Spearman (S) and Pearson (P) correlation coefficients are reported on top of each panel. Blue-dashed lines show the best-fit linear relations determined with the LTSFIT Python package (Cappellari et al. 2013), with the blue-shaded region showing the resulting intrinsic scatter σint. Values for the line slope, m, intercept, c, and σint are reported in each panel. |
We find that galaxies in the DWALIN-19 sample have ionised gas outflow rates ranging from 10−4 to 10−1 M⊙ yr−1, corresponding to loading factors of 10−3 − 101, with a median β of 0.02. These values are remarkably small compared to those predicted by galaxy evolutionary models (see Sect. 5.2 for further discussion). Also, Fig. 8 clearly shows that the properties of the ionised wind are tightly related to those of the host galaxy. Ṁwind (β) correlate (anti-correlate) with M⋆, SFR, and ΣSFR, with Spearman (S) and Pearson (P) correlation coefficients typically in the range 0.4 − 0.7 (in modulus). Specific SFRs show instead a somewhat weaker correlation with Ṁwind, but remain highly anti-correlated with β. We point out that these correlations are at least partially driven by the fact that the quantities compared are not fully independent, as Ṁwind ∝ vwind = f(M⋆), and β ∝ (SFR)−1 by construction. On the other hand, similar trends have been reported in other studies that make use of absorption line techniques to measure outflow rates (Chisholm et al. 2017; Xu et al. 2022a). We used the LTSFIT Python package from Cappellari et al. (2013) to make a linear fit to these relations in the logarithmic space, finding an intrinsic perpendicular scatter ranging from 0.28 dex (for the β–sSFR relation) to 0.68 dex (for the Ṁwind–sSFR relation). We stress that most of the observed scatter is driven by two galaxies, ESO 489−G56 and He 2-10 (ID number 2 and 4, respectively), for which SFRs have been determined without UV information (Table 1). More accurate measurements for their SFRs may bring these two systems in better agreement with the general trends, with possible further reduction of the scatter.
5. Discussion
5.1. Comparison with previous studies
Previous studies based on H I, Hα, or Na I D data have found that gas in dwarf galaxies exhibits outflow velocities that are too small to escape the gravitational potential well of their host (Martin 1996; Schwartz & Martin 2004; van Eymeren et al. 2009b, 2010, 2009a; Lelli et al. 2014b). Our work confirms this result: we find that the fraction of gas that can potentially escape the virial radius is ≲ a few percent.
However, more recent estimates for mass outflow rates and loading factors of warm ionised gas in star forming galaxies are quite controversial; this can be appreciated by comparing the various observational studies shown in Fig. 9. Works that make use of UV absorption lines from the Cosmic Origins Spectrograph on board of the Hubble Space Telescope tend to find values for β in the range 1 − 10 for M⋆ ∼ 108 M⊙ systems (e.g. Chisholm et al. 2017, brown circles in Fig. 9), which are factors of 100 − 1000 larger than those reported in this study. An extreme case is that of the galaxy Haro 11, for which Chisholm et al. (2017) reported log β = 0.08 ± 0.15, whereas our estimate is log β ∼ −3.4, namely, about 2 × 103 times smaller. Comparatively large outflow rates were also found by Xu et al. (2022a), who inferred ∼3.3 M⊙ yr−1 for CGCG007-025 and ∼1.8 M⊙ yr−1 for Haro 11, which are factors of ∼70 and ∼2600 larger than our measurements, respectively. On the other hand, the kinematic modelling results of stacked optical emission lines in gravitationally lensed star-forming galaxies at 1.2 < z < 2.6 have shown that objects with 8.0 < log(M⋆/M⊙) < 9.6 have velocity profiles consistent with those expected from regularly rotating discs, suggesting a typical log(β) < − 1.6 for these systems (Concas et al. 2022, purple stars in Fig. 9), which is in excellent agreement with our local analysis. Also, spatially resolved gas kinematics in the small (M⋆ ∼ 105 M⊙) starburst dwarf Pox 186 indicates a mass-loading factors of 0.5 (Eggen et al. 2021), which is compatible with the trends shown in Fig. 8 for galaxies at such low M⋆.
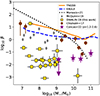 |
Fig. 9. Wind mass-loading factor β as a function of galaxy M⋆ from different studies. Markers show observational results from Chisholm et al. (2017, brown circles), McQuinn et al. (2019, grey diamonds), Concas et al. (2022, purple stars), and the present study (yellow squares). Lines show theoretical predictions from the EAGLE (Mitchell et al. 2020, blue-dashed) and the Illustris TNG 50 (Nelson et al. 2019, orange-solid) cosmological simulations, and from the evolutionary model of Marasco et al. (2021, black-dotted). |
Pinpointing the dominant source of these discrepancies is not trivial, since the quoted studies largely differ in terms of methodology, sample selection and atomic species considered. By construction, absorption line studies infer flow rates from a small number of pencil-beam observations along sparse sight-lines, thus lack any spatial information and rely on strong assumptions on the geometry, kinematics and filling factor of the wind. Even when hundreds of sight-lines are available, as in the case of the Milky Way, the interpretation of the gas flow outside the disc varies depending on such assumptions (e.g., Clark et al. 2022; Marasco et al. 2022). Overall, the impression is that low values of β are found when gas kinematics are modelled in some detail, as in the current study as well as in that of Concas et al. (2022).
The study conducted by McQuinn et al. (2019) provided one of the first systematic investigations of ionised galactic winds in nearby, low-mass (M⋆ ∼ 107 − 109.3 M⊙) starburst galaxies from Hα narrow-band imaging. The main results of that work are that winds are spatially confined within the innermost 10% of galaxy virial radii, indicating that most of material expelled from dwarf galaxies remains in the halo and can be eventually re-accreted onto their discs. These findings align with our own and support a scenario where baryonic feedback in dwarfs stimulates a gentle gas cycle rather than producing a massive blowout. However, in McQuinn et al. (2019), typical values quoted for mass-loading factors β are in the range 0.5 − 3 (grey diamonds in Fig. 9), approximately a factor 100 larger than those inferred in our study.
A key difference between our work and that of McQuinn et al. (2019) is the selection of the wind component. Both studies rely on the Hα line to characterise the wind, but while our approach focuses on the Hα kinematics in relation to the galaxy escape speed (Sect. 4.1), the criterion used by McQuinn et al. (2019) is based on the Hα morphology, and specifically on the Hα radial extent compared to that of the H I component: ionised gas located beyond an H I surface density contour-level of 5 × 1020 cm−2 is selected as the wind, to which an expansion velocity of 25 − 50 km s−1 (typical for the Hα velocity dispersion in the ISM of these systems) is assigned. Such an approach has the advantage of relying on a visual identification of the wind component, intended as ionised gas beyond some scale radius. Related shortcomings include the fact that the definition of such radius is arbitrary and that the gas expansion speed must be assumed. Velocities of 25 − 50 km s−1 are typically insufficient to gravitationally unbind the wind material (see our vwind estimates based on vesc in Table 3), which will eventually fall back onto the galaxy in a galactic fountain cycle or join the CGM. Hence, β values estimated with this approach likely refer to gas that participates to the disc-halo cycle, rather than to baryons that get permanently expelled from galaxy halos. Models of the galactic fountain (e.g., Fraternali & Binney 2006; Marasco et al. 2019a) require β greater than unity in order to reproduce the properties of extra-planar gas in nearby galaxies.
We stress that some of the galaxies in the DWALIN-19 sample have been studied individually in separate works. Thuan & Izotov (1997) found P-Cygni profiles in the stellar UV absorption lines of SBS 0335-052 and Tol 1214-277, suggesting the presence of a stellar wind from massive stars in these two systems. The terminal velocities measured for the stellar winds in SBS 0335-052 and Tol 1214-277 were ∼500 and ∼2000 km s−1, respectively. Interestingly, while we do not infer terminal velocities in our study, our estimates for mass outflow rates and loading factors in Tol 1214-277 are about one order of magnitude larger than for SBS 0335-052. Cresci et al. (2017) carried out a detailed investigation of the ionised gas properties in He 2-10 using the same MUSE data analysed here. These authors estimated a mass outflow rate of 0.3 M⊙ yr−1 that is consistent with our measurement, although our uncertainties are particularly large for this system.
Cohen et al. (2018) studied the kinematics of the Brackett α emission line towards a supernebula in NGC 5253 to quantify the effects of feedback from its embedded super star cluster. Based on the absence of a massive outflow, these authors concluded that feedback is ineffective at dispersing gas around the cluster, in line with our findings. Using MUSE data and a dynamical approach that is conceptually similar to that adopted here, Menacho et al. (2019) inferred the ionised gas fraction that could escape the gravitational potential in Haro 11, finding values between 0.1 and 0.3. In our study, the flux fraction of the wind component in Haro 11 is, instead, only 0.01. This discrepancy is largely driven by the different dark matter halo mass assumed for this galaxy: we used 4 × 1011 M⊙ from the SHMR of Moster et al. (2013), while Menacho et al. (2019) adopt 7–9 × 1010 M⊙, from the estimate of Östlin et al. (2015) based on the rotational speed of the ionised gas in the galaxy outskirts. As discussed in Sect. 3, the DWALIN-19 galaxies are characterised by irregular velocity fields. This complicates any possible estimate for their circular velocity (and, hence, for their dynamical mass) from the ionised gas kinematics, which pushed us opt for a different approach.
Galaxy winds in J1044+0353 and J1418+2102, two galaxies in the DWALIN sample (but not in the DWALIN-19 sub-sample), have recently been detected using deep optical slit-spectroscopy by Xu et al. (2022b), who inferred mass loading factors of 0.44 and 0.36 for the two systems, respectively. These values are in excellent agreement with the β–SFR and β–M⋆ relations found in our study (Fig. 8), given the M⋆ and SFRs of these two galaxies listed in Table 1.
5.2. Comparison with theoretical expectations
A scenario where the outflow mass-loading anti-correlates with the galaxy stellar (or dynamical) mass, as we find here (see Fig. 8), is supported by arguments based on energy- and momentum- driven winds as well as, in general, by theoretical models of galaxy evolution in the ΛCDM framework (e.g., Somerville et al. 2008; Somerville & Davé 2015; Bower et al. 2017; Zhang 2018). This scenario is based on the simple expectation that more massive galaxies prevent gas from escaping due to the depth of their gravitational potential well. Unfortunately, the comparison between theoretical predictions and observational measurements of outflow rates is not trivial: observations are limited by projection effects and can provide only an instantaneous measurement of the outflow rate for a given gas phase (which is, in this study, the warm-ionised phase traced by optical emission lines), whereas theoretical predictions are robust only for time-averaged wind properties and seldom distinguish between the different gas phases. It is therefore very likely that the theory will provide higher outflow rates than observational determinations.
Figure 9 shows the predictions for β as a function of M⋆ from the EAGLE (Schaye et al. 2015) and Illustris TNG50 (Pillepich et al. 2018) suites of cosmological hydrodynamical simulations (dashed-blue and solid-orange lines, respectively), and that of the analytical model of galaxy evolution from Marasco et al. (2021). These predictions make use of very different prescriptions for determining Ṁwind. Mitchell et al. (2020) derived Ṁwind in EAGLE using all gas particles whose time-averaged radial speeds exceed a given fraction of the halo maximum circular velocity. Nelson et al. (2019) computed outflow rates in TNG50 at a fixed galactocentric radius (r = 10 kpc) by considering all gas particles with radial velocity above 5× the halo virial velocity (see their Appendix A7). In the analytical evolutionary model of Marasco et al. (2021), β is parameterised as (Mh/Mcrit)−α, where Mh is the galaxy halo virial mass and Mcrit and α are free parameters that control the efficiency of stellar feedback in driving winds. These parameters, along with others controlling feedback from supermassive black holes, are adjusted to reproduce the relation between black hole masses, M⋆ and Mh observed in nearby galaxies (Mcrit = 2.5 × 1011 and α = 1.7 in their fiducial model). However, in spite of these diversities, all predictions must be re-scaled by at least two orders of magnitude in order to match the DWALIN-19 data points. A similar result seems to hold even at a higher redshift, as found by Concas et al. (2022) via the modelling of stacked optical emission lines from lensed KMOS data at 1.2 < z < 2.6. Taken at face value, this result suggests that either theory drastically over-predicts outflow rates in star-forming galaxies by more than two orders of magnitudes or, otherwise, that warm ionised gas accounts for less than 1% of the wind mass – as seems to be the case in local ultra-luminous infrared galaxies (Fluetsch et al. 2021). We remark, however, that the tension between theory and observations is alleviated when the higher values of β determined by Chisholm et al. (2017) and McQuinn et al. (2019) are considered. On the other hand, recent high-resolution simulations of isolated galaxy formation indicate that a feedback efficiency lower than often employed in cosmological models is required in order to correctly reproduce the chemical and morphological properties of stellar discs in Milky Way-like systems (e.g., Clarke et al. 2019; Beraldo e Silva et al. 2020).
6. Conclusions
Feedback from star formation and/or AGN (‘baryonic’ feedback) is expected to strongly affect the evolution of low-mass galaxies by launching multi-phase, galaxy-scale winds characterised by large (1 − 50) mass-loading factors (Somerville et al. 2008; Muratov et al. 2015; Nelson et al. 2019; Mitchell et al. 2020). Feedback models predict that most of the wind mass is expected to be found in the warm (T ∼ 104 K) phase (Kim et al. 2017; Kim & Ostriker 2018), thus, spatially resolved optical spectroscopy of local starburst dwarfs has the potential to put key constraints on the wind properties (and therefore on the role of baryonic feedback) in galaxies at the low-mass end of the M⋆ function.
In this paper, we study the properties of the warm ionised winds in a sample of 19 nearby starburst galaxies, namely, the DWALIN-19 sample, using archival MUSE at VLT data. Our results can be summarised as follows.
-
We determined M⋆ and SFRs for all the galaxies in the DWALIN sample (Fig. 1) in a homogeneous way, using the method outlined by Leroy et al. (2019). This makes use of photometric measurements in various bands, ranging from the FUV to the MIR, which we obtained by processing GALEX, WISE, and Spitzer images with an ad-hoc pipeline based on the extraction of cumulative light profiles (Fig. A.1). We find that as expected, the vast majority of our galaxies lie above the star-forming main-sequence, so they may be considered low-mass starbursts.
-
Detailed modelling of the Hα velocity profiles from the MUSE data shows that starburst galaxies feature complex velocity fields characterised by irregular velocity gradients (Fig. 4), indicating the presence of non-circular motions with speeds of a few tens km s−1, which are well below the galaxy escape speed. The typical velocity dispersion for the ionised gas is 40 − 60 km s−1 (Fig. 5), slightly larger than that of typical star forming galaxies (30 ± 10 km s−1), in line with the idea of feedback injecting turbulence into the ISM.
-
A wind component for the ionised gas is determined spaxel-by-spaxel from the Hα velocity profiles, by comparing the gas distribution in the phase-space with simple models for the escape speed radial profile. To better assess the uncertainties in our measurements we adopt two approaches to extract the wind component based on two different feedback scenarios (Fig. 6). We find ionised gas outflow rates in the range of 10−4 − 10−1 M⊙ yr−1, corresponding to mass-loading factors of 10−3 − 101, with a typical value of 0.02.
-
Outflow rates (loading factors) are tightly correlated (anti-correlated) with M⋆, SFRs, SFR densities, and specific SFRs (Fig. 8). While these trends are in qualitative agreement with expectations from hydrodynamical and analytical models of galaxy evolution, model predictions exceed the observed values by at least two orders of magnitude.
Our findings suggest that baryonic feedback in starburst dwarfs stimulates a gentle gas cycle, rather than producing a large-scale blow-out, in line with previous results based on interferometric H I observations (Lelli et al. 2014b) and deep Hα imaging (McQuinn et al. 2019). An open question remains regarding whether most of the wind mass in these systems is confined to the colder, denser molecular phase. Deep observations with radio or sub-mm interferometers like ALMA are available for some of the DWALIN galaxies. However, studies that used such data (e.g., Hunt et al. 2014, 2015; Amorín et al. 2016; Cormier et al. 2017; Gao et al. 2022) have mostly focused on determining molecular gas fractions, gas depletion time-scales, and dust properties, while little attention has been dedicated to quantify the properties of molecular outflows. A homogeneous study of the molecular gas kinematics in DWALIN, analogous to that presented in this work, will be mandatory to definitively infer whether the coldest gas phase plays a dominant role in starburst-driven galactic winds.
Defined as 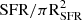 , where RSFR is taken from Table 1.
, where RSFR is taken from Table 1.
Amongst the various prescriptions adopted by Nelson et al. (2019) this is the one that comes closer to our approach, as in our mass models vesc ≃ 4 − 5× the halo virial velocity.
Acknowledgments
The authors thank an anonymous referee for a prompt and constructive report. AM and GC acknowledge the support by INAF/Frontiera through the “Progetti Premiali” funding scheme of the Italian Ministry of Education, University, and Research. GV acknowledges support from ANID program FONDECYT Postdoctorado 3200802.
References
- Altintas, I., Barney, O., Cheng, Z., et al. 2006, J. Phys. Conf. Ser., 46, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Amorín, R., Muñoz-Tuñón, C., Aguerri, J. A. L., & Planesas, P. 2016, A&A, 588, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anand, G. S., Rizzi, L., Tully, R. B., et al. 2021, AJ, 162, 80 [CrossRef] [Google Scholar]
- Armillotta, L., Fraternali, F., Werk, J. K., Prochaska, J. X., & Marinacci, F. 2017, MNRAS, 470, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Colina, L., Bellocchi, E., Maiolino, R., & Villar-Martín, M. 2014, A&A, 568, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacchini, C., Fraternali, F., Iorio, G., et al. 2020, A&A, 641, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldassare, V. F., Reines, A. E., Gallo, E., & Greene, J. E. 2017, ApJ, 836, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Baldassare, V. F., Geha, M., & Greene, J. 2018, ApJ, 868, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K. 2008, MNRAS, 388, L10 [Google Scholar]
- Bekki, K., & Freeman, K. C. 2002, ApJ, 574, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Beraldo e Silva, L., Debattista, V. P., Khachaturyants, T., & Nidever, D. 2020, MNRAS, 492, 4716 [CrossRef] [Google Scholar]
- Berg, D. A., Skillman, E. D., Marble, A. R., et al. 2012, ApJ, 754, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Birchall, K. L., Watson, M. G., & Aird, J. 2020, MNRAS, 492, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouché, N., Carfantan, H., Schroetter, I., Michel-Dansac, L., & Contini, T. 2015, AJ, 150, 92 [Google Scholar]
- Bower, R. G., Schaye, J., Frenk, C. S., et al. 2017, MNRAS, 465, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G., Gibson, B. K., et al. 2012, MNRAS, 419, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [Google Scholar]
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
- Chae, K.-H., Desmond, H., Lelli, F., McGaugh, S. S., & Schombert, J. M. 2021, ApJ, 921, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Y.-Y., van der Wel, A., da Cunha, E., & Rix, H.-W. 2015, ApJS, 219, 8 [Google Scholar]
- Chisholm, J., Tremonti Christy, A., Leitherer, C., & Chen, Y. 2016, MNRAS, 463, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Chisholm, J., Tremonti, C. A., Leitherer, C., & Chen, Y. 2017, MNRAS, 469, 4831 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S., Bordoloi, R., & Fox, A. J. 2022, MNRAS, 512, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, A. J., Debattista, V. P., Nidever, D. L., et al. 2019, MNRAS, 484, 3476 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, D. P., Turner, J. L., Consiglio, S. M., Martin, E. C., & Beck, S. C. 2018, ApJ, 860, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, M. L. M., & Read, J. I. 2022, Nat. Astron., 6, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Concas, A., Popesso, P., Brusa, M., Mainieri, V., & Thomas, D. 2019, A&A, 622, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Concas, A., Maiolino, R., Curti, M., et al. 2022, MNRAS, 513, 2535 [NASA ADS] [CrossRef] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2015, A&A, 578, A53 [CrossRef] [EDP Sciences] [Google Scholar]
- Cormier, D., Bendo, G. J., Hony, S., et al. 2017, MNRAS, 468, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, T., Pakmor, R., & Springel, V. 2020, MNRAS, 497, 5229 [Google Scholar]
- Cresci, G., Mainieri, V., Brusa, M., et al. 2015, ApJ, 799, 82 [Google Scholar]
- Cresci, G., Vanzi, L., Telles, E., et al. 2017, A&A, 604, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R., Baron, D., Shimizu, T., et al. 2020, MNRAS, 498, 4150 [Google Scholar]
- de Blok, W. J. G. 2010, Adv. Astron., 2010, 789293 [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [Google Scholar]
- Di Teodoro, E. M., McClure-Griffiths, N. M., De Breuck, C., et al. 2019, ApJ, 885, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Eggen, N. R., Scarlata, C., Skillman, E., & Jaskot, A. 2021, ApJ, 912, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Zhang, H.-X., & Hunter, D. A. 2012, ApJ, 747, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Amram, P., Balkowski, C., & Marcelin, M. 2010, MNRAS, 401, 2113 [Google Scholar]
- Eskew, M., Zaritsky, D., & Meidt, S. 2012, AJ, 143, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2019, MNRAS, 483, 4586 [NASA ADS] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2021, MNRAS, 505, 5753 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F. 2017, in Gas Accretion onto Galaxies, eds. A. Fox, & R. Davé, Astrophys. Space Sci. Lib., 430, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., & Binney, J. J. 2006, MNRAS, 366, 449 [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, Y., Gu, Q., Shi, Y., et al. 2022, A&A, 661, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil de Paz, A., Boissier, S., Madore, B. F., et al. 2007, ApJS, 173, 185 [Google Scholar]
- Governato, F., Brook, C., Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Zolotov, A., Pontzen, A., et al. 2012, MNRAS, 422, 1231 [Google Scholar]
- Green, A. W., Glazebrook, K., McGregor, P. J., et al. 2014, MNRAS, 437, 1070 [Google Scholar]
- Heckman, T. M., Dahlem, M., Lehnert, M. D., et al. 1995, ApJ, 448, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Alexandroff, R. M., Borthakur, S., Overzier, R., & Leitherer, C. 2015, ApJ, 809, 147 [Google Scholar]
- Herrmann, K. A., Hunter, D. A., Zhang, H.-X., & Elmegreen, B. G. 2016, AJ, 152, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J., Tadhunter, C. N., Morganti, R., & Emonts, B. H. C. 2011, MNRAS, 410, 1527 [NASA ADS] [Google Scholar]
- Hunt, L. K., Testi, L., Casasola, V., et al. 2014, A&A, 561, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., García-Burillo, S., Casasola, V., et al. 2015, A&A, 583, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Tortora, C., Ginolfi, M., & Schneider, R. 2020, A&A, 643, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishibashi, W., & Fabian, A. C. 2016, MNRAS, 463, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, B. A., Rizzi, L., Tully, R. B., et al. 2009, AJ, 138, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [Google Scholar]
- Katz, H., Lelli, F., McGaugh, S. S., et al. 2017, MNRAS, 466, 1648 [Google Scholar]
- Kaviraj, S., Martin, G., & Silk, J. 2019, MNRAS, 489, L12 [Google Scholar]
- Keller, B. W., Wadsley, J., Benincasa, S. M., & Couchman, H. M. P. 2014, MNRAS, 442, 3013 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., & Ostriker, E. C. 2018, ApJ, 853, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., Ostriker, E. C., & Raileanu, R. 2017, ApJ, 834, 25 [Google Scholar]
- King, A. R. 2010, MNRAS, 402, 1516 [Google Scholar]
- King, A., & Pounds, K. 2015, ARA&A, 53, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [Google Scholar]
- Kobulnicky, H. A., & Skillman, E. D. 2008, AJ, 135, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Koudmani, S., Henden, N. A., & Sijacki, D. 2021, MNRAS, 503, 3568 [CrossRef] [Google Scholar]
- Kourkchi, E., Courtois, H. M., Graziani, R., et al. 2020, AJ, 159, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kourkchi, E., Tully, R. B., Courtois, H. M., Dupuy, A., & Guinet, D. 2022, MNRAS, 511, 6160 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., Fraternali, F., & Sancisi, R. 2012, A&A, 537, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014a, A&A, 566, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014b, MNRAS, 445, 1694 [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016a, ApJ, 816, L14 [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2016b, ApJ, 827, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Sandstrom, K. M., Lang, D., et al. 2019, ApJS, 244, 24 [Google Scholar]
- Liu, G., Zakamska, N. L., Greene, J. E., Nesvadba, N. P. H., & Liu, X. 2013, MNRAS, 436, 2576 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Sturm, E., Janssen, A., et al. 2020, A&A, 633, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&A Rev., 27, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Oman, K. A., Navarro, J. F., Frenk, C. S., & Oosterloo, T. 2018, MNRAS, 476, 2168 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Fraternali, F., Heald, G., et al. 2019a, A&A, 631, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marasco, A., Fraternali, F., Posti, L., et al. 2019b, A&A, 621, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marasco, A., Cresci, G., Nardini, E., et al. 2020, A&A, 644, A15 [EDP Sciences] [Google Scholar]
- Marasco, A., Cresci, G., Posti, L., et al. 2021, MNRAS, 507, 4274 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Fraternali, F., Lehner, N., & Howk, J. C. 2022, MNRAS, 515, 4176 [NASA ADS] [CrossRef] [Google Scholar]
- Marlowe, A. T., Heckman, T. M., Wyse, R. F. G., & Schommer, R. 1995, ApJ, 438, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L. 1996, ApJ, 465, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L. 1998, ApJ, 506, 222 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2015, ApJ, 802, 18 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Schombert, J. M., & Lelli, F. 2017, ApJ, 851, 22 [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Dolphin, A., et al. 2015, ApJ, 812, 158 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., van Zee, L., & Skillman, E. D. 2019, ApJ, 886, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., van de Ven, G., et al. 2014, ApJ, 788, 144 [Google Scholar]
- Menacho, V., Östlin, G., Bik, A., et al. 2019, MNRAS, 487, 3183 [CrossRef] [Google Scholar]
- Mingozzi, M., Cresci, G., Venturi, G., et al. 2019, A&A, 622, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitchell, P. D., Schaye, J., Bower, R. G., & Crain, R. A. 2020, MNRAS, 494, 3971 [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [Google Scholar]
- Muratov, A. L., Kereš, D., Faucher-Giguère, C.-A., et al. 2015, MNRAS, 454, 2691 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Nelson, D., Pillepich, A., Springel, V., et al. 2019, MNRAS, 490, 3234 [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Noguchi, M. 1988, A&A, 203, 259 [NASA ADS] [Google Scholar]
- Norris, M. A., Van de Ven, G., Schinnerer, E., et al. 2016, ApJ, 832, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito: University Science Books) [Google Scholar]
- Östlin, G., Marquart, T., Cumming, R. J., et al. 2015, A&A, 583, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, J., Walter, F., & Brinks, E. 2005, MNRAS, 358, 1453 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, M., Lanzuisi, G., Brusa, M., Cresci, G., & Mignoli, M. 2017, A&A, 606, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Popesso, P., Concas, A., Morselli, L., et al. 2019, MNRAS, 483, 3213 [Google Scholar]
- Posti, L., Fraternali, F., & Marasco, A. 2019, A&A, 626, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richings, A. J., & Faucher-Giguère, C.-A. 2018, MNRAS, 474, 3673 [Google Scholar]
- Röck, B., Vazdekis, A., Ricciardelli, E., et al. 2016, A&A, 589, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogstad, D. H., Lockhart, I. A., & Wright, M. C. H. 1974, ApJ, 193, 309 [Google Scholar]
- Rose, M., Tadhunter, C., Ramos Almeida, C., et al. 2018, MNRAS, 474, 128 [Google Scholar]
- Saito, M. 1979, PASJ, 31, 193 [NASA ADS] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [Google Scholar]
- Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016, ApJ, 816, 23 [Google Scholar]
- Sawala, T., Frenk, C. S., Fattahi, A., et al. 2016, MNRAS, 457, 1931 [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Schombert, J., McGaugh, S., & Lelli, F. 2019, MNRAS, 483, 1496 [NASA ADS] [Google Scholar]
- Schwartz, C. M., & Martin, C. L. 2004, ApJ, 610, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2017, ApJ, 839, L13 [Google Scholar]
- Smith, B. J., & Hancock, M. 2009, AJ, 138, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., & Davé, R. 2015, ARA&A, 53, 51 [Google Scholar]
- Somerville, R. S., Hopkins, P. F., Cox, T. J., Robertson, B. E., & Hernquist, L. 2008, MNRAS, 391, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, L. K., Stevens, I. R., Strickland, D. K., & Heckman, T. M. 2003, MNRAS, 342, 690 [CrossRef] [Google Scholar]
- Thuan, T. X., & Izotov, Y. I. 1997, ApJ, 489, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., Hunt, L. K., & Ginolfi, M. 2022, A&A, 657, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tozzi, G., Cresci, G., Marasco, A., et al. 2021, A&A, 648, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Tully, R. B., Rizzi, L., Shaya, E. J., et al. 2009, AJ, 138, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Courtois, H. M., & Sorce, J. G. 2016, AJ, 152, 50 [Google Scholar]
- van der Kruit, P. C., & Freeman, K. C. 2011, ARA&A, 49, 301 [Google Scholar]
- van Eymeren, J., Marcelin, M., Koribalski, B., et al. 2009a, A&A, 493, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Eymeren, J., Marcelin, M., Koribalski, B. S., et al. 2009b, A&A, 505, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Eymeren, J., Koribalski, B. S., López-Sánchez, Á. R., Dettmar, R.-J., & Bomans, D. J. 2010, MNRAS, 407, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Combes, F., Rubio, M., & Kunth, D. 2009, A&A, 496, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Villar Martín, M., Emonts, B., Humphrey, A., Cabrera Lavers, A., & Binette, L. 2014, MNRAS, 440, 3202 [CrossRef] [Google Scholar]
- Walter, F., Weiss, A., & Scoville, N. 2002, ApJ, 580, L21 [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Xu, X., Heckman, T., Henry, A., et al. 2022a, ApJ, 933, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Ouchi, M., Rauch, M., et al. 2022b, ApJ, 929, 134 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr, et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zhang, D. 2018, Galaxies, 6, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H.-X., Puzia, T. H., & Weisz, D. R. 2017, ApJS, 233, 13 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Photometric analysis
The method employed for our photometric analysis is an upgraded version of that used by Marasco et al. (2019b) and is based on the extraction of the cumulative light profile from sky-subtracted images after the removal of contamination from point-like sources such as foreground stars and background galaxies. This approach is more refined than measurements based on traditional aperture photometry, which (as we show below) may lead to significantly different results,
We describe our procedure below, and show an illustrative application to the IRAC 3.6 μm data of NGC 2915 in Fig. A.1. We anticipate that several of the parameters that regulate our method are set by eye, image-by-image, on the basis of the credibility of the resulting mask and of the final light profile. However, as we discuss below, variations in our choices are accounted for in the estimates of the uncertainties on our M⋆ and SFR measurements.
 |
Fig. A.1. Example of our photometric analysis on the IRAC 3.6 μm data of NGC 2915. First panel: IRAC image, with the ellipse marking the division between galaxy and sky regions. Second panel: Pixel intensity distribution within the sky region (black histogram). The red curve shows the best-fit model made by the sum of a Gaussian and a Schechter component (individually shown by light-blue dashed curves). The vertical dotted line shows the mean of the Gaussian component, corresponding to the sky background value. Third panel: IRAC image filtered with our point-source masking technique (see text). The division in concentric annuli is also shown. Fourth panel: Final radial intensity profile in image units (black circles with error-bars) and normalised growth curve (red solid curve). |
We first defined a region of the image where the contribution of the galaxy is sufficiently small that it can be assumed to be largely dominated by the sky. This region is defined via an ellipse, centred at the coordinates given in Table 1, and with an axial ratio and orientation that are defined by eye from either the IRAC 3.6 μm image or (when these data are not available) the W1 images (first panel in Fig. A.1). Ideally, the ellipse should define the overall galaxy radial extent, inclination, and position angle. Once set, the ellipse parameters are maintained also for the images of the same system in the other bands, while the radial extent of the ellipse is manually adjusted depending on the spatial extent and quality of the data.
Pixels external to the ellipse are used to characterise the ‘sky’ region of the image. This is composed by a combination of a smooth background, point-like sources (i.e. unresolved background stars and galaxies) and, in some rare cases, resolved nearby systems. Point-like sources are very rare in UV images but strongly contaminate W1 and IRAC 3.6 μm images. As we are mainly interested in determining the sky background b and rms-noise σ, we employ an automatic approach that allows us to filter out the contamination from the other components. We model the pixel intensity (I) distribution in the sky region, nsky(I), with a two component model made by the sum of a Gaussian and a Schechter function:
where x ≡ (I − b), and nG, nS, IS and α are free parameters of the fit along with b and σ. This approach allows us to account for the positive tail in the intensity distribution introduced by point-like sources: a Schechter function is the optimal choice for pure stellar contamination and, in general, is flexible enough to describe complex tails. The second panel of Fig. A.1 shows that the observed distribution (black histogram) is well fitted by our two-component model (red curve). The determined background intensity b is subtracted from the image before the next analysis step.
We stress that the fit of our model to the sky intensity distribution does not always converge. In these occurrences we determine b and σ as the mean and standard deviation of the nsky(I) after filtering the original distribution with a sigma-rejection method. Finally, in some cases, we are forced to adjust the background value manually until the cumulative intensity profile converges (see below). This mainly occurs in the W4 band, where sky fluctuations across the image can be severe and difficult to deal with our automatic approach.
We now move to the analysis of the region within the initial ellipse (‘galaxy’ region). Here, the galactic emission (ideally smooth and axi-symmetric) is also contaminated by point-like sources that, if not filtered out correctly, can significantly affect the radial profile especially in the outermost regions where the galaxy surface brightness is low. To tackle this, we first divide the galaxy region into a series of concentric ellipses, all with the same centre, orientation and axial ratios of the initial ellipse, and with inter-ellipse separation given by the image resolution. The intensity distribution in each ring is filtered with a sigma-rejection technique (with a clip imposed at 3 or 4 rms, depending on the image), which allows us to mask pixels that are too bright or too dim with respect to the typical intensity value of that annulus. To further clean the image, the mask obtained is then broadened by a few pixels. The resulting ‘cleaned’ image obtained for NGC 2915 is shown in the third panel of Fig. A.1. Using this map, we extract the radial profile by computing the mean intensity of all the non-masked pixels in each ring. The outermost ring considered is defined by the initial ellipse, but we stop tracking the profile when the signal-to-noise ratio8 falls below unity.
Using the derived intensity profile, we built the cumulative radial profile (or ‘growth curve’), for which the masked pixels in a given ring are replaced with the mean intensity computed in that ring. The progressive flattening of the growth curve (shown as a solid red curve in the rightmost panel of Fig. A.1) is a key check for the goodness of our photometry, as it indicates both that the sky background has been correctly determined and that no additional flux from the galaxy can be measured in regions beyond the outermost annulus considered. This is only an a posteriori check that is done by visual inspection, and we stress that we have not tuned our approach to output a flat cumulative profile a priori to avoid introducing bias into our analysis. The outermost value of the growth curve gives the galaxy flux in image units, which is then converted to physical units using conversion factors that depend on the instrument and, finally, to a luminosity using distances reported in Table 1.
The lack of flattening in the growth curve can be caused by different factors, the most crucial of which is the poor masking of point-like sources. To appreciate this effect, in Fig. A.2 we compare the growth curves obtained with and without masking. The two curves are similar only for R < 1 kpc, beyond which the one derived without masking, rather than flattening, grows linearly with R due to the contribution of the many point-like sources that simulate the effect of an additional background. The final flux determined with this approach is ≈50% larger than that computed with the mask, and can reach up to a factor of 2 in some galaxies. This exemplifies the importance of a correct treatment for the contamination of point sources very well.
 |
Fig. A.2. Flux growth curves for NGC 2915 in the IRAC 3.6 μm band. The solid red (dashed black) curve shows the growth determined with (without) masking of the point-like sources. The approach without masking outputs a growth curve that does not flatten and an overestimation of the total flux. |
Further complications are induced by small errors in the sky background estimate, which produce a flattening (if the background is underestimated) or a steepening (if the background is overestimated) of the outer data points in the radial profile. While we cannot exclude a change of slope in the outer region of the galaxy surface brightness profile, a perfectly flat or an abruptly truncated profile indicate a mistake in the background calculation. In these rare occurrences, we manually adjust the background value (typically by a few percent only), so that the profile slope does not show strong discontinuities at large radii.
A risk associated with the masking of point-like sources within the galaxy region is the removal of bright star clusters that belongs to the galaxy itself. To minimise this risk, we have selected the parameter of our masking method so that the fractions of masked pixels in the sky region and in galaxy region are similar to each other. This ensures that in a statistical sense, we are not filtering out genuine galaxy features. Clearly, less features are masked close to the galaxy centre, where the galaxy surface brightness is larger than that of possible contaminants.
A.1. Estimate of the uncertainties
We compute the uncertainty associated with our flux measurements (ϵflux) as the quadratic sum of two errors, the first being due to the image noise (ϵσ) and the second being due to the method (ϵmet).
To determine (ϵσ), we produced a series of N stochastic realisation of the cleaned, background-subtracted image by replacing each pixel intensity I in the galaxy region with a value randomly extracted from a normal distribution with a mean equal to I and variance given by σ2(I + b)/b, where b and σ are the sky background and rms-noise determined as discussed above. The formulation adopted for the variance ensures that the image noise scales as the square root of the signal, being equal to σ at the background level, as expected. For each of these N images we determine a value for the galaxy flux as described above, and set ϵσ equal to the standard deviation of the resulting flux distribution.
To determine ϵmet, we repeated M times the whole photometric analysis procedure using each time different values for the main parameters that regulate our method. The parameters are randomly extracted from either normal or uniform distributions, centred around the values adopted in the initial photometric calculation. Table A.1 lists the parameters subject of this procedure and their variation range. Also in this case we get M flux measurements and set ϵmet equal to the standard deviation of these estimates.
Parameters that are varied in the computation of ϵmet, type of distribution adopted, and range considered.
We use N = 250 and M = 100, which we found to be a good compromise between sampling accuracy and computation speed. As expected, ϵmet is the dominant source of uncertainty in most images, while ϵσ is relevant only in images with very low signal-to-noise ratio, typical of FUV and W4 images of the faintest galaxies.
Appendix B: Phase-space distribution and wind maps
In Fig. B.1, we present the phase-space analysis used to extract the wind component from the Hα velocity cubes in the 19 galaxies of the DWALIN-19 sample. For each system, we show the same panels (a), (d1), (d2), (e1), and (e2) shown in Fig. 6 for He 2-10. We refer to the caption of Fig. 6 for detailed information on each panel.
 |
Fig. B.1. Extraction of the wind component from the Hα line in four galaxies of the DWALIN-19 sample. The individual panels are analogous to those shown in Fig. 6, with the galaxy name indicated on top of panel (a). To improve their visualisation, the intensity maps have been smoothed to a resolution (FWHM) of ∼1.5″. Iso-intensity contours in panels (e1) and (e2) are spaced by a factor of three, with the outermost being at an intensity level indicated in the bottom-left corner of panel (e1) (in units of erg s−1 cm−2, corresponding to 4σnoise), both for the whole emission (grey contours) and for the wind component alone (black contours). No contours are shown when fluxes are below such value. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
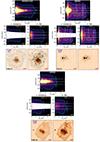 |
Fig. B.1. continued. |
All Tables
Methods used to determine M⋆ and SFR in this work, in descending order of preference.
Parameters that are varied in the computation of ϵmet, type of distribution adopted, and range considered.
All Figures
 |
Fig. 1. Optical DSS or SDSS images (2′ on a side) of the DWALIN sample of starburst galaxies, with the MUSE field of view overlaid (squared overlays). Green overlays show the MUSE data that have been re-reduced and analysed and are discussed in the current study. Red overlays are used for the MUSE data that will be analysed in a future study. Galaxies are ordered by their M⋆, with lowest-mass galaxies at the top left. |
| In the text | |
 |
Fig. 2. SFR vs. M⋆ plot for the DWALIN galaxy sample. Green squares, brown triangles, and blue circles indicate galaxies whose SFR measurements come from the combination of UV and MIR data, MIR data alone, or UV data alone, respectively (see text for details). ID numbers are shown for the DWALIN-19 sample studied with MUSE in this work. Gray dots show the sample of ≈15 750 nearby galaxies studied by Leroy et al. (2019). We also show the SFR–M⋆ trends at z ≃ 0 from the SDSS (Chang et al. 2015, dashed line), from the LMLVL sample (Berg et al. 2012, dotted line), and the relation derived by McGaugh et al. (2017) for a sample of low-surface brightness galaxies (dot-dashed line). |
| In the text | |
 |
Fig. 3. Multi-Gaussian modelling of the Hα line in He 2-10. Top panel shows the total Hα intensity map and the six representative slices (blue-dashed segments) used to extract the position-velocity plots. These are shown in the panels below (left column: data, middle column: model, right column: residual), using a width of three spaxels. Iso-intensity contours are at 2, 5, 10, 20, 102, 103, 104 times the rms noise σ. An additional contour at −2σ is shown in grey. Arrows mark the regions where emission from the [N II] doublet leaks into the Hα cube. |
| In the text | |
 |
Fig. 4. Hα velocity fields of the DWALIN-19 galaxies, as derived from our multi-Gaussian modelling of the MUSE data. |
| In the text | |
 |
Fig. 5. Hα velocity dispersion fields of the DWALIN-19 galaxies, as derived from our multi-Gaussian modelling of the MUSE data. Only the intrinsic line broadening is shown (see Sect. 3.2). |
| In the text | |
 |
Fig. 6. Scheme illustrating the extraction of the wind component from the Hα velocity cube of He 2-10. (a): phase-space distribution for the whole Hα emission. Instrumental broadening is removed via the multi-Gaussian decomposition. Cyan contours encompass 50%, 70%, and 90% of the total Hα flux. White-dashed lines show the escape speed radial profile (see Sect. 4.1). (b): the two feedback scenarios of Sect. 4.2. In (b1) feedback injects turbulence in the ISM, but produces no bulk flow. In (b2) feedback produces the spherical expansion of a turbulent shell of gas (TES). (c): illustration of the effects of feedback on a single velocity profile. For both scenarios we assume vesc of 100 km s−1, a systemic velocity of 0 km s−1, and velocity dispersion of 30 km s−1 for the unperturbed gas (blue-dashed curve). The component perturbed by feedback (red-dashed curve) is derived by assuming a shell expansion speed, v, and a velocity dispersion, σ, indicated in the top-right corner. Both scenarios feature very similar broad components. In the turbulent case (c1), only the flux at |v|> vesc (highlighted in yellow) is eligible as ‘wind’. In the TES case, given that v > vesc, the whole component will be associated with a wind. (d): phase-space plots for the wind component alone, extracted by processing each Hα velocity profile as discussed in Sect. 4.2. Contours are defined as in panel a. (e): integrated Hα intensity maps of the wind component. Iso-intensity contours for the total Hα emission are shown in grey, as a reference. |
| In the text | |
 |
Fig. 7. Extinction A(Hα) (top panel) and electron density ne (bottom panel) distribution in our sample. The grey-shaded histograms show mean values representative for the whole galaxy. The solid green and red lines refer to the wind component computed in the turbulence and TES scenarios, respectively. Winds are characterised by higher A(Hα) and ne than in the rest of the galaxy. |
| In the text | |
 |
Fig. 8. Summary of the wind properties in the DWALIN-19 sample. Ionised gas outflow rate, Ṁwind, (left-hand panels) and mass-loading factors β (right-hand panels) as a function of galaxy M⋆ (first row), SFR (second row), mean SFR surface density (third row), and sSFR (fourth row). Each galaxy is labelled with an ID number (see legend on top). Data points are based on the average of values from the turbulence and TES scenarios; error-bars account both for the difference between the two scenarios and for the uncertainties associated with each of them (see text). Spearman (S) and Pearson (P) correlation coefficients are reported on top of each panel. Blue-dashed lines show the best-fit linear relations determined with the LTSFIT Python package (Cappellari et al. 2013), with the blue-shaded region showing the resulting intrinsic scatter σint. Values for the line slope, m, intercept, c, and σint are reported in each panel. |
| In the text | |
 |
Fig. 9. Wind mass-loading factor β as a function of galaxy M⋆ from different studies. Markers show observational results from Chisholm et al. (2017, brown circles), McQuinn et al. (2019, grey diamonds), Concas et al. (2022, purple stars), and the present study (yellow squares). Lines show theoretical predictions from the EAGLE (Mitchell et al. 2020, blue-dashed) and the Illustris TNG 50 (Nelson et al. 2019, orange-solid) cosmological simulations, and from the evolutionary model of Marasco et al. (2021, black-dotted). |
| In the text | |
 |
Fig. A.1. Example of our photometric analysis on the IRAC 3.6 μm data of NGC 2915. First panel: IRAC image, with the ellipse marking the division between galaxy and sky regions. Second panel: Pixel intensity distribution within the sky region (black histogram). The red curve shows the best-fit model made by the sum of a Gaussian and a Schechter component (individually shown by light-blue dashed curves). The vertical dotted line shows the mean of the Gaussian component, corresponding to the sky background value. Third panel: IRAC image filtered with our point-source masking technique (see text). The division in concentric annuli is also shown. Fourth panel: Final radial intensity profile in image units (black circles with error-bars) and normalised growth curve (red solid curve). |
| In the text | |
 |
Fig. A.2. Flux growth curves for NGC 2915 in the IRAC 3.6 μm band. The solid red (dashed black) curve shows the growth determined with (without) masking of the point-like sources. The approach without masking outputs a growth curve that does not flatten and an overestimation of the total flux. |
| In the text | |
 |
Fig. B.1. Extraction of the wind component from the Hα line in four galaxies of the DWALIN-19 sample. The individual panels are analogous to those shown in Fig. 6, with the galaxy name indicated on top of panel (a). To improve their visualisation, the intensity maps have been smoothed to a resolution (FWHM) of ∼1.5″. Iso-intensity contours in panels (e1) and (e2) are spaced by a factor of three, with the outermost being at an intensity level indicated in the bottom-left corner of panel (e1) (in units of erg s−1 cm−2, corresponding to 4σnoise), both for the whole emission (grey contours) and for the wind component alone (black contours). No contours are shown when fluxes are below such value. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.