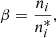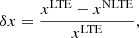| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245130 | |
| Published online | 24 January 2023 | |
Non-LTE formation of the Fe I 6173 Å line in the solar atmosphere
1
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: smitha@mps.mpg.de, narayanamurthy@mps.mpg.de
2
School of Space Research, Kyung Hee University, Yongin, Gyeonggi 446-701, Republic of Korea
Received:
4
October
2022
Accepted:
18
November
2022
The current analysis is dedicated to a detailed investigation of the non-local thermodynamic equilibrium (NLTE) effects influencing the formation of the Fe I 6173 Å line, which is widely used by many instruments, including the Helioseismic and Magnetic Imager (HMI) on board the Solar Dynamics Observatory (SDO) and the Polarimetric and Helioseismic Imager on board the Solar Orbiter. We synthesize the Stokes profiles in a snapshot of a three-dimensional magnetohydrodynamic simulation of the solar photosphere under both LTE and NLTE conditions. The simulation cube contains a sunspot and a plage region around it. The LTE and NLTE Stokes profiles formed in different features are compared and analysed. NLTE effects are evident in both intensity and polarization profiles. For the 6173 Å line, UV overionization is the dominant NLTE mechanism, and scattering effects are much less important. In addition to Fe, an NLTE treatment of Si, Mg, and Al is necessary to set the right photon density in the UV. This is found to further enhance the LTE departures compared to the case where Fe alone is treated in NLTE. These effects in the Stokes profiles survive even when the profiles are averaged spatially or sampled on a coarse wavelength grid such as that used by the SDO/HMI and other magnetographs. The deviations from the LTE profiles are stronger in the Fe I 6173 Å compared to the 6301 Å–6302 Å lines because in the latter case, line scattering compensates the effect of UV overionization. Based on the nature of departures from LTE, treating the 6173 Å line in LTE will likely result in an overestimation of temperature and an underestimation of the magnetic field strength.
Key words: radiative transfer / line: formation / line: profiles / Sun: magnetic fields / Sun: photosphere / polarization
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model.
Open access funding provided by Max Planck Society.
1. Introduction
Iron lines crowd the solar spectrum from ultraviolet (UV) to infrared (IR) wavelengths. Lines of neutral iron are among the most widely used diagnostic lines for the solar photosphere and in particular for photospheric magnetism (Rutten & Kostik 1982; Solanki & Steenbock 1988; Rutten et al. 1988). The photospheric iron lines are routinely modelled assuming local thermodynamic equilibrium (LTE) conditions.
Lites (1972) and Athay & Lites (1972) were among the first to discover the departure from LTE in Fe I lines due to imbalances in radiative bound-free transitions. UV photons with energies that match the bound-free jumps of the well-populated atomic levels overionize these levels. Although the overionization mainly occurs from higher levels with energies around 4 eV, its effects get shared over all atomic levels, due to strong collisional and radiative coupling (Rutten et al. 1988). As a result, the atomic level populations are no longer given by Saha-Boltzmann statistics. The signatures of this non-LTE (NLTE) effect are imprinted in all iron lines observed in the UV, visible, and infrared wavelength regions. UV overionization is not just limited to iron atoms, but affects all minority species, including alkalis (Rutten & Kostik 1982; Bruls et al. 1992; Rutten 2021). In addition to UV overionization, the spectral lines can also be affected by other NLTE mechanisms such as the resonance scattering that is specific to particular spectral lines (Bruls et al. 1992). The observed spectral profiles are shaped by a combination of different NLTE mechanisms. Depending on the atmospheric conditions and the properties of the individual line, the resulting profile can have a shape close to its LTE equivalent, or it can be significantly different.
A number of studies have investigated the role of NLTE effects in the formation of the famous Fe I 6301 Å – 6302 Å line pair (also refereed to as the 6300 Å pair) and their influence on the inferred atmospheric models (see Rutten & Kostik 1982; Shchukina & Trujillo Bueno 2001; Holzreuter & Solanki 2012, 2013, 2015; Smitha et al. 2020, 2021). In the present study we investigate the formation of Fe I 6173 Å, another widely utilized line. This line has been extensively used to infer solar properties because it is a clean line without any blends, which makes it advantageous for velocity measurements (e.g. for helioseismic applications) and because it is a normal Zeeman triplet (Jl = 1, Ju = 0) with a large Landé factor (geff = 2.5), which makes it favourable for measuring magnetic fields. It is used by the Helioseismic and Magnetic Imager (HMI; Scherrer et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) to capture full-disk images of the Sun nearly continuously. It is also used by the Polarimetric and Helioseismic Imager (PHI; Solanki et al. 2020) on the recently launched Solar Orbiter (Müller 2020). The Photospheric Magnetic Field Imager (PMI) on ESA’s Vigil mission to the Lagrange point L5 is also designed to observe the Sun in this line (Staub et al. 2020).
Ground-based observatories, such as the Swedish Solar Telescope (SST; Scharmer et al. 2003) and the Daniel K. Inouye Solar Telescope (DKIST; Elmore et al. 2014), also observe this line. However, the modelling of the 6173 Å line is often done under the assumption of LTE (e.g., Bello González et al. 2009; Felipe et al. 2017; Pastor Yabar et al. 2020; Yadav et al. 2021) or by using the even simpler Milne-Eddington approximation (e.g., Borrero et al. 2011; Centeno et al. 2014; Joshi et al. 2020; Vissers et al. 2022; Joshi & Rouppe van der Voort 2022). The 6173 Å line has been treated in NLTE in only a few papers, including Sadykov et al. (2020), Monson et al. (2021), and da Silva Santos et al. (2022), and also by Harker & Pevtsov (2013) and Hong et al. (2018) for flare diagnostics.
The present study is dedicated to understanding the different sources of NLTE effects influencing the formation of the Fe I 6173 Å line. We find that these effects are prominently seen in the Stokes profiles of this line. Interestingly, they even survive when the profiles are spatially averaged or spectrally sampled over a coarse grid. The deviations from LTE in this line can be stronger than for the Fe I 6301 Å–6302 Å line pair. The details are presented in the sections below.
2. MHD cube and profile synthesis
To investigate the NLTE effects in the Fe I 6173 Å line, we computed its Stokes profiles from a three-dimensional radiation magnetohydrodynamic (MHD) cube. We chose a high-resolution non-grey sunspot cube by Rempel (2012) 1 generated using the MURaM code (Vögler et al. 2005). The cube has a grid spacing of 12 km in the horizontal direction, and 8 km in the vertical direction.
To save computing time, we synthesized the profiles over a small patch of the cube, covering the sunspot and the plage region around it. The temperature, vertical velocity, and magnetic field strength maps at z = 0 km are plotted in the first three panels of Fig. 1. Here z = 0 km corresponds to the layer where log(τ5000) in the part of the simulation box outside the sunspot is zero, on average. The Stokes profiles were computed at the heliocentric angle μ = 1 in LTE and NLTE along every column using the RH 1.5D code (Uitenbroek 2001; Pereira & Uitenbroek 2015). No additional microturbulent velocity was used to broaden the line profiles. The continuum intensity image of this patch at 6170 Å is shown in the bottom panel of Fig. 1. The four pixels labelled in this figure, P1 to P4, are sample pixels at which we later discuss the Stokes profiles in detail.
 |
Fig. 1. Maps of temperature (first panel), line-of-sight velocity (second panel), and magnetic field strength (third panel) over the chosen region in the MHD cube at a geometric height z = 0 km. Positive velocities denote downflows. The continuum intensity image at 6170 Å is shown in the bottom panel. Here the points P1, P2, P3, and P4 are the four pixels used for a detailed comparison between the Stokes profiles computed in LTE and NLTE. |
According to Rutten (2021), a proper NLTE treatment of the iron lines demands a large Fe atom model; treatment of Si, Al, and Mg in NLTE to set the radiation field in the UV; and the UV line haze. For iron we here use a 33-level atom model, which is a part of the RH 1D code2 (Uitenbroek 2001). In this model 31 levels belong to Fe I. The other two levels are the ground states of Fe II and Fe III. The atomic levels are coupled by 63 bound-bound and 31 bound-free transitions. The atom includes photo-ionization cross-sections of the bound-free transitions computed using the hydrogenic approximation.
Metals such as Si, Mg, Fe, and Al have ionization edges in the UV. They play an important role in setting the level of angle averaged mean intensity Jν in the UV. Additionally, they are also the most abundant electron-donor atoms in the solar temperature minimum (Vernazza et al. 1981; Rutten 2003, 2021). The electrons contributed by them affect the formation of H−. For a complete NLTE treatment, it is important to treat all these metals in NLTE, and also self-consistently compute the electron densities in NLTE. However, in the present study we restricted ourselves to only treating the former effect. That is, the electron densities are computed by assuming LTE ionization. Additionally, for the greater part of the cube we treat only Fe in NLTE to save computing time. Over a small stripe of the cube we compute the Stokes profiles by also treating the other metals (Si, Mg, and Al) explicitly in NLTE. A detailed discussion on this is presented in Sect. 5.4.
The effects of the UV line haze are incorporated using the opacity fudging described in Bruls et al. (1992). The fudge factors include frequency-dependent multiplication factors to the total H− opacity for λ > 210 nm, and at shorter wavelengths the metal opacity is enhanced. These factors were derived by Bruls et al. (1992) by fitting the continuum computed from the VAL3C model atmosphere (Vernazza et al. 1981) with the observed continuum.
3. NLTE mechanisms
According to Bruls et al. (1992), five important NLTE mechanisms affect minority species. They are resonance line scattering and photon loss, photon suction, UV overionization, infrared over recombination, and UV line pumping. For iron, UV overionization and resonance scattering are the two dominant mechanisms (Shchukina & Trujillo Bueno 2001). We briefly describe them below. More details can be found in Rutten & Kostik (1982), Rutten et al. (1988), Bruls et al. (1992), Bruls & Rutten (1992), Rutten (2021).
UV overionization: The radiation temperature at wavelengths between 200 nm and 500 nm exceed the electron temperature, Te (Avrett et al. 1985; Rutten et al. 1988; Bruls et al. 1992). Hence the UV photons are superthermal with angle-averaged mean intensity Jν exceeding the Planck function Bν(Te). This excess UV radiation incident onto the photosphere from the cool temperature minimum region is absorbed by the minority species, including iron, which have well-populated atomic levels with energies between 2 eV and 4 eV from the continuum, resulting in UV overionization. Excess ionization leads to line opacity deficits in Fe I, and an opacity excess in Fe II.
Resonance scattering in lines: The second dominant NLTE mechanism affecting iron lines is resonance scattering in atomic bound-bound transitions. This is a property of the individual lines. According to Shchukina & Trujillo Bueno (2001), for iron lines with intermediate to high excitation potential (> 2 eV) the source function deviates from the Planck function; when the excitation potential is < 2 eV, the source function follows the Planck function (see also Rutten et al. 1988; Solanki & Steenbock 1988). A source function deficit results from the upper level departure coefficient being less than that of the lower-level. This is due to outward photon-losses. Scattering propagates this to layers below the surface where the optical depth at the line centre is greater than unity (Bruls et al. 1992; Carlsson et al. 1994). Source function deficit makes the NLTE line stronger than the LTE line.
The line opacity deficit due to UV overionization and the source function deficit due to scattering affect the spectral profiles in opposite ways. The former makes the spectral line shallower, while the latter makes the line stronger and deeper than the LTE line. For the iron line pair at 6301 Å–6302 Å, with an excitation potential of 3.6 eV, these two effects both play a role (Smitha et al. 2020). Depending on the atmospheric conditions and the dominant NLTE mechanism, the profile computed in NLTE can either be stronger or weaker than the LTE line. In some cases when the two effects are equally strong, the NLTE line can be identical to the LTE line.
The Fe I 6173 Å line has an excitation potential of 2.2 eV. Its radiative width (Einstein A coefficient) is an order of magnitude smaller than that of the 6301 Å line. The collisional coupling is stronger and the photon destruction probability is much higher. Furthermore, the line interlocking effects forces the source function to follow the Planck function by setting the upper-level departure coefficient equal to that of the lower-level. Therefore, the 6173 Å line is not affected as much by scattering as the 6300 Å line pair, and UV overionization is the only dominant NLTE mechanism affecting it.
4. Departure coefficients
The departure coefficient, β, is defined as the deviation of an atomic level population from its LTE value (Wijbenga & Zwaan 1972)
where ni and 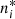 are the NLTE and LTE populations of level i, respectively.
are the NLTE and LTE populations of level i, respectively.
The line opacity deficit from the excess UV ionization scales with the lower level departure coefficient, βlow. It changes height where the line optical depth reaches unity: the τ(λ0)=1 surface with λ0 being the rest wavelength of the line. We denote this height as hLTE and hNLTE for LTE and NLTE computations, respectively. In the rest of this paper, hLTE and hNLTE are used as reference heights to compare different physical quantities, and are sometimes referred to as the height of formation of the line. However, we are aware of the limitations and uncertainties introduced by such a definition (Sanchez Almeida et al. 1996). It is used here only for simplicity. More discussion on this can be found in Sect. 5.3.
A map of the lower-level departure coefficient βlow at hNLTE over the region of interest for the 6173 Å line is shown in the top panel of Fig. 2. The βlow at hNLTE is less than one in granules, intergranular lanes, penumbral filaments, and umbral dots. This is due to UV overionization. Over hotter granules, βlow is lower than over cool intergranular lanes because the UV radiation is more superthermal (Jν > Bν) over granules than over intergranular lanes (Bruls & Rutten 1992). The βlow at hNLTE is close to unity in the umbra and in regions of strong magnetic field outside the sunspot, seen by comparing Fig. 2 to the third panel of Fig. 1. Even though βlow is close to one in bright magnetic structures, later in Sects. 5.1 and 5.3, we discuss how the LTE departures in the Stokes profiles can still be quite strong.
 |
Fig. 2. Maps of departure coefficients at heights where τλ0 = 1, with λ0 being the rest wavelength of the Fe I 6173 Å line. Top panel: departure coefficients of the lower level (βlow). Middle panel: departure coefficient of the upper level (βup). Bottom panel: ratio of βup to βlow. Heights corresponding to τλ0 = 1 surface computed from LTE (white line) and NLTE (blue line) are plotted in panel d. In the background is the temperature map of the slice marked by the horizontal yellow line in Fig. 1. The positions of the four sample pixels chosen for detailed analysis are marked by vertical lines in panel d. |
The line opacity deficit translates into hNLTE < hLTE (Shchukina & Trujillo Bueno 2001). Panel d of Fig. 2 shows hNLTE and hLTE, overplotted on a vertical slice through the atmosphere, indicated by the yellow line in the continuum image in Fig. 1. Outside the sunspot, hNLTE is lower than hLTE, while within the sunspot hNLTE is close to hLTE.
The deviations in the line source function 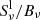 due to bound-bound scattering is proportional to βup/βlow (Bruls et al. 1992). Panels b and c in Fig. 2 show maps of βup and βup/βlow, respectively. Almost everywhere within the chosen region of the cube, βup follows βlow and the ratio βup/βlow is close to one. The line source function follows the Planck function, indicating the weaker role of resonance scattering for the 6173 Å line. In panel c we see a few patches where βup/βlow is slightly greater than one. In these pixels, the MHD cube has strong gradients in temperature, and the steep increase in T around hNLTE gives rise to βup/βlow > 1. This increase is localized and occurs only over a narrow range of heights in the cube. It does not have an impact on the overall line formation.
due to bound-bound scattering is proportional to βup/βlow (Bruls et al. 1992). Panels b and c in Fig. 2 show maps of βup and βup/βlow, respectively. Almost everywhere within the chosen region of the cube, βup follows βlow and the ratio βup/βlow is close to one. The line source function follows the Planck function, indicating the weaker role of resonance scattering for the 6173 Å line. In panel c we see a few patches where βup/βlow is slightly greater than one. In these pixels, the MHD cube has strong gradients in temperature, and the steep increase in T around hNLTE gives rise to βup/βlow > 1. This increase is localized and occurs only over a narrow range of heights in the cube. It does not have an impact on the overall line formation.
5. Effects on Stokes profiles
The NLTE effects alter the equivalent widths (EW) and depths of the intensity profiles (Rutten & Kostik 1982; Solanki & Steenbock 1988; Shchukina & Trujillo Bueno 2001; Holzreuter & Solanki 2015), and also the strength of the polarization profiles (Smitha et al. 2020). In Fig. 3 we compare the LTE and NLTE profiles using their EW, and Q/Ic, U/Ic, or V/Ic peak amplitudes, denoted as Qmax, Umax, or Vmax, respectively. Relative changes in these quantities due to the NLTE effects are given by
where x can be EW, Qmax, Umax, or Vmax. A positive value of δx indicates line weakening due to overionization, while a negative value indicates line strengthening mainly due to resonance scattering.
 |
Fig. 3. Comparison between the intensity, linear polarization, and circular polarization profiles computed in LTE and NLTE. Panels a–c show maps of relative differences δEW, δQmax, and δVmax, respectively, for the Fe I 6173 Å line (these quantities are defined in Eq. (2)). Panels g-l show the same for the 6301 Å – 6302 Å line pair, but over a smaller region outside the sunspot indicated by the orange boxes in panels a–c. Panels d–f display scatter plots between various quantities for pixels from within the orange box. They demonstrate the variation in δEW as a function of temperature (T at z = 0 km), and the variation in δQmax and δVmax as a function of the magnetic field strength B at z = 0 km. Panels m–o show similar scatter plots for the 6301 Å line. The stokes profiles of the 6173 Å line spatially averaged over the orange box are plotted in panels 1–3; those of the similarly averaged 6301 Å line are plotted in panels 4–6. |
In the same figure we also show maps of the corresponding quantities for the 6301 Å–6302 Å line pair. For this comparison, we selected a small region, indicated by the orange rectangle over which the Stokes profiles of this line pair were computed. This region was chosen outside the sunspot because the 6173 Å line is not affected by NLTE effects in the umbra (see Fig. 2). The details are discussed in the sections below.
5.1. Intensity
In panel a of Fig. 3, the δEW is predominantly greater than zero. For the pixels within the orange box, we show a scatter plot of δEW as a function of temperature at z = 0 km in panel d. Clearly, the relative change in δEW becomes larger as the temperature increases. This is due to the increase in (Jν − Bν) excess as the region becomes hotter, a correlation noted by Bruls & Rutten (1992), Carlsson et al. (1994). Due to the higher contrast between hotter and cooler regions in layers close to the surface, this correlation is best seen when we consider the temperature at z = 0 km (the surface at which the optical depth at 5000 Å is unity) in panel d of Fig. 3, especially over the orange box outside the sunspot.
In brighter features such as granules, penumbral filaments, and umbral dots, the δEW is found to be as high as 30% (Fig. 3, panel a). In the magnetic structures embedded in the intergranular lanes, the relative change can also be higher than 30%, indicating the strong influence of NLTE effects in such regions. This is also consistent with the findings of Solanki & Steenbock (1988), who investigated the NLTE effects in both quiet Sun and flux tube models for over 200 iron lines, including the one at 6173 Å. From their analysis, the authors conclude that the departures from LTE in the flux tube models are larger than in the quiet Sun models. In contrast to this, the values of departure coefficients βlow and βup in the magnetic structures seen from Fig. 2 are close to one at hNLTE. We try to resolve this interesting discrepancy in Sect. 5.3.
In darker features such as the umbra, intergranular lanes, and penumbral spines, the δEW is close to zero. This is consistent with the departure coefficients also being close to one in these features (Fig. 2), indicating that the ratios of neutral to ionized iron in such regions are close to their LTE predictions near the heights of formation of the line. The pixels P3 and P4 are two examples, which will be discussed in detail in Sect. 5.4 (see also Fig. 6). If one observes closely, faint red patches can be seen in the umbra where δEW is marginally less than zero. This is due to line strengthening by resonance scattering. Although they are weak, its effects become apparent in the absence of UV overionization.
In comparison, the line pair at 6300 Å shows a slightly different behaviour. Its δEW maps are presented in Fig. 3, panels g and h. The maps contain a mix of grey and red patches; the grey patches are much lighter compared to those in panel a for the 6173 Å line. The LTE departures for the 6300 Å line pair are less than the departures measured for the 6173 Å line. The δEW is greater than zero in the granules due to the dominance of UV overionization effects. In the intergranular lanes and magnetic structures the δEW can be greater or less than zero depending on the extent to which resonance scattering compensates for the UV overionization effects. Similar conclusions can also be drawn from the scatter plot in panel m.
For the 6173 Å line, the departures from LTE in the intensity can be clearly seen even when the profiles are spatially averaged (Fig. 3, panel 1). Here we average over the orange box since outside it the NLTE effects are either absent or quite weak. Interestingly, similar spatial averaging of the intensity profiles for the 6301 Å line, over the same patch, cancels out the NLTE effects from UV overionization and resonance scattering. This is clear from Fig. 3, panel 4, where the LTE and NLTE profiles are nearly identical. We note that these profiles do not yet include the effects of Si, Al, and Mg atoms, which set the right photon density in the UV and further enhance the overionization effects (see Sect. 5.4).
5.2. Polarization
For the 6173 Å line the maps of δQmax and δVmax (Fig. 3, panels b and c) are similar to the δEW maps; in other words, the departures from LTE are the largest in the granules. In the intergranular lanes and magnetic structures we mostly see grey and white patches, and only a few pixels are coloured red. Consequently, in most of the pixels, the NLTE polarization profiles are weaker than the LTE profiles. This is confirmed by the scatter plots in Fig. 3 (panels e and f) of δQmax and δVmax, over the area marked by the orange box, plotted as a function of B at z = 0 km. Here again, we see a clear trend. For a majority of the pixels, the relative change in the polarization is positive, indicating the dominance of UV overionization effects. Inverting these profiles in LTE results in an underestimation of the magnetic field strength. Recently, da Silva Santos et al. (2022) used a 16-level Fe atom model, and found that NLTE effects in the 6173 Å line can introduce differences of up to 60% in the inverted magnetic field strength.
In the umbra we again see faint red patches where the amplitudes of the LTE Q and V profiles are larger than in the NLTE case. In the absence of UV overionizaton, weak signatures of resonance scattering start to show up.
The δQmax and δVmax maps for the 6300 Å line pair show more red patches in the intergranular lanes in between the grey patches in the granules (Fig. 3, panels i–l). These red patches are also stronger and larger. For this line pair, NLTE effects can make the profiles stronger or weaker depending on the atmospheric conditions. Accordingly, the scatter plots in panels n and o of Fig. 3 show a much larger spread in both δQmax and δVmax on either side of zero.
Similar to the intensity profiles, the spatially averaged polarization profiles of the 6173 Å line retain the effects of UV overionization, see Fig. 3, panels 2 and 3. This is particularly striking for Stokes Q. For the 6301 Å line, the spatial averaging dampens the NLTE effects. Over the region chosen in Fig. 3, the NLTE effects are no longer apparent in spatially averaged V/Ic, but do survive in Q/Ic.
5.3. Detailed comparison of the Stokes profiles
We chose four sample pixels (P1–P4, labelled on the continuum intensity map in Fig. 1) to analyse the NLTE effects in detail. Their Stokes profiles computed in NLTE and in LTE are plotted in Fig. 4. Pixel P1 is in a granule, P2 is in a small-scale magnetic concentration (or magnetic element), P3 lies in the dark umbra, and P4 is at an umbral dot. In this section we compare the LTE profiles (in black) with the NLTE profiles plotted in blue. These correspond to the case when only iron is treated in NLTE. In the same panels, the red curves were computed by also treating Si, Al, and Mg in NLTE, and are discussed in Sect. 5.4.
 |
Fig. 4. Comparison between the Stokes profiles computed in LTE and NLTE at the four sample pixels P1, P2, P3, and P4 indicated in Fig. 1. The black curves are computed in LTE. The blue curves are computed by treating only iron in NLTE. The red curves are computed by treating Fe as well as Si, Al, and Mg in NLTE. The four columns show Stokes I/Ic, Q/Ic, U/Ic, and V/Ic, expressed as percentages, where Ic is the spatially averaged continuum intensity over the non-spot region of the cube. The six vertical lines give the positions of the grid points sampled by HMI onto which the Stokes profiles are interpolated in Fig. 7. The numbers in the bottom right corner of each panel are the δEW, δQmax, δUmax, and δVmax, respectively, for the profiles in red and blue. |
In Fig. 5, panels a and b show temperature and line-of-sight magnetic field variation across the slice from where the four pixels were chosen. The four pixels are marked by vertical lines. The δEW for the case with only iron in NLTE is indicated by the blue curve. The δEW is close to zero in the umbral region with variations seen at the locations of the umbral dots. Outside the spot, the relative change is greater than zero, in agreement with Fig. 3.
 |
Fig. 5. Temperature and line-of-sight magnetic field variation over a slice of the atmosphere from where the four sample pixels were chosen. The pixel positions are given by vertical lines. The variation in δEW (panel a) and δVmax (panel b) across this slice are shown as blue and red curves. The former represents the case where only Fe is in NLTE, while in the latter Si, Al, and Mg are also treated in NLTE (see Sects. 5.3 and 5.4 for more details). |
The differences in the Stokes profiles are clear at P1 and P2. In P1 the NLTE effects decrease the EW by 17%; in P2 they decrease by 50%. The change in amplitude is close to 70% in P1 for all three polarized Stokes profiles, all of which admittedly have rather small amplitudes. More interestingly, the amplitudes of the two orders of magnitude stronger Q/Ic and U/Ic profiles in P2 are also reduced by ≈70%. Here the NLTE Stokes V/Ic profile is weakened by 40%, and there is also a qualitative change in its shape (from a multi-lobed complex profile to a simple V profile). This is due the strong velocity gradients in that pixel (see panel 2b, Fig. 6). In P3, the LTE and NLTE profiles nearly match. Finally, in the umbral dot pixel P4 we again see differences, the most pronounced of which are in the U/Ic.
In Fig. 6 we plot various quantities, such as the temperature, vertical velocity, departure coefficients, ratio of neutral to ionized iron atoms, total opacity, and normalized contribution function, at these four pixels. The heights hNLTE and hLTE are indicated by vertical solid and dashed lines, respectively. According to this figure, the departure coefficients βlow and βup follow the temperature stratification, as noted earlier by Bruls et al. (1992). On average, the upper level departure coefficient βup follows βlow up to roughly 400 km above the formation height of the local continuum in that pixel. Strong gradients and fluctuations in the temperature stratification, typical of high-resolution MHD cubes, makes it challenging to discern a general correlation between the behaviour of the departure coefficients and atmospheric variations. This is not the case in the one-dimensional atmospheres, such as the VALC model, used in previous studies (Bruls et al. 1992; Bruls & Rutten 1992; Carlsson et al. 1994)
 |
Fig. 6. Variation in different physical quantities as a function of height at the four sample pixels. The first two rows show temperature and vertical velocity. The third and fourth rows show the departure coefficients and the ratio of neutral iron atoms to ionized iron atoms (Fe I/[Fe II + Fe III]), respectively, for LTE and NLTE computations for the case where only iron is in NLTE (blue) and where the Si, Al, and Mg are also treated in NLTE (red). The total opacity at the rest wavelength of the line (λ0) is plotted in the fifth row. Finally, the LTE and NLTE normalized contribution functions are shown in the bottom row. The vertical lines indicate the height where τλ0 = 1 when the line is formed in LTE (hLTE, dashed line) and in NLTE (hNLTE, solid line) conditions. |
In pixel P1, both βlow and βup are much less than one near the formation heights of the 6173 Å line. However, their ratio stays close to one at these heights (panel 1c). Here hLTE − hNLTE ≈ 100 km. A drop in the ratio of neutral to ionized iron due to UV overionization, compared to their LTE values, can be seen in panel 1d. When the UV line haze is not taken into account, the ratio drops further, enhancing the NLTE effects to unrealistically large values (not shown in the figure). The red curve in panel 1d represents the neutral to ionized iron ratio when Si, Al, and Mg are explicitly treated in NLTE. A detailed discussion of this is presented in Sect. 5.4. The NLTE total opacity at λ0 (plotted in panel 1e) shows a drop compared to its LTE value around hNLTE. Since there is no change in the continuum opacity around 6173 Å, this drop is due to the change in line opacity. The normalized contribution function is plotted in panel 1f. Although it peaks close to hNLTE, the contribution function itself is quite broad, implying that the line samples a range of heights around hNLTE.
Pixel P2 presents quite an interesting case. This pixel is at the edge of a magnetic structure where the temperature and velocity profiles show strong gradients (panels 2a and 2b). The different parameters plotted in panels 2c–2e, are close to their LTE values at hNLTE, and yet we see departures from LTE in the Stokes profiles (Fig. 4). The hLTE − hNLTE is around 50 km. This can be explained by the multiple peaks in its contribution function (panel 2f). The fragmented nature of this function could arise due to the velocity, which has similar multiple peaks at those heights (panel 1b). Such steep gradients give rise to a highly asymmetric and distorted intensity profile such as the one plotted in Fig. 4 at P2. At the locations of the secondary peaks in the contribution function βlow < 1, and we see departures from LTE in other parameters as well, all of which affect the formation of the line. We find similar multiple peaked contribution functions in and around other magnetic structures. This explains why the δEW in Fig. 3 is greater than zero in magnetic regions (Fig. 4, panels a and b), even though the departure coefficients βlow and βup are close to unity at the locations in Fig. 2.
Because spectral lines are formed over a range of heights, the physical conditions alone at the reference height, hNLTE, provide an incomplete picture on what influences the formation of a spectral line. Defining a height of formation or looking at the atmospheric conditions at a single height could be misleading (Sanchez Almeida et al. 1996), but making use of reference heights, such as hNLTE and hLTE, helps us compare different quantities to explain the complex NLTE mechanisms. It gives us a rough idea of the different atmospheric layers sampled by the spectral line. In addition, the wavelength chosen to define τλ = 1 introduces further uncertainty. Here we chose λ = λ0, the rest wavelength of the line, but the actual line core wavelength need not coincide with the rest wavelength of the line.
In the umbra we find that the effect of UV overionization is negligible. The UV photons are much less superthermal over the cooler regions (Bruls & Rutten 1992). At pixel P3 chosen from the umbra, the departure coefficients are close to unity and the ratio of neutral to ionized iron is close to its LTE value around the height of formation of the line (see panels 3c and 3d in Fig. 6). The striking thing about the umbra is that it is the only place within the range of line formation where Fe I is the dominant ionization stage of iron (see panel 3d of Fig. 6). This also partly explains why there is no overionization there. Since there is so much Fe I, changing the ionization rate by a factor of two still leaves it as the dominant species and largely unchanged, while the number of atoms of the minority species, Fe II in this case, changes by nearly a factor of 2.
Another interesting feature in the umbra is seen in panel 3e of Fig. 6, where the NLTE total opacity is slightly higher than the LTE opacity up to 180 km. As discussed in Sect. 5.1, this is due to resonance scattering. Its effects become apparent in the absence of UV overionization. For the 6173 Å line, this is quite weak. From Fig. 4, the LTE and NLTE profiles nearly match.
The umbral dots are brighter than their surrounding dark umbra and we see signatures of UV overionization in them although not as strongly as in the granules. At hNLTE, the parameters in panels 4c–4e do not show much deviation from their LTE values. The broad contribution function implies that the line is also sampling layers higher than hNLTE, and that at these heights the NLTE parameters deviate from their LTE values. This explains the differences in Stokes profiles observed in Fig. 4.
5.4. Importance of treating Si, Al, and Mg in NLTE
The amount of excess photoionization of the iron atoms is set by the radiation field in the UV. For a proper NLTE treatment of the iron line, it is therefore crucial to compute the correct photon density in the UV. The metals Si, Al, and Mg all have ionization edges in the UV and they have a strong influence on Jν, which in turn affects the ionization equilibrium of iron. In addition, these metals are the most important electron donors in the temperature minimum region, where hydrogen is not fully ionized (Vernazza et al. 1981). A full NLTE computation of the iron lines would involve a NLTE treatment of the metals Fe, Si, Mg, and Al, along with electron densities being computed in NLTE. The latter is beyond the scope of this present study. To ensure that we use the correct levels of Jν in the UV, we add the contributions from Si, Al, and Mg by treating them in NLTE while setting the electron densities to their LTE values.
Over the stripe indicated by the yellow line in the continuum image shown in Fig. 1, we computed the Stokes profiles by treating Si I, Mg I, and Al I in NLTE in addition to Fe I. For Si we used a 16-level model atom (15 Si I levels + 1 ground state of Si II) coupled by 28 line transitions and 15 continuum transitions. We included Mg using a model atom with 11 Mg I levels plus the ground state of Mg II. The model atom includes 15 bound-bound and 11 bound-free transitions. For Al we used an 18-level model atom of which 9 levels belong to Al I, 8 levels to Al II, and the last level is the ground state of Al III. These levels are coupled by 19 bound-bound and 17 bound-free transitions.
The Stokes profiles computed by treating Si, Al, and Mg atoms in NLTE at the four sample pixels are shown by the red curves in Fig. 4. The δEW over the whole stripe are plotted in the bottom two panels of Fig. 5. The NLTE effects are clearly much stronger now compared to the case when only Fe was in NLTE. The intensity profiles are shallower and the δEW values are larger, as shown in panel a of Fig. 5. Similarly, the polarization profiles are also affected. Inclusion of Si, Al, and Mg in NLTE further weakens the Stokes V amplitude. The trend over the whole stripe can be seen in panel b of Fig. 5. The iron overionization and the line opacity deficit has increased. This is also evident from the reduced ratio of neutral to ionized iron at the four sample pixels plotted in Fig. 6 (red curves, panels 1d, 2d, 3d, and 4d).
In pixel P1 the relative change in polarization amplitudes with respect to the LTE values are now as high as 90%. In the four Stokes profiles, the inclusion of Si, Al, and Mg in NLTE has increased the LTE departures by nearly 20% compared to the case when only iron was treated in NLTE. In P2, the δEW is now 61% which is a 10% increase. In the polarization profiles, δQmax, δUmax, and δVmax increase between 5% and 10%. In P3 and P4, the enhancement in relative change is quite small except in the U/Ic profile at P4, where we see a nearly 25% increase.
Thus, for a better treatment of NLTE, it is important to also treat Si, Al, and Mg in NLTE, in addition to Fe. Their impact on the Stokes profiles is once again dependent on the atmosphere.
5.5. Effects of spectral degradation
The observations in the Fe I 6173 Å line from both ground-based and space-based telescopes are at a much lower spectral resolution than we used in this study. To investigate the effects of spectral degradation, we chose the coarse wavelength grid used by the SDO/HMI instrument. The effects of different filter curves were approximated by convolving with a single Gaussian of FWHM 75 mÅ, and interpolating the profiles onto the six wavelength points sampled by HMI (neglecting shifts introduced by the relative spacecraft–Sun velocity). This was done for both LTE and NLTE profiles (Fe only). The comparison is presented in Fig. 7. The degradation in the profile shape due to coarse wavelength sampling and the large effects of departure from LTE are both clearly seen in the figure. Comparing the profiles in Figs. 4 and 7 highlights that when the spectrum is sampled with such a coarse grid, the poor spectral sampling of the line has a bigger effect on the Stokes profiles than the NLTE effects. Nevertheless, the fact that NLTE effects survive spectral degradation indicates that they will likely survive in observations from other telescopes such as Solar Orbiter/PHI or Vigil/PMI, and also in SST and DKIST, which can observe this line at higher spectral resolutions. Analysis or inversions of such observations assuming LTE will introduce errors in the inverted atmosphere.
 |
Fig. 7. Stokes profiles at the four sample pixels P1, P2, P3, and P4 after degradation onto a coarse wavelength grid with only six spectral points used by the SDO/HMI instrument. These six points are indicated by the vertical lines in Fig. 4. The NLTE profiles used for degradation were computed by treating only Fe in NLTE. |
6. Conclusions
In this paper we have for the first time presented a detailed analysis of the NLTE formation of the widely used photospheric iron line at 6173 Å by synthesizing its Stokes profiles in both LTE and NLTE using a 3D MHD cube. Understanding its formation in an MHD cube is quite complex. In particular, the strong gradients in the cube make it challenging to correlate the LTE departures seen in the spectra to the nature of NLTE effects playing a role.
The line 6173 Å is an LTE line considering its source function. That is, resonance scattering in the line is quite weak due to its low excitation potential and line interlocking effects. However, the NLTE effects acting on the iron species as a whole, namely the UV overionization, plays an important role in shaping its Stokes profiles.
In comparison, the iron line pair at 6301 Å–6302 Å are not only affected by UV overionization, but also by scattering (Shchukina & Trujillo Bueno 2001; Rutten 2021). The UV overionization introduces a line opacity deficit while scattering results in a line source function deficit. They affect the line profiles in opposite ways, reducing the net deviation from LTE profiles.
The departures from LTE for the 6173 Å line are stronger compared to the 6301 Å–6302 Å line pair. For the 6173 Å line, the NLTE intensity and polarization profiles tend to be weaker than the LTE profiles. This is particularly clear in the bright features, such as granules and bright magnetic structures, but to some extent also in penumbral filaments and umbral dots. In the darker regions, such as intergranular lanes, dark umbra, and penumbral spines, the NLTE profiles match the LTE profiles closely.
In order to reproduce the right amount of UV overionization in the Fe lines, it is necessary to treat other prominent metals such as Si, Mg, and Al in NLTE as well. This is important in order to set the right ionization equilibrium for iron through Jν. We find that this increases the departure from LTE compared to the case where only Fe is treated in NLTE. Table 9 and Fig. 36 of Vernazza et al. (1981) suggest that Si I and Mg I are the most important in setting the right Jν in the UV (see also Rutten 2021). Hence, it is important to treat at least these two species in NLTE along with Fe to properly account for the UV overionization effects in the atmosphere. These metals are also dominant electron donors in the temperature minimum. In the present paper, however, we do not take this into account; instead, we compute the electron densities in LTE. Consequently, our NLTE treatment is still incomplete. For chromospheric lines such as Mg II k, Bjørgen et al. (2019) showed that the differences in electron densities between LTE and NLTE computations have an impact on the intensity profiles. For the photospheric iron lines such as the Fe I 6173 Å, this remains to be investigated.
The NLTE effects in the 6173 Å line continue to survive even when the Stokes profiles are spatially averaged or spectrally degraded. In the present paper this was tested only on profiles computed by treating the iron atom alone in NLTE. Since the treatment of Si, Al, and Mg in NLTE enhances the LTE departure in spatially resolved profiles, it will likely have a similar effect on the spatially averaged profiles as well. This means that when a complete treatment of NLTE is carried out over the whole cube, then the spatially averaged NLTE profile will likely show a larger deviation from LTE compared to the case presented in Fig. 3 (panels 1–3).
Modelling the observed iron profiles using LTE inversion codes will compensate for the above NLTE effects by tweaking the temperature and other atmospheric parameters, an effect known as NLTE-masking (Rutten & Kostik 1982; Rutten et al. 1988). In the case of the 6173 Å line, since the NLTE effects act in a unidirectional manner, its LTE inversions are expected to result in an overestimation of the temperature and an underestimation of the magnetic field strength.
Acknowledgments
This work has greatly benefited from the discussions with R. J. Rutten. H.N.S. would also like to thank L. P. Chitta and D. Przybylski for their valuable inputs.
References
- Athay, R. G., & Lites, B. W. 1972, ApJ, 176, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H. 1985, in Chromospheric Diagnostics and Modelling. ed. B. W. Lites, 67 [Google Scholar]
- Bello González, N., Yelles Chaouche, L., Okunev, O., & Kneer, F. 2009, A&A, 494, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjørgen, J. P., Leenaarts, J., Rempel, M., et al. 2019, A&A, 631, A33 [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Bruls, J. H. M. J., & Rutten, R. J. 1992, A&A, 265, 257 [NASA ADS] [Google Scholar]
- Bruls, J. H. M. J., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 265, 237 [NASA ADS] [Google Scholar]
- Carlsson, M., Rutten, R. J., Bruls, J. H. M. J., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
- Centeno, R., Schou, J., Hayashi, K., et al. 2014, Sol. Phys., 289, 3531 [Google Scholar]
- da Silva Santos, J. M., Danilovic, S., Leenaarts, J., et al. 2022, A&A, 661, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmore, D. F., Rimmele, T. R., Casini, R., et al. 2014, Proc SPIE, 9147, 914707 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Collados, M., Khomenko, E., et al. 2017, A&A, 608, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harker, B. J., & Pevtsov, A. A. 2013, ApJ, 778, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Holzreuter, R., & Solanki, S. K. 2012, A&A, 547, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzreuter, R., & Solanki, S. K. 2013, A&A, 558, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzreuter, R., & Solanki, S. K. 2015, A&A, 582, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hong, J., Ding, M. D., Li, Y., & Carlsson, M. 2018, ApJ, 857, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, J., & Rouppe van der Voort, L. H. M. 2022, A&A, 664, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J., Rouppe van der Voort, L. H. M., & de la Cruz Rodríguez, J. 2020, A&A, 641, L5 [Google Scholar]
- Lites, B. W. 1972, Ph.D. Thesis, University of Colorado, Boulder, USA [Google Scholar]
- Monson, A. J., Mathioudakis, M., Reid, A., Milligan, R., & Kuridze, D. 2021, ApJ, 915, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Pastor Yabar, A., Martínez González, M. J., & Collados, M. 2020, A&A, 635, A210 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., & Uitenbroek, H. 2015, A&A, 574, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Rempel, M. 2012, ApJ, 750, 62 [Google Scholar]
- Rutten, R. J. 1988, in IAU Colloq. 94, eds. R. Viotti, A. Vittone, & M. Friedjung, Astrophys. Space Sci. Lib., 138, 185 [NASA ADS] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres, Lecture Notes, Utrecht University, The Netherlands [Google Scholar]
- Rutten, R. J. 2021, ArXiv e-prints [arXiv:2103.02369] [Google Scholar]
- Rutten, R. J., & Kostik, R. I. 1982, A&A, 115, 104 [NASA ADS] [Google Scholar]
- Sadykov, V. M., Kosovichev, A. G., Kitiashvili, I. N., & Kerr, G. S. 2020, ApJ, 893, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez Almeida, J., Ruiz Cobo, B., & del Toro Iniesta, J. C. 1996, A&A, 314, 295 [NASA ADS] [Google Scholar]
- Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, SPIE Conf. Ser., 4853, 341 [NASA ADS] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Smitha, H. N., Holzreuter, R., van Noort, M., & Solanki, S. K. 2020, A&A, 633, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smitha, H. N., Holzreuter, R., van Noort, M., & Solanki, S. K. 2021, A&A, 647, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., & Steenbock, W. 1988, A&A, 189, 243 [NASA ADS] [Google Scholar]
- Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staub, J., Fernandez-Rico, G., Gandorfer, A., et al. 2020, J. Space Weather Space Clim., 10, 54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uitenbroek, H. 2001, ApJ, 557, 389 [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
- Vissers, G. J. M., Danilovic, S., Zhu, X., et al. 2022, A&A, 662, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
- Wijbenga, J. W., & Zwaan, C. 1972, Sol. Phys., 23, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R., Díaz Baso, C. J., de la Cruz Rodríguez, J., Calvo, F., & Morosin, R. 2021, A&A, 649, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Maps of temperature (first panel), line-of-sight velocity (second panel), and magnetic field strength (third panel) over the chosen region in the MHD cube at a geometric height z = 0 km. Positive velocities denote downflows. The continuum intensity image at 6170 Å is shown in the bottom panel. Here the points P1, P2, P3, and P4 are the four pixels used for a detailed comparison between the Stokes profiles computed in LTE and NLTE. |
| In the text | |
 |
Fig. 2. Maps of departure coefficients at heights where τλ0 = 1, with λ0 being the rest wavelength of the Fe I 6173 Å line. Top panel: departure coefficients of the lower level (βlow). Middle panel: departure coefficient of the upper level (βup). Bottom panel: ratio of βup to βlow. Heights corresponding to τλ0 = 1 surface computed from LTE (white line) and NLTE (blue line) are plotted in panel d. In the background is the temperature map of the slice marked by the horizontal yellow line in Fig. 1. The positions of the four sample pixels chosen for detailed analysis are marked by vertical lines in panel d. |
| In the text | |
 |
Fig. 3. Comparison between the intensity, linear polarization, and circular polarization profiles computed in LTE and NLTE. Panels a–c show maps of relative differences δEW, δQmax, and δVmax, respectively, for the Fe I 6173 Å line (these quantities are defined in Eq. (2)). Panels g-l show the same for the 6301 Å – 6302 Å line pair, but over a smaller region outside the sunspot indicated by the orange boxes in panels a–c. Panels d–f display scatter plots between various quantities for pixels from within the orange box. They demonstrate the variation in δEW as a function of temperature (T at z = 0 km), and the variation in δQmax and δVmax as a function of the magnetic field strength B at z = 0 km. Panels m–o show similar scatter plots for the 6301 Å line. The stokes profiles of the 6173 Å line spatially averaged over the orange box are plotted in panels 1–3; those of the similarly averaged 6301 Å line are plotted in panels 4–6. |
| In the text | |
 |
Fig. 4. Comparison between the Stokes profiles computed in LTE and NLTE at the four sample pixels P1, P2, P3, and P4 indicated in Fig. 1. The black curves are computed in LTE. The blue curves are computed by treating only iron in NLTE. The red curves are computed by treating Fe as well as Si, Al, and Mg in NLTE. The four columns show Stokes I/Ic, Q/Ic, U/Ic, and V/Ic, expressed as percentages, where Ic is the spatially averaged continuum intensity over the non-spot region of the cube. The six vertical lines give the positions of the grid points sampled by HMI onto which the Stokes profiles are interpolated in Fig. 7. The numbers in the bottom right corner of each panel are the δEW, δQmax, δUmax, and δVmax, respectively, for the profiles in red and blue. |
| In the text | |
 |
Fig. 5. Temperature and line-of-sight magnetic field variation over a slice of the atmosphere from where the four sample pixels were chosen. The pixel positions are given by vertical lines. The variation in δEW (panel a) and δVmax (panel b) across this slice are shown as blue and red curves. The former represents the case where only Fe is in NLTE, while in the latter Si, Al, and Mg are also treated in NLTE (see Sects. 5.3 and 5.4 for more details). |
| In the text | |
 |
Fig. 6. Variation in different physical quantities as a function of height at the four sample pixels. The first two rows show temperature and vertical velocity. The third and fourth rows show the departure coefficients and the ratio of neutral iron atoms to ionized iron atoms (Fe I/[Fe II + Fe III]), respectively, for LTE and NLTE computations for the case where only iron is in NLTE (blue) and where the Si, Al, and Mg are also treated in NLTE (red). The total opacity at the rest wavelength of the line (λ0) is plotted in the fifth row. Finally, the LTE and NLTE normalized contribution functions are shown in the bottom row. The vertical lines indicate the height where τλ0 = 1 when the line is formed in LTE (hLTE, dashed line) and in NLTE (hNLTE, solid line) conditions. |
| In the text | |
 |
Fig. 7. Stokes profiles at the four sample pixels P1, P2, P3, and P4 after degradation onto a coarse wavelength grid with only six spectral points used by the SDO/HMI instrument. These six points are indicated by the vertical lines in Fig. 4. The NLTE profiles used for degradation were computed by treating only Fe in NLTE. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.