| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 27 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202244316 | |
| Published online | 23 December 2022 | |
Assessing the impact of two independent direction-dependent calibration algorithms on the LOFAR 21 cm signal power spectrum
And applications to an observation of a field flanking the north celestial pole
1
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700AV
Groningen, The Netherlands
e-mail: hgan@astro.rug.nl
2
LERMA (Laboratoire d’Études du Rayonnement et de la Matière en Astrophysique et Atmosphères), Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université,
75014
Paris, France
3
The Netherlands Institute for Radio Astronomy (ASTRON),
PO Box 2,
7990AA
Dwingeloo, The Netherlands
4
Max-Planck Institute for Astrophysics,
Karl-Schwarzschild-Straße 1,
85748
Garching, Germany
5
School of Earth and Space Exploration, Arizona State University,
Tempe,
AZ 85281, USA
6
Astrophysics Research Center (ARCO), Department of Natural Sciences, The Open University of Israel,
1 University Road,
PO Box 808,
Ra’anana
4353701, Israel
7
Department of Physics,
Technion, Haifa
32000, Israel
8
Institute for Computational Science, University of Zurich,
Winterthurerstraße 190,
8057
Zurich, Switzerland
9
Astronomy Centre, Department of Physics and Astronomy, University of Sussex,
Pevensey II Building,
Brighton BN1 9QH,
UK
Received:
21
June
2022
Accepted:
12
September
2022
Context. Detecting the 21 cm signal from the epoch of reionisation (EoR) has been highly challenging due to the strong astrophysical foregrounds, ionospheric effects, radio frequency interference (RFI), and instrumental effects. Better characterisation of their effects and precise calibration are, therefore, crucial for the 21 cm EoR signal detection.
Aims. In this work we introduce a newly developed direction-dependent calibration algorithm called DDECAL, and compare its performance with an existing direction-dependent calibration algorithm called SAGECAL, in the context of the LOFAR-EoR 21 cm power spectrum experiment.
Methods. We process one night of data from LOFAR observed by the HBA system. The observing frequency ranges between 114 and 127 MHz, corresponding to the redshift from 11.5 and 10.2. The north celestial pole (NCP) and its flanking fields were observed simultaneously in this data set. We analyse the NCP and one of the flanking fields. While the NCP field is calibrated by the standard LOFAR-EoR processing pipeline, using SAGECAL for the direction-dependent calibration with an extensive sky model and 122 directions, for the RA 18h flanking field, DDECAL and SAGECAL are used with a relatively simple sky model and 22 directions. Additionally, two different strategies are used for the subtraction of the very bright and far sources Cassiopeia A and Cygnus A.
Results. The resulting estimated 21 cm power spectra show that DDECAL performs better at subtracting sources in the primary beam region, due to the application of a beam model, while SAGECAL performs better at subtracting Cassiopeia A and Cygnus A. The analysis shows that including a beam model during the direction-dependent calibration process significantly improves its overall performance. The benefit is obvious in the primary beam region. We also compare the 21 cm power spectra results on two different fields. The results show that the RA 18h flanking field produces better upper limits compared to the NCP for this particular observation.
Conclusions. Despite the minor differences between DDECAL and SAGECAL, due to the beam application, we find that the two algorithms yield comparable 21 cm power spectra on the LOFAR-EoR data after foreground removal. Hence, the current LOFAR-EoR 21 cm power spectrum limits are not likely to depend on the direction-dependent calibration method. For this particular observation, the RA 18h flanking field seems to produce improved upper limits (~30%) compared to the NCP.
Key words: cosmology: observations / methods: data analysis / dark ages, reionization, first stars / techniques: interferometric
© The Authors 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Observation of the 21 cm signal of neutral hydrogen from the epoch of reionisation (EoR) is one of the most promising methods of revealing the formation and evolution history of the Universe (Furlanetto et al. 2006; Morales & Wyithe 2010; Pritchard & Loeb 2012; Liu & Shaw 2020). Many experiments have been designed to detect the 21 cm signal from the EoR, including global experiments whose aim is measuring the sky-averaged spectrum of the 21 cm signal with a single receiver, such as EDGES1 (Bowman et al. 2018), LEDA2 (Greenhill & Bernardi 2012), PRIZM3 (Philip et al. 2019), and SARAS4 (Singh et al. 2017; Thekkeppattu et al. 2021), and interferometric experiments whose aim is measuring the spatial brightness-temperature fluctuations of the 21 cm signal with a radio interferometer, such as GMRT5 (Paciga et al. 2011, 2013), LOFAR6 (van Haarlem et al. 2013; Patil et al. 2017; Mertens et al. 2020), MWA7 (Bowman et al. 2013; Barry et al. 2019; Li et al. 2019), and PAPER8 (Parsons et al. 2012; Cheng et al. 2018; Kolopanis et al. 2019), as well as the second-generation instruments HERA9 (DeBoer et al. 2017; HERA Collaboration 2022) and SKA10 (Mellema et al. 2013; Koopmans et al. 2015).
However, the detection of the 21 cm signal is very challenging because the observed measurements are contaminated by the astrophysical foregrounds that are about four to five orders of magnitude stronger than the expected 21 cm signal (Bowman et al. 2009; Mertens et al. 2018; Gan et al. 2022), by the ionosphere (Mevius et al. 2016; Vedantham & Koopmans 2016; Edler et al. 2021) and radio frequency interference (RFI; Offringa et al. 2012, 2019a), and by instrumental effects (Offringa et al. 2019b). Hence, suppressing these effects during calibration is crucial for detection (Barry et al. 2016).
The calibration of the LOFAR-EoR KSP (Key Science Project) data uses the sky-based calibration approach. The processing pipeline of data has been developed and improved over a decade (Yatawatta et al. 2013; Patil et al. 2016, 2017; Mertens et al. 2020; Mevius et al. 2022). Due to the wide field of view of LOFAR, the data need to be calibrated depending on direction to correct for different errors from the varying beam and ionospheric effects. This direction-dependent (DD) calibration step, in particular, was carried out by SAGECAL (Yatawatta 2011, 2015, 2019). While SAGECAL has shown excellent calibration performance, no other DD calibration code has yet been applied to LOFAR-EoR data.
This study introduces a newly developed DD calibration algorithm called DDECAL (van Diepen et al. 2018), and compares the performance of this new algorithm with an existing DD calibration algorithm called SAGECAL, in the context of LOFAR-EoR 21 cm power spectra. The two algorithms have some differences, especially in the beam application and constraining the gain smoothness in frequency, which could result in different calibration performance. To study the differences between the two algorithms, we processed one night of raw data obtained with the LOFAR High-Band Antenna (HBA) system on an unexplored flanking field of the north celestial pole (NCP) following steps similar to those in the standard LOFAR-EoR pipeline (Patil et al. 2017; Mertens et al. 2020). We used two different DD calibration algorithms, DDECAL and SAGECAL, with a more limited sky model and fewer directions compared to the current analysis of the NCP field. The goal of the paper is not to compare the two DD calibration algorithms using an identical sky model, clustering, and settings, but to test the full end-to-end processing in terms of the resulting power spectra when the current best settings and models for the two algorithms are used, within the limits of their implementation. The observation covers the unexplored frequency range from 114 to 127 MHz, corresponding to the redshift range z = 11.5−10.2, pointing at RA 18h, Dec +86°.
For DD calibration, we used fewer directions (~20) compared to the standard 122 directions used for the NCP analysis (Patil et al. 2017; Mertens et al. 2020). The DD calibration step is performed by two algorithms, DDECAL and SAGECAL. In addition to varying the calibration scheme, we also tested a ‘peeling’ scheme. The peeling scheme, first proposed by Noordam & Oschmann (2004), calibrates and subtracts bright sources sequentially in decreasing order of brightness. In Gan et al. (2022) we found that residuals of two very far and bright sources, Cassiopeia A and Cygnus A (hereafter Cas A and Cyg A) may be among the sources of the excess power in the 21 cm power spectra. In this work we model and subtract these two bright sources separately from the full sky model to improve the calibration performance. Similar approaches have been taken for the bright sources (Patil et al. 2017; Gehlot et al. 2019; Mertens et al. 2020).
The paper is arranged as follows. In Sect. 2, we describe the data and the observational set-up. In Sect. 3, the strategy of the DD calibration with LOFAR is described in detail and we summarise the two DD calibration algorithms, DDECAL and SAGECAL. Section 4 is dedicated to the description of the processing of LOFAR-EoR data. In Sect. 5, we present the DD calibration results with different algorithms and strategies including residual images and power spectra. Different gain smoothness constraints between DDECAL and SAGECAL are discussed in more depth in Sect. 5.2.3. In Sect. 6, we summarise the results and present our conclusions.
Summary of observational details of L612832.
2 Observation
The data analysed in this work have been obtained by the LOFAR High-Band Antenna (HBA) system (van Haarlem et al. 2013). The observational details of the data are summarised in Table 1. The LOFAR-EoR KSP has two target fields: the NCP (Yatawatta et al. 2013) and a field centred on the bright compact radio source 3C196 (Bernardi et al. 2010). From the LOFAR observation Cycles 0 to 10, about 2450 h (more than 100 nights) and ~1100 h of data have been collected on these two fields, respectively. Around 75% of the collected data are assumed to be of good quality. In later observation cycles, the main fields have a configuration with a target field in the centre surrounded by a hexagonal ring of six flanking fields. For the NCP field, flanking fields are at an angular distance of 4°. The observing configuration is shown in Fig. 1 with the core station FWHM (-4.8° at 120 MHz van Haarlem et al. 2013). The pointing directions of the NCP flanking fields are summarised in Table A.1. The flanking field data are collected in addition to the main field data to increase the data volume (-6 times that of the main field per observation) and to build a deep and wide sky model for the NCP. In principle, observing six flanking fields enables the errors to be lowered in the 21 cm power spectrum by a square root of seven for a fixed bandwidth. The frequency range was chosen based on the best results from Patil et al. (2017). One disadvantage is that by observing multiple fields on a fixed bandwidth, the range of bandwidth will be limited. Because the main field and flanking fields share the same or very similar RFI, ionospheric environment, and systematics, the flanking field data can be used to cross-check the NCP results. The flanking field data are also useful for calibration (e.g. for constructing better sky models for the main field), improving ionospheric modelling, and expanding the field of view for polarisation images (Patil et al. 2017).
To date, the two published LOFAR-EoR KSP upper limits on the 21 cm signal power spectra (Patil et al. 2017; Mertens et al. 2020) are based solely on NCP observations. In this work, for the first time, we analyse one night of data on one of the six NCP flanking fields from the LOFAR observation Cycle 5, the RA 18h flanking field (see blue circle in Fig. 1). We created a new sky model on the chosen field, calibrated the data using the new sky model, and estimated a 21 cm power spectrum. The 21 cm power spectrum is compared with the spectrum on the NCP field for a cross-check.
While Patil et al. (2017) and Mertens et al. (2020) focused on the frequency range from 121.8 to 159.3 MHz (corresponding to z = 10.6−7.9), we analyse the frequency range from 113.4 to 127.1 MHz, corresponding to a slightly higher redshift range from 11.5 to 10.2. We chose the RA 18h flanking field for analysis because this field has never been analysed at this frequency range before. The data were obtained during nighttime to minimise ionospheric effects and to avoid the Sun, using all core stations and remote stations, with a spectral resolution of 3.05 kHz and a temporal resolution of 2 s. The observation duration was approximately 11.6 h. The observational details are summarised in Table 1.
 |
Fig. 1 Observing configuration of the NCP field in LOFAR-EoR. The main target field NCP is located in the centre, and six flanking fields are distributed from the centre at an angular distance of 4° (indicated by circles of radius 4°). The bright radio source 3C61.1 is inside the RA 2h flanking field (SAP001). The image is constructed from a single observation night L612832 (~11.6-h duration) using full sub-bands. In this work, one night of data on the RA 18h field (blue circle) is analysed. |
3 Direction-dependent calibration
The propagation of the signal from radio sources to the radio interferometer is often described by the Radio Interferometric Measurement Equation (RIME, Hamaker et al. 1996; Smirnov 2011). Considering an array of N elements, the correlation of signals between the ith and jth elements at frequency v and time t produces the observed visibility matrix Vijvt, which can be described as
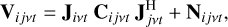 (1)
(1)
where Jivt and 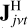 are 2 × 2 Jones matrices at frequency v and time t for element i and j, and Cijvt is a 2 × 2 coherency matrix of the intrinsic signal in a certain direction at the ith and jth elements (i.e. baseline ij). The Jones matrices describe the electromagnetic interaction of the intrinsic signal, such as the instrumental effects, including the beam shape and receiver response, and propagation effects, including ionospheric distortions (Hamaker et al. 1996; Born et al. 1999). The matrix Nijvt is a 2 × 2 noise matrix of baseline ij.
are 2 × 2 Jones matrices at frequency v and time t for element i and j, and Cijvt is a 2 × 2 coherency matrix of the intrinsic signal in a certain direction at the ith and jth elements (i.e. baseline ij). The Jones matrices describe the electromagnetic interaction of the intrinsic signal, such as the instrumental effects, including the beam shape and receiver response, and propagation effects, including ionospheric distortions (Hamaker et al. 1996; Born et al. 1999). The matrix Nijvt is a 2 × 2 noise matrix of baseline ij.
Due to the wide field of view of LOFAR11, the LOFAR data need to be calibrated direction-dependently to compensate for different errors from varying beam and ionospheric effects. The sky model consists of many thousands of bright (a few Jy) and faint (a few mJy) discrete sources. These sources therefore need to be clustered to K directions for the DD calibration. Each cluster must have a sufficient integrated flux so that a DD gain solution can be obtained in a given time and frequency range with a high enough signal-to-noise ratio (S/N). The observed visibility matrix for elements i and j in Eq. (1) then replaces the true sky with the sky model, becoming
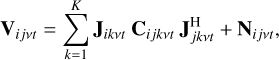 (2)
(2)
where k indicates the specific direction for which gains are solved. The goal of calibration is to estimate a set of parameters θ describing the Jones matrices at a given time t, frequency v, and element (i or j) in Eq. (1). The solutions can be applied to the data to correct for the non-signal effects such as the ionosphere and instrumental errors, or the solutions predicted from a sky model can be subtracted from the data to calculate the residuals. Direction-independent (DI) gains are often applied to the data, whereas direction-dependent (DD) gains are used during the subtraction of the sky model.
The parameter θ can be estimated by minimising the least-square’s cost function
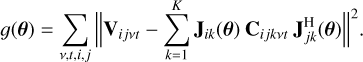 (3)
(3)
In the calibration process, the gain solutions are assumed to be invariant over a small but finite time and frequency interval.
One of the main assumptions used for calibration is that other effects, including instrumental and ionospheric effects, are intrinsically smooth as a function of frequency, while the 21 cm EoR signal is not. Enforcing spectral smoothness can therefore drastically improve the calibration performance by avoiding overfitting and signal suppression (Mouri Sardarabadi & Koopmans 2018; Mevius et al. 2022). Known spectrally unsmooth effects, such as RFI and cable reflections, are handled by RFI excision or are treated as a DI bandpass error that can be solved at the DI calibration step.
There are many calibration algorithms for solving the RIME in Eq. (2) (e.g. Kazemi et al. 2011; Kazemi & Yatawatta 2013; Tasse 2014; Ollier et al. 2018; Arras et al. 2019). In this work, we focus on two algorithms, DDECAL and SAGECAL, and compare their performance in the context of LOFAR-EoR 21 cm power spectra.
3.1 DDECAL
We use DDECAL as one of our DD calibration tools in the analyses of this work. DDECAL is part of the Default Preprocessing Pipeline (DP3) processing software (van Diepen et al. 2018)12. DP3 performs streaming operations on an astronomical data set, such as flagging, averaging, calibration, compression, and statistical and various other corrections. DP3 is configured by providing a parameter set (parset) that defines the operations to be performed, as well as their parameters. DDECAL is implemented into DP3 with the purpose of having a flexible framework to integrate constrained calibration algorithms. At present, it integrates four algorithms: a directional solving algorithm (Smirnov & Tasse 2015); a direction-iterative algorithm (Offringa et al. 2016); the Limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm (Liu & Nocedal 1989; Yatawatta et al. 2019), and a hybrid algorithm that can combine methods. In this work we only use the directional-solving algorithm, which we describe in the next section.
3.1.1 Directional solving in DDECAL
In each iteration, the directional-solving algorithm finds the solution of all directions for a single element from the measurement equation of Eq. (1). It is an extension of the iterative single-directional solve algorithm (Mitchell et al. 2008; Salvini & Wijnholds 2014). If we define 𝒥i to be a matrix consisting of the 2 × 2 matrices for element i and all the solved directions, stacked in the row direction,
 (4)
(4)
the solve algorithm finds the least-squares solution for 𝒥i (i.e. the calibration solutions for a single element but all directions at once):
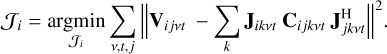 (5)
(5)
During one iteration the solutions for every element are calculated one by one, and are updated by moving the old value towards the new value, and this is iterated until convergence. This is the algorithm described by Smirnov & Tasse (2015).
To solve Eq. (5), we define matrices 𝒱 and ℳ that contain the multi-directional data visibilities and corrected model visibilities for one element. When we introduce an index symbol w that enumerates over all values of v and t inside the solution interval13, these two matrices can be defined by
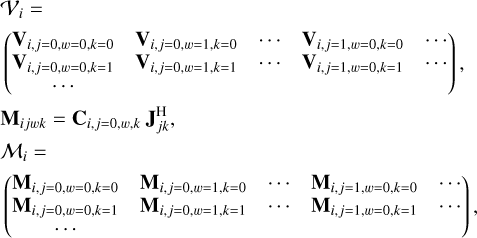 (6)
(6)
where the columns of the 𝒱 and ℳ enumerate all combinations of w and j (excluding i = j), and the directions are stacked in rows. With these definitions, the solution to Eq. (5) is simplified to
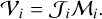 (7)
(7)
This results in a 2Nw × 2 matrix 𝒱, a 2Nk × 2 matrix 𝒥, and a 2Nw × 2Nk matrix ℳ, with Nk the number of directions and Nw the number of timesteps × frequencies inside the solution interval.
Equation (7) is a standard linear equation, and 𝒥i can be solved for by standard linear algebra techniques, such as using the normal equations 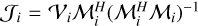 or QR decomposition or singular-value decomposition of ℳi. DDECAL supports these three methods, and we have found that QR decomposition generally results in a good compromise between accuracy and speed.
or QR decomposition or singular-value decomposition of ℳi. DDECAL supports these three methods, and we have found that QR decomposition generally results in a good compromise between accuracy and speed.
In addition to the full Jones problem shown here, DDECAL has specialisations of this algorithm to find diagonal and scalar solutions, and can optionally constrain the algorithm to find phase-only or amplitude-only solutions, or solve for differential Faraday rotation.
3.1.2 Applying constraints to the algorithms
DDECAL allows the application of constraints on its four algorithms, including the directional-solving algorithm which is used in this paper. The implemented algorithms are written such that they iteratively step towards the solution. Updated solutions are used in the next iteration, leading again to more accurate solutions (as long as the algorithm converges), which repeats until the accuracy tolerance has been reached. Such iterative algorithms make it relatively easy to find constrained solutions; after moving the solutions towards the direction given by Eq. (7), a constraint can be applied.
DDECAL allows the application of different types of constraints, including spatial, temporal and spectral constraints. In this work we use a constraint that forces the solutions to be spectrally smooth. DDECAL implements this by Gaussian smoothing the solutions with a requested width. When applying a spectral smoothness constraint, DDECAL calculates the next solution step independently for a number of channels, applies the smoothness constraint to all solutions simultaneously, and then continues with the next iteration for each channel, repeating until the channels simultaneously reach the stopping criterion.
3.2 SAGECAL
The space alternating generalised expectation maximisation (SAGE) algorithm (Fessler & Hero 1994; Kazemi et al. 2011) can be used to estimate the parameters describing Jik for all possible values of i and k in Eq. (2).
3.2.1 SAGE algorithm
The ‘expectation’ step of the SAGE algorithm calculates the effective observed data along the mth direction in a finite time interval, using
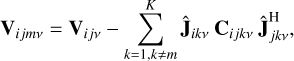 (8)
(8)
where 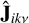 and
and 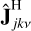 , are the estimated Jones matrices. The ‘maximisation’ step minimises the objective function only for the mth direction defined under a Gaussian noise model as
, are the estimated Jones matrices. The ‘maximisation’ step minimises the objective function only for the mth direction defined under a Gaussian noise model as
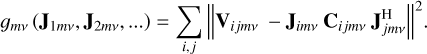 (9)
(9)
Using the SAGE algorithm, Eq. (2) can be simplified from a simultaneous calibration along K directions to K single-direction sub-problems (Kazemi et al. 2011; Yatawatta 2016). For simplicity, we consider the calibration along one direction only, and drop the subscript m, such that Eq. (9) becomes
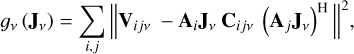 (10)
(10)
where Jv are the Jones matrices for all elements along the mth direction and Ai is the canonical selection matrix to choose ith element among N elements,
![$\matrix{ {{{\bf{J}}_v}} \hfill & \buildrel \Delta \over = \hfill & {{{\left[ {{\bf{J}}_{1mv}^{\rm{T}},{\bf{J}}_{2mv}^{\rm{T}}, \ldots ,{\bf{J}}_{Nmv}^{\rm{T}}} \right]}^{\rm{T}}},} \hfill \cr {{{\bf{A}}_i}} \hfill & \buildrel \Delta \over = \hfill & {\left[ {{\bf{0}},{\bf{0}}, \ldots ,I, \ldots ,{\bf{0}}} \right],} \hfill \cr }$](/articles/aa/full_html/2023/01/aa44316-22/aa44316-22-eq15.png) (11)
(11)
where only the ith matrix of Ai is an identity matrix divided in time or frequency in Eq. (11).
3.2.2 Applying constraints to solutions
An observation with P data sets is distributed over C compute agents (typically, P ≫ C). Each data set has several frequency channels and each channel can be identified by its central frequency. Given that all known effects are spectrally smooth, SAGECAL constrains the continuity of Jv over frequency to improve the calibration performance by applying the consensus alternating direction method of multipliers algorithm (C-ADMM; Boyd et al. 2011; Yatawatta 2015, 2016). The objective function in Eq. (10) is then modified to an augmented Lagrangian with a regularisation parameter to guide solutions to approach the smooth regularisation function of choice BvZ,
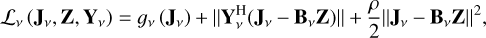 (12)
(12)
where ℒv denotes the Lagrange multiplier and the continuity of frequency is constrained by the frequency model described by a set of basis functions Bv. SAGECAL uses third-order Bernstein polynomials (Farouki & Rajan 1988) as the basis functions (Yatawatta 2019). The parameter Z is a global variable shared by all frequencies in the data. The nth ADMM iteration solves Eq. (12) in the following three steps for all frequencies in parallel:
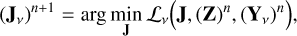 (13)
(13)
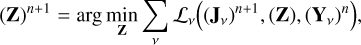 (14)
(14)
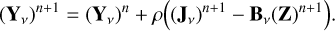 (15)
(15)
Here the superscript (·)n denotes the nth iteration and ρ is a regularisation parameter that determines the level of smoothness in frequency for each iteration. For our observation, ρ ~ 1000 is found to be optimal for 30 ADMM iterations. For more discussions about the selection of p, we refer readers to Yatawatta (2015, 2016); Mertens et al. (2020); and Mevius et al. (2022).
3.3 Differences between DDECAL and SAGECAL
Mathematically, both DDECAL and SAGECAL find gain solutions by minimising the least square’s cost function given by Eq. (3). Their detailed implementations are different, however. In this work, DDECAL applies the direction-solving algorithm to find solutions for all directions at a given element (i.e. an antenna), while SAGECAL applies the SAGE algorithm to find solutions for all elements at a fixed direction.
The frequency smoothness of gains is constrained differently in the two methods. DDECAL smooths gains by convolving them with a Gaussian kernel of a chosen bandwidth during each iteration of the optimisation, while SAGECAL uses an augmented Lagrangian with a regularisation parameter to enforce the gain smoothness.
Another important difference between DDECAL and SAGECAL is the application of beam. DDECAL supports the LOFAR HBA station beam (with usebeammodel in DP3), and for this reason an intrinsic sky model is used for calibration. SAGECAL currently does not support the LOFAR station beam model14. Hence, an apparent sky model (which folds the average beam into the sky model) is used for calibration.
In theory, DD calibration is supposed to solve gains for an optimal number of directions and solution intervals to take care of beam variations and ionospheric phase shifts. However, this process is not perfect and there are errors. In this work DDECAL uses an intrinsic sky model with an HBA beam model, while SAGECAL uses an apparent model without a beam model. We focus on how these differences affect the results of DD calibration and 21 cm signal power spectra.
4 Outline of the data processing
The observed data are processed on the dedicated high performance computing (HPC) cluster DAWN which consists of 124 NVIDIA K40 GPUs (Patil et al. 2017; Pandey et al. 2020). Because we are analysing data on a flanking field of the NCP and our main purpose is to compare the performance of two different DD calibration algorithms, we use a slightly different data processing strategy from the LOFAR-EoR data processing pipeline adopted in Patil et al. (2017) and Mertens et al. (2020), especially for the DI and DD calibration steps. The main processing steps in this work are (1) pre-processing, including data averaging and RFI flagging; (2) self-calibration iterations and imaging to create a sky model; (3) averaging and DI calibration to correct the flux of sources; (4) DD calibration with the two different algorithms described in Sects. 3.1 and 3.2 to subtract the sky model; (5) imaging; (6) visibility cube conversion; (7) residual foreground removal; and (8) power spectrum estimation. Figure 2 shows an overview of the RA 18h flanking field data processing pipeline of this work. Each step will be described in more detail in the following.
4.1 Pre-processing
RFI flagging is performed by AOFLAGGER (Offringa et al. 2012) on the highest time and spectral resolution of 2 sec and 3.05 kHz (64 channels per sub-band, 183 kHz). In this step, the four edge channels 0, 1, 62, and 63 of sub-bands are flagged to avoid aliasing effects from the polyphase filter (Patil et al. 2017). After the first RFI flagging, the remaining 60 channels are averaged to 15 channels (12.2 kHz per channel) and the data are archived in the LOFAR LTA at SURFsara in Amsterdam and Poznan in Poland (Mertens et al. 2020). On this averaged data we perform a second RFI flagging, and subsequently the data are averaged to three channels (61 kHz per channel) per sub-band and 2 s resolution. This initial RFI-flagging results in a ~5% loss of the LOFAR-EoR HBA data (Offringa et al. 2013). This pre-processing step is identical to that used in the standard LOFAR-EoR pipeline (Mertens et al. 2020).
4.2 Direction-independent calibration
The first step of calibration begins with a self-calibration (Cornwell & Wilkinson 1981; Pearson & Readhead 1984), and the main goal is to correct the source fluxes and build up a sky model for the DD calibration. We perform a first gain calibration on the averaged visibilities with a sky model consisting of 355 bright point sources from the NCP sky model. The gain calibration is carried out by GAINCAL in DP3. Using the usebeammodel option in GAINCAL, we apply the LOFAR-HBA beam model during calibration and use the initial sky model with intrinsic fluxes. To reduce the data volume and accelerate the calibration process we first average the data to a ten-second time resolution and gain solutions are calculated on the same timescale per sub-band with the LOFAR-HBA beam model15. We note that baselines are not limited during the first DI calibration of self-calibration. Based on our test, if we use the same 50λ cut for self-calibration and for the subsequent DI calibration, data on baselines close to the 50λ cut are not well calibrated. For this reason, we decided not to apply a baseline cut when creating a sky model (during self-calibration). The 50λ cut is applied during DI calibration after the self-calibration step. We combine all 69 sub-bands and limit baselines up to 10 000λ to create a high-resolution image with a pixel size of 6 arcsec. The calibrated visibilities are imaged and deconvolved by the multi-scale CLEAN feature of WSCLEAN (Offringa et al. 2014; Offringa & Smirnov 2017). The obtained CLEAN components are saved as two types of sky models: an apparent model and an intrinsic model. The sources in the apparent model are attenuated by the average beam. The two models are used in the next calibration steps with combinations of two DD calibration algorithms. DDECAL can apply the LOFAR-HBA beam model in calibration, so we can use an intrinsic sky model. SAGECAL requires an apparent sky model because the beam model is not applied.
At this stage we compare the intrinsic flux of four known bright sources (J190401.7+8536, 6C B184741+851139, 6C B174711+844656, and 6C B163113+855559) around the phase centre (ideally within ~4.75°, being the FWHM of the LOFAR core stations at 120 MHz; van Haarlem et al. 2013) to the ones from the catalogues to check whether their fluxes match. The details of sources used for flux scaling and their catalogues are summarised in Table B.1. We aim for an intrinsic flux calibration accuracy of 10% or better. An additional calibration factor is applied to match the intrinsic sky model to the catalogue fluxes. Finally, we perform a DI calibration using the extended CLEAN component model on the pre-processed data. It is similar to the first DI calibration step. The data is first averaged to a ten-second time resolution and the CLEAN component model (intrinsic) is used with the LOFAR-HBA beam model. Baselines are limited to 50–9500λ this time. The lower baseline cut is applied to avoid the diffuse emission (Patil et al. 2017), while the upper baseline cut comes from the constraint (of 10 000λ) on the sky model.
 |
Fig. 2 Processing pipeline of the LOFAR-EoR flanking field data in this work to obtain the 21 cm power spectra with two different DD calibration algorithms. The pipeline is slightly different from the standard LOFAR-EoR HBA processing pipeline (Pandey et al. 2020; Mertens et al. 2020) because the main purpose is comparing the performance of two DD calibration algorithms. Two different clustering approaches are adopted for the DD calibration (i.e. the one-step and two-step methods) to investigate how different clustering impacts the subtraction of the sky model. |
4.3 Direction-dependent calibration
After we create the new sky model and re-scale the flux in the DI calibration step, we perform a DD calibration. The main goal is to subtract sources in the sky with their DD calibration gains. In this work we perform this task with two different DD calibration algorithms, DDECAL and SAGECAL, described in Sects. 3.1 and 3.2. Because Cas A and Cyg A are very bright and far away from the phase centre, their solutions can be distinctive from those of the remaining sources close to the phase centre. Hence, they need to be calibrated in a separate cluster, a similar approach to that used for calibrating the bright source 3C61.1 in the NCP field by Patil et al. (2017) and Mertens et al. (2020). Hence, we test two methods for the subtraction of the sky model. In the one-step method the CLEAN component model with a Cas A and Cyg A model is divided into 22 clusters (20 clusters for the CLEAN model and one cluster each for Cas A and Cyg A), and all the sources are predicted and subtracted simultaneously in one step. In the two-step method the CLEAN model, Cas A, and Cyg A are divided into three clusters. Cas A and Cyg A are predicted and subtracted first, after which the CLEAN model is again divided into 20 clusters, predicted and subtracted from the data. Solutions are calculated for 10 min time intervals and each sub-band for the two DD calibration algorithms and two different approaches to subtracting the sources.
We adopt the same baseline cut applied in the standard LOFAR-EoR pipeline (i.e. 250–5000λ). The lower baseline cut is used to reduce signal suppression on the baselines of 50–250λ used for the 21 cm signal power spectrum extraction, to avoid the effects from the diffuse emission, and to include enough baselines for the required S/N. The upper baseline cut is applied to avoid sky model error and ionospheric phase fluctuations on longer baselines leaking into the short baseline gain solutions (Patil et al. 2016; Mertens et al. 2020; Mevius et al. 2022).
4.4 Imaging and conversion to brightness temperature
After DI and DD calibration, imaging, removal of residual foreground, and power spectrum estimation are similar to those performed in the standard LOFAR-EoR pipeline (see Mertens et al. 2020, for more details). The residual visibilities after the DD calibration are gridded and imaged per sub-band to create an image cube using WSCLEAN. We adopt identical imaging parameters used by Mertens et al. (2020), a Kaiser-Bessel anti-aliasing filter with a kernel size of 15 pixels, an oversampling of 4096, and 32 w-layers. According to Offringa et al. (2019b), these parameters are chosen to confine the systematics from gridding below the predicted 21 cm signal.
At this stage, we create even and odd ten-second time-differenced images to estimate the thermal noise of the data. We estimate the thermal noise for the NCP and RA 18h flanking field, and use them for the flux scale cross-check.The power spectrum is corrected by a factor of two downwards to account for the increase in noise level due to the differencing. The results are discussed in more detail in the following section.
The image cube with a field of view of 12° × 12° and a pixel size of 0.5 arcmin is then multiplied by a Tukey function with a diameter of 4° to concentrate on the beam centre. The image cube has units of Jy per PSF. To estimate the power spectrum, the image cube is transformed into a gridded visibility cube by a spatial Fourier transform and is converted to units of Kelvin, as described in Offringa et al. (2019b).
Parameter set-up for the multiscale deconvolution algorithm with WSCLEAN.
4.5 Foreground removal and power spectrum estimation
The remaining foregrounds in the residual Stokes-I visibilities are further removed by the Gaussian process regression (GPR) foreground removal technique (Mertens et al. 2018, 2020). GPR enables a separation between different components in observations including smooth astrophysical foregrounds, mode-mixing contaminants, noise and the 21 cm signal by modelling each of them as a Gaussian process (GP), assuming they can be described by Gaussian processes to first order. GPR properly accounts for degeneracies between the signal components by marginalising other components.
Finally, the variations in the 21 cm signal as a function of wavenumber k (at different scales) are obtained by a power spectrum. It is estimated by taking the Fourier transform of the foreground-subtracted visibility cube in the frequency direction and converting angle and frequency, to comoving distances (Morales & Hewitt 2004; McQuinn et al. 2006). We can average the power spectrum in k-bins to create the spherically averaged dimensionless power spectrum or define the cylindrically averaged power spectrum, as a function of angular k⊥ versus line-of-sight k‖.
5 Results
In this section, we present the results of processing one night observation from LOFAR-EoR with DDECAL and SAGECAL. We present the results of each step following the data processing pipeline introduced in Sect. 4. We also compare differences in their performance in terms of removing sources in Sects. 5.2–5.4. In Sect. 5.5, we compare sky images, power spectra, and upper limits on the RA 18h flanking field and NCP field.
5.1 The RA 18h flanking field sky model and DI calibration
The sky model of the RA 18h flanking field is built by the multi-scale deconvolution algorithm of WSCLEAN with the parameters listed in Table 2. The intrinsic flux of the CLEAN model is then scaled to match the fluxes of the four bright sources around the phase centre listed in Table B.1 at the central observing frequency 119.725 MHz with a spectral index α = −0.6. With a flux scaling factor of 1.91, we find a mean ratio of 0.997 between the intrinsic CLEAN flux and the references with a standard deviation of 0.0861. In addition, we compare the estimated thermal noise on the RA 18h flanking field and NCP (scaled by NVSS J011732+892848 Patil et al. 2017; Mertens et al. 2020) from the same observation. Their estimated thermal noise should closely match if the absolute flux scale is performed accurately. The average ratio of the estimated thermal noise between the NCP and RA 18h flanking field is found to be 1.06, showing that the absolute flux scaling is well performed and the estimated thermal noise values on the two fields are comparable. We note that due to the 4° difference in pointing the sensitivity is slightly different between the two fields. The noise in part is set by the total power in the beam, which is also partly contributed by sources in the field and diffuse emission. Hence, a perfect flux agreement is not expected. The top panel of Fig. 3 shows images of the RA 18h flanking field after DI calibration.
Sky model set-ups for DDECAL and SAGECAL.
5.2 Direction-dependent gain calibration
In the DD gain calibration step, we cluster the sky model into a number of directions, predict visibilities in each direction, and subtract the clustered sky model sources with their DD gain applied from the data. An example of the obtained DD gain power spectra for one station is presented in Appendix E. In this subsection we discuss the sky model we use for the DD calibration, and compare its performance using two algorithms, DDECAL and SAGECAL, and two different approaches regarding the subtraction of Cas A and Cyg A.
5.2.1 Clustering of the sky model
The 3389 CLEAN components after self-calibration are clustered into 20 directions identically for the two algorithms, as shown in Fig. 4. We make sure that clustering does not contribute to the DD calibration difference between the two algorithms. The detailed clustering information of the sky model is summarised in Table B.2 and the differences between the two sky models are summarised in Table 3. Finally, we add Cas A and Cyg A into the two sky models as these bright radio sources, even located outside the field of view, will enter via side lobes and leave residuals in the power spectrum if not included in the sky model (Patil et al. 2017; Mertens et al. 2020). For DDECAL we use the Cas A and Cyg A model (14 components) from the low-resolution A-team sky model16. For SAGECAL, we use shapelet models created from wide-band LOFAR-LBA and HBA observations with ~350 components (Yatawatta 2011)17. The additional Cas A and Cyg A components are clustered into their respective directions.
 |
Fig. 3 LOFAR-HBA 5° × 5° Stokes-I residual images after DI and DD calibration with four different calibration scenarios on the RA 18h flanking field at frequency 113.9–127.1 MHz. The images are created with a pixel size of 0.2 arcmin using baselines 50–5000λ, combining 69 sub-bands and a single observation night L612832 (~11.6-h). Top: after DI calibration. Middle: calibrated by DDECAL (left) and SAGECAL (right) with the one-step method. Bottom: calibrated by DDECAL (left) and SAGECAL (right) with the two-step method. Different DD calibration scenarios also show different residuals. A source close to the centre is indicated by a dashed blue circle as reference. The residuals of the reference source look different in the four scenarios. |
5.2.2 Images
In Fig. 3, we show 5° × 5° images of the Stokes-I residuals after DD calibration with four different scenarios using DDECAL and SAGECAL (middle and bottom). Compared to the Stokes-I images before DD calibration (top), most bright sources are removed well after DD calibration (middle and bottom). In the primary beam region, DDECAL (middle left and bottom left) removes more power compared to SAGECAL (middle right and bottom right) for both the one-step and two-step methods.
However, depending on the strategy, there are some differences in their residuals. In Fig. 3, the images calibrated by DDECAL (middle left and bottom left) have more compact residual sources than the images calibrated by SAGECAL (middle right and bottom right). Notably, DDECAL shows better performance with the one-step method in the primary beam region, and the residual power is lower with the one-step method (middle left) than with the two-step method (bottom left). The difference between the one-step and two-step methods is marginal for SAGECAL (middle right and bottom right).
We chose a reference source close to the centre to compare the residuals after DD calibration with the four scenarios. The reference source is indicated by a dashed blue circle in Fig. 3. The flux of the source is largely reduced after DD calibration in all four scenarios. DDECAL shows an oversubtraction where the source appears as negative (in blue). The oversubtraction is stronger in the two-step method than in the one-step method. On the other hand, the residuals of SAGECAL are positive (in red) and not as compact as those from DDECAL. Difference images between the DD calibration scenarios subtracted by the DDECAL and one-step scenario (middle left) are shown in Fig. C.1.
Overall, DDECAL shows better performance than SAGECAL in the primary beam region, especially when carried out by the one-step method. This difference between DDECAL and SAGECAL may be explained by the application of the LOFAR-HBA beam in DDECAL which enables more realistic prediction and subtraction of visibilities.
In principle, the number of directions and the time or frequency interval of solutions in DD calibration are chosen to naturally capture the direction-dependent effects, including beam variations and ionospheric phase fluctuations. However, this calibration process is not perfect (e.g. due to the incomplete sky model or a bad choice of solution intervals) and there are errors. Increasing the solution resolution (i.e. using a finer time or frequency interval for solutions) can be useful for capturing rapid varying beam variations and ionospheric fluctuations to a certain extent; however, it could also introduce extra noise into the data and add extra structures in time and frequency. This point is also partially shown in Fig. E.4 where we use different time intervals, 5 min and 10 min, to calibrate Cas A and Cyg A. The 5 min interval results (bottom panel) did not show an improvement compared to the 10 min interval results (middle panel). What we found in this work is that having a physical beam model during DD calibration improves the performance of calibration, especially in the primary beam region.
To compare the subtraction performance of distant sources, such as Cas A and Cyg A, we create full sky Stokes-I residual images (120° × 120°) after DI calibration and four different DD calibration scenarios. The images are created by combining all sub-bands, integrating the full observation, and applying a 50–300λ baseline cut (comparable to the cut used for the power spectrum estimation later on).
Figure 5 shows the residual Stokes-I images after DI calibration (top left), Cas A and Cyg A subtraction with DDECAL (bottom left), and DD calibration with the four scenarios (second and third columns) on the RA 18h flanking field. By comparing the two images in the first column, before and after the subtraction of Cas A and Cyg A, we find that this extra step taken by DDECAL significantly reduces the power from Cas A and Cyg A without changing the power around the phase centre. The subtraction of Cas A and Cyg A is not as efficient with the one-step DDECAL method (top middle panel), showing more residuals from Cas A and Cyg A after the DD calibration compared to the other three scenarios.
This difference in the performance of the subtraction of Cas A and Cyg A between the one-step and two-step methods is very evident in DDECAL (second column in Fig. 5), but not as much in SAGECAL (last column in Fig. 5). It is still unclear why the one-step method performs better in subtracting sources in the primary beam than the two-step method for DDECAL in this specific case, and whether the existence of distant and bright sources (such as Cas A and Cyg A, in this case) in the sky model improves the prediction of nearby sources within the field of view.
However, this different performance of DDECAL between the one-step and two-step methods shows the importance of optimising parameters during the DD calibration. With the same calibration algorithm and sky model, the calibration performance can be different, depending on the exact parameters used and the order in which the directions are solved.
The one-step SAGECAL method shows the best subtraction of Cyg A compared to others, leaving the lowest power in the image (second panel on bottom in Fig. 5). One of the major differences between DDECAL and SAGECAL is the application of time and frequency smearing correction and this correction is only applied for SAGECAL in this work. The better Cas A and Cyg A subtraction of SAGECAL could be due to this smearing correction.
In the far field in Fig. 5, Cas A and Cyg A are by far the most dominant sources of residuals, even after DD calibration. This is in line with the previous study on sources of excess variance in the LOFAR-EoR 21 cm power spectra (Gan et al. 2022). The dominant imprint of Cas A and Cyg A are perhaps contributors to the excess power in the wedge.
 |
Fig. 4 Flanking field sky model from CLEAN components with the LOFAR beam applied clustered into 20 directions for the DD calibration. The different colours denote different solving directions. Each cluster has an angular radius of 1–2°. |
 |
Fig. 5 Full sky (120° × 120°) Stokes-I residual images created by using 69 sub-bands and 50–300λ baseline cut, and integrating the full observation after DI calibration, Cas A and Cyg A subtraction, and DD calibration with four different strategies with DDECAL and SAGECAL on the RA 18h flanking field. Shown are the residuals after DI calibration (top left). After DI calibration, all sources are subtracted, including Cas A and Cyg A in one step (i.e. the one-step method, top middle and right), or first Cas A and Cyg A are subtracted (i.e. the two-step method, bottom left) and sources in the centre are subtracted (bottom middle and right). The flux of Cas A and Cyg A is largely reduced after Cas A and Cyg A subtraction (bottom left), while sources in the centre remain. The one-step method with SAGECAL shows comparable performance in Cas A and Cyg A subtraction (top right), while DDECAL still shows a high level of residuals (top middle). |
5.2.3 Gain smoothness difference in DDECAL and SAGECAL
One of the main differences between the two DD calibration algorithms is the implementation of frequency smoothness constraints. As discussed in Sect. 3, all sky signals, apart from the 21 cm signal are supposed to be smooth in frequency. By enforcing gains to be smooth in frequency, we can minimise signal suppression and avoid enhancing the noise variance introduced by calibration (Mevius et al. 2022). DDECAL enforces this gain smoothness by convolving solutions with a Gaussian kernel of a given size for each iteration.
We test two different kernel sizes, 1 MHz and 4 MHz, and find that the 4 MHz kernel is better for the analysis (i.e. better subtraction of the sky model). On the other hand, SAGECAL iteratively penalises solutions that deviate from a frequency smoothness prior by a quadratic term of a third-order Bernstein polynomial over the full bandwidth (~13 MHz in this case).
To understand the effects of different frequency constraints in DDECAL and SAGECAL, we compare the delay τ transformed and peak-normalised (at τ = 0 ns) gains obtained by the two algorithms. Figure 6 shows the normalised gains obtained by DDECAL (on top) and SAGECAL (on bottom) with the two-step method for the first five clusters (from left to right) and core stations (in different colours) in delay space. For all clusters and stations, SAGECAL gain distributions show slightly narrower widths compared to those from DDECAL. A more noticeable difference is shown in the tails of gains at large delays. Gains from DDECAL hit a noise floor (|G| ~ 10−4) at |τ| > 1000 ns, while gains from SAGECAL continue to drop. However, gains from DDECAL and SAGECAL have similar distributions in delay space, despite the difference in the flux of the sky model and application of the beam model. We assume that the different frequency constraints used in the two algorithms have comparable effects in this analysis.
5.3 Foreground removal: Gaussian process regression (GPR)
In this subsection, we show the results of the GPR foreground removal after the four different DD calibration scenarios. The residual foregrounds after the DD calibration can be further removed by GPR. GPR models each component in observation as a GP (Rasmussen & Williams 2005). The parametric GP model has five components: the foreground residuals that are composed of intrinsic sky emission and mode mixing contaminants related to the chromaticity of the instrument and calibration errors; the 21 cm signal; the spectrally uncorrelated noise; and the spectrally correlated excess noise.
The modelled GP components are summarised for the four different DD calibration scenarios in Table 4. We refer readers to Mertens et al. (2020) for the detailed selection of the covariance model. GPR uses a Matern covariance function to model different components in the residuals. A Matern covariance function is defined with three hyperparameters, η, σ, and l. The parameter η constrains the smoothness of the function, σ2 is the variance, and l is the spectral coherence scale of each component. Mertens et al. (2018) have found the most probable setting of GP and hyperparameter priors and the found values are used in this work.
We note that the coherence scales l converge to similar values, especially for the excess noise and 21 cm signal components (i.e. lex and l21), given the four different DD calibration scenarios. This is expected because the four scenarios are based on the same observation and the DD calibration step should not bias the excess variance and 21 cm signal18. On the other hand, the intrinsic sky and mix coherence scales (i.e. lsky and lmix) depend on the calibration method in Table 4. For instance, DDECAL shows longer intrinsic sky coherence scales (82–85 MHz) compared to SAGECAL (39–41 MHz).
This again can be explained by the difference in the residuals after the application of DDECAL and SAGECAL. As we discussed earlier, due to the application of the beam model, DDECAL and SAGECAL end up with different residuals in the primary beam after DD calibration. The sky and mix components are used to model these residuals. Hence it is reasonable to assume that the estimated parameters of the same calibration algorithm converge to similar values for the sky and mix components.
 |
Fig. 6 Peak-normalised gain solutions in delay space per station and cluster obtained by DDECAL (top) and SAGECAL (bottom) with the two-step method. The different colours denote solutions for different stations. Each polarisation component is added in quadrature. |
Summary of the GP model for each DD calibration case.
 |
Fig. 7 Cylindrical Stokes-I power spectra after DD calibration (top) and GPR foreground removal (bottom) with four DD calibration scenarios using DDECAL and SAGECAL. The dashed lines, from bottom to top, correspond to the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre. From the top to the bottom row, the GPR foreground removal technique efficiently removes the residual power in the primary beam region. As in the residual images in Fig. 3 (middle and bottom), SAGECAL (last two panels on top) leaves slightly higher power in the primary beam region than DDECAL (first two panels on top) after DD calibration. However, this difference in the primary beam disappears after the application of GPR (bottom). In addition, the power spectrum of DDECAL and one-step method before GPR (first panel on top) has higher residual power between 20° and 90° delay lines compared to the rest, which indicates poor subtraction of Cas A and Cyg A. However, after GPR, the residual Stokes-I power spectra from the four different DD calibration scenarios show very similar results. |
5.4 Power spectra
Figure 7 shows the resulting cylindrical power spectra after the DD calibration and foreground removal with four DD calibration scenarios using DDECAL and SAGECAL. Figure 8 shows the cylindrical Stokes-I power-spectra ratio after DD calibration of DDECAL to SAGECAL for the one-step or two-step method (top), and the ratio of the one-step to two-step calibration method for the fixed DD calibration algorithm (bottom). In the top panel, red indicates excess power from DDECAL, while blue indicates excess power from SAGECAL. In the bottom panel, red indicates excess power from the one-step method, and blue from the two-step method. If the colour is close to white, it means that the ratio of the two methods is close to 1 and the difference is marginal. The dashed lines, from bottom to top, indicate the 5° (the primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre.
The major difference between DDECAL and SAGECAL is seen in the region of the primary beam (for both one-step and two-step methods in Fig. 7 top, and in Fig. 8 top). We find that the power in the primary beam region is lower when calibrated by DDECAL. SAGECAL subtracts Cas A and Cyg A better than DDECAL when the one-step method is used (top left in Fig. 8); however, the difference disappears when the two-step method is used (top right in Fig. 8). This different performance between the one-step and two-step methods with DDECAL is also reflected in the bottom left panel in Fig. 8. DDECAL with the one-step method shows significantly higher power between the 20° and 90° delay lines compared to the two-step method. However, the difference between the one-step and two-step methods is marginal for SAGECAL (bottom right in Fig. 8).
After the GPR foreground removal, which is well suited to remove foreground in the primary beam region, the difference in the primary beam region between DDECAL and SAGECAL is significantly reduced, as shown in the bottom row of Fig. 7.
 |
Fig. 8 Cylindrical Stokes-I power spectra ratio after DD calibration of DDECAL to SAGECAL given a calibration strategy, the one-step or two-step method (top), and of the one-step to two-step methods given a DD calibration algorithm, DDECAL or SAGECAL (on bottom). The dashed lines indicate the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre from bottom to top. Top: red indicates excess power from DDECAL and blue indicates excess power from SAGECAL. Bottom: red indicates excess power from the one-step method and blue indicates excess power from the two-step method. |
5.5 The north celestial pole results
In this subsection, we present the DD calibration results on the NCP processed by the standard LOFAR-EoR pipeline. The main differences between the DD calibration examined in this work and the standard pipeline are summarised in Table 5. The NCP sky images after DI and DD calibration can be found in Appendix D.
5.5.1 Images
Figure 9 shows the full sky Stokes-I residual images on the NCP after the DI (top left) and DD calibration (top right). The residual images after DI and DD calibration (with SAGECAL and two-step method) are shown for comparison (bottom). Most sources show significantly reduced power after the DD calibration on the NCP; however, we still see the imprint of Cas A and Cyg A in the residuals.
Compared to the residuals of the RA 18h flanking field in Fig. 5 (bottom right), the residual power around the phase centre is significantly lower on the NCP, due to the application of the extensive sky model and more directions during the DD calibration in the NCP processing.
However, the subtraction of Cas A and Cyg A does not show better performance on the NCP compared to the RA 18h flanking field. While the residuals of Cas A are slightly more compact on the NCP than the RA 18h flanking field, the residuals of Cyg A have significantly lower power on the RA 18h flanking field.
In Table 6, we summarise the calibration set-up details forthe Cas A and Cyg A subtraction on the NCP with the standard processing and flanking field with the best results using SAGECAL and the one-step method. In both cases the calibration is carried out by SAGECAL using the shapelet model. One main difference is the time interval of solutions in the two fields. The NCP uses a higher resolution, one solution per 2.5 min, compared to the 10 min interval of the RA 18h flanking field in this particular case. This also indicates that solving gains for a finer time interval does not always improve the calibration performance because it is more likely to overfit the data and increase noise. Hence, finding an optimal calibration set-up is crucial for the calibration performance, given a calibration algorithm and a sky model.
5.5.2 Power spectra
Figure 10 shows the cylindrical Stokes-I power spectra after the DD calibration and GPR foreground removal on the NCP. A few kj_ modes are flagged, due to bad data quality. Compared to the cylindrical Stokes-I residual power spectra of the RA 18h flanking field in Fig. 7 bottom, the NCP has higher power on short baselines (k⊥ ~ 0.05–0.13 h cMpc−1), in particular between the 20° and 90° delay lines and around the 90° delay line.
Figure 11 shows the ratio of cylindrical Stokes-I power spectra of the flanking field to the NCP field after DD calibration (top) and after GPR foreground removal (bottom). Red indicates excess power from the flanking field and blue indicates excess power from the NCP field. Again, a few k⊥ modes are flagged, due to bad data quality after GPR foreground removal (bottom). As we have already found, the flanking field has higher residual power in the foreground region (below the 20° delay line) after DD calibration (top). This power is stronger with SAGECAL (top, last two panels) than with DDECAL (top, first two panels). However, after GPR foreground removal, the excess power is largely removed (bottom). Finally, the major difference comes from the excess power from the NCP on short baselines (k⊥ ~ 0.05–0.13 h cMpc−1) around the 90° delay line, as we show in Fig. 10.
It is unclear where this extra power originates. Because the data on the two fields are from the same observing run, but with the station beams and array phased up differently, they are supposed to have similar RFI and systematics. The NCP has a known disadvantage that stationary RFI sources can add coherently via its side lobes. We therefore perform an extra RFI flagging step after DD calibration to mitigate this effect on the NCP. However, this extra flagging step does not show a significant improvement.
5.6 Spherically averaged power spectra and upper limits
Figure 12 shows the spherically averaged Stokes-I power spectra of the RA 18h flanking field with four different DD calibration scenarios and the NCP at different stages of the processing, the DI calibration, DD calibration, and foreground removal (in green, red, and blue). After the DI calibration the Stokes-I power is higher in the RA 18h flanking field than in the NCP; however, this tendency reverses after the DD calibration (up to k ~ 0.7 h c Mpc−1), as we discussed earlier, likely due to the extensive sky model and clustering used for the DD calibration on the NCP. However, this advantage disappears once we apply the GPR foreground removal technique. The Stokes-I power of the RA 18h flanking field is lower than that of the NCP by a factor of 1.2–2 over k = 0.075–0.6 h c Mpc−1.
We also compare the 2σ upper limits of the 21 cm signal on the RA 18h flanking field and NCP (in Table 7). Compared to the NCP results, the RA 18h flanking field shows around 1030% improved upper limits overall k values considered for the four different calibration scenarios.
The 2σ upper limits on the 21 cm signal after the calibration and foreground removal by the four different DD calibration scenarios are summarised in Table 7. The two-step SAGECAL method presents the best upper limit results compared to others. Within the four cases studied, SAGECAL provides 5-10% better upper limits compared to DDECAL given a calibration strategy, either one-step or two-step. The two-step method produces 3–8% better upper limits given a calibration algorithm, either DDECAL or SAGECAL. This difference is minor and could also come from the different model assumptions (e.g. between apparent and intrinsic flux models, and/or between different Cas A and Cyg A models), apart from the difference in the model clustering and the application of the primary beam model.
Main differences between the DD calibrations used in this work and in the standard LOFAR-EoR pipeline.
 |
Fig. 9 Comparison of full sky (120° × 120°) Stokes-I residual images created by using 69 sub-bands and 50–300λ baseline cut, and integrating the full observation after DI (first column) and DD calibration (second column) on the NCP (top) and on the RA 18h flanking field (bottom). The DD calibration is performed by SAGECAL with an extensive sky model (~28 000 sources) on the NCP and with a simpler sky model (~3400 sources) on the RA 18h flanking field. The residual power around the centre is substantially lower on the NCP (top right) than the flanking field (bottom right), due to using an extensive sky model with more directions during the DD calibration. The power from Cas A and Cyg A is significantly reduced after DD calibration. The residuals of Cas A are stronger on the NCP (top right) than on the flanking field (bottom right). Unphysical sources below the horizon are masked. |
Comparison of the Cas A and Cyg A subtraction set-up of the NCP in the standard processing with SAGECAL and the RA 18h flanking field with SAGECAL and the one-step method.
 |
Fig. 10 Cylindrical Stokes-I power spectra after DD calibration (left) processed by the standard LOFAR-EoR pipeline with SAGECAL and GPR foreground removal (right) of a single observation night on the NCP. The dashed lines indicate the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre (from bottom to top). Some bad quality data are flagged on the right. |
2σ upper limit of the 21 cm signal 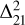 from a single observation night on the RA 18h flanking field with different DD calibration scenarios and the NCP calibrated by the standard pipeline with SAGECAL.
from a single observation night on the RA 18h flanking field with different DD calibration scenarios and the NCP calibrated by the standard pipeline with SAGECAL.
6 Conclusions
In this work we have compared the performance of two DD calibration algorithms, DDECAL and SAGECAL, in the context of LOFAR-EoR 21 cm power spectra by processing a single observation night on a flanking field of the north celestial pole (NCP) obtained by Low-Frequency Array (LOFAR). We applied two different strategies for subtracting the very bright sources Cas A and Cyg A, predicting and subtracting the two sources simultaneously with the sky model in the one-step method, or in a separate step before predicting and subtracting the sky model, namely the two-step method. We conclude the following:
- (1)
We find that there are differences between the two DD calibration algorithms. DDECAL shows better performance in subtracting sources in the primary beam region, probably due to the application of the beam model during the DD calibration. This suggests that having a beam model during the DD calibration significantly improves the calibration performance, especially in the primary beam region.
- (2)
SAGECAL, on the other hand, shows better performance in subtracting Cas A and Cyg A. While predicting and subtracting Cas A and Cyg A in a separate step does not change the DD calibration results significantly for SAGECAL, it does make a significant difference for DDECAL. The time and frequency smearing correction is applied for SAGECAL but not for DDECAL in this work. The difference in subtracting Cas A and Cyg A could be due to the application of this smearing correction.
- (3)
The difference of the residual power in the primary beam region between DDECAL and SAGECAL becomes marginal when the GPR foreground removal is applied after DD calibration.
- (4)
We also compare the results on the RA 18h flanking field with the NCP results processed by the standard LOFAR-EoR pipeline. The standard processing pipeline uses a very extended sky model (with ~28 000 sources) and 122 directions for the DD calibration, which makes the processing computationally expensive.
- (5)
For the four different DD calibration scenarios studied, comparable upper limits on the 21 cm power spectra on the NCP flanking field are achieved, using a simpler sky model (with ~3500 sources including Cas A and Cyg A) and fewer directions (20 directions), when the foreground removal technique known as Gaussian process pegression (GPR) is used after DD calibration.
- (6)
In both NCP and RA 18h flanking field results, even after DD calibration, Cas A and Cyg A are the most dominant sources of residuals in the far field in full sky images in Figs. 9 and 5, which agrees with the previous study on sources of excess variance in the LOFAR-EoR 21 cm power spectra (Gan et al. 2022). They may be contributors to the excess noise in the wedge.
Based on our analysis, we suggest the following strategies for future improvements:
Apply time and frequency smearing corrections for DDECAL. The latest version of DDECAL corrects for the time and frequency smearing. This correction is not applied during the DD calibration process in this work. In the future, we would like to include the smearing correction during the DD calibration and investigate whether it further improves the calibration performance, especially the subtraction of Cas A and Cyg A.
Apply a beam model for SAGECAL. The future versions of SAGECAL will support the LOFAR beam model. Our results with DDECAL show that applying a beam model is likely to improve the source subtraction around the phase centre substantially. We expect to achieve similar source subtraction performance with SAGECAL once we apply a beam model for SAGECAL.
Process flanking fields for cross-checks. In this work we have processed a single observation night on two different fields, the NCP and one of its flanking fields, using different calibration set-ups, and have compared the results. While the data sets from the same observation share the same or very similar RFI, ionosphere, and systematics, we note that the residuals in the two fields look rather different than expected. In particular, the NCP shows extra power above the wedge on short baselines that is not present in the RA 18h flanking field. We suspect that this power partially comes from the residuals of Cas A and Cyg A; however, more investigations are needed to clarify the source(s) of the extra power. By processing other flanking fields of the same observation and imaging ground planes, we will be able to identify whether this is a particular problem of the NCP field that is related to the beam or a calibration issue.
Optimise DD calibration parameters. By comparing the performance of the four different DD calibration scenarios, even with the same sky model, the calibration outcome can be significantly different depending on the calibration parameters and strategies we use, such as frequency smoothing constraints or the number of clusters for particularly bright sources. While there are some studies on the regularisation of frequency in the DD calibration (Yatawatta 2015, 2016; Mevius et al. 2022), more studies are needed, in particular for the selection of the number of clusters and solution intervals. Different calibration parameters can be tested relatively straightforwardly because it does not require modifying the existing sky model or pipeline.
 |
Fig. 11 Cylindrical Stokes-I power spectra ratio after DD calibration (top) and GPR foreground removal (bottom) of the flanking field to the NCP field. The dashed lines, from bottom to top, correspond to the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre. Red indicates excess power from the flanking field and blue indicates excess power from the NCP field. Some bad data are flagged at the bottom. From top to bottom, the residual foregrounds below the 20° delay line (i.e. excess power from the flanking field) are largely removed after GPR foreground removal. |
 |
Fig. 12 Spherically averaged Stokes-I power spectra on the NCP calibrated by the standard LOFAR-EoR pipeline with SAGECAL (dotted lines) and the RA 18h flanking field calibrated by DDECAL (solid lines) or SAGECAL (dashed lines) with the one-step (top) or two-step (bottom) method. The different colours denote different processing stages. Green, red, and blue denote the Stokes-I power spectra after DI calibration, DD calibration, and GPR foreground removal, respectively. After each calibration stage, the Stokes-I power is reduced significantly. The NCP results show lower power after DD calibration at low k (< 0.3 h cMpc−1) compared to the RA 18h flanking field (in red), due to using an extensive sky model; however, after the GPR foreground removal, the RA 18h flanking field has lower power compared to the NCP (in blue). DDECAL (solid lines) shows better subtraction of sources after DD calibration (in red) compared to SAGECAL (dashed lines) in the one-step and the two-step method, due to the application of the beam model; however, this advantage disappears after GPR (in blue). |
Acknowledgements
H.G. and L.V.E.K. would like to acknowledge support from the Centre for Data Science and Systems Complexity (DSSC) at the University of Groningen and a Marie Sklodowska-Curie COFUND grant, no. 754315. BKG and LVEK acknowledge the financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement no. 884760, “CoDEX”). Data availability: The data underlying this article will be shared upon request by the corresponding author.
Appendix A NCP Flanking Field Configuration
In Table A.1 the pointing and beam number of the NCP and six flanking fields are summarised. The phase centres of the six flanking fields are located 4° from the NCP field. In this work we focus on the RA 18h field.
Summary of the NCP flanking field positions (SAP stands for sub-array pointing).
Appendix B Sky Model Details
Here we provide detailed information about the sky model on the RA 18h flanking field. The flux of the model is scaled using four calibrators summarised in Table B.1. The details of sky model clustering are summarised in Table B.2.
Four bright radio sources around the position of RA 18h flanking field selected to set the absolute flux of the sky model.
Summary of the CLEAN component model and its clustering.
Appendix C Difference Images of DD Calibration Residuals
In Fig. C.1 we show the difference in residuals after different calibration scenarios. The Stokes-I residual images after DD calibration with the four scenarios in Fig. 3 are subtracted by the residual image of the DDECAL and one-step method (middle left in Fig. 3).
In Fig. C.1 red indicates undersubtraction and blue indicates oversubtraction of sources, compared to the DD calibration scenario with DDECAL and the one-step method. We use the same reference source (dashed blue circle) to compare residuals after DD calibration. Residuals of the source are lighter blue (indicating marginal oversubtraction) in the DDECAL and two-step method scenario (bottom left), while residuals are red in the two SAGECAL scenarios (top and bottom right), indicating undersubtraction.
Overall, DDECAL with the two-step method shows undersubtraction with most sources appearing red and relatively compact. SAGECAL shows rather scattered residuals with a mixture of oversubtraction and undersubtraction for sources. The difference between the one-step and two-step methods is rather small for SAGECAL.
 |
Fig. C.1 Difference of LOFAR-HBA 5° × 5° Stokes-I residual images after DD calibration with different calibration scenarios on the RA 18h flanking field at frequency 113.9–127.1 MHz shown in Fig. 3. The images are created with a pixel size of 0.2 arcmin using baselines 50 – 5000λ, combining 69 sub-bands and a single observation night L612832 (~ 11.6-hour). The residual images with different DD calibration scenarios are subtracted by the residual image of the DDECAL and one-step scenario. A reference source is shown (dashed blue circle), which is identical to the one in Fig. 3 to compare different DD calibration residuals. |
Appendix D NCP Sky Images after DI and DD Calibration
In Fig. D.1 we present the 20° × 20° and zoomed (4° × 4°) images on the NCP after DI calibration (top) and after DD calibration (bottom). Compared to the RA 18h flanking field results in Fig. 3, the NCP shows better subtraction of the foregrounds in the primary beam region. This is likely due to the application of an extended sky model (~ 8 times more components compared to the RA 18h flanking field sky model) and more directions (~ 6 times more directions compared to the RA 18h flanking field) during the DD calibration. The downside is that using an extended sky model and solving gains for more direction can be computationally much more expensive (the NCP standard processing time is ~ 5 times longer compared to the flanking field processing time). In this work we note that power spectra similar to those obtained by the NCP processing can be achieved with a relatively simple sky model and fewer directions during the DD calibration if the GPR foreground removal technique is applied.
 |
Fig. D.1 LOFAR-HBA Stokes-I images of the NCP at frequency 113.9 – 127.1 MHz. All 69 sub-bands are combined for imaging after the DI calibration (top row) and DD calibration (bottom row). The DI and DD calibrations are performed by SAGECAL and the images are deconvolved by WSCLEAN. Left column: 20° × 20° image with a pixel size of of 0.8 arcmin with baselines between 50–1000λ after DI calibration (top) and after DD calibration (bottom). Right column: Zoomed 4° × 4° image with a pixel size of of 0.2 arcmin with baselines between 50–5000λ after DI calibration (top) and after DD calibration (bottom). |
Appendix E Gain Dynamic Spectra
Here we present the gain spectra of one station (CS001HBA0) per cluster obtained with the one-step method (top) and the two-step method (bottom) achieved by the calibration algorithm, either DDECAL (Fig. E.1) or SAGECAL (Fig. E.2). From each figure, by comparing the gain spectra between the one-step and two-step methods, we can find how the subtraction of Cas A and Cyg A impacts the gains of the remaining sources in the phase centre.
Depending on the flux type of the sky model used for the calibration, obtained gains show distinct values. DDECAL uses an intrinsic sky model and SAGECAL uses an apparent model, average gain values are higher for SAGECAL than DDECAL. The gain spectra of DDECAL are also flatter than SAGECAL, due to the application of the beam model.
To investigate the difference between the one-step and two-step methods, we create gain ratio spectra for the two methods given a calibration algorithm in Fig. E.3 for CS001HBA0 per cluster. We find that the gain difference between the one-step and two-step methods is rather big in SAGECAL than in DDECAL. While this difference is more concentrated in the clusters close to the phase centre (clusters 2–7) for DDECAL, the difference is more obvious in the outer clusters (clusters 11–20) for SAGECAL.
We also present the Cas A and Cyg A gain spectra from different calibration set-ups in Fig. E.4. We compare the gain spectra obtained by the one-step method using DDECAL (in the first row) and SAGECAL (in the second row). The solution interval is 10 min for both cases. The gains vary more rapidly over time for DDECAL in this case, and the gains from SAGECAL are rather flat. In particular, the gains from SAGECAL are smoother in frequency compared to DDECAL. This improved smoothness in frequency of SAGECAL possibly contributed to the better performance of the subtraction of Cas A and Cyg A in Fig. 5.
In the last row of Fig. E.4 we present the Cas A and Cyg A gain spectra obtained by DDECAL and the two-step method. The solutions have a higher resolution (i.e. a 5 min interval), and the gain spectra have more structures in time compared to the lower resolution solutions in the first two rows. While SAGECAL with the one-step method (in the second row) and DDECAL with the two-step method (in the last row) show comparable performance in subtracting Cas A and Cyg A, it is still unclear whether the added structures in the gain spectra obtained by DDECAL and the two-step method are physical or noise. More studies are needed to determine the optimal frequency constraints and solution time intervals for calibration.
 |
Fig. E.1 Gain dynamic spectra obtained by DDECAL algorithm for 20 clusters around the phase centre, using the one-step method (top) and two-step method (bottom) for one station (CS001HBA0). The different polarisation components are added in quadrature. |
 |
Fig. E.2 Gain dynamic spectra obtained by SAGECAL algorithm for 20 clusters around the phase centre, using the one-step method (top) and two-step method (bottom) for one station (CS001HBA0). The different polarisation components are added in quadrature. |
 |
Fig. E.3 Gain dynamic spectra ratio of the one-step to two-step method for 20 clusters around the phase centre for one station (CS001HBA0), obtained by DDECAL algorithm (top) and SAGECAL algorithm (bottom). Different polarisation components are added in quadrature. While gain differences between the one-step and two-step methods are more prominent in the phase centre for DDECAL (in clusters 2-7, top), the difference is more obvious outside the phase centre for SAGECAL (in clusters 11-20, bottom). |
 |
Fig. E.4 Gain spectra of Cas A (left) and Cyg A (right) obtained by different calibration strategies for one station (CS001HBA0). The different polarisation components are added in quadrature. |
References
- Arras, P., Frank, P., Leike, R. H., Westermann, R., & Ensslin, T. A. 2019, A&A, 627, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. E., Boysen, R. C., Hales, S. E. G., et al. 1985, MNRAS, 217, 717 [NASA ADS] [Google Scholar]
- Barry, N., Hazelton, B., Sullivan, I., Morales, M. F., & Pober, J. C. 2016, MNRAS, 461, 3135 [CrossRef] [Google Scholar]
- Barry, N., Wilensky, M., Trott, C. M., et al. 2019, ApJ, 884, 1 [Google Scholar]
- Bernardi, G., de Bruyn, A. G., Harker, G., et al. 2010, A&A, 522, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Born, M., Wolf, E., Bhatia, A. B., et al. 1999, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th edn. (Cambridge University Press) [Google Scholar]
- Bowman, J. D., Morales, M. F., & Hewitt, J. N. 2009, ApJ, 695, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, J. D., Cairns, I., Kaplan, D. L., et al. 2013, PASA, 30, e031 [Google Scholar]
- Bowman, J. D., Rogers, A. E. E., Monsalve, R. A., Mozdzen, T. J., & Mahesh, N. 2018, Nature, 555, 67 [Google Scholar]
- Boyd, S., Parikh, N., Chu, E., Peleato, B., & Eckstein, J. 2011, Found. Trends Mach. Learn., 3, 1 [Google Scholar]
- Cheng, C., Parsons, A. R., Kolopanis, M., et al. 2018, ApJ, 868, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Cornwell, T. J., & Wilkinson, P. N. 1981, MNRAS, 196, 1067 [NASA ADS] [Google Scholar]
- DeBoer, D. R., Parsons, A. R., Aguirre, J. E., et al. 2017, PASP, 129, 045001 [NASA ADS] [CrossRef] [Google Scholar]
- Edler, H. W., de Gasperin, F., & Rafferty, D. 2021, A&A, 652, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farouki, R., & Rajan, V. 1988, Comput. Aided Geom. Des., 5, 1 [CrossRef] [Google Scholar]
- Fessler, J., & Hero, A. 1994, IEEE Trans. Signal Process., 42, 2664 [CrossRef] [Google Scholar]
- Furlanetto, S. R., Peng Oh, S., & Briggs, F. H. 2006, Phys. Rep., 433, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gan, H., E. Koopmans, Mertens, F.G.L.V., et al. 2022, A&A, 663, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehlot, B. K., Mertens, F. G., Koopmans, L. V. E., et al. 2019, MNRAS, 488, 4271 [Google Scholar]
- Greenhill, L. J., & Bernardi, G. 2012, arXiv e-print [arXiv: 1201.1700] [Google Scholar]
- Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HERA Collaboration (Abdurashidova, Z., et al.) 2022, ApJ, 924, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Kazemi, S., & Yatawatta, S. 2013, MNRAS, 435, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Kazemi, S., Yatawatta, S., Zaroubi, S., et al. 2011, MNRAS, 414, 1656 [Google Scholar]
- Kolopanis, M., Jacobs, D. C., Cheng, C., et al. 2019, ApJ, 883, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Pritchard, J., Mellema, G., et al. 2015, The Cosmic Dawn and Epoch of Reionization with the Square Kilometre Array, Proceedings of science, 215 [Google Scholar]
- Li, W., Pober, J. C., Barry, N., et al. 2019, ApJ, 887, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., & Nocedal, J. 1989, Math. Program. 45, 503 [CrossRef] [Google Scholar]
- Liu, A., & Shaw, J. R. 2020, PASP, 132, 062001 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M., Zahn, O., Zaldarriaga, M., Hernquist, L., & Furlanetto, S. R. 2006, ApJ, 653, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G., Koopmans, L. V. E., Abdalla, F. A., et al. 2013, Exp. Astron., 36, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Mertens, F. G., Ghosh, A., & Koopmans, L. V. E. 2018, MNRAS, 478, 3640 [NASA ADS] [Google Scholar]
- Mertens, F. G., Mevius, M., Koopmans, L. V. E., et al. 2020, MNRAS, 493, 1662 [Google Scholar]
- Mevius, M., van der Tol, S., Pandey, V. N., et al. 2016, Radio Sci., 51, 927 [Google Scholar]
- Mevius, M., Mertens, F., Koopmans, L. V. E., et al. 2022, MNRAS, 509, 3693 [Google Scholar]
- Mitchell, D., Greenhill, L., Wayth, R., et al. 2008, Sel. Top. Sig. Proc. IEEE J., 2, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Morales, M. F., & Hewitt, J. 2004, ApJ, 615, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Morales, M. F., & Wyithe, J. S. B. 2010, ARA&A, 48, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Mouri Sardarabadi, A., & Koopmans, L. V. E. 2018, MNRAS, 483, 5480 [Google Scholar]
- Noordam, J., & Oschmann, J. 2004, Proc. SPIE Conf. Ser., Ground-based Telescopes, 5489 [Google Scholar]
- Offringa, A. R., & Smirnov, O. 2017, MNRAS, 471, 301 [Google Scholar]
- Offringa, A. R., van de Gronde, J. J., & Roerdink, J. B. T. M. 2012, A&A, 539, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R., de Bruyn, A. G., Zaroubi, S., et al. 2013, A&A, 549, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [Google Scholar]
- Offringa, A. R., Trott, C. M., Hurley-Walker, N., et al. 2016, MNRAS, 458, 1057 [Google Scholar]
- Offringa, A. R., Mertens, F., & Koopmans, L. V. E. 2019a, MNRAS, 484, 2866 [CrossRef] [Google Scholar]
- Offringa, A. R., Mertens, F., van der Tol, S., et al. 2019b, A&A, 631, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ollier, V., El Korso, M. N., Ferrari, A., Boyer, R., & Larzabal, P. 2018, Signal Process., 153, 348 [CrossRef] [Google Scholar]
- Paciga, G., Chang, T.-C., Gupta, Y., et al. 2011, MNRAS, 413, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Paciga, G., Albert, J. G., Bandura, K., et al. 2013, MNRAS, 433, 639 [CrossRef] [Google Scholar]
- Pandey, V., Koopmans, L., Tiesinga, E., et al. 2020, ADASS XXIX. ASP Conference Series, 524 [Google Scholar]
- Parsons, A. R., Pober, J. C., Aguirre, J. E., et al. 2012, ApJ, 756, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Patil, A. H., Yatawatta, S., Zaroubi, S., et al. 2016, MNRAS, 463, 4317 [NASA ADS] [CrossRef] [Google Scholar]
- Patil, A. H., Yatawatta, S., Koopmans, L. V. E., et al. 2017, ApJ, 838, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, T. J., & Readhead, A. C. S. 1984, ARA&A, 22, 97 [Google Scholar]
- Philip, L., Abdurashidova, Z., Chiang, H., et al. 2019, Journal of Astronomical Instrumentation, 8, 1950004 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchard, J. R., & Loeb, A. 2012, Rep. Progr. Phys., 75, 086901 [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2005, Gaussian Processes for Machine Learning (The MIT Press) [Google Scholar]
- Salvini, S., & Wijnholds, S. J. 2014, in 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), 1 [Google Scholar]
- Singh, S., Subrahmanyan, R., Shankar, N. U., et al. 2017, AJ, 845, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Smirnov, O. M. 2011, A&A, 527, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M., & Tasse, C. 2015, MNRAS, 449, 2668 [Google Scholar]
- Tasse, C. 2014, A&A, 566, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thekkeppattu, J. N., Subrahmanyan, R., Somashekar, R., et al. 2021, Exp. Astron., 51, 193 [CrossRef] [Google Scholar]
- van Diepen, G., Dijkema, T. J., & Offringa, A. 2018, Astrophysics Source Code Library [record ascl:1804.003] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vedantham, H. K., & Koopmans, L. V. E. 2016, MNRAS, 458, 3099 [NASA ADS] [CrossRef] [Google Scholar]
- Yatawatta, S. 2011, URSI General Assembly and Scientific Symposium, 1 [Google Scholar]
- Yatawatta, S. 2015, MNRAS, 449, 4506 [Google Scholar]
- Yatawatta, S. 2016, arXiv e-prints [arXiv: 1605.09219] [Google Scholar]
- Yatawatta, S. 2019, MNRAS, 486, 5646 [NASA ADS] [CrossRef] [Google Scholar]
- Yatawatta, S., de Bruyn, A. G., Brentjens, M. A., et al. 2013, A&A, 550, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yatawatta, S., Clercq, L. D., Spreeuw, H., & Diblen, F. 2019, IEEE Data Science Workshop (DSW), 208 [CrossRef] [Google Scholar]
- Zheng, Q., Wu, X.-P., Johnston-Hollitt, M., Gu, J.-H., & Xu, H. 2016, ApJ, 832, 190 [NASA ADS] [CrossRef] [Google Scholar]
The Large-aperture Experiment to detect the Dark Ages, http://www.tauceti.caltech.edu/leda/
Giant Metrewave Radio Telescope, http://gmrt.ncra.tifr.res.in
Low-Frequency Array, http://www.lofar.org
Murchison Widefield Array, http://www.mwatelescope.org
The Donald C. Backer Precision Array for Probing the Epoch of Reionisation, http://eor.berkeley.edu
Hydrogen Epoch of Reionisation Array, http://reionization.org/
The Square Kilometer Array, http://www.skatelescope.org
The LOFAR core station field of view is ~ 17.73 deg2 at 120 MHz (van Haarlem et al. 2013).
The source code for DP3 can be found at https://github.com/lofar-astron/DP3, and the DP3 documentation can be found at https://www.astron.nl/lofarwiki/doku.php?id=public:user_software:documentation:ndppp
The latest version of SAGECAL only supports the LOFAR dipole beam model; in the future more beam options will be supported: http://sagecal.sourceforge.net/
In the standard LOFAR-EoR pipeline the DI calibration is conducted on the high-resolution data before averaging. We also performed a test on calibrating the higher resolution data before averaging, but the results were almost identical to those after averaging. In this case, calibrating on the higher resolution increases the computing time by a factor of 4–5 without a significant improvement. Hence, for this work we decided to calibrate the data after averaging.
We also tested the calibration performance with a high-resolution Cas A and Cyg A sky model with more components with DDECAL. However, using more components did not significantly improve the subtraction of the sources. Hence, we decided to use the low-resolution model to reduce the computing time.
The excess variance by definition is the extra noise that is above the thermal noise level and cannot be removed easily with DD calibration or GPR (Mertens et al. 2018; Gan et al. 2022).
All Tables
Main differences between the DD calibrations used in this work and in the standard LOFAR-EoR pipeline.
Comparison of the Cas A and Cyg A subtraction set-up of the NCP in the standard processing with SAGECAL and the RA 18h flanking field with SAGECAL and the one-step method.
2σ upper limit of the 21 cm signal  from a single observation night on the RA 18h flanking field with different DD calibration scenarios and the NCP calibrated by the standard pipeline with SAGECAL.
from a single observation night on the RA 18h flanking field with different DD calibration scenarios and the NCP calibrated by the standard pipeline with SAGECAL.
Summary of the NCP flanking field positions (SAP stands for sub-array pointing).
Four bright radio sources around the position of RA 18h flanking field selected to set the absolute flux of the sky model.
All Figures
 |
Fig. 1 Observing configuration of the NCP field in LOFAR-EoR. The main target field NCP is located in the centre, and six flanking fields are distributed from the centre at an angular distance of 4° (indicated by circles of radius 4°). The bright radio source 3C61.1 is inside the RA 2h flanking field (SAP001). The image is constructed from a single observation night L612832 (~11.6-h duration) using full sub-bands. In this work, one night of data on the RA 18h field (blue circle) is analysed. |
| In the text | |
 |
Fig. 2 Processing pipeline of the LOFAR-EoR flanking field data in this work to obtain the 21 cm power spectra with two different DD calibration algorithms. The pipeline is slightly different from the standard LOFAR-EoR HBA processing pipeline (Pandey et al. 2020; Mertens et al. 2020) because the main purpose is comparing the performance of two DD calibration algorithms. Two different clustering approaches are adopted for the DD calibration (i.e. the one-step and two-step methods) to investigate how different clustering impacts the subtraction of the sky model. |
| In the text | |
 |
Fig. 3 LOFAR-HBA 5° × 5° Stokes-I residual images after DI and DD calibration with four different calibration scenarios on the RA 18h flanking field at frequency 113.9–127.1 MHz. The images are created with a pixel size of 0.2 arcmin using baselines 50–5000λ, combining 69 sub-bands and a single observation night L612832 (~11.6-h). Top: after DI calibration. Middle: calibrated by DDECAL (left) and SAGECAL (right) with the one-step method. Bottom: calibrated by DDECAL (left) and SAGECAL (right) with the two-step method. Different DD calibration scenarios also show different residuals. A source close to the centre is indicated by a dashed blue circle as reference. The residuals of the reference source look different in the four scenarios. |
| In the text | |
 |
Fig. 4 Flanking field sky model from CLEAN components with the LOFAR beam applied clustered into 20 directions for the DD calibration. The different colours denote different solving directions. Each cluster has an angular radius of 1–2°. |
| In the text | |
 |
Fig. 5 Full sky (120° × 120°) Stokes-I residual images created by using 69 sub-bands and 50–300λ baseline cut, and integrating the full observation after DI calibration, Cas A and Cyg A subtraction, and DD calibration with four different strategies with DDECAL and SAGECAL on the RA 18h flanking field. Shown are the residuals after DI calibration (top left). After DI calibration, all sources are subtracted, including Cas A and Cyg A in one step (i.e. the one-step method, top middle and right), or first Cas A and Cyg A are subtracted (i.e. the two-step method, bottom left) and sources in the centre are subtracted (bottom middle and right). The flux of Cas A and Cyg A is largely reduced after Cas A and Cyg A subtraction (bottom left), while sources in the centre remain. The one-step method with SAGECAL shows comparable performance in Cas A and Cyg A subtraction (top right), while DDECAL still shows a high level of residuals (top middle). |
| In the text | |
 |
Fig. 6 Peak-normalised gain solutions in delay space per station and cluster obtained by DDECAL (top) and SAGECAL (bottom) with the two-step method. The different colours denote solutions for different stations. Each polarisation component is added in quadrature. |
| In the text | |
 |
Fig. 7 Cylindrical Stokes-I power spectra after DD calibration (top) and GPR foreground removal (bottom) with four DD calibration scenarios using DDECAL and SAGECAL. The dashed lines, from bottom to top, correspond to the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre. From the top to the bottom row, the GPR foreground removal technique efficiently removes the residual power in the primary beam region. As in the residual images in Fig. 3 (middle and bottom), SAGECAL (last two panels on top) leaves slightly higher power in the primary beam region than DDECAL (first two panels on top) after DD calibration. However, this difference in the primary beam disappears after the application of GPR (bottom). In addition, the power spectrum of DDECAL and one-step method before GPR (first panel on top) has higher residual power between 20° and 90° delay lines compared to the rest, which indicates poor subtraction of Cas A and Cyg A. However, after GPR, the residual Stokes-I power spectra from the four different DD calibration scenarios show very similar results. |
| In the text | |
 |
Fig. 8 Cylindrical Stokes-I power spectra ratio after DD calibration of DDECAL to SAGECAL given a calibration strategy, the one-step or two-step method (top), and of the one-step to two-step methods given a DD calibration algorithm, DDECAL or SAGECAL (on bottom). The dashed lines indicate the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre from bottom to top. Top: red indicates excess power from DDECAL and blue indicates excess power from SAGECAL. Bottom: red indicates excess power from the one-step method and blue indicates excess power from the two-step method. |
| In the text | |
 |
Fig. 9 Comparison of full sky (120° × 120°) Stokes-I residual images created by using 69 sub-bands and 50–300λ baseline cut, and integrating the full observation after DI (first column) and DD calibration (second column) on the NCP (top) and on the RA 18h flanking field (bottom). The DD calibration is performed by SAGECAL with an extensive sky model (~28 000 sources) on the NCP and with a simpler sky model (~3400 sources) on the RA 18h flanking field. The residual power around the centre is substantially lower on the NCP (top right) than the flanking field (bottom right), due to using an extensive sky model with more directions during the DD calibration. The power from Cas A and Cyg A is significantly reduced after DD calibration. The residuals of Cas A are stronger on the NCP (top right) than on the flanking field (bottom right). Unphysical sources below the horizon are masked. |
| In the text | |
 |
Fig. 10 Cylindrical Stokes-I power spectra after DD calibration (left) processed by the standard LOFAR-EoR pipeline with SAGECAL and GPR foreground removal (right) of a single observation night on the NCP. The dashed lines indicate the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre (from bottom to top). Some bad quality data are flagged on the right. |
| In the text | |
 |
Fig. 11 Cylindrical Stokes-I power spectra ratio after DD calibration (top) and GPR foreground removal (bottom) of the flanking field to the NCP field. The dashed lines, from bottom to top, correspond to the 5° (primary beam), 20°, and 90° (instrumental horizon) delay lines from the phase centre. Red indicates excess power from the flanking field and blue indicates excess power from the NCP field. Some bad data are flagged at the bottom. From top to bottom, the residual foregrounds below the 20° delay line (i.e. excess power from the flanking field) are largely removed after GPR foreground removal. |
| In the text | |
 |
Fig. 12 Spherically averaged Stokes-I power spectra on the NCP calibrated by the standard LOFAR-EoR pipeline with SAGECAL (dotted lines) and the RA 18h flanking field calibrated by DDECAL (solid lines) or SAGECAL (dashed lines) with the one-step (top) or two-step (bottom) method. The different colours denote different processing stages. Green, red, and blue denote the Stokes-I power spectra after DI calibration, DD calibration, and GPR foreground removal, respectively. After each calibration stage, the Stokes-I power is reduced significantly. The NCP results show lower power after DD calibration at low k (< 0.3 h cMpc−1) compared to the RA 18h flanking field (in red), due to using an extensive sky model; however, after the GPR foreground removal, the RA 18h flanking field has lower power compared to the NCP (in blue). DDECAL (solid lines) shows better subtraction of sources after DD calibration (in red) compared to SAGECAL (dashed lines) in the one-step and the two-step method, due to the application of the beam model; however, this advantage disappears after GPR (in blue). |
| In the text | |
 |
Fig. C.1 Difference of LOFAR-HBA 5° × 5° Stokes-I residual images after DD calibration with different calibration scenarios on the RA 18h flanking field at frequency 113.9–127.1 MHz shown in Fig. 3. The images are created with a pixel size of 0.2 arcmin using baselines 50 – 5000λ, combining 69 sub-bands and a single observation night L612832 (~ 11.6-hour). The residual images with different DD calibration scenarios are subtracted by the residual image of the DDECAL and one-step scenario. A reference source is shown (dashed blue circle), which is identical to the one in Fig. 3 to compare different DD calibration residuals. |
| In the text | |
 |
Fig. D.1 LOFAR-HBA Stokes-I images of the NCP at frequency 113.9 – 127.1 MHz. All 69 sub-bands are combined for imaging after the DI calibration (top row) and DD calibration (bottom row). The DI and DD calibrations are performed by SAGECAL and the images are deconvolved by WSCLEAN. Left column: 20° × 20° image with a pixel size of of 0.8 arcmin with baselines between 50–1000λ after DI calibration (top) and after DD calibration (bottom). Right column: Zoomed 4° × 4° image with a pixel size of of 0.2 arcmin with baselines between 50–5000λ after DI calibration (top) and after DD calibration (bottom). |
| In the text | |
 |
Fig. E.1 Gain dynamic spectra obtained by DDECAL algorithm for 20 clusters around the phase centre, using the one-step method (top) and two-step method (bottom) for one station (CS001HBA0). The different polarisation components are added in quadrature. |
| In the text | |
 |
Fig. E.2 Gain dynamic spectra obtained by SAGECAL algorithm for 20 clusters around the phase centre, using the one-step method (top) and two-step method (bottom) for one station (CS001HBA0). The different polarisation components are added in quadrature. |
| In the text | |
 |
Fig. E.3 Gain dynamic spectra ratio of the one-step to two-step method for 20 clusters around the phase centre for one station (CS001HBA0), obtained by DDECAL algorithm (top) and SAGECAL algorithm (bottom). Different polarisation components are added in quadrature. While gain differences between the one-step and two-step methods are more prominent in the phase centre for DDECAL (in clusters 2-7, top), the difference is more obvious outside the phase centre for SAGECAL (in clusters 11-20, bottom). |
| In the text | |
 |
Fig. E.4 Gain spectra of Cas A (left) and Cyg A (right) obtained by different calibration strategies for one station (CS001HBA0). The different polarisation components are added in quadrature. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


